Walter Tydecks
Die Wende zur absoluten Idee
– Der Schluss von der Lebendigkeit über den Satz des Pythagoras auf die dialektische Methode
Vortrag bei der Tagung des Internationalen Arbeitskreises zu Hegels Naturphilosophie am Freitag und Samstag, dem 27. und 28. November 2015 an der TU Kaiserslautern. Erschienen in: Wolfgang Neuser, Pirmin Stekeler-Weithofer (Hg.): Idee, Geist, Freiheit: Hegel und die zweite Natur, Würzburg 2017, S. 155-162
Abstract Seit seinen frühen Systementwürfen steht für Hegel der Satz des Pythagoras an der Wende von der Logik und Metaphysik zur Naturphilosophie. In der Wissenschaft der Logik steht er in der Mitte einer Bewegung vom Leben über das Erkennen zur absoluten Idee. Das Leben ist für Hegel keine abstrakte Idee wie das transzendentale Subjekt bei Kant, sondern zeigt sich in jedem konkreten lebendigen Individuum, seinem Lebensprozess (seiner Biographie) und seiner Aufgehobenheit in der Gattung (Geburt, Tod, über das Individuum hinausgehende Selbsterhaltung der Gattung). Wird jedoch die Idee des Lebens als ein logischer Schluss verstanden, der zur absoluten Idee führt, dann basiert sie zwar auf der reichen Fülle des Lebens, aber ein Schluss ist logisch betrachtet mehr als ein Lebensprozess. Was im Lebensprozess unmittelbar erlebt wird, wird auf die neue Ebene des Erkennens gehoben. Das Erkennen findet nichts Neues, was nicht bereits im Leben unmittelbar enthalten ist, aber es gibt ihm eine neue Gestalt, die Hegel als die »Begriffsform« bezeichnet (HW 6.487). Das Erkennen entfernt sich zunächst vom Leben und seiner Fülle, stellt sich ihm gegenüber und zieht sich zurück in die Welt der Gedanken und des Denkens. Aber dort erkennt es an seinen eigenen Gedanken wiederum deren innere Lebendigkeit. Dieser Wendepunkt gelingt mit dem Satz des Pythagoras. Wenn mit ihm die innere Lebendigkeit der Gedanken ergriffen wird, gelingt der Schluss zur absoluten Idee, in der das Leben und Erkennen in einer neuen Einheit aufgehoben sind. Das öffnet den Weg in die Naturphilosophie.
Der Satz des Pythagoras befindet sich für Hegel mit dem Erkennen an der Schwelle von Verstand und Vernunft: An ihm zeigt sich »die als Verstand tätige Vernunft«, hier steht der Verstand »in seinem äußerlichen Tun unter der Leitung des Begriffs, und dessen Bestimmungen machen den inneren Faden des Fortgangs aus« (Enz. § 226, HW 8.379). Daher werden an dieser Stelle alle herangezogenen Begriffe (wie z.B. Definition oder Gleichung) mehrdeutig, wenn sie zum einen in der uns gewohnten Bedeutung aus Sicht des Verstandes und zum anderen aus Sicht der Vernunft gesehen werden. Wird das Erkennen vom Verstand her betrachtet, führt es notwendig in Widersprüche. Geleitet von der Vernunft gelangt der Verstand zu Ergebnissen, die die Endlichkeit überschreiten. Der Verstand kann sein eigenes Ergebnis nicht zusammenhalten, und es kommt zum »Zusammenfallen« der von ihm gewonnenen Resultate (HW 6.500). Das lässt nicht nur an Faust denken, dem das innere Band seiner Erkenntnisse entgleitet, sondern auch an den realen Zustand der modernen Naturwissenschaft.
Der Verstand wird im Prozess des Erkennens über alle inneren Widersprüche hinweg getragen von einem »Trieb«, der aus dem »Keim des Lebendigen« erwächst und den »Fortgang« des Erkennens bestimmt (HW 6.555f). Die Vernunft steht nicht jenseits des Verstandes, sondern wirkt über sein Innern, wenn sie ihn zum Fortgehen beflügelt. Sie offenbart sich nicht als eine äußere Erscheinung, sondern in seinem eigenen Tun. Sie gibt seinem Fortgang die Wende, über alle Paradoxien hinaus zu gehen. Dieser Wendepunkt ist für Hegel nicht eine unbestimmte Idee, sondern zeigt sich für ihn an einer in der Geschichte der Wissenschaft vorgefundenen Einsicht: Der Satz des Pythagoras. Das Anliegen dieses Beitrags ist, den Satz des Pythagoras im Horizont dieser Bewegung zu sehen und an ihm zu zeigen, wie vom Verstand scheinbar entgegen aller Vernunft und zugleich mit der Vernunft der »Überfluss der Realität« (HW 6.531) ergriffen wird.
Hegel bewegt sich hier bewusst an einer Grenze, an der er aus entgegengesetzten Richtungen sowohl von der Mathematik und dem Verstand wie von der Philosophie und der Vernunft mit Unverständnis und Kritik rechnen muss. Deren Vertreter wollen beide nicht glauben, dass der eine auf den anderen angewiesen ist. Hegel wollte beiden einen Ausweg aus ihrer jeweiligen Beschränktheit zeigen.
Von den Kongruenzsätzen zum Satz des Pythagoras
Auch ohne den Satz des Pythagoras ist die euklidische Geometrie zu erstaunlichen Leistungen fähig. Ihr gelingt es, die Geometrie auf einfachste Elemente zurückzuführen und mit ihnen zu operieren. Sie zeigt, wie sich im euklidischen Raum Figuren verschieben und drehen lassen und erkennt deren Bewegungsgesetze (die Kongruenzsätze, vgl. HW 6.531). Wenn z.B. die Länge der Grundseite, die Länge einer anliegenden Seite und die Größe des eingeschlossenen Winkels bekannt sind, genügt das, um daraus unter Anwendung der Kongruenzsätze eindeutig mit Lineal und Zirkel das Dreieck zu konstruieren, ohne irgendwelche Rechnungen ausführen zu müssen (für Details siehe die Lehrbücher über Elementargeometrie und Online-Seiten wie z.B. mathematik-wissen). An dieser Stelle sind auch noch keine Gleichungen möglich, denn sie setzen bereits den Satz des Pythagoras voraus.
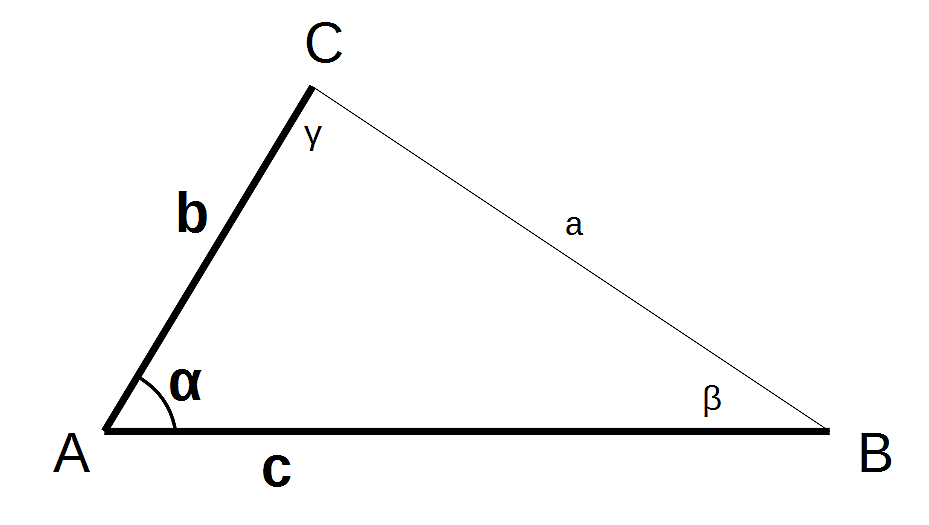
Definition des Dreiecks – ein Beispiel
Ein Dreieck ist vollständig durch die Längen der Grundseite c und der linken Seite b sowie den von ihnen eingeschlossenen Winkel α bestimmt.
Wenn sowohl in der Naturwissenschaft der Neuzeit wie auch bei Kant in den Metaphysischen Anfangsgründen der Naturwissenschaft die euklidische Geometrie als das große Vorbild gilt, ist damit die Kongruenzgeometrie gemeint: Alle Wissenschaften definieren nach dem Muster der Geometrie ihre elementaren Einheiten (Partikel, Elektronen, Atome, Zellen, Teilchen usf.) und deren elementare Bewegungen (Rotation und Translation, Anziehung und Abstoßung, Aufbau und Zerfall), und deduzieren aus ihnen ihre Sätze und Erkenntnisse. Der Satz des Pythagoras wird hierfür nicht gebraucht und wird z.B. bei Kant nirgends erwähnt. Bei dieser Herangehensweise liegt die Aktivität ausschließlich aufseiten der Wissenschaft. Ihr Gegenstand darf keine eigene Lebendigkeit besitzen, die die Analyse und Konstruktion nur stören würde.
»Das vollständig Bestimmende nämlich, z.B. die zwei Seiten und der eingeschlossene Winkel, ist bereits das ganze Dreieck für den Verstand: es bedarf zur vollständigen Bestimmtheit desselben nichts weiter; die übrigen zwei Winkel und die dritte Seite ist der Überfluß der Realität über die Bestimmtheit des Begriffs.« (HW 6.531)
Der Ausdruck ‘Überfluß der Realität’ kann mehrfach gedeutet werden und hat für mich einen ironischen Unterton: Für den Verstand ist alles überflüssig, was er nicht für seine Definitionen und Konstruktionen braucht (so versteht es auch Liebrucks, S. 555). Klaus Hartmann hält aus dessen Perspektive Hegel vor, dass er »den Zweck der Reduktion – die Erzielung von Eindeutigkeit mit einem Minimum an Begriffsbestimmungen – zu erwähnen unterlässt« (Hartmann, S. 418 mit Bezug auf HW 6.513).
An dieser Stelle mehr zu "sehen" und eine Intuition zu entwickeln, wie in der Überfülle des Dreiecks etwas verborgen liegt, das über die Symmetrien der Kongruenz hinausgeht, das zeichnet gegenüber dem Verstand die Idee des Erkennens aus. Die weitergehende Bedeutung als Überfülle (hyperplêres), welche über das Eine überfließt (hypererrhyê), fand Hegel bei Plotin vor (Enneaden V 2, 3-9, vgl. Halfwassen 2004, S. 89). Dies Überfließen wahrzunehmen und in ihm eine eigene Ordnung zu erwarten, die es zu erkennen gilt, kann nicht anders beschrieben werden als eine innere Unruhe, die sich nicht mit den Kongruenzsätzen zufrieden gibt. Stattdessen wird mit den bekannten Konstruktionsmethoden ohne bestimmtes Ziel experimentiert und gespielt, bis in den mehr oder weniger beliebig entworfenen Zeichnungen etwas entdeckt wird, das an den bloßen Dreiecken nicht zu erkennen war. So muss jemand mehr oder weniger durch Zufall darauf gekommen sein, an den Außenseiten des Dreiecks Quadrate zu konstruieren und diese mit den Kongruenzsätzen zu teilen und zu verschieben, bis die Übereinstimmung des Quadrats der Hypotenuse mit den beiden Quadraten über die Katheten gefunden war. (Anregung gaben möglicherweise die bereits in der babylonischen Mathematik bekannten pythagoreischen Tripel.)
Hegel stellt das Ergebnis fast provozierend in einer Sprache dar, die jeden verwirren muss und soll, der die üblichen Darstellungen kennt. Obwohl er natürlich weiß, dass der Satz des Pythagoras eine Gleichung über die Quadrate der Außenseiten ist und nicht über die Seiten, schreibt er:
»Die völlige Bestimmtheit aber der Größe des Dreiecks nach seinen Seiten in sich selbst enthält der Pythagoreische Lehrsatz; dieser ist erst die Gleichung der Seiten des Dreiecks, da die vorhergehenden Seiten es nur im allgemeinen zu einer Bestimmtheit seiner Stücke gegeneinander, nicht zu einer Gleichung bringen. Dieser Satz ist daher die vollkommene, reelle Definition des Dreiecks, nämlich zunächst des rechtwinkligen, des in seinen Unterschieden einfachsten und daher regelmäßigsten.« (HW 6.531f)
Es ist mathematisch wahr, dass erst mit dem Satz des Pythagoras Gleichungen gefunden wurden, während mit den Kongruenzsätzen lediglich geometrisch operiert wird. Aber was soll es heißen, dass erst dieser Satz zeigt, dass das Dreieck »in sich selbst« etwas enthält, das als seine »reelle Definition« gilt? Und was ist mit der »Gleichung der Seiten des Dreiecks« gemeint, obwohl der Satz des Pythagoras anders lautet? (Für Schäfer sind daher Hegels Ausführungen »in mehrfacher Hinsicht fragwürdig«, Schäfer, S. 142f, Fn. 159.)
Statt eine Antwort zu geben, erhöht Hegel mit seiner Kritik an den üblichen Beweisen die Spannung. Wer die euklidische Geometrie lernt, fühlt sich von ihren Konstruktionen überrumpelt und denkt im ersten Moment an eine Art Taschenspielertrick, mit dem auf nicht nachvollziehbaren Wegen etwas hin und her geschoben wird, bis ein Ergebnis herauskommt, das niemand erwartet hätte. Hegel gab sich nie damit zufrieden. Sie »verunstalten und zerreißen« die ursprüngliche Figur (JLMN, S. 118). Sie erscheinen als »ein sinnloses Tun für denjenigen, der den Zweck noch nicht kennt« (HW 6.534, vgl. auch Phänomenologie des Geistes, HW 3.42f). Ähnlich spricht Schopenhauer vom »Euklidische(n) Mausefallenbeweis« (Schopenhauer § 39 über Geometrie).
Definition durch Erkenntnis der Selbsterhaltung
Statt mithilfe der überlieferten Wissenschaft von außen die Sachen zu konstruieren, fragt Hegel nach ihrer inneren Bewegung. Die innere Bewegung gemäß der eigenen Natur einer Sache zu verstehen und in Worte zu bringen, das ist für Hegel die reelle Definition. In seinen frühen Systementwürfen brachte er es programmatisch auf den Punkt: »Die Selbsterhaltung oder die Definition hat als unmittelbar Eins, was bisher getrennt oder nur unsere Reflexion war.« (JLMN, S. 109) Was ist die »Natur« der mit dem Satz des Pythagoras beschriebenen Aufgabe?
In einer schwierigen Passage dieses von Hegel nicht veröffentlichten Textes sah er den Satz des Pythagoras als typisches Beispiel für eine Selbsterhaltung und hatte offenbar schon früh ein völlig anderes Verständnis dieses Satzes als Euklid und die ihm folgende Mathematikgeschichte.
»Die in sich reflektierte Bestimmtheit ist die der Selbsterhaltung, welche an sich nach außen gegen anderes gerichtet ist, in sich zurückgekehrt auf sich selbst bezogen, die Ungleichheit an sich aufgehoben hat. So ist die Definition des rechtwinkligen Dreiecks die, daß ein rechtwinkliges Dreieck das Quadrat der seinem Rechten entgegengesetzten Seite gleich hat der Summe der Quadrate seiner Katheten. Jene [ist] die Bestimmung der bestimmten Qualität, diese der Reflexion, in dem es aus dem Gegensatze der einen Seite gegen die andern die Rückkehr oder die Gleichheit ausdrückt; der Gegensatz ist nach seiner Weise der von einer Seite gegen zwei.« (JLMN, S. 117f)
Ich verstehe das so: Schon im Ansatz kehrt Hegel das übliche Verhältnis von Definition und Satz genau um. Er definiert nicht zuerst, was Kreise, Geraden, Punkte, Quadrate etc. sind, um dann aus diesen Definitionen den Satz des Pythagoras zu folgern, sondern er erkennt umgekehrt, dass im Satz des Pythagoras eine Selbsterhaltung formuliert ist: Die Fläche eines Quadrats bleibt erhalten, wenn eine Außenseite aufgeklappt wird und die beiden neu entstandenen Flügel im rechten Winkel zueinander stehen.
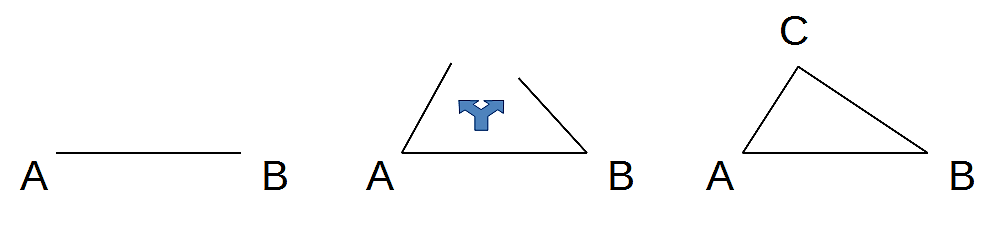
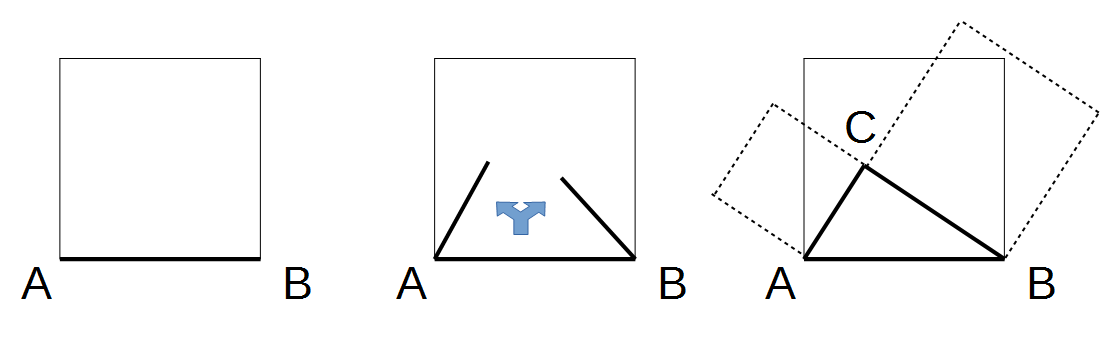
Aufklappen einer Linie in ein rechtwinkliges Dreieck
Das obere Bild zeigt das Aufklappen der Grundlinie. Das untere Bild zeigt die Erhaltung des Flächeninhalts: Die beiden neu entstehenden gestrichelt umrandeten Flächen haben den gleichen Inhalt wie das ursprüngliche schwarz umrandete Quadrat.
Das rechtwinklige Dreieck wird als das Ergebnis einer Bewegung verstanden, die von einer Geraden zu einem Dreieck führt, und hierbei einen Erhaltungssatz erfüllt: Die Größe des Quadrats der Grundlinie bleibt erhalten und ist gleich der Größe der beiden Quadrate über die Katheten. Die Natur der Sache liegt in der Bewegung, und der Satz des Pythagoras wird als Selbsterhaltung verstanden. Das ist die gesuchte reelle Definition. Sie geht aus von der Bewegung, und die formelle Definition der an ihr beteiligten Elemente ergibt sich daraus: Weil die Selbsterhaltung vorausgesetzt wird, entsteht in ihrer Bewegung der rechte Winkel der Katheten. Abschließend ist es nur noch eine Art Kontrollrechnung oder Gegenprobe, wenn bewiesen werden soll, dass sich auch umgekehrt der Satz des Pythagoras aus den Elementen folgern lässt, die mit der reellen Definition aus ihm gewonnen wurden.
Das ist ein völlig anderer Begriff der Definition als in der gewöhnlichen Wissenschaft. Ähnlich beim Begriff der Gleichung: Mit Gleichung kann eine übliche mathematische Gleichung gemeint sein, mit der z.B. aus den Längen zweier Seiten und der Größe des eingeschlossenen Winkels die Länge der dritten Seite berechnet wird. – Oder der Ausdruck ‘Gleichung’ ist abwertend gemeint, wenn zwei Sachen entgegen ihrer wahren Fülle gewaltsam einander gleichgemacht und dadurch gegenüber ihrem wahren Maß zurechtgestutzt werden. Dieser abwertende Ton schwingt in Hegels Kritik am Verstand mit (und wird meines Erachtens im Kommentar von Liebrucks absolut gesetzt, weswegen er dem Gedanken von Hegel nur teilweise gerecht wird, siehe Liebrucks, S. 554ff). – In meinem Verständnis ist bei Hegel mit ‘Gleichung’ der Inhalt einer Selbsterhaltung gemeint: In diesem Sinne spricht Hegel von der Gleichung, die für ihn erst im Satz des Pythagoras gegeben ist.
Schäfer widerspricht dieser Deutung. »Das Dreieck als solches ist keine allgemeine Einheit, die sich selbst in besondere Merkmale einteilt und sich tätig als Einheit im Beweis selbst wiederherstellt.« (Schäfer, S. 142f, Fn. 159). Doch genau in diesem Sinne verstehe ich die Aussage von Hegel. Für ihn zeigt der Satz des Pythagoras, dass hier innerhalb der Geometrie eine Eigenschaft beschrieben ist, die alle Anforderungen an eine lebendige Gattung und ihre Fähigkeit der Selbsterhaltung erfüllt. Das Unbefriedigende an den üblichen Beweisen des Satzes des Pythagoras löst sich auf, wenn er in diesem größeren Horizont gesehen wird.
Der Satz des Pythagoras im Gesamtbau der Wissenschaft der Logik
Wenn der Satz des Pythagoras für Hegel nicht nur eine Anmerkung oder ein vorausschauender Hinweis auf die Realphilosophie ist, sondern maßgeblich zur Logik der Idee gehört, dann muss sich zeigen lassen, dass er bereits in allen vorangegangenen Erkenntnisschritten implizit enthalten ist, auch wenn er erst in der Logik der Idee manifest wird. Das soll abschließend stichwortartig angedeutet werden.
– Seinslogik. Der Satz des Pythagoras wurde unausgesprochen herangezogen, wenn in den rechtwinkligen Steigungsdreiecken des Differentialkalkül die Tangente angenähert wird und ebenso bei der Berechnung der inneren Faktoren einer absoluten Indifferenz, die senkrecht aufeinander stehen wie z.B. bei der Zentripetal- und Zentrifugalkraft. (Vgl hierzu JLMN, S. 116-122 und kommentierend Richli 1978, S. 74-78 sowie Schäfer, S. 141-144.)
– Reflexionslogik. Hegel zeigt, wie es zum Widerspruch kommen muß, wenn sich Gegensätze in zwei Pole aufteilen, die einander frontal gegenüberstehen. Das führt zum Widerspruch, der entlang einer neuen Achse zu Grunde geht, die senkrecht zum Gegensatzpaar verläuft.
– Mechanismus. Hegel deutet die Impulsübertragung als eine Mitteilung. Das ist ein Beispiel für einen materiellen Prozess, der etwas Immaterielles erhält. Der Impuls zeigt sich im Zustand eines Objekts, ist aber für sich kein materielles Ding. Auf analoge Weise lässt sich auch die Übertragung des Flächeninhalts vom Quadrat der Hypotenuse zu den Quadraten der Katheten als immaterielle Mitteilung verstehen. Es sprengt die Grenze des Verstandes, zwar das Gesetz der Mitteilung zu erkennen (den Satz des Pythagoras), aber ihn nicht als Mitteilung im Sinne einer Offenbarung zu verstehen.
– Chemismus. Das chemische Medium ist ein Katalysator, der Prozesse ermöglicht und beschleunigt. Das kann formal auch vom Satz des Pythagoras gesagt werden, durch den die Aufteilung einer Grundseite in Katheten bei Erhaltung der Quadratfläche ermöglicht wird. Für Hegel ist dies aber anders als beim Chemismus ein lebendiger Prozess. Dieser Gedanke entfernt sich am weitesten vom gewöhnlichen Verständnis, für das unvorstellbar ist, dass der Satz des Pythagoras nur die äußere Erscheinung eines sich selbst erhaltenden Organismus ist, dessen Handeln im Ganzen der Mensch nicht überschauen und verstehen kann.
– Methode. Wenn der Satz des Pythagoras als Definition des Dreiecks verstanden wird, ist er ein Beispiel, wie sich eine Erkenntnis ihre eigenen Voraussetzungen und Definitionen schafft und in diesem Sinn selbstbezüglich ist (vgl. Richli 1982, S. 107).
– Überfließen. Mit dem Satz des Pythagoras wird in meiner Deutung der »Überfluss der Realität« ergriffen. Das gehört für Hegel zum Fortgang des Erkennens. Es ist das vielleicht schlagende Beispiel, wie nicht der Fortgang der Methode ein Überfluss ist, sondern sich das Erkennen dem Überfluss der Realität nähert. Darin liegt der Unterschied von Hegel zum Neuplatonismus, von dem er sich mit der absoluten Idee absetzt. (HW 6.555f, siehe auch die Interpretationen bei Halfwassen 1999, S. 289 und Schäfer, S. 212).
– Zusammenfallen. Nicht nur dem Verstand fallen seine Ergebnisse zusammen, sondern auf ganz andere Art kommt es Zusammenfallen der Logik, wenn sie vollständig abgeschritten und ausgeschöpft ist und übergeht in die neue Unmittelbarkeit der Naturphilosophie (siehe Richli 1978, S. 81ff mit Bezug auf JLMN, S. 185). Der Satz des Pythagoras scheint mir dasjenige zu zeigen, was im Zusammenfallen erhalten bleibt und in der Naturphilosophie aufgehoben ist.
Literatur
Andreas Arndt: Wer denkt absolut? Die absolute Idee in Hegels "Wissenschaft der Logik"
in: Revista Eletrônica Estudos Hegelianos, Ano 9, Nr. 16, Juni 2012, S. 22-33; Link
Ludovicus de Vos: Hegels Wissenschaft der Logik: Die absolute Idee, Bonn 1983
Hans Friedrich Fulda: Hegels Logik der Idee und ihre epistemologische Bedeutung
in: Christoph Halbig (Hg.): Hegels Erbe, Frankfurt am Main 2004, S. 78-137; Link
Klaus Hartmann: Hegels Logik, Berlin 1999
Jens Halfwassen: Hegel und der spätantike Neuplatonismus, Bonn 1999
Jens Halfwassen: Plotin und der Neuplatonismus, München 2004
Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971 (zitiert als HW); Link
Georg Wilhelm Friedrich Hegel: Jenenser Logik, Metaphysik und Naturphilosophie, Leipzig 1923 (zitiert als JLMN)
Gottfried Wilhelm Leibniz: Aus den Metaphysischen Anfangsgründen der Mathematik
in: Leibniz: Hauptschriften zur Grundlegung der Philosophie, Bd. 1, Hamburg 1996, S. 35-48
Bruno Liebrucks: Sprache und Bewußtsein, Band 6 Teil 3, Frankfurt am Main und Bern 1974
Kurt Reidemeister: Raum und Zahl, Berlin u.a. 1957
Urs Richli 1978: Die Bewegung des Erkennens in Hegels Jenenser Logik und Metaphysik
in: Philosophisches Jahrbuch, 85, 1978, S. 71-86
Urs Richli 1982: Form und Inhalt in G.W.F. Hegels »Wissenschaft der Logik«, Wien, München 1982
Rainer Schäfer: Die Dialektik und ihre besonderen Formen in Hegels Logik, Hamburg 2001
Arthur Schopenhauer: Ueber die vierfache Wurzel des Satzes vom zureichenden Grunde. 1813 (Dissertation Schopenhauers). Zweite, sehr verbesserte und beträchtlich vermehrte Auflage 1847. (zeno.org)
2015
© tydecks.info 2015


