Die Frage nach einer Dynamik der Maße der Natur

Dieser Beitrag soll die Frage nach einer Dynamik der Maße der Natur aufwerfen. Im Zentrum steht die Relativitätstheorie. Einstein hatte beschrieben, wie sich Zeit und Raum vergrößern und verkleinern, drehen und krümmen können. Allerdings hat er bewusst jede Frage ausgeklammert, was die Ursache einer solchen Dynamik sein kann. Fragen dieser Art tragen seiner Meinung nach nichts bei zu einem besseren Verständnis. Es genügt, alle Ergebnisse der Naturforschung zu sammeln und aus ihnen eine Theorie zu entwerfen, die mit dem geringsten Einsatz von Mitteln und Aufwand alles widerspruchsfrei erklären kann. Als einziges Prinzip ließ er "Occams Rasiermesser" gelten.

Das hat im Ergebnis jedoch zum Gegenteil geführt. Es wurden unterschiedliche Methoden der Veranschaulichung gesucht, um möglichst viel in komplexen Bildern zu verdichten. In den Minkowski-Diagrammen werden Koordinaten-Kreuze ineinander verdreht. Raum und Zeit einerseits und Geschwindigkeit durch Raum und Zeit andererseits gehen oft durcheinander. Prinzipien der Physik wie das Trägheitsprinzip werden in die Konstruktion des Koordinatensystems aufgenommen (Inertialsystem), so dass sie nicht mehr als eigenständige Prinzipien zu erkennen sind. Beschleunigung erscheint als die Verdichtung von Geodätischen in einem gekrümmten Gravitationsfeld, das sich in sich selbst krümmt, da kein absoluter Raum mehr zur Verfügung steht, um seine Krümmung darstellen zu können.

Um die Frage nach der Dynamik der Maße der Natur stellen zu können, ist dies schrittweise zu entwirren und auseinander zu legen, auch auf die Gefahr hin, bisweilen ins Unbestimmte zu fragen. Anregung gaben die Deutungen von Epstein und Hansen.

Lewis C. Epsteins Deutung der Speziellen Relativitätstheorie

Bewegungen werden üblicherweise durch Raum-Zeit-Diagramme dargestellt, in denen die x-Achse den Raum und die t-Achse die Zeit bedeutet. Eine Kurve im Diagramm verläuft grundsätzlich von unten nach oben und zeigt, zu welcher Zeit sich ein Körper an welcher Stelle befindet. Das ist seine Weltlinie.

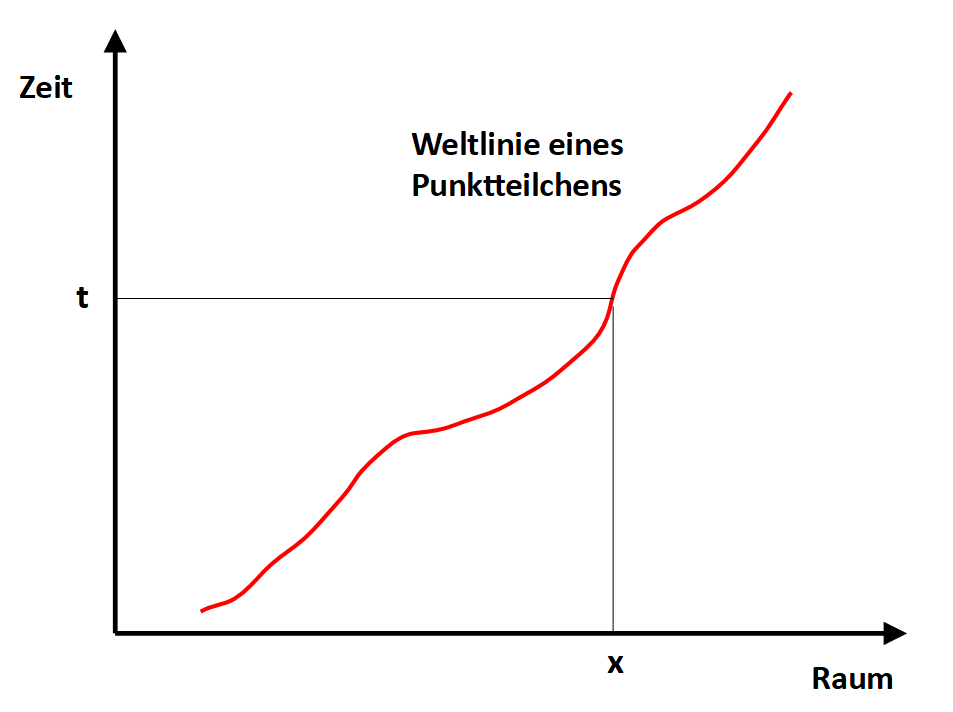
Figur 1 Weltlinie im Raumzeit-Diagramm

"Jeder Punkt der Zeichenebene entspricht einem Ereignis. (In diesem Sinn stellt die Zeichenebene die - auf zwei Dimensionen reduzierte - Raumzeit dar). Die rot eingezeichnete Linie wird Weltlinie des Teilchens genannt. Sie gibt darüber Auskunft, wo das Teilchen wann ist. Das Inverse der Steigung der Weltlinie in einem Ereignis ist die (Momentan-)Geschwindigkeit. Bewegt sich das Teilchen gleichförmig, so ist seine Weltlinie eine Gerade (deren Steigung gleich dem Inversen der Geschwindigkeit ist). Derartige grafische Darstellungen werden Raumzeit-Diagramme genannt." Auszug aus der sehr empfehlenswerten Darstellung der Speziellen Relativitätstheorie durch Franz Embacher.
Urheber: eigene Zeichnung

Diagramme dieser Art genügen vollständig, um alle Bewegungen in der vertrauten Umgebung zu beschreiben. Zwar gibt es einige auffallende Phänomene: Wenn z.B. in einem fahrenden Schiff etwas zu Boden fällt, wird seine Bewegung nicht gemäß der Geschwindigkeit des Schiffes zur Seite abgelenkt, sondern es fällt genau so, als ob das Schiff stehen würde. Innerhalb des Schiffes ist nicht zu erkennen, ob das Schiff im Ganzen bewegt ist. Bereits Aristoteles kannte dies Phänomen (Phys. 212a). Galilei hat es systematisch analysiert und mathematische Beschreibungen zu seiner Darstellung gefunden (Galilei-Transformationen). - Etwas ähnliches geschieht, wenn die Insassen in einem stehenden Zug sehen, wie ein benachbarter Zug anfährt und den Eindruck haben, sie selbst würden in Bewegung versetzt und der andere Zug würde stehen bleiben. - Für alle Phänomene dieser Art lassen sich Regeln finden, die die Bewegung im Ganzen widerspruchsfrei beschreiben.

Eine völlig neue Situation ergab sich erst, als im Gegensatz zu diesen Regeln festgestellt wurde, dass die Lichtgeschwindigkeit immer konstant ist. Das durchbrach alle bis dahin geltenden Transformationen und führte zu einem völlig neuen Formalismus: Wenn sich ein Beobachter bewegt, verändern sich für ihn die Maße von Raum, Zeit und Masse: Bei größerer Geschwindigkeit erscheinen der Raum kürzer (Längenkontraktion), die Zeit länger (Zeitdilatation), die Masse und Energie größer. Durch diese Änderung des Bezugssystems wird garantiert, dass die Lichtgeschwindigkeit Grenzgeschwindigkeit bleibt.

Am extremsten stellt es sich dar, wenn die Welt aus der Sicht eines mit Lichtgeschwindigkeit fliegenden Photons betrachtet wird. Nichts kann sich dem Photon nähern oder von ihm entfernen, denn diese Bewegungen würden Überlicht-Geschwindigkeit erreichen. Alle Abstände zu anderen Objekten sind durch die Längenkontraktion auf 0 geschrumpft, d.h. das Photon umfasst in einem einzigen Punkt die Welt. Masse und Energie haben sich in diesem Punkt unendlich verdichtet, sind unendlich-groß geworden. Das Photon sieht so aus wie der Kosmos im Moment des Urknalls oder wie ein unendlich-großes Schwarzes Loch. Die Welt um das Photon herum altert jedoch aufgrund der Zeitdilatation unendlich-schnell, d.h. dieser Zustand dauert nur unendlich-kurz an. Das Photon selbst altert jedoch überhaupt nicht, es bleibt ewig in diesem Zustand. Es umfasst in ewiger Dauer die vollständige Zeit und zugleich in einem einzigen unendlich-kurzen Zeitmoment den vollständigen Raum. Das Photon verwirklicht damit die von Nikolaus von Kues aufgestellten Gesetze des Zusammenfalls der Gegensätze zu einer Einheit (coincidentia oppositorum), die sich nun nicht mehr als Ergebnis philosophischer und religiöser Überlegungen, sondern als strenge Konsequenz aus der Speziellen Relativitätstheorie ergeben. (Helmut Hansen ergänzt in einem Kommentar: "Dieser Zustand dauert nur unendlich-kurz an, um einem neuen Zustand Platz zu machen, der wiederum nur unendlich-kurz andauert. Kurzum: Alles ändert sich in jedem Augenblick. Und genau das ist der begriffliche Sinn des  Ewigen Jetzt".)

Das ist für den menschlichen Verstand schwer zu verstehen, denn wie kann der gleiche Raum für den einen Beobachter größer, für den anderen kleiner sein? Epstein veröffentlichte 1984 einen neuen Ansatz ("Relativity visualized"). "What makes time desynchronize? What makes space contract? What makes time run slow? What makes the speed of light unexceedable" (Epstein, S. 76).

Das Gesetz von der Konstanz der Lichtgeschwindigkeit ist eine Aussage über Geschwindigkeiten und nicht über Raum und Zeit. Daher liegt es näher, nach Symmetrien im Tangentialraum zu suchen, in dem für jeden Punkt des Raums die dort möglichen Geschwindigkeiten eingetragen sind, statt im Raum selbst. Epstein ersetzt daher das Raum-Zeit-Diagramm durch ein Geschwindigkeits-Diagramm, dessen Achsen nicht mehr Raum und Zeit, sondern die Geschwindigkeiten durch Raum und Zeit sind, d.h. er wechselt mathematisch gesprochen vom Raum zu dessen Tangentialraum. Allerdings wird dieser Übergang oft nicht klar ausgesprochen und Aussagen über den Tangentialraum der Geschwindigkeiten als Aussagen über den zugrundeliegenden Raum dargestellt. Das Koordinatenkreuz des Tangentialraums TxM ist die Stelle x, wo der Tangentialraum am Raum M "angebracht" ist. Im Ganzen ergibt sich ein Tangentialbündel aller Tangentialräume zur Raumzeit.

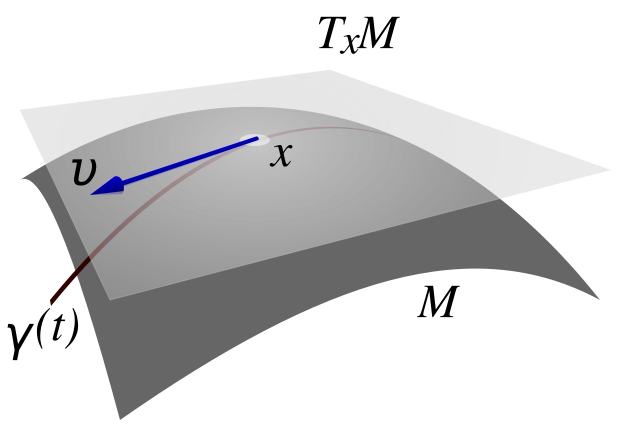
Figur 2 Tangentialraum

Die ebene Fläche TxM ist an der Stelle x der Tangentialraum einer differenzierbaren Mannigfaltigkeit M.; Wikipedia
Urheber: Von derivative work: McSush (talk)Tangentialvektor.png: TN Der ursprünglich hochladende Benutzer war TN in der Wikipedia auf Deutsch - Tangentialvektor.png, Gemeinfrei, Link

Das Epstein-Diagramm beschreibt einen Tangentialraum. Um Verwirrung zu vermeiden, sollen im folgenden die Achsen in der zugrundeliegenden Mannigfaltigkeit M mit x für den Raum und t für die Zeit und die Achsen im Tangentialraum TxM mit vx und vt bezeichnet werden. Die vx-Achse des Tangentialraums zeigt nicht mehr die jeweilige Stelle im Raum, sondern die jeweilige Geschwindigkeit an der Stelle x. An jeder Stelle sind unterschiedliche Geschwindigkeiten möglich: "Weiter draußen" ist im Tangentialraum auf der vx-Achse nicht ein räumlich weiter entfernter Punkt der zugrundeliegenden Mannigfaltigkeit M, sondern eine größere Geschwindigkeit. Der Nullpunkt des Tangentialraums markiert den Ruhepunkt, an dem der Tangentialraum in der Raumzeit angebracht ist, d.h. die Stelle, an der die Geschwindigkeiten gemessen werden. Zum Beispiel kann sich an der Stelle x im Raum M ein Fußgänger, ein Flugzeug, eine Rakete oder ein Licht befinden. Sie unterscheiden sich unter anderem durch ihre jeweilige Geschwindigkeit, und dies Merkmal wird im Tangentialraum eingetragen. Die vx-Achse ist daher zunächst nicht unendlich-lang wie die x-Achse des Raums, sondern hat eine endliche Länge von 0 bis zur Lichtgeschwindigkeit c.

Entsprechend zeigt im Tangentialraum die vt-Achse nicht mehr die Zeit, sondern das Altern, d.h. die "Geschwindigkeit durch die Zeit". Dieser Begriff ist missverständlich, da es sich um eine Übertragung (Metapher) der zunächst nur für den Raum bekannten Geschwindigkeit vx handelt. Am Nullpunkt befindet sich das Licht, das überhaupt nicht altert. Je langsamer sich etwas durch den Raum bewegt, desto schneller altert es in seiner Bewegung durch die Zeit. (Das ist die Umkehrung des bekannten Satzes aus der Speziellen Relativitätstheorie: Schnellere Uhren ticken langsamer.) Am schnellsten altert, was sich räumlich in absoluter Ruhe befindet, was sich also weder selbst räumlich bewegt noch in einer Umgebung befindet, die räumlich bewegt wird.

Wie kann ein Maß des Alterns, d.h. der Geschwindigkeit vt gefunden werden? Die räumliche Geschwindigkeit vx ist die übliche Geschwindigkeit, das Verhältnis von Raum und Zeit, aber das Maß des Altern kann nur aus dem übergeordneten Prinzip abgeleitet werden, das Epstein als Verallgemeinerung der Konstanz der Lichtgeschwindigkeit formuliert: Die Gesamtgeschwindigkeit durch Raum und Zeit ist immer konstant! Es können sich nur die Anteile der zeitlichen und räumlichen Geschwindigkeit verändern. Wenn die Geschwindigkeiten im Tangentialraum eingetragen werden, müssen sie auf einem Viertelkreis liegen, der die vx- und vt-Achse verbindet und die vx-Achse an der Stelle c für die Lichtgeschwindigkeit trifft. Dann kann die allgemeine Formel für den Einheitskreis

(1)    x2 + y2 = 1

durch Übertragen auf die vx- und vy-Achse und für einen Durchmesser c umgewandelt werden in:

(2)    vx2 + vt2 = c2

Wenn eine Geschwindigkeit vx gegeben ist, errechnet sich daraus das Altern, d.h. die Geschwindigkeit vt:

(3)    vt = √(c2 - vx2)

Mit diesem Viertelkreis erscheint das Symbol des Mandala in der Physik, dem Helmut Hansen in seinen Büchern systematisch weiter nachgeht. Die Konstanz der Lichtgeschwindigkeit beschreibt nur den Grenzfall einer Bewegung mit Ruhemasse Null, die keinen zeitlichen Anteil hat.

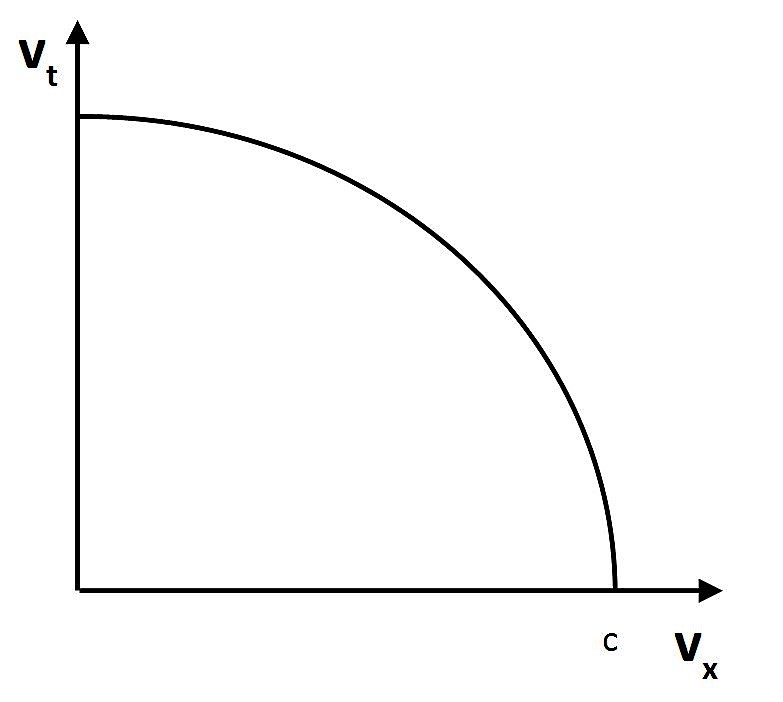
Figur 3 Epstein-Kreis

Die Zeichnung ist aus dem Buch von Helmut Hansen "Linien des Alten", S. 51 übernommen. Abweichend werden hier die Achsen mit vx und vt bezeichnet und sind analog den üblichen Raumzeit-Diagrammen gedreht.

Dieses Diagramm ist zu verstehen als die Darstellung eines Tangentialraums mit den Achsen vx und vt. Theoretisch könnten in dem Tangentialraum beliebige Kombinationen von Raumgeschwindigkeiten vx und Altern vt möglich sein. Das Prinzip der Konstanz der Lichtgeschwindigkeit besagt jedoch, dass nur die Kombinationen möglich sind, die auf dem hier dargestellten Epstein-Kreis liegen. Wenn im Grenzfall die Lichtgeschwindigkeit c erreicht wird, beträgt vt=0. Ansonsten wird jeder Geschwindigkeit vx eindeutig eine Geschwindigkeit vt zugeordnet. Alle Geschwindigkeiten liegen auf dem Kreis und erfüllen dadurch eine Symmetrie, die identisch ist mit der Symmetrie der Elektrodynamik, U(1), was später erläutert wird.

Das Maß des Alterns ergibt sich als der "Rest-Anteil", um dieses Gesetz einhalten zu können. Die vt-Achse beschreibt als Maß des Alterns eine Bewegung in absoluter räumlicher Ruhe, die ausschließlich einen zeitlichen Anteil hat, die Ruhe-Energie. Bei geeigneter Wahl der Koordinaten können aus diesen Diagrammen die wichtigen Schlussfolgerungen wie E = m · c2 direkt abgelesen werden, wobei E0 auf der vt-Achse und c als Geschwindigkeit auf der vx-Achse liegt. Eckstein wählt daher eine Darstellung, in der als Einheit der vx-Achse die Geschwindigkeit vx multipliziert wird mit den Konstanten m und c. m steht für eine vorgegebene Masse, m · vx ist also der Impuls, und c ist die Lichtgeschwindigkeit. Einheit der vt-Achse ist die Ruhe-Masse für den gleichen Wert m. Dann lässt sich an der Stelle c die Formel E = m · c2 ablesen. Im Ganzen zeigt diese Darstellung, dass die von Epstein formulierte Konstanz der Geschwindigkeit eine Konsequenz der Energie-Erhaltung ist. Raum- und Zeit-Anteil der Geschwindigkeit müssen in Summe immer die gleiche Geschwindigkeit ergeben, damit die Gesamt-Energie erhalten bleibt.

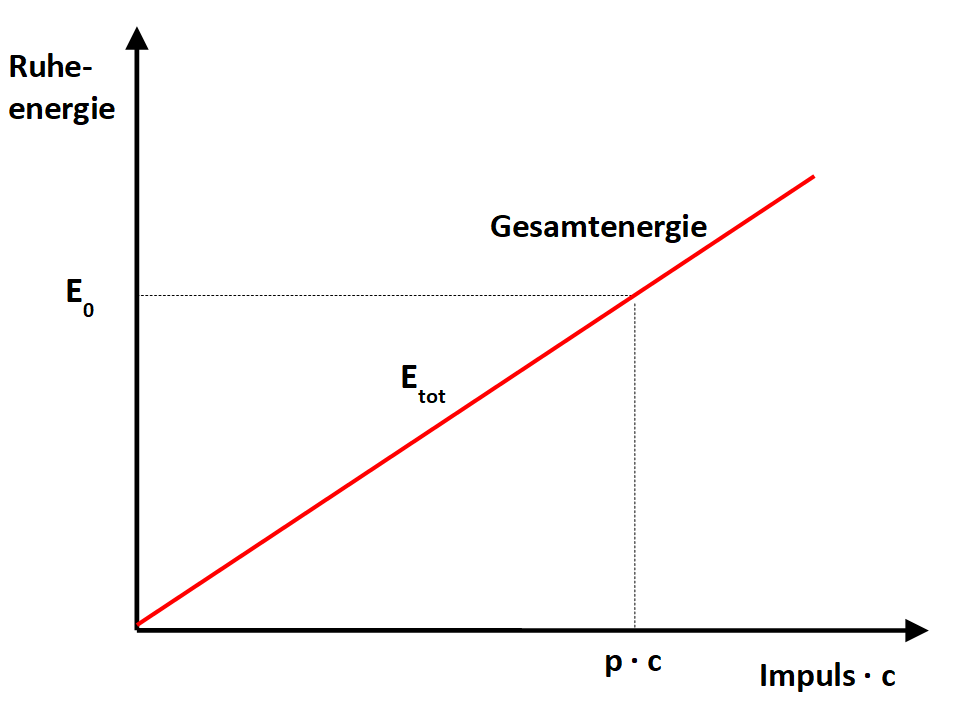
Figur 4 Gesamtenergie

E0 ist die Ruhe-Energie, Etot die Gesamtenergie, p · c die reine Bewegungsenergie. Gemäß Energie-Erhaltung muss Etot konstant sein. (Die Idee für die Zeichnung stammt aus dem Online-Skript von David Eckstein.) Quelle

Epstein und Eckstein können mit dieser Darstellung sehr intuitiv und anschaulich alle Schlußfolgerungen von Einstein nachvollziehen. Allerdings scheint ihnen die Tragweite ihrer Erkenntnis nicht bewußt zu sein. Während Einstein Aussagen über die Raumzeit treffen wollte, wonach sich z.B. Längen und Zeit verändern können (Zeitdilatation, Längenkontraktion), verstehen sie sein Prinzip als Aussagen über Tangentialräume. Nicht die Länge kontrahiert sich, sondern die Bewegung durch den Raum wird größer oder kleiner, und nicht die Zeit dilatiert, sondern die Geschwindigkeit durch die Zeit (das Altern) wird größer oder kleiner.

Einstein wollte mit der Vorstellung der Raumkrümmung die Geschwindigkeiten durch den Raum im Raum selbst darstellen. Statt an jedem Punkt im Raum den dort angebrachten Tangentialraum zu betrachten und dort darzustellen, mit welchen Geschwindigkeiten sich Teilchen durch diesen Raum bewegen, verstand er die Geschwindigkeit durch den Raum als Raumkrümmung. Das Krümmungsmaß ist mathematisch identisch mit der Geschwindigkeit vx.

Nachdem es vieler Jahrzehnte bedurft hatte, um sich an die Relativitätstheorie zu "gewöhnen", muss dieses neuerliche Umdenken sicher schwer fallen. Aber es wird eine wesentliche klarere Darstellung ermöglichen.

Jeder Tangentialraum zeigt die Geschwindigkeit an einer jeweils bestimmten Stelle. Wird weiter gefragt, ob sich die Geschwindigkeit ändern kann (Beschleunigung), dann ist das die Frage, wie benachbarte Tangentialräume miteinander verknüpft werden können. Wenn sich etwas auf einer Weltlinie durch den Raum bewegt, können sich gleichzeitig seine Geschwindigkeiten ändern. Dafür wird nicht mehr die Weltlinie betrachtet, sondern die Linie durch die zugehörigen Tangentialräume. Diese Linie wird von der Mathematik als Zusammenhang im Tangentialbündel bezeichnet.

Physik des Mandala (Helmut Hansen)

Helmut Hansen möchte zeigen, dass ausgehend von dieser Deutung ein Verständnis von Geschwindigkeiten größer als der Lichtgeschwindigkeit möglich wird. Das könnte sowohl einen Weg öffnen, quantenmechanische Tunneleffekte zu verstehen, wie es auch religiösen Überzeugungen wie Allgegenwart und Synchronizität von Ereignissen entgegenkommt.

Im wesentlichen scheint es mir um eine neue Deutung des Zwillings-Paradoxons zu gehen. Wenn ein Raumfahrer die Erde verlässt, kann von der Erde aus gemessen werden, wie weit die Bewegung führt und wie lange sie dauert. In dieser Messung von der Erde aus überschreitet der Raumfahrer nicht die Lichtgeschwindigkeit. Wenn er zurückkehrt, ist er jedoch aufgrund seines langsameren Alterns wesentlich jünger geblieben im Vergleich zu seinem Zwilling, der auf der Erde zurückblieb. Wird nun seine Geschwindigkeit berechnet als Verhältnis der von ihm gemessenen Zeit (um wie viel er während der Reise gealtert ist) und des von der Erde aus gemessenen Wegs seiner Reise, dann kann er sich weit schneller als mit Lichtgeschwindigkeit bewegt haben. Eckstein kommentiert entsprechend der Deutung von Epstein: "Da B einen Teil dieser Raumzeit-Strecke für den Raum beansprucht, bleibt bei ihm weniger für die Bewegung in der Zeit übrig. So einfach ist das." (Eckstein, C7, Link). Die höhere Geschwindigkeit ergibt sich daraus, dass zwar die Zeitdilatation des bewegten Objekts, aber nicht die von ihm gemessene Längenkontraktion berücksichtigt wird. Daher sei diese Geschwindigkeit mit vra bezeichnet: Sie berücksichtigt in gebrochener Weise die relativistischen Effekte der Zeitdilatation beim bewegten Objekt und zugleich die absolute Messung der Länge ohne Längenkontraktion vom ruhenden Beobachter aus. Gibt es Gründe, und lässt sich ein mathematischer Raum konstruieren, in dem diese unterschiedlichen Berechnungsweisen darstellbar sind? Das würde den Schritt von Epstein nochmals erweitern.

Hansen stellt die Geschwindigkeiten vra auf einer weiteren Achse dar, die parallel zur vx-Achse verläuft. Er ordnet jedem Wert auf der vx-Achse durch eine vertikale Abbildung den zugehörigen Wert vra zu. Dadurch wird der Viertelkreis durch ein Quadrat umschlossen und das Mandala ist perfekt. Hansen bezeichnet dies Quadrat als "Einstein-Quadrat".

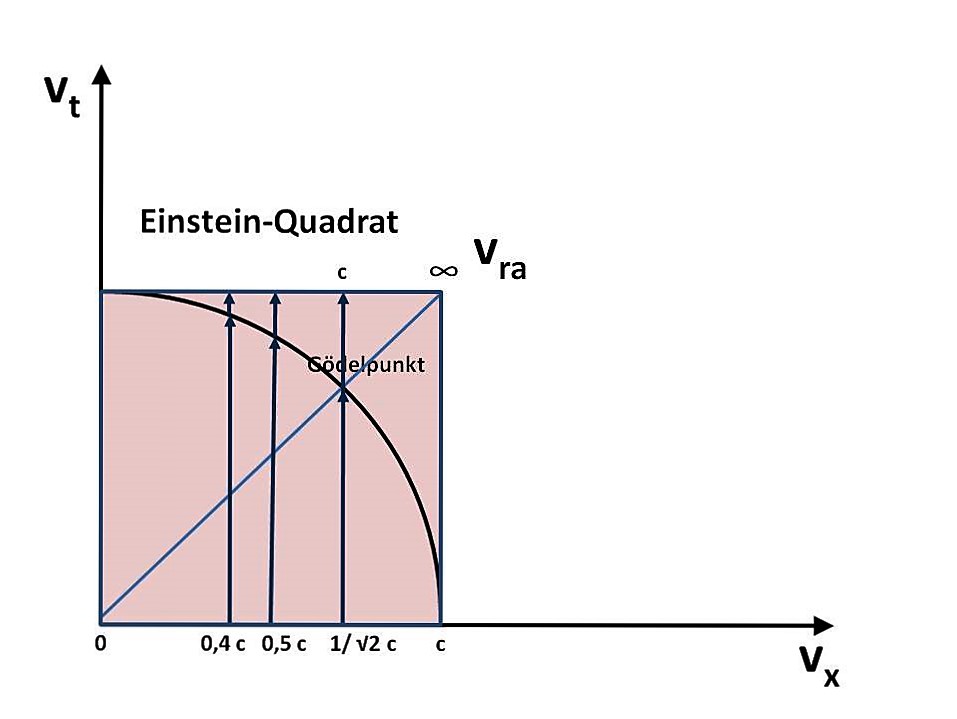
Figur 5 Mandala-Code (Epstein-Kreis im Einstein-Quadrat)

Quelle: Helmut Hansen "Linien des Alten", S.59. Hier wurden ebenfalls die Beschriftungen der Achsen und ihre Drehung geändert.

Die auf der vx-Achse eingetragenen Geschwindigkeiten werden auf die obere Seite des Quadrats projiziert. Dort wird jeder Geschwindigkeit vx die zugehörige Geschwindigkeit vra zugeordnet. Der Umrechnungsfaktor ist der von Einstein übernommene Gamma-Wert:

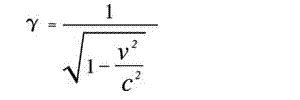
Wichtige Punkte:

• 0 wird auf 0 abgebildet, also vra(0) = 0.

• Die Grenzgeschwindigkeit c wird auf ∞ abgebildet, also vra(c) = ∞.

• Die Geschwindigkeit 1/√2 · c wird auf c abgebildet, also vra(1/√2 · c) = c.

  Diese Abbildung schneidet den Epstein-Viertelkreis an der gleichen Stelle, an der die Diagonale des Quadrats den Viertelkreis schneidet. D.h. an dieser Stelle sind Zeit- und Raum-Anteil der Geschwindigkeit identisch. Das ist die Grenze, ab der vra die Lichtgeschwindigkeit überschreitet. Bereits Gödel hatte diesen Punkt gefunden. Hansen bezeichnet ihn daher als Gödel-Punkt.

Dass dieser direkte Vergleich von Zeitmessung durch das bewegte Objekt und Längenmessung von der Erde aus sehr praktische Konsequenzen hat, zeigen ausgerechnet die experimentellen Nachweise für die Relativitätstheorie. Wenn 15 km oberhalb der Erde kosmische Höhenstrahlung auf Atome der Erdatmosphäre treffen, entstehen Myonen. Aufgrund ihrer Halbwertszeit müssten sie so schnell zerfallen, dass sie die Erde nicht erreichen. Da sie langsamer altern, verlängert sich für sie von der Erde aus gemessen die Halbwertszeit und viele von ihnen vermögen bis zur Erde zu gelangen.

Helmut Hansens Darstellung widerspricht allen heute üblichen Ansätzen der Theoretischen Physik. Sie wird aus der intuitiven Einsicht gerechtfertigt, dass das hier erscheinende Symbol des Mandala eine eigene, höhere Symbolkraft hat. Auf ähnliche Weise hatte auch Kepler seine Analysen der Planetenbewegungen begonnen, als er intuitiv versucht hatte, sie auf die Kugeln von ineinander geschachtelten platonischen Körpern zu projizieren.

Die Konstruktion des Einstein-Quadrats und die Umschließung des Epstein-Kreises durch dies Quadrat deutet auf eine grundsätzlich neue mathematische und physikalische Herangehensweise. Heute werden alle Quantenfeldtheorien mathematisch als Faserbündel dargestellt. Die besondere Bedeutung der Lichtgeschwindigkeit wurde mit der Aufstellung der Feldgleichungen der Elektrodynamik durch Maxwell erkannt. Als Symmetriegruppe der Quantenelektrodynamik gilt heute die unitäre Gruppe U(1) aller komplexen Zahlen auf dem Einheitskreis, d.h. aller komplexen Zahlen mit Betrag 1 (vgl Wikipedia). Kaum eine Theorie ist experimentell so gut nachgewiesen wie diese. Die Symmetriegruppe U(1) ähnelt dem Epstein-Kreis, wobei hier die vx- und die vt-Achse als die reelle und imaginäre Achse der komplexen Zahlen verstanden werden. Mir ist nicht bekannt, ob der innere Zusammenhang der Epstein-Deutung und der Quantenelektrodynamik bereits näher betrachtet worden ist.

Das Einstein-Quadrat mit seinen beiden parallelen Geschwindigkeits-Achsen läßt sich mathematisch nicht auf diese Weise als Faserbündel darstellen. Helmut Hansen begründet die Verschränkung von Epstein-Kreis und Einstein-Quadrat, weil die Lichtgeschwindigkeit sowohl von der Richtung (Isotropie) als auch von dem Betrag unabhängig ist, mit der sich ein Beobachter durch den Raum bewegt. Seiner Meinung nach müssen beide voneinander unterschieden werden und sind auch nur durch jeweils eigene Experimente nachweisbar (Michelson-Morley 1887 die Richtung, Kennedy-Thorndike 1932 den Betrag). Für ihn gilt: Richtung = Kreis, Betrag = Quadrat, die gemeinsam den Mandala-Code ergeben.

Mir ist an seinem Ansatz wichtig, dass er hiermit den Welle-Teilchen-Dualismus auflöst in einen gleitenden Übergang von einem teilchen-artigen in einen wellen-artigen Bereich. In einem erweiterten Mandala-Code werden die beiden Seiten des Einstein-Quadrats verlängert zu zwei Geraden vx# ("vx erhöht/sharp") und vt#, die parallel zur vx- bzw. zur vt-Achse verlaufen (die Bezeichnungen habe ich ergänzt). Die Projektion der räumlichen Geschwindigkeit vx auf die Geschwindigkeit vra kann hier geometrisch abgelesen werden:

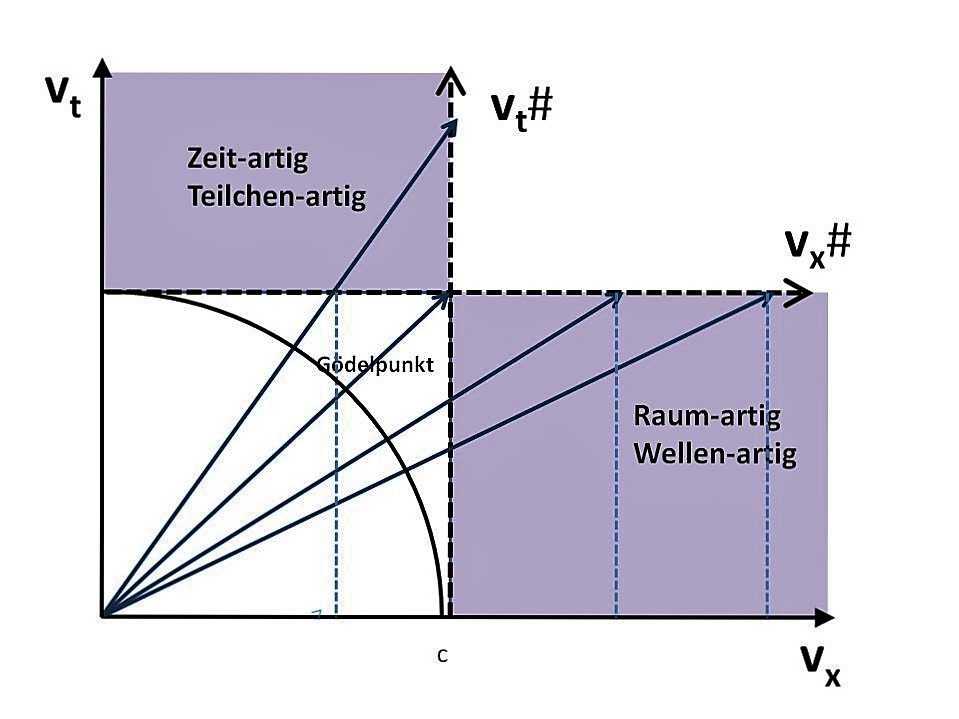
Figur 6 Entfalteter Mandala-Code (Einstein-Quadrat entfaltet in teilchen- und wellen-artige Bereiche)

Quelle: Helmut Hansen "About the Dual Parametrization of c", Figur 23, S. 12. Beschriftung und Drehung der Achsen wurde geändert. Geschwindigkeitspfeile in die Bereiche "Zeit-artig" und "Raum-artig" wurden ergänzt.

In dem erweiterten Mandala-Code werden nicht mehr die Geschwindigkeiten vx senkrecht auf die obere Seite des Einstein-Quadrats abgebildet, sondern hier wird von Nullpunkt aus eine Gerade gezeichnet, die erst den Epstein-Kreis schneidet und dann die Gerade vx# trifft. Wird dort eine Senkrechte zur vx-Achse gezogen (hier blau-gepunktet dargestellt), dann kann auf der vx-Achse der Wert abgelesen werden, der als Geschwindigkeit vra zu interpretieren ist. Aus der Darstellung geht deutlich hervor, wie für alle Geschwindigkeiten, deren räumlicher Anteil vx größer als 1/√2 ist (abzulesen an der Stelle, an der der Epstein-Kreis geschnitten wird), für vra Geschwindigkeiten größer als c erreicht werden.

Hansen bezeichnet den Bereich rechts von c als wellen- und raum-artig, den Bereich oberhalb von vx# als teilchen- und zeit-artig. Das veranlasst mich zu der weitergehenden Vermutung, dass im Epstein-Kreis sowohl eine Überschneidung von Raum und Zeit als auch eine Überschneidung von Teilchen und Partikel vorliegt. Diese beiden Überschneidungen können solange nicht voneinander unterschieden werden, wie sie innerhalb einer einzigen Darstellung übereinander gelegt werden. Um eine Unterscheidung zu ermöglichen, ist daher eine weitere Achse notwendig, die den Übergang von teilchen- zu wellen-artigen Phänomenen darstellt. Das soll im folgenden durch die Einführung der Größen-Achse und der Idee einer "Geschwindigkeit durch die Größe" erreicht werden, die von einer Diskussion der Inertialsyssteme ausgeht.

Die Abbildung des Intervalls [0,c] auf das Intervall [0,∞] von der unteren Seite des Einstein-Quadrats auf dessen obere Seite werde ich in einem weiteren Schritt als ein Beispiel für zwei verschiedene Geschwindigkeiten des Zählens interpretieren. Auf diese Weise soll aus der dichten Darstellung des Mandala-Code neben der Größe eine weitere Achse abgeleitet werden, so dass sich im Ganzen eine Erweiterung des Epstein-Kreises vx-vt zu einer Kugel ergibt.

Zuvor sei ergänzend darauf hingewiesen, dass Epstein auf eine verblüffend ähnliche Darstellung kommt. In einem Kapitel über den Urknall (Bigbang) stellt er die Frage, wie alt das Weltall ist. Ergebnis: Es gibt kein eindeutiges Alter des Weltalls. Im Urknall bewegen sich alle Teilchen mit Lichtgeschwindigkeit auseinander, wobei jedoch die Lichtgeschwindigkeit wiederum die Gesamtgeschwindigkeit ist. Die Teilchen, die sich räumlich schneller bewegen, altern langsamer. Sie sind gemessen vom Urknall aus daher bereits sehr weit entfernt, aber noch sehr jung. So kommt es zum paradoxen Ergebnis, dass die Teile des Universums, die am weitesten von uns entfernt sind, zugleich am jüngsten sind. Würde sich alles mit einer Geschwindigkeit vx = c bewegen, wäre die maximale räumliche Größe des Kosmos erreicht, aber zeitlich wäre alles beim Urknall stehen geblieben. Dies ist eine andere Darstellung der oben genannten Betrachtung, dass aus Sicht des Photons der Urknall zeitlich noch gar nicht verlassen ist.

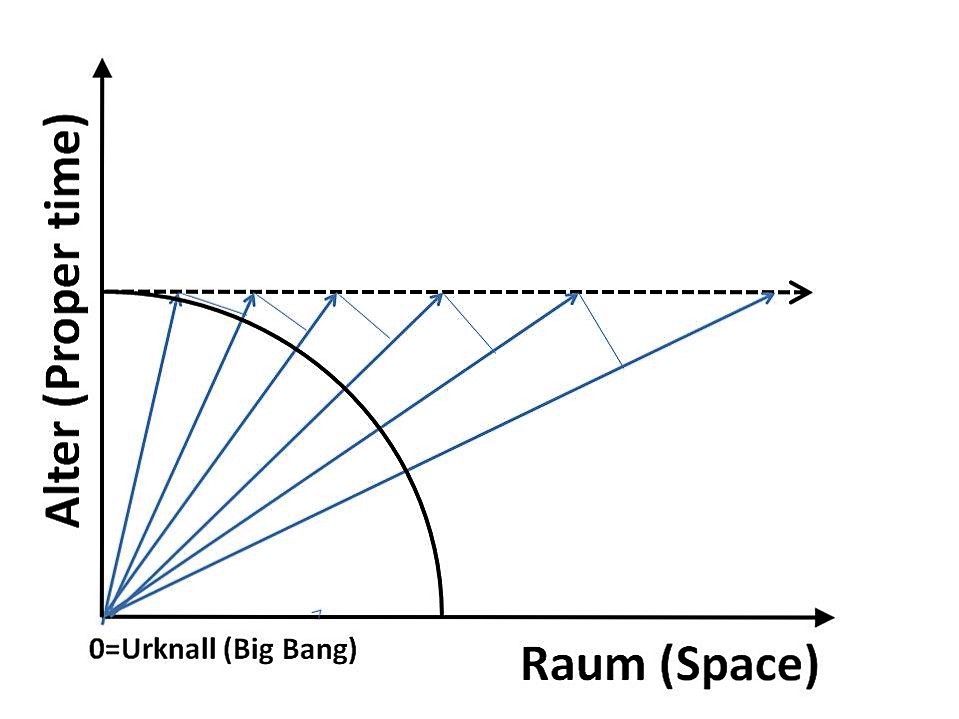
Figur 7 Der Allerletzte Horizont (Ultimate Horizon)

Quelle: Epstein, "Relativity Visualized", Figure 6-5, s. 105 Epstein versteht hier den Nullpunkt als den Urknall. Das Diagramm zeigt, wie weit vom Ort des Urknalls die Teilchen entfernt sind, wenn sie alle das gleiche Alter erreicht haben. Je schneller sich ein Teilchen durch den Raum bewegt, desto langsamer altert es. Daher sind die schnelleren Teilchen viel weiter entfernt, wenn sie gleich alt sind wie die langsameren Teilchen. Es gibt nicht "das Alter" des Weltalls. Als Maß kann das Alter derjenigen Telchen gewählt werden, die sich räumlich nicht bewegen, also räumlich am Ort des Urknalls stehen bleiben.

Bei einer genaueren Betrachtung zeigt sich, dass dies Diagramm ähnlich wie die Konstruktion der Geschwindigkeit vra einen absoluten und einen relativistischen Aspekt mischt. Der Begriff "Alter (Proper time)" ist missverständlich. Das zeigt nicht die absolute Zeit seit dem Urknall, sondern das jeweilige Alter, dass sich für jedes bewegte Partikel entsprechend seiner Geschwindigkeit ergibt. Daher ist diese Achse im Grunde eine Variante der vt-Achse. Epstein hat hier eine Mischung des Raum-Zeit-Diagramm und des vx-vt-Diagramm gewählt und kommt daher zu ähnlichen Ergebnissen wie Helmut Hansen im erweiterten Mandala-Code.

Synchronizität

Gibt es auch andere Möglichkeiten, Synchronizität darzustellen? Ich sehe fünf mögliche Ansätze:

(1) Das Licht ist als Grenzgeschwindigkeit zunächst nur in der Raumzeit nachgewiesen, in der sich Wirkungen durch Wechselwirkungsteilchen ausbreiten, die sich nicht schneller als das Licht bewegen können. Anders kann es im Tangentialbündel sein. Möglicherweise können sich dort Wirkungen über benachbarte Tangentialräume schneller fortpflanzen und würden damit bereits vorab das Umfeld beeinflussen, bevor die Bewegung in der Raumzeit dort angekommen ist.

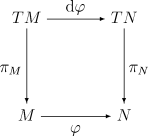
Figur 8 Abbildungen von einem Tangentialbündel auf ein anderes

Hier kann auch vereinfachend eine Abbildung von M auf M und entsprechend von TM auf TM gewählt werden. Wenn sich in TM Symmetrien ausbreiten, könnte das in M als Synchronizität wahrgenommen werden. Quelle
Urheber: By User:Fropuff~commonswiki - , Public Domain, Link

(2) Raumzeit und Tangentialbündel sind ihrerseits Objekte in einem übergeordneten unendlich-dimensionalen Raum (Hilbertraum), der als Achsen sowohl die Raum- und Zeit-Achse in M wie auch alle vx- und vt-Achsen der Tangentialräume TxM des Tangentialbündel TM enthält. Nur in einem solchen Raum können direkte Wechselwirkungen zwischen den Raumzeit-Achsen und den Geschwindigkeits-Achsen betrachtet werden, also auch Symmetrien, die relativistische und absolute Aspekte frei miteinander verknüpfen, wie es Hansen nahe legt. Wird nun in einem weiteren Schritt dieser übergeordnete Raum seinerseits als Mannigfaltigkeit betrachtet, die sich verändert und daher ihrerseits ein Tangentialbündel hat, können dort Entstehen und Vergehen von Symmetrien studiert werden. (Überlegungen solcher Art werden herangezogen zum Beweis der Poincaré-Vermutung).

Die Quantentheorie geht schon lange nach dieser Methode vor. Sie betrachtet nicht die möglichen Geschwindigkeiten, die ein Teilchen an der Stelle x haben kann und die im Tangentialraum TxM eingetragen sind, sondern die möglichen Quantenzustände des Teilchens an der Stelle x. Die Quantenzustände werden in einer Faser Fx in einem Faserbündel FM eingetragen. Das Faserbündel FM ist ein unendlichdimensionaler Raum.

(3) Bisher wurde implizit vorausgesetzt, dass sich die Erde in absoluter Ruhe befindet und Synchronizität hergestellt werden könnte durch ein Objekt, das sich schneller als die Erde bewegt und wieder zurückkehrt. Kann es nicht genau umgekehrt sein? Die Erde hat eine eigene Bewegung, und es ist denkbar, umgekehrt zu einem bewegten Objekt zu wechseln, das wesentlich langsamer ist. Wenn es sich zurückmeldet, ist die Erde kaum älter geworden, im Grenzübergang unverändert geblieben.

(4) Das Zwillingsparadoxon - gleich in welcher Richtung - führt zur Identitätsfrage: Welche Umgebung ist bei der Rückkehr gültig? Wie lassen sich im Moment des Verlassens und der Wiederkehr die beiden unterschiedlichen Bewegungen mit ihren unterschiedlichen Maßen in Zeit, Länge und Masse wieder zusammenführen? Diese Frage führt zur Allgemeinen Relativitätstheorie, da im Moment des Starts und der Rückkehr große Beschleunigungen bzw. Abbremsen notwendig sind. Positive und negative Beschleunigung stellen die Identitätsfrage neu. Weitergedacht ist es nicht nur eine Frage des unterschiedlichen Alterns, sondern möglicherweise auch unterschiedlichen Zählens, das in diesen Momenten zusammentrifft und in der Einheit der Eins integriert werden muß.

(5) Daraus ergibt sich abschließend der Ansatz: Es sind zusätzlich zu Raum und Zeit weitere Dimensionen notwendig, um Fragen dieser Art zu betrachten. Aus systematischen Gründen sind das vorrangig die Zahl und die Größe, um die es im weiteren gehen soll.

Transzendentale Deutung im Sinne von Kant

Die fest an einem Ort installierte, also "unbewegte" Uhr (Raumanteil = 0) gilt simultan überall. Sie beschreibt exakt die reine Wechselwirkung, von der Kant in der "Kritik der reinen Vernunft" sprach. Ihre Signale sind "unendlich schnell", ihre Reichweite unendlich groß. Wird dagegen die Uhr räumlich bewegt, gilt sie nur noch in einem lokalen Bereich, der um so kleiner wird, je schneller sich die Uhr bewegt. Im anderen Grenzfall wird der Zeitanteil = 0, so dass die Uhr mit der Zeitachse zusammenfällt. Das hat Kant mit der reinen Kausalität gemeint. Hier bedingt in einer eindimensionalen Folge ein Ereignis das nächste. Alles hat einen eindeutigen Grund und eine eindeutige Wirkung. Zusammenfassend können die vx-Achse mit der Kausalität und die vt-Achse mit der Wechselwirkung identifiziert werden.

Die Relativitätstheorie beschreibt beim Gödelpunkt, d.h. der Geschwindigkeit 1/√2 · c einen dritten, mittleren Grenzfall, wenn Raum- und Zeitanteil anteilig gleich sind. An dieser Stelle nimmt der Vorwärtskegel die Gestalt wie in der Speziellen Relativitätstheorie ein. An dieser Stelle beschreibt die Physik des Mandala den Grenzfall der Speziellen Relativitätstheorie. Damit ist die Physik von Einstein ebenso als Grenzwert dargestellt und "eingeordnet" wie die Physik von Newton. Allerdings gilt jetzt nicht mehr, dass die Physik von Newton ein Grenzfall der Physik von Einstein ist, sondern beide sind unterschiedliche Grenzfälle einer höheren Physik.

Das Prinzip der Relativität muss genau umgekehrt werden: Reichweite und Neigung der Vorwärtskegel sind abhängig von der jeweiligen Geschwindigkeit der Uhr, also relativ. Sie sind nicht - wie bisher in der Speziellen Relativitätstheorie postuliert - überall identisch geneigt mit dem Winkel der Lichtgeschwindigkeit, also nicht absolut. Die Vorwärtskegel werden immer "steiler", restriktiver, je schneller die Uhr bewegt ist. Umgekehrt werden sie immer flacher, je langsamer die Uhr bewegt ist. In den beiden Extremen fallen die Vorwärtskegel entweder mit der reinen Wechselwirkung oder der reinen Kausalität zusammen. Einstein hat daher nicht nur eine Physik geliefert, für die Newton der Grenzfall ist, sondern er kann vermittelt über die Interpretation durch Epstein auch einen philosophischen Neuansatz zum Verständnis von Raum und Zeit liefern, für den Kant der Grenzfall ist. Und mit Kant wird auch der euklidische Raum als Grenzfall erkannt: Die euklidische Geometrie gilt im flachen Bereich der reinen Wechselwirkung auf der vt-Achse. Die euklidische Geometrie kennt keine Zeit, sie liegt vollständig innerhalb der Zeit, wenn der Raumanteil = 0 ist. Die nicht-euklidischen Geometrien liegen in den geneigten Räumen mit Raumanteil > 0.

Die Gravitationstheorie in ihrer heutigen Form beschreibt "Fernwirkungen", gilt also simultan und liegt damit umgekehrt vollständig innerhalb des Raums, wenn der Zeitanteil = 0 ist, auf der vx-Achse. Sie wird von keinem Wechselwirkungsteilchen übertragen, das sich wie jedes andere Teilchen bewegen müsste. Es kann daher keine Gravitonen gehen (wie es auch umgekehrt auf der reinen Zeitachse keine Tachyonen gibt). Die Quantenmechanik beschreibt Natureigenschaften, die von Wechselwirkungsteilchen übertragen werden, die jeweils bestimmte Geschwindigkeiten und Reichweiten haben. Daher ist es strukturell unmöglich, Gravitations- und Quantentheorie in Deckung zu bringen. Der Epstein-Kreis liefert einen Ansatz, diese Theorien in einen größeren Zusammenhang zu bringen.

Helmut Hansen vermutet, dass sich durch eine Bifurkation vom Gödelpunkt aus ein Hyperraum öffnet, den er Gödel-Graben nennt, und von dem aus extreme Beschleunigungen möglich sind. Das muss noch intensiver betrachtet werden.

Größe und Zahl

Kann die Dynamik von Raum und Zeit erweitert werden zu einer Dynamik aller vier Maße der Natur? Hierfür ist die zugrundeliegende Mannigfaltigkeit zu erweitern: Größe und Zahl ergänzen Raum und Zeit. Zur x- und t- müssen zwei weitere Achsen hinzutreten, die als z-Achse für die Zahl und g-Achse für die Größe bezeichnet seien. Im Tangentialraum ist zu fragen, was die Geschwindigkeiten durch die Zahl und durch die Größe sind, entsprechend dem Altern als Geschwindigkeit durch die Zeit und der räumlichen Geschwindigkeit. Der Kreis im Raum des Alterns und der räumlichen Geschwindigkeit ist zu erweitern durch einen dazu senkrecht stehenden zweiten Kreis der Dynamik von Größe und Zahl mit den beiden zusätzlichen vz- und vg-Achsen. Das ergibt zusammengesetzt eine Kugel.

"Die Geschwindigkeit vg durch die Größe" ist die Geschwindigkeit des Übergangs zwischen den verschiedenen Größen wie Festes, Flüssiges, Gasförmiges, Chaotisches. Das ist nicht mit der Entropie zu verwechseln. Die Entropie zeigt das Maß der inneren Bewegtheit. Hier geht es dagegen um die Dynamik, wie sich dies Maß ändern kann, also ein Zustand höherer Entropie in einen mit niedriger übergeht und umgekehrt. Das ist die jeweilige Stabilität, wie schnell etwas stabilisiert bzw. wie schnell es zu zerfallen droht.

Noch ungewohnter ist es, die "Geschwindigkeit vz durch die Zahl" zu finden. Das ist das Zählen. Es ist also auf einer vierten Achse nicht die Zahlengerade einzutragen, sondern die Dynamik des Zählens, die "Zählgeschwindigkeit". Beispiele für unterschiedliche Zählgeschwindigkeiten: Das langsame, bedenkende philosophische Zählen oder gar die intuitive Versenkung in die Eins. Es folgt das einfache Abzählen. Das wird bescheunigt durch Multiplizieren und Potenzieren. Reelle Zahlen fassen ganze Grenzprozesse zusammen, komplexe Zahlen durchlaufen Kreise und Blätter, Funktionen durchlaufen Funktionswerte, es folgen Räume und Funktionsräume und schließlich als das heute äußerste Extrem die virtuelle Mathematik mit ihrer Konstruktion von Problem- und Lösungsräumen.

Ein anderer Ansatz, die Geschwindigkeit vz durch die Zahl zu messen, könnte die Komplexität sein, entsprechend den verschiedenen Größen. Auf der vz-Achse sind dann nicht die unterschiedlichen Zahlen und auch nicht die Zahlenklassen wie natürliche, ganze, rationale, irrationale, reelle und komplexe Zahlen einzutragen, sondern die Komplexität. Ihr Maß könnte die Vielfältigkeit (Multiplizität) der Eins sein, ausgehend von der einfachen Eins der natürlichen Zahlen über das Plus-Minus der ganzen Zahlen, die Brüche n/n, Eins als Grenzwert bis zur Eins auf der Einheitskugel. Hier schlägt die Komplexität der Zahlen um in das Symbol des Kreises, das zugleich eine bestimmte Stufe der Auflösung der Größe zeigt und das innere Prinzip der gesamten Darstellung ist.

Für die Erweiterung um die Dynamik von Größe und Zahl sprechen zunächst prinzipielle Überlegungen: Kant hat neben der Kausalität und der Wechselwirkung als dritten gleichberechtigten Begriff die Substanz eingeführt. Das ist dasjenige, was in der Zeit unverändert bleibt. Wechselwirkung gibt es innerhalb der Substanz.

Die Neuplatoniker sprachen am Ende - mit Simplikios - von vier Maßen der Natur: Neben Zeit und Ort sind das Zahl und Größe. Substanz sehe ich in ähnlicher Weise zwischen vz und vg aufgespannt wie die Gesamt-Energie im Epstein-Kreis zwischen vx und vt. Impuls und Energie sind Funktionen der Geschwindigkeit, mv bzw. mv2. Die reinen Gesetze von Impuls und Energie gelten jedoch nur für Masse-Punkte, d.h. für eine Ebene, in der die Masse punktuell gilt. Dies widerspricht der Natur und führt in der Physik zu den unlösbaren Problemen, dass bei Integralen über die Masse beim Übergang zum Massenpunkt unendlichgroße Werte entstehen. Diese können nur durch die rein hypothetisch getroffene Annahme von gegenläufigen virtuellen Teilchen ausgeglichen werden. Der zweidimensionale Tangentialraum mit der vx- und vt-Achse zeigt eine Welt, in der Masse auf Massepunkte reduziert ist. Um von den Massenpunkten zu zusammenhängenden Massen zu gelangen, sind die zusätzlichen Achsen vg für die Größe und vz für die Zählung von Zeiten, Räumen und Größen notwendig.

Umgekehrt gibt es bei Zahl und Größe ähnliche Komplementaritäten wie bei Raum und Zeit. Eine "reine Zahl" hat paradoxerweise keine Größe, sondern ist eine reine Existenz-Aussage: etwas, das in Eins-Zahl, Zwei-Zahl, ... vorkommt. Daraus lässt sich nichts über dessen Größe aussagen. Es ist ein Grundgesetz der Arithmetik, dass ihre Regeln unabhängig von der Größe der Dinge gelten, die gezählt, addiert, multipliziert, und allgemeiner: mit denen gerechnet wird. Physikalisch gesprochen ist die Arithmetik vollständig skalen-invariant, was jedoch nirgends in der Natur zutrifft.

Auf der anderen Seite hat "reine Größe" keine Zahl. Eine Größe ist dadurch bestimmt, dass sie innerlich zusammenhängend ist, dass sie nicht in Teile zerrissen werden kann. Eine Größe ist als Größe ihr eigenes Maß. Das wird am deutlichsten an den Grenzfragen, die ebenfalls bereits Kant betrachtet hat: Die Größe des Alls oder die Größe des Individuums. Reine Größen sind daher nicht zählbar, sie sind - wie in voller Klarheit die Quantentheorie gezeigt hat -, un-unterscheidbar. Ihre Zahl ist unbestimmbar.

Zwischen diesen beiden Extremen gibt es wie im Fall von Raum und Zeit einen Kreis voller Zwischenwerte: Das sind die Wahrscheinlichkeiten. Heute betrachtet die Wahrscheinlichkeitstheorie allerdings nur ein einziges Wahrscheinlichkeitsmaß und das darauf aufbauende Gesetz der Großen Zahlen. Ich vermute daher, dass es entsprechend dem Epstein-Kreis einen weiteren vz-vg-Kreis gibt, auf dem die Wahrscheinlichkeiten liegen mit jeweils unterschiedlichen Zahl-Anteilen und Größen-Anteilen. Je größer der Größen-Anteil wird, desto verschwommener ist das Bild, und desto ungenauer lassen sich auch nur die Wahrscheinlichkeiten berechnen. Je größer der Zahl-Anteil wird, desto schwächer wird die innere Bindung, die in der Größe durch den inneren Zusammenhang gegeben ist.

Um Relativitäts-, Gravitations- und Quantentheorie zusammenzubringen, scheint mir eine solche weitere Achse erforderlich. Einstein hatte mit seinen Bedenken gegen die Wahrscheinlichkeitstheorie keineswegs unrecht. Sie müssen ernst genommen und berücksichtigt werden, indem die Wahrscheinlichkeitstheorie in dieser Weise ein Grenzfall wird, mit dem Einstein vielleicht auch "leben" könnte.

Die größten Schwierigkeiten scheinen mir nach wie vor zu sein, den Größen-Begriff und die Geschwindigkeit vz des Zählens überzeugend zu klären.

Im Ergebnis würde eine ganz andere Struktur der Mathematik begründet werden können als es heute üblich ist und seit Bourbaki unverändert gilt: (a) Durch den Epstein-Kreis die besonderen Zahlen des Kreises wie π und damit e, (b) durch das Einstein-Quadrat die irrationalen Zahlen, hier √2*c als Länge der Diagonale im Verhältnis zur Seitenlänge des Einheitsquadrats, (c) die imaginären Zahlen durch Einbeziehung der Gruppe U(1), (d) orthogonale Zahlen (möglicherweise symplektische Form, Energie-Begriff), falls auf diese Weise der Hyperraum entsteht.

Eine andere Architektur der Mathematik würde auch ein neues Verständnis physikalischer Räume bedeuten. Das könnte zu einer Rückkehr zu älteren Überlegungen von Kepler und Proklos führen: Die Mathematik wird systematisch aus Prinzipien wie der Grenze und dem Unbegrenzten aufgebaut, daraus ergeben sich sowohl die geometrischen Objekte wie Punkt, Gerade, Kreis usf. als auch die Zahlklassen wie natürliche, rationale, reelle, komplexe Zahlen. Die Zahlklassen werden auseinander entwickelt. Mit der Entwicklung entstehen schrittweise Symmetrien. Gebilde wie Punkt, Gerade, Kreis und Quadrat entwickeln sich ihrerseits: Anfangs handelt es sich um die elementaren Figuren der Geometrie, später um Symmetrien in größeren Räumen. Erst aus solch einem neuen Zugang zur Mathematik könnte ein intuitiver Einfall wie das Mandala, das Hansen betrachtet, systematisch verstanden werden.

Lokale und globale Betrachtung: Die globale Betrachtung erfolgt von der Grundlinie aus. Dies ist die Linie, die völlig unbewegt ist und damit für Erde, Schwere oder Gewicht steht. Von hier aus kann alles beobachtet werden, was sich in der Zeit abspielt. Die Überlichtgeschwindigkeit entsteht nur dadurch, wenn die Geschwindigkeit des bewegten Körpers gemessen wird als Verhältnis der lokalen Eigenzeit (der bewegte Körper altert langsamer als der ruhende Körper) und der globalen, durchlaufenen Strecke, wie sie von der Grundlinie aus gesehen wird. Um ein solches Verhältnis erkennen und bestimmen zu können, ist ein Standort außerhalb dieses Diagramms notwendig. Um zu diesem Standort zu gelangen, könnte eine weitere Dimension notwendig sein, die möglicherweise als die Substanz-Achse zu verstehen ist und den Hyperraum öffnen könnte.

In der Mathematik wird seit langem nicht mehr nur von Zahlen und Punkten, sondern von Funktionen und Funktionsräumen gesprochen. Funktionen können ähnlich addiert und abgeleitet werden wie Zahlen, es gibt Grenzfunktionen von Funktionen-Folgen, wie es Grenzwerte von Zahlen-Folgen gibt. Noch einen Schritt weiter gibt es dann Grenz-Räume von Raum-Folgen und qualitative Eigenschaften von solchen Folgen. Und es gibt seit der genialen Idee von Galois Grenz-Konstruktionen von Konstruktions-Folgen. In welchem Zusammenhang steht das zu den hier entwickelten Ideen. Eine Schlüsselstellung könnten die Fourier-Reihen haben. Ist es denkbar, dass innerhalb der oben definierten Kugel eine Struktur entsteht, die mit Folgen dieser Art zu tun hat?

Und ist es möglich, dass innerhalb dieser Kugel das Resonanz-Phänomen beschrieben werden kann? Gibt es bestimmte Bereiche, möglicherweise Ebenen in dieser Kugel, in denen Resonanz-Effekte rein bzw. unrein auftreten, und die daher unterschiedliche Grade von Stabilität zeigen?

Ist mit diesen Bildern die von Dürer gezeichnete Schraubenlinie zu vereinbaren? Ist die Schraubenlinie auf die Kugel zu projizieren?

Schließlich sollte auch das Trägheitsprinzip als noch zu definierender Grenzfall in bestimmten Bereichen dieser Kugel gelten. Das könnte bedeuten, dass die von Aristoteles unterschiedenen Stoff-Arten der proto hyle, hyle topike und hyle noete möglicherweise hier ebenfalls ihren Platz finden und vielleicht sogar ineinander übergehen..

Mathematik der Größe (Größe und Inertialsystem)

Größe soll hier nicht als eine Kategorie, sondern als ein Maß der Natur wie Raum und Zeit verstanden werden. Diesen Unterschied zu erkennen macht zunächst die größte Schwierigkeit aus. In der Regel wird gefragt: Welche Größe hat etwas, wie groß ist etwas. Diese Frage ist vergleichbar der Bestimmung von anderen Kategorien: Wo ist etwas, wie alt ist es, welche Farbe hat es, wie schmeckt es, welche anderen Eigenschaften hat es. Wird die Größe als Kategorie verstanden, dann ist sie im Grunde identisch mit dem Volumen von etwas im Raum: Etwas ist so groß, wie viel Platz es im Raum einnimmt. Größe als Kategorie bedeutet: Es wird gefragt, welche Größe eine vorgegebene Substanz hat. Größe als Maß dagegen bedeutet: Es wird nicht mehr gefragt, wie groß etwas ist, sondern ob es überhaupt Größe hat, in welchem Maß es Größe hat.

Anschaulich hat etwas Festes eher Größe als etwas Durchlöchertes, als eine Gruppe einzelner, voneinander getrennter Elemente. Wie groß ist ein Vogelschwarm? Müssen für seine Größe auch alle einzeln fliegenden Vögel berücksichtigt werden, die möglicherweise gerade dabei sind, sich ganz vom Schwarm zu trennen? Wie groß ist eine Flüssigkeit? Zählen auch alle Tropfen in der Umgebung dazu, die verspritzt wurden, und was ist mit dem Teil der Flüssigkeit, der gerade verdunstet? Wie groß ist eine Flamme? Größe als Maß verstanden mißt nicht die jeweilige Größe, sondern mißt, mit welcher Genauigkeit die Größe gemessen werden kann.

Es fällt schwer, den Begriff Größe in zwei unterschiedliche Begriffe aufzuteilen und zu unterscheiden, um hier Missverständnisse zu vermeiden. Die Relativitätstheorie zeigt jedoch einen Ansatz. Dort übernimmt auf eine überraschende Art und Weise das Inertialsystem das Maß der Größe.

Das Relativitätsprinzip setzt voraus, dass alle Inertialsysteme gleichberechtigt sind und sich relativ zueinander bewegen. Stillschweigend wird dabei weiter vorausgesetzt, dass sich die Inertialsysteme klar und eindeutig voneinander abgrenzen lassen und nicht ineinander übergehen, sich nicht auflösen oder neu entstehen, also jeweils für sich absolut sind.

Das scheint aufgrund der gängigen Beispiele selbstverständlich zu sein: Bewegung auf der Erde, in einem Schiff, in einer Eisenbahn oder einem Auto. Überall bestätigt sich, dass innerhalb des jeweiligen Inertialsystems alles senkrecht nach unten fällt und nicht abgelenkt wird. Jedes Inertialsystem erscheint als ein für sich bestehender Raum, in dem eindeutig Innen und Außen zu unterscheiden sind. Die einzigen Schwierigkeiten, die bisher diskutiert wurden, betrafen Fragen, ob sich das Inertialsystem beschleunigen kann oder eine rotierende Bewegung vollzieht. Immer wurde aber vorausgesetzt, dass Inertialsysteme erhalten bleiben.

Ohne große Experimente durchführen zu müssen, können zahlreiche Gegenbeispiele genannt werden:

(1) Inertialsysteme können durchlässig sein. In einem Auto mit offenen Verdeck werden sich im offenen Bereich das Inertialsystem des Autos und der umgebenden Atmosphäre vermischen. Wenn hier etwas zum Autoboden fällt, wird es teils vom Inertialsystem Auto mitgeführt, teils vom Inertialsystem der umgebenden Luft abgelenkt. - Der Asteroidengürtel kann als ein Inertialsystem angesehen werden: wenn von einem Asteroid etwas herunterfällt, wird es in Richtung der Gesamtbewegung des Gürtels mitgeführt. Wie groß können die Abstände der Asteroiden werden, bis das Inertialsystem zerfällt in die einzelnen kleineren Inertialsysteme der einzelnen Asteroiden und des umgebenden Raums? - Epstein nennt ein Gedankenexperiment von Galilei: Ein großer Stein fällt gleich schnell wie ein kleiner Stein, da der große Stein als Haufen kleiner Steine gedacht werden kann, die ein gemeinsames Inertialsystem bilden. Wie weit müssen die einzelnen Steine voneinander entfernt sein, damit sich zwischen ihnen beherrschend der äußere Wind oder vorbeiziehende Wolken mit Sturm und Hagelschlag durchsetzen können? - Neutrinos sind so klein und schnell, dass ein Neutrinostrom alles durchdringt. Sind Fälle denkbar, bei denen der Neutrinostrom dennoch in den jeweiligen von ihm durchdrungenen Inertialsystemen Änderungen hervorruft?

(2) Inertialsysteme können sich auflösen. In einem Gedankenexperiment sei ein Flugzeug aus Wachs vorgestellt, das sich wie die Flügel des Ikaros in der Sonne auflöst. Wie lange bleibt der Charakter des Inertialsystems erhalten, wann machen sich die einzelnen Teile des sich auflösenden Flugzeugs selbständig und bilden ihre jeweils eigenen Inertialsysteme? - Andere Beispiele sind kleinere Flüsse, die mit einer eigenen Geschwindigkeit in einen größeren Fluß strömen und sich dort auflösen. Während des Einströmens überlagern sich die beiden voneinander unabhängigen Inertialsysteme bis schließlich der größere Strom dominiert. Übergangsweise kann es zu Turbulenzen kommen, die für eine Weile eine eigene innere Stabilität besitzen, also ihrerseits als ein Inertialsystem angesehen werden können.

Aus diesen Beispielen ergibt sich, dass das Maß der Größe nicht "ihre Größe" ist, also das in einem umgebenden absoluten Raum gemessene Volumen (die Grenzen des jeweiligen absolut gedachten Inertialsystems), sondern die Stabilität und Durchlässigkeit, d.h. die Eindeutigkeit und der Bestand der Grenze, wodurch Innen von Außen unterschieden sind. Bevor gefragt wird, welche Größe größer als eine andere ist, sie also beim direkten Anlegen überragt, muss gefragt werden, wie konsistent das jeweilige Große ist. Damit ist auch nicht die spezifische Dichte gemeint. Wenn z.B. Getreidekörner sehr eng aneinander gepresst sind, werden sie dennoch sofort auseinanderfallen sowie der von außen angelegte Druck gelockert wird. Ein Ziegelstück hat dagegen für sich Bestand.

Diese Beispiele sollen ausreichend gezeigt haben, dass bis heute in der Regel nach Maßen gesucht wird, um die Größe zu messen, während es hier umgekehrt darum geht, die Größe als ein Maß zu verstehen, mit dem etwas gemessen wird. Heute werden in der Regel das Feste und das Flüssige oder allgemeiner die verschiedenen Aggregatzustände starr voneinander abgegrenzt. Eine Wissenschaft der Maße soll dagegen erforschen, nach welchen Kriterien die Größe als Maß anzulegen ist. Da bieten sich unterschiedliche Übergänge an: Vom Partikel-artigen zum Wellen-artigen. Von einer regelmäßigen Binnenstruktur zu einer unregelmäßigen. Von einer größeren Dichte innerer Verknüpfungen zu einer geringeren Dichte. Als Grenzbegriff kann aufgenommen werden, wie Schelling das Schwere beschrieben hat: Das Schwere ist das in sich Verhangene, Untransparente, das sogar Licht schluckt und nicht mehr freigibt.

Gegenseitige Durchlässigkeit und unterschiedliche Dauerhaftigkeit sind intuitiv die einfachsten Parameter, um zu bestimmen, was unterschiedliche Grade von Größe ausmacht.

Auch Entropie oder Wärme können lediglich dazu dienen, die Größe als Maß zu beschreiben. Sie helfen, die innere Beweglichkeit der einzelnen Komponenten zu bestimmen, wodurch der Zusammenhalt einer Größe gegeben ist. Naheliegender erscheint mir, das elektromagnetische Feld als Paradigma zu wählen. Jede Größe hat einen Durchfluss (die Divergenz), der ihre Durchlässigkeit zeigt, und eine Rotation, durch die ihr Zusammenhalt hergestellt und gesichert wird. Unterschiedliche Größe kann dadurch erkannt werden, dass Divergenz und Rotation gemessen werden. Bei einem festen Stoff ist die zusammenhaltende Rotation gewissermaßen unendlich schnell, die ständig die Oberfläche sichert. Beim elektromagnetischen Feld vermittelt die Lichtgeschwindigkeit den Zusammenhalt von Magnetismus und Elektrizität.

Die "Geschwindigkeit durch die Größe" ist daher, wie schnell sich etwas Großes auflöst bzw. aufbaut. Diese Geschwindigkeit darf nicht verwechselt werden mit den Binnengeschwindigkeiten, durch die die Grenze des Großen erhalten wird.

Soll der Begriff der Größe in dieser Weise definiert und möglichst klar von dem traditionellen Verständnis der Größe als Volumen unterschieden werden, bietet sich kein Begriff so sehr an wie das Inertialsystem. Das Inertialsystem ist das Große, also dasjenige, das Größe hat. Die "Geschwindigkeit durch die Größe" ist die "Geschwindigkeit durch die Inertialsysteme", d.h. die Geschwindigkeit, mit der Inertialsysteme entstehen und vergehen können.

Im Ergebnis wird damit das Relativitätsprinzip nochmals erweitert. Die Inertialsysteme sind nicht nur relativ gegeneinander, sondern sie gelten auch nur relativ im Prozess ihres Entstehens und Vergehens.

Wie der Begriff des Alterns als der "Geschwindigkeit durch die Zeit" missverständlich ist und daher von "Eigenzeit" gesprochen wird, so auch der Zerfall/Aufbau einer Größe. Es ist die größende bzw. entgrößende Größe.

Im entfalteten Mandala-Code von Helmut Hansen sind das Verhältnis von Raum und Zeit und das Verhältnis von Teilchen und Welle übereinander gelegt. Hier sollen sie voneinander getrennt und entkoppelt werden. Wenn nach der Gesamtgeschwindigkeit gefragt wird, hat sie nicht nur einen Raum- und einen Zeit-Anteil, sondern auch einen Größen-Anteil, der aussagt, wie stark sich die Größe in dem hier beschriebenen Sinn verändert.

Die Mathematik der Größe (und also nicht die Lehre der mathematischen Größe) wird vermutlich zum einen fragen, wie das Große im Innern strukturiert und wie es nach außen gewickelt und dadurch zusammengehalten ist. In diesem Sinne erwarte ich eine Mathematik der Größe, die ebenbürtig neben der Geometrie (einschließlich Topologie und Differentialgeometrie, also der Mathematik des Raums) und der Arithmetik (Mathematik der Zahl) stehen wird. Sie wird ihre eigenen Elemente (Struktur- und Aufbauelemente, Verwindungs- und Verknotungselemente) haben. Es sieht so aus, als ob in der gesamten Mathematik des 20. Jahrhunderts unterschiedliche Vorarbeiten geleistet wurden, die in einer Mathematik der Größe systematisch ihren Platz finden können: Differentialtopologie, Parkettierung, Graphentheorie, Knotentheorie, fraktale Geometrie.

Die Mathematik der Größe wird ebenso in Anwendungsgebiete (etwa der Materialfestigkeit, mathematischen Lehre von Makro- und/oder Nano-Molekülen etc.) übergehen wie die Analysis in die Mechanik oder die Funktionentheorie in die Elektrodynamik.

Dies sind erste Ideen. Konsequent wird weiter gefragt werden müssen, ob es auch eine Mathematik der Zeit gibt, die sich von der Mathematik des Raums (Geometrie, Topologie) unterscheidet. Heute wird innerhalb der Mathematik nicht einmal eine solche Frage gestellt. Unter diesem Gesichtspunkt sollen die Arbeiten von Aristoteles und den Neuplatonikern zum Zeitbegriff gelesen werden. - Die Arithmetik wird als eine Mathematik der Zahl ebenfalls völlig ihren Charakter ändern. Im Ganzen wird sich eine neue Architektur der Mathematik ergeben.

Wird fortgesetzt.

2010

[Version 21. November 2010]

Schraubenlinie

Mathematische Basteleien

Literaturhinweise

David Eckstein: Epstein erklärt Einstein, Online

Franz Embacher: Spezielle Relativitätstheorie, Online

Lewis C. Epstein: Relativity Visualized: The Gold Nugget of Relativity Books, San Francisco 1991 [1981]

Lewis C. Epstein: What is the Principle of Relativity?, San Francisco 1982

Helmut Hansen: Die Physik des Mandala, Aitrang 2007

Helmut Hansen: Die Linien des Alten, Norderstedt 2009 (Online)

Helmut Hansen: About the Dual Parametrization of c, in: Proceedings of the Natural Philosophy Alliance Vol 7, Long Beach 2010

 

© tydecks.info 2011