Ruhende und bewegende Zeit

– Miniatur über die Dialektik des Widerspruchs am Beispiel der Venusbahn

Einleitung

Warum die Venusbahn? Die Venus ist die hellste sternartige Erscheinung am Himmel. Sie ist entweder als Abendstern im Westen oder als Morgenstern im Osten zu sehen. Das Venusjahr beträgt 224,7 Tage und ist daher verblüffend genau mit dem Erdjahr synchronisiert: Wenn die Erde 8 mal um die Sonne gelaufen ist, ist die Venus fast auf die Stunde genau 13 mal um die Sonne gelaufen (8 · 365,25 = 13 · 224,7), d.h. alle 8 Jahre ist die Venus von der Erde aus an genau der gleichen Stelle am Himmel zu sehen. Die Venus ist schneller als die Erde. 5 mal wird die Erde im Verlaufe von 8 Jahren überrundet, als Abendstern holt die Venus die Erde ein, als Morgenstern läuft sie ihr davon. Bei Tagesanbruch ist sie als letzter Stern noch sichtbar und erscheint daher als Lichtbringer, und wenn es abends zu dunkeln beginnt, ist sie als erster Stern zu sehen, der den Blick vom sichtbaren Schein auf das dahinter verborgene Wesen lenkt. In der griechischen Mythologie wurden Abendstern und Morgenstern auch dann noch mit zwei unterschiedlichen Figuren verbunden, als ihre Einheit bekannt war: Der Lichtbringer heißt Phosphoros (in der lateinischen Übersetzung Luzifer), der Abendstern Hesperos, etymologisch verwandt mit Vesper, Westen, dem Wesen (siehe hierzu den Eintrag in Wikipedia).

Abendstern und Morgenstern sind geradezu überladen mit einander entgegengesetzten Sinnzuschreibungen, so dass es mehr als nur ein naives Beispiel ist, wenn 1892 der Logiker Gottlob Frege (1848-1925) die Einheit von Abendstern und Morgenstern als schlagendes Beispiel für das Verhältnis von Sinn und Bedeutung wählt: Beide haben ihren eigenen (in den meisten Fällen entgegengesetzten) Sinn, aber in der Venus ihre gemeinsame Bedeutung. Die Venus verkörpert auf elementare Weise Identität und Nicht-Identität des Widerspruchs.

Worin besteht die Einheit von Abendstern und Morgenstern, und wie läßt sie sich nachweisen? Beide sehen ähnlich aus. Sie sind fast gleich hell, vor bzw. nach den anderen Sternen zu sehen, aber sie treten nie gleichzeitig auf. Beide erscheinen in bestimmten Zyklen, und das legte schon früh die Vermutung nahe, dass der gleiche Stern abwechselnd mal als Abendstern und mal als Morgenstern zu sehen ist. Um das nachzuweisen muß es gelingen, die gemeinsame Bahn zu finden, auf der mal der eine und mal der andere zu sehen ist. Ihre gemeinsame Bahn muss aus den jeweiligen sichtbaren Phasen berechnet und interpoliert werden, bis der Nachweis geführt ist, dass bei Berücksichtigung der Zeitverzögerung der Abendstern und Morgenstern widerspruchsfrei ineinander übergehen können. Solange es nicht möglich ist, von einem Standort außerhalb des Sonnensystems die Gesamtbewegung von Erde und Venus zu überschauen, kann jedoch ihre Identität nur hypothetisch behauptet werden. (Erst 1922 hat Kurt Lewin den Begriff Genidentität eingeführt, mit dem Fragen dieser Art systematisch erfasst werden können.)

Von der Erde aus gesehen ist der 8-jährige Zyklus der sichtbaren (geozentrischen) Venusbahn außerordentlich komplex, jedoch von verblüffender Symmetrie und Schönheit.

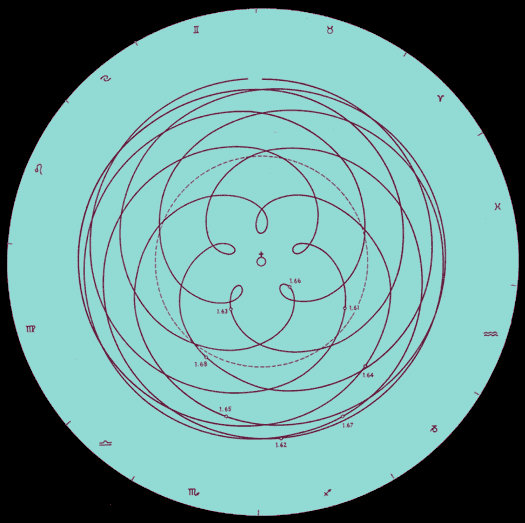
Figur 1: Die geozentrische Venusbahn

Die geozentrische Sonnenbahn ergibt sich, wenn an einem festen Punkt auf der Erde an jedem Tag der höchste Sonnenstand gemessen und in einer Zeitkurve eingetragen wird. Im Sommer steigt die Sonne am höchsten, im Winter am wenigsten. Zwischen den beiden Sonnenwenden im Juni und Dezember werden die Tage gleichmäßig kürzer bzw. länger. Die Sonne scheint daher im Ganzen auf einem Kreis um die Erde zu wandern, der gegenüber dem Erdäquator geneigt ist (die Ekliptik), in dieser Figur im mittleren Bereich gestrichelt gezeichnet. Weit komplizierter ist die geozentrische Venusbahn. Das hat zwei Ursachen: Die Venus wandert schneller um die Sonne als die Erde (das Venusjahr ist daher kürzer als das Erdjahr) und die Venusbahn ist anders geneigt als die Erdbahn. Wird an jedem Tag von einem festen Punkt auf der Erde der größte sichtbare Abstand zwischen Venus und Sonne gemessen (das heißt der höchste Venusstand im Vergleich zum Sonnenstand), zeigt sich ein 8-jähriger Zyklus.
Dessen Symmetrie wird am besten erkennbar, wenn er 8-fach um den einjährigen Sonnenkreis geflochten wird. Da die Venusbahn anders geneigt ist als die Erdbahn, verläuft von der Erde aus gesehen die Venusbahn teils oberhalb und teils unterhalb der Sonnenbahn, die in dieser Figur als Maßstab der Symmetrie gewählt wurde. Innerhalb der Sonnenbahn liegen die fünf unteren Sonne-Venus-Konjunktionen, wenn die Venus den Bereich zwischen Erde und Sonne durchläuft und die Erde überholt. Sie steht aufgrund der Neigung der Venusbahn jedoch nur selten direkt zwischen Erde und Sonne (Venustransit). Nach jeweils 4 Jahren kommt es am entgegengesetzten Punkt zu einer oberen Sonne-Venus-Konjunktion, wenn umgekehrt die Venus von der Erde aus gesehen hinter der Sonne steht und dort die Gerade überschreitet, auf der Erde und Sonne liegen, wenn also die Venus von der Erde am weitesten entfernt ist. Mit jeder unteren Konjunktion wandelt sich der Abendstern in den Morgenstern und mit jeder oberen Konjunktion wieder zurück.
In dieser Figur ist das Jahr nicht in 12 Monate, sondern in die 12 Tierzeichen aufgeteilt. Wird vom Mittelpunkt eine Verbindung zum äußeren Tierzeichenkreis gezogen, schneidet sie 8-mal die Venusbahn. Die 8 Schnittpunkte zeigen die 8 Abstände von Sonne und Venus, die im Verlaufe von 8 Jahren jeweils am gleichen Kalendardatum (z.B. jeweils am 1. Mai) gemessen werden. Diese Figur zeigt allerdings nicht, wann die Venus als Morgenstern bzw. Abendstern sichtbar ist. Dafür müsste die Venusbahn abwechselnd alle 292 Tage gefärbt werden. Außerdem wurden alle von der Erde aus nicht sichtbaren Abschnitte ergänzt, um die volle Symmetrie zeigen zu können.
Die Venusrose wurde erstmals 1948 von dem Anthroposophen Joachim Schultz (1902-1953) dargestellt und veröffentlicht (siehe zur Geschichte der Venusrose den Beitrag von Liesbeth Bisterbosch).
Figur 1 zeigt eine von Fritz Dobretzberger optisch aufbereitete Darstellung.
(Eine sehr anschauliche Darstellung, warum sich ein innerer Plant vom äußeren Planeten aus gesehen auf einer Schleife bewegt, d.h. zeitweise zurückzugehen scheint, wenn er den äußeren Planeten überholt, ist in Wikipedia am Beispiel der Mars-Schleifen zu finden. Das erklärt die 5 nach innen gerichteten Schleifen der Venus-Rose, da die Venus im Verlaufe des 8-jährigen Zyklus 5 mal die Erde überholt.)

Die geozentrische Venusbahn ist zwar symmetrisch, aber sehr kompliziert. Daher war es sehr schwer, mithilfe dieser Bahn die Identität von Abendstern und Morgenstern nachzuweisen. Der Durchbruch gelang mit dem Wechsel zur heliozentrischen Bahn, bei der nicht mehr die Erde, sondern die Sonne als fester Bezugspunkt der Bewegung angesehen wird. Sowohl die Erde wie die Venus durchlaufen jeweils eine Ellipse um die Sonne. Erst mit diesem Verständnis wurden die eingangs genannten Erkenntnisse gewonnen: Die Symmetrien ergeben sich aus der unterschiedlichen Gestalt der Erd- und Venusbahn und dem Verhältnis ihrer Umlaufgeschwindigkeiten.

Erhaltungsgrößen der ruhenden Zeit

Während die geozentrische Bahn der Venus wie ein unveränderliches Mandala aussieht, wurde mit den heliozentrischen Bahnen der gleichmäßig bewegten Planeten eine höhere Symmetrie entdeckt: Das 2. Keplersche Gesetz stellt einen Zusammenhang zwischen den durchlaufenen Flächen und Zeiten eines Planeten her.

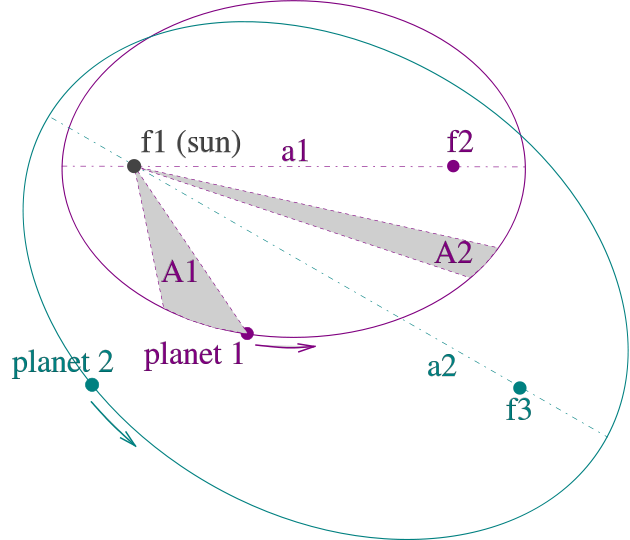
Figur 2: Die Keplerschen Gesetze

2. Keplersches Gesetz: Jeder Planet bewegt sich auf einer Ellipse um die Sonne. Die Bewegungsbahnen sind hier violett und grün gezeichnet. Er ändert jedoch fortlaufend seine Geschwindigkeit. Wenn ein Planet der Sonne sehr nahe ist, bewegt er sich sehr schnell. Dagegen ist er am langsamsten, wenn er der Sonne am weitesten entfernt ist. Kepler hat entdeckt, dass es hierfür eine verblüffend einfache Formel gibt: Innerhalb der Ellipse können Teilflächen markiert werden, die hier grau schattiert sind. Wenn zwei Flächen gleich groß sind, dann benötigt der Planet die gleiche Zeit, wenn er die eine oder die andere Fläche durchläuft. In dieser Figur sind als Beispiel die beiden gleich großen Flächen A1 und A2 grau hervorgehoben. Bei der Fläche A1 ist der Rand entlang der Ellipse deutlich länger als bei A2. Dennoch durchläuft der Planet den längeren Abschnitt bei A1 in der gleichen Zeit wie den Abschnitt bei A2. Er ist also wesentlich schneller, wenn er bei A1 der Sonne näher steht. Das Besondere an dieser Formel ist, dass Kepler hier einen direkten Zusammenhang zwischen Zeit und Raum entdeckt hat: Die Flächen A1 und A2 sind reine Raumgebiete, die Bewegungsdauer für den Planeten eine rein zeitliche Aussage.
3. Keplersches Gesetz: Dies Gesetz ist noch weit überraschender. Wenn a₁ und a₂ die jeweils größten Entfernungen der Planeten 1 und 2 von der Sonne sind, dann verhalten sich die Gesamtumlaufzeiten der Planeten 1 und 2 zueinander wie a₁^3/2 : a₂^3/2. (Der Exponent 3/2 bedeutet ausgeschrieben: Die Wurzel aus a₁³ bzw. aus a₂³). Auch dies Gesetz stellt einen direkten Zusammenhang zwischen Raum und Zeit her. Die Entfernungen a₁ und a₂ sind eine rein räumliche Größe, die Umlaufgeschwindigkeiten dagegen in der Zeit gemessen. Wikipedia

Werden die Planetenbahnen gemäß den Keplerschen Gesetzen betrachtet, dann verlaufen sie natürlich innerhalb der Zeit. Jeder Planet hat sein eigenes Jahr, das ist die Umlaufzeit seiner Bahn um die Sonne. Die Zeit geht ein in die Berechnung der zugrunde liegenden Erhaltungsgröße (der Planet »überstreicht in gleichen Zeiten gleich große Flächen«). Und über die Zeit ergibt sich das Verhältnis der verschiedenen Planeten zueinander (das dritte Gesetz formuliert einen inneren Zusammenhang der jeweiligen Umlaufgeschwindigkeiten und Halbachsen, aus denen sich beispielsweise die Symmetrie der geozentrischen Venusbahn für einen Beobachter auf der Erde ergibt, aber genau so gut die relativen Symmetrien aller anderen Planetenbahnen zueinander).

Jedoch handelt es sich hier um eine »ruhende Zeit«. Im Ganzen verändert sich im Verlaufe der Zeit nichts an den Bahnen. Die Keplerschen Gesetze galten schon vor 1000 Jahren so und werden auch in 1000 Jahren noch so gelten. Im Fall der Venus- und der Erdbahn wiederholt sich alles völlig identisch alle 8 Jahre. Daher kann von Erhaltungsgrößen oder von Symmetrie gesprochen werden. Alles gilt innerhalb der Zeit (im Verlaufe der Zeit) und zugleich unabhängig von der Zeit (in die Keplerschen Gesetze geht nicht ein, für welches Jahr sie gelten sollen).

Zeit und Raum in vergleichbarer Weise als Dimensionen zu verstehen, das kannte schon die Antike und insbesondere Aristoteles (siehe seine Physik). Völlig neu ist jedoch bei Kepler der Gedanke, dass Zeit und Raum in einem direkten Verhältnis zueinander stehen. Raum und Zeit werden als gleichberechtigte Dimensionen betrachtet. Kepler entdeckte eine höherdimensionale Symmetrie. Das ist keine körperliche, dreidimensionale Symmetrie (wie z.B. die Symmetrie einer Bienenwabe, Schneeflocke, Lotusblume), sondern eine vierdimensionale Symmetrie in Raum und Zeit von Bewegungsverläufen. Nicht mehr der bewegte Körper (der klassische Gegenstand), sondern sein raum-zeitliches Bewegungsmuster wird zum »höheren Gegenstand« der neuzeitlichen Naturwissenschaft.

Daher können nicht mehr bloß Gegenstände (oder Lebewesen) in Opposition zueinander kommen, sondern ihre Bewegungsverläufe. Abendstern und Morgenstern stehen einander nie gegenüber, denn es handelt sich um den gleichen Stern (die Venus). Aber Abendstern und Morgenstern sind zwei verschiedene Namen der Venus, die jeweils unterschiedliche Phasen der Venusbahn betreffen. Wird die gesamte Bahn geometrisch aufgezeichnet, dann stehen auf dieser Bahn die Phasen des Abendsterns und des Morgensterns einander gegenüber, die unterschiedliche Abschnitte der Venusbahn bezeichnen. Das bedeutet, dass der überlieferte Gegenstands-Begriff entweder entsprechend erweitert oder durch einen neuen Begriff wie den hier gebrauchten Begriff des Bewegungsverlaufes ersetzt werden muß.

Die Symmetrieebene der Venusbahn

Der Vergleich der heliozentrischen mit der geozentrischen Venusbahn zeigt einen offenen Punkt, den Hegel zwar berührt, aber nicht ausgeführt hat. Die heliozentrische Bahn ist nicht nur eine wesentlich einfachere Kurve als die komplexe Gestalt der doppelten fünfblättrigen Lotusblume, sondern sie liegt auf einer Symmetrieebene, während die geozentrische Venusbahn eine verschlungene dreidimensionale Kurve innerhalb der dem Menschen sichtbaren Himmelskugel darstellt (wovon Figur 1 nur ein zweidimensionales Abbild zeigt, in dem die unterschiedlichen Entfernungen der Venus zur Erde nicht dargestellt sind).

Heute ist die Einsicht völlig selbstverständlich geworden, dass die Planeten auf Ellipsen verlaufen, die zweidimensional sind. Bis zu den frühen Arbeiten von Kepler war jedoch immer angenommen worden, dass die Bahnen der Planeten wesentlich komplizierteren Figuren folgen, die grundsätzlich dreidimensional sind. Der Himmel und alle seine Erscheinungen galten als dreidimensionale Bewegungen. Erst durch die Erkenntnis der Symmetrieebene wurde es Kepler möglich, seine Gesetze der Planetenbewegungen aufzustellen, die Newton dann wesentlich verallgemeinern konnte.

Noch überraschender ist, dass die Symmetrieebenen der meisten Planeten nahezu in einer gemeinsamen Ebene liegen. Nur der Planet Pluto fällt erkennbar aus dem Rahmen und wird daher inzwischen nicht mehr als Planet angesehen.

Figur 3: Die Ebene der Planetenbahnen im Sonnensystem

»Die Bahnen der Planeten um die Sonne liegen ungefähr in einer gemeinsamen Ebene. Diese Auffälligkeit wird durch die Entstehung des Sonnensystems erklärt« Wikipedia.

Die Erkenntnis der Symmetrieebenen der Planeten und die mit ihnen gewonnene Vereinfachung der Darstellungsmethoden wurde ihrerseits zum Vorbild, dann auch bei allen anderen Naturphänomenen auf ähnliche Weise nach Symmetrieebenen zu suchen, um ihre inneren Eigenschaften erkennen zu können. Hatte früher die axiomatische Methode von Euklid als Vorbild gedient, ein Gebiet auf seine selbst-evidenten Eigenschaften zurückzuführen, wird seit den astronomischen Rechnungen von Kepler versucht, einen komplexen Zusammenhang auf seine inneren Symmtrieebenen zurückzuführen. Dadurch werden die voneinander unabhängigen Freiheitsgrade entkoppelt. Newton hat diese Vorgehensweise zur Grundlage der Kräfte-Parallelogramme genommen, deren Achsen die entkoppelten Kraftanteile sind. In der Mathematik wird seither versucht, komplizierte Gleichungen durch Erkenntnis der verborgenen inneren Dimensionen zu entwirren und aufzulösen. Ganz allgemein wird bei Analyse von Merkmalen versucht, diejenigen Merkmale zusammenzustellen, die einen inneren Zusammenhang bilden und dadurch für sich im übertragenen Sinn eine Symmetrieebene bilden. Durch die Symmetrieebene wird der Bereich einer Symmetrie erkannt bzw. festgelegt. Es soll im weiteren gezeigt werden, wie Hegel diese Anschauung aufgenommen hat, wenn er von der »Achse« spricht, auf der die Gegensätze liegen (HW 6.61), und in ihrer Mitte der Nullpunkt, auf den sich der Widerspruch zusammenzieht (HW 6.67), bzw. in der formalen Logik von der »Sphäre« (HW 6.321ff).

Die Geschichte des Planetensystem entlang der Symmetrieachse durch die Sonne

Das Beispiel der gemeinsamen Ebene der Planetenbahnen zeigt schließlich, wie es hier zum Umschlag in einen anderen Zeitbegriff kommt, die bewegende Zeit. Die Entstehung und die Symmetrie der Planetenbahnen kann nur erklärt werden aus der Geschichte des Planetensystems.

Die Symmetrieebene erzeugt in ihrem Zentrum eine senkrecht zu ihr stehende Symmetrieachse. Das ist im Falle der Spiegelsymmetrie der Spiegel, im Falle der Zahlenachse der Nullpunkt, bei der Balkenwaage die Drehachse, für die Planetenbahnen die Sonne in einem der beiden Brennpunkte der Ellipse. (Vgl. hierzu auch die Figura paradigmatica von Nikolaus von Kues in Von den Mutmaßungen, um 1442, die den doppelten Lichtkegel der Speziellen Relativitätstheorie vorweggenommen zu haben scheint, der senkrecht auf der Ebene der Gegenwart steht.)

Werden die Planetenbahnen über kosmische Zeiten hinweg beobachtet, dann ist zu erkennen, wie sich ihre Bahnen verändert haben. Im Verlaufe der Zeit haben sich Resonanzen zwischen den Planetenbahnen gebildet. Die Symmetrie der geozentrischen Venusbahn ist dafür das großartigste bekannte Beispiel. Erst diese Analyse kann all die offenen Fragen der Planetenbahnen erklären (warum und wie lange sind sie stabil, gab es Resonanzkatastrophen, warum liegen sie in einer Ebene, etc.).

Das führt zu mathematischen Darstellungen, die entlang der Symmetrieachse eine weitere Dimension ergänzen und zeigen, wie sich die Planetenbahnen im Verlaufe der Zeit verändern und historisch aus einer Urwolke entstanden sind (Nebularhypothese von Kant, 1755).

Der Punkt, an dem sich Symmetrieachse und Symmetrieebene kreuzen, lässt sich zwar genau berechnen, aber er führt zu einer Unbestimmtheit, die innerhalb der Symmetrieebene unlösbar ist. Dieser Punkt lässt sich an keinem Etalon (Musterstück, Maßverkörperung) innerhalb der Symmetrieebene messen, er fällt außerhalb ihres Maßes, bleibt ihr gegenüber Null, »nichts«. Die Konstruktion der Regeln, die einem universellen Urteil bzw. der Bildung von Äquivalenzklassen zugrunde liegen, gelten nur innerhalb des durch eine Symmetrieebene bestimmten Bereiches und werden am Kreuzungspunkt mit der Symmetrieachse unbestimmt (Singularitäten).

Jede Symmetrie kann aber zurückgeführt werden auf einen Strom, der entlang dieser Symmetrieachse quer zur Symmetrieebene verläuft (Satz von Emmy Noether). Der Übergang von der Symmetrieebene zur Symmetrieachse ist die von Hegel gemeinte Auflösung eines Gegensatzes im Widerspruch, die zu ihrem Grund führt (in diesem Beispiel zur Entstehungsgeschichte des Sonnensystems, der der Grund ihrer typischen Eigenschaften ist, vgl. HW 6.67f).

Figur 4: Konvektionsströme (Frenet-Serret Frames of an Arter Flow)

Der Strom durch die Symmetrieebene kann vollständig das lokale Koordinatensystem ändern. In dieser Figur zeigen die schwarzen Bewegungslinien den Strom, dessen lokale Bewegungskoordinaten sich ständig ändern. Sie sind jeweils farblich durch die Tangente T, die auf ihr senkrecht stehende Normale N und das zu beiden senkrecht stehende äußere Produkt B=T⊗N eingetragen.
Auf diese Weise ließe sich auch die Entstehung der Resonanzen zwischen Planetenbahnen darstellen, wenn sich zum Beispiel die Neigung der Planetenbahnen zueinander ändert. Im Verlaufe dieser Entwicklung entstehen stabile Muster, die für eine bestimmte Zeit das System optimieren, bis sie aufgrund von Änderungen des übergreifenden Stroms wieder aufgelöst werden; in dieser Figur gut erkennbar durch den in der Mitte dargestellten Wirbel und eine länger andauernde Stabilität am rechten Rand.
»The Arter flow is a sum of two integrable Hamiltonian flows in ℝ³ that is not integrable in general« (Quelle); Bildquelle.

Zeit und Macht

Während Kant von einer geschichtlichen Entwicklung des Planetensystems überzeugt war, stellten für Hegel die Bewegungsmuster der Planeten Absoluta dar, die nicht nur unabhängig von den physikalischen Prinzipien gelten (HW 9.85), sondern aus denen diese herzuleiten sind. Daher will Hegel zeigen, dass die von Newton entwickelten Prinzipien nichts anderes sind als eine neue mathematische Darstellung der von Kepler entdeckten Bewegungsgesetze der Planeten (HW 9.85-106).

Hegels Ideal war die ruhende Zeit. Ähnlich dem Mandala der Venusrose vollendet sich für ihn die Wissenschaft der Logik in einem »Kreis von Kreisen«, die sich ineinander und im Ganzen »zurückschlingen« (HW 6.571), Figuren größter Schönheit hervorbringen können, und alle Widersprüche plan, d.h. innerhalb ihrer eigenen Ebene lösen. Hier ist Kepler sein großes Vorbild: Er hat mit seinen Bewegungsgesetzen exemplarisch gezeigt, wie ein komplexes Äußeres (das sind die sichtbaren und seinerzeit von Tycho Brahe aufgezeichneten Bewegungsbilder am Himmel einschließlich ihrer von Kant betrachteten realen Oppositionen einander gegenüberstehender Planeten) auf ein verborgenes Inneres zurückgeführt werden kann, wobei Inneres und Äußeres den gleichen Inhalt haben. Die Identität von Innerem und Äußerem ist für Hegel in seiner Wesenslogik der Übergang zum Absoluten (HW 6.186f).

Mit dem Absoluten ist für Hegel eine absolute Grenzlinie gezogen, mit der der drohende unendliche Regreß vermieden wird, dass die Bewegung von Kräften aus einem zugrunde liegenden Strom erklärt wird, und dessen pulsierende Bewegung wiederum aus tiefer liegenden Kräften usf. Ohne Zweifel wird die empirische Forschung fortlaufend neue Erkenntnisse über die Kräfte und ihr Zusammenspiel zutage fördern. Hegel fragt, ob es innerhalb dieser unendlichen Bewegung des naturwissenschaftlichen Fortschritts eine absolute Basis gibt, auf die sich alles weitere bezieht. Ein Beispiel waren für ihn die Keplerschen Gesetze. Die heutige Physik stößt in einer bis auf Pythagoras zurückgehenden Tradition von einer ganz anderen Seite auf das Absolute. Für sie haben stabilisierende Muster wie die Venusrose zwar nur begrenzte Dauer und sind zu erklären aus einer übergreifenden Strömung, wodurch sie aufgebaut und später wieder aufgelöst werden. Aber in diesen Mustern kommen absolute Bilder zum Vorschein wie das Pentagramm, und es ist eine noch ungelöste Frage an die Mathematik, warum Muster wie das Pentagramm eine stabilisierende Wirkung haben. Auch wenn dessen Dauer nur begrenzt ist, kehrt es wahrscheinlich auf allen Ebenen wieder und zeigt innerhalb der Physik etwas Absolutes.

Hier scheint sich die Physik Hegel zu nähern. Doch er folgt zwar Keplers Ansatz, im Innern für sich unanschauliche, rein mathematisch-physikalische Gesetze zu entdecken, die dem sichtbaren Äußern zugrunde liegen, lehnt aber alle Überlegungen ab, die mit Symbolen wie zum Beispiel dem Pentagramm arbeiten. Er vermeidet das Wort »Naturmagie«, hält aber diese Art von Symbolen für ein »widerspenstiges und inadäquates Medium«, Gedanken Ausdruck zu verleihen (HW 9.53).

Er versteht genau, dass mit Symbolen ein Machtanspruch verbunden ist, den er jedoch ausschließlich für den Begriff in Anspruch nimmt. Aus dem gleichen Grund lehnt er den Ansatz von Kant ab. Während Hegel nach einer absoluten Grundlage gesucht hatte, auf der die Naturwissenschaft errichtet werden kann, hat Kant nach dem inneren Prinzip gefragt, das allen Naturgesetzen zugrunde liegt und es im Begriff der Zeit gefunden. Aus der Zeit erklärt er die Grundbegriffe der Naturwissenschaft. Das sind in seinem System die Kategorien der Relation (Substanz, Kausalität, Wechselwirkung): Substanz ist das Dauerhafte, das in der Zeit unverändert bleibt. Das ist hier verallgemeinert zur ruhenden Zeit und dort insbesondere die Erhaltungsgröße. Kausalität ist die Abfolge in der Zeit. Das muss differenziert werden. Es gibt sowohl eine »ruhende«, ewig kreisförmige Abfolge, als auch eine bewegende mit zerstörender und aufbauender Kraft. Mit Wechselwirkung meint Kant dasjenige, das im Zeitmoment gemeinschaftlich, d.h. räumlich auftritt. Daraus wird hier die Symmetrieebene.

Der Begriff darf nach Hegels Überzeugung jedoch nicht der Macht der Zeit unterworfen werden, sondern »er ist vielmehr die Macht der Zeit« (HW 9.49). Daher entwickelt Hegel den Begriff der Zeit noch nicht in der Wissenschaft der Logik, sondern erst nachfolgend in der Naturphilosophie.

Innerhalb der Wissenschaft der Logik bereitet Hegel lediglich die von Kant betrachteten Kategorien der Relation vor. Aber er versteht sie als rein logische Beziehungen, die in der Substanzlogik aus dem Absoluten hervorgehen. Genau genommen entwickelt er in der Logik nicht die Substanz, sondern die Substantialität, das ist dasjenige, was Substanz werden kann (treffender wäre ein umständlicher Ausdruck wie das »Substanzbare«, und entsprechend das »Kausalitätsbare« und »Wechselwirkungsbare«, so wie vom Wahrnehmbaren oder Denkbaren gesprochen wird, d.h. jeweils dasjenige, was Substanz, Kausalität und Wechselwirkung werden kann). Erst im Übergang von der Logik zur Naturphilosophie sollen aus ihnen Substanz, Kausalität und Wechselwirkung in dem Sinn hervortreten, wie die Naturwissenschaft sie kennt und Kant sie betrachtet hat.

Auch wenn es auf diese Weise gelingt, Hegel einen Rückfall in neuplatonisches Denken (Proklos, Simplikios) nachzuweisen, wenn aus seinem Begriff des Absoluten zwar die ruhende Zeit, aber nicht die bewegende Zeit hervorgeht und er dadurch in Widerspruch zur neuzeitlichen Naturwissenschaft geriet und von ihr »überholt« wurde, entwickelt er zugleich einen Gedanken, der diese Kritik wieder sprengt: Mit dem Absoluten sieht er nicht nur die Macht, sondern auch die Freiheit entstehen. Mit Freiheit ist weit mehr gemeint als die Freiheit des Mächtigen, sich alles erlauben zu können. Wird ein System wie der in Figur 4 dargestellte Konvektionsstrom betrachtet, ist der Übergang zu spüren, wie solch ein System zum Leuchten gebracht werden kann. Das Absolute enthält in sich die »orientalische Vorstellung« des »sich selbst erleuchtenden Lichts«. »Allein es erleuchtet sich nicht nur, sondern strömt auch aus« (HW 6.198).

Um zu verstehen, was mit dieser Ausströmung gemeint ist, unterscheidet Hegel mit Spinoza am Absoluten dessen Attribute und Modi. Ein Modus ist die Verfaßtheit eines Zustands. Der Zustand wird dann nicht nur objektiv durch seine Gegebenheit beschrieben (seine objektiven Merkmale), sondern darüber hinaus durch etwas, was grundsätzlich nicht materiell beschrieben werden kann, wenn zum Beispiel ein Zustand der Freundlichkeit, der Ängstlichkeit, der Verzweiflung, des Tatendrangs oder der Stockung beschrieben wird. Solche Modi entziehen sich der physikalischen (oder neurophysiologischen Darstellung), und nur hier liegt für mich der Wert von Hegels absoluter Grenzziehung. – Hegel selbst hätte eine solche Folgerung vermutlich abgelehnt. Er wendet sich kritisch oder mindestens skeptisch gegen die »orientalischen« oder »morgenländischen« Ideen »der substantiellen Identität des Geistigen und des Natürlichen« im Licht (HW 9.116). Das Licht ist mit seiner Fähigkeit, etwas zum Leuchten zu bringen oder umgekehrt in die Finsternis versinken zu lassen das Paradigma, wie Änderungen der Modi vorzustellen sind.

Gegen Hegel möchte ich an seinem eigenen Gedanken festhalten. Dafür kann die Kunst ein Beispiel geben. Jan Vermeer (1632-1675) stand dem aufklärerischen (erleuchtenden) Denken nahe und hat in seinen Gemälden gezeigt, wie das Erleuchtende zur Geltung gebracht werden kann. Eins der bekanntesten und am meisten diskutierte Beispiele ist die Ansicht von Delft. Dort sind sowohl auf der Wasseroberfläche Strömungen zu sehen, in denen sich tiefere Wasserbewegungen, Wind, Sonnenreflexe und Spiegelbilder kreuzen, wie auch Gebäudeteile, die teils im Schatten und teils im Licht liegen. Vermeer ist es gelungen, buchstäblich auf Partikelebene mehrfach übereinander aufgetragener Farben die einzelnen Farbkörner so anzusetzen und gegeneinander auszurichten, dass sowohl ein Bild wie das in Figur 4 nachgebildet erscheint als auch dank seiner künstlerischen Freiheit das Ausströmen des Lichts und die dadurch hervorgebrachten Wirkungen zu sehen sind.

Ist es ihm gelungen, auf der untersten Ebene der Materialität des Farbauftrags spontan Regeln zu folgen, die über die bekannten physikalischen Gesetzmäßigkeiten hinausgehen? Mit einer faszinierenden Idee fragte Proust, ob es nach dem Vorbild von Vermeer auch Regeln der Satzbildung geben könnte, denen ein Schriftsteller folgen kann. Gehen in diesem Sinn Regeln der Satzbildung den in den Sätzen eingetragenen Begriffen voraus? Das würde Hegels Machtverständnis des Begriffs elementar erschüttern. Zu diesem Thema sind zwei weitere Beiträge geplant, warum in Hegels Logik ein Kapitel über formale Systeme (Kalküle) fehlt und ob es sich aus seinen Ansätzen rekonstruieren lässt, und zu seinem Verständnis der Objektivität (Mitteilung, Medium, Mittel).

Figur 5: Jan Vermeer (1632-1675), Ansicht von Delft (1660-61), Ausschnitt Link

»Wie ein Fenster von Licht öffnet sich denn auch in Vermeers Gemälde die gelbe Mauerecke (un petit pan de mur, eigentlich Wandfeld), die doch in der rechten Bildhälfte gar nicht auffindbar ist, es sei denn, man begnügte sich mit dem leuchtenden Dach, das in Prousts Beschreibung schon ganz entstofflicht ist. ... Da gestand er sich ein, daß er mit solchen Farben hätte schreiben sollen und 'seine Satzbildung in sich selber hätte kostbar machen müssen, so kostbar wie diese kleine Mauerecke'« (Belting, S. 267, mit einer eigenen Übersetzung von Proust, Auf der Suche nach der verlorenen Zeit, Band 5 Die Gefangene). Proust schildert, wie der Schriftsteller Bergotte ein letztes Mal vor dem Gemälde von Vermeer steht, bevor er an einem Schlaganfall stirbt. Siehe in der Suhrkamp Taschenbuchausgabe von 1983 S. 246f.)

Literaturhinweise

Hans Belting: Das unsichtbare Meisterwerk, München 1998

Georges Didi-Huberman: Die leibhaftige Malerei, München 2002

Gottlob Frege: Über Sinn und Bedeutung,
in: Zeitschrift für Philosophie und philosophische Kritik, NF 100, 1892, S. 25-50; Link

Byung-Chul Han: Hegel und die Macht, München 2005; Link

Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971 (zitiert als HW); Link

Peter Manchester: The Syntax of Time, Leiden, Boston 2005

John McTaggart: A Commentary on Hegel's Logic, Cambridge 1910 (Neudruck durch "Forgotten Books" 2012); Link

Peter Ruben: Prädikationstheorie und Widerspruchsproblem,
in: Wissenschaftliche Zeitschrift der Humboldt-Universität zu Berlin, Ges.-Sprachw. R. XXV(1976)1, S. 53-63;

2013