Information und Grund-Rauschen

Einleitung

Nachdem alle Atomtheorien gescheitert sind, auf materieller Ebene eine kleinste Einheit zu finden, seien dies die mechanischen Partikel, elektrischen Ladungsträger, Atome, Protonen, Elektronen und Neutronen, Elementarteilchen, Quarks oder auf vorerst unterster Ebene die Präonen, kann nach dem Erfolg der Quantenmechanik und Informationstheorie die Frage auf einer Metaebene anders gestellt werden: Enthält jede physikalische Theorie eine Information, und kann diese auf eine nicht mehr teilbare kleinste Einheit zurückgeführt werden, unterhalb derer das prinzipiell Nicht-Wissbare und Akausale folgt? Der Beitrag von Helmut Hansen diskutiert die Möglichkeit, diese letzte Einheit im Natural Digit (Nit) zu sehen. Diese kleinste Informationsaussage darf nicht verwechselt werden mit einer elementaren Aussage (Proposition) ›S ist p‹, an die wohl Wittgenstein im Tractatus logico-philosophicus gedacht hat, und aus der alle weiteren, komplexen Aussagen gebildet werden, sondern es handelt sich um den kleinsten Informationswert einer beliebigen Zeichenkette, sei dies ein philosophischer Text, eine Gen-Sequenz, eine Folge von Ereignissen in einem Experiment oder einem Spiel oder sonst eine Gestalt, aus der eine Information abgelesen werden kann.

Anmerkung: Das Nit ist definiert als Lösung der Gleichung 2Nit = e und geht über die Eulersche Formel ei · π + 1 = 0 zurück auf die Kreisfunktionen und die imaginären Zahlen. Weiter ist die Zahl e eine Art Neutralitätspunkt innerhalb der Ableitung: Die e-Funktion f(x) = ex ist die einzige Funktion, bei der an jeder Stelle die Ableitung mit dem jeweiligen Funktionswert übereinstimmt: f(x) = f '(x) = ex.

Helmut Hansen beruft sich einleitend auf John Archibald Wheeler und Anton Zeilinger, die 1990 bzw. 1999 ausgehend von den Erfolgen der Thermodynamik und Quantentheorie eine durchgehende Begründung der Physik auf der Informationstheorie vorschlugen. Er führt ihren Gedanken weiter, indem er als Dritten Louis de Broglie hinzunimmt, der in seinen späten Arbeiten über isolierte Teilchen eine Analogie von mechanischen und thermodynamischen Größen zeigen wollte, die auf einem Subquanten-Milieu (Subquanten-Medium, Subquanten-Energiefeld, subquantum level) gilt. Mit ihm kann das Resultat dieses Beitrags zusammengefasst werden: Das Subquanten-Milieu ist der Grenzbereich zwischen Wissbarem und Nicht-Wissbarem, zwischen Wirklichem und Möglichem. Die Hinzufügung oder Entfernung eines Nit ist die kleinste Einheit, durch die Ordnung in Energie oder Energie in Ordnung umgewandelt werden kann.

Wem die mathematischen Gleichungen Schwierigkeiten bereiten, der kann sie getrost überspringen und sollte dennoch in der Lage sein, dem Grundgedanken zu folgen.

Shannon-Einheit und Natural Digit (Nit)

Auszugehen ist von der reinen Informationstheorie, die auf Claude Shannon (1916-2001) und dessen 1948 erschienene Arbeit Mathematische Grundlagen in der Informationstheorie zurückgeht. Dort wird der Informationsbegriff formal definiert. Information wird völlig unabhängig gesehen von natürlichen Prozessen oder von einem Gespräch, in dem eine Information im wechselseitigen Aufeinandereingehen weitergegeben und durch Rückfragen bestätigt wird. Es wird weder nach Semantik, Syntax oder Pragmatik gefragt, sondern ausschließlich nach dem Informationswert einer beliebigen Folge von Zeichen oder Ereignissen. Ihm genügt ein Alphabet, wobei das Alphabet sowohl im üblichen Sinn ein Zeichensatz (von Buchstaben und Satzzeichen wie Punkt, Komma, Anführungsstriche usf.) sein kann wie auch eine mit symbolischen Zeichen dargestellte Gesamtheit unterschiedlicher Ereignisse. Das können die beiden Seiten einer Münze, die 6 Flächen eines Würfels, die Karten eines Skatblatts, aber auch die Gesamtheit aller Zustände sein, die einem quantenmechanisch betrachteten Objekt möglich sind. Das Alphabet ist daher im weiteren Sinn ein Möglichkeitsraum (Ereignisraum), mit dem die Gesamtheit aller Informationen in einem gegebenen Kontext darstellbar ist. Für jedes einzelne Zeichen (Ereignis) des Alphabets kann die Häufigkeit seines Auftretens gezählt werden. Liegt nun eine Folge von Zeichen vor (das kann sowohl ein Text sein, der aus vielen Zeichen besteht, wie auch die Folge von Ereignissen, die in einem Experiment oder im Verlaufe eines Spiels aufgezeichnet werden), dann kann auf sehr abstrakte Weise der Informationsgehalt dieser Zeichenfolge definiert werden.

Shannon bildet die Summe der Wahrscheinlichkeiten, mit der die einzelnen Ereignisse auftreten können, und gewichtet sie mit dem Logarithmus zur Basis 2. Das hat keine inhaltliche Bedeutung, sondern dient nur dazu, allzu große Zahlen zu vermeiden. Er nennt die Summe ‘Entropie’ und geht damit auf einen Begriff aus der Wärmelehre zurück. Ein früherer Begriff für Entropie war das Caloricum, das ist die Menge an Wärme, die in einem Gegenstand enthalten ist. Shannon verallgemeinert das auf beliebige Reihen von Informationstexten. Daher ist hier besser von Ordnung zu sprechen, und es wird im Weiteren zu zeigen sein, in welchem Wechselverhältnis die Ordnung (Entropie, Information) zur Energie steht. Eine sehr klare Darstellung gibt Wikibooks, abgerufen am 27.12.2016, [Zählung der Gleichung als (1) ergänzt, t.]:

»Shannon definierte die Entropie H einer gegebenen Information I über einem Alphabet Z durch

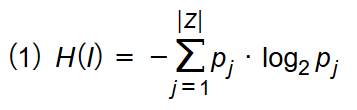
wobei pj die Wahrscheinlichkeit ist, mit der das j-te Symbol zj des Alphabets Z im Informationstext I auftritt.«

Die mathematische Formel bedeutet: Für jedes Element j aus dem Alphabet Z wird die Häufigkeit pj gezählt, wie oft es auftritt. Diese Häufigkeit wird multipliziert mit dem Logarithmus zur Basis 2 von dieser Häufigkeit, um kleinere Zahlen zu erhalten. Die Summe aller Produkte der Häufigkeiten und ihrer Logarithmen zur Basis 2 ergibt die Entropie. Das sei im Folgenden an einigen einfachen Beispielen erläutert:

Ein von Wikibooks genanntes Beispiel: Wenn eine Reißzwecke zu Boden fällt, kann sie entweder genau auf den Kopf oder schräg zum Liegen kommen: Fall 1 tritt mit einer Wahrscheinlichkeit von 30% ein, Fall 2 mit einer Wahrscheinlichkeit von 70%. Daraus ergibt sich gemäß der Formel von Shannon die Rechnung:

H(Reißzwecke)	= − (0,3 · log20,3 + 0,7 · log20,7)	| Definition
	= − (0,3 · −1,737 + 0,7 · −0,515)	| Logarithmus abgelesen aus Logarithmenrechner
	= − (−0,5211 − 0,3605)	| Produkte ausgerechnet
	= 0,8816	| Summe gebildet und Vorzeichen beachtet

Damit beträgt die Entropie H des Reißzwecke-Wurfs 0,8816.

Die Rechnung vereinfacht sich wesentlich, wenn alle Fälle mit der gleichen Wahrscheinlichkeit auftreten. Wird zum Beispiel mit einem Würfel gewürfelt, der 6 Augen hat, dann sind alle Fälle gleichwahrscheinlich und betragen jeweils 1/6. Werden alle 6 Fälle aufaddiert, dann kürzt sich die Anzahl der Fälle gegen die Wahrscheinlichkeit der einzelnen Fälle:

H(Würfel)	= − (1/6 · log21/6 + 1/6 · log21/6 + 1/6 · log21/6 + 1/6 · log21/6 + 1/6 · log21/6 + 1/6 · log21/6)	| Definition
	= − (6 · (1/6 · log21/6))
	= − log21/6
	= − log20,167
	= − (−2,582)

Die Entropie H des Würfels beträgt damit 2,5825. Sie ist wesentlich größer als die Entropie der Reißzwecke. Das bedeutet anschaulich: Es lässt sich schlechter voraussagen, welche Augenzahl als nächste gewürfelt wird im Vergleich zur Voraussage, ob die nächste untersuchte Reißzwecke auf dem Kopf oder schräg liegt.

Das wichtigste Anwendungsgebiet der Entropie ist die Analyse von Texten. Bisher wurden nur Beispiele mit einem Ereignis betrachtet. In einem Text gilt jedes Zeichen in der Zeichenkette als ein eigenes Ereignis, und die Entropie errechnet sich als Summe daraus. Zum Beispiel kann folgender genetischer Code analysiert werden (Wikibooks):

AGCTTTTCATTCTGACTGCAACGGGCAATATGTCTCTGTGTGGATTAAAAAAAGAGTGTCTGATAGCAGC

Der Text enthält 70 Zeichen, davon 20 mal A, 12 mal C, 17 mal G und 21 mal T. Die Häufigkeit jedes Zeichens ist das Verhältnis seiner Anzahl zur Gesamtanzahl, d.h.:
pA = 20 / 70 = 0,29
pC = 12 / 70 = 0,17
pG = 17 / 70 = 0,24
pT = 21 / 70 = 0,3

Daraus ergibt sich die Entropie:

H(genetischer Code)	= − (0,29 · log20,29 + 0,17 · log20,17 + 0,24 · log20,24 + 0,30 · log20,30)
	= − (0,29 · −1,786 + 0,17 · −2,556 + 0,24 · −2,059 + 0,30 · −1,737)
	= − (−0,518 + −0,435 + −0,494 + −0,521)
	= 1,968

Die Entropie H dieses genetischen Codes beträgt damit 1,986. Dieses Beispiel zeigt zugleich besonders deutlich, was mit Entropie gemeint ist: Die Unsicherheit, welches Zeichen als nächstes Zeichen folgen wird. Bei großer Entropie lässt sich in einer Zeichenkette kaum voraussagen, wie es weitergehen wird, bei geringer Entropie ist es weniger zufällig. Da Systeme mit höherer Anzahl von Mikrozuständen statistisch wahrscheinlicher sind, tendiert jedes System zu einem Zustand maximaler Entropie (das heißt maximaler Unordnung und Unvorhersehbarkeit). Umgekehrt gilt es seit Schrödinger als typisches Merkmal des Lebens, dass lebendige Systeme aus ihrer Umgebung Energie aufnehmen und mit ihr die innere Ordnung vergrößern und Entropie abbauen können (negative Entropie, Negentropie).

Um die Entropie zu berechnen, sind drei Schritte notwendig:

–    Bestimmung des Ereignisraums. Das sind alle unterschiedlichen Fälle, die vorkommen können. Im Beispiel der Reißzwecke die beiden Möglichkeiten, wie die Reißzwecke am Boden liegt. Bei einem Würfel die 6 Seiten. Bei einem Text die Gesamtheit aller auftretenden Zeichen (der Zeichensatz). In der thermodynamischen Informationstheorie die Gesamtheit aller Mikrozustände (jeder Mikrozustand beschreibt für alle beteiligten Teilchen ihren Ort und Impuls). Daraus verallgemeinert für die Quantenmechanik jeweils ein Vektor |n⟩ (Zustandsraum) im Hilbertraum, der alle Zustände enthält, die ein Objekt annehmen kann.
–    Bestimmung der Wahrscheinlichkeiten, mit der die jeweiligen Ereignisse eintreten.
–    Ausrechnen der Entropie gemäß der Formel von Shannon.

Neben der Shannon-Einheit wurden zahlreiche andere Einheiten für die Entropie betrachtet, um in unterschiedlichen Situationen das Rechnen zu vereinfachen, so das Trit, das Ban oder das natural digit Nit, um das es im Folgenden gehen soll. Während das Bit der Informationsgehalt bei Auswahl von zwei (und das Ban von zehn) gleichwahrscheinlichen Möglichkeiten ist, liegt dem Nit die Auswahl von 2,886 = 2 · 1,443 gleichwahrscheinlichen Möglichkeiten zugrunde. 1 Nit entspricht daher 1,443 Bit. Diese ungewöhnliche Anzahl ergibt sich aus der Definition des Nit, die auf die eulersche Zahl e zurückgeht.

(Def.) Nit = loge2. Das ist die Zahl, die die Gleichung 2Nit = e erfüllt. Es gilt: Nit ≈ 1,443

Die oben genannte Gleichung (1) für die Entropie kann für gleichverteilte Ereignisse formuliert werden:

(2) H = log2 Z = ln Z / ln 2

Der Ausdruck ‘ln‘ steht für den natürlichen Logarithmus, das ist der Logarithmus zur Basis e. Die Übersetzung von log2 Z in ln z / ln 2 ergibt sich aus den für Logarithmen geltenden Regeln. (2) kann gemäß Definition des Nit umgewandelt werden in:

(3) H = ln Z · Nit

Thermodynamische Informationstheorie und Boltzmannkonstante k

Die Informationstheorie nach Shannon gilt unabhängig von allen physikalischen Beobachtungen. In ihrem Licht kann rückblickend die wesentlich früher entstandene thermodynamische Informationstheorie gedeutet werden. Ludwig Boltzmann (1844-1906) hatte 1877 mit der Arbeit Über die Beziehung zwischen dem zweiten Hauptsatz der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht einen Zusammenhang zwischen dem Makrozustand und den Mikrozuständen eines thermodynamischen Systems erkannt. Sie lautet in der von Max Planck (1858-1947) präzisierten Form:

(4) S = kB ln Ω

»Die Entropie S eines Makrozustands eines abgeschlossenen Systems im thermischen Gleichgewicht ist proportional zum natürlichen Logarithmus der Anzahl Ω (Ergebnisraum) der entsprechend möglichen Mikrozustände (bzw. anders ausgedrückt zum Maß der 'Unordnung' des Makrozustands). Das statistische Gewicht Ω ist ein Maß für die Wahrscheinlichkeit eines bestimmten Mikrozustandes.« (Wikipedia zur Boltzmann-Konstante, abgerufen am 28.12.2016)

Gleichung (4) geht durch zwei charakteristische Änderungen aus Gleichung (3) hervor: Während bei Shannon ein Ereignisraum betrachtet wird, der aus endlich vielen Elementen z.B. eines Alphabets oder einer Reihe von Ereignissen besteht, betrachtet Boltzmann einen kontinuierlichen Raum. Das sind alle Mikrozustände eines idealen Gases.

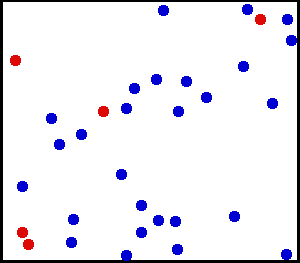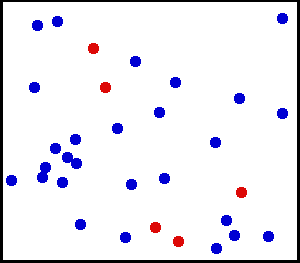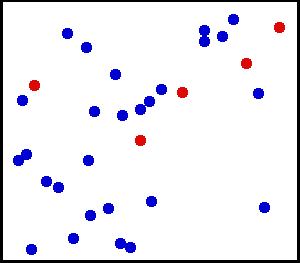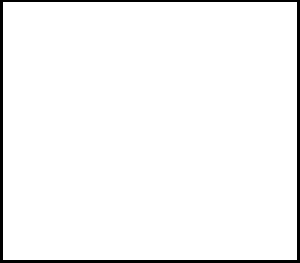
Mikrozustände eines idealen Gases
»Simulation eines idealen Gases in zwei Dimensionen. Einige Moleküle sind rot gezeichnet, damit sich ihre Bewegung leichter verfolgen lässt.« (Wikipedia, abgerufen am 28.12.2016 unter Verwendung eines Bildes von Greg L aus der englischsprachigen Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=1325234)

Jede Momentaufnahme dieser Animation zeigt einen Mikrozustand. Er ist definiert durch die jeweilige Position und Geschwindigkeit aller beteiligten Partikel des Gases. Kommt es zu Kollisionen zweier Partikel miteinander oder an der Wand, ändert sich der Mikrozustand.

In Gleichung (4) ist nicht nur der Übergang zu einem kontinuierlichen Ereignisraum zu sehen, sondern weiter die Boltzmann-Konstante k. Anders als bei Shannon ist die Entropie nicht einfach die Summe der Elemente des Ereignisraums, sondern sie wird mit dieser Konstante gewichtet. Sie ist eine übergreifende Systemeigenschaft, die für alle Gase gilt. In dieser Formel kommt – wie bei den Keplerschen Gesetzen für die Planetenbewegung – keine Masse m vor, sondern die Partikel werden ausdrücklich als materiefrei gedacht, jedoch mit der Eigenschaft, dass bei den Kollisionen in einer übertragenen Weise die Impulserhaltung gilt. Diese Formel ist daher für mich wie die Keplerschen Gesetze nur als Ergebnis eines Grenzprozesses zu verstehen, der aus materiellen Systemen gewonnen wurde, jedoch im Grenzübergang keine Materie mehr hat. Daher hat diese Formel in meiner Deutung eine ähnliche Stellung wie die Keplerschen Gesetze: Sie steht an der Grenze von Mathematik und Physik. Sie ist rein mathematisch formuliert, aber nur als Grenzprozess aus physikalischen Vorgängen verständlich.

Was bedeutet die Konstante k inhaltlich? Sie wird als die Temperatur eines Systems bezeichnet. In einem überhitzten System ist die Unordnung groß. Beruhigen sich die Bewegungen und sinkt die Temperatur, dann kehrt wieder Ordnung ein. Alles verläuft langsamer und es kann besser erkannt werden, welche Muster (Ordnungen) der Bewegung zugrunde liegen. Kommt das System völlig zur Ruhe (absoluter Kältepunkt), dann besteht es nur noch aus der starren Ordnung, wie sich die Elemente in diesem Moment angeordnet haben. Lebendigkeit liegt irgendwo zwischen Überhitzung und Erstarrung.

»Die Boltzmannkonstante k ist die Energie, die bei der Kollision von 2 Teilchen in einem Gas frei wird. Sie hängt natürlich von der Temperatur des Gases ab und ist pro Grad K konstant. Woher stammt diese frei werdende Energie? Sie entstammt der Unordnung des Systems.« (Walter Rella, E-Mail vom 22.9.2016)

Das verstehe ich so: Wenn in einem thermodynamischen System (d.h. einem System, in dem die Temperatur als übergreifende Eigenschaft gilt, die die innere Bewegtheit des Systems zeigt) zwei Elemente kollidieren, wird Energie frei. Mit dem Ereignis der Kollision ist eine Information gegeben, die genau das Auftreten dieses Ereignisses beschreibt. Dadurch verringert sich jedoch die Unordnung des Systems. Jede auftretende Information kann als Zeichen einer Ordnung verstanden werden. Die Vergrößerung der Ordnung wird ausgeglichen durch eine Verkleinerung der Energie, die in diesem Moment frei wird. Es ist äquivalent zu sagen: ›Eine Information tritt ein‹ und ›Eine Energie wird frei und verringert die Gesamtenergie‹.

Damit wird der Unterschied zur Informationstheorie von Shannon deutlich. Hier kommt die Bewegtheit des Systems hinzu, die nicht direkt erkannt wird, sondern indirekt an der Boltzmannkonstante erklärt wird. Es ist eine übergreifende Eigenschaft des Systems, die alle Bewegungen innerhalb des Systems beeinflusst. Rella vergleicht für mich überzeugend diese Systemeigenschaft mit der Bewegtheit eines mechanischen Systems, wenn sich dort der Raum im Ganzen ausdehnt oder zusammenzieht und mit dieser Bewegung alle Bewegungen innerhalb des Raums überlagert und beeinflusst. Das wird im Folgenden näher betrachtet.

Léon Nicolas Brillouin und der Maxwellsche Dämon

Léon Nicolas Brillouin lebte 1889-1969. Er prägte den Begriff Negentropie, den Gegenbegriff zur Entropie. Ordnung (Negentropie, Synentropie) und Energie befinden sich im umgekehrten Verhältnis zueinander: Ordnung nimmt ab, wenn Energie zugeführt und ein Zustand »heißer« wird, und Ordnung wird aufgebaut, wenn Energie verloren geht. Ordnung kann daher als gebundene Energie verstanden werden und Energie als das Potential, Ordnung zu schaffen.

Wasser: Wenn gefrorenes Wasser (Eis) erwärmt wird, dann erhöht sich die Energie, die einzelnen Wassermoleküle werden beweglicher, der feste Eisblock löst sich auf. Damit geht zugleich die Ordnung verloren, die im Eiskristall gegeben ist. Energie- (Temperatur-) Zufuhr wird durch Ordnungsverlust ausgeglichen. Die Erhaltungsgröße ist also lokal nicht die Energie, sondern die Summe von Energie und Ordnung.

Wenn umgekehrt Energie verloren geht, bildet sich eine höhere Ordnung. Diese Selbstorganisation ist eine Kraft, die meist übersehen wird. Energie wandelt sich in Negentropie.

Von einem höheren Standpunkt gleichen sich Temperaturveränderungen aus: Um an einer Stelle Energie zuführen zu können, muss an anderer Stelle Energie verbraucht werden. Wird daher an einer Stelle Ordnung aufgelöst, entsteht an anderer Stelle Ordnung (dort, wo der Energieverbrauch die Negentropie erhöht).

Brillouin war in den 1920ern neben de Broglie einer der wenigen Physiker in Frankreich, die sich mit Quantenmechanik beschäftigten. Beide standen in engem Kontakt, als de Broglie über Photonen arbeitete und intensiv die Ergebnisse von Einstein heranzog. So besaß Brillouin beste Vorkenntnisse, als er sich um 1950 der Frage nach dem Maxwellschen Dämon zuwandte und in diesem Zusammenhang die neu bekannt gewordene Informationstheorie von Shannon nutzen konnte. Maxwell hatte 1870 folgendes Gedankenexperiment entworfen: Zwei unterschiedlich warme Flüssigkeiten sind durch eine Öffnung verbunden, an der ein Dämon sitzt, der in einer Richtung nur die warmen Stoffe und in der anderen Richtung nur die kalten Stoffe durchlässt. Dadurch würde die Wärme getrennt und der Hauptsatz der Thermodynamik wäre verletzt.

»Der 'Dämon' öffnet und schließt die Klappe, um Teilchen größerer Geschwindigkeit (rot) von A nach B und solche kleinerer (blau) von B nach A durchzulassen.« (Wikipedia, abgerufen am 29.12.2016 mit einem Bild von User:Htkym - Eigenes Werk, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=1625737)

»Brillouin fragte 1951 genauer nach der Messung, dem 'Sehen' des Dämons. Sehen im wörtlichen Sinn bedeutet letztlich eine Abtastung der Moleküle mit Licht, auch wenn ganz andere Wellenlängen denkbar sind. Diese Abtastung bedeutet bei Berücksichtigung der Quantennatur des Lichts die Wechselwirkung zweier Teilchen, eines Moleküls und eines Photons, durch Stoß. Brillouin konnte nun relativ einfach zeigen, dass bei diesem Stoß immer genügend Entropie frei wird, um den zweiten Hauptsatz einzuhalten, wenn vorausgesetzt wird, dass die Energie der Photonen groß genug sein muss, um dem Dämon überhaupt Information liefern zu können. Der Dämon schien erledigt, die bei Szilárd noch offene Frage nach dem genauen Ort der Entropieerzeugung auf unspektakuläre Weise geklärt.

Brillouin ging in seiner Interpretation aber weiter, er sah die Photonen als Übermittler von ('gebundener') Information und postulierte erstmals einen direkten Zusammenhang zwischen der von Shannon eingeführten Entropie der Information und thermodynamischer Entropie, wozu er Shannons Entropie mit einer Konstanten multiplizierte. Er formulierte dann das 'Negentropie-Prinzip der Information', das umstritten blieb: Die Information selbst ist negative Entropie (Negentropie) und bewirkt im Sinne einer Erhaltung eine entsprechende Entropieerhöhung im Gas. Der Dämon kann diese anschließend höchstens gerade wieder ausgleichen.« (Wikipedia, abgerufen am 29.12.2016)

Für diese Betrachtung hat Brillouin die Gleichungen nach Shannon und Boltzmann, das sind die Gleichungen (2) und (4), direkt in Verhältnis zueinander gesetzt und dies als μ bezeichnet:

(5) μ = S / H = k · ln 2 ≈ 0.956 · 10⁻¹³ erg/grad, mit k = Boltzmann-Konstante

μ wird interpretiert als der kleinst-mögliche Anstieg der informations-theoretischen Entropie (Unordnung) bei Änderung eines Bit.

In (5) ist mit ›ln 2‹ der Kehrwert von Nit enthalten. Es gilt daher:

(6) μ =

k Nit

(7) k = μ · Nit

Die Boltzmann-Konstante k ist damit geschrieben als das Produkt der kleinst-möglichen Änderung der Ordnung, gemessen in Nit.

Thermodynamik eines isolierten Teilchens nach de Broglie

Louis de Broglie (1892-1987) erhielt 1929 den Nobelpreis für die Theorie der Materiewellen. Er nahm den Gedanken von Brillouin auf und führte ihn wesentlich weiter. Er setzte nicht nur die thermodynamische Entropie mit der Entropie in der Quantenmechanik in Beziehung, sondern er postulierte zwischen ihnen eine Analogie und fand einen Weg, wie sie nachzuweisen ist: Durch Untersuchung der Thermodynamik eines isolierten Teilchens. Es wird sich zeigen, dass sein Ergebnis noch weiter reicht: Ihr liegt eine übergreifende Analogie zu Grunde, wodurch sie auch zur Entropie nach Shannon in Analogie tritt. Im Grenzübergang stimmen die unterschiedlichen Entropien überein.

»Der Titel klingt paradox, denn bekanntlich kann die Thermodynamik nur statistische Eigenschaften zusammengesetzter Systeme behandeln, z.B. das durchschnittliche Verhalten der Atome oder Moleküle eines materiellen Elements. Doch wenn ein isoliertes Teilchen, d.h. ein Teilchen, das von jedem anderen Teilchen weit entfernt ist, mit einem in ungeordneter Bewegung befindlichen, verborgenen Milieu in Wechselwirkung steht, so ergibt sich daraus ein Chaos, das dem molekularen Chaos von Boltzmann analog ist.« (Andrade a Silva, Lochak, S. 228)

Das soll schrittweise näher betrachtet werden. Die von ihm aufgestellte Gleichung ist nicht im wörtlichen Sinn eine Gleichung, in der die linke Seite mithilfe der Operation auf der rechten Seite ausgerechnet wird, sondern eine Analogie: Das Quantenpotential A verhält sich zur Planck-Konstante h wie die Entropie S eines isolierten Teilchens zur Boltzmann-Konstante k:

(8)

A h

=

S k

Um diese Analogie zu finden, konstruierte er einen Grenzfall: Ähnlich wie Brillouin betrachtete er den Fall, dass in einem System eine minimale Änderung erfolgt, wenn ein einziges Teilchen hinzugefügt wird. In seinem Gedankenexperiment liegt ein System vor, dass völlig leer ist, in dem aber die thermodynamische Entropie gelten soll. Er betrachtet damit genau den Grenzfall, wenn im Übergang aus den Beobachtungen von materiehaltigen Systemen mit vielen Partikeln ein Grenzzustand erreicht wird, der materiefrei ist. Es wird hierbei nach einer mathematischen Funktion gesucht, die übergreifend sowohl für die materiehaltigen Systeme wie den materiefreien Grenzfall gilt. In materiehaltigen Systemen ist die mathematische Funktion durch die Wechselwirkung der Teilchen gestört und gilt nicht vollkommen. Mathematisch gilt sie nur im Grenzfall, wenn es keine Materie gibt, aber sie zeigt in diesem Grenzfall eine Struktur, die aus der Betrachtung von materiehaltigen Systemen gewonnen wurde. (Das entspricht den Keplerschen Gesetzen der Planetenbewegung: Kepler fand diese Gesetze durch Beobachtung der Planeten, die von der Erde aus sichtbar sind. Genau genommen gelten dort diese Gesetze nur in Annäherung, da sie gestört sind durch andere Kräfte. Aber an ihnen konnte eine Struktur erkannt werden, die erst im Grenzfall zutrifft, wenn es keine Materie mehr gibt.) Unmittelbar vor der Grenze befindet sich ein einziges Teilchen im System, und de Broglie untersuchte, wie sich dies Teilchen verhält.

Wird Gleichung (8) umgeformt und werden anschließend die Konstanten und der für die thermodynamische Entropie S eines isolierten Teilchens bestimmte Wert eingesetzt, ergibt sich für das Quantenpotential A:

(9) A =

S · h k

≈ 4,59 · 10−27 ergsec

Bevor diese Gleichung weiter umgeformt wird, um zu zeigen, wie sie mit dem Ergebnis von Brillouin und damit mit der Entropie von Shannon übereinstimmt, ist näher zu betrachten, was eigentlich mit dem Quantenpotential A gemeint ist.

»Die Planckkonstante h ist die Energie, die an einem Photon über einen definierten Zeitraum hinweg frei wird. Sie hängt natürlich von der Frequenz bzw. der Wellenlänge ab. Woher stammt diese am Photon erscheinende Energie? Sie entstammt dem Quantenpotential A – eine reichlich obskure und von niemandem noch beobachtete Größe. Um eine Ähnlichkeit mit S herzustellen – das ist notwendig um die Analogie zu rechtfertigen – muss man davon ausgehen, dass das Quantenpotential ebenfalls einen maximal ungeordneten Zustand repräsentiert, den die Physiker Raumzeit nennen und der ein Energiepotential beinhaltet, aus dem das Photon je und je seine Energie schöpft, indem es sich mit Lichtgeschwindigkeit bewegt, die gleichzeitig die Mitteilungsgeschwindigkeit des Systems ist.« (Walter Rella, E-Mail vom 22.9.2016)

Das ist eine weitreichende Aussage, die im abschließenden Teil über die philosophische Deutung der von Brillouin und de Broglie gefundenen Ergebnisse weiter untersucht werden soll. Für Rella gibt es eine Übereinstimmung zwischen Thermodynamik und der Bewegung des Photons, da in beiden Fällen unterhalb einer genau bestimmbaren Grenze ein Grund (Potential) vorhanden ist, der sich aus Sicht des Menschen in reiner Unordnung (Chaos) befindet. Es lassen sich keinerlei Aussagen machen, was dort geschieht. Für mich kann dieser Grund verglichen werden mit dem ursprünglichen Raum, den Platon als chora bezeichnet hatte, in dem letztlich alle Vorgänge, an denen eine Form (d.h. eine Ordnung) erkannt werden kann, ihren Boden haben. Es gibt unterschiedliche Welten, die aus diesem Grund hervorgehen. Sie können nicht auseinander erklärt werden, sondern sie befinden sich in Analogie zueinander, weil sie unabhängig voneinander doch auf analoge Weise aus diesem Grund hervorgehen. In thermodynamischer Betrachtung wandelt auf der untersten Ebene ein Teilchen einen Teil der Unordnung des Systems um in die Ordnung, die sich an diesem Teilchen zeigt, oder anders gesagt, durch die sich das Teilchen zeigt. Die zugrunde liegende Unordnung des thermodynamischen Systems wird als dessen Temperatur bezeichnet. In raumzeitlicher Betrachtung wandelt auf unterster Ebene ein einzelnes Photon einen Teil der im zugrunde liegenden Raum enthaltenen Bewegtheit (das ist aus heutiger Sicht die Ausdehnung des Raums im Ganzen) um in seine Bewegung innerhalb dieses Raums. So wie die kleinste Einheit der Umwandlung des thermodynamischen Rauschens in Ordnung die Boltzmann-Konstante ist, so ist die kleinste Umwandlung der Bewegtheit des umgebenden Raums in die Bewegung des Photons das Plancksche Wirkungsquantum. Alle weiteren Bewegungen in der Raumzeit beruhen darauf und werden gemäß der Lehre von Einstein übertragen durch Lichtsignale. In beiden Fällen gibt es an der Grenze ein Verhältnis zwischen dem Potential (der Unordnung) des zugrunde liegenden Systems und dem Ereignis (dem Akt, der Wirklichkeit, der Information), wenn aus dem Chaos ein isoliertes Teilchen hervortritt und sich bewegt. Für Rella kann die von de Broglie betrachtete Analogie nur deshalb gebildet werden, weil beide Verhältnisse ‘A zu h’ wie ‘S zu k’ unterschiedliche Ausprägungen eines übergreifenden Verhältnisses von Potential zu Akt sind.

Planck-Konstante und Natural digit

Der in Gleichung (9) aufgeschriebene Wert 4,59 · 10⁻²⁷ ergsec liegt bereits dem Wert der Planck-Konstanten h ungewöhnlich nahe. Der Beitrag von Hansen liegt in dem verblüffend einfachen und zugleich schlagenden Hinweis: Völlige Übereinstimmung wird erzielt, wenn A mit Nit multipliziert wird:

(10) h = A · Nit ≈ 4,592 · 10⁻²⁷ ergsec · 1,443 = 6,626 · 10⁻²⁷ ergsec

Dies Ergebnis ist aus einer zahlenmäßigen Übereinstimmung, also gewissermaßen als Beobachtung an den Formeln gewonnen. Es liefert noch keine Erklärung, warum es sich so verhält.

Formel (10) kann wiederum in (8) eingesetzt werden. Wenn dort im Nenner statt h der hier gefundene Wert A · Nit eingesetzt wird, ergibt sich:

(11)

A A · Nit

=

S k

Wird auf der linken Seite A gekürzt und die Gleichung nach k aufgelöst:

(12) k = S · Nit

Da zugleich gemäß (7) k = μ · Nit gilt, führt (12) zum Ergebnis:

(13) S = μ

Damit ist Übereinstimmung mit dem Ergebnis von Brillouin erreicht. Es bedeutet: Der Entropie-Zustand S eines isolierten Partikel ist identisch mit der kleinst-möglichen (d.h. bit-weisen) Veränderung der informationstheoretischen Entropie. Oder umgekehrt formuliert: Die kleinst-mögliche Veränderung der Entropie ergibt sich durch Aufnahme oder Abgabe eines isolierten Partikels.

Letztlich war das nicht anders zu erwarten. Wenn ein thermodynamisches System sich völlig entleert, geht es schließlich im Übergang zum Nichts in ein leeres System über, das über keine innere Bewegtheit verfügt und für das ausschließlich die Informationstheorie nach Shannon gilt. Entscheidend ist jedoch, was an dieser Grenze geschieht: Es herrscht nicht völlige Willkür oder Zufall, sondern es treten das Plancksche Wirkungsquantum und die Boltzmann Konstante hervor. Mit der von de Broglie betrachteten Thermodynamik des isolierten Teilchens ist es ihm gelungen, die Paradoxien des Maxwell Dämon zurückzuführen auf einen Grund, aus dem die uns bekannten und in der Natur beobachteten Naturkonstanten hervorgehen. Der Wert dieser Konstanten kann nicht theoretisch konstruiert, sondern nur gemessen werden. Aber es ist der Punkt gefunden, an dem dieser Wert rein hervortritt und nicht gestört ist durch andere Einflüsse.

Vorläufige Fragen zur philosophischen Deutung

Wie ist dies Ergebnis zu deuten?

Gibt es unterhalb des physischen Geschehens im subquanten Milieu einen Grund, der sich völlig der Rationalität entzieht?

Ist die Vernunft fähig, mithilfe von Analogien etwas zu erkennen, das prinzipiell über der Physik liegt?

Ist der Grenzübergang ins Nichts der entscheidende Punkt, an dem die Naturwissenschaft ihren Grund findet? Stimmt das überein mit Hegels Ausführungen, wenn sich die Maßlogik in absolute Indifferenz auflöst und an dieser Stelle ihre inneren Voraussetzungen zutage treten, das sind die Reflexionsbegriffe?

Lässt sich das über Shannon verbinden mit einem anderen Verständnis des Grundes, in den die Information eingeschrieben ist, so wie das Blatt Papier der Grund für die Schrift oder ein Stück Sand der Grund für die in ihn gezeichneten Spuren ist?

Sind mit Rella und letztlich mit Aristoteles Dynamik und Akt die entscheidenden Ideen?

Ist dieser Grund der Möglichkeitsraum, von dem auch in der Arbeit zu Gödel und Leibniz die Rede war?

Gilt im Grenzübergang nichts als der Satz des Pythagoras, wie es möglicherweise Hegel sah? Ist dieser Satz daher letztlich dasjenige, worauf sich die Analogien stützen können? Das würde bedeuten, dass der Raum, in dem Analogien wie die von Rella gebildet werden, als übergreifende Systemeigenschaft die Gültigkeit des Satzes von Pythagoras haben. In diese Richtung deuten bereits die Überlegungen, dass die von Hegel in der Maßlogik betrachtete Gesamtheit der Zustände mit dem Hilbertraum verglichen werden kann, der seinerseits durch das Merkmal definiert ist, dass in ihm der Satz des Pythagoras gilt. Ist also im Satz von Pythagoras mit der Forderung, dass die beiden Katheten senkrecht (im rechten Winkel) aufeinander stehen, die Anforderung gefunden, die über die bloße Aussage hinausgeht, dass etwas durch Nichts miteinander vermittelt ist? Enthält der Satz des Pythagoras also den materialen Inhalt, der über die Einsicht Hegels in der Maßlogik hinausgeht, dass Wahlverwandtschaften und Knotenlinie voneinander unabhängig sind und wäre damit innerhalb der von Hegel gebrauchten Begrifflichkeit ein Unterscheidungskriterium zwischen Maß und Idee?

Welche Bedeutung bekommen hier die Gesetze der Form von Spencer-Brown? Ist der hier genannte Grund in seiner vielfachen Bedeutung das Substrat, an dem Formen erkannt und in den Informationen eingeschrieben sind? Wie unterscheidet sich Formbestimmung und Information?

Ist Nikolaus von Cues folgend der Grund unterhalb des subquanten Milieu das Eine, an dem sich keinerlei Unterscheidungen mehr treffen lassen, das als das Kleinste zugleich überall enthalten ist und daher alles umfasst?

Literatur

Joao Andrade e Silva und Georges Lochak: Wellen und Teilchen, Frankfurt 1974

Louis de Broglie: The Thermodynamics of the isolated particle, Paris 1964

Helmut Hansen: Is the Planck constant itself the natural digit?
in: fqxi-forum, 2013

Walter Rella: Der Schritt in die Analogie
in: Wiener Jahrbuch für Philosophie Band XVI/1984 S. 129-138 und Band XVII/1985 S. 141-158

Dezember 2016