Walter Tydecks
Hegel und Hilbert – das Maßlose (Substrat) als Keim der Quantenzahl
Version 3.1.2014, überarbeitete Fassung eines Vortrags am 1.11.2013 im Internationalen Arbeitskreis zu Hegels Naturphilosophie in Kaiserslautern
Abstract Dieser Beitrag entwickelt Hegels Lehre des Substrats und seiner Zustände als neuen Ansatz zur Klärung der philosophischen Grundlagenfragen der Quantenmechanik. Auszugehen ist von Kant. Dessen kritische Wende wurde durch den Schock ausgelöst, als Kant entdeckte, dass die Chiralität (Händigkeit) weder mit der euklidischen Geometrie noch mit den naturphilosophischen Prinzipien Newtons oder den metaphysischen Ideen von Leibniz erklärt werden kann. Die Händigkeit ist – modern gesprochen – eine zusätzliche Quantenzahl, die über Ort und Impuls hinausgeht und damit den Rahmen der klassischen Mechanik sprengt. Im folgenden wird die These vertreten, dass sich mit ihr der Übergang in eine nicht-mechanische Logik verstehen lässt, den Hegel mit seinem Verständnis der Knotenlinien und des Maßlosen angedeutet hat.
Die Entdeckung der »philosophischen Anwendung« der Chiralität (Händigkeit) durch Kant
Auf den ersten Blick scheint es recht einfach zu sein, die Mechanik nach dem Vorbild der euklidischen Geometrie zu begründen. So wie der Mensch die Natur in Gestalt dreidimensionaler Körper wahrnimmt, geht Kant in seiner metaphysischen Grundlegung der Naturwissenschaften von der Mechanik 3-dimensionaler starrer Körper aus. Die Gestalt der Körper wird durch ihre dreidimensionale Geometrie beschrieben und ihre Bewegung erfolgt in 6 Freiheitsgraden: Geradlinige Bewegungen (Translationen) entlang der 3 Raumrichtungen und Rotationen um 3 voneinander unabhängige Drehachsen, die den Geraden und Kreisen der euklidischen Geometrie entsprechen.
Wenn weiter gezeigt werden kann, wie die Mechanik starrer Körper im Grenzfall in die Punktmechanik übergeht, in der ein einzelner Punkt für einen Körper steht bzw. ein ausgedehnter Körper aus einer Menge von Punkten und ihren Verbindungslinien konstruiert werden kann, dann ist die Aufgabe gelöst. Bewegungen lassen sich als Kurven oder als Strömungen von Kurvenbündeln durch den Raum beschreiben. Übergreifend bleibt nur die Frage, ob es einen absoluten Raum gibt, der alles enthält, was an mechanischen Bewegungen möglich ist (deduktiver Ansatz), oder ob umgekehrt aus allen beobachtbaren Bewegungen schrittweise der Raum zu entwickeln ist, der als Gesamtheit der wirklich vorkommenden Bewegungen verstanden wird (induktiver Ansatz). Kant war in seinen jungen Jahren der Überzeugung, dass beide Ansätze zwei Seiten der gleichen Sache sind. Es sollte daher möglich sein, die metaphysischen Grundbegriffe zu finden, in denen beide übereinstimmen. Im später von Frege eingeführten Sprachgebrauch haben der absolute und der relative Raum die gleiche Bedeutung.
Da wirkte es wie ein Schock, als er eine Eigenschaft entdeckte, die sich grundsätzlich nicht auf diese Weise darstellen lässt. Er konnte von ganz einfachen Phänomenen ausgehen, deren Tragweite jedoch vor ihm niemand erkannt hatte.
»Aller Hopfen windet sich von der Linken gegen die Rechte um seine Stange; die Bohnen aber nehmen eine entgegengesetzte Wendung« (Kant, GUGR, AA 02: 380.09-11).
Wird die Windung berücksichtigt, dann können unterschiedliche Gebilde entstehen, die von der Oberfläche her völlig gleich (isometrisch) sind, jedoch nicht ineinander überführt werden können, »man mag ihn drehen und wenden, wie man will« (Kant, GUGR, AA 02: 382.30-31). Ein linksgedrehtes Schraubengewinde passt in keine rechtsgedrehte Mutter.
Mir scheint, dass Kant bis heute der einzige Philosoph ist, der die Tragweite dieser Eigenschaft gesehen hat und nach ihrer »philosophischen Anwendung« fragte (Kant, GUGR, AA 02: 382.24). Er erkannte, dass mit diesem Beispiel sowohl die Grundlagen des absoluten Raums von Newton wie die Raumtheorie von Leibniz hinfällig werden. Beide haben auf unterschiedliche Weise darauf vertraut, dass die euklidische Geometrie eine ausreichende Grundlage ist. Aber das Beispiel der Händigkeit (Chiralität) zeigt, dass die euklidische Geometrie nicht alle beobachtbaren geometrischen Phänomene erfasst und daher in eine höhere Geometrie eingebettet werden muss.
Kant betont, dass seine Entdeckung der Händigkeit letztlich die kritische Wende ausgelöst hat (Kant, MAN AA 04: 484.12-19, vgl. auch die detaillierte Darstellung durch Brigitte Falkenburg). Sie brachte ihn dazu, mit der transzendentalen Ästhetik einen völlig neuen Ansatz vorzulegen, um Raum und Zeit zu verstehen.
Als das gelungen war, kam er in den Metaphysischen Anfangsgründen der Naturwissenschaft auf diese Frage zurück. Er versucht, die Grundbegriffe der von Newton axiomatisierten Physik entsprechend der Urteilstafel der Kritik der reinen Vernunft zu ordnen. Die Händigkeit fällt jedoch heraus. Kant erwähnt sie zwar, versteht sie aber als eine »Abschweifung« außerhalb der Anfangsgründe der Naturwissenschaft (Kant, MAN, AA 04: 484.19).
Sie ist ein »innerer Unterschied« der Dinge (Kant, MAN, AA 04: 484.09), der zusätzlich zu Ort und Impuls herangezogen werden muss. Sie sprengt daher den Rahmen der klassischen Mechanik und gehört für Kant weder in das Gebiet der transzendentalen Ästhetik noch zu den metaphysischen Anfangsgründen der Naturwissenschaft. Er findet für sie in seinem System keinen rechten Ort. Daher blieb ihm nichts anderes als die Behauptung, dass die Händigkeit eine empirische Eigenschaft des absoluten Raums ist, die wahrgenommen, aber nicht weiter begründet werden kann (Kant, GUGR, AA 02: 383).
1858 fanden unabhängig voneinander Möbius und Listing eine mathematische Darstellung, mit der es gelingt, die beiden Zustände der Händigkeit kontinuierlich ineinander zu überführen. Hierfür ist gegenüber dem euklidischen Raum eine zusätzliche Dimension notwendig, in dem von links nach rechts umgeblättert werden kann. Am vereinfachten Beispiel einer zweidimensionalen Fläche ist das das Möbiusband. Inzwischen sind verschiedene weitere Naturphänomene entdeckt, die eine Händigkeit aufweisen. Es wird vermutet, dass es auch eine höherdimensionale Händigkeit (Chiralität) gibt.
Poincaré und Hilbert gelang es, eine übergreifende Geometrie zu entwerfen, die die euklidische, nicht-euklidische und orientierbare Geometrie als jeweils spezifische Ausprägungen enthalten sollte. Die Händigkeit wird als eine eigene Symmetrie verstanden, wobei Linksdrehung und Rechtsdrehung ihre beiden Zustände sind. Damit war ein Raum gefunden – der Hilbert-Raum –, in dem sich sowohl die bekannten mechanischen wie auch die »inneren Unterschiede« der Dinge einheitlich darstellen lassen. Nach Überzeugung der überwiegenden Mehrheit der Physiker hat sich damit die Frage von Kant erledigt. Wenn es gelingt, die klassische Mechanik dahin zu erweitern, dass einheitlich alle geometrischen Eigenschaften einschließlich der Händigkeit dargestellt werden können, entfällt der von Kant für seine transzendentale Ästhetik genannte Beweggrund. Die Händigkeit ist keine »Abschweifung« mehr, sondern eine eigene Quantenzahl (Messgröße) zur Beschreibung von physikalischen Zuständen, die gleichberechtigt neben anderen Quantenzahlen wie Ort, elektrische Ladung, Baryonenzahl etc steht (siehe z.B. Solstice).
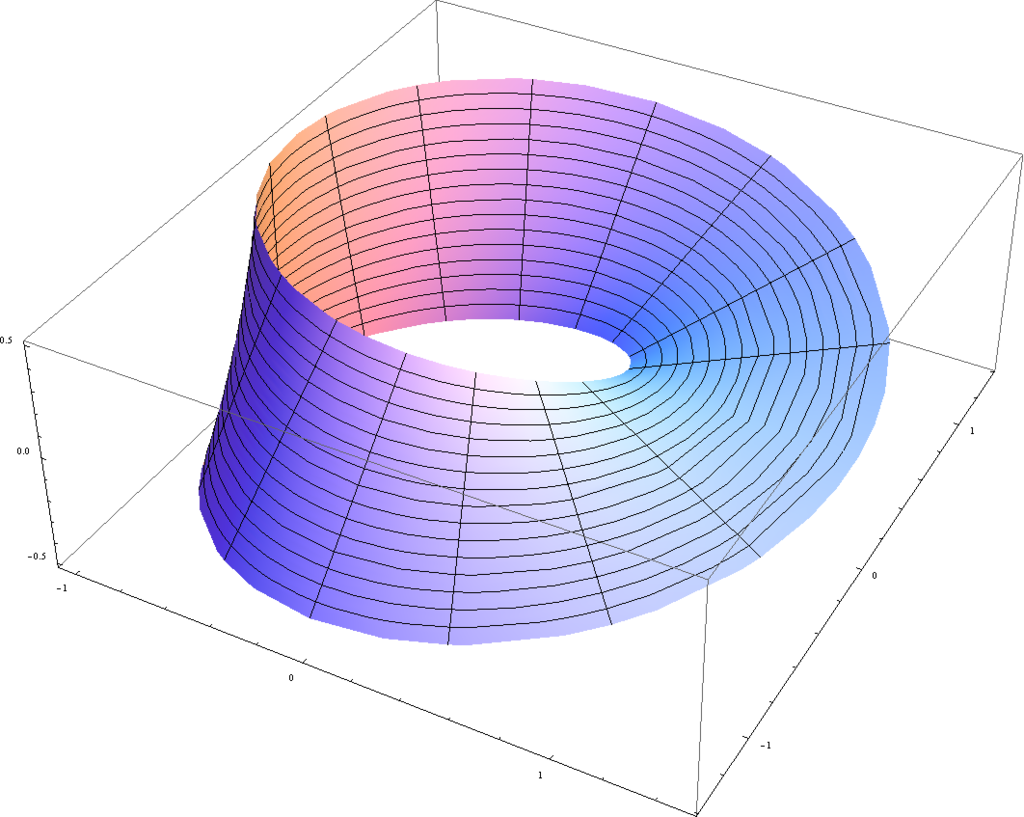
Figur 1: Möbiusband
»Einmal rundherum krabbeln genügt für eine Ameise nicht, um am selben Ort des Möbiusbandes zu sein. Entsprechend muss auch der Quantenspin des Elektrons zweimal rotiert werden, bis er wieder in seinen Ausgangszustand zurückkehrt. Dieser Effekt führt zu Chiralität in Quantenspinsystemen, wie ein ETH Forscher herausfand« (Christoph Meier Versteckte Händigkeit, dort auch eine Abbildung des Möbiusbandes nach Escher mit Ameisen, Link). Quelle des Bildes aus Wikipedia: CC BY-SA 3.0
Das Zeigen des Substrats bei Hegel
Oder hat Kant doch etwas gesehen, was seinen Kritikern entgeht? Die Händigkeit ist das kritische Beispiel, das für sich völlig anschaulich ist, jedoch an der Grenze steht zur Unanschaulichkeit der modernen Mathematik, ohne die heute die Physik nicht mehr auskommt. Kant fasste diese Frage in die paradoxe Formulierung, dass sich in der Händigkeit der absolute Raum empirisch zeigt. Die modernen Physiker glauben zwar an keinen absoluten Raum, müssen aber zugeben, dass sich die von ihnen beschriebenen Eigenschaften der Anschauung entziehen und nur mit der Widerspruchsfreiheit des mathematischen Raums begründet werden können. Sie sprechen stattdessen vom Kollaps der Wellenfunktion oder der Dekohärenz, durch den im Prozess der Messung die Unanschaulichkeit und letztlich Unterbestimmung der im Hilbert-Raum dargestellten mathematischen Objekte übergeht in »vertraute, klassische Objekte«, die wahrnehmbar und anschaulich sind. Bis heute hat niemand erklären können, was beim Kollaps oder der Dekohärenz geschieht. Es geht letztlich um die gleiche Frage wie bei Kant: Wie ist es möglich, dass sich das Unanschauliche (oder das Absolute) zeigt? Das Zeigen bedarf einer Vermittlung. Hierfür führt Hegel in seiner Maßlogik den Begriff des Substrats ein. Das Substrat stellt in seiner Wissenschaft der Logik den Dreh- und Angelpunkt dar, um vom Sein zum Wesen zu gelangen. Die folgenden Ausführungen sollen helfen, mit den Fragestellungen der Quantenphysik den Gedanken von Hegel zu erläutern, und umgekehrt ausgehend von Hegels Begriffsklärungen der Diskussion um den ontologischen Status der Grundlagenbegriffe der Quantenmechanik eine neue Richtung zu öffnen.
Statt zwischen »anschaulich« und »unanschaulich« oder zwischen klassischen Objekten und Quantenobjekten unterscheidet Hegel innerhalb des Maßlosen nochmals zwischen dem »abstrakt Maßlosen«, das einer Knotenlinie von Zuständen zugrunde liegt, und der »bloßen Ordnung«, der »Beziehung-auf-sich«, die sich im Maßlosen zeigt und gesetzt ist (HW 5.445, HW 8.229). Diese beiden Begriffe sind nicht unmittelbar eingängig. Und es kommt hinzu, dass das Verhältnis zwischen beiden zum einen noch wie die Übergänge innerhalb der Lehre vom Sein verstanden wird. Hegel vergleicht es mit dem Übergang von der quantitativen zur qualitativen Unendlichkeit (HW 5.442, HW 8.229). Zum anderen stehen sie aber an der Grenze zur Lehre vom Wesen und für sie gilt bereits: »Im Wesen findet kein Übergehen mehr statt sondern nur Beziehung« (HW 8.229). Das Beispiel der Händigkeit soll helfen, diese Vermittlung und die mit ihr verbundene Widersprüchlichkeit zu verstehen. – Mit Blick auf die Physik soll mit dieser Unterscheidung klarer gemacht werden, warum die aktuell vorherrschenden Modelle der Quantentheorie in die Irre gehen, wenn sie Symmetrien, die auf Teilchenprozessen beruhen, und rein geometrische Symmetrien einander gleichstellen. Die ersteren verstehe ich als Beispiele für das »abstrakt Maßlose«, die geometrischen Symmetrien als Beispiele für die mit dem Maßlosen gegebene »bloße Ordnung«. Der Kollaps der Wellenfunktion oder die Dekohärenz werden als Wechsel des theoretischen Horizonts verstanden statt als mysteriöses Ereignis im Prozess des Messens.
Das abstrakt Maßlose in der chemischen Sphäre
Entsprechend dem Stand der Naturwissenschaft seiner Zeit geht Hegel von Beispielen in der Chemie aus und nennt die Bühne, auf der sich das Substrat zeigen kann, die »chemische Sphäre« (HW 5.420). In der Chemie wird der klassische Begriff des Gegenstands überwunden. Als Gegenstand gilt nicht mehr ein den mechanischen Gesetzen gehorchender, starrer, dreidimensionaler Körper, sondern die Chemie entwickelt einen ersten Begriff des Substrats. Das typische Beispiel ist das Wasser, in dem sich andere Stoffe auflösen und das in unterschiedlichen Aggregatzuständen auftreten kann (Eis, Flüssigkeit, Dampf). Mit dem Substrat Wasser ist nicht eine bestimmte Menge von Wasser gemeint mit klaren Grenzen und fester Gestalt, – wie ein Eimer Wasser oder ein Eiswürfel –, sondern die Gesamtheit von Wasser, die dem allem zugrunde liegt. Die Gesamtheit des Wassers ist maßlos. Sie lässt sich weder räumlich noch stofflich klar abgrenzen. Dennoch hat sie Eigenschaften. Das Substrat ist kontinuierlich, beständig und materiell, wobei diese Eigenschaften bisweilen nicht klar voneinander getrennt werden. Hegel nennt es »bleibendes, materielles Substrat« (HW 5.436), das den verschiedenen Zuständen und ihren qualitativen Umschlägen zugrunde liegt.
Die verschiedenen Zustände eines Substrats lassen sich entlang einer Knotenlinie anordnen, wobei ein bestimmter Systemparameter kontinuierlich geändert wird. Im Beispiel des Wassers gehen die unterschiedlichen Zustände auseinander hervor, wenn Temperatur, Druck oder Teilchenzahl verändert werden. Auf ähnliche Weise kann der Zustand eines Gemisches von Stoffen in einem Reaktionsbehälter verändert werden, wenn z.B. der Anteil eines Stoffes erhöht, ein Katalysator zugeführt oder das Gemisch erhitzt oder umgerührt wird. Wie beim Wasser ergibt sich für jede Änderung eines Parameters eine Knotenlinie, in der unterschiedliche Zustände aufeinander folgen und das Reaktionsverhalten der Stoffe im Gemisch radikal umschlagen kann. Auf diesen Erkenntnissen beruhen die Verfahren der chemischen Produktion.
Wenn Hegel die Knotenlinie als »bleibendes, materielles Substrat« bezeichnet, ist mit dem Substrat ein bestimmter, zugrundeliegender Stoff ausgezeichnet, dessen Zustand sich ändert. Es ist leicht zu erkennen, wie sich hier vergleichbar der schlechten Unendlichkeit auf zweifache Weise ein unendlicher Regreß wiederholt. So wie entlang der natürlichen Zahlengerade immer weiter gezählt werden kann, kann z.B. die Temperatur eines Stoffes über alle Grenzen erhöht werden, wodurch ständig neue Zustände entstehen bis schließlich der ursprüngliche Stoff völlig aufgelöst ist. Wird dieser Prozess gedanklich immer weiter getrieben und auf alle Knotenlinien verallgemeinert, dann wird im Ergebnis ein rein abstraktes Substrat erreicht, um das es Hegel geht. In ihm sind alle Stoffe und ihre Beschaffenheiten ununterscheidbar. Heute geht die Physik den gleichen Weg rückwärts und beschreibt gedanklich den Urknall als Zustand ohne jegliche innere Unterscheidung vor aller Aufteilung in gebrochene Symmetrien.
Zugleich können stufenweise immer weiter für jedes Substrat zugrundeliegende Substrate gefunden werden. Ist das Wasser als Substrat von Eis, Flüssigkeit und Dampf erkannt, kann im nächsten Schritt nach dem Substrat von Wasser, Erde, Luft und Feuer gefragt werden. Das führt zu den chemischen Elementen. Als deren Substrat erweist sich das Atom, das sich seinerseits aus den Elementarteilchen zusammensetzt. Eine Ende ist nicht abzusehen.
Das Gemeinsame der Knotenlinien ist, dass es sich in allen Fällen um materielle Prozesse handelt. Auf jeder Stufe liegt ein neues Substrat vor. Dessen Zustände werden mathematisch als Symmetrien beschrieben, die von Hegel angesprochene Knotenlinie als Strömung (vgl. das Noether-Theorem von 1918). Alle hier betrachteten Symmetrien befinden sich innerhalb des »abstrakt Maßlosen«, Mathematisch wird das durch die Symmetrie-Gruppen der Eichtheorien dargestellt.
Die »bloße Ordnung« und »Beziehung-auf-sich«
Was unterscheidet die Knoten auf einer Knotenlinie, dem »abstrakt Maßlosen«, von den Zuständen einer »bloßen Ordnung«, die »nur Substrat« ist (HW 5.445)? Alle bisher genannten Beispiele waren »unmittelbare qualitative Etwas (die spezifischen Schweren, oder die chemischen Stoffe)« (HW 5.444). Gibt es ein striking example, das zwar eine »bloße Ordnung« darstellt, aber kein »unmittelbar qualitatives Etwas«? Das ist nach meiner Überzeugung die Händigkeit.
Eine rechte Hand kann sich nicht in eine linke Hand verändern. Es gibt auch weder eine Ur-Hand, die sich mal in eine rechte Hand und mal in eine linke Hand entwickeln kann, noch einen Grundzustand, der in einen linksdrehenden oder rechtsdrehenden Zustand gebrochen werden kann. Das Rechtsdrehende lässt sich ausschließlich definieren durch seine Beziehung zum Linksdrehenden. Am nächsten kommt dem die Embryologie, die nach den Keimen fragt, über die sich aus der einfachen geometrischen Struktur der befruchteten Eizelle entlang verschiedener Verzweigungspunkte die links- und rechtsdrehenden Gliedmaßen entwickeln. In der Mathematik wird nach dem übergreifenden Raum gefragt, in dem sich dieser Entwicklungsgang darstellen lässt (siehe hierzu die Arbeit von René Thom).
Was wäre im Beispiel der Händigkeit das Substrat? Die Gesamtheit aller Gegenstände, die die Eigenschaft der Händigkeit aufweisen, also Hände, Schneckenhäuser, Schrauben, Hopfen, Bergkristall, Thalidomide (Contergan), Helicene etc? Da die Händigkeit eine geometrische Eigenschaft ist, müsste eine rein geometrische Entität das Substrat sein, das allen konkreten Dingen, die das Merkmal der Händigkeit tragen, zugrunde liegt. Die Gesamtheit der händigen Figuren müsste innerhalb der Gesamtheit aller geometrischen Figuren auf ähnliche Weise ausgezeichnet werden wie etwa die Primzahlen innerhalb der natürlichen Zahlen.
Mit einem Wort: Es gibt kein »unmittelbar qualitatives Etwas«, das an sich rechts- oder linksdrehend wäre, sondern es kann lediglich an einem Etwas eine Eigenschaft nachgewiesen werden, die die Händigkeit aufweist, d.h. ein isometrisches Gegenstück besitzt, das gegenläufig gedreht ist. Die Händigkeit ist ihr eigenes Substrat. Die Händigkeit ist sowohl eine beobachtbare Eigenschaft wie das Prinzip, das dieser Eigenschaft zugrunde liegt.
Nach meinem Verständnis geht es Hegel genau um einen paradoxen Fall dieser Art. Hier drohen sich Meta- und Sachebene (die Händigkeit als Phänomen und als Substrat) zu verschlingen. Da jeder sieht, dass es die Händigkeit gibt, ist das kein Fehler, den es nicht geben kann, sondern zeichnet umgekehrt die Händigkeit als vermittelndes Glied (terminus medius) aus, über das vom Sein auf das Wesen geschlossen werden kann. Hegel wählt eine Formulierung, die bereits auf Wittgenstein vorausdeutet:
»Dies Übergehen des Qualitativen und des Quantitativen ineinander geht auf dem Boden ihrer Einheit vor, und der Sinn dieses Prozesses ist nur das Dasein, das Zeigen oder Setzen, daß demselben ein solches Substrat zugrunde liegt, welches ihre Einheit sei« (HW 5.444).
Die Formulierung ist sehr bedacht gewählt: Innerhalb seiner Wissenschaft der Logik übernimmt das Sich-Zeigen des Substrats den Übergangspunkt, um vom Dasein der Seinslogik zum Setzen der Reflexionslogik zu gelangen.
Das ist etwas anderes als die Übergänge in der Daseinslogik. Etwas Wohlriechendes kann übelriechend werden, etwas Rotes kann verwelken und Schwarz werden, aber etwas Linksdrehendes kann nicht rechtsdrehend werden. Es kann nur als linksdrehend erkannt werden, weil es auf etwas Rechtsdrehendes verweist. Linksdrehend und rechtsdrehend sind zwei Zustände einer Symmetrie, zwischen denen es keinen Übergang gibt, sondern nur einen Perspektivwechsel, durch den beide ihre Seiten tauschen, aber die Beziehung links-rechts erhalten bleibt.
Wenn die Vermutung zutrifft, dass die Händigkeit das Besondere des Maßlosen zeigt, was sind ihre charakteristischen, verallgemeinerbaren Merkmale? Es sollte möglich sein, eine Eigenschaft zu bestimmen, in der Kontinuität, Beharrlichkeit und Ordnung aufgehoben sind und deren Verhältnis zur Materialität erkannt werden kann. Einige Hinweise:
 Links und Rechts als austauschbare Beziehung vergleichbar dem Verhältnis von positiv und negativ (vgl. HW 8.230).
Links und Rechts als austauschbare Beziehung vergleichbar dem Verhältnis von positiv und negativ (vgl. HW 8.230).
 Händigkeit erzwingt ein Umblättern in einer höheren Dimension. Händigkeit verweist auf eine höhere Potenz, enthält diese aber noch nicht an sich selbst. Die lokale Eigenschaft der Händigkeit verweist auf eine globale Eigenschaft des Raums, seine Orientierung.
Händigkeit erzwingt ein Umblättern in einer höheren Dimension. Händigkeit verweist auf eine höhere Potenz, enthält diese aber noch nicht an sich selbst. Die lokale Eigenschaft der Händigkeit verweist auf eine globale Eigenschaft des Raums, seine Orientierung.
 Gebrochene Symmetrie. Es gibt einerseits eine Spiegelachse, andererseits versperrt die Undurchdringlichkeit des Außenrandes das Umstülpen. Asymmetrie. Innen und außen.
Gebrochene Symmetrie. Es gibt einerseits eine Spiegelachse, andererseits versperrt die Undurchdringlichkeit des Außenrandes das Umstülpen. Asymmetrie. Innen und außen.
 Da Händigkeit auf keinen materiellen Träger verweist, sollte es möglich sein, Symmetrien wie die Händigkeit systematisch zu unterscheiden von Eich-Symmetrien, die jeweils mit einem Substrat und Austauschteilchen verbunden sind. Das könnte den Weg öffnen, um die Eichtheorien zu verknüpfen mit den Prinzipien der Speziellen und Allgemeinen Relativitätstheorie. Kombinatorisches Unterscheidungsmerkmal ist die Anti-Symmetrie (ungerade Permutationen). Dies scheint nicht auszureichen, wie die bisher erfolglosen Bemühungen mit den Supersymmetrien zeigen.
Da Händigkeit auf keinen materiellen Träger verweist, sollte es möglich sein, Symmetrien wie die Händigkeit systematisch zu unterscheiden von Eich-Symmetrien, die jeweils mit einem Substrat und Austauschteilchen verbunden sind. Das könnte den Weg öffnen, um die Eichtheorien zu verknüpfen mit den Prinzipien der Speziellen und Allgemeinen Relativitätstheorie. Kombinatorisches Unterscheidungsmerkmal ist die Anti-Symmetrie (ungerade Permutationen). Dies scheint nicht auszureichen, wie die bisher erfolglosen Bemühungen mit den Supersymmetrien zeigen.
 Analytizität. Mit ihr ließe sich erklären, warum die Gesetzmäßigkeiten der Ausbreitung von Zuständen im Bereich der komplexen Zahlen liegt und die Zustände nach dem Vorbild der Klang- und Farbspektren polarisiert werden können. Möglicherweise ist die Analytizität zu verallgemeinern von den komplexen Zahlen auf äußere Algebren, die auch anti-symmetrische Elemente enthalten.
Analytizität. Mit ihr ließe sich erklären, warum die Gesetzmäßigkeiten der Ausbreitung von Zuständen im Bereich der komplexen Zahlen liegt und die Zustände nach dem Vorbild der Klang- und Farbspektren polarisiert werden können. Möglicherweise ist die Analytizität zu verallgemeinern von den komplexen Zahlen auf äußere Algebren, die auch anti-symmetrische Elemente enthalten.
 Ist Händigkeit mit Lebendigkeit verbunden? Die ursprünglichen Beispiele stammen aus der Pflanzen- und Tierwelt. Gibt es eine spontane geometrische Optimierung, warum Pflanzen gleichmäßig drehen und warum bestimmte lebende Organismen händige Organe ausbilden, um die Orientierung und Sicherheit räumlicher Wahrnehmungen und Bewegungen zu verbessern? Vermeidung von Knotenbildungen. Zugleich verleiht die Händigkeit eine besondere Festigkeit. Daher wird Händigkeit in Schrauben genutzt. Doppelhelix. Gibt es hierfür eigene mathematische Maße?
Ist Händigkeit mit Lebendigkeit verbunden? Die ursprünglichen Beispiele stammen aus der Pflanzen- und Tierwelt. Gibt es eine spontane geometrische Optimierung, warum Pflanzen gleichmäßig drehen und warum bestimmte lebende Organismen händige Organe ausbilden, um die Orientierung und Sicherheit räumlicher Wahrnehmungen und Bewegungen zu verbessern? Vermeidung von Knotenbildungen. Zugleich verleiht die Händigkeit eine besondere Festigkeit. Daher wird Händigkeit in Schrauben genutzt. Doppelhelix. Gibt es hierfür eigene mathematische Maße?
Ausblick
Das Verhältnis von Hegel und Hilbert ist mit der Frage des Substrats noch nicht erschöpfend beantwortet. Es bedarf entlang des Gedankengangs seiner Logik weiterer Überlegungen, die in vier Thesen skizziert werden sollen.
1. Gegenläufigkeit. Im Substrat ist die durchgehende Einheit oder der Boden gefunden, auf den die einzelnen realen Maße und Quantenzahlen zurückbezogen sind. Die Zustände sind durch Indifferenzpunkte voneinander getrennt. Hegel betrachtet als Beispiel das Pendel: Im äußersten Punkt ruht es, jedoch bleibt die Bewegung damit nicht stehen, sondern im Hintergrund kehrt sich das Verhältnis der Kräfte um und lässt es zurückschwingen. Es geht um diese Kraft, die im Ganzen das System in einen übergreifenden Zustand der Oszillation versetzt. Die Gegenläufigkeit geht implizit in die Konstruktion des Hilbert-Raums ein, indem angenommen wird, dass sich der Grundzustand und die Zustände zueinander verhalten wie Grundton und Oberton einer Schwingung (Polarisation). Im Beispiel des Möbius-Bandes zeigt sie sich in der Verwindung (Krümmung) des Bandes.
Für Hegel sind mit Kontinuation und Gegenläufigkeit (Umkehr) die beiden Bestimmungen gefunden, wodurch das Substrat als Terminus Medius dienen kann, um den Schluss vom Sein zum Wesen zu ziehen. Sie kehren innerhalb der Reflexionslogik wieder, wenn dort gezeigt wird, wie der Gegensatz schließlich zum Gegensatz des »an sich Positiven« (Kontinuation) und des »an sich Negativen« (Umkehr) wird, wodurch der Gegensatz als Widerspruch gesetzt wird und zu Grunde geht. Erst dann kann die bereits in der Maßlogik genannte »Sache« aus dem Grund in die Existenz treten (HW 6.122f). Kontinuation und Umkehr stehen gewissermaßen auf beiden Seiten, sowohl in der Logik des Seins wie in der Logik der Reflexion, und können im Sinne eines Analogieschlusses zwischen beiden vermitteln.
2. Ausgehend von der Prädikationstheorie von Peter Ruben soll ein neues Verständnis der Schluss-Lehre von Hegel vorgelegt werden. Ruben interpretiert die aus der Ur-Teilung von Sätzen entstehenden reduzierten Sätze als Namen, mit denen die Gesamtheit aller Eigenschaften eines Subjekts, das ist dessen Realität, bzw. die Gesamtheit aller Subjekte einer Eigenschaft, das ist formal dessen Substrat, bezeichnet werden. Der Schluss vom Einzelnen zum Allgemeinen gelingt dann auf dem Weg, dass für ein charakteristisches Einzelnes ein treffender Name gefunden wird, der zugleich der Name der Allgemeinheit ist.
3. Darauf aufbauend soll das Chemismus-Kapitel neu gelesen werden, in dem Hegel von der Analogie des Wassers als Medium im Körperlichen und der Sprache als Medium im Geistigen spricht. Idee: Der äußere Rahmen des Hilbert-Raums kann gefüllt werden mit Objekten, die miteinander verwandt sind, wobei die Verwandtschaft sowohl durch ihren gemeinsamen Namen wie ihre Affinität zueinander gegeben sein kann.
4. In einem letzten Schritt ist zurückzukommen auf Hegels Ausführungen über die euklidische Geometrie im Methoden-Kapitel. Sie werden meist als eine zu lang geratene Anmerkung verstanden. Eine Gegenposition vertritt Richli. Für ihn erweist sich in der Konstruktion die eigenständige Leistung des Denkens. Mit dem Schluss des Seins über das Maß zum Wesen wurde ein Beispiel gezeigt, wie das Denken konstruiert. Lässt sich das Methodenkapitel mit Blick auf den Hilbert-Raum neu verstehen? Erst mit dieser Frage ist das Verhältnis Hegel und Hilbert umfassend erschöpft. Innerhalb des Systems von Hegel wird an dieser Stelle der Übergang von der Wissenschaft der Logik zur Naturphilosophie vollzogen.
Anhang
Kurt Reidemeister zur Händigkeit
Kurt Reidemeister hat in Kritik an Kant gezeigt, dass sich innerhalb der euklidischen Geometrie geeignete Definitionen und Axiome aufstellen lassen, mit denen chirale Figuren durch Spiegelung ineinander überführt werden können. Seine Kritik macht deutlich, dass weitere mathematische Beschreibungen notwendig sind, um zu erklären, worin sich die Händigkeit von den üblichen geometrischen Eigenschaften unterscheidet. Das ist ihre Topologie: Wenn innerhalb des euklidischen Raums eine rechtsdrehende dreidimensionale Figur in eine linksdrehende dreidimensionale Figur umgestülpt werden soll, ist ein Bruch ihrer topologischen Eigenschaften notwendig. Sie muss entweder in eine zweidimensionale Figur projiziert und dann seitenverkehrt aus hier herausgeklappt werden, oder es muss in der Phase der Umstülpung Punkte geben, an denen sich die Wege der rechtsliegenden Punkte mit denen der linksliegenden Punkte kreuzen, wenn sie von der rechtsdrehenden auf die linksdrehende Figur abgebildet werden. Mit den Kreuzungspunkten wird im Übergang eine andere Topologie erzeugt.
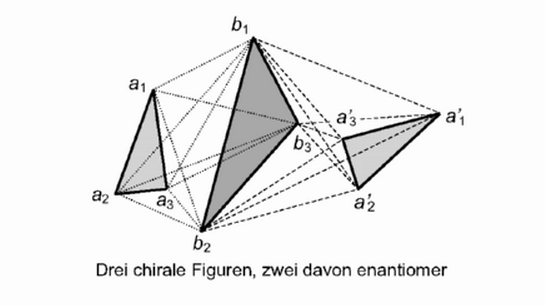
Figur 2: Enantiomere Figuren
Diese Darstellung soll die Konstruktionsidee von Reidemeister veranschaulichen. Von links nach rechts gelesen zeigt sie sehr gut, wie die Linie a1— a2 durch die Ebene hindurchgeführt werden muss, auf der a3 liegt, damit dann im Spiegelbild a3' links von der Linie a1' — a2' liegen kann. Quelle: Wirth und Dreiding, S. 12 Figur 3
Am Beispiel der Knoten relativiert Reidemeister seine eigene Aussage wieder. Hier betrachtet er »die kombinatorische Topologie des dreidimensionalen Raums« (Reidemeister 1957, S. 97) und analysiert verknotete Fäden, für die alle Deformationen erlaubt sind, jedoch nicht, sich selbst zu durchdringen. Genau das geschieht aber bei der Umstülpung.
Im Hintergrund steht eine philosophische Frage. Hat Kant recht, wenn er mit dem Beispiel der Händigkeit die Existenz eines absoluten Raums erwiesen sieht? Reidemeister ist überzeugt, dass Kant nur aus der Not heraus zum absoluten Raum greift, da er die »Irreduzibilität von Relationen« nicht anerkennt (Reidemeister 1957, S. 55). Da es weder einen Gegenstand noch ein Substrat gibt, als dessen Eigenschaft die Händigkeit erklärt werden kann, bleibt Kant nichts anderes als der absolute Raum. Während zum Beispiel übelriechend und wohlriechend auf einen riechenden Gegenstand bezogen werden können, müssen für Kant rechtshändig und linkshändig auf den absoluten Raum bezogen werden, weil es keinen »händigen Gegenstand« gibt, der einem riechenden Gegenstand vergleichbar wäre. Reidemeister erkennt, dass Kant implizit voraussetzt, dass es immer einen Gegenstand geben muss, auf den Eigenschaften bezogen werden können. Er vertritt dagegen, dass auch Relationen (und verallgemeinert Strukturen) Träger von Eigenschaften sein können und will zeigen, »dass der wahre Gegenstand des mathematischen Denkens die Struktur von Eigenschafts- oder Sachverhaltsbereichen ist« (Reidemeister 1957, S. 112).
Anmerkung: Damit kommt Reidemeister – ohne ihn zu kennen – dem Gedanken Hegels sehr nahe, der im Wesen »nur Beziehung« sieht (HW 8.229). Allerdings unterscheidet Hegel sehr genau zwischen einer Ordnung, die »grundlos« und nur »auf unmittelbare Weise« erkennbar ist, und einer Ordnung, mit der diese »Gleichgültigkeit« überwunden ist (HW 5.448 und 456). Diese subtile Unterscheidung lässt sich nach meiner Meinung sehr gut am Verhältnis von links-rechts und positiv-negativ nachvollziehen. Während links-rechts eine reine Ordnungsstruktur ist, innerhalb derer es keinen Grund für die Auszeichnung einer Seite gibt, ist bei positiv-negativ jede Seite mit einer besondere Bedeutung verbunden, die Hegel im Abschnitt über den Widerspruch ausführt und dort »in seinen Grund« gehen lässt (HW 6.68).
Die angelsächsische Diskussion der Händigkeit seit 1973
Einen sehr klaren Überblick gibt Annette Garbe. Hervorgehoben seien die Positionen von Graham Nerlich und Lawrence Sklar.
Der Australier Nerlich eröffnet 1973 die Diskussion. Er vereinfacht den Fall, indem er die dreidimensionalen Beispiele (wie Hand, Hopfen, Schneckenhaus) auf zwei Dimensionen reduziert: Zwei asymmetrische Eckstücke. Sie lassen sich innerhalb der Ebene nicht ineinander überführen, sondern nur, wenn sie durch den Raum »umgeblättert« werden.

Figur 3: Linkes »Knie« und Rechtes »Knie« nach Graham Nerlich
Zwei Figuren, die teils symmetrisch und teils asymmetrisch sind. Sie sind im Ganzen spiegelsymmetrisch zueinander, aber jeweils im Innern asymmetrisch, da die Seite a kürzer ist als die Seite b. Quelle: Garbe, Abbildung 1, S. 25 und eigene Ergänzung für das 'L' mit den beiden unterschiedlich langen Seiten a und b.
Entscheidend ist der Symmetriebruch. Wären die Seiten a und b gleich lang, dann könnte innerhalb der Ebene die eine Figur in die andere gedreht werden. Die Asymmetrie der beiden Seiten a und b erzwingt eine weitere Raumachse.
Nerlich gibt daher Kant insofern unrecht, als Kant sich explizit auf Figuren im dreidimensionalen Raum bezieht.
»Nach Nerlich läßt sich aber Kants Argument in dem Sinne verallgemeinern, daß man behauptet, der jeweilige Raum als ganzer (seine globale topologische Struktur) lege fest, ob die in ihm enthaltenen Objekte bestimmt oder unbestimmt sind bezüglich Händigkeit, d.h. ob sie enantiomorph oder homomorph sind« (Garbe, S. 27).
Hiervon ausgehend lässt sich die Lösung durch das Möbius-Band relativieren. Wenn ein Streifen Papier lückenlos und gleichmäßig mit Figuren wie dem linken Knie parkettiert ist, dann kann das Möbius-Band nicht hergestellt werden.
»Denn wenn wir den Zylinder an der Grenze zweier benachbarter (eingelegter roter) 'Knie' zerschneiden, verdrehen und zu einem Möbiusband verkleben, so gibt es an der Schnittstelle ein Paar ungleichartiger 'Knie', d.h. zwei benachbarte 'Knie', von denen eines ein linkes und das andere ein rechtes ist« (Garbe, S. 27f).
Lawrence Sklar: Sklar gibt weitere Beispiele von teils symmetrisch, teils asymmetrischen Figuren, die sich innerhalb der Ebene nicht ineinander überführen lassen.
»Nach Sklar gibt es viele Eigenschaften der Dinge (und nicht allein die Händigkeit), die auf der globalen (topologischen) Struktur der Natur ('nature') des Raumes, in dem sie sich befinden, in sehr engem Zusammenhang stehen« (Garbe, S. 35). »Als abschließendes Resultat seiner detaillierten Analyse ergibt sich für Sklar, daß zur Klärung der Frage, ob der Raum absolut ist, ob er eine Substanz ist, ob er primitiv ist, ob eine absolute Bewegung existiert etc., die Begriffe der Orientierung vollkommen bedeutungslos und irrelevant sind« (Garbe, S. 39).
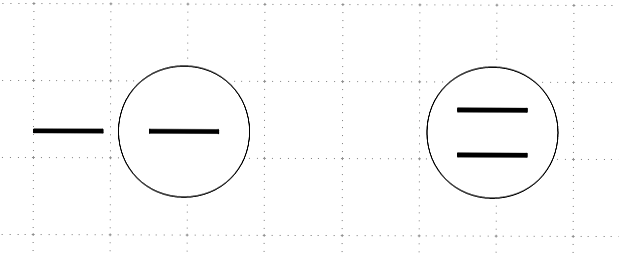
Figur 4: »Opposite-sided« und »Same-sided« nach Lawrence Sklar
Zwei Figuren, die teils symmetrisch und teils asymmetrisch sind. Alle Einzelelemente sind identisch, jedoch links innerhalb und außerhalb des Kreises, rechts beide innerhalb des Kreises Quelle: Garbe, Abbildung 2, S. 35
Auch in diesem Beispiel ist es nicht möglich, beide Figuren innerhalb der Ebene ineinander zu überführen, da der außenliegende Strich nicht über die Kreislinie »gehoben« werden kann.
Wittgenstein zur Händigkeit
Garbe lässt allerdings Ludwig Wittgenstein aus, der das Argument von Nerlich vorweggenommen und verallgemeinert hat. Wittgenstein begründet im Tractatus logico-philosophicus eine Philosophie, die an der Theoretischen Mechanik von Hertz orientiert ist. Anders als Kant will er die Kausalität nicht auf die Zeit zurückführen, sondern auf Asymmetrien zwischen mechanisch beschreibbaren zeitlichen Vorgängen und räumlichen Gegenständen.
»Wir können keinen Vorgang mit dem 'Ablauf der Zeit' vergleichen – diesen gibt es nicht –, sondern nur mit einem anderen Vorgang (etwa mit dem Gang des Chronometers).
Daher ist die Beschreibung des zeitlichen Verlaufs nur so möglich, dass wir uns auf einen anderen Vorgang stützen. Ganz Analoges gilt für den Raum.
Wo man z.B. sagt, es könne keines von zwei Ereignissen (die sich gegenseitig ausschließen) eintreten, weil keine Ursache vorhanden sei, warum das eine eher als das andere eintreten solle, da handelt es sich in Wirklichkeit darum, dass man gar nicht eines der beiden Ereignisse beschreiben kann, wenn nicht irgendeine Asymmetrie vorhanden ist. Und wenn eine solche Asymmetrie vorhanden ist, so können wir diese als Ursache des Eintreffens des einen und Nicht- Eintreffens des anderen auffassen.« (TLP, 6.3611)
Wittgenstein übernimmt das Beispiel der Händigkeit, aber er deutet es genau entgegensetzt zu Kant. Die Händigkeit ist für ihn ein elementarer Fall einer partiellen Asymmetrie. Er versteht sie daher als Muster für seinen Begriff der Kausalität. Kants Bedenken gegen die Händigkeit sind für ihn mit der Erkenntnis, wie sich Asymmetrien in einer zusätzlichen Dimension ineinander überführen lassen, ausreichend geklärt. Es ist daher nur konsequent, wenn er in seiner Kritik an Kant nicht direkt auf dessen Kritik der reinen Vernunft eingeht, sondern auf die Frage der Händigkeit. Er nimmt als einziger ernst, dass sie für Kant dessen kritische Wende ausgelöst hat. Daher ist er überzeugt, dass die Kritik der reinen Vernunft hinfällig wird, wenn für die Händigkeit eine andere Deutung gefunden ist.
»Das Kantsche Problem von der rechten und linken Hand, die man nicht zur Deckung bringen kann, besteht schon in der Ebene, ja im eindimensionalen Raum, wo die beiden kongruenten Figuren a und b auch nicht zur Deckung gebracht werden können, ohne aus diesem Raum
– – –o————x – – x————o– – –
a b
herausbewegt zu werden. Rechte und linke Hand sind tatsächlich vollkommen kongruent. Und dass man sie nicht zur Deckung bringen kann, hat damit nichts zu tun.
Den rechten Handschuh könnte man an die linke Hand ziehen, wenn man ihn im vierdimensionalen Raum umdrehen könnte« (TLP, 6.36111).
Während für Wittgenstein die Händigkeit gegenüber Kant zum schlagenden Argument wird, warum sich die formale Logik überzeugender aus der Theoretischen Mechanik als aus dem Zeitbegriff begründen lässt, zeigt sich nach meiner Meinung hier umgekehrt die Begrenztheit der Mechanik. Wittgenstein bemerkt nicht, dass mit der Händigkeit der mechanische Gegenstandsbegriff und die auf ihn aufbauende formale Logik infrage gestellt sind und die Händigkeit über die Mechanik hinausführt in eine nicht-mechanische Logik, in der der mechanische Gegenstandsbegriff verlassen wird. Hegel spricht von der »chemischen Sphäre«, siehe den Beitrag Das reale Maß – die Logik der chemischen Sphäre.
Geometrische Grundlagenbegriffe im Hilbert-Raum
Die aus der euklidischen Geometrie bekannten Begriffe der Länge und des Abstandes erhalten im Hilbert-Raum eine verallgemeinerte Bedeutung. Der Länge eines euklidischen Objekts entspricht bei einem Zustand φ die Wahrscheinlichkeit, dass ein Teilchen diesen Zustand annimmt. Entsprechend wird als Abstand zwischen zwei Zuständen φ und φ' die Übergangswahrscheinlichkeit definiert, dass ein Teilchen von einem Zustand in den anderen Zustand wechselt.
Mit diesem Verständnis von Länge und Abstand können die Objekte der euklidischen Geometrie (Gebilde, die aus Geraden und Kreisen zusammengesetzt sind) erweitert werden zu den Objekten der Quantenmechanik (Gesamtzustände, wobei sich jeder Gesamtzustand zusammensetzt aus den Komponenten der einzelnen Zustände und ihrer jeweiligen Wahrscheinlichkeiten).
Gemessen werden die jeweils tatsächlich auftretenden Zustände. Wenn große Mengen von Messungen vorliegen, kann ihre Wahrscheinlichkeitsverteilung als Integral über die Häufigkeit aller gemessenen Ergebnisse aufgeschrieben werden. Daher wird in der Quantenmechanik der Hilbert-Raum aller Funktionen betrachtet, die als Wahrscheinlichkeitsmaß gelten können. Sie beschreiben eine Fläche von 1. Das ist mit dem Normierungsintegral ∫ φφ' = 1 gemeint (vgl. hierzu Ruschig, S. 172f).
Die Zustände werden als Energieniveaus bezeichnet. In der mathematischen Darstellung entsprechen die Energieniveaus den Obertönen eines Grundtons. Die Verteilung eines Systems auf unterschiedliche Energieniveaus kann daher als die Klangfarbe oder als das Farb-Spektrum des Systems bezeichnet werden.
Knotentheorie und Katastrophentheorie
Die mathematischen Verfahren lassen sich nahezu unbegrenzt ausbauen. So kann gefragt werden, ob es Bedingungen gibt, unter denen sich die gemessenen Wahrscheinlichkeitsmaße verändern. Das führt zu Maßverhältnissen oder Knotenlinien in dem Sinn, wie Hegel dies ausgehend von den frühen chemischen und elektrischen Beobachtungen seiner Zeit bereits kannte. Innerhalb der Knotenlinien kann wiederum gefragt werden, ob die Knoten bestimmte mathematische Eigenschaften haben (Knotentheorie) und ob die Knotenlinien nach bestimmten Gesetzmäßigkeiten Brüche aufweisen (Katastrophentheorie).
Um die Vielzahl der Möglichkeiten zu demonstrieren, mögen zwei Figuren genügen. Sie zeigen, welches nahezu unerschöpfliche Potential in der einfachen Beobachtung der unterschiedlichen Windungen besteht.
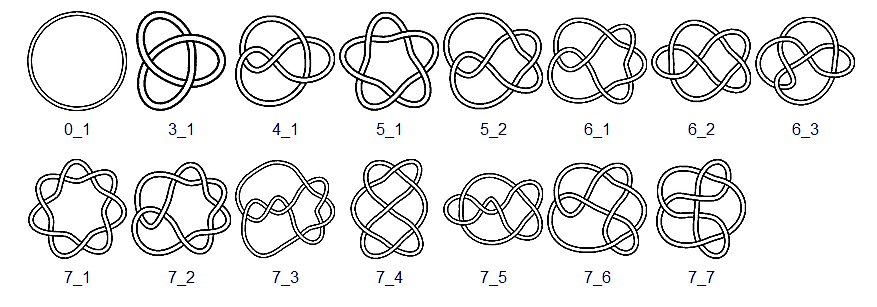
Figur 5: Knoten mit bis zu 7 Kreuzungen
Auszug aus einem Knotenatlas; Link)
Während mit Knoten-Typen die im Möbiusband erstmals betrachteten Windungen systematisch fortgeführt werden, zeigt die Katastrophentheorie, wie sich aus einfachen Bahnverläufen Knoten entwickeln können. Die Entstehung der Knoten wird als Kastrophe verstanden, durch die eine neue Quantenzahl entsteht, wodurch die Dimensionszahl des betrachteten Raums bruchartig vergrößert wird. Mit dieser Methode kann in der Embryologie die Entstehung organischer Formen dargestellt werden.

Figur 6: Spitzen-Kastrophe (Cusp)
»Diagramm einer im Dreidimensionalen verlaufenden Cusp-Katastrophe mit Kurven (braun, rot) kritischer Punkte in x bei Variation der Parameter a und b.
Außerhalb des Cusps (blau) gibt es nur ein Extremum, innerhalb gibt es zwei« (Wikipedia).
Urheber: <a href="//commons.wikimedia.org/wiki/User:Jheald" title="User:Jheald">Jheald</a> - Made in OpenOffice Draw, exported as SVG., Gemeinfrei, Link
Siglen
GUGR = Immanuel Kant: Von dem ersten Grunde des Unterschiedes der Gegenden im Raume (1768)
in: Akademie-Ausgabe Bd. II, Berlin 1905, S. 375-383; Link
HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971; Link
KrV = Immanuel Kant: Kritik der reinen Vernunft (1781, 1787)
MAN = Immanuel Kant: Metaphysische Anfangsgründe der Naturwissenschaft (1786) (zitiert als MAN)
in: Akademie-Ausgabe, Bd. IV, Berlin 1911; Link Volltext
ND = Immanuel Kant: Versuch den Begriff der negativen Größen in die Weltweisheit einzuführen (1763)
in: Akademie-Ausgabe Bd. II, Berlin 1905, S. 165-204; Link; zeno
Prol. = Kant, Immanuel: Prolegomena zu einer jeden künftigen Metaphysik, die als Wissenschaft wird auftreten können, Riga 1783
in: Akademie-Ausgabe Band IV, Berlin 1911 AA IV
TLP = Ludwig Wittgenstein: Tractatus logico-philosophicus
in: Werke Band 1, Frankfurt am Main 1984; Link
Literaturhinweise
Brigitte Falkenburg: Kants Kosmologie, Frankfurt am Main 2000
Annette Garbe: Die partiell konventional, partiell empirisch bestimmte Realität physikalischer RaumZeiten, Würzburg 2001
Karen Gloy: Die Kantische Differenz von Begriff und Anschauung und ihre Begründung
in: Kant-Studien, 75:1-37, 1984
Heinrich Lange: Über den Unterschied der Gegenden im Raum
in: Kant-Studien, 50:479-499, 1958/59
Holger Lyre: Metaphysik im "Handumdrehen"
in: Philosophia naturalis 42:1 (2005) 49-76; Link
Holger Lyre: Händigkeit und Ontologie des Raumes, Vortrag Ulm 8.11.2011; Link, mit Co-Referat durch Erhard Scholz.
Christoph Meier: Versteckte Händigkeit, Chirale Solitonen in Quanten-Spinsystemen (Tagungsbericht), 2006; Link
Peter Mittelstaedt: Philosophische Probleme der modernen Physik, Mannheim 1972
Kurt Reidemeister: Über den Unterschied der Gegenden im Raum
in: Zeitschrift für philosophische Forschung, 2:131-150, 1947
Kurt Reidemeister: Raum und Zahl, Berlin u.a. 1957
Urs Richli: Form und Inhalt in G.W.F. Hegels »Wissenschaft der Logik«, Wien, München 1982
Ulrich Ruschig: Hegels Logik und die Chemie, Bonn 1997
Arthur Schopenhauer: Über die vierfache Wurzel des Satzes vom zureichenden Grunde
in: Kleinere Schriften Bd. 1, Zürich 1977; Link
Josef Simon: Sprache und Raum, Berlin 1969
René Thom: Topological Models in Biology
in: Topology 8:313-335, 1969 ; Link
Dieter Wandschneider: Raum, Zeit, Relativität, Frankfurt am Main 1982
Carf Friedrich von Weizsäcker: Die Einheit der Natur, München 1981 [1971]
Karl Wirth und André S. Dreiding: Kants Hand, Chiralität und konvexe Polytope
in: Elemente der Mathematik 62:8-29, 2007; Link
2013-2014
© tydecks.info 2014


