Walter Tydecks
Das reale Maß – die Logik der chemischen Sphäre
– Kommentar zu Ulrich Ruschig Hegels Logik und die Chemie
Inhaltsverzeichnis
Einleitung
Modelle für Wahlverwandtschaften und Knotenlinien
Chemie
Energie und Entropie
Musik
Quantenmechanik
Geometrie der Hilberträume
Das Maßlose
Auflösung der chemischen Sphäre
Anhang: Zwei frühere Einleitungen
Neue Fassung, Version 5.3.2019
Einleitung – von einer statischen Logik der Dinge zu einer dynamischen Logik der Beziehungen
Auf den ersten Blick kann etwas dann am besten bestehen und gedeihen, wenn es keinerlei Störungen unterworfen ist und keiner Realität unterliegt, der es sich anpassen muss. Es befindet sich mit seiner Natur im Reinen und hat einen ausgeglichenen Zustand der Ruhe erreicht. Seine Idealität und Realität sind eins. Es gibt keine Art von Negativität oder Veränderung. Das scheint das Ideal sowohl von Aristoteles wie der östlichen Religionen zu sein. Aus dem Blick der Neuzeit zeigt sich jedoch die Natur von Etwas darin, wie es mit seiner Umgebung in Wechselwirkung treten, störende Einflüsse abwehren und belebende Impulse aufnehmen kann. Mit dem formalen Maß wird eine Sache statisch an sich selbst gemessen, mit dem realen Maß an ihrer Dynamik, mit der sie umgebenden Realität in Beziehung treten und in der Wechselwirkung mit ihr über sich selbst hinausgehen zu können. – Das gilt nicht nur für die Gegenstände der Philosophie, sondern auch für sie selbst. Eine dynamische Logik kann sich nicht darauf beschränken, die Dynamik der von ihr untersuchten Beziehungen zu erkennen, sondern sie wird nur Erfolg haben, wenn sie sich ihrerseits in einer dynamischen Wechselbeziehung mit ihrer Umgebung befindet. Eine Lehre der realen Maße muss auch die tradierten formalen Maße verlassen, die die Philosophie an sich selbst angelegt und sich gemessen hat an ihrer inneren Kohärenz, Durchsichtigkeit und Sprachfähigkeit, letztlich an einem Ideal des absoluten, statischen Wissens. Eine Lehre der realen Maße zeigt eine Philosophie, die in Wechselwirkung mit ihren Gegenständen über sich hinauszugehen vermag. Sie vermag in das Verständnis und den Entwurf ihrer eigenen Denkbestimmungen die Bewegungen ihrer Gegenstände aufzunehmen. Sie erkennt an sich Denkbestimmungen, die von der Realwissenschaft übernommen sind. Hegel wählt mit den Wahlverwandtschaften und Knotenlinien Begriffe aus der Chemie. »Denn in der chemischen Sphäre hat wesentlich das Materielle seine spezifische Bestimmtheit in der Beziehung auf sein Anderes; es existiert nur als diese Differenz.« (HW 5.420)
Der aus dem Altgriechischem stammende Ausdruck chemeia bezeichnet die Scheidekunst, mit der in Gießereien und in verschiedensten Verfahren des Waschens, Mischens, Kochens, Rührens usf. Stoffe zusammen gebracht, zerlegt und daraus neue Stoffe mit neuen Eigenschaften erzeugt werden können. In der chemischen Sphäre öffnet sich etwas nach außen wie nach innen: Nach innen werden bisher verborgene Seiten sichtbar und können hervortreten. Im Ergebnis wird sich zeigen, dass jedes Etwas schon immer das Andere an sich selbst enthalten hat. Nach außen werden neue Verbindungen eingegangen, bis sich das gegebene Etwas auflöst und über sich hinausgeht. Erst hierüber tritt die wahre Natur einer Sache hervor. Für Aristoteles war die Relation (pros ti) ebenso eine Kategorie wie Qualität und Quantität. Leibniz sprach vom Streben (appetitus) der Monaden, in einen anderen Zustand überzugehen (Monadologie, § 15), Kant von der Affinität (»dem Grund der Möglichkeit der Assoziation des Mannigfaltigen«; KrV, A 113), und Hegel übernimmt von der Chemie und der Naturphilosophie seiner Zeit den Begriff der Wahlverwandtschaften. Sachen sind mit anderen wahlverwandt und neigen dazu, die entsprechenden Verbindungen einzugehen.
Die chemische Scheidekunst stand in der Antike der Philosophie zweifellos recht fern, und auch ihr Gott Hephaistos war von eher zweifelhaftem Ruf. Es gibt jedoch eine Tradition sowohl von den Orphikern aus dem 6./5. Jahrhundert v. Chr. wie auch unterschiedlichen Quellen im Osten über die verschiedensten Strömungen der Alchemie bis weit in die Neuzeit. Die Alchemisten hatten auf naive Weise gehofft, mit Verfahren dieser Art nicht nur die Natur einer Sache, sondern nicht weniger als den Stein der Weisen (Lapis philosophorum) zu finden, eine sprichwörtliche Verkörperung, in der sich das Niedrigste (Gedankenloseste) der Natur, ihre zu Stein gewordene und erstarrte Gestalt verbindet mit dem höchsten Ziel des Denkens, der Weisheit.
Eine Wende in der Einstellung gegenüber Fragen dieser Art brachte überraschend das Christentum. Was die Alchemisten in ihren Experimenten mithilfe der Natur bewerkstelligen wollten, gilt seit dem Christentum als ein göttlicher Vorgang der Transsubstantiation von Brot und Wasser in Leib und Blut Christi im Verlaufe der Heiligen Messe. Beide Richtungen unterscheiden sich deutlich und bekämpften und verfolgten sich oft genug, aber im Ergebnis hat sich gegenüber der Antike die Grundeinstellung zur Bedeutung chemischer Vorgänge und ihrer Wandlungsprozesse geändert. So wurde im Verborgenen der Einfluss der Alchemie auf die neu entstehende Naturwissenschaft größer als sich diese im Rückblick eingestehen möchte. Sowohl Newton wie Leibniz haben sich intensiv damit beschäftigt, jedoch kaum öffentlich darüber gesprochen, da sie Angst haben mussten, in Widerspruch zur Kirche zu geraten. Die alchemistischen Neigungen Newtons wurden erst nach 1945 bekannt. Ihre Frage war: Offenbart sich Gott nicht nur in der Absolutheit von Raum und Zeit und der Substanz der Dinge, sondern auch in den chemischen Wandlungsvorgängen der Natur?
Erst seit der Entmachtung der Kirche durch die Französische Revolution können Fragen dieser Art offen in der Philosophie diskutiert werden. Um 1800 wurde der Weg frei für Naturromantiker wie Novalis (1772-1801) und William Blake (1757-1827), und darauf suchten Philosophen wie Schelling und Hegel eine Antwort. Wird eine völlig neue Kategorienlehre und Logik, ja sogar eine neue Art von Logik notwendig, wenn nicht nur statische Verhältnisse, sondern dynamische Beziehungen und Verwandlungen betrachtet und hierfür die geeigneten Denkbestimmungen gefunden werden sollen? Wie ändert sich das Verhältnis der ersten Kategorie, der für sich unwandelbaren Substanz (ousia) und ihrer Eigenschaften (Attribute), das sind die zweiten Kategorien (symbebekoi) wie Qualität, Quantität, Ort und Zeit? Die Relation (das Maß, die Beziehung) ist nicht einfach eine weitere Kategorie wie Quantität und Qualität, sondern mit ihr wird das Denken statischer Eigenschaften verlassen und der Raum der Möglichkeiten und der Bewegung eröffnet. In den Relationen des realen Maßes zeigen sich die äußeren Möglichkeiten, die sich einer Sache bieten, und die inneren Möglichkeiten, sie zu ergreifen und darüber über sich hinaus zu gehen. Das reale Maß trifft den Punkt, an dem eine Sache nicht nur ihrer Natur gemäß wird, sondern sich zu wandeln vermag. Heute würde von Emergenz gesprochen werden. Mit dem realen Maß wird ein Übermaß erreicht, in der die Sache in einem widersprüchlichen Vorgang in dem Maß ihr eigenes Maß trifft, wie sie in dieser Bewegung über ihr Maß hinauszugehen vermag. Das Übermaß ist aus Perspektive des realen Maßes maßlos. Die Maßlosigkeit ist der kritische Begriff, in den sich das Maß auflöst und darüber in einer heute fast altertümlich klingenden Sprache vom Sein zum Wesen übergeht.
Das Denken und seine Gegenstände werden in einem neuen Licht gesehen. Wo ist die innere Einheit, an der sich Naturwissenschaften wie die Chemie und die Philosophie treffen können? Hegel fragt nicht nur nach den in der Natur beobachtbaren Neigungen der Dinge zueinander, ihren Wahlverwandtschaften und Abneigungen, sondern nach der wechselseitigen Neigung und Wahlverwandtschaft der Naturwissenschaft und der Philosophie zueinander. Er fragt, wann sowohl die Naturwissenschaft als auch die Logik von sich aus entsprechend ihrer eigenen inneren Entwicklung an einen Punkt kommen, an dem sie sich berühren und einander wechselseitig zuneigen. Das ist mehr als die wechselseitige Bedingung, von der östliche Lehren wie der Buddhismus sprechen. Es ist ein dynamischer Prozess. In einfachen Worten: Der Gedanke drängt zur Sache, und die Sache drängt zum Gedanken. Die Philosophie stößt an einen Punkt, an dem sie nicht nur der Anregung durch die Realwissenschaft bedarf, sondern sich dessen bewusst wird und sich von sich aus der Naturwissenschaft zuwendet und dort nach Lösungen sucht. Auf der anderen Seite stößt die Naturwissenschaft an einen Punkt, an dem sie sich nicht nur ohne Reflexion ihrer eigenen Methode verfängt, sondern sich ihrerseits dieser Lage bewusst wird und die Philosophie nicht mehr als ungeliebten Fremdkörper abstößt, sondern mit ihr zu verbinden sucht. Das Verständnis und der Begriff der Beziehung (Relation, Maß) können nur auf mehreren Ebenen gleichzeitig entwickelt werden: Die realen Beziehungen, der Begriff der Beziehung, und die Beziehung dieser beiden Arten von Beziehung. Daher ist für mich die Lehre vom realen Maß das Herzstück der Wissenschaft der Logik von Hegel.
Wird sich die Philosophie dessen bewusst, kann das zu einer Wende in mystisches Denken führen, die Schelling in den gleichen Jahren zwischen 1804 und 1812 vollzog, als Hegel die Wissenschaft der Logik schrieb. Hegel enthält sich aller Hinweise auf Alchemie und Magie. Aber ihm ist aufgefallen, wie selbst ein Denker wie Kant an dieser Stelle ins Straucheln gerät. Die von Kant angestrebte Ordnung der Kategorientafel kam durcheinander, als er »die Modalität unter den Kategorien des transzendentalen Idealismus nach der Quantität und Qualität, auf Einschiebung der Relation, aufgeführt« hat (HW 5.387). Mit Modalität ist die Unterscheidung von etwas in die Modi (Zustände) der Möglichkeit, Wirklichkeit und Notwendigkeit gemeint. Relationen begeben sich in das Gebiet des Möglichen, in Beziehung zu Anderen über die gegebene Wirklichkeit hinausgehen zu können, und Kant gelang es noch nicht, den inneren Zusammenhang von Relation und Modalität zu treffen, da er im Ganzen noch im Rahmen einer statischen Logik blieb, die er in festen Tafeln ordnen wollte. Das war angesichts des Aufschwungs der neuzeitlichen Wissenschaft nicht mehr möglich. Aber Kant ist es zu verdanken, diese Frage so deutlich wie möglich aufgeworfen zu haben. Er riss das Denken auseinander in die Vielzahl der wahrnehmbaren Erscheinungen (Phänomene) und ihrer möglichen Beziehungen einerseits und den unerreichbaren Fixpunkt eines Dinges-an-sich, das ihnen in seiner Wirklichkeit als innerer Bezugspunkt zugrunde liegt, andererseits. Beide Seiten lassen sich nur im Denken erfassen: Nur im Denken lässt sich entwerfen, was Etwas im Geflecht seiner Beziehungen werden kann, auch wenn es das im Moment noch nicht ist, und nur im Denken lässt sich ein negativ bestimmter Begriff wie das Ding-an-sich bilden, der sich gemäß seiner eigenen Definition jeder unmittelbaren Erfahrung entzieht.
Wenn ich ihn richtig verstehe, will Hegel zeigen, dass sich Erscheinung und Ding-an-sich zueinander verhalten wie ein Substrat und seine Zustände. Die Idee hierfür hat er nicht aus der Philosophie gewonnen, sondern dank der Leistungen der Naturwissenschaften. Aber ihm gelang es, sie auf die Philosophie zu übertragen. Die chemische Sphäre ist für ihn der Horizont, in dem sich schrittweise und systematisch entwickeln lässt, was mit dem Substrat und seinen Zuständen gemeint ist. Wenn es gelingt, in einer Logik der Beziehungen zunächst das Substrat und seine Zustände begrifflich voneinander zu trennen und davon ausgehend in einer zweiten Negation dieser Trennung die innere Einheit der voneinander getrennten Momente zu erkennen, wird darüber für Hegel die grundlegende Frage jeder Logik gelöst, die »Beziehung des Gegenstandes auf das Denken« (HW 5.387). Das Denken wird sich seiner selbst bewusst, wenn es sich als die Möglichkeit versteht, dank seiner Vorstellungskraft und Phantasie Gegenstände nicht nur so zu sehen, wie sie in der gegebenen Wirklichkeit sind, sondern sie in ihren Möglichkeiten zu erfassen, ihrer Fähigkeit, ihren aktuellen Zustand zu negieren und in Beziehung zu anderen über sich selbst hinauszugehen. Im Denken wird erfasst, was in den Gegenständen bereits als Entwicklungskeim angelegt ist. Die Gegenstände erhalten ihre Fähigkeiten nicht vom Denken, aber erst mit dem Denken ist die Fähigkeit gegeben, die an den Dingen bereits enthaltenen Fähigkeiten und die in ihnen angelegten Entwicklungsbahnen zu erkennen. Um so denken zu können, muss sich das Denken aus einer statischen Logik lösen und einer dynamischen Logik fähig werden. Das ist für die Logik ein Quantensprung, den sie nicht auf sich zurückgezogen und isoliert aus sich selbst heraus vollziehen kann, sondern nur in Wechselbeziehung mit ihrem Gegenstand. In einer reflexiven Bewegung erkennt das Denken an der Dynamik seines Gegenstands seine eigene Dynamik. Es projiziert nicht eine Dynamik oder gar bestimmte Resultate einer Bewegung in den Gegenstand hinein, sondern an der Dynamik des Gegenstands erkennt es sich selbst und wird fähig, den Gegenstand zu verstehen.
Auch wenn ich verstehe und gut nachvollziehen kann, gegen welche Art von Hegel-Deutung sich Ruschig wehrt, kann ich daher seine Kritik nicht teilen: »Hegel erklärt das von ihm im und für den 'Fortgang' herbeizitierte Material zum lediglich illustrierenden Beispiel für eine im Begriff gegründete und auch unabhängig von den Beispielen zu konstruierende Entwicklung.« (R, 16) Das will er später im Einzelnen näher ausführen, wenn aus seiner Sicht für Hegel logische Begriffe wie die ‘negative Einheit’ oder das ‘Kontinuieren’ aus sich heraus chemische Prozesse vorantreiben oder gar erzeugen können (R, 190, 196). Diese Kritik trifft meines Erachtens sicher zahlreiche Hegel-Interpreten, aber nicht Hegels eigene Ausführungen zum realen Maß, in denen umgekehrt das »illustrierende Beispiel« bewusst im Haupttext steht, weswegen diese Ausführungen von vielen Hegelianern ignoriert und nur selten zitiert werden, da sie nicht in das Bild passen, das sie sich von Hegel gemacht haben, und das – wie mir scheint – Ruschig indirekt von ihnen übernommen hat. Vielmehr ist sich Hegel bewusst, mit der »Entwicklung des Maßes [...] eine der schwierigsten Materien« vor sich zu haben, da »die verschiedenen Formen, in welchen sich das Maß realisiert, auch verschiedenen Sphären der natürlichen Realität angehören« (HW 5.392). Nirgends sonst sind in seiner Wissenschaft der Logik aus der Realwissenschaft übernommene Begriffe wie die Wahlverwandtschaften und Beispiele aus der Chemie und anderen Naturwissenschaft so ineins mit den Denkbestimmungen, mit denen sie gedacht werden. Damit ist die Gefahr eines doppelten Missverständnisses verbunden: Es kann zum einen so aussehen, als wären in reduktionistischer Weise mechanische oder chemische Prozesse unmittelbar identisch mit dem Denken, mit dem sie wahrgenommen und gedacht werden, oder umgekehrt, als bedürfe es des Denkens (oder des Beobachters, wie Quantenphysiker glauben), damit sich an den Dingen Prozesse vollziehen, die ohne das Denken (den Beobachter) nicht möglich wären. Hegel begibt sich in die Gefahr dieser Missverständnisse und will die innere Einheit zeigen, die sich für ihn an dieser Stelle zwischen dem Gegenstand und dem Denken zeigt.
Wahlverwandtschaften sind nicht starr, sondern ändern sich ihrerseits dynamisch in verschiedenen Umgebungen. Das klassische Beispiel ist die Temperatur. Viele chemische Reaktionsstärken ändern sich, wenn Wärme zugeführt bzw. entzogen wird. Durch die Änderung von Systemparametern wie der Temperatur werden unterschiedliche Zustände erzeugt, in denen jeweils spezifische Wahlverwandtschaften gelten. Hegel hat die mit den jeweiligen Zuständen gegebenen realen Maße auf einer Knotenlinie angeordnet. Für ihn sind es zwei voneinander unabhängige Kräfte, wenn zum einen innerhalb eines gegebenen Zustands von den Reaktionsstärken der jeweiligen Wahlverwandtschaften gesprochen wird, und zum anderen von den Kräften, durch die ein Zustand in einen anderen übergeht und sich die Reaktionsstärken der Wahlverwandtschaften mit diesem Übergang ändern. Diese Unterscheidung in Wahlverwandtschaften innerhalb eines Zustands und Übergängen von einem Zustand in einen anderen entlang einer Knotenlinie ist seine wesentliche Neuerung gegenüber der Naturphilosophie seiner Zeit, mit der es ihm gelang, an zahlreichen bereits bekannten Phänomenen aus der Chemie, den Aggregatzuständen von Wasser, und aus der Musik eine einheitliche Logik zu erkennen.
Die verschiedenen Zustände sind in ähnlicher Weise auf der Knotenlinie angeordnet wie die Zahlen auf der Zahlengerade. Und so, wie bei den Zahlen und dem Zählen übergegangen wurde von den Eigenschaften der Zahlen zu den Eigenschaften der Gerade, auf der sie angeordnet sind (das ist insbesondere die Kontinuität der Linie, aus der sich die Eigenschaften der reellen Zahlen ergeben), so ist für die Knotenlinie zu fragen, welche Eigenschaften es sind, dank derer auf ihr die Zustände angeordnet werden können. Während Hegel für die Zahlen aus der Mathematik mit dem Zusammenhang (der Kontinuität) eine bereits bekannte Eigenschaft der Linie übernehmen konnte (siehe HW 5.160), war ihm das für die Knotenlinie noch nicht möglich. Es ist auf Anhieb nicht einmal klar, welche Entität es sein soll, aus deren Eigenschaften die Übergänge der Zustände auf der Knotenlinie auf ähnliche Weise zu begründen sind wie die Relationen der Zahlen aus der Transitivität und Kontinuität der Zahlengerade. Er konnte nur die entsprechende Frage aufwerfen. Es sollte etwas geben, das vergleichbar der Zahlengerade über Eigenschaften verfügt, mit denen die Übergänge der Zustände begründet werden können. Die Naturwissenschaft und Mathematik haben erst später mögliche Lösungen gefunden wie den Hilbert-Raum und die komplexen Zahlen, mit denen sich Knotenlinien darstellen lassen.
Hegel setzt für diese Entität in gewisser Weise provisorisch mal den Begriff des Maßlosen und mal noch elementarer den Begriff der Sache ein, aus deren Eigenschaften die Übergänge der Zustände zu erklären sind. In einer diffizilen Unterscheidung spricht er (a) vom »bleibende(n), materielle(n) Substrat«, dank dessen sich die verschiedenen Maße einheitlich auf einer Knotenlinie anordnen lassen (HW 5.436), (b) der »Materie, Sache« als der inneren Einheit der verschiedenen realen Maße (HW 5.443), (c) der Unterscheidung in das Substrat von seinen Zuständen, durch die die unterschiedlichen Maße zu Zuständen herabgesetzt werden (HW 5.444) und (d) der »Ordnung« als der inneren Einheit des Substrats und seiner Zustände, dank derer sich das Substrat in seinen Zuständen zeigen kann (HW 5.445). Diese Ordnung ist für ihn (e) als spezifizierendes Prinzip zunächst ihrerseits »nur Substrat, eine Materie« (HW 5.445), die jedoch bereits die Anlage enthält, sich zum Subjekt und zum lebendigen Begriff zu entfalten. So wie in der Naturwissenschaft nachgewiesen werden kann, wie sich reale Maße auseinander entwickeln und in höhere Ordnungen emergieren, so will Hegel in einer analogen Entwicklung zeigen, wie sich in den Denkbestimmungen, mit denen diese Emergenzen erfasst werden können, ihrerseits eine Emergenz zeigt, die vom abstrakten Substrat über die Sache, die Ordnung, das Prinzip der Ordnung schließlich zum Begriff führt.
Im Folgenden werden Modelle der Wahlverwandtschaften und Knotenlinien vorgestellt, mit denen diese Frage schrittweise angenähert werden soll. Es wird begonnen mit der Chemie. Das ist das von Hegel herangezogene Modell. Es folgen direkt darauf aufbauend Energie und Entropie, mit denen ein besseres Verständnis gelingt. Mit der Musik wird ein Modell gewählt, mit dem sich bereits Hegel intensiv beschäftigt hat. Es ist vor allem dank der Funktionstheorie von Hugo Riemann entscheidend erweitert worden. Mit der Funktionstheorie lässt sich die Musik als ein endliches Modell verstehen, in dem die Frage des Maßlosen deutlicher wird. Hegel hatte für das Maßlose keine Illustrationen gefunden. Die Quantenmechanik lässt sich wiederum in ihrer mathematischen Darstellung formal als eine Erweiterung der Musik verstehen, und mit der Geometrie der Hilbert-Räume wird im Bereich der Realwissenschaften der abschließende Schritt erreicht, von dem aus für mich das Anliegen verständlicher werden kann, um das es Hegel beim Maßlosen geht. Davon ausgehend kann als These formuliert werden, dass für die Maßlogik die Ordnung auf der Zahlengerade mit den genannten Eigenschaften der Transitivität und Kontinuität erweitert werden muss zur Ordnung des Hilbert-Raums und der komplexen Zahlen. Dort sind die Analytizität und die Auflösbarkeit die Eigenschaften, die der Kontinuität für die wahre Unendlichkeit entsprechen und diese weiter führen. Mit der Auflösbarkeit wird der Übergang vom Maßlosen zur absoluten Indifferenz und ihrer inneren Faktoren verständlicher. Hier wird nicht einfach ein Übergang vollzogen, sondern der bereits für die wahre Unendlichkeit eingeführte Begriff des Übergangs (HW 5.166) zum Übergang in das Wesen (HW 5.456) voll entfaltet.
Die Auflösbarkeit geht über in Neutralisation und absolute Indifferenz. Diese deuten bereits voraus auf spätere Ausführungen über den Chemismus. Daraus ergibt sich im Ganzen ein Blick auf die Logik der chemischen Sphäre und ihren Stellenwert innerhalb der Wissenschaft der Logik.
Die Logik der chemischen Sphäre ist eine Logik der Negativität, der Relationen und der sich mit ihnen eröffnenden Möglichkeiten. Nach meinem Verständnis hat Hegel alle Grundbegriffe der Logik so umgestaltet, dass in ihrem Zentrum die Logik der chemischen Sphäre hervortreten kann. Er hat ausgehend von der chemischen Sphäre gewissermaßen rückwirkend auch an den Grundbegriffen wie Sein und Nichts, Etwas und Anderes usf. die an ihnen bereits enthaltenen chemischen Eigenschaften gezeigt, ihre innere Negativität und ihre Neigung, über sich hinaus zu gehen. Da die Logik der chemischen Sphäre eine Logik des Werdens und Vergehens ist, ist sie im wörtlichen Sinn die natürliche (physische) Logik, die Logik der Natur. Das Denken wird sich seiner eigenen Logik (der Logik der Worte, der Logik im wörtlichen Sinn) bewusst, wenn es sich in Wechselbeziehung zur Logik der Natur zu verstehen beginnt und die geeigneten Denkbestimmungen zu bilden vermag.
Modelle für Wahlverwandtschaften und Knotenlinien
Ausgehend vom heutigen Wissensstand vermag Ruschig die von Hegel herangezogenen chemischen Modelle wesentlich klarer darzustellen. Und es kommen neue Modelle wie die Entropie und die Quantenmechanik hinzu, mit denen die von Hegel entworfene Logik fortgeführt und ausgebaut werden kann.
(1) Für jeden Stoff wird untersucht, mit welchen anderen Stoffen er reagiert. Stoffe haben Zuneigung oder Abneigung zueinander oder sind einander gleichgültig. Sie suchen einander oder meiden sich. Es ist kein Zufall, wenn diese von Hegel in die Logik eingeführten Begriffe an menschliches Verhalten und ihre Psychologie erinnern. Als er die Wissenschaft der Logik schrieb, erschien im Jahr 1809 der Roman Die Wahlverwandtschaften von Goethe, in dem beide Partner einer Vernunftehe sich in neue Partner verlieben und Goethe die Frage nach den tieferen, letztlich mystisch verstandenen Kräften stellt, die hier wirken. Es besteht für mich kein Zweifel, dass Hegel in diesem Roman eine tiefe philosophische Aussage sah, die er in seiner Logik herausarbeiten wollte.
(2) Trifft ein Stoff auf zwei oder mehrere wahlverwandte Stoffe, dann muss es zu einer Entscheidung kommen und der Reaktionsstärkste von ihnen setzt sich durch und verdrängt die anderen. Ist die Reaktionsstärke und die von ihr bewirkte Verdrängung der anderen wahlverwandten Stoffe eine eigenständige Qualität? Hat sie ihr eigenes Maß? Hegel kannte zu seiner Zeit aus der Chemie nur das Phänomen unterschiedlicher Reaktionsstärken. Mit der Quantenmechanik wurde es möglich, die Reaktionsstärke wesentlich klarer zu beschreiben. Statt von Reaktionsstärken wird von Übergangswahrscheinlichkeiten gesprochen. Wenn ein Stoff mit mehreren Stoffen wahlverwandt ist, beschreibt die Übergangswahrscheinlichkeit, welche der Reaktionsmöglichkeiten sich durchsetzen wird.
(3) Können sich unter bestimmten Bedingungen die Reaktionsstärken (Übergangswahrscheinlichkeiten) verändern? Zum Beispiel sollte erwartet werden, dass die Wahrscheinlichkeit einer Reaktion größer wird, wenn der betreffende Stoff in einem Stoffgemisch in einem Übermaß vorhanden ist und durch seine reine Präsenz Reaktionen gefördert werden (wenn also umgangssprachlich eine große Menge von Gelegenheiten für eine Reaktion besteht). Welche Parameter können identifiziert werden, unter deren Einfluss sich Reaktionsstärken verändern? Wenn es dazu kommt, spricht Hegel von Knotenlinien. Entlang der Knotenlinien kann es zu Umschlägen kommen. Dominiert bis zu einem bestimmten Punkt der eine Stoff, kann sich anschließend ein anderer Stoff durchsetzen. Das wichtigste Beispiel ist die Temperatur. Bei Temperaturerhöhung können sich die Reaktionsstärken gravierend ändern. Andere Beispiele sind die Zufuhr von Katalysatoren oder Rührbewegungen. Wichtig ist zu verstehen, dass die Parameter der Knotenlinien unabhängig sind sowohl von den Wahlverwandtschaften wie von den Reaktionsstärken.
(4) Entlang der Knotenlinien bilden sich zwischen den jeweiligen Umschlägen Makrozustände heraus, in denen das System relativ stabil ist und die jeweiligen Wahlverwandtschaften (Übergangswahrscheinlichkeiten) erhalten bleiben. Selbst wenn sich im Innern bereits die Parameter ändern und auf eine Umwälzung hin tendieren, überwiegen noch die konservativen Erhaltungskräfte des Systems. Lässt sich ein höheres Maß bestimmen, wie lange sie wirksam bleiben und den gegebenen Zustand erhalten, und an welchem Punkt sie zusammenbrechen und sich auflösen?
(5) Mit der Erkenntnis der unterschiedlichen Reaktionsstärken (Übergangswahrscheinlichkeiten) von Wahlverwandtschaften in den jeweiligen Zuständen geht die anfangs gegebene Unmittelbarkeit der Wahlverwandtschaft verloren. Es gibt nicht mehr das eindeutig gegebene reale Maß, mit dem Stoffe miteinander reagieren, sondern es wird aufgebrochen in ein Substrat und dessen Zustände. Mit dem Substrat wird erkannt, warum es überhaupt zu einer Wahlverwandtschaft kommt, mit dem Zustand, welche Reaktionsstärke die Wahlverwandtschaft jeweils annimmt. Am Beispiel der Aggregatzustände des Wassers ist zu unterscheiden, was das Wasser als Substrat ist, und was seinen jeweiligen Zustand als Eis, Flüssigkeit oder Gas ausmacht. Diese Unterscheidung ist keineswegs selbstverständlich, und es war ein großer Erfolg der Naturwissenschaft zu erkennen, dass Eis, Flüssigkeit und Gas nicht verschiedene Stoffe, sondern verschiedene Zustände eines gemeinsamen Substrats sind. Es ist ein Unterschied, ob ein Stoff seinen Zustand ändert oder sich in einen anderen Stoff verwandelt. In der logischen Sprache von Hegel kann gesagt werden: Anfangs wird eine bestimmte Wahlverwandtschaft wahrgenommen und gemessen. Mit der Erkenntnis ihrer Veränderung in verschiedenen Zuständen wird die Unmittelbarkeit negiert und das reale Maß aufgeteilt (ge-ur-teilt) in Substrat und Zustände. Die Knotenlinie mit ihrer Unterscheidung der Wahlverwandtschaften in verschiedene Zustände kann daher als Negation der unmittelbar gegebenen realen Maße verstanden werden.
(6) Setzt sich die Knotenlinie unendlich weit fort und führt in unendlich viele, neue Zustände, oder droht am Ende eine völlige Auflösung, mit der die jeweiligen Wahlverwandtschaften in absolute Indifferenz übergehen und ein Grenzzustand erreicht wird, der sich in völligem Stillstand befindet, in der Sprache der nachfolgenden Physik der absolute Wärmetod? Die Knotenlinie würde auslaufen in eine schlechte Unendlichkeit, wie Hegel sie bereits am Beispiel der natürlichen Zahlen untersucht hatte. So wie dort am Ende die unbestimmten Pünktchen ›…‹ stehen, würde hier am Ende die leere Maßlosigkeit stehen. Daher ist die Negation der unmittelbaren Wahlverwandtschaften in die verschiedenen Zustände eines Substrats entlang der Knotenlinie nochmals zu negieren und zu fragen, welches die innere Einheit eines Substrats und seiner Zustände ist. Am Beispiel der Zahlen war die schlechte Unendlichkeit negiert worden, indem gefragt wurde, welche Eigenschaft der Zahlengerade die Unendlichkeit der Zahlen ermöglicht. Das ist deren Kontinuität. Und so ist hier zu fragen, welche Eigenschaft der Knotenlinie es ist, mit der entlang der Knotenlinie die Unterscheidung eines Substrats in seine Zustände gelingt. Wenn diese Eigenschaft gefunden wird, löst sich die Frage der drohenden Maßlosigkeit auf und die nachfolgende absolute Indifferenz ist nicht das Ende der Natur und der Naturwissenschaft, sondern umgekehrt ein höherer Gesichtspunkt, ihre Einheit zu verstehen und die Naturwissenschaft fortzuführen.
Chemie
Für Hegel war die Chemie der Ausgangspunkt. Dort ist zu sehen, wie sich verschiedene Stoffe suchen oder abstoßen, miteinander reagieren und aus den Reaktionen neue Stoffe hervorgehen.
– Wahlverwandtschaften
Experimentell kann beobachtet werden, mit welchen anderen Stoffen ein bestimmter Stoff reagiert. Die Ergebnisse werden in Reaktionsgleichungen aufgeschrieben. Ruschig findet bei Hegel drei wichtige Beispiele aus der Chemie.
Neutralisation der Schwefelsäure
Schwefelsäure kann durch Natronlauge, Kalk, Magnesia oder Ammoniak neutralisiert werden. Hier gelten jedoch unterschiedliche Massenrelationen. »1000 g Schwefelsäure werden durch 816 g Natronlauge oder 572 g Kalk oder 408 g Magnesia oder 714 g Ammoniak neutralisiert« (R, S. 83). Hegel kannte noch nicht die Molekül-Darstellung der Stoffe und ihre Summenformeln. Mit ihnen lassen sich die Reaktionen übersichtlich aufschreiben:
H2SO4 + 2 NaOH → 2 H2O + Na2SO4
lies: 1 Mol Schwefelsäure und 2 Mol Natronlauge ergibt 2 Mol Wasser und 1 Mol Natriumsulfat
H2SO4 + {Mg} → MgSO4 + H2
lies: 1 Mol Schwefelsäure und Magnesium ergibt 1 Mol Magnesiumsulfat und 1 Mol molekularen Wasserstoff
H2SO4 + CaCO3 → H2O + CO2 + CaSO4
lies: 1 Mol Schwefelsäure und 1 Mol Kalk (Calciumcarbonat) ergibt 1 Mol Wasser und 1 Mol Kohlenstoffdioxid und 1 Mol Calziumsulfat
H2SO4 + 2 NH3 → (NH4)2SO4
lies: 1 Mol Schwefelsäure und 2 Mol Ammoniak ergibt 1 Mol Ammoniumsulfat
Mit der Molekül-Darstellung lassen sich die Massenrelationen bestimmen (siehe z.B. den Molekulargewicht-Rechner von Tobias Schmidt). Schwefelsäure hat das Molekulargewicht 98 (2 x Wasserstoff mit Atomgewicht 1, 1 x Schwefel mit Atomgewicht 32, 4 x Sauerstoff mit Atomgewicht 16). Natronlauge hat das Molekulargewicht 40, so dass 1000 g Schwefelsäure mit 816 g Natronlauge reagieren. Dies stimmt teilweise mit den von Ruschig genannten Werten überein.
Reaktionen mit Natronlauge
Umgekehrt kann untersucht werden, was geschieht, wenn unterschiedliche Säuren mit einer bestimmten Lauge zusammengebracht werden. Nicht nur die Schwefelsäure reagiert mit Natronlauge, sondern auch die Salzsäure:
HCl + 2 NaOH → 2 H2O + NaCl
lies: 1 Mol Salzsäure und 1 Mol Natronlauge ergibt 2 Mol Wasser und 1 Mol Kochsalz
Reaktionen des Löschkalk
Ein weiteres Beispiel ist der Löschkalk (Calciumhydroxid). In diesem Fall gibt Ruschig die Reaktionsgleichungen (siehe R, S. 164):
Ca(OH)2 + CO2 ⇄ CaCO3 + H2
lies: 1 Mol Löschkalk und 1 Mol Kohlenstoffdioxid ergeben 1 Mol Calciumcarbonat und 1 Mol molekularen Wasserstoff
Ca(OH)2 + 2 HCl ⇄ CaCl2 + 2 H2O
lies: 1 Mol Löschkalk und 2 Mol Chlorwasserstoff ergeben 1 Mol Calciumchloridund 2 Mol Wasser
Ca(OH)2 + H2SO4 ⇄ CaSO4 + 2 H2O
lies: 1 Mol Löschkalk und 1 Mol Schwefelsäure ergeben 1 Mol Calciumsulfat und 2 Mol Wasser
Mit Reaktionsgleichungen werden die Ergebnisse chemischen Experimentierens protokolliert. Sie zeigen, welche Stoffe miteinander reagieren und welche Massenverhältnisse auftreten. Zum Beispiel reagiert in der ersten Zeile ein Mol Löschkalk mit einem Mol Kohlenstoffdioxid, dagegen in der zweiten Zeile ein Mol Löschkalk mit zwei Mol Chlorwasserstoff. In allen Fällen, in denen es zu einer Reaktion kommt, wird von Wahlverwandtschaft gesprochen. Die jeweiligen Stoffe ziehen sich an, finden zueinander und reagieren miteinander.
Diese Art der Reaktionsgleichungen heben die Summenformeln hervor. Sie zeigen, wie in der Reaktion zweier oder mehrerer Stoffe Atome aus den jeweiligen Molekülen ausgetauscht und aus ihnen neue Stoffe gebildet werden. Die experimentell beobachteten Massenverhältnisse in Mol können erklärt werden aus den zugrundeliegenden Verhältnissen der Atome in den beteiligten Molekülen. Zum Beispiel muss ein Mol Löschkalk mit zwei Mol Chlorwasserstoff reagieren, damit im Ergebnis Calciumchlorid entstehen kann, das zwei Chlor-Atome enthält.
Dieser Prozess wird seit der Formulierung des Pauli-Prinzips von 1924, wonach nicht mehr als zwei Elektronen ein Orbital besetzen können, nochmals genauer beschrieben als Reaktion der Ionen, aus denen sich die Moleküle zusammensetzen. Die in den Molekülen enthaltenen Atome werden aufgeteilt in Atomkerne (aus Neutronen und Protonen) und Elektronen, und die Elektronen werden wiederum gruppiert in Elektronenorbitale. Ist das äußerste Elektronenorbital teilweise unbesetzt, dann kann es zu einem Austausch kommen, bei dem ein einsames Elektron von einem Stoff sich mit dem einsamen Elektron eines anderen Stoffs zusammenschließt und dadurch ein stabilerer Zustand erreicht wird, in dem alle Elektronenorbitale voll besetzt sind. So wird z.B. die Neutralisierung von Schwefelsäure und Natronlauge aufgeteilt in eine Reaktion der jeweiligen Ionen.
Die Schwefelsäure H2SO4 setzt sich zusammen aus den Ionen 2 H+ und SO4-.
Die Natronlauge NaOH setzt sich zusammen aus den Ionen Na+ und OH-
Daraus ergibt sich die verfeinerte Reaktionsgleichung:
{2 H+ + SO4-} + {2 Na+ + 2 OH-} → 2 {H2O} + {2 Na+ + SO4-}
An dieser Gleichung ist zu erkennen, wie nicht die Atome ausgetauscht wurden, sondern sich die auf der linken Seite der Gleichung aufgeschriebenen Ionen neu miteinander kombiniert haben. Das SO4--Ion hat seine Verbindung mit den H+-Ionen verlassen und zum Na+-Ion gefunden. Die dadurch frei werdenden Ionen haben sich ihrerseits zu Wassermolekülen zusammengeschlossen. Diese Darstellung kommt dem literarischen Vorbild von Goethe wesentlich näher, bei dem sich zwei Paare treffen und wechselweise ihre Partner tauschen.
Bei genauerer Untersuchung kann die Reaktionsgleichung weiter zerlegt werden (vgl. chemie-master), doch ändert sich gegenüber Hegel nichts an der grundlegenden Idee der Wahlverwandtschaft. Niemand kann ausschließen, dass in der Zukunft nochmals eine Stufe tiefer erklärt werden kann, warum das Pauli-Prinzip gilt und dann der Ablauf bei chemischen Reaktionen weiter zerlegt werden kann in Teilprozesse. Das wird nichts am Prinzip ändern, um das es Hegel geht: Die Natur ist polar aufgebaut, wodurch es zu Anziehungskräften (Affinität, Wahlverwandtschaft) kommt.
– Knotenlinien
Knotenlinien von Konzentrationen eines Stoffs in Gemischen
Hegel hat das Bild der Knotenlinien von den Chladnischen Klangfiguren übernommen (siehe hierzu in seiner Naturphilosophie in der Enzyklopädie die Ausführungen zu den »Schwingungsknoten« von Tönen nach Chladni, Enz. § 301, HW 9.176), und der Ausdruck »Knotenlinien« wird bis heute vor allem benutzt, um zweidimensionale Wellenmuster zu beschreiben, bei denen es zu typischen Knotenbildungen der Wellenzüge kommt.
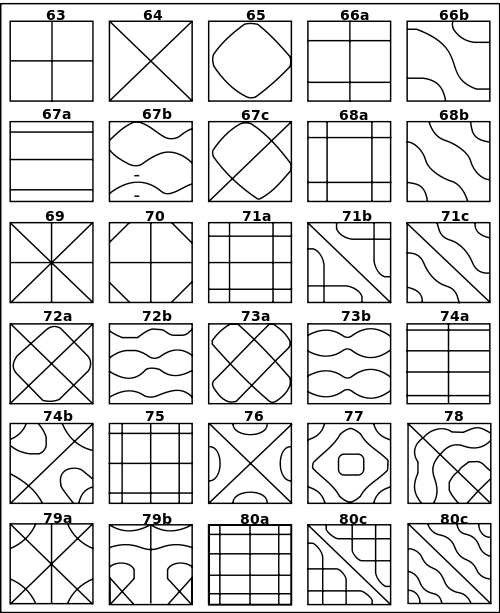
Figur 1: Chladnische Klangfiguren
»Chladnische Klangfiguren sind Muster, die auf einer mit Sand bestreuten dünnen Platte (am besten aus Metall) entstehen, wenn diese in Schwingungen versetzt wird. Dieses geschieht, indem die Platte an einer Kante mit einem Geigenbogen bestrichen oder einer schwingenden Stimmgabel berührt wird«. Sie wurden erstmals 1787 von Ernst Florens Friedrich Chladni (1756-1827) in seinem Werk Entdeckungen über die Theorie des Klanges veröffentlicht und gelten bis heute in der Atomphysik als eins der besten Mittel, das Verhalten mehrdimensionaler Wellen zu veranschaulichen. Wikipedia
Urheber: Von E.F.F.Chladni – From the book "Die Akustik" from E.F.F.Chladni. Originally from de.wikipedia; description page is/was here., Gemeinfrei, Link
(1) An den Knotenlinien ist für Hegel wichtig, dass mit ihnen ein zweidimensionaler Sachverhalt beschrieben werden kann, der auf zwei voneinander unabhängigen Qualitäten beruht. Seine Ausgangsfrage war, warum die Wahlverwandtschaften eines gegebenen Stoffes mit anderen Stoffen unterschiedlich stark sind. Beispiel: Kochsalz NaCl und Glaubersalz Na2SO4 reagieren sowohl mit Schwefelsäure H2SO4 wie auch mit Salzsäure HCl und sind daher mit beiden wahlverwandt. Aber obwohl Salzsäure die stärkere Säure ist (ihre Säurekonstante, der pKS-Wert ist −6 gegenüber −3 der Schwefelsäure), setzt sich die Schwefelsäure durch. Das liegt in diesem Beispiel daran, dass die Salzsäure flüchtiger ist und daher eher entweicht als die Schwefelsäure. In diesem Beispiel ist die Flüchtigkeit die von der Wahlverwandtschaft unabhängige zweite Qualität, warum einer der beiden Stoffe reaktionsstärker als der andere ist. Chemiker sagen, dass Schwefelsäure aus Kochsalz Salzsäure verdrängt, aber Salzsäure kann nicht aus Glaubersalz Schwefelsäure verdrängen (R, S. 132).
Ein weiteres Beispiel sind die Reaktionen des Löschkalks Ca(OH)2. Der Löschkalk kann u.a. mit Kohlenstoffdioxid CO2 und mit Schwefelsäure H2SO4 reagieren, ist also mit beiden wahlverwandt. In beiden Fällen gibt es aufgrund der unterschiedlichen Molekulargewichte jeweils bestimmte Massenrelationen (Äquivalentgewichte) für die Reaktion. Die Massenrelationen legen fest, wie groß die Mengen sein müssen, wenn die Stoffe im Verlauf der Reaktion vollkommen aufgebraucht werden sollen. Aber mit den Massenrelationen lässt sich nicht die Frage beantworten, welcher Stoff reaktionsstärker ist und sich daher durchsetzt. Dafür ist eine zweite Eigenschaft notwendig. Dies ist nach neuerer Erkenntnis die Freie Bindungsenthalpie der entstehenden Stoffe, das sind in diesem Beispiel Calciumsulfat CaSO4 bzw. Calciumcarbonat CaCO3. Es wird sich die Reaktion durchsetzen, deren Endprodukte eine größere Freie Bindungsenthalpie haben. Das ist angesprochen, wenn Ruschig schreibt:
»Das Verhältnis der Freien Bindungsenthalpien von CaSO4 und CaCO3 ist nicht gleich dem Verhältnis der diese Verbindungen herstellenden Äquivalente von H2SO4 und CO2; reagiert Ca(OH)2 mit einer Mischung von H2SO4 und CO2, so ist das Gleichgewicht nicht durch jenes der Äquivalentgewichte bestimmt« (R, S. 170f).
Die Freien Bindungsenthalpien können aus Tabellen abgelesen werden (z.B. Wikibooks) und betragen für Calciumsulfat −1320,5 kJ/mol und für Calciumcarbonat 1128,8 kJ/mol. Die Säurekonstante wird mithilfe der Freien Bindungsenthalpie berechnet. Zusammenfassend schreibt Ruschig:
»Dann aber muss eine von den Massenrelationen spezifisch unterschiedene und nicht aus ihnen entwickelbare Qualität existieren, welche die Rangfolge unter den Affinitäten / Wahlverwandtschaften regelt. Diese Qualität kann quantifiziert werden: Die Freie Bindungsenthalpie ist das Maß, das angibt, welche Reaktionen bevorzugt oder benachteiligt sind und in welchem Ausmaß Bevorzugungen bzw. Benachteiligungen stattfinden« (R, S. 172).
Was die Freie Enthalpie bedeutet, wird weiter unten näher ausgeführt. Hier genügt die Erkenntnis, dass mit ihr eine unabhängige Qualität gefunden ist, mit der das Maß der Wahlverwandtschaft erklärt werden kann. Das Beispiel von Schwefelsäure und Salzsäure zeigt weiter, dass es Ausnahmesituationen geben kann, in denen andere Eigenschaften dominieren.
(2) Zum zweiten stellt sich die Frage, ob es möglich ist, bestimmte Bedingungen zu ändern, so dass der vorher reaktionsschwächere Stoff zum reaktionsstärkeren werden kann. Das kann am einfachsten dadurch erreicht werden, dass der Anteil des reaktionsschwächeren Stoffs kontinuierlich erhöht wird, bis das Reaktionsverhalten umschlägt und der schwächere Stoff sich aufgrund seiner größeren Präsenz durchsetzen kann. Hegel bezeichnet die kontinuierliche Veränderung eines Parameters als Knotenlinie. Wenn es im Verlaufe dieser Veränderung zu qualitativen Sprüngen kommt, ergeben sich Knoten, durch die unterschiedliche Zustände voneinander getrennt sind.
Hegel wusste nicht, welche Kraft es ist, die den Übergang von einem Zustand in den nächsten entlang einer Knotenlinie bewirkt. Es genügt ihm, einen grundsätzlichen Ansatz zu finden, um rein algebraisch aus den Messergebnissen die Zweidimensionalität der Ordnungsstruktur zu erkennen. Diese Frage wurde zu seiner Zeit intensiv und konträr diskutiert. Viele Chemiker glaubten, dass es die gleiche Qualität sei, die sowohl zu einer Wahlverwandtschaft wie auch zum Umschlag von einer Wahlverwandtschaft in eine andere führen kann. Hegel erkannte, dass dies buchstäblich "rein logisch" nicht möglich ist. Etwas kann nicht zugleich eine Qualität (die Wahlverwandtschaft) und den Übergang von einer Qualität in eine andere (die Kraft, die entlang der Knotenlinie an bestimmten Stellen Knoten bildet) bestimmen. Dieser Ansatz ist im weiteren von der naturwissenschaftlichen Forschung voll bestätigt wurden, als erkannt wurde, worin der Grund der Umschläge besteht (die Entropie, siehe dazu weiter unten).
Sein Kapitel über Knotenlinien hat daher weit grundsätzlichere Bedeutung. Es zeigt, wie in einer unübersichtlichen Fülle von Mess-Ergebnissen dadurch Ordnung geschaffen werden kann, dass voneinander unabhängige Kräfte erkannt und entkoppelt werden. Er hat damit das Modell der mechanischen Freiheitsgrade (drei Raumrichtungen und drei Drehachsen) übertragen auf die Suche nach Symmetrien in nicht-mechanischen Naturwissenschaften wie der Chemie. Das ist bis heute die Vorgehensweise der Naturwissenschaft und hat sich in der Quantenmechanik völlig durchgesetzt.
Unabhängig davon, wie diese – Hegel noch unbekannte – Eigenschaft genau aussieht, hat Ruschig den grundsätzlichen Punkt getroffen, um den es Hegel geht. Er bemerkt, dass Hegel eine heute kaum mehr gebräuchliche und daher meist überlesene Formulierung wählt, die aus der Webtechnik übernommen ist. Wenn Hegel davon spricht, »das ausschließende, negative Verhalten leidet zugleich diesen Eintrag von der quantitativen Seite her« (HW 5.422, zitiert R, S. 179), erläutert Ruschig:
»Das anschauliche Bild für die Metapher 'Eintrag erleiden' stammt aus der Weberei. Demgemäß ist die qualitative Seite ('das ausschließende, negative Verhalten') von der quantitativen durchwirkt, welche als querliegender Faden das Gewebe durchschießt« (R, S. 180).
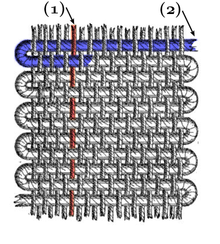
Figur 2: Kettfaden (1) und Schussfaden (2)
»Die Kettfäden (auch Kette, Zettel, Aufzug, altertümlich Werft genannt) sind die Fäden, die in der Weberei in einem Webstuhl in Längsrichtung aufgespannt werden. Im fertigen Gewebe liegen sie parallel zur Webkante, während die Schussfäden quer dazu verlaufen« (Wikipedia).
Urheber: Von Kette_und_Schuß.jpg: http://commons.wikimedia.org/wiki/User:Ryj / *derivative work: Derwok (talk) - Kette_und_Schuß.jpg, CC BY-SA 3.0, Link
Mathematisch gesprochen sind die Wahlverwandtschaften und der Übergang von einer Reaktion zu einer anderen voneinander unabhängig und bilden ein Kreuzprodukt. Sie lassen sich nicht auf eine gemeinsame Einheit zurückführen, sondern spannen eine zweidimensionale Fläche auf. Hierfür ist das Bild des Webens ausgesprochen anschaulich, in dem Kettfaden und Schussfaden in zwei voneinander unabhängigen Richtungen geküpft sind.
Säure-Lauge-Titration
Noch elementarer ist das Beispiel, wenn in einem Säure-Lauge-Gemisch tröpfchenweise der Anteil der Säure bzw. der Lauge erhöht wird. In diesem Fall kommt es zu markanten Umschlagpunkten, an denen sich die Farbe des Gemischs ändert. Der Umschlag der Farbe ist das Vorbild, an dem der Begriff des Umschlags von Quantität in Qualität gefunden wurde (siehe hierzu R, S. 252ff).

Figur 3: Ph-Indikatoren und ihre Farbskala
Wird einer Lauge tröpfchenweise eine Säure zugeführt (Säure-Base-Titration), verändert sich das Maß des sauren Charakters (ph-Wert). Der Farbumschlag liegt in den Bereichen des senkrechten Verlaufs des Äquivalenzpunktes. Sein Wert gilt spezifisch für die jeweiligen Stoffe. Bei Zuführung von Lackmus (Lackmus-Test) ändert sich die Farbe von rot nach blau, bei Zuführung von Methylorange von rot nach orange usw. Wikipedia
Urheber: Von Säuren und Laugen - Farbspektrum verschiedener Indikatoren.png: de:Benutzer:MarkusZi derivative work: MarkusZi (talk) Diese W3C-unbestimmte Vektorgrafik wurde mit CorelDRAW erstellt. - Säuren und Laugen - Farbspektrum verschiedener Indikatoren.png, Gemeinfrei, Link
Die Ursachen für den Farbumschlag sind äußerst komplex. Das ist schon daran zu erkennen, dass die hier genannten ph-Indikatoren ihrerseits sehr komplex sind. Zum Beispiel ist Lackmus seinerseits ein Stoffgemisch aus 10 - 15 Komponenten.
Aggregat-Zustände des Wasser (Temperaturänderungen)
Etwas überraschend wechselt Hegel von den Wahlverwandtschaften der Chemie zu den Aggregat-Zuständen des Wassers. Beide Phänomene galten jedoch seinerzeit als verwandt, wie Ruschig anhand eines Zitats von Berzelius belegt. Berzelius schreibt auf den einleitenden Seiten seines Lehrbuch der Chemie:
»Diese Verwandtschaften sind von doppelter Art. Die eine, kraft welcher die kleinsten Teilchen (Moleküle) der Körper unter einander zusammenhängen, nennt man Zusammenhangs-Verwandtschaft oder Cohäsionskraft. ... Die andere Art der Verwandtschaft heißt Vereinigungs-Verwandtschaft« (Berzelius, Lehrbuch der Chemie, Bd. 1, Dresden 1825, S. 3f, zitiert R, S. 285).
Die Wahlverwandtschaften sind ein anderer Name für die Vereinigungs-Verwandtschaft. Die Aggregat-Zustände des Wassers sind das wichtigste Beispiel für die Zusammenhangs-Verwandtschaft. Im Eis sind alle Teile starr aneinander gebunden. In der Flüssigkeit gibt es einen lockeren Verband, durch den ein innerer Zusammenhang und nach außen eine Oberfläche gebildet wird. Beim Dampf ist freie Beweglichkeit und Unabhängigkeit gegeben. So hat jeder Aggregat-Zustand seine eigene Zusammenhangs-Intensität, die sich mit dem Wechsel der Aggregat-Zustände schlagartig ändert.
Ruschig kritisiert die Darstellung bei Hegel und fasst sie genauer. Der Grundgedanke von Hegel wird jedoch meiner Meinung nach dadurch nicht geändert.
»So resultiert bei kontinuierliche Wärmezufuhr eine Funktion, die streng monoton wachsend ist. Hingegen zeigt die Temperaturkurve in Abhängigkeit von der Zeit einen Knick (eine nicht differenzierbare Stetigkeitsstelle) am Kochpunkt, jedoch keinen Sprung, während andere Eigenschaften wie Dichte, Brechungsindex etc dort eine Unstetigkeitsstelle besitzen« (R, S. 286). »Die kontinuierliche Veränderung selbst (die Zufuhr von Wärme und dadurch verursacht das kontinuierliche Ansteigen des Dampfdrucks) enthält schon die beiden Qualitäten (die neue Qualität, der gasförmige Zustand, tritt eben nicht erst am Kochpunkt ein). ... Die Bewegung eines Moleküls im Flüssigkeitsverband ist durch seine kinetische Energie und die Van-der-Wals-Kräfte zu den umgebenden Molekülen bestimmt. ... Die Auflösung des Flüssigkeitsverbandes ist der 'Sprung'« (R, S. 287).
Heute können die Grenzübergänge wesentlich genauer beschrieben werden. Beim Schmelzen gibt es einen Moment, in dem sich zwar der Zustand von fest in flüssig ändert, jedoch die kinetische Energie noch nicht erhöht wird. Die Wassermoleküle befinden sich bereits in einem neuen Zustand des Zusammenhangs, nutzen ihn aber noch nicht. Experimentell konnte die Schmelzwärme (Schmelzenthalpie) gemessen werden, die für diesen Teilschritt notwendig ist, um Bindungskräfte zwischen Molekülen bzw. Atomen zu überwinden, aber die kinetische Energie noch nicht zu erhöhen. Das erklärt, warum umgekehrt im gleichen Betrag eine Erstarrungswärme abgegeben wird, wenn ein Körper kristallisiert. Dadurch kann beim Vereisen kurzzeitig die Umgebung erwärmt werden, was z.B. von Pflanzen genutzt wird, wenn sie entsprechende Bedingungen herstellen und dadurch eine lokale Wärme erzeugen.
Im flüssigen Zustand bestehen Van der Wals Kräfte. Innerhalb der Moleküle sind die Elektronen nicht völlig symmetrisch verteilt, weswegen die Moleküle an der Oberfläche eine elektrische Ladungsverteilung aufweisen und sich entsprechend gegenseitig anziehen und einen lockeren Verband bilden.
Energie und Entropie
Die chemischen Modelle haben eine Gemeinsamkeit: In allen Fällen gibt es stabile Phasen (Zustände), in denen sich eine bestimmte Ordnung erhält, obwohl kontinuierlich ein Stoff oder Energie zugeführt wird, bis in einem Sprung eine neue Ordnung an ihre Stelle tritt. Mit jeder Ordnung werden bestimmte Kräfte wirksam, die sich erst innerhalb dieser Ordnung durchsetzen können und ihrerseits durch eine Barriere gegen Auflösung geschützt sind. So gesehen ist für jede Ordnung eine bestimmte Kraft spezifisch, die nur unter diesen Bedingungen dominieren kann und ein lokales Gleichgewicht herstellt.
Systemzustände dieser Art werden systematisch von der Thermodynamik untersucht. Unter diesem Gesichtspunkt kann Hegel neu gedeutet werden.
Gibbs-Energie (Freie Enthalpie, Gibbs-Helmholtz-Energie)
Was ist die Freie Enthalpie bzw. Enthalpiedifferenz? Bereits das scheinbar einfache Beispiel der Wassererwärmung zeigt die Schwierigkeit zu verstehen, was Enthalpie ist. Was bedeutet die Aussage, dass dem Wasser »Wärme zugeführt« wird, bis es schmilzt bzw. im nächsten Sprung verdampft? Es gibt drei völlig verschiedene Verfahren, und mit der Enthalpie soll das Gemeinsame erkannt werden: (a) Dem flüssigen Wasser kann Dampf zugeführt werden, d.h. Wasser, das heißer als 100° ist. Dadurch entsteht ein Gemisch aus Wassermolekülen unterschiedlicher Temperatur, das sich auf einer mittleren Temperatur ausgleicht. Die Wassermenge ist vergrößert worden, und die am Ende erreichte Durchschnittstemperatur der größeren Wassermenge liegt über 100°, weswegen das Wasser im Ganzen verdampft. (b) Eine nicht aus Wasser bestehende Grenzfläche zum Wasser, z.B. das Metall eines Kochtopfs, kann erhitzt werden. Dadurch kommt es zu Schwingungen des Metalls. Das schwingende Metall vermischt sich nicht mit dem Wasser, aber es bringt das angrenzende Wasser ebenfalls zum Schwingen. Die Wassermenge wird nicht wie im vorher genannten Fall erhöht, aber durch die Schwingungen der Wassermoleküle wird deren kinetische Energie so weit erhöht, bis die Van-der-Waals-Kräfte überwunden sind, die den Flüssigkeitsverband des Wassers hergestellt haben. Daher verdampft das Wasser. (c) Schließlich kann ohne Zufuhr von Dampf oder Erhitzung der Außenwand die Temperatur dadurch erhöht werden, dass das Wasser zusammengepresst wird.
Daraus ergibt sich der komplexe Begriff der Gibbs-Energie. Josiah Willard Gibbs (1839-1903) hat 1876-1878 seine entscheidenden Erkenntnisse veröffentlicht, die jedoch erst in den 1890ern in Europa bekannt und dort mit ähnlichen Forschungen von Hermann von Helmholtz (1821-1894) zusammengeführt wurden. Die Gibbs-Energie ist »ein thermodynamisches Potential mit den natürlichen unabhängigen Variablen Temperatur T, Druck p und Stoffmenge n oder alternativ Teilchenzahl N« (Wikipedia). Damit fasst sie alle Parameter zusammen, mit denen einem Stoff wie Wasser Energie zugeführt werden kann und resultiert in einer einheitlichen Funktion. Sie zeigt, wie sich nach jedem Sprung ein Potentialtopf entwickelt: Die neue Ordnung erreicht ein neues lokales Minimum und ist nach außen durch Potentialdifferenzen geschützt. Das bedeutet: Sie hat zum einen die Kraft, die für ihre Umgebung spezifischen Bedingungen zu optimieren, und es ist zum anderen ein hohes Maß an Aktivierungsenergie notwendig, um die Potentialgrenzen überwinden und die Ordnung auflösen zu können.
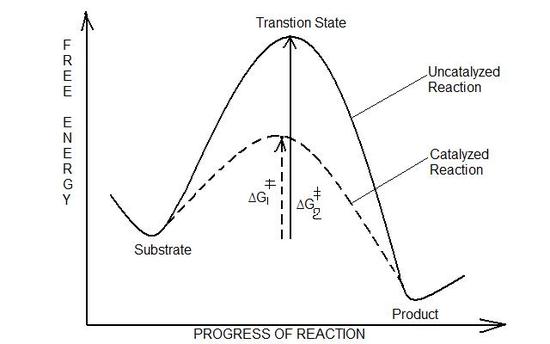
Figur 4: Übergangszustand (Transition State)
Das Diagramm zeigt zwei lokale Minima: Den Ausgangszustand, in dem sich der Ausgangsstoff (Substrate) vor der Reaktion befindet und das neue lokale Minimum, das im Endzustand erreicht wird, wenn ein neues Produkt (Product) hergestellt ist. Im Übergangszustand ist die Freie Gibbs-Energie größer als im Ausgangs- und im Endzustand. Durch einen Katalysator kann die Aktivierungsenergie verringert werden. libretexts
Mit diesem Ansatz können die zuvor genannten chemischen Modelle einheitlich gedeutet und verstanden werden:
(a) Wenn in einem Gemisch kontinuierlich ein reaktionsschwächerer Stoff zugeführt wird, entsteht ein Übergewicht, und die Entropie (Unordnung) verringert sich. Das System bekommt die Neigung, die Entropie wieder zu erhöhen und diesen Stoff aufzulösen. Wenn bei einer Reaktion mit diesem Stoff der Zugewinn an Entropie größer ist als die Differenz zum reaktionsstärkeren Stoff, dann kann es zu einer Reaktion kommen, da sie im Ganzen die Entropie erhöht. Das ist mit der Enthalpiedifferenz gemeint.
Atkins beschreibt einen ähnlichen Prozess: Die Selbstbeschränkung von chemischen Reaktionen. Zu Beginn vergrößert sich während einer Reaktion die Unordnung, wenn die Ausgangsstoffe und Produkte nebeneinander existieren. Werden jedoch allmählich alle Ausgangsstoffe aufgebraucht, erhält das neue Produkt ein Übergewicht und die Unordnung verringert sich wieder. Der Prozess beginnt sich selbst zu bremsen.
»Die Reaktion hat solange eine spontane Neigung zur Bildung von Produkten, bis die Zusammensetzung den Punkt erreicht hat, der einer größtmöglichen Unordnung des Universums entspricht. Dann ist die Hinreaktion nicht länger spontan. Die Produktkonzentration steigt nicht mehr weiter, und die Reaktion geht in das dynamische Gleichgewicht über. Das Produkt hat sowohl selbst die Voraussetzungen für seine Bildung geschaffen als auch seine eigene Bildung beschränkt« (Atkins, S. 109).
Das lässt sich auf den von Hegel diskutierten Fall übertragen. Die thermodynamischen Gesetze liegen den von ihm betrachteten Reaktionen und ihren Knotenlienien zugrunde.
(b) Bis ins Detail sind alle Prozesse erforscht und gemessen worden, die beim Übergang von flüssigem Wasser in Dampf auftreten, um Dampfkraftwerke optimieren zu können (siehe die aussagekräftigen Tabellen bei Wikipedia). Bei siedendem Wasser erhöht sich sprunghaft die Entropie (die Bewegung der Wassermoleküle ist im Dampf wesentlich ungeordneter als in der Flüssigkeit) und das spezifische Volumen (m³/kg) steigt steil an (der Dampf dehnt sich aus). Im Dampf bildet sich eine neue Ordnung, die wesentlich geringer ist als die Ordnung des flüssigen Wassers. Der Übergang zum Dampf setzt sich schlagartig durch, wenn der Gewinn an Entropie in der neuen Ordnung größer ist als die Energie (Temperaturerhöhung), um ihn zu erreichen.
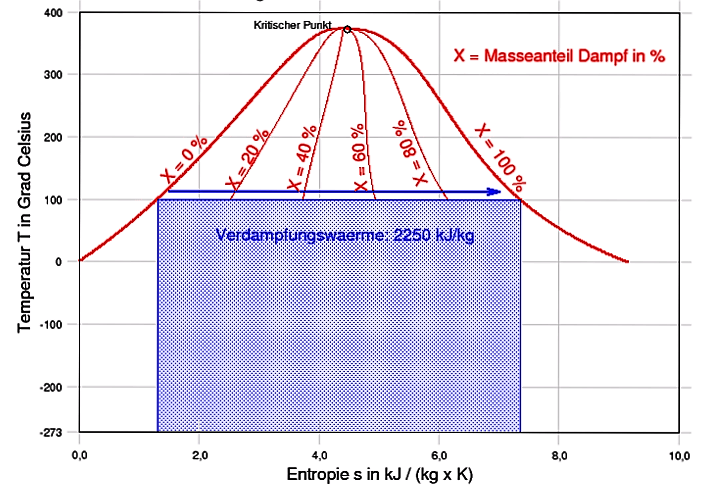
Figur 5: Zustandsänderung von Wasserdampf bei 100 Grad Celsius und 1 bar Druck
»Bei einem normalen Umgebungsdruck von 1,013 bar (101,325 kPa) siedet Wasser bei 100 Grad Celsius. Wird dem verbliebenen Wasser darüber hinaus Energie (Wärme) zugeführt, verdampft es, ohne dass es zu einem weiteren Temperaturanstieg kommt. Aus 1 Liter (entsprechend 1 kg) Wasser entstehen 1673 Liter Wasserdampf (unter Normalbedingungen), wofür eine Energiezufuhr von 2257 kJ benötigt wird. ... Das hier abgebildete Diagramm stellt die für die Verdampfung notwendige Wärme in Form der gepunkteten blauen Fläche dar«. Wenn es nicht zur Verdampfung kommt, weil sich das Wasser in einem geschlossenen Raum befindet, dann steigt die Temperatur weiter an, bis sie am kritischen Punkt von 374,12 Grad Celsius und einen Druck von mindestens 221,2 bar den Zusammenhangscharakter der Flüssigkeit verliert und in überkritisches Wasser übergeht. Wikipedia
Urheber: CC BY-SA 3.0, Link
Musik
Die Musik zeigt das an der Sprache und der Mathematik Verborgene, sie lässt es hören. Der Tonos der Musik geht allen Symbolbildungen der von Menschen gebildeten Zeichensysteme voraus und verleiht ihnen ihren inneren Zusammenhang, den sie aus sich selbst heraus nicht zu fassen vermögen. Ruschig hat 2012 in seinem Beitrag Vom Sinn des Tones sehr übersichtlich zusammengetragen, was Hegel zur Musik geschrieben hat. Mir geht es in diesem Abschnitt vor allem darum, am Modell der Musik die schwierige Unterscheidung in Beziehungen, Wahlverwandtschaften, Knotenlinien, Substrat, Sache, Ordnung und Prinzipien der Ordnung zu verdeutlichen. Die Musik ist mit ihren Tonsystemen ein Beispiel für eine Sache, an deren Ordnung die Eigenschaften zu erkennen sind, aus denen sich die Übergänge der einzelnen Zustände (das sind im Beispiel der Musik die Gebrauchstonleitern) eines gegebenen Substrats (dem Tonvorrat, der Materialtonleiter) begründen lassen. Die Ordnung der Musik erscheint gegenüber den Maßen der einzelnen Tonleitern maßlos. Wer versucht, direkt auf der Ebene der Materialtonleiter und ihrer Ordnung zu komponieren (die Zwölftonmusik), erzeugt eine Musik, die entgegen ihrem eigenen Anspruch das innere Maß verloren hat, und begeht innerhalb der Sache der Musik hörbar einen Kategorienfehler. Zugleich ist die Ordnung der Musik wie keine andere Ordnung eingebettet in die übergeordneten Ordnungen des Kosmos. Die zwölf Töne verweisen auf die zwölf Tierkreiszeichen und das grundlegende, babylonische Sexagesimalsystem und seiner Aufteilung des Jahres in zwölf Monate und des Tages in zwei mal zwölf Stunden mit jeweils 60 Minuten.
Intervalle und ihre harmonischen Verwandtschaften (Funktionen)
Die Intervalle zwischen zwei Tönen wie z.B. die Prim, Sekunde, Terz, Quarte, Oktave sind zunächst noch keine Wahlverwandtschaften, sondern einfach Beziehungen (Relationen) von jeweils zwei Tönen. Von einer Wahlverwandtschaft kann erst gesprochen werden, wenn ein Ton von sich aus zu einem anderen Ton neigt, zu dem er übergehen möchte. Wer den Beginn einer Melodie hört, erwartet nach jedem Ton den nachfolgenden Ton, zu dem über ein bestimmtes Intervall übergegangen wird. Mit zwei aufeinander folgenden Tönen kann eine Spannung erzeugt werden, die von sich aus zu einem weiteren Ton neigt, mit dem sie aufgelöst wird. Das kann als Wahlverwandtschaft bezeichnet werden und wird systematisch mit der 1893 von Hugo Riemann (1849-1919) begründeten Funktionstheorie untersucht. Mit ihr lassen sich die Spannungen und Auflösungen innerhalb eines Musikwerks nachvollziehen.
Für Husserl ist das Hören von Musik das maßgebliche Beispiel für das innere Zeitbewusstsein. Wer ein Musikstück hört, bewegt sich auf zwei Zeitebenen: Zum einen hört er in der Jetzt-Zeit den jeweils erklingenden Ton. Zum anderen erinnert er sich an die vergangenen Töne, vielleicht auch an vergangene Hörerlebnisse des gleichen Musikstücks und anderer Musikstücke, und bildet mit seinem Vorstellungsvermögen eine Erwartung, welche Töne folgen werden. Diese beiden Ebenen unterscheiden an der Zeit die Modi des Wirklichen und des Möglichen: Was im Moment gehört wird, ist wirklich, und was zu hören erwartet wird, ist im Moment der Erwartung möglich. Mit diesen beiden Modi lassen sich die von Hegel gebrauchten Begriffe des Substrats und der Sache unterscheiden: Das Substrat bezieht sich auf die wirklich zu hörenden Töne. Wenn nach dem Substrat der Töne gefragt wird, so ist das der Tonvorrat der jeweiligen Musik. In der Vorstellungswelt kann dagegen weit über den verfügbaren Tonvorrat hinausgegangen werden. Es wird nicht nur in jedem Moment ein Ton erwartet, der noch nicht erklingt und in diesem Moment erst möglich ist, sondern es können in der Vorstellung ausgehend von den gegebenen Melodien auch »überirdische« Klänge »gehört« werden, die in einer eigenen Ordnung über den gegebenen Tonvorrat hinausgehen. Sie verlassen den sinnlich hörbaren Tonvorrat und werden daher nie als wirkliche Töne zu hören sein, aber die Musik im Ganzen lässt sie im inneren Ohr (dem »göttlichen Ohr«) erklingen. An ihnen ist der Unterschied von Substrat und Sache zu erkennen: Das Substrat ist der Fundus, aus dem alle wirklich hörbaren Töne hervorgehen. Wird gefragt, wie es möglich ist, über das Substrat hinauszugehen, so definiert diese Frage, was mit der Sache der Musik gemeint ist. Es ist die Ordnung der Musik, dank derer der Tonvorrat verlassen werden kann ohne in Chaos oder Kakophonie zu verfallen, sondern in höhere Klänge. Honoré Balzac (1799-1850) hat in seinen Erzählungen Das unbekannte Meisterwerk (1831) und Seraphita (1835) für die Darstellung einer solchen Kunst die unübertroffenen Worte gefunden.
Kulturelle Präferenzen für bestimmte Intervalle (Knotenlinie)
Die im Moment des Musikhörens erwarteten Töne befinden sich im Modus des Möglichen. In der Regel gibt es unterschiedliche Töne, die folgen können, und oft spielen der Komponist und der Interpret mit der Möglichkeit, die Erwartungen des Hörers bewusst zu täuschen und in die Irre zu führen. Daher kann im Moment des Musikhörens genau genommen für alle im gegebenen Tonvorrat verfügbaren Töne nur ihre jeweilige Wahrscheinlichkeit bestimmt werden, mit der sie auftreten werden. In Anlehnung an den von der Quantenmechanik gebrauchten Begriff kann von der Übergangswahrscheinlichkeit gesprochen werden, welches Intervall dem aktuell gehörten Ton folgen wird.
Diese Übergangswahrscheinlichkeiten von einem Intervall zum nächsten sind gebunden an die jeweilige Musikkultur und haben sich historisch gravierend geändert. In bestimmten Kulturen und Tonsystemen werden jeweils bestimmte Intervalle bevorzugt oder sogar verboten. Zum Beispiel gilt in unserer Kultur der Tritonus als dissonant und kommt nur selten vor, während die Quart (das Martinshorn, der Tusch beim Karneval) sehr häufig zu hören ist.
So wie sich die Wahlverwandtschaften entlang einer Knotenlinie von einem Zustand in den nachfolgenden ändern können, gilt das auch für die erwarteten Intervalle. Das wichtigste Beispiel ist die Terz. In der antiken Musik Griechenlands waren nur Oktaven, Quinten und Quarten erlaubt, weil nur sie in die pythagoreischen Verhältnisse passen. Erst seit ungefähr 700 n.Chr. wurden in England Terzen eingeführt und galten aus Sicht der früheren Musik als barbarisch. Erst mit der Terz wurde jedoch Mehrstimmigkeit möglich. Seither ist die Terz eine der häufigsten Intervalle. Am Beispiel der Terz können daher sehr gut die Begriffe Wahlverwandtschaft, Übergangswahrscheinlichkeit und Knotenlinie veranschaulicht werden: Für sich ist die Terz eine Beziehung. Die gefühlte Nähe (Übergangswahrscheinlichkeit, Wahlverwandtschaft) zweier Töne im Terz-Intervall hat sich kulturell radikal geändert und zeigt den typischen Verlauf einer Knotenlinie. Es kann ganz deutlich von einem Systemwechsel mit einem qualitativen Sprung von der antiken zur modernen Musik gesprochen werden.
Tonsysteme und ihre realen Maße (Harmonien)
Wenn das gleiche Intervall in einer Umgebung als Konsonanz und in einer anderen Umgebung als Dissonanz empfunden wird, liegt das am jeweiligen Tonsystem und seinen Harmonien. Das ursprüngliche und in allen Kulturen nachweisbare Tonsystem ist die Pentatonik (siehe auch musicacademy). Bei der Pentatonik beschränkt sich der Tonvorrat auf 5 Töne, die in genau definierten Intervallen zueinander stehen. Wer sich einmal an ein Klavier gesetzt hat, kennt das Phänomen, dass jede beliebige Folge von Tönen, die nur auf den schwarzen Tasten gespielt wird, auf eine elementare Weise harmonisch klingt. Die Gesamtheit der schwarzen Tasten und die ihr zugrunde liegenden Regeln der Tonabstände ist ein Beispiel für ein System, dessen Eigenschaften ein bestimmtes Schönheits-Maß erfüllen. In der Pentatonik sind alle Intervalle gleichberechtigt. In gewisser Weise gibt es keine Unterscheidung in Konsonanzen und Dissonanzen. Alles klingt schön.
Der Übergang von der Pentatonik zur Heptatonik, deren Tonvorrat von 5 auf 7 Töne erweitert ist, wird mit der Legende von Pythagoras in der Schmiede verbunden und darüber mit der noch älteren mythischen Erzählung der Idäischen Daktylen. Das sind »dämonenartige Gestalten, denen die Auffindung und erste Bearbeitung des Eisens und Kupfers zugeschrieben wird« (Wikipedia, abgerufen am 27.1.2019). Mit ihnen ist zugleich der Ursprung des Begriffs ‘Chemie’ erreicht, der nichts anderes beschreibt als die frühe Schmiedekunst. Wenn man so will, ist es die Sache der Chemie, die Pythagoras in der Schmiede hörte und die ihn zum Bruch von der Pentatonik zur Heptatonik führte. Spätere Beispiele für Heptatonik sind die üblichen Dur- und Moll-Tonleitern, die Kirchentonarten, aber auch die Zigeunertonleitern und die meisten Bluestonleitern. Sie umfassen jeweils 7 Töne und unterscheiden sich dadurch voneinander, in welchen Intervallen die Töne angeordnet sind.
Amboss und Hammer sind in wörtlichem Sinn das ursprüngliche physische Material, aus dem die Musik hervorgeht. Komponisten sind sich dessen immer bewusst. Wenn in einem Musikstück auf die elementare Gewalt der Musik zurückgegangen werden soll, kehren sie wieder, so bei Richard Wagner in den Opern Rheingold und Siegfried und im Hammerschlag der 6. Sinfonie von Gustav Mahler, ganz zu schweigen von der Wiederverwendung von Amboss und Hammer in der Punkmusik, etwa durch FM Einheit, dem Schlagzeuger der Musikgruppe Einstürzende Neubauten.
Auf welche höhere Ordnung verweisen die unterschiedlichen Tonsysteme wie Pentatonik und Heptatonik, aus deren Eigenschaften sie sich unterscheiden lassen? Gibt es überhaupt eine solche Ordnung, oder führen die Tonsysteme entlang der Knotenlinie in einen unbestimmten, maßlosen Grenzzustand? Zumindest in der neuzeitlichen, westlichen Musik gelten als Tonvorrat der höheren Ordnung wiederum in Berufung auf Pythagoras die 12 Töne, die ursprünglich in pythagoreischer Stimmung und später in temperierter Stimmung angeordnet werden. Die Pythagoras zugeschriebene Ordnung ging noch nicht auf und enthielt störende Momente wie die sogenannten Wolfsquinten und das pythagoreische Komma. Die heute übliche Lösung wurde erst 1681 von Andreas Werckmeister (1645-1706) in seiner Schrift Orgel-Probe oder kurtze Beschreibung … wie … ein Clavier wohl zu temperiren … sey eingeführt (Werckmeister-Stimmung). Das sind die 12 Töne im temperierten System mit zwölfgeteilter Oktav, wobei alle Töne zusammengefasst sind, die durch enharmonische Verwechslungen aufeinander fallen. Zwischen den verschiedenen Dur- und Moll-Tonleitern der temperierten Stimmung kann nach festen Regeln moduliert werden, z.B. von C-Dur nach a-Moll. Alles jenseits dieser Tonleitern gilt als maßlos.
Seit dem 19. Jahrhundert wird mit weiteren Möglichkeiten experimentiert. Legendär ist der Tristan-Akkord von Wagner, der sich allen bekannten Tonleitern entzieht und daraus seinen besonderen Klangreiz gewinnt. Es gibt auch Tonarten mit einem Tonvorrat von 6 Tönen wie z.B. der von Skrjabin genutzte und von der Theosophie aufgenommene Mystische Akkord und bestimmte Bluestonleitern, die die Pentatonik um einen Tritonus ergänzen. Andere Beispiele finden sich bei Liszt, Debussy, Ravel und Bartok. Olivier Messiaen (1908-1992) hat 7 Modi mit begrenzten Transpositionsmöglichkeiten unterschieden (nicht zu verwechseln mit den logischen Modi von Wirklichkeit, Möglichkeit und Notwendigkeit). Der 1. Modus ist eine Unterteilung in 6 Töne, die jeweils durch einen Ganztonabstand getrennt sind, der 2. Modus ist eine Unterteilung in 8 Töne mit alternierenden Halb- und Ganztonschritten. Auf Grundlage weiterer mathematischer Studien insbesondere von Rudolf Wille (1937-2017) und neuer kompositorischer Experimente hat Martin Münch eine systematische Darstellung aller kombinatorischen Möglichkeiten vorgeschlagen. Die 12 Töne werden wie gewohnt auf einem regelmäßigen Zwölfeck angeordnet. Innerhalb dieses Systems können alle kombinatorisch möglichen Modi unterschieden werden. Ein Modus enthält »einen Klang, der aus n Tönen besteht und den Ambitus (Tonumfang) einer Oktave nicht überschreitet« (Münch, S. 188). Mit diesen Regeln lassen sich 354 Modi finden, wenn auch die Grenzfälle, dass kein Ton erklingt (Pause), dass nur ein Ton für sich klingt und dass alle Töne erklingen mitgezählt werden. Innerhalb dieser Modi gibt es 66 Fünf-Klänge (darunter Ganztöne, Ondine, Raga, Pentatonik). In der systematischen Darstellung von Münch ist die Pentatonik derjenige Modus, der sich innerhalb der 66 verschiedenen Fünf-Klänge durch das höchste Maß an Gleichverteilung der 5 Töne auszeichnet.
Auf dem Klavier werden mit der Pentatonik die schwarzen Tasten belegt und mit der C-Dur-Tonleiter auf den weißen Tasten die 7 Töne des einfachsten heptatonischen Systems.
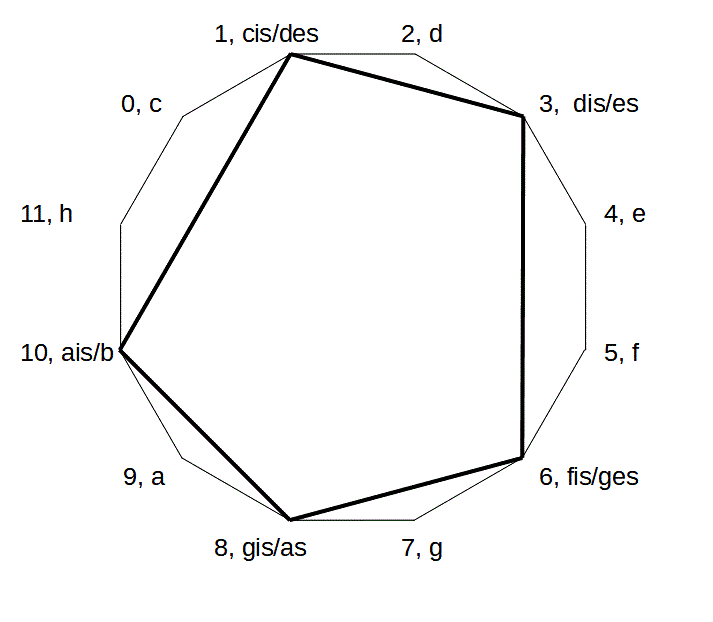
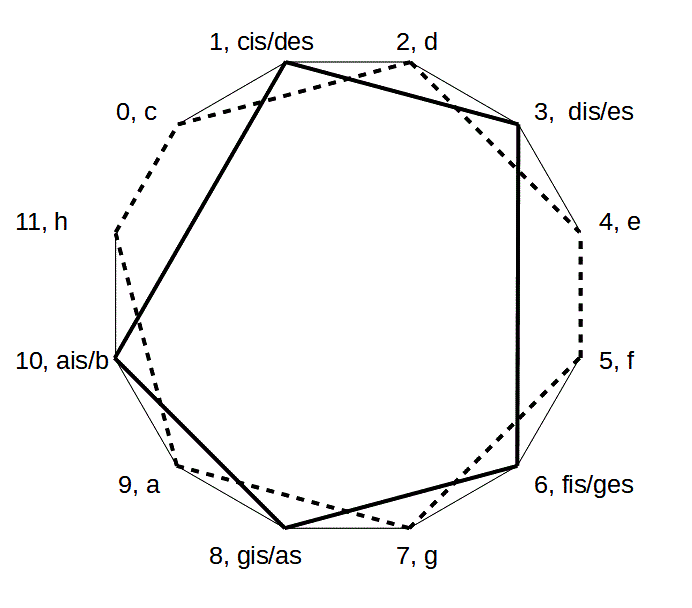
Figur 7 a,b: Pentatonik und C-Dur-Tonleiter innerhalb der 12 Töne des temperierten Systems
Das Zwölfeck zeigt den gesamten Tonvorrat. Die Pentatonik wählt 5 Töne daraus aus, das sind auf dem Klavier die schwarzen Tasten. Die C-Dur-Tonleiter wählt die anderen 7 Töne, das sind auf dem Klavier die weißen Tasten.
Auf diese Weise kann im Ganzen zwischen Substrat, Ordnung und den Prinzipien der Ordnung unterschieden werden. Das Substrat sind die Töne, die z.B. mit Hammer und Amboss oder in verfeinerter Form mit einem Klavier zum Klingen gebracht werden können, wenn dort das »Spielwerk von Tasten, Federn, Zungen, Stößeln, Dämpfern und Hämmern, die beim Tastendruck die Saiten anschlagen und damit den Klang erzeugen« (Wikipeida, abgerufen am 27.1.2019). Die Ordnung ist die Frage, welcher übergreifende Tonvorrat für alle Tonsysteme ausgewählt wird und nach welchen Regeln er aufgebaut ist. In der westlichen Musik fallen die Gesamtheit der Pentatonik (schwarze Tasten) und der Heptatonik der C-Dur-Tonleiter (weiße Tasten) direkt mit den 12 Tönen der Ordnung zusammen. Allerdings wäre auch denkbar, dass für die Ordnung ein abstrakter Tonvorrat angenommen wird, der aus Gründen für die Herstellung der Ordnung Elemente enthält, die niemals erklingen werden und nicht zum Substrat des Tonvorrats eines Tonsystems gehören. Heute sind aus anderen Kulturen weitere Ordnungen bekannt, so die mikrotonale Musik mit weit mehr als 12 Tönen.
Wie lassen sich die Ordnungen und ihre Prinzipien unterscheiden? Das sind im Beispiel der Musik die jeweiligen Stimmungen. So gilt für die pythagoreische Stimmung die Quintenreinheit. Die Quinte leitet sich von der Fünf her, die für Pythagoras das Prinzip des Kosmos ist. Dagegen gilt für die wohltemperierte Stimmung das Prinzip der Gleichverteilung innerhalb der Oktave. Das deutet auf das für die Neuzeit gültige Prinzip der Harmonie. Diese Harmonie wird jedoch meist statisch und in festen mathematischen Abständen gedacht. Hegel möchte darüber hinaus gehen und strebt eine dynamische Logik an, deren Prinzip nicht mehr die Fünf oder ein bestimmtes Maß wie der Goldene Schnitt ist, sondern die Lebendigkeit. Wird dafür nach einem Beispiel in der Musik gesucht, wäre dies in meinem Verständnis eine improvisierende Musik, die im richtigen Maß frei zu improvisieren und zwischen unterschiedlichsten Modi zu wechseln vermag.
Johannes Kepler (1571-1630) befand sich auf der Schwelle zur Neuzeit. Er hat nicht nur das bis heute maßgebliche Werk über die Weltharmonie und die Sphärenmusik geschrieben, sondern ihm ist es mit den nach ihm benannten Keplerschen Gesetzen erstmals gelungen, den Gedanken der Prinzipien einer Ordnung zu übertragen auf die Naturwissenschaft. Er ist daher für Hegel das große Vorbild nicht nur der Naturwissenschaft, sondern auch des philosophischen Denkens und ihrer gemeinsamen inneren Einheit. Kepler ging vom empirischen Material aus, entdeckte dort die inneren Ordnungen und an ihnen die ihnen zugrunde liegenden Prinzipien. An seinem System lässt sich die abschließende Frage der Logik der realen Maße erkennen: Welche Eigenschaften muss eine Ordnung haben, damit sich an ihr ihre inneren Prinzipien erkennen lassen? Die Ordnung muss auflösbar sein in eine absolute Indifferenz, die keineswegs leer ist, sondern sich in ihre inneren Faktoren zerlegen lässt. Die Knotenlinie der Zustände mit ihren jeweiligen Maßen geht in einen unendlich-fernen Grenzzustand über, der an sich die Prinzipien enthält, die der Unterscheidung in die verschiedenen Zustände zugrunde liegt.
In einer zusammenfassenden methodischen Überlegung können die sieben Grundbegriffe Beziehung, Wahlverwandtschaft, Knotenlinie, Substrat, Sache, Ordnung und Prinzip der Ordnung als eine Heptade verstanden werden, die über die übliche Triade (etwa von These, Anti-These und Synthese oder von Begriff, Urteil und Schluss) oder Tetrade (Allgemeines, Besonderes, Einzelnes, Rückkehr zum Allgemeinen in Hegels Entwurf der dialektischen Methode als Abschluss seiner Wissenschaft der Logik, HW 6.564) hinausgeht. Die Heptade kann mit Novalis als »Krumme Regel« oder »Krumme Linie« bezeichnet werden (siehe hierzu die Darstellung von Ulrich Gaier, der die zahlreichen Quellen von Novalis zusammenstellt). Mit der Heptade würde sich die Heptatonik auf methodischer Ebene reflektieren.
Zustände und ihre Übergangswahrscheinlichkeiten in der Quantenmechanik
Die von Hegel aus der Chemie und von Goethes gleichnamigem Raum übernommene Ausdrucksweise von Wahlverwandtschaften und Knotenlinien hat sich weder in der Philosophie noch in der Naturwissenschaft durchgesetzt. Stattdessen spricht die Quantenmechanik von Übergangswahrscheinlichkeit. Die wichtigste Erkenntnis der Quantenmechanik liegt jedoch im Übergang von Stoffen zu Zuständen. Während in der Chemie betrachtet wird, welche Stoffe miteinander wahlverwandt sind und miteinander reagieren können, spricht die Quantenmechanik von Zuständen. So kann ein Elektron sich nicht nur in Reaktion mit anderen Teilchen in ein neues Teilchen umwandeln, sondern seinen Zustand verändern. Allerdings hat sich nach meinem Eindruck in der Wissenschaft eine Sprachverwirrung ergeben, die bis zu impliziten Kategorienfehlern führt. Was ist mit Zustand gemeint, und wie lässt sich der Begriff des quantenmechanischen Zustands verbinden mit Hegels Unterscheidung in das Substrat und seine Zustände? Der Ausdruck »Zustand« wird auf mehreren Abstraktionsstufen gebraucht:
(a) Niveaus. Die Quantenmechanik bezeichnet die voneinander unabhängigen Eigenschaften eines Objekts (seine Messgrößen) sowohl als Quantenzahlen wie auch als Dimensionen (Achsen), so z.B. Ort, Impuls, Spin, Leptonenzahl. Innerhalb einer Dimension sind nur bestimmte Werte möglich, die bisweilen als Niveaus oder Zustände bezeichnet werden.
(b) Vektor-Zustände. Statt von Dingen wird von messbaren Objekten gesprochen. Die Gesamtheit der Messungen in allen Dimensionen (Quantenzahlen) gilt als der Zustand des Objekts, in dem es sich zum Zeitpunkt der Messung befindet. Die Gesamtheit wird als Vektor (Liste aller gemessenen Merkmale) dargestellt.
(c) Systemzustände. Es gibt übergreifende Systemzustände (vergleichbar den Aggregat-Zuständen und den von Hegel gemeinten Zuständen), bei denen sich das Verhalten der messbaren Objekte ändert und ihre Übergangswahrscheinlichkeiten ändern.
(a) Niveaus
Die Quantenmechanik bezeichnet die von ihr an ihren Objekten beobachteten und beschriebenen, voneinander unabhängigen Eigenschaften als Dimensionen, Messgrößen oder als Quantenzahlen. Innerhalb jeder Dimension (Quantenzahl) sind experimentell nur bestimmte Mess-Ergebnisse nachgewiesen worden, was mit dem Ausdruck ‘Quantenzahl’ im Unterschied zu einer Dimension hervorgehoben werden soll, deren Werte sich kontinuierlich ändern können. Die einzelnen diskreten Werte werden als Niveaus und manchmal auch als Zustände bezeichnet. Die Physiker suchen daher nach Modellen, mit denen erklärt werden kann, warum nur diese Ergebnisse auftreten, d.h. innerhalb des Modells möglich sind. Das klassische Beispiel sind die Elektronenbahnen im Bohrschen Atommodell. In diesem Modell kann sich ein Elektron nur auf bestimmten Bahnen bewegen. Wie der Sprung von einer Bahn zu einer anderen erfolgt, kann in diesem Modell nicht beschrieben werden. Die unterschiedlichen Bahnen (Niveaus, Zustände) verhalten sich mathematisch zueinander wie der Grundton und die Obertöne in der Musik. Für jedes Elektron kann indirekt gemessen werden, auf welcher Bahn es sich befindet, da beim Sprung von einer Bahn auf eine andere entweder Licht ausgestrahlt oder absorbiert wird.

Figur 6: Das Bohrsche Atommodell des Wasserstoffatoms
»Dem Elektron steht von allen klassisch möglichen Bahnen nur eine kleine Auswahl zur Verfügung. Auf diesen Bahnen behält das Elektron seine Energie, denn es erzeugt keine elektromagnetischen Wellen. Dies sind die stationären Zustände des Atoms« Wikipedia. ›n = 1‹ beschreibt den Grundzustand, ›n = 2‹ etc. die höheren Zustände (die Obertöne). Beim Sprung von einer Bahn auf eine andere (hier mit dem blauen Pfeil gezeichnet) wird eine Energiedifferenz frei oder absorbiert, die als Licht erscheint (dargestellt durch die rote Wellenlinie) und wahrgenommen werden kann.
Urheber: Von JabberWok, CC BY-SA 3.0, Link
Auch wenn das Atommodell von Bohr aufgegeben wurde, hat sich diese Methode der Modell-Bildung durchgesetzt. Wenn experimentell nur eine bestimmte Folge von Messwerten nachgewiesen werden kann, wird eine mathematische Funktion gesucht, die Werte liefert, die wie ein Grundton und seine Obertöne angeordnet sind (mathematisch handelt es sich um eine Fourier-Analyse). Diese Funktionen sind die kleinste Einheit des Hilbert-Raums, mit dem die Quantenmechanik dargestellt wird. Der Hilbert-Raum setzt sich daher aus Funktionen statt aus Punkten zusammen.
(b) Zustands-Vektoren |φ⟩
Jedes Teilchen wird beschrieben durch die voneinander unabhängigen Eigenschaften, die an ihm gemessen werden können. In der Messtheorie werden diese Eigenschaften als Messgrößen, in der Quantenmechanik als Quantenzahlen bezeichnet. Der Zustands-Vektor eines Teilchens ist die Liste dieser Eigenschaften. Sprachlich wird bisweilen nicht genau unterschieden zwischen (1) der Liste der Eigenschaften, (2) der Liste von Messwerten eines einzelnen gemessenen Objekts und (3) der Liste von Durchschnittswerten der Messungen eines Ensembles von messbaren Objekten.
(1) Systematisch ist auszugehen von der Liste der Eigenschaften. Das klassische Beispiel ist die Beschreibung des Elektronenzustands durch vier Quantenzahlen. An einem Elektron können mithilfe der heute verfügbaren Messmethoden nur vier voneinander unabhängige Eigenschaften gemessen werden. Sie werden als seine Quantenzahlen bezeichnet. Die Liste der Eigenschaften des Elektrons sieht daher so aus:
Liste der Eigenschaften des Elektrons (Elektronenzustand mit 4 Quantenzahlen)
1) die Schale n = 1,2,3, ..., auf der sich das Elektron befindet (Hauptquantenzahl)
2) das Orbital 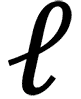 = 1,2,3,..., n−1 innerhalb der Schale n (Nebenquantenzahl)
= 1,2,3,..., n−1 innerhalb der Schale n (Nebenquantenzahl)
3) die z-Komponente des Drehimpulses m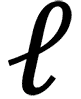 = −
= −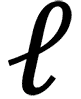 , −
, −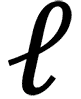 +1, ..., 0, ...,
+1, ..., 0, ..., 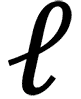 −1,
−1, 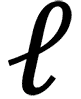 (magnetische Quantenzahl)
(magnetische Quantenzahl)
4) der Spin mS = +½, −½
Der Zustandsraum des Elektrons wird durch die vier voneinander unabhängigen Achsen n, 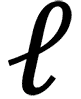 , m
, m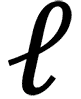 , mS (Schale, Orbital, Drehimpuls, Spin) beschrieben. Jede Kombination von Schale, Orbital, Drehimpuls, Spin ergibt einen theoretisch möglichen Zustand des Elektrons. Warum es gerade diese vier Achsen gibt und warum sie voneinander unabhängig sind, wird in der Quantenmechanik nicht erklärt, sondern als experimentelles Ergebnis der Messprozesse verstanden.
, mS (Schale, Orbital, Drehimpuls, Spin) beschrieben. Jede Kombination von Schale, Orbital, Drehimpuls, Spin ergibt einen theoretisch möglichen Zustand des Elektrons. Warum es gerade diese vier Achsen gibt und warum sie voneinander unabhängig sind, wird in der Quantenmechanik nicht erklärt, sondern als experimentelles Ergebnis der Messprozesse verstanden.
(2) Jede einzelne Messung identifiziert einen Zustand und kann als ein Punkt innerhalb des Zustandsraums dargestellt werden. Das ist die Bedeutung des Zustands-Vektors im engeren Sinn. Hiermit erklärt sich auch die sprachlich in die Irre führende Bezeichnung »Quantenzahl«. Unter einer Zahl wird gewöhnlich ein bestimmter einzelner Wert (hier ein konkreter Messwert) verstanden. Die Quantenmechanik bezeichnet mit »Quantenzahl« jedoch sowohl die einzelnen gemessenen Werte wie auch die Dimensionen (Messgrößen), innerhalb derer sie gemessen wurden.
(3) Um die Verwirrung perfekt zu machen, werden häufig im Zustands-Vektor als Quantenzahlen nicht die Ergebnisse einer einzelnen Messung, sondern die statistischen Durchschnittswerte einer Vielzahl von Messergebnissen eingetragen. Eine einzelne Messung zeigt, welche Eigenschaft für das bestimmte gemessene Objekt gilt. Wenn eine Vielzahl von Messungen durchgeführt wurde, kann ermittelt werden, welche Durchschnittswerte auftreten.
In dieser Gesamtheit von Zuständen treten Zustände auf, die in der klassischen Physik als unmöglich galten. Die klassische Physik hat nur solche Zustände "erlaubt", für die sie erklären konnte, wie ein Objekt in diesen Zustand gelangen kann. Anders gesagt: Die klassische Physik hat nur solche Modelle gesucht, mithilfe derer alle Zustände und die Übergänge von einem Zustand in einen anderen erklärbar sind. Die Quantenmechanik hat diese strenge Forderung an Modelle aufgeben müssen, da sie ständig Zustände nachgewiesen hat, für die nicht erklärbar ist, wie sie erreicht werden können. Sie begnügt sich daher mit Modellen, mit denen es mathematisch möglich ist, alle Zustände zu beschreiben und aufzuzählen, die experimentell nachgewiesen werden können, auch wenn es keine Erklärungen gibt, warum diese Zustände auftreten können. (Die Quantenmechanik bewegt sich daher in einer Situation, die mit der von Tycho Brahe vergleichbar ist. Er hat alle Himmelsbeobachtungen aufgezeichnet, die er beobachten konnte. Erst nach ihm konnten Kepler und Newton Gesetze finden, mit denen die Gesamtheit der Beobachtungen beschrieben und erklärt werden konnte. Vergleichbare Gesetze fehlen bis heute in der Quantenmechanik.)
Anmerkung 1: Wenn jede Quantenzahl als eine Funktion verstanden wird, die einen Grundton und seine Obertöne beschreibt, dann ist der Zustands-Vektor ein Akkord, der aus dem Zusammenklang der Quantenzahlen besteht, die im Zustands-Vektor beschrieben werden. Zum Beispiel ist der Elektronen-Zustand mit seinen vier Quantenzahlen ein Vierer-Akkord. Wird zusätzlich die Anordnung (die Reihenfolge) der vier Töne berücksichtigt, dann ist der Elektronen-Zustand eine Melodie aus vier Tönen.
Anmerkung 2: Paul Dirac führte 1930 die Bra-Ket Darstellung ein: |φ⟩ beschreibt einen Zustand im Ganzen. Es können auch die einzelnen Quantenzahlen aufgezählt werden, also z.B. für den Elektronenzustand |n, 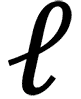 , m
, m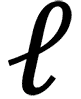 , mS⟩.
, mS⟩.
(c) Übergangswahrscheinlichkeiten ⟨φ|φ'⟩ (Wahlverwandtschaft)
Die Übergangswahrscheinlichkeiten beziehen sich auf die Zustands-Vektoren. Mit der Darstellung ⟨φ|φ'⟩ wird die Wahrscheinlichkeit beschrieben, dass ein Zustand ∣φ⟩ in den Zustand ∣φ'⟩ wechselt.
Die Übergangswahrscheinlichkeit ist die gesuchte Verallgemeinerung der Wahlverwandtschaft, mit der eine mathematische Darstellung möglich wird. Die Wahlverwandtschaft beschreibt die Wahrscheinlichkeit, dass zwei Stoffe miteinander reagieren und einen oder mehrere neue Stoffe erzeugen. Die Zustände vor und nach der Reaktion lassen sich als Vektor-Zustände beschreiben, wobei das Gemisch der verschiedenen Stoffe, die miteinander reagieren können, das messbare Objekt ist. Der Zustands-Vektor beschreibt den Zustand des Gemischs, d.h. die Konzentrationen der einzelnen Stoffe, die im Gemisch enthalten sind. Die Reaktionsgleichungen werden interpretiert als Übergänge von einem Zustand in einen anderen. Je größer die Wahrscheinlichkeit ist, dass zwei Stoffe miteinander reagieren, desto größer ist die Wahrscheinlichkeit, dass sie in einen Zustand wechseln, der dem Ergebnis der Reaktionsgleichung entspricht. Zum Beispiel kann eine Reaktionsgleichung
HCl + 2 NaOH → 2 H2O + NaCl
lies: 1 Mol Salzsäure und 1 Mol Natronlauge ergibt 2 Mol Wasser und 1 Mol Kochsalz
"übersetzt" werden in eine Darstellung
⟨HCl, 2 NaOH|2 H2O, NaCl⟩
lies: Ein Zustand aus 1 Mol Salzsäure und 1 Mol Natronlauge geht über in einen Zustand aus 2 Mol Wasser und 1 Mol Kochsalz
Verändern sich durch die Reaktion weitere Parameter wie z.B. die Temperatur des Systems, dann lässt sich das sehr übersichtlich in dieser Art der Darstellung ergänzen.
Damit können die von Hegel betrachteten chemischen Modelle verallgemeinert werden in die Schreibweise, die für die Quantenmechanik entwickelt wurde. Hier darf der Ausdruck »Quantenmechanik« nicht verwirren. Mit dieser Methode lassen sich alle messbaren Vorgänge beschreiben, nicht nur quantenmechanische, sondern auch chemische, biologische, neurologische etc. Daher wird sie dem allgemeinen Ansatz von Hegel am besten gerecht.
Geometrie der Hilberträume
Die Quantenmechanik spricht nicht von Veränderungen von Übergangswahrscheinlichkeiten in verschiedenen Systemzuständen entlang einer Knotenlinie, sondern von Symmetrien mit bestimmten Reichweiten. Wird die Reichweite überschritten, kommt es zum Symmetriebruch. Auf diese Weise sind die Symmetrien entlang der Reichweite angeordnet wie die Wahlverwandtschaften entlang der Knotenlinie. Für die Gesamtheit der Symmetrien wurde ein allgemeiner mathematischer Formalismus gefunden, doch gelingt es bis heute nicht, die Gravitation und die Aussagen der Allgemeinen Relativitätstheorie in diesen Entwurf aufzunehmen. Mit jeder Symmetrie werden statische Verhältnisse beschrieben, die innerhalb der jeweiligen Reichweite gelten, während die Relativitätstheorie Krümmungen des Raums betrachtet. Daher möchte ich die These vertreten, dass sich die Quantenmechanik und die Allgemeine Relativitätstheorie zueinander verhalten wie die Wahlverwandtschaften und die Knotenlinien. So wie Hegel gegenüber der Chemie seiner Zeit nachgewiesen hat, dass es nicht möglich ist, für die Wahlverwandtschaften und ihre Änderungen ein gemeinsames Maß zu finden, sondern beide unabhängig voneinander sind, so verhält es sich nach meiner Meinung auch für die Quantenmechanik und die Allgemeine Relativitätstheorie. Eine übergreifende Theorie wird daher keinen Erfolg haben, wenn sie versucht, die Aussagen der Allgemeinen Relativitätstheorie innerhalb einer erweiterten Quantenmechanik als eine eigene Symmetrie darzustellen, sondern es ist ein Ansatz notwendig, für beide einen übergreifenden Raum zu definieren, der in einer Analogie-Bildung aufgespannt ist auf den beiden Achsen der Quantenmechanik und der Allgemeinen Relativitätstheorie.
Vielleicht hilft zum besseren Verständnis der Vergleich mit der Musik.
– An die Stelle der Intervalle zwischen zwei Tönen treten die Übergangswahrscheinlichkeiten zwischen zwei Zuständen. Mit der Übergangswahrscheinlichkeit wird allerdings nicht mehr zwischen Beziehung und Wahlverwandtschaft unterschieden. Eine hohe Übergangswahrscheinlichkeit bedeutet eine enge Wahlverwandtschaft, eine niedrige Übergangswahrscheinlichkeit eine bloße Beziehung, die fast nie eintritt.
– So wie es in der Musik Tonleitern gibt, sind in der Quantenmechanik Symmetrien zu unterscheiden. Jede Symmetrie umfasst eine bestimmte Anzahl von Zuständen, für deren Übergänge es bestimmte Regeln gibt wie z.B. das Pauli-Verbot. Der Modulation von einer Tonart in eine andere entspricht der Übergang von einer Symmetrie in eine andere.
– In der westlichen Musik sind alle Tonleitern (Symmetrien) hergeleitet aus den 12 Tönen, mit denen eine Oktave unterteilt wird. Mir erscheint bis heute nicht ganz eindeutig, welcher mathematische Raum ihnen in der Quantenmechanik entspricht. Das ist naheliegenderweise der Hilbertraum aller Zustände, zugleich wird jedoch auch z.B. in der Schrödinger-Gleichung auf die Eigenschaften der imaginären Zahlen und damit auf die Zahlenebene der komplexen Zahlen Bezug genommen.
– Die pythagoreische bzw. temperierte Stimmung sind Ordnungen der Musik. Ihnen entsprechen geometrische Eigenschaften, die für die Abstandsfunktion im Hilbertraum formuliert werden, sowie die Ordnungsregeln komplexen Zahlen. Das ist im Hilbertraum der Satz des Pythagoras (wonach in einem rechtwinkligen Dreieck die Summe der Quadrate über die Katheten gleich dem Quadrat über der Hypotenuse ist) und bei den komplexen Zahlen die besondere Eigenschaft der imaginären Achse, mit der sie sich von üblichen Achsen mehrdimensionaler Räume unterscheidet.
– Schließlich kann nach den Prinzipien der Ordnung gefragt werden. Das sind analog zur Quintenreinheit bzw. gleichmäßigen Verteilung der musikalischen Stimmungen die Prinzipien, aus denen der Satz des Pythagoras bzw. das Besondere der imaginären Achse begründet wird. Eine solche Frage wird in der Mathematik und Naturwissenschaft nicht einmal gestellt, geschweige denn, in welchem Verhältnis die Prinzipien des Satzes von Pythagoras und der imaginären Achse zueinander stehen, und ob es ein beiden zugrunde liegendes einheitliches Prinzip gibt. Hegel kommt darauf zurück, wenn er in seiner Logik der Ideen nach dem Stellenwert des Satzes von Pythagoras fragt.
Die Geometrie des Hilbertraums wird in drei Schritten skizziert, wobei das Verhältnis zu den imaginären Zahlen und deren Eigenschaften offen bleibt. Das ersetzt keine genaue Ausarbeitung, sondern kann nur die Richtung zeigen, in der diese möglich sein kann.
(1) So wie in der temperierten Stimmung die Töne gleichmäßig entlang der Tasten eines Klaviers angeordnet werden können, und so wie die natürlichen Zahlen auf der Zahlengerade ℕ liegen, liegen die quantenmechanischen Zustände φ in einem unendlich-dimensionalen Raum, den ich mit dem Buchstaben  bezeichne, den Raum aller Zustände. So wie zwei benachbarte Töne in der Beziehung (Intervall) einer Prim stehen und auf der Zahlengerade jeweils zwei benachbarte Zahlen durch den Abstand 1 voneinander getrennt sind, kann in
bezeichne, den Raum aller Zustände. So wie zwei benachbarte Töne in der Beziehung (Intervall) einer Prim stehen und auf der Zahlengerade jeweils zwei benachbarte Zahlen durch den Abstand 1 voneinander getrennt sind, kann in  eine Abstandsfunktion eingeführt werden: Die Übergangswahrscheinlichkeit von einem Zustand φ zu einem anderen Zustand φ' wird als ihr Abstand definiert. Hilbert hat gezeigt, dass in diesem Raum in verallgemeinerter Weise der Satz des Pythagoras gilt.
eine Abstandsfunktion eingeführt werden: Die Übergangswahrscheinlichkeit von einem Zustand φ zu einem anderen Zustand φ' wird als ihr Abstand definiert. Hilbert hat gezeigt, dass in diesem Raum in verallgemeinerter Weise der Satz des Pythagoras gilt.
(2) Wird nach den Eigenschaften der Übergangswahrscheinlichkeiten gefragt, so ist der Raum aller Übergangswahrscheinlichkeiten zu untersuchen und zu fragen, welche geometrischen Eigenschaften dort bestimmt werden können. Es wird skizziert, wie dieser Raum analog zum Raum ℕ  ℕ entworfen werden kann:
ℕ entworfen werden kann: 

 . Das ist der Raum aller Wahlverwandtschaften (Übergangswahrscheinlichkeiten). Ich nenne ihn
. Das ist der Raum aller Wahlverwandtschaften (Übergangswahrscheinlichkeiten). Ich nenne ihn  .
.
(3) Um Knotenlinien zu beschreiben, entlang derer sich die Übergangswahrscheinlichkeiten (Wahlverwandtschaften) ändern, ist abschließend der Raum  aller Parameter τ zu betrachten, die sich entlang einer Knotenlinie ändern können. Das ergibt den Raum aller Knotenlinien, der als
aller Parameter τ zu betrachten, die sich entlang einer Knotenlinie ändern können. Das ergibt den Raum aller Knotenlinien, der als  bezeichnet werden kann. Da die Übergangswahrscheinlichkeiten als Abstände angesehen werden, kann dieser Raum verstanden werden als ein gekrümmter Raum, in dem sich die Abstände verändern, d.h. krümmen. Erst in diesem Raum ist eine Vereinheitlichung von Allgemeiner Relativitätstheorie und Quantenmechanik darstellbar. Dies ist für mich zugleich der Raum, den Hegel mit der Frage nach dem Maßlosen angesprochen hat. Seine Geometrie beschreibt die von Hegel gesuchten Eigenschaften (Ordnungen) und deren Prinzipien, aus denen sich die Übergänge der Wahlverwandtschaften entlang der Knotenlinie erklären lassen.
bezeichnet werden kann. Da die Übergangswahrscheinlichkeiten als Abstände angesehen werden, kann dieser Raum verstanden werden als ein gekrümmter Raum, in dem sich die Abstände verändern, d.h. krümmen. Erst in diesem Raum ist eine Vereinheitlichung von Allgemeiner Relativitätstheorie und Quantenmechanik darstellbar. Dies ist für mich zugleich der Raum, den Hegel mit der Frage nach dem Maßlosen angesprochen hat. Seine Geometrie beschreibt die von Hegel gesuchten Eigenschaften (Ordnungen) und deren Prinzipien, aus denen sich die Übergänge der Wahlverwandtschaften entlang der Knotenlinie erklären lassen.
(1) Der Raum aller Zustände 
Während die klassische Mechanik als kleinste Einheit dimensionslose Partikel (Objekte) annimmt, die formal mit mathematischen Punkten übereinstimmen, geht die Quantenmechanik von mehrdimensionalen Zuständen als kleinster Einheit aus, im Beispiel des Elektrons ein Zustand aus 4 Quantenzahlen. Die Zustände können daher nicht wie die Zahlen auf einer eindimensionalen Gerade angeordnet werden, sondern erst in einem größeren Raum.
In diesem Raum kann dennoch eine Geometrie definiert werden, in dem die Übergänge ⟨φ | φ'⟩ als Abstand zwischen je zwei Zuständen φ und φ' gedeutet werden. Bei einem kleineren Abstand stehen sich beide Zustände näher und die Übergangswahrscheinlichkeit ist größer, bei einem größeren Abstand sind sie einander ferner und die Übergangswahrscheinlichkeit ist kleiner. Damit wird eine Geometrie möglich, die unmittelbar auf Wahlverwandtschaften aufgebaut ist. Die Wahlverwandtschaft wird als Abstand beschrieben, die Knotenlinie als Krümmung, entlang derer sich die Abstände ändern. Führt die Krümmung zu Brüchen, dann liegen Wechsel von System-Zuständen vor.
Mit dem Hilbert-Raum ist es gelungen zu zeigen, dass diese Geometrie eine Verallgemeinerung der euklidischen Geometrie ist und diese als Grenzfall enthält.
Anmerkung (Wellenfunktion): In der Physik wird häufig gesagt, dass die Objekte der Quantenmechanik nicht mehr wie in der klassischen Physik sinnlich wahrnehmbare Gegenstände, sondern Wellenfunktionen seien. Beim Begriff ‘Wellenfunktion’ wiederholt sich die Mehrdeutigkeit des Begriffs ‘Zustand’. Es ist zu unterscheiden: (1) Mit Wellenfunktionen können physische Wellen wie z.B. Wasser-, Schall- oder Lichtwellen beschrieben werden. (2) Mit einer Wellenfunktion kann beschrieben werden, welche unterschiedlichen Niveaus (Werte) innerhalb einer Quantenzahl (Dimension) möglich sind. (3) Sind die unterschiedlichen Niveaus innerhalb einer Messgröße (Dimension, Quantenzahl) gefunden, dann kann mit einer Wellenfunktion die Wahrscheinlichkeitsverteilung beschrieben werden, wie sich die gemessenen Werte auf die unterschiedlichen Niveaus verteilen. In diesem Sinn werden die Objekte ersetzt durch Wellenfunktionen, und die Wellenfunktionen sind die kleinste Einheit des Hilbert-Raums. (Siehe hierzu Claus Kiefer Quantengravitation in Esfeld.)
(2) Der Raum aller Wahlverwandtschaften (Übergangswahrscheinlichkeiten) 
Die Übergangswahrscheinlichkeit kann als der Abstand (Relation) zwischen zwei Zuständen verstanden werden. Gibt es auch andere Relationen zwischen Zuständen? Für die Quantenmechanik genügt es bisher, die Übergangswahrscheinlichkeiten experimentell auszuwerten und zu messen und keine weiteren Relationen zwischen den Zuständen zu betrachten. Schon die Beispiele der Chemie und Entropie legen nahe, eine Vielfalt von Relationen in Betracht zu ziehen, aus denen die Reaktionsstärke als eine komplexe Resultierende hervorgeht, wie z.B. den Aufbau der Moleküle, der beteiligten Ionen und der geometrischen Anordnung der Stoffe im jeweiligen Medium. Die Festkörperphysik und die Materialwissenschaft zeigen ständig neue Relationen, und es ist für mich davon auszugehen, dass wir erst am Beginn der Entwicklung stehen. Das elementarste Beispiel sind die natürlichen Zahlen. Im einfachsten Fall gilt als Relation zweier Zahlen ihr Abstand voneinander: Der Abstand der beiden Zahlen 18 und 23 ist 5, der Abstand zweier benachbarter Zahlen wie z.B. 7 und 8 ist 1. Es können aber auch andere Relationen zwischen je zwei Zahlen bestimmt werden, z.B. das Vielfache. So stehen in einem einfachen Beispiel die beiden Zahlen 13 und 39 im Verhältnis 3 zueinander, da 39 = 3 · 13 gilt. Weitere Relationen zwischen je zwei Zahlen sind der größte gemeinsame Teiler und das kleinste gemeinsame Vielfache. Es gibt befreundete Zahlen und teilerfremde Zahlen sowie eine Vielfalt von Eigenschaften, die darauf aufbauen. An dieser Stelle soll genügen hervorzuheben, dass es zwischen den Zahlen eine Vielzahl von Relationen gibt und daher naheliegt, einen eigenen Raum zu entwerfen, der alle Relationen zwischen den Zahlen enthält. Es kann vermutet werden, dass für diesen Raum im Ganzen geometrische Eigenschaften gelten, so wie die Zahlengerade nicht nur die einzelnen Zahlen enthält, sondern durch Eigenschaften wie die Transitivität und Kontinuität bestimmt ist.
Um die Geometrie aller Relationen zu beschreiben, wird übergegangen vom Raum der natürlichen Zahlen in den Raum aller Relationen zwischen jeweils zwei natürlichen Zahlen. Mathematisch ist das am Beispiel der natürlichen Zahlen der Übergang von der Zahlengeraden ℕ zum Zahlengitter ℕ  ℕ. Es ist kein Zufall, dass das Zahlengitter anschaulich sehr ähnlich aussieht wie das Kreuzmuster von Kettfaden und Schussfaden in der Webtechnik, auf die sich Hegel bezog.
ℕ. Es ist kein Zufall, dass das Zahlengitter anschaulich sehr ähnlich aussieht wie das Kreuzmuster von Kettfaden und Schussfaden in der Webtechnik, auf die sich Hegel bezog.
Entsprechend sind die Wahlverwandtschaften (Übergangswahrscheinlichkeiten) darzustellen. Wird der Raum aller Zustände mit  bezeichnet, dann liegen die Übergangswahrscheinlichkeiten im Raum
bezeichnet, dann liegen die Übergangswahrscheinlichkeiten im Raum 

 . Dieser Raum sei mit
. Dieser Raum sei mit  bezeichnet. Es gilt also:
bezeichnet. Es gilt also: 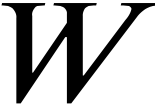 =
= 

 , wobei W für Wahlverwandtschaft steht.
, wobei W für Wahlverwandtschaft steht.
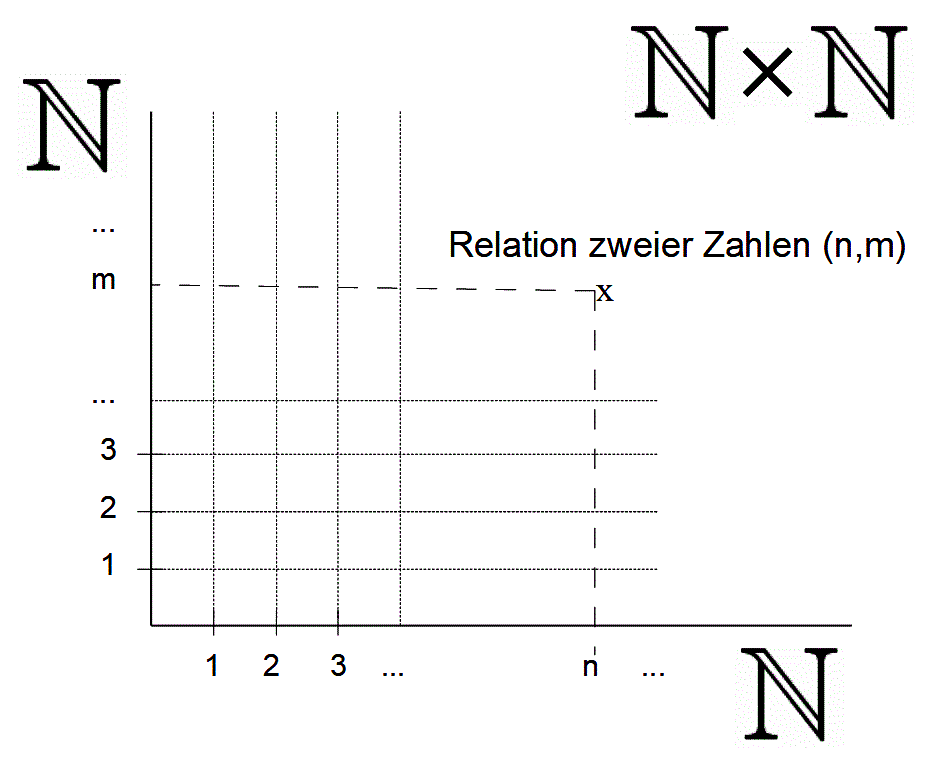
Figur 8 a,b: Zahlengitter, Wahlverwandtschaft
Auf der horizontalen und vertikalen Achse sind jeweils alle natürlichen Zahlen bzw. alle Zustände φ und φ' aus  eingetragen. Die Gesamtheit aller Wahlverwandtschaften ist die Fläche
eingetragen. Die Gesamtheit aller Wahlverwandtschaften ist die Fläche  . Jeder Punkt stellt ein Paar (φ,φ') dar, welches die Übergangswahrscheinlichkeit von φ zu φ' ist.
. Jeder Punkt stellt ein Paar (φ,φ') dar, welches die Übergangswahrscheinlichkeit von φ zu φ' ist.
Diese Schreibweise ist auf den ersten Blick umständlich und ungewohnt, aber sie zeigt das Wesentliche, worauf es hier ankommt: Die Nachfolger-Relation kann nicht in dem Raum liegen, dessen Elemente in Relation zueinander gesetzt werden. Sie liegt in einem größeren Raum, der den Raum der Elemente der Relation als Grenzfall enthält. Während Kategorien wie Qualität und Quantität auf einzelne Substanzen bezogen werden können und deren Eigenschaften beschreiben, gilt die Kategorie der Relation in einem größeren Raum. Erst dort wird sich die Systembewegtheit im Ganzen beschreiben lassen.
Mit dieser Darstellung sind zwei mögliche Missverständnisse verbunden.
(1) Es ist nicht einfach zu verstehen, dass die meisten Relationen r(n,m) zwar eine Beziehung zweier Zahlen n und m darstellen, aber wertmäßig eine Zahl ergeben wie z.B. den Abstand, den größten gemeinsamen Teiler oder eine Übergangswahrscheinlichkeit. Diese Werte sind ihrerseits Zahlen, die auch auf der Zahlengerade eingetragen sind. (Es gibt auch komplexe Relationen, deren Wert keine natürliche oder reelle Zahl, sondern wiederum eine komplexe Zahl mit zwei Koordinaten ist. Darauf wird an anderer Stelle in einem Beitrag über imaginäre Zahlen näher eingegangen.) Wenn die Werte der reellen Relationen wiederum gewöhnliche Zahlen sind, warum ist dann die Unterscheidung in Zahlengerade und Zahlengitter notwendig? Das soll am einfachsten Beispiel verdeutlicht werden, wenn als Relation der Abstand gewählt wird. Im Zahlengitter ist an jedem Punkt (m,n) der Wert der Abstandsrelation r(n,m) = |n - m| der beiden Zahlen m und n einzutragen. Das Ergebnis ist ein Skalarfeld, das allen Punkten im Zahlengitter eine Zahl zuordnet.

Figur 9: Zahlengitter mit den Werten der Abstands-Relation
Zum Beispiel ist der Abstand der Zahlen 3 und 2 mit 1 gegeben, oder von 2 und 0 mit 2.
Figur 9 zeigt, wie die Werte der Abstände im Zahlengitter symmetrisch angeordnet sind. Auf jeder Diagonale liegen jeweils identische Werte, und die Werte wiederholen sich nach links oben und nach rechts unten, da für den Abstand die Symmtrie angenommen wird, dass für den Abstand zweier Zahlen n und m gleichbedeutend ist, den Abstand von n nach m oder von m nach n zu messen. Diese geometrischen Verhältnisse zeigen in einem einfachen Beispiel, wie in der Zahlenebene Eigenschaften von Relationen erkannt werden können, die Verlaufsformen und Symmetrien ihrer Werte. Wird statt des Abstandes eine andere Relation gewählt, sind identische Werte nicht mehr auf geradlinigen Diagonalen und symmetrisch angeordnet, sondern können ganz andere Verläufe nehmen. Schon das Beispiel der Teiler-Relation zeigt ein weit komplexeres Bild. In diesem Beispiel ist im Zahlengitter für jeweils zwei Zahlen n und m ihr Teiler eingetragen, z.B. für die beiden Zahlen 2 und 3 der Teiler 2 / 3 = 0,67 oder für die beiden Zahlen 2 und 1 der Teiler 2 / 1 = 2. Weil Teilen durch 0 nicht möglich ist, ist für den Teiler 0 n / 0 = n.a. gesetzt, wobei ‘n.a.’ für ‘nicht anwendbar’ steht.

Figur 10: Zahlengitter mit den Werten der Teiler-Relation
Jeder Relation liegt eine Rechenoperation zugrunde. Der Abstand zweier Zahlen n, m ist ihre Differenz n − m. Wird als Relation das Vielfache gewählt, dann stehen zwei Zahlen n und m in der Beziehung n / m. Die Gesamtheit aller Operationen, die aus zwei Zahlen n und m eine neue Zahl r(n,m) bildet, ist identisch mit der Gesamtheit aller Relationen.
Wird eine Vielzahl von Relationen und ihrer geometrischen Verhältnisse betrachtet, ist übergeordnet zu fragen, ob es gemeinsame geometrische Eigenschaften gibt, die für alle Relationen gelten. In welchen Beziehungen stehen Relationen zueinander, und kann es Übergänge von einer Relation zu einer anderen geben? (Der Physiker David Bohm hat Fragen dieser Art am Beispiel des Verlaufs von möglichen Teilchenbahnen gestellt. Er hat sich damit aber offenbar zu weit vom Grundverständnis der heutigen Physik entfernt. Siehe den Beitrag über Quantenphysik.)
(2) Jeder verbindet mit graphischen Darstellungen spontan die Vorstellung einer Funktion, die jedem Wert x (dem Argument) einen Funktionswert f(x) zuordnet. Das führt jedoch bei der Gesamtheit aller Relationen zu einem Missverständnis. Hier wird nicht jedem Wert n ein anderer Wert m(n) zugeordnet, sondern im Zahlengitter jedem Zahlenpaar (m,n) ein Wert r(m,n). Das bedeutet, dass jedem Punkt (m,n) auf der Ebene ein eigener Wert zugeordnet wird. Hier ergeben sich völlig neue mathematische Verhältnisse. Die Zahlenebene hat eigene Eigenschaften, die sie von der Zahlengerade unterscheiden. Sie kann als Ebene der komplexen Zahlen verstanden werden mit eigenen Regeln für Addition und Multiplikation, die im Grenzübergang auf die reellen Zahlen mit den üblichen Regeln übereinstimmen. Die hier betrachteten Funktionen r(m,n) sind ein Beispiel einer reell-wertigen, komplexen Funktion und erfordern ein völlig neues anschauliches Verständnis. Siehe hierzu den Beitrag über die imaginären Zahlen.
Hegel hat zwar die imaginären Zahlen gekannt, sich aber meines Wissens nirgends zu ihnen geäußert. Diese Darstellung soll zeigen, dass er mit seiner Unterscheidung in Stoffe, Wahlverwandtschaften, Knotenlinien, Ordnungen und deren Prinzipien implizit ein Verständnis nahegelegt hat, das zu den imaginären Zahlen führt.
Der Unterschied von ℕ und ℕ  ℕ ist das Modell, an dem die verschiedenen Begriffe des Substrats differenziert werden können.
ℕ ist das Modell, an dem die verschiedenen Begriffe des Substrats differenziert werden können.
– Das Substrat der Zahlen ist die Zahlengerade ℕ, auf der die Zahlen liegen.
– Das Substrat der Relationen ist das Zahlengitter ℕ  ℕ , auf dem alle Relationen eingetragen sind.
ℕ , auf dem alle Relationen eingetragen sind.
– Die von Hegel im Kapitel über das Maßlose angesprochene Ordnung ist die Geometrie des Zahlengitters. Deren Eigenschaften sind zu unterscheiden von den Eigenschaften der einzelnen Punkte, die im geometrischen Raum liegen. Im euklidischen Raum haben Punkte die Eigenschaft der Dimensionslosigkeit, und in der Quantenmechanik haben die Zustände die mit den Quantenzahlen gegebenen Eigenschaften. Diese Eigenschaften sind zu unterscheiden von den Eigenschaften der Ordnung der Geometrie, in der sie angeordnet sind. Die Ordnung hat Eigenschaften wie den Satz des Pythagoras oder die algebraischen Regeln der komplexen Zahlen.
(3) Der Raum aller Kotenlinien 
Abschließend ist zu berücksichtigen, dass sich die Wahlverwandtschaften (φ, φ') verändern können, wenn sich der übergreifende Systemzustand durch die Variation eines Parameters τ verändert. Beispiele können die Temperaturerhöhung oder das Zutropfen von anderen Stoffen sein.
Wird das verallgemeinert auf die Gesamtheit aller Zustände, ihrer Wahlverwandtschaften und Umgebungsparameter τ, dann ergibt sich der Raum  , in dem alle Knotenlinien dargestellt werden können:
, in dem alle Knotenlinien dargestellt werden können:
 =
= 



lies: eine Knotenlinie k ∈  zeigt die Veränderung einer Wahlverwandtschaft w = (φ,φ') ∈
zeigt die Veränderung einer Wahlverwandtschaft w = (φ,φ') ∈  in eine neue Wahlverwandtschaft w' = (φ,φ') ∈
in eine neue Wahlverwandtschaft w' = (φ,φ') ∈  abhängig von einem veränderten Systemparameter τ ∈
abhängig von einem veränderten Systemparameter τ ∈ 
Die folgende Figur soll veranschaulichen, wie sich für einen bestimmten Zustand φ die Übergangswahrscheinlichkeit in einen anderen Zustand φ' ändert, wenn für den Zustand φ ein bestimmter Parameter τ verändert wird.
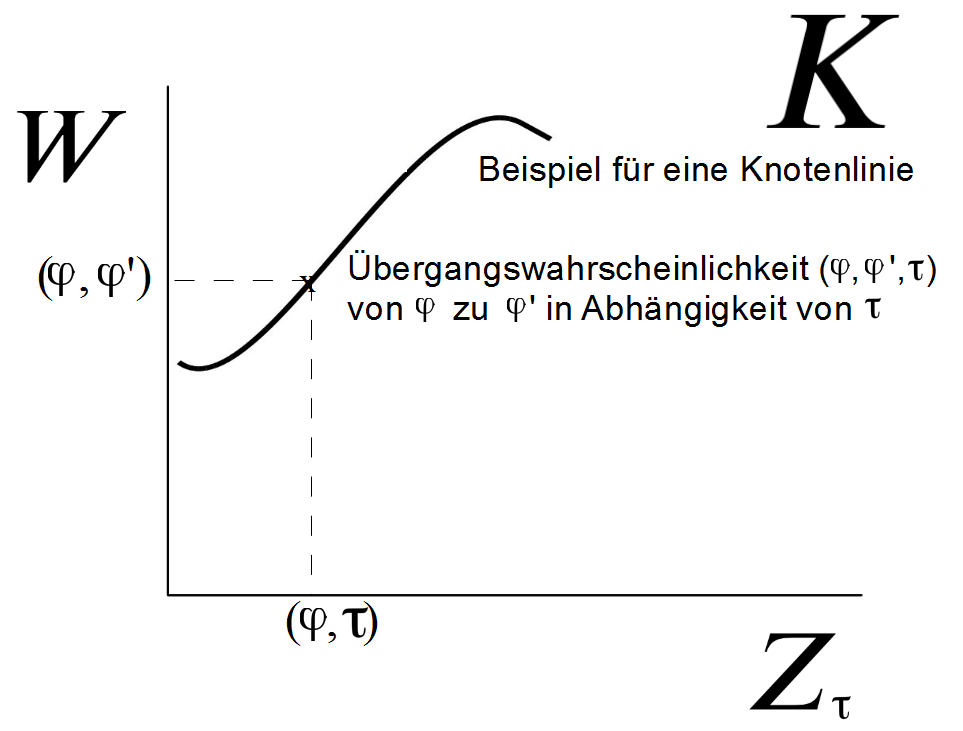
Figur 11: Knotenlinie für eine bestimmte Wahlverwandtschaft (φ,φ')
Auf der horizontalen Achse ist ein Zustand φ eingetragen, für den sich ein Umgebungsparameter τ ändert. Auf der vertikalen Achse sind die unterschiedlichen Übergangswahrscheinlichkeiten von φ in einen bestimmten anderen Zustand φ', d.h. die Werte (φ,φ') eingetragen. Beispiel: Die horizontale Achse  τ kann die Gesamtheit der Zustände des flüssigen Wassers mit jeweils unterschiedlichen Temperaturen sein. Die vertikale Achse
τ kann die Gesamtheit der Zustände des flüssigen Wassers mit jeweils unterschiedlichen Temperaturen sein. Die vertikale Achse 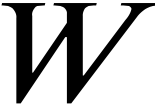 (φ,φ') zeigt die unterschiedlichen Übergangswahrscheinlichkeiten, mit denen einzelne Wassermoleküle aus dem flüssigen in den gasförmigen Zustand wechseln. Die Knotenlinie zeigt, wie sich die Übergangswahrscheinlichkeit abhängig von der Veränderung von τ entwickelt.
(φ,φ') zeigt die unterschiedlichen Übergangswahrscheinlichkeiten, mit denen einzelne Wassermoleküle aus dem flüssigen in den gasförmigen Zustand wechseln. Die Knotenlinie zeigt, wie sich die Übergangswahrscheinlichkeit abhängig von der Veränderung von τ entwickelt.
Wichtig ist zu verstehen, dass Knotenlinien Veränderungen von Übergangswahrscheinlichkeiten zeigen. Innerhalb des Raums 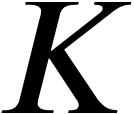 können die Umschläge von Qualitäten abgelesen werden, die Hegel gemeint hat. Von der Mathematik werden sie heute in der Katastrophentheorie untersucht.
können die Umschläge von Qualitäten abgelesen werden, die Hegel gemeint hat. Von der Mathematik werden sie heute in der Katastrophentheorie untersucht.
Ausgehend von den Modellen der Chemie, der natürlichen Zahlen und der Musik scheint Hegel unausgesprochen angenommen zu haben, dass es für jede Sache genau eine Knotenlinie gibt und entsprechend einen eindeutigen Parameter, entlang dessen sie sich ändert. Seine eigenen Beispiele zeigen dagegen bereits eine Vielfalt von Parametern wie die Temperatur und die Anteile der Stoffe in einem Stoffgemisch. Die Vorstellung eines Raums aller Knotenlinien geht daher über Hegel hinaus, ist aber in seinen Ausführungen bereits angelegt. Ich gehe davon aus, dass die Kräfte, die zur Veränderung von einer Knotenlinie zu einer anderen führen, wiederum unabhängig sind von den Kräften, die zu einer Wahlverwandtschaft und zur Veränderung von einer Wahlverwandtschaft zu einer anderen führen. Das ergibt eine Dreidimensionalität, die im Grunde den Grundüberzeugungen von Hegel näher kommt.
Anmerkung (Proto-Zeit): Es fällt auf, dass in der hier betrachteten Geometrie nicht ausdrücklich die Zeit erwähnt wird. Es werden zwar Veränderungen eines Umgebungsparameters τ analysiert, aber unabhängig von einem bestimmten Zeitmaß. Der Begriff von (physischem) Raum und Zeit soll erst im weiteren aus der Gesamtheit der Zustände und ihrer Wahlverwandtschaften, Knotenlinien und Harmonien entwickelt werden. Hegel hat damit im Prinzip bereits die Lösung vorweggenommen, die heute in der Physik als Quantengravitation oder Quantisierung der Raumzeit gesucht wird. Die Quantenmechanik spricht von Quantensubstrat oder Prägeometrie. Siehe dazu z.B. Reiner Hedrich Hat die Raumzeit Quanteneigenschaften? in Esfeld (Hg.) Philosophie der Physik.
Das Maßlose
Umgangssprachlich werden das Maßlose und die Maßlosigkeit abwertend gesehen, Zeichen von Gier (einer Kardinalsünde), unstillbarer Unzufriedenheit, von Luxus und Prasserei, Kontrollverlust und Dekadenz. Auch wenn diese Bedeutungen bei Hegel anklingen, ist für ihn dagegen in einer fast provokativen Wende das Maßlose eine Umkehr, an der etwas von allen seinen endlichen Erscheinungen und den mit ihnen gegebenen Maßen übergeht und zur Sache selbst findet. Wenn Kant zwischen den Erscheinungen und dem Ding-an-sich und Spinoza zwischen der Substanz und ihren Modi eine unüberbrückbare Kluft sahen, ist für Hegel das Maßlose der Begriff, der den Weg von den Erscheinungen zum Ding-an-sich und von den Modi zur Substanz weist. Das Ding-an-sich und seine Erscheinungen und die Substanz und ihre Modi werden verstanden wie das Substrat und seine Zustände. Ihr Verhältnis verliert dadurch seine Absolutheit. Es wird im Kontext von Maß und Maßlosigkeit gesehen, in dem sie sich vermitteln lassen.
Daher sollen einleitend mit Ruschig einige Ansichten des Maßlosen vorgestellt werden, die bei Hegel mit angesprochen sind, von denen er aber seinen Begriff des Maßlosen unterscheiden will, auch wenn das nicht immer ganz deutlich gelungen sein sollte.
(1) Selbstzerstörung. Ruschig nennt drei Beispiele, an denen das Maß selbstzerstörerisch in Maßlosigkeit umschlägt und sich dadurch seiner eigenen Grundlage beraubt (R, S. 311): (a) Temperatur-Erhöhung einer Flüssigkeit in einem geschlossenen System. Ist der gasförmige Zustand erreicht, gibt es keine weiteren Änderungen mehr. Insofern ist der gasförmige Zustand maßlos. (b) Wenn Uran 235 eine kritische Masse überschreitet, kommt es zur Explosion. »Er (der Uranblock) explodiert in einem prinzipiell untechnischen und so maßlosen Prozeß« (c) Schwerekollaps beim Schwarzen Loch. Bei diesen drei Beispielen wird ein Parameter so lange vergrößert, bis im Ergebnis nicht mehr ein neuer Zustand mit einem neuem Maß gefunden ist, sondern die Knotenlinie der Zustände sich selbst zerstört hat und daher auch keine Möglichkeit einer Umkehr mehr besteht.
Das geht entsprechend dem negativen Vorverständnis des Maßlosen weit über das hinaus, was Hegel meint. Für Hegel kommt es nicht zur Selbstzerstörung der Knotenlinie, sondern nur eines jeweiligen Zustandes, der durch einen neuen Zustand abgelöst wird. Zwar schreibt Hegel: »Die Größe ist die Beschaffenheit, an der ein Dasein mit dem Scheine von Unverfänglichkeit ergriffen und wodurch es zerstört werden kann.« (HW 5.442) Doch ist damit nicht die Zerstörung aller Größen gemeint, sondern nur für die Maßverhältnisse im jeweiligen Zustand, die durch neue Maßverhältnisse abgelöst werden. »Das neue Maßverhältnis, in welches das zuerst vorhandene übergeht, ist ein Maßloses in Rücksicht auf dieses.« (HW 5.442) Im Ganzen ergibt sich eine schrittweise Unendlichkeit, in der ein Zustand den anderen ablöst und jeder gegenüber den anderen maßlos erscheint.
Auch wenn der Gedanke einer völligen Selbstzerstörung über das Ziel hinaus schießt, ist er hilfreich, um zu erkennen, dass hier etwas anderes geschieht als beim schrittweisen Übergang von einer Zahl zur nächsten entlang der Zahlengerade. Während entlang der Zahlengerade gilt, dass für jede noch so große Zahl n dennoch die Nachfolger-Relation bestehen bleibt und ihr Nachfolger n + 1 von ihr mit dem gleichen Abstand 1 getrennt ist, wie es für die ersten Zahlen 1, 2, 3, … gilt, verhält es sich bei den Maßen anders. Während entlang der Zahlengerade das Maß der Abstände zwischen zwei einander folgenden Zahlen erhalten bleibt, ändern sich beim Übergang von einem Zustand zum anderen die Maße. Es gibt innerhalb der Zahlengerade keine maßlos große Zahl. Der Begriff der Maßlosigkeit entsteht erst mit der Unterscheidung der Zustände. Erst einige Jahrzehnte nach Hegel hat der Mathematiker Georg Cantor auch für die Mathematik maßlos große Zahlen eingeführt. Für ihn befindet sich die transfinite Zahl ω jenseits aller Zahlen 1, 2, 3, … und ist ihnen gegenüber maßlos. Die von Cantor unterschiedenen Zahlklassen mit ihren jeweiligen Mächtigkeiten beschreiben innerhalb der Mathematik die Maßlosigkeit, die Hegel gemeint hat. Jede neue Mächtigkeit ist maßlos gegenüber der vorangehenden.
Während Ruschig die Gefahr einer völligen Selbstzerstörung sieht, stellt sich für Hegel um so dringlicher die Frage nach der inneren Einheit, die entlang der Knotenlinie gegeben ist, obwohl jeder Zustand gegenüber dem vorangehenden maßlos erscheint. Diese innere Einheit sieht er im Substrat. Das Substrat ist daher für ihn im wörtlichen Sinn das Maßlose, der Träger unterschiedlicher Maße, die einander gegenüber maßlos sind.
(2) Verlust jeder Kontrolle. Ruschig nennt Beispiele aus der Wirtschaftsgeschichte und der Maßlosigkeit des Kapitalismus.
»Das progressive Wachstum des Kapitals ist prinzipiell unbeschränkt (maßlos). Da es notwendig auf materielle Voraussetzungen (die natürlichen Ressourcen der Produktion) verwiesen ist, die prinzipiell beschränkt sind, treibt es in einen überkritischen Zustand mit der Zerstörung der natürlichen Ressourcen. Die Rückführbarkeit einzelner solcher in das 'Maaßlose' führender Prozesse steht dahin (point of no return).« (R, 312 Fn. 2)
Das hat sich für ihn mit der Entwicklung von Massenvernichtungs-Waffen in bedrohlicher Weise radikalisiert, mit denen »die Zerstörung der gesamten Erde möglich wird« (R, 312 Fn. 2). Für ihn ist Maßlosigkeit der Verlust jedes inneren Maßes bis zur vollständigen Selbstauslöschung. Für ihn verliert die Maßlosigkeit die Fähigkeit der selbstbezüglichen Negativität. Es ist entfesselt und im wörtlichen Sinn absolut.
(3) Unabhängigkeit vom Material.
Hegel vertraut darauf, dass es trotz der Maßlosigkeit beim Übergang von einem Zustand zum nächsten dennoch eine übergreifende innere Einheit gibt.
»Hegel unterstellt Verallgemeinerbarkeit der Modelle für kritische Größen. Diese Unterstellung der Verallgemeinerbarkeit liegt darin begründet, daß für Hegel das Über-sich-hinaus-in-das-Maßlose-Getriebenwerden nicht mit dem jeweiligen besonderen Material und mit der besonderen Konstellation von Maßgrößen zusammenhängt, sondern an einem völlig unbestimmten, allen Maßgrößen zugrundeliegenden und für alle identischen Substrat (der 'Indifferenz').« (R, 312)
Was Ruschig als »Unterstellung« kritisiert, ist der Gedanke, um den es Hegel geht. Allerdings will Hegel die Indifferenz nicht mittels einer Unterstellung aus dem Reich des Denkens von außen in das Reich der Gegenstände tragen, sondern umgekehrt zeigen, wie sich aus der Bewegung der Übergänge der Zustände die Indifferenz ergibt. Mit dem Maßlosen ist nach einer Eigenschaft der Maßlosigkeit gefragt, die aus dem Maßlosen von sich aus zur Indifferenz führt und nicht von außen von der Logik oder dem Denken in sie hinein gesetzt werden muss. Ruschig sieht hier jedoch eine Art von Widerspruch:
»Dann ließen sich über den Zustand des Maßlosen von jeder Maßgröße alle anderen Maßgrößen und – wegen der Ersetzung der Qualitäten durch Maßgrößen – von jeder Qualität alle anderen Qualitäten erreichen.« (R, 312)
Vom »Zustand des Maßlosen« zu sprechen ist widersprüchlich und eine negative Selbstbezüglichkeit. Der Zustand des Maßlosen ist einerseits die Negation aller Zustände, die jeweils durch ihr Maß bestimmt sind, und andererseits für sich selbst wiederum ein Zustand, der sich in seiner Maßlosigkeit selbstbezüglich als Zustand negiert. »Das Maßlose (ist) gleichfalls ein Maß« (Enz. § 109, HW 8.229). Um diesen Widerspruch geht es Hegel. An ihm will er die Auflösung der chemischen Sphäre zeigen, wenn sich die Indifferenz »zum Widerspruch entwickelt« (HW 5.449) bis »der allseitige Widerspruch« (HW 5.551) hervortritt.
Der Begriff des Maßlosen wird von Hegel streng logisch entwickelt:
– Das Maßlose ist die innere Einheit, die beim Übergang der realen Maße entlang der Knotenlinie erhalten bleibt. Während sich die Zustände und mit ihnen die realen Maße ändern, ist die Einheit für sich maß-los. Materie, Sache.
– Die Maßlosigkeit teilt sich auf in das Substrat und seine Zustände. Das ist der entscheidende Schritt, um die Unvermitteltheit von Maß und Maßlosigkeit zu überwinden.
– In einer zweiten Negation wird gefragt: Wenn sich das Maßlose in Substrat und dessen Zustände geteilt hat, was ist dann die innere Einheit des Substrats und seiner Zustände? Das kann nicht wiederum ein Substrat sein, sondern ist für Hegel die gemeinsame Ordnung. Damit trifft er den Punkt, entlang dessen die Knotenlinie der Zustände bis zum Grenzzustand entwickelt werden kann, an dem die stoffliche Materialität in einem mathematischen Modell aufgehoben wird.
Mir geht es vor allem um die Frage, welche mathematischen Eigenschaften sich am Maßlosen und der Ordnung erkennen lassen. Das sind für mich die Händigkeit und die Eigenschaften der imaginären Zahlen, ihre Analytizität und Auflösbarkeit. Mit ihnen gelingt der Übergang in den Grenzzustand der Indifferenz, ohne mit der Indifferenz in völligen Stillstand zu geraten.
Der Begriff des Maßlosen (das abstrakte Maßlose und die Sache)
Textgrundlage: HW 5.442f
Von Maßlosigkeit kann nur solange im abwertenden Sinn gesprochen werden, wie es ein eindeutiges, natürliches Maß gibt. Eine Inschrift am Eingang zur Orakelstätte von Delphi lautete: »Nichts im Übermaß« (medèn ágan). Wer sein Maß verfehlt und nicht Maß zu halten versteht, wird maßlos. Das ist auch für Hegel der Ausgangspunkt der Maßlogik. Maße dieser Art sind statisch. Lassen sich dagegen in den vielfältigen Beziehungen einer Sache zu ihrer Umgebung und zu anderen Dingen viele Maße unterscheiden, und lassen diese sich sogar in ihrer Affinitätsstärke messen und vergleichen, dann spricht Hegel vom realen Maß. Ihm gegenüber bekommt die Negation des Maßes als Maßlosigkeit eine neue Bedeutung. Gegenüber realen Maßen ist Maßlosigkeit nicht der Verlust jeden Maßes, sondern dasjenige, das den unterschiedlichen Maßen gemeinsam ist und daher für sich nicht seinerseits ein Maß sein kann. Hegel führt daher den Begriff des Maßlosen nicht bereits als Negation des Maßes ein, sondern erst, nachdem das Maß sich differenziert hat in die Vielfalt der realen Maße.
So zu argumentieren, ist bewusst rein formal. Hegel bringt es auf den Punkt:
»Das abstrakte Maßlose ist das Quantum überhaupt als in sich bestimmungslos und als nur gleichgültige Bestimmtheit, durch welche das Maß nicht verändert wird.« (5.442)
Nach jedem Übergang ist der neue Zustand jeweils aus Sicht des alten Qualitativen maßlos, da es dessen Maß überschritten hat. Darauf beziehen sich die von Friedrich Engels in seinen Arbeiten über Dialektik und Natur genannten Beispiele aus den Naturwissenschaften: Das Molekül ist maßlos groß gegen das Atom, das Atom maßlos klein gegen das Molekül. Das gasförmige Wasser ist maßlos beweglich gegen das flüssige Wasser. In der Mathematik ist das Unendlich-Kleine des Differentials maßlos klein gegenüber den üblichen Zahlen. Die Menge der reellen Zahlen ist maßlos groß gegenüber der Menge der natürlichen Zahlen.
Auf den ersten Blick scheint sich zu wiederholen, was bereits zum Übergang von der Endlichkeit zur Unendlichkeit gesagt wurde. Wenn entlang der natürlichen Zahlen immer weiter gezählt wurde, hat sich im Ergebnis der Blick umgekehrt und nicht nach der größten natürlichen Zahl gefragt (die es nicht geben kann, denn jede beliebige Zahl n hat wiederum einen Nachfolger), sondern nach der Eigenschaft der Zahlengerade. Das ist die Kontinuität. Aus der Kontinuität ergibt sich die Menge der gegenüber den natürlichen Zahlen maßlos vielen reellen Zahlen, die dicht auf der Zahlengerade liegen.
Hegel erwähnt allerdings nicht explizit das Argument von Aristoteles, dass auch die kontinuierliche Unendlichkeit noch keine zusammenhängende Linie hervorbringen kann, sondern diese erst dann gegeben ist, wenn die Punkte auf der Linie nicht nur kontinuierlich angeordnet sind, sondern beweglich sind. Während die natürlichen Zahlen 1, 2, 3, … jeweils mit einem Abstand von 1 getrennt und voneinander diskret sind, kann bei den reellen Zahlen metaphorisch von ihrer Fluidität (Flüssigkeit) gesprochen werden. Dieser Begriff ist in der Mathematik bis heute nicht systematisch eingeführt worden, obwohl er logisch dem Grundgedanken von Euler zugrunde liegt, der von einer Mathematik diskreter Größen zu einer Mathematik der Strömungen überging.
Offenbar fehlt der Mathematik bis heute der entscheidende Begriff, um diese Unterscheidung treffen zu können. Anschaulich ist jedoch deutlich, dass sich die natürlichen und die reellen Zahlen analog zueinander verhalten wie die starre Struktur des Eises und die flüssige Struktur des fließenden Wassers. Werden diese als Zustände eines gemeinsamen Substrats (des Wassers) verstanden, wird deutlich, wie die Unterscheidung in Substrat und Zustand auch die grundlegende Frage der Mathematik lösen kann: Die natürlichen Zahlen und die reellen Zahlen sind unterschiedliche Zustände der Zahlen mit ihren jeweils eigenen Maßen. Der abstrakte Zahlbegriff ist ihnen gegenüber maßlos.
Daher ist mit dem Maß ein Begriff gefunden, der nicht einfach den Übergang von der schlechten zur wahren Unendlichkeit wiederholt, sondern ihn neu verstehen lässt. Mit einem subtilen Gedanken will Hegel zeigen, dass beim Übergang der Endlichkeit zur Unendlichkeit, wie sie »am Dasein« hervorbrachen, beide Seiten noch auseinander gefallen waren. Auf der einen Seite stand die quantitative Bewegung des Immer-weiter-Zählens der schlechten Unendlichkeit, auf der anderen Seite die qualitative Erkenntnis, dass das Unendliche gegenüber dem Endlichen eine eigene Qualität (Eigenschaft) hat, seine Kontinuität. Für diese beiden Seiten des Quantitativen und des Qualitativen wird mit dem Maß und dem Maßlosen eine innere Einheit gefunden. Das qualitative Unendliche war »das Hervorbrechen des Unendlichen am Endlichen«, das quantitative Unendliche »die Kontinuität des Quantums ... über sich hinaus« (HW 5.442). Demgegenüber ist das Maß »die erste, unmittelbare Einheit derselben« (HW 5.443). Das führt ihn zum Ergebnis:
»Diese so sich in ihrem Wechsel der Maße in sich selbst kontinuierende Einheit ist die wahrhaft bestehenbleibende, selbständige Materie, Sache.« (HW 5.443)
Mit dem Begriff der Materie oder Sache sucht Hegel nach einem neuen Begriff, der sich sowohl vom Begriff der Natur wie dem Begriff des abstrakten Maßlosen unterscheidet. Das natürliche Maß ist das statische Maß, wenn Etwas zur Ruhe kommt und zu sich selbst und seiner eigenen Natur findet. Mit der Sache ist dagegen die Bewegung (Dynamik) gemeint, wenn etwas seine Fähigkeit verwirklicht, über sich selbst hinausgehen zu können.
Hegel konnte alle Elemente dieses Gedankengangs bei Aristoteles vorfinden, nicht zuletzt den Begriff der Dynamik selbst (dynamis). Aber erst bei ihm hat sich daraus der Entwurf einer neuen Wissenschaft der Logik ergeben.
Die Ur-Teilung des Maßlosen in das Substrat und seine Zustände
Textgrundlage: Absatz HW 5.443f
Wenn das Maßlose die innere Einheit ist, die den verschiedenen realen Maßen entlang einer Knotenlinie gemeinsam ist, sind am Maßlosen drei Momente zu unterscheiden: Das Übergreifende, das über die einzelnen Maße hinausgeht, dasjenige, das an jedem einzelnen Maß auf das zugrunde liegende Maßlose verweist und umgekehrt dasjenige, worin dennoch das Maßlose mit jedem einzelnen realen Maß eine Einheit bilden kann. Das sind für Hegel das Substrat, seine Zustände und das wechselseitige Aufeinander-Zeigen der Zustände auf das Substrat und des Substrats in seinen Zuständen. An jedem Zustand zeigt sich das Substrat, oder umgekehrt formuliert: Der Zustand ist dasjenige, worin sich das für sich nicht wahrnehmbare Substrat in den verschiedenen Maßen seiner Zustände zeigen kann.
Das Substrat ist dasjenige, dessen Dieselbigkeit hervorgehoben wird. Es ist dasjenige, das »sich in dies sein Unterscheiden kontinuiert« (HW 4.443)
Auf der anderen Seite stehen die verschiedenen Qualitäten und Quantitäten der unterschiedlichen realen Maße.
Die realen Maße sind vom Maßlosen getrennt, und beide schließen sich gegenseitig aus. Ein Maß kann nicht maßlos sein, und das Maßlose ist kein Maß. Wenn dennoch die realen Maße im Substrat eine gemeinsame Grundlage haben, muss es am realen Maß etwas geben, worin die Verbindung zum Substrat besteht. Werden als Beispiel das Wasser und seine Aggregatzustände gewählt, so kann es etwa am Zustand des Eises kein besonderer Stoff sein, weswegen das Eis ein Zustand des Substrats Wassers ist. Alle Zustände des Wassers bestehen stofflich nur aus Wasser. Es kann daher nur etwas an der Form des Eises sein, weswegen Eis als Aggregatzustand des Wassers gilt. Jeder Zustand des Wassers (Eis, Flüssigkeit, Gas) muss in seiner Form etwas enthalten, worin er als Zustand des Wassers erkennbar ist. In den Worten von Hegel: An jedem Zustand muss sich das Substrat zeigen.
»Dies Übergehen des Qualitativen und des Quantitativen ineinander geht auf dem Boden ihrer Einheit vor, und der Sinn dieses Prozesses ist nur das Dasein, das Zeigen oder Setzen, daß demselben ein solches Substrat zugrunde liegt, welches ihre Einheit sei.« (HW 5.444)
Am Beispiel des Wassers lässt sich in der Feinstruktur aller Zustände zeigen, wie sich sowohl im Kristall des Eises, der lockeren Beweglichkeit des Flüssigen wie der freien Beweglichkeit des Gases dennoch Feinunterschiede ergeben, die auf die Eigenschaften des Wassers verweisen: Seinen Molekülaufbau, seine elektrische Ladungsverteilung usf. Doch soll es nicht um illustrierende Beispiele gehen, sondern um die Einsicht in die besondere Natur des Verhältnisses des Substrats zu seinen Zuständen: Das Substrat zeigt sich in seinen Zuständen.
Mit dem Zeigen ist ein Verhältnis gefunden, das sich von den anderen bisher entwickelten Verhältnissen unterscheidet. Es wäre unsinnig zu sagen, dass das Substrat in seine Zustände übergeht, sondern es befindet sich immer in einem Zustand, die nur untereinander ineinander übergehen können. Die Zustände sind nicht das Andere gegenüber einem Substrat. Die Zustände ergeben sich nicht aus einer inneren Bewegung des Substrats, und sie sind nicht gegenüber dem Unendlichen des Substrats das Endliche. Jeder Zustand hat sein eigenes Maß, und an diesem Maß muss sich das Substrat zeigen.
Hegel hat mit dem unscheinbaren Begriff des Zeigens einen Gedanken vorweggenommen, den später Kierkegaard und insbesondere Wittgenstein fortgeführt haben. An jeder Sprache zeigt sich, was die Sprache ist. Wir kennen in unserem Sprechen nur jeweils einen bestimmten Zustand der Sprache, an dem sich jedoch die Sprache im Ganzen zeigt.
Hegel hat diesen Gedanken sicher übernommen vom Begriff der religiösen Offenbarung. Niemand kann den Kosmos überblicken, sondern nur jeweils den bestimmten Zustand, in dem er sich befindet. Am Kosmos zeigt sich jedoch das Göttliche, das in übertragenem Sinn das Substrat des Kosmos ist.
Wenn sich am Zustand dessen Substrat zeigt, hat Hegel an dieser Stelle bereits in nuce den Begriff des Scheins und der Erscheinung getroffen. Das ist der grundsätzliche Gedanke, um die bei Kant noch bestehende Dichotomie des Ding-an-sich und seiner Erscheinungen aufzulösen: An den Erscheinungen zeigt sich das Ding-an-sich. Alle Ideen, die Kant als überfliegend abgelehnt hat, treten in ein neues Licht, wenn sie in diesem Verhältnis des Zeigens gesehen werden. Um diesen Gedanken auszuführen, bleiben noch einige Schritte offen, von denen die ersten nachfolgend skizziert werden.
Zusammenfassend:
»Nun sind solche Verhältnisse nur als Knoten eines und desselben Substrats bestimmt. Damit sind die Maße und die damit gesetzten Selbständigkeiten zu Zuständen herabgesetzt. Die Veränderung ist nur Änderung eines Zustandes, und das Übergehende ist als darin dasselbe bleibend gesetzt.« (HW 5.444)
Der Schluss auf die Ordnung und ihre Prinzipien
Textgrundlage: Absatz HW 5.444f
Wenn sich das Substrat an den Zuständen in der doppelten Bedeutung zeigt, dass sich das Substrat in seinen Zuständen offenbart und an den Zuständen deren Substrat gezeigt werden kann, kann das Sich-Zeigende für sich betrachtet werden: Was ist es am Zeigenden, weswegen es sich zeigen kann?
Das ist für Hegel an diesem Punkt des Gedankengangs in einer ersten Näherung die »bloße Ordnung, noch ganz äußerliche Einheit« (HW 5.445). Deren »Prinzip ist zunächst nur Substrat« (HW 5.445).
Daher ist für ihn mit diesem Prinzip noch nicht der Begriff erreicht. Um den Begriff zu erreichen, wird erforderlich, dass das Substrat nicht nur als Prinzip verstanden wird, sondern als Setzung, und dass die Setzung sich weiter entwickelt zum Subjekt mit einer eigenen Lebendigkeit und Freiheit. Erst dann werden der Begriff und die Idee erreicht.
»Aber das spezifizierende Prinzip ist noch nicht der freie Begriff, welcher allein seinen Unterschieden immanente Bestimmung gibt, sondern das Prinzip ist zunächst nur Substrat, eine Materie, für deren Unterschiede, um als Totalitäten zu sein, d. i. die Natur des sich selbst gleich bleibenden Substrats in sich zu haben, nur die äußerliche quantitative Bestimmung vorhanden ist, die sich als Verschiedenheit der Qualität zugleich zeigt. Die Maßbestimmung ist in dieser Einheit des Substrats mit sich selbst eine aufgehobene, ihre Qualität ein durch das Quantum bestimmter, äußerlicher Zustand. – Dieser Verlauf ist ebensowohl die realisierende Fortbestimmung des Maßes, als sie das Herabsetzen desselben zu einem Momente ist.« (HW 5.445)
Daher sieht Hegel das alles noch in der Seinslogik, jedoch bereits im Übergang zur Wesenslogik. Die verschiedenen Zustände sind innerlich zusammengehalten und haben eine gemeinsame Einheit, weil sie Zustände eines Substrats sind. Aber sie sind noch nicht gesetzt. Hier ist es nicht anders möglich, als von Substraten zu sprechen.
Wenn an dieser Stelle bloß von einer Ordnung gesprochen wird, sollte es möglich sein, spezifische mathematische Eigenschaften dieser Ordnung zu identifizieren. Das sind für mich die Händigkeit und die Eigenschaften der imaginären Zahlen.
Händigkeit: Leibniz hatte den absoluten, starren Raum von Newton abgelöst durch einen dynamischen Raum der Relationen. Das öffnete den Weg für den Übergang von der Physik Newtons zur Relativitätstheorie von Einstein. Gibt es eine spezifische Eigenschaft, an der sich dieser Übergang zeigen lässt? Das ist für mich die Eigenschaft der Händigkeit. Darauf war bereits Kant gestoßen, als er die Prinzipien verglich, nach denen Newton und Leibniz vorgegangen sind. Erst mit der Quantenmechanik ist die Händigkeit systematisch untersucht worden und zu einer Eigenschaft (Quantenzahl) der Physik geworden. In der Händigkeit zeigt sich exemplarisch, was mit Zuständen gemeint ist. Händigkeit ist weder ein Stoff noch eine Reflexion, weder ein Sein noch ein Gesetztes. Der umständliche Ausdruck Händigkeit substantiviert einfach das Spezifische der beiden Zustände des Linkshändigen und des Rechtshändigen. Das gilt ebenso für alle anderen Zustände, die seit dem 20. Jahrhundert von der Quantenmechanik betrachtet werden. Es müßte von der Ladigkeit, der Baryonenzahligkeit etc. gesprochen werden. Was kann das Substrat zweier solcher Zustände wie Rechtswindigkeit und Linkswindigkeit sein? Siehe hierzu den Beitrag Hegel und Hilbert
Imaginäre Zahlen: Mit den Relationen wird der Raum der Etwase (Dinge) verlassen und ein umfassender Raum betreten, dessen kleinste Einheit nicht mehr die einzelnen Etwase, sondern ihre jeweiligen Beziehungen sind. Auf den ersten Blick sollte es naheliegen, dass dort letztlich die gleichen mathematischen Eigenschaften gelten wie für die einzelnen Etwase, wenn jede Beziehung ebenso als ein Objekt betrachtet wird wie jedes einzelne Dinge, das zu anderen in Beziehung tritt. Mit der Einführung der imaginären Zahlen hat sich jedoch gezeigt, das hier neue Regeln gelten.
An dieser Stelle sei als These vertreten, welche Eigenschaften das sein können. Das sind für mich die Analytizität und die Auflösbarkeit.
Die Analytizität stellt sicher, dass Funktionen aus konvergenten Potenzreihen gebildet werden können (Vorbild ist der Klang, der die Potenzreihe des Grundtons und seiner Obertöne ist), und sie sollte die Eigenschaft begründen, dass die für System-Veränderungen wesentlichen Erkenntnisse im Bereich der komplexen Zahlen liegen (das gilt sowohl für die Wärmeleitungs-Gleichung wie für die Schrödinger-Gleichung). Sie begründet, warum die im Hilbert-Raum dargestellten Eigenschaften nach dem Vorbild der Zerlegung der Farbe in ein Farbspektrum und eines Klangs in das Spektrum der Obertöne polarisiert werden können. Daraus ergibt sich die mit diesem Beitrag begründete, aber noch nicht konstruktiv nachgewiesene These:
Die Analytizität ist die spezifische innere Eigenschaft der chemischen Sphäre. In ihr sind Kontinuität und Beharrlichkeit aufgehoben. Sie kann philosophisch und mathematisch konstruiert und in naturwissenschaftlichen Experimenten überprüft und nachgewiesen werden. Die chemische Sphäre ist der Bereich, in dem die Analytizität gültig ist.
Diese Frage wird fortgeführt werden, wenn Hegels Ausführungen über den Chemismus in der Begriffslogik näher betrachtet werden. Als Ansatz kann bereits vorweggenommen werden, dass wesentlich für den Chemismus das Medium ist. Mit dem Verständnis der chemischen Sphäre wird die Einsicht vorbereitet, dass anders als in mechanischen Verhältnissen nicht von den voneinander isolierten Bausteinen (mathematisch gesprochen nicht von den einzelnen Zahlen oder Elementen der Geometrie wie Punkt und Strecke), sondern von dem Medium auszugehen ist, in dem sie sich befinden (mathematisch gesprochen der Strömung oder dem Raum). Mit der Analytizität könnte eine Eigenschaft gegeben sein, die das Medium bestimmt und nicht mehr nur wie die Kontinuität die Reihe der reellen Zahlen.
Zugleich kann für mich mit dem Hinweis auf die imaginären Zahlen das Thema aufgegriffen werden, das Hegel ein wenig aus den Augen verloren zu haben scheint: Die Modalität. Der für die imaginären Zahlen herangezogene Begriff der Imagination (Vorstellungskraft) verweist darauf, dass mit den imaginären Zahlen ein Möglichkeitsraum betrachtet wird, der in sich die Eigenschaft besitzen muss, sowohl das Reich der Möglichkeiten betreten zu können, wie auch dort den Umkehrpunkt zu finden, der sich nicht in der bloßen Phantasie verliert, sondern zur Wirklichkeit zurückfindet. Das ist die Analytizität, durch die die verschiedenen, bloß möglichen Wege in diesem Raum innerlich zusammenhängen. Die Analytizität hat wiederum ihre sachliche Grundlage in der Zyklizität der imaginären Zahlen. Werden zwei imaginäre Zahlen multipliziert, ergibt das nicht nur eine Translation entlang einer Geraden wie bei den üblichen Zahlen, sondern eine Drehung, durch die benachbarte komplexe Zahlen ineinander überführt werden.
Auflösung der chemischen Sphäre
So wie die mechanische Sphäre im Unbestimmten der schlechten Unendlichkeit ausläuft, die mit drei Pünktchen ›…‹, dem Unendlichkeitszeichen ∞ oder dem Übergang von ›n‹ zu ›n + 1‹ bezeichnet wird, löst sich die aus der mechanischen Sphäre hervorgegangene chemische Sphäre ihrerseits in Indifferenz und Neutralisierung auf, woraus die organische Sphäre hervorgeht.
- Die chemische Sphäre beschreibt die Auflösung von Stoffen in einem Medium. Das gängigste Medium hierfür ist nach wie vor das Wasser.
- Mit der Auflösung wird eine Neutralisation erreicht. Das kann sowohl das Endresultat sein, wenn sich Stoffe völlig in einem Medium aufgelöst haben, wie auch der Endpunkt, wenn entlang einer Knotenlinie ein Grenzzustand erreicht ist, in dem es keine inneren Differenzen mehr gibt. Die Urknall-Theorie verfolgt dies rückwärts und konstruiert den Urknall als einen Anfangspunkt, der keine inneren Differenzen enthält und über eine Phase von Symmetrie-Brüchen zerfällt. Am Ende würde ein anderer Grenz-Zustand stehen, wenn das aus dem Urknall hervorgegangene Universum völlig asymmetrisch (chaotisch) ist.
- Innerhalb jedes einzelnen Übergangs von einem Zustand in einen anderen gibt es einen Indifferenzpunkt, in dem sich die Ordnung auflöst. In diesem Moment gilt die alte Ordnung nicht mehr, die neue noch nicht.
Es ist die Kunst der Logik der chemischen Sphäre, Wahlverwandtschaften und ihre Knotenlinien in einer Weise zu verstehen, dass die aus ihnen hervorgehenden Indifferenzen sich im Innern in verschiedene Faktoren zerlegen (auflösen) lassen. Das stellt Hegel im abschließenden Kapitel über den »Übergang zum Wesen« genauer dar.
(1) Die Logik der chemischen Sphäre muss in einer Weise entfaltet werden, dass es im Ergebnis zu einer Auflösung kommt, die nicht bei einer Leeraussage wie ›0 ≡ 0‹ stehen bleibt, sondern eine Zerlegung in aussagekräftige, innere Faktoren ermöglicht.
(2) Die inneren Faktoren sind nach außen indifferent. Sie stehen im umgekehrten Verhältnis zueinander. Es muss möglich sein, sowohl diejenige Indifferenz zu finden, die sich nach innen in Faktoren zerlegen lässt, wie auch die Faktoren, die in ihrem wechselseitigen Ausgleich nach außen indifferent sind.
(3) Die inneren Faktoren sind Setzungen. Sie erscheinen nach außen indifferent und sind daher nicht direkt wahrnehmbar. Sie entsprechen insofern den von Kant eingeführten regulativen Ideen. Mit ihrer Hilfe lässt sich etwas verstehen, was für sich indifferent aussieht. Aber anders als bei Kant sind es nicht einfach Ideen, sondern einander gegenüberstehende Faktoren, die in einem Wechselverhältnis zueinander stehen. Das ist im einfachsten Beispiel das Wechselverhältnis von kinetischer und potentieller Energie am Pendel. Hegel interpretiert in diesem Sinn auch das 2. Keplersche Gesetz, das er als Wechselverhältnis von Geschwindigkeit der Planeten und ihrer Entfernung zur Sonne versteht. Die moderne Teilchenphysik arbeitet fast ausschließlich mit Setzungen dieser Art, wenn sie von Quarks oder von virtuellen Teilchen spricht, die nur als innere, nach außen einander ausgleichende Faktoren zu verstehen sind.
(4) Die zuvor betrachteten Zustände eines zugrundeliegenden Substrats erscheinen jetzt als Spezifikationen der inneren Faktoren. Je nach dem, in welchem Verhältnis die inneren Faktoren zueinander stehen, ergeben sich die verschiedenen Zustände.
Das erzeugt den Anschein, als sei die beobachtbare Realität das Ergebnis der nachträglich rein theoretisch gefundenen Spezifikation. Es kann so scheinen, dass die mit der nachträglichen Analyse gewonnenen inneren Faktoren eigenständige Subjekte innerhalb der Natur sind, die das Geschehen steuern. Einige Naturforscher sitzen nach Ruschig einem solchem Missverständnis auf und geraten damit in seiner Sicht in einen ähnlichen Idealismus wie Hegel. Viele Chemiker glaubten, dass die Schrödinger-Gleichung aus sich selbst heraus das Spezifikationsprinzip entwickelt, während sie nur eine Formel ist, um das in der Natur zu entdeckende Spezifikationsprinzip darzustellen. Ihnen gegenüber macht Ruschig zurecht geltend, dass die Gültigkeit und Nachweisbarkeit von Gleichungen dieser Art abhängig sind von den materiellen Prozessen, die mit ihnen beschrieben werden und bei deren Beobachtung sie sich überprüfen lassen.
»Substrat ist für sie (Chemiker des 20. Jahrhunderts, t.) die Energie. Die Lösung der Schrödinger-Gleichung für das Wasserstoffatom, welche Quantenzahlen, Eigenfunktionen und Energieniveaus ergibt, wird von ihnen fälschlich als Selbst-Spezifikation der Schrödinger-Gleichung interpretiert« (R, S. 230). »Systematisch stecken im Separationsansatz physikalische Voraussetzungen, die selbst nicht aus der Schrödinger-Gleichung folgen: Die Aufteilung in zeitabhängige und zeitunabhängige Schrödinger-Gleichung wäre ohne die Existenz von in der Zeit stabilen Atomen bedeutungslos; die Einführung von Polarkoordinaten, ohne die die Differentialgleichung nicht lösbar ist, impliziert ein kugelsymmetrisches Feld; in den Hamilton-Operator geht das Coulomb-Anziehungsgesetz und damit die Konstellation Proton-Elektron ein« (R, S. 231).
Aber Ruschig scheint zu übersehen, dass es an diesem Punkt der naturwissenschaftlichen Entwicklung unvermeidlich ist, die chemische Sphäre aufzulösen und Lösungen zu setzen, die als innere Faktoren für sich anschaulich nicht nachweisbar sind, mit denen aber die in der chemischen Sphäre auftretenden Indifferenzpunkte und die aus ihnen hervorgehenden Zustände beschrieben werden können. Sie beschreiben im Prinzip eine unendliche Vielfalt von Lösungen. Das beobachtbare Material kann gedeutet werden, wenn zusätzlich bestimmte Randbedingungen erkannt und eingesetzt werden. Das gilt bereits für die Planetengesetze von Kepler. Diese Gesetze sind nicht am Himmel ablesbar. Sie gelten im Prinzip für unendlich viele mögliche Planetensysteme, und es müssen zusätzlich bestimmte Randbedingungen (wie die konkret zu messenden Daten unserer Sonne und ihrer Planeten) beobachtet und gemessen werden, um von den Keplerschen Gesetzen zu den Beobachtungsdaten zu gelangen, wie sie am Himmel gesehen werden können. Das gilt entsprechend auch für die Schrödinger- und die anderen übergreifenden Feldgleichungen.
Mit Hegel kann verstanden werden, an welchem Punkt der chemischen Sphäre Indifferenzen auftreten, die von Gleichungen dieser Art aufgelöst werden können.
Um dies zu erreichen, ist zweierlei notwendig. Das Beobachtungsmaterial muss in eine Gestalt gebracht werden, in der nicht nur Indifferenzen auftreten, sondern ihre inneren Faktoren erkennbar waren. Im Beispiel von Kepler war das das 1. Keplersche Gesetz, wonach sich die Planeten auf elliptischen Bahnen und nicht auf Kreisbahnen bewegen. Erst für elliptische Bahnen lassen sich die weiteren Keplerschen Gesetze formulieren. Und es müssen im weiteren diese Gesetze gefunden werden, im Beispiel von Kepler das 2. und 3. Keplersche Gesetze.
Daher kommt zu den bereits genannten Eigenschaften der Kontinuität, Beharrlichkeit und Affinität die Eigenschaft der Auflösbarkeit hinzu. Das ist im Ergebnis für mich die eigentlich spannende Frage, die sowohl eine philosophische wie eine mathematische Herausforderung ist. Der Mathematiker Evariste Galois (1811-1832) hat am Beispiel der offenen Fragen der griechischen und mittelalterlichen Mathematik zeigen können, dass bestimmte Aufgabenstellungen (wie die Quadrierung des Kreises) nur auflösbar sind, wenn sie bestimmte mathematische Eigenschaften erfüllen. Das sollte sich übertragen und anwenden lassen auf die Frage der Auflösbarkeit in der chemischen Sphäre. Für die Auflösbarkeit sollte wie für Kontinuität, Beharrlichkeit und Affinität gelten, dass sie sowohl innerhalb der Mannigfaltigkeit angelegt (präformiert) ist, wie auch zur Verfassung des Verstandes gehören muss, der eine Auflösung denken können muss. Im Einzelnen kommt Galois der hier genannten Fragestellung insofern nahe, als er Faktorgruppen betrachtet, die eine gewisse Analogie zu den hier genannten inneren Faktoren bilden könnten. Mit dieser Analogie könnte es möglich werden, für die Logik der chemischen Sphäre eine Formalisierung zu finden. Das würde bedeuten, aus den bei Galois angelegten Ideen einen eigenen Kalkül zu entwickeln, der auf ähnliche Weise über den Differentialkalkül hinausgeht, wie die chemische Sphäre über die mechanische Sphäre hinausgeht. Dann wäre positiv gezeigt, welchen Stellenwert der Differentialkalkül von Leibniz hat, wie er zur mechanischen Sphäre gehört und auf welche Weise er von einem weiter führenden Kalkül abgelöst werden kann. Erst damit wäre für mich der bei Hegel bereits implizit angelegte Gedankengang ausgeführt, der im ersten Band der Wissenschaft der Logik den Differentialkalkül innerhalb des Abschnitts über die Größe (Quantität) ausführt, über das der Abschnitt über das Maß hinausgeht und daher recht verstanden auch eine Aufhebung des Differentialkalküls erfordern und ermöglichen sollte.
Wenn Hegels Intuition vertraut werden kann, scheint zum Abschluss die Frage nach dem Satz des Pythagoras auf. Der Übergang des Maßlosen in die absolute Indifferenz wiederholt sich in der Auflösung des Mediums des Chemismus in das Organische. Die Auflösbarkeit wird in neuem Licht gesehen. Sie löst sich nicht mehr nur in innere Faktoren auf, die im Verhältnis der Umkehrung stehen, sondern in deren organische Beziehung. Der Satz des Pythagoras verweist für Hegel auf die Lebendigkeit eines organischen Wesens, das sich in der Bewegung zeigt, die vom Satz des Pythagoras beschrieben wird. Das legt die Idee nahe, dass es das Prinzip der Lebendigkeit ist, welches dem Satz des Pythagoras und den mit ihm begründeten Ordnungen zu Grunde liegt. Siehe hierzu den Beitrag über die Wende zum absoluten Wissen.
Anhang: Frühere Einleitungen
Logik der chemischen Sphäre und der Harmonien
Hegels Ausführungen zum realen Maß lassen die Grundlinien einer neuen, nicht-formalen Logik erkennen, die weder verwechselt werden darf mit späteren Entwürfen einer mehr-wertigen, »dialektischen« Logik – zum Beispiel von Gotthard Günther –, noch mit parakonsistenten Logiken. Hegel geht davon aus, dass die bestehenden Logiken am mechanischen Denken orientiert sind und entwirft die Idee, wie sie aufgehoben werden können in einer weiter reichenden Logik der chemischen Sphäre. Während in den traditionellen Logiken atomare Bestandteile definiert und äußerlich miteinander verknüpft werden, – so gelten Subjekt und Prädikat als kleinste Einheiten von Aussagensätzen, und es wird nach den Wahrheitsregeln ihrer Verknüpfung in den verschiedenen Arten von Urteilen gefragt –, und im weiteren die Verknüpfungen mit bestimmten Wahrscheinlichkeiten relativiert werden können (Unsicheres Wissen, Fuzzylogik), sowie höherstufige Meta-Logiken diese Verknüpfungen ihrerseits als Elemente verstehen, zwischen denen Verknüpfungen erfolgen (also Verknüpfungen von Verknüpfungen, oder mathematisch gesprochen Funktionen von Funktionen), will Hegel nach dem Vorbild der sich zu seiner Zeit entwickelnden Chemie eine andere Art von Logik entwerfen, die die mechanische Logik als Grenzfall enthält. Dort wird unterschieden zwischen Wahlverwandtschaften miteinander reagierender Objekte, über die unterschiedliche Zustände eines zugrundeliegenden Substrats konstituiert werden. Jeder Zustand hat seine eigene Ordnung und seine eigene Stabilität, und kann entlang einer Knotenlinie in andere Zustände umschlagen.
Hegel entwickelt diese Logik jedoch nicht in einem zusammenhängenden Handbuch, das den früheren logischen Arbeiten etwa von Aristoteles oder später entstandenen Logiken in der Tradition von Frege vergleichbar ist, sondern in mehreren Schritten entlang seiner Wissenschaft der Logik. Er entwickelt noch nicht zusammenhängend eine neue nicht-mechanische Logik, sondern ich verstehe seine Wissenschaft der Logik so, dass er mit ihr eine Wissenschaft begründet hat, die in dieser Richtung tätig werden kann (auch wenn er selbst sicher der Überzeugung war, bereits ein abschließendes System vorgelegt zu haben). Der vorliegende Beitrag soll dieses Anliegen anhand Hegels Ausführungen zum realen Maß herausarbeiten, worauf sich weitere Beiträge zur Klärung elementarer Begriffe der Logik beziehen können. Das Ergebnis könnte in Zukunft eine andere Logik sein, in der die von Hegel insbesondere in den Kapiteln über das reale Maß und die Objektivität angedeuteten Grundlinien ausgeführt werden. In diesem Beitrag werden erste Thesen aufgestellt, welche neuen Begriffe hilfreich sein könnten (Analytizität, Auflösbarkeit).
Der Ausdruck »Logik der chemischen Sphäre« (mit Bezug auf HW 5.420) soll verdeutlichen, welche Schwierigkeiten und möglicherweise Missverständnisse damit verbunden sind. Gibt es in der Natur eine chemische Sphäre, die über eine eigene Logik verfügt, so wie zum Beispiel von der »Sprache der Blumen« gesprochen werden kann, und die zu erkennen und in Worte zu bringen Anliegen einer neuen Wissenschaft der Logik ist? Oder ist umgekehrt der menschliche Geist fähig, aus Betrachtung seiner eigenen transzendentalen Strukturen eine höhere Logik zu entwerfen, die nicht adäquat durch die mechanische Wissenschaft dargestellt werden kann, und für die er nun dank der neuen chemischen Experimente seit dem 18. Jahrhundert gleichsam das Illustrationsmaterial geschenkt bekommt, worauf er zur Darstellung seiner Ideen lange hatte warten müssen?
Die Idee einer Logik der chemischen Sphäre sieht sich beiden Vorwürfen ausgesetzt. Wer an Hegel die Geistesphilosophie schätzt, wird kaum verstehen, warum er in der Maßlogik so intensiv Beispiele aus der chemischen Wissenschaft heranzieht und keineswegs ausschließlich in illustrierende Anmerkungen verbannt. Daher werden diese Ausführungen und erst recht die später folgenden über den Chemismus von dieser philosophischen Richtung überwiegend schlicht ignoriert. – Und umgekehrt kann Hegel vorgehalten werden, er wolle schulmeisterlich von außen der Chemie sagen, wie sie denken könne und solle. Ihm kann vorgeworfen werden, dass er die experimentellen Leistungen der Chemie zu gering schätzt. Dieser Vorwurf sieht sich bestätigt, wenn später von vielen Hegelianern die »Realwissenschaft« als geringerwertig angesehen wird im Vergleich zum absoluten Wissen. – Eine solche kritische Haltung vertritt auch Ulrich Ruschig. Er ist dennoch in einer Weise von den Ergebnissen der hegelschen Ausführungen fasziniert, dass sein Kommentar tiefer als andere mir bekannte Arbeiten in die Ausführungen von Hegel eindringt und im folgenden zum Ausgangspunkt genommen wird.
Rückblickend muss gesagt werden, dass die von Hegel eingeführten Begriffe »chemische Sphäre« und »Chemismus« von der Philosophie nicht angenommen wurden. Auch der dialektische Materialismus hat sie ignoriert, obwohl Friedrich Engels zahlreiche Aussagen der chemischen Sphäre als »Gesetze« einer Dialektik der Natur versteht. Niemand spricht mehr von »chemischer Sphäre«, und »Chemismus« taucht bestenfalls als selten benutzter Fachbegriff in der Biologie, Medizin oder Ökologie auf. Sie scheinen völlig durch die Entwicklung einer wissenschaftlichen Chemie im 19. Jahrhundert überholt worden zu sein.
Für Hegel geht die chemische Sphäre aus der mechanischen Sphäre hervor und bedeutet einen notwendigen Vermittlungsschritt, um zur Sphäre des Lebendigen zu gelangen. Er ist damit wesentlich über Kant hinausgegangen, dem es noch unmöglich erschienen war, dass die Chemie jemals zu einer »eigentlichen Wissenschaft«, d.h. mathematik-fähig werden könne (Kant, MAN, AA 04: 471.05-10). Wenn mit Hegel der Logik der chemischen Sphäre nachgegangen wird, bedeutet das, dass nicht nur mit Kant der Monismus der Leibnizschen Monadologie überwunden wird, sondern auch Kants Dualismus. Kant hatte bereits 1746 in seiner ersten Veröffentlichung Gedanken von der wahren Schätzung der lebendigen Kräfte gegenüber Leibniz zwischen toten und lebendigen Kräften unterschieden und in weiteren Arbeiten nahegelegt, dass ihnen zum einen ein eindimensional verbleibender Verstand und zum anderen eine zu höheren Einsichten fähige Vernunft entsprechen, oder ein Dualismus zwischen der im Mechanischen verhafteten reinen Vernunft und eine darüber hinausgehende Urteilskraft, die zu Einsichten in das Organische fähig ist. Als Analogie diente ihm die physikalische Unterscheidung zwischen der dem Impuls zugrunde liegenden toten Kraft, die als ›m · v‹ gemessen wird, in der die Zeit mit ›v = t / s‹ eindimensional auftritt, und die der Energie zugrunde liegende lebendige Kraft durch das Maß ›m · v2‹, in der die Zeit quadratisch, also in einer höheren Dimension auftritt.
Obwohl Hegel mit der chemischen Sphäre diesen Dualismus im Prinzip aufgebrochen hat, fällt er dennoch immer wieder in das dualistische Denken zurück, wenn er zwischen dem endlichen Verstand und der »höheren« Vernunft unterscheidet. Daher konnte den Lesern Hegels die weitreichende Bedeutung der chemischen Sphäre verborgen bleiben. Bonsiepen fasst es in einem Satz zusammen: »Insgesamt ist festzuhalten, daß Hegel zu keiner positiven Aufnahme der neueren Chemie gelangt, obwohl er die zeitgenössischen Entwicklungen verfolgt« (Bonsiepen, S. 536).
Demgegenüber eröffnet nach meiner Überzeugung die chemische Sphäre einen neuen Horizont. Um das zu verstehen ist zunächst zu entwickeln, was mit chemischer Sphäre gemeint ist und dann in weiteren Beiträgen zu zeigen, wie auch die anderen philosophischen Begriffe im Licht der chemischen Sphäre neu gedeutet werden können. Das wird exemplarisch am Begriff der Trägheit und dort weiterführend am Begriff der Zeit ausgeführt, sowie in weiteren Beiträgen zum Chemismus und zur Teleologie (in Vorbereitung), d.h. zu den drei Kapiteln über die Objektivität in Hegels Wissenschaft der Logik.
Heute wird dagegen in Kants Tradition das mechanische Denken oder das mechanische Weltbild direkt mit dem organischen oder dem holistischen Denken konfrontiert. Daher scheint es heute eine Alternative zu sein, sich entweder für das eine oder das andere entscheiden zu müssen. Das führt in der Tendenz dazu, das mechanische Weltbild völlig abzulehnen und das holistische Weltbild zu verklären.
Ohne Zweifel ist eine Kritik des mechanischen Denkens notwendig, aber sie soll auf eine Weise erfolgen, die im Ergebnis das mechanische Denken nicht einfach für rundum falsch erklärt, sondern in der Lage ist, seine Leistungen im positiven Sinn aufzuheben. Andernfalls droht bei aller Kritik am mechanischen Denken ein Rückfall auf Positionen des Aberglaubens und Irrationalismus, gegen die sich das mechanische Denken ursprünglich zurecht entwickelt hatte.
Ohne Kritik an der Willkür und den Absonderlichkeiten des mittelalterlichen Analogie-Denkens hätte die neuzeitliche Naturwissenschaft nicht entstehen können und wäre gegenüber weltabgewandten Weltanschauungen in einer hilflosen Position geblieben. Erst nachdem es ihr gelungen war, sich innerlich zu festigen, konnte in einem weiteren Schritt in einem Gegenzug eine Selbstüberprüfung des mechanischen Denkens erfolgen, mit der verschiedene Ideen des zuvor kritisierten Analogie-Denkens neu aufgegriffen werden. Die Logik der chemischen Sphäre hat die Aufgabe, das zu leisten, ohne in Positionen des vor-aufklärerischen Denkens zurückzufallen.
Mit der Logik der chemischen Sphäre erfolgt gewissermaßen ein kontrollierter Bruch des geschlossenen mechanischen Systems. Der klassische Begriff des mechanischen (dreidimensionalen, starren) Gegenstands muss ebenso aufgegeben und durch den Begriff des Substrats ersetzt werden, wie sich weder ein rein beschreibendes (qualitatives, deskriptives, analytisches) noch ein rein messendes (quantitatives, formales, konstruktives) Denken halten lässt. Ihre Methoden erweisen sich als gebunden an den mechanischen Kontext.
Das ist die Aufgabenstellung, um die es im Kapitel über das reale Maß geht. Statt von Analogien spricht Hegel von Wahlverwandtschaften und übernimmt damit einen Fachbegriff aus der sich zu seiner Zeit neu begründenden Chemie. Stoffe sind miteinander wahlverwandt, wenn sie zu gemeinsamen Reaktionen neigen. Wahlverwandtschaften können sich wiederum ihrerseits bei Veränderung der Rahmenbedingungen wandeln, wobei es Phasen stabiler Wahlverwandtschaften und qualitativer Sprünge gibt.
Hegel hat diese Frage in die Wissenschaft der Logik aufgenommen. Er erkennt, dass alle überlieferten formalen Systeme an der Mechanik orientiert waren. Sie operieren mit autonomen, frei beweglichen Bausteinen. Sie gehen von unveränderlichen letzten Bausteinen aus. Diese können zwar ihre Eigenschaften verändern, aber nicht direkt miteinander reagieren und sich ineinander verwandeln, sondern einander nur berühren. Es ist nur ein äußerlicher Übergang vom einen zum anderen möglich.
Dagegen entwickelt sich in der chemischen Sphäre ein System von Beziehungen (Familienähnlichkeiten). Beziehungen können enger oder lockerer sein, und das Beziehungsgeflecht im Ganzen kann sich entlang von Knotenlinien verändern. Hegel will nicht die chemische Sphäre äußerlich neben die mechanische Sphäre stellen und insofern dann doch wieder dem äußerlichen, mechanischen Denken verfallen bleiben, sondern er zeigt, wie die mechanische Sphäre von sich aus in die chemische Sphäre führt. Er fragte, wie unter solchen Verhältnissen eine Wissenschaft der Logik möglich bleibt, ohne in die Beliebigkeit des früheren Analogie-Denkens zurückzufallen.
Anmerkung (Wittgenstein): Nach Hegel hat mit der Industrialisierung die Mechanik trotz der Erfolge der neueren Wissenschaften wie Chemie und Elektrodynamik einen unerwarteten Aufschwung genommen. Sie konnte daher überraschenderweise Ende des 19. Jahrhunderts nochmals zu einer Art Leitwissenschaft aufsteigen. Wittgensteins Philosophie zeigt die Faszination, die von dieser zweiten Blüte ausging. Er will im Tractatus logico-philosophicus die Logik ein letztes Mal auf die Mechanik zurückführen. Die Wahrheitsfunktion wird auf Elementarsätze angewendet. Die Frage nach den Eigenschaften des Raums, in dem sich die Elementarsätze befinden, wird noch nicht gestellt. Diese Frage entsteht erst mit einem Verständnis der chemischen Sphäre, wie es von Hegel begründet wurde.
»6 Die allgemeine Form der Wahrheitsfunktion ist [p, ξ, N(ξ)].
6.001 Dies sagt nichts anderes, als dass jeder Satz ein Resultat der successiven Anwendung der Operation N(ξ) auf die Elementarsätze ist. [...]
6.341 Die Mechanik bestimmt eine Form der Weltbeschreibung, indem sie sagt: Alle Sätze der Weltbeschreibung müssen aus einer Anzahl gegebener Sätze – den mechanischen Axiomen – auf eine gegebene Art und Weise erhalten werden. Hierdurch liefert sie die Bausteine zum Bau des wissenschaftlichen Gebäudes und sagt: Welches Gebäude immer du aufführen willst, jedes musst du irgendwie mit diesen und nur diesen Bausteinen zusammenbringen« (Wittgenstein, Tractatus logico-philosophicus).
Ur-Teilung des Maßes
Der Begriff des Maßes ergibt sich aus den »Etwas – geläufiger: Dinge(n)« (HW 5.412) selbst, indem an ihnen Maß genommen wird. Jedes Ding hat sein natürliches Maß. Die Maßlogik beginnt mit der »spezifischen Quantität«. Das ist im wesentlichen das spezifische Quantum (die Größe), das an einem anderen natürlichen Maßstab (z.B. der Elle oder dem Fuß) gemessen wird, die räumliche und zeitliche Gestalt eines Dinges.
In der Realität werden aber die Dinge meist nicht so vorgefunden, wie sie ihrem natürlichen Maß entsprechen würden, sondern in der einen oder anderen Anpassung an ihre Umgebung oder auch Verzerrung. Es ist Aufgabe der Kunst, hinter der erscheinenden Hülle der Dinge ihr inneres Maß zu sehen und zu gestalten, und es ist entsprechend die Aufgabe der Wissenschaft, die Regeln zu finden, wodurch sich Maße auszeichnen. Sogar in der Vielfalt der Maße kann es natürliche Maße geben, an denen die anderen Maße gemessen werden wie z.B. der Kreis oder das Goldene Maß. Was ein Maß ist, wird daher im Grunde erst verständlich durch Abgrenzung gegen das Übermaß, wenn etwas sein Maß verfehlt oder verliert. Das Maß eines Dinges ist seine natürliche Größe, die sich positiv von allen Abweichungen unterscheidet. Erst wenn etwas in einem übergreifenden Horizont gesehen wird, der sowohl das Maß wie das Verfehlen des Maßes übersieht, dann wird es für sich als Maß verstanden. Hegel spricht von »negativer Einheit«, die sowohl das Maß wie das Verfehlen des Maßes umfasst und das Maß gleichermaßen von innen und von außen sieht.
»Diese negative Einheit ist reales Fürsichsein, die Kategorie eines Etwas, als Einheit von Qualitäten, die im Maßverhältnisse sind, – eine volle Selbständigkeit« (HW 5.411)
Das Maß wird von außen betrachtet (einer äußerlichen Reflexion unterzogen). Das ist innerhalb der Maßlogik die Aufgabe des zweiten Kapitels über das reale Maß. Der im ersten Kapitel entwickelte Begriff des Maßes, der am natürlichen Maß der jeweiligen Dinge gewonnen wurde, wird negiert durch eine Ur-Teilung des Maßes. Jedes Maß wird verstanden als Verhältnis zweier Aspekte, die in der Beziehung zueinander ihr Maß finden. Auf diese Weise kann das Maß gegenüber dem Übermaß positioniert und mit ihm in einer negativen Einheit gesehen werden, wenn es gelingt, die inneren Bestandteile zu erkennen, die sich im Maß angemessen zusammenfügen, während sie im Übermaß in der einen oder anderen Weise das Maß über- oder unterschreiten.
Genauer ist zu betrachten: (1) Ein Maß kann nur gebildet werden als Verhältnis zwischen zwei Seiten, die bereits eine innere Beziehung zueinander haben. Sie müsssen in gewisser Weise zusammengehören und zueinander passen. Hegel bezeichnet das im Sprachgebrauch der romantischen Naturphilosophie als Wahlverwandtschaft. Ein reales Maß kann nur zwischen zwei Dingen bestehen, die miteinander wahlverwandt sind. Damit greift er den Begriff der Affinität auf, den Kant noch in der ersten Auflage der Kritik der reinen Vernunft gebraucht hatte. Wenn zwischen zwei Dingen oder zwei Momenten einer Sache eine Affinität besteht, dann kann es zwischen ihnen ein reales Maß geben. Wenn sie nicht wahlverwandt sind, stellt sich die Frage nach ihrem realen Maß erst gar nicht.
(2) Bei genauerer Betrachtung zeigt sich, dass die Wahlverwandtschaft kein festes Verhältnis ist, sondern von jeweils bestimmten Bedingungen abhängt. Etwas kann unter bestimmten Bedingungen miteinander verwandt sein, in anderen jedoch noch nicht oder nicht mehr. Hegel sucht nach einem Ansatz, um die Parameter zu bestimmen, wodurch sich diese Bedingungen ändern. Mit ihnen soll unterschieden werden, wann alles "stimmt", um ein reales Maß herstellen zu können, und wann nicht. Der Verlauf dieser Bedingungen sind die von ihm so genannten Knotenlinien. Zum Beispiel können manche chemischen Stoffe nur miteinander reagieren, wenn eine bestimmte Temperatur gegeben ist, oder wenn die Konzentration der Stoffe im vorliegenden Gemisch innerhalb bestimmter kritischer Grenzen liegt. In diesen Beispielen ergeben sich Knotenlinien entlang der Erhöhung der Temperatur bzw. des prozentualen Anteils (der Konzentration) eines Stoffs in einem Gemisch. Hegel hofft, auf einer höheren Ebene Eigenschaften zu finden, die für alle Knotenlinien gelten und mit denen allgemein die Veränderungen von Wahlverwandtschaften verstanden werden können.
(3) Sind die Knotenlinien gefunden, dann kann abschließend gefragt werden, was es ist, das sich zwar im Verlaufe der Knotenlinie verändert, aber als zugrunde liegendes Substrat erhalten bleibt. Hegel bezeichnet diese Erhaltungsgröße als die Sache selbst. Sie ist insofern maßlos, weil sie das Maß erhält unter den sich verändernden Zuständen, aber sich nicht selbst mißt. Wenn z.B. das Wasser als Substrat des gefrorenen, flüssigen und gasförmigen Wassers verstanden wird, dann befindet sich das Substrat als solches in keinem eigenen Aggregatzustand, sondern liegt allen zugrunde.
(4) Mit der Sache selbst wird im nachfolgenden Schritt der Übergang zum Wesen erfolgen, und dort wird der Schritt zur Existenz der Sache gezeigt werden
Daraus ergibt sich als Arbeitshypothese für diesen Beitrag:
Die chemische Sphäre ist für Hegel der Horizont des Maßes. Die Logik der chemischen Sphäre zeigt, wie sich Maße bilden und auflösen. Das reale Maß ist das Maß verstanden aus seiner Entstehung in der chemischen Sphäre.
Das kann in anderen Worten auch so gesagt werden, dass Hegel im Kapitel über das reale Maß den Prozess betrachtet, aus dem ein Maß hervorgeht oder verfehlt wird. Das verstehe ich ganz anschaulich: Unmittelbar liegen meist Gemische vor, z.B. Geräusche in der Tonwelt oder Mischungen in der stofflichen Welt (etwa Erde, die sich aus zahlreichen Stoffen zusammensetzt, Flüssigkeiten, in denen verschiedene Stoffe in einem anderen Stoff gelöst sind, etc.). Hegel verallgemeinert das in die Aussage, dass das Etwas eine »Einheit von Qualitäten« ist, die im folgenden voneinander zu differenzieren sind, um erkennen zu können, in welchem Verhältnis sie zueinander stehen müssen, um ein Maß zu ergeben.
Den schwierigsten Punkt lässt Hegel an dieser Stelle allerdings weg: Wie gelingt es, innerhalb eines Gemisch dessen anfangs noch verborgenen, charakteristischen Bestandteile zu erkennen? Hegel spricht davon, dass hier die »chemische Sphäre« betreten wird, in der »das Materielle seine spezifische Bestimmtheit in der Beziehung auf sein Anderes (hat); es existiert nur als diese Differenz« (HW 5.420). Damit meint er nicht nur chemische Vorgänge, sondern alle Vorgänge, in denen sich Maße bilden, also insbesondere auch in der Ästhetik (z.B. Harmonie-Maße in der Musik) oder der Politik (so hat »der Staat ein Maß seiner Größe, über welches hinausgetrieben er haltungslos in sich zerfällt", HW 5.441f).
Dennoch bleibt die Frage, wie diese inneren Bestandteile der Maße gefunden werden. Im Beispiel der Musik waren es die Pythagoreer, denen mit dem Monochord die Zerlegung eines Klangs in Grundtöne und deren Zahlenverhältnisse gelungen war. Alle Geräusche lassen sich aus ihnen zusammensetzen. In der Chemie liegt eine lange Tradition vor, in der die unterschiedlichen Stoffe isoliert und wieder zusammengefügt worden sind. Es hat sehr lange gedauert und unterschiedlichste Klassifikationsversuche gegeben, bis einigermaßen erkannt war, welche Stoffe sich aus anderen zusammensetzen und welche Stoffe als grundlegende, reine Stoffe angesehen werden können. Naheliegenderweise übernimmt Hegel den in seiner seiner Zeit erreichten Erkenntnisstand und geht davon aus, dass die chemischen Stoffe, wie sie damals bekannt waren, eine geeignete Aufteilung der chemischen Sphäre darstellen. Neuere Ideen wie Daltons Atomtheorie (A New System of Chemical Philosophy, 1808) kannte er zwar bereits, aber obwohl er die von Dalton beschriebenen Befunde anerkennt, lehnt er dessen Atomtheorie ab (siehe hierzu R, S. 280 mit Verweis auf Hegel, Enz. Zusatz zu § 333, HW 9.326).
An dieser kritischen Stelle formuliert Ruschig eine grundsätzliche Kritik: Es bedarf experimenteller Arbeit, um in einer langwierigen Kette von gelingenden und fehlschlagenden Versuchen schließlich zu den Ergebnissen zu kommen, wie sie hier bei Hegel vorausgesetzt werden. Ruschig kritisiert am Beispiel der Auflösung eines Salzes (Na2SO4) in Wasser:
»Ein Dispositionsprädikat wie 'löslich in Wasser' kann ohne die Beziehung auf eine durch einen Zweck dirigierte Tätigkeit gar nicht bestimmt werden. Allein die Deskription dieser Tätigkeit reicht nicht hin, wie der gescheiterte Versuch des Positivismus zeigt, solche Dispositionsprädikate 'subjektivitätsfrei' – so durch den Wenn-Dann-Satz 'wenn immer x ins Wasser gegeben wird, löst es sich darin auf' – zu definieren« (R, S. 196).
Hegel setzt an dieser Stelle voraus, dass die Ur-Teilung des Etwas in seine Bestandteile bereits gefunden ist und in experimentellen Versuchen überprüft und verfeinert werden kann. Er fragt nicht, wie das möglich war. Sein Ziel ist an dieser Stelle nur, einen einzelnen – allerdings wesentlichen – Schritt in der Gesamtbewegung wissenschaftlichen Arbeitens zu erkennen: Welche Bestimmungen sind notwendig, um ein zunächst unübersichtliches Gemisch von Erkenntnissen in voneinander unabhängige Faktoren zu zerlegen. Darauf aufbauend werden weitere Schritte folgen, die er abschließend im Methoden-Kapitel zusammenfasst und zur analytischen und synthetischen Methode Stellung nimmt. Erst dann wird sich klären lassen, ob und wie weit die Kritik von Ruschig berechtigt ist.
Siglen
HW: Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971
KrV: Immanuel Kant: Kritik der reinen Vernunft (1781, 1787)
MAN: Immanuel Kant: Metaphysische Anfangsgründe der Naturwissenschaft (1786)
in: Akademie-Ausgabe, Bd. IV, Berlin 1911; Link Volltext
R: Ulrich Ruschig: Hegels Logik und die Chemie, Bonn 1997
Literatur
Peter William Atkins: Chemie des Wandels, Heidelberg u.a. 1993 [1991]
Wolfgang Bonsiepen: Die Begründung einer Naturphilosophie bei Kant, Schelling, Fries und Hegel, Frankfurt 1997
Michael Esfeld (Hg.): Philosophie der Physik, Berlin 2012
Ulrich Gaier: Krumme Regel, Tübingen 1970
Edmund Husserl: Vorlesungen zur Phänomenologie des inneren Zeitbewußtseins, Tübingen 2000 [1928]
Martin Münch: Die Klaviersonaten und späten Préludes Alexander Skrjabins, Berlin 2004
Gerhard Nestler: Geschichte der Musik, München 1993 [1962]
Lorenz Bruno Puntel: Darstellung, Methode und Struktur, Bonn 1973
Urs Richli: Form und Inhalt in G.W.F. Hegels »Wissenschaft der Logik«, Wien, München 1982
Ulrich Ruschig 2000: Die “Knotenlinie von Maaßverhältnißen” und materialistische Dialektik
in: Andreas Arndt, Christian Iber (Hg.): Hegels Seinslogik, Berlin 2000, S. 301-314
Ulrich Ruschig 2010: Randglossen zur "Bewegung des Begriffs"
in: Johann Kreuzer (Hg.): Hegels Aktualität, München 2010, S. 67-82; Link
Ulrich Ruschig 2012: Vom Sinn des Tones
in: Georg Mohr und Johann Kreuzer (Hg.): Vom Sinn des Hörens, Würzburg 2012, S. 109 - 126; Link
Ludwig Wittgenstein: Tractatus logico-philosophicus
in: Werke Band 1, Frankfurt am Main 1984; Link
2013-2014, 2019
© tydecks.info 2014


