Mathematik und Ökonomie - Thesen und Arbeitsprogramm

Basistrends in der Volkswirtschaftsrechnung

Ökonomische Ströme im Welthandel

Im Welthandel (und entsprechend auch in kleineren ökonomischen Einheiten) werden Ströme von Waren und zugehörigen Daten und Informationen betrachtet. Zum Beispiel: Handelsströme, Kapitalströme, Wechselkurse, Zinsen, Preisindizes, Gewinne. Hier interessiert weniger, dass die Ströme in Zahlenmaterial ausgedrückt werden, sondern der Begriff Strom selbst hat ein Gegenstück in der Mathematik. Es ist also nicht nur im Einzelnen zu verfolgen, welche Zahlenwerte die Ströme annehmen, sondern die qualitativen Eigenschaften der Ströme sind zu betrachten:

• Wie stabil und gleichmäßig sind die Ströme?

• Gibt es labile, gefährdete Zonen?

• Gibt es absolute Grenzwerte (z.B. natürliche Grenzen der Rohstoffe)?

Strukturverschiebungen

Die Ökonomie betrachtet mindestens im 20. Jahrhundert verschiedene Strukturverschiebungen. Zum Beispiel:

Kostenstruktur: Gegenüber direkten Kosten gewinnen abgeleitete Kosten wachsende Bedeutung, etwa Gesundheit, Ökologie, Bildung, Dienstleistungen.

Kreditstruktur: Die Grenzen von Sach- und Geldanlagen verschwimmen. Der Kreditsektor gewinnt an Bedeutung, innerhalb des Sektors verlagert sich der Schwerpunkt von Kreditgewährung zu Anleihen. Die Konkurrenz unter den Banken wächst, Großunternehmen wachsen bisweilen aus der Rolle von Kreditnehmern zu Kreditgebern. Insgesamt wächst die Spekulation.

Mathematisch wäre zu bestimmen, wie diese Strukturen und ihre signifikanten Änderungen in den Strömen qualitativ wiederkehren. Ändern die Strukturverschiebungen die qualitativen Eigenschaften der Ströme, z.B. die Stabilität? Wenn ja, in welchem Maß?

Arbeitsteilung

Die ökonomische Arbeitsteilung verändert sich deutlich in allen Gesichtspunkten.

Stofflich: Rohstoffe, Landwirtschaft, Industrie, Dienstleistungen

Geographisch: Neue und größere Ballungszentren, Branchenverteilung.

Wieder ist nach den Rückwirkungen auf die ökonomischen Ströme zu fragen.

Stabilität

Die Stabilität ist jedoch nicht nur durch Strukturveränderungen und fließende Arbeitsteilung beeinflußt, sondern zahlreiche weitere direkte Prozesse kommen hinzu:

• Auflösung autarker Einheiten und der Subsistenzwirtschaft

• Wachsende Verflechtung (in verschiedenen Komponenten)

• Zunahme und Abnahme bestimmter Fixwerte (Staatskosten für Infrastruktur, fixe Kosten der Unternehmen, evtl. weitere)

• mehr oder weniger Flexibilität

• Zunahme und Abnahme von Liquidität und Mobilität

Stoffliche Grundlagen

Worin liegt eigentlich die "stoffliche Grundlage" für mathematische Methoden (welche Aspekte der Ökonomie liegen in einer Form vor, dass sie mathematisiert werden können):

• Planung der Ökonomie (und dadurch Ansatzpunkte für Gleichmäßigkeiten und Quantifizierung)

• Endlichkeit der Ökonomie (und damit endliche Zahlen wie Anzahl der Menschen, Menge der Arbeitszeit, Anzahl der Produkte, Konsumvolumen etc.)

• Starke Zeitabhängigkeit ökonomischer Prozesse

• Möglicherweise Autonomie von ökonomischen Prozessen gegenüber anderen (Naturbearbeitung, Politik, Kultur), wodurch mathematische Modelle möglich werden

Wie weit reichen die mathematischen Modelle: Zeithorizont, Genauigkeit, branchenübergreifend, länderübergreifend, Raumhorizont.

Elementare Ideen aus der Mathematik (Mutterstrukturen)

Basiselemente

Bisher gibt es in der mathematischen Ökonomie nur äußerst wenig Basiselemente. In der auf Ricardo zurückgehenden Ökonomie der Zeit ist es nur die eine Zeitdimension. Die mechanistischen Angebots-Nachfrage-Modelle reduzieren bewußt alles auf die Produktions- und Kaufkraft, ausgedrückt in der einen Gelddimension.

Zwar gibt es also verschiedene, sich gegenseitig ausschließende Modelle. Im Grunde bestand aber der Ehrgeiz der politischen Ökonomie darin, möglichst die gesamte Theorie auf ein einziges Basiselement aufzubauen, wodurch alle diese Theorien einen stark axiomatischen Charakter bekommen und mathematischen Methoden nur wenig Spielraum lassen. Zugleich zerfällt die ökonomische Diskussion in einander gegenüberstehende Positionen, deren Vertreter einander nicht einmal zitieren.

Verhältnis lokal / global

In der Mathematik ist das Verhältnis lokaler und globaler Ereignisse präzise bestimmt. Auch in der Ökonomie gibt es Fragen in dieser Richtung:

Am interessantesten ist die Frage nach der Synchronisierung verschieden langer Wirtschaftszyklen. Ist der kurze Zyklus einfach nur eine präzisere Form des längeren, oder bildet sich die Struktur des Zyklus rekursiv in kleineren Einheiten immer wieder ab? Oder gibt es zwischen den Zykluslängen charakteristische Maßzahlen (wie in der Physik), so dass jeder Zyklus seine eigene Qualität hat? Grundsätzlich weist die Existenz von Zyklen auf mehr als eine Dimension, und je mehr spezifische Zyklen es gibt, desto mehr Dimensionen.

Ströme

Die Mehrdimensionalität führt direkt zur Frage der simultanen Wechselwirkung. Wenn zu der einen Zeit- bzw. Gelddimension weitere Dimensionen hinzukommen, kann es simultane Wechselwirkung im Zeitmoment geben. Kann diese Wechselwirkung mit Selbstorganisationsmodellen erfaßt werden? Die Ausbreitung von Ereignissen erfolgt als Informationsverbreitung, auf die Märkte reagieren, und dabei nicht nur das quantitative Wachsen von Geldwerten in Betracht ziehen. Überhaupt ist die reine Betrachtung von Größenwachstum aufzugeben.

Wenn es Wechselwirkung im Zeitmoment gibt, können schon rein mathematisch Katastrophenprozesse in ganz anderen Formen beschrieben werden (Konstellationen) als im bisher ausschließlich zeitorientierten Krisenbegriff. (Die Krise nur als Ergebnis einer zeitlichen Entwicklung, zyklisch oder chronisch).

Muster

Als Darstellungstechniken kennt die VWL im Grunde nur die Graphik und die Tabelle, wenn sie sich überhaupt auf mathematische Darstellungen einlässt. In der Regel sind es Säulen- und Tortendiagramme, so wie sie jeden Tag auf den Wirtschaftsseiten in der Zeitung zu sehen sind. Es fehlen geometrische Methoden, d.h. es gibt ausschließlich zeitorientierte Betrachtungen.

Es fehlen erst recht differentialtopologische Methoden, um die komplexeren Strukturen von Stabilität zu erfassen.

Nur wenige neuartige Muster wie etwa point-and-figure-Methoden in der Chartanalyse sind neu eingeführt worden.

Algebra

Auch komplexere algebraische Ansätze fehlen, es gibt im Grunde nur die reelle Analysis aus dem 18. Jahrhundert, da eben nur eindimensionale Zeitfunktionen betrachtet werden. Mehrdimensionale Methoden wie komplexe Analysis, Lie-Algebra, äußere Algebra, Superstrukturen, harmonische Analyse sind aber in der Mathematik reichlich vorhanden und in allen Gebieten der Physik bestens eingeführt.

Der Begriff Zyklus (Kreis)

Dimensionen

Ein Kreis ist immer zweidimensional. Es kann sogar 3 Dimensionen geben, falls bei mehrfachem Durchlauf der Kreis nicht einfach wiederholt wird, sondern Unterschiede auftreten. So kann der Kreis die Form einer Spirale annehmen (mathematisch gesprochen kann der Kreis auch in einem mehrblättrigem Raum liegen, wobei jeder Durchlauf in ein anderes Blatt führt).

Kräfte

Den 2 Dimensionen entsprechen 2 Kräfte, die in der Kreisbewegung wirken: Eine Gravitationskraft, die zum Zentrum hin wirkt und eine periphere Kraft, die tangential von der Kreislinie wegstrebt.

Die Gravitationskraft wirkt im weitesten Sinn erhaltend, konservativ.

Im Zentrum liegen Kapazitäten, Widerstandslinien, die verhindern, dass die Bewegung sich verselbständigt und maßlos wirkt. Sowohl der maßlose überhitzte Aufschwung werden verhindert, wie der bodenlose Fall. Bei den Kapazitäten im Zentrum kann es sich um Bodengröße, Bevölkerungszahl, natürliche Bevölkerungsentwicklung, klimatische Rahmenbedingungen, Produktionsstock (vorhandene Anlagen und Werkzeuge), liquide Reserven handeln.

Im äußersten Fall bewirkt die Gravitationskraft die Rückkehr in die Subsistenzwirtschaft (die Überlebenden ernähren sich vom Eigenanbau).

Die periphere Kraft wirkt dagegen verändernd, innovativ, progressiv. Jede einmal ausgelöste Bewegung tendiert in eine unbegrenzte, entfesselte Dynamik. Ist ein Produkt einmal eingeführt, will es jeder haben. Ist eine neue Produktionsmethode erfolgreich pilotiert, soll sie überall eingesetzt werden.

Langfristig unterstellt die Kreisbewegung einen Ausgleich der beiden Kräfte. Ist auf Dauer eine Kraft stärker, kann es in der dritten Dimension zu einer spiralenförmigen Bewegung kommen (Trend).

Kreisunterteilung

Die Kreisbewegung kann in gleichmäßige Abschnitte unterteilt werden, indem z.B. ein Dreieck, Viereck, Fünfeck etc. in den Kreis einbeschrieben werden.

Mathematisch sind am interessantesten die Fälle, wo die Anzahl der Abschnitte eine Primzahl ist (2, 3, 5, 7 etc.). (In diesen Fällen kann der Kreisteilungskörper aus dem ersten Element vollständig erzeugt werden.)

Kreisunterteilungen werden in den Naturwissenschaften systematisch als Symmetrien untersucht.

Rotation

Der Kreis kann die Rotation eines Stroms darstellen, wodurch die Trenddimension eine neue Interpretation erhält. Der Kreis erfüllt dann eine Extremaleigenschaft: maximale Durchflußmöglichkeit.

Weitere mathematische Ansatzpunkte

Projektion des Kreises auf die Kugel.

Quaternionen.

Kreisfunktionen

Schwingungskurve

Die Kreisbewegung scheint überall gleich zu sein, beliebig, welcher Punkt betrachtet wird. Dieser Eindruck entsteht, da zunächst nur das räumliche Bild des Zyklus als Kreis, die Kreisgestalt, betrachtet wurde.

Durch die Zeit kommt die Darstellung als Schwingungsfunktion hinzu:

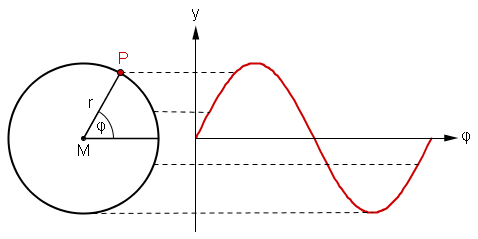
Figur 1: Welle am Beispiel der Sinusschwingung in der Musik
"Bewegt sich ein Punkt P auf einer kreisförmigen Bahn mit Radius r, so lässt sich jedem Phasenwinkel φ aus dem Intervall  [0,2π] der Wert der zugehörigen Auslenkung y zuordnen. Diese Werte werden entlang der Ordinaten-Achse eines Koordinatensystems aufgetragen, wodurch eine Sinuskurve entsteht." Quelle Die horizontale Achse (φ-Achse) ist die Zeitachse, entlang derer die Welle fortschreitet. Sie wird auch häufig als Nulllinie, Trendlinie oder Gleichgewichtslage bezeichnet.

Mathematisch als Formel:

	K(t) = A sin (wt + p)
	K	Kurvenfunktion
	t	Zeit
	A	Amplitude, auslenkende Kraft (Abweichung vom Trend) (wird auch als Elongation bezeichnet, maximaler Wert von der Nulllinie bis zum Wellenberg bzw. Wellental, mathematisch gesprochen bis zum lokalen Maximum bzw. Minimum)
	sin	Sinus (Kreisfunktion)
	w	Frequenz, rückholende Kraft (in ökonomischen Zyklen wird die Frequenz in Jahren ausgedrückt)
	p	Phasenverschiebung

Die vier Abschnitte eines Zyklus

Die Schwingungsgestalt lässt gegenüber der Kreisgestalt qualitative Unterscheidungen zu:

An die Stelle des Mittelpunktes im Kreis tritt die eindimensionale, resultierende, langfristige Trendentwicklung (im einfachsten Fall die waagerechte Gerade, um die die Schwingung oszilliert).

Abweichend vom Trend können Tiefs und Hochs unterschieden werden.

Durch die Extrem- und Wendepunkte wird die Schwingung in 4 Phasen geteilt. Zwar stimmen alle Ökonomen darin überein, den Zyklus in vier Phasen zu unterteilen, doch gibt es unterschiedliche Präferenzen, in welcher Reihenfolge die Phasen dargestellt werden. Das führt vor allem bei langfristigen Zyklen (wie dem 60-jährigen Kondratieff-Zyklus) zu Verwirrungen, wenn Anfang und Ende der Zyklen verschieden datiert werden. Ich folge dem Gabler-Wirtschaftslexikon. Hier wird jeder Zyklus mit der Erholungsphase begonnen:

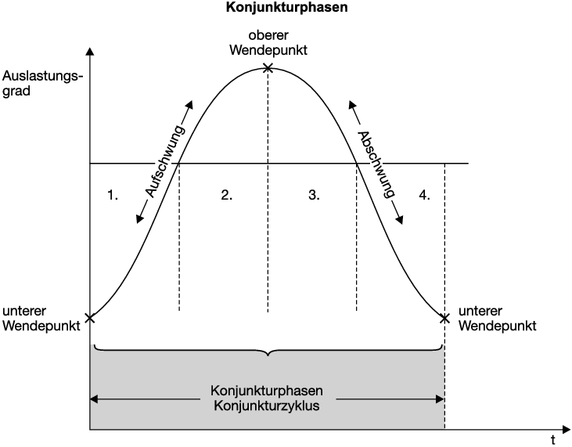
Figur 2: Konjunkturphasen
"(1) Die Aufschwungsphase nach dem unteren Wendepunkt wird als Erholung oder Expansionsphase bezeichnet, gekennzeichnet durch verbesserte Kapazitätsauslastung, steigende private Investitionen und Lohnsumme, zunehmendes Volkseinkommen und erhöhten privaten Konsum.
(2) Die Erholung geht in den Boom (Hochkonjunktur, Prosperität) über, sobald die Produktionsfaktoren voll beschäftigt sind, eine Erhöhung des realen Volkseinkommens ist nicht mehr möglich, es kommt zu starken Preissteigerungen und Störungen auf dem Geld- und Kapitalmarkt.
(3) Nach Erreichen des oberen Wendepunktes geht die Entwicklung in die Rezession (Kontraktion, Abschwung) über, die in der Boomphase bei überhöhtem Zinsniveau durchgeführten Investitionen erweisen sich bei jetzt vorherrschender relativer Preisstabilität als unrentabel, es kommt zu einem Rückgang der privaten Investitionen und zu einer Stagnation des privaten Konsums. Gewinne und Lohnsumme sinken, zahlreiche Unternehmen geraten in Schwierigkeiten.
(4) Die Phase vor dem unteren Wendepunkt ist die Depression (Krise), gekennzeichnet durch hohe Arbeitslosigkeit, geringe Kapazitätsauslastung, geringe Investitionstätigkeit und hohe Bankenliquidität." Quelle

Hierbei verhalten sich Wachstum und Wachstumsraten jeweils spiegelbildlich: Während des Booms und der Rezession befindet sich die Wirtschaftskurve oberhalb der Nulllinie, jedoch nehmen die Wachstumsraten während dieser Zeit ab, bewegen sich also negativ. Umgekehrt steigen die Wachstumsraten in den Phasen der Depression und Erholung, wenn das Wellental durchlaufen wird.

Beispiel: Im Nachkriegsaufschwung der 50er und 60er des 20. Jahrhunderts waren die absoluten Zahlen der Produktion usw. ständig am steigen, aber die Veränderungsraten gingen laufend nach unten, bis sie auf dem Höhepunkt auch die absoluten Zahlen nach unten zwangen.

(Mathematischer Hintergrund: Die cosinus-Funktion ist die Ableitung der sinus-Funktion und umgekehrt.)

Vor- und nachlaufende Zyklen (Phasenverschiebungen)

Der Kreis wurde durch Hinzunahme der Zeitdimension in die Schwingungskurve umgewandelt. Das heißt aber nicht, dass beide Bilder identisch sind, im Grunde nichts Spezifisches haben. Vielmehr resultiert in der ökonomischen Realität eine Bewegung aus 3 Schwingungskurven, wobei der Hauptkurve (Produktionsleistung) eine anstoßende Kurve vorausläuft, die der Kraft der Eigenbewegung entspricht (innovativ), und eine bremsende Kurve nachläuft, wodurch sich die Auswirkungen des Zentrums bemerkbar machen (konservativ).

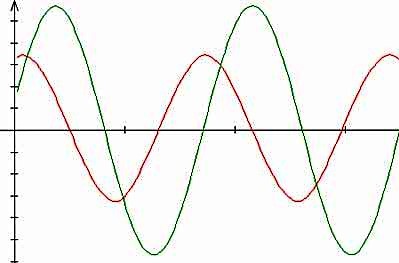
Figur 3: Anregung und Resonanz
Die rote Kurve läuft voran und erzwingt eine Resonanz, die als grüne Kurve nachläuft. Für dieses Phänomen gibt es zahlreiche biologische und technische Beispiele. In der Ökonomie stößt die Innovation den Wirtschaftszyklus an.Quelle

In der Ökonomie werden jedoch nicht 2, sondern 3 phasenverschobene Kurven betrachtet. Die vorlaufende Kurve wird in unterschiedlichen Theorien als Innovations- oder als Gewinnkurve interpretiert. Die nachlaufende Kurve beschreibt den Zinszyklus. Das stiftet nochmals Verwirrung, wenn unterschiedliche Ökonomen "den Wirtschaftsyklus" mal als den Produktions- und mal als den Zinszyklus interpretieren. Untersuchungen langfristiger zyklischer Prozesse gehen in der Regel von Preiszyklen aus, die dem Wirtschaftszyklus nachlaufen.

Empirisch lassen sich alle drei Kurven nachweisen. Es gibt auch intuitive Begründungen für ihre gegenseitigen Wirkungen. Mathematisch ließe sich sicher noch weit mehr über den inneren Zusammenhang dieser drei Kurven herausarbeiten. Das gesamte Gefüge aus unterschiedlichen kurz- und längerfristigen Zyklen, die jeweils wiederum aus drei phasenverschobenen (zeitversetzten) Zyklen bestehen, wird sehr schnell recht komplex. Werden weiter zeitversetzte Zyklen verschiedener Länder auf dem Weltmarkt und unterschiedliche Zyklen einzelner Wirtschaftszweige (z.B. Erneuerungszyklen im Wohnungsmarkt, Modellwechsel der Autoindustrie, Zyklen von Erschließung und Abbau verschiedener Rohstoffquellen) berücksichtigt, kommt es zu zahlreichen Wechselwirkungen (und Resonanzen), die die Standard-Dauern typischer Wirtschaftszyklen verändern.

Die Phasenverschiebung der 3 Kurven muss ausreichend eng sein, dass nicht zwei Kurven einander wie Spiegelbilder folgen. Die Phasenverschiebung darf nicht der halben oder der ganzen Wellenlänge entsprechen.

Beispiele und ökonomische Interpretation:

8-10-jähriger Zyklus (Konjunkturzyklus):

• Vorlauf: Gewinne, ca. 1/2 bis 1 Phase früher, d.h. 1/2 – 1 Jahr. Während die Produktion noch fällt, erholen sich die Gewinne bereits wieder, da Löhne und Zinsen sinken und Lagerbestände abgebaut werden. Umgekehrt beginnen die Gewinne bereits vor dem Konjunkturhöhepunkt wieder zu fallen. Die Gewinnentwicklung löst mit einer halbjährigen Verzögerung die Veränderungen der Produktionsentwicklung aus.

• Hauptlauf: absolute Produktion

• Nachlauf: Preise, Zinsen, ca. 1 Phase später, d.h. 1 Jahr. Erst wenn der Aufschwung bereits 1 Jahr begonnen hat, beginnen auch die Preise wieder zu steigen. Am anderen Ende steigen die Preise selbst nach dem Konjunkturhöhepunkt weiter, da angesichts des Aufschwungs viele Marktteilnehmer Kredite aufgenommen haben und nun weiter Geld für die Kreditfinanzierung brauchen.

55-60-jähriger Zyklus (Kondratieff-Zyklus):

• Vorlauf: Gewinne, Innovationen ca. 1/2 Phase früher, d.h. 5-8 Jahre

• Hauptlauf: absolute Produktion

• Nachlauf: Preise, Zinsen, Monopol, Protektionismus ca. 1 Phase später, d.h. 13 Jahre

Ananaszyklen

Wie sind Zyklen mit unterschiedlicher Zeitdauer synchronisiert? Ein Ansatz könnten Ananaszyklen sein, mit denen 3 Zyklen in einem dreidimensionalen Bild (der Ananas) verknüpft werden.

Jede Schuppe auf der Ananas ist 6-eckig, so dass durch jede Schuppe 3 Bänder hindurchlaufen: aufsteigend von links unten nach rechts oben (blau), aufsteigend von rechts unten nach links oben (rot) und senkrecht von unten nach oben (grün):

Figur 4: Ananaszyklus (Phyllotaxis)
"Wie diese Abbildung zeigt, sind die sechseckigen Pseudoschuppen der Ananas so angeordnet, dass durch die Zentren nebeneinander liegender Schuppen Spiralen gezogen werden können, die in drei Richtungen orientiert sind. Verblüffend ist, dass sich dabei 8, 13 und 21 jeweils gleich orientierte Spiralen ergeben. Die Zahl der Spiralen ist also in allen drei Orientierungsrichtungen eine Fibonaccizahl. - Eigene Untersuchungen ergaben jedoch auch Abweichungen von der Regel. Eine leicht deformierte Ananas wies 8, 9 und 17 jeweils gleich orientierte Spiralen auf." Quelle

Der Mathematiker Harold Coxeter (1907-2003) brachte die Darstellung der Ananas-Zyklen in eine stärker mathematische Form. Er projizierte die dreidimensionale Gestalt in eine rechteckige Form, wobei die Elemente am linken und am rechten Rand in jeder Zeile jeweils identisch sind. Die Natur hat mit der Abfolge gemäß den Fibonacci-Zahlen sichergestellt, dass jedes Blatt auf einem insgesamt beschränkten Raum beim 3-dimensionalen Wachstum optimalen Platz erhält.

Das Bild der Ananas kann zweidimensional veranschaulicht werden:

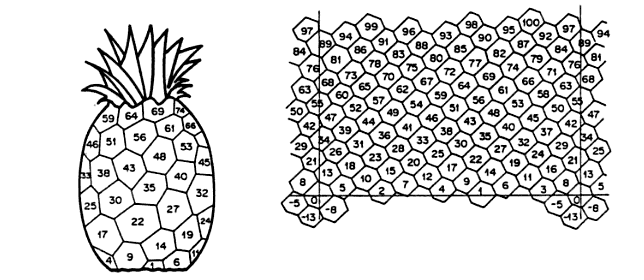
Figur 5: Ananaszyklus (Coxeter)
Harold Coxeter veröffentlichte diese Graphik in "Introduction to Geometry" (1961, deutsch "Unvergängliche Geometrie"). Online ist sie einsehbar bei Jay Kappraff "The Relationship between Mathematics and Mysticism of the Golden Mean Through History" in: István Hargittai (ed.): "Fivefold Symmetry", Singapore 1992, S. 52; GoogleBooks

Das Besondere an der Ananas ist, dass hier drei Zyklen verknüpft werden. Beim Aufbau von Muscheln werden einfache Zyklen nachgewiesen, die dem Goldenen Schnitt und den Fibonacci-Zahlen folgen, bei Samen, Kieferzapfen, den Einzelblüten der Sonnenblume jeweils zwei Spiralsysteme.

Mathematisch kann der Ansatz der Ananas verallgemeinert werden. Basis ist die Anzahl der Schuppen, die direkt am Boden stehen. Dann ergibt sich für das Verhältnis der drei Zyklen (wobei n größer als 2 sein muß):

Hauptzyklus	n	= Anzahl der Schuppen auf der Bodenfläche
1. Nebenzyklus	2 · n − 1	= Rechtswindung
2. Nebenzyklus	((n − 1) · 2) · n	= senkrechte Steigung

Das führt beispielsweise zu diesen Zahlen:

Hauptzyklus	3	5	6	10	23	50	60	100
1. Nebenzyklus	5	9	11	19	45	99	119	199
2. Nebenzyklus	12	40	60	180	1023	4900	7080	19800

Diese Zahlen liegen verblüffend nahe an den Werten der wirklichen Zyklen, wenn z.B. ein 6-jähriger Lagerzyklus, ein 11-jähriger Konjunkturzyklus und ein 60-jähriger Kondratieff-Zyklus angenommen werden.

Beispiel 1 (n = 3):

Die Schuppen 1, 2 und 3 stehen am Boden; n = 3
von links unten nach rechts oben ergibt sich ein 5-er Zyklus; 5 = 2·3 − 1
die Endpunkte in jeder Zeile liegen 12 auseinander; 12 = (3 − 1) · 2 · 3

Das ergibt von unten nach oben gelesen die Ringe:

11 14 17 20 23
6 9 12 15 18
1 4 7 10 13
2 5 8
3

In diesem Beispiel sind zwei initiale verkürzte Zyklen erforderlich, bis ab dem dritten Zyklus volle Reife erreicht ist. Ab diesem Zyklus wird beim Übergang von einem Platz rechts außen jeweils der Wert 2.Nebenzyklus - 1.Nebenzyklus abgezogen, hier: 12-5=7). Das ergibt den Übergang von 13 zu 6 und von 18 zu 11.

Beispiel 2 (n = 6):

Die Schuppen 1, 2, 3, 4, 5 und 6 stehen am Boden; n = 6
von links unten nach rechts oben ergibt sich ein 11-er Zyklus; 11 = 2·6 − 1
die Endpunkte in jeder Zeile liegen 60 auseinander; 60 = (6 − 1) · 2 · 6

Das ergibt von unten nach oben gelesen die Ringe:

12 18 24 30 36 42 48 54 60 66 72
1 7 13 19 25 31 37 43 49 55 61
2 8 14 20 26 32 38 44 60
3 9 15 21 27 33 39
4 10 16 22 28
5 11 17
6

In diesem Beispiel sind fünf initiale verkürzte Zyklen erforderlich, bis ab dem sechsten Zyklus volle Reife erreicht ist. Ab diesem Zyklus wird beim Übergang von einem Platz rechts außen jeweils der Wert 2.Nebenzyklus - 1.Nebenzyklus abgezogen, hier: 60-11=49. Das ergibt den Übergang von 61 zu 12.

Beispiel 3 (Konstruktionsregel für beliebiges n):

Aus diesen Beispielen kann verallgemeinert werden:

Berechne die beiden Nebenzyklen entsprechend den bekannten Formeln.

Baue die Ringe von unten nach oben auf:
(1) Eine Zeile mit einem Element [n]
(2) Zweite Zeile mit den 3 Elementen [n-1], [n-1]+n, [n-1]+n+n
(3) Dritte Zeile mit den 5 Elementen [n-2], [n-2]+n, [n-2]+n+n, [n-2]+n+n+n, [n-2]+n+n+n+n
(i) Nach diesem Schema so weit fortfahren, bis die Zeile beginnend mit 1 erreicht ist
Damit ist die "Reife" erreicht und alle weiteren Zyklen ergeben sich fortlaufend.
Ab diesem Zyklus wird beim Übergang von einem Platz rechts außen zum nächsten Ring links außen jeweils der Wert 2.Nebenzyklus - 1.Nebenzyklus abgezogen, allgemein:
[((n − 1) · 2) · n] - [2 · n − 1] = (2n-2) · n - 2n + 1 = 2n² - 4n + 1

Bemerkung

Auch mathematisch ist der Ananaszyklus sehr interessant. Er liefert eine ungewöhnliche Methode des Zählens aller natürlichen Zahlen, die nicht mehr auf der Zahlengerade, sondern auf den Ringen der Ananas dargestellt werden. Die Anordnung hängt von der Vorgabe des jeweiligen n ab. Die Regel ist so gewählt, dass lückenlos alle natürlichen Zahlen abgezählt werden. Jedoch ist die auf der Zahlengerade bekannte Nachfolger-Regel offensichtlich verletzt, da ab der vollen Reife bei jedem Übergang von einem Ring zum nächst-höheren Ring 2n²-4n+1 zurückgesprungen wird und der Abstand zweier benachbarter Zahlen innerhalb eines Rings jeweils n beträgt.

Diese Anordnung verletzt daher die strikte Nachfolgerbeziehung und damit auch die Transitivität. Stattdessen folgt sie einer höheren Symmetrie, die sich aus der Optimierung der Flächen für die Schuppen der Ananas ergibt (Phyllotaxis). Sie genügt über die Beziehung zu den Fibonacci-Zahlen dem Goldenen Schnitt und damit der inneren Symmetrie des Fünfecks.

Es kann versucht werden, hieraus mit den Methoden der axiomatischen Mengenlehre Verallgemeinerungen und Konsequenzen abzuleiten.

1989 - 1993
2011 (verbesserte Darstellung der Figuren und des Ananaszyklus)

© tydecks.info 2013