Walter Tydecks
Symmetrie und Verzweigung
Inhaltsverzeichnis
Zufall und Notwendigkeit
Lokale Symmetrie
Strom
Verzweigung
1. Zufall und Notwendigkeit
Im 20. Jahrhundert entwickelt sich die Mathematik zunehmend aus einer Größenlehre in eine Strömungslehre. Bisher war sie den Umgang mit diskreten, isolierten Objekten gewohnt, seien es die einzelnen natürlichen Zahlen, symbolisiert durch Finger, Steine, Perlen. Striche, Zahlzeichen oder neuerdings durch Schaltungen im Computer, oder seien es die endlichen geometrischen Figuren wie Kreis, Dreieck, Gerade, Kugel etc., mit denen der Mathematiker wie ein Handwerker arbeiten konnte. Größenlehre basierte auf dem Zählen und Messen starrer Gegenstände. Innerhalb der Mathematik wurde dies durch die Differentialrechnung durchbrochen, die Newton auch konsequent als Fluxionenrechnung bezeichnet. Sie basiert auf dem Grenzübergang, wo ein mathematischer Prozess nicht in allen endlich vielen Schritten von Anfang bis Ende durchgeführt werden kann, wie es bei den arithmetischen Beweisen und geometrischen Konstruktionen der Fall gewesen war. Der Prozess wird nicht selbst Schritt für Schritt vollzogen, sondern er wird sprachlich benannt. Statt einen Beweis oder eine Konstruktion auszuführen wird vom Grenzübergang gesprochen. Im Grenzübergang wechseln die Rechenmethoden und die Rechensymbole, bei der Ableitung treten an die Stelle der Zahlsymbole x, y, z, .... die Differentialsymbole dx, dy, dz,..., bei der Integration an die Stelle des Summensymbols 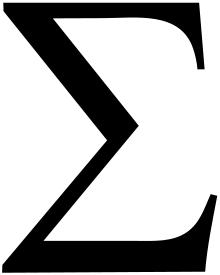 das Integralsymbol ∫. Das Vollständigkeitsaxiom hat im wesentlichen nur die Aussage, dass in der jeweiligen Zahlenmenge dieser Umschlag der Methode und Symbole möglich ist.
das Integralsymbol ∫. Das Vollständigkeitsaxiom hat im wesentlichen nur die Aussage, dass in der jeweiligen Zahlenmenge dieser Umschlag der Methode und Symbole möglich ist.
Hier entsteht innerhalb der Mathematik die Idee der Strömung. Anschauliches Vorbild der Zahlenmenge, in der abgeleitet werden kann, sind der Zeitfluss, bzw. der Raum, in dem die stetige, fließende Bewegung stattfindet. Dass der Grenzprozess wirklich erfolgt und nicht wie im Paradox von Achilles und der Schildkröte immer nur ohne Ende angenähert wird, liegt daran, dass eine fließende, kontinuierliche, stetige Bewegung vorausgesetzt wird. Strömung, Kontinuum, Stetigkeit sind hierbei in der Anschauung zunächst identische Begriffe.
Mit der Strömung entsteht der Gegensatz von Zufall und Notwendigkeit. Im Grenzübergang wechseln die Rechensymbole. Das führt prinzipiell zu einer Unbestimmtheit, wenn versucht wird, die neuen Symbole dx, dy, dz, ... im Raum der alten Symbole x,y,z, ... anzusiedeln. Wird z.B. die Funktion
y = x2
bei x0 abgeleitet und der Differentialausdruck gefunden:
dy / dx = 2x0 + dx
so kann gefragt werden, welchen Zahlenwert denn dy und dx haben sollen. Die Antwort der Mathematik ist: Sie liegen beliebig nahe bei x0 und 2x0, wo sie genau liegen, ist gleichgültig, zufällig. Dagegen ist das Resultat gesetzmäßig, notwendig: Die Ableitung hat an der Stelle x0 genau den Wert 2x0.
Das Maß bezeichnet den Grenzfall, wo die Bewegung isolierter, diskreter Dinge in die Strömung übergeht. Zu ihrer Beschreibung ist von der Größenlehre zur Strömungslehre zu gehen und die beiden mathematischen Symbolsprachen können als Größensymbole und Strömungssymbole bezeichnet werden. Newton sprach von Zahlen und Fluxionen, Leibniz von Differenzen und Differentialen, Summen und Integralen. In der Mathematik ist dieser Übergang in seiner allgemeinsten Weise bestimmt, es wurde ein Weg gefunden, konkrete Grenzübergänge in der Natur in einem allgemeinen Zeichensystem darzustellen. Das Maß hat daher in der Mathematik keinen bestimmten Zahlenwert, sondern nur eine allgemeine Bezeichnung, deren Festlegung Konvention ist. Es wird mal als lim (von Limes) bezeichnet, mal als epsilon-Umgebung oder epsilon-Kugel. Die epsilon-Umgebung ist hierbei der anschaulichere Begriff. Gerät ein Grenzprozess in die epsilon-Umgebung, dann ist das Maß zwischen Größen- und Strömungssymbolen erreicht und der Umschlag erfolgt.
In der Natur ist die Wasserströmung die leitende Anschauung. Zwar ist bekannt, dass sich das Wasser aus einzelnen Molekülen zusammensetzt und insofern als bewegliche Punktmenge veranschaulicht werden sollte, aber es erscheint als eine raumfüllende Flüssigkeit mit Welleneigenschaften. Offensichtlich liegt ein Maß zugrunde, wo das Wasser nicht bloß die Summe einzelner Moleküle ist, sondern eher wie das mathematische Integral ein zusammenhängendes Ganzes. Im Unterschied zur Mathematik kann aber für das Wasser das Maß genau bestimmt werden, wann aus einer Menge isolierter Wassermoleküle eine zusammenhängende Flüssigkeit wird. Hierfür müssen die Moleküle genügend dicht zusammenrücken und sich entsprechend der inneren elektrischen Ladungsverteilung der Moleküle anordnen. Die Anordnung muss in einem bestimmten Wärmezustand stabil bleiben (das Wasser darf nicht frieren oder verdampfen). Die Winkel der Ladungsverteilung, die Abstände der Moleküle und ihr Bewegungsspielraum im Wärmezustand können gemessen werden. So ergeben sich Maßzahlen, wo aus einer Menge von Wassermolekülen eine Flüssigkeit wird.
Das Verhältnis von Zufall und Notwendigkeit wird am Beispiel des Wassers anschaulicher. Wenn Wasser z.B. verdampft, kann ein Gesetz beschrieben werden, wie schnell das Wasser insgesamt bei bestimmten Temperaturen, bestimmter Wärmezufuhr, bestimmter Oberfläche verdampft. Wie schnell dagegen ein einzelnes Wassermolekül das Wasser verlässt, ist zufällig, hierfür kann nur eine Wahrscheinlichkeit berechnet werden. So verhält es sich bei allen Bewegungen des Wassers wie Turbulenzen, Wellen, Vereisung etc. Der Gesamtprozess ist gesetzmäßig, die Bewegung des einzelnen Molekül zufällig. Das folgt daraus, weil die einzelnen Wassermoleküle Bestandteil einer Strömung geworden sind.
Wird die Bewegung eines einzelnen Molekül betrachtet, können nur Wahrscheinlichkeiten berechnet werden. Wenn immer mehr einzelne Moleküle in der Wahrscheinlichkeitsrechnung berücksichtigt werden, führt das zum Gesetz der großen Zahlen, wonach für hinreichend viele Einzelgegenstände aus der Zufallsbewegung eine gesetzmäßige Bewegung wird. Dies ist offenbar der gleiche Grenzübergang in die Strömung. Und er führt zur Annahme, dass alle Bewegungen, aus hinreichender Entfernung gesehen (für den Abstand gelten wiederum spezifische Maße), als Strömungen erscheinen. Das entspricht auch der Alltagserfahrung, wo z.B. große Menschenmengen von weitem als Menschenstrom erscheinen.
Dies ist Ansatzpunkt für eine teleologische Überlegung. Denn hier wissen wir, wie wir uns als Elemente einer Strömung verhalten, die von außen durch den Gegensatz von Zufall und Notwendigkeit charakterisiert ist. Auch für Menschenströme lassen sich Gesetzmäßigkeiten formulieren, wie sie sich z.B. verhalten, wenn Ströme aufeinandertreffen, sich auflösen, von außen gesteuert werden sollen. Dies wird schon allein daher erforscht, um im Kriegsfall Flüchtlingsströme lenken zu können. Jeder kennt die Erfahrung, wenn durch einen Menschenstrom ein Ruck geht, der im Extremfall Panik auslösen kann. Aus dem Autoverkehr können andere Strömungserfahrungen gewonnen werden. Von außen scheint der Strom inneren Gesetzen zu folgen, für den einzelnen beteiligten Menschen kann von außen aber nur die Wahrscheinlichkeit berechnet werden, wie er sich verhält. Jeder selbst weiß dagegen sehr wohl, mit welchem Ziel und warum er sich in dem Gedränge bewegt. Der Gegensatz von Zufall und Notwendigkeit in der Strömung kann aufgelöst werden, dass die einzelnen Elemente nicht einfach gemäß Zufall agieren, sondern gemäß inneren Triebkräften, mit denen sie sich in der Strömung orientieren. In die resultierende Bewegung gehen sowohl die Dynamik der Strömung (der Strom) als auch die Eigenbewegung des einzelnen Element ein, das sich mitreißen lässt, oder gegen den Strom zu steuern versucht, oder in der Strömung einen anderen Platz zu erreichen versucht.
Mathematisch wird dies durch die Unterscheidung von lokalen und globalen Eigenschaften erfasst. Werden die globalen Eigenschaften einfach auf die lokale Ebene projiziert, dann werden aus den Bewegungsgesetzen der Strömung die Wahrscheinlichkeitsgesetze der Elemente. Mathematisch sind sie identisch. Lokal gilt aber mehr als nur der Zufall, der Zufall umschreibt genau den Freiraum, den das Element in der Strömung hat. Um zu klären, wie er ausgefüllt wird, sind die inneren Bewegungen des Elements zu erkennen. Im Beispiel der Wasserströmung ist dies der Unterschied zwischen der mechanischen Gesetzmäßigkeit der Flüssigkeit und den chemischen und elektrischen Gesetzmäßigkeiten der Moleküle. Das zeigt weiter, dass die Strömungslehre darauf basiert, dass die Bewegungen einer Bewegungsform der Natur sich zu Komplexen in einer höheren Bewegungsform zusammenschließen, wenn sie ein bestimmtes Maß überschreiten. Im Verband der Moleküle im Wasser weitet sich die chemische Bewegung zur mechanischen aus. Die Gesamtmenge des Wassers erscheint für das einzelne Molekül maßlos groß, umgekehrt gilt das einzelne Molekül als Teil des Wassers unendlich-klein. Der Symbolwechsel in der Differentialrechnung dient als Zeichensystem für Wechsel von Bewegungsformen in der Natur. Damit erwirbt sich die Mathematik das Verdienst, Wissenschaft der Maße zu werden.
Der gleiche Vorgang liegt den Experimenten der Quantenmechanik zugrunde. Im wesentlichen gibt es zwei Experimente: In der Spektroskopie werden die Wellenlängen des Lichts gemessen, die ein Atom oder ein Molekül ausstrahlt. In Streuprozessen werden Elektronen durch einen Spalt oder durch ein Gitter geschickt und auf einer dahinterstehenden Wand gemessen, wie sie sich verteilen. In beiden Fällen liegen Strömungen vor: der Lichtstrom, der von einem Atom ausgeht, bzw. der Elektronenstrom, der gebrochen wird. Für die Strömung können eindeutige Gesetzmäßigkeiten gefunden werden, für das einzelne Photon bzw. Elektron gelten nur Wahrscheinlichkeitsaussagen.
Während aber niemand auf die Idee gekommen ist, beim Wasser von einem unerklärlichen Welle-Korpuskel-Dualismus zu sprechen, eine Unbestimmtheitsrelation zu formulieren oder gar von einer Grenze menschlicher Erkenntnis zu reden, Substanz und Kausalität in Frage zu stellen, gibt es das alles in der Quantenmechanik. Von den berühmten Forschern suchten nur Einstein, Bohm, de Broglie und Vigier von Anfang an nach "inneren Parametern", wie sie es nannten, um die inneren Triebkräfte der Elemente der Quantenmechanik zu erforschen. Selbst Havemann wollte ihnen hier nicht folgen. So wie die Entstehung der Differentialrechnung von den alten Paradoxen der Griechen begleitet war, überschatteten die Paradoxa der Kopenhagener Deutung die Quantenmechanik. Dies ist nur aus dem philosophischen Umfeld zu erklären, in dem diese Physiker standen. Im 19. Jahrhundert sollten alle Naturwissenschaften mechanisiert werden, jede Wissenschaft suchte nach den für sie spezifischen Elementen und deren mechanischen Bewegungen. Für die Wellenmechanik des Wassers waren das anschaulich zunächst eher die einzelnen Wassertropfen als die Moleküle. Die Einheit der Natur und Naturwissenschaft wurde nicht inhaltlich gesehen, sondern in der Gemeinsamkeit der mechanisierenden Methode. Die Unbestimmtheitsrelation gilt keineswegs nur in der Quantenmechanik, sondern in jeder Strömung mit Welleneigenschaften. Der konkrete Wert der Unbestimmtheit ist nichts als die Kehrseite des Gesetzes der großen Zahlen.
Daher kann auch nicht gesagt werden, dass durch die Quantenmechanik das Weltbild von Newton umgestoßen wird und gar New-Age-Horizonte eröffnet werden. Vielmehr geschah der Bruch durch die Strömungslehre, und daran war Newton nicht gerade unbeteiligt. Während sie jedoch zunächst nur eine mathematische Theorie war, entworfen zur Beschreibung mechanischer Prozesse, ist sie im 20. Jahrhundert zu einer Wissenschaft geworden, die die Zusammenhänge zwischen den Bewegungsformen der Natur klärt. Gerade die Quantenmechanik mit ihrer Umwälzung des Atommodells, mit dem vertieften Verständnis molekularer Prozesse, der Feinanalyse des Verhaltens in Werkstoffen etc. hat bedeutend dazu beigetragen.
2. Lokale Symmetrie
In Mathematik und Physik sollten mit lokaler Symmetrie komplizierte Bewegungen auf einfache Bestandteile zurückgeführt werden. Die Atomtheorie kann als erste Theorie lokaler Symmetrie angesehen werden. Die Vielfalt aller Körper wurde zurückgeführt auf ihre innere Zusammensetzung aus Atomen, die ihrerseits viel einfacher, symmetrischer sind. Ein Atom wurde als Kugel angesehen oder als eine andere einfache geometrische Figur wie Kubus, Pyramide etc. Platons Ideenlehre gab die philosophische Theorie dazu, wonach die komplexe sichtbare Welt auf einfachen, schönen, geometrischen Formen beruht, die die wahre Kristallisation der Natur gemäß einem logischen Muster darstellen. Vertreter der modernen Atomtheorie wie Heisenberg oder Weizsäcker gehen ebenso von Platons Ideen aus wie Wittgenstein in seinem frühen, an der Mathematik orientierten "Tractatus logico-philosophicus".
Auch die Differential- und Integralrechnung kann als eine Theorie lokaler Symmetrie verstanden werden. Frühe Ideen lagen in der griechischen Wissenschaft vor. Um den Kreis zu quadrieren, wurde lokal der Kreisbogen durch Geraden angenähert:
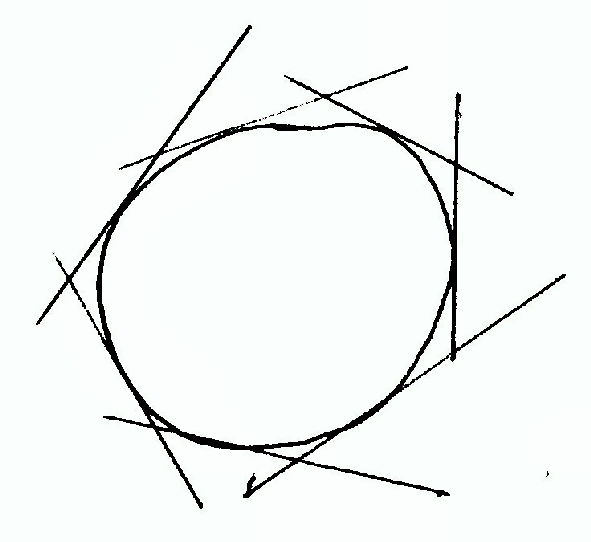
Figur 1 Kreis mit Tangenten
Freihandzeichnung
Jede einzelne Gerade ist symmetrischer (da geradlinig) als der angenäherte gekrümmte Kreisbogen.
Diese Anschauung leitet die Differentialrechnung. Jetzt wird allgemein die Kurve als Bewegungskurve verstanden. Insgesamt, also global, handelt es sich um eine komplizierte gekrümmte Bahn. Aber lokal, d.h. in einem einzelnen Zeitmoment, kann die Bewegung durch die Gerade angenähert werden, die Tangente. In der Mechanik kann die Steigung der Tangente als die Momentangeschwindigkeit interpretiert werden, die der Körper zu diesem Zeitpunkt hat. Mathematisch ist die Tangente die Ableitung der Kurve an diesem Punkt.
Die physikalischen Voraussetzungen dieser Theorie seien am Beispiel der Planetenbewegung dargestellt. Jeder Planet bewegt sich auf einer komplizierten Kurve rund um die Sonne. Andere Planeten und Monde wirken ihrerseits anziehend auf den Planeten, so dass seine Bewegungskurve keinesfalls ein einfacher Kreis oder eine einfache Ellipse ist. Wie auch immer, es wird aber angenommen, dass der Planet sich lokal geradlinig bewegt, also auf einer Geraden, deren Maß einzig durch seine momentane Geschwindigkeit gegeben ist. Für die lokale Bewegung gelten nur innere Eigenschaften (Masse und Geschwindigkeit des Planeten) und das Wirkungsgesetz, wonach jede Bewegung den einfachsten Weg geht. Die äußeren Einflüsse wirken erst auf den Vertauf der globalen Bewegung.
Es wird unterstellt, dass die inneren Eigenschaften des Atoms wesentlich einfacher sind als die Eigenschaften eines von vielen Atomen zusammengesetzten Systems. Die Unteilbarkeit des Atoms und die Symmetrie erzeugenden Wirkungsgesetze (hier das Trägheitsgesetz) waren die Voraussetzungen der frühen Theorie lokaler Symmetrie. Damit schien ein Ausweg gefunden aus der schwierigen Situation, als sich zeigte, dass der Raum insgesamt nicht euklidisch ist. Er sollte wenigstens lokal euklidisch sein.
Diese Hoffnung zersprang mit der Erkenntnis der Teilbarkeit der Atome. Bis dahin standen die verschiedenen Naturwissenschaften schön nebeneinander, jede suchte nach ihrem atomaren Baustein und seiner lokal symmetrischen Bewegung. Nun sind die Naturwissenschaften ineinander verschachtelt. Die inneren Eigenschaften des Atoms sind keineswegs einfacher als die Eigenschaften eines mechanischen Systems aus vielen Atomen, sondern hier tut sich eine Vielfalt der inneratomaren Prozesse auf. Und möglicherweise sind die Teile des Atoms wie Proton, Elektron, Neutron etc. ihrerseits aus anderen Teilen aufgebaut (den Elementarteilchen), die wiederum keineswegs einfacher sind als der atomare Prozess im Ganzen.
Lokale Symmetrie strukturiert die in der Natur gefundenen Maße. Um die mechanische Bewegung eines Planeten im Sonnensystem zu beschreiben, kann die Eigenbewegung der vielen Moleküle vernachlässigt werden, aus denen er sich zusammensetzt, und erst recht die Eigenbewegung der Protonen, Elektronen, etc, die das Molekül umfasst, usw. Dass diese Vernachlässigung vorgenommen werden kann, wird durch ein Maß geregelt, wonach die mechanische Bewegung sich in einer bestimmten Größenordnung bewegt. Alles, was kleiner ist, kann für die mechanische Bewegung als Atom, als unteilbar, als einfach, als symmetrisch angesehen werden. Der Ansatz für lokale Symmetrie ergibt sich aus der Existenz der Maße. Unterhalb dieses Maßes beginnt gewissermaßen ein neues Leben, mit eigenen Bewegungsgesetzen und eigener Vielfalt. Nach außen erscheint es einfach und kann darauf reduziert werden, dass bestimmte Erhaltungsgesetze erfüllt sind, z.B. in der Mechanik die Impulserhaltung.
Und weiter hat auch das mechanische System als Ganzes nach außen eine symmetrische Erhaltungsgröße: die Energie. Wird die mechanische Bewegung als Ganze genommen, kann gesagt werden, unabhängig von allen Einzelbewegungen ändert sich nichts, bleibt der Prozess im Gleichgewicht (oder in Symmetrie), da die Gesamtenergie erhalten bleibt.
Ausgehend von der mechanischen Bewegung können Schritt für Schritt in die Tiefe gehend Symmetrien der verschiedenen Bewegungsformen erkannt werden. Hierbei hat jede Bewegungsform ihr eigenes Längenmaß und ihre eigentümliche Symmetrie. Ein sehr anschauliches Bild ergibt sich z.B. für die inneratomare Symmetrie. Während am mechanischen System im Prinzip unendlich viele verschiedengroße Körper im Weltall beteiligt sind in Größenordnungen von Galaxien bis zu Staubkörnern, gibt es im inneratomaren Prozess nur eine endliche Anzahl von Bausteinen, wie Neutron, Proton, Meson, Elektron etc. Sie können sich in bestimmten Grenzen zu großen Atomen zusammenballen, in der Natur bis zum Uran, aber alle größeren Komplexe sind unstabil und zerfallen wieder. Auf der anderen Seite können sie kaum mehr unterteilt werden. Ein Neutron zerfällt nicht in zwei halbe Neutronen, sondern in verschiedenen Prozessen in jeweils verschiedene andere Teile vergleichbarer Größenordnung. So scheint paradoxerweise jedes Teilchen als Bestandteil jedes beliebige andere Teilchen zu enthalten, da es in verschiedenen Prozessen unter verschiedener Energiezufuhr in praktisch alle möglichen anderen Teilchen zerfallen kann. Anders gesagt besteht die Bewegung darin, dass sich die Teilchen nach gewissen Gesetzen ineinander verwandeln. Die lokale Symmetrie ist darin erkannt worden, dass alle Teilchen symmetrisch danach geordnet werden können, wie sie sich ineinander verwandeln. Was im Einzelnen die Umwandlungen bewirkt, wie sie ablaufen, ist ungeklärt. Bekannt ist nur als Symmetrie, dass alle Umwandlungen eine gewisse Ordnung erhalten.
Wird nun ausgehend von der mechanischen Bewegung die lokale Symmetrie inneratomarer Prozesse studiert, so handelt es sich zum einen um die mechanische Momentangeschwindigkeit tangential zur Bewegungskurve, zum anderen kann sich das Teilchen dabei umwandeln entsprechend den Symmetrien der Teilchenphysik. Es kann z.B. Photonen aufnehmen oder abgeben usw. Die lokale Bewegung zerfällt in verschiedene, voneinander als unabhängig angenommene symmetrische Bewegungen. Die gesamte lokale Bewegung ist ein Produkt mehrerer Symmetrien.
In der Physik werden Theorien lokaler Symmetrie als Eichtheorien bezeichnet. Die Grundideen gehen auf Einsteins Feldtheorien zurück. Erstmals gelang 1950 Yang und Mills die Theorie der Radioaktivität als Eichtheorie, in den 1960er Jahren gelang es, Radioaktivität und Elektrodynamik einheitlich als Eichtheorie zu beschreiben. Seither wird daran gearbeitet, auch die inneratomaren Prozesse als Eichtheorie darzustellen (Quantenchromodynamik) und daraus eine einheitliche Theorie aller bekannten Bewegungsformen und Symmetrien bis zur Gravitation zu finden. Das wäre nach der euklidischen Geometrie eine neue Theorie der Einheit der Natur.
Die Substanz oder Identität eines Teilchens liegt darin, dass es an allen Bewegungsformen der Natur zugleich teilnimmt, dass also z.B. ein Meson gleichzeitig an der inneratomaren Wechselwirkung, der Elektrodynamik, der Radioaktivität, der Gravitation teilnimmt, dass es sich gleichzeitig mechanisch und elektrisch bewegt, etc. Wenn für jede Bewegungsform in einem Zeitmoment eine spezifische lokale Symmetrie gilt, gelten für das eine Teilchen alle Symmetrien gleichzeitig. Und das, obwohl z.B. seine Bewegung im radioaktiven Feld vernachlässigbar klein ist für die mechanische Bewegung des mechanischen Körpers, dem dies Meson angehört. Diese Identität kann daher nur philosophisch als Substanzgesetz postuliert und der Physik als Axiom zugrundegelegt werden. Und ganz im Sinne von Kant gilt das Substanzgesetz im Zeitmoment.
Kann von einer mechanischen Bewegung etwa des Mesons gesprochen werden? Zweifellos, nur ist die Frage, wie sie zu messen ist. Der Mensch kann nur mechanisch messen (er bewegt sich in der Größenordnung der mechanischen Bewegung), und für die mechanische Bewegung ist das Meson unendlichklein, seine Bewegung vernachlässigbar. Es gilt das Unbestimmtheitsprinzip. Eine Messung der mechanischen Bewegung des Meson ist nur denkbar, wenn die Messung innerhalb der für das Meson charakteristischen Bewegungsform, also innerhalb der inneratomaren Prozesse erfolgt. Das bedeutet, dass ein Messprozess in Gang gesetzt wird, der sich selbständig innerhalb dieser Bewegungsform zu orientieren vermag und die Resultate zurückmelden kann. Dafür ist Künstliche Intelligenz erforderlich.
Von außen kann lediglich per Wahrscheinlichkeitsrechnung eine Interpolation der mechanischen Gesetze in Bereiche vorgenommen werden, wo diese im Grunde vernachlässigbar sind. Dass dies überhaupt geschieht, ist einem anderen philosophischen Axiom zu verdanken, dass der Raum homogen ist, dass der Raum an sich, in dem die Bewegungsgesetze dargestellt werden, also der mathematische Raum, keine begrenzenden Längenmaße kennt. Für den mathematischen Raum ist diese Annahme notwendig, denn in ihm sollen ja verschiedene Bewegungen mit verschiedenen Maßen dargestellt werden. Das Maß der Differentialrechnung ist wie gesehen unbestimmt. Wird also zuerst die mechanische Bewegung im mathematischen Raum dargestellt, scheint sie in dieser Darstellung ihr konkretes Maß zu verlieren. Obwohl es in der Natur ein Maß für die mechanische Bewegung gibt, und sogar der konkrete Wert in einiger Genauigkeit bestimmt werden kann, gilt dies Maß in der mathematischen Darstellung nicht mehr. Daher kann in der mathematischen Darstellung die mechanische Bewegung auch auf Größenbereiche projiziert werden, wo sie so in der Natur nicht nachweisbar ist. Der Preis ist, dass nur noch Wahrscheinlichkeitsgesetze gelten.
Auch die Idee einer einheitlichen Feldtheorie der Natur ist daher ein mathematisches Konstrukt. Sie wird nie vollständig sein, da die Naturerkenntnis nie abgeschlossen ist, und sie wird zum überwiegenden Teil auf Wahrscheinlichkeitsaussagen beruhen. Einstein hat als erster leidenschaftlich nach einer einheitlichen (allgemeinen) Feldtheorie gesucht, aber zugleich wollte er sich mit dem Wahrscheinlichkeitscharakter nicht abfinden: Gott würfelt nicht. Aber seine eigene Gottesidee ist gebunden an den homogenen mathematischen Raum, während frühere Naturphilosophen das Göttliche in der Harmonie der Maße ausgeführt sahen.
Wie ist von der mechanischen Bewegung in die Größe gehend die Gravitation einzuordnen? Zunächst handelt es sich um die Anziehungskräfte zwischen mechanischen Körpern, deren Gesetz seit Newton bekannt ist. Sie vollziehen sich aber in einem Raum, der als ganzer gekrümmt ist. Von daher ist es naheliegend anzunehmen, dass die Gravitation ihrerseits gegenüber der Raumkrümmung eine lokale Bewegung ist. Lokal, also in einem bestimmten Zeitpunkt und bestimmten Raumpunkt, wirkt sie so, als wäre der Raum nicht gekrümmt. Wie weit reicht hier "lokal"? Für die Bewegung des ganzen Planetensystems im Zeitraum von Millionen Jahren kann die Raumkrümmung vernachlässigt werden, also dies alles ist lokal. Der Wechsel der Größenordnung in eine globale Betrachtung, wo die Raumkrümmung wesentlich wird, scheint durch die Lichtgeschwindigkeit gegeben zu sein. Das legt die Relativitätstheorie nahe, wonach die Masse und Geschwindigkeit, also genau die inneren Eigenschaften der mechanischen Körper, in einem bestimmten Verhältnis stehen, solange die Lichtgeschwindigkeit als Grenzgeschwindigkeit gilt. Die Grenzen der Gravitation erscheinen daher auch als Stellen der Unsichtbarkeit, als Schwarze Löcher, wo offenbar höhere Bewegungsformen dominieren. Für eine Bewegung, deren Grenze die Lichtgeschwindigkeit ist, erscheinen sie unsichtbar, unerreichbar. Dies ist gerade so, wie für ein Teilchen der inneratomaren Prozesse die mechanischen Partikel unerreichbar sind, da sie sich nicht direkt in ein mechanisches Partikel umwandeln können. Die Eigenschaften der höheren Bewegungsform können in der Mechanik nur an ihrer raumkrümmenden Wirkung abgelesen werden.
Abschließend ist auf die Zeit zu kommen. Jede Symmetrie ist die Darstellung einer Bewegung in den für sie wesentlichen Dimensionen. Die mechanische Bewegung wird in den euklidischen Raumdimensionen dargestellt, die inneratomaren Prozesse in den als Dimensionen wirkenden Basisteilchen. Wo ist die Zeitdimension angesiedelt? Zunächst als undefinierte allgemeine Bewegungsdefinition. Lokal heißt immer: zu einem Zeitpunkt. Die Zeitdimension scheint allerdings wesentlich zu sein für die raumkrümmende Bewegung, gegenüber der auch die mechanische Bewegung nur lokal, vernachlässigbar klein gilt. Das wird auch dadurch untermauert, dass für die Mechanik die Lichtgeschwindigkeit (also ein Zeitfaktor) als Maß gilt.
Dieses Maß regelt den Umfang, wie weit gegenüber höheren Bewegungsformen die mechanische Bewegung vernachlässigbar klein ist, wie weit ihr lokaler Spielraum reicht. Die charakteristischen Längenmaße der Bewegungsformen sind zugleich Zeitmaße. Wenn lokale Symmetrie im Zeitmoment gilt, ist zu fragen, wie lange dieser Zeitmoment dauert. Das scheint paradox. Aber zieht sich das Zeitmoment auf die Null zusammen, ist im Zeitmoment keine Dynamik möglich, die lokale Symmetrie bliebe starr, tot. Im Grunde kann gesagt werden: Für eine bestimmte Zeit und für ein bestimmtes Raumgebiet kann eine Bewegung für sich betrachtet werden, alles andere ist vernachlässigbar klein. Im Falle der mechanischen Bewegung fallen diese Maße in die Größenordnung der menschlichen Sinne. Die menschliche Lebenszeit ist nur so lang, dass sie ganz in den lokalen Bereich der Mechanik passt, aber doch so lang, dass die Zeitmaße etwa der Elektrodynamik vernachlässigbar klein sind. Alltagserfahrung ist daher mechanische Erfahrung.
Aber dies alles gilt nur für die lokale Symmetrie. Wird die globale Bewegung betrachtet, ragt sie in andere Bewegungsformen hinein. Der elektrodynamische Fluss z.B. erfolgt mit Lichtgeschwindigkeit und steht so an der Grenze zwischen mechanischer und raumkrümmender lokaler Symmetrie. Das Bild der Staffelung der Bewegungsformen in die Tiefe gilt nur für lokale Symmetrie.
3. Strom
In lokaler Symmetrie scheint eine einheitliche Feldtheorie in greifbarer Nähe. Aber wie hängen in der zeitlichen Abfolge die lokal symmetrischen Momentaufnahmen zusammen? Am vertrautesten und daher anschaulichsten ist die Situation in der Mechanik.
Lokal ist die Bewegung jeweils durch Masse und Geschwindigkeit definiert und liegt auf einer Tangente. Die gesamte Bewegung erfolgt jedoch im Zeitverlauf auf einer gekrümmten Bahn. Das Maß der Krümmung ist durch zwei Komponenten gegeben: Das Wirkungsgesetz legt fest, dass die Bewegung den Weg mit dem geringsten Kraftaufwand geht, und das Energieerhaltungsgesetz, dass dabei die Gesamtenergie unverändert bleibt. Mathematisch kann gezeigt werden, dass diese beiden Gesetze ausreichen, um die Bewegung eindeutig zu beschreiben (das Wirkungsgesetz erscheint mathematisch als Hauptsatz der Variationsrechnung, das Erhaltungsgesetz als kovariante Ableitung der symplektischen Form, vgl. die ausführliche Darstellung bei Arnold). Und mehr noch: In dieser mathematischen Verallgemeinerung können diese Gesetze auch auf die anderen Bewegungsformen übertragen werden, sie gelten allgemein für den mathematischen Raum, in dem die Bewegungsformen dargestellt werden. Erst hierdurch wurde es mit Eichtheorien möglich, sowohl die lokale Symmetrie als auch deren globalen Verlauf darzustellen (mathematisch wird die lokale Symmetrie als Strukturgruppe in einem Hauptfaserbündel dargestellt, wobei der Zusammenhang die globale Bewegung beschreibt).
In den anderen Bewegungsformen kommen aber Besonderheiten hinzu, die weit über den mechanischen Fall hinausgehen und schon in elementaren Fragen noch ungeklärt sind. Mechanisch wird für den globalen Zusammenhang die Bewegung eines einzelnen Körper beschrieben. In der Elektrodynamik und so weit bekannt den anderen Bewegungsformen handelt es sich bei der globalen Bewegung immer um einen Strom, an dem eine Vielzahl von einzelnen Elementen beteiligt ist. Statt einer einzelnen Bewegungskurve handelt es sich um eine Strömung, deren Querschnitt mindestens zweidimensional ist.
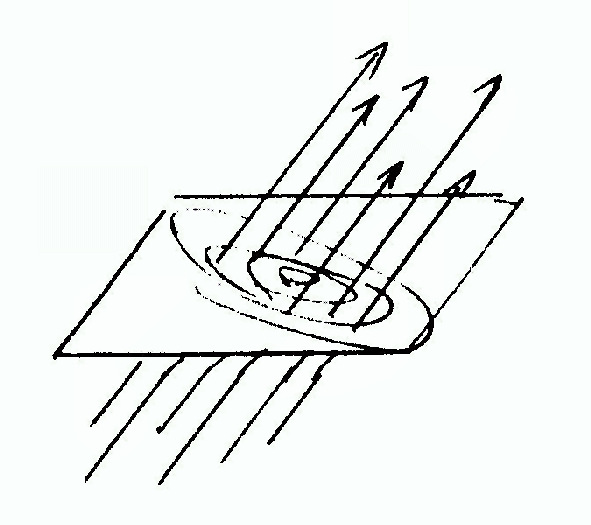
Figur 2 Strom
Strom durch zweidimensionalen Querschnitt nach dem Vorbild des elektrischen Flusses, der ein Magnetfeld induziert, Freihandzeichnung
Auch der Strom als Ganzer erhält die Energie und geht den kürzesten Weg, erfüllt damit die Bestimmungen der globalen mechanischen Bewegung. Da jedoch an Stelle einer eindimensionalen Bewegungskurve ein mehrdimensionaler Strom vorliegt, sind innerhalb des Stroms zusätzlich Eigenbewegungen zu berücksichtigen wie Flussdichte, innere Rotation etc. Für die Elektrodynamik sind sie durch die Maxwell-Gleichungen beschrieben.
Diese Gleichungen gelten als Feldgleichungen (mathematisch handelt es sich um partielle Differentialgleichungen). Sofort fällt auf, dass der klassische Begriff von Kausalität in diesem Zusammenhang versagen muss. Denn die Feldgleichungen gelten in einem mehrdimensionalen Raum, in der Skizze als Querschnittebene dargestellt, die quer zur Zeitachse liegt. Dennoch gibt es in diesem Raum Querbeziehungen zwischen den verschiedenen am Strom beteiligten Elementen. Diese Beziehungen gelten innerhalb eines Zeitmoment, die Wirkung vollzieht sich damit in Gleichzeitigkeit. Genau dieser Fall war für Newton unerklärlich und sollte von Kant ausgeschlossen werden, für den Kausalität eine Eigenschaft der fließenden Zeit ist, während bei reiner Gleichzeitigkeit in seiner Terminologie Wechselwirkung in Unterscheidung von Kausalität gelten soll.
In der Elektrodynamik hat dies zu keinen unerklärlichen Effekten geführt, wohl aber in der Quantenmechanik. Da gibt es eine Reihe von offenen Fragen, die als Phänomene dieser Gleichzeitigkeit gedeutet werden können.
Die mechanische Bewegung des Elektrons im Atom kann nur durch Wahrscheinlichkeitsrechnung beschrieben werden. Obwohl weder berechnet noch experimentell gemessen werden kann, wo genau das Elektron zu einem Zeitpunkt zu finden ist, kann aber doch vorausgesagt werden, dass es sich auf ganz bestimmten Bahnen bewegen muss, damit das Atom im Ganzen stabil bleibt und das Elektron weder in den Kern stürzt noch das Atom verlässt. Die Beschreibung der Bewegung des Atom kann nicht zerlegt werden in die Beschreibung voneinander unabhängiger Teile. In jedem Zeitmoment befindet sich das Atom in einem bestimmten Zustand, in dem die Bewegungen der verschiedenen Teile des Atoms in bestimmter Relation zueinander stehen. Die Zustände, in denen sich das Atom bewegen kann, können berechnet werden und ebenso die Wahrscheinlichkeiten, in welchen Zustand es jeweils übergeht. Eine Zustandsänderung liegt z.B. vor, wenn ein Elektron ein Photon abstrahlt oder aufnimmt, und dadurch auf eine andere Bewegungsbahn springt. Für jedes Atom gibt es einen spezifischen Satz von möglichen Zuständen und eine spezifische Wahrscheinlichkeitsverteilung, in welchen Zuständen es sich aufhält. Dies kann an den Intensitäten der Spektrallinien des Farbspektrums abgelesen werden, welches das Atom durch Abgabe von Photonen erzeugt. Die Gesamtbewegung des Atoms kann als ein Strom gedeutet werden, an dem alle Teile des Atoms beteiligt sind. Jeder Zustand des Atoms ist ein Querschnittsmuster in diesem Strom, der Strom hat nur die Möglichkeit, durch eine endliche Anzahl verschiedener Muster hindurchzuströmen. Was geschieht aber beim Wechsel von einem Zustand in einen anderen? Hier liegt ein Bruch vor, und die Lücke kann durch keine mathematische Beschreibung geschlossen werden. Insbesondere kann z.B. nicht der mechanische Weg eines Elektrons von einem Zustand in einen anderen Zustand beschrieben werden, nicht einmal durch Wahrscheinlichkeitsrechnung. Die Beschreibung des Stroms durch seine Muster kann nicht zurückgeführt werden auf die Beschreibung der Bewegungskurven der einzelnen Teile in diesem Strom.
Die Quantenmechanik ist voll von ähnlichen Strömen, wo sich ein System durch verschiedene Zustände, verschiedene Muster bewegt. Hier treten sogenannte Tunneleffekte auf, d.h. der Übergang von einem Zustand in einen anderen ist nur möglich, wenn verschiedene beteiligte Teile "wissen", wie sich die anderen in diesem Zeitmoment verhalten, in welchen anderen Zustand sie wechseln "wollen". Die Quantenmechanik schwillt über mit teleologischen Überlegungen dieser Art. Zustandsänderungen sind nur möglich, wenn mehrere Teile gleichzeitig in bestimmter Weise ihr Verhalten ändern. Ihr Verhalten ist damit aneinander gekoppelt. Der Strom ist nicht nur durch die verschiedenen Muster beschrieben, sondern auch durch die wechselseitigen Abhängigkeiten, die genau erfasst werden können. In einer Hilfskonstruktion werden sie bisweilen als Austausch von Instantonen bezeichnet, d.h. als interne Kommunikation in einem Zeitmoment. Das ist Wechselwirkung. Diese Kommunikation hat jeweils ihre eigene genaue Struktur, in wie viele Richtungen ein Teil zugleich kommunizieren kann, welche Teile kommunizieren können etc.
Es gibt Prozesse, in denen die Zustandsänderungen bestimmte Reihenfolgen einhalten müssen. Teleologisch wurde dies so interpretiert, dass die Teile ein Gedächtnis haben. Beispiele sind bestimmte Zerfallsprozesse von Kaonen.
In neueren Theorien zur Selbstorganisation wird ein höherer globaler Zusammenhang beschrieben. Nicht nur weist die Strömung in jedem Moment ein Muster auf, sondern im Zeitverlauf kommt es zu periodischen Bewegungsmustern, Turbulenzmustern. Im klassischen Beispiel geht ein Wärmestrom durch eine besondere Flüssigkeit und ordnet sie in Turbulenzmuster, wodurch der Wärmedurchfluss optimiert wird. Selbstorganisation erfolgt nie im Gleichgewicht, sondern in einer globalen Strömung. Letztendlich genügt auch sie den grundlegenden Gesetzen, die Energie zu erhalten und den Weg mit dem geringsten Kraftaufwand zu wählen. Und wie im elektrischen Strom gibt es in jedem Zeitmoment ein charakteristisches Muster. Aber bei Selbstorganisation liegt ein dynamisches Muster vor, das nicht mehr einfach quer zur Zeitdimension steht, sondern seine eigene Entwicklung in der Zeit hat.
Mit der Selbstorganisation stellt sich noch dringender die Frage der Kausalität. Um klassische Kausalität kann es sich nicht handeln, da im Muster gewissermaßen jedes einzelne Teil weiß, was alle anderen tun und sich demgemäß bewegt. Wie ist diese Gleichzeitigkeit, dies Wissen zu deuten? Göttlicher Plan, magische Eigenschaft, inneres Bewusstsein der Dinge sind nur andere Bezeichnungen für diese Eigenschaft, keine Erklärung. Hier setzt mitten in der Naturwissenschaft und der Mathematik die Informationstheorie an und dies ist der Punkt, worauf sich Künstliche Intelligenz wird beziehen können.
4. Verzweigung
Die Verzweigungsmöglichkeit ist die allgemeinste Eigenschaft, die mehrdimensionale Systeme von eindimensionalen unterscheidet. Daher sind als Ausgangs- und Abgrenzungspunkt zuerst die eindimensionalen Systeme zu charakterisieren. Für abzählbare Mengen ist wesentlich, dass sie nicht nur auf einer eindimensionalen Kurve angeordnet sind, sondern dass ihre Anordnung durch eine einzige, eindeutige, sequentielle Vorschrift gegeben ist. Diese Vorschrift ist die Definition des jeweiligen eindimensionalen Systems. Der einfachste Fall sind die natürlichen Zahlen, die durch das sequentielle Zählen 1, 2, 3, angeordnet sind. Die ganzen Zahlen können durch die Sequenz 0, 1, -1, 2, -2, ... angeordnet werden, und auch die rationalen Zahlen (alle Brüche) lassen sich nach einer entsprechenden Vorschrift anordnen. Im Prinzip gibt es für jede abzählbare Menge beliebig viele Verfahren der Anordnung, wesentlich ist aber, dass durch eine einzige Anordnung alle Elemente geordnet werden können.
Zu den abzählbaren Mengen gehören die arithmetischen Operationen, die alle in bestimmter Weise mehrfache endliche Abzählungen kombinieren: Addieren als mehrfaches Abzählen nacheinander, Subtrahieren als mehrfaches Abzählen vor und zurück, Multiplizieren als mehrfaches Addieren, etc. Umgekehrt kann dann jede einzelne Zahl qualitativ durch die arithmetischen Operationen ausgezeichnet werden, durch die sie erreichbar ist. Die ganzen Zahlen erlauben Division durch 2 ohne Rest, Primzahlen können nicht ohne Rest geteilt werden etc. Diese Untersuchungen sind Gegenstand der Zahlentheorie und Zahlenmythologie. Einzelne Zahlen haben Eigenschaften, durch die sie sich von allen anderen unterscheiden. Beispiele:
Die Eins ist das Produkt mit sich selbst
1 = 1 * 1.
Die Drei ist die Summe aller kleineren Zahlen
3 = 1 + 2.
Die Sechs ist Produkt und Summe ihrer Teiler
6 = 1 * 2 * 3 = 1 + 2 + 3.
Die EDV zeigt das Ausmaß der Möglichkeiten, die in den abzählbaren Mengen stecken. Rein theoretisch kann jedes Programm als ein einziger arithmetischer Ausdruck
y = f(x)
dargestellt werden, worin x die Eingabe, y die Ausgabe ist und f sich aus arithmetischen Funktionen zusammensetzt. x und y sind natürliche Zahlen. In der Praxis werden natürlich Ein- und Ausgabe in mehrere Variablen zerlegt, aber theoretisch könnte jede Eingabe- und Ausgabekonstellation durch eine natürliche Zahl dargestellt werden. EDV-Programme zerlegen den einen überaus komplexen arithmetischen Ausdruck f in eine Vielfalt verschachtelter einfacher arithmetischer Ausdrücke. Dafür wird aber in Kauf genommen, dass größere Programme praktisch nicht vollständig getestet werden können, da es unmöglich ist, alle Eingabekonstellationen zu berücksichtigen. Außer Schreibfehlern können daher arithmetisch gesehen EDV-Programme auch keine Fehler enthalten. Sie berechnen immer aus vorgegebenen Zahlen neue Zahlen. Eine andere Frage ist, ob das Programm das gewünschte Ergebnis liefert und ob die Eingabekonstellation richtig gewählt war.
EDV-Programme enthalten daher im strengen Sinn keine Verzweigungspunkte. Zwar gibt es in ihnen wenn-dann-Abfragen (die IF-Befehle), aber die dienen lediglich zur Auswertung von Zwischenergebnissen und haben im Grunde nur die Aufgabe, die Eingabekonstellation zu bestimmen. Zu jeder bestimmten Eingabe kann es nur eine eindeutig bestimmte Ausgabe geben, es gibt in EDV-Programme keine Verzweigungen, wo eine Eingabe zu verschiedenen Resultaten führen kann.
Die reellen Zahlen stellen zwischen den ein- und mehrdimensionalen Mengen den Grenzfall dar. Sie lassen sich wie die zählbaren Mengen auf einer eindimensionalen Gerade darstellen, aber sie sind nicht abzählbar. Cantor hat dies durch die Konstruktion der transfiniten Zahlen zu veranschaulichen versucht. Es gibt danach so viele reelle Zahlen, als könnte hinter den natürlichen Zahlen beliebig weiter gezählt werden:
1, 2, 3, ... w
w, w+1, w+2, ... 2w
2w, 2w+1, ... 3w
w, 2w, 3w, ... e
e, e+1, ... 2e
w, e etc. symbolisieren unendlich große natürliche Zahlen. Die Konstruktion der transfiniten Zahlen kann so gedeutet werden, dass sich die abzählbaren Mengen durch eine einzige Anordnung darstellen lassen, während dies für die reellen Zahlen unmöglich ist. Sie liegen zwar wie die natürlichen Zahlen auf einer eindimensionalen Strecke, sind aber für quantitative Operationen nicht fassbar, solange ihre Anordnung nicht geklärt ist. Reelle Zahlen werden einzeln durch Grenzprozesse definiert, etwa durch die Längenbestimmung der Kreislinie mit Radius r: die Länge ist 2 * pi * r, wobei pi eine nicht-rationale, reelle Zahl ist. Die genaue Lage, d.h. die Anordnung dieser Zahl auf der Zahlengerade kann aber nicht durch eine Dezimalzahl (d.h. eine Zahl aus einer abzählbaren Menge) angegeben werden, sondern es gibt nur eine Zahlenfolge, die dieser Zahl beliebig nahe kommt.
Der Unterschied zwischen den eindimensionalen abzählbaren und den reellen Zahlen ist daher so zu verdeutlichen: die abzählbaren Mengen werden durch ein Verfahren Punkt für Punkt definiert. Wenn etwa die natürlichen Zahlen aufgezeichnet werden, ist jeder neue Punkt die Grenze der kontinuierlichen eindimensionalen Bewegung, die zu ihm hinführt, z.B. der zeichnenden Handbewegung. Die reellen Zahlen können dagegen nicht Punkt für Punkt dargestellt werden, sondern nur als der gesamte Prozess der eindimensionalen Bewegung selbst. Abzählbare Mengen markieren Grenzen (Größen) von eindimensionalen Bewegungen, die als Messprozesse verstanden werden können. Reelle Zahlen sind das Abbild von kontinuierlichen Prozessen, von Strömungen. Zwar liegen sie wie die abzählbaren Mengen auf einer Gerade, aber einmal dient die Gerade als Hintergrund, als Messlatte, auf der die Punkte der abzählbaren Menge eingetragen sind, das andere Mal ist die Gerade selbst die betrachtete Menge, die sich ihrerseits vor einem Hintergrund abheben muss, die erst im mindestens zweidimensionalen Raum Kontur gewinnt. Um Geraden und allgemein eindimensionale Kurven darstellen zu können, wird mindestens die zweidimensionale Zeichenebene benötigt.
In der zweidimensionalen Ebene kann die Verzweigungssituation anschaulich am einfachsten dargestellt werden. Hierfür wird die Ebene durch ein kontinuierliches Muster strukturiert, etwa durch die Höhenlinien, also durch einen Abdruck einer Figur aus dem dreidimensionalen Raum, oder durch Strömungslinien.
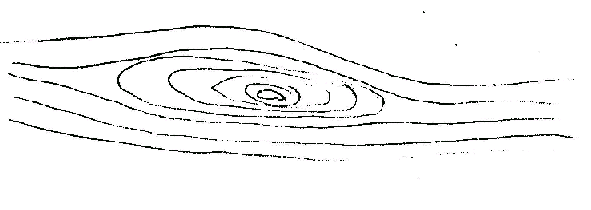
Figur 3 Basin
Beispiel für einen singulären Punkt: Basin, Freihandzeichnung
In diesem Muster gibt es zwei qualitativ verschiedene Gruppen von Linien: Geschlossene und offene Kurven. Wenn das Muster kontinuierlich ist, gibt es dann notwendig Verzweigungspunkte, wo offene Kurven in geschlossene Kurven übergehen, und es gibt als Gegenstück isolierte Punkte, um die sich die geschlossenen Kurven zusammenziehen. Wird dies Muster als Höhenlinienzeichnung interpretiert, können die Verzweigungspunkte als Punkte gedeutet werden, wo eine Kammlinie durch eine Senke unterbrochen wird und die isolierten Punkte sind Bergspitzen bzw. Talgrundpunkte. Bewegt sich eine Kugel mit gleichbleibender Geschwindigkeit entlang einer Kammlinie, wird sie an Verzweigungspunkten radikal ihre Bewegung ändern und mit wachsender Geschwindigkeit ins Tal rollen.
Es gibt in der Ebene auch andere Typen von Verzweigungspunkten, etwa eine Kammlinie selbst:

Figur 4 Kammlinie
Beispiel für eine singuläre Strecke: Kammlinie, Freihandzeichnung
Hier liegt nicht ein einzelner Verzweigungspunkt vor, sondern eine ganz Verzweigungsstrecke mit Anfangs- und Endpunkt.
In der Katastrophentheorie werden für jede Dimension alle möglichen Typen von Verzweigungen klassifiziert. Im zweidimensionalen Fall gibt es genau 2 Möglichkeiten:
der Übergang von einer geschlossenen Kurve zu einer offenen und umgekehrt der Übergang von einer geschlossenen Kurve zu einer anderen geschlossenen Kurve, die sich um einen anderen isolierten Punkt schließt. Für diesen Fall hat Thom die Terminologie geschaffen: isolierte Punkte heißen Attraktoren, Systeme von geschlossenen Kurven um einen Attraktor heißen Basins, die Grenzlinien von Basins heißen Wasserscheiden.
In höheren Dimensionen ergeben sich entsprechend vielfältigere Verzweigungsmöglichkeiten.
Verzweigungen sind nur in mehrdimensionalen Räumen möglich. Dort ergeben sie nur dann einen Sinn, wenn nicht isolierte Punkte oder Kurven betrachtet werden, sondern Strömungen. Verzweigungspunkte markieren in der Strömung die Stellen, wo Symmetrien gebrochen werden, wo sich die qualitativen Eigenschaften der Strömung ändern. Dies können Turbulenzen sein, es können Materialrisse sein, der Übergang von einem Schwerefeld in ein anderes, von einer Bewegungsform in eine andere etc. Unabhängig von dem konkreten Vorgang, der mathematisch dargestellt wird, werden die Verzweigungsmöglichkeiten analysiert. Hier kommt es wieder nur zu einer Annäherung zwischen mathematischer Darstellung mit wirklichem Geschehen.
Denn entsprechend den spezifischen Längenmaßen der Bewegungsformen können die Verzweigungspunkte nicht mathematisch punktgenau lokalisiert werden. Z.B. kann die Oberfläche von Wasser nicht exakt bestimmt werden, einzelne Moleküle lösen sich ständig oder werden umgekehrt ständig neu aufgenommen. Die Oberfläche ist in permanenter Bewegung und für ein vorbeikommendes Wassermolekül kann kein genauer Punkt bestimmt werden, wo die Kräfte, die es ins Wasser ziehen, die Oberhand gewinnen. Die Oberfläche, also die Grenzlinie, bewegt sich innerhalb einer Bandbreite, deren Größe durch das spezifische Maß des Wassers und allgemeiner des zu begrenzenden Inhalts bestimmt ist.
Aber unabhängig davon gilt dennoch die rein mathematische Erkenntnis, dass durch die Anzahl der Dimensionen qualitativ die Verzweigungsmöglichkeiten festgelegt sind. Bewegungsformen können folglich nicht nur durch lokale Symmetrien charakterisiert werden. So ist es denkbar, dass die lokale Symmetrie einer Bewegungsform zweidimensional ist. Die Strömung kann also durch zweidimensionale Querschnitte beschrieben werden (siehe oben Figur 2).
Wichtig ist nun auch, wie in dieser Bewegungsform die Verzweigungen aussehen. Kann es überhaupt Verzweigungen geben, wie sehen in den Verzweigungen die Brüche aus? Bleibt etwa das Muster auf der Ebene erhalten und nur die Ebene ändert ihre Richtung? Oder kann es Brüche geben, wo die Strömung aufgeteilt wird, wo sie in Chaos auseinander läuft, wo sie sich verändert und neu ordnet? Die quantenmechanischen Streuexperimente sind ein Beispiel, wo solche Eigenschaften untersucht werden.
Wenn die Strömung bestimmte endliche Muster enthält, kann diese Frage genauer ausgeführt werden.
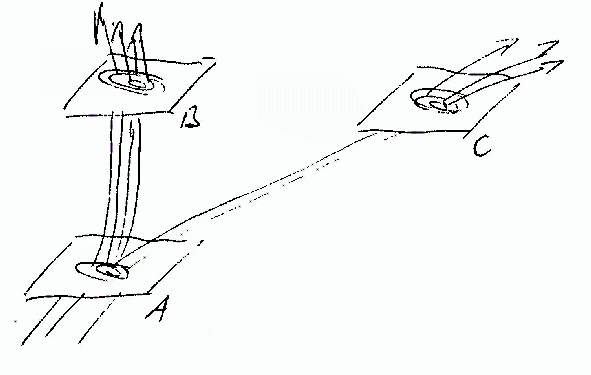
Figur 5 Verzweigungsprozess eines Stroms
Freihandzeichnung
Welche Muster, welche Konstellationen sind in einer Bewegungsform erreichbar? Gibt es bestimmte stabile Muster, die nicht mehr verändert werden können, gibt es unerreichbare Muster, gibt es unveränderbare stabile Bestandteile in den Mustern? Welche Änderungen im Muster können ausgeglichen werden, welche bleiben isoliert bestehen, welche weiten sich aus zum Systembruch? Entsprechend kompliziert sind die Verzweigungssituationen. Und da jeder Verzweigungstyp einem Raum mit bestimmter Anzahl von Dimensionen zugeordnet werden kann, ist diese Dimensionszahl wesentlich für die Bewegungsform mit ihren Verzweigungsmöglichkeiten.
Die Raumdimensionen haben nicht mehr nur quantitative Bedeutung (indem einfach gezählt wird: eindimensionaler Raum, zweidimensionaler Raum, dreidimensionaler Raum, etc), sondern entsprechend ihren Verzweigungsmöglichkeiten qualitative Bedeutung. Hegel hielt einen dreidimensionalen Raum für notwendig für die Darstellung von Dialektik in der Natur. Der Begriff Aufhebung bedeutet anschaulich, dass in einer zweidimensionalen Ebene eine unlösbare Konstellation, eine unentscheidbare Verzweigungssituation entsteht, die durch eine räumliche Verzweigung weg von dieser Ebene in eine andere, höhere Ebene gelöst wird.
Allgemein kann gefragt werden, ob und in welcher Strömung ein bestimmtes Muster in ein anderes bestimmtes Muster umgewandelt werden kann. Hierfür ist die richtige Bewegungsform mit den richtigen Randbedingungen und der richtigen Dimensionszahl zu finden.
Auch wenn für Verzweigungsprozesse je nach ihrem Charakter bestimmte Dimensionen notwendig sind, können sie in weniger Dimensionen ihre Spuren hinterlassen. Das Beispiel der Höhenlinien ist ein Modell dafür, wie eine dreidimensionale Figur in der Ebene abgebildet werden kann. Hierdurch entstehen Mehrdeutigkeiten, z.B. kann nicht erkannt werden, ob die geschlossenen Kurven ein Tal oder einen Berg darstellen. In Kartenwerken wird daher die absolute Höhenzahl neben die Linie geschrieben oder durch Einfärbung der Unterschied kenntlich gemacht. Im Extremfall wird alles auf einen einzigen Punkt projiziert, womit jede Aussage verschwindet. Die ersten Aussagen werden also möglich durch Projektion auf die eindimensionale Zahlengerade. Wie im Fall der Projektion in die Ebene verschwindet jede Tiefen- und Breitenkontur. Aber es bleibt möglich, aus der Verteilung der Punkte auf die Anzahl der Dimensionen des Raumes zu schließen, wo die Figur steht.
In der experimentellen Katastrophentheorie dient hierfür die Untersuchung von Zeitreihen. Von einer unerforschten Bewegung wird die Veränderung eines Parameters in der Zeit aufgezeichnet. Für die Bewegung wird zunächst angenommen, dass sie möglicherweise chaotisch ist. Die Daten werden dann danach untersucht, ob sich in der Zeitreihe bestimmte Zustände häufen oder zumindest Zustände auftreten, die in der Nähe von früheren Zuständen liegen. Die Zeitreihe wird danach untersucht, wie periodisch sie ist, ob es in ihrem Verlauf Grenzprozesse gibt. Aus der Häufigkeit der Perioden und der Dichte der Häufigkeit kann ein Maß abgeleitet werden, wie viele Dimensionen der Raum hat, in dem die Bewegung abläuft. Während in der Katastrophentheorie systematisch von der qualitativen Darstellung aller möglichen Verzweigungstypen auf ihre Projektion in Räumen mit geringerer Dimension geschlossen werden kann, verhält es sich in allen Experimenten genau umgekehrt. Dort ist aus der Fülle der empirischen Daten die innere Regelmäßigkeit (ein Naturgesetz) herauszufiltern, und dann das Maß dieser Bewegung, ihre Verzweigungstypen, ihre spezifische Dimension, ihre Figur in dem Raum mit dieser Dimension.
Die Darstellung einer komplizierten Bewegung erfolgt in einer Dimension oder in mehreren eindimensionalen Bewegungsachsen. Für die Darstellung sind die Eigenschaften der reellen Zahlen erforderlich, da die reellen Zahlen allgemein durch Grenzprozesse definiert sind und hier konkrete Grenzprozesse erkannt werden sollen. Schon bei den rationalen Zahlen lassen sich topologisch Häufungs- und Grenzprozesse darstellen, aber erst bei den reellen Zahlen gilt das Vollständigkeitsaxiom, dass der Grenzwert bzw. Häufungspunkt (und das ist in der dargestellten Bewegung der Attraktor) in der Menge existiert.
Auch wenn die Verzweigungs- und Grenzpunkte einer Bewegung zunächst in den reellen Zahlen dargestellt werden, wird doch angenommen, dass zwischen diesen Punkten bestimmte feste Korrelationen bestehen, bestimmte Harmonieverhältnisse, Maß- und Periodenzahlen. Hierdurch erfolgt im letzten Schritt die Darstellung der Bewegung in den natürlichen Zahlen, indem ganz bestimmte, feste Werte charakteristisch sind, wie die Lichtgeschwindigkeit, ein Längenmaß, der Goldene Schnitt, die Anzahl Tage im Mond- oder Sonnenzyklus, etc. Zahlenmystik beruht auf der Annahme, dass qualitative Eigenschaften der natürlichen Zahlen Ausdruck von Eigenschaften höherer Bewegungen sind. Als Paradox wird sich zeigen, dass Künstliche Intelligenz nur Erfolg haben kann, wenn es Zahlenmystik gibt, wenn also die unübersehbaren, nicht nachvollziehbaren Berechnungen der Künstlichen Intelligenz sich rückvermitteln lassen in einfache Zahlenverhältnisse.
Literaturhinweise
1985 - 1987
© tydecks.info 2002