Walter Tydecks
Mathematik und Philosophie
Inhaltsverzeichnis
Orientierung bei Kant
Hegels Idee einer Mathematik der Natur
Axiomatische Methode
Dialektische Methode
Mathematik der Natur
1. Orientierung bei Kant
Angesichts der offenen Fragen der Naturphilosophie diskutiert Kant das Verhältnis von Mathematik und Philosophie. Hat die Welt einen zeitlichen und kausalen Anfang? Hat sie ein räumliches Ende? Besteht die Materie aus kleinsten Bausteinen? Herrscht in der Natur Notwendigkeit? Kant sah genau, dass die vorherrschende populäre, dogmatische Naturphilosophie in allem die Existenz von Grenze und Notwendigkeit behauptet. Allerdings konnte er nicht ahnen, welch grenzenlosen Siegeszug sie ausgerechnet unter den Flaggen Materialismus und Anti-Metaphysik antreten sollte. Heute ist es so weit, dass gesagt wird, wieviel Jahre seit dem Anfang der Welt vergangen sind, wieviel Kilometer der Durchmesser der Welt beträgt. Alle Elementarteilchen gelten als Kombinationen von 6 Quarks, deren Gewicht, Durchmesser etc. gemessen sind. Die Entstehung aller Teile der Natur wird in der Evolutionstheorie in einer einzigen Zeitreihe geordnet und mit mehr oder weniger Notwendigkeit postuliert. Den logischen Abschluß bildet die evolutionäre Erkenntnistheorie, wonach der Schlußpunkt der Evolution ihre eigene Selbsterkenntnis in Form der modernen Naturwissenschaften ist. Da kann etwas nicht stimmen.
Kant wollte den dogmatischen Weg ebenso vermeiden wie den entgegengesetzten empiristischen, der jede Existenz von Naturgesetzmäßigkeiten leugnet und sich auf eine im Prinzip unendliche Menge von Einzelanalysen beschränkt. In der Mathematik und der Philosophie sieht er zwei mögliche Auswege. Der Mathematik fällt es leichter, und sie ist zunächst erfolgreicher.
Sie steht nicht so gespannt im Gegensatz von Dogmatismus und Empirismus, da sie sich von der unmittelbaren Anschauung leiten lassen kann. Ohne Untersuchung konkreter Eigenschaften reicht ihr zum Zählen als Anschauung die Hand mit den fünf Fingern und für die Geometrie die Anschauung der einfachen Figuren wie Dreieck, Kreis etc. Sie beschränkt sich im weiteren ganz auf die Konstruktion von Größenbegriffen, wie Zahlenwerte, Flächeninhalte, Längen, Winkel etc. Dadurch wird sie nicht empiristisch, da alle ihre Ergebnisse allgemeingültig sind, und auch nicht dogmatisch, da sie keine einschränkenden Voraussetzungen über ihre Größenbegriffe trifft. Und dennoch gelingen ihr mit den strengen Konstruktionsmethoden der Arithmetik und Geometrie immer wieder überraschende Erkenntnisse, die kein Philosoph durch bloßes Nachdenken hätte erwarten, geschweige denn beweisen können.
Trotzdem ist Kants Faszination von der Mathematik gebrochen. Historisch gesehen folgt er dem platonischen Verständnis der Mathematik, wonach sie die ewigen Ideen der reinen geometrischen Objekte zum Gegenstand hat, sich von ihnen aber auch nicht lösen kann. Trotz aller Erfolge ist sie hiernach eine erstarrte Wissenschaft, die nur die äußerste Oberfläche erkennen kann.
"Wir haben zwei Ausdrücke: Welt und Natur, welche bisweilen ineinander laufen. Das erste bedeutet das mathematische Ganze aller Erscheinungen und die Totalität ihrer Synthesis, im Großen sowohl als im Kleinen, d.i. sowohl im Fortschritt derselben durch Zusammensetzung, als durch Teilung. Eben dieselbe wird aber Natur genannt, so fern sie als ein dynamisches Ganzes betrachtet wird, und man nicht auf die Aggregation im Raume oder der Zeit, um sie als eine Größe zu Stande zu bringen, sondern auf die Einheit im Dasein der Erscheinungen sieht." (Kant, Kritik der reinen Vernunft, B 446/A 418)
Im Zeitalter der Postmoderne und der Simulation mag das für die Mathematik sprechen. Auch in der EDV wird nur noch von Welten gesprochen: Unix-Welt, PC-Welt, IBM-Welt etc. Aber Kant ist das natürlich zu wenig. Wittgenstein hat dies später auf den Punkt gebracht:
"Wir fühlen, dass, selbst wenn alle möglichen wissenschaftlichen Fragen beantwortet sind, unsere Lebensprobleme noch gar nicht berührt sind." (Wittgenstein, Werke Bd. 1, S. 85)
Und Kant sagt, die Mathematik würde sofort ihr Geschäft aufgeben, könnte sie die großen naturphilosophischen Fragen lösen.
So gelingt es zwar in der Mathematik der Vernunft, ohne Dogmatismus und Empirismus in der Naturerkenntnis immer neue Erfolge zu erzielen, aber sie bleibt bei der bloßen Quantität stehen. Mathematik bleibt Größenlehre und Meßkunst. Die Philosophie umgekehrt kann zwar erhabene Ideen formulieren, verfängt sich bei deren Lösung aber in Dogmatismus, Empirismus oder Skeptizismus. Den Ausweg sieht Kant im regulativen Gebrauch der philosophischen Ideen. Die Philosophie soll gar nicht lehren, wie die Natur ist. Sie soll sich nicht von außen in die Naturwissenschaft einmischen und so tun, als könne sie besser als diese die Natur erkennen. Sie soll auch nicht so tun, als könne sie ins Herz der Natur sehen und deren inneres Geheimnis enträtseln, also eine neue Theologie oder Mythologie entwerfen. Sie soll den Leitfaden liefern, an dem sich die Naturwissenschaft orientieren kann. Denn der Orientierung bedarf eine zugleich nicht-dogmatische und nicht-empiristische Wissenschaft, die sich nicht wie die Mathematik auf die unmittelbare Anschauung verlassen kann. Sie soll weder in der Fülle des Materials versinken, noch vom Korsett dogmatischer Ideen eingezwängt werden oder die Natur einzwängen. Verfehlt die aufgeklärte Wissenschaft die Orientierungsfähigkeit, oder büßt sie sie ein, dann verfängt sie sich unweigerlich in einem Prozeß, der ebenso maßlos ist wie die erhabenen Ideen über das Ganze der Natur, der jeden Halt niederreißt und am Ende den einen als entfesselte Naturwissenschaft erscheint, den anderen als unentrinnbare Dialektik der Aufklärung.
Auf den ersten Blick gerät die Orientierung jedoch widersprüchlich. Kant formuliert in der "Kritik der Urteilskraft" diesen Widerspruch: Die Naturwissenschaft soll einerseits überall nach Kausalketten suchen, andererseits ein teleologisches Verständnis für die Natur gewinnen. Der Orientierung liegen in den Modellen der Maschine und des Organismus zwei verschiedene Muster vor. Es ist zu einfach, diesen Gegensatz durch Verweis auf zwei verschiedene Bewegungsformen der Natur aufzulösen, die Maschine auf die mechanische Physik, den Organismus auf die Biologie. Sie beziehen sich in Kants Anleitung für die Orientierung auf zwei verschiedene Situationen.
Teleologische Urteilskraft ist verlangt, um ein grundsätzliches Verständnis von der Natur zu gewinnen. Es handelt sich um Interpretation und kann daher nicht in Naturgesetzen oder anderen mathematischen Zeichensystemen ausgedrückt werden. Im einfachsten Fall geht teleologische Naturerkläreng nach der Frage vor: Wie würde ich mich verhalten? In der Biologie ist das natürlich am naheliegendsten. Bei Beobachtungen von Lebewesen kann deren Verhalten danach beurteilt oder damit verglichen werden, wie Menschen handeln. Sei es bei der Kommunikation von Ameisen oder im Energiehaushalt einer Pflanze. Aber auch in die Physik gehen teleologische Überlegungen ein. Zum Beispiel, wenn strukturell-stabile Systeme betrachtet werden, in denen kleine Abweichungen ausgeglichen werden, oder beim Wirkungsprinzip, wonach der Weg mit dem kleinsten Kraftaufwand gegangen wird. Die Physik ist voll von Erhaltungs- und Optimierungsgesetzen. Nicht diese Gesetze selbst sind teleologische Naturerklärung, aber sie nehmen bei teleologischen Interpretationen wie Ausgleich, Harmonie, Erhaltung, Optimierung ihren Anfang.
Hierbei steht für die Orientierung die Teleologie keineswegs allein, auch wenn sie bei Kant den wichtigsten Platz einnimmt. Es braucht ja nicht nur gefragt zu werden: Wie würde ich mich verhalten? Es kann auch umgekehrt Versenkung stattfinden, um so weit wie möglich nachzuerleben, wie in der Natur anderes Verhalten stattfindet als das gewöhnliche menschliche. Statt Teleologie kann Ästhetik der Orientierung dienen. In der Natur werden bestimmte Zusammenhänge dadurch hervorgehoben, dass sie als schön, erhaben, oder umgekehrt als bedrohlich, erschreckend, eigenartig wahrgenommen werden. In allen Fällen führt die Orientierung dazu, dass eine Ordnung, Zuordnung, Strukturierung der Realität erfolgt. Es handelt sich aber nur um Interpretation, nur um Bewußtwerden, wie die Natur auf den Menschen wirkt, auch wenn die Ergebnisse zu praktischen Erfolgen in Experimenten oder industrieller Anwendung führen. Es geht nicht um Erkenntnis der Form: Der Stein fällt so, weil er möglichst wenig Arbeit leisten will. Es geht nicht um den eigenen Willen, das eigene Schönheitsempfinden der Natur. Darüber kann nichts ausgesagt werden, es sei denn, der Mensch geht von Allmachtsphantasien aus, in seinem Bewußtsein werde sich die ganze Natur ihrer selbst bewußt, sein Leib sei die höchste Organisation der sich selbstorganisierenden Natur, oder aber die Natur existiere nur in seinem Bewußtsein. Auch ist nicht zu sehen, welchen Erkenntnisgewinn Aussagen über die inneren Antriebe der Natur bringen sollen. Es geht nur um Orientierung, was gehört wohin, welche Teile bilden einen gemeinsamen Apparat oder einen gemeinsamen Organismus, welche Töne klingen schön zusammen usw. Über die Natur wird nur vorausgesetzt, dass es in ihr eine objektive Grundlage für diese Interpretation gibt. Orientierung ist der Versuch, sich in der Natur zurechtzufinden und sich nur an das zu halten, wie der Mensch die Natur erlebt. Die Klippen der Dialektik der Aufklärung werden gar nicht erreicht, wenn weder mythologisch (etwa durch Schöpfungsmythen) noch durch die erhabenen Ideen der Naturphilosophie versucht wird, aus der Natur herauszuspringen und sie von außen als Ganze zu beurteilen.
Auf die Orientierung kann eine Darstellung der Natur in den verschiedensten Zeichensystemen folgen. Orientierung und Darstellung werden einander wechselseitig beeinflussen. In der Kunst kann der ästhetische Eindruck komponiert, visualisiert oder ausgesprochen werden. In der Naturwissenschaft wird eine Gesetzmäßigkeit für die Beobachtungen gesucht, deren Zusammenhang in der Orientierung bereits erkannt worden ist. Und hier wird eine Orientierung anderer Art erforderlich, auf die Kant in der "Kritik der reinen Vernunft" eine Antwort geben will. Diese Orientierung ist notwendig, aber keineswegs selbstverständlich oder eindeutig, wie die Geschichte der Mathematik zeigt. Die Phythagoreer gingen von ästhetischen Urteilen in ihren Musikexperimenten aus (was klingt schön zusammen), und ließen sich dann von der Vorstellung leiten, dass alle Zusammenhänge in der Natur durch Zahlenverhältnisse ausgedrückt werden können (insofern besteht die Welt aus Zahlen). Kant will eine andere Orientierung geben. Ausgehend von teleologischen Urteilen zerfällt der gefundene Zusammenhang in einzelne Komponenten, die in Form von Kausalketten als Naturgesetze dargestellt werden können. Die Zeit ist ihm die Orientierung, in der Naturgesetze mathematisch formuliert werden können.
Damit ist inhaltlich der Punkt gefunden, wo in der kritischen Philosophie von Kant Mathematik und Philosophie einander berühren. Durch eine erste Orientierung wird qualitativ erkannt, welche Zusammenhänge, inneren Bezüge in der Natur existieren. Dann geht es darum, diese Zusammenhänge auch quantitativ zu erfassen. Im einfachsten Fall, bei starren Naturgebilden, genügt es, zuerst qualitativ zu bestimmen, was zu dem Gebilde gehört und was nicht, und dann einen Meßstab anzulegen, und die Aufgabe der Mathematik ist, für die Messung ein verbindliches Größenmaß zu finden und Aufgaben der Art zu lösen, wie aus äußeren Abmessungen Flächen- oder Rauminhalt, Materiedichte, Gewicht etc. berechnet werden können. Bei dynamischen Prozessen kommt die Zeit hinzu, die Uhr dient als Meßinstrument. Die Mathematik arbeitet an einem abstrakten Raum mit 3 Raumachsen und 1 Zeitachse, dessen allgemeine Eigenschaften unabhängig davon erkannt werden, welche Naturprozesse in ihm dargestellt werden. Das Größenraster wird rein quantitativ unabhängig von konkreten Naturprozessen untersucht. In der Naturwissenschaft wird umgekehrt rein qualitativ untersucht, welche Naturprozesse die Eigenschaft haben, dass sie in diesem Raster dargestellt werden können. Die philosophische Orientierung muß zum einen anleiten, wie in der Natur qualitative Eigenschaften gefunden werden können, und sie muß zum anderen erkennen, welche Eigenschaft in der Natur es ist, wo Natur und Welt der Mathematik übereinstimmen, wo die Natur also mathematisch dargestellt werden kann. Dies war für die Pythagoreer das Zahlenverhältnis, für Plato die ideale geometrische Figur, für Kant ist es die reine Zeit (siehe das Schematismus-Kapitel in der "Kritik der reinen Vernunft", dort B 184/A 145).
Aber hier verwickelt er sich doch in Widersprüche. Die Orientierung an der Zeit ist nicht eindeutig. Kant beschreibt 3 Modi der Zeit, die die Grundlagenbegriffe der Naturwissenschaft sind: Substanz als das, was in der Zeit erhalten bleibt; Kausalität als das, was notwendig einander in der Zeit nachfolgt; Wechselwirkung als das, was notwendig gleichzeitig (gemeinschaftlich) auftritt. Während Substanz und Kausalität in der Zeitreihe liegen (als Veränderliches oder Unveränderliches), steht die Wechselwirkung quer zur Zeit. Sie wird zwar als Eigenschaft der Zeit erkannt, bleibt dann aber folgenlos. Das ist schrittweise nachzuzeichnen.
I Die Antithetik der erhabenen naturphilosophischen Ideen handelt von den Widersprüchen einer maßlosen, überfliegenden Betrachtung der Zeitreihe, wenn geglaubt wird, es sei dem Menschen möglich, die Zeitreihe im Ganzen zu überschauen und über sie Aussagen zu treffen. Eigenschaften der Wechselwirkung lässt Kant hierbei ausdrücklich beiseite. Aber all die großen Ideen erscheinen unter einem ganz anderen Licht, wenn die Möglichkeit von Wechselwirkung berücksichtigt wird. Wenn in jedem einzelnen Zeitmoment notwendig viele verschiedene Dinge gleichzeitig passieren, kann eine Kausalkette bestenfalls einen Querschnitt erfassen. In aller Regel werden viele Kausalketten gleichzeitig nebeneinander verlaufen. Und es kommt zu Schnittpunkten, zu Verzweigungen, von wo die Entwicklung in verschiedene Richtungen weiterlaufen kann. Das Gesetz der Kausalität, wonach bestimmte Dinge einander in der Zeit notwendig nachfolgen, bleibt dabei erhalten. Aber das Verhältnis von Notwendigkeit und Freiheit ist neu gestellt. Und wenn die Kausalketten in Zukunftsrichtung und in jeder Gegenwart Verzweigungsmöglichkeiten haben, gilt das auch für die naturhistorische Betrachtung zurück in die Vergangenheit, wo jeder einmal erreichte Zustand Teil einer Wechselwirkung ist und durch verschiedene Kausalketten erklärt werden kann, die zu ihm hinführen. Das betrifft die Frage des kausalen und zeitlichen Anfangs aller Dinge.
Wenn Wechselwirkung berücksichtigt wird, kann auch nicht mehr beliebig geteilt werden. Selbst Aggregate wie ein Sandklumpen können nicht beliebig geteilt werden. Zunächst führt das Teilen zwar zu kleineren Klümpchen, zu Sandkörnern usw., dies hatte Kant vor Augen. Aber mit der Teilung geht es zu Ende, wenn das Molekül erreicht wird. Wird das Molekül geteilt, entstehen nicht halbe Moleküle, sondern diese Teilung ist ein chemischer Prozeß, der zu anderen Molekülen und Atomen mit anderen chemischen Eigenschaften führt, da hier die Teilung einen Verband von Atomen zerreißt, die in Wechselwirkung zueinander stehen. Kant hatte die Teilung als mechanischen Prozeß vor Augen, aber die führt an die Grenze, wenn eine tieferliegende Bewegungsform der Materie erreicht wird, und so geht es weiter. Auch die Quarks werden bestenfalls eine Zwischenstation sein. Die Antithetik ist hier daher anders aufzulösen. Die Quantenmechanik traf experimentell auf dies Problem. Im Umkreis von Weizsäcker wurde daraus jedoch vorschnell geschlossen, Kausalität und Substanz gibt es gar nicht mehr, wo in der Natur Zufallsprozesse und Unbestimmtheiten angetroffen wurden, die ihrerseits nur eine Zwischenstation im Erkenntnisprozeß sind. In Berücksichtigung von Wechselwirkung sind diese Phänomene aber ganz anders zu beurteilen, so dass Substanz und Kausalität ihre Bedeutung behalten.
II In jedem Zeitmoment existiert notwendig der gesamte Raum, den Kant daher konsequent als die reine Wechselwirkung, die reine Gemeinschaft bezeichnet. Wenn der reine Raum Gegenstand der Mathematik ist, sollte daher die Wechselwirkung von grundsätzlicher Bedeutung sein. Kant wendet das dadurch ab, dass er den Gegenstand hinter der Vorgehensweise der Mathematik verschwinden lässt. Mathematik ist für ihn letztlich Zählen, geometrisches Konstruieren und Messen. Das alles erfolgt aber schrittweise in der Zeitreihe. Die Ergebnisse sind jeweils feste, starre Größen (die Zahl oder die Figur). Wenn Kant die Mathematik dermaßen einschränkt und nicht sieht, wie z.B. sein großes Vorbild Newton mathematisch die Wechselwirkung von mechanischen Körpern durch die Gravitation beschrieben hat, kann die Mathematik genau das nicht leisten, was Kant ihr zuweist: die Darstellung von dynamischen Prozessen in der Zeitreihe.
III Im "Opus postumum" ist die Gravitation sogleich die Kernfrage für das nächste Problem. In welchem Verhältnis steht der reine Raum der Mathematik zum wirklichen Raum, in dem das Naturgeschehen stattfindet? Anschaulich hat Kant das zweifellos so gedacht, dass der reine Raum der leere Raum ist, in den die Naturdinge hineingestellt sind, dass also der Zwischenraum zwischen den Naturdingen leer ist. Kausalität vollzieht sich bei Berührung, wenn mindestens zwei Dinge sich treffen und verändern. Nach Newton wirkt aber Gravitation durch den leeren Raum. Das ist zunächst Bestätigung für die Existenz des leeren Raum. Aber für Kant entsteht ein Problem: "Newtons Anziehungskräfte durch den leeren Raum. Wie wird der leere Raum selbst wahrgenommen, denn die Kräfte können ja nicht ohne physische Realität für sich sein." (Kant, Opus postumum, Bd. 1, S. 19). Kant entscheidet dies dahin, dass Kräfte durch den leeren Raum nicht möglich sind und dass es einen leeren Raum damit nicht gibt. Das zerreißt aber die Verbindung von Wirklichkeit und reinem Raum der Mathematik, eine Frage, der Kant nicht mehr nachgegangen ist.
Die Alternative ist der gefüllte Raum. Und hier zieht Kant all die Naturprozesse zu Rate, die Gegenstand der mittelalterlichen Naturforschung waren, wie Blasenbildung, Tropfenbildung, Elastizität, Kristallisation, Schmiedbarkeit, Sprödigkeit, Erschütterung, Porosität, Erstarrung, Reibung, Affinität, Wellenschwingung, Textur, Verwerfung. Als gemeinsames bewegendes Prinzip erkennt er den Wärmefluß, durch den die verschiedensten Erstarrungs- und Flüssigkeitsgestalten erzeugt werden. Ein Strom tritt an die Stelle der eindimensionalen Reihe, das ist von grundsätzlicher Bedeutung. Denn im Strom (wie im einzelnen in der Tropfenbildung, Blasenbildung, Verwerfung etc.) wird die zeitliche Bewegung von räumlich ausgedehnten Naturdingen betrachtet, also von Gemeinschaften, von Wechselwirkungen, die sich zeitlich entwickeln. Wenn der Raum als die reine Wechselwirkung gefüllt ist, muß das so sein. "Durch Licht und Wärme setzen sich Welten in Gemeinschaft, als gewisse Stoffe, welche den Raum erfüllen, nicht bloß in ihm wirksam sind." (ebd., S. 105) Das entspricht bereits sehr der physikalischen Vorstellung von Teilchenfeldern.
IV Mit dem leeren Raum fällt aber auch das Leitbild der modernen Naturwissenschaft, die Maschine, nach der die Natur darzustellen und zu bearbeiten ist.
"Das Gefühl der Wärme (das Leben), der Kälte (der Tod). Keine der beiden sind Stoffe, sondern nur Verhältnisse von Kräften. Luft, Licht, Wärme; positive und negative Elektrizität." (ebd., S. 118) "Licht, Wärme, Elektrizität und Nervenfluß sind die bewegenden Kräfte, welche ein Leben im Universum gleich dem Galvanismus bewirken." (ebd., S. 136)
Das sind alles nur Notizen, im "Opus postumum" eingestreut zwischen Kants Speiseplänen und Ausflugszielen, und sie widersprechen sich bisweilen von Seite zu Seite (mal ist Wärme ein Stoff, dann wieder nicht). Und doch setzt sich die Erkenntnis durch, dass ein mit Wärme gefüllter Raum lebt, dass er vom Menschen mit allen Sinnen wahrgenommen wird (nicht nur mit dem Auge), und dass er keine Maschine sein kann. Wie ist dann zu erklären, dass dennoch die Bewegung der Planeten in ihrer Gleichmäßigkeit und Regel wie eine Maschine, rein mechanisch, wirkt? Kant durchdenkt das Verhältnis von Maschine und Organismus neu. "Organische Körper sind solche, welche aus eigenen Kräften als Maschinen wirken." (ebd., S. 194). Maschine ist hier ein Körper, in dem verschiedene Kausalketten planmäßig aufeinander abgestimmt sind und zu bestimmten Resultaten führen. Insofern kann jedes Lebewesen als Maschine angesehen werden, das Nahrungsmittel verarbeitet. Landwirtschaft nutzt das schon immer, Biotechnologie soll das weitertreiben. Diese Überlegungen führen Kant direkt in die Naturromantik.
"Ein immaterielles bewegendes Prinzip in einem organischen Körper ist dessen Seele, und von diesem kann man, wenn man sie als Weltseele denken will, annehmen, dass sie ihren Körper und selbst das Gehäuse desselben (die Welt) baue." (Bd. 2, S. 97)
Von hier aus löst sich auch die Frage, warum die Himmelsmechanik als Maschine erscheint.
"Amphibolie (Doppeldeutigkeit, t.) der Reflexionsbegriffe in Ansehung der Physik, da das, was gemacht wird, a priori synthetisch als Gegebenes gedacht ist." (ebd. 2, S. 285)
Die Himmelsmechanik wird als Gewordenes vorgefunden. In ihr paßt alles zusammen, so erscheint sie als Maschine, als Gegebenes. In Wahrheit ist sie historisch Gewordenes, in dem die Natur als organischer Körper sich auf diese Weise organisiert hat und weiter organisiert. An die Stelle des leeren Raums als reiner Wechselwirkung tritt die Natur als wirkliche Wechselwirkung, die in ständiger Änderung und Entwicklung begriffen ist. Organismus und Maschine taugen beide als Leitideen, indem entweder die entstehende, planende, vorbereitende, steuernde Wechselwirkung betrachtet wird oder die Wechselwirkung an sich, als Gesamtgefüge von aufeinander bezogenen Kräften.
Das muß auch Auswirkungen auf den reinen Raum der Mathematik haben. Kant war davon ausgegangen, dass der reine Raum euklidisch ist und von der Mathematik Objekte nur in diesem Raum konstruiert werden. Wird dagegen vom gefüllten Raum ausgegangen, so ist es die erste Aufgabe der Mathematik, die allgemeinen Eigenschaften des Raums zu erkennen und dann in diesem Raum zu konstruieren. Beispiele für mathematisch erkannte qualitative Eigenschaften des Raums sind aus der weiteren Entwicklung der Himmelsmechanik bekannt, wo studiert wird, ob der Raum gekrümmt ist, ob er sich ausdehnt etc. In gewisser Weise hat Kant eine Ahnung davon, wo er nach einem Beispiel für die synthetische Methode der Geometrie sucht.
"Dass die gerade Linie zwischen zwei Punkten die kürzeste sei, ist ein synthetischer Satz. Denn mein Begriff vom Geraden enthält nichts von der Größe, sondern nur eine Qualität. Der Begriff des Kürzesten kommt also gänzlich hinzu, und kann durch keine Zergliederung aus dem Begriff der geraden Linie gezogen werden. Anschauung muß also hier zu Hilfe genommen werden." (Kant, Kritik der reinen Vernunft, S. 816)
Hier wird mathematisch eine qualitative Eigenschaft des gesamten euklidischen Raums erkannt, ihre Ebenheit, wodurch er sich qualitativ unterscheidet von anderen Räumen wie der Kugel oder dem gekrümmten Weltall. Damit ist die Mathematik keine bloße Größenlehre mehr, sondern untersucht auch qualitative Eigenschaften. Das führte jedoch nicht dazu, dass sie von Philosophie und Geschichte unabhängig wird. Weiterhin ist philosophisch zu bestimmen, welchen Ort die Mathematik in der Naturerkenntnis einnimmt und von welchen Grundlagen sie ausgeht.
2. Hegels Idee einer Mathematik der Natur
2.1. Das Unendlichkeitsaxiom im Differentialkalkül
Für Hegel besteht die überwältigende Leistung der Philosophie im Entwurf der Methode. Mit ihr kann er sich überall orientieren und jedes Problem lösen. Das Verhältnis von Mathematik und Philosophie wird zum Methodenvergleich: hier axiomatisch, dort dialektisch. Die euklidische Geometrie dient als glänzendes Beispiel für die Erfolge der axiomatischen Methode, und zu Recht erkennt Hegel sie in allen Naturwissenschaften wieder, die die euklidische Geometrie nachahmen, wie die klassische Mechanik.
Und doch geht in der "Wissenschaft der Logik" die Mathematik nicht in der Geometrie auf. Dem Differentialkalkül räumt Hegel eine Sonderstellung ein. Während die Axiomatik von Euklid seit über 2000 Jahren galt, wurde für den Differentialkalkül erst zur Zeit von Hegel, systematisch erst im 20. Jahrhundert ein Axiomsystem aufgestellt.
(a) Messungen und geometrische Intuition
Dem Differentialkalkül waren geometrische Untersuchungen vorausgegangen, die auf die Frage nach der Quadratur des Kreises zurückgingen. Systematisch wurden gekrümmte Kurven durch gerade Tangenten angenähert mit dem Ziel, den Kreis durch ein Tangentensystem, durch ein Vieleck, auszudrücken. Bei einfachen Funktionen wie y = x² konnte mit geometrischen Methoden die Ableitung gewissermaßen erraten werden, indem an vielen Punkten gemessen wurde, dass die Steigung der Tangente an der Stelle x₀ den Wert 2x₀ hat.
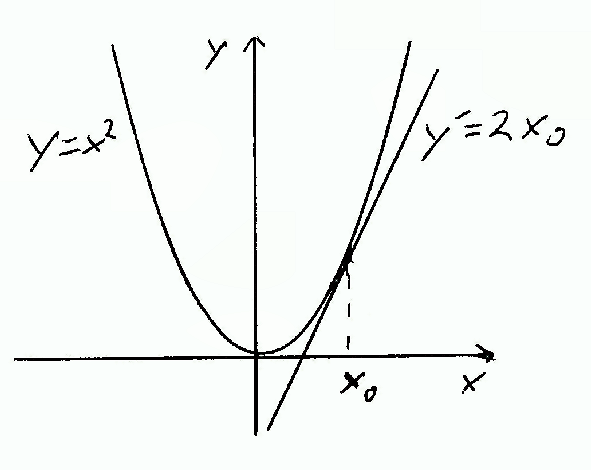
Figur 1 Parabel
Funktionsverlauf von y = x², Freihandzeichnung
Es lässt sich auch genau die Gerade angeben, die an der Stelle x₀ die Tangente ist: Sie muss entsprechend den Messergebnissen die Steigung 2x₀ haben, also im ersten Ansatz:
(1) y = 2x₀x + C
Die Verschiebung C auf der y-Achse muss so gewählt werden, dass an der Stelle x₀ genau der gewünschte Funktionswert erreicht wird:
(2) y₀ = x₀² = 2x₀x
Daraus ergibt sich für die Gerade, die die Tangente an der Stelle x₀ liefert, die Lösung:
(3) y = 2x₀x - x₀²
Bei komplexeren Funktionen ist die Rechnung natürlich aufwändiger.
Diese geometrische Anschauung liegt bis heute der Ableitung zugrunde. Sie wurde auf andere Räume und mehrdimensionale Figuren verallgemeinert, indem z.B. eine Kugel an jedem Punkt ihrer Oberfläche eine Tangentialfläche definiert, die hier die Kugeloberfläche annähert. So kommt auch der euklidische Raum weiter zu seinem Recht, indem der Weltraum lokal durch den euklidischen Raum angenähert werden kann. Werden Bewegungskurven im wirklichen Raum abgeleitet, d.h. durch gerade Linien angenähert, so liegen diese im euklidischen oder vergleichbaren Raum.
(b) Algebraische Operationen und Stoßen an die Schranken des traditionellen Kalküls
Im nächsten Schritt wurde versucht, mit arithmetischen Methoden die Ableitung auszurechnen. Grundidee war, dass die Steigung der Tangente durch das Verhältnis der beiden Seiten im Steigungsdreieck angenähert werden kann: y / x.
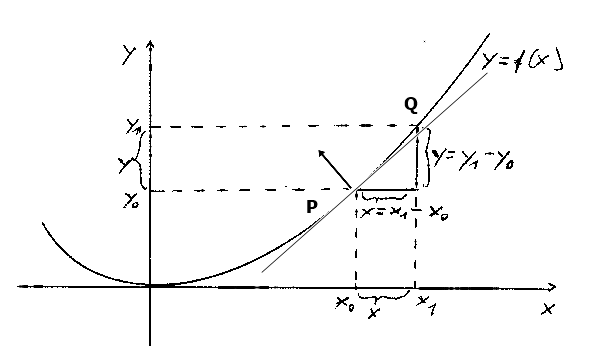
Figur 2 Steigungsdreieck
Freihandzeichnung
Hier soll die Funktion an der Stelle x₀ abgeleitet werden, wobei y die Differenz zu einem Funktionswert y₁ in der Nähe von y₀ ist. Es gilt der Ansatz:
| (4) |
|
= |
|
= x + 2x₀ |
Dies ist ein arithmetischer Ausdruck und er kann durch arithmetische Rechnung gelöst werden. Als Beispiel diene weiter die Funktion y = x².
Es soll der Funktionswert y₁ ein kleines Stück oberhalb von y₀ berechnet werden.
(5) y₁ = y + y₀ = f(x + x₀) = f(x₁)
In diesem Beispiel gilt f(x) = x², folglich eingesetzt:
(6) y + y₀ = (x + x₀)²
Auf der rechten Seite entsprechend der binomischen Formel ausmultipliziert:
(7) y + y₀ = x² + 2xx₀ + x₀²
Da an der Stelle x₀ nun gilt: y₀ = x₀², bleibt die Gleichung gültig, wenn links y₀ und rechts x₀² abgezogen wird mit dem Resultat:
(8) y = x² + 2xx₀
Jetzt braucht nur noch die Gleichung auf beiden Seiten durch x geteilt zu werden, und der gesuchte arithmetische Ausdruck y / x ist gefunden:
| (9) |
|
= |
|
= |
|
+ |
|
= x + 2x₀ |
Aus den geometrischen Untersuchungen war bekannt, dass auf der rechten Seite mit 2x₀ in der Tat die Lösung ausgerechnet worden war. Dafür ist nur anzunehmen, dass im Grenzprozeß die Differenz
x₁ - x₀ = x = 0 wird und damit auch die Differenz
y₁ - y₀ = y = 0 wird mit dem gesuchten Endresultat:
| (10) |
|
= 0 + 2x₀ = 2x₀ |
Lagrange hat die arithmetische Methode systematisch zu Ende geführt und gezeigt, dass auf ähnliche Weise alle Polynome
(11) y = a₀ +a₁x+ ... anxn
und auch unendliche Reihen wie
(12) y = a₀ +a₁x+ ... anxn + ...
abgeleitet werden können. Da sich die trigonometrischen Funktionen und die Exponentialfunktion als unendliche Reihen schreiben lassen, sind sie auch ableitbar.
Andere Funktionen können nicht abgeleitet werden (es gibt jedenfalls kein Verfahren dafür). Aber es wurde bewiesen: Wenn irgendwie gezeigt werden kann, dass eine Funktion die qualitative Eigenschaft der Ableitbarkeit besitzt (d.h., dass sie lokal, also im Kleinen durch Geraden angenähert werden kann), dann kann diese Funktion stückweise beliebig genau durch Polynome angenähert werden (Satz von Stones-Weierstrass).
(c) Grenzprozess und Begründung durch eine erweitere Axiomatik der Zahlenmengen
Hegel und Marx gingen in ihren Studien zum Differentialkalkül von den Arbeiten von Lagrange aus. Die oben entwickelte arithmetische Resultierende von der Gestalt
| (9) |
|
= x + 2x₀ |
bezeichnet Marx als "vorläufig Abgeleitete", da hier die arithmetische Operation abgeschlossen ist und nur noch der Grenzprozeß durchzuführen ist, in dem x = 0 und y = 0 gesetzt werden.
Der Grenzprozeß steht aber im Gegensatz zur Arithmetik, in der ein Ausdruck der Gestalt 0 / 0 nicht berechnet werden kann ("Teilen durch Null geht nicht"). Dies Problem wurde zunächst von Leibniz mit einer neuen Symbolik umgangen, indem er den arithmetischen Ausdruck der "vorläufigen Abgeleiteten" im Grenzprozeß symbolisch umformt zu
| (13) |
|
= dx + 2x₀ |
Die Umformung der Symbolik sagt aus, dass die Rechenregeln der Arithmetik verlassen werden und neue Regeln gelten. Lagrange übernimmt diese Symbolik. Leibniz formulierte den Differentialkalkül, in dem definiert ist, wie mit diesen Symbolen gerechnet werden kann, ohne dass beim Teilen durch Null Widersprüche auftreten.
Als aber Cauchy den Differentialkalkül auf andere Zahlenmengen (die komplexen Zahlen) anwandte, wurde deutlich, dass die Gültigkeit des Differentialkalkül eine Eigenschaft der Zahlenmenge ist, in der abgeleitet wird, und daher in die Axiomatik dieser Zahlenmenge gehört. Zum Beispiel kann in der Menge der natürlichen Zahlen nicht abgeleitet werden, da der Grenzprozeß nicht möglich ist, wenn der Abstand zwischen zwei benachbarten natürlichen Zahlen immer Eins ist. Das führte in der weiteren Entwicklung dahin, dass Räume konstruiert wurden, die genau diese Eigenschaft der Ableitbarkeit haben (normierte Räume). Insbesondere konnte gezeigt werden, dass im euklidischen Raum und im Bewegungsraum der Mechanik abgeleitet werden kann. Umgekehrt gibt es aber normierte Räume, die nicht euklidisch sind. Die Vorstellung von Kant und Newton, dass der euklidische Raum, der Raum der Natur und der Raum, in dem abgeleitet werden kann, identisch sind, war damit endgültig dahin. Die axiomatische Methode hatte zuerst die differenzierende Wirkung, dass verschiedene Räume konstruiert werden konnten, in denen jeweils bestimmte Axiome gelten und andere nicht, woraus dann verschiedene Eigenschaften dieser Räume folgen.
Bemerkenswert war der Gang der Axiomatisierung. Am Anfang stehen bekannte mathematische Operationen (wie geometrisches Konstruieren und arithmetisches Rechnen), die unter Umständen das Gebiet verlassen können, das bis dahin durch Axiome abgedeckt war. Das hat dazu geführt, dass neue Operationen definiert wurden (arithmetisches Rechnen im Differentialkalkül), für die das verletzte Axiom nicht gilt. Und von den neuen Operationen wurde zurückgeschlossen auf die Axiomatik der Zahlenmenge und diese um Axiome erweitert, unter denen die neuen Operationen zulässig sind.
In ihrer fertigen Gestalt besteht das axiomatische System aus den Definitionen, die die Zahlenmenge oder Punktmenge bestimmen, den Axiomen, die deren grundlegende Eigenschaften festhalten, und den Operationen, wie in der Menge konstruiert werden kann. Bisher hat sich immer erwiesen, dass zwischen den Definitionen und Axiomen einerseits und den Operationen andererseits ein Spannungsverhältnis besteht. Sei es, dass unklar ist, welche Operationen überhaupt möglich sind (z.B. in der euklidischen Geometrie die Frage, ob der Kreis quadriert werden kann), sei es, dass wie beim Ableiten die Operationen den Rahmen der Axiome sprengen.
2.2. Dialektische Methode
Gewissermaßen stehen wir schon mittendrin in der dialektischen Methode, indem so etwas wie die Dialektik der Axiomatik aufgezeigt wurde. Die axiomatische Methode springt immer wieder über ihre Grenzen, und wenn neue Axiome gesucht werden, kann diese Suche selbst nicht mehr als axiomatisch bezeichnet werden. Aber im Resultat führt das wieder zu neuer Axiomatik, und die axiomatische Methode lässt sich nicht wie von Hegel gewünscht in der dialektischen Methode aufheben. Das ist zu begründen.
Die Kritik der axiomatischen Methode fällt Hegel leicht. Die Axiome stehen ohne erkennbaren inneren Zusammenhang nebeneinander, sie sind nicht aus dem Begriff der Sache hergeleitet (z.B. dem Begriff der Zahlen oder dem Begriff des Raumes), einen solchen Begriff scheint sie gar nicht zu kennen. Den Lehrsätzen bescheinigt Hegel zwar synthetischen Charakter, d.h. sie führen zu echt neuen Resultaten gegenüber den Axiomen und Definitionen, aber auch sie sind nicht aus dem Begriff der Sache entwickelt, sondern ergeben sich aus einem mechanisch anmutenden Operieren mit den Axiomen. Angesichts des Dogmatismus der Hochschulwissenschaft hat seine Kritik einiges für sich. Da gelten die Axiome als Grundgesetz des Staatsgebäudes der Wissenschaften, und wer sie anzweifelt als dumm oder als Scharlatan. Jeder Bezug zur Wirklichkeit und zur praktischen Arbeit wird triumphierend verstellt, die autonome und freie Wissenschaft begnügt sich im Umkreis ihrer Axiome mit sich selbst.
In Wahrheit sind die Axiome in aller Regel Lehrsätze aus der Philosophie (meistens aus der Logik), bemerkt Hegel. Der Differentialkalkül führte zum Vollständigkeitsaxiom: Wenn ein Grenzprozeß durchgeführt wird, existiert der Grenzwert, die Zahlen sind insofern vollständig. Mit der Entwicklung des Differentialkalkül wurde dies Axiom neu aufgestellt. In dieser Form wurde es natürlich nirgends vorgefunden, auch nicht in der Philosophie. Aber es gab in der Philosophie eine lange Debatte seit Aristoteles über das Kontinuum und verschiedene Unendlichkeitsbegriffe. In den physikalischen Experimenten und Beobachtungen wurde der Begriff der stetigen Bewegung gefunden. Dies alles ermöglichte es den Mathematikern, für den Differentialkalkül ein geeignetes Axiom zu finden. Einer der einflußreichsten Axiomatiker, Cantor, bezog sich ausdrücklich auf die scholastische Auseinandersetzung über den Unendlichkeitsbegriff. Leibniz und Newton stellten den Differentialkalkül in den Kontext naturphilosophischer Betrachtungen. Dass Axiome auf Lehrsätze in der Philosophie zurückgehen, kann gar nicht als Mangel angesehen werden. Sofern die axiomatische Wissenschaft nicht in den toten Buchstaben des Dogmatismus erstarrt, lebt sie von der Spannung zwischen den wissenschaftlichen Operationen und den Axiomen. Sie drängt zu ständig neuen Axiomen. Da ergibt sich aus dem Gang der Naturwissenschaft selbst die Notwendigkeit der Klärung ihrer philosophischen Grundlagen.
Der dialektischen Methode geht es im Grunde nicht anders, wenn auch in umgekehrter Richtung. Als Beispiel diene, wie Hegel den Differentialkalkül interpretiert. Er hat ein philosophisch motiviertes Interesse an dieser Frage, um die "Vexierfrage" seiner Logik zu lösen (Hegel, Logik Bd. 1, 169), wie Unendliches in Endliches; Quantitatives in Qualitatives umschlägt. Die Lösung findet er nicht in der Philosophie - vielmehr will er in dieser Frage die Philosophie ein gut Stück weiterbringen -, sondern im Differentialkalkül. Die Suche nach der Ableitung führt dazu, die Steigung der Tangente zu finden, und die wird ausgedrückt durch das Größenverhältnis y/x der Seiten im Steigungsdreieck. Ist dies bestimmte Größenverhältnis gefunden, kommt es zum Grenzübergang, der eine neue Qualität bringt. Im Grenzprozeß werden y und x durch die neuen Symbole dy und dx ersetzt.
"dx, dy sind keine Quanta mehr, noch sollen sie solche bedeuten, sondern haben allein in ihrer Beziehung eine Bedeutung, einen Sinn bloß als Momente. Sie sind nicht mehr Etwas, das Etwas als Quantum genommen, nicht endliche Differenzen; aber auch nicht Nichts, nicht die bestimmungslose Null. Außer ihrem Verhältnisse sind sie reine Nullen, aber sie sollen nur als Momente des Verhältnisses, als Bestimmungen des Differentialkoeffizienten dx/dy genommen werden. In diesem Begriff des Unendlichen ist das Quantum wahrhaft zu einem qualitativen Dasein vollendet; es ist als wirklich unendlich gesetzt; es ist nicht nur als dieses oder jenes Quantum aufgehoben, sondern als Quantum überhaupt." (Hegel, Logik Bd. 1, S. 295f)
Sichtlich vollzieht Hegel die Operation des Differentialkalkül nach: Er versucht, sie in der Sprache der Philosophie darzustellen. Er kann sie keineswegs ersetzen, seine Philosophie liefert keine Ableitungen und entwickelt auch den Differentialkalkül nicht weiter (wie es sein Zeitgenosse, der Mathematiker Cauchy tat). Aber dafür gelingt ihm genau das, was in der Mathematik nicht gelingt: Die Bewußtwerdung über den inneren Zusammenhang der verschiedenen benutzten Begriffe, der verschiedenen Operationen und ihrer Resultate. Wie Kant von der Philosophie verlangt, wirkt er orientierend, das Ergebnis ist die Idee einer Mathematik der Natur.
Die Philosophie kann nur von dem Material ausgehen, dass ihr von den Naturwissenschaften gegeben wird. Sie kann es interpretieren. Wenn es ihr gelingt, dadurch neue Zusammenhänge aufzuklären, für die Wissenschaft neue Horizonte zu öffnen, drängt sie danach, dass dies zum Programm wird und ausgeführt wird. Sie selbst kann das nicht. So wie sie der Axiomatik deren Begrifflosigkeit vorwirft, muß sie sich sagen lassen: Die Philosophen haben die Welt nur interpretiert, es kommt darauf an, sie zu verändern.
Ähnlich wie Ästhetik und Teleologie erhält die Dialektik eine orientierende Aufgabe, wobei diese verschiedenen Herangehensweisen an die Natur nicht aufeinander zurückgeführt werden können, das Ergebnis wäre Dogmatismus. Kant hatte richtig gesehen, dass die Philosophie die Methoden der Mathematik nicht nachahmen kann. Die charakteristische Leistung der Dialektik wird von Hegel darin gesehen, im Erkenntnisgegenstand eine innere Differenzierung aufzuspüren, den typischen inneren Widerspruch zu bestimmen. Aber nicht als starre Paradoxie wie bei den vorsokratischen Griechen, sondern als Bewegungsquell. Der Widerspruch treibt zur Aufhebung, zum qualitativen Sprung. Auf diese Weise wirkt die Dialektik analytisch, wo sie den Gegenstand differenziert, und synthetisch, wo sie im Prozeß der Aufhebung seine Beziehung zu anderen Qualitäten erkennt.
Wie in der Teleologie führt es zu nichts, die Interpretation als unmittelbare Natureigenschaft auszugeben, also zu sagen, die Natur ist dialektisch. Das führt zum Kurzschluß, dass jede einmal gewonnene Erkenntnis die Weihe erhält, die Natur ist so und nicht anders, und daher nicht weiter entwickelt werden kann. Dann blockiert die Methode mit ihren ersten Erkenntnissen die weitere Orientierung. In Nachfolge von Hegel und Engels ist dies dem dialektischen Materialismus zugestoßen. Plötzlich stand er jeder neuen naturwissenschaftlichen Erkenntnis (wie der Relativitätstheorie, Quantentheorie, Kybernetik) mißtrauisch gegenüber, sie paßte nicht ins System. Irgendwann wurden ihre Lehrbücher genau so langweilig und öde wie die der bekämpften bürgerlichen Wissenschaft. Das fatale Ergebnis war, dass die dialektische Methode ihre orientierende Kraft nicht entfalten konnte, was dazu beitrug, dass die Grundlagenkrise der Naturwissenschaften in diesem Jahrhundert im Pragmatismus endete.
2.3. Mathematik der Natur
Schon Hegel hat mit seiner Naturphilosophie kräftig zu dieser Fehlentwicklung beigetragen. Aber in der "Wissenschaft der Logik" findet sich mit der Idee einer Mathematik der Natur ein Beweis für die orientierenden Fähigkeiten der Philosophie.
Wenn Quantität in Qualität umschlägt, wird positiv ein Maß definiert. Mit der Ableitung wird ein Maß der Bewegung gefunden. Physikalisch wird es als Geschwindigkeit und Impuls, bei zweifacher Ableitung als Beschleunigung und Kraft, beim Integrieren des Impulses über die Zeit als Energie definiert. Wo die Mathematik selbst nur um ein Unendlichkeitsaxiom bereichert wurde, erkennt Hegel, dass der Mathematik mit ihrer Fähigkeit, Maße zu finden, völlig neue Welten offen stehen.
"In Rücksicht auf die absoluten Maßverhältnisse darf wohl erinnert werden, daß die Mathematik der Natur, wenn sie des Namens von Wissenschaft würdig sein will, wesentlich die Wissenschaft der Maße sein müsse – eine Wissenschaft, für welche empirisch wohl viel, aber eigentlich wissenschaftlich, d. i. philosophisch noch wenig getan ist. Mathematische Prinzipien der Naturphilosophie – wie Newton sein Werk genannt hat –, wenn sie diese Bestimmung in einem tieferen Sinn erfüllen sollten, als er und das ganze Baconsche Geschlecht von Philosophie und Wissenschaft hatte, müßten ganz andere Dinge enthalten, um ein Licht In diese noch dunklen, aber höchst betrachtungswürdigen Regionen zu bringen. – Es ist ein großes Verdienst, die empirischen Zahlen der Natur kennenzulernen, z.B. Entfernungen der Planeten voneinander, aber ein unendlich größeres, die empirischen Quanta verschwinden zu machen und sie in eine allgemeine Form von Quantitätsbestimmungen zu erheben, so daß sie Momente eines Gesetzes oder Maßes werden; – unsterbliche Verdienste, die sich z.B. Galilei in Rücksicht auf den Fall und Kepler in Rücksicht auf die Bewegung der himmlischen Körper erworben hat. Sie haben die Gesetze, die sie gefunden haben, so erwiesen, daß sie gezeigt haben, daß ihnen der Umfang der Einzelheiten der Wahrnehmung entspricht. Es muß aber noch ein höheres Beweisen dieser Gesetze gefordert werden, nämlich nichts anderes, als daß ihre Quantitätsbestimmungen aus den Qualitäten oder bestimmten Begriffen, die bezogen sind (wie Zeit und Raum), erkannt werden." (Hegel, Logik Bd. 1, S. 406f)
Unverkennbar ist der Gedankengang angelehnt an die Darstellung des Differentialkalkül. (a) Zuerst wurden die Steigungen einzelner Tangenten gemessen (mit geometrischen Methoden), das entspricht der Beobachtung einzelner empirischer Zahlen etwa durch astronomische Messungen. (b) Dann wurden Formeln für die Ableitung bestimmter Funktionen gefunden (mit arithmetischen Methoden, die zur vorläufig Abgeleiteten führten), was etwa den Keplerschen Gesetzen der Planetenbewegung entspricht. (c) Schließlich wurden Grenzprozeß und Differentialkalkül eingeführt, und dies erweitert Hegel zum Programm einer Mathematik der Natur. Nach Kenntnis der weiteren naturwissenschaftlichen Forschungen ist es genauer zu fassen.
Seit den Arbeiten von Poincaré werden die Keplerschen Gesetze in der Himmelsmechanik erklärt aus qualitativen Eigenschaften des mechanischen Bewegungsraums. Wenn ein Raum die Eigenschaft hat, dass in ihm die kürzesten Verbindungslinien Geraden sind, ist das gleichbedeutend damit, dass dieser Raum weder wächst noch schrumpft. Unter dieser Bedingung wirkt die Gravitation in der Weise, dass die Keplerschen Gesetze erfüllt sind. Hat der Raum andere qualitative Eigenschaften, nehmen auch die Bewegungsgesetze der Körper eine andere Gestalt an.
Die Quantenmechanik ist eher in einem Übergangsstadium. Eine Unmasse empirischer Daten und eine ganze Reihe von Gesetzmäßigkeiten liegen vor, aber ein unumstrittenes qualitatives Naturverständnis liegt noch nicht vor. Die Eigenschaften des Raumes werden untersucht, in dem die Quantenmechanik gilt. Das ist Gegenstand der Quantenfeld- und Gittereichtheorien. Die Quarktheorie ist eine mögliche Lösung.
Auch die Katastrophentheorie geht diesen Weg. Anfangs gab es zahlreiche empirische Beobachtungen von Turbulenzen, Unregelmäßigkeiten, chaotischen Situationen. Erst sehr spät gelang es überhaupt, in diesem Gewirr Gesetzmäßigkeiten zu entdecken. Seit den 1950er Jahren (und verstärkt seit den Arbeiten von Thom) wird daran geforscht, die Räume zu qualifizieren, in denen sich Katastrophen ereignen, das sind gefaltete Räume, gebrochene Räume, Räume mit Singularitäten (Punkte, in denen das Vollständigkeitsaxiom verletzt wird: wird ein Singularitätspunkt in einem Grenzprozeß angenähert, gerät der Grenzprozeß in einen Strudel und stürzt in einem Raum mit qualitativ anderen Eigenschaften).
Kant hatte die reine Zeit und den reinen Raum als den Berührungspunkt zwischen der qualitativen Naturwissenschaft und der quantitativen Mathematik bestimmt. Ist der Raum gefüllt, geht das Konzept so nicht mehr auf. Nach der Orientierung von Hegel sind es die Maßverhältnisse, wo Naturwissenschaft und Mathematik zusammenkommen. In der Naturwissenschaft können die Maße gefunden werden (wie die Lichtgeschwindigkeit als Grenzgeschwindigkeit, das Plancksche Wirkungsquantum, die Größenordnung der Moleküle, wo mechanische in chemische Bewegung umschlägt usw.). Jedes dieser Maße ist eine Herausforderung der Mathematik, den Umkreis zu bestimmen, wo das Maß wirksam ist und wie damit gerechnet werden kann. Diese Orientierung steht eher in der phytagoreeischen Tradition, die die Zahlenverhältnisse suchten, welche Harmonie ausdrücken.
Literaturhinweise
1982 - 1984
© tydecks.info 2002