Walter Tydecks
Nicht-homogene Koordinatensystem
Inhaltsverzeichnis
Kugelpackungen
Parkette
Vierfarbenproblem
Bewegungen und Grenzübergänge
Wie geht es nun weiter? Die Polarisation führt gegenwärtig in der Teilchenphysik bis zur Supersymmetrie, in der kommutative und anti-kommutative Symmetrien verknüpft werden, um für alle bekannten physikalischen Kräfte von der Gravitation bis zur Quantenchromodynamik (Wechselwirkung zwischen den Quarkteilchen) einen einheitlichen Ansatz zu finden. Eine Lösungsmöglichkeit könnte ein neuer Differentialkalkül auf Basis der äußeren Algebra sein, die ebenfalls mathematisch in allgemeinster Form kommutative und anti-kommutative Elemente enthält. In der Diplomarbeit habe ich gezeigt, dass ein solcher Kalkül ähnlich entworfen und ausgearbeitet werden kann, wie es mit der Funktionentheorie als Differentialkalkül auf Basis der Algebra der komplexen Zahlen gelungen ist, und Querbeziehungen zu allgemeinen Systemen partieller Differentialgleichungen (Pfaffschen Systemen) existieren.
Bei dem Versuch, Gravitation und Quantentheorien zusammenzuführen, kommt es allerdings zu einem grundsätzlichen Problem, das die Frage nach den qualitativen Eigenschaften des Raums neu aufwirft. Die Gravitation wird bis heute durch die Allgemeine Relativitätstheorie von Einstein beschrieben. Gegenüber der Allgemeinen Relativitätstheorie sind die verschiedenen Quantentheorien jedoch insofern klassisch, als sie physikalisches Geschehen innerhalb von Raum und Zeit darstellen. Wie die klassische Mechanik gehen sie von der Vorstellung aus, dass die Grundelemente und die Feldquanten (z.B. Elektron, Quarkteilchen, Photon, Gluonen) kleine Partikel sind, die frei durch den Raum fliegen und nur beim Zusammenstoß in direkte Wechselwirkung treten. Anders als in der klassischen Mechanik können sie sich dann aber beim Zusammenprall ineinander umwandeln und nicht nur Energie (bzw. Impuls) übertragen. (Die "Welleneigenschaft" ist keine "körperliche" Eigenschaft dieser Teilchen, sondern beschreibt die Wahrscheinlichkeitsverteilung, in welche Zustände die Feldquanten wechseln können.)
Eine Frage aber blieb offen: Was geschieht in dem Moment, wo sich zwei Teilchen im Zusammenstoß ineinander umwandeln? Im einfachsten Fall kann z.B. das Elektron durch Aufnahme eines Photons seine Energie vergrößern und auf eine andere Umlaufbahn um den Atomkern springen. Aber welchen Weg nimmt der Sprung? Anschaulich wird vermutet, dass die verschiedenen möglichen Bahnen wie Zwiebelschalen um den Atomkern liegen. Wenn das Elektron Energie in Gestalt eines Photons aufnimmt, springt es in eine Schale, die vom Atomkern weiter entfernt ist, bis es sich schließlich ganz vom Atomkern lösen kann. Wie lange dauert es aber, wenn ein Elektron ein Photon aufnimmt bzw. abgibt? Wieviel Zeit hat es für den Sprung? Die heute formulierten Naturgesetze schließen einen kontinuierlichen Prozeß aus. Die Energieveränderung und der zugehörige Sprung zwischen den Bahnen können in keiner zeitlichen Entwicklung dargestellt werden. Es gibt keinen Weg und keinen Zeitraum für die Änderung. Das Elektron kann das Photon nicht aufnehmen wie eine Schlange, die ihr Opfer schnappt und dann herunterschlingt. So wie eine mathematische Addition keine Zeit kennt, werden hier zwei physikalische Größen addiert und die Summe ist dann sofort "da".
Für diesen Moment legt die Quantentheorie daher nahe, die Vorstellung des homogenen mathematischen Raums aufzugeben, der sich unendlich weiter teilen lässt. Auf der untersten Ebene gibt es Quanten mit festen Energiewerten, und diese können bei den Wechselwirkungen nicht weiter in zeitliche und räumliche Prozesse geteilt werden. Nach allem Bisherigen ist jedoch stark zu vermuten, dass wiederum nur eine Zwischenstufe erreicht ist. So wie für die mechanischen Gesetze ganzer Körper die Bewegungen der einzelnen Atome im Körper vernachlässigbar klein sind, wird es hier ähnlich sein: Innerhalb des Elektrons, des Photons usw. wird es wiederum eine Binnenstruktur geben, die für die Bewegung des Elektrons vernachlässigbar klein ist. Der Sprung des Elektrons ist nicht unendlich-schnell, sondern er wird durch innere Prozesse gesteuert, die bisher unbekannt sind und für die Beschreibung des Elektrons im Ganzen vernachlässigbar klein bleiben.
Das macht noch deutlicher, auf welche Weise die Quantentheorie ähnlich wie die klassische Mechanik Naturprozesse beschreibt, die im mathematischen Raum abgebildet werden können. Der mathematische Raum wird als leerer Raum vorausgesetzt und er wird dann mit den Teilchen der Quantentheorien gefüllt. Diese Teilchen bewegen sich im Raum. Es gibt aber keinerlei Wechselwirkung zwischen der Bewegung dieser Teilchen und dem mathematischen Raum, in dem sie beschrieben werden. Die Teilchen können den mathematischen Raum nicht ändern. Unterhalb eines charakteristischen Längenmaßes bleibt für sie alles vernachlässigbar klein. Die Mathematik hat zunächst nur die Aufgabe, in ihren Rechnungen die Existenz eines solchen Längenmaßes zu berücksichtigen und nimmt es als Symbol des Unendlich-Kleinen wahr. Während für die Physik entscheidend ist, welche wirkliche Größe das Längenmaß hat (welchen Zahlenwert), wird diese Größe in der Vorstellung des mathematischen Symbols negiert. Es ist als Symbol des Unendlich-Kleinen so abstrakt definiert, dass es keinen bestimmten Zahlenwert annehmen kann (siehe hierzu die oben bereits erläuterte negative Definition der Unendlichkeit).
Genau das ändert sich mit der Allgemeinen Relativitätstheorie, so wie sie von Einstein entworfen wurde. Hier wird ganz bewußt versucht, physikalische und geometrische Eigenschaften zu identifizieren. Ihr Ausgangspunkt ist die Äquivalenz zwischen Schwerefeld und Beschleunigung. Ist eine Schwerkraft zu spüren (oder experimentell meßbar), kann diese ihre Ursache sowohl in der Anziehung durch eine andere Masse haben, als auch in der Beschleunigung des messenden Systems. Wer schnell im Auto startet, wird in den Sitz gedrückt, und es wirkt genau so, wie die Schwerkraft der Erde alles zu Boden zieht. Um eine allgemeine Lösung zu finden, stellte Einstein die Allgemeine Relativitätstheorie koordinateninvariant auf mit der Konsequenz, dass hier eine physikalische Eigenschaft (die Schwerkraft) aus einer geometrischen Eigenschaft der Raumzeit (ihrer Krümmung) erklärt werden soll.
Einstein kehrte den ursprünglichen Ansatz von Newton genau um, der zur Einführung der Infinetisimalrechnung geführt hatte. Während da mechanische Bewegungen aus der Physik in der Mathematik dargestellt worden waren und ihre Beschleunigung mathematisch als Krümmung (das ist die zweite Ableitung der Bewegungsfunktion) interpretiert worden war, will er nun umgekehrt die Schwerkraft in der Physik daraus erklären, dass der mathematische Raum, in dem alle Bewegungen dargestellt werden, selbst gekrümmt ist.
Mit dieser Umkehrung kehrt er zu der griechischen Vorstellung zurück, dass der mathematische und der natürliche Raum unmittelbar identisch sind. Denn er will ja aus den Eigenschaften des mathematischen Raums eine physikalische Eigenschaft direkt ableiten. Dies Vorgehen erscheint fraglich. In den Schwierigkeiten, die Gravitation als Quantentheorie zu deuten, treten die Widersprüche der Allgemeinen Relativitätstheorie offen zutage. Wirklich nachgewiesen ist genau gesehen nur so viel: Wenn der mathematische Raum gekrümmt ist, wirkt sich die Krümmung wie eine eigene zusätzliche Kraft auf alle Bewegungen aus, die im mathematischen Raum dargestellt werden. Und es ist denkbar, die in der Natur wirkende Schwerkraft auf diese Weise als eine Krümmung des mathematischen Raums zu beschreiben.
Worin krümmt sich aber der mathematische Raum? (Wenn z.B. ein zweidimensionales Blatt Papier gekrümmt wird, wölbt es sich in die dritte Dimension des Raumes.) Entweder muß der Raum um weitere "innere" Dimensionen ergänzt werden, die zusätzliche Eigenschaften darstellen können. Oder die Krümmung führt zu einer weiteren Dimension, in die sich der Raum hineinkrümmt. Der größere Raum wird als Kaluza-Klein-Raum bezeichnet und führt in der Mathematik zu den Faserbündeln. Dieser Ansatz wurde von Einstein favorisiert, auch wenn es ihm nicht gelang, auf diesem Weg zu einer befriedigenden Lösung zu gelangen.
In den letzten Jahrzehnten wurde stärker in die andere Richtung geforscht, dem Raum zusätzliche innere Dimensionen zu verleihen. Hier wird angenommen, dass der mathematische Raum unterhalb einer sehr kleinen Distanz seine Homogenität verliert. Der Raum im Kleinen wird porös oder schäumig, oder er setzt sich aus Strings oder Twistoren zusammen. Ähnlich wie in der Allgemeinen Relativitätstheorie von Einstein wird danach gesucht, im mathematischen Raum eine Eigenschaft zu konstruieren, die dann die physikalische Eigenschaft der Schwerkraft erklären soll.
Der naheliegendste Ausweg ist, die Frage der Schwerkraft so in Angriff zu nehmen wie die offenen Fragen der Bewegung des Elektrons. Es muß vergleichbar den Elektronen Grundelemente in der Natur geben, die diese Kraft tragen. Sie werden naheliegenderweise als Gravitonen bezeichnet. Die spannende Frage ist nun, von welchen Kraftquellen in der Natur die Schwerkraft erzeugt wird, die so gleichmäßíg wie eine Raumkrümmung wahrgenommen wird. Können diese Kraftquellen sich ändern und mit ihnen die "Raumkrümmung"? Das würde alle heute gängigen Theorien über die Struktur und die Entstehung des Weltalls infrage stellen.
Mit seiner Identifizierung des physikalischen und mathematischen Raums hat Einstein diese Fragen geschickt umgangen. Seine Aussage ist eigentlich: Die Kraftquellen des Schwerefeldes und ihre Veränderungen sind für die menschliche Erkenntnis unendlich-groß, sie gelten im Sinne von Kant a priori für den Raum an sich, so dass sie wiederum vernachlässigt werden können. Das klingt paradox. Aber damit ist gemeint, dass ihr Wirken als "Ansatz" in die Krümmung des Raums der Mathematik aufgenommen wird. Sie können nicht ihrerseits wiederum aus einer tieferen Naturerkenntnis erklärt werden und stellen daher wirklich ganz im Sinne der griechischen Mathematik ein neues Axiomensystem dar. Wenn der mathematische Raum, in dem alle Bewegungen dargestellt werden soll, selbst schon gekrümmt ist, gewinnt diese Krümmung die Bedeutung einer unveränderlichen Größe. Diese "Unveränderlichkeit" bedeutet aber eben nichts anderes als die präzisere Aussage: Entweder können ihre Veränderungen vernachlässigt werden, oder sie werden so groß, dass alle anderen physikalischen Gesetze ihnen gegenüber verschwinden. Das ist der Fall, wenn die Raumkrümmung ein bestimmtes Maß überschreitet und die Gravitation kollabiert (Schwarze Löcher). Diese Möglichkeit ergibt sich zwangsläufig , wenn der mathematische Raum als Träger einer bestimmten physikalischen Kraft konstruiert wird.
In gewisser Hinsicht hat Einstein sicher recht: Es wird sich nie vermeiden lassen, eine gewisse Krümmung des mathematischen Raums zu unterstellen. Diese Krümmung wird immer den Rest ausdrücken, wo die naturwissenschaftliche Erkenntnis an ihre Grenze stößt. Denn wie kann die Erkenntnis der aktuell bekannten Raumkrümmung weitergehen? Vielleicht gelingt es, die theoretisch postulierten Gravitonen nachzuweisen und ihre Bewegungsgesetze zu erkennen. Vielleicht hat der Ansatz der Supersymmetrien Erfolg und wird die heute bekannten Quantentheorien erweitern. Damit wäre die Erkenntnis wiederum einen Schritt weiter.
Aber prinzipiell wird sich nicht vermeiden lassen, dass die Naturerkenntnis an zwei Enden immer auf Unbestimmtheiten oder Uneindeutigkeiten stößt: Zum einen im Kleinen, wo die inneren Bewegungsgesetze der kleinsten, bekannten Teilchen noch unbekannt sind. Diese Situation ist heute bei der Frage der Bewegung der Elektronen gegeben. Zum anderen im Großen, wo sich im Grunde die gleiche Frage bei den Kräften stellt, die in den längsten Zeiträumen wirken. Denn was würde geschehen, wenn das Graviton entdeckt und beschrieben sein sollte: Dann wird sich wieder die Frage stellen, welche Kräfte es sind, die seine Bewegung steuern.
Einsteins Idee der Raumkrümmung war übernommen von den mathematischen Erkenntnissen der Krümmung, die den Bewegungsgesetzen der Geometrie zugrunde liegen. Während jedoch die Mathematik der Einsicht nahe kam, die griechische Vorstellung von der Identifizierung von natürlichem und mathematischem Raum ganz aufzugeben, suchte Einstein nach einer Erklärung, mit welcher physikalischen Eigenschaft diese neu gefundene mathematische Eigenschaft der Raumkrümmung korrespondiert.
Mindestens können aus der Allgemeinen Relativitätstheorie zwei Lehren gezogen werden:
Der ideale mathematische Raum muß durch eine Raumkrümmung gebrochen werden, die ein Maß für die noch unbekannten Naturkräfte ist. Nur diese unbekannten Kräfte gelten mathematisch koordinaten-invariant.
Jede bekannte Naturkraft wirkt nur bis zu einem bestimmten Längenmaß, und "ihr Raum" ist daher grundsätzlich nicht-homogen. Aufgabe der Mathematik kann es aber sein, die qualitativen Eigenschaften der jeweiligen Nicht-Homogenität zu beschreiben. Dies ist der Ansatz für die im folgenden anzudeutenden möglichen weiteren Entwicklungsrichtungen der anschaulichen Geometrie.
Erstens. Der mathematische Raum ist ein idealer Raum, der zunächst absolut flach ist. Wenn in ihm physikalisches Geschehen dargestellt werden soll, muß der ideale Zustand gebrochen und eine Raumkrümmung konstruiert werden. Diese Raumkrümmung ist keineswegs symbolisch, sondern sie muß ganz bestimmte Zahlenwerte annehmen, wobei die Krümmung das Maß der noch unbekannnten, weitreichenden Kräfte ist. Diese Zahlenwerte können nicht mathematisch gefolgert oder philosophisch abgeleitet werden, sondern sie müssen aus der empirischen Beobachtung kommen. Mit jeder neuen Erkenntnis wird der Bruch des idealen flachen mathematischen Raums ein Stück weniger. Wenn z.B. die durch das Schwerefeld auftretenden Wechselwirkungen quantentheoretisch dargestellt werden können, entsteht unter Einbeziehung der Gravitation eine neue Symmetriegruppe, die im mathematischen Raum dargestellt werden kann. Das Schwerefeld würde dann nicht mehr aus der Krümmung des mathematischen Raums erklärt, wie von Einstein unterstellt, sondern mit der neuen Symmetriegruppe beschrieben. Der "verbleibende" mathematische Raum als Träger der Symmetriegruppe würde dadurch wesentlich flacher, da auch die Gravitation als die Wirkung von Teilchen innerhalb dieses Raums beschrieben werden kann.
Aber auch dieser Raum wäre nicht absolut flach, da das Schwerefeld keineswegs die letzte weitreichende Kraft sein wird. Der absolut flache Raum ist das unerreichbare Ideal, in dem alles erklärt und beschrieben werden kann. Die griechische Mathematik mit ihrer Identifizierung von natürlichem und mathematischen Raum hat also genau dann "recht", wenn dieser Idealzustand hergestellt wäre und keine Brechung des Raums durch eine Krümmung notwendig wird.
Und weiter ist von Einstein zu lernen: Nur für die Raumkrümmung und der mit ihr korrespondierenden noch unbekannten Naturkraft kann die Koordinateninvarianz gelten. Die grundsätzliche Erkenntnis der Allgemeinen Relativitätstheorie gewinnt dann eine ganz andere qualitative Bedeutung, wenn sie nicht mehr konkret auf die Schwerkraft bezogen wird, sondern auf "die verbleibende Unbekannte". Koordinateninvarianz ist die mathematische Beschreibung für die Offenheit des Universums.
Die jeweils bekannten Naturgesetze gelten grundsätzlich nur in einem nicht-homogenen Raum. Lediglich die Mechanik unterstellte die Existenz eines homogenen Raums, solange die Physiker noch der Meinung waren, es wäre möglich, die Partikel als Träger der Mechanik unbegrenzt zu teilen. Inzwischen ist jedoch klar, dass bei immer weiterer Teilung schließlich die molekulare Ebene erreicht wird, wo die chemischen Gesetze dominieren, und dann die atomare Ebene und so weiter.
Der homogene mathematische Raum hat seine Bedeutung daher im wesentlichen nur für die Grenzphänomene, sei es die Raumkrümmung oder der Grenzübergang. Immer erfolgversprechender wird inzwischen aber die Untersuchung der qualitativen Eigenschaften von nicht-homogenen Räumen, die mit nicht-homogenen Koordinatensystemen zu beschreiben sind.
Zweitens. Wenn jede wirkliche Naturkraft ab einer bestimmten Stufe nicht-homogen ist, gewinnt die Untersuchung nicht-homogener Räume besonderes Interesse. Die oben gestellte Frage wird dann umgekehrt: Wenn es nicht möglich ist, den Weg und den Prozeß zu beschreiben, wie ein Elektron "springt" und nur beschrieben werden kann, welche Gesetzmäßigkeiten beim Sprung gewahrt bleiben müssen, führt das zu einer Frage an einen nicht-homogenen Raum.
Der nicht-homogene Raum ist aus kleinen Bausteinen aufgebaut, deren Inneres unbekannt ist. Aber es wird angenommen: Was an den Grenzen geschieht, bestimmt das Innere. Mit diesem Ansatz konnten erfolgreich die Bewegungsgesetze der Elektrodynamik formuliert werden, als Gesetzmäßigkeiten gefunden wurden, wie die kleinsten Bausteine in einer Strömung rotieren bzw. wie intensiv der Stromfluß durch sie hindurchgeht (Rotation und Divergenz). Maxwell stellte sich ganz anschaulich vor, dass das elektrische Feld aus kleinen Rollen besteht, die sich bewegen.
Von der Mathematik wurde diese Anschauung in verschiedener Hinsicht verallgemeinert. Die Theorie elektromagnetischer Felder führte schließlich zur Polarisation, wodurch die kleinsten Bausteine der Natur als Oszillatoren gedeutet werden. Und der Ansatz, das Innere durch seine Grenzen zu beschreiben, wurde in der topologischen Beweisidee aufgegriffen, ein kompliziertes System durch ein einfacheres, endliches System zu überdecken, wodurch innere Eigenschaften beschrieben werden können wie das Maß an Kompaktheit (materieller Dichte) oder eine fraktale Dimension (um z. B. zu klären, wie die Grenzlinie einer Insel, einer Galaxis, einer festeren Flüssigkeit in einer weniger festen Flüssigkeit ausfranst).
Diese Fragen können noch keineswegs wirklich klassifiziert werden. Vielleicht wird aber klarer, wie die drohende Sackgasse verlassen werden kann, in die die Polarisation mit der Teilchenphysik zu geraten droht. Durch die Abgrenzung gegen die koordinaten-invarianten Raumeigenschaften wird ihr systematischer Stellenwert innerhalb des mathematischen Raums deutlicher und es sollte klar werden, von welchen übertriebenen Fragen (Weltformeln, Theorien über Alles) die Polarisation sich zu befreien hat. - Und mit der Entwicklung neuer geometrischer Ansätze könnte ein Weg gefunden werden, neue innere Beziehungen zwischen den jeweiligen Grundelementen zu finden.
Hierzu kann zunächst nur etwas Material zusammengestellt werden. Und der beste Einstiegspunkt ist die letzte Arbeit von Hilbert. Nach den weniger erfolgreichen Versuchen mit der Metamathematik erschien 1932 die "Anschauliche Geometrie", redigiert von Cohn-Vossen. Im Kern geht es genau um die Suche nach Koordinatensystemen in nicht-homogenen Räumen, und es wird sich zeigen, dass sie in letzter Konsequenz den Aufbau der Mathematik auf Basis der reellen Zahlen infrage stellen.
Kugelpackungen
Das übliche (kartesische) Koordinatensystem unterteilt die Gerade in gleichmäßige Abschnitte, die Ebene in gleichmäßige Quadrate, den Raum in gleichmäßige Würfel. Gerade, Ebene und Raum (und verallgemeinert höherdimensionale Räume) sind dadurch restlos strukturiert. Die Achsen stehen jeweils senkrecht aufeinander. Andere Koordinatensysteme (Zerlegung der Ebene in Dreiecke, des Raums in Pyramiden oder Tetraeder, sphärische und elliptische Koordinaten etc.) lassen sich eindeutig auf das kartesische Koordinatensystem beziehen, ermöglichen jedoch in speziellen Fällen einfacheres Rechnen.
Auch bei Kugelpackungen sollen alle Bausteine untereinander gleich sein und sich in gleichmäßiger Anordnung über den gesamten Raum erstrecken. Sie können aber nie den Raum restlos füllen. Es gilt nur die Bedingung, dass jede Kugel mindestens zwei Nachbarkugeln berührt (also Grenzen ausgeschlossen sind).
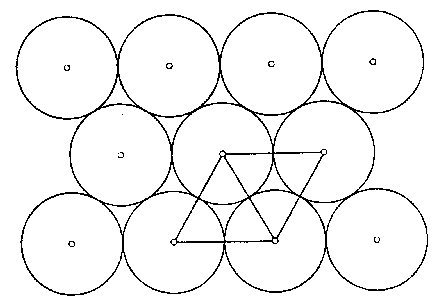
Figur 1 Ebene Kugelpackung
Freihandzeichnung
Einige qualitative Eigenschaften lassen sich für ebene Kugelpackungen, in denen alle Kugeln gleich groß sind, sofort ablesen:
In der dichtesten Kugelpackung hat jede Kugel 6 Nachbarn. Es ist unmöglich, eine Kugelpackung zu finden, in der jede Kugel mehr als 6 Nachbarn hat.
Wenn von der dichtesten Kugelpackung ausgegangen wird, ist es nicht möglich, innerhalb jeder Kugel Unterkugeln so zu konstruieren, so dass weiter jede Kugel 6 Nachbarn hat. Es gibt nur die Möglichkeiten, Unterkugeln so anzulegen, dass jede Kugel 3 oder 2 Nachbarn hat. Die dichteste Kugelpackung kann nicht selbstähnlich nach innen fortgeführt werden.
Wenn eine Kugelpackung gefunden ist, wo jede Kugel 3 Nachbarn hat, können dann aber immer weiter Unterkugeln konstruiert werden, die wiederum jeweils 3 Nachbarn haben. Diese Möglichkeit der Konstruktion nach innen gibt es auch bei Kugelpackungen mit je 4 Nachbarn. Sie erinnern an das kartesische Koordinatensystem. In diesen Fällen gelingt eine selbstähnliche Bauweise und die Kugelpackung kann nach innen und außen homogen erweitert werden.
Der Übergang zu einer Packung, wo jede Kugel 2 Nachbarn hat, ist immer möglich. Es entsteht dann eine sequentielle Abfolge, die in nebeneinander liegenden Linien die Fläche füllt.
Zwischen Kugelsystemen mit 3 und 6 Nachbarn bzw. 4 Nachbarn kann nicht gewechselt werden, da die Kugeln im einen Fall in Winkeln von 90 Grad, im anderen Fall von 60 Grad angeordnet sind.
Aus der dichtesten Kugelpackung kann eine Kugelpackung mit jeweils 5 Nachbarn entwickelt werden. In diesem Fall sind geeignet Kugeln herauszunehmen. Im Ergebnis zeigt sich, dass dies innerhalb der dichtesten Kugelpackung gerade die Packung ist, wo die Lücken am dichtesten gesät sind, ohne dass zwei Lücken einander berühren.
Die dichteste Kugelpackung entsteht gewissermaßen von selbst, wenn frei bewegliche, feste Kugeln in einen abgegrenzten Raum gelegt werden. Hier äußert sich eine Eigenschaft, die als "Zusammenhalt" bezeichnet werden kann und ähnlich elementar gilt wie die Ebenheit für die euklidische Geometrie. Ist es möglich, diese Eigenschaft weiter zu beschreiben und gibt es eine andere Eigenschaft, wodurch sie variiert werden kann (wodurch also der freie Zusammenhalt eingeschränkt oder mit zusätzlichen Ordnungsstrukturen versehen wird, die wie Bindungskräfte wirken)?
Die Frage nach der dünnsten Kugelpackung ist dagegen bis heute ungelöst. In der "Anschaulichen Geometrie" ist die dünnste bisher bekannte Packung vorgestellt (die von Laves und Heesch gefunden worden war).
Ihre Konstruktion zeigt die Besonderheiten beim Arbeiten mit Kugelpackungen:
Zuerst wird in den Raum ein gleichmäßiges Tetraeder-Gitter gelegt (also ein klassisches Koordinatensystem).
Um jeden Gitterpunkt wird eine Kugel gelegt, so dass sich die benachbarten Kugeln berühren.
Innerhalb jeder Kugel werden 4 Kugeln konstruiert, die sich untereinander berühren und nach außen die Unterkugeln der Nachbarkugeln.

Figur 2 Räumliche Kugelpackung
Quelle: Hans-Günther Bigalke: Heinrich Heesch, Basel u.a. 1988, S. 88, Abb. 30
Grundsätzlich entsteht die Vielfalt der Möglichkeiten durch zwei Eigenschaften der Kugelpackungen:
Sie füllen den Raum nicht restlos aus. Bei frei beweglichen Kugeln ist die dichteste Packung die einzige stabile Packung. Ansonsten sind Befestigungen oder Anziehungskräfte notwendig. Die Kugelpackung könnte daher auch als ein geometrisches Bild solcher Kräfte interpretiert werden.
Die Kugeln als kleinste Einheit sind 3-dimensional und besitzen endliche Größen. Zwischen Innen und Außen kann unterschieden werden und der Raum im Innern kann weiter durch eigene Kugelpackungen gefüllt werden. Diese können dann ihrerseits weiter unterteilt werden und so fort. Die kartesischen Koordinaten beruhen dagegen auf dimensionslosen Punkten.
Kugelpackungen bilden sicher den anschaulich naheliegendsten nicht-homogenen Raum. Molekularbiologie, Chemie, Kristallographie, Makromoleküle bieten ein schier unübersehbares Material. Sie können Modell stehen für mathematische Kugelpackungen und Anregung geben zur mathematischen Konstruktion bestimmter Eigenschaften wie Festigkeit, Verbiegbarkeit, Durchlässigkeit, die aus der Grundeigenschaft des Zusammenhalts zu entwickeln wären. Die Quanten können nur von einer Kugel zu einer anderen springen. In den Kugelpackungen können Geodätische konstruiert werden, auf denen die Energie erhalten bleibt. Der Sprung von einer Kugel zu einer anderen erfolgt zeitlos, die Energieänderung simultan. Durch die Gestalt geeigneter Kugelpackungen sollte es gelingen, die aus den Naturwissenschaften bekannten Symmetrien und qualitativen Eigenschaften darzustellen
Parkette
Statt Kugeln können den Kugeln einbeschriebene Polyeder als Bausteine genommen werden, die den Raum ebenfalls nicht restlos füllen, z.B. Oktaeder. Während die Kugeln sich nur punktweise berühren, kann es Berührungsflächen geben. Oder es können sogar unterschiedliche Polyeder kombiniert werden. Bedingung bleibt nur, dass das entstehende Muster insgesamt gleichförmig ist.
Soll der Raum (bzw. im einfachsten Fall die Fläche) restlos aufgeteilt werden, sind geeignete Parkettierungen (Kartierungen) zu konstruieren. Üblicherweise wird von einem Parkett verlangt, dass alle Parkettsteine gleich sind. Typische Parketts sind aus Elementen mit quadratischer, sechseckiger oder dreieckiger Grundfläche aufgebaut. Erstaunlicherweise sind erst im 20. Jahrhundert die Parkettierungen mathematisch klassifiziert worden.
Parkette entstehen durch regelmäßige Anbauweise und sind insofern Kristallstrukturen verwandt. Sie können als zweidimensionale, flache Kristalle angesehen werden. Mit den Kristallen teilen sie die Eigenschaft, dass nur 2-, 3-, 4- und 6-fache Symmetrien möglich sind. Typische Beispiele: 2-fache Symmetrie ist die Rechts-Links-Symmetrie, 4-fache Symmetrie das Quadratmuster, 6-fache Symmetrie die Bienenwabe (und die Schneeflocke).
Die schier unendlichen Möglichkeiten von Parketten sind durch Mosaike und in neuerer Zeit durch die Kunst von Escher demonstriert worden. Wird 3-dimensional gebaut, bildet die Ananas ein bemerkenswertes Beispiel, wie aus untereinander weitgehend gleichen Bausteinen ein stabiles System geschaffen werden kann.
Spannend wird die Frage nach nicht-periodischen, eingeschränkt symmetrischen Mustern, die im einfachsten Fall auf der 5-fachen Symmetrie beruhen. Sie werden seit den 60er Jahren insbesondere von Penrose untersucht und sind von ihm von Anfang an konsequent in Beziehung zu kosmologischen Modellen gestellt worden.
Obwohl 5-fache Symmetrien prinzipiell den Raum nicht restlos mit untereinander identischen Parkettsteinen bedecken können, zeigen die Beispiele von Penrose, dass sie dennoch erstaunlicherweise die Eigenschaft haben, dass sich ihr Symmetriebild hierarchisch wiederholt:

Figur 4 Ebene 5-fache Symmetrie
Quelle: Roger Penrose: Hermann Weyl, Space-Time and Conformal Geometriy, S. 30
in: K. Chandrasekharan (Hg.): Hermann Weyl 1885 - 1985, Berlin u.a. 1986
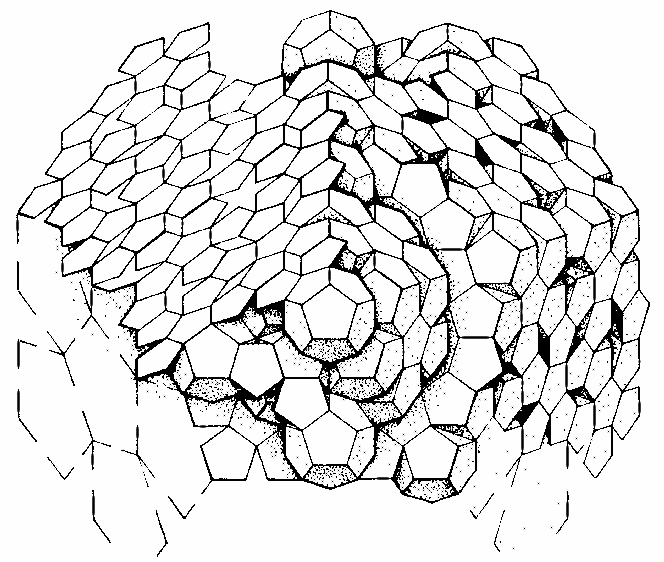
Figur 5 Räumliche 5-fache Symmetrie
Quelle: ebd., S. 34
Auch hier wird jedoch die Homogenität der kartesischen Koordinaten verlassen, indem zwar die Muster einander selbstähnlich sind, jedoch auf charakteristische Weise gegeneinander verschoben.
Ein Vergleich der 5-fachen Muster mit Kugelpackungen zeigt:
Die Grundbausteine sind jeweils von endlicher Ausdehnung.
In beiden Fällen werden orthogonale Koordinaten verlassen (bei denen die Koordinaten senkrecht aufeinander stehen).
Zwar treten gleichmäßige Bausteine auf, sie füllen den Raum aber nicht restlos. Allerdings sind Kugelpackungen im Ganzen periodisch, was für die 5-fachen Muster nicht gilt.
Dafür können sich bei den 5-fachen Mustern die Symmetrien hierarchisch wiederholen, während bei Kugelpackungen bewußt in verschiedenen Hierarchieebenen unterschiedliche Bauprinzipien angewandt werden können.
(Penrose zieht die Verbindung zu kosmologischen Modellen reichlich spekulativ, aber sein Ansatz zeigt doch, wie nach neuen Anwendungsmöglichkeiten gesucht wird: Er teilt den Weltraum auf in zwei Teile A und B. Alle Schwarzen Löcher sollen in A liegen. Also gibt es in A Punkte, in denen Information und Raum verschwinden, destruiert werden. Umgekehrt muß es in B dann Punkte geben, in denen Raum und Information erzeugt werden. Solche Punkte können als Verzweigungspunkte gedeutet werden, in denen sonst gleichförmige Bewegungen verschiedene Alternativen besitzen. Die Wahlfreiheit ist der Raum, in dem neue Information entstehen kann.
Ein Beispiel hierfür: Wenn ein zerfallendes Atom Elektronen abgibt, kann die wahrscheinliche Bewegungskurve des Elektrons berechnet werden. In konkreten Experimenten treten jedoch Abweichungen auf. Diese Fälle interpretiert Penrose nun so, dass die Elektronenbahn offenbar Verzweigungspunkte durchläuft, die über die übliche Wahrscheinlichkeitsverteilung hinaus zusätzlicher Informationen bedarf.
Für solche Fälle könnten die unperiodischen Muster dienen, in denen die üblichen Perioden ebenfalls nur gebrochen auftreten. Auch wenn Penrose hierfür noch keine konkreten Rechnungen angeben kann, gibt es immerhin Verteilungsmuster von Elektronenbeugungen, die eher 5-fache Muster aufweisen.)
Im Unterschied zu den 3-, 4- und 6-eckigen Bausteinen in architektonischen Systemen gilt die 5-fache Symmetrie traditionell als typisch für lebendige Organismen, z.B. in Blütengestalten. Die 3-, 4- und 6-fach symmetrischen Parkette sind noch sehr eng den klassischen Koordinaten verwandt. Die Interpretation des Koordinatensystems als quadratisches Parkett liefert damit den systematischen Übergang zu mehr biologisch orientierten Systemen. In dieser Richtung erscheint eine qualitative Weiterentwicklung der Mathematik denkbar.
Vierfarbenproblem
"Es sei auf einer Fläche eine Anzahl von Gebieten eingezeichnet. Jedes dieser Gebiete soll mit einer bestimmten Farbe bemalt werden, aber nie zwei Gebiete, die längs einer Kurve aneinandergrenzen, mit derselben Farbe. Wenn dagegen zwei Gebiete nur in einzelnen Punkten aneinanderstoßen, dürfen sie die gleiche Farbe haben. Es soll nun für eine gegebene Fläche die Mindestanzahl der Farben bestimmt werden, die zu einer derartigen Färbung für jede auf der Fläche mögliche Gebietseinteilung ausreichen."(Hilbert und Cohn-Vossen, s. 296).
Anschaulich geht es darum, in einer Landkarte alle Länder so zu färben, dass nie zwei Länder mit gleicher Farbe nebeneinander liegen. Deutschland und Frankreich dürfen also nicht die gleiche Farbe haben. Für Polen könnte dagegen die Farbe von Frankreich wiederverwendet werden. Nach einigem Probieren drängt sich die Vermutung auf, dass 4 Farben ausreichen. Hierzu die Beispiele von Hilbert und Cohn-Vossen:
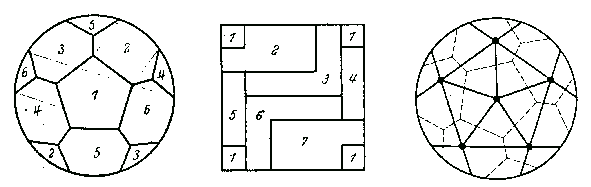
Figur 6 Vierfarbenproblem I
Quelle: Stefan Cohn-Vossen und David Hilbert: Anschauliche Geometrie, Berlin u.a. 1932, S. 296
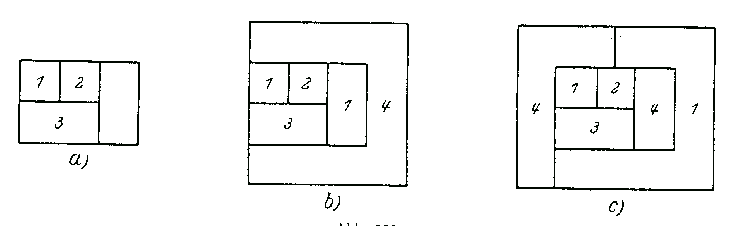
Figur 7 Vierfarbenproblem II
Quelle: ebd., S. 297
"Man erkennt aus diesen Beispielen, dass die Färbung der ersten vier Gebiete durch die Anordnung der weiteren Gebiete mitbestimmt wird. Wir müssen, wenn ein neues Gebiet hinzukommt, unter Umständen die bereits gefärbten Gebiete noch einmal umfärben und daraus ergibt sich die ganze Schwierigkeit des Problems." (ebd., s. 297)
Damit ist wieder, aber in völlig anderer Weise, die Homogenität durchbrochen. Die homogenen Koordinatensysteme stellen sicher, dass auf ihrer Grundlage stetig und folgerichtig konstruiert werden kann. (Das Induktionsaxiom stellt sicher, dass vom ersten zum n-ten Schritt keine strukturelle Änderung auftritt.)
Beim Vierfarbenproblem ist der grundlegende Konstruktionsgedanke infrage gestellt. Dies Problem wurde in den 70er Jahren so gelöst, dass gezeigt wurde, dass es einige Tausend echt verschiedene Kartentypen gibt, aus denen jede beliebige Karte zusammengesetzt werden kann, und dass jeder Kartentyp für sich mit 4 Farben auskommt. Die Rechnungen konnten allerdings nur per EDV ausgeführt werden, und im Grunde ist unklar, ob irgendwo in dem sehr komplexen Programm Fehler verborgen sind.
Vor allem aber stehen die verschiedenen Kartentypen mehr oder weniger isoliert nebeneinander und es konnte bisher keine innere Gesetzmäßigkeit gefunden werden. Mit einem Wort: Es sind keine Symmetrien gefunden worden, die die Kartentypen miteinander verbinden. Das Vierfarbenproblem scheint also auf eine nicht-polarisierbare Eigenschaft der Natur hinzudeuten. Es sind bisher auch keine anderen Eigenschaften der Kartentypen gefunden worden, wodurch die Lösung des Vierfarbenproblems in Verbindung mit geometrischen oder sonstigen Fragen gebracht werden könnte, obwohl anschaulich naheliegt, dass es sich hier um ein Standardproblem handelt, dass auch in anderen Gebieten der Geometrie Konsequenzen haben müßte.
So weist das Vierfarbenproblem letztlich nur darauf hin, dass es Eigenschaften der Ebene gibt, die bisher ungeklärt sind. Es fehlt ein Koordinatensystem, mit dessen Hilfe dies Problem konstruktiv gelöst werden kann. Die Situation ähnelt der, vor der Galois stand, als er an die offenen Fragen der griechischen Geometrie ging. Die Darstellung der Konstruktionsebene als komplexe Zahlenebene, d.h. die Erarbeitung der komplexen Koordinaten seit Gauß brachte damals die Lösung. Und so ist auch hier zu fragen, ob sich ein geeignetes Koordinatensystem finden lässt, in dem die verschiedenen Kartentypen eingeordnet werden können.
Bewegungen und Grenzübergänge
Die hier vorgestellten Koordinatensysteme ähneln stark der endlichen, lokalen Betrachtungsweise der molekularen Chemie. Daher ist weiter nach Grenzübergängen zu fragen, indem die Kugeln, Polyeder bzw. gefärbten Polyeder unendlich klein werden. Schon anläßlich der Quantengeometrie war die Möglichkeit neuer Differentialkalküle etwa auf Basis der äußeren Algebra gesehen worden. Bei Grenzübergängen in den neuen Koordinatensystemen ist erst recht mit veränderten algebraischen Strukturen und Differentialkalkülen zu rechnen.
Die Grenzübergänge können aber auch anders entstehen, wenn es sich um Ströme innerhalb des Koordinatengitters handelt, z.B. Rotation um die einzelnen Elemente oder Wirbelmuster. Maxwell schwebte bei Entwicklung der Wellengleichungen für die Elektrodynamik ein solches Bild vor. Die Physik der Selbstorganisation kennt Flüssigkeiten, wo bei Wärmezufuhr eine derartige Wirbelstruktur spontan entsteht und einen neuen optimierten Zustand herstellt.
Schließlich können auch andere Konstruktionsregeln eingeführt werden:
Widerstände und Speicher als Eigenschaften der Kugeln (Petri-Netze, elektrische Schaltpläne)
Spielfiguren mit speziellen Bewegungsmöglichkeiten (Werkzeuge wie Lineal und Zirkel, Figuren wie bei Schach etc.)
Ausbreitung nach symmetrischen Mustern (wie Wärme, Flüssigkeiten etc.)
Ausbreitung bei Resonanzeffekten (Supraleitfähigkeit etc.)
Abgrenzungsregeln (z.B. Färbungen, Schwarz/Weiß-Muster, etc.)
Muster mit zusätzlichen Eigenschaften (chemische Moleküle, architektonische Muster, Kristalle etc.)
Der Phantasie sind hier keine Grenzen gesetzt und es kann also nicht im geringsten gesagt werden, dass die anschaulichen Möglichkeiten für eine weitere Entwicklung der Mathematik bereits ausgeschöpft wären.
Literaturhinweise
© tydecks.info 2002