Anschauliche Geometrie

Die Mathematik wird jedoch nicht einfach nur unanschaulicher. Es gibt auch eine Geschichte der Anschaulichkeit. Hierbei geht es weniger um die Entdeckung einzelner neuer Symbole, sondern um die Frage, wo mathematische Symbole gesucht werden, also um die Frage von Leitbildern oder Leitvorstellungen für Symbole.

Im tiefsten Innern ist die Mathematik sich sehr wohl des Problems bewußt, mit welcher Berechtigung und auf welche Anwendungsgebiete Ergebnisse des Rechnens mit mathematischen Symbolen zurückübertragen werden können. Es ist immer zu fragen, welche Eigenschaften der Natur in den mathematischen Symbolen angesprochen sind, was das Symbolisierte in den Symbolen ist.

Die Symbole entstehen durch Intuition. Intuitiv werden zwischen verschiedenen offenen Fragen Gemeinsamkeiten ("Wahlverwandtschaften", "Familienähnlichkeiten") wahrgenommen. Ein neues Symbol ist zunächst nur eine Anregung, in der sich die Intuition äußert. Mit dem Symbol soll eine Verbindung zwischen verschiedenen ungelösten Problemen hergestellt werden, die in Sackgassen zu laufen drohen und für die nun ein Ausweg gesucht wird. Wenn ein neues Symbol von der Mathematik aufgenommen wird, wirkt es dort natürlich zuerst wie ein Fremdkörper, wie eine neue Spielfigur, die in die Mathematik geworfen wurde, und die nun sehen muß, was sie damit anfangen kann. Erst mit den Resultaten, die nach und nach gewonnen werden, werden der wahre Umfang und die wahre Gültigkeit des Symbols deutlich.

Als z.B. das Koordinatenkreuz zur Beschreibung von Punkten und Figuren auf einer Fläche eingeführt wurde, konnte niemand ahnen, dass es später auch für die Darstellung der komplexen Zahlen und zur Veranschaulichung von Zeitreihen dienen würde, wobei die y-Achse mal als Achse der imaginären Zahlen und mal als Zeitachse verstanden wird.

In jedem Einzelfall ist es wieder spannend zu sehen, welche Änderungen in der Mathematik durch ein neues Symbol ausgelöst werden. Welche Eigenschaften befähigen ein Symbol, den weiteren Weg der Mathematik zu öffnen und von ihr integriert zu werden? Symbole entstehen zwar in der Intuition, aber auch die Intuition lässt sich von bestimmten Fragen und Vorstellungen leiten. Zuerst waren die Kurven eine solche Leitvorstellung. Die Mathematiker gingen regelrecht in der Natur auf die Suche nach neuen Kurven (z.B. Wurfparabeln, Höhenlinien etc), die für die Mathematik symbolische Bedeutung bekommen sollten. Intuition wurde gebraucht, um aus den unendlich vielen Kurven in der Natur die "interessanten" herauszufinden.

Wenn zuerst Kurven (wie Parabel, Hyperbel oder Ellipse) die Rolle einer Leitvorstellung übernehmen, geht es danach irgendwann nicht so weiter, dass immer neue Kurven entdeckt werden, sondern es stellt sich die Frage, durch welche Eigenschaften die Kurven auf der einen Seite mathematisch berechenbar werden und auf der anderen Seite sichergestellt bleibt, dass sie wirklich in der Natur vorkommen und nicht nur ein mathematisches Konstrukt sind. Das führt zur Erkenntnis ihrer inneren Symmetrie, die dadurch zur neuen Leitvorstellung für die mathematischen Symbole wird.

Diese neu gewonnene Symmetrie geht weit über Platons Anschauung symmetrischer, geometrischer Figuren hinaus. Symmetrie wird nicht nur als räumliche Eigenschaft, sondern auch als zeitliche Symmetrie verstanden. In die Erkenntnis von Symmetrie gehen sowohl Beobachtungen zyklischer Prozesse als auch räumlicher Regelmäßigkeiten in der Natur ein. Mit der Symmetrie als Leitbild gelang daher mathematisch die volle Integration des reinen Raumes und der reinen Zeit, die Kant philosophisch unter dem Titel der "transzendentalen Ästhetik" vorausgesehen hatte. Die Zeit erhält sogar wie bei Kant eine herausgehobene Bedeutung, indem die physikalischen Grundbegriffe Kraft, Impuls und Energie an Ableitungen der Bewegung nach der Zeit gebunden sind. Die Integration von Raum und Zeit führt zur Umwälzung der mathematischen Raumvorstellung. Felder und schließlich differenzierbare Mannigfaltigkeiten treten an die Stelle des euklidischen Raums.

Aber auch an die Symmetrie ist die Frage zu stellen, was eigentlich das "Symmetrische" ist, oder: was an der Symmetrie zwischen Natur und Mathematik vermitteln kann, und das führt zu der mathematischen Technik der Polarisation, des Aufbaus komplexer Funktionen und Funktionssystemen aus einfachen periodischen Funktionen. Hier kann nun wiederum weiter gefragt werden, welche Eigenschaft der Natur die Polarisation erlaubt und ob es vielleicht auch andere Eigenschaften gibt, die nicht polarisiert werden können. Polarisation setzt die Existenz regelmäßiger Pulsgeber (Oszillatoren) voraus und ist an deren Wirkungsfeld gebunden. Beispiele sind rotierende Himmelskörper, die Lichtstrahlen aussenden, oder die periodische Bewegung der Elektronen um den Atomkern. Die Frage, ob das gesamte Geschehen in der Natur auf das Wirken von Pulsgebern zurückgeführt werden kann, ist jedoch offen, und daher steht an dieser Stelle vorläufig ein programmatischer Begründungszusammenhang, der keine andere Aufgabe hat, als den aktuellen Stand so genau wie möglich zu kennzeichnen und für weitere Fragestellungen anzuregen.

Mit der Symmetrie und der Polarisation als neuen Leitvorstellungen für Symbole sind jeweils philosophische Ideen verbunden. Die enge Verwandschaft des modernen Symmetrie-Gedankens mit den platonischen Ideen und Kants transzendentaler Ästhetik (Lehre von der reinen Zeit und dem reinen Raum) war allen beteiligten Physikern und Mathematikern immer bewußt. Siehe hierzu insbesondere die Arbeiten von Heisenberg, Weizsäcker und Forschern in ihrem Umfeld. Die Herausarbeitung der neuen Raumvorstellung zur Beschreibung von Feldern hat dann zu Recht den Anstoß für die neu-kantianische Richtung gegeben, zu der maßgeblich auch die frühen Arbeiten von Wittgenstein zu zählen sind.

Mit der Polarisation als neuester Leitvorstellung wird dagegen oft die abendländische Philosophie verlassen, und Vorbilder werden in östlichen Religionen gesucht. Mir scheint jedoch treffender zu sein, dass die Polarisation und die zugehörigen Resonanzuntersuchungen ("sound") als eine wissenschaftlicher Neuaufnahme und Weiterführung der Vorgehensweise der Alchemie verstanden werden können. (Der Verweis auf die östlichen Religionen ist häufig einfach ein erster Schritt in dieser Richtung, denn oft dienen die östlichen Religionen dann ihrerseits nur als Ansatzpunkt, um in ihnen alchemistisches Gedankengut zu entdecken.)

Im Unterschied zur Trinität der dialektischen Methode durchmißt das Opus der Alchemie eine Quaternität, deren 4 Schritte als Schwärzung (Nigredo), Weißung (Albedo), Gelbung (Citrinitas) und Rötung (Rubedo) bezeichnet werden. So zeigt schon die Vorgehensweise selbst das Bild einer optischen Brechung in Farben. Und weiter kann der Schritt der Gelbung direkt als Vorläufer der Polarisation angesehen werden: Nach Auflösung des bearbeiteten Stoffes (Nigredo), Auffinden des inneren Ideals aus den Bruchstücken des zersetzten Stoffes (Albedo), wird dann nochmals das Ideal gebrochen und so zum Aufleuchten gebracht. Wie die Polarisation zum Farb- oder Tonspektrum führt, ist das Ergebnis der Citrinitas ein Farbenkranz um die Farben Gelb und Grün, der von den Alchemisten gern in Symbolen wie Pfauenrad oder Iris (Regenbogenhaut) vorgestellt wird. Abschließend wird in dem Spektrum der gefundenen Farben und Möglichkeiten der Grundton herausgehört und zum Leben gebracht (symbolisch die Farbe Rot, daher Rubedo als Bezeichnung dieses letzten Schritts). Das kann mathematisch so gedeutet werden, dass die Resonanzeigenschaften des Spektrums entdeckt werden, oder musikalisch, dass der "sound" getroffen wird und eine Wechselbeziehung zwischen Musik, Spieler und Hörer lebendig wird.

Der Hinweis auf alchemistische Ideen birgt natürlich die Gefahr des Mißverständnisses, nun solle auch das komplette Ideengut reaktiviert werden, in dessen Umfeld sich die Alchemie bewegte. Es sind schon genügend Versuche in Umlauf, eine neue Geheimwissenschaft zu schaffen, theosophisches Denken zu popularisieren oder in einem neuen Zeitalter die Ideen der Individualität und Autonomie freiwillig aufzugeben. Die Alchemie kann nicht wiederbelebt werden, als sei zwischendurch nichts gesehen. Die Alchemie hat aber zumindest in einigen Teilströmungen ein Verständnis und eine Intuition für Zusammenhänge in der Natur bewiesen, die es durchaus lohnt, wieder freizulegen und die der weiteren Entwicklung der Mathematik Anregung geben können.

Aber auch das ist sicherlich nicht der Endpunkt. In möglicherweise ganz andere Richtungen weisen die Entwicklungen neuer Koordinatensysteme für nicht-homogene Räume, die von Hilbert und seinen Mitarbeitern als Beispiele für "Anschauliche Geometrie" vorgestellt wurden und hier erst anschließend im nächsten Abschnitt besprochen werden sollen.

Kurven

Die seit den Lehrbüchern von Euklid axiomatisch aufgebaute Geometrie ging von einfachsten Figuren aus (Punkt, Gerade, Kreis) und versuchte daraus mit möglichst einfachen Regeln alle komplizierteren Figuren zu entwickeln. Das legte ein normierendes, atomistisches Verständnis der mathematischen Symbole nahe.

Daneben gibt es aber unendlich vielfältige komplizierte Figuren in der Natur, die zwar durch einfachere Figuren angenähert werden können, aber doch als eigenständige Objekte angesehen wurden. Zur Analyse ihrer inneren Struktur ging daher die Mathematik den umgekehrten Weg: Ausgehend von den Eigenheiten jeder einzelnen Figur wurde jeweils eine neue, bisher unbekannte mathematische Gleichung gesucht, um das Charakteristikum zu treffen. Der Lösungsweg bestand dann darin, die Gleichung solange mathematisch umzuwandeln, bis sie in eine Gestalt gebracht war, die herkömmlich gelöst werden konnte.

Am wichtigsten sind die Kurven. Beispiele: Schwingungen von Saiten, Wurfparabeln, Bewegungskurven von Gestirnen durch nachgewiesene Beobachtungspunkte, Isothermen der Wärmeausbreitung, Höhenlinien in geologischen Bewegungen, Wellenverlauf in Strudeln, Bruchlinien in Materialien. Bis ins 19. Jahrhundert war es nicht für möglich gehalten worden, solche speziellen Kurven rein mathematisch unabhängig von ihrem Kontext in der jeweiligen Naturwissenschaft darzustellen.

Der Bruch in der Mathematik war so tief, dass systematisch unterschieden wurde zwischen der reinen (axiomatischen) Mathematik und der angewandten Mathematik, die eng in Zusammenarbeit mit der jeweiligen Naturwissenschaft stand.

Hier bedeutet bis ins 19. Jahrhundert angewandte Mathematik keineswegs Mathematik in direktem Bezug zur Produktion, wie es für die heute vorherrschende pragmatische Ausrichtung der Mathematik typisch ist. Vielmehr wurden diese Fragen eher wie Rätsel aufgeworfen und oft regelrecht in der Form von Preisausschreiben gestellt.

Aufgabe der Mathematik war, die vorgegebenen Kurven durch eine mathematische Funktion zu beschreiben, in der Regel durch eine Differentialgleichung. Dann wurde nach der Lösung der Gleichung gesucht. Es war auch nicht nach Strenge im Beweisverfahren oder möglichst großer Allgemeinheit gefragt, sondern im Grunde genügte es, irgendwie die gestellte Aufgabe zu lösen. (Leonhard Euler steht exemplarisch für diese Mathematik.)

Letztlich gab es soviel mathematische Verfahren wie Aufgaben. Der mathematische Lösungsweg wurde mehr oder weniger mit der jeweils konkret gestellten Aufgabe identifiziert und teilte dessen Anschaulichkeit. Natürlich entging den Mathematikern nicht, dass bestimmte Lösungsmethoden erfolgreicher waren als andere und wiederverwendet werden konnten. Das galt aber eher als zufällig und wurde von den einzelnen Mathematiker als "Geheimwaffe" bewahrt, um in der wissenschaftlichen Konkurrenz obenauf zu bleiben. Heute würde gesagt werden: Es wurde nicht ingenieurmäßig, nicht technisch geforscht.

Im Ergebnis standen immer mehr mathematische Gleichungen nebeneinander, so die Wellengleichung, Wärmegleichung, später die Maxwellgleichungen für die Elektrodynamik usw. Jede Gleichung ging auf einen eigenen anschaulichen Naturprozeß zurück. Es gab keinen Weg, sie auseinander axiomatisch abzuleiten.

Ursprünglich übernehmen sie die Rolle der qualitativen Symbole. Sie sind durch Beobachtung in der Natur gefunden und brauchen daher nicht weiter hinterfragt zu werden. Die Mathematik hat hier zunächst nichts weiter als die Aufgabe, ihre Größenbestimmung zu finden.

Das Nebeneinander der verschiedenen Wellengleichungen mit ihrer jeweils symbolischen Bedeutung erinnert stark an die Gleichwertigkeit der verschiedenen Zahlzeichen, wenn diese als Ausdruck verschiedener Qualitäten gesehen werden (qualitatives Verständnis der Zahlsymbole). Auch bei ihnen liegt das Symbolische in der jeweils spezifischen geometrischen Gestalt, wobei die Zahlzeichen als Symbol für typisierte Kurven stehen (wenn z.B. die "1" einen Strich symbolisiert, die "2" eine Aufteilung in 2 Hälften etwa in Gestalt der Trennlinie im yin-yang-Zeichen, die "3" die Verbindung dreier Ebenen, die "4" das Koordinatenkreuz mit den 4 Quadranten).

Wird gefragt, wie Symbole zwischen der Natur und der Mathematik vermitteln, geben die Kurven die einfachste und erste Antwort: Die Symbole der Mathematik sind den Objekten in der Natur ähnlich.

Gruppen

Lösen von Gleichungen wurde zum Hauptgeschäft der Mathematik. Was geschieht dabei? Im Mittelpunkt steht die Beweisidee. Einer Gleichung muß "angesehen" werden, wie sie geeignet so umzuformen ist, dass in einer Nebenrechnung oder durch Rückgriff auf Methoden aus anderen Gebieten die Vereinfachung gelingt. Ein Beispiel war die Gleichung

y = ax² + bx + c,

die durch die Nebenrechnung a² + 2ab + b² = (a + b)² gelöst wird.

Andere Gleichungen konnten vereinfacht werden, indem sie für bestimmte einfachere Teilgebiete gelöst wurden und gezeigt wurde, dass diese Lösung überall gilt. Werden z.B. Gleichungen gesucht, wie eine Strömung durch ein Raumgebiet fließt, genügt es herauszufinden, wie sie durch die Oberfläche strömt.

Mathematische Arbeit erfordert also Intuition (für die Beweisidee) und Erfahrung und Übung (für die Ausführung der Rechnung). "Genies" zeichneten sich durch ihre Intuition aus. Intuition hilft beim Aufdecken verborgener Regelmäßigkeiten. Es genügt nicht, eine komplizierte Kurve durch irgendeinen Linienzug anzunähern, sondern durch eine "geschickte" regelmäßige Figur. Der Vereinfachungsschritt erfolgt von der zusammengesetzten Figur zu der Figur, die in ihr in regelmäßiger Wiederholung enthalten ist.

So kann ein System aus unendlich vielen Punkten überdeckt werden durch endlich viele regelmäßige Kreise (topologische Beweisidee). Oder eine räumliche Figur durch ihre Oberfläche. Oder eine Oberfläche durch ein Netz mit regelmäßiger Zellenstruktur.

Alle diese möglichen Regelmäßigkeiten wurden um 1830 von Galois im Begriff der mathematischen Gruppe zusammengefaßt. Eine Gruppe ist eine Menge, deren Elemente Regelmäßigkeiten aufweisen, oder anschaulicher gesprochen, deren Elemente untereinander symmetrisch sind.

In dem Maß, in dem mit Gruppen bzw. Symmetrien eine höhere Ordnung gefunden wurde, entstand die Hoffnung auf eine neue Art von Anschaulichkeit. 1872 veröffentlichte Felix Klein das Erlanger Programm: Die Mathematik soll nach Symmetrien (gruppentheoretisch) aufgebaut werden. Die Symmetrie wird zum Angelpunkt der Anwendbarkeit und ersetzt paradigmatisch die Betrachtung von Kurven in der Geometrie und Differentialrechnung.

Symmetrien: Die mathematische Forschung stößt auf mathematische Objekte mit symmetrischen Eigenschaften, etwa die Drehungen und Spiegelungen geometrischer Figuren, oder auch auf Gruppen gleichwertiger Lösungen vorgegebener Gleichungen, die untereinander symmetrisch sind und sucht dann nach wirklichen Objekten, die diese Symmetrie teilen. Umgekehrt können in der Naturbeobachtung Symmetrien gefunden werden und die Mathematik prüft, ob es in ihrem Bereich Ähnliches gibt.

1870 - 1920 wurden die mathematischen Axiome neu geschrieben (Dedekind, Cantor), entstanden die Differentialgeometrie (Poincare, Einstein) und neue Algebren mit bisher unerforschten Symmetrien (Tensorkalkül, Lie-Algebra, Kristallographie). Während die Axiomatik in die Grundlagenkrise steuerte, erlebte der Symmetriegedanke immer neue Triumphe.

So lösten 1920 - 1930 die Experimente der Atom- und Quantenphysik einen wahren Begeisterungssturm aus. Elektronenstrahlen wurden an Gittern gebrochen und die Physik lieferte genau das Anschauungsmaterial an Symmetrie, welches die Mathematik 100 Jahre lang vorbereitet und vermißt hatte. Die Relativitätstheorie trug das ihre dazu bei, auch die Raumvorstellung umzuwälzen und das Weltall als symmetrisch geordnetes Feld zu begreifen. Bis heute zielen alle Experimente der Teilchenphysik darauf, weitere Symmetrien und Gruppen von Teilchen in der Natur zu entdecken bzw. nachzuweisen.

Der Methodenwechsel kann am deutlichsten in der Theorie der Differentialgleichungen abgelesen werden. Aus dem großen Fundus einzelner Lösungen entwickelte sich eine systematische Theorie, die ihrerseits die neu gewonnenen gruppentheoretischen Lösungen an zentraler Stelle einsetzte.

Endlich gelang die Verknüpfung der Ideen der euklidischen Geometrie mit den Techniken zur Lösung von Differentialgleichungen.

1920 - 1940 wurde der Kanon der mathematischen Disziplinen neu konzipiert (wegweisend im Aufbau der "Elemente der Mathematik" von Bourbaki). Die Trennung in reine und angewandte Mathematik wurde im Grunde überwunden. Beide Gebiete wurden auf gemeinsamen "Mutterstrukturen" aufgebaut (Topologie, Algebra, Verbandstheorie), die an die Stelle der Axiomensysteme traten. Bis heute hat diese Umwälzung ihre Gültigkeit behalten können.

War es damit aber nicht letztlich zu einem Rückfall in die griechische Geometrie gekommen? Mit den Kurven als Leitvorstellung für Symbole sollte bewußt die Einschränkung durchbrochen werden, die durch die euklidische Geometrie nahegelegt wurde, als sie die Geometrie auf das beschränkte, was sich aus Gerade und Kreis konstruieren lässt. Entsteht nun nicht eine ähnliche Einschränkung, wenn nach den Kurven die Symmetrie neue Leitvorstellung wird und nur das zählt, was mit den Axiomen und Beweistechniken aus Topologie, Algebra und Verbandstheorie gefolgert werden kann?

Felder und Mannigfaltigkeiten

Angewandte und reine Mathematik paßten aber auch daher nicht zusammen, da ihnen unvereinbare Raumvorstellungen zugrunde lagen. Die reine Mathematik ging von Koordinaten aus, die mathematisch transparent waren und mit denen gerechnet werden konnte. Für arithmetische Operationen genügt der eindimensionale Zahlenstrahl, auf dem die Zahlen liegen, für die Geometrie die ebene Fläche mit den Koordinaten Breite und Höhe. Der dreidimensionale Raum der Mechanik erschließt sich unproblematisch durch Ergänzung um die z-Achse. Kant faßt dies als "Welt der Mathematik" zusammen.

Dagegen stand in der Begrifflichkeit von Kant das "System der Natur", wo all die verschiedenen unterschiedlichen Kurven beobachtet und gelöst werden können. Während die Welt der mathematischen Koordinaten immer leer und unbewegt vorgestellt wird, ist das System der Natur gefüllt mit Strömen wie Luft, Wasser, Wärme, Licht etc. Das System der Natur schließt Leere geradezu aus ("horror vacui").

Natürlich stellte sich Kant die Frage, wie es möglich ist, in der Welt der Mathematik zu Ergebnissen zu gelangen, die im System der Natur stimmen, - oder umgekehrt: wie es möglich ist, das System der Natur in der Welt der Mathematik abzubilden. Im Grunde reicht die Erkenntnisfähigkeit des Menschen nur so weit, wie es die Welt der Mathematik zulässt. Für Kant ist die Welt der Mathematik identisch mit dem Erkenntnishorizont des Menschen und er war sich bewußt, dass damit nur ein Ausschnitt der Natur erreicht wird. Allerdings hat er nicht sehen wollen, dass es dem Menschen in der Auseinandersetzung mit der Natur möglich ist, diesen Ausschnitt zu vergrößern. Oder anders gesagt: Die Wahrnehmungsfähigkeit des Menschen ist sicherlich weit umfassender als die wissenschaftliche Erkenntnisfähigkeit und bietet der Erkenntnisfähigkeit immer unbegrenzten Entwicklungsraum. Kant hat dagegen die Welt der Mathematik und das System der Natur als unveränderliche Räume einander gegenübergestellt und nur das Axiom aufgestellt, dass alle Erkenntnisse aus der Welt der Mathematik auch im System der Natur Gültigkeit haben, ohne dies System damit vollständig beschreiben zu können.

Wie genau Kant sich dieser Probleme bewußt war, zeigt sein Begriff der Mannigfaltigkeit. In seiner Philosophie ist die "unverbundene Mannigfaltigkeit" die verstandesmäßig noch unverarbeitete Rohform der sinnlichen Natureindrücke (siehe hierzu die "Transzendentale Deduktion der Verstandesbegriffe" in der "Kritik der reinen Vernunft" und die Interpretation von K.Heinrich in "arbeiten mit oedipus"). dass die Mannigfaltigkeit keineswegs ein leerer Begriff ist, zeigt das Problem des Zinnobers, mit dem Kant sich ausführlich beschäftigt. Der Zinnober ist für Kant das charakteristische Beispiel für Erscheinungen, die in der "unverbundenen Mannigfaltigkeit" auftauchen und vom Menschen wahrgenommen werden können, aber keinen Platz in der Welt der Mathematik finden und sich jeder wissenschaftlichen Erkenntnis entziehen. Der Zinnober mit seinen schillernden, auf keine Eindeutigkeit festlegbaren qualitativen Eigenschaften ist aber zugleich ein typisches Symbol der Alchemie und umfaßt wesentlich mehr als das Quecksilbererz, das später als sein materielles Substrat entdeckt wurde. Bevor im nächsten Abschnitt über die Polarisation noch intensiver auf die Alchemie als "geheime", unbewußte Vorlage moderner mathematischer Methoden zurückgekommen wird, ist hier bereits festzuhalten, dass historisch der Begriff der Mannigfaltigkeit zuerst von Kant eingeführt wurde, um die Gebiete der Alchemie und der Mathematik voneinander zu scheiden, und dann doch der neue Bezugspunkt für die weitere Entwicklung des mathematischen Raumbegriffs wurde.

Entsprechend dem damaligen Stand der Mathematik gab es für Kant nur räumliche Koordinaten und die eine Zeitkoordinate, die ohne innere Beziehung zueinander standen. Im weiteren Verlauf der Mathematik wurde aber durchaus an den Grenzen dieser Mathematik gerüttelt. Die bahnbrechende Erkenntnis von Kant kann hier also genauer so verstanden werden, dass er überhaupt klar herausgearbeitet hat, dass es einen Unterschied zwischen der Welt der Mathematik und dem System der Natur gibt. Bis dahin waren beide grundsätzlich "naiv" ineins gesehen worden. Er hat also das Bewußtsein für die Grenzen der Mathematik geweckt, und steht damit genau an dem Punkt, wo die weitere Mathematik dann daran ging, diese Grenzen infrage zu stellen und zu verändern. Diesen Schritt wagte Kant allerdings noch nicht. Die Mannigfaltigkeit blieb für ihn ein Reich außerhalb der Wissenschaft, während die Mathematik im folgenden immer bewußter daran ging, ihr Gebiet in dieser Richtung zu erweitern.

Die "Reibungen" zwischen der Welt der Mathematik und dem System der Natur wurden immer deutlicher bewußt und konzentrierten sich schnell auf das Problem, dass das System der räumlichen Koordinaten nicht ausreicht. Für die Darstellung von Strömungen sind außer den räumlichen Koordinaten weitere Bewegungsparameter nötig, die Stärke, Dichte, Rotationen und Wirbelbildung beschreiben. Im Gegensatz zu den räumlichen Koordinaten kennen diese keinen absoluten Nullpunkt, sondern ändern sich mit dem Verlauf des Stroms.

Die Übertragung von Methoden der reinen Mathematik auf die angewandte Mathematik setzte daher eine Überwindung der starren räumlichen Koordinatensysteme voraus:

Erstens. Die Zeitachse setzt sich als gleichberechtigte Achse durch. Das Koordinatenkreuz wird in der Regel sogar so verstanden, dass eine Achse "den Raum" und die zweite Achse "die Zeit" darstellt. Es wird dann nicht mehr die Bewegungskurve im Raum, sondern ihr zeitlicher Ablauf dargestellt.

Diese Vorstellung ist mit dem Ableitungsbegriff entstanden. Ableitungen wurden ursprünglich als Berechnungen von Geschwindigkeit und Beschleunigung verstanden, d.h. es wurde "nach der Zeit" abgeleitet. Zur Veranschaulichung entstanden die Bewegungskurven, die in einer Achse anzeigen, wie weit der bewegte Körper im Raum gekommen ist, und in der anderen Achse, wieviel Zeit hierfür vergeht.

Heute sind solche Diagramme derart verbreitet, dass sie als selbstverständlich gelten. Daher wird kaum mehr wahrgenommen, dass sie die Anschauung für die Mathematik völlig umgewälzt haben. Bis zur Entstehung des Ableitungsbegriffs hatten alle Zeichnungen in der Mathematik den Charakter von Bildern, und sie unterschieden sich prinzipiell nicht von Zeichnungen in der Kunst. Sie verdeutlichten ausschließlich räumliche Maßverhältnisse, etwa in der Geometrie oder der Architektur. Auch das perspektivische Zeichnen änderte im Prinzip an diesen Diagrammen nichts, da lediglich die räumlichen Verhältnisse anders dargestellt wurden (nämlich so, wie sie subjektiv dem Auge erscheinen).

Diese Anschauung lag so tief der Mathematik zugrunde, dass sie sogar zur Leitvorstellung der Symbole wurde und damit auch die mathematische Intuition prägte: Symbole sind Kurven, die durch ihre äußere, rein räumliche Gestalt zwischen dem System der Natur und der Welt der Mathematik vermitteln.

Bewegungskurven entstanden zunächst in der Mechanik zur Beschreibung der Bewegungsabläufe fester Körper und wurden dann auch in allen anderen Wissenschaften eingesetzt, um Wachstumsprozesse darzustellen. In allen Fällen werden Beobachtungswerte, die nacheinander in der Zeit gemessen wurden, eingetragen und durch eine Kurve verbunden. Bei Bewegungskurven wird zunächst eine in der Natur wirklich beobachtbare Kurve auf diese Weise nachgezeichnet. Wenn diese Methode auf andere Wissenschaften wie Geschichte oder Ökonomie übertragen wird (z.B. in Kurven der Geldwertentwicklung zur Beschreibung von Inflation, u.ä.), zeigt das, wie stark diese neue Anschauung aus der Mathematik allmählich auch prägend auf alle Gebiete des Denkens übergriff. Und es zeigt, wie sich die symbolische Bedeutung der Kuven wandelt, indem nun wie selbstverständlich akzeptiert wird, dass mit der Mathematik Bewegungskurven entdeckt werden, die in dieser Gestalt sicher nicht in der Natur vorkommen, die aber dennoch Naturprozesse treffend veranschaulichen. Die symbolische Bedeutung der Kurve ist nicht mehr an ihre geometrische Gestalt gebunden, sondern an die geeignete mathematische Darstellung eines Prozesses in Raum- und Zeitkoordinaten.

Dies ist der Umschlagpunkt in der frühen Neuzeit, auf den sich Arendt kritisch bezieht. Aber jetzt wird ganz deutlich, dass nicht der Erdstandpunkt verlassen und ein fiktiver außerirdischer Standpunkt eingenommen wurde, sondern dass die Zeitachse mit den Raumachsen integriert wird und dadurch Kurven gezeichnet werden können, die keine räumlichen Vorbilder haben. Diese Bewegungskurven beziehen sich aber zunächst durchaus auf Vorgänge, die auf der Erde mit den üblichen menschlichen Sinnen wahrgenommen werden.

Zeichnungen in der Kunst und in der Mathematik fielen damit erstmals auseinander. Bis heute werden Bilder aus der Malerei danach analysiert, welche inneren geometrischen Verhältnisse in ihnen ausgedrückt werden, ob sie dem Goldenen Schnitt folgen und ähnliches. Die "verborgene Geometrie" machte einen guten Teil des Symbolgehalts dieser Bilder aus. Während dann aber in der Mathematik die Technik der Bewegungskurven entstand, gab es in der Malerei nur wenig Ansätze, dies nachzubilden (etwa in den Bildern "Bewegte Frau" von Duchamp). Statt dessen kam es eher insofern zu einer Analogie von Mathematik und Malerei, als der unanschaulicher werdenden Mathematik die abstrakte Malerei entspricht.

Zweitens. Mit rein räumlichen Koordinaten werden sogenannte Vektorfelder dargestellt. In diesem Fall wird in der Fläche an jedem Punkt ein Pfeil ergänzt, in welche Richtung und mit welcher Stärke sich eine Strömung bewegt. Der einfachste Fall sind Magnetfelder, da in einem einfachen Experiment mit Metallspänen unmittelbar das anschauliche Bild des Feldes erzeugt werden kann. Ebenso direkt lassen sich Wellenmuster auf bewegten Gewässeroberflächen beobachten, oder durch Wasser und Wind erzeugte Sandmuster im Watt bzw. auf Dünen.

Als Vorlage für die Anschauung kann sehr gut ein wirkliches Feld dienen. Der Erdboden steht für den "natürlichen Raum", und auf ihm wachsen als Feld die vielen Halme. Wenn Wind weht, wird das Feld bewegt, und von oben gesehen ergibt sich das typische Bild eines mathematischen Feldes. Die Halme neigen sich nach der Windrichtung, der Neigungswinkel gibt die Windstärke an.

Mit Vektorfeldern kann die Eigenbasis einer Bewegung gefunden werden. Die Eigenbasis bezieht sich immer auf einen Punkt in einem bestimmten Zeitmoment und definiert in einer Achse die Richtung der Bewegung, mit der Länge des Pfeils die Stärke der Strömung an dieser Stelle und in der komplementären Achse die Frontlinie der Strömung.

Anschaulich handelt es sich um die Freiheitsgrade einer Bewegung. In den einfachsten, die Anschauung prägenden Fällen sind Freiheitsgrade und Raumachsen identisch. So z.B. bei einem frei hängenden Pendel. Es kann in alle Raumrichtungen schwingen und angestoßen werden.

Schon die Möglichkeiten des Doppelpendels können rein anschaulich ohne Experimente kaum erschlossen werden. In diesem Fall ist ein Pendel frei aufgehängt, und an der Pendelkugel wiederum ein zweites Pendel. Beide Pendelkörper können frei in allen 3 Raumrichtungen schwingen. Dennoch ist klar, dass die Bewegung des unteren Pendels von dem oberen, an dem es aufgehängt ist, beeinflußt wird und umgekehrt dessen Bewegung beeinflußt. Die Freiheitsgrade können also nicht einfach multipliziert werden. Vielmehr bedarf es aufwendiger Rechnungen, alle Bewegungsmöglichkeiten zu ermitteln.

Bei der Berechnung von mehr als 2 miteinander gekoppelten Pendeln (allgemein: Mehr-Körper-Problem) stößt bis heute die Mathematik schnell an ihre Grenzen.

Im Ergebnis entsteht die Anschauung, dass es zum einen den Basisraum gibt, in dem die Bewegung erfolgt (der natürliche Raum), und an jedem Bewegungspunkt einen Bewegungsraum, dessen Achsen die Eigenbasis (Freiheitsgrade) der Bewegung darstellen. Das Vektorfeld ist gerade die einfachste Veranschaulichung hierfür, indem jeder Pfeil die Hauptachse des Bewegungsraums anzeigt. In der Mathematik werden die hier entstehenden Raumkonstruktionen als differenzierbare Mannigfaltigkeiten bezeichnet und systematisch untersucht.

Die Bewegung verläuft entlang der Achsen der Eigenbasis jeweils linear. Die Eigenbasis ist die innere Symmetrie der Bewegung. Die Theorie der Diffentialgleichungen konnte erheblich transparenter gestaltet werden, indem konsequent die Differentialgleichungen entlang der Achsen der Eigenbasis aufgestellt und gelöst wurden.

An die Stelle intuitiver Lösungen tritt der systematische Einsatz der linearen Algebra in der Theorie der Differentialgleichungen. Am klarsten ist dies in den Lehrbüchern von Arnold herausgearbeitet. Im nachhinein wird deutlich, dass die intuitiven Lösungen im Grunde darin bestanden haben, dass für eine bestimmte Bewegung die Eigenbasis erraten worden war.

Besonders in den 50er Jahren gab es in der Kunst zahlreiche Versuche, mathematische Strömungen in Bildern darzustellen, so auf ganz verschiedene Weisen im action painting von Pollock, den Nagelfeldern von Uecker oder verschiedenen orphischen Bildern, die eher Lichtströme zeigen.

Polarisation und Resonanz (Pfauenrad und sound)

Trotz allem bleibt die anschauliche Vorstellung der differenzierbaren Mannigfaltigkeiten irgendwie schwerfällig. Der Basisraum ist so etwas wie ein großer Kasten, durch den sich die Bewegungskurve zieht. An jedem Punkt der Bewegungskurve kann wieder ein (anschaulich kleinerer) Kasten montiert werden, der alle Punkte enthält, zu denen hin von hier aus die Bewegung weitergehen kann. Schon das einfache Beispiel mehrerer gekoppelter Pendel zeigt aber, wie diese Darstellungsweise in unübersichtlich viele Freiheitsgrade zu explodieren droht und dadurch unanschaulich und der wirklichen Realität unangemessen wird.

Ein ganz anderer Ansatz entsteht, wenn eine Bewegungskurve als Überlagerung (Summe) einfacher Sinus-Funktionen dargestellt wird:

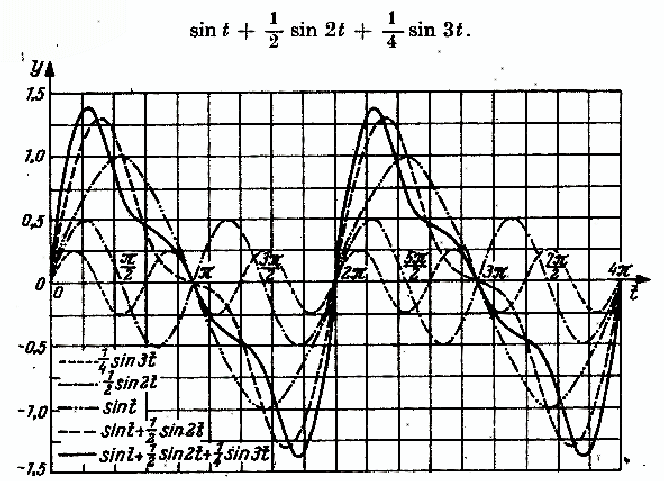
Figur 1 Überlagerung von Sinuskurven

aus: G.M. Fichtenholz: Differential- und Integralrechnung, Band III, Berlin 1974, S. 409, Abb. 121

Durch einen Lehrsatz der Mathematik (Satz von Weierstraß) wird nachgewiesen, dass wirklich alle denkbaren Kurven zumindest abschnittsweise durch einfache Sinus-Funktionen beliebig genau angenähert werden können.

Und ohne auf weitere mathematische Fragen einzugehen legt dies Beispiel den Ansatz nahe, dass jede mathematische Funktion f(x) durch folgende Formel "entwickelt" werden kann (Fourier-Reihe):

f(x) = a₁*sin x + b₁*cos x + a₂*sin 2x + b₂*cos 2x + a₃*sin 3x + b₃ *cos 3x + ...

Das bedeutet, dass zumindest abschnittsweise alle Funktionen f(x) aus den gleichen "Bausteinen" sin x, cos x, sin 2x, cos 2x, ... aufgebaut sind und sich nur darin unterscheiden, mit welchen Faktoren a₁, b₁, a₂, b₂ ... die Bausteine gewichtet sind.

Variationen der Bewegungskurve werden in dieser Vorstellung nicht mehr dadurch veranschaulicht, dass die Kurve auf ihrem Weg durch den Raum an jedem Punkt einen neuen Bewegungsraum betritt, der alle offenen Möglichkeiten für die weitere Fortsetzung des Weges bereithält, sondern indem die Zusammensetzung aus den Bausteinen sin x, cos x, sin 2x, cos 2x ... geändert wird.

Für diese Änderung sind zwei Möglichkeiten denkbar:

• Die Zusammensetzung der gesamten Funktion wird geändert. Das soll sich so auswirken, dass das Erscheinungsbild der Kurve im bisherigen Verlauf unverändert bleibt, dann aber die gewünschte neue Richtung genommen wird. Dadurch bleibt eine einheitliche Funktion für die gesamte Bewegung erhalten, aber es ist klar, dass dies in der Regel nur mit großem Rechenaufwand und einer sehr komplizierten Darstellung möglich ist.

• Die Funktion wechselt in einen neuen Abschnitt, in dem sich gegenüber dem vorigen die innere Zusammensetzung ändert. In diesem Fall liegen im Grunde zwei verschiedene Funktionen vor, die dann aber geeignet "verklebt" werden müssen, was mathematisch möglich ist. Im Grenzübergang werden die einzelnen Abschnitte immer kürzer und "schrumpfen" schließlich auf Punkte zusammen, und die Funktion wird punktweise durch Sinus-Funktionen angenähert. In diesem Grenzfall ist wieder das ursprüngliche Bild der differenzierbaren Mannigfaltigkeit erreicht, indem jetzt aber die Eigenbasis des Bewegungsraums die Bausteine aus den Sinus- und Cosinus-Funktionen sin x, cos x, sin 2x, cos 2x ... sind, aus denen die Bewegung an dieser Stelle zusammengesetzt wird. (Räume mit dieser Struktur werden als Hilbert-Räume bezeichnet und systematisch in der Funktionalanalysis studiert.)

Noch deutlicher wird die veränderte Anschauung vielleicht im zweidimensionalen Fall. Hier werden zweidimensionale Wellenmuster als Überlagerung einfacher Wellenmuster "aufgebaut". Ohne mathematische Rechnungen ist das in einfachen Experimenten z.B. dadurch möglich, dass am Rande eines Wasserbeckens Pulsgeber (Oszillatoren) angebracht werden, die sich regelmäßig bewegen und dadurch Wellen erzeugen. Wird nur ein Pulsgeber bewegt, entsteht ein sehr einfaches Muster. Wenn mehrere bewegt werden, überlagern sich die von ihnen erzeugten Muster. Unendlich viele Variationen können sehr einfach erzeugt werden, indem die Anzahl der Pulsgeber und ihre Bewegungsperioden verändert werden.

Die Funktionen sin x, cos x, sin 2x, cos 2x ... zur Darstellung der mathematischen Funktion sind hier technisch durch die Pulsgeber (Oszillatoren) ersetzt, und die Faktoren a₁, b₁, a₂, b₂ ... erhalten die anschauliche Bedeutung, wie viele der jeweiligen Pulsgeber angeschaltet sind. Schon im zweidimensionalen Fall kommt allerdings zusätzlich hinzu, dass die Pulsgeber nicht alle an einem einzigen Punkt "aufeinander" (bzw. übereinander) angebracht sind, sondern in einer bestimmten räumlichen Verteilung, die ebenfalls bei der Berechnung des entstehenden Wellenmusters berücksichtigt werden muß.

Auch viele der heute gängigen Bildschirmschoner am PC nutzen dieses Prinzip und zeigen, wie mit einfachen mathematischen Funktionen eine unglaubliche Vielfalt von Bildern gezeichnet werden kann.

In der Physik war diese Vorstellung schon lange bei der Zerlegung von Tönen in Obertöne bzw. des Lichts in das Farbspektrum bekannt. Wenn auf verschiedenen Instrumenten der gleiche Ton gespielt wird, entsteht doch jedes Mal eine andere Klangfarbe, da die Obertöne verschieden stark mitschwingen. Die Zerlegung des Klangs in den Ton und die Obertöne entspricht mathematisch genau der oben dargestellten Entwicklung einer Funktion in die Bausteine sin x, cos x, sin 2x, cos 2x, ... , wobei hier für x der Grundton und für 2x, 3x, ... die Obertöne eingesetzt werden. Die Faktoren a₁, b₁, a₂, b₂ ... geben dann die Intensitäten an, mit denen auf dem jeweiligen Instrument der Grundton und die Obertöne schwingen.

Im 20. Jahrhundert wurde dieser Ansatz in der Physik in weiteren Gebieten zunächst in der Atomspektroskopie und dann allgemeiner in der Quantenfeldtheorie eingeführt und dient heute praktisch als allgemeine Grundlage aller physikalischen Naturbeschreibungen. In der Atomspektroskopie wird das Licht gemessen, das von den verschiedenen chemischen Elementen ausgestrahlt wird. Die Messungen zeigen, dass jedes Element sein eigenes typisches Farbspektrum hat, d.h. es strahlt nur Licht mit bestimmten Wellenlängen aus. Das wird so erklärt, dass in jedem chemischen Element die Elektronen nur auf bestimmten Bahnen um den Atomkern kreisen können. Durch Aufnahme bzw. Abgabe von Photonen vergrößern bzw. verkleinern sie ihre Energie und springen von einer der möglichen Bahnen auf eine andere. Die möglichen Bahnen des Elektrons werden als seine Zustände bezeichnet. Im Grundzustand hat es die geringste Energie, bei Aufnahme von Photonen springt es in Zustände mit höherer Energie. Die Wellenlängen des ausgestrahlten Lichts ergeben sich aus den Energiedifferenzen zwischen den Zuständen, in denen sich das Elektron befinden kann.

So wie ein Klang in den Grundton x und die Obertöne 2x, 3x, ... zerlegt wurde, wird in der Quantenfeldtheorie der Zustand eines Teilchens (z.B. eines Elektrons) zerlegt in einen Grundzustand x und höhere Zustände 2x, 3x, ... usw. Der Grundzustand bedeutet den stabilsten Zustand mit der geringsten Energie, wo das Teilchen keine Energie abgeben kann. Die höheren Zustände (die auch als angeregte Zustände oder mißverständlich als Resonanzen bezeichnet werden) zeigen dagegen Situationen, in denen das Teilchen Energie aufgenommen hat und daher auch wieder Energie abgeben kann. Die Zustände sind bezogen auf den Grundzustand durch ganzzahlige "Abstände" 2x, 3x, ... usw. unterschieden.

Insgesamt können nun die Wahrscheinlichkeiten a₁, b₁, a₂, b₂ ... gemessen werden, mit denen sich das Elektron in einem der möglichen Zustände befindet. Das Farbspektrum eines chemischen Elements zeigt an, mit welchen Häufigkeiten die Elektronen dieses Elements bestimmte Energiepakete in Form von Licht abstrahlen, d.h. zwischen den verschiedenen möglichen Zuständen im jeweiligen chemischen Element wechseln. Wann und wie ein Elektron von einem Zustand in einen anderen springt, kann nicht erklärt, sondern eben nur gemessen werden. Wie die Aufnahme bzw. Abgabe des Photons wirklich ablaufen, ist ebenfalls unbekannt. Und weiter ist unbekannt, wie der Weg des Elektrons aussieht, wenn es von einer Umlaufbahn in eine andere springt.

Dennoch ist mit der Polarisation ein Ansatz gefunden, einen komplexen Zustand (wie einen Klang oder die Wahrscheinlichkeitsverteilung der Zustände eines Teilchens) zu zerlegen und ihn mit anderen komplexen Zuständen zu vergleichen und die Möglichkeiten seiner Veränderung zu erkennen. Die Geschichte der Polarisation zeigt einige Parallelen zur Entstehung des Ableitungsbegriffs: So wie dort durch Messungen der Geschwindigkeit die Ergebnisse der Ableitung geprüft und bestätigt werden konnten, können hier die Wahrscheinlichkeitsverteilungen der Zustände oder die Schwingungen der Obertöne gemessen werden und zeigen dadurch die Richtigkeit des Ansatzes, den Zustand durch Funktionen sin x, cos x, sin 2x, cos 2x, ... aufzubrechen.

Entsprechend ist der mathematische Ansatz zur Beschreibung einer Bewegungskurve im Quantenfeld zu erweitern. Zunächst einmal bewegt sich ein Teilchen wie gewöhnlich entlang einer räumlichen Kurve. An jedem Punkt ist jedoch zusätzlich durch die Polarisation (physikalisch durch Streu- und Beugungsverteilungen) zu messen, mit welchen Wahrscheinlichkeiten sich das Teilchen an dieser Stelle in einem der Zustände befindet. Wenn sich das Teilchen bewegt, verändert es zum einen seine räumliche Lage, zum anderen kann es Energie aufnehmen oder abgeben und dadurch zwischen den Energiezuständen hin und her springen. Mit welchen Wahrscheinlichkeiten es von einem Zustand in einen anderen wechseln kann, wird in physikalischen Experimenten gemessen und als Übergangswahrscheinlichkeit bezeichnet. Hier können experimentell zahlreiche Regelmäßigkeiten bzw. Ausschließungsprinzipien (unmögliche Zustandsänderungen) nachgewiesen werden. In allen Fällen interpretiert die Quantenfeldtheorie den Vorgang nach dem Muster, das zuerst in der Atomspektroskopie entdeckt worden war: Zustandsänderungen sind möglich, indem das jeweilige Teilchen ein Feldquantum (z.B. das Photon im elektrodynamischen Feld) aufnimmt bzw. abstrahlt.

Damit wird konsequent die Vorstellung aufgegriffen, dass Variationen einer Bewegungskurve möglich sind, indem die Zusammensetzung ihrer Bausteine geändert wird. Die mathematischen Funktionen sin x, cos x, sin 2x, cox 2x, sin 3x etc., aus denen die Funktion zusammengesetzt wird, erhalten systematisch die physikalische Bedeutung, welche Energie ein Teilchen hat. Wenn es sich im Quantenfeld bewegt, ändern sich die Wahrscheinlichkeiten, in welchen Zuständen es sich aufhalten kann. Auf diese Weise können Wechselwirkungen und Anziehungskräfte beschrieben werden. Wird zum Beispiel die Energiezufuhr von außen immer größer, wächst die Wahrscheinlichkeit, dass ein Elektron seine Energie vergrößert und auf äußere Bahnen im Atom springt, bis es schließlich genug Energie hat, sich ganz vom Atomverband (bzw. vom Atomgitter in einem Kristall) zu lösen.

Mit diesem Ansatz werden auch Phänomene beschrieben, für die es zunächst noch keine Erklärung gibt. Wenn etwa ein Teilchen mit einer gewissen (meist natürlich sehr geringen) Wahrscheinlichkeit einen Ort oder einen Zustand erreicht, der nach allen bekannten Theorien unerreichbar fern ist, wird diese Messung nicht verworfen, sondern von einem Tunneleffekt gesprochen. Auch dieser Weg wird mit der gemessenen Häufigkeit bewertet und in die mathematische Gleichung zur Beschreibung der Zustandsverteilung aufgenommen. Wenn diese Gleichung insgesamt dennoch bestimmte Eigenschaften bewahrt, die die Gültigkeit der physikalischen Grundprinzipien sicherstellen, kann der Tunneleffekt wenigstens formal integriert werden. Gerade diese Fälle zeigen aber besonders deutlich, dass der Ansatz der Polarisation zunächst lediglich ein Weg ist, um in einer ersten Form vollständig das gefundene Beobachtungsmaterial zu ordnen.

Für das Konzept der Polarisation genügt aber nicht die Zerlegung in Funktionen sin x, cos x, sin 2x, cos 2x, ... und das Bestimmen der Koeffizienten a₁, b₁, a₂, b₂ ..., sondern es sind ganze Systeme von Grundtönen, Grundfarben bzw. allgemeiner Grundzuständen zu finden, die alle einzeln polarisiert werden können und insgesamt notwendig sind für die Beschreibung eines mehrdimensionalen Wellenmusters. Der Fall der Atomspektroskopie und der auf ihr aufgebauten Quantenelektrodynamik, wo es nur ein Bewegungsteilchen (das Elektron) und nur ein Feldquantum (das Photon) gibt, ist eine einmalige Ausnahme.

Auch bei der Suche nach Systemen von Grundzuständen dient die Musik als bestes Anschauungsmaterial. Wenn verschiedene Töne miteinander verglichen werden, genügt es, wie bisher ausgeführt, die Schwingungsdauern der jeweiligen Grundtöne und die Intensitäten der zugehörigen Obertöne zu vergleichen. Dann stellt sich aber heraus, dass keineswegs alle Töne schön zusammenklingen, sondern nur die, wo die Grundtöne in bestimmten festen Zahlenverhältnissen zueinander stehen. Die Tonsysteme (wie Pentatonik, Quintenzirkel der Dur- und Moll-Tonarten, aber auch Naturton- oder Mikroton-Systeme) legen die innere Symmetrie der Musik fest. Eine Melodie ist eine Gruppe von Tönen, die der Symmetrie genügen.

Auf ähnliche Weise klingen nur Instrumente mit bestimmten Verhältnissen der Obertöne schön und der Komponist muß intuitiv Melodie, Instrumentation und Rhythmus kombinieren. (Dies sind gewissermaßen die Freiheitsgrade der Musik.) Seine Kompositionstechnik ähnelt insofern der Arbeitsweise des Mathematikers oder Physikers, der ebenfalls nach der geeigneten "Komposition" von Grundbausteinen (fundamentalen Teilchen und Quanten) und Sinus-Funktionen (Wahrscheinlichkeitsverteilung des Quantenaustauschs zwischen den Teilchen) sucht, um die gewünschte Bewegungskurve oder das gesuchte Wellenmuster zu erhalten.

Was für die Musik gesagt ist, ist anschaulich ohne weiteres auf die Malerei zu übertragen. Aus den unendlich vielen verschiedenen Farben sollen Grundfarben ausgewählt werden, die in bestimmten harmonischen (schönen oder häßlichen) Beziehungen zueinander stehen. Hierfür kann z.B. das volle Farbspektrum auf einem Farbenkreis dargestellt werden und es zeigt sich, dass gegenüberliegende Farben gut zusammenpassen. Andere Möglichkeiten sind das Farbdreieck mit den Grund- und Komplementärfarben oder die von Goethe vorgeschlagenen Komplementärfarben. Der Maler muß nun intuitiv ein Bild entwerfen, in dem geometrische Formverhältnisse, die Farbzusammenstellung und die Farbkraft der ausgewählten Farbtypen eine gelungene Komposition ergeben.

Während die Tonsysteme als Schöpfungen der Musikgeschichte noch klar erkennbar sind, gilt das System der Grundfarben (rot, blau, gelb) als so selbstverständlich, dass es einer eigenen Überlegung bedarf, seine Besonderheiten zu entdecken. Wenn dies aber gelingt, wird von einer anderen Seite aus die tiefe Bedeutung der Polarisation bewußt. Sehr deutlich hat Wittgenstein in seinen späten Schriften auf dies Problem hingewiesen. In den "Philosophischen Untersuchungen" heißt es z.B. in Punkt 239: "Wie soll er wissen, welche Farbe er zu wählen hat, wenn er 'rot' hört? - Sehr einfach: er soll die Farbe nehmen, deren Bild ihm beim Hören des Wortes einfällt. - Aber wie soll er wissen, welche Farbe das ist, 'deren Bild ihm einfällt'? Braucht es dafür ein weiteres Kriterium? (Es gibt allerdings einen Vorgang: die Farbe wählen, die einem beim Wort .... einfällt.) ''Rot' bedeutet die Farbe, die mir beim Hören des Wortes 'rot' einfällt' - wäre eine Definition. Keine Erklärung des Wesens der Bezeichnung durch ein Wort." (Wittgenstein, Werkausgabe Bd. 1, s. 355) Und so beleuchtet er von immer neuen Seiten die Frage, wie es möglich ist, dass sich alle verstehen und offensichtlich dasselbe meinen, wenn von den Grundfarben wie 'rot' die Rede ist. Wenn zum Wort 'rot' ein 'Bild einfällt', hat die Grundfarbe 'rot' offenbar die Bedeutung eines Symbols mit einer Aussagekraft, die weit über die Wellenlänge hinausgeht, mit der die Physiker die Farbe 'rot' identifizieren mögen. Denn niemand braucht diese Wellenlänge nachzumessen, damit zu 'rot' ein Bild einfällt.

Polarisation in ein Farbspektrum gewinnt damit die qualitative Bedeutung, einen komplexen Zustand in seine 'rote', 'grüne', 'gelbe', 'blaue' usw. Seite zu zerlegen, und zwar so, dass jeder unmittelbar die symbolische Bedeutung der Farben versteht. "Und so weiter ...": Allein die Frage, wieviel Grundelemente, in diesem Fall, wieviel Grundfarben es gibt, ist von größtem Interesse. Sind es 3 ('rot', 'gelb', blau') oder 4 (wie im System der Elemente, wo es 'braune Erde', 'gelbe Luft', blaues Wasser', 'rotes Feuer' gibt) oder 5 (indem 'schwarz' und 'weiß' zu den 3 Grundfarben hinzukommen, was oft in der chinesischen Tradition angeommen wird), oder doch 4 (wie im Opus der Alchemie mit 'scharz', 'weiß', 'gelb', 'rot') ?

Die Anzahl der Grundfarben kann sicher nur verstanden werden, wenn transparent ist, wodurch aus den potentiell unendlich vielen (beliebig fein abgestuften) Farben ein endliches System von Grundfarben ausgewählt wird, das sich durch eine innere Harmonie und allgemein verständliche Symbolkraft auszeichnet. Wie einfach hat es da doch die Musik, wo in den verschiedenen Tonsystemen in der Regel sogar mathematisch präzise definiert ist, in welchem Verhältnis die Grundtöne zueinander stehen und alle anderen Töne ausgeschlossen sind. Wird der Frage von Wittgenstein weiter nachgegangen, ist es also nicht einfach das Problem, dass zu einer einzelnen Farbe wie 'rot' ein 'Bild einfällt', sondern dass intuitiv die Farbe 'rot' im Zusammenhang eines Systems von Grundfarben gesehen wird, in dem 'rot' seinen bestimmten Stellenwert hat. Denn nur dann ist sichergestellt, dass alle unter 'rot' das gleiche meinen, auch wenn dem einen vielleicht das Bild der Morgensonne, dem nächsten die Rose oder das Haltesignal der Ampel dazu einfällt. Sicherlich handelt es sich in allen Fällen um Farben mit unterschiedlicher Wellenlänge, und doch sind sie durch ihren Standort im System der Grundfarben deutlich genug identifiziert. Im Extremfall ist sogar vorstellbar, dass dem einen ein Bild zu 'blau' einfällt, welches ein anderer eher unter 'rot' sehen würde, und sich doch beide verstehen.

Dies erklärt auch, warum alchemistische Texte im ersten Moment so furchtbar wirr erscheinen und jedes Symbol in unterschiedlichen Zusammenhängen geradezu einander widersprechende Bedeutungen erhalten wird, und sich die Alchemisten dennoch gut verständigen konnten. Genau hiermit schlug sich Kant herum, als der "Zinnober" nicht in die Systeme der "Kritik der reinen Vernunft" passen wollte. Entgegen vorschneller Kritik an Kant ist aber zu betonen, dass er damit die Existenz des Zinnober keineswegs abgestritten, sondern im Gegenteil sehr präzise eine Frage aufgeworfen hat, der sich die Mathematik in ihrer weiteren Geschichte mit dem Begriff der differenzierbaren Mannigfaltigkeit ein wenig genähert hat. Bei der Polarisation stellt sie sich nun dringender und es kann die These aufgestellt werden, dass die Polarisation für differenzierbare Mannigfaltigkeiten die Bedeutung erhält, die der Sprung (und die dialektische Aufhebung) für die klassische Mathematik hatte.

Denn hier wird genau das alte Problem der Chemie und allgemeiner der Mathematik aufgegriffen, das sich beim Übergang von der lokalen zur globalen Ebene stellte. Nun wird nicht mehr einfach von den unendlich vielen Farben oder Tönen auf der globalen Ebene zu einer lokalen Betrachtung gesprungen, sondern aus den unendlich vielen Farben oder Tönen wird ein endliches System qualitativ ausgezeichnet und mit Symbolen angesprochen, die eine unmittelbare Anschauungskraft entfalten. Zwischen ihnen werden harmonischen Beziehungen studiert, die dann lokal gemessen werden können.

Die Systeme der Grundelemente übernehmen die lokale Seite und die aus ihnen nach dem Vorbild der Fourier-Reihe entwickelten zusammengesetzten Funktionen (bzw. komplexen Klänge oder Mischfarben) die globale Seite. Zwischen der lokalen und globalen Ebene vermittelt die Fourier-Reihe. Wenn es wie im Fall der Elektrodynamik nur ein Grundelement gibt, ist der Weg sehr einfach. Wenn es dagegen mehrere Elemente gibt, nimmt die Funktion die mehrdimensionale Gestalt an:

f(x₁, x₂, x₃, ...) = a₁₁*sin x₁ + b₁₁*cos x₁ + a₁₂*sin 2x₁ + b₁₂*cos 2x₁ + a₁₃*sin 3x₁ + ...

+ a₂₁*sin x₂ + b₂₁*cos x₂ + a₂₂*sin 2x₂ + b₂₂*cos 2x₂ + a₂₃*sin 3x₂ + ...

+ a₃₁*sin x₃ + b₃₁*cos x₃ + a₃₂*sin 2x₃ + b₃₂*cos 2x₃ + a₃₃*sin 3x₃ + ...

Hier bedeuten x₁, x₂, x₃, ... die Grundelemente, die ihrerseits wiederum jeweils in Grund- und Obertöne zerlegt werden. Gleichzeitig zeigt diese mehrfache Entwicklung sehr deutlich die beiden verschiedenen Seiten der Polarisation, die leicht zu Verwechslung führen können (im Opus der Alchemie werden sie als Nigredo und citrinitas bezeichnet). Auf der einen Seite (oder am Anfang) steht die qualitative Zerlegung in Grundelemente, dann folgt für jedes Grundelement die Zerlegung in die Obertonreihe (mathematisch die Fourier-Reihe).

Genau an diese Fragen stößt die Physik seit Formulierung der Quantenfeldtheorie und der Suche nach inneren Symmetrien zwischen den Grundelementen. (In der Physik werden solche Symmetrien als Eichgruppen bezeichnet, in der Mathematik als Hauptgruppen, wo in differenzierbaren Mannigfaltigkeiten an allen Punkten Fasern ergänzt werden, die die Gruppeneigenschaft tragen.) Die unendlich vielen verschiedenen Partikel als kleinste Bausteine der Physik sollen eine innere Struktur, eine innere Symmetrie erhalten, und zwar so, dass sie die Methode der Polarisation erlauben. Die Partikel sollen qualitativ gebrochen werden in die Grundelemente einer tiefer liegenden Schicht, und für dieses tiefer liegende System von Elementarteilchen sucht die Physik nach Begriffen mit symbolischer Kraft.

Zur Zeit ist für die Teilchen auf der untersten und noch recht unklaren Ebene für das System der Grundelemente der Ausdruck "Quarkteilchen" nach dem Bild des "Dreikäsehoch" im Roman "Finnegans Wake" von James Joyce eingeführt. Während das Elektron nur eine einzige Ladung besitzt (die elektrische Ladung), werden bei den Quarkteilchen ursprünglich drei verschiedene Ladungen unterschieden, die als Farbladungen oder, um die sprachliche Verwirrung perfekt zu machen, als Aromen bezeichnet werden. So wie Quark in Rot-, Blau- und Grüntönen schimmert, die jedoch insgesamt zur weißen Farbe resultieren, enthält jedes Quarkteilchen Rot-, Blau- und Grünladungen, die zuammengenommen die Quarkteilchen unsichtbar machen.

Die Teilchen der nächsthöheren Ebene, die Hadronen (zu denen z.B. das Neutron und Proton im Atomkern gehören), können dann ähnlich wie die chemischen Elemente danach klassifiziert werden, aus welchen Quarkteilchen sie sich zusammensetzen. Und Hadronen, die sich aus den gleichen Quarkteilchen zusammensetzen, sind dann weiter danach zu unterscheiden, wie stark die jeweiligen Quarkteilchen farblich "aufgeladen" sind, d.h. welche Farbladungen sie tragen.

So wie das Elektron seine Ladung durch Aufnahme oder Abgabe von Photonen ändern kann und hierdurch das elektrodynamische Feld aufgebaut wird, sind für die Farbladungen 3 Gluonen (Klebteilchen) postuliert, die die Farbladung zwischen den Quarkteilchen austauschen. Mit der Existenz von 3 Farbladungen und 3 zugehörigen Gluonen als Feldquanten wird jedoch die Situation gegenüber der Quantenelektrodynamik wesentlich komplexer, die mit dem Photon nur ein Feldquant kennt, da nun auch die Gluonen untereinander wechselwirken können.

Und während es in der Quantenelektrodynamik mit dem Elektron nur ein fundamentales Teilchen gibt, wurde hier schon immer mindestens die Existenz von 3 Quarkteilchen angenommen, die mit den symbolischen Eigenschaften 'up', 'down' und 'strange' (seltsam) bezeichnet wurden. Dann zeigte sich aber, dass die nicht ausreichen, und es kamen ein Zauberteilchen ('charm'), ein Basisteilchen ('bottom', das manchmal auch als Schönheitsteilchen bezeichnet wird, 'beauty') und schließlich ein Spitzenteilchen ('top') hinzu. Nun kann die Zahl 6 ihre symbolische Bedeutung geltend machen, die schon immer als ideal für Bausteine in großen Systemen galt (nach dem Vorbild der sechseckigen Bienenwabe).

Insgesamt entsprechen einander:

	Quantenelektrodynamik	Quantenchromodynamik
Grundelement	Elektron	6 Quarks
Elementarladung	elektrische Ladung	3 Farbladungen
Feldteilchen	Photon	3 Gluonen
angeregte Zustände	Elektron auf höherer Energiebahn	Quarks mit höherer Farbladung
Symmetriegruppe	U(1)	SU(3)

Der Clou an der ganzen Quantenchromodynamik ist aber, dass alle diese Teilchen experimentell nicht isoliert und direkt nachgewiesen werden können, sondern ausschließlich der besseren theoretischen Darstellung der Ergebnisse physikalischer Messungen dienen. Sie lassen sich bis jetzt nur indirekt nachweisen (durch die Widerspruchsfreiheit der zugrunde liegenden Theorie und der experimentellen Bestätigung ihrer verschiedenen Vorhersagen). Durch die zahlreichen Streuprozesse in den Teilchenbeschleunigern, wo Elementarteilchen aufeinander geschossen werden, ist direkt nur nachgewiesen, dass die Elementarteilchen im Innern keine homogene Masse haben, sondern eine körnige Struktur. Konkret stimmen alle Forscher auf dem Gebiet der Teilchenphysik darin überein, dass es noch nicht gelungen ist, die Harmonien zwischen den Quarkteilchen zu beschreiben (z.B. die Unterschiede in ihrer Masse), so dass die Quarkteilchen zwar eine Menge von Grundelementen bilden, aber noch keineswegs ein System. Bisher lassen sie sich nur als Elemente bestimmter mathematischer Gruppen beschreiben, die aber nur für einen Teil der zu erklärenden Eigenschaften eine innere Symmetrie aufzeigen.

Inzwischen wird von einigen Theoretikern daher auch wieder infrage gestellt, ob die 6 postulierten Quarkteilchen wirklich ein System von Grundzuständen bilden und nicht eventuell ihrerseits aus noch kleineren Bausteinen zusammengesetzt sind. Das könnte in der Konsequenz bedeuten, dass einzelne sehr einfache Quarkteilchen die wahren Grundzustände bilden (vergleichbar dem Elektron oder den einfachsten Atomkernen), und die anderen höhere Zustände, die durch Aufnahme neuer Feldquanten entstehen (vergleichbar den Photonen oder Gluonen).

Von den Physikern werden damit nahezu alle bisher bekannten Symbolsysteme zitiert. Mal sind es die Farben (rot, blau, grün), mal Buchstaben (u, d, s, c, b, t), mal symbolische Eigenschaften (strange, charm, beauty, etc.), als Begriff kommen auch noch die Aromen hinzu, für eine noch unterhalb der Quarks liegende Struktur wurden die Bezeichnungen 'tohu' und 'wabohu' aus der Schöpfungsgeschichte im Alten Testament vorgeschlagen. Das zeigt eine tiefe Unsicherheit. Wie im einzelnen die Theorie auch weiter entwickelt werden wird, auf jeden Fall ist die Naturwissenschaft damit an einen Punkt gekommen, wo sie nicht mehr einfach wie bisher mit den vorgefundenen Symbolsystemen auskommt und lediglich durch immer bessere, genauere, differenziertere Messungen zu neuen Erkenntnissen gelangt, sondern ein neues, eigenes Symbolsystem schaffen muß. Bezeichnungen wie seltsame Teilchen oder Zauberteilchen werden zwar gewissermaßen augenzwinkernd eingeführt, als witzige Abkürzungen in komplizierten Rechnungen, die nicht unbedingt ernst genommen werden sollen. Aber dann kommt es doch vor, dass die gleichen Physiker unvermittelt und ohne Vorwarnung in religiöse Deutungen springen, sei es, dass sie buddhistisches Gedankengut ansprechen, oder sich selbst in die Position des ursprünglichen Schöpfers begeben wollen. Da erscheint es doch naheliegender, nach dem Vorbild von Wittgenstein die Situation genauer zu betrachten, die zur Anrufung von Symbolen führt, und sie mit ähnlichen Entwicklungen in der Wissenschaftsgeschichte zu vergleichen.

Im Unterschied zur Mathematik und Physik sind sicherlich in der Musik und der Malerei die Techniken der Intuition und Bildung von Symbolen besser erkennbar und nachvollziehbar. Musik und Bilder haben eine direkte sinnliche Wirkung, während in der Mathematik die geeignete Veranschaulichung erst gefunden werden muß.

Dadurch sind Musik und Malerei gut geeignet, auch für die Mathematik die Techniken der Intuition verständlich zu machen. Letzten Endes geht es um die Frage, ob überhaupt die Suche nach einem neuen Symbolsystem in der Physik erfolgversprechend ist, d.h. um die Frage, ob die Methoden der Polarisation eine Korrespondenz zwischen Aussagen der Theorie und wirklichen Prozessen in der Natur herstellen können. Als Antwort gibt es bis heute nur die Möglichkeit, von einigen nicht weiter erklärbaren Grundannahmen auszugehen, die für die Symbolsysteme einen Begründungszusammenhang liefern und für die Mathematik orientierend wirken. Hierbei ist besonders wichtig die Unterscheidung der verschiedenen Seiten der Polarisation. Sie hat sowohl die qualitative Bedeutung, Systeme von Grundzuständen oder Grundeigenschaften zu erkennen, als auch die quantitativ meßbare und mathematisch berechenbare Aussage, wenn zwischen einem Grundzustand und den höheren Zuständen unterschieden wird, die zur Entwicklung in die Funktionen sin x, cos x, sin 2x, cos 2x, sin 3x, ... führt.

A	Bei allen Bewegungen in der Natur gibt es Bewegungsparameter, wonach die Bewegung qualitativ so in endliche Grundbausteine gebrochen (polarisiert) werden kann, dass die komplexe Bewegung sich durch eine Obertonreihe (mathematisch: Fourier-Reihe) des Bewegungsparameters entwickeln lässt.
B	Die Grundtöne (Grundfarben, Grundelemente etc.) bilden ein endliches System. Beispiele: Tonsystem, Grundfarben, System der Elementarteilchen bzw. eine Ebene tiefer der Quarks.
C	Zwischen den Grundelementen gibt es Harmonien. Beispiele: Terz, Quint etc. in der Musik, Komplementärfarben, algebraische Strukturen der Teilchen und Quarks.
D	Die Grundelemente werden durch Pulsgeber (Oszillatoren) erzeugt, z.B. die Töne durch Instrumente, die Farbspektren durch die periodische Bewegung des Elektrons usw.
E	Die Pulsgeber (Instrumente, chemische Elemente etc.) befinden sich ihrerseits in einem System, in dem sie sich wechselseitig durch Resonanzwirkungen beeinflussen. In der Musik wird ein solches Resonanzsystem als sound bezeichnet und stellt eine Wechselwirkung zwischen Spielern, Hörern und der gespielten Musik her.
F	Hermetische Systeme gehen weiter, indem die qualitative Bedeutung der Grundelemente hervorgehoben wird und Relationen zwischen den Grundelementen verschiedener Naturbereiche hergestellt werden. Die Möglichkeiten sind schier unendlich und charakterisieren die jeweiligen Systeme. Beispiele: D-Dur ist blau, A-Dur ist rot, Planeten werden Wochentagen, Jahreszeiten Charaktertypen, Temperamente chemischen Elementen zugeordnet usw.

Letztlich kann einfach gesagt werden: Naturforschung kann immer von intuitiver Erfassung der Naturschönheit ausgehen und findet mit der Polarisation ein geeignetes mathematisches Hilfsmittel.

Während in vielen Fällen die Zustände und Bewegungen einzelner Teilchen bereits mathematisch mit Faserbündeln (und physikalisch mit Eichfeldern) beschrieben werden können, bereitet der im Axiom E angesprochene Übergang zum Resonanzsystem noch größte Schwierigkeiten. Wieder ist die Musik das beste Beispiel. Jedes Konzert zeigt, wie zwischen den Spielern und den Hörern ein "Funke überspringen" kann oder auch nicht, wie gut den Spielern das Zusammenspiel gelingt und schließlich, wie weit jeder Spieler der Musik einen "Ausdruck" zu verleihen vermag, der über die bloße Werktreue hinausgeht. (Wittgenstein hierzu in den "Philosophischen Untersuchungen": "Sing dies Lied mit Ausdruck! Und nun sing es nicht, aber wiederhole den Ausdruck." ebd., s. 384)

In der Physik werden jedoch zunehmend Erscheinungen beobachtet, die die Existenz von Resonanzsystemen zeigen:

Supraleitfähigkeit: Wenn ein Metall erhitzt wird, verlangsamt sich die Bewegung der freien Elektronen in dem Metall, ohne dass dadurch die Leitfähigkeit wesentlich verändert wird. Wird dann aber ein kritischer Wert überschritten, ordnen sich die Elektronen neu und das Elektronengas kann ohne Streuung und elektrischen Widerstand durch das Metallgitter strömen. Dadurch wird die Leitfähigkeit sprunghaft verbessert und die Supraleitfähigkeit hergestellt.

Plasma: In diesem Fall wird einem Gas Energie zugeführt. Zunächst geschieht dadurch nicht viel. "Doch wenn die Energie auf eine bestimmte Weise zugeführt wird, ist die Wirkung geradezu spektakulär. Es ist, als hätte man ein Musikinstrument angeschlagen oder als beginne ein Weinglas in Resonanz mit der Stimme eines Sängers zu schwingen. In diesem Fall beginnt das Elektronengas nämlich, sich als Ganzes zu bewegen. Es schwingt wie eine riesige Sprungfeder und wie im Falle des Supraleiters tragen alle Elektronen im Gas zu diesem neuen allgemeinen Tanz bei. (...) Die Plasmaschwingung in einem Metall ist feiner verästelt und komplizierter als der supraleitende Zustand, weil eine neue Beschreibungsebene erforderlich ist, auf der sich die Elektronen in einem Metall teilweise als Individuen verhalten, aber gleichzeitig zu einer großräumigen, kohärenten Schwingung beitragen. Die Wellenfunktion für das Plasma wurde ursprünglich von David Bohm entdeckt, der sagte, er habe im ersten Augenblick das Gefühl gehabt, das Plasma sei lebendig." (F. David Peat: "Der Stein der Weisen", s. 102f)

Gravitation: Nach diesen Vorbildern hat Penrose seine Idee für die Entstehung des Graviton entworfen. "In seiner allgemeinen Relativitätstheorie hatte Einstein behauptet, die Gegenwart von Materie - oder Energie - bewirke eine Krümmung der Raumzeit. In Anlehnung daran meint Penrose, der Urkristall erreiche an einem bestimmten Punkt seines Wachstums eine Größe, die ihm erlaube, in seiner Umgebung eine winzige Region gekrümmter Raumzeit zu schaffen. Zunächst gibt es viele verschiedene gekrümmte Raumzeiten, jede von mikroskopischen Ausmaßen, die sich alle überlagern. Doch an irgendeinem Punkt im Zuge des Wachstums wird die Raumzeit so groß, dass ein einzelnes Gravitationsquantum - Graviton genannt - entsteht. Nach Penroses Auffassung gibt es, sobald diese Region der Raumzeit geschaffen worden ist, kein Zurück mehr. Dieser Vorgang, so Penrose, bewirkt den Kollaps der Wellenfunktion von der Mehrdeutigkeit zur Eindeutigkeit." (ebd, s. 116)

In allen diesen Fällen erfolgt ein Umschlag durch den Aufbau eines Resonanzsystems. Das Resonanzsystem bringt "unendlich viele" Teilchen auf der lokalen Ebene in Übereinklang und erzeugt dadurch eine Wirkung, die auch auf der globalen Ebene deutlich sichtbar und meßbar ist. Während z.B. die Bewegung des einzelnen Elektron im erhitzten Metall aus Sicht der klassischen Mechanik "unendlich klein", vernachlässigbar klein ist, erzielt die aus den koordinierten Elektronen erzeugte Supraleitfähigkeit Wirkungen, die in mechanischen Geräten direkt eingesetzt und genutzt werden können.

Mit der Obertonreihe (Fourier-Reihe) war ein erster Ansatz gefunden, den Wechsel von der lokalen zur globalen Ebene zu berechnen und quantitativ meßbar zu machen. Wenn auf Grundlage ganzer Systeme von Grundzuständen die Obertonreihen mehrerer Grundzustände verknüpft werden, können bereits überaus komplexe Übergänge geschaffen werden. Die Symmetrie zwischen den Grundzuständen liefert aber nur den ersten Ansatz, der zu einer Koordination auf lokaler Ebene mit Wirkungen in den globalen Bereich hinein führt. Durch Resonanz können auch zwischen gleichartigen Grundelementen potenzierte Wirkungen erzielt werden. Die Resonanz stellt insofern gewissermaßen eine höhere Form von Symmetrie dar. Ihre besondere Bedeutung wird treffend durch den "Eindruck" belegt, dass Resonanzsysteme erste Formen von Leben darstellen. In anderen Theorien werden solche Übergänge auch als Selbstorganisation bezeichnet, um anzudeuten, wie sich hier Bewußtsein und Subjektivität entwickeln.

Bisher kannte die Mathematik zur Schließung "offener Stellen" nur den Begriff des Sprunges, womit von der lokalen zur globalen Ebene (und umgekehrt) gewechselt werden kann und womit der Wechsel der Symbole im Grenzübergang gedeutet wird. Was im Moment des Sprungs wirklich geschieht (ob z.B. etwas bewußt zu einem Sprung ansetzt oder wie von einer überwältigenden Welle in einen Sprung fortgerissen wird), war unklar und wurde aus der Wissenschaft ausgeklammert. Beim Aufbau von Resonanzsystemen ist die Wechselwirkung zwischen vielen beteiligten Elementen unübersehbar. Hier gibt es nicht mehr einen einzigen Sprung, und mit einem Schlag ist alles da, sondern es wird eine neue Berechnung nötig und möglich. Die Polarisation gibt daher Anlaß, die bisherige Begriffsbildung erneut zu überprüfen und in einen größeren historischen Zusammenhang zu stellen. Das wird auch daher notwendig, wo die Physik seit langem wieder gezwungen ist, neue Symbole zu finden. Alle weggeschobenen "unwissenschaftlichen" Fragen kehren wieder, wie zum Beispiel, was Leben ist und wie Subjektivität entstehen kann.

Literaturhinweise

© tydecks.info 2002