Drei Fragen der Quantenphysik
an den Buddhismus

Beitrag für den Themenkreis Naturwissenschaft und Technik von 50plus aktiv an der Bergstraße am 23.5.2018 in Bensheim

 

Einleitung

Seit gut 100 Jahren wurde mit der Quantenphysik die klassische Naturwissenschaft abgelöst, und doch kann bis heute niemand für alle überzeugend sagen, was sie bedeutet. Stattdessen gibt es vier Erklärungsansätze, die sich wechselweise ausschließen. Kann der Buddhismus eine Antwort geben, was ein solches Tetralemma über den Menschen und sein Denken aussagt? Bestätigt es tiefe Grundannahmen des Bedingten Entstehens (pratitya-samutpada), und kann es zu einer religiösen Neuorientierung der Naturwissenschaftler führen, deren aufgeklärte Grundhaltung eng mit der klassischen Physik Newtons verbunden war?

Die Naturgesetze der Quantenphysik beziehen sich ausschließlich auf Möglichkeiten. Experimentell beobachtet und gemessen werden kann dagegen nur, was wirklich geschieht. Im Moment der Messung kommt es zu einem sogenannten Kollaps des Möglichkeitsraums und der nur in ihm gültigen Gesetze der Quantenphysik. Aber sind diese Gesetze nicht auf ihre Art ebenso wirklich, wenn sich alle ihr Vorhersagen bestätigen, auch wenn sie nur für statistische Gesamtheiten von wahrscheinlichen Ereignissen formuliert sind? Die Quantenphysik fragt nach einem neuen Verständnis des Möglichen, und diese Frage ist bis heute von der westlichen Philosophie noch nicht einmal zur Kenntnis genommen worden. Daraus ergibt sich die zweite Frage an den Buddhismus: Gibt es Wege (karana, samtana), den Raum der Möglichkeiten als solchen zu erfahren, bevor er kollabiert in die jeweilige Wirklichkeit?

Das würde bedeuten, dass es gelingt, in einer kreisförmigen Bewegung in den Raum der Möglichkeiten einzutauchen ohne die Verankerung (alaya-vijnana) im Wirklichen aufzugeben und von dort in die Wirklichkeit zurückzukehren. Was sagt die Quantenphysik dazu? Und was lehrt der Buddhismus über eine zyklische Bewegung in den Bereich des Möglichen und zurück zur Wirklichkeit, der offensichtlich weit über die bekannten Zyklen von Tag und Nacht, der Jahreszeiten und des Lebens und Sterbens hinausgeht?

Fachkenntnisse sind nicht vorausgesetzt, wohl aber Freude an Rätseln der Natur und ungewohnten Arten zu denken. Fragen sind ausdrücklich erwünscht.

Das Tetralemma der Quantenphysik und die buddhistische Logik

Angesichts der Quantenphysik stößt das Denken an Grenzen. Kann etwas zugleich Welle und Teilchen sein? Wir könnten nichts sehen, wenn nicht mittels der Photonen in unserem Auge eine Art Schattenwurf der äußeren Dinge entstehen würde. 2016 konnte nachgewiesen werden, dass unser Auge sogar einzelne Photonen erkennen kann (scinexx vom 20.7.2016). Bei Schallwellen ist es anders. Geräusche verbreiten sich wellenförmig, und daher kann sie das Ohr nur schwer lokalisieren. Aber die Photonen verhalten sich mal wie Teilchen und mal wie Wellen. Beim Doppelspaltexperiment werden Photonen (oder andere Teilchen) durch zwei Öffnungen einer Mauer geschossen. Statt ihre Bahn geradlinig fortzusetzen, erscheint jede Öffnung wie eine Quelle, aus der wellenförmig die einzelnen Wege hervorgehen. Dadurch wird auf einem rückwärtigen Schirm von den auftreffenden Teilchen ein Interferenzmuster erzeugt, das aus Sicht der klassischen Physik unerklärlich ist.

Jeder kennt das Doppelspaltexperiment vom Fußballtraining beim Schießen durch eine Torwand mit zwei Öffnungen. Es braucht nur hinter der Torwand ein Netz aufgespannt zu werden. Wer scharf genug schießt und trifft, dessen Ball wird auf einer geraden Linie durch eine Öffnung hindurch fliegen und auf das dahinter aufgespannte Netz treffen. Dort werden alle Bälle in zwei kleinen Kreisen landen, die wie ein Schatten hinter den beiden Öffnungen sind. Völlig anders verhält es sich in der Quantenwelt.

      

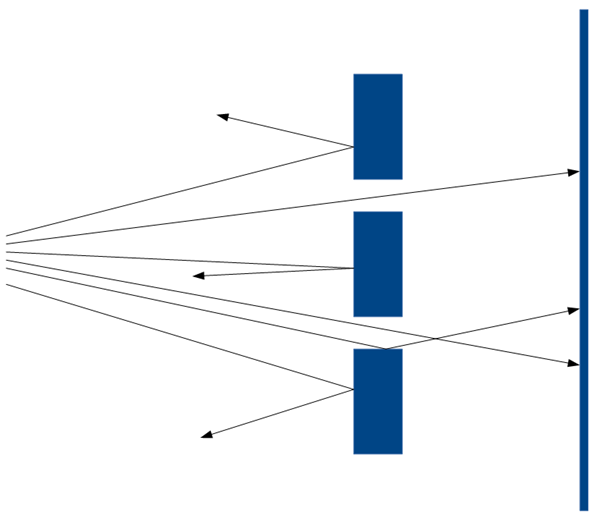
Abb. 1a, 1b: Doppelspalt-Versuch: Diskretes und Interferenz-Muster
Diskret: Die Objekte werden wie bei der Torwand nach den Reflexionsgesetzen von der Wand zurückprallen, von den Innenwänden reflektiert oder fliegen geradlinig hindurch.
Welle: Die Objekte breiten sich wie eine Welle aus und erzeugen ein Interferenzmuster

Wie ist das zu erklären? (i) Es wird einfach physikalisch beschrieben, was hier geschieht, ohne zu verstehen, warum es so ist. (ii) Oder es wird nach einer mathematischen Formel gesucht, mit der sich die Messergebnisse einheitlich beschreiben lassen, ohne zu verstehen, warum diese Formel gültig ist. (iii) Schließlich kann angenommen werden, dass die beteiligten Teilchen über eine bisher unbekannte Eigenschaft verfügen, durch die es zum beobachteten Phänomen kommt. Diese Eigenschaft bekommt den Namen Spin. Ausgerechnet ein ausgewiesener und anerkannter Mathematiker und Physiker wie Roger Penrose (* 1931) spricht von Quantenmagie und Quantengeheimnis (Penrose, 218, Kapitelüberschrift) und schreibt: »Viele Physiker verzweifeln an der Aufgabe, dafür jemals ein Bild zu finden. Statt dessen geben sie sich mit der Ansicht zufrieden, die Quantentheorie liefere kein objektives Bild der physikalischen Welt, sondern bloß ein Berechnungsverfahren für Wahrscheinlichkeiten.« (Penrose, 235) Wenn die Physiker in ihrer Not von Spin sprechen, verbergen sie unter diesem Namen einfach ihr Unwissen: »Doch wie wir sehen werden, zeigt der Spin eines einzelnen quantenmechanischen Teilchens einige höchst seltsame Eigenschaften, die wir nach unserer Erfahrung mit rotierenden Billardkugeln und ähnlichen Dingen ganz und gar nicht erwarten würden.« (Penrose, 257)

Bis heute ist keine für alle überzeugende Antwort gefunden. Zeigt sich hier ein tiefgehendes Tetralemma, in dem sich nach Überzeugung des indischen Philosophen und Buddhisten Nagarjuna (2. Jahrhundert n. Chr.) jedes menschliche Denken befindet? Solange das westliche Denken und nicht zuletzt die Physik in klassischen Bahnen verlief, hat kaum jemand das von ihm aufgestellte Tetralemma (Sanskrit: Catuskoti) verstanden und ernst genommen. Es sieht aus wie ein logisches Rätsel. Wird gefragt, ob eine Aussage A wahr ist, gibt es rein formal vier Möglichkeiten, über die Wahrheit von A zu urteilen:

– A ist wahr
– A ist falsch
– A ist wahr und falsch
– A ist weder wahr noch falsch

Für gewöhnlich werden das dritte und vierte Urteil als unsinnig ausgeschlossen, und für die Logik bleibt der Dualismus übrig: Entweder ist A wahr, oder A ist falsch. Etwas Drittes gibt es nicht (tertium non datur). Nagarjuna behauptet nicht nur, dass auch das dritte und das vierte Urteil gelten können, sondern dass für das menschliche Denken alle vier zugleich gelten und sich gegenseitig bedingen! (Er unterläuft damit zugleich die wenigen Ansätze einer nicht-aristotelischen oder einer dialektischen Logik, die zusätzlich das vierte Urteil ›A ist weder wahr noch falsch‹ zulassen wollen, aber wie die traditionelle Logik davon ausgehen, dass für eine bestimmte Aussage A jeweils nur eins der Urteile gelten kann.) Von einem Tetralemma kann erst dann gesprochen werden, wenn es für alle vier Urteile gute Gründe gibt und keine Entscheidung möglich ist. Das geschieht bei einer Aussage wie ›das Photon ist ein Teilchen‹ oder der komplementären Aussage ›das Photon ist eine Welle‹ oder ›das Photon ist sowohl ein Teilchen wie eine Welle‹ oder ›das Photon ist weder ein Teilchen noch eine Welle›. Bei diesen Aussagen trifft keine der vier Urteilsmöglichkeiten über ihre Wahrheit zu. Was der westlichen Tradition als Tetralemma erscheint, d.h. als eine unauflösbare Blockade in vier sich gegenseitig ausschließende Möglichkeiten, ist für Nagarjuna die einzig richtige Beschreibung des menschlichen Denkens in seiner inneren Vielfalt.

Niemand konnte sich vorstellen, dass die westliche Naturwissenschaft jemals in ein Tetralemma dieser Art geraten könnte. Doch genau das ist mit der Quantenphysik geschehen. Im 20. Jahrhundert haben sich verschiedene Deutungen der Quantenphysik entwickelt, die diesen vier Möglichkeiten entsprechen und unentscheidbar sind. Darauf hat erstmals 2005 Christian Thomas Kohl (* 1945) in seinem Buch Quantenphysik und Buddhismus aufmerksam gemacht. Für ihn ergibt sich die Konsequenz, dass die Deutungen der Quantenphysik ein Beispiel für Bedingtes Entstehen im Sinne des Buddhismus sind. Keine Aussage A und kein Urteil über eine Aussage A kann für sich allein bestehen ohne zugleich die gegenteiligen und über sie hinausführenden Aussagen und Urteile mit zu bedenken. Jede Aussage A und jedes Urteil über die Wahrheit der Aussage A ist daher für sich allein gesehen ‘nichts’. Alle Aussagen und Urteile über Aussagen bedingen sich gegenseitig und hängen voneinander ab.

(1) Objektivismus, Reduktionismus. Irgendwo gibt es eine absolute Substanz, die allem zugrunde liegt, seien dies nun die kleinsten Teilchen, »Quantenobjekte, Energien, Kraftfelder, Naturgesetze & Symmetrien« (Kohl, 194). Wenn wir sie noch nicht kennen, zeigt das nur die Unvollständigkeit unseres aktuellen Wissens. So hatte Einstein gegen die Quantenphysik argumentiert. Weitere typische Vertreter sind bei allen Unterschieden neben Einstein der objektive Idealismus von Platon, die Aufklärung und ihre wichtigsten Vertreter wie der Enzyklopädist d'Alembert, Rutherford, Carnap, die Quantenmechanik von de Broglie und Bohm, Feynman, Koyré, und in der neueren Zeit David Layzer, Henry J. Folse u.v.a. Wittgenstein hat diese Haltung auf den Punkt gebracht und kritisiert: »So bleiben sie bei den Naturgesetzen als bei etwas Unantastbarem stehen, wie die älteren bei Gott und dem Schicksal.« (TLP 6.372) Das Ergebnis sind »wechselwirkungsfreie Grundbausteine der Materie« (Kohl, 195), auf die alles andere zurückgeführt (reduziert) werden kann.

(2) Subjektivismus. Niemand kann mit Sicherheit sagen, ob es eine objektive Welt gibt. Alles besteht nur in unseren Modellen und Konzepten und ist subjektiv. Der britische Physiker und Sachbuchautor Paul C.W. Davies (* 1946) schrieb 1984 programmatisch einen Beitrag Elementary Particles Do Not Exist. Typische Vertreter dieser Richtung sind George Berkeley (1685-1753), der große Gegen-Aufklärer, der dennoch mit seiner Kritik die Philosophie wie kaum ein anderer zu beflügeln vermochte, Ernst Mach (1838-1916), Anreger der Gestaltpsychologie und von großer Bedeutung für Einstein, in neuerer Zeit Nicholas Rescher (* 1928) und John (Johann) Bernhard Stallo.

Bohr: "Es gibt keine Quantenwelt. Es gibt nur eine abstrakte quantenmechanische Beschreibung. Es ist falsch zu denken, dass es die Aufgabe der Physik ist, herauszufinden wie die Natur ist. Physik befasst sich damit, was wir über die Natur sagen können."
Heisenberg: "Atome oder Elementarteilchen sind nicht so real; sie formen eine Welt von Eventualitäten oder Möglichkeiten, anstelle von Dingen oder Fakten."
"Jordan erklärte mit Nachdruck, dass Beobachtungen das, was zu messen ist, nicht nur stören, sondern es produzieren." (Zitate nach Bell, 161)

(3) Sowohl-als-auch, Holismus. Nach der 1927 entstandenen Kopenhagener Deutung werden Objektivismus und Subjektivismus gleichermaßen abgelehnt zugunsten einer Lehre des übergreifenden Holismus. Der Zufall, die Unschärfe und die Komplementarität von Welle und Teilchen gehören ebenso zur Natur der Dinge, wie es zur Natur des subjektiven Beobachters gehört, die von ihm beobachteten Gegenstände ungewollt zu beeinflussen. Für Niels Bohr (1885-1962) gibt es keinen reinen Messprozess, der einfach vor den Augen des Experimentators abläuft und von diesem protokolliert werden kann, sondern es kommt immer zu einer Wechselwirkung der Objekte und den subjektiv gesteuerten Experimenten. Das war schon das Argument von Kant, warum niemals eine reine, das ist mathematische Psychologie möglich ist: Wer von einem Psychologen beobachtet wird, spürt das und verhält sich anders als gewohnt (Kant Metaphysische Anfangsgründe der Naturwissenschaft, Vorwort). Das gilt nach Bohr auch für die Quantenprozesse. Sie verhalten sich unter Beobachtung anders als wenn sie ausschließlich für sich selbst ablaufen. Daher bleibt nur, sich dessen bewusst zu werden und die Wechselwirkung von Subjekt und Objekt bei den Messergebnissen und den auf ihn aufbauenden Theorien zu berücksichtigen. Auch wenn es kaum vorstellbar zu sein scheint, sind umfangreiche mathematische Modelle entwickelt worden, um diesen Bruch (Kollaps) des unbeobachteten Verhaltens im Moment der Beobachtung mathematisch beschreiben zu können. Historisch kann sich diese Richtung auf den griechischen Philosophen Heraklit berufen (»Alles fließt«). Die Romantiker griffen das auf, sowohl Hölderlin wie innerhalb der Philosophie Schelling. Im 20. Jahrhundert stehen Heidegger und dessen Schüler Hans-Georg Gadamer (1900-2002) für diese Richtung wie auch das New-Age-Denken seit den 1970ern. Kohl zitiert Gadamer: »Die schärfere These ist das Zugleich des Einen und des Vielen.« (Gadamer Der Anfang des Wissens, Stuttgart 1999, 4, zitiert bei Kohl, 201). In der Physik sind neben Niels Bohr aus neuerer Zeit Klaus Michael Meyer-Abich (* 1936) und die späteren Arbeiten von David Bohm zu nennen, der »vom Holomovement« spricht (Bohm Die implizite Ordnung, München 1985, 200, zitiert bei Kohl, 204). Über Vertreter wie diese hat der Holismus großen Einfluss bis weit in die Kirchen, die ökologische Bewegung und alle Arten alternativen Denkens bekommen, und in diesem Umfeld ist ein neues Interesse am Buddhismus geweckt worden. Wichtigster Vertreter ist bis heute der aus Österreich stammende kalifornische Physiker Fritjof Capra (* 1939), dessen Bücher Tao der Physik (1975) und Wendezeit (1983) eine neue Generation von Naturwissenschaftlern prägte.

(4) Weder-Noch, Konstruktivismus, Instrumentalismus. Auch wenn sich der Holismus in der 2. Hälfte des 20. Jahrhunderts durchgesetzt hat, muss er sich fragen, worauf er seine Prinzipien gründen will, wenn er weder Objekt noch Subjekt anerkennt. Bleibt die Ganzheitlichkeit in der Luft hängen, wenn es weder Objekte noch subjektive Ideen sind, aus denen sie hervorgeht? Neue Begriffe wie Emergenz helfen nur bedingt weiter, denn was ist es, was da emergiert: Es darf im Sinne des Holismus weder ein Objekt sein, aus dessen Eigenschaften die Emergenz erklärt wird, noch ein Subjekt, in dessen Vorstellung ein Geschehen als Emergenz erscheint. Wie kann der Holismus seine eigenen Prinzipien wie zum Beispiel den Gestalt-Gedanken begründen? Es bleibt nur noch, das jeweilige Modell rein instrumentell (konventionalistisch) zu begründen: Ein Modell ist dann gelungen, wenn es in sich widerspruchsfrei und möglichst einfach ist, und sich zugleich bei der Erklärung der bekannten Phänomene bewährt. Das mathematische Modell und das physikalische Konzept liefern keine physikalische Erklärung. Darauf wird ganz verzichtet. Begriffe gewinnen ihre Bedeutung ausschließlich dadurch, dass sich mit ihnen Modelle konstruieren lassen, die besser als andere alle experimentellen Ergebnisse mathematisch beschreiben können. Daher sind häufig aus Vertretern des Holismus Konstruktivisten und Instrumentalisten geworden. Sie gaben den Anspruch auf, unabhängig von Objekt oder Subjekt für das Ganze und die Ganzheitlichkeit einen eigenen Grund zu suchen, und beschränken sich bewusst darauf, auf die technische Überlegenheit ihrer Modelle zu setzen. Für sie bleibt die Frage nach Objekt oder Subjekt oder beiden nicht nur unbeantwortbar, sondern letztlich auch als wenig hilfreich, um in der Forschung Fortschritte zu erziehen. Für Kohl tendierten schon Bohr und unter den Philosophen Ernst Cassirer (1874-1945) in diese Richtung. Eine eigenständige Richtung formierte sich mit dem Systemtheoretiker Niklas Luhmann (1927-1998) und in der Physik Stephen Hawking (1942-2018), Anton Zeilinger (* 1945) u.a. (Kohl, 12). Für Kohl ist es vor allem Luhmann, »der den Konstruktivismus interessant macht und ihn zu einem führenden Modell für neue Wissenschaft werden ließ, die durch die Stichwörter der Selbstorganisation, Komplexität, Nichtlinearität, Rückkopplung etc. gekennzeichnet sind« (Kohl, 208). Dieser Richtung folgt Ernst Pöppel »Was uns als Realität erscheint, ist eine durch uns selbst bedingte Konstruktion der Realität« (Pöppel Grenzen des Bewusstseins, Frankfurt am Main 2000, 167, zitiert bei Kohl, 208). Kohl nennt weiter Harry Collins, Trevor Pinch, Peter Janich, Wolf Singer, Kuno Lorenz, Hugo Dingler.

Ist es möglich, eine dieser Richtungen mithilfe des Buddhismus aufzuwerten? Diese Gefahr sieht Kohl zum einen bei Capra, der in Tao der Physik den Holismus favorisiert und eine besonders in verschiedenen Kreisen Kaliforniens populäre Philosophie von Holismus, New Age und Buddhismus vertritt, und zum anderen bei Konstruktivisten und Instrumentalisten, wenn diese ihr weder-noch auf die Leere im Sinne des Buddhismus begründen wollen. Dafür steht z.B. der Indologe Kuno Lorenz (* 1932), der 1970 als Professor der Philosophie Nachfolger von Weizsäcker in Hamburg wurde, ein Vertreter des Konstruktivismus von Paul Lorenzen und der dialogischen Logik. Für Lorenz sind die Begriffe und deren mathematische Beziehungen der modernen Naturwissenschaft im Vergleich zu den »wirklichen Dingen« leer und substanzlos und gewinnen ihre Bedeutung nur innerhalb der mathematischen Modelle. Diese Art von Leere und Substanzlosigkeit hat nach Lorenz bereits Nagarjuna vorweggenommen. Für Kohl ist beides eine unzulässige Vereinfachung und einseitige Sicht auf Nagarjuna. Der Buddhismus findet nicht  innerhalb  des Tetralemma seinen Platz, sei es in der Rubrik des Holismus oder des Konstruktivismus, sondern ergibt sich aus der Erfahrung der Unauflöslichkeit des Tetralemma.

Auf ähnliche Weise redeten der Physiker Anton Zeilinger und der 1959 aus Tibet geflohene Tenzin Gyatso (* 1936), der 14. Dalai Lama aneinander vorbei, als sie sich nicht über die Frage von Kausalität und Bedingung einigen konnten. Anton Zeilinger bewegt sich innerhalb des Konstruktivismus und sieht nicht, wie sein Ansatz für eine buddhistische Sicht nur eine Seite innerhalb eines übergreifenden Bedingten Entstehens ist. Mit Bedingtem Entstehen ist nicht gemeint, dass in einem deterministischen, eindimensionalen Verständnis A die Bedingung für B ist (A → B), sondern mit Nagarjuna kann gesagt werden: So wie es kein Gehen gibt, wenn es niemanden gibt, der gehen kann, oder wenn es keine Strecke gibt, entlang derer gegangen werden kann, und umgekehrt keinen Gehenden gibt, wenn es nicht die Bewegung des Gehens gibt oder keine Strecke, entlang derer er gehen kann, und es schließlich keine Strecke für das Gehen gibt, wenn es niemand gibt, der sie geht und keine Bewegung des Gehens, so lässt sich das auf die Quantentheorie übertragen: die sich ausbreitenden Teilchen entsprechen dem Geher, die Ausbreitung dem Gehen und der Raum, über den sie sich ausbreiten, dem gegangenen Weg. Jedes von ihnen kann nur bestehen, wenn es die jeweils beiden anderen gibt und ist durch sie bedingt.

Diese Art zu denken mag als Spielerei erscheinen, aber sie legt zwei Gedanken nahe: Möglichkeit und Zyklizität. Es kann nur ein Gehen geben, wenn es Wege gibt, die gegangen werden können (auf denen das Gehen möglich ist). Die wechselseitige Bedingung aller drei Momente deutet eine innere Zyklizität an, durch die diese Momente miteinander verbunden sind. Im Weiteren wird es darum gehen, die hier angelegten Ideen aufzugreifen, die über das übliche Verständnis von Möglichkeit und Zyklizität hinausgehen.

Kollaps der Möglichkeit in die Wirklichkeit

Gibt es einen sachlichen Grund, warum sich erst die Quantenphysik in ein Tetralemma verfängt, und nicht bereits die klassische Physik? Das erklärt sich für mich aus dem neuen und völlig ungewohnten Verhältnis von Möglichkeit und Wirklichkeit. John Bell hat aus seiner Sicht 1989 kurz vor seinem Tod in einem Beitrag mit dem programmatischen Titel Wider die ‘Messung‘ eine faire Einschätzung gegeben. Schrödinger verstand die Welle ursprünglich ganz anschaulich. »Er versuchte, sich das Elektron als Wellenpaket vorzustellen - eine Wellenfunktion, die nur in einem kleinen Raumbereich nennenswert von Null verschieden ist.« (Bell, 255) Das ließ sich nicht halten. Es folgte 1926 die Wahrscheinlichkeitsinterpretation durch Max Born (1882-1970) als Wahrscheinlichkeitswelle, aus der die Kopenhagener Deutung hervorging. Born war »1921 bis 1933 Professor in Göttingen. Hier entwickelte er unter anderem mit Wolfgang Pauli, Werner Heisenberg, Pascual Jordan und Friedrich Hund große Teile der modernen Quantenmechanik« (Wikipedia-Eintrag zu Born, abgerufen am 18.5.2018). Bell betont:

»Die Wellenfunktion gibt nicht die Dichte von Stoff, sondern vielmehr (als Quadrat ihres Betrages) die Dichte von Wahrscheinlichkeit. Wahrscheinlichkeit wovon genau? Nicht davon, dass das Elektron dort ist, sondern dass es dort gefunden wird, wenn seine Position 'gemessen' wird. Warum diese Abneigung gegen 'sein' und das Bestehen auf 'finden'? Die Gründungsväter konnten kein klares Bild von den Dingen in den entfernten, atomaren Größenordnungen formen. Sie wurden sich des dazwischenliegenden Apparates deutlich bewusst; und der Notwendigkeit für eine 'klassische' Basis, von der aus auf das Quantensystem eingewirkt wird. Deshalb die fragwürdige Spaltung« in beobachtetes System und beobachtenden Messapparat. (Bell, 255)

Physiker wie Paul Dirac waren sich der Mängel bewusst, stellten sie aber erst einmal zurück und hofften, das später lösen zu können. »Er erwartete Entwicklungen in der Theorie, die diese Probleme in völlig neuem Licht erscheinen lassen würden. Es wäre Verschwendung von Mühe, sich darüber übermäßig den Kopf zu zerbrechen, insbesondere, da wir in der Praxis sehr gut zurechtkommen, ohne sie zu lösen.« (Bell, 241) Doch kam es völlig anders. Statt später nach einer für alle überzeugenden Lösung zu suchen, werden seither die mathematischen Formeln hingenommen und ihre Bedeutung nicht erklärt. Es soll genügen, wenn ihre Ergebnisse mit den Messresultaten übereinstimmen. Alle weitergehenden Fragen werden für überflüssig erklärt. Ist das Denkfaulheit, ein selbstgerechter Konservativismus, der jede Art von Umsturz scheut, oder eine angemessene Bescheidenheit, die sich der Grenzen des menschlichen Denkens bewusst ist und sie zu akzeptieren gelernt hat?

Die Quantenphysik kann in ihrer Theorie ausschließlich Möglichkeitsräume (Mannigfaltigkeiten von Möglichkeiten) beschreiben, obwohl wie in der klassischen Physik nur das gemessen und protokolliert werden kann, was im Moment der Messung wirklich gegeben ist. Zugleich handelt es sich um einen bisher unbekannten Typ von Möglichkeiten: Die von der Quantenphysik unterschiedenen Möglichkeiten sind nicht voneinander unabhängig, sondern verschränkt. Sie bilden  als Möglichkeiten  eine eigentümliche Gesamtheit, die einem lebenden Organismus vergleichbar ist, und sich doch nie als Ganze, sondern immer nur in einzelnen Ereignissen zeigt, deren innerer Zusammenhang im Reich der Möglichkeiten verborgen bleibt und nur indirekt erschlossen werden kann. Das auch nur einigermaßen anschaulich zu beschreiben und dafür eine Erklärung zu finden, ist eine ungewohnte Herausforderung für eine Wissenschaft, die so gut wie gar nicht darauf vorbereitet ist. Die westliche Wissenschaft ist seit ihren Anfängen bei den Sumerern und der griechischen Antike am Vorrang des Wirklichen orientiert und zieht einen klaren Trennstrich gegenüber allem Dunklen und Ungewissen, wofür sie Mythos und Religion zuständig sieht und als unwissenschaftlich abgrenzt. Sie hat bis heute keinen überzeugenden Ansatz gefunden, wie es zum Übergang vom Möglichen zum Wirklichen kommt. Stattdessen wird seit der Kopenhagener Deutung von den meisten Quantenmechanikern übereinstimmend vom Kollaps der Wellenfunktion gesprochen. Da mit der Wellenfunktion die Wahrscheinlichkeitsverteilung der Messergebnisse beschrieben wird, ist der Kollaps der Möglichkeit in die Wirklichkeit gemeint. (Wem das Wort ‘Kollaps’ zu hart klingt, der spricht von ‘Dekohärenz’. Die Quantensysteme verhalten sich nur im Modus der Möglichkeit kohärent und schlagen beim Übergang in die Wirklichkeit um in Dekohärenz).

Was geschieht im Kollaps? Hier halten es die meisten Quantenphysiker mit Wittgenstein: »Wovon man nicht sprechen kann, darüber muss man schweigen.« (TLP 7). Es gibt keinen zeitlichen Verlauf des Kollaps. Er erfolgt gleichzeitig an allen Stellen der Wellenfunktion. Bell bringt es in die trockene Sprache der Quantenphysik: »Eine der augenscheinlichen Nichtlokalitäten der Quantenmechanik ist der augenblickliche – überall im Raum stattfindende – ‘Kollaps der Wellenfunktion‘ bei der ‘Messung‘. (Bell, 58) Im folgenden Abschnitt möchte ich zeigen, dass es jedoch durchaus einen Subtext philosophischer Überzeugungen gibt. Gerade weil über ihn nicht gesprochen wurde, hat er auf eine verborgene Weise die Entwicklung der Quantenphysik geprägt und eingeengt. Das soll an vier Etappen der Geschichte der Quantenphysik ausgeführt werden:

• der verborgene Existenzialismus der Kopenhagener Deutung nach Niels Bohr
• die Deutung der Quantenmechanik als Glücksspiel nach John v. Neumann
• der Versuch, zu den Prinzipien der Aufklärung und der klassischen Physik zurückzukehren bei David Bohm
• die neuartige Experimentalstrategie nach John Bell, die zur Erkenntnis der Quantenverschränkung geführt hat

– Der Existenzialismus der Kopenhagener Deutung

Warum kennt die Quantenphysik nur Möglichkeiten? Seit den legendären Gesprächen 1927 von Niels Bohr (1885-1962) und Werner Heisenberg (1901-1975), – in deren Folge Heisenberg im gleichen Jahr die Unschärfe-Relation formulierte –, wird das mit dem  Messproblem  erklärt. In der Quantenphysik geht es um Teilchen, die in der gleichen Größenordnung liegen wie die Teilchen, mit denen sie gemessen werden. Jede Messung begibt sich in das Quantengeschehen und beeinflusst es. Das unterscheidet sich völlig von der alltäglichen Erfahrung. Wenn wir zum Beispiel den Mond anschauen, glaubt niemand, dass von unseren Augen oder einem Teleskop am Mond eine Änderung vorgenommen wird, wodurch der Mond beim Anschauen anders aussieht als vor dem Anschauen. Bei einer quantenphysikalischen Messung wird dagegen der gemessene Gegenstand verändert, und es kann nur noch indirekt geschlossen werden, wie er möglicherweise unabhängig und vor jeder Messung ausgesehen haben kann.

Aber ist das überzeugend? Warum kann das Messen nicht wie alle anderen Vorgänge als ein physikalischer Prozess beschrieben, in den Modellen berücksichtigt und sein störender Einfluss herausgerechnet werden, so wie beispielsweise bei den Fotografien der kosmischen Hintergrundstrahlung der Einfluss der Messgeräte, der Atmosphäre der Erde usf. berücksichtigt wird? Inzwischen scheint mir die Kopenhagener Deutung auch experimentell widerlegt zu sein. Zeilinger berichtet von Experimenten, mit denen nachgewiesen werden konnte, dass das Interferenzmuster beim Doppelspaltversuch nicht immer auftritt. Wird die Bewegung von Fullerenmolekülen durch einen Doppelspalt beobachtet, zeigt sich dort zunächst das bekannte Interferenzmuster. Dies gilt jedoch nicht mehr, wenn sie heißer als 3.000 Grad Celsius sind (Zeilinger, 105). Das ist ein Hinweis, dass der Wellencharakter sich nicht ausschließlich aus der Einwirkung des Beobachters beim Messen ergibt, sondern auch aus Eigenschaften der Objekte, die durch den Doppelspalt geleitet werden.

Wenn Physiker über das Messen und dessen störende Einflüsse nachdenken, verändern sie ihren Standort. Sie betrachten nicht mehr einen Gegenstand, sondern ihr eigenes Experimentieren. In diesem Moment der Selbstreflexion geben viele ihren wissenschaftlichen Anspruch auf. Sie behaupten, dass die Wirklichkeit des Messens ein einzigartiger Vorgang ist, in dem sich ein Subjekt (der Beobachter) und ein Objekt (sein Gegenstand) aufeinander beziehen, der nicht seinerseits wiederum wissenschaftlich beschrieben und in seinen Wirkungen berücksichtigt werden kann. Der Messvorgang bekommt einen existenzialen Status, der sich jedem Wissen entzieht. Letztlich wird mit einer unhintergehbaren Wirklichkeit des Messens argumentiert. Dafür gibt es weder eine weitere philosophische Erklärung noch eine Art Meta-Experiment, um es nachzuweisen. Über diese Grundhaltung wurde weder gesprochen noch offen im Austausch mit anderen Meinungen diskutiert. »It is a fact of the history of modern physics that Bohr never spent a word in trying to justify his philosophical position, which he adopted under the well documented influence of S. Kierkegaard, H. Høffding, and W. James.« (So der italienische Physiker Franco Selleri [1936-2013] in einem Beitrag 1994 [zitiert nach Löfgren, 6]. Löfgren hat einige Jahre bei v. Foerster am Biological Computer Laboratory gearbeitet.).

Mit den beiden dänischen Philosophen Søren Kierkegaard (1813-1855) und Harald Høffding (1843-1931) ist ein Hinweis auf den Existenzialismus gegeben, der in den 1920ern seine Blüte erlebte (so bei Rudolf Bultmann, Karl Barth, Karl Jaspers, Martin Heidegger, Paul Tillich, die in den 1880ern geboren der gleichen Generation wie Niels Bohr angehörten). Nach dieser aus der protestantischen Tradition entstandenen Richtung zählt für den Menschen vorrangig seine Lebenswirklichkeit, seine individuell erlebte Existenz, die sich jeder wissenschaftlichen (kategorialen) Beschreibung entzieht. Auch die Wissenschaft ist nur ein Aspekt des Menschen und seiner Existenz. Der Existenzialismus beansprucht, das menschliche Dasein in einer Tiefe zu erfassen, die jeder Wissenschaft vorausgeht. Er ist daher nicht seinerseits wissenschaftlich zu erklären, sondern begründet umgekehrt die Grundlinien allen wissenschaftlichen Denkens und Arbeitens, deren sich die Wissenschaft aus sich selbst heraus nicht bewusst zu werden vermag. In diesem Sinn kann das Messen als eine existenziale Wirklichkeit verstanden werden, die zu verstehen sich für die Wissenschaft wie ein blinder Fleck entzieht. Anders gesagt: Die Wirklichkeit des Messens steht höher als die  innerhalb  der Quantenphysik betrachteten Möglichkeiten. Wie aber ist es Niels Bohr gelungen, den Bogen zu schlagen vom Existenzialismus zur Quantenphysik? Es gibt keinen Text und keine überlieferten Gespräche, aus denen das klar hervorgeht. Stattdessen gibt es eine Vielzahl von Positionen, die sich in unterschiedlicher Weise auf Bohr und die Gespräche mit ihm beziehen und sich jeweils als die Kopenhagener Deutung ausgeben. Mir scheinen die hier angesprochenen philosophischen Fragen weitgehend offen und ungeklärt zu sein. So ist zum Beispiel zu fragen, wie Heidegger vom Existenzialismus zum Vorrang des Möglichen fand, ob und wie er mit seiner Philosophie die Quantenphysik beeinflusst hat, oder welche Entwicklungslinien es bei den deutschen Physikern Heisenberg, Weizsäcker und deren Schülern gibt, etwa Thomas Görnitz und Holger Lyre, die mit wichtigen Beiträgen über die Philosophie der Quantenphysik hervorgetreten sind.

– Quantenmechanik als Glücksspiel (v. Neumann)

In dieser Situation boten sich zwei Alternativen: Die klassische Vorstellung einer Bewegungsbahn ganz aufzugeben und die Quantenmechanik wie ein Glücksspiel anzusehen, oder mit mathematischen Methoden virtuelle Bahnen zu entwerfen und die Wellenfunktion der Wahrscheinlichkeit als eine verborgene Wechselwirkung der virtuellen Bahnen untereinander zu verstehen. Für den ersten Weg steht John v. Neumann, für den zweiten Louis de Broglie und David Bohm.

John von Neumann (1903-1957) stammte aus einer jüdischen Familie in Ungarn, wurde jedoch auf protestantische Schulen geschickt und erwies sich seit jungen Jahren als ein mathematisches Universalgenie mit legendärem Ruf. Er arbeitete 1926-27 in Göttingen mit Hilbert zusammen. Das waren die Jahre, als dort die mathematische Theorie der Quantenphysik entstand, und deren Entwicklung er von Anfang an aus der Perspektive des von Hilbert begründeten geometrischen und axiomatischen Denkens zu sehen lernte. Er wurde bereits 1929 in die USA eingeladen und unterstützte Gödel bei dessen später Ausreise 1940 von Österreich in die USA. Seine Beiträge reichen von der Logik und Mengenlehre über die Funktionalanalysis bis zur Spieltheorie und der nach ihm benannten Architektur der modernen Computer, leider auch mit zweifelhaftem politischen Engagement für die Atom- und Wasserstoffbombe und paranoiden Reaktionen beim Wettrüsten mit der Sowjetunion (Stanley Kubrick hat 1964 im Film Dr. Seltsam oder: Wie ich lernte, die Bombe zu lieben nicht zuletzt an v. Neumann gedacht).

Die 1932 veröffentlichten Mathematischen Grundlagen der Quantenmechanik standen zwar anfangs im Schatten des Werks von Paul Dirac (1902-1984), dem sowohl erste Schritte für eine Zusammenführung der Einsteinschen Relativitätstheorie und der Quantenmechanik wie auch der unterschiedlichen Ansätze von Schrödinger und Heisenberg gelungen waren, und der mit dem Nachweis von Antimaterie Furore machen. Doch spätestens mit dem Erfolg differentialgeometrischer Methoden in den 1950ern setzte sich v. Neumanns streng an der Geometrie von Hilbert entworfener Ansatz durch, sehr zum Leidwesen all der Physikstudenten, die sich fortan mit Hilberträumen und selbstadjungierten Operatoren herumschlagen müssen. Seine Richtung dominierte mindestens zwei Generationen von Physikern und gerät erst heute in eine Krise, seit sich die Stringtheorien und Supersymmetrien nicht experimentell nachweisen lassen. Mit ihnen hätte der Ansatz von v. Neumann gekrönt werden sollen.

Dirac und v. Neumann waren Vertreter einer neuen Generation, die sich nicht mehr wie Planck, Einstein, Bohr und Born in harten Kontroversen von den Prinzipien der klassischen Physik und der Aufklärung lösen mussten, sondern sie vermochten sich mit geradezu traumwandlerischer Sicherheit auf dem neuen Boden zu bewegen. Ihre Parole war Ockhams Rasiermesser: So wie sich die neue Kunst ihrer Zeit gegen Ornamente und den Plüsch des Jugendstil wandte, und so wie Carnap 1935 postulierte »In der Logik gibt es keine Moral« (Carnap, 45), lehnten sie alle aus ihrer Sicht überflüssigen nicht-mathematischen Deutungen, Erklärungen und Veranschaulichungen ab und beschränkten sich auf die rein mathematischen Strukturen der Quantenmechanik. Die Quantenmechanik beschreibt für sie eine Welt singulärer, voneinander unabhängiger Ereignisse. Es ist für sie sinnlos zu fragen, welcher Weg oder welche Begründung von einem Ereignis zu einem anderen führt, und welche Motive oder Gefühle eine Rolle spielen könnten. Jedes Ereignis steht für sich, und es kann nur gefragt werden, nach welchen formalen Regeln Ereignisse einander ähnlich sind und mit welchen Übergangswahrscheinlichkeiten ein Ereignis einem anderen folgt. Sie kritisierten nicht mehr die klassischen Begriffe wie Substanz, Kausalität und Wechselwirkung oder Materie, Trägheit, Freiheit und Notwendigkeit, sondern hielten sie schlicht für überflüssiges Beiwerk, um etwas nochmals mit zusätzlichen metaphysischen Begriffen zu beschreiben, dessen mathematische Struktur bereits bekannt und geklärt ist.

Es war nur konsequent, als v. Neumann von der Theorie unabhängiger Ereignisse weiter ging zur Spieltheorie. Mit Spieltheorie ist nicht die Theorie eines Lebensstils nach dem Vorbild des homo ludens gemeint, oder Schillers Begeisterung, der Mensch »ist nur da ganz Mensch, wo er spielt«. Sondern es geht um unkooperative Glücks- und Kartenspiele wie Würfeln, Roulette, Pokern usf. Bereits 1928 war v. Neumann auf diesem Gebiet mit einem wichtigen Beitrag hervorgetreten und brachte 1944 mit Oskar Morgenstern das Standardwerk The Theory of Games and Economic Behavior heraus. Der Titel ist Programm: Der nur an seinem Eigennutz interessierte Homo oeconomicus wird zum Maß aller Dinge, und seine Art der Kosten-Nutzen-Maximierung das Urbild aller Mathematik. Nicht ohne Zufall warf zur gleichen Zeit der aus dem Existenzialismus hervorgegangene Heidegger der Mathematik ihre be-rechnende Vorgehensweise vor, in der doppelten Bedeutung des Rechnens und der ausschließlichen Orientierung am eigenen Vorteil. Die Spieltheorie und Heideggers Kritik an aller Mathematik sind zwei Seiten einer Medaille.

Als nach 1989 viele Quantenphysiker als sogenannte Quants bei den Banken eine neue Beschäftigung fanden und die als Finanzinnovationen bekannt gewordenen Konstrukte entwarfen, mit denen nach allen Regeln der Kunst sichere und spekulative Werte nach dem Modell guter und schlechter Karten gemischt und für den Gegner [das sind die Käufer] ununterscheidbar verknüpft sind, konnten sie daher im Grunde dort fortfahren, was sie ursprünglich bei v. Neumann gelernt hatten. Und während die Stringtheorien empirisch nicht verifiziert werden konnten, erlebt dieser Ansatz mit Big Data einen unerwarteten, neuen Aufschwung. Deren Algorithmen zur Steuerung menschlichen Verhaltens sind nach dem gleichem Menschenbild v. Neumanns gestrickt und wollen das Leben der Menschen mit den Techniken von Smartphones und elektronisch gesteuerten, sozialen Netzen umfassend nach den Regeln der Spieltheorie organisieren. Das Leben scheint in eine Fülle unabhängiger Ereignisse und Glücks-Entscheidungen (Like-Buttons) zu zerfallen, die – ohne dass es den einzelnen Anwendern bewusst wird – von Datenbank-Anwendungen präformiert werden.

Mir ist nicht bekannt, ob v. Neumann irgendwo sein Menschenbild oder seine Philosophie veröffentlicht hat. Aber es gibt viele Berichte, dass er persönlich ein leidenschaftlicher Pokerspieler war, für sich selbst schon sehr früh astronomische Gehälter ausgehandelt hat und in seinem politischen Engagement seit der Mitarbeit am Manhattan-Projekt zur Entwicklung der Atombombe und später der Wasserstoffbombe entschiedener Verfechter der Spieltheorie war. Die Spieltheorie galt lange Zeit als eine Art Geheimwaffe im Kalten Krieg, und als v. Neumann im Sterben lag (an einem Krebsleiden, das er sich möglicherweise durch die Strahlenbelastung bei der Entwicklung der Atombombe zugezogen hatte), wurde im Krankenhaus sein Zimmer bewacht, damit er nicht im geschwächten Zustand Spionen gegenüber Geheimnisse verrät.

So wie der Existenzialismus von Bohr nur im Verborgenen vertreten wurde, war es mit dem Menschenbild und der Ethik von v. Neumann. Frank Schirrmacher hat deren weitreichenden Einfluss 2013 in seinem Buch Ego – das Spiel des Lebens hervorgehoben. Hier soll nicht auf mathematische Details eingegangen werden. Ich vermute jedoch, dass die Theorie der Glücksspiele der innere Bezugspunkt der Arbeiten von v. Neumann ist. V. Neumann ging vom Zufall aus und lehnte konsequent die für ihn deterministischen Theorien verborgener Parameter ab und mit ihnen die gesamte Richtung von de Broglie und später Bohm. Ähnlich ist es in der Spieltheorie. Es ist ein reiner Glücks- (oder Unglücks-)fall, wie jemand ins Leben geworfen wurde und mit welchen Situationen er konfrontiert ist. Das Leben gilt als eine Art Lotterie oder genauer ein Kartenspiel, bei dem jeder durch seine Geburt das Los gezogen hat, in welchen Verhältnissen er aufwächst und welches Erbe und welche Fähigkeit ihm mitgegeben wurden. Bei Kartenspielen entscheidet das Glück, welche Karten ausgegeben werden, aber nur jeder Spieler weiß für sich, welche Karten er auf der Hand hat. Die Spieltheorie empfiehlt in solchen Fällen unkooperativer Spiele mit unvollständiger (asymmetrischer) Information nach dem Vorbild des Pokerns Bluff und Täuschung. Andere Strategien sind bei Glücksspielen dieser Art nicht möglich. Die gesellschaftliche Wirkung kann kaum überschätzt werden. In einer säkularen Gesellschaft, in der keinerlei Weltanschauungen mehr zählen, sieht sich der Mensch zurückgeworfen auf einen Zustand, wie ihn die Spieltheorie beschreibt. Daran halten sich die Politiker der westlichen Staaten nicht weniger als der ausschließlich am persönlichen Nutzen orientierte homo oeconomicus. Wenn v. Neumann recht hat, liefert die Quantenphysik hierfür eine naturwissenschaftliche Erklärung, die sich in den 1920ern und 1930ern gut verbinden konnte mit einer Richtung der Biologie, die die Evolutionstheorie Darwins mit statistischen Methoden weiterführen wollte. – Von diesem Standort aus, dem jede Art von Mitgefühl, Religion oder Spiritualität fremd ist, ergeben sich sicher keine Fragen der Quantenphysik an den Buddhismus. Wer eine religiöse Sprache liebt, kann sagen, die Physik hat sich nie weiter in das Reich der Finsternis verloren. Ich bin überzeugt, dass es auf diesem Weg zu einem Rückschlag wie der von Kierkegaard beschriebenen Krankheit zum Tode kommen wird.

– Quantenmechanik nach Bohm

Auch wenn sich offiziell die Kopenhagener Deutung durchgesetzt hat – zumindest in der Bohr zugeschriebenen »Ansicht, dass es in der Natur eines Teilchens liege, ihm unterhalb gewisser Grenzen (die durch die Unschärferelation gegeben sind) Ort und Impuls nicht mehr zuordnen zu können« (Wikipedia abgerufen am 2.5.2018) –, und das Standardmodell der Teilchenphysik auf die Mathematik von v. Neumann zurückgeht, tendiert ein Naturwissenschaftler intuitiv zu der von Louis de Broglie (1892-1987) und David Bohm (1917-1992) entwickelten Theorie der Führungswellen. Zwar lassen sich die Wege der Teilchen im Doppelexperiment nicht beobachten, aber ohne es auszusprechen geht jeder davon aus, dass es solche Wege gibt. De Broglie und Bohm ist es gelungen, ein entsprechendes mathematisches Modell aufzustellen, das ebenfalls perfekt mit den Messergebnissen übereinstimmt. Die Wege sind im Modell für alle Teilchen eindeutig, und sie überschneiden sich nicht. Sie erfüllen damit die elementaren Voraussetzungen für ein physikalisches Feld mit Feldlinien.

Abb. 2: Wellenmuster dargestellt in Bewegungsbahnen (Trajektorien) nach Bohm
»Simulation einiger bohmscher Trajektorien beim Doppelspalt. Die Teilchen werden durch die Wellenfunktion geleitet, die am Doppelspalt interferiert. Auf diese Weise kommt es zu dem bekannten Interferenzmuster, obwohl eine Bewegung von Teilchen beschrieben wird.« (Wikipedia, abgerufen am 20.4.2018)
Urheber: Von Doppelspalt.jpg: Opassonderivative work: Malyszkz (talk) - Doppelspalt.jpg, Gemeinfrei, Link

Dieses Bild ist für mich nach wie vor die beste Möglichkeit, die Mathematik der Quantenphysik anschaulich darzustellen. Das Interferenzmuster wird aufgelöst mit dem ungewöhnlichen Verlauf der Bewegungsbahnen. Es ist anschaulich zu sehen, wie es im Übergang von einer Bewegungsbahn zu einer anderen eine Art innere Welle (eine Verstauchung oder ein Erzittern) gibt. Die Führungswelle verläuft senkrecht zu den Wegen und gibt ihnen ihre eigentümliche Gestalt. Das Bild zeigt alle Wege, die dem Teilchen möglich sind. Welchen Weg es tatsächlich einschlägt, kann nicht beobachtet werden. Aber es lassen sich mathematisch die Eigenschaften der Gesamtheit aller Wege erkennen, die das Teilchen gehen kann, und aus diesen Eigenschaften ergibt sich das Interferenzmuster, das auf dem Schirm hinter dem Doppelspalt gemessen werden kann. Daher ist dieses Bild zugleich eine gute Veranschaulichung, was mit der Gesamtheit aller Möglichkeiten und seinen mathematischen Eigenschaften gemeint ist.

Mit David Bohm begann sich immerhin eine Minderheit unter den Quantenphysikern von den unausgesprochenen philosophischen und ethischen Ansichten in der Tradition von Bohr und v. Neumann zu lösen und wieder der Aufklärung zuzuwenden. Das hatte auch einen politischen Kontext. Während der Existenzialismus und die Spieltheorie Varianten die beiden eines mal konservativ und mal modern agierenden bürgerlichen Denkens waren, war Bohm interessiert an der Philosophie von Hegel und Marx, hatte 1939 bei Oppenheimer studiert, neigte politisch pazifistischen und kommunistischen Ideen zu und arbeitete nach 1945 mit Einstein zusammen. Wegen seiner politischen Überzeugungen musste er 1951 trotz Fürsprache durch Einstein die USA verlassen und ging über Brasilien und Israel nach Großbritannien. (Einen Vorläufer sehe ich bei Lew Landau. Landau [1908-1968] stammte aus einer jüdischen Familie im heutigen Aserbaidschan, »aus der viele namhafte Rabbiner und Gelehrte hervorgegangen sind« [Wikipedia, abgerufen am 20.5.2018]. Er ging 1929-31 zu Max Born in Göttingen, war 1929 und 1933-34 bei Bohr in Kopenhagen, und arbeitete Ende der 1940er und in den 1950ern mit Sacharow am sowjetischen Wasserstoffbombenprojekt. In seinem gemeinsam mit Jewgeni Lifschitz in den 1930ern in der Sowjetunion geschriebenen Lehrbuch heißt es: »Unter einer Messung versteht man in der Quantenmechanik jeden Wechselwirkungsprozess zwischen einem klassischen und einem Quantenobjekt, der unabhängig von irgendeinem Beobachter abläuft.« [zitiert nach Bell, 245]. Zwar konnte er keine klare Grenze ziehen, was ein klassisches Objekt von einem Quantenobjekt unterscheidet, doch ist die Rückwende vom Existenzialismus und der Spieltheorie zu einer Wissenschaft in der Tradition der Aufklärung klar erkennbar.)

Zur Enttäuschung von Bohm schloss sich Einstein dieser Richtung nicht an, obwohl er bekanntlich ebenfalls der Meinung war, »Gott würfelt nicht« (Brief von Einstein an Max Born vom 4.12.1926). Am 12. Mai 1952 schrieb Einstein in einem späteren Brief an Max Born: »Hast Du gesehen, dass der Bohm (wie übrigens vor 25 Jahren schon de Broglie) glaubt, dass er die Quantentheorie deterministisch umdeuten kann? Der Weg scheint mir zu billig.« (Wikipedia, abgerufen am 1.5.2018)

Bohm hatte für ihn zu einseitig die Frage nach Möglichkeit und Determinismus entschieden. Auch wenn Einstein der vorherrschenden Ansicht in der Quantenphysik widersprach, musste es für ihn eine Lösung geben, warum sie ihre Gesetze nur in Möglichkeitsräumen formulieren kann. Bohm hatte den Möglichkeitsraum auf wirkliche Wege zurückgeführt und hoffte, die Quantenphysik völlig auf den Boden der klassischen Physik zu stellen. Das war Einstein nach seiner eigenen Kritik an der Physik Newtons zu wenig. Bohm nahm in gewisser Weise die Kritik von Einstein an. Er sah ein, dass die Quantenmechanik weiterer Prinzipien bedarf, die über die klassische Physik hinausgehen. Doch sah er keinen Ansatzpunkt, dies innerhalb der Mathematik und der Physik zu leisten und orientierte sich in seinen späteren Jahren neu und vollzog eine Wende in Richtung Theosophie und Buddhismus. Er arbeitete viele Jahre mit dem Theosophen Jiddu Krishnamurti (1895-1986) zusammen und hatte eine Reihe von Treffen mit dem Dalai Lama, der ihn als »one of my scientific 'gurus'« bezeichnete (Lee Nichol [Hg.] The essential David Bohm, London, New York 2003, x). Doch scheint er mir in religiösen Fragen keinen festen Boden unter den Füßen gefunden zu haben, wie seine Sympathien für theosophische Richtungen zeigen. Er blieb ein Suchender, dem der sichere religiöse Instinkt fehlte, und der daher dem in Großbritannien unter Naturwissenschaftlern neu entstehenden Atheismus etwa bei Penrose, Dawkins und Hawking keine ausreichende Überzeugungskraft entgegensetzen konnte (siehe die Gespräche von Renée Weber mit Bohm, dem Dalai Lama, Krishnamurti und anderen in ihrem Buch Alles Leben ist eins).

– Quantenverschränkung (John Bell)

Es ist schwer zu sagen, ob Einstein die weitere Entwicklung positiver beurteilt hätte. Für mich gelang dem nordirischen Physiker John Bell (1928-1990) die Wende. Er ging in den 1950ern an das Forschungszentrum CERN und setzte sich von Beginn an für die Theorie von Bohm ein. Wie kein anderer hat er die Schwächen der ersten beiden Generationen von Quantenphysik nach Bohr und v. Neumann gesehen, ohne sich im Weiteren wie Bohm ganz von der Physik zu entfernen und bei der Theosophie und dem Buddhismus eine nicht-physikalische Antwort zu suchen. Für mich hat mit ihm die Quantenphysik die Dialog-Fähigkeit mit dem Buddhismus erworben: Der Buddhismus wird nie auf eine physikalische Frage eine physikalische Antwort geben und z.B. eine neue Formel liefern können, aber er könnte helfen, ein besseres Verständnis der Grundlagenbegriffe der Physik zu finden. Dafür ist es notwendig, die richtigen Fragen zu stellen, und das scheint mir seit Bell möglich. Wie das Beispiel des Dalai Lama zeigt, besteht umgekehrt auf Seiten des Buddhismus die Bereitschaft, Anregungen der modernen Physik aufzunehmen und das eigene Weltverständnis zu bereichern.

Für lange Zeit war Bell im Vergleich zu den anderen führenden Quantenphysikern nahezu unbekannt, und die Richtung von de Broglie, Bohm und Bell galt als nicht besonders ernst zu nehmende Nischenentwicklung abseits vom mainstream der Standardtheorien, während alle über die Quarks und den Achtfachen Weg der Teilchenphysik sprachen, mit dem Murray Gell-Mann (* 1929) eine oberflächliche Verbindung der neuen Teilchenphysik zum Achtfachen Weg des Buddhismus schlagen wollte, im Ganzen aber die in den 1930ern entworfenen Grundlagen der Quantenmechanik nicht in Frage stellte. Erst in den letzten Jahren zeichnet sich ein Umdenken ab, wie die Beiträge in dem von Friebe u.a. herausgegebenen Sammelband Philosophie der Quantenphysik zeigen.

Bell traf den kritischen Punkt: In der Axiomatik v. Neumanns müssen die Ereignisse der Quantenphysik voneinander unabhängig sein. Das ist übernommen von der Geometrie in der Tradition von Euklid bis Hilbert. Niemand bezweifelt, dass die einzelnen Punkte, Geraden und Figuren der Geometrie voneinander unabhängig sind und sich nicht gegenseitig beeinflussen. Keine Gerade biegt von sich aus eine andere Gerade, und es gibt keine geometrischen Punkte, die in irgendeiner Weise miteinander verschränkt sind. Es kann nur nach ihren äußeren Beziehungen untereinander gefragt werden, die vom Geometer mit seinen Konstruktionen aufgezeigt und hergestellt werden. Hilbert und v. Neumann war es mit überwältigendem Erfolg gelungen, diesen Ansatz auf die Quantenmechanik, die Spieltheorie und damit letztlich die Ethik und die religiösen Überzeugungen des Menschen zu übertragen. Für einen Außenstehenden ist es möglicherweise schwer nachzuvollziehen, wie radikal demgegenüber der neue Ansatz von Bell ist. Er fragte: Kann wirklich das statische Modell der Geometrie übertragen werden auf eine dynamische Lehre von Ereignissen? Könnte es stattdessen so sein, dass zwar jedes einzelne mögliche Ereignis für sich nur nach den üblichen Wahrscheinlichkeitserwartungen zu berechnen ist, zugleich aber zwischen den Möglichkeiten innere Abhängigkeiten bestehen, die im Folgenden als Quantenverschränkung bezeichnet wurden? Bell nahm den Ansatz eines Glücksspiels ernst und entwarf eine Art Ratespiel. Er konnte eine mathematische Bedingung formulieren, mithilfe derer an einem Glücksspiel erkannt werden kann, ob dessen Ereignisse wirklich unabhängig voneinander sind. Mit dieser Idee bewegt er sich völlig innerhalb der Theorie v. Neumanns und fand den Punkt, an dem von innen heraus gezeigt werden kann, dass ihr Anspruch in Widerspruch gerät zu den Messergebnissen.

Das kann am Beispiel eines typischen Glücksspiels erläutert werden. Angenommen, 6 Spieler würfeln gleichzeitig, und die Würfel sind wie üblich voneinander unabhängig. Wären die Würfel quantenverschränkt, dann müssten über die bekannte Wahrscheinlichkeitsverteilung hinaus zusätzliche Regeln über die Gesamtheit aller 6 Würfe nachweisbar sein. Zum Beispiel könnte der Fall eintreten, dass in jeder Runde jede Zahl genau einmal auftritt. Zwar weiß niemand, wer welche Zahl würfelt, aber es ergibt sich, dass keine Zahl doppelt fällt. Das Würfelspiel hätte ungewollt den Charakter eines  kooperativen Spiels  angenommen, bei dem es es darum geht, dass alle gemeinsam ein vorgegebenes Muster von Würfen erzielen, im einfachsten Beispiel 1, 2, 3, 4, 5, 6. Bei einem kooperativen Spiel gewinnt nicht einer gegen die anderen, sondern nur die Gruppe kann gewinnen, wenn sie als Gruppe eine Aufgabe erhält, die von niemandem allein, aber von allen gemeinsam gelöst werden kann. Ein solcher Spielverlauf widerspricht allen Grundannahmen der Spieltheorie von v. Neumann und der auf ihr aufgebauten Ethik. Mathematiker würden ergänzen: Es widerspricht auch dem Gesetz der großen Zahlen, wonach erst nach sehr vielen Würfen die statistischen Durchschnittswerte beliebig genau angenähert, in der Regel aber nie perfekt erreicht werden. Wer aus der Erfahrung mit nicht-kooperativen Spielen misstrauisch gegenüber Betrug und Intrige ist, würde sofort fragen: Woher weiß ein Würfel (oder der jeweilige Würfelspieler), wie die anderen Würfel fallen, und trifft genau die richtige? Das sieht nach Magie, geheimen Absprachen oder einem Zaubertrick aus, denen niemand glauben will. – Wer sich dagegen auf die naive Logik eines Kindes zurückbegibt, wird zugeben, es ist doch klar, dass bei 6 Würfeln alle Zahlen jeweils einmal fallen. Nachdem sich die Wahrscheinlichkeitstheorie mit viel Mühe vom naiven Standpunkt befreit hatte, muss es jetzt wieder einen Weg zurück geben, um eine höhere Einsicht zu erlangen, aufgrund welcher Bedingungen Glücksspiele kooperativ bzw. nicht-kooperativ ablaufen und die jeweiligen Wahrscheinlichkeitsgesetze gelten.

Der erste Schritt gelang Bell 1964 mit der nach ihm benannten Bellschen Ungleichung. Die Ungleichung stellt mathematisch die Bedingung auf, wann sich an einer experimentell erkannten Wahrscheinlichkeitsverteilung eine Quantenverschränkung zeigt, und wann nur zufällig alle Ereignisse höheren Regeln zu folgen scheinen. Diese Formel war nicht die einzige Schwierigkeit. Es könnte auch verborgene äußere Bedingungen geben, mit denen die Abhängigkeit der Ereignisse zu erklären ist. Die Spieler könnten sich vorher abgesprochen und ihre Würfel manipuliert haben. Sie könnten sich im Verlauf des Spiels miteinander abstimmen (Informationen über den jeweiligen Verlauf austauschen) und den jeweiligen Wurf geschickt beeinflussen. Oder es könnte ein drittes Ereignis geben, an dem sie sich unabhängig voneinander orientieren und dadurch zu aufeinander abgestimmten Ereignissen kommen. Der Durchbruch kam 1982. Der französischen Physiker Alain Aspect (* 1947) konnte an verschränkten Photonen experimentell nachweisen, dass es in der Quantenphysik Prozesse gibt, die nicht dem Modell des Glücksspiels entsprechen, sondern die Bedingung von Bell erfüllen. Das wurde inzwischen in zahlreichen weiteren Experimenten u.a. von Zeilinger bestätigt. Mittlerweile können die Zahl der miteinander verschränkten Quanten fortlaufend erhöht und ihre Entfernung voneinander vergrößert sowie die experimentellen Nachweise vereinfacht werden. Aktueller Stand: Ein Team in Warschau konnte ein Photon mit Billionen von Atomen verschränken (scinexx vom 3.3.2017), chinesischen Wissenschaftlern gelang per Satellit eine Verschränkung über 1.200 km (Spektrum der Wissenschaft vom 16.6.2017).

Die Folgen sind kaum absehbar, weder für die Physik noch für die Philosophie und vielleicht sogar die Religion. Einige sprechen von einer neuen kopernikanischen Wende. Bell widerspricht mit seiner Kritik an v. Neumann einem Grundprinzip der Naturwissenschaft, das Wittgenstein zutreffend auf die einfache Formel gebracht hatte: »Die Sachverhalte sind von einander unabhängig.« (TLP, 2.061) Für den Fall miteinander verschränkter Möglichkeiten gilt das nicht mehr, und erst hier wird von Quanteninformation gesprochen. Bei üblichen Informationen gibt es entweder eine klare Ereignis- und Bedingungskette A → B → …, oder sie sind voneinander unabhängig. Für Quanteninformationen gilt weder das eine noch das andere. Die Besonderheit des Quantenkalküls und darauf aufbauender Algorithmen bis hin zum Quantencomputer nutzt die Verschränkung aus.

Auf eine für mich noch ungeklärte Weise ist die Quantenverschränkung mit der metaphysischen Frage nach Identität, Verschiedenheit, Widerspruch und Grund verbunden. Was ist im Falle von Quantenverschränkung die Identität: Die jeweils einzelnen miteinander verschränkten Quanten oder die Gesamtheit aller verschränkten Quanten? Zeilinger konnte experimentell nachweisen, dass Interferenzmuster nur dann auftreten, wenn die einzelnen Teilchen nicht voneinander unterscheidbar sind. Das ist seine Erklärung für die Experimente mit Fullerenmolekülen, bei denen mit steigender Temperatur das Interferenzmuster verschwindet. »Wenn die Fullerenmoleküle sehr heiß sind, in unserem Fall etwa 3.000 Grad Celsius, dann senden sie so viele Photonen aus, dass das Interferenzbild tatsächlich verschwindet.« (Zeilinger, 105) Dank der ausgesendeten Photonen werden sie unterscheidbar. Im Umkehrschluss bedeutet das, dass das Interferenzmuster nur auftritt, wenn die Teilchen ununterscheidbar sind. Schon Bell vermutete, dass es bei der Quantenverschränkung keine Signalübertragung gibt. Die Teilchen sind miteinander korreliert, ohne sich wechselweise in ihrem Verhalten zu beeinflussen. In dem Beispiel der 6 Würfel würde das bedeuten, dass die Würfel im Moment des Würfelns ununterscheidbar sind, und dennoch für sich eine Möglichkeit finden sich so abzustimmen, dass im Ergebnis keine Zahl doppelt auftritt. Bell ist überzeugt: »Einstein hatte keine Schwierigkeit damit, zu akzeptieren, dass Zustände an verschiedenen Orten korreliert sein können. Was er nicht akzeptieren konnte, war, dass ein Eingriff an einem Ort den Zustand an einem anderen Ort unmittelbar beeinflussen konnte.« (Bell, 163)

Ein Paradigmen-Wechsel von nicht-kooperativen zu kooperativen Spielen könnte eingeleitet werden durch Strategiespiele. Schon bei Strategiespielen wie Schach und Go ist auf völlig neue Art zu unterscheiden zwischen den Spielregeln und der Strategie des Spiels. Hier versagt alles, was von den Glücksspielen bekannt ist: Alle Karten liegen offen auf dem Tisch und jeder hat im Spiel ganz demokratisch die gleichen Ausgangschancen, so dass kaum Täuschungsmanöver möglich sind. Zugleich versagt aufgrund der exponentiell wachsenden Anzahl möglicher Spielzüge der Versuch, alle Möglichkeiten durchzurechnen und die beste auszuwählen. Stattdessen werden ohne Bewertung diejenigen Spielverläufe positiv gewichtet und für weitere Spielentscheidungen verstärkt, die sich als erfolgreich erwiesen haben. Vermutlich geht auch das menschliche Gehirn so vor. Erst seit dieser Weg mit Methoden neuronaler Netze eingeschlagen wird, ist es möglich geworden, dass Computer auch bei Strategiespielen wie Go unschlagbar sind. Sie können erfolgreicher spielen, weil sie besser die Muster von überlegenen Spielverläufen wie eine Erinnerung in der Vernetzung der Neuronen aufzeichnen und für sich nutzen können. Dennoch unterscheidet intuitiv jeder zwischen dem Schachbrett und den Schachfiguren oder dem Go-Brett und den Go-Steinen einerseits, die vor mir liegen, die ich in die Hand nehmen und werfen bzw. setzen kann, und dem mathematischen Modell und dem neuronalen Netz andererseits, welche Spielverläufe möglich sind bzw. mit welchen Methoden erfolgreiche Spielverläufe aufgezeichnet werden. Jeder einzelne Zug ist ein Ereignis. Eine Strategie berücksichtigt eine Vielzahl von Zügen und möglichen Antworten des Gegenspielers. Eine Strategie baut allmählich eine Lösung auf, die anfangs noch unfertig und mit vielen Unwägbarkeiten verbunden ist, bis sie schließlich eine Eigendynamik zu entwickeln vermag, der sich der Gegner nicht zu entziehen vermag. Um vom Strategiespiel zur Quantenphysik zurückzukommen, ist anzunehmen, dass es weder den Zufall noch einen äußeren Spieler gibt, der nach seiner Strategie die Figuren oder Steine zieht, sondern in ihnen selbst ist ihre Strategie angelegt. Jede Figur weiß von sich aus, was die anderen tun und welchen Weg sie zu gehen hat. – Ohne Frage können auch die Strategiespiele nur ein Zwischenschritt sein. Es gelten nicht mehr die bloßen Regeln von Glück und Zufall, aber auch sie sind noch nicht kooperativ. Im gemeinsamen Nachdenken über Strategien und Heuristiken zeigen sich aber bereits Züge eines kooperativen Spiels.

Wege des Möglichen und des kreativen Denkens

Mit der Quantenverschränkung ergeben sich neue Fragen an den Buddhismus.

• Weg und Ereignis.
  Was geschieht zwischen zwei Ereignissen?
  Kann ein Teilchen gleichzeitig zwei oder mehrere Wege gehen?
  Gibt es Wege in verbotene Bereiche (Tunnel-Effekt)?
  
  

  ---

• Verankerung der Wege.
  Wie können die vielen Wege miteinander verankert werden, so dass sie nicht auseinander laufen oder sich kreuzen oder blockieren?
  Gibt es Wege erster und zweiter Ordnung: Ein Weg zweiter Ordnung entsteht aus dem Weg erster Ordnung, betrachtet oder überwacht ihn von außen und kann ihn durch einen Re-entry beeinflussen. Wie sind die Wege zweiter Ordnung in den Wegen erster Ordnung verankert? Welche Arten von Wegen zweiter Ordnung gibt es? Beispiele sind Träume, Tagträume, bewusste Reflexion, therapeutische Übungen usf.

– Weg und Ereignis

Wer sich nicht auf die nur schwer fassbaren existenzialistischen Ideen der Kopenhagener Deutung einlassen wollte, beschränkte sich lieber auf Fakten und eine reine Mathematik, diese zu beschreiben. Das Neue der Quantenphysik liegt nicht einfach darin, dass niemand die Messergebnisse im Einzelnen vorhersagen kann. Sie gleichen nur auf den ersten Blick einem Glücksspiel. Wie beim Würfeln oder beim Roulette weiß beim Doppelspaltexperiment niemand, wo das Teilchen auf dem Schirm auftreffen wird, und erst bei einer Vielzahl von Teilchen lässt sich an deren kollektivem Verhalten ein festes, vorhersagbares Muster erkennen und mathematisch beschreiben. Und doch gibt es einen wesentlichen Unterschied: Zwar ist in beiden Fällen nicht vorhersagbar, welches Ereignis eintreten wird. Aber beim Glücksspiel kann jeder direkt zuschauen, welchen Weg der Würfel, die Roulette-Kugel oder die Münze nehmen bis das Ereignis eintritt. Der Weg kann nicht vorhergesagt werden, aber er lässt sich in seinem aktuellen Verlauf mit verfolgen und eindeutig identifizieren. Das ist in der Quantenphysik nicht möglich.

Damit unterscheidet sie sich radikal von jeder alltäglichen Erfahrung und nicht weniger von der klassischen Physik und Logik. Dort können physikalische Bewegungen und Prozesse mathematisch als Ereignisketten entlang von Wegen beschrieben werden, auf denen nach festen Regeln ein Ereignis dem anderen folgt. Um von einem gegebenen Zustand A zu einem gewünschten Zustand Z zu gelangen, muss hierfür ein Weg gefunden werden. Das kann eine Folge klar voneinander zu unterscheidender Schritte A → B → C → … → Z wie auch eine kontinuierliche Bewegungsbahn 𝔨 sein. Beispiele sind die natürlichen Zahlen 1, 2, 3, …, die auf dem Weg der Zahlengerade liegen, die Buchstaben A, B, C, …, wenn ihre Anordnung in einem Text oder im Alphabet in einem übertragenen Sinn als Weg gilt, oder die Bewegungsbahnen, entlang derer z.B. die Teilchen bei einer Elektron-Positron-Erzeugung beobachtet werden (siehe Titelbild). Wenn die Frage nach den bislang unbeobachtbaren Wegen in den Ereignisräumen der Quantenphysik gestellt wird, ist das für die Mathematik die Frage, ob und wie die von den mechanischen Räumen bekannten Bewegungsbahnen in höherdimensionale Ereignisräume verallgemeinert werden können, und es auch dort auf vergleichbare Art virtuelle Wege gibt, wie sie z.B. Bohm entworfen hatte.

Die Aufgabenstellung ist in gewisser Weise paradox: Üblicherweise werden der Mathematik Bruchstücke vorgegeben, und es ist ihre Aufgabe, sie wie ein Mosaik zusammen zu setzen und als Fragmente eines von der Mathematik zu findenden Musters oder Weges in einer einheitlichen Formel oder einem zusammenhängenden Formelsystem zu bestimmen. Die Mathematik nimmt anhand einzelner Anzeichen eine Spur auf und schließt von ihr auf den Weg, die Art der Fortbewegung, die sich in der Spur zeigt und die Eigenschaften des Wesens, dessen Spur zu sehen ist. Mathematik ist wie alle menschliche Erkenntnis Spurenlese. Historisch ist eins der berühmtesten Beispiele, wie Kepler aus den Beobachtungsdaten der Sterne und Planeten durch Tycho Brahe deren Bewegungsgesetze fand.

In der Quantenphysik ist es nahezu umgekehrt: Mit den Messergebnissen sind die Lösungen bekannt, und mathematisch wird die Aufgabe gesucht, deren Lösung sie sind. Das Ergebnis ist bekannt, aber es hat seine Spuren verwischt, oder sie liegen in einem Bereich, in dem sie niemand vermutet. Es ist z.B. bekannt, wie viel Energie gebraucht wurde (oder welche Arbeit geleistet werden musste), um einen bestimmten Weg zu gehen, aber es ist nicht bekannt, welcher Weg es war, entlang dessen diese Leistung erfolgreich vollbracht werden konnte. Um es mathematisch genauer zu formulieren: Es sind die Integrale bekannt, und damit ist auch bekannt, dass es Wege geben muss, entlang derer das Integral gebildet werden kann, aber die Wege selbst sind unbekannt. An dieser Stelle gibt es mehrere Möglichkeiten: Die Integrale sind auf eine bisher unbekannte Weise gebildet worden. Oder es gibt keine einzelnen Wege, entlang derer sie gebildet werden, sondern es sind räumlich übergreifende geometrische Eigenschaften, aus denen die Integrale hergeleitet werden. In beiden Fällen wird eine Grundannahme verletzt, die für die klassische Mathematik und Physik gilt: Für mathematische Rechnungen ist entscheidend, dass die Aufgabenstellung entlang eines Weges verläuft, dessen formale Eigenschaften mittels der Mathematik aufgeklärt werden können, und die mathematische Rechnung erfolgt ihrerseits entlang eines Lösungsweges, der Schritt für Schritt entwickelt und nachgeprüft werden kann. Es galt das Axiom: Was wirklich ist, dessen Weg kann mitverfolgt und optimiert werden.

Dieser Ansatz hat nicht nur die Quantenphysik erschüttert, sondern zugleich kam es zu zwei ähnlichen Erschütterungen innerhalb der Mathematik: Bei den komplexen Zahlen und der Wahrscheinlichkeitstheorie. Bei komplexen Zahlen ist nach dem 1814 formulierten Cauchyschen Integralsatz in regulären Gebieten das Integral über alle Wege gleich, die zwei vorgegebene Punkte miteinander verbinden. Umgekehrt bedeutet das, dass aus dem Wert eines Integrals nicht eindeutig auf den Weg geschlossen werden kann, über den integriert wurde, denn das gleiche Integral ergibt sich entlang aller Wege zwischen den jeweils betrachteten Anfangs- und Endpunkten. So gesehen stimmt die Situation in der Funktionentheorie genau überein mit der Quantenphysik, widerspricht aber allem, wovon bisher die Mathematik und die Physik ausgegangen waren. Als die Mathematiker noch versuchten, für unerwartete Ergebnisse Erklärungen zu finden und sich nicht mit der formalen Widerspruchsfreiheit zufrieden gaben, war das für sie ein Rätsel. So heißt es in der erstmals 1924 veröffentlichten und für lange Zeit als Standard-Lehrbuch anerkannten Funktionentheorie von Konrad Knopp (1882-1957): »Wie aus dieser Interpretation hervorgeht, ist der Satz außerordentlich merkwürdig und zeigt, daß die Werte einer regulären Funktion durch ein sehr starkes inneres Band miteinander verknüpft sind.« (Knopp, 64) Knopp stieß in der Funktionentheorie (der Lehre des Rechnens mit komplexen Zahlen) auf ein Phänomen, das zu gleichen Zeit auch in der Quantenmechanik auftrat, wenn dort im Doppelspaltexperiment die Teilchen auf vielen Bahnen ihren Weg finden, die irgendwie miteinander verknüpft sind. Fast im gleichen Jahr erriet 1926 Ernst Schrödinger (1887-1961) die nach ihm benannte Schrödinger-Gleichung, mit der die zeitliche Entwicklung der Wahrscheinlichkeitsverteilung von Objekten der Quantenphysik beschrieben wird. Sie operiert mit imaginären Zahlen. Konsequent ergab sich daraus das vor allem von Feynman in den 1940ern entwickelte Pfadintegral, das alle für ein Teilchen möglichen Wege (Pfade) von einem Zustand in einen anderen berücksichtigt.

In diesem Fall war Mathematik nicht als Abstraktion aus empirischen und physikalischen Beobachtungen entstanden, sondern Mathematik und Physik entwickelten sich in enger Nachbarschaft synchron. Wie durch Zufall lieferte die Mathematik genau im rechten Moment das, was die Physik brauchte, und beide gerieten parallel in die gleiche Krise ihrer überlieferten Grundüberzeugungen. Niemand kann das bis heute erklären. Die Mathematiker waren fasziniert von der Einfachheit und Schönheit der Funktionentheorie, die mit dem Übergang von den reellen zu den komplexen Zahlen nicht schwieriger, sondern einfacher geworden war, und sprachen von der Königin der Wissenschaft. Ich vermute, dass Mathematik und Physik von zwei Seiten auf ein größeres Phänomen stießen, das einer philosophischen Aufklärung bedarf: Die Zyklizität, die sich sowohl in der Multiplikation der komplexen Zahlen wie der Abläufe der Quantenphysik zeigt. Mit der Zyklizität könnte ein neuer Begriff gefunden sein, der von gleicher Bedeutung ist wie Transitivität und Kontinuität. Doch das ist bis heute von der Philosophie noch nicht einmal wahrgenommen worden. Offensichtlich gibt es eine Art Denksperre.

Ebenso unverständlich ist das aus der Statistik bekannte Gesetz der großen Zahlen. Es besagt, dass in allen Glücksspielen jede Pech- oder Glückssträhne irgendwann zu Ende geht, aber niemand weiß, wann das geschehen wird. Es widerspricht der Intuition, dass z.B. beim Würfeln auch nach 10 nacheinander gewürfelten Sechsern im elften Wurf wiederum mit einer Wahrscheinlichkeit von 1 : 6 eine Sechs fallen wird. Jeder vermutet intuitiv, dass die Wahrscheinlichkeit, nochmals die gleiche Zahl zu würfeln, geringer werden sollte. Und diese Intuition hat in gewisser Weise recht: Das Gesetz der großen Zahlen besagt, dass sich irgendwann bei großen Zahlen die durchschnittliche Wahrscheinlichkeit durchsetzt. Aber wie setzt sie sich durch, und kann vorausgesagt werden, wann sie sich durchsetzt? Das ist bis heute völlig unmöglich, und es gibt nicht einmal Ansätze für eine Lösung. Häufig wird nicht einmal die Frage verstanden. Denn selbst wenn noch so oft nacheinander die gleiche Zahl gewürfelt wurde, gilt für jeden neuen Wurf wiederum die gleiche Wahrscheinlichkeit von einem Sechstel, so als wäre nichts vorausgegangen. Es ist unmöglich, an der Wahrscheinlichkeit einzelner Würfe zu erkennen, dass ein Ausgleich von vorangegangenen, sehr unwahrscheinlichen Ereignisfolgen stattfinden muss. Für den einzelnen Wurf ändert sich nie die jeweilige Wahrscheinlichkeit. Und dennoch setzt sich über alle einzelnen Würfe hinweg das Gesetz der großen Zahlen durch. Gibt es eine Art verborgenes Gedächtnis, wenn Pech- oder Glückssträhnen ausgeglichen werden? Kann mathematisch ein Weg beschrieben werden, der von den einzelnen Ereignissen zum Gesetz der großen Zahlen führt?

– Keimbahnen

Lange Zeit hatte die Quantenphysik gehofft, von der Mathematik formale Operationen übernehmen zu können, die gleichermaßen für Mögliches und Wirkliches gelten. An einer mathematischen Formel ist nicht zu erkennen, ob ihre Variablen für Mögliches, Wirkliches oder beides gelten. Sie gilt nur, wenn dieser Unterschied keine Rolle spielt. Heute sehe ich genau eine Umkehrung: Können die Mathematik und die Logik von den neuen Erfahrungen und Ideen der Quantenverschränkung lernen, ihrerseits systematisch zwischen Möglichem und Wirklichem zu unterscheiden? Auch dieser Gedanke geht auf Bell zurück, der ihn allerdings aus physikalischer Sicht anders begründete. Für ihn war es unbefriedigend, wie die Physiker in den physikalischen Gleichungen zwischen solchen Variablen unterscheiden, die nur wie in der Mathematik als Rechengrößen dienen, und solchen, die sich als Observable auf beobachtbare Größen beziehen. Diese Unterscheidung geht für ihn zwar grundsätzlich in eine richtige Richtung, aber sie legt mit dem Ausdruck ‘Observable’ nahe, als würden die Gleichungen nur für einen Beobachter (observer) und seine Beobachtungsmöglichkeiten (Observationen) gelten. Stattdessen schlug er vor, von beables (‘be-able’, oder noch genauer ‘maybe-ables’, wörtlich übersetzt ‘Sei-bare’) zu sprechen, die ich als Reable bezeichnen würde, da sie im Unterschied zu den Observablen nicht auf den Beobachter, sondern auf etwas Reales Bezug nehmen (Bell, 196).

Die von Bell eingeführte Unterscheidung in Observable und Reable (beables) ist meines Wissens bisher nicht aufgegriffen worden. Ich möchte sie dagegen verallgemeinern und ihnen eine neue Wendung geben. Es geht nicht nur um die Unterscheidung von Reablen und Observablen mit Bezug auf das Objekt bzw. den Beobachter. Sondern es kann allgemeiner gefragt werden: Ist eine dynamische Logik möglich, die schrittweise den Weg vom Möglichen zum Wirklichen verfolgt und im Bereich des Möglichen unterschiedliche Stufen erkennt, die jeweils halbfertig sind und aus sich heraus nach dem Modell der Emergenz stufenweise genauer werden und sich der Wirklichkeit annähern? Dann würde nicht mehr von einem Kollaps des Möglichen in das Wirkliche gesprochen werden, sondern von einer Genese des Wirklichen aus dem Möglichen. Der schrittweise Lernvorgang der neuronalen Netz kann ein Ansatzpunkt sein.

Ein erstes Gedankenexperiment in diese Richtung hat der Physiker John Archibald Wheeler (1911-2008) vorgeschlagen: In einem üblichen Ratespiel überlegt sich eine Gruppe einen bestimmten Begriff, den der Ratende Zug um Zug erschließt, zum Beispiel: Lebewesen? Ja. Fliegt? Nein. Schwimmt? Ja. Fisch? Nein. Säugetier? Nein. Grün? Ja. Krokodil? Ja. Statt sich im Vorfeld auf etwas wie das Krokodil zu einigen, kann auch vereinbart werden: Die Antwortenden lassen den zu ratenden Begriff bewusst offen, aber es gilt die Regel, dass keine Antwort einer vorherigen widersprechen darf. So gibt es am Anfang einen nahezu unendlichen Möglichkeitsraum, was gemeint sein kann, der sich dynamisch Schritt für Schritt einschränkt, bis schließlich eine Möglichkeit hervortritt, an die wahrscheinlich anfangs noch niemand gedacht hat (Zeilinger, 211f). Ist es möglich, am Beispiel solcher Entscheidungsfindungen aus dem Ungewissen eine erfolgreiche inhärente Logik zu erkennen, die zielgerichtet den Horizont des Gebiets zu erkunden versucht und auf Verzweigungspunkte drängt, an denen die Vielzahl der Möglichkeiten eingeschränkt werden kann?

Gibt es anschauliche Vorbilder, um auf diesem Weg weiter zu kommen? Das könnten die Embryologie, die Immunologie und in der Mathematik die ununterscheidbar großen natürlichen Zahlen und die imaginären Zahlen sein.

– In der embryologischen Entwicklung gibt es eine fortlaufende Kette von Verzweigungspunkten, an denen anfangs noch viele Möglichkeiten offen sind. Lässt sich eine übergreifende Geometrie erkennen, die möglicherweise mit heute noch unbekannten qualitativen Methoden arbeiten, und wie gelingt es den Lebewesen, die embryologische Entwicklung über die Verzweigungspunkte hinweg zu stabilisieren?

– Die Immunologie betrachtet ein Immunsystem, das auf eine im Prinzip unbegrenzte Vielzahl möglicher Bedrohungen reagieren kann. Es muss sowohl fähig sein, auch auf bisher unbekannte Gefährdungen reagieren zu können, wie auch in jedem Krankheitsfall zügig eine wirksame Abwehr zu finden.

– Wie lässt sich das Paradox lösen, dass zum einen die natürlichen Zahlen irgendwo ununterscheidbar groß werden, zum anderen jede konkret genannte natürliche Zahl n sich eindeutig von ihren Nachbarn n − 1 und n + 1 unterscheiden lässt? Das führt zum Gesetz der Großen Zahlen. Lässt sich das von Zeilinger nachgewiesene Phänomen einer Grenze für ununterscheidbare Teilchen in Umkehrung auf die natürlichen Zahlen übertragen?

– Mit den imaginären Zahlen könnte ein Modell vorliegen, die Übergänge aus dem imaginären Bereich auf die reelle Zahlenachse als Vorbild für den Übergang vom Möglichen zum Wirklichen zu nehmen.

Offensichtlich fällt es dem westlich orientierten Denken bisher schwer, sich auf diesem Gebiet zu bewegen. Das scheint mir die größte Hürde für weitere Fortschritte zu sein. Daher lautet die zweite Frage an den Buddhismus: Kann der Buddhismus helfen, hier eine Antwort zu finden? Die grundsätzliche Frage scheint mir zu sein, ein neues Verständnis von Möglichkeiten zu gewinnen, das sich vom Modell der Glücksspiele löst.

– Gibt es einen Überschuss des Raums der Möglichkeiten gegenüber der Wirklichkeit, der in irgendeiner Weise für sich erfahrbar ist? Ist mit dem Buddhismus ein Weg gangbar, um sich aus der gewöhnlichen Wirklichkeit zu erheben und den Raum aller Möglichkeiten als solchen zu erleben? Mit einer solchen Erfahrung würde im eigenen Erleben nach- und mitvollzogen, was die große Neuerung der Quantenphysik ist: Den Raum der Möglichkeit als eine eigene Entität für sich zu verstehen und zu erfahren.

– Ist es möglich, den Indifferenzpunkt zu treffen und zu erleben, an dem sich die Innensicht und die Distanzsicht auf das eigene Agieren voneinander trennen und einander treffen? An diesem Indifferenzpunkt erscheinen beide Wege ‘leer’ – ‘leer’ nicht gemeint als depressives Nichts oder Nihilismus, sondern als eine Erfahrung des Shunyata im Sinne des buddhistischen Philosophen Nagarjuna.

– Wie kann das Halbfertige und Keimhafte mathematisch beschrieben werden? Es gibt in der Mathematik Ansätze wie das Differential, das Imaginäre oder in einem mathematisch technischen Sinn Halme und Keime. Kann der Buddhismus lehren, für das Halbfertige und Keimhafte einen innere Zugang zu gewinnen, der mathematische Intuitionen beflügelt?

– Offenbar muss für die Entwicklungslinien in einer dynamischen Logik ein anderer Begriff des Weges gefunden werden als bei den Wegen für Beweis- und Ereignisketten. Biologen sprechen von Keimbahnen. Können die vom Buddhismus gefundenen Begriffe wie karana für den Bewegungsverlauf und samtana in der doppelten Bedeutung als Reifeprozess und Bewusstseinsstrom weiterhelfen?

Wege erster und Zweiter Ordnung

Jeder kennt aus eigener Erfahrung die Gefährdung, wenn sich das Denken in den Bereich des Möglichen begibt und sich dort auf die eine oder andere Weise verlieren kann, sei es in einem unrealistischen Wunschdenken oder zwanghaften Grübeleien. Gibt es eine dynamische Logik, das ist eine Logik zweiter Ordnung, ob und wie es dem Denken in Möglichkeiten gelingt, im ersten Schritt den Handlungsspielraum aller Alternativen zu erkennen, und anschließend wieder umzukehren und entsprechend zu handeln? Verfügt das Denken über eine innere Zyklizität, die aus der unmittelbaren Nähe und dem unbedachten, spontanen Reagieren hinausführt, der Reflexion fähig ist, und anschließend in einer zweiten Verneinung das bloß Mögliche wieder von sich abzustoßen vermag und realitätstüchtig ist? Die westliche Philosophie bezeichnet das mit Aristoteles als Besonnenheit, mit Kant als Urteilskraft oder mit Hegel als Lebendigkeit. In ihrer starren Orientierung am Wirklichen (Realismus, Positivismus) steht die westliche Philosophie möglicherweise zu streng unter dem Erfolgsdruck nachweisbarer und messbarer Ergebnisse (Anwendungen) und löst sich daher nicht konsequent genug von der Logik erster Ordnung, wenn es darum geht, nicht nur die Ergebnisse, sondern auch die Eigenschaften des Denkweges zu erkennen. Das Denken wird zu eng nach einem Input-Output-Modell gemessen (was investiere ich, was erhalte ich dafür zurück), statt ihm größere Freiheit zu lassen und zu untersuchen, welchen eigenen Regeln es folgt. Welche Antwort gibt der Buddhismus? Hier könnten vor allem die Arbeiten von Vasubandhu über den Gedankenstrom und dessen Eigenschaften helfen.

Übersteigt die Situation in der Quantenphysik die Möglichkeiten des bewussten Denkens? Hat Kant recht, dass wir nur in Substanzen mit ihren kategorialen Eigenschaften, Kausalität und Wechselwirkung denken können?

Können Mathematiker in anderen Zeiten und Räumen denken? Das war die Frage von Einstein und Gödel an Kant. Bietet der Buddhismus eine weiter gehende Antwort? Vasubandhu sprach von alaya vijnana. Das ist die Fähigkeit, an Dingen und Vorstellungen ihre Verwurzelung zu erkennen und über ihren Grund innere Seelenverwandtschaften (Wahlverwandtschaften) mit anderen Dingen und Vorstellungen. Auch im Westen gibt es Erfahrungen dieser Art, wenn z.B. jemand spürt, wie zur gleichen Zeit ein anderer ihm räumlich weit entfernter, aber persönlich nahe stehender Mensch großes Glück oder Leid empfindet, wenn Gartenblumen auf die Zuneigung der Gärtner reagieren u.ä., doch wird das meist als Schwärmerei, wenn nicht gar als psychische Krankheit abgetan. Wann hat sich das westliche Denken in diese Richtung entwickelt, und sind im Buddhismus andere Traditionen überliefert, die auf die gleichen Erfahrungen andere Antworten geben? Mit der Idee der Verankerung könnte sowohl der innere Zusammenhalt von Bewegungsbahnen der Elemente eines Kollektivs beschrieben werden, den Bohm mit den Führungswellen meinte, als auch die Stabilisierung von Bewusstseinsprozessen, die frei assoziieren können ohne sich dabei in Beliebigkeit zu verlieren und nicht wieder in die Realität zurück zu finden.

Für mich stehen wir am Anfang eines Dialogs. Es genügt nicht, einfach wie fremde Bilder Ergebnisse aus einer anderen Kultur zu bewundern. Das wird erst dann zu einem eigenen Umdenken führen, wenn schrittweise der blinde Fleck im eigenen Denken erkannt ist. Daher soll nach dieser ersten Infragestellung des eigenen Denkens im Weiteren an zwei zentralen Begriffen nach den Grundlagen des westlichen Denkens gefragt werden, um den Dialog mit dem Buddhismus fortführen zu können: Welche Keimbahnen hat Platon in seinem Modell der Entstehung der Welt im Timaios gesehen, und mit welchem Verständnis von Zahl und Zeit hat Aristoteles die abendländische Physik begründet. Das bereitet vor auf das nächste Thema: Die Fragen der Relativitätstheorie an den Buddhismus.

Literatur

Adam Becker: What is real? The unfinished quest for the meaning of quantum physics, London 2018

John S. Bell: Quantenmechanik, Berlin, Boston 2015

Fritjof Capra: Das Tao der Physik, Bern, München, Wien 1983 [1975]

Rudolf Carnap: Logische Syntax der Sprache, Wien, New York 1968 [1934]

Dalai Lama: Die Welt in einem einzigen Atom, Berlin 2005

Detlef Dürr, Dustin Lazarovici: Quantenphysik ohne Quantenphilosophie
in: Michael Esfeld (Hg.): Philosophie der Physik, Berlin 2012, 110-134

Michael Esfeld: Der Messproblem der Quantenmechanik heute: Übersicht und Bewertung
in: Michael Esfeld (Hg.): Philosophie der Physik, Berlin 2012, 88-109

Cord Friebe u.a.: Philosophie der Quantenphysik, Berlin 2018 [2015]

Konrad Knopp: Funktionentheorie I, Berlin New York 1976, 13. Auflage

Christian Thomas Kohl: Buddhismus und Quantenphysik, Oberstdorf 2015 [2005]

Lars Löfgren: Shadows of language in physics and cybernetics
in: Systems Research, Vol. 13, Issue 3, 1996, 329-340; Link

Nationale Akademie der Wissenschaften Leopoldina: Perspektiven der Quantentechnologie; Link

Roger Penrose: Computerdenken, Heidelberg 1991 [1989]

Renée Weber: Alles Leben ist Eins, Die Begegnung von Quantenphysik und Mystik, Amerang 2012 [1986]

Bernhard Weber-Brosamer, Dieter M. Back: Die Philosophie der Leere – Nagarjunas Mulamadhaymaka-Karikas, Wiesbaden 2005 (Harrasowitz) [1997]

Ludwig Wittgenstein: Tractatus logico-philosophicus (zitiert als TLP)
in: Ludwig Wittgenstein: Werke Band 1, Frankfurt am Main 1984

Anton Zeilinger: Max Planck, Einstein und der Dalai Lama, Interview mit der Welt vom 12.12.2000

Anton Zeilinger: Einsteins Schleier, München 2005 [2003]

Anton Zeilinger: Die zweite Quantenrevolution
in: SWR2 Aula - Manuskriptdienst: Sendung: Sonntag, 12. Mai 2013, 8:30 Uhr, SWR 2

Bildnachweis des Titelbildes: Von Paarbildung_gamma_p_Desy_Blasenkammer_Rekonstruiert.png: Ivan Baev (DESY-Blasenkammer)derivative work: Pro2 (talk) - Paarbildung_gamma_p_Desy_Blasenkammer_Rekonstruiert.png, CC BY-SA 3.0, Link

2018