Zyklizität der imaginären Zahlen

Vortrag beim 41. Internationalen Wittgenstein-Symposium 2018, Kirchberg am Wechsel am 10.8.2018

Einleitung

Der Beitrag über die Zyklizität der imaginären Zahlen ist für mich ein wenig überraschend in die Sektion über den Begriff der Unendlichkeit aufgenommen worden, doch von hier ergibt sich ein guter Einstieg: Den verschiedenen Zahlklassen entsprechen jeweils eigene Vorstellungen des Unendlichen, und darüber ist ein erster Eindruck zu gewinnen, was das Besondere an den imaginären Zahlen ist:

– Die natürlichen Zahlen 1, 2, 3, … lassen sich unbegrenzt weiter zählen. Das führt zum Begriff der schlechten Unendlichkeit. Er ergibt sich aus der Transitivität der natürlichen Zahlen.

– Die reellen Zahlen sind überabzählbar. Sie bilden ein Kontinuum. Erst mit der Kontinuität wird seit Hegel von der wahren Unendlichkeit gesprochen.

– Mit der Differentialrechnung werden für die verschwindenden Größen symbolische Zahlen eingeführt wie dx und dy. Für sie gelten eigene Rechengesetze. Insbesondere ist das Teilen durch 0 erlaubt. Das erfordert einen besonderen Differentialkalkül, der sich vom üblichen Kalkül der Zahlen unterscheidet. Und nicht nur das Teilen durch 0 ist erlaubt, sondern für diese Zahlen gelten eigene Prinzipien wie die Ununterscheidbarkeit verschiedener Größen. Der Differentialkalkül und dessen Prinzipien sind von Leibniz eingeführt worden.

– Bei den komplexen Zahlen ist durch ihre Zyklizität eine neue Art von Unendlichkeit gegeben. Sie gehen über den Bereich der reellen Zahlen hinaus und kehren dank geeigneter Rechenregeln wieder zurück. Im Verlaufe der Kreisfunktionen kann es zu unendlichen Oszillationen kommen. Für diese neue Situation sind die geeigneten Begriffe und Prinzipien zu finden, worum es in diesem Vortrag gehen soll.

Der Vortrag gliedert sich in drei Teile:
Im ersten Teil gebe ich einen Überblick über die Geschichte der imaginären Zahlen.
Der zweite Teil präsentiert die überraschenden Lösungsvorschläge von Spencer-Brown zur Russellschen Antinomie und dem Lügner-Paradoxon.
Der dritte Teil skizziert den Entwurf eines Zyklizitäts-Denkens.

Zur Geschichte der komplexen Zahlen

Üblicherweise gelten die imaginären Zahlen als der Abschluss einer Entwicklung, mit der schrittweise die Umkehrung mathematischer Operationen gelang: Die negativen Zahlen ergeben sich aus der Subtraktion, die rationalen Zahlen aus der Division, die irrationalen Zahlen aus dem Wurzelziehen und die imaginären Zahlen als Wurzeln aus negativen Zahlen. Das ist ohne Zweifel im Rückblick richtig, doch geht darüber der Blick auf die spezifische Eigenschaft verloren, die erst mit den imaginären Zahlen erreicht ist: Ihre Zyklizität. So wie die ganzen Zahlen nicht nur dem Addieren und dem Subtrahieren dienen, sondern an sich transitiv (additiv) sind, und so wie nicht nur mit reellen Zahlen kontinuierliche Bewegungen beschrieben werden, sondern sie an sich ein Kontinuum bilden, so werden die imaginären Zahlen nicht nur genutzt, um elektrische Schwingungen, Fraktale oder die periodischen Welleneigenschaften von Quantenobjekten zu beschreiben, sondern sie tragen an sich die Eigenschaft der Zyklizität. Ihre Zyklizität ergibt sich nicht aus der äußeren Anordnung einer endlichen Algebra wie z.B. bei den ersten zwölf natürlichen Zahlen auf der Uhr, sondern aus den Rechenregeln für eine Zahlenmenge, die eine echte Erweiterung der bekannten Zahlen darstellt.

Die Idee imaginärer Zahlen entstand bei Universalgelehrten der Renaissance wie Girolamo Cardano (1501-1576). Aktiv auf so verschiedenen Gebieten wie Medizin, Ingenieurwesen, Philosophie oder das Stellen von Horoskopen kam er in der Mathematik auf eine typische Rätselaufgabe seiner Zeit: Gibt es zwei Zahlen a und b, so dass gilt:

a + b = 10
a · b = 40

Einfache Lösungsversuche zeigen schnell, dass es auf der gewöhnlichen Zahlengerade keine Lösung gibt. Niemand weiß, dank welcher Imagination Cardano die richtigen Lösungen fand, die oberhalb und unterhalb der Zahlenachse in der Zahlenebene liegen: 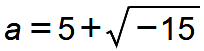und 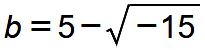. Cardano dachte noch nicht an Wurzeln aus negativen Zahlen, sondern er blieb dabei, irgendwie die gewöhnlichen Zahlen zu verlassen und zugleich für die neuen Zahlen Operationen zu definieren, die nicht im Widerspruch zu den gewöhnlichen Zahlen stehen, sondern zu ihnen zurückführen. Die von ihm gefundenen Lösungen müssen irgendwie aus der Zahlenachse herausgedreht sein und im Verlaufe der gleichen Drehung wieder in einem Re-entry zu ihr zurückkehren.

Ungefähr 200 Jahre später fand 1748 der Mathematiker Leonhard Euler (1707-1783) mit der nach ihm benannten Eulerschen Formel den Zusammenhang der imaginären Zahlen mit den Kreisfunktionen Sinus und Cosinus. Von da war es nur noch ein kleiner Schritt, bis in den Jahren um 1800 der norwegisch-dänische Kartograph Caspar Wessel (1745-1818) und der aus Genf stammende Buchhändler, republikanische Revolutionär und Hobbymathematiker Jean-Robert Argand (1768-1822) die Rechenregeln für das Addieren und Multiplizieren komplexer Zahlen entwickelten, und darauf folgten 1811 die Gaußsche Zahlenebene und 1857 die Riemannsche Zahlenkugel, mit denen das Verhältnis der komplexen Zahlen zu den reellen Zahlen geklärt wurde. Wessel schuf die bis heute gültige anschauliche Darstellung und versteht die Multiplikation zweier komplexer Zahlen als »Richtungsänderung« (Drehung) (Wessel, § 4).

Damit lagen die mathematischen Werkzeuge bereit. Es bedurfte nur noch des Anstoßes durch die ab 1880 rasant entstehende Elektrotechnik. Deren Schwingkreise lassen sich am einfachsten mit komplexen Zahlen beschreiben. Das führte 1920-1940 zur Ausarbeitung der Funktionentheorie mit komplexen Variablen, wie sie bis heute gelehrt wird. Sie gilt aufgrund der Reinheit ihrer Sätze bisweilen als »Königin der Analysis«.

Das Wurzelziehen aus negativen Zahlen ergibt sich in diesem Kontext wie von selbst als Drehung der komplexen Zahlen. Im einfachsten Fall 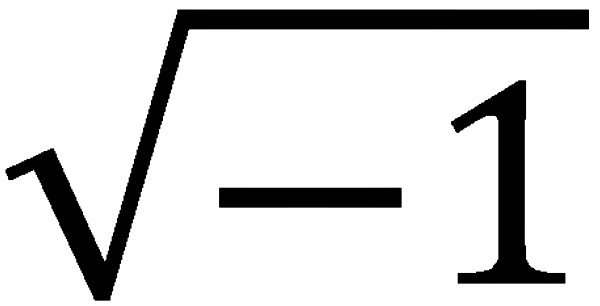wird das Produkt i · i betrachtet: In diesem Fall haben beide Faktoren (jeweils die Zahl i) einen Winkel von 90° relativ zur reellen Achse. Werden die beiden Winkel addiert, ergibt das den Winkel von 180° und das Produkt fällt durch die Drehung auf die Zahl −1. Daher ergibt i · i = −1 und es gilt nach Wurzelziehen auf beiden Seiten i = .

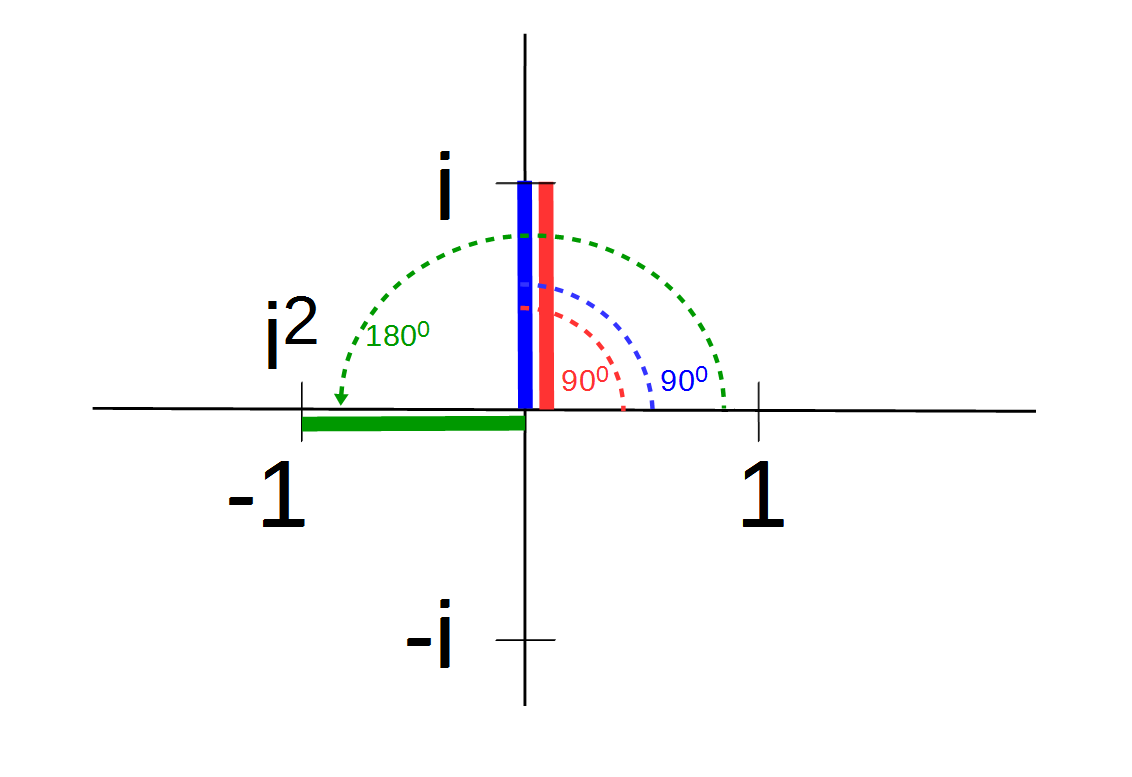
i · i als Drehung auf −1

Wird diese Bewegung im Ganzen betrachtet, dann zeigt sie, wie im Übergang zur Zahl i die reelle Zahlenachse verlassen und durch Weiterdrehen bei den negativen Zahlen wieder erreicht wird. Die Zyklizität öffnet einen neuen Zahlenraum und stellt zugleich sicher, wie er widerspruchsfrei die bekannten Zahlen enthält.

Russellsche Antinomie und Lügner-Paradox

Wird diese Bewegung, aus den reellen Zahlen hervorzutreten und wieder zu ihnen zurückzukehren, für sich betrachtet, erschließt sich mit ihr eine völlig neue Art zu denken. Das ist in allgemeiner Weise bereits bei Hegel angelegt, wenn er die Pulsation der in Widersprüchen denkenden dialektischen Methode einführt, doch es war die große Leistung des nach wie vor zu Unrecht kaum bekannten britischen Mathematikers, Psychologen, Dichters und Songwriters George Spencer-Brown (1923-2016), die Verbindung der Zyklizität der imaginären Zahlen mit den unlösbar scheinenden Paradoxen der Logik gefunden zu haben. Er war durch seine Arbeit als Funker und Nachrichtentechniker im 2. Weltkrieg und anschließend bei der Programmierung von Schaltkreisen mit komplexen Zahlen bestens vertraut. Daneben hat er 1950-51 bei Ludwig Wittgenstein (1889-1951) studiert und war ab 1960 mit dem Mathematiker und Philosophen Bertrand Russell (1872-1970) bekannt.

Das Denken droht sich in logischen Paradoxien zu verfangen, wenn es wie in der von Russell betrachteten Menge aller Mengen, die sich nicht selbst enthalten, zu einer negativen Selbstbezüglichkeit zwischen den Eigenschaften eines Systems und seinen Elementen kommt. Russell und Whitehead wollten daher in der Typen-Theorie mit dem Verbot selbstbezüglich definierter Elemente alle Antinomien ausschließen (Vicious circle principle). Aus Wien kam von verschiedenen Seiten Kritik, sowohl von Wittgenstein wie auch von Gödel. Sie wiesen nach, dass sich dieser Anspruch nicht konsequent durchhalten lässt, und dass er die Möglichkeiten der Wissenschaft zu stark einschränkt. Gödel hat gezeigt, wie sich in jedem ausreichend komplexen System Meta- und Objektebene verschlingen und der Satz ›dieser Satz ist falsch‹ formal korrekt formuliert werden kann. Mit Spencer-Brown bietet das Zyklizitäts-Denken einen Ausweg. Spencer-Brown berichtet, dass er Russell 1967 getroffen und ihm gezeigt hat, wie er ohne diesen Ausschluss arbeiten kann, was nach seiner Aussage von Russell begeistert aufgenommen wurde (Spencer-Brown, x).

Spencer-Brown ging in zwei Schritten vor: Ihm gelingt eine einfache arithmetische Darstellung der Russellschen Antinomie, die er sodann mithilfe der imaginären Zahlen auflöst:

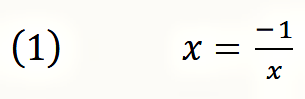
Mit dieser Gleichung ist die negative Selbstbezüglichkeit formalisiert: Der Kehrwert steht für den Selbstbezug, das Minuszeichen für die Negation. Das in ihr enthaltene Paradox wird sichtbar, wenn für x der Wert 1 oder der Wert −1 eingesetzt wird:

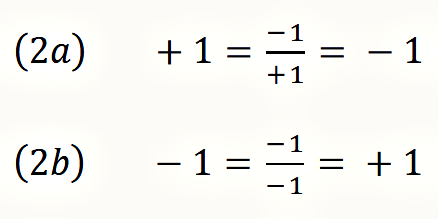
1 und −1 sind die einfachst-möglichen Zahlen, und sie zeigen, dass es für diese Formel keine natürliche Zahl als Lösung gibt. Dagegen ergibt sich mit imaginären Zahlen die Lösung:

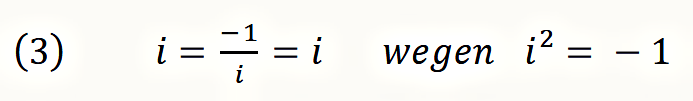
Das ist in einem Analogie-Schluss zu übertragen auf die Russellsche Antinomie. Whitehead und Russell hatten nur den Ausweg gesehen, Fragen dieser Art mit einem dritten Wahrheitswert ‘bedeutungslos‘ (meaningless) zu versehen und auszuschließen. Spencer-Brown stellt stattdessen den beiden Wahrheitswerten ‘wahr’ und ‘falsch’ den dritten Wahrheitswert ‘imaginary’ gegenüber. Während ‘meaningless’ lediglich unbestimmt die Leerheit bezeichnet, die jenseits von ‘wahr’ und ‘falsch’ liegt, öffnet sich mit ‘imaginary’ ein Möglichkeitsraum, der als solcher nur im Denken besteht. Dieser Möglichkeitsraum ist nicht mehr leer oder beliebig, sondern in ihm gelten die für die komplexen Zahlen eingeführten Regeln. Der Status oder erweiterte Wahrheitswert ‘imaginary’ ist daher der Schlüsselbegriff, um die Fähigkeit des Denkens formal zu beschreiben, sich Möglichkeiten vorstellen und aus ihnen auswählen zu können.

Mit diesem Ansatz löst sich für Spencer-Brown auch das Lügner-Paradox, das aus dem einfachen Satz besteht: ›dieser Satz ist falsch‹. Wenn der Satz falsch ist, ist er laut eigener Aussage wahr, und wenn er wahr ist, ist er laut eigener Aussage falsch. Das ergibt eine unendliche Oszillation der beiden Wahrheitswerte ‘wahr’ und ‘falsch’. Spencer-Brown löst die Oszillation nicht erneut durch den dritten Wahrheitswert ‘imaginary’, sondern er stellt den Verlauf der Oszillation der beiden Wahrheitswerte in der komplexen Zahlenebene dar. Für Spencer-Brown ist das formal ein Beispiel für einen Re-entry und vergleichbar einer Zuweisung in einem Computer-Programm: Dem Satz wird abwechselnd der Wahrheitswert ‘wahr’ und ‘falsch’ zugewiesen. Das ergibt im Sinne der Programmierung eine Endlos-Schleife, die fortwährend zwischen zwei Werten hin und her springt:

Spencer-Brown entwickelte für komplexe oszillierende Figuren der Logik graphische Schalt-Pläne, die seiner früheren Programmierung technischer Anwendungen und den heute bekannten Ablaufplänen mit Rückkopplungen sehr nahe kommen, und im Weiteren von der Kybernetik, dem radikalen Konstruktivismus und der Systemtheorie von Luhmann fortgeführt wurden.

Zyklizität als eigene Figur des Schließens und eigener Seins-Modus

Die Zyklizität passt weder in die traditionellen Figuren des Schließens noch in die überlieferte Unterscheidung der Seins-Modi von Möglichkeit, Wirklichkeit und Notwendigkeit. Das Tautologie-Denken des Mythos und der Religionen konnte sich auf heilige Texte berufen. Es hat nicht einfach nur tautologisch wiederholt, was in diesen bereits enthalten ist, sondern ihm ist es gelungen, ausgehend von einem übergreifenden, universalen Entwurf eine kosmologische Ordnung zu finden und mit ihr der Wissenschaft den Boden zu bereiten. Das ist bereits bei Pythagoras zu sehen und setzt sich fort über die regulativen Ideen bei Kant bis zu den bewusst tautologischen Formulierungen Heideggers wie ›die Sprache spricht‹, mit denen er die impliziten Grundzüge des Denkens aufdecken wollte. – Das Homologie-Denken verlässt sich auf eine vorgegebene, prinzipielle Übereinstimmung der jeweiligen Elemente (Objekte) der Wissenschaft. Eine Wissenschaft kann begründet werden, wenn es gelingt, aus der Vielfalt des Gegebenen diese Elemente zu erkennen, ihre Regelmäßigkeit nachzuweisen und entlang der homologen Reihe der Elemente und ihrer enzyklopädischen Ordnung deduktiv wie induktiv zu schließen. Wittgenstein hat mit dem Tractatus logico-philosophicus die Grundzüge und Grenzen dieser Art des Denkens aufgezeigt. In der Realität verfahren kreative Kunst und Wissenschaft jedoch mit einem Analogie-Denken. Sie bilden Metaphern, mit denen Muster von einem Bereich auf einen anderen übertragen werden, um bisher ungelöste Fragen unter neuen Perspektiven sehen zu können und verborgene Strukturen aufscheinen zu lassen. Wenn das gelingt, können aus den Analogien neue Offenbarungen im Sinne des Tautologie-Denkens wie auch die Erkenntnis neuartiger Grundelemente für das Homologie-Denken hervorgehen.

Aber erst mit dem Zyklizitäts-Denken gelingt es, mit einer an den imaginären Zahlen gewonnenen Methode nicht nur die Beziehungen der Elemente untereinander, sondern die Beziehung zwischen den Eigenschaften der Elemente und den Eigenschaften des Systems im Ganzen aufzuzeigen. Das wird möglich, wenn nicht mehr wie in der Mengenlehre nur die statischen Eigenschaften, sondern die  Bewegungseigenschaften  auf System- und Element-Ebene untersucht und miteinander in Beziehung gesetzt werden: Die Bewegtheit des Systems im Ganzen und die Bewegungsgesetze der einzelnen Elemente innerhalb des Systems. Die Thermodynamik war das erste Beispiel, als sie an der Bewegung der nur statistisch unterscheidbaren Elemente einer Gesamtheit das Grundrauschen des Systems und die mechanische Bewegung seiner einzelnen Elemente voneinander trennen konnte. Analog wird mit der Allgemeinen Relativitätstheorie unterschieden zwischen den mechanischen Bewegungen von Körpern innerhalb eines Raums (ihren Translationen und Rotationen), sowie der Bewegtheit des Raums im Ganzen (seiner Ausdehnung, Kontraktion oder Drehung). Einstein suchte nach Feldgleichungen, beide einheitlich darstellen zu können. Die Lösung zeichnet sich unerwartet von der Quantenphysik her ab. Es war eine intuitive Eingebung, als Schrödinger 1926 mit seiner auf den imaginären Zahlen beruhenden Gleichung ein Bewegungsgesetz der Quantenobjekte erriet, das sich bisher mit äußerster Genauigkeit in allen Experimenten bestätigt hat. De Broglie vollzog 1964 den letzten Schritt, als er aus einer nur statistisch messbaren Gesamtheit von Objekten die Bewegung isolierter Partikel zu separieren und an ihr die Bewegtheit des Systems im Ganzen darzustellen vermochte. Erfolge dieser Art werden maßgeblich durch Analogien vorbereitet, etwa von Quantenobjekten und Wellen oder dem Planckschen Wirkungsquantum h aus der Quantendynamik und der Boltzmann-Konstante k aus der Thermodynamik bei de Broglie. Sie führen im Ergebnis zur Erkenntnis der inneren Zyklizität eines Systems mit seinen Elementen.

In einer nochmals übergreifenden Analogie wird die Zyklizität des Systems und seiner Elemente verstanden als Zyklizität des Raums aller Möglichkeiten und der jeweiligen Wirklichkeit. Dadurch wird die überlieferte Unterscheidung von Möglichkeit und Wirklichkeit unterlaufen. Mit Möglichkeit ist nicht mehr eine bloße Aufzählung von Alternativen gemeint, wie sie bereits dem disjunktiven Urteil bekannt war, der Theorie von Glücksspielen oder den mechanischen Phasen- und Konfigurationsräumen, auf die sich Wittgenstein in seinem Tractatus bezieht. Sondern so wie Wittgenstein später mit den Sprachspielen der Philosophie einen neuen Horizont öffnen wollte, ist hier der mit imaginären Zahlen beschriebene Möglichkeitsraum der spezifische Raum, in dem die Praxis eines Systems im Ganzen für sich formalisiert und als die Gesamtheit der mit dem System gegebenen Möglichkeiten erkannt werden kann. Möglichkeit und Wirklichkeit sind nicht mehr zwei voneinander getrennte Seins-Modi, sondern in ihrer jeweils spezifischen Tätigkeit über die Zyklizität der imaginären Zahlen aufeinander bezogen.

Mit dem Zyklizitäts-Denken lässt sich die negative Selbstbezüglichkeit auf die Modallogik von Möglichkeit und Wirklichkeit übertragen. Walter Rella hat beim Wittgenstein-Symposium 1999 den Begriff eines negativen Ereignisses (neguent, negvent) vorgestellt. Das ist das Ereignis des Nicht-Ereignisses. Das negative Ereignis tritt aus der traditionellen Unterscheidung von Möglichkeit und Wirklichkeit heraus und vollzieht wie die imaginären Zahlen eine Bewegung durch einen imaginären Raum, der jenseits der üblichen Möglichkeit und Wirklichkeit liegt und in den Bereich der Wirklichkeit zurückkehrt (Re-entry). Es bewegt sich in der Sprache der Quantenphysik in einem subquanten Milieu, wobei im Verlaufe der Drehung imaginäre Informationseinheiten auftreten, die jenseits der Grenze von einem Bit liegen. Möglicherweise kommen wiederum aus der Physik weiterführende Anstöße und Hinweise, wenn sie bei den Higgs-Feldern die Erhaltung negativer Massequadrate nachweist. Das könnte in Erweiterung der traditionellen Erhaltungsgrößen von Impuls und Energie die Invariante sein, die die innere Drehung und Rückkehr von negativen Ereignissen auf ähnliche Weise stabilisiert wie die Rechenregeln der komplexen Zahlen die Drehung durch die imaginäre Einheit i. Im Ergebnis entsteht eine neue Ontologie, die die klassische Ontologie auf ähnliche Weise enthält wie die reellen Zahlen eingebettet sind in den komplexen Zahlen.

Literatur

Rella, Walter (1999): "Beyond Analysis and Synthesis", in: Meixner, Uwe; Simons, Peter (Hg.) Metaphysik im postmetaphysischen Zeitalter, Beiträge des 22. Internationalen Wittgenstein Symposiums 15.-21. August 1999, Kirchberg am Wechsel: Hölder-Pichler-Tempsky, 161-167

Remmert, Reinhold (1985): "Komplexe Zahlen" in: Ebbinghaus u.a. (Hg.) Zahlen, Darmstadt: Wissenschaftliche Buchgesellschaft, 45-77

Spencer-Brown, George (1972) Laws of Form, New York: Julian Press

Tydecks, Walter (2017) Imaginäre Zahlen, Bensheim, unter: http://www.tydecks.info/online/themen_zahlen_imaginaer.html

Wessel, Caspar (1797) Über die analytische Repräsentation der Richtung, unter: http://1iz.heimat.eu/theart-Dateien/Wessel.pdf