Das Lochargument in der Allgemeinen Relativitätstheorie

– Fußnote / Zusatz zum Beitrag Sphäre des Begriffs und Logik der Sphäre

Wenn in der Speziellen Relativitätstheorie die Zeit definiert wird über den Austausch von Signalen zwischen verschiedenen Lichtquellen, kann das in einem abstrakten Sinn als eine Wahlverwandtschaft verstanden werden: Zwei Ereignisse sind in einem elementaren Sinn verwandt, wenn sie sich durch eine Mitteilung verständigen können. Und wie bei chemischen Reaktionen kann gefragt werden, ob sich die Rahmenbedingungen für die Verwandtschaft ändern, d.h. in diesem Fall für den Austausch von Signalen. Dieser Frage ging Einstein in der Allgemeinen Relativitätstheorie nach und fand in der Raumkrümmung das verborgene Maß, welches die Bedingungen für den Austausch von Lichtsignalen ändert. Die von Einstein gefundene Krümmung des Raums entspricht daher den Knotenlinien bei Hegel, entlang derer sich für Hegel die Bedingungen für die Wahlverwandtschaften in chemischen Reaktionen ändern.

Die Wahlverwandtschaft erfolgt sowohl in chemischen Prozessen wie in der Gravitationstheorie in einem Medium. Chemische Reaktionen spielen sich meist im Wasser oder vergleichbaren Lösungen ab, für die Übertragung von Licht wurde als Medium der Äther gewählt. Die allgemeine Relativitätstheorie liefert daher mit ihren Einsichten in die Krümmung des Mediums das heute geltende Paradigma, in dem die Krümmung der Sphäre des Begriffs ihr anschauliches Modell findet.

Einstein stieß an diesem Punkt seiner Arbeiten schon 1915 auf eine Paradoxie, die bis heute im Grunde ungelöst ist. Er fragte, wie die Krümmung des Raums dargestellt werden kann. Wenn der Raum selbst gekrümmt ist, in welchem Gebilde oder vor welchem Hintergrund kann seine Krümmung dann erkennbar sein? Wird dafür wiederum ein umfassender Raum gewählt, kann auch der gekrümmt sein, und so weiter ad infinitum. Um aus dieser Sackgasse hinauszukommen wählte Einstein eine Methode, die im 19. Jahrhundert in der Mathematik eingeführt worden war: Er wechselte von der Aufgabe zum Lösungsraum, in dem alle Lösungen der Aufgabe enthalten sind, unabhängig davon, ob sie in der Natur nachgewiesen werden können oder nicht. Das heißt in diesem Fall: Er wechselte vom Raum, dessen Krümmung dargestellt werden soll, zur Gesamtheit aller Koordinatensysteme, mit denen sich die Geometrie eines Raumes darstellen lässt. Vereinfacht gesagt: Er wechselte vom gekrümmten Raum zur Gesamtheit aller Geometrien, mit denen eine Krümmung gezeichnet werden kann. Diese Vorgehensweise entsprach ähnlichen Überlegungen, die zur gleichen Zeit der Mathematiker David Hilbert in seinen Axiomatisierungen der Geometrie vortrug.

Für die Gesamtheit aller Geometrien sind einige Anforderungen zu stellen. Anschaulich gesprochen geht es darum, dass alle Geometrien den gleichen Sachverhalt im Prinzip ähnlich darstellen, obwohl sie mit unterschiedlichen Koordinatensystemen arbeiten. Hierfür gibt es einige fast banale Beispiele. Angenommen, alles in der Welt wäre um 5 Meter nach rechts verschoben, dann sollte sich an der Geometrie nichts ändern und alles so aussehen wie vorher. Wenn also von einem rechtwinklingen (kartesischen) Koordinatensystem in ein anderes gewechselt wird, das sich nur darin unterscheidet, dass der Nullpunkt gegenüber dem ersten ein wenig verschoben ist, sollten dennoch beide Koordinatensysteme der Sache nach nichts ändern.

Und ebenso sollte nichts geändert werden, wenn die rechtwinkligen Koordinaten durch Polarkoordinaten ersetzt werden. Bei Polarkoordinaten wird jeder räumliche Punkt bestimmt durch seinen direkten Abstand zum Mittelpunkt und die Winkel der Verbindungslinie des Punktes zum Mittelpunkt gegenüber einer festen Ebene.

Diese Beispiele können dahin verallgemeinert werden, dass in der Gesamtheit der Geometrien die unterschiedlichen Koordinatensysteme diffeomorph (bijektiv und stetig differenzierbar) ineinander übergehen.

Figur 1: Rechtwinkliges Netz
"Bild eines rechtwinkligen Netzes auf einem Quadrat unter einem Diffeomorphismus vom Quadrat auf sich selbst."(Wikipedia)

Das lässt sich verallgemeinern auf beliebige krummlinige Koordinatensysteme, solange nur die Anforderung erhalten bleibt, dass ein diffeomorpher Übergang in das Koordinatensystem möglich ist.

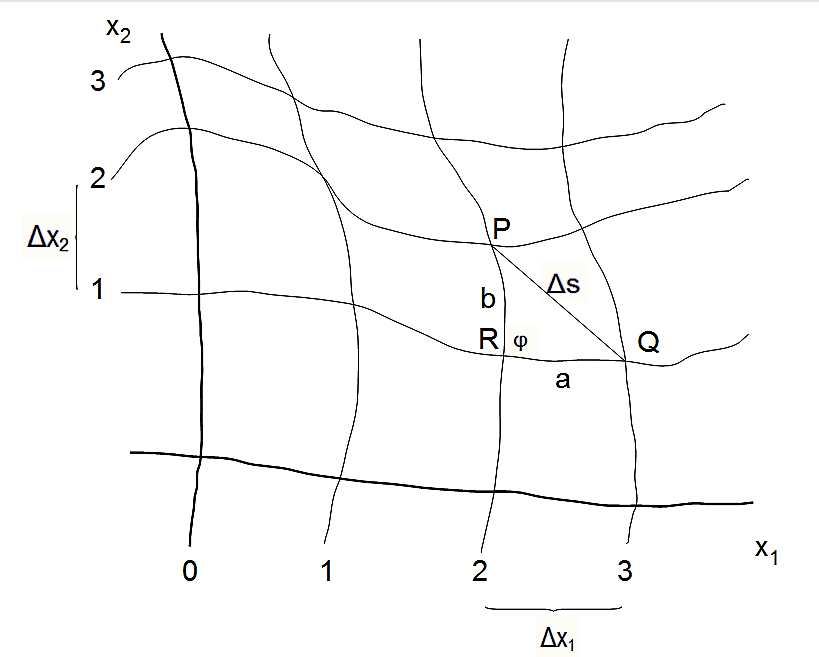
Figur 2: Zur Bestimmung der Riemannschen Metrik
In einem krummlinigen Koordinatensystem mit den Achsen x₁ und x₂ wird zwischen den Punkten P und Q ein Abstand Δs betrachtet. P hat die Koordinaten (2,2) und Q hat die Koordinaten (3,1). Der Abstand Δs bildet ein Dreieck mit dem Punkt R mit den Koordinaten (2,1). Der Punkt R stimmt in jeweils einer Koordinate mit P und Q überein: R und P haben den gleichen Wert 2 auf der x₁-Achse und R und Q haben den gleichen Wert 1 auf der x₂-Achse. Daher wird angenommen, dass für dieses Dreieck der Satz des Pythagoras gelten soll:
    (Δs)² = a² + b².
Das ist nur möglich, wenn drei Grenzübergänge gelten: die Länge a entspricht der Länge Δx₁ auf der x₁-Achse, die Länge b entspricht der Länge Δx₂ auf der x₂-Achse, der Winkel φ zwischen a und b ist rechtwinklig. Darauf aufbauend gilt schließlich im Grenzübergang der Satz von Pythagoras. Quelle: Freihandzeichnung ausgehend von Garbe "Die partiell konventional, partiell empirisch bestimmte Realität physikalischer RaumZeiten" Würzburg 2001, Abbildung 4.29, S. 187

Einstein hoffte, auf diese Weise die Frage nach dem Raum, in dem ein gekrümmter Raum dargestellt werden kann, zu ersetzen durch die Anforderung, dass es für die Krümmung ein Maß gibt, das in der Gesamtheit aller Geometrien erhalten bleibt. (Diese Anforderung wird als "Freiheit der allgemeinen Kovarianz", Freedom of General Coviance bezeichnet.) (Auch dieser Gedanke ähnelt sehr der Vorstellung, die Hegels Betrachtung der Knotenlinien zugrunde liegt. Siehe hierzu die Logik-Studie zum realen Maß und dort die Figuren 7 und 8, in denen Wahlverwandtschaften und Knotenlinien als geometrische Figuren innerhalb der Gesamtheiten von Zuständen und Wahlverwandtschaften betrachtet werden, Link).

Aber Einstein musste erkennen, dass es innerhalb der Gesamtheit von Geometrien zu Singularitäten (Katastrophen) kommen kann, die einen Übergang in eine Geometrie ermöglichen, der zwar die Anforderungen der Diffeomorphie erfüllt, aber in Bereiche führt, in denen die Lichtsignale verschluckt werden.

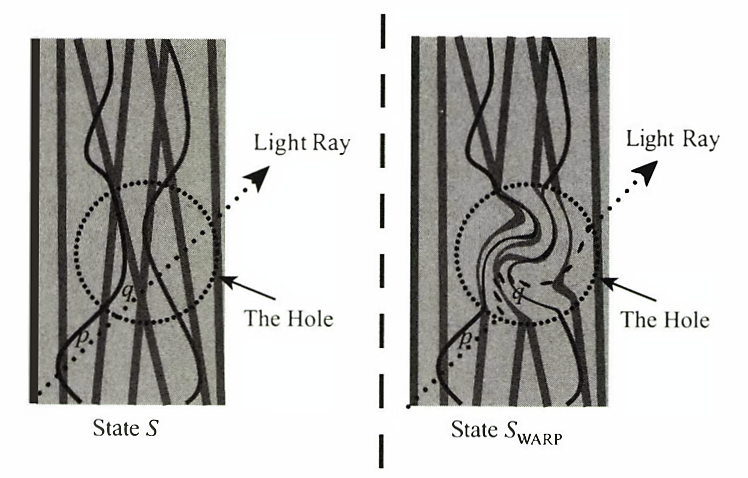
Figur 3: Loch und Verwerfung in einem Medium
Im links dargestellten Zustand S kreuzt ein Lichtstrahl eine komplexe Situation ohne sich von ihr ablenken zu lassen. Im rechts dargestellten Zustand S_WARP tritt dagegen im Zustand eine Verwerfung (warp) auf, wodurch der Lichtstrahl im Extrem in eine unendliche Kreiselbewegung gerät. Quelle: Maudlin, S. 148 Figur 28. Maudlin bezieht sich hier auf John Earman and John Norton "What Price Space-Time Substantivalism? The Hole Story" British Journal for the Philosophy of Science 38:515-525 (1987).

Die Verwerfung erzeugt eine neue Dimension. Sie kann auch als Knoten verstanden werden. Siehe im Deutschen die Doppelbedeutung von Verwerfung im Sinne von Faltung oder Nichtanerkennung, englisch übersetzt in warping bzw. disavowal.

Maudlin sieht hier eine Grenze zur Metaphysik.

"The heart of the hole argument is evidently a deeply metaphysical proposition, namely, that S and S_WARP can be interpreted as representing two metaphysically distinct and yet physically possible situations. Since the differences between S and S_WARP can only be stated in terms of individual, named events (rather than qualitative features, such as the existence of a pair of colliding particles, or a black hole), the metaphysical issue of the identity of individuals in different 'possible worlds' must be addressed. One line of reply to the hole argument, presented by Jeremy Butterfield (1989), argues that S and S_WARP (which are merely mathematical representations) cannot represent metaphysically distinct situations, since an event in S can only be identified with an event in S_WARP by means of some counterpart relation. But any counterpart relation will match up the event p in S with the event that the diffeomorphism maps p to in S_WARP and the same for q. So if p and q are light-like related in S, their counterparts are light-like related in S_WARP. According to David Lewis's semantics for modal locutions, this means that if p and q are actually light-like related, there is no possible world according to which they are not light-like related." (Maudlin, S. 150)

Da sich das Loch diffeomorph in die Mannigfaltigkeit einschmiegt, erfüllt es alle an die Koordinatentransformationen gestellten Anforderungen und ist eine der möglichen Koordinatensysteme. Einstein erkannte das und war nahe am Verzweifeln. Er stand kurz davor, die Forderung der allgemeinen Kovarianz aufzugeben, um eine solche Situation zu vermeiden. 1915 half ihm der 17 Jahre ältere David Hilbert (1862-1943). Einstein glaubte, er habe eine Lösung gefunden, aber 1980 bemerkte John Stachel (* 1928), dass diese Frage keineswegs so trivial ist wie sie aussah. Durch die Theorie der Schwarzen Löcher war mittlerweile auf diesem Gebiet das Wissen weit besser ausgearbeitet.

Ergänzung 1 (Eich-Freiheit): Eine verwandte Frage ist die Eich-Freiheit (Gauge Freedom, Symmetrie). Das gibt es seit Newton. Seine Feldtheorie kann äuqivalent durch einen Testkörper beschrieben werden, auf den Anziehungskräfte wirken, wie auch durch ein Potential U. Das Potential U ändert sich nicht, wenn überall ein bestimmter Wert hinzugefügt wird, der sich in gewissem Maß sogar in der Zeit ändern kann.

Ergänzung 2 (Unabhängigkeit der Kräfte): Hegel kritisierte Newtons Kräfte-Parallelogramm. Das Kräfte-Parallelogramm setzt voraus, dass die beiden betrachteten Kräfte voneinander unabhängig sind, ohne zu erklären, warum und wann diese Unabhängigkeit gelten soll (Ihmig, S. 32).

Hegel konnte sich auf die Arbeiten des französischen Mathematikers Lagrange beziehen. Lagrange zeigte, dass letztlich eine Unabhängigkeit der Koordinatenachsen gegeben sein muss, auf die sich die voneinander unabhängigen Kräfte beziehen.

"Die mathematische Beschreibung einer Bewegungsbahn wird zurückgeführt auf die Bestimmung der Projektion dieser Bahn auf die jeweiligen Koordinatenachsen. Jede Bewegung, die auf ein bestimmtes (rechtwinkliges) Koordinatensystem bezogen wird, kann damit natürlicherweise zerlegt werden in die den Projektionen auf die Achsen entsprechenden Komponenten, und sie kann dann ebenso daraus zusammengesetzt werden." (Ihmig, S. 36)

Zum einen ergibt sich ein Kräfteparallelogramm von allein, wenn die Kräfte in einem Koordinatensystem dargestellt und entsprechend der Koordinaten zerlegt werden. Zum anderen wird umgekehrt versucht, ausgehend von komplexen Kräften ein geeignetes Koordinatensystem zu finden, in dem die Kräfte zerlegt werden können. Die voneinander unabhängigen Koordinaten werden als voneinander unabhängige Freiheitsgrade der Bewegung der jeweiligen Kräfte verstanden.

Newton übertrug das auf die Momentanbewegung entlang einer Kurve wie z.B. der Bewegungsbahn der Planeten und zerlegt sie in die Achsen des Tangentialraums. Eine Achse zeigt tangential entlang der Bahn, die andere senkrecht in die Richtung ihrer stärksten Krümmung.

Wird nun gefragt, ob die Zerlegung von Kräften einfach aus der Wahl des Koordinatensystems herrührt und insofern zirkulär begründet ist (die Zerlegung der Kräfte führt zu entsprechenden Koordinaten, und die Koordinaten führen zu einer Zerlegung der Kräfte), was der Kritik von Hegel an Newton entspricht, dann kann eine Antwort gefunden werden, wenn gezeigt wird, dass sich die Kräfte auf ähnliche Weise in allen Koordinatensystemen zerlegen lassen. Wenn das gilt, kann angenommen werden, dass es zur Natur der Kräfte gilt, dass sie sich zerlegen lassen. Damit ist im Prinzip die Frage von Einstein erreicht, wie die Krümmung eines gekrümmten Raums nicht-zirkulär dargestellt werden kann.

Ergänzung 3 (Materialität des Mediums): Es wird sowohl von Einstein wie von Newton vorausgesetzt, dass die geometrische Darstellung auch physikalisch gilt. Daher spricht Ihmig von

"Hegels Kritik, Newton habe nicht exakt zwischen den mathematisch zu beweisenden Größenverhältnissen geometrisch konstruierter Linien und ihrer physikalischen Bedeutung als in der Natur wirkenden Kräften unterschieden und auf diese Weise ein 'aus Physik und Mathematik gemischtes Bauwerk' errichtet. [...] Kant sieht, ebenso wie Hegel, die Notwendigkeit, die geometrische Konstruktion der Größen von der, wie Kant es nennt, 'mechanischen' Konstruktion der Kräfte genau zu unterscheiden." (Ihmig, S. 34)

Diese Kritik trifft die Sache auf den Punkt. Jede mathematische Darstellung einer Krümmung "sieht eben aus". Die Koordinatensysteme (Figur 1 - 3)  zeigen  nur eine Krümmung und  sind nicht  selbst gekrümmt: Weder der Bildschirm noch der Ausdruck, auf dem sie zu sehen ist, ist gekrümmt. Das gezeigte Objekt kann nur gekrümmt sein, wenn es mit einem zusammenhängenden Stoff erfüllt ist, der krümmbar ist. Auch die hier abgebildeten Figuren sind eben auf dem Bildschirm oder auf dem Papier eines Ausdrucks. Das ändert sich erst, wenn die Materialität hinzugenommen wird, was durch den Übergang in ein physikalisches System erfolgt. Das Prinzip der Materialität kann dann wiederum abstrahiert und auf die Sphäre des Begriffs übertragen werden.

Literatur

Annette Garbe: Die partiell konventional, partiell empirisch bestimmte Realität physikalischer RaumZeiten, Würzburg 2001

Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971 (zitiert als HW); Link

Karl-Norbert Ihmig: Hegels Deutung der Gravitation, Frankfurt 1989

Immanuel Kant: Kritik der reinen Vernunft (1781, 1787) (zitiert als KrV)

Tim Maudlin: Philosophy of Physics, Space and Time, Princeton 2012

John Norton: "The Hole Argument" (2008)
In: Edward N. Zalta, ed., Stanford Encyclopedia of Philosophy. Link

Georg Picht: Von der Zeit, Stuttgart 1999

2014