Walter Tydecks
Hegels Idee eines »höheren Widerspruchs«
– Von der Kontinuation und Umkehr zur »Pulsation« des Widerspruchs
Inhaltsverzeichnis
Einleitung
Von der absoluten Indifferenz zum »allseitigen Widerspruch«
Die Identität »in ihrer höheren Wahrheit«
Die negative Einheit
Die Kraft des Minus
Die »Pulsation« des sich auflösenden Widerspruchs
Die Kraft den Widerspruch auszuhalten
Anhang 1: Trendelenburg und Marx zu Hegels Logik
Anhang 2: M. Wolff über die Stufen des Gegensatzes
Version 4.1.2019
Einleitung
Am Begriff des Widerspruchs misst Hegel den Erfolg seiner Philosophie. Programmatisch schreibt er in der Einleitung der Wissenschaft der Logik, »daß der Widerspruch eben das Erheben der Vernunft über die Beschränkungen des Verstandes und das Auflösen derselben ist« (HW 5.39). Der Verstand gerät in seiner eigenen Entwicklung notwendig in Widersprüche, und der Vernunft gelingt es, dies aufzugreifen und ihm eine neue Wendung zu geben. Hegel fragt nicht mehr, ob eine Theorie einen Widerspruch enthält und daher falsch ist und korrigiert werden muss, sondern ob und wie es einer Theorie gelingt, die Bewegung des Widerspruchs zu ergreifen und mit ihr ihre Begriffe zu entfalten.
In diesem Beitrag soll gezeigt werden, wie Hegel innerhalb der Entwicklung der modernen Naturwissenschaft und ihrer Logik auf die Bewegungsform des Widerspruchs stößt, das Wechselspiel von Kontinuität und Umkehr. Was anfangs wie eine empirische Beobachtung aussieht (die regelmäßigen Bahnen der Himmelsläufe mit ihren Phasen der Entfernung und Umkehr, der Sichtbarkeit und Unsichtbarkeit) erweist sich für Hegel als eine Denkbestimmung, die aller Wissenschaft zugrunde liegt. Diese zu erkennen und den Widerspruch als ihren kreativen Wendepunkt zu bestimmen, das führt zur Idee des höheren Widerspruchs. Die mit dem Widerspruch verbundene Negativität wird nicht mehr als bloß zerstörerisch, sondern als die wahre Kraft der Logik verstanden im Wechselspiel der Kraft des Minus und der Kraft, den Widerspruch auszuhalten.
Von der absoluten Indifferenz zum »allseitigen Widerspruch«
Einführend soll am Beispiel des zweiten Keplerschen Gesetzes gezeigt werden, wie die moderne Naturwissenschaft von sich aus auf die absolute Indifferenz stößt und sie nicht vermeiden kann. Aus heutiger Sicht mögen die Keplerschen Gesetze ein Randgebiet der Physik sein. Für Hegel waren sie die größte Leistung, die der Physik in ihrer Geschichte gelungen ist. Mit ihr hat sie alle überlieferten Denktraditionen und Dogmen überwunden und den Weg geöffnet für die neuzeitliche Physik, wie wir sie kennen. Wenn Hegel an den Keplerschen Gesetzen zeigen will, wie sie schließlich in einen »allseitigen Widerspruch« geraten, ist das nicht als Kritik gemeint, sondern im Gegenteil ist Hegel überzeugt, nirgends besser als auf dem Höhepunkt der ihm bekannten Physik-Geschichte seinen neuen Gedanken zu entwickeln. Er will in der Logik als dem Herz der Philosophie nach- und mitvollziehen, was Kepler gelungen ist: Die Abkehr von allen überlieferten Grundüberzeugungen, und das nicht mit einer von außen vorgetragenen Kritik, sondern am Gang der Naturwissenschaft selbst. So wie für Kepler die von Tycho Brahe gefundenen empirischen Daten die Grundlage waren, die ihm die Sicherheit in seiner Umwälzung der Astronomie gaben, so sind auf einer höheren Abstraktionsebene für Hegel die Keplerschen Gesetze und ihr Erfolg die Grundlage, auf der er seinen Begriff des Widerspruchs ausführen will und sich sicher ist, gegenüber allen Kritikern der Sache nach recht zu haben.
Kepler hatte festgestellt, dass sich die Planeten auf Ellipsen und nicht auf Kreisen bewegen (1. Keplersches Gesetz). Auf den Ellipsen ändert sich fortlaufend ihre Geschwindigkeit: In der Nähe der Sonne sind sie schneller, weiter entfernt dagegen langsamer. Kepler fand die mathematische Beziehung, wie sich Geschwindigkeit und Abstand gegenläufig verändern (2. Keplersches Gesetz). Das Überraschende liegt darin, dass seine Gesetze unabhängig von der Masse gelten und damit auch unabhängig von der Kraft (wenn die Kraft gemäß der Formel ›Kraft gleich Masse mal Beschleunigung‹ als eine Funktion der Masse verstanden wird). Wie ist dann aber zu verstehen, dass es offenbar dennoch Kräfte geben muss, wenn sich die Bewegung entlang der Ellipsenbahn abwechselnd beschleunigt und verlangsamt? Die Keplerschen Gesetze gelten in einem masse- und kraftfreien Raum. Sie können aber auch nicht wie die zahlreichen Sätze der euklidischen Geometrie aus den Axiomen der Geometrie hergeleitet werden, sondern wurden am empirischen Datenmaterial der Himmelsbeobachtungen gewonnen. Sie konstituieren ein eigenes »Reich« zwischen Physik und Mathematik. Sie sind aus der Betrachtung von Himmelskörpern gewonnen, gelten aber nur in einem rein geometrischen Raum, in dem es keine Materie gibt. Offenbar liegt keine geometrische Konstruktion vor, sondern ein Grenzübergang, der aus den an Himmelskörpern beobachtbaren Verhältnissen auf Gesetze schließt, die unabhängig von Kraft und Masse gelten. Wie ist das möglich? Diese Frage wird bis heute weder von Mathematikern, Physikern noch Philosophen diskutiert. Für Hegel war es dagegen bereits das Thema seiner 1801 veröffentlichten Habilitationsarbeit Dissertatio philosophica de Orbitis Planetarum, und er hat im Weiteren danach gesucht, einen »höheren« Begriff von Kraft, Materie und Bewegung (Lebendigkeit) zu finden, der für Hegel in das Gebiet der Logik fällt. Für mich ist diese Frage entscheidend um zu verstehen, worin Hegel sowohl über Newton wie Kant hinausgegangen ist bzw. ihnen gegenüber neue Erkenntnisse gewinnen wollte. Aus seiner Untersuchung der Keplerschen Gesetze hat Hegel ein neues Verständnis von Gegensatz und Widerspruch gefunden, mit dem er gegenüber Kants Arbeit über die positiven und negativen Größen eine eigene Position gefunden hat, was Gegensatz und Widerspruch bedeuten.
Wenn die Keplerschen Gesetze unabhängig von Kraft und Masse gelten, aber mit ihnen dennoch Bewegungen und Kräfte von Massen beschrieben werden sollen, haben sie für Hegel objektiv den Status absoluter Indifferenz. Ohne Kraft und Masse versagen die klassischen Kategorien der Substanz, Qualität, Quantität und deren Relationen, und dennoch lassen sich ihre Bewegungen und deren Maße beschreiben und sie aus inneren Faktoren zu konstruieren. Das ist möglich, wenn es gelingt, die absolute Indifferenz als Grenzzustand einer Knotenlinie von Zuständen zu verstehen, für die jeweils die üblichen Kategorien gelten und gemessen und naturwissenschaftlich ausgewertet werden können, entlang derer übergreifend eine Erhaltungsgröße besteht und sich daher auch im Grenzfall der absoluten Indifferenz formulieren lässt. Das sind im Beispiel der Keplerschen Gesetze die Erhaltungsgrößen, die im Grenzzustand die Bewegungsform von Massen und ihren Kräften in einem Raum zeigen, in dem es keine Massen gibt.
(a) In jahrelanger Arbeit hatte Kepler in den von Tycho Brahe gelieferten Beobachtungsdaten der Himmelsbewegungen nach neuen Regelmäßigkeiten gesucht, nachdem sich für ihn empirisch erwiesen hatte, dass alle bekannten und aus der Tradition überlieferten Ansätze nicht bestätigt werden können. Er musste mit allen überlieferten Vorstellungen und Ideen brechen. An dem ihm vorliegenden Material entdeckte er, dass sich die Planeten auf Ellipsen und nicht auf Kreisen bewegen (Erstes Keplersches Gesetz), und dass sich die Geschwindigkeiten der Planeten periodisch ändern. Je weiter ein Planet von der Sonne entfernt ist, desto langsamer ist er, und je näher er ihr kommt, desto schneller wird er. Das widersprach allen Erwartungen. Niemand konnte sich vorstellen, mithilfe welcher Kraft sich die Planeten mal von der Sonne entfernen und sich ihr dann wieder nähern und mal beschleunigen und dann wieder verlangsamen. Kepler konnte auf diese Fragen keine Antwort geben, aber er entdeckte, dass es in der Bewegung der Planeten eine innere Erhaltungsgröße gibt: In gleichen Zeiten werden gleiche Flächen überstrichen.
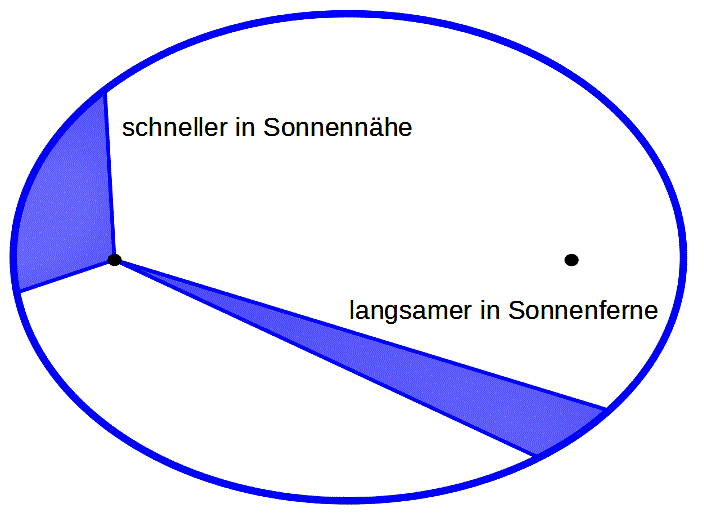
Figur 1 Zweites Keplersches Gesetz
»Zieht man einen Radiusvektor von der Sonne zum Planeten, so überstreicht dieser Fahrstrahl in gleichen Zeiten gleiche Flächen. Das 2. Keplersche Gesetz beschreibt die Drehimpulserhaltung« (uni würzburg). Je näher der Planet der Sonne ist, desto schneller ist er; je weiter entfernt, desto langsamer. Es gibt zwei Extrempunkte des größten bzw. kleinsten Abstandes zur Sonne, an denen sich die Bewegung umkehrt.
Urheber: Die Autorenschaft wurde nicht in einer maschinell lesbaren Form angegeben. Es wird Harp als Autor angenommen (basierend auf den Rechteinhaber-Angaben). - Die Autorenschaft wurde nicht in einer maschinell lesbaren Form angegeben. Es wird angenommen, dass es sich um ein eigenes Werk handelt (basierend auf den Rechteinhaber-Angaben)., CC BY-SA 3.0, Link. – Beschriftungen von mir ergänzt.
Obwohl die Keplerschen Gesetze nur für materielle Körper gelten, kommt in ihren Formeln die Masse nicht als Faktor vor. Sie gelten unabhängig von den Massen der Sonne und des betrachteten Planeten und damit auch unabhängig von den üblichen Kräften im Sinne von Newton (die gemäß der Formel ›Kraft ist gleich Masse mal Beschleunigung‹ an die Masse gebunden sind). Die Keplerschen Gesetze beschreiben ausschließlich die Geometrie der Planetenbewegung, sind aber auch nicht aus der Geometrie abgeleitet. Sie können nicht wie zum Beispiel der Satz des Pythagoras mit den geometrischen Konstruktionsmethoden aus den Axiomen der Geometrie abgeleitet werden. Sie konnten nur aus der Beobachtung der Himmelskörper und ihrer Regelmäßigkeit gewonnen werden. Andererseits gelten sie nur in einem Raum ohne Massen, d.h. in einem rein geometrischen Raum. Wird eine beliebige Masse für die Sonne und die Planeten angenommen, dann ergeben sich daraus störende Einflüsse. Da die Planeten und die Sonne Massen haben, wirken sie aufeinander, verformen sich gegenseitig (z.B. durch die vom Mond auf der Erde ausgelösten Gezeiten) und verändern ihre Abstände. So kann heute empirisch gemessen werden, dass sich die Umlaufbahn der Erde jedes Jahr 15 cm von der Sonne entfernt (siehe z.B. Welt der Physik), sich also genau gesehen auf einer spiralförmigen Kurve von der Sonne weg bewegt. Im Zeitraum von Milliarden von Jahren führt das zu deutlichen Änderungen.
Figur 2: Indifferenzpunkt auf der Planetenbahn
Wenn sich ein Planet auf seiner Bahn um die Sonne bewegt, kann jeder Bewegungspunkt als Indifferenzpunkt angesehen werden, von dem aus auch andere Wege möglich sind, die anfangs nur unendlich-wenig von der Ellipse abweichen. Die Erde könnte auf die rot gezeichnete Bahn einschwenken und würde sich entsprechend der Gravitationskraft immer direkter der Sonne nähern und schließlich senkrecht in sie hineinstürzen. Oder sie bricht entlang der grünen Bahn aus dem Kräftesystem der Sonne aus. Anfangs ist die Sonnengravitation noch sehr stark, weswegen sich die Erde nur wenig entfernt. Diese Kurve enthält wiederum Indifferenzpunkte: Entweder löst sich die Erde auf einer spiralförmigen Bahn völlig von der Sonne, oder sie wird gewissermaßen wieder eingefangen und die grüne Bewegungsform schließt sich zu einer neuen Ellipse, die einen weiter ausholenden Bogen um die Sonne schlägt.
Die Keplerschen Gesetze beschreiben einen Grenzfall, der nur ohne Materie gilt und daher nie in der Realität vorkommt. Um diesen Widerspruch geht es Hegel: Alle Beobachtungsdaten sind »gestört«, weil sie an massehaltigen Himmelskörpern gemessen wurden. Werden die Massen immer kleiner, dann wird im Grenzfall der Zustand erreicht, in dem die Keplerschen Gesetze gelten. Dieser Zustand gilt in einer Geometrie absoluter Indifferenz. Es handelt sich um masselose Punkte, die keinerlei Anziehung aufeinander ausüben und keinen Impuls übertragen können. Sie verfügen über keine Kräfte. Wird dieser Grenzzustand für sich betrachtet, dann befinden sich die Punkte in vollständiger Gleichgültigkeit. Und doch lassen sich nur in diesem Zustand die Keplerschen Gesetze formulieren. Das liegt darin begründet, dass sie aus einem Grenzprozess hervorgegangen sind: Ihre Bedeutung ergibt sich ausschließlich daraus, dass sie zwar keine Masse mehr enthalten, aber auf Zustände verweisen, in denen es Masse gibt. Sie befinden sich in dem Paradox, dass sie dort, wo sie gelten, nicht existieren, und dort, wo sie realisiert werden, gebrochen sind durch Störungen, die sich aus den Massen ergeben. Hegel beschreibt in äußerster Abstraktion den Widerspruch, den Einstein mit dem Paradox des gekrümmten Raums veranschaulicht hat.
Der Widerspruch kann auch so formuliert werden: Wenn es Materie gibt, gelten die Keplerschen Gesetze nur angenähert. Und wenn es keine Materie gibt, ist im Ergebnis eines Grenzprozesses mit den Keplerschen Gesetzen in einem höheren Sinn die »Materie, Sache« gefunden, um die es bei den Bewegungen des Planetensystems geht.
Hier lässt sich bereits anschaulich zeigen, was Hegel im Weiteren als die Bestimmungen des Gegensatzes und des Widerspruchs herausarbeiten will: Es gibt zwei Seiten, die jeweils aufeinander verweisen und sich gleichzeitig wechselweise ausschließen: Die Keplerschen Gesetze sind geometrisch formuliert, aber sie lassen sich weder aus den Axiomen der Geometrie beweisen noch gelten sie für rein geometrische Punkte, die sich nicht bewegen, sondern sie verweisen auf dynamische Körper. Sie gelten für dynamische Körper, aber die dynamischen Körper bewegen sich keineswegs – wie noch die antike Naturphilosophie dachte – auf zeitlosen, unveränderlichen Bahnen, sondern haben ihre eigene Geschichte, aber die an ihnen erkennbaren Bewegungsmuster verweisen auf geometrische Gesetze, die unabhängig von den Massen und der geschichtlichen Entwicklung der Himmelskörper gelten.
Dieser Grenzübergang kann verglichen werden mit dem Grenzübergang des Differentialkalküls. So wie sich dort die Differenzen der Steigungsdreiecke der Tangente annähern, so hier die mit Masse erfüllten Zustände an den Grenzzustand ohne Masse. Der wesentliche Unterschied ist jedoch, dass die Übergänge des Differentialkalküls aus anderen Kategorien hergeleitet werden konnten (sie führen zum Übergang von der Kategorie ‘Quantität’ zur Kategorie ‘Maß’), während hier in der absoluten Indifferenz des Grenzzustands keine Herleitung aus anderen Kategorien mehr möglich ist. Stattdessen muss der Verstand innerhalb der Figur, die aus dem Grenzprozess im Zustand der absoluten Indifferenz gefunden wurde, nach inneren Faktoren suchen, aus denen sich diese Figur zusammensetzt. (Für Kepler war ein solcher Grenzübergang noch nicht erkennbar, da die ihm vorliegenden Messdaten zwar genau genug waren, um die überlieferten Deutungen der Planetenbewegungen zu widerlegen, aber noch nicht genau genug, um die Störungen am beobachtbaren Himmel gegenüber dem Grenzfall zu erkennen, in dem es keine Massen gibt.)
Der Verstand kann sich nicht damit abfinden, dass mit den Keplerschen Gesetzen ein Beispiel vorliegt, in dem keine Herleitung aus Kategorien möglich ist. Er sucht daher nach Erklärungen, die jedoch immer nur innerhalb von Systemen gelten, in denen das Vorhandensein von Masse ausschlaggebend ist. Am überzeugendsten ist der von Kant vorgetragene Gedanke, dass sich die Rotation der Planeten aus dem Drehimpuls eines ursprünglichen Nebels ergibt, aus dem die Sonne und die Planeten hervorgegangen sind. Die ursprüngliche Eigendrehung des Nebels wirkt weiter im Bahndrehimpuls (Schwung), mit dem sich die Planeten auf den ihnen ursprünglich im rotierenden Nebel mitgegebenen Ellipsen bewegen. Kant vermutete, dass nach wie vor ein innerer materieller Zusammenhalt des Planetensystems aus den Zeiten des Urnebels besteht und alle Elemente des Systems dazu bringt, auf den uns bekannten Bahnen zu bleiben. Mit neueren Ideen könnte versucht werden zu zeigen, dass ein rotierender Nebel ein energetisches Minimum erreicht, wenn er eine Gestalt wie das uns bekannte Planetensystem annimmt und daher aufgrund des Gesetzes des geringsten Kraftaufwandes in diesen Zustand gelangt und dort solange verbleibt, bis größere Kräfte ihn daraus verdrängen. – Kants Nebularhypothese hat sich nach einigem hin und her in der Wissenschaft durchgesetzt. Sie beschreibt, wie es naturhistorisch gewesen sein wird. Aber sie kann nicht das Paradox lösen, warum die Keplerschen Gesetze nur in einem materiefreien Raum gelten. Kant und die ihm folgenden Naturwissenschaftler sehen nicht einmal dieses Paradox.
Newton war sich dessen dagegen völlig bewusst. Sein intuitives Bild, dass der Planet sich lokal in die Richtung der Diagonale bewegt, die aus dem Parallelogramm der Anziehungskraft der Sonne und der Trägheitskraft des Planeten entsteht, setzt Kräfte und Massen voraus. Wird in einem Grenzübergang ausschließlich die Geometrie von Tangente und direkter Verbindungslinie zum Brennpunkt betrachtet, dann ist es im Grenzzustand mathematisch äquivalent mit dem Gesetz von Kepler. Newton sah sehr deutlich, dass in seinem Modell der Planet in diesem materielosen Grenzzustand absolute Bewegungsfreiheit hat, da keinerlei Gravitationskräfte wirken, und daher neben der Gravitationskraft eine zusätzliche Kraft (die später so genannten Randbedingungen) gegeben sein muss, die ihn in die "richtige" Richtung "schubst" (siehe den Brief von Newton an Richard Bentley vom 10.12.1692 und Linhard, S. 2). – Später ist er wegen solcher Gedanken verspottet worden, weil die nachfolgenden Naturwissenschaftler nicht einmal das Problem sahen, für das er nach einer Lösung suchte. Ihnen genügte, dass sich die physikalischen Gesetze beliebig genau empirisch bestätigen lassen.
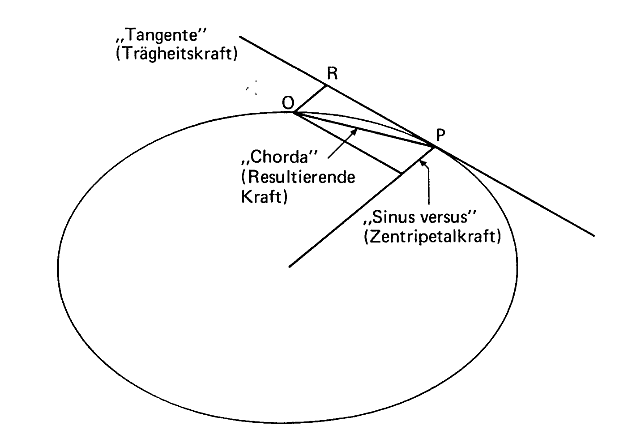
Figur 3: Trägheitskraft nach Newton Newton zerlegt die Kraft der Planeten an jeder Stelle mit einem Kräfteparallelogramm in zwei Komponenten: Eine wirkt tangential entlang der Bahn und wird von ihm als »Trägheitskraft« bezeichnet, die andere ist zur Sonne gerichtet (»Sinus versus«, Zentripetalkraft). Hieraus bildet sich resultierend die Diagonale (»Chorda«), die zu dem nächsten Punkt auf der Bewegungsbahn verweist, den der Planet erreichen wird. Quelle: Neuser, S. 14.
(b) Wie ist das Keplersche Gesetz konstruiert? Im Grenzübergang ist aus der Beobachtung massehaltiger Systeme die Figur der Ellipse und das in ihr geltende zweite Keplersche Gesetze hervorgegangen. Diese Figur ist die wahre Erhaltungsgröße, die anschließend in innere Faktoren zerlegt und aus ihnen konstruiert werden kann. Diesen Ansatz hat Hegel auf die größtmögliche Weise verallgemeinert. Für ihn hat Kepler mit der materiefreien Geometrie in einem übertragenen Sinn das Substrat beschrieben, das allen beobachteten und beobachtbaren Bewegungszuständen des Planetensystems zugrunde liegt und auf der Ebene des Substrats das spezifizierende Prinzip gefunden, aus dem sich die Ordnung der Zustände ergibt. Mit Substrat ist hier nicht mehr wie im Beispiel des Wassers ein Stoff gemeint, der in unterschiedlichen Aggregatzuständen auftreten kann, sondern eine Erhaltungsgröße, die übergreifend sowohl im materiefreien Grenzzustand wie in den beobachtbaren physischen Zuständen gilt. Die an stofflichen Beispielen für das reale Maß gefundene Unterscheidung in Substrat und seine Zustände kann übertragen werden, um das von Kepler gefundene Gesetz als ein Substrat zu verstehen, dessen innere Faktoren betrachtet werden. Der materielose Grenzzustand kann formal auf ähnliche Weise auf eine Art Grenz-Substrat bezogen werden wie sich die physischen Zustände auf ein Substrat beziehen. Um dieses Grenz-Substrat oder Substrat in einem höheren Sinn geht es Hegel. Es enthält im physischen Sinn keine Materie, aber es ist die Sache und damit im höheren Sinn die Materie, die den Keplerschen Gesetzen im Grenzzustand zugrunde liegt. Jeder sieht die Widersprüchlichkeit dieser Situation. Sie lässt sich nicht mehr in den Kategorien beschreiben, die auf ein Substrat im üblichen Sinn bezogen sind, sondern enthält für Hegel den Keim für einen eigenen Träger: die Substanz, die zugleich als Subjekt verstanden wird. Die Keplerschen Gesetze gelten nur für materiefreie Punkte, aber sie haben ihre eigene Substanz, die wiederum ihre eigene Lebendigkeit hat, mit der sie sich in den Keplerschen Gesetzen zeigt.
In diesem Sinn versteht Hegel die Zerlegung der Bewegung der Planeten in zwei innere Faktoren als Beispiel, wie »zwei unterschiedene Quanta eines und desselben Substrats« (HW 5.447) unterschieden und als zwei »qualitativ gegeneinander bestimmter Faktoren« (HW 5.451) erkannt werden. Die beiden Quanta sind »veränderlich, gleichgültig, größer oder kleiner, gegeneinander«, und sie »sie sind danach im umgekehrten Verhältnisse zueinander« (HW 5.447). Sie müssen in umgekehrten Verhältnis zueinander stehen, da ihnen die Erhaltungsgröße, »dies feste Maß« (HW 5.447) vorgegeben ist, innerhalb dessen sie sich bewegen. (Diesen Punkt hat Carlson in seiner Interpretation hervorgehoben. Er versteht die von Kepler untersuchte Planetenbahn als ein Beispiel für ein vorgegebenes Maß, innerhalb dessen die Unterscheidung in zwei Faktoren erfolgt, die sich im umgekehrten Verhältnis zueinander verändern. Siehe Carlson, S. 286f.)
Jede einzelne dieser Aussagen enthält einen Widerspruch. Für gewöhnlich bedeutet die Kategorie der Quantität, dass es etwas gibt, das dieses Quantum hat. Hier wird nun im Grenzzustand die absolute Indifferenz ihrerseits in zwei Faktoren aufgeteilt mit dem widersprüchlichen Ergebnis, dass ein Substrat zwei Quanta hat. Jedes dieser Quanta kann unter gewöhnlichen Umständen nur so verstanden werden, dass es das Quantum eines zugrunde liegenden Substrats ist, und das würde bedeuten, dass hier mit der Zerlegung der absoluten Indifferenz ein Substrat zerlegt wird in Momente, die wiederum auf eigene Substrate verweisen. Das ist ein Widerspruch. Er kann nur so gelöst werden, dass bei Betrachtung der beiden Quanta der inneren Faktoren nicht neue Substrate gefunden werden, sondern die beiden Quanta können nur an sich selbst ihr Substrat enthalten. Das ist kein gewöhnliches Substrat mehr. Es sind wörtlich genommen Quanta, ohne dass es etwas gibt, dessen Größe sie sind. Wird gefragt, welches Substrat sich in den Keplerschen Gesetzen zeigt, dann kann dies weder ein materielles noch ein nicht-materielles Substrat sein, da es sich sowohl in physischen materiellen wie in einem nicht-materiellen Grenzzustand zeigt. Das widerspricht jeder Anschauung, weil sich in der Anschauung nur Zustände vorstellen lassen, die noch nicht in den materiefreien Grenzzustand übergegangen sind, für den absolute Indifferenz gilt. Für die Anschauung ist es keine Schwierigkeit, aus der Menge materieller Zustände auf ein gemeinsames materielles Substrat zu schließen, das ihnen zugrunde liegt. Doch versagt dieser Schluss, wenn ausdrücklich auch der materiefreie Grenzzustand als ein möglicher Zustand zugelassen werden soll. Für Hegel zeigt sich hier in der Naturwissenschaft ein Widerspruch, den er im Weiteren genauer ausarbeiten wird: So wie sich an den Quanta der inneren Faktoren ihr Substrat zeigt und nicht unabhängig von ihnen, so will Hegel zeigen, dass sich an den Reflexionsbestimmungen Identität, Verschiedenheit, Widerspruch und Grund das Substrat zeigt, als dessen Zustände die Reflexionsbestimmungen gedeutet werden können. Die Keplerschen Gesetze sind das einzige Beispiel, an dem sich dieser Widerspruch zeigen lässt. Alle anderen Beispiele wie Soll und Haben, Osten und Westen, rot und schwarz, wohl- und übelriechend beziehen sich dagegen auf bestimmte Qualitäten (Farbe, Geruch) oder Quantitäten (Betrag, Richtung) und damit auf Kategorien. Sie zeigen nur negativ, was mit dem neuen Verständnis des Substrats und seiner inneren Faktoren, das für Hegel in der absoluten Indifferenz hervortritt, nicht gemeint ist.
Der gleiche Widerspruch gilt für die qualitativ gegeneinander bestimmten Faktoren. Das Substrat liegt allen qualitativen Änderungen zugrunde. Wird es seinerseits aus Faktoren konstruiert, die über bestimmte Qualitäten verfügen, durch die sie sich voneinander unterscheiden, dann gibt es nichts, das diese qualitativen Eigenschaften haben könnte. Wenn sich die Faktoren qualitativ voneinander unterscheiden, kann das nicht damit verglichen werden, wie etwas Daseiendes unterschiedliche Qualitäten haben kann (z.B. Farb- und Geruchseigenschaften), sondern jeder einzelne Faktor ist in übertragenem Sinn ein Daseiendes, das dem Substrat als innerer Faktor zugrunde liegen müsste. Das widerspricht dem grundlegenden Verständnis der Kategorien, mit denen eine Erste Kategorie dadurch ausgezeichnet wurde, dass sie nicht ihrerseits eine Eigenschaft von etwas Zugrundeliegendem ist. Mit der Setzung innerer Faktoren eines Substrats wird der Rahmen der Kategorien gesprengt. Die inneren Faktoren können keine Kategorien mehr sein, sondern es muss sich um innere Voraussetzungen handeln, die von Hegel im Weiteren als Reflexionsbestimmungen nachgewiesen werden sollen. Dieses Argument steht bewusst in Widerspruch zur gewöhnlichen Vorstellung und ist die entscheidende Wende, mit der Hegel von den Kategorien zu den Reflexionsbestimmungen überleiten will.
Das Beispiel des zweiten Keplerschen Gesetzes zeigt sowohl anschaulich wie zugleich entgegen aller üblichen Anschauung, dass für die inneren Faktoren alle Vorstellungen versagen, die üblicherweise mit Kontinuität und Umkehrung verbunden werden. Die Geschwindigkeit des Planeten kontinuiert sich nicht in den Abstand zur Sonne, sondern der Anteil der Geschwindigkeit wird größer zulasten des Anteils des Abstandes der Sonne und umgekehrt. Die beiden inneren Faktoren Geschwindigkeit und lokale Geschwindigkeit stehen zwar in umgekehrtem Verhältnis, aber sie verhalten sich nicht zueinander wie die auf einer gemeinsamen Achse in entgegengesetzten Richtungen angeordneten negativen und positiven Zahlen oder all die anderen Beispiele, die Kant im Versuch den Begriff der negativen Größen in die Weltweisheit einzuführen herangezogen hat (Osten und Westen, Soll und Haben, oben und unten). Wer sein Vermögen betrachtet und sieht, wie dessen Bestand kontinuierlich kleiner wird und schließlich am Nullpunkt in Schulden umschlägt, die kontinuierlich anwachsen, erlebt, wie eine kontinuierliche Bewegung von Haben in Soll erfolgt. Das Haben geht kontinuierlich in Soll über. Nichts dergleichen gilt für das Verhältnis von Abstand und Geschwindigkeit: Der Abstand wird nicht so klein, bis er bei einem Durchgang durch einen Nullpunkt in Geschwindigkeit übergeht. Abstand und Geschwindigkeit lassen sich nicht auf einer gemeinsamen Achse anordnen, wie es für Soll und Haben, Osten und Westen und die anderen von Kant betrachteten Beispiele möglich ist.
Dennoch enthält der Ansatz von Kant etwas Treffendes, das Hegel übernehmen kann. Vor Kant hatte sich niemand vorstellen können, was negative Zahlen sein sollen. Sie müssten weniger als Nichts sein, was ein offenbarer Unsinn ist. Kant löste das, indem er erkannte, dass negative Zahlen sich in einer Gesamtheit befinden können, in der sie mit positiven Zahlen ausgeglichen werden. Die Bilanz geht immer auf: Die Schulden des einen sind die Forderungen des anderen. Senkt sich am Hebel ein Hebelarm, dann hebt sich der andere. Es gibt eine übergreifende Einheit, innerhalb derer negative und positive Seiten unterschieden werden können, die im umgekehrten Verhältnis zueinander stehen. In den von Kant genannten Beispielen stehen diese noch nebeneinander wie ein Etwas und ein Anderes: Auf dieser Seite ist Westen, auf der anderen Seite ist Osten. Rechts ist das Andere zu Links usf. Alle von Kant genannten Beispiele lassen sich in das Schema von Etwas und Anderes bringen, die durch eine Grenze getrennt sind. Völlig anders verhält es sich bei den inneren Faktoren der Keplerschen Gesetze. Der Abstand zur Sonne ist nicht das Andere der Geschwindigkeit des Planeten. Es gibt keine Grenze, durch die der Abstand und die Geschwindigkeit voneinander getrennt sind. Würde unterschieden werden, dass die einen Planeten linksherum und die anderen in entgegengesetzter Richtung rechtsherum um die Sonne laufen, dann wäre das ein Beispiel, das wie diejenigen von Kant konstruiert ist. Das Verhältnis von Abstand und Geschwindigkeit lässt sich nicht auf diese Weise entwerfen. Abstand und Geschwindigkeit sind zwar anschauliche Größen, aber die Zerlegung der Planetenbahn in die inneren Faktoren von Abstand und Geschwindigkeit ist kein materieller Vorgang, der in Worte gefasst und nachvollzogen wird, sondern eine rein theoretische Operation, die von Kepler vorgenommen wurde, um die Erhaltungsgröße der Planetenbahnen zu erkennen. Das war für Hegel die einzigartige Leistung von Kepler, die sich von allen Messungen empirischer Größen unterscheidet und seither eine neue Epoche des Denkens begründet hat. (Vergleichbar mit den von Kant betrachteten positiven und negativen Größen ist nur die Veränderung eines einzelnen der beiden Faktoren. So gilt zum Beispiel für die Geschwindigkeit: Bewegt sich ein Planet auf einem Bahn-Abschnitt, auf dem die Abstände zur Sonne kürzer werden, dann erhöht sich die Geschwindigkeit. Er hat daher eine positive Beschleunigung. Doch kommt es an einer Stelle zu einer Umkehr: Die Beschleunigung fällt auf Null und wird negativ, wenn der Planet auf seiner Umlaufbahn so weit fortgeschritten ist, dass die Abstände zur Sonne wieder größer und die Geschwindigkeit kleiner werden. Hier gilt eine negative Beschleunigung, der Planet wird gebremst. Das Verhältnis der positiven und negativen Beschleunigung kann im Ganzen mit Kant als ein Ausgleichsprozeß betrachtet werden.)
Beobachtet werden kann nur, wie sich die Größen von Abstand und Geschwindigkeit verändern (das eine wird größer, wenn das andere kleiner wird), aber nicht, wie sie aufeinander wirken. Während bei der Impulsübertragung ein Körper an den anderen stößt, wodurch er langsamer wird und der andere schneller, gibt es hier keinen vergleichbaren Vorgang, wodurch der Abstand auf die Geschwindigkeit wirkt und sie vergrößert, wenn er sich verkleinert. Es gibt keinen nachvollziehbaren Funktionszusammenhang, der das Verhältnis von Abstand und Geschwindigkeit erklärt, sondern es ist ein mathematisches Verhältnis zwischen den Größen der Geschwindigkeit und des Abstandes. Für Naturwissenschaftler ist dies einfach eine empirisch überprüfbare mathematische Beschreibung, ein Gesetz (siehe hierzu HW 6.152-156). Kepler war bei Betrachtung aller Beobachtungsdaten aufgefallen, dass sich das eine vergrößert, wenn sich das andere verkleinert. Das gilt als die spezifische Fähigkeit der Mathematik, ihre Gegenstände in ihren rein quantitativen Verhältnissen zu untersuchen ohne zu fragen, welche qualitativen Ursachen oder Eigenschaften den quantitativen Beziehungen zugrunde liegen. Kant sah hierin die Freiheit der mathematischen Konstruktion. Hegel ging einen Schritt weiter und fragte, worin diese Freiheit ihren Grund hat und von welchen impliziten Voraussetzungen sie auch dann ausgeht, wenn ihr selbst ihr Vorgehen als völlig frei erscheint. Er fragte nach der Fähigkeit der menschlichen Vernunft, dank derer in diesem Beispiel Kepler vermochte, beliebige Verknüpfungen zwischen den von ihm untersuchten Daten herzustellen bis er eine Formel fand, die »aufging«. Diese Fähigkeit sieht Hegel in der Reflexion. Sie beschränkt sich nicht auf das sinnlich wahrnehmbare Sein, sondern geht auf das Wesen. Mit gutem Grund vergleicht Hegel das Wesen mit der Quantität: »Das Wesen ist im Ganzen das, was die Quantität in der Sphäre des Seins war.« (HW 6.15) Kepler hat nicht eine beobachtbare Wirkung von etwas auf etwas anderes beschrieben, sondern Verhältnisse von Zahlenreihen. Dem Naturwissenschaftler erscheint das selbstverständlich, weil er aus der Geschichte seiner Wissenschaft weiß, dass es oft genug zu solchen Einfällen gekommen ist. Aber er versucht nicht zu verstehen, wie das möglich ist. Für ihn ist es ein glücklicher Zufall, dass Kepler eine innere Verbindung zwischen Abstand und Geschwindigkeit aufgefallen war, auch wenn sie sachlich nie begründet werden kann.
Abstand und Geschwindigkeit verhalten sich im 2. Keplerschen Gesetz nicht wie positive und negative Zahlen zueinander, sondern wie Kontinuation und Umkehr:
- »Diese Seiten selbst kontinuieren sich so auch nach ihren qualitativen Bestimmungen ineinander« (5.448). Das darf allerdings nicht in der Weise missverstanden werden, als würde sich der Abstand in die Geschwindigkeit oder die Geschwindigkeit in den Abstand verwandeln, sondern jeder von ihnen kann sich nur kontinuieren dank der gegenläufigen Bewegung des anderen. Die Geschwindigkeit wird so klein, bis der Abstand so groß geworden ist, dass die Geschwindigkeit wieder anwachsen muss. Sie verdankt ihre eigene Kontinuität der Kontinuität der anderen. Es gibt erkennbar keinen Nulldurchgang: Weder wird jemals ein Abstand gleich Null erreicht (das wäre eine Berührung der Sonne) noch am äußersten von der Sonne entfernten Punkt eine Ruhe (das wäre ein Stillstand des Planeten).
- »Die beiden Momente sind in umgekehrtem quantitativen Verhältnisse« (HW 5.449). Sie bilden einen »unmittelbaren Gegensatz, welcher sich zum Widerspruch entwickelt« (HW 5.449). Aus dem Gegensatz entwickelt sich ein Widerspruch, weil die eine Seite nur in Beziehung auf die andere Seite bestimmt werden kann, und zugleich jede Seite in dem Maße verringert wird, wie die andere vermehrt wird, d.h. durch die jeweils andere Seite zum Verschwinden gebracht wird. So ist einerseits jede Seite von der anderen abhängig, weil sie ohne sie nicht bestehen könnte, und tendiert zugleich dazu, sie zu vernichten. In paradoxen Bezügen dieser Art entwickelt Hegel den mit den inneren Faktoren der Indifferenz verbundenen Widerspruch.
Diese Situation kann nicht anders beschrieben werden als »der allseitige Widerspruch« (HW 5.451), in dem sich die absolute Indifferenz befindet. Und doch steht für Hegel die absolute Indifferenz noch in der Seinslogik, wenn auch an der Grenze zum Wesen. Sie beschreibt Verhältnisse, die im Grenzübergang aus der sinnlich gewissen Erfahrung hervorgegangen sind. Im Grenzzustand gelten diese zwar nur widersprüchlich, aber sie stehen noch im klaren Bezug auf den Prozess, aus dem sie hervorgegangen sind. Es lässt sich anschaulich nicht besser treffen als in dem oft genannten Gleichnis: Stell Dir eine Katze vor, die lächelt, und nun stell Dir das Lächeln der Katze vor ohne die Katze.
Daraus ergibt sich die These dieses Beitrags: In der Reflexionslogik wird Hegel zwar den Kontext der absoluten Indifferenz verlassen, aber die beiden Beziehungen der Kontinuation und der Umkehr festhalten, die sich hier ergeben haben. Er zieht einen Analogie-Schluss: So wie sich im Grenzübergang von den physischen materiehaltigen Zuständen zum geometrischen, materiefreien Grenzzustand die verborgenen inneren Gesetze zeigen, so kann nochmals übergreifend die Seinslogik in ihren Übergängen von einer Kategorie zur nächsten als ein Prozess verstanden werden, der im Grenzübergang durch die absolute Indifferenz in die Reflexion führt, in der es nur noch eine Bewegung von Nichts durch Nichts zu Nichts gibt. Eine solche Formulierung erscheint auf den ersten Blick leer und sinnlos, aber sie wird verständlich, wenn die Reflexion ihrerseits als Grenzzustand gegenüber den Kategorien des Seins verstanden wird, wie sich die Geometrie als Grenzzustand gegenüber den physischen Systemen ergeben hatte. – Und so, wie sich in der Lehre des Seins der materielose Grenzzustand aus inneren Faktoren bilden ließ, so lässt sich auch die Reflexion auf innere Faktoren zurückführen. Hegel wird zeigen, wie an jeder Reflexionsbestimmung eine innere Bewegung nachzuweisen ist, die sich aus Kontinuation und Umkehr zusammensetzt. Während sich die Untersuchung des Keplerschen Gesetzes immer noch auf physische Zustände und konkrete Messungen von Himmelskörpern beziehen konnte, ist dies für die Reflexion nicht mehr möglich. Die Untersuchung ihrer Bewegungen kann nur an den Reflexionsbestimmungen selbst erfolgen. Wenn gefragt wird, ob einander entgegengesetzte Reflexionsbestimmungen wie z.B. Identität und Unterschied als unterschiedliche Zustände eines gemeinsamen Substrats verstanden werden können, dann kann in übertragenen Sinn nur die Reflexionsbestimmung ‘Widerspruch’ das gemeinsame Substrat sein, da sich beide im Zustand des Widerspruchs befinden bzw. sich als Zustände des Widerspruchs verstehen lassen. Wird an der inneren Bewegung der einzelnen Reflexionsbestimmung wiederum ein Widerspruch nachgewiesen, dann gerät der Widerspruch mit sich selbst in Widerspruch. Auf diesen Punkt kommt es Hegel an. In ihm zeigt sich der höhere Widerspruch: Der Widerspruch widerspricht sich selbst, was zur Auflösung des Widerspruchs führt. Wenn Hegel sagt, dass der Widerspruch zu Grunde geht, ist beides gemeint: Der Widerspruch wendet sich gegen sich selbst (er löst sich auf und geht zugrunde in der Bedeutung, dass er verschwindet), und zugleich führt er dazu, dass sich der Widerspruch auf den Weg macht und den Grund erreicht. Wird an dem Ausdruck ‘geht zu Grunde’ das Gehen betrachtet, dann ist dies eine Kontinuation, in der der Widerspruch über sich hinausgeht und den Grund erreicht. – Und so, wie Hegel das im 2. Keplerschen Gesetz gefundene Übergreifende als Sustrat bezeichnet hat, das sowohl für materielle wie materielose System gilt, so spricht er am Ende dieser Bewegung in einem weiteren Analogie-Schluss von dem Substrat, das übergreifend für alle Stationen entlang des Weges in den Widerspruch, durch den Widerspruch und seine Auflösung hindurch zum Grund geführt hat (HW 6.85).
Anmerkung. Aus mathematischer Sicht ist äußerst interessant, in welcher Weise Hegel die Besonderheiten unterschiedlicher mathematischer Gesetze erkennt und voneinander unterscheidet. Die Regeln des arithmetischen Rechnens einschließlich des Differentialkalküls bewegen sich innerhalb der Kategorie der Größe (Quantität) und führen zu Übergängen zwischen den einzelnen Kategorien, mit denen sich die Größe näher bestimmen lässt. – Die Keplerschen Gesetze und alle anderen Gesetze dieser Art liegen wie hier dargestellt in einem Grenzzustand, der aus einer Knotenlinie von Zuständen mithilfe der dort geltenden übergreifenden Erhaltungsgrößen erschlossen werden kann. – Von mathematischen Gesetzen dieser Art werden in weiteren Schritten zu unterscheiden sein die Kraft des Minus (siehe dazu weiter unten), die Impulsgesetze und der Satz des Pythagoras. Die Impulsgesetze sind zunächst ähnlich wie die Keplerschen Gesetze in einem Grenzzustand definiert. Aber dort wird nicht völlig von der Materie abstrahiert, sondern lediglich gesetzt, dass die Materie aus ausdehnungslosen Punkten besteht, die über eine Mitteilungsfähigkeit verfügen, etwa die Mitteilung des Impulses. – Abschließend wird in der Wissenschaft der Logik der Satz des Pythagoras angeführt. Er liegt für Hegel nicht, wie ein Mathematiker erwarten würde, den geometrischen Verhältnissen zugrunde, von denen die Keplerschen Gesetze handeln, sondern zeigt für Hegel eine übergreifende Lebendigkeit, die im Satz des Pythagoras nur aus einer eingeschränkten Perspektive wahrgenommen, aber nicht im Ganzen überschaut werden kann. Hegel steht damit unverkennbar in Widerspruch zum Selbstverständnis der Mathematik und kann zu einer völlig anderen Philosophie der Mathematik anregen, die er jedoch nirgends ausgearbeitet und kaum angedeutet hat.
(c) Newtons Frage, welche Kraft die Planeten auf der richtigen Bahn hält, ist für mich das beste Beispiel um zu verstehen, warum für Hegel die Kraft eine Denkbestimmung (eine Wesensbestimmung) ist, auch wenn Hegel meines Wissens das Problem Newtons zwar in seiner Habilitationsschrift Dissertatio Philosophica de Orbitis Planetarum angesprochen, aber später nirgends mehr direkt aufgenommen hat. Hegel spricht in seiner Lehre des Seins unterschiedliche Kräfte an, so die Repulsiv- und Attraktivkraft (HW 5.201-207, 255f), die Kraft der Schwere und die Kraft der Trägheit (HW 5.309f, 319, 346, 407, 410) und schließlich die Zentripetal- und Zentrifugalkraft (HW 5.451-454). Das sind Kräfte, die er bestimmten Kategorien zuordnet: Anziehung und Abstoßung der Qualität, Schwere der Quantität, Zentripetal- und Zentrifugalkraft dem Maß. Völlig anders verhält es sich mit der Kraft, nach der Newton fragt. Für sie gibt es keine Kategorien, mithilfe derer sie gedeutet werden kann. Sie ergibt sich ausschließlich als Denkbestimmung, um die Verhältnisse im Grenzzustand der absoluten Indifferenz verstehen zu können.
Was stellt sicher, dass noch im Grenzzustand der absoluten Indifferenz die übergreifenden Erhaltungssätze gelten, die nur an physischen Zuständen beobachtet und gemessen werden können? Das kann nicht der mit der Nebularhypothese genannte Drehimpuls sein, der nicht mehr gilt, wenn es keine Massen gibt. Das kann nur eine übergreifende Kraft sein, die sicherstellt, dass die Übertragung von den physischen Systemen zum materiefreien geometrischen System angenommen werden kann. Diese Situation kann verglichen werden mit dem Paradox von Achilles und der Schildkröte. So wie es eine übergreifende Energie gibt, dank derer Achilles die unendlich vielen kleiner werdenden Abstände zur Schildkröte »nebenbei« durchläuft, muss es eine übergreifende Energie geben, dank derer die Unterschiede zwischen den verschiedenen physischen Zuständen und dem Grenzzustand nebenbei durchlaufen werden. Diese Kraft kann aus Sicht der einzelnen, messbaren Zustände nur wie ein äußerer Eingriff verstanden werden, der auf eine Kraft außerhalb des Systems deutet, ein deus ex machina oder in der Ausdrucksweise von Newton ein »spirit«. Für Hegel ist dies eine Kraft, die nur von der Reflexion gesetzt werden kann. Kein Weg führt an dem Paradox vorbei, dass im Grenzzustand zum einen wie von Newton gefordert eine Kraft wirken soll, zum anderen keine Kraft wirken kann, wenn ein materiefreier Zustand betrachtet wird. Mathematisch müsste gemäß der von Newton eingeführten Formel ›Kraft ist gleich Masse mal Beschleunigung‹ gelten, dass die Kraft verschwindet, wenn es keine Masse mehr gibt. Dieser Widerspruch kann nur gelöst werden, wenn ein anderer Kraft-Begriff eingeführt wird.
Der andere Kraftbegriff kann nicht an die Stelle des Widerspruchs gesetzt werden, sondern ist aus der Auflösung des Widerspruchs zu begreifen. Hegel versteht die Kraft als negative Einheit. »Die Kraft ist die negative Einheit, in welche sich der Widerspruch des Ganzen und der Teile aufgelöst hat, die Wahrheit jenes ersten Verhältnisses.« (HW 6.172) Die von Newton gesuchte Kraft kann nicht gemessen werden, sondern sie ergibt sich als Forderung, dass übergreifend im Grenzzustand und in den physischen Zustände vergleichbare Verhältnisse bestehen. Wie diese Kraft aussehen soll, ist völlig unbestimmt, aber es ist nachvollziehbar, warum sie angenommen und gesetzt werden muss. So verstehe ich, was Hegel mit »negativer Einheit« meint: Es wird in diesem Beispiel eine übergreifende Einheit gesetzt, die für alle Zustände einschließlich des Grenzzustands gilt, aber sie kann nur negativ bestimmt werden durch eine Art indirekten Beweis: Wenn sie fehlen würde, wären die Keplerschen Gesetze nicht möglich.
Auch auf die Gefahr hin, missverstanden zu werden, kann gesagt werden: Es geht um eine Kraft, die sich sogar in einem materiefreien Grenzzustand in den Keplerschen Gesetzen zeigt. Auf eine ähnliche Weise, wie Kant gegenüber Hume gesagt hatte, dass sich die Kausalität nicht aus empirischen Daten beweisen lässt, sondern nur als eine grundlegende Denkbestimmung anzunehmen ist, spricht auch Hegel von der »Denkbestimmung der Kraft« (HW 5.21). Das Denken kann aufgrund seiner eigenen Bestimmungen nicht anders, als in einer solchen Situation eine Kraft anzunehmen. Den meisten Naturwissenschaftlern wird das nicht bewusst, da sie von Symmetrien, Erhaltungsgrößen, Invarianzen etc. sprechen, und nur Newton ist darauf gestoßen. Für ihn war klar, dass es nicht nur eine Kraft, sondern auch einen Träger der Kraft geben muss, den er in den »spirits« sah, oder anschaulich gesprochen in Engeln, die von außen eingreifen und die Planeten in die richtige Richtung lenken. Hegel kannte aus der Naturwissenschaft seiner Zeit ähnliche Vorstellungen, wenn statt von »spirits« von bestimmten »Materien« wie z.B. dem »feinen Äther« gesprochen wurde (HW 6.174), oder von Fluida u.ä. Daran hat sich bis heute nichts geändert, wenn Austauschteilchen, virtuelle Teilchen u.ä. eingeführt werden. Allem liegt der gleiche Gedanke zugrunde: Physische Systeme können mathematisch nur in Grenzzuständen materieloser Geometrien beschrieben werden, und dort muss es eigene Kräfte mit eigenen immateriellen Trägern geben, die den Zusammenhalt sicherstellen.
Anmerkung 1: Das ist für mich damit vergleichbar, wie Husserl vom Korrelat des Gedankens gesprochen hat. Jeder Gedanke ist mit einem Korrelat verbunden, das als sein Gegenstand gilt, selbst dann, wenn völlig klar ist, dass dieser Gedanke sich auf keinen realen Gegenstand bezieht, wie z.B. der Gedanke des Kentaur, des Inhalts eines erzählten Traums, des Absoluten, des Einen oder der Seele. Auf ähnliche Weise kann hier gesagt werden, dass selbst da, wo im Moment der absoluten Indifferenz der Kraft-Begriff keinerlei Bedeutung mehr zu haben scheint, von einer Kraft im Sinne einer Korrelation gesprochen werden kann. Wenn Husserl erkannt hat, dass jedem Gedanken ein Korrelat entspricht, geht es hier um die weitergehende Einsicht, dass es eine Kraft geben muss, die sicherstellt, dass alle Gedanken so formuliert werden, dass ihnen ein Korrelat entsprechen kann. Das ist die Frage nach der Sprachmächtigkeit: Es kann nichts anderes gedacht werden als etwas, für das es ein Korrelat geben kann.
Anmerkung 2: Für Collmer ist mit »negativer Einheit« eine Offenheit gemeint: Es besteht eine Einheit, die zunächst nur negativ bestimmt werden kann, wobei noch offen ist, worin sie für sich betrachtet besteht. Möglicherweise entzieht sich ihr Verständnis sogar der menschlichen Vernunft, die nur erkennen kann, dass es eine solche Einheit geben muss. Hegel nähert sich damit der negativen Theologie von Kant an: Es muss eine Einheit geben, die für sich nicht erkennbar ist. Collmer bezieht sich ausdrücklich auf Hegels Ausführungen zur Kraft (Collmer 2002, S. 629). Das kann auch als Neue Metaphysik bezeichnet werden: Die negative Einheit ergibt sich denknotwendig aus der Physik und verweist auf eine Metaphysik.
Anmerkung 3: Was sagt die Realwissenschaft über unterschiedliche physische Zustände und einen rein geometrischen, materielosen Grenzzustand? Sowohl beim Übergang ins Große wie ins Kleine wird der Raum immer leerer. Zum Beispiel gilt für das Wasserstoffatom: »Der Atomkern nimmt davon nur ein Hundertbillionstel ein.« (chemieunterricht.de). Und umgekehrt wird das Vakuum fortlaufend größer, je größere Räume im Weltall betrachtet werden. Nur in unserer unmittelbaren Umgebung ist alles von sichtbaren Körpern bevölkert. Es liegt nahe, dies für eine Täuschung zu halten, die sich aus der sinnlichen Wahrnehmungsfähigkeit des Menschen ergibt. Das Gehirn fügt die uns erfahrbaren Eindrücke, mit denen wir seit der Kindheit aufwachsen, in Aggregate zusammen, die als zusammengehörige Körper gelten. Von den Philosophen wurde meist das Sehen für die wichtigste sinnliche Erfahrung gehalten, aber die tieferliegende Erfahrung von Körpern geht zweifellos auf den Tastsinn zurück, mit dem die jeweilige Festigkeit der uns umgebenden Materie erkannt wird. Aus diesen Erfahrungen können in mehreren Schritten zunächst unterschiedliche Aggregatzustände wie fest, flüssig und gasförmig unterschieden werden, dann unterschiedliche Materiedichten wie in den genannten Beispielen des Atomkerns, eines Festkörpers oder großräumiger Strukturen im Weltall und schließlich mit Hegel die Denkbestimmung, dass das Denken nicht anders kann, als physische Zustände entlang ihrer Festigkeit zu ordnen bis zu einem Grenzzustand, der materiefrei ist (Geometrie).
Wird gefragt, unter welchen Bedingungen materielle Strukturen auf den Grenzzustand übertragen werden können, versucht die Mathematik dies seit einigen Jahrzehnten mithilfe der Chaostheorie, Katastrophentheorie bzw. der Theorie dynamischer Systeme zu beschreiben. Ein Grenzzustand kann als Singularität angesehen werden, die in unterschiedlichen Typen angenähert wird. Dies ändert nichts an der hier grundsätzlicher betrachteten Frage, wie Grenzzustände mit physischen Zuständen zusammenhängen.
Für mich stellt sich umgekehrt die Frage, ob an den algebraischen (symmetrischen) Strukturen einer rein mathematischen Zahlen- und Punktmenge zu erkennen ist, dass sie der Grenzzustand physischer Systeme ist, für die bestimmte Kräfte gelten. Oder anders gefragt: Ist die Schönheit rein mathematischer Strukturen Zeichen einer Kraft, mit der sich die Teile rein mathematischer Figuren zu Ganzheiten fügen, die als Schönheit empfunden werden? Das ist die Frage der Objektivität, die an anderer Stelle fortgeführt werden soll: Gibt es eine Mitteilung, mit der in der Schönheit übergreifende Kräfte erscheinen, die an »imponderable Agentien« gebunden (HW 6.416) oder in modernerer Sprachweise als reine Informationsausbreitung zu verstehen sind?
Anmerkung 4: Wenn Hegel die Kraft als die negative Einheit versteht, »in welche sich der Widerspruch des Ganzen und der Teile aufgelöst hat«, erinnert sein Verweis auf das Ganze und seine Teile an eine Lehre aus der Kunsttheorie. Zu Beginn der Renaissance hat der italienische Gelehrte Leon Battista Alberti (1404-1472) die übergreifende Bedeutung des Verhältnisses des Ganzen und seiner Teile für Mathematik, Kunst und Philosophie hervorgehoben: »Die Schönheit ist eine Art Übereinstimmung (consensus) und Einklang (conspiratio) der zugehörigen Teile in Bezug auf eine bestimmte Anzahl (numerus), Beziehung (finitio) und Anordnung (collocatio), so wie es die Harmonie (concinnitas), das vollkommene und ursprüngliche Naturgesetz, verlangt.« (Alberti, zitiert nach Wikipedia) Das Besondere liegt in der paradoxen Selbstähnlichkeit: Ein Ganzes kann sich nur aus Teilen zusammensetzen, wenn sowohl das Ganze seinen Teilen wie auch die Teile untereinander in bestimmter Weise ähnlich sind. Und das gilt nicht nur für den Gegenstand selbst, sondern auch für den Wahrnehmungsprozess: Die Regelmäßigkeit eines Gegenstands kann nur erkannt werden, wenn es eine Symmetrie zwischen dem Gegenstand und dem Wahrnehmungsorgan gibt. Wird diese Symmetrie für sich betrachtet, dann handelt es sich um eine Kraft, die sowohl auf Seiten des Gegenstands eine gewisse Einheitlichkeit der Teile sowie des Ganzen herstellt, wie auch im Wahrnehmungsprozess um eine Kraft, wodurch sich das Wahrnehmungsorgan und der wahrgenommene Gegenstand aktiv aufeinander beziehen. Es ist daher nicht nur wie für Kant eine transzendentale Eigenschaft des Denkens, dass es nur das denken kann, was seinen Denkbestimmungen entspricht, sondern während des Wahrnehmens und Denkens wirkt eine Kraft, die zwischen beiden steht und den Gegenstand auf das Denken ausrichtet bzw. umgekehrt das Denken auf den Gegenstand fokussiert (Intentionalität im Sinne von Husserl). Es gibt Versuche, diesen Vorgang experimentell nachzuweisen. Sie sehen sich allerdings wie Newtons Frage nach einem »spirit« dem tiefen Misstrauen gegenüber jeder Art von echter oder vermeintlicher Parapsychologie ausgesetzt. Hier ging es darum zu zeigen, dass sich an ihnen ähnlich der Scheidung der Magie in helle und dunkle Magie ein vernünftiger Kern nachweisen lässt, den Hegel getroffen hat, wenn er von der Kraft sprach, die sich als negative Einheit aus dem Widerspruch des Ganzen und seiner Teile ergibt.
Die Physik ist diesem Verständnis mit ihrer Untersuchung von Symmetrien und Kräften weit näher als sie bisweilen glaubt. Sie sagt, dass jeder Symmetrie eine Strömung entspricht (Theorem von Noether), wobei für mein Verständnis die hier angesprochene Strömung der von Hegel gemeinten Kraft sehr nahe kommt.
Daher ersetzt Hegel die Frage nach einem übergreifenden Substrat durch ein übergreifendes Ganzes. Dieses ist im Gang seiner Logik ein Zwischenschritt, der im Weiteren zur Substanz, dem Begriff und der Idee führt
Die Identität »in ihrer höheren Wahrheit«
Die Identität ist die erste von Hegel eingeführte Reflexionsbestimmung. Hier sollte sich daher am besten erkennen lassen, wie der Übergang von der Seinslogik zur Wesenslogik gelingt.
Hegel grenzt den Begriff der Identität ab von der »Abstraktion«, die für ihn lediglich »Verstandesidentität« ist, und vom Reduktionismus, für den alles »bloße Identität« ist, und der z.B. »die organischen Prozesse der Verdauung und Assimilation als bloß chemischer Prozeß betrachtet« (Enz. § 115, 118 Zusatz, HW 8.236 und 8.243). Damit stellt er sich radikal gegen den Trend, der seither die weitere Entwicklung der Wissenschaft dominiert und mit dem Einsatz EDV-gestützter Informationssysteme zur Auswertung, Spracherkennung, Ordnung und Dokumentation nahezu unbegrenzter Datenmengen einen ungeahnten Aufschwung genommen hat. Das von Hegel genannte Beispiel, organische Prozesse auf chemische Prozesse zurückzuführen ist harmlos im Vergleich zu den Ansichten, die heute beispielsweise in der Kognitionswissenschaft vertreten werden, um mit ihnen Künstliche Intelligenz entwickeln zu können: Das Denken ist »bloß« eine Verknüpfung chemischer und elektrischer Synapsen im Nervensystem.
Was lässt sich dem entgegensetzen? Hegel findet mit dem Positiven einen elementaren Begriff, der sein Verständnis der Identität von allen anderen unterscheidet: »Das Positive ist wieder die Identität, aber in ihrer höheren Wahrheit« (Enz. § 119 Zusatz 1, HW 8.245).
In diesem Kapitel soll mithilfe des Begriff des Positiven gezeigt werden, wie sich das Verständnis der Identität entwickelt von der Seinslogik zur Wesenslogik. Der Begriff des Positiven soll in seiner von Hegel gemeinten Bedeutung als Reflexionsbestimmung erkennbar werden, um verstehen zu können, wie er erst in Gegensatz und dann in Widerspruch gerät mit dem Negativen.
Qualitätslogik: Jeder gebraucht das Eigenschaftswort »positiv« und versteht zugleich, dass es im Grunde keine Eigenschaft ist wie Farbe, Geruch, Größe, Gestalt. Das Positive ist keine Kategorie und gehört keiner Kategorie an. Wenn überhaupt, dann kann umgangssprachlich die Haltung eines Menschen als positiv bezeichnet werden im Sinne von »glücklich, optimistisch, bejahend« (Wikipedia ). Im Sinne der Qualitätslogik bedeutet positiv, dass etwas die Eigenschaft hat, sich in innerer Übereinstimmung mit seinen Eigenschaften zu befinden und daraus die Kraft zu ziehen, die positiven Eigenschaften fortlaufend verstärken zu können. So entsteht bereits in der Qualitätslogik und in der Umgangssprache ein selbstreflexiver Gebrauch des Wortes »positiv« und zeigt elementar, welch anderer Begriff von Identität sich mit ihm gewinnen lässt als mit der leeren Aussage ›A = A‹.
Maßlogik: Was mit »positiv« gemeint ist, erschließt sich genauer, wenn Zustände als positiv beschrieben werden. In der Medizin kann ein Zustand als positiv gelten, wenn gute Heilungschancen bestehen. Meist wird jedoch dann von einem »positivem Befund« gesprochen, wenn ein Krankheitserreger nachgewiesen werden kann und daher der gesamte Zustand im Grunde negativ, d.h. durch einen Erreger belastet ist. Ein Zustand kann in zweierlei Weise als positiv gelten: Er ist stabil, oder er hat in sich die Neigung, einen kritischen Grenzwert zu überwinden und sich in einen höheren Zustand zu verändern. Wenn »positiv« in dieser Weise verstanden wird, dann lässt sich der Begriff über die Medizin hinaus verallgemeinern und z.B. auch auf chemische und physikalische Prozesse beziehen, in denen mit den Methoden der Chaos-Theorie Zustände unterschieden werden können, die in unterschiedlichem Grad stabil und unstabil, selbst-erhaltend und selbst-auflösend, robust oder anfällig gegen Störungen sind.
So verstanden entsteht mit dem Substrat, das sich in verschiedenen Zuständen zeigen kann, ein neuer Begriff der Identität: Das Substrat bleibt in den verschiedenen Zuständen identisch. Die Identität geht so weit, dass sie auch den Grenzzustand erreicht, wie ihn zum Beispiel die Keplerschen Gesetze beschrieben haben. Innerhalb der absoluten Indifferenz sind nur daher Gesetze erkennbar, weil es eine übergreifende Identität gibt, die die Verlaufsform der jeweils betrachteten Bewegung (wie z.B. der Planetenbewegung) auch noch in einem Grenzzustand sicherstellt, in dem es keine Materie gibt oder die Materie auf ausdehnungslose Punkte reduziert ist. Doch enthält der Begriff des Positiven mehr als diese formale Identität. In ihm ist die weitergehende Aussage enthalten, dass die Identität innerhalb einer Vielfalt von Zuständen in der Neigung besteht, denjenigen Zustand zu erreichen, der seiner Natur am besten entspricht. In dieser Weise können Grundbegriffe von Aristoteles übernommen werden. Ein Zustand ist negativ, wenn dem Substrat in diesem Zustand etwas fehlt (siehe bei Aristoteles den Begriff des Mangels, steresis), und entsprechend positiv, wenn das Fehlen überwunden ist. Aristoteles hat seine Lehre zweifellos von der Beobachtung von Krankheits- und Gesundheitszuständen entwickelt.
Die naheliegende Gleichsetzung von »positiv« mit »gesund« wäre jedoch verkürzt. So wie im Bereich der Medizin die Gesundheit ein Maß ist, an dem die medizinisch bewerteten Zustände gemessen werden, so gibt es in allen anderen Bereichen deren eigene spezifischen Maße. Und bereits in der Medizin ist nicht nur ein stabiler Zustand gesund, sondern im Grunde erst eine Gesamtsituation, die über genügend Selbstheilungskräfte verfügt, die auch in kranken Zuständen eine positive Entwicklung ermöglichen.
Wird nach einer formalen Definition gefragt, dann erscheint mir für die Verwendung des Begriffs »positiv« für Zustände der Ausdruck »Wiederholungsschleife« am geeignetsten, der als ein mögliches Synonym für »Kontinuation« angeboten wurde. Das klingt zwar ein wenig schwerfällig und ungewohnt, zeigt aber am besten in einem Begriff, worum es geht: Ein Zustand vermag sich entweder dank einer inneren Wiederholungsschleife zu erhalten, oder es gibt im Innern von benachbarten Zuständen Wiederholungsschleifen, die diese Zustände in den Zustand »kontinuieren«, in dem die größtmögliche Stabilität erreicht ist. (Hegel gebraucht den Ausdruck »Kontinuation«, um zu beschreiben, wie sich die inneren Faktoren eines Zustands, aus deren Wirken die Zustandsänderungen erklärt werden sollen, ineinander kontinuieren. Wenn die Kontinuation der Faktoren gelingt, kann über die Zustände übergreifend die Identität des ihnen zugrundeliegenden Substrats gewahrt werden.)
In diesem Sinn lässt sich das von Hegel genannte Beispiel der Himmelsmechanik völlig anders interpretieren. Jetzt wird nicht der einzelne Planet, z.B. die Venus, als ein Substrat betrachtet, das sich um die Sonne bewegt und in jedem einzelnen Bewegungszustand der Anziehung zur Sonne und der eigenen Trägheit ausgesetzt ist, sondern das gesamte Planetensystem ist das Substrat. Seine Zustände sind die Momentaufnahmen, in denen sich die Gesamtheit von Sonne, Planeten, Monden etc. jeweils befindet. Die Umlaufbahnen sind die Wiederholungsschleifen, durch die sich dies Substrat im Ganzen stabil erhält. Mathematisch handelt es sich um ein Mehrkörperproblem, welches mithilfe der Keplerschen Gesetze nur für 2 Körper lösbar ist. Bei mehr Körpern erscheint es mathematisch chaotisch (d.h. indifferent), und es sind höhere Erklärungen als durch eine mechanische Beschreibung notwendig, um die Stabilität des Systems zu erklären. Für eine mechanische Lösung gibt es nur Ansätze, z.B. das Kolmogorow-Arnold-Moser-Theorem.
Mit dem Begriff der Identität vollzieht Hegel den entscheidenden Schritt, der im Ganzen der Wissenschaft der Logik vom Etwas über die Identität zum Begriff führt. Für den Verstand ist die Identität das gleiche wie das jeweils endliche Etwas. Hegel spottet über Leibniz, für den jedes einzelne Blatt, das er in den Herrenhäuser Gärten bei Hannover gefunden und identifiziert hat, einzigartig ist. Mit jedem Etwas ist zugleich die Identität gegeben, dass das jeweilige Etwas mit sich selbst identisch ist und alles andere von ihm unterschieden werden kann.
Dagegen führt Hegel bereits in der Seinslogik aus, dass zwar zweifellos auf den ersten Blick jedem Etwas viele Andere gegenüberstehen, die sich jeweils in mindestens einer Qualität vom Etwas unterscheiden. Der blaue Ball ist anders als der rote Ball. Alle diese Anderen befinden sich außerhalb des Etwas und sind von ihm unterschieden. Dennoch spricht Hegel zugleich vom Anderen »an ihm selbst« (HW 5.127). Das verstehe ich so, dass Hegel hiermit Realität und Idealität unterscheidet. Jedes Etwas verfehlt in seiner Realität dasjenige, was es entsprechend seiner Natur sein könnte und nur in der Idealität erreichen würde. Aber es trägt in seiner Realität die Idealität an sich, obwohl es nicht seiner Idealität entspricht. Diesen Unterschied zu erkennen ist für Hegel die Aufgabe der Philosophie. Am Endlichen zeigt sich das Unendliche, das zugleich weit über es hinausgeht. »Die Idealität kann die Qualität der Unendlichkeit genannt werden« (HW 5.166).
Die bloße Verstandesidentität bleibt innerhalb der Realität stehen und sieht nicht, wie das Etwas zugleich das Andere an ihm selbst enthält und insofern für den Verstand die Forderung nach der Identität verletzt. Daher ist es für Hegel unangemessen, den von der Metaphysik entwickelten Begriff der Identität zu übernehmen. Für ihn muss die Identität weiter gehen und sowohl ermöglichen, dass das Etwas nicht nur in seiner Realität, sondern auch in der an ihm erkennbaren Idealität verstanden werden kann. Und es muss möglich sein, diese Unterscheidung von Realität und Idealität des Etwas fortzuführen bei Betrachtung des Substrats: Es sind nicht nur die Zustände zu betrachten, die es real in der materiellen Welt gibt, sondern die Identität des Substrats soll auch den Grenzfall mit umfassen, an dem sich erst das Substrat in seiner wahren Ordnung zeigt.
Im Begriff der Identität wird der Begriff des Etwas aufgenommen, an dem dessen Realität und Idealität, das Etwas selbst und das Andere am ihm selbst unterschieden werden. Und der Begriff der Identität deutet bereits voraus auf den Begriff des Begriffs, der im weiteren Fortgang der Wissenschaft der Logik aus ihm entwickelt werden wird. Mit dem Begriff wird die wahre Identität erreicht.
Die negative Einheit
Was kann angemessen gegen ein Positives gesetzt werden, das sich als die höhere Wahrheit der Identität erwiesen hat, und diesen Gegensatz gegen das Positive bis zum höheren Widerspruch treiben? Der Gegensatz zum Positiven muss bereits im Positiven enthalten sein. Hegel versteht ihn als die »negative Einheit«. Als die »höhere Wahrheit« des Positiven hat sich gezeigt, dass das Positive auch das mit enthält, was sich noch außerhalb seiner befindet, aber zu ihm hin tendiert. Hier konnte sich Hegel auf den Natur-Begriff von Aristoteles beziehen, für den die Natur einer Sache auch den vorübergehenden Mangel enthält, der entsprechend seiner eigenen Natur zur Überwindung des Mangels drängt. Hegel konnte sich weiter auf den Neuplatonismus beziehen und dort insbesondere auf Proklos. Proklos vertrat die dreifache Bewegung, wie etwas im Einen verharrt (mone), darüber hinausgeht (daraus hervortritt) (prohodos) und wieder zurückkehrt (epistrophe).
Ausgangspunkt ist nochmals die Unterscheidung in das Substrat und seine Zustände. Wenn sich ein Substrat in verschiedenen Zuständen zeigt, kann das als ein Beispiel für das Heraustreten (prohodos) verstanden werden. Das Substrat an sich ist verborgen, aber es zeigt sich in seinen Zuständen. (Zum Beispiel kann niemand das Wasser sehen, sondern nur jeweils einen bestimmten Zustand des Wassers. Umgangssprachlich wird das Substrat Wasser häufig gleichgesetzt mit seinem flüssigen Zustand.) Und auf der anderen Seite enthält jeder Zustand in sich einen Verweis, der auf das Substrat deutet. (Wird Eis, eine Flüssigkeit oder Dampf analysiert, dann enthält es bestimmte Eigenschaften, an denen erkennbar ist, dass es sich um Wasser handelt.) Das führt zu einer Umkehrung vom Zustand zurück zum Substrat. Hegel hatte dies selbstreflexiv für die Indifferenzpunkte beschrieben. Sie werden zerlegt in innere Faktoren, die sich einerseits ineinander kontinuieren, andererseits wieder zu sich selbst zurückkehren und dadurch im Ganzen den Übergang von einem Zustand in einen anderen beschreiben.
Mit dem Begriff dieser Rückkehr (der epistrophe im Sinne von Proklos) kann derjenige Begriff der Grenze überwunden werden, an dem der Verstand in seinen Versuchen Widersprüche zu verstehen scheitert. Die Grenze schließt einen endlichen Bereich ab und setzt, dass es jenseits der Grenze etwas Anderes gibt, das dem Verstand unzugänglich bleibt. Mit den Begriffen des Hinausgehens und der Umkehr ist dagegen ein Verständnis gewonnen, das die Grenze überschreitet, sich dort jedoch weder im Beliebigen verliert noch endgültig verschwindet, sondern die Kraft behält, den Widerspruch auszuhalten und umzukehren. Wenn eine solche Kraft der Umkehrung gegeben ist, dann kann von einer negativen Einheit gesprochen werden. Mit der negativen Einheit ist in einer Einheit zusammen gedacht, was zuvor diesseits und jenseits der Grenze getrennt war. Die Einheit kann nur negativ sein, da sie einen Widerspruch umschließt. Eine solche negative Einheit kann für sich nicht beobachtet werden, sondern nur in ihren Auswirkungen (der Rückkehr dessen, das sich phasenweise entzieht). Ich bin der Überzeugung, dass die negative Einheit (die Umkehr) für Hegel den Rang einer transzendentalen Bestimmung annimmt. Die Vernunft kann weder etwas denken, das immer da ist, sondern nur, wenn es sich zeitweise entzieht. Und genau so wenig kann sie etwas denken, das sich völlig entzieht und nie wieder zurückkehrt.
Um es noch abstrakter zu formulieren: Hegel nimmt die Probleme, an die der Verstand stößt und mit denen er kämpft, so ernst wie möglich. Der Verstand hat zurecht die Befürchtung, dass ein Hinausgehen über die Grenze in das Nichts führt. Hegel verfolgt kein geringeres Ziel, als für diesen Weg in das Nichts und die Umkehr aus dem Nichts die geeigneten Begriffe zu finden. Das sind die negative Einheit und die Umkehrung, die in Gegensatz und in Widerspruch zum Positiven geraten.
Das klang bereits an bei der Beschreibung der Planetenbewegung (Kontinuation und Umkehr) und lässt sich nach meiner Überzeugung noch elementarer veranschaulichen am Verhältnis von Hell und Dunkel, von Sichtbarkeit und Unsichtbarkeit. Hierfür kann das Beispiel der Sonnenbahn genommen werden. Die Sonne ist an wolkenfreien Tagen tagsüber sichtbar. Dann kann ihre Bahn beobachtet werden einschließlich des Umkehrpunktes zur Mittagszeit, wenn die Sonne wieder abzusteigen beginnt. Im Jahresverlauf kann beobachtet werden, wie die Tage immer länger werden, bis sich diese Bewegung am Tag der Sonnenwende wieder umkehrt. Daraus wird geschlossen, dass etwas gleiches in den Phasen geschieht, wenn die Sonne nachts nicht zu sehen ist. Es wird unterstellt, dass sie in diesen Phasen einen Durchgang durch das Nichts macht und dort erneut umkehrt. In dieser elementaren Anschauung gilt alles, was nicht sichtbar ist, als Nichts. Mit den bloßen Augen ist in diesen Phasen buchstäblich nichts zu sehen. Aber die Vernunft kann setzen, dass sich die Sonne in diesen Phasen nicht in Nichts auflöst, sondern sich in dem für den Menschen unsichtbaren Bereich weiter bewegt, dort umkehrt und am nächsten Morgen wieder aufgeht.
Diese Art zu denken erscheint heute völlig selbstverständlich, ist aber das Ergebnis einer langen Entwicklung, in der die menschliche Vernunft aus dem magischen Denken hervorging. Noch Aristoteles spricht von der »Herrschaft und Leitung ... der ursprünglichen Götter, z.B. der Nacht und dem Himmel oder dem Chaos oder dem Okeanos«, von der sich die frühen Dichter Griechenlands befreit haben (Aristoteles, Metaphysik, 1091b). Für Hegel übernimmt die negative Einheit die Aufgabe, die die frühen Dichter Griechenlands bei den Göttern der Nacht oder des Chaos gesehen haben. So wie die Göttin der Nacht sicherstellt, dass die Sonne nicht verschwindet, wenn sie in der Nacht untergegangen ist, sondern in ihrem Verschwundensein umkehrt und am nächsten Morgen wieder erscheint, leistet das gleiche die negative Einheit. Die negative Einheit als solche kann prinzipiell nicht empirisch beobachtet werden, sondern wird von der Wissenschaft unbemerkt als Prinzip vorausgesetzt, wenn sie aus bruchstückhaft vorhandenen Beobachtungsdaten zusammenhängende Bewegungen interpoliert, die teils sichtbar und teils unsichtbar sind.
Es muss eine negative Einheit geben, die das Sichtbare und Unsichtbare, die Bewegung durch das Dunkle und das Helle miteinander verbindet. Mit der negativen Einheit ist Hegel bis an die innerste Wurzel gelangt, aus der Wissenschaft hervorgeht. Er hat damit den Ansatz von Kant aufgegriffen und wesentlich weiter geführt. Kant war dabei stehen geblieben, innerhalb der Wissenschaft nach den Begriffen zu suchen, aus denen sie sich konstituiert, das sind Raum und Zeit, Substanz, Kausalität und Wechselwirkung. Hegel hat weiter gefragt, auf welchen Voraussetzungen diese Begriffe beruhen. Das ist für ihn die negative Einheit. Kant hatte bereits von der Reflexion gesprochen und den Reflexionsbegriffen. Hegel hatte gefragt, was wiederum die Bestimmung der Reflexion ist, die Reflexionsbestimmung. Im Ergebnis will er zeigen, wie es zunächst ein Verständnis der negativen Einheit geben muß und dann daraus die Reflexionsbegriffe entstehen können. Er lässt nicht, wie es scheinen kann – und auch mir lange erschienen ist – Begriffe wie Raum und Zeit aus der Logik hervorgehen, sondern er zeigt, wie ein Denken beschaffen sein muß, das der Bildung und dem Gebrauch solcher Begriffe fähig ist. Das ist die Frage nach den Denkbestimmungen. Hier bleibt er im Prinzip Kant treu, wenn er mit den Denkbestimmungen ausschließlich regulative Bestimmungen entwickelt, die die Methode der Wissenschaft ermöglichen, aber nicht aus sich heraus bereits deren Inhalt festlegen. (Ob er seinerseits diesem Ansatz in seiner Naturphilosophie gerecht wird, und ob dies noch für seine Schüler gilt, ist eine andere Frage.)
Hegel kritisierte daher an Newton und anderen Physikern nicht, dass und wie sie Naturvorgänge beschrieben haben, sondern bewundert diese Leistung in höchstem Maß. Ihm geht es nur darum zu zeigen, dass die Physiker in die Irre gehen, wenn sie die von ihnen konstruierten inneren Faktoren der Indifferenzpunkte als voneinander unabhängige, endliche Kräfte verstehen und dann gezwungen sind, eine zusätzliche dritte Kraft zu fordern, die die Umkehrung der beiden voneinander getrennten, umgekehrten Faktoren hervorruft. Hegel hält dagegen fest, dass es eine solche »dritte Kraft« prinzipiell nicht gibt, und dass sie sich daher empirisch nicht beobachten oder nachweisen lässt. Sie ist mit der negativen Einheit gegeben, die als Denkbestimmung im Denken immer bereits vorausgesetzt und enthalten ist. So wie bereits die beiden inneren Faktoren der Indifferenz nur gesetzt werden konnten (bei Kepler die Geschwindigkeit und der Abstand des Planeten zur Sonne, bei Newton die Zerlegung der Kraft in ein Kräfteparallelogramm), so lässt sich auch nur setzen, dass sie im umgekehrten Verhältnis zueinander stehen. Sie befinden sich in einer negativen Einheit, die grundsätzlich nicht beobachtet werden kann und daher nicht ins Gebiet der Lehre vom Sein fällt. Sie lassen sich prinzipiell nicht in Kategorien fassen.
So wie Kant gegenüber Hume argumentierte, dass sich die Kausalität nicht empirisch nachweisen lässt, sondern dass weit grundsätzlicher kein Denken möglich ist, das nicht in Kausalitäten denkt, so verstehe ich Hegels Argument gegenüber Newton: Die Kraft der Umkehrung lässt sich nicht durch eine empirisch beobachtbare Kraft nachweisen, sondern sie gilt im Gegenteil in einem Bereich, der sich der empirischen Beobachtung entzieht. Sie ist wie die Kausalität ein Prinzip des Denkens, ohne dass das Denken keine Gesetze aufstellen könnte. Anders als die Kausalität ist es jedoch nicht in der Zeit und deren innerer Kontinuität gegründet, sondern steht vielmehr der Kontinuität gegenüber und führt zur Umkehr einer kontinuierlich gleichartigen Bewegung. Die Umkehr ist für Hegel nicht in der Zeit, sondern in der bereits von Proklos und anderen Neuplatonikern genannten übergreifenden Bewegung des Einen zum Vielen und des Vielen zurück zum Einen begründet. Darin gründet die dialektische Methode, wenn es ihr gelingt, in der Vielfalt der dem einheitlichen Allgemeinen gegenüber stehenden Besonderen das Einzelne zu finden, in dem das Allgemeine und Besondere eine höhere Einheit finden. In diesem Einzelnen erfolgt innerhalb der zerstreuten Mannigfaltigkeit des Besonderen, die sich in das völlig zusammenhanglose und chaotische Nichts aufzulösen droht, die Umkehrung, die zu einen Allgemeinheit zurückführt.
In diesem Sinn bestimmt Hegel im Weiteren den Unterschied und unterscheidet ihn ebenso von der Ungleichheit, wie er die Identität von der Gleichheit unterschieden hat. Der Unterschied stellt in seiner höheren Wahrheit die negative Einheit her.
»Das Vergleichende geht von der Gleichheit zur Ungleichheit und von dieser zu jener zurück, lässt also das eine im andern verschwinden und ist in der Tat die negative Einheit beider. Sie ist zunächst jenseits des Verglichenen sowie jenseits der Momente der Vergleichung, als ein subjektives, außerhalb ihrer fallendes Tun. Aber diese negative Einheit ist in der Tat die Natur der Gleichheit und Ungleichheit selbst, wie sich ergeben hat. Eben die selbständige Rücksicht, die eine jede ist, ist vielmehr die ihre Unterschiedenheit und damit sie selbst aufhebende Beziehung auf sich. [...] Aber diese ihre negative Einheit ist ferner auch an ihnen gesetzt« (HW 6.51).
Wenn verstanden ist, welchen Unterschied Hegel zwischen dem Unterschied im umgangssprachlichen Verständnis (der Ungleichheit) und dem von ihm gemeinten Unterschied sieht, dann kann gefragt werden, ob das Besondere des reflexionslogischen Unterschiedes für sich betrachtet werden kann. Das ist für Hegel das Positive und das Negative.
»Das Positive und Negative aber sind der gesetzte Widerspruch, weil sie als negative Einheiten selbst das Setzen ihrer [sind] und darin jedes das Aufheben seiner und das Setzen seines Gegenteils ist« (HW 6.65).
Dies alles zusammenfassend wird klar, was mit dem Übergang vom Widerspruch zum höheren Widerspruch gemeint ist.
»Dieses Widersprechende löst sich allerdings in nichts auf, es geht in seine negative Einheit zurück. Das Ding, das Subjekt, der Begriff ist nun eben diese negative Einheit selbst; es ist ein an sich selbst Widersprechendes, aber ebensosehr der aufgelöste Widerspruch; es ist der Grund, der seine Bestimmungen enthält und trägt. Das Ding, das Subjekt oder der Begriff ist als in seiner Sphäre in sich reflektiert sein aufgelöster Widerspruch, aber seine ganze Sphäre ist auch wieder eine bestimmte, verschiedene; so ist sie eine endliche, und dies heißt eine widersprechende. Von diesem höheren Widerspruche ist nicht sie selbst die Auflösung, sondern hat eine höhere Sphäre zu ihrer negativen Einheit, zu ihrem Grunde. Die endlichen Dinge in ihrer gleichgültigen Mannigfaltigkeit sind daher überhaupt dies, widersprechend an sich selbst, in sich gebrochen zu sein und in ihren Grund zurückzugehen« (HW 6.79).
Hegel unterscheidet sorgfältig zwischen dem Widerspruch innerhalb der jeweiligen Sphäre und dem höheren Widerspruch in der höheren Sphäre. Die höhere Sphäre kann nur als negative Einheit verstanden werden. Vorausschauend sei angemerkt, dass von hier der Weg nicht mehr weit ist, bis Hegel in der subjektiven Logik fast gleichlautend vom »Begriff« und »der negativen Einheit des Begriffs« sprechen wird. Mit der negativen Einheit ist der Begriff bereits gesetzt und es fehlt nur noch die Freiheit, mit dieser Setzung frei operieren zu können (siehe dazu den Beitrag zum Begriff des Subjekts).
Anmerkung 1: Diese Ausführungen zur negativen Einheit haben eine gewisse Verwandtschaft mit Heideggers Verständnis der Wahrheit als Unverborgenheit (aletheia), siehe seinen Vortrag Vom Wesen der Wahrheit (1930). Ohne Heidegger wäre das hier entwickelte Verständnis kaum oder nur schwerer möglich geworden, aber es zeigt, dass Hegel inhaltlich über die von Heidegger formulierte Position hinausgegangen ist. Wahrheit ist entsprechend dem hier entwickelten Gedanken nicht einfach die Unverborgenheit, sondern Hegel hat mit dem Verständnis der negativen Einheit gezeigt, wie sich das Verborgene denken lässt. Es bleibt den Sinnen und der Erfahrung und jeder Darstellung in Kategorien verborgen, aber es lässt sich durch die Reflexion setzen. Mit den Reflexionsbestimmungen will Hegel die Frage beantworten, warum und wie der Reflexion das möglich ist.
Anmerkung 2: Für Thomas Collmer löst Hegel den Satz der Identität in eine Operation (Bewegung) der Selbstbezüglichkeit auf. Hegel verweist darauf, dass in der scheinbar tautologischen Formulierung ›A ist A‹ das A doppelt auftritt und sich wie an einem Spiegel selbst gegenübergestellt wird. Statt einfach von »A« zu sprechen, setzt der Satz der Identität einen Raum voraus, in dem A mit Anderem verglichen wird, und eine Operation des Vergleichs mit sich selbst.
»A ist, ist ein Beginnen, dem ein Verschiedenes vorschwebt, zu dem hinausgegangen werde; aber es kommt nicht zu dem Verschiedenen; A ist – A; die Verschiedenheit ist nur ein Verschwinden; die Bewegung geht in sich selbst zurück.« (HW 6.44)
Im Sinne dieses Hinausgehens und Zurückgehens ist der Satz der Identität für Collmer das Ergebnis einer selbstbezüglichen Operation, die er als eine »basale Selbstreferenz« versteht und mit einem eigenen Operationszeichen versieht: ◻a (Collmer 2011, S. 90, Hervorhebung t.). Das soll betonen, dass diese Operation an A erfolgt: Sie wird an A vorgenommen und führt zu A zurück. Formal ist es eine einstellige Operation. Sie kennt als Operanden nur A, aber sie geht einen Weg durch einen Möglichkeitsraum, in dem sich A befindet.
Mit der basalen Selbstreferenz geht Collmer an einem entscheidenden Punkt über Hegel hinaus. Die Operation ◻a verweist auf einen Möglichkeitsraum, der innerhalb von A eröffnet wird. Während Hegel nur davon spricht, dass dem »Beginnen ... ein Verschiedenes vorschwebt«, wird bei Collmer die Gesamtheit der Verschiedenen als ein Möglichkeitsraum angesehen, der A umgibt. Die A umgebenden Möglichkeiten bezeichnen die Verschiedenen, die im Satz ›A ist‹ ergänzt werden können.
»Insofern hat jede holistische Konzeption einen Möglichkeitsgrund, der ihr äußerlich bleibt und auf den sie nur verweisen kann – genau darin besteht, näher betrachtet, ihr ›Beweisen‹.« (Collmer 2011, S. 109)
Niemand kann sagen, welche Möglichkeiten im Möglichkeitsgrund enthalten sind. Der Möglichkeitsgrund ist daher eine negative Einheit, mit der alles zusammengefasst ist, das in dem begonnenen Halbsatz ›A ist‹ für einen Moment vorschwebt. Für Hegel scheint das Vorschweben ein Vorgang zu sein, der nur im Denken stattfindet, damit es aus ihm heraus in der Rückkehr zur Identität gelangen kann. Die im Vorschweben gestreiften Verschiedenen scheinen eine Ausgeburt des Denkens zu sein, das nicht anders als auf diese Weise denken kann, während der von Collmer angesprochene Möglichkeitsgrund an A eine Vielfalt von Möglichkeiten enthält, die in A angelegt sind, und von denen aktuell nur eine wirklich geworden ist. Es ist für Hegel erkennbar eine transzendentale Bestimmung, dass durch diese Operation die Identität von A nicht in einer Vielfalt von Möglichkeiten zerstreut wird, sondern eine Rückkehr zu A erfolgt. Für ihn ist es die Aussage des Satzes der Identität, dass A festgehalten werden kann und sich nicht in Beliebigkeit verliert.
Mit der Unterscheidung in Identität und Möglichkeitsgrund gelingt Collmer die formal-logische Grundlage, mithilfe derer die Unterscheidung in Realität und Idealität, Mangel und Natur möglich wird. Damit hat er in meinem Verständnis das Anliegen von Hegel getroffen, der in der Reflexionslogik die impliziten Voraussetzungen aufdecken will, die in der Seinslogik noch nicht offen zutage lagen. Nur weil es im Denken einen Möglichkeitsraum gibt, innerhalb dessen die Identität von A identifiziert werden kann, können die aktuelle Realität von A und seine Natur unterschieden werden, wie es in der Seinslogik intuitiv erfolgt war. Realität und Idealität befinden sich im Möglichkeitsgrund, und es bedarf eines weiteren Prinzips, das aus der Vielzahl der Möglichkeiten eine herausgreift, zu der hin sich das A in seiner Realität bewegt. Das war für Aristoteles schlicht die Natur, die von sich aus alles dazu bringt, einen Zustand anzustreben, in dem es mit der eigenen Natur übereinstimmt. Für Leibniz ist es das Harmonie-Prinzip, für ein Denken in der Tradition von Empedokles oder dem Christentum das Prinzip der Liebe.
In seiner Dissertation sprach Collmer bereits im Untertitel von einer »negativen Totalisierung«. Bei Hegel bleibt mindestens offen, ob der Weg der Kontinuation und Umkehr durch die negative Einheit eindeutig festgelegt ist oder durch einen Möglichkeitsraum verläuft. Hegel neigt in Collmers Einschätzung zu einer geschlossenen Dialektik, während er eine offene Dialektik vertritt. »Von 'offener' Dialektik zu sprechen, besagt immer auch, dass mit dem Verhältnis von Zirkularität und Linearität, Selbstabstraktion und Selbstanreicherung anders operiert werden muß als bei Hegel.« (Collmer 1992, S. 258) Für ihn bleibt in der negativen Einheit prinzipiell eine »Lücke«, die das System offen hält. Er bezieht sich auf Lacans Verständnis der Lücke, und kann sich meiner Meinung nach noch deutlicher auf die Unvollständigkeitssätze von Gödel berufen.
Anmerkung 3: Die Eröffnung eines Möglichkeitsgrundes kann mit Scheier als der Übergang vom metaphysischen zum anti-metaphysischen Denken verstanden werden.
"Das metaphysische Denken hatte sein Prinzip am Actus purus und darum an der Plentitudo entis der Gegenwart. Daß die Möglichkeit höher steht als die Wirklichkeit (Heidegger Sein und Zeit, S. 38) – dies Axiom des anti-metaphysischen Denkens wird wahr, sobald die Wirklichkeit, seit der Restauration, sich gegen sich selber als gegen ihre eigne Möglichkeit kehrt und sie provoziert. Die eine Tendenz ist geschichtlich als Verdinglichung der wirklichen Welt, die andre als Utopie der möglichen Welt zum Vorschein gekommen: Baudelaires Spleen et Idéal." (Scheier, S. 11)
Obwohl Hegel den Satz der Identität operationalisiert, ist er überzeugt, dass das anfangs noch verworrene Denken sich dessen Schritt für Schritt bewusst wird, alle seine impliziten Voraussetzungen zu durchschauen lernt und schließlich fähig wird zu erkennen, was es idealiter bereits ergriffen, aber sich noch nicht klar vor Augen gestellt hat. In diesem Sinn hält er am Identitäts-Denken fest, was ihm Heidegger, Adorno und andere vorhalten. Es lässt sich nicht klarer als in den Worten von Scheier sagen, dass nach den Erfahrungen des 19. und 20. Jahrhunderts die Aufklärung mit ihrem Glauben an eine höhere Vernunft und ihrer Bereitschaft, im Namen dieser Vernunft Opfer und Verbrechen aller Art zu legitimieren, fragwürdig geworden ist. Stattdessen ist an jeder einzelnen Erscheinung die sich in ihr zeigende Vielfalt und Möglichkeit anderer und neuer Entwicklungen zu schätzen und zu fördern.
Das gilt auch für Frege und die ihm folgenden Logiker. Wenn Frege exemplarisch von den verschiedenen Namen wie “Abendstern” und “Morgenstern” die ‘Venus’ als ihre Bedeutung unterscheidet, setzt er voraus, dass es eine solche eindeutige Bedeutung gibt, die die gemeinsame Identität aller unterschiedlichen Namen ist, die das ‘gleiche’ meinen und eine Äquivalenzklasse bilden. Wird dagegen der Möglichkeitsgrund als eine negative Einheit verstanden, gibt es eine solche Sicherheit nicht mehr. Die Identität ist wie das Absolute nur eine regulative Idee, derer das Denken bedarf, um denken zu können, an die es sich jedoch niemals binden darf und die ständig von Neuem infrage zu stellen ist.
Die Kraft des Minus
Den meisten Lesern Hegels war gar nicht klar, an was für einem dramatischen Punkt sich die Wissenschaft der Logik im Kapitel über den Gegensatz befindet. Es droht, dass mit dem Begriff des Unterschiedes alles beziehungslos auseinander fällt. Es droht, dass die Welt auseinanderfällt in eine beliebige Vielzahl von Polaritäten, die einander starr gegenüber stehen. Mit den Polaritäten droht, dass beide Seiten, die im polaren Gegensatz zueinander stehen, vollständig austauschbar werden, so dass es nichts mehr gibt, das in dieser Situation aus dieser Spannung herausführen könnte.
An diesem entscheidenden Punkt findet Hegel mit den Begriffen des ‘an sich Positiven’ und des ‘an sich Negativen’ einen solchen Gegensatz, der einerseits wie alle anderen Gegensätze aussieht, aber zugleich in sich die Umkehrung enthält, die aus der Gefahr der Erstarrung in den Widerspruch führt. Das ist nur möglich, wenn innerhalb dieses einzelnen Gegensatzes von an sich Positivem und an sich Negativem beide Seiten nicht völlig gleichwertig sind, sondern die negative Einheit von größerer Macht ist. Daher sind alle üblicherweise gewählten Beispiele wie Westen und Osten, positive und negative Ladung oder Spannung eines Magneten in die Irre führend, da sich mit ihnen dieses Ungleichgewicht nicht zeigen lässt. Überraschenderweise findet Hegel dagegen in der Arithmetik der positiven und negativen Zahlen ein Beispiel, das diese Umkehr zeigen soll.
Um das aufzeigen zu können, entwickelt Hegel im Kapitel über den Gegensatz drei »Bestimmungen, welche das Positive und Negative konstituieren« (HW 6.57): (a) Es wird gesetzt, »dass das Positive und das Negative erstens absolute Momente des Gegensatzes sind; ihr Bestehen ist untrennbar eine Reflexion« (HW 6.57). (b) Bei Bestimmung des Positiven und Negativen wird vorausgesetzt, dass sie »verwechselt werden« können (HW 6.58). (c) Positives und Negatives treten in zwei Beziehungen zueinander, die wiederum positiv und negativ sind. In ihnen sehe ich die beiden Bestimmungen fortgeführt, die Hegel bei Analyse der inneren Faktoren der Indifferenz eingeführt hat: Kontinuation als positive Beziehung, umgekehrtes Verhältnis (Umkehrung) als negative Beziehung.
Diese beiden Beziehungen sind jedoch nicht gleichwertig, sondern Hegel sieht am Beispiel der positiven und der negativen Zahlen und ihren Multiplikationsregeln in der negativen Beziehung mit der Kraft des Minus eine Hervorhebung. Diese Hervorhebung ist das Prinzip der Negativität, die an Hegels Wissenschaft der Logik nachgewiesen werden kann (siehe dazu Collmer Hegels Dialektik der Negativität).
Bevor das näher betrachtet wird, ist ein mögliches Missverständnis auszuräumen. Wenn Hegel in der Anmerkung zum Gegensatz das Besondere des Negativen als die Kraft des Minus beschreiben will, die sich in den mathematischen Multiplikationsregeln der negativen Zahlen zeigt, kann das zur Vermutung führen, Hegel würde hier zurückfallen auf die von Kant betrachteten realen Oppositionen und die negative Einheit reduzieren auf die mathematische negative Einheit, das Minus. Ich verstehe diese Anmerkung so, dass Hegel zeigen will, wie die Denkbestimmungen des Positiven und Negativen nicht nur in der Physik als regulative Ideen wirken, sondern auch in der Mathematik. Das Plus und Minus der positiven und negativen Zahlen ist nicht gleichzusetzen mit den Reflexionsbestimmungen des Positiven und des Negativen und ihren konstitutiven Bestimmungen, sondern sie zeigen, wie diese Denkbestimmungen im Gebiet der Mathematik erfolgreich angewandt werden können.
Hegel will am Beispiel der negativen Zahlen zeigen, welche Bedeutung Austauschbarkeit und Umkehrung innerhalb der Mathematik annehmen. Um seinen Gedanken zu verstehen ist zurückzukehren in die Situation, wie und warum die negativen Zahlen entstanden sind. Heute ist ihr Gebrauch so selbstverständlich geworden, dass sich kaum jemand mehr vorstellen kann, dass sie systematisch erst 1762 durch Kant mit seinem Versuch den Begriff der negativen Größen in die Weltweisheit einzuführen begründet wurden. Vorher galt: Es kann nichts Kleineres als Nichts geben, daher gibt es keine Zahlen, die kleiner als 0 sind.
Für ihre Einführung sind zwei Vorstellungen wichtig: (a) Das Verhältnis der positiven und der negativen Zahlen ähnelt dem Verhältnis der sichtbaren und unsichtbaren Phasen, wie es am Beispiel der Sonnen- und der Venusbahn dargestellt wurde.
(b) Kant hat als Beispiel das Gleichgewicht gegeneinander wirkender Kräfte gewählt. So wird in der Lagerwirtschaft von negativen Beständen gesprochen. Natürlich gibt es keine negativen physischen Bestände: Eine Ware kann in einer bestimmten Menge vorrätig sein oder nicht. Aber es ist möglich, zusätzlich die Anfragen (den Bedarf) zu berücksichtigen. Es ist ein Unterschied, ob für eine nicht vorrätige Ware kein Bedarf, ein kleiner oder ein großer Bedarf besteht. Der Bedarf nach einer nicht vorrätigen Ware wird als ihr negativer Bestand bezeichnet. Entsprechend kann von negativem Kapital gesprochen werden, womit Schulden gemeint sind, die in Zukunft zurückgezahlt werden müssen.
Diese Beispiele legen einen Gedanken nahe, der heute von den meisten als abwegig empfunden werden wird: Während die positiven Zahlen endlos weiter gezählt werden können, ist bei den negativen Zahlen Schritt für Schritt zu prüfen, ob sie in einen Bereich führen, der sich des Ausgleichs entzieht, weil es keine Möglichkeit der Umkehrung mehr gibt. Wenn z.B. in Dürrejahren der negative Bestand so groß wird, dass die Menschen verhungern, ist der Ökonomie im Ganzen der Boden entzogen und es wird zu keiner Umkehr kommen. Etwas weniger dramatisch können die Schulden (das negative Kapital) so groß werden, dass ein Unternehmen Konkurs anmelden muß und die Schulden nie zurückgezahlt werden können, sondern abgeschrieben werden müssen. In solchen Fällen schlägt ein negativer Bestand direkt in Vernichtung um und macht offensichtlich, dass die negativen Zahlen einen völlig anderen Charakter haben als die positiven Zahlen. Die Kraft des Minus bedeutet daher zunächst elementar, dass eine solche Vernichtung vermieden werden kann und eine Umkehrung möglich ist.
Hegel hat auf einen anderen Aspekt aufmerksam gemacht. Mit der Einführung der negativen Zahlen bekommen die Vorzeichen eine doppelte Bedeutung. Wie das gemeint ist, erschließt sich aus dem Verständnis der Austauschbarkeit. Wenn das Positive und das Negative austauschbar sind, enthalten sie etwas Gemeinsames. In der Sprache der Mathematik enthält jede Symmetrie etwas Invariantes, das beim Austausch erhalten bleibt. Am Beispiel der ganzen Zahlen heißt das: Der Abstand der beiden einander entgegengesetzten Zahlen +a und −a zur Null ist jeweils gleich und wird als Betrag von a bezeichnet: |a|. Dennoch lassen sie sich voneinander unterscheiden. Dafür dienen die Vorzeichen + und −.
Entsprechend den ersten beiden Bestimmungen des Positiven und Negativen bestehen jetzt zwischen Positiv und Negativ zwei Beziehungen: Sie sind einander entgegengesetzt, was durch die Vorzeichen + und − gekennzeichnet wird, und sie stimmen überein, was mit dem Symbol a beschrieben wird. Hegel nennt die Übereinstimmung der ursprünglich einander Entgegengesetzten das Positive an sich und ihre Entgegensetzung das Negative an sich.
Es ist nicht einfach, diese fast gleich klingenden Bestimmungen auseinanderzuhalten. Ursprünglich wurde etwas Entgegengesetztes betrachtet, zum Beispiel die beiden Zahlen +a und −a. Jetzt wird davon als das Negative an sich ihre Entgegensetzung unterschieden. Mit Entgegensetzung ist nicht mehr eine der beiden Seiten gemeint, also nicht das +a oder −a, sondern eine Beziehung zwischen +a und −a.
Dass Entgegengesetztes und Entgegensetzung tatsächlich zweierlei sind, demonstriert Hegel am Beispiel der Mathematik. Dort wird unterschieden zwischen + und − als Vorzeichen und + und − als Operationszeichen. Hegel nennt das Beispiel: 8 − (−3) (HW 6.26). Zur besseren Unterscheidung ist hier das Minus-Zeichen in der Bedeutung als Vorzeichen grün hervorgehoben und in der Bedeutung als Operationszeichen rot. Die erste Bestimmung des Positiven und Negativen meint + und − als Vorzeichen. In der dritten Bestimmung ist dagegen Minus als Operationszeichen gemeint.
Das mag spitzfindig erscheinen, doch zeigt die Mathematik, wie Operationszeichen und Vorzeichen zusammengeführt werden können. »Näher tritt dies bei der Multiplikation und Division hervor; hier ist das Positive wesentlich als das Nichtentgegengesetzte, das Negative hingegen als das Entgegengesetzte zu nehmen« (HW 6.63). Erst jetzt tritt in Reinheit hervor, worauf Hegel hinauswollte. Denn hier zeigt sich, dass sich das Positive und das Negative charakteristisch voneinander unterscheiden. Bei den Multiplikationsregeln ergibt sich eine besondere »Kraft des Minus« (HW 6.64), durch die das Negative vom Positiven hervorgehoben wird.
»Dem Minus wird im ersten Falle die Kraft zugeschrieben, das Plus zu verändern; aber im anderen sollte Plus nicht dieselbe Kraft über Minus haben. [...] Eine Bestimmung als Negation kommt also allein durch das Negative herein, nicht durch das Positive« (HW 6.64).
Diesen Gedanken hat meines Wissens erstmals Okochi in voller Klarheit herausgearbeitet. Hegel bezieht sich auf die bekannten Multiplikations-Regeln (wobei die sich ändernden Vorzeichen rot hervorgehoben sind):
+ · + = +
+ · − = −
− · + = −
− · − = +
Wird der linke Faktor als Anzahl (Multiplikator) und der rechte Faktor als Einheit (Multiplikand) bezeichnet, dann ist zu erkennen, wie ein Multiplikator mit positivem Vorzeichen das Vorzeichen des Multiplikanden erhält, während ein Multiplikator mit negativem Vorzeichen das Vorzeichen des Multiplikanden umkehrt. Auf diese Weise lassen sich auch scheinbar paradoxe Aufgaben lösen wie: Berechne das (-7)-fache von 3: In einem ersten Schritt ist das 7-fache von 3 zu berechnen, im zweiten Schritt das Vorzeichen des Ergebnisses umzukehren.
Diese Regeln werden jedem Grundschüler eingepaukt und dann nur noch mechanisch nachvollzogen. Heute kann sich niemand mehr eine Vorstellung davon machen, wie schwierig es war, sie einzuführen. Taiju Okochi ist es gelungen, Hegel folgend diesen scheinbar einfachen Sachverhalt wieder in die nötige Schwierigkeit zurück zu übersetzen. Das folgende Zitat ist eine wahre Kniffel-Aufgabe und sollte jedem ermöglichen, die nötige Aufmerksamkeit für diese Verhältnisse zurück zu gewinnen.
»Das nächste Beispiel der Multiplikation scheint noch überzeugender zu sein. In diesem Beispiel wird deutlich, dass dem Verstand ein Fehler unterläuft, wenn er davon ausgeht, dass, wenn ›−a · +a = −a2‹ ist, umgekehrt ›+a · −a = +a2‹ sei, der auf diese Weise die qualitativen Bestimmungen der beiden Zahlen verkennt und 'Plus und Minus nur als entgegengesetzte Größen überhaupt' (GW XI 278, HW 6.64) nimmt. Hegel zufolge bedeutet jedoch Minus die Entgegensetzung an und für sich selbst und Plus die Nichtentgegensetzung an und für sich selbst. ›−a · +a = −a2‹ heißt entsprechend: Es gibt '−a' Einheiten von '+a', d.h. Hegel zufolge dasselbe wie 'a' Einheiten von '+a', jedoch auf entgegengesetzte Weise. Aus diesem Grund muß ›−a · +a = −a2‹ sein. Wenn diese Entgegensetzung nur relativ, d.h. von der Beziehung abhängig wäre, ergäbe sich ›+a · −a = +a2‹, weil '−a' auf die entgegengesetzte Weise von '−a' mit a multipliziert werden soll. Jedoch muss ›+a · −a = −a2‹ sein, weil laut Hegel '+' und '-' an und für sich selbst als positiv oder negativ verstanden werden müssen. Das Plus hat keine Kraft, eine jeweilige Qualität zu verändern, während das Minus sie hat. ›−a · −a = +a2‹ kann auch auf die gleiche Weise verstanden werden, weil hier '−a' auf die entgegengesetzte Weise mit 'a' multipliziert wird. In diesem Kalkül der Multiplikation von zwei negativen Zahlen sieht Hegel ein Beispiel für seine Theorie der Negation der Negation: 'Die Negation der Negation aber ist das Positive' (ebd.)« (Okochi, S. 191).
Wird dies alles im Zusammenhang überblickt, dann ist zu sehen, wie der Mathematik der Übergang in eine höhere Dimension gelungen ist. Mit höherer Dimension ist hier nicht gemeint, dass die eindimensionale Zahlengerade in die zweidimensionale Zahlenebene der komplexen übergeht oder der Differentialkalkül hergeleitet werden kann aus der höheren Dimensionalität des Tangentialbündels (was an anderer Stelle wichtig ist), sondern dass sich weit grundsätzlicher die Ebene der Zahlen mit der Ebene der Operationen kreuzt. Die Mathematik enthält eine Achse, auf der ihre Zahlen liegen, und eine andere Achse, auf der die Operationsregeln mit den Zahlen liegen. Lange galten diese Sphären völlig getrennt und gerieten daher nicht in Widerspruch. Ein Widerspruch trat erst in dem Moment auf, als beide Achsen in gleicher Weise formalisiert werden konnten und es daher formal möglich wurde, sie aufeinander abzubilden. Diese Abbildung ist der Grundgedanke, mit dem Kurt Gödel die prinzipielle Offenheit der Mathematik bewiesen hat (oder negativ formuliert, mit dem er nachgewiesen hat, dass es kein abgeschlossenes formales System der Mathematik geben kann).
Hegel hat lange vor Gödel erkannt, dass diese beiden Achsen der Mathematik sich kreuzen im Doppelcharakter des Minus-Zeichens. Als Vorzeichen dient es der Ordnung innerhalb der Achse der Zahlen, als Operationszeichen der Ordnung innerhalb der Regeln der Operationen, von denen hier die Multiplikations-Regeln wichtig sind. (Eine ähnliche Unterscheidung trifft Hegel bereits bei Betrachtung der Wahlverwandtschaften und Knotenlinien in der chemischen Sphäre, siehe hierzu den Beitrag über das reale Maß.)
Erst angeregt von dem durch Gödel ausgelösten Schock hat die Mathematik begonnen, sich mit ihren verschiedenen Entwürfen der axiomatisierten Mengenlehre, Modelltheorie und Kategorientheorie ihrer Grundbegriffe klar zu werden, aber ein systematischer, von Hegel angeregter Ansatz steht meines Wissens noch aus. Von einer anderen Seite haben sich McTaggart mit seiner Unterscheidung von zwei Zeitreihen und Husserl in seinen Untersuchungen zum inneren Zeitbewußtsein dieser Frage genähert, als sie ebenfalls eine zweite Dimension einführen wollten, die sich in vergleichbarer Weise von der ersten Dimension unterscheidet, wie ich es bei Hegel herauslese.
Exkurs zur positiven und negativen Dialektik
Die Kraft des Minus ist der entscheidende Punkt, an dem sich positive und negative Dialektik voneinander trennen. Die positive Dialektik unterstellt, dass es einen Formalismus gibt, der immer zu einem Negativen das zugehörige Positive bestimmen kann. Die positive Dialektik sagt daher, dass es im Grunde keine Gefahr, sondern nur handwerkliche Fehler gibt, diesen Formalismus nicht korrekt auszuführen. Eine negative Dialektik kehrt das Argument der Umkehrung um. Sie setzt, dass der Punkt der Umkehrung verloren gegangen ist und sich die gesamte Bewegung in eine Logik des Zerfalls begibt, die in die völlige Katastrophe führt.
Formal ist beides innerhalb der Hegelschen Logik darstellbar.
Doppelte Bedeutung einer Negativen Dialektik: Sie kann eine Beschreibung sein, wie eine Entwicklung den kritischen Punkt überschritten und sich in eine Logik des Zerfalls verwandelt hat. Alles befindet sich in Dekadenz. Sie kann auch eine kritische Darstellung einer Situation sein, in der scheinbar noch alles stimmt: Alle sind überzeugt von der Kraft des Positiven und gehen davon aus, dass kraft eines höheren Gesetzes für jede Fehlentwicklung im Laufe der Zeit ein Lösungsweg gefunden werden wird. Das führt zu einem Zwangsverhalten, alles zu machen, was technisch möglich (machbar) ist und darauf zu vertrauen, dass es sich von selbst auspendeln wird. Dies Verhalten ist nicht nur unbesonnen, sondern überheblich gegen alle Kritiker ("Bedenkenträger"), die an einer Überprüfung festhalten wollen. Es ist ohne es zu merken bereits in eine Sucht umgeschlagen und hat innerlich (mental) den kritischen Punkt bereits überschritten, während es äußerlich noch eine gute Weile zu laufen scheint. Diese Situation befindet sich daher auf eine andere Weise durch innere Aushöhlung ebenfalls in Zerfall und Katastrophe.
Becketts Endspiel schildert eine Lage, in der keine Umkehrung mehr gelingt. Becketts Figuren sind deutlich polar aufgebaut, spiegeln einander in gewisser Weise, sind auf ihre Art symmetrisch. Aber es gelingt ihnen nicht selbständig zu werden. Weder wird eine prä-substanzielle Einheit sichtbar, die Hegel in der Symmetrie des Sichtbaren und Unsichtbaren, des Positiven und Negativen unterstellt, noch gibt es bei der einen oder anderen Figur eine Umkehrung. Daher wird kein Widerspruch erreicht. Das ist gewissermaßen die Implosion sowohl der fortschrittsorientierten wie der marxistischen Sicht des Widerspruchs.
Die »Pulsation« des sich auflösenden Widerspruchs
Der Widerspruch entsteht aus der Bewegung der Entgegengesetzten gegeneinander. Hegel betont die Dramatik und unterscheidet drei Momente dieser Bewegung:
(a) Die Entgegengesetzten bewegen sich gegeneinander und verschwinden in dieser Bewegung beim Übergang in die Null.
»Dies rastlose Verschwinden der Entgegengesetzten in ihnen selbst ist die nächste Einheit, welche durch den Widerspruch zustande kommt; sie ist die Null« (HW 6.67).
(b) Am Ort ihres Aufeinandertreffens kommt es zu einer Pulsation.
»Der Widerspruch enthält aber nicht bloß das Negative, sondern auch das Positive; oder die sich selbst ausschließende Reflexion ist zugleich setzende Reflexion; das Resultat des Widerspruchs ist nicht nur Null« (HW 6.67).
»Die Mannigfaltigen werden erst auf die Spitze des Widerspruchs getrieben regsam und lebendig gegeneinander und erhalten in ihm die Negativität, welche die inwohnende Pulsation der Selbstbewegung und Lebendigkeit ist« (HW 6.78).
»Der gewöhnliche horror, den das vorstellende, nicht spekulative Denken – wie die Natur vor dem vacuum – vor dem Widerspruche hat, verwirft diese Konsequenz; denn es bleibt bei der einseitigen Betrachtung der Auflösung des Widerspruchs in nichts stehen und erkennt die positive Seite desselben nicht, nach welcher er absolute Tätigkeit und absoluter Grund wird« (HW 6.78).
(c) Mit der Pulsation geht der Widerspruch zu Grunde und dieser wird aus sich zum Hervorgang der Sache führen.
»Der sich widersprechende selbständige Gegensatz war also bereits selbst der Grund; es kam nur die Bestimmung der Einheit mit sich selbst hinzu, welche dadurch hervortritt, daß die selbständigen Entgegengesetzten jedes sich selbst aufhebt und sich zu dem Anderen seiner macht, somit zugrunde geht, aber darin zugleich nur mit sich selbst zusammengeht, also in seinem Untergange« (HW 6.70).
Ausgehend von der Anmerkung Hegels zur Arithmetik soll versucht werden, diesen Vorgang in einer geometrischen Figur darzustellen:
Figur 4: Pulsation der Null
(a) Die positiven und negativen Zahlen sind wie auf der Zahlengerade angeordnet. Die Größe der Zahlen ist nicht nur durch den Zahlenwert (1, −1, 2, −2, 3, −3, 4, −4, ...), sondern auch durch die Größe der schwarzen bzw. roten Kreise dargestellt, um besser das »Verschwinden« der einander Entgegengesetzten zu zeigen.
(b) Entsprechend ist die Null nicht nur durch den Größenwert 0, sondern durch eine angedeutete pulsierende Bewegung dargestellt.
(c) Im Grenzübergang bei der Null bleibt der reine innere Zusammenhalt der Strecke übrig, auf der die Kugeln angeordnet sind. Das ist die reine Krümmung der Strecke. Die senkrecht zur Zahlenachse stehende Gerade verweist auf den Punkt, um den die Zahlenachse an dieser Stelle gekrümmt ist.
In der Null ist es wiederum zu einer Indifferenz gekommen. Doch jetzt bleibt sie nicht einfach stehen und wird nicht in innere Faktoren zerlegt, sondern sie erzeugt eine Lebendigkeit, wird zum »springenden Punkt«, der aus der Achse der Entgegengesetzung hinausführt und den Weg in den Grund eröffnet.
»Der aufgelöste Widerspruch ist also der Grund, das Wesen als Einheit des Positiven und Negativen« (HW 6.69).
»Das spekulative Denken besteht nur darin, daß das Denken den Widerspruch und in ihm sich selbst festhält, nicht aber, daß es sich, wie es dem Vorstellen geht, von ihm beherrschen und durch ihn sich seine Bestimmungen nur in andere oder in nichts auflösen läßt« (HW 6.76)
Die folgenden drei Anmerkungen sollen zeigen, auf welche Weise Hegel Ideen von Leibniz, Kant und der Natur- und Religionsphilosophie seiner Zeit übernehmen und in sein Verständnis des Widerspruchs integrieren konnte.
Anmerkung 1: Leibniz hat von der »Lebendigkeit« des »metaphysischen Punktes« gesprochen, aus dem später die Monade wird.
»Man könnte sie metaphysische Punkte nennen: sie tragen etwas wie Leben und eine Art von Perzeption in sich, und die mathematischen Punkte sind ihre Gesichtspunkte, denen gemäß sie das Universum ausdrücken. Wenn aber die körperlichen Substanzen sich in zusammengedrängtem Zustande befinden, dann bilden alle ihre Organe für uns nur einen physischen Punkt. Demnach sind die physischen Punkte nur scheinbar unteilbar, während die mathematischen Punkte zwar exakt, aber bloße modale Bestimmungen sind« (Leibniz Neues System der Natur, S. 453).
Anmerkung 2: Für Kant hat die Vernunft die Aufgabe, »dem Verstande sein Feld (zu bereiten)« (KrV, B 670, B 685). Dies Feld wird mehr oder weniger synonym als »Sphäre des Begriffs« oder als »Horizont« bezeichnet. Es ist »nicht etwa eine unbestimmbar-weit ausgebreitete Ebene«, sondern hat die Eigenschaft einer »Krümmung« (KrV B 790). Der Brennpunkt der Krümmung ist dem Verstand nicht sichtbar und wird von Kant als »focus imaginarius« bezeichnet (KrV, B 672). Siehe hierzu den Beitrag Späre des Begriffs.
Anmerkung 3: Markus Semm ist in seiner Arbeit Der springende Punkt in Hegels System dem Gebrauch der Ausdrücke »Pulsieren« und »Puls« bei Hegel nachgegangen. Der Puls ist verbunden mit dem Puls des Blutes, und lässt sich bei Hegel bereits in den frühen natur- und religionsphilosophischen Arbeiten nachweisen (»das Phänomen des springend-pulsierenden Blutpunktes« und »vom Blut als dem Symbol und der Substanz des Lebens zur Inkorporation des heiligen Blutes«, so zwei Kapitelüberschriften bei Semm, S. 35 und 48).
In der Phänomenologie des Geistes schreibt Hegel programmatisch:
»Der absolute Begriff ist [...] die Seele der Welt, das allgemeine Blut, [...] welches [...] in sich pulsiert, ohne sich zu bewegen, in sich erzittert, ohne unruhig zu sein« (HW 3.132, zitiert bei Semm, S. 9).
Von hier ausgehend lässt sich mit Semm in nahezu allen Werken Hegels die elementare Bedeutung des Pulsierens nachweisen. Semm tritt bereits in seiner Einleitung dem zu erwartenden Einwand entgegen, dies sei bestenfalls als eine »bloß metaphorische Rede« zu verstehen, und Metaphern wie Puls und Blut seien nicht mehr als eine »nur äußerliche und uneigentliche Hülle« (Semm, S. 11, 12).
Nur auf die Ausführung Hegels zur Pulsation des Widerspruchs geht Semm nicht ein, so dass das vorliegende Kapitel als eine Abrundung seiner Arbeit verstanden werden kann.
Die Kraft den Widerspruch auszuhalten
Die am weitesten gehende Kritik an Hegel kam von Kierkegaard und ihm folgend in ähnlicher Weise von Wittgenstein, die Hegel vorhielten, dass die Vernunft nur scheinbar die Grenze des Verstandes durchbrechen kann. Sie kann sich nicht vom Paradox befreien, weil sie letztlich immer an Veranschaulichungen wie z.B. das Bild einer höheren Sphäre gebunden ist.
Hegel war sich dessen bewußt, wie die zitierten dramatischen Formulierungen zeigen, die vom »rastlose(n) Verschwinden der Entgegengesetzten« und ihrem »Untergange« sprechen.
In der dritten Anmerkung zum Widerspruch kommt er darauf zurück. An einer Stelle, deren Deutung für mich letztlich offen bleibt, bewegt er sich in der Nähe einer negativen Theologie. Kann der Mensch sich vom Absoluten ergreifen und an ihm teilhaben lassen, oder ist er in seiner Existenz darauf beschränkt, die Kraft zu erfahren, den Widerspruch auszuhalten zu können? Hegel beschreibt sehr genau die Differenz zwischen Zugrundegehen und den eigenen Grund finden.
»Ebenso ist die innere, die eigentliche Selbstbewegung, der Trieb überhaupt (Appetit oder Nisus der Monade, die Entelechie des absolut einfachen Wesens) nichts anderes, als daß Etwas in sich selbst und der Mangel, das Negative seiner selbst, in einer und derselben Rücksicht ist. Die abstrakte Identität mit sich ist noch keine Lebendigkeit, sondern daß das Positive an sich selbst die Negativität ist, dadurch geht es außer sich und setzt sich in Veränderung. Etwas ist also lebendig, nur insofern es den Widerspruch in sich enthält, und zwar diese Kraft ist, den Widerspruch in sich zu fassen und auszuhalten. Wenn aber ein Existierendes nicht in seiner positiven Bestimmung zugleich über seine negative überzugreifen und eine in der anderen festzuhalten, den Widerspruch nicht in ihm selbst zu haben vermag, so ist es nicht die lebendige Einheit selbst, nicht Grund, sondern geht in dem Widerspruche zugrunde« (HW 6.76).
Damit ist auch die Frage nach der positiven und negativen Dialektik beantwortet. Hegel erkennt, dass es nicht genügt, über Bestimmungen wie Kontinuität (Wiederholungsschleife) und Umkehrung zu verfügen, damit Wissenschaft möglich werden kann, sondern es muß in der Logik die genannte Kraft enthalten sein, den Widerspruch auszuhalten. Diese Kraft entsteht nicht in der Logik und kann erst recht nicht von ihr erzeugt werden, sondern wird von ihr vorausgesetzt.
Anhang 1: Trendelenburg und Marx über Hegels Wissenschaft der Logik
1840 veröffentlichte Friedrich Adolf Trendelenburg (1802-1872) den ersten Band der Logischen Untersuchungen, der eine umfassende Kritik an Hegels Wissenschaft der Logik enthält. Auch wenn Trendelenburg nur selten unter die großen deutschen Philosophen gezählt wird, ist die von ihm ausgehende Wirkung kaum zu überschätzen. Über seine Schüler Franz Brentano und Hermann Cohen hat er das Denken von Husserl, Cassirer und Heidegger mit geprägt. Auf der anderen Seite war der junge Karl Marx von den Logischen Untersuchungen tief beeindruckt und hatte zeitlebens vor, gegenüber Trendelenburgs Kritik an Hegels Logik eine eigene Darstellung zu schreiben, wozu es jedoch nie gekommen ist. So ist es bei einer Reihe verstreuter Bemerkungen geblieben, die Andreas Arndt in seinem Buch über Marx übersichtlich zusammengestellt hat.
Im Grundsatz stimmen jedoch Trendelenburg und Marx in ihrer Kritik überein, dass Hegel in seiner Wissenschaft der Logik nicht von der Fülle des Seins ausgeht, sondern von den von ihm gefundenen Denkbestimmungen und diese absolut setzt, weswegen sie keiner weiteren Voraussetzungen mehr bedürfen. Sie vertreten dagegen, dass der Mensch in seiner Arbeit einschließlich dem wissenschaftlichen Denken aus dem Vollen der Natur schöpfen kann und daher in seiner Entwicklung nie stillstehen wird. In diesem Sinn bewundern sie zwar die Leistung, wie es Kant mit der transzendentalen Ästhetik und Analytik und Hegel mit den Reflexionsbestimmungen gelungen ist, die von aller Wissenschaft implizit vorausgesetzten Denkbestimmungen zu durchschauen und transparent zu machen, schränken aber ein, dass auch die von ihnen gefundenen Denkbestimmungen ihrerseits nur Ergebnis eines bestimmten historischen Fortschritts und keineswegs endgültig sind. Nie kann der Mensch die Fülle des Seins erschöpfen, sondern nur immer neue Seiten in ihr erkennen. Seine eigene Arbeits- und Denkfähigkeit gehört zur umfassenden Bewegung, die in der Natur vorhanden ist und der er sich nie in einem vermeintlich absoluten Standpunkt von außen gegenüberstellen kann. Nicht nur die Wissenschaft, sondern auch die Erkenntnis der ihr zugrundeliegenden Denkbestimmungen sind niemals abgeschlossen.
Trendelenburg will zeigen, dass auch Hegel letztlich nicht daran vorbeikommt, dies anzuerkennen. Er muss versteckt den Begriff der Bewegung und verschiedene räumliche Anschauungen voraussetzen, zum Beispiel im Begriff der Verneinung, die eine Bewegung vollzieht (Trendelenburg, S. 43). Ohne räumliche Anschauungen wären Begriffe wie Grenze, Repulsion und Attraktion, die Natur »außer sich« und der Geist »bei sich« nicht möglich. Mit »außer« und »bei« wird »stillschweigend geschöpft« aus räumlichen Vorstellungen (Trendelenburg, S. 52). Vor allem aber enthält Hegels Wissenschaft der Logik in dem scheinbar leeren Begriff des Nichts in Wahrheit die Fülle des Seins, die im Dasein hervortritt.
»Es gibt also kein reines Sein, es ist nichts. Das Nichts ist hier nur gewonnen, inwiefern das reine Sein des Denkens mit dem vollen Sein der Anschauung verglichen ist. Das Denken hat also etwas Anderes ausser der ersten Bestimmung in seinem Busen versteckt (die Anschauung des vollen Seins) und gewinnt die neue Bestimmung durch reflektierende Vergleichung mit diesem unrechtmässigen Begriffe« (Trendelenburg, S. 45).
Marx radikalisiert das bereits 1843 in seiner Kritik der Hegelschen Rechtsphilosophie. Dort wendet er sich gegen das von Hegel gebrauchte Abstraktionsverfahren. Im einzelnen lässt sich seine Kritik zweifellos widerlegen, doch bleibt sein Grundanliegen erkennbar, sich auf die Wirklichkeit statt auf Denkbestimmungen zu berufen. Zugleich hat er anfangs noch geglaubt, den bürgerlichen Ökonomen dank der dialektischen Methode überlegen zu sein und geschult an Hegels Wissenschaft der Logik die höheren Gesetze der Ökonomie verstehen und aus ihnen Voraussagen über revolutionäre Umwälzungen ableiten zu können, doch wurde er durch den Verlauf der wirklichen Geschichte widerlegt. Nach dem Scheitern der 1848er Revolution ging er nach England und verdiente ein wenig Geld mit Zeitungs-Artikeln über die aktuelle Geschichte. Während dieser Arbeit wurde ihm klar, dass die Empirie weit komplexer ist als alle Spekulationen. Marx fragte sich, ob die Revolution im Zentrum oder in der Peripherie ausbricht, welche Wirkung die starken Überreste vergangener Epochen haben etc. In Summe entstand die Idee einer Formation, die weit mehr ist als Form.
»Das Bild der Formation ist interpretierbar. In dem Übereinanderlagern von Schichten drückt sich die einfache Kontinuität aus, durch die jede Generation gezwungen ist, unter den vorgefundenen Bedingungen weiterzuarbeiten. Die Produktion und Reproduktion des Lebensprozesses vollzieht sich aber, den Bedingungen entsprechend, in strukturierten, voneinander qualitativ unterschiedenen Einheiten: Schichten und Formationen. Dabei ist keine absolute Notwendigkeit einer gleichförmigen Folge des Ablagerns gegeben: die Schichten können sich verschieben, ineinanderlagern usw. Auf der Oberfläche entsteht das Bild einer Vielfalt von Formationstypen, die die Basis einer neuen Formation bilden können. Sicher hat das Bild seine Grenzen. Es verdeutlicht aber, was Marx unter einem naturgeschichtlichen Prozeß eigentlich verstanden wissen will, den er als Metapher für gesellschaftliche Prozesse immer wieder bemüht« (Arndt, S. 102).
Marx griff daher zwar immer wieder zu Hegels Wissenschaft der Logik, um aus ihrer Darstellung der Reflexionsbestimmungen insbesondere des Widerspruchs und des Grunds Anregungen für seine wissenschaftliche Arbeit zu gewinnen, aber er sah ein, dass in der Wirklichkeit die Widersprüche aus sich selbst eine Verlaufsform finden, die von keiner Analyse der Denkbestimmungen vollständig vorausgesagt werden kann. Daher betont er in den 1857-58 entstandenen Grundrissen der Kritik der politischen Ökonomie in einer Anmerkung:
»Es wird später nötig sein, eh von dieser Frage abgebrochen wird, die idealistische Manier der Darstellung zu korrigieren, die den Schein hervorbringt, als handle es sich nur um Begriffsbestimmungen und die Dialektik //86/ dieser Begriffe« (MEW 42.85f zitiert bei Arndt, S. 12).
Anhang 2: Michael Wolff über die Stufen des Gegensatzes zum Widerspruch
Wolff wollte die verhärteten Fronten zwischen den auf Kant und Hegel zurückgehenden Traditionen auflockern, und damit die Fronten zwischen der dialektischen und der analytischen Philosophie. Für ihn suchten Kant und Hegel wie auch die Begründer einer neuen mathematischen Logik im 19. Jahrhundert Antworten »auf eine vergangene philosophie- und wissenschaftshistorische Problemsituation« und befanden sich »in derselben mathematikhistorischen Situation« (W, S. 10). Wolff will den Anspruch einer »höheren Logik« vermeiden, den er als Vorwurf »mit ironischem Unterton« versteht (W, S. 9). Er unterscheidet daher nicht wie Hegel zwischen dem Widerspruch und dem »höheren Widerspruch«, sondern will zeigen, wie sich der Widerspruch schrittweise aus einem Verständnis des Gegensatzes ergibt, das bereits Kant in den Grundzügen entwickelt hatte. Er will zugleich in angemessener Form Methoden mathematischer Symbolisierung übernehmen. Er will mit einem Wort potentielle Gemeinsamkeiten zwischen Kant, Hegel und den neuen mathematischen Logikkalkülen herausarbeiten. Dies Anliegen hat er gemeinsam mit Burkhard Tuschling recht offensiv auf einer Kant-Tagung 1981 in Marburg vorgetragen. Dort waren jedoch die Kantianer nicht bereit, in Hegels »Bewegung des Begriffs« eine Antwort auf die Fragen zu sehen, die Kant sehr offen in den aus dem Nachlass veröffentlichten Notizen des Opus postumum angesprochen hat.
Die erste Gegensatzform – Bestimmungspaare und ihr reflexionslogisches Substrat
Im Zentrum der Studie von Wolff steht eine Interpretation des Kapitels über den Gegensatz aus Hegels Wissenschaft der Logik. Wolff versteht die von Hegel genannten drei »Bestimmungen, welche das Positive und Negative konstituieren« (HW 5.57-59) als drei Formen bzw. Stufen des Gegensatzes, die im Ergebnis zum Begriff des Widerspruchs führen.
Die erste Stufe beschreibt Bestimmungspaare, die jeweils einen sachlichen Gegensatz darstellen wie z.B. wohlriechend / übelriechend oder Westen / Osten. Sie stehen einander gegenüber wie positiv und negativ und können nach dem Vorbild der Arithmetik mit den Vorzeichen Plus und Minus voneinander getrennt werden, wobei es gleichgültig ist, welche von beiden Bestimmungen das Plus und welche das Minus erhält. Doch damit ist für Wolff die erste Stufe »noch nicht hinreichend erklärt« (W, S. 112). Für ihn ist eine weitere Bedingung, dass »sie Bestimmungen eines bestimmten Gegenstandes sind«, den er als ihr »reflexionslogisches Substrat« bezeichnet (W, S. 113). Zum Beispiel ist das reflexionslogische Substrat des Gegensatzes ›wohlriechend / übelriechend‹ ein »bestimmter Gegenstand, [...] der ein riechender Gegenstand« ist. Für den Gegensatz ›6 Meilen nach Westen / 6 Meilen nach Osten‹ ist der Weg das reflexionslogische Substrat, der mal in die eine Richtung und mal in die entgegengesetzte Richtung durchlaufen wird. Ich vermute, dass er diese Bedingung fordert, um mit ihr sicher zu stellen, dass sich die beiden Bestimmungen des Bestimmungspaares auf einer gemeinsamen Ebene befinden.
Wolff hat den Ausdruck »reflexionslogisches Substrat« neu eingeführt und will mit ihm die innere Verbindung aufzeigen, die aus seiner Sicht zwischen den Arbeiten von Kant zur Einführung der negativen Größen und den Ausführungen von Hegel zum Gegensatz besteht.
(a) Negative Größen. Der Ausgangspunkt von Wolff ist Kants Versuch den Begriff der negativen Größen in die Weltweisheit einzuführen von 1763. Kant betrachtet neben logischen Oppositionen reale Oppositionen, bei denen jeweils »zwei Prädikate eines Dings« aufeinander treffen, die beide »bejahend« sind, aber in einer »Realrepugnanz« stehen (Kant, NG, AA 02: 172.07-18).
Wolff stellt einleitend eine Liste von Beispielen zusammen, um zu zeigen, was er unter Bestimmungspaaren versteht, wobei er offen lässt, »ob alle diese Bestimmungen einen reflexionslogischen Gegensatz bilden können«, d.h. für ihn, ob sie über ein reflexionslogisches Substrat verfügen. Die Beispiele stammen zum Teil aus Kants Einführung der negativen Größen und sind ergänzt um Bestimmungspaare aus der Kritik der reinen Vernunft (»wohlriechend / übelriechend«, in KrV B 531 f), einen Grundbegriff der Kritik der reinen Vernunft (»Ding an sich / Erscheinung«), ein Begriffspaar aus der Hegelschen Seinslogik (»endlich / unendlich«), ein von Hegel in der Urteilslehre diskutiertes Beispiel (»blau / gelb«), die Frage nach der Bewegung und etwas überraschend das Thema der Spontaneität.
»Wohlriechend / übelriechend,
endlich / unendlich,
Weg nach Osten / Weg nach Westen,
negatives Kapital / positives Kapital,
Ding an sich / Erscheinung,
im Zeitpunkt T am Ort L / im Zeitpunkt T nicht am Ort L,
spontan wirkend / nicht spontan wirkend,
blau / gelb« (W, S. 112).
Im weiteren werden aus dieser Liste jedoch nur noch die Bestimmungspaare betrachtet, die sich auf Qualitäten wie Farbe und Geruch beziehen. Wolff lässt offen, nach welchen Kriterien ein Bestimmungspaar reflexionslogisch ist oder nicht, d.h. für ihn, wann ein Bestimmungspaar über ein reflexionslogisches Substrat verfügt und wann nicht. Er glaubt nicht, dass es ein »allgemeines Verfahren (gibt), mit dessen Hilfe man ausgehend von zwei als entgegengesetzt angenommenen Bestimmungen zum reflexionslogischen Substrat dieser Bestimmungen gelangen kann« (W, S. 113). Mir scheint deutlich zu sein, dass Wolff ohne es ausdrücklich zu begründen solche Bestimmungspaare auswählt, die sich im Sinne der aristotelischen Kategorienlehre als Akzidenzien (symbebekoi, zweite Kategorien) auf eine Substanz (ousia, erste Kategorie) beziehen und zugleich wie die Prädikate eines negativen Urteils einander entgegengerichtet sind.
(b) Transzendentales und reflexionslogisches Substrat. Warum spricht Wolff von einem Substrat? Er scheint mir einen ähnlichen, aber allgemeineren Gedanken von Kant zu übernehmen und auf Bestimmungspaare anzuwenden. Kant spricht in der Kritik der reinen Vernunft vom »transzendentalen Substratum«, das der »durchgängigen Bestimmung« eines »Ding« durch »Paare einander entgegengesetzter ... Prädikate« »zum Grunde gelegt wird« (Kant KrV B 601-603). Das ist nahezu wörtlich identisch mit den Formulierungen von Wolff. Wolff erwähnt zwar die durchgängige Bestimmung bei Kant (W, S. 115, 120), jedoch nicht das transzendentale Substratum. Der Unterschied zwischen dem transzendentalen Substratum bei Kant und dem reflexionslogischen Substrat bei Wolff besteht darin, dass für Kant das transzendentale Substratum »den ganzen Vorrat des Stoffes, daher alle mögliche Prädikate der Dinge genommen werden können, enthält« (Kant KrV B 603). Dagegen schränkt Wolff das »reflexionslogische Substrat« auf jeweils ein Bestimmungspaar ein. So ist z.B. ein riechender Gegenstand das reflexionslogische Substrat von wohlriechend / übelriechend. Es gibt für ihn daher so viele reflexionslogische Substrate wie es reflexionslogische Bestimmungspaare gibt. Und darüber hinaus wird sich in den folgenden Stufen des Gegensatzes zeigen, dass Wolff jeden einzelnen Gegenstand, der Träger eines reflexionslogischen Bestimmungspaares ist, als ein reflexionslogisches Substrat ansieht.
In seinem Beitrag für den von Henrich herausgegebenen Band Probleme der Hegelschen Logik schreibt er noch deutlicher als in dem Buch über den Begriff des Widerspruchs:
»Es handelt sich um Paare von Prädikaten ausschließlich affirmativer Subjekt-Prädikat-Urteile, die trotz ihres affirmativen Charakters Entgegensetzungen zum Inhalt haben. Aber die Entgegensetzung resultiert nicht aus der logischen Negation prädikativer Urteile, sondern aus der Negativität der zugrundeliegenden 'realen' Prädikate, d.h. der Bestimmungen des Urteilsgegenstandes«. »Beide legen dem Gegenstand eine Bestimmung bei. Nur ist jede dieser Bestimmungen die negative der anderen« (Wolff 1986b, S. 119, 123).
(c) Plus und Minus. Obwohl Wolff den Gegensatz nicht auf positive und negative Größen einschränken will (W, S. 110), übernimmt er aus den Anmerkungen von Hegel zu den positiven und negativen Größen in der Arithmetik eine Symbolsprache, die an der Ordnung der ganzen Zahlen auf der Zahlengeraden orientiert ist.
»In Anlehnung an die von Hegel selbst in den Anmerkungen zur Reflexionslogik gebrauchten Zeichensprache können wir zwei entgegengesetzte Bestimmungen eines Paares durch die Symbole »+A« und »−A« bezeichnen« (W, S. 111).
Das ist für ihn möglich, da nach seinem Verständnis die Arithmetik mit dem Betrag (|A|) etwas meint, was dem reflexionslogischen Substrat entspricht.
»Wohlriechend (+A) und übelriechend (−A) sind entgegengesetzt (und nicht bloß verschieden) erst dann, wenn sie als Bestimmungen eines bestimmten Gegenstandes gedacht werden, der ein riechender Gegenstand (|A|) ist« (W, S. 113).
Zum einen bestätigt das, dass das reflexionslogische Substrat für Wolff ein Gegenstand ist. Zum anderen ist der Vergleich mit der Arithmetik problematisch. Als Betrag wird der Abstand einer Zahl zum Nullpunkt verstanden. Zum Beispiel haben die beiden Zahlen 12 und −12 den gleichen Betrag 12, da sie beide zur 0 den Abstand 12 haben. Es ist jedoch zumindest nicht üblich, in der Arithmetik die Abstände als eigene Gegenstände zu betrachten, die wahlweise auf der Zahlengeraden auf der einen oder der anderen Seite des Nullpunktes liegen. Wenn hier überhaupt von einem Substrat gesprochen werden soll, wäre die Zahlengerade (Zahlenachse) im Ganzen das Substrat aller Zahlen. Hegel deutet das an, wenn er von der »Achse« spricht, auf der die positiven und negativen Zahlen liegen (HW 6.61).
(d) Negatives Urteil. Die Bestimmungspaare sind nach dem Muster konstruiert, wie Hegel in der Urteilslehre das negative Urteil einführt. Einem Prädikat in einem positiven Urteil (ein Gegenstand S ist wohlriechend, endlich, führt nach Osten, positives Kapital, ein Ding an sich, im Zeitpunkt T am Ort L, spontan wirkend, blau) wird im negativen Urteil das entgegengesetzte Prädikat gegenübergestellt (S ist nicht wohlriechend, nicht endlich, führt nicht nach Osten, etc.). Beide Urteile bilden jeweils ein Bestimmungspaar. Hegel betont, dass mit einem negativen Urteil der Art ›die Rose ist nicht rot‹ gemeint ist, dass die Rose zwar nicht rot ist, jedoch eine andere Farbe hat. Wird der gleiche Satz ›die Rose ist nicht rot‹ als unendliches Urteil verstanden, dann ist gemeint, dass sie möglicherweise gar keine Farbe hat. Beim negativen Urteil ist vorausgesetzt, dass die Rose, die nicht rot ist, dennoch zur Sphäre des Farbigen gehört. »Das Negative ist somit in einer umschlossenen Sphäre gehalten, worin das, was das eine nicht ist, etwas Bestimmtes ist« (HW 6.321). Das unendliche Urteil besagt dagegen, dass »die allgemeine Sphäre ... negiert« ist (HW 6.325).
Obwohl das negative Urteil den von Wolff gemeinten Bestimmungspaaren sehr nahe kommt, zieht er es nicht heran. Der Unterschied zwischen dem negativen Urteil und den Bestimmungspaaren liegt darin, dass Hegel nicht nach einem Substrat fragt, auf welches das positive und negative Urteil zutreffen, sondern nach der umschlossenen Sphäre. Ich vermute, dass dieser Unterschied der Grund ist, warum Wolff trotz aller sachlichen Ähnlichkeiten bei Bestimmungspaaren und negativen Urteilen eine klare Grenze zieht: »Diese Reflexion hat aber mit begriffs- und urteilslogischen Strukturen gar nichts zu tun« (W, S. 113).
(e) Sphäre und Spektrum. Wolff bildet die Bestimmungspaare auf die gleiche Weise wie Hegel negative Urteile einführt, aber statt von einer »umschlossenen Sphäre« spricht er vom »reflexionslogischen Substrat« (und später vom »Bereich« und dem »ganzen Reflexionszusammenhang inhaltlich bestimmter Gegensatzrelate mit dem dazugehörigen inhaltlich bestimmten reflexionslogischen Substrat«, W, S. 147f). Er sucht nicht wie Hegel in der Begriffslogik die allgemeine Sphäre von Begriffen, innerhalb derer positive und negative Urteile unterschieden werden können, und unter ihnen solche, die eine Entgegensetzung enthalten, sondern er geht von Gegenständen aus, die unterschiedliche Bestimmungen annehmen können. Wolff vermeidet den Gebrauch eines negativen Urteils und seiner umschlossenen Sphäre, da es ihm um etwas Anderes geht: Statt beispielsweise von der Sphäre der Farbe zu sprechen, geht er von Gegenständen aus, die dank ihrer stofflichen Eigenschaften ein bestimmtes Spektrum von Farben annehmen können. Das kann z.B. die Gesamtheit aller Farben sein, die eine Rosenblüte im Verlaufe ihres Wachstums und Verwelkens annimmt, oder die Gesamtheit aller Wellenlängen, die ein bestimmter Stoff abstrahlt. Ein reflexionslogisches Substrat liegt für Wolff dann vor, wenn es innerhalb des Spektrums zwei Bestimmungen gibt, die einander entgegengesetzt sind. Entsprechend ist nicht von der Sphäre des Geruchs, sondern von dem spezifischen Spektrum der Geruchsbestimmungen zu sprechen, die jeweils auf einen bestimmten riechenden Gegenstand zutreffen können.
(f) Substrat in der Maßlogik. Das legt nahe, dass sich Wolff mit dem Begriff »reflexionslogisches Substrat« auf das Substrat bezieht, das Hegel in der Maßlogik eingeführt und von seinen Zuständen unterschieden hat (z.B. das Wasser als Substrat, das in den Zuständen Eis, Flüssigkeit und Dampf auftreten kann). In diesem Sinn kann der »riechende Gegenstand«, den Wolff als Beispiel für ein reflexionslogisches Substrat wählt, als ein riechendes Substrat verstanden werden, das unterschiedliche Geruchszustände annehmen kann, etwa wohlriechend oder übelriechend. Und ähnlich kann eine Rosenblüte als ein farbiges Substrat verstanden werden, das unterschiedliche Farbzustände annehmen kann. – Hegel spricht allerdings in der Maßlogik nicht von einzelnen Gegenständen, sondern versteht das Substrat als das »spezifizierende Prinzip«, durch welches die unterschiedlichen Zustände voneinander unterschieden sind (HW 5.445).
(g) Schließlich bleibt bei Wolff wie bereits bei Kant offen, ob mit dem Bestimmungspaar eine Entgegensetzung gemeint ist, die eine Begriffssphäre vollständig beschreibt, oder ob es sich um einen konträren Gegensatz innerhalb einer umfassenderen Begriffssphäre handelt. Wohlriechend und übelriechend sind entgegengesetzte Ausprägungen innerhalb einer Sphäre zahlreicher weiterer Geruchsbestimmungen wie faulig, aromatisch, fruchtig, beißig, erdig, rauchig etc. Blau und gelb sind Konträrfarben innerhalb einer umfassenderen Farbskala. Westen und Osten sind einander entgegengesetzte Himmelsrichtungen innerhalb des Gevierts der Himmelsrichtungen. Auch bei den positiven und negativen Zahlen wurden unmittelbar nach Kant weitere Zahlen eingeführt, die auf einer zusätzlichen Achse liegen (die imaginären Zahlen). Die anderen von Wolff genannten Bestimmungspaare sind dagegen unmittelbar als negative Urteile gebildet (endlich / unendlich, spontan / nicht spontan etc.).
(h) Satz vom ausgeschlossenen Dritten. Wolff schließt seine Darstellung der ersten Gegensatzform ab mit einem Hinweis auf den »Satz des ausgeschlossenen Dritten. Etwas ist entweder A oder Nicht-A; es gibt kein Drittes« (HW 6.73), über den Hegel im Kapitel über den Widerspruch eine Anmerkung geschrieben hat, die die Betrachtung der positiven und negativen Größen in der Arithmetik ein zweites Mal aufgreift. Wolff will zeigen, dass Hegel diesen Satz nicht für falsch hält, sondern schlicht für trivial. Hegel meint damit: Wenn ich sage, etwas ist grün oder nicht grün, ist diese Aussage wertlos, da unbestimmt bleibt, ob »nicht grün« bedeutet, dass das Etwas rot ist (d.h. die Konträrfarbe zu grün innerhalb der Sphäre der Farben), oder irgendeine andere Farbe hat, oder gar keine Farbe hat. Hegel meint mit der Trivialität daher gerade nicht, dass es ein Bestimmungspaar gibt, sondern dass die Alternative zum Prädikat grün unbestimmt bleibt.
Während Hegel den Satz vom ausgeschlossenen Dritten für trivial hält und ihn daher »unterscheidet ... vom ... Satz der Identität oder des Widerspruchs, der so hieß: es gibt nicht etwas, das zugleich A und Nicht-A ist« (HW 6.74), auf den er sich im weiteren in seiner Anmerkung bezieht, hält Wolff Hegels Ausführungen zum Satz des Widerspruchs für Hegels »Deutung« vom »Satz vom ausgeschlossenen Dritten« (W, S. 116), um Hegels Anmerkung auf die Bestimmungspaare beziehen zu können, d.h. für ihn die erste Gegensatzform.
Davon abgesehen ist dies auch inhaltlich nicht angemessen. Denn Wolff beachtet nicht, dass sich bei Hegel diese Anmerkung auf den Widerspruch bezieht und damit auf die dritte Bestimmung des Positiven und Negativen. Wenn Hegel zum Satz des Widerspruchs sagt, dass es sehr wohl etwas Drittes gibt, das zugleich +A und −A ist, nämlich A (HW 6.74), dann ist das nicht das reflexionslogische Substrat oder ein Gegenstand |A|, der entweder die eine Bestimmung +A oder die andere Bestimmung −A haben kann, sondern »tiefer genommen die Einheit der Reflexion, in welche als in den Grund die Entgegensetzung zurückgeht« (HW 6.74). Mit »Einheit der Reflexion« ist zweifellos nicht ein Gegenstand gemeint, der eine Eigenschaft hat, die in entgegengesetzten Ausprägungen vorkommen kann. Sondern Hegel bezieht sich implizit kritisch auf die Aussage Kants, wonach das »transzendentale Substratum« den entgegengesetzten Prädikaten »zum Grunde gelegt wird« (KrV B 603). Stattdessen versteht er den sich herausbildenden Widerspruch als eine Reflexionsbestimmung, die zum Grund als einer resultierenden weiteren Reflexionsbestimmung führt, die Hegel hier als »Einheit der Reflexion« einführt. Hegel betrachtet eine innere Bewegung von Reflexionsbestimmungen, ein »Scheinen in Anderes« (Enz. § 161, HW 8.308), während sich Kant und ihm folgend Wolff auf Prädikatsbestimmungen von Gegenständen beziehen.
(i) Grund als Substrat. Vielleicht wollte Wolff auch mit dem reflexionslogischen Substrat den nächsten Schritt im Gedankengang der Wissenschaft der Logik vorbereiten. Hegel will zeigen, wie der Widerspruch zu Grunde geht. Über den Grund schreibt er: »Erst als Grund hat es (das Wesen) eine feste Unmittelbarkeit oder ist Substrat« (HW 6.85). Wird die Erste Kategorie von Aristoteles (ousia) entsprechend der ursprünglichen Bedeutung des griechischen Wortes ousia als Grund oder Boden verstanden, könnte daraus eine Rechtfertigung abgeleitet werden, warum Wolff das reflexionslogische Substrat auf ähnliche Weise versteht wie die Erste Kategorie. Solche Bezüge werden von ihm jedoch nicht ausgeführt, und es muss daher daher Spekulation bleiben, wenn versucht wird, seinen Text in dieser Weise zu verstehen.
Zusammenfassend vermute ich, dass Wolff in seinem Begriff des reflexionslogischen Substrats Bestimmungen zusammengefügt hat, die er vom transzendentalen Substratum bei Kant, dem Substrat in der Maßlogik von Hegel und dem negativen Urteil übernommen hat. Im Ergebnis bleibt stehen, dass er die erste Stufe des Gegensatzes an ein reflexionslogisches Substrat bindet, welches weitgehend den Charakter eines daseienden Gegenstandes hat und daher in die Sphäre des Seins und nicht in die Sphäre des Wesens gehört.
2. Gegensatzform – der amphibolische Gegensatz
Bei der zweiten Gegensatzform entfernt sich Wolff weiter von Hegel. Das hat zu tun mit einem sprachlichen Missverständnis, was mit dem Ausdruck »verwechseln« gemeint ist. Hegel will zeigen, dass der Gegensatz nicht nur die Momente des Positiven und des Negativen an sich hat, sondern dass sie »verwechselt« werden können. »Jede Seite ist von der Art, daß sie ebensogut als positiv wie als negativ genommen werden kann« (HW 6.58). Diese Bestimmung hat Wolff bereits in seine Konstruktion der 1. Gegensatzform aufgenommen und gesagt, dass es beliebig ist, welche Bestimmung eines Bestimmungspaares als positiv oder negativ bezeichnet wird.
Für die 2. Gegensatzform sucht er nach einer anderen Bedeutung von Verwechselbarkeit: Das eine kann im Sinne eines Trugschlusses (Amphibolie) für das andere gehalten werden und wird in diesem Sinn mit dem anderen verwechselt. Wie ist eine solche Verwechslung möglich? Bestimmungspaare wie wohlriechend und übelriechend oder blau und gelb sind so angelegt, dass ihre beiden Seiten nicht austauschbar sind. Es gibt nicht zwei Sichtweisen auf die gleichen farbigen Körper, wonach sie mal als blau und mal als gelb erscheinen, oder zwei Sichtweisen auf riechende Körper, wonach sie mal als wohlriechend und mal als übelriechend erscheinen. (Es kann nur sein, dass der eine als übelriechend empfindet, was dem anderen wohlriechend erscheint, doch ist diese Unterscheidung des Geschmacks hier nicht gemeint.)
Um dennoch dem Text von Hegel folgend eine Verwechselbarkeit der beiden Seiten des Bestimmungspaares nachzuweisen, muss Wolff für die zweite Gegensatzform das Bestimmungspaar verlassen und zu ihren reflexionslogischen Substraten übergehen:
»Während beim Gegensatzverhältnis erster Stufe ein und dasselbe reflexionslogische Substrat |A| beliebig als Bestimmtheit eines positiv oder negativ bestimmten Gegenstands aufgefasst werden kann, so sind beim Gegensatz zweiter Stufe der positiv und der negativ bestimmte Gegenstand verschiedene Gegenstände, aber sie können »verwechselt« werden. [...] Die äußere Reflexion gelangt zur zweiten Stufe der Entgegensetzung dadurch, daß sie erstens den Gegensatz (erster Stufe) zwischen Bestimmungen wie wohlriechend/übelriechend, blau/gelb etc. voraussetzt; zweitens verschiedene Gegenstände annimmt, die teils wohlriechend, teils übelriechend, teils blau, teils gelb usw. sind; und schließlich diese Gegenstände (aufgrund ihrer Bestimmtheit und aufgrund des vorausgesetzten Gegensatzes erster Stufe) zu einerseits positiv, andererseits negativ bestimmten Gegenständen erklärt: Wenn z.B. Blau und Gelb einander entgegengesetzt sind, so ist auch das Blaue dem Gelben entgegengesetzt und vice versa« (W, S. 117f).
Das hilft zunächst noch nicht weiter. Denn das Blaue und das Gelbe sind ebenso wenig zu verwechseln wie blau und gelb. Eine Verwechslung ist erst dann gegeben, wenn recht trickreich im nächsten Schritt vom Blauen und vom Gelben wieder zurückgegangen wird zu den jeweiligen Substraten. Es seien zum Beispiel ein wohlriechender Gegenstand A1 und ein übelriechender Gegenstand A2 verglichen. Beide Gegenstände können auch als reflexionslogische Substrate angesehen werden, d.h. in diesem Fall als riechende Gegenstände, und diese beiden reflexionslogischen Substrate lassen sich nicht mehr hinsichtlich wohlriechend / übelriechend unterscheiden, da von dieser Bestimmung gerade abgesehen wurde. Wolff konstruiert deswegen aus dem Grund zunächst zwei unterschiedliche Gegenstände, um anschließend die Verwechselbarkeit ihrer reflexionslogischen Substrate zeigen zu können. »Wenn wir daher zwei Substrate mit entgegengesetzten Bestimmungen annehmen, so kann jedes von ihnen, wie Hegel sagt, 'eben so gut als positiv wie als negativ genommen werden'« (W, S. 118).
Er bezeichnet diese Gegensatzform als »amphibolischen Gegensatz«, wodurch das Missverständnis gegenüber Hegel nochmals deutlicher wird. Eine Amphibolie ist ein Trugschluss, wenn etwas für A gehalten wird, obwohl es in Wahrheit etwas Anderes, z.B. B ist. Darum geht es bei Hegel nicht, sondern um die Austauschbarkeit. Dagegen kann in Wolffs Deutung sehr wohl von der Gefahr eines Trugschlusses gesprochen werden: Wenn zum Beispiel für einen Gegenstand A2 nur dessen reflexionslogisches Substrat »riechender Gegenstand« betrachtet wird, kann nicht erkannt werden, dass es sich in diesem Fall um einen übelriechenden Gegenstand handelt, und das kann zum Trugschluss führen, dieser Gegenstand sei wohlriechend, was sich erst bei näherer Bestimmung als falsch herausstellen wird. Im Ganzen erscheint mir das recht konstruiert und ist aus der Not geboren, für Hegels zweite Bestimmung des Positiven und Negativen eine eigene Gegensatzform zu finden, die in das Schema der Bestimmungspaare passt.
3. Gegensatzform – das an sich Positive und das an sich Negative
Da Wolff von Anfang an das »reflexionslogische Substrat« nach dem Vorbild der Arithmetik als Betrag von A konstruiert, sollte seine Deutung für die dritte Bestimmung sehr gut passen, die Hegel in der Anmerkung ausführlich am Beispiel der positiven und der negativen Zahlen erläutert. Das ist jedoch nicht der Fall, da er das reflexionslogische Substrat als eine eigene Entität vom Positiven und Negativen trennt. Zwar kritisiert er an anderer Stelle diese Vorgehensweise, wenn er schreibt:
»Riechende Körper, Wege, die zwei Orte im Osten und Westen verbinden, Kapital, Dinge überhaupt usw. halten wir gewöhnlich für selbständige Dinge, und zwar für selbständig in dem Sinne, dass sie unabhängig von einer der auf sie bezüglichen entgegengesetzten Bestimmungen bestehen können. Obgleich diese Dinge immer schon durch eine dieser entgegengesetzten Bestimmungen bestimmt sind und obgleich diese Dinge, als diesen Bestimmungen 'zugrundeliegende' Gegenstände, erst aufgrund einer besonderen Reflexion ihrer Bestimmungen ein möglicher Gegenstand unseres Nachdenkens werden, stellen wir uns vor, dass diese Dinge selbständig 'zugrunde liegen' und die entgegengesetzten Bestimmungen nur äußerlich hinzukommen« (W, S. 127).
Aber genau auf diese Weise versteht er die dritte Gegensatzform. Sie ist für ihn »das Verhältnis zwischen den entgegengesetzten Bestimmungen einerseits und ihren reflexionslogischen Substraten andererseits« (W, S. 124), und das auf eine Weise, in der beide Seiten gegenüber selbständig werden. Um kein Missverständnis aufkommen zu lassen, entwickelt er eine formalisierte Darstellung, in der er einerseits die beiden Bestimmungen des Bestimmungspaares und andererseits die beiden reflexionslogischen Substrate, die diesen Bestimmungen zugrunde liegen, aufschreibt (W, S. 124). Wie bereits in der 2. Gegensatzform gesehen, versteht er die beiden reflexionslogischen Substrate als »verschiedene Gegenstände« (W, S. 117), die jetzt gemeinsam einen Gegensatz gegen das Bestimmungspaar bilden. Wenn er in den Ausführungen zu »Hegels Exposition des Widerspruchsbegriffs« (W, S. 146ff) darauf zurückkommt, betont er nochmals: »Die Identität des Übelriechenden mit dem Nichtwohlriechenden ergibt sich erst unter Voraussetzung des reflexionslogischen Substrats riechender Körper (zu denen die weder wohl- noch übelriechenden Körper nicht gehören mögen)« (W, S. 148).
Diese Beispiele verdeutlichen, dass damit zwei Gegenstände gemeint sind, die einerseits darin übereinstimmen, dass sie die gleiche Eigenschaft haben (z.B. riechend oder farbig zu sein), die sich aber dann unterscheiden, wenn erkannt wird, dass diese Eigenschaft entgegengesetzte Ausprägungen erhalten kann (z.B. wohlriechend und übelriechend). Er betont ausdrücklich, dass die Gesamtheiten dieser beiden Gruppen von Gegenständen identisch sind: »Die wohl- und übel-riechenden Körper zusammengenommen sind die riechenden Körper etc.« (W, S. 148). Der Gegensatz besteht darin, dass für die gleiche Menge von Gegenständen auf der einen Seite eine gemeinsame Eigenschaft, auf der anderen Seite die entgegengesetzten Ausprägungen dieser Eigenschaft hervorgehoben wird.
Wird für diesen Gegensatz wiederum nach dessen reflexionslogischem Substrat gefragt, dann führt das in das logische Paradox, dass es ein reflexionslogisches Substrat geben muss, dass der Unterscheidung in reflexionslogische Substrate und Bestimmungspaare zugrunde liegt. Da ein Gegensatz von reflexionslogischen Substraten einerseits und Bestimmungspaaren andererseits konstruiert wurde, würde sich das reflexionslogische Substrat dieses Gegensatzes auf beiden Seiten befinden: Einerseits als Substrat dieses Gegensatzes, und andererseits als eine Seite des Gegensatzes, dessen Substrat gesucht wird. Das reflexionslogische Substrat wäre sein eigenes reflexionslogisches Substrat, oder aber ein »reflexionslogisches Substrat höherer Stufe«, was Wolff jedoch vermeiden möchte (W, S. 148).
Daraus schließt er, dass es sich in diesem Fall um eine »substratfreie Negativität« handelt, die zum »Ausschließen« der beiden Entgegengesetzten (W, S. 149) führt. Da es kein gemeinsames Substrat gibt, schließt die eine Seite des Gegensatzes die andere aus. Diese »Ausschlußbeziehung [...] ist nun der unmittelbare Ausgangspunkt für (Hegels) Exposition des Begriffs 'Widerspruch'« (W, S. 150).
Nach meinem Eindruck hat Wolff im Grunde gezeigt, dass seine Konstruktion einen Fehler enthält. Sein Ansatz lässt sich nicht durchhalten, allen Gegensätzen ein reflexionslogisches Substrat zu unterlegen, denn er hat selbst einen Gegensatz bilden können, für den das nicht möglich ist. – Damit hat er gezeigt, dass sein Begriff des reflexionslogischen Substrats in einen Widerspruch führt. Statt nun zu prüfen, wie dieser Begriff gebildet wurde, versteht er diesen Widerspruch, in den das von ihm eingeführte reflexionslogische Substrat führt, nicht als Nachweis, dass er fehlerhaft entworfen wurde, sondern als den Untergang in den Widerspruch, um den es Hegel geht. – In dem Moment, in dem Hegel die Selbständigkeit des Positiven und Negativen im Widerspruch zu Grunde gehen und das Wesen im Grund sein Substrat gewinnen lässt (HW 6.85), sieht Wolff eine »substratfreie Negativität«
Nachdem Wolff gezeigt hat, dass es für ihn in der 3. Gegensatzform kein reflexionslogisches Substrat mehr gibt und die beiden Seiten des Gegensatzes selbständig werden, geht er in der Darstellung des Widerspruchs auf die Bestimmungspaare wie blau / gelb etc. nicht mehr ein und beschränkt sich darauf, Hegels Lehre in eigenen Worten wiederzugeben.
Die Kritik von Urs Richli an Wolffs Studie über den Widerspruch
Als dieser Beitrag bereits im wesentlichen geschrieben war, bin ich von Bernd Seestaedt auf den Artikel von Urs Richli aufmerksam gemacht worden, der schon 1989 in ähnlicher Weise argumentiert hat. Bis heute hat weder Michael Wolff noch einer der Philosophen, die sich positiv auf seine Studie beziehen, auf diese Kritik geantwortet.
Während hier versucht wurde zu verstehen, wie Wolff ausgehend von Kants Einführung der negativen Größen seinen Begriff des Gegensatzes entwickelt und sich dabei immer weiter von Hegel entfernt hat, argumentiert Richli weit grundsätzlicher, jedoch in der Sache ähnlich. Er hält Wolff vor, dass er den Begriff des Widerspruchs nicht als Denkbestimmung versteht, sondern an Gegenstände bindet.
Die Bestimmungen des reinen Denkens »an und für sich zu betrachten, heißt sie nicht auf Gegenstände und exemplarisch verwendete Prädikate zu beziehen. Da Wolff dieses methodische Prinzip nicht beachtet, gerät seine Rekonstruktion zum Zerrbild der logischen Darstellung« (Richli 1989, S. 40).
Richli versteht das von Wolff eingeführte reflexionslogische Substrat als eine Gattung und das Bestimmungspaar als deren Arten. So sind z.B. »wohlriechend« und »übelriechend« Arten der Gattung »riechend« Häufig wählt Wolff Bestimmungspaare, »die eine vollständige Disjunktion bilden« (Richli 1989, S. 38).
»Auf der ersten Stufe des Gegensatzes würden die beiden Prädikate auf einen einzigen Gegenstand bezogen, dem entweder das eine oder andere zukomme, auf der zweiten komme jedes Prädikat einem andern Gegenstand zu. [...] Auf der dritten Stufe seien dagegen die Gattung als an sich Positives, d. h. als an sich Nicht-Entgegengesetztes, und das kontradiktorisch-entgegengesetzte Prädikat als an sich Negatives einander entgegengesetzt. [...] Er exemplifiziert übrigens die Reflexionsbestimmungen ausschließlich an materialen Prädikaten« (Richli 1989, S. 39).
In der von Richli gewählten Darstellung werden die Kategorienfehler sehr deutlich, die Wolff unterlaufen, wenn er die Reflexionsbestimmungen auf Gegenstände bezieht. In der zweiten Stufe sieht er einen Gegensatz der Gattung zu sich selbst (z.B. einen Gegensatz zwischen einem riechenden Gegenstand und einem anderen riechenden Gegenstand, weil auf Ebene der Gattung nicht unterschieden wird, dass der eine wohlriecht und der andere übelriecht), in der dritten Stufe einen Gegensatz zwischen einer Art und der übergeordneten Gattung im Ganzen (z.B. einen Gegensatz zwischen wohlriechend und riechend). Beides ist innerhalb der Betrachtung von Gegenständen jeweils ein Kategorienfehler. Wird nur die Gattung betrachtet, dann wird gerade abgesehen von möglicherweise entgegengesetzten bestimmten Merkmalen. Hinsichtlich der Gattung sind die betrachteten Gegenstände gleich (und daher verwechselbar, worauf es Wolff ankommt), und bilden keinen Gegensatz.
Und es kann nicht ein Gegensatz zwischen einer einzelnen Art und der Gattung konstruiert werden. Wolff spürt, dass seine Konstruktion der dritten Stufe in einen Kategorienfehler läuft. Eine Art steht nicht im Gegensatz zur Gattung, sondern ist in ihr enthalten. Um dennoch von Gegensatz sprechen zu können, muß er erläutern, warum hier die übliche »Metapher des »Enthaltens«« (W, S. 151) nicht zutreffen soll. Er argumentiert, dass innerhalb eines Bestimmungspaares jeder einzelne Begriff per Definition das Entgegengesetzte des anderen Begriffs und insofern negativ ist, während die Gattung von den einander negierenden Merkmalen absieht und insofern positiv (frei von Negativität) ist. Etwas Negatives (die Art, die jeweils eine entgegengesetzte Art negiert) kann aber nicht in etwas Positivem (der Gattung, die von den Entgegensetzungen absieht) enthalten sein. – So zu argumentieren ist nicht weniger spitzfindig als die zweite Gegensatzform, auf der nach Wolff die reflexionslogischen Substrate verwechselt werden können. Seine eigenen Beispiele zeigen, dass diese Art der Argumentation nicht stimmen kann. Es würde z.B. bedeuten, dass die positiven und negativen Zahlen nicht in den ganzen Zahlen enthalten sind, und auch die Vorstellung etwas Wohlriechenden, das nicht im Bereich des Riechenden enthalten sein soll, ist widersinnig. Wolff gerät hier in Widerspruch mit eigenen Ausführungen, wenn er nur wenige Seiten zuvor schreibt: »Die wohl- und übel- riechenden Körper zusammengenommen sind die riechenden Körper etc.« (W, S. 148).
Siglen
HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971; Link
KrV = Immanuel Kant: Kritik der reinen Vernunft (1781, 1787)
NG = Immanuel Kant: Versuch den Begriff der negativen Größen in die Weltweisheit einzuführen
in: Immanuel Kant: Akademie-Ausgabe Bd. II, Berlin 1905, S. 165-204; Link
W = Michael Wolff: Der Begriff des Widerspruchs, Frankfurt am Main 2010 [1981]
Quellen
Andreas Arndt: Karl Marx, Berlin 2012 [1985]
Horst-Heino v. Borzeszkowski, Renate Wahsner: Infinitesimalkalkül und neuzeitlicher Bewegungsbegriff oder: Prozeß als Größe
in: Jahrbuch für Hegelforschung Band 8/9, 2002/2003, Sankt Augustin 2004 (Academia), S. 197-271
David Gray Carlson: Hegel and the Becoming of Essence
in: Cosmos and History: The Journal of Natural and Social Philosophy, Bd. 3, Nr. 2-3, 2007, S. 276-290; Link
Thomas Collmer 1992: Aktuelle Perspektiven einer immanenten Hegel-Kritik, Gießen 1992
Thomas Collmer 2002: Hegels Dialektik der Negativität, Gießen 2002
Thomas Collmer 2011: Hegel und Gödel, Wenzendorf 2011
Georg Wilhelm Friedrich Hegel: Philosophische Erörterung über die Planetenbahnen, Weinheim 1986
Dieter Henrich: Hegels Logik der Reflexion. Neue Fassung.
in: Hegel-Tage Chantilly 1971 Die Wissenschaft der Logik und die Logik der Reflexion, Hrsg. von Dieter Henrich 1978, (Hegel-Studien, Beiheft 18), S. 203-324
Christian Iber: Metaphysik absoluter Relationalität, Berlin, New York 1990
Karl Kerényi: Hermes der Seelenführer, Zürich 1944
Gottfried Wilhelm Leibniz: Neues System der Natur und der Gemeinschaft der Substanzen, wie der Vereinigung zwischen Körper und Seele
in: ders.: Philosophische Werke in vier Bänden, Bd. 2, herausgegeben von Ernst Cassirer, Hamburg 1996 [1904]
Frank Linhard: Newtons "spirits" und der Leibnizsche Raum, Hildesheim 2008
John McTaggart: A Commentary on Hegel's Logic, Cambridge 1910 (Neudruck durch "Forgotten Books" 2012); Link
Wolfgang Neuser: Einleitung und Übersetzung von Georg Wilhelm Friedrich Hegel: Philosophische Erörterung über die Planetenbahnen, Weinheim 1986
Taiju Okochi: Ontologie und Reflexionsbestimmungen, Würzburg 2008
Thomas Posch: Hegels Kritik am Newtonschen Kraftbegriff und seine Verteidigung Keplers
in: Sitzungsberichte der Leibniz-Sozietät der Wissenschaften zu Berlin 103(2009), S. 49-59; Link
Urs Richli 1982: Form und Inhalt in G.W.F. Hegels „Wissenschaft der Logik”, Wien, München 1982
Urs Richli 1989: Dialektik im Sinn der Betrachtung der Denkbestimmungen an und für sich, zu MichaeI WoIffs Rekonstruktion der Kategorie 'Widerspruch' in Hegels Wissenschaft der Logik
in: Allgemeine Zeitschrift für Philosophie 14.2, Stuttgart 1989, S. 37-44
Rainer Schäfer: Die Dialektik und ihre besonderen Formen in Hegels Logik, Hamburg 2001
Claus-Artur Scheier: Ästhetik der medialen Moderne, Vorlesung Wintersemester 2015/16 (unveröffentlichtes Typoskript)
Klaus J. Schmidt: G.W.F. Hegel: ›Wissenschaft der Logik – Die Lehre vom Wesen‹, Paderborn u.a. 1997
Markus Semm: Der springende Punkt in Hegels System, München 1994
Adolf Trendelenburg: Logische Untersuchungen, Bd. 1, Leipzig 1862 [1840]
Michael Wolff 1984: Der Begriff des Widerspruchs in der 'Kritik der reinen Vernunft'
in: Burkhard Tuschling (Hg.): Probleme der 'Kritik der reinen Vernunft', Kant-Tagung Marburg 1981, Berlin, New York 1984, S. 178-202
Michael Wolff 1986a: Der Satz vom Grund oder: Was ist philosophische Argumentation?
in: Neue Hefte für Philosophie 26 (1986) S. 89-114
Michael Wolff 1986b: Über Hegels Lehre vom Widerspruch
in: Dieter Henrich (Hg.): Probleme der Hegelschen Logik, Stuttgart 1986, S. 107-128
2012-2014, 2016
© tydecks.info 2014


