Walter Tydecks
6. Mathematik auf den Spuren des sich zurückziehenden Gottes
Inhaltsverzeichnis
Der Begriff Spur in der Philosophie und Mathematik bei Leibniz - Kontinuitätsprinzip und algebraische Kalküle
Zimzum, die Spur Gottes
Mathematische Existenz
Bildintentionen, der mathematisch-technische Begriff der Spur
Die Tiefe der nordisch bestimmten Forschung und das ungeschrieben gebliebene "Buch der Natur"
Der Begriff Spur in der Philosophie und Mathematik bei Leibniz - Kontinuitätsprinzip und algebraische Kalküle
In gewisser Weise hat Leibniz ganz ähnlich begonnen wie Kepler. So wie Kepler in den Beobachtungsdaten von Tycho Brahe die Anregung fand, sie als Punkte auf einer Ellipse statt auf einem Kreis zu deuten, so entdeckte Leibniz in den Studien von Blaise Pascal die frühe Form von etwas Neuem, der Infinitesimalrechnung. Pascal hatte sich mit der mathematischen Darstellung gekrümmter Kurven und ihrer Tangenten beschäftigt und war bis zur Idee der Steigungsdreiecke gekommen. Der erst 25-jährige Leibniz lernte sie 1672 10 Jahre nach dessen Tod bei einem Aufenthalt in Paris kennen. In diesem Material hat er entdeckt, dass hier eine völlig neue Herangehensweise in der Geometrie am Entstehen war. Waren seit Euklid so konsequent wie möglich die geometrischen Konstruktionen in einzelne Schritte zerlegt worden, die Zug um Zug aufeinander aufbauen und nach einer endlichen Kette zu neuen Figuren und Beweisen führen, ging es jetzt darum, über die einzelnen endlichen Schritte hinaus zu gehen, sie im Zusammenhang zu analysieren und zu erkennen, dass sie nur den Grenzfall einer kontinuierlichen Veränderung darstellen.
Und da ging ihm auf: Dies Herauslesen aus vorgefundenen Texten ist die neue wissenschaftliche Methode. Sie unterscheidet sich deutlich vom Induktionsprinzip, mit dem Francis Bacon 1620 die neuzeitliche Wissenschaft begründet hatte. Leibniz selbst verstand es so, dass in der Natur Spuren entdeckt werden, und dass der Wissenschaftler aus den Spuren größere Zusammenhänge erschließen kann. Dieser Grundgedanke der Monadologie findet sich bereits 1686 in der "Metaphysischen Abhandlung":
"So kann man sagen, dass in der Seele Alexanders jederzeit Nachwirkungen von allem, was ihm zugestoßen ist, und ebenso Anzeichen von dem, was er noch erleben wird, vorhanden sind, ja sogar Spuren von allem, was im Universum vor sich geht, wenngleich es allein Gott zukommt, sie sämtlich zu erkennen." Das heißt, "dass unsere Seele alles virtuell weiß, und daß es nur der Aufmerksamkeit bedarf, um die Wahrheiten zu erkennen." (Leibniz, Metaphysische Abhandlung, in: Hauptschriften, Bd. 2, S. 351, 374)
Die Idee der Spur so allgemein wie möglich und in allen Konsequenzen zu formulieren, verstehe ich als die eigentliche Leistung von Leibniz. Wenn eine Spur aufgenommen wird, ist am Anfang noch vollkommen offen, in welchen Raum sie führt. Im einfachsten Fall ist es eine Gerade, und auf der Spur kann gleichmäßig Schritt für Schritt vorangegangen werden. In diesem Fall gilt das Induktionsprinzip und mit ihm können allgemeine Aussagen getroffen werden, die bis in den Bereich der unendlich großen Zahlen gelten. Der Verlauf der Spur kann aber auch von äußeren Einflüssen geprägt sein, und dann ist der Weg der Spur nur zu verstehen, wenn ihre Umgebung mit berücksichtigt wird.
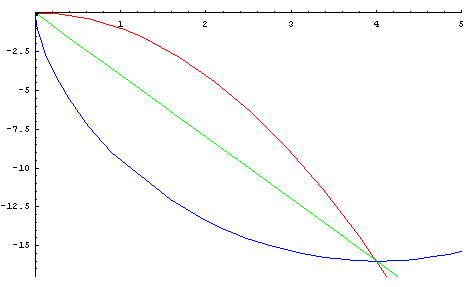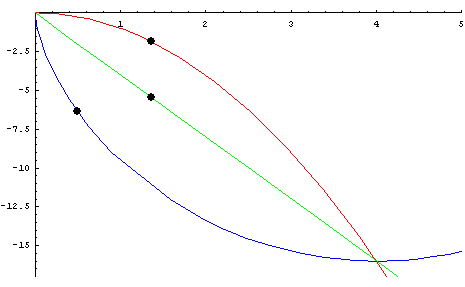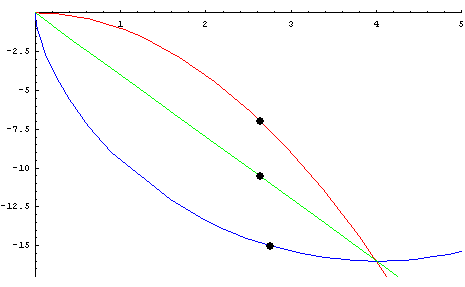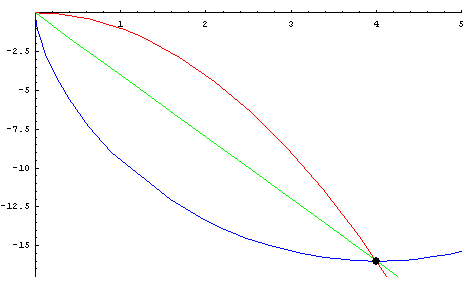
Figur 1: Brachistochrone-Problem
Gesucht ist der schnellste Weg, auf dem nur unter Berücksichtigung der Schwerkraft ein Körper von einem Punkt A zu einem anderen, seitwärts tiefer gelegenen Punkt B laufen kann (gr. brachistos kürzeste, chronos Zeit). Galilei hatte 1636 erkannt, dass dies keineswegs die gerade Verbindungslinie ist. Johann Bernoulli, ein Schüler von Leibniz, hatte dazu 1696 eine Preisfrage veröffentlicht. Hiervon ausgehend kann weiter gefragt werden, wie ein höherer Raum mit zusätzlichen Dimensionen bzw Parametern zu versehen ist, so dass dort die Brachistochrone der kürzeste Weg ist. Auch diese Lösung kann dann ihrerseits als der lineare Grenzfall eines nochmals größeren Raums interpretiert werden, der weitere Störeffekte und ihre möglichen Resonanzen enthält. Auf solche Weise dient das Kontinuitätsprinzip als "Prinzip für die Entdeckung neuer Wahrheiten" (Leibniz, Hauptschriften, Bd. 1, S. 78). Quelle
Im Kleinen (lokal) erscheint jede Spur geradlinig. Wird ihr weiterer Verlauf betrachtet, liegt es wiederum immer nahe, möglichst einfache Figuren wie einen Kreis als Annäherung zu wählen. Doch eine Spur kann auch wieder verloren werden. Dann ist eine gründliche Untersuchung der ganzen Umgebung notwendig, möglicherweise auch in größerer Entfernung, wo sie wieder erscheinen kann. Mit einem Wort: Spuren lassen sich nicht in das Schema von Platon bringen, wo schön unterschieden ist zwischen den verschiedenen Grundformen der Bewegung (dem Kreis und der Geraden). Auch wenn Leibniz große Sympathien für Platon gehegt und ihn als wissenschaftlich denkenden Philosophen verehrt hat, hat er im Grunde die Gegenposition zu Ende gedacht, die bereits bei Kepler angelegt war und bis heute das neuzeitliche Denken bestimmt.
Für Leibniz stellt sich daher im Grunde eine einzige Frage: Was kann den Wissenschaftler leiten, wenn er eine Spur verfolgt? Und darauf kennt er am Ende nur eine einzige Antwort: Es ist das Kontinuitätsgesetz. Ohne dies ausdrücklich zu sagen, tritt es für ihn an die Stelle des Induktionsaxioms und damit überhaupt an die Stelle einer Logik, die nur zwischen Induktion und Deduktion zu unterscheiden vermag. Entsprechend weit wird es gefaßt:
-
Ausgangspunkt sind sicher die kontinuierlichen Veränderungen bei stetigen Funktionen, die Infinitesimalrechnung im engeren Sinn. In den endlichen Größen zeigt sich die Spur der unendlich-kleinen Größen. Für die menschliche Erfahrung haben aber natürlich nur die endlichen Größen Realität. Die unendlich-kleinen Größen sind so gesehen nur ideell. Die Spur zeigt die Grenze, wo Idealität in Realität übergeht.
-
Was für das Verhältnis von endlichen und unendlich-kleinen Größen gilt, gilt aber auch ganz allgemein für das Verhältnis zwischen Mathematik und der Natur. Die Grundbegriffe der Mathematik wie die Zahl, der Raum, insofern auch die Zeit, kommen als solche nicht unmittelbar in der Natur vor, sondern zeigen sich nur in der Realität. Provokativ kann daher gesagt werden: Die Natur ist voller Spuren, die die Mathematik in ihr hinterlässt. Die Mathematik selbst liegt in dem Sinn dahinter oder darunter, wie die unendlich-kleinen Größen sich in der kontinuierlichen Bewegung zeigen. Dies Verhältnis von Idealität und Realität kann auch als Verhältnis von Möglichkeit und Wirklichkeit gedeutet werden. Die Mathematik enthält idealiter alles, was möglich ist, und die Natur das, was wirklich geworden ist.
-
Mit dieser Idee hat Leibniz tatsächlich die weitere Entwicklung der Mathematik vorweggenommen. Der Raumbegriff wurde Schritt um Schritt erweitert zur Theorie der differenzierbaren Mannigfaltigkeiten. Zu jedem Punkt in diesen verallgemeinerten Räumen gehört ein Tangentialraum. Der Tangentialraum ist der Raum aller Richtungen, wohin die Kurven verlaufen können, die durch diesen Punkt gehen.
-
Spuren sind auch umgekehrt der Grenzfall ins Unendlich-Große. Sie weisen nicht nur zurück zum Unendlich-Kleinen, zum Keimhaften, sondern die endlichen Kurven sind der dem Menschen erfahrbare Grenzfall unendlich-großer Bewegungen, die er im Ganzen auch nicht annähernd überschauen kann.
-
Dann wieder hat Leibniz sich dies Verhältnis ganz anschaulich gedacht. Das Prinzip der Kontinuität besagt, dass nichts übergangslos entstehen kann. Voller Konsequenz lehnt er daher sowohl die Theorie vom leeren Raum wie auch die Atomistik ab, wobei die Atomistik bedeutet, dass die Atome absolut kompakte Einheiten im leeren Raum sind. Beide Extreme werden von Leibniz bestritten. Der Raum ist grundsätzlich kontinuierlich gefüllt. Es wäre jedoch falsch, als den zugrundeliegenden feinen Stoff den Äther anzusehen als das fehlende 5. Element neben Erde, Wasser, Luft und Feuer. Der von Leibniz gemeinte Stoff liegt in dem Sinn zugrunde, wie die Mathematik als Raum der Möglichkeiten der Natur zugrundeliegt. Wenn im 20. Jahrhundert in der Teilchenphysik diese Idee von Leibniz wieder aufzuleben scheint, wo von virtuellen Teilchen, Materie-Antimaterie-Paaren und ähnlichem gesprochen wird, ist sehr genau die Grenze zu beachten, dass diese Theorien dahin tendieren, das Unmögliche nachweisen zu wollen, nämlich die letzten Bausteine der Materie. Das wären dann aber am Ende auch wieder Atome, nur gewissermaßen einige Ebenen tiefer. Mit dem leeren Raum lehnt Leibniz auch die Atome ab. Sie müßten eine gewisse räumliche Ausdehnung haben, ohne eine innere Mannigfaltigkeit enthalten zu können. Schon der Begriff des Atoms an sich führt immer in einen logischen Widerspruch. Das lässt sich nur in der von Leibniz angegebenen Richtung auflösen.
-
In Auseinandersetzung mit Descartes betont Leibniz, dass der zugrundeliegende Raum der Mathematik nicht nur aus bloßen Ausdehnungen bestehen kann, sondern ein Kraftfeld sein muß. Auch hier hat er wieder viel von der weiteren Entwicklung vorweggenommen. An die Stelle ebener euklidischer Räume treten Vektorfelder mit einer reichen, dynamischen Struktur. Aber wieder gilt die gleiche Anmerkung wie zu den virtuellen Teilchen, dass es ein Mißverständnis wäre, konkrete, reale Vektorfelder wie z.B. das elektromagnetische Feld für das Kraftfeld zu halten, das Leibniz meint. Es ist nur eine Äußerung im Übergang vom mathematischen Raum zur Natur. Es lag Leibniz völlig fern, irgendein absolutes, letztes, alles erklärendes Kraftfeld als Basis der Naturwissenschaft anzunehmen. Mit seinem Verständnis von Kraftfeldern wollte er nur die Richtung, die Orientierung geben, wohin die Naturwissenschaft sich entwickeln kann.
-
Leibniz hat aber auch auf ganz andere Weise seine Ideen zu veranschaulichen versucht. Die Seele gilt ihm nicht als tabula rasa, auf die das Leben seine Geschichte einträgt, sondern eher wie ein Marmorblock, der auf den ersten Blick hart und glatt erscheint, dann aber Fasern und Muster zeigt, denen nachgespürt wird. Leben bedeutet Aufmerksamkeit für diese Strukturen. Im Grunde ist das ganze Leben und die Selbstfindung der eigenen Persönlichkeit damit etwas Ähnliches wie die Gewinnung der wissenschaftlichen Erkenntnisse entlang vorgefundener Strukturen. Die Seele liegt als Raum von Möglichkeiten und Idealität dem realen Leben so zugrunde wie die Mathematik der Natur.
-
Ein anderes anschauliches Bild ist das diffuse Geräusch des Meeres. Wer am Meer lebt, nimmt es irgendwann gar nicht mehr wahr. Wer zum Meer kommt, hört es nur unbestimmt. In Wahrheit enthält es eine Unendlichkeit von Stimmen und Stimmungen, die sich zusammensetzt aus den einzelnen Wellen, Meeresströmungen, Windverhältnissen und den Küstenlinien, an denen sich das Meer bricht. Und ganz ähnlich hört die Seele auf den Körper. Der Körper äußert sich in einer Unendlichkeit der verschiedensten Regungen, sei es der Blutkreislauf, die Atmung, Verdauung, aber auch Assoziationen, die durch Erinnerungen an frühere Erlebnisse ständig wachgerufen werden. Auf diese Äußerungen ist meist gar keine besondere Aufmerksamkeit mehr gerichtet, sie werden schlicht nicht wahrgenommen. Aber Leibniz weist den Weg, sich dessen bewußt zu werden. Und so ist es kein Zufall, dass seine Ideen nicht nur die weitere Geschichte der Mathematik beeinflußt haben, sondern indirekt auch die der Kunst, wenn etwa an die Romane von Proust und Joyce gedacht wird.
-
Nicht nur der absolute Gegensatz zwischen leerem Raum und undurchdringlichen Atomen wird aufgelöst, sondern auch der zwischen Wachen und Schlafen, Denken und Träumen, Menschen und Tieren, Tieren und Pflanzen, Tod und Leben. Das ist seine Antwort auf den cartesianischen Zweifel. Selbst wenn ich nicht weiß, ob ich wache oder schlafe, ist das am Ende unerheblich, wo es doch nur darum geht, Beständiges und Veränderliches wahrzunehmen. Im Schlaf zeigen sich Symbole, die im Grunde übergangslos in das Wache übergehen und auch dort dem Denken zugrundeliegen.
-
Wenn es weder Atome noch den leeren Raum gibt, ist für Leibniz jedes Einzelne sowohl einmalig als auch mit allem anderen verbunden (Monadologie). Nichts kann sich vollständig identisch woanders wiederholen oder an zwei Orten zugleich sein. Aber es geschieht auch nichts, was nicht überall wahrgenommen wird. Das denkt Leibniz so konsequent, dass mit "überall" auch die Grenzen von Tod und Leben überschritten sind. Was heute geschieht, nimmt alles Frühere auf und wirkt auf alles Zukünftige weiter. In diesem Sinn vertritt Leibniz die These der Unsterblichkeit der Seele.
-
Vielleicht waren auch Fragen der Sprache der Ausgangspunkt. Leibniz war immer fasziniert von der Beobachtung, wie in jeder Sprache mehrere Schichten einander überlagern, wenn etwa in Folge von Eroberungswellen oder hegemonialen Vorherrschaften die Sprache des Alltags mit der Sprache von Verwaltung und Militärwesen konfrontiert wird. Meist verweisen die Eigennamen wie z.B. die Namen von Flüssen auf die ältesten Quellen. Diese Sicht auf die Sprache war der Anfang einer langen Geschichte von Textanalysen, in denen alle "großen Texte" wie das Alte Testament oder die Epen von Homer auf unterschiedliche Sprachschichten analysiert wurden.
Sprache kann aber auch im Ganzen als eine eigene Schicht gesehen werden, der wiederum räumliche Vorstellungsweisen unterliegen. Daran erinnern insbesondere die Präpositionen wie "zu, von, mit, über, gegen" etc, die von einer räumlichen Anschauung ausgehen, dann aber in übertragenem Sinne für alle Beziehungen gebraucht werden. Selbst bei nicht räumlich gemeinten Zusammenhängen greift der Sprachfluß immer auf räumliche Vorstellungen zurück. Am Ende können ja auch die Ideen der Spur und der Kontinuität nur räumlich gedacht werden.
Leibniz kennt bereits die Vorstellung von Sprachwurzeln. Die Analyse der verschiedenen Sprachen und die Versuche, sie auf Sprachfamilien und ursprünglichere Sprachen zurückzuführen, kamen erst später. Ganz intuitiv will Leibniz aber zeigen, wie bestimmte Buchstaben oft aufbauend auf lautmalerische Ursprünge den jeweiligen Worten, in denen sie vorkommen, einen bestimmten Charakter geben. Zum Beispiel weist das R auf abrupte Bewegungen, das L auf sanfte Bewegungen.
All dies kommt zusammen, wenn bestimmte herausgehobene Worte betrachtet werden, die fast schon als Symbole angesehen werden können. In den "Neuen Abhandlungen über den menschlichen Verstand" wird ausführlich das Wort "Auge" behandelt. Die Wurzel A verweist z.B. auf Atem oder Odem, aber auch auf Wasser (aqua), woran auch ganz direkt die Auen erinnern, wasserüberflutete Wiesen. Vom äußeren Erscheinungsbild ähnelt das Auge im Gesicht dem Fettauge, der Insel im Meer, die als Oeland bezeichnet wird, oder dem Ägaischen Meer, bildhaft gesprochen einem Meer voller Augen. Im Spanischen bedeutet "ojo" Loch. Über Leibniz hinaus lassen sich weitere Bezüge nennen, etwa das Auge als Organ der Seele oder das Pfauenauge und die große Bedeutung dieses Begriffs in der Alchemie. Leibniz war immer an Fragen der Alchemie und der rosenkreuzerischen Tradition interessiert.
Erst vor dem Hintergrund des so weit verstandenen Kontinuitätsprinzips wird die Bedeutung der algebraischen Kalküle für Leibniz verständlich. Sie definieren eine Struktur genau an der Grenze, wo Idealität in Realität, wo Möglichkeit in Wirklichkeit übergeht, die "Ordnung der Dinge". Das Kontinuitätsprinzip stellt sicher, dass in diesem Übergang etwas erhalten bleibt. Erhalten bleibt ein Kalkül, der Beziehungen zwischen Größen definiert, die sowohl vor wie nach dem Übergang gelten und das sogar dann, wenn wie in der Infinitesimalrechnung die Größen im Grenzübergang völlig verschwinden. Mathematisch gesprochen bilden sie lokale Koordinatensysteme für Wahrscheinlichkeitsräume in einem Bereich, wo es aus Sicht der Philosophie bei einer absoluten Gegenüberstellung von Ruhe und Bewegung, Sein und Nicht-Sein nichts geben könnte. (Siehe dazu von Leibniz die "Rechtfertigung der Infinitesimalrechnung durch den gewöhnlichen algebraischen Kalkül" von 1702, in "Hauptschriften" Bd. 1).
Das Kontinuitätsprinzip nimmt insofern das Induktionsaxiom auf, als es aus einer begrenzten Erfahrung von Spuren auf größere Zusammenhänge schließt, in die diese Spuren eingebettet sind. Mithilfe des Kontinuitätsprinzips vermag sich die Seele schrittweise das Umfeld zu erschließend, aus der die Ordnung der Dinge verständlich wird. Das ist allerdings ein unendlicher, dem Menschen labyrinthisch erscheinender Prozess, denn nie vermag der Mensch vollständig die Sicht Gottes einzunehmen. Er kann nur darauf vertrauen, dass Gott ihm die Orientierungsfähigkeit gegeben hat, auf diesem Weg erfolgreich weiter zu gehen.
Das Kontinuitätsprinzip unterscheidet sich aber wesentlich vom Induktionsaxiom, weil das Induktionsaxiom auf diskrete Mengen beschränkt ist, während das Kontinuitätsprinzip gerade den Übergang von diskreten zu unendlich-kleinen Größen betrachtet. Das Kontinuitätsprinzip liegt dem Induktionsaxiom in dem Sinn zugrunde, wie die Mathematik der Natur. Das Schließen des Induktionsaxioms ist nur möglich, wenn angenommen wird, dass die Menge endlicher Größen, über die mit dem Induktionsaxiom Aussagen gemacht werden, im Sinne des Kontinuitätsprinzips zusammenhängen. Umgekehrt ist aber das Induktionsaxiom der einzige mathematische Weg, um aus den begrenzten Spuren Aussagen über unbegrenzte Kurven machen zu können, auf die die Spuren hinweisen. (Mathematisch ist mit dem Begriff der Kompaktheit der Weg definiert, zusammenhängende Mengen durch diskrete Teilmengen zu überdecken. Alle Sätze der Differentialrechnung gehen letztlich immer auf das Induktionsaxiom zurück, das für Aussagen über die begrenzten Teilmengen der Überdeckung gebraucht wird.)
Leibniz hat damit ein System entwickelt, das von den mathematischen Entdeckungen seiner Zeit ausging und bis heute der Mathematik und Naturwissenschft zugrunde liegt. Das wird immer deutlicher, je weiter diese fortgeschritten sind. Daher stellt sich im Grunde umgekehrt die Frage, warum er von Anfang an bis heute eher im Hintergrund geblieben ist und im Ganzen nie solche Anerkennung gefunden hat wie seine Nachfolger Kant oder Hegel.
In erster Beantwortung war Leibniz einfach zu radikal. Wenn Kepler es gewagt hatte, für die Planetenbahnen Ellipsen statt Kreise anzunehmen, hatte Leibniz alle überlieferten Gegensatzbegriffe der Philosophie und Religion in Frage gestellt. Diese Radikalität war um so schwerer zu akzeptieren, als der gleiche Leibniz ansonsten ein oft eher kleinlicher Vertreter des Absolutismus und der Gegenreformation war und häufig genug seine Gegner mit hinterhältigen Briefwechseln traktieren konnte.
Vor allem aber war es sein grenzenloser Optimismus über unsere Welt als die beste aller möglichen Welten. Ein solches Maß an Beschönigung und Selbstgefälligkeit ist kaum zu ertragen. Und so wurde seine Philosophie jedes Mal mit Hohn und Spott bedacht, wenn es Naturkatastrophen wie das Erdbeben in Lissabon oder andere Einbrüche des Bösen gab. Mit einem Wort: Sein System scheint zu glatt, zu stimmig, insofern irgendwie reduziert zu sein. Es scheint alles zu enthalten, aber zugleich scheint auch alles zu entschwinden, ungreifbar zu werden. Er selbst spricht dies an, wenn er am Beispiel eines Begriffes wie "das Blaue" einräumen muß, dass zwar jeder weiß, was gemeint ist, aber trotzdem unmöglich jemandem gesagt werden kann, wie er "das Blaue" wahrnehmen kann. Sein System setzt auf ungeheuer viel Intuition. Das ist zugleich eine Stärke wie eine Schwäche. Mit der Intuition ist es offen und erlaubt eine Unendlichkeit an Möglichkeiten. Zugleich droht es ständig sich selbst zu neutralisieren. Auf sein eigenes System trifft zu, was er scharfsinnig schon bei seiner ersten Lektüre der "Ethik" 1678 gegenüber Spinoza bemerkt hat: Das System seiner unendlichen Möglichkeiten ist ständig in Gefahr, da unsicher bleibt, ob es nicht auf inneren Widersprüchen beruht, die sich gegenseitig neutralisieren.
Dennoch kann kein Zweifel bestehen, dass nicht sein System, sondern alle anderen Systeme letztlich gescheitert sind. Immer neu wurde versucht, gegenüber Leibniz etwas Absolutes festzuhalten bzw. die Grenzen der von ihm skizzierten Bewegung zu fixieren. Immer wieder neu wurde geglaubt, dass die Entwicklung der Naturwissenschaft an einen Punkt gekommen ist, wo etwas qualitativ Neues erreicht wurde und die allgemeinen Bahnen, die Leibniz gewiesen hatte, an ihr Ende stoßen. So suchte Kant die Grenzen der mechanischen Wissenschaft zu definieren mit seiner transzendentalen Ästhetik. Schelling glaubte, dass die neuen Entdeckungen seiner Zeit etwa in den Gebieten Elektrizität und Optik eine solche Grenze darstellen und er sich daher nach erfolgreich getaner Arbeit von der Naturphilosophie ein für alle Mal abwenden könne. Ganz ähnlich dachte Hegel, die Naturwissenschaft in einer Naturphilosophie auf Basis seines Systems umfassend und abschließend darstellen zu können. Dann folgten im 19. Jahrhundert die Energetik und der Evolutionismus, die genau so schnell verstaubt und altmodisch wirkten, wie sie als der alles erklärende Fundamentalansatz erschienen waren. Auf der anderen Seite folgten die Naturdialektik bei Engels (und eingeschränkt Marx) und der dialektische Materialismus in der Sowjetunion, die nun aus ihrer weltanschaulichen Haltung heraus glaubten, die unveränderlichen Grundwidersprüche und Bewegungsgesetze der Natur gefunden zu haben, über die keine Naturwissenschaft mehr hinaus kann.
Zimzum, die Spur Gottes
Der religiöse Hintergrund bei Leibniz ist jedoch weit komplexer als es die banale Aussage scheinen lässt, Gott sei der Schöpfer der besten aller möglichen Welten. Überhaupt ist die persönliche Stellung von Leibniz keineswegs so durchsichtig, wie es die klare Darstellung des Kontinuitätsprinzips erwarten lässt. Er war ein Vertreter des Absolutismus in Preußen, mochte aber die Absolutisten in Paris nicht. Mit dem 14 Jahre älteren Spinoza konnte er sich nicht anfreunden, wohl wegen dessen republikanischer Gesinnung. Aber kann ein Zweifel bestehen, dass von Spinoza die entscheidenden Anstöße ausgingen?
Leibniz lebte in einer Zeit, als das Judentum eine tiefe Krise durchmachte. Mit Isaak Luria (1533 - 1572) hatte nach der Vertreibung der Juden aus Spanien die Kabbala in Palästina einen letzten Aufschwung erlebt. Der kurze Auftritt 1665 - 66 des Sabbatai Zwi als Messias in Palästina und seine direkt anschließende Bekehrung zum Islam hatte das Judentum ratlos zurückgelassen. Aber nun bestand die Chance, dass sich das Judentum einer in der Renaissance entstandenen neuen Geistesrichtung öffnete, die nach einer höheren Vernunftreligion suchte, in der Christentum, Judentum, Islam, heidnische Antike und altorientalische Überlieferungen insbesondere aus Ägypten vereinbart werden. Spinoza trug mit seinem "Traktat" wesentlich dazu bei. Leibniz war befreundet mit Christian Knorr von Rosenroth (1636 - 1689), der 1677 - 1684 an der "Kabbala denudata" arbeitete, die als die beste zusammenfassende Darstellung der kabbalistischen Ideen gilt. Ein Mitarbeiter von Rosenroth war Henry More (1614 - 1687), der zum kleinen Kreis der Cambridger Platoniker gehörte. Diese sahen Platon geradezu als "attischen Moses" an. Und dort erschien um 1678 das monumentale Werk "The intellectual system of the Universe" von Cudworth (1617 - 1684), wo in großem Stil die Geschichte der ägyptischen Überlieferungen zusammengestellt ist und die Formel "Hen kai Pan" ("Alles ist Eins") wiederentdeckt wurde. Vermittelt durch Herder wurde "Hen kai Pan" das Losungswort, auf das sich die christlichen und jüdischen Aufklärer in Deutschland in der zweiten Hälfte des 18. Jahrhunderts einigen konnten. Cudworth hatte auch in Vergessenheit geratene Quellen über die vorsokratischen Philosophen wieder gelesen und veröffentlicht. Hölscher vermutet, dass Hölderlin von ihm sein Wissen über Empedokles bezog.
Dies alles wird hier zusammengetragen, um schließlich die Vermutung zu äußern, dass sich trotz der berühmten Auseinandersetzung über den Begriff des Raums in Wahrheit Newton und Leibniz bei dem kabbalistischen Grundgedanken getroffen haben, der von Isaak Luria stammte: die Idee des Zimzum, des sich aus der Welt zurückziehenden Gottes. "John Locke jedoch, der mit ihr (der Newtonschen Theorie, t.) unmittelbar vertraut war, machte die - so Locke wörtlich - eigenartige Meinung Newtons bekannt: die Materie konnte aus der göttlichen Unendlichkeit nur hervortreten, weil Gott sich zuvor aus einem Teil von ihr zurückgezogen hat." (Hutin in: Koslowski, S. 173) Und sind nicht die Spuren, denen Leibniz nachgeht, die Spuren des Gottes, die dieser beim Rückzug hinterlassen hat und die in den Momenten der Intuition und der Erkenntnis ein Glücksgefühl wachrufen, das an die frühere Gegenwart Gottes erinnert?
Newton und Leibniz vertreten beide eine negative Theologie. Newton sieht den Raum keineswegs als ein göttliches Ding, das wie andere Dinge vor uns steht und wie andere Dinge mathematisch und physikalisch untersucht, beschrieben und dargestellt werden kann. Das wäre ein Widerspruch, den Raum selbst als Ding zu sehen, in den zugleich alle Dinge hineingestellt sind. Der Nachweis dieses Widerspruchs ist das wesentliche Argument, das Leibniz gegen Newton ins Feld führt. Aber er versteht Newton nicht und konnte ihn nicht verstehen, weil Newton den Gedanken nicht veröffentlichte, dass der Raum, der der Physik zugänglich ist, das Gebiet der göttlichen Unendlichkeit ist, aus der Gott sich zurückgezogen hat. Physik und Mathematik sind daher negative Theologie.
Dies ist zugleich die radikalste Kritik an Platon, auch wenn Leibniz von ihm fasziniert war und ihn konsequent als Wissenschaftler und nicht als Mythologen sah. Wenn die Naturwissenschaft genau den Bereich des All erkennen kann, aus dem Gott sich zurückgezogen hat, erscheinen nicht mehr am Ende des Weges der Erkenntnis göttliche Ideen, sondern der Weg ist prinzipiell unendlich und verliert sich immer in der Nacht. Exklusive Durchblicke oder gar Bemächtigungen eines reinen Reiches der Ideen, wie noch Platon sie vertreten hatte, gibt es nicht. Es gibt keine "Auserwählten". Die von Leibniz eingeführten Vorstellungen wie das Unendlich-Kleine, die Mathematik als Raum der Möglichkeiten, die der Natur zugrunde liegt, die universelle Sprache, erscheinen zwar im Anschaulichen, sind aber selbst unanschaulich und entziehen sich jedem Versuch, sie in der Weise zu fixieren, wie nach Euklid die Geometrie auf Punkt, Kreis und Gerade aufbauen konnte. Welche geometrische Gestalt hat das Unendlich-Kleine? Aus welchen Buchstaben setzt sich die universelle Sprache zusammen? Welcher Stoff füllt den reinen mathematischen Raum, der doch nicht leer sein darf?
Leibniz selbst hatte das Gefühl, in ein Labyrinth geraten zu sein. Er versuchte daher auch erst gar nicht, ein eigenes System zu entwickeln. Selbst die "Neuen Abhandlungen" wurden erst 50 Jahre nach seinem Tod veröffentlicht.
So konnte es kommen, dass er fast 100 Jahre lang im Schatten von Kant stand. Wem dann später Kant nicht genügte, der ging weiter zu Fichte, Schelling und Hegel oder gleich zu Nietzsche, aber kaum zurück zu Leibniz. Der Anstoß für eine Wende kam von der Mathematik. Als diese sich völlig von den angeblich a priori vorgegebenen Raum- und Zeitvorstellungen gelöst hatte, sah als einer der ersten Frege in den "Grundlagen der Arithmetik" (1884) in Leibniz statt Kant den Vorläufer seiner Ideen. Aber Leibniz' großer "Förderer" war unumstritten Ernst Cassirer, der ab 1904 die "Hauptschriften" von Leibniz in deutscher Übersetzung herausgab. Womit Cassirer jedoch sicher am wenigsten gerechnet hatte, war die Wirkung dieser Werke auf eine neue Generation von Philosophen, die bei Husserl lernten, auf Martin Heidegger und Oskar Becker, die dann in den 1920er Jahren seine großen Herausforderer wurden und ausgerechnet mit Leibniz gegen den Neukantianismus auftraten.
Zunächst schien aber im Gegenteil mit den Erfolgen der Algebra, den neuen axiomatischen Beweistechniken und der Einführung der Mengenlehre die "mathesis universalis" zum Greifen nahe zu sein. Hinzu kamen die bahnbrechenden Erfolge der mathematischen Physik (Relativitätstheorie, Quantentheorie) und die neue Atomtheorie. Trotz aller Ernüchterungen ist diese Hoffnung bis heute nicht aufgegeben worden, wo in immer neuen Anläufen versucht wird, direkt das "Buch der Natur" entziffern, lesen und dann darin schreiben zu können, sei es durch Entdeckung der letzten Elementarteilchen, aus denen sich dann alles zusammensetzt, oder die Entschlüsselung der Gene. Der Ausweg aus dem Labyrinth schien möglich, und das mit den Mitteln, die Leibniz selbst angeregt hatte.
Und so schien er in den Jahren nach 1900 ganz eingeholt zu werden von der platonischen Tradition in England, die in Russell und Whitehead eine Wiedergeburt erlebte. Für sie war alles Mystizismus, wo Leibniz sich von Platon unterschied, und diese mystischen Tendenzen waren ihrer Meinung nach ausschließlich zeitbedingt zu erklären, da Leibniz sich noch nicht radikal genug von den Meinungen hatte trennen können, die im weiteren Verlauf der Aufklärung durchschaut wurden. Sie wollten daher Leibniz von allem Mystizismus befreien und gewissermaßen einen "reinen Leibniz" präparieren, der als der neue Platon auf der Höhe der Neuzeit verstanden werden könnte.
Das konnte nicht gut gehen. Es war auch gar nicht nötig, lange darauf zu warten, was kommen mußte: bis jemand streng logisch die innere Paradoxie solcher Systeme nachwies (Gödels Erkenntnis der Unbestimmtheit der Grundlagen der Mathematik). Sondern Leibniz wurde in Deutschland von dem in den 1920er Jahren entstehenden Existenzialismus neu und anders gelesen. Die Verwicklung dieser neuen Sichtweise in die Vorgeschichte des Faschismus ist allerdings unübersehbar.
Mathematische Existenz
Leibniz hatte die Grundfragen der Mathematik bis an einen Punkt gebracht, wo es ihm unmöglich wurde, diese noch mit den ihm geläufigen wissenschaftlichen Begriffen zu beschreiben. Er musste erkennen, dass weder das Kontinuitätsprinzip noch die Idee einer universellen Algebra sich nach den seit Euklid bekannten Methoden ordnen oder gar axiomatisieren lassen würden. Sie verwirren sich in einem Labyrinth, da sich diese Prinzipien immer zugleich auf das Objekt der Wissenschaft, was sie erkennen will, und den Erkenntnisprozess, d.h. die Reflexion, wie beim Erkennen vorgegangen wird, beziehen. Sie sind eher Leitideen, die dem Erkennen vorauseilen, wobei dem Erkennen bewusst ist, dass diese Leitideen nie verwirklicht werden können und sogar in gewisser Weise jeder Realitätserfahrung widersprechen. Was ist z.B. von der Vorstellung zu halten, dass die kontinuierlichen Zusammenhänge der Natur nichts anderes sind als die Spuren, die die Mathematik in ihr hinterlassen haben? Eine solche Leitidee kann zwar vom Verstand nachvollzogen werden, indem die Metapher der Spur hilft zu verstehen, was gemeint ist und wie diese Leitvorstellung helfen kann, die Naturforschung zu orientieren. Aber dennoch wird niemand im Ernst vertreten, die Natur sei nichts als die Spuren der Mathematik.
Erst die phänomenologischen Untersuchungen von Husserl haben den Ansatz gefunden, um Fragen dieser Art aufklären zu können. Mit seinem Begriff der Intentionalität, die das Denken leitet und prägt, hat er den "logischen Untersuchungen" einen Weg eröffnet, um hier klarer zu sehen. Mit seinen Forschungen über die Intentionen ist er gerade so weit über Kant hinausgegangen, dass nun ein Verständnis möglich wurde, was Leibniz vorgeschwebt hat. Auch Kant hatte nach regulativen Ideen gefragt, die aller Naturforschung vorausgehen müssen, und war sich ebenfalls bewusst, dass diese regulativen Ideen selbst niemals bewiesen werden können. Aber seine regulativen Ideen waren Leitvorstellungen über die Natur im Ganzen, d.h. Vorstellungen, wie die Natur im Ganzen aussehen könnte, auch wenn sich das nie wirklich beweisen lassen wird und alle Erfolge der Naturwissenschaft immer nur Schritte auf dem Weg zu solcher Gesamterkenntnis sein können. Die Leitvorstellungen von Leibniz dagegen sind keine Vorstellungen über die Natur, sondern sind Leitvorstellungen über Leitvorstellungen des Denkens, die sich ausschließlich im und während des Denkens verwirklichen.
Hier droht der unendliche Prozess der Meta-...-Meta-Logiken der Selbstreflexion, wenn von Vorstellungen von Vorstellungen ... von Vorstellungen gesprochen wird. Das wird dadurch verhindert, dass die Metapher der Spur nicht einfach ein "bloßes Bild" ist, sondern eine religiöse Erfahrung. Die von der Kabbala übernommene Einsicht, dass die Physik und Mathematik dort ihren Gegenstand finden, wo Gott sich zurückgezogen hat, ist nicht eine Wahrheit, die durch eine theoretische Erkenntnis oder als Ergebnis von Denken gefunden werden kann, sondern eine Wahrheit, die dem Menschen in seiner Existenz zustoßen muss.
Diese Begriffe haben Husserl und Kierkegaard folgend Heidegger in den 1920er Jahren entwickelt. Heidegger hat die Struktur solcher Fragen aus ihrem religiösen Kontext entnommen und als Verhältnis von Sein und Seiendes dargestellt. Wie Husserl versteht Heidegger Denken immer als "Denken von etwas". Auch alles Denken in der Mathematik und Naturwissenschaft bleibt in dieser Struktur, einschließlich den regulativen Ideen von Kant. Hier wird immer "von etwas" oder "über etwas" gedacht. Was aber das Sein dieses Etwas ist, kann nicht selbst wieder ein Etwas sein, es ist daher formal-logisch genommen für das Denken Nichts und wird vom Denken nicht erreicht. Es ist dem Menschen nur zugänglich als Ereignis des Seins, das den Menschen in seiner Existenz trifft. Heidegger hat in "Sein und Zeit" Angst und Sorge als Beispiele beschrieben, wodurch der Mensch in seiner Existenz für solche Ereignisse empfänglich wird.
Husserl hat die Tragweite der Ideen seiner Schüler erkannt und entsprechend gefördert. Und es war nur konsequent, als er 1927 Heideggers "Sein und Zeit" in einer Ausgabe des "Jahrbuch für Philosophie und phänomenologische Forschung" gemeinsam mit Oskar Beckers Schrift "Mathematische Existenz" veröffentlichte.
"Mathematische Existenz": Während Heidegger die Grundfragen des Denkens von der Ontologie her lösen will, lässt sich Becker noch viel direkter auf Leibniz ein. Becker beruft sich in allen grundlegenden philosophischen Passagen immer auf Heidegger, insbesondere dessen Vortrag über die Fragen der Zeit, gehalten 1924 in Marburg. Dort bekennt Heidegger sich zur neuen Generation und meint damit die Generation, die von der Jugendbewegung herkommend auf dem Weg zum Faschismus war.
Becker versteht "Mathematische Existenz" als "Mathematisieren", das er wie Philosophieren oder Musizieren als eine "Weise des lebendigen Daseins" (Becker, Mathematische Existenz, S. 441) ansieht, wodurch der Mensch empfänglich wird für die Grundfragen der Mathematik, wie sie Leibniz entwickelt hatte. Aus dem Verständnis der Mathematischen Existenz wird ebenso wenig eine konkrete mathematische Erkenntnis entspringen wie aus dem Verständnis der Angst oder der Sorge eine Erkenntnis im alltäglichen Leben des Menschen. Mathematik vom Mathematisieren her zu verstehen, das setzt bewußt einen Widerspruch zu einer Auffassung, wonach vor allem deshalb geforscht wird, um bestimmte Ergebnisse zu erreichen ("Zielorientierung"). Ergebnisse: Dies wären zunächst mathematische Ergebnisse im engeren Sinn (erfolgreich gelöste Gleichungen, Entdeckung neuer Sätze usw.), dann die damit zu erreichenden persönlichen Ziele wie Ruhm oder materieller Gewinn und schließlich die dem allem zugrunde liegenden Leitideen wie Unsterblichkeit und Allmacht, so wie Platon das konsequent zuende gedacht hat. Solches Forschen läuft immer seinen Zielen hinterher.
Mathematische Existenz kann nicht übersetzt werden in ein neues, umfassendes Axiomensystem, wie es zur gleichen Zeit in den 1920er und 1930er Jahren von der französischen Mathematikergruppe Bourbaki konzipiert wurde ("Architektur der Mathematik"). Mathematische Existenz kann aber erklären, wie im Mathematisieren ein Grundverständnis der Welt "aufgehen" kann, so wie es Leibniz geschehen ist. In diesem Sinn ließe sich die Mathematik von Leibniz viel treffender als barocke Mathematik bezeichnen, um das Lebens- und Weltgefühl anzusprechen, aus dem heraus sie zu verstehen ist.
Bildintentionen, der mathematisch-technische Begriff der Spur
Welchen Fortschritt die Erkenntnis der phänomenologischen Methode bringen konnte, lässt sich aber durchaus genauer beschreiben. Becker nahm Bezug auf die Grundlagendiskussion der Mathematik. Die Fronten von Formalismus und Intuitionismus hatten sich 1927 schon verhärtet, und es war bereits absehbar, dass sie entlang dieses Gegensatzes nicht zu lösen sein würde. Becker neigt zwar eher zum Intuitionismus, wonach die Mathematik immer vom Bereich des sinnlich Anschaulichen, des praktisch Verwirklichbaren ausgehen muß und sich von absoluten Ideen wie dem Unendlichen zu enthalten hat. Aber Becker ist nicht bereit, die Vorstellung des Unendlichen deswegen aufzugeben. Während Russell aus der Perspektive des zu seiner Zeit erfolgreichen Formalismus Leibniz liest, fragt Becker aus der umgekehrten Richtung: Wie kann ausgehend von der Grundposition des Intuitionismus dennoch der Begriff des Unendlichen bestimmt werden?
Als erstes entdeckt er, dass auch Leibniz immer von der anschaulichen Erfahrung ausgegangen ist. Leibniz kannte also das Problem. Und er hatte die Lösung gesehen in der Einführung von Symbolen für das Unendliche (den Differential-Symbolen). "Aber die transfiniten Beziehungen, als solche dem menschlichen Geist unzugänglich, sind in finiten Symbol-Zusammenhängen darstellbar." (Becker, Mathematische Existenz, S. 727)
Worin besteht dann der Unterschied zum Formalismus? Die Formalisten setzen "formal" das Endliche und das Unendliche gleich. Aus ihrer Sicht gelten die Aussagen der Mathematik gleichbedeutend für das Endliche und das Unendliche. Das Endliche und das Unendliche haben die gleiche innere Struktur, philosophisch gesprochen die gleiche Substanz. Nach ihrer Meinung gelten die Aussagen der Mathematik in einer Allgemeinheit, die sich gewissermaßen "anwenden" lässt sowohl auf das Endliche wie das Unendliche. Das ist der Grundgedanke insbesondere der Mengenlehre, woraus dann all ihre Paradoxien erwachsen: Wenn von Mengen gesprochen wird, können darunter sowohl Mengen mit endlich vielen wie auch mit unendlich vielen Elementen verstanden werden, also z.B. die Menge von endlich vielen einzelnen Gegenständen ebenso gut wie die Menge der unendlich vielen natürlichen Zahlen. Die Gesetzmäßigkeiten der Mengenlehre sollen für alle Mengen gelten, unabhängig von der Anzahl ihrer Elemente. Und was für die Mengenlehre gilt, soll sich dann in streng logischer Schlußfolgerung auch auf alle anderen Gebiete der Mathematik auswirken.
Für Leibniz war es dagegen nie eine Frage, dass Unendliches und Endliches qualitativ verschieden sind und daher unmöglich für die Mathematik gleichbedeutend sein können. Aber im Gegensatz zu seinen Vorgängern wollte Leibniz diesen Gegensatz nicht erstarren lassen, Endliches und Unendliches nicht absolut einander gegenüberstellen. Becker versteht Leibniz sehr gut, wenn er von einem Übergang "von der transfiniten (aktual-unendlichen) Ideenwelt Gottes bis zur bloß indefiniten Welt des menschlichen Geistes" spricht (Becker, Mathematische Existenz, S. 727).
"Der zentralste Punkt ist aber vielleicht, dass das Problem der 'universellen Charakteristik', der Darstellung abstrakter, ja jeglicher (menschlicher) Anschauung transzendenten Zusammenhänge durch sinnlich-anschauliche Symbole in den Mittelpunkt seiner Philosophie tritt. Wenn man einen Begriff als den tragenden und eigentlich ausschlaggebenden der Leibnizschen Systeme bezeichnen darf, so ist es der der Repräsentation. In ihm laufen alle Fäden der verschlungenen Motivation des gigantischen Gewebes der Leibnizschen Philosophie zusammen: der grundlegende mathematische Begriff der Abbildung (nicht nur zwischen gleichartigen, sondern auch zwischen [anscheinend] verschiedenartigen Gefügen), der uralte mythisch-magische Gedanke der universellen 'Sympathie' aller Dinge." (Becker, Mathematische Existenz, S. 715)
Das ist die entscheidende Stelle, wo die Übereinstimmung mit Leibniz umkippt. Kritisch ist das Verständnis des Symbols. Während Leibniz dahin tendiert, das Symbol als Spur zu verstehen, die sich am Ende immer entzieht oder wie in einem Labyrinth zu verlieren droht und den menschlichen Geist immer von neuem ratlos zurück lässt, glaubt Becker den Angelpunkt gefunden zu haben, wo sich das Leibnizsche System festigen kann. Bewußt setzt er an dieser Stelle genau den Mystizismus ein, den Russell verbannen wollte, den "uralten mythisch-magischen Gedanken der universellen 'Sympathie' aller Dinge". Dieser Irrweg und seine Konsequenzen werden noch zu betrachten sein.
Denn zugleich gelingt es Becker, die Frage des Differentialsymbols phänomenologisch zu verstehen, und dies enthält im Keim die Lösung des Problems. Das Differentialsymbol bei Leibniz ist zunächst nur ein Zeichen (dx für die Ableitung und ∫ für das Integral). Dies Zeichen ist für sich ebenso ein "finites Symbol" wie die 1 für die elementare Anzahl oder das + für das Addieren. Nur für sich genommen legt es den Fehlschluss der Formalisten nahe, dass es die Mathematik lediglich mit finiten Symbolen zu tun hat, die für sie alle gleichwertig sind, gleichgültig ob sie einen endlichen oder unendlichen Inhalt darstellen.
Doch ist noch einmal zu erinnern, wie Leibniz auf dies Symbol gekommen war: Er war von den geometrischen Skizzen Pascals ausgegangen. Dort hatte er an den Steigungsdreiecken und den an Kurven angelegten Tangenten "gesehen", was gemeint war. Er hatte Pascals Intention verstanden und aufgegriffen. Allerdings hat er dann nicht versucht, diese "Bildintention" als solche zu fassen und klarer darzustellen, sondern hat die "geometrische Ableitung" in der "algebraischen Ableitung" nachvollzogen und dort die Differentialsymbole eingesetzt.
Ohne explizit auf diesen Ursprungspunkt der Differentialrechnung bei Leibniz einzugehen, greift Becker dennoch genau dies auf. Er entwickelt im Abschnitt § 5 a) II B, also an ziemlich untergeordneter Stelle in seiner Arbeit, die "Stufen der Bildgegebenheit". Das sind iterative Bildfolgen, die er "ineinandergeschachtelte Bildintentionen" nennt. Mit ihnen kann anschaulich ein Grenzprozeß dargestellt werden, z.B. die fortschreitende Unterteilung eines Kreises, oder später die Darstellung von überall nicht-stetigen Funktionen. Diese Art von Darstellung ist inzwischen so selbstverständlich geworden, dass kaum mehr zu glauben ist, dass sie erst 1927 von Becker im "Jahrbuch für Philosophie und phänomenologische Forschung" eingeführt wurde. Um deutlicher zu machen, worum es geht, sei ein späteres und bewusst komplizierter gewähltes Beispiel vorgestellt:
Figur 2: Swap Diagram
Quelle: George K. Francis: "Topological Picturebook", Berlin, Heidelberg, New York 1987, S. 141
Mit diesen "Bildintentionen" soll die Idee erklärt werden, wie eine Spirale im Innern "immer spiraliger" wird. Sie zieht sich nicht nur wie in einem Trichter in immer engeren Kreisen zusammen, sondern verknotet sich auch immer komplexer. Je näher an diese kritische Stelle herangegangen wird ("heran-zoomen"), desto komplizierter wird sie. Die Idee des "Ineinanderschachtelns" selbst soll dargestellt werden. Es zeigt sich, wie dafür auch fortschreitend immer mehr Dimensionen notwendig werden. Liegen anfangs zwei Geraden übereinander, so verschieben sich dann Ebenen und schließlich räumliche Figuren ineinander, so dass die Idee einer im Prinzip unendlichen "Dimensions-Explosion" anschaulich vermittelt werden kann.
Zunächst ist einfach verblüffend, gegen welche Widerstände und doch wie unwiderstehlich sich diese bildliche Darstellungsweise der Mathematik behauptet hat. Der "Siegeszug" erfolgte in den 1970er Jahren, als sich unter den Mathematik-Studenten gegen die Literaturvorschläge der Professoren jene Lehrbücher durchsetzten, die auf diesem Weg den Lehrstoff anschaulich aufbereiteten. Sie galten den Professoren als nicht streng genug und fielen unter den Verdacht des Comic-Niveaus, dem Geist der Mathematik unangemessen. Das Mathematisieren drohte aus ihrer Sicht wieder auf die geometrische Anschauung zurückzufallen, aus der sie gerade durch die Axiomatiker von Frege bis Bourbaki befreit worden war. Und tatsächlich geht es auch um Grundsätzliches. Denn es handelt sich keineswegs bloß um eine Frage der Hochschuldidaktik.
Volkert hat im einzelnen nachgewiesen, wie es erst mit den von Becker entworfenen Bildfolgen möglich geworden war, alle die Funktionen anschaulich zu beschreiben, die im 19. Jahrhundert zwar bereits studiert worden waren, aber wegen ihrer Unanschaulichkeit als "Monsterfunktionen" galten. Das am meisten diskutierte Monster trug am 18.7.1872 Weierstraß vor:
f(x) = ![]() bn cos (an xp
)
bn cos (an xp
)
"wobei a eine ungerade Zahl, b eine Zahl zwischen 0 und 1 sein soll und ab > 1 + 3/2p " (Volkert, S. 106)
Eine solche Funktion sieht zwar auf diese Weise hingeschrieben sicher kompliziert, aber im Prinzip völlig normal aus. Wenn aber versucht wird, den zugehörigen Graph zu zeichnen, zeigt sich, dass ihr Verlauf völlig unberechenbar erscheint. Mathematisch gesprochen kann sie nicht abgeleitet werden. Das heißt: Die von Leibniz vorausgesetzte "Urimpression" der Ableitung versagt, wonach die Ableitung die Steigungstangente ist, die durch Steigungsdreiecke angenähert wird.
Die spontane Reaktion der Mathematiker war, wie solche "Monster" ausgeschlossen werden können. Was geometrisch nicht veranschaulicht werden kann, konnte ihrer Meinung nicht "als legitime Bewohner des mathematischen Reiches akzeptiert" werden (Volkert, S. 203). So wurde 25 Jahre lang erfolglos diskutiert, ob nicht eher der Funktionsbegriff entsprechend eingeschränkt werden muß, um solche Monster auszuschließen, bis dann allgemein der Rang solcher Funktionen anerkannt war.
Mit dem Erfolg der Axiomatiker und der frühen Mengenlehre um 1880 - 1910 wendete sich die Grundhaltung unter den Mathematikern vollständig. Nun galten die Monster nicht mehr als bedrohliche Monster, sondern umgekehrt als Beweis, dass es in der Mathematik etwas gibt, was nicht anschaulich darstellbar ist, und daher als Beweis, dass die Mathematik nicht von der Anschauung ausgehen darf. In diesem Sinn berief sich noch 1933 Hans Hahn auf die Monster, um von einer Krise der Anschauung zu sprechen und damit das Programm der Wiener Schule zu begründen.
Becker ist es dagegen mit seinem Ansatz gelungen, auch für Funktionen dieser Art einen Weg für die Veranschaulichung zu finden. Mit den "ineinandergeschachtelten Bildintentionen" lassen sich auch Funktionen beschreiben, die anders als etwa der Wellenverlauf der Sinus-Funktion oder die Parabel der Funktion y = x2 nicht mehr in das Bild eines festen Graphen passen, sondern nur in ähnlicher Weise anschaulich nachvollzogen werden können, wie das oben dargestellte topologische Beispiel.
Inzwischen werden auch alle komplizierteren Techniken bei rekursiven Funktionen oder in objektorientierten Methoden nur auf diese Weise dargestellt. Mit der Verbreitung der elektronischen Datenverarbeitung wurden sie geradezu selbstverständlich und inzwischen ist es umgekehrt notwendig, sich der grundsätzlichen Fragen bewusst zu bleiben, die mit ihrer Einführung verbunden sind (was ist der Geist der Mathematik, wo liegen die Grenzen des mathematischen Reiches).
Becker hatte die Vorgehensweise von Leibniz im Kern getroffen. Wenn erinnert wird, wie weitreichend die Ideen von Leibniz angelegt sind, braucht nicht groß spekuliert zu werden, was diese Erkenntnis in voller Konsequenz bedeuten kann. Ich bin überzeugt, dass diese Art der Darstellungen eine völlige Neuorientierung der Mathematik anzeigen. Alle am Ende des Beitrags über "Symbolische Mathematik" genannten Beispiele weisen in diese Richtung. Becker hatte die Grundidee der fraktalen Geometrie vorweggenommen und befand sich ganz in der Nähe der zur gleichen Zeit von Hilbert und Cohn-Vossen begonnenen "Anschaulichen Geometrie". Hilbert hatte ebenfalls eingesehen, dass es unmöglich sein würde, mithilfe des Formalismus oder einer formalistischen Meta-Mathematik die Grundlagenkrise der Mathematik zu lösen. Auch die möglichen Anregungen für Ästhetik oder Medientheorie sind noch nicht einmal im Ansatz ergriffen.
Die Tiefe der nordisch bestimmten Forschung und das ungeschrieben gebliebene "Buch der Natur"
Aber Oskar Becker scheint nicht bewusst geworden zu sein, welchen Schlüssel er da in Händen hielt. Er hat daher die Phänomenologie um einen ihrer größten Triumphe gebracht. Wie ist das zu erklären? Hierfür ist auf das Zitat zur "universellen Charakteristik" bei Leibniz zurückzukommen. Statt die Darstellungs-Methode der "ineinandergeschachtelten Bildintentionen" als inneren Wesenszug der von Leibniz anvisierten Mathematik zu verstehen, glaubt Becker, den "uralten mythisch-magischen Gedanken der universellen 'Sympathie' aller Dinge" auf der Spur zu sein. Hier liegt die gleiche Kehre vor wie bei Paulis Entscheidung für das Renaissance-Denken eines Robert Fludd gegen die Ideen von Kepler. So hat Becker dann im tiefsten Innern doch wieder zurückgefunden in die platonische Tradition.
Leibniz war an solchen Ideen wie "der universellen 'Sympathie' aller Dinge" keineswegs uninteressiert, sondern hat im Gegenteil in der "Monadologie" versucht, sie mit größter Konsequenz zu Ende zu führen. Aber es stellt sich immer die Frage, wie die Vermittlung zwischen derartigen transzendenten Zusammenhängen und dem menschlichen Anschauungsvermögen hergestellt werden kann. Und da sah Leibniz schließlich keine Möglichkeit mehr, dies voll überschauen zu können. Daher beschränkte er sich auf das Aufdecken von Spuren und sah sich nie in der Lage, seine eigene Idee einer "mathesis universalis" so weit auszuführen, dass sie den eigenen Ansprüchen auch nur annähernd hätte gerecht werden können.
Die größere Zuversicht von Becker stützt sich zunächst - natürlich - auf die gleichen Beispiele, auf die sich auch Russell und Whitehead berufen hatten, als sie vom genau entgegengesetzten Ausgangspunkt herkommend Leibniz' Ideen in ein geschlossenes System umwandeln wollten: die Relativitätstheorie, die nicht-euklidischen Räumlichkeiten, die vieldimensionalen Räume und schließlich die immer abstrakter und unanschaulicher werdenden Theorien etwa der Hilbert-Räume, mit einem Wort auf die Erfolge der Mathematik und Naturwissenschaften im 19. und beginnenden 20. Jahrhundert. Während aber Russell darin die Erkennbarkeit der transzendenten Ideen bestätigt sah, sieht Becker hier die prinzipielle Überlegenheit von Volksgruppen, die neu in die Geschichte der Naturwissenschaft eingetreten sind und wesentlich erfolgreicher mathematisieren können:
"Die abendländische (so stark nordisch bestimmte) Forschung dringt in die 'Tiefe' der Natur in einem der gestalthaft denkenden Antike ganz fremden Maße ein und gelangt schrittweise zu immer weniger anschaulichen Sachverhalten." (Becker, Mathematische Existenz, S. 703)
Das erinnert deutlich an die "Jugendlichkeit der germanischen Seele" bei Jung und den "prometheisch selbstvertrauenden Intellekt" bei Rothacker. Wer von Becker eine etwas präzisere Auskunft bekommen will, worin die neue Qualität des "Nordischen" liegen soll, wird wie nicht anders zu erwarten enttäuscht. So bleibt als ihre spezifische Fähigkeit nur ihr Vermögen, nicht mehr gestalthaft zu denken.
Steht dies nicht im Widerspruch zu seiner eigenen Leistung mit der Einführung der Bildintentionen? Und zugleich geriet er mit seinem Ansatz in Widerspruch zu der unter dem Nationalsozialismus vorherrschenden Strömung der "Deutschen Mathematik", die genau umgekehrt darin die Überlegenheit des Nordischen oder Deutschen sah, "dass die wohlentwickelte Raumanschauung ein vorherrschendes Merkmal der Deutschen Rassen ist, während der rein logische Sinn bei den romanischen und hebräischen Rassen reicher entwickelt ist." (Bieberbach, S. 357) Bieberbach war ein Begründer der Differentialgeometrie, und deren anschauliche Vorstellungsweise war es dann, von wo aus über den Weg der Differentialtopologie einige Jahrzehnte später die Methode der Bildfolgen buchstäblich wiederentdeckt werden musste. Becker fühlte sich in eine Sackgasse geraten und stellte die mathematische Forschung immer mehr zurück zugunsten ästhetischer und fundamentalontologischer Arbeiten, in denen er Heidegger noch an "Tiefe" übertreffen wollte ("Dasein und Dawesen").
Aber nicht nur Husserl hatte die mögliche Tragweite der Ergebnisse des Ansatzes von Oskar Becker erkannt. In Freiburg war Becker bei Husserl Nachfolger auf der Assistentenstelle von Heidegger geworden. 1931 wurde Becker auf Wunsch von Rothacker nach Bonn berufen.
Rothacker hatte zweifellos eine sehr konkrete Vorstellung, als er Becker zu sich nach Bonn holte. Seine Arbeiten gingen in eine ganz ähnliche Richtung. In seinen psychologischen Experimenten arbeitete er mit Filmstudien von Buytendijk, die in kurzen Sequenzen typische Bewegungsabläufe zeigen, z.B. den Kampf einer Kobra und eines Mungo, ein Tennisturnier oder ein tanzendes Paar (mit einem aufdringlichen männlichen und einem abweisenden weiblichen Partner). Rothacker wollte anhand dieser Beispiele zeigen, wie sich das Handeln intuitiv an ganzen vorgeprägten Bildern und Handlungssequenzen orientiert. Er bezeichnete dies als "Imagines" oder "imagomotorische Reaktionen" (Rothacker, Genealogie).
Für mich besteht kein Zweifel, dass Rothacker hier weit ausgreifend einen neuen Ansatz für die Mathematik suchte und dies als Grundlage für sein Lieblingsprojekt zum "Buch der Natur" nehmen wollte. Offenbar war seine unbestimmte Absicht, sowohl Ideen von Jung ("Imago") wie über Becker aus der phänomenologischen Forschung aufzugreifen. Denn es ist klar zu erkennen, dass sich die "ineinandergeschachtelteten Bildintentionen" und die Idee der "imagomotorischen Reaktionen" zu einer gemeinsamen Methode hätten entwickeln lassen, die der Philosophie von Rothacker eine klare Grundlage hätten geben können. Aber so ist es für sein "Buch der Natur" bei einer Skizzensammlung geblieben, die erst nach seinem Tod veröffentlicht wurde.
"Zum Ziele führen könnte hier aber nur eine eingehende geistesgeschichtliche Untersuchung. Sie müßte einmal die Gedankenwelt der spätantik-mittelalterlichen 'Typologien', wie des Platonismus, Neupythagoräismus, der Logos-Philosophie, der Sympathie-Metaphorik, der Apokalyptik, Gnosis und Patristik, der hermetischen und kabbalistischen Traditionen umfassen, aber auch deren Renaissance im frühen Pietismus und die von Friedrich von Bezold und dem Kreise um Aby Warburg erforschten astrologischen und alchimistischen Weltbilder. Die Untersuchung hätte nicht zuletzt noch das Analogieproblem methodisch in Angriff zu nehmen." (Rothacker, Buch der Natur, S. 27)
Auch Rothacker hätte Becker in seiner Kehre zur platonischen Tradition bestärkt. Letztlich wurde als das "Nordische" die Hoffnung verstanden, zum direkten Blick in die Natur und ihre Rätsel zu finden, wie er bei den Alchemisten der Renaissance vermutet wurde. Die Philosophen des "Herrenvolks" hofften, ähnlich in den Kreis der "Auserwählten" aufgenommen zu werden, wo sie trotz aller Kritik am Anfang ihrer neuen Ideen Platon sahen. Die Mathematik-Vision von Leibniz war wie die von Kepler einmal kurz angerührt, und wurde dann ebenso schnell wieder fallen gelassen.
Literaturhinweise
© tydecks.info 2002, 2003