Walter Tydecks
Zur Geschichte der Geometrie
Inhaltsverzeichnis
Pythagoreeische und euklidische Geometrie
Arithmetik in der Renaissance
Galois-Theorie
Differentialgeometrie
1. Pythagoreeische und euklidische Geometrie
Die pythagoreeische Geometrie entstand am Ende einer 300 Jahre dauernden Umwälzung der griechischen Gesellschaft. Gegen die Grundbesitzer und Kriegskönige revoltierten die Bauern, zunehmend unterstützt von den Bergarbeitern und Handwerkern in den Städten. Anders als im Mittelalter spielte sich das Geschehen allerdings ideologisch nicht innerhalb der vorgefundenen Weltanschauung ab. Im Gegenteil schuf fast jede Generation ihre eigene Götter- und Weltanschauung, ihre eigene Naturkunde. Und verschiedene Weltanschauungen standen neben- und gegeneinander. In den bäuerlich beeinflußten Kosmogonien von Hesiod und den nachfolgenden orphischen Mythen wurden die elementaren Naturprozesse dargestellt. Mit wachsendem Selbstbewußtsein gewann die wissenschaftliche Methode an Bedeutung. Erst so um 540 v.u.Z konnte der Erfolg der demokratischen Bewegung konsolidiert werden. Zu dieser Zeit schufen Thales und sein Schüler Anaximander die ersten rein naturphilosophischen Systeme.
In dieser Tradition entstand unmittelbar nachfolgend etwa 500 v.u.Z. die phythagoreeische Geometrie. Mathematik war bis dahin im wesentlichen in Asien entwickelt worden. Sie hatte da überwiegend den Rang einer angewandten Verwaltungswissenschaft, mit der verschiedene im alltäglichen Leben anfallende Probleme gelöst wurden: einfache oder auch kompliziertere Rechenaufgaben in Erbschaftsregelungen, Berechnungen von Dammbauten, Sternenbewegungen etc. Die asiatischen Kenntnisse waren in Griechenland teilweise bekannt. Die Phythagoreer gingen jedoch vollkommen anders an die Mathematik heran. Sie waren Demokraten. Pythagoras kam aus einer Handwerkerfamilie. Sie verstanden sich als eine Art Sekte, die eine neue freiere Lebensform verwirklichen wollte. Unter ihrem Einfluß entstanden kleine Stadtrepubliken. Wie bei anderen griechischen Bewegungen waren ihre politischen und ethischen Ideen untrennbar mit ihrer Naturanschauung verbunden. Die Naturwissenschaft hatte sich noch nicht spezialisiert. Die Phythagoreer vertreten ein Lebensgefühl, das Leben in der Natur und gesellschaftliches Leben umfaßte. Oft wird vom Geborgenheitsgefühl der Griechen in der sie umgebenden Natur und Gemeinschaft gesprochen, wogegen der Individualismus und die Einsamkeit des modernen Menschen abfallen. Wenn es das gab, dann haben die Phythagoreer es bewußt ausgesprochen.
Die Grundlage der Welt war für sie die Zahl. Das klingt paradox für eine naturverbundene Weltanschauung. Aber Zahl ist bei ihnen als Maß zu verstehen. Sie gingen davon aus, dass Natur und Gemeinschaft harmonisch sind und die Harmonie sich in festen Maßzahlen ausdrückt, die durch Naturbeobachtung und Berechnung gefunden werden können. Mathematik war für sie der Zusammenklang der Maße, was ganz wörtlich zu verstehen ist. Ihre mathematischen Untersuchungen entstanden in musikalischen Experimenten mit Saiteninstrumenten und Hohlgefäßen. Da entdeckten sie, dass die schön klingenden Melodien auf einer Tonleiter von 12 Tönen basieren, die in einem gleichmäßigen Verhältnis zueinander stehen. Und zwischen diesen Tönen gibt es wiederum ausgezeichnete Harmonien, die Oktav, Quint, Quart, Terz, die alle durch mathematische Proportionen zu beschreiben sind. Die mathematische Musikästhetik ist das Urbild der pythagoreeischen Mathematik.
Im nächsten Schritt suchten sie nach Zwischentönen, die im harmonischen Verhältnis zu zwei vorgegebenen Tönen stehen. So wurde für das Quartverhältnis 4 : 3 ein Zwischenton x gesucht, für den gelten soll:
4 : x = x : 3
Diese Gleichung kann in eine quadratische Gleichung umgeformt werden:
x · x = 3 · 4 bzw. gleichbedeutend: x2 = 12
Und für diese Gleichung gibt es nur Lösungen durch die Irrationalzahlen +√12 und -√12.
Von hier führte der Weg direkt zur Geometrie. Das Verhältnis 4 : x = x : 3 konnte zu a : x = x : b verallgemeinert und in die Gleichung x2 = a · b umgeformt werden. Da die Griechen keine arithmetischen Methoden zu ihrer Lösung kannten, schlugen sie einen geometrischen Weg ein. Die Gleichung x2 = a · b kann auch als geometrische Aufgabe formuliert werden: Zu einem Rechteck mit den Kantenlängen a und b ein Quadrat mit der Kantenlänge x zu finden, das den gleichen Flächeninhalt hat. Und diese Aufgabe konnte geometrisch mit Lineal und Zirkel gelöst werden.
Die Ideale der pythagoreeischen Mathematik waren jedoch nur von kurzer Dauer. Griechenland wurde zur Sklavenhaltergesellschaft. Wissenschaft und Kultur verselbständigten sich von der unmittelbaren Produktion. Der historisch einmalige Impuls der pythagoreeischen Bewegung war vorbei. Er hinterließ aber die Idee einer in Axiomen wohlgeordneten Mathematik, die die Harmonien der Natur ausdrückt. Nach den Pythagoreern folgten zunächst scharfe Kritiker, die auf innere Widersprüche hinwiesen und sie zu Paradoxien zuspitzten. Parmenides war anfangs selbst Pythagoreer gewesen. Er und Zenon bewiesen die inneren Widersprüche einer Philosophie, die auf den abstrakten Begriffen vom Einen, Ganzen, vom Sein und der Bewegung aufgebaut ist. Platon verflüchtigte dagegen die Idee einer harmonischen Mathematik zur geometrisch orientierten Ideenlehre.
In Nachfolge der Pythagoreer wurde in den über 100 Jahren von 440 bis 303 v.u.Z. die euklidische Geometrie entworfen. Die "Elemente der Geometrie" von Euklid sind ein abschließendes Werk, in dem die Kenntnisse der griechischen Geometrie zusammengefaßt sind. Erste Arbeiten stammten von Oinipides, der erste systematische Entwurf 430 v.u.Z. von Hippokrates, ganze Teile schufen Archytas und Eudoxos. Ins Zentrum der Forschung rückten das Studium des Unendlichkeitsbegriffs und der offenen Fragen, die innerhalb der Geometrie unbeantwortet blieben.
Die Geometrie geht keineswegs nur von Axiomen aus. Fast noch interessanter sind die Definitionen und Postulate. In den Definitionen sind die Objekte der Geometrie erklärt, in den Postulaten die Konstruktionsmethoden. Die Axiomatik umfaßt nicht weiter beweisbare Eigenschaften der Objekte, z.B. dass das Ganze größer ist als eins seiner Teile. Definitionen und Axiome sind aber nicht klar voneinander zu trennen, da auch die Definitionen Eigenschaften der Objekte beschreiben.
Es ist eine Idee der euklidischen Geometrie, die Frage der Unendlichkeit nicht weiter philosophisch zu diskutieren, wie es zur gleichen Zeit Platon und Aristoteles taten, sondern ihren Umfang in Definitionen zu umschreiben und durch die Konstruktion mit Lineal und Zirkel festzulegen, wie widerspruchslos damit gearbeitet werden kann. Schon hieraus geht hervor, dass es sich bei der euklidischen Geometrie in Wahrheit um ein offenes System handelt.
"Definitionen. 1. Ein Punkt ist, was keine Teile hat. ... 23. Parallel sind gerade Linien, die in derselben Ebene liegen und dabei, wenn man sie nach beiden Seiten ins Unendliche verlängert, auf keiner einander treffen." (zitiert nach Becker "Grundlagen der Mathematik", S. 88f)
Dies sind die beiden entscheidenden Definitionen, in denen eine mathematische Theorie der Unendlichkeit vorausgesetzt wird. Die Definition des Punktes entspricht ganz der Definition eines Atoms. Der Punkt ist gegenüber der Linie unendlichkurz, wie die Fläche gegenüber dem Körper unendlichflach ist. Im anderen Extrem verlangt die Definition der Parallelität die Vorstellung einer unendlichweiten Ebene. Ob diese Unendlichkeit wirklich existiert, wird ausdrücklich außer Acht gelassen. Und obwohl Mathematiker wie Archytas und Eudoxos im engen Zusammenhang zu Platon standen und alle Mathematiker ihrer Zeit von Parmenides beeindruckt waren, wird auf die philosophische Definition offenbar bewußt verzichtet.
Der Sinn dieser rein mathematischen Definitionen zeigt sich in den Postulaten, mit denen die Konstruktionsverfahren mit Lineal und Zirkel festgelegt werden. Die philosophischen Paradoxien der Bewegung und des Unendlichen hatten zwar das Bewußtsein über die Eigentümlichkeiten dieser Begriffe schlagartig erhellen können, führten aber auch in eine gewisse Erstarrung. Die wurde durch die euklidische Geometrie überwunden. Der spätere neuplatonische Kommentator Proklos (410 - 485) hat dies genau erkannt. Szabo zitiert:
"Die Möglichkeit, von jedem beliebigen Punkt zu jedem beliebigen Punkt eine Gerade zu ziehen, folgt daraus, dass die Linie ein Fließen des Punktes ist, und die Gerade ein gerichtetes und unablenkbares Fließen. Stellen wir uns also vor, der Punkt führe eine gleichgerichtete und kürzeste Bewegung aus, so werden wir zu dem anderen Punkte hingelangen ... Würde aber jemand Schwierigkeiten geltend machen durch die Frage, wie wir Bewegung hineintragen in die unbewegte geometrische Welt und wie wir das, was keinen Teil hat (nämlich den Punkt) bewegen: denn das sei völlig undenkbar - so wollen wir ihn bitten, sich nicht allzu sehr zu grämen ... Die Bewegung müssen wir uns nicht körperlich, sondern vorstellungsmäßig vorstellen; und wir dürfen nicht zugeben, dass das, was keinen Teil hat (der Punkt) körperlicher Bewegung unterworfen sei, dass es vielmehr Bewegungen der Phantasie unterliege." (Proklos, zitiert nach Szabo "Die Anfänge der griechischen Mathematik", S. 374-376)
Dass der euklidischen Geometrie dennoch ein tiefer philosophischer Anspruch zugrunde lag, ist an der Konsequenz zu erkennen, mit der die axiomatische Methode durchgehalten wurde. Sie wurde in der Mathematik regelrecht zur Grenzlinie, zum Prüfstein, wie weit die auf Axiomen abgesicherten Konstruktionsverfahren tragen. Auf drei unlösbare Probleme stieß die euklidische Geometrie:
-
Kann der Kreis quadriert werden, d.h. gibt es ein Verfahren, mit Lineal und Zirkel aus dem Durchmesser eines Kreises die Kantenlänge eines Quadrates mit dem gleichen Flächeninhalt zu konstruieren. Insbesondere Eudoxos entwickelte exakte Verfahren, den Kreis durch einbeschriebene und umschriebene Vielecke anzunähern und lieferte damit die Beweisidee, mit der im 19. Jahrhundert Riemann die Integralrechnung begründete.
-
Kann der Würfel verdoppelt werden, d.h. gibt es ein Verfahren, aus einer Strecke eine andere größere Strecke zu konstruieren, so dass der Würfel mit der Kantenlänge der größeren Strecke genau das doppelte Volumen hat wie der Würfel mit der Kantenlänge der Ausgangsstrecke. Archytas hatte ein kompliziertes Verfahren hierfür gefunden, das jedoch nicht mit Lineal und Zirkel auskam.
-
Kann ein beliebiger Winkel in drei gleichgroße Teile geteilt werden.
Erst Galois konnte Anfang des 19. Jahrhunderts diese Fragen beantworten. Die euklidische Geometrie war in dem Sinne als ein offenes System entworfen worden, als sie gerade nicht einfach eine platte Zusammenstellung des damals bekannten mathematischen Wissens war, sondern ein Entwurf, dessen Grenzen unbekannt waren und innerhalb der Geometrie nur als offene Fragen erkannt werden konnten.
2. Arithmetik in der Renaissance
Über 2000 Jahre blieben die offenen Fragen der euklidischen Geometrie ungelöst. In Europa geriet Euklid bis ins 12. Jahrhundert regelrecht in Vergessenheit. Anders in Arabien. Die mathematische Schule in Bagdad begann um 700 ihre Arbeit mit Übersetzungen der antiken Texte, u.a. von Euklid, Archimedes, Appolonios, Heron, Ptolemaios, Diophantos. Bei den Arabern stand die Mathematik stets in engem Zusammenhang zu Astronomie und Landvermessung, d.h. zu Aufgabenstellungen, die aus der Landwirtschaft erwuchsen. Naturgemäß richtete sich daher ihr Interesse auf die Geometrie. Erwähnt seien die "Kommentare zu den Schwierigkeiten in den Einführungen des Buches von Euklid" von Ummar al-Hayyam aus dem Jahr 1077. Ausgehend von den griechischen Betrachtungen zu den Irrationalzahlen wurde hier der weiterreichende Begriff der positiven reellen Zahlen entwickelt, d.h. die Menge aller Zahlen, die durch Grenzverfahren angenähert werden können. Hierbei entwickelten die arabischen Mathematiker ungewöhnliche Fähigkeiten. 1424 gelang es Al-Kasi, die reelle Zahl π (pi) bis auf 17 Stellen hinter dem Komma anzunähern. Die Araber führten das Wurzelzeichen und die Trigonometrie ein. Und besonders in der Arithmetik gelangen ihnen große Erfolge. Sie lösten zahlreiche kubische Gleichungen (Gleichungen der Gestalt ax3 + bx2 + cx + d = 0) und mit arithmetischen Methoden konnte Al-Kasi auch die Frage der Dreiteilung des Winkels lösen. Hieran ist sowohl bemerkenswert, dass erkannt wurde, dass dies geometrische Problem durch eine kubische Gleichung ausgedrückt werden kann, und dass diese dann tatsächlich auch gelöst werden konnte.
Als aber Euklid in Europa wieder bekannt wurde, feierte er einen ungewöhnlichen Siegeszug. Bis zu Beginn des 20. Jahrhunderts waren seine "Elemente" neben der Bibel das meistgedruckte Buch und von den "Principia" des Newton bis zu den "Elementen der Mathematik" von Bourbaki orientierten sich alle systematischen Entwürfe in der Mathematik daran.
In der Renaissance wurde Euklid auf dem Umweg über Arabien bekannt. Allerdings gab es in der Renaissance keine reinen Mathematiker, geschweige denn reine Geometer. Während die Naturforscher sich mit den verschiedensten ausgefallenen Mustern in der Natur beschäftigten, fiel die Mathematik jetzt weit stärker noch als in Griechenland in den Bereich der Geisteswissenschaft, ja im Grunde in die Sprachwissenschaft. Dies schon allein deswegen, da damals die Mathematiker die arabische Sprache beherrschen mußten, so wie heute die englische.
Und wieder richtete sich das Interesse auf eigentümliche Zeichensysteme und Muster, also auf ägyptische Hieroglyphen, auf die Schriftvirtuosität der Araber, und das mathematische Zeichensystem erschien als eine Sprache unter anderen. Mathematik war ein Forschungszweig wie Papyrologie oder Archäologie. So wurden in der Renaissance in der Mathematik eher asiatische als griechische Traditionen fortgeführt. Weit im Hintergrund stand die chinesische Mathematik, Quelle und Motor der Mathematikgeschichte bis in die Neuzeit. Von dort kommen die ältesten mathematischen Zeichen, überliefert auf Zauberwürfeln aus dem 14. bis 11. Jahrhundert v.u.Z. Und noch im 14. Jahrhundert, also zeitgleich zur Renaissance, erschien eine der bemerkenswertesten mathematischen Arbeiten von Zhu Shie-jie unter dem Titel "Jaspisspiegel der vier Elemente", in dem die ungewöhnliche Leistung gelang, einige nicht-lineare Gleichungen mit 4 Unbekannten zu lösen.
In der Renaissance wurde zwar die Axiomatik des Euklid bewundert, aber die eigene Forschung ging andere Wege. Es sollten keine neuen Systeme entworfen werden, sondern mit den Zeichensystemen wurde rumexperimentiert, zahlenmystische Spekulationen angestellt etc. Hier lagen die überaus verwickelten arithmetischen Rechnungen der Araber näher als die Geradlinigkeit der euklidischen Geometrie. Die Gedankenwege dieser Mathematik sind praktisch nicht nachvollziehbar, sie führten aber zu klaren, überprüfbaren Ergebnissen. Hatten die Araber einzelne kubische Gleichungen gelöst, so gelang es nun, allgemeingültige Lösungsalgorithmen für alle Gleichungen 3. und 4. Grades zu finden. Auch dies ist in der Mathematikgeschichte eine einmalige Leistung, die so wohl nur im Umkreis des eigenartigen Tiefgangs der Renaissance-Forschung möglich war.
Schon vor den Griechen war bekannt, wie eine quadratische Gleichung ax2 + bx + c = 0 allgemein gelöst werden kann. Allgemeine Lösung bedeutet, dass ein allgemeingültiger Algorithmus gefunden wird, der aus den Koeffizienten der Gleichung (hier a, b und c) nur mit den Methoden der rationalen Operationen (Addieren, Subtrahieren, Multiplizieren, Dividieren) und Wurzelziehen die Lösung findet. Nach diesem Algorithmus kann die Gleichung in die Gestalt x = ... umgeformt werden, wobei auf der rechten Seite ein arithmetischer Ausdruck steht, der nur noch die Koeffizienten enthält. In diesem Fall lautet die Lösung:
| (1) | ax2 + bx + c = 0 | |
| (2) | ax2 + bx = − c | | auf beiden Seiten c abziehen |
| (3) | x2 + (b/a)x = − (c/a) | | auf beiden Seiten durch a teilen |
| (4) | x2 + (b/a)x + (b/2a)2 = − (c/a) + (b/2a)2 | | auf beiden Seiten (b/2a)2 addieren |
| (5) | (x + b/2a)2 = − (c/a) + (b/2a)2 | | Anwendung der Formel (a + b)2 = a2 + 2ab + b2 |
| (6) | (x + b/2a) = √(− (c/a) + (b/2a)2) | | auf beiden Seiten Wurzel ziehen |
| (7) | x = √(− (c/a) + (b/2a)2) − b/2a | | auf beiden Seiten b/2a abziehen |
Weitaus komplizierter sind entsprechende Algorithmen für die Gleichungen 3. und 4. Grades:
ax3 + bx2 + cx + d = 0
ax4 + bx3 + cx2 +dx + e = 0
Bei der Lösung der Gleichung 2. Grades bestand die Beweisidee darin, die Formel (a + b)2 = a2 + 2ab + b2 anzuwenden. Zur Lösung der Gleichungen 3. und 4. Grades wird x geschickt durch einen anderen Ausdruck ersetzt, wodurch die Gleichung zunächst komplizierter wird, dann aber in einem Gegenlauf wieder vereinfacht werden kann. (Heute werden Gleichungen dieses Typs durch Exponentialfunktionen gelöst.) Die allgemeine Lösung der Gleichung 3. Grades fanden 1515 die Italiener Ferro und Fontana, die Lösung der Gleichung 4. Grades 1545 Cardano. Damit war die Arithmetik der Renaissance erheblich über die Kenntnisse der arabischen Arithmetik hinausgekommen. Natürlich stellte sich die Frage, ob es auch für Gleichungen 5. Grades und höheren Grades arithmetische Lösungsverfahren gibt. Trotz aller Suche wurde nichts gefunden und folglich sollte umgekehrt bewiesen werden, dass ein solcher Algorithmus nicht existieren kann. Auch das konnte aber nicht gezeigt werden. Wie die euklidische Geometrie war die Arithmetik an eine offene Frage gestoßen. Allerdings war den Mathematikern der Renaissance nicht bewußt, wie nahe beieinander die Lösungen auf beiden Gebieten liegen. Dies zu erkennen und damit auf einem Schlag auf beiden Gebieten die Lösungen zu finden, war die Leistung von Evariste Galois.
3. Galois-Theorie
Im 19. Jahrhundert dominierte an den Universitäten die euklidische Geometrie alle Naturwissenschaften. Mit der Französischen Revolution entstand an der neugegründeten École polytechnique unter Federführung von Lagrange und Laplace die Idee, zunächst die Physik und die Elektrostatik nach dem Vorbild von Euklid zu axiomatisieren. Hierfür mußte Euklid nur geringfügig neu gelesen werden. Die Definition des Punktes wurde endgültig als Definition eines Atoms verstanden. Die Beschreibung der Konstruktionsverfahren mit Lineal und Zirkel durch die Postulate wurde so interpretiert, dass alle Bewegungen des Punktes auf Rotation (Kreis) und lineare Bewegung (Gerade) zurückzuführen sind. In diesem Verständnis ließ sich die Geometrie von Euklid auf die Physik übertragen. An die Stelle des Punktes tritt das Basiselement, das die jeweilige Naturwissenschaft charakterisiert, so das Massepartikel in der Mechanik oder die Elementarladung in der Elektrostatik. An die Stelle der Konstruktion mit Lineal und Zirkel treten jeweilige Naturgesetze, die wiederum wie in der euklidischen Geometrie alle Bewegungen auf Rotation und lineare Bewegung zurückführen. In der Mechanik legen das Trägheits- und das Wirkungsgesetz fest, dass ein Partikel ohne Krafteinwirkung geradlinig durch den Raum fliegt und alle Bewegung den kürzesten Weg geht, also auf Geraden verläuft. Mit dem Gravitationsgesetz ist gesetzt, dass die Anziehungskräfte vom Abstand zwischen den anziehenden Körpern abhängig sind. Hieraus ergibt sich für zusammengesetzte Bewegungen in der Nähe eines Gravitationszentrums (z.B. von Planeten im Sonnensystem) die Rotation, indem Trägheits- und Gravitationsgesetz zusammenwirken und in der Kreis- bzw. Ellipsenbewegung resultieren. Und damit war eine Vorstellung verwirklicht, die den Griechen (insbesondere Archimedes) immer vorschwebte: die Geometrie mit mechanischen Gesetzmäßigkeiten statt mit Lineal und Zirkel zu betreiben.
Nach diesem Erfolg in der Physik sollten alle Naturwissenschaften ähnlich axiomatisiert werden. In allen Fällen sollte die Materie auf die Zusammensetzung endlich vieler Atome zurückgeführt werden und jede Bewegung auf Rotation und lineare Bewegung der Atome. Dies ist der Kern der Mechanisierung der Naturwissenschaften. Er blendete auch eine ganze Strömung von Kritikern der Naturwissenschaft, ausgehend von Nietzsche, für die Naturwissenschaft nicht anders denkbar und daher prinzipiell zu kritisieren war.
Aber schon zu Anfang des 19. Jahrhunderts stellte Galois die Gültigkeit der euklidischen Geometrie grundlegend in Frage. Er bewegte sich weitab vom universitären Forschungsstrom und wurde nie an die Universität aufgenommen. Er nahm an der bürgerlichen Revolution 1830 in Paris teil und wurde wahrscheinlich deswegen in verschiedene Intrigen verwickelt, die zu seinem frühen Tod in einem Duell führten. Seine mathematischen Arbeiten liegen im wesentlichen nur als Skizzen vor.
Ausgangspunkt ist die Erkenntnis, dass die offenen Fragen der Arithmetik aus der Renaissance und die offenen geometrischen Fragen im Prinzip den gleichen Charakter haben. Vielleicht ist er einfach so vorgegangen, dass er versucht hat, auch die Arithmetik nach dem Vorbild der euklidischen Geometrie zu axiomatisieren und dabei überraschende Parallelen aufgedeckt hat. Das Ergebnis seiner Forschung war, dass die euklidische Geometrie ihrerseits auf ein anderes Axiomsystem zurückgeführt werden kann: die Arithmetik der komplexen Zahlen. Hierdurch erschienen aber die Bewegungen in der euklidischen Geometrie unter einem neuen Gesichtspunkt. Sie lassen sich als arithmetische Operationen mit komplexen Zahlen darstellen. Mehr noch: Es kann genau gezeigt werden, welche arithmetischen Operationen den geometrischen Bewegungen entsprechen und welche nicht. Damit war die Grenze der euklidischen Geometrie gefunden. Als Teilresultat ergab sich, dass die offenen Fragen der Griechen innerhalb der euklidischen Geometrie unlösbar sind wie auch die Gleichungen ab dem 5. Grad.
Damit ist der Absolutheitsanspruch der Axiomatik erschüttert. Es gibt nicht nur nicht-euklidische Geometrien (Geometrien, in denen sich Parallelen schneiden, z.B. Geometrie auf der Kugel), sondern es ist am Beispiel der euklidischen Geometrie gezeigt, wie eine Axiomatik auf eine andere zurückgeführt werden kann, deren Horizont weiter ist.
In Geometrie und Arithmetik sind jeweils ganz bestimmte einfache Beweisschritte zugelassen: in der Geometrie Kreis und Gerade, in der Arithmetik Addition, Subtraktion, Produkt, Division, Wurzelziehen. Der gesamte Beweisgang setzt sich aus endlich vielen einfachen, aufeinander aufbauenden Beweisschritten zusammen. In der Geometrie ist das Ziel, aus einer Figur eine andere zu konstruieren, z.B. aus einem Kreis ein Quadrat. In der Arithmetik ist eine Gleichung so umzuformen, dass auf der einen Seite nur die Variable steht und auf der anderen ein arithmetischer Ausdruck der Koeffizienten.
Galois ging es nun nicht direkt um die Lösung eines einzelnen Problems, einer einzelnen Gleichung oder einer einzelnen Konstruktionsaufgabe, sondern er wollte allgemein untersuchen, welche Lösungsmöglichkeiten überhaupt in einem mathematischen Gebiet vorkommen können. Er untersuchte daher die Eigenschaften des Lösungsweges statt der Eigenschaften einer einzelnen zu lösenden Aufgabe.
Dafür waren zunächst die geeigneten Begriffe zu finden (die moderne Algebra). Ausgangspunkt ist der (mathematische) Körper. Eine Menge von Zahlen (Punkten) bildet einen Körper, wenn alle Summen, Differenzen, Produkte und Brüche von Elementen dieser Menge wieder zur Menge gehören. Und die Elemente müssen natürlich Eigenschaften haben, dass mit ihnen diese Rechenoperationen ausgeführt werden können. Die ganzen Zahlen sind kein Körper, da viele Brüche von ganzen Zahlen einen Rest ergeben. Während 10 / 5 = 2 wieder ganz ist, ergibt 7 / 4 die ganze Zahl 1 mit Rest 3. Musterbeispiel für einen Körper sind die rationalen Zahlen, die gewissermaßen per Definition alle Produkte und Brüche enthalten.
Um den allgemeinen Charakter des Körperbegriffs zu verdeutlichen, soll ein anderes Beispiel vorgestellt werden, ein Körper mit endlich viel Elementen, die auf einem Kreis angeordnet sind.
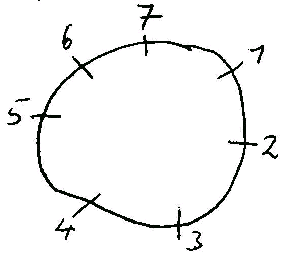
Figur 1 Körper mit 7 Elementen, die auf einem Kreis angeordnet sind
Freihandzeichnung
Die bekannten arithmetischen Operationen können leicht übertragen werden. Übersteigen Summe oder Produkt zweier Zahlen den Maximalwert 7, dann wird einfach der Kreis nochmals oder mehrfach durchlaufen, bis das Resultat gefunden ist. Z.B. gilt 2 · 6 = 5, wobei als Umrechnung vorgenommen wurde: 2 · 6 würde gewöhnlich 12 ergeben, d.h. hier muß über die 7 hinaus bis zur 5 weiter gegangen werden gemäß: 2 · 6 = 12 = 7 + 5. Auf diese Weise ist gesichert, dass Summen und Produkte nicht aus der Menge der Zahlen 1, 2, 3 ,4 ,5 ,6 ,7 hinausführen.
Die Umkehroperationen sind auf diese beiden Operationen zurückzuführen. So kann die Gleichung x = 7 / 3 durch die Umkehrung in 3 · x = 7 gelöst werden. Es ist also ein x zu finden, so dass das Produkt 3x nach eventuell mehrmaligen Durchlaufen des Kreises auf die 7 fällt. Eine Lösung ist 7 da 3 · 7 = 21 = 7 + 7 + 7 gilt. Auch die Brüche führen also nicht über die vorgegebene Menge hinaus. Schon anschaulich wird klar, dass die Idee des Körpers darin liegt, dass die Zahlen nicht nur auf der Zahlengerade liegen müssen wie in der klassischen Arithmetik, sondern auch räumlich angeordnet werden können wie in diesem Beispiel auf einem Kreis. Mit dem Körper wird die alte Vorstellung der Zahlen verlassen. Oder umgekehrt: Es wird erkannt, dass die Anordnung der Zahlen auf der Zahlengerade nicht nur ein anschauliches Hilfsmittel ist, sondern eine geometrische Eigenschaft der Zahlen, die Auswirkungen auf die Lösungen von Gleichungen hat.
Beim Lösen von Gleichungen ist aber auch das Wurzelziehen zugelassen. Hierdurch kann eine Irrationalzahl entstehen, die über den Körper der rationalen Zahlen hinausgeht, in ihm nicht enthalten ist. Dadurch entsteht ein neuer Körper, der außer den rationalen Zahlen auch alle Produkte von rationalen Zahlen mit dieser einen neuen Irrationalzahl umfaßt. Dieser Körper enthält als Teilmenge den Körper der rationalen Zahlen und gilt daher als Erweiterungskörper.
Damit kann der Beweisgang beim Lösen von Gleichungen beschrieben. werden. Ausgangspunkt ist der Körper der rationalen Zahlen, dem alle Koeffizienten entnommen sind. Dann folgen zwei Typen von Beweisschritten: entweder wird eine Wurzel gezogen, und damit ein Erweiterungskörper erreicht. Oder es wird addiert, subtrahiert, dividiert, multipliziert, und damit innerhalb des jeweils erreichten Erweiterungskörper eine Operation ausgeführt. Der ganze Beweisgang kann dargestellt werden als Kette aufeinander folgender Erweiterungskörper.
Die Frage der Lösbarkeit von Gleichungen ist damit die Frage, ob die Lösungen in einem Körper liegen, der durch eine Kette von Erweiterungskörpern erreicht werden kann. Genau das ist bei Gleichungen 5. und höheren Grades im allgemeinen ausgeschlossen. Galois konnte das beweisen, indem er die Kette der Erweiterungen ihrerseits als selbständiges mathematisches Objekt auffaßte (Galois-Gruppe) und ihre Eigenschaften untersuchte. Nur unter bestimmten Bedingungen (Endlichkeit, Auflösbarkeit) führen sie zum Ziel. Rückblickend können die Eigenschaften dann bereits an den Gleichungen überprüft werden, bevor ein Lösungsweg gesucht wird.
Auf die gleiche Weise konnten die offenen Fragen der Geometrie entschieden werden. Dafür ist die Punktmenge als Körper zu beschreiben, die Konstruktionsschritte als Körpererweiterungen und die Eigenschaften der Ketten von Körpererweiterungen sind zu überprüfen. Die Operationen der euklidischen Geometrie erweisen sich als arithmetische Operationen im Körper der komplexen Zahlen.
Die komplexen Zahlen sind alle Punkte in einer Ebene, die durch die zwei Koordinaten auf der x- und y-Achse beschrieben werden. Die Summe zweier komplexer Zahlen ist zu erhalten, indem jeweils die Summen der beiden Koordinaten gebildet werden und dadurch die Lage eines neuen Punktes bestimmt wird. Das Produkt ist etwas komplizierter: zunächst ist von beiden Zahlen eine Gerade zum Nullpunkt zu legen, dann werden die beiden Winkel zur x-Achse addiert und durch die Winkelsumme kann eine neue Gerade konstruiert werden. Weiter sind die Abstände der beiden Punkte zum Nullpunkt zu multiplizieren und dies Produkt auf der neuen Gerade abzutragen, was die gesuchte neue komplexe Zahl liefert. Wie im Beispiel des endlichen Körpers geht in diese arithmetischen Operationen eindeutig die räumliche Eigenschaft der Ebene ein. Und diese beiden Operationen lassen sich auch durch Lineal und Zirkel ausführen, womit die Verbindung zur Geometrie hergestellt ist.
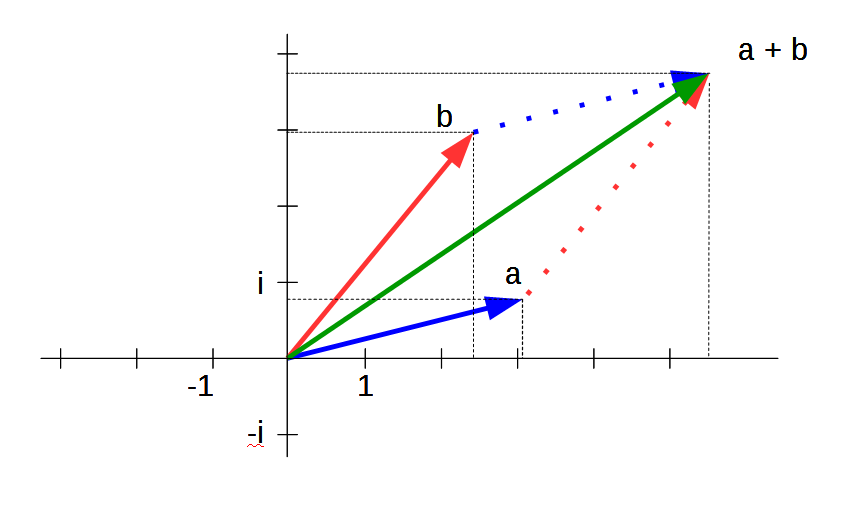
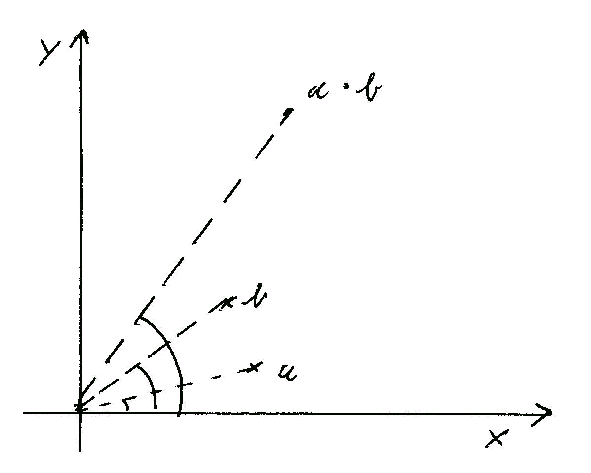
Figur 2a und 2b Addition und Multiplikation komplexer Zahlen
Addition komplexer Zahlen: Addition der x- und y-Koordinaten;
Multiplikation komplexer Zahlen: Addition der Winkel zur x-Achse, Multiplikation der Abstände zum Nullpunkt; Freihandzeichnungen
Ist eine geometrische Figur gegeben, ist es auch möglich, mithilfe Lineal und Zirkel alle Summen, Differenzen, Produkte und Brüche aller Punkte zu konstruieren, die in dieser Figur liegen. Die Menge aller dieser Punkte bildet einen Körper, der aus lauter Punkten in der Ebene besteht, also ein Unterkörper der komplexen Zahlen ist. Mit jedem Konstruktionsschritt wird die Figur vergrößert, und entsprechend ein Erweiterungskörper erreicht. Die Kette der Konstruktionsschritte ist wiederum eine Kette von Erweiterungskörpern, deren Ausgangsfiguren Kreis und Gerade sind.
Die Untersuchung der Erweiterungskörper ergab, dass mit jeder Erweiterung nur eine rationale Zahl oder eine Quadratzahl erreicht werden kann. Für die Winkeldreiteilung und die Würfelverdoppelung sind aber Kubikwurzeln zu erreichen, für die Quadratur des Kreises die reelle Zahl π (pi). Beides ist durch keine Kette von Körpererweiterungen in der euklidischen Geometrie möglich.
Die Galois-Theorie legte nahe, neue Räume zu untersuchen, die über die euklidische Geometrie hinausgehen. Der Körper der komplexen Zahlen enthält alle Räume, die mithilfe der euklidischen Geometrie konstruiert werden können, und wurde daher als erster untersucht. Es wurde aber auch möglich, Räume durch andere mathematische Operationen zu definieren. Physikalisch wurde es möglich, Räume mit anderen Werkzeugen als Lineal und Zirkel zu messen. Die Probleme, die sich dabei ergeben, sind der Gegenstand der Relativitätstheorie. Soll zwischen klassischer und moderner Geometrie unterschienen werden, hat Galois die moderne Geometrie eingeleitet.
4. Differentialgeometrie
Galois hat aber auch das charakteristische Problem der modernen Mathematik herausgestellt: eine gewisse Orientierungslosigkeit. Die euklidische Geometrie hatte einen inneren Zusammenhang hergestellt. Wenn Galilei sagte, das Buch der Natur sei in Mathematik geschrieben, hieß das, der euklidische Raum ist identisch mit dem wirklichen Raum der Natur. Für Newton ist die Differentialrechnung Fluxionentheorie, d.h. die Theorie der fließenden Bewegung des Punktes in der Geometrie. Kant sah in der euklidischen Geometrie nicht nur die innere Einheit der Natur und der Naturwissenschaften, sondern für ihn war sie auch der Raum der menschlichen Anschauung. Damit sah er einerseits gesichert, dass menschliche Erkenntnis mit der Realität der Natur übereinstimmt, andererseits aber auch ihre Grenzen.
Indem Galois die euklidische Geometrie in die Arithmetik der komplexen Zahlen einbettete, erzwang er eine Umorientierung. Der feste Boden unter den Füßen wankte. Keiner konnte mehr sagen, dass die Axiomatik der komplexen Zahlen einen neuen Zusammenhalt stiftet. Im Gegenteil wurde im 20. Jahrhundert schrittweise gezeigt, dass der euklidische Raum, der Raum der Mechanik, der Raum der Differentialrechnung und der menschliche Anschauungsraum jeweils verschieden sind. Und in anderen Wissenszweigen treten weitere Räume hinzu. Mit der Relativitätstheorie wurde gezeigt, dass überhaupt Raum und Zeit nicht klar voneinander getrennt werden können. Insofern wurde wirklich alles relativ, die ursprüngliche Einheit wurde fragmentiert. Nach außen hin wurde die Naturwissenschaft undurchsichtig, die moderne (oder postmoderne?) Kultur sucht nach Bildern. Im Innern wurden neue Axiomsysteme gesucht, aber nicht gefunden. So blieb nichts übrig, als sich wieder ganz auf die Naturforschung zu verlassen und zu hoffen, aus der Natur neue Maßstäbe zu finden. Noch nie seit den Griechen war die Mathematik so stark auf die physikalischen und technologischen Anwendungen orientiert. Das enthält immer die Gefahr des Pragmatismus, aber auch die Möglichkeit einer eher pythagoreeisch, eher naturromantisch orientierten Naturforschung.
Ausgehend von den Umwälzungen der Himmelsmechanik wird auch ein neues Verständnis der euklidischen Geometrie gewonnen, das die neue Orientierung auf die Physik anzeigt und an den zwei Beispielen Raumkrümmung und Resonanz vorgestellt werden soll.
Experimentell ergab sich, dass im Weltall das Parallelenaxiom nicht gilt. Gemäß dem Trägheitsgesetz bewegen sich starre Körper nicht auf Geraden, sondern auf gekrümmten Linien, die als Geodätische bezeichnet werden. Im vereinfachten Modell der Bewegung auf der Kugeloberfläche sind die Geodätischen die Kreise, deren Zentrum im Mittelpunkt der Kugel liegt, wie der Äquator und die Längengrade.
Auch der wirkliche Raum ist gekrümmt, der sich zusammenzieht (positive Krümmung) oder ausdehnt (negative Krümmung). Im Fall der positiven Krümmung bewegen sich alle Körper aufeinander zu, bis sie sich im Zentrum treffen (wenn der Raum sich auf seinen Mittelpunkt zusammengezogen hat), im Fall negativer Krümmung bewegen sie sich voneinander weg, da die Abstände untereinander schon allein aufgrund des Raumwachstums größer werden.
Gemäß der Allgemeinen Relativitätstheorie ist das Weltall ein sich ausdehnender Raum. Diese Theorie ist vielfach experimentell überprüft und gilt als gesichert.
War früher das Parallelenaxiom im wesentlichen unter dem Gesichtspunkt der Vollständigkeit der euklidischen Axiomatik diskutiert worden, bekam es eine völlig neue Bedeutung, nachdem der euklidische Raum mit dem mechanischen Bewegungsraum identifiziert worden war. In diesem Zusammenhang wurde klar, dass durch das Parallelenaxiom eine Raumeigenschaft bestimmt wird: der Raum als ganzer ist unbewegt. In der Allgemeinen Relativitätstheorie verliert der Raum diese Starrheit und wird dynamisch, er bewegt sich. Daraus folgt notwendig, dass die strikte Trennung von Raum und Zeit nicht aufrechterhalten werden kann, denn Bewegung vollzieht sich in der Zeit.
Die Probleme entstehen damit aber erst. Denn wenn sich im ebenen, unbewegten Raum alles schön auf Geraden bewegt, kann der Verlauf der Bewegungen gut vorausberechnet werden. Das war ja die Stärke der klassischen Mechanik, dass sie von ihren Anfangsdaten ausgehend alles weitere voraussagen konnte. Mehr noch: Es konnte bewiesen werden, dass eine kleine Veränderung der Anfangsdaten die Voraussagen nicht wesentlich verändert, der Fehler bei den vorausgesagten Daten ist nicht größer als die Abweichung bei den Anfangsdaten. Ist die Krümmung des Raums bekannt, so können auch dort die Bewegungskurven ausgehend von Ausgangsdaten berechnet werden. Lange war offen, ob durch die Raumkrümmung eine kleine Änderung der Anfangsdaten zu gewaltigen Fehlern führt. Erst 1967 konnte Anosov überraschend beweisen, dass auch negativ gekrümmte Räume strukturell stabil sind.
Das System kann aber auch von anderer Seite her aus den Angeln gehoben werden. Durch Resonanzwirkungen können durch kleine Einflüsse größte Systeme in Schwingung und zum Absturz geführt werden. Dieser Effekt ist bekannt vom Schaukeln und Aufschaukeln, von klingenden und zerspringenden Gläsern, von vibrierenden und einstürzenden Neubauten. Die Resonanzeffekte ziehen sich als inneres Band durch Hofstadters "Gödel Escher Bach", wo er die Konstruktion eines Plattenspielers diskutiert, dessen Musik die aufgelegte Schallplatte und den Spieler zum Schwingen und Zerbrechen bringt.
Die Wirkungsweise der Resonanz sei am Pendel erläutert. Ein Pendel hängt im Wind und schwingt gleichmäßig langsam vor sich hin. Um es zum Schaukeln zu bringen ist zu beachten: Es muß in genau der Richtung angestoßen werden, in der es bereits schwingt. Andernfalls würden die Eigenschwingung und die einwirkende Kraft in einer anderen, torkelnden Bewegung resultieren. Und die Einwirkung muß rhythmisch genau so erfolgen, dass das Pendel möglichst in dem Moment angestoßen wird, wo es sich in seiner Eigenschwingung am äußersten Punkt in momentaner Ruhe (in einem labilen Gleichgewicht) befindet. Andernfalls wird es eher gebremst und könnte vielleicht sogar in Ruhe kommen. Resonanz liegt also vor, wenn eine äußere Einwirkung die Richtung und Periode einer Eigenschwingung trifft und verstärkt.
In periodisch bewegten Systemen wie dem Planetensystem drohen überall Resonanzkatastrophen. Diese Wirkung ist durch die vorher besprochene strukturelle Stabilität keineswegs ausgeschlossen. Katastrophen dieser Art beschäftigen derzeit mehr und mehr Superrechner, können bisher aber auch nicht annähernd simuliert, geschweige denn ausgeschlossen werden. Es konnten nur umgekehrt einige Planetenbahnen bzw. Asteroidenbahnen berechnet werden, die mit Sicherheit zur Resonanz führen würden und es wurde beobachtet, dass auf diesen "verbotenen" Bahnen auch wirklich kein Asteroid steht.
Im Grunde ist zu vermuten, dass es bisher unbekannte Raumeigenschaften gibt, die diese Resonanzfälle steuern und hier ein ähnliches offenes Problem vorliegt wie für die Griechen innerhalb ihrer Geometrie. Schon der euklidischen Geometrie lagen implizite Axiome zugrunde, wie die fehlende Raumkrümmung (woraus das Parallelenaxiom folgt) und Resonanzfreiheit (woraus die Stabilität der Bewegungen folgt). Im wirklichen Raum der Natur mit ihren bewegten Massen statt unteilbaren Punkten wirken offensichtlich bisher unbekannte Naturgesetze. Die Geschichte der Geometrie bleibt offen.
Literaturhinweise
1982 - 1986
© tydecks.info 2002