Walter TydecksWie aus den Bildern Zahlen wurden |
|
Beitrag für den Themenkreis Naturwissenschaft und Technik von 50plus aktiv an der Bergstraße am 28.1.2015 in Bensheim
Inhaltsverzeichnis
Einleitung
Anschreiben auf Kerbholz (30.000 v.Chr.)
Calculi – die ersten Zählsteine (3.500 v.Chr)
Ägyptische Zahlen – Bilder je Zehnerpotenz (3.000 v.Chr.)
Das babylonische Sexagesimalsystem (2.000 v.Chr.)
Verwaltungsaufgaben – Papyrus Rhind (um 1.550 v.Chr.)
"Ägyptisch": Stufen der Unendlichkeit nach Georg Cantor
"Babylonisch": Algorithmen als erweitertes Stellenwertsystem
Einleitung
»Die meisten Hochkulturen haben es schon frühzeitig geschafft Sprache in Schrift umzusetzen. Hierfür waren fast immer die „Lagerbuchhalter” Pioniere: wie viele Sack Korn habe ich im Lager, wie viel Tonkrüge Öl? Zahlen und Schrift zur Konservierung von Informationen. Die Anfänge der Schrift waren meist Bilder, die zu Buchstaben wurden« (Dierk Haase).
Die ältesten Zahlzeichen können bereits in den frühesten Kerbhölzern gesehen werden, die bis 30.000 v. Chr. zurückgehen. Im engeren Sinn kann jedoch erst bei den Sumerern und Ägyptern von Zahlen gesprochen werden, die um das Jahr 3.000 v. Chr. entstanden sind.
Die Beschäftigung mit den frühesten Zahlen kann zu einem besseren Verständnis der Zahlen führen. Je sicherer und selbstverständlicher mit Zahlen gerechnet werden kann, desto mehr ist das ursprüngliche Zahlverständnis verloren gegangen. Kaum jemand macht sich heute noch klar, aus welchen Bildern die Zahlen hervorgegangen sind und was sie bedeuten. Das lässt sich besonders gut an den ägyptischen Zahlzeichen zeigen, sei es ein Symbol für die Anzahl von Blütenblättern, das Gewimmel von Kaulquappen oder der die unfassbare Weite des Himmels anzeigende Gott der Unendlichkeit.
In diesem Beitrag geht es um folgende Themen:
- Zahlen als eigene Objekte (Zählsteine, calculi)
- Erstes Verständnis von Größenordnungen. Die für Zahlen ausgewählten Bilder zeigen nicht einfach Objekte, sondern veranschaulichen Eigenschaften, die für Mengen in bestimmten Größenordnungen typisch sind.
- Das erste Stellenwertsystem: Babylonisches Sexagesimalsystem (die Babylonier waren die Nachfolger der Sumerer). Es wird bis heute für Zeitangaben genutzt (Stunde, Minute, Sekunde)
- Erste Rechenaufgaben für Verwaltungsarbeiten am Beispiel des Papyrus Rhind
Im Anhang wird ein Ausblick auf die Entwicklung der Mengenlehre durch Cantor und die Wende zu einer algorithmischen Mathematik im 20. Jahrhundert gegeben, mit der Zahlen durch Regeln zur Erzeugung von Zahlen ersetzt werden. Die von den Ägyptern und Babyloniern eingeführten Zahlen erweisen sich bis heute als zwei Grundrichtungen, die die Entwicklung der Mathematik prägen. Philosophisch stellen sich seit Einführung der Zahlen die Fragen nach dem Verständnis der Unendlichkeit einerseits und drohender Endlosschleifen und Paradoxien andererseits.
Anschreiben auf Kerbholz (30.000 v.Chr.)
Das Wort »Zahl« entwickelte sich aus dem althochdeutschen Wort zala, welches »eingekerbtes Merkzeichen« bedeutet (Duden).
Die ältesten gefundenen Kerbhölzer gehen bis 40.000 v.Chr. zurück. Diese Art des Zählens oder Anschreibens war bis ins 19. Jahrhundert in Europa weit verbreitet und ist heute noch üblich auf Bierdeckeln.


Quelle: Krömer, S. 17 und Wikipedia: Von Scan:de:Benutzer:Superbass - eigener Scan, Gemeinfrei, Link
Kerbhölzer sind offenbar auf allen fünf Kontinenten unabhängig voneinander entstanden. Älteste Ausgrabungsstätten in Europa sind zum Beispiel ein »etwa 40.000 Jahre alter Knochen aus einem Neandertalergrab von La Ferrassie in Frankreich« und ein »25.000 Jahre alter Wolfsknochen mit in zwei Gruppen unterteilter Kerbenreihe aus Dolní Věstonice in Mähren« (Kuckenburg, S. 103).
Letztlich ist schwer entscheidbar, welches Zahlenverständnis hier bereits vorlag. Jeder Strich symbolisiert einen Gegenstand, aber gab es schon Vorstellungen wie ›ein Gegenstand‹, ›zwei Gegenstände‹, ›drei Gegenstände‹, ...? Die Einkerbungen sind gebündelt, und es lassen sich auf eine gewisse Art rhythmische Anordnungen erkennen. Darin kann ein erstes Zahlenverständnis vermutet werden, die in der Zeichnung mit den Zahlen angedeutet sind. Von den Griechen wurde die Zahl als arithmos bezeichnet, als dasjenige, was innerhalb des Rhythmus erhalten bleibt und für sich selbst nicht rhythmisch ist, a-rhythmisch.
Calculi – die ersten Zählsteine (3.500 v.Chr.)
Die ersten Zahlen waren keine Zeichen, sondern Zählsteine (Calculus). Sie sind jeweils 1 bis 3 cm groß. Wenn jemand etwas gekauft hat, wurden in einer hohlen, aus Lehm gekneteten Bulle Zahlzeichen hinterlegt, die die Anzahl festhielten. Sollte es später zu Streit kommen, wie viel geliefert worden war, wurde zum Nachweis die Bulle aufgeschlagen und die Anzahl überprüft. Für Ifrah ist das ein Beleg, wie die Buchhalter die Schrift erfunden haben. Bullen und calculi sind älter als die ersten Schriftzeichen und gelten als Proto-Keilschrift. Es wird vermutet, dass später die ersten Keilzeichen die Gestalt der calculi nachgeahmt haben.
Älteste Ausgrabungen in Susa, siehe Ifrah, S. 190f. (Zu Susa siehe: Uruk-Zeit und Elam)

Quelle: Ifrah, S. 191
Diese Zahlen waren ganz anschaulich. Man konnte sie buchstäblich in die Hand nehmen. Niemand stellte sich die Frage, ob es Zahlen in der Natur oder nur im Denken, also im Kopf gibt. Damerow und Schmidt sprechen von »Repräsentationen erster Ordnung«, das sind »Objekte oder Symbole [...], mit denen gemäß gewisse(r) Transformationsregeln die gleichen Handlungen ausgeführt werden können wie mit den realen Objekten selbst« (Damerow, Schmidt, S. 19).
Anmerkung: Bei den Calculi handelt es sich noch um keine Münzen, die erst ab 650 v.Chr. geprägt wurden. Sie hatten die Funktion von Kreditgeld und verpflichteten den Schuldner, nach Ablauf einer vereinbarten Zeit die ausgeliehenen Güter zurückzuerstatten. Siehe hierzu ausführlich David Graeber über die Geschichte der Schulden (zu Mesopotamien Graeber, S. 221-234, 272-276).
Ägyptische Zahlen – Bilder je Zehnerpotenz (3.000 v.Chr.)
Der nächste wesentliche Schritt zur Herausbildung der Zahlen lässt sich besonders gut an den ägyptischen Zahlen erkennen. Die Ägypter ordneten die Zahlen in Größenordnungen. Mengen wurden in Größenklassen eingeteilt: Es gibt Mengen, die sind ungefähr so groß wie eine Menge, die aus einzelnen Strichen besteht, oder wie die Menge der Enden einer gebogenen Linie, die Anzahl Knoten auf einem Strick, Anzahl Blütenblätter, Anzahl Finger, das Gewimmel der Kaulquappen und schließlich die Unendlichkeit des Weltalls.

Quelle: Krömer, S. 42
Jede Größenklasse wird bildlich durch den jeweils typischen Repräsentanten dargestellt. Statt »2.375.486« könnte daher gesagt werden: »Eine Zahl so groß wie die Summe
aus zwei Mengen der Größenklasse Unendlichkeit und
drei Mengen der Größenklasse Kaulquappe
sieben Mengen der Größenklasse Finger
fünf Mengen der Größenklasse Lotosblume
vier Mengen der Größenklasse Strick
acht Mengen der Größenklasse Bügel
und schließlich 6 einzelne Striche«.
Sehr schöne Beispiele finden sich im Tempel von Edfu. Siehe z.B. die Darstellung der Zahl 1.333.330 auf der Seite medu-netscher.de.
Das klingt ungewohnt und auf den ersten Blick kompliziert, aber wer weiter darüber nachdenkt, erkennt die Ideen, die der Ausbildung von Zahlen zugrunde liegen. Zahlen erstrecken sich über zahlreiche Größenordnungen.
- Für jede Größenordnung wird ein anschauliches Maß gewählt.
- Die Größenordnungen werden durch Zehner-Potenzen miteinander verknüpft.
Das Beispiel »Finger« zeigt die Abstraktionsleistung, die den Ägyptern gelungen ist. Mit »Finger« ist nicht die Anzahl 5 oder 10 gemeint, wie naheliegenderweise vermutet werden könnte. Sondern mit »Finger« ist eine bestimmte Größenordnung gemeint, die zwischen den Größenordnungen der Blütenblätter einer Lotosblume und dem Gewimmel der Kaulquappen liegt.
Wenn wir heute Zahlen nur noch in der Weise aussprechen wie »2 Millionen und 3 Hunderttausend und 7 Zehntausend und 5 Tausend und 4 Hundert und 8 Zehner und 6 Einzelne«, ist in den einzelnen Bestandteilen Millionen, Hunderttausend, etc. die gleiche Aufteilung in Größenordnungen enthalten, wie sie von den Ägyptern eingeführt wurde. Nur ist das heute so selbstverständlich geworden, dass sich niemand mehr über diesen Aufbau der Zahlen Gedanken macht. Auch in der Schule werden die Zahlen nicht auf diese Weise eingeführt, was im Weiteren wesentlich dazu beiträgt, dass erst das Rechnen und später die Mathematik als etwas Schwieriges und Unverständliches gelten.
Es ist keineswegs selbstverständlich, dass Mengen aus unterschiedlichen Größenordnungen einheitlich zusammengesetzt werden können. Ursprünglich waren die Zahlen der verschiedenen Größenordnungen qualitativ voneinander getrennt, und es wäre nicht weniger absurd erschienen, Kaulquappen und Lotosblüten zusammen zu zählen, als wenn Äpfel und Birnen addiert werden. Den übergreifenden, inneren Bezug aller Zahlen zu erkennen, war eine große Abstraktionsleistung. Für die Ägypter war das der Zehnerübergang. Die verschiedenen Zahlräume sind jeweils durch den Faktor Zehn voneinander getrennt. Warum das so ist, lässt sich kaum erklären und kann letztlich nur mit der Existenz einer übergreifenden Ordnung des Kosmos begründet werden, auf den die Ägypter vertrauten. Nicht ohne Grund haben die meisten Kinder beim Erlernen von Zahlen Schwierigkeiten beim Zehnerübergang: Warum muss nach der Zehn nochmal "von vorne" gezählt werden, ›ein Zehner und Eins‹, ›ein Zehner und Zwei‹, usw.? Warum gibt es noch für 11 und 12 eigene Namen, – »Elf« und »Zwölf« –, bis dann die Namen zusammengesetzt werden in »Dreizehn«, »Vierzehn« usw., mit denen wiederum nicht ›Drei Zehner‹ oder ›Vier Zehner‹ gemeint sind, sondern ›Zehn und Drei‹ bzw. ›Zehn und Vier‹? Wie ist zu verstehen, dass z.B. bei der Aufgabe ›7 + 5 = 12‹ eine Zahl entsteht, deren Ziffern 1 und 2 kleiner sind als 5 und 7, aus der sie hervorgegangen ist? Hier geht es um die Frage, wie unterschiedliche Größenordnungen ("Zehner" und "Einer") miteinander verknüpft werden können. Das wird häufig nur durch Auswendiglernen beigebracht, wodurch das Zahlverständnis verloren geht.
Mathematisch scheint es einfach zu sein: Entscheidend ist nur, dass ohne Widersprüche die Zahlen gezählt und mit ihnen gerechnet werden kann. Doch zeigen die Veranschaulichungen der Ägypter, dass ursprünglich unterschiedliche Arten von Mengen (einzelne Striche, Paare, Knoten an einem Strick, Blütenkränze, Finger einer Hand, Schwärme) zusammengezählt wurden. Anschaulich kann die Frage gestellt werden: Wie soll aus zehn Stricken mit Knoten ein Blütenkranz entstehen, wenn gerechnet wird, dass zehn Hunderter einen Tausender ergeben? Ein Strick mit Knoten kann sich nicht in einen Bütenkranz verwandeln, aber die Menge kann so groß werden, dass sie als Menge eher der Menge eines Blütenkranzes als der Menge eines Stricks mit Knoten entspricht. An dieser Stelle haben die Ägypter den schwierigen und für alles Weitere entscheidenden Übergang von der Betrachtung Einzelner zur Betrachtung von Mengen vollzogen. Sie haben erkannt, dass verschiedene Größenordnungen jeweils eigene Eigenschaften haben und ineinander umschlagen, wenn die Elemente innerhalb einer Menge einer Größenordnung so viele oder so wenige werden, dass ein Übergang in eine andere Größenordnung mit anderen Eigenschaften erfolgt.
Ergänzung: Der Umschlag sich verändernder Quantitäten aus einer Größenordnung in eine andere Größenordnung mit einer neuen Qualität beschäftigt die Philosophie von der Antike bis zur Gegenwart. Die Griechen fragten, wie viele Haare ausfallen müssen, bis aus einem Haarschopf eine Glatze geworden ist. – Wahrscheinlich ohne sich dessen bewusst zu sein, dass bereits die Ägypter die Knotenlinie als Zahlzeichen nutzten, sprach Hegel in einem übertragenen Sinn von einer Knotenlinie: Eine Knotenlinie liegt vor, wenn durch eine quantitative Entwicklung Ordnungen mit unterschiedlichen Qualitäten auseinander hervorgehen. Die ägyptischen Zahlen sind das beste Beispiel: Ihre Symbole bilden im Sinne von Hegel eine Knotenlinie, entlang derer beim jeweiligen Zehnerübergang ein Symbol aus dem anderen hervorgeht. Die Knotenlinie tritt doppelt auf: Sie ist einerseits gleichberechtigt mit den anderen Bildern für Größenordnungen, und sie ist das übergreifende Bild der Anordnung aller Größenordnungen. Wenn gefragt wird, welches Substrat diesen Übergängen zugrunde liegt, dann kann es nur in der Ordnung selbst gesehen werden, mithilfe derer die Übergänge spezifiert sind, in diesem Beispiel die Ordnung der Zahlen und dem Zehnerübergang als ihrem inneren Maß (siehe hierzu weiterführend den Beitrag über das reale Maß).
Das babylonische Sexagesimalsystem (2.000 v.Chr.)
Die ägyptischen Zahlen sind dekadisch und sehen daher ähnlich aus wie das uns vertraute Dezimalsystem, aber es ist noch kein Stellenwertsystem. Jede Größenklasse ist zwar zehnfach so groß wie die vorangehende (dekadisch), aber für jede Größenklasse werden eigene Zeichen gewählt (Gott mit erhobenen Armen, Kaulquappe etc.). Ein Stellenwertsystem liegt erst dann vor, wenn für alle Größenordnungen die gleichen Zeichen genommen werden, und die Größenordnung ausschließlich durch die Stelle in der Zahl erkennbar wird: Die letzte Ziffer einer Zahl steht für die Einzelnen, die Vorletzte für die Zehner, die Drittletzte für die Hunderte etc. Würde jemand bei einer ägyptischen Zahl die Reihenfolge durcheinander bringen und z.B. erst eine Kaulquappe zeichnen, dann einen Strich, dann zwei weitere Kaulquappen und schließlich eine Blüte, so wäre es dennoch möglich, an den jeweiligen Bildern zu erkennen, welche Zahl gemeint ist und die Zahl zu ordnen und richtig zusammenzusetzen. Das ist im Stellenwertsystem nicht mehr möglich. Wird dort die Reihenfolge der Ziffern vertauscht, entsteht eine andere Zahl. So sind z.B. im Dezimalsystem die Zahlen 5473 und 7435 verschieden, obwohl sie die gleichen Ziffern enthalten, die sich nur in ihrer Ordnung unterscheiden.
Die anschauliche Darstellung der verschiedenen Größenordnungen (vom Strich bis zur segnenden Geste des Gottes der Unendlichkeit) war nicht nur eine Stärke der ägyptischen Zahlen, sondern auch eine Schwäche. Sie verhinderte, dass ein übergreifendes System von Zahlen geschaffen wurde. Das gelang erst den Babylonieren, den Nachfahren der Sumerer. Sie lösten sich von der Anschauung bestimmter charakteristischer Mengen und ihrer Größenordnungen und fanden in der Zeit eine übergreifende Ordnung. Die Zeit steht an der Grenze der Wahrnehmbarkeit. Sie kann nicht unmittelbar sinnlich wahrgenommen werden, aber jeder hat ein intuitives Verständnis, was mit der Länge des Jahres, eines Monats, eines Tages, einer Stunde und der Minuten gemeint ist. Daraus ergab sich, dass die Babylonier als erstes Stellenwertsystem nicht das Dezimalsystem wählten, was nach dem dekadischen System der Ägypter naheliegend gewesen wäre, sondern das auf der Zahl 60 beruhende Sexagesimalsystem.
Für das Sexagesimalsystem suchten sie nach keiner bildlichen Darstellung wie die Ägypter, sondern ein Zeichensystem, das vermutlich aus den Zählsteinen (calculi) entstanden ist und in sumerischen Keilschriften nachgewiesen werden kann, die bis 2.650 v. Chr. zurückgehen. Daraus entstand die babylonische Mathematik, die seit 2.000 v. Chr. nachweisbar ist. (Damerow und Schmidt haben detailliert gezeigt, wie bereits in den bis 3.200 v. Chr. zurückgehenden archaischen Zahlen der sumerischen Protokeilschrift frühe Formen des Stellenwertsystems zu erkennen sind, die jedoch erst ab 2.000 v. Chr. von den Babyloniern systematisiert wurden. Siehe Damerow, Schmidt, S. 22ff)
Damit wurden neben der Idee der Größenordnungen zwei weitere wesentliche Eigenschaften der Zahlen entwickelt:
- Zahlen, Zählen und Zeit gehören zusammen. Das fasste später Aristoteles in seiner Begründung der Physik zusammen: »Nicht gleich Bewegung ist die Zeit, sondern insoweit die Bewegung Zahl an sich hat« (Aristoteles Physik, Buch IV Kapitel 11 Absatz 5, 219b).
- Stellenwertsystem
Das Stellenwertsystem lässt sich sehr einfach veranschaulichen, da es sich für Zeitangaben bis heute erhalten hat. Wer zum Beispiel sagt, jetzt ist es »9:34:12 Uhr«, meint damit ausgesprochen »9 Uhr und 34 Minuten und 12 Sekunden«. Niemand macht sich die Mühe, dies in das Dezimalsystem zu übersetzen, da bezüglich der Zeit jeder intuitiv das Sexagesimalsystem versteht. Für eine Übersetzung ist es notwendig, auf die kleinste Einheit zu wechseln. Das sind die Sekunden:
9:34:12 = 9 Std. + 34 Min. + 12 Sek. = 9 · (60 · 60) + 34 · 60 + 12 = 34.452 Sek.
Hier tritt wie bei den ägyptischen Zahlen deutlich der Gedanke hervor, auf welche Weise unterschiedliche Größenordnungen miteinander summiert werden. Stunden, Minuten und Sekunden sind verschiedene Größenordnungen der Zeit, die im Alltag niemand mehr auf eine einzige Einheit wie die Sekunde bringt. Erst recht nicht, wenn weiter gegangen wird zu Tagen, Monaten und Jahren.
Wird das babylonische Zahlensystem im Ganzen betrachtet, ähnelt es mehr den Strichen auf den Kerbhölzern und den Figuren der Zählsteine als den ägyptischen Hieroglyphen:

Quelle: Grandt, S. 4
Die erste Zeile entspricht noch dem ägyptischen System: Einer und Zehner werden aufgezählt und z.B. bei der 11 nebeneinander geschrieben (›
 ‹ bedeutet ›ein Zehner und ein Einer‹). Das Neue entsteht am Ende der ersten Zeile: Hier kehrt das gleiche Zeichen wieder, mit dem begonnen wurde:
‹ bedeutet ›ein Zehner und ein Einer‹). Das Neue entsteht am Ende der ersten Zeile: Hier kehrt das gleiche Zeichen wieder, mit dem begonnen wurde:  . Jetzt hat es jedoch die Bedeutung 60. Wenn 60 Minuten durchlaufen sind, ist 1 Stunde vollendet. 60 Minuten verwandeln sich in 1 Stunde und werden in der nächsten Stunde neu gezählt. Daher geht es mit der zweiten und dritten Zeile weiter:
. Jetzt hat es jedoch die Bedeutung 60. Wenn 60 Minuten durchlaufen sind, ist 1 Stunde vollendet. 60 Minuten verwandeln sich in 1 Stunde und werden in der nächsten Stunde neu gezählt. Daher geht es mit der zweiten und dritten Zeile weiter:
  |
61 = 1 · 60 + 1 · 1 |
   |
121 = 2 · 60 + 1 · 1 |
Um die Zahl ›
 ‹ (61) von der Zahl ›
‹ (61) von der Zahl ›
 ‹ (2) zu unterscheiden, ist der Abstand zwischen den beiden Ziffern etwas größer. Für die Zahl ›
‹ (2) zu unterscheiden, ist der Abstand zwischen den beiden Ziffern etwas größer. Für die Zahl › ‹ (60) wird im Unterschied zur Zahl ›
‹ (60) wird im Unterschied zur Zahl › ‹ (1) hinter der ersten Ziffer eine kleine Lücke gelassen. Die Babylonier kannten zwar noch kein Symbol für die 0, haben sie aber durch die Lücke (ein Leerzeichen) dargestellt.
‹ (1) hinter der ersten Ziffer eine kleine Lücke gelassen. Die Babylonier kannten zwar noch kein Symbol für die 0, haben sie aber durch die Lücke (ein Leerzeichen) dargestellt.
Mögliche Gründe für die Wahl der Basis 60 durch die Babylonier (nach Krömer, S. 79)
- Für einen Mathematiker ist es ganz klar: Kaum eine Zahl hat so viele Teiler wie die 60. 60 kann durch 2, 3, 4, 5, 6, 10, 12, 20, 30 geteilt werden. Das erleichtert das Rechnen in diesem System enorm.
- Die Natur legt ein Sechziger-System nahe, wenn das Sonnenjahr angenähert 360 = 6 · 60 Tage und der Mondzyklus angenähert 30 Tage hat.
Probleme: Auch die Babylonier werden bemerkt haben, dass das Jahr 365 Tage hat und der Mondzyklus etwas kürzer als 30 Tage ist. Und war ihnen klar, dass die Himmelskörper einander auf Kreisbahnen umrunden? - Über den Jahreszyklus ergibt sich die Aufteilung des Kreises: Der Kreis besteht aus 360 Grad und jedes Grad wiederum aus 60 Minuten, jede Minute aus 60 Sekunden. Winkel werden sexagesimal geschrieben: ggg° mm' ss''. Wenn der Himmel als Halbkreis mit 180° verstanden wird, beträgt die Größe der sichtbaren Sonnenscheibe ungefähr ein halbes Grad, oder anders gesagt: Der Umfang des sichtbaren Himmelsbogens ist 360 mal so groß wie der Durchmesser der sichtbaren Sonnenscheibe. Der Sonnenuntergang dauert in Europa 3 bis 4 Minuten.
Zeichnet ein Mensch von seinem Auge aus zwei Geraden zum linken und zum rechten Rand der sichtbaren Sonne, dann beträgt der Winkel zwischen den Geraden ungefähr 0,5 Grad
Auf diese Weise sind Jahreszyklus, Kreiszyklus und Sonne vielfach miteinander verknüpft, wobei die Sonne doppelt auftritt: Im Sonnenzyklus des Jahres und als sichtbares Objekt am Himmelsbogen. Das innere Maß dieser Beziehungen kann in der 60 gesehen werden. - Möglicherweise ging eine Verschmelzung zweier Völker voraus, von denen eines das Dezimalsystem nutze und ein anderes ein System mit Basis 6.
- Im vorderasiatischen Raum wurden zum Zählen die Fingerglieder genutzt. Das ergibt bei vier Fingern an einer Hand (ohne Berücksichtigung des Daumens) und je drei Gliedern je Finger die Basis 12.
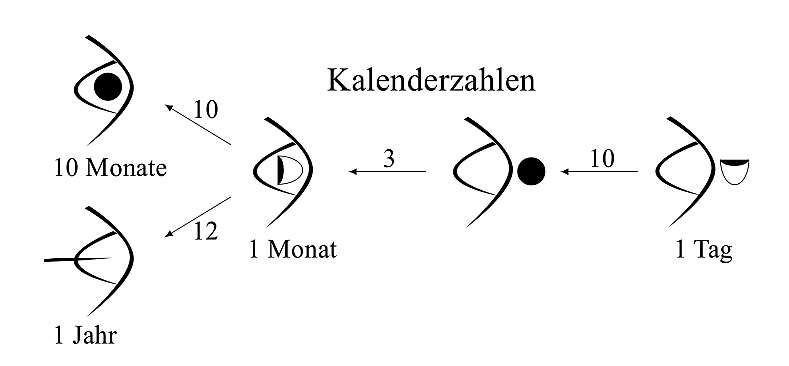
Die frühesten sumerischen Zeichen für Zeiteinheiten zeigen sehr anschaulich die Schwierigkeiten, ein einheitliches Stellenwertsystem zu finden.
Quelle: Damerow, Schmidt, S. 23
Weil 30 Tage einen Monat und 12 Monate ein Jahr ergeben, kreuzen sich Dreier-, Zehner- und Zwölferübergänge. Das Zeichen für einen Tag  wandelt sich in das Zeichen für 10 Tage
wandelt sich in das Zeichen für 10 Tage  , indem rechts der Trichter in einen Vollkreis umgewandelt wird. Aus 10 Tagen wird durch einen Dreierübergang der Monat mit 30 Tagen, indem der Vollkreis als Symbol für die 10 wieder verschwindet und durch einen liegenden Trichter ersetzt wird. Von einem Monat wird zu 10 Monaten übergegangen, indem der Vollkreis als Symbol der 10 wieder aufgenommen, jedoch an anderer Stelle gezeichnet wird. Um das Jahr mit 12 Monaten zu erreichen, ist im Zeichen für 10 Monate das Symbol für die 10 durch ein anderes Symbol für 12 zu ersetzen, den waagerechten Keil. In einem Zeitraum von 1.000 Jahren hat sich hieraus sowie aus verschiedenen anderen Zahlenübergängen schließlich das einheitliche Sexagesimalsystem entwickelt.
, indem rechts der Trichter in einen Vollkreis umgewandelt wird. Aus 10 Tagen wird durch einen Dreierübergang der Monat mit 30 Tagen, indem der Vollkreis als Symbol für die 10 wieder verschwindet und durch einen liegenden Trichter ersetzt wird. Von einem Monat wird zu 10 Monaten übergegangen, indem der Vollkreis als Symbol der 10 wieder aufgenommen, jedoch an anderer Stelle gezeichnet wird. Um das Jahr mit 12 Monaten zu erreichen, ist im Zeichen für 10 Monate das Symbol für die 10 durch ein anderes Symbol für 12 zu ersetzen, den waagerechten Keil. In einem Zeitraum von 1.000 Jahren hat sich hieraus sowie aus verschiedenen anderen Zahlenübergängen schließlich das einheitliche Sexagesimalsystem entwickelt.
Ergänzung: Die Ausführung von Aristoteles zu Zahl und Zeit beschäftigt bis heute die Philosophie. Im wesentlichen geht es um die Frage, ob die Zahlen und die Zeit etwas Objektives sind, das es in der Natur gibt und das wahrgenommen werden kann, oder ob es sich bei Zahl und Zeit um etwas handelt, das es nur im Denken gibt. Im Ergebnis hat der Philosoph Simplikios (480-560) unterschieden zwischen dem Zählbaren (alles, was gezählt werden kann) und dem Zählenkönnenden (alles, was zählen kann, wie der Mensch). Wenn es zum Zählen kommt, kann unterschieden werden zwischen dem Gezählten (alles, was gezählt worden ist) und dem Zählenden (alles, was aktiv zählt).
Ähnlich kann die Zeit verstanden werden: Es gibt das Bewegbare (alles, was sich bewegen und dessen Änderung in der Zeit wahrgenommen werden kann), und das Erinnernkönnende (alles, was sich an frühere Zustände erinnern und dadurch eine Veränderung erkennen kann). Wenn es zum Erinnern kommt, kann unterschieden werden zwischen dem Vergangenen (alles, dessen früherer Zustand sich vom gegenwärtigen Zustand unterscheidet, und dessen Veränderung in der Zeit erinnert worden ist) und dem Erinnernden (alles, was aktiv frühere Zustände erinnert, mit der Gegenwart vergleicht, Entwicklungen erkennt und auf die Zukunft schließt). Wörtlich müsste von »Zeitigen« statt »Erinnern« gesprochen werden, um die Analogie zum »Zählen« hervorzuheben. Heidegger hat daher konsequenterweise Ausdrücke wie »Zeitigen« geprägt und in seinem Philosophieren eingesetzt. In ähnlicher Weise hat der Musikwissenschaftler Georgiades die Ursprünge des Zählens, des Zeitgefühls und der Musikalität untersucht.
»Das grundlegende Phänomen ist also das Zählen (sc. der Jetzte: deren Bestimmung durch die gegebene gleichfömig wiederkehrende Bewegung). Und nun wird dieses Zählen - durch Wenden der Aufmerksamkeit auf die Dauer des einen Umlaufs, allgemein: des wiederkehrenden gleichen Zeitintervalls - auch zum Messen verwendet.«
»Es ist, als ob wir ein Organ für die Wiederkehrstruktur des Jetzt, für das gleichmäßige Zählen besäßen. (...) Unser Zeitorgan betätigt sich als Gleichgewichtsorgan, es reguliert unser Zählen nach der Wiederkehr-Ordnung des Jetzt, nach dem Rhythmus der Jetzt-Wiederkehr. (...) Und ich bändige sie (die Zeit), indem auch ich, von mir aus, das wiederkehrende Jetzt durch mein Gleichgewichts- oder Zählorgan treffe: indem mein Sinn für Rhythmus sich spontan meldet« (Georgiades, S. 45, 46).
Werden das Zählen und die Erinnerung zur Gewohnheit, dann entsteht spontan der Eindruck, als gäbe es die Zahl und die Zeit unabhängig vom Menschen, der sich gewissermaßen nur in ihnen bewegt. Dann scheint es so, als habe der Mensch entdeckt, dass es Zeit gibt, und auch ganz konkret, als habe er Zahlen entdeckt. Ein Kind empfindet Freude, wenn es entdeckt, dass es immer größere Zahlen sagen und verstehen kann. Es ist in einer bestimmten Phase ein beliebtes Spiel, dass sich zwei Kinder jeweils eine Zahl vorstellen, diese dann sagen, und das Kind "gewonnen" hat, dessen Zahl größer ist. Beide müssen darüber lachen, wenn sie den Witz dieses Spiels verstanden haben und wiederholen es immer wieder neu.
Wird auf diese Weise eingesehen, was die Zahlen sind, dann entspricht das dem Verständnis, das die Babylonier eingeführt haben, und das überraschenderweise bis heute philosophische Diskussionen entzündet, obwohl es doch so einfach aussieht. Es muss nur jemand wie Zenon kommen und sagen, dass die Zeit nicht gemessen werden kann, da es nichts gibt, woran sie sich messen lässt, dass der fliegende Pfeil steht, also die Zeit nicht vergeht. Wie für die ägyptischen Zahlen gilt für die Zeit, dass sie sich im Sinne von Hegel als Knotenlinie verstehen lässt, auf der unterschiedliche Größenordnungen der Zeit miteinander verknüpft sind. Ihr inneres Maß ist jedoch nicht der Zehnerübergang, sondern der Sechzigerübergang. Ihr Substrat ist die Ordnung der Zeit. Davon handelt bereits der älteste schriftlich überlieferte Spruch eines westlichen Philosophen, in dem Anaximander ungefähr 580 v.Chr. von der »Ordnung der Zeit« (chronou taxis) spricht.
Verwaltungsaufgaben – Papyrus Rhind, um 1.550 v.Chr.
Abschließend sei gezeigt, welche Aufgaben mit diesen Zahlen gelöst wurden. Der Papyrus Rhind enthält 84 Aufgaben für Feldmesser und Verwaltungsbeamte: Verteilung von Löhnen, Berechnung von Getreidebedarf, Ermittlung von Flächen- und Rauminhalten, Umrechnung von Maßen. Weitere typische Aufgaben: Vermessung von Feldern, Projektierung von Bauwerken, Berechnung des Proviant fürs Heer, von Getreidemengen für Brot und Bier, Buchhaltung über Vorräte, Schulden, Zinsen (nach Pester, S. 24)
Ein Beispiel für eine solche Aufgabe:

Quelle: Krömer, S. 55
Anhang: Neuere Entwicklungen
"Ägyptisch": Stufen der Unendlichkeit nach Georg Cantor
Innerhalb der ägyptischen Zahlzeichen stellt Heh, der Gott der Unendlichkeit einen Grenzfall dar. Zum einen steht er für eine Größenordnung, die nochmals um den Faktor 10 das Gewimmel von Kaulquappen übersteigt und innerhalb der zählbaren Zahlen verbleibt. Zum anderen steht er als Unendliches allen Zahlen gegenüber, die jeweils nur endlich sind. Daher ist es eine berechtigte Frage, ob sich die Unendlichkeit ihrerseits vervielfältigen lässt. Die Unendlichkeit sollte unverändert bleiben, auch wenn es eine größere Anzahl von Bildern gibt, die den Gott der Unendlichkeit zeigen. (Ergänzung: Es wird vermutet, dass aus den Namen des Heh und seiner Gattin Hehet der Ausdruck tohu wabohu hervorgegangen ist, der im zweiten Vers des Alten Testaments gebraucht wird, »Und die Erde war wüst und leer«, Genesis 1.2. Botterweck u.a., S. 572.)
Um 1880 hat Cantor die mit der Unendlichkeit verbundenen Zahlen weit genauer unterschieden:
- Die durch das Zählen nie erreichbare unendliche Zahl, die meist durch drei Pünktchen … oder die liegende Acht ∞ symbolisiert wird.
- Ein Unendliches, das sich wie das ägyptische Zahlzeichen
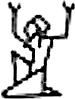 vervielfachen lässt. Für ihn ist jedoch das Unendliche nicht das Zehnfache von Hunderttausend, sondern für ihn ist die Gesamtzahl aller natürlichen Zahlen die erste transfinite Zahl, die sich nie durch Zählen erreichen lässt, und er bezeichnet sie mit dem letzten Buchstaben des griechischen Alphabets ω (Omega). Damit will er veranschaulichen, dass dort weiter gezählt wird, wo das gewöhnliche Zählen nicht hinkommt, wo die Buchstaben zuende sind. Mit den transfiniten Zahlen kann er z.B. ›3 · ω‹ rechnen, so wie die Ägypter mit dem Bild
vervielfachen lässt. Für ihn ist jedoch das Unendliche nicht das Zehnfache von Hunderttausend, sondern für ihn ist die Gesamtzahl aller natürlichen Zahlen die erste transfinite Zahl, die sich nie durch Zählen erreichen lässt, und er bezeichnet sie mit dem letzten Buchstaben des griechischen Alphabets ω (Omega). Damit will er veranschaulichen, dass dort weiter gezählt wird, wo das gewöhnliche Zählen nicht hinkommt, wo die Buchstaben zuende sind. Mit den transfiniten Zahlen kann er z.B. ›3 · ω‹ rechnen, so wie die Ägypter mit dem Bild 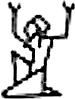
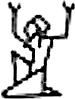
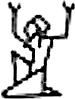 ein dreifaches Unendliches dargestellt und damit die Zahl 3.000.000 gemeint hatten.
ein dreifaches Unendliches dargestellt und damit die Zahl 3.000.000 gemeint hatten.
Für die transfiniten Zahlen gibt es bis heute kein Anwendungsbeispiel. Cantor vermutete, dass die natürlichen Zahlen mit den Körper-Atomen und die transfiniten Zahlen mit den von ihm so genannten Äther-Atomen, d.h. Wellen- und Strömungsphänomenen zu tun haben. Mathematische Eigenschaften der transfiniten Zahlen könnten daher helfen, physikalische Eigenschaften des Äthers besser zu verstehen. Dieser Ansatz ist nicht mehr fortgeführt worden, seit mit der Relativitätstheorie die Äthertheorie aufgegeben wurde. Ich könnte mir vorstellen, dass es zu einer Renaissance der transfiniten Zahlen kommt, wenn es gelingt, im Zuge einer Zusammenführung von Relativitäts- und Quantentheorie den Begriff des Äthers in geeigneter Form wieder aufzunehmen. - Der ägyptische Gott Heh der Unendlichkeit »versinnbildlicht die räumliche wie zeitliche Endlosigkeit. Insofern war der Gott auch Inbegriff für die Erdatmosphäre (Luft) und galt auch als Träger des Himmelszeltes« (Wikipedia, abgerufen 20.1.2015). Cantor wählt als elementaren Repräsentanten der räumlichen und zeitlichen Endlosigkeit das Linearkontinuum, das ist die eindimensionale Strecke, und fragt nach der Anzahl der Punkte auf dieser Strecke. Ist es möglich, den Grundbegriff der Geometrie (den Punkt) mit dem Grundbegriff der Arithmetik (der natürlichen Zahl) in ein mathematisches Verhältnis zu bringen?
- Schließlich unterscheidet Cantor diese verschiedenen Stufen durch ihre jeweilige Mächtigkeit, für die er als Symbol den ersten Buchstaben des hebräischen Alphabets wählt, das Aleph
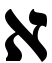 .
. - Die Mächtigkeiten sind für Cantor Stufen auf dem Weg zu Gott. 1885 hat er in Über die verschiedenen Standpunkte in bezug auf das aktuelle Unendliche mit Bezug auf Thomas von Aquin (Summa Theologica Prima I, Qaestio 7, Articulus 4) deutlich unterschieden zwischen dem aktual Unendlichen im Bereich der geschaffenen Welt (natura creata), das ein »noch Vermehrbares« (multiplicabilis) ist, und dem Absoluten, welches »wesentlich als unvermehrbar und daher mathematisch undeterminierbar zu denken ist« (Cantor, Abhandlungen, S. 375). Er wirft dem Pantheismus und Philosophen wie z.B. Kant vor, dass sie diese Unterscheidung ignorieren.
Damit hat Cantor den Grundgedanken der ägyptischen Zahlen wieder aufgegriffen und für die Frage nach dem Unendlichen eine religiös begründbare Lösung gefunden. Er unterscheidet wie die Ägypter verschiedene Größenordnungen und verleiht jeder Größenordnung ein eigenes Symbol. Jedoch sind die Größenordnungen nicht mehr wie bei den Ägyptern durch Zehnerpotenzen, sondern durch Stufen der Mächtigkeit voneinander getrennt.
Daraus ergibt sich sein Aufbau der Zahlen.
| endliche Zahlen | Zahlzeichen | 1, 2, 3, … |
| natürliche Zahlen
abzählbare Zahlen |
lateinisches Alphabet | 1, 2, 3, … n, …
1, 1/2, 2, 1/3, 2/3, 3, … n/m, … |
| transfinite Zahlen | griechisches Alphabet | ω, ω + 1, … 2 · ω, … n · ω + m, … ωω, …
Hier steht ω für die Anzahl aller natürlichen Zahlen. Es wird jenseits der natürlichen Zahlen weitergezählt. |
| reelle Zahlen | Sonderzeichen | z.B.  und e und e
Cantor konnte zeigen, dass es mehr reelle Zahlen als natürliche Zahlen gibt. Offen ist, ob die Anzahl der transfiniten Zahlen, der reellen Zahlen und der Punkte auf einer Gerade gleich ist. |
| Punkte einer Gerade | Geometrie |  |
| Mächtigkeiten | hebräische Zahlen mit Index | 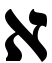 0, 0, 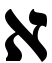 1, … 1, …
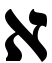 0 ist die Mächtigkeit der natürlichen Zahlen. 0 ist die Mächtigkeit der natürlichen Zahlen.
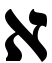 1 ist die kleinste Mächtigkeit, die größer als 1 ist die kleinste Mächtigkeit, die größer als 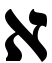 0 ist. 0 ist. |
Wie bei den ägyptischen Zahlen gibt es für jede Größenordnung eigene Symbole (Zahlzeichen, lateinisches, griechisches und hebräisches Alphabet sowie Sonderzeichen wie die Zahl e, geometrische Bilder wie Punkt und Gerade). Cantor verlässt damit die reinen Stellenwertsysteme wie das babylonische Sexagesimalsystem, das heute übliche Dezimalsystem oder das von der EDV genutzte Dualsystem, welche auf allen Stufen gleiche Zahlzeichen verwenden und sie nur durch ihre Stelle unterscheiden. Er sieht diese Systeme alle im Bereich der ersten Größenordnung der abzählbaren Zahlen.
Die Konstruktion der Zahlklassen und hier zunächst der transfiniten Zahlen ist nach dem Vorbild des Zehnerübergangs gestaltet. So wie nach jedem Zehnerübergang weitergezählt und in gewisser Weise wieder "von vorn" angefangen wird, zählt Cantor nach dem "Mächtigkeits-Übergang" weiter: Wird nach dem Übergang zur Zehn weitergezählt 10 + 1, 10 + 2, …, dann ersetzt Cantor die 10 durch die Anzahl aller Zahlen der Zahlklasse mit der nächstgeringeren Mächtigkeit und zählt bei den transfiniten Zahlen weiter mit ω + 1, ω + 2, …, wobei ω die Anzahl aller natürlichen Zahlen bedeutet. Wenn mit  (der hebräische Buchstabe tav) die Anzahl aller transfiniten Zahlen bezeichnet sei, wird nach dem nächsten Mächtigkeits-Übergang weitergezählt mit
(der hebräische Buchstabe tav) die Anzahl aller transfiniten Zahlen bezeichnet sei, wird nach dem nächsten Mächtigkeits-Übergang weitergezählt mit  + 1,
+ 1,  + 2, …, usf.
+ 2, …, usf.
Cantor vermutete, dass es so viele transfinite Zahlen gibt wie reelle Zahlen, und so viele reelle Zahlen wie Punkte einer Gerade (Linearkontinuum), oder anders gesagt: Es gibt keine Menge von Zahlen, die von größerer Mächtigkeit ist als die natürlichen Zahlen und von kleinerer Mächtigkeit als die Punkte auf einer Gerade (Kontinuumshypothese). Gödel hat gezeigt, dass diese Vermutung nicht in Widerspruch zu den Axiomen der Mengenlehre steht. In den 1960ern hat umgekehrt Paul Cohen gezeigt, dass auch die Negation der Kontinuumshypothese nicht den Axiomen der Mengenlehre widerspricht. Daher kann diese Vermutung nicht innerhalb der bekannten Axiomensysteme der Mengenlehre entschieden werden.
Im Sinne von Hegel kann gefragt werden, ob und wie die von Cantor eingeführten Stufen der Mächtigkeit eine Knotenlinie bilden. Für Cantor zeigt bereits jede einzelne Stufe eine bestimmte Ordnung, und es ist zu fragen, ob es eine übergreifende Ordnung gibt, aus der diese hervorgehen, die als das »Substrat der Mächtigkeit« verstanden werden kann. Es ist zu vermuten, dass es eine innere Beziehung dieser Ordnung zur Ordnung der Zeit gibt.
"Babylonisch": Algorithmen als erweitertes Stellenwertsystem
Ein Algorithmus ist eine Folge einfacher, maschinell ausführbarer Schritte. Das von den Babyloniern eingeführte Stellenwertsystem kann als ein elementarer Algorithmus verstanden werden:
| (1) | Gehe zur letzten Ziffer, lies die Ziffer und setze sie als Summe s, setze Anzahl Schritte k = 0. |
| (2) | Gehe eine Stelle nach links, erhöhe die Anzahl Schritte von k auf k + 1, lies die dort stehende Ziffer und multipliziere sie mit 60k und addiere das Ergebnis zur Zwischensumme. |
| (3) | Wiederhole Schritt 2 solange, bis die erste Ziffer erreicht ist und zeige das Ergebnis an. |
Zum Beispiel werde die folgende sumerische Zahl betrachtet, die aus drei Ziffern besteht:


Dann ergeben sich die Schritte:
| (1) | Gehe zur letzten Ziffer. Das ist  , sie bedeutet übersetzt in das Dezimalsystem 10. , sie bedeutet übersetzt in das Dezimalsystem 10.
Daher wird begonnen mit s = 10 und k = 0. |
| (2a) | Gehe eine Stelle nach links,
erhöhe die Anzahl Schritte k von 0 auf 1, lies die dort stehende Ziffer, das ist  , sie bedeutet übersetzt in das Dezimalsystem 3, , sie bedeutet übersetzt in das Dezimalsystem 3,
multipliziere sie mit 60k und addiere das Ergebnis zur Summe s. Da s nach Schritt 1 den Wert 10 hat und k auf 1 erhöht wurde, ergibt sich: s = 10 + 3 · 60k = s = 10 + 3 · 60 1 = 10 + 3 · 60 = 190 |
| (2b) | Gehe eine Stelle nach links,
erhöhe die Anzahl Schritte k von 1 auf 2, lies die dort stehende Ziffer, das ist  , sie bedeutet übersetzt in das Dezimalsystem 9, , sie bedeutet übersetzt in das Dezimalsystem 9,
multipliziere sie mit 60k und addiere das Ergebnis zur Summe s. Da s nach Schritt 2a den Wert 190 hat und k auf 2 erhöht wurde, ergibt sich: s = 190 + 9 · 60k = s = 190 + 9 · 60 2 = 190 + 9 · 3.600 = 32.590 |
In dieser Form ist der Algorithmus jedoch noch nicht maschinenlesbar. Für eine Maschine (z.B. einen Computer oder eine numerisch gesteuerte Anlage) sind auch die Operations-Schritte wie Gehe, Setze oder Erhöhe in maschinenlesbare Zahlen zu übersetzen, die von der Maschine erkannt und ausgeführt werden können.
Das ist der entscheidende Punkt: Es werden nicht nur die üblichen Zahlen gebraucht wie 0, 1, 2, 3, … 9 im Dezimalsystem, sondern weitere Zahlzeichen, die als Operationen und nicht als Ziffern zu verstehen sind. Daher ist der Zahlenvorrat entsprechend zu erweitern. So kann zum Beispiel das heute übliche Dezimalsystem erweitert werden in ein Hexadezimalsystem, das 16 Zahlzeichen kennt, wobei zusätzlich die Buchstaben A, B, C, D, E, F ergänzt werden. Mit ihnen können die Operationen bezeichnet werden. Im Ergebnis entsteht eine Zeichenfolge wie z.B. 576CAG, wobei mit den Zeichen CAG verschlüsselt ist, welche Schritte auszuführen sind, und mit 576 die auszuwertende Zahl. Die Maschine ist so programmiert, dass Zeichen, die größer als 9 sind, als Befehle erkannt und ausgeführt werden, während die üblichen Zeichen von 0 bis 9 als Zahlen interpretiert werden.
Diese Vorgehensweise kann schrittweise erweitert werden. Es können Operationen hinzukommen, aus der Umgebung bestimmte Werte einzulesen, die zum Beispiel von einem Sensor geliefert werden, Ergebnisse an einem Bildschirm anzuzeigen oder an Maschinen bestimmte Schalter an- oder auszuschalten.
Das Prinzip des Stellenwertsystems bleibt erhalten und ist lediglich ausgebaut:
Ein Algorithmus kann als eine Verallgemeinerung von Zahlen verstanden werden. Die Idee des Algorithmus ist bereits in der Idee des Stellenwertsystems enthalten, wenn die Interpretation einer Stelle als die elementare Operation eines Algorithmus verstanden wird.
So wie in einer Zahl schrittweise die Ziffern gelesen werden, werden in einem Algorithmus schrittweise die Befehle ausgeführt oder die Zahlen gelesen. Das Lesen von Zahlen wird als eine Operation verstanden, die gleichwertig ist mit anderen Operationen.
Als Beispiel können das Notensystem und die darauf aufbauenden Walzen und Lochstreifen für Drehorgeln dienen. Im Notentext gibt es sowohl Zeichen, welcher Ton zu singen oder zu spielen ist (die Noten), wie auch Ausführungszeichen, wenn z.B. eine bestimmte Passage zu wiederholen ist. Der Ausführende versteht, dass er hier im Notentext wieder zurückzugehen und den betreffenden Abschnitt ein zweites Mal vorzutragen hat. Das Notensystem enthält daher sowohl eine Art Zahlwerte, wenn die Linien und Zwischenräume als Zählwert verstanden werden (der erste, zweite, dritte, ... Ton in einem Tonsystem) wie Aufführungsanweisungen.
Algorithmus und Maschinenlesbarkeit sind nur möglich, wenn die beteiligten Zeichen und ihre Ausführung austauschbar sind. Die Maschine muss auf eine Weise konstruiert sein, dass sie austauschbare Zeichenfolgen nach einem einheitlichen Verfahren verarbeiten kann, so wie z.B. eine Drehorgel unterschiedlche Drehwalzen zum Klingen bringen kann. Und die Deutung der Zeichen muss so allgemein sein, dass sich die Maschinen austauschen lassen. Wenn ein Notentext so eindeutig aufgezeichnet ist, dass er immer gleich klingt, von wem auch immer er ausgeführt wird, also die Ausführenden und Ausführungen ausgetauscht werden können, dann kann an die Stelle der spielenden Menschen auch eine Maschine eingesetzt werden, die ihn genauso gut zum Klingen bringt. Im ersten Schritt sind unterschiedliche Menschen austauschbar, im zweiten Schritt Mensch und Maschine. Es ist die Frage zu stellen, ob mit der Forderung der Austauschbarkeit eine inhaltliche Beschränkung des Gedankens oder der Melodien verbunden ist, die dieser Bedingung genügen.
Die Möglichkeiten von Algorithmen werden bei einem weiteren Treffen zum Thema Big Data näher untersucht. Mit Big Data sind Datenmengen gemeint, die so groß sind, dass sie nur mithilfe von Algorithmen maschinell verarbeitet werden können. Es kann sich um eine Auswertung aller Suchanfragen bei Google handeln, eine Analyse aller Käufe in einem bestimmten Marktsegment, technischer Veränderungen an komplexen Systemen und so weiter.
Kurt Gödel hat die Möglichkeiten von Algorithmen genutzt, um mit ihnen zu zeigen, in welcher Weise auch selbstbezügliche Aufgaben entstehen können. Zum Beispiel kann ein Programm die Aufgabe bekommen, seinen eigenen Maschinencode einzulesen, auszuwerten und zu verändern. Mithilfe solcher Ideen konnte Gödel zeigen, dass mit jeder formalen Sprache Paradoxien entstehen. In einem System, das Selbstbezüglichkeit zulässt, ist es möglich, einen Satz zu bilden, der sich selbst widerruft: ›dieser Satz ist falsch‹. Das führt in den bekannten Widerspruch: Wenn dieser Satz falsch ist, ist er richtig, und wenn er richtig ist, ist er falsch.
Während die Ägypter eine maximal größte Zahl kannten (9.999.999), haben die Babylonier ein Zahlensystem entwickelt, das im Prinzip unbegrenzt ist, wenn fortlaufend neue Stellen ergänzt werden. Dadurch wurde es ihnen möglich, rein formal Zahlen aufzuschreiben, die sich jeder Anschauung entziehen. Während das ägyptische System zu den Stufen der Unendlichkeit durch Georg Cantor führte, sind im babylonischen System im Prinzip sowohl die unbegrenzten Möglichkeiten wie auch die inneren Paradoxien und Endlosschleifen angelegt, die die Mathematik des 20. Jahrhunderts beschäftigen. Endlosschleifen entstehen, wenn für eine Aufgabe ein Algorithmus gebildet wird, für die es prinzipiell keine Lösung gibt. Ein Beispiel ist ein »System aus zwei nicht-linearen, gekoppelten Differentialgleichungen erster Ordnung«, mit denen die »Wechselwirkung von Räuber- und Beutepopulationen« beschrieben wird (Lotka-Volterra-Gleichungen). Dies Thema wird fortgeführt bei dem geplanten Beitrag zu Big Data, bei dem es um den Einsatz von Algorithmen und ihre Deutung gehen wird.
Literatur
Oskar Becker: Grundlagen der Mathematik in geschichtlicher Entwicklung, Frankfurt am Main 1971
G. Johannes Botterweck, Helmer Ringgren, Heinz-Josef Fabry (Hg.): Theological Dictionary of the Old Testament, Band 8, Cambridge 1996; Auszüge zum Wort tohu in GoogleBooks, abgerufen 5.2.2015
Georg Cantor: Über die verschiedenen Standpunkte in bezug auf das actuale Unendliche (1886)
in: Georg Cantor: Gesammelte Abhandlungen mathematischen und philosophischen Inhalts, Berlin 1932, S. 370-377; Link
Georg Cantor: Briefe, Berlin u.a. 1991
Peter Damerow, Siegbert Schmidt: Arithmetik im historischen Prozeß: Wie „natürlich” sind die „natürlichen Zahlen”?, Stuttgart 2001; Link
Thrasybulos Georgiades: Nennen und Erklingen, Göttingen 1985
David Graeber: Schulden, München 2014
Christoph Grandt: Das Babylonische Sexagesimalsystem; Link
Dörte Haftendorn: Mathematik hat Geschichte, Teil 3, Alte Völker; Link
Georges Ifrah: Universalgeschichte der Zahlen, Frankfurt New York 1986
Ralf Krömer: Geschichte der Mathematik I, Vorlesung Universität Siegen 2009; Link
Martin Kuckenburg: Wer sprach das erste Wort?, Stuttgart 2010; Link
Andreas Pester: Vom Zählen zu den Zahlen, Spittal (Kärnten) 2002; Link
Jochen Ziegenbalg: Woher kommen die Zahlen?, PH Karlsruhe; Link
Bildnachweis des Titelbildes: Von Ochmann-HH - Eigenes Werk (own foto), CC BY 2.5, Link
© tydecks.info 2015