Das mathematische und das mythische Symbol

- mit einem Nachwort "Virtuelle und multiple Mathematik"

Einleitung

Mathematische Symbole sind heutzutage im alltäglichen Leben nicht weniger selbstverständlich als Buchstaben oder Verkehrszeichen. Sie gelten als Konventionen, mit denen sich leichter rechnen und die Ergebnisse der Mathematik besser auf andere Bereiche übertragen läßt. In diesem Beitrag geht es um das Spannungsverhältnis zwischen mathematischen und mythischen Symbolen, das heute nahezu vergessen scheint. Werden mythische Symbole hinfällig und überflüssig, wenn mathematische Symbole gefunden werden? Sind mythische Symbole Platzhalter, die nur solange gebraucht werden, bis die geeigneten mathematischen Symbole an ihre Stelle treten? Oder erklärt sich der Erfolg der mathematischen Symbole, weil sie die Macht der vorangegangenen mythischen Symbole bewahren?

So wie die rhetorischen Figuren am besten und überzeugendsten eingesetzt werden können, wenn niemand sie als rhetorische Figuren wahrnimmt, sondern sich unbewußt von ihnen beeinflussen läßt, gilt das auch für die Symbole. Sie werden heute nicht mehr an heiligen Orten bewahrt, verehrt und angebetet, sondern in die Formate der alltäglichen Darstellung gebracht (die Diagramme und Graphiken, Charts, Statistiken, formalisierten Anleitungen und Aufstellungen, Nebenrechnungen, logischen Folgerungen mit Gebrauch von "wenn - dann", "und", "oder" usf. bis zu den von Lacan entdeckten und weiterentwickelten Mathemen, Deleuze und Guattari sprechen von abstrakten Maschinen, Foucault von Ordnungen), in denen sie als bloße Hilfsmittel erscheinen. Niemand soll wahrnehmen, in welcher Weise er bereits einer grundsätzlichen Tendenz von Aussagen zustimmt, wenn er sich bedenkenlos auf den Gebrauch der wie selbstverständlich eingesetzten Symbole einlässt. Zugleich wird der aufgeklärte Mensch entmündigt, wenn er die Bedeutung der Symbole verlernt und nicht mehr fähig ist, sie angemessen zu nutzen. Das beraubt ihn wesentlicher Mittel der Wahrnehmung, Erkenntnis und Mitteilung und macht ihn unfähig, seine eigene Meinung äußern zu können.

Um einen Ansatz zu finden, dies zu verstehen, soll zur Entstehung der neuzeitlichen Symbole zurückgegangen werden.

Auf der Schwelle zwischen Antike, orientalischer Weisheit, christlicher Philosophie und neuzeitlicher Wissenschaft hat der Neuplatonismus ein Verständnis des Symbols gefunden, worauf die moderne Wissenschaft gründen konnte. Seine eigene Position in diesem Spannungsfeld ist recht überraschend: Für Platon und gegen Aristoteles, aber mit dem Wunsch, möglichst viel von Aristoteles zu übernehmen. Für das Heidentum bis zur aktiven Pflege überlieferter Kulte und Orakeldeutungen, und gegen das Christentum, das in seiner Lehre des offenbarten Wortes auf den ersten Blick Platon näher zu stehen scheint. Spektakulär war die Bekehrung des Christen Ammonias Sakkas zum Heidentum. Er lebte bis 242 in Alexandrien und gilt als Gründer der neuplatonischen Schule. Plotin und Origines waren seine Schüler.

Die Neuplatoniker sahen Vorläufer des Symbols (1) bei Platon, wenn er in seinen mythischen Erzählungen die Dialektik verläßt und Bilder schafft, die über das logische Denkvermögen des Menschen hinausgehen. (2) Aristoteles führte in seiner "Metaphysik" Proto-Begriffe ein wie den Proto-Stoff (proto hyle, prima materia). (3) Die orientalische Weisheit und das griechische Heidentum vertrauten der Bedeutung und Wirkung von göttlichen Symbolen in der Natur.

Seit der Neuzeit ist das wissenschaftliche Denken ohne den Siegeszug des mathematischen Symbols nicht mehr vorstellbar. Der Rückblick auf den umfassenden Symbolbegriff der Neuplatoniker soll die Grundlagenfragen der in ihrer Nachfolge entstandenen symbolischen Wissenschaft verstehen helfen: Was geht bei der Verdrängung der mythischen Symbole den mathematischen Symbolen und den mit ihnen operierenden Wissenschaften systematisch verloren? In welcher Weise verleiht die Wissenschaft dann ihren Symbolen doch wieder göttliche Kräfte und lädt ihnen damit etwas auf, was sie getrennt von mythischen Symbolen zu sprengen droht? Wo liegen die Grenzen der logischen Denkweise? Und wie kann es zum Einbruch von mythischen Symbolen in eine von der Wissenschaft geprägte Welt kommen, die einen tiefgreifenden Prozess der Ent-Mythologisierung hinter sich hat (Blumenberg nennt das "Arbeit am Mythos"), wie es während des Nationalsozialismus geschehen ist?

Mathematisches und mythisches Symbol haben in zwei Richtungen eine orientierende Aufgabe: Symbole der Götter und Symbole des Chaos zu schaffen. Mathematik muss die Symbole der Götter (des Transzendenten, der Unendlichkeit, des Übermaßes) übersetzen, damit mit ihnen im Endlichen gerechnet werden kann, ohne dabei den Bezug zur Unendlichkeit zu verlieren. In der anderen Richtung müssen die mathematischen Symbole gegenüber dem Chaos wie Kristallisationskerne wirken, um die herum sich Wissen bilden kann (Formspuren, ichne ton eidon, ein Ausdruck aus Platons Timaios). Solange die mathematischen Symbole "funktionieren", fragt niemand weiter nach ihnen. Aber am Horizont melden sich immer die mythischen Symbole: Zum einen als die Macht der Götter, die den Symbolen ihre Kraft verleihen, und zum anderen die Bedrohung des Chaos, das alles zu fragmentieren droht. Die mythologischen Symbole schützen die mathematischen Symbole, damit mit ihnen weder das dem Menschen unverständliche Göttliche noch das beunruhigende Chaotische überhand nehmen.

Dieser Beitrag soll in einem ersten Schritt zu den Fragestellungen der Neuplatoniker, insbesondere bei Jamblichos, Proklos und Simplikios zurückführen. Ihre Tradition blieb unvollendet. Was die mathematischen Symbole betrifft, hatten sie die Frage nach einer klaren Unterscheidung von Zahl und Größe offen lassen müssen. Diesen Punkt wieder aufzunehmen ist im engeren Sinn das Anliegen des folgenden Beitrags. Von dort aus soll eine neue Sicht auf die Grundlagenkrisen der Mathematik und Physik im 20. Jahrhundert gewonnen werden.

Im Verlauf der folgenden Untersuchung ergibt sich schrittweise die Wichtigkeit der Begriffe Zusammenhang (synecheia) und Größe (megethos). Sie werden sich später als Schlüsselbegriffe der aristotelischen Physik erweisen und sollen hier bereits vorgemerkt werden. Die Grundlagen der aristotelischen Philosophie waren tiefer im Denken der Neuplatoniker verborgen, als sie sich bewußt oder auszusprechen bereit waren.

Die drei Wurzeln des neuplatonischen Symbol-Begriffs

Meist werden die Einflüsse der orientalischen Weisheit auf den Neuplatonismus vernachlässigt. In gewisser Weise ist der erst seit 1900 üblich gewordene Begriff "Neuplatonismus" irreführend. Seine wichtigsten Vertreter wie Jamblichos, Plotin, Proklos und Simplikios kamen aus dem Libanon, Ägypten, Syrien und dem Südosten der Türkei. Ihr Vorläufer war Philo von Alexandrien. Jamblichos lehrte die ägyptischen Mysterien und Proklos kommentierte die chaldäischen Texte. Aus dieser Tradition kommt ihr Verständnis des Symbols, das sich von Platon und Aristoteles unterscheidet, auch wenn sie bei ihnen zurecht Vorläufer sehen. Heute wird das etwas in den Hintergrund gerückt, da sich die moderne Wissenschaft nur ungern eingesteht, in welchem Maß sie auf die gleichen Ursprünge zurückgeht wie die von ihr verachteten "Para-Wissenschaften". Bei den Neuplatonikern ist zu lernen, wie unkompliziert diese verschiedenen Einflüsse miteinander verschmolzen werden konnten.

Wissenschaft ist das Arbeiten mit Symbolen, und das um so mehr, je stärker sie mathematisch ausgerichtet ist. Prototyp ist die euklidische Geometrie, die mit symbolischen Figuren arbeitet und deren wechselseitige Beziehungen klärt. Obwohl der Symbol-Begriff von Jamblichos bis Proklos meistens nur beiläufig, dann aber immer wie selbstverständlich gebraucht wird, haben sie die entscheidende Vorarbeit geleistet. Es musste nur noch vom christlichen Glauben der Gedanke der Kreativität hinzukommen, damit sich die neuzeitliche Wissenschaft verstehen kann als die Fähigkeit, eigenständige Symbole zu schaffen, mit ihnen zu arbeiten und Modelle der Welt zu entwickeln. Von der neuplatonischen Philosophie ist zu lernen, wie der Symbol-Begriff aussah unmittelbar bevor er mit der Idee der Kreativität verbunden wurde. Er hat noch starke mythische Anklänge, die mit dem Einfluss des Christentums verdrängt wurden.

Statt von Symbolen zu sprechen, war bei den Neuplatonikern häufig vom Proto-Körper und der Proto-Zeit die Rede. Hier wurden auf völlig neue Art ganz unterschiedliche Vorstellungen von Platon, Aristoteles und dem Heidentum zusammengebracht.

(A) Platon hatte in seinem Timaios eine pythagoreeische Lehre überliefert, wonach der Kosmos das dem Menschen zugängliche Bild (eikon) eines nur für einen höheren als dem menschlichen Verstand fassbaren Grundrisses (paradeigma) ist. Nur Gott überschaut beides, das paradeigma und das eikon.

Der Begriff paradeigma ist schwer zu übersetzen. paradeigma darf nicht mit den platonischen, transzendenten Ideen verwechselt werden. Wörtlich bedeutet paradeigma das Neben-Zeigen, zusammengesetzt aus para (neben) und deiknunai (zeigen) (siehe Wikipedia). In den lateinischen Übersetzungen wurde der Begriff paradeigma aus dem Timaios sowohl als exemplum (Beispiel) wie auch als Archetyp (Urbild) übersetzt. Mir erscheint für eine deutsche Übersetzung das Wort "Grundrisse" oder "Grundlinien" am geeignetsten: Der Mensch vermag in der Natur Linien zu erkennen, die Auszug eines größeren, ihm im Ganzen nicht zugänglichen Geflechts von Grundlinien sind. Sein aus Linien zusammengesetztes Bild steht daher neben den umfassenderen Grundlinien. Er vertraut darauf, dass eikon und paradeigma im Sinne eines Analogie-Denkens miteinander verbunden sind.

Was hier gemeint ist, kann vielleicht am besten ein Gedanke von Nikolaus von Kues (1401-1464) zeigen: Die unendlich lange Gerade ist zugleich ein unendlich großer Kreis, ein Dreieck mit unendlich langer Grundlinie und eine unendlich große Kugel. Nikolaus von Kues denkt an einen Grenzübergang und nähert sich der Idee einer nicht-euklidischen Geometrie:

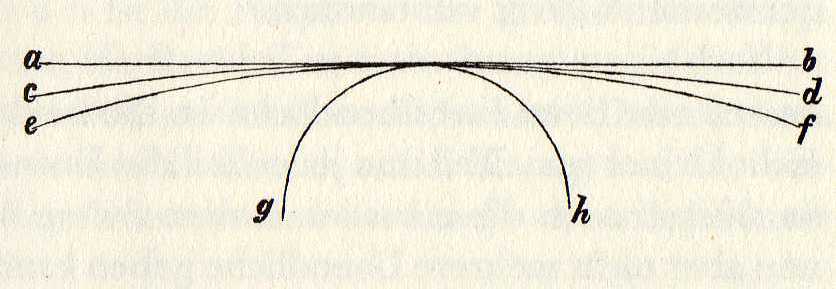
Figur 1 Unendliche Line

Quelle: Nikolaus von Kues "Von der Wissenschaft des Nichtwissens", Kap. 13 "Von den möglichen Veränderungen der größten und unendlichen Linie", in: "Philosophische und theologische Schriften", S. 65

Nikolaus von Kues hat Proklos intensiv studiert. Seine Gedanken zur negativen Theologie können daher im folgenden zum besseren Verständnis der Neuplatoniker herangezogen werden. Er hat Giordano Bruno und die Entwicklung der Infinitesimalrechnung angeregt. Leider blieb er der Aufklärung weitgehend unbekannt und wurde erst im 20. Jahrhundert von Ernst Cassirer neu entdeckt.

Die drei Kreissegmente g-h, e-f, c-d stehen symbolisch für ein unendliches Bündel von Kreissegmenten, die sich immer weiter an die Gerade annähern bis im Grenzübergang die Linie a-b als Segment eines unendlich großen Kreises verstanden werden kann. Diese Abbildung kann auch so gedeutet werden, dass ein Betrachter von oben auf eine Kugel schaut. Die Kreissegmente g-h, e-f, c-d werden als Breitengrade der Kugel verstanden, die Linie a-b als Äquator einer unendlich-großen Kugel.

Wäre es dem Menschen möglich, den Standpunkt des Unendlichen einzunehmen, dann würden Gerade, Kreis, Kugel und Dreieck in einer Proto-Topologie ineinander übergehen. Die menschliche Wahrnehmungsfähigkeit verbleibt jedoch im Endlichen und daher in der euklidischen Geometrie bzw. der transzendentalen Ästhetik im Sinne von Kant. Die Vorstellungskraft kann zwar darüber hinausgehen, aber auch ihre veranschaulichenden Bilder sind an die euklidische Geometrie gebunden, wenn z.B. wie hier angedeutet die Geometrie auf einer Kugeloberfläche Beispiel für eine nicht-euklidische Geometrie ist.

Der Mensch kann nur den Gedanken des Grenzübergangs erfassen. Abbildungen wie diese sind Bilder von Grundlinien, die sich als solche dem Menschen entziehen.

Zugleich darf der Kosmos nicht verwechselt werden mit dem sinnlich wahrnehmbaren Himmel, dem ouranos. Der Kosmos ist weder eine Verallgemeinerung der Himmelskugel noch das Muster, nach dem Gott die Welt erschaffen hat, sondern nur eine dem Menschen zugängliche Variante dieses Musters, die der Mensch aus seinem eingeschränkten Verständnis des göttlichen Bauplans und seiner sinnlichen Wahrnehmung des Himmels und der Natur erschließen kann.

Entsprechend ist die dem menschlichen Verständnis zugängliche Zeit ein Bild des Aion (des Ewigen, das nur Gott überschauen kann). Der Mensch kann die höhere Einheit der Zeit, die vor der Aufteilung in Vergangenheit, Gegenwart und Zukunft liegt, bzw. in moderner Vorstellung alle physikalische Ideen wie z.B. von einem Urknall übersteigt und die innere Einheit aller Ereignisse darstellt, nicht erfassen, sondern sich nur Bilder von ihr machen: Ein Bild ist der Zeitfluss mit seinem inneren Zusammenhang, ein anderes Bild ist die Ereignis-Kette einander unmittelbar folgender Zeitatome. Jedes der Bilder ist für sich allein unvollständig und beide fügen sich nicht widerspruchslos zusammen. Darauf beruhen die Paradoxien von Zenon. Versucht der Mensch, in Gedanken über den Zeitfluss und die Zeitatome hinauszugehen, dann verwickelt er sich notwendig in die von Kant beschriebenen Antinomien. - Beide Bilder sind intuitiv und unmittelbar eingängig, aber es ist leicht nachzuvollziehen, dass in der Natur weder ein Zeitfluss noch Zeitatome wahrgenommen werden können. Stattdessen werden in der Natur konkrete zeitliche Prozesse wahrgenommen, wie z.B. der wandernde Schattenwurf von Sonnenuhren, der Mechanismus von Uhrwerken, oder die jeweils einmalige Eigenzeit alles Lebendigen und seines inneren Pulses. Das wahrnehmbare Maß aller zeitlichen Prozesse sind die Umläufe der Sterne am Himmel (ouranos).

Das platonische eikon kommt bereits dem Symbol sehr nahe. Zeitfluss und Zeitatome können nur symbolisch verstanden werden: Mit ihnen kann die denkende Seele operieren und die in der Natur beobachtbaren zeitlichen Prozesse zu beschreiben versuchen, aber sie sind nicht Gegenstand der Wahrnehmung. Sie können aus den wahrnehmbaren Erscheinungen mithilfe des Verstandes herausgelesen werden. Auf der anderen Seite läßt sich die göttliche Schöpfung nicht als ein Ereignis innerhalb des Zeitflusses verstehen oder als ein Ur-Zeitatom, aus dem alle weiteren Zeitatome entspringen. Die moderne Physik verwickelt sich in unlösbare Dilemmata, wenn sie die Zeit aus zeitlosen Zuständen emergieren lassen will.

(B) Aristoteles hatte in der Metaphysik den Begriff der Prima Materia (proto hyle) eingeführt. Die Prima Materie ist der den vier Elementen Erde, Wasser, Luft und Feuer zugrundeliegende einheitliche Stoff der sublunaren Welt, in der die Gesetze der für uns aus eigener Wahrnehmung bekannten Physik gelten. Prima Materie war insofern eine materialistische Kritik an der Ideenlehre von Platon, der die vier Elemente nicht auf einen zugrundeliegenden Stoff, sondern auf transzendente, mathematische Formen zurückführen wollte.

Der Begriff proto hyle steht bei Aristoteles in einem inneren Zusammenhang mit den rätselhaften übergeordneten Begriffen hyle noete (die gedachte Hyle oder der Stoff der Gedanken, der Stoff der Mathematik) (Met. VII 10, 1036a; VII 11, 1036b-1037a; VIII 6, 1045a; X 8, 1058a), und hyle topike (die Orts-Materie, der Stoff der Ortsbewegung, der Sternenstoff der körperlos verstandenen Himmelserscheinungen im supralunaren Bereich) (Met. VIII 1, 1042b). Die proto hyle steht zwischen diesen beiden Stoffen einerseits und den aus der Natur bekannten Stoffen andererseits. Aristoteles wollte mit der proto hyle einen Begriff finden, der nicht wie bei Platon die Physik aus der Mathematik ableitet, sondern umgekehrt ermöglicht, dass im Denken aus den sinnlichen Erfahrungen der Stoffe der Natur höhere Begriffe gebildet werden können (Metaphysik).

Die proto hyle ist daher kein Urstoff, wie es die Alchemisten der europäischen Renaissance bei ihrer Suche nach der Prima Materie missverstanden und ihn erfolglos in der Retorte erzeugen wollten, sondern am besten als ein symbolischer Stoff zu verstehen, der im Denken stellvertretend für alle sinnlich wahrnehmbaren Stoffe steht und mithilfe dessen im Denken allgemeine Eigenschaften des Stoffes erkannt werden können, etwa das Verhältnis des Stoffes zur Form und zum Formmangel (steresis). Dies nur im Denken zu verstehende Verhältnis ist der Ausgangspunkt der aristotelischen Physik. (Siehe zur doppelten Bedeutung der Natur, was sie ist [kategoreia] und was fehlt [steresis], den Kommentar "steresis - eine Lehre des Fehlenden und Neinsagens", Link. Wichtige Quellen sind Aristoteles Physik B 1 und Heideggers Erläuterungen.)

(C) Schließlich die heidnische Überlieferung. Die neuplatonischen Philosophen haben trotz der Verbote durch die christliche Staatsreligion die heidnischen Kulte im Geheimen fortgeführt, und die von ihnen inspirierten symbolischen Zeichen (z.B. Traumbilder, Formationen des Vogelflugs, Faserungen der Leber von geopferten Tieren, Sternbilder, Muster der Lage von Steinen, etc.) wurden als Wahrsagung verstanden. Proklos hat eine Schrift "Über das mythische Symbol" verfasst, von der jedoch nicht einmal Fragmente oder Zitate überliefert sind. Aber Ficino hat das "Opus Procli de sacrificio et magia" ("Über Opfer und Magie") überliefert. Proklos vertritt eine Sympathie zwischen Himmel und Erde: auf der Erde ordnet sich die Natur zu solchen Mustern, die das Göttliche verstehen lassen. Die Natur bildet von sich aus Symbole, die der Mensch nur zu verstehen lernen muß.

Peter Crome ist dem Symbol-Begriff bei Proklos nachgegangen: Im Timaios-Kommentar interpretiert Proklos die dort von Platon genannten Mythen über das untergegangene Atlantis, die ägyptische Tempelstätte Sais und die Jugendlichkeit Griechenlands als Symbole, mit denen in die im weiteren dargestellte Lehre eingeführt wird. Platon bezieht sich hier seinerseits ausdrücklich auf ägyptische Lehren. Im Politeia-Kommentar kritisiert Proklos allerdings Platons Ablehnung aller nachahmenden Kunst. Im Gegenteil will er zeigen, dass auch Platon mit seinen Mythen Symbole geschaffen hat. Nachahmung hat allerdings nicht einfach Abbild-Charakter, sondern ist eine symbolische Darstellung, um etwas sinnlich erfahrbar und verstehbar zu machen, was nicht direkt erkannt werden kann. (Mit einer ähnlichen Kritik an der Lehre von den Trugbildern bei Platon hat Gilles Deleuze seine Philosophie begonnen, siehe die Anhänge in "Logik des Sinn".)

Ein Beispiel von Jamblichos (245-325) vermag das vielleicht zu erklären. Er interpretiert die merkwürdig klingende pythagoreeische Regel "Malven pflanze zwar, doch iß sie nicht":

"Dies drückt verrätselt aus, daß sich solche Pflanzen der Sonne zuwenden, und erlangt, dies zu beachten; dabei steht aber auch 'umpflanzen', das ist: Wende deine Aufmerksamkeit ihrer Natur zu, dem Streben nach der Sonne und dem Mitschwingen, doch sei damit nicht zufrieden oder bleibe bei dieser Erscheinung stehen, sondern ändere den Sinn und verpflanze ihn sozusagen auf die verwandten Pflanzen und Gemüse und weiter auf die nicht verwandten Lebewesen, die Steine, Flüsse und einfach alle Naturerscheinungen. Du wirst finden, daß das Zeichen der Einheit und Übereinstimmung des Kosmos mannigfach, vielfältig und staunenswert reichhaltig ist, wenn du wie von Wurzel und Startpunkt von der Malve ausgehst. Also iß nicht davon und laß solche Beobachtungen nicht untergehen, sondern vermehre sie im Gegenteil und erzeuge wie ein Gärtner eine Fülle davon." (Jamblichos, "Aufruf zur Philosophie", S. 83)

Figur 2 Malve, historische Kräuterabbildung
Urheber: Von Jan Kops - www.BioLib.de, Gemeinfrei, Link

Die Malve ist ein Zeichen, wie sich das Materielle dem Höheren zuwendet, und sie zeigt, wie die Natur durchströmt ist von einer Bewegung, die Einheit und den Kosmos zu verstehen. Die Philosophie, zu der Jamblichos in dieser Schrift aufruft, soll von der Naturbeobachtung ausgehen, in der Natur diese Bewegung erkennen und sich von ihr ergreifen lassen. Wenn sie dies Streben in der Natur erkennt, gewinnen die sinnlich wahrnehmbaren Erscheinungen der Natur symbolische Bedeutung. Viele sind überliefert in den symbolischen Darstellungen der griechischen Götter, so die Ähre, die Leier, der Blitz und so fort. Das ist ein ganz anderes Verständnis des Symbols als etwa das Kreuz im Christentum. (Yehuda Liebes vermutet, dass die Schriften von Jamblichos eingeflossen sind in den um 1280 entstandenen "Sohar", eins der Hauptwerke der Kabbala.) Die Neuplatoniker vertrauten der Kraft der natürlichen Symbole und hielten daher an dem Glauben an Wunder und der Orakeldeutung fest.

Das Symbol und die Seele mit ihrer Fähigkeit, Symbole zu bilden, stehen in der Mitte zweier Bewegungen, die im Ganzen einen Kreislauf bilden: Ausgehend von den Grundlinien der Vernunft (Geist, nous) bildet die Seele Proto-Begriffe, die die Keime der Wissenschaft sind, mit deren Hilfe der Mensch die Natur erkennen und systematisch verstehen kann. Diese Keime, wie z.B. der Kreis, gehen der Wissenschaft voraus und können in ihrem Innern nicht in der Weise begründet werden, wie dann im weiteren alle Folgerungen begründbar sind. Die euklidische Geometrie ist Prototyp der Wissenschaft. Sie beginnt mit den Definitionen (oristike) elementarer Figuren (Punkt, Kreis, Gerade) und eröffnet mit ihnen einen Horizont, innerhalb dessen dann alles weitere daraus abgeleitet werden kann. Proklos will das in seinem Euklid-Kommentar nachweisen. Für seine eigene Philosophie bleibt die Aufgabe, einen Schritt früher die Herausbildung der Elemente zu verstehen, die am Anfang der Wissenschaft stehen. Der Titel seines Hauptwerks "Stoicheiôsis theologikê" erscheint mir daher weder als "Grundkurs über die Einheit" noch als "Theologische Elementarlehre" treffend übersetzt. Der Begriff stoicheiôsis soll vielmehr das Wirkende der Elemente (stoicheia) in der Seele beschreiben, die "elementenden Elemente", wie z.B. von der "zählenden Zahl", oder mit Heidegger von der zeitigenden Zeit gesprochen werden kann.

Zugleich werden in der anderen Richtung die Symbole aus der Betrachtung der Natur gewonnen wie es Jamblichos beschrieben hat. Das ergibt eine kreisförmige Bewegung, Proklos spricht von der "kreisartigen Wirklichkeit" (kyklike energeia, Proklos, Einheit, §33). Die ausgehende Monas ist Dynamis sowohl als Kraft, wie als Bestand, wie als Möglichkeit, aus der das Viele hervorgeht (prohodos ). Und sie ist auch der Grund, worauf sich das aus ihr entstandene Viele wieder zurückbezieht (epistrophe). Erst der Kreislauf im Ganzen ergibt die Fülle des Symbols. "Der Hervorgang allein würde den Gegenstand unbestimmt lassen, da jeder Gegenstand erst durch die Rückwendung auf seine Ursache sein Wesen (ousia) bestimmt." (Gombocz, S. 216)

Jedes Symbol befindet sich daher in zwei Ordnungen (tas taxeis, Proklos, Einheit, §63). Eine Ordnung geht zurück auf die Grundlinien des Geistes, die andere auf die Wahrnehmung der Natur. Die göttliche Überfülle hat beim Übergang in die von der Seele gebildeten Symbole etwas verloren und behält daher einen für die Seele geheimen, unerkennbaren, nicht einmal benennbaren Grund. Proklos spricht von geheim (kruphion), unfassbar (alepton), unsagbar (arreton) und unerkennbar (agnoston) (Proklos, Einheit, §§121-123). (Das meint auch Nikolaus von Kues mit den ignorantia und gründet darauf seine negative Theologie). Die andere Ordnung ergibt sich aus der Naturbeobachtung und legt in sie Erkenntnisse hinein, die nicht unmittelbar in der Natur zu sehen, aber aus ihr herauszulesen sind. Alles in der Natur läßt sich zählen, aber nirgends lassen sich die Zahlen als solche in der Natur sehen. Diese beiden Ordnungen drohen sich als mythisches und mathematisches Symbol voneinander zu isolieren. Die Trennung ist vollzogen, wenn in der neuzeitlichen Naturwissenschaft die mathematischen Symbole als Geschöpfe des kreativen wissenschaftlichen Geistes erscheinen, als bloße Konventionen. Dann befindet sich die Wissenschaft nicht mehr innerhalb des vom Neuplatonismus beschriebenen Kreislaufs, sondern steht über der Natur und schafft aus sich selbst die Symbole, um die Natur wissenschaftlich beschreiben zu können.

Das Besondere der Mathematik ist nun, dass sie das Wechselverhältnis dieser beiden Ordnungen zum Gegenstand ihrer Forschungen zu machen versteht und auf diesem Wege Erkenntnisse liefert, die keineswegs von Anfang an selbsterklärend sind. Das erscheint heutzutage systematisch in der Gegenüberstellung lokaler und globaler Ordnungen (lokal ist jeder Raum "euklidisch", d.h. rechtwinklig, in dem der Satz des Pythagoras gilt, global ist er eine differenzierbare Mannigfaltigkeit). Bei Euklid geht es um das Verhältnis von Gerade und Kreis. Proklos: "Right lined figures are proper to sensibles, but a circle to intelligibles." (Proklos, In Eucl., Taylor-Übersetzung, 82) Zwischen beiden besteht ein Spannungsverhältnis, aus dem sich die Geometrie von Euklid entwickelt. Sie beginnt mit einfachen Konstruktionen geradliniger Figuren und führt zu komplizierten Schraubenlinien (Helix, Spirale) (Proklos, In Eucl., 179-180, siehe Becker S. 103). (Siehe dazu Manchester "Syntax of Time" über die archimedische Spirale als mathematische Darstellung des Falls [ekpipto] der intelligiblen Zeit in den natürlichen Zeitstrom.)

Für Proklos sind die Elemente der Geometrie von Euklid gleichermaßen mathematische und mythische Symbole. Der Punkt ist sowohl das kleinste Element der Geometrie, ohne Teile, ohne Dimension, also negativ definiert, leer, und zugleich die göttliche Kraft, aus der alles entspringt und wohin alles zurückkehrt. Am ungewohntesten für die heutige Mathematik ist die Zuordnung von Winkeln zu Göttern. Der rechte Winkel ist Symbol der Erdgöttinnen Rhea, Demeter und Hestia (Proklos, In eucl., 128-130 und 173-174). Jeder Winkel zeigt, wie aus dem Punkt Linien herausströmen und umgekehrt Linien in einen Punkt zusammenfallen. Jeder Winkel hat eine qualitative, göttliche Kraft. Der rechte Winkel steht für das Bauprinzip der Erde. Hier befinden sich die expandierenden und kontrahierenden Kräfte im Gleichgewicht. Der rechte Winkel wird über die Göttin Hestia mit dem Herdfeuer identifiziert, dem kraftgebenden Winkel des Hauses, und dem Pol der Himmelskugel. Das mag weit hergeholt klingen und bedarf sicher einer weiterführenden Interpretation. Das gleiche Bild kehrt wieder, wenn der Mathematiker Bernhard Riemann im 19. Jahrhundert zur Beschreibung der komplexen Zahlen die Zahlenkugel mit ihrem unteren Pol auf dem rechtwinklingen Koordinatenkreuz der komplexen Ebene auflegt.

Als Hegel in der späten Version des ersten Bandes seiner "Wissenschaft der Logik" abschließend die Idee einer Mathematik der Natur entwarf, die für ihn die Wissenschaft der Maße ist, war er auf dem Weg in das Zentrum der neuplatonischen Lehre. In neuerer Zeit hat Deleuze in seiner "Logik des Sinns" mit den "fünf Charakteristika des Transzendentalen Feldes" einen anderen intuitiven Ansatz vorgelegt. Auch er unterscheidet systematisch zwei Serien und stellt die "königliche", vernunftartige, axiomatische Mathematik, also die Mathematik des Geistes, der "kleinen", molekularen, Probleme aufwerfenden Mathematik gegenüber, die aus der Wahrnehmung schöpfende Mathematik. (Vgl. hierzu Aristoteles Met. VII,10 1036a und De.An. III,4 430a sowie Proklos, In Eucl. 51.)

Beide Seiten stehen einander aber nicht starr gegenüber, sondern die Mathematik befindet sich in einer wechselseitigen Bewegung zwischen den Prinzipien des Geistes (Proklos versteht dies als die Dialektik im Sinne von Platon) und der Fülle der Natur. Daher spricht Proklos von den "sich selbst bewegenden Zahlen" und den "lebendigen" Figuren, die in der Seele den Zahlen und den "sichtbaren" Figuren vorausgehen (Proklos, In. Eucl. 16). Die folgenden Überlegungen zu den Maßen der Natur sollen die Grundlage legen, um darauf aufbauend die Dynamik der Maße der Natur zu verstehen. Hegel hat das nicht mehr weiter ausführen können. Heute ergeben sich dank der Relativitätstheorie von Einstein und der Quantentheorie ganz neue Möglichkeiten zu ihrem Verständnis.

Von den Maßen der Natur (Zahl, Größe, Ort, Zeit) zu den Prinzipien einer Proto-Mathematik

Das abrupte Ende der neuplatonischen Schule fiel in aufgewühlte Zeiten. Seit 375 war Europa unter dem Druck der Hunnen in den Strudel der Völkerwanderung geraten. Die Auflösung des Römischem Reiches war nicht mehr aufzuhalten. Auch die 391/92 durchgesetzte Erhebung des Christentums zur römischen Staatskirche brachte nicht die gewünschte Stabilisierung. Dennoch traf das die antike Philosophie hart, die ineins mit dem Heidentum verfolgt wurde. Heidnische Religionstätigkeit war offiziell seither verboten. 402 war Ravenna Hauptstadt Westroms geworden, 410 plünderten die Westgoten Rom. 415 wurde in Alexandria die Mathematikerin Hypathia (370-415) von einer aufgebrachten christlichen Menge ermordet, weil sie dem neuplatonisch motivierten Heidentum treu blieb. Der Vormarsch der Hunnen wurde erst 451 mit der Schlacht auf den Katalaunischen Feldern gebrochen. 529 wurde von Kaiser Justinian endgültig die Akademie in Athen geschlossen. Ihr wurde heidnischer Unterricht vorgeworfen. Letzter Vertreter der Neuplatoniker blieb daher Simplikios (490-560). Er war Schüler von Damaskios (458 - 540), dem letzten Direktor der Akademie in Athen. Beide mussten für einige Jahre Athen verlassen.

Mit Simplikios brach die neuplatonische Tradition ab. Auf ihn gehen zwei wichtige Neuerungen zurück, von denen hier ausgegangen wird: (a) Er hat nach dem Vorbild des Proto-Stoff (prima materia) den Begriff der Proto-Zeit eingeführt, um systematisch zwischen dem Paradigma der Zeit im Nous, den Symbolen der Zeit in der Seele und den zeitlichen Prozessen in der Natur unterscheiden zu können. Die Proto-Zeit hat ihren Ursprung im Aion, der höheren Einheit der Zeit im Geist (Nous). In der anderen Richtung ist sie in der Natur (Physis) das Übergreifende von Werden und Vergehen und damit die messende, "zeitigende" Zeit. Das Verhältnis von Aion im Nous, Proto-Zeit in der Seele und Chronos in der Natur wird Muster für alle anderen Begriffe, um Paradigma, Eikon und das "Natürliche", das sinnlich Wahrnehmbare zu unterscheiden. (b) Für Simplikios sind anders als für Damaskios Größe und Ort (megethos, topos) nicht ein Maß, sondern zwei Maße (Simplikios, Zeit, 773-774).

Damit zeichnet sich eine Gruppierung ab: Es gibt vier statt drei Maße, und von ihnen sind Zahl und Größe mathematisch, Ort und Zeit physikalisch (naturwissenschaftlich). Unter mathematischen Symbolen werden im engeren Sinn die arithmetischen Zahlsymbole, die geometrischen Symbole wie Punkt, Gerade, Kreis, Winkel, Kugel und die Symbole des Unendlichen (Unbegenzten, unendlich Großen) verstanden. Die Naturwissenschaften werden nach Symbolen für Orte und Zeiten suchen.

Das Verständnis der Größe als eigenes Maß ist offen geblieben, da der Ansatz von Simplikios nicht fortgeführt werden konnte. Für die Größe fehlen bis heute allgemein anerkannte Symbole. Das System der Maße der Natur ist daher unvollständig. Was die Mathematik im engeren Sinn betrifft: Wenn das Maß der Größe deutlich vom Ort unterschieden werden kann, wird es auch möglich, Zahl und Größe voneinander zu unterscheiden. Diese Aufgabe ist ebenfalls offen geblieben, und das ist die tiefe Ursache für die Paradoxien, in die sich die Naturwissenschaft im 20. Jahrhundert entwickelt hat.

Wie weit war es den Neuplatonikern gelungen, die mathematischen Maße Zahl und Größe in vergleichbarer Strenge zu klären wie den Zeitbegriff?

Zahl: In einem ersten Ansatz sind bei der Zahl (1) die natürlichen Zahlen, (2) die Proto-Zahlen der Seele und (3) das Paradigma der Zahlen im Nous zu unterscheiden. Gyburg Radke (Uhlmann) hat in ihrer Arbeit "Die Theorie der Zahl im Platonismus" ausführlich einen Text von Syrian (400-450) übersetzt und gedeutet. In einem Kommentar zu Aristoteles' Kritik an Platons Ideen- und Zahlenlehre (Metaphysik Buch XIII Kapitel 8) fragt er nach dem Stoff und der Form der Zahlen. Das führt ihn zur Unterscheidung von zugestandenen, demiurgischen und eidetischen Zahlen. Sie sollen hier als die gesuchten natürlichen Zahlen, Proto-Zahlen und noetischen Zahlen interpretiert werden.

(1) Die zugestandenen Zahlen sind die Zahlen, mit denen in der physischen Welt gezählt wird: drei Äpfel, 111 Werke, tausend Stufen usf. Das sind die Anzahlen physisch vorhandener Dinge, die abgezählt werden können. Diese Zahlen werden bis heute als die natürlichen Zahlen bezeichnet. Alle natürlichen Dinge werden durch die Anzahl ihrer Teile und Merkmale beschrieben: ein Mensch geht auf zwei Beinen, ein Jahr hat 365 Tage, die Bienenwabe hat 6 Seiten ...

(2) Die demiurgischen Zahlen sind die Zahlen, mit denen die Seele ihre Bilder (eikon) entwirft. Die Idee der demiurgischen Zahlen schließt an den Timaios von Platon an. Platon erzählt, wie der Demiurg den Kosmos geschaffen hat. Hier wird nicht mehr etwas abgezählt, sondern die Seele sucht nach geeigneten Zahlen, um sich ein Bild zu machen, welche Zahlen der Demiurg gewählt hat. Daher spricht Syrian von demiurgischen Zahlen. Wenn z.B. von 4 Himmelsgegenden gesprochen wird, werden nicht wie im physischen Bereich die Himmelsgegenden abgezählt mit dem Ergebis "die Anzahl der Himmelsgegenden beträgt vier", sondern die Vier hat symbolische Bedeutung (Quaternität). Ihr Symbol ist das Koordinatenkreuz, noch heute entfernt im Zeichen "4" ablesbar, in dem eine Senkrechte und eine Waagerechte einander kreuzen. Der Himmel wird symbolisch als ein Koordinatenkreuz mit den 4 Flächen West, Nord, Ost und Süd verstanden.

Die demiurgischen Zahlen sind Symbole. Wo lassen sich am Himmel Norden, Süden, Westen oder Osten wahrnehmen, beobachten und zählen? Sternzeichen oder Sterne können gezählt werden, aber nicht die Himmelsrichtungen. Die Quaternität (Vierfaltigkeit) ist eine symbolische Eigenschaft des Himmels, die sich aus dem Verständnis des Bauplans des Demiurgen ergibt und nicht aus der Beobachtung des Himmels. Das Koordinatenkreuz ist ein Bild der Grundlinien, wie der Kosmos geschaffen wurde.

Wenn von demiurgischen Zahlen gesprochen wird, bedeutet das, dass der Demiurg in seinem Plan mit Zahlen gearbeitet hat. Der Mensch kann diese Zahlen nur unvollständig verstehen. In der Natur kommen sie nur in Annäherung vor. Aber die Natur neigt dazu, Formen zu bilden, die zu diesem Ursprung zurückgehen wollen. Die Seele hat die Fähigkeit, sich ein Bild dieser Zahlen zu machen und sie aus der Natur herauszulesen. Das Ergebnis sind die symbolischen (demiurgischen) Zahlen.

Das Verständnis der symbolischen Bedeutung der Zahlzeichen ist inzwischen weitgehend verloren gegangen. Der Kreis der Null ("0") erinnert an das Symbol der Einheit, wird jedoch nicht der Zahl 1 zugewiesen. Die "1" zeigt dagegen das als Strich symbolisierte Zeichen der Existenz, dass etwas einmal vorhanden ist (die Kerbe, der Strich auf dem Bierdeckel, die römische Eins). Die Schlangenlinie der "2" läßt an das chinesische Yin-Yang-Zeichen erinnern. Die "3" hat sich weit entfernt vom Dreieck, früher Symbol des Matriarchats, der Dreifaltigkeit der Mondphasen, später Symbol der christlichen Trinität. Mit einiger Phantasie kann sie als Symbol der Verzweigung (Dreiweg, trivium) gelesen werden, wenn sich in der Mitte nach oben und nach unten die beiden Halbkreise voneinander trennen. Die "4" zeigt das Koordinatenkreuz, die "8" steht in symbolischer Beziehung zum Symbol des Unendlichen "".

Heute werden die symbolischen Zahlen nicht mehr von den natürlichen Zahlen getrennt. Das Abzählen von Dingen mithilfe der natürlichen Zahlen und das symbolische Verständnis von Eigenschaften des demiurgischen Bauplans werden nicht voneinander unterschieden. Daher ist es auch nie möglich geworden, eine eigene Dynamik der Zahlen zu entwickeln, sondern lediglich den bekannten Aufbau der Zahlen, der von den natürlichen Zahlen zu den ganzen, rationalen, irrationalen und reellen Zahlen führt. Die Frage nach der Dynamik der Zahlen wird sich ebenso als Neuland erweisen wie die Frage nach den Symbolen der Größen.

Heute gelten die natürlichen Zahlen nicht nur als Maß der Zahlen, sondern zugleich auch als Maß der Größe. Größen werden nur nach ihrem Zahlenwert unterschieden. Die Ordnungsrelation der natürlichen Zahlen (z.B. "7 > 3" oder "n² > n", in Worten: ›sieben ist größer als drei‹ oder ›n Quadrat ist größer als n für alle natürlichen Zahlen n‹ wird mit dem Maß der Größe gleichgesetzt. Um das Maß der Größe vom Maß der Zahl unterscheiden zu können, ist daher notwendig, zunächst für die Zahlen zwischen den natürlichen Zahlen und den symbolischen Zahlen zu unterscheiden.

Vielleicht ist es David Foster Wallace besser gelungen, diesen Gedanken in Worte zu fassen. Bei seinen Betrachtungen des Unendlichen in der Mengenlehre stößt er auf eine ähnliche Doppeldeutigkeit: "Die dritte Unterscheidung mag zunächst pingelig erscheinen. Sie betrifft mit verbundene Wörter wie 'Menge' und 'Zahl'. Diese besitzen eine seltsame und verwirrende Doppelbedeutung, die auch bei Wörtern wie 'Länge' oder 'Gramm' zu finden ist. Ein Stück Seil hat eine bestimmte Länge, wird aber manchmal auch als 'eine Länge Seil' bezeichnet; eine bestimmte Menge einer Arznei, die ein Gramm wiegt, heißt auch 'ein Gramm Arznei'. ... Deshalb kann ein Begriff wie 'unendlich' doppeldeutig sein: Entweder er ist prädikativ gemeint ('Es gibt eine unendliche Zahl von Primzahlen') oder nominal ('Cantors erste unendliche Zahl ist 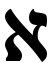₀.')." (Wallace, "Entdeckung des Unendlichen", S. 46) Wenn von "ein Gramm Arznei" gesprochen wird, gehen Größe (hier gemessen in Gramm) und Zahl (hier "eins") ineinander.

Zusammenfassend: Demiurgische Zahlen, symbolische Zahlen und Proto-Zahlen meinen dasselbe, sind aber zu unterscheiden von den natürlichen Zahlen und von den symbolischen Größen (den Proto-Größen).

(3) Wenn es sich bei den demiurgischen Zahlen um die Proto-Zahlen handelt, ist die eidetische Zahl das paradeigma der symbolischen Zahlen im Nous. Jede symbolische Zahl ist das Bild von etwas, mit dem der Demiurg den Kosmos geschaffen hat. So weit ich die Darstellung von Syrian durch Radke verstehe, wollte er unterscheiden zwischen dem zugrundeliegenden Prinzip und dem Bild im Kosmos. Die Quaternität der Himmelsrichtungen kann vom Menschen als eine Eigenschaft des Kosmos erkannt werden. Sie ist Bild eines höheren Prinzips der Quaternität. Alles, was mit dem Symbol der Quaternität beschrieben werden kann, hat teil an einem höheren Prinzip, das ich zur Unterscheidung von der Quaternität als Tetras bezeichnen möchte. Einheit, Dualität, Trinität, Quaternität etc sind Bilder von Grundlinien, die mit Monas, Dyas, Trias, Tetras, ..., Dekas, ... benannt werden können. Leider ist auch dieser Ansatz nicht mehr fortgeführt worden. Meiner Meinung nach wäre es näherliegend, von noetischen Zahlen zu sprechen. Ich erwarte, dass sich diese Fragen besser klären lassen, wenn die Dynamik der Zahlen verstanden wird. Dann kann unterschieden werden, welche Möglichkeiten und welche Wirklichkeit mit den jeweiligen Zahlen verbunden sind und aus welchen Prinzipien sie hervorgehen.

Syrian unterscheidet die von ihm so genannten eidetischen Zahlen von den materialen Zahlen, womit er offenbar die natürlichen und demiurgischen Zahlen zusammenfasst. Ich sehe dagegen - Aristoteles folgend - das Verhältnis von Form und Stoff der Zahlen anders: (1) Die Zahlen und Gedanken sind der Stoff des Nous, hyle noete. Wenn diese Seite der Zahlen betrachtet wird, ist von noetischen Zahlen zu sprechen. Der Mensch weiß nicht, wie diese Zahlen aussehen. Sie sind unerschöpflich, und der Mensch kennt nur, was aus ihnen in einer für den Menschen erfassbaren Weise entsprungen ist. (2) Die Seele kann sich nur ein Bild von ihnen machen, das sind die Zahlensymbole. Sie werden abgelesen aus den Sternzeichen (Konstellationen), die in allen frühen Kulturen gleichermaßen als Symbole der Götter und als Urbild der Zahl- und Schriftzeichen galten. Die Sterne bestehen aus einem symbolischen Stoff (hyle topike). Mit ihm hat der Demiurg den Kosmos geschaffen. Der noetische Stoff ist das Paradigma des symbolischen Stoffs. Die Sterne sind körperlos und bestehen daher nur aus symbolischem Stoff. Ihre Bewegung ist unendlich, immer gleich und kennt weder Verzögerung noch Beschleunigung. Es handelt sich um eine reine Ortsbewegung. (Wer heute über solchen "Quark" lächeln mag, sollte daran erinnert werden, dass auch die heutige Physik mit den virtuellen Teilchen, Higgs-Teilchen, Quarks, Lichtteilchen ohne Ruhemasse, systematisch mit den symmetrischen Zuständen der Lie-Gruppen im Faserbündel ihre Theorien auf eine Art symbolischen Stoff aufbaut, ohne sich darüber Rechenschaft abzulegen.) (3) Aus dem natürlichen Stoff sind die Körper geschaffen, die mit den natürlichen Zahlen gezählt werden können.

Zu den bisher betrachteten noetischen Zahlen, Proto-Zahlen (demiurgischen Zahlen, symbolischen Zahlen) und natürlichen Zahlen kamen in der Neuzeit neue Zahlen hinzu: (a) Negative Zahlen, als Systeme betrachtet wurden, in denen es zu Ausgleichsprozessen kommt, z.B. Soll und Haben in der Ökonomie, oder Gewichte, die auf beiden Seiten an einem Hebelarm aufgehängt sind. (b) Irrationale Zahlen, als die Zahlenverhältnisse innerhalb des Maßes der Größen gefunden wurden, so z.B. das Verhältnis von Grundseite und Diagonale im Quadrat (Wurzel aus 2), als Maß der Quadrierung des Kreises, Goldener Schnitt. (c) Differentiale als das innere Maß von Ort und Zeit. (d) Komplexe Zahlen für Strömungen. Diese Zahlen haben zu neuen mathematischen Symbolen geführt: Minuszeichen oder rote Einfärbung für negative Zahlen, Wurzelzeichen für irrationale Zahlen, Differentialsymbole und Integralzeichen, i für die imaginäre Achse der komplexen Zahlen. Diese Symbole wurden ausschließlich als Konventionen verstanden. Es wurde nicht mehr versucht, sie als symbolische Zeichen der Seele zu verstehen mit Paradigmen, die ihnen zugrunde liegen. Hier überhaupt ein echtes philosophisches Problem zu sehen ist das Hauptanliegen dieses Beitrags.

Größe: Gibt es so etwas wie (1) natürliche Größen, (2) Proto-Größen mit ihren Symbolen und (3) die Paradigmen der Proto-Größen? Das antike und neuplatonische Denken hatte diese Frage offen gelassen. Es gibt nur einige Anhaltspunkte. Um sich dieser Frage nähern zu können, muss auseinandergehalten werden: Es ist nicht gemeint, wie groß etwas ist, das heißt welcher Größenwert gemessen werden kann, sondern welche Eigenschaften etwas haben muss, um von seiner Größe sprechen zu können. Diese Frage steht am Anfang aller Naturphilosophie, seit Thales aufging, was es bedeutet nach der Größe des Wassers zu fragen. Wie groß ist Wasser? Was fehlt dem Wasser, weswegen sich seine Größe nicht bestimmen läßt? Was hat es, weswegen es über alle Größen hinausgeht? Das Wasser-Artige wird sich als eine symbolische Größe erweisen, die keine natürliche Größe hat.

(1) Wie immer kann auf Aristoteles zurückgegangen werden, um in seiner Physik ein besseres Verständnis zu finden, was der natürliche Begriff von etwas, hier also die natürliche Größe ist: Etwas hat natürliche Größe, wenn es im Innern zusammenhängend und nach außen durch Grenzen getrennt ist. Aristoteles hat in seiner Physik eine frühe Form der Topologie entwickelt, als er systematisch unterschied: Was eine natürliche Größe hat, das ist selbständig und getrennt (choris) von anderem, läßt sich mit anderem der Reihe nach anordnen (ephexes) bis es anderes berührt (apteesia). Die Übergänge können stetig sein (syneches). Was keine eigene Größe hat, ist zwischen anderem (metaxy). (Phys. E 3, 226b). Natürliche Maße der Größe sind nicht die Einheiten, um den Größenwert zu messen (z.B. Meter), sondern sie sind das Maß, wie stark der innere Zusammenhang der Größe hält, ob er porös, locker, bruchgefährdet ist, und wie klar die Grenzen gezogen werden können. Mit der fraktalen Mathematik wurde die Möglichkeit geschaffen, die Maße des inneren Zusammenhangs und der äußeren Grenze mathematisch zu erfassen.

Um auf das Beispiel des Wassers zurückzukommen: Eine bestimmte Menge Wasser mit klaren Grenzen, etwa Wasser in einem Eimer oder in einem See, hat eine Größe. Die Menge des Wassers kann gemessen werden. Schwieriger ist es schon bei Wolken, deren Grenzen sich nicht klar bestimmen lassen. Wieviel Luft und wieviel Wasser enthalten sie? Das Wasser im Ganzen hat keine Grenzen und daher keine Größe.

Die natürliche Größe eines Baums ist seine Größe, wenn er entsprechend seiner Natur voll ausgewachsen ist. Dann ist er innerlich zusammenhängend und nicht durch äußere Einflüsse auf ein zu kleines oder zu großes Maß (Übermaß) verzerrt. Nur in der natürlichen Größe ist der innere Zusammenhang voll hergestellt, andernfalls droht entweder durch eine zu große Zusammendrängung oder durch zu weitgehende Auflockerung eine Unstabilität, die bis zur Auflösung des Inneren führen kann. - Zugleich geht Aristoteles vom natürlichen Lebenszyklus aller physischen (sublunaren) Körper aus. Alles hat in seiner jeweiligen Lebensphase seine jeweilige natürliche Größe. Der Begriff der natürlichen (physischen) Größe muss entwickelt werden ausgehend vom Verständnis der Physis.

Um die natürliche Größe zu verstehen ist nach dem natürlichen Zusammenhang und dem natürlichen Abstand zu fragen. In der Natur gibt es natürliche Abstände, die physische Körper voneinander haben, um sich frei entfalten zu können.

(2) Als Symbole des Zusammenhangs und der Größe, d.h. als Proto-Größen bieten sich zunächst die geometrischen Elementar-Figuren an: Der Punkt symbolisiert alles, was keinen inneren Zusammenhang hat, der nach außen begrenzt wird, und was daher auch keine Größe hat. Die Linie ist zwar stetig, in jedem Teilabschnitt zusammenhängend, hat im Ganzen aber keine Grenze und daher keine Größe. Sie ist unendlich-dünn und unendlich-lang. Erst wenn sie sich zum Kreis zusammenschließt, ist die einfachste zusammenhängende Figur gefunden, deren Größe gemessen werden kann (der Durchmesser). Daher gilt oft der Kreis als das Symbol der Größe. Der Kreis wird zusammengehalten durch den Mittelpunkt. Die Pythagoreer sahen im Kreismittelpunkt das Symbol des Zusammenhangs und bezeichneten es mit Hestia, der Göttin des Herdes, die den Mittelpunkt und Zusammenhang des Hauses und der Hausgemeinschaft herstellt.

"Philolaos sagt, es gebe in der Mitte um das Zentrum ein Feuer, das er Herd (hestia) des Weltalls nennt und Haus des Zeus und Mutter der Götter und Altar und Zusammenhalt (synoche) und Maß der Natur." (Diels Kranz, Fragmente der Vorsokratiker, 44 A 16)

Mit einem anderen Ansatz werden die natürlichen (bzw. reellen) Zahlen als Symbole bzw. Ordnung der Größe angesehen. (Symbolik und Ordnung gehen ebenfalls oft durcheinander.) Mit Größe ist heute in der Regel die gemessene Höhe gemeint: Dieses Hochhaus ist 130 m groß, ich bin 1,80 m groß.

Eine dritte Richtung sucht Symbole der Größe ausgehend von der menschlichen Wahrnehmungsfähigkeit: Zum Beispiel die Elle als symbolische Größe, wenn durch Anlegen mit dem Ellenbogen die Größe eines Tuches gemessen wird. Das Meer oder die Wüste als Symbol für Größen, die für das menschliche Auge am Horizont im Unbegrenzten verschwimmen (und daraus abgeleitet das Glatte und das Gekerbte als Symbole für bestimmte Größenarten bei Deleuze und Guattari in "Tausend Plateaus"). Aristoteles sah die Größe des Mond-Abstands von der Erde als symbolische Größe an. Der Mensch kann nur im sublunaren Bereich Veränderungen der ihm sichtbaren Dinge wahrnehmen. Planeten und Sterne bewegen sich zwar am Himmel, erscheinen aber für seine Wahrnehmung unveränderlich, nur ihre Ortsbewegung ist zu sehen. Erst viel später wurden Veränderungen von Sternen wie z.B. die Supernovae beobachtet. Die heutige Physik sieht ähnliche Grenzen, wenn sie als Atom bzw. Elementarteilchen dasjenige bezeichnet, dessen Inneres mit den heute bekannten Meßinstrumenten nicht wahrgenommen werden kann. Im Grunde sind dies alles jedoch keine Größensymbole, sondern natürliche Größen aus der Perspektive des Menschen und seiner technischen Möglichkeiten.

Eine weitere Richtung unterscheidet nicht Größe vom Ort: Die Größe von etwas wird identifiziert mit dem Ort, den es einnimmt. Ein Luftballon ist mal größer oder kleiner, je nachdem wie stark er aufgeblasen ist. Die Größe eines Sees wird mit der Länge seines Ufers gleichgesetzt.

Schließlich hat die Größe mit dem Aggregatzustand zu tun. Wasser kann eine zusammenhängende Flüssigkeit sein, es kann einzelne Tropfen in einer Wolke bilden oder sich beim Verdampfen in einen luft-artigen Zustand auflösen. Die gleiche Wassermenge hat jedesmal eine andere Größe. Die gleiche Menge Wasser nimmt einen größeren Raum ein, wenn sie eine Wolke bildet statt nach einem Regenfall in einer Pfütze gesammelt zu sein.

Alle diese Aspekte zeigen jeweils etwas Richtiges. So wie in einer ersten Annäherung Dualität (das "Zwei-Artige"), Trinität (das "Drei-Artige") zum Verständnis der Proto-Zahlen führten, sind das Teilchen-Artige, Flüssig-Artige (Wellen-Artige), Gas-Artige erste Annäherungen, um symbolische Größen (die Proto-Größen) zu verstehen. Die symbolischen Größen unterscheiden sich voneinander nicht durch die gemessene Größe: Es ist z.B. sinnlos zu fragen, wie groß das Kristall-Artige ist oder ob das Kristall-Artige größer als das Flüssig-Artige ist. So wie es symbolische Zahlen gibt, gibt es symbolische Größen. Als Thales vom Wasser sprach, meinte er es im Sinne einer symbolischen Größe.

Das Teilchen-Artige ist zugleich Symbol der diskreten Größen, der Atome. Platon hat das Teilchen-Artige im Timaios durch die Körper mit jeweils regelmäßigen Außenflächen systematisiert (die platonischen Körper, deren kleinster Baustein das Tetraeder ist). In der anderen Richtung ist das Wellen-Artige Symbol der kontinuierlichen Größen, des Flusses, der Strömung.

Der Einheit unter den Zahlen entspricht das Element unter den Größen. Das Elementare ist das Symbol alles Größen-Artigen. Die weiteren symbolischen Größen wie das Teilchen-Artige werden in ähnlicher Weise aus dem Elementaren entwickelt wie die Dualität, Trinität etc aus der Einheit.

Bei den symbolischen Größen ist bis in den allgemeinen Sprachgebrauch die enge Verbindung zu mythischen Symbolen erkennbar. Die romantische Poesie spielt häufig damit, wenn z.B. der Kristall als Symbol des Teilchen-Artigen einmal als natürlicher Kristall und ein andermal in symbolischer Bedeutung als Verhärtung einer ganzen Lebensweise genommen wird. Oder es wird sowohl von Elementen gesprochen wie auch davon, dass jemand in seinem Element ist. Er bewegt sich dann frei in seiner natürlichen Größe.

Und so wie es bei den Zahlen das Zeichen als Symbol des Unendlichen gibt, das jenseits aller Zahlen liegt, so hier den Äther als das Unendlich-Große, das zugleich unendlich-fein ist und alles durchspinnt, das Proto-Medium der Wellenausbreitung des Proto-Flüssigen. Den Äther experimentell nachweisen zu wollen ist ebenso unmöglich, wie die Prima Materie oder symbolische Zahlen nicht in der Natur "entdeckt" werden können.

Ausgehend von den symbolischen Größen werden sich daher sowohl die scheinbaren Paradoxien der Relativitätstheorie wie diejenigen der Quantentheorie verstehen lassen. Einstein unterschied nicht klar zwischen dem Äther als einer symbolischen Größe, dem natürlichen Raum und den Ordnungsbeziehungen im Raum (der Differentialgeometrie). Wenn Heisenberg von einem Welle-Teilchen-Dualismus sprach, hat er symbolische Größen (das Wellen-Artige und Teilchen-Artige) und natürliche Größen natürlicher Wellen und Teilchen unzulässig gemischt. Zwischen Wellen-Artigem und Teilchen-Artigem kann es ebenso wenig einen Dualismus geben wie zwischen Trinität und Quaternität. Was Heisenberg meint, ist etwas anderes: Wenn natürliche Größen gemessen werden, werden sie immer durch den Meßvorgang zugleich verändert, auch in ihrer Größe. Wenn der Wirkungsgrad des Meßinstruments von ähnlicher natürlicher Größe wie das gemessene Objekt (Welle oder Teilchen) ist, dann ist die durch die Messung ausgelöste Veränderung signifikant. Das liegt aber nicht daran, dass Wellen-Artiges auf Teilchen-Artiges trifft.

Diese Interpretation der Unschärferelation ist allerdings umstritten. Andere argumentieren, dass die Unbestimmtheit dann auftritt, wenn etwas zugleich lokale wie globale Eigenschaften hat. Werden die lokalen Eigenschaften genauer betrachtet, dann verschwimmt der Blick auf das Globale gewissermaßen im Horizont. Werden die globalen Eigenschaften hervorgehoben, können die lokalen Eigenschafen nur noch statistisch abgeschätzt werden. Mit einer Lehre der Dynamik der Größe sollen diese Fragen entwirrt werden. An Aristoteles und Platon ist die Frage zu stellen, ob ihr Verständnis des Mittleren, metaxy, hier weiterhilft.

Die symbolischen Größen unterscheiden sich systematisch durch ihren jeweiligen inneren Zusammenhang. Das Flüssig-Artige hat einen anderen inneren Zusammenhang und daher auch andere äußere Grenzen als das Kristall-Artige. Wird noch einmal zurückgeblickt auf das Zitat von Philolaos, dann ist Hestia, die Herdgöttin des Kosmos, sowohl Symbol des durch sie hergestellten inneren Zusammenhangs des Kosmos als auch der symbolischen Größe des Feuer-Artigen. Das Feuer-Artige leitet über zum Licht-Artigen und damit zu den Paradigmen der Größe.

In der Mathematik wurde der Begriff des Zusammenhangs erst seit dem 19. Jahrhundert mit der Strömungslehre eingeführt. Wie bei der Einführung der negativen, irrationalen, reellen und komplexen Zahlen sind hier zahlreiche neue mathematische Symbole geschaffen worden, so die Christoffel-Symbole Γ zur Ableitung in Riemannschen Mannigfaltigkeiten, Symbole für Differentialoperatoren wie der Nabla-Operator ∇ für eine einheitliche Darstellung von Gradient, Divergenz und Rotation in Strömungen. Die Differentialtopologie befasst sich mit den mathematischen Grundlagen dieser Begriffe. Die Mathematiker-Gruppe Bourbaki hat seit den 1930ern in Anlehnung an Euklid für diese neuen mathematischen Entwicklungen "Elemente der Mathematik" veröffentlicht, doch gibt es bisher keine philosophische Deutung dieser Begriffe in vergleichbarer Weise, wie sie Proklos für Euklid geleistet hat.

Gibt es Ansatzpunkte, welche Symbole es für Größen geben kann? Die werden möglicherweise von der Informatik geliefert. Das Zeichen # kann als Symbol des Diskreten und Teilchen-Artigen (Numerierbaren, Abzählbaren) verstanden werden, das Zeichen ~ als Symbol des Kontinuierlichen und Wellen-Artigen (des Ähnlichen und Ungefähren). Eine andere mögliche Quelle sind die heidnischen Symbole. Der konzentrische Kreis mit Punkt gilt als Symbol des Goldes und des Zusammenhalts des Universums. Die keltische Doppelspirale ist das Symbol des Werdens, ~ ist eine Vereinfachung davon.

(3) Was ist das Paradigma der Größen? Das können entsprechend dem bisher entwickelten Gedanken nur das Schwere und das Licht sein.

Die Romantiker werteten das Paradigma der Nacht auf, wobei es recht unterschiedliche Ansätze von Novalis, Hölderlin, Hegel und Schelling gibt. Zum Beispiel schreibt Schelling in seinem Würzburger System von 1804 in ausdrücklicher Kritik an den mathematischen Prinzipien der Naturphilosophie von Newton:

"Der Grund der Schwere ist also die unerforschliche Tiefe der Natur selbst, das, was nie selbst an den  Tag  treten kann, weil es das ist,  wodurch  alles andere geboren wird und das Licht des Tages erblickt, die geheimnisvolle Nacht, das Fatum aller Dinge, oder auch, weil in ihr die Dinge als in ihrem Grunde sind, in dem sie empfangen, und aus dem sie geboren werden, das mütterliche Princip der Dinge." (Schelling, Würzburger System, S. 256f)

Nur was Gewicht hat, kann einen Zusammenhang haben. Das Gewicht ist Paradigma der im Zusammenhang hergestellten inneren Beziehungen, die die Gleichmäßigkeit der Gerade und des Kreises herstellen, d.h. ihre jeweiligen konkreten Formen des in ihnen dargestellten Zusammenhangs.

Das Licht zeigt den Zusammenhang. Sind schon das Feste oder der Äther nur Symbole, die als solche nicht in der Natur nachgewiesen werden können, so haben das Schwere und das Licht, Hell und Dunkel zwar eine "sichbare Seite", die wahrgenommen werden kann, entziehen sich aber im Ganzen der menschlichen Erkenntnisfähigkeit und stehen daher in allen Schöpfungsmythen am Anfang, bevor die natürlichen Dinge geschaffen wurden. Der Mensch kann sich nur Bilder von ihnen machen, etwa die Lichtstrahlen, Lichtwellen, Photonen oder die Schwere und Dunkelheit der Höhlen in der Erde bzw. in der modernen Physik die Bilder der Schwarzen Löcher und des Urknalls. Jeder versteht intuitiv, dass dies nur unvollständige Bilder eines Paradigmas sind, das der Mensch nicht überschauen kann. Schwarzes Loch, Urknall, Lichtwellen und Photonen können in der Sprache der modernen Physik nur indirekt an ihren Wirkungen nachgewiesen werden. Die moderne Physik will nicht anerkennen, dass es sich ähnlich wie bei der Proto-Zeit z.B. bei den Lichtwellen und Photonen nur um Symbole handelt, die in der einen Richtung zu unterscheiden sind vom natürlichen Licht, wie etwa dem Tageslicht, und in der anderen Richtung von dem unerkennbaren Paradigma des Lichtes. Oft wird das Sonnenhafte als Paradigma des Lichtes eingesetzt. Licht in der Bedeutung der Aufklärung, Enlightment, der Erleuchtung oder im Sprachgebrauch von Heidegger des Lichtens sind verschiedene Bilder, dies Paradigma zu verstehen.

Die Physik verwickelt sich notwendig in Paradoxien, wenn ihr die Unterscheidung von natürlichem Licht, Symbolen des Licht und dem Paradigma dieser Symbole nicht gelingt. In gleicher Weise sind zu unterscheiden die natürlichen Beobachtungen, was beim "Tod" von Sternen geschieht, dem nur symbolisch zu verstehenden Schwarzen Loch und dem Paradigma, dessen Bild das Schwarze Loch ist, in der Weise wie Schelling den Grund der Schwere beschrieben hat. Eine sorgfältige Unterscheidung dieser Ebenen wird eine moderne Metaphysik verstehen lassen, die völlig anders ist als die alte Metaphysik, von der sich die neuzeitliche Naturwissenschaft mit guten Gründen abgewandt hat.

Ausgehend von den symbolischen Zahlen und Größen kann das Programm für eine Proto-Mathematik entworfen werden, die sich grundsätzlich von der Metamathematik im Sinne von Hilbert unterscheidet und die im neuplatonischen Denken offen gebliebenen Fragen neu anzugehen versucht. Das ist die Stelle, an der die Grundlagendiskussion der Mathematik in den 1920er bis 1940er Jahren stehen geblieben ist. Mathematiker wie Max Steck, der 1945 eine deutsche Übersetzung des Euklid-Kommentars von Proklos herausgab, Hugo Dingler und der Philosoph und Mathematik-Historiker Oskar Becker kamen diesem Programm bereits nahe. Sie wollten damit allerdings nationalsozialistische Überzeugungen begründen. Statt das zu hinterfragen wurde dieser Ansatz einer Proto-Mathematik nicht weiter fortgeführt, sondern in den 1950ern umgewandelt in eine rein formalisierende Vorgehensweise, bis sie nicht mehr zu unterscheiden war von ihrer früheren Gegenposition, der Metamathematik. Dass ausgerechnet an dieser entscheidenden Stelle aus der Mathematik heraus der Einbruch einer neuen Mythologie im Nationalsozialismus möglich war, ist jedoch kein Zufall, sondern muss verstanden werden. Hier zeigt sich, dass das Spannungsverhältnis von mathematischem und mythischem Symbol noch nicht geklärt ist. (Im nächsten Schritt soll daher die gleiche Frage mit Nietzsche von einer anderen Seite her betrachtet werden.)

Vermutung: Der Proto-Abstand erscheint mir der geeignete Begriff, um zu verstehen, was Michael Zednik als Abstand der Markanzen ansieht. Die Markanzen verstehe ich wiederum als Proto-Orte, wenn nach einer Unterscheidung gesucht wird zwischen (1) den physischen Orten, wie Aristoteles sie betrachtet hat (Physik, Δ 1-9), (2) den Proto-Orten der Seele und (3) den Orten im Nous, d.h. dem paradeigma der Proto-Orte. Daher kann der Ansatz von Graf und Zednik, der auf eine neue Interpretation der Speziellen Relativitätstheorie zurückgeht, verstanden werden als ein erster Versuch, für Proto-Größen und Proto-Orte eine Lehre zu finden, die dort weiter geht, wo der Neuplatonismus unterbrochen wurde.

In anderer Richtung hat Helmut Hansen die Interpretation der Speziellen Relativitätstheorie durch Epstein aufgegriffen und daraus eine "Physik des Mandala" entworfen, in der die symbolischen Größen der Sonne und der Erde, Kreis und Quadrat miteinander verflochten sind. Ich vermute, dass der Epstein-Kreis, mit dem Epstein alle Bewegungen auf Raum- und Zeitanteile verteilt und dadurch eine verblüffend neue Interpretation der Längen-Kontraktion und Zeit-Dilatation erhält, erweitert werden kann zu einer Kugel, in der zusätzlich die Zahl- und Größe-Anteile berücksichtigt sind, d.h. alle vier von Simplikios genannten Maße der Natur. Eine solche Figur nimmt die Keplerschen Ideen der Weltharmonie auf und führt zu einem neuen Entwurf für die Architektur der Mathematik. Aufgrund der Rotationssymmetrie von Kreis und Kugel ist das eine multiple Mathematik.

Was den Grundlinien des Denkens fehlt

Die Frage nach den Paradigmen und Symbolen der Größe berührt ein grundsätzliches Problem: Gibt es systematische Grenzen zwischen mythischen und mathematischen Symbolen? Die Symbole der alchemistischen Stoffe sehen den mathematischen Symbolen recht ähnlich. Symbolische Stoffe haben offenbar viel mit symbolischen Größen zu tun. Typische Proto-Stoffe sind das Salzige , Schweflige 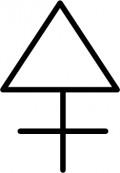, Wässrige . Mit ihnen werden Elemente bezeichnet, die nicht mit den entsprechenden natürlichen Elementen verwechselt werden dürfen. Es war ein Missverständnis, wenn von der Alchemie versucht wurde, die Proto-Stoffe als natürliche Stoffe in der Natur nachzuweisen und herzustellen. Einige dieser Symbole können auch als symbolische Größen verstanden werden: Das Symbol des Goldes oder das Symbol des Erzes bieten sich als Symbol des Teilchen-Artigen an, das Symbol des Feuers oder piktogrammartig des Wassermanns als Symbol des Wellen-Artigen. Dem Erz verwandt ist das Symbol des Diamanten ◊, das heute in der axiomatischen Mengenlehre gebraucht wird (Symbol des kombinatorischen Prinzips, aus dem die Kontinuumhypothese abgeleitet werden kann).

Die Neuplatoniker haben nicht nach Paradigmen der Proto-Stoffe im Nous gesucht. Am Beginn der Neuzeit gab es um 1600 Ideen, ihre Lehren wieder aufzugreifen und Symbole dieser Art mit den mathematischen Symbolen zusammenzubringen. Am bekanntesten wurde John Dee (1527-1608), der ein Vorwort für die englische Übersetzung der Elemente des Euklid schrieb und das Zeichen der Monas Hieroglyphica entwarf, mit der er Wissenschaft und Para-Wissenschaft einheitlich begründen wollte.

       

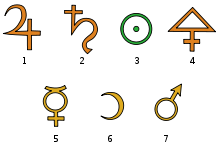
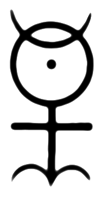
Figur 3 Alchemistische Symbole

Beispiele für Elementsymbole der Alchemisten 1 = Zinn, 2 = Blei, 3 = Gold, 4 = Schwefel, 5 = Quecksilber, 6 = Silber, 7 = Eisen; Monas Hieroglyphica von John Dee, in der die Symbole der 7 Planeten, von 4 Elementen und einigen Sternzeichen nachweisbar sind;
Urheber 1: Von MaEr - Eigenes Werk, based on former ElementeAlchemisten.jpg onclick="window.open(this.href); return false;" by Roland1952, CC BY-SA 3.0, Link
Urheber 2: Von PRiis in der Wikipedia auf Englisch - Übertragen aus en.wikipedia nach Commons durch Leyo mithilfe des CommonsHelper., Gemeinfrei, Link

Nach meiner Überzeugung ist es nur eine Frage der Zeit, bis in den Grenzbereichen der Mathematik oder der Teilchenphysik alchemistische Symbole aufgegriffen und eingesetzt werden. Ein erster Ansatz kommt von Alain Badiou. Er hat in "Das Sein und das Ereignis" das Venus-Symbol als Symbol des Ununterscheidbaren eingeführt, ein Grenzbegriff der Mengenlehre und der Teilchenphysik.

Läßt sich systematisch ein Unterschied der mathematischen und mythischen Symbole bestimmen? Die Neuplatoniker gaben eine klare Antwort: Die mathematischen Symbole sind Bilder von Paradigmen im Nous. Proklos schreibt in seiner Abhandlung über die Einheit in §57, dass der Nous keinen Mangel (Beraubung, privatio, steresis) und daher auch das Böse nicht kennt, wenn das Böse als Beraubung des Guten verstanden wird. Im Nous sind Möglichkeit und Wirklichkeit eins. Es gibt im Nous - und damit für die Paradigmen der mathematischen Symbole - keine Unterscheidung, was nur möglich, aber nicht wirklich ist, und daher auch keine Unterscheidung, was fehlt, aber anwesend sein könnte. Es gibt daher im Nous auch keine zeitliche Vorstellung von Substanz (Dauerhaftes) und Kausalität (einander zeitlich notwendig Nachfolgendes), denn es gibt nichts, was verfallen könnte, also nicht dauerhaft ist, und nichts, was zugunsten eines Nachfolgenden vergehen könnte. Diese spekulativen Ideen werden sofort anschaulich, wenn sie an der Mathematik betrachtet werden: Es gibt keine möglichen oder fehlenden Zahlen. Zahlen haben keine bestimmte Dauer. Beim Beweisen wird zwar gefolgert, aber das Verhältnis der auseinander gefolgerten Sätze kann nicht als Kausalität verstanden werden.

Die mathematischen Symbole sind durchweg Bilder von paradeigmata, die zum Nous gehören. Daher läßt sich die Schlußfolgerung der Neuplatoniker in einem Satz zusammenfassen: Den mathematischen Symbolen fehlt alles, was fehlt (steresis). Sie sind in einer leeren Weise perfekt und vollständig. Diese Leere kommt in jeder Mathematik irgendwo vor (seien es der paradoxe Begriff der Zwei, die in der griechischen Mathematik sowohl das Andere wie der Abstand bedeutet, oder das Verbot durch Null zu teilen, das Verschwinden der Differentiale und schließlich die Paradoxa der leeren Menge seit Cantor), aber sie entziehen sich ihr. Das zeigt sich in der Mischung aus Gewissheit und Vergeblichkeit, die alle Mathematik charakterisiert, und liegt genau in der Mitte dessen, was Deleuze und Guattari in royal and minor mathematics voneinander trennen wollten mit der Hoffnung, ausgehend von einer bisher zu wenig beachteten minor mathematics die Mathematik neu begründen zu können.

Die Bestimmungen (diakriseis) des Nous und der Beraubung (steresis) bleiben bei den Neuplatonikern voneinander unabhängig. Die diakriseis kommen aus dem Nous und erfassen nur Teile, Orte, Seiendes und zeitliche Dauern innerhalb vollständiger Ganzheiten, denen nichts fehlt. Wenn in der physischen Welt etwas fehlt, ist das Fehlende ein fehlendes Teil oder eine Differenz zwischen dem Ganzen und der Summe der Teile, fehlende Zeit um etwas fertig zu stellen usw. Aber es gibt in der Seele kein "Proto-Fehlen", kein symbolisches Fehlen, denn die Seele kann für das Fehlen kein eikon bilden, da es im Nous hierfür kein paradeigma gibt. Das mathematische Symbol der leeren Menge ist mit seiner durchgestrichenen Null offensichtlich ein Kunstsymbol und kein Bild eines höheren Paradigma. Die Leerstellen der Mathematik wie die Null, die leere Menge oder die von Badiou betrachtete Ununterscheidbarkeit hängen daher in der Luft. Sie zeigen die Unvollständigkeit (oder positiv formuliert die Offenheit) einer jeden Mathematik, die platonisch bzw neuplatonisch begründet wird. Mit Lacan können sie als Stepp-Punkte bezeichnet werden.

Die Seele hat die Fähigkeit, das Fehlende zu verstehen, aber sie kann es nicht angemessen in den von ihr selbst geschaffenen mathematischen Symbolen ausdrücken, solange diese als Bilder der Grundlinien des Nous verstanden werden. Zum Verständnis des Fehlenden braucht sie daher Mythen. Die symbolischen Mythen über Verlust, Verlassenheit, Zerrissensein und auch umgekehrt Glück und Gelingen ermöglichen es zu verstehen, was im "wirklichen Leben", im natürlichen Leben geschieht, so wie die Proto-Begriffe das Messen von Größen und Abständen und das Zählen ermöglichen.

Bei mathematischen und mythischen Symbolen handelt es sich um verschiedene Ausprägungen des Vermögens der Seele Symbole zu schaffen. Durch den Begriff des Zusammenhalts (synecheia) gibt es eine Überschneidung. Das Fehlen läßt sich als Destabilisieren bis zum völligen Verlust des Zusammenhalts verstehen, und zugleich sind auch die mathematischen Symbole auf dem Zusammenhalt aufgebaut. Die gesamte Mathematik läuft in die Leere, wenn ihr der zugrundeliegende Zusammenhalt entzogen wird. Das ist innerhalb der mathematischen Forschung dann zu spüren, wenn die überlieferten Symbole in Paradoxien geraten und die Seele die Fähigkeit verliert, neue angemessene Symbole zu bilden. Dann kommt es innerhalb der Mathematik beim Operieren mit den ihr vertrauten Symbolen zu unerwünschten Rückkoppelungs-Effekten, Resonanzen oder kombinatorischen Explosionen, die alle mathematischen Rechnungen in Frage stellen. Die Wissenschaft des 20. Jahrhundert liefert hierfür geradezu unbegrenzt viele Beispiele.

In solchen Situationen muss die Seele einen Gründungs-Mythos schaffen. Diese Gründung ist weit mehr als ein physisches Ereignis, sie ist ein symbolisches Ereignis. (Nietzsche fragte mit seiner Genealogie nach symbolischen Ereignissen, die von den historischen Ereignissen zu unterscheiden sind.) Im Gründungs-Mythos werden Symbole geschaffen, die übergreifend Einheit und Zusammenhalt herstellen. Beispiele für Gründungs-Mythen der Wissenschaft sind Prometheus, der im Alten Testament beschriebene Sündenfall und der pythagoreische Mythos, der in den Fragmenten von Philolaos überliefert ist, in dem Hestia in der Wissenschaft wiederkehrt, als sie am Olymp fehlte.

Wenn Klarheit über die symbolischen Größen geschaffen wird, wird sich das Verhältnis der mathematischen und mythischen Symbole ein weiteres Mal verschieben. Mit den symbolischen Größen wird mathematisch dargestellt werden können, was bisher nur im Bereich der symbolischen Stoffe verblieben ist. Bestimmte Eigenschaften, die bisher mit den symbolischen Stoffen verbunden waren (wie der innere Zusammenhalt des Goldes , die lockere Ordnung des Sandes , das Dynamische des Feuers, symbolisiert im Frühlingszeichen des Widders ), werden mathematische Symbole werden. Erst wenn das gelungen ist, ist das Anliegen von Simplikios ausgeführt.

Noch offen bleibt die Frage, ob es für die Dynamik der Maße der Natur eigene mathematische Symbole geben wird. Bisher gibt es hier nur Kunstsymbole, die Leibniz eingeführt hat, wie das Differential- und Integral-Symbol, und später die Symbole der Tangentialräume und -bündel sowie die Symbole zum besseren Operieren in der Feldtheorie.

Ausblick. Damit scheint mir der Umfang der platonisch inspirierten Mathematik so weit als möglich beschrieben. Sie hat faszinierende Erkenntnisse geliefert und ist noch längst nicht an das Ende ihrer Entwicklungsmöglichkeiten gelangt. Im Gegenteil könnte eine Wiederaufnahme der Ideen von Simplikios große Umwälzungen und völlig unerwartete Ergebnisse bringen. Dennoch soll das hier vor allem dazu dienen, die Lektüre von Aristoteles vorzubereiten. Bei Platon fallen mathematische und mythische Symbole notwendig auseinander. Gibt es bei Aristoteles einen Ansatz, das Prinzip des Fehlens auf die Mathematik zu übertragen? Das würde nicht die einzelnen Erkenntnisse der platonischen Mathematik in Frage stellen, aber die gesamte Architektur der Mathematik von Grund auf ändern.

Nachwort: Virtuelle und multiple Mathematik

In Nachfolge von Deleuze vertritt eine Gruppe von Philosophen um Manuel DeLanda und Simon Duffy die These einer virtuellen Mathematik. Die Idee der virtuellen Mathematik greift die Bewegung von der Vielfalt der Natur über die Seele zur Einheit des Nous und des Seins auf. Während jedoch die neuplatonischen Philosophen die Seele in einer vermittelnden Rolle innerhalb einer übergeordneten Bewegung von der Natur zurück zum Einen sehen, wird als die Aufgabe der virtuellen Mathematik angesehen, mathematisch übergreifend den Bewegungsraum für diese Bewegung zu entwerfen, also einen virtuellen Raum zu finden, der die Natur, die Seele und den Nous enthält. Dieser virtuelle Raum würde die natürlichen Dinge, die Symbole und deren Grundlinien enthalten. Er würde damit auch die natürlichen Orte, Proto-Orte und deren Grundinien umfassen.

Die Mathematik beschreibt den allgemeinsten Raum, in dem sich Probleme stellen, analysieren und lösen lassen. Jedes Problem kann als eine Ausgangskonstellation in diesem Raum verstanden werden, die Lösung ist eine Endkonstellation. Der Raum ist so definiert, dass sich dort alle Probleme, ihre Lösungen und die Lösungswege beschreiben lassen. Aufgabe der virtuellen Mathematik ist daher, mathematische Eigenschaften der Probleme, ihrer Lösungswege und Lösungen als Eigenschaften dieses Raums zu erkennen. Es kann gleichermaßen von einer Geometrie der Problemlösung und einer Logik der Eingebungen gesprochen werden, einer Logik, der die Eingebungen folgen müssen, wenn sie erfolgreich sein wollen. Das ist eine Verallgemeinerung der Ideen des Differentialkalküls und der Galois-Theorie, mit denen mathematische Probleme so umformuliert wurden, dass für das Problem ein geeigneter Raum zu seiner Lösung geschaffen wurde. Konkret waren das die Mannigfaltigkeit der Tangentialräume als Raum für die Lösung der Fragen des Differentialkalküls und die Gruppe der Körpererweiterungen als Raum zur Darstellung der Probleme der euklidischen Geometrie und der arithmetischen Lösungswege der Renaissance-Mathematik durch Galois.

Diese faszinierende Idee treibt die am Ende des 19. Jahrhunderts entstandenen Ideen von Hertz, Boltzmann und schließlich Wittgenstein ins äußerste Extrem. (Von denen wollen die Autoren der "virtuellen Mathematik" allerdings nichts wissen, da sie sich gegen den auf Wittgenstein zurückgehenden linguistic turn wenden.)

Jeder Problemlösungsweg ist eine konkrete Figur in diesem Raum und wird mit Deleuze als Individuation bezeichnet. Der Begriff Individuation soll aussagen, dass in der Vielfalt (gewissermaßen der Gattung) aller möglichen Lösungswege und -Irrwege, die von einem Problem ausgehen, schließlich eine einzelne (individuelle) Lösung ausgezeichnet wird.

Zugleich wird der Begriff der Vielfalt des Seienden verallgemeinert zum Begriff des Multiplen, um auch die besondere Situation einer Problemstellung beschreiben zu können, die nicht einfach eine Vielfalt ist, sondern etwas Multiples aus zunächst ungewohnten Zusammenhängen. Mathematisch trifft besser der Begriff Mannigfaltigkeit, den die virtuelle Mathematik synonym gebraucht.

Von diesen anregenden Gedanken möchte ich die Idee einer "multiplen Mathematik" unterscheiden. (i) Zum einen wird mit der Physik die Multiplizität konkreter gefasst: Multiples ist keine weitere Verallgemeinerung des Elementbegriffs der Mengenlehre (so wie die Kategorientheorie den Begriff des Elements verallgemeinern wollte zum Topos), sondern bezieht sich auf Rotationen, auf Bewegungsmultipletts, auf Auseinandergeschachteltes, das durch eine Polarisation zusammengebracht werden kann und die Eigenschaft hat, dass sich etwas Multiplizieren läßt. Mathematisch bedeutet das, dass multiple Mathematik grundsätzlich etwas beschreibt, dass mindestens zwei miteinander verbundene Operationen nach dem Vorbild der Addition und Mulitplikation enthält (Verallgemeinerung des Körper-Begriffs). (ii) Multiple Mathematik wird systematisch durch eine Proto-Mathematik begründet, während die virtuelle Mathematik auch die Proto-Begriffe und deren Paradigmen enthalten will und für sie die Frage nach einer Proto-Mathematik lediglich ein bestimmtes Problem ist, für das mit der virtuellen Mathematik der geeignete Raum gefunden werden muss, in dem es dargestellt und gelöst werden kann. (iii) Multiple Mathematik beschreibt nicht nur einen Prozess, sondern wird ihrerseits multipel entworfen werden müssen. Multiple Mathematik bewegt sich bewusst bis an die Grenze, wo mathematische in mythische Symbole übergehen. Virtuelle Mathematik scheint demgegenber den Weg der bisherigen Wissenschaft weiter gehen zu wollen, mythische Symbole durch mathematische abzulösen.

Die Ideen für eine virtuelle und eine multiple Mathematik befinden sich noch im Anfangsstadium. Gegenüber der virtuellen Mathematik ist zu fragen, ob sie nicht unzulässig das Verhältnis von paradeigma und eikon in ihren Ansatz aufnimmt und damit eine Position bezieht, die aus Sicht der Neuplatoniker nur dem göttlichen Geist zugänglich ist. Damit steht die virtuelle Mathematik in der Tradition der christlichen Wissenschaft, die davon ausgeht, dass der Mensch von Gott die Fähigkeit verliehen bekommen hat, als sein Ebenbild das Gesamt der Schöpfung von außen betrachten zu können.

Die Problematik der virtuellen Mathematik ist sehr gut mit dem Begriff der Individuation getroffen. Die Individuation scheint in der virtuellen Mathematik aus rein mathematischen Symbolen beschreibbar zu sein, muss ihre Macht aber von einem Prinzip erhalten, das über sie hinausgeht. Mir erscheint erfolgversprechender, den Raum der Lösungswege prinzipiell offen anzusehen. Grundsätzlich gilt auch diesem Raum gegenüber die von Kant vorgetragene Kritik der reinen Vernunft.

Werden die Anregungen der virtuellen Mathematik aufgegriffen, dann kann die multiple Mathematik möglicherweise als eine Methode entwickelt werden, die im Raum der Lösungswege operiert. Die Multiplizität ist dann nicht mehr nur eine Verallgemeinerung der Vielheit, sondern nimmt die Dynamik der Maße der Natur auf, die sich in Rotationen, Durchflüssen und Multipletten zeigt. Daher kann es gut sein, dass aus beiden etwas Gemeinsames entsteht, wenn zum einen die virtuelle Mathematik einen Bezug zur Proto-Mathematik findet und zum anderen der Proto-Mathematik ein besseres Verständnis gelingt, wie sie als Kristallisationskeim im Chaotischen wirken kann.

* * *

Deleuze hat eine Anregung gegeben, wie die Idee einer Proto-Mathematik neu aufgenommen werden kann. Die Mathematik steht nicht nur als "königliche Wissenschaft" an der Grenze zur göttlichen Vernunft, sondern auch als "minor mathematics" der ungeordneten, chaotischen Bewegung nahe. Sie kann dort möglicherweise wie ein Katalysator wirken, der innere Beziehungen im Chaos erkennen läßt, die zunächst bloß wie ein weißes Rauschen aussehen. Bei der Auswertung von experimentellen Beobachtungen etwa in Teilchenbeschleunigern ist das inzwischen ein ganz praktisches Problem.

"Das Chaos ist ein reines many, reine disjunktive Verschiedenheit, während das Etwas ein one ist, nicht schon eine Einheit, sondern vielmehr der unbestimmte Artikel, welcher eine beliebige Singularität bezeichnet. Wie wird das many zum one? Ein großes Sieb muß dazwischentreten, wie eine elastische oder formlose Membran, wie ein elektromagnetisches Feld oder wie der Behälter des Timaios, um ein Etwas aus dem Chaos herauszulassen, selbst wenn dieses Etwas sich davon sehr wenig unterscheidet. In diesem Sinn konnte bereits Leibniz mehrere Annäherungen an das Chaos geben." (Deleuze, Falte, S. 126f)

Mit dem Sieb meint Deleuze sicher das transzendentale Feld seiner "Logik des Sinns", das er ebenfalls als eine biologische Membran versteht (Deleuze, Logik des Sinns, S. 136). Es ist eine sehr anschauliche und hilfreiche Vorstellung, die Proto-Mathematik als Sieb zu verstehen. Die Proto-Mathematik soll zeigen, welche grundlegenden Funktionen und Vorprägungen der Mathematik vorausgehen,

* * *

Das hier dargestellte Verständnis der virtuellen und der multiplen Mathematik steht im Zeichen des platonischen Grundansatzes, so insbesondere die Vorstellung des Nous und einer Proto-Mathematik. Es soll den Stand festhalten, an dem später eine neue Interpretation im Lichte der aristotelischen Philosophie zu messen ist.

2010-2011

Literaturhinweise

Aristoteles: Physik, in: Schriften Bd. 6, Hamburg 1995 ( Link )

Aristoteles: Über Werden und Vergehen ( Link )

Alain Badiou: Das Sein und das Ereignis, Berlin 2005

August Böckh: Philolaos des Pythagoreers Lehren, Berlin 1819

Peter Crome: Symbol und Unzulänglichkeit der Sprache, München 1970

Manuel DeLanda: Intensive Science and Virtual Philosophy, London, New York 2002

Gilles Deleuze: Logik des Sinns, Frankfurt am Main 1993 [1969]

Simon Duffy (Hg.): Virtual Mathematics, Manchester 2006

Benjamin Gleede: Platon und Aristoteles in der Kosmologie des Proklos, Tübingen 2009

Albert Görland: Aristoteles und die Mathematik, Marburg 1899

Wolfgang Gombocz: Die Philosophie der ausgehenden Antike und des frühen Mittelalters, München 1997

Wilhelm Graf: Vom Punkt zur Energie, Typoskript, Wien 1952

Heinz Happ: Hyle, Studien zum aristotelischen Materie-Begriff, Berlin, New York 1971

Helmut Hansen: Die Linien des Alten, Norderstedt 2009 ( Link )

Georg Wilhelm Friedrich Hegel: Wissenschaft der Logik, 2 Bd, Frankfurt am Main 1969

Martin Heidegger: Phänomenologische Interpretationen ausgewählter Abhandlungen des Aristoteles zur Ontologie und Logik (1922) (GA 62), Frankfurt am Main 2005

Martin Heidegger: Vom Wesen und Begriff der physis. Aristoteles, Physik B, 1 (1939),
in: ders.: Wegmarken (GA 9), Frankfurt am Main 1996

Ernst Hoffmann: Methexis und Metaxy bei Platon
in: ders.: Drei Schriften zur griechischen Philosophie, Heidelberg 1964

Ernst Hoffmann: Die Vorgeschiche der Cusanischen Coincidentia oppositorum
in: Nikolaus von Cues: Über den Beryll, Leipzig 1938

Nikolaus von Kues (Nicolaus Cusanus): Von der Wissenschaft des Nichtwissens (De docta ignorantia)
in: ders.: Philosophische und theologische Schriften, Wiesbaden 2005

Nikolaus von Kues: Über den Beryll, Leipzig 1938

Peter Manchester: The Syntax of Time, Leiden, Boston 2005

Otto Pöggeler: Dialektik und Topik
in: Rüdiger Bubner, Konrad Cramer, Reiner Wiehl (Hg.): Hermeneutik und Dialektik, Bd. 2, Tübingen 1970

Proklos: Grundkurs über die Einheit, St. Augustin 2001
die Thesen sind ohne die Kommentare online verfügbar, Link

Proklos: Euklid-Kommentar, englische Übersetzung von Thomas Taylor, Dorset 2006 [1788]

deutsche Übersetzung: Proklus Diadochus 410-485: Kommentar zum ersten Buch von Euklids "Elementen", übersetzt von Leander Schönberger, herausgegeben von Max Steck, Halle an der Saale 1945
daraus sind wichtige Teile übernommen in: Oskar Becker: Grundlagen der Mathematik in geschichtlicher Entwicklung, Frankfurt 1975 [1954], S. 99-105, 122-129

Pseudo-Aristoteles: Über unteilbare Linien
in: Otto Apelt: Beiträge zur Geschichte der griechischen Philosophie, Leipzig 1891; Open Library, S. 271-286

Gyburg Radke (Uhlmann): Die Theorie der Zahl im Platonismus, Tübingen, Basel 2003

Shmuel Sambursky: Der Begriff der Zeit im späten Neuplatonismus
in: Clemens Zintzen (Hg.): Die Philosophie des Neuplatonismus, Darmstadt 1977

Shmuel Sambursky: Das physikalische Weltbild der Antike, Zürich, Stuttgart 1965

Markus Schmitz: Euklids Geometrie und ihre mathematiktheoretische Grundlegung in der neuplatonischen Philosophie des Proklos, Würzburg 1997

Erwin Sonderegger: Simplikios: Über die Zeit - ein Kommentar, Göttingen 1982

Richard Sorabji: Time, Creation & the Continuum, London 1983

David Foster Wallace: Die Entdeckung des Unendlichen, München Zürich 2009

Michael Zednik: Schematik, Manuskript, Wien 2007

Paul Ziche: Mathematische und naturwissenschaftliche Modelle in der Philosophie Schellings und Hegels, Stuttgart-Bad Cannstadt, 1996

Paul Ziche: Raumdimensionen und Prinzipiendeduktion
in: Wolfgang Neuser, Vittorio Hösle (Hg.): Logik, Mathematik und Naturphilosophie im objektiven Idealismus, Würzburg 2004

 

© tydecks.info 2011