Die Selbst-Organisation des Mediums in Spencer-Browns Schaltkreisen – sieben Thesen

Impuls-Beitrag für das Panel 1 bei der The Unmarked State Conference celebrating the 50th Anniversary of the First Publication of George Spencer-Brown's ‘Laws of Form’ in Liverpool, 9.8.2019; Video in Vimeo oder YouTube

In meinen späten Jahren bin ich ein begeisterter Neuling und Quereinsteiger auf dem Gebiet von Spencer-Brown geworden und freue mich sehr, hier sprechen zu können und sicher vieles zu lernen. Mein Thema sind die von Spencer-Brown entwickelten Schaltkreise (circuits). In gewisser Weise ist das eine Fortführung des Beitrags von Bernie Lewin. So wie er aus den Grundregeln der Laws of Form die Grundlagen der klassischen Geometrie hergeleitet hat, möchte ich zeigen, wie aus den in Kapitel 11 eingeführten Schaltkreisen ein Bogen zur Mathematik des 20. Jahrhunderts geschlagen werden kann. Während er seine Arbeit weitgehend abgeschlossen hat, stehe ich am Anfang und möchte in diesem kurzen Impuls sieben einleitende Thesen formulieren.

              

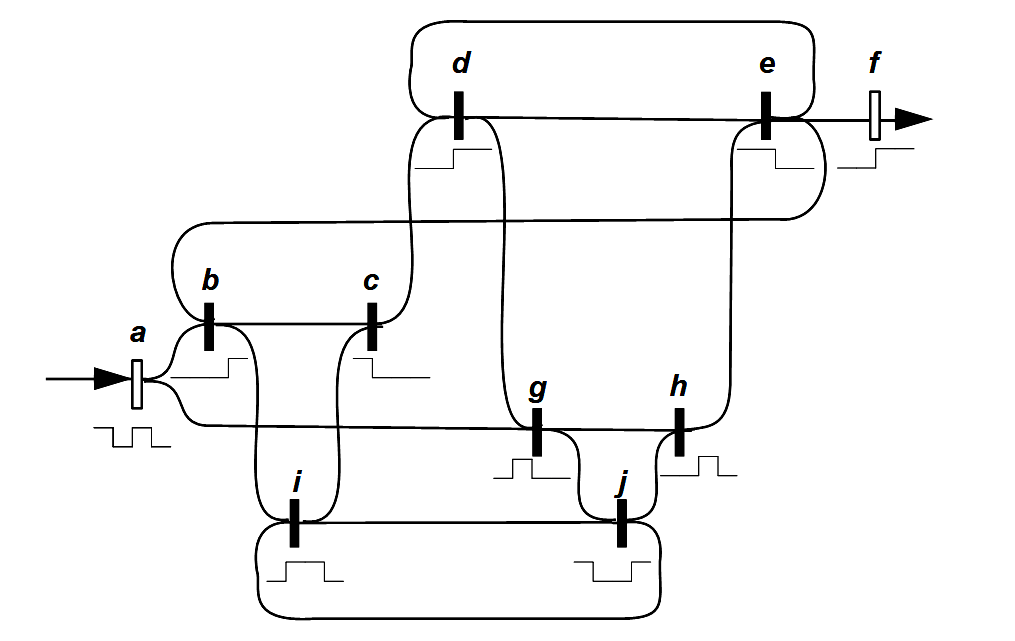
                  Modulator Funktion (LoF, 67), Benennung der Schaltelemente ergänzt

Legende
Volles Rechteck: Schaltelement
Leeres Rechteck: Eingang bzw. Ausgang
Oberhalb des Rechtecks steht dessen Name
Unterhalb des Rechtecks steht die ein- bzw. ausgehende Welle und bei Schaltelementen deren Konversionsregel

(1) Was besagt dieser Schaltkreis? Als erstes ist zu erklären, warum Spencer-Brown den Eingang mit a und den Ausgang mit f bezeichnet. Wird das Kapitel 11 im Ganzen gesehen, steht für mich a für Argument und f für Funktion. Sein Kalkül kennt für die Variable a nur die beiden Argumente Haken  ⃧   (markierter Zustand) und ein Leerzeichen (unmarkierter Zustand, Ɔ), die er in diesem Diagramm mit einem Wellenberg (up) und einem Wellental (down) darstellt. Das Kapitel handelt davon, wie Argumente a, deren Eigenschaften und Regeln in der vorhergehenden Primary Arithmetic und Primary Algebra eingeführt und studiert werden, auf selbstbezügliche Weise in Funktionen f übergehen, deren Argumente sie sind. Um das zu zeigen, führt Spencer-Brown Grenzübergänge ein, die nach dem Vorbild der Nachfolger-Relation der natürlichen Zahlen gebildet sind. Der Übergang von a zu f erfolgt formal ähnlich wie in der traditionellen Mathematik mit Cantor die transfiniten Zahlen erreicht werden und den Raum der natürlichen Zahlen erweitern. Analog entsteht bei Spencer-Brown mit dem Grenzübergang von a zu f ein neuer Typ von Objekten, der durch Re-entry in den Raum der Argumente a aufgenommen werden kann und diesen erweitert.

Kommt es zum Re-entry von f, durchläuft eine Erschütterung (oscillation) die Menge der Argumente, wodurch innerhalb ihrer Logik Zeit entsteht und formal dargestellt werden kann. Wenn das geschieht und ein logischer Begriff der Zeit gefunden ist, kann in einem abschließenden Schritt untersucht werden, welche zeitlichen Prozesse im Übergang von den Argumenten a zu den Funktionen f erfolgen. Sie sind das Thema meines Impuls-Vortrags. Es sind für Spencer-Brown keine linearen Prozesse mehr, wie sie aus den Schlussketten und Kausalfolgen der klassischen Logik und Naturwissenschaft bekannt sind, sondern Netzwerke in der Art, wie er sie aus seiner Zeit als Entwickler von Schaltkreisen kannte, und wie sie in den 1930ern und 1940ern von der Neurophysiologie und Kybernetik eingeführt worden waren. Er untersucht, wie von Netzwerken ein Input a in einen Output f moduliert wird. Er beschränkt sich auf den einfachsten Fall, wenn aus einer eingehenden Welle eine neue Welle mit doppelter Wellenlänge erzeugt wird. Alles weitere sollte sich daraus entwickeln lassen.

(2) Es ist kein Zufall, dass er Netzwerke betrachtet, mit denen Wellen moduliert werden. Im 19. Jahrhundert wurde mit dem Satz von Stokes und Weierstrass gezeigt, dass jede Funktion als Approximation einfacher Wellen gedeutet werden kann. Hilbert hat daraus den Hilbert-Raum konstruiert, der von grundlegender Bedeutung für die Quantenmechanik und Spieltheorie wurde. Spencer-Brown entwirft daher – in meinem Verständnis – mit der Modulation von Wellen den Nukleus, aus dem schrittweise die Grundlagen der modernen Mathematik entwickelt werden können.

(3) Wie läuft die eingehende Welle durch das Netzwerk? Um seinen Ansatz zu verstehen, ist wichtig: Die Modulation einer Welle in einem Netzwerk erfolgt nicht für die Welle im Ganzen, sondern abschnittweise je Wellenberg und Wellental. Jeder Abschnitt ergibt einen einzelnen Input, den Spencer-Brown als stroke (Impuls) bezeichnet. Jeder einzelne stroke muss für sich einen eigenen Weg durch das Netzwerk finden.

(4) Was geschieht an den Schaltelementen (markers) im Innern des Netzwerks? Jedes Schaltelement legt fest, in welcher Weise ankommende Wellenberge und Wellentäler konvertiert oder blockiert werden. Es ist die Kunst des Ingenieurs, die Schaltelemente geschickt anzuordnen, wobei offen ist, ob er hier implizit vorausgesetzten, verborgenen Regeln folgt. Im Ergebnis ist das Netzwerk so entworfen, dass fast immer zwei einander folgende strokes den gleichen Weg gehen können. Jeder stroke bestimmt mit seinem individuellen Weg einen Zustand des Netzwerks. Die Welle wird bei ihrem Weg durch das Netzwerk aufgespalten (gestreut) und im Ergebnis zu der resultierenden Welle zusammengefügt. Das Netzwerk beschreibt daher nicht mehr einfach eine  Differenz  ›f | a‹ zwischen dem Input a und dem Output f, sondern ein  Differenzfeld ›f ▒ a‹ (den Gebrauch der Symbole | und ▒ übernehme ich von Scheier, 18f).

Als Beispiel werden die Wege der ersten beiden strokes dargestellt:

              

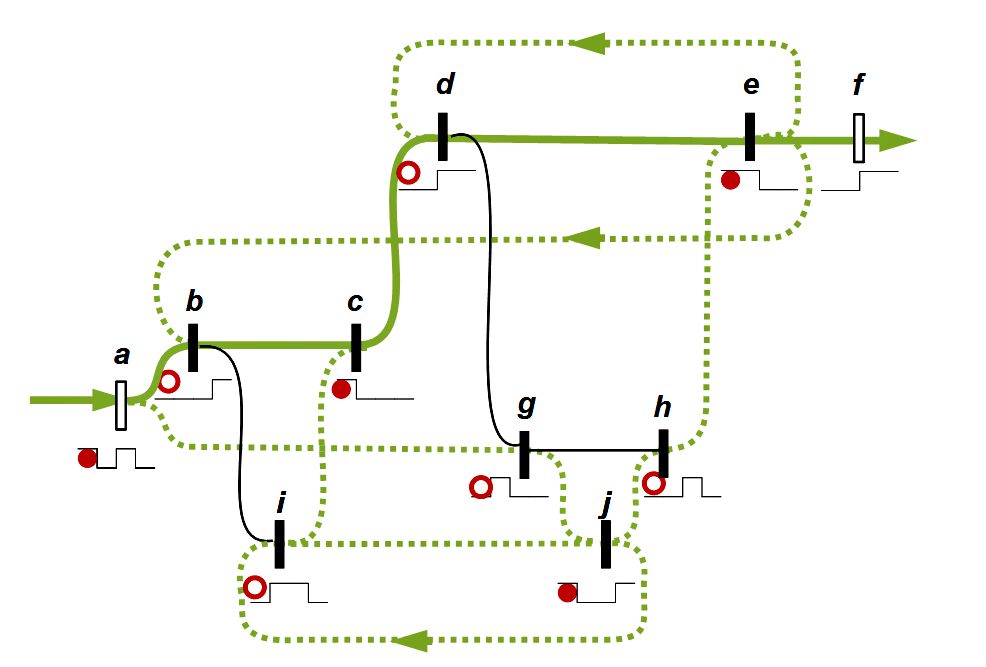
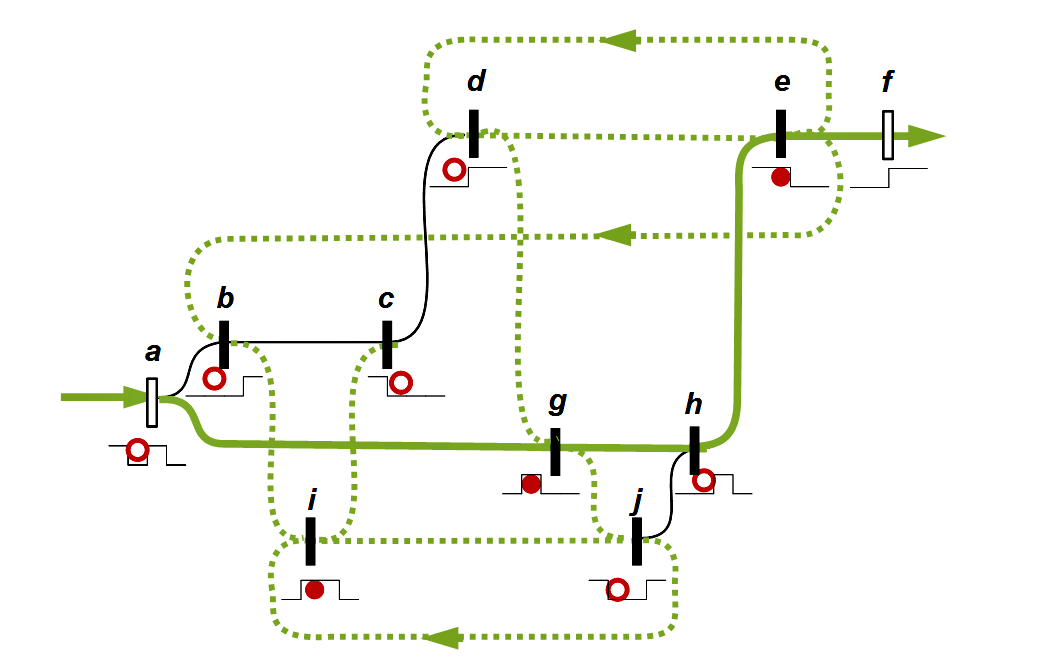
                  Wege nach dem ersten und nach dem zweiten Stroke

Legende
Unterhalb der Marker: Roter Vollkreis zeigt einen Wellenberg an, Leerer Vollkreis ein Wellental (nach Kauffman 2006, 115ff)
Olivgrün: Standardwege, die direkt zum Ausgang führen
Olivgrün gestrichelt: Weitere mögliche Wege
Schwarz: Diese Wege sind im jeweiligen Zustand blockiert, da ein leerer Kreis auf einen leeren Kreis bzw. ein Vollkreis auf einen Vollkreis trifft
Linksgerichtete Pfeile auf einem Weg zeigen mögliche Rückläufe an
Beobachtung: Auf jedem möglichen Weg wechseln Vollkreise und Leerkreise einander regelmäßig ab

(5) Das System ist so eingerichtet, dass es in der Oszillation seiner Systemzustände auf die Oszillation des Inputs reagieren kann und im Ganzen eine Art Fließgleichgewicht herstellt, von dem Bertalannfy sprach, und das mit Maturana und Varela als Selbstorganisation (Autopoiesis) bezeichnet werden kann.

(6) Der Entwickler entwirft das System in "Zusammenarbeit" mit dem von ihm geschaffenen Netzwerk. Er weiß im Voraus weder, welche Inputs erfolgen werden, noch kann er vollständig planen, welchen Weg sie im Netzwerk finden werden. Er kann das Verhalten des Netzwerks nur vage voraussagen und verlässt sich auf die Selbstorganisation durch das System. Das Netzwerk kann als das Medium (Grund) verstanden werden, sein jeweiliger Zustand als seine Form.

Mit den Netzwerken wird die einseitige Vorgehensweise verlassen, die am Anfang von Laws of Form steht: Es ist nicht mehr ein einseitig handelndes Subjekt, das in einen Grund eine Form zeichnet (»draw a distinction«), sondern das Subjekt entwirft ein Netzwerk, das seine eigene Form findet, die im Weiteren vom Subjekt verbessert werden kann. Das Verhältnis von Medium und Form, oder in der Sprache von Spencer-Brown: das Verhältnis von cross (marked space) und »unmarked space« (ock) wird dynamisch. Spencer-Brown zeigt im Detail, wie das Netzwerk alternativ entsprechend den Regeln der Laws of Form als eine Form konstruiert werden kann, die nur aus Haken (crosses) und Feedbacks durch Re-entries gebildet wird.

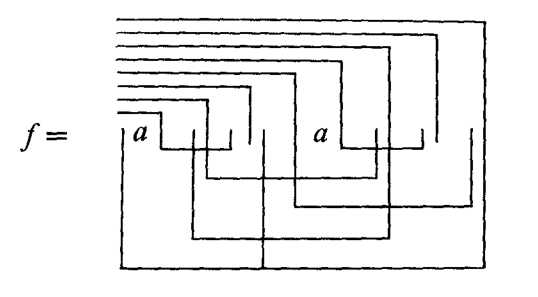
Modulator Funktion (LoF, 66)

Aber seine spezifische Eigenschaft als Netzwerk zeigt sich besser in der üblichen graphischen Gestalt. So gelingt Spencer-Brown mit den Netzwerken ein Übergang von den einfachen Formen im Haupttext von Laws of Form in einen neuen Entwurf einer Logik, deren Grundelemente Netzwerke sind. Weiter gedacht ergeben sie die Idee einer Mathematik, die nicht mehr nur auf Zahlen und den elementaren geometrischen Figuren (Punkt, Kreis, Gerade) beruht.

(7) Die Anwendungsgebiete sind vielfältig und im Grunde unbegrenzt. Die Netzwerke stehen daher für mich für eine Logik der medialen Moderne. In diesem Panel möchte ich als Beispiel die Organisationstheorie nennen.

Jede Organisation ist ein Netzwerk, das bestimmte Ressourcen (ihren Input) verarbeitet, um ein Ergebnis zu erzielen (den Output). Innerhalb der Organisation kann jedes Schaltelement als eine Stelle bezeichnet werden, die von einem oder mehreren Mitgliedern der Organisation besetzt wird. Jede Stelle schafft einen Wert, und der Netzplan ist eine Verallgemeinerung linear gedachter Wertschöpfungsketten. Entscheidend ist die Einsicht, nicht nur ein Schema der Organisation zu entwerfen, sondern zu verstehen, in welcher Weise mit diesem Schema die Selbstorganisation der Organisation getroffen und auf theoretischer Ebene zum Leben erweckt wird. Hierfür hat Spencer-Brown einen Formalismus geschaffen, mit dem es möglich werden könnte, die Algorithmen zu verstehen und zu entwickeln, die der gegebenen Organisation zu Grunde liegen. Das war in den verschiedenen Anwendungsgebieten wie in diesem Beispiel der Organisationstheorie bisher nicht möglich.

Hinweis: Siehe weiterführend den ausführlichen Kommentar zu Spencer-Brown Laws of Form (deutsch, englisch).

Anhang

Aus der Diskussion im Panel und weiteren Beiträgen und Gesprächen im Verlaufe der Konferenz ergeben sich für mich vor allem drei weiterführende Punkte zum Thema Netzwerke bei Spencer-Brown:

Erzählstrukturen und ihre Netzwerke Wie ist Nicht-Mathematikern zu erklären, was das Besondere beim zirkulären Übergang von Argumenten a zu Funktionen f ist, deren Argumente sie sind, und was ist zu antworten, wenn die meisten Mathematiker diese bewusst paradoxe Idee von Spencer-Brown für absurd erklären? Eine überraschende andere Sicht ergibt sich mit Leon Conrad, und sie kann einiges klarer und anschaulicher machen. Er nutzt die Grundsymbole von Spencer-Brown, um mit ihnen auf einer Meta-Ebene die Strukturen unterschiedlicher Typen von Erzählungen zu beschreiben (analysis of sentence types and story structures). Mit Erzählungen können auch Musikstücke gemeint sein, die etwas zu erzählen haben, mathematische Beweise oder Vorträge.

 : Einstieg und Ausstieg in und aus einer Erzählung. Per Re-entry wird die übliche Alltagssituation gebrochen, in der sich der Hörer (bzw. Leser) befindet. Der Erzähler richtet liebevoll die Umgebung ein, in der er erzählen möchte, so dass der Hörer schon beim Eintreten weiß, dass ihn eine andere als die gewöhnliche Welt erwartet. Im Konzertsaal stimmen die Spieler ihre Instrumente, bis Ruhe einkehrt, wenn der Dirigent eintritt und den Taktstock hebt. Der Leser macht es sich gemütlich, bevor er zu einem Buch greift, liest vielleicht am Anfang den Klappentext, das Literaturverzeichnis, bis er mit der Lektüre beginnt. In neueren Formen des Storytelling wird das Publikum wie in einem Rock-Konzert zu einer besonderen Begrüßung aufgefordert (Beispiel). – Die jeweilige Stimmung springt zugleich auf den Erzähler über, der seinerseits spürt, dass dies ein besonderer Abend zu werden verspricht. – Und umgekehrt muss am Ende der Erzählung der Ausstieg gelingen und die Erzählung vom Hörer mit einem Re-entry in seine Alltagssituation übernommen und dort vernäht werden. Erst jetzt entscheidet sich über Erfolg oder Misserfolg der Erzählung.

 ⃧  : Ort, Zeit und Situation, in der die Erzählung spielt. Mit ihnen wird die Umgebung der Erzählung bestimmt, und zugleich der Horizont, vor dem sie zu verstehen ist. Der Erzähler beginnt bewusst auf zwei Ebenen gleichzeitig: Er reagiert auf die Situation der Hörer und vermischt sie geschickt mit dem Inhalt, den er erzählen möchte. Das kann ein bewusster Paukenschlag sein, wie z.B. die beiden ersten, diffus klingenden Schläge, mit denen Beethoven die Eroica beginnt, oder umgekehrt ein Anfang wie aus dem Nichts zu Beginn seiner 9. Sinfonie. Märchenerzähler beginnen mit Floskeln wie "Es war einmal vor langer, langer Zeit", die in einem getragenen Ton vorgetragen werden, und beziehen manchmal zu Beginn das Publikum mit Rückfragen ein, bis jeder innerlich dabei ist. Jeder spürt, dass jetzt etwas Neues anfängt. Viele Rhetoriker empfehlen, eine Rede mit einer Anekdote zu beginnen, um den Hörer auf das Kommende einzustimmen.

 : Im Verlaufe der Erzählung treten Ereignisse ein ...

⇀: die die Erzählfiguren näher zur Lösung ihres Problems bringen, und Erwartungen werden erfüllt ...

↽: ... oder Rückschritte, Spannung wird aufgebaut ...

⇌: ... oder es wird eine vorübergehende Dissonanz (Schwebezustand) erzeugt.

Mit diesen Elementen kann z.B. folgender Typ einer Erzählung beschrieben werden:

    ↽ ⇀ ↽ ⇌ ↽ ⇌

Das ist ein linearer Prozess und beschreibt eine sehr einfach aufgebaute Erzählung. Im Verlaufe der Erzählung können Nebenfiguren mit Seitenhandlungen eingeführt und in die Haupthandlung übernommen werden. So ergibt sich ein Netzwerk. Ein berühmtes Beispiel ist der Roman Erziehung des Herzens (L’Éducation sentimentale) von Gustave Flaubert. Er hatte auf einer großen an der Wand aufgehängten Zeichnung die Struktur des Romans entworfen und beim Schreiben ständig vor Augen. Der Leser ist dagegen verblüfft über die Zeitsprünge im Roman und die Vielzahl der Figuren, die wie im wirklichen Leben scheinbar zufällig kommen, gehen und wiederkehren.

In der Regel identifiziert sich der Hörer mit der Hauptfigur, nimmt dessen Standort ein, erlebt die Geschichte aus dessen Perspektive, geht im Flow der Erzählung auf und erreicht am Ende eine Einsicht, in der er nicht mehr einzelne Ereignisse hört, sondern versteht, wie die Erzählung im Ganzen heißt und was sie bedeutet. Ein gelungenes Beispiel ist Peter und der Wolf von Prokofjew: Erst lassen sich die meist jungen Hörer von der Geschichte gefangen nehmen, bis sie am Ende wissen, dass es eine Geschichte war, was sie bedeutet und was sie von ihr gelernt haben. Dieser Übergang von den einzelnen Ereignissen innerhalb einer Erzählung zum Ereignis, die Erzählung als Erzählung verstanden, identifiziert und benannt zu haben, ist eine anschauliche Beschreibung, was mit dem Übergang von den Argumenten a zur Funktion f gemeint ist.

Für mich ergibt das die Anregung, im Netzwerk nicht nur von Input und Output zu sprechen, sondern Input und Output weitergehend als die Re-entries zu verstehen, mit denen das Netzwerk mit seiner Umgebung verbunden ist. Innerhalb des Netzwerks können die Funktionsweisen der Schaltelemente erweitert werden. Sie sind nicht darauf zu beschränken, ein einlaufendes Signal zu konvertieren oder zu blockieren, sondern aus der Konvertierung wird ein Fortschritt ⇀, aus der Blockade ein Rückschritt ↼ und möglicherweise ein kurzfristiger Stillstand ⇌, ein Moment des Nachdenkens, aus dem sich unterschiedliche Wege ergeben können.

Parallele Wege und ihre Verfilzung Arthur Collings erweitert nicht nur die duale Logik von  ⃧   (cross) und   (recrossing) in eine quaternionen-artige zirkuläre Struktur eines in vier Viertelkreise unterteilten Kreises, sondern er betrachtet Netzwerke mit nicht nur einem Input, sondern zwei voneinander unabhängigen Inputs, die zu zwei voneinander unabhängigen Outputs führen. Im einfachsten Fall laufen zwei parallele Wege von jeweils einem Input zu einem Output, doch kann es auch zu Verfilzungen (Flechten, Zöpfen, braids) kommen, die zu einer eigenen Flechtfrisur von Rastazöpfen führen, und ihrer mathematischen Struktur, den braid groups.

In einem sehr einfachen Beispiel gibt es zwei Inputs mit den Argumenten a und b, die als Output zu  ⃧a  und  ⃧b  führen. Sie können sich miteinander verflechten.

Der Phantasie sind keine Grenzen gesetzt, welche weiteren – aus der Quantenmechanik bekannten – Möglichkeiten denkbar sind: So können zwei Wege einander durch Resonanz beeinflussen. Oder es sind virtuelle Sprünge in die Vergangenheit und Zukunft denkbar, wenn ein Weg durch ein Ereignis beeinflusst wird, das auf dem anderen Weg in der Vergangenheit bzw. in der Zukunft liegt. Die moderne Literatur kennt unbegrenzt viele Beispiele, wie sich Vorgänge dieser Art erzählen lassen.

Mit der Theorie der Schaltkreise sollte es möglich sein, aus dieser Vielzahl bestimmte Grundstrukturen zu ermitteln.

Genesis von Netzwerken Mit Josef Freystetter lässt sich die biblische Schöpfungsgeschichte Genesis 1,1 - 2,4a Vers für Vers als ein sich entwickelndes Netzwerk im Sinne von Laws of Form lesen. So handelt z.B. Gen.1,4 von der Scheidung (distinction) von Licht und Finsternis, wobei Freystetter zyklisch wechselnd am Tag das Licht als den markierten Bereich und das Dunkel als den unmarkierten Bereich deutet und in der Nacht das Dunkel als den markierten Bereich und das Licht als den unmarkierten Bereich.

Der Wechsel von Tag und Nacht ist der elementare Zyklus in der Zeit. Im nächsten Schritt wird das Wasser auch räumlich in verschiedene Bereiche getrennt (Meere, Wolken, Flüsse) und von ihm scheidet sich die Erde, die sowohl zum fruchtbaren Boden wird, auf dem Pflanzen und Tiere leben können, wie im übertragenen Sinn zum Grund, in dem die Formen eingetragen werden. Am Himmel entstehen Zeichen und Konstellationen, die zum Vorbild der Schaltelemente (marker) in den Netzwerken werden.

Die biblische Schöpfungsgeschichte ist jedoch nicht einfach eine klassische Naturgeschichte in Kurzform an sieben Tagen, sondern mit den natürlichen Dingen entstehen zugleich die Bilder und der Sprache, in denen sie dargestellt werden. Es lässt sich nicht sagen, was zuerst kam: Die Sprache und die Bilder oder ihr Inhalt. Die Bilder und die von ihnen dargestellten Inhalte bedingen einander gegenseitig (siehe Lof, 42). Gott hat dem Menschen die Vorstellungskraft und die Sprachfähigkeit verliehen, mit denen er sich ein Bild dieser Entwicklung machen kann (Gen. 1,26 und 2,19).

Es geht Freystetter nicht nur darum, mit Spencer-Brown das Netzwerk der Ereignisse in der biblischen Genesis zu verstehen, sondern nach dem Vorbild der Genesis die Genesis (die Entstehung) eines Netzwerks mitzuvollziehen. Das Netzwerk entwickelt sich nach meinem Verständnis nicht wie eine lineare Erzählung – wie es der Aufbau von Gen. 1-2 nahelegt –, in der aus einem Punkt schrittweise eine Differenz, ein einfacher Zyklus, die Verschränkung zweier Zyklen und schließlich ein Netzwerk mit 6 Schaltelementen entstehen, sondern aus einem unterliegenden Bereich, in dem die verwendeten Formen anfangs noch unscharf, halb-fertig, gestrichelt gezeichnet sind oder in der Vorstellungsweise der Teilchenphysik von Elektronenwolken gesprochen werden kann. Sie befinden sich im Sinne von Leibniz im Zustand der Differentiale, der dem Bereich der gewohnten Zahlen vorausgeht. Jedes noch in Entwicklung begriffene Spurenelement (das noch keine abgeschlossene Form hat und noch keine ausgebildete Spur hinterlässt) sucht sich seine Partner, bis aus dieser Entwicklung die Formen und ihre Spuren hervorgehen. Die Vorstellung der Spur ist vieldeutig. Für Freystetter zieht sich Gott am Ende der Schöpfung aus der von ihm geschaffenen Welt zurück. Diese Idee wurde auch von Leibniz vertreten, doch sprach Leibniz von den Spuren, die Gott in der Welt hinterlassen hat. Diese Spuren sind für mich der Bereich, aus denen das menschliche Vorstellen, Denken, Sprechen und Verstehen hervorgeht und damit auch die Laws of Form. Spencer-Brown trifft besser und genauer als alle anderen mir bekannten Logiken diesen Punkt, der allen weiteren Unterscheidungen etwa in Mathematik und Sprache vorausgeht.

Wenn Spencer-Brown innerhalb komplexer Formen Verschachtelungsebenen sᵢ unterscheidet und die ihnen unterliegende Realität s₀ nennt (LoF, 7), handelt es sich bei den vorausgehenden Möglichkeitsräumen um Ebenen s₋₁ und abwärts (s₋ᵢ). Es scheint mir die größte Herausforderung und zugleich interessanteste Arbeit zu sein, hierfür einen geeigneten Kalkül zu finden, der den von Leibniz entwickelten Differentialkalkül aufgreift und fortführt, bis im Ergebnis aus einem Raum möglicher Netzwerke und ihrer möglichen Verknüpfungen die wirklichen Netzwerke und ihre tatsächlichen Verknüpfungen entstehen.

Danksagung Ich möchte mich bei Bernie Lewin und Lars Clausen für die Vorbereitung und Gestaltung des Panels bedanken und bei Leon Conrad für zahlreiche weiterführende Fragen und Anmerkungen sowie die Unterstützung bei der graphischen Gestaltung der Netzwerke und der Übersetzung ins Englische.

Literatur

Leon Conrad: The Unknown Storyteller, Liverpool 2019; academia.edu; Video (oder YouTube)

Louis H. Kauffman 2006: Laws of Form – An Exploration in Mathematics and Foundations, Rough Draft; PDF

Louis H. Kauffman, Arthur M. Collings: The BF Calculus and the Square Root of Negation, 2019; ResearchGate

Bernie Lewin: Enthusiastic Mathematics, Melbourne 2018

Claus-Artur Scheier: Luhmanns Schatten, Hamburg 2016

George Spencer-Brown: Laws of Form, New York 1972 (Julian Press) [1969]; archive.org

George Spencer-Brown: An Introduction to Reductors, unveröffentlichtes Typoscript 1992

 

© tydecks.info 2019