A commentary on Laws of Form from Spencer-Brown

Based on a contribution to the Philosophical Colloquium of the Akademie 55plus Darmstadt on March 13 and 27, 2017, Version July 12th, 2019

 

 

Introduction

George Spencer-Brown (1923-2016) was from England and came from the same county of Lincolnshire as Newton. He worked early in parallel and overlapping on questions of mathematics, engineering and psychology, e.g. in World War II as a radio operator, communications engineer and hypno-pain therapist with the Royal Navy, 1950-51 at Trinity College Cambridge with Ludwig Wittgenstein (1889-1951), from 1960 with the mathematician and philosopher Bertrand Russell (1872-1970), in the field of psychotherapy and child-education with Ronald D. Laing (1927-1987), who was his therapist and whom he taught mathematics, and he was also a writer, songwriter, chess player, game inventor, glider pilot (with two world records), a quite unusual personality. 1959-61 Chief Logic Designer at Mullard Equipment, 1963-64 Advisor at British Rail, 1963-1968 projects at mathematical institutes in England, 1968-69 full-time employment as psychotherapist with hypnosis techniques, later only part-time. From 1976 temporary professorships at universities in Australia and USA. 1977-78 consulting for Xerox. In later years he became impoverished and withdrew himself, but was able to live on the property of the Marquess of Bath, a former student of his. – Laws of Form was published in 1969 thanks to promotion by Bertrand Russell. A positive review by Heinz von Foerster (1911-2002) attracted some attention, but it has remained a marginal phenomenon in mathematics, computer science and philosophy to this day. In Germany, the sociologist Niklas Luhmann (1927-1998) took up Spencer-Brown's ideas and saw them as a new approach to systems theory which, in his view, enabled a liberation from traditional philosophy. A first introduction to his logic can be found at Wikipedia. Louis Kauffman (* 1945), University of Chicago, has further developed the approach. There are references to computer science (von Foerster), cybernetics (Norbert Wiener), antipsychiatry (Laing), anthropology (Bateson), psychology (Piaget) and communication science (Watzlawick), systems science (Luhmann, Baecker), self-referential systems (Maturana, Varela). – Spencer-Brown is said to have been rather difficult to deal with personally, which probably has something to do with the fact that – as I think rightly – he saw his works on a par with those of Aristotle and Frege and was disappointed by the lack of recognition.

Accordingly, there is little secondary literature. Spencer-Brown's texts are composed extraordinarily compactly. The Laws of Form comprise 77 pages in the main text, supplemented by some prefaces and self-comments. In 1973 a conference took place at the Esalen Institute at the californian pacific coast, attended by Spencer-Brown, Bateson, von Foerster and others (American University of Masters Conference, abbreviated AUM-Conference). This already lists the source texts. Dirk Baecker sent me an unpublished typescript An Introduction to Reductors written by Spencer-Brown in 1992. In Germany, following Luhmann, there are circles at the anthroposophically influenced private university Witten/Herdecke in the Ruhr area, in Heidelberg and Munich that regularly are working on Spencer-Brown. As secondary literature, I have therefore used Luhmann's complex chapter on observation from his 1990 work Wissenschaft der Gesellschaft (Science as a Social System), in which he presents his position on Spencer-Brown, and, building on this, an anthology Kalkül der Form (Calculus of Form), edited by his student Dirk Baecker in 1993, which also contains Heinz von Foerster's review, as well as Luhmann's 1995 lecture Die neuzeitlichen Wissenschaften und die Phänomenologie (Modern Sciences and Phenomenology) in Vienna, in which he explains his philosophical position on Husserl and Spencer-Brown. In 2016, Claus-Artur Scheier, in Luhmanns Schatten (Luhmann's shadow), linked his approach to the newer French philosophy and formalized it in his own way. In Heidelberg a short introduction to the logic of Spencer-Brown by Felix Lau was published in 2005 and in Munich in 2004 an extended introduction by Tatjana Schönwälder-Kuntze, Katrin Wille and Thomas Hölscher was published in 2009. They are associated with Matthias Varga von Kibéd (* 1950), who studied with the logician Ulrich Blau (* 1940). Blau has written standard books on new directions in logic, in which, however, he does not mention Spencer-Brown. Varga von Kibéd has turned to Far Eastern traditions and has become active in the founding, introduction and marketing of new methods of systemic structures, which refer to Spencer-Brown.

In summary, Spencer-Brown has mainly influenced the theory of self-referential systems and new methods of systemic therapy, but is largely ignored and unknown in traditional philosophy, mathematics and computer science.

This contribution is also for me a first beginning and introduction and can only try to approach further philosophical questions. However, I suspect that his idea contains a potential that is far from exhausted.

Motives

In his highly self-reflexive work, Spencer-Brown stresses »There can be no distinction without motive« (LoF, 1). This seems to me to be the best approach to this unusual work. In order to understand his thoughts, it is hardly possible to rely on what has been learned and practiced in mathematics, logic or philosophy so far. On the contrary, he encourages us to unlearn much of it and to become aware again of the deeper motives which originally underlie our enthusiasm for mathematics and which have largely been lost.

– Liar paradox and negative self-reference

The first motive is surely the concern with the liar paradox ›This sentence is wrong‹. With it, the logical foundations of mathematics and thus of all natural science were fundamentally questioned. This caused a deep sense of uncertainty, that is hardly imaginable today – since we have become »accustomed« to it. At the same time, with the decline of all traditional religious and mythical beliefs, mathematics and natural science had become the only force promising identity and security. If their foundations are shaken too, every hold is in danger of being lost. Robert Musil has written about this marvellously in his novel Die Verwirrungen des Zöglings Törleß (The Confusions of Young Törless), published in 1902. Anyone who studied mathematics between 1900 and 1980 was almost inevitably confronted with Russell's paradox and was plunged into a crisis comparable to the skeptical challenge to philosophy. Only the long-lasting economic upswing in the Western countries after 1945 was able, at least for a while, to push all concerns and questions of this kind into the background and establish bare pragmatism and ordinary materialism as new values. What danger should such a paradox pose when the applications of the same science are so successful around it? In such times, Spencer-Brown's questions have little chance of resonating, since they threaten to stir up the questions that had just been laboriously swept under the carpet.

The liar paradox is the most famous example of negative self-reference: the sentence refers to itself, and it negates itself. This leads to the paradox: If this statement is right, it is wrong, and if it is wrong, it is right.

This paradox can be brought into many different forms, which has driven Ulrich Blau to the outermost ramifications with the result that there is nothing in the usual logic that leads out of this paradox.

The sentence is by no means just a logical gimmick that every teenager between the ages of 12 and 16 goes through, but in the original formulation »a Cretan says that all Cretans lie« it is of mythological importance when Cretans had to cope with the fear that they might have killed God on the island of Crete. In philosophy Hegel gave it systematic significance and it is considered the decisive characteristic of the dialectical method.

Bertrand Russell was initially Hegelian, but could not be satisfied with Hegel's speculative sentences on contradiction. For him, there had to be a formal solution that could withstand the demands of traditional logic. He succeeded only negatively with the prohibition of self-referential sentences, and he was therefore enthusiastic when Spencer-Brown was able to present a completely new formal solution.

– Imaginary numbers

Spencer-Brown was looking for a way out based on the example of imaginary numbers. The imaginary numbers are still a strange, mysterious foreign body within mathematics. Already the name ‘imaginary’ is completely untypical for the usual mathematical thinking. Are these numbers imaginary like a dream, or are they mere images, virtual objects of thought, born out of the imagery (fantasy) of the soul? What distinguishes a mathematical imago from a psychological imago? Questions of this kind certainly moved Spencer-Brown a lot after his therapy at Laing.

The expression ‘imaginary number’ goes back to Descartes and Euler. For mathematicians it is a consistent formalism to extend the space of numbers, and for engineers and physicists it is an extremely helpful tool to simplify complex equations, even if they can usually hardly answer the question of why this is possible with imaginary numbers. As a communications engineer, Spencer-Brown was undoubtedly familiar with this meaning and had learned how engineers and scientists simply calculate with such numbers, because it works well and proves itself without asking about the mathematical basics.

In the preface to the first American edition of Laws of Form in 1972, he saw an amazing relationship between imaginary numbers and the question of Russell's paradox. Russell and Whitehead wanted to exclude the threat of paradox in type theory by prohibiting self-referential elements. Spencer-Brown considered this a mistake. »Mistakenly, as it now turns out.« (LoF, ix) Spencer-Brown reports that he met Russell in 1967 and showed him how to work without this exclusion. »The Theory was, he said, the most arbitrary thing he and Whitehead had ever had to do, not really a theory but a stopgap, and he was glad to have lived long enough to see the matter resolved.« (LoF, x)

In order to define a negative self-reference within arithmetic, an equation must be established in which a variable x appears as its own reciprocal value and is negated with the minus sign:

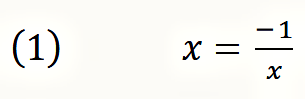
With this equation the negative self-reference is formalized: The reciprocal stands for the self-reference, the minus sign for the negation.

At first glance, this equation looks just as harmless as if someone heard the sentence ›this sentence is wrong‹ for the first time. Everybody considers this at first a common statement about another sentence (one says »the heaven is green« and another answers «this sentence is wrong«) until its inner explosive force is seen through when it refers to itself. So formula (1) does not look unusual at first sight. The paradox it contains becomes visible when x is set to 1 or −1:

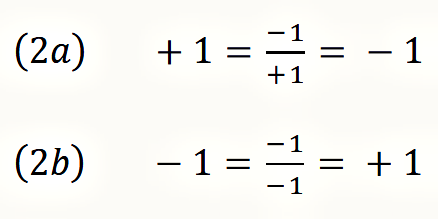
1 and −1 are the simplest possible integers, and they show that there is no integer as solution for this formula. With it, Spencer-Brown has recreated the paradox of negative self-reference within arithmetic. (Scientists trained in traditional logic and analytical philosophy, however, deny that it is permissible to transform Russel's paradox, originally formulated in set theory, in this way and to find an astonishing solution. This was my experience at the Wittgenstein Symposium 2018 in Kirchberg am Wechsel.)

Whitehead and Russell had only seen the way out to provide and exclude questions of this kind with the indefinite, third truth value ‘meaningless’. While it is not possible to operate logically and mathematically with this truth value, a solution can be found with the imaginary numbers, which allows calculating with an additional truth value. Like the y-axis, the imaginary numbers are perpendicular to the number axis. Their unit is the newly introduced number i. Both i and −i are solutions of equation (1).

That's what Spencer-Brown is about. He wonders whether, following the example of imaginary numbers in arithmetic, imaginary numbers can also be introduced into logic with far-reaching consequences for logical thinking.

»What we do in Chapter 11 is extend the concept of Boolean algebras, which means that a valid argument may contain not just three classes of statement, but four: true, false, meaningless, and imaginary.« (LoF, xi)

– Traditional logic is both too simple and too complex.

These examples already show the new approach to logic by Spencer-Brown. He was completely dissatisfied with the traditional logic. For him it is banal, not to say childish, and at the same time unnecessarily complicated.

(1) On the one hand, traditional logic is too simple, almost childish.

Anyone who has ever read textbooks of logic with their examples understands what Spencer-Brown means. A typical logical task is: »Which of the following assertions is true: Some apples are bananas. All apples are bananas. Some bananas are not apples. Some bananas are apples.« The correct solution is hidden in the sentence »Some bananas are not apples.« No one does realize that immediatly, because no one would say so in everyday life, as everyone would spontaneously understand that sentence to imply that there are some bananas that are apples. But formally this sentence is correct. It is intended to teach an abstract understanding of logic that is independent of a prior understanding of content and a feeling for language.

Is logic nothing more than the search for funny brain teasers that everyone has to smile about? This can be expanded at will: Is a sentence like »the number 2 is yellow« true or false, and what can be deduced from this sentence? What is to be thought of the conclusion: »If John has no children, both the statement ‘All John's children sleep’ and the contrary statement ‘None of John's children sleep’ are true«? Does this refute the contradiction? Analytical philosophy continues to think up new examples according to this pattern and has been struggling with questions of this kind for decades, although Herbert Marcuse (1898-1979) had already mocked this way of thinking in the 1960s (One-dimensional Man, 1964) and basically sees in it a certain kind of education for stupidity, which unfortunately dominates almost all western philosophical faculties at which philosophers of this direction are preferentially employed. Obviously, people and especially teachers who can teach in schools with this kind of logic are to be trained on a large scale at the universities.

Because of his training in logic, Spencer-Brown had been given a job to program circuits, and quickly noticed:

»The logic questions in university degree papers were childishly easy compared with the questions I had to answer, and answer rightly, in engineering. We had to devise machinery which not only involved translation into logic sentences with as many as two hundred variables and a thousand logical constants--AND's, OR's, IMPLIES, etc.--not only had to do this, but also had to do them in a way that would be as simple as possible to make them economically possible to construct--and furthermore, since in many cases lives depended upon our getting it right, we had to be sure that we did get it right.« (AUM, Session One)

As a result, although he and the other developers could generally rely on their logical thinking, they started programming and very quickly gave up systematically designing and checking their programs according to the rules of learned logic, but were satisfied when they saw that the circuits they had programmed worked without being able to explain or prove it logically. In my experience, this is the way most programmers do it, and yet it leaves a feeling of unease that there must be another kind of logic that comes closer to the practice of programming and is more helpful. (Who hasn't struggled as a programmer with methods such as the logically structured program flowchart and dropped it at some point because the effort to replicate program extensions in methods of this kind is greater than programming and testing? With complex programs, logical methods of this kind are more complicated than the program text itself, and in reality a simple pseudo code has become established for documentation, which represents the algorithms in an easy-to-read language.)

(2) At the same time, logic is far too complex.

At the beginning of every Logic and Mathematics lecture a lot of effort is put into introducing different characters, although everyone understands them intuitively. These are own characters for constants, variables, logical operators like ∧, ∨, ¬ and quantifiers like ∀ and ∃. The various professors and textbooks outdo each other in introducing the necessary conceptual apparatus as abstractly as possible. One example is the lecture Finite Model Theory of Geschke (online in the German original):

»1.1. Structures. A vacabulary is a finite set consisting of relation symbols P, Q, R, …, function symbols f, g, h, … and constant symbols c, d, … Each relation and function carries a natural number, its arity (Stelligkeit).
   Fix a vokabulary . A structure for (a -structure) is a set A together with
   (S1) relations ⊆ An for each n-digit relation symbol ∈ ,
   (S2) functions : Am → A for m-digit function symbol ∈ and
   (S3) constants ∈ A for each constantsymbol ∈ .
   Often you identify a structure with its underlying set A, so you write A instead of .« (Geschke,1, my translation)

Anyone who has studied mathematics and logic understands why a lecture is introduced in this way, and yet everyone has the feeling that there is something wrong with this way of approaching things. In the end, the attempt is made to deduce everything from a single teaching. That does not succeed. Instead, the view seems to have prevailed today that set theory, model theory and the theory of formal languages are more or less equal at the beginning. Set theory cannot do without a formal language, formal language uses set theory, each theory can be understood as a model, which in turn requires a formal language and set theoretical operations, as can be seen in this example. The result is the impression that it has not been possible to trace the different doctrines back to their simplest elements, and that the great abstraction and the complex technical apparatus are basically an escape to avoid this question.

For Spencer-Brown, this whole tendency is on the wrong path. His first basic decision is therefore to make a substantial reduction and thus open up an area that can be described as proto-logic or proto-mathematics (primary logic, primary arithmetic). He understands his approach as »perfect continence« (LoF, 1), a moderation and self-control in clarifying the logical foundations.

– Logic and Time

Classical logic is independent of time. Only statements that are timeless in themselves are made and linked with it. A fact or an observation always remains, even with sentences that refer to a certain point in time. A sentence like »On 24th February 2017 the first crocuses of the year 2017 blossomed in Bensheim« is still valid even if the crocuses have long since faded again. It is valid even if it proves to be a deception, because this sentence in itself is a fact of my thinking. Wittgenstein founded the Tractatus logico-philosophicus in 1921: »1 The world is everything that is the case. […] 1.13 The facts in logical space are the world.« For him, the world is the totality of all protocol propositions. Spencer-Brown had witnessed in 1950-51 how Wittgenstein wanted to go beyond this approach. It is too little to base logic on propositions of this kind and their connections.

Now logic has not stood still. Thus in 1954 Paul Lorenzen (1915-1994) developed the operative modal logic with which the differences between possibility, reality and necessity are to be logically included and formalized. The technical apparatus is as far as possible adapted to traditional logic. This direction has taken a certain upswing in connection with quantum logic. – Even in modal logic the consideration of time is still missing. At the same time, in the 1950s, this was attempted to be solved with a temporal logic. If one takes a look at the results of both modal logic and temporal logic, one will understand why this is not what Spencer-Brown was looking for. He took a completely different approach from the practical experience that, in programming, the equal sign is understood context-dependently as an assignment or as an agreement.

Elena Esposito has pointed out this aspect (Esposito in Baecker Kalkül der Form, 108-110). When programming, it is neither a contradiction nor a paradox when you write:

(4a)    i = i + 1
(4b)    a = f(a)

In the programming line (4a), the character i does not stand for a variable, as in a mathematical equation, for which an arbitrary number can be used, but which then has to be included in the course of the calculation. Instead, the character i stands for a storage location, the contents of which can be changed during the execution of the program. With both allocations, the result is on the left side later than the arithmetic operation on the right side. The assignment ›i = i + 1‹ is one of the most frequently used programming lines, if in a loop in the course of a temporal repetition it is counted, how often the loop was passed through. – The statement ›a = f(a)‹ is also a temporal operation that reads the current value stored from storage location a, recalculates it with a function f(a), and then reassigns the result to memory location a. The result of this operation is then used to calculate the value. The a on the left side therefore usually has a different value than the a on the right side. If, for example, in an asset management system, the value of an asset is located at storage location a and recalculated with function f, the content of storage location a changes as a result. The »old a« is located on the right-hand side and the »new a« calculated with function f is located on the left-hand side. This difficulty in understanding arises because abbreviations are used in programming: The character a stands both for the storage location and for the value stored at this storage location.

To explain what happens during programming and to find a suitable logic for it is in my opinion one of the strongest motives of Spencer-Brown. If his work has so far been almost completely ignored by computer science, it only shows to what extent computer science is incapable of finding something like a transcendental turn from its own actions, as Kant had done within philosophy, and how it looked for my impression of Spencer-Brown for programming. Especially for a mathematician and computer scientist, Spencer-Brown's book is not easy to read. Although he is more familiar than others with formal considerations of this kind, he must free himself from entrenched prejudices. He must – as Spencer-Brown said – unlearn a lot, and approach the unlearning step by step, in order not to get into too much confusion already at the first step.

Spencer-Brown answered a question from John Lilly (1915-2001) (neurophysiologist, dolphin research, study of drugs and their effects like LSD, influence on New Age):

»LILLY: Have you formulated or recommended an order of unlearning?
SPENCER BROWN: I can't remember having done so. I think that, having considered the question, the order of unlearning is different for each person, because what we unlearn first is what we learned last. I guess that's the order of unlearning. If you dig too deep too soon you will have a catastrophe; because if you unlearn something really important, in the sense of deeply imported in you, without first unlearning the more superficial importation, then you undermine the whole structure of your personality, which will collapse. Therefore, you proceed by stages, the last learned is the first unlearned, and this way you could proceed safely.« (AUM, first session)

– The influence of the observer

Kant's transcendental turn is a new kind of self-observation with which thinking examines its own actions. Kant was aware that he was following with it a turning point that had already occurred in astronomy with the Copernican turn, when he had become clear how the world view is dependent on the respective position of the observer. The world presents itself differently when it is no longer seen in thought from the earth, but from the sun. Materially everything remains the same, but the movements of the sun, the planets and the moon are mathematically much easier to bring into equations of motion. They indicate patterns (Kepler's laws), which cannot be seen from the earth with bare eyes.

With Einstein, the speed at which an observer moves plays a role in how he perceives other movements. In quantum mechanics it is feared that nothing can be measured as it is because it is changed by the measurement, i.e. the measuring process interferes with the measurement.

The observer is of even greater importance for psychology and sociology, and it is not without reason that Spencer-Brown's teachings have been taken up there. Kant considered scientific psychology to be impossible. For him it was questionable whether chemistry could ever become a science with mathematical methods, but for psychology he considered that to be completely impossible. Every thinking being will notice when it is observed and react accordingly. Therefore, the observer can never be sure that the other is only behaving the way he does because he's attuned to him. Psychoanalysis has partially taken this into account since it is aware of the phenomenon of the transference (Übertragung) recognized by Freud, when a patient adapts unnoticed to the analyst's expectations and the analyst behaves unconsciously as the patient expects of him (countertransference, Gegenübertragung).

»But not even as a systematic art of analysis, or experimental doctrine, can it (psychology, t.) ever approach chemistry, because in it the manifold of internal observation is only separated in thought, but cannot be kept separate and be connected again at pleasure; still less is another thinking subject amenable to investigations of this kind, and even the observation itself, alters and distorts the state of the object observed. It can never therefore be anything more than an historical, and as such, as far as possible systematic natural doctrine of the internal sense, i.e. a natural description of the soul, but not a science of the soul, nor even a psychological experimental doctrine. « (Kant The Metaphysical Foundations of Natural Science, Preface, MAN, AA 04:471.22-32, translated by Ernest Belfort Bax)

Has this been confirmed for Spencer-Brown in his own psychotherapeutic experience? In contrast to Kant's belief, can patterns be recognized in the behavior of the observer and the observed in psychological practice that go beyond the respective personality? I do not know whether and how intensively Spencer-Brown was known about the teachings of Husserl, Heidegger, Sartre and others, who have investigated this question. Luhmann and Scheier understand the logic of Spencer-Brown from this context.

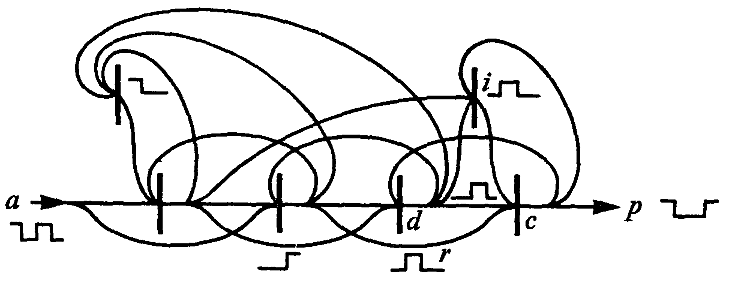
Here the question of re-entry takes on a new meaning. In psychological and sociological practice, re-entry is not simply a possibly purely mechanical resonance, feedback, or feedback that, as in self-referential systems, takes place almost automatically, but the observer receives feedback from the observed on his behavior and reacts to it.

– Process and result

When Spencer-Brown emphasizes pragmatic action from his professional experience, he questions the traditional relationship between process and result. Since traditional logic knows only timeless statements that are always valid and never change, it has not examined the logic of processes. For Aristotle, logic and physics were clearly separated. He systematically examined the timeless statements in his both works on the Analytics (Analytica protera and Analytiká hystera), whereas in physics, as the doctrine of ephemeral things and beings subject to Coming to Be and Passing Away (the title of another text from Aristotle, Peri geneseôs kai phthoras), time, movement and change occur. In his Physics he introduced with energeia and entelecheia new concepts that apply only to the course of processes and consciously leave the framework of the Analytics and come close to a new logical understanding. (They have since become basic concepts in physics and biology as energy and entelechy. Heidegger had described them as existentials (Existentialien), but considered it impossible to find a formalization comparable to traditional logic.)

Spencer-Brown wants to base logic on concepts in which process and result are not yet clearly separated. He shares this concern with Hegel, who has systematically used such concepts. 'Beginning': This can be both the process of beginning and the result that was started. Similar to determination, development, measurement etc.: A measurement can be the process of measuring, as well as the value that was measured. Determination can be the process of determining as well as the result that something is so and not differently determined.

Spencer-Brown bases his logic with distinction and indication on similar terms. This can be the process of naming and distinguishing as well as the result when a distinction is made and a name is given. It is the process of distinguishing something, and in the result the sign (mark) and the value that is given to the something with the distinction.

If one begins with concepts in which the distinction between process and result is consciously kept open, then there must be a clearly recognizable and comprehensible way within logic to introduce time and movement there and to separate this openness into its two components. I see this motive especially in the distinction between primary arithmetic and primary algebra as in the introduction of re-entry and the time given with re-entry.

– The signs and their medium

If it is unusual for a mathematician to accept the changed meaning of variables in the temporal course of assignment in the programming and logic of Spencer-Brown on the one hand and the timelessly conceived mathematical equations on the other hand, it requires an even more radical rethinking to regard the relationship between sign and medium as a reciprocal process. It is almost absurd for a mathematician to assume that the medium in which the mathematical signs are inscribed could influence the signs and their operations. Basically, every mathematician sees the signs of his formulas completely independently of the medium in which they are represented, preferably as objects in an entirely immaterial, purely intellectual space. If he needs a blackboard or a sheet of paper or a screen to write down his formulas there, these are only tools without influence on the contents of calculation and proof. It is possible that a formula is made blurred on a bad background and is therefore misread with results that are misleading. But this is nothing more than a disruptive factor that can ideally be excluded. The statements of mathematical propositions apply in principle independently of the medium in which they are written.

This attitude was shaken in 1948 by the work of Claude Shannon (1916-2001) on the mathematical foundations in information theory. Shannon was like Spencer-Brown a mathematician and electrical engineer. In his study of data transmissions, he has demonstrated how any medium generates background noise that interferes with the transmitted characters. To this day, mathematics has not perceived or not wanted to perceive the elementary consequences of this for mathematics and logic. To this day, mathematics is regarded as a teaching that is independent of the medium in which it is written and through which it is transmitted. Nobody can imagine that the medium could have an influence on the signs and their statements. Mathematics is regarded as a teaching that is developed in a basically motionless mind.

For Spencer-Brown, this relativizes itself. For Spencer-Brown, the design of circuits added a fundamentally new experience that goes far beyond mere programming. At first glance, schematics are nothing more than a graphic, descriptive language of formulas whose logical status should resemble the signs of mathematics and ultimately correspond to them. But for him, the circuits that he designed and worked with showed that each circuit contains its own dynamics that support the statements and results designed with the circuit. It is possible to describe in words and formulas which input a circuit processes and to which output it leads, but it is not possible to fully explain how these results come about. Obviously, the circuit contains a kind of self-organization that influences the result by itself. Whoever designs a circuit has a clear target in mind and can design and realize the circuit, but he cannot completely predict what will happen in the circuit. On the contrary, he relies on the circuit itself to stabilise, giving the result the expected certainty. Even if on closer examination many of the processes that have led to the desired result in the circuit can be explained, there is always a residual. This property does not result from the graphic form and its formal elements, but from the medium in which the circuit is realized. Spencer-Brown compares it with chemistry: chemical formulas can never be used to describe completely what happens in a chemical reaction. The real chemical process has its own dynamics that can always lead to surprises despite all the precautions taken. From today's perspective, cell biology can be cited as another example. It has been shown that even the complete decoding of the DNA does not lead to a comprehensive prediction of the processes in a cell. All these examples are texts or text-like forms (the schematic diagram, the chemical reaction equations, the DNA code) which are fundamentally incomplete and cannot completely represent the medium in which they are realized. Is this experience in a kind of limit process also to be transferred to mathematics and logic, or at least to be taken into account there?

This leads Spencer-Brown to the fundamental question of the relationship between the signs and the medium. The result is certainly not that the mathematics known today becomes »wrong« because it has overlooked its medium and its interaction. Rather, the result is that mathematics must be understood before the horizon of an overarching doctrine of medium and sign, from which the special status of mathematics and the conditions for why it applies in the way we know it can be understood.

For me, this is the most difficult motif of Spencer-Brown to understand and at the same time the one with the most serious consequences. If a logic is designed that self-reflectively understands its own medium, in which it is founded, inscribed and transmitted, then this can lead to the design of a Logic of medial Modernity that does justice to man's constitution today. Scheier in Luhmanns Schatten in particular pointed out the importance of the medium for understanding our culture. Spencer-Brown can help to work this out further.

– Neural Networks

While the paradoxes and antinomies of Russell and Gödel are intensively discussed in philosophy, the development of a new logic, which was based on an upswing in neurophysiological research and led to neural circuits, remained largely unnoticed. Only with spectacular successes such as the Go playing program AlphaGo from 2015-16 does this change abruptly. Programs like these are the result of more than 100 years of development. I see Spencer-Brown in this tradition too.

Warren McCulloch (1898-1969) played a key role. He studied philosophy, psychology and medicine, worked primarily as a neurophysiologist and sees himself both in the tradition of American philosophy, which has always been practically oriented and pragmatically thinking, and in the neurophysiology that emerged around 1900. Of American philosophy, he names Charles Sanders Peirce (1839-1914) and Josiah Willard Gibbs (1839-1903) in particular, then, based on them, the discussion during the 1940s with Norbert Wiener (1894-1964), Arturo Rosenblueth (1900-1970), John von Neumann (1903-1957) and Walter Pitts (1923-1969). Most of them certainly saw themselves more as specialists than philosophers, because they no longer expected any stimulating impulses from the philosophy of their time. Many of them deliberately remained outside the academic field or were not accepted there (e.g. Norbert Wiener). If, nevertheless, deep philosophical questions and conversations did arise and were discussed, it is mainly thanks to McCulloch.

For decades McCulloch had been searching for a new logic with ever new approaches that went beyond the tradition of Aristotle to Frege and Russell. In 1920 he wanted to extend the copula 'is', which appears in all classical statements according to the pattern ›S is P‹, into three groups of verbs: (i) verbs that lead from an object to a subject and come from the past, while the copula 'is' occurs only in a timeless present; (ii) verbs that lead from a subject to an object and thus into the future; (iii) verbs that describe an ongoing state. But this attempt did not lead to success. This was followed by efforts to search for the smallest units in psychic thought in a similar way as physics had done with electrons, photons and other physical elements: He called them psychons. They should be connected in a way other than the traditional objects and relationships of logic in order to represent the psychic events and the diseases examined by psychiatry and to find therapies. This, too, did not lead to the expected results. The turning point came when he became familiar with the work of neurophysiology and took an active part in it as a researcher. From the very beginning, he saw the possibility of giving Kant's transcendental logic a new ground with them (when the network of neurons from the sense organs to the brain takes the place of transcendental apperception and explains the pre-influence of all sensual stimuli before it comes to thinking in ideas and concepts). At the end of his life he published an anthology of important works with the programmatic title Embodiments of Mind. From 1946 to 1953 he was a leading participant in the Macy conferences. Many ideas had arisen during the Second World War within the framework of the Office of Strategic Services (OSS) founded in 1941 by US President Roosevelt, in which Marcuse, Bateson, Sweezy and other representatives of the later New Left also participated. After 1945, the OSS gave rise to the CIA on the one hand, and on the other, many participants sought to continue their work within the framework of a civilian application. They were convinced that they were at the beginning of a completely new development.

Already in 1931 McCulloch had heard about the new findings of Kurt Gödel (1906-1978) and from the beginning he dealt with the results of Alan Turing (1912-1954), which were published since 1937. That was the beginning of a completely new kind of logic, and it is undoubtedly McCulloch's special achievement to have linked the diversity of these currents together.

His breakthrough came with neurophysiology. It began with the physician Ramón y Cajal (1852-1934). He draw the first diagrams of sensory organs and the nerve pathways they emanated from, which he had obtained from thorough studies of the nervous system and thorough dissections of frogs and other animals. The physician, psychiatrist and psychoanalyst Lawrence Kubie (1896-1973) used their example 1930-41 to describe for the first time circuits (closed reverberating circuits) in order to understand memory.

For me, two results are particularly important with regard to Spencer-Brown: Two important principles were recognized in the example of the nerve tracts from the frog's eye to the frog's brain, which have an indirect effect on the Laws of Form.

Principle of Additivity: Only when a sufficient number of neural pathways report an input is it passed on to the brain. Individual, isolated inputs, on the other hand, are ignored. If the selection does not work, the brain is flooded and overtaxed. This is one cause of epilepsy.

  

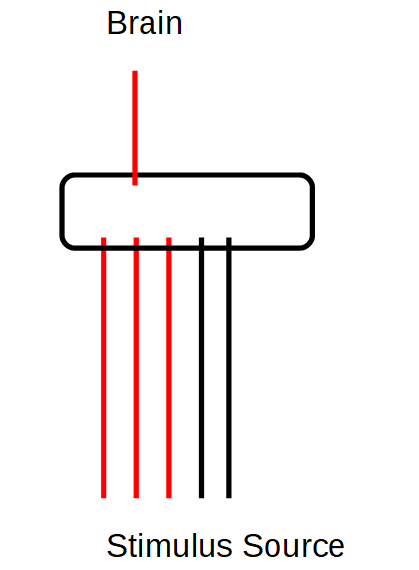
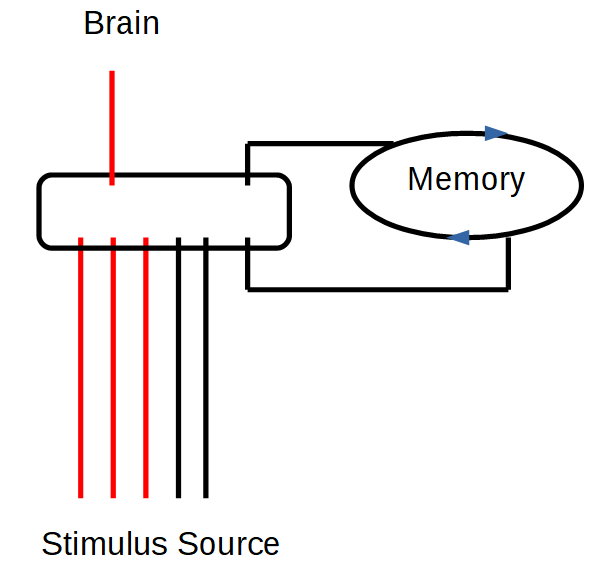
Memory: In addition, a spinning top is set up when a threshold is exceeded. There, information runs in a circle and each return reminds us that there was originally a stimulus that triggered this cycle. The activated circle remembers that something has happened. It serves as additional input in the nervous system. It not only indicates that enough neural pathways have been stimulated by the same event, but that this event has already taken place in the past. This is the technical basis and realization of a learning system.

In a similar way, Spencer-Brown speaks of the memory function and represents it through closed circuits. Spencer-Brown has sought a more abstract level that fits within the framework of logic. I don't know if he explicitly referred to this tradition, but it is clear to me how he stands in this tradition. He was no longer able to elaborate these ideas, but they appear in decisive places in the Laws of Form. In England he may have been more impressed by the Homeostat introduced in 1948 than by neurophysiology. The developer was the English psychiatrist and biochemist William Ross Ashby (1903-1972). Spencer-Brown has in a strange way brought elements of the new findings of neurophysiology in his remarks on re-entry and circuits, without it becoming clear which intuition had led him.

McCulloch had in 1945, in a short but fundamental article The heterarchy of values determined by the topology of nervous nets, pointed to fundamental philosophical aspects of the new circuits that arose in the context of the first ideas for neural networks. In a network there is no longer a controlling, hierarchical centre, but a heterarchy of concurrent and circularly interconnected developments. This seems to me to be the basic idea that Niklas Luhmann (1927-1998) has taken up in his work on systems theory – even if he only makes very marginal reference to McCulloch (as in Soziale Systeme, 565 and Wissenschaft der Gesellschaft, 365), and why he hoped with Spencer-Brown to be able to give his systems theory a new logical basis that differs from traditional subject philosophies and their paradoxes.

– The Gordian knot

Is it possible to solve all these questions together as in a Gordian knot? That seems to me to be Spencer-Brown's motive.

Spencer-Brown's motto is a verse from Laozi Tao Te Ching. Laozi begins his writing with four verses, of which Spencer-Brown has chosen the third verse.

Wu ming tian di zhi shi
Nothing/Without Name Heaven Earth from Beginning

»Since Chinese is an isolating language and not an inflectional language, the Chinese sentence has an ambiguity that is lost in Western languages through the choice of a word type. Ambiguity depends on the grammatical role of the first word 'wu:' 'not, without, nothing'«. (SWH, 65, my translation)

The verse can therefore be translated in two ways:

– Without name is the beginning of heaven and earth
– 'Nothing' is the name of the beginning of heaven and earth.

All four verses are related:

The way that is really the way is different from the unchangeable way.
The names that are real names are other than unchangeable names.
Nameless/Nothing is the beginning of heaven and earth.
The name is the mother of ten thousand things. (quotes SWH, 65, my translation)

»Distinction is Perfect Continence«

Somewhere, Spencer-Brown's logic must begin with basic concepts that cannot be further questioned. He searches for them below the usual mathematics and language. Before every speaking and arithmetic, there are indication and distinction. With them he wants to establish a proto-logic and proto-mathematics (primary logic, primary mathematics), a calculus of indication and distinction.

»We take as given the idea of distinction and the idea of indication. We take, therefore, the form of distinction for the form.« (LoF, 1)

Without having made distinctions, neither language nor calculations are possible: In order to be able to calculate and to form sentences, the characters used in calculating and writing must be differentiated from each other. In an equation like ›2 + 3 = 5‹ operands (in this example the numbers 2, 3 and 5) and operators (operation signs) (in this example + and = for addition and equation) are linked and a statement is formed with them. Similar it is in the language. In a proposition like ›S is p‹ S and p are operands and the copula ‘is’ an operator. The signs 2, 3, 5, = and + must be distinguishable from each other, and it must be assumed that they do not change during the calculation. If this were not possible, then the equation would be meaningless. Therefore it is obvious to start with differentiation as the proto-operation before the operations of calculating and speaking and to develop the usual logic and arithmetic from it step by step.

For Spencer-Brown there must be a sign that this level meets and precedes the known signs for operands (numbers and letters) and linking verbs (like the copula ‘is’ and arithmetic symbols like +). He goes even a step beyond: He looks for a sign that precedes the differentiation into operands and operators and can serve as both operator and operand. For him, this elementary sign is the cross:

   

This sign has a multiple meaning:
– Execution of an elementary operation (drawing this character, draw a distinction)
– Highlighting an interior (mark)
– Marking of an inner area (marked space) (asymmetry of inside and outside)
– Drawing a boundary (boundary with separate sides)
– Distinguishing a ground from the sign drawn in the ground (ground, medium)
– Calling the border the sign  ⃧   (indication, call)

In the latter meaning, it is self-referential: With its outward appearance, it clearly shows the difference between an inside and an outside, and at the same time this sign is the name for this difference. This gives value to the inside.

The amazing thing is that with this single character not only the operands but also the operators can be represented. Unlike traditional logic and mathematics, Spencer-Brown does not distinguish between signs for operands and operators, but implicitly defines the operations (the calculation and the formation of statements) by the mere arrangement of the operands: These are the two operations 'repetition' and 'nesting'. With them the further logic can be constructed completely.

             

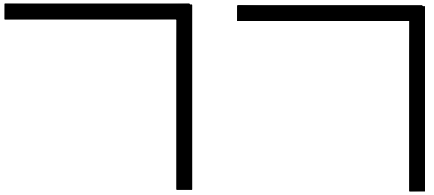
All further signs are constructed step by step from these two signs and their two arrangement possibilities, just as in Euclidean geometry all constructions result from straight lines and circles.

»Axiom 1: The law of calling.
The value of a call made again is the value of the call.« (LoF, 1)

 ⃧   ⃧   =   ⃧    

Read: If something is mentioned twice by its name, the name does not change.

»Axiom 2: The law of crossing
The value of crossing made again is not the value of the crossing« (LoF, 2)

  =     .

Read: If the boundary is crossed twice, the initial state is restored. The repetition of the crossing has a different value than the simple crossing. This is because there is a reversal in between. With crossing the side is changed, with recrossing this action is undone.

The introduction of these two axioms may be more understandable if one remembers that Spencer-Brown has been starting from circuits. (1) If a switch is opened in a circuit on a connection, the distance is interrupted and changes from the 'on' state to the 'off' state. If several switches are opened, the 'off' state is retained. The result is the same as opening one or more switches. (2) If a switch is first opened and then closed again, the original state 'on' is restored.

Axiom 2 implicitly introduces the medium: If the Recrossing is understood as reflection, with which in the literal sense a border crossing is reflected (thrown back), then Axiom 2 results in the empty space. It is what remains when something is undertaken and undone. What remains behind is no longer simply nothing: It is the space that has arisen through the double movement of becoming and passing: the border was drawn first. That is becoming. Then the becoming was undone by a passing. What remains is the ground on which this movement of becoming and passing away took place. – In other words, an observer may not see anything, but he can remember the movement of crossing and recrossing. A trace on which the memory is based can remain in his memory. Compare Hegel's statements about the sublation of becoming:

»This result is a vanishedness, but it is not nothing; as such, it would be only a relapse into one of the already sublated determinations and not the result of nothing and of being. It is the unity of being and nothing that has become quiescent simplicity. But this quiescent simplicity is being, yet no longer for itself but as determination of the whole.« HW 5.113, translated by George di Giovanni)

With the becoming and passing of the boundary in crossing and recrossing, time is implicitly set from the beginning. It is already contained in the original prompt »draw a distinction«. Spencer-Brown is even more consistent than Hegel: He not only chooses, like Hegel, terms that simultaneously describe a movement and its result (differentiation, designation can be understood both as the process of differentiating and designating as well as the result, that is the differentiation and designation achieved by the process of the differentiating and designating), but with the cross he chooses a sign that simultaneously describes the operation (movement) as well as the operand.

Remark: In the two operations of recalling and recrossing I formally see the two movements of continuing and turnabout (reversal, Umkehrung) which Hegel distinguished (HW 5.446, 453) which are central for me for the understanding of absolute indifference as well as the transition from the doctrine of being to the doctrine of essence and further the concept of idea.

But how should the sign be named in German? Spencer-Brown introduces it as »crossing the boundary« and as »calling« (LoF, 1), and after the first drawing calls it a »mark« (LoF, 3). In German translations the English word 'cross' is sometimes retained or a neutral expression like 'token', 'mark' or 'character' is chosen. The literal German translation 'Kreuz' (cross) is mostly avoided, because the outward appearance is not a cross , but an angle. However, an angle is in typically intuition seen as opened to the right and presented with an opening of less than 90°, as is the angle sign in the HTML markup language: ∠. The word 'hook' is also possible. However, all this does not apply to Spencer-Brown's double meaning of a sign and a movement (cross, crossing). Also the German word 'Quere' (transverse) is misleading, because a transverse is rather a sign like \ or / that runs transversely, and by traversing is often meant another kind of movement, such as traversing an empty square, a river, or possibly a shortcut if a rectangle is traversed along the diagonal. Despite reservations, the name 'hook' is the most catchy for me in conversations and demonstrations on a blackboard, because it best hits the outer shape. Therefore I use it in German original. In the English translation I keep the expression 'cross' despite all reservations, because it is the most common expression in the works on Spencer-Brown.

For the other sign, which consists only of a void, Spencer-Brown has long searched for a suitable name. Only in the 2nd edition of the German translation of 1999 did he introduce the term 'ock' and the sign Ɔ.

»Shortly after it was first published, I received a telephone call from a girl named Juliet who, while expressing her enthusiasm for what I had done, also expressed her frustration at not being able to speak the empty space over the telephone. [...] She was absolutely right, and I subsequently invented the word ock (from the Indo-European okw = the eye), symbolized by a rotated lower-case letter Ɔ, to indicate in a speakable form the universal recessive constant that all systems have in common. Ordinary number systems naturally have two ocks, zero for addition and the unit for multiplication. [...] But in this book, in which its true nature was made clear for the first time, it was important to leave the ock nameless and empty, because it was the next one I could reach to emphasize that it is nothing at all, not even empty. His invention was more powerful than the invention of zero, and sent shock waves through the entire mathematical community, which have not yet subsided.« (Spencer-Brown, 1999, xvf, quoted by Rathgeb, 118, my translation)

In the secondary literature on Spencer-Brown, this has not been taken into account to this day, with the exception of Rathgeb, but I will follow him as it seems to me the easiest and best way to name the two basic signs and in words.

Summary: Spencer-Brown explains the intention of these first steps:

»Definition
   Distinction is perfect continence.« (LoF, 1)

What is meant by the unusual word 'continence': SWH comment: (a) It can mean abstinence, moderation and self-control (continent as the opposite of incontinent). In this sense continence ensures that something does not diverge and disperses, becomes frayed and loses its own identity. (b) And it can mean cohesion in the sense of the continuum, whereby for example in geometry the infinity of points is held together on a line. (SWH, 70) This seems to me to meet Spencer-Brown's concern very well.

»Distinction is Perfect Continence«

Spencer-Brown presented and discussed his understanding of arithmetic and algebra at the AUM conference in Session Two on March 19th, 1973.

– Arithmetic is demonstrated on physical objects. Already in kindergarten or primary school it is learned by examples like ›3 apples and 2 apples are 5 apples‹. Everyone can take the two smaller amounts of 2 and 3 apples, combine them and recount that there are 5 apples now. Examples of this kind are so intuitive and striking that hardly anyone notices what is implicitly assumed and learned as if incidentally. The individual apples remain independent and do not change through counting. If they would react and merge with each other like in a chemical process, or transform or divide into other objects, counting would be impossible. Spencer-Brown therefore formulates his own rules to ensure this (what he calls canons).

Only gradually does this become abstract arithmetic with numbers, in which no explicit reference is made to specific objects. The numbers themselves are not physical objects. At school this is implicitly learned, and it is still an undecided question whether numbers exist independently of counted objects, whether they are one of the properties of counted objects, or whether numbers exist only in the mind of rational beings such as humans, who have introduced numbers in the course of their development and can operate with them in thought. Philosophers and logicians have never reached agreement on this. I agree with Aristotle, for whom numbers consist only in thinking.

In what way can be spoken of proto numbers in proto arithmetic, and how can they be illustrated in a similar way to counting apples on concrete objects? Spencer-Brown goes one level deeper and understands the two signs cross  ⃧   and ock Ɔ in a double meaning, in which they serve both as numbers and as operation signs. The usual arithmetic knows expressions like ›7 + 5‹ or ›120 − 13‹. For Spencer-Brown these are character strings, which are formed according to fixed rules from a certain character set, which consists of the digits 0, 1, 2, …, 9 and the operation signs like + and − in the decimal system. In the proto-arithmetic, it reduces the character set to the two characters cross  ⃧   and ock Ɔ, from which the arithmetic expressions are composed. Strictly speaking, they are neither proto-digits nor proto-numbers, but mathematical proto-characters, from which mathematical expressions are formed, in which they get both the meaning of digits (and the numbers composed of them according to the positional notation) and of operation signs. In order not to complicate the way of expression too much, one can still speak of proto-numbers, even if this is literally wrong. Spencer-Brown says that proto-arithmetic calculates with them. From the two characters cross  ⃧   and ock Ɔ more complex characters are composed according to the two rules of repetition and nesting. In an inaccurate sense, these are the proto-numbers. Spencer-Brown does not speak of arithmetic operations, but of transformations (»primitive equations«, »procedue«, »changes«; LoF, 10f) and introduces the sign ⇀ (LoF, 8). It means that the second expression is derived from the first expression by a transformation (LoF, 11).

The ordinary numbers are illustrated and understood as abstraction from counting objects. With the two signs cross  ⃧   and ock Ɔ, objects are not counted in the first step, but just differentiated. Distinguishing precedes counting. If objects are not distinguished (sortal), they cannot be counted. The cross  ⃧   describes that there is a difference from something to something else, and the ock Ɔ describes the background against which the boundary of something stands out from its exterior. The process of abstraction, however, remains similar: just as the understanding of numbers is gained by counting objects, the understanding of the two signs cross  ⃧   and ock Ɔ is gained by distinguishing objects from each other and against the respective background.

Just as conventional arithmetic introduces the natural numbers 0, 1, 2, 3, …, 9, and forms numbers and calculates with them, Spencer-Brown regards his primary arithmetic as a simplified and preceding arithmetic, which only knows the two signs cross  ⃧   and ock Ɔ. With these two signs we shall calculate in a comparable way, as we are familiar with ordinary arithmetic, in order to recognize deeper arithmetic connections, from which the ordinary arithmetic can be derived step by step.

– The arithmetic takes into account the individuality of the respective numbers. In number theory every single number is something special. What has been proven in arithmetic for a certain number cannot be easily transferred to the other numbers. Only algebra will study rules that apply to all numbers independent of their individual properties. This is also the case with proto-arithmetic, with which the special features of the two signs cross  ⃧   and ock Ɔ as well as the signs composed of them are examined.

Spencer-Brown wants to return to the original understanding of numbers, which is contained in arithmetic and precedes algebra. If you learn to calculate and use numbers, you will initially appreciate the peculiarities of each number. Each new number has something of its own. For example, children learn how the two and the multiples of two, the three and the multiples of three, the five and the multiples of five each have something special. So for example all multiples of five have as last digit only the 0 or the 5 (5, 10, 15, 20, …), with the multiples of 3 the checksum is divisible by 3 (the checksum is the sum of all digits, e.g. the checksum of 75342 is calculated as ›7 + 5 + 3 + 4 + 2 = 21‹, and since 21 is divisible by 3, 75342 is divisible by 3 too). Another example is the number 6, which is identical with the sum of its divisors ›6 = 1 · 2 · 3 = 1 + 2 + 3‹. Thus, specific properties can be recognized for each number. Everyone who is enthusiastic about mathematics is fascinated by playing with numbers and thinking about the peculiarities of the individual numbers (thaumazein, or ‘wondering’ from ‘wonder’) and has his favourite numbers and numbers that somehow seem strange to him. Even if an outsider may hardly be able to understand it, this way of playing with numbers shows me the same spontaneous joy and attitude as with canon singing. The apt example comes from the Piaget school: I say a number and you say a number. Whoever said the greater number won. Both have to laugh when they understand the trick of why the second player wins all the time, and yet repeat the same game over and over again, with continuing pleasure. For me, this is the first and simplest example of an arithmetic proof idea with which the children without knowing it found a procedure for proving that there are infinitely many numbers.

The result are rules like the so-called donkey bridges, which apply to certain numbers and are not transferable to other numbers. Everyone will have his or her favourite calculation methods, which he or she succeeds in using particularly well, comparable to their favourite colours. Spencer-Brown wants to return to this original (naive, magical) way of handling numbers, because it is only from this that he will be able to see the formal way in which numbers were operated in the 20th century in a new light.

In Piaget's view, arithmetic belongs to the second phase of symbolic and pre-conceptual thought, which he wants to preserve in its peculiarity and uniqueness. The transition to algebra will therefore in many ways be similar to the transition to operational arithmetic in the III. phase (at the age of 7 to 12 years).

– Within arithmetic there are propositions (theorems). Theorems for Spencer-Brown are ideas that are found in individual, unique elements. They show mathematics in the stricter (proper) sense. Algebra, on the other hand, is formulated for variables independent of the individuality of the values used in each of the variables. Therefore proto-arithmetic for Spencer-Brown cannot formally derive theorems from the axioms, but only intuitively grasp them and only in the second step prove them with formal methods and deduce consequences. On the other hand, the approach of algebra can in principle be adopted by computers. In the 20th century, mathematicians like Russell equated mathematics with the algebraic way of operating. For Spencer-Brown, this is a great step backwards, which atrophied mathematics, mathematical skills and the joy of mathematics.

What is meant by theorems is best illustrated by the example given by Spencer-Brown: Euclid proved the theorem that there are infinitely many prime numbers. His proof was: If there are only finitely many prime numbers, there is one largest prime number. Its name would be N. If the product of all prime numbers from 1 to N is formed, the result is ›M = 1 · 2 · 3 · 5 · 7 · 11 · … · N‹. For M it can be shown that ›M + 1‹ is a prime number. Therefore there is another prime number that is greater than N, and so on. This idea cannot be deduced as a consequence of the arithmetic rules, but had to be found. Two things are important for Spencer-Brown: The proof shows both an original idea of proof and a procedure with which the idea of proof is presented. Most people will only be convinced of the procedure, why the sentence is correct, and understand the idea of proof from it. Such an idea of proof results from the arithmetic typical way of calculating, which has a deep understanding (not to say compassion) of the numbers and their inner rhythms and infinitely diverse relationships and kinships. No computer can do that. Computers, on the other hand, provide a different kind of insight, which for Spencer-Brown belongs to algebra.

– Spencer-Brown had started from the two-element Boolean algebra and had sought the arithmetic which precedes it and whose algebra it is. Usually we learn arithmetic from natural and real numbers and then all the algebraic rules how to calculate with them. George Boole (1815-1864) had found a simplified algebra in 1847, which calculates with the elementary logical operations AND and OR and whose variables in the simplest case only stand for the two numbers 0 and 1 (or in the Boolean algebra for 'on' and 'off'). This was Spencer-Brown's starting point and he wanted to go one step further: Just as the arithmetic of natural and real numbers underlies the complex theories of number theory and analysis, it should be possible to find a simplified arithmetic for Boolean algebra which is only formulated for the numbers 0 and 1. As primary arithmetic (proto-arithmetic), it precedes the usual arithmetic just as much as Boolean algebra precedes ordinary algebra. In this way, he succeeded in developing an arithmetic whose character set is further restricted by the two characters cross  ⃧   and ock Ɔ, and which therefore precedes Boolean algebra.

– From Spencer-Brown's point of view, Gödel's groundbreaking statements can be read differently and anew: Kurt Gödel (1906-1978) showed in 1931 that algebra is no longer able to say everything that is possible in the arithmetic that precedes it when a certain complexity of numbers is given. Arithmetic, with the individuality of its signs, contains a surplus that cannot be completely grasped and captured by any algebra. Compared to arithmetic, algebra is fundamentally incomplete. However far algebra may be developed, arithmetic and the infinite stock of its individual numbers can provide new insights that go beyond the known algebra. – When Spencer-Brown speaks of completeness in Chapter 9, he means something else. Theorem 17 says: »The primary algebra is complete« (LoF, 50). This does not mean, however, that it contains everything that can be obtained in arithmetic discoveries, but only that every arithmetic discovery can also be formulated algebraically. »That is to say, if a = ß can be proved as a theorem about the primary arithmetic, than it can be demonstrated as a consequence for all a, ß in the primary algebra.« (LoF, 50) Spencer-Brown therefore deliberately speaks of a theorem and not of a consequence, i.e. of a statement that can be proved with the methods of arithmetic and not with those of algebra.

»So, to find the arithmetic of the algebra of logic, as it is called, is to find the constant of which the algebra is an exposition of the variables--no more, no less. Not, just to find the constants, because that would be, in terms of arithmetic of numbers, only to find the number. But to find out how they combine, and how they relate -- and that is the arithmetic. So in finding -- I think for the first time, I don't think it was found before, I haven't found it -- the arithmetic to the algebra of logic -- or better, since logic is not necessary to the algebra, in finding the arithmetic to Boolean algebra, all I did was to seek and find a) the constants, and b) how they perform.« (AUM, Session Two)

– An example of calculating and proving from proto arithmetic

»Theorem 1. Form The form of any finite cardinal number of crosses can be taken as the form of an expression.« (LoF, 12)

The statement is hardly to be understood directly in this choice of words. It means that any form constructed from a finite number of crosses and ocks can be converted into either a single cross or a single ock. This statement can also be formulated differently: Any shape, however complicated, composed of crosses and ocks, can be considered as a whole form. This can be illustrated by an example that Spencer-Brown later cites for the 3rd theorem (LoF, 17):

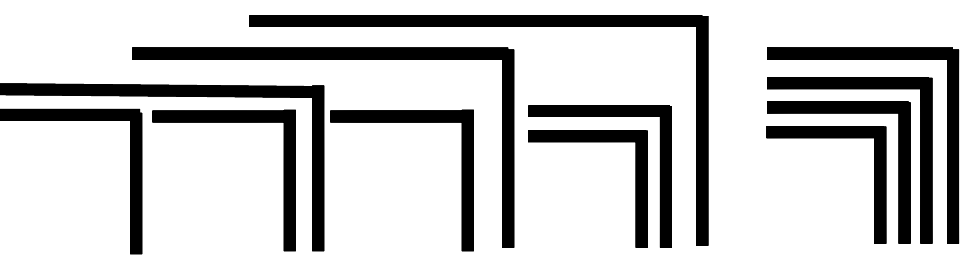
It is shall be shown how this figure can be reduced to a cross or an ock. The idea of proof is to go to the deepest nesting level. There are only two possibilities: Either a cross repeats itself several times, or two crosses are nested into each other. If it repeats itself, it can be condensed into a single cross according to axiom 1. If two crosses are nested, they can be converted into an ock according to axiom 2 (cancellation). The example also gives an impression of how the proto-arithmetic calculates. The crosses that can be contracted or deleted in the next step are highlighted in red. The character ⇀ introduced by Spencer-Brown is used for the conversions.

       

       

       

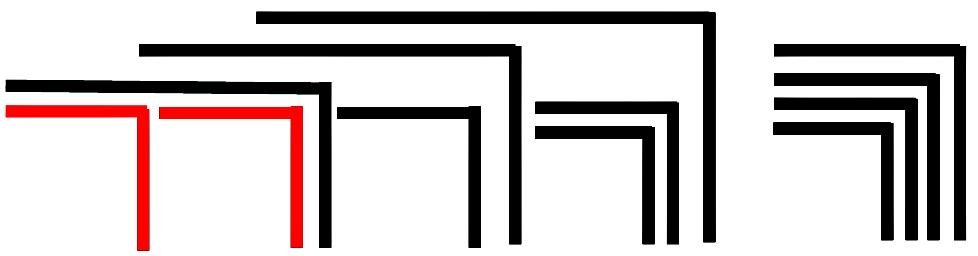
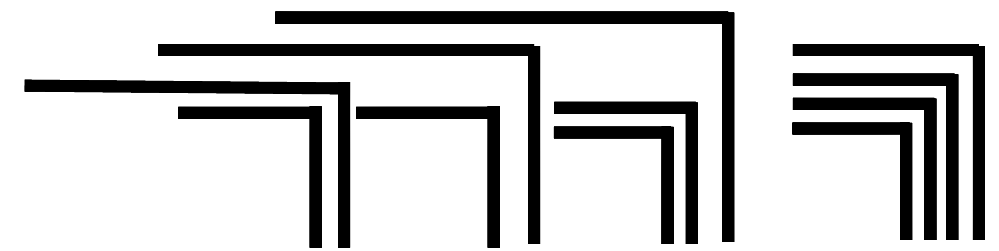
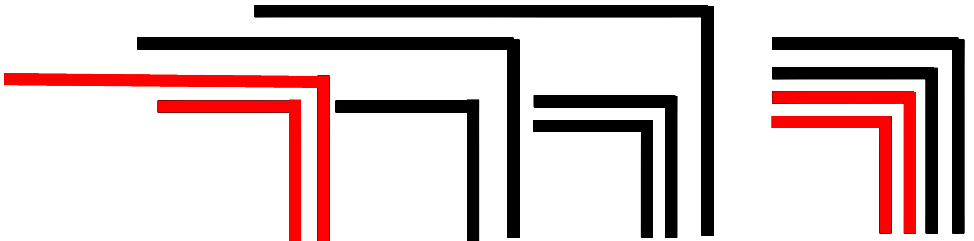
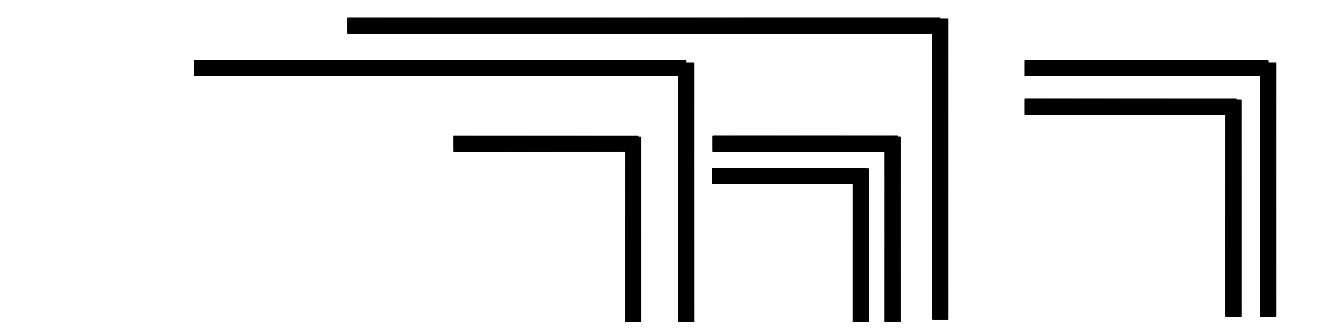
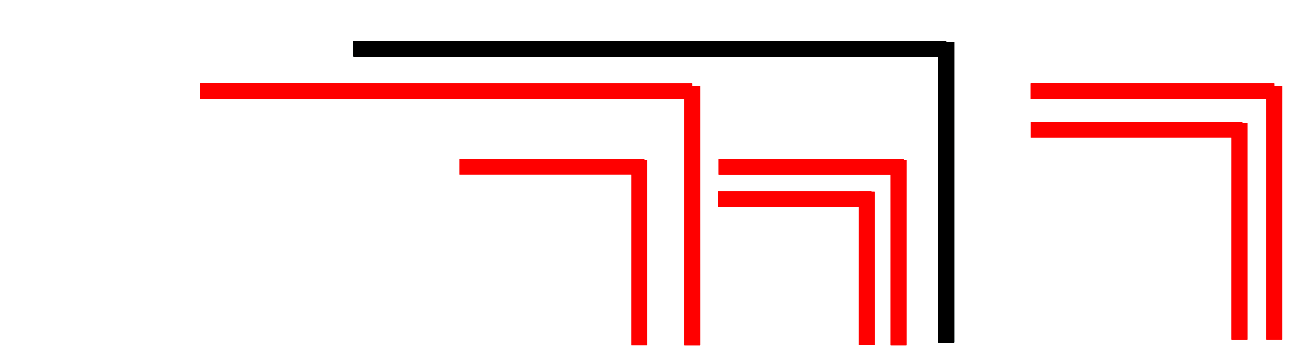
A comparison with networks shows how important this result is. If you have a confusing network and want to simplify it in a similar way, deadlocks can occur where any further simplification is blocked, see as an example the possibility of deadlocks in petri nets. This is not possible in the calculation chosen by Spencer-Brown. Each complex character can be converted to one of the two basic characters.

– Successor ordinal

The main difference between proto-arithmetic in Spencer-Brown and the usual arithmetic is in the successor ordinal and the mathematical induction. All natural numbers n have the property that they have a successor n + 1. This means that the natural numbers can be arranged on the number line. Multiple execution of the successor relation leads to adding, and from this result the further arithmetic operations and with them the extensions of the natural numbers by the negative and rational numbers and so on. The induction-axiom says: If a statement A is valid for an initial element n₀ (beginning of induction, base case) and if it can be shown that it can be concluded from A(n) to A(n + 1) (induction step), then it is valid for all natural numbers.

However, Spencer-Brown does not even ask the question about the arrangement of all characters of proto-arithmetic. In a first attempt, the characters resulting from the repetitions of the crosses can be arranged like the strokes on a beer mat:

    |, ||, |||, …

     ⃧  ,  ⃧   ⃧  ,  ⃧   ⃧   ⃧  , …

But there is also the nesting of the crosses. While the multiplication and the higher arithmetic operations can be reduced step by step to the addition, it is not possible to derive the nesting from the repetition. Both are independent. Instead, it is reasonable to choose a lexicographical (canonical) order for the arrangement of all characters considered in proto-arithmetic, as for two independent letters a and b:

    a, b, aa, ab, bb, ba, aaa, aab, …

   

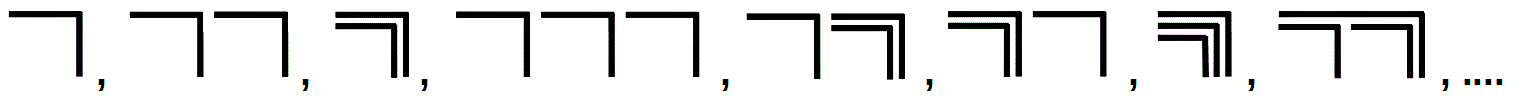
In this order, there is no simple successor relation that can be used to describe the relationship between the following character and its predecessor. Correspondingly, there is no simple linking rule with which a new character can be formed from two characters. Bernie Lewin, however, in Enthusiastic Mathematics, has explained numerous further possibilities of the arrangements of the two symbols of Spencer-Brown's calculus, which go back to the original ideas of Pythagoras and his school, and has shown how they can be used to derive the operations of the usual arithmetic. His book also shows that arithmetic has not only an inexhaustible wealth of ideas of proof and sentences, but also of symbolic and graphic signs with which new ideas of proof can be created.

– Opacity and transparency of arithmetic and algebra

The relationship between arithmetic and algebra raises far-reaching philosophical questions: Arithmetic is unique and opaque (dark, blurred, impervious to light), algebra is transparent and translucent. Within algebra, everything can be derived from the given basic rules, which Spencer-Brown calls initials. For him, the algebraic derivations are not proofs with their own ideas of proof, but just consequences which result formally from the initials and which can also be derived by a computer. In arithmetic, on the other hand, there is an infinite abundance of possibilities which can never be fully exhausted by a finite being like man and his art of arithmetic. There are always still unknown possibilities that can be discovered by new coming mathematicians. This corresponds to the statement of Gödel's incompleteness theorems: Arithmetic will never be able to fully describe all the possibilities it offers. Thus it always contains something that remains hidden (opaque) for algebra.

Arithmetic is used to recognize value charts and their underlying rules. The simplest case is the axiom of natural numbers, according to which two adjacent natural numbers are separated by a distance of 1. On the other hand, it is still unclear what efficient formula for prime numbers exists. Euclid proved that there are infinitely many prime numbers, but nobody knows how their distances evolve. One of the most researched and yet unproven mathematical assumptions comes from the mathematician Bernhard Riemann (1826-1866), who postulated an important estimate for the distribution of prime numbers based on imaginary numbers in 1859.

The prime numbers and their properties are the best example of what Spencer-Brown means by the opacity of arithmetic. Despite all the advanced methods of mathematics, no solution is found. For Spencer-Brown, this is an indication that it will never be possible to completely overlook the abundance of arithmetic. He brought this into the unimposing statement: »Principle of transmission: With regard to the oscillation of a variable, the space outside the variable is either transparent or opaque.« (LoF, 48). The term »oscillation of a variable« refers to the value progression of prime numbers, for example.

This understanding has radically changed the relationship between mathematics and philosophy. Since Descartes, modern philosophy has been convinced that it must be possible for a completely transparent method to see through all things. It is the task of philosophers to develop this method, and things were assumed to be transparent in principle, i.e. metaphorically speaking, not to resist the light of a superior method. Perhaps, it is even in the history of nature that man's task is to find such a method and to free things from their concealment. In a way, they are waiting to be released from their darkness by man.

The opposite position goes back to Heraclitus, from whom the aphorism is preserved: »Nature loves to conceal Herself« (Fragments, B 123, others translate: »Concealment accompanies Physis«). While since Descartes the philosophers have expected support from mathematics to find a method with mathematical rigour that opens everything up, it is Spencer-Brown who reverses the relationship. For him, the relationship between opacity and transparency is not only repeated within mathematics, which is why mathematics cannot simply be taken on the side of transparency, but for him it was fatal and a radical paralysis of mathematical creativity to seek only what is transparent in and with mathematics. For him, the triumph of the mathematized sciences since the 19th century has been like a house of cards that immediately collapses when one looks at how mathematics works inside. It has lost its vitality for him with the dominance of the mere derivation of consequences in an algebra. For him, the Principia Mathematica by Russell and Whitehead, published in 1910-13, are an example of this way of thinking.

Kant was the first to question Descartes' prospects of success with his doctrine of the thing in itself, but he left open the question of whether the unfathomability of the thing in itself can nevertheless be determined paradoxically. For him, mathematics stood on the side of transparent science and was the guarantor of reason. Whenever he wanted to describe the freedom of reason, he reverted to images from mathematics, e.g. in his idea of a sphere of the concept that can be overlooked from a certain location and is thus transparent (KrV, B 886). However, he recognized that this is only true if the sphere is not curved. If knowledge is arranged on a curved surface, there is no point from which it can be completely overlooked. The curvature of the point prevents one from seeing what lies beyond the horizon. Therefore, there are good reasons to understand curvature as the elementary property of the opacity of things.

In the sense of Spencer-Brown, arithmetic is located on a curved surface, and with algebra you can never overlook everything that exists on the curved surface. Nothing else remains to be done but to change one's position on the curved surface. Whoever moves on the curved surface may open up new areas that become visible, but with the same movement other areas withdraw again and disappear behind the horizon. Never everything can be overlooked.

After Kant, the paths of philosophy and the natural sciences diverged in two directions: (i) Some are looking for a new method from which no object can escape. Most important are Hegel with the dialectical method (HW 6.551) and all those who follow him. Or they hope to install mathematical functions that would guarantee their full transparency. (ii) The others drew the consequence from the doctrine of the thing in itself that in thinking its principal limits are provable. Nietzsche hit the nail on the head when he spoke of the »superstition of logicians«, they could recognize with Descartes from their own thinking that there is an 'I' who thinks, while for him it is just as conceivable »that a thought comes when 'it' wishes, and not when 'I' wish« (Nietzsche Beyond Good And Evil, Part 1, Chapter 17). The ego can never overlook the overabundance of all thoughts and must always reckon with the fact that new thoughts will appear of their own accord and become accessible to the ego.

(i) To this day, the natural sciences after Kant hope to find a mathematical measure for the curvature of the system and to be able to transform its opacity into transparency by recognizing and using the measure of the curvature. Whoever succeeds in changing his position that he no longer looks at the curved surface but at its measures, could obtain a full overview of the measures on the way. I see first ideas in this direction in Hegel's theory of real measures, but so far there have been no realizations.

Another approach was developed by the theory of self-referential systems. If, in a curved system, various observers succeed in matching their respective local views to a global image, then a global image would be possible for them all together. This shifts the original question to a new level: Although the local horizons of all observers cover the entire system as a whole, the question arises as to which rules their views can be coordinated with each other.

Luhmann can be seen from a higher perspective in the tradition of Hegel. He assumes that the system as a whole emerges into a self-description that is no longer bound to individual participants of the system, but results from the laws of movement (Hegel would say: reason) of the system as a whole. He expects this path to be opened with the help of the logic introduced by Spencer-Brown and in particular its self-reference given with re-entry (Luhmann Gesellschaft der Gesellschaft, 877 and in numerous other places in Gesellschaft der Gesellschaft and Wissenschaft der Gesellschaft). It is planned to take a closer look at this in a separate section.

(ii) Conversely, Nietzsche's successors speak of the opacity of thought. For them it necessarily follows from the opacity of things that thinking also loses its transparency, which Descartes still believed when thinking is able to investigate itself as its own object. Contrary to Descartes, Heidegger sees in Being and Time »the identity of human life [...] not only in the transparency of purely rational self-representation and self-determination, but also in the unavailable opacity of its moods, for which the state of mind is supposed to be the ontological condition of possibility«. (Volpi, 43, my translation). For Sartre »the reflective consciousness reifies its je to a centre of compression (centre d'opacité), which seems to lead a life of its own in the reflected consciousness as 'the psyche' (Moi/Ego): consciousness (je) - Moi - body« (Scheier, Luhmanns Schatten, 69 with reference to Sartre Transcendence of the Ego). And Adorno turns directly against Hegel:

»He [Hegel, t.] did not need language in the emphatic sense, because to him everything, even what is devoid of language and opaque, is supposed to be Spirit and the Spirit, the context. This supposition is beyond salvation. That which is resolvable, which is not in any previously-thought context, does indeed transcend its self-enclosed nature out of itself, as what is non-identical. It communicates with that from which the concept separated it. It is opaque only for the totality-claim of identity; it resists the latter's pressure. As such however it seeks expression. Through language it dispels the bane of its selfness.«. (Adorno Negative Dialectic, 162, Translation by Dennis Redmond)

At Spencer-Brown, this conflict is taken up in mathematics. For Spencer-Brown, mathematics can only awaken to new life when it gives up the claim to complete transparency and the associated self-limitation to methods that satisfy this claim. And philosophy does not have to stop at either demanding or denying the opacity of things, but can, thanks to its own creativity and the creativity of other sciences such as mathematics, see this question from ever new angles. For me, it shows the deplorable condition in which not only mathematics, but also philosophy finds itself today, when it does not even take note of Spencer-Brown's work except through the philosophical-sceptical sociologist Luhmann.

Re-entry

The doctrine of re-entry is at the heart of the Laws of Form. It is also the only idea of Spencer-Brown that has gained a certain popularity. In a first approach, re-entry can be understood as something like resonance, recursion, feedback, self-reference as well as reflexivity of terms or of people communicating with each other who refer to each other. It has been taken up above all by the theory of self-referential systems as well as by applications in sociology and psychology, in particular by radical constructivism and system theories of various kinds up to systemic psychology.

These applications dissolve the idea of re-entry from the context of proto-arithmetic and proto-algebra in which it stands at Spencer-Brown. Without further concern for the difficult arithmetic and algebraic operations in the Laws of Form, they adopt the basic idea that Spencer-Brown considers a movement that detaches itself from a system and can return to it by re-entry. When it returns, it is not only picked up again by the system, but the re-entry induces an inner movement there and must – in Lacan's parlance – be sutured. What happens here in detail is examined more closely in the context of the system under consideration, be it a family, a company organization or society as a whole. In all cases, something can be pushed aside and isolated until it decouples. This causes a crisis both in the system and in the isolated element, which can be solved by re-entry. Since Spencer-Brown was very interested in questions of psychology, I assume that he always had examples and applications of this kind in mind. In Laws of Form, however, he does not refer to them, but limits himself to questions of logic and mathematics. Two things are therefore important to me:

(i) To which mathematical questions does Spencer-Brown give a completely new and original answer? For me, these are above all the transition from natural numbers to transfinite numbers and the algorithms with which irrational numbers are arbitrarily approximated but never reached. In both cases there are  processes  which differ fundamentally from the usual arithmetic operations. A re-entry for Spencer-Brown is only possible with infinite processes and not with ordinary, finite arithmetic operations.

(ii) What requirements must be met for Spencer-Brown to be re-entryable? A re-entry is only possible for him if a figure repeats itself infinitely often uniformly, while arithmetic basically only works with constructions that contain a finite number of steps (9th canon; LoF, 54). The transition to infinity only succeeds if variables are considered in algebra that are independent of their respective content, and if, thanks to the transparency within algebra, there is the certainty that there are no side effects and internal deviations in the infinite number of repetitions. The individual repetitions are completely independent of each other. Re-entry shows the originality (and thus the relative autonomy) of algebra in relation to arithmetic. In proto-arithmetic there is still no re-entry. On the contrary: Re-entry leads to »loss of connexion with arithmetic« (LoF, 58).

With the process that leads to re-entry, there is a kind of inner musicality that is introduced with re-entry into the order from which it emerges. It is not only a scar or a crack that is sutured at the place of re-entry, but the system, previously examined only in its spatial, timeless relationships, is set into vibration as a whole (begins to oscillate), from which time emerges and with it a new order (emergence).

With the transitions to transfinite and irrational numbers are connected not only the two concepts of infinity common in mathematics (Hegel calls them simple – often, but for me not correctly translated as »bad« or »spurious« – and true infinity), but also the two elementary properties of numbers known since Aristotle: The transitivity of the numbers arranged on the number axis and the continuity of the real numbers. (The less-than-relation is an example of transitivity: If x < y and y < z, x < z also applies). Transitivity ensures that counting can continue indefinitely, and thanks to continuity, the limit value of approximation processes to irrational numbers exists. If Spencer-Brown's idea of re-entry hits the heart of mathematics and the philosophy dealing with mathematics, this should have fundamental consequences for the basic understanding of mathematics. These can only become visible if the re-entry is not only seen as a general property of systems with feedback, but with Spencer-Brown more precisely as a specific interrelation of the internal arithmetic and algebra given with these systems.

– Processes in ordinary mathematics and at Spencer-Brown

In my opinion, models for the re-entry are the construction of the first transfinite number ω at Cantor and the limit crossing that leads to the approximation of irrational numbers such as .

Transfinite numbers When counting 1, 2, 3, … n, n+1, … the same successor relation from n to n + 1 is repeated infinitely. Beyond all countable natural numbers lies the transfinite number ω. It can never be reached by counting and has no predecessor, but it can be formally defined as the result of the rule of counting in whole. There must be an overarching number class (a ground) into which the limit value can be included by re-entry.

Where is ω located, and how is ω included in the set of numbers? The mathematician Riemann had found a very descriptive idea for this: If a sphere is placed on the number line at the zero point, whose center is identical with the number zero and whose surface intersects the number axis at the two points −1 and 1, a point on the sphere can be clearly assigned to each number by drawing a connecting line between the north or south pole and the respective number, which intersects the sphere at exactly one point. For numbers outside the sphere (in the following figure these numbers are greater than 1 or less than −1) the intersection is on the upper hemisphere, for numbers inside the sphere (the numbers in the interval [−1, 1]) on the lower hemisphere. The north pole corresponds to the number ω which is infinitely distant on the number line and is included in the number class of all points on the sphere with this construction method. On the south pole the 0 is mapped.

Source: Wikipedia, called on March, 4th, 2017
Origin by Jean-Christophe BENOIST - Eigenes Werk. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV., CC BY-SA 3.0, Link

The picture clearly shows how ω is infinitely far away on the number line, but finds its place on the number sphere at P(ω). How is this possible? The number sphere implicitly introduced new properties of numbers that are not yet given in the number line: The number sphere has a second, independent dimension (its height, which can also be interpreted as an imaginary axis or as the time-axis), it is symmetrical to rotations (cyclic), and it is curved. These are properties that go beyond the previously known properties of numbers (transitivity, continuity) and already descriptivly suggest that an extension and new definition of numbers is necessary if processes are to be allowed that lead to a re-entry. (It will be shown further how this image and these properties lead to the innovative theory of Spencer-Brown about observers).

Irrational numbers For irrational numbers like there is no decimal representation. It is approximately 1.414… and can only be determined step by step more accurately. With each step, the interval in which it must lie is defined more precisely. For example, the expression 1.414… says that it lies somewhere in the interval [1.414, 1.415]. And just as Cantor had to find its own symbols for the transfinite numbers with ω, its own symbol had to be agreed for the irrational numbers with the root sign .

Spencer-Brown mentions the irrational numbers in the Notes when he speaks of second-degree equations there. He demonstrates this at the square function x² or in his calculus aa = a and then executes it at the elementary polynomial of second order. (LoF, 97f)

What happens at the two transitions to the transfinite and irrational numbers? It is no longer an ordinary arithmetic operation. An arithmetic operation like ›7 + (10 − 3) / 91‹ can be arbitrarily complicated. Ultimately, however, it is always a finite string consisting of operands and operators (in the simplest case of the natural numbers as operands and the usual rules of calculation +, −, · and / as operators), which leads to a clearly defined rational number. With infinite incrementing and with the approximation algorithms for determining irrational numbers, on the other hand, an arithmetic operation is  repeated  (iterated) infinitely often. Only the repetition (iteration) creates a process. – Mathematics has so far not been noticed, – or it does not want to notice -, that the process of repetition implicitly implies time. To this day, mathematics insists that its formulas are basically timeless. It was Spencer-Brown who made the long overdue turn and consistently developed how time is implicitly contained in the process leading to re-entry. This will be explained in more detail below.

In the arithmetic operations, the respective number class is not left. It returns a new number and can be identified with it. It is the same to say ›12‹ or to say ›5 + 7‹. With processes, on the other hand, a new number is defined that was not yet contained in the number class previously considered. Neither ω is a natural number nor 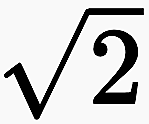is a rational number. With them a new concept of numbers emerges: Numbers are all elements with which one can calculate like with natural and rational numbers. What is a number and belongs to the totality of numbers is opened up step by step. The idea of numbers is in itself infinite, and it can be assumed that new processes are always found to recognize new numbers with properties that were previously unknown.

Echelon without limit How can Spencer-Brown transfer the infinite processes of counting or approximation to an irrational number into his calculus? In proto-arithmetic, there is no successor relation as in natural numbers, but a variety of possibilities to convert one sign into another. When Spencer-Brown speaks of calculation, he means conversion. Calculating with natural numbers is for him an example of transformations, which he generalizes in his logic. In order to find a process which corresponds to the infinite counting of natural numbers, a transformation must be determined which, like counting, can be repeated infinitely often, whereby all individual steps are formally the same (self-similar). In proto-algebra, Spencer-Brown constructs a rule which, comparable to the of the continuously repeated (iterated) successor relation from n to n + 1, can be continued arbitrarily and for which, analogous to the successor relation, an infinite-far element can be defined and included in a larger number space by re-entry: He explains how a sequence of 5 single steps can be applied to the string whereby the string doubles. (These are in his terminology the 5 single steps C5 iteration, C1 reflection, J2 distribution, C4 occultation, C1 reflection; LoF, 55). If this sequence is executed, the output character is appended at the end with the result (LoF, 56):

    ⇀ .

The symbol ⇀ indicates that both signs (forms) have the same value. The same sequence of 5 single steps can again be applied to the new sign (form), whereby it is extended again. In this way, a sequence of steps is achieved that corresponds to the successor relation and can be repeated infinitely. The result for Spencer-Brown is »an echelon without limit«, which is derived from the »Consequence C7 Echelon« proven for proto-algebra (LoF, 34).

»The next decisive step is to imagine, if possible (let us imagine, if we can, LoF, 55), that the process of this sequence of steps continues end- or timelessly. In space this would result in an echelon of a's and b's without limit. [...] Since the determination of the value of an expression is bound to the rule of finite demonstrability, no statement can be made about the value of an echelon without limits.« (SWH, 175, my translation)

With these steps not all signs (forms) of the proto-algebra are enumerated and put in an order, but only a certain subset. It is to be assumed that there are infinitely many other possibilities of similarly forming infinite consequences from the inexhaustible reservoir of forms. However, it is sufficient to have found an example as simple as possible and to use it to introduce re-entry into proto-algebra.

As a result, Spencer-Brown writes down a diagram with which the re-entry is defined:

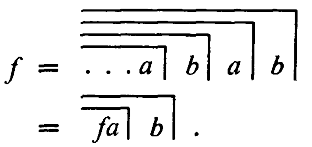
E1 Re-entry
(LoF, 56)

The diagram E1 is unusually to be read block by block from right to left. Spencer-Brown considers in E1 the stepwise crossing from a to b to a to b … a and b stand as variables of proto-algebra for values that can be used from proto-arithmetic: In Spencer-Brown's calculus these are only the cross and the ock. The transition from a to b is repeated as often as desired. For the repetition Spencer-Brown introduces first with the three dots … and then with f two new symbols, which until now were neither known in his proto-arithmetic nor in his proto-algebra. He takes over the three dots from the corresponding processes known from ordinary arithmetic, when there, beyond n and n + 1, counting is continued without limit or an irrational number is approximated arbitrarily exactly.

The symbol f describes the result of a limit crossing. For Spencer-Brown, a can be regarded as an input that can be saturated with the two values possible from proto-arithmetic: the cross and the ock. For this input a rule is found which is repeated infinitely often. The result is an output f which cannot simply be re-entried into the same set of numbers where the input a was, but which expands this set of numbers in a similar way as the transfinite numbers expand the set of natural numbers and the roots expand the set of rational numbers.

By f is meant both the function (the algorithm, the process) with which a limit value is approximated in infinitely many steps, and the result of the process (this limit value itself). Spencer-Brown consistently holds out his idea of introducing symbols which, in multiple meanings, can be both an operation and the result of that operation.

The summary of the infinite number of crossings from a to b to a to b etc. in f is bound to three conditions:

(a) »a clearly defined sequence of steps, so there is a clear construction instruction«,
(b) it »shall be continued continuously«,
(c) it contains a »pattern of self-equality« (SWH, 175, my translation).

»The key is to see that the crossed part of the expression at every even depth is identical with the whole expression, which can thus be regarded as re-entering its own inner space at any even depth.« (LoF, 56)

The symbol f reminds of the functions f(x) introduced in the usual mathematics. f is defined by the value progression of an infinite sequence of formally identical steps that approach a limit value. But unlike the usual function f(x), f is at the same time the limit value itself. Like the transfinite number ω or the root , f is a limit value which was not present in the previous character set. f is neither the cross nor the ock. With f the set of signs (forms) in proto-arithmetic is extended in a similar way as the character set of natural numbers by transfinite numbers and rational numbers by roots.

Spencer-Brown formulates this negatively: There is no clear place for the re-entry. It is indefinite in the given calculus where it can be taken up (»indeterminacy« LoF, 57). In this context, Spencer-Brown describes the transition from a to f in greater generality as the transition from an expression e (for expression) to an expression e', which is to be included by re-entry:

»We have just introduced to e' a degree of indeterminacy in respect of its value which is not (as it was in the case of indeterminacy introduced merely by cause of using independent variables) necessarily resolved by fixing the value of each independent variable.« (LoF, 57)

There is no value for f in the initial quantity where it could be included. Therefore, there are only two possibilities: Either the initial set is extended for the re-entry of f (following the example of ω and ), or f errs around and cannot find a defined place. This indefinite wandering around will lead Spencer-Brown to the oscillation with which he introduces the concept of time. (So I understand how he comes from re-entry to time. In a final step, he will extend the path from a form a to a limit f to circuits that convert an input a into an output f.)

It is therefore misleading if the re-entry is interpreted as if somehow a process would emerge from a base set that separates itself from the base set until it delivers a value that leads back to the base set and meets a value already present there. Instead, the re-entry of f extends the already known set of signs (forms). However, the old rules of the base set remain valid, and it must be ensured that with f can be calculated as with all other numbers. For Spencer-Brown this is given in his calculation: »It is evident that J1 and J2 hold for all equations, whatever their degree.« (LoF, 57)

More accurate is the comparison of f with the imaginary numbers. To understand this, two steps are necessary. In a first step the set of all arguments is to be extended into a set, in which all value courses of the functions can be represented, which operate on the basis set. Based on this, the second step is to understand how to get from the set of all arguments a to the set of all functions f operating on them and how to return from it to the set of arguments by a re-entry.

(i) Transition from arguments to value courses: On one axis all signs (forms) of the proto-arithmetic are arranged, and on the axis perpendicular to it all signs (forms), into which they can be transformed, are arranged, like in the usual mathematics on the x-axis all arguments and on the y-axis all function values y = f(x) are represented. This results in a two-dimensional tableau in which the values courses can be entered.

(ii) The value courses can be considered for-themselves. Each value course f is in itself a mathematical object, and the set of all value courses f can be examined. The set of value courses f is independent of the set of arguments x on which the functions f operate. (Scheier speaks of a difference between the functions and their arguments. [Scheier Luhmanns Schatten, 67]). I understand the fundamental thought of Spencer-Brown to mean that there is a way for him by which the set of arguments emerges into the set of functions perpendicular to the set of arguments. This is a movement which leads from the set of arguments into the set of functions and from it through a re-entry back into the set of arguments. This is only possible if the arguments can be regarded as rudimentary functions (by understanding each argument a as an identity function a = a), and if there is an operation in the set of all functions which leads back to the set of arguments. If I understand it correctly, Spencer-Brown sees a model for this in the imaginary numbers. Just as the rules of complex algebra with the imaginary numbers lead to a rotation, which goes from the real numbers o the imaginary numbers and from there back to the real numbers, there is for him a way from the arguments a to the functions f and through a re-entry back into a new argument. This thought is only hinted by Spencer-Brown, and it seems to me a fruitful task to formalise it more mathematically. It is a completely new view on the mathematical theory of the function spaces. It could lead further thought to embed the Hilbert space into another space, which preserves the properties of the Hilbert space, but is based on the proto-arithmetic introduced by Spencer-Brown and with the re-entry lets understand new properties, which are not given in the usual Hilbert space. Since Hilbert space is also the mathematical tool for quantum theory, a new view on quantum theory can result, which could resolve the known aporia in a similar way as Spencer-Brown resolved Russell's paradox.

For Spencer-Brown, Russell's paradox exists only at the level of the set of all arguments and is unsolvable there. It becomes solvable for him only with the transition to the imaginary numbers, and he has given the basic idea how this is possible in the already quoted preface to the American edition of Laws of Form. The arguments a and the functions f may have a similar relationship as the real and the complex numbers. As shown, the transition into the imaginary space of all functions is not arbitrary, but bound to fixed rules. Thanks to these rules, a return to the space of arguments is possible, generating new arguments there, and in this way the paradoxes which Russell and Whitehead wanted to avoid, so to speak, with the brute force method with the prohibition of negative self-referential, impredicative judgements (vicious circle principle) can be avoided. Re-entry takes the critical place of negative self-reference and should therefore enable the often requested formalization of the dialectical method, if it is defined by its negative self-reference. (It was often attempted to find a formalization for Hegel's method of Aufhebung [sublate, abolish, preserve, transcend]. In my opinion this is possible on the path opened by Spencer-Brown, with which he went far beyond the ideas of Gotthard Günther, who pursued a similar goal.)

It is certainly still a long way to go to work out these ideas. Before this can be started, further ideas from Spencer-Brown need to be understood in order to overview his intentions in their full extent. These are his comments on the introduction of time and the circuits he designed.

– Waves and their time (Time)

With the 3 dots ‘…’ and the variable f Spencer-Brown is obviously oriented on symbols known from the usual mathematics. The peculiarity of his calculation, however, lies in the fact that instead of the usual numbers and calculation symbols (operation signs) he knows only the two signs  ⃧   and Ɔ for cross and ock, which he uses in the double meaning as operand and operator. Thanks to this simplification he succeeds in showing properties at limit crossings (Grenzübergänge) which go far beyond the known mathematics. This leads to a shift in perspective in two steps:

– For him, the smallest units of the limit crossing are no longer the points along which the process underlying the limit crossing runs until it determines the border value as a new point – as is known from the example when Achilles approaches the turtle in front of him point by point –, but the  shape  of the limit course as a whole. That's the wave to him. What makes him think that? If the limit value f is wandering around at the moment of re-entry and does not find a fixed place, this can be understood as a swinging motion that oscillates continuously between cross and ock. This results in a wave, where the wave crest stands for the cross and the wave trough for the ock. There are no more signs in his proto-arithmetic. Limit crossings can move directly to a certain point or oscillate constantly between the two values available in the proto-algebra. Spencer-Brown anticipates what was later explained in more detail in catastrophe theory with its bifurcations and attractors, and in a sense describes their innermost logic.

– When he separates himself using the image of the wave from the traditional symbols of the limit crossing and takes a new view of its course, he is able to nest limit crossings for the first time. This does not mean that limit crossings are considered uniformly in several dimensions, as in the case of multiple integrals, but that within a limit crossing a contrary limit crossing of second or higher order can occur (which he calls equations of second degree). From the interrelationship of two limit crossings time arises for him.

The wave representation and the time contained in it are introduced in a complex diagram which is to be read and interpreted line by line:

Time as a Key
Quelle: LoF, 63, Figure 3

In the first line the echelon without limit is drawn with the variables a and b. Its result is the output f. In the following lines, special values are used for a and b. m and n do not stand for new variables, but m (marked state) refers to the cross, n (unmarked state) to the ock. The two constants m and n were first introduced for the Rule of dominance (LoF, 15) and then taken up again in LoF, 56. The accumulation of names and symbols for cross and ock is confusing and puzzling at first glance. Although Spencer-Brown has good reasons to emphasize certain aspects more clearly with these different names and representations, it would be easier to stick as far as possible with the two original signs cross  ⃧   and ock Ɔ.

In the second line, the ock (n, unmarked state) is used for both a and b. The continuous crossing of the infinite echelon 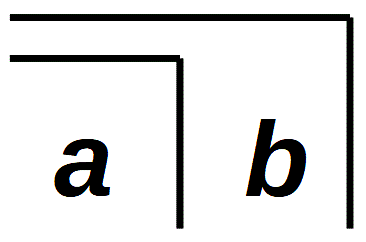starts with the unmarked state (wave below), changes to the marked state (wave above) and so on, until after an odd number of steps the unmarked state n is reached again.

In the third line the cross (marked state, m) for a and the ock (unmarked state, n) for b are inserted. In this case the wave starts at the top with the marked state and ends after an odd number of steps back at the top with the marked state.

The decisive step takes place in the fourth to sixth line: Waves can overlap each other. Spencer-Brown vividly speaks of a »dominant pulse« and a »short pulse« (LoF, 63, 64). The dominant pulse describes a fundamental which is preserved, and the short pulse runs recognizably through the fundamental. Lines 4 to 6 show how the run through can be read at the three points in time t₁, t₂, t₃.

With the nesting of contrary limit crossings, time is created within logic. For him, the first limit crossing is spatial (as depicted in the spatial figure of infinite staggering), while the second is temporal.

»Since we do not wish, if we can avoid it, to leave the form, the state we envisage is not in space but in time.« (LoF, 58)

Without the distinction between dominant pulse and short pulse, the time would remain incomplete. It would remain at a level that Felix Lau aptly describes:

»In his review of the Laws of Form, Heinz von Foerster euphorically pointed to the discovery or development of time from the axioms. (Lau, 93) [...] Oscillation is not accompanied by a measure that is indispensable for our common concept of time. This 'first time' has no duration, no measure; it is merely the change, the back and forth between the states. Oscillation does not yet have a speed for which units of space and time are needed.« (Lau, 94, my translation)

Note: Only by using the short pulse can the measure of time be described. Dominant pulse and short pulse for me can be understood as the background noise of a system (system dynamism, dominant pulse) and movement within the system (short pulse). However, Spencer-Brown does not further consider their relationship. In extension of his work, a common inner measure can be found for both pulses based on the mechanics with the square. (See on the concept of square and the square of velocity the two articles Force, Impulse, Energy and Dynamic Numbers).

This corresponds to the classical idea of time and is brought to the most general possible level of logic by Spencer-Brown: Time and motion can only be described if a single object moves against a background that is either resting or moving uniformly, such as the motion of the moon against the background of the starry sky.

Spencer-Brown is aware that his symbols ‘…’ and ‘f’ are misleading for re-entry. He therefore forms his own symbol for the re-entry with great suggestive power:

   

The symbol shows the movement that is running back. Spencer-Brown was convinced that with this discovery he had found the Gordian knot he was looking for. He found a uniform formalization of limit crossings, which can also be nested into each other. With them he developed the imaginary numbers and, within logic, time in its distinction from space. And he is able to integrate complex oscillating figures in circuit diagrams, which are already very close to the kind of programming he was doing in technical applications.

Remark: In another vivid picture he understood the re-entry as tunneling. This is already shown by the symbol when the new character undercuts the two variables a and b and returns to the beginning as if through a tunnel. A further commentary explains how a deeper understanding of reason and medium can be found with the tunnel and the tunneling.

– Inertia and self-organization of circuits

Mathematics starts from counting. With counting the numbers are introduced step by step. In the simplest case, counting creates a reduced model, the origin of numbering: If you count glasses of beer, you draw a line on a beer mat for each glass of beer and see from the lines how much beer has been drunk and how much is to be paid for. This seems so self-evident that until the end of the 19th century, nobody doubted that counting could be used to justify mathematics and arithmetic. Hidden paradoxes first appeared in 1877 when Georg Cantor (1845-1918) was able to prove with the Second Diagonal Argument that the path of mathematics leads to uncountable numbers. This is a contradiction of a completely new kind: It is no longer an exterior contradiction when a property or a statement A is opposed by an opposite property or statement not-A, but numbers are found that contradict themselves: numbers that cannot be numbered. Formally, this looks like the classical liar paradox ›this sentence is false‹. But while this sentence can be understood as a joke that can easily be avoided in everyday language, the uncountable numbers are at the heart of mathematics and question its consistency.

With Bertrand Russell (1872-1970) it became clear that the paradox goes much further. He examined sets of all sets that do not contain themselves (the Russell paradox named after him) and in 1902 he communicated his findings to the logician Gottlob Frege (1848-1925). This threw mathematics into a fundamental crisis. The negative self-reference is not only a limiting case of uncountable numbers, which occurs somewhere in the structure of numbers at a high level, but already occurs in the basic concepts of mathematics. In response, Russell together with Whitehead formulated as an additional axiom of mathematics the prohibition of negative self-reference statements (vicious circle principle).

Mathematics can never accept this. Spencer-Brown has found a completely new way. He questioned the usual understanding of counting. Counting means that a subject has the ability to count objects given to him. Counting is only possible if the counting subject and the countable objects are distinguished from each other and can be related to each other in the process of counting. Of course, the case can arise where a subject counts itself and appears in the double role of counting and being counted. Since Aristotle, mathematics has been asking, due to which properties a subject can count (the ability to count, to arithmetikon), objects can be counted (arithmeton) and what occurs in the process (procedure) of being counted (arithmeisthai). Countable objects are named sortal. Science is only possible if it deals with sortal objects. »One must count and remember in order to technically fix a selection range and keep it open contextually.« (Baecker 2000, 330, my translation)

But it was first in 1961 that Warren McCulloch (1898-1969) investigated the technical aspects of counting: What Is a Number, that a Man May Know It, and a Man, that He May Know a Number? was the title of his groundbreaking essay. Is there a logic of the number that precedes the number and a logic of signal transmission and communication of the nerves that meet? He asks for the first time how in a network an input (the sensory stimuli) can be processed in such a way that at the end there is the knowledge of a number in the brain. This should be clarified by a neurophysiological examination of the neural pathways. With McCulloch, we can see how the question of logic changes direction. Logic is no longer seen, as in Neoplatonism, as the visible and experiential expression of a higher spirit, but is rooted in a deeper logic in the body and its processes.

From this horizon I understand Spencer-Brown. He comes from mathematics, logic and programming and asks for a function that enables objects to count themselves. This is how I interpret the inconspicuous sentence with which he introduces his explanations about networks: »We can find a function which will not only remember, but count« (LoF, 65). With this approach it is no longer a subject that sees something coming from outside and counts it, but in an object (a machine, a body) it is a function that receives an input a and provides an output f that results from counting the input.

How can a machine be imagined that can count a given quantity of balls, for example? It has to scan the balls and detect when a boundary occurs between two balls. With each boundary a new ball is reached which can be counted. And it must recognize whether the balls are arranged in a circle like the numbers on a clock and must not be counted several times, or whether they move back and forth and therefore come into view several times. Spencer-Brown was given a similar task during his time as a programmer in the early 1960s. He was commissioned by a British railway company to write a program to count the wagons that enter a tunnel and possibly move back and forth. Without explaining it further, he understands counting elementarily as modulation of an incoming wave into an outgoing wave with a changed frequency, in the simplest case with a frequency halved (dividing by 2). This task led to his design of the circuits. He therefore calls the function »modulator function« (LoF, 65) or in other works »reductor«. Although I do not yet fully understand how counting can be justified in the modulation of waves, I would like to approach this question with some remarks on the circuits Spencer-Brown considered.

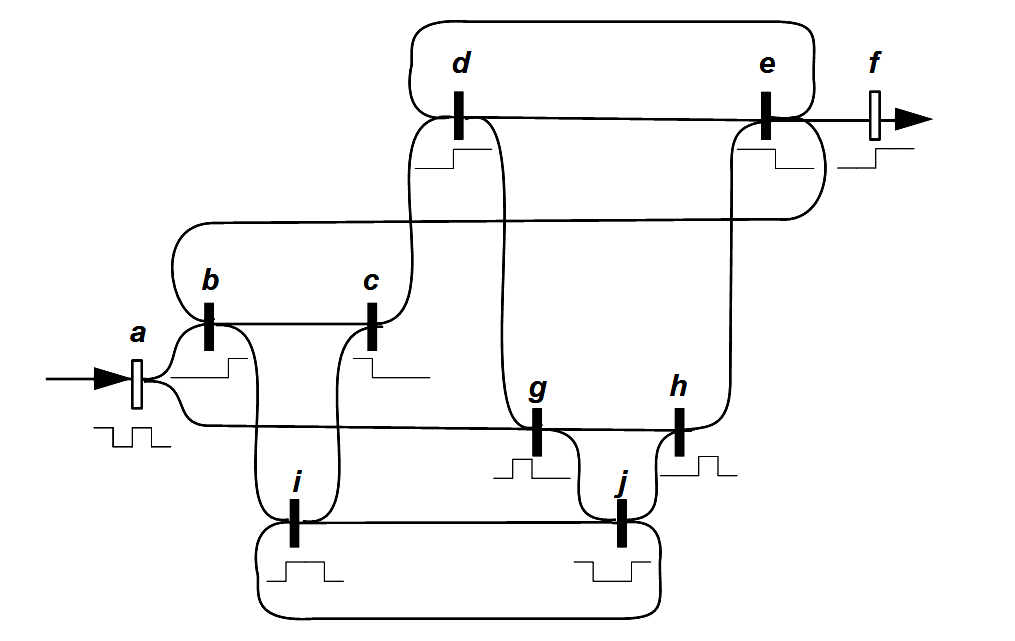
Modulator function (LoF, 67), naming of the switch elements added
Legend
Full rectangle: Switching element (marker)
Empty rectangle: input or output
Above the rectangle is the name of the switching element
Below the rectangle is the incoming or outgoing wave and for switching elements their conversion rule.

In this contribution, details of the network and various consequences will be explained, showing in what way they open up a completely new understanding of logic:

– (1) Functioning of the network: The input is processed step by step. What happens at the switching elements.

– (2) Time delays (inertia) in the network

– (3) Nodal line of system states

– (4) Self-organisation of the network

– (5) From linear processes to the logic of evolutionary production

– (6) Dynamic equilibrium of states of the network and its inputs

– (7) Converting an argument into a function that passes through the argument

– (8) Interaction of object and subject

– (9) Possible applications

(1) Functioning of the network

The circuit contains an input a, an output f and 8 switching elements (markers) b, c, d, e, g, h, i, j. At each element a wave is added. It will be shown that it has two meanings: At the input a and at the output f it describes the form of the wave entering or leaving the network. Inside the network it describes the rule with which waves arriving at the respective marker are converted. In Spencer-Brown's calculation, the only values are a cross (marked state,  ⃧  ) or an ock (the outside of the cross, unmarked state, Ɔ). There are no other values in his calculus. In the schematic, the cross is shown as a wave crest and the unmarked outside as a wave trough. If a wave crest meets a marker which converts into a wave trough, the conversion can take place. If a wave crest meets a marker which converts into a wave crest, the conversion is not possible and the path is blocked by the marker at this point. Accordingly, a wave trough that hits a marker is blocked or converted into a wave crest.

The task of the circuit is clearly recognizable and can be intuitively understood: An incoming wave a is to be converted into an outgoing wave f of half the frequency. But what happens at the individual switching elements? Here, spontaneous intuition is misleading: The complete incoming wave is not transformed step by step at each switching element into another wave as shown in the circuit diagram until the output f is reached. Instead, in order to understand the circuit diagram, a hidden  third dimension  has to be recognized. Spencer-Brown only explained this later in an unpublished text. Above all, Louis Kauffman succeeded in clarifying the facts of the matter better.

The incoming wave a does not enter the circuit in one go, but step by step. In this example, it consists of 4 elements (4 elementary inputs): Wave crest - wave trough - wave crest - wave trough. Each element of the incoming wave enters the circuit individually. Spencer-Brown therefore speaks of 4 strokes (impulses) (R, 10). For each individual stroke it is necessary to consider how it is converted at the individual switching elements and in which state it puts the circuit. When this idea is understood, the picture of E4 shows what happens with the first stroke. For this purpose, the first section of the waves drawn in the diagram must be analysed. In the graphical representation I follow Kauffman 2006, who displays the wave crest (cross) of each stroke by a full circle and the wave trough (ock) by an empty circle. The result is very illustrative, because it shows how each switching element converts full circles into empty circles and empty circles into full circles.

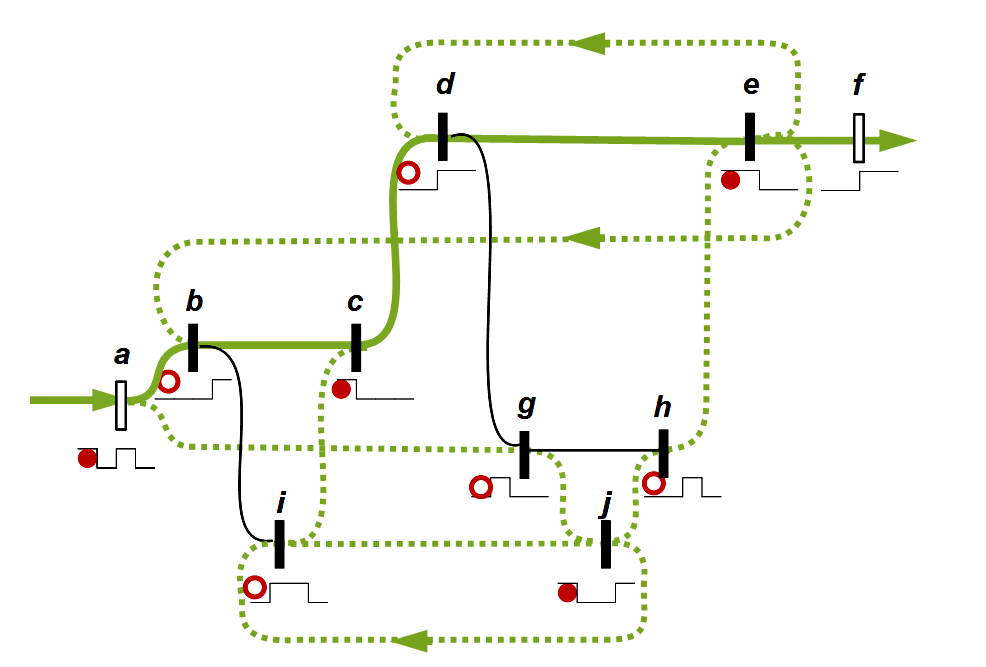
E4-1 Possible paths after the first stroke
Legend
Below the markers: Red full circle indicates a wave crest, empty circle a wave trough (according to Kauffman 2006, 115ff)
Olive green: standard paths leading directly to the output
Olive green dashed: Further possible paths
Black: These paths are blocked in their respective states, since an empty circle meets an empty circle and a full circle meets a full circle.
Left arrows on a path indicate possible returns
Observation: On every possible way full circles and empty circles alternate regularly.

This complex diagram is to be explained step by step:

– The easiest way from input a to output f for the first stroke is highlighted with a continuous green line:

a → b → c → d → e → f

At each marker, either a full circle is converted to an empty circle, or an empty circle is converted to a full circle. This way was probably the starting point from which Spencer-Brown constructed the schematic.

The four markers g, h, i and j are not yet used. They will only be needed in the following steps when this path is blocked and detours have to be taken.

– Additional paths are also possible, which are highlighted with green dashes. For example, it is possible to reach the output f also on another way:

a → g → j → h → e → f

– And feedback loops are possible, which are marked with arrows pointing to the left.

d → e → d … and i → j → i …
Loops of this type are constantly rotating around themselves and never reach the output. They are called memory by Spencer-Brown, because the same value is repeated over and over again in their circular course. To reach the output f, these loops are not necessary. I suspect that Spencer-Brown attached them in the style of the homeostat introduced by Ross Ashby in 1948, which similarly has two memory units attached to it to stabilize the system (Ashby, 101). It will be shown that for the modulation sought by Spencer-Brown a path via the two markers i and j is never absolutely necessary. He could therefore have left them out. I suspect that he included them because he expected them to provide the stabilization known from homeostates. It may also be that he very consciously wanted to design a network that, like the neural networks McCulloch was looking at, artfully combines linear and circular (heterarchic) elements. I am not aware of any texts in which he elaborates on this, but at this point it seems obvious to me to continue his approach.

e → b
This setback enables further loops. It is just as unnecessary as the memory units. While the memory units remember Ashby's homeostates, the setbacks are similar to the feedback loops of cybernetic systems. Spencer-Brown's circuit diagram thus contains all the ideas that revolutionized scientific research in his day. Spencer-Brown gives no indication as to whether and how homeostatic or cybernetic systems can be systematically derived from his circuit diagram. But he has obviously prepared this possibility.

In summary, there are many paths and internal loops for the first stroke. The actual path taken is found according to the principle of the shortest path.

From this first insights result:

(i) Spencer-Brown already vividly continues the basic idea of Frege's conceptual writing. He does not limit logic to one-dimensional final chains, but designs two-dimensional final chains with branches and alternatives. The network therefore no longer simply describes a  difference  ›f | a‹ between the input a and the output f, but a  difference field ›f ▒ a‹ (the use of the symbols | and ▒ is taken over from Scheier 2016, 18f).

(ii) He succeeded in transferring the principle of the shortest path known from classical physics into a finite (discrete) representation and breaking it down to the level of elementary logic. Classical physics considered continuous movements of mass particles moving through time and space. It can be imagined that, according to this principle, the reductor independently finds the shortest path on its own and can be called self-organization.

The paths possible for the first stroke are no longer possible for the second stroke. Example: At the switches a, b, c and d empty circuits follow each other, which must be excluded. Instead, the following paths are found for the second stroke:

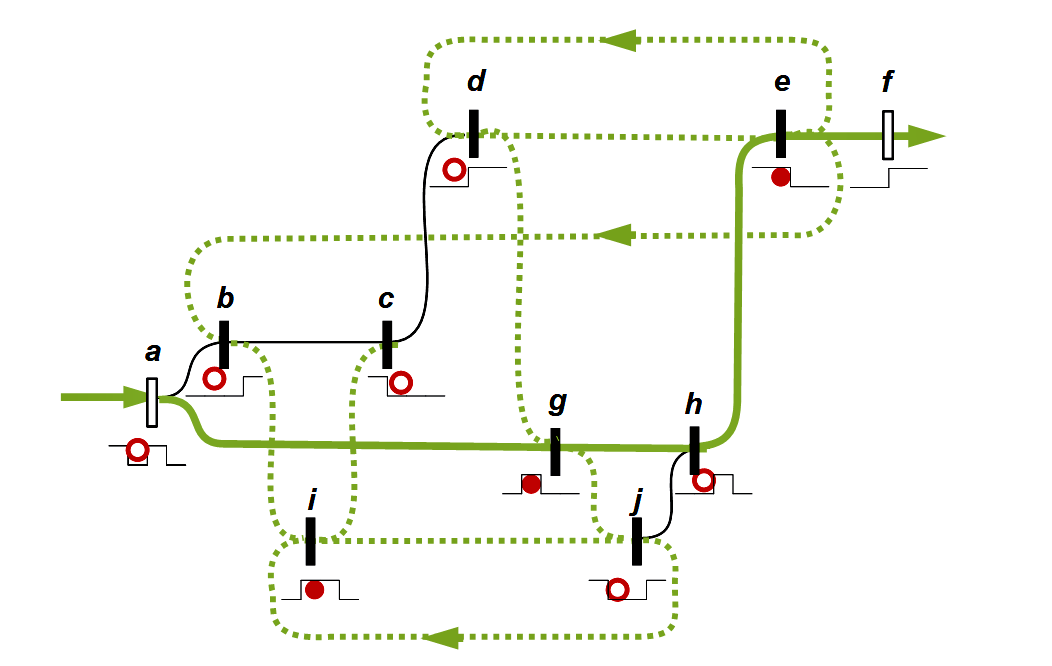
E4-2 Possible paths after the second stroke

In order to achieve the required output at f, the two elements g and h, which have not yet been absolutely necessary, must be used now. With them the path is obtained:

a → g → h → e → f

Further ways are not possible for the second stroke, because the way from a to b is blocked and only the way from a to g can be taken. Also the return from e to b does not help, because from there all possible ways are blocked somewhere. The second stroke is therefore a critical section in this circuit.

With the second stroke the third essential insight becomes apparent:

(iii) It is not possible to follow the same path for all strokes. Instead, each stroke changes the state of the circuit diagram. Each new stroke must find its own way.

This becomes even clearer with the third stroke. It could be expected that with the third stroke, the first stroke will simply be repeated, because at a, another wave crest enters the circuit. If this were the case, however, the target would be missed, because at f another wave crest (full circle) would be generated. Instead of generating a wave of half the frequency, a wave would be generated that consists of only wave crests in a straight line.

Instead, it turns out that for the third stroke the path of the second stroke can be repeated:

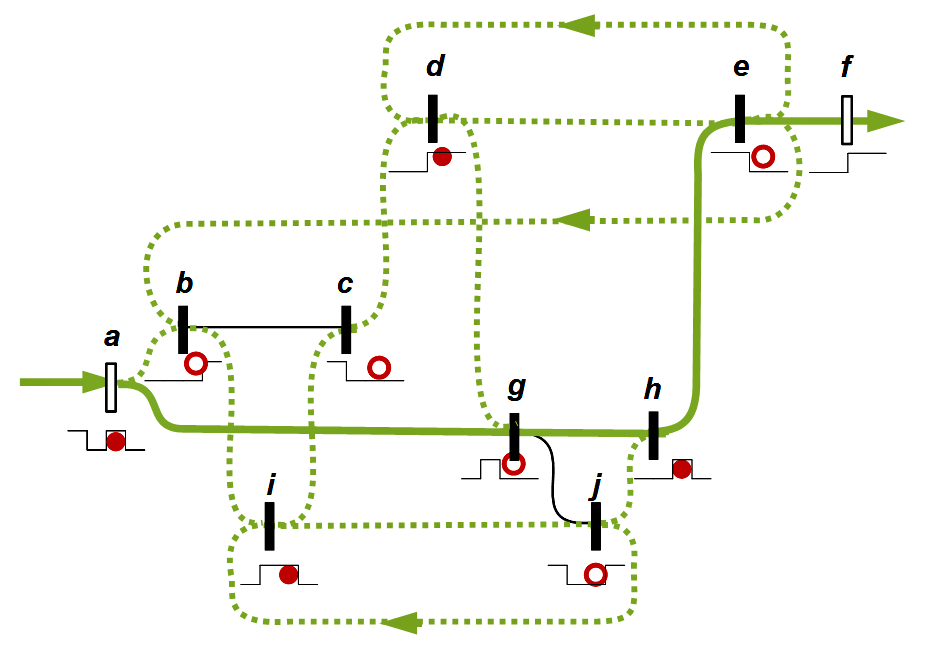
E4-3 Possible paths after the third stroke

If the previously unused marker i is taken into account, further possible paths emerge:

a → b → i → j → h → e → f

a → b → i → c → d → e → f

For the fourth stroke, the path known from the first stroke can be chosen again:

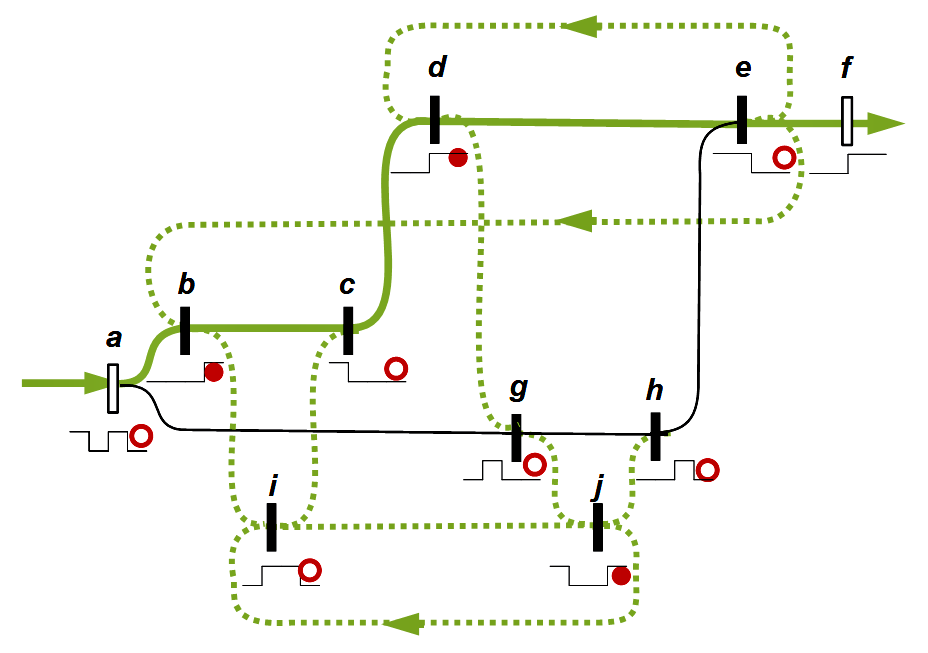
E4-4 Possible paths after the fourth stroke

a → b → c → d → e → f

Spencer-Brown describes a dodge of the kind at b via i to c or in a corresponding manner at g via j to h as the introduction of an imaginary axis. The direct connection has to be left and a new (imaginary) axis has to be added to mark the detour. The return to the original chain of evidence can be explained by the rotation of the imaginary numbers.

Who wants to deepen this topic with the works of Kauffman should pay attention: While it is very vivid for the graphical representation to show cross and ock as full circle and empty circle, it is easier for a more mathematical notation in list form to set the cross as 1 and the ock as 0. Then the respective state of the circuit can be described by the values 0 and 1, which are assumed at the respective markers. For this purpose, a tuple of numbers of the input and the 8 switching elements is formed (Kauffman ignores the output f, because there is no conversion from e to f):

{a, b, c, d, e, g, h, i, j}

After each stroke the specific values are inserted. If 1 is set for the full circle (cross, marked) and 0 for the empty circle (ock, unmarked), the following overview is given:

	a, b, c, d, e, g, h,  i,  j	Path from a to f
Stroke 1	1, 0, 1, 0, 1, 0, 0, 0, 1	a → b → c → d → e → f
Stroke 2	0, 0, 0, 0, 1, 1, 0, 1, 0	a → g → h → e → f
Stroke 3	1, 0, 0, 1, 0, 0, 1, 1, 0	a → g → h → e → f
Stroke 4	0, 1, 0, 1, 0, 0, 0, 0, 1	a → b → c → d → e → f

The values at a and e are highlighted in semi-bold to make input and output visible, and it is easy to see how the frequency of the incoming wave at a and at marker e before the output in f is halved. This is how the circuit is shown in Kauffman 2006. Spencer-Brown originally wrote the circuit in a similar way (see R, 7, Figure 1.1).

(2) Time delays (inertia) in the network

If several paths are possible in a network, and if it is possible for a path to get into a cycle for an indefinite period of time, how is it then to be determined which path leads first to the goal? The simplest answer is: the shortest way. But how is the length of the path measured? Is it the number of markers that are taken along this path? This was assumed in the previous section, and is to be relativised step by step in the following. Is it the sum of all distances between the markers on this path? Is it the task of engineering to arrange the markers in such a way that all distances are as equal as possible, or is it the task of the designer to arrange the markers in such a way that their logical relationships become as clear as possible, even if different distances occur? This is how Spencer-Brown has done it: In his graphic representations, the distances between the markers are very different. And how are the circuits to be evaluated: Do they have to consider an additional variable that is increased with each cycle until it exceeds a limit value and the cycle can be left? Does the length of a path through a circuit result from the sum of all passes?

Once the length of the path is known, the question of time must be asked: at what speed will the path be traversed. Is the same speed valid everywhere? Can the speed increase if there is an higher voltage between two adjacent markers, and what causes the voltage to increase? Spencer-Brown and Kauffman deliberately leave these questions open. But they do assume that there are time delays when passing from one marker to the next and possibly also when passing through a marker. While in common mathematics all calculations are instantaneous, there is an inertia in the network which causes a time delay. This manifests the materiality of the network. The network is not a pure calculation, not a mere design or blueprint, but it is a material medium. Its material properties determine how fast the medium can be traversed.

Spencer-Brown calls the timelessness of the usual calculations »imaginary«, because at first it looks as »magical« as the properties of imaginary numbers. Never before has a mathematician asked which properties make calculations timeless, and whether these properties possibly influence the calculation. However, for the imaginary numbers their arithmetic laws have been found and they are no longer considered magic. Should this also be possible for timelessness? In the opposite direction, from the perspective of traditional mathematics, the inertia of the network appears as a danger. It is a threat as long as its causes and effects are unknown. Spencer-Brown does not yet provide a solution, but he sets mathematics a completely new task.

»Mathematically, since there is no time in mathematical expressions, everything happens all at once, the short signal from i to j is never there, since there is no time for it to exist. The propagation-time of the signal through the leads and markers has not just become very small: in mathematics it has vanished completely, and this why we say the signal is ‘imaginary’. But like the other imaginary i in numerical algebra, which has similar 'magical' characteristics, the fact that it exists in the mathematical circuit, not as a reality, but as a threat, should j even consider doing the wrong thing, is sufficient to keep j honest. The threat never has to be carried out in reality, in fact mathematically it cannot be. But its mere presence is sufficient. It is what we mean, in chess, when we say 'the threat is more powerful than the execution'.« (R, 9)

Network designers and engineers face the same question. In their designs of networks they assume an ideal circuit, for whose understanding the time delays can be neglected. All they need to know is the logical order in which the switching elements are passed through. In reality it is different. The circuit can develop a »life of its own«. It is even possible that the logical design of the circuit contains errors which are compensated and corrected by the realized circuit.

»In hardware the mark behaves like an idealized transistor 'nor' gate: If any of its inputs is connected to an EMF (say 1 or mark), then its output is grounded (say 0 or ock).
    Some engineering designs with these units will 'work' even if their mathematics is incorrect, because of delays in signal travel-time etc. These are bad designs: they might suddenly fail if the material are improved.
    The beauty of the present mathematics is this: if it is correct, anything designed from it in transistor units will certainly work.« (R, 5)

Kauffman looks at the inertia of the network from an other point of view. It is not possible for each stroke to follow the same path from input a to output f. The change of the paths can be understood as a change of state of the network. The network can change state with each new stroke. For Kauffman, time must pass when one stroke follows another for the network to change state during this time. Sound engineers know the problem: the network has to level out until optimum sound transmission and modulation can be achieved.

»As a model for action we assume that each change in z (Kauffman, unlike Spencer-Brown, refers to the input as z rather than a, t.) is held fixed long enough for the automaton to accomplish its transition to the next state. In terms of applications this means that the model assumes delays associated with each inverter. There are no delays associated with the connecting lines in the graph. This method of distributing the delays is a mathematical abstraction, but it is sufficiently realistic so that these circuits can actually work at the hardware level. In any given instantiation the delays are given up to the variation in the components. If the automaton is mathematically determinate (as in this example), then it will behave in the same way for any choice of actual delays – so long as the input varies more slowly than the time needed for internal balancing.« (Kauffman 1995, 91f)

For him too, however, it ultimately remains »a black box B with input line z and output line d with this behaviour« (Kauffman 1995, 92).

As long as the causes and the measurement of inertia (time delay) are unknown, it is left to the skill of the engineer to design the network in the given medium in such a way that there is enough time for the states to change after each new stroke. For Spencer-Brown this is »the art of making a reductor« and the »ingenuity« of network designers (R, 10, 13)

Ultimately, it is necessary to test whether the network works as expected. It is understandable why the success of these circuits was taken up incredulously. Spencer-Brown writes about the reaction of his colleagues when he first constructed a circuit of this kind in 1961: »My colleagues were so shocked that they wouldn't look, even though we constructed it in transistor hardware and watched it counting on the cathode-ray tube. 'There must be something wrong with it.'« (R, 7)

He compares the work of engineers with that of chemists. They also test different chemical processes and ultimately cannot say exactly why the process they have found is successful. It is not possible to fully describe and understand the multitude of processes and substances that may act as catalysts. (When I spoke to researchers in the chemical industry, this was confirmed to me. The reality of chemical research and its successes is very different from what an outsider would expect).

»As in a chemical formula, it gives the number of elements (markers and leads) without saying how they are actually connected, so if they can be connected a different way in the same formula we call it an isomer« (R, 21)
    »The same is true for reductors, as mathematical entities. Like numbers, they don't actually exist in any space we call Euclidean. Yet unless we draw them in some way, even though no way we can draw them is relevant to what they actually are, we cannot use them, nor can we even imagine them. Even the specification of the reductor is not, mathematically, what it really is: it is just a more succinct way of drawing it, getting rid of all the irrelevant ways it can be diagrammed as a circuit.« (R, 21)

It is similar in music. »Mathematics, like musics, is meaningless unless it is performed.« (R, 23) The comment on music seems to me to be striking: just as a composer and a musician can never completely calculate in advance what sound an instrument will produce, but must try it out and be prepared for the special, often unexpected sound effects of the given instrument (anyone who plays a new instrument must first get used to it and learn about its characteristics), so too do researchers. It is a great achievement for me to not simply contrast the creative process with logical repetition and routine, in the course of which it will gradually become clear why which states occur (this is undoubtedly the way a circuit is designed today not so much into the indefinite after it has proven itself many times over), but to show a way to think about the interaction between the developer and his instruments and materials right down to the logic and to present it paradigmatically using examples such as the circuits mentioned by Spencer-Brown.

(3) Nodal line of system states

When talking about a sequence of states of the network, a third dimension is needed for this: By the first dimension, a path is determined that is one-dimensional in itself; the second dimension opens up the possibility of parallel paths with which barriers can be bypassed; and with the third dimension the course of state changes can be described. Each state is two-dimensional inside, its change takes place in the third dimension. Spencer-Brown incidentally hints at the introduction of a new dimension, but he does not investigate its consequences further: »We are now in difficulties through attempting to write in two dimensions what is clearly represented in three dimensions.« (LoF, 66)

The relationship of a circuit to its states can be compared with the relationship of a material substrate to its aggregate states. Standard example is the substrate water with the states ice, liquid and gas. With every change of state a new order is created. To explain why and how state changes occur, a new dimension is necessary: In the example of water it is the supply or withdrawal of heat. In other chemical processes it can be the stirring or the supply of catalysts. The transition from one state to the other is understood as emergence. The respective order can be explained by a self-organisation of the substrate in the new state. The entirety of all changes of state can be described according to Hegel as a nodal line (HW 5.435), even if this term was no longer used after Hegel. The nodal line describes the third dimension. I can imagine that it should be possible to continue Spencer-Brown's remarks in this direction and give the theory of self-organisation and emergence a logical basis.

(4) Self-organisation of the network

It doesn't have to be inertia. It is possible that the input does not run like a sphere or like the focus of the observer's gaze on a fixed path, which gradually examines all paths, reverses at blocked markers and takes the next possible path until it can finally decide on the optimal path. But it is also possible that the input spreads out in waves in the network, as in the experiments in quantum mechanics, and runs through all possible paths in parallel until the optimal path emerges from them. This means that after passing through a marker, all paths starting from the marker are entered in parallel, and loops can be passed through endlessly. When this type of propagation occurs, there may be interactions between the different paths. And possibly the loops provided in the network will have an influence on the propagation of the signals on the other paths. They may be able to stabilize, as in the homeostat of Ashby, or their effect may enter into a higher-level process of self-organization and balancing. So far nothing is known about this. Spencer-Brown describes the situation in which it can only be observed empirically how the network behaves in the final result.

Furthermore, it is conceivable that the network may interact with the ground in which it is inscribed. If it comes along a path to a loop to an earlier point on the path, this can be understood as a re-entry. In his comments on the re-entry, Spencer-Brown showed how the medium can be set in motion (restlessness, vibrations) by the re-entry. If this is transferred to the networks, loops can cause the ground to shake and with it the paths entered into the ground.

(5) From linear processes to the logic of evolutionary production

Spencer-Brown has already gone far beyond the scope of traditional logic with the introduction of re-entry and the waveform of time. However, if they are considered in detail, they remain within their sequence in a linear, causal order: The re-entry results from an iteration whose individual steps strictly follow each other and are formally similar and countable among each other. Likewise, the waveform of time describes a one-dimensional curve that oscillates regularly up and down. This changes radically with the circuits. They cannot be restricted to a fixed path, but contain redundancy (concurrency) and circularity. Compared to linear orders, they contain a surplus of possible paths, of which one will dominate.

In Luhmann's terminology this corresponds to the logic of an evolutionary system. From an evolutionary point of view, the continuous oscillation of the input a entering the circuit can be understood as the given situation of the genetic material; the different pathways of the network describe the variety of single or possibly step-by-step mutations of the genetic material, from which one is chosen by a selection. When this has stabilised (retention), new genetic material is produced which will assert itself in the course of evolution. It is the product of an evolutionary change, in the terminology of the networks considered by Spencer-Brown the output f. Or in other words: The processing of the given resources (input) does not follow a fixed, predetermined workflow, but the schematic opens up a multitude of possible paths that lead to the output (the product). The system is able to make a choice (selection) from the multitude of paths. The circuit can change between different states, with which it optimizes its behavior according to the given input (adaptation). However, there are two important limitations compared to evolution: (i) Although there is a variety of paths, they are predetermined in the design of the network. Mutations in evolution, on the other hand, can also result in unexpected (random) changes. Although the network can also show unexpected behaviour, it remains within the framework of the given paths. (ii) And it is not yet a learning system, which, like the human brain, can form new links in the course of its activity or remove or downgrade their priority. Spencer-Brown's networks are a necessary intermediate step that leads from linear, causally determined systems, the re-entries and waveforms of time to learning and evolutionary systems.

»We want to speak of production when some, but not all, of the causes necessary to produce certain effects can be used under the control of a system. [...] To understand production, one must therefore not start from natural laws, but from the advantages of selection.« (Luhmann 1984, 40, my translation)

In a way, this already applies to the networks. Their behavior cannot be predicted completely. They are consciously designed in such a way that their inertia and self-organisation contain a degree of freedom that already points to an evolutionary process.

The understanding of production is shifting. In the civic epoch of commodity production, it was a concern to revalue the importance of vital (dynamic) human labor over mere (static) ownership. Production was understood as the creation of value through the transfer of human labour to the man-made product (Philoponos, Adam Smith, Marx). The model for this was craftsmanship, in which, for example, a table is made from various pieces of wood or, in larger projects, a ship is built. The product is worth as much as the working time required to make it and that was transferred to the product. With the knowledge of evolutionary development, the view of natural production processes is broadened. Just as Spencer-Brown asks for a function that can count on its own, evolution is about an independent process of production. The initiative lies with evolution. Material processes were already planned and controlled in agricultural and industrial production, be it the growth of plants, the rearing of animals or the use of mechanical and chemical processes in industrial production. However, the formative power was seen in humans. Although he can never fully foresee whether there will be disturbances that can lead to complete loss. But it is up to him to learn from it and to avoid deviations with improved production methods. In evolution, on the other hand, deviations are no longer seen as disturbances only, but as the creativity of the process. The question is, by what cybernetic mechanisms is creativity able to control itself? The result is a production oriented to evolution, which is no longer merely a transfer of value from the human being to the product, but leads to products created by evolution.

What is produced by the circuits? Spencer-Brown has consciously limited himself to the simplest and most elementary case of counting. It is no coincidence that he considers networks with which waves are modulated. In the 19th century, Stokes and Weierstrass's theorem showed that any function can be interpreted as an approximation of simple waves, i.e. »produced« from them. Hilbert constructed the mathematical concept of a Hilbert space from this, which became fundamentally important to quantum mechanics and game theory. In my understanding, Spencer-Brown therefore uses the modulation of a given wave into a double wavelength wave to design the nucleus from which the foundations of modern mathematics can gradually be developed. Spencer-Brown deliberately limits himself to the elementary step: In the simplest case, the frequency is halved from a pattern like 'abab' to a pattern like 'aabb'. From this simple modulation, modulations of any complexity can be assembled. This is literally audible when, in sound engineering, sounds can be modulated with networks such as those studied by Spencer-Brown and music can be created (produced) with them.

(6) Dynamic equilibrium of states of the network and its inputs

The system is set up in such a way that in the oscillation of its system states it can react to the oscillation of the input and, as a whole, produces a kind of dynamic equilibrium of which Bertalanffy spoke, and which can be described as Maturana and Varela as self-organization (autopoiesis).

(7) Object and meta level

While traditional logic wanted to avoid paradoxes by strictly separating the object and meta-levels, Spencer-Brown consciously uses their inner interweaving. This makes it difficult to understand his designs, as we have learned to think in traditional logic and are used to it. Kauffman has considered this in the circuit diagrams: the waves attached to the markers have a double meaning: they can be read both as elements of a process and as its results. Each marker is both an element in the circuit diagram and at the same time the marker shows into which value the character arriving at the marker is to be converted or a blockage occurs.

»In using the interlock algebra, one regards the link diagram as a circuit whose parts (the arcs in the diagram) are both carriers of circuit values and operators that process these values. This duality is the core of the interrelationship with topology. In actual applications of digital circuitry, there is usually a sharp distinction between circuit elements as operators and circuit elements as carriers of signals.« (Kauffman 1995, 88)

This method is used throughout the Laws of Form. The cross  ⃧   is both comparable to the numbers as an operand that can be included in a calculation, and comparable to the arithmetic symbols like +, -, / etc. as the operator with which the calculation is executed. The cross  ⃧   is both an operation, with which a distinction is drawn, as well as the product of this operation, which can be used for further calculations. In Frege's terminology, the cross is at the same time an argument a as a function f, which is used to operate on arguments a. This is a paradox, which should be avoided especially by the type theory of Russell and Whitehead. Spencer-Brown, on the other hand, wants to demonstrate in Chapter 11 of the Laws of Form how arguments a and functions f originate from one another in his calculus. He shows this in the process form of the re-entry, by which an argument a is transformed into a new form, which he calls f. How he succeeds in this is a subject in itself. At this point it is sufficient to note that he adopts the symbols a and f for his networks from the re-entry if he designates the input as a and the output as f.

The networks used to modulate an input a into an output f are therefore a more detailed elaboration of the re-entry. However, while the sequence of iterations leading to re-entry is linear, the network contains branches and loops. If the network is considered as a whole, it leads, like the re-entry, from an argument a to a result f, which is also the process of this production. If the arguments a are called objects, the functions (processes) f belong to the meta-level on which the objects a are referred to.

At a higher level, which Spencer-Brown has not investigated any further, the network as a whole can be regarded as a re-entry. Then the output f is no longer just a product that can be further processed in subsequent steps, but returns to the network as a re-entry and can change it. In this understanding it can not only change the form of the paths in the re-entry, but also the medium in which the paths are inscribed. From this point of view the full understanding of an evolutionary production is achieved, as it was meant by Luhmann. Man's task is limited to one part of this process, working together with his natural environment. The evolutionary process can change both the natural environment and man himself.

(8) Interaction of object and subject

The inertia and self-organisation of the networks demonstrate: It is no longer true, as it was for Kant, »that the objects must conform to our cognition, which would agree better with the requested possibility of an a priori cognition of them, which is to establish something about objects before they are given to us« (Kant, KrV, B XVI), but both are equal and mutually dependent on each other. Anyone who designs a circuit like Spencer-Brown cannot be sure at the beginning whether and how it will work. It is known from chemical research that most discoveries are unexpected and surprising, and this is how Spencer-Brown sees it when designing circuits, and he cautiously seeks the basic logic for this approach, which takes him into a still unknown area. The circuit diagrams he designs contain a degree of freedom that gives sufficient leeway to the actual flow of the technical systems implemented with them. Anyone who has programmed himself or worked with engineers will at some point be surprised by the experience that his own programs and technical systems are used in a completely different way and exhibit characteristics that the developer had not originally expected.

With the interaction of object and meta-level as well as object and subject, everything is prepared to determine the relationship between the observed process and its observer in a fourth dimension.

(9) Possible applications

The schematic can be transferred to chemical process chains. Input a describes the external resources that must be introduced into the process, output f the outgoing materials that are to be produced with the process. Each marker describes a chemical reaction that occurs at this point. All in all, the schematic diagrams describe chemical process chains and their possible branching patterns.

In the terminology introduced by Hegel according to chemistry, each state can be understood as elective affinity (Wahlverwandtschaft), in which the chemical reactions that are elective are linked with each other. The transition from one state to the next can be called Hegel's nodal line.

The schematic can stand for organization models. Input and output describe the external resources and the product produced by the organization. Each marker is literally a position in the organization that assumes a certain task and interacts with the other positions.

Within the organization, there are sub-processes that are processed sequentially, as well as branches that can lead to equivalent products. In terms of organisation, the task can be set to optimise the paths for the individual strokes in such a way that, as far as possible, no point is on the critical path several times in succession, but can regenerate itself.

There is no controlling unit in the process, but self-organization, which takes place after certain principles like e.g. the principle of the shortest way. Instead of a central control system, a decentralized control system can be assumed if each unit searches for local paths in its own environment until the individual local paths originating from the units connect with each other and result in a system solution.

It is assumed that the process has organized itself over the four steps. But it is possible to ask an external consultant to analyze the process for possible weaknesses and improve the spontaneous result of the self-organization. This can go as far as modifying the network plan or even creating additional virtual jobs that allow ways that were previously closed.

Neural networks and cybernetics: The overall solution can be programmed recursively: Starting from a, every possible path is examined recursively. If it runs into a cul-de-sac, this branch is marked and the next possible path is searched for until the first continuous solution is found. This is similar to recursive programming when on a chess board for a horse the path is searched on which it enters all fields exactly once.

The significance of the two memory units introduced by Spencer-Brown as well as the feedback loops are to be examined more closely and make an application to cybernetics and neural networks possible.

Physics and Cosmology: Spencer-Brown describes bypasses that lead him into the imaginary axis. It is also conceivable that tunnels and wormholes could be allowed, with which points that are far away from each other can be directly connected under conditions that must be precisely defined. A possible example of wormholes are re-entries: If a circular path in the schematic is traversed infinitely often using feedback in the network, this re-entry iteration can create a direct connection between two points opposite each other in a circle.

Conclusion To sum up, for me the innovation in this logic consists of three points:

– Introduction of the imaginary axis

Spencer-Brown particularly emphasises this point. By imaginary axis is meant that the linear inference is left in the circuit. A distinction is made between different paths, some of which run parallel and some of which are connected and fed back. This requires a new axis compared to the linear inference. For Spencer-Brown this is compared to the introduction of imaginary numbers, although he does not calculate with imaginary numbers anywhere.

– Inertia and self-organisation of the circuit

If a state has balanced in the circuit after a stroke, there seems to be a tendency to maintain this state with the next stroke. However, conflicts cannot be avoided. This leads to a kind of self-organization: The circuit breaks down into sections, each of which is free of conflict, and only certain transitions are allowed. They result in a harmony of their own accord, which Spencer-Brown called musicality.

– Interaction of the developer and the works of art created by him

Note (musicality and technique): What Spencer-Brown has written down in logic and circuitry was surprisingly introduced into music at the same time as an avant-garde technique: Loops. Their models were mechanical instruments like music clocks. This technique is what makes minimalism so appealing and is for me, especially in the pieces by Steve Reich (* 1936), immediately audible and almost a musical counterpart to the Laws of Form. See for example at YouTube with a very clear visualization the 1973 piece Music for Pieces of Wood. Those who find it difficult to understand Spencer-Brown's ideas should start with this film sequence. There you can immediately see and hear how further rhythms are built up on a canonical basic rhythm, until step by step a sound impression of its own is created. While at the beginning the individual rhythmic lines are clearly distinguishable from the ear, at a certain point this jumps over into an overall impression of a harmonic acoustic pattern, in which the statically recorded basic rhythm also seems to vibrate.

Observer

»An observer, since he distinguishes the space he occupies, is also a mark.« (LoF, 76)

Spencer-Brown wants to follow the Copernican turn consistently into logic and design a logic within which the position of the observer and his relativity can be represented. In order to better illustrate this, he chooses new signs: instead of a cross, a circle stands for the boundary of something. Repetition is represented by two circles lying side by side, nesting by circles lying inside each other. In a presentation by Kauffman Laws of Form and the Logic of Non-Duality, 31, the two axioms take shape:

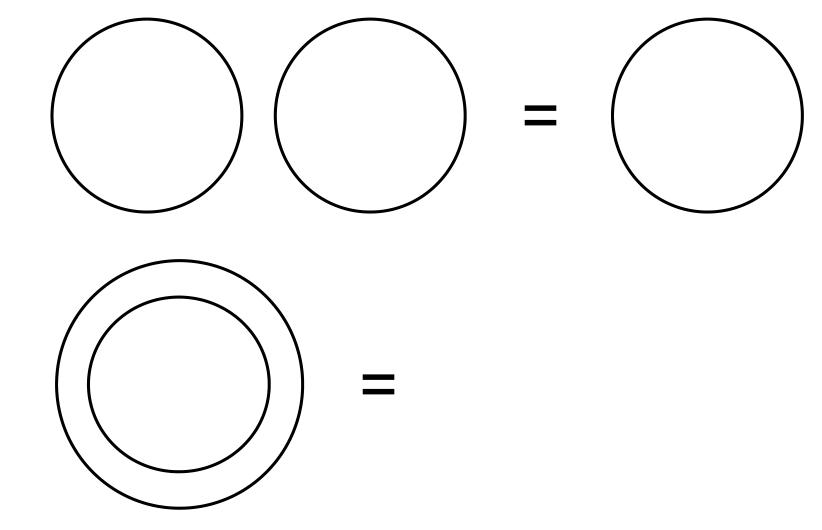
At first this does not result in any new knowledge, but in the representation with circles it is better to show that different observers see the same nesting and repetitions differently. What looks like a nesting to one observer may look like a repetition to another from another position. If, for example, the equator on earth is chosen as a circle and an arbitrary circle, which is completely on the southern hemisphere, is chosen as a second circle, then this second circle for an observer viewing from the northern hemisphere lies within the equator. For an observer in the southern hemisphere, who is between the equator and the second circle, both circles are side by side (see LoF, 102f). In the following pictures the respective position of the observer is marked with a blue square and with a small square, where he sees the other observer:

2 circles from different perspectives
left: An observer in the northern hemisphere sees the two circles in each other and the second observer in the space between the circles.
right: An observer in the southern hemisphere sees the two circles next to each other and the first observer in the larger circle.

Each representation of logical elements and their relationships and operations is dependent on the perspective of the observer, who at the same time makes himself an image of his own position within logic. Spencer-Brown calls this kind of observer-dependent representation »experiments« (LoF, 70-75).

The inclusion of an observer leads into a new infinite loop. In the first step, an observer draws an image of how he sees the system from his position. In a second step, the observer enters his own location, i.e. the place where he is within the map. Everyone knows this from walking maps attached to nature, which show with a highlighted point the location where the map is located within the landscape. In the third step, you can ask from which location a map containing the location could be drawn. It must be beyond the observer and his environment. A map can also be drawn for this location from a location even further away, e.g. a location on the left.

This becomes just as clear in structural arrangements. The patient places a representative of himself in the room and surrounds him with other figures from his social system. The patient now sees himself, as it were, in the system surrounding him. The therapist, in turn, sees from the outside how the patient reacts to his self-image and interacts with it, when the people in the room begin to express themselves and the patient shifts or changes their position. A supervisor can observe the therapist's work, etc. – In debates it is a popular game when the disputants alternately want to step out of the clinch and judge the other from a meta-level. This provokes a corresponding reaction, until a cycle without end occurs. – In meetings, the process is sometimes disrupted when someone raises both arms and asks procedural questions. Then someone else can come forward and question the admissibility of procedural questions and so on.

   

Therefore, a final step is needed to demonstrate that the results are valid regardless of the location of the observers. There must be transformation rules that translate one position into another. What transformations are there between the different representations and what are their properties? For Einstein this was the question about the Lorentz transformations, in economics it is the question about the currency transformations and for me there is a related question about the truth transformations at Wittgenstein.

Equally important is the question of the lowest system that Spencer-Brown called (s₋₁). Here, too, a reference to the psychotherapeutic applications should suffice at the moment. How is it to be explained that the persons involved in a structural arrangement can feel and say how the person they represent feels and what changes in the system they wish to see (e.g. that other persons should be closer or further away from them, or that there are further persons who are missing and are to be included in the arrangement) although they have not received any further information about the persons set up? Apparently on the lowest level – in this example this is the physicality (body) of the involved persons – there is a level of perception which in its openness and infinity goes beyond all conscious information. For me, this is an example of the small perceptions meant by Leibniz.

Luhmann, on the other hand, seems to be primarily concerned with the fact that logic and truth only emerge from the communication between observers. True is no longer in the classical sense what corresponds to the thing, but what is established in the communication of the observers.

»With the re-entry we generally mean the reintroduction of a distinction into the realm that allows it to be distinguished. An example: According to Niklas Luhmann's systems theory, the scientific system is differentiated on the basis of the distinction true/not-true. If one develops a theory of science that observes the use of this distinction with the distinction true/not-true, a re-entry is carried out with the theory of science. With regard to the system of science, one finds oneself in such a theory of science on a meta-level, since one can now ask the question about the truth of the operation of science - the truth of the distinction true/not-true. By being the same distinction that is applied to itself, a situation arises 'in which the distinction is simultaneously the same (as the particular distinction of the operations of this system) and another (as the observed distinction)'. (Claudio Baraldi, Giancarlo Corsi, Elena Esposito GLU: Glossary of Niklas Luhmann's Theory of Social Systems, Frankfurt am Main 1997: 152).« (Lau, 55f, my translation)

Sigles

AUM = The G. Spencer-Brown – AUM-Conference 1973, Esalen 1973; Link

HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971; Link

KrV = Immanuel Kant: Kritik der reinen Vernunft (1781, 1787)

LoF = George Spencer-Brown: Laws of Form, New York 1972 (Julian Press) [1969]; archive.org

R = George Spencer-Brown: An Introduction to Reductors, unveröffentlichtes Typoscript 1992

SWH = Tatjana Schönwälder-Kuntze, Katrin Wille, Thomas Hölscher: George Spencer Brown, Wiesbaden 2009 [2004]

Literature

W. Ross Ashby: Design for a Brain, New York 1960 [1952]

Gregory Bateson: Ökologie des Geistes, Frankfurt am Main 1981 [1972]

Dirk Baecker 1993 (Hg.): Kalkül der Form, Frankfurt am Main 2016 [1993]

Dirk Baecker 2000: System
erstveröffentlicht in: Christian Bermes und Ulrich Dierse (Hrsg.), Schlüsselbegriffe der Philosophie des 20. Jahrhunderts, Archiv für Begriffsgeschichte, Sonderheft 6, Hamburg 2010, 389-405; vordenker Neuss 2018

Dirk Baecker 2013: George Spencer-Brown wird 90; catjects

Ulrich Blau: Die Logik der Unbestimmtheiten und Paradoxien, Heidelberg 2008

Thomas Collmer: Hegels Dialektik der Negativität, Gießen 2002

Louis H. Kauffman und Francisco J. Varela: Form Dynamics
in: Journal of Social and Biological Structures 1980 3, S. 171-206

Louis H. Kauffman 1995: Knot Logic
in: ders. (Hg.): Knots and Applications, Singapore 1995, 1-110

Louis H. Kauffman 2000: What is a Number?; Link

Louis H. Kauffman 2006: Laws of Form – An Exploration in Mathematics and Foundations, Rough Draft

Louis H. Kauffman 2009: Laws of Form and the Logic of Non-Duality, San Rafael 2009; Link

Felix Lau: Die Form der Paradoxie, Heidelberg 2012 [2005]

Bernie Lewin: Enthusiastic Mathematics, Melbourne 2018

Niklas Luhmann: Beobachten
in: Luhmann: Die Wissenschaft der Gesellschaft, Frankfurt 1992 [1990], S. 68-122

Niklas Luhmann: Die neuzeitlichen Wissenschaften und die Phänomenologie, Wien 1996

Niklas Luhmann: Die Gesellschaft der Gesellschaft, Frankfurt am Main 1998 [1997]

Warren McCulloch: Verkörperungen des Geistes, Wien, New York 2000 [1965]

Warren McCulloch: The heterarchy of values determined by the topology of nervous nets
in: The Bulletin of Mathematical Biophysics 7(1945), 89-93; deutsche Übersetzung bei Vordenker

Martin Rathgeb: George Spencer Browns Laws of Form zwischen Mathematik und Philosophie, Siegen 2016; Link

Claus-Artur Scheier: Ästhetik der Simulation, Hamburg 2000

Claus-Artur Scheier: Luhmanns Schatten, Hamburg 2016

The Telegraph: George Spencer-Brown, polymath who wrote the landmark maths book Laws of Form – obituary; Telegraph vom 13.9.2016

Franco Volpi: Der Status der existenzialen Analytik (§§ 9-13)
in: Thomas Rentsch (Hg.): Martin Heidegger - Sein und Zeit, Berlin 2001, S. 29-50

 

© tydecks.info 2017-2019