Spencer-Brown Gesetze der Form

Beitrag für das Philosophische Colloquium der Akademie 55plus Darmstadt am 13. und 27. März 2017 (wesentlich erweiterte Fassung, Version 12.7.2019)

 

 

Einleitung

George Spencer-Brown (1923-2016) kommt aus England und stammt aus der gleichen Grafschaft Lincolnshire wie Newton. Er hat schon früh parallel und übergreifend an Fragen der Mathematik, Ingenieurstechnik und Psychologie gearbeitet, so im 2. Weltkrieg als Funker, Nachrichtentechniker und Hypno-Schmerztherapeut bei der Royal Navy, 1950-51 am Trinity College Cambridge bei Ludwig Wittgenstein (1889-1951), ab 1960 mit dem Mathematiker und Philosophen Bertrand Russell (1872-1970), auf dem Gebiet der Psychotherapie und Kindererziehung mit Ronald D. Laing (1927-1987), bei dem er an einer Therapie teilnahm und ihn umgekehrt in Mathematik unterrichtete, und daneben war er Schriftsteller, Liedermacher, Schachspieler, Spieleerfinder, Segelflieger (mit zwei Weltrekorden), also eine durchaus ungewöhnliche Persönlichkeit. 1959-61 Chief Logic Designer bei Mullard Equipment, 1963-64 Advisor bei British Rail, 1963-1968 Projekte an Mathematischen Instituten in England, 1968-69 Vollzeitbeschäftigung als Psychotherapeut mit Hypnose-Techniken, später nur noch in Teilzeit. Ab 1976 befristete Professorentätigkeiten an Universitäten in Australien und USA. 1977-78 Beratung für Xerox. In späteren Jahren verarmte er und zog sich zurück, konnte jedoch auf dem Grundstück des Marquess of Bath leben, einem früheren Schüler von ihm. – Gesetze der Form erschien 1969 dank Förderung durch Bertrand Russell. Durch eine positive Rezension von Heinz von Foerster (1911-2002) gewann es eine gewisse Aufmerksamkeit, ist aber dennoch in der Mathematik, Informatik und Philosophie bis heute im Grunde ein Randphänomen geblieben, das kaum jemandem bekannt ist. In Deutschland hat vor allem der Soziologe Niklas Luhmann (1927-1998) die Ideen von Spencer-Brown aufgegriffen und sah in ihnen einen neuen Zugang zur Systemtheorie, der aus seiner Sicht eine Befreiung von der traditionellen Philosophie ermöglicht. Eine erste Einführung in die Logik gibt es bei Wikipedia. Louis Kauffman (* 1945), Uni Chicago, hat den Ansatz weiter ausgebaut. Es gibt Bezüge zur Informatik (von Foerster), Kybernetik (Wiener), Antipsychiatrie (Laing), Anthropologie (Bateson), Psychologie (Piaget) und Kommunikationswissenschaft (Watzlawick), Systemwissenschaft (Luhmann, Baecker), selbstreferenzielle Systeme (Maturana, Varela). – Im persönlichen Umgang soll Spencer-Brown eher schwierig gewesen sein, was wohl damit zusammenhängt, dass er – wie ich meine zurecht – seine Arbeiten auf einem Rang mit denen von Aristoteles und Frege gesehen hat und über die fehlende Anerkennung enttäuscht war.

Entsprechend gibt es nur wenig Sekundärliteratur. Die Texte von Spencer-Brown sind außerordentlich dicht geschrieben. Die Gesetze der Form umfassen im Haupttext 77 Seiten, die mit einigen Vorworten und Eigenkommentaren ergänzt wurden. 1973 fand am Esalen-Institut an der kalifornischen Pazifikkünste eine Tagung statt, an der Spencer-Brown, Bateson, von Foerster u.a. teilnahmen (American University of Masters Conference, abgekürzt AUM-Konferenz). Damit sind die Quellentexte bereits aufgezählt. Von Dirk Baecker erhielt ich ein 1992 von Spencer-Brown geschriebenes, unveröffentlichtes Typoscript An Introduction to Reductors. In Deutschland gibt es in Nachfolge von Luhmann an der anthroposophisch geprägten Privatuniversität Witten/Herdecke im Ruhrgebiet sowie in Heidelberg und München Kreise, die sich regelmäßig mit Spencer-Brown beschäftigen. Als Sekundärliteratur habe ich daher von Luhman das komplexe Kapitel über Beobachtung aus seinem 1990 erschienenen Werk Wissenschaft der Gesellschaft herangezogen, in dem er seine Position zu Spencer-Brown darstellt, darauf aufbauend einen von seinem Schüler Dirk Baecker 1993 herausgegebenen Sammelband Kalkül der Form, der unter anderem auch die Rezension von Heinz von Foerster enthält, sowie den von Luhmann 1995 in Wien gehaltenen Vortrag Die neuzeitlichen Wissenschaften und die Phänomenologie, in dem er seine philosophische Position gegenüber Husserl und Spencer-Brown ausführt. Claus-Artur Scheier hat 2016 in Luhmanns Schatten dessen Ansatz mit der neueren französischen Philosophie in Verbindung gebracht und auf eine eigene Weise formalisiert. In Heidelberg erschien 2005 eine kurze Einführung in die Logik von Spencer-Brown durch Felix Lau und in München wesentlich ausführlicher 2004 eine 2009 erweiterte Einführung durch Tatjana Schönwälder-Kuntze, Katrin Wille, Thomas Hölscher. Sie kommen aus dem Umfeld von Matthias Varga von Kibéd (* 1950), der wiederum Schüler des Logikers Ulrich Blau (* 1940) ist. Blau hat Standardbücher über neue Richtungen der Logik verfasst, in denen er jedoch auf Spencer-Brown nicht eingeht. Varga von Kibéd hat sich fernöstlichen Traditionen zugewandt und ist vor allem aktiv geworden in der Gründung, Einführung und Vermarktung neuer Methoden der Systemischen Strukturaufstellung, die sich im weitesten Sinn auf Spencer-Brown berufen. Zusammenfassend kann gesagt werden, dass Spencer-Brown vor allem auf die Theorie selbstreferenzieller Systeme und auf neue Methoden der systemischen Therapie Einfluss gewonnen hat, jedoch in der traditionellen Philosophie, Mathematik und Informatik weitgehend ignoriert wird und unbekannt geblieben ist.

Dieser Beitrag ist auch für mich eine erste Annäherung und Einführung und kann nur versuchen, sich weitergehenden philosophischen Fragen zu nähern. Ich vermute jedoch, dass in seinem Ansatz ein Potential enthalten ist, das noch bei weitem nicht erschöpft ist. Einige weiterführende Gedanken finden sich im Beitrag Freiheit des Grundes.

Motive

In seiner äußerst selbstreflektierten Arbeit betont Spencer-Brown, dass es keine Unterscheidung ohne ein bestimmtes Motiv gibt (»There can be no distinction without motive«, LoF, 1). Das scheint mir der beste Zugang zu diesem ungewöhnlichen Werk zu sein. Um seine Gedanken zu verstehen, ist es kaum möglich, sich auf das zu stützen, was bisher in Mathematik, Logik oder Philosophie gelernt und praktiziert wurde. Im Gegenteil regt er dazu an, vieles davon mühsam wieder zu verlernen und sich der tieferen Motive wieder bewusst zu werden, die ursprünglich der Begeisterung für die Mathematik zugrunde lagen und weitgehend verschüttet worden sind.

Lügner-Paradoxon und negative Selbstbezüglichkeit

Das erste Motiv ist sicher die Beschäftigung mit dem Lügner-Paradox ›Dieser Satz ist falsch‹. Mit ihm waren die logischen Grundlagen der Mathematik und damit aller Naturwissenschaft elementar in Frage gestellt. Das löste eine tiefe Verunsicherung aus, die heute – seit wir uns daran »gewöhnt« haben – kaum mehr vorstellbar ist. Denn zur gleichen Zeit waren mit dem Niedergang aller überlieferten religiösen und mythischen Glaubensvorstellungen die Mathematik und die Naturwissenschaft zur einzigen Kraft geworden, die Identität und Sicherheit zu geben versprach. Wenn nun auch ihre Grundlagen erschüttert werden, droht jeder Halt verloren zu gehen. Robert Musil hat das 1902 in Die Verwirrungen des Zöglings Törleß wunderbar gestaltet. Jeder, der zwischen 1900 und 1980 Mathematik studierte, stieß nahezu zwangsläufig auf die Russellschen Antinomien und wurde in eine Krise gestoßen vergleichbar der skeptizistischen Herausforderung an die Philosophie. Erst der lang anhaltende ökonomische Aufschwung in den westlichen Ländern nach 1945 hat zumindest für eine Weile alle Bedenken und Fragen dieser Art in den Hintergrund drängen können und blanken Pragmatismus und gewöhnlichen Materialismus als neue Werte etabliert. Welche Gefahr soll von einer solchen Antinomie ausgehen, wenn doch drum herum die Anwendungen der gleichen Wissenschaft so erfolgreich sind? In solchen Zeiten haben die Fragen eines Spencer-Brown kaum Aussicht auf Resonanz, drohen sie doch die Fragen wieder aufzurühren, die gerade mühsam unter den Teppich gekehrt worden waren.

Das Lügner-Paradoxon ist das berühmteste Beispiel für negative Selbstbezüglichkeit: Der Satz bezieht sich auf sich selbst, und er verneint sich. Das führt zum Paradox: Wenn seine Aussage richtig ist, ist er falsch, und wenn seine Aussage falsch ist, ist er richtig.

Dies Paradox kann in die unterschiedlichsten Formen gebracht werden, was Ulrich Blau bis in die äußersten Verästelungen getrieben hat mit dem Ergebnis, dass es in der gewohnten Logik nichts gibt, was aus diesem Paradox herausführt.

Der Satz ist keineswegs nur eine logische Spielerei, die jeder Jugendliche irgendwann im Alter von 12 bis 16 Jahren durchmacht und damit die IV. Stufe des kognitiven Denkens (das formale Denken) im Sinne von Jean Piaget (1896-1980) erreicht, sondern ist in der ursprünglichen Formulierung »ein Kreter sagt, dass alle Kreter lügen« von mythologischer Bedeutung, als die Kreter mit der Angst fertig werden mussten, dass sie auf der Insel Kreta Gott getötet haben könnten. In der Philosophie hat er bei Hegel systematische Bedeutung erhalten und gilt als das entscheidende Merkmal der dialektischen Methode.

Bertrand Russell war anfangs Hegelianer, konnte sich aber mit den spekulativen Sätzen Hegels über den Widerspruch nicht zufrieden geben. Für ihn musste es auch eine formale Lösung geben, die den Anforderungen der traditionellen Logik standhält. Das ist ihm mit dem Verbot selbstbezüglicher Sätze nur negativ gelungen, und er war daher begeistert, als Spencer-Brown eine völlig neue, formale Lösung präsentieren konnte.

Imaginäre Zahlen

Spencer-Brown suchte einen Ausweg nach dem Vorbild der imaginären Zahlen. Die imaginären Zahlen sind innerhalb der Mathematik ein eigenartiger, geheimnisvoller Fremdkörper. Schon der Name imaginär ist völlig untypisch für das übliche mathematische Denken. Sind diese Zahlen imaginär wie ein bloßer Traum, oder sind sie bloße Bilder, virtuelle Objekte des Denkens, entsprungen aus der Imagination (Einbildungskraft, Phantasie) der Seele? Was zeichnet eine mathematische Imago gegenüber einer psychologischen Imago aus? Fragen dieser Art haben Spencer-Brown nach seiner Therapie bei Laing sicher sehr bewegt.

Der Ausdruck imaginäre Zahl geht auf Descartes und Euler zurück. Für Mathematiker ist es ein in sich widerspruchsfreier Formalismus, den Zahlenraum zu erweitern, und für Ingenieure und Physiker ist es ein überaus hilfreiches Werkzeug, komplexe Gleichungen zu vereinfachen, auch wenn sie in der Regel kaum die Frage beantworten können, warum das mit den imaginären Zahlen möglich ist. Als Nachrichtentechniker war Spencer-Brown zweifellos mit dieser Bedeutung vertraut und hatte gelernt, wie Ingenieure und Naturwissenschaftler einfach mit solchen Zahlen rechnen, weil das gut geht und sich bewährt, ohne nach den mathematischen Grundlagen zu fragen.

Im Vorwort zur ersten amerikanischen Ausgabe von Laws of Form hat er 1972 eine verblüffende Beziehung der imaginären Zahlen zur Frage der Russellschen Antinomie gesehen. Russell und Whitehead wollten die drohende Antinomie in der Typen-Theorie mit dem Verbot selbstbezüglicher Elemente ausschließen. Das hielt Spencer-Brown für einen Fehler. »Mistakenly, as it now turns out.« (LoF, ix) Spencer-Brown berichtet, dass er Russell 1967 getroffen und ihm gezeigt hat, wie er ohne diesen Ausschluss arbeiten kann. »The Theory was, he said, the most arbitrary thing he and Whitehead had ever had to do, not really a theory but a stopgap, and he was glad to have lived long enough to see the matter resolved.« (LoF, x)

Um innerhalb der Arithmetik eine negative Selbstbezüglichkeit zu definieren, ist eine Gleichung aufzustellen, in der eine Variable x als ihr eigener Kehrwert auftritt und mit dem Minus-Zeichen negiert wird:

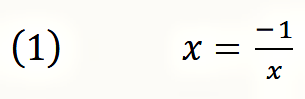
Mit dieser Gleichung ist die negative Selbstbezüglichkeit formalisiert: Der Kehrwert steht für den Selbstbezug, das Minuszeichen für die Negation.

Diese Gleichung sieht auf den ersten Blick ebenso harmlos aus wie wenn jemand zum ersten Mal den Satz hört ›dieser Satz ist falsch‹. Jeder hält das im ersten Moment für eine gewöhnliche Aussage über einen anderen Satz (einer sagt, ›der Himmmel ist grün‹ und ein anderer antwortet darauf ›dieser Satz ist falsch‹), bis dessen innere Sprengkraft durchschaut wird, wenn er sich auf sich selbst bezieht. So sieht auch Formel (1) auf den ersten Blick nicht ungewöhnlich aus. Das in ihr enthaltene Paradox wird sichtbar, wenn für x der Wert 1 oder der Wert −1 eingesetzt wird:

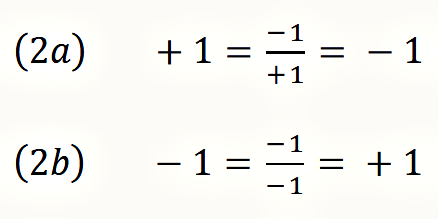
1 und −1 sind die einfachst-möglichen Zahlen, und sie zeigen, dass es für diese Formel keine natürliche Zahl als Lösung gibt. Mit ihr hat Spencer-Brown das Paradox der negativen Selbstbezüglichkeit innerhalb der Arithmetik nachgebildet. (In der tradionellen Logik und der analytischen Philosophie geschulte Wissenschaftler bestreiten allerdings, dass es zulässig ist, auf diese Weise das ursprünglich mengentheoretisch formulierte Russellsche Paradoxon zu transformieren und eine verblüffende Lösung zu finden. So habe ich es beim Wittgenstein-Symposium 2018 in Kirchberg am Wechsel erlebt.)

Whitehead und Russell hatten nur den Ausweg gesehen, Fragen dieser Art mit dem unbestimmten, dritten »Wahrheitswert« ‘bedeutungslos‘ (meaningless) zu versehen und auszuschließen. Während mit diesem Wahrheitswert logisch und mathematisch nicht operiert werden kann, kann eine Lösung mit den imaginären Zahlen gefunden werden, die das Rechnen mit einem zusätzlich Wahrheitswert erlaubt. Die imaginären Zahlen stehen wie die y-Achse senkrecht zur Zahlenachse. Ihre Einheit ist die neu eingeführte Zahl i. Sowohl i wie auch −i sind Lösungen von Gleichung (1).

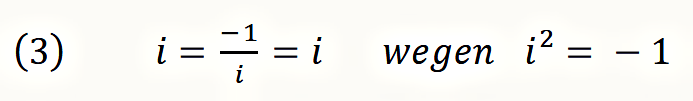
Darum geht es Spencer-Brown. Er fragt sich, ob nach dem Vorbild der imaginären Zahlen in der Arithmetik auch imaginäre Zahlen in der Logik eingeführt werden können mit weitreichenden Folgen für das logische Denken.

»What we do in Chapter 11 is extend the concept of Boolean algebras, which means that a valid argument may contain not just three classes of statement, but four: true, false, meaningless, and imaginary.« (LoF, xi)

Die traditionelle Logik ist zugleich zu einfach und zu komplex

Diese Beispiele zeigen bereits den neuen Zugang zur Logik bei Spencer-Brown. Er war mit der überlieferten Logik völlig unzufrieden. Die ist für ihn banal, um nicht zu sagen kindisch, und zugleich unnötig kompliziert.

(1) Die traditionelle Logik ist einerseits zu einfach, geradezu kindisch.

Wer einmal Lehrbücher der Logik gelesen hat mit ihren Beispielen, versteht was Spencer-Brown meint. Eine typische logische Aufgabe lautet: »Welche der folgenden Behauptungen ist wahr: Einige Äpfel sind Bananen. Alle Äpfel sind Bananen. Einige Bananen sind keine Äpfel. Manche Bananen sind Äpfel.« Die richtige Lösung ist versteckt in dem Satz »Einige Bananen sind keine Äpfel.« Darauf kommt niemand gleich, weil das niemand im alltäglichen Leben so sagen würde, denn jeder würde spontan diesen Satz so verstehen, dass er implizit auch die falsche Aussage enthält, dass es einige Bananen gibt, die Äpfel sind. Aber formal ist dieser Satz richtig, und das soll eine Aufgabe wie diese zeigen. Sie soll ein abstraktes Verständnis für Logik lehren, das unabhängig ist von einem inhaltlichen Vorverständnis und Sprachgefühl.

Ist Logik nichts weiter als die Suche nach witzigen Logeleien, über die jeder schmunzeln muss? Das kann beliebig ausgebaut werden: Ist ein Satz wie »die Zahl 2 ist gelb« wahr oder falsch, und was kann aus diesem Satz gefolgert werden? Was ist von dem Schluss zu halten: »Wenn John keine Kinder hat, ist sowohl die Aussage wahr, ›Alle Kinder von John schlafen‹ wie auch die konträre Aussage ›Keins von Johns Kindern schläft‘.« Ist damit der Satz des Widerspruchs widerlegt? Die analytische Philosophie denkt sich nach diesem Muster bis heute immer neue Beispiele aus und schlägt sich seit Jahrzehnten mit Fragen dieser Art herum, obwohl bereits Herbert Marc#use (1898-1979) diese Art zu denken in den 1960ern verspottet hatte (Der eindimensionale Mensch, 1964) und darin im Grunde eine bestimmte Art der Erziehung zur Dummheit sieht, die leider auch an den Universitäten nahezu alle philosophischen Fakultäten dominiert, an denen Philosophen dieser Richtung bevorzugt eingestellt werden. Offenbar sollen in großem Stil an den Universitäten Menschen und vor allem Lehrer ausgebildet werden, die mit dieser Art von Logik in den Schulen Unterricht erteilen können.

Aufgrund seiner Ausbildung in Logik hatte Spencer-Brown eine Stelle bekommen, um Schaltkreise zu programmieren, und merkte schnell:

»The logic questions in university degree papers were childishly easy compared with the questions I had to answer, and answer rightly, in engineering. We had to devise machinery which not only involved translation into logic sentences with as many as two hundred variables and a thousand logical constants--AND's, OR's, IMPLIES, etc.--not only had to do this, but also had to do them in a way that would be as simple as possible to make them economically possible to construct--and furthermore, since in many cases lives depended upon our getting it right, we had to be sure that we did get it right.« (AUM, Session One)

Im Ergebnis konnten er und die anderen Entwickler sich zwar allgemein auf ihr logisches Denkvermögen verlassen, programmierten aber drauf los und gaben es sehr schnell auf, ihre Programme systematisch gemäß den Regeln der gelernten Logik zu entwerfen und zu überprüfen, sondern waren zufrieden als sie sahen, dass die von ihnen programmierten Schaltkreise funktionieren, ohne das logisch erklären oder beweisen zu können. So geht es nach meiner Erfahrung den meisten Programmierern, und es hinterlässt dennoch ein Unbehagen, dass es eine andere Art von Logik geben müsste, die der Praxis des Programmierens näher kommt und hilfreicher ist. (Wer hat sich als Programmierer nicht mit Methoden wie z.B. dem logisch aufgebauten Programmablaufplan herumgeschlagen und es irgendwann fallen gelassen, weil der Aufwand, Programmerweiterungen in Methoden dieser Art nachzubilden größer ist als die Programmierung und das Austesten. Bei komplexen Programmen sind logische Methoden dieser Art komplizierter als der Programmtext selbst, und in der Realität hat sich für Dokumentationen ein übersichtlicher Pseudocode durchgesetzt, der die Algorithmen in einer einfach zu lesenden Sprache darstellt.)

(2) Zugleich ist die Logik viel zu komplex.

Fast gebetsmühlenartig wird am Anfang jeder Logik- und Mathematik-Vorlesung ein großer Aufwand mit der Einführung unterschiedlichster Zeichen getrieben, obwohl die jeder intuitiv versteht. Das sind eigene Zeichen für Konstanten, Variablen, logische Operationen wie ∧, ∨, ¬ und Quantoren wie ∀ und ∃. Die unterschiedlichen Professoren und Lehrbücher überbieten einander darin, den erforderlichen Begriffsapparat so abstrakt wie möglich einzuführen. Ein Beispiel ist die online verfügbare Vorlesung Endliche Modelltheorie von Geschke:

»1.1. Strukturen. Ein Vokabular ist eine endliche Menge bestehend aus Relationssymbolen P, Q, R, …, Funktionssymbolen f, g, h, … und Konstantensymbolen c, d, … Jedes Relations- und Funktionssymbol trägt eine natürliche Zahl ≥ 1, seine Stelligkeit.
   Fixiere ein Vokabular . Eine Struktur für (eine -Struktur) ist eine Menge A zusammen mit
   (S1) Relationen ⊆ An für jedes n-stellige Relationssymbol ∈ ,
   (S2) Funktionen : Am → A für jedes m-stellige Funktionssymbol ∈ und
   (S3) Konstanten 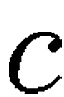∈ A für jedes Konstantensymbol ∈ .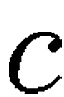
   Oft identifiziert man eine Struktur mit ihrer unterliegenden Menge A, schreibt also A anstatt .« (Geschke, S. 1)

Wer Mathematik und Logik studiert hat, versteht, warum auf solche Weise eine Vorlesung eingeleitet wird, und doch hat jeder das Gefühl, dass an dieser Art an die Sache heranzugehen etwas nicht stimmen kann. Am Ende wird versucht, alles deduktiv aus einer einzigen Lehre abzuleiten. Das gelingt nicht. Stattdessen scheint sich heute die Ansicht durchgesetzt zu haben, dass am Anfang mehr oder weniger gleichberechtigt die Mengenlehre, die Modelltheorie und die Theorie formaler Sprachen stehen. Die Mengenlehre kommt nicht aus ohne eine formale Sprache, die formale Sprache nutzt die Mengenlehre, jede Lehre kann als ein Modell verstanden werden, das aber wiederum wie an diesem Beispiel zu sehen einer formalen Sprache und mengentheoretischer Operationen bedarf. Im Ergebnis entsteht der Eindruck, dass es nicht gelungen ist, die unterschiedlichen Lehren auf ihre einfachsten Elemente zurückzuführen, und die große Abstraktheit und der komplexe technische Apparat im Grunde eine Flucht sind, um dieser Frage auszuweichen.

Für Spencer-Brown ist diese ganze Richtung ein Irrweg. Seine erste Grundentscheidung ist daher, eine wesentliche Reduktion vorzunehmen und damit einen Bereich zu eröffnen, der als Proto-Logik oder als Proto-Mathematik bezeichnet werden kann. Er versteht seine Herangehensweise als »perfect continence« (LoF, 1), eine Mäßigkeit und Selbstkontrolle bei Klärung der logischen Grundlagen.

Logik und Zeit

Die klassische Logik gilt unabhängig von der Zeit. Mit ihr werden nur Aussagen getroffen und verknüpft, die für sich zeitlos gültig sind. Eine Tatsache oder eine Beobachtung bleibt immer bestehen, selbst bei Sätzen, die sich auf einen bestimmten Zeitpunkt beziehen. Ein Satz wie ›Am 24.2.2017 sind in Bensheim die ersten Krokusse des Jahres 2017 aufgeblüht‹ gilt auch dann noch, wenn die Krokusse längst wieder verblüht sind. Er gilt selbst dann, wenn er sich als eine Täuschung erweist, denn dieser Satz ist für sich genommen eine Gegebenheit meines Denkens. So hatte Wittgenstein 1921 den Tractatus logico-philosophicus begründet: »1 Die Welt ist alles, was der Fall ist. [...] 1.13 Die Tatsachen im logischen Raum sind die Welt.« Für ihn ist die Welt die Gesamtheit aller Protokollsätze. Spencer-Brown hatte 1950-51 miterlebt, wie Wittgenstein über diesen Ansatz hinausgehen wollte. Es ist zu wenig, die Logik auf Sätzen dieser Art und ihren Verknüpfungen zu begründen.

Nun ist die Logik dabei nicht stehen geblieben. So wurde 1954 von Paul Lorenzen (1915-1994) die operative Modallogik entwickelt, mit der die Unterschiede von Möglichkeit, Wirklichkeit und Notwendigkeit logisch erfasst und formalisiert werden sollen. Der technische Apparat ist so weit wie möglich angepasst an die traditionelle Logik. Diese Richtung hat in Verbindung mit der Quantenlogik einen gewissen Aufschwung genommen. – Auch in der Modallogik fehlt noch die Berücksichtigung der Zeit. Das wurde zur gleichen Zeit in den 1950ern mit einer Temporalen Logik zu lösen versucht. Wer sich die bisher vorliegenden Ergebnisse sowohl der Modallogik wie der temporalen Logik ansieht, wird verstehen, warum das nicht das ist, was Spencer-Brown suchte. Er ging auf einem ganz anderen Weg von der praktischen Erfahrung aus, dass beim Programmieren das Gleichheitszeichen kontextabhängig als Zuweisung oder als Übereinstimmung verstanden wird.

Auf diesen Aspekt hat Elena Esposito hingewiesen (Esposito in Baecker Kalkül der Form, 108-110). Bei Computer-Anweisungen ist es weder ein Widerspruch noch ein Paradox, wenn geschrieben wird:
(4a)    i = i + 1
(4b)    a = f(a)

In der Zuweisung (4a) steht das Zeichen i anders als in mathematischen Gleichungen nicht für eine Variable, für die zwar eine beliebige Zahl eingesetzt werden kann, die dann aber im Verlaufe der Rechnung festzuhalten ist, sondern für einen Speicherplatz, dessen Inhalt im Verlaufe der Programm-Ausführung verändert werden kann. Bei beiden Zuweisungen liegt das Ergebnis auf der linken Seite zeitlich später als die Rechenoperation auf der rechten Seite. Die Zuweisung ›i = i + 1‹ ist eine der am häufigsten verwendeten Programmierzeilen, wenn in einer Schleife im Verlaufe einer zeitlichen Wiederholung mitgezählt wird, wie oft die Schleife durchlaufen wurde. Und ebenso ist die Anweisung ›a = f(a)‹ eine zeitliche Operation, die aus dem Speicherplatz a den dort aktuell gespeicherten Wert einliest, ihn mit einer Funktion f(a) neu berechnet und anschließend das Ergebnis dem Speicherplatz a neu zuweist. Das a auf der linken Seite hat daher in der Regel einen anderen Wert als das a auf der rechten Seite. Wenn z.B. in einer Anlagenbuchhaltung am Speicherplatz a der Wert einer Anlage steht und mit der Funktion f neu berechnet wird, verändert sich dadurch der Inhalt am Speicherplatz a. Auf der rechten Seite steht das »alte a«, auf der linken Seite das mit einer Funktion f berechnete »neue a«. Die Verständnisschwierigkeit entsteht, weil in der Programmierung abgekürzt wird: Das Zeichen a steht sowohl für den Speicherplatz wie für den Wert, der an diesem Speicherplatz gespeichert ist.

Aufzuklären, was hier beim Programmieren geschieht und dafür eine geeignete Logik zu finden, ist für mich eins der stärksten Motive von Spencer-Brown. Wenn seine Arbeiten bisher von der Informatik nahezu vollständig ignoriert werden, zeigt das für mich nur, in welchem Ausmaß die Informatik unfähig ist, gegenüber ihrem eigenen Tun so etwas wie eine transzendentale Wende zu finden, wie es Kant innerhalb der Philosophie geleistet hatte, und wie es nach meinem Eindruck Spencer-Brown für die Programmierung suchte. Gerade für einen Mathematiker und Informatiker ist das Buch von Spencer-Brown nicht einfach zu lesen. Er ist zwar besser vertraut als andere mit formalen Überlegungen dieser Art, muss sich aber von festgefahrenen Vorurteilen befreien. Er muss – wie Spencer-Brown sagte – viel verlernen, und das Verlernen schrittweise angehen, um nicht bereits beim ersten Schritt in zu große Verwirrung zu geraten.

Spencer-Brown antwortete auf eine Frage von John Lilly (1915-2001) (Neurophysiologe, Delfin-Forschung, Untersuchung von Drogen und ihren Wirkungen wie LSD, Einfluss auf New Age):

»LILLY: Have you formulated or recommended an order of unlearning?
SPENCER BROWN: I can't remember having done so. I think that, having considered the question, the order of unlearning is different for each person, because what we unlearn first is what we learned last. I guess that's the order of unlearning. If you dig too deep too soon you will have a catastrophe; because if you unlearn something really important, in the sense of deeply imported in you, without first unlearning the more superficial importation, then you undermine the whole structure of your personality, which will collapse. Therefore, you proceed by stages, the last learned is the first unlearned, and this way you could proceed safely.« (AUM, first session)

Der Einfluss des Beobachters

Die transzendentale Wende von Kant ist eine neue Art von Selbstbeobachtung, mit der das Denken sein eigenes Tun untersucht. Kant war sich bewusst, dass er mit ihr eine Wende nachvollzog, die sich bereits in der Astronomie mit der kopernikanischen Wende ereignet hatte, als deutlich geworden war, in welcher Weise das Weltbild vom jeweiligen Standort des Beobachters abhängig ist. Die Welt stellt sich anders dar, wenn sie in Gedanken nicht mehr von der Erde aus, sondern von der Sonne aus gesehen wird. Sachlich bleibt alles gleich, aber die Bewegungen der Sonne, Planeten und des Mondes sind mathematisch wesentlich einfacher in Bewegungsgleichungen zu bringen. An ihnen werden Muster erkennbar (die Keplerschen Gesetze), die mit bloßem Augenschein von der Erde aus nicht zu sehen sind.

Bei Einstein spielt die Geschwindigkeit, mit der sich ein Beobachter bewegt, eine Rolle, wie er andere Bewegungen wahrnimmt. In der Quantenmechanik wird befürchtet, dass nichts so gemessen werden kann, wie es ist, da es durch die Messung verändert wird, also der Messvorgang in die Messung eingreift.

Von noch größerer Bedeutung ist der Beobachter für die Psychologie und Soziologie, und nicht ohne Grund ist vor allem dort die Lehre von Spencer-Brown aufgegriffen worden. Kant hielt eine wissenschaftliche Psychologie für unmöglich. Für ihn war schon fraglich, ob die Chemie jemals eine Wissenschaft mit mathematischen Methoden werden kann, aber für die Psychologie hielt er das für ganz ausgeschlossen. Jedes denkende Wesen wird merken, wenn es beobachtet wird, und entsprechend reagieren. Daher kann der Beobachter nie sicher sein, ob der andere nur deshalb so ist, wie er ist, weil er sich auf ihn einstellt. Die Psychoanalyse berücksichtigt das teilweise, seit sie mit Freud das Phänomen der Übertragung kennt, wenn ein Patient sich unbemerkt den Erwartungen des Analytikers anpasst und dieser sich umgekehrt unbewusst so verhält, wie es der Patient von ihm erwartet (Gegenübertragung).

»Aber auch nicht einmal als systematische Zergliederungskunst, oder Experimentallehre, kann sie (die Psychologie, t.) der Chemie jemals nahe kommen, weil sich in ihr das Mannigfaltige der inneren Beobachtung nur durch bloße Gedankenteilung von einander absondern, nicht aber abgesondert auf behalten und beliebig wiederum verknüpfen, noch weniger aber ein anderes denkendes Subjekt sich unseren Versuchen der Absicht angemessen von uns unterwerfen läßt, und selbst die Beobachtung an sich schon den Zustand des beobachteten Gegenstandes alteriert und verstellt. Sie kann daher niemals etwas mehr als eine historische, und, als solche, so viel möglich systematische Naturlehre des inneren Sinnes, d.i. eine Naturbeschreibung der Seele, aber nicht Seelenwissenschaft, ja nicht einmal psychologische Experimentallehre werden.« (Kant Metaphysische Anfangsgründe der Naturwissenschaften, Vorrede, MAN, AA 04:471.22-32)

Hat sich das für Spencer-Brown in seiner eigenen psychotherapeutischen Erfahrung bestätigt? Lassen sich anders als Kant glaubt im Verhalten des Beobachters und des Beobachteten in der psychologischen Praxis Muster erkennen, die über die jeweilige Persönlichkeit hinausgehen? Mir ist nicht bekannt, ob und wie intensiv sich Spencer-Brown mit den Lehren etwa von Husserl, Heidegger, Sartre und anderen beschäftigt hat, die dieser Frage nachgegangen sind. Luhmann und Scheier stellen die Logik von Spencer-Brown in diesen Kontext und versuchen ihn von dort aus zu verstehen.

Hier erhält die Frage nach dem Re-entry eine neue Bedeutung. In der psychologischen und soziologischen Praxis ist Re-entry nicht einfach eine möglicherweise rein mechanische Resonanz, Feedback oder eine wie in selbst-referentiellen Systemen nahezu automatisch ablaufende Rückkopplung, sondern der Beobachtete bekommt vom Beobachter auf sein Verhalten eine Rückmeldung und reagiert darauf.

Prozess und Resultat

Wenn Spencer-Brown von seiner Berufserfahrung her das pragmatische Tun hervorhebt, stellt er damit das überlieferte Verhältnis von Prozess und Resultat in Frage. Da die traditionelle Logik nur zeitlose Aussagen kennt, die immer gelten und sich nie ändern, hat sie nicht die Logik von Prozessen untersucht. Für Aristoteles waren Logik und Physik klar getrennt. Die zeitlosen Aussagen hat er systematisch in den beiden Analytiken (Analytica protera und Analytiká hystera) untersucht, wogegen es in der Physik als der Lehre von den vergänglichen Dingen und Wesen, die Werden und Vergehen unterworfen sind, zu Zeit, Bewegung und Veränderung kommt (so auch der Titel seiner Schrift über das Werden und Vergehen, peri geneseôs kai phthoras). In der Physik bildete er mit energeia und entelecheia neue Begriffe, die nur für den Verlauf von Prozessen gelten und bewusst den Rahmen der Analytiken verlassen und einem neuen logischen Verständnis nahekommen. (Sie sind seither als Energie und Entelechie zu Grundlagenbegriffen in der Physik und Biologie geworden. Heidegger hatte sie als Existenzialien bezeichnet, es aber für unmöglich gehalten, für sie eine der traditionellen Logik vergleichbare Formalisierung zu finden.)

Spencer-Brown will die Logik begründen auf Begriffen, in denen Prozess und Resultat noch nicht klar getrennt sind. Dies Anliegen teilt er mit Hegel, der systematisch solche Begriffe benutzt hat. ‘Anfang’: Das kann sowohl der Vorgang des Anfangens wie das Resultat sein, das angefangen wurde. Ähnlich Bestimmung, Entwicklung, Messung usf.: Eine Messung kann der Vorgang des Messens sein, wie auch der Messwert, der gemessen wurde. Bestimmung kann der Vorgang des Bestimmens sein wie das Ergebnis, dass etwas so und nicht anders bestimmt ist.

Spencer-Brown gründet seine Logik mit Distinction (Unterscheidung) und Indication (Anzeige, Hinweis) auf ähnliche Begriffe. Das kann sowohl der Vorgang des Bezeichnens und Unterscheidens sein wie auch das Ergebnis, wenn eine Unterscheidung getroffen ist und eine Bezeichnung gefunden wurde. Es ist der Vorgang, etwas zu unterscheiden, und im Ergebnis das Zeichen (mark) und der Wert (value), der dem Etwas mit der Unterscheidung verliehen wird.

Wenn mit Begriffen begonnen wird, bei denen die Unterscheidung in Prozess und Resultat bewusst offen gehalten wird, dann muss es innerhalb der Logik einen klar erkennbaren und nachvollziehbaren Weg geben, dort Zeit und Bewegung einzuführen und diese Offenheit in ihre beiden Bestandteile auseinander zu legen. Dies Motiv sehe ich besonders in der Unterscheidung der primären Arithmetik und primären Algebra wie in der Einführung des Re-entry und der mit dem Re-entry gegebenen Zeit.

Die Zeichen und ihr Medium

Ist es für einen Mathematiker schon ungewohnt, die veränderte Bedeutung von Variablen im zeitlichen Verlauf von Zuweisungen in der Programmierung und der Logik von Spencer-Brown einerseits und den zeitlos gedachten mathematischen Gleichungen andererseits zu akzeptieren, so erfordert es ein noch weiter gehendes Umdenken, das Verhältnis von Zeichen und Medium als wechselseitigen Prozess anzusehen. Es ist für einen Mathematiker geradezu absurd anzunehmen, dass das Medium, in das die mathematischen Zeichen eingeschrieben sind, Einfluss auf die Zeichen und ihre Operationen nehmen könnte. Im Grunde stellt sich jeder Mathematiker die Zeichen seiner Formeln völlig unabhängig vom Medium vor, in dem sie dargestellt sind, am besten als Objekte in einem gänzlich immateriellen, rein geistigen Raum. Wenn er eine Tafel oder ein Blatt Papier oder einen Bildschirm braucht, um dort seine Formeln aufschreiben zu können, sind das nur Hilfsmittel ohne Einfluss auf die Inhalte des Rechnens und Beweisens. Es kann sein, dass eine Formel auf einem schlechten Hintergrund verschwimmt und daher falsch gelesen wird mit Ergebnissen, die in die Irre führen. Doch ist das nichts weiter als ein Störfaktor, der idealerweise ausgeschlossen werden kann. Die Aussagen mathematischer Sätze gelten prinzipiell unabhängig vom Medium, in dem sie aufgeschrieben werden.

Diese Einstellung ist 1948 mit der Arbeit von Claude Shannon (1916-2001) über die Mathematischen Grundlagen in der Informationstheorie erschüttert worden. Shannon war wie Spencer-Brown Mathematiker und Elektrotechniker. Er hat in seiner Untersuchung von Datenübertragungen nachgewiesen, wie jedes Medium ein Grundrauschen erzeugt, das die übertragenen Zeichen stört. Die Mathematik hat bis heute nicht wahrgenommen oder nicht wahrnehmen wollen, welche elementaren Konsequenzen sich daraus auch für die Mathematik und die Logik ergeben. Die Mathematik gilt bis heute als eine Lehre, die unabhängig vom Medium gilt, in dem sie geschrieben und über das sie übertragen wird. Niemand kann sich vorstellen, dass das Medium einen Einfluss auf die Zeichen und ihre Aussagen haben könnte. Mathematik gilt als eine Lehre, die im prinzipiell unbewegten Geist entwickelt wird.

Für Spencer-Brown relativiert sich das. Für ihn kam mit dem Entwurf von Schaltkreisen eine prinzipiell neue Erfahrung hinzu, die noch weit über das bloße Programmieren hinausgeht. Schaltkreise sind auf den ersten Blick nichts anderes als eine graphische, anschauliche Formelsprache, die in ihrem logischen Status den Zeichen der Mathematik ähneln und ihnen letztlich entsprechen sollten. Doch zeigte sich für ihn bei den Schaltkreisen, die er entworfen und mit denen er gerechnet hat, dass jeder Schaltkreis eine Eigendynamik enthält, die die mit dem Schaltkreis entworfenen Aussagen und Ergebnisse mit tragen. Es lässt sich in Worten und Formeln beschreiben, welchen Input ein Schaltkreis verarbeitet und zu welchem Output er führt, aber es lässt sich nicht restlos erklären, wie es zu diesen Ergebnissen kommt. Offenbar enthält der Schaltkreis eine Art von Selbstorganisation, die aus sich heraus das Ergebnis beeinflusst. Wer einen Schaltkreis entwirft, hat zwar ein klares Ziel vor Augen und kann den Schaltkreis gestalten und realisieren, aber er kann nicht völlig voraussagen, was im Schaltkreis geschieht. Im Gegenteil verlässt er sich darauf, dass der Schaltkreis von sich aus eine Stabilisierung bewirkt, die dem Ergebnis erst die erwartete Sicherheit verleiht. Auch wenn sich bei näherer Untersuchung viele der Prozesse erklären lassen, die im Schaltkreis zum gewünschten Ergebnis geführt haben, bleibt immer ein Rest zurück. Diese Eigenschaft ergibt sich nicht aus der graphischen Gestalt und ihrer Formelemente, sondern aus dem Medium, in dem der Schaltkreis verwirklicht wird. Spencer-Brown vergleicht es mit der Chemie: Niemals kann mit chemischen Formeln vollständig beschrieben werden, was in einer chemischen Reaktion geschieht. Im realen chemischen Prozess steckt eine Eigendynamik, die trotz aller Vorkehrungen immer zu Überraschungen führen kann. Aus heutiger Sicht kann die Zellbiologie als weiteres Beispiel genannt werden. Es hat sich gezeigt, dass selbst die vollständige Aufschlüsselung des DNA-Codes nicht dazu führt, die Vorgänge in einer Zelle umfassend voraussagen zu können. In allen diesen Beispielen handelt es sich um Texte oder textähnliche Formen (die Graphik des Schaltplans, die chemischen Reaktionsgleichungen, der DNA-Code), die grundsätzlich unvollständig sind und das Medium, in dem sie realisiert werden, nicht vollständig abbilden können. Ist diese Erfahrung in einer Art von Grenzprozess auch auf die Mathematik und die Logik zu übertragen, oder zumindest dort geeignet zu berücksichtigen?

Das führt Spencer-Brown zur grundsätzlichen Frage nach dem Verhältnis der Zeichen und des Mediums. Das Ergebnis ist sicher nicht, dass die heute bekannte Mathematik »falsch« wird, weil sie ihr Medium und dessen Mitwirkung übersehen hat. Sondern das Ergebnis ist, dass die Mathematik vor dem Horizont einer übergreifenden Lehre von Medium und Zeichen zu verstehen ist, aus der heraus der besondere Status der Mathematik und die Bedingungen verständlich werden, warum sie in der uns bekannten Weise gilt.

Für mich ist dies das am schwersten zu verstehende und zugleich folgenschwerste Motiv von Spencer-Brown. Wird eine Logik entworfen, die selbstreflexiv ihr eigenes Medium versteht, in dem sie sich gründet, eingeschrieben ist und übertragen wird, dann kann das zum Entwurf einer Logik der medialen Moderne führen, die der heutigen Verfassung des Menschen gerecht wird. Auf den Stellenwert des Mediums zum Verständnis unserer Kultur hat insbesondere Scheier in Luhmanns Schatten hingewiesen. Spencer-Brown kann helfen, das weiter auszuarbeiten.

Neuronale Netze

Während die Paradoxa und Antinomien von Russell und Gödel bis in die Philosophie intensiv diskutiert werden, blieb die Entwicklung einer neuen Logik weitgehend unbeachtet, die von einem Aufschwung neurophysiologischer Forschungen ausging und zu den Neuronalen Netzen führte. Erst mit spektakulären Erfolgen wie dem Go spielenden Programm AlphaGo von 2015-16 ändert sich das schlagartig. Programme wie diese sind das Ergebnis einer inzwischen mehr als 100 Jahre andauernden Entwicklung. In dieser Tradition sehe ich auch Spencer-Brown.

Eine Schlüsselrolle spielte Warren McCulloch (1898-1969). Er studierte Philosophie, Psychologie und Medizin, arbeitete vor allem als Neurophysiologe und sieht sich sowohl in der Tradition der schon immer praktisch orientierten und pragmatisch denkenden amerikanischen Philosophie wie auch der um 1900 entstehenden Neurophysiologie. Von der amerikanischen Philosophie nennt er insbesondere Charles Sanders Peirce (1839-1914) und Josiah Willard Gibbs (1839-1903), sodann auf sie aufbauend die Diskussion während der 1940er mit Norbert Wiener (1894-1964), Arturo Rosenblueth (1900-1970), John von Neumann (1903-1957) und Walter Pitts (1923-1969). Die meisten von ihnen haben sich sicher eher als Fachwissenschaftler denn als Philosophen verstanden, weil sie von der Philosophie ihrer Zeit keine anregenden Impulse mehr erwarteten. Viele von ihnen blieben bewusst außerhalb des akademischen Bereichs bzw. wurden dort nicht aufgenommen (so Norbert Wiener). Wenn es dennoch zu tiefen philosophischen Fragen und Gesprächen kam, ist das vor allem McCulloch zu verdanken.

McCulloch hatte über Jahrzehnte mit immer neuen Ansätzen nach einer neuen Logik gesucht, die über die Tradition von Aristoteles bis Frege und Russell hinausgeht. 1920 wollte er die in allen klassischen Aussagen nach dem Muster ›S ist P‹ auftretende Copula ‘ist’ erweitern in drei Gruppen von Verben: (i) Verben, die von einem Objekt zu einem Subjekt führen und aus der Vergangenheit kommen, während die Copula ‘ist’ nur in einer zeitlosen Gegenwart auftritt; (ii) Verben, die von einem Subjekt zu einem Objekt und damit in die Zukunft führen; (iii) Verben, die einen andauernden Zustand beschreiben. Doch führte das nicht zum Erfolg. Es folgten Bemühungen, für das psychische Denken auf ähnliche Weise nach kleinsten Einheiten zu fahnden, wie es der Physik mit den Elektronen, Photonen und anderen physikalischen Elementen gelungen war: Er nannte sie Psychone. Sie sollten in anderer Weise als die traditionellen Objekte und Beziehungen der Logik miteinander verknüpft sein, um mit ihnen das psychische Geschehen und die von der Psychiatrie untersuchten Krankheiten darstellen und Therapien finden zu können. Auch das lieferte nicht die gewünschten Ergebnisse. Die Wende kam erst, als er mit den Arbeiten der Neurophysiologie vertraut wurde und sich aktiv als Forscher an dieser Richtung beteiligte. Er sah von Anfang an die Möglichkeit, mit ihnen der transzendentalen Logik von Kant einen neuen Boden zu geben (wenn das Netzwerk von den Sinnesorganen zum Gehirn an die Stelle der transzendentalen Apperzeption tritt und die Vorprägung aller sinnlichen Reize erklärt, bevor es zum Denken in Vorstellungen und Begriffen kommt). An seinem Lebensende veröffentlichte er einen Sammelband wichtiger Arbeiten mit dem programmatischen Titel Verkörperungen des Geistes. Er nahm 1946-1953 federführend an den Macy-Konferenzen teil. Viele Ideen waren im Verlaufe des 2. Weltkriegs im Rahmen des 1941 vom US-Präsidenten Roosevelt gegründeten Office of Strategic Services (OSS) entstanden, an dem auch Marcuse, Bateson, Sweezy und andere Vertreter der späteren Neuen Linken mitarbeiteten. Nach 1945 ging aus dem OSS zum einen der CIA hervor, zum anderen suchten viele Beteiligte nach einer Fortführung ihrer Arbeit im Rahmen einer zivilen Anwendung. Sie waren überzeugt am Beginn einer völlig neuen Entwicklung zu stehen.

Bereits 1931 hatte McCulloch von den neuen Arbeiten von Kurt Gödel (1906-1978) erfahren und beschäftigte sich von Anfang mit den Ergebnissen von Alan Turing (1912-1954), die seit 1937 veröffentlicht wurden. Dort war der Beginn einer völlig neuen Art von Logik zu erkennen, und es ist ohne Zweifel die besondere Leistung von McCulloch, die Vielfalt dieser Strömungen miteinander in Verbindung gebracht zu haben.

Der Durchbruch kam für ihn mit der Neurophysiologie. Sie nahm ihren Anfang mit dem Mediziner Ramón y Cajal (1852-1934). Von ihm stammen die ersten Diagramme von Sinnesorganen und den von ihnen ausgehenden Nervenbahnen, die er aus gründlichen Untersuchungen des Nervensystems und dem Sezieren von Fröschen und anderen Tieren gewonnen hatte. Der Mediziner, Psychiater und Psychoanalytiker Lawrence Kubie (1896-1973) beschrieb an ihrem Beispiel 1930-41 erstmals Schaltkreise, geschlossene Nachhall-Kreise (closed reverberating circuits), um das Gedächtnis zu verstehen.

Für mich sind in Hinblick auf Spencer-Brown vor allem zwei Ergebnisse wichtig: Am Beispiel der Nervenbahnen vom Froschauge zum Froschgehirn wurden zwei wichtige Prinzipien erkannt, die indirekt in den Gesetzen der Form nachwirken.

Prinzip der Additivität: Erst wenn ausreichend viele Nervenbahnen einen Input melden, wird er zum Gehirn weiter geleitet. Einzelne, isolierte Inputs werden dagegen ignoriert. Wenn die Selektion nicht funktioniert, wird das Gehirn gleichsam überschwemmt und darüber überfordert. Das ist eine Ursache für Epilepsie.

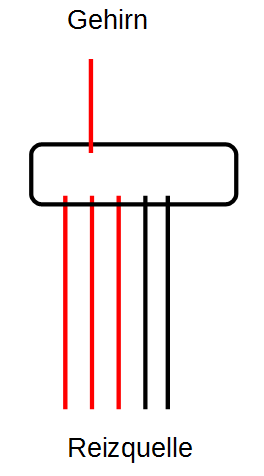
Gedächtnis: Zusätzlich wird bei Überschreiten einer Grenzschwelle ein Kreisel eingerichtet. Dort läuft eine Information im Kreis und jede Wiederkehr erinnert daran, dass es ursprünglich einen Reiz gab, der diesen Kreislauf ausgelöst hat. Der aktivierte Kreis merkt sich, dass etwas geschehen ist. Er dient im Nervensystem als zusätzlicher Input. Mit ihm wird nicht nur gemeldet, dass ausreichend viele Nervenbahnen vom gleichen Ereignis angeregt wurden, sondern dass dieses Ereignis bereits in der Vergangenheit stattgefunden hat. Das ist die technische Grundlage und Realisierung eines lernenden Systems.

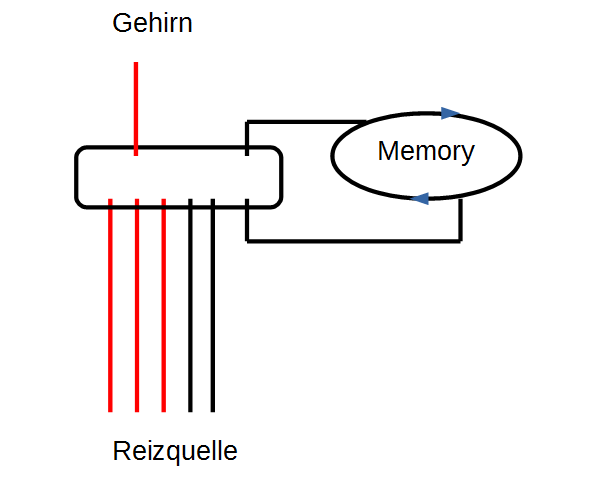
Auf ähnliche Weise spricht Spencer-Brown von der memory function und stellt sie durch geschlossene Schaltkreise dar. Spencer-Brown hat eine abstraktere Ebene gesucht, die in den Rahmen einer Logik passt. Mir ist nicht bekannt, ob er sich ausdrücklich auf diese Tradition bezogen hat, aber für mich ist deutlich, wie er in dieser Tradition steht. Er hat diese Ideen nicht mehr ausarbeiten können, aber sie tauchen an entscheidenden Stellen in den Gesetzen der Form auf. In England war er möglicherweise stärker von dem 1948 vorgestellten Homöostaten beeindruckt als von der Neurophysiologie. Urheber war der englische Psychiater und Biochemiker William Ross Ashby (1903-1972). Spencer-Brown hat auf eigenartige Weise in seine Ausführungen zum Re-entry und zu Schaltkreisen (circuits) Elemente der neuen Erkenntnisse der Neurophysiologie aufgenommen, ohne das klar wird, welche Intuition ihn geleitet hat.

McCulloch hatte 1945 in einem kurzen, aber grundlegenden Artikel Heterarchie und Hierarchie auf grundlegende philosophische Aspekte der neuen Schaltkreise hingewiesen, die im Rahmen der ersten Ideen für neuronale Netze entstanden. In einem Netzwerk gibt es kein steuerndes, hierarchisches Zentrum mehr, sondern eine Heterarchie nebenläufiger und zirkulär miteinander verbundener Entwicklungen. Das scheint mir die Grundidee zu sein, die wiederum Niklas Luhmann (1927-1998) in seinen Arbeiten zur Systemtheorie aufgenommen hat – auch wenn er nur sehr am Rande auf McCulloch Bezug nimmt (so in Soziale Systeme, Frankfurt am Main 1984, 565 und Wissenschaft der Gesellschaft, Frankfurt am Main 1990, 365), und warum er hoffte, mit Spencer-Brown seiner Systemtheorie eine neue logische Basis geben zu können, die sich von der traditionellen Subjektphilosophe und deren Paradoxien unterscheidet.

Der gordische Knoten

Ist es möglich, alle diese Fragen gemeinsam wie in einem gordischen Knoten zu lösen? Das scheint mir letztlich das Motiv von Spencer-Brown zu sein.

Spencer-Brown stellt als Motto einen Vers aus dem Daodejing von Lao-Tse voran. Lao-Tse beginnt seine Schrift mit vier Versen, von denen Spencer-Brown den dritten Vers ausgewählt hat.

Wu ming tian di zhi shi
Nichts/Ohne Name Himmel Erde von Anfang

»Da das Chinesische eine isolierende und keine flektierende Sprache ist, gehört zu dem chinesischen Satz eine Ambiguität, die in den westlichen Sprachen durch die Entscheidung für eine Wortart verloren geht. Die Ambiguität hängt an der grammatischen Rolle des ersten Wortes wu: nicht, ohne, Nichts.« (SWH, 65)

Der Vers kann daher in zweierlei Weise übersetzt werden:

– Ohne Name ist der Anfang des Himmels und der Erde
– 'Nichts' ist Name des Anfangs von Himmel und Erde.

Alle vier Verse lauten im Zusammenhang:

Der Weg, der wirklich Weg ist, ist ein anderer als der unwandelbare Weg.
Die Namen, die wirklich Namen sind, sind andere als unwandelbare Namen.
Namenlos/Nichts ist der Anfang von Himmel und Erde.
Der Name ist die Mutter der zehntausend Dinge. (zitiert SWH, 65)

»Distinction is Perfect Continence«

Irgenwo muss auch Spencer-Brown in seiner Logik mit nicht weiter hinterfragbaren Grundbegriffen anfangen. Er sucht sie noch unterhalb der gewöhnlichen Mathematik und Sprache. Vor jedem Sprechen und Rechnen stehen für ihn Indication (Hinweis) und Distinction (Unterscheidung). Mit ihnen möchte er eine Proto-Logik und Proto-Mathematik begründen, einen Kalkül der Indikation und Distinktion.

»We take as given the idea of distinction and the idea of indication. We take, therefore, the form of distinction for the form.« (LoF, 1)

Ohne Unterscheidungen getroffen zu haben, sind weder Sprache noch Rechnungen möglich: Um rechnen und Sätze bilden zu können, müssen bereits im Vorfeld die beim Rechnen und Schreiben verwendeten Zeichen voneinander unterschieden sein. In einer Gleichung wie ›2 + 3 = 5‹ werden Operanden (in diesem Beispiel die Zahlen 2, 3 und 5) und Operatoren (Operationszeichen) (hier + und = für Addition und Gleichsetzung) verknüpft und aus ihnen eine Aussage gebildet. Ähnlich ist es in der Sprache. In einem Satz wie ›S ist p‹ sind S und p als Operanden und die Copula ‘ist’ als Operator zu verstehen. Die Zeichen 2, 3, 5, + und = müssen voneinander unterscheidbar sein, und es muss vorausgesetzt werden, dass sie sich während der Rechnung nicht ändern. Wäre das nicht möglich, dann wäre die Gleichung sinnlos. Daher liegt es nahe, die Proto-Operation des Unterscheidens noch vor den Operationen des Rechnens und Sprechens anzusetzen und aus ihr schrittweise die übliche Logik und Arithmetik zu entwickeln.

Für Spencer-Brown muss es ein Zeichen geben, dass diese Ebene trifft und den bekannten Zeichen für Operanden (Zahlen und Buchstaben) sowie Bindeverben (Satzbändern wie z.B. die Kopula ‘ist’ und Rechensymbolen wie +) vorausgeht. Er geht noch weiter: Er sucht ein Zeichen, dass sogar der Unterscheidung in Operanden und Operatoren vorausgeht und sowohl als Operator wie als Operand dienen kann. Dies elementare Zeichen ist für ihn der Haken (Winkel, cross):

   

Dies Zeichen hat eine vielfache Bedeutung:

– Ausführung einer elementaren Operation (das Zeichnen dieses Zeichens, draw a distinction)

– Hervorheben eines Inneren (mark)

– Auszeichnen eines inneren Bereichs (marked space) (Asymmetrie von Innen und Außen)

– Ziehen einer Grenze (boundary with separate sides)

– Unterscheiden eines Grundes vom Zeichen, das in den Grund gezeichnet ist (ground, medium)

– Benennen der Grenze durch das Zeichen  ⃧   (indication, call)

In der letztgenannten Bedeutung ist es selbst-bezüglich: Es zeigt sowohl mit seiner äußeren Gestalt anschaulich den Unterschied zwischen einem Innen und einem Außen, und zugleich ist dies Zeichen der Name für diesen Unterschied. Dadurch wird dem Innen ein Wert verliehen.

Das Verblüffende ist nun, dass mit diesem einzigen Zeichen nicht nur die Operanden, sondern auch die Operatoren dargestellt werden können. Spencer-Brown unterscheidet nicht wie die traditionelle Logik und Mathematik zwischen Zeichen für Operanden und Operatoren, sondern definiert die Operationen (das Rechnen und die Bildung von Aussagen) implizit durch die bloße Anordnung der Operanden: Das sind die beiden Operationen ‘Wiederholung’ und ‘Verschachtelung’. Mit ihnen lässt sich die weitere Logik vollständig aufbauen.

             

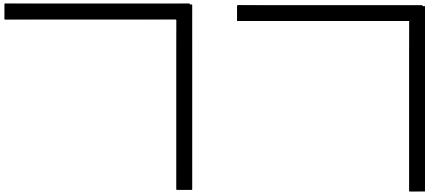
Alle weiteren Zeichen werden schrittweise aus diesen beiden Zeichen und ihren beiden Anordnungsmöglichkeiten zusammengesetzt, so wie in der euklidischen Geometrie alle Konstruktionen aus Geraden und Kreisen hervorgehen.

Für diese beiden Operationen setzt Spencer-Brown zwei Axiome:

»Axiom 1: The law of calling.
The value of a call made again is the value of the call.« (LoF, 1)

 ⃧   ⃧   =   ⃧    

lies: Wird etwas zweimal bei seinem Namen genannt, ändert sich der Name dadurch nicht.

»Axiom 2: The law of crossing
The value of crossing made again is not the value of the crossing« (LoF, 2)

  =     .

lies: Wird zweimal die Grenze gewechselt, dann wird der Anfangszustand wiederhergestellt. Die Wiederholung des Crossing hat einen anderen Wert als das einfache Crossing. Das liegt daran, dass zwischendurch eine Umkehr erfolgt. Beim Crossing wird die Seite gewechselt, beim Recrossing wird diese Aktion rückgängig gemacht.

Die Einführung dieser beiden Axiome wird vielleicht verständlicher, wenn daran erinnert wird, dass Spencer-Brown von Schaltkreisen ausging. (1) Wird in einem Schaltkreis auf einer Verbindung ein Schalter geöffnet, dann ist die Strecke unterbrochen und wechselt vom Zustand ‘an’ in den Zustand ‘aus’. Werden mehrere Schalter geöffnet, bleibt der Zustand ‘aus’ erhalten. Es ist im Ergebnis das gleiche, einen Schalter oder mehrere Schalter zu öffnen. (2) Wird ein Schalter erst geöffnet und dann wieder geschlossen, ist der Ursprungszustand ‘an’ wieder hergestellt.

Mit Axiom 2 ist implizit das Medium eingeführt: Wird das Recrossing als Reflexion verstanden, mit der im wörtlichen Sinn eine Grenzüberschreitung reflektiert (zurückgeworfen) wird, dann entsteht mit Axiom 2 als Ergebnis der leere Raum. Er ist das, was übrig bleibt, wenn etwas unternommen und wieder rückgängig gemacht wird. Was zurück bleibt ist nicht mehr einfach das Nichts: Es ist der Raum, der durch die zweifache Bewegung eines Werdens und eines Vergehens entstanden ist: Die Grenze wurde zuerst gezeichnet. Das ist ein Werden. Sodann wurde das Werden durch ein Vergehen rückgängig gemacht. Übrig bleibt der Grund, auf dem diese Bewegung von Werden und Vergehen stattgefunden hat. – Oder anders gesagt: Ein Beobachter sieht zwar nichts mehr, aber er kann sich an die Bewegung des Crossing und Recrossing erinnern. In seinem Gedächtnis kann eine Spur zurückbleiben, auf die sich die Erinnerung stützt. (Vergleiche hierzu die Ausführungen von Hegel: »Das Resultat ist das Verschwundensein, aber nicht als Nichts.« HW 5.113)

Mit Werden und Vergehen der Grenze im Crossing und Recrossing ist implizit von Anfang an die Zeit gesetzt. Sie ist bereits in der ursprünglichen Aufforderung enthalten »triff eine Unterscheidung, draw a distinction«. Spencer-Brown ist noch konsequenter als Hegel: Er wählt nicht nur wie Hegel Begriffe, die zugleich eine Bewegung wie ihr Resultat beschreiben (Unterscheidung, Bezeichnung kann sowohl verstanden werden als das Unterscheiden und Bezeichnen wie auch als das Ergebnis, die mit dem Unterscheiden und Bezeichnen erreichte Unterscheidung und Bezeichnung), sondern er wählt mit dem Haken ein Zeichen, das zugleich die Operation (Bewegung) wie den Operand beschreibt.

Anmerkung: In den beiden Operationen der Wiederholung (Recalling) und der Rückkehr zurück über die Grenze (Recrossing) sehe ich formal die beiden von Hegel unterschiedenen Bewegungen der Kontinuation und der Umkehr, die für mich zentral sind für das Verständnis sowohl der absoluten Indifferenz, wie des Übergangs von der Seinslogik zur Wesenslogik und im Weiteren des Begriffs der Idee (siehe hierzu den Beitrag Idee des höheren Widerspruchs).

Aber wie soll das Zeichen  ⃧   im Deutschen benannt werden? Spencer-Brown führt es ein als »crossing the boundary« und als »calling« (LoF, 1), und nennt es nach dem ersten Aufzeichnen ein »mark« (LoF, 3). In deutschen Übersetzungen wird bisweilen das englische Wort ‘cross’ beibehalten oder ein neutraler Ausdruck gewählt wie ‘Token’, ‘Markierung’ oder ‘Zeichen’. Die wörtliche deutsche Übersetzung ‘Kreuz’ wird meist vermieden, da es sich äußerlich nicht um ein Kreuz , sondern um einen Winkel handelt. Ein Winkel wird jedoch meist nach rechts geöffnet und mit einer Öffnung von weniger als 90° vorgestellt, so auch das Zeichen für Winkel in der Auszeichnungssprache HTML: ∠. Möglich ist auch das Wort ‘Haken’. Das alles trifft jedoch nicht die von Spencer-Brown gemeinte Doppelbedeutung eines Zeichens und einer Bewegung (cross, crossing, in deutscher Übersetzung: Kreuz und Kreuzen). Auch das Wort ‘Quere’ ist missverständlich, denn unter einer Quere ist eher ein Zeichen wie \ oder / zu verstehen, das quer verläuft, und mit Überqueren ist oft eine andere Art von Bewegung gemeint, etwa das Überqueren eines leeren Platzes, eines Flusses, eventuell auch eine Abkürzung, wenn ein Rechteck entlang der Diagonale durchquert wird. Trotz Bedenken ist für mich in Gesprächen und bei Demonstrationen an einer Tafel der Name ‘Haken’ am eingängigsten, weil er am besten die äußere Gestalt trifft. In der englischen Übersetzung behalte ich trotz aller Bedenken den Ausdruck ‘cross’ bei, da er in den Arbeiten zu Spencer-Brown am weitesten verbreitet ist.

Für das andere Zeichen, das nur aus einer Leere besteht, hat Spencer-Brown lange nach einem geeigneten Namen gesucht. Erst in der 2. Auflage der deutschen Übersetzung von 1999 führt er den Ausdruck Ock ein.

»Kurz nachdem es das erstemal veröffentlicht wurde, erhielt ich einen Telephonanruf von einem Mädchen namens Juliet, die, während sie ihre Begeisterung über das, was ich getan hatte, ausdrückte, ebenso ihrer Frustration Ausdruck verlieh, nicht den leeren Raum über das Telephon sprechen zu können. [...] Sie hatte völlig recht, und ich erfand in der Folge das Wort Ock (vom Indoeuropäischen okw = das Auge), symbolisiert durch einen umgekehrten Kleinbuchstaben Ɔ um in einer sprechbaren Form die universelle rezessive Konstante zu kennzeichnen, die alle Systeme gemeinsam haben. Gewöhnliche Zahlensysteme haben natürlich zwei Ocks, null für die Addition und die Einheit für die Multiplikation. [...] In diesem Buch, in dem seine wahre Natur erstmals klargemacht wurde, war es aber wichtig, das Ock namenlos und leer zu lassen, weil es das nächste war, an das ich gelangen konnte, um hervorzuheben, daß es überhaupt nichts ist, nicht einmal leer. Seine Erfindung war mächtiger als die Erfindung der Null, und sandte Schockwellen durch die gesamte mathematische Gemeinde, die selbst jetzt noch nicht abgeklungen sind.« (Spencer-Brown, 1999, xvf, zitiert bei Rathgeb, 118)

In der Sekundärliteratur zu Spencer-Brown ist das bis heute außer bei Rathgeb nicht aufgenommen worden. Aber ich werde mich ihm im Folgenden anschließen, da mir das die einfachste und beste Weise scheint, die beiden Grundzeichen in Worten zu benennen.

Zusammenfassung: Das Anliegen dieser ersten Schritte nennt Spencer-Brown:

»Definition
   Distinction is perfect continence.« (LoF, 1)

Was ist mit dem ungewöhnlichen Wort continence gemeint: SWH erläutern: (a) Es kann Enthaltsamkeit, Mäßigkeit und Selbstkontrolle bedeuten (kontinent als Gegenteil von inkontinent). In dieser Bedeutung wird mit continence gesichert, dass etwas nicht auseinanderläuft und sich zerstreut, verfranst und die eigene Identität verliert. (b) Und es kann Zusammenhalt bedeuten im Sinne des Kontinuum, wodurch zum Beispiel in der Geometrie die Unendlichkeit von Punkten auf einer Linie zusammengehalten wird. (SWH, 70) Das scheint mir das Anliegen von Spencer-Brown sehr gut zu treffen.

Proto-Arithmetik und Proto-Algebra

Spencer-Brown hat sein Verständnis von Arithmetik und Algebra auf der AUM-Konferenz in der Session Two am 19.3.1973 dargelegt und zur Diskussion gestellt.

–    Eine Arithmetik wird demonstriert an physischen Gegenständen. Schon im Kindergarten oder der Grundschule wird sie an Beispielen gelernt wie ›3 Äpfel und 2 Äpfel sind 5 Äpfel‹. Jeder kann die beiden kleineren Mengen von 2 und von 3 Äpfeln nehmen, sie zusammenlegen und nachzählen, dass es jetzt 5 Äpfel sind. Beispiele dieser Art sind so intuitiv und "schlagend", dass kaum jemand bemerkt, was implizit vorausgesetzt und unter der Hand mitgelernt wird. Die einzelnen Äpfel bleiben selbständig und verändern sich nicht durch das Zählen. Würden sie wie bei einem chemischen Prozess miteinander reagieren und verschmelzen oder sich in andere Objekte umwandeln oder aufteilen, dann wäre das Zählen unmöglich. Spencer-Brown formuliert daher eigene Regeln, die das sicherstellen (die von ihm so genannten Kanons).

Erst allmählich wird daraus das abstrakte Rechnen mit Zahlen, bei dem nicht mehr ausdrücklich auf bestimmte Gegenstände hingewiesen wird. Die Zahlen selbst sind keine physischen Gegenstände. In der Schule wird das implizit mitgelernt, und es ist bis heute eine unentschiedene Frage, ob die Zahlen unabhängig von den gezählten Gegenständen bestehen, ob sie eine der Eigenschaften der gezählten Gegenstände sind, oder ob es die Zahlen nur im Denken von vernunftbegabten Wesen wie den Menschen gibt, die im Laufe ihrer Entwicklung Zahlen eingeführt haben und mit ihnen in Gedanken operieren können. Die Philosophen und Logiker haben hierüber nie Einigkeit erzielt. Ich schließe mich der Ansicht von Aristoteles an, für den die Zahlen nur im Denken bestehen.

In welcher Weise kann in der Proto-Arithmetik von Proto-Zahlen gesprochen werden, und wie lassen sie sich vergleichbar dem Zählen von Äpfeln an konkreten Gegenständen veranschaulichen? Spencer-Brown geht eine Ebene tiefer und versteht die beiden Zeichen  ⃧   und Ɔ (Ock) in einer doppelten Bedeutung, in der sie sowohl als Zahlen wie als Operationszeichen dienen. Die gewöhnliche Arithmetik kennt Ausdrücke wie ›7 + 5‹ oder ›120 − 13‹. Für Spencer-Brown handelt es sich bei ihnen um Zeichenketten, die nach festen Regeln aus einem bestimmten Zeichenvorrat gebildet werden, der im Dezimalsystem aus den Ziffern 0, 1, 2, …, 9 und den Operationszeichen wie + und − besteht. In seiner Proto-Arithmetik reduziert er den Zeichenvorrat auf die beiden Zeichen  ⃧   und Ɔ (Ock), aus denen die arithmetischen Ausdrücke zusammengesetzt werden. Genau genommen sind sie weder Proto-Ziffern noch Proto-Zahlen, sondern mathematische Proto-Zeichen, aus denen mathematische Ausdrücke gebildet werden, in denen sie sowohl die Bedeutung von Ziffern (und den aus ihnen nach dem Stellenwertsystem zusammengesetzten Zahlen) als auch von Operationszeichen erhalten. Um die Ausdrucksweise nicht zu kompliziert werden zu lassen, kann dennoch von Proto-Zahlen gesprochen werden, auch wenn das wörtlich genommen falsch ist. Spencer-Brown sagt, dass die Proto-Arithmetik mit ihnen rechnet (calculates, siehe das Kapitel Calculation; LoF, 11). Aus den beiden Zeichen  ⃧   und Ɔ (Ock) werden nach den beiden Regeln der Mehrfach-Ausführung und Verschachtelung komplexere Zeichen zusammengesetzt. Das sind in einem ungenauen Sinn die Proto-Zahlen. Spencer-Brown spricht nicht von Rechenoperationen, sondern von Umwandlungen (»primitive equations«, »procedue«, »changes«; LoF, 10f) und führt hierfür das Zeichen ⇀ ein (LoF, 8). Mit diesem Zeichen werden zwei arithmetische Ausdrücke voneinander getrennt. Es bedeutet, dass der zweite Ausdruck durch eine Umwandlung aus dem ersten Ausdruck hervorgegangen ist (LoF, 11).

Die gewöhnlichen Zahlen werden als Abstraktion aus dem Zählen von Gegenständen veranschaulicht und verstanden. Mit den beiden Zeichen  ⃧   und Ɔ werden im ersten Schritt noch nicht Gegenstände gezählt, sondern unterschieden. Das Unterscheiden geht dem Zählen voraus. Wenn Gegenstände nicht unterschieden werden (nicht sortal sind), können sie auch nicht gezählt werden. Das Zeichen  ⃧   beschreibt, dass es einen Unterschied von etwas zu etwas anderem gibt, und das nur als leere Fläche gedachte Zeichen Ɔ beschreibt den Hintergrund, vor dem sich die Grenze eines Etwas von seinem Äußeren abhebt. Der Abstraktionsprozess bleibt jedoch ähnlich: So wie aus dem Zählen von Gegenständen das Verständnis der Zahlen gewonnen wird, so wird aus dem Unterscheiden von Gegenständen voneinander und vor dem jeweiligen Hintergrund das Verständnis der beiden Zeichen  ⃧   und Ɔ gewonnen.

So wie die herkömmliche Arithmetik die natürlichen Ziffern 0, 1, 2, 3, …, 9 einführt und mit ihnen Zahlen bildet und rechnet, sieht Spencer-Brown seine primary arithmetic als eine vereinfachte und vorlaufende Arithmetik an, die nur die beiden Zeichen  ⃧   und Ɔ (Ock) kennt. Mit diesen beiden Zeichen soll auf eine vergleichbare Art gerechnet werden, wie wir es aus der gewöhnlichen Arithmetik gewohnt sind, um tieferliegende arithmetische Zusammenhänge zu erkennen, aus denen schrittweise die gewöhnliche Arithmetik hergeleitet werden kann.

–    Die Arithmetik berücksichtigt die Individualität der jeweiligen Zahlen. In der Zahlentheorie ist jede einzelne Zahl etwas Besonderes. Was in der Arithmetik für eine bestimmte Zahl bewiesen wurde, lässt sich nicht ohne Weiteres auf die anderen Zahlen übertragen. Erst die Algebra wird Regeln studieren, die grundsätzlich für alle Zahlen gelten. So ist es auch bei der Proto-Arithmetik, mit der die Besonderheiten der beiden Zeichen  ⃧   und Ɔ (Ock) sowie der aus ihnen zusammengesetzten Zeichen untersucht werden.

Spencer-Brown will zurückkehren zu dem ursprünglichen Zahlenverständnis, das in der Arithmetik enthalten ist und der Algebra vorausgeht. Wer das Rechnen und den Umgang mit Zahlen lernt, wird anfangs jede Zahl in ihrer Besonderheit erfassen. Jede neue Zahl hat etwas Eigenes. Kinder lernen, wie z.B. die Zwei und die Vielfachen von Zwei, die Drei und die Vielfachen von Drei, die Fünf und die Vielfachen von Fünf jeweils etwas Besonders haben. So haben z.B. alle Vielfachen von Fünf als letzte Ziffer nur die 0 oder die 5 (5, 10, 15, 20, …), bei den Vielfachen der 3 ist die Quersumme durch 3 teilbar (die Quersumme ist die Summe aller Ziffern, z.B. wird die Quersumme von 75342 berechnet als ›7 + 5 + 3 + 4 + 2 = 21‹, und da 21 durch 3 teilbar ist, ist auch 75342 durch 3 teilbar). Ein anderes Beispiel ist die Zahl 6, die mit der Summe ihrer Teiler identisch ist ›6 = 1 · 2 · 3 = 1 + 2 + 3‹. So lassen sich für jede Zahl spezifische Eigenschaften erkennen. Jeder, der von Mathematik begeistert ist, ist von Zahlenspielereien und Gedanken über die Besonderheiten der einzelnen Zahlen fasziniert (thaumazein, in einem altertümlichen Ausdruck ‘verwundert’) und hat seine Lieblingszahlen und Zahlen, die irgendwie fremd wirken. Auch wenn es ein Außenstehender vielleicht kaum nachvollziehen kann, zeigt sich für mich in dieser Art mit Zahlen zu spielen die gleiche Haltung und spontane Freude wie beim Kanon-Singen. Aus der Schule von Piaget stammt das Beispiel: Ich sage eine Zahl und du sagst eine Zahl. Wer die größere Zahl gesagt hat, hat gewonnen. Beide müssen lachen, wenn sie den Trick verstehen, warum ständig der zweite gewinnt, und wiederholen doch voller Übermut das gleiche Spiel immer neu. Das ist für mich das erste und einfachste Beispiel einer arithmetischen Beweisidee, mit der die Kinder ohne es wissen eine Prozedur für den Beweis gefunden haben, dass es unendlich viele Zahlen gibt.

Im Ergebnis entstehen Regeln wie die sogenannten Eselsbrücken, die jeweils für bestimmte Zahlen gelten und nicht auf andere Zahlen übertragbar sind. Jeder wird seine favorisierten Rechenverfahren haben, die ihm besonders gut gelingen, vergleichbar den Lieblingsfarben. Spencer-Brown will zu diesem ursprünglichen (naiven, magischen) Umgang mit den Zahlen zurück, denn nur aus ihm heraus ergeben sich für ihn die Möglichkeiten, den im 20. Jahrhundert entstandenen formalen Umgang mit Zahlen in einem neuen Licht zu sehen.

Im Sinne von Piaget gehört für ihn die Arithmetik zur II. Phase des symbolischen und vorbegrifflichen Denkens, die er in ihrer Besonderheit und Eigenheit erhalten will. Der Übergang zur Algebra wird daher in Vielem den Übergang zum operationalen Rechnen in der III. Phase (im Alter von 7 bis 12 Jahren) ähneln.

–    Innerhalb der Arithmetik gibt es Sätze (Theoreme). Theoreme sind für Spencer-Brown Ideen, die an individuellen, einzigartigen Elementen gefunden werden. In ihnen zeigt sich die Mathematik im engeren (eigentlichen) Sinn. Die Algebra wird dagegen formuliert für Variable unabhängig von der Individualität der jeweils in die Variablen eingesetzten Werte. Daher kann die Proto-Arithmetik für Spencer-Brown keine Theoreme formal aus den Axiomen ableiten, sondern nur intuitiv erfassen und erst im zweiten Schritt mit formalen Methoden nachweisen und Konsequenzen ziehen. Dagegen kann die Vorgehensweise der Algebra im Prinzip von Computern übernommen werden. Im 20. Jahrhundert wird seit Mathematikern wie Russell die Mathematik mit der algebraischen Art zu operieren gleichgesetzt. Das ist für Spencer-Brown ein großer Rückschritt, der die Mathematik, die mathematischen Fähigkeiten und die Freude an der Mathematik verkümmern lässt.

Was mit Theoremen gemeint ist, wird am besten klar an dem von Spencer-Brown genannten Beispiel: Euklid hat den Satz bewiesen, dass es unendlich viele Primzahlen gibt. Sein Beweis war: Wenn es nur endlich viele Primzahlen gibt, gibt es eine größte Primzahl. Sie heiße N. Wird das Produkt aller Primzahlen von 1 bis N gebildet, ergibt sich ›M = 1 · 2 · 3 · 5 · 7 · 11 · …· N‹. Für M lässt sich zeigen, dass ›M + 1‹ eine Primzahl ist. Daher gibt es eine weitere Primzahl, die größer als N ist, und so fort. Diese Idee kann nicht als Konsequenz aus den arithmetischen Regeln gefolgert werden, sondern sie musste gefunden werden. Wichtig ist für Spencer-Brown zweierlei: Der Beweis zeigt sowohl eine originelle Beweisidee wie auch ein Verfahren (procedure), mit dem die Beweisidee vorgeführt wird. Die meisten werden erst vom Verfahren überzeugt sein, warum der Satz richtig ist, und von ihm ausgehend die Beweisidee verstehen. Eine solche Beweisidee ergibt sich aus der für die Arithmetik typischen Art des Rechnens, die ein tiefes Verständnis (um nicht zu sagen Mitgefühl) mit den Zahlen und ihren inneren Rhythmen und unendlich vielfältigen Beziehungen und Verwandtschaften hat. Das kann kein Computer. Computer liefern dagegen eine andere Art von Erkenntnissen, die für Spencer-Brown zur Algebra gehören.

–    Spencer-Brown war von der Schalt-Algebra und der Booleschen Algebra ausgegangen und hatte die Arithmetik gesucht, die ihr vorausgeht und deren Algebra sie ist. Gewöhnlich lernen wir die Arithmetik anhand der natürlichen und reellen Zahlen kennen und anschließend all die algebraischen Regeln, wie mit ihnen gerechnet wird. George Boole (1815-1864) hatte 1847 eine vereinfachte Algebra gefunden, die mit den elementaren logischen Operationen wie UND und ODER rechnet und deren Variablen im einfachsten Fall nur für die zwei Zahlen 0 und 1 (oder in der Schalt-Algebra für ‘an’ und ‘aus’) stehen. Das war für Spencer-Brown der Ausgangspunkt, und er wollte auf diesem Weg noch einen Schritt weiter gehen: So wie die Arithmetik der natürlichen und reellen Zahlen den komplexen Theorien der Zahlentheorie und der Analysis zugrunde liegt, sollte es möglich sein, für die Boolesche Algebra eine eigene vereinfachte Arithmetik zu finden, die nur für die Zahlen 0 und 1 formuliert ist. Sie geht als primary arithmetic (Proto-Arithmetik) der üblichen Arithmetik ebenso voraus wie die Boolesche Algebra der gewöhnlichen Algebra. Auf diesem Weg ist ihm im Ergebnis eine Arithmetik gelungen, deren Zeichenvorrat mit den beiden Zeichen  ⃧   und Ock noch weiter eingeschränkt ist, und die daher auch der Booleschen Algebra vorausgeht.

–    Aus Sicht von Spencer-Brown können die bahnbrechenden Aussagen von Gödel anders und neu gelesen werden: Kurt Gödel (1906-1978) hat 1931 gezeigt, dass die Algebra ab einer bestimmten Komplexität der Zahlen nicht mehr alles zu sagen vermag, was in der ihr vorausgehenden Arithmetik möglich ist. Die Arithmetik enthält mit der Individualität ihrer Zeichen einen  Überschuss, der von keiner Algebra vollständig erfasst und eingefangen werden kann. Die Algebra ist gegenüber der Arithmetik grundsätzlich unvollständig. Wie weit auch die Algebra entwickelt sein mag, aus der Arithmetik und dem unendlichen Vorrat ihrer jeweils individuellen Zahlen können neue Erkenntnisse kommen, die über die jeweils bekannte Algebra hinausgehen. – Wenn Spencer-Brown in Kapitel 9 von der Completeness (Vollständigkeit) spricht, meint er etwas anderes. Theorem 17 besagt: »The primary algebra is complete« (LoF, 50). Das besagt jedoch nicht, dass sie alles enthält, was an arithmetischen Entdeckungen gewonnen werden kann, sondern nur, dass jede arithmetische Entdeckung sich auch algebraisch formulieren lässt. »That is to say, if α = β can be proved as a theorem about the primary arithmetic, than it can be demonstrated as a consequence for all α, β in the primary algebra.« (LoF, 50) Mit Bedacht spricht Spencer-Brown daher von einem Theorem und nicht von einer Konsequenz, d.h. von einer Aussage, die mit den Methoden der Arithmetik und nicht mit denen der Algebra zu beweisen ist.

»So, to find the arithmetic of the algebra of logic, as it is called, is to find the constant of which the algebra is an exposition of the variables--no more, no less. Not, just to find the constants, because that would be, in terms of arithmetic of numbers, only to find the number. But to find out how they combine, and how they relate -- and that is the arithmetic. So in finding -- I think for the first time, I don't think it was found before, I haven't found it -- the arithmetic to the algebra of logic -- or better, since logic is not necessary to the algebra, in finding the arithmetic to Boolean algebra, all I did was to seek and find a) the constants, and b) how they perform.« (AUM, Session Two)

– Ein Beispiel für das Rechnen und Beweisen aus der Proto-Arithmetik

»Theorem 1. Form The form of any finite cardinal number of crosses can be taken as the form of an expression.« (LoF, 12) »Die Form jeder endlichen ganzen Zahl von Kreuzen kann als Form eines Ausdrucks aufgefasst werden.« (Spencer-Brown, übersetzt bei Lau, 68) Die Aussage ist in dieser Wortwahl kaum direkt zu verstehen. Sie bedeutet, dass eine beliebige Form, die aus endlich vielen Haken und Ocks konstruiert ist, entweder in einen einzigen Haken oder in ein einziges Ock umgewandelt werden kann. Diese Aussage kann auch anders formuliert werden: Jede noch so komplizierte aus Haken und Ocks zusammengesetzte Form kann im Ganzen als eine Form angesehen werden. Das lässt sich an einem Beispiel verdeutlichen, das Spencer-Brown später für das 3. Theorem anführt (LoF, 17):

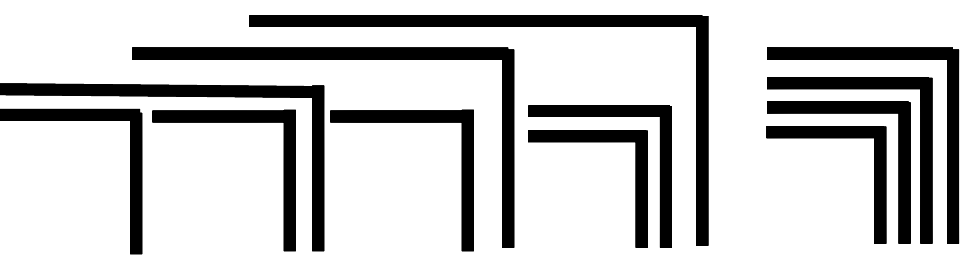
Es soll gezeigt werden, wie diese Figur auf einen Haken oder ein Ock reduziert werden kann. Die Beweisidee besteht darin, auf die tiefste Verschachtelungsstufe zu gehen. Dort gibt es nur zwei Möglichkeiten: Entweder wiederholt sich ein Haken mehrfach, oder zwei Haken sind ineinander geschachtelt. Wenn es sich wiederholt, kann es nach Axiom 1 in einen einzigen Haken zusammengefasst werden (condensation). Wenn sich zwei Haken verschachteln, können diese nach Axiom 2 in ein Ock umgewandelt werden (cancellation). Das Beispiel gibt zugleich einen Eindruck, wie in der Proto-Arithmetik gerechnet wird. Mit rot sind jeweils die Haken hervorgehoben, die im nächsten Schritt zusammengezogen oder ausgelöscht werden können. Für die Umwandlungen wird das von Spencer-Brown eingeführte Zeichen ⇀ verwendet.

       

       

       

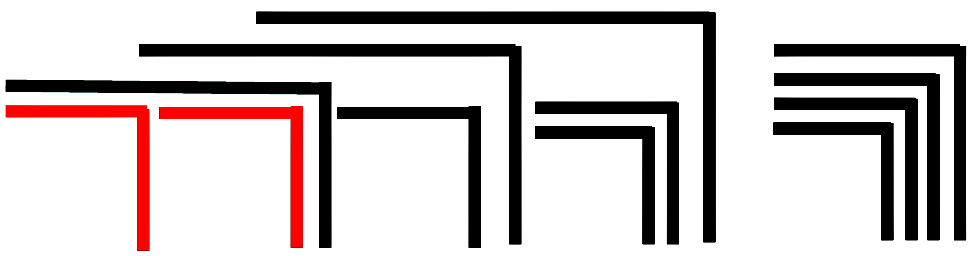
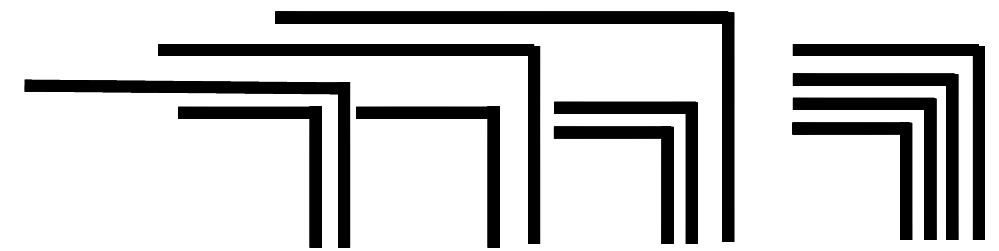
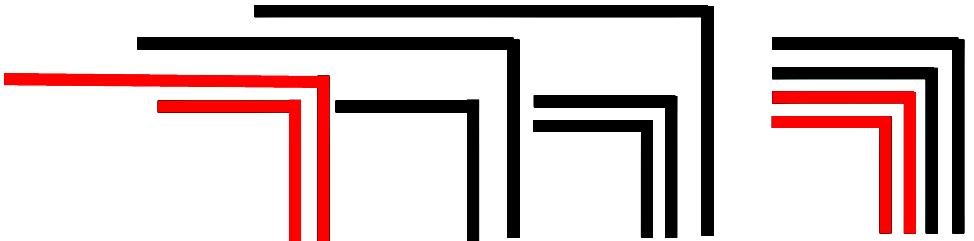
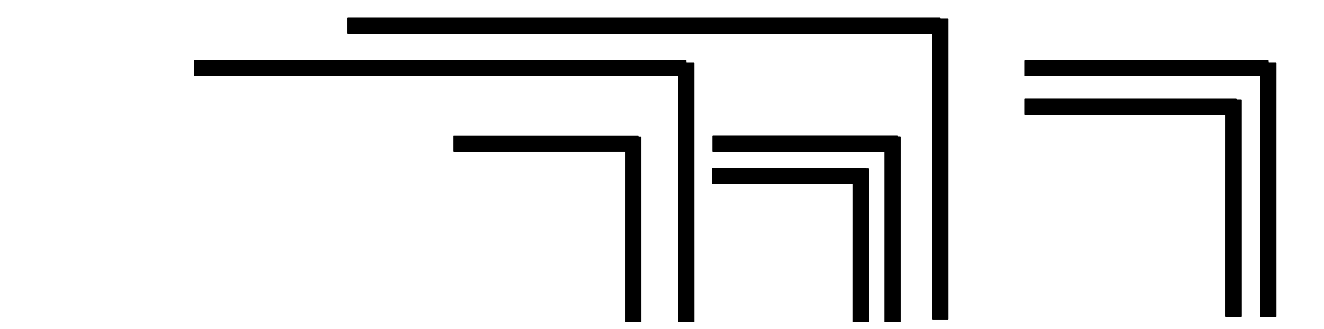
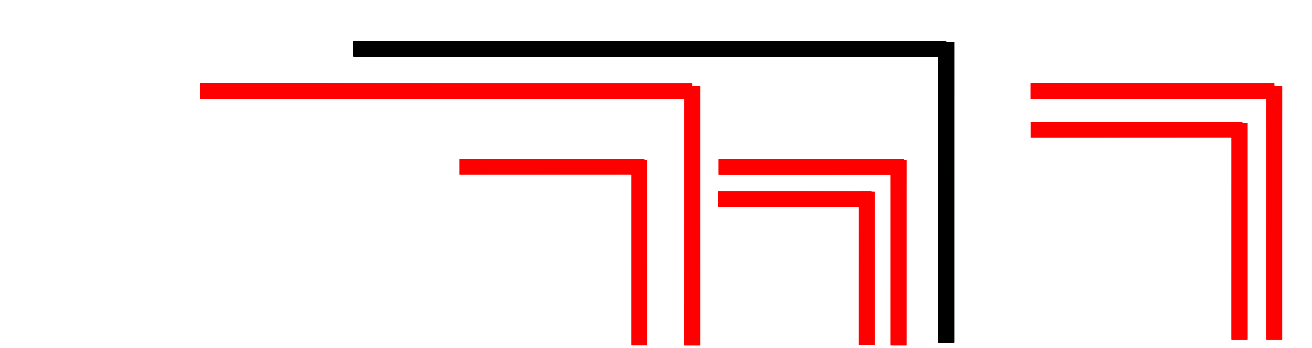
Wie wichtig dies Ergebnis ist, zeigt ein Vergleich mit Netzwerken. Wenn ein unübersichtliches Netzwerk vorliegt und auf ähnliche Weise vereinfacht werden soll, können Deadlocks auftreten, bei denen jede weitere Vereinfachung blockiert ist, siehe als Beispiel die Möglichkeit von Deadlocks in Petri-Netzen. Das ist in dem von Spencer-Brown gewählten Kalkül nicht möglich. Jedes komplexe Zeichen lässt sich bis auf eins der beiden Grundzeichen umwandeln.

– Nachfolger-Relation

Der wesentliche Unterschied zwischen der Proto-Arithmetik bei Spencer-Brown und der üblichen Arithmetik liegt in der Nachfolger-Relation (successor ordinal) und der auf sie gründenden vollständigen Induktion (mathematical induction). Für alle natürlichen Zahlen n gilt die Eigenschaft, dass sie einen Nachfolger n + 1 hat. Daraus ergibt sich, dass die natürlichen Zahlen auf der Zahlengerade angeordnet werden können. Mehrfaches Ausführen der Nachfolger-Relation führt zum Addieren, und daraus ergeben sich die weiteren Rechenoperationen und mit ihnen die Erweiterungen der natürlichen Zahlen durch die negativen und rationalen Zahlen usf. Das Induktions-Axiom besagt: Wenn eine Aussage A für ein Anfangselement n0 gilt (Induktionsanfang, base case) und gezeigt werden kann, dass sie von A(n) auf A(n + 1) gefolgert werden kann (Induktionsschritt, induction step), dann gilt sie für alle natürlichen Zahlen.

Spencer-Brown stellt jedoch nicht einmal die Frage nach der Anordnung aller Zeichen der Proto-Arithmetik. In einem ersten Versuch können die aus den Wiederholungen der Haken entstehenden Zeichen angeordnet werden wie die Striche auf einem Bierdeckel:

    |, ||, |||, …

     ⃧  ,  ⃧   ⃧  ,  ⃧   ⃧   ⃧  , …

Aber es gibt auch die Verschachtelung des Crossing. Während sich die Multiplikation und die höheren Rechenoperationen schrittweise auf die Addition zurückführen lassen, ist es nicht möglich, die Verschachtelung aus der Wiederholung herzuleiten. Beide sind unabhängig. Stattdessen bietet sich an, für die Anordnung aller in der Proto-Arithmetik betrachteten Zeichen eine lexikographische (kanonische) Ordnung wie für zwei voneinander unabhängige Buchstaben a und b zu wählen:

    a, b, aa, ab, bb, ba, aaa, aab, …

   

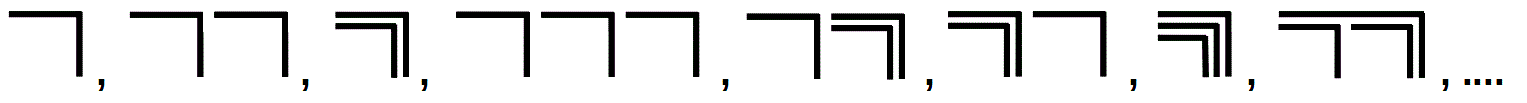
In dieser Reihenfolge gibt es keine einfache Nachfolger-Relation, mit der übergreifend beschrieben werden kann, in welchem Verhältnis das jeweils nachfolgende Zeichen zu seinem Vorgänger steht. Entsprechend gibt es keine einfache Verknüpfungs-Regel, mit der aus zwei Zeichen ein neues gebildet werden kann. Bernie Lewin hat jedoch in Enthusiastic Mathematics zahlreiche weitere Möglichkeiten der Anordnungen der beiden Symbole des Kalküls von Spencer-Brown ausgeführt, die auf die ursprünglichen Ideen von Pythagoras und seiner Schule zurückgehen, und gezeigt, wie sich mit ihnen die Operationen der üblichen Arithmetik herleiten lassen. Sein Buch zeigt zugleich, dass es für die Arithmetik nicht nur eine unerschöpfliche Fülle an Beweisideen und Sätzen gibt, sondern auch an symbolischen und graphischen Zeichen, mit denen neue Beweisideen entworfen werden können.

– Opazität und Transparenz von Arithmetik und Algebra

Das Verhältnis von Arithmetik und Algebra wirft weitreichende philosophische Fragen auf: Die Arithmetik ist einzigartig und opak (dunkel, verschwommen, lichtundurchlässig), die Algebra ist transparent und durchsichtig. Innerhalb der Algebra lässt sich alles aus den vorgegebenen Grundregeln ableiten, die Spencer-Brown als Initiale bezeichnet. Die algebraischen Ableitungen sind für ihn keine Beweise mit jeweils eigenen Beweisideen, sondern lediglich Konsequenzen, die sich formal aus den Initialien ergeben, und die auch ein Computer ausführen kann. In der Arithmetik gibt es dagegen eine unendliche Fülle von Möglichkeiten, die von einem endlichen Wesen wie dem Menschen und seiner Rechenkunst nie vollständig ausgeschöpft werden kann. Es gibt immer bislang unbekannte Möglichkeiten, die von neuen Mathematikergenerationen entdeckt werden können. Das entspricht der Aussage von Gödels Unvollständigkeitssätzen: Die Arithmetik wird nie alle in ihr angelegten Möglichkeiten beschreiben können. So enthält sie immer etwas, das für die Algebra verborgen (opak) bleibt.

Mit der Arithmetik werden Werteverläufe und die ihnen zugrundeliegenden Regeln erkannt. Der einfachste Fall ist das Axiom der natürlichen Zahlen, wonach jeweils zwei benachbarte natürliche Zahlen durch den Abstand 1 voneinander getrennt sind. Dagegen ist bis heute ungeklärt, wie der Werteverlauf der Primzahlen aussieht. Mit Euklid ist zwar bewiesen, dass es unendlich viele Primzahlen gibt, aber keiner weiß, wie sich ihre Abstände entwickeln. Eine der am meisten erforschten und dennoch unbewiesenen mathematischen Vermutungen stammt von dem Mathematiker Bernhard Riemann (1826-1866), der 1859 mithilfe der imaginären Zahlen immerhin eine wichtige Abschätzung für die Verteilung der Primzahlen postulierte.

Die Primzahlen und ihre Eigenschaften sind das beste Beispiel, was Spencer-Brown mit der Opazität der Arithmetik meint. Trotz aller fortgeschrittenen Methoden der Mathematik gelingt keine Lösung. Für Spencer-Brown ist das eine Indikation, dass es nach seiner Überzeugung nie gelingen wird, die Fülle der Arithmetik völlig zu überschauen. Er brachte das in die unscheinbare Aussage: »Principle of transmission: With regard to the oscillation of a variable, the space outside the variable is either transparent or opaque.« (LoF, 48). Mit »oscillation of a variable« ist der Werteverlauf beispielweise der Primzahlen gemeint.

Damit hat sich das Verhältnis von Mathematik und Philosophie radikal verschoben. Seit Descartes war die neuzeitliche Philosophie überzeugt, dass es einer in sich völlig transparenten Methode möglich sein müsste, alle Dinge zu durchschauen. Aufgabe der Philosophen ist es, diese Methode zu entwickeln, und von den Dingen wurde angenommen, dass sie im Prinzip transparent sind, d.h. metaphorisch gesprochen, sich dem Licht einer überlegenen Methode nicht widersetzen. Möglicherweise ist es sogar in der Geschichte der Natur die Aufgabe des Menschen, eine solche Methode zu finden und die Dinge aus ihrer Verborgenheit zu befreien. Sie warten gewissermaßen darauf, vom Menschen aus ihrer Dunkelheit erlöst zu werden.

Die Gegenposition geht bis zu Heraklit zurück, von dem der Spruch überliefert ist, »die Natur liebt es sich zu ververbergen« (Fragmente, B 123). Während sich seit Descartes die Philosophen von der Mathematik Unterstützung versprochen haben, mit mathematischer Strenge eine Methode zu finden, der sich alles öffnet, kehrt erst Spencer-Brown das Verhältnis um. Für ihn wiederholt sich nicht nur  innerhalb  der Mathematik das Verhältnis von Opazität und Transparenz, weswegen die Mathematik nicht einfach auf die Seite der Transparenz geschlagen werden kann, sondern für ihn war es fatal und eine durchgreifende Lähmung der mathematischen Kreativität, an und mit der Mathematik nur dasjenige zu suchen, was transparent ist. Der Siegeszug der mathematisierten Wissenschaften seit dem 19. Jahrhundert ist für ihn ein Kartenhaus, welches sofort zusammenfällt, wenn betrachtet wird, wie die Mathematik im Innern vorgeht. Sie hat für ihn mit der Dominanz der bloßen Herleitung von Konsequenzen in einer Algebra ihre Lebendigkeit verloren. Für diese Richtung stehen für ihn exemplarisch die 1910-13 veröffentlichten Principia Mathematica von Russell und Whitehead.

Kant hatte mit seiner Lehre des Ding-an-sich als erster die Erfolgsaussichten von Descartes in Frage gestellt, aber offen gelassen, ob sich die Unergründlichkeit des Dinges-an-sich dennoch paradoxerweise bestimmen lässt. Die Mathematik stand für ihn auf Seiten einer transparenten Wissenschaft und war für ihn der Garant der Vernunft. Wann immer er die Freiheit der Vernunft beschreiben wollte, griff er auf Bilder aus der Mathematik zurück, so z.B. in seiner Idee einer Sphäre des Begriffs, die sich von einem bestimmten Standort aus überschauen lässt und insofern transparent ist (Kant Kritik der reinen Vernunft, B 886). Allerdings erkannte er, dass das nur gilt, wenn die Sphäre nicht gekrümmt ist. Wenn das Wissen auf einer gekrümmten Fläche angeordnet ist, gibt es keinen Punkt, von dem aus es sich völlig überschauen lässt. Durch die Krümmung entzieht sich dem Blick, was jenseits des Horizonts liegt. Daher gibt es gute Gründe, die Krümmung als die elementare Eigenschaft der Opazität der Dinge zu verstehen.

Im Sinne von Spencer-Brown befindet sich die Arithmetik auf einer gekrümmten Fläche, und mit der Algebra lässt sich nie alles übersehen, was es auf der gekrümmten Fläche gibt. Es bleibt nichts anderes übrig, als den eigenen Standort auf der gekrümmten Fläche zu verändern. Wer sich auf der gekrümmten Fläche bewegt, dem erschließen sich zwar neue Bereiche, die sichtbar werden, aber mit der gleichen Bewegung entziehen sich andere Bereiche wieder und verschwinden hinter dem Horizont. Nie ist alles zu übersehen.

Nach Kant trennten sich die Wege der Philosophie und der Naturwissenschaften in zwei Richtungen. (i) Die einen suchen nach einer Methode, der sich kein Objekt entziehen kann. Hauptvertreter sind Hegel mit der dialektischen Methode (HW 6.551) und alle diejenigen, die ihm folgen. Oder sie hoffen, innerhalb der Mathematik Sicherungen einzubauen, die ihre volle Transparenz garantiert. (ii) Die anderen zogen aus der Lehre vom Ding-an-sich die Konsequenz, dass am Denken dessen prinzipielle Grenzen nachweisbar sind. Nietzsche traf es auf den Punkt, als er vom »Aberglauben der Logiker« sprach, sie könnten mit Descartes an ihrem eigenen Denken erkennen, dass es ein ‘Ich’, gibt, das denkt, während es für ihn genauso denkbar ist, »dass ein Gedanke kommt, wenn ‘er’ will, und nicht wenn ‘ich’ will« (Nietzsche Jenseits von Gut und Böse, 1. Hauptstück, Kapitel 17). Das Ich kann nie die Überfülle aller Gedanken überschauen und muss immer damit rechnen, dass sich neue Gedanken von sich aus melden und dem Ich zugänglich werden.

(i) Die Kant nachfolgende Naturwissenschaft hofft bis heute, für die Krümmung des Systems ein mathematisches Maß zu finden und mit dem Erkennen des Maßes der Krümmung deren Opazität in Transparenz wandeln zu können. Wem es gelingt, seinen Standort so zu ändern, dass er nicht mehr auf die gekrümmte Fläche, sondern auf ihre Maße schaut, der könnte auf dem Weg über die Maße eine Gesamtübersicht erhalten. Erste Ideen in diese Richtung sehe ich in Hegels Theorie der realen Maße, doch gibt bisher keine Umsetzungen.

Ein anderer Ansatz ist mit der Theorie selbst-referentieller Systeme entstanden. Wenn es in einem gekrümmten System unterschiedlichen Beobachtern gelingt, ihre jeweils lokalen Sichten auf ein globales Bild abzustimmen, dann wäre ihnen gemeinsam ein globales Bild möglich. Damit verlagert sich die ursprüngliche Frage auf eine neue Ebene: Zwar überdecken die lokalen Horizonte aller Beobachter im Ganzen das gesamte System, doch fragt sich, nach welchen Regeln ihre Sichten miteinander koordiniert werden können.

Luhmann kann aus einer höheren Perspektive in der Tradition von Hegel gesehen werden. Er nimmt an, dass das System im Ganzen in eine Selbstbeschreibung emergiert, die nicht mehr an einzelne Teilnehmer des Systems gebunden ist, sondern sich aus den Bewegungsgesetzen (Hegel würde sagen: der Vernunft) des Systems im Ganzen ergibt. Er erwartet, dass dieser Weg mithilfe der von Spencer-Brown eingeführten Logik und insbesondere ihrer mit dem Re-entry gegebenen Selbstbezüglichkeit eröffnet wird (Luhmann 1997, 877 und an zahlreichen anderen Stellen). Es ist geplant, dies in einem eigenen Abschnitt genauer zu betrachten.

(ii) Umgekehrt wird von den Nachfolgern Nietzsches von der Opazität des Denkens gesprochen. Für sie folgt aus der Opazität der Dinge zwangsläufig, dass auch das Denken seine Transparenz verliert, an die noch Descartes glaubte, wenn es sich selbstbezüglich als sein eigenes Objekt zu untersuchen vermag. Entgegen Descartes sieht Heidegger in Sein und Zeit »die Identität des menschlichen Lebens [...] nicht allein in der Transparenz rein rationaler Selbstdarstellung und Selbstbestimmung, sondern ebenso in der unverfügbaren Opazität seiner Stimmungen, für welche die Befindlichkeit die ontologische Möglichkeitsbedingung sein soll.« (Volpi, 43). Für Sartre »verdinglicht das reflektierende Bewußtsein sein Je zu einem Verdichtungszentrum (centre d'opacité), das im reflektierten Bewußtsein als 'die Psyche' (Moi/Ego) ein Eigenleben zu führen scheint: Bewußtsein (Je) – Moi – Leib.« (Scheier 2016, 69 mit Bezug auf Sartre Transzendenz des Ego). Und Adorno wendet sich direkt gegen Hegel:

»Im emphatischen Sinn bedurfte er (Hegel) der Sprache nicht, weil bei ihm alles, auch das Sprachlose und Opake, Geist sein sollte. Jene Supposition ist nicht zu retten. Wohl aber transzendiert das in keinen vorgedachten Zusammenhang Auflösliche als Nichtidentisches von sich aus seine Verschlossenheit. Es kommuniziert mit dem, wovon der Begriff es trennte. Opak ist es nur für den Totalitätsanspruch der Identität; seinem Druck widersteht es. Als solches jedoch sucht es nach dem Laut. Durch die Sprache lost es sich aus dem Bann seiner Selbstheit.« (Adorno Negative Dialektik, 162)

Bei Spencer-Brown ist dieser Konflikt in die Mathematik hineingenommen. Für ihn kann die Mathematik erst wieder zu neuem Leben erwachen, wenn sie den Anspruch auf restlose Transparenz aufgibt und die damit verbundene Selbstbeschränkung auf Methoden, die diesem Anspruch genügen. Und die Philosophie muss nicht dabei stehen bleiben, entweder die Opazität der Dinge zu fordern oder zu negieren, sondern sie kann dank ihrer eigenen Kreativität und der Kreativät anderer Wissenschaften wie der Mathematik diese Frage von immer neuen Seiten sehen, wenn erst einmal wieder Bewegung in die Mathematik kommt. Es zeigt für mich den betrüblichen Zustand, in dem sich heute nicht nur die Mathematik, sondern auch die Philosophie befindet, wenn diese außer durch den philosophie-skeptischen Soziologen Luhmann die Arbeiten von Spencer-Brown nicht einmal zur Kenntnis nimmt.

Re-entry

Zwar gibt es für die Proto-Arithmetik und Proto-Algebra keine Nachfolger-Relation. Aber Spencer-Brown führt mit dem Re-entry eine Prozedur ein, die von ähnlich fundamentaler Bedeutung ist wie die Nachfolger-Relation und das Induktions-Axiom.

Die Lehre vom Re-entry ist das Herzstück der Laws of Form. Sie ist zugleich die einzige Idee von Spencer-Brown, die eine gewisse Popularität gewonnen hat. Re-entry kann in einer ersten Annäherung sowohl als Resonanz, Rekursion, Feedback, Rückkopplung, Selbstreferenz wie auch als Reflexivität von Begriffen oder von miteinander kommunizierenden Menschen verstanden werden, die aufeinander Bezug nehmen. Sie ist vor allem von der Theorie selbstreferentieller Systeme wie von Anwendungen in der Soziologie und Psychologie aufgenommen worden, insbesondere dem radikalen Konstruktivismus und Systemtheorien verschiedenster Art bis zur systemischen Psychologie.

Diese Anwendungen lösen die Idee des Re-entry aus dem Kontext von Proto-Arithmetik und Proto-Algebra, in dem er bei Spencer-Brown steht. Ohne sich weiter um die diffizilen arithmetischen und algebraischen Operationen in den Laws of Form zu kümmern, übernehmen sie den Grundgedanken, dass Spencer-Brown eine Bewegung betrachtet, die sich von einem System löst und per Re-entry wieder in sie zurückzukehren vermag. Wenn sie zurückkehrt, wird sie nicht nur von dem System wieder aufgenommen, sondern der Re-entry erzeugt dort eine innere Bewegung und muss – im Sprachgebrauch von Lacan – vernäht werden. Was hier im Einzelnen geschieht, wird im Kontext des jeweils betrachteten Systems genauer untersucht, sei es eine Familie, eine Betriebsorganisation oder die Gesellschaft im Ganzen. In allen Fällen kann etwas abgedrängt und isoliert werden, bis es sich abkoppelt. Das löst sowohl im System wie in dem isolierten Element eine Krise aus, die durch den Re-entry gelöst werden kann. Da Spencer-Brown sehr an Fragen der Psychologie interessiert war, gehe ich davon aus, dass er immer Beispiele und Anwendungen dieser Art im Blick hatte. In den Laws of Form nimmt er darauf jedoch keinen Bezug, sondern beschränkt sich auf Fragestellungen der Logik und der Mathematik. Mir ist daher zweierlei wichtig:

(i) Auf welche Fragen der Mathematik gibt Spencer-Brown eine völlig neue und originelle Antwort? Das sind für mich vor allem der Übergang von den natürlichen zu den transfiniten Zahlen und die Algorithmen, mit denen irrationale Zahlen beliebig angenähert, aber nie erreicht werden. In beiden Fällen liegen  Prozesse  vor, die sich grundsätzlich von den gewöhnlichen arithmetischen Operationen unterscheiden. Einen Re-entry kann es für Spencer-Brown nur bei unendlichen Prozessen und nicht bei gewöhnlichen, endlichen arithmetischen Operationen geben.

(ii) Welche Voraussetzungen müssen für Spencer-Brown gegeben sein, damit es zu einem Re-entry kommen kann? Ein Re-entry ist für ihn nur möglich, wenn sich eine Figur unendlich oft gleichförmig wiederholt, während die Arithmetik grundsätzlich nur mit Konstruktionen arbeitet, die endlich viele Schritte enthalten (9. Kanon; LoF, 54). Der Übergang zur Unendlichkeit gelingt erst, wenn in der Algebra Variablen betrachtet werden, die unabhängig von ihrem jeweiligen Inhalt sind, und wenn dank der Transparenz innerhalb der Algebra die Sicherheit besteht, dass es bei den unendlich vielen Wiederholungen zu keinen Nebenwirkungen und inneren Abweichungen kommt. Die einzelnen Wiederholungen sind völlig unabhängig voneinander. Mit dem Re-entry zeigt sich das Neue (und damit die relative Autonomie) der Algebra gegenüber der Arithmetik. In der Proto-Arithmetik gibt es noch keinen Re-entry. Im Gegenteil: Mit dem Re-entry kommt es zum »loss of connexion with arithmetic« (LoF, 58).

Mit dem Prozess, der zum Re-entry führt, ist eine Art innere Musikalität gegeben, die mit dem Re-entry in die Ordnung eingeführt wird, aus der sie hervorgeht. Es ist nicht nur eine Narbe oder ein Riss, die am Ort des Re-entry vernäht werden, sondern das bisher nur in seinen räumlichen, zeitlosen Beziehungen untersuchte System wird im Ganzen in eine Schwingung versetzt (beginnt zu oszillieren), woraus die Zeit und mit ihr eine neue Ordnung hervorgehen (die Emergenz).

Mit den Übergängen zu den transfiniten und irrationalen Zahlen sind nicht nur die beiden in der Mathematik geläufigen Unendlichkeitsbegriffe verbunden (von Hegel als schlechte und wahre Unendlichkeit bezeichnet), sondern auch die beiden seit Aristoteles bekannten elementaren Eigenschaften der Zahlen: Die Transitivität der auf der Zahlenachse angeordneten Zahlen und die Kontinuität der reellen Zahlen. (Die kleiner-als-Relation ist ein Beispiel für Transitivität: Wenn x < y und y < z, gilt auch x < z.) Mit der Transitivität wird sichergestellt, dass unbegrenzt weitergezählt werden kann, und dank der Kontinuität existiert der Grenzwert der Annäherungsprozesse an Irrationalzahlen. Wenn Spencer-Brown mit seiner Idee des Re-entry dies Herzstück der Mathematik und der sich mit der Mathematik beschäftigenden Philosophie trifft, sollte das prinzipielle Konsequenzen für das Grundverständnis der Mathematik haben. Diese können erst sichtbar werden, wenn der Re-entry nicht nur als eine allgemeine Eigenschaft von Systemen angesehen wird, die über Rückkopplung verfügen, sondern mit Spencer-Brown genauer als eine spezifische Wechselbeziehung der mit diesen Systemen gegebenen internen Arithmetik und Algebra.

– Prozesse in der gewöhnlichen Mathematik und bei Spencer-Brown

Vorbilder (Modelle) für den Re-entry sind nach meinem Eindruck die Konstruktion der ersten transfiniten Zahl ω bei Cantor und der Grenzübergang, der zur Annäherung von Irrationalzahlen wie 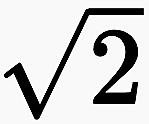führt.

Transfinite Zahlen Beim Zählen 1, 2, 3, … n, n+1, … wird formal betrachtet unendlich oft die jeweils gleiche Nachfolger-Relation von n zu n + 1 wiederholt. Jenseits von allen abzählbaren natürlichen Zahlen liegt die transfinite Zahl ω. Sie kann nie durch Zählen erreicht werden und hat keinen Vorgänger, aber sie kann formal als Ergebnis der Regel des Zählens-im-Ganzen definiert werden. Es muss eine übergreifende Zahlenklasse (einen Grund) geben, in den der Grenzwert per Re-entry aufgenommen werden kann.

Wo liegt ω, und wie wird ω in die Zahlen aufgenommen? Der Mathematiker Riemann hatte dafür eine sehr anschauliche Vorstellung gefunden: Wenn auf der Zahlengerade im Nullpunkt eine Kugel aufgelegt wird, deren Mittelpunkt mit der Zahl Null identisch ist und deren Kugeloberfläche die Zahlenachse an den beiden Punkten −1 und 1 schneidet, kann eindeutig jeder Zahl ein Punkt auf der Kugel zugeordnet werden, indem eine Verbindungslinie zwischen dem Nord- bzw. Südpol und der jeweiligen Zahl gezogen wird, die an genau einer Stelle die Kugel schneidet. Für Zahlen außerhalb der Kugel (das sind in der folgenden Abbildung die Zahlen größer als 1 oder kleiner als −1) liegt der Schnittpunkt auf der oberen Halbkugel, für Zahlen innerhalb der Kugel (das sind die Zahlen im Intervall [−1, 1]) auf der unteren Halbkugel. Der Nordpol entspricht der auf der Zahlengerade unendlich-fernen Zahl ω und ist mit diesem Konstruktionsverfahren in die Zahlenklasse aller Punkte auf der Kugel aufgenommen. Auf den Südpol wird die 0 abgebildet.

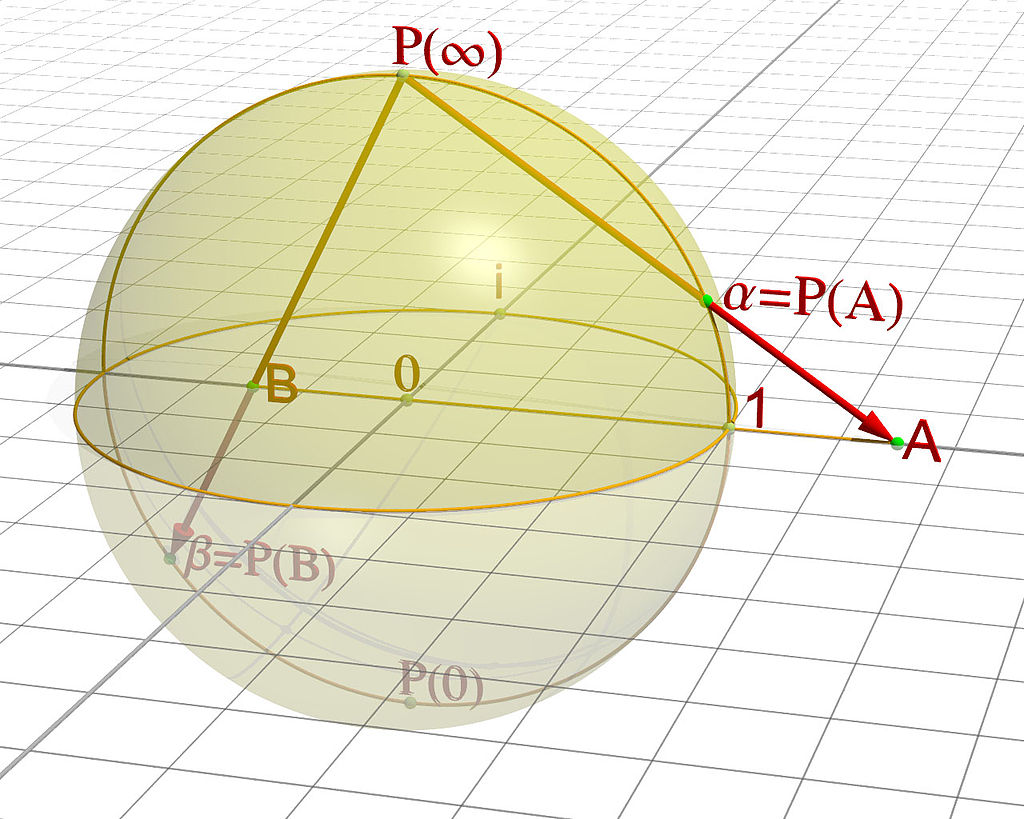
Quelle: Wikipedia, abgerufen am 4.3.2017
Urheber: Von Jean-Christophe BENOIST - Eigenes Werk. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV., CC BY-SA 3.0, Link

An dem Bild ist anschaulich zu sehen, wie ω auf der Zahlengerade unendlich weit weg liegt, jedoch auf der Zahlenkugel bei P(ω) ihren Ort findet. Wie ist das möglich? Mit der Zahlenkugel wurden implizit neue Eigenschaften der Zahlen eingeführt, die bei der Zahlengerade noch nicht gegeben sind: Die Zahlenkugel verfügt über eine zweite, unabhängige Dimension (ihre Höhe, die auch als imaginäre Achse oder als Zeitachse interpretiert werden kann), sie ist symmetrisch gegenüber Drehungen (zyklisch), und sie ist gekrümmt. Das sind Eigenschaften, die über die bisher bekannten Eigenschaften der Zahlen (Transitivität, Kontinuität) hinausgehen und bereits anschaulich nahelegen, dass eine Erweiterung und neue Definition der Zahlen notwendig wird, wenn Prozesse zugelassen werden sollen, die zu einem Re-entry führen. (Im Weiteren wird gezeigt werden, wie dieses Bild und diese Eigenschaften zu der neuartigen Theorie von Beobachtern bei Spencer-Brown führen.)

Irrationalzahlen Für Irrationalzahlen wie 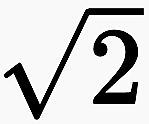gibt es keine Dezimaldarstellung. Sie beträgt ungefähr 1,414… und kann nur fortlaufend genauer bestimmt werden. Mit jedem Schritt wird das Intervall genauer eingegrenzt, in dem sie liegen muss. Zum Beispiel wird mit dem Ausdruck 1,414… gesagt, dass sie irgendwo im Intervall [1,414, 1,415] liegt. Und so wie Cantor mit ω für die transfiniten Zahlen eigene Symbole finden musste, musste für die Irrationalzahlen mit dem Wurzelzeichen ein eigenes Symbol vereinbart werden.

Spencer-Brown erwähnt die Irrationalzahlen in den Notes, wenn er dort von Gleichungen zweiten Grades spricht. Er demonstriert das an der Quadratfunktion x² oder in seinem Kalkül aa = a und führt es am elementaren Polynom zweiter Ordnung aus. (LoF, 97f)

Was geschieht bei den beiden Übergängen zu den transfiniten und den Irrationalzahlen? Es handelt sich nicht mehr um eine gewöhnliche arithmetische Operation. Eine arithmetische Operation wie z.B. ›7 + (10 · 3) / 91‹ kann zwar beliebig kompliziert sein. Letztlich handelt es sich jedoch immer um eine endliche Zeichenkette, die aus Operanden und Operatoren besteht (im einfachsten Fall aus den natürlichen Zahlen als Operanden und den üblichen Rechenregeln +, −, · und / als Operatoren), und die zu einer eindeutig bestimmten rationalen Zahl führt. Bei dem unendlichen Weiterzählen und bei den Annäherungs-Algorithmen zur Bestimmung von Irrationalzahlen wird dagegen eine arithmetische Operation unendlich oft  wiederholt  (iteriert). Erst die Wiederholung (Iteration) erzeugt einen Prozess. Der Mathematik blieb bis heute unbemerkt, oder sie will es nicht wahrhaben, dass im Prozess der Wiederholung implizit die Zeit enthalten ist. – Die Mathematik besteht bis heute darauf, dass ihre Formeln grundsätzlich zeitlos gelten. Erst Spencer-Brown vollzog die längst überfällige Wende und entwickelte konsequent, wie im Prozess, der zum Re-entry führt, implizit die Zeit enthalten ist. Das wird im Weiteren näher ausgeführt.

Bei den arithmetischen Operationen wird die jeweilige Zahlenklasse nicht verlassen. Sie liefert eine neue Zahl und kann mit dieser identifiziert werden. Es ist gleichbedeutend, ob von 12 oder von 5 + 7 gesprochen wird. Bei Prozessen wird dagegen eine neue Zahl definiert, die in der vorher betrachteten Zahlenklasse noch nicht enthalten war. Weder ist ω eine natürliche Zahl noch 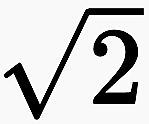eine rationale Zahl. Mit ihnen entsteht ein neuer Begriff von Zahlen: Zahlen sind alle Elemente, mit denen wie mit natürlichen und rationalen Zahlen gerechnet werden kann. Was eine Zahl ist und zur Gesamtheit der Zahlen gehört, wird schrittweise erschlossen. Die Idee der Zahl ist in sich unendlich, und es kann davon ausgegangen werden, dass immer neue Prozesse gefunden werden, um neue Zahlen mit Eigenschaften zu erkennen, die bisher unbekannt waren.

Unendliche Staffelung (echelon without limit) Wie kann Spencer-Brown die unendlichen Prozesse des Zählens oder der Annäherung an eine Irrationalzahl in seinen Formenkalkül übertragen? In der Proto-Arithmetik gibt es keine Nachfolger-Relation wie bei den natürlichen Zahlen, sondern eine Vielfalt von Möglichkeiten, ein Zeichen in ein anderes umzuwandeln. Wenn Spencer-Brown von Kalkulation spricht, meint er das Umwandeln. Das Rechnen mit den natürlichen Zahlen ist für ihn ein Beispiel von Umwandlungen, das er in seiner Logik verallgemeinert. Um einen Prozess zu finden, der dem unendlichen Weiterzählen bei den natürlichen Zahlen entspricht, ist in seinem Kalkül eine Umwandlung zu bestimmen, die ebenfalls wie das Zählen unendlich oft wiederholt werden kann, wobei alle einzelnen Schritte formal gleich (selbstähnlich) sind. Spencer-Brown konstruiert in der Proto-Algebra eine Regel, die vergleichbar der fortlaufend wiederholten (iterierten) Nachfolger-Relation von n nach n + 1 beliebig fortgesetzt und für die analog zur Nachfolger-Relation ein unendlich-fernes Element definiert und per Re-entry in einen größeren Zahlenraum aufgenommen werden kann. Er zeigt, wie auf das Zeichen 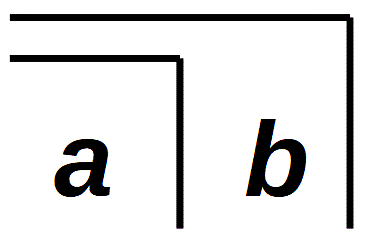eine Sequenz von 5 Einzelschritten angewandt werden kann, wodurch sich das Zeichen verdoppelt. (Das sind in seiner Terminologie die 5 Einzelschritte C5 Iteration, C1 Reflektion, J2 Distribution, C4 Occultation, C1 Reflektion; LoF 55). Wird diese Sequenz ausgeführt, so wird das Ausgangszeichen am Ende angehängt mit dem Ergebnis (LoF, 56):

    ⇀ .

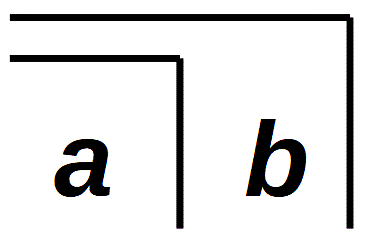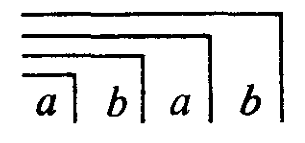Mit dem Symbol ⇀ ist ausgesagt, dass beide Zeichen (Formen) wertgleich sind. Auf das neue Zeichen (Form) kann wiederum die gleiche Sequenz aus 5 Einzelschritten angewandt werden, wodurch es sich erneut verlängert. Auf diese Weise gelingt eine Folge von Schritten, die der Nachfolger-Relation entspricht und unendlich oft wiederholt werden kann. Das Ergebnis ist für Spencer-Brown »an echelon without limit«, das aus der für die Proto-Algebra nachgewiesenen »Consequence C7 Echelon« (Staffelung) hervorgeht (LoF, 34).

»Der nächste entscheidende Schritt besteht darin, sich vorzustellen, wenn es möglich ist (let us imagine, if we can, LoF, 55), dass der Prozess dieser Schrittsequenz end- oder zeitlos (timelessly) weiterläuft. Im Raum würde das ein Echelon (Staffelung) von a's und b's ohne Grenze ergeben. [...] Da die Bestimmung des Wertes eines Ausdrucks an die Regel der endlichen Demonstrierbarkeit gebunden ist, kann über den Wert eines Echelons ohne Grenzen keine Aussage gemacht werden.« (SWH, 175)

Mit diesen Schritten sind nicht alle Zeichen der Proto-Algebra aufgezählt und in eine Reihenfolge gebracht, sondern nur eine bestimmte Teilmenge. Es ist davon auszugehen, dass es unendlich viele weitere Möglichkeiten gibt, aus dem unerschöpflichen Vorrat der Formen auf ähnliche Weise unendliche Folgen zu bilden. Es genügt jedoch, ein möglichst einfaches Beispiel gefunden zu haben und an ihm den Re-entry in die Proto-Algebra einzuführen.

Im Ergebnis schreibt Spencer-Brown ein Diagramm auf, mit dem der Re-entry definiert wird:

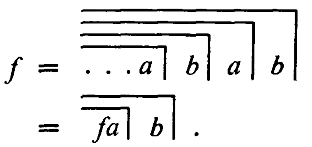
E1 Re-entry
(LoF, 56)

Das Diagramm E1 ist ungewohnterweise blockweise von rechts nach links zu lesen. Spencer-Brown betrachtet in E1 das schrittweise Crossing von a zu b zu a zu b usf. a und b stehen als Variable der Proto-Algebra für Werte, die aus der Proto-Arithmetik eingesetzt werden können: Das sind im Kalkül von Spencer-Brown nur der Haken und das Ock. Der Übergang von a zu b wird beliebig oft wiederholt. Für die Wiederholung führt Spencer-Brown erst mit den drei Pünktchen … und dann mit f zwei neue Symbole ein, die bisher weder in seiner Proto-Arithmetik noch in seiner Proto-Algebra bekannt waren. Die drei Pünktchen übernimmt er von den entsprechenden, aus der gewöhnlichen Arithmetik bekannten Prozessen, wenn dort über n und n + 1 hinaus immer weiter gezählt oder eine Irrationalzahl beliebig genau angenähert wird.

Mit dem Symbol f wird das Ergebnis eines Grenzübergangs beschrieben. Für Spencer-Brown kann a als ein Input angesehen werden, der mit den beiden aus der Proto-Arithmetik möglichen Werten gesättigt werden kann, dem Haken oder dem Ock. Für diesen Input wird eine Regel gefunden, die unendlich oft wiederholt wird. Im Ergebnis entsteht ein Output f, der per Re-entry nicht einfach in die gleiche Zahlenmenge aufgenommen werden kann, in der der Input a lag, sondern diese Zahlenmenge auf ähnliche Weise erweitert wie die transfiniten Zahlen die Menge der natürlichen Zahlen und die Wurzeln die Menge der Rationalzahlen erweitern.

Mit f ist sowohl die Funktion (der Algorithmus, der Prozess) gemeint, mit dem in unendlich vielen Schritten ein Grenzwert angenähert wird, wie das Resultat des Prozesses (dieser Grenzwert selbst). Spencer-Brown hält konsequent seine Idee durch, Symbole einzuführen, die in Mehrfachbedeutungen sowohl eine Operation wie das Ergebnis dieser Operation sein können.

Die Zusammenfassung der unendlich vielen Crossings von a zu b zu a zu b usw. in f ist an drei Bedingungen gebunden:

(a) »eine klar bestimmte Folge von Schritten, es gibt also eine klare Konstruktionsanweisung«,
(b) sie »soll kontinuierlich fortgesetzt werden«,
(c) sie enthält ein »Muster der Sich-selbst-Gleichheit« (SWH, 175).

»The key is to see that the crossed part of the expression at every even depth is identical with the whole expression, which can thus be regarded as re-entering its own inner space at any even depth.« (LoF, 56)

Das Symbol f erinnert an die in der gewohnten Mathematik eingeführten Funktionen f(x). f ist definiert über den Werteverlauf einer unendlichen Folge untereinander formal gleicher Schritte, die sich einem Grenzwert nähern. Aber anders als bei den gewohnten Funktion f(x) ist f zugleich der Grenzwert selbst. f ist wie die transfinite Zahl ω oder die Wurzel 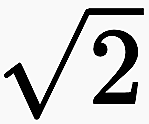ein Grenzwert, der in dem bisherigen Zeichenvorrat nicht vorhanden war. f ist weder der Haken noch das Ock. Mit f wird der Zeichenvorrat der Proto-Arithmetik in ähnlicher Weise erweitert wie der Zeichenvorrat der natürlichen Zahlen durch die transfiniten Zahlen und der rationalen Zahlen durch die Wurzeln.

Spencer-Brown formuliert das negativ: Für den Re-entry f gibt es keinen eindeutigen Platz. Es ist in dem gegebenen Kalkül unbestimmt, wo es aufgenommen werden kann (»indeterminacy« LoF, 57). Spencer-Brown bezeichnet in diesem Zusammenhang den Übergang von a zu f in größerer Allgemeinheit als Übergang von einem Ausdruck e (für expression) zu einem Ausdruck e', der per Re-entry aufgenommen werden soll:

»We have just introduced to e' a degree of indeterminacy in respect of its value which is not (as it was in the case of indeterminacy introduced merely by cause of using independent variables) necessarily resolved by fixing the value of each independent variable.« (LoF, 57)

Es gibt für f in der Ausgangsmenge keinen Wert, wo es aufgenommen werden könnte. Daher gibt es nur zwei Möglichkeiten: Entweder wird für den Re-entry von f die Ausgangsmenge erweitert (nach dem Vorbild von ω und 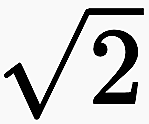), oder f irrt gleichsam umher und findet keinen festen Platz. Dies Umherirren wird Spencer-Brown zur Oszillation führen, mit der er den Begriff der Zeit einführt. (So verstehe ich, wie er vom Re-entry zur Zeit kommt. In einem abschließenden Schritt wird er den Weg von einer Form a zu einem Grenzwert f erweitern zu Schaltkreisen, die einen Input a in einen Output f umwandeln.)

Es ist daher missverständlich, wenn der Re-entry so gedeutet wird, als würde irgendwie aus einer Basismenge ein Prozess hervorgehen, der sich von der Basismenge entfernt, bis er im Ergebnis einen Wert liefert, der wieder in die Basismenge zurückführt und auf einen dort bereits bekannten Wert trifft. Stattdessen wird mit dem Re-entry von f die bereits bekannte Zahlenmenge erweitert. Aber es gilt, dass alle bisher gültigen Regeln der Zahlenmenge erhalten bleiben, und es ist sicher zu stellen, dass mit f auf die gleiche Weise gerechnet werden kann wie mit allen anderen Zahlen. Für Spencer-Brown ist das in seinem Kalkül gegeben: »It is evident that J1 and J2 hold for all equations, whatever their degree.« (LoF, 57)

Treffender ist daher der Vergleich mit der Erweiterung von den reellen Zahlen zu den imaginären Zahlen. Um das zu verstehen, sind zwei Schritte notwendig. In einem ersten Schritt ist die Menge aller Argumente a zu erweitern in eine Menge, in der alle Werteverläufe der Funktionen f dargestellt werden können, die auf den Argumenten a operieren. Darauf aufbauend ist in einem zweiten Schritt zu verstehen, wie von der Menge aller Argumente a zur Menge aller auf ihnen operierenden Funktionen f gelangt und aus ihr durch einen Re-entry in die Menge der Argumente zurückgekehrt werden kann.

(i) Übergang von den Argumenten zu den Wertverläufen: Auf einer Achse sind alle Zeichen der Proto-Arithmetik angeordnet, und auf der senkrecht zu ihr stehenden Achse alle Zeichen, in die sie umgewandelt werden können, so wie in der gewöhnlichen Mathematik auf der x-Achse alle Argumente und auf der y-Achse alle Funktionswerte y = f(x) dargestellt werden. Das ergibt ein zweidimensionales Tableau, in dem der Werteverlauf eingetragen werden kann.

(ii) Die Werteverläufe können wiederum für sich betrachtet werden. Jeder Werteverlauf f ist für sich ein eigenes mathematisches Objekt, und es kann die Menge aller Werteverläufe f untersucht werden. Diese Menge der Werteverläufe f ist unabhängig von der Menge der Argumente x, auf denen die Funktionen f operieren. (Scheier spricht von einer Differenz zwischen den Funktionen und ihren Argumenten. [Scheier 2016, 67]). Ich verstehe den Grundgedanken von Spencer-Brown so, dass es für ihn einen Weg gibt, auf dem die Menge der Argumente emergiert in die Menge der Funktionen, die senkrecht zur Menge der Argumente steht. Das ist eine Bewegung, die aus der Menge der Argumente in die Menge der Funktionen führt und aus ihr durch einen Re-entry in die Menge der Argumente zurück. Das ist nur möglich, wenn die Argumente als rudimentäre Funktionen angesehen werden können (indem jedes Argument a als eine Identitätsfunktion a = a verstanden wird), und wenn es in der Menge aller Funktionen eine Operation gibt, die in die Menge der Argumente zurückführt. Wenn ich ihn richtig verstehe, sieht Spencer-Brown hierfür ein Vorbild in den imaginären Zahlen. So wie nach den Regeln der komplexen Algebra mit den imaginären Zahlen eine Drehung erfolgt, die von den reellen Zahlen in die imaginären Zahlen und von dort zurück zu den reellen Zahlen führt, so gibt es für ihn einen Weg von den Argumenten a zu den Funktionen f und durch einen Re-entry zurück in ein neues Argument. Dieser Gedanke ist bei Spencer-Brown bestenfalls angedeutet, und es erscheint mir eine lohnende Aufgabe, ihn mathematischer genauer zu formalisieren. Es ist eine völlig neue Sicht auf die mathematische Theorie der Räume von Funktionen und könnte weiter gedacht dazu führen, den Hilbert-Raum in einen anderen Raum einzubetten, der die Eigenschaften des Hilbert-Raums bewahrt, aber auf der von Spencer-Brown eingeführten Proto-Arithmetik beruht und mit dem Re-entry neue Eigenschaften verstehen lässt, die im gewöhnlichen Hilbert-Raum nicht gegeben sind. Da der Hilbert-Raum wiederum das mathematische Werkzeug für die Quantentheorie ist, kann sich daraus eine neue Sicht auf die Quantentheorie ergeben, die dort auf ähnliche Weise die bekannten Aporien auflöst wie Spencer-Brown die Russellsche Antinomie aufgelöst hat.

Die Russellsche Antinomie besteht für Spencer-Brown nur auf der Ebene der Menge aller Argumente und ist dort unlösbar. Sie wird für ihn erst mit dem Übergang in die imaginären Zahlen lösbar, und er hat im bereits zitierten Vorwort zur amerikanischen Ausgabe von Laws of Form die grundlegende Idee gegeben, wie das möglich ist. Ähnlich kann es sich bei den Argumenten a und den Funktionen f verhalten. Der Übergang in den imaginären Raum aller Funktionen ist wie gezeigt nicht beliebig, sondern an feste Regeln gebunden. Dank dieser Regeln ist eine Rückkehr in den Raum der Argumente möglich, erzeugt dort neue Argumente, und auf diesem Wege können die Paradoxien vermieden werden, die Russell und Whitehead gewissermaßen mit der Holzhammermethode mit dem Verbot negativ selbstbezüglicher, imprädikativer Urteile (vicious circle principle) vermeiden wollten. Der Re-entry tritt an die kritische Stelle negativer Selbstbezüglichkeit und sollte daher in einem weiteren Horizont die oft gesuchte Formalisierung der dialektischen Methode ermöglichen, wenn diese mit ihrer negativen Selbstbezüglichkeit definiert wird. (Oft wurde versucht, für Hegels Methode der Aufhebung eine Formalisierung zu finden. Das ist nach meinem Eindruck auf dem von Spencer-Brown geöffneten Weg möglich, mit dem er für mich weit über die Ideen von Gotthard Günther hinausging, der ein ähnliches Ziel verfolgte.)

Es ist sicher noch ein weiter Weg, diese Ideen auszuarbeiten. Bevor das begonnen wird, sind weitere Ideen von Spencer-Brown zu verstehen, um sein Anliegen in ihrem ganzen Umfang zu überschauen. Das sind seine Ausführungen zur Einführung der Zeit und die von ihm entworfenen Schaltkreise.

– Wellen und ihre Zeit (Time)

Mit den 3 Pünktchen ‘…’ und der Variable f hat sich Spencer-Brown naheliegenderweise an Symbolen orientiert, die aus der gewohnten Mathematik bekannt sind. Die Besonderheit seines Kalküls liegt jedoch darin, dass er statt der üblichen Ziffern und Rechensymbole (Operationszeichen) nur die beiden Zeichen für Haken und Ock kennt, die er in der Doppelbedeutung als Operand und Operator gebraucht. Dank dieser Vereinfachung gelingt es ihm, an Grenzübergängen Eigenschaften aufzuzeigen, die weit über die bekannte Mathematik hinausgehen. Das führt in zwei Schritten zu einem Perspektivwechsel:

– Die kleinste Einheit des Grenzübergangs sind für ihn nicht mehr die Punkte, entlang derer der dem Grenzübergang zugrunde liegende Prozess verläuft, bis er den Grenzwert als einen neuen Punkt bestimmt, – so wie es aus dem Beispiel bekannt ist, wenn sich Achilles Punkt für Punkt der ihm vorauslaufenden Schildkröte nähert –, sondern die  Gestalt  des Grenzverlaufs im Ganzen. Das ist für ihn die Welle. Wie kommt er darauf? Wenn der Grenzwert f im Moment des Re-entry umherirrt und keinen festen Platz findet, kann das verstanden werden als eine Hin- und Herbewegung, die fortlaufend zwischen Haken und Ock pendelt. Das ergibt eine Welle, wobei der Wellenberg für den Haken steht und das Wellental für das Ock. Mehr Zeichen gibt es in seiner Proto-Arithmetik nicht. Grenzübergänge können direkt auf einen bestimmten Punkt zusteuern oder aber ständig zwischen den beiden in der Proto-Algebra verfügbaren Werten oszillieren. Spencer-Brown nimmt vorweg, was später in der Katastrophentheorie mit ihren Bifurkationen und Attraktoren genauer ausgeführt wurde, und beschreibt gewissermaßen deren innerste Logik.

– Wenn er sich mit dem Bild der Welle von den überlieferten Symbolen des Grenzübergangs löst und eine neue Sicht auf ihren Verlauf gewinnt, vermag er erstmals Grenzübergänge zu verschachteln. Damit ist nicht gemeint, dass wie z.B. bei Mehrfachintegralen Grenzübergänge einheitlich in mehreren Dimensionen betrachtet werden, sondern es kann innerhalb eines Grenzübergangs zu einem konträren Grenzübergang zweiter oder höherer Ordnung kommen (die er Gleichungen zweiten Grades nennt). Aus dem Wechselverhältnis zweier Grenzübergänge entsteht für ihn die Zeit.

Die Wellendarstellung und die in ihr enthaltene Zeit werden in einem komplexen Diagramm eingeführt, das zeilenweise zu lesen ist:

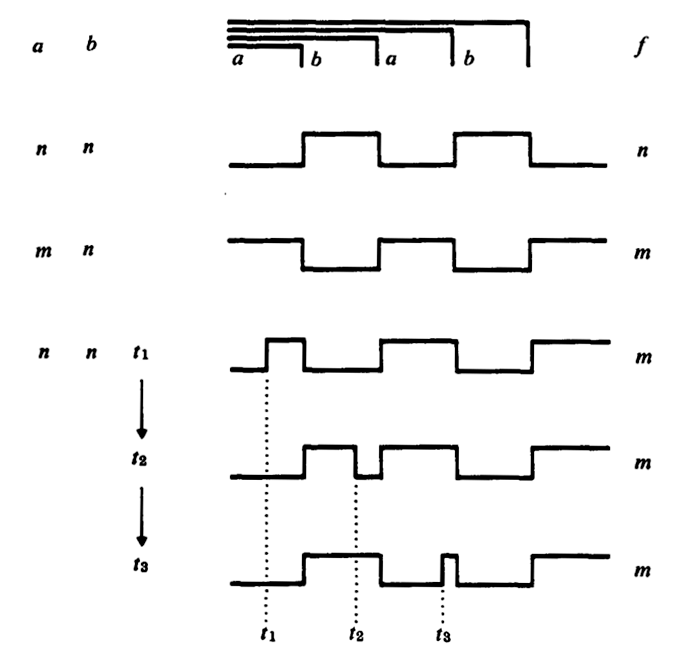
Time as a Key
Quelle: LoF, 63, Figure 3

In der ersten Zeile ist die unendliche Staffelung mit den Variablen a und b gezeichnet. Ihr Ergebnis ist der Output f. In den weiteren Zeilen werden für a und b spezielle Werte eingesetzt. m und n stehen nicht für neue Variable, sondern mit m (marked state) ist der Haken gemeint, mit n (unmarked state) das Ock. Die beiden Konstanten m und n wurden erstmals für die Rule of dominance definiert (LoF, 15) und wieder aufgegriffen in LoF, 56. Die Häufung von Namen und Symbolen für Haken und Ock ist auf den ersten Blick verwirrend und unübersichtlich. Spencer-Brown hat zwar gute Gründe, mit diesen verschiedenen Bezeichnungen und Darstellungen jeweils bestimmte Aspekte klarer hervorzuheben, doch wäre es einfacher, so weit als möglich bei den beiden Urzeichen Haken und Ock zu bleiben.

In der zweiten Zeile werden sowohl für a wie auch für b jeweils das Ock (n, unmarked state) eingesetzt. Das fortlaufende Crossing der unendlichen Staffelung 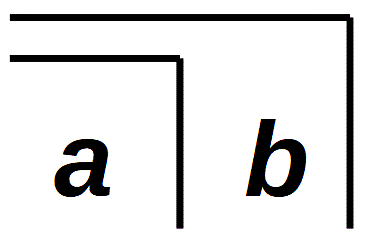wird mit dem unmarked state (Welle unten) begonnen, in den marked state gewechselt (Welle oben) usf., bis nach einer ungeraden Anzahl von Schritten wieder der unmarked state n erreicht ist.

In der dritten Zeile wird für a der Haken (marked state, m) und für b das Ock (unmarked state, n) eingesetzt. In diesem Fall beginnt die Welle oben mit dem marked state und endet nach einer ungeraden Anzahl von Schritten wieder oben im marked state.

Der entscheidende Schritt erfolgt in der vierten bis sechsten Zeile: Wellen können einander überlagern. Spencer-Brown spricht anschaulich von einem »dominant pulse« (LoF, 63) und einem »short pulse« (LoF, 64). Der dominant pulse beschreibt eine Grundschwingung, die erhalten bleibt, und der short pulse läuft erkennbar durch die Grundschwingung hindurch. In den Zeilen 4 bis 6 wird gezeigt, wie das Durchlaufen an den drei Zeitpunkten t₁, t₂, t₃ abzulesen ist.

Mit der Verschachtelung konträrer Grenzübergänge entsteht innerhalb der Logik die Zeit. Der erste Grenzübergang erfolgt für ihn räumlich (so wie es in der räumlichen Figur der unendlichen Staffelung dargestellt wurde), der zweite dagegen zeitlich.

»Since we do not wish, if we can avoid it, to leave the form, the state we envisage is not in space but in time.« (LoF, 58)

Ohne die Unterscheidung in dominant pulse und short pulse bliebe die Zeit unvollständig. Sie bliebe auf einem Stand, den Felix Lau treffend beschreibt:

»In seiner Rezension der Laws of Form hat Heinz von Foerster auf die Entdeckung bzw. Entwicklung der Zeit aus den Axiomen euphorisch hingewiesen. (Lau, 93) [...] Mit der Oszillation geht kein Maß einher, was für unser gängiges Konzept von Zeit unentbehrlich ist. Diese 'erste Zeit' hat keine Dauer, kein Maß; sie ist lediglich der Wechsel, das Hin-und-her zwischen den Zuständen. Die Oszillation hat eben noch keine Geschwindigkeit, für die man Maßeinheiten von Raum und Zeit bräuchte.« (Lau, 94)

Erst mit dem short pulse kann das Maß der Zeit beschrieben werden. dominant pulse und short pulse lassen sich für mich als Grundrauschen eines Systems (die Systembewegtheit) und Bewegung innerhalb des Systems verstehen. Spencer-Brown betrachtet jedoch nicht weiter ihr Verhältnis. In Erweiterung seiner Arbeit kann ausgehend von der Mechanik mit dem Quadrat für beide Pulse ein gemeinsames, inneres Maß gefunden werden. (Siehe zum Quadrat den Beitrag über dynamische Zahlen).

Das entspricht der klassischen Vorstellung der Zeit und wird bei Spencer-Brown bis in die allgemeinst-mögliche Ebene der Logik gebracht: Zeit und Bewegung können nur beschrieben werden, wenn sich ein einzelnes Objekt vor einem Hintergrund bewegt, der entweder ruht oder sich gleichmäßig bewegt, wie z.B. die Bewegung des Mondes vor dem Hintergrund des Sternenhimmels.

Spencer-Brown ist sich bewusst, dass die von ihm bisher benutzten Symbole ‘…’ und f für den Re-entry missverständlich sind. Er bildet daher für den Re-entry ein eigenes Symbol mit großer Suggestivkraft:

   

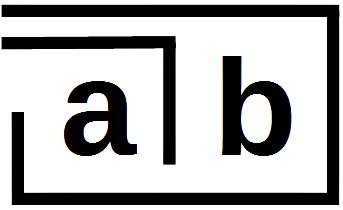
Das Symbol zeigt die zurücklaufende Bewegung. Spencer-Brown war überzeugt, mit dieser Entdeckung den gesuchten gordischen Knoten gefunden zu haben. Er hat eine einheitliche Formalisierung von Grenzübergängen gefunden, die zudem ineinander verschachtelt werden können. Mit ihnen hat er die imaginären Zahlen und innerhalb der Logik die Zeit in ihrer Unterscheidung vom Raum entwickelt. Und er kommt in die Lage, komplexe oszillierende Figuren in Schaltplänen aufzuzeichnen, die bereits der Art der von ihm betriebenen Programmierung in technischen Anwendungen sehr nahe kommt.

Anmerkung: In einem weiteren anschaulichen Bild hat er den Re-entry als Tunnellung verstanden. Das zeigt bereits das Symbol, wenn das neue Zeichen die beiden Variablen a und b unterläuft und wie durch einen Tunnel an den Anfang zurückkehrt. In einem weiterführenden Kommentar wird ausgeführt, wie mit dem Tunnel und der Tunnellung ein vertieftes Verständnis von Grund und Medium gefunden werden.

– Trägheit und Selbstorganisation der Schaltkreise

Die Mathematik geht vom Zählen aus. Mit dem Zählen werden schrittweise die Zahlen eingeführt. Im einfachsten Fall wird beim Zählen ein vereinfachtes Abbild geschaffen: Wer Gläser Bier zählt, zeichnet auf einem Bierdeckel für jedes Glas Bier einen Strich und sieht an den Strichen, wie viel Bier getrunken wurde und zu bezahlen ist. Das erscheint so selbstverständlich, dass bis Ende des 19. Jahrhundert niemand daran zweifelte, mit dem Zählen die Mathematik und das Rechnen begründen zu können. Verborgene Paradoxien traten erst auf, als 1877 Georg Cantor (1845-1918) mit dem Zweiten Diagonalargument nachweisen konnte, dass der Weg der Mathematik zu über-abzählbaren Zahlen führt. Das ist ein Widerspruch völlig neuer Art: Es handelt sich nicht mehr um einen äußeren Gegensatz, wenn einer Eigenschaft oder einer Aussage A eine gegenteilige Eigenschaft oder Aussage Nicht-A gegenübersteht, sondern es sind Zahlen gefunden, die sich an sich selbst widersprechen: Zahlen, die nicht zählbar sind. Formal ähnelt das dem klassischen Lügner-Paradoxon ›dieser Satz ist falsch‹. Doch während dieser Satz als Scherz verstanden werden kann, der sich ohne Probleme in der alltäglichen Sprache vermeiden lässt, befinden sich die über-abzählbaren Zahlen im Herzen der Mathematik und stellen ihre Konsistenz in Frage.

Mit Bertrand Russell (1872-1970) wurde klar, dass das Paradox viel weiter geht. Er untersuchte Mengen aller Mengen, die sich nicht selbst enthalten (die nach ihm benannte Russellsche Antinomie) und teilte seine Erkenntnis 1902 dem Logiker Gottlob Frege (1848-1925) mit. Das stürzte die Mathematik in eine Grundlagenkrise. Die negative Selbstbezüglichkeit ist nicht nur ein Grenzfall über-abzählbarer Zahlen, der irgendwo im Aufbau der Zahlen auf einer hohen Stufe vorkommt, sondern tritt bereits in den Grundbegriffen der Mathematik auf. Als Antwort formulierte Russell gemeinsam mit Whitehead als ein zusätzliches Axiom der Mathematik das Verbot negativ-selbstbezüglicher Aussagen (vicious circle principle).

Damit kann sich die Mathematik nie abfinden. Spencer-Brown fand einen völlig neuen Weg. Er hinterfragte das übliche Verständnis des Zählens. Mit Zählen ist gemeint, dass ein Subjekt über die Fähigkeit verfügt, ihm gegebene Objekte zählen zu können. Zählen ist nur möglich, wenn das zählende Subjekt und die zählbaren Objekte voneinander unterschieden sind und im Prozess des Zählens aufeinander bezogen werden können, wobei natürlich der Fall auftreten kann, dass ein Subjekt sich selbst mitzählt und in der Doppelrolle als Zählendes und Gezähltes auftritt. Seit Aristoteles fragt die Mathematik, dank welcher Eigenschaften ein Subjekt zählen kann (das Zählenkönnende, to arithmetikon), Objekte zählbar sind (arithmeton) und was beim Prozess (Vorgang) des Gezähltwerdens (arithmeisthai) geschieht. Zählbare Objekte werden als sortal bezeichnet. Wissenschaft ist nur möglich, wenn sie von sortalen Objekten handelt. »Man muss zählen und erinnern, um einen Auswahlbereich technisch zu fixieren und kontextuell offen zu halten.« (Baecker 2000, 330)

Aber erst Warren McCulloch (1898-1969) untersuchte 1961 die technischen Aspekte des Gezähltwerdens: Was ist eine Zahl, daß ein Mensch sie kennen kann, und ein Mensch, daß er eine Zahl kennen kann?, so der Titel seines bahnbrechenden Essays. Gibt es eine Logik der Zahl, die der Zahl vorausgeht, und eine Logik der Signalübertragung und Kommunikation der Nerven, die sich treffen? Er fragt erstmals, wie in einem Netzwerk ein Input (die sinnlichen Reize) auf eine Weise verarbeitet werden können, so dass am Ende im Gehirn die Erkenntnis einer Zahl steht. Das sollte sich durch eine neurophysiologische Untersuchung der Nervenbahnen klären lassen. Bei McCulloch ist zu erleben, in welcher Weise die Frage nach der Logik ihre Richtung ändert. Logik wird nicht mehr wie im Neuplatonismus als der uns sichtbare und erfahrbare Ausdruck eines höheren Geistes gesehen, sondern begründet in einer tiefer liegenden Logik im Körper und dessen Prozessen.

Aus diesem Horizont verstehe ich Spencer-Brown. Er kommt von der Mathematik, der Logik und der Programmierung und fragt nach einer Funktion, mithilfe derer Objekte sich selbst zu zählen vermögen. So deute ich den unscheinbaren Satz, mit dem er seine Ausführungen über die Netzwerke einleitet: »We can find a function which will not only remember, but count« (LoF, 65). Mit diesem Ansatz ist es nicht mehr ein Subjekt, das von außen kommend etwas sieht und es zählt, sondern in einem Objekt (einer Maschine, einem Körper) eine Funktion, die einen Input a erhält und einen Output f liefert, der aus dem Zählen des Input hervorgeht.

Wie lässt sich eine Maschine vorstellen, die beispielsweise eine gegebene Menge von Kugeln zählen kann? Sie muss die Kugeln abtasten und erkennen, wann zwischen zwei Kugeln eine Grenze auftritt. Mit jeder Grenze wird eine neue Kugel erreicht, die gezählt werden kann. Und sie muss erkennen, ob die Kugeln wie die Ziffern auf einer Uhr in einem Kreis angeordnet sind und nicht mehrfach gezählt werden dürfen, oder ob sie sich vor und zurück bewegen und daher mehrfach in das Blickfeld treten. Eine ähnliche Aufgabe erhielt Spencer-Brown in seiner Zeit als Programmierer Anfang der 1960er. Er sollte im Auftrag einer britischen Eisenbahngesellschaft ein Programm schreiben, mit dem die Waggons gezählt werden, die in einen Tunnel fahren und möglicherweise vor und zurück kommen. Ohne es weiter zu erläutern versteht er das Zählen elementar als Modulation einer einlaufenden Welle in eine auslaufende Welle mit einer veränderten Frequenz, im einfachsten Fall mit einer halbierten Frequenz (Teilen durch 2). Aus dieser Aufgabe entstand sein Entwurf der Schaltkreise. Er nennt daher die Funktion »modulator function« (LoF, 65) oder in anderen Arbeiten »reductor«. Auch wenn ich noch nicht ganz überschaue, wie das Zählen in der Modulation von Wellen begründet werden kann, möchte ich mich dieser Frage mit einigen Ausführungen zu den von Spencer-Brown betrachteten Schaltkreisen nähern.

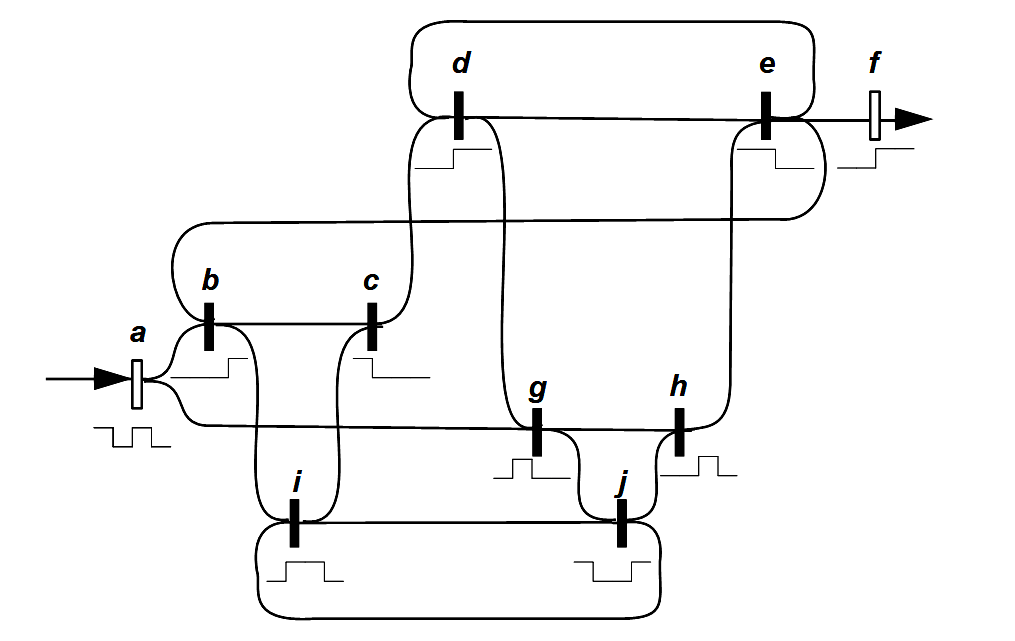
E4 Schaltplan eines Reduktor (Modulation)
Legende
Volles Rechteck: Schaltelement
Leeres Rechteck: Eingang bzw. Ausgang
Oberhalb des Rechteck steht dessen Name
Unterhalb des Rechteck steht die ein- bzw. ausgehende Welle und bei Schaltelementen deren Konversionsregel
Der Reduktor (reductor) reduziert (moduliert) die Frequenz einer Welle a auf die Hälfte und erzeugt mit f eine Welle von halb so großer Frequenz.
Quelle: LoF, 67 mit eigener Ergänzung der Namen für die marker

In diesem Beitrag sollen Einzelheiten des Netzwerks und verschiedene Konsequenzen erläutert werden, die zeigen, in welcher Weise mit ihnen ein völlig neues Verständnis der Logik eröffnet wird:

– (1) Funktionsweise des Netzwerks: Der Input wird schrittweise verarbeitet. Was geschieht an den Schaltelementen.

– (2) Zeitverzögerungen (Trägheit) im Netzwerk

– (3) Knotenlinie von Systemzuständen

– (4) Selbstorganisation des Netzwerks

– (5) Mit der Vielfalt möglicher Wege und der Auswahl aus ihnen ist die Logik einer evolutionären Produktion entworfen.

– (6) Fließgleichgewicht von Zuständen des Netzwerks und seinen Inputs

– (7) Umwandlung eines Arguments in eine Funktion, die über das Argument verläuft

– (8) Wechselwirkung von Objekt und Subjekt

– (9) Mögliche Anwendungen

(1) Funktionsweise des Netzwerks

Der Schaltkreis enthält einen Eingang a, einen Ausgang f sowie 8 Schaltelemente (marker) b, c, d, e, g, h, i, j. An jedem Element ist eine Welle ergänzt. Es wird sich zeigen, dass sie zweierlei Bedeutung hat: Sie beschreibt am Eingang a und am Ausgang f die Gestalt der Welle, die in das Netzwerk eintritt bzw. das Netzwerk verlässt. Im Innern des Netzwerks beschreibt sie die Regel, mit der am jeweiligen marker dort eintreffende Wellen konvertiert werden. Als Werte sind im Kalkül von Spencer-Brown nur ein Haken (Kreuz, markierter Zustand,  ⃧  ) oder ein Ock (das Äußere des Haken, unmarkierter Zustand, Ɔ) möglich. Andere Werte gibt es in seinem Kalkül nicht. Im Schaltplan wird der Haken als Wellenberg und das unmarkierte Äußere als Wellental dargestellt. Trifft ein Wellenberg auf einen marker, der in ein Wellental umwandelt, dann kann die Umwandlung erfolgen. Trifft ein Wellenberg dagegen auf einen marker, der in einen Wellenberg umwandelt, dann ist die Umwandlung nicht möglich und der Weg an dieser Stelle durch den marker versperrt. Entsprechend wird ein auf einen marker treffendes Wellental blockiert oder in einen Wellenberg umgewandelt.

Die Aufgabenstellung des Schaltkreises ist klar erkennbar und erschließt sich intuitiv: Eine einlaufende Welle a soll in eine auslaufende Welle f von halber Frequenz umgewandelt werden. Doch was geschieht an den einzelnen Schaltelementen? Hier führt die spontane Intuition in die Irre: Es wird nicht schrittweise an jedem Schaltelement die vollständige einlaufende Welle in eine andere Welle verwandelt, wie sie im Schaltplan dargestellt ist, bis der Output f erreicht ist. Sondern um den Schaltplan zu verstehen, ist eine verborgene  dritte Dimension  zu erkennen. Das hat Spencer-Brown erst später in einem unveröffentlichten Text näher ausgeführt. Vor allem aber ist es Louis Kauffman gelungen, den Sachverhalt besser aufzuklären.

Die einlaufende Welle a betritt den Schaltkreis nicht auf einen Schlag, sondern schrittweise. Sie setzt sich in diesem Beispiel aus 4 Elementen (4 elementaren Inputs) zusammen: Wellenberg - Wellental - Wellenberg - Wellental. Jedes Element der einlaufenden Welle betritt einzeln den Schaltkreis. Spencer-Brown spricht daher von 4 strokes (Impulsen) (R, 10). Für jeden einzelnen stroke ist zu betrachten, wie er an den einzelnen Schaltelementen umgewandelt wird und in welchen Zustand er den Schaltkreis versetzt. Wenn diese Idee verstanden ist, kann aus dem Bild von E4 abgelesen werden, was beim ersten stroke geschieht. Dafür ist jeweils der erste Abschnitt der in dem Diagramm eingezeichneten Wellen auszuwerten. In der graphischen Darstellung folge ich Kauffman 2006. Er stellt für die einzelnen strokes den Wellenberg (Haken) durch einen Vollkreis und das Wellental (Ock) durch einen Leerkreis dar. Das Ergebnis ist sehr anschaulich, denn es zeigt, wie jedes Schaltelement Vollkreise in Leerkreise und Leerkreise in Vollkreise umwandelt.

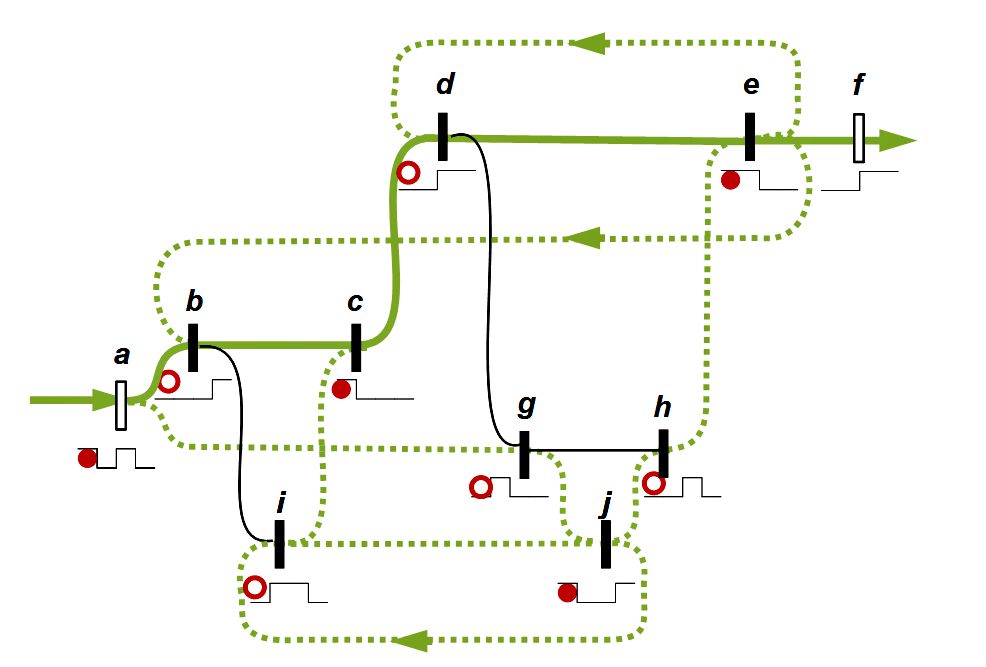
E4-1 Mögliche Wege nach dem ersten stroke
Legende
Unterhalb der Marker: Roter Vollkreis zeigt einen Wellenberg an, Leerer Vollkreis ein Wellental (nach Kauffman 2006, 115ff)
Olivgrün: Standardwege, die direkt zum Ausgang führen
Olivgrün gestrichelt: Weitere mögliche Wege
Schwarz: Diese Wege sind im jeweiligen Zustand blockiert, da ein leerer Kreis auf einen leeren Kreis bzw. ein Vollkreis auf einen Vollkreis trifft
Linksgerichtete Pfeile auf einem Weg zeigen mögliche Rückläufe an
Beobachtung: Auf jedem möglichen Weg wechseln Vollkreise und Leerkreise einander regelmäßig ab

Dieses komplexe Diagramm ist schrittweise zu erklären:

– Mit einer durchgehenden grünen Linie ist der einfachste Weg hervorgehoben, der für den ersten stroke vom Input a zum Output f führt:

a → b → c → d → e → f

An jedem marker wird entweder ein Vollkreis in einen Leerkreis, oder ein Leerkreis in einen Vollkreis umgewandelt. Dieser Weg war vermutlich der Ausgangspunkt, von dem aus Spencer-Brown den Schaltplan konstruiert hat.

Die vier marker g, h, i und j werden noch nicht gebraucht. Sie werden erst bei den folgenden Schritten notwendig, wenn dieser Weg blockiert ist und Umwege gegangen werden müssen.

– Zusätzlich sind weitere Wege möglich, die grün-gestrichelt hervorgehoben sind. Zum Beispiel ist es möglich, den Output f auch auf einem anderen Weg zu erreichen:

a → g → j → h → e → f

– Und es sind Feedback-Schleifen möglich, die mit nach links gerichteten Pfeilen gekennzeichnet sind.

d → e → d … sowie i → j → i …
Schleifen dieser Art drehen sich ständig um sich selbst und gelangen nie zum Output. Sie werden von Spencer-Brown als Gedächtnis (memory) bezeichnet, da in ihrem zirkulären Verlauf der gleiche Wert immer neu wiederkehrt. Um den Output f zu erreichen, sind diese Schleifen nicht notwendig. Ich vermute, dass Spencer-Brown sie angebracht hat in Anlehnung an den von Ross Ashby 1948 eingeführten Homöostaten, an dem in ähnlicher Weise zwei Memory-Units angebracht sind, um das System zu stabilisieren (Ashby, 101). Es wird sich zeigen, dass für die von Spencer-Brown gesuchte Modulation niemals ein Weg über die beiden marker i und j zwingend erforderlich ist. Er hätte sie daher auch weglassen können. Ich vermute, dass er sie aufgenommen hat, weil er sich von ihnen die vom Homöostaten bekannte Stabilisierung versprochen hat. Es kann auch sein, dass er sehr bewusst ein Netzwerk entwerfen wollte, dass wie die von McCulloch betrachteten neuronalen Netze kunstvoll lineare und zirkuläre (heterarchische) Elemente miteinander kombiniert. Mir sind keine Texte bekannt, in denen er das weiter ausführt, aber an dieser Stelle scheint es mir nahezuliegen, seinen Ansatz fortzuführen.

e → b
Dieser Rücksprung ermöglicht weitere Schleifen. Er ist ebensowenig notwendig wie die Memory-Units. Während die Memory-Units an den Homöostaten von Ashby erinnern, ist bei den Rücksprüngen an die Feedback-Schleifen kybernetischer Systeme zu denken. Damit enthält der Schaltplan von Spencer-Brown alle Ideen, die zu seiner Zeit die naturwissenschaftliche Forschung revolutioniert haben. Spencer-Brown gibt keine Hinweise, ob und wie aus seinem Schaltplan systematisch homöostatische oder kybernetische Systeme hergeleitet werden können. Aber er hat offensichtlich diese Möglichkeit vorbereitet.

Zusammenfassend: Es gibt für den ersten stroke viele Wege und interne Schleifen. Der tatsächlich gegangene Weg wird nach dem Prinzip des kürzesten Weges gefunden.

Daraus ergeben sich erste Einsichten:

(i) Spencer-Brown führt schon anschaulich die Grundidee der Begriffsschrift von Frege weiter. Er beschränkt die Logik nicht auf eindimensionale Schluss-Ketten, sondern entwirft zweidimensionale Schluss-Ketten mit Verzweigungen und Alternativen. Das Netzwerk beschreibt daher nicht mehr einfach eine  Differenz  ›f | a‹ zwischen dem Input a und dem Output f, sondern ein  Differenzfeld ›f ▒ a‹ (den Gebrauch der Symbole | und ▒ übernehme ich von Scheier 2016, 18f).

(ii) Ihm ist es gelungen, das aus der klassischen Physik bekannte Prinzip des kürzesten Wege in eine endliche (diskrete) Darstellung zu übertragen und bis auf die Ebene der elementaren Logik herunterzubrechen. Die klassische Physik betrachtete kontinuierliche Bewegungen von Massenpartikeln, die sich durch Zeit und Raum bewegen. Es lässt sich vorstellen, dass der Reductor gemäß dieses Prinzips von sich aus selbständig den kürzesten Weg findet und von einer Selbstorganisation gesprochen werden kann.

Die für den ersten stroke möglichen Wege sind für den zweiten stroke nicht mehr möglich. Beispiel: An den Schaltern a, b, c und d folgen jeweils Leerkreise aufeinander, was ausgeschlossen werden muss. Stattdessen werden für den zweiten stroke die folgenden Wege gefunden:

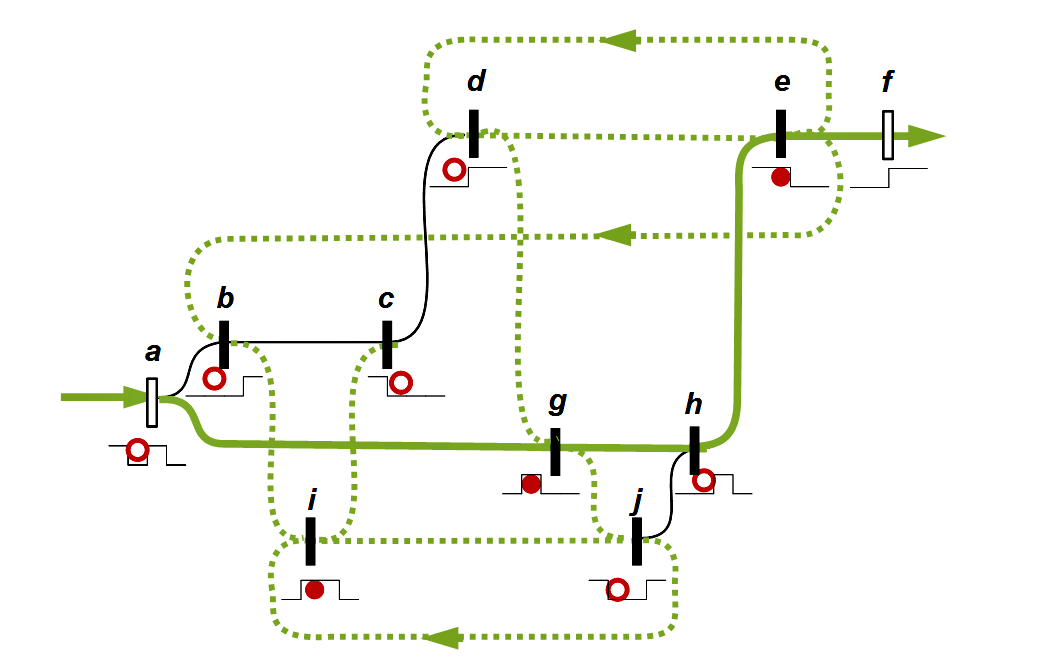
E4-2 Mögliche Wege nach dem zweiten stroke

Um bei f den gewünschten Output zu erzielen, müssen gegenüber den im ersten stroke genutzten Schaltelementen die beiden bisher nicht zwingend erforderlichen Elemente g und h herangezogen werden. Mit ihnen ergibt sich der Weg:

a → g → h → e → f

Weitere Wege sind für den 2. stroke nicht möglich, da der Weg von a nach b versperrt ist und nur der Weg von a nach g gegangen werden kann. Auch der Rücksprung von e nach b hilft nicht weiter, da von dort aus alle möglichen Wege irgendwo versperrt sind. Der 2. stroke ist daher in diesem Schaltkreis ein kritischer Abschnitt.

Mit dem zweiten stroke zeigt sich die dritte wesentliche Einsicht:

(iii) Es ist nicht möglich, für alle strokes die gleichen Wege gehen zu können. Stattdessen erfolgt mit jedem stroke eine Zustandsänderung des Schaltplans. Jeder neue stroke muss für sich seinen eigenen Weg finden.

Das wird noch deutlicher beim 3. stroke. Es könnte erwartet werden, dass sich mit dem 3. stroke einfach der 1. stroke wiederholt, da bei a erneut ein Wellenberg den Schaltkreis betritt. Wenn es so wäre, würde jedoch das Ziel verfehlt, denn dann würde bei f erneut ein Wellenberg (Vollkreis) erzeugt. Statt eine Welle von halber Frequenz zu erzeugen, würde eine Welle erzeugt, die geradlinig nur aus Wellenbergen besteht.

Stattdessen zeigt sich, dass für den dritten stroke der Weg des zweiten stroke wiederholt werden kann:

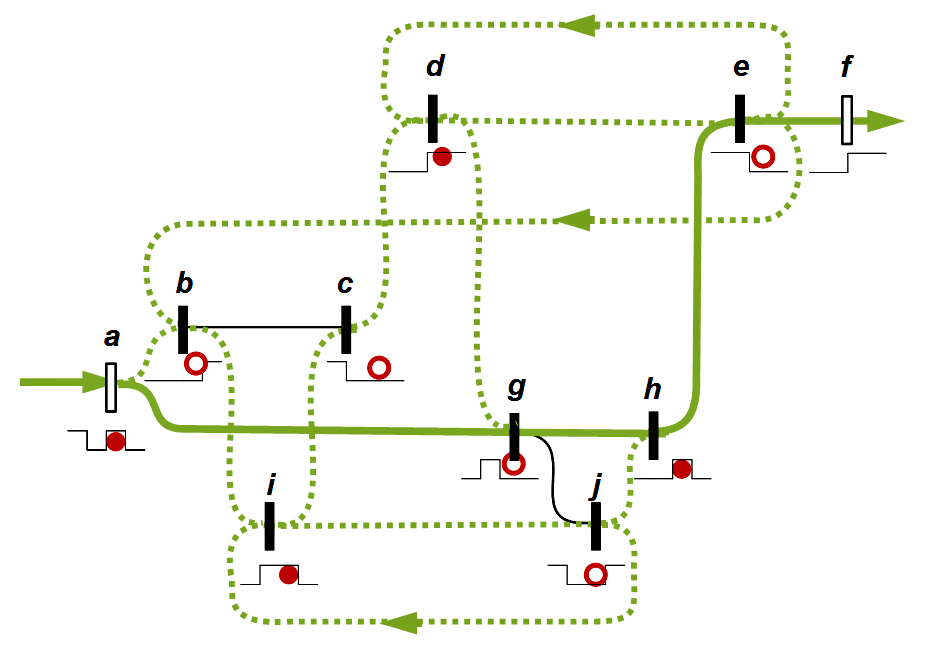
E4-3 Mögliche Wege nach dem dritten stroke

Wird der bisher nicht genutzte marker i berücksichtigt, ergeben sich weitere mögliche Wege:

a → b → i → j → h → e → f

a → b → i → c → d → e → f

Für den vierten stroke kann wiederum der aus dem ersten stroke bekannte Weg gewählt werden:

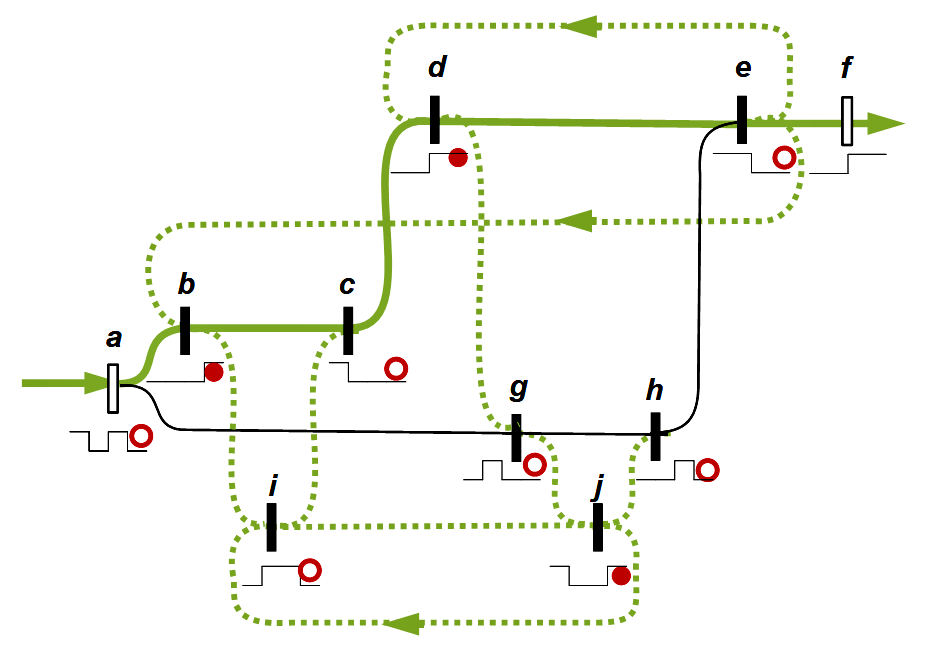
E4-4 Mögliche Wege nach dem vierten stroke

a → b → c → d → e → f

Einen Schlenker von der Art wie bei b über i zu c bzw. in entsprechender Weise bei g über j zu h bezeichnet Spencer-Brown als Einführung einer imaginären Achse. Die direkte Verbindung muss verlassen werden, und es ist eine neue (die imaginäre) Achse aufzuschlagen, um den Umweg einzeichnen zu können. Die Rückkehr zur ursprünglichen Beweiskette kann mit der Drehbewegung der imaginären Zahlen erklärt werden.

Wer dieses Thema mit den Arbeiten von Kauffman vertiefen möchte, sollte beachten: Während es für die graphische Darstellung sehr anschaulich ist, Haken und Ock als Vollkreis und Leerkreis darzustellen, ist es für eine stärker mathematische Schreibweise in Listenform einfacher, den Haken als 1 und das Ock als 0 zu setzen. Dann kann der jeweilige Zustand des Schaltkreises beschrieben werden durch die Werte 0 und 1, die an den jeweiligen markers angenommen werden. Hierfür wird ein Zahlentupel des Input und der 8 Schaltelemente gebildet (wobei Kauffman den Output f ignoriert, da es keine Konversion von e zu f gibt):

{a, b, c, d, e, g, h, i, j}

Nach jedem stroke werden die konkreten Werte eingesetzt. Wird für den Vollkreis (Haken, marked) 1 gesetzt und für den Leerkreis (Ock, unmarked) 0, ergibt das folgende Übersicht:

	a, b, c, d, e, g, h,  i,  j	Weg von a zu f
Stroke 1	1, 0, 1, 0, 1, 0, 0, 0, 1	a → b → c → d → e → f
Stroke 2	0, 0, 0, 0, 1, 1, 0, 1, 0	a → g → h → e → f
Stroke 3	1, 0, 0, 1, 0, 0, 1, 1, 0	a → g → h → e → f
Stroke 4	0, 1, 0, 1, 0, 0, 0, 0, 1	a → b → c → d → e → f

Die Werte bei a und e sind halbfett hervorgehoben, um Input und Output deutlich zu machen, und es ist gut zu sehen, wie sich die Frequenz der einlaufenden Welle bei a und am marker e vor dem Ausgang in f halbiert. In dieser Weise wird der Schaltkreis in Kauffman 2006 dargestellt. Auch Spencer-Brown hat den Schaltkreis ursprünglich auf ähnliche Weise aufgeschrieben (siehe R, 7, Figure 1.1).

(2) Zeitverzögerungen (Trägheit) im Netzwerk

Wenn in einem Netzwerk mehrere Wege möglich sind, und wenn es geschehen kann, dass ein Weg auf unbestimmte Zeit in einen Kreislauf gerät, wie ist dann zu bestimmen, welcher Weg als erster zum Ziel führt? Die einfachste Antwortet lautet: Der kürzeste Weg. Doch woran wird die Länge des Weges gemessen? Ist es die Anzahl der marker, die auf diesem Weg durchlaufen werden? Davon wurde im vorigen Abschnitt ausgegangen, und es ist im Folgenden schrittweise zu relativieren. Ist es die Summe aller Abstände zwischen den markers auf diesem Weg? Ist es eine Aufgabe der Ingenieurskunst, die marker so zu anzuordnen, dass alle Abstände möglichst gleich sind, oder ist es die Aufgabe des Designers, die marker so zu anzuordnen, dass ihre logischen Beziehungen möglichst anschaulich werden, auch wenn dabei unterschiedliche Abstände auftreten? So ist Spencer-Brown verfahren: In seinen graphischen Darstellungen sind die Abstände zwischen den marker sehr unterschiedlich. Und wie sind die Kreisläufe zu bewerten: Ist bei ihnen eine zusätzliche Größe zu berücksichtigen, die bei jedem Durchlauf erhöht wird, bis sie einen Grenzwert überschreitet und der Kreislauf verlassen werden kann? Ergibt sich also die Länge eines Weges durch einen Kreislauf aus der Summe aller Durchläufe?

Wenn die Länge des Weges bekannt ist, stellt sich die Frage nach der Zeit: Mit welcher Geschwindigkeit wird der Weg durchlaufen. Gilt überall die gleiche Geschwindigkeit? Kann sich die Geschwindigkeit erhöhen, wenn es zwischen zwei benachbarten markers eine erhöhte Spannung gibt, und wodurch wird die Spannung erhöht? Spencer-Brown und Kauffman lassen diese Fragen bewusst offen. Aber sie gehen grundsätzlich davon aus, dass es beim Durchgang von einem marker zum nächsten und möglicherweise auch beim Durchqueren eines marker Zeitverzögerungen (time delays) gibt. Während in der üblichen Mathematik alle Rechnungen instantan erfolgen, gibt es im Netzwerk eine Trägheit, die zur Zeitverzögerung führt. Darin zeigt sich die Materialität des Netzwerks. Das Netzwerk ist keine reine Rechnung, kein bloßes Design oder eine Blaupause, sondern es ist ein materielles Medium. Dessen Materialeigenschaften bestimmen, wie schnell das Medium durchquert werden kann.

Spencer-Brown bezeichnet die Zeitlosigkeit der üblichen Rechnungen als »imaginär«, da sie auf den ersten Blick ähnlich »magisch« ist wie die Eigenschaften der imaginären Zahlen. Noch nie hat ein Mathematiker gefragt, dank welcher Eigenschaften das Rechnen zeitlos ist, und ob diese Eigenschaften möglicherweise das Rechnen beeinflussen. Dagegen sind für die imaginären Zahlen deren Rechengesetze gefunden worden und sie gelten nicht mehr als magisch. Sollte das auch für die Zeitlosigkeit möglich sein? Umgekehrt erscheint aus der Perspektive der herkömmlichen Mathematik die Trägheit des Netzwerks als Bedrohung (threat). Sie ist solange eine Bedrohung, wie ihre Ursachen und Wirkungen ungeklärt sind. Spencer-Brown gibt noch keine Lösung, aber er stellt der Mathematik eine völlig neue Aufgabe.

»Mathematically, since there is no time in mathematical expressions, everything happens all at once, the short signal from i to j is never there, since there is no time for it to exist. The propagation-time of the signal through the leads and markers has not just become very small: in mathematics it has vanished completely, and this why we say the signal is ‘imaginary’. But like the other imaginary i in numerical algebra, which has similar 'magical' characteristics, the fact that it exists in the mathematical circuit, not as a reality, but as a threat, should j even consider doing the wrong thing, is sufficient to keep j honest. The threat never has to be carried out in reality, in fact mathematically it cannot be. But its mere presence is sufficient. It is what we mean, in chess, when we say 'the threat is more powerful than the execution'.« (R, 9)

Den Netzwerkdesignern und Ingenieuren stellt sich die gleiche Frage. In ihren Entwürfen von Netzwerken unterstellen sie einen idealen Schaltkreis, für dessen Verständnis die Zeitverzögerungen vernachlässigt werden können. Ihnen genügt die Erkenntnis, in welcher Reihenfolge die Schaltelemente durchlaufen werden. In der Realität ist es anders. Der Schaltkreis kann ein »Eigenleben« entwickeln. Es ist sogar möglich, dass der logische Entwurf des Schaltkreises Fehler enthält, die vom realisierten Schaltkreis ausgeglichen und behoben werden.

»In hardware the mark behaves like an idealized transistor 'nor' gate: If any of its inputs is connected to an EMF (say 1 or mark), then its output is grounded (say 0 or ock).
    Some engineering designs with these units will 'work' even if their mathematics is incorrect, because of delays in signal travel-time etc. These are bad designs: they might suddenly fail if the material are improved.
    The beauty of the present mathematics is this: if it is correct, anything designed from it in transistor units will certainly work.« (R, 5)

Kauffman betrachtet die Trägheit des Netzwerks aus einer anderen Perspektive. Es ist nicht möglich, dass für jeden stroke die gleichen Wege gegangen werden können, die vom Input a zum Output f führen. Die Änderung der Wege kann als Zustandsänderung des Netzwerks bezeichnet werden. Das Netzwerk kann bei jedem neuen stroke in einen neuen Zustand wechseln. Für Kauffman muss Zeit vergehen, wenn ein stroke dem anderen folgt, damit das Netzwerk in dieser Zeit seinen Zustand ändern kann. Tontechniker kennen das Problem: Das Netzwerk muss sich jeweils einpendeln, bis eine optimale Tonübertragung und Modulation erreicht werden kann. (Kauffman bezeichnet den Input abweichend von Spencer-Brown als z und nicht als a.)

»As a model for action we assume that each change in z is held fixed long enough for the automaton to accomplish its transition to the next state. In terms of applications this means that the model assumes delays associated with each inverter. There are no delays associated with the connecting lines in the graph. This method of distributing the delays is a mathematical abstraction, but it is sufficiently realistic so that these circuits can actually work at the hardware level. In any given instantiation the delays are given up to the variation in the components. If the automaton is mathematically determinate (as in this example), then it will behave in the same way for any choice of actual delays – so long as the input varies more slowly than the time needed for internal balancing.« (Kauffman 1995, 91f)

Auch für ihn bleibt es jedoch letztlich »a black box B with input line z and output line d with this behaviour« (Kauffman 1995, 92).

Solange die Ursachen und das Maß der Trägheit (Zeitverzögerung) unbekannt sind, bleibt es dem Geschick des Ingenieurs überlassen, das Netzwerk im jeweils gegebenen Medium auf eine Weise zu entwerfen, dass genügend Zeit besteht für den Wechsel der Zustände nach jedem neuen stroke. Das ist für Spencer-Brown »the art of making a reductor« und die »ingenuity« der Netzwerk-Designer (R, 10, 13)

Letztlich muss ausprobiert werden, ob das Netzwerk so funktioniert wie erwartet. Es ist gut zu verstehen, warum der Erfolg dieser Schaltkreise ungläubig aufgenommen wurde. Spencer-Brown berichtet von der Reaktion der Kollegen, als er 1961 erstmals einen Schaltkreis dieser Art realisiert hat: »My colleagues were so shocked that they wouldn't look, even though we constructed it in transistor hardware and watched it counting on the cathode-ray tube. 'There must be something wrong with it.'« (R, 7)

Er vergleicht die Arbeit der Ingenieure mit der von Chemikern. Auch sie testen unterschiedliche chemische Prozesse aus und können letztlich nicht genau sagen, warum der von ihnen gefundene Prozess gelingt. Es ist nicht möglich, die Vielzahl von Abläufen und möglicherweise wie Katalysatoren wirkender Stoffe vollständig zu beschreiben und zu verstehen. (Als ich in der chemischen Industrie mit Forschern sprach, wurde mir das bestätigt. Die Realität der chemischen Forschung und ihrer Erfolge unterscheidet sich deutlich von dem, was ein Außenstehender erwarten würde.)

"As in a chemical formula, it gives the number of elements (markers and leads) without saying how they are actually connected, so if they can be connected a different way in the same formula we call it an isomer" (R, 21)
    "The same is true for reductors, as mathematical entities. Like numbers, they don't actually exist in any space we call Euclidean. Yet unless we draw them in some way, even though no way we can draw them is relevant to what they actually are, we cannot use them, nor can we even imagine them. Even the specification of the reductor is not, mathematically, what it really is: it is just a more succinct way of drawing it, getting rid of all the irrelevant ways it can be diagrammed as a circuit." (R, 21)

Ähnlich ist es in der Musik. "Mathematics, like musics, is meaningless unless it is performed." (R, 23)

Der Hinweis zur Musik erscheint mir schlagend: So wie ein Komponist und ein Musiker niemals vollständig im Voraus berechnen können, welchen Klang ein Instrument erzeugen wird, sondern es ausprobieren und mit den speziellen, oft unerwarteten Klangwirkungen des Instruments rechnen müssen (wer ein neues Instrument spielt, muss sich erst einmal darauf einspielen und dessen Eigenarten kennen lernen), so gehen auch die Forscher vor. Es ist für mich eine großartige Leistung, den kreativen Prozess nicht einfach der logischen Wiederholung und Routine gegenüberzustellen, in deren Verlauf sich nach und nach klären wird, warum welche Zustände auftreten (so wird heute zweifellos nicht mehr so ins Unbestimmte hinein ein Schaltkreis entworfen, nachdem er sich viele Male bewährt hat), sondern bis in die Logik einen Weg aufzuzeigen, wie das Zusammenwirken des Entwicklers und seiner Instrumente und Stoffe zu denken und paradigmatisch an Beispielen wie den von Spencer-Brown genannten Schaltkreisen darzustellen ist.

(3) Knotenlinie von Systemzuständen

Wird mit Kauffman von einer Abfolge von Zuständen des Netzwerks gesprochen, so ist dafür eine dritte Dimension notwendig: Mit der ersten Dimension wird jeweils ein Weg betrachtet, der für sich eindimensional ist; die zweite Dimension öffnet die Möglichkeit nebenläufiger Wege, mit denen Hindernisse umgangen werden können; und mit der dritten Dimension lässt sich der Verlauf von Zustandsänderungen beschreiben. Jeder Zustand ist im Innern zweidimensional, seine Veränderung verläuft in der dritten Dimension. Spencer-Brown deutet die Einführung einer neuen Dimension beiläufig an, aber er untersucht deren Konsequenzen nicht weiter: »We are now in difficulties through attempting to write in two dimensions what is clearly represented in three dimensions.« (LoF, 66)

Das Verhältnis eines Schaltkreises zu seinen Zuständen kann verglichen werden mit dem Verhältnis eines materiellen Substrats zu seinen Aggregat-Zuständen. Standardbeispiel ist das Substrat Wasser mit den Zuständen Eis, Flüssigkeit und Gas. Mit jeder Zustandsänderung entsteht eine neue Ordnung. Um zu erklären, warum und wie es zu Zustandsänderungen kommt, ist eine neue Dimension notwendig: Im Beispiel des Wassers ist es die Zufuhr oder der Entzug von Wärme. Bei anderen chemischen Prozessen kann es das Durchrühren oder die Zufuhr von Katalysatoren sein. Der Übergang von einem Zustand in den anderen wird als Emergenz verstanden. Die jeweilige Ordnung ist zu erklären aus einer Selbstorganisation des Substrats im neuen Zustand. Die Gesamtheit aller Zustandsänderungen kann mit Hegel als Knotenlinie bezeichnet werden (HW 5.435), auch wenn dieser Ausdruck nach Hegel nicht mehr aufgegriffen wurde. Die Knotenlinie beschreibt die dritte Dimension. Ich kann mir vorstellen, dass es möglich sein sollte, die Ausführungen von Spencer-Brown in dieser Richtung fortzuführen und der Theorie der Selbstorganisation und Emergenz eine logische Grundlage zu geben.

(4) Selbstorganisation des Netzwerks

Es muss nicht bei der Trägheit bleiben. Möglicherweise verläuft der Input nicht wie eine Kugel oder wie der Focus des Beobachterblicks auf einer festen Bahn, die nach und nach alle Wege testet, an blockierten markers umkehrt und den nächsten möglichen Weg einschlägt, bis sie sich schließlich für den optimalen Weg entscheiden kann, sondern es kann auch sein, dass sich der Input wie in den Experimenten der Quantenmechanik wellenförmig im Netz ausbreitet und alle möglichen Wege parallel durchläuft, bis sich aus ihnen der optimale Weg herausbildet. Das bedeutet: Nach dem Durchgang durch einen marker werden alle vom marker ausgehenden Wege parallel betreten, und Schleifen können endlos durchlaufen werden. Bei einer Ausbreitung dieser Art kann es zu Wechselwirkungen zwischen den verschiedenen Wegen kommen. Und möglicherweise entfalten die im Netzwerk vorgesehenen Kreisläufe einen Einfluss auf die Ausbreitung der Signale auf den anderen Wegen. Eventuell gelingt mit ihnen wie beim Homöostat von Ashby ein Stabilisieren, oder ihre Wirkung geht in ein übergeordnetes Geschehen der Selbstorganisation und Ausbalancierung ein. Darüber ist bisher nichts bekannt. Spencer-Brown beschreibt die Situation, in der lediglich empirisch beobachtet werden kann, wie sich das Netzwerk im Ergebnis verhält.

Darüber hinaus ist es denkbar, dass das Netzwerk in Wechselwirkung mit dem Grund tritt, in den es eingeschrieben ist. Kommt es entlang eines Weges zu einer Schleife zu einem früheren Punkt auf dem Weg, kann dies als Re-entry verstanden werden. In seinen Ausführungen zum Re-entry hat Spencer-Brown gezeigt, wie durch den Re-entry das Medium in Bewegung (Unruhe, Schwingungen) versetzt werden kann. Wird das auf die Netzwerke übertragen, so kann es bei Schleifen zu einer Erschütterung des Grundes und mit ihm der in den Grund eingetragenen Wege kommen.

(5) Von linearen Prozessen zur Logik einer evolutionären Produktion

Spencer-Brown ist bereits mit der Einführung des Re-entry und dem Wellenverlauf der Zeit weit über den Rahmen der traditionellen Logik hinausgegangen. Werden sie jedoch im Einzelnen betrachtet, verbleiben sie innerhalb ihres Ablaufs in einer linearen, kausalen Ordnung: Der Re-entry geht aus einer Iteration hervor, deren einzelne Schritte streng einander folgen und untereinander formal ähnlich und abzählbar sind. Und ebenso beschreibt der Wellenverlauf der Zeit eine eindimensionale Kurve, die regelmäßig zwischen ihren Auf's und Ab's hin und her schwingt. Das ändert sich radikal mit den Schaltkreisen (circuits). Sie lassen sich nicht auf einen fest vorgegebenen Weg beschränken, sondern enthalten Redundanz (Nebenläufigkeit) und Zirkularität. Sie enthalten gegenüber linearen Ordnungen einen Überschuss an möglichen Wegen, von denen sich einer durchsetzt.

In der Begrifflichkeit von Luhmann entspricht das der Logik eines evolutionären Systems. Aus Sicht der Evolution kann die fortlaufende Schwingung des in den Schaltkreis eintretenden Input a als die gegebene Situation des Genmaterials verstanden werden; die verschiedenen Wege des Netzwerks beschreiben die Vielfalt der einmaligen oder möglicherweise stufenweise erfolgenden Mutationen des Erbmaterials, aus denen mit einer Selektion eine ausgewählt wird. Wenn diese sich stabilisiert hat (Retention), ist ein neues Erbmaterial erzeugt, welches sich im Fortgang der Evolution durchsetzen wird. Es ist das Produkt einer evolutionären Veränderung, in der Sprache der hier betrachteten Netzwerke der Output f. Oder in anderen Worten: Die Verarbeitung der gegebenen Ressourcen (Input) folgt nicht einem festen, vorgegebenen Arbeitsablauf, sondern der Schaltplan eröffnet eine Vielzahl von möglichen Wegen, die zum Output (dem Produkt) führen. Das System ist in der Lage, aus der Vielzahl der Wege eine Auswahl (Selektion) zu treffen. Der Schaltkreis kann zwischen verschiedenen Zuständen wechseln, mit denen er jeweils sein Verhalten entsprechend des gegebenen Inputs optimiert (Anpassung). Allerdings gibt es gegenüber der Evolution zwei wichtige Einschränkungen: (i) Es gibt zwar eine Vielfalt von Wegen, doch sind sie im Entwurf des Netzwerks vorgegeben. Bei den Mutationen der Evolution können dagegen auch unerwartete (zufällige) Mutationen auftreten. Zwar kann auch das Netzwerk ein unerwartetes Verhalten zeigen, doch bleibt es innerhalb des Rahmens der vorgegebenen Wege. (ii) Und es handelt sich noch nicht um ein lernendes System, das wie das menschliche Gehirn im Verlaufe seiner Tätigkeit neue Verknüpfungen bilden bzw. in ihrer Priorität herabsetzen und abbauen kann. Die Netzwerke von Spencer-Brown sind ein notwendiger Zwischenschritt, der von linearen, kausal bestimmten Systemen, den Re-entries und Wellenverläufen der Zeit überleitet zu lernenden und evolutionären Systemen.

"Von Produktion wollen wir sprechen, wenn einige, aber nicht alle Ursachen, die zum Bewirken bestimmter Wirkungen nötig sind, unter Kontrolle durch ein System eingesetzt werden können. [...] Um Produktion zu begreifen, muß man deshalb nicht von Naturgesetzen ausgehen, sondern von den Vorteilen der Selektion." (Luhmann 1984, 40)

Das gilt in gewisser Weise bereits für die Netzwerke. Ihr Verhalten kann nicht vollständig vorausgesagt werden. Sie sind bewusst auf eine Weise gestaltet, dass sie in ihrer Trägheit und Selbstorganisation einen Freiheitsgrad enthalten, der bereits auf einen evolutionären Prozess deutet.

Das Verständnis der Produktion ändert sich. In der bürgerlichen Epoche der Warenproduktion ging es darum, gegenüber dem bloßen (statischen) Besitz von Ressourcen die Bedeutung der lebendigen (dynamischen), menschlichen Arbeit aufzuwerten. Produktion wurde verstanden als Wertschöpfung durch die Übertragung von menschlicher Arbeit auf das vom Menschen geschaffene Produkt (Philoponos, Adam Smith, Marx). Vorbild war die handwerkliche Arbeit, bei der z.B. aus verschiedenen Holzstücken ein Tisch gezimmert oder in größeren Vorhaben ein Schiff gebaut wird. Das Produkt ist so viel wert wie zu seiner Herstellung Arbeitszeit erforderlich war und auf das Produkt übertragen wurde. Mit der Erkenntnis der evolutionären Entwicklung erweitert sich der Blick auf natürliche Produkionsvorgänge. So wie Spencer-Brown nach einer Funktion fragt, die aus sich selbst heraus zu zählen vermag, geht es in der Evolution um einen eigenständigen Prozess des Produzierens. Die Initiative liegt bei der Evolution. Bereits in der agrarischen und industriellen Produktion wurden materielle Prozesse geplant und gesteuert, sei es das Wachstum von Pflanzen, die Aufzucht von Tieren oder die Nutzung mechanischer und chemischer Prozesse in der industriellen Fertigung. Die gestaltende Kraft wurde jedoch beim Menschen gesehen. Er kann zwar nie vollständig voraussehen, ob es Störungen geben wird, die bis zum vollständigen Verlust führen können. Doch es liegt bei ihm, daraus zu lernen und mit verbesserten Produktionsmethoden Abweichungen zu vermeiden. In der Evolution werden dagegen Abweichungen nicht mehr nur als Störungen angesehen, sondern als die Kreativität des Prozesses. Es wird gefragt, dank welcher kybernetischen Mechanismen die Kreativität sich selbst zu steuern vermag. Im Ergebnis entsteht orientiert an der Evolution eine Produktion, die nicht mehr nur Wertübertragung des Menschen an das Produkt ist, sondern zu Produkten führt, die durch die Evolution geschaffen werden.

Was wird mit den Schaltkreisen produziert? Spencer-Brown hat sich bewusst auf den einfachsten und elementaren Fall des Zählens beschränkt. Es ist kein Zufall, dass er Netzwerke betrachtet, mit denen Wellen moduliert werden. Im 19. Jahrhundert wurde 1885 mit dem Satz von Stone-Weierstraß gezeigt, wie alle stetigen Funktionen beliebig genau durch Wellenfunktionen angenähert, d.h. aus ihnen "produziert" werden können. Hilbert hat daraus den Hilbert-Raum konstruiert, der von grundlegender Bedeutung für die Quantenmechanik und Spieltheorie wurde. Spencer-Brown entwirft daher – in meinem Verständnis – mit der Modulation von Wellen den Nukleus, aus dem schrittweise die Grundlagen der modernen Mathematik entwickelt werden können. Spencer-Brown beschränkt sich bewusst auf den elementaren Schritt: Im einfachsten Fall wird die Frequenz von einem Muster wie ›abab‹ in ein Muster wie ›aabb‹ halbiert. Aus dieser einfachen Modulation lassen sich beliebig komplexe Modulationen zusammensetzen. Das ist buchstäblich hörbar, wenn in der Tontechnik mit Netzwerken, wie sie Spencer-Brown studiert hat, Klänge moduliert und mit ihnen Musik erzeugt (produziert) werden kann.

(6) Fließgleichgewicht

Das System ist so eingerichtet, dass es in der Oszillation seiner Systemzustände auf die Oszillation des Inputs reagieren kann und im Ganzen eine Art Fließgleichgewicht herstellt, von dem Bertalannfy sprach, und das mit Maturana und Varela als Selbstorganisation (Autopoiesis) bezeichnet werden kann.

(7) Objekt- und Meta-Ebene

Während die traditionelle Logik Paradoxien durch konsequente Trennung der Objekt- und Meta-Ebenen vermeiden wollte, setzt Spencer-Brown bewusst deren innere Verschlingung ein. Das erschwert das Verständnis seiner Entwürfe, da wir in der traditionellen Logik zu denken gelernt haben und diese gewohnt sind. Kauffman zeigt das an den Schaltplänen: Die bei den markers angefügten Wellen haben eine Doppelbedeutung: Sie können sowohl als Elemente eines Prozesses wie auch als dessen Ergebnisse gelesen werden. Jeder marker ist sowohl ein Element im Schaltplan, und zugleich zeigt der marker, in welchen Wert das am marker ankommende Zeichen umgewandelt werden soll bzw. eine Blockade eintritt.

»In using the interlock algebra, one regards the link diagram as a circuit whose parts (the arcs in the diagram) are both carriers of circuit values and operators that process these values. This duality is the core of the interrelationship with topology. In actual applications of digital circuitry, there is usually a sharp distinction between circuit elements as operators and circuit elements as carriers of signals.« (Kauffman 1995, 88)

Diese Methode gilt für das gesamte Werk Laws of Form. Der Haken  ⃧   ist sowohl vergleichbar den Zahlen ein Operand, der in eine Rechnung eingehen kann, wie auch vergleichbar den Rechenzeichen +, −, / etc. der Operator, mit dem die Rechnung ausgeführt wird. Der Haken  ⃧   ist zugleich eine Operation, mit der eine Grenze gezogen wird, wie das Produkt dieser Operation, mit dem seinerseits weiter gerechnet werden kann. In der Begriffssprache von Frege ist der Haken zugleich ein Argument a wie eine Funktion f, mit der auf Argumenten a operiert wird. Das ist ein Paradox, das insbesondere mit der Typentheorie von Russell und Whitehead vermieden werden sollte. Spencer-Brown will dagegen in Kapitel 11 der Laws of Form zeigen, wie in seinem Kalkül Argumente a und Funktionen f auseinander hervorgehen. Er zeigt das mit dem Re-entry, mit dem ein Argument a in eine neue Form umgewandelt wird, die er als f bezeichnet. Wie ihm das gelingt, ist ein Thema für sich. An dieser Stelle genügt es festzuhalten, dass er für seine Netzwerke vom Re-entry die Symbole a und f übernimmt, wenn er den Input als a und den Output als f bezeichnet.

Die Netzwerke, mit denen ein Input a in einen Output f moduliert werden, sind daher eine nähere Ausarbeitung des Re-entry. Während jedoch die Folge der Iterationen, die zum Re-entry führen, linear ist, enthält das Netzwerk Verzweigungen und Kreisläufe. Wird das Netzwerk im Ganzen betrachtet, dann führt es wiederum wie der Re-entry von einem Argument a zu einem Ergebnis f, das zugleich der Prozess dieser Produktion ist. Werden die Argumente a als Objekte bezeichnet, so gehören die Funktionen (Prozesse) f zur Meta-Ebene, auf der über die Objekte a gesprochen wird.

Auf einer höheren, von Spencer-Brown nicht mehr untersuchten Ebene kann das Netzwerk im Ganzen als ein Re-entry betrachtet werden. Dann ist der Output f nicht mehr nur ein Produkt, das in Folgeschritten weiter verarbeitet werden kann, sondern er kehrt als Re-entry in das Netzwerk zurück und kann es verändern. Er kann in diesem Verständnis nicht nur die Form der Wege im Re-entry verändern, sondern auch das Medium, in das die Wege eingetragen sind. Mit dieser Erweiterung ist das volle Verständnis einer evolutionären Produktion erreicht, an die Luhmann gedacht hat. Die Aufgabe des Menschen beschränkt sich auf ein Glied in diesem Prozess, der mit seiner natürlichen Umwelt zusammenarbeitet. Der evolutionäre Prozess kann sowohl die natürliche Umgebung wie auch den Menschen selbst verändern.

(8) Wechselwirkung von Objekt und Subjekt

Die Trägheit und die Selbstorganisation der Netzwerke zeigen: Es gilt nicht mehr wie für Kant, dass sich »der Gegenstand (als Objekt der Sinne) nach der Beschaffenheit unseres Anschauungsvermögens« richten müsse (Kant, KrV, B XVI), sondern beide sind gleichberechtigt und bedingen einander gegenseitig. Wer wie Spencer-Brown einen Schaltkreis entwirft, kann sich am Anfang nicht sicher sein, ob und wie er funktionieren wird. Aus der chemischen Forschung ist bekannt, dass die meisten Entdeckungen unerwartet und überraschend kamen, und so sieht es Spencer-Brown auch im Entwurf von Schaltkreisen und sucht für diese sich vorsichtig in ein noch unbekanntes Gebiet vortastende Vorgehensweise die grundlegende Logik. Die von ihm entworfenen Schaltpläne enthalten einen Freiheitsgrad, der dem tatsächlichen Ablauf der mit ihnen realisierten technischen Systeme ausreichend Spielraum gibt. Wer selbst programmiert oder mit Ingenieuren zusammengearbeitet hat, wird irgendwann von der Erfahrung überrascht, dass die eigenen Programme und technischen Systeme völlig anders genutzt werden und Eigenschaften zeigen, mit denen der Entwickler ursprünglich nicht gerechnet hatte.

Mit der Wechselwirkung von Objekt- und Meta-Ebene sowie von Objekt und Subjekt ist alles vorbereitet, um in einer vierten Dimension das Verhältnis des beobachteten Prozesses und seines Beobachters zu bestimmen.

(9) Mögliche Anwendungen

Der Schaltplan lässt sich auf chemische Prozessketten übertragen. Der Input a beschreibt die externen Ressourcen, die in den Prozess eingeführt werden müssen, der Output f die Ausgangsstoffe, die mit dem Prozess erzeugt werden sollen. Jeder marker beschreibt eine chemische Reaktion, die an dieser Stelle erfolgt. Es kann nur zu Reaktionen kommen, wenn sich wahlverwandte Stoffe finden. Im Ganzen beschreiben die Schaltpläne chemische Prozessketten und ihre möglichen Verzweigungen.

Das System kann im Ganzen in unterschiedliche Systemzustände emergieren, wenn z.B. Wärme zugeführt oder entzogen wird, wenn das System umgerührt wird usw. Mit der Änderung des Systemzustand können sich die Bedingungen für chemische Reaktionen ändern.

In der Begrifflichkeit von Hegel kann jeder Zustand als eine Wahlverwandtschaft und der Übergang von einem Zustand in einen anderen als Knotenlinie bezeichnet werden.

Der Schaltplan kann für Organisationsmodelle stehen. Input und Output beschreiben die externen Ressourcen und das von der Organisation hervorgebrachte Produkt. Jeder marker ist im wörtlichen Sinn eine Stelle in der Organisation, die eine bestimmte Aufgabe übernimmt und mit den anderen Stellen zusammenwirkt.

Innerhalb der Organisation gibt es Teilprozesse, die fließbandartig (sequentiell) abgearbeitet werden, sowie auch Verzweigungen, die zu gleichwertigen Produkten führen können. Ökonomisch werden die Prozesse als Wertschöpfungsketten verstanden. Organisatorisch kann die Aufgabe gestellt werden, die Wege für die einzelnen strokes in der Weise zu optimieren, dass der kürzeste Weg gefunden wird, oder dass möglichst keine Stelle mehrfach nacheinander auf dem kritischen Weg liegt, sondern sich regenerieren kann.

Es gibt keine steuernde Stelle im Prozess, sondern Selbstorganisation, die nach bestimmten Prinzipien erfolgt wie z.B. das Prinzip des kürzesten Weges. Statt einer zentralen Steuerung kann eine dezentrale Steuerung angenommen werden, wenn jede Stelle für sich in ihrer Umgebung nach lokalen Wegen sucht, bis sich die einzelnen von den Stellen ausgehenden lokale Wege miteinander verbinden und eine Systemlösung ergeben.

Es wird angenommen, dass sich der Ablauf über die vier Schritte selbst organisiert hat. Aber es ist denkbar, eine externe Beratung hinzuzuziehen, die den Ablauf auf mögliche Schwachstellen analysiert und das spontane Ergebnis der Selbstorganisation verbessert. Das kann so weit gehen, dass der Netzplan verändert oder sogar zusätzliche virtuelle Stellen geschaffen werden, mithilfe derer Wege möglich werden, die vorher verschlossen waren.

Neuronale Netze und Kybernetik Die übergreifende Lösung kann mit Backtracking (Rücksetzverfahren) programmiert werden: Ausgehend von a wird schrittweise jeder mögliche Weg untersucht. Läuft er in eine Sackgasse, wird die Verzweigung in die Sackgasse markiert und der nächste mögliche Weg gesucht, bis die erste durchgehende Lösung gefunden ist. Das ähnelt der Programmierung des Springer-Problems, »für einen Springer auf einem leeren Schachbrett eine Route zu finden, auf der dieser jedes Feld genau einmal besucht«.

Die Bedeutung der beiden von Spencer-Brown eingeführten Memory-Units sowie die Feedback-Schleifen sind näher zu untersuchen und machen eine Anwendung auf Kybernetik und neuronale Netze möglich.

Physik und Kosmologie Spencer-Brown beschreibt Umgehungen, die für ihn in die imaginäre Achse führen. Ebenso ist denkbar, Tunnellungen und Wurmlöcher zuzulassen, mit denen fern voneinander liegende Stellen unter genau zu definierenden Bedingungen direkt miteinander verbunden werden können. Ein mögliches Beispiel für Wurmlöcher sind Re-entries: Wenn im Schaltplan mithilfe eines Feedbacks im Netzwerk ein kreisförmiger Weg unendlich oft durchlaufenden wird, kann diese Iteration per Re-entry eine direkte Verbindung zwischen zwei einander im Kreis konträr gegenüber liegenden Stellen erzeugen.

Zusammenfassend besteht für mich das Neue an dieser Logik in drei Punkten:

– Einführung der imaginären Achse

Diesen Punkt hebt Spencer-Brown besonders hervor. Mit imaginärer Achse ist gemeint, dass im Schaltkreis das lineare Folgern verlassen wird. Es wird zwischen unterschiedlichen Wegen differenziert, die teils parallel verlaufen und teils miteinander verbunden und rückgekoppelt sind. Das erfordert gegenüber dem linearen Schließen eine neue Achse, die für Spencer-Brown mit der Einführung imaginärer Zahlen verglichen wird, obwohl er nirgends mit imaginären Zahlen rechnet.

– Trägheit und Selbstorganisation des Schaltkreises

Wenn sich im Schaltkreis nach einem stroke ein Zustand ausbalanciert hat, scheint zum einen die Neigung zu bestehen, diesen Zustand beim nächsten stroke zu erhalten. Es können jedoch keine Konflikte vermieden werden. Das führt zu einer Art Selbstorganisation: Der Schaltkreis zerfällt in Teilbereiche, die jeweils in sich konfliktfrei sind, und nur bestimmte Übergänge sind zulässig. Sie ergeben von sich aus eine Harmonie, die Spencer-Brown als Musikalität bezeichnet hat.

– Wechselwirkung des Entwicklers und der von ihm geschaffenen Kunstwerke

Anmerkung (Musikalität und Technik): Was Spencer-Brown in der Logik und an Schaltkreisen aufgezeichnet hat, wurde überraschenderweise zur gleichen Zeit als eine avantgardistische Technik in die Musik eingeführt: Loops. Deren Vorbild waren mechanische Instrumente wie Spieluhren. Diese Technik macht den Reiz des Minimalismus aus und ist für mich besonders in den Stücken von Steve Reich (* 1936) unmittelbar hörbar und geradezu ein musikalisches Gegenstück zu den Laws of Form. Siehe z.B. bei YouTube mit einer sehr klaren Visualisierung das 1973 entstandene Stück Music for Pieces of Wood; YouTube. Wem es schwer fällt, die Ideen von Spencer-Brown zu verstehen, der sollte mit dieser Filmsequenz anfangen. Dort ist unmittelbar zu sehen und zu hören, wie auf einem kanonischen Grundrhythmus weitere Rhythmen aufgebaut werden, bis schrittweise ein eigener für sich stehender Klangeindruck aufgebaut wird. Während anfangs die einzelnen rhythmischen Linien vom Ohr klar zu unterscheiden sind, springt dies an einem bestimmten Punkt um in einen Gesamteindruck eines harmonischen akustischen Gesamt-Bildes, in dem auch der statisch festgehaltene Grundrhythmus zu schwingen scheint.

Beobachter

»An observer, since he distinguishes the space he occupies, is also a mark.« (LoF, 76)

Spencer-Brown will die kopernikanische Wende konsequent bis in die Logik nachvollziehen und eine Logik entwerfen, innerhalb derer der Standort des Beobachters und dessen Relativität dargestellt werden kann. Um das besser veranschaulichen zu können, wählt er neue Zeichen: Statt eines Hakens steht ein Kreis für die Grenze von Etwas. Wiederholung wird durch zwei nebeneinander liegende Kreise dargestellt, Verschachtelung durch ineinander liegende Kreise. In einer Präsentation von Kauffman Laws of Form and the Logic of Non-Duality, 31 nehmen die beiden Axiome die Form an:

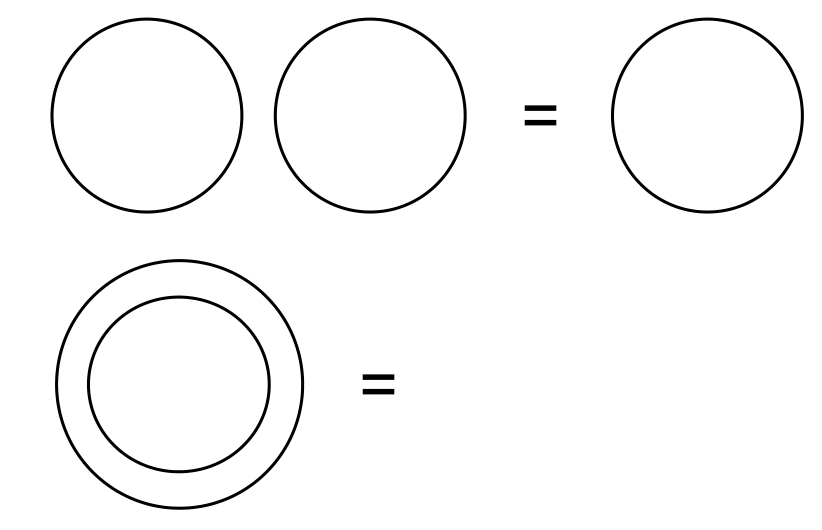
Das ergibt zunächst keine neue Erkenntnis, doch lässt sich in der Darstellung mit Kreisen besser zeigen, dass unterschiedliche Beobachter die gleichen Verschachtelungen und Wiederholungen verschieden sehen. Was für den einen wie eine Verschachtelung aussieht, kann für einen anderen von einer anderen Position aus wie eine Wiederholung aussehen usf. Wird z.B. als ein Kreis der Äquator auf der Erde gewählt und als zweiter Kreis ein beliebiger Kreis, der sich vollständig auf der Südhalbkugel befindet, dann liegt dieser zweite Kreis für einen Beobachter von der Nordhalbkugel aus gesehen innerhalb des Äquators. Für einen Beobachter auf der Südhalbkugel, der sich zwischen dem Äquator und dem zweiten Kreis befindet, liegen beide Kreise dagegen nebeneinander (siehe hierzu LoF, 102f). In den folgenden Bildern ist mit einem blauen Quadrat der jeweilige Standort des Beobachters eingetragen und mit einem kleinen Quadrat, wo er den anderen Beobachter sieht:

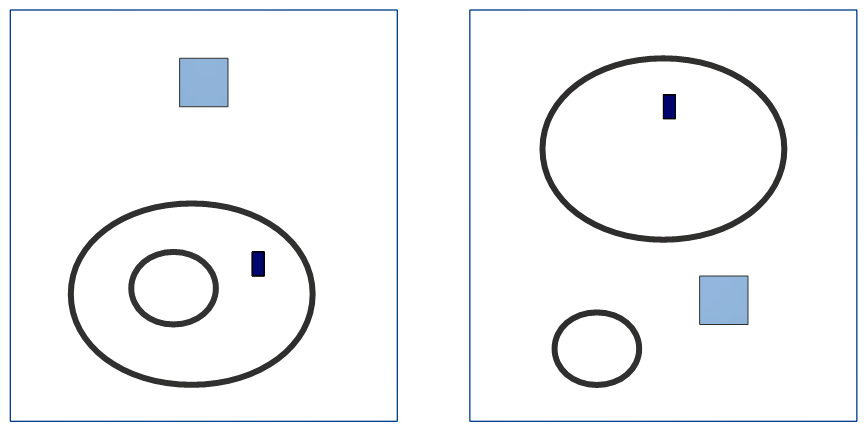
2 Kreise aus unterschiedlichen Perspektiven
links: Ein Beobachter auf der Nordhalbkugel sieht die beiden Kreise ineinander und den zweiten Beobachter im Zwischenraum zwischen den Kreisen.
rechts: Ein Beobachter auf der Südhalbkugel sieht die beiden Kreise nebeneinander und den ersten Beobachter im größeren Kreis.

Jede Darstellung logischer Elemente und ihrer Verhältnisse und Operationen ist abhängig von der Perspektive des jeweiligen Beobachters, der sich zugleich ein Bild macht, welches sein eigener Standort innerhalb der Logik ist. Diese Art von beobachter-abhängigen Darstellungen bezeichnet Spencer-Brown als »experiments« (LoF, 70-75).

Die Einbeziehung eines Beobachters führt in eine neue Endlosschleife. Im ersten Schritt zeichnet ein Beobachter ein Bild, wie er von seinem Standort aus das System sieht. In einem zweiten Schritt trägt er in diesem Bild den eigenen Standort ein, d.h. den Ort, wo er sich innerhalb der Karte befindet. Jeder kennt das von in der Natur angebrachten Wanderkarten, die mit einem hervorgehobenen Punkt den Standort zeigen, an dem sich die Karte innerhalb der Landschaft befindet. Im dritten Schritt kann gefragt werden, von welchem Standort aus eine Karte gezeichnet werden konnte, die den Standort enthält. Er muss sich jenseits des Beobachters und seiner Umgebung befinden. Auch für diesen Standort kann wiederum eine Karte gezeichnet werden von einem noch weiter außerhalb liegenden Standort aus, usf.

In Strukturaufstellungen wird das ebenso deutlich. Der Patient stellt einen Repräsentanten seiner selbst in den Raum und umgibt ihn mit weiteren Figuren aus seinem sozialen System. Der Patient sieht sich jetzt gleichsam selbst in dem ihn umgebenden System. Der Therapeut sieht wiederum von außen, wie der Patient auf sein Selbstbild reagiert und mit ihm interagiert, wenn die aufgestellten Personen sich zu äußern beginnen und der Patient ihre Stellung verschiebt oder verändert. Ein Supervisor kann die Arbeit des Therapeuten beobachten usw. – In Streitgesprächen ist es ein beliebtes Spiel, wenn die streitenden Parteien wechselweise aus dem Clinch heraustreten wollen und den anderen von einer Meta-Ebene aus beurteilen. Das provoziert eine entsprechende Reaktion, bis ein Kreislauf ohne Ende eintritt. – In Versammlungen wird bisweilen der Ablauf gestört, wenn jemand beide Arme hebt und Verfahrensfragen stellt. Dann kann sich jemand anders melden und die Zulässigkeit von Verfahrensfragen in Frage stellen usf.

   

Daher wird ein abschließender Schritt notwendig, mit dem gezeigt wird, dass die Ergebnisse unabhängig vom Standort der Beobachter gelten. Es muss Transformationsregeln geben, die einen Standort in einen anderen übersetzen. Welche Transformationen zwischen den verschiedenen Darstellungen gibt es und welche Eigenschaften haben sie? Das war für Einstein die Frage nach den Lorentz-Transformationen, in der Ökonomie ist es die Frage nach den Währungs-Transformationen und für mich gibt es eine verwandte Frage nach den Wahrheits-Transformationen bei Wittgenstein.

Ebenso wichtig ist die Frage nach dem untersten System, das Spencer-Brown mit (s₋₁) bezeichnet hat. Auch hier soll im Moment ein Hinweis auf die psychotherapeutischen Anwendungen genügen. Wie ist es zu erklären, dass die in einer Strukturaufstellung aufgestellten Personen spüren und sagen können, wie sich die von ihnen vertretene Person fühlt, und welche Veränderungen am System sie wünscht (z.B. dass andere Personen ihnen näher oder ferner stehen sollten, oder dass es weitere Personen gibt, die fehlen und in die Aufstellung aufgenommen werden sollen), obwohl sie keine weiteren Informationen über die aufgestellten Personen erhalten haben? Offenbar gibt es auf der untersten Ebene, – das ist in diesem Beispiel die Körperlichkeit (Leib) der Personen –, eine Wahrnehmungsebene, die in ihrer Offenheit und Unendlichkeit über alle bewussten Informationen hinausgeht. Das ist für mich ein Beispiel für die von Leibniz gemeinten kleinen Perzeptionen.

Luhmann scheint es dagegen vor allem darum zu gehen, dass erst aus der Kommunikation von Beobachtern untereinander Logik und Wahrheit entstehen. Wahr ist nicht mehr im klassischen Sinn dasjenige, was mit der Sache übereinstimmt, sondern was sich in der Kommunikation der Beobachter etabliert.

»Mit dem re-entry bezeichnen wir ganz allgemein die Wiedereinführung einer Unterscheidung in den Bereich, den sie zu unterscheiden erlaubt. Ein Beispiel: Das Wissenschaftssystem ist nach der Systemtheorie von Niklas Luhmann auf der Grundlage der Unterscheidung wahr/nicht-wahr ausdifferenziert. Wenn man eine Wissenschaftstheorie erarbeitet, die die Verwendung dieser Unterscheidung wiederum mit der Unterscheidung wahr/nicht-wahr beobachtet, wird mit der Wissenschaftstheorie ein re-entry vollzogen. Bezüglich des Wissenschaftssystems befindet man sich in einer solchen Wissenschaftstheorie auf einer Meta-Ebene, da man nun die Frage nach der Wahrheit der Operation der Wissenschaft – also der Wahrheit der Unterscheidung wahr/nicht-wahr – stellen kann. Dadurch, dass es die gleiche Unterscheidung ist, die auf sich selbst angewendet wird, entsteht eine Situation, 'in der die Unterscheidung gleichzeitig dieselbe (als die besondere Unterscheidung der Operationen dieses Systems) und eine andere (als beobachtete Unterscheidung) ist'. (Claudio Baraldi, Giancarlo Corsi, Elena Esposito GLU: Glossar zu Niklas Luhmanns Theorie sozialer Systeme, Frankfurt am Main 1997: 152)« (Lau, 55f)

– Ergänzungen zur Strukturaufstellung

Varga von Kibéd hat die Methode systemischer Strukturaufstellungen weiter ausgebaut bis zu einer anonymisierten Form: Der Patient lässt sich auf der Bühne aufstellen und um ‘sich’ herum weitere Personen, die für ‘das Problem’, ‘den größten Widerstand’, ‘mögliche Hilfe’, ‘einen unbekannten Einflussfaktor’ usf. stehen. Nur der Patient weiß, was damit gemeint ist, und dennoch können die aufgestellten Personen überraschende Erkenntnisse liefern: Sie können sagen, ob noch etwas fehlt, welche Figur falsch steht u.ä. So können Probleme aufgestellt werden, die den sich aufstellenden Personen unbekannt (verdeckt) sind. Das schließt mögliche Beeinflussungen durch die Erzählungen des Patienten und Kommentare des Therapeuten noch weiter aus.

Den Familienaufstellungen wurde oft der Vorwurf gemacht, dass ihr Erfolg von einem Moderator mit charismatischen Fähigkeiten abhängt, der mithilfe von Suggestion das Verhalten der Gruppe steuert. Möglicherweise sind es auch verdeckte Gruppenprozesse, die die Ergebnisse in eine bestimmte Richtung drängen, Angst vor Selbstentblößung, Freude am Narzissmus, Lust am Fabulieren. Varga von Kibéd beruft sich ausdrücklich auf Hypnose-Techniken. Mir ist unbekannt, ob und in welcher Weise die Hypnose-Arbeit von Spencer-Brown in seine Arbeiten zur Logik eingeflossen sind.

Varga von Kibéd nannte bei einem Weiterbildungsseminar 2010 (veröffentlicht in YouTube) den Madhyamaka-Buddhismus und dort insbesondere das Gesetz des Bedingten Entstehens (pratitya-samutpada, das in wechselseitiger Abhängigkeit voneinander Entstehende) als eine Grundlage seiner Arbeit, die er mit den Ideen von Spencer-Brown zusammenbringen will. Er beruft sich auf Nagarjuna (2. Jh. n.Chr.) und Vasubandhu (4. Jh. n.Chr.) und dessen drei Prinzipien, die aus seiner Sicht den heutigen radikalen Konstruktivismus etwa von Heinz von Förster noch unterlaufen. Alles geht nicht nur auf eine ousia (einer allem anderen unterliegenden Substanz) zurück, wie Aristoteles gelehrt hatte, sondern auf drei Prinzipien: (a) das, was erscheint (b) das, wie es erscheint im jeweiligen Modell, (c) dasjenige an (a), das in (b) nicht erscheint und daher eine ewige Bewegung neuer Modelle auslöst.

Lässt sich die Methode der Systemischen Strukturaufstellung auf andere naturwissenschaftliche Gebiete übertragen? Evolutionstheorie: Stehen die einzelnen, zufällig entstandenen Mutationen wie die in einer Strukturaufstellung aufgestellten Personen auf einer Art Bühne und beginnen dank ihrer Körperlichkeit ihre Beziehungen untereinander zu erkennen, woraus sich etwas Neues ergibt? Das wäre ein neuartiger Versuch, den Verlauf von Emergenz und Evolution zu beschreiben und zugleich ein Ansatz, der Monadologie von Leibniz eine zeitliche Verlaufsform zu geben, wenn die Monaden als Einheiten auf einer Bühne verstanden werden und dort ihre Positionen verändern können.

Ein anderes Beispiel könnte die Quantenverschränkung sein: Stehen die verschränkten Quanten auf einer gemeinsamen Bühne und gelangen dank ihrer Körperlichkeit zu einer gemeinsamen, übergreifenden Bewegung, einem Tanz der Quanten?

Anhang

– Die Grenze bei Hegel und Spencer-Brown (Stichworte und Fragen)

Das Etwas ist durch eine Grenze vom Anderen getrennt. Die Grenze unterteilt bei Spencer-Brown den Raum in den durch Etwas markierten Bereich und den Bereich alles anderen.

Das Etwas ist aber zugleich das Andere-an-im-selbst. Das Hinausgehen zum Anderen kehrt zurück. Dies ist bei Spencer-Brown der Re-entry.

Hegel betrachtet den Fall, wenn nicht nur von einem einzelnen Etwas, sondern von vielen Etwasen zum jeweils Anderen hinausgegangen wird. Für ihn geht die Wiederholung des Hinausgehens von verschiedenen Etwasen zu ihrem jeweils Anderen über in das Hinausgehen des Einen zu den Vielen entlang einer Reihe, auf der die Etwase angeordnet sind. Dadurch erfolgt zugleich ein Hinausgehen zweiter Stufe: Es wird über die einzelnen Schritte des Hinausgehens hinausgegangen auf die Reihe und deren Eigenschaften, entlang derer das Hinausgehen erfolgt. Die einzelnen Schritte des Hinausgehens wenden sich in sich selbst und führen zum Grund, in dem das Hinausgehen erfolgt. Vorbild ist die Zahlenreihe der natürlichen Zahlen. Die Einen sind entlang der Reihe untereinander ähnlich. Zunächst werden die einzelnen Schritte betrachtet (Nachfolger-Relation, wobei der Abstand von einem Etwas zu seinem Vorgänger und zu seinem Nachfolger jeweils Eins beträgt), anschließend die Reihe der Schritte für sich. Sie ist transitiv und euklidisch geordnet.

Spencer-Brown betrachtet dagegen den Fall, wenn von einem markierten Bereich aus das Hinausgehen über die Grenze wiederholt wird. Wird nur das einzelne Hinausgehen wiederholt, verändert sich nichts, denn jedes neue Hinausgehen führt wieder zum gleichen Anderen. Kommt es jedoch zu einer unendlich häufigen Wiederholung, dann führt das zum Re-entry. Damit das möglich ist, muss die Wiederholung formal geregelt und selbstähnlich sein. Das führt im Ergebnis von der eindimensionalen Reihe zur Welle bzw. zum Gedächtnis: Beim Gedächtnis wird immer der gleiche Wert erreicht, bei der Welle (Oszillation) werden abwechselnd mindestens zwei unterschiedliche Werte erreicht. Dieser Gedanke ist nochmals aufzunehmen, wenn auch Hegel von Oszillationen (Pulsation) spricht.

Knotenlinie und Wahlverwandtschaft: Ist die Knotenlinie eine Folge von Grund-Bereichen, in die im Sinne von Spencer-Brown eine Form, d.h. eine Unterscheidung eines markierten Bereichs von seinem Anderen eingetragen wird? Jeder Grundbereich stabilisiert sich durch einen Re-entry, das ist eine innere zirkuläre Bewegung. (Das müsste näher ausgeführt werden. Wie stabilisieren sich chemische Prozesse oder Wärmeaustausch, und wann kippt das System um?) Jeder Zustand ist durch eine Grenze von einem anderen Zustand getrennt. Kommt es zur Grenzüberschreitung, so wird diese zurückgekoppelt und verstärkt als Rückkopplung nochmals den Zustand.

Der Re-entry im Sinne von Spencer-Brown kann in der Ausdrucksweise von Hegel als Wechselspiel von Kontinuation und Umkehr verstanden werden. In der Systemtheorie wird dies beschrieben als Entkopplung und Kopplung.

Identität und Verschiedenes: Jedes A ist von der Gesamtheit aller Nicht-A getrennt. Es gibt jedoch ein Hinausgehen zu den von A Verschiedenen, der Gesamtheit der Nicht-A-s und ein Zurückkehren. Erst durch die Bewegung von beiden wird die Identität hergestellt.

Gegensatz und Widerspruch: A und ¬A bilden einen Gegensatz. Sie sind durch viele Beziehungen miteinander verbunden. Jede Beziehung geht zum anderen hinaus und kehrt zurück, wodurch der Gegensatz gefunden wird.

Lässt sich der Übergang vom Gegensatz und dem Widerspruch zum Grund verstehen im Sinn von Spencer-Browns Einführung der imaginären Werte? Ist der Grund das Imaginäre? Sind der Grund und die Ebene, auf der der Gegensatz liegt, voneinander auf imaginäre Weise getrennt, die nach Spencer-Brown das Gedächtnis und die Oszillation hervorbringt und mit ihnen die Zeit?

Der Grund ist zunächst der Grund, in den diese Figur eingeschrieben (in-formiert) ist. Ist von hier ausgehend der Begriff der Information zu entwickeln, und warum kennt Hegel diesen Begriff nicht? Ist der Grund mit Hegel der Rückverweis auf die Seinslogik und dort die Bewegung von Kontinuation und Umkehr?

Wie verändert sich der Grund, wenn er erst einen Re-entry ermöglicht und dann einen Re-entry aufnimmt? Wird der Re-entry »vernäht«, und ist die Vernähung zu spüren?

– Syntax und Semantik

Das Verhältnis von Proto-Arithmetik und Proto-Algebra ähnelt dem Verhältnis von Semantik und Syntax. Es gibt eine unendliche Fülle semantischer Aussagen, die nie abreißen wird. Aber so viele semantische Aussagen es auch geben mag, sie sollten einer endlichen Anzahl syntaktischer Regeln genügen. Syntaktische Regeln sehen formal wie übliche Sätze aus, haben jedoch eine prinzipiell andere Bedeutung. Wenn Hilbert gehofft hatte, die Mathematik in einer formalen Metamathematik begründen zu können, hatte er im Grunde nach einer Syntax der Mathematik gesucht. Das haben Carnap und Gödel gesehen und daher die Frage nach der Metamathematik umgewandelt in die Frage nach der Syntax der Sprache.

Hegel diskutiert das Verhältnis von Semantik und Syntax im Übergang von der Seins- zur Wesenslogik. Die Seinslogik untersucht die Kategorien, mit denen semantisch etwas über ein Seiendes ausgesagt werden kann (Qualität, Quantität, Relation bzw. bei Hegel Maß). Demgegenüber ist die Logik der Reflexionsbestimmungen (der erste Abschnitt der Wesenslogik) ein Übergang von der Semantik zur Syntax der Sprache (siehe seine Anmerkung in der Wissenschaft der Logik zum Satz der Identität, HW 6.41-45).

Mit dem Identitätssatz ›A = A‹ wird das Sprachspiel fundamental verändert: Aus semantischen Sätzen über etwas wird ein Beispiel-Satz, an dem die Struktur (Syntax) der Sprache aufgezeigt wird, also ein selbstbezüglicher Satz der Sprache über sich. Der Satz sagt jedoch nicht etwas Inhaltliches über andere Sätze, sondern an seiner Form wird etwas demonstriert. Der tautologische Satz ›A = A‹ liefert offensichtlich kein neues Wissen, sondern erscheint geradezu sinnlos und völlig überflüssig. Aber  an diesem Satz  wird etwas deutlich über die Syntax (und damit das Wesen) aller Sätze. (Collmer beschreibt das in angedeuteter Mathematik kategorientheoretisch, wenn er vom Einsatz des »Funktor 'selbst'« spricht und mit dem Funktor die Meta-Ebene erreicht; Collmer, 125.)

Wird das leere ›A ist A‹ beliebig erweitert in ›A ist A ist A ist A ist …‹, ergeben sich aus dieser ins Leere laufenden Bewegung verborgene weitere Bedeutungen: Es kann nach dem Vorbild von die Rose ist eine Rose ist eine Rose (Gertrude Stein Sacred Emily, 1913) »ein artifizielles Muster« im Sinne des Dadaismus sein, bei endloser Wiederholung eine Verschwendung von Ressourcen an Papier oder Speicherkapazität, die irgendwann an die »Macht des Faktischen« stößt und abgebrochen werden muss oder eine Bewegung des Verinnerlichen und der Versunkenheit in einem Gebet (Collmer, 126).

Die Reflexionsbestimmungen sind für Hegel Sätze, jedoch nicht im Sinne von Antworten auf Was-Fragen (›Was ist die Identität‹), sondern sie zeigen an sich selbst (selbstbezüglich) eine bestimmte Struktur, die allen Sätzen zugrunde liegt. Es sind keine prädikativen Aussagesätze, sondern Sätze auf einer abstrakteren Ebene (Collmer, 129).

Hegel hat die transzendentale Logik von Kant radikalisiert, und sein Wechsel von Semantik und Syntax vollzieht eine Wende, die später im 20. Jahrhundert sowohl von Wittgenstein wie von Heidegger in einem jeweils anderen Kontext neu formuliert, aber erst von Carnap und Gödel mit der Syntax der Sprache in aller Klarheit gefasst wurde.

Scheier sieht diesen Wechsel in Ästhetik der Simulation in einem größeren Horizont, von dem aus die kulturellen und philosophischen Veränderungen der industriellen Moderne im 19. Jahrhunderts überschaubar werden. Franz Schubert hat in seinen späten Werken nicht mehr einfach neue zeitliche, musikalische Abläufe komponiert, sondern versucht, mit seinen Werken den Verlauf der Zeit an sich darzustellen (siehe hierzu im Beitrag Von Schubert zu Klimt – die Verräumlichung der Musik den Abschnitt über die Klaviersonate in c-Moll D958, ein Finale an den Grenzen der Zeit, mit Bezug auf Peter Gülke Franz Schubert und seine Zeit, Laaber 1991, wobei der Titel bewusst doppeldeutig gewählt ist). Ein anderes Beispiel ist die Poetik von Stéphane Mallarmé. Er suchte nach dem »Gesang unter dem Text«, der »'Musik' in den Buchstaben«, den »Kraftlinien der fließenden, heterogenen, doch semiotisierbaren chora«, dem » Ort der Sprache«, in den hinein die Arbeit am Text erfolgen kann (Kristeva Die Revolution der poetischen Sprache, Frankfurt am Main, 1978, S. 41, 72, 184, 205).

Siglenverzeichnis

AUM = The G. Spencer-Brown – AUM-Conference 1973, Esalen 1973; Link

HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971; Link

KrV = Immanuel Kant: Kritik der reinen Vernunft (1781, 1787)

LoF = George Spencer-Brown: Laws of Form, New York 1972 (Julian Press) [1969]; archive.org

R = George Spencer-Brown: An Introduction to Reductors, unveröffentlichtes Typoscript 1992

SWH = Tatjana Schönwälder-Kuntze, Katrin Wille, Thomas Hölscher: George Spencer Brown, Wiesbaden 2009 [2004]

Literatur

W. Ross Ashby: Design for a Brain, New York 1960 [1952]

Gregory Bateson: Ökologie des Geistes, Frankfurt am Main 1981 [1972]

Dirk Baecker 1993 (Hg.): Kalkül der Form, Frankfurt am Main 2016 [1993]

Dirk Baecker 2000: System
erstveröffentlicht in: Christian Bermes und Ulrich Dierse (Hrsg.), Schlüsselbegriffe der Philosophie des 20. Jahrhunderts, Archiv für Begriffsgeschichte, Sonderheft 6, Hamburg 2010, 389-405; vordenker Neuss 2018

Dirk Baecker 2013: George Spencer-Brown wird 90; catjects

Ulrich Blau: Die Logik der Unbestimmtheiten und Paradoxien, Heidelberg 2008

Thomas Collmer: Hegels Dialektik der Negativität, Gießen 2002

Louis H. Kauffman und Francisco J. Varela: Form Dynamics
in: Journal of Social and Biological Structures 1980 3, S. 171-206

Louis H. Kauffman 1995: Knot Logic
in: ders. (Hg.): Knots and Applications, Singapore 1995, 1-110

Louis H. Kauffman 2000: What is a Number?; Link

Louis H. Kauffman 2006: Laws of Form – An Exploration in Mathematics and Foundations, Rough Draft

Louis H. Kauffman 2009: Laws of Form and the Logic of Non-Duality, San Rafael 2009; Link

Felix Lau: Die Form der Paradoxie, Heidelberg 2012 [2005]

Bernie Lewin: Enthusiastic Mathematics, Melbourne 2018

Niklas Luhmann 1984: Soziale Systeme, Frankfurt 1991 [1984]

Niklas Luhmann 1990: Die Wissenschaft der Gesellschaft, Frankfurt 1992 [1990]

Niklas Luhmann 1996: Die neuzeitlichen Wissenschaften und die Phänomenologie, Wien 1996

Niklas Luhmann 1997: Die Gesellschaft der Gesellschaft, Frankfurt am Main 1998 [1997]

Warren McCulloch: Verkörperungen des Geistes, Wien, New York 2000 [1965]

Warren McCulloch: The heterarchy of values determined by the topology of nervous nets
in: The Bulletin of Mathematical Biophysics 7(1945), 89-93; deutsche Übersetzung bei Vordenker

Martin Rathgeb: George Spencer Browns Laws of Form zwischen Mathematik und Philosophie, Siegen 2016; Link

Claus-Artur Scheier 2000: Ästhetik der Simulation, Hamburg 2000

Claus-Artur Scheier 2016: Luhmanns Schatten, Hamburg 2016

The Telegraph: George Spencer-Brown, polymath who wrote the landmark maths book Laws of Form – obituary; Telegraph vom 13.9.2016

Franco Volpi: Der Status der existenzialen Analytik (§§ 9-13)
in: Thomas Rentsch (Hg.): Martin Heidegger - Sein und Zeit, Berlin 2001, S. 29-50

Bildnachweis des Titelbildes: Spencer-Brown Laws of Form S. 68

 

© tydecks.info 2017-2020