Walter Tydecks
The Self-organisation of the Medium in Spencer-Brown's Circuits – seven Theses
Impulse topic for "Panel Discussion 1" of The Unmarked State Conference celebrating the 50th Anniversary of the First Publication of George Spencer-Brown's ‘Laws of Form’ in Liverpool, 9th August, 2019; Video in Vimeo or YouTube
In my late years I am an enthusiastic newcomer and a lateral entrant in the field of Spencer-Brown and I am very happy to have the chance to speak here and certainly to learn a lot. My topic concerns the circuits developed by Spencer-Brown. In a way, this is a continuation of Bernie Lewin's contribution. Just as he showed how the foundations of classical geometry can be derived from the basic rules of Laws of Form, I would like to show how the circuits introduced in Chapter 11 can be turned into mathematics of the 20th century. While he has largely completed his work, I am at the beginning and I want to present seven theses in this short impulse
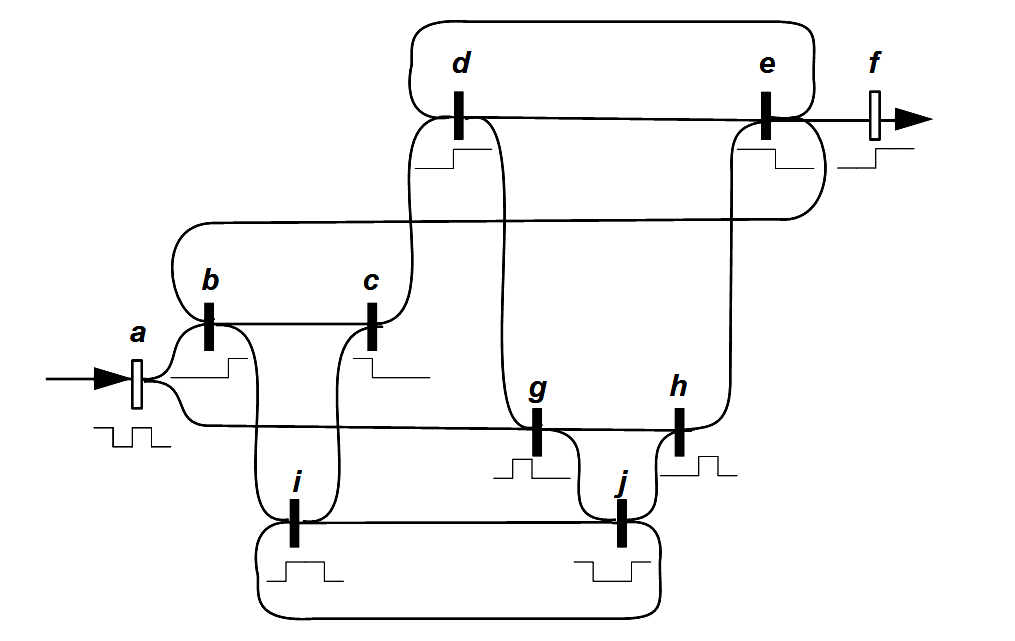
Modulator function (LoF, 67), naming of the switch elements added
Legend
Full rectangle: Switching element (marker)
Empty rectangle: input or output
Above the rectangle is the name of the switching element
Below the rectangle is the incoming or outgoing wave and for switching elements their
conversion rule.
(1) What does this circuit mean? First of all, it is necessary to explain why Spencer-Brown indicates the input with a and the output with f. In my opinion, if chapter 11 is seen as a whole, a stands for argument and f for function. His calculus recognizes only two conditions for a: a cross ⃧ (a marked state) and an empty space (an unmarked state), which he represents in this diagram with a wave trough and a wave crest. Chapter 11 deals with how the oscillation between the two conditions of argument a, whose properties and rules are introduced and studied in the preceding primary arithmetic and primary algebra, self-refer to functions f, to which they relate. To show this, Spencer-Brown introduces limit crossings (Grenzübergänge) that are formed like the successor relation of natural numbers. The transition from a to f is formally similar to that in traditional mathematics, where Cantor achieves transfinite numbers and expands the space of natural numbers. Similarly, Spencer-Brown creates a new type of object in transforming a to f, by including f in the space of argument a by re-entry and extending it.
If the re-entry of f occurs, a vibration (oscillation) passes through the set of arguments, whereby time arises within its logic and can be represented formally. When this happens and a logical concept of time is found, the temporal processes which occur in the transition from the arguments a to the functions f can be identified. They are the topic of my impulse lecture. For Spencer-Brown they are no longer linear processes, as they are known from the final chains and causal sequences of classical logic and natural science, but networks in the way he knew them from his time as a developer of circuits, and as they had been introduced by neurophysiology and cybernetics in the 1930s and 1940s. He examines how an input a is modulated by networks into an output f. He restricts himself to the simplest case, when a new wave of double wavelength is generated from an incoming wave. Everything else should develop from this.
(2) It is no coincidence that he considers networks with which waves are modulated. In the 19th century, Stokes and Weierstrass's theorem showed that any function can be interpreted as an approximation of simple waves. Hilbert constructed the mathematical concept of a Hilbert space from this, which became fundamentally important to quantum mechanics and game theory. In my understanding, Spencer-Brown therefore uses the modulation of a given wave into a double wavelength wave to design the nucleus from which the foundations of modern mathematics can gradually be developed.
(3) How does the incoming wave pass through the network? In order to understand his approach, it is important to understand that the modulation of a wave in a network does not apply to the wave as a whole, but independently for each wave crest (up) and wave trough (down) individually. Each section (either a crest or a trough) is seen as a single input, which Spencer-Brown calls stroke. Each stroke must find its own way through the network.
(4) What happens at the switching elements (markers) inside the network? Each switching element determines how incoming wave crests or troughs are converted or blocked. It is the engineer's art to carefully arrange the switching elements, whereby it is open whether he follows implicitly assumed, hidden rules here. As a result, the network is designed in such a way that two consecutive strokes will almost never follow the same path. Each stroke determines a state of the network with its individual path. The wave is split (dispersed) as it travels through the network and an output wave is created which carries the effect of its journey through the network. The network therefore no longer simply describes a difference ›f | a‹ between the input a and the output f, but a difference field ›f ▒ a‹ (the use of the symbols ‘|’ and ‘▒’ I take from Scheier, 18ff).
The paths of the first two strokes are shown as an example:
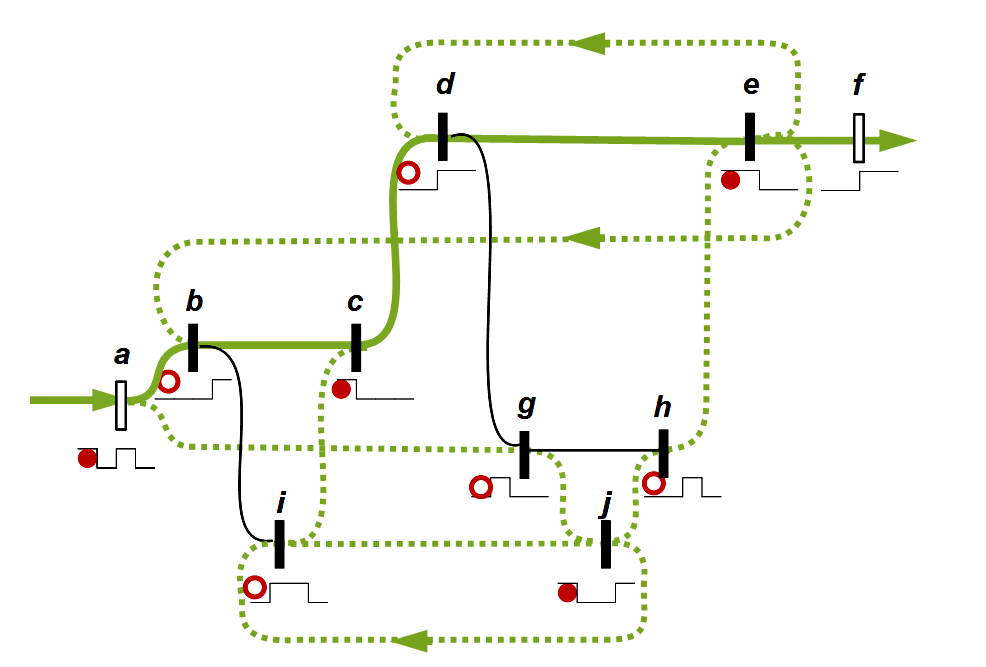
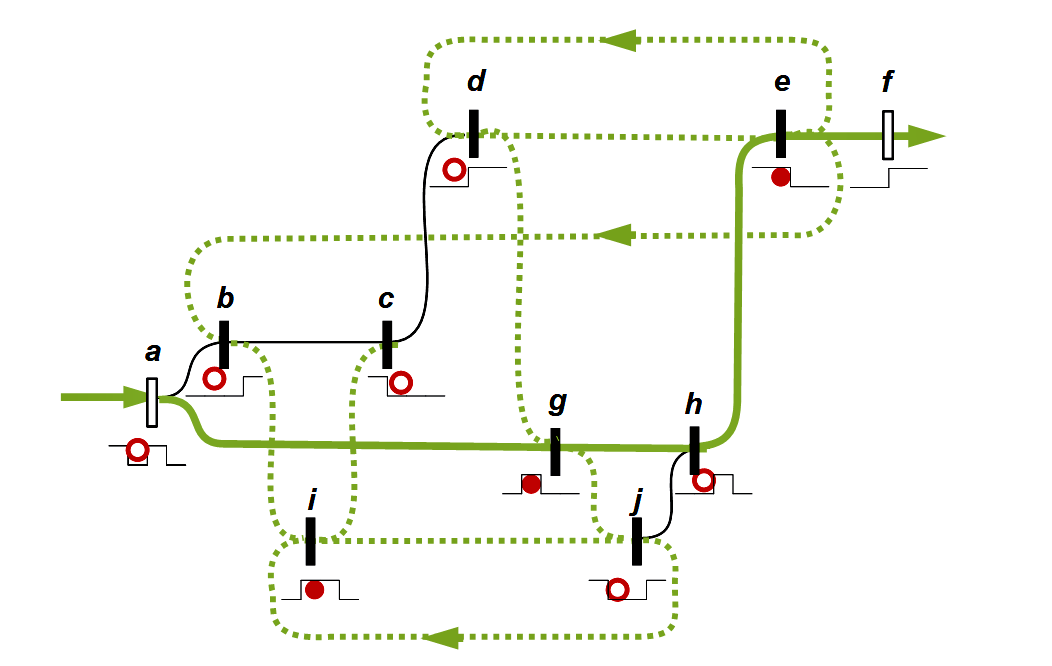
Paths of the first two strokes
Legend
Below the markers: Red full circle indicates a wave crest, empty circle a wave trough (according to Kauffman 2006, 115ff)
Olive green: standard paths leading directly to the output
Olive green dashed: Further possible paths
Black: These paths are blocked in their respective states, since an empty circle meets an empty circle and a full circle meets a full circle.
Left arrows on a path indicate possible returns
Observation: On every possible way full circles and empty circles alternate regularly.
(5) The system is set up in such a way that in the oscillation of its system states it can react to the oscillation of the input and, as a whole, produces a kind of dynamic equilibrium of which Bertalanffy spoke, and which can be described as Maturana and Varela as self-organization (autopoiesis).
(6) A developer designs the system in collaboration with the network. Developers do not know in advance what inputs will be made, nor can they fully plan which paths the inputs will follow through the network. Developers can only vaguely predict the network's behavior and they rely on the system's self-organization. The network can be understood as the medium (ground); its respective state as its form.
With networks, the one-way procedure at the beginning of Laws of Form is left behind: It is no longer a single-directional acting subject that draws a form onto a ground (»draw a distinction«), but the subject designs a network that finds its own form, which can then be improved by the subject. The relationship between medium and form, or in Spencer-Brown's language: the relationship between cross and unmarked space (ock) becomes dynamic. Spencer-Brown shows in detail how the network can alternatively be constructed according to the rules of Laws of Form as a form that is only formed of crossings and feedback by re-entries into the form:
Modulator function (LoF, 66)
But its specific property as a network is better shown only in its usual graphical form. Thus Spencer-Brown succeeds with the networks in a transition from the simple forms in the main text of Laws of Form to a new design of logic whose basic elements are networks. Thinking further, they result in the idea of a mathematics that is no longer based only on numbers and the elementary geometric figures (point, circle, straight line).
(7) The fields of application are diverse and basically unlimited. For me, therefore, networks stand for a logic of medial modernity. In this panel, I would like to discuss the application of these points in relation to the field of organisational theory.
Every organisation is a network that processes certain resources (its input) in order to achieve a result (its output). Within the organisation, each switching element can be described as a position occupied by one or more members of the organisation. Each job creates value, and the network plan is a generalisation of linearly envisioned value chains. What is crucial is the insight not only to design a scheme of the organisation, but to understand how this scheme affects the self-organisation of the organisation and brings it to life on a theoretical level. To this end, Spencer-Brown has created a formalism that could make it possible to develop the necessary algorithms to achieve this, which was not previously possible in organisational theory, to give just one example of a key field of application.
Note: See also the detailed commentary on Spencer-Brown's Laws of Form (German, English).
Appendix
From the discussion in the panel and further contributions and talks in the course of the conference, I would like to highlight three further points on the topic of networks related to Spencer-Brow's work:
Story structures and their networks How to explain to non-mathematicians what is special about the circular transition from arguments a to functions f, whose arguments they are, and what to answer if most mathematicians declare Spencer-Brown's conscious paradoxical idea absurd? A surprisingly different view emerges with Leon Conrad, and it can make things clearer and more vivid. He uses the basic symbols of Spencer-Brown to describe, on a meta-level, the structures of different types of narratives (analysis of sentence types and story structures). Stories can also mean pieces of music that have something to tell, mathematical proofs or lectures.
 : Openings and closings. Re-entry breaks the usual everyday situation in which the listener (or reader) finds himself. The narrator carefully sets up the environment in which he wants to tell the story, so that the listener already knows when he enters that a different world awaits him than the usual one. In the concert hall, the players tune their instruments until calm returns when the conductor enters and raises the baton. The reader makes himself comfortable before he picks up a book, perhaps looking at the cover text first, the bibliography, until he begins reading. In traditional forms of storytelling, the audience is invited to a special greeting (example). At the same time, the respective mood leaps over to the narrator, who reacts to it and feels that this is going to be a special evening. Conversely, at the end of the narrative, the listener has to succeed in getting out and re-entering the narrative into his ‘everyday life’ and sew it up there. It is on this that the success or failure of the narrative depends.
: Openings and closings. Re-entry breaks the usual everyday situation in which the listener (or reader) finds himself. The narrator carefully sets up the environment in which he wants to tell the story, so that the listener already knows when he enters that a different world awaits him than the usual one. In the concert hall, the players tune their instruments until calm returns when the conductor enters and raises the baton. The reader makes himself comfortable before he picks up a book, perhaps looking at the cover text first, the bibliography, until he begins reading. In traditional forms of storytelling, the audience is invited to a special greeting (example). At the same time, the respective mood leaps over to the narrator, who reacts to it and feels that this is going to be a special evening. Conversely, at the end of the narrative, the listener has to succeed in getting out and re-entering the narrative into his ‘everyday life’ and sew it up there. It is on this that the success or failure of the narrative depends.
⃧ : A character in a specific time and space. This determines the environment of the narrative and at the same time the horizon in front of which it is to be understood. The narrator consciously begins on two levels at the same time: he reacts to the situation of the listeners and skillfully mixes it with the content he wants to tell. This can be a conscious introduction, such as the first two diffusely sounding drumbeats with which Beethoven begins the Eroica, or the chords at the start of his 9th Symphony. Storytellers can introduce stories (particularly wonder tales) with phrases like "Once upon a time, a long, long time ago," which are recited in a solemn tone, and sometimes at the beginning they involve the audience with questions until everyone is inwardly present. Everyone feels that something new is starting now. Many rhetoricians recommend starting a speech with an anecdote to get the listener in the mood for what is to come.
 : In the course of the narrative there are events that can ...
: In the course of the narrative there are events that can ...
⇀: bring characters closer to solving a problem, or fulfill their expectations ...
↽: ... create setbacks, build up tension, or ...
⇌: ... create transitional dissonance.
With these elements, for example, the following type of narrative can be described:
 ↽ ⇀ ↽ ⇌ ↽ ⇌
↽ ⇀ ↽ ⇌ ↽ ⇌ 
This is a linear process and describes a very simple narrative. In the course of the narrative, secondary characters can be introduced with side plots and integrated into the main plot. This results in a network. A famous example is the novel Sentimental Education (L’Éducation sentimentale)by Gustave Flaubert. He designed the structure of the novel on a large drawing hanging on the wall and had it always in mind when writing. The reader, on the other hand, is amazed by the leaps in time in the novel and the multitude of characters that seem to come, go and return as if by chance, as in real life.
Usually the listener identifies himself with the main character, takes his position, experiences the story from his perspective, is absorbed in the flow of the narrative and at the end reaches an insight in which he no longer hears individual events but understands what the narrative as a whole is called and what it means. A good example is Peter and the Wolf of Prokofiev: First the mostly young listeners let themselves be captivated by the story, until they finally know that it was a story, what it means and what they have learned from it. This transition from the individual events within a narrative to the event, having understood, identified and named the narrative as a narrative, is a vivid description of what is meant by the transition from the arguments a to the function f.
For me, this gives the impulse not only to speak of input and output in the network, but to further understand input and output as the re-entries with which the network is connected to its environment. Within the network, the functions of the switching elements can be extended. They are not to be limited to converting or blocking an incoming signal, but the conversion becomes progress ⇀, the blockade becomes a step back ↼ and possibly a short-term standstill ⇌, a moment of reflection from which different paths can result.
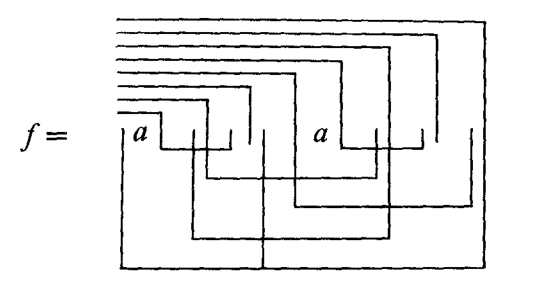
Parallel paths and their matting Arthur Collings not only expands the dual logic of ⃧ (cross) and  (recrossing) into a quaternion-like circular structure of a circle divided into four quarter circles, but also considers networks with not just one input, but two independent inputs leading to two independent outputs. In the simplest case, two parallel paths run from one input to one output each, but there can also be felting (braiding, plaits), which leads to a braiding hairstyle of Rasta plaits of their own, and their mathematical structure, the braid groups.
(recrossing) into a quaternion-like circular structure of a circle divided into four quarter circles, but also considers networks with not just one input, but two independent inputs leading to two independent outputs. In the simplest case, two parallel paths run from one input to one output each, but there can also be felting (braiding, plaits), which leads to a braiding hairstyle of Rasta plaits of their own, and their mathematical structure, the braid groups.
In a very simple example there are two inputs with the arguments a and b, which lead to ⃧a and ⃧b as output. They can intertwine with each other.

There are no limits to the imagination, which further possibilities are conceivable - known from quantum mechanics: Thus two ways can influence each other by resonance. Or virtual leaps into the past and the future are conceivable if one path is influenced by an event that lies on the other path in the past or in the future. Modern literature knows an unlimited number of examples of how processes of this kind can be told.
With the theory of circuits it should be possible to determine certain basic structures from this multitude.
Genesis of Networks With Josef Freystetter the biblical creation story Genesis 1:1 - 2:4a can be read verse by verse as a developing network in the sense of Laws of Form. Gen. 1:4, for example, deals with the distinction between light and darkness, with Freystetter cyclically interpreting light as the marked area and darkness as the unmarked area during the day and darkness as the marked area and light as the unmarked area during the night.
The change of day and night is the elementary cycle in time. In the next step the water is also spatially separated into different areas (oceans, clouds, rivers) and from it separates the earth, which becomes both the fertile soil on which plants and animals can live, and in the figurative sense the ground in which the forms are inscribed. In the sky, signs and constellations emerge that become models for the switching elements (markers) in the networks.
However, the biblical story of creation is not simply a classical natural history in a short version over seven days, but the symbolic images/language and the things symbolized emerge together. It is impossible to say what came first: the symbolic images/language or the things symbolized. The symbols and the things symbolised are of dependent origination (see LoF, 42). God has given man the imagination and the faculty of speech with which he can form an image of this development (Gen 1:26 and 2:19).
Freystetter is not only concerned with understanding the network of events in the biblical Genesis with Spencer-Brown, but also with following the example of Genesis to understand the Genesis (the origin) of a network. In my understanding, the network does not develop like a linear narrative – as suggested by the structure of Gen. 1-2 – in which a point gradually becomes a difference, a simple cycle, the entanglement of two cycles and finally a network with 6 switching elements, but from an underlying area in which the forms used are initially still blurred, half-finished, dotted or can be spoken of as clouds of electrons as in particle physics. They are as Leibniz described them as differentials, which precede the domain of natural numbers. Every trace element still in development (which has no completed form and leaves no completed trace) looks for its partners until the forms and their traces emerge from this development. The idea of the trace is ambiguous. For Freystetter, God withdraws at the end of creation from the world created by him. This idea was also shared by Leibniz, but Leibniz spoke of the traces that God left in the world. For me, these traces are the area from which the human imagination, thinking, speaking and understanding emerge, and thus also the Laws of Form. Spencer-Brown hits this point better and more accurately than any other logic I know, which precedes all further distinctions, for example in mathematics and language.
If Spencer-Brown distinguishes between nesting levels within complex forms sᵢ and calls the underlying reality s₀ (LoF, 7), the preceding possibility spaces are levels s₋₁ and downwards (s₋ᵢ). It seems to me that the greatest challenge and at the same time the most interesting work is to find a suitable calculus for this, which takes up the differential calculus developed by Leibniz and continues it until, as a result of a space of possible networks and their possible connections, the real networks and their actual connections emerge.
Acknowledgement I want to thank Bernie Lewin and Lars Clausen for the preparation and presentation of the panel and Leon Conrad for numerous further questions and comments as well as support in the graphic design of the networks and the translation into English.
Bibliography
Leon Conrad: The Unknown Storyteller, Liverpool 2019; academia.edu; Video (or YouTube)
Louis H. Kauffman 2006: Laws of Form – An Exploration in Mathematics and Foundations, Rough Draft; PDF
Louis H. Kauffman, Arthur M. Collings: The BF Calculus and the Square Root of Negation, 2019; ResearchGate
Bernie Lewin: Enthusiastic Mathematics, Melbourne 2018
Claus-Artur Scheier: Luhmanns Schatten, Hamburg 2016
George Spencer-Brown: Laws of Form, New York 1972 (Julian Press) [1969]; archive.org
George Spencer-Brown: An Introduction to Reductors, unpublished Typoscript 1992
© tydecks.info 2019