Dynamische, geträumte und imaginäre Zahlen

Version 6.12.2018

Auszüge aus der Einleitung und dem Teil über dynamische Zahlen wurden beim Arbeitskreis zu Hegels Naturphilosophie Anthropologie und Psychologie in der Naturphilosophie Hegels, Leipzig am 1.12.2018 vorgetragen.

Einleitung

Die Einbildungskraft nimmt in der Entwicklungsgeschichte des Geistes eine Schlüsselrolle ein. Mit der Einbildungskraft löst sich der Geist von der Bindung an die unmittelbar gegebenen Eindrücke und Wahrnehmungen und vermag Abstand von ihnen zu gewinnen. Er bleibt nicht bei dem stehen, was er vorfindet, sondern malt sich dank seiner Phantasie aus, wie etwas so geworden sein kann, wie es jetzt ist, und welche Möglichkeiten für die weitere Entwicklung bestehen. Die Möglichkeiten existieren vor ihrer Verwirklichung nur virtuell in der Einbildungskraft. Sie bilden ein Möglichkeitsfeld, und sich in ihm bewegen zu können, lässt den Geist den Weg zu sich selber und seiner eigenen Freiheit finden und betreten. »Die Vorstellung ist die Mitte in dem Schlusse der Erhebung der Intelligenz« (HW 10.263). Der Geist bleibt nicht bei den Bildern und Sprachelementen stehen, die er vorfindet, sondern beginnt seine eigene Sprache zu sprechen. Seine Einbildungskraft schwingt sich auf bis zur »Zeichen erschaffende(n) Tätigkeit«, mit denen sie »ihren selbständigen Vorstellungen ein bestimmtes Dasein aus sich gibt« (HW 10.270) und erzeugt die Sprache und die Buchstabenschrift einschließlich aller mathematischen Symbole.

Das sieht nach einem zirkulären Schluss aus: Wie kann ohne bereits über Sprache und Zeichen zu verfügen an etwas dessen Sprache und Bedeutung erkannt werden? Wir finden in der Natur weder Zahlen noch Worte oder Namen vor, aber wir vermögen es mit unserer Einbildungskraft, aus und in der Anschauung der Natur nicht nur deren Zahlen, Worte und Namen zu finden, sondern mit ihnen die Sprache, mithilfe derer das möglich ist. Der Zirkel kann durchbrochen werden, wenn er in einem größeren Horizont gesehen wird. Dafür wählt Hegel bewusst eigenartige und umstrittene Ausdrücke. Die Vorstellungen entstehen für ihn aus einem »nächtlichen Schacht, in welchem eine Welt unendlich vieler Bilder und Vorstellungen aufbewahrt ist, ohne daß sie im Bewußtsein wären« (HW 10.259). Sie sind anfangs in einem Zustand wie ein »Keim«, bevor sie »zur Existenz kommen, in virtueller Möglichkeit« (HW 10.259).

Hegel vertraut auf die Kraft der von ihm gewählten Bilder wie Schacht und Pyramide (HW 10.270). Sie erinnern an die romantische Todes- und Nachtsymbolik von Novalis, Hölderlin und bei einiger Phantasie an die Gemälde von Caspar David Friedrich. Warum kann sich Hegel sicher sein, dass er dem Schicksal der Romantik entgeht, wenn sich deren Einbildungskraft in leere Phantastereien verliert und später zum Spottbild eines überfliegenden, rein subjektiven spekulativen Denkens wurde? Er verlässt sich auf die Sicherheit der philosophischen Begriffsbildung. Und diese stützt sich trotz aller anderslautenden Bekenntnisse an wichtigen Punkten auf die mathematische Einbildungskraft.

Wenn es gelingt, an den mathematischen Zahlen zu zeigen, dass sie nicht nur formal, diskret und letztlich tot, sondern lebendig und dynamisch sind, ist am Beispiel der Mathematik der Weg der Einbildungskraft nachvollzogen. Dafür gibt es im Werk von Hegel positive wie negative Hinweise. Er sieht an den verschwindenden Größen der Differentialrechnung eine innere Bewegung, die sich an den Differentialen als den kleinsten Einheiten dieser Rechnung selbst zeigt und sieht mit dem mathematischen Begriff des Differentials die »Vexierfrage« der Philosophie nach der Unendlichkeit beantwortet (HW 5.169). Auf der anderen Seite war Hegel überaus skeptisch gegenüber allen überlieferten Ansichten, die die Mathematik in den Bereich der Einbildungskraft führen. Obwohl er die imaginären Zahlen und sogar weitergehende Erkenntnisse des eine Generation jüngeren Augustin-Louis Cauchy (1789-1857) über die komplexe Analysis kannte, hat er sie nirgends erwähnt, geschweige denn sich die Frage gestellt, was aus den imaginären Zahlen über die mathematische Einbildungskraft gelernt werden kann. Das Verhältnis von Mathematik und Philosophie geht für Hegel nur in eine Richtung. Für einen Mathematiker ist es ernüchternd, wenn nicht frustrierend, wenn Hegel schreibt: »Die Philosophie bedarf solche Hilfe nicht, weder aus der sinnlichen Welt, noch aus der vorstellenden Einbildungskraft«, und wer sie annimmt, für den ist es »nichts als ein bequemes Mittel, es zu ersparen, die Begriffsbestimmungen zu fassen, anzugeben und zu rechtfertigen« (HW 5.386). Immerhin sieht er es als Aufgabe der Philosophie gegenüber den mathematischen Vorstellungen, »so müßte vor allem ihre philosophische Bedeutung, d. i. ihre Begriffsbestimmtheit aufgezeigt werden« (HW 5.386).

Ein näherer Blick auf Hegels Werk zeigt für mich, wie eng sich für ihn trotz aller anderslautenden Bekenntnisse die philosophische und mathematische Einbildungskraft verflechten. Das soll am Beispiel des Quadrats und der mit dessen Diagonale gegebenen Frage nach den Irrationalzahlen gezeigt werden. Was auf den ersten Blick wie ein spezielles Thema der Mathematikgeschichte aussehen mag, soll zeigen, wie Hegel – auch wenn er das nicht wahrhaben möchte – in einer Tradition steht, die von der babylonischen Mathematik über Pythagoras, Platon und Aristoteles bis zu deren Interpreten im 20. Jahrhundert reicht, von denen insbesondere Stenzel, Heidegger und Szabo zu nennen sind. Am Begriff der dynamischen Zahlen soll inhaltlich ausgeführt werden, was mit Hegel unter Einbildungskraft zu verstehen ist und diese von Phantasterei unterscheidet.

Dynamische Zahlen

In der Wissenschaft der Logik und der Naturphilosophie will Hegel bestimmte empirische Erkenntnisse wie zum Beispiel die Bewegungsgleichung des freien Falls s = ½ · g · t² begrifflich herleiten. Wenn in dieser Gleichung die Zeit t im Quadrat auftritt, ist das für ihn nicht einfach eine empirisch beobachtete Gesetzmäßigkeit, sondern der Hinweis, diese Gleichung umgekehrt mit dem »Quadrat« aus dem »Begriffe der Sache« zu verstehen (HW 5.347, HW 9.78f). Das Quadrat tritt nicht nur in der Bewegungsgleichung auf. Am Steigungsverhalten der Parabel der Quadratfunktion f(x) = x² können die Regeln des Differentialkalkül abgelesen und anschließend verallgemeinert werden. Der Satz des Pythagoras lässt sich verstehen als eine Erhaltungsgröße, bei der im Übergang vom Quadrat über der Hypotenuse zu den Quadraten über den Katheten der Flächeninhalt erhalten bleibt. Das mag wie eine willkürliche Sammlung von Beispielen aussehen, und doch stellt sich die Frage: Deutet das auf einen übergreifenden Begriff des Quadrats, der zwar eindeutig aus der Mathematik stammt, aber nur mit philosophischer Begriffsbildung zu klären ist und den die Mathematik als gegeben hinnehmen muss, um mit ihm operieren zu können?

Mit dem Begriff des Quadrats ist sicher weder das umgangssprachliche, griechische Wort für Quadrat gemeint, platys, platt, breit, eben, so wie auch im Deutschen vom ‘Plattdeutsch’ gesprochen wird, oder auf englisch flat, level, plane, plaine, platform, tier, noch ist damit der tetragonos gemeint, das Viereck, bisweilen auch »vierschrötig; zunächst von dickem, gedrungenem Wuchse, so breit wie lang, homo quadratus; auch übertr., von fester, kräftiger, unerschütterlicher Gemüthsart« (Wilhelm Pape Handwörterbuch der griechischen Sprache, Braunschweig 1914, S. 1097). Sondern es ist an den Begriff dynamis zu denken, den Platon im Dialog Theaitetos gebraucht, und der für Aristoteles zu einem Schlüsselbegriff wurde.

Für den Altphilologen Árpád Szabó (1913-2001) besteht kein Zweifel: »Das Quadrat hieß in der Alltagssprache griechisch nie dynamis!« (Szabó, 47) Warum wird es dennoch von Platon wie selbstverständlich so genannt? Auch wenn sich dafür außer einem späteren Text von Eudemos über die Möndchen des Hippokrates keine weiteren historischen Belege finden ließen, scheint es unter Mathematikern gängig gewesen zu sein. Was ist das Besondere, wodurch sich dynamis von den üblichen Worten für das Quadrat unterscheidet?

Was ist am Quadrat dynamisch? Szabó erläutert es mit einer Analogie zu den Wechselkursen unterschiedlicher Währungen.

»Man vergleiche bei Xenophon (Anab I 5, 6): 'der siglos (eine asiatische Münze, das hebräische Seckel) macht aus, gilt oder hat den Wert (dynatai) von siebenundeinhalb attischen Obolen; oder Demosthenes (34, 23): 'der Stater von Kyzikos hatte dort den Wert (idynato) von 28 Drachmen'.« (Szabó, 46 Fn. 20)

So wie in der Finanzwirtschaft gefragt wird, welchen Obolos-Wert ein Siglos hat (heute könnte als Beispiel genannt werden: welchen Dollar-Wert ein Euro hat, und jeder kennt von Marx die Beispiele aus der Tauschwirtschaft, wie viel Ellen Leinwand ein Rock wert ist, usf.), so wird in der Geometrie gefragt, welchen Quadrat-Wert ein Rechteck hat. Um eine Währung in eine andere umrechnen zu können, muss es einen gemeinsamen, vermittelnden Maßstab geben. Das ist z.B. der Goldstandard, wenn beide Währungen am Gold gemessen werden, oder eine andere internationale Übereinkunft. Es muss eine  Transformation  geben, mit der eine Währung in eine andere gewechselt werden kann. Analog muss es eine Transformation geben, mit der ein Rechteck in ein Quadrat umgewandelt werden kann, um – in einer sicher ungewohnten Ausdrucksweise – zu erkennen, wie viel Quadrat ein Rechteck wert ist. Daher bedeutet dynamis für Szabó genau genommen nicht das Quadrat, sondern den Quadratwert, und es ist für ihn ein Fehler, dynamis als ‘Quadratwurzel’ oder ‘Quadratseite’ zu übersetzen (Szabó, 47).

Es muss eine Transformation geben, die ein Rechteck in ein Quadrat überführt. Das ist der tetragonismos bzw. als Verb tetragonizein. Theaitetos unterscheidet im gleichnamigen Dialog von Platon zwei Fälle: Bei manchen Rechtecken ist es geometrisch möglich, sie direkt in ein Quadrat mit ganzzahliger Seitenlänge umzuwandeln und dort an der Seitenlänge (mekos) abzulesen, um welches Quadrat es sich handelt. Zum Beispiel kann ein Rechteck mit den Seitenlängen 2 und 8 und dem Flächeninhalt 2 · 8 = 16 in das Quadrat mit der Seitenlänge 4 umgewandelt werden mit dem Ergebnis 2 · 8 = 16 = 4². Aufgaben dieser Art können bereits in der Vorschule unterrichtet werden, wenn Kinder die Aufgabe bekommen, ein aus 16 quadratischen Bausteinen bestehendes Rechteck so zu verschieben, dass ein Quadrat entsteht. Bei anderen Rechtecken wie zum Beispiel mit den Seitenlängen 3 und 5 und dem Flächeninhalt 15 ist das nicht möglich. Die Seitenlänge 3 ist zu klein, da das Quadrat von 3 nur die 9 ergibt, die Seitenlänge 4 ist dagegen bereits zu groß, da das Quadrat von 4 die 16 ergibt. Zwischen 3 und 4 gibt es aber keine weitere natürliche Zahl. Wurzel aus 15 beträgt 3,879… und liegt zwischen 3 und 4. In diesen Fällen gibt es kein Quadrat mit gleichem Flächeninhalt, dessen Seitenlänge (mekos) ganzzahlig ist, und an der der Quadratwert abgelesen werden kann. Nur für diesen Fall sprach Theaitetos von dynamis und nicht von mekos und hat damit wie von Sokrates aufgefordert eine klare Begriffsdefinition geliefert.

»Diejenigen Strecken nun, die eine gleichseitige Quadratzahl viereckig machen (tetragonizein), bezeichneten wir mit dem Wort mekos; diejenigen Strecken dagegen, die eine Rechteckzahl in ein Quadrat verwandeln, bezeichneten wir als dynameis.« (Platon Theaitetos, 148ab, in der Übersetzung von Szabó, 51).

Es führt daher nach Szabó in die Irre, wenn tetragonizein als ‘quadrieren’ übersetzt wird. Es geht nicht um die arithmetische Rechenoperation, eine Zahl mit sich selbst zu multiplizieren, sondern um eine Umwandlung eines Rechtecks in ein Quadrat, dessen Seitenlänge keine natürliche Zahl ist. (Szabó, 58) In diesen Fällen kann die Seitenlänge des Quadrats nicht durch geometrische Konstruktion gefunden werden, sondern es ist mathematische Einbildungskraft erforderlich, sich einen Wert vorzustellen, der diese Aufgabe löst.

Der dänische Mathematikhistoriker Jens Høyrup (* 1943) ist dem weiter nachgegangen und konnte nachweisen, dass es zwar für mekos einen Vorläufer in der babylonischen Mathematik und bei den Sumerern gibt, der bei den Babyloniern mithartum und bei den Sumerern ibsi heißt, während der entsprechende Ausdruck mahirum für dynamis bei den Babyloniern nur im ökonomischen Denken und nicht in der Mathematik gebraucht wurde. Beide gehen auf die gleiche Sprachwurzel maharum zurück (Høyrup, 208). Während also die griechischen Mathematiker von der babylonischen Mathematik den Begriff der Seitenlänge mithartum übernehmen und in das griechische Wort mekos übersetzen konnten, war es ihre eigene Leistung, den Begriff mahirum auf die Mathematik zu übertragen und dafür das Wort dynamis zu wählen. Platon konnte davon ausgehen.

»As already stated, the link between dynamis as commercial worth and as confrontation of force is a feature shared with the Babylonian mithartum. No Babylonian mathematical term equivalent to dynasthai exists, however. Nor does there appear to be any concept or procedure in Babylonian mathematics which necessitates such a word. So, even if the dynamis may be imported from or inspired by Babylonia, the term dynasthai appears to be a genuine Greek development due to the integration of the dynamis concept into the theoretical structure of Greek geometry. We see in Theaetetus 148b2 a possible explanation for such a development, when Plato speaks of 'the plane figures' which the lines dynantai, i.e., 'have in their power to form when seen dynamei' or 'are worth' under the same aspect.« (Høyrup, 211)

Daraus ergeben sich die ersten Hinweise, was unter dynamischen Zahlen zu verstehen ist:

(i) Es muss eine Umwandlung existieren, bei der aus etwas Gegebenem etwas Neues entsteht, in diesem Beispiel aus Rechtecken Quadrate, oder im Beispiel der Finanzen aus einer Währung eine andere Währung.

(ii) Es muss einen Wert geben, der bei der Umwandlung erhalten bleibt. Beim Geld ist das der Wert des Geldes (ohne an dieser Stelle der Frage weiter nachzugehen, wie der gemessen werden kann), bei der Umwandlung des Rechtecks in das Quadrat der Flächeninhalt.

(iii) Und es muss eine Transformation (eine Umrechnung bzw. eine geometrische Konstruktion) geben, mit der die Umwandlung algorithmisch durchgeführt werden kann. Das sind in der Finanzwirtschaft die Währungskurse, in der Mathematik die Algorithmen bzw. geometrischen Konstruktionen, mit denen Irrationalzahlen beliebig genau angenähert werden können.

Mit diesen Eigenschaften ist für mich jedoch noch nicht der Begriff der dynamischen Zahlen erschöpft. Das Bedeutungsspektrum von dynamis umfasst auch Macht und Möglichkeit.

(iv) Es muss eine Macht (dynamis) geben, mithilfe derer die Umwandlung vollzogen werden kann.

In der Finanzwirtschaft ist das die Macht einer von allen anerkannten internationalen Behörde oder die Macht des stärkeren Landes, das die Regeln festlegt, wie Währungskurse gebildet und durchgesetzt werden. In der Mathematik ist das die Macht, die sicherstellt, dass die Transformation gelingt. Hier ist zweierlei zu unterscheiden:

(iv-a) Mit der mathematischen Einbildungskraft (wobei mit ‘Kraft’ der Aspekt von Macht, Kraft, Vermögen, dynamis hinzukommt) ist gemeint, dass sich der Mathematiker auch dort eine Zahl  vorstellen  und ihren Begriff finden kann, wo es für die beliebig genaue Annäherung dieser Zahl nur ein Konstruktionsverfahren gibt, die Zahl selbst jedoch nie greifbar ist.

(iv-b) Über die Einbildungskraft hinaus muss es einen Kalkül geben, in dem sicher und fehlerfrei gerechnet werden kann. Ohne ihn bliebe die Einbildungskraft bloße Phantasie. An diesem Kalkül war die Philosophie allerdings mit Ausnahme von Leibniz nie sonderlich interessiert. Weder Sokrates noch Theaitetos wollten genau wissen, wie Theodoros (der Lehrer von Theaitetos) im Einzelnen die Umwandlung eines Rechtecks mit einem bestimmten Flächeninhalt in ein Quadrat gelungen oder nicht gelungen ist. Das haben erst spätere Interpreten gefragt, so 1941 J. H. Anderhub in Joco-Seria, aus den Papieren eines reisenden Kaufmanns, für den Theodorus bereits über die Methode der Wurzelschnecke verfügt, was sich jedoch nach Szabó aus dem Dialog nicht ausreichend begründen lässt (Szabó, 72).

Erst Leibniz ging in seiner Monadologie (1714) der Frage nach, welche Einheit es für einen Kalkül geben kann, mit dem Zahlen berechnet werden, die sich nur annähern lassen. Das ist für ihn die Monade, die an die Stelle der Eins tritt. Die Monade ist für ihn nicht nur eine philosophische Idee, sondern er hat diesen Gedanken mathematisch mit der Einführung der Differentiale dx, dy, … umgesetzt und mit dem Differentialkalkül eine neue Rechenmethode entwickelt, die diesem Anliegen gerecht wird. Während die natürlichen Zahlen 1, 2, 3, … an konkreten Gegenständen demonstriert werden können, indem z.B. 1, 2, 3, … Äpfel gezählt werden, bestehen die Differentiale ausschließlich in der mathematischen Einbildungskraft. Sie können nur durch Symbole wie dx, dy (nach Leibniz), ẋ, ẏ (Schreibweise der Fluxionen nach Newton) oder ε (für die Annäherung durch ε-Kugeln) dargestellt werden. Sachlich gehen sie auf die Annäherungen zurück, mit denen die Frage beantwortet werden sollte, welche Länge ein Quadrat hat, das einem Rechteck mit den Außenseiten 3 und 5 in der Fläche äquivalent ist.

Hegel teilte diese Sicht von Leibniz nicht. Er ging in der Phänomenologie des Geistes so weit zu sagen, dass die Philosophie die Mathematik »verschmähen« muss. Für ihn beschränken sich die Axiomatik und der Kalkül der Mathematik auf eine der Sache äußerlich bleibende Vorgehensweise: »Ein äußerer Zweck regiert diese Bewegung« der Konstruktion, der nur »blindlings zu gehorchen« ist. (HW 3.43f.) Nur aus dieser einseitigen Haltung heraus ist für mich zu erklären, warum Hegel in der Wissenschaft der Logik in der Anmerkung zum Kapitel über das Potenzenverhältnis schreibt: »Es ist bei diesen Potenzen nicht an die potentia, dynamis des Aristoteles gedacht« (HW 5.385). Sicher geht der aristotelische Begriff der dynamis weit über die quantitativen Potenzen hinaus, und doch ist in den quantitativen Potenzen bereits die von Aristoteles gemeinte Bedeutung angelegt. Hegels pauschale Abwehr ist für mich sachlich nicht zu halten und widerspricht im übrigen seiner eigenen wichtigen Herleitung des Differentialkalkül aus der qualitativen Potenzbestimmung (siehe hierzu den Kommentar). Ich kann es mir nur aus seiner – für mich im Prinzip berechtigten, aber weit über das Ziel hinausschießenden – Abgrenzung gegen all diejenigen verstehen, die für ihn unter Berufung auf Pythagoras ein esoterisches Denken verfolgen, womit er insbesondere Schelling und dessen Potenzenlehre meint. Schelling hat sich angesprochen gefühlt und in einer handschriftlichen Randnote im Manuskript zu seiner Philosophie der Mythologie darauf Bezug genommen, siehe die in GoogleBooks verfügbare Ausgabe, Stuttgart und Augsburg 1857, Anmerkung des Herausgebers K.F.A. Schelling zu S. 60.

Die mathematische Einbildungskraft ist so selbstverständlich geworden, dass sie für sich als eigenständige Leistung kaum mehr wahrgenommen wird. Jeder geht dank seiner Einbildungskraft davon aus, dass die Irrationalzahlen so wie die natürlichen und rationalen Zahlen eindeutige Punkte auf der Zahlengerade sind. Zwar ist an der Diagonale des Einheitsquadrats unmittelbar anschaulich zu sehen, dass es eine solche Zahl geben muss, aber es ist unmöglich, auf der Zahlengerade ihren genauen Ort zu ermitteln, sondern es kann lediglich ein Intervall angegeben werden, in dem die Zahl liegt. Dies Intervall kann zwar beliebig genau eingegrenzt werden, aber es wird nie auf einen eindeutigen Punkt reduziert werden können. Irrationalzahlen sind daher genau genommen keine Zahlen, sondern beliebig genau bestimmbare Zahlenmengen, von denen eine die gesuchte Irrationalzahl ist. Es muss eine spezifische Eigenschaft geben, die diese Mengen jeweils zusammenhält und ihnen eine innere Richtung gibt, die auf den Grenzfall der Irrationalzahl verweist, ihr tonos. Mit der mathematischen Einbildungskraft wird dieser Prozess im Ganzen erfasst. Der Mathematiker stellt sich die Irrationalzahl als Grenzfall vor, obwohl er ihn nie exakt greifen kann. Das birgt jedoch die Gefahr, dass das Bewusstsein der Besonderheit der Irrationalzahlen verloren geht und nicht einmal nach Eigenschaften wie dem tonos gefragt wird, dank derer sie möglich sind. Daher ist es heute so schwierig, gewissermaßen gegen die gewohnte mathematische Einbildungskraft wieder zur ursprünglichen Differenzierung in mekos und dynamis zurückzukehren und zu verstehen, was Platon damit gemeint hat. (Die Frage nach dem tonos und dessen Beziehung zu mathematischen Begriffen wie Dichte, Kompaktheit, Zusammenhang soll an dieser Stelle zurückgestellt werden. Sie ist jedoch entscheidend für ein qualitatives Verständnis der Zahlen.)

Es muss eine Macht geben, die sicherstellt, dass der Annäherungsprozess an die gesuchte Zahl erfolgreich ist. Diese Macht kann mathematisch nicht beschrieben werden, sondern die Mathematiker müssen sie voraussetzen. Als sie sich dessen bewusst wurden, führten sie ein eigenes Axiom ein, das das garantiert. Platon legt in meinem Verständnis nahe, dass es die Macht der Begrifflichkeit ist, dank derer eine Umwandlung von etwas in den mit dem Begriff verbundenen Begriffswert gelingt. Wenn der Begriff des Rechtecks und der Begriff des Quadrats gefunden sind, liegt es für ihn an der Macht des Begriffs, dass begrifflich gesehen jedes Rechteck einen Quadratwert hat, selbst wenn dieser sich nicht geometrisch mit Figuren aus ganzzahligen Seitenlängen konstruieren lässt. Ich vermute, dass für Platon mit ‘Idee’ dasjenige gemeint ist, das dem Begriff diese Macht verleiht. Diese Macht gehört nicht dem einzelnen Menschen an, der diesen Begriff denkt, sondern der Mensch hat in seinem Denken an dieser Macht teil. Bei Hegel ist es in meiner Deutung sein Verständnis der ‘Sache selbst’ und ihres Tun, worin sich diese Macht zeigt (HW 3.304, 5.25, 6.119). Das Tun der Sache selbst darf für Hegel nicht verwechselt werden mit dem Tun des Denkenden, der diese Sache denkt. Die Sache selbst gibt mit ihrem Tun etwas hinzu. Das ist die Macht, um die es in diesem Zusammenhang geht.

Was bei Platon und Hegel nur vermutet und hinein interpretiert werden kann, wird mit Aristoteles explizit. Er unterschied das »unvernünftige« und das »vernünftige« Können / Vermögen (dynameis alogoi, dynameis meta logon, Met. IX 2, 1046a36-b2). Das unvernünftige Können ist nicht gegen die Vernunft, sondern bereits ohne Vernunft gegeben. Beispiele sind schon genannt: Das sind die Rechtecke, die direkt in ein Quadrat mit einer ganzzahligen Seitenlänge umgewandelt werden können. Ihr Quadratwert lässt sich an der Seite (mekos) messen. Dafür ist keine besondere Vernunft erforderlich. Umgekehrt gibt es auf dieser Ebene der dynameis alogoi auch den negativen Fall, dass etwas als unvermögend, unkräftig, adynata erkannt wird. Aristoteles nennt das Standardbeispiel: »Z.B. ist die Diagonale im Quadrat unkräftig (adynata) dazu, mit der Quadratseite das gleiche Maß zu haben« (Met. V 12, 1019b, in der Übersetzung durch Heidegger, 62). Die Diagonale ist unkräftig oder unmöglich in dem Sinne, da sie ohne eine hinzutretende Vernunft nicht mit den üblichen geometrischen Verfahren aus sich selbst heraus erfassbar ist.

Was unterscheidet davon das vernünftige Vermögen (dynameis meta logon)? Für Heidegger kommt bei Aristoteles mit dem logos die Fähigkeit hinzu, etwas nicht nur so zu sehen, wie es gerade ist und über welche Kraft es bereits aktuell verfügt, sondern im Denken über es hinauszugehen, es von allen Seiten zu sehen, seinen inneren Mangel (steresis) wie auch sein größeres Umfeld und die in ihm enthaltenen Möglichkeiten zu erkunden, Wege einzuschlagen, die über etwas hinausgehen und wieder zurückkehren (Heidegger, 145f). dynameis meta logon geht über die geometrische Konstruktion hinaus und erkennt die Quadratwerte als einen reinen Begriff, für den es keine geometrische Transformation und keine natürliche Zahl gibt. Wenn heute die Wurzeln als Irrationalzahlen bezeichnet werden, würde Aristoteles widersprechen. Sie sind nicht irrational, sondern im Gegenteil handelt es sich um diejenigen Quadratwerte, die ausschließlich mittels der Vernunft als dynameis meta logon bestimmt werden können. Wird Theaitets Unterscheidung in mekos und dynamis festgehalten, handelt es sich erst bei ihnen um dynamische Zahlen. Sie können nicht bereits aus der jeweiligen Sache ohne Vernunft erzeugt werden, sondern nur dank der Einbildungskraft der Vernunft, die über die jeweiligen sachlichen Prozesse (wie z.B. die geometrische Transformationen) hinaus zu einer eigenen begrifflichen Transformation fähig ist, mit der sie ihre Werte findet.

Mit Aristoteles wird der fünfte Aspekt der dynamischen Zahlen sichtbar. Sie haben nicht einfach eine unbestimmbare Macht, die sich in der Fähigkeit zeigt, sich auch dort Zahlen vorstellen zu können, wo diese sich nicht geometrisch konstruieren lassen, sondern sie liegt in der Fähigkeit der Vernunft, über das Gegebene hinaus etwas im Raum seiner Möglichkeiten sehen zu können. Das ergibt die 5. Bestimmung der dynamischen Zahlen:

(v) Es muss einen Möglichkeitsraum (Potential, dynamis) geben, aus dem heraus die dynamischen Zahlen entstehen und in dem sie mittels des logos in ihrer Lebendigkeit beschrieben werden können, wobei es einiger begrifflicher und mathematischer Einbildungskraft bedarf, sich unter lebendigen Zahlen etwas vorstellen zu können.

Hegel nähert sich diesem Gedanken an anderer Stelle, wenn er in der Phänomenologie des Geistes ausführt, wie das handelnde Bewusstsein erst dann zu sich selbst findet, wenn es in der Lage ist, ein Werk zu schaffen. »Es geht also über sich als Werk hinaus und ist selbst der bestimmtheitslose Raum, der sich von seinem Werke nicht erfüllt findet.« (HW 3.300). Dieser am Beispiel des Werks gegebene »bestimmtheitslose Raum« ist der größere Horizont, in dem sich das begriffliche Denken bewegen kann und vom einseitigen, bloß zweck-orientierten Handeln unterscheidet. Hegels eigene Vorstellungskraft ist an dieser Stelle subtil und komplex: Mit dem Werk schafft das Bewusstsein in einem bereits gegebenen, aber noch bestimmtslosen Raum etwas, das zugleich über sich selbst hinausgeht. Das ist für mich der Schlüssel, um die spätere Aussage über den Schacht zu verstehen: Die Vernunft verfügt über einen Möglichkeitsraum mit ihr anfangs unbewusst gegebenen Vorstellungen, und sie vermag in diesem Raum etwas zu schaffen, das über sie selbst hinausgeht. Das, was über die Vernunft hinausgeht, muss etwas sein, das mit den inneren Eigenschaften des Möglichkeitsraums gegeben ist, die zwar für die Vernunft als Handlungshorizont erschließbar sind, aber im Ganzen nie überschaut werden können. Mathematisch sehe ich das mit den imaginären Zahlen und den von Cantor untersuchten Mächtigkeiten höherer Stufe gegeben.

Die dynamischen Zahlen öffnen einen Raum, der über die gegebenen natürlichen, ganzen und rationalen Zahlen hinausgeht. Sie erschließen sich nach Aristoteles nur einer Vernunft (logos), die in Möglichkeiten zu denken vermag. Niemand überschaut, was an den Irrationalzahlen enthalten ist. Enthalten ihre unendlich langen, nicht-periodischen Dezimaldarstellungen Muster, die auf verborgene Eigenschaften deuten? Wie ist die besondere Bedeutung von bestimmten Irrationalzahlen wie Wurzel aus 2 oder dem auf der Wurzel aus 5 beruhenden Goldenen Schnitt zu deuten?

Eine rein quantitativ denkende Mathematik gibt sich damit zufrieden, dass es Irrationalzahlen gibt, und dass es möglich ist, ihren Ort auf der Zahlengerade beliebig genau zu bestimmen. Dennoch weiß sie, dass dies keine Zahlen wie die natürlichen und ganzen Zahlen sind. Daher nutzt sie für die Irrationalzahlen eigene Symbole: Das sind entweder die drei Punkte, mit denen jede Dezimaldarstellung abbricht, oder das neue Symbol für die Irrationalzahlen, das  Wurzelzeichen  .

Die mathematische Einbildungskraft verbindet mit diesem Symbol genaue Vorstellungen. Es muss ein Verfahren geben, die mit diesem Zeichen bestimmte Zahl beliebig genau anzunähern. Es muss auf der Zahlenebene einen Ort für sie geben, der mit keiner anderen Zahl kollidiert. Und es muss einen Kalkül geben, in dem mit Zahlen dieser Art genau so gerechnet werden kann wie mit den anderen Zahlen. Für diese Zahlen sollen die gleichen Rechenregeln gelten wie für alle üblichen Zahlen, obwohl sie genau genommen nie exakt bestimmt werden können. Das ist eine Eigenschaft des neu definierten Körpers aller Irrationalzahlen, der sowohl die rationalen wie die irrationalen Zahlen umfasst. Diese Eigenschaft kann nicht hergeleitet, sondern muss axiomatisch  gesetzt  werden. Diese Setzung erfolgt in einem Möglichkeitsraum, über dessen Eigenschaften sich die Mathematik keinerlei Gedanken macht. Sie nimmt einfach hin, dass ihr dank ihrer Einbildungskraft diese Setzung möglich ist.

Wenn all diese Aspekte der dynamischen Zahlen erkannt sind, bleibt dennoch ein gewisses Unbehagen zurück: Ist damit wirklich der Begriff des Quadrats bestimmt, oder nur der allgemeinere, von Platon verwendete Begriff der dynamis? Alle diese Momente gehören zum Quadrat, aber dessen Inhalt ist die einfache Aussage, dass etwas  mit sich selbst ins Verhältnis gesetzt  wird. Hegel spricht vom Potenzverhältnis: »Das Quantum ist so in der Potenz als in sich selbst zurückgekehrt gesetzt; es ist unmittelbar es selbst und auch sein Anderssein.« (HW 5.382) An diesem kritischen Punkt geht für Hegel das Quantum im Potenzverhältnis über in »die Wahrheit des Quantums, Maß zu sein« (HW 5.384).

Mir ist es wichtig, den Gedanken des Selbstbezugs und des Übergangs zum Maß nicht nur auf die beiden Faktoren in einer arithmetischen Gleichung y = x · x oder auf die vier Seitenlängen eines quadratischen Rechtecks □ zu beziehen, sondern auf den voll entfalteten Begriff von dynamis. Während die Finanzwissenschaft Währungen an einem Maßstab wie dem Gold misst und bewertet, oder die Geometrie den Quadratwert von Rechtecken konstruiert, enthält der Begriff des Quadrats für sich betrachtet an sich selbst den Übergang zum Maß. Er wird paradoxerweise an sich selbst gemessen. Er erzeugt aus sich das ihm zu Grunde liegende Maß. Das ist seine Lebendigkeit. Erst mit ihr ist der volle Begriff der dynamischen Zahlen gefunden:

(vi) Es muss einen Selbstbezug geben, mit dem eine dynamis an sich selbst gemessen werden kann und ihr Maß findet. Dies Maß ist das Quadrat.

Ein solcher Selbstbezug erscheint dem gewöhnlichen Denken als Paradox, Zirkel oder Widerspruch. Für Hegel wird mit ihm die innere Lebendigkeit des Quantums gefunden und der Weg zu einer Mathematik als »Wissenschaft der Maße« geöffnet (HW 5.406). Das ist die Erklärung, warum der Quadratwert (die Irrationalzahlen) weder arithmetisch ausgerechnet noch geometrisch konstruiert, sondern nur begrifflich bestimmt werden kann. Die dynamischen Zahlen lassen sich ebenso wenig als Punkte auf der Zahlengerade fixieren, wie die einzelnen Zeitmomente auf der Zeitgeraden. Sie tragen an sich die gleiche Bewegung (Dynamik) wie die Zeit.

Wird zurückgekehrt zur Ausgangsfrage der Bewegungsgleichung des freien Falls, in der die Zeit im Quadrat auftritt, ist das für Hegel nicht einfach ein Zufall oder ein als gegeben hinzunehmendes empirisches factum brutum, sondern in diesem Quadrat zeigt sich der Begriff der Sache. Er hat allerdings bestenfalls angedeutet, wie das zu verstehen ist. Für mich zeigt sich im Quadrat der Zeit, wie die Zeit im Quadrat an sich selbst gemessen wird und darüber zu ihrem eigenen Maß findet. ›Die Zeit wird an sich selbst gemessen‹: Das fällt keinem Physiker auf, solange er die Bewegungsgleichung einfach als eine intuitiv geratene Formel ansieht, deren Wahrheit sich empirisch beliebig genau bestätigen lässt. Erst mit etwas Abstand kann deutlich werden, was hier geschieht. Dem Physiker genügt es zu sagen, dass und wie in dieser Gleichung der Ort s und die Zeit t in Relation gesetzt sind. Mit dieser Formel wird der jeweilige Ort s aus der jeweils abgelaufenen Zeit t ausgerechnet, wobei in dieser Formel die Zeit im Quadrat auftritt. Doch was soll es heißen, die Zeit in einen Ort umzurechnen, und warum tritt hier die Zeit im Quadrat auf? Wenn qualitativ verschiedene Begriffe wie Zeit und Ort ineinander umgerechnet werden, muss es sich um eine  Transformation  handeln, so wie es im Dialog Theaitetos um die Umwandlung von Rechtecken in Quadraten ging. Genau genommen wird in einer sprachlich ungewohnten und schwerfälligen Ausdrucksweise nach dem Ort-Wert der Zeit im Verlaufe einer Bewegung (oder in mathematischer Umkehrung nach dem Zeit-Wert des Orts) gefragt. Da wir uns hier in der Physik befinden, handelt es sich um keinen arithmetischen Algorithmus oder eine geometrische Konstruktion, sondern um einen physikalischen Vorgang, dessen Verlaufsform mathematisch zu beschreiben ist. Den hat in voller Klarheit erst Galilei gefunden. Mit den von ihm erdachten und ausgeführten Experimenten und der an ihnen gemessenen Bewegungsgleichung ist in der Physik eine Transformation gefunden, an einer Bewegung deren quadratischen Zeit-Wert (und mit ihm das Maß der Zeit) zu finden. Der in dieser Gleichung auftretende Quadratwert erfüllt die volle Definition von dynamis. Das ist nach meiner Überzeugung die Lösung der von Hegel in seiner Naturphilosophie aufgeworfenen Frage nach dem Begriff der Bewegung. Er ist ihr zwar nahe gekommen, hat sich jedoch zugleich aufgrund seiner skeptischen Haltung gegenüber der Mathematik und insbesondere der auf Pythagoras zurückgehenden Tradition das volle Verständnis verbaut. Die entsprechenden Passagen in seiner Naturphilosophie bleiben bloße Andeutungen.

Diese Art zu fragen bewegt sich zweifellos weitab von der uns heute vertrauten Physik. Wird in dieser Weise konsequent weiter gedacht, ist nach der Macht zu fragen, mit der diese Transformation gelingt. Das ist für mich die Energie, die sich in der Bewegung zeigt. Es ist in einem elementaren Sinn die Wirkung selbst, deren Wirk-lichkeit (energeia) die Bewegung aufrecht erhält und zum Ziel kommen lässt. Physikalisch gesprochen wird mit ihr das Maß der kinetischen Energie E = ½ · m · v² gefunden. Für mich ergibt sich das Quadrat der Geschwindigkeit (v²) inhaltlich aus dem Zusammentreffen der Systembewegtheit im Ganzen und der lokalen Bewegung, die jeweils in einer übereinstimmenden Variable v gemessen werden können. (Das ist an anderer Stelle ausführlich entwickelt.) Warum ist das möglich? Wieder kann gefragt werden, welche Macht es möglich macht, die lokale Bewegung einzelner Elemente und die Systembewegtheit des Systems im Ganzen auf identische Einheiten zu bringen und an ihnen das Maß der Bewegung zu finden. Das ist mathematisch gesprochen der gleiche tonos, durch den in der Physik die bewegten Elemente miteinander und zugleich mit der übergreifenden Systembewegtheit verbunden sind, wie es in den Zahlen einen tonos geben muss, durch den die verschiedenen Zahlen, die im Laufe einer Annäherung an den Grenzwert durchlaufen werden, untereinander und mit der Gesamtheit der Zahlen verbunden sind und darüber sicherstellen, dass der Grenzwert erreicht wird. Aristoteles wählte für diesen Zusammenhang der Zahlen den Begriff synecheia (Kontinuität, wörtlich das Verwachsene oder Zusammengewachsene, siehe verschiedene Stellen der Physik von Aristoteles, Buch III, V, VI und VIII, sowie in Zusammenhang mit der Mathematik Metaphysik VII.11 1036b). Das Maß der kinetischen Energie E = ½ · m · v² ist zugleich das Maß der Energieumwandlung, wenn die kinetische Energie in eine andere Art von Energie übergeht, sei es potentielle Energie, Wärme oder eine andere. Der zugrunde liegende Begriff ist gefunden, wenn die Macht verstanden ist, dank derer das möglich ist.

Kann mit der Differentialrechnung der Übergang von einer Funktion f zur abgeleiteten Funktion f ' (die Ableitungsregel) wiederum als eine Transformation verstanden werden, die eine Funktion in eine andere Funktion umwandelt, so wie Rechtecke in Quadrate transformiert werden, und kann die Fragestellung der Differentialrechnung so formuliert werden, welche Steigung von Tangenten ein Funktionsverlauf wert ist? So verstehe ich Hegels Ausführungen zum Differentialkalkül, den er aus der qualitativen Potenzbestimmung herleiten will (siehe den Beitrag). Mathematisch wird mit der Differentialrechnung an jedem Punkt der Kurve der Raum aller Möglichkeiten betreten, wie sich die Kurve an dieser Stelle verändern kann. Das ist mathematisch der Tangentialraum. Die innere Freiheit dieses Raum entspricht den freien Wahlfolgen von Brouwer.

Diese Ideen erfordern ein völliges Umdenken. Sie werden sicher nicht dazu führen, bereits bekannte Ergebnisse der Mathematik oder Physik inhaltlich zu revidieren. Aber sie lassen sie möglicherweise unter neuem Licht sehen und könnten Anregung geben für bisher unbekannte neue Entwicklungen. Das Ergebnis ist eine qualitative Mathematik, die die heute bekannte und praktizierte quantitative Mathematik als Grenzfall enthält und sich mit Hegel als Wissenschaft der Maße verstehen lässt. Mit ihr ist für mich zugleich die einleitend gestellte Frage nach der Einbildungskraft beantwortet. Vermögen die Mathematik und die Physik diesen Weg zu gehen, dann demonstrieren sie, wie für und mit der Einbildungskraft der Bogen geschlagen werden kann aus einem Entwurf von Möglichkeiten und den in ihm angelegten, noch nicht oder erst teilweise bewussten Vorstellungen, über empirisch überprüfbare Transformationen bis hin zu den mit ihnen als inneren Voraussetzungen gegebenen Maßen.

Geträumte Zahlen

Geraten Mathematiker ins Träumen, wenn sie so denken, und können sie nur so denken, wenn sie ins Träumen geraten? Müssen sogar Philosophen bisweilen ins Träumen geraten, wie es Sokrates im bereits genannten Dialog Theaitetos geschieht, wenn er seine heute als »Traumtheorie« bezeichnete Aufforderung ausspricht: »Höre also einen Traum (oneiratos) für einen Traum« (Platon, Theaitetos, 201d)? Hegel war da skeptisch. Er glaubt nicht an Träume, und Träume gibt es für ihn nur als Phänomen des Schlafes, aus denen aber keine Erkenntnis gewonnen werden kann.

Hegel schreibt in der Phänomenologie des Geistes recht ironisch: »Indem sie sich dem ungebändigten Gären der Substanz überlassen, meinen sie, durch die Einhüllung des Selbstbewußtseins und Aufgeben des Verstandes die Seinen zu sein, denen Gott die Weisheit im Schlafe gibt; was sie so in der Tat im Schlafe empfangen und gebären, sind darum auch Träume.« (HW 3.18) Auch in der Enzyklopädie beschränkt er sich in seiner Anthropologie auf das natürliche Träumen, wie wir es vom Schlafen kennen. »Im Traume ist es nur unser vorstellendes, nicht unser verständiges Denken, dessen Interesse erregt wird.« (HW 10.92) »Das bloße Vorstellen reißt aber die Dinge aus ihrem konkreten Zusammenhange völlig heraus, vereinzelt dieselben. Daher fließt im Traume alles auseinander, durchkreuzt sich in wilder Unordnung, verlieren die Gegenstände allen notwendigen, objektiven, verständigen, vernünftigen Zusammenhang und kommen nur in eine ganz oberflächliche, zufällige, subjektive Verbindung.« (HW 10.93f und zum natürlichen Träumen HW 10.130). Was er im Weiteren über die assoziative Einbildungskraft schreibt, kommt zwar den Träumereien nahe, wird aber von ihm nicht so genannt oder damit verglichen.

Dagegen ist für mich das von Platon genannte Träumen (oneirôxeôs) eine Umschreibung der spezifisch mathematischen Einbildungskraft und erhielt erst aus späterer Sicht einen abwertenden Klang. Zweierlei ist möglich: Wenn Mathematiker ihre Theorien entwickeln, können sie glauben, dass das, was sie da denken, zugleich unmittelbar wirklich sei. Wetzel spricht vom »de facto um Realität unbekümmerten, aber gleichwohl und pauschal auf sie Ansprüche erhebenden Mathematiker« (E-Mail vom 9.4.2016). Er führt später genauer aus:

»Ad Platons Timaios erachte ich den eikòs lógos für zentral, der besagt, das Ideale ist in's Reale immer nur unvollständig, unvollkommen, nur näherungsweise und mit Wahrscheinlichkeit eingelassen, weshalb aus reiner – idealer Mathematik für die Realität noch schlechthin gar nichts folgt – das gilt nicht nur für die Physik, sondern auch für die Ökonomik. Insbesondere Einstein hat hier ganz klar gesehen: 'Insofern sich die Sätze der Mathematik auf die Wirklichkeit beziehen, sind sie nicht sicher, und insofern sie sicher sind, beziehen sie sich nicht auf die Wirklichkeit.' Genau dies wollte Platon nach meinem Verständnis mit seinem Gleichnis von den 'träumenden Mathematikern' sagen, indem er ihnen vorhält, nicht zu sehen, was Einstein gut 2300 Jahre später sagte.« (E-Mail vom 1.11.2016)

Der Vorhalt ist berechtigt, und doch kann der Gedanke genau umgekehrt werden: Wenn Mathematiker träumen, sehen sie an der Realität etwas, was dort empirisch nicht zu sehen, aber als zugrunde liegende Struktur enthalten ist. Wer fallende Körper untersucht, wird dort nie wie ein Menetekel die Formel s = ½ · g · t² aufgeschrieben sehen, und diese Formel wird nie ohne Störeinflüsse perfekt nachweisbar sein, aber der Mathematiker kann sie aus dem empirischen Material gewinnen. Er wandelt in seinem Denken (seinen Träumereien) die harten empirischen Fakten um in geträumte Zahlen, mit denen er rechnen kann. Geträumte Zahlen sind bei Platon die demiurgischen Zahlen oder Proto-Zahlen. Sie gehen über das hinaus, was sinnlich erfahren und empirisch gezählt werden kann. Sie bezeichnen einen vorhergehenden Zustand, aus dem nach Platon der Schöpfer erst die zählbaren Objekte und die Zahlen geschaffen hat.

»Eine dritte Gattung sei ferner immer die des Raumes, Vergehen nicht annehmend, allem, dem ein Entstehen zukommt, eine Stelle gewährend, selbst aber ohne Sinneswahrnehmung durch ein gewisses Afterdenken (logismôi tini nothô mit der Wurzel nothos logismos, wörtlich ein Fehl- oder Trugschluss) erfaßbar, kaum glaubhaft erscheinend. Darauf hinblickend, überlassen wir uns dann Träumereien (oneiropoloumen) und behaupten, alles Seiende müsse notwendig an einer Stelle sich befinden und einen Raum einnehmen, dasjenige aber, bei dem das weder auf Erden noch irgendwo am Himmel der Fall sei, das sei nichts. Dieses alles also und anderes diesem Verwandtes auch in bezug auf die schlaflose und wahrhaft bestehende Natur festsetzend, werden wir auf Grund dieses Träumens (oneirôxeôs, von oneiroi, Träume) unvermögend, wachend das Wahre zu sagen.« (Platin Timaios, 52a-b)

»Da sie aber weder mit ähnlichen noch mit im Gleichgewicht stehenden Kräften angefüllt wurde, befindet sich nichts in ihr im Gleichgewicht, sondern als überall ungleichmäßig schwebend (anômalôs pantê talantoumenên) wird sie selbst durch jene erschüttert und erschüttert, in Bewegung gesetzt, umgekehrt jene.« (52e)

»Ehe das aber geschah, sei alles dies ohne Maß und Verhältnis (alogôs kai ametrôs) gewesen. Als jedoch Gott das Ganze zu ordnen unternahm, haben sich anfangs Feuer, Wasser, Luft und Erde, die aber bereits gewisse Spuren von sich selbst besaßen (ichnê men echonta hautô atta), durchaus in einem Zustande befunden, wie er bei allem, über welches kein Gott waltet, sich erwarten läßt. Diese von Natur also Beschaffenen formte zunächst Gott durch Gestaltungen und Zahlen (eidesi te kai arithmois).« (53a-b)

Mit geträumten Zahlen sind die Proto-Zahlen gemeint, wenn die anfangs chaotische Bewegung bereits die Spuren enthält, aus denen Gott die Gestalten und Zahlen schaffen konnte. Diese Zahlen entziehen sich prinzipiell der sinnlichen Erfahrung und sind nur der Seele zugänglich. Es ist ihre Einbildungskraft, oder ihre Fähigkeit, träumen zu können, an den Zahlen die Spuren zu erkennen, aus denen sie hervorgegangen sind.

Für Platon ist das ein notwendiger Zwischenschritt, um von den Zahlen, wie wir sie vom Zählen kennen – den natürlichen Zahlen –, zu den Ideen der Zahlen zu kommen. Aristoteles machte es sich einfacher und durchschlug gewissermaßen den gordischen Knoten: Er spricht nicht mehr von Träumereien, sondern für ihn bestehen die Objekte der Mathematik  im Denken. Es sind weder jenseitige Ideen noch liegen sie unmittelbar in der Realität vor, sondern sie können vom Menschen dank seiner Einbildungskraft im Denken gebildet werden. Hier verschiebt sich unmerklich die Bedeutung des Begriffs dynamis von Macht zu Möglichkeit: Aristoteles geht es zwar darum, an den Erscheinungen und Regeln die Macht (Kraft) nachzuweisen, die sich an ihnen zeigt (dynameis alogoi), aber mit der Macht der Begriffe (dynameis meta logon) ist nicht gemeint, dass die Begriffe wie die platonischen Ideen an sich eine eigene Macht haben, sondern an ihnen zeigt sich die Fähigkeit des menschlichen Denkens, in Möglichkeiten zu denken. Mit den Möglichkeiten erhebt es sich über die jeweils gegebene Realität und kann an den Möglichkeiten studieren, welche inneren Bewegungsgesetze, Trends und Erwartungswerte gegeben sind.

Ogkische (gewichtige) Zahlen

Wie kann es nach dynamis weitergehen? Diophantos von Alexandria sprach in seinen im dritten Jahrhundert n. Chr. erschienenen Arithmetica von »square and cube numbers as 'tetragons' (tetragonoi) and 'cubes' (kuboi)« (Høyrup, 207). Doch das ist hier nicht gemeint. Szabó betont, dass die Griechen keinen allgemeinen Begriff der Potenz kannten. Im Grunde ist am Beispiel der Quadratzahlen alles gesagt, was sich bei den höheren Potenzen nur noch wiederholt. Der allgemeine Begriff einer Potenz wäre in Rückübersetzung aus dem Lateinischen potentia wiederum dynamis. Nach den dynamischen Zahlen geht es daher nicht mit Kubikzahlen und möglicherweise Zahlen in höheren Dimensionen weiter, sondern es sind völlig neue Zahlenwerte zu erwarten. Das sind nach meiner Vermutung ogkos (Umfang, Masse, Gewicht, auch Bug, Krümmung, Winkel, Widerhaken, auf englisch bulk, size, mass, body, weight, digity, particle) und tetraktys (die Zahl 4 in der pythagoreischen Bedeutung als Wurzel, rhizoma und Quelle aller Dinge). Der Grundgedanke der dynamischen Zahlen als Quadrat-Wert wird jedoch festgehalten und auf Schwere- und Harmonie-Werte übertragen.

Während der Kubus der Würfel und damit einer der platonischen Körper ist, bedeutet ogkos Masse, Umfang, Volumen, Gewicht. Dieser Ausdruck wird von Platon im Timaios und Aristoteles in den Meteorologica gebraucht.

»The use of the term ogkos, I think, may be in fact less puzzling than it appears to be. The occasional mentions of (seemingly minimal) ogkoi (of water etc.) do not necessarily point to the spurious nature of parts of Meteor. IV. The notion of ogkos may simply have an empirical foundation, i.e. it may rely on the observation that the more fluid and elusive a stuff is (in increasing order: viscous liquids, watery liquids, mist, air, fire), the easier it is for it to penetrate another body. Thus it is not the case that, for instance, some solid, earthy stuff is not (theoretically) divisible ad infinitum, just like a quantity of water or pneuma etc.; it is simply that, empirically and practically speaking, some utterly fluid stuffs are very easily divided into minuscule (but not atomic) particles or portions, whereas other, more viscous or solid stuffs are not.« (Popa, 28 Fn. 36)
    »Timaeus: 59a3 (ton hugron ogkon); 59b7 morion oligon); 60c3 (toi tes ges ogkoi); 60e4 (ges ogkous - diexodon - particles of air and fire are smaller than the interstices in a mass of earth and do not dissolve it, like the particles of water). Also: 385b20-21 porous meizous ton tou hudatos ogkon.« (Popa, 132 Fn. 182)

ogkos ist die Schwere, Gewichtigkeit, in gewisser Weise Dichte von etwas. So wie nach dem Quadratwert des Rechtecks gefragt wurde, kann nach dem Massewert von etwas gefragt werden. Ist es ein Prinzip der Mathematik, dass ihre Objekte grundsätzlich den Massewert 0 haben? Niemand wird einer Zahl oder einem Quadrat und auch nicht einem platonischen Körper ein Gewicht oder eine Masse zuschreiben. Wie erfolgt aber der Übergang von den mathematischen Gebilden zu den tatsächlichen Körpern, die ein Gewicht haben? Beispiele sind der Übergang von der Oberfläche zum Inhalt, vom Durchfluss an den Rändern zu den Quellen und Strömen im Innern und vor allem der Übergang von Geometrie zu Mechanik wie beim Fallgesetz und den Keplerschen Gesetzen. Hegel trifft es auf den Punkt, wenn er zum Fallgesetz schreibt:

»Der Beweis aber besteht in der Verwandlung der Momente der mathematischen Formel in physikalische Kräfte, in eine beschleunigende Kraft, welche in jedem Zeitmoment einen (denselben) Impuls mache*, und in eine Kraft der Trägheit.« (HW 9.75)

In diesen Beispielen geht es um den Massewert einer geometrischen Figur. Die von Platon und Aristoteles genannten Beispiele legen nahe, für den Massewert eine Eigenschaft zu suchen, die den unterschiedlichen Aggregatzuständen wie fest, flüssig oder flüchtig unterliegt. Es genügt nicht, das Substrat zu erkennen, das sich in verschiedenen Aggregatzuständen zeigt, sondern am Substrat ist eine kleinste Einheit zu bestimmen, mittels derer die verschiedenen Bewegungsformen der unterschiedlichen Aggregatzustände ineinander übergehen. Diese Einheit (ogkos) erlaubt nicht nur, den Übergang der verschiedenen Aggregatzustände ineinander chemisch und mathematisch zu beschreiben, sondern ist zugleich der gesuchte Begriff, um die Massigkeit von etwas zu bestimmen. Gesucht ist eine Transformation, die ein arithmetisches oder geometrisches Objekt in einen ogkos umwandelt. (Für mich stößt Hegel in der Wissenschaft der Logik auf diese Frage, wenn er vom Begriff des Substrats im Kapitel über das Maßlose zum Begriff der »Indifferenz als umgekehrtes Verhältnis ihrer Faktoren« übergeht. Doch ist dies bei Hegel bestenfalls angedeutet und bedarf einer weiteren Ausarbeitung.)

Auf diese Frage scheint mir auch die Allgemeine Relativitätstheorie von Einstein zu stoßen. Raumkrümmung und Verteilung der Masse werden auseinander erklärt. Das droht in einen Zirkel zu geraten, und ogkos könnte in seiner Mehrfachbedeutung, die von Masse bis Krümmung reicht, der gesuchte Begriff sein, um Umwandlungen dieser Art zu beschreiben und die Macht zu verstehen, dank derer sie erfolgen.

Ist ogkos die Trägheit? Mir scheint ogkos eine Ebene tiefer das Prinzip zu sein, dank dessen Trägheit und Lebendigkeit ineinander umschlagen. Ogkische Zahlen sind so gesehen nicht die trägen Zahlen, sondern solche Zahlen, an denen es zum Umschlag von Trägheit und Lebendigkeit kommen kann.

Was unterscheidet ogkische Zahlen von naturwissenschaftlichen Maßeinheiten, mit denen jeweils eine bestimmte Dimension definiert wird, wie z.B. Kilogramm (kg) für mechanische Gewichte oder im Bereich der Elektrizitätslehre Volt (V), Ampere (A) und Ohm (Ω) als Einheiten für Spannung, Stromstärke und Widerstand? Was unterscheidet sie insbesondere am Beispiel der Quantenmechanik von den Quantenzahlen? Die Quantenzahlen haben ähnlich wie die Grundbegriffe der Relativitätstheorie eine mehrfache Bedeutung. Ein Beispiel ist der Spin.

»Der Spin ist eine Dimension, innerhalb der Dimension ist das reduzierte Plancksche 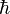eine Maßeinheit, und nur die Größe der Maßeinheit und ihre Vielfachen sind Zahlen. In Texten über die Quantenmechanik ist bisweilen generell unklar, ob mit der Quantenzahl ein Merkmal eines Objekts gemeint ist, oder eine Maßeinheit, oder eine Dimension wie z.B. der Spin, oder der jeweilige Messwert, z.B. der Spin eines bestimmten Teilchens.« (Tydecks Dialektische Theorie des Satzes; Link).

Naturwissenschaftliche Maßeinheiten wie die Messgrößen oder Quantenzahlen sind sowohl ein Hinweis auf die jeweilige Dimension, in dessen Horizont etwas gesehen wird, wie die Maßeinheit dieser Dimension und zugleich der konkrete Zahlenwert (Größe), die etwas in dieser Dimension angenommen hat, und die gemessen werden kann. Wird diese Mehrfachbedeutung philosophisch (sprachkritisch) untersucht, dann ist für mich deutlich, dass ein unterscheidender Begriff fehlt, mit dem die Mehrfachbedeutung auseinander gelegt werden kann. Das könnten die ogkischen Zahlen leisten.

Mit ogkischen Zahlen ist eine gemeinsame Eigenschaft gemeint, die an den üblichen Zahlen abzulesen ist und von sich aus hindeutet auf naturwissenschaftliche Zusammenhänge. Üblicherweise wird angenommen, dass alle Zahlen auf der Zahlengerade oder in höheren Zahlenräumen völlig symmetrisch, homogen und isotrop angeordnet sind. Es ist kein Unterschied, ob die Umgebung einer Zahl wie 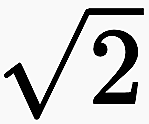, 100 oder eine Million betrachtet wird. Für jede Zahl wird angenommen, dass sie so wie alle anderen Zahlen in ihrer Umgebung eingebettet ist. Das ist der Grenzfall, wenn alle Zahlen den gleichen ogkischen Wert haben. Wenn sich dagegen herausstellt, dass es innerhalb der Zahlen bestimmte Verdichtungen und Verschiebungen gibt, die sich nicht in den üblichen Maßen wie Abstand, Kompaktheit oder Vollständigkeit messen lassen, dann ist das ein Hinweis auf ogkische Werte. Einstein stieß mit seiner Vorstellung des gekrümmten Raums auf diese Grenzsituation. In dem von ihm betrachteten Raum sind einerseits alle Punkte geometrisch gesehen in gleicher Weise verteilt, wie es aus der gewöhnlichen Geometrie bekannt ist. Und doch tragen sie an sich eine Krümmung, die auf eine Krümmung des Raums im Ganzen verweist.

Mit ogkischen Zahlen ist dieser Grenzübergang gemeint: Die üblichen Zahlen werden jeweils lokal betrachtet, und es wird angenommen, dass sich die Regeln für ihre Abstände zu ihren Vorgängern, Nachfolgern, Häufigkeiten etc. nirgends ändern. Wenn es Aristoteles gelungen ist, den Begriff der Zahlen klar zu trennen von den Begriffen ihrer Merkmale wie Anordnung auf einer Reihe und Kontinuität, hat er dabei mit guten Grund angeommen, dass diese Eigenschaften überall und für alle Zahlen gelten. Sie sind unabhängig von der jeweiligen einzelnen Zahl. Mit ogkischen Zahlen ist gemeint, dass es eine darüber hinaus gehende Umgebung gibt, die zusätzlich zur gleichmäßigen Ordnung und Kontinuität eine höhere Ordnung darstellt.

Wieder sind für mich die Keplerschen Gesetze das beste Beispiel. Wenn die Punkte auf einer elliptischen Bahn betrachtet werden, gelten für sie zunächst alle aus der Geometrie bekannten Gesetze: Die Punkte gehorchen bestimmten Ordnungs-Prinzipien, und sie liegen kontinuierlich nebeneinander. Und dennoch ist zugleich an der Bahn zu erkennen, dass es in der Nähe der beiden Brennpunkte zu auffälligen Verdichtungen kommt: An dem einen Brennpunkt wird alles intensiver, schneller, stärker bewegt, am anderen Brennpunkt wird es dagegen träger, ruhiger und gemächlicher. Wird für diese Unterscheidung ein Maß gesucht, kann es nicht mehr eins der üblichen geometrischen Maße sein, sondern ist für mich ein Beispiel für einen ogkischen Wert. Aus Sicht von Einstein ist der Raum an dem einen Brennpunkt, an dem sich die Sonne befindet, stärker gekrümmt, am anderen Brennpunkt dagegen weniger.

Das soll an anderer Stelle am Beispiel der Relativitätstheorie näher ausgeführt werden. Wenn dort die Photonen die Ruhemasse 0 haben, ist für mich der Begriff der Ruhemasse diejenige Vorstellung, die meinem Verständnis der ogkischen Zahlen am nächsten kommt. Wird die Bewegung eines Photons beschrieben, tritt grundsätzlich ein Konflikt, wenn nicht eine Antinomie auf: Diese Bewegung kann einerseits lokal wie für alle anderen Teilchen beschrieben werden, und zugleich zeigt sich am Photon die Systembewegtheit des Raums im Ganzen. Daher soll am Beispiel des Photons gezeigt werden, was es bedeutet, wenn in einem System Zahlen mit unterschiedlichem ogkischen Wert auftreten und zugleich mit ihnen gerechnet werden soll. So wie für die verschwindenden Größen dx und dy im Differentialkalkül eigene Regeln notwendig waren, gilt das auch für das Rechnen mit unterschiedlichen ogkischen Zahlen. Einstein hat mit seinen Transformationsformeln intuitiv eine Lösung gefunden. Diese Lösung muss jedoch für sich weiter ausgearbeitet werden und bedarf zusätzlicher, stabilisierender Annahmen. Andernfalls drohen Paradoxien wie das Lochargument oder die von Gödel betrachteten rotierenden Universen. Es ist kein Zufall, dass sich diese Fragen im Rahmen der üblichen Mathematik nicht einmal von Hilbert beantworten ließen. Zu ihrer Lösung bedarf es zusätzlicher Begriffe und Unterscheidungen.

Harmonische Zahlen

Und was folgt danach? Das könnte mit den Pythagoreern die tetraktys sein, die Weltharmonie. Die ogkischen Zahlen sind ihrerseits eingebettet in die harmonischen Zahlen. So wie nach dem Quadratwert und dem Massewert gefragt wird, wird nach dem Harmoniewert von etwas gefragt. Wie weit ist es von Harmonie entfernt, und gibt es eine Transformation, etwas in die in ihm verborgene Harmonie zu transformieren? Der von Leibniz geprägte Ausdruck der besten aller möglichen Welten erhielte damit eine klarere Bedeutung: Es ist nicht nur unter allen möglichen Welten die beste auszuzeichnen, sondern nach der Transformation zu fragen, mit der der Übergang von einer der vielen möglichen Welten in die beste erfolgt, und nach der Macht, die diese Transformation sicherstellt.

Tektraktys ist der Zahlenaspekt an der Harmonie. Wenn die Pythagoreer die Tetraktys verehrten, war es nicht einfach eine höhere Zahl oder das Pentagramm, sondern ein eigener Zahlenwert, der Harmoniewert. Sie waren überzeugt, dass sich diese Art von Zahlen sowohl den Sinnen wie dem Denken entziehen und nur indirekt zu erschließen sind. Sie zeigen sich in Phänomenen wie dem Goldenen Schnitt, der geometrisch mit dem Pentagramm verbunden ist.

Høyrup erläutert anschaulich, wie die Vorstellung der Tektraktys mit der Frage nach den Quadrat-Werten in Verbindung steht (Høyrup, 213f).

Abb. 1: mekos, dynamis, tetraktys

Das Bild links zeigt am Beispiel des Rechtecks mit den Längen 2 und 8, wie der Quadratwert an einer Länge (mekos) des Quadrats gemessen werden kann. Das Bild in der Mitte zeigt, wie dies für ein Rechteck mit den Längen 3 und 5 misslingt. Das Bild rechts zeigt die auf die Pythagoreer zurückgehende Veranschaulichung der Tetraktys. In diesem Bild besteht zwar die Grundlinie gleichfalls aus 4 Elementen, doch geht es nicht mehr darum, einen Quadratwert zu finden, sondern ein Bild von vollendeter Harmonie.

Führt so zu denken zu einem Rückfall von Aristoteles zu Pythagoras und Platon, vor dem Hegel implizit oft genug gewarnt hatte?

Ursprünglich waren Zahlen, Buchstaben und einzelne Symbole für bestimmte Zahlen wie die hier aufgezeichnete Tetraktys nicht klar getrennt. Es gab noch keinen eindeutigen Begriff der Zahl. Zahlen wurden so gebraucht, wie es im jeweiligen Zusammenhang gerade sinnvoll erschien, und es gab fließende Grenzen zwischen Zahlen und anderen Zeichen. Es war auch nicht eindeutig, ob mit bestimmten Zahlen zugleich spezifische qualitative Eigenschaften gemeint waren oder nur die gezählte Anzahl. Zahlen hatten eine Mehrfachbedeutung als mathematische Zahlen zum Zählen, zur Unterscheidung der aufeinander aufbauenden Dimensionen wie Punkt, Linie und Körper, und als Prinzipien wie die Eins und das Andere (die Zwei). Aristoteles vertrat demgegenüber als erster die bis heute vorherrschende Vorstellung von den Zahlen. So wie er den Begriff der Größe megethos allgemein bestimmte und nicht mehr an qualitative Bestimmungen der jeweils unterschiedlichen Größen und ihrer Maße für Längen, Höhen, Flächen, Töne etc. band, so fand er den allgemeinen mathematischen Begriff der Zahl und unterschied davon philosophische Begriffe, um mit ihnen Zahlen beschreiben zu können. Das sind für ihn Begriffe wie die Reihe, auf der alle Zahlen angeordnet sind, der Zusammenhang (syneches, continuum) der Zahlen und ihre Beweglichkeit. Erst Jahrhunderte später wurde von den Neuplatonikern wie Jamblichos, Syrian, Proklos und Simplikios zunehmend deutlicher zwischen natürlichen Zahlen, Proto-Zahlen (wie Monas, Dyas, Trias, Tetras, Pentas, Dekas) und ihren für den Menschen unsichtbaren Urbildern (paradeigmata) im nous unterschieden. Sie suchten nach einem Ausgleich zwischen der Philosophie von Aristoteles und Platon.

»Mit unermüdlicher Hartnäckigkeit verteidigt Aristoteles die uns natürliche Auffassung der Zahlen als gleicher, in den arithmetischen Operationen grundsätzlich gleichartiger und vereinbarter Einheiten gegen einen ganz anderen Zahlenbegriff, der gerade durch die Unvereinbarkeit der Zahlen im Sinne irgendwelcher rechnerischer Verwendung ausgezeichnet sein muß: wenn die Vierheit die Idee von etwas ist, z.B. des Pferdes oder des Weißen, so ist der Mensch 'ein Teil des Pferdes, wenn die Zweiheit der Mensch ist' (Met. M8 1084 a 23).« (Stenzel, 7)

Für mich kann mit den harmonischen Zahlen zugleich eine Harmonie zwischen den Ansätzen von Aristoteles und seiner Vorläufer gefunden werden:

– Niemand wird mehr den von Aristoteles erzielten Fortschritt aufgeben wollen. Er trennte klar zwischen den Zahlen und ihren Eigenschaften wie Abstand auf einer Reihe, Kontinuum usf. In Abwandlung von Hilbert kann gesagt werden: Aus diesem Paradies lassen wir uns nicht mehr vertreiben.

– Ebenso wird niemand den von den Neuplatonikern erzielten Fortschritt aufgeben wollen mit ihrer Unterscheidung in Zahlen, Proto-Zahlen und deren Urbilder.

– Wichtig ist mir, dass mit den harmonischen Zahlen Bewegung in diese Unterscheidung kommt. Zahlen und Proto-Zahlen liegen nicht mehr in verschiedenen Ebenen getrennt von- oder übereinander, sondern es wird gewissermaßen nach dem Monas-Wert, dem Dyas-Wert und allgemeiner dem Harmonie-Wert von Zahlen gefragt. Auf diese Weise scheint sich mir mit den harmonischen Zahlen das in den dynamischen Zahlen bereits angelegte Konzept einer Selbstbeziehung der Zahlen aufeinander und die Frage nach ihrem eigenen, inneren Maß zu erfüllen. Mit den Harmoniewerten werden an den Zahlen ihre eigenen Maße gefunden und sogar ein Weg eröffnet, der eine Transformation von den Zahlen zu ihren eigenen Maßen vollzieht. Darin kann eine Renaissance des Pythagoreismus gesehen werden, ohne auf die Einsichten von Aristoteles verzichten zu müssen.

Imaginäre Zahlen und Schaltkreise

Niemand kann in der Natur Zahlen sehen, aber wenn etwas gezählt oder gemessen wird, ergeben sich Zahlen. Das gilt für die Irrationalzahlen nicht mehr. Sie lassen sich weder durch Zählen noch durch Messen bestimmen, sondern nur von der Vernunft als Vorstellungen denken. Zwar ist beispielsweise die Diagonale im Einheitsquadrat mit der Länge 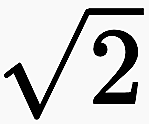zu "sehen" und daher auf elementare Weise klar, dass sie eine messbare Größe hat, doch gibt es im uns vertrauten metrischen System keinen Maßstab, um sie genau messen zu können. Beim Messen wird eine kleinste Einheit vorgegeben und gezählt, wie oft diese Einheit in der zu messenden Länge vorkommt. Wer ein Lineal mit der kleinsten Einheit Millimeter an die Diagonale anlegt, wird ihre Länge nicht genau messen können. Wird die kleinste Einheit fortlaufend verkleinert auf Nano-, Pico- oder noch kleinere Einheiten, bleibt dennoch immer ein Rest übrig. Daher kann eine Irrationalzahl niemals exakt gemessen werden. Diese Situation ähnelt Hegels Bild des Schachts, in dem die Vorstellungen liegen. Die fortlaufende Verkleinerung von Umgebungen, in denen die Irrationalzahl liegt, kann mit einem Schacht verglichen werden, an dessen Tiefpunkt sich die Irrationalzahl befindet, ohne je erreicht werden zu können. Es ist nur mithilfe der Einbildungskraft möglich sich vorzustellen, dass und wo in diesem Schacht die Irrationalzahl liegt.

Ist es möglich, einen solchen Schacht zu betreten, seine inneren qualitativen Eigenschaften zu erkennen, ohne sich wie in einem Schwarzen Loch in der Unendlichkeit zu verlieren und niemals zurückzukehren? Gibt es einen Weg, die vom Zählen und Messen bekannten und identifizierbaren Zahlen in der Vorstellung zu verlassen, und aus dem Bereich der virtuellen Zahlen zu den bekannten Zahlen zurückzukehren? Bei den Irrationalzahlen erscheint das nicht notwendig, da es einen Algorithmus gibt, mit dem sie beliebig genau bestimmt werden können. Aber es hat auch noch nie jemand versucht, an den Ziffern ihrer Dezimaldarstellung Muster und Regeln zu erkennen. Diese Frage gleicht der Frage nach dem Möglichkeitsraum. Gibt es mögliche Muster für die Ziffern der Dezimaldarstellung, und lassen sich an der Gesamtheit dieser Muster Eigenschften erkennen, die sich in der Rückkehr an der tatsächlichen Dezimaldarstellung nachweisen lassen?

Auf diese Weise zu fragen ist der Mathematik bisher nur bei der Verteilung der Primzahlen bekannt. So wie nach Mustern der Dezimaldarstellung von Irrationalzahlen gefragt werden kann, wird nach der Verteilung der Primzahlen gefragt. Jeder vermutet, dass es solche Muster gibt (d.h. kann sich die Existenz solcher Muster vorstellen), aber sie ließen sich bisher nicht nachweisen. Offenbar fehlen klare Anhaltspunkte, wie solche Muster bestimmt werden könnten. Könnte es sich um eine Art Fraktale handeln? Lassen sich an ihnen Folgen wie die Fibonacci-Zahlen (und mit ihnen der Goldene Schnitt) nachweisen?

Was bei der Verteilung von Zahlen und Ziffern vielleicht nur schwer vorzustellen ist, gelingt seit einigen Jahrzehnten immer besser bei den Mustern auf der Ebene. Dort wird gefragt, ob es nicht-periodische Muster gibt, die dennoch bestimmten Regeln folgen. Das sind insbesondere die 1973 und 1974 unabhängig voneinander von Roger Penrose und Robert Ammann entdeckten Penrose Parkettierungen. Könnte es möglich sein, an und aus den zweidimensionalen Mustern auf eindimensionale Muster und die sich an ihnen zeigende Verteilung von Zahlen zu schließen?

In allen diesen Fällen handelt es sich um Beispiele, bei denen Vielfalten möglicher Muster, deren Eigenschaften und daraus gefolgert die Eigenschaften realer Muster betrachtet werden.

Mathematisch geht es für mich um die allen diesen Beispielen zu Grunde liegende Frage nach den imaginären Zahlen. Mit den imaginären Zahlen wurden erstmals von Girolamo Cardano (1501-1576) und anderen im 16. Jahrhundert einfache mathematische Aufgaben gelöst, für die es keine Lösungen im Bereich der natürlichen, ganzen und rationalen Zahlen gibt. Sie erweiterten diese Zahlen um imaginäre Zahlen, die es nur in der mathematischen Einbildungskraft gibt, erkannten deren Rechengesetze und zeigten, wie sich mit ihnen nicht nur die mit den herkömmlichen Zahlen unlösbaren Aufgaben dennoch lösen ließen, sondern wie es eine Bewegung gibt, die aus dem Bereich der imaginären Zahlen in den Bereich der herkömmlichen Zahlen zurückführt und sich mit ihr deren Lösungen dort darstellen lassen. Das ist die Zyklizität der imaginären Zahlen. Erst mit ihnen lässt sich für mich die Frage beantworten, ob und wie sich mit der mathematischen Einbildungskraft ein Weg finden lässt, der in den Schacht der Vorstellungen hinein- und wieder zurückführt.

Nun mag eingewendet werden, dass sich inzwischen gezeigt hat, wie sich mit den imaginären Zahlen beispielsweise die Elektrizität oder bestimmte Eigenschaften der Quantenmechanik darstellen lassen. Entsprechen also die klassischen Zahlen der Mechanik und die imaginären Zahlen neueren Gebieten der Physik, und sind sie mit ihnen letztlich genau so natürlich wie die herkömmlichen, an der Mechanik orientierten Zahlen? Wer sich näher anschaut, wie beispielsweise die Elektronen, auf denen die Elektrizität beruht, oder die Elementarteilchen der Quantenmechanik vorzustellen sind, wird feststellen, dass sie sich der gewöhnlichen Vorstellung genau so entziehen wie die imaginären Zahlen. Sie sind also kein Mittel, um die vermeintliche Wirklichkeit der imaginären Zahlen zu erkennen, sondern umgekehrt leisten die imaginären Zahlen in der Elektrizität und der Quantenmechanik die Aufgabe, auch dort dasjenige beschreiben und sich vorstellen zu können, was sich der üblichen Vorstellung entzieht.

Die imaginären Zahlen sind daher für mich die Grundlage, um alle bisher aufgeworfenen Fragen weiter vertiefen zu können. Was ist ein Schacht? Welche Fluktuationen gibt es dort? Wo findet er seinen Grund und welche Eigenschaften hat dieser?

Um Fragen dieser Art beantworten zu können, muss das Denken bis in die Logik radikal erweitert werden. Die Logik kann nicht wie bisher geschehen ausschließlich und einfach entlang von Schlussketten stets voranschreiten. Sondern sie muss sowohl in der Lage sein, sich aus dem Bereich des Bekannten entfernen und wieder zurückkehren zu können (wofür der Logiker George Spencer-Brown [1923-2016] 1969 in seinen Laws of Form den Begriff des Re-entry eingeführt hat), und sie muss ihr eigenes Medium verstehen lernen, in dem sie sich vorwärts und rückwärts bewegen kann wie auch einer Bewegung fähig ist, die in einen Grund eingetragen wird und an anderer Stelle wieder aufscheint. Dafür gibt es erste Hinweise bei Edmund Husserl (1859-1938), der wie kein anderer Philosoph die Aufbruchjahre der Physik und Mathematik um 1910 in Göttingen miterlebt hat. Er entwickelte in seinen 1928 von Heidegger herausgegebenen Vorlesungen zur Phänomenologie des inneren Zeitbewusstseins ein erstes halb-formales Verständnis, wie sich in der Einbildungskraft Erinnerungen und Erwartungen kreuzen, und hat für mich als erster einen Ansatz gefunden, die von Hegel zur Einbildungskraft und ihrer Vorstellungsräume aufgeworfenen Fragen weiter auszuführen, auch wenn er sich kaum auf Hegel bezieht. Er hat als erster die Idee entwickelt, wie das Denken im Zeitbewusstsein nicht nur eindimensional vorwärts schließt, sondern gleichermaßen vorwärts wie rückwärts, woraus sich eine Vielfalt von Möglichkeiten ergibt. Für ihn ist die Zeit das Medium, in das Erinnerungen und Erwartungen eingetragen werden.

In seiner Tradition hat Claus-Artur Scheier (* 1942) 2016 mit Luhmanns Schatten einen Versuch veröffentlicht, ausgehend von der Systemtheorie von Luhmann formale Darstellungen für eine neue Logik zu entwickeln, die sowohl die gegenläufigen Bewegungen der Erinnerung und Erwartung wie auch des Zu-Grunde-Gehens enthält. Spuren können in einen Grund eingezeichnet und später sowohl rückwärts- wie vorwärtslesend wieder aufgenommen werden. Wenn nur noch die Spur zu sehen ist, kann sie »gelesen«, d.h. nach dem Ereignis gefragt werden, das die Spur hinterlassen hat und nach dem Ziel, wo die Spur hinführt. Aus den Spuren kann sich das Bild eines Rhythmus, ja eines labyrinthischen Tanzes ergeben, der seine eigene Dynamik entwickelt, sich aufschwingt und auf elementarer logischer Ebene die Bewegung einer Oszillation und ihres Aufblühens zeigen kann. Das verstehe ich nicht als Konkurrenz-Projekt gegenüber Spencer-Brown, sondern als einen eigenen Ansatz. Für mich kommt es darauf an, aus der Vielfalt dieser Vorschläge die Grundlinien einer neuen Logik zu erkennen, die von Scheier als Philosophie in der medialen Moderne verstanden wird. Um dies Vorhaben in seinem vollen Umfang zu verstehen, können als ein dritter Ansatz die von Slavoj Zizek (* 1949) 2012 in Weniger als nichts ausgeführten Ideen einer Logik des Futur II gesehen werden, – wobei er sich auf Hegel und Lacan beruft –, wenn in einer komplexen logischen Bewegung zunächst etwas wie gewohnt in einem Nachfolger-Schritt gesetzt wird, und anschließend die Bewegung wiederum umkehrend alle Voraussetzungen zu prüfen sind, die in der Setzung implizit bereits enthalten waren. Logische Schlüsse erfolgen dann nicht mehr ausschließlich Punkt für Punkt entlang einer Kette, sondern mit jedem neuen Punkt wird zugleich die komplette Vergangenheit und mit ihr die Erwartung an neue zukünftige Punkte völlig neu gesehen.

Für einen Mathematiker sind jedoch ohne Frage die Ideen von Spencer-Brown am interessantesten. Er versteht den Re-entry als das Ergebnis eines periodisch arbeitenden Schaltkreises, für den es einfache und komplexe Beispiele gibt. Schaltkreise können nur als Netzwerke entworfen und realisiert werden, in denen das klassische eindimensionale Schließen entlang einer Reihe aufgegeben wird zugunsten einer vielfältigen Struktur von Vor- und Rückbezügen. Und dennoch lassen sie sich von außen als eine Black-Box verstehen, die einen Input-Strom von Daten verarbeitet und aus ihnen einen Output-Strom von Daten erzeugt. Während der Phase der Verarbeitung entfernt sich der Schaltkreis von der eindimensionalen Zahlenachse, liefert jedoch im Ergebnis mit dem Output neue Zahlenwerte, die per Re-entry in die Zahlenachse aufgenommen werden können. Hier stellen sich viele Fragen: Sind die bekannten Regeln der komplexen (imaginären) Zahlen ein elementares Beispiel für einen Schaltkreis, wie er Spencer-Brown vorgeschwebt hat? Geht die Vielfalt der von ihm betrachteten Schaltkreise über die Regeln der komplexen Zahlen hinaus und enthält diese als einen Grenzfall? Wann und wie treten in Schaltkreisen intern systematisch imaginäre Zahlen auf: Das scheint nach den Arbeiten von Spencer-Brown dann der Fall zu sein, wenn stabile Kreisläufe durch zusätzliche Eingaben von außen gestört zu werden drohen und der Konflikt (die drohende Antinomie) durch eine imaginäre Schleife umgangen werden kann.

Welche Eigenschaften gibt es, die den Erfolg von Schaltkreisen sicherstellen? Zu Ende gedacht können die Schaltkreise im Sinne von Spencer-Brown als eine höhere Zahlenklasse betrachtet werden. Viele Schaltkreise verfügen intern über unterschiedliche Zustände, und Spencer-Brown fragt sich, wie diese ineinander übergehen. Können eine Ebene höher betrachtet auch ganze Schaltkreise ineinander übergehen? Gibt es also Zyklen von Schaltkreisen? So wie Aristoteles den Begriff der Zahlen gefunden hat, indem er ihn klar getrennt hat von den Eigenschaften der Zahlen wie Transitivität und Kontinuität, ist auch der Begriff von imaginären Zahlen und möglicherweise noch allgemeiner von Schaltkreisen zu trennen von ihren Eigenschaften. Die elementare Eigenschaft ist sicher – nahezu tautologisch gesagt – ihre Zyklizität, d.h. ihre Fähigkeit, sich von etwas zu entfernen (Supplement-Bildung) und wieder zurückzukehren (Re-entry). Wenn ich Spencer-Brown richtig verstehe, kommt für ihn eine Reduktivität hinzu. Er gebraucht Schaltkreise prinzipiell nur als reductors, die einen komplexen Input vereinfachen. Das ist im einfachsten Fall ein Schaltkreis, der als Input einen Wellenverlauf verarbeitet und als Output einen neuen, einfacheren Wellenverlauf zurückgibt, der sich z.B. vom Input darin unterscheidet, dass die Periode (Frequenz) nur noch halb so groß ist. Das sollte sich dahin verallgemeinern lassen, an einem Input wiederkehrende Muster zu erkennen, die für sich einfacher sind als der Input im Ganzen.

Kann es auf einer Meta-Ebene zu einer Wechselwirkung zwischen Input, Ouput und möglicherweise sogar den internen Zuständen der Schaltkreise kommen? Kann diese Wechselwirkung den Charakter eines Spiels oder Tanzes annehmen? Den Weg zu Fragen dieser Art hat für mich Luhmanns Schatten von Scheier geöffnet. Auch wenn er sich kaum explizit zur Logik von Spencer-Brown äußert, hat für mich Luhmanns Schatten erstmals den Fragehorizont gezeigt, aus dem heraus die neuen Ideen von Spencer-Brown weiter zu diskutieren sind.

Siglenverzeichnis

HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971 (zitiert als HW); Link

Literatur

Francis M. Cornford: Plato's Theory of Knowledge: the Theaetetus and Sophist of Plato, London 1935

Englische Übersetzung mit einigen Kommentaren. Er übersetzt dynamis als square roots. An der kritischen Textstelle 148ab übersetzt er mekos als length und dynameis als 'roots' (surds). In einem Kommentar auf S. 22 Fn. 1 verweist er auf Thomas Heath A History of Greek Mathematics I, 155, von dem er diese Übersetzung übernimmt. Heath schreibt dort: "While it was Theaetetus who, inspired by Theodorus's investigation of these particular 'roots' (or surds), was the first to generalize the theory, seeking terms to cover all such incommensurables; this is confirmed by the continuation of the passage from Pappus's commentary, which says that the theory was 'considerably developed by Theaetetus'." Cornford nennt einen weiteren Text von Heath The Thirteen Books of Euclid's Elements, II, 288. Dort wird dynameis ebenfalls als roots übersetzt.

Jacques Derrida: Der Schacht und die Pyramide
in: Derrida: Die différance, Stuttgart 2004 [1968]

Klaus Düsing: Hegels Theorie der Einbildungskraft
in: Franz Hespe, Burkhard Tuschling (Hg.): Psychologie und Anthropologie oder Philosophie des Geistes, Stuttgart-Bad Cannstatt, 1991, 297-320

Aden Evans: The surd
in: Simon Duffy (ed.): Virtual Mathematics, Manchester 2006, 209-234

Martin Heidegger: Aristoteles, Metaphysik Θ 1-3, Frankfurt am Main 2006

Jens Høyrup: Dynamis, the Babylonians, and Theaetetus 147c7-148d7
in: Historia Mathematica 17 (1990), 201-222; Link

Tiberiu M. Popa: Aristotle on material dispositions in Meteorology IV, Pittsburgh 2005; Link

Pirmin Stekeler-Weithofer: Hegels Philosophie der Mathematik
Unterlage für eine Vorlesung 2011/2012, ursprünglich in: Ch. Demmerling und F. Kambartel (Hg.): Analytische Interpretationen zur Dialektik Hegels, Frankfurt am Main 1992, 139-197; Link

Julius Stenzel: Zahl und Gestalt bei Platon und Aristoteles, Darmstadt 1959 [1924]

Arpad Szabó: Die Anfänge der griechischen Mathematik, Wien 1969

Walter Tydecks 2013: Hegels Herleitung des Differentialkalküls aus der qualitativen Potenzbestimmung, Bensheim 2013
unter: http://www.tydecks.info/online/logik_kraft_diff.html

Walter Tydecks 2016: Kraft, Impuls, Energie, Bensheim 2016
unter: http://www.tydecks.info/online/themen_kraft_impuls_energie.html

Michael Wolff: Hegel und Cauchy
in: R.P. Horstmann & J.M. Petry (Hgg.) "Hegel und die Naturwissenschaften", Stuttgart 1986, S. 197 - 263

2018