Walter TydecksKraft, Impuls, Energie |
Beitrag für den Themenkreis Naturwissenschaft und Technik von 50plus aktiv an der Bergstraße am 26.10.2016 in Bensheim, stark erweiterte Fassung
Inhaltsverzeichnis
Einleitung
Einfache Beispiele
Die Unvergänglichkeit des Impulses
Die höhere Mächtigkeit (Potenz) der Energie
Die Allgegenwart der Kraft (und ein Schluss durch die Mitte)
Das Beispiel Radioaktivität
Einleitung
Niemand kann Kraft, Impuls oder Energie sehen, aber jeder kennt und spürt sie: Kraft ist die Fähigkeit etwas zu verändern, z.B. die Kraft, einen Stein von einem Ort zu einem anderen zu bewegen. Unter Impuls wird meist ein äußerer Anstoß verstanden, etwas zu tun und auf den Impuls zu reagieren. Wird intuitiv versucht, Energie von Kraft zu unterscheiden, gilt Energie als das Vermögen, eigene oder fremde Kräfte erfolgreich mobilisieren zu können und an einer Aufgabe so lange dran zu bleiben, bis sie erfolgreich zu Ende gebracht ist. Energie, das sind im weiteren Sinn die Triebe, die Libido, Vitalität und die aufmerksame Lebendigkeit, die heute für die meisten das Glück bedeuten, das sie bis ins hohe Lebensalter genießen möchten.
Fachwissenschaftlich wird jedoch unter Kraft, Impuls und Energie etwas ganz Anderes verstanden, und das macht das Verständnis naturwissenschaftlicher Vorträge häufig sehr schwer. Pädagogische Lernkontrollen bestätigen, dass an den Gymnasien höchstens ein Drittel der Schüler versteht, was in der Physik damit gemeint ist. Daran haben alle Unterrichtsreformen nichts ändern können. Didaktiker klagen »Aristoteles siegt immer noch über Newton« und meinen damit, dass bis heute die neuen Ideen der neuzeitlichen Wissenschaft bei der Mehrheit der Menschen nicht angekommen sind.
Woran liegt das? Die Griechen hatten eine anschauliche Vorstellung von Kraft (Fähigkeit, Möglichkeit), Schwung und Energie. Im Mittelalter wandelten sich diese Begriffe mit dem Siegeszug monotheistischer Religionen in Eigenschaften, mit denen das Höchste Wesen beschrieben werden kann: Die Unvergänglichkeit (Unsterblichkeit) des Impulses, die höhere Mächtigkeit (Potenz) der Energie (»Energie ist Masse mal Geschwindigkeit zum Quadrat«) und die Allgegenwärtigkeit (Omnipräsenz) von Kraft. Als das gelungen war, war es nur noch ein kleiner Schritt, seit Galilei und seine Nachfolger Kraft, Impuls und Energie lediglich als Rechengrößen ansehen und einsetzen, mit denen mathematisch die Verlaufsform von Bewegungen optimal gemessen und beschrieben wird, ohne zu fragen, was sie genau bedeuten.
Dieser Beitrag führt die mit den Vorträgen über ägyptische, babylonische und griechische Mathematik begonnene Reihe über die Wissenschaftsgeschichte fort. Da es weniger um Mathematik und Physik, sondern ausgehend von einfachen Beispielen vor allem um die ihnen zugrundeliegenden, philosophisch und theologisch geprägten Grundbegriffe geht, sind mathematische Vorkenntnisse nicht erforderlich und werden Formeln nur zur Verdeutlichung gebraucht.
Einfache Beispiele
Zusammenstoß zweier starrer Körper
Das einfachste Beispiel für Kraft und Impuls ist der Zusammenstoß zweier starrer Körper. Würde die Welt nur aus einer Linie bestehen, auf der sich zwei starre, punktförmige Körper bewegen, könnten diese sich höchstens einmal treffen. Entweder stoßen sie zentral zusammen und fliegen anschließend in entgegengesetzte Richtungen voneinander weg, oder der schnellere Körper stößt den langsameren an und beschleunigt ihn, so dass dieser sich mit größerer Geschwindigkeit stetig von ihm entfernt.
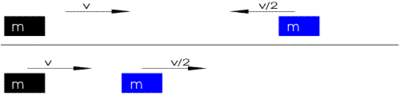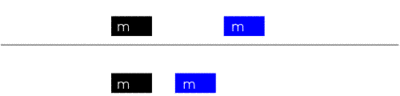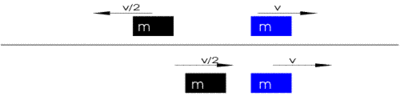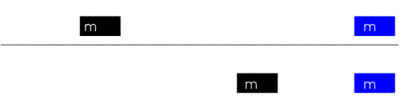
Elastische Stöße mit verschiedenen Anfangsgeschwindigkeiten
Zwei mechanische Körper mit gleicher Masse stoßen aufeinander. Im Moment des Zusammenstoßes kommt es zur Impulsübertragung, wodurch sich die Bewegungszustände der beiden Körper verändern.
Urheber: Von Simon Steinmann - Eigenes Werk, CC BY-SA 2.5, Link
Für die Bewegung zweier starrer, punktförmiger Körper gilt das euklidische Axiom: Mit zwei Punkten ist eindeutig eine Gerade definiert, auf der diese Punkte liegen. Bewegen sich die beiden Punkte, können sie nur aufeinander stoßen, wenn sich beide entlang der Gerade bewegen. Beide können diese Gerade nicht verlassen.
Pendelkette
Dies Beispiel kann einfach ausgebaut werden. In der Pendelkette hängen mehrere Kugeln entlang einer geradlinigen Achse nebeneinander. Wird eine der äußersten Kugeln angestoßen, gibt sie den Impuls über die anderen Kugeln weiter bis am anderen Ende die letzte Kugel davonfliegt. Das widerspricht der Erwartung. Jeder würde vermuten, dass beim Anstoß durch eine der äußeren Kugeln alle Kugeln wie eine Schaukel miteinander in Bewegung versetzt werden. Was geschieht in den mittleren Kugeln, die unbewegt bleiben, aber irgendwie den Impuls weiter geben?

Pendelkette
Urheber: Von DemonDeLuxe (Dominique Toussaint) - Image:Newtons cradle animation book.gif, CC BY-SA 3.0, Link
Stoßwelle
Was in den mittleren Kugeln der Pendelkette vorgeht, wird klarer, wenn die Anzahl der Kugeln fortlaufend erhöht wird und die Kugeln dichter hängen bis in einem Grenzübergang im Ergebnis ein kontinuierliches Seil erreicht wird. Erfolgt an einem Ende ein Impuls, dann setzt dieser sich als Stoßwelle durch das Seil fort. – Das folgende Bild unterscheidet sich allerdings insofern von einer Pendelkette, da die Bewegung am rechten Rand nicht umgekehrt wird, sondern in einer ständigen Wiederholung von links eine Welle nach rechts läuft. Hier geht es nur darum zu zeigen, wie man sich eine Stoßwelle vorstellen kann.

Eine Stoßwelle durchquert ein zweidimensionales Gitter.
Urheber: Von Christophe Dang Ngoc Chan (cdang) - Eigenes Werk, CC BY-SA 3.0, Link
Eine Stoßwelle ist nicht das übliche Ausschwingen eines Seils, sondern eine nach außen kaum sichtbare Impuls-Welle, die im Innern durch das Seil zieht. Das Gitternetz veranschaulicht die horizontal durch das Seil laufenden Fasern und ihre vertikale Verknüpfung.
Wie die Stoßwelle bei einem nicht völlig gleichmäßigen Träger beschrieben werden kann, ist bis heute eine der größten ungelösten mathematischen Aufgaben.
Rückstoß
Während ein Zusammenstoß zweier Objekte nur von außen gesehen werden kann und beim Wurf das geworfene Objekte mit dem Arm beschleunigt und dann losgelassen wird, ist beim Gewehrschuss der Rückstoß unmittelbar zu spüren. In diesem Fall dient die Schulter als Stütze, an der das Gewehr anliegt und mit einem eigenen Mechanismus die Kugel anstößt. Erst in diesem Beispiel ist die Gegenkraft bei einer Impulsübertragung unmittelbar wahrzunehmen. Sie wirkt sich genau so aus wie wenn ein von außen kommendes Objekt mit genügend Impuls auf den eigenen Körper trifft und ihn ins Wanken bringt.
Billard
Jeder kann den Impuls sehr gut beim Billard beobachten. Mit dem Queue wird ein Impuls auf eine Kugel übertragen, die zu rollen beginnt. Wenn sie auf andere Kugeln trifft, gibt sie den Impuls weiter. Eine Kugel darf nicht mehrfach angestoßen oder geschoben werden. Wenn der Kontakt des Queue mit der Kugel zu lange fortgeführt wird, handelt es sich um keinen Impuls mehr, sondern entgegen den Spielregeln um eine Arbeit, mit der die Kugel gelenkt wird.
Impuls und Energie einer Wasserwelle
Wer in eine umstürzende Welle springt, wird deren Impuls spüren: Die Welle schlägt mit ihrem vollem Gewicht unmittelbar auf und wirft einen um, wenn sie stark genug ist. An diesem Beispiel lassen sich die beiden Faktoren beschreiben, aus denen sich der Impuls zusammensetzt: Der Impuls ist um so größer, je größer die Masse und die Geschwindigkeit des Objekts ist. Eine größere oder eine schnellere Welle haut einen stärker um.
Das Beispiel der Welle lässt den Unterschied zwischen Impuls und Energie verstehen. Der Impuls wird in einem Augenblick übertragen, Energie wirkt über einen längeren Zeitverlauf. Wer in eine herantreibende Welle springt, die noch nicht überschlägt, wird spüren, wie sie ihn mit fortlaufend stärkerer Kraft mitreißt. Wer einer Welle standhält bis die nächste Welle kommt, wird spüren, wie viel Arbeit notwendig ist. Wird ausgerechnet, wie viel Arbeit verrichtet werden muss, um gegen heranströmenden Wellengang zu rudern, ergeben sich anschaulich die wesentlichen Faktoren: Das ist zum einen der Impuls jeder einzelnen Welle (ihre Masse und ihre Geschwindigkeit), und das ist zum anderen die Häufigkeit, wie schnell Welle auf Welle folgt. Wer sich das mathematisch vorstellt, wird verstehen, dass die Wellenlänge (oder die Frequenz der Wellen) das Maß ist, mit welcher Energie heranströmende Wellen alles mit sich reißen, was sich ihnen entgegenstellt.
Im Extrem kann ein Tsunami entstehen.
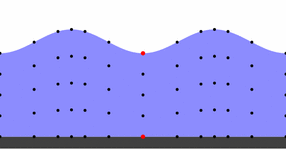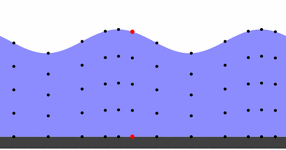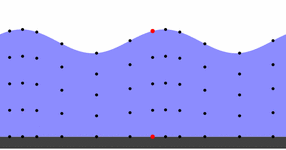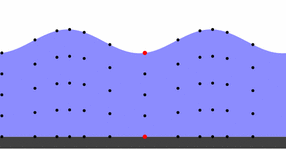
Bewegung eines Tsunami
Urheber: Von Auteur : Original uploader was Régis Lachaume (Lachaume) at fr.wikipedia - Transferred from fr.wikipedia; transferred to Commons by User:Korrigan using CommonsHelper., CC BY-SA 3.0, Link
Jede einzelne Welle verläuft von links nach rechts. Ihr Impuls ergibt sich aus ihrer Masse und Geschwindigkeit. Wird die Bewegung des roten Punktes betrachtet ist zu erkennen, wie die Bewegtheit der See kreisförmig erfolgt. Jeder spürt das beim Baden in offener See, wenn zwischen den Wellen ein Sog in die See erfolgt, dem ebenso standgehalten werden muss wie der anbrandenden Welle. Viele haben beim Baden mehr Angst vor dem Sog, und bei durch Tsunamis ausgelösten Katastrophen entstehen häufig die größeren Schäden durch den Sog, der alles ins Meer reißt und hin und her schleudert.
Zusammenfassend ergeben sich zwei Geschwindigkeiten: Die Ortsbewegung jeder einzelnen Welle, mit der sie auf den Strand läuft. Sie kann wie jede Bewegung gemessen werden in Stundenkilometern (Wegstrecke je Zeiteinheit). Und die Bewegtheit, das ist die Häufigkeit (Frequenz), mit der die Wellen einander folgen. Sie kann als Anzahl Wellen je Zeiteinheit gemessen werden. Das Beispiel des roten Punktes zeigt, wie diese zweite Bewegung ebenfalls als Ortsbewegung in Stundenkilometern gemessen werden kann: Das ist die Geschwindigkeit, wie schnell sich der rote Punkt hin und her bewegt. Dadurch können beide Geschwindigkeit auf eine gemeinsame Einheit gebracht werden.
Optik und Radioaktivität
So viel sei schon jetzt gesagt, dass bei Optik und Radioaktivität im Grunde das gleiche geschieht. Es gibt eine Quelle, die periodisch Wellen aussendet. Für jede einzelne Welle kann ihr Impuls und für die Gesamtheit aller Wellen ihre Energie berechnet werden.
Ausblick
Und es sei schon angedeutet, dass an diesen Beispielen gewissermaßen bereits zu sehen ist, warum bei der Berechnung der Energie E = ½ · m · v2 die Geschwindigkeit im Quadrat auftritt: Zum einen ergibt sich der Impuls jeder einzelnen Welle aus ihrer eigenen Geschwindigkeit, und zum anderen gibt es die Geschwindigkeit, wie schnell die Wellen einander folgen. Es scheint naheliegend zu sein, beide Geschwindigkeiten zu addieren und den Gesamtimpuls der einzelnen Welle zu ermitteln aus der Summe der Geschwindigkeit der Welle für sich und der Frequenz des Wellengangs. Es wird noch genauer ausgeführt, warum das nicht so ist. Beide Geschwindigkeiten sind voneinander unabhängig und müssen daher multipliziert werden, um die Energie des Wellengangs im Ganzen zu berechnen. Wenn es in der Rechnung so aussieht, als sei in der Größe v2 die Geschwindigkeit v mit sich selbst multipliziert, ist das ein irreführender Schein, der darauf zurückgeht, dass die Rechnung mathematisch auf den Sonderfall vereinfacht wird, wenn beide Geschwindigkeiten gleich groß sind bzw. in den gleichen Maßeinheiten gemessen werden.
Die Unvergänglichkeit des Impulses
Impuls und neuzeitliche Wissenschaft
Mit den einfachen Beispielen scheint alles klar zu sein oder zumindest sieht es so aus, als ließe es sich einfach ausarbeiten. Wer näher hinschaut, stößt auf eine völlig ungewohnte Vorstellungswelt. Sie geht auf eine jahrhundertelange Diskussion zwischen den monotheistischen Religionen (Judentum, Christentum, Islam) einerseits, und den überlieferten heidnischen Traditionen andererseits zurück. Aristoteles (384 v.Chr. - 322 v. Chr.) hatte in seinen Schriften die Physik im heutigen Sinn begründet. Er unterschied die objektiv gegebenen Möglichkeiten (Anlagen, Fähigkeiten, dynamis, potentia) und den Vorgang, sie zu ergreifen und zu verwirklichen (energeia, actualitas). Physik beschreibt, was möglich ist und wie es wirklich werden kann. Wird gefragt, warum es überhaupt zu einer Bewegung kommt, war seine Antwort, dass etwas dann zu einer Bewegung neigt, wenn es sich im Zustand des Mangels (steresis, privatio) gegenüber seiner eigenen Natur befindet. Dann kann es sich entweder selbst umwandeln (zum Beispiel beim Wachstum einer Pflanze), oder anderes von außen technisch in seinem Sinn verändern. Wird ein Stein künstlich in die Höhe gehalten, hat er die Neigung, sich zu seinem natürlichen Ort am Boden zu bewegen. Befindet sich eine Pflanze in einer ungünstigen Position, neigt sich ihre Blüte so weit sie kann dem Sonnenlicht zu. Die Bewegung ist beendet, wenn sich etwas in Übereinklang mit seiner Natur befindet. Das kann auch übertragen werden auf die Ethik und Grenzfragen des Lebens. Wem es gelingt, ein Leben in Übereinklang mit seiner Natur zu leben (und das heißt nach Aristoteles für den Menschen: bei Erfüllung aller seiner Grundbedürfnisse, in Freundschaft und Gesellschaft mit anderen Menschen und bei Verwirklichung aller seiner Fähigkeiten), dessen Leben gilt als gut und gelungen. Zur Natur eines vergänglichen Wesens zählt auch sein Tod. Es gehört daher zum guten Leben, dem Tod gegenüber eine natürliche Einstellung zu finden, die den Tod als Teil der eigenen Natur versteht.
In diesem Verständnis ist die Natur das Maß aller Dinge. Demgegenüber vertreten die monotheistischen Religionen ein Höchstes Wesen als Maß. Bewegung entsteht nicht aus dem Mangel gegenüber der eigenen Natur, sondern geht auf Gott zurück. Alle Wesen wollen sich von den Zwängen der eigenen Natur befreien und so weit sie können dem Höchsten Wesen zuneigen und ihm ähnlich werden. Gott ist seinerseits an keinerlei Naturgesetze oder Maße der Natur gebunden. Er kann in seiner Härte wie auch Gnade, seiner Gewalt wie auch Ausdauer und Sanftheit über alle physikalischen oder moralischen Gesetze hinweggehen und steht über ihnen. Der Mensch befindet sich in der Zerreißprobe, ob er seiner eingeschränkten Natur folgt oder sich Gott zuwenden und ein Leben führen kann, in dem alles Gott dient.
Was hat das mit Physik zu tun? Johannes Philoponos (490-575) war einer der ersten, der in ausführlichen Kommentaren zu den Schriften von Aristoteles und dort insbesondere auch der Physik eine umfassende und in sich schlüssige Gegenposition vertrat. Er lebte in einer Zeit, als im Römischen Reich das Christentum Staatsreligion geworden war und die antiken Überlieferungen als heidnische Religionen verworfen wurden. Zu seiner Zeit wurde von dem oströmischen, christlichen Kaiser Justinian I (482-565) die auf Platon zurückgehende Akademie in Athen geschlossen und ihre letzten Vertreter mussten nach Osten auswandern.
Bei Philoponos liegen die Anfänge einer völlig neuen Physik, deren Grundbegriffe Eigenschaften sind, die aus Sicht der antiken Philosophie ausschließlich Gott zukommen und nicht Maß einer dem Menschen zugänglichen Lebensweise oder Wissenschaft sein können. Philoponos vertiefte sich in das Werk von Aristoteles und dessen späteren Kommentatoren und stieß dort auf Fragen, die für ihn eine völlig neue Antwort verlangen und erst im Rahmen der monotheistischen Religion möglich werden. Er hat keineswegs einfach konträr der aristotelischen Philosophie eine eigene Position entgegengesetzt, sondern ging von Fragen aus, die er in der aristotelischen Tradition vorfand und die für ihn dort ungeklärt geblieben waren. Daher sind seine Ergebnisse sowohl für die weitere Entwicklung der Theologie wie der Physik von großer Bedeutung. Das war vor allem die Frage, was bei einem Wurf geschieht. Warum fliegt der Speer weiter, wenn er den werfenden Arm verlässt? Offenbar wurde ihm etwas mitgegeben, weswegen er fliegen kann. Das ist für Philoponos der Impetus. Er hat diesen Begriff gegenüber der antiken Tradition neu eingeführt, der heute als Vorläufer des Impulses verstanden wird. Impetus kann wörtlich als Schwung oder Antrieb übersetzt werden und bedeutet das Gegenteil von Trägheit.
Die Geschichte der christlichen Gegenposition verlief jedoch nicht geradlinig. Die Ideen von Philoponos gerieten in Vergessenheit, weil er trotz seiner umfassenden Kritik am antiken, heidnischen Denken in christliche Dogmenstreitigkeiten verwickelt war und von seinen Gegnern ins geistige Abseits gedrängt wurde. In den nachfolgenden Jahrhunderten stagnierte das physikalische Denken im Gebiet des Christentums, während die weiteren Fortschritte in den Schulen und Denkstätten gelangen, die unter dem Druck des Christentums Griechenland hatten verlassen müssen, in den Nahen Osten ausgewichen waren und dort im aufstrebenden arabischen Reich eine neue Blüte erlebten. Erst ab ungefähr 1200 kamen die aristotelischen Lehren auf diesem Umweg zurück nach Europa und wurden unter veränderten Bedingungen neuer Kritik unterzogen. Was Philoponos über den Impetus wusste, wurde neu entdeckt. Es wurden neue Begriffe eingeführt wie vis derelicta (verlassene Kraft) und als Gegenstück vis impressa (eingedrückte Kraft): Wer z.B. einen Speer wirft und ihm einen Impuls überträgt, gibt etwas vom eigenen Impuls ab (es verlässt ihn) und drückt es dem Speer ein, der dank diesem von außen erworbenen (eingedrückten) Impuls eine gewisse Strecke frei zu fliegen vermag. Im Ausdruck vis, der meist als ‘Kraft’ übersetzt wird, ist noch nicht klar zwischen Kraft und Impuls unterschieden. Erst mit Galilei und Newton hat sich daraus die heute übliche Bedeutung von Impuls durchgesetzt, wobei im Englischen unterschieden wird zwischen Momentum (was im Deutschen Impuls bedeutet) und Impulse, dem Impulsübertrag.
Anmerkung: »Das Wort Impuls von lat. Impellere = stoßen, antreiben bedeutet etwas Aktives, Dynamisches, während momentum, eigentlich movimentum von movere = bewegen, etwas in Gang setzen, nicht ganz so stark, sondern eher behäbig wirkt. (Newton spricht ja auch viel vom Fließen und nicht vom Gestoßenwerden.) Im übrigen ist die auch im Deutschen gelegentlich anzutreffende Verwendung von momentum (= das Moment) für Impuls nicht unproblematisch, da es bei uns auch noch den Moment für ‘Zeitpunkt’ gibt. Leider nur selten wird im Deutschen für Impuls der m. E. sehr treffende Ausdruck ‘Kraftstoß’ verwendet.« (Zuschrift von Hans-Jürgen Caspar am 31.8.2016)
Die Unvergänglichkeit des Impulses
Während heute der Impuls ganz selbstverständlich als ein Grundbegriff der Physik gilt, war er aus Sicht der griechischen Naturphilosophie eine völlig un-natürliche Erscheinung, die nur den Göttern zukommen kann: Er ist nicht vergänglich. Er unterliegt nicht Werden und Vergehen, Geburt und Tod. Diese Bedeutung ist kaum mehr erkennbar, wenn heute von Impulserhaltung gesprochen wird, aber deren sachliche Begründung.
Wird ein neues Lebewesen geboren, bekommt es den Impuls nicht wie alle anderen Eigenschaften durch seine Anlagen oder Gene mit, sondern erhält ihn von außen. Es wird jedem Vertreter der Impulstheorie schwer fallen genau zu beschreiben und zu erklären, woher ein Neugeborenes seinen Impuls hat: Das ist auf den ersten Blick nichts weiter als der mechanische Stoß, der ihm beim Verlassen des Mutterkörpers mitgegeben wird, und bei genauerer Betrachtung die mechanische Grundlage aller seiner inneren organischen Bewegungen, die sich als ein realer mechanischer Prozess entwickelt haben, wenn das Blut fließt, Knochen in Bewegung sind usf. Umgekehrt gibt ein Lebewesen beim Tod seinen Impuls wieder komplett an die Umgebung ab, wenn es in eine liegende Position kommt und durch Erkalten des Leichnams alle inneren mechanischen Impulse als Wärme nach außen gibt. Eine solche Sicht auf Geburt, Leben und Tod klingt so ungewöhnlich und nahezu phantastisch, dass es von den frühen Naturphilosophen nicht akzeptiert wurde und auch heute kaum verstanden wird. Die meisten wissen gar nicht oder machen sich nicht klar, wie sich der Impuls von allen anderen Eigenschaften und Stoffen unterscheidet.
Für alle vorchristlichen Religionen ist Unvergänglichkeit das wichtigste Merkmal der Götter. Wird vom unvergänglichen Impuls gesprochen, ist das für sie eine unzulässige Vermischung von Religion und Physik. Darauf kam es aber Philoponos und seinen Nachfolgern an: Sie wollten sich vom antiken Bild einer nicht-göttlichen, sterblichen und vergänglichen Natur trennen und zeigen, wie die Natur an sich göttliche Züge trägt, wodurch sie als Ebenbild Gottes geschaffen ist. Das Vorbild war die Lehre der Transsubstantiation: Seit Philoponos wird der physikalische Begriff des Impulses verglichen mit der Wandlung von Brot und Wein, wenn dort auf vergleichbare Art in vergängliche Dinge etwas Unvergängliches (Leib und Blut Jesu) eingeht. Die Konsequenzen dieses Weltbildes sind kaum abzuschätzen und wurden erstmals von Kant in ihrer ganzen Tragweite erfasst: Sie reichen von der gedanklichen Konstruktion aller Naturerscheinungen aus unvergänglichen, mathematisierbaren Elementen bis zur unbedingten Lehre der Unverletzlichkeit des menschlichen Körpers: Für einen überzeugten Christen sind nicht nur Leib und Seele, sondern aufgrund der Göttlichkeit der Natur auch sein Körper als ein Sakrament anzusehen bis zum Verbot von körperlicher Grausamkeit und Folter wie auch Selbstmord.
Ein anschauliches Bild für die Impulsübertragung ist der Staffellauf. Der erste Läufer startet, gibt am Ende seiner Wegstrecke das Staffelholz weiter und bleibt stehen, während sein Nachfolger den Lauf fortführt. So wie das Staffelholz durchgereicht wird, wird der Impuls weitergegeben. Das kann sowohl ein Bild für den physikalischen Vorgang der Impulsübertragung sein wie auch für die Seelenwanderung: Die Seele wandert weiter von einer Materialisierung in die nächste. Jeder Mensch ist in seinem Leben nur eine Materialisierung einer übergreifenden Seele. Während er körperlich stirbt, lebt seine Seele weiter und ist unsterblich. Mit Philoponos erfolgt erstmals ein Perspektivwechsel von den einzelnen, vergänglichen Körpern zu den übergreifenden Eigenschaften, die deren sterbliches Leben überdauern. Das war in dieser Konsequenz erst möglich im Rahmen einer monotheistischen Religion. Als einmal diese Begriffe entstanden waren, konnten sie mit der Aufklärung im 18. Jahrhundert ihre religiöse Vergangenheit abwerfen und erscheinen seither als rein mathematische Rechengrößen. Geht das historische Bewusstsein über ihre Entstehung verloren, dann wird auch nicht mehr verstanden, was sie eigentlich bedeuten, und sie können nur auswendig gelernt und in der praktischen Arbeit angewandt werden.
(+) Die Vergänglichkeit der Dinge. Für die Griechen handelt die Physik grundsätzlich von vergänglichen Dingen. Vergängliche Dinge verfügen über Kräfte, können sich bewegen und verändern, aber sie vergehen irgendwann. Zwar gab es für die Griechen auch unvergängliche Dinge wie die Fixsterne oder die Objekte der Mathematik (Punkt, Gerade, Kreis), doch waren sie überzeugt, dass die physikalischen Gesetze nur für vergängliche Dinge gelten.
Alle vergänglichen Dinge haben auch nur vergängliche Eigenschaften. Farben blühen auf und verblassen, Geruch und Größe entwickeln sich und vergehen wieder. Alle Eigenschaften der Dinge haben ihrerseits stoffliche Träger und vergehen mit ihnen. Im Gegensatz dazu ist der Impuls eine unvergängliche Eigenschaft. Er wird übertragen, bleibt im Prinzip ewig erhalten und kann nur verschwinden, wenn er durch äußere Einwirkung wie zum Beispiel Reibung aktiv gebremst und verdrängt wird. Der Impuls ist aber auch kein Stoff, der ebenfalls insofern unvergänglich ist, als er nach dem Tod verwest und aus ihm Neues entsteht.
(+) Unerschöpfbare Kraft (vis infatigabilis). Der Impuls ist daher unerschöpfbar. Die vis infatigabilis ist eine Kraft, die »sich nicht erschöpft und nicht verbraucht und darum in der gleichen Weise in alle Ewigkeit weiter bewegen und immer dieselbe konstante Geschwindigkeit hervorbringen kann« (Maier, Bd. II, S. 473). Gegenüber den vergänglichen Eigenschaften vergänglicher Dinge galt eine solche Eigenschaft als göttlich. Über solche Eigenschaften verfügten aus Sicht der antiken Philosophie nur die Kräfte, welche der Erste Beweger, d.h. im christlichen Verständnis Gott, unmittelbar auslösen konnte, »d.h. die die Himmel bewegenden Intelligenzen (oder Engel) und die von ihnen abgeleiteten natürlichen Bewegungstendenzen gravitas und levitas.« (Maier, Bd. II, S. 473)
(+) Natürliche Kräfte Stattdessen gab es für die Griechen natürliche Kräfte, die keiner Impulsübertragung bedürfen. Feuer lodert nach oben, ohne dass ihm ein Impuls übertragen und mitgegeben wird. Steine sinken von allein durch das Wasser an den Boden. Alles bewegt sich von sich aus zu seinem natürlichen Ort. Ein Impuls ist nur notwendig, wenn etwas entgegen seiner natürlichen Bewegung bewegt werden soll. Das klassische Beispiel ist der Speer, der nicht von allein fliegt, sondern geworfen werden muss. Er hat keinen eigenen Antrieb, bewegt sich nicht während des Fluges, und fliegt dennoch eine Weile weiter, wenn er sich von der werfenden Hand gelöst hat. Wie das möglich ist, war für die Griechen kaum zu verstehen. Aristoteles vermutete, dass der Werfer nicht nur den Speer beschleunigt, sondern auch Druck auf die Luft ausübt und dadurch die den Speer umgebenden Luftschichten aufwirbelt, wodurch der Speer eine Weile weiter getragen wird. Es konnte nicht erklärt werden, welche innere Eigenschaft dem geworfenen Speer durch den Wurf übertragen wurde, sondern es wurde nach einer Übertragung über das Medium gesucht, durch das der Speer fliegt. Aristoteles versuchte es sich so zu erklären, dass der Speer auf ähnliche Weise fliegt, wie Schall oder Licht durch ein Medium übertragen werden. So wie Schall und Licht im Laufe ihrer Übertragung an Intensität verlieren, stellte sich Aristoteles auch den Impuls vor: Er verliert an Geschwindigkeit, und es setzt sich die natürliche Bewegung des jeweiligen Gegenstandes durch, die zu ihrem natürlichen Ort führt. Der Speer fällt zu Boden. Auch wenn diese Erklärung lange Zeit für ein Beispiel des heute überholten, vorwissenschaftlichen Denkens der griechischen Naturphilosophen galt, hat sie sich in der Quantenmechanik wieder durchgesetzt: Impulse breiten sich wellenförmig aus und verlieren mit der ständig größer werdenden Ausdehnung der Welle an Betrag.
Sich-Ähnlich-Machen (similitudo) und Symmetrie
Für die Griechen erfolgt eine Wirkung von etwas auf etwas anderes, wenn beide in mindestens einer genau bestimmbaren Hinsicht ähnlich sind und dadurch zueinander passen. Die Wirkung erfolgt, wenn sich das Eine dem Anderen weiter annähert und ihm ähnlich wird. So erklärten sie sich bereits die Wahrnehmung: Etwas kann nur wahrgenommen werden, wenn das Wahrnehmungsorgan (das Auge, das Ohr, die Nase, ...) in einer bestimmten Weise dem Wahrgenommenen ähnlich ist. Das Trommelfell schwingt ähnlich wie der übertragene Schall. Dieser Ansatz versagt gegenüber dem Impuls. Der Impuls eines Körpers kann nicht unmittelbar wahrgenommen werden, sondern es ist nur die körperliche Erschütterung zu spüren, wenn ein anderer Körper auf den eigenen Körper auftrifft. Die neuzeitliche Physik gab daher den überlieferten Ansatz völlig auf, Wirkung durch Sich-Ähnlich-Machen zu erklären.
(+) Wirkung durch Sich-Ähnlich-Machen (similitudo). Etwas wirkt auf etwas anderes, indem es das andere sich ähnlich macht. Aus Sicht der frühen Naturphilosophen gibt nicht ein warmer Körper seine Wärme an einen anderen Körper ab, der in seiner Nähe erwärmt wird, sondern Wärme hat die Fähigkeit, dass warme Körper andere Körper in ihrer Nähe sich ihnen angleichen lassen können. In übertragenem Sinn könnte gesagt werden, Wirkung erfolgt nicht durch äußere Einwirkung bis hin zur Gewalt, sondern durch innere Einfühlung und Sympathie, die im anderen eine innere Bewegung hervorzurufen vermag, wodurch beide einander ähnlich werden. So hat auch noch der mittelalterliche Philosoph und Physiker Ockham angenommen, »dass die Farben imstande sind, eigentliche Farben in der Luft hervorzubringen, oder, anders gesagt, sich selbst – wie die primae qualitates – im Medium zu vervielfältigen. Er wird geführt mit einer neuen und ausführlichen Beschreibung der experimentia von dem Sonnenstrahl, der durch rotes oder diesmal auch grünes Glas geht und einen verus color auf oder vor der gegenüberliegenden Wand verursacht.« (Maier, Bd. II, S. 441) Eine solche Wirkung ist bei der Impulsübertragung nicht zu erkennen. Wenn ein Mensch einen Speer wirft, wird der Speer dem Menschen nicht ähnlich. Es könnte nur in einer etwas weit hergeholten Analogie gesagt werden, dass der Mensch mit seiner Wurfbewegung erst seinen Arm bewegt und darüber den Speer dem Arm in der Weise ähnlich macht, dass er sich im Weiteren wie der Arm bewegt. Dies Bild stößt jedoch schnell an Grenzen und so blieb den frühen Naturphilosophen unklar, was geschieht, wenn der Werfer den Speer wirft.
Was auf den ersten Blick abwegig klingt, hat sich im Grunde dennoch in der modernen Philosophie und Physik auf einer abstrakteren Ebene durchgesetzt. Bei jeder Bewegung bleibt eine Symmetrie erhalten, und es ist für jede Bewegung zu erkennen, um welche Symmetrie es sich jeweils handelt. Das liegt bereits dem Harmonie-Gedanken bei Leibniz zugrunde: Leibniz suchte nach einer inneren Harmonie, die in einer Bewegung erhalten bleibt und die Bewegung mathematisch beschreiben lässt. Durch eine Harmonie werden die harmonisch miteinander verbundenen Elemente einander ähnlich.
Trotz aller Kritik an Leibniz haben das um 1800 die Naturromantiker fortgeführt, und von ihnen inspiriert am überzeugendsten Hegel. Er entwickelt einen äußerst abstrakten und daher ungewohnten Gedanken: Für ihn ist nicht die Frage, warum in der Formel für die Energie die Geschwindigkeit im Quadrat auftritt, sondern für ihn ist umgekehrt das Quadrat eine elementare Symmetrie, die in der Bewegung erhalten bleibt. Er wollte nicht mit mathematischen Formeln entwickeln, wie und warum in den Gleichungen von Kepler, Galilei und Newton Quadrate auftreten, wenn dort mit dem Quadrat der Zeit oder dem Quadrat der Geschwindigkeit gerechnet wird, sondern für ihn war umgekehrt das Auftreten der Quadrate in den Formeln die äußere Erscheinung einer inneren Ähnlichkeit. Er kehrte damit im Prinzip zur griechischen Naturphilosophie und zum Harmonie-Gedanken von Leibniz zurück und entwickelte sie weiter. (Dem liegt ein sehr weit reichender Gedanke zugrunde: Hegel ist überzeugt, dass das Denken zwei unterschiedliche Begriffe oder Gedanken nur vermitteln kann, wenn das Denken ein Mittel – das ist ein vermittelnder terminus medius – einsetzen kann, das über eine höhere innere Symmetrie verfügt, mit der beide Seiten unter einem abstrakten Gesichtspunkt als einander ähnlich erkannt und daher in ihrer Kausalität oder Wechselwirkung beschrieben werden können. Das soll an anderer Stelle näher ausgeführt werden und geht zurück auf Hegels Lehre der Objektivität in der Wissenschaft der Logik und korrespondierende Ausführungen in seiner Naturphilosophie.)
Doch wurde so zu denken als abwegiges Beispiel einer im schlechten Sinn spekulativen Naturphilosophie angesehen, die ins Blaue spekuliert statt empirischen Beobachtungen und rationalen Erkenntnissen zu folgen. – Trotz aller Kritik an der vorchristlichen Naturphilosophie und ihren Nachfolgern unter den Naturromantikern hat sich in der Physik des 20. Jahrhunderts der Gedanke des Sich-Ähnlich-Machen wieder durchgesetzt, jedoch wird heute von Symmetrien, Invarianzen oder Erhaltungsgrößen statt Harmonie gesprochen, siehe dazu im Folgenden die Hinweise auf Lagrange und seine Nachfolger.
(+) Damit ist die Frage nach Mathematik und Physik angesprochen. Das Prinzip der Similitudo reicht sehr weit. Aristoteles war überzeugt, Gleiches kann nur durch Gleiches erkannt werden, d.h. Denkbares durch Denken, Wahrnehmbares durch Wahrnehmung, Mathematisches durch Mathematik, Physikalisches durch Physik usw. Dagegen vertritt die sich herausbildende neuzeitliche Naturwissenschaft in Abkehr vom antiken Denken:
»Nicht alle Prinzipien wahrnehmbarer Dinge müssen wahrnehmbar sein; denn Materie, die ein Prinzip der wahrnehmbaren Dinge bildet, entzieht sich der Wahrnehmung.« (Simplikios, Kommentar zur Schrift von Aristoteles über den Himmel [in cael.] 642,22, zitiert bei Sambursky, S. 432)
Das sieht Sambursky heute in der Quantentheorie bestätigt, wenn sich die Quantentheorie völlig von der Anschauung entfernt und ganz auf mathematische Methoden verlässt. Für ihn sind die Neuplatoniker wie insbesondere Jamblichos (240-320) und Simplikios (480-550) die Wegbereiter der modernen Naturwissenschaft, auch wenn sie sich selbst dem antiken Denken verbunden sahen. Für Sambursky, der sich wie Max Jammer der jüdischen Tradition verpflichtet fühlt, haben sich die Neuplatoniker weit stärker dem jüdischen Denken zugewandt als ihnen bewusst war und als sie zugeben wollten. (Daher konnte Philoponos inhaltlich viele Grundideen von ihnen übernehmen, auch wenn er ihnen vorwarf, sich nicht zum Christentum zu bekehren. Sie sahen sich zur Zeit von Philoponos der Verfolgung durch die christlichen Kaiser ausgesetzt, die die von Platon in Athen gegründete Akademie schließen und die dort vertretenen Lehren nach Persien vertreiben ließen.)
Paradoxien der Bewegung
Schließlich war die griechische Naturwissenschaft in eine Reihe von Paradoxien geraten, die mit dem Begriff der Bewegung zusammenhängen. Die Antworten durch Aristoteles wurden für unvollständig angesehen, und erst mit dem Impuls gelten sie für gelöst.
Wie kann eine Bewegung anfangen? Gibt es nicht im Anfang einen Punkt, an dem etwas gleichzeitig noch ruht und sich bereits bewegt, was ein Widerspruch ist? Der Widerspruch wird gelöst, wenn mit der Impulsübertragung beschrieben werden kann, was im Anfang der Bewegung geschieht. Die Impulsübertragung ist der Anfang der Bewegung. Wenn ein Körper an einen anderen stößt und dieser sich zu bewegen beginnt, ist mit der Impulserhaltung der Widerspruch gelöst: Der eine bewegt sich um so viel mehr, wie sich der andere weniger bewegt.
Wie kann Achilles die Schildkröte einholen, wenn es möglich ist, fortlaufend kleinere Abstände zur Schildkröte zu betrachten? Auch hier liefert der Impuls die Antwort: Es ist der größere Schwung, der Achilles an der Schildkröte vorbeiträgt.
Der Impuls galt daher bis ungefähr um die Jahrhundertwende 1900 als die gesuchte Antwort auf die Paradoxien der Bewegung. Erst mit den seither neu entstandenen Paradoxien der Mengenlehre, Quantentheorie und Kosmologie wurde ein neuer Blick auf die antiken Paradoxien gewonnen. Doch hat das bis heute nicht dazu geführt, auch die Grundbegriffe wie Kraft, Impuls und Energie neu zu begründen. Dieses Missverhältnis macht die Schwierigkeit aus, die sich in den Verständnisschwierigkeiten über die Grundlagen der Physik zeigt.
Ökonomische und politische Gründe
Die Grenzen der antiken Naturphilosophie können auch in den Grenzen der Gesellschaft gesehen werden, in der sie entstand. Diesen Gesichtspunkt hat vor allem Michael Wolff in seiner Studie über die Geschichte der Impetustheorie hervorgehoben. Er sieht die von Philoponos und seinen Nachfolgern neu entwickelten physikalischen Grundbegriffe in Verbindung mit sozialrevolutionären und ökonomischen Ideen. Wenn Philoponos von der Übertragung der Kraft vom Menschen an das von ihm geschaffene Produkt spricht, gehört das für Wolff »einer spezifisch spätantiken Emanzipationsideologie« an und «soll die Tätigkeit der Produzenten als Entäußerung seiner eigenen Kraft« anerkennen (Wolff, S. 133). Bei Philoponos war das noch eingebettet in eine christliche Theologie, die die Ebenbildlichkeit des Menschen als Übertragung von Gott an den Menschen verstand. – Im Mittelalter wurde die Impetus-Theorie erneut von radikalen Christen aufgenommen (den Franziskanern bzw. den Spiritualen), deren Theoretiker Petrus Olivi (1247/48-1296/98) den Kapital-Begriff begründete. Geld ist nicht mehr wie bei Aristoteles bloß ein Tauschmittel, sondern es zeigt einen Wert an, der durch Übertragung von Arbeitskraft vermehrt wurde. Wie Philoponos und Olivi entwickelten auch Nikolaus von Oresme (vor 1330-1382) und Johannes Buridan (1300-1358, Begründer der Impetus-Theorie) klare ökonomische Lehren von Kraft, Arbeit, Kapital, Wert und Geld mit der Stoßrichtung, die feudale Willkür (die sich zum Beispiel in Geldfälschungen zeigte) zu bekämpfen zugunsten einer Wirtschaftsordnung, in der nur Kraft und Leistung belohnt werden. – Der Übertragungsbegriff steht für Wolff zugleich am Beginn der neuzeitlichen Produktionstechniken, die Marx im 1. Band des Kapital beschrieben hat. Der Impetus ist ein Quantum, das weiter gegeben wird. Es ging darum, unterschiedliche Arbeitsprozesse mechanisch miteinander zu verknüpfen. Das Prinzip dieser vorindustriellen Zeit war der Transmissionsmechanismus. »Der Transmissionsmechanismus, zusammengesetzt aus Schwungrädern, Treibwellen, Zahnrädern, Kreiselrädern, Schäften, Schnüren, Riemen, Zwischengeschirr und Vorgelege der verschiedensten Art, regelt die Bewegung, verwandelt, wo es nötig, ihre Form, z.B. aus einer perpendikulären in eine kreisförmige, verteilt und überträgt sie auf die Werkzeugmaschinerie« (Marx Kapital, MEW 23, S. 393, Link).
Das formale Modell der Mechanik nach Euler und Lagrange
Die seit Galilei und Newton eingeführten physikalischen Begriffe hatten eine eigentümliche Doppelbedeutung: Zum einen bezogen sie sich auf anschauliche Erfahrung und ließen sich experimentell überprüfen. Zum anderen waren sie nach wie vor in einer an der Theologie orientierten Sprache geschrieben. Das änderte sich endgültig erst mit der Aufklärung, in der um 1750-1800 die bis heute übliche Physik entstand. Helmut Pulte zeigt in seiner Studie Das Prinzip der kleinsten Wirkung und die Kraftkonzeptionen der rationalen Mechanik, wie Leonhard Euler (1707-1783) auf dem Höhepunkt der Aufklärung eine neue Synthese gelang: (a) Von Descartes übernimmt er die Vorstellung des gefüllten Raums und lehnt den leeren Raum und die Atome als kleinste Bausteine ab. Er geht von Flüssigkeiten aus, die einen Raum kontinuierlich füllen, und nicht von einer Vielzahl isolierter, punktförmiger Atome, die im Raum verteilt sind. (b) Von Newton greift er die mathematische Methode auf, Kräfte in voneinander unabhängige Komponenten zu zerlegen und in einem Kräfteparallelogramm darzustellen, in dem die Komponenten der Kräfte senkrecht aufeinander stehen (Vektordarstellung statt skalare Zahlenwerte). (c) Von Leibniz stammen die Bewegungsprinzipien: Die den Raum füllenden Flüssigkeiten bewegen sich nicht chaotisch, sondern ihre Bewegungen folgen Prinzipien wie dem Prinzip der kleinsten Wirkung. Mit den Bewegungsprinzipien ist eine innere Harmonie in der Strömung gegeben, wodurch die mathematische Rechnung vereinfacht wird. Seit dem 20. Jahrhundert werden die inneren Harmonien einer Strömung als die Symmetrien bezeichnet, die in einer Bewegung erhalten bleiben. (Wer an fachlichen Details interessiert ist, schaue sich das Noether-Theorem an, das 1918 von Emmy Noether ausgehend von einer weiteren Verallgemeinerung des Ansatzes von Lagrange, dem Lagrange-Formalismus, formuliert wurde und heute als das grundlegendste Gesetz der Physik gilt.)
Im Ergebnis geht Euler nicht mehr von starren Körpern aus, deren Bewegung zu untersuchen ist, sondern von Strömungen und der mathematischen Darstellung ihrer Verlaufsform. In einer Flüssigkeit gibt es ständig Strömungen, Turbulenzen, eine innere Bewegung. Diese Bewegung ist für Euler der Ausgangspunkt. Aus ihr will er die Bewegungsgleichungen erklären. Aus der Bewegung heraus entsteht die Kraft.
Sein Programm ließ sich jedoch aufgrund mathematischer Schwierigkeiten nur teilweise umsetzen. Den gordischen Knoten durchschlug erst sein Nachfolger Joseph-Louis Lagrange (1736-1813), der nach der Französischen Revolution in Paris hohe Ämter erhielt: Er entwickelte eine rein mathematische, überwiegend algebraisch (in mathematischen Formeln) und nicht mehr geometrisch (in Zeichnungen und Konstruktionen) geschriebene Lehre und gab alle Bezüge zur Theologie auf. Ihn interessierten weder die jahrzehntelang ausgetragene Diskussion von Leibnizianern und Kartesianern über Impuls- oder Energie-Erhaltung noch Fragen nach ausgedehnter, träger oder undurchdringlicher Materie oder die Frage, wie im Gegensatz zur Nahewirkung eine Fernwirkung zu verstehen ist. Seit ihm gilt: Was sich mathematisch klar darstellen und experimentell überprüfen lässt, gewinnt aus der Klarheit und Einfachheit (Eleganz, Schönheit) und der empirischen Bestätigung seine ausreichende Rechtfertigung. Weitergehende philosophische und / oder theologische Begründungen sind für ihn überflüssig und verwirren im Grunde nur das Verständnis. Er war daher überzeugt, dass sich Lehren dieser Art auch pädagogisch am einfachsten vermitteln lassen und hat damit den bis heute gültigen Physik-Unterricht an Schulen, Fachhochschulen und Universitäten geprägt. Er konnte nicht ahnen, welch ernüchternde Ergebnisse die Erfolgskontrolle dieser Art von Unterricht zeigen würde, wenn die Mehrheit der Schüler und Studenten die ihnen vorgetragenen Formeln einfach auswendig lernt.
Die höhere Mächtigkeit (Potenz) der Energie
Vor diesem Hintergrund sind die Formeln der Mathematik und Physik neu aufzunehmen und zu diskutieren. Aus dem Schulunterricht sind die beiden Formeln bekannt:
(1) p = m · v
lies: der Impuls p beträgt Masse mal Geschwindigkeit
(2) Ekin = ½ · m · v2
lies: die kinetische Energie Ekin beträgt ein Halb mal Masse mal Geschwindigkeit zum Quadrat
Heute werden diese Formeln aus den Axiomen von Newton abgeleitet, doch war es historisch genau umgekehrt: Zuerst wurden Impuls und Energie gemessen, und dann wurden ausgehend von den beiden empirisch gefundenen Formeln (1) und (2) sowie weiteren empirischen Erkenntnissen die Axiome der Mechanik und die Regeln des Differentialkalkül gefunden, verallgemeinert und in allen bisher bekannten Anwendungen bestätigt. – Früher waren sich die Mathematiker dieser historischen Entwicklung bewusst, und erst seit dem 20. Jahrhundert wird das vergessen. Siehe hierzu die bei Hegel genannten Zitate von Lagrange (HW 5.347, HW 9.77 Fußnote).
Die erste Formel ist unmittelbar anschaulich und entspricht der Alltagserfahrung: Der Impuls eines Objekts ist um so größer, je schwerer und je schneller es ist. Aber wie erfolgt der Übergang zur kinetischen Energie und welche Bedeutung hat dort die im Quadrat auftretende Geschwindigkeit? Welche Geschwindigkeit ist das, die mit sich selbst multipliziert wird, und warum werden hier Geschwindigkeiten multipliziert und nicht wie üblich addiert? Wenn jemand in einer fahrenden Eisenbahn in Fahrtrichtung nach vorne geht, ergibt sich seine Gesamtgeschwindigkeit aus der Summe der Geschwindigkeit der Eisenbahn und seiner eigenen Geschwindigkeit innerhalb der Eisenbahn. Warum werden dagegen in der Formel der Energie die Geschwindigkeiten multipliziert? Handelt es sich um eine Geschwindigkeit, die mit sich selbst multipliziert wird oder um zwei verschiedene Geschwindigkeiten von gleicher Größe? In diesem Abschnitt soll schrittweise die These entwickelt werden, dass sich in der Quadrierung der Geschwindigkeit eine besondere Eigenschaft der Mechanik verbirgt, mit der sie über die Geometrie und die Arithmetik (das Rechnen mit reellen Zahlen) hinausgeht. Innerhalb eines Systems werden Geschwindigkeiten addiert. Eine Multiplikation von Geschwindigkeiten liegt vor, wenn auf eine noch genauer zu erklärende Weise Geschwindigkeiten innerhalb eines Systems und die Geschwindigkeit des Systems im Ganzen miteinander verknüpft werden. So gesehen ist das Neue der Mechanik gegenüber der Mathematik, Eigenschaften des System-Ganzen mit Eigenschaften der Elemente eines Systems direkt verbinden zu können. Mithilfe der Energie gelingt die Vermittlung. Das ist in meinem Verständnis der sachliche Inhalt, warum von der höheren Potenz der Energie gegenüber den Elementen des Systems gesprochen werden kann.
Die Mathematik betrachtet ruhig nebeneinander liegende Objekte (Zahlen, Punkte, Figuren) und ihre Verhältnisse zueinander. Wenn sie mit diesen Objekten operiert, ist die Reihenfolge der Operationen (die Rechenschritte bzw. geometrischen Konstruktionsschritte) wichtig, das heißt ihre logische Ordnung, aber es gibt keine innere Bewegung der einzelnen Objekte (der Zahlen oder der Figuren) oder der umfassenden Systeme von Zahlen bzw. geometrischen Gebilden. In der Physik wird dagegen von einer inneren Bewegtheit ihrer Objekte ausgegangen. Sie befinden sich im Fluss, und alle einzelnen Teilchen bewegen sich innerhalb der Strömung. Es soll der Gedanke entwickelt werden, dass die beiden in der Energie auftretenden Geschwindigkeiten zum einen die Geschwindigkeit der Strömung (das Strömen) und zum anderen die Geschwindigkeit der einzelnen Teilchen innerhalb der Strömung sind (ihr hin und her Flitzen). Das Strömen zeigt sich in der Energie, die Einzelbewegung im Impuls. Während ein Impuls in einem unendlich-kurzen Zeitmoment übertragen wird (in einer einzelnen Aktion oder physikalisch gesprochen in einem Kraftstoß), ist die Energie zu verstehen als eine kontinuierliche Folge von Impulsen über eine bestimmte Zeitdauer. Wird die Summe über alle Impulse gebildet, ergibt das die Energie. (Es können auch negative Impulse auftreten, wenn sich die Bewegungsrichtung umkehrt.)
Die Energie ist das Neue, das sich in der Mechanik gegenüber der Geometrie und Arithmetik zeigt. In der Energie lassen sich eigene Bewegungsmuster (Erhaltungsgrößen, Symmetrien) nachweisen, die es in der Geometrie und Arithmetik noch nicht gibt. Diese Unterscheidung droht aus zwei Gründen unsichtbar und unkenntlich zu werden: Die spezifischen Eigenschaften der Energie erhalten den Rang göttlicher oder höherer Bedeutung (so zum Beispiel »der von Gott eingehauchte Atem«, der Sturm und das »Brausen des Geistes«, die größere »Vitalität«, dank derer sich manche Menschen glauben über andere erheben zu können, usf.), und die Eigenschaften der Energie können ihrerseits mathematisch beschrieben werden, so dass nicht mehr erkennbar wird, was sich in ihnen gegenüber der Mathematik Neues zeigt.
Rückblickend kann gesagt werden, dass die griechische Philosophie zwar bereits die Idee der Energie hatte (dieser Begriff geht auf Aristoteles zurück und war eine von ihm in die Philosophie eingeführte eigene Wortschöpfung), aber noch nicht naturwissenschaftlich und mathematisch ausgearbeitet wurde. Das wurde erst möglich, als mit dem Monotheismus neue übergreifende Ideen entstanden, mit denen Fragen dieser Art formuliert und gelöst werden konnten, und als sich anders als in Griechenland die Naturwissenschaft mit dem Handwerk verband und messende Verfahren einführte, mithilfe derer die spezifischen Eigenschaften von Impuls und Energie genauer beschrieben und identifiziert werden konnten. Nach diesem historischen Erfolg besteht jedoch die Gefahr, dass dieser Entwicklungsweg verabsolutiert wird, was Alternativen und neue Entwicklungsrichtungen erschwert. Das ist nach meinem Eindruck auch der Grund für die Schwierigkeiten des Physik-Unterrichts, wenn den Pädagogen (den Entwicklern des Lehrplans, Schulbuch-Autoren und Lehrern) dieser Weg für so selbstverständlich gilt, dass sie nicht mehr offen sind für die Fragen der Schüler und alle Schwierigkeiten mit diesem Stoff als Unfähigkeit ansehen, mathematisch und physikalisch denken zu können.
Der einzelne Impuls verhält sich zur Energie wie ein Punkt zur Linie oder wie eine einzelne Zahl zu einem umgebenden Intervall von Zahlen. Doch kommt in der Mechanik gegenüber der Geometrie etwas hinzu, was in all den physikalischen Lehren vernachlässigt wird, die sich an der euklidischen Geometrie und dem mathematischen Kontinuum orientieren: Es gibt nicht nur einen kontinuierlichen Zusammenhang zwischen den einander folgenden Impulsen, sondern eine innere Geschwindigkeit, mit der die Impulse einander folgen. Das ist nicht zu erkennen, wenn die Kontinuität der einander folgenden Impulse ausschließlich nach dem Vorbild der kontinuierlich verbundenen reellen Zahlen auf der Zahlengerade oder der kontinuierlich auf einer Linie nebeneinander liegenden Punkte betrachtet wird. Ohne die mathematische Kontinuität zu zerreißen, gibt es in der Mechanik zusätzlich eine innere Geschwindigkeit des Systemzustandes.
Die Umgangssprache bietet eine Lösung an, die die Sache besser trifft als viele physikalische Erklärungen: Es ist zu unterscheiden zwischen Bewegung und Bewegtheit, die beide in einer jeweils eigenen Geschwindigkeit gemessen werden. Zur Vereinfachung der Rechnung wird in der Regel angenommen, dass sie die gleiche Größe haben (gleich schnell sind), wodurch jedoch unkenntlich zu werden droht, dass es sich um zwei verschiedene Arten von Geschwindigkeit handelt.
Um das anschaulich zu erklären, ist vom Beispiel der einander folgenden Wasserwellen zum Beispiel des Drucks in einem Kessel überzugehen. Hier kann schrittweise entwickelt werden: Zunächst wird ein System endlich vieler isolierter Punkte und ihrer chaotischen Bewegungen betrachtet. Kommt es zum Grenzübergang zu unendlich vielen, aber nach wie vor bewegten Partikeln, dann füllen sie mit einer inneren Bewegtheit kontinuierlich den von ihnen bedeckten Raum, und zugleich verfügt jedes einzelne Partikel weiter über einen eigenen Impuls. (Das scheint mir auch die Vorstellung zu sein, nach der Euler die Mechanik entwickelt hat.)
Während sich in den einander folgenden Wasserwellen und in der Stoßwelle in einem Seil regelmäßig Impulse fortpflanzen, wird für ein System in einen Kessel zunächst eine völlig chaotische Bewegung aller Teilchen im System angenommen. Schrittweise werden daraus bestimmte statistische Regelmäßigkeiten und Harmonien abgeleitet und eingeführt.
Im einfachsten Fall bewegen sich mehrere Teilchen auf einer gemeinsamen Gerade, die rechts und links durch zwei Wände abgesperrt ist. Wenn ein Teilchen an eine der Wände stößt, wird es reflektiert und kehrt seine Bewegungsrichtung um. In diesem Modell können nur die beiden äußersten Teilchen die Wände erreichen, wogegen alle Teilchen in der Mitte vorher auf andere Teilchen stoßen, bevor sie bis zu einer der Wände kommen könnten. (Hierbei ist in einem idealisierten Modell vorausgesetzt, dass die Wand völlig starr ist. In der Realität besteht die Wand ihrerseits aus Molekülen, die durch das Anstoßen der Teilchen an die Wand in Bewegung versetzt werden, wodurch sich die Wand aufwärmt und Wärme abgibt. Auf diese Weise gelangt in der Realität ein Teil der Impulse der Teilchen als Strahlung nach außen und auf sehr lange Dauer wird sich ein Gleichgewicht zwischen Innen und Außen herstellen.)

Bewegungen von Teilchen auf einer Linie
Teilchen bewegen sich entlang einer Linie hin und her. Nur die beiden äußeren Teilchen können an die Ränder stoßen. Die inneren Teilchen stoßen mit den jeweils benachbarten Teilchen zusammen und ändern dadurch ihre Bewegungsrichtung. Beim Stoß an die Wand wird Impuls an die Wand übertragen. Das ist mit den beiden roten Pfeilen gemeint.
Urheber: eigene Zeichnung
Es ist sicher möglich, für dies Modell den Impuls zu berechnen, der auf die beiden Wände ausgeübt wird, aber anschaulicher ist es wie in den heute üblichen Lehrbüchern und Lernhilfen mehrdimensionale Beispiele zu betrachten, in denen sich die Teilchen freier bewegen können.
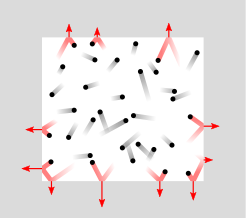
Bewegungen von Teilchen in einer quadratischen Fläche
Teilchen bewegen sich mit unterschiedlichen Geschwindigkeiten frei in einem flachen Kessel. Stoßen sie an eine Wand, werden sie reflektiert. Das Anstoßen erzeugt den Druck im Kessel.
Urheber: Von Becarlson - Eigenes Werk, see http://www.becarlson.com/, CC BY-SA 3.0, Link
An diesen Bildern sind die beiden unterschiedlichen Geschwindigkeiten zu erkennen: Zum einen die Geschwindigkeit der einzelnen Teilchen, aus der sich ihr Impuls ergibt, und zum anderen die Wiederholrate (Frequenz) der Stöße an der Wand. Die Frequenz hängt davon ab, wie viele Teilchen sich im Kessel befinden, wie dicht also der Kessel mit Teilchen gefüllt ist, wie viel Druck im Kessel ist.
Im einfachsten Fall sind alle Geschwindigkeiten gleich groß: Alle Teilchen bewegen sich mit der gleichen Durchschnittsgeschwindigkeit, die zugleich die Geschwindigkeit der Wiederholungen ist. Das sind Annahmen, die das Rechnen vereinfachen, aber das Verständnis erschweren, da die Unterschiede nicht klar hervortreten.
Jedes Teilchen, das an eine Wand stößt, wird reflektiert und kehrt wieder um. Bewegt es sich mit dem Impuls ›m · v‹ zur Wand, dann kehrt es mit dem Impuls ›− m · v‹ zurück. Die Differenz zwischen diesen beiden Werten beträgt:
(m · v) − (− m · v) = 2 · m · v
Das ist der Impuls, der dem Teilchen an der Wand mitgegeben wurde, damit es umkehren und anschließend mit der gleichen Geschwindigkeit und Masse in entgegengesetzter Richtung zurückfliegen kann. Entsprechend der Impulserhaltung nimmt die Wand bei jedem Aufprall eines Teilchen einen Impuls in gleicher Größenordnung auf, jedoch mit umgekehrtem Vorzeichen. In Summe ändert sich der Gesamtimpuls des Systems nicht.
Erster Erklärungsansatz: Summe kontinuierlich folgender Impulse
Werden für alle beteiligten Teilchen die Impulse mi · vi durchnummeriert und zusammengezählt, dann ergibt das die Summe
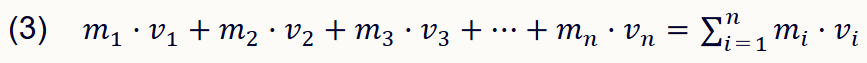
In Formel (3) wird lediglich das in der Mathematik übliche Symbol für eine Summe von n Zahlen eingesetzt.
Wird die Anzahl der Teilchen größer und geht schließlich gegen Unendlich, und wird vereinfachend angenommen, dass alle einzelnen Teilchen ununterscheidbar werden und sich mit gleicher Masse und gleicher Geschwindigkeit bewegen (bzw. ihre Abweichungen von der Durchschnittsmasse und der Durchschnittsgeschwindigkeit vernachlässigt werden können), dann ergibt sich im Grenzübergang aus der unendlichen Summe ein Integral über alle Impulse, die innere Energie:
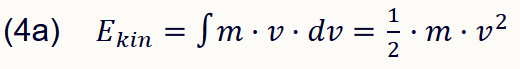
lies: Die innere Energie E eines nach außen abgeschlossenen Systems ist das Integral über die Impulse aller Teilchen in seinem Innern
In diesem vereinfachten Modell werden Bedingungen angenommen, unter denen die innere Energie identisch ist mit der rechnerisch ermittelbaren gesamten Ruheenergie aller Teilchen des Systems.
Wie erklärt sich der mathematische Inhalt der Formel? In der historischen Entwicklung der Mathematik wurden zuerst Impuls und Energie gemessen, und dann wurde der mathematische Zusammenhang erkannt, wie diese beiden empirisch gefundenen Formeln auseinander berechnet werden können. Das war wiederum der Ursprung des Differentialkalkül, nach dessen Regeln die Integration erfolgt. In diesem Beispiel genügt die Potenzregel, die aus der empirisch gefundenen Ableitung von Quadratfunktionen verallgemeinert wurde.
Was hier am Beispiel eines Systems mit vielen und im Grenzübergang unendlich-vielen Teilchen und ihren einzelnen Impulsen gezeigt wurde, kann übertragen werden auf ein einzelnes Teilchen, das einer kontinuierlichen Folge von unendlich-vielen Impulsen ausgesetzt ist. Soll die Energie dieses einzelnen Teilchens berechnet werden, ist das wiederum zunächst die Summe und im Grenzübergang das Integral über alle Impulse, die kontinuierlich einander folgen. Aus diesen Impulsen erklärt sich die Bewegung des Teilchens. Um eine mathematische Darstellung zu finden, ist der einfachste Fall zu betrachten, wenn das Teilchen durch die Vielzahl der Impulse seine Geschwindigkeit von einer Anfangsgeschwindigkeit va zu einer Endgeschwindigkeit ve ändert:
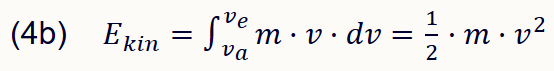
lies: Die kinetische Energie Ekin eines Teilchens ist das Integral über alle Impulse, durch die es seine Geschwindigkeit von einer Anfangsgeschwindigkeit va bis zu seiner Endgeschwindigkeit ve ändert.
Zweiter Erklärungsansatz: Der auf die Systemgrenze wirkende Druck
Wie kann dieser Übergang ohne Rückgriff auf die Integral-Rechnung erklärt werden? Hierfür ist zu erklären, warum das Quadrat v · v gebildet werden kann und wie der Faktor ½ entsteht. Anschaulich wird die innere Energie eines Kessels ermittelt aus der Summe aller Impulsübertragungen an die Außenwand. Wenn ein Teilchen durch die Reflexion an der Wand eine Impulsübertragung 2 · m · v erhält, erfolgt mit dem gleichen Betrag ebenfalls eine Impulsübertragung von 2 · m · v auf die Wand. Das ist aus Sicht der Wand der Rückstoß, der durch die Reflexion eines Teilchens erfolgt. Das wird in der Regel für ein Volumen ausgerechnet (siehe z.B. Lernhelfer), kann aber auch im vereinfachten Fall an einem Einheitsquadrat betrachtet werden. Hier werden mit M die Summe der Massen aller Teilchen und mit v ihre Durchschnittsgeschwindigkeit eingesetzt:
| (5a) | 2 · M · v | Rückstoß aller Teilchen an allen vier Außenseiten |
| (5b) | ¼ · 2 · M · v = ½ · M · v | Rückstoß an einer der vier Außenseiten (ein Viertel von [5a]) |
| (5c) | v · ½ · M · v = ½ · M · v2 | Menge aller Rückstöße im Verlaufe einer Einheitszeit, wenn die Bewegtheit des Systems ebenfalls v beträgt, wiederum bezogen auf eine der vier Außenseiten ([5b] multipliziert mit v) |
Diese Art einer Erklärung ist ähnlich verblüffend wie die Konstruktionen nach Euklid. Sie arbeitet mit zahlreichen Annahmen, die demjenigen unplausibel erscheinen, der die heute üblichen Rechnungen gewohnt ist. Es sieht so aus, als wären die Annahmen so gewählt worden, um mit ihnen das gewünschte Ergebnis zu erzielen. Im Grunde gehen aber die heute üblichen Erklärungen genauso vor. Sie wurden jedoch so oft wiederholt und von Autoritäten beglaubigt, dass sie nicht mehr hinterfragt werden. Der 2. Erklärungsansatz wurde daher bewusst eingefügt, um an einem einfachen Beispiel zu demonstrieren, wie Ableitungen dieser Art entstehen.
Anmerkung: Auch Hegel hat bisweilen versucht, komplizierte Ableitungen der mathematischen Physik zu ersetzen durch einfache Rechnungen, die ohne Integral auskommen, obwohl er die Differential- und Integralrechnung gut kannte. So verweist Ihmig in seiner Studie Hegels Deutung der Gravitation auf das »Kuriosum« (Ihmig, S. 170), dass Hegel in Enz. § 270 (HW 9.86) zeigt, dass die Newtonschen Gesetze auf direktem algebraischen Weg aus den Keplerschen Gesetzen gefolgert werden können und hierfür nicht eine infinitesimale Zerlegung der Bewegung in das infinitesimale Kräfteparallelogramm erforderlich ist. Umgekehrt vertrat später Thüring die Ansicht, dass die Newtonschen Gesetze nicht aus den Keplerschen abgeleitet werden können, »weil bei Kepler der Massebegriff nicht auftrete« (Ihmig, S. 172).
Dritter Erklärungsansatz: Zustände in einem System und System-Zustand
Philosophische Erklärungen wollen die von der Physik intuitiv eingeführten Begriffe aufklären ohne direkt auf theologische Argumente zurückzugehen. Theologie wird erst erreicht, wenn die philosophischen Begriffe ihrerseits zurückbezogen werden auf metaphysische Ideen.
Aristoteles hat nicht nur den Begriff der Energie eingeführt, sondern bei ihm sehe ich auch in seiner Diskussion der Zenonschen Paradoxien den ersten philosophischen Ansatz für die systematische Unterscheidung von Mechanik und Mathematik. Das Argument von Zenon, dass sich Achilles trotz seiner größeren Geschwindigkeit der Schildkröte immer weiter annähert und sie daher nie überholen kann, zeigt genau die innere Grenze der Mathematik, um die es hier geht. Zenon hat vollkommen recht, wenn innerhalb der Mathematik geblieben wird. Der Abstand von Achilles zur Schildkröte kann unendlich weiter geteilt werden, ohne dass es zum Überholen kommt. Überholen ist kein mathematischer, sondern ein physischer Vorgang. Zahlen und geometrische Figuren bewegen sich nicht und können einander nicht überholen. Das Überholen wird erst erklärbar, wenn nicht mehr rein mathematisch die Abstände zwischen Achilles und der Schildkröte verglichen werden, sondern ein Perspektivwechsel erfolgt und die Bewegung als physischer Vorgang für sich betrachtet wird. Aus Perspektive der Bewegung werden alle unendlich-kleinen Abstände »nebenbei« durchlaufen, wie Aristoteles unübertrefflich formulierte (Aristoteles, Physik, VIII.8, 263b). Es ist der Schwung der Bewegung, der Achilles an der Schildkröte vorbeiträgt. Die Bewegung ist nicht nur kontinuierlich, sondern hat einen eigenen inneren Zusammenhang und eigene innere Eigenschaften. (Siehe hierzu auch die Beiträge zur Russellschen Antinomie und zum Begriff des Zwischen bei Aristoteles.)
Kant blieb mit der Antinomie über die Teilung des Raums auf dem Standpunkt von Zenon: »Eine jede zusammengesetzte Substanz in der Welt besteht aus einfachen Teilen, und es existiert überall nichts als das Einfache, oder das, was aus diesem zusammengesetzt ist.« (Kant, Kritik der reinen Vernunft, B462) Hegel hat das zurecht kritisiert und ist im Prinzip zu Aristoteles zurückgekehrt. Für ihn ergibt sich der Differentialkalkül, wenn über die Linearität der Zahlengerade und der Schrittfolge bei geometrischen Konstruktionen hinausgegangen und eine neue Dimension (eine höhere Potenz) erschlossen wird, in der die Tangenten und Steigungsdreiecke sowie ihr Grenzübergang ausgeführt werden können (siehe hierzu den Beitrag über den Differentialkalkül bei Hegel). Er hat damit inhaltlich vorweggenommen, wie seit der 2. Hälfte des 20. Jahrhunderts von der Physik die Energie interpretiert wird. Für fachlich Interessierte: Es wird unterschieden zwischen dem gewöhnlichen Raum und den an den Raum angehefteten Faserbündeln, in denen die Symmetrien der Bewegung einschließlich der Energie-Erhaltung dargestellt werden.
Noch einen Schritt näher an der Naturwissenschaft hat Hegel aus der Chemie die Unterscheidung in Wahlverwandtschaften und Knotenlinien übernommen. Mit Wahlverwandtschaften ist in der Chemie gemeint, welche chemischen Stoffe dazu neigen, miteinander zu reagieren. Zugleich hat die Chemie gezeigt, dass sich die Wahlverwandtschaften in unterschiedlichen Systemumgebungen ändern können. Manche Stoffe reagieren erst miteinander, wenn die Temperatur erhöht wurde oder die stoffliche Zusammensetzung des Systems verändert ist. Daher hat Hegel unterschieden zwischen den Wahlverwandtschaften innerhalb eines Zustands und den verschiedenen Zuständen eines Systems. Die Systemzustände sind für ihn angeordnet entlang einer Knotenlinie, in der sich bestimmte Systemparameter wie der Druck oder die Temperatur verändern.
Diese Unterscheidung lässt sich auf die Mechanik erweitern und letztlich aus ihr begründen (siehe hierzu den Beitrag zum realen Maß, in dem gezeigt wird, wie heute die chemischen Systemzustände aus der Gibbs-Energie und damit mechanisch erklärt werden). Wichtig ist die klare Unterscheidung zwischen Bewegungen innerhalb des Systems und der Bewegtheit des Systems im Ganzen. So wie in der Chemie chemische Reaktionen innerhalb eines Systems betrachtet werden, sind die Stöße und Bewegungen der Teilchen innerhalb eines Systems zu verstehen. Und so wie die Chemie Systemparameter unterscheidet wie die Temperatur, den Druck oder den Aggregatzustand (gefroren, flüssig, gasförmig), sind auf analoge Weise mechanische Systemzustände zu unterscheiden. Das erklärt für mich die beiden Geschwindigkeiten, die in der Energie miteinander multipliziert werden: Das sind zum einen die Geschwindigkeiten der Teilchen innerhalb eines Zustands, wodurch ihr Impuls gegeben ist, und zum anderen die Geschwindigkeit des Zustands, was als Bewegtheit bezeichnet werden kann.
Diese Unterscheidung zweier Geschwindigkeiten eines Systems entspricht der Unterscheidung der Relativitätstheorie von Einstein, wenn Einstein zum einen Bewegungen in einem Raum und zum anderen Bewegungen des Raums (z.B. die Ausdehnung des Raums im Ganzen) unterscheidet (siehe hierzu den Beitrag über die Paradoxien der Kosmologie). (Anmerkung: Genau auf der Grenze liegt das Photon. Es hat zwar Energie und Impuls und kann wie "normale" Teilchen mit anderen zusammenstoßen, was am photoelektrischen Effekt zu erkennen ist, wenn das Photon beim Aufprallen an ein Metall einzelne Moleküle herauszubrechen vermag, aber es hat keine Ruhemasse. Es kann niemals zur Ruhe kommen und weder seine Geschwindigkeit noch seinen Impuls ändern. Einstein hat ausgehend von diesem Grenzfall die Gleichungen der Relativitätstheorie mathematisch so konstruiert, dass sich mit der Geschwindigkeit die Masse verändert bis bei der Lichtgeschwindigkeit ein Grenzwert erreicht ist. Die sicht- und messbare Geschwindigkeit des Photons ist daher ausschließlich aus der Bewegtheit des Raumzeitkontinuums zu erklären, erscheint jedoch innerhalb des Systems wie eine übliche Bewegung. Daraus ergeben sich die Paradoxien.)
Vierter Erklärungsansatz: Mitteilung
Wie ist es möglich, die Eigenschaften von Elementen innerhalb eines System direkt zu verknüpfen mit Eigenschaften des Systems im Ganzen? Warum ist es “erlaubt”, die Geschwindigkeiten der einzelnen Elemente zu multiplizieren mit der Geschwindigkeit des Systems im Ganzen? (Und warum ist es umgekehrt in der Relativitätstheorie verboten, Geschwindigkeiten innerhalb des Systems mit der Geschwindigkeit des Systems im Ganzen, d.h. der Geschwindigkeit der Raumausdehnung zu verknüpfen, wodurch Geschwindigkeiten entstehen würden, die weit über die Lichtgeschwindigkeit hinausgehen?) Die meisten Physiker und Mathematiker verstehen nicht einmal diese Frage, da für sie ausreicht, dass sich die Formel E = ½ · m · v2 in allen Messungen empirisch bestätigt und in allen darauf aufbauenden Anwendungen praktisch bewährt hat.
Wird jedoch in andere Wissenschaftsgebiete geschaut, zeigt sich die Brisanz der Frage: Man stelle sich vor, in der Mathematik würde die Größe der einzelnen Zahlen multipliziert mit Eigenschaften der Größe der übergeordneten Menge wie z.B. der Mächtigkeit der jeweiligen Zahlklasse, in der die Zahlen liegen. Wer auch nur in die Nähe eines solchen Versuchs kommt, stößt an Widersprüche wie die Russellsche Antinomie, mit der Eigenschaften einzelner Mengen mit Eigenschaften der Klasse aller Mengen widersprüchlich auf sich selbst bezogen werden. – In der Linguistik wird die Frage gestellt, ob zum Verständnis einer Sprache das Verständnis ihrer einzelnen Elemente (wie z.B. der Laute, Buchstaben, Worte, syntaktischen Regeln) zu verknüpfen ist mit einem Gesamtverständnis der Sprache. Für Wittgenstein stößt ein Nachdenken über Fragen dieser Art an eine unüberwindbare Grenze und wird sinnlos, da sich keine Worte dafür finden lassen. – In der Theologie stellt sich die Frage, wie ein alles durchwaltender monotheistischer Gott sich seinen eigenen Geschöpfen offenbaren kann. Er muss eine Sprache finden, die physikalisch gesprochen für die Elemente eines Systems verständlich ist, und zugleich mit ihr eine Offenbarung möglich machen, die das System im Ganzen verstehen lässt. Mit dieser theologischen Frage, die sich erst im Monotheismus stellt (da für polytheistische Religionen und Mythen wie z.B. den Göttern des griechischen Olymp völlig problemlos angenommen werden kann, wie sie sich unter den Menschen bewegen), ist für Hegel der Rahmen gefunden, mit der sich diese Frage der Physik fassen und lösen lässt: Es ist die Frage nach der Mitteilung. Die Physiker haben das intuitiv getroffen, als sie von der Mitteilung von Impulsen sprachen.
Das sind Beispiele, wie durch die Energie eine Einheit von Geschwindigkeiten (Impulsen) der Elemente eines Systems und des System-Ganzen (der Systembewegtheit) aufgebaut wird und wieder zusammenfallen kann. Dadurch werden zwei Wirkungen hervorgerufen, die nur dank der Energie möglich sind: Jeder System-Zustand garantiert für eine gewisse Spannbreite eine Stabilität. Ist zum Beispiel Wasser bei 0° Celsius flüssig geworden, wird der Zustand der Flüssigkeit beibehalten bis zur nächsten Grenze bei 100° Celsius. Und zum anderen kann durch die Energie ein Qualitäts-Wechsel erfolgen, wenn z.B. der quantitative Anstieg der Temperatur umschlägt in einen qualitativen Wechsel von Flüssigkeit in Gas. Diese Eigenschaften können mit Hegel anschaulich als Knotenlinie bezeichnet werden: Jeder Umschlag von einer Qualität in eine andere ist ein Knotenpunkt auf einer Knotenlinie, auf der alle Systemzustände eingetragen sind. Die Knotenlinie hat eigene Eigenschaften gegenüber den Eigenschaften innerhalb jedes einzelnen Zustands.
Anmerkung 1: Hat die Mitteilung eine Aussage unabhängig von der jeweils einzelnen Person oder dem jeweils einzelnen Objekt, von und an den sie übertragen wird? Vergleiche die Frage nach der Unsterblichkeit großer Kunstwerke oder religiöser Texte, deren Wert sich unabhängig von den jeweiligen Sendern und Empfängern ergibt. Oft hat ein Schriftsteller oder ein Komponist das Gefühl, das er nur zum Sprachrohr einer Mitteilung wird, die durch ihn Wirklichkeit wird. Richard Dawkins hat das erweitert zur Theorie der Meme: Vergleichbar den Genen breiten sich Meme über die Gehirne aus. Sie nehmen von ihnen Besitz, steuern die vom Gehirn veranlassten Mitteilungen bzw. machen einen Menschen empfänglich für bestimmte Mitteilungen, wodurch diese sich immer weiter ausbreiten können. Diese Theorie klingt nach science fiction und ist entsprechend umstritten, aber sie zeigt gut die Grundidee, um die es geht: Die Perspektive wird gewechselt von den einzelnen Sendern und Empfängern, die eine Mitteilung abgeben und empfangen zur Mitteilung selbst, die sich über die Gesamtheit der Sender und Empfänger ausbreitet.
Anmerkung 2: Es ist noch einmal zurückzukommen auf die Frage nach der Offenbarung. Wie konnte Moses wissen, dass die Gesetzestafeln, die er auf dem Berg Sinai erhielt, keine gewöhnlichen Tafeln sind? Auf den ersten Blick unterscheidet sie nichts von allen anderen Gesetzestafeln. An ihnen sind keine Eigenschaften zu erkennen, die anders wären. Sie sind aus Stein, haben die üblichen Eigenschaften wie Gewicht, Farbe, Porosität usw., und auch die Buchstaben und Worte unterscheiden sich nicht von anderen Texten. Ihre Göttlichkeit kann nur erkannt werden durch eine besondere Art der inneren Erschütterung, die Moses erlebt hat und an die anderen Juden weiterzugeben vermochte. In gewisser Weise ist es eine Art Autoritäts-Beweis, dass manche Texte für heilig gelten und andere als Machwerke von Möchtegern-Heiligen. Die Wirkung heiliger Texte ist an der Macht zu erkennen, die von ihnen ausgeht. Dieser Vorgang lässt sich nur wie von einem Ethnologen beschreiben, aber nicht beweisen. Aber die Energie liefert eine einzigartige Analogie. Die Energie zeigt, wie in der Natur völlig selbstverständlich die Bewegtheit eines übergreifenden Systems und die Bewegung der einzelnen Elemente des Systems eine gemeinsame Sprache finden, in der sie sich verstehen und mit ihnen in einer einheitlichen Formel gerechnet werden kann. Für Richard Dawkins ist daher die Religion ein Super-Meme.
Die Allgegenwart der Kraft (und ein Schluss durch die Mitte)
Wie kann der freie Fall eines Steins zur Erde erklärt werden? Mit dem freien Fall ist eine Bewegung gemeint, die nicht von außen durch einen Impuls (Kraftstoß) verursacht wird, sondern auf den ersten Blick von selbst erfolgt. Aristoteles erklärte sie aus einem inneren Mangel, wenn sich etwas in einer anderen Lage befindet als es seiner Natur entspricht. Ein Stein fällt herab, weil es zur Natur des Steins gehört, auf dem Boden zu liegen. Feuer lodert nach oben, weil es zur Natur des Feuers gehört, nicht am Boden zu bleiben, sondern in den Bereich der Luft überzugehen. Diese Art von Erklärungen wurde mit dem Monotheismus und ihm folgend der neuzeitlichen Physik kritisiert. Kräfte werden nicht mit der inneren Natur der physischen Gegenstände erklärt, sondern mit Eigenschaften, die sich aus dem System im Ganzen ergeben. In diesem Beispiel eines fallenden Steins gilt seit Galilei die Gewichtskraft der Erde als Ursache, obwohl sie nicht direkt wahrzunehmen ist, und er konnte mathematisch den Verlauf des freien Falls beschreiben, bei dem eine konstante Fallbeschleunigung in Richtung der Erdoberfläche von ca. 9,81 m/s2 messbar ist. Masse und Beschleunigung können gemessen werden, und seit Newton wird die Kraft als das Produkt von Masse und Beschleunigung definiert:
(6) F = m · a
lies: Kraft (Force) ist gleich Masse (mass) mal Beschleunigung (acceleration)
Newton konnte rein mathematisch zeigen, dass sich die Kraft zum Impuls verhält wie der Impuls zur Energie: So wie der Impuls als Grenzübergang zu verstehen ist, wenn für immer kleinere Zeiträume betrachtet wird, wie sich die Energie verändert, so ergibt sich die Kraft aus dem Grenzübergang, wenn für immer kleinere Zeiträume die Veränderung des Impulses betrachtet wird. Gleichbedeutend ergibt sich: So wie die Energie die Summe aller kontinuierlich in einem Zeitraum erfolgenden Impulse ist, so ist der Impuls die Summe einer kontinuierlich über einen bestimmten Zeitraum wirkenden Kraft. Newton konnte zeigen, dass sich die von Galilei empirisch nachgewiesene Bewegungsgleichung s = ½ · g · t2 als zweifaches Integral über die Definition der Kraft F = m · a ergibt.
Die Entdeckung dieses mathematischen Zusammenhangs und der Entwurf einer völlig neuen Rechenart, um diesen Zusammenhang mathematisch formulieren zu können (die Differential- und Integralrechnung) war der Wendepunkt, mit dem die neuzeitlichen Naturwissenschaften begründet wurden. Sie gehören daher zurecht zum Standardstoff des Schulunterrichts und werden von allen Schülern auswendig gelernt und in Prüfungen abgefragt. Dennoch ergeben alle Nachprüfungen, dass kaum jemand diese Formeln und ihren inneren Zusammenhang versteht und erklären kann, und im Alltagsbewusstsein mit Kraft etwas anderes meint. Die meisten glauben, dass ein Körper, der fortlaufend beschleunigt wird, dadurch auch an Kraft gewinnt, obwohl sich mit der zunehmenden Geschwindigkeit nur sein Impuls vergrößert. Die Gewichtskraft, von der Galilei ausging, und die Verallgemeinerung zur Kraft im Sinne von Newton sind als solche ebenso wenig sinnlich wahrzunehmen wie die Art und Weise, mit der sie andere Körper zu ihrer Bewegung veranlassen. Niemand sieht, wie die Erde den fallenden Stein anzieht. Es ist nur zu sehen, auf welchem Weg und mit welcher Geschwindigkeit und Beschleunigung er fällt. Nur der von der Gewichtskraft der Erde bewirkte Bewegungsverlauf kann beobachtet und gemessen werden. Sie wirkt über die Ferne auf einen Stein, der sich oberhalb der Erdoberfläche befindet, ohne irgendeine Art von direktem Kontakt oder vermittelndem Mechanismus auf die Körper, die von ihr angezogen werden. Sie wird daher oft als ‘Fernkraft’ bezeichnet, um den Ausdruck ‘Magie’ zu vermeiden, mit dem früher fernwirkende Kräfte benannt wurden. Der Ausdruck ‘Fernkraft’ verdeckt, welche theologische Erklärung im Hintergrund steht: Die Kraft ist allgegenwärtig. Dank ihrer Allgegenwart kann die Gewichtskraft der Erde auf Steine wirken, die sich vor dem Fall von der Erde entfernt befinden. Sie gilt unabhängig von Raum und Zeit, und es ist lediglich zu messen, wie sie bei wachsendem Abstand zur Kraftquelle schwächer wird. Die Allgegenwart (Omnipräsenz) ist eine Eigenschaft, mit der in monotheistischen Religionen das Höchste Wesen (Gott) beschrieben wird: Gott ist allgegenwärtig, und ebenso die von ihm mit der Schöpfung konstituierten Kräfte. Es war daher ein Argument von Newton gegen Leibniz, warum es einen absoluten Raum und eine absolute Zeit gibt: In ihnen zeigt sich die Allgegenwart Gottes.
Die Allgegenwart der Kraft und ihre Wechselwirkung zu verstehen, das ist die eigentliche Schwierigkeit. Wenn Kräfte allgegenwärtig sind, muss sich alles mit allem überall und immer in Wechselwirkung befinden. Die neuzeitliche Physik beschränkt sich darauf, mit ihr zu rechnen und sie fortlaufend genauer zu differenzieren. Für die neuzeitliche Physik wirken auf jeden Punkt im Raum alle Körper, die im Raum existieren, jedoch nimmt die Kraft mit der Entfernung ab. In jedem einzelnen Punkt sind zwar theoretisch alle Körper des Weltalls durch ihre Fernwirkung zu spüren, jedoch können die meisten vernachlässigt werden, da ihre Wirkung im Vergleich zu anderen zu klein ist. Aber auch wenn sich die Wissenschaft auf diese Körper beschränkt, deren Wirkung unmittelbar spürbar und messbar ist, gelingt es nicht, ein Modell der Wechselwirkung der Kräfte der verschiedenen Körper zu entwickeln, die auf einen Punkt wirken. In welcher Weise gleichen sie sich aus, verstärken sich, lenken sich gegenseitig ab und führen zu einem stabilen Verhalten des Körpers, auf den sie einwirken? Das rein mathematische Modell der Wechselwirkung versagt schon im einfachen Fall von drei Körpern, wenn keine weiteren Zusatzbedingungen ergänzt werden (Dreikörperproblem). Daher wurden unterschiedliche Konzepte entwickelt, verschiedene Kräfte nach ihrer Reichweite zu unterscheiden und zusätzliche Symmetrien zu bestimmen, die bei der Wechselwirkung erhalten bleiben. Für diese Symmetrien sind keine Ursachen bekannt, sondern sie sind ausschließlich das Ergebnis empirischer Beobachtungen. Von besonderer und weitgehend ungeklärter Bedeutung ist die in Wechselwirkungen auftretende Resonanz: Selbst mit geringer Kraft kann etwas bewegt werden, wenn dessen Eigenschwingung getroffen wird.
.gif)
Die chaotischen Bewegungen dreier Körper
Urheber: Gemeinfrei, Link
Da die Physik im 20. Jahrhundert weitgehend die ursprünglichen Ideen "vergessen" hat, die zu ihrer Gründung geführt hatten, und sich innerlich sowohl von den theologischen wie philosophischen Fragen befreit glaubt, denen sie in Wahrheit ihr Entstehen verdankt, sucht sie einen Ausweg in immer komplizierteren mathematischen Rechnungen. Sie bewährt sich in technischen Fragen mit ingenieur-mäßigem Charakter und gerät in Grundlagenkrisen und Unsicherheit in theoretischen Fragen. Kein Schüler lernt heute in der Schule, dass der von ihm gebrauchte Kraftbegriff mit Allgegenwärtigkeit zu tun hat und bekommt nur noch die mathematischen und physikalischen Formeln vorgesetzt, die es auswendig zu lernen gilt, ohne sie zu verstehen. Wer glaubt, dass sich das an der Universität ändert, täuscht sich. Auch dort beschränkt sich das Studium auf die mathematischen Formeln, mit denen Bewegungen beschrieben werden, und fragt nicht nach der Herkunft und Bedeutung der Begriffe, mit denen gerechnet wird. Ein Physiker lernt statt einer Erklärung nur, wie er sie experimentell überprüfen kann und dass sie mit deren Ergebnissen übereinstimmen.
Wer über den üblichen Schulunterricht und das Physik-Studium hinaus die Texte liest, mit denen Philosophie und Theologie der Physik eine Begründung geben wollen, wird wiederum enttäuscht sein. Ihnen ist es nicht gelungen, selbst auf die elementaren Fragen wie Kraft, Impuls und Energie eine Antwort zu geben, die von den Naturwissenschaften akzeptiert werden kann. Am weitesten gekommen sind sicher Leibniz und Hegel. Für Leibniz war es nur ein kleiner Schritt von der Allgegenwart der Kräfte zur Monadologie. Er konstruiert eine Welt aus Monaden, die es zunächst nur als Modell im Denken gibt. Die Lehre der Monaden gibt eine Orientierung, wohin sich die physikalische Forschung entwickeln kann. Leibniz postuliert für die Monaden: Anders als die Physik vernachlässigen die Monaden die Kräfte sehr weit entfernter Körper nicht, sondern können dank der kleinen Perzeptionen die Allgegenwart aller noch so weit entfernten Objekte wahrnehmen und aus ihnen ein umfassendes Bild der Welt gewinnen. Das ist den Monaden weitgehend unbewusst, aber sie haben die Möglichkeit, dies schrittweise aufzuklären. Während für Newton mit dem absoluten Raum die Allgegenwart Gottes gegeben ist, hat Leibniz ein dynamisches Bild entworfen, in dem die Allgegenwart aller Kräfte zu spüren und aus ihnen dank übergeordneter Prinzipien (Prinzip der kleinsten Wirkung, Harmonie-Prinzip) ein übergreifendes Weltbild zu gewinnen ist. Anders als Newton hat der konservative Leibniz erkannt, dass in der Gleichberechtigung und Allgegenwart aller Körper und ihrer Kräfte ein demokratisches Prinzip enthalten ist, das der Individualität der einzelnen Körper umfassende Entfaltungsmöglichkeiten gibt und objektiv im Gegensatz zur feudalen Ordnung und ihrer hierarchischen Stände steht. Es ist nicht die Frage, wer sich durchsetzt und Macht (Kraft) über die anderen gewinnt, sondern nach welchen gemeinsamen Prinzipien ein Ausgleich gefunden werden kann, der für alle optimal ist.
Auf den ersten Blick vollzog Hegel gegenüber Leibniz eine Wende zurück zur Restauration früherer Verhältnisse und entspricht damit dem politischen Zeitgeist des Biedermeier, nachdem Napoleon und mit ihm die letzten Reste der Französischen Revolution besiegt waren. Für ihn zeigt sich im freien Fall das übergeordnete Prinzip einer allgegenwärtigen Bewegung zum Zentrum oder noch allgemeiner gesprochen zur Mitte (HW 6.423-427, HW 9.75-108). Wenn eine Fallbewegung beobachtet werden kann, muss es ein Zentrum geben, wohin alles fällt. Doch was ist mit Zentrum und Mitte gemeint? Es gibt bei Hegel genügend Ausführungen, die im politischen Kontext die Mitte als eine konstitutionelle Monarchie verstehen lassen. In seinen logischen und naturphilosophischen Arbeiten lässt sich jedoch auch eine andere Lesart entdecken, die Mitte als einen Konsens zu verstehen, die allen gerecht wird und ihnen im freien Zusammenspiel ihrer Kräfte größte Entfaltungsspielräume gibt, was dem Harmonie-Prinzip von Leibniz entspricht.
Sein Verständnis der Schwerkraft lässt sich in mehreren Schritten entwickeln:
(i) Gibt es in einem System ein dominierendes Zentrum wie z.B. die Erde innerhalb der sie umgebenden Sphäre, dann bewegt sich alles zu diesem Zentrum. Gibt es ein Zweikörpersystem bestehend aus einer Sonne und einem Planeten, dann gelten die Keplerschen Gesetze und ermöglichen eine relativ freie, andauernde Bewegung entlang der elliptischen Planetenbahn, auf der sich der Planet der Sonne in abwechselnden Phasen nähert und entfernt und in regelmäßigen Abschnitten sowohl seine Bewegung fortführt (kontinuiert) wie auch umkehrt (revolutioniert). Gibt es ein System aus endlich und im Grenzübergang unendlich vielen ungefähr gleich großen Körpern, dann bewegen sich die Körper zur rechnerisch bestimmten Mitte des Systems. Hegel hat betont, dass die Mitte kein tatsächlich vorhandener Zentralkörper sein muss, sondern in einem höheren Sinn die Mitte des Systems, in dem es seinen Ausgleich findet.
(ii) Das bedeutet zuende gedacht, dass es nicht nur die Gravitationskraft gibt, die alles zu einem Zentrum führt, sondern dass es in Verallgemeinerung der Zentrifugal- und Zentripetalkraft im Planetensystem zugleich eine gegenläufige Kraft geben muss. Die Mitte ist nicht mehr ein Zentralkörper, der alles anzieht, sondern der Ausgleich der beiden gegenläufigen Kräfte. Inhaltlich wird für mich damit wieder die Philosophie von Aristoteles erreicht: Jedes System strebt danach, sich entsprechend seiner Natur zu optimieren. Allerdings wird heute anders als von Aristoteles nicht mehr von der Erde als Mitte gesprochen, um die sich die anderen Elemente Wasser, Luft und Feuer aufbauen und alles zu seinem natürlichen Ort strebt, sondern als Ausgleich der Wechselwirkung der allgegenwärtigen Kräfte. Unter diesen Kräften muss es Kräfte geben, die als ordnende Prinzipien wirken. Ohne auf Hegel Bezug zu nehmen, hat Einstein das weiter ausgearbeitet und in eine mathematische Form gebracht: Er erkannte, dass es im Weltall neben der Gravitationskraft eine gegenläufige, sich nach außen ausdehnende (expandierende) Kraft geben muss, die er neutral als Lambda-Konstante bezeichnete, ohne die über lange Zeiträume betrachtet alles in sich zusammenstürzen würde und ohne die heute kein Modell des Universums mehr auskommt.
(iii) In einer naturromantischen Sprache hat Hegel der Schwerkraft, d.h. der Schwere und dem Gewicht der Materie, die Lichtkraft des Aufstrahlens und der Aufklärung gegenübergestellt. Er hat in seiner umfassenden Arbeit zur Neubegründung einer Wissenschaft der Logik versucht nachzuweisen, wie in den Prinzipien, die allem Denken zugrunde liegen, bereits die Unterscheidung von Anziehung und Abstoßung (Attraktion und Repulsion) und darauf aufbauend von Schwere und Licht enthalten ist. Er hat ähnlich wie Kant nachweisen wollen, dass wir gar nicht anders können, als in den Begriffen von Schwere und Licht, von Trägheit und Erleuchtung zu denken. Er hat für mich letztlich ähnlich wie Leibniz zeigen wollen, welche Prinzipien dem Denken zugrunde liegen und ihm volle Freiheit gewähren, statt es wie in der vorgefundenen formalen Logik auf starre Regeln einzuschränken.
(iv) Der Clou seiner Ausführungen zur Schwerkraft liegt daher für mich dort verborgen, wo er die Mitte, in deren Ausgleich die einander widerstrebenden Kräfte sich sammeln, interpretiert als die Mitte eines Schlusses: Sie ist für ihn »die objektiv allgemeine Mitte, welche das Insichsein des relativen Individuums und seine Äußerlichkeit zusammenschließt und festhält« (HW 6.425), was er in diesem Zusammenhang ausdrücklich als die Mitte eines Schlusses versteht. Mit der Mitte eines Schlusses ist der terminus medius gemeint, über den von A auf B geschlossen werden kann. Um das in eigene Worte zu übersetzen: Die einander entgegengerichteten Kräfte bewegen die Dinge auf eine ausgleichende Mitte, die vom Denken als solche erkannt werden kann. Gelingt es dem Denken, diese Mitte zu erkennen und zu ergreifen, dann kann sie als Mitte für einen Schluss dienen, mit dem von denen einzelnen Dingen und den auf sie wirkenden Kräfte über diese Mitte sowohl auf andere Dinge im gleichen System wie auch auf die Prinzipien des Systems im Ganzen geschlossen werden kann. Galilei und Newton geben für ihn Beispiele, wie ein solcher Schluss anhand der objektiv vorliegenden Daten gezogen werden konnte. Er sieht seine eigene Aufgabe als Philosoph darin zu erkennen, dass ihnen dieser Schluss möglich war, weil sie der gegebenen Bewegung der Dinge folgen konnten und weil sie – wie alle Menschen – über eine von Gott verliehene Fähigkeit des Denkens und Schließens verfügten. Bleiben beide unverbunden, versagt das Denken. Damit hat er aus meiner Sicht den von Leibniz eingeführten Gedanken der Monaden, ihrer Perzeptionen und ihres Strebens (appetitus), die dem Harmonieprinzip folgen, fortgeführt.
(v) Was Hegel über die Mitte sagt, zu der objektiv alle Körper streben und die im Innern der Denkbestimmungen angelegt ist, ist für ihn nach meinem Eindruck zugleich ein Gleichnis, wie er seine eigene Philosophie versteht: Er untersucht, auf welche gemeinsame Mitte alle Realwissenschaften von sich aus tendieren, ohne sich dessen bewusst zu sein, und will in einem nochmals übergreifenden Schluss über diese Mitte auf die allen Denkprozessen immanent zugrunde liegenden Denkbestimmungen schließen. Das ist der übergreifende Schluss, auf dem die Wissenschaft der Logik beruht, und der von Hegel in knappen Worten am Ende der Enzyklopädie angesprochen ist (Enz., §§ 575-577, HW 10.393f).
Das Beispiel Radioaktivität
Vorbereitend: Wie schwierig es ist, die Begriffe Kraft, Impuls und Energie zu verstehen und anzuwenden, soll zusammenfassend am Beispiel der Radioaktivität gezeigt werden. Oft wird gesagt, Radioaktivität überträgt Energie an eine menschliche Zelle und beschädigt dadurch das in ihr enthaltene Erbgut. Das ist ungenau. Erstens wird hier sprachlich nicht unterschieden zwischen drei unterschiedlichen Vorgängen: Die Umwandlung eines Atomkerns, die dabei freiwerdende Strahlung und die von der Strahlung im organischen Gewebe verursachten Schäden. Mit Kraft, Impuls und Energie der Radioaktivität werden meistens ausschließlich die Eigenschaften der freigewordenen ionisierenden Strahlung gemeint, aber weder die Kraft, der Impuls und die Energie, die zur Umwandlung eines Atoms geführt haben, noch die Kräfte, die im Verlaufe dieser Umwandlung die Strahlung abgeben und mit ihrem Impuls versehen. – Zweitens wird gesagt, dass Energie an die Zelle mitgeteilt wird. Die Strahlung teilt beim Stoß den Elementen im Gewebe, auf die sie trifft, einen Impuls mit und verändert dadurch ihre Geschwindigkeit und ihre kinetische Energie. Das können einzelne Elektronen in den biologischen Makromolekülen sein, die aus ihrer Umgebung herausgeschlagen werden, wodurch das Gewebe bzw. Erbgut durchlöchert und beschädigt wird. Es kann zu unerwünschten chemischen Folgeprozessen kommen und zu langfristig wirkenden Spätfolgen, wenn die in der Zelle ablaufenden Prozesse gestört sind und zum Beispiel Krebs entsteht.
Der Vergleich mit den üblichen Begriffen von Kraft, Impuls und Energie wird weiter dadurch erschwert, dass nicht die Energie der ionisierenden Strahlung, sondern die Gefährdung gemessen wird: Statt von Energie wird von Dosis (oder genauer: Strahlendosis) gesprochen. Das ist nicht die Energie der Strahlung oder des strahlenden Objekts, sondern die vom bestrahlten Objekt je kg aufgenommene Energie. "Die Einheit ist der Quotient aus der aufgenommenen Energie und der Masse des Körpers." Das wurde früher in der Maßeinheit Röntgen gemessen. Heute hat sich die Maßeinheit Gray durchgesetzt. Letztlich interessiert aber auch nicht die Dosis oder Dosisleistung (das ist die Dosis je Zeiteinheit), sondern die Gefährdung, die wiederum abhängt von den Eigenschaften der jeweiligen bestrahlten Gewebe. Daher wird die Dosis nochmals gewichtet mit biologisch bestimmbaren Faktoren, und im Ergebnis wird mit der Einheit Sievert gemessen, wie groß die Gefährdung auf ein typisches biologisches Gewebe ist. Das Sievert ist für alle gesundheitlichen Fragen die kennzeichnende Maßeinheit, doch darf sie nicht verwechselt werden mit Kraft, Impuls oder Energie, sondern misst in einer mehrstufigen Rechnung das von der Strahlung ausgehende Gesundheitsrisiko.
Bei dieser Betrachtung wird die radioaktive Strahlung als ein Strom mechanischer Partikel betrachtet, auf die die üblichen mechanischen Eigenschaften zutreffen. Wird dagegen die Kraft betrachtet, die diesen Strom auslöst, ist ein abstrakteres Modell zu verwenden, mit dem die in der Mechanik entwickelten Begriffe von Kraft, Impuls und Energie auf andere physikalische Vorgänge übertragen werden. Die der Radioaktivität zugrundeliegende Kraft wird als schwache Kernkraft bezeichnet und hat viele Eigenschaften mit der starken Kernkraft gemeinsam. (Besonders interessant sind die erstmals 1930 von Pauli vorhergesagten Neutrinos, da sie nur der schwachen und nicht der starken Kernkraft unterliegen, aber über eine eigene Energie verfügen. An ihnen können daher besonders gut die spezifischen Eigenschaften der schwachen Kernkraft untersucht werden.)
Was ist bei der Radioaktivität der Impuls: Während in der Mechanik eine Ortsbewegung betrachtet wird, die in Metern gemessen werden kann, liegt der Radioaktivität die schwache Wechselwirkung zugrunde. Die bei der schwachen Wechselwirkung hervorgerufene Bewegung ist keine Ortsveränderung, sondern eine innere Umwandlung der wechselwirkenden Teilchen (es wäre von metabole statt kinesis zu sprechen). Die Geschwindigkeit ist daher bei dieser Wechselwirkung nicht das Verhältnis von Weg zu Zeit, sondern das Verhältnis der Anzahl von Umwandlungen (Ereignissen) zur Zeit. Die kleinste Einheit ist das Becquerel: 1 Bq ist eine Umwandlung (Ereignis) pro Sekunde. Wird weiter an die Stelle der Masse in der Mechanik die Anzahl der Elementarladungen der sich umwandelnden Teilchen gesetzt, dann ergibt sich der Impuls aus dem Produkt der Umwandlungen pro Sekunde (der Geschwindigkeit) und der Anzahl der beteiligten Elementarladungen (der Masse).
Warum und wie häufig kann es zu Umwandlungen eines Atoms kommen? Die Physiker unterscheiden innere und äußere Ursachen. Die Wahrscheinlichkeit einer Umwandlung eines Atomkerns wird als dessen Instabilität bezeichnet und mit der Halbwertszeit gemessen. Das sind verschiedene Ausdrücke, die alle dasselbe bedeuten: Die Geschwindigkeit der radioaktiven Umwandlung. Ursachen können die Größe des Atoms und äußere Einflüsse sein. Bei größeren Atomen werden gegenüber der von der starken Wechselwirkung ausgelösten Bindungsenergie die elektrostatischen Kräfte zunehmend stärker, durch die sich die jeweils elektrisch positiv geladenen Protonen im Atomkern voneinander abstoßen. Das führt zur Instabilität und kann die Umwandlung des großen Atomkerns in kleinere Atomkerne bewirken, die einzeln jeweils eine höhere Bindungsenergie haben. In der Bilanz (Summe) verringert sich durch die Spaltung die Energie und die Energie-Differenz wird frei. Der genaue Ablauf hängt davon ab, welche Atome sich umwandeln und in welche Bestandteile sie zerfallen. Das Ergebnis kann sowohl die freiwerdende ionisierende Strahlung sein, wie auch die in Kernkraftwerken genutzte freiwerdende Wärme oder die Zerstörungskraft in Atombomben. Wichtig ist mir an dieser Stelle nur der Gedanke, dass es eine Geschwindigkeit (Häufigkeit) der Umwandlungen gibt, die zusammen mit der Anzahl der beteiligten Elemente als der Impuls der Radioaktivität bezeichnet werden kann. Dieser Sprachgebrauch ist heute jedoch nicht üblich, und stattdessen gibt es eine verwirrende Vielfalt unterschiedlicher Begriffe für das gleiche Phänomen. (Ergänzung: Andere Ursachen für die Instabilität eines Atomkerns können der Beschuss eines Atoms durch Teilchen von außen wie das Einfangen von Elektronen durch den Atomkern sein, wodurch ebenfalls die Stabilität durcheinander gebracht wird.)
Anmerkung: Beim Freisetzen der Strahlung im Verlaufe einer Atomumwandlung entsteht im Atom wie bei einem Gewehrschuss ein Rückstoß. Der Impuls, der der Strahlung mitgegeben wird, wird ausgeglichen durch einen entgegengesetzten Impuls, der auf das abgebende Atom wirkt. Das Atom wird in Bewegung versetzt, wodurch für lange Zeit eine genauere Untersuchung der Vorgänge im Atom erschwert wurde. Erst Rudolf Mößbauer (1929-2011) ist es durch seine Arbeiten 1955 bis 1957 am Max-Planck-Institut für medizinische Forschung in Heidelberg gelungen, die Wirkung des Rückstoßes aufzuklären und mathematisch zu beschreiben (Mößbauer-Effekt).
Was ist die Kraft: Eine Kraft erhöht oder bremst eine Geschwindigkeit und enthält daher als einen Faktor die Beschleunigung. Im Fall der Radioaktivität bewirkt eine Kraft, dass die Häufigkeit der Umwandlungen pro Zeit erhöht oder verringert wird. Diese Kraft wird als schwache Kernkraft bezeichnet. Ihre Reichweite ist extrem kurz und beträgt 10−16 Meter. Das bedeutet nicht, dass die Kraft außerhalb dieser Reichweite völlig entfällt, aber sie ist vernachlässigbar klein. Nur Teilchen, die sich so nahe kommen und hierbei die elektrische Abstoßung überwinden, üben die schwache Kernkraft aufeinander aus. Die Physik geht daher davon aus, dass diese Kraft nur innerhalb von Elementarteilchen wie dem Elektron und Proton spürbar ist und zu Umwandlungen der Quarks, – das sind die Bestandteile der Elementarteilchen –, führt.
Die Aufgabe der Kernphysik ist daher, die geeigneten Kräfte zu finden und die Instrumente und Möglichkeiten zu verstehen, wie sie zu steuern sind, um die Geschwindigkeit der Umwandlungen in den Atomkernen zu erhöhen und wieder zu bremsen.
Was ist die Energie: Mit der Energie der Radioaktivität wird irreführend meist die Energie der freiwerdenden Strahlung und nicht die Energie der schwachen Kernkraft gemeint. (Das liegt daran, dass sowohl bei Atombomben wie bei Kernkraftwerken im Grunde nur die als Nebeneffekt freiwerdende Energie von Interesse ist, sei es aufgrund ihrer zerstörerischen Kraft oder als nutzbare Energie.) Eine "richtige" Bestimmung der radioaktiven Energie muss nach dem Vorbild der Mechanik anders erfolgen: Sie setzt sich zusammen aus dem Produkt der Bewegung der einzelnen Elemente und der Bewegtheit des Systems. Die Bewegung der einzelnen Elemente wird in Becquerel gemessen. Die Bewegtheit des Systems zeigt wie in der Mechanik, wie sich übergreifend das System im Ganzen bewegt.
Mathematisch handelt es sich um einen inneren Zusammenhang, der die verschiedenen einzelnen Bewegungen aller Elemente des Systems verbindet. Wird das System wie üblich in einem Raumzeit-System beschrieben, in dem eingetragen ist, wie sich alle Teilchen im Laufe der Zeit umwandeln, dann kann zum einen an jedem einzelnen Punkt dieses Systems die jeweils lokale Bewegung gemessen werden (das ist hier die Häufigkeit von Umwandlungen, quantenmechanisch gesprochen die Übergangswahrscheinlichkeit von einem Zustand in einen anderen Zustand) und zum anderen das innere Band zwischen den lokalen Zuständen. Das klingt sehr komplex, lässt sich aber am Beispiel eines schwingenden Seils veranschaulichen: Wenn ein Seil schwingt, kann zum einen in jedem Zeitmoment an jeder Stelle gemessen werden, welche kinetische und potentielle Energie das betreffende Teilchen des schwingenden Seiles hat, und zum anderen, welche innere Spannung es im gesamten Seil gibt, die die einzelnen Teile eines Seils zusammenhält. So ist es auch bei der schwachen Kernkraft. Zum einen hat jedes Teilchen seinen eigenen Impuls (die Häufigkeit der Umwandlungen), und zum anderen sind durch das System die räumlich und zeitlich benachbarten Abschnitte durch eine übergreifende Spannung miteinander verbunden. (Für an der Mathematik Interessierte: Mathematisch ist der lokale Zustand beschrieben durch eine Faser, die am jeweiligen Punkt in der Raumzeit angebracht ist, und die Gesamtheit aller Zustände durch das Bündel der Fasern, das Faserbündel, und den im Faserbündel zu beschreibenden Zusammenhang. Hier stimmt der in Mathematik gebrauchte Fachausdruck ‘Zusammenhang’ mit seiner philosophischen Deutung überein.)
Die Kernphysik muss daher nicht nur die Kräfte verstehen, mit denen die Umwandlungen im Atomkern ausgelöst und wieder gebremst werden können, sondern auch die übergreifende Energie dieses Prozesses.
Anhang 1: Newton über das Momentum
Der lateinische und im Englischen übernommene Ausdruck ‘momentum’ zeigt die innere Begriffsvielfalt besser als das im Deutschen gebräuchliche ‘Impuls’. Mit Moment ist sowohl der Zeitmoment gemeint, der Augenblick als kleinste Einheit innerhalb des kontinuierlichen Zeitflusses, wie auch die kleinste Einheit, die nur im Zusammenhang mit anderen Momenten verstanden werden kann und die übergreifende Einheit ergibt. In diesem Sinn spricht Hegel von Momenten eines einheitlichen Begriffs, die nicht – wie meist üblich – voneinander isoliert betrachtet werden dürfen. Momente können nur innerhalb eines Kontinuums verstanden werden und sind daher Beispiele für imprädikative Urteile (siehe hierzu die Ausführungen zur Russellschen Antinomie).
In der Originalveröffentlichung wird sehr deutlich, wie für Newton Impuls nahezu synonym gebraucht wird mit ‘verschwindender Größe’ oder in seinen eigenen Worten »principia jamjam nascentia finitarum magnitudinum«. Das würde ich wörtlich übersetzen als »Keim und Prinzip der gerade entstehenden endlichen Größen«, wobei »principia« gedeutet wird als lateinische Übersetzung von arché (Anfang, Prinzip, Herrschaft).
»Produkte, Quotienten, Wurzeln, Rechtecke, Quadrate, Kuben, Quadratseiten, Würfelseiten und ähnliche. Diese Größen betrachte ich hier als unbestimmt und veränderlich (indeterminatas & instabiles), und gleichsam durch eine beständige Bewegung oder Fluß fortwährend wachsend oder abnehmend (quasi motu fluxuve perpetuo crescentes vel decrescentes). Ihr augenblickliches Inkrement oder Dekrement begreife ich unter der Benennung Moment (sub nomine momentorum), so daß die Inkremente als additive oder positive, die Dekremente als subtraktive oder negative Momente angesehen werden. Die Momente hören auf, Momente zu sein, sobald sie eine endliche Größe erhalten. Man hat unter ihnen die eben entstehenden Anfänge endlicher Größen zu verstehen (principia jamjam nascentia finitarum magnitudinum).« (Newton, Mathematische Principien der Naturlehre Buch II, Abschnitt 2, § 10, S. 243, zitiert bei Büchel, S. 227f; Wikisource)
Anhang 2: Übergang von Impuls und Energie
Walter Rella weist in einer Zuschrift vom 6.10.2016 auf den Übergang von Impuls zu Arbeit hin. Wie das Beispiel des Billard zeigt, erfolgt eine reine Impulsübertragung nur dann, wenn der Stoß "in einem Augenblick" erfolgt (was von den Physikern abweichend von der Umgangssprache als "elastisch" bezeichnet wird), während ein länger andauerndes Führen der Billardkugel eine Arbeit ist. Das kann verallgemeinert werden: Eine Impulsübertragung erfolgt durch den elastischen Stoß, Energieübertragung durch zeitlich andauernde Arbeit. Bei einer Arbeit wird die Grenze wichtig: Wenn zum Beispiel in einem Kessel fortdauernd von Innen Partikel an die Außenwand stoßen, leisten sie eine Arbeit, die als der Druck auf den Rand erkennbar ist. Es könnte sein, dass auf ähnliche Weise in einem größeren Atom zwischen einem Inneren und einem Rand unterschieden werden kann: Es gibt eine instabile Bewegtheit im Innern, die auf einen Rand so lange Druck ausübt, bis sich der Rand zumindest teilweise auflöst und die Strahlung durchlässt. Die nach außen durchtretende radioaktive Strahlung entspricht der an einem sich aufheizenden Kessel nach außen austretenden Wärme.
Die Bewegtheit eines Systems ist erst zu erkennen, wenn am System ein Innen und eine Grenze unterschieden werden können. An der Grenze multiplizieren sich die Geschwindigkeit der einzelnen Elemente und die Geschwindigkeit des Systems und äußern sich als Energie. Energie ist daher eine Übertragung, die dann auftritt, wenn ein System fortlaufend auf eine Grenze trifft. Logisch kann die Energie mit den Begriffen von An-sich-Sein, Grenze und Sein-für-Anderes beschrieben werden: Energie tritt erst dann auf, wenn ein System in Wechselwirkung mit einem Anderen tritt, von dem es durch eine Grenze getrennt ist. Für die Energie ist daher zweierlei notwendig: Es muss sich um ein System handeln, das viele Elemente mit einer Eigenbewegung enthält, und um ein System, das in Wechselwirkung mit einem Außen tritt. In der Energie werden die Geschwindigkeiten multipliziert, die gewissermaßen hierarchisch verschachtelt sind: Die Geschwindigkeit der Wechselwirkung von Elementen in einem System, und die Geschwindigkeit der Wechselwirkung des Systems mit einem anderen System.
Diese beiden Geschwindigkeiten werden nach Louis de Broglie (1892-1987) unterschieden als Wirkungsquantum h innerhalb des Systems und Einwirkungsquantum k (Boltzmann-Konstante) von außen. De Broglie vermutet, dass es zwischen beiden eine mathematische Beziehung gibt, die letztlich auf die aus den Kreisfunktionen zurückgehende Eulersche Zahl e zurückgeht. Mit der Eulerschen Zahl e und ihrer Deutung über das natürliche Bit nbit wäre eine Größe gefunden, die für das System der Natur im Ganzen übergreifende Bedeutung hat, und damit ein konkreter Nachweis für eine neue Metaphysik.
Siglen
HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971; Link
KrV = Immanuel Kant: Kritik der reinen Vernunft (1781, 1787)
Literatur
Arbeitsgruppe Didaktik der Physik (Universität Regensburg, Fakultät für Physik): Der Weg zum physikalischen Kraftbegriff von Aristoteles bis Newton; PDF
Udo Backhaus und Hans-Joachim Schlichting: Didaktische Überlegungen zur Einführung von Kraft und Masse
in: Der Physikunterricht 13/1, 7 (1979); PDF
Wolfgang Bonsiepen: Die Begründung einer Naturphilosophie bei Kant, Schelling, Fries und Hegel, Frankfurt 1997
Gregor Büchel: Geometrie und Philosophie, Berlin 1987
Hans-Jürgen Caspar: Umlaufzeit einer Mondfähre (mit einer anschaulichen Erläuterung von Kraft, Geschwindigkeit und Beschleunigung); Link
Stefan Goessner: Dynamik, Lehrveranstaltung 2006; Link
Dieter Heuer und Thomas Wilhelm: Aristoteles siegt immer noch über Newton – Unzulängliches Dynamikverstehen in Klasse 11
in: Der mathematische und naturwissenschaftliche Unterricht 50, Nr. 5, 1997, S. 280 - 285; PDF
Karl-Norbert Ihmig: Hegels Deutung der Gravitation, Frankfurt 1989
Max Jammer: Der Begriff der Masse in der Physik, Darmstadt 1964
Thomas Leinkauf: Einheit, innere Kraft und substantielle Form. Der Begriff der Substanz bei Giordano
Bruno und Gottfried Wilhelm Leibniz
in: La filosofia di Giordano Bruno, Rom 2003, S. 417-449; PDF
Anneliese Maier: Ausgehendes Mittelalter, 2 Bd., Rom 1964, 1967
Erhard Oeser: Die Kontroverse mit Hegel
in: Heinz Paetzold, Helmut Schneider (Hg.): Schellings Denken der Freiheit, Kassel 2010, S. 195-211
Helmut Pulte: Das Prinzip der kleinsten Wirkung und die Kraftkonzeptionen der rationalen Mechanik, Stuttgart 1989
Shmuel Sambursky: Das physikalische Weltbild der Antike, Zürich, Stuttgart 1965
Michael Wolff: Geschichte der Impetustheorie, Frankfurt 1978
2016
© tydecks.info 2016



