Walter Tydecks
synecheia – der aristotelische Begriff des Continuums
– der Zusammenhang als Stoff der Größe
Inhaltsverzeichnis
Entwicklung des Prinzips Kontinuum
(1) Das Kontinuum ist das unbegrenzt Teilbare
Ordnung (taxis) und Reihenfolge der Zahlen
Lage (thesis) und Reihenfolge der Figuren
(2) Das Kontinuum ist das Zusammengewachsene
(3) Das Kontinuum besteht nicht aus Punkten
Der Zusammenhang als Stoff der Größe
Entwicklung des Prinzips Kontinuum bei Aristoteles (nach Dehn, Waschkies und Seidel)
Der Begriff des Zusammenhangs (synecheia, lat. continuum, wörtlich das Verwachsene, Zusammengewachsene) hat für Aristoteles eine Schlüsselrolle. Wie der Begriff der Größe geht der Begriff des Zusammenhangs weit über die Mathematik hinaus, auch wenn vor allem dank Cantor und anderen die mathematische Bedeutung des potentiell und aktual Unendlichen des Continuums wieder intensiv diskutiert wurde. Ursprünglich ist mit Zusammenhang das Zusammenhängende der Welt im Ganzen gemeint. Heidegger und Benjamin sprechen in ähnlicher Weise vom »Waltenden« oder »Durchwaltenden«.
Mit diesem Begriff hat Aristoteles seine Position in der naturphilosophischen Tradition gefunden. Er unterscheidet als erster die Natur (physis) von ihrem Stoff (hyle), wobei er als Ausdruck für den Stoff mit hyle wörtlich das Holz, Gewächs wählt, das heißt einen biologischen Ausdruck mit innerer Lebendigkeit. Das Verwachsene (synecheia) zeigt die Eigenschaft des Holzes, an der Aristoteles gelegen ist. Im folgenden Kommentar soll gezeigt werden, wie sich Zusammenhang und Größe zueinander verhalten wie Stoff und Form. Während Aristoteles jedoch für den Begriff der Größe in der Figur (schema) eine mathematische Verselbständigung (chorizein) gesehen hat (Phys. II.2, 193b31), hat er keinen vergleichbaren Begriff zur mathematischen Verselbständigung des Zusammenhangs eingeführt. In diesem Kommentar soll die These entwickelt werden, dass dies die Dimension (diasthema) ist.
Welche Macht mit dem Zusammenhang verbunden ist, zeigen die Vorgänger von Aristoteles. Den Ursprüngen am nächsten stehen wohl die Phythagoreer. Für Philolaos wird durch das Herdfeuer (hestia) die Mitte, der Zusammenhalt (synoche) und das Maß der Natur (metron physeos) hergestellt und gesichert. (»Philolaos sagt, es gebe in der Mitte um das Zentrum ein Feuer, das er Herd (hestia) des Weltalls nennt und Haus des Zeus und Mutter der Götter und Altar und Zusammenhalt (synoche) und Maß der Natur ((metron physeos)«, Diels Kranz, Fragmente der Vorsokratiker, 44 A 16). Mit Hestia bezieht sich Philolaos auf die ursprüngliche Götterwelt. Die Herdgöttin Hestia ist nicht einfach für die Einheit der Welt, sondern mit dem Herdfeuer für den Zusammenhang, das Erwärmende und Belebende verantwortlich. Wenn sie das Herdfeuer schützt, sichert sie die Grundlagen des Lebens. Zugleich steht Hestia für die größte Krise der griechischen Geschichte. Sie hatte den Olymp verlassen, als sich mit der Ankunft des Dionysos dort die Verhältnisse radikal geändert hatten. Wenn Philolaos dennoch auf Hestia Bezug nimmt, will er mit seiner Vorstellung des Zusammenhalts auf eine ursprüngliche Weltordnung zurückgehen, die durch die neuen Verhältnisse nach dem Weggang von Hestia tief erschüttert war. Als Hestia den Olymp verlassen hatte, drohte der ursprüngliche Zusammenhang und mit ihm der Schutz der Welt unterzugehen. Wenn Philolaos ihren Namen wieder aufgreift, möchte er mit seiner Naturphilosophie diese Weltordnung in ihrem Namen wieder beleben. Er könnte hier in der Tradition der orphischen Überlieferungen stehen, die er auf seine Art fortführen will.
Bei Parmenides ist von solch einer Grundhaltung nur noch wenig zu spüren, aber auch er gebraucht den Begriff Zusammenhang. In dem von ihm überlieferten Fragment 8 des Lehrstücks über die Natur heißt es, »niemals war es, nie wird es sein, da es jetzt ist, alles zugleich, das Eine, kontinuierlich« (oude pot' ên oud' estai, epei nun estin homou pan, hen, suneches; Quelle). Das Zusammenhängende stellt die innere Einheit des Einen her, also dasjenige an der Einheit, wodurch sie zum Eins wird.
Heraklit erwähnt zwar in Fragment 30 nicht mehr direkt den Zusammenhang (syneches), sondern spricht nur noch von Maßen (metra). Um so deutlicher geht er auf die Bedeutung des Feuers zurück. Allerdings ruft er nicht mehr den Namen der Hestia an, sondern spricht stattdessen vom »ewig lebendigen Feuer (pur aeizôon): »Diese Weltordnung (kosmon tonde), dieselbige für alle Wesen, schuf weder einer der Götter noch der Menschen, sondern das ewig lebendige Feuer war immerdar und ist und wird sein, erglimmend nach Maßen (metra) und erlöschend nach Maßen« (Quelle).
Das alles nimmt Aristoteles auf. Mit dem Zusammenhang sieht er aus der Physik ein Prinzip hervorgehen, das für ihn die Stelle einnimmt, die bei Platon die Zahl hat. Während für Platon die Zahl der Stoff ist, aus dem die Mathematik gemacht ist, ist das für Aristoteles der Zusammenhang. Statt wie Platon die Idee der Zahl der Wahrnehmung der Natur gegenüberzustellen, will er zeigen, wie aus dem Verständnis der Natur das Prinzip des Zusammenhangs gewonnen werden kann.
Dieser Ansatz kann als gelungen gelten, wenn sich das Zusammenhängende als Stoff der Größen verstehen lässt, wobei sich Aristoteles ausdrücklich auf den seit Eudoxos neu eingeführten Begriff der Größe (megethos) bezieht. Damit hat er zugleich eine Antwort auf den Atomismus gefunden, der sich letztlich nie entscheiden konnte, ob nun das Leere oder das Volle der Stoff der Größe ist. Die moderne Naturwissenschaft folgt dem Atomismus und versteht in der Regel die Atome als den Stoff der Größe, neigt dann aber wieder dem geordneten Raum zu und spricht z.B. von einem Strukturenrealismus, der den räumlichen Strukturen ontologisches Gewicht verleiht. Die moderne Mathematik sieht im übertragenen Sinn die Zahlen und die einfachsten geometrischen Figuren als ihre Atome und damit als den Stoff der mathematischen Größe an, im 20. Jahrhundert die Menge und ihre Elemente. Diese Richtung soll im folgenden mit Aristoteles grundsätzlich in Frage gestellt werden.
Allerdings ist von Aristoteles keine geschlossene Darstellung der Begriffe Zusammenhang, Größe und Zwischen überliefert. Der Begriff Zusammenhang (synecheia, Kontinuum) wird in den verschiedenen Büchern der Physik fortlaufend weiterentwickelt (Phys. III, V, VI und VIII). An anderen Stellen wie z.B. der Himmelskunde wird er vorausgesetzt. Hier können – mit Dehn und Waschkies – drei unterschiedliche Definitionen des Kontinuums nachgewiesen werden, wobei Waschkies davon ausgeht, dass die Bücher der Physik entsprechend ihrer Entstehung angeordnet sind und aufeinander aufbauen.
Um den Zusammenhang zu verstehen, entwickelt Aristoteles eine frühe Form der Topologie. Er unterscheidet voneinander getrennte, einander nächstfolgende und schließlich zusammengewachsene Dinge. Erst bei ihnen sieht er einen Zusammenhang gegeben. Dieser Ansatz ist jedoch noch nicht systematisch zusammengeführt mit seinen Ideen über die Ordnung der Zahlen und die Lagen der Figuren.
Da Aristoteles noch nicht systematisch zwischen Zusammenhang und ihrer mathematischen Verselbständigung unterscheidet, bleiben bei ihm andere weiterführende Ideen unverbunden. (Das kann natürlich auch daran liegen, dass große Teile seines Werks verloren gegangen sind.) Mit der Unterscheidung der Ordnung der Zahlen und der Lage der Figuren suchte Aristoteles offenbar nach einem Ansatz, von dem aus die in der griechischen Mathematik aufgebrochene Krise beantwortet werden kann: Größen und Zahlen sind unvereinbar. Für Aristoteles geht ihre Unvereinbarkeit darauf zurück, dass die Ordnung der Zahlen und die Lage der Figuren systematisch voneinander unterschieden werden müssen.
Ihr Verhältnis ist bis heute offen und hat mit der Kontinuum-Hypothese von Cantor zur Grundlagenkrise der neuzeitlichen Mathematik geführt, in der sich auf einer neuen Ebene die griechische Grundlagenkrise der Mathematik wiederholt. Im folgenden sollen daher nach einer kurzen Wiederholung der ersten Definition des Kontinuums als des Unteilbaren die Ordnung der Zahlen und die Lage der Figuren erläutert werden, um dann zu zeigen, wie in dieses Problemfeld hinein das Prinzip des Zusammenhängenden eingeführt wurde. Die Ordnung der Zahlen und die Lage der Figuren werden als Ansatz verstanden, in welcher Weise am Zusammenhang eine mathematische Verselbständigung gefunden werden kann, die dem Verhältnis von Größe und Figur entspricht. – Das soll in weiteren Kommentaren zum Zwischen (metaxy), zu den Prinzipien der Mathematik und zum Begriff der Zeit fortgeführt werden.
(I) Das Kontinuum ist das unbegrenzt Teilbare
Die unbegrenzte Teilbarkeit war als das Unterscheidungsmerkmal der Größe von der natürlichen Zahl erkannt worden. Wird diese Eigenschaft für sich betrachtet und als eigenes Prinzip hervorgehoben, dann ergibt das die erste Definition: Das Kontinuum (syneches) ist das unbegrenzt Teilbare. Was unbegrenzt teilbar ist, muss ein Kontinuum sein. Das ist für Max Dehn der analytische Begriff des Kontinuums.
Dieser Begriff des Kontinuums wird in Phys. III angesprochen. Er wird dort vorausgesetzt und nicht weiter begründet. Ebenso unvermittelt wird vorausgesetzt, dass das mit Eudoxos gewonnene Verständnis der Größe bekannt ist. Das sind die Stellen, über die jeder unvoreingenommene Leser stolpern muss. Seidel hat völlig recht, wenn für ihn hier die Größe ganz unvermutet in den Gedankengang »hineingepoltert« kommt (Seidel, S. 209). Aristoteles' Formulierungen zeigen, dass hier nicht viel mehr vorliegt als eine Skizze, den Gedankengang zu ordnen.
Die Bewegung »scheint in den Bereich des Zusammenhängenden zu gehören, in dem Begriff 'zusammenhängend' erscheint allerdings (die Bestimmung) 'unbegrenzt'; wenn man nämlich 'zusammenhängend' bestimmt, tritt nebenbei ein, daß man oftmals den Begriff 'unbegrenzt' mitbenutzt, denn 'unbegrenzt teilbar' – das ist eben 'zusammenhängend'« (Phys., III.1, 200b).
»Die Bedeutung von 'unbegrenzt' ist nicht dieselbe in Anwendung auf (Raum-)Größe, Veränderung und Zeit, – als wäre dies ein einziger Naturgegenstand (physis) –, sondern hier wird das Nachgeordnete (acholondein) nach Maßgabe des sachlich Vorangehenden ausgesagt, z.B. Veränderung (ist ein unbegrenzt sich vollziehender Vorgang), weil die (Raum-)Größe, an der sich Ortsbewegung, Eigenschaftsveränderung und Wachstum vollziehen, (dies unbegrenzt tut); die Zeit dann ist es wegen der Veränderung« (Phys. III.7, 207b, vgl. auch Phys. III.4, 202b, Phys. III.6,206a und nochmals im Rückblick Phys., IV.11, 219a).
Die Größe ist unbegrenzt teilbar. Sie ist kontinuierlich. Weil sich die Größe kontinuierlich ändert (und nicht in diskreten Quantensprüngen), ist auch die Bewegung kontinuierlich. Und weil die Bewegung kontinuierlich ist, ist es auch die Zeit, in der die Bewegung erfolgt.
Anmerkung: Hier ist bei Aristoteles bereits in Grundzügen der Gedankengang entworfen, mit dem auch Hegel in seiner Wissenschaft der Logik schrittweise aus der Größe die Zeit entwickelt, oder vielleicht besser gesagt, den Begriff der Zeit konstruiert. Siehe hierzu die Logik-Studien zu Hegel.
Aristoteles begründet allerdings nicht, warum er in dieser Reihenfolge die Nachordnung (acholondein) bildet. Denn es kann auch umgekehrt argumentiert werden, dass die Bewegung kontinuierlich ist und daher die sich in und mit der Bewegung verändernde Größe ebenfalls kontinuierlich sein muß. Es kann gesagt werden, dass die Zeit kontinuierlich ist, und daher die in ihr abfolgende Bewegung. Ganz offensichtlich handelt es sich um erste Skizzen, das zugrundeliegende Prinzip (arche) zu erkennen.
Wie auch immer die Nachordnung gebildet werden mag, es ist das unbegrenzt Teilbare des Zusammenhängenden, worin Größe, Bewegung und Zeit etwas gemeinsam haben. Größe, Bewegung und Zeit sind kontinuierlich.
Die Aussage »die Größe unterscheidet sich von der Zahl, weil sie unbegrenzt teilbar ist« wird jetzt neu formuliert in »die Größe unterscheidet sich von der Zahl, weil sie kontinuierlich und nicht diskret ist«. Damit ist inhaltlich noch keine neue Erkenntnis gewonnen, aber eine erste Definition für das Kontinuum gefunden und ein Ansatz, diese Begriffe in eine innerliche Reihenfolge zu bringen, die noch genauer zu erläutern ist.
Ordnung (taxis) und Reihenfolge der Zahlen
Die Ordnung der Zahlen (eins, zwei, drei, ...) scheint selbstverständlich zu sein. Sie bildet geradezu prototypisch das Muster einer Reihe. Das Verständnis erweist sich jedoch als voreilig, wenn scheinbar wider jede Vernunft eingesehen werden muß, dass die Ordnung der Zahlen nicht geometrisch veranschaulicht werden kann. Der Verstand sperrt sich gegen drei Einsichten: (i) Zahlen sind keine Größen und sie haben keine Größe. Es ist sinnlos zu fragen, welche Größe die Zahl 7 hat. Die 7 ist weder hoch, breit, farbig, salzig oder rauh, sie ist keine Fläche und keine Kugel. Die Zahlen haben keine Dimension. Diese Erkenntnis hat nicht erst Frege vertreten, sondern sie ist bei Aristoteles implizit enthalten. Zahlen gibt es nur beim Zählen, innerhalb des Vorgangs des Zählens. (ii) Daher gibt es auch umgekehrt nichts, das eine Zahl als Eigenschaft hätte. Es ist zum Beispiel sinnlos zu sagen, dass etwas die Größe 7 habe. Die Größe bezieht sich immer auf eine Dimension. Es kann gemessen werden, dass ein Haus 7 m hoch oder 7 m breit ist, dass es eine Grundfläche von 7 Quadratmetern oder einen umbauten Raum von 7 Kubikmetern hat, aber es hat nicht »die Größe 7«. (iii) Obwohl jede Zahl um 1 größer ist als ihr Vorgänger, gibt es keinen Abstand zwischen zwei benachbarten Zahlen. Eine Zahl folgt unmittelbar der anderen, es gibt zwischen zwei benachbarten natürlichen Zahlen keine weitere natürliche Zahl. (Nur für die Größen gilt, dass es zwischen zwei beliebigen Größen stets mindestens eine weitere Größe gibt.) Wenn versucht wird, die Zahlen z.B. als Punkte auf einer Zahlengeraden geometrisch darzustellen, müsste einerseits der Abstand dargestellt werden, andererseits dürfte er nichts enthalten.
Aber niemand kann sich der geometrischen Veranschaulichung entziehen, weil sonst ein Kreislauf droht: Zahlen sind notwendig um zu beschreiben, was Zahlen sind. Die Eins hat eine doppelte Bedeutung: Die Eins ist (i) die erste Zahl, die Eins, und sie ist (ii) der Abstand zwischen zwei benachbarten Zahlen. Jede Zahl ist um Eins größer als ihr Vorgänger. Die gleiche Eins wird gebraucht als Zahl und zur Beschreibung einer Eigenschaft von Zahlen. Um diese Doppeldeutigkeit zu vermeiden, ergibt sich zwangsläufig die geometrische Intuition, die Zahlen durch Punkte und ihre Abstände durch Längen zwischen den Punkten darzustellen. Das ist weder eine optische Täuschung noch ein Trug- oder Traumbild, sondern die Einbildungskraft der Seele wird gegenüber den Zahlen prinzipiell in die Irre geführt.
Um die geometrische Intuition zu vermeiden, kann versucht werden, die beiden Bedeutungen farblich zu unterscheiden wie Seidel es vorgeschlagen hat. Jede Zahl hat einen Größenwert und zwei Zahlen sind voneinander getrennt durch einen Abstand. Zum Beispiel haben die Zahlen 12 und 5 den Abstand 7, oder die Zahlen 1 und 2 den Abstand 1. Der Abstand zweier Zahlen kann nicht gemessen werden, da weder die Zahlen eine Größe haben noch zwischen zwei benachbarten Zahlen eine andere Zahl liegt, sondern er kann nur als die Differenz berechnet werden.
Niemand wird das Unbehagen leugnen können, wenn akzeptiert werden muss, dass und wie sich die Zahlen allen spontanen Versuchen entziehen, Vorstellungsbilder und eine räumliche Anschauung zu bilden. Zur Mathematik wird nur finden können, wer diese Krise der spontanen Wahrnehmungsfähigkeit durchgemacht hat. Zahlen und ihre Gesetze sind prinzipiell nicht wahrnehmbar, aber jede Wahrnehmung folgt den Gesetzen der Zahlen, wenn sie Gegenstände zählt und gezählte Gegenstände vergleicht. Nicht einmal im Traum können die elementaren Regeln der Zahlen verletzt werden. Der Mensch ist unfähig, sich etwas vorzustellen, das im Widerspruch zu den Zahlen steht. Wenn er dennoch auf so etwas trifft wie die Länge der Diagonale im Vergleich zur Außenseite, ist das Vorstellungsvermögen vollends in die Krise geraten. Diese Länge ist zu »sehen«, aber sie kann nicht gezählt werden, obwohl ansonsten gilt, dass der Mensch nichts sehen kann, das er nicht zählen kann.
Lage (thesis) und Reihenfolge der Figuren
Bevor darauf im einzelnen eingegangen und das Besondere des Verwachsenen untersucht wird, ist der Begriff der Reihenfolge zu klären. Allgemein gilt für Aristoteles, dass zwei geometrische Figuren der gleichen Gattung, zum Beispiel zwei Punkte, zwei Linien oder zwei Flächen, dann voneinander getrennt sind, wenn zwischen ihnen eine geometrische Figur einer anderen Gattung liegt, zum Beispiel eine Strecke zwischen zwei getrennten Punkten, eine Fläche zwischen zwei getrennten Linien, ein Raum zwischen zwei getrennten Flächen.
Damit ist der Fall der Reihenfolge ausgeschlossen, denn z.B. zwei Strecken bilden eine Reihenfolge, wenn sie auf einer gemeinsamen Gerade liegen. In diesem Sonderfall sind sie nicht durch eine Fläche, sondern durch eine dritte Strecke voneinander getrennt. Und entsprechend können zwei Flächen auf einer gemeinsamen Grundfläche nebeneinander liegen. Dann sind sie durch eine dritte Fläce und nicht durch einen Raum voneinander getrennt.
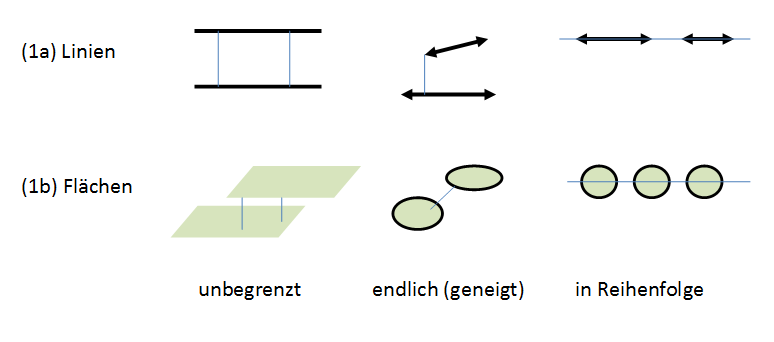
Figur 1: Lagen von Linien und Flächen
(1a) Linien: Voneinander getrennte unendlich-lange Linien müssen parallel verlaufen, sonst würden sie sich schneiden. Zwischen ihnen liegt eine Fläche. Der Abstand ist überall gleich. - Endlich-lange Linien (Strecken) müssen nicht parallel verlaufen. Wenn sie zueinander geneigt sind, gibt es zwei einander gegenüberliegende Punkte, an der sie den kürzesten Abstand haben. - Endlich-lange Linien können auf einer gemeinsamen unendlich-langen Linie leigen. Ihr Abstand ist durch den Abstand der einander gegenüber liegenden Endpunkte gegeben.
(1b) Flächen: Unendlich-große Flächen müssen parallel zueinander liegen. Zwischen ihnen liegt ein Raum, dessen Höhe ihr Abstand ist. - Endlich-große Flächen (z.B. Kreise) können zueinander geneigt liegen. - Endlich-große Flächen (z.B. Kreise) liegen in Reihenfolge, wenn ihre Abstande endlich-lange Linien sind, die auf einer gemeinsamen unendlich-langen Linie liegen.
Diese Beispiele zeigen, dass im Falle der Reihenfolge Figuren durch den Abstand ihrer Grenzpunkte voneinander getrennt sind.
(II) Das Kontinuum ist das Zusammengewachsene
Die Definition der Größe durch Eudoxos, Euklid und ihre Verallgemeinerung durch Hilbert kann nahelegen, dass das Zusammenhängende bereits gegeben sei, wenn sich Punkte dicht – »ohne Unterbrechung«, lückenlos – der Reihe nach anordnen lassen. Aristoteles widerspricht deutlich und unterscheidet zur besseren Klarheit: Etwas kann (a) "getrennt", choris, "in Reihe folgend", ephexes angeordnet sein, (b) es kann einander unmittelbar "angrenzend", echomenos sein, so dass die einzelnen Elemente sich "berühren", haptesthai (mit der Wurzel hapto, berühren, ergreifen), bis es (c) "zusammenhängend", "zusammengewachsen", syneches bzw. in einem für die Zeitlehre wichtigen Grundverständnis »zugleich«, ama ist.
Aristoteles legt durch die Art seiner Darstellung nahe, dass das Verwachsene wie ein Grenzübergang aus der Reihenfolge hervorgeht. Um die von Aristoteles betrachteten Begriffe ephexes, echomenos, haptesthai und syneches klarer unterscheiden zu können, ist zuerst der Sonderfall der Zahlen zu betrachten, die keine eigene Größe haben, dann das Besondere der Reihenfolge und schließlich das Zusammengewachsene.
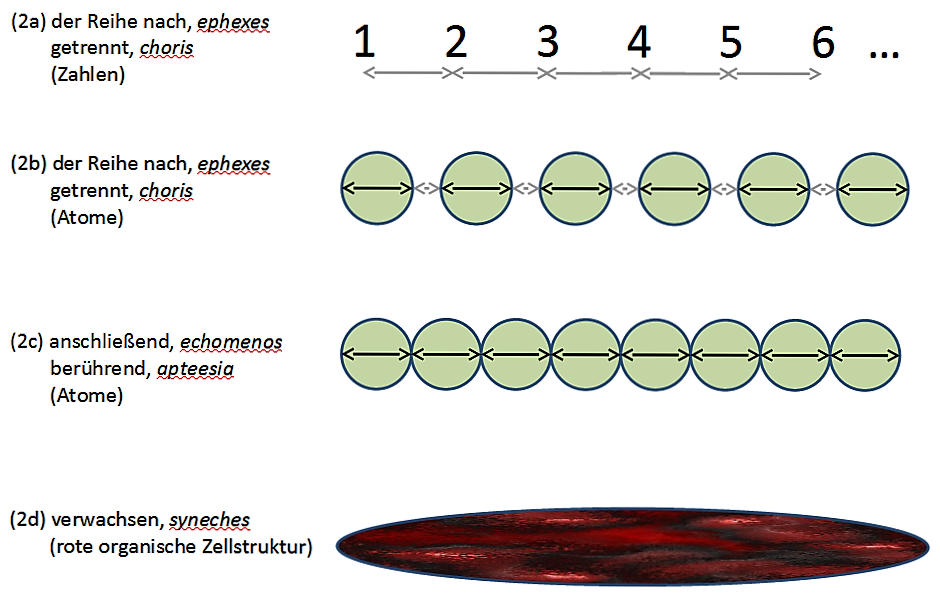
Figur 2: Zahlen, Atome und Punkte
(2a) Natürliche Zahlen haben keinen inneren Abstand (sie haben für sich keine Größe, sondern sind Größenwerte) und sind jeweils durch einen äußeren Abstand voneinander getrennt.
(2b) Atome haben einen inneren unteilbaren Abstand (sie haben eine Größe und sind im Inneren »voll«) und können durch einen äußeren Abstand getrennt sein.
(2c) Atome können linear geordnet und so nahe aneinander gerückt werden, dass sie sich an Grenzpunkten berühren, aber nicht durchdringen oder überschneiden. Sie liegen dann dicht aneinander.
(2d) Verwachsener Zusammenhang (am Beispiel einer roten organischen Zellstruktur) (Kompaktheit)
Hier entfaltet sich ein wahres Gedankenspiel, das von zahlreichen Mehrfachbedeutungen und der systematischen Unterscheidung von Zahlen, Größen und Größenwerten, Punkten, inneren und äußeren Abständen sowie verschwindenden Mengen (den »Zwischen«) lebt. Erst mit dem Begriff des Verwachsenen gewinnt Aristoteles die besondere Bedeutung des Zusammenhängenden, das weit mehr ist als nur das unbegrenzt Teilbare.
(2b) Werden Figuren (Linien, Flächen oder Körper) betrachtet, gibt es sowohl einen inneren Abstand zwischen den einander am weitesten entfernten Außenpunkten der Figur (die ein Zwischen innerhalb der Figur beschreiben), als auch einen äußeren Abstand zwischen den verschiedenen Figuren. Sie sind hier durch schwarze und graue Doppelpfeile unterschieden. Werden diese beiden Arten von Abständen nicht klar auseinander gehalten, führt das in eine Reihe von Widersprüchen. Die inneren Abstände sind die Größe der Figuren, die äußeren Abstände die Größe ihrer Entfernung voneinander.
(2b) kann aus (2a) hervorgehen, wenn jede Zahl durch eine Figur ersetzt wird. Im einfachsten Fall sind alle inneren Abstände (Durchmesser) und alle äußeren Abstände gleich.
(2c) Wenn die äußeren Abstände verschwinden, berühren die verschiedenen Figuren einander. Sie »halten sich zusammen«, wie Heidegger sehr anschaulich das Wort echomenos übersetzt hat. Wie so häufig wählt Aristoteles eine sehr komplexe Formulierung, um den Sachverhalt in größter Allgemeinheit zu treffen.
»Von (etwas) Nächstfolgendem (spreche ich), wenn zwischen dem, was nach der Lage oder natürlicherweise oder auf Grund irgendeiner anderen (Regel) abgetrennt nach dem Anfang kommt und dem, auf das es nächstfolgend sein soll, nichts aus derselben Gattung liegt. Damit meine ich beispielsweise, daß (man zwischen) einer Linie (und ihrem unmittelbaren Nachfolger) weder eine Linie noch mehrere Linien aufzeigen kann (und daß zwischen zwei unmittelbar benachbarten Einheiten) weder eine Einheit noch mehrere Einheiten (liegen dürfen)« (Phys. V.3 226b34-227a3, zitiert und übersetzt Waschkies, S. 226f).
Die Schwierigkeit entsteht, weil Aristoteles hier mit einer einzigen Formulierung sowohl die Reihenfolge einander berührender Figuren wie auch die Reihenfolge der Zahlen beschreiben will. Für die Figuren ist die Aussage einsichtig: Wenn wie in diesem Beispiel Kreise einander berühren, folgt Kreis auf Kreis und keine andere Gattung schiebt sich dazwischen. Sind dagegen die Kreise durch einen Abstand getrennt, dann folgen Kreis, Abstand, Kreis, Abstand, ... einander. Der Abstand zweier Kreise ist kein Kreis, sondern eine Länge, also von anderer Gattung.
Dagegen ist es weit schwerer zu verstehen, dass auch bei Einheiten, die eine Reihenfolge bilden, keine andere Gattung zwischen einander folgenden Einheiten liegt. Gemeint ist, dass zwischen zwei Zahlen keine andere Zahl liegt wie es bereits anhand Figur (2a) erläutert wurde. Die Tatsache, dass Aristoteles diese beiden Fälle einander folgender geometrischer Figuren und einander folgender natürlicher Zahlen nicht klar voneinander trennt, ist für mich ein Hinweis, dass er auch die Prinzipien von Größe und Dimension noch nicht in aller Klarheit voneinander getrennt hat. (Das hat bereits Max Dehn vermutet, der bei aller Zustimmung zu Aristoteles einwendet, »ob aber die Unabhängigkeit des Begriffes 'Größe' von der Dimension erkannt ist, ist sehr zweifelhaft», Dehn, S. 20).
Nachdem zunächst das Gemeinsame der einander nächstfolgenden Zahlen und Figuren betont ist, will Aristoteles im zweiten Schritt ihren Unterschied klären. Während sich geometrische Figuren in gemeinsamen Randpunkten berühren können (wenn etwa ein Kreis den nachfolgenden berührt), ist keine Berührung zwischen Zahlen denkbar. Sie folgen zwar einander dicht – es gibt keine Zahl zwischen zwei benachbarten Zahlen –, aber sie berühren sich nicht.
»Also wenn es Punkt und Einheit in der Weise geben sollte, wie man sie so als Für-sich-Bestehende ansetzt, dann ist es nicht möglich, daß Einheit und Punkt dasselbe wären: den (Punkten) nämlich steht Berührung zu, den Einheiten (nur) Reihenfolge, und bei den (Punkten) kann etwas dazwischen liegen - jede Strecke liegt ja zwischen Punkten -, bei den (Einheiten) ist diese Notwendigkeit nicht: es gibt ja kein 'inmitten' zwischen Zweiheit und Einheit« (Phys. V.3, 227a).
Etwas klarer ist vielleicht die knappere Formulierung in der Metaphysik:
»Es ist also der Punkt und die Eins nicht identisch. Denn für Punkte gibt es Berührung, für Einsen aber nicht, sondern nur Aufeinanderfolge; bei Punkten gibt es ein Mittleres (metaxy), bei Einsen aber nicht« (Metaphysik XI, 12, zitiert bei Seidel, S. 318).
Dennoch provoziert Aristoteles mit dieser ungenauen – wörtlich genommen falschen – Aussage ein Missverständnis. (2c) zeigt, dass hier nicht Punkte einander berühren, sondern Figuren berühren einander in ihren Grenzpunkten. Seidel hakt daher sogleich ein: »Hab ich dich! Die einzige Stelle in der Physik, in der Aristoteles sagt, dass Punkte sich berühren können« (Seidel, S. 287). Nach meinem Verständnis hat das Aristoteles nicht gemeint, aber wörtlich genommen hat Seidel recht.
(2d) Aus Sicht der Mathematik des 20. Jahrhundert ist die eigentlich spannende Frage, ob es in (2c) so etwas wie einen Grenzübergang gibt, wenn die inneren Abstände der Kreise immer kleiner werden und schließlich gegen 0 konvergieren. Das würde im Grenzübergang bedeuten, dass die jeweils endlichen Kreise in die reellen Zahlen übergehen, die weder einen inneren Abstand noch einen äußeren Abstand voneinander hätten. Eine kleinste Einheit kann es nicht geben, denn wie bereits gesehen, lassen sich die rationalen Zahlen und die irrationalen Zahlen nicht auf eine gemeinsame Einheit zurückführen. Eine kleinste Einheit würde auch der Voraussetzung widersprechen, dass die kontinuierliche Menge der reellen Zahlen unbegrenzt teilbar sein soll. Bevor Aristoteles in seiner dritten Definition des Kontinuums diese Annahme eindeutig ablehnt, führt er hier stattdessen eine positive Definition des Kontinuum ein.
Den Begriff synecheia (Zusammenhang) hat Aristoteles aus der Medizin übernommen. Mit Synechie sind heute Missbildungen gemeint, wenn beim Zusammenwachsen von Organen etwas misslingt. Das Krankheitsbild der Synechie zeigt, worauf es Aristoteles ankommt: Wenn es gut geht, entsteht durch das Verwachsen ein Zusammenhang, der eine große Belastbarkeit gegenüber äußeren Störungen herstellt.
Ursprünglich war syneches, was zusammengeheftet ist. So gebrauchten es die Atomisten, wenn mehrere Atome zusammengeheftet sind. So gebraucht es auch noch Proklos in seinem Euklid-Kommentar (In Eucl., S. 278.9-9.2, zitiert und übersetzt bei Waschkies, S. 382f), der hier den Weg von Aristoteles nicht mitgeht. Vom Zusammengehefteten unterscheidet Aristoteles das Verwachsene. Das Verwachsene lässt sich nicht aufteilen in die einzelnen Elemente, die verheftet sind, sondern es ist ein Ganzes geworden mit neuen Eigenschaften. Für Max Dehn ist das der synthetische Begriff des Kontinuums.
(III) Das Kontinuum besteht nicht aus Punkten
Das ist allerdings zunächst nur ein intuitives Verständnis, das weitere Überlegungen anregen kann. Intuitiv ist klar, was beim Verwachsen von Organen geschieht, aber was sind »verwachsene Zahlen« oder »verwachsene Punkte«? Aristoteles gibt darauf keine Antwort, sondern stellt in seiner abschließenden dritten Definition lediglich klar, dass ein Kontinuum nicht aus bloßen dimensionslosen Punkten zusammengesetzt werden kann.
»Wenn aber das Continuierliche und Sichberührende und das Nächstfolgende sich so verhält, wie wir oben festgestellt haben, nämlich dass continuierlich jene Dinge sind, deren äußerste Grenzen Eins ('verwachsen') sind, sich berührend aber jene, deren äußerste Grenzen örtlich zugleich und nächstfolgend jene, zwischen welchen Nichts ihnen gleichartiges liegt, so ist es unmöglich, dass aus Unteilbarem etwas ein Continuierliches bestehe, wie z.B. dass eine Linie aus Punkten bestehe, wofern die Linie ein Continuierliches, der Punkt aber ein Unteilbares ist« (Phys. VI.1, 231a, Prantl-Übersetzung nach Seidel, S. 313. Zekl übersetzt: »deren Ränder eine Einheit bilden«).
Das Stetige besteht nicht aus Diskretem. Aristoteles entwickelt die Definition des Zusammenhängenden vom Verständnis des Zusammenhängenden aus und nicht mehr von der Frage der Teilbarkeit oder der Größe. Dehn und Waschkies betonen, dass damit eine neue selbständige Definition des Kontinuum gefunden ist, die sich von den früheren in der Physik unterscheidet.
Von der modernen Mathematik wurde hierfür in der Toplogie der Begriff der Kompaktheit gefunden. So wie in einer organischen Zellstruktur Zellfasern gebildet werden, die jeweils einen ganzen Bereich überdecken, gilt für kompakte Mengen, dass es innerhalb aller Überdeckungen, d.h. aller Mengen von Mengen, die zusammengenommen die Menge enthalten (»überdecken«), eine Teilmenge von endlich vielen Mengen gibt, die bereits die Menge überdecken. Damit ist der Ansatz von Aristoteles ernst genommen. Die kompakte Menge wird nicht durch die Punkte definiert, die sie enthält, sondern durch die Mengen, von denen sie überdeckt wird. Diese Mengen können noch so klein gewählt werden, endlich viele von ihnen reichen aus. Das beste anschauliche Beispiele ist die Überdeckung der reellen Zahlen durch Kreise. Wenn zum Beispiel das Zahlenintervall von 0 bis 1 durch eine beliebige Anzahl von Kreisen überdeckt wird, gibt es unter diesen Kreisen endlich viele, die sich ausreichend stark überlappen oder einander berühren und das Intervall komplett überdecken. Das scheint auf den ersten Blick selbstverständlich zu sein. Die Idee besteht darin, dass dies auch dann noch gilt, wenn die einzelnen Mengen der Überdeckung immer kleiner werden. Da es sich jedoch immer um Mengen handelt, werden sie nie so klein wie dimensionslose Punkte. Alle grundlegenden Sätze der Analysis werden mit dieser Eigenschaft bewiesen.
Der Zusammenhang als Stoff der Größe (nach Happ, Waschkies und Seidel)
Happ und Waschkies sind überzeugt, »daß Aristoteles das syneches schließlich mit der hyle der megethi identifiziert hat« (Waschkies, S. 368). Wie kann das begründet werden?
Es ist an die Unterscheidung der beiden Bedeutungen der Zahl durch Seidel zu erinnern. Seidel verallgemeinert das auf die weiteren Dimensionen.
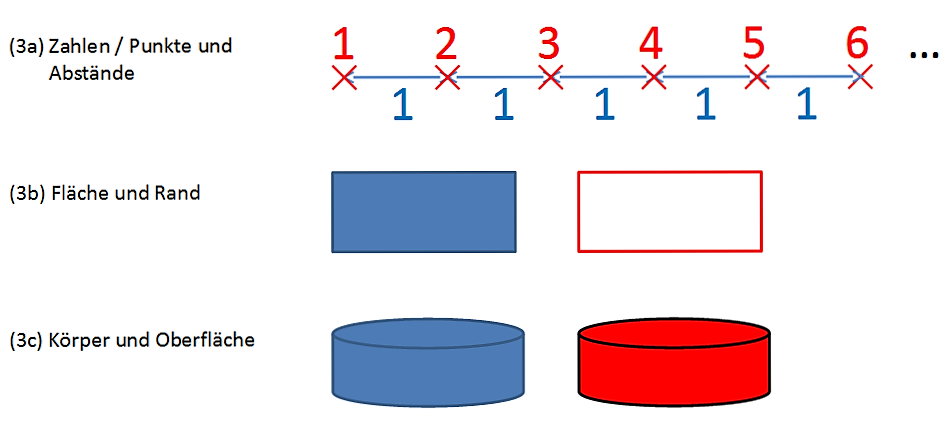
Figur 3: Dimension und Größe
(3a) Die eindimensionale Gerade wird durch Punkte unterteilt in gleich lange Abschnitte. Jeder Punkt hat die Größe 0 (er ist nicht ausgedehnt). Jeder Abstand hat die Größe 1 gemessen als die Länge des Abstandes. Im Innern ist jeder Abschnitt zusammenhängend, nach außen durch einen Punkt begrenzt. Werden die Punkte zur Unterscheidung durchgezählt und als ›1, 2, 3, ...‹ bezeichnet, ergibt sich die übliche Darstellung der natürliche Zahlen.
(3b) Flächen sind zweidimensional. Ihr Rand ist ihre Form. Die Größe der Fläche wird durch ihren Flächeninhalt gemessen (im einfachsten Fall bei Rechtecken aus Höhe mal Breite), die Größe des Randes ist die Länge der Außenlinie.
(3c) Körper sind dreidimensional. Ihre Oberfläche ist ihre Form. Die Größe des Körpers wird durch sein Volumen gemessen und ergibt sich aus den inneren Abständen, zum Beispiel beim Zylinder aus Höhe mal Durchmesser mal 2 mal pi. Die Größe der Form ist der Flächeninhalt der Oberfläche.
Die Beispiele zeigen, dass die äußere Grenze (der Rand) jeweils eine Dimension kleiner ist als der Inhalt. Da sowohl die Größe des Inhalts wie die Größe des Randes jeweils ausgerechnet werden können und eine Zahl ergeben, stellt sich die Frage, ob es eine allgemeine Formel gibt, um die Größe des Inhalts aus der Größe des Randes und umgekehrt die Größe des Randes aus der Größe des Inhalts zu berechnen. Das leistet die Differential- und Integralrechnung. Seidel kann daher vereinfachend sagen:
»Die erste Ableitung des Stoffs ergibt die Form. (...) Zum Hinunterdeklinieren ... auf eine für den Physiker handhabbare Form, haben wir das Werk Isaac Newtons, wo die Fläche die erste Ableitung des Körpers, der Weg die erste Ableitung der Fläche und der Punkt die erste Ableitung des Weges ist« (Seidel, S. 241, 243).
Hier überspringt Seidel bewusst die mathematische Verselbständigung von Stoff und Form und setzt Stoff und Form direkt in ein mathematisches Verhältnis: Die Form ist gegenüber dem Stoff jeweils um eine Dimension kleiner. Die Form ist die Ableitung des Stoffs und der Stoff ist das Integral über die Form. (Später wird nochmals darauf zurückgekommen, wenn es um die Quadrate der Zeit und die Keplerschen Gesetze geht, deren Verhältnis Seidel zurecht bei Aristoteles vorausgeahnt sieht.)
Diese Aussage, »die erste Ableitung des Stoffs ergibt die Form« trifft den wahren Kern, ist jedoch in mehrere Teilaussagen auseinander zu legen, um Doppeldeutigkeiten und Missverständnisse zu vermeiden. Integral und Ableitung gibt es nur innerhalb der Mathematik, wenn also nicht mehr Stoff und Form, sondern ihre mathematischen Verselbständigungen betrachtet werden. Davon ausgehend können jedoch folgende Aussagen betrachtet werden, zwischen denen innere Analogien bestehen:
(a) Innerhalb der Mathematik gilt: Die Ableitung von f(x) = xn ist f '(x) = n · xn-1. Aus dieser einfachen Formel werden in der Mathematik schrittweise die Regeln des Differentialkalkül und sein Geltungsbereich erklärt.
(b) Die Ableitung einer globalen Figur einer Funktion (zum Beispiel der Parabel als Figur der Funktion f(x) = x²) ergibt die lokale Figur an jeder einzelnen Stelle x0 dieser Funktion. Mathematiker sagen: Die Funktion y = x² sieht im Ganzen aus wie eine Parabel, an jeder einzelnen Stelle jedoch wie eine Tangente. Das kann verallgemeinert werden zu: Lokale Eigenschaften sind die Ableitungen von globalen Eigenschaften.
(c) Innerhalb der Geometrie und Differentialgeometrie gilt: Die Ableitung des Inhalts einer Figur ergibt den Rand der Figur. Wird der Inhalt als die Ausgedehntheit der Figur verstanden und der Rand der Figur vereinfacht gesagt als »die Figur«, dann lässt sich sagen: Die Ableitung der Ausgedehntheit ergibt die Figur. An dieser entscheidenden Stelle ist die Doppeldeutigkeit zu beachten: »Rand einer Figur« und »Figur« werden gleichgesetzt. – Statt »Rand einer Figur« wird auch bisweilen von »Gestalt einer Figur« gesprochen mit einer ähnlichen Doppeldeutigkeit: »Gestalt« und »Gestalt einer Figur« werden in der Regel sprachlich gleichgesetzt.
(d) Werden in der Meta-Mathematik Größen definiert als etwas, das im Innern zusammenhängend und nach außen begrenzt ist, dann kann gesagt werden: Die äußere Begrenzung ist die Ableitung des inneren Zusammenhangs, oder noch einfacher gesagt: Die Grenze ist die Ableitung des Zusammenhangs. Was außerhalb der Grenze liegt, das hängt nicht mehr zusammen mit dem, was innerhalb der Grenze liegt. Das ist nur eine andere Formulierung der Definition von Grenze.
Um die Verwirrung perfekt zu machen, wird zwar in der Geometrie in der Regel unter der Größe einer Figur ihr Inhalt verstanden (zum Beispiel ist die Größe eines Rechtecks der umschlossene Inhalt und nicht die Länge seines Randes), aber in der Lehre der Wahrnehmung und darauf aufbauend der Psychologie und Philosophie der äußere Rand: Ein Gegenstand ist so groß, wie ich ihn sehe (wahrnehme). Da ich sein Äußeres sehe (z.B. die Höhe eines Gebäudes) und nicht sein Inneres, gilt die (sichtbare) äußere Grenze als die Größe. – Daher kann hier gesagt werden: Die Größe (der äußere sichtbare Rand) ist die Ableitung des Zusammenhangs (des im Inneren und von außen nicht sichtbaren Zusammenhängenden). Kant bezeichnet das von außen Sichtbare als das »Phänomen« (das Erscheinende) und das im Innern nicht Sichtbare als das »Ding an sich«. Insofern kann gesagt werden, dass das Phänomen die Ableitung des Dings an sich ist.
(e) Werden schließlich die Größe als die Form und das Innere als der Stoff verstanden, dann ergibt sich: Die Form ist die Ableitung des Stoffs. Form und Stoff sind Prinzipien der Physik. Wenn auf sie der mathematische Begriff der Ableitung anwendbar ist, dann ist mit der Ableitung im wahrsten Sinn des Wortes ein mathematisches Prinzip der Physik gefunden, was das Anliegen von Newton war.
Aristoteles war sich offenbar der hier angesprochenen Mehrdeutigkeiten bewusst, ist jedoch nicht dazu gekommen, eine Klärung herbeizuführen. Happ und Waschkies gehen davon aus, dass er in diese Richtung gedacht hat, aber solange sehr vorsichtig blieb, wie für ihn die zugrunde liegenden Begriffe noch nicht geklärt waren. Es gibt keinen überlieferten Text, in dem Aristoteles sich systematisch mit dieser Frage beschäftigt, aber Waschkies und Happ nennen zwei Stellen, an denen sie angesprochen wird:
»Es könnte mithin scheinen, die Form und Gestalt eines jeden sei sein Ort, wodurch doch die (Raum-)Größe und der Stoff dieser Größe (e hyle e tou megethous) begrenzt wird; das ist doch (äußere) Abgrenzung eines jeden« Phys. IV.2, 209b4).
»So kommen manche in Zweifel auch über den Kreis und das Dreieck, als gehöre es sich nicht, diese durch Linien und durch Stetiges (syneches) zu definieren, sondern ... führen alles auf Zahlen zurück und behaupten, der Begriff der Linie sei der der Zwei« (Met. VII.11 1036b).
Das legt nahe, dass Aristoteles die geometrischen Figuren wie Kreis und Dreieck durch Stetiges (syneches) definieren und nicht auf Zahlen zurückführen wollte, und dass er ausdrücklich von einem Stoff der Größe (e hyle e tou megethous) ausging und die unbestimmte Vorstellung hatte, dass die äußere Figur die Form dieses Stoffes ist.
Happ kommentiert:
»Man unterscheidet also in jeder Größe das Bestimmbare vom Bestimmenden. Da an unserer Stelle keine anderen Körpereigenschaften außer der Ausdehnung in den Blick gefaßt werden, ist die hyle hier reine unbestimmte Ausdehnung. Das wird zur Gewißheit erhoben durch den Schlußsatz unseres Abschnitts, der ein Abstraktionsverfahren schildert: (Das Bestimmbare hyle zu nennen ist richtig), 'denn wenn man einem Körper (z.B.) einer Kugel) die Begrenzung und seine Eigenschaften (pade) wegnimmt, bleibt nichts übrig außer der Hyle'. Ergebnis dieses Substraktionsverfahrens ist ohne Zweifel nicht die absolut eigenschaftslose Hyle, sondern die Hyle als unbestimmtes poson, mit anderen Worten: die Hyle der mathematischen Gegenstände« (Happ, S. 606f).
»Die hyle noete ist also die unbegrenzte mathematische Ausdehnung, die vom Denken aus dem sinnlich Wahrnehmbaren herausgehoben wird und als Gedachtes nicht an die Einschränkungen gebunden ist, denen der kosmos aistetos nach der Auffassung des Aristoteles unterliegt« (Happ, S. 609).
2006-2011, 2014
Prinzipien einer Meta-Mathematik nach Aristoteles
Einleitung
megethos – Größe und Krise der griechischen Mathematik
synecheia – der aristotelische Begriff des Continuums
» metaxy - das Zwischen als Größenmangel
Literaturhinweise
 |
 |
 |
 |
|---|
© tydecks.info 2014
