metaxy - das Zwischen als Größenmangel

 

Version 6.12.2014

Einleitung

Das Zwischen (metaxy) ist  die  große Herausforderung für das logische (vernünftige, rationale) Denken und seine Grenzen. Es enthält etwas, das sich der Vernunft entzieht. Um hierfür einen Ansatz zu finden, hat Aristoteles in seinem Begriff der Natur die beiden Prinzipien Stoff und Form ergänzt durch ein drittes Prinzip, den Formmangel (steresis), aus dem das Zwischen entwickelt werden soll.

Die Mathematiker unterscheiden zwischen natürlichen Zahlen (1, 2, 3, …), rationalen (vernünftigen, logischen) Zahlen (welche aus Verhältnissen von natürlichen Zahlen gebildet werden wie 1:1, 1:2, 1:3, 2:3, 1:4, 3:4 …) und irrationalen Zahlen. Die irrationalen Zahlen sind nicht »unvernünftig«, sondern sie entziehen sich der Vernunft. Das ist in der Mathematik auf eine derart unmittelbare Weise anschaulich, dass es sehr schwer fällt, sich der Suggestivkraft dieses Bildes zu entziehen: Zwischen je zwei benachbarten natürlichen Zahlen – z.B. zwischen der 12 und der 13 – gibt es keine andere natürliche Zahl. Irrationale Zahlen wie (Wurzel aus 2) liegen dagegen prinzipiell zwischen natürlichen Zahlen, z.B. zwischen 1 und 2. Obwohl bei Betrachtung eines Quadrats unmittelbar zu sehen ist, dass dessen Diagonale eine vollgültige Größe aufweist wie alle anderen Längen auch, ist es nicht möglich, für die Diagonale und die Außenseite des Quadrats eine gemeinsame Einheit zu finden. Wenn im einfachsten Fall die Außenseite des Quadrats die Länge 1 hat (z.B. 1 cm), dann ist die Diagonale = 1,41421… cm lang. Diese Zahl lässt sich nie vollständig ausschreiben. Es bleibt immer ein Rest übrig, der mit den drei Pünktchen ›…‹ symbolisiert werden muss. An dieser Stelle »verschmiert« die Zahl. Sie liegt in diesem Beispiel mit 5 Nachkommastellen irgendwo  zwischen  1,41421 und 1,41422. Wie genau auch ausgerechnet wird, am Ende bleibt immer ein Zwischen stehen. Und das, obwohl doch klar ist, dass die Größe der Diagonale eindeutig ist. – Daraus ergeben sich die ersten Fragen:

(+) Das Zwischen ist mehr als »keine Größe«, d.h. mehr als der Punkt oder die Null, und doch zugleich weniger als eine »echte Größe«. Es wird daher von Mathematikern und Physikern als »verschmierter« Punkt, als »verschwindende« Größe, als »Wolke«, als »Umgebung«, als »beliebig klein« bezeichnet. Kann dieser Zustand eines Größen-Mangels, d.h. einer unfertigen Größe, der noch etwas fehlt an einer »vollendeten, ausgewachsenen« Größe, und die dennoch auf dem Weg zu einer Größe ist, verstanden werden als eine Variante des Form-Mangels (steresis), wie es in der Physik entwickelt wurde?

(+) Das Zwischen ist eine unlösbare Herausforderung für ein streng logisches Denken, das nur ›Ja oder Nein‹, nur ›A oder nicht-A‹ kennt und nichts dazwischen. Aristoteles war sich daher völlig bewusst, dass das Verständnis des Zwischen in logische Paradoxien führen muss, wenn die Logik nicht aus diesem eingeschränkten Denken herausfindet.

Aristoteles hat keine Lehre des Zwischen ausgearbeitet, aber aus seinen überlieferten Texten lassen sich die wesentlichen Schritte ableiten, mit denen in diesem Kommentar eine solche Lehre skizziert werden soll:

(1) Es muss ein Ausweg aus einem kontradiktorischen Denken, das nur ›Ja oder Nein‹ kennt, in ein konträres Denken gefunden werden, indem die formale Gegenüberstellung von »A« und »nicht-A« ersetzt wird durch konträre Widersprüche, die zwischen »A« und dem Gegenteil von »A« ein Zwischen aufspannen. Mit Max Dehn wird als wichtige Eigenschaft des Zwischen verstanden, dass es in seine Extreme (eschaton) übergehen kann. Von hier aus ergibt sich ein Ansatz, die Frage nach der Länge der Diagonale als das Äußerste aller Verbindungslinien innerhalb eines Quadrats zu verstehen.

(2) Spektakulär sind die Paradoxien von Zenon, die im wesentlichen in der kritischen Darstellung durch Aristoteles überliefert sind. Bleibt zwischen der vorauseilenden Schildkröte und dem ihr folgenden Achilles immer ein Abstand bestehen, so dass sie nie eingeholt werden kann? Aristoteles entwickelt in Auseinandersetzung mit diesem Paradox die Idee, dass im Verlaufe einer Bewegung unendlich viele Punkte »nebenbei« durchlaufen werden, also die Unendlichkeit der Punkte gewissermaßen »zwischendurch« passiert wird, ohne von der Wahrnehmung und dem Bewusstsein voll aufgenommen zu werden. Das Bewusstsein erreicht in diesem Moment einen schwebenden Zwischenzustand, von dem später auch Leibniz, Fichte und Hegel sprachen.

(3) Cantor greift die Ideen von Aristoteles auf, wenn er einerseits das Verschwinden des Zwischen zeigt und bestätigt, andererseits als Kontinuum nicht nur eine Menge von unendlich vielen Punkten versteht, sondern versehen mit einer bestimmten Ordnung. Anne Newstead hat unter diesem Aspekt die Lehren von Cantor und Aristoteles verglichen.

(4) Wenn es nicht nur um statische Mengen geht, sondern auch um das Zwischen innerhalb einer Bewegung, kann die Ordnung des Zwischen als Rhythmus verstanden werden.

(5) Wird das Zwischen innerhalb einer Bewegung für sich betrachtet, kann mit Aristoteles vom »Inmitten« der Bewegung gesprochen werden. Etwas befindet sich zwischen Möglichkeit und Wirklichkeit: Es ist mehr als bloße Möglichkeit, da es sich bereits zu verwirklichen beginnt, und weniger als Wirklichkeit, da die Bewegung noch nicht abgeschlossen und das Ziel (telos) noch nicht wirklich geworden ist.

(7) Die Lehre des Zwischen wird abgeschlossen, wenn umgekehrt nicht mehr das Äußerste innerhalb eines gegebenen Zwischen, sondern für eine vorliegende Sache das Zwischen gesucht wird, innerhalb dessen sie sich befindet, der Horizont der Sache. In diesem Sinn deutet Heidegger die Ausführungen von Aristoteles in der Metaphysik über die spezifische Fähigkeit des »vernünftigen Wissens«, das zu einer Sache ihr Umfeld und damit ihre Entwicklungsmöglichkeiten und äußeren Widerstände zu erkunden vermag. In einer Anmerkung wird in diesem Sinn der Begriff der Haltung (hexis) gedeutet, in der sich zeigt, wie eine Sache sich innerhalb ihrer Umgebung, also innerhalb ihrer Möglichkeiten in bestimmten Gewohnheiten eingerichtet hat.

(8) Damit ist Aristoteles eine »Umwertung« der Philosophie der Mathematik von Platon gelungen. Während für Platon die Mathematik im Ganzen in einem Zwischenbereich (metaxy) zwischen Wahrnehmung und Denken liegt und die Mitteilung göttlicher Ideen ermöglicht, ist für Aristoteles das Zwischen ein Prinzip, das der Mathematik vorausgeht und sie ermöglicht.

Abschließend sei angemerkt, dass das Zwischen seit Ende des 20. Jahrhunderts dank der Medienphilosophie eine gewisse Renaissance erlebt, allerdings weitgehend eingeschränkt auf philosophische Fragen der neu entstandenen technischen Medien wie Rundfunk, Film, Fernsehen, Internet.

Das Zwischen und das Äußerste (eschaton) im konträren Widerspruch (nach Dehn)

Während im 20. Jahrhundert von vielen Logikern nach einer nicht- oder nach-aristotelischen Logik gesucht wurde, die die zwei-wertige Logik des ›A oder nicht-A‹ durch eine drei-wertige Logik des ›A oder nicht-A oder unbekannt‹ ersetzen wollen und damit das Zwischen auf einen dritten Wert beschränken, der gleichen Rang wie A und nicht-A hat, lässt sich bei Aristoteles ein anderer Ansatz erkennen. Für ihn unterscheidet sich das Zwischen, das zwischen A und nicht-A liegt, in seinen Eigenschaften prinzipiell vom A und nicht-A. Es erzeugt eine höhere Dimension. Zwischen zwei Punkten liegt nicht wieder ein Punkt, sondern eine Strecke. Zwischen zwei Strecken liegt nicht wiederum eine Strecke, sondern eine Fläche.

Max Dehn hat meines Wissens bis heute als einziger an die systematische Bedeutung des Zwischen bei Aristoteles erinnert. Er hat hervorgehoben, in welcher Weise Aristoteles den Begriff des Zwischen mit dem Begriff des Äußersten (eschaton) verbindet. Die maßgebliche Stelle aus der Physik lautet in seiner Übersetzung:

»Zwischen ist das, zu welchem das sich Verändernde früher (prosteron, wie in älteren Ausgaben, statt proton in der Akademie-Ausgabe) kommt, bevor es zu dem, was das Äußerste (Letzte, eschaton) ist, sich verändert, falls es seiner Natur nach ein sich stetig Veränderndes ist« (Phys. V.3, 226b18ff, übersetzt und zitiert Dehn, S. 14).

Bevor auf den Kommentar durch Dehn eingegangen wird, soll an einigen Beispielen gezeigt werden, wie das verstanden werden könnte. Aristoteles unterscheidet sorgfältig: Das Zwischen ist nicht das Äußerste, aber es hat die Eigenschaft, sich in das Äußerste verändern zu können. Mit dieser Eigenschaft des Zwischen ist diejenige Eigenschaft getroffen, durch die sich der konträre Widerspruch vom kontradiktorischen Widerspruch unterscheiden lässt. Werden A und nicht-A einander direkt gegenübergestellt, dann ist ihre Beziehung eindeutig: Beide schließen sich wechselseitig aus. Es ist sinnlos, nach ihrer äußersten Entfernung zu fragen, da es nur eine einzige Relation zwischen ihnen beiden gibt, die unmittelbare Gegenüberstellung. In einem konträren Widerspruch, bei dem etwas in seinen Gegensatz übergeht, gibt es dagegen ein mannigfaltiges Zwischen zwischen zwei konträren Punkten, innerhalb dessen es eine äußerste Entfernung gibt.

Mit dem Zwischen zwischen zwei Punkten kann zweierlei gemeint sein: Die Menge aller Punkte, die zwischen den beiden vorgegebenen Punkten liegen, oder die Gesamtheit aller Verbindungslinien, die von einem zum anderen Punkt führen, und von denen eine als die Äußerste hervorgehoben werden soll. Wenn Aristoteles den Begriff des Zwischen mit dem des Äußersten verbindet, denkt er offenbar an die zweite Bedeutung.

»'Gegenüberliegend' in Hinsicht auf den Ort ist das, was über eine Gerade am weitesten von einander entfernt ist: sie (ist) ja die kürzeste (Strecke und) begrenzt, und Begrenztes dient als Maß« (Phys., V.3, 226b).

Hier kommen zwei Gesichtspunkte zusammen: Zum einen wird zwischen jeweils zwei Punkten die kürzeste Verbindung gesucht, zum anderen werden in einer Menge von Punkten die beiden gegenüberliegenden Punkte gesucht, deren kürzeste Verbindung im Vergleich zu allen anderen Verbindungen einen Extremwert annimmt. Das sei an einigen Beispielen verdeutlicht.

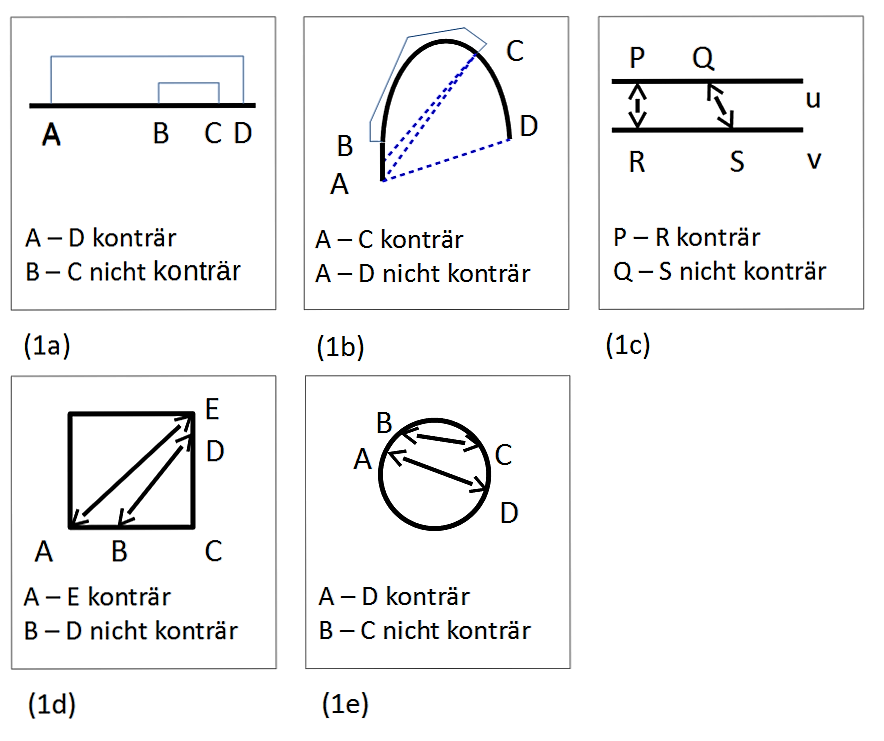
Figur 1: Konträr und nicht-konträr

(1a) Zwischen zwei Punkten A und D auf einer Geraden bildet das geschlossene Intervall [A,D] die Gesamtheit aller Punkte, die zwischen A und D liegen, wobei die Randpunkte im geschlossenen Intervall mitgezählt werden. Das Intervall enthält unendlich viele Punkte. Innerhalb des Zwischen zwischen A und D gelten diejenigen Punkte als konträr, die den größten Abstand zueinander haben. Die Abstände zwischen zwei Punkten sind durch die blauen Hilfslinien eingetragen. In diesem einfachen Beispiel sind nur die beiden Grenzpunkte A und D konträr zueinander. Alle anderen Punkte, die zwischen A und D liegen, sind zwar voneinander unterschieden, jedoch nicht konträr. Es gibt keine Punkte B und C zwischen A und D, deren Abstand größer wäre als der zwischen A und D.

(1b) Im Beispiel (1a) ist noch nicht der Unterschied erkennbar, ob Punkte zwischen zwei Grenzpunkten oder die Gesamtheit aller Grenzlinien zwischen zwei Punkten das Zwischen definieren. Da in (1a) die Grenzpunkte und alle Punkte zwischen ihnen auf einer Geraden liegen, gibt es nur jeweils eine Verbindungslinie zwischen zwei Punkten, die entlang dieser Gerade verläuft.

Ist dagegen das Intervall zwischen A und D gekrümmt, dann gibt es zwei mögliche Arten von Verbindungen: Zum einen können zwei Punkte verbunden werden, indem zwischen ihnen ein Weg entlang der gekrümmten Strecke gewählt wird. Das ist am Beispiel der Punkte B und C in Analogie zu (1a) mit der blauen Hilfslinie angedeutet. Wenn auf diese Weise Wege und Abstände bestimmt werden, bleiben topologisch alle Verhältnisse von (1a) erhalten: Die längste Verbindung besteht zwischen den beiden Endpunkten A und D, und die Verbindungen aller anderen Punkte zwischen A und D bilden Teilstrecken auf dieser Verbindung.

Es können aber auch andere Verbindungslinien zugelassen werden, die in (1b) mit blauen, gestrichelten Linien eingetragen sind. Dann sind z.B. die beiden Punkte B und C weiter voneinander entfernt als A und D, obwohl sie auf der gekrümmten Strecke zwischen A und D liegen.

Schon anschaulich ist deutlich, dass es keineswegs trivial ist, den Punkt C zu finden, der am weitesten von A entfernt ist. (Fragen dieser Art wurden erst seit dem 18. Jahrhundert mit der Variationsrechnung gelöst und stehen bis heute im Zentrum der mathematischen Physik, wobei für die Begriffe der Verbindungslinien und ihrer Gesamtheit fortlaufend abstraktere Räume gesucht werden.)

Zwischen (1a) und (1b) ist der systematische Unterschied zu erkennen: Während in (1a) die  Punkte  betrachtet werden, die im gegebenen Intervall [A,D] zwischen A und D liegen, werden in (1b) alle  Verbindungslinien  betrachtet, die zwischen jeweils zwei Punkten liegen. Während in (1a) unmittelbar zu sehen ist, dass die Randpunkte A und D zugleich die konträren Punkte sind, sind in (1b) die konträren Punkte A und C erst zu finden, indem aus der Gesamtheit aller Verbindungslinien die längste ausgewählt wird, und die beiden Punkte als konträr erkannt werden, die sich an den Enden dieser Linie befinden. Erst in diesem Beispiel wird der Übergang in eine höhere Dimension notwendig und erkennbar: In (1a) liegen alle Verbindungslinien zwischen zwei Punkten auf der gleichen Strecke, auf der die Punkte angeordnet sind und führen noch in keine neue Dimension. In (1b) liegen die Verbindungslinien außerhalb der Strecke, auf der die Punkte liegen. Mit ihnen gelingt eine  Abkürzung .

(1c) Im Beispiel zweier Parallelen u und v können alle Verbindungslinien betrachtet werden, die zwischen den Parallelen liegen. In diesem Kontext gelten zwei Punkte auf den beiden Parallelen als konträr, wenn sie einander gegenüberliegen. Ihre Verbindungslinien sind kürzer als alle anderen Verbindungslinien seitlich voneinander versetzter Punkte.

(1d) In einem Quadrat bilden jeweils zwei einander gegenüberliegende Eckpunkte einen konträren Gegensatz. Alle anderen Punkte innerhalb der Seiten wie z.B. B und D wie auch die Endpunkte auf einer Seite wie z.B. A und C sind durch kürzere Strecken miteinander verbunden. Beträgt die Seitenlänge 1, dann ist die Diagonale von der Länge das Äußerste des Zwischen innerhalb des Quadrats.

Mit diesem Beispiel ist der Horizont gefunden, aus dem heraus die besondere Bedeutung der Diagonale und mit ihr der irrationalen Zahlen wie verstanden werden kann. Sie entstehen nicht wie die natürlichen Zahlen aus dem Zählen, sondern aus der Betrachtung des Äußersten innerhalb eines Zwischen.

(1e) Wird von einer Kreislinie ausgegangen, dann können alle Verbindungslinien betrachtet werden, die zwischen den Punkten auf dem Kreis bestehen. Hier gelten diejenigen Punkte auf der Kreislinie als konträr, deren Verbindungslinie durch den Kreismittelpunkt führt. Ihre Länge ist der Durchmesser des Kreises. Alle anderen Verbindungslinien sind kürzer.

In dem hier betrachteten Übergang von den Punkten zwischen zwei Randpunkten auf einer gegebenen Strecke zu den Verbindungslinien zwischen zwei Randpunkten ist der Grundgedanke der Differential- und Integralrechnung enthalten. Durch die konträren Punkte wird innerhalb des Zwischen eine Achse ausgezeichnet, entlang derer ein Grenzübergang möglich ist, mit dem das Zwischen zum Verschwinden gebracht wird. (Oder dramatischer formuliert: entlang derer es zu Grunde geht. Die Wortwahl ist bewusst an Hegels Ausführungen zum Widerspruch angelehnt, siehe den Beitrag über den Begriff des höheren Widerspruchs). In den hier genannten Beispielen können sich die Strecke oder der Kreis im Grenzübergang auf einen Punkt zusammenziehen, bzw. die beiden parallel verlaufenden Geraden auf eine einzige Gerade. Ein Grenzübergang ist nur ausgehend von einem konträren Gegensatz möglich.

Bei diesem Grenzübergang verschwindet die Unterscheidung der zuvor sorgfältig unterschiedenen Fälle (1a) und (1b), da im Grenzübergang die Aussagen über die Krümmung der geraden Linie verloren geht. Daran läßt sich in nuce erkennen, wie im Grenzübergang nicht nur das Zwischen zu Grunde geht, sondern in der paradoxen Formulierung von Hegel im Grenzübergang der Grund gefunden wird. Das ist in diesem Beispiel die Krümmung. Sie ist der Grund, warum in es (1b) unterschiedliche Verbindungslinien zwischen zwei Punkten gibt, nicht dagegen in (1a).

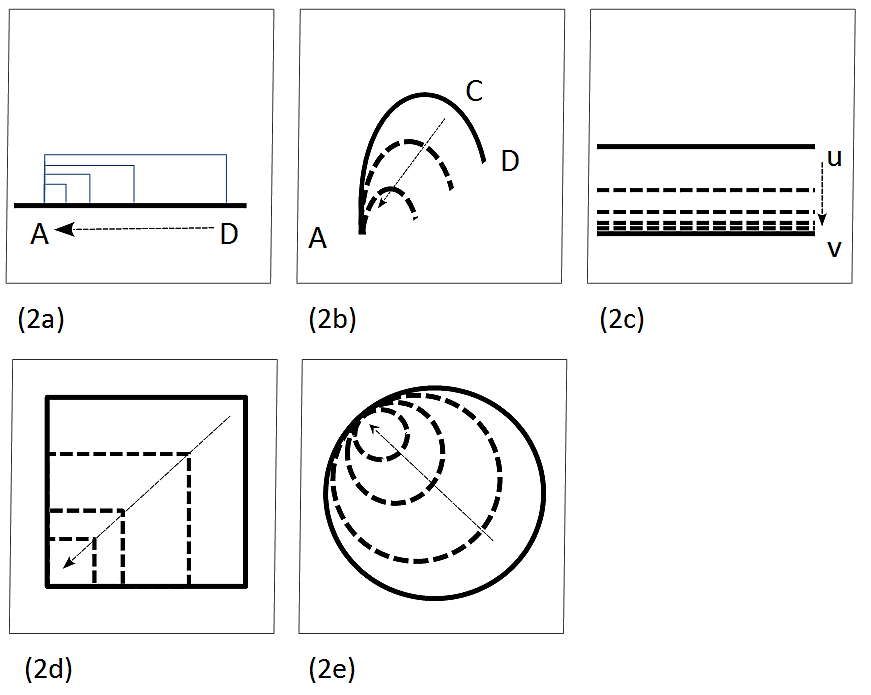
Figur 2: Grenzübergang im konträren Gegensatz

(2a) Der konträre Abstand zweier Punkte A und D zieht sich zusammen bis beide Punkte aufeinander fallen.

(2b) Ebenso zieht sich auf einer gekrümmten Linie der konträre Abstand zweier Punkte zusammen, wodurch die gekrümmte Linie schließlich in einen Randpunkt übergeht. Die Linie, entlang derer der Grenzübergang erfolgt, ist jetzt jedoch nicht wie in (1a) die Verbindungslinie zwischen den beiden Randpunkten A und D, sondern zwischen den beiden konträren Punkten A und C.

(2c) Zwei Parallelen nähern sich entlang ihres konträren Abstandes einander an bis sie sich decken.

(2d) Ein Quadrat wird entlang der Diagonale auf einen Eckpunkt verkleinert.

(2e) Ein Kreis wird entlang eines Durchmessers verkleinert bis er auf einen Punkt schrumpft.

Nur ein konträrer Gegensatz erzeugt eine Richtung, entlang derer ein Grenzübergang erfolgen kann.

Diese Bewegung kann auch in der anderen Richtung gelesen werden, wenn aus einem Punkt zwei Punkte entstehen, die konträr zueinander liegen, oder aus einer Gerade zwei parallele Geraden. Hier entsteht systematisch das Zwischen, denn diese Richtung eröffnet einen Raum (eine neue Dimension).

(2a) Aus einem Punkt entfernt sich auf einer geraden Strecke ein anderer Punkt, wodurch ein Abstand zweier konträrer Punkte auf einer Gerade entsteht.

(2b) Von einem Punkt löst sich ein anderer Punkt, der auf einer gekrümmten Kurve der konträre Punkt gegenüber dem Ausgangspunkt ist.

(2c) Von einer Gerade entfernt sich eine Parallele, wodurch eine Fläche entsteht.

(2d) Aus einem Punkt entsteht entlang der Diagonale ein Quadrat, das fortlaufend wächst.

(2e) Aus einem Punkt entsteht entlang des Durchmessers ein Kreis, der fortlaufend wächst.

Werden die in diesen Beispielen herangezogenen Elementarfiguren (Gerade, gekrümmte Kurve, Parallelen, Quadrat, Kreis) ersetzt durch ein freies System geschlossener, gekrümmter Kurven, dann entsteht die Vorstellung der Vektorfelder. Das anschaulichste Beispiel liefern die geographischen Höhenlinien einer Landkarte. Auf jeweils zwei benachbarten Höhenlinien sind diejenigen Punkte konträr, zwischen denen die kürzeste Verbindungslinie besteht. Das ist in geographischer Deutung der steilste Anstieg bzw. Abstieg, in mathematischer Sprache der Gradient.

Zugleich kann die Tangente betrachtet werden, die in die Richtung weist, in der entlang der Höhenlinie die Höhe unverändert bleibt.

  

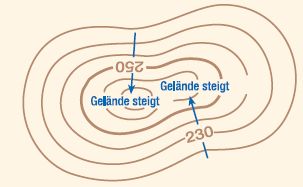
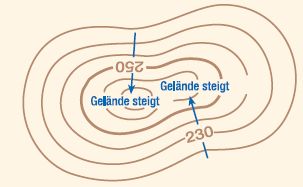
Figur 3a 3b: Höhenlinien
»Höhenlinien auf einer Karte haben immer einen gleichen Höhenabstand zueinander (man nennt das auch eine 'Äquidistanz'). Würde man die wirkliche Landschaft entlang der Höhenlinien aufschneiden, erhielte man immer gleich dicke Scheiben. [...]
Die Beschriftung der Höhenlinien auf einer Karte ist so angebracht, dass man sie in Richtung des steigenden Geländes lesen kann. Durch die Höhenlinien werden Form und Steigung in einem Gelände sichtbar. Je enger die Linien zusammen liegen, desto steiler ist das Gelände, je weiter sie auseinander liegen, desto flacher ist es« (geolinde.)

Das Zwischen kann nur aus einer Bewegung heraus entstehen, die durch eine konträre Spannung aufgebaut wird. Aristoteles hat nach meinem Verständnis mit dem Äußersten (eschaton) auf einer rein geometrischen Ebene den Grundbegriff gefunden, aus dem in weiteren Schritten die Spannung im engeren Sinn entwickelt werden kann (der tonos). Insofern ist sein Ansatz allgemeiner als der der Stoa, für die die Spannung der grundlegende Begriff war. Aristoteles ist es im Ansatz gelungen, mit dem Zwischen und dem Äußersten, in das sich das Zwischen verändert, ein Prinzip der Meta-Mathematik zu finden. Es gilt wie in den hier gewählten Darstellungen innerhalb der Mathematik, geht jedoch weit über sie hinaus.

Bis heute gibt es in der Mathematik und Physik Verständnisschwierigkeiten, wenn das Zwischen gleichgesetzt wird mit der größten bzw. kleinsten Verbindungslinie, in die es übergeht. So wird z.B. gesagt, das Zwischen zwischen zwei Parallelen ist der Abstand zwischen den beiden Parallelen, und der Abstand wird wiederum gleichgesetzt mit dem jeweiligen Größenwert, z.B. 2 cm, wenn zwei Parallelen 2 cm voneinander entfernt sind. Hier wiederholen sich ähnliche begriffliche Ungenauigkeiten wie im Verhältnis von Form, Größe, Figur und Größenwert. Es kommt jedoch darauf an, diese drei Schritte sorgfältig zu unterscheiden: Das Zwischen ist die Gesamtheit aller Verbindungslinien. Diese Gesamtheit hat die Eigenschaft, dass es in ihr eine größte Verbindungslinie gibt. Und diese größte Verbindungslinie kann wiederum gemessen werden.

Im anderen Extrem identifiziert Seidel das Zwischen nicht mit der äußersten Verbindungslinie, sondern mit dem Moment, wenn es im Grenzübergang verschwindet und sich die Figuren berühren. Er denkt an das Jetzt als der kleinsten Einheit der Zeit und versteht das Zwischen als kleinste Einheit des Kontinuums (des Zusammenhangs), wobei er sich deutlich gegen die gegenteilige Aussage von Aristoteles wendet, wonach im Moment der Berührung kein Zwischen mehr existiert (Seidel, S. 281). So wie sich das Zwischen in einem Grenzübergang in das Äußerste (eschaton) wandelt, so wandelt es sich im anderen Grenzübergang in die Berührung (apteesia). In diesem Grenzübergang kann nur noch in einem übertragenen Sinn die gemeinsame Grenze »zwischen« ihnen als Zwischen (metaxy) bezeichnet werden, und für diesen Grenzfall kann Seidel sagen: »Das Zwischen hat keine Grösse« (Seidel, S. 287). Auch wenn es meiner Meinung nach an der Intention von Aristoteles vorbeigeht, das Zwischen mit der Berührung gleichzusetzen, trifft Seidel dennoch etwas Richtiges: Es gehört zum Begriff des Zwischen, sich in diese Übergänge der Berührung und des Äußersten zu verändern, und insofern hat das Zwischen selbst keine eigene Größe. Es gewinnt erst dann eine eigene Größe, wenn es sich entweder in die Größe des Äußersten oder in den Null-Wert der Berührung wandelt. Diesen Mangel an eigener Größe zu verstehen, der jedoch zugleich in eine Größe übergeht, ist das wesentliche Anliegen dieses Beitrags über das Zwischen.

Aristoteles hat diese Begriffe nur angedeutet. Dehn hebt hervor, dass Aristoteles seiner Meinung nach hier mit dem Begriff »früher« auf die Zeit und die mit ihr verbundene stetige Bewegung Bezug nimmt und nicht auf den kontinuierlichen Raum. So geht nach seiner Überzeugung heute die Wissenschaft vor, wenn sie die Zahlen, Töne oder Farbveränderungen »'durchlaufen' denkt, d.h. auf diesen Bereich ein Zeitintervall abbildet« (Dehn, S. 14).

»Damit nun die aristotelische Definition von 'zwischen' einen Sinn bekommt, muss die stetige Bewegung definiert werden und zwar ohne Benutzung des Zwischenbegriffes« (Dehn, S. 15).

Das gelingt Aristoteles zwar aus Sicht von Dehn noch nicht, aber dennoch bewundert er das Ergebnis, zu dem Aristoteles bereits gelangt ist:

»'Stetig ist das, was kein (oder das allerkleinste) Intervall des Bereiches auslässt (dialeipon)' (Phys. V.3 226b). Es ist klar, dass bei dieser Definition wieder der Begriff 'zwischen' stillschweigend gebraucht wird, denn das Intervall ist das, was dazwischen liegt. ... Also ist die Definition eine Zirkeldefinition. Sie hat trotzdem Anrecht auf unsere größte Bewunderung. Denn sie spricht die wichtigste Eigenschaft der stetigen Bewegung aus. ... Die wichtigste Eigenschaft der stetigen Funktion ist nun, daß sie keinen Zwischenwert ausläßt« (Dehn, S. 15).

Auf diese Frage wird im weiteren zurückgekommen, wenn es um die Einheitlichkeit einer stetigen Bewegung geht, die »nebenbei« die überabzählbar vielen Punkte eines Kontinuum durchläuft. Trotz dieser kritischen Bemerkung kommt Dehn zum Ergebnis:

»Aristoteles untersucht auch den in der Erklärung von 'zwischen' vorkommenden Begriff 'das Äußerste' (eschaton): 'Äußerst ist das (dem Anfang) Entgegengesetzte der Bewegung.' Mit dem Wort 'entgegengesetzt' ist Aristoteles nun auf dem ihm behaglichen Boden der Logik und zwar wählt er, wie er sagt, die Bezeichnung to enantion, weil es sich um einen konträren Gegensatz handelt. Denn konträr muss der Gegensatz von Anfang und Ende sein, weil von etwas Mittlerem (dazwischen) nur bei konträr Gegensätzlichem, nicht aber bei bloss kontradiktorisch, kata antiphasis Gegensätzliches die Rede sein kann. Schließlich genügt ihm aber diese Berufung auf das Logische noch nicht, sondern er führt das 'Äußerste' auf etwas Geometrisches zurück, etwa bei einer Kurve auf den Punkt mit der weitesten Entfernung vom Anfangspunkt» (Dehn, S. 16).

Anmerkung 1: Die Unterscheidung zwischen der Betrachtung von Verbindungslinien innerhalb einer Figur (1a) und der Gesamtheit aller möglichen Verbindungslinien, die auch die Figur verlassen können (1b), kehrte wieder in den Theorien von Demokrit und Epikur. Während es für Demokrit nur geradlinige Bewegungen gab und damit jeweils nur eine einzige mögliche Verbindungslinie zwischen zwei Bewegungszuständen, betrachtete Epikur auch andere Verbindungslinien zwischen einem Anfangs- und Endpunkt, die gegenüber der geradlinigen Verbindungslinie abweichen. Innerhalb dieser Gesamtheit von Verbindungslinien kann es unter einem höheren Aspekt eine andere als die geradlinige Bewegung geben, entlang derer die Bewegung erfolgt, weil auf diesem Weg unter einem zusätzlichen Gesichtspunkt eine Optimierung erfolgt. Insofern gilt für Epikur ähnlich wie für Aristoteles die Gesamtheit der Verbindungslinien als das Zwischen, innerhalb dessen es ein Äußerstes gibt.

Anmerkung 2: Der Übergang zum Zwischen kann mit Hegels Untersuchung der Wahlverwandtschaften verglichen werden. Zwischen zwei Stoffen A und B besteht eine Wahlverwandtschaft, d.h. im übertragenen Sinn eine Verbindungslinie, wenn es zu einer Reaktion kommen kann, in deren Verlauf die Stoffe A und B sich aus den vorhandenen Bindungen lösen und eine neue Bindung miteinander eingehen. Hegel betrachtet auch den Fall, dass mehrere Verbindungslinien möglich sind, und fragt, welche von ihnen sich durchsetzt (das ist in der Sprache von Aristoteles das Äußerste innerhalb einer Gesamtheit von Verbindungslinien). Siehe hierzu den Beitrag zum realen Maß.

Anmerkung 3: Das anschaulichste Beispiel für eine optimierte Bewegung entlang einer nicht-geradlinigen Bewegungsbahn ist die Brachistochrone, deren Lösung 1696 Johan Bernoulli fand. »Die Brachistochrone (gr. brachistos kürzeste, chronos Zeit) ist eine reibungsfreie Bahn zwischen einem Anfangs- und einem gleich hoch oder tiefer gelegenen Endpunkt, auf der ein Massenpunkt unter dem Einfluss der Gravitationskraft am schnellsten zum Endpunkt gleitet. Der Tiefpunkt der Bahn kann tiefer liegen als der Endpunkt« (Wikipedia).

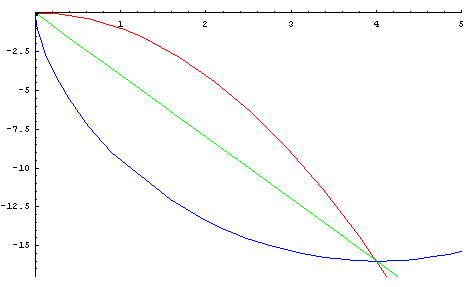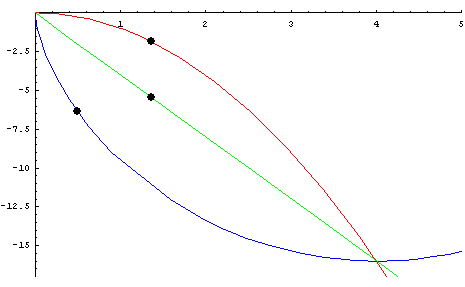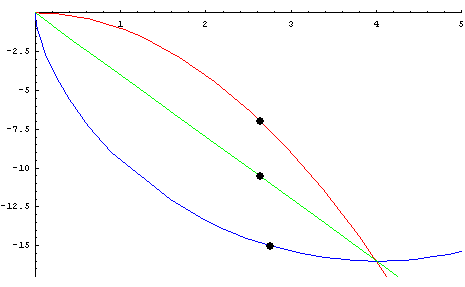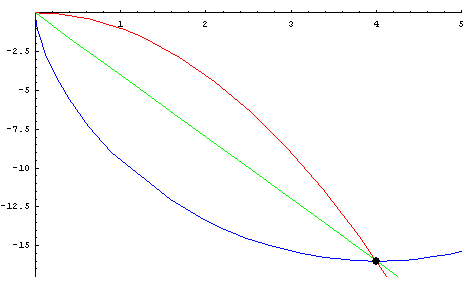
Figur 4: Brachistochrone
Quelle: National Curve Bank. Eine gute Einführung mit vielen weiteren Beispielen findet sich auch bei Matroids Matheplanet.

Die Gravitationskraft wird am besten entlang der tiefer gelegenen blauen Kurve genutzt. (Die am Bildschirm zu sehende Animation zeigt den Verlauf entlang der drei Bahnen.) Während geometrisch in einem euklidischen Raum ohne Kraftwirkungen zwischen zwei Punkten die geradlinige Verbindung am kürzesten ist, entsteht mit der Gravitationskraft neben den Raumdimensionen ein zusätzlicher Parameter, der bei der Lösung der Brachistochrone zu berücksichtigen ist. Mathematisch werden alle Parameter dieser Art als gleichberechtigte Dimensionen ergänzend zu den Raumdimensionen konstruiert.

Aufgaben dieser Art lösten am Beginn der neuzeitlichen Mathematik eine Diskussion zwischen Descartes, Newton, Leibniz, Maupertuis, Euler und anderen aus, in welcher Weise die Axiome der euklidischen Geometrie zu erweitern sind (siehe hierzu Helmut Pulte Das Prinzip der kleinsten Wirkung und die Kraftkonzeptionen der rationalen Mechanik). Im Ergebnis wurde klar herausgearbeitet, dass für die Auswahl der kürzesten Verbindungslinie aus einer Gesamtheit unendlich vieler Verbindungslinien ein eigenes Prinzip formuliert werden muss. Das kann dazu führen, dass eine Strecke gewählt wird, die nicht geradlinig verläuft, wenn entlang dieser Strecke der gesamte Kraftaufwand geringer ist als entlang einer geradlinigen Strecke. Dies Prinzip geht über die Mathematik hinaus und kann daher in der ersten Verallgemeinerung als physikalisches Prinzip (Natur-Prinzip) und in weiterer Übertragung als meta-mathematisches Prinzip bezeichnet werden. (Siehe weiterführend Frank Linhard Historische Elemente einer Prinzipienphysik.) Es wird angenommen, dass sich dies Prinzip auch auf andere Bereiche übertragen lässt, sei es die Verhaltensforschung, Ästhetik oder Ethik.

Das Unendliche »nebenbei« durchlaufen

Wie lassen sich die Paradoxien von Zenon beantworten, wenn das Zwischen nicht als unendliche Menge von Punkten verstanden werden soll? Die Argumentation von Aristoteles kann in drei Punkte aufgeteilt werden:

(a) Die Bewegung ist von ihrem Gesamtablauf (ihrer Kontinuität) und nicht von einzelnen Abschnitten her zu verstehen.

(b) Die Bewegung enthält unendlich viele Punkte, besteht aber nicht aus unendlich vielen Punkten.

(c) Die unendlich vielen Punkte werden während der Bewegung nicht einzeln »gepackt«, sondern »nebenbei« durchlaufen.

Um auf Zenon eine Antwort zu finden, geht Aristoteles grundsätzlich davon aus, dass die betrachteten Bewegungen als Einheiten verstanden werden müssen (vgl. auch Met. V.6, 1015b-1016a über das Eine und das Kontinuum). Werden der Lauf von Achilles und der Schildkröte verglichen, dann ist jeder Lauf zunächst im Ganzen als eine Ortsveränderung von einem Ort AX zu einem Ort BX zu verstehen. Wenn Achilles und die Schildkröte zur gleichen Zeit an bestimmten Orten AA und AS starten, um zu den Orten BA und BS zu gelangen, dann ist jeweils der gesamte Bewegungsablauf zu betrachten, und innerhalb dieses Ablaufs kann die Frage gestellt werden, ob es einen Punkt ÜAS gibt, an dem Achilles die Schildkröte überholt. – Grünbaum hat für diese Unterscheidung das intuitive Bild des »Legato-Lauf« und des »Staccato-Lauf« geprägt (legato-run, staccato-run, Grünbaum, S. 205). Während Aristoteles die gebundene, zusammenhängende Bewegung betrachtet, versteht Zenon den Lauf als Staccato einzelner Schritte, die sich einzeln zählen lassen.

Wenn der Punkt gesucht wird, an dem sich Achilles und die Schildkröte treffen, kann das Paradox entstehen, wie es Zenon formuliert hat. Die beiden Bewegungskurven werden fortlaufend unterteilt, um den Punkt zu finden, an dem beide sich schneiden. Und so wie es nicht möglich ist, das Verhältnis der Längen von Diagonale und der Außenseite eines Quadrats ohne Rest als Verhältnis zweier natürlicher Zahlen zu bestimmen, kann der Fall eintreten, dass es nicht gelingt, die Längen der Wege von Achilles und der Schildkröte bis zu dem Punkt, an dem sie sich treffen, ohne Rest als Verhältnis natürlicher Zahlen zu beschreiben.

Zenon hat diese Frage ein wenig anders formuliert. Er hat schrittweise betrachtet, wie sich die Bewegung des Achilles der Schildkröte annähert, jedoch bei Unterteilung in kleinere Einheiten immer ein Zwischen (ein Rest) übrig bleibt zwischen dem Punkt, den Achilles erreicht hat, und dem Punkt, den die Schildkröte weiter gelangt ist.

Aristoteles betont gegenüber Zenon, dass das Kontinuum unendlich viele Punkte enthält und damit auch einen Punkt, an dem sich Achilles und die Schildkröte treffen, selbst wenn es nicht möglich ist, diesen Punkt exakt zu bestimmen. Dies Argument entspricht dem von Dehn genannten Mittelwertsatz und der Betrachtung der Diagonale: Die Definition des Kontinuum mit dem Mittelwertsatz besagt, dass im Kontinuum jeder Wert angenommen wird, auch wenn er nicht in rationalen Zahlen bestimmt werden kann.

Entsprechend hat die Lösung von Aristoteles im mathematischen Sinn große Verwandtschaft mit der Frage nach dem Zwischen und dem Äußersten. So wie in einer Gesamtheit von Linien gefragt werden kann, welche die längste ist, so kann gefragt werden, was zwischen zwei Bewegungskurven liegt. Wird für jeden Zeitpunkt der räumliche Abstand zwischen Achilles und der Schildkröte gemessen, ergibt sich eine Gesamtheit von Verbindungslinien zwischen den sich bewegenden Achilles und der Schildkröte, die in dem Moment ein Minimum erreicht, wenn sich ihre Wege kreuzen und Achilles die Schildkröte überholt.

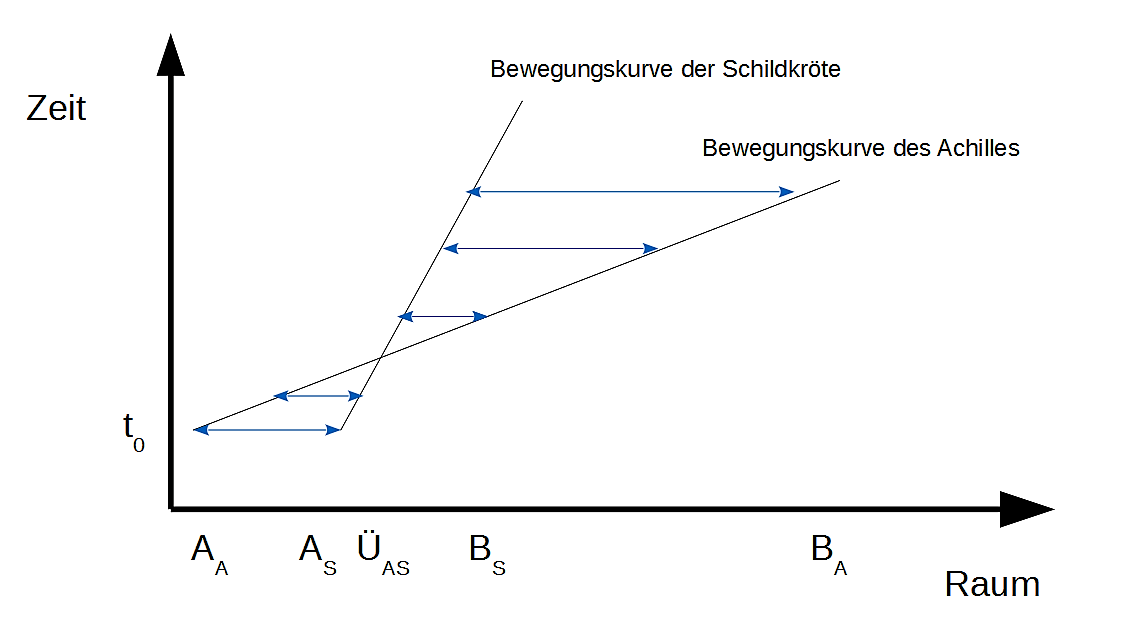
Figur 5: Achilles und die Schildkröte
Mit den schwarzen Geraden sind die Bewegungskurven von Achilles und der Schildkröte gezeichnet. Achilles und die Schildkröte starten zur gleichen Zeit t0, wobei Achilles der Schildkröte einen gewissen Vorsprung lässt, weswegen der Startpunkt der Schildkröte AS rechts vom Startpunkt von Achilles AA liegt. Die blauen Pfeile zeigen die Verbindungslinien zwischen den beiden Bewegungskurven: Jeder blaue Pfeil zeigt den Abstand von Achilles zur Schildkröte zu einem bestimmten Zeitpunkt. In dem Moment, wenn Achilles die Schildkröte überholt, ist der Abstand Null.

Aristoteles erkennt, an welcher Stelle der kritische Punkt im Argument von Zenon liegt. Zenon geht davon aus, dass im Verlaufe der Bewegung unendlich viele Punkte passiert werden müssen, und dass sie jeweils einzeln erfasst werden sollen, was nicht möglich ist.

»Es sei nicht möglich, das Unendliche (apeiron) durchzugehen (di-elthein) oder das unendlich Viele Punkt für Punkt einzeln zu packen (hapsastai) in begrenzter Zeit (peperasmenou chronos)« (Phys., VI.2, 233a).

Aristoteles ist in der Wortwahl sehr genau: haphastai geht zurück auf haphê, den Tastsinn, den er in der Seelenkunde als die erste Wahrnehmung bezeichnet, weil sich vor allem mithilfe dieses Sinns die Tiere orientieren und hierin von den Pflanzen unterscheiden (Aristoteles, De anima, II.2, 413b). Der Tastsinn geht jeder Bewegung voraus, um den Weg der Bewegung zu erkunden. Zenon behauptet in der Darstellung durch Aristoteles, dass in diesem Sinn im Verlaufe der Bewegung alle Punkte einzeln ertastet (gepackt, berührt) werden, die zu durchlaufen wird.

Der Unendlichkeit (apeiron) der Punkte steht gegenüber die »begrenzte Zeit (peperasmenou chronos)«. Der Ausdruck peperasmenou hat seine Wurzel in peras, der Grenze, dem Gegenteil der Unendlichkeit (apeiron) (siehe hierzu Cherubin, Mannucci, S. 189f). Peperasmenos ist das Partizip Medium und Passiv des Perfekts zum Verb peraino und bedeutet »zu Ende bringen, beenden, ausführen, erreichen«. (Die Hinweise zur griechischen Übersetzung verdanke ich Gabriele Stumpp.) peperasmenou chronos kann daher auch genauer übersetzt werden als »die beendete oder abgelaufene Zeit«. Es ist nicht möglich, im Ablauf einer endlicher Zeit unendlich viele Punkte zu erkunden.

Diesen Gedanken hat Adolf Grünbaum weiter ausgeführt. Zellini fasst es zusammen:

»In neuerer Zeit hat Adolf Grünbaum Can an Infinitude of Operations be performed in a Finite Time gezeigt, dass die Anwendung der arithmetischen Theorie der Grenzwerte zur Auflösung der Paradoxes durch die Maßstruktur der physikalischen Zeit gerechtfertigt wird. Das menschliche Zeitbewußtsein gibt der Wahrnehmung eine untere Schwelle vor, eine Untergrenze, unterhalb der zeitliche Abstände wegen ihrer Kürze nicht mehr vorstellbar sind. Wenn man sich bewusst 'alle' Abstände der Folge (a) vorzustellen versuchte, würde man konkret zählbare, unendlich viele mentale Akte realisieren, deren Dauer aber stets oberhalb der von der Wahrnehmungsschwelle vorgegebenen Spanne bleibt. Dies nicht zu unterschreitende 'Minimum' ist indes eine archimedische Größe. Zu sich selbst unendliche Male hinzuaddiert, ergäbe es ein unendliches Ergebnis. Folglich würde die Vorstellung der gesamten Folge dadurch unmöglich gemacht, dass es einen unbegrenzten Zeitraum benötigt, zum Beispiel dann, wenn man die Abstände (a) einzeln 'durchzählte' und ihnen jeweils eine Ordnungszahl zuwiese, die allein dadurch, dass sie gedacht (oder gesagt) wird, mehr Zeit in Anspruch nähme als das besagte Minimum dauert. (Allerdings, so hatte Aristoteles eingewendet, sei es doch widersinnig, anzunehmen, dass das, was sich bewege, zählenderweise voranschreite. Phys. 263a-263b.) Zenon, der die Möglichkeit bezweifelt, dass sich die Strecke [0,1] zurücklegen lässt, beruft sich auf die Verzögerung, die dadurch entsteht, dass die Folge (a) auf die entsprechenden geistigen Akte des Zählens bezogen wird, verschweigt dabei aber, dass dieser Prozess nicht genau das Maß der physischen Zeit abbildet, die für das tatsächliche Ablaufen der Strecke benötigt wird.
  So ist für Grünbaum Zenons Argument deshalb unzulässig, weil es im Grunde auf einem Zeitmaß aufbaut, das zwangsläufig eine Verwechslung zwischen unvereinbaren Formen des Denkens darstellt. Demnach nehmen wir die Unterabstände, in die wir die Gesamtstrecke unterteilen, nicht in einem Zeitmaß wahr, das ihrer Natur entspricht. Vielmehr beziehen wir den Eindruck ihrer Dauer aus der Zeit, die unsere Vorstellungsakte einnehmen, eine Zeitspanne, die für jeden gedachten Teilabschnitt zwangsläufig immer über der Wahrnehmungsschwelle oder der unteren Wahrnehmungsgrenze liegt« (Zellini, S. 38f).

Dies Zitat zeigt, wie schwierig es bis heute ist, für das Paradox von Zenon die geeigneten Worte zu finden. Ich möchte versuchen, es in zwei Fälle aufzuteilen:

• Wenn Achilles und die Schildkröte in der Lage sind, alle Punkte wahrzunehmen und zu zählen, die sie im Verlaufe ihrer Bewegung passieren, dann zählen sie in gleicher Zeit gleich viele Punkte, obwohl Achilles schneller ist und eine größere Strecke zurücklegt. Das ist mathematisch darin begründet, dass zwei Kontinua unterschiedlicher Länge die gleiche Mächtigkeit haben. Es ist möglich, alle Punkte der kürzeren Strecke eindeutig auf alle Punkte der längeren Strecke abzubilden, obwohl die längere Strecke die kürzere enthalten kann. Jedoch kann keine Zahl genannt werden, wie viele Punkte das sind. Stattdessen setzen die Mathematiker ein Symbol ein und sagen, dass die Mächtigkeit des Kontinuum 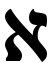1 beträgt. In diesem Sinn ist das Kontinuum größen-los: Seine Größe kann nicht durch die Anzahl Punkte gemessen werden, die in ihm enthalten sind. Cantor hat es auf den Begriff gebracht: Das Kontinuum ist über-abzählbar.
  
  Wird die Geschwindigkeit von Achilles und der Schildkröte daran gemessen, wie viele Punkte sie im Verlaufe einer Zeiteinheit durchlaufen, dann sind sie gleich schnell, da sie in der gleichen Zeiteinheit gleich viele Punkte durchlaufen, und Achilles wird die Schildkröte nie einholen. Das Argument von Zenon liegt darin versteckt, dass er unausgesprochen das Maß für die Geschwindigkeit durch die Anzahl der durchlaufenen Punkte bestimmt und voraussetzt, dass sich das Kontinuum lückenlos in Punkte aufteilen lässt.
  
  Aristoteles hat daraus die Konsequenz gezogen, dass sich das Kontinuum nicht aus dimensionslosen Punkten zusammensetzen kann. Es  enthält  zwar unendlich viele Punkte, aber es  besteht  nicht aus unendlich vielen Punkten. Wie genau auch immer die Strecke in Abschnitte und deren Grenzpunkte aufgeteilt wird, es bleibt immer eine Strecke  zwischen  zwei benachbarten Grenzpunkten. Aristoteles nimmt damit das Argument von Zenon in gewisser Weise auf: Zenon hat recht, wenn er zeigt, dass das Zwischen nie verschwinden wird. Aber Zenon zieht daraus den falschen Schluss, dass es möglich sein muss, dennoch alle Punkte zählen zu können, d.h. in endlicher Zeit das jeweilige Zwischen immer weiter zu unterteilen und zu zählen bis es ausgeschöpft ist.
  
  
• Gibt es dagegen entsprechend dem Argument von Grünbaum für die Wahrnehmungsfähigkeit und die mentale Fähigkeit zu zählen eine Wahrnehmungsschwelle, dann sind weder Achilles noch die Schildkröte in der Lage, alle Punkte wahrzunehmen und zu zählen, die sie durchlaufen. Sie können nur so viele einzelne Strecken wahrnehmen, wie es entsprechend der unteren zeitlichen Begrenzung der Wahrnehmungsfähigkeit möglich ist. Die Wahrnehmungsschwelle beträgt ca. 30 Millisekunden (siehe Zeitwahrnehmung). Da die Wahrnehmungsschwelle unabhängig von der Geschwindigkeit gilt, wie schnell sich ein Mensch bewegt, nehmen Achilles und die Schildkröte in der gleichen Zeit gleich viele Strecken wahr (wobei unterstellt wird, dass die Wahrnehmungsschwelle von Schildkröte und Mensch gleich sind). Da sich Achilles schneller bewegt, ist die kürzeste einzelne Strecke, die er wahrnehmen und zählen kann, länger als die kürzeste Strecke, die die Schildkröte wahrnehmen kann.
  
  Hier ist die Unschärferelation vorgeprägt: Während Achilles an der unteren Grenze seiner Wahrnehmungsschwelle längere Strecken sieht, sieht die Schildkröte in der gleichen kürzesten Zeiteinheit kürzere Strecken, und diese entsprechend schärfer. Im Ganzen sehen sie gleich viel, jedoch setzt sich das Gesehene zusammen aus zwei inneren Faktoren, die in umgekehrten Verhältnis zueinander stehen: Die Schärfe und die Länge der einzelnen Strecken.

In Buch VIII geht Aristoteles einen wesentlichen Schritt weiter, was insbesondere von Waschkies hervorgehoben wird. Für ihn werden die Paradoxien von Zenon »in Phys. VIII.8 263a4-b9 im Rahmen einer ganz neuen Theorie diskutiert« und lassen sowohl »die älteren Überlegungen aus Phys. VI.2« wie auch die Ausführungen in Über Werden und Entstehen hinter sich (Waschkies, S. 334). Zwar wurde in Buch VI »eine Lösung gefunden dadurch, dass die Zeit unendlich viele (Jetztpunkte) in sich enthält, [...] hingegen für die Wahrheit der Sache (pros to pragma kai ten aletheian) reicht sie nicht« (Phys. VIII.8, 263a). (Wörtlich übersetzt heißt pros to pragma kai ten aletheian »gemäß der Sache und der Wahrheit«, oder auch »Tat und Wahrheit«, wenn an die Bedeutung von pragma als Handlung oder Tat gedacht wird.) Denn jetzt will Aristoteles nicht mehr wie im Beispiel von Achilles und der Schildkröte zwei verschiedene Bewegungen miteinander vergleichen, sondern er will »das nun für die Zeit selbst wissen« (Phys. VIII.8, 263a). Es wird also nicht die Bewegung eines Objekts mit der Bewegung eines anderen Objekts verglichen, sondern mit der Zeit selbst. Daher kann nicht mehr wie mit Grünbaum auf die Wahrnehmungsschwelle des Menschen verwiesen werden, denn diese gilt für die Zeit nicht. Für die Zeit gilt, dass sie kontinuierlich vergeht, ohne etwas wahrzunehmen und zu zählen.

Aristoteles fragt, was geschieht, wenn beide Aspekte zusammenkommen (das Legato und Staccato im Bild von Grünbaum), zum einen die Betrachtung der Bewegung im Ganzen und zum anderen die Untersuchung aller Punkte, die im Verlaufe der Bewegung durchlaufen werden.

»Wer eine fortlaufende Bewegung macht, hat nebenbei auch Unendliches durchlaufen, im eigentlichen Sinne aber nicht. Es trifft der Linie doch nur nebenbei zu, unendlich viele Halbstücke zu sein, ihr wesentliches Sein ist ganz etwas anderes« (Phys., VIII.8, 263b).

Mit dem »Nebenbei« (symbebêkos) ist nach meinem Verständnis an dieser Stelle zweierlei gemeint: Aristoteles gebraucht den Ausdruck symbebêkos im Sinne von Akzidenz und unterscheidet damit die erste Kategorie (Substanz, ousia) von den zweiten Kategorien wie Qualität, Quantität, Ort etc, die in der Metaphysik als symbebêkota bezeichnet werden (Met. V.7 1017a, Met V.30 1025a). Wenn mit der Bewegung nebenbei alle Punkte durchlaufen werden, ist das nicht die wesentliche Bedeutung der Bewegung, sondern eine Eigenschaft, die ihr akzidentell zukommt.

Zugleich verstehe ich »nebenbei« in dem Sinn, dass das Durchlaufen der Punkte »nebenbei« erfolgt, ohne vom Bewusstsein voll wahrgenommen zu werden. Es merkt nicht, wie jeder Punkt auf der Bewegungsbahn einzeln durchlaufen wird. Das gilt auch für die Wahrnehmung. Wer sehr schnell eine Baum-Allee entlang fährt und nach rechts oder links auf die Baumreihen schaut, für den werden ab einer bestimmten Geschwindigkeit die einzelnen gesehenen Bäumen verschwimmen zu einer Art Schleier oder Nebel, der zwar den Hintergrund durchschimmern lässt, aber nicht mehr in einzelne Objekte unterschieden werden kann. Das Bewusstsein gelangt in einen Zwischen- oder Schwebezustand zwischen genauer und summarischer Wahrnehmung. Es nimmt etwas wahr, von dem es weiß, dass es unendlich viele Punkte enthält, ohne diese unterscheiden zu können.

Ähnliche Beispiele hatte Leibniz genannt, wenn er von der Wahrnehmung des Meeresrauschens sprach. In Wahrheit ist das unbestimmte Rauschen zerlegbar in die Geräusche der einzelnen Wasserpartikel, die am Meer zu hören sind, aber der Mensch hört mit seiner begrenzten Wahrnehmungsfähigkeit nur noch ein unbestimmtes Rauschen. Leibniz hat daher sorgfältig unterschieden zwischen der Wahrnehmung und den »kleinen Wahrnehmungen«.

»Ist aber eine gewaltige Menge kleiner Perzeptionen vorhanden, in der sich nichts deutlich abhebt, so ist man betäubt, wie wenn man sich mehrmals in derselben Richtung herumdreht, wobei einen ein Schwindel überkommt, durch den man das Bewußtsein verlieren kann und der es einem unmöglich macht, Etwas zu unterscheiden« (Leibniz Monadologie, § 21).

Die »gewaltige Menge kleiner Perzeptionen« erreicht zwar die Wahrnehmungsfähigkeit, aber nicht das Bewusstsein. Hier sehe ich bei Leibniz den gleichen Gedanken wie bei Aristoteles. Was Aristoteles als »nebenbei« bezeichnet, nennt Leibniz die »kleinen Perzeptionen«.

Die einzelnen Bestandteile des Rauschens können nur statistisch unterschieden werden. Sie sind für sich ununterscheidbar. Das Zwischen setzt sich unterhalb der Wahrnehmungsschwelle zusammen aus ununterscheidbaren Teilen. Die Ununterscheidbarkeit ist ein anderer Ausdruck dafür, dass sie in einem genau definierten Sinn größen-los sind: Sie haben eine Größe, aber diese Größe kann nur statistisch ermittelt und nicht genau bestimmt werden. In diesem Sinn verstehe ich das Zwischen als die gesuchte mathematische Verselbständigung des Formmangel (steresis). Das Zwischen enthält ununterscheidbare Teile. Das bedeutet anders gesagt: Diese Teile sind austauschbar. Da sie nicht unterschieden werden können, verändert sich nichts, wenn sie ausgetauscht werden. Die einzelnen austauschbaren Teile können nicht identifiziert werden, aber es können Regeln der Austauschbarkeit erkannt werden. So geht das Zwischen als Prinzip der Meta-Mathematik über in die Austauschbarkeit als Prinzip der Mathematik.

So gesehen hat die Unschärfe-Relation ihren tiefsten Grund im Wechselverhältnis von Form und Formmangel, das meta-mathematisch als Wechselverhältnis von Größe und Größen-Mangel verstanden werden kann, wie es sich am Zwischen zeigt, oder mathematisch als Verhältnis von Dimension und Austauschbarkeit. Davon sollen weitere geplante Kommentare handeln.

Erst mit diesem Verständnis ist für Aristoteles »Sache und Wahrheit« erreicht.

Anmerkung: Auf ähnliche Weise beschreiben Fichte und Hegel den besonderen Zustand einer höheren Erkenntnis, wenn Fichte in der Darstellung der Wissenschaftslehre von 1801 den »Mittel- und Wendepunkt des absoluten Wissens« als »ein Schweben zwischen Sein und Nichtsein des Wissens« bezeichnet (Fichte, WL 1801, § 24, S. 51), und Hegel in der Phänomenologie des Geistes 1807 von der »schwebenden Mitte und Vereinigung« von Rhythmus und Metrum im philosophischen Satz spricht (HW 3.59).

Das unsichtbare Zwischen (nach Newstead)

Die Wiederentdeckung Aristoteles' durch die Mathematik geht auf Georg Cantor zurück. Cantor wendet sich zwar gegen das Argument von Aristoteles, dass die Unendlichkeit des Kontinuum nur potential und nicht aktual besteht, aber er sieht zugleich bei Aristoteles die entscheidenden Anregungen, wie den Paradoxien von Zenon entgangen werden kann. Newstead zitiert einen Brief von Cantor an den französischen Mathematiker Paul Tannery:

"Mit Recht heben Sie hervor, dass ich gewissermaßen die Auffassung der Pythagoreer erneuere, sofern ich eine reale Zusammensetzung des geometrischen Continuums aus getrennten Punkten als geometrischen Einheiten lehre, analog dem, wie der Wald aus Bäumen zusammengesetzt ist; aber während von den Pythagoreern das Continuum als eine Summe von Punkten gefasst wird, gegen welche die Beweise Zenons von Elea volle Kraft besitzen, ist es bei mir eine Punktmenge (ensemble of points) von bestimmter, genau angegebener Beschaffenheit.
   Meine Fassung des geometrischen (und zeitlichen) Continuums ist eine solche, welche die Vorzüge der Aristotelischen mit dem, was an der Pythagoreischen Auffassungsweise wahr ist, harmonisch vereinigt, sodass es keinem Zeno gelingen wird, mir in meinem wohlerwogenen Continuumsbegriff irgendwelche Widersprüche nachzuweisen." (Georg Cantor an Paul Tannery am 5. Oktober 1888, Cantor, Briefe, S. 323, zitiert in englischer Übersetzung bei Newstead, S. 11f)

Cantor versteht zwar das Kontinuum als eine Menge von Punkten, jedoch versehen mit einer bestimmten mathematischen Ordnung. Für ihn kann den Paradoxien von Zenon begegnet werden, wenn gezeigt wird, dass die Argumente von Zenon nur für solche Punktmengen zutreffen, denen eine solche Ordnung fehlt.

Wie kann innerhalb des unbestimmten Zwischen eine Ordnung gefunden werden? Auf diese Frage ist bereits Aristoteles gestoßen, und Newstead will zeigen, wie Cantor das allgemeine Argument von Aristoteles in eine exakte mathematische Gestalt gebracht hat. Aristoteles betrachtet die Aufteilung eines physischen Körpers in immer kleinere Teile, bis er am Ende in einen neuen Zustand übergeht, den Aristoteles in großer Anschaulichkeit als »Sägemehl« bezeichnet. Ist etwas in Sägemehl zerfallen, dann ist das Sägemehl zwar stofflich identisch mit dem Gegenstand, der zerkleinert wurde, aber es hat die innere Spannung, im wörtlichen Sinn das Zusammengewachsene verloren, das vorher das Holz ausgezeichnet hatte.

Aristoteles schreibt in Über Werden und Vergehen (peri geneseôs kai phthoras, De generatione et corruptione):

»Aber auch wenn bei einer Teilung des Körpers so etwas entstünde wie Sägemehl (prisma) (wörtlich: das Zersägte, Zerschnittene, siehe Duden, t.) und sich auf diese Weise aus der Größe ein Körper davonmachte, griffe das gleiche Argument: wie ist denn jenes teilbar? Wenn es aber kein Körper ist, sondern ein getrenntes Charakteristikum oder ein Zustand (pathos), der sich davongemacht hat, und die Größe sich aus Punkten oder Berührungen bildet, die in einem solchen Zustand (pathos) sind, so ist es doch ungereimt, daß Größe aus Größelosem sein soll« (Aristoteles, Werden und Vergehen, 316a34-316b5, bei Newstead in englischer Übersetzung zitiert S. 16).

Aristoteles wählt den Ausdruck »Sägemehl« mit Bedacht, da er das Holz (hyle) als Metapher für den Stoff gebraucht. Wenn etwas so weit zerkleinert wird, dass es aus einem kompakten Zustand wie Holz in einen pulverisierten Zustand wie Sägemehl übergeht, ist damit ein Wandel verbunden, der der Frage entspricht, ob und wie ein Kontinuum aus Punkten zusammengesetzt werden kann. Im Sägemehl ist die Ordnung verloren, um deren mathematisches Schema es Cantor geht.

Cantor löst sich von den stofflichen Vorgängen und trifft das mathematische Schema der von Aristoteles beschriebenen Aufteilung eines Stückes Holz in Sägemehl, wenn er den Cantor-Staub konstruiert. Der Cantor-Staub ist gewissermaßen das Sägemehl, das übrig bleibt, wenn das zusammenhängende Kontinuum unendlich oft zerschnitten und die jeweils mittleren Teile weggeworfen werden. Obwohl der Cantor-Staub in dieser Hinsicht dem Sägemehl gleicht, gibt es einen wesentlichen Unterschied: Durch die feste Regel, wie der Cantor-Staub konstruiert ist, bleibt selbst im Übergang bis zur völligen Zerstreuung eine Ordnung erhalten. Mathematisch gesehen ist der Cantor-Staub ein erstes Beispiel für ein Fraktal, d.h. eine Menge mit einer gebrochenen Dimension.

Figur 6: Cantor-Staub

Der Cantor-Staub entsteht, wenn aus einer endlichen Strecke erst das mittlere Drittel, dann aus den verbleibenden Dritteln schrittweise wieder jeweils das mittlere Drittel herausgenommen wird und so fort. Der Cantor-Staub besteht auf jeder Stufe der Aufteilung aus voneinander getrennten, in sich zusammenhängenden Abschnitten. Im Ergebnis bleiben isolierte Punkte stehen. Wird im einfachsten Fall das Intervall [0,1] schrittweise aufgeteilt, dann sind dies die Punkte 1/3, 2/3, 1/9, 2/9, 7/9, 8/9, 1/27, 2/27, …. Cantor hat für die Gesamtheit dieser Punkte eine mathematische Darstellung gefunden und gezeigt, dass es eine eineindeutige Zuordnung gibt, die jeder reellen Zahl einen dieser Punkte zuordnet. Daher ist die Cantor-Menge von gleicher Mächtigkeit wie die reellen Zahlen (siehe Newstead, S. 15f).

Dennoch ist zugleich klar, dass im Ergebnis mit der Wegnahme der mittleren Drittel die komplette Länge des Intervalls verschwunden ist. Übriggeblieben sind nur dimensionslose Punkte. Die Cantor-Menge ist damit einerseits von gleicher Mächtigkeit wie die reellen Zahlen, hat andererseits aber ihre Länge und ihren Zusammenhang verloren. Für solche Situationen wurde der Begriff der Dimension erweitert. Die Cantor-Menge hat eine gebrochene Dimension. Sie beträgt ›ln(2) / ln(3) = 0,6309…‹ (Wikipedia).

Mit der Cantor-Menge und der gebrochenen Dimension ist nach meinem Verständnis genau die Art von Größenlosigkeit gemeint, um die es Aristoteles ging. Das Zwischen ist ein verschwindender Bereich. Es hat keine eigene Größe im üblichen Sinn, sondern verschwindet in dem Maß, wie versucht wird, es zu greifen. Während Aristoteles jedoch bei der Gegenüberstellung von Punkt, Kontinuum und Zwischen stehen blieb, hat Cantor nach den Eigenschaften gesucht, mit denen das Kontinuum beschrieben werden kann.

Newstead will zeigen, dass Cantor vier Eigenschaften des Kontinuum bestimmt hat, von denen drei auch bei Aristoteles nachweisbar sind: Dichte, Zusammenhängendes (im Sinne von lückenlos, Mittelwertsatz), Abgeschlossenheit (Closure). Der Unterschied liegt für sie erst bei der Wohlordnung, die Cantor für die überabzählbaren Zahlen eingeführt hat. Eine Menge ist wohlgeordnet, wenn jede Teilmenge bezüglich der Ordnung ein kleinstes Element enthält. Diese Definition ist in der Mathematik umstritten, da sich keine Regel angeben lässt, wie das kleinste Element zu finden ist.

Das Wohlordnungs-Axiom kann in zweierlei Sinn auf Aristoteles bezogen werden: Wenn in einer Untermenge einer wohlgeordneten Menge das kleinste Element gesucht wird, ist das ein Beispiel für die Eigenschaft des Äußersten (eschaton), von der Aristoteles sprach. Wenn jede Menge ein kleinstes Element enthält, ist sie wohlgeordnet. Im Grunde benutzt Aristoteles dies Argument, wenn er gegenüber Zenon festhält, dass es in der Menge der Verbindungslinien zwischen Achilles und der Schildkröte ein kleinstes Element geben muss, welches den Punkt bezeichnet, an dem sie sich treffen.

Anmerkung: Einige Jahrzehnte vor Cantor hat der Schriftsteller Balzac die Idee des schrittweisen Wegnehmens vorweggenommen und damit zugleich die Grundidee der modernen Kunst getroffen. Er lässt in seiner Erzählung Das unbekannte Meisterwerk den Maler Frenhofer sein Verständnis der Malerei entwickeln. Frenhofer sucht eine Malerei, die »zwischen Zeichnung und Farbe, zwischen der sorgfältigen Ruhe und exakten Strenge der alten deutschen Meister und der fulminanten Glut und glückseligen Üppigkeit der Italiener« die Mitte trifft. Denn »die Natur setzt sich aus einer Reihe von Rundungen zusammen, die einander umhüllen. Strenggenommen gibt es die Zeichnung gar nicht. ... In der Natur, in der alles ausgefüllt ist, gibt es keine Linien! ... Allein die Verteilung des Lichts lässt den Körper als Körper erscheinen!« (Balzac, S. 130, 141f) Lichtflecken überdecken den erhellten Körper, umhüllen (überdecken) einander statt aneinander geheftet zu werden, und der Maler hat aus ihnen sein Bild des Körpers zusammenzusetzen, statt es aus atomaren kleinsten Bausteinen zusammenzufügen. Wenn ein Maler in einem Gemälde erst den Hintergrund und dann davon getrennt die Figuren im Vordergrund zeichnet, oder erst den Vordergrund, und dann in den Lücken zwischen den Figuren des Vordergrunds die sichtbaren Abschnitte des Hintergrunds, dann entstehen starre Bilder, wie Delacroix sie am Beispiel der Bilder von Ingres kritisiert hat. Lichtflecken dagegen liegen in einem unbestimmbaren Zwischenbereich zwischen dem Vordergrund und dem Hintergrund und verleihen der Figur ihre einzigartige Freiheit und Beweglichkeit im Raum. Diese Ansicht blieb natürlich nicht unwidersprochen. Die künstlerische Gegenposition vertrat im 20. Jahrhundert der Kubismus, der mit dem Siegeszug des Atomismus in der Naturwissenschaft entstand. - Wen Beispiele interessieren, der vergleiche, wie starr Ödipus auf dem berühmten Bild von Ingres vom Hintergrund abgetrennt ist, wie fremd er in dieser Welt bleibt ( Link ), während sich die von Delacroix gemalte Frau mit dem Papagei völlig im Einklang mit ihrer Umgebung und ihrer Situation befindet, ein Bild vollendeten Glücks ( Link ).

Der Rhythmus des Zwischen

Wenn die Wahrnehmung der einzelnen Ereignisse zu verschwimmen beginnt und den Wahrnehmenden eine Art Taumel ergreift, von dem Leibniz sprach, dann wandeln sich die einzelnen Wahrnehmungen in einen neuen Zustand, der als Schwindel, Schwebung, Strömung oder flow bezeichnet werden kann, wohl auch als die Leere des Nirwana. In all diesen Erfahrungen gewinnt das Zwischen, das sich nicht mehr aus einzelnen, unterscheidbaren Punkten zusammensetzt, eine eigene Lebendigkeit. Es wird nicht einfach etwas Anderes erfahren, sondern ein anderer Wahrnehmungszustand erreicht. Für Aristoteles geht daher konsequenterweise an dieser Stelle die Physik über in die Psychologie (Seelenkunde, De Anima), die dem VIII. Buch der Physik folgt.

Im Übergang ist nur noch der Rhythmus der einzelnen Wahrnehmungen zu spüren. Das kann das kontinuierliche Geräusch der scheinbar »vorbeifliegenden« Bäume bei der schnellen Fahrt durch eine Allee sein. Das Geräusch ändert sich, wenn sich der Abstand der einzelnen Bäume ändert, auch wenn die einzelnen Bäume nach wie vor nicht zu unterscheiden sind. Ähnlich gilt es für das Auf und Ab des Meeresrauschens, von dem Leibniz sprach.

Mit Wahrnehmungen dieser Art hat sich Aristoteles nicht mehr beschäftigt. An dieser Stelle ist Cantor weiter gegangen, wenn er nicht mehr nach den Eigenschaften der einzelnen Elemente, sondern ihrer übergreifenden Struktur gefragt hat. Sein Hinweis auf Pythagoras kann auch so verstanden werden, dass die Pythagoreer mit ihrer mathematischen Lehre der Harmonien ein erstes Verständnis gewonnen haben, welcher Art diese Eindrücke sind.

Heute wird mit Emergenztheorien versucht, die spontane Entstehung neuer Ordnungen zu verstehen, die im Übergang einer tieferliegenden Schicht in eine höhere Schicht auftreten.

Hinweis auf die Austauschbarkeit: Ununterscheidbarkeit liegt vor, wenn die einzelnen ununterscheidbaren Elemente austauschbar sind. Wären sie nicht austauschbar, könnten sie unterschieden werden. Für die Austauschbarkeit gilt statistisch, dass sie bestimmten Regeln folgt. Diese können als Rhythmen verstanden werden.

»Inmitten« der Bewegung zwischen Möglichkeit und Wirklichkeit

Aristoteles ist jedoch von einer anderen Seite auf die Frage des Zusammenhalts im Schwebezustand des Zwischen einer Bewegung gekommen. Wurde bisher die Bewegung als Ortsbewegung betrachtet und gemessen an den für sich unveränderlichen Orten, die von ihr durchlaufen werden, so kann sie auch für sich betrachtet werden. Jede Bewegung ist ein Übergang von einem Zustand in einen anderen, und innerhalb dieses Übergangs durchläuft sie ein Zwischen, in dem sie gefährdet ist. Während im Griechischen von Aristoteles der gleiche Ausdruck metaxy gebraucht wird, kann bei Übersetzung in das Deutsche unterschieden werden in »Zwischen« und »Inmitten«.

»Zwischen nennt man den Zustand, in dem bei stetiger Wandlung der sich wandelnde Gegenstand kommen muss, bevor er das Ziel der Wandlung erreicht« (Phys. V.3, 226b, Gohlke; Zekl übersetzt »inmitten« statt »zwischen«).

Diese Übersetzung kann missverstanden werden: Das Zwischen ist kein dritter Zustand zwischen dem Anfangs- und dem Endzustand und diesen insofern gleichberechtigt, sondern das Bewegte befindet sich im Zwischen in einem völlig anderen Schwebezustand, der nicht wie die festen Zustände vor und nach der Bewegung beschrieben werden kann.

»Dafür, daß Veränderung unbestimmbar (aoriston) zu sein scheint, liegt die Ursache darin, daß man sie im Bereich des Seienden weder auf der Seite der Möglichkeit noch unter die wirkende Tätigkeit einordnen kann: weder, was ein 'irgend-wieviel' sein kann, verändert sich mit Notwendigkeit, noch das, was schon wirklich ein 'so-und-so-viel' ist, und Veränderung scheint zwar eine Art Wirksamkeit zu sein, aber eine noch nicht zu Ende gebrachte. Ursache davon ist: Noch unvollkommen (ateles) ist das Mögliche, dessen Verwirklichung sie ist« (Phys. III.2, 201b).

Wenn die Bewegung unterwegs zu dem ist, was noch fehlt, mittendrin ist, ist sie unfertig. Würde sie hier abgebrochen oder durch äußere Einflüsse unterbrochen werden, käme es wahrscheinlich sogar zu einem Rückfall hinter den Ausgangszustand. Während der Veränderung sind die betroffenen Bestandteile des zu Ändernden in einem frei-beweglichen Zustand, um sie anders und neu zusammenfügen zu können. In diesem Veränderungszustand versagen die Kategorien. In diesem Moment befinden sich Substanz, Qualität, Quantität und Ort in einem undefinierbaren Schwebezustand.

Am Beispiel der Kategorie Quantität hat Aristoteles die Lehre vom Differential vorweggenommen. Im Grenzübergang ist das Differential genau in dem Sinn unbestimmbar (aoriston), wie Aristoteles hier beschreibt. Im Grenzübergang gibt es »verschwindend« kleine Größen. Sie dürfen nicht 0 sein, aber auch keinen festen Wert annehmen. Ohne Aristoteles zu erwähnen geht Hegel davon in seiner Wissenschaft der Logik im Kapitel über die Aufhebung des Quantums aus (Hegel, HW 5.295f). Im Moment der Aufhebung verschwindet die alte Größe und eine neue Qualität entsteht. Das lässt sich weder in der Kategorie der Quantität noch der Qualität fassen. (Auch die Kategorie der Relation zwischen unterschiedlichen Größen hilft nicht, denn im Grenzübergang gibt es zwar immer ein Verhältnis zweier Größen im Steigungsdreieck, aber dies Verhältnis verschwindet ebenso wie die beiden Größen verschwinden. Im Grenzübergang wandelt sich das zweidimensionale Steigungsdreieck in die Tangente und die Relation ist aufgehoben.)

Anmerkung 1: Seidel erhebt Einspruch:

»Nein, das Sein der Bewegung ist nicht unvollständig, sondern die Bewegung hat wie alles Stetige zwei Definitionen, die 'in' einem Jetzt und die zwischen zwei Jetzt« (Seidel, S. 112).

Das ist aber nur halb richtig. Er stimmt Aristoteles zu, zwischen dem Jetzt und dem »Zwischen zwei Jetzten« zu unterscheiden (und arbeitet es graphisch sehr klar heraus, wenn das »Jetzt« zur rot dargestellten Form und das »Zwischen« zum blau dargestellten Stoff gehört), aber er umgeht die Frage des Grenzübergangs. Während die frühen Naturphilosophen hier ein Paradox sahen, das sich dem Denken entzieht, reißt Seidel den Übergang auseinander in zwei Definitionen.

Anmerkung 2: Die Gefährungen inmitten einer Entwicklung werden naturgemäß besonders intensiv für die Embryogenese untersucht. Im Verlaufe der Embryogenese gibt es zahlreiche kritische Punkte, an denen äußere Einflüsse die Herausbildung des Menschen negativ beeinträchtigen können. Siehe z.B. Medikamente in der Schwangerschaft. Lassen sich im Verlaufe der Embryogenese mathematische Strukturen erkennen, die die Entstehung des Embryo stabilisieren, z.B. bestimmte geometrische Muster, zeitliche Zyklen, topologische Umbildungen? Fragen dieser Art hat René Thom aufgeworfen. Biomathematik und Bioinformatik.

Erkundung im Raum des Möglichen (nach Heidegger)

Bisher wurde davon ausgegangen, dass es innerhalb eines Zwischen ein Äußerstes gibt, in das übergehen zu können eine Eigenschaft des Zwischen ist. Das Äußerste befindet sich innerhalb eines Zwischen zwischen den beiden Elementen, die einen konträren Gegensatz bilden. In der Metaphysik ist Aristoteles an anderer Stelle von einer ganz anderen Seite auf diese Frage gekommen. Hier geht er nicht von einem vorliegenden Zwischen aus, dessen Eigenschaften zu bestimmen sind, sondern von einer Sache, für die das Zwischen zu finden ist, innerhalb derer sie sich befindet. Er sieht als die besondere Fähigkeit eines vernünftigen Vermögens (dynameis meta logon), die er von dem unvernünftigen Vermögen unterscheidet (dynameis alogoi, Met. IX.2, 1046a36-b2), für eine vorliegende Sache das Zwischen zu finden, innerhalb dessen sie sich befindet, oder anders gesagt, für die Sache einen Horizont zu erkennen, in dem sie steht. Der Horizont ist aufgespannt durch die einander konträr Entgegengesetzten (enantion).

Kunstvoll wird die zweifache Bedeutung von dynamis genutzt: Sie ist zum einen das Vermögen, eine Sache zu verstehen, und zum anderen wird mittels dieser Fähigkeit der Möglichkeitsraum erkundet, innerhalb dessen sich die vorliegende Sache befindet. Die Möglichkeiten, die für die Sache bestehen, enthalten ihrerseits einen konträren Gegensatz, der zwischen einer vollendeten Ausbildung aller Möglichkeiten und einem Entzug (steresis) bestimmter Möglichkeiten besteht.

Diese Deutung des Kapitel IX.2, 1046ab geht auf Heidegger zurück (siehe dessen Vorlesung Aristoteles, Metaphysik Θ 1-3 in Freiburg 1931, GA 33). Eine Sache wird erkundet, indem von ihr ausgehend die Sphäre gefunden wird, innerhalb derer sie sich befindet.

Heidegger übersetzt Aristoteles in eine komplexe Sprache, die die Vielfältigkeit der inneren Bezüge festhält und nicht glättet.

»Der Grund dafür (dass gewisse dynameis auf Gegenliegendes gehen) ist der, dass das Sichverstehen-auf-etwas (in sich) eine Kundschaft (die Kunde) ist; die Erkundigung aber, und zwar ein und dieselbe, macht offenbar das, womit man es je zu tun hat, und den Entzug; freilich das nicht in derselben Weise; in gewisser Weise nämlich zwar betrifft die Erkundigung beides, in gewisser Weise aber mehr das (je schon) Vorliegende. Daher die Notwendigkeit, daß auch die so beschaffenen (logos-geführten) Weisen des Sichverstehens-auf-etwas in einer Hinsicht zwar auf Gegenliegendes (das eine und dessen anderes) sich beziehen, in anderer Hinsicht aber auf das eine des Gegenliegenden, und zwar von sich aus (unmittelbar, gemäß ihrer Ausrichtung), auf das andere nicht in der genannten Weise; denn auch die Kunde geht auf das eine an ihm selbst, auf das andere gewissermaßen nur beiläufig. Durch Absprechen nämlich und Wegbringen macht sie das Gegenliegende offenbar; das Gegenliegende ist nämlich das in erster Linie Entzogene, dieses aber ist der Wegtrag des anderen (gegenüber dem einen)« (Met IX.2, 1046b7-15, in Heideggers Übersetzung, S. 134f).

Der logos erkundet das Umfeld, den Weg und seine Alternativen. Nur wenn das Umfeld verstanden wird, kann logos in seiner ursprünglichen Bedeutung verstanden werden als das Sammeln, Einlesen, den inneren Zusammenhang des Ganzen Erkennen. Dadurch werden auch Gefährdungen vorausgesehen, es müssen Entscheidungen für und gegen etwas getroffen werden, und es besteht immer die Gefahr des Scheiterns. Kraft und Macht sind daher grundsätzlich gefährdet und endlich.

Heidegger versteht logos ausdrücklich nicht als Begriff (Heidegger, S. 141), sondern als »Bürgschaft der Größe des Einsatzes menschlicher Existenz« (Heidegger, S. 145), wie das Herstellen als »Grundstellung zur Welt« (Heidegger, S. 146) und unterscheidet es vom Verständnis des logos »aus gnostisch-orientalischen Weisheitslehren«, wie es in den ersten Zeilen des Johannes-Evangelium über das Wort (logos) mitschwingt (Heidegger, S. 147).

Sachlich kann er sich besonders da auf Aristoteles berufen, wo der direkt die Seele erwähnt. Die Schlüsselstelle in diesem Text von Aristoteles ist daher:

»Da das in der äußersten Nachbarschaft Liegende sich nicht (zugleich) einbildet in dasselbe Seiende, das Sich-auf-etwas-verstehen aber eine Kraft ist auf Grund des Geführtseins durch die Rede, Kundschaft, und da die Seele einen Ausgang für Bewegung in sich vor-hält, so kann zwar das Gesunde lediglich Gesundheit befördern, das Warmgebende Wärme, das Kühlende nur Kühle, dagegen bezieht sich das, das sich auf etwas versteht, auf beides (das Entgegenliegende). Denn eine Kunde geht immer auf beides, aber nicht in gleicher Weise, und sie gehört (ihrer Seinsart nach) in eine Seele, die selbst (als solche) ein Von-wo-aus für Bewegung in sich vor-hält. Daher wird sie beides in Bewegung bringen und zwar ausgehend von demselben Ausgang und so, daß sie beides auf solches, was als dasselbe erkundet ist, zusammen zurücknimmt« (Met. Θ 2, 1046 b 15-22, in Heideggers Übersetzung, S. 149).

Durch die Seele gewinnt die Kraft erst ihre eigentümliche Kraft, wodurch sie sich von den anderen Kräften in der Natur unterscheidet. Kräfte in der Natur können etwas anderes beeinflussen und verändern. Aber sie sind »kundschaftslos« (alogoi, unvernünftig) und unbeseelt. Davon unterschieden ist das vernünftige Können (meta logon, schließlich die Wissenschaft), das seelische Können. Durch die Seele erhält es ein eigenes Streben, eine Orientierung an Zielen, und mit der Vernunft (Kundschaft, Sprache, logos) vermag es sich im Gelände der unterschiedlichen Wege, Alternativen und Gefährdungen zu orientieren.

Anmerkung 1: Die hier beschriebene Erkundung einer Sache kann verglichen werden mit der äußeren Reflexion bei Hegel. Auch die äußere Reflexion geht über die Sache hinaus und vermag es, sie von außen zu sehen und dadurch in einen größeren Zusammenhang zu stellen. Hegel selbst sieht jedoch die Mangelhaftigkeit der äußeren Reflexion. Sie entfernt sich von der Sache und droht, ihr einen äußerlichen Maßstab anzulegen. Daher bedarf sie ihrerseits einer zweiten Negation, um zur Sache zurück zu finden und diese in der bestimmenden Reflexion genauer zu treffen.

Aristoteles entfernt sich dagegen nicht in dieser Weise von der Sache. Er geht aus von den Möglichkeiten, die in ihr enthalten sind und vermag selbst im Entzug (steresis) bestimmter Möglichkeiten die Beziehung auf die Sache zu erkennen. Statt die äußere Reflexion ihrerseits wieder zu negieren, kann er die Eigenschaften untersuchen, die dem Möglichkeitsraum im Ganzen zugrunde liegen.

Anmerkung 2: Weiter kann untersucht werden, in welcher inneren Beziehung dies zum ersten Teil der Wissenschaftslehre von 1794/95 von Fichte steht, wenn er schreibt:

»Wir heben demnach mit einer Deduction an, und gehen mit ihr, so weit wir können. Die Unmöglichkeit sie fortzusetzen wird uns ohne Zweifel zeigen, wo wir sie abzubrechen und uns auf jenen unbedingten Machtspruch der Vernunft, der sich aus der Aufgabe ergeben wird, zu berufen haben« (Fichte, WL 1794, § 3 Einleitung, S. 18).

Mit einer solchen Deduktion scheint mir Fichte eine ähnliche Erkundung vorzunehmen, wie Aristoteles sie skizziert und Heidegger gedeutet hat. Die Deduktion beendet ihren Weg, wenn sie ihren Bereich »erschöpft« hat (Fichte, WL 1794, §3 D, S. 21).

Anmerkung 3: Im Ergebnis wird eine Sache irgendwo im Raum ihrer Möglichkeiten liegen und eine Zwischenstellung erlangen, die mit Aristoteles als hexis (Haltung) bezeichnet werden kann. Aristoteles führt den Begriff hexis in etwas anderer Bedeutung ein und versteht sie im wörtlichen Sinn als »Halten«, so wie jemand ein Kleid hält, oder als »Disposition, nach welcher das in einem bestimmten Zustand Befindliche sich gut oder schlecht befindet« (Met. V.20, 1022b). Mit dieser Disposition ist nach meiner Deutung die Position einer Sache innerhalb ihres Möglichkeitsraums gemeint.

Das kann ganz anschaulich verstanden werden. Wenn sich eine Sache entwickelt, muss sie in einer Umgebung und einem Lebensumfeld ihren Platz finden, der den äußeren Einflüssen gerecht wird und den inneren Fähigkeiten so viel Entfaltungsraum als möglich gibt. Die Haltung eines Menschen zeigt, wie er in seinen Gesten und alltäglichen Lebensgewohnheiten seinen Weg gefunden hat. In die Ausbildung der Haltung fließen unendlich viele und verschiedene äußere Einflüsse ein, die ihm nur teilweise bewusst sind. Mit der Haltung hat er seine in gewisser Weise stilisierte (schematisierte) Lösung für sein Lebensgeschick ausgebildet, und an ihr lassen sich sowohl seine Fähigkeiten wie auch die Rückschläge und Widerstände, das heißt die Entzüge (Mängel, steresia) erkennen, denen er ausgesetzt ist und auf die er eine Antwort gefunden hat. (Siehe hierzu Peter Nickl Ordnung der Gefühle).

Es ist für mich eine offene Frage, ob sich in der Herausbildung von Haltungen gewissermaßen mathematische Strukturen erkennen lassen, die die unendliche Vielfalt des Möglichkeitsraums vereinfachen. Das ist die Grundthese aller Lehren von Charaktertypen, die letztlich auf die pseudoaristotelische Schrift Physiognomonika aus dem 3. Jahrhundert vor Christus zurückgehen (Wikipedia).

Der Bedeutungswandel des Zwischen (metaxy) von Platon zu Aristoteles

Mit seinem Verständnis der Verselbständigung (chorizein) der mathematischen Figuren (schemata) und des Zwischen (metaxy) hat Aristoteles zentrale Themen von Platons Philosophie der Mathematik aufgenommen und völlig neu gedeutet. Platon sah die Mathematik zwischen der Wahrnehmungsfähigkeit und dem Denken. Mithilfe der Mathematik kann in dem Wahrgenommenen dasjenige identifiziert werden, das Gegenstand des Denkens wird. Ganz allgemein kann gesagt werden, dass es selbst im Chaos bereits Formspuren gibt, die noch keine ausgeprägte Form haben, aber mithilfe der Mathematik erfasst werden und das Denken anregen, mit seinen Ideen die Formen zu verstehen. Und umgekehrt bedarf das Denken der Mathematik, um seine rein idealen Ergebnisse in eine »mathematische Form« zu bringen, in der sie sich in der natürlichen Welt der Wahrnehmung wiedererkennen lassen. Nur auf diesem Weg können die »Eingeweihten« ihr Denken der »unwissenden Menge« verständlich machen. Daher empfahl Platon allen Wissenden, Mathematik zu lernen.

Für Platon befähigt die Mathematik den Menschen, in der sinnlichen Natur die höheren göttlichen Ideen zu erkennen und umgekehrt die von ihm erkannten Ideen den anderen Menschen mitzuteilen. Die Mathematik löst für Platon die Frage, in welcher Weise sich das Göttliche dem Menschen offenbaren kann. Das ist nur möglich, wenn es am sinnlich Wahrnehmbaren etwas gibt, woran der Mensch die göttliche Mitteilung erkennen kann. Das ist dessen mathematische Gestalt.

Anmerkung: Vergleiche die Ausführungen von Hegel zum Begriff der Mitteilung, den Hegel aus dem mittleren Glied (lat. terminus medius, gr. mesos horos) entwickelt, über das Schlüsse gezogen werden können. Hegel denkt an Beispiele wie die Mitteilung des Impulses von einem mechanischen Objekt an ein anderes, betont aber zugleich die weitreichende Bedeutung bis hin zur göttlichen Mitteilung. Siehe hierzu den Beitrag über die Kraft der Trägheit.

Aristoteles beschreibt den gleichen Vorgang, wenn er von der Verselbständigung der mathematischen Figuren spricht. Doch sieht Aristoteles hier nicht eine Offenbarung göttlicher Ideen, sondern eine Leistung des menschlichen Denkens, das an den Formen der Natur die dort bereits angelegten Figuren erkennen und in seinem Denken verselbständigt darstellen kann. Die mathematischen Figuren sind keine Ideen, sondern sie zeigen an den in der Welt vorkommenden Formen dasjenige, das unabhängig vom Stoff betrachtet werden kann. Diese Figuren gibt es nur im Denken der Menschen, der sie an den Sachen (pragma) seiner Umgebung erkennt, und nicht in einem eigenen Reich der Ideen.

Platon suchte eine besondere Eigenschaft des Menschen, mithilfe derer er zu Erkenntnissen dieser Art fähig ist. Das ist für ihn die Seele, die wie die Mathematik in einem Zwischenbereich (metaxy) liegt zwischen den körperlichen Regungen und ihren Trieben und dem Geist mit seiner Fähigkeit zu denken. Anschaulich wird das in Platons Verständnis der Liebe. Die Liebe beginnt mit körperlichem Begehren, aber sie kann weit darüber hinaus tragen. Die Liebe verleiht Flügel, sie ist eine Muse (siehe hierzu Pechriggl Chiasmen).

Daher hat für Aristoteles die Auseinandersetzung mit Zenon exemplarischen Charakter. Er will zeigen, dass das Unendliche und die Bewegung keine Ideen sind, die letztlich jenseits der wirklichen Erfahrung stehen und bei Betrachtung physischer Vorgänge das Denken ratlos in Paradoxien geraten lassen, sondern gerade an den von Zenon gewählten Beispielen vorführen, in welcher Weise die Verselbständigung der mathematischen Theorien erfolgt.

2006 - 2011, 2014

© tydecks.info 2014