megethos – Größe und Krise der griechischen Mathematik

 

 

Größe und Dimension (erste Fragestellungen)

(1) Ursprünglich wurde von Größe nur in einem jeweils spezifischen Kontext gesprochen, wie hoch, breit, tief etwas ist, wie lange etwas dauert, um das Wievielfache das eine größer als das andere ist. Wenn von Größe die Rede war, musste aus dem jeweiligen Zusammenhang erschlossen werden, ob die Höhe, das Volumen, die Breite, Tiefe oder Oberfläche gemeint war, im übertragenen Sinn die Macht, Kreativität oder ihre Folgen, wenn etwa von »großen Philosophen« oder »großen Ereignissen« gesprochen wird. Umgangssprachlich hat sich das bis heute gehalten, wenn z.B. gesagt wird, dass jemand 1,80 m »groß« ist, womit seine Höhe gemeint ist. Erst der Mathematiker Eudoxos hat erkannt, dass es allgemeine Gesetze der Größe gibt, die in allen Dimensionen gelten. Dafür wurde der Begriff megethos eingeführt, um sprachliche Verwirrung zu vermeiden, wie sie noch heute im Deutschen vorkommt. Diesen Begriff hat Aristoteles übernommen.

(2) Größe muss vom Ort getrennt werden. Anschaulich ist es gleichbedeutend zu sagen, welchen Ort etwas einnimmt und welche Größe es hat, womit die räumliche Größe (das Volumen) gemeint ist. Niemand wusste, wie die räumliche Größe von unregelmäßigen Körpern zu messen ist, bis Archimedes auf die verblüffende Erkenntnis kam, dass er so »groß« ist wie das Wasser, das er beim Eintauchen in eine randvoll gefüllte Badewanne verdrängt, und seine Körpergröße gemessen werden kann durch das Wasser, das nach dem Überlaufen in einem Eimer aufgefangen wird. Das ist ein Beispiel, wie eine bestimmte Größe (hier das Volumen) als »die Größe« genommen wird. Aber auch für die Raumgröße gilt nicht, dass sie identisch mit dem Ort ist. Aristoteles hat es überzeugend widerlegt: Am gleichen Ort können nacheinander verschiedene Dinge sein, die einander ablösen. Umgekehrt kann etwas am gleichen Ort bleiben, dort aber wie ein Ballon seine Größe verändern (sich ausdehnen oder schrumpfen). Nur wenn alles statisch wäre, könnten Ort und Größe gleichgesetzt werden. – Solange Aristoteles den Eindruck hatte, dass die Mathematiker Ort und Größe nicht unterscheiden, traute er ihren Erkenntnissen nicht.

(3) Erst als der Begriff Größe in dieser Allgemeinheit erkannt und unabhängig vom Ort definiert war, konnte die Größe als ein eigenes Prinzip verstanden werden. Im nächsten Schritt war die Größe zu unterscheiden von der Zahl, womit ursprünglich nur die natürlichen Zahlen gemeint waren. Die Zahlen haben in der Eins eine kleinste Einheit und sind in festen Abständen voneinander getrennt. Zwei einander nachfolgende Zahlen haben immer den Abstand Eins. Zahlen sind entweder unteilbar oder in eine endliche Anzahl von Primfaktoren teilbar. Größen sind dagegen beliebig teilbar. Mit der unterschiedlichen Teilbarkeit war ein klares Unterscheidungsmerkmal zwischen Zahl und Größe gefunden. (Das droht erst später wieder verloren zu gehen, als mit Zahl nicht nur die natürlichen und rationalen, sondern auch die reellen Zahlen gemeint sind. Darauf wird zurückzukommen sein.)

(4) Die unendliche Teilbarkeit war der erste Begriff des Kontinuums (syneches), der Stetigkeit in heutiger Sprechweise. Der Mittelwertsatz besagt, dass eine stetige Funktion, die nicht konstant ist, kontinuierlich alle Werte zwischen Minimum und Maximum durchläuft und keinen überspringen kann.

(5) Aristoteles verstand jedoch, dass das Kontinuum zwar alle Punkte zwischen einem Anfangs- und Endpunkt durchläuft, dennoch aber nicht aus Punkten zusammengesetzt werden kann. Das war seine Schlussfolgerung aus den Paradoxien Zenons. Stattdessen ist das Kontinuum als etwas Eigenes zu verstehen, das mehr ist als die Summe der von ihm durchlaufenen Punkte.

(6) Wenn das Kontinuum auf diese Weise definiert ist, dann wird es möglich, es als den Stoff der Größe zu verstehen.

(7) Damit ist zugleich ein allgemeineres Verständnis des Stoffes gefunden als es in der Physik möglich war. Das Prinzip des Stoffs ist so allgemein, dass es nicht nur um den physischen Stoff geht (den »wirklichen«, anfassbaren Stoff), sondern auch vom Stoff der Gedanken, der Träume oder der Zahlen gesprochen werden kann. In weiterer Konsequenz gibt es dann auch große und kleine Gedanken, große und kleine Träume und sogar große und kleine Zahlen, womit nicht ihr Zahlenwert gemeint ist, sondern ihre »absolute Größe«. Zum Beispiel gelten traditionell die 4, die 8 oder die 40 als große Zahlen. (In primitiven Kulturen wird gezählt ›eins, zwei, drei, viele‹, wobei »viele« alles ist, was mehr als 3 ist. In der Geometrie ist das Achteck das größte regelmäßige Vieleck, das unmittelbar anschaulich ist. Jeder hat vom Achteck ein anschauliches Bild, aber nicht vom Neuneck, Zehneck und so weiter. Bei den Hebräern steht die Zahl 40 für das Unendliche.) Ein anderes Beispiel gibt Balzac: »Die Drei und die Sieben sind die beiden größten geistigen Zahlen« (Balzac, Louis Lambert).

(8) Um den Stoff der Zahlen zu verstehen, ist mithilfe des Zusammenhangs die mathematische Verselbständigung des physischen Stoffs zu finden, die Ausgedehntheit.

(9) Dennoch bleibt etwas offen. Die Lehre ist nicht abgeschlossen, wenn Zusammenhang und Größe sich wie Stoff und Form verhalten. Das Zusammenhängende kann nicht allein aus Punkten zusammengesetzt werden, die streng genommen alle aufeinander liegen würden (zwei Punkte, die sich berühren, sind identisch, und das gilt auch für unendlich viele Punkte). Es muss etwas hinzukommen, das sich einerseits dem Zusammenhängenden und der Größe entzieht, andererseits aber erst das Zusammenhängende vollständig macht. Das ist das Zwischen (metaxy). Das Zwischen ist das Gegenstück zum Formmangel (steresis) und entsprechend schwierig zu erfassen. Solange es ungeklärt bleibt, wird sich das Denken nicht den von Zenon aufgestellten Widersprüchen entziehen können. Da Aristoteles das Prinzip des Zwischen nicht klar hat definieren können, blieben auch seine Widerlegungen des Zenon unvollständig und konnten nicht richtig überzeugen.

Größe und Phänomen

Der Weg zum Verständnis des Prinzips Größe wird meistens dadurch verbaut, dass die Größe als das grundlegende Prinzip der Mathematik gilt und nicht als  Prinzip des Übergangs zur Mathematik. Die Mathematik erscheint als Größenlehre, obwohl sie die Lehre der Zahlen und geometrischen Figuren (schemata) ist. Um zu verstehen, wie die Größe (in Gedanken) eine Bewegung von der Physik zur Mathematik ermöglicht, ist zu erkennen, was der Größe systematisch fehlt, denn das stößt die Bewegung zur Mathematik an. Das ist die leitende Frage, mit der zunächst die historische Entstehung des mathematischen und philosophischen Begriffs der Größe durch Eudoxos und Aristoteles nachvollzogen werden soll, und im weiteren, wie das Prinzip der Größe nur innerhalb der Gruppe der drei Prinzipien von Zusammenhang, Größe und Zwischen verständlich wird.

Die neuplatonische Diskussion der Größe als viertes Maß neben Ort, Zeit und Zahl durch Simplikios muss an dieser Stelle systematisch "vergessen" werden, um zur ursprünglichen Fragestellung von Aristoteles zurückzufinden. In den Folgerungen wird darauf zurückgekommen.

Umgangssprachlich macht es keine Schwierigkeit von der »Größe« von etwas zu sprechen. Jeder versteht, was damit gemeint ist. Und doch ist hier einiges an Vorverständnis verborgen, das systematisch auseinander gelegt werden muss. (i) Größen können nicht gezählt, sondern sie müssen  gemessen  werden. Etwas hat immer nur  eine Größe, oder einfacher gesagt »seine Größe«. Es wäre sinnlos von einer halben oder einer dreifachen Größe zu sprechen. (ii) Beim Messen handelt es sich um eine  Analogie, die zwischen der zu messenden Größe und einem Maßstab hergestellt wird. (iii) Die Analogie kann nur hergestellt werden, wenn die zu messende Größe und der Maßstab in Hinsicht auf eine  Dimension  übereinstimmen. Sie müssen eine gemeinsame Ebene haben. (iv) Jede Größe muss sich von der Dimension abheben wie ein Vordergrund von einem Hintergrund. In diesem Sinn ist jede Größe ein  Phänomen, etwas Sichtbares und Erscheinendes in dem genauen Sinn, wie Husserl es verstanden hat. (v) Die Seele integriert jede wahrgenommene Größe in einen umfassenden Zusammenhang und verändert dadurch die Größenverhältnisse. Spektakuläre Beispiele sind die  perspektivische Verzerrung  der Längen, Höhen und Breiten und die  Wohltemperierung  der Töne. In beiden Fällen wird jede einzelne Größe "verfälscht", um die Größe des Ganzen richtig zu treffen. (vi) Schließlich interpretiert die Seele jede wahrgenommene Größe im Zusammenhang ihres gesamten  Erlebnishorizonts. Was dem einen groß erscheinen mag, erscheint dem anderen klein. Was der eine als Zwischenton wahrnimmt und in das Gesamtbild aufnimmt und dadurch ihre Größenverhältnisse ändert, kritisiert der andere als willkürliches Hinein-Interpretieren.

In erster Annäherung ist an der Größe das Messbare das Mathematische, ihre »absolute Größe«. In zweiter Näherung werden – wie besonders anschaulich die harmonischen Intervalle zeigen – Glättungen notwendig, die jeden einzelnen Messwert gewichten, um seinen Stellenwert im jeweiligen Zusammenhang erkennen zu können. Das zeigt schließlich im dritten Schritt, dass zu unterscheiden ist zwischen der »gemeinten Größe« und der wahrnehmbaren Größe. So kann zum Beispiel ein Maler mit bestimmten Farbkontrasten einen Farbeindruck hervorrufen, der sich nicht »photographisch« messen, sondern nur in seiner Wirkung im Rahmen des Gesamteindrucks erkennen lässt. Auf ähnliche Weise können »große Musikwerke« in ihrer Wirkung eine Gewalt erzeugen, die sich nur unangemessen durch Tonhöhe, Lautstärke etc. messen lässt.

Das kann im Ergebnis dazu führen, dass außergewöhnliche Meisterwerke ein eigenes Raum- oder Zeitempfinden hervorrufen können, dass sie ein eigenes Verständnis, was Größe ist, erzeugen können. (Hier wird jeder entsprechend seinem persönlichen Geschmack Beispiele kennen. Ich nenne aus meiner Sicht den Beginn der Reprise im ersten Satz der 9. Sinfonie von Beethoven und die Drei Tänze für Orgel von Jehan Alain.)

Worum es geht ist verstehen zu lassen, dass Größe dieser Art sich ablöst von der Form besonderer Stoffe und danach drängt, eine mathematische Gestalt anzunehmen.

Bei näherem Hinsehen ist oft nicht einmal eindeutig, was mit Größe genau gemeint ist. Wird zum Beispiel mit der Größe eines Apfels sein Gewicht gemeint, muss er in Gramm gewogen werden, wird seine Höhe gemeint, ist er an einem Maßband zu messen, wird sein räumliches Volumen gemeint, kann er in ein Gefäß mit Wasser eingetaucht und am gestiegenen Wasserspiegel seine Größe gemessen werden.

Für jede Eigenschaft wurden historisch jeweils spezifische Messverfahren eingeführt, die Waage für das Gewicht, die Sonnenuhr für die Zeit, die Elle für die Länge, ... Jedem Messverfahren liegt eine Analogie zugrunde: Die Hebelgesetze der Waage, die Strahlengesetze dem Schattenwurf auf der Sonnenuhr oder dem Anlegen eines Maßstabs. Größe muss im Grunde etwas umständlicher formuliert werden, indem jeweils das Objekt, die Dimension und der Maßstab genannt werden: ›Dieser Stoffballen ist so breit wie 7 Ellen‹, ›der Schatten auf der Sonnenuhr ist so weit fortgeschritten wie die Sonne im Laufe des Tages bis zum Messzeitpunkt um die Erde gewandert ist‹, ›der Apfel ist so schwer wie 3 Einheitsgewichte auf der Waage‹. Länge, Umlauf und Gewicht sind in diesen Beispielen die jeweiligen Dimensionen, wodurch die Analogie hergestellt werden kann.

In den meisten Fällen ist jedoch keine Messung an einem äußeren Maßstab notwendig, sondern die menschliche Sinneswahrnehmung nimmt die Messung direkt vor, wenn etwa im Auge die von außen kommenden Bilder gemessen werden, im Ohr das Trommelfell schwingt und dadurch die Schallwellen misst, die Geschmacksknospen auf der Zunge die Gestalt der aufgenommenen Stoffe messen und so fort. Die menschliche Wahrnehmung ist ein Messvorgang, der mit Analogien arbeitet und darüber hinaus die verschiedenen Aspekte des wahrgenommenen Gegenstands miteinander verknüpft. Die Fähigkeit der Seele besteht darin, alle äußeren Dinge in ihrer  Größe  zu erkennen, im direkten wie im übertragenen Sinn. Zugleich wird jede Größe nicht nur an einem Maßstab gemessen, sei es ein äußerlich angelegter Maßstab oder das Sinnesorgan selbst, sondern gewissermaßen an sich selbst im Vergleich zur früheren Größe und zur erwarteten Größe. Dieser Vergleich ist notwendig, um die Größe vor einem Hintergrund abheben zu können. Es wäre unmöglich etwas zu erkennen und seine Größe zu messen, das sich nie ändert. Die Menschen merken erst, dass die Erdoberfläche gekrümmt und nicht eben ist, wenn es ihnen gelingt, von der Erde ausreichend Abstand zu gewinnen und sie in ihrer Bewegung vor einem Hintergrund zu sehen oder zu sehen, wie am Horizont bewegte Dinge auftauchen und erst allmählich in ihrer vollen Größe zu sehen sind. Die Größe ist nie fix. Sie ist relativ in Bezug auf den Maßstab, die Sinne, ihre Vergangenheit und ihre Zukunft.

Die Philosophie fand daher in dem Moment einen völlig neuen Zugang zu Aristoteles, als sie mit Husserl systematisch den Begriff der Größe durch den Begriff des Phänomens verstand. Der Mensch ist keine Maschine, die Größen registriert, sondern hat eine Seele, die Phänomene wahrnimmt. Das Phänomen umfasst und verfehlt die Größe. Es gibt immer etwas  zwischen  der Größe und dem Phänomen. Die Seele erkennt im Phänomen dasjenige an der Größe, was gegenüber ihren Änderungen in der Wahrnehmung Bestand hat. Diesen seelischen Blick auf das Phänomen durch die Wahrnehmung hindurch nennt Husserl Intentionalität. Das Phänomen ist zum Verständnis von Größe und Größenmangel ebenso wichtig wie die Physis zum Verständnis von Form und Formmangel. So wie die Physik fragt, was etwas seiner Natur (physis) nach ist, auch wenn es gegenwärtig nicht diese Form hat, so fragt die Phänomenologie, was etwas seiner Intention nach ist, auch wenn es diese Intention gegenwärtig nicht darzustellen vermag.

Daher lässt sich gegenüber dem Phänomen das Wechselspiel von Größe und Größenmangel verstehen. Es ist zu unterscheiden zwischen der intendierten und der tatsächlich vorliegenden Größe. Mit der Phänomenologie hat Husserl die Lehre begründet, die hier fortgeführt werden soll und an der sich alles weitere orientieren kann. Wäre der Begriff Phänomenologie nicht bereits zu stark vorbelegt, wäre es angemessen, hier von Phänomenologie statt von Meta-Mathematik zu sprechen.

Der Begriff der Größe musste durch den Begriff des Phänomens erschüttert werden, um ihn dann im Rückgang richtig verstehen zu können. Ein Beispiel für eine solche Erschütterung sollte der frühere Kommentar zur Kunst des Hörens leisten. Entscheidend ist mir herauszuarbeiten, wie alle Prinzipien der Meta-Mathematik die Wahrnehmung und den Verstand in scheinbar unlösbare Zweifel stürzen. Die Seele muss beim Verständnis der wahrgenommenen Reize, ihrer Größe, ihres Zusammenhangs und des nur zu ahnenden Zwischen eine  Krise  durchmachen, um zur Verselbständigung der Mathematik finden zu können. Im folgenden wird es vor allem darum gehen, diesen Moment der Krise genau zu erkennen und zu verstehen, wie daraus die mathematische Verselbständigung hervorgeht, die gegenüber der phänomenologischen Wahrnehmungsfähigkeit (der Intentionalität) sowohl etwas verliert wie gewinnt.

Entstehung des Prinzips Größe aus der Proportionenlehre (nach Waschkies)

Das kann am besten verdeutlicht werden an der Entstehung des Begriffs der Größe selbst. Hier folge ich im Grundzug der Arbeit von Waschkies über Eudoxos und Aristoteles. An ihrem Anfang stand die Proportionen-Lehre (Analogie): Wann verhält sich a zu b wie c zu d?

Zunächst wurden unabhängig voneinander die Proportionen von Zahlen, Strecken, Flächen etc. betrachtet. Lange wurde vermutet, dass es jeweils unterschiedliche Regeln der Proportionen gibt, und dass sich die Regeln von Proportionen ändern, wenn größere oder kleinere Dinge verglichen werden, wenn die Anzahl der verglichenen Dinge sehr groß wird etc. Proportionen galten oft als eine qualitative Aussage und als Geschmacksurteile, die häufig auch eine emotionsgeladene Bedeutung hatten (›ich mag a so gern wie b‹, ›a ist um so viel schöner als b wie c im Vergleich mit d‹). Erst Eudoxos erkannte in voller Klarheit, dass allen Proportionen eine gemeinsame mathematische Struktur zugrunde liegt, wodurch es möglich wird, die Proportionen unterschiedlichster Figuren direkt einander gleichzusetzen. Der vereinheitlichende Begriff ist die Größe. Im einfachsten Fall wird mathematisch die Größe als Flächeninhalt definiert:

a · d = b · c =def a : b ∷ c : d

lies: Wenn für zwei Rechtecke mit unterschiedlichen Seiten a und d bzw. b und c gilt, dass sie die gleiche »Größe« (den gleichen Flächeninhalt) haben, d.h. wenn a · d = b · c gilt, dann verhält sich a : b wie c : d. (Dies ergibt sich mathematisch, wenn die Gleichung a · d = b · c auf beiden Seiten durch b und durch d geteilt wird.)

Entscheidend war, zunächst Größe (megethos) und Größenbetrag (schema) zu unterscheiden und dann zu verstehen, in welcher Weise der Größenbetrag mit Dimension und Austauschbarkeit zu tun hat. Beides ist auch bei Aristoteles nur angedeutet und droht bisweilen durcheinander zu gehen.

In diesem Beispiel sind die Seiten a, b, c und d und ihre Produkte a · b und c · d Größen. Bei den Seiten handelt es sich um Längen, bei den Produkten um Flächen. Davon zu unterscheiden sind die Messergebnisse, wenn die Seiten gemessen und die Flächen daraus errechnet oder direkt gemessen werden (z.B. durch Auszählen von Einheitsquadraten, die in der Fläche enthalten sind). Im Griechischen fällt die Unterscheidung leichter, da die Größe im Dativ und der Größenbetrag im Nominativ stehen kann. Im Deutschen würde das heißen: Das Größen-bare und die Größe, so wie vom Messbaren und der Messung oder vom Zählbaren und der Zahl gesprochen werden kann. In diesem Beispiel sind Längen und Flächen »größen-bar«, d.h. ihre Größe lässt sich ermitteln. Bei bestimmten Objekten ist »größen-bar« und »messbar« identisch: Längen und Flächen können gemessen werden, womit ihre Größe bestimmt wird. Das gilt jedoch beispielsweise nicht für Ereignisse oder für Kunstwerke. Sie sind zwar »größen-bar«, weil von ihrer Größe gesprochen werden kann, aber nicht messbar. Sprachlich ist zu unterscheiden: Etwas hat Größe (z.B. es hat eine Höhe), und es ist x Maßeinheiten groß (z.B. es ist 7 m hoch).

Diese Ungenauigkeit lässt sich im folgenden nicht völlig vermeiden. Daher wird nur an Stellen, wo direkt Missverständnisse drohen, auf die Unterscheidung hingewiesen.

Bevor ein allgemeines Verständnis der Größe gefunden werden konnte, musste der Sonderfall der drei räumlichen Dimensionen Höhe, Breite und Tiefe verstanden werden. Im Unterschied zu allen anderen Dimensionen werden sie in einer gemeinsamen Einheit (Meter) gemessen und können daher direkt miteinander verglichen werden. Wenn etwas 4 m hoch und 8 m breit ist, kann ohne weiteres gesagt werden, dass es doppelt so breit wie hoch ist. Das gilt aber keineswegs für die anderen Dimensionen (etwas kann nicht doppelt so viel Volumen haben wie es breit ist, oder doppelt so hell sein wie es hoch ist). Es hat lange gebraucht einzusehen, dass dies nur deswegen möglich ist, da die Raumdimensionen senkrecht (orthogonal) zueinander stehen und gleiche Eigenschaften (Isotropie) haben. Höhe, Breite und Tiefe sind in einem genau zu bestimmenden Sinn austauschbar, während z.B. für andere Dimensionen wie Fläche und Farbe völlig andere Austauschregeln gelten.

Werden andere Dimensionen als Höhe, Breite und Tiefe betrachtet, dann wird deutlicher: Zwei Größenbeträge können dann ins Verhältnis gesetzt werden, wenn sie sich auf die gleiche Ausgedehntheit (missverständlich gesagt: auf die gleiche Größe) und dort auf die gleiche Einheit beziehen. Zum Beispiel können Flächen in Quadratmeter gemessen und dann verglichen werden, etwa eine 4 qm große Fläche und eine 2 qm große Fläche. Hier gilt: ›4 qm : 2 qm = 4 : 2 = 2‹. Das gleiche gilt für alle anderen Dimensionen: Längen können mit Längen, Volumen mit Volumen verglichen werden usw. Was in der jeweiligen Dimension gemessen wird, das ist der Größenbetrag (der Flächeninhalt, der Rauminhalt, für Höhe und Breite und Tiefe jeweils der Längeninhalt, der Farbwert, die Tonhöhe etc).

Dagegen wäre es sinnlos zu fragen, ob eine Farbe größer als eine Fläche, eine Zahl kleiner oder größer als bitterer Geschmack ist. Das zu betonen war der richtige Kern der Grundlagen der Arithmetik von Frege. Sein Ansatz wird erst dann problematisch, wenn er die Möglichkeit der Analogie ebenfalls verweigert: C-Dur ist nicht rot, aber C-Dur kann sich zu E-Dur verhalten wie die Farbe rot zur Farbe grün. C-Dur ist dann nicht rot, aber C-Dur ist innerhalb der Tonarten was Rot innerhalb der Farbskala ist. Analogien dieser Art werden von der Seele ständig gebildet. Manche Menschen sind sogar fähig, Analogien dieser Art unmittelbar zu erleben (Synästhesie, die ihrerseits nur als ein besonderes Phänomen beschrieben werden kann). Sie hören nicht, dass C-Dur rot ist, aber sie sehen in ihrer inneren Wahrnehmung etwas Rotes, wenn sie C-Dur hören. Das ist ein Beispiel, wie Analogien Resonanzen hervorrufen.

Die Besonderheiten der anderen Dimensionen neben Höhe, Breite und Tiefe wie z.B. die Farbe haben Konsequenzen bis in die Grundlagen der Logik, was an anderer Stelle ausgeführt wird. Frege fand keinen Ansatz für nicht-aristotelische Logiken, weil er diese Besonderheiten nicht sah und hier stärker der Tradition verhaftet blieb als er sich bewusst war.

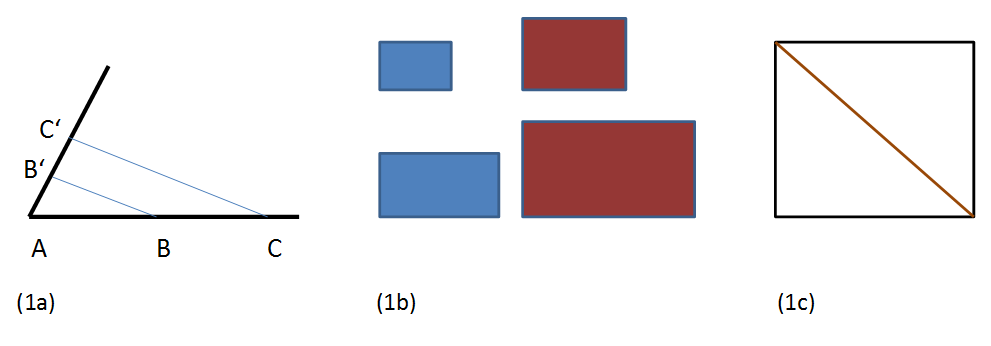
Figur 1: Proportionen
(1a) Die klassische Proportionenlehre betrachtet Proportionen von Abschnitten auf Geraden. Beispiel für einen Strahlensatz: Es verhalten sich die Längen AB zu BC auf der unteren Gerade wie die Längen AB' zu B'C' auf der angewinkelten Gerade, wenn die Verbindungslinien BB' und CC' parallel verlaufen.
(1b) Die beiden blauen Flächen stehen im gleichen Verhältnis zueinander wie die beiden dunkelroten Flächen.
(1c) Im Quadrat verhalten sich Außenseite zur Diagonale wie 1 zu √2

Wird nach dieser Regel vorgegangen, dann können die Größenverhältnisse unterschiedlicher Dimensionen direkt miteinander gleichgesetzt werden. Zum Beispiel gilt: Eine Fläche von 4 Quadratmetern verhält sich zu einer Fläche von 2 Quadratmetern wie ein Volumen von 125 Kubikmetern zu einem Volumen von 62,5 Kubikmetern, da in beiden Verhältnissen jeweils die Dimension (Quadratmeter bzw. Kubikmeter) gekürzt werden kann und daher eine Aussage über reine Größen übrig bleibt:

4 m² : 2 m² = 4 : 2 = 2 und 125 m³ : 62,5 m³ = 125 : 65,5 = 2

also 4 m² : 2 m² = 125 m³ : 62,5m ³ = 2

Dass in dieser Weise gekürzt werden darf und die Ergebnisse der Kürzungen direkt einander gleichgesetzt werden können, erscheint heute völlig selbstverständlich. Das ist jedoch nur möglich, weil – so eigenartig das auch klingen mag – die hier betrachteten Verhältnisse mathematisch sind. Höhen, Flächen, Farben, elektrische Ladungen stehen jeweils untereinander in gleichartigen mathematischen Verhältnissen, und nur das erlaubt diese Art zu rechnen. Das zu ermöglichen ist in einem übertragenen Sinn die »Größe der Mathematik«. Aristoteles hat es versucht so zu sagen, dass an jeder Form etwas Mathematisches ist, ihre Größe (Phys. II.1).

Das ist die Antwort von Aristoteles auf Platon, der die Mathematik unabhängig von den Dingen gesehen hat.

Die Physiker stoßen oft genug auf Situationen, in denen Kürzungen dieser Art nur eingeschränkt möglich sind, und formulieren daher ergänzende Regeln, unter denen Kürzungen möglich sind. Ein Beispiel ist das Pauli-Prinzip. Das wird mathematisch übersetzt in die verschiedenen Quantenstatistiken und schränkt die Regeln der Proportionen ein.

Das Prinzip Austauschbarkeit und seine Regeln werden noch intensiv zu betrachten sein, denn sie führen zu Regeln der Ununterscheidbarkeit. Das stellt die Anschaulichkeit und – wenn man so will – die Größe der Mathematik vor eine echte Herausforderung.

Die Proportionenlehre brachte den Durchbruch, dass nicht nur Proportionen von natürlichen Zahlen betrachtet werden können (etwa die elementaren musikalischen Intervalle wie die Oktave 1 : 2, die Quarte 3 : 4, die Quinte 2 : 3), sondern auch Proportionen von irrationalen Zahlen wie das Verhältnis von Diagonale und Außenseite im Einheitsquadrat √2 : 1 (im Quadrat ist die Diagonale √2-mal so lang wie die Außenseite). Die Lehre der Pythagoreer, die nur Verhältnisse von natürlichen Zahlen gelten ließen, musste aufgegeben werden. Erst damit war der Weg frei zu Euklid, der in seinen Elementen die diskreten arithmetischen Zahlen und die kontinuierlichen geometrischen Figuren zusammenbringen konnte.

Der entscheidende Übergangsschritt wurde von Eudoxos geleistet. Mithilfe seines allgemeinen Begriffs der Größe (megethos) war er in der Lage, das Gemeinsame von rationalen Verhältnissen (wie bei den musikalischen Intervallen) und irrationalen Verhältnissen (wie das Verhältnis der Diagonale zur Außenseite im Quadrat, oder in einem anderen Beispiel das Verhältnis des Goldenen Schnitts) zu erkennen. Die Definition der Größe in Euklid V.4 geht direkt auf Eudoxos zurück und gilt sowohl für diskrete wie für kontinuierliche Größen.

Die Krise der Pythagoreer und ihre Lösung durch Eudoxos ist paradigmatisch für das Verständnis der Verselbständigung der Mathematik. Vorher konnte es so scheinen, als seien die mathematischen Eigenschaften auf eine ähnliche Weise natürlich wie alle anderen Eigenschaften, etwa die Farbe oder der Geschmack. Das war die Meinung der Pythagoreer: Sie lassen als Zahlenverhältnisse nur gelten, was an den Dingen direkt wahrzunehmen ist. Ihre musikalischen Intervalle waren experimentell gefunden, indem an einem Monochord die Längen der schön klingenden Intervalle gemessen wurde. Der Begriff der Größe von Eudoxos trifft dagegen etwas Gemeinsames, das in dieser Weise nur im Denken besteht. – So schwierig es seinerzeit war, diesen Weg zu finden, so schwierig ist es umgekehrt heute, sich wieder in die Situation dieser Krise zurückzuversetzen, um von dort aus die Entstehung der Prinzipien der Mathematik nachvollziehen zu können.

Die Folgerungen gehen weit über die Mathematik hinaus. Als es einmal möglich geworden war, mithilfe der Mathematik ein Verständnis für irrationale Proportionen zu finden, bot sich die Aussicht, auch für andere philosophische Streitfragen eine Lösung zu finden, die sich bis dahin einem streng rationalen Denken entzogen hatten und daher von den Sophisten und anderen Vernunft-Kritikern als Beweis für ihren Skeptizismus herangezogen werden konnten. Aristoteles gibt Andeutungen in der Nikomachischen Ethik, wenn er in Buch II.5 über die irrationalen Regungen wie z.B. Angst, Mut, Begehren und Zorn schreibt. Bei ihnen geht es darum, sie angemessen und zur richtigen Zeit einzusetzen. Als Maß dient ihm das geometrische Mittel.

Aristoteles verfolgte die mathematische Diskussion des Größen-Begriffs mit großem Interesse und nahm an zahlreichen Stellen auf die Definition der Größe (megethos) von Eudoxos Bezug. Waschkies nennt: Ana.Post. II.17, 99a8-10, Phys. I.4, 187b25-6 und b32-4, III.6, 206b7-12, VIII.10 266b2-3, De sensu 6,445b27-29, mangelhaft überliefert Phys. III.7 207b27-34 (Waschkies, S. 132 Anm. 27). (Stellen zur irrationalen Größe der Diagonale im Quadrat nennt Newsteadt: Ana.Pr. 41a23-40 und 50a37-38, Phys. 221b23-5 und 223a3-7, De Cael. 281a-b, Meta. 1019b24-7, GA 742b27-8, Meta. 983a12-21, Meta. 1053a17-8, Newsteadt S. 5 Fn. 8).

Wie genau Aristoteles die offene Frage der Mathematiker verstanden hat, zeigt die Zweite Analytik:

»Ebenso würde es sich mit dem Satze verhalten, dass die Glieder einer Proportion sich versetzen lassen, mögen diese Glieder Zahlen oder Linien, oder Körper, oder Zeiten sein, wenn dieser Satz etwa für jede dieser Arten besonders bewiesen würde, während es doch ausführbar ist, dass der Satz für alle Arten durch einen Beweis dargelegt werden kann. Da jedoch die Zahlen, Längen, Zeiten und Körper für das, worin sie alle Eins sind, keinen Namen haben und da sie selbst der Art nach verschieden sind, so wurde es an den einzelnen Arten bewiesen; jetzt wird aber der Beweis allgemein geführt, denn jene Bestimmung wohnt ihnen nicht als Linien oder Zahlen ein, sondern insofern sie das sind, was als Allgemeines in ihnen enthalten angenommen wird« (Ana.Post. I.5 74a18-25).

Waschkies vermutet, dass die Mathematiker ursprünglich für das hier von Aristoteles angesprochene »Allgemeine» den Begriff »Topos« einsetzten. Aristoteles wollte jedoch mit guten Gründen den Topos-Begriff anders benutzen und lässt das daher vorerst offen. Die Begriffsbildung war noch im Fluss.

Die Mathematiker erkannten, dass die Größen anders als die natürlichen Zahlen beliebig teilbar sind. Die naheliegendste Erklärung war, dass es auch Größen von Dingen gibt, die sich stetig verändern, z.B. die Größe von wachsenden Pflanzen oder die Größe von Bewegungen (Geschwindigkeiten). Aber warum ändern sie sich nicht sprunghaft oder in moderner Sprachweise gequantelt? Selbst wenn die Bewegung in Sprüngen erfolgt, ist es unabhängig von der Bewegung eine rein mathematische Erkenntnis, dass im Quadrat die Diagonale und die Außenseite unkommensurabel sind. Die Erklärung muss viel allgemeiner in den Eigenschaften der Fläche und der Quadrate gesucht werden. Es muss sich um eine grundlegende Eigenschaft handeln, die mit der zweiten Dimension (mit dem Quadrat, der Potenz »hoch zwei«) zu tun hat, und ist bis heute nicht systematisch erforscht.

Größen werden nicht gezählt, sondern gemessen. Daher wird es möglich, dass sich ihr Zahlenwert von den natürlichen Zahlen unterscheidet und – wie schon früh erkannt wurde – auch irrationale Zahlen möglich sind.

Wie dramatisch für die Griechen die Unterscheidung der kontinuierlichen Größe von der natürlichen Zahl war, muss heute erst wieder erschlossen werden. Irrationale Zahlen wie √2 »gab« es für die Griechen nicht. Die natürlichen Zahlen »gibt« es, denn sie ergeben sich aus dem Zählen: Hier sind zwei Dinge, und dort sind zwei andere Dinge. Sie haben etwas Gemeinsames, beide haben die Anzahl Zwei (Zweiheit). Aber √2 kommt als solches nicht vor, kann nicht durch Zählen erreicht werden. Es gibt nichts, dessen Anzahl √2 ist. (Es ist nicht möglich, etwas abzuzählen und im Ergebnis zu sagen: Ich habe bis √2 gezählt.) √2 kommt nur in Proportionen vor, wie dem Verhältnis der Diagonale zur Außenseite im Quadrat. Die neuzeitliche Mathematik ist weitgehend unfähig, hier überhaupt ein Problem zu sehen. Für sie ist es völlig unproblematisch, statt √2 zu schreiben: 1,414213562..., und sie fragt sich nicht, was das Neue an ›...‹ ist. Heute wird nur gesagt: Es gibt keine Dezimaldarstellung von √2 mit endlich vielen Stellen hinter dem Komma. Das klingt weit harmloser als es ist, denn es gibt auch keine Dual-, Oktal- oder sonstige Darstellung, die auf einer natürlichen Zahl beruht. Die Irrationalzahlen sind inkommensurabel mit den natürlichen und gebrochenen Zahlen und lassen sich nie ohne Rest durch sie darstellen. Dieser »nie weg zu rechnende Rest« wird entscheidend sein, um ein tieferes Verständnis für das Kontinuum und das Zwischen zu gewinnen.

Hier wird auch deshalb nicht weiter nachgefragt, weil es den Atomismus erschüttert, der bis heute die anerkannte Grundlage aller Naturwissenschaft ist. Der Atomismus geht von der Existenz kleinster Atome aus. Wenn zum Beispiel ein Quadrat mit einer Seitenlänge von 10 cm gezeichnet wird, kann die Seitenlänge in kleine Einheiten von z.B. Millimetern geteilt werden mit dem Ergebnis, dass sich die Seite aus der Anzahl von 100 mm zusammensetzt. Wird nun gefragt, aus wie vielen Millimetern die Diagonale besteht, sind das 142 mm und ein Rest, der größer als 0 und kleiner als 1 mm ist. Das ändert sich auch nicht, wenn die Einheit immer kleiner gewählt wird, und sei es bis zur Planck-Länge. Es ist unmöglich, für Seite und Diagonale eine gemeinsame Einheit zu finden, nach der beide abgezählt werden können. Und dennoch ist zu "sehen", dass die Diagonale eine genaue Länge hat, die ohne jede Unschärfe oder jeden »Rest« von einem Eckpunkt des Quadrats zum gegenüberliegenden Eckpunkt gezeichnet werden kann. Wenn also die natürlichen Zahlen zu den irrationalen Zahlen erweitert werden sollen, gibt es keine kleinste Einheit der Zahlen mehr. Um sicherzustellen, dass die neue Zahlenklasse nicht beliebig oder widersprüchlich bestimmt ist, kann nicht auf eine Einheitslänge zurückgegriffen werden, sondern es muss ein gemeinsames Prinzip gefunden werden, das Prinzip der Größe. Das Prinzip der Größe ist jedoch unmöglich ein Atom.

Die Griechen lösten das Problem, indem sie √2 nur in Proportionen zuließen. (Damit nahmen sie bereits den Grundgedanken des Differentialkalküls vorweg, als Leibniz in ganz ähnlicher Weise auf das Problem stieß, dass sich die »verschwindenden Größen« im Differentialquotienten nicht absolut, sondern nur relativ innerhalb der Proportion dx : dy schreiben lassen.) Das bedeutet aber, dass die Glieder der Proportion nicht als Zahlen, sondern nur durch die Regeln definiert werden können, wie mit der Proportion zu rechnen ist. (Ohne sich das einzugestehen, geht so auch die neuzeitliche Mathematik vor. Ihr genügt es, eine Regel zu kennen, wie die Dezimaldarstellung von √2 beliebig genau ausgerechnet werden kann, also fortlaufend weitere Stellen hinter dem Komma gefunden werden können, ohne je alle Stellen zu finden.)

Anmerkung: Kant nahm diese Frage auf, als er Begriffe durch Regeln definierte. Bei Hegel wird diese Frage beim realen Maß aufgenommen, wenn er Wahlverwandtschaften und Knotenlinie betrachtet. Der von ihm gesuchte Übergang in eine »höhere« Dimension meint den Übergang von den Dingen zu den Beziehungen zwischen den Dingen.

Definition von Mengen durch ihren Umfang (paratasis)

Der Begriff Größe (megethos) bezeichnet die neu gefundenen mathematischen Objekte wie z.B. √2, die innerhalb von Proportionen auftreten, aber nicht für sich allein stehen können.  Für die Griechen hat die Diagonale im Quadrat eine Größe, aber keine Zahl. Euklid definiert Eudoxos folgend die Größen durch ihre Verhältnisse zueinander, d.h. durch Regeln.

Euklid Definition V.4: »Man sagt, dass Größen (megethe), die einander vervielfältigt übertreffen können, ein Verhältnis zueinander haben.«
In heutiger Schreibweise: Wenn es zu zwei Größen G und K natürliche Zahlen m und n gibt, so dass gilt m · G > K und n · K > G, dann gilt G > K oder G < K. G und K lassen sich entsprechend ihrer Größe ordnen.

Dieses Axiom verbirgt allerdings den entscheidenden Gedanken, dass G und K nur dann miteinander verglichen werden können, wenn sie der gleichen Ausgedehntheit angehören. Stattdessen soll umgekehrt die Ausgedehntheit aus der Ordnung der Größen erschlossen werden: Alle Größen, die sich in dieser Weise ordnen lassen, ergeben in ihrer Gesamtheit die Linearität.

Waschkies zeigt, wie Hilbert das mit größter Konsequenz verallgemeinert hat. Hilbert setzt als Axiom, dass mit der Gesamtheit aller G und K, die diese Regel erfüllen, der Umfang aller Punkte einer Geraden beschrieben ist, auch wenn weder die kleinste Größe noch die größte Größe bekannt sind. Mit diesem Axiom werden nicht alle Größen G, K, ... aufgezählt, die auf der Geraden liegen. Das ist nicht möglich. Sondern es wird die Gesamtheit aller Punkte betrachtet, die diese Regel erfüllen. Diese Gesamtheit ergibt – per Axiom – die Gerade. Regeln liefern keine Anzahlen, sondern nur Eigenschaften wie die Linearität oder die Vollständigkeit.

»Hilberts Axiom der linearen Vollständigkeit, das ich hier zum Vergleich zitieren will: 'Axiom V: Das System der Punkte einer Geraden mit seinen Anordnungs- und Kongruenzbeziehungen ist keiner solchen Erweiterung fähig, bei welcher die zwischen den vorigen Elementen bestehenden Beziehungen sowie auch die aus den (übrigen Axiomen der euklidischen Geometrie) folgenden Grundeigenschaften der linearen Anordnung und Kongruenz (sowie das Axiom des Messens gültig) bleiben.' Dieses Axiom erfordert also quasi, daß das System der Punkte schon alle Stellen auf den Geraden belegt, die im Rahmen der euklidischen Geometrie zum Gegenstand einer sinnvollen Aussage gemacht werden können, während die Def. K.1 aus Phys. VI.2 eine viel schwächere Forderung zum Ausdruck bringt, die beispielsweise schon erfüllt wäre, wenn man die Geraden nur mit der Mengen der rationalen Punkte ausstatten würde« (Waschkies, S. 387f).

Der Gedanke ist großartig, jedoch gut versteckt in einer negativen Formulierung. Die Wissenschaft wird seit Eudoxos durch Regeln definiert. Er zählt nicht mehr die Zahlen nach dem Vorbild der natürlichen Zahlen auf (1,2,3,...), sondern beschreibt die Eigenschaften von Proportionen und erklärt damit als Objekte der Mathematik alle »Größen«, die diese Regeln erfüllen. Dabei bleibt im Grunde unklar (oder offen), welche und wie viele Objekte diese Regeln erfüllen und wie groß also die Menge dieser Objekte ist. Statt von einer Menge aller Objekte zu sprechen, wird vom Umfang (paratasis) gesprochen.

Hilbert argumentiert direkt mit der Paratasis, dem Umfang der Menge aller Punkte auf einer Gerade. Sein Axiom besagt: Das System der Punkte hat vollen Umfang. Es kann nicht erweitert werden ohne das neue Regeln geschaffen werden. Regeln ergeben keine anschauliche Reihe von Objekten (wie die natürlichen Zahlen). Die von ihnen begründeten Objekte bleiben grundsätzlich unscharf, wenn sie innerhalb des Dezimalsystems dargestellt werden sollen.

Erst mit der Mächtigkeit 0 der natürlichen Zahlen wurde eine Größe gefunden, die sich der euklidischen Definition der Größe entzieht, denn es gibt keine Größe G, für die es eine natürliche Zahl m gibt mit m · G > 0. Die Mächtigkeit kann nicht auf das Prinzip der Größe zurückgeführt werden, sondern bedarf eines anderen Prinzips.

Newstead zitiert Arbeiten von Bostock und Stein, dass die Gesamtheit der Eudoxischen Proportionen als Ersatz für die reellen Zahlen stehen kann:

»Bostock (Logic and Arithmetic, Oxford 1979) shows that if we introduce arithmetical operations on Eudoxean ratios, we can derive the same results in geometry that we would now state using real numbers. Finally, Stein (Eudoxos and Dedekind in W. Demopoulos (ed.) Frege's Philosophy of Mathematics, Cambridge 1995) shows that there is a one to one mapping of Eudoxean ratios onto the set of positive real numbers as defined by Dedekind cuts. In light of these results it seems undeniable that the the Eudoxean theory of ratios can act as a surrogate for the theory of real numbers, but it does not follow, in my opinion, that the ancient Greeks had the theory of real numbers« (Newstead, S.7).

Ich würde einen Schritt weiter gehen. Die Analogien von Eudoxos sind ein Beispiel, wie Zahlen durch Regeln statt durch Zählen definiert werden können. Wird nun weiter jede Regel als Bestandteil eines Spiels verstanden und nach der  Gesamtheit aller Regeln  gefragt, dann kann vermutet werden, dass die Gesamtheit der Regeln einen zweidimensionalen Raum aufspannt. Das legt bereits das Beispiel der Eudoxischen Analogien nahe. Bostock und Stein verstehen sie (Cantor und der Hauptströmung der Mathematik folgend) als gleichmächtig wie die reellen Zahlen. Aber ihre Zweidimensionalität ergibt sich durch eine elementare Umformung: a verhält sich zu b wie c zu d, wenn gilt: ›a : b = c : d‹. Diese Gleichung kann auf beiden Seiten mit b und mit d multipliziert werden und ist daher äquivalent zur Aussage: ›a · d = c · b‹. Analogien vergleichen Flächen mit unterschiedlichen Längen und Breiten, aber identischem Flächeninhalt. Verallgemeinert soll gezeigt werden, dass auf ähnliche Weise die Menge aller Regeln die Mächtigkeit 2 hat. Wenn dann gezeigt werden kann, dass die Menge der reellen Zahlen und die Menge der Regeln gleichmächtig sind, dann ist die Kontinuum-Hypothese von Cantor widerlegt, der annahm, dass die reellen Zahlen die Mächtigkeit 1 haben. (Siehe hierzu den sehr gut lesbaren Artikel von Schindler über Große Kardinalzahlen, der zeigt, wie die hier aufgeworfenen Fragen von größter Aktualität sind).

Alle Versuche, das Neue am Prinzip der Größe zu beschreiben, bewegen sich am Rande der Verständlichkeit. Jeder versteht unter Größen alles dasjenige, dessen Größe er kennt. Dass das Prinzip der Größe auch alles dasjenige umfasst, was er nicht kennt, was aber eine Größe hat, also auch das Größte und das Kleinste, ist schwindelerregend. Was später alle Physiker den Physik-Studenten gesagt haben, die am Verständnis der Quantenphysik verzweifelten, gilt bereits hier: Nur wer durch diesen Zweifel hindurchgeht, seinen Verstand verlieren zu können, hat eine Chance, dies Prinzip zu verstehen. Der Zweifel wird sich auch bei allem Verständnis nie mehr beruhigen lassen. Das Prinzip Größe führt in eine Krise, die zu diesem Prinzip gehört und den Weg zur Verselbständigung der Mathematik öffnet. Die Mathematik wird eine Lösung finden, die jedoch ihren Preis hat, der in einer noch abzuschätzenden Ununterscheidbarkeit liegt.

2006-2011

© tydecks.info 2014