Die Freiheit des Grundes nach Spencer-Brown

 

In Arbeit, Version 10.7.2017

Einleitung

Die Abhandlung Gesetze der Form (Laws of Form) könnte ebenso gut Freiheit des Grundes heißen, wenn unter Freiheit die Freiheitsgrade und Bewegungsmöglichkeiten des Grundes verstanden werden, aus dem die Formen hervorgehen, von dem sie sich abheben und in den sie zurückkehren. In der Einführung in die Logik von Spencer-Brown lag naturgemäß der Schwerpunkt auf den Gesetzen (Axiomen, Sätzen, Konsequenzen, Bedingungen für Re-entry und Beobachterstandorte) der Formen. In dieser Fortführung soll umgekehrt gefragt werden, wie sich aus den Eigenschaften des Grundes die Freiheit des Denkens erklären und möglicherweise in bestimmten Grenzen abstecken lässt. Das ist zugleich eine Umkehrung der traditionellen Perspektive: Die Freiheit des Denkens wird nicht mehr darin gesehen, dass dem Denken Flügel verliehen sind, womit es sich von seinem Grund zu lösen und bis in ein eigenständiges Reich der Ideen aufzusteigen vermag, sondern auch für diese Fähigkeit wird nach ihrem inneren Grund gefragt, aus dem sie hervorgeht und in den sie zurückkehrt. Das Denken muss zwar alle Schritte des Überschreitens (Transzendierens) selbst vollziehen, aber es droht sich in überfliegendes Denken zu verflüchtigen und innerlich zu entleeren, wenn der Bezug zum Grund verloren geht. Die Frage nach der Freiheit des Grundes soll beides leisten: Wie sind im Grund die Handlungsmöglichkeiten des Denkens angelegt, und wie bleibt das Denken auf den Grund bezogen. Wird zum Beispiel nach dem kanonischen Denken gefragt, so kann mit Kanon ein einschränkendes Dogma gemeint sein, das vom Denken nicht verlassen werden kann, oder der Kanon ist wie im Gesang eine Bewegungsform des Denkens, die über eine eigene Rhythmik und innere Freude verfügt, die das Denken beflügelt und zugleich in bestimmten Bahnen hält

Das ist auszuführen entlang den aufeinander aufbauenden Bestimmungen des Grundes bei Spencer-Brown. Zunächst verweist jede Form auf ihren Grund. Dann kommt es innerhalb der Logik zur Unterscheidung von Arithmetik und Algebra. Die Algebra hat in der Arithmetik ihren Grund und gewinnt zugleich in ihren formalen Argumenten einen eigenen Grund, der sich in der Fähigkeit zeigt, ohne Umweg durch eine Transzendenz einen Re-entry zu ermöglichen, eine Neujustierung des Systems aus sich selbst. Soll ein Re-entry innerhalb eines Systems möglich sein, so müssen sich die Schleifen des Re-entry durch den Unter-Grund tunneln. Der Grund gewinnt dadurch eine eigene Dicke und kann sich wölben, Wellen werfen und schwingen. Wenn er sich wölbt, entstehen für die unterschiedlichen Beobachter Horizonte und voneinander abweichende Sichtweisen.

Form und Grund

Aus gutem Grund wird der Grund einer Form meist übersehen. Ein Grund soll so beschaffen sein, dass sich Formen in und aus ihm frei entfalten können und es höchstens klar definierte Wechselwirkungen zwischen beiden gibt. Spencer-Brown setzt das implizit voraus und beginnt mit drei Operationen, von denen nur die ersten beiden explizit genannt werden: Hinweisen (indication), Unterscheiden (distinction), einen Raum Öffnen (space-opening).

Am Anfang steht die Aufforderung »draw a distinction« (LoF, 3) (»Triff/ziehe/zeichne eine Unterscheidung«).

(i) Es gibt ein A (einen marked space), das mit der Unterscheidung hervorgehoben und auf das hingewiesen wird.
(ii) Es gibt ein B, das von A unterschieden wird (nicht-A).
(iii) Es gibt eine Grenze zwischen A und B, dargestellt durch das Zeichen .
(iv) Es gibt einen Kontext (Raum), in dem die Unterscheidung erfolgt.

Meist wird der vierte Aspekt übersehen. SWH heben hervor, dass der Raum nicht einfach da ist, also kein vorhandener Grund ist, in den etwas eingeschrieben wird, sondern dass er durch das Treffen der Unterscheidung eröffnet wird.

Die Grenze kann durchlässig und ein eigenes System sein. Maturana erweitert (oder konfrontiert) die Grenze zur Membran (SWH, 75). Eine Membran ist eine lebende und teils durchlässige Grenze. Diese Grenze ist ein Netzwerk, mit der der Austausch von beiden Seiten geregelt wird. Siehe hierzu die Arbeit von Karafillidis, der soziologisch ausführt, wie jede Grenze und jede Identität durch ein Netzwerk mit dem Anderen hergestellt und gesichert wird. Etwas kann von Anderem nur abgegrenzt werden, wenn zugleich das Andere bekannt ist und insofern eine kommunikativer Austausch mit dem Anderen erfolgt.

SWH weisen darauf hin, dass bei der Rückkehr über die Grenze (recrossing) weder der Wert des Überschreitens (cross, crossing) noch einfach dessen Umkehrung (Negation) erhalten werden, sondern ein neuer Wert entsteht, der nicht Null ist, sondern eine eigene innere Dimension (Freiheitsgrad) hat. Er wird sich als der imaginäre Wert erweisen, der aus der Bewegung des Recrossing hervorgeht. Er ist eine Eigenschaft des Grundes. Im Grund muss die Möglichkeit gegeben sein, hinausgehen und wieder umkehren zu können.

»Wenn beide Absichten, die Grenze einmal zu überschreiten und die Grenze nochmal zu überschreiten, zusammen genommen werden, dann weist dies auf einen Wert hin, der weder der Wert der Überschreitung noch der Rücküberschreitung ist, sondern ein Wert, auf den durch keine von beiden hingewiesen wird (the value indicated by none of them).« (SWH, 84 mit Zitat LoF, 2)

Daraus ergeben sich die ersten elementaren Eigenschaften des Grundes:

–    Der Grund soll in dem Sinn transparent sein, dass beim Betrachten einer Form der Grund nicht wahrgenommen wird. Er soll im Hintergrund stehen und keinen direkten Einfluss auf die Form haben. Wenn ein Text gelesen wird, soll der Grund sicherstellen, dass der Text unabhängig vom jeweils spezifischen Grund verstanden wird. Werden zum Beispiel Worte wie ›Heute ist Dienstag, der 4. April 2017‹ auf ein Blatt Papier geschrieben, so ist das Blatt Papier nur als Grund für diesen Text geeignet, wenn es den Text nicht ändert und der gleiche Text genau so gut zum Beispiel in eine elektronische Datei oder auf eine Baumrinde geschrieben werden könnte ohne dadurch seine Bedeutung zu ändern.

–    Der Grund soll der Form eine gewisse Stabilität geben. Würde etwas in Wasser geschrieben und sich dort sofort auflösen, ist der Grund ungeeignet.

–    Der Grund muss wieder-beschreibbar sein. Es muss möglich sein, eine Form einzutragen, auszulöschen und durch eine andere Form zu überschreiben. Zusätzlich kann die Eigenschaft verlangt werden, dass Reste der früheren Formen als Palimpsest zurückbleiben und an der Form ihre Geschichte erkennen lassen.

–    Der Grund muss feinkörniger als der Text sein. Andernfalls würde die Form wie durch ein Sieb hindurchfallen. Während die Form diskret ist, erscheint der Grund ihr gegenüber kontinuierlich. So sind z.B. die natürlichen Zahlen als diskrete Punkte auf der kontinuierlichen Gerade der reellen Zahlen eingetragen.

Die Eigenschaften zeigen die elementaren Freiheiten des Grundes. Der Grund sichert der Form eine Unabhängigkeit vom Grund, eine Dauerhaftigkeit, einen Formenwechsel und eine räumliche Gestalt.

Wird in dieser Weise nach dem Grund gefragt, verallgemeinert das den Ansatz von Kant, die Sachen im Horizont der Zeit zu sehen. Eine Form hat Substanz, weil es einen Grund gibt, auf dem sie auf- oder in den sie eingetragen wird. Es ist eine Kausalität möglich, die von einer Form A zu einer anderen Form B führt, weil es einen Grund gibt, auf dem eine Form eingetragen und später überschrieben werden kann. (Ein typisches Beispiel für Überschreiben ist die wiederkehrende Zuweisung von Variablen in EDV-Programmen, wenn etwa in der Instruktion ›i = i + 1‹ ein Zähler i beim mehrfachen Durchlaufen einer Schleife jeweils erhöht wird.) Wechselbeziehungen mehrerer diskreter Formen sind möglich, weil es für sie einen gemeinsamen, übergreifenden kontinuierlichen Grund gibt, auf dem sie miteinander in Resonanz treten oder einander überlagern können. So ist z.B. das Wasser der Grund (das Medium) für die vielfältigen Formen von Wellen oder die Sprache der Grund (das Medium) für die Kommunikation in allen ihren Formen.

Was sind Kanons?

Spencer-Brown führt mit der Grenze und dem leeren Raum, in den die Grenze gezeichnet wird, zwei elementare Proto-Zahlen ein, mit denen in einer Proto-Arithmetik und Proto-Algebra gerechnet werden soll: Der Haken (Winkel, cross, call) und Ock . Wie ihm das im Einzelnen gelingt, ist dargestellt im Parallelbeitrag Gesetze der Form.

Um arithmetisch und algebraisch rechnen zu können, sieht sich Spencer-Brown gezwungen, die mathematischen und logischen Operationen zu unterscheiden von einem Grund an Vorwissen und impliziten Annahmen, die er als Kanons bezeichnet.

Der griechische Ausdruck canon (siehe auch Wikipedia) ist sehr weit gefasst und hat möglicherweise im englischen canon einen etwas anderen Klang als im Deutschen. So wird vom Bildungskanon gesprochen, dem Bibelkanon, einem Kanon von Standardregeln in der Kunst. In der Mathematik und Physik sind Kanonische Gleichungen meist die Standardgleichungen, die direkt aus einem Prinzip erfolgen. Kanonisch bedeutet etwas wie ein Standard, eine Norm, in seiner ursprünglichen griechischen Bedeutung »kanón 'Rohr[stab], Stange, Messstab, Richtschnur', daraus lat. canon 'Maßstab, festgesetzte Ordnung, Regel')« (Wikipedia, abgerufen am 28.2.2017). In der Mathematik sind Standardform und kanonische Form synonym. Möglicherweise denkt Spencer-Brown auch an die verschachtelten Figuren des Kanons in der Musik, ein spielerisches, fröhliches »Zusammen-drauf-los-Singen« mit einer belebenden und aufmunternden Wirkung. (Thomas Mann lässt im Doktor Faustus mit dem Kanon-Singen die Freude an der Musik und dem Komponieren beginnen, so wie für Spencer-Brown in den logischen Kanons die Begeisterung für Mathematik und Logik ihren Anfang nimmt.)

Für Felix Lau sind bei Spencer-Brown die Kanons »Regeln, die außerhalb des Kalküls stehen, weil sie durch nichts als ihre Plausibilität zu rechtfertigen sind« (Lau, 50). Sie sind klar von den Axiomen zu unterscheiden, mit denen die Arithmetik beginnt.

»Es liegt also in der Verantwortung des Autors, die Kanons so zu wählen, dass sie unmittelbar einleuchten. Und deshalb halte ich die Vorgehensweise von George Spencer Brown, die Kanons an Ort und Stelle ihres ersten Gebrauchs einzuführen, statt sie – wie sonst auch üblich – am Anfang aufzulisten, für sehr hilfreich und einleuchtend.« (Lau, 61)

Kanons werden von Spencer-Brown immer dann eingeführt, wenn er spürt, dass eine intuitive Vorgehensweise eingeschlagen wird, die für sich nicht weiter zu begründen ist. Bereits die Aussage »There can be no distinction without motive« (LoF, 1) versteht er als den ersten Kanon.

Weitere wichtige Kanons, die zugleich die Bedeutung und den Umgang mit Kanons bei Spencer-Brown zeigen:

2. Kanon, »Contraction of reference« (LoF, 8) Es ist möglich, einen durchaus komplexen Ausdruck mit einem einfachen Namen zu benennen und sich den Ausdruck in seiner Gesamtheit mit dem Namen zu vergegenwärtigen.

Das klingt banal, ist aber eine tiefgehende Aussage. Bisweilen wird die Frage gestellt, ob ein Zeichen an sich selbst das zeigen muss, was es ausdrücken soll. Dagegen sagt dieser Kanon, dass auch mit einem einfachen Wort ein schwieriger Sachverhalt benannt werden kann. Die Ebene der Worte und die Ebene der von ihnen benannten Sachverhalte sind voneinander unabhängig.

3. Kanon, »Convention of substitution« (LoF, 9) Ein Ausdruck bleibt erhalten, wenn in ihm ein Teilausdruck durch einen identischen anderen Teilausdruck ersetzt wird.

Das ist von ähnlich elementarer Bedeutung wie die ersten beiden Kanons. Die einzelnen Teilausdrücke eines komplexen Zeichens sind unabhängig (modular) voneinander. Beim Austausch eines Teilausdrucks kommt es zu keinen unerwünschten Nebenwirkungen. Es gibt zwar einen inneren Zusammenhang des vollständigen Zeichens, aber er lässt die Substitution von Teilausdrücken zu.

Das ist keineswegs selbstverständlich. Oft sind in einem Teilausdruck implizit und unbemerkt Wirkungen auf andere Teilausdrücke enthalten. Wird der Teilausdruck ausgetauscht, können sie verloren gehen, und das Gesamtgefüge kann dadurch verändert werden. Das gilt insbesondere für mechanische, chemische und organische Systeme: Wird in einem Schwerkraft-System ein Körper durch einen anderen ausgetauscht, der zwar die gleiche Form, aber ein anderes Gewicht hat, dann hat das Auswirkungen auf das gesamte System. Wenn in einem chemischen System chemische Stoffe ausgetauscht werden, verändert das die chemischen Prozesse. In einem organischen System sind alle Teile mit jeweils bestimmten Funktionen aufeinander abgestimmt. Wenn eines ausgetauscht wird, ist der Organismus gestört und muss das Zusammenspiel seiner Organe neu ordnen. Auf philosophischer Ebene gilt in der Monadologie, dass jede Monade ein Bild aller anderen Monaden enthält. Wenn eine Monade ausgetauscht wird, hat das unmittelbar Auswirkungen auf alle anderen Monaden. – Der von Spencer-Brown genannte 3. Kanon ist daher keineswegs selbstverständlich, sondern ein Merkmal von formalen Systemen, wie sie insbesondere beim Rechnen in Kalkülen und bei symbolischer Verarbeitung in Computern gegeben sind.

7. Kanon, »Principle of relevance« (LoF, 43) Wenn eine Aussage für alle Elemente gilt, braucht sie nicht gesondert genannt zu werden. Das beschreibt implizites Wissen: Mit implizitem Wissen sind Eigenschaften gemeint, die für alle Elemente gelten und daher nicht gesondert aufgeführt werden.

8. Kanon, »Principle of transmission« (LoF, 48) Eine Transmission kann entweder transparent oder opak erfolgen.

9. Kanon, »Rule of demonstration« (LoF, 54) Eine Demonstration besteht aus endlich vielen Schritten. (Da der Re-entry für Spencer-Brown aus unendlich vielen Schritten hervorgeht, entzieht er sich der Demonstration.)

Die Unterscheidung in opak und transparent hat für Spencer-Brown den Rang eines Kanons. Was inhaltlich mit Transparenz, Opazität und Transmission gemeint ist, wird im Folgenden weiter ausgeführt.

Spencer-Brown bezeichnet Canons als »constellations«, weil mit ihnen Anweisungen vorliegen, die nur in ihrer Gesamtheit im Bezug zueinander verständlich sind. Jede für sich bliebe sinnlos.

»The more important structures of command are sometimes called canons. They are the ways in which the guiding injunctions appear to group themselves in constellations, and are thus by no means independent of each other. A canon bears the distinction of being outside (i.e., describing) the system under construction, but a command to construct (e.g., 'draw a distinction'), even though it may be of central importance, is not a canon. A canon is an order, or set of orders, to permit or allow, but not to construct or create.« (LoF, 80)

Und umgekehrt bleibt jede logische oder mathematische Aussage sinnlos (»useless«), wenn nicht ihr Hintergrund verstanden ist. Spencer-Brown nennt die Goldbach-Vermutung als Beispiel, da niemand weiß, wofür sie gut sein soll. Daraus schließt er,

»... that their apparent uselessness is not exactly a reason why such theorems cannot be proved, but is a reason for supposing that if a valid proof were given today, nobody would recognize it as such, since nobody is yet familiar with the ground on which such a proof would rest.« (LoF, 85)

So gesehen will Spencer-Brown mit den Kanons zeigen, welcher Grund für vertraute Rechnungen mit den zuvor entwickelten Axiomen gelegt worden ist. Eine Aussage ohne einen Grund wird von niemandem verstanden.

Was ist der Grund der Proto-Algebra?

Wenn der Grund des arithmetischen Rechnens die unerschöpfliche Freude im Umgang mit den jeweiligen Zeichen ist (so wie die Poesie aus den Worten neue Gedichte zu bilden vermag), was ist der Grund der Proto-Algebra? Am naheliegendsten ist es, den Grund der Proto-Algebra in den Initialen zu sehen, aus denen alle Konsequenzen der Proto-Algebra hergeleitet werden. Spencer-Brown bezeichnet als Initialen, was sonst unter Axiomen verstanden wird. Er wählt diesen Begriff, um die Besonderheit der Proto-Algebra zu betonen, die für ihn nicht aus Sätzen besteht, sondern eben nur aus Konsequenzen, die sich letztlich auch mit Computer-Methoden aus den Initialen berechnen lässt.

Doch enthält die Proto-Algebra weit mehr. Spencer-Brown verbindet mit jeder Konsequenz einen philosophischen Begriff. Welchen Grund gibt es für diese Zuordnung, und kann die Proto-Algebra als eine höhere Art einer Enzyklopädie angesehen werden, deren Vollständigkeit sich aus der Vielfalt der Konsequenzen einer Proto-Algebra ergibt? So gesehen ist auch jedes philosophische System (etwa von Kant oder Hegel) eine Proto-Algebra, die aus den jeweiligen Grundbegriffen des Systems hergeleitet wird.

Innerhalb der Konsequenzen haben die Generierung (generation) und Integration eine hervorgehobene Bedeutung. Mit ihnen lassen sich neue Ergebnisse erzeugen und wieder zusammenführen. Spencer-Brown vergleicht das mit dem Neuplatonismus von Proklos, und Luhmann sieht hierin ein Wechselspiel von Überschussproduktion und Selektion. Ist dies der wahre Grund für die Proto-Algebra?

Eine andere Konsequenz gewinnt ähnlich wichtige Bedeutung, die Staffelung (echelon), aus der eine unendliche Folge und mit ihr der Re-entry hervorgehen wird. Sie kann daher ebenfalls als Grund der Proto-Algebra angesehen werden.

Werden Proto-Algebra und Proto-Arithmetik verglichen, erweist sich die Proto-Arithmetik gegenüber der Proto-Algebra als opak und diese für sich selbst als transparent (siehe hierzu den Parallel-Beitrag zu Spencer-Brown). Ist die Transparenz der Grund der Proto-Algebra?

– Initiale als Grund der Proto-Algebra

Die Proto-Arithmetik ist für Spencer-Brown der Grund der Proto-Algebra. In der Proto-Arithmetik werden die Sätze aufgestellt, auf die sich im Weiteren die Proto-Algebra beziehen kann. Vollständigkeit (completeness) der Proto-Algebra bedeutet für ihn nicht, dass die Proto-Algebra alles abdeckt, was aus der Proto-Arithmetik kommen kann (sie kann nur in vollständiger Weise alle Konsequenzen aus den ihr gegebenen Initialen ziehen), sondern dass sich als Theorem beweisen lässt, dass alle Sätze aus der Proto-Arithmetik in die Proto-Algebra übertragen werden können (Theorem 17; LoF, 50). Aufgrund der Unerschöpflichkeit der Proto-Arithmetik wird immer Neues gefunden und an die Proto-Algebra weiter gegeben werden.

Arithmetische Gesetze werden in der Sprachweise von Spencer-Brown algebraisch, wenn sie nicht nur für einzelne Zahlen gelten (etwa ein Theorem über alle Vielfachen von 5 oder ein Theorem über die Primzahlen), sondern für alle Zahlen. Daher erfolgt der Übergang von der Proto-Arithmetik zur Proto-Algebra über diejenigen Theoreme, die für alle Zahlen gelten. Die Zahlen können durch Variablen ersetzt werden, für die wiederum alle Zahlen eingesetzt werden können. Sie werden identisch von der Proto-Algebra übernommen und fungieren dort als Initiale. Hierbei ist wichtig zu beachten, dass in der von Spencer-Brown eingeführten Proto-Arithmetik die Variablen als Werte nur die beiden Zeichen und Ock annehmen können. Daher kommt Spencer-Brown erstmals auf den Gebrauch einer Variable p, als er in der Proto-Arithmetik mit den Theoremen 8 und 9 Erkenntnisse gewinnt und beweist, die in formaler Übereinstimmung sowohl für wie für das Ock gelten. Sie sind im engeren Sinn der Grund der Proto-Algebra, da sich aus ihnen schrittweise alle Konsequenzen der Proto-Algebra ziehen lassen. Werden sie näher betrachtet, können sie als Gesetz des ausgeschlossenen Widerspruchs (Theorem 8) und als Distributivgesetz (Theorem 9) gedeutet werden. Diese beiden Gesetze sind in einer ersten Annäherung der Grund der Proto-Algebra.

       

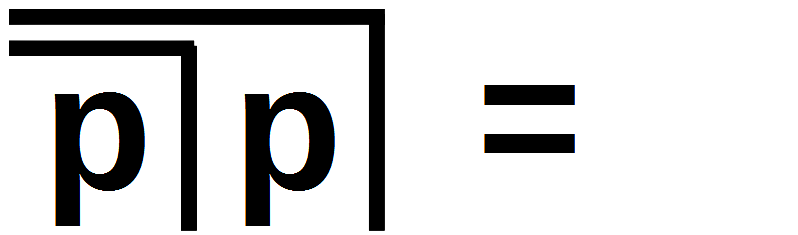
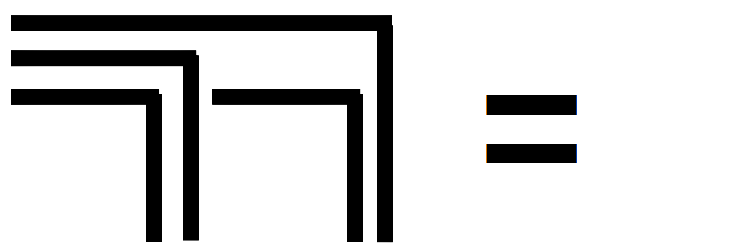
T8, Invariance; LoF, 22
Links steht die Formel mit der Variable p, im mittleren Bild ist für p der Haken eingesetzt und im rechten Bild ist für p der leere Raum eingesetzt.

»Theorem 8. Invariance.
If successive spaces sn, sn+1, sn+2 are distinguished by two crosses, and sn+1 pervades an expression identical with the whole expression in sn+2, then the value of the resultant expression in sn is the unmarked space.« (LoF, 22)

Das ist bei näherem Hinsehen eine wörtliche Beschreibung der Form, mit der im Bild links das Theorem T8 dargestellt ist. Was damit gemeint ist, wird am besten klar, wenn die zugehörige Formel betrachtet und in ihr zuerst für die Variable p das Zeichen und anschließend alternativ für die Variable p das Ock eingesetzt wird (Bild in der Mitte und Bild rechts). An diesen Bildern ist der Beweis direkt abzulesen. Beim Bild in der Mitte ist zuerst gemäß Axiom 2 das links unten stehende Recrossing zu annihilieren und anschließend das übrig bleibende Recrossing. Das Bild rechts zeigt direkt die Aussage von Axiom 2.

Ich vermute, dass Spencer-Brown von dem mittleren Bild ausgegangen ist und hier eine Eigenschaft des Zeichens gesehen hat. Wird anschließend wie in dem Bild rechts für die Variable p das Zeichen des leeren Raums eingesetzt, ergibt sich die Aussage unmittelbar. Aus beiden Fällen folgt Theorem 8, da für die Variable p in der Proto-Arithmetik nur die beiden Zeichen und Ock zur Verfügung stehen.

So ergibt sich sehr anschaulich und nachvollziehbar aus einer Eigenschaft für das Zeichen eine Eigenschaft, die für beide möglichen Zeichen gibt, die daher stellvertretend durch die Variable p dargestellt werden kann.

Varga von Kibéd und Matzka verstehen diesen harmlos aussehenden Satz als den Satz vom ausgeschlossenen Widerspruch. Sie gehen in zwei Schritten vor: 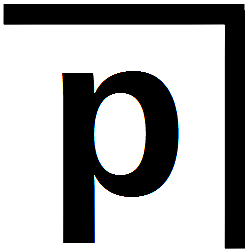wird als Zeichen desjenigen verstanden, was außerhalb von p ist, also ¬p (nicht-p). Daraus wird der zusammengesetzte Ausdruck 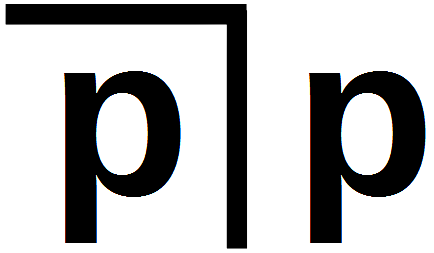gebildet, der für ›p ∨ ¬p‹ (p oder nicht-p) steht, und dieser Ausdruck wird nochmals im Ganzen negiert. Wenn gesagt wird, dass die Negation dieses gesamten Ausdrucks leer ist, ist das ihre Deutung von Theorem 8:

»Damit kann die Positionsgleichung

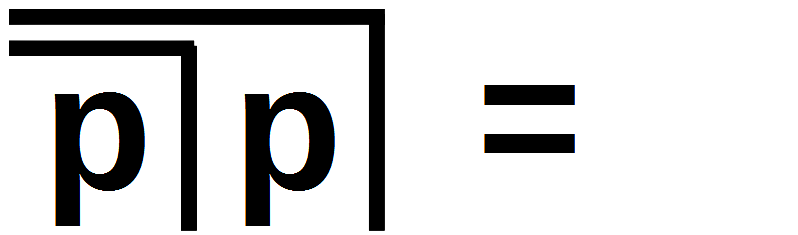
interpretiert werden als die wechselseitige Ableitbarkeit des nullstelligen Falsums und der Negation von ›nicht-p oder p‹, also als eine Version des Satzes vom ausgeschlossenen Widerspruch.« (Varga von Kibéd und Matzka in Baecker Kalkül der Form, 81)

Theorem 9 zeigt eine Präform des Distributivgesetzes für die Proto-Arithmetik.

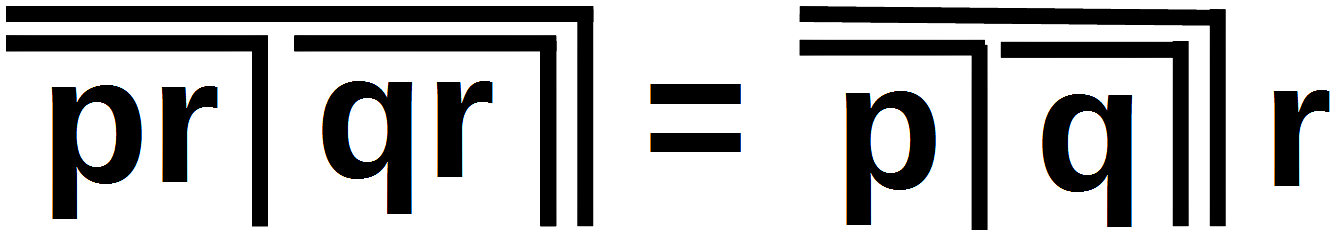
T9 Variance; LoF, 22f

Wenn in einer Form dieser Gestalt die Variable r zweimal auftritt, kann sie "ausgeklammert" werden, bzw. in umgekehrter Richtung kann die Variable r von außen auf die beiden Variablen im Innern der Form verteilt werden. Der Beweis erfolgt, indem für die drei Variablen p, q und r die 8 Möglichkeiten, für p, q und r jeweils einen Haken oder einen Ock einzusetzen, aufgeschrieben und umgewandelt werden, bis sich im Ergebnis zeigt, dass das Theorem für alle 8 Möglichkeiten erfüllt ist.

Für Spencer-Brown genügt, dass er in der intuitiven Untersuchung arithmetischer Regeln auf solche Sätze gestoßen ist, die übergreifend für beide Zeichen gelten. Bei Sätzen mit Variablen handelt es sich in meinem Verständnis um die Einführung von  Regeln, die übergreifend für alle Werte gelten, die in die Variablen eingesetzt werden können. Es geht Spencer-Brown um den Übergang von der Betrachtung einzelner Zeichen zur Betrachtung von Regeln. Die Proto-Algebra kann daher verstanden werden als Lehre der Regeln, während die Proto-Arithmetik eine Lehre über die Eigenschaften der Zeichen ist.

– Sprachfähigkeit

Die Konsequenzen der Proto-Algebra werden rein formal aus den beiden Theoremen 8 und 9 abgeleitet. Sie erfordern keine Beweisidee mehr, sondern eine gewisse Arbeit und Ausdauer, um alle Konsequenzen dieser Theoreme zu erkennen. Die Ableitungen geschehen mechanisch und könnten durch einen Computer übernommen werden. Und dennoch liefert die Proto-Algebra weit mehr als nur technische Ergebnisse. Spencer-Brown deutet das wiederum nur implizit an, indem er jeder Konsequenz einen  Namen  verleiht, der zugleich ein elementarer philosophischer Begriff ist. Er vergibt der Reihe nach den Konsequenzen folgende Namen: Reflexion, Erzeugung (Generierung, generation), Integration, Verdeckung (occultation), gleichmäßige Wiederholung (Iteration), Ausdehnung (Extension), Staffelung (Staffel, echelon), veränderter Austausch (modified transposition), Sammlung und Austeilung (crosstransposition). In den Notes erläutert er:

»One of the most beautiful facts emerging from mathematical studies is this very potent relationship between the mathematical process and ordinary language. There seems to be not mathematical idea of any importance or profundity that is not mirrored, with an almost uncanny accuracy, in the common use of words, and this appears especially true when we consider words in their original, and sometimes long forgotten, sense.« (LoF, 90f)

Weitergedacht bedeutet das, dass mit der Proto-Algebra das Prinzip für ein lexikographisches System gefunden wird. Im einfachsten Fall werden in einem System die Begriffe entweder entsprechend ihren Buchstaben alphabetisch angeordnet, oder nach einer hierarchischen Aufteilung nach Gattungen und Arten. Ein logisches System ist dagegen so angeordnet, dass alle Begriffe auseinander hergeleitet werden können. Der Grund eines solchen Systems liegt in der Fähigkeit, den einzelnen Konsequenzen die angemessenen Namen vergeben und sie darüber auseinander herleiten zu können.

Damit hat Spencer-Brown aus meiner Sicht die klassische Idee aller philosophischen Systeme getroffen. Sie haben den Anspruch, alle philosophischen Begriffe in einer Weise zu ordnen, in der sie logisch auseinander hervorgehen. Am weitesten ausgearbeitet hat das ohne Zweifel Hegel in seiner Wissenschaft der Logik. Für Spencer-Brown sind alle Systeme dieser Art Beispiele für Proto-Algebren. Er hat zugleich den Grundgedanken dieser Systeme erfasst wie auch die schlagende Kritik formuliert: Jedes System erscheint für sich vollständig – und wie im Weiteren ausgeführt wird: transparent –, aber es ist gegründet auf einer Proto-Arithmetik, die prinzipiell offen ist und fortlaufend neue Erkenntnisse liefern wird, weswegen die darauf begründete Proto-Algebra ihrerseits nie abgeschlossen sein kann. – Und Spencer-Brown hat das nicht nur in einer reflektierenden (um nicht zu sagen: räsonierenden) Sprache geäußert, sondern mit den Laws of Form einen Formalismus gefunden, der das angemessen beschreibt.

– Hinausgehen und Rückkehr (prohodos und epistrophe)

Die ersten drei Konsequenzen zeigen, wie Spencer-Brown das meint. Sie stellen eine Methodenlehre in Kurzform dar. So gesehen ist nicht einfach die Sprachfähigkeit, sondern das methodische Denken der Grund der Proto-Algebra.

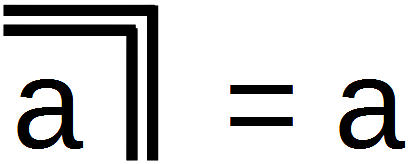
C1 Reflexion; LoF, 28

Eine Reflexion liegt vor, wenn von einer Variable a zu dem hinausgegangen wird, was jenseits von a liegt, und anschließend eine Umkehr erfolgt. Inhaltlich bedeutet die Konsequenz C1 (consequence 1), dass durch die Reflexion keine inhaltliche Veränderung erfolgt. Diese Figur bereitet bereits den Re-entry vor, wenn etwas nicht nur verlassen, sondern durch einen Wiedereintritt neu aufgenommen wird.

Spencer-Brown hatte nicht für möglich gehalten hatte, die Reflexion aus den beiden Initialen J1 und J2 formal ableiten zu können. Das gelang 1965 einem seiner Studenten (LoF, 89). Die Reflexion gehört für ihn zur Proto-Algebra, aber ihre Herleitung gelingt aus den Initialen, die bereits in der Proto-Arithmetik gefunden worden waren. Der Grund der Reflexion liegt damit in der Proto-Arithmetik. – Das ist für mich eine überaus überraschende Konsequenz, mit der die Proto-Algebra begonnen wird. Sie zeigt, dass in grober Annäherung die Proto-Arithmetik von Spencer-Brown mit der Seinslogik von Hegel und die Proto-Algebra mit der Reflexionslogik verglichen werden kann. Mit der Herleitung ist Spencer-Brown eine Formalisierung dieses Verhältnisses gelungen. Die Seinslogik ist der Grund der Reflexionslogik.

Mithilfe der Reflexion lassen sich in der Proto-Algebra beliebig neue Zeichen erzeugen. Hier handelt es sich nicht mehr um das Wiederholen oder Verschachteln von Haken, wie es in den beiden Axiomen formuliert wurde,

   

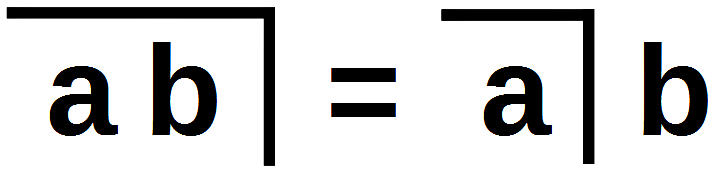
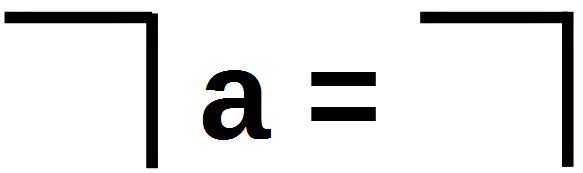
C2 Generation (Erzeugung), C3 (Integration); LoF, 32

C2 ist der erste Schritt einer systematischen Darstellung, die im Weiteren mit C7 fortgeführt werden wird und im Ergebnis den unendlichen Progress ergibt, aus dem der Re-entry hervorgeht. Ohne es auszusprechen legt Spencer-Brown implizit eine Normalisierung nahe, in der alle Variablen schrittweise durch einen Haken getrennt werden. C2 zeigt den ersten Schritt, auf den alle weiteren Schritte aufbauen werden. Stehen zwei Variable a und b innerhalb eines Haken, können sie aufgeteilt werden, so dass beide Variablen durch einen Haken getrennt werden. Das ist eine Formalisierung der impliziten Aussage, dass sich beide Variablen voneinander unterscheiden und daher die eine im Äußeren der anderen steht. (Mathematisch entspricht dies Verfahren der Normalisierung der Umwandlung von Matrizen in die Diagonalgestalt.)

Die Konsequenz C3 (Integration) sieht eigenartig aus, aber sie ist formal äquivalent der üblichen Logik, wonach mit einer Aussage m auch die Aussage ›m oder n‹ gilt, wobei n eine beliebige andere Aussage ist. Das wird in der üblichen Logik formalisiert mit ›m ∨ n = m‹. In der Darstellung der traditionellen Logik und der Alltagssprache erscheint es banal, in der verallgemeinernden Darstellung bei Spencer-Brown in der Proto-Algebra verblüffend und ungewohnt.

In den Anmerkungen sieht Spencer-Brown in diesen beiden Konsequenzen sowohl eine Formalisierung der von Proklos (412-485) eingeführten Begriffe prohodos und epistrophe wie auch typischer Ausdrücke aus der Alltagssprache von Ingenieuren.

»I do not suppose all the names will always stick. Familiarity tends to produce a kind of in-slang, often more appropriate, in its place, than what is deemed to be academically proper or seemly. For example, the engineering application of consequence 2 has produce the more homely ‘breed’ for ‘regenerate’ and ‘revert’ for ‘degeneration’, and it is of interest to note that the transformations of this consequence are immediate images of what Proclus called prohodos and epistrophe, translated by Dodds into procession and reversion.« (LoF, 90)

Das Wechselspiel von prohodos and epistrophe wurde von Hegel als frühe Gestalt der Dialektik gesehen, die mit einer Negation (äußeren Reflexion) über eine gegebene These (Setzung) hinausgeht und in einer Negation der Negation (bestimmende Reflexion) zu ihr zurückkehrt. Ingenieure dachten weit praktischer. ‘Breed’ und ‘revert’ kann ungefähr in ‘Brut’ und ‘Rückkehr, Rückfall’ übersetzt werden: Erst wird aus etwas Gegebenem etwas Neues ausgebrütet, möglicherweise eine Vielfalt von Varianten. Vieles davon wird verworfen, aber einiges kann verwertet werden und wird übernommen. Luhmann hatte daher zurecht von einer Bewegung von Überschuss-Produktion und Selektion gesprochen (Luhmann Wissenschaft der Gesellschaft, 81).

Für Spencer-Brown sind Reflexion, Hinausgehen (generation) und Rückkehr (integration) die ersten drei Konsequenzen. Für ihn beschreibt die Proto-Algebra mit diesen drei Begriffen die Methode des wissenschaftlichen Denkens. Spencer-Brown entwickelt eine Vielzahl von Konsequenzen, und er legt intuitiv nahe, dass mit ihnen ein System philosophischer Grundbegriffe entworfen werden kann, das bis in die Grundlagen des Neuplatonismus (Proklos) zurückreicht. Mir erscheint der Ansatz vielversprechend, aber noch nicht voll ausgearbeitet. Einen Vorläufer sehe ich in Platons Sophistes, in dem Platon auf vergleichbare Weise die fünf Hauptbegriffe (mégista géne) seiner Philosophie entlang der ersten fünf Zahlen durch eine Art philosophisches Zählen begründen und motivieren wollte (siehe dazu den Beitrag Mathematik und Dikalektik in Platons Sophistes).

– Staffelung

Spencer-Brown vergibt den Konsequenzen nicht nur Namen aus der überlieferten Philosophie, sondern kreiert eigene Begriffe, deren Tragweite für mich noch nicht ganz erkennbar ist. Die Staffelung stellt einen Zwischenschritt von der Reflexion zum unendlichen Progress dar.

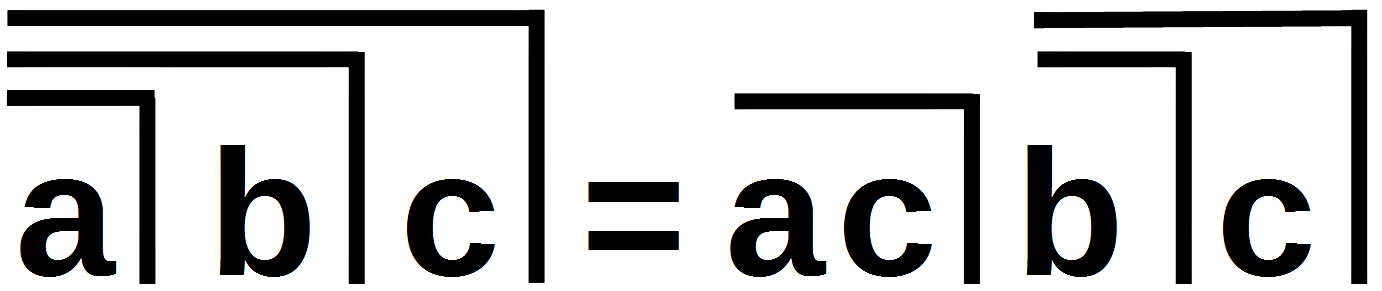
C7 Echelon; LoF, 34

Diese Form sieht wie eine Standardform (kanonische Form) aus. Alle Variablen sind auf ähnliche Weise angeordnet wie es in der Mathematik üblich ist, wenn eine Matrix in eine Diagonalgestalt gebracht wird, in der alle Werte auf der Hauptdiagonale von links oben nach rechts unten angeordnet sind. Das ist die einzige Gestalt, in der alle Variablen völlig voneinander entkoppelt sind und Operationen ohne Nebenwirkungen ausgeführt werden können.

»Es geht hier um die Möglichkeit, eine geordnete Menge, ein geordnetes Hinter-, Neben- oder Nacheinander herzustellen, in dem so viele 'Tiefen' hergestellt werden, wie verschiedene Variablen vorhanden sind. Andererseits kann aber auch die Tiefe eines Ausdrucks oder Gefüges um eine Tiefe reduziert, d.h. um ein 'cross' verringert werden.« (SWH, 146)

Werden die ersten drei Konsequenzen als eine elementare Methodenlehre verstanden, so kann diese Konsequenz als Modell des kanonischen Denkens gesehen werden. Bei Spencer-Brown finden sich jedoch keine Hinweise, die einen Zusammenhang herstellen zwischen den von ihm eingeführten Canons und dem kanonischen Denken. So muss diese Deutung Spekulation bleiben. Für mich scheint dennoch erkennbar, wie Spencer-Brown in der Staffelung die Methode des infiniten Progresses als Konsequenz innerhalb der Proto-Algebra einführt, aus der der Re-entry hervorgeht.

– Transparenz

In welchem Verhältnis stehen der Grund und die in ihn eingetragenen Formen? Wie wirken sich Änderungen im Grund auf die Formen aus? Wenn mit Topologie die mathematische Lehre gemeint ist, wie sich Formen ineinander verwandeln, geht es hier um eine Proto-Topologie. Spencer-Brown unterscheidet zwischen Inhalt, Bild und Reflexion und fragt, wann sich Änderungen im Inhalt in entsprechenden Änderungen der Bilder auswirken, die sich der Mensch von den Inhalten macht. Dem Begriff der stetigen Funktion in der Topologie entspricht hier nach dem Vorbild von Optik und Akustik die Transmission. Mit der Opazität wird gemessen, ob und wie Änderungen im Werteverlauf einer Variable innerhalb eines Grundes nach außen durchsichtig (transparent) sind.

Wird für einen beliebigen Ausdruck e (expression) sein Inhalt gleichlautend mit e bezeichnet, dann können von ihm mit den bisher eingeführten Methoden sein Bild und seine Reflexion unterschieden werden (content, image, reflexion; LoF, 42):

Beispiel: Der Inhalt e sei ein bestimmtes Muster von Strichen auf einem Stein. Um zu verstehen, was der Inhalt bedeutet, wird er als Bild interpretiert. Er kann als Verwitterung, als eine Beschädigung des Steins bei einem Transport, als Spuren von Tieren oder als eine von Menschen in den Stein eingeritzte Hieroglyphe gedeutet werden. Diese Bilder sind nicht Teil des Inhalts: Der Inhalt besagt nicht ›dies ist eine Verwitterung‹ oder ›ich bin eine Hieroglyphe‹, sondern das Bild ist eine Deutung des Inhalts im Denken, das diesen Inhalt als ein Bild für eine Verwitterung, Spuren, Hieroglyphen oder sonst etwas versteht. Das Bild ist eine Markierung, die vom Denken an den Inhalt von außen herangetragen wird. Daher schreibt Spencer-Brown (LoF, 42):

Es muss vom Inhalt zu dem gewechselt werden, was nicht zum Inhalt gehört, sich also im Außen des Inhalts befindet, um dort den Inhalt als ein Bild zu erkennen. Was bei diesem Vorgang geschieht, kann seinerseits betrachtet werden. Es ist zum Beispiel eine archäologische oder eine stilistische Untersuchung. Um es als solche zu erkennen, ist nochmals in das Außen des Bildes zu gehen. Es wird als ein bestimmter Inhalt erkannt. Das ist der Inhalt, woran in diesem Beispiel ein Zeichen als Hieroglyphe nachgewiesen wird.

Das lässt sich beliebig weiterführen und auf andere Beispiele übertragen. So kann der Inhalt das Leben eines Menschen sein. Andere Menschen sehen ihn und machen sich ein Bild von ihm. Wird weiter gefragt, wie und warum ein solches Bild entstanden ist, handelt es sich wiederum um einen bestimmten Inhalt, der dieses Bild als Bild charakterisiert, z.B. bestimmte Merkmale des Habitus oder psychologisch klassifizierte Verhaltensweisen. (Beispiele dieser Art erklären, warum Spencer-Brown unter Soziologen und Psychologen weit größeren Einfluss gewinnen konnte als unter Mathematikern oder Philosophen.)

Schönwalder-Kuntze wählt in ihrem Kommentar bewusst die Geometrie als ein mathematisches Beispiel. Gegeben sei eine bestimmte Figur, die unmittelbar wahrgenommen wird. »Dann heißt das, dass der Inhalt des Kreises erst als Kreisinhalt sichtbar wird, wenn wir auf die ihn umgebende Grenze, die seine Form 'shaped', schauen.« (SWH, 156)

Ein anderes Beispiel ist eine Landkarte (SWH, 161). Hier ist auf einem Stück Papier ein Bild gezeichnet, das eine bestimmte Landschaft repräsentiert. Es ist wichtig, dass für den jeweiligen Kontext (etwa bei einer Wanderung) die wesentlichen Änderungen des Geländes auf der Karte erkennbar sind, wie z.B. Entfernungen, Anstiege, Straßen, Aussichtspunkte etc. Der Nutzer einer Karte orientiert sich: Er vergleicht die unmittelbar gesehene Umgebung mit der Karte und wechselt im Moment der Orientierung zwischen Inhalt (der wirklichen Landschaft) und Bild (Landkarte) hin und her. »'Ebenensprung' beim Kartenlesen.« (SWH, 162)

Wird eine Form im Ganzen betrachtet, nennt Spencer-Brown mit s0 sowohl den vollständigen Raum, den dies Zeichen einnimmt (pervasive space), wie auch das Zeichen selbst als den anzeigenden Raum (indicative space). Innerhalb des Zeichens können schrittweise weitere Zeichen eingetragen werden, die stufenweise mit s1, …, sn, sn+1, … bezeichnet werden. Zugleich verweist das Zeichen im Ganzen auf einen äußeren Raum s−1, der sowohl den Beobachter wie die gegebene Form umgibt.

»In evaluating e we imagine ourselves in s0 with e and thus surrounded by the unwritten cross which is the boundary to sn+1.« (LoF, 42)

Mit s−1 wird die Gesamtheit aller Formen verlassen und die Ebene der Wirklichkeit erreicht (die Landschaft um uns herum, das Leben eines anderen Menschen, die tatsächlichen Zeichen auf einem Stein, usf.).

An dieser Stelle fragt Spencer-Brown, ob sich innere Veränderungen einer Form nach außen zeigen. Ich verstehe das auch als die Frage, ob es gelungen ist, sich auf eine Weise von einem Inhalt ein Bild zu machen, die auf Änderungen des Inhalts mitlaufend zu reagieren vermag.

»Eighth Canon. Principle of transmission
With regard to the oscillation of a variable, the space outside the variable is either transparent or opaque.« (LoF, 48)

Das ist für mich der entscheidende Punkt, um den es mir bei der Beschäftigung mit Spencer-Brown geht. Mit einem ähnlichen Index −1 konnte bei Betrachtung des Möglichkeitsraums bei Leibniz argumentiert werden (der Gesamtheit aller möglichen Welten, siehe hierzu den Beitrag Dynamische Logik nach Leibniz und Gödel). Bei Spencer-Brown kommt zweierlei hinzu: Ihm gelingt eine Formalisierung, die über Leibniz hinausgeht, und er stellt die Frage nach der paradoxen (selbstbezüglichen) Verknüpfung von Inhalt, Bild und Reflexion beim Beobachter, wie sie in anderer Weise später von Autoren wie Lacan u.a. aufgenommen wurde. Während alle anzeigenden Räume auseinander konstruiert und daher transparent sind, entzieht sich der Raum s−1 der Transparenz des Denkens und ist ihm gegenüber opak.

Wenn es im Inhalt Veränderungen gibt, also formal gesprochen innerhalb des Inhalts einzelne oder mehrere Variablen oszillieren, ist zu fragen, ob diese Änderungen durch die Transmission angemessen in den Bildern erfasst werden. Bei Transparenz ist die Transmission von Inhalten zu Bildern nicht unterbrochen und die Veränderungen im Werteverlauf können in den Bildern mitvollzogen werden. Wenn sich zum Beispiel bei genauerer Säuberung eines Steins die dort freigelegten Zeichen ändern, ist es bei transparenter Transmission dennoch möglich, sie im Bildbereich der Hieroglyphen als eine andere Hieroglyphe zu verstehen. Wird jedoch dieser Zusammenhang unterbrochen, muss vollständig die Interpretation des Zeichens als Hieroglyphe aufgegeben werden. – Oder wenn ein Mensch signifikant sein Verhalten ändert, bleibt dies zunächst innerhalb der üblichen Menschenkenntnis transparent und kann verstanden werden. Fällt er jedoch völlig aus dem Rahmen gewohnten Verhaltens, sind andere Bilder notwendig, etwa durch die Psychiatrie oder sonstige medizinische Erklärungsversuche bis hin zu religiösen Deutungen als Besessenheit.

Im Kommentar schreibt Spencer-Brown, dass auf diese Weise jeder Beweis in eine neue Ebene führt.

»We do not fully understand a theorem until we are able to contain it in a more general theorem. We nevertheless follow its proof, in the sense of coming to see its evidence, without understanding it in the wider sense in which it may rest.« (LoF, 95)

Re-entry getunnelt durch den Grund

Dank ihrer Transparenz ist es der Proto-Algebra möglich, ausgehend von Generation und Echelon eine infinite, gleichförmige Sequenz zu finden, die im Ergebnis zu einem Re-entry der unendlich verschachtelten Form in eine endliche Form findet.

Spencer-Brown wählte hierfür das Ikon . Schon an diesem Bild ist die Untertunnelung zu erkennen: Der Re-entry führt unterhalb der Zeichenreihe zurück von einem Element, das transfinit jenseits aller aufzählbaren Zeichen liegt, an einen Punkt im endlichen Zeichenbereich.

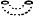
Equations of the Second Degree; LoF, 60

Das wird inhaltlich nicht weiter ausgeführt, aber es ist offensichtlich, dass der Re-entry verbunden ist mit einer Eigenschaft des Grundes, durch den in der dargestellten Weise Tunnel gegraben werden können. Der Grund muss über eine eigene Ausdehnung verfügen, durch den der Tunnel führen kann, und er muss zusammenhängend und kompakt sein, um den Weg des Tunnels stabilisieren zu können.

In einem anderen Bild kann gesagt werden, dass der Grund wie ein Tanzboden schwingt. Die infinite Bewegung löst auf dem Grund, in den sie eingetragen wird, einen Rhythmus aus, der überall zu spüren ist. Der Grund verfügt über eine Musikalität und der Re-entry kann als Resonanz-Phänomen gedeutet werden. Der Grund erweist sich als Medium mit einem eigenen Klang.

Beobachter auf einem gekrümmten Grund

Wenn der Grund untertunnelt und ins Schwingen gebracht werden kann, verfügt er über eine eigene Tiefe, die auf einer vertikalen Achse zur Oberfläche des Grundes verläuft, auf der die Formen eingetragen sind. Und wenn diese Tiefe nicht starr ist, kann sie sich wölben. Der Grund ist gekrümmt.

Werden auf einem gekrümmten Grund sowohl die Formen wie die Positionen der Beobachter eingetragen, dann ergibt sich aus der Krümmung die Relativität der Beobachterstandorte. Was dem einen Beobachter als zwei verschachtelte Kreise erscheint, sieht für den anderen Beobachter so aus, als würden zwei Kreise nebeneinander liegen. Beide Beobachter machen sich von der gleichen Sache völlig verschiedene Bilder.

Wird nun gefragt, wie sich die unterschiedlichen Bilder der verschiedenen Beobachter ineinander transformieren lassen, dann sind die Transformationen aus den Eigenschaften des Grundes zu erklären. Wie das gelingen und formalisiert werden kann, ist für mich die Frage, auf die die Logik von Spencer-Brown am Ende hinausläuft. Von der Freiheit des Grundes zu sprechen besagt genauer, dass der Grund ebenso viele Transformationen enthält wie Formen. Welche Transformation aus dem unerschöpflichen Vorrat an Transformationen ausgewählt ist und die Regeln der uns bekannten Wirklichkeit ausmacht, das ist die Frage nach der Existenz und der Faktizität.

Siglenverzeichnis

AUM = The G. Spencer-Brown – AUM-Conference 1973, Esalen 1973; Link

LoF = George Spencer-Brown: Laws of Form, New York 1972 (Julian Press) [1969]; Link

SWH = Tatjana Schönwälder-Kuntze, Katrin Wille, Thomas Hölscher: George Spencer Brown, Wiesbaden 2009 [2004]

Literatur

Dirk Baecker (Hg.): Kalkül der Form, Frankfurt am Main 2016 [1993]

Felix Lau: Die Form der Paradoxie, Heidelberg 2012 [2005]

Niklas Luhmann: Beobachten
in: Luhmann: Die Wissenschaft der Gesellschaft, Frankfurt 1992 [1990], S. 68-122

Niklas Luhmann: Die neuzeitlichen Wissenschaften und die Phänomenologie, Wien 1996

 

© tydecks.info 2017