Russellsche Antinomie und die Paradoxien des Denkens

Beitrag für das Philosophische Colloquium der Akademie 55plus Darmstadt am 4. Juli 2016, erweiterte Version

 

Die Russellsche Antinomie

Die Russellsche Antinomie beschäftigt seit ihrer Veröffentlichung im Jahre 1903 die Mathematik, die Logik und die Philosophie. Seither ist das Vertrauen in die Sicherheit der Logik von Grund auf erschüttert mit Auswirkungen auf alle Wissenschaften und Künste bis hin zur Ethik und Glaubensfragen, die sich ebenfalls auf die Unumstößlichkeit der scholastischen Logik verlassen hatten. Russell gehörte zu einer größeren Gruppe von Intellektuellen in England, die aus unterschiedlichsten Bereichen kamen und das Gefühl teilten, am Anbruch einer neuen Zeit zu stehen. Das waren die Cambridge Apostles und der Bloomsbury Kreis, zu ihnen zählten u.a. T.S. Eliot, Eric Hobsbawm, Aldous Huxley, John Maynard Keynes, John McTaggart, Katherine Mansfield, Vita Sackville-West, Ludwig Wittgenstein, Virginia Woolf. Ist ein Boden in Sicht, von wo aus sich das Denken neu erfinden kann? Kann er woanders liegen als wiederum in der Logik? Ein Blick auf die bisher bekannten Antinomien und ihre Beziehungen zueinander soll zeigen, wie es zur Russellsche Antinomie kommt und in welchem Zusammenhang sie steht. Aus ihm ergibt sich möglicherweise eine neue Perspektive für die weitere Entwicklung der Logik.

Was Russell meint, wird am einfachsten verständlich in einer neueren Version: »Alle Bürgermeister dürfen nicht in ihrer eigenen Stadt leben, sondern müssen in die eigens dafür eingerichtete Bürgermeister-Stadt Bümstädt ziehen. Wo nun lebt der Bürgermeister von Bümstädt?« (Duden Unnützes Sprachwissen 2012, zitiert nach Wikipedia, hier wie im Folgenden abgerufen am 5.6.2016). Für Ulrich Blau kommen Paradoxien dieser Art in allen Kulturen vor. Er zitiert frei den buddhistischen Lehrer Nagarjuna, der im 2. Jahrhundert gelebt hat: »Buddha hat nie ein wahres Wort gesprochen. Wer meine Worte als Theorie versteht, ist unheilbar.« (Blau, S. 445)

Eine der anregendsten Arbeiten zu diesem Thema ist für mich das 1984 erschienene Buch Die Produktivität der Antinomie von Thomas Kesselring (im Folgenden zitiert als K). Er zieht eine Verbindung zur Entwicklungspsychologie von Jean Piaget. Piaget lebte 1896-1980, war von Haus aus Biologe und wirkte in Genf. Seine Arbeiten waren bahnbrechend für die Mathematikpädagogik. Er hat versucht zu zeigen, in welchem Alter die Kinder und Jugendlichen empfänglich werden für mathematische Ideen. Statt sie zu früh mit Stoff zu konfrontieren, den sie noch nicht aufnehmen können, sollten in jeder Altersstufe die jeweiligen Fähigkeiten gefördert werden, wovon der Mathematikunterricht heute nach wie vor weit entfernt ist. Das würde eine freiere Sicht auf die Mathematik und darüber auch die Logik und Philosophie ermöglichen. Hegel hatte er nicht gelesen, soll sich aber sehr interessiert gezeigt haben, als Kesselring mit ihm kurz vor seinem Tod über sein Vorhaben gesprochen hat. Hegels Phänomenologie des Geistes liegt ein vergleichbares Entwicklungsmodell zugrunde.

Kesselring vertritt die These: Die vier von Piaget unterschiedenen Stadien der Entwicklung des Denkens stoßen jeweils an eine Antinomie, die erst mit der nachfolgenden Stufe gelöst werden kann. Mit der Russellschen Antinomie wird die IV. Stufe des formalen Denkens erreicht und mit ihr – laut Kesselring – auch die Dialektik. Im Folgenden werden die 4 Phasen und ihre Antinomien vorgestellt, bis sich zeigen wird, dass der Russellschen Antinomie weitere Antinomien folgen: das Lügner-Paradoxon (›alles, was ich sage, ist falsch‹), das Gleichnis von Achilles und der Schildkröte und die Cantorsche Antinomie. Sie lassen sich nicht mehr in den vier von Piaget unterschiedenen Stufen lösen, sondern erst in nachfolgenden Stufen, in denen das Denken einen Begriff der Unendlichkeit entwickelt. Inhaltlich beziehe ich mich bei den Stufen V und VI auf die beiden von Cantor eingeführten Unendlichkeitsbegriffe der transfiniten Zahlen und des Kontinuums, sowie auf die von Hegel in seiner Wissenschaft der Logik ausgeführten Antinomien der Unendlichkeit. Abschließend folgt ein Ausblick auf die weitere Entwicklung der Logik.

Bekannt geworden ist die Russellsche Antinomie als Barbier-Paradoxon: »Man kann einen Barbier als einen definieren, der all jene und nur jene rasiert, die sich nicht selbst rasieren« (Wikipedia). Es ist nicht unmittelbar einleuchtend, dass diese Definition in sich widersprüchlich ist. Wo liegt ein Widerspruch, wenn die Menge aller Barbiere betrachtet wird, die sich nicht selbst barbieren? Der springende Punkt liegt in der Verschärfung, »der all jene und nur jene rasiert«. Der genannte Wikipedia-Eintrag erläutert: »Angenommen der Barbier rasiert sich selbst, dann gehört er zu denen, die er laut Definition nicht rasiert, was der Annahme widerspricht. Angenommen es gilt das Gegenteil und der Barbier rasiert sich nicht selbst, dann erfüllt er selbst die Eigenschaft derer, die er rasiert, entgegen der Annahme.«

Die ersten vier Stufen der kognitiven Entwicklung nach Piaget

Piaget spricht nicht von Widerspruch oder Antinomie, sondern vom Widerstand, die jeweilige Stufe zu verlassen. Auf jeder Stufe folgt das Denken einem bestimmten  Schema. Wird dieses Schema seinerseits zum Inhalt, und soll mithilfe des Schemas die Frage beantwortet werden, wann das Schema  nicht  gilt, führt das in eine Antinomie. Das Kind hat sich aber an das Schema gewöhnt und möchte daran festhalten. Das führt in eine Entwicklungskrise, die mit der nachfolgenden Stufe gelöst wird.

I: Sensomotorisch, Alter: 0 - 2 Jahre, Säuglingsalter

Niemand kann sich an das erinnern, was in der Phase der ersten beiden Lebensjahre geschah. Sie fällt unter die Infantile Amnesie und wirkt auf einer Ebene unterhalb des Bewusstseins. Unmittelbar nach der Geburt reagiert der Säugling mit angeborenen Reflexen auf seine Umwelt. Das sind motorische Abläufe, die jeweils einem bestimmten Verhaltensmuster (Schema) folgen. Beispiele: Saug- und Schluckreflex, Greifreflex, reflexartiges Fokussieren der Augen auf einen hell hervorgehobenen Gegenstand. – Reflexe dieser Art können zwar später durchschaut, aber nicht vermieden werden. Mit dem Libet-Experiment wird nachgewiesen, wie auch Erwachsene spontan auf bestimmte Reize reagieren, bevor sie sich des Reizes und der Antwort darauf bewusst werden. Daraus wurden weitreichende Schlüsse über die Grenzen der menschlichen Willensfreiheit und Selbsttäuschungen des Bewusstseins gezogen. Sie zeigen für mich lediglich den Bereich, in dem die Schemata der I. Stufe lebenslang gültig bleiben.

Ursprünglich selektiert die Wahrnehmung aus allen Reizen diejenigen aus, für die es ein angeborenes Reaktions-Schema gibt. »Man schätzt, daß der Mensch pro Sekunde 10.000 exterozeptive und propriozeptive Sinneswahrnehmungen aufnimmt.« (Watzlawick 1967, zitiert K, S. 385, siehe Begriffsdefinitionen Exterozeption und Propiozeption) Davon wird das meiste nicht bewusst wahrgenommen und löst keine Reaktion aus. Leibniz bezeichnet die Gesamtheit aller sinnlichen Reize als Kleine Perzeptionen, von denen nur ein Teil ins Bewusstsein dringt. Nomadisches Denken ist die Fähigkeit, dennoch unterhalb der Bewusstseinsebene auf Reize dieser Art reagieren zu können. Metzinger vermutet, dass es einen zweiten Prozess höherer Ordnung gibt, der dem Prozess der Selektion der Reize nachfolgt und dem Bewusstsein verdeckt, wie viel ausgefiltert wurde (Metzinger Der Ego-Tunnel, München, Zürich 2014, S. 71f).

In dieser frühen Phase kann der Säugling nur zwei Situationen unterscheiden: Fülle oder Mangel. Wenn irgendetwas fehlt, ist er völlig hilflos. Seine bodenlose Verzweiflung kann andere täuschen, die nicht verstehen, was ihm genau fehlt. Und umgekehrt: Wenn alle Bedürfnisse erfüllt sind, ist er zeitlos glücklich und kann sich nicht vorstellen, dass es je anders sein könnte. Er spürt nur, wie sich der Zustand verändert: Es verschwindet etwas, es kommt etwas. Wenn etwas verschwindet, kann er sich nicht vorstellen, dass es je wieder kommt, und wenn etwas da ist, scheint es für immer da zu sein.

In dieser frühesten Entwicklung lernt das Kind allmählich bestimmte sensorische Bilder zu unterscheiden und kann zum Beispiel ein menschliches Gesicht erkennen. Aber auch hier gilt: Wenn etwas aus dem Gesichtsfeld verschwindet, ist es endgültig fort. Wenn die Sonne untergeht, wird sie nie wiederkommen, wenn sie scheint, nie untergehen. Großartig das Bild in der Abenddämmerung von Baudelaire: In der Regel freuen sich die »erschöpften Seelen« auf den Abend, »oh erquickliche Finsternis! Ihr seid für mich die Ankündigung eines inneren Festes«, aber es gibt Geisteskranke in einer Irrenanstalt, die dann laut schreien und »das Kommen der Nacht für die Ankündigung eines Hexensabbats halten« (Baudelaire, Pariser Spleen, XXII). Sie verhalten sich noch so wie der Säugling beim Verlust der Fülle. In dieser ersten Phase lässt sich logisch bereits das Muster aller Antinomien erkennen:  Das Verschwinden des Verschwindens. Wenn etwas verschwindet, ist es verschwunden und nicht mehr das Verschwinden. Wenn es nicht-verschwindet, ist es kein Verschwinden mehr.

Im Laufe der weiteren Entwicklung können allmählich einzelne Situationen deutlicher voneinander differenziert werden. Das Kind muss erfahren, dass sein angeborenes Reaktionsverhalten nicht immer zu der erwarteten Bedürfnisbefriedigung führt. Beispiel: Es lutscht an allem, was dem sensorischen Bild der Mutterbrust entspricht, und erlebt, dass das bisweilen keine Nahrung gibt. Das Kind lernt Enttäuschung und Freude. Daraus entsteht für Kesselring die erste Antinomie: »Es ist so, wie es nicht ist.« (K, S.192) Etwas scheint eine Nahrungsquelle zu sein, ist es aber nicht.

Das Kind lernt, dass das, was im sensorischen Bild zu sehen ist, möglicherweise nur Schein ist. Das Kind macht die Erfahrung, dass Bilder zwar täuschen können, aber Bilder zu sehen ist kein Schein. Was macht die Konstanz des Sehens aus? Darauf wird das Kind mit der nächsten Entwicklungsstufe eine Antwort finden.

Das Kind muss lernen, zwischen Schein und Nicht-Schein zu unterscheiden. Es sucht nach neuen Erkennungsmerkmalen. Es erlebt Situationen, für die noch kein Schema verfügbar ist. Das sind nicht mehr die Reize, die ausgefiltert werden, weil es keine angeborene Antwort auf sie gibt, sondern die Reize, bei denen das Kind nicht mehr sicher ist, ob sie Schein sind oder nicht. Das Kind kann in Situationen der Indifferenz geraten, in denen es nicht schematisch reagieren kann. Welches Schema setzt sich dann durch? Verhält es sich spontan vorsichtig, abwehrend, ängstlich, offen, aufmerksam, depressiv? Das hängt sowohl von seinen persönlichen Eigenarten wie der Unterstützung durch seine Umgebung ab. Ich vermute, dass sich in diesen Situationen sein spezifischer  Habitus  herausbildet. Jeder Mensch ist an seinem Habitus zu erkennen, seinen spezifischen und zugleich schematisierten Gesten und Verhaltensmustern, und er selbst erfährt seinen Habitus von innen als den Schatten, über den er nicht zu springen vermag.

Beginnt das Kind diese Stufe zu überschreiten, wird das trotz aller vorangegangenen Erfahrung der eigenen Hilflosigkeit als Verlust erlebt, aus der Geborgenheit eines Paradieses zu fallen und ist mit entsprechendem Widerstand verbunden. Piaget sieht hier erstmals Ersatzbefriedigungen auftreten, wenn das Kind – meist im Alter von 4 bis 5 Jahren – lernt, auch von Enttäuschungen Gebrauch zu machen und sich z.B. angewöhnt, auf alle unbehaglichen Situationen mit Daumenlutschen oder Nagelbeißen zu reagieren. – Der Habitus entsteht zwar aus einem Mangel (einer Enttäuschung), aber er muss keineswegs in eine Regression führen, sondern umgekehrt können auch alle positiven Eigenschaften des Denkens wie Intentionalität, Spiritualität, Offenheit usw. mit Überschreiten der I. Stufe nur aus einem Habitus hervorgehen.

II: Präoperational (symbolisch oder vorbegrifflich), Alter: 2 - 7 Jahre, Kindergarten und Vorschule

Mit der Erfahrung von Enttäuschung und Freude lernt das Kind den Unterschied von Gegenstand und Symbolen. Es lernt, dass nicht alles eine milchgebende Mutterbrust ist, das sich so anfühlt und woran es saugen kann, sondern dass die Mutterbrust ein bestimmter Gegenstand ist, der sich sowohl von anderen Gegenständen unterscheidet wie auch von dem Schein (dem Bild), eine Mutterbrust zu sein. Das Kind lernt in einem  einheitlichen  Prozess, wie die einzelnen Gegenstände an ihrer jeweiligen Beschaffenheit zu erkennen und zu unterscheiden sind, und wie es diese sprachlich benennen kann. In diesem Alter erfolgt der Spracherwerb. Die sprachlichen Symbole sind anders beschaffen als das, was sie aussagen. Sie sind von anderer Natur als das, was sie bezeichnen. Das Wort ”gelb“ ist nicht gelb. Das Wort ”Abendstern“ ist nicht der Abendstern. In diese Phase fällt auch das erste Verständnis von Begriffen, Urteilen, Zahlen. (K, S. 201) Eine Zahl ist nicht das, was mit ihr gezählt wird, ein Urteil nicht das, was mit ihm ausgesagt wird.

Die vorangegangene Antinomie wird aufgelöst: Der Schein hat Permanenz, weil er anders als der von ihm dargestellte Inhalt ein Symbol ist, das sich von seinem Inhalt unterscheidet. Die Inhalte können kommen und verschwinden, aber das Symbol bleibt erhalten. Diese Einsicht ist Grundlage der frühesten philosophischen Systeme (siehe Platons Reich der Ideen, die anders als das von ihnen Dargestellte nicht vergänglich sind, und Hegel über das Entstehen der Sprache in der ersten Entwicklungsstufe der Phänomenologie des Geistes, der sinnlichen Gewissheit).

Eigenartigerweise fällt es wesentlich schwerer, sich in diese Phase zurückzuversetzen als in die vorangegangene Phase der Reize und Empfindungen. Das Kind lernt in dieser Phase noch nicht auf eine systematische Weise wie später in der Schulzeit. Kinder diesen Alters verstecken und verkleiden sich gern und sind begeistert vom Zirkus und märchenhaften Figuren wie dem Struwwelpeter. Die III. Phase wird später derart dominant, dass auf alles herabgesehen wird, was vorher geschah. Das Kind befindet sich im Vorschulalter in einer Phase  magischen Denkens, wie Piaget mit vielen Übungsaufgaben zeigen wollte.

Umschüttaufgabe: Wenn eine Flüssigkeit von einem breiten in einen schmaleren Topf gegossen wird und dort der Pegel höher steht, glaubt das Kind, die Menge habe sich vergrößert, obwohl es gesehen hat, dass nichts hinzugekommen ist. Ihm kann gezeigt werden, wie die gleiche Flüssigkeit zurückgeschüttet werden kann, das Experiment kann beliebig oft wiederholt werden, dennoch wird das Kind bei seiner Überzeugung bleiben, dass sich die Menge verändert. – Werden von einer Perlenkette die Perlen ausgefädelt und in ein Glas gelegt, sind es für das Kind neue Perlen geworden. Trägt die Schwester ein ungewohntes Kleid, ist sie jemand anders, bis sie sich wieder wie üblich kleidet und die alte ist.

Dies Denken gilt als magisch, weil es für das Kind eine verborgene Verwandlungsmacht gibt: Wenn sich die Eigenschaften von Dingen ändern, verwandeln sich die Dinge ebenfalls. Das Kind muss zu unterscheiden lernen, welche Veränderungen eines Gegenstandes auf innere Veränderungen und welche auf Änderungen der Umgebung zurückgehen, die den Gegenstand selbst unverändert lassen.

Kein Stellvertreter: Wenn in diesem Alter einem Kind drei Kugeln gezeigt werden mit der Aufzählung »eins, zwei, drei« und das Kind anschließend gebeten wird, drei Kugeln zu geben, gibt es nicht alle drei Kugeln, sondern die dritte, die bei der Aufzählung mit »drei« bezeichnet worden war.

Unfähigkeit, etwas aus einer anderen Perspektive zu sehen. Ist das dein Bruder? Ja. Hat er auch einen Bruder? Nein.

Es ist schwer, die in dieser Phase auftretende Schwierigkeit und Antinomie in Worte zu fassen. Das Kind lernt, das sich manches verändern kann und manches nicht. Fort-Da-Spiel: Der Ball kann zum Boden fallen, und bleibt doch ein Ball. Sein Ort hat sich verändert, aber nicht sein Wesen als Ball.

Rückblickend mag diese Phase als Unvollkommenheit erscheinen, und wer daran festhält oder bisweilen dahin zurückfällt, gilt als durcheinander. Sie hat aber ihren eigenen Zauber und Poesie. Besser als die Philosophen und Pädagogen vermögen bisweilen die Schriftsteller daran zu erinnern. Das war nicht nur das Anliegen der Romantiker. Es ist auch zu denken an die Verwandlung von Kafka oder an Musil. Er beschreibt einen Mann, der sich in seinen Gefühlen gegenüber einer Frau verwirrt. Das überträgt sich auf seine Wahrnehmung der alltäglichen Dinge in dem Zimmer, in dem er sich gerade aufhält, die Tapete, die Türen, der Samtstuhl. »Von ihnen galt, daß der Glaube an sie früher da sein mußte als sie selbst; wenn man die Welt nicht mit den Augen der Welt ansieht und sie schon im Blick hat, so zerfällt sie in sinnlose Einzelheiten.« (Robert Musil Drei Frauen, zitiert bei Kulenkampff, S. 9 Fn. *, Text verfügbar bei Projekt Gutenberg). Aber niemand hat für mich die Stimmung dieser Phase besser getroffen als Katherine Mansfield (1888-1923), die seit 1916 mit Russell gut bekannt war und in ihren Erzählungen ihre Kindheit erinnert.

Die zugrunde liegende Frage ist bis heute in der Philosophie umstritten. Für Kant ist dasjenige, was unveränderlich allen veränderten Erscheinungen als Bezugspunkt erhalten bleibt, das »Ding an sich«. Es geht sogar den Erscheinungen in Raum und Zeit voraus und birgt bei unvoreingenommener Betrachtung eine magische Qualität, wie am besten aus der Perspektive des Kindes in der II. Stufe zu sehen ist. Nur ein Beispiel: Wenn die Mutter für eine längere Zeit wegfährt, gibt sie dem Kind ein Symbol (einen Fetisch), damit das Kind ihre Gegenwart weiter spüren kann, sei das eine Puppe, ein Foto oder ein anderes Erinnerungsstück. Solange das Kind sieht, wie es dem Fetisch "gut geht", ist es beruhigt, aber wenn es zerbricht oder verloren geht, ist es verzweifelt, als sei die Mutter gestorben. Der Fetisch ist nur eine Erscheinung der Mutter, aber das Kind glaubt daran, und der "realen" Mutter und der Erscheinung liegt etwas zugrunde, was mit Kant als »Ding an sich« bezeichnet werden kann, außerhalb von Raum und Zeit. Mit der Erfahrung der III. Stufe wird das niemand mehr so sehen wollen, und es wird jeder nur bei ehrlicher Sicht sich selbst gegenüber eingestehen müssen, wie oft auch im Erwachsenenleben noch auf Magie vertraut und zurückgegriffen wird. Psychologen wie C.G. Jung haben dies Phänomen als Synchronizität bezeichnet und in ihrer Praxis herangezogen, so auch in der Behandlung des Physikers Wolfgang Pauli, der sich zum Zeitpunkt seiner bahnbrechenden physikalischen Erkenntnisse in einer psychischen Krise befand.

Hegel fand dafür in einer neuen, verblüffenden Wendung den abstrakt klingenden Begriff des »Anderen an ihm selbst«. Damit ist gemeint, dass z.B. eine in einer kargen Umgebung wachsende Blume dennoch von Natur aus blühen kann, selbst wenn ihr das in den gegebenen widrigen Umständen nicht möglich ist. In einem großen Gedanken versteht Hegel unter Idealismus die Fähigkeit, an einem Menschen oder an einer Sache dasjenige zu erkennen, was sie entsprechend ihrer Natur oder inneren Bestimmung potentiell an sich enthalten, selbst wenn sie es aktuell nicht verwirklichen können. Das ist der Grundgedanke der Humanität, auch im Menschen, der in seinem Elend eine traurige Gestalt abgibt, seine wahre Gestalt sehen und ihm die Zuneigung geben zu können, die er braucht, um sich daraus zu lösen.

Das Kind lernt zu unterscheiden, was etwas ist, so wie es ist, und was es seiner Bestimmung nach sein kann. Das führt in eine Antinomie, wenn es seinerseits negiert wird:  Gibt es etwas, dessen Bestimmung es ist, nicht das zu sein, was es ist?  Das kann als eine rein logische Antinomie verstanden werden: Der Begriff des Widerspruchs. Es ist die Bestimmung des Widerspruchs, nicht das zu sein, was er ist. Die Bestimmung, einen Widerspruch nachzuweisen, liegt darin, den Widerspruch aufzulösen. Es ist die Bestimmung des Widerspruchs, zugrunde zu gehen, d.h. den Weg (den Ausweg) zu weisen, welcher Grund dem Widerspruch zugrunde liegt und seinerseits kein Widerspruch mehr ist. Das wird nahezu unweigerlich mit moralischen Werten verbunden. Das Kind lernt in diesem Alter nicht nur Gegenstände zu differenzieren und über sie zu sprechen, sondern es beginnt auch wahrzunehmen, wie sich verschiedene Menschen unterschiedlich verhalten, wie sich die Mutter oder der Vater in bestimmten Situationen keineswegs mehr so verhalten, wie es vom Kind erwartet wird, und wie sie von anderen Menschen völlig anders gesehen werden als von ihren Kindern. Das Kind spürt, wie es seinerseits auf andere Menschen unterschiedlich wirkt und bei den einen Sympathie und bei anderen Aggression auslöst. Es gerät in double-bind-Situationen, wenn es einander widersprechenden Erwartungen ausgesetzt ist, und es lernt, seinerseits andere Menschen gegeneinander auszuspielen. Mit der Frage nach dem Etwas, dessen Bestimmung es ist, nicht das zu sein, was es ist, ist die Frage nach dem Bösen gestellt. Gibt es etwas, dessen Wesen es ist, anderes zu zerstören, bis es sich in negativer Selbstbezüglichkeit selbst zerstört? Wie unterscheiden sich davon die Negation der Negation und die Antinomie, die ebenfalls etwas negieren, aber sich in der negativen Selbstbezüglichkeit nicht auslöschen, sondern in einer höhere Ebene aufgehoben werden? Die Antwort wird im Begriff der Grenze liegen, die nicht etwas in einen Käfig einsperrt und dort verhungern lässt, sondern in deren Wesen das Hinausgehen über die Grenze liegt.

Wie bei der I. Phase ist die Überschreitung der II. Phase mit Trennungsängsten und Widerstand verbunden. Wenn das Kind die Verkleidungen (den Weihnachtsmann) und den Fetisch als Täuschung zu durchschauen lernt, ist es mit einem Schlag mit der Härte der Erwachsenenwelt und der unerträglichen Macht des Realen konfrontiert und erlebt das als Desillusionierung und Entzauberung. Im Innern bleibt der geheime Wunsch: Ich möchte nie erwachsen sein.

Gibt es Möglichkeiten, etwas aus der II. Phase aufzuheben, ohne damit den Übergang in die III. Phase zu blockieren? In den 1920ern entstanden Kunstströmungen wie der Magische Realismus und der Surrealismus, die sich das zur Aufgabe gemacht haben und insbesondere in der Literatur bis in die Gegenwart reichen. Auswirkungen auf die Logik blieben nahezu völlig aus, wenn von wenigen Ausnahmen im Umfeld von Ronald Laing oder Jacques Lacan abgesehen wird, die jedoch kaum über erste Ansätze hinausgekommen sind. Das magische Denken aufzuheben ist nicht weniger wichtig als das in der I. Stufe wurzelnde nomadische Denken. Die mit einer einseitigen Dominanz der III. und IV. Stufe verbundenen Katastrophen belegen das eindringlich.

III: Operational, Alter: 7 - 12 Jahre, Grundschulalter

Mit der Einschulung beginnt das Kind systematisch zu lernen, Wissen zu erwerben und in gewissem Maß die vorangegangenen schwierigen Fragen zurückzustellen (um nicht zu sagen: zu verdrängen). Freud spricht in einem anderen Kontext von einer Latenz. Das Kind lernt auf allen Gebieten Gegenstände und Sachverhalte kennen und ihnen ihre Eigenschaften zuzuordnen. Es eignet sich in großem Maß Faktenwissen an. Es versteht die Zusammenhänge und ihre Ordnung. Es ist begeistert von einer Welt, in der alles verständlich ist und seinen klaren Platz hat. Es ist empfänglich für neue Ideen und Erfahrungen wie sonst nie im Leben. Es ist von einer ursprünglichen Demokratie aller Menschen und Sachen überzeugt: Gegenüber der Wahrheit ist alles im positiven Sinn gleich wert und von gleicher Gültigkeit. Es fühlt sich geborgen in einem Glauben an ein höheres Wesen, das alles so eingerichtet hat, dass es in Harmonie aufgeht.

Die vorangegangene Antinomie wird aufgelöst: Die Gegenstände und ihre Namen, das Gezählte und die Zahlen sind nicht von gleicher Natur und können nicht verwechselt werden, weil es gelingt, sie einheitlich in einem übergreifenden System zu ordnen, ohne dass es zu Widersprüchen kommt. Den Gegenständen und den Namen, den Individuen und den Eigenschaften, dem Gezählten und den Zahlen werden jeweils eigene Prädikate zugeordnet, wodurch sie voneinander unterscheidbar sind und nicht in Konflikt miteinander geraten. Die Prädikationsfunktion (das Erkennen und Zusprechen von Prädikaten zu Subjekten in Urteilen von der Gestalt ›S ist p‹) ist das durchgehende Prinzip. Wenn Ungereimtheiten auftreten, lassen sie sich als Täuschungen, Tricks oder Flüchtigkeitsfehler durchschauen und problemlos bereinigen. Wer nicht alles allein wissen oder lernen kann, fragt die anderen und  verständigt  sich mit ihnen. Das ist die Welt der Aufklärung, des Empirismus von Aristoteles und der englischen Experimentalphilosophie, der französischen Enzyklopädisten, der Logiker wie Frege oder Carnap, der analytischen Philosophie und des amerikanischen Optimismus, der Sozialdemokratie und des Vertrauens in eine gemeinschaftliche kommunikative Vernunft bei Habermas. Wer schätzt sich nicht glücklich, wenigstens einmal im Leben an diesem Projekt teilgenommen zu haben?

Wären da nicht die immer wiederkehrenden Zweifel! Das beginnt mit Descartes, ob nicht möglicherweise alles eine Täuschung ist, und kulminiert in Paradoxien bei Russell. Frege hat sein Vorhaben für gescheitert erklärt, als er davon erfuhr. Piaget nennt typische paradoxe Aussagen von Kindern dieses Alters, die den eigenen inneren Widerspruch nicht wahrnehmen und mit ehrlicher Überzeugung sagen:

»Ich habe die Zwiebeln nicht gern, und ich bin froh darüber, denn wenn ich sie gern hätte, dann würde ich immer wieder Zwiebeln essen, wo ich doch Zwiebeln absolut nicht mag.«
»Ich bin nicht stolz, denn ich glaube, nicht halb so intelligent zu sein, als ich es in Wirklichkeit bin.« (zitiert K, S. 244)

Sätze wie diese müssen zweimal gelesen werden, um sie zu verstehen. Wer in seinem Leben zum ersten Mal erlebt, Sätze dieser Art bilden zu können, fühlt sich von einem ozeanischen Gefühl ergriffen, in völliger Freiheit über sich und der Welt zu stehen und an übergreifender Weisheit teilzuhaben. Um so größer die Enttäuschung und tiefe Verunsicherung, wenn andere darüber lachen (müssen). Da bricht eine Welt zusammen, und es droht die Gefahr zum Zyniker zu werden.

Was geschieht hier? Die vorige Stufe war auf die Frage gestoßen, wie an einer Sache ihre natürliche Bestimmung erkannt werden kann, selbst wenn diese aktuell nicht verwirklicht ist. Diese Antinomie kann aufgelöst werden, wenn an einer Sache zwei verschiedene Beschaffenheiten unterschieden werden: Zum einen ist sie so beschaffen, wie es sich unter dem Druck der äußeren Einflüsse ergeben hat. An der Beschaffenheit von etwas zeigen sich die Spuren, wie sie gefördert und bedrängt worden ist. In einem abstrakten Gedanken kann Hegel sagen, dass die Beschaffenheit »die dem Andern offene Seite« ist (Hegel, WL A, S. 70). Weil die Sachen keine theoretischen Konstrukte sind, sondern hervorgegangen aus einem physischen Prozess der Zeugung, Geburt und Entwicklung, verfügen sie über eine körperliche Beschaffenheit, die ihnen Bestand und Verletzlichkeit gibt. Hegel unterscheidet die jeweilige Beschaffenheit von etwas, wie es sich in seiner konkreten Umgebung entwickelt hat, von dem Begriff der Beschaffenheit: Wenn auf paradox klingende Weise gesagt wird, dass etwas so beschaffen ist, beschaffen zu sein, dass es über die Eigenschaft der Beschaffenheit verfügt, ist damit gemeint, dass es die Eigenschaft hat, in seiner Beschaffenheit von Anderem geprägt werden zu können. Es ist in dem Maß veränderlich, wie es der Veränderung ausgesetzt ist. – Zugleich aber enthält jedes Etwas an sich seine Bestimmung nicht als eine transzendente Sache, die irgendwo weit draußen in einem fernen Jenseits liegt, sondern es ist so beschaffen, dass es sich seiner Bestimmung gemäß verändern kann. Zu seiner Beschaffenheit gehören die innere Unruhe und das Vermögen, das zu werden, was es noch nicht ist, aber seiner Bestimmung nach sein sollte. »Die andere Bestimmung ist die Unruhe des Etwas in seiner Grenze, in der es immanent ist, der Widerspruch zu sein, der es über sich selbst hinausschickt.« (Hegel Werke, HW 5.138) Die Bestimmung kann nicht von außen belehrt werden (»sei, wie du nicht bist«, »sei endlich du selbst«). Sie ist nur auf dem Weg einer neuen Antinomie möglich: »Zunächst ist es also die Beschaffenheit, welche sich so ändert, daß sie nur eine andere Beschaffenheit wird« (Hegel, Logik, 1. Auflage, S. 71) Die Beschaffenheit ist so beschaffen, sich selbst umzukehren und eine andere Beschaffenheit zu werden.

Diese Antinomie kann genauer gefasst werden als Widerspruch der inneren Grenze. Wenn das Etwas in seiner Beschaffenheit sowohl das enthält, was äußeren Einflüssen preisgegeben ist, wie das, was es über seinen aktuellen Zustand hinausschickt, dann muss es zwischen beiden eine innere Grenze geben. Hegel fand dafür die treffende Formulierung vom »Aufhören eines Anderen an ihm«. (HW 5.135) Das kann in zweierlei Sinn verstanden werden: Wenn das Andere das Etwas beeinflusst und möglicherweise bedrängt, gibt es im Etwas dennoch eine innere Grenze, an der der Einfluss ohnmächtig wird. Und zugleich enthält das Etwas seine Bestimmung an sich, so dass diese in ihm aufhört und dort als Potential vorliegt. Wer das werden will, was er seiner Bestimmung nach schon ist, muss nicht ein Anderer werden, sondern die innere Grenze überschreiten, die ihn bisher davon abgehalten hat.

Mit dieser Unterscheidung löst sich jedoch der Ordnungsgedanke eines jeden Systems auf. In einem System gilt, dass ein Element dann in zwei Arten unterteilt werden kann, wenn es eine Eigenschaft hat, die in zwei oder mehr unterschiedlichen Ausprägungen auftritt. Wenn es rote und gelbe Rosen gibt, dann gibt es Arten, die innerhalb ihrer Art jeweils alle gelb bzw. rot sind. Hier nun tritt die Beschaffenheit von Etwas in zwei Ausprägungen auf, die durch eine Grenze getrennt sind: Zum einen die Beschaffenheit, wie etwas gemäß seiner Biographie in seiner Einmaligkeit geworden ist, und zum anderen die Beschaffenheit, wodurch es gemäß seiner Bestimmung zur nächsthöheren Gattung gehört. Jeder Mensch kann in seiner Einzigartigkeit gesehen werden, die ihn von allen anderen unterscheidet, und bleibt doch seiner Bestimmung nach ein Wesen der Gattung Mensch. Werden diese beiden Ausprägungen der Beschaffenheit isoliert, bringt jede für sich das System zu Fall: (+) Wird die eine Beschaffenheit isoliert, durch die Etwas ein Einzelnes und Einmaliges wird, dann fällt es ganz aus dem System. Diesen Gedanken hat Adorno mit der negativen Dialektik des Nicht-Identischen radikalisiert. Für ihn ist das Ganze das Unwahre und jedes Etwas hat seine Würde darin, in kein System zu passen. Das System fällt auseinander. (-) Wird dagegen die andere Eigenschaft isoliert, durch die Etwas zur übergeordneten Gattung gehört, dann entsteht eine Definition von etwas, die sich nur auf die nächsthöhere Ordnung beruft. Das sind die von Poincaré, Russell, Carnap und Gödel untersuchten imprädikativen Urteile. »Ein Term heißt imprädikativ (definiert / definierbar), wenn er mittels einer Gesamtheit, zu der er selbst gehört, definiert ist (oder: nur definiert werden kann).« (Roland Hagebücher und Volker Geyer Das Paradox, Würzburg 2002, S. 120). Zum Beispiel ist das Element ’größte Stadt‘ imprädikativ definiert: Es bezieht sich auf die Gesamtheit aller Städte und bezeichnet dort das größte Element. Bei endlichen Mengen ist das problemlos, doch führt es in Unbestimmtheiten bei unendlichen Mengen. Zum Beispiel versteht jeder, was mit dem Ausdruck ’größte Primzahl‘ gemeint ist, aber es gibt keine größte Primzahl. Imprädikative Definitionen können ins Leere greifen und eine Ordnung aushöhlen.

Mit den imprädikativen Definitionen wird die Russellsche Antinomie erreicht. Sie ist eine imprädikative Definition, die sich zugleich negativ auf sich selbst bezieht. Kesselring hat die Russellsche Antinomie in eine allgemeinere Formulierung gebracht: "Der Begriff ›... fällt nicht unter sich selbst‹ bedeutet in Bezug auf Begriffe dasselbe wie der Begriff ›... erfüllt sich nicht selbst‹." (K, S. 212) Wird der Begriff ‘Erfüllt-sich-nicht-selbst’ analysiert, erweist er sich als eine Antinomie: Wenn sich das Nicht-Erfüllen erfüllt, bedeutet es, dass es sich erfüllt, im Widerspruch zu sich selbst. Wenn es sich nicht-erfüllt, ist es kein Erfüllen mehr. Es ist deutlich zu erkennen, wie sich die Antinomie des Verschwindens des Verschwindens wiederholt und das Lügner-Paradox (›dieser Satz ist falsch‹) bereits andeutet.

Mit der Russellschen Antinomie ist gezeigt, wie der für die III. Stufe konstitutive Systemgedanke aus sich heraus in eine Antinomie führt. Wenn es nicht gelingt, diese Antinomie aufzulösen, dann schlägt der Empirismus in Dogmatismus um. Jedem Einzelnen wird in seiner Einmaligkeit dogmatisch übergestülpt, wie es in das System zu passen hat. Die Russellsche Antinomie soll durch ein Verbot bereinigt werden: Es wird ein Axiom aufgestellt, mit dem negativ selbstbezügliche, imprädikative Urteile ausgeschlossen werden sollen. – In einer empirisch dominierten Wissenschaft entstehen heute überall Dogmen dieser Art. Die Physik lehrt uns: Der Urknall ist die Grenze und das Prinzip des Kosmos, über die nicht weiter hinausgefragt werden darf. Die Neurowissenschaft will alles Denken auf das endliche System der Neuronen und ihrer Synapsen zurückführen. Jedes Kind stößt in diesem Alter mit seinem unbefangenen Fragen auf Dogmen und Paradoxien dieser Art. Meistens wird ihm gesagt: »Lerne das auswendig! Später wirst Du es verstehen.« Aufklärung schlägt um in Autoritäts-Denken. Das gleiche macht heute jeder Mathematik- und Physik-Student durch, dem irgendwann zugemutet wird, das zu glauben, was er lernt. Die Hälfte aller Studenten bricht daher diese Studienrichtungen ab. Nur wenige konnten es wagen offen auszusprechen, »dass niemand die Quantenmechanik versteht« (Richard Feynman, Begründer der Quantenelektrodynamik und einer der einflussreichsten Physiker des 20. Jahrhunderts).

Mit Empirismus und Dogmatismus stößt die III. Stufe an ihre Grenze. Wer anfangs mit großer Begeisterung am Wissenserwerb und dem Projekt der Aufklärung teilgenommen hat, sieht sich und seine Freunde und Verbündeten irgendwann unmerklich auf die Bahn des Empirismus oder Dogmatismus geraten und weiß nicht recht, wie das geschehen konnte. An dieser Stelle entsteht der Wunsch, sich daraus in etwas »Höheres« zu befreien, und wenn das mit der IV. Stufe gelingt, bleibt der III. Stufe gegenüber nur noch Hohn und Spott übrig. Die III. Stufe gilt dann nur noch als der »gesunde Menschenverstand« oder einfach »der Verstand«, der Bildungsphilister oder der Stammtisch-Schwätzer. In dieser Herablassung ist verdeckt die Enttäuschung, dass das Projekt der III. Stufe nicht verwirklicht werden konnte. Unausgesprochen sehnt sich jeder dahin zurück, die Welt noch einmal mit offenen Augen wie beim »ersten Mal« sehen zu können, unbefangen und in der naiven Überzeugung, die Unendlichkeit frei von allen Antinomien zu fassen.

Kaum jemand hat die mit der III. Stufe einhergehende Dummheit und Selbstgerechtigkeit so gut getroffen wie Flaubert (Madame Bovary), wobei die nahezu enzyklopädische Detailtreue und -vielfalt seiner Werke ihn zugleich als geheimen Vertreter dieser Stufe zeigen. Von ihm stammt die Kapitänsaufgabe, die die bei jedem Schüler so unbeliebten »eingekleideten Rechenaufgaben« dieses Schulalters auf den Punkt bringt:

"Ein von Boston kommendes mit Baumwolle beladenes Schiff von 200 Registertonnen segelt nach LeHavre, auf der Back befindet sich ein Schiffsjunge, zwölf Passagiere sind an Bord, der Wind steht Ostnordost, die Schiffsuhr zeigt viertel nach drei am Nachmittag und es ist Mai ... Wie alt ist der Kapitän?" (Brief von Flaubert an seine Schwester Caroline, 1843)

Was wie ein Scherz aussieht, wurde seit 1980 in vereinfachter Form Grundschülern als Übungsaufgabe vorgelegt mit dem verblüffenden Ergebnis, dass sie im Laufe des Schulbesuchs verlernen, Aufgaben dieser Art zu lösen. Der Anteil richtiger Antworten fiel vom Vorschulalter bis zur 4. Klasse von 90 auf 30% (Holger Dambeck Schulmathematik absurd in: Spiegel Online vom 17.1.2012). Das Wissenserwerb der III. Stufe hat die Folge, sich ganz auf Schematismen zu verlassen und den unbefangenen Blick zu verlieren. Was zeigt den Verlust besser als das einfache Märchen von Des Kaisers neue Kleider: Der König ist nackt.

IV: Formales Denken, Alter: ab 12 Jahre, Jugendalter

Und doch gibt es eine Lösung für die Antinomie der III. Stufe: Die formalen Systeme. Selbst wenn es unmöglich ist, alles, was in der Natur empirisch gefunden werden kann, und alles, was sich als Text aufschreiben oder sagen lässt, durchgehend zu klassifizieren, und selbst wenn sich jede Ordnung als vergänglich erweist, die nach einem Paradigmenwechsel durch eine neue Ordnung abgelöst wird, bleibt doch die Idee, dass es ein höheres System von endlich vielen  Regeln  gibt, mit denen immer neue Sätze gesprochen und Kunstwerke geschaffen werden können.

Das naheliegendste Beispiel ist die Sprache. Niemals werden sich alle Sätze beschreiben lassen, die gesprochen werden können. Aber es gibt eine endliche Anzahl von Buchstaben und eine endliche Anzahl grammatischer Regeln, aus denen alle Sätze gebildet werden. Ähnlich kann die unendliche Vielfalt musikalischer Melodien zurückgeführt werden auf einen endlichen Tonvorrat und eine endliche Anzahl von Intervallen, Tonleitern und Modi, mit denen komponiert oder spontan gesungen werden kann. Das legt den Gedanken nahe, dass dies auch für die Mathematik und die Logik möglich sein sollte.

So argumentierten Hilbert und Carnap. Niemand wird bezweifeln, dass das mathematische Wissen nie an eine absolute Grenze stößt, aber gibt es nicht übergreifende Regeln, mit denen alle Mathematiker arbeiten? Das war die Idee einer Metamathematik von Hilbert, der nach dem Vorbild der euklidischen Geometrie nach einer endlichen Menge von Regeln und Methoden suchte, auf die alle mathematischen Beweise zurückgehen. Und Carnap wollte trotz der Russellschen Antinomie die imprädikativen Urteile rehabilitieren, indem er zurückging von den Inhalten (der Semantik) der Sprache, in der sich widersprüchliche Aussagen wie die von Russell sagen lassen, zu ihrer Syntax. Auch wenn es möglich ist, etwas Unsinniges oder Paradoxes zu sagen, folgt dies dennoch der Syntax. Wird von dieser weiteren Perspektive aus gedacht, dann sieht Carnap keine Schwierigkeiten mit imprädikativen Sätzen: Sie beziehen sich zwar auf die jeweils nächsthöhere Ordnung (die Gattung), aber sie sind nicht – offen oder verborgen – abhängig von individuellen Eigenschaften einzelner Elemente, und sie ermöglichen es, mit endlich vielen Beweisschritten ein System aufzubauen (Carnap, S. 116). Das wichtigste Beispiel sind die reellen Zahlen. Jede reelle Zahl ist das Element einer übergreifenden Menge. Sie kann nur imprädikativ definiert werden durch Eigenschaften der Menge, der sie angehört. In dieser Menge muss ein Grenzübergang möglich sein, der zur reellen Zahl führt. Ein typisches Beispiel für imprädikative Bestimmungen reeller Zahlen: »Zu jeder reellen Zahl x lässt sich also eine offene Umgebung angeben, deren Abschluss kompakt ist.« (Wikipedia). Hier ist jede offene Umgebung von x eine Menge, die x enthält.

Formale Systeme dieser Art werden ab dem Alter von 12 Jahren gelernt und sind der wichtigste Stoff der Oberstufe ab der 11. Klasse. Piaget nennt ein typisches Beispiel für die Fähigkeit zum formalen, hypothetischen Denken, die sich in diesem Alter entwickelt:

»John ist dünner als Bill; John ist dicker als Sam; wer ist der Dickste von den dreien? Kinder, die jünger als 11 oder 12 Jahre sind, haben große Schwierigkeiten mit solchen Aufgaben, außer wenn es sich um Objekte handelt, die sie sehen können. Der Grund ist, daß die Lösung der Aufgabe propositionales Denken erfordert, d. h. Nachdenken über hypothetische Aussagen.« (Guy R. Lefrancois, Psychologie des Lernens, Berlin u.a. 1994, S. 138, zitiert nach psychologie.de, abgerufen am 5.6.2016)

Der Jugendliche erkennt die abstrakte Struktur der einzelnen Aussagen und kann übergreifende Schlüsse ziehen. Er befreit sich aus dem »Blind drauflosrechnen« (Dambeck in dem zitierten Artikel in Spiegel Online) der III. Stufe.

Sie verstehen die Unterscheidung in Objekt- und Metaebene. Es ist ein Unterschied zu sagen »Der Schnee ist weiß« oder »Die Behauptung ›der Schnee ist weiß‹ ist wahr«. Waren die Kinder in der III. Stufe naiv davon ausgegangen, dass alles, was sie sehen, erfahren und lernen wahr ist, entwickeln sie im Alter ab 12 Jahren das Verständnis, zwischen der Prädikationsfunktion (der Zuordnung von Prädikaten zu Subjekten) und der Wahrheitsfunktion (der Behauptung, dass ein Urteil wahr oder falsch ist) zu unterscheiden. Die Wahrheitsfunktion ist das elementare Beispiel für eine Metaebene: Es wird von außen geprüft, ob die Aussagen der Objektebene wahr sind.

Die Russellsche Antinomie lässt sich nach diesem Modell auflösen: Aussagen auf der Objektebene (Menge aller Barbiere, die sich nicht selbst barbieren) und auf der Metaebene (die Frage, ob es eine solche Menge gibt oder nicht) können getrennt werden. Russell entwarf ein System aufeinander aufbauender Metaebenen, nummerierte sie durch in die Ebenen 1., 2., 3. Ordnung usf. (bzw. gleichbedeutend von Typ 1, 2, 3, …) und forderte, dass jedes Urteil innerhalb seiner Ordnung verbleiben muss.

Damit schien alles klar. Statt weiter an einer starren, dogmatischen Systematik zu arbeiten, die ihren enzyklopädischen Anspruch nie einhalten kann, wurde nach einer überschaubaren und in der Praxis erfolgreichen Sammlung von Regeln gesucht, die ihrerseits endlich vielen Regeln folgt. Diese Haltung bestimmt bis heute das Selbstverständnis der Wissenschaft. Für Piaget ist die kognitive Entwicklung mit dieser Stufe abgeschlossen, und auch Kesselring ist in Bezug auf Hegel überzeugt, »daß der genetische Standort seiner Dialektik gleichfalls in die IV. Stufe fällt« (K, S. 316). Das würde bedeuten, dass die Dialektik vergleichbar der Metamathematik oder der axiomatischen Mengenlehre über eine in endlich vielen Schritten ausführbare Methode verfügt, mit der sie alles durchschauen und verstehen kann. (Hegel hätte eine solche Interpretation wohl als »formellen Idealismus« kritisiert, vgl. HW 5.173.)

Kesselring sieht zwar, wie auch die IV. Stufe in eine Antinomie gerät. Sie beruft sich zum einen auf die endliche Anzahl der einzelnen Regeln und Methoden, über die sie verfügt, kann jedoch auf der anderen Seite nicht vermeiden, dass ihre Unterscheidung in Objekt- und Metaebenen in einen unendlichen Progress ständig neuer Metaebenen führt. Aber die Erkenntnis und Beschreibung von Antinomien erfolgt für ihn wiederum innerhalb einer formalen Methode, die mit endlich vielen Schritten erfolgt, und ist daher für ihn in sich schlüssig. Im Gegensatz zu Popper ist für ihn die dialektische Methode kein Anstoß und Ärgernis für das wissenschaftliche Denken, sondern im Gegeneil gewissermaßen dessen Krönung.

Kurt Gödel (1906-1978) hatte jedoch 1931 gezeigt, dass die Unterscheidung in Objekt- und Metaebenen in eine innere unauflösbare Antinomie führt. Ihm ist es gelungen nachzuweisen, dass sich das Lügnerparadox ›Dieser Satz ist falsch‹ nicht durch die Unterscheidung in Meta- und Objektebenen ausgrenzen lässt. Mit diesem Paradoxon liegt erneut eine typische negative Selbstbezüglichkeit vor. Trifft der Satz zu, dann behauptet er seine eigene Unwahrheit. Trifft der Satz nicht zu, dann ist er wahr und widerspricht seiner eigenen Aussage. Gödel konnte zeigen, wie es möglich ist, diesen Satz  innerhalb  eines jeden formalen Systems zu formulieren und damit in diesem System einen Widerspruch zu zeigen. Diese Antinomie geht wesentlich weiter als die von Russell. Sie formuliert nicht nur einen in sich widersprüchlichen Satz, sondern sie zeigt darüber hinaus, dass es unmöglich ist, ein widerspruchsfreies System zu finden.

Jeder kann sich vorstellen, wie unbeliebt sich Gödel mit dieser Erkenntnis machte. Völlig unverzeihlich wurde es, als er auch noch gemeinsam mit seinem Freund Einstein nachwies, dass dies kein abseitiges Konstrukt weltfremder Logiker ist, sondern sich innerhalb der am weitesten fortgeschrittenen physikalischen Systeme reproduzieren lässt und diese damit ebenfalls aushebelt (Paradoxien der Kosmologie).

Der Widerstand, die IV. Stufe zu verlassen, bleibt groß. Die Wissenschaft kann sich bis heute nicht damit abfinden und sucht nach Auswegen innerhalb der IV. Stufe. Mithilfe der Modelltheorie, der Theorie formaler Sprachen und der Mengenlehre soll das Programm von Carnap eingelöst werden. Ulrich Blau hat sich über Jahrzehnte damit beschäftigt und stellt eine beeindruckende Liste von Regeln zusammen, mit denen das Lügner-Paradoxon mal ausgeschlossen und mal aufgenommen werden sollte. Sie haben sich nach seiner Überzeugung alle als Sackgassen erwiesen (Blau, S. 451-454).

L1 Selbstreferentielle Sätze werden durch Hierarchien ausgeschlossen.

L2 Solche Sätze werden zugelassen, aber als falsch bezeichnet.

L3 Sie erhalten einen eigenen, dritten Wahrheitswert.

L4 Sie erhalten mehrere zusätzliche Wahrheitswerte.

L5 Sätze ohne Wahrheitswert werden zugelassen.

L6 Paradoxe Sätze werden zugelassen, die zugleich wahr und falsch sind.

L7 Beliebig viele (selbst überabzählbare viele) Wahrheitswerte werden zugelassen.

L8 Parakonsistente oder dialektische Logik.

»Man führt eine nicht-wahrheitsfunktionale, evtl. partiell wahrheitsfunktionale, Negation ein und läßt zu, dass Sätze wie (1) (›Dieser Satz ist nicht wahr‹, t.) zugleich mit ihrer Negation wahr, oder vielleicht beide falsch sind. Das geschieht z.B. in Systemen der sog. 'dialektischen' oder der 'parakonsistenten' Logik (z.B. Da Costa 1974 und Routley 1979). Keins dieser Systeme hat eine Semantik, die diesen Namen verdient. Man möchte wissen, welche Sätze bei Negation ihren Wahrheitswert behalten, welche nicht, und vor allem, warum. Als Antwort erhält man - nun ja, einen Index für mögliche Welten oder Ähnliches mit ein paar formalen Eigenschaften. Dergleichen Semantik zu nennen ist kühn, aber leider noch ziemlich üblich.« (Blau, S. 453)

L9 Bivalenz wird relativiert »auf Situationen, Kontexte oder was immer. Vielleicht ist der Lügner wahr in manchen Situation s₁ und falsch in anderen Situationen s₂.« (Blau, S. 453)

L10 Es wird ganz auf Wahrheitswerte verzichtet.

Die V. und VI. Stufe – Antinomien der Unendlichkeit

Die formalen Systeme der IV. Stufe führen unvermeidlich in eine unendliche Progression. Jeder Metaebene folgt eine weitere. Jedes System enthält eine offene Stelle oder einen blinden Fleck, an dem es in eine neue Stufe erweitert werden muss. Wird der Widerstand gegen die Einsicht aufgegeben, dass sich keine übergreifenden, widerspruchsfreien, formalen Systeme finden lassen, dann stellt sich umgekehrt die Frage, was beim Übergang in die Unendlichkeit eigentlich geschieht. Für Hegel beginnt hier die Philosophie: »Der Grundbegriff der Philosophie (ist) das wahrhafte Unendliche« (HW 8.203, Enz. § 95).

V: Das Unendliche überhaupt, die transfiniten Zahlen

Wo liegt die Grenze vom Endlichen zum Unendlichen und wie bestimmen sich beide wechselseitig? Das Endliche treibt über sich hinaus, und wird ‘das Unendliche’ als eine innere Einheit betrachtet, ist es als Einheit seinerseits endlich. Hegel unterscheidet (a) den Umschlag vom Endlichen in das Unendliche und (b) die unendliche Progression vom Endlichen in das Unendliche, ihre Wechselbestimmung. Wird die unendliche Progression negativ auf sich selbst bezogen, ergibt sich aus meiner Sicht (c) eine neue Antinomie, das von Zenon aufgestellte Paradox von Achilles und der Schildkröte.

(a) Es kommt zu einem Umschlag, wenn das Endliche bis zu einer bestimmten Grenze reicht, hinter der sich das Unendliche befindet. Primitive Völker zählen »eins, zwei, drei, viele« und sehen den Umschlag bei der ‘Drei’. Im griechischen Alphabet gilt der letzte Buchstabe Ω als Umschlag und wurde daher von Cantor als Bezeichnung für die transfiniten Zahlen übernommen. Im hebräischen Alphabet hat jeder Buchstabe unmittelbar einen Zahlenwert. Der letzte Buchstabe ‘Taw’ mit dem Zeichen hat den Zahlenwert 400. Für die Ägypter wurde die größte Zahl mit der Million erreicht, dargestellt mit einer Hieroglyphe für Heh, den Gott der Unendlichkeit: 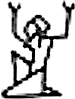. Während das Omega- und das Taw-Zeichen den Himmelsbogen darstellen, bis wohin die Endlichkeit reicht und hinter der die Unendlichkeit liegt, zeigt die ägyptische Hieroglyphe die Anbetung der offenen Unendlichkeit. Heute gilt die Bremermann-Grenze, mit der die größte, physikalisch mögliche Geschwindigkeit abgeschätzt wird, Zahlen mit Computern zu berechnen. Das sind 1,35639·1050 bit/Kilogramm/Sekunde. Größere Zahlen, die sich technisch nicht darstellen lassen und mit denen daher nicht gerechnet werden kann, können als sinnlos angesehen werden.

Innerhalb der auf der IV. Stufe basierenden heutigen Wissenschaften stellt sich die Frage des Umschlags in die Unendlichkeit als Induktionsproblem. Ist es möglich, nach einer endlichen Anzahl von Erkenntnissen induktiv auf eine übergreifende Erkenntnis zu schließen? Die Verneinung des Induktionsaxioms ist eine genauere Fassung der von Adorno geforderten Nicht-Identität des Einmaligen. Das Induktionsaxiom besagt, dass nach einer endlichen Anzahl von Schritten auf eine Regel geschlossen werden kann, die sich induktiv auf eine unendliche Menge erweitern lässt. Jede Induktion vollzieht einen Umschlag vom Endlichen in das Unendliche. Eine der für mich verblüffendsten neueren Erkenntnisse auf diesem Gebiet hat der Mathematiker Manjul Bhargava (*1974) gezeigt: Er konnte gemeinsam mit Jonathan Hanke nachweisen, dass für Fragestellungen wie z.B. ›Läßt sich jede natürliche Zahl als Summe von 4 Quadratzahlen darstellen‹ »ein Test mit genau 29 Zahlen genügt, um die Frage zu beantworten. [...] Hier sind die 29 Zahlen: 1, 2, 3, 5, 6, 7, 10, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 34, 35, 37, 42, 58, 93, 110, 145, 203, 290« (Spiegel-Online vom 15.8.2014).

(b) Wenn es zu einem Umschlag vom Endlichen ins Unendliche kommt, muss es ein inneres Maß geben, wodurch der Umschlag vermittelt wird. Es muss etwas geben, weswegen behauptet werden kann, warum es im Unendlichen so weiter geht wie in den zuvor endlich vielen Beobachtungen. Wenn oft genug erlebt wurde, dass jeden Morgen ein neuer Tag anbricht, wird induktiv gefolgert, dass es eine übergreifende, ewige Regelmäßigkeit gibt. Der »Progress ins Unendliche« (HW 5.155) bleibt nicht an der Grenze zum Unendlichen stehen, sondern wird im Unendlichen fortgeführt. Um das mathematisch zu beschreiben, hat wenige Jahrzehnte nach Hegel der Mathematiker Georg Cantor (1845-1918) die transfiniten Zahlen eingeführt. Das entscheidende Argument war der Nachweis, dass es überabzählbar viele Zahlen gibt, also auch Zahlen, die nicht zu den natürlichen Zahlen gehören, und dennoch Zahlen sind. Daher entwickelte Cantor die transfiniten Zahlen, um mit ihnen jenseits der natürlichen Zahlen weiterzuzählen. Dies kann als der erste Ansatz gelten, eine innere Gemeinsamkeit zwischen den endlichen und unendlichen Zahlen zu finden, auch wenn die Darstellung auf den ersten Blick wenig spektakulär aussieht:

1, 2, 3, … ω, ω + 1, ω + 2, … 2 · ω, 2 · ω + 1, …

Hier kommt es nicht mehr zu einem eindeutigen Umschlag des Endlichen in das Unendliche, sondern zu einem Wechselspiel des auf jeder Ebene neu wiederholten Zählens 1, 2, 3, … einerseits und der Einführung transfiniter Zahlen wie ω – die Ganzheiten von unendlichen Zählprozessen umfassen – andererseits. Das trifft meines Erachtens genau die von Hegel gemeinte Wechselbestimmung von Endlichem und Unendlichem. Sie läuft erkennbar in eine Antinomie. Mit dem unendlichen Progress wird zwar immer wieder neu jede Grenze überschritten, aber es gelingt nie, zu einem Abschluss zu kommen. Es müßte »über dies Hinausgehen [...] selbst hinausgegangen werden« (HW 5.155, zitiert K, S. 309).

Cantor hat bereits 1873 und auf neue Weise 1877 mit seinem zweiten Diagonalargument beweisen können, dass mit dieser Methode nicht alle Zahlen erreicht werden können. Es bleibt immer ein nicht-leerer Rest übrig, den er als überabzählbare Zahlen bezeichnet hat. Sie liegen jenseits der transfiniten Zahlen und lassen sich auch nicht mit der Wechselbestimmung des Endlichen und Unendlichen erreichen. Um sie zu bestimmen, ist eine neue Methode notwendig: Der Grenzübergang, der mit der VI. Stufe eingeführt wird.

(c) Wie löst der mit der V. Stufe gewonnene Begriff der Unendlichkeit die Antinomie der IV. Stufe? Das gelingt wie auf den vorherigen Stufen durch eine neue Antinomie. Die V. Stufe hat zur unendlichen Progression geführt, und diese ist negativ auf sich selbst zu beziehen: Statt immer weiter zu zählen, wie es von den natürlichen Zahlen bekannt ist, ist das Zählen gewissermaßen gegen sich selbst zu kehren. Das ist auf sehr anschauliche Art mit dem Paradox von Achilles und der Schildkröte gelungen. Achilles kann die Schildkröte nie einholen, denn jedesmal, wenn er dort angekommen ist, wo sie einen Moment vorher war, ist sie ihrerseits eine kleine Strecke weitergelaufen. Jeder spürt, was hier geschieht: Es wird zwar immer weiter gezählt, wie sich Achilles fortlaufend der Schildkröte nähert, aber er erreicht sie nie, weil zugleich die jeweils betrachteten Strecken kürzer werden. Zwei Vorgänge streben auseinander: Das Weiterzählen der jeweils betrachteten Abstände, und das Kürzerwerden dieser Abstände. Wird im Rahmen der unendlichen Progression geblieben, lässt sich dies Paradox nicht lösen.

Aber mit diesem Paradox beginnt sich die vorangegangene Antinomie aufzulösen. Auch wenn noch offen bleibt, wie mathematisch formuliert werden kann, dass Achilles in endlicher Zeit die unendlich vielen unendlich kleiner werdenden Abstände zur Schildkröte überschreitet und sie überholt, ist dies ein Beispiel, »wie das Unendliche aus sich heraus und zur Endlichkeit komme« (HW 5.168f). Achilles durchläuft unendlich viele Abstände, bis er in einer endlichen Zeit die Schildkröte überholt. Die Unendlichkeit kann widerspruchsfrei in einen endlichen Kalkül eingebunden werden, wenn es gelingt, auf die mit dem Beispiel von Achilles und der Schildkröte beschriebene Weise die unendliche Progression negativ auf sich selbst zu beziehen. Die Frage, wie das Unendliche endlich werden kann, war aber die »Vexierfrage« (HW 5.169), mit der aus Sicht der IV. Stufe jede Philosophie im Ansatz unmöglich gemacht werden sollte. Für formale Systeme der IV. Stufe gibt es keine Unendlichkeit, sondern nur endlich viele Regeln und letztlich auch nur endlich viele Modelle, die aus diesen Regeln gebildet werden können. Wenn dagegen am Beispiel von Achilles und der Schildkröte gezeigt wird, wie ein unendlicher Prozess der Annäherung im Moment des Überholens endlich wird, ist ex negativo gezeigt, dass das Lügner-Paradoxon nur innerhalb einer Logik Gültigkeit hat, die über keine Unendlichkeit verfügt. Es wird weiterer Schritte bedürfen zu zeigen, wie mithilfe des Gedankens der Unendlichkeit das Lügner-Paradoxon auch inhaltlich aufgelöst werden kann.

Wird die negative Selbstbezüglichkeit des transfiniten Zählens fortlaufend kleinerer Beträge für sich betrachtet, führt das zur Kontinuum-Hypothese: Die Menge der überabzählbaren Zahlen entspricht der Menge der reellen Zahlen.

VI: Die wahrhafte Unendlichkeit, das Kontinuum der reellen Zahlen

Aristoteles hat die Antwort gefunden. Der Weg der Schildkröte und des Achilles setzt sich nicht aus Schritten zusammen, die jeweils eine gleichbleibende Schrittlänge haben. Während beim Zählen angenommen wird, dass der Abstand von einer Zahl ‘n’ zu ihrem Nachfolger ‘n + 1’ immer 1 beträgt, wird der reale Abstand von Achilles zur Schildkröte immer kürzer. Die Zahlenwerte der fortlaufend kleiner werdenden Abstände liegen auf einer anderen Zahlenklasse als die natürlichen Zahlen. Diese andere Zahlenklasse hat eine Eigenschaft, die sie von den natürlichen Zahlen unterscheidet: Das ist ihr »Zusammenhang« (HW 5.161), die Kontinuität. Mit dem Zusammenhang ist ein neuer Term gefunden, der über die bisher eingeführten Terme hinausgeht. (Das ist in Kritik an Kesselring formuliert. Da für ihn die dialektische Methode zur IV. Stufe gehört, sieht er auf den nachfolgenden Stufen nichts Neues mehr, sondern nur eine nachträgliche Reflexion. Konsequenterweise wendet er »kritisch gegen Hegel« ein, dass Hegel auf den nachfolgenden Stufen »keine neuen Terme mehr in die Dialektik eingeführt hat« [K, S. 315]. Für mich ergibt dagegen bereits die vorangegangene Unterscheidung in Umschlag und Progression und die folgende Unterscheidung in Kontinuität, Prozess und Übergang neue Terme, die innerhalb der IV. Stufe noch nicht erreichbar waren.)

Zur Auflösung der Antinomie von Achilles und der Schildkröte genügt nicht, auf die fortlaufend kleiner werdenden Abstände hinzuweisen. Es gibt zugleich etwas, das mit einem eigenen inneren Maßstab über diese Abstände hinweggeht: Die Bewegung des Achilles. Er bremst nicht und kommt nicht zum Stehen, wenn er sich der Schildkröte nähert, sondern er hält den  Schwung  seiner Bewegung bei, so dass er sie mühelos überholt (vgl. hierzu auch Hegel in seinen Vorlesungen über die Geschichte der Philosophie, Bd. 1, HW 18.310).

»Wer eine fortlaufende Bewegung macht, hat nebenbei (symbebêkos) auch Unendliches durchlaufen, im eigentlichen Sinne aber nicht. Es trifft der Linie doch nur nebenbei zu, unendlich viele Halbstücke zu sein, ihr wesentliches Sein ist ganz etwas anderes.« (Aristoteles, Physik, VIII.8, 263b)

Ohne diese Stelle ausführlich zu kommentieren (siehe dazu den entsprechenden Aristoteles-Kommentar) sei zweierlei hervorgehoben: Die Bewegung wird in ihrer Einheitlichkeit betrachtet. In einer feinen Unterscheidung ist zu sagen, dass sie nicht aus unendlich vielen Punkten besteht, sondern unendlich viele Punkte enthält, die durch ihre Kontinuität miteinander verbunden sind. Die Bewegung wird als das Sein (im wörtlichen Sinn als das Subjekt, mit Aristoteles als erste Kategorie, ousia) betrachtet, und die Unendlichkeit ihrer Punkte als Eigenschaft (zweite Kategorie, symbebêkos), die sie an sich trägt. Zugleich berührt Achilles in seinem Lauf die unendlich vielen Punkte nur »nebenbei«. Sie verschwimmen in seiner bewussten Wahrnehmung. Ihre Vielzahl und Unendlichkeit ist ein Beispiel der Kleinen Perzeptionen, die zwar in ihrer Fülle berührt werden, aber nicht als Wahrgenommene ins Bewusstsein dringen.

Wird die Bewegung für sich betrachtet, handelt es sich um einen »Übergang« (HW 5.166). Mit Übergang kann in einfachen Beispielen das Überholen gemeint sein. Weiter kann der Vorgang gemeint sein, wie in der kontinuierlichen Bewegung die einzelnen Punkte nebenbei »übergangen« werden. Und schließlich ist mit Übergang der Wechsel von einer Kategorie zur nächsten gemeint. Hegel gebraucht den Ausdruck ‘Übergang’ im strengen Sinn nur, wenn es um den Übergang von einer Kategorie zur nächsten geht. Die Seinslogik ist abgeschlossen, wenn alle Kategorien durch Übergänge abgeschritten sind. Am Ende der VI. Stufe erfolgt nicht nur erstmals ein Übergang von einer Zweiten Kategorie (symbebêkos) zur nächsten, sondern selbstbezüglich der Übergang zum Übergang.

Die VI. Stufe führt in eine Antinomie, die Cantor 1897 gefunden hat. Cantor hat nach einem Begriff gesucht, die verschiedenen Stufen der Unendlichkeit voneinander zu trennen: Das ist die Mächtigkeit. Endliche Mengen, die Menge der natürlichen Zahlen und die Menge der kontinuierlichen, reellen Zahlen haben jeweils ihre eigene Mächtigkeit. Wird gefragt, ob die Gesamtheit der Mächtigkeiten wiederum eine Menge bildet, führt das in die Cantorsche Antinomie: Die Gesamtheit der Mächtigkeiten kann keine Menge bilden. Die Antinomie wird in der Mathematik daduch gelöst, dass sie Mengen dieser Art einen eigenen Namen gibt und sie als ‘Klassen’ bezeichnet. Klassen werden nicht mit der Mengenlehre, sondern in Anspielung auf Aristoteles mit der Kategorientheorie untersucht.

Ausblick: Die Bewegung des Begriffs und ihre Objektivität

Für mich ist die Lösung der Cantorschen Antinomie durch einen neuen Namen (‘Klasse’ statt ‘Menge’) unbefriedigend. Aber sie weist auf die allgemeinere Frage, mithilfe derer eine Lösung gefunden werden kann: Die Bildung von Begriffen und Namen. In der Begriffslogik wird nicht mehr nach der Beschaffenheit der Gegenstände des Denkens, ihren Zugangsweisen (Kategorien) und den Übergängen von einer Kategorie zur nächsten gefragt, sondern nach der Beschaffenheit des Denkens.

Mit dieser Frage wird erneut ein Perspektivwechsel vollzogen wie bei der Lösung des Paradoxons von Achilles und der Schildkröte. So wie es dort darum ging, die Bewegung-an-sich als das Subjekt zu erkennen und die Kontinuität als ihre Eigenschaft, ist hier das Denken-an-und-für-sich als Subjekt zu bestimmen und die Regeln seines formalen Schließens als seine Eigenschaft. Während sich das Denken der IV. Stufe damit zufrieden gibt, ein System formaler Regeln aufzustellen, fragt Hegel nach dem Subjekt, das sich in diesen Regeln im Ganzen zeigt. Damit sind nicht mehr die Satzsubjekte gemeint, also die einzelnen Inhalte, die mit Begriffen, Urteilen und Schlüssen beschrieben werden, sondern ein sich im Denken und dessen Regeln zeigendes Subjekt. Das entspricht dem Ansatz von Wittgenstein, der ebenfalls nach Etwas fragt, das sich in der Sprache zeigt, statt nach dem zu fragen, was mit der Sprache ausgedrückt und gezeigt werden kann.

Um das herauszuarbeiten, werden die Sätze ihrerseits auf ähnliche Weise in zwei Momente aufgeteilt, wie in der III. Phase die beiden Ausprägungen der Beschaffenheit von Etwas unterschieden worden waren: Die wörtliche Aussage (Semantik) und der unmittelbare Gebrauch (Pragmatik), wie und warum etwas gesagt wird einerseits, und die  Spur  etwas Anderen, das sich in dieser Aussage zeigt (in übertragenem Sinn die Bestimmung oder die eigene Poesie eines Satzes, die von einem Satz ausgehende Erschütterung und Offenbarung, die weit über den wörtlichen Inhalt des Gesagten hinausgeht) andererseits. So verstehe ich auch Wittgenstein. Er kritisierte sowohl die Typen-Theorie von Russell wie die Syntax-Theorie von Carnap, da sie bei der wörtlichen Bedeutung eines Satzes stehen bleiben und für sie die formalen Strukturen suchen. Für ihn ist es dagegen nicht denkbar, dass die Sprache in eigenen Worten sagt, was sie ist, sondern sich an der Sprache nur  zeigen  kann, was die Sprache übersteigt, das Andere der Sprache, so wie die Kontinuität der Bewegung die Einzelschritte übersteigt, aus der sie sich zusammensetzt. Wird dennoch versucht, die im Satz verborgene Bestimmung als Satz zu formulieren, kann das Ergebnis mit Hegel als ‘spekulativer Satz’ bezeichnet werden. In ihm zeigt sich die Natur des Satzes. "Formell kann das Gesagte so ausgedrückt werden, daß die Natur des Urteils oder Satzes überhaupt, die den Unterschied des Subjekts und Prädikats in sich schließt, durch den spekulativen Satz zerstört wird und der identische Satz, zu dem der erstere wird, den Gegenstoß zu jenem Verhältnisse enthält." (HW 3.59, zitiert bei Kulenkampff, S. 1). Erst mit dem spekulativen Satz scheint es mir möglich, eine umfassende Lösung der Russellschen Antinomie und des Lügner-Paradoxons zu finden, wobei sich sogleich die Frage stellt, ob auch ‘spekulativ’ wiederum nichts weiter als ein neuer Name ist, der mit Inhalt zu füllen ist (siehe hierzu einführend Kulenkampff Antinomie und Dialektik).

Daraus ergeben sich weiterführende Fragen, die an dieser Stelle nur thesenhaft genannt werden sollen. Ihnen soll am Beispiel der Logik von Spencer-Brown und seinen Interpreten weiter nachgegangen werden.

(1) Innerhalb der Eindimensionalität einer Zeichenkette gelingt Erinnerung nur durch Weitergabe einer Spur.

(2) Wie kann eine Spur als Spur und nicht als zufällige Ansammlung von Gegenständen erkannt werden? Beispiel: Wie können die Spuren auf frühesten Kunstwerken oder Tontafeln als Sprache und nicht als zufällige Kritzeleien oder Reibungen von Steinen aneinander erkannt werden? Was kann aus Spuren über das Denken und die Lebendigkeit der Wesen geschlossen werden, die diese Spur hinterlassen haben?

(3) Re-Entry (Wiedereintritt) und Vernähen einer Spur. Was ist das Medium (der Grund), in dem nicht nur die Spur, sondern auch die mit ihr überlieferte Offenbarung eingetragen werden kann.

Fazit Lässt sich ein Fazit ziehen? Für mich besteht es in der Einsicht in die  Einheit  des Denkens, das zerfällt, wenn einzelne Stufen verabsolutiert werden. Die Stufen sind durch Antinomien voneinander getrennt. Zwar kann jede neue Stufe die Antinomie der vorangehenden auflösen, doch lebt sie weiter in einer neuen Antinomie. Nach einer Phase der Dominanz der III. und IV. Stufe sind die anderen aufzuwerten. Das kann nicht durch eine Art Entscheidung erfolgen nach dem Muster Sei spontan!, sondern nur durch Offenheit und Aufmerksamkeit für unterschiedlichste Entwicklungen in allen Gebieten.

Siglen

HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971 (zitiert als HW); Link

K = Thomas Kesselring: Die Produktivität der Antinomie, Frankfurt am Main 1984 (zitiert als K)

WL A = Georg Wilhelm Friedrich Hegel: Wissenschaft der Logik, Erster Band: Die objektive Logik. Erstes Buch, 1. Auflage, Nürnberg 1812; Link

Literatur

Aristoteles: Physik, in: Schriften Bd. 6, Hamburg 1995 ( Link )

Ulrich Blau: Die Logik der Unbestimmtheiten und Paradoxien, Heidelberg 2008

Rudolf Carnap: Logische Syntax der Sprache, Wien, New York 1968 [1934]

Kurt Gödel: Russell's mathematical logic
in: Kurt Gödel: Collected Works II, Oxford 1990, S. 119-141 [1944]

Kurt Gödel: Is mathematics syntax of language
in: Kurt Gödel: Collected Works, Volume III, Oxford u.a. 1995, S. 334-362 [1953-1959]

Heiko Knoll, Jürgen Ritsert: Das Prinzip der Dialektik, Münster 2006

Arend Kulenkampff: Antinomie und Dialektik, Stuttgart 1970

psychologie.de: Das Entwicklungsstufenmodell nach Piaget; Link

Urs Richli: Kritische Bemerkungen zu Thomas Kesselrings Rekonstruktion der Hegelschen Dialektik im Lichte der genetischen Erkenntnistheorie und der formalen Logik
in: Philosophisches Jahrbuch, 1988 1. Halbband, Freiburg / München 1988, S. 131-143

Dieter Wandschneider: Grundzüge einer Theorie der Dialektik, Stuttgart 1995

Bildnachweis des Titelbildes: Wikipedia