Walter Tydecks
Imaginäre Zahlen
– Wie aus der Wissenschaft mathematische Intuition wird
Beitrag für den Themenkreis Naturwissenschaft und Technik von 50plus aktiv an der Bergstraße am 22.11.2017 in Bensheim, stark erweiterte Version, Stand 13.1.2019
Inhaltsverzeichnis
Einleitung
Komplexe Zahlen als mathematisches Spiel (Cardano)
Drehung komplexer Zahlen (Zyklizität)
Anwendungen der komplexen Zahlen
Dynamische Farbverläufe
Zyklizitäts-Denken
Einleitung
Warum sind die imaginären Zahlen imaginär oder unmöglich? Welche Einbildungskraft (Imagination) zeigt sich an ihnen? Und warum sind für die meisten Laien die imaginären Zahlen die unüberwindbare Hürde um zu verstehen, mit welchen neuen Inhalten die moderne Mathematik und Naturwissenschaft befasst sind? Ist es möglich, das mit einfachen Beispielen aufzulösen?
Sind sie einfach nur eine hilfreiche Abkürzung, damit Elektroingenieure und Quantenphysiker leichter rechnen können, oder ein unglaublicher Juwel (»amazing jewel«), von dem der legendäre Nobelpreisträger Richard Feynman in seinen Physik-Vorlesungen schwärmt?
Warum liegen hier die größten offenen Fragen der Mathematik wie die Riemannsche Vermutung über die Verteilung der Primzahlen, und lohnt es sich überhaupt, Themen dieser Art verstehen zu wollen?
Besteht die Welt aus reellen oder komplexen Zahlen, oder möglicherweise noch exoterischen Zahlen wie die Quaternionen oder die Elemente der Lie-Gruppe E8, die sich aus 248 komplexen Dimensionen zusammensetzt?
Für mich zeigt sich in den imaginären Zahlen der neue Beitrag Europas in der Geschichte der Mathematik: So wie die Entstehung der Mathematik bei Ägyptern und Sumerern unter die Überschrift Wie aus den Bildern Zahlen wurden gestellt werden konnte und die antike Mathematik von Pythagoras, Euklid und anderen den Titel trägt Wie aus den Zahlen Wissenschaft wurde, kennzeichnet die europäische Mathematik Wie aus der Wissenschaft intuitive Mathematik wurde. Während die natürlichen Zahlen aus dem Zählen und die reellen Zahlen aus dem Messen hervorgehen, sind die imaginären Zahlen das Ergebnis mathematischer Einbildungskraft, sogar noch in solchen Bereichen mathematische Beziehungen zu konstruieren und mit ihnen nachprüfbare Erkenntnisse zu gewinnen, die für alle sinnlichen Erfahrungen verdeckt sind und den gegebenen Regeln des Denkens widersprechen.
Das soll an der Entwicklung der imaginären Zahlen vom italienischen Universalgelehrten Cardano (1501-1576) bis in die Gegenwart gezeigt werden, an den verschiedenen Anwendungsgebieten der imaginären Zahlen und führt zur Frage, welche neue Art zu denken mit den imaginären Zahlen verbunden ist. Überraschenderweise hat sich die moderne Philosophie mit diesem Thema bisher kaum befasst, die Religion und Theologie schon gar nicht, wohl aber Schriftsteller wie Robert Musil und Psychologen wie C.G. Jung und Lacan. An diesem Vormittag soll versucht werden, ein wenig Licht auf das Geheimnis zu werfen, das die imaginären Zahlen umgibt.
Komplexe Zahlen als mathematisches Spiel (Cardano)
Die imaginären Zahlen gehen zurück auf typische Universal-Gelehrte des Renaissance-Humanismus wie Girolamo Cardano (1501-1576), der auf unterschiedlichen Gebieten hervorgetreten ist von der Medizin über die Philosophie bis zur Mathematik, daneben astrologische Interessen und Traumdeutung. Heute ist sein Name vielleicht am ehesten bekannt über die nach ihm benannte Kardanwelle und die Kardanische Aufhängung. Renaissance-Denker wie Cardano standen damit zum einen in der Tradition arabischer Gelehrte wie Avicenna (980-1037) oder Averroës (1126-1198) aus dem 10. bis 12. Jahrhundert, die über eine ähnliche Bildung und Wissensfülle verfügten, gingen aber in einem entscheidenden Punkt über sie hinaus: Das ist ihre mathematische Intuition, um die es in diesem Beitrag gehen soll.
Cardano »hat zahlreiche Horoskope (u. a. für Francesco Petrarca, Erasmus von Rotterdam und Albrecht Dürer) gestellt und sich mit der Deutung von Vorzeichen und Vorahnungen beschäftigt. Dies hat ihm im 18. Jahrhundert den Ruf eines Schwärmers eingebracht. So urteilt später Leibniz über ihn: 'Es scheint, das Wissen hat einen Zauber, den die nicht begreifen können, die von ihm nie ergriffen worden sind. Ich meine nicht bloß Tatsachenwissen, das keine Gründe kennt, sondern ein Wissen wie dasjenige Cardanos. Der war wirklich ein großer Mann, trotz aller seiner Fehler; ohne die wäre er unvergleichlich gewesen.' (Leibniz: Essais de théodicée, 1710)«. (Wikipedia, abgerufen am 26.8.2017)
Seine Bedeutung für die Geschichte der Mathematik kann verglichen werden mit den ersten Mathematikern in Babylonien und den Pythagoreern. Hatten sie die ersten Zahlsysteme und das geometrische Beweisverfahren eingeführt, so steht Cardano noch 100 Jahr vor Descartes und Kepler für das intuitive Denken oder genauer die mathematische Intuition, die das Paradigma für die neuzeitliche, europäische Mathematik wurde, auch wenn diese paradoxerweise zwar damit gearbeitet hat, sich aber dessen nie recht bewusst wurde. Seine Neuerung scheint mir noch nicht annähernd gewürdigt zu sein. Bis heute blieb in der westlichen Philosophie die Frage der imaginären Zahlen nahezu unbeachtet.
Seine Herangehensweise mutet wie ein Spiel an, – ein Gedankenexperiment oder ein »Glasperlenspiel« (Hermann Hesse): Er ging von einer Aufgabe aus, die von keiner praktischen Bedeutung ist, sondern dazu hilft, an einer präzise gestellten Frage bisher unbekannte Wege zu gehen: Gibt es zwei Zahlen a und b, so dass gilt:
a + b = 10
a · b = 40
An dieser Aufgabe lassen sich alle Grundzüge der imaginären Zahlen verdeutlichen. Wer verschiedene Zahlen ausprobiert, wird schnell merken, dass es im Bereich der üblichen Zahlen keine Lösung gibt: Zum Beispiel gilt für 1 und 9 zwar 1 + 9 = 10, aber nur 1 · 9 = 9. Im anderen Extrem gilt zwar 5 + 5 = 10, aber 5 · 5 = 25 erreicht wiederum nicht die 40.
Erst mit komplexen Zahlen ist eine Lösung möglich:
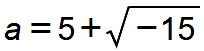
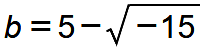
Es gilt offensichtlich a + b = 10, da die Wurzel aus −15 einmal addiert und dann wieder subtrahiert wird. Und wer nachrechnet, wird für das Produkt a · b finden (nach Gill, 1):
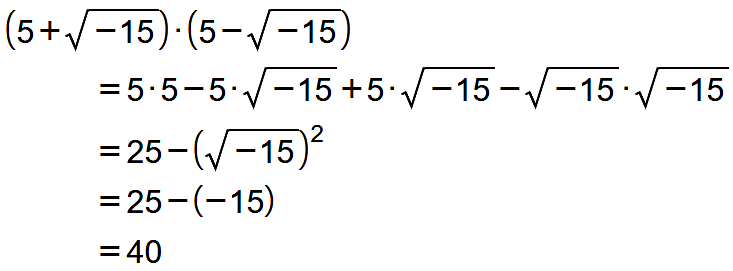
Welche Idee liegt dieser Lösung zugrunde? Cardano erkannte, dass die Lösung nicht auf der Zahlengerade liegen kann, sondern dass die Lösungen außerhalb der Zahlengerade liegen müssen. Er sprach unter der Kapitelüberschrift »De Regula falsum ponendi« (Regeln falschen Setzens) von einer »unmöglichen Aufgabe« (quaestio est impossibilis) und von »quantitas sophistica«. Es ist nicht bekannt, wie er die Lösung gefunden hat. Verschiedene Äußerungen deuten darauf hin, dass er bei der Beschäftigung mit quadratischen und kubischen Gleichungen von einer algebraischen Vorstellung ausging. So sprach er von »dimissis incruciationibus«, was von den einen als »Überwindung geistiger Qualen«, von anderen als »kreuzweise entstehende Produkte« übersetzt wird und möglicherweise ein bewusst gewähltes Sprachspiel enthält. Ich will versuchen, es geometrisch an einer Zeichnung zu verdeutlichen und wähle eine eigene Intuition, die im Weiteren dabei helfen wird, die unterschiedlichen Möglichkeiten des Multiplizierens miteinander zu vergleichen.
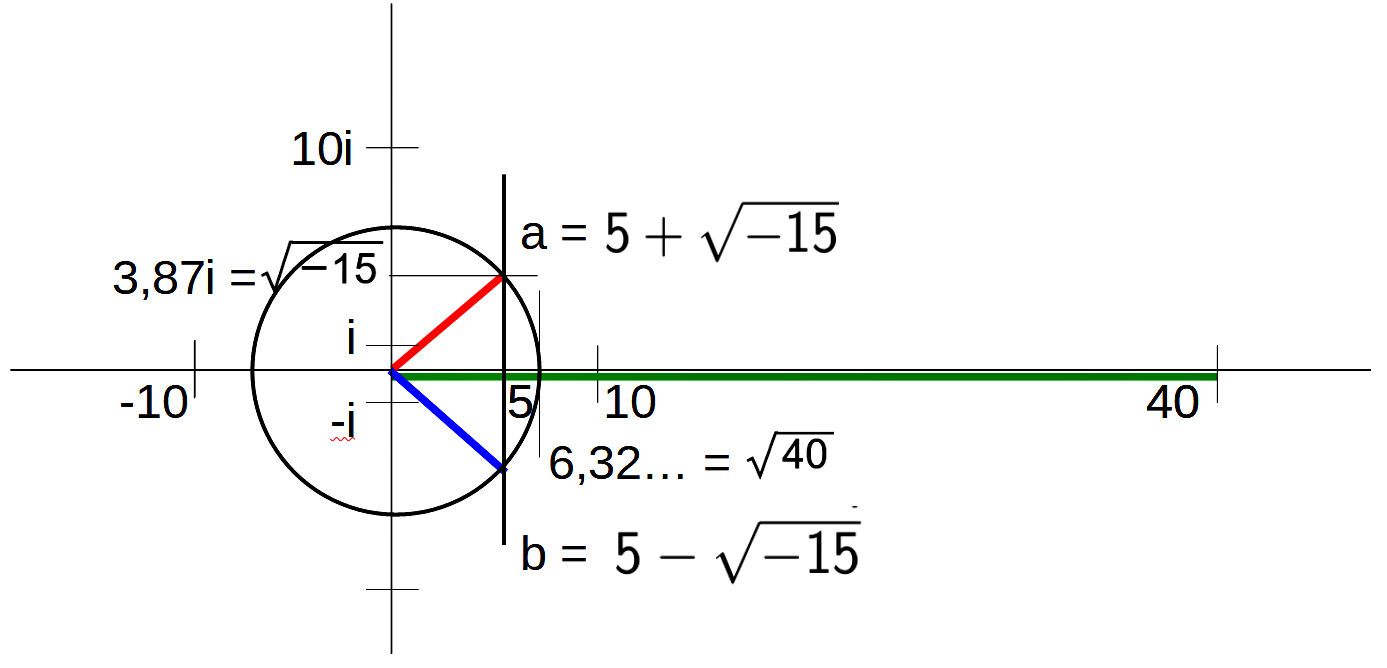
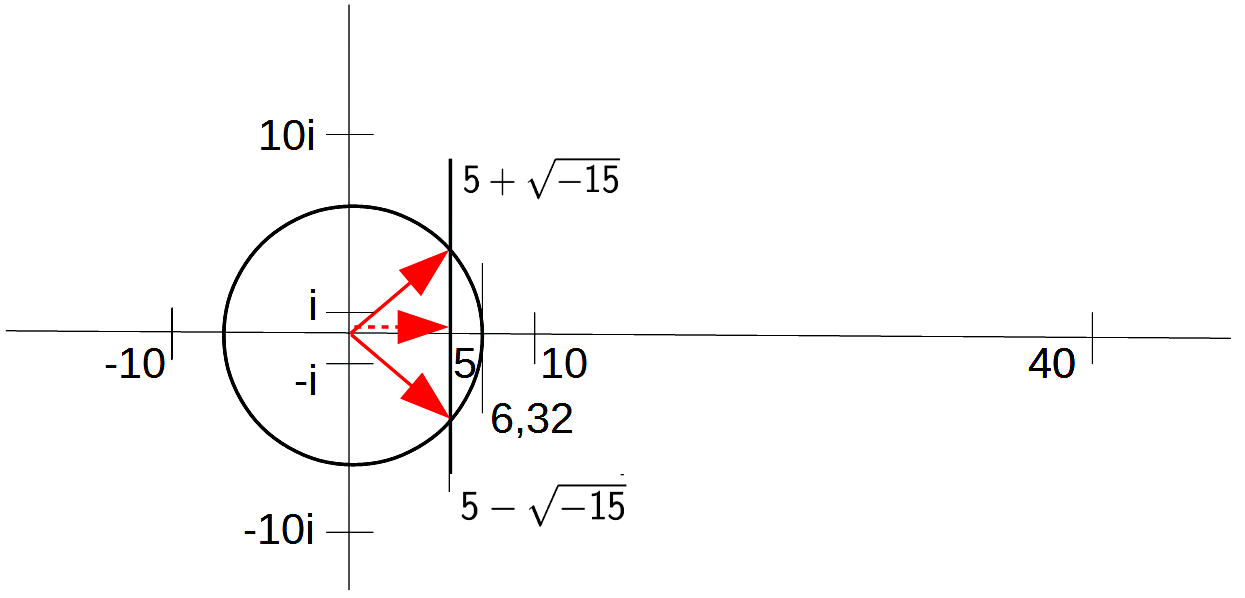
Cardanos Lösung mit imaginären Zahlen in meiner geometrischen Darstellung
Die Zeichnung erfolgt in zwei Schritten:
– Um für die Aufgabe a · b = 40 eine Lösung zu finden, kann im einfachsten Fall angenommen werden, dass a = b gelten soll. Es wird also die Zahl a gesucht, für die a · a = a2 = 40 gelten soll. Das ist Wurzel aus 40. Wurzel aus 40 beträgt angenähert 6,32. Diese Zahl wird auf der reellen Achse eingetragen. Das kann noch nicht die Lösung sein, denn es gilt 6,32 + 6,32 = 12,64 ≠ 10, so dass die erste Bedingung verletzt wird. An dieser Stelle ist es die Intuition der Mathematik, sich nicht auf die Zahlengerade zu beschränken, sondern eine neue Dimension zu öffnen und einen Kreis um den Nullpunkt zu schlagen, der die reelle Achse bei 6,32 schneidet. Alle Punkte auf dem Kreis haben den Abstand 6,32 zum Nullpunkt. Die Lösung muss irgendwo auf dem Kreis liegen, aber nicht auf der reellen Zahlengerade.
– Um auf dem Kreis die gesuchten Punkte zu finden, wird eine Gerade gezeichnet, die an der Zahl 5 senkrecht zur reellen Zahlengerade steht. Sie schneidet an zwei Punkten den Kreis, der den Radius 6,32 hat, und diese beiden Schnittpunkte sind die gesuchte Lösung!
Cardano hat die imaginären Zahlen noch nicht mit dem Buchstaben i bezeichnet, aber er hat intuitiv die Rechenregeln der imaginären Zahlen vorweggenommen. Die Rechenregeln für imaginäre Zahlen müssen zwei Anforderungen erfüllen:
(i) Sie dürfen nicht die bekannten Regeln für natürliche und reelle Zahlen verletzen. Werden zwei reelle Zahlen addiert oder multipliziert, dann sollen die bisher bekannten Ergebnisse gültig bleiben.
(ii) Werden dagegen zwei komplexe Zahlen addiert oder multipliziert, die nicht auf der reellen Zahlengerade liegen, dann sollen die Rechenregeln in sich widerspruchsfrei sein und die Aufgabe erfüllen, die sich Cardano gestellt hatte.
Schon am Beispiel der Aufgabe von Cardano lässt sich »sehen«, wie mit komplexen Zahlen gerechnet wird:
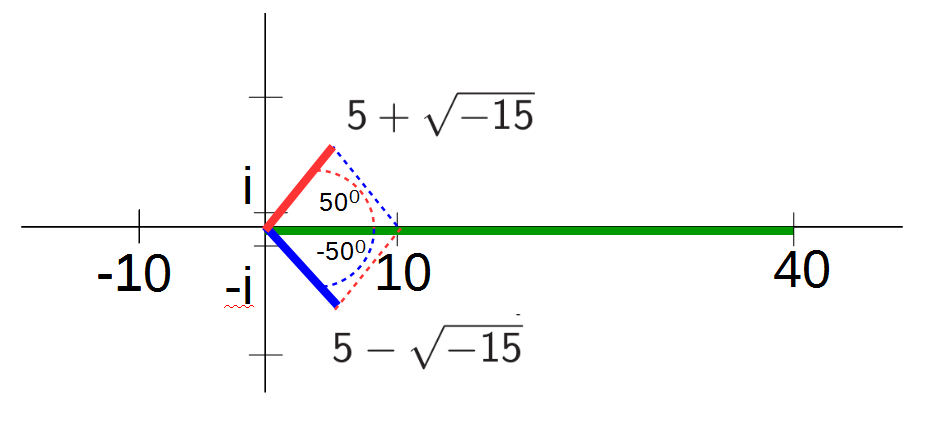
Addition und Multiplikation imaginärer Zahlen am Beispiel der Cardano-Aufgabe
Addition: Für die Addition werden die beiden Strecken, die vom Nullpunkt zur jeweiligen komplexen Zahl führen, hintereinander ausgeführt. In diesem Beispiel wird zuerst die rote Strecke bis zur Zahl 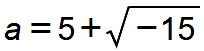 gegangen, und anschließend die blaue Strecke zur Zahl
gegangen, und anschließend die blaue Strecke zur Zahl 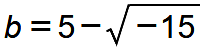 mit einer Parallel-Verschiebung angefügt (blau-punktiert angedeutet), wodurch im Ergebnis wie gewünscht die Zahl 10 erreicht wird. (Gleichbedeutend kann erst die blaue und dann die rot-punktierte Strecke ausgeführt werden, wobei ebenfalls die 10 erreicht wird.)
mit einer Parallel-Verschiebung angefügt (blau-punktiert angedeutet), wodurch im Ergebnis wie gewünscht die Zahl 10 erreicht wird. (Gleichbedeutend kann erst die blaue und dann die rot-punktierte Strecke ausgeführt werden, wobei ebenfalls die 10 erreicht wird.)
Multiplikation: Für die Multiplikation erfolgen zwei Schritte:
(a) Für jede Strecke, die zu einer komplexen Zahl führt, wird der Winkel gegenüber der reellen Zahlenachse ermittelt. In diesem Beispiel ist die rote Strecke ungefähr im Winkel von 50° gegenüber der reellen Zahlenachse gedreht, die blaue Strecke im Winkel von −50°. Beim Multiplizieren werden beide Windel addiert, wodurch sich in diesem Beispiel ein Winkel von 0° ergibt, da beide Zahlen spiegelbildlich oberhalb und unterhalb der reellen Zahlenachse liegen. Das war die Lösungsidee anhand der Aufgabe von Cardano: Werden die Winkel addiert, dann fällt die Lösung auf die reelle Zahlenachse.
(b) Zugleich werden die Längen der beiden Faktoren multipliziert, das sind die Abstände der beiden imaginären Zahlen zum Nullpunkt. In diesem Beispiel ergibt das 6,32 · 6,32 = 40, da beide Zahlen auf dem Kreis mit dem Radius 6,32 liegen.
Es ist nicht einfach, die mathematische Sprache zu verstehen, in der Cardano diese Lösung fand. Für ihn war klar, dass es solche Zahlen nicht gibt, sondern dass sie ausschließlich Ergebnis einer mathematischen Vorstellungskraft (Phantasie, Imagination) sind. Er hat auf nahezu spielerische Weise die Regeln der komplexen Zahlen vorweggenommen, die erst im Verlaufe der Jahrhunderte nach ihm im Einzelnen ausgearbeitet wurden. Die bis heutige gültige Darstellung führte erst 300 Jahre später Bernhard Riemann ein. Für mich ist die Arbeit von Cardano ein herausragendes Beispiel, welcher Leistungen die mathematische Intuition fähig ist.
Drehung komplexer Zahlen (Zyklizität)
Die Rechenregeln der imaginären Zahlen ergeben sich ausgehend von dem Cardano-Beispiel sehr einfach. Mir geht es vor allem um die Frage: Was ist das Neue der komplexen Zahlen, wodurch sich die imaginären Zahlen von gewöhnlichen Zahlen unterscheiden: Die Besonderheit der komplexen Zahlen liegt in der Multiplikation zweier komplexen Zahlen, bei der die beiden Faktoren gedreht werden. Um das zu verstehen, ist am einfachsten jede komplexe Zahl als ein Zeiger zu deuten, der vom Nullpunkt auf den Punkt der komplexen Zahl auf der zweidimensionalen Zahlenebene verweist.
Darauf sind um 1800 unabhängig voneinander der norwegisch-dänische Kartograph Caspar Wessel (1745-1818) und der aus Genf stammende Buchhändler, republikanische Revolutionär und Hobbymathematiker Jean-Robert Argand (1768-1822) gekommen. Ihr Ansatz lässt sich bis heute nicht anschaulicher als in den Worten von Wessel formulieren.
Addition: »Zwei gerade Linien werden addiert, wenn wir sie auf solche Weise vereinigen, daß die zweite Linie beginnt, wo die erste endet, und dann eine gerade Linie von dem ersten zu dem letzten Punkt der vereinigten Linien ziehen. Diese Linie ist die Sume der vereinigten Linien.« (Wessel, § 1). Das verallgemeinert anschaulich das Addieren gewöhnlicher Zahlen, bei dem die beiden Zeiger zu den reellen Zahlen auf der Zahlengerade nebeneinander gelegt werden. Im zweidimensionalen Fall ergibt das ein Parallelogramm, dessen Diagonale die gesuchte Summe ist. (Die Bezeichnung i für die imaginäre Achse geht auf Euler 1777 zurück. Von komplexen Zahlen wird erst seit Gauß 1831 gesprochen.)
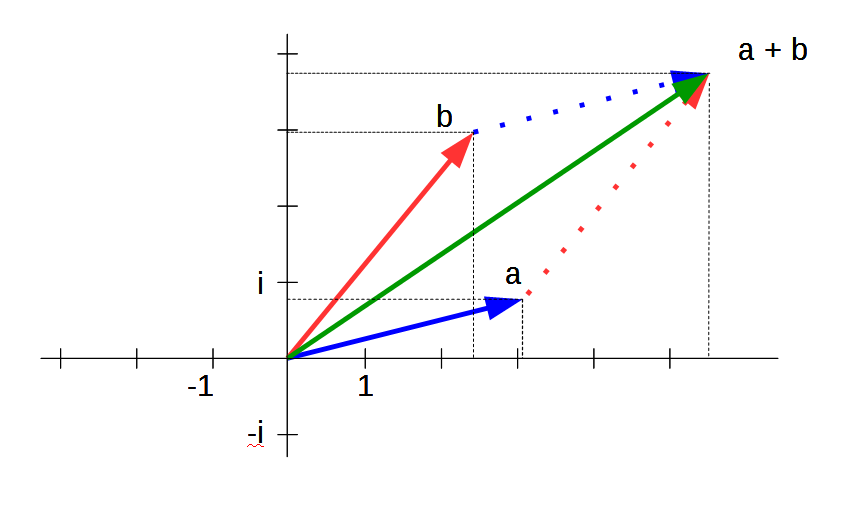
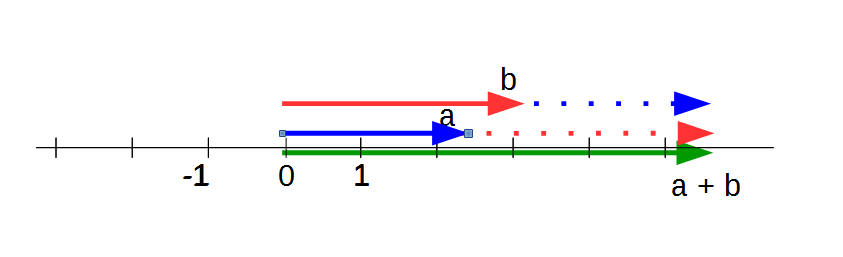


Summe zweier komplexer und zweier reeller Zahlen in Zeigerdarstellung
Die komplexen Zahlen werden mit Zeigern (Vektoren) dargestellt: Der rote und der blaue Vektor werden addiert, indem jeweils ihre beiden Koordinaten addiert werden. Erst wird die Strecke des roten Vektors gegangen, anschließend die Strecke des blauen Vektors, oder gleichbedeutend: Erst die Strecke des blauen Vektors, anschließend die Strecke des roten Vektors. Es entsteht ein Parallelogramm. Dessen Diagonale ist der grüne Vektor. Er ist die Summe der beiden Vektoren a und b, bzw. gleichbedeutend der beiden komplexen Zahlen a und b. Die schwarz gestrichelten Linien bezeichnen die Koordinaten, die jeweils addiert werden.
Bei der Addition reeller Zahlen geschieht das gleiche, nur liegen in diesem Fall der rote und der blaue Vektor auf der gleichen Linie. Sie werden nacheinander ausgeführt. Im Ergebnis ergibt sich als Summe der grüne Vektor. (Genau genommen liegen der blaue, rote und grüne Vektor jeweils aufeinander auf der horizontalen Achse. In der Zeichnung müssen sie übereinander dargestellt werden, um sie unterscheiden zu können.)
Multiplikation: Für die Multiplikation zweier komplexer Zahlen gilt in den Worten von Wessel eine »Richtungsänderung« (Drehung). Werden zwei komplexe Zahlen multipliziert, ergibt das wie beim Addieren einen neuen Zeiger. Seine Länge ist das Produkt der Längen der beiden Faktoren. Hinzu kommt die »Richtungsänderung«, wobei der Richtungswinkel des Produkts »der Summe der Richtungswinkel der Faktoren gleich werden« soll (Wessel, § 4).
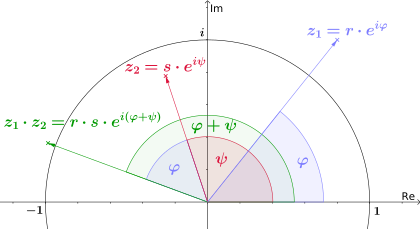
Produkt zweier komplexer Zahlen
Urheber: von Kmhkmh - Eigenes Werk, CC-BY 4.0, Link
Die beiden komplexen Faktoren werden mit einem blauen bzw. roten Zeiger dargestellt, das Produkt mit einem grünen Zeiger. Die Drehung ergibt sich durch Addition der Winkel φ der beiden Zeiger, die Länge als Produkt der Längen des blauen und roten Zeigers. In diesem Beispiel ist die Länge des blauen Zeigers größer als 1 und die Länge des roten Zeigers kleiner als 1. Daher ergibt ihr Produkt einen Wert, der zwischen den Längen der beiden Faktoren liegt. Das Produkt zweier komplexer Zahlen ergibt durch eine Drehstreckung eine neue komplexe Zahl (grün).
Wie bei der Addition stimmen die Regeln für das Multiplizieren komplexer Zahlen mit den Regeln für das Multiplizieren reeller Zahlen überein: Positive reelle Zahlen können als komplexe Zahlen angesehen werden, die um einen Winkel von 0° (bzw. bei den negativen Zahlen von 180°) gedreht sind. Werden zwei reelle Zahlen multipliziert, dann ergeben sich die Multiplikationsregeln direkt aus der Lage auf der reellen Zahlenachse:
| Multiplikationsregel | Addition der Winkel | Deutung |
| + · + = + | 0° + 0° = 0° | |
| + · − = − | 0° + 180° = 180° | Spiegelung |
| − · + = − | 180° + 0° = 180° | Spiegelung in der anderen Richtung |
| − · − = + | 180° + 180° = 360° = 0° | volle Drehung zum Anfangspunkt |
Das Produkt reeller Zahlen liegt wieder auf der reellen Zahlenachse. Es bleibt, nach den üblichen Regeln die Beträge (die Abstände zum Nullpunkt) der beiden reellen Zahlen miteinander zu multiplizieren und die Vorzeichen zu berücksichtigen.
Um zu erkennen, wie außergewöhnlich eine Drehung (Richtungsänderung) bei mathematischen Operationen ist, ist die Idee zur geometrischen Darstellung der Aufgabe von Cardano einen Schritt genauer zu untersuchen. Sie enthält zwei Momente: Das Skalarprodukt und das Vektorprodukt. Das Skalarprodukt kann mit einem Schattenbild, das Vektorprodukt mit der Errichtung einer neuen Achse und das Produkt komplexer Zahlen als Drehstreckung verstanden werden, die das Skalarprodukt und das Vektorprodukt als innere Momente enthält. Wer heute Mathematik, Physik oder technische Fächer lernt, wird meist mit einer Vielfalt von Begriffen wie diesen konfrontiert, und das oft in unterschiedlichen Zusammenhängen. Daher kann der Eindruck entstehen, als seien das einfach verschiedene Möglichkeiten, mit denen jeweils das gewünschte Ergebnis nachgewiesen werden soll, welches im Vorfeld schon bekannt ist. Ausgehend von der Multiplikation komplexer Zahlen lässt sich jedoch verstehen, wie diese verschiedenen Arten des Multiplizierens innerlich zusammen gehören und was sie unterscheidet.
(i) Skalarprodukt: Anschaulich kann gesagt werden: Zwei Zeiger, die in verschiedene Richtungen weisen, können nicht direkt miteinander multipliziert werden, da sie gegeneinander verdreht sind. Mit dem Skalarprodukt zweier Zeiger wird ein Weg gefunden, die Drehung beider Zeiger zueinander zu berücksichtigen und sie so zu multiplizieren, als würden beide auf der reellen Zahlenachse liegen. Um sie multiplizieren zu können, muss ein Zeiger auf den anderen projiziert werden, so dass beide aufeinander liegen und in die gleiche Richtung weisen. Wenn das erfolgt ist, können sie wie gewöhnliche Zahlen miteinander multipliziert werden. Das wird am klarsten an einer einfachen Zeichnung:
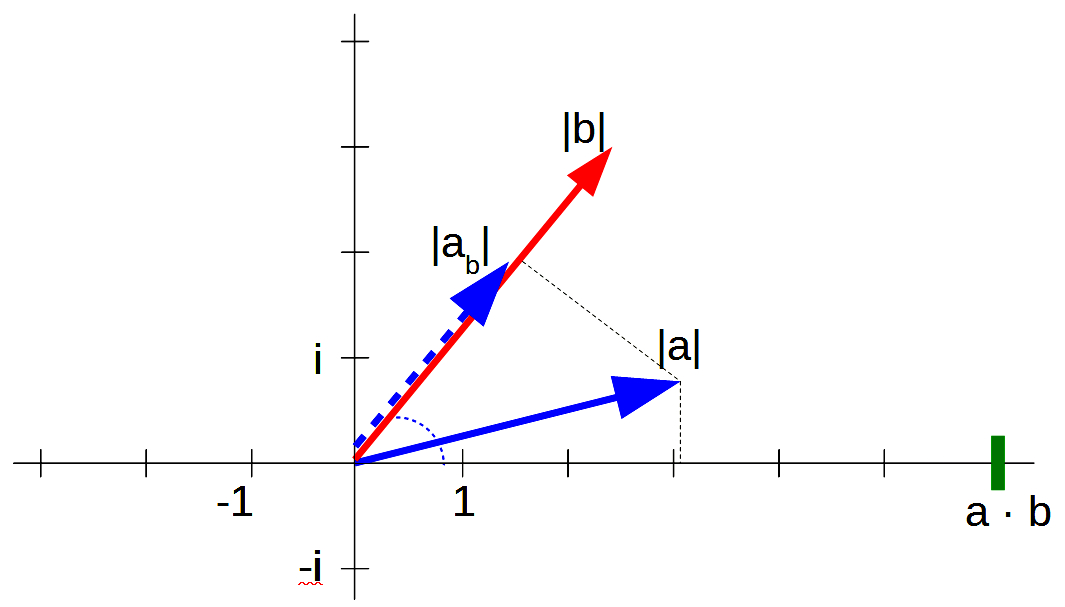


Skalarprodukt
Linkes Bild: Der kürzere Zeiger – das ist in diesem Beispiel der blaue Zeiger a mit der Länge |a| – wird auf den längeren Zeiger projiziert. Wichtig ist, den Unterschied einer Drehung und einer Projektion zu erkennen. Bei einer Drehung verändert sich die Länge nicht, bei einer Projektion wird sie verkürzt. Die Projektion kann mit einem Schattenwurf verglichen werden: Die Projektion ist der Schatten des einen Zeigers auf dem anderen. Das ergibt in diesem Bild den blau gestrichelten Zeiger ab mit der Länge |ab|. Es ist an der Zeichnung zu sehen, dass mit der Projektion die Länge kürzer geworden ist: |ab| ist kleiner als |a|. Das grün hervorgehobene Skalar a · b ist das Produkt der Länge des längeren Vektors, – bezeichnet als |b| –, und der Länge des auf den längeren Vektor projizierten kürzeren Vektors |ab|. Das ergibt in diesem Beispiel: a · b = |ab| · |b| .
Wenn im Grenzfall der Winkel zwischen beiden Zeigern 0° beträgt und sie aufeinander liegen, dann ist keine Projektion notwendig und es muss nicht unterschieden werden zwischen der Länge des Zeigers vor der Projektion – das ist in diesem Beispiel |a| – und der Länge der Projektion – das ist in diesem Beispiel |ab|. In diesem Grenzfall gilt direkt: a · b = |a| · |b|.
Rechtes Bild: Die Idee des Skalarprodukts ist bereits in der Intuition zu Cardano enthalten. Wird die senkrechte Linie betrachtet, die von der reellen Zahl 5 ausgeht, dann erfolgt entlang dieser Senkrechte der Schattenwurf der beiden Zeiger, die auf die Zahlen 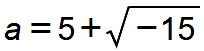 und
und 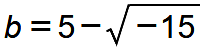 zeigen, auf die reelle Zahlenachse. Während die beiden Zeiger jeweils die Länge 6,32 haben (das ist der Radius des Kreises), hat ihr Schattenwurf nur die Länge 5. Das lässt sich auch in der anderen Richtung "lesen": Statt den Schattenwurf der Zeiger auf die reelle Zahlenachse zu "sehen", kann umgekehrt entlang der Senkrechte eine Verlängerung gesehen werden, die von dem Zeiger auf die Zahl 5 durch eine Projektion auf die beiden Zeiger zu den Zahlen
zeigen, auf die reelle Zahlenachse. Während die beiden Zeiger jeweils die Länge 6,32 haben (das ist der Radius des Kreises), hat ihr Schattenwurf nur die Länge 5. Das lässt sich auch in der anderen Richtung "lesen": Statt den Schattenwurf der Zeiger auf die reelle Zahlenachse zu "sehen", kann umgekehrt entlang der Senkrechte eine Verlängerung gesehen werden, die von dem Zeiger auf die Zahl 5 durch eine Projektion auf die beiden Zeiger zu den Zahlen 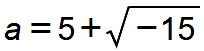 und
und 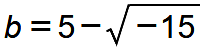 führt. Mit dieser Operation sind die Zahlen gefunden, die die gestellte Aufgabe lösen: Das Produkt ihrer Längen ergibt wie gewünscht 6,32 · 6,32 = 40, während ihr Skalarprodukt (das ist das Produkt ihrer Schatten auf der reellen Zahlenachse jeweils mit der Länge 5) nur 5 · 5 = 25 ergibt. Mit dieser Operation ist es gelungen, aus ›5 · 5 = 25‹ das gesuchte Ergebnis ›6,32 · 6,32 = 40‹ zu "machen".
führt. Mit dieser Operation sind die Zahlen gefunden, die die gestellte Aufgabe lösen: Das Produkt ihrer Längen ergibt wie gewünscht 6,32 · 6,32 = 40, während ihr Skalarprodukt (das ist das Produkt ihrer Schatten auf der reellen Zahlenachse jeweils mit der Länge 5) nur 5 · 5 = 25 ergibt. Mit dieser Operation ist es gelungen, aus ›5 · 5 = 25‹ das gesuchte Ergebnis ›6,32 · 6,32 = 40‹ zu "machen".
Als Ausblick sei ergänzt, dass jetzt nur noch jemand mit einer zugleich mathematischen wie physikalischen Phantasie begabter Wissenschaftler wie Einstein kommen musste, um das hier dargestellte Spiel der mathematischen Intuition der Zahlen zu übertragen auf den Bewegungsraum der Mechanik und zu erkennen, dass die im Verhältnis vom Skalarprodukt und dem Produkt komplexer Zahlen auftretenden Verkürzungen und Verlängerungen physikalisch gedeutet werden können. Das ergibt den Übergang zu Räumen, bei denen es in der Speziellen Relativitätstheorie zur Längenkontraktion und in der Allgemeinen Relativitätstheorie zur Krümmung kommt. Der gekrümmte Raum verhält sich zum ebenen Raum wie der in die komplexe Ebene gedrehte Zeiger zu seinem Schattenwurf auf der reellen Zahlenachse. Allerdings haben diesen Zusammenhang offenbar weder Einstein noch Gödel bemerkt. Das bis in seine philosophischen Konsequenzen auszuarbeiten und zum Beispiel für elementare philosophische Begriffe wie Reflexion, Abschattung und Imagination ihren über die imaginären Zahlen erkennbaren inneren Bezug zu finden, ist das langfristige Ziel der mit diesem Beitrag begonnenen Arbeit.
(ii) Vektorprodukt: Der Grundgedanke von Cardano war zweifellos, sich von der eindimensionalen Zahlengerade zu lösen und eine neue Dimension zu öffnen, in der die imaginären Zahlen liegen. Dieser Grundgedanke wird klarer, wenn er auf höhere Dimensionen verallgemeinert und insbesondere am Übergang von Flächen in den Raum veranschaulicht wird. Das liefert in der Physik die Drei-Finger-Regel, bisweilen auch als Korkenzieherregel oder Rechter-Daumen-Regel bezeichnet. Hier wird anschaulich gezeigt, wie aus zwei Dimensionen eine senkrecht auf ihnen stehende neue Dimension hervorgeht.
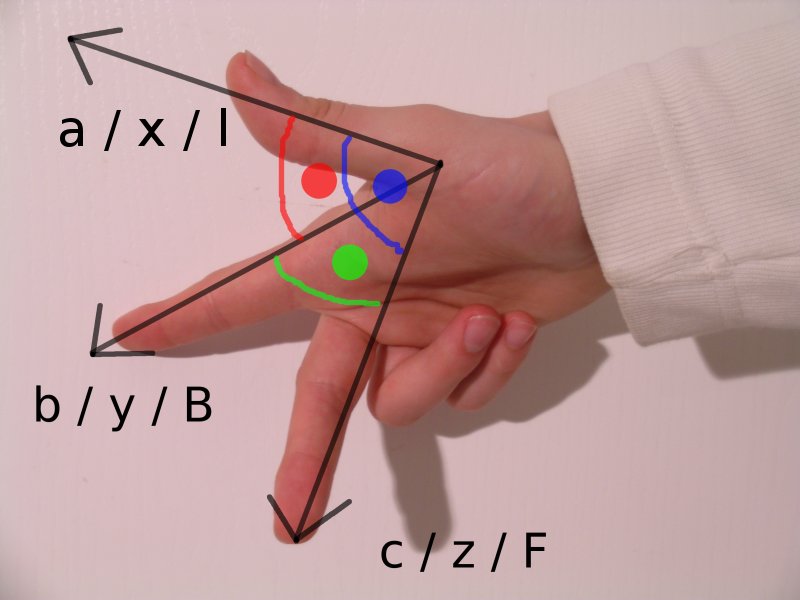
Rechter-Daumen-Regel
Zeigefinger und Mittelfinger bestimmen eine Fläche. Der Daumen steht senkrecht auf der Fläche.
Urheber: Von Abdull - Eigenes Werk, CC BY-SA 3.0, Link
Elektrotechniker machen sich mit der Daumenregel klar, in welche Richtung in einem Magnetfeld der Strom fließt. Das sind bereits Beispiele für die Anwendungen der imaginären Zahlen in die Naturwissenschaft und Technik.
Mathematisch wird das verallgemeinert zum Vektorprodukt oder Kreuzprodukt. Während das Skalarprodukt ein Skalar ergibt, – das ist eine reelle Zahl –, ergibt das Vektorprodukt einen Vektor. Zwei Vektoren, die nicht in die gleiche Richtung weisen, bilden eine Fläche. Das Kreuzprodukt zweier Vektoren erzeugt einen Vektor, der senkrecht auf dieser Ebene steht. (Das Kreuzprodukt wird bisweilen missverständlich auch als äußeres Produkt beschrieben. Das äußere Produkt gilt in äußeren Algebren mit eigenen Rechenregeln. Darauf soll in einem späteren Teil näher eingegangen werden.)
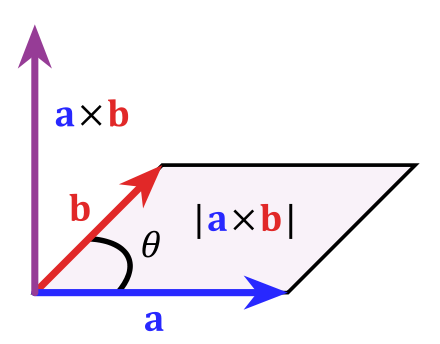
Kreuz-Produkt
Das Kreuzprodukt (Vektorprodukt) zweier Vektoren: Zwei nicht in die gleiche Richtung weisende Vektoren bilden eine Ebene. Das Vektorprodukt a  b hat eine Richtung, die senkrecht auf der von den beiden Vektoren gebildeten Ebene steht. Der Zahlenwert des Vektorprodukts entspricht dem Flächeninhalt der von den beiden Vektoren gebildeten Fläche.
b hat eine Richtung, die senkrecht auf der von den beiden Vektoren gebildeten Ebene steht. Der Zahlenwert des Vektorprodukts entspricht dem Flächeninhalt der von den beiden Vektoren gebildeten Fläche.
Urheber: von MartinThoma - Eigenes Werk, CC BY 3.0, Link
Ergebnis Diese Darstellung soll zweierlei zeigen: (i) Das Skalarprodukt und das Kreuz-Produkt lassen sich verstehen als Momente des Produkts imaginärer Zahlen. Das Skalarprodukt verallgemeinert die Projektion (den Schattenwurf) zweier Geraden aufeinander, das Kreuz-Produkt verallgemeinert das Eröffnen einer Dimension und der Regeln, die hierbei einzuhalten sind. (ii) Aber weder das Skalarprodukt noch das Kreuz-Produkt ergeben die Drehung (die Richtungsänderung), die erst für die imaginären Zahlen typisch ist und diese von allen anderen Zahlen unterscheidet. (Die meisten dieser Erkenntnisse gehen auf den irischen Mathematiker William Rowan Hamilton, 1805-1865, zurück. Er hat nicht nur das Verständnis der komplexen Zahlen vertieft und darauf aufbauend weitere Zahlen wie die Quaternionen eingeführt, sondern auch die Vektorrechnung klarer formuliert.)
Die drei Arten der Multiplikation seien zusammenfassend nebeneinander gestellt, um die Gemeinsamkeiten und Unterschiede zu sehen:






Produkt zweier Vektoren und zweier komplexer Zahlen – Übersicht
(a) Das Skalarprodukt zweier Zeiger (Vektor) ergibt eine reelle Zahl (grün hervorgehoben)
(b) Das Vektorprodukt zweier Zeiger (Vektoren) ergibt einen senkrecht zu ihnen stehenden Zeiger (violett)
(c) Das Produkt zweier komplexer Zahlen ergibt durch eine Drehung eine komplexe Zahl (grün)
Wurzel aus minus 1 Nach diesen Vorbereitungen ist auf die Definition der imaginären Zahlen als ‘Wurzel aus minus 1’ zurückzukommen. Durch die Drehung wird es möglich, eine Zahl zu finden, die mit sich selbst multipliziert eine negative Zahl ergibt. Im einfachsten Fall 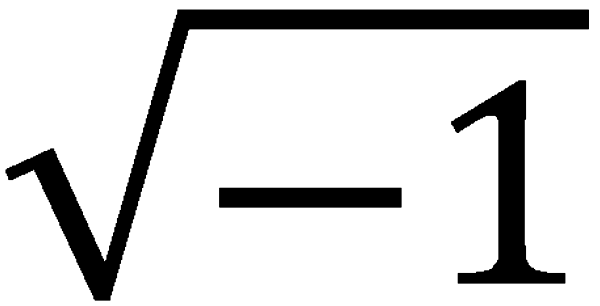 wird das Produkt i · i betrachtet: In diesem Fall haben beide Faktoren (jeweils die Zahl i) einen Winkel von 90° relativ zur reellen Achse. Werden die beiden Winkel addiert, ergibt das den Winkel von 180° und das Produkt fällt durch die Drehung auf die Zahl −1. Daher ergibt i · i = −1 und es gilt nach Wurzelziehen auf beiden Seiten i =
wird das Produkt i · i betrachtet: In diesem Fall haben beide Faktoren (jeweils die Zahl i) einen Winkel von 90° relativ zur reellen Achse. Werden die beiden Winkel addiert, ergibt das den Winkel von 180° und das Produkt fällt durch die Drehung auf die Zahl −1. Daher ergibt i · i = −1 und es gilt nach Wurzelziehen auf beiden Seiten i =  .
.
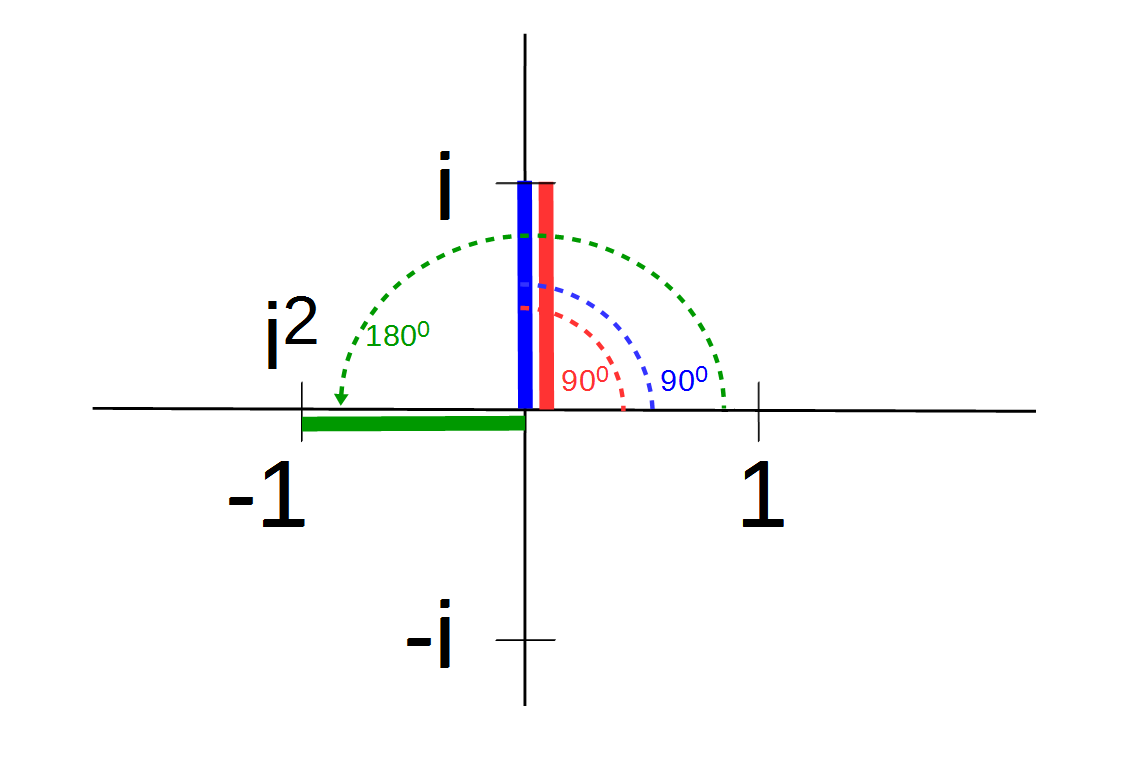
i · i als Drehung auf −1
In diesem Fall handelt es sich bei beiden Faktoren (rot und blau) jeweils um die komplexe Zahl i und einem Winkel von 90° relativ zur reellen Achse. Das Produkt i · i = i2 = −1 ergibt sich durch Addition der beiden Winkel auf 180° = 90° + 90°.
Daher führt es in die Irre, wenn gesagt wird, das die imaginären Zahlen so etwas wie negative Flächen sind. Sie ergeben sich nicht aus Flächen, sondern aus der Drehung.
Wenn komplexe Zahlen miteinander multipliziert werden, kann das dazu führen, dass die Drehung wie bei einer Uhr an den Anfangspunkt zurückkehrt und ihn überschreitet. Während jedoch auf der Uhr nach jeweils 12 Stunden die gleichen Zahlen neu durchlaufen werden, soll das bei den komplexen Zahlen vermieden werden. Jede komplexe Zahl soll eindeutig bleiben. Das führt in eine Überlagerung von unendlich vielen Flächen, die wie in einer Spirale angeordnet sind:
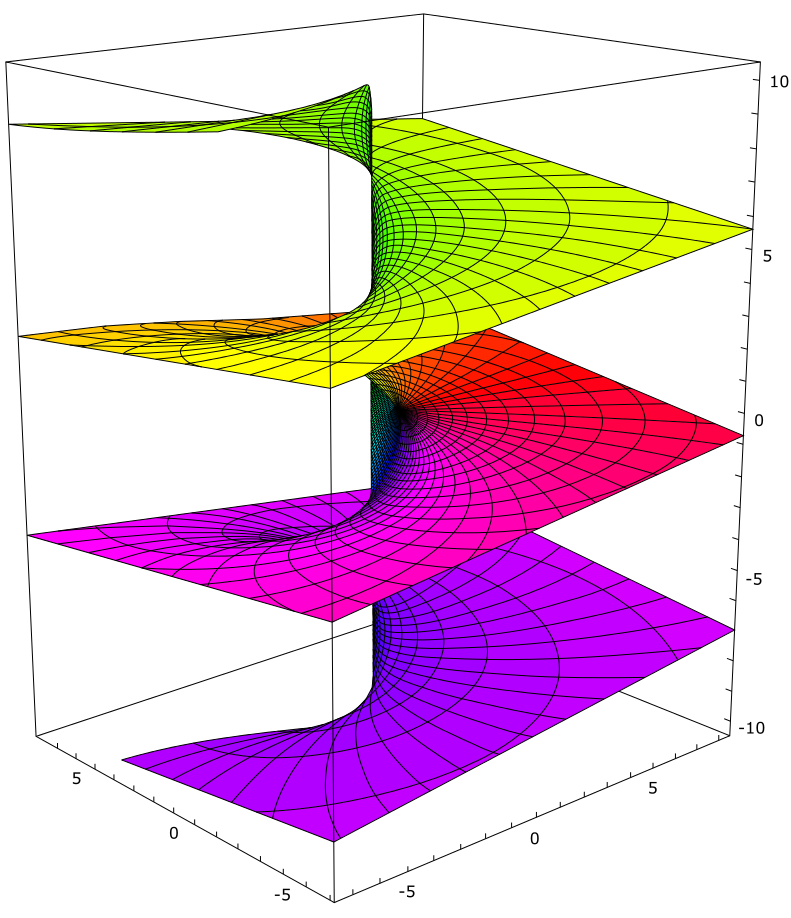
Riemannsche Fläche des komplexen Logarithmus
Urheber: Von Leonid 2 - Eigenes Werk, CC BY-SA 3.0, Link
Mit dieser Darstellung ist das Besondere der komplexen Zahlen getroffen. Die komplexen Zahlen zeichnen sich durch eine Multiplikation aus, bei der zwei komplexen Zahlen gedreht werden, und die Drehung kann spiralförmig in fortlaufend neue Blätter führen. Anschaulich entsteht das Bild einer Schraube, die von unten nach oben strömt, oder in der Sprache des Fernen Ostens einer Schlange, die durch eine Reihe von Rädern aufsteigt und mit jedem Rad neue Energie gewinnt und sich wandelt. Komplexe Zahlen sind daher besonders geeignet zur mathematischen Beschreibung von Prozessen, die sowohl rotieren wie strömen.
Anwendungen der komplexen Zahlen
Strömungslehre nach Euler
Waren die komplexen Zahlen für Cardano noch eine Art Spielerei und Herausforderung für die mathematische Intuition, so hat 200 Jahre später Leonhard Euler (1707-1783) den Übergang in vielfältige Anwendungsgebiete der Mathematik und Physik vollzogen. Er geht in der Mechanik nicht mehr von starren Körpern und in der Mathematik nicht mehr von dimensionslosen Punkten aus, sondern von Strömungen und ihrer mathematischen Gestalt in mindestens zwei Dimensionen. In einer Strömung gibt es ständig Turbulenzen und eine innere Bewegtheit. Die Strömung kann sowohl in einer Flussrichtung fließen wie sich auch um die eigene Fließ-Achse drehen (was insbesondere bei elektrischen Strömen zu berücksichtigen ist).
Das Strömungsverhalten soll an einem aktuellen Beispiel veranschaulicht werden:
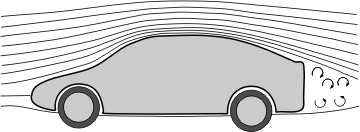
Stromlinienverlauf um ein Auto
Urheber: Von AndreHuppertz, CC BY-SA 3.0, Link
Die Luftströmung ist nicht punktförmig, sondern anschaulich wird von einer Stromröhre und in deren Innern von einem Stromfaden gesprochen, die mit Windkanälen nachgebildet und simuliert werden können. Auf der Rückseite des Autos bilden sich Verwirbelungen, die das Fahrverhalten beeinträchtigen.
Euler beschäftigte sich mit zahlreichen Anwendungsbeispielen dieser Art. Aus heutiger Sicht hat er den Paradigmenwechsel der Mathematik des 20. Jahrhunderts zur Differentialgeometrie und Theorie differenzierbarer Mannigfaltigkeiten vorweggenommen. Er selbst war Praktiker, der sich ganz auf die Lösung einer Vielzahl konkret gegebener Aufgaben konzentrierte. Er hat dafür noch keinen theoretischen Rahmen entwickelt, aber eine Vielzahl bis heute genutzter Symbole eingeführt, mit denen er sich das Rechnen vereinfachte, darunter die Symbole  , i und e für die Kreisfunktionen, zirkulierende Bewegungen und die imaginären Zahlen (Eulersche Formel). Sein pragmatischer Ansatz ist wohl die Erklärung, warum er zwar als äußerst produktiver Mathematiker anerkannt ist, aber die Tragweite seiner Neubegründung der Mathematik und Mechanik als Strömungslehre unerkannt bleibt. Hegel bezieht sich auf Euler nur über Lagrange bezüglich des Differentialkalküls (HW 5.303-306), geht jedoch nirgends auf die komplexen Zahlen und die neuen Ideen von Euler ein. Im Grunde werden die imaginären Zahlen bis heute überwiegend wie bereits bei Euler als eine Art technisches Hilfsmittel gesehen und nicht als eine völlig neue Denkweise der Mathematik (Zyklizitäts-Denken).
, i und e für die Kreisfunktionen, zirkulierende Bewegungen und die imaginären Zahlen (Eulersche Formel). Sein pragmatischer Ansatz ist wohl die Erklärung, warum er zwar als äußerst produktiver Mathematiker anerkannt ist, aber die Tragweite seiner Neubegründung der Mathematik und Mechanik als Strömungslehre unerkannt bleibt. Hegel bezieht sich auf Euler nur über Lagrange bezüglich des Differentialkalküls (HW 5.303-306), geht jedoch nirgends auf die komplexen Zahlen und die neuen Ideen von Euler ein. Im Grunde werden die imaginären Zahlen bis heute überwiegend wie bereits bei Euler als eine Art technisches Hilfsmittel gesehen und nicht als eine völlig neue Denkweise der Mathematik (Zyklizitäts-Denken).
Zeigermodell: Komplexe Zahlen in Naturwissenschaft und Technik seit 1900
Daran hat sich auch nichts mit dem nächsten großen Anwendungsgebiet geändert, der Elektrotechnik. Im Gegenteil hat sich mit ihr der Ruf der imaginären Zahlen als Werkzeug für Ingenieure und Techniker verfestigt. Die ersten technischen Erfindungen gehen auf die Zeit um 1880 zurück und haben seither die Wirtschaft wie auch unser Leben bis in den Alltag völlig umgekrempelt. Mit der Elektrotechnik und der Elektrifizierung wurden elektrische Ströme genutzt von der Energieverteilung über Elektromotoren bis zum Einsatz von Funkgeräten. In allen Fällen wurde es notwendig, die Größe und Einflussfaktoren der Ströme genau zu bestimmen und zu regulieren, und meist ist das Rechnen mit komplexen Zahlen am einfachsten. Hier entstand die Daumenregel.
Grundgedanke ist das Zeigermodell, mit dem die Eulersche Formel für Kreisfunktionen erweitert wird. Periodische Schwingungen etwa von elektrischen Schaltkreisen werden interpretiert als der zeitliche Ablauf eines Zeigers, der sich wie ein Uhrzeiger kreisförmig dreht. Wird der Zeiger verstanden als die Drehung in der komplexen Ebene, dann können die zeitlich periodischen Abläufe vergleichsweise einfach als komplexe Funktion aufgeschrieben werden.
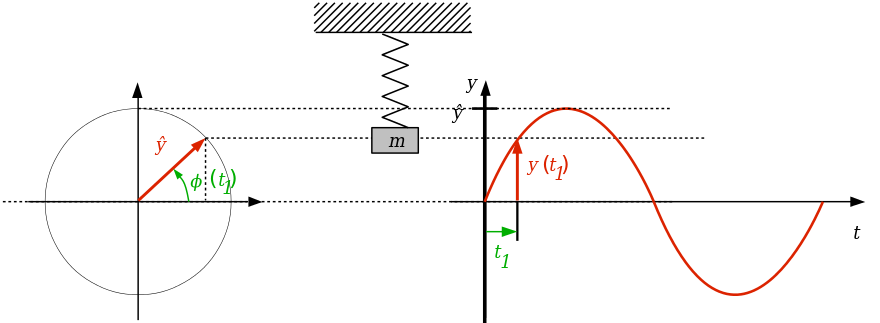
Zeigermodell
»Das Zeigerdiagramm (links) am Beispiel eines Federpendels: Im Diagramm (rechts) wurde die Momentanauslenkung y(t) des Pendels über der Zeit aufgetragen. Wie man sieht, entspricht sie der Projektion des Zeigers auf die y-Achse.« (abgerufen am 27.8.2017)
Urheber: Von Pyrrhocorax in der Wikipedia auf Deutsch - Eigenes Werk des ursprünglichen Hochladers, Gemeinfrei, Link
Die komplexe Wechselstromrechnung wurde erstmals 1893 eingeführt und 1937 zusammenfassend ausgearbeitet. In einem elektrischen Schwingkreis »wird Energie zwischen dem magnetischen Feld der Spule und dem elektrischen Feld des Kondensators periodisch ausgetauscht, wodurch abwechselnd hohe Stromstärke oder hohe Spannung vorliegen« (Wikipedia-Eintrag, abgerufen am 27.8.2017). Der zyklische Prozess lässt sich am einfachsten mit komplexen Zahlen beschreiben. Die Anwendungen reichen quer durch die gesamte Elektrotechnik.
Quantentheorie
Erst mit der Quantentheorie beginnt sich die Einstellung zu den imaginären Zahlen zu ändern. Zwar ist der Grundgedanke der gleiche geblieben, wenn das Atom wie ein elektrischer Schaltkreis als ein schwingendes System verstanden wird, das sich am besten mit komplexen Zahlen beschreiben lässt. Wer aber erstmals Formeln wie die Schrödinger-Gleichung sieht, in der die imaginäre Einheit i auftritt, hat elementare Schwierigkeiten sich vorzustellen, was und wie das gemeint ist. Hier kommt zweierlei zusammen: Erstens versteht kaum jemand, warum die Quantenphysik nur Wahrscheinlichkeiten kennt, und zweitens ist es schwer sich vorzustellen, wie sich Wahrscheinlichkeiten periodisch ändern und daher am einfachsten mit imaginären Zahlen formulieren lassen.
(i) Das beginnt mit der Frage der Quantenphysik, an welchem Ort ein Teilchen nachgewiesen und gemessen werden kann, seiner Aufenthaltswahrscheinlichkeit. Bei einem frei schwingenden Pendel kann unter idealen Bedingungen genau berechnet werden, an welcher Stelle sich das Pendel befindet. Es gibt entsprechend dem Zeigermodell eine Sinus-Funktion, mit der beschrieben wird, wie das Pendel auf- und abschwingt. In der heute gültigen Quantentheorie ist es nicht mehr möglich, für ein einzelnes Teilchen genau zu beschreiben, wo es sich aufhalten wird (alternative Modelle wie das von David Bohm werden überwiegend abgelehnt, siehe hierzu den Beitrag über Grundfragen der Quantenphysik). Aber es ist möglich, die Wahrscheinlichkeit zu berechnen, an welchem Ort es nachgewiesen werden kann. Die Aufenthaltswahrscheinlichkeit ist jedoch wiederum nicht immer gleich, sondern verändert sich wie die Bewegung eines Pendels periodisch und wird daher entsprechend dem Zeigermodell mit imaginären Zahlen beschrieben. Auch das muss zunächst einfach als eine empirisch bestätigte Tatsache hingenommen werden.
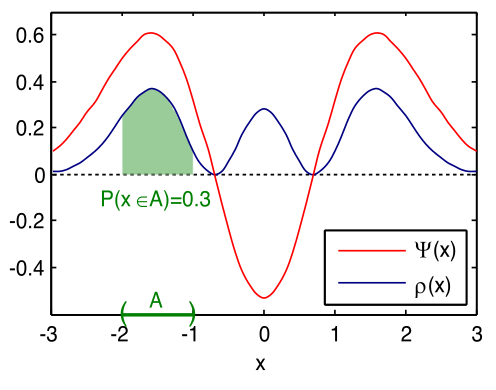
Aufenthaltswahrscheinlichkeit
»Wellenfunktion (in rot), Wahrscheinlichkeitsdichte (blau) und Aufenthaltswahrscheinlichkeit (grün) des zweiten angeregten Zustandes (n=2) eines eindimensionalen harmonischen Oszillators.
Die Wahrscheinlichkeit, ein Teilchen im Intervall A (grüner Bereich: -2<x<-1) zu finden, ist ungefähr 30 Prozent.« (abgerufen am 7.11.2017)
Urheber: Von Debenben - Eigenes Werk, CC BY-SA 3.0, Link
Die Aufenthaltswahrscheinlichkeit hängt von dem jeweiligen Zeitintervall ab. Sie ist in diesem Diagramm als grüne Fläche dargestellt, die für das jeweils betrachtete Zeitintervall der sich periodisch ändernden Wahrscheinlichkeitsdichte (blaue Kurve) gilt.
(ii) Noch komplizierter wird es, wenn nicht nur der Ort, sondern der Zustand eines Teilchens der Quantenphysik betrachtet wird. Der Zustand kann nur eine endliche Anzahl möglicher Werte annehmen, und es lässt sich nur die Übergangswahrscheinlichkeit berechnet, mit der das Teilchen aus einem Zustand in einen anderen springt. Die Übergangswahrscheinlichkeit verändert sich wiederum periodisch und wird daher wie die Aufenthaltswahrscheinlichkeit mit Kreisfunktionen dargestellt.
Dynamische Farbverläufe
Trotz aller Erfahrungen in den Anwendungen sind die besonderen Eigenschaften komplexer Zahlen schwer zu verstehen, da es ein großes Umdenken erfordert sich vorstellen zu können, wie eine Funktion von komplexen Variablen verläuft. Jeder kennt die Graphen (Wertverläufe) reeller Funktionen, sei es die Wurfparabel, bei der Ort und Zeit die beiden Koordinaten einer Bewegung sind, oder Darstellungen ökonomischer Veränderungen im Zeitverlauf, wenn z.B. die Entwicklung des Bruttoinlandsprodukts eines Landes in der Zeit dargestellt wird. Bei reellen Funktionen wird einem punktförmigen, veränderlichen Wert x ein anderer punktförmiger Wert y = f(x) zugeordnet, und beide ergeben die Punkte (x,y) der Bewegungskurve. Aber wie soll es möglich sein sich eine Funktion vorzustellen, bei der das punktförmige x ersetzt wird durch eine komplexe Zahl z mit 2 Koordinaten (ihrem Real- und Imaginärteil), und ebenso der Funktionswert f(z) zwei Koordinaten hat?
Hierfür sind heute die dynamischen Farbverläufe die Standardmethode. Ihre Grundidee ist, auf einer Fläche allen Punkten, die jeweils durch ihre x- und y-Koordinaten definiert sind, einen Farbwert zuzuordnen, der ebenfalls zwei Koordinaten hat: Den Farbton und die Helligkeit. Mithilfe von Animationen kann die Veränderung von Farbverläufen dargestellt werden. Das kann als der Verlauf einer komplexen Funktion verstanden werden, mit der jedem Punkt (x,y) ein Farbwert (Farbton, Helligkeit) zugeordnet wird. Das wird bei den bildgebenden Verfahren genutzt und ist inzwischen zu einem der wichtigsten Anwendungsgebiete der imaginären Zahlen geworden, die nicht nur in der Medizin, sondern von nahezu allen Wissenschaften genutzt werden. Wer die Darstellung von Farbverläufen »lesen« kann, versteht den Verlauf einer komplexen Funktion. Eine Variante sind die Fraktale, mit denen ebenfalls allen Punkten einer zweidimensionalen Figur Farbwerte zugeordnet werden.
Es gibt Vorläufer, die das Verständnis komplexer Funktionen erleichtern helfen. Das älteste Beispiel sind die seit dem 18. Jahrhundert eingeführten topographischen Karten. Jeder Ort (topos) hat wie die komplexen Zahlen zwei Koordinaten (den Höhen- und den Breitengrad). Mit der Farbe wird die jeweilige Höhe eingetragen, und bisweilen mit einem angedeuteten Schattenwurf (Schummerung) die jeweilige Steigung. Die topographische Karte mit Schummerung ist ein Beispiel für eine komplexe Funktion: Eine Zahl mit zwei Koordinaten (Längengrad, Breitengrad) wird abgebildet auf einen Wert mit ebenfalls zwei Koordinaten (Höhe als Farbe, Steigung als Schummerung). Mathematisch handelt es sich um die Darstellung eines vierdimensionalen Raums (Längengrad, Breitengrad, Höhe, Steigung) auf einer zweidimensionalen Fläche (dem Kartenblatt).
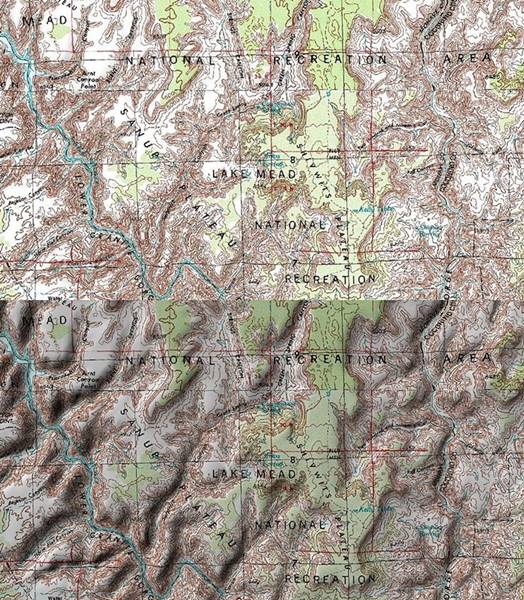
Karte mit und ohne Schummerung
»Lake Mead, USA
Oben:Karte ohne Schummerung;
Unten: Karte mit Schräglichtschummerung (Screenshot aus der NASA World Wind Software)« (Wikipedia, abgerufen am 22.11.2017)
Urheber: Gemeinfrei, Link
Noch beeindruckender sind die seit 1787 bekannten Chladnischen Klangfiguren. Eine mit dünnem Sand bestreute Platte wird mit einer Violinsaite angestrichen und beginnt zu vibrieren. Die Sandkörner ordnen sich zu symmetrischen Mustern. An jedem einzelnen Punkt ist zu erkennen, in welcher Richtung sich ein Sandkorn anordnet und wie dicht an dieser Stelle das Muster ist. Daher ist es wie die topographischen Karten ein weiteres Beispiel für eine komplexe Funktion: Jedem Ort auf der schwingenden Fläche wird ein Wert mit zwei Koordinaten zugeordnet: Die Richtung des Sandkorn und die Dichte der Sandkörner an dieser Stelle. Die Richtung der Sandkörner ist dargestellt durch die Richtung der Linien, die Dichte durch die Größe der leeren Flächen zwischen den Linien.
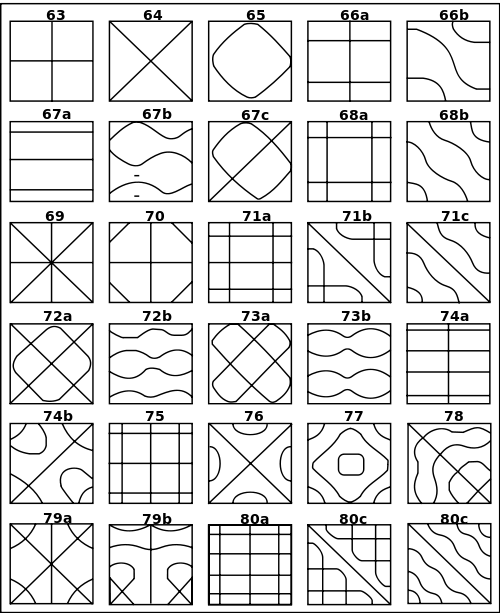
Chladnische Klangfiguren
Urheber: Von E.F.F.Chladni - From the book "Die Akustik" from E.F.F.Chladni. Originally from de.wikipedia; description page is/was here., Gemeinfrei, Link
Figuren dieser Art waren Hegel, Schopenhauer und Nietzsche bekannt. Hegel erwähnt in seiner Naturphilosophie zum Begriff der Töne die »Schwingungsknoten« nach Chladni (Hegel Enz. § 301, HW 9.176) und hat in der Wissenschaft der Logik möglicherweise nach ihrem Vorbild den Begriff der Knotenlinien entwickelt (HW 5.435). Schopenhauer nennt in Die Welt als Wille und Vorstellung § 52 die Akustik von Chladni (in der von den Klangfiguren gehandelt wird), wenn er von den harmonischen Systemen und den Dissonanzen der Töne spricht. Nietzsche spricht in Über Wahrheit und Lüge im außermoralischen Sinne (1873) von einem tauben Menschen, der »die chladnischen Klangfiguren im Sande anstaunt, ihre Ursachen im Erzittern der Saite findet und nun darauf schwören wird, jetzt müsse er wissen, was die Menschen den 'Ton' nennen«. So haben sie sich zwar einem Phänomen genähert, das zur Frage der imaginären Zahlen führt, aber für sie blieb das offenbar nichts als eins von vielen kuriosen Beispielen, mit denen sich die Naturromantik gern beschäftigte. Sie erkannten noch nicht die in ihnen verborgenen Eigenschaften der komplexen Zahlen und deren Funktionen, die Zyklizität, die an Bedeutung weit über diese Beispiele hinausgeht und eine erneuerte Philosophie der Mathematik erforderlich macht.
Ingenieure und Techniker bevorzugten eine andere Darstellung, die bereits einer mathematischen Darstellung näher kommt. Sie tragen auf einer Fläche Pfeile ein, wobei jeder Pfeil durch seine Richtung und Größe (Länge) definiert ist und zugleich die Dichte der Pfeile variiert werden kann.
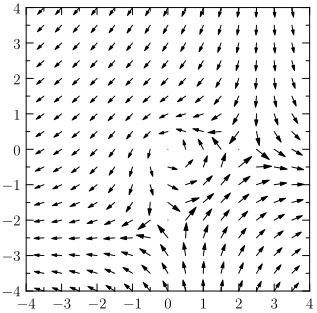
Funktionsgraph von 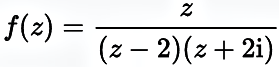
In der Darstellung ist an der Stelle jeder komplexen Zahl das Bild der komplexen Funktion eingezeichnet. Ihr Realteil ist die Pfeillänge, ihr Imaginärteil die Richtung des Pfeils. Entsprechend der Funktion sind zwei Pole erkennbar. Das kann als die Beschreibung eines elektrischen oder eines magnetischen Feldes gedeutet werden.
Quelle: Wikibook, abgerufen am 21.11.2017
Zahlreiche weitere Beispiele finden sich auf dem in Entstehung begriffenen Wikibook über komplexe Zahlen. Dort wird schrittweise von der Darstellung reeller zu komplexen Funktionen übergegangen und die Komplexität der Funktionen stufenweise erhöht.
Erst mit der freien Verwendung der Farbe und den technischen Möglichkeiten der Computergraphik werden der Reichtum und die Anwendungsmöglichkeiten komplexer Funktionen deutlich. In diesen Beispielen wird jedem Ort ein Farbwert mit den zwei Koordinaten Farbton und Helligkeit zugeordnet.
(z-2-3i)z)over((z+2i+4)(z+3i-2).png)
Funktionsgraph von (z-2-3i)z)over((z+2i+4)(z+3i-2) f.png)
In der Darstellung ist an der Stelle jeder komplexen Zahl das Bild der komplexen Funktion eingezeichnet. Ihr Realteil ist die Farbe, ihr Imaginärteil die Helligkeit.
Quelle: Wikibook, abgerufen am 21.11.2017
Mit Animationen ist es möglich, darüber hinaus zeitliche Verläufe komplexer Zahlen zu veranschaulichen. Es kommt entweder zu einer Veränderung des Farbverlaufs oder zu einer Bewegung der Fläche, auf der die Farben und ihre Helligkeiten eingetragen sind. Ein schönes Beispiel ist die komplexe Tangential-Funktion, wenn deren Real- und Imaginärteil zeitlich verändert werden:
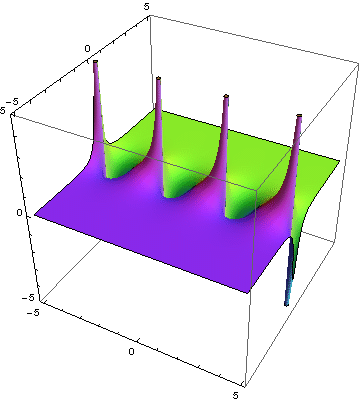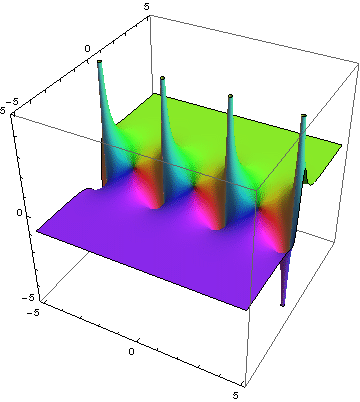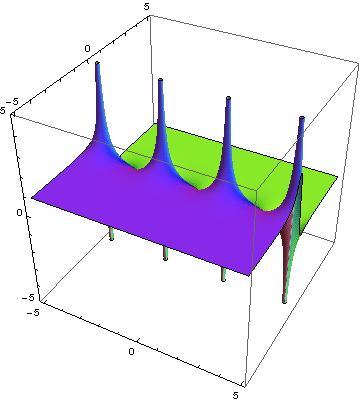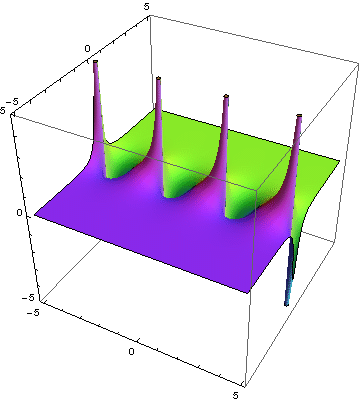
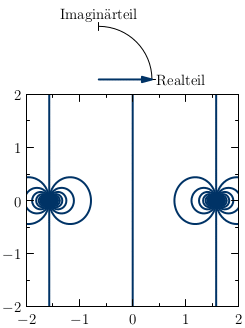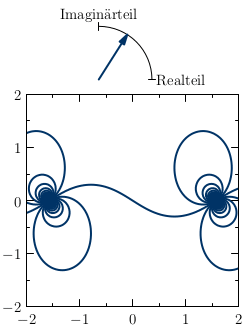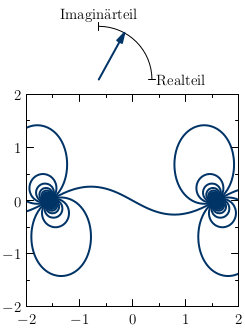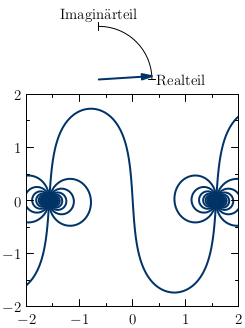


Funktionsgraph von tan z
Quelle: Wikibook, abgerufen am 21.11.2017
Aufgrund ihrer Zyklizität haben die komplexen Zahlen besondere Bedeutung für Fraktale. Werden solche Zahlen gewählt, die spiralartige Entwicklungen hervorrufen, kann sehr einfach Selbstähnlichkeit entstehen.
»Die Mandelbrot-Menge ist die Menge aller komplexen Zahlen c, für welche die durch
z0 = 0
zn+1 = zn2
rekursiv definierte Folge beschränkt ist. Bilder der Mandelbrot-Menge können erzeugt werden, indem für jeden Wert des Parameters c, der gemäß obiger Rekursion endlich bleibt, ein Farbwert in der komplexen Ebene zugeordnet wird.« (Wikipedia Eintrag zur Mandelbrot-Menge, abgerufen am 27.8.2017)

Mandelbrot-Menge
Urheber: Die Autorenschaft wurde nicht in einer maschinell lesbaren Form angegeben. Es wird Wolfgangbeyer als Autor angenommen (basierend auf den Rechteinhaber-Angaben). - Die Autorenschaft wurde nicht in einer maschinell lesbaren Form angegeben. Es wird angenommen, dass es sich um ein eigenes Werk handelt (basierend auf den Rechteinhaber-Angaben)., CC BY-SA 3.0, Link
Besonders beeindruckend sind Filmsequenzen, die in Mandelbrot-Mengen hineinzoomen. Siehe eine Auswahl in YouTube mit Suchbegriff "mandelbrot fraktale zoom".
Zyklizitäts-Denken
Trotz aller Anwendungen und der wesentlich verbesserten Möglichkeiten graphischer Darstellung sind die imaginären Zahlen bis heute so ungewöhnlich, dass nicht nur Laien mit ihnen Schwierigkeiten haben, sondern auch die Philosophie, Psychologie oder Theologie haben sie bisher weitgehend ignoriert oder können nichts mit ihr anfangen. Wer sich mit diesem Thema beschäftigt, betritt Neuland. Ich möchte die These vertreten, dass mit den imaginären Zahlen eine eigene Art des Denkens verbunden ist, die nicht weniger bedeutsam als das Kausalitäts- und das Prinzipien-Denken ist, welche an den natürlichen bzw. reellen Zahlen orientiert sind. Es geht nicht nur darum, dass sich mit komplexen Zahlen die Verlaufsform von Turbulenzen oder anderen kreiselnden Bewegungen optimal formulieren lässt, sondern die Zyklizität ist zugleich als eine Eigenschaft des Denkens selbst zu verstehen: So wie sich die komplexen Zahlen aus dem reellen Bereich entfernen, bis es im imaginären Bereich zu einer Umkehr kommt, die zu den reellen Zahlen zurückfindet, so gelingt dem Zyklizitäts-Denken eine Abkehr von der engen Bindung an das Wirkliche (den Tatsachen) in ein Möglichkeitsfeld, und dort eine Umkehr zurück in das Denken des Wirklichen. So wie dies für die imaginären Zahlen möglich ist durch eine klare Multiplikationsregel, so ist für das Zyklizitäts-Denken eine neue Logik zu entwerfen, bahnbrechend die Gesetze der Form (Laws of Form) von Spencer-Brown. Kommentare zu seiner Arbeit sind daher für mich der erste Schritt in das Zyklizitäts-Denken.
An dieser Stelle sollen zunächst nur die wenigen Ausnahmen vorgestellt werden, mit denen in Literatur, Philosophie und Psychologie über komplexe Zahlen gesprochen wurde. Die darauf aufbauenden und weiter führenden eigenen Ideen über das Zyklizitäts-Denken sollen in weiteren Beiträgen ausgearbeitet werden. Bisher liegen vor:
– Ein Kommentar zur Logik von Spencer-Brown, in der auf völlig neue Art von imaginären Zahlen gesprochen wird.
– Ein Beitrag über die Zyklizität der imaginären Zahlen beim 41. Internationalen Wittgenstein-Symposium in Kirchberg am Wechsel am 10.8.2018
– Ein Beitrag über Dynamische, geträumte und imaginäre Zahlen von 2018
Geplant sind weitere Beiträge zum Zyklizitäts-Denken nach Raymond Swing, zu Fragen der modernen Naturwissenschaft an den Buddhismus, die auch zyklisches Denken betreffen, und zum Ausbau dieses Ansatzes.
Robert Musil über imaginäre Zahlen in Die Verwirrungen des Zöglings Törleß (1906)
Vor der Philosophie wurde die Literatur auf die imaginären Zahlen aufmerksam. Sogar Philosophen wie Hegel, Schopenhauer, Frege oder Husserl, die sich intensiv mit Mathematik beschäftigt hatten, übersahen sie schlicht und einfach, und selbst Russell und Gödel erwähnen sie nicht. Aber als sich im 19. Jahrhundert entgegen dem materialistischen Zeitgeist eine Wende vom Realismus zum Irrealismus vollzog und die Literatur sich mit dem Symbolismus ihrer eigenständigen Position bewusst zu werden begann, ließ Robert Musil (1880-1942) beide in seinem ersten, 1906 veröffentlichten Roman Die Verwirrungen des Zöglings Törleß direkt aufeinander treffen. Anders als die meisten Schriftsteller und Philosophen seiner Zeit hatte Musil eine Ausbildung an einer Technischen Hochschule durchlaufen und 1901 die zweite Ingenieurprüfung mit der Gesamtnote »sehr befähigt« absolviert. Er spürte, dass mit den imaginären Zahlen etwas Neues entstand, das weit über bloße Rechenkonventionen hinausgeht, erhielt darauf jedoch keine Antwort. Im Törleß legt er diese Frage seiner Romanfigur in den Mund.
Törleß hat eine unbestimmte Erwartung über »die fürchterlichen Dinge«, die in der Mathematik geschehen. Schon als er das Zimmer seines Lehrers betritt und dessen einfache Einrichtung sieht, »(begann) sein Respekt [...] mißtrauischen Widerstreben zu weichen« – nicht nur gegenüber dem Lehrer, sondern auch gegenüber der Mathematik. Der Lehrer spürt die Frage nach dem Transzendenten und Übernatürlichen und wehrt sie ab. Er antwortet, was jeder wahrscheinlich schon einmal so oder ähnlich gehört hat:
»Was also die Mathematik anlangt, ist es ganz gewiß, daß hier auch ein natürlicher und nur mathematischer Zusammenhang besteht. Nur müßte ich – um streng wissenschaftlich zu sein – Voraussetzungen machen, die Sie kaum noch verstehen dürften, auch fehlt uns die Zeit dazu«.
»Ich gebe ja gerne zu, daß zum Beispiel diese imaginären, diese gar nicht wirklich existierenden Zahlwerte, ha ha, gar keine kleine Nuß für einen jungen Studenten sind. Sie müssen sich damit zufrieden geben, daß solche mathematische Begriffe eben rein mathematische Denknotwendigkeiten sind.«
Der Lehrer sieht seine Schüler »von der Wissenschaft weg zu religiösen Gesichtspunkten gezogen« und erkennt bei ihnen »ein empfängliches Gemüt für das feinere, ich möchte sagen göttliche und über uns hinausgehende Wesen der Moral«, worauf für ihn die Mathematik keine Antwort zu geben hat, auch nicht mit den imaginären Zahlen.
Der Roman von Musil blieb jedoch in der Literatur eine Ausnahme. Erst 100 Jahre später nahm der amerikanische Schriftsteller Thomas Pynchon (* 1937) das Thema wieder auf. Pynchon hatte zunächst Physik studiert und nach dem Krieg als technischer Redakteur beim Luftfahrtkonzern Boeing gearbeitet. In seinem großen Roman Gegen den Tag (2006) schreibt er in ausführlichen Darstellungen von der Begeisterung über komplexe Zahlen, Quaternionen und die Riemannsche Vermutung, die 1900 eine ganze Generation von Wissenschaftlern erfasst hatte und nicht zuletzt in Oxford und Göttingen eine fast magische Stimmung erzeugte, aus der sowohl die physikalischen Anschauungen der Relativitäts- und Quantentheorie wie auch die neue philostophische Strömung der Phänomenologie hervorgingen.
Cassirer zum Imaginären (1910 und ca. 1930)
Für den 6 Jahre älteren Ernst Cassirer (1874-1945) war wie für die meisten Philosophen seiner Zeit Kant das große Vorbild, aber ihm gelang früh eine Wende von Kant zu Leibniz, der gegenüber Kant nahezu in Vergessenheit geraten war. Mit Leibniz gewann Cassirer einen neuen Blick auf die Mathematik und hat in seinem frühen Hauptwerk Substanzbegriff und Funktionsbegriff von 1910 am Beispiel der von Leibniz eingeführten Symbole für den Differentialkalkül eine Wende in der Mathematik vom Operieren mit Zahlen zum Operieren mit Symbolen gesehen. Natürliche Zahlen beziehen sich unmittelbar auf natürliche Gegenstände (Substanzen) und deren Anzahlen, während mit mathematischen Symbolen Relationen zwischen mathematischen Objekten betrachtet werden, die es nur im Denken und der Einbildungskraft (Imagination) der Mathematik gibt.
Hätte es da nicht nahe gelegen, die von Euler eingeführten Symbole für imaginäre Zahlen näher zu betrachten? Allerdings sind schon von Leibniz nur wenige Bemerkungen über die imaginären Zahlen bekannt. Er hat mit ihnen gerechnet und verblüffende Ergebnisse gefunden, sie 1702 als »feine und wunderbare Zuflucht des göttlichen Geistes, beinahe ein Zwitterwesen zwischen Sein und Nichtsein« (»taque elegans et mirabile effugium reperit in illo analyseos miraculo, idealis mondi monstro, pene inter Ens et non Ens amphibium quo radicem imaginariam apellamus«) gesehen (Wikipedia abgerufen am 17.11.2017, deutsche Übersetzung durch Remmert, 48), und er hatte im Ganzen eine hohe Meinung von Cardano.
Cassirer sah jedoch in den imaginären Zahlen keine neue Denkart der Mathematik und vielleicht sogar der menschlichen Vernunft insgesamt, sondern für ihn vollendet sich mit den imaginären Zahlen eine Entwicklung, die bereits zur Einführung der negativen, irrationalen und transfiniten Zahlen geführt hat. Mit Berufung auf Gauß unterscheidet er zwischen Zahlen, die einen Substanzcharakter haben, und Zahlen mit einem Relationscharakter. Zum einen gibt es anfassbare Gegenstände mit einer eigenen Substanz, die gezählt werden können. Wer von Zahlen wie 2 oder 4 spricht, kann sich mühelos Gegenstände mit einer Anzahl von 2 oder 4 vorstellen. Anders ist es bereits bei den negativen Zahlen. Es gibt keine Gegenstände mit einer negativen Anzahl. Die negativen Zahlen entstehen erst im Denken und in der Einbildungskraft der Mathematiker, wenn diese sich auf rein formale Weise Zahlen vorstellen, die den bekannten positiven Zahlen entgegengesetzt sind. Cassirer zitiert Gauß:
»Positive und negative Zahlen können nur da eine Anwendung finden, wo das Gezählte ein Entgegengesetztes hat, was mit ihm vereinigt der Vernichtung gleich zu stellen ist. Genau besehen findet diese Voraussetzung nur da statt, wo nicht Substanzen (für sich denkbare Gegenstände), sondern Relationen zwischen je zwei Gegenständen das Gezählte sind.« (Cassirer, 72 mit einem Zitat aus einer Anzeige von Gauß über die Metaphysik der imaginären Zahlen von 1831).
Das wiederholt sich für Cassirer bei den Irrationalzahlen, den transfiniten und schließlich den imaginären Zahlen. Wer z.B. die Diagonale in einem Quadrat betrachtet, kann in ihr einen Gegenstand mit einer Anzahl 1 sehen, »eine Diagonale«. Aber ihre Länge ergibt sich nicht aus ihrem Gegenstandscharakter, sondern als Relation der Diagonale zur Außenseite des Quadrats, wie sie entsprechend der geometrischen Konstruktion gezeichnet wurde. Erst in der geometrischen Konstruktion treten im Bereich der Relationen Irrationalzahlen auf, die sich grundsätzlich von einfachen Anzahlen anfassbarer Gegenstände (Substanzen) unterscheiden. Ähnlich hat Cantor die transfiniten Zahlen konstruiert, und auf diese Weise versteht Cassirer die imaginären Zahlen. Sie ergeben sich nicht aus der Betrachtung realer Gegenstände, sondern aus einer mathematischen Konstruktion mit einer reellen und einer imaginären Achse, die es so nur im Denken der Mathematik gibt.
»Der Begriff und die Bezeichnung der 'imaginären' Zahl ist der Ausdruck eines Gedankens, der seinem ersten Ansatz nach bereits in jeder der neuen Zahlarten wirksam ist und der ihr das charakteristische Gepräge gibt. Es sind Urteile und Aussagen über 'Nicht-Wirkliches', die hier dennoch einen bestimmten, unentbehrlichen Erkenntniswert für sich in Anspruch nehmen.« (Cassirer, 71)
Damit hat Cassirer eine Grundeigenschaft der imaginären Zahlen getroffen, unterscheidet aber bewusst nicht die Besonderheiten der imaginären Zahlen etwa von den Irrationalzahlen. Alle diese Zahlen sind für ihn dem Denken der Mathematik entsprungen und beschreiben Relationen. Im Weiteren trat für ihn die Frage nach dem Imaginären in den Hintergrund. Erst aus dem Nachlass wurden die Vorarbeiten für einen geplanten 4. Band für die Philosophie der symbolischen Formen bekannt, aus denen Philipp Stoellger (* 1967) in seinem Beitrag Das Imaginäre der Philosophie der symbolischen Formen mit dem Untertitel Zum Imaginären als Figur des Dritten zwischen Symbolischen und Realem zitiert. Dort geht Cassirer noch weiter: Er sieht die imaginären Zahlen nicht nur in Gemeinsamkeit mit den negativen, irrationalen und transfiniten Zahlen, sondern mit der Kultur insgesamt.
»[D]ie Kultur ist [...] niemals eine reelle [,] sondern eine komplexe Größe (a + bi)[,] denn sie enthält eine ›imaginäre‹ (Sinn-)Einheit[.]« (Cassirer Nachgelassene Manuskripte und Texte Bd. 1 Zur Metaphysik der symbolischen Formen, Hamburg 1995, 245, zitiert nach Stoellger, 393).
Nach Stoellger sind für Cassirer die imaginären Zahlen weit über die Mathematik hinaus das Vorbild für den besonderen Status jeder Kultur. Die Kultur ist im reellen Leben verankert und geht aus ihm hervor, vermag sich daraus zu lösen und ein eigenes Reich der Vorstellung und Imagination zu schaffen, das jedoch nicht einfach im Nichts schwebt oder durch eine magische Grenze vom reellen Leben getrennt ist, sondern mit ihm verbunden bleibt und in es zurückführt. Nach Stoellger ist bei Cassirer »das Imaginäre als Figur des Dritten zwischen Symbolischem und Realem zu verstehen. Dass sich im Zeichen des ›Imaginären‹ auch Religion und Kunst anders verstehen lassen als allein im Verhältnis von Symbolischem und Realem« ist daraus eine Konsequenz« (Stoellger, 395). Was Cassirer mit Kultur meint, die sich vom realen Leben entfernt und wieder in es zurückkehrt, kann ungefähr verglichen werden mit der Idee des Zyklizitäts-Denkens, setzt aber den Schwerpunkt anders und entfernt sich stärker von dem Anliegen, hierfür eine eigene Logik zu finden.
Auf diesem Stand blieb die Philosophie seither stehen. Eine Generation nach Cassirer suchte der amerikanische Philosoph William Van Orman Quine (1908-2000) nach einer eigenen Antwort. Für ihn sind die imaginären Zahlen ein Beispiel für den Holismus. Für sich wirken sie unmöglich, und erst im Ganzen des Systems ergeben sich ihre Bedeutung und ihr Nutzen. Das ist bereits bei Cassirer angedeutet, wenn er von der Gesamtheit des Realen, Symbolischen und Imaginären spricht. Michael Otte gibt 2014 Hinweise zur philosophischen Diskussion der imaginären Zahlen.
»Die imaginären Zahlen blieben vom 17. bis zum 19. Jahrhundert sogar bloße Rechenmarken, bis Gauß u.a. eine geometrische Modellierung dafür vorschlugen, und dieses Modell wiederum gewann seine Bestätigung aus interner Kohärenz und externer Anwendung. Es ist es sehr häufig der Sinn und nicht die Bedeutung, der wichtig ist und zunächst weiterhilft!« (Otte, 117)
»In der Algebra Cardanos (1545) und Bombellis (1572) wird mit 'imaginären' Zahlen gerechnet, deren Bedeutung (Sinn) rein in ihrem Gebrauch liegt und die, wie ihr Name schon sagt, nichts empirisch Größenartiges darstellen.« (Otte, 165f)
Lacan zu den imaginären Zahlen (1958-1962)
Auch die Psychologie hat überraschend spät auf die imaginären Zahlen reagiert, obwohl Fragen der Einbildungskraft wie auch im engeren Sinn der Imago zu den Grundbegriffen der Psychologie zählen. Sigmund Freud (1856-1939) hat zwar auf dem Gebiet der Traumdeutung einen Paradigmen-Wechsel vollzogen und die Traumdeutung erstmals wissenschaftlicher Forschung zugänglich gemacht, indem er an den Träumen eine eigene Sprache oder Traumlogik nachweisen wollte (Verdichtung und Verschiebung von Trauminhalten), aber er scheint nie einen möglichen Zusammenhang zu den imaginären Zahlen gesehen zu haben. Carl Gustav Jung (1875-1961) hat zwar über die Imago gearbeitet und war seit 1931 mit dem Physiker Wolfgang Pauli (1900-1958) bekannt. Pauli kam zu ihm in psychologische Behandlung. Ihn verfolgte die Zyklizität der Quantenmechanik bis in die Träume. In einem Brief an Jung berichtet er von folgendem Traum:
»Traum: (...) Da spricht der Blonde: 'Die Männer, deren Frauen die Rotation objektiviert haben, sind angeklagt.' (...) Bald nachdem der Neger mit dem Zettel fortgegangen war, kommt wirklich meine Frau und sagt zu mir: 'Du hast vergessen mir gute Nacht zu sagen'. (...) Mit dem eindringlichen Ton eines Lehrers fährt er (der Blonde, t.) fort: 'Aber Sie wissen doch, was Rotation ist!' 'Natürlich' sage ich sofort 'der Kreislauf und die Zirkulation des Lichtes das gehört doch zu den Anfangsgründen'. (Da spricht der Blonde: 'Jetzt verstehen Sie die Männer, deren Frauen ihnen die Rotation objektiviert haben'. Nun küsse ich meine Frau und sage ihr: 'Gute Nacht! Es ist ganz entsetzlich, was diese armen Menschen leiden, die da angeklagt sind!' Ich werde sehr traurig und weine. Aber der Blonde sagt lächelnd: 'Nun halten Sie den ersten Schlüssel in der Hand.« (Brief von Pauli an Jung 28.10.46, zitiert in Pauli, 34f)
Es kam auch zu einer wissenschaftlichen Zusammenarbeit. In einer gemeinsamen Broschüre veröffentlichten Pauli eine Arbeit über Kepler und Jung über die Synchronizität. Doch wurde das Thema der imaginären Zahlen nicht aufgegriffen. Dazu kam es erst mit Lacan mit verblüffenderweise ähnlichen Ergebnissen wie bereits bei Cassirer.
Jacques Lacan (1901-1981) entwickelt einen weit über die Mathematik hinausgehenden Begriff des Imaginären, der für ihn die menschliche Existenz und das Denken im Ganzen bestimmt. Für ihn sind das Reale, das Symbolische und das Imaginäre drei Bereiche, die aufeinander angewiesen sind und nur wechselweise aus- und miteinander erklärt werden können. So gesehen führt Lacan im Strukturalismus konsequent den Holismus von Quine weiter, jedoch beschränkt er seine Untersuchung nicht auf die Stellung der imaginären Zahlen innerhalb mathematischer Kalküle. Aber an den imaginären Zahlen lässt sich klarer als an anderen Beispielen zeigen, was er meint: Die imaginären Zahlen blieben bloße Traumgebilde, wenn sie nicht nach klaren Regeln auf dem Boden der reellen Zahlen entstehen und zu ihnen zurückkehren würden. Diese Regeln lassen sich nur formulieren, wenn eine eigene Symbolsprache gefunden wird. Auf der anderen Seite blieben die reellen Zahlen (das Reale) flach und tot, gäbe es nicht die Einbildungskraft, mit der die Bewegung der aus ihnen hervorgehenden imaginären Zahlen beschrieben werden kann. Und ebenso würden die Symbole wie e, i oder  nichts-sagend bleiben, gäbe es nicht die Bewegung und die Operationen der imaginären Zahlen, mit und an denen sie ausgeführt werden.
nichts-sagend bleiben, gäbe es nicht die Bewegung und die Operationen der imaginären Zahlen, mit und an denen sie ausgeführt werden.
Rolf Nemitz stellt die Stellen zusammen, an denen Lacan von imaginären Zahlen spricht:
»Eine imaginäre Zahl ist eine Zahl, deren Quadrat eine negative reelle Zahl ist, beispielsweise  . Statt von 'imaginären Zahlen' sprach man früher von 'unmöglichen Zahlen' (vgl. Lacan: 'Das Reale ist das Unmögliche').
. Statt von 'imaginären Zahlen' sprach man früher von 'unmöglichen Zahlen' (vgl. Lacan: 'Das Reale ist das Unmögliche').
Auf imaginäre Zahlen bezieht Lacan sich erstmals in Seminar 6, Das Begehren und seine Deutung, 1958/59 (Sitzung vom 22. April 1959), er sagt hier, das menschliche Leben könne als ein Kalkül definiert werden, dessen Null irrational wäre, und er fügt hinzu, dies sei eine mathematische Metapher und der Ausdruck 'irrational' beziehe sich auf eine imaginäre Zahl,  . Er erläutert dann, dass er darunter einen Signifikanten versteht, der nicht subjektiviert werden kann. (Vgl. Seminar 6, Version Miller S. 387 f.)
. Er erläutert dann, dass er darunter einen Signifikanten versteht, der nicht subjektiviert werden kann. (Vgl. Seminar 6, Version Miller S. 387 f.)
Im Aufsatz Subversion des Subjekts und Dialektik des Begehrens im Freud'schen Unbewussten (geschrieben 1962) heißt es über  : 'Es ist das, was dem Subjekt fehlt, um sich durch sein Cogito ausgeschöpft zu denken, nämlich das, was es an Undenkbarem ist', ein 'Fehlen im Meer der Eigennamen' (J. Lacan: Schriften. Band II. Vollständiger Text. Übersetzt von Hans-Dieter Gondek. Turia und Kant, Wien 2015, S. 325-368, hier: S. 358). Näher ausgeführt wird das in Seminar 9, Die Identifizierung, 1961/62, in den Sitzungen vom 10. Januar 1962 und vom 2. April 1962.
: 'Es ist das, was dem Subjekt fehlt, um sich durch sein Cogito ausgeschöpft zu denken, nämlich das, was es an Undenkbarem ist', ein 'Fehlen im Meer der Eigennamen' (J. Lacan: Schriften. Band II. Vollständiger Text. Übersetzt von Hans-Dieter Gondek. Turia und Kant, Wien 2015, S. 325-368, hier: S. 358). Näher ausgeführt wird das in Seminar 9, Die Identifizierung, 1961/62, in den Sitzungen vom 10. Januar 1962 und vom 2. April 1962.
Der Ausdruck 'Funktion der reellen Zahlen' steht hier für die Funktion, durch die – wie Lacan annimmt – die reellen Zahlen definiert werden können.« (Nemitz Imaginäre Zahlen bei Jacques Lacan, Fußnote 36)
Alain Sokal (* 1955) kritisierte, dass Lacan in Seminar 6 irrationale und imaginäre Zahlen gleichsetzt und offenbar »die Materie, auf die er seine Behauptungen gründe, nicht verstanden habe« (Marius Erdt Eleganter Unsinn, Koblenz 2004, 13). Aus Perspektive von Cassirer wird jedoch klar, wie Lacan das gemeint hat.
Inhaltlich hat Lacan den Grundgedanken von Cassirer mit vielen Beispielen aus der Psychologie füllen können und fand beeindruckende Bilder wie den borromäischen Knoten, um die wechselseitige Abhängigkeit des Realen, Imaginären und Symbolischen darzustellen, doch ist auch er nicht tiefer auf die mathematischen Eigenschaften der imaginären Zahlen eingegangen.
Literatur
Hans-Jürgen Caspar: Imaginärer Kreis, Link
Ernst Cassirer: Substanzbegriff und Funktionsbegriff, Berlin 1910
Richard Feynman: The Feynman Lectures on Physics, Volume 1, Chapter 22: Algebra; Link
Wilhelm Forst und Dieter Hoffmann: Funktionentheorie erkunden mit Maple; Link
Klaus Fritzsche: Grundkurs Funktionentheorie, Heidelberg 2009
Auszüge und Bonusmaterial auf der Seite des Springer-Verlag
Lutz Führer: Kubische Gleichungen und die widerwillige Entdeckung der komplexen Zahlen; Link
Helmut Gericke: Mathematik im Abendland, Berlin u.a. 1990
Brian Gill: Why i? The Historical Roots of 'Imaginary' Numbers, Link
Thomas und Brigitte Görnitz: Der kreative Kosmos, Heidelberg, Berlin 2006
Hans Humenberger: Wie können die komplexen Zahlen in die Mathematik gekommen sein?; Link
Jacques Lacan: Seminar XVIII, 8. Sitzung (19. Mai 1971); Link
Christian B. Lang, Norbert Pucker: Mathematische Methoden in der Physik, Heidelberg 2010 [2005]
Matheplanet: Funktionentheorie existenziell - Sartres Residuensatz; Link
Rolf Nemitz: Imaginäre Zahlen bei Jacques Lacan; lacan_entziffern vom 27.1.2017
Max Neunhöffer: Wie schaffte es E8 in die Schlagzeigen?; Link
Michael Otte: Analytische Philosophie, Hamburg 2014
Wolfgang Pauli, C.G. Jung: Ein Briefwechsel 1932 - 1958, Heidelberg u.a. 1992
Helmut Pulte: Das Prinzip der kleinsten Wirkung und die Kraftkonzeptionen der rationalen Mechanik, Stuttgart 1989
Reinhold Remmert: Komplexe Zahlen
in: Ebbinghaus u.a. (Hg.) Zahlen, Berlin, Heidelberg 1983
Jürgen Roth: Die Zahl i - phantastisch, praktisch, anschaulich
in: Mathematik lehren, Heft 121, Dezember 2003, S. 47-49; Link
George Spencer-Brown: Laws of Form, New York 1972 (Julian Press) [1969]; Link
Philipp Stoellger: Das Imaginäre der Philosophie der symbolischen Formen
in: Birgit Recki (Hg), Philosophie der Kultur - Kultur des Philosophierens, Hamburg 2012, 393-420; Link
Raymond Swing: Formale und generative Dialektik, Kopenhagen 2006; online
Caspar Wessel: Über die analytische Repräsentation der Richtung, [1797]; Link
Wikibooks: Komplexe Zahlen: Darstellung komplexwertiger Funktionen – Mathe für Nicht-Freaks; Link