Die Kraft der Trägheit in Hegels Wissenschaft der Logik

Version 28.6.2020

Was ist Trägheit? Eine mechanische Eigenschaft der Materie oder ein psychischer Charakterzug eines antriebsarmen Menschen, eine Kraft, die alles auszubremsen vermag oder der erfolgreiche Widerstand, der vor innerem und äußerem Zerfall bewahrt, ein Gesetz, ein Axiom oder ein Prinzip? Wie wirkt sie mit und gegen andere Kräfte? Ein klassisches Beispiel: Intuitiv scheint die Trägheit einen Planeten in Richtung der Tangente von seiner geschlossenen Bewegungsbahn aus dem Sonnensystem hinaus ins All zu tragen, gäbe es nicht die entgegenwirkende Anziehungskraft zur Sonne hin. So sah es Newton, aber diese Vorstellung lässt sich weder mathematisch noch physikalisch halten. Oder sollte eine »träge Rotation« von sich aus stur auf ihrer Kreisbahn verharren und sich ewig weiter drehen, ein »träges Leben«, sich allem Neuen und Unerwartetem verweigernd? Trägheit, Schwere und Masse scheinen sich zirkulär aufeinander zu beziehen. Unterliegt die Trägheit einer Art begrifflich-unbegrifflicher Schwammigkeit, wodurch sie erfolgreich jede vernünftige Begriffsbildung unterläuft? In diesem Beitrag sollen die verschiedenen Ebenen und Gesichtspunkte entwirrt werden, die bisher den Zugang zu Hegels Verständnis der Trägheit erschweren. Es soll gezeigt werden, wie ausgehend von Hegels Ansatz eine Klärung der physikalischen Grundlagenbegriffe von Zeit, Relativitäts- und Quantentheorie gelingen könnte.

Ausblick: Gewissermaßen mitlaufend soll deutlich werden, wie Hegel die klassische Vorgehensweise der Mathematik und Naturwissenschaft umkehrt. Beispiel: Statt einfach festzustellen, wie in den Formeln der Fallbewegung und der kinetischen Energie ½ · m · v² die Geschwindigkeit v im Quadrat auftritt oder die Planeten auf Ellipsen verlaufen, bereitet Hegel den Gedanken vor, dass umgekehrt aus den Begriffen des Quadrats bzw. der Ellipse die entsprechenden Gesetze zu bestimmen sind. Das sind für ihn Beispiele einer begrifflichen Herleitung. Sie werden hier zusammengetragen und sollen in einem weiteren Beitrag systematisch entwickelt werden, wofür als Grundlage Hegels Ausführungen zur Objektivität und zur Idee dienen werden. An diesem Punkt ist jedoch aus meiner Sicht der Ansatz von Hegel zu verlassen. Sicher ist es notwendig, erst einmal zu verstehen, wie er das gemeint hat. Für mich ergeben sich jedoch aus der weiteren Entwicklung der Naturwissenschaft im 20. Jahrhundert neue Ansätze, um zu erklären, warum die Zeit und die Geschwindigkeit im Quadrat auftreten, und es ist eine offene Frage, welche Konsequenzen das für eine Weiterentwicklung der Hegelschen Naturphilosophie hat.

Einleitung

Die Trägheit ist für Hegel kein Randphänomen oder Spezialthema der Mechanik, sondern steht im Zentrum seiner Philosophie. Er sah in der Trägheit der Materie eine grundsätzliche Schranke, an der letztlich jede Aufklärung scheitert, die sich nur auf ihre eigene Vernunft verlässt. Im Sinne des christlichen Glaubens vermag sich für ihn ein Denken nicht aus der Trägheit der Materie und des Verstandes zu befreien, solange es nicht von einem göttlichen Geist beflügelt ist. Schon in seiner ersten größeren Veröffentlichung 1801 über die Differenz des Fichteschen und Schellingschen Systems der Philosophie zieht er die Grenzlinie zwischen der »Hartnäckigkeit des gesunden Menschenverstandes« und der »Kraft seiner Trägheit« einerseits und dem »Bewußtsein« andererseits (HW 2.35). Das war auch politisch gegen seine Vorgänger Kant und Fichte gemeint. 1799 hatte Fichte nach dem Atheismus-Streit seinen Lehrstuhl in Jena verlassen müssen, als er an den Zielen der Aufklärung und der Französischen Revolution festhielt. Gegen die aufklärerische Religionskritik wollten Schelling und Hegel die Philosophie wieder an das Absolute als ihren Ausgangspunkt binden, will sie nicht in Verstandesdenken und Materialismus hängen bleiben. Das trifft für Hegel letztlich auch auf Kant zu, weswegen dessen Philosophie nun »vom Buchstaben geschieden und das rein spekulative Prinzip aus dem Übrigen herausgehoben« werden muss (HW 2.9).

In jungen Jahren hatte sich Hegel vom »Sturm« der Französischen Revolution und der Philosophie von Kant mitreißen lassen. Wer davon ergriffen war, den ließ er nicht mehr los. »Diesem Sturm gibt Hegel den Namen 'Geist'« (Picht, S. 406). Hegel wollte seine früheren Ideale nicht verraten, sondern in sein System der Philosophie aufnehmen und in gewisser Weise sogar mit größerer Konsequenz weiter führen. Daher steht und fällt sein Anliegen damit, ob und wie es ihm gelingt, die Differenz zwischen der Materie als dem Träger der Trägheit und dem Bewußtsein »in einer höheren Potenz wieder zur Synthese zu  konstruieren« (HW 2.35, Hervorhebung von mir). Die Kraft der Trägheit kann nicht einfach zurückgewiesen, überwunden oder gebrochen werden, sondern sie ist in die Konstruktion einer höheren Philosophie aufzunehmen und muss dort in der gesuchten Synthese ihre tragende Bedeutung erlangen.

Bevor der Frage nach der  Kraft der Konstruktion  nachgegangen wird, mit der die Kraft der Trägheit überwunden und zugleich genutzt und aufgehoben werden kann, soll in diesem Beitrag gezeigt werden, wie Hegel in der Wissenschaft der Logik schrittweise den Begriff der Trägheit aufwertet und entwickelt, bis er im Kapitel über den mechanischen Prozess zur Erkenntnis kommt, auf welche Weise mechanische Objekte dank ihrer Widerstandsfähigkeit Mitteilungen einer höheren Ordnung aufnehmen und sich von ihnen in Bewegung setzen lassen können. Erst hier ist für ihn das Thema Trägheit umfassend erschlossen. Das Verstandesdenken wird mit seiner Kraft der Trägheit als ein (bloß) mechanisches Denken beschrieben, das gleichwohl im Gang der Wissenschaft der Logik einen notwendigen Schritt darstellt. Hegel will nachweisen, wie der Mechanismus mit seiner Fähigkeit, Mitteilungen aufnehmen und weiter geben zu können, gerade dank seiner Trägheit einen unerlässlichen Schritt für die Entwicklung zu einer objektiven Logik darstellt und zugleich aus sich selbst heraus weiter drängt zum Chemismus und Organismus und schließlich zur Idee. Damit hat für ihn die Kraft der Trägheit ihren genau bestimmten Beitrag geleistet. Sie kehrt im weiteren nur noch wieder als immanente Kraft innerhalb der höheren Objektivität und der Idee, wenn sie den Zusammenhalt des Mediums des Chemismus sichert, den Bestand und die Wirkungsweise der Arbeitsmittel (Organon) garantiert, die während ihres Gebrauchs der Vernutzung Widerstand leisten und dadurch einsatzfähig sind, und schließlich in der Konstruktion der absoluten Idee und der Beständigkeit ihrer Werke aufgehoben wird.

(1) Trägheit als Verzögerung. In der sinnlichen Wahrnehmung und in experimentellen Beobachtungen kann Trägheit nur als Verzögerung (Hemmung) sichtbar werden. Gäbe es keine Trägheit, dann würden alle Kräfte instantan wirken, und es gäbe keine Zeit. Ein Stein, der von der Erde angezogen wird, würde ohne Trägheit nicht entlang einer zeitlichen Bewegungsbahn auf die Erde fallen, sondern er würde ohne zeitliche Dauer in dem Moment seinen Ort wechseln von seinem Anfangsort zu einem neuen Ort auf der Erdoberfläche, in dem die Gewichtskraft wirkt. Dagegen haben alle experimentellen Beobachtungen und die auf ihnen aufbauenden mathematischen Darstellungen gezeigt, dass die Bewegung eine Funktion der Zeit ist. Dass es überhaupt zu einem zeitlichen Ablauf kommt, liegt an der Trägheit der Körper, die erst in Bewegung gebracht und dann in fortlaufender Beschleunigung zu ihrem neuen Ort bewegt werden müssen.

Die Kraft der Trägheit ist daher keine Kraft, die zu den anderen Kräften hinzukommt und gemeinsam mit ihnen in die Erhaltungsgröße aller Kräfte aufgenommen werden muss, sondern sie ist im Gegenteil rechnerisch gleich groß wie alle anderen Kräfte und stellt ein dynamisches Gleichgewicht her, in dem sich Aktion und Reaktion auf ähnliche Weise wie Soll und Haben ausgleichen (Prinzip von d'Alembert). Es wird keine zusätzliche Kraft verbraucht, um etwas träge zu machen und in seiner Trägheit zu erhalten, und es geht umgekehrt keine Kraft verloren, um die Trägheit zu überwinden. Die Trägheitskraft bewirkt lediglich, dass sich alle anderen Kräfte im Widerspiel mit der Trägheit im Zeitverlauf entwickeln und nur dadurch zeigen können. Gäbe es keine Trägheit, würden alle anderen Kräfte unmittelbar wirken und wären nicht wahrnehmbar. Ohne Trägheit gäbe es nur Geometrie und keine Mechanik.

Schon dieses Verständnis zeigt, in welcher Weise über Kant hinauszugehen ist. Kant hatte die Eigenschaften der Zeit in Dauer, Kausalität und Gleichzeitigkeit gesehen. Trägheit liegt ihnen zugrunde. (a) Ohne Trägheit gäbe es keine Dauer und keine Zeit. An der Dauer kann die Trägheit empirisch gemessen werden. Etwas dauert so lange, wie es die Kraft der Trägheit erfordert. (b) Kausalität wird sich im mechanischen Prozess als Mitteilung einander widerstehender (träger, elastischer) Körper erweisen: Es kommt nur zu Kausalität, wenn ein Körper träge genug ist, eine Mitteilung aufnehmen und durch sie seinen Bewegungszustand ändern zu können. Gäbe es keine Trägheit, würden äußere Impulse wirkungslos durch ein Objekt hindurchgehen und verpuffen. (c) Gleichzeitigkeit wird bereits von Kant als die Gemeinschaft gedeutet, in der zwei Objekte miteinander kommunizieren und sich mechanische Eigenschaften wie den Impuls mitteilen. Im Ergebnis wird nicht Trägheit aus den Eigenschaften der Zeit, sondern diese aus der Trägheit erklärt. Dadurch bekommt Trägheit eine übergreifende Bedeutung, die nicht nur die Eigenschaften der Zeit, sondern auch andere Phänomene als die Zeit erklären kann. Die Trägheit geht der Zeit in logischem Sinn voraus. Wenn Hegel aus der Logik die Grundbegriffe der Natur entwickeln will, ist die Trägheit der Schlüsselbegriff. Plakativ gesagt ist die Trägheit innerhalb der Logik die Proto-Zeit, mithilfe derer aus der Logik der Übergang zur Natur und der dort waltenden Zeit gelingt. (Es wird sich zeigen, dass Kant diesen Sichtwechsel bereits vermutet und in seiner Schrift über die Metaphysischen Anfangsgründe der Naturwissenschaft vorbereitet hat, ohne ihn konsequent ausführen zu können.)

Trägheit bekommt in diesem Sinn eine Bedeutung, die dem neuplatonischen Begriff des Abstandes (gr. diastema, lat. distantia, engl. distance) ähnelt und damit der vom Neuplatonismus betrachteten Proto-Zeit. Trägheit verändert nicht Ursache und Wirkung und fordert keine zusätzlichen Kräfte heraus, sondern Trägheit führt ausschließlich dazu, dass zwischen Ursache und Wirkung ein zeitlicher Abstand aufgerissen wird. Ursache und Wirkung fallen nicht zeitlich ineins, sondern der Beginn und der Abschluss der Wirkung sind durch eine zeitliche Distanz voneinander getrennt. Das wäre ohne die Trägheit nicht möglich.

Anmerkung: Hegel nimmt den Begriff des Abstandes nicht in seine Wissenschaft der Logik auf, sondern spricht von Anziehung und Abstoßung (Repulsion und Attraktion), wodurch für ihn die Größe entsteht. Es bleibt daher vorerst offen, in welchem Verhältnis der räumliche (euklidische) Abstand der Geometrie und der durch Trägheit hervorgerufene zeitliche Abstand dynamischer Ereignisse in der Mechanik stehen. Seit Hilbert wird versucht, eine übergreifende Geometrie zu entwerfen, innerhalb derer ein Abstand definiert werden kann, der gleichermaßen für Zeit und Raum gilt. Wird an eine Rekonstruktion der Hegelschen Wissenschaft der Logik und Naturphilosophie gedacht, scheint mir der Begriff des Abstandes maßgeblich zu sein. Wenn es gelingt, ihn wie ein Prinzip an den Beginn der Philosophie zu stellen, dann kann im Weiteren auch eine Alternative gefunden werden, anders als Hegel die Grundbegriffe der Naturwissenschaft nicht aus den Begriffen des Quadrats, des Kubus und der Ellipse zu entwickeln, sondern aus Begriffen wie dem des Abstandes. Die hier aufgeworfenen philosophischen Fragen sind in den Kommentaren zu den Prinzipien einer Meta-Mathematik bzw. Mathematik nach Aristoteles weiter ausgeführt.

(2) Trägheit als negative Beschleunigung (das Maß der Trägheit). Die verzögernde Wirkung der Trägheit lässt sich nicht direkt nachweisen, sondern nur indirekt. Das gelang Newton mit einer einzigartigen Leistung, die zurecht als Gründungsakt der modernen Naturwissenschaft angesehen wird: Er trennte die Begriffe Kraft, Impuls und Energie voneinander und zeigte zugleich ihren inneren, mathematisch bestimmbaren Zusammenhang: Sie verhalten sich mathematisch zueinander wie eine Funktion zu ihrer ersten und zweiten Ableitung. Für ihn galten Mathematik und Naturphilosophie nicht unabhängig voneinander, sondern er verstand die von ihm erstmals aufgezeigten mathematischen Beziehungen zwischen den Grundbegriffen der Mechanik als die Mathematischen Prinzipien der Naturphilosophie. Empirisch lassen sich Kraft, Impuls und Energie nicht unmittelbar wahrnehmen, sondern wahrgenommen werden Bewegungskurven von Objekten (z.B. die Bewegungsbahnen der Planeten, fallender Körper, etwa wenn ein Apfel vom Baum fällt, Kugeln auf einer schiefen Ebene, etc.). Die Bewegungsbahnen lassen sich mathematisch beschreiben, wofür bereits Galilei und Kepler wichtige Vorarbeiten geleistet hatten. Aber erst Newton erkannte, dass es sich nicht nur um die sichtbare Bewegungsbahn handelt, sondern dass mithilfe der von ihm eingeführten mathematischen Ableitung aus diesen Bewegungsbahnen die Veränderung und Erhaltung der zugrunde liegenden Kraft, Impuls und Energie berechnet werden können. Erst als auf diese Weise die Kraft bestimmt werden konnte, die einer beobachteten Bewegung zugrunde liegt, konnte auch in Negation dieser Kraft die ihr entgegenwirkende Kraft der Trägheit bestimmt werden.

Wie im Weiteren näher ausgeführt werden wird, konnte Newton zeigen, dass sich ausgehend von der Bewegungsgleichung des freien Falls ›s(t) = ½ g · t^²‹ als erste Ableitung die Momentangeschwindigkeit ›v(t) = g · t‹ und als zweite Ableitung die Kraft ›F = m · a‹ ergeben. Hier stehen s für distance, t für time, v für velocity, F für force, m für mass, a für acceleration und die Konstante g für die empirisch messbare Fallbeschleunigung. Die Bewegungsgleichung beschreibt, welche Strecke s ein Objekt nach Ablauf einer Zeit t gefallen ist. – Die Trägheit ergibt sich rein formal als die der Kraft entgegenstehende Trägheitskraft
›FT = −F = −(m · a)‹.

Niemand bezweifelt die Wahrheit dieser Gleichungen, und die Physik hat sie im Weiteren fortlaufend verallgemeinern und für andere Rahmenbedingungen konkretisieren können. Aber es kann auch niemand sagen, was der Ausdruck t^² bedeuten soll, d.h. was man sich unter der Zeit im Quadrat vorzustellen hat. Das wird einfach als notwendige Konsequenz der mathematischen Formeln und ihrer Rechenregeln hingenommen. An diesem Punkt setzt Hegel an. Er kehrte die Perspektive um: Für ihn ist es nicht eine rein mathematische Erkenntnis, dass die Zeit im Quadrat auftritt, sondern er fragt, warum der Differentialkalkül als mathematisches Arbeitsmittel für die Beschreibung der Bewegung anwendbar ist. In einem für die Naturwissenschaft und Mathematik bis heute völlig ungewohnten Gedanken vertritt Hegel die Überzeugung, dass sich innerhalb des von Newton und Leibniz betrachteten Grenzübergangs die  Figur des Quadrats  erhält, d.h. gegenüber dem Grenzübergang träge ist, und dies sogar im Nulldurchgang verschwindender Größen. Daher ist für Hegel nicht die Frage, warum sich aus der mathematischen Darstellung der Bewegung die Potenzierung der Zeit ins Quadrat ergibt (und nicht einmal diese Frage wird heute gestellt, sondern es wird erwartet, die mathematischen Formeln als gegeben zu akzeptieren), sondern er will umgekehrt zeigen, wie sich aus dem Quadrat und seinen qualitativen Eigenschaften die Bewegungsformel ergibt. Das setzt ein völlig anderes Verständnis des Differentialkalküls voraus, siehe hierzu den Beitrag Hegels Herleitung des Differentialkalküls aus der qualitativen Potenzbestimmung.

(3) Trägheit als Umkehrung. Doch es gibt nicht nur Kräfte entlang der Verbindungslinien zwischen zwei Körpern, die einander abstoßen und anziehen, sondern auch mehrdimensionale Gebilde können sich im Ganzen ändern. Eine Platte kann sich erwärmen, das Gleichgewicht eines chemischen Gemisches kann bei Zutropfen bestimmter Stoffe schlagartig umkippen, Wasser kann großflächig zu Eis gefrieren oder verdampfen usw. Mit dem Übergang in höhere Dimensionen scheint sich eine grenzenlose Freiheit aufzutun, die unendlich viele Bewegungsmuster und keinerlei Regelmäßigkeit erkennen lässt und dadurch der Wissenschaft unzugänglich bleibt. So hat es auch noch Kant gesehen, für den die zeitgenössische Chemie »zuletzt bloß empirisch« vorzugehen vermochte und »daher eher systematische Kunst, als Wissenschaft« sei (MAN, AA 04: 468.24 und 468.29). Hegel ist es mit seinen Ausführungen über das reale Maß gelungen, hier Ordnungen zu erkennen. Er hat die ihm vorliegenden Ergebnisse der Chemie auf ihre logische Struktur analysiert und in ihnen Wahlverwandtschaften und Knotenlinien unterschieden mit dem Ergebnis, dass sich unterschiedliche Zustände herausbilden, die sich jeweils durch eine eigene Ordnung stabilisieren. In jedem Zustand lassen sich innere Faktoren unterscheiden, die nicht voneinander unabhängig sind, sondern in umgekehrten Verhältnis zueinander stehen. Wird der eine Faktor größer, dann wird der andere kleiner. Dadurch ergibt sich im Ganzen auch für höherdimensionale Bewegungen eine Trägheit, die das unkontrollierte Ausbrechen einzelner Parameter verhindert. Das klassische Beispiel ist das schwingende Pendel: Wird die kinetische Energie größer, dann wird die potentielle Energie kleiner. Beide gleichen sich genau aus, und im Ganzen wird die Energie erhalten (ist träge gegenüber dem Bewegungsverlauf).

In diesem Sinn versteht Hegel das Trägheits-Phänomen der die Sonne umkreisenden Planeten anders als Newton. Newton sieht hier einen eindimensionalen, mechanischen Vorgang, bei dem eine Kraft und ihr entgegen eine Trägheitskraft wirken. Newton zerlegt jeden Punkt der Bewegungsbahn in ein Parallelogramm voneinander unabhängiger Kräfte, die auf diesen Punkt wirken (Tangential- und Radialkraft, die entlang der Tangente bzw. zum Zentrum gerichtet sind). Er deutet die Tangentialkraft als Trägheitskraft, was sich jedoch weder mathematisch noch mechanisch halten lässt (siehe dazu unten Anmerkung 3 und 4 zum Trägheitsprinzip). Hegel folgt dagegen Kepler und betrachtet die Bewegung des Planeten im Ganzen. Für ihn ist nicht die Trägheit des Planeten, sondern die Erhaltung (Trägheit) der elliptischen Bewegungsbahn und mit ihr das als Einheit verstandene Bewegungssystem aus Sonne und Planeten das Bewegungsprinzip. Es setzt sich nach Kepler zusammen aus zwei inneren Faktoren, die im umgekehrten Verhältnis zueinander stehen: Das sind nicht wie bei Newton zwei voneinander unabhängige Kräfte, sondern die Momentangeschwindigkeit des Planeten und sein jeweiliger Abstand zur Sonne. Wenn der Abstand eines Planeten zur Sonne kleiner wird, wird seine Geschwindigkeit größer, und umgekehrt. Dadurch bleibt die Figur der Bewegungsbahn als Ellipse erhalten. Das kann mit Kepler auch so formuliert werden, dass in gleichen Zeiteinheiten die von der Verbindungslinie des Planeten zur Sonne überstrichene  Fläche  immer gleich ist.

Anders als Newton vermag Hegel mit Kepler das Phänomen der Planetenbewegung mathematisch zutreffend zu beschreiben: Die in der Planetenbewegung auftretende Trägheit liegt nicht in einer Kraft, die entlang der Tangente der Bewegungsbahn wirkt, sondern in der Erhaltung der in gleichen Zeiteinheiten überstrichenen Fläche (Invarianz, Symmetrieerhaltung). Diese Erhaltung ist gegeben, weil sich der Abstand zur Sonne und die Momentangeschwindigkeit im umgekehrten Verhältnis zueinander befinden. Mit der Umkehrung wird sichergestellt wird, dass die Planetenbahn auf einer geschlossenen Ellipse verläuft und nicht ausbricht. Die Änderung des einen Faktors wird dadurch ausgeglichen, dass sich der andere Faktor gegenläufig verändert. Dieser Erkenntnis wäre nicht möglich, wenn die Planeten auf Kreisen verliefen, da sich auf dem Kreis der Abstand zur Sonne nie ändert. Hegel bringt es auf den Punkt: In der Darstellung von Newton könnten die Planeten auch auf Kreisen verlaufen, in der Darstellung von Kepler nicht (Erstes Keplersches Gesetz, siehe hierzu Enz. § 270, HW 9.86).

Eine andere Frage ist, welche Ursache die Trägheit der Planetenbewegung hat und ob sie ewig fortdauern wird. Seit Kant ist die Astrophysik überzeugt, dass das Planetensystem eine eigene Geschichte hat. Es ist entstanden aus der Urwolke und wird sich wieder auflösen, wenn die Sonne einen Großteil ihrer Energie verbraucht hat. Hegel lehnt Kants Theorie der Geschichte des Himmels ab und scheint von der Ewigkeit des Planetensystems überzeugt zu sein.

Hegel konnte nicht voraussehen, wie es mit der Relativitätstheorie gelingen sollte, auch für die Zeit drei innere Dimensionen zu erkennen. Die Zeit ist damit ebenfalls ein mehrdimensionales Phänomen, das sich mit den Begriffen des realen Maßes beschreiben lässt. Das soll in diesem Beitrag im Abschnitt über die Ordnung der Zeit ausgeführt werden. Auch die Zeit lässt sich in innere Faktoren zerlegen. Alles, was in einer Beziehung schneller wird, wird zugleich in anderer Beziehung langsamer. Mithilfe der neueren Erkenntnisse der Relativitätstheorie und Astrophysik kann die Zeit auf ähnliche Weise beschrieben werden, wie Hegel in der Wissenschaft der Logik die Wahlverwandtschaften, Knotenlinien und die Ordnung der chemischen Sphäre entwickelt hat. Auch für die Zeit gibt es Dimensionalität, reale Maße, Umschlag von Quantität in Qualität, Kontinuität, Umkehrung, Ordnung. Die Trägheit ist dann keine spezifische Eigenschaft der Zeit mehr, sondern gehört zur logischen Ordnung, mit der alle realen Phänomene darzustellen sind.

Mit diesem Ansatz lässt sich meines Erachtens die Frage nach dem begrifflichem Verhältnis von Relativitätstheorie und Quantentheorie klären. Die logische Struktur der Quantenzustände kann auf die gleiche Weise wie die chemische Wahlverwandtschaft und deren Zustände beschrieben werden (siehe den Beitrag Das reale Maß). Wenn es gelingt, auch die Ordnung der Zeit auf diese Weise darzustellen, dann ist gezeigt, dass Chemie, Quantentheorie und Theorie der Zeit auf die gleichen Grundlagen zurückgehen. Es handelt sich bei ihnen allen entgegen dem üblichen Verständnis nicht um ein mechanisches, sondern um ein chemisches Phänomen, wenn Chemie in dem weiten Sinn verstanden wird, wie Hegel in der Lehre vom realen Maß die »Logik der chemischen Sphäre« begründet.

(4) Trägheit als Widerstand. Der logisch voll entwickelte Begriff der Trägheit wird für Hegel erst mit dem Begriff des Widerstandes erreicht. Erst wenn im Gang der Wissenschaft der Logik vom daseienden Etwas über die zur Existenz gekommenen Dinge und ihre Wirklichkeit schließlich das formal-logische Subjekt erreicht ist, dem Prädikate zugeschrieben werden, über das Urteile gefällt und mit dem Schlüsse gezogen werden können, kann der Begriff eines konkreten, vollständigen und selbständigen  Objekts  entfaltet werden. Das Neue am Objekt liegt darin, dass es Mitteilungen aufnehmen und weiter geben kann. Das ist auf den ersten Blick »ganz mechanisch« gedacht: Einem mechanischen Objekt wird ein Impuls »mitgeteilt«, den es aufnimmt und weiter gibt.

Für Hegel geht der von der Mechanik verwendete Begriff der Mitteilung jedoch wesentlich weiter. Ein Objekt kann nur eine Mitteilung aufnehmen, weil es dem anderen Objekt einen Widerstand leistet. Andernfalls würde die Mitteilung ungehört verhallen und spurlos durch das Objekt hindurchgehen. Wenn der Widerstand des Objekts überwältigt wird, liegt das jedoch nicht an der Übermacht eines anderen Objekts, wie die Formulierungen Hegels bisweilen nahelegen und missverstanden werden können, sondern an der höheren Macht der Sprache, in der die Mitteilung formuliert ist. Es hat nicht ein Objekt A ein anderes Objekt B überwältigt, sondern A ist einer Sprache mächtig, mit der es B erreichen und ansprechen kann. Es ist die Eigendynamik der Sprache, über die sowohl A wie auch B verfügen, durch die die Mitteilung ankommt, der sich B nicht entziehen kann.

Auf diese Weise wird der Widerstand für Hegel zum entscheidenden Argument für seinen ontologischen Gottesbeweis: Der Mensch wird dank seines Widerstands nicht einfach von der göttlichen Mitteilung überwältigt, sondern kann ihr standhalten und sie aufnehmen. Und zugleich ist es dem Widerstand verdankt, dass die Botschaft den Menschen nicht wirkungslos erreicht, sondern ihn berührt und existenziell erzittern lässt. Durch die höhere Macht der Sprache (und nicht durch die überwältigende Übermacht einzelner Objekte A gegenüber anderen Objekten B) gelangt der Mensch in eine gemeinsame Sphäre mit Gott, in der Gott ihn ansprechen kann. So wie im mechanischen Prozess nicht mechanische Gesetze mitgeteilt werden, sondern Impulse, so werden im Gespräch nicht die dem Menschen unzugänglichen göttlichen Gesetze der Sprache mitgeteilt, sondern diese  zeigen  sich im Gelingen der Kommunikation. Wittgenstein hat es auf den Punkt gebracht: »Was sich in der Sprache ausdrückt, können wir nicht durch sie ausdrücken.« (TLP, 4.121) Der Mensch erbebt unter der Mitteilung und gewinnt eine negative Vorstellung der Übermacht dessen, der ihn angesprochen hat.

Trägheit erweist sich als das gesuchte Zwischenglied, um von der euklidischen Geometrie zur Mechanik zu gelangen. In der euklidischen Geometrie gibt es keinen Widerstand. Jeder Punkt und jede Figur können frei durchschnitten werden. Eine Gerade verläuft durch Punkte, sie kann einen Kreis schneiden etc. Erhält dagegen jeder Punkt einen Widerstand, mit dem die auf ihn auftreffenden anderen Punkte konfrontiert werden und ihn nicht wie in der Geometrie durchdringen, sondern ihn nur beiseite schieben können, dann wird aus dem Punkt der Geometrie das punktförmige Partikel der Mechanik und verallgemeinert der Physik. Dort treten an die Stelle der einander schneidenden Figuren der Geometrie die Feldlinien, die sich nirgends schneiden. (Einstein hat diesen Gedanken umgekehrt, wenn für ihn eine Geometrie, in der sich die Feldlinien nirgends schneiden, Ausdruck eines mit Materie gefüllten Raums ist.) (Dieser Begriff des Widerstandes soll bis auf die Ebene der Zahlen untersucht werden: Wenn die Mathematik in dieser Weise in die Mechanik übergeht, wandeln sich nicht nur die masselosen, geometrischen Punkte in mechanische Partikel, sondern auch die einzelnen Zahlen werden mit jeweils einem eigenen Gewicht aufgeladen. Das führt zur Idee von ogkischen, gewichtigen Zahlen.)

(5) Trägheit als Autonomie. Mit Trägheit ist ein bestimmter Freiheits-Begriff verbunden, der nur im mechanischen Prozess gilt (Autonomie des mechanischen Objekts, Multitude der mechanisch verbundenen Gesamtheiten von Objekten, die jeweils ihre innere Freiheit bewahren). Im mechanischen Prozess sind die aufeinander wirkenden Objekte völlig gleichberechtigt. Es gibt zwar ein Zentrum, aber dies liegt im mathematisch berechenbaren Schwerpunkt, der sich außerhalb aller beteiligten Objekte befinden kann. Nur unter sehr vereinfachten Bedingungen, – wenn ein einzelnes Objekt wesentlich größer als alle anderen ist (wie die Sonne gegenüber den Planeten) –, fallen das Zentrum des mechanischen Systems und ein bestimmtes Objekt des Systems zusammen. Im Ganzen gilt aber die volle Autonomie (Selbständigkeit) der einzelnen Objekte. Keins von ihnen verfügt über eine dominierende Macht, sondern die Macht liegt in der außer ihnen liegenden Sprache, in der die Mitteilungen des Systems formuliert werden. Jedem einzelnen Objekt erscheint die Sprache als etwas Jenseitiges. Und zugleich bleiben die Objekte einander fremd, da keins die Autonomie des anderen durchbrechen und sich an dessen Stelle setzen oder es auch nur von innen verstehen kann.

Diese Sicht legt nahe, den von Kant und seinen Nachfolgern vertretenen spezifischen Freiheits-Gedanken auf die mechanische Sphäre zu beschränken. Sie ist notwendig, aber begrenzt. Hegel ist überzeugt, dass hier und nur hier ein strenges moralisches Reglement gelten kann, wie Kant es formuliert hat. Hegel nennt für den mechanischen Prozess ausdrücklich auch die »Sitten« als eine der höheren Mächte, die sich in der von ihnen formulierten Sprache (den sittlichen Forderungen) mitteilen (HW 6.416). Kein einzelner Mensch kann beanspruchen, für sich als Instanz der moralischen Ordnung zu gelten und sich über die anderen zu erheben. Sie können einander nur die moralischen Forderungen mitteilen, aber deren Macht ergibt sich aus dem Sittengesetz und nicht aus deren Wächtern. Das bedeutet weiter, dass eine negative Theologie im Sinne von Kierkegaard und Wittgenstein aus Sicht von Hegel nur für die mechanische Sphäre gilt, da nur hier dem einzelnen mechanischen Objekt die ihm mitteilbare allgemeine Sprache transzendent bleibt. Für Hegel gilt das Christentum in einer anderen Sphäre. Zwischen mechanischen Objekten gibt es keine Liebe. Diese erfordert weitere Momente, die erst mit der Wahlverwandtschaft und Geschlechtsbeziehung der chemischen Sphäre und der Lebendigkeit der organischen Sphäre entstehen. (In seiner Konstellation der ästhetischen, ethischen und religiösen Sphäre hat Kierkegaard sich auf Grundlage des christlichen Glaubens dieser Überzeugung von Hegel wieder angenähert, wobei die ethische Sphäre mit der mechanischen Sphäre verglichen werden kann.)

(6) Trägheit als Auflösung. Trägheit richtet sich letztlich auch gegen sich selbst. Was in einen Zustand der Erstarrung gerät, verliert seine Widerstands-Kraft und damit seine Trägheit. Es erschöpft sich. Der Mechanismus geht über in den Chemismus. Dort bekommt die Trägheit als Zusammenhalt des Mediums eine völlig neue Bedeutung.

Die empirisch beobachtbare Bewegungsbahn des freien Falls

Um Hegels Gedanken zu verstehen, soll von einer Betrachtung der Bewegungsbahn des freien Falls und einer typischen Darstellung durch die zeitgenössische Physik ausgegangen werden. Mit dem bloßen Auge sind der genaue Bewegungsverlauf eines Steines oder die Parabel eines Wurfgeschosses nur schwer zu erkennen. Galilei führte daher zahlreiche Experimente durch, mit denen er untersuchte, wie z.B. eine Kugel auf einer schiefen Ebene beschleunigt wird. Sie wird durch die Reibung verlangsamt, und wenn dieser Effekt wieder herausgerechnet wird, kann die Bewegung des freien Falls berechnet werden.

Im Ergebnis zeigt sich, dass die Bewegung eines fallenden Körpers durch drei Komponenten beeinflusst wird: (a) Der Ort sA, an dem die Bewegung beginnt, (b) die Anfangsgeschwindigkeit vA, die der Gegenstand bei Beginn der Bewegung bereits hat, (c) die Anziehung zur Erde. Im folgenden Diagramm können idealtypisch einige Fälle unterschieden werden, um schrittweise die Zerlegung der Bewegungsbahn zu verstehen:

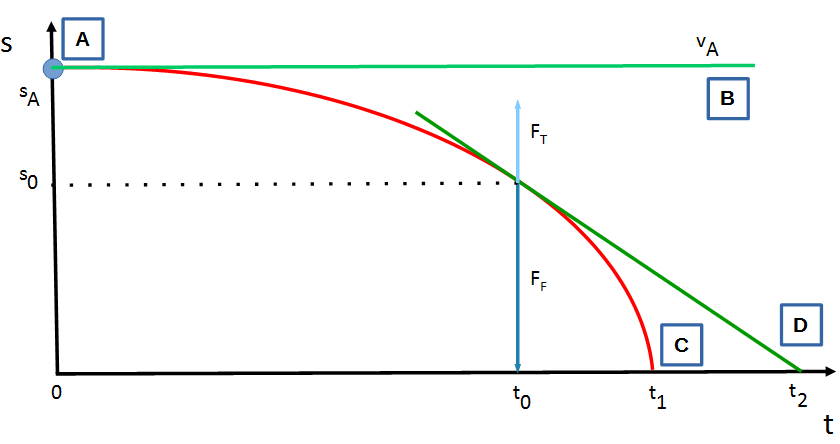
Figur 1  Bewegungsbahn des freien Falls
Die nach oben gerichtete s-Achse zeigt den Abstand (die Strecke s) eines fallenden Körpers von der Erdoberfläche, die nach rechts gerichtete t-Achse den Zeitverlauf. Die rot gezeichnete Parabel zeigt, wie der Körper mit fortlaufend größerer Geschwindigkeit zur Erde fällt.

[A] Eine Kugel befindet sich zur Zeit t=0 in einer Anfangsentfernung sA von der Erde. Wenn die Kugel ruht und keinerlei Kräfte auf sie wirken, würde sie diese Position unverändert beibehalten und sich nicht von der Stelle rühren. Der Abstand des Körpers zur Erdoberfläche bleibt unverändert. Das ist graphisch durch die hellgrüne Gerade dargestellt, die parallel zur t-Achse verläuft.

[B] Wenn sich die Kugel mit der Anfangs-Geschwindigkeit vA parallel zum Erdboden in eine beliebige Richtung bewegt, würde sie ausgehend von der gleichen Position sA wie in [A] diese Bewegung unendlich beibehalten, sofern keine sonstigen Anziehungskräfte auf sie wirken. Mit [B] ist daher die Aussage von [A] dahin erweitert, dass jeder Körper seinen aktuellen Bewegungszustand erhält, wenn keine äußeren Kräfte auf ihn wirken. Das wird als seine Trägheit bezeichnet. Der Bewegungsverlauf ist in diesem Diagramm identisch mit dem Bewegungslauf von [A], da in beiden Fällen der Gegenstand den Abstand zur Erdoberfläche nicht ändert.

[C] Wenn jedoch zusätzlich eine Gewichtskraft FF wirkt, die die Kugel zum Fall auf die Erde bewegt, dann entsteht eine Bewegung, die sich aus seiner eigenen Anfangsgeschwindigkeit und der Gewichtskraft zur Erde zusammensetzt. Würde die Kugel zur Zeit 0 keine eigene Bewegung haben, dann würde sie senkrecht zur Erde fallen. Die resultierende Bewegungsbahn ist mit der roten Parabel dargestellt. Die Kugel wird im Zeitpunkt t1 auf dem Erdboden auftreffen.

Die Zerlegung der resultierenden Bewegung in innere Faktoren kann an jedem beliebigen Zeitpunkt erfolgen. Hier ist als Beispiel die Zeit t0 gewählt. In diesem Moment befindet sich der Gegenstand im Abstand s0 von der Erde (durch die gepunktete Linie angedeutet), und es wirkt die Gewichtskraft FF, die senkrecht zur Bodenfläche gerichtet und mit einem blauen Strich dargestellt ist. Gleichzeitig ist die Anfangsgeschwindigkeit vA erhalten geblieben. Die Kugel fliegt aber jetzt nicht mehr wie zur Zeit t=0 parallel zur Erde, sondern ihre Bewegungsrichtung ist durch den Fall in der Zeit von t=0 bis t0 verändert worden und erfolgt in diesem Zeitmoment in Richtung der dunkelgrün eingezeichneten Tangente.

[D] Würde im Zeitmoment t0 die Gewichtskraft aufhören zu wirken, dann würde die Kugel entlang der dunkelgrünen Tangente weiterfliegen und zum Zeitpunkt t2 auf der Erde auftreffen.

Anmerkung: Die blau gezeichneten Kräfte FT und FF zeigen die auf den Körper wirkende Gewichtskraft und Trägheitskraft (gestichelt). Die Kraft FF ist auf die Erde gerichtet, FT in die entgegengesetzte Richtung von der Erde weg. Beide Kräfte sind gleich groß und werden werden in späteren Kapiteln genauer erläutert.

Die mathematische Bewegungsgleichung

Im Ergebnis zahlreicher Beobachtungen konnte der Bewegungsverlauf mathematisch beschrieben werden. Diese Formel hat sich in allen Experimenten bestätigt.

(1)   s(t) = ½ g · t^² + vA· t + sA

lies: Die Funktion s(t) beschreibt die Bewegungskurve eines fallenden Körpers. Sie zeigt die Veränderung des Abstandes zur Erdoberfläche, der entsprechend allgemeiner Nomenklatur mit ›s‹ bezeichnet wird (distance, Strecke) im Zeitverlauf t. Sie setzt sich von rechts nach links gelesen aus drei Summanden zusammen:
– sA ist der Anfangspunkt. Das ist die Höhe, aus der der Körper zu fallen beginnt.
– Die Strecke vA· t, die der Körper aufgrund seiner Anfangsgeschwindigkeit vA im Verlaufe der Zeit t zurückgelegt hat.
– Und schließlich die Strecke, die der Körper aufgrund der Gewichtskraft im Verlaufe der Zeit t in Richtung Erdoberfläche gefallen ist, das ist ½ g · t^². Die Konstante ›g‹ steht für die empirisch gemessene Fallbeschleunigung.

In dieser Darstellung ist sehr klar zu erkennen, wie sich der Anteil der Anfangsgeschwindigkeit nur linear mit der Zeit auswirkt: ›vA· t‹, während der von der Gewichtskraft bewirkte Anteil mit dem Quadrat der Zeit wächst: ›½ g · t^²‹. Daher setzt sich der Anteil der Gewichtskraft im Verlaufe der Zeit immer mehr durch und die Bewegungsbahn beugt sich zur Erde hin.

Diese Gleichung kann auf spezielle Fälle angewendet werden:

Fall 1, Bewegung zum Zeitpunkt t=0:

(2)   s(0) = ½ g · 0^² + vA· 0 + sA = sA

lies: Im Anfangspunkt befindet sich der Körper im Abstand sA von der Erde und bewegt sich noch nicht.

Fall 2, Bewegung zum Zeitpunkt t0:

(3)   s(t0) = ½ g · t0^² + vA· t0 + sA

lies: Zum Zeitpunkt t0 bewegt sich der Körper entsprechend der Bewegungsgleichung.

Fall 3, der Körper befindet sich anfangs in Ruhe, d.h. es gilt vA = 0:

(4)   s(t) = ½ g · t^² + 0 · t + sA = ½ g · t^² + sA

lies: Wenn der fallende Körper am Anfang ruht und keine Geschwindigkeit hat, vereinfacht sich die Bewegungsgleichung.

Hegel betrachtet den Fall 3 eines Körpers, der aus einer Position der Ruhe heraus zu fallen beginnt, und er vereinfacht nochmals die Schreibweise. Er vernachlässigt den Anfangsort sA, um den reinen Bewegungsverlauf unabhängig vom Anfangsort zu beschreiben, und setzt a = ½ g. Statt s(t) schreibt er abgekürzt s. Daraus ergibt sich die von ihm zitierte Bewegungsgleichung (HW 5.346):

(5)   s = a · t^²

lies: Gegenüber Gleichung (4) wird der Anfangsort sA nicht berücksichtigt, und es wird a statt ½ g gesetzt. Dadurch wird erkennbar, dass die Bewegungsbahn des frei fallenden Körpers eine Parabel ist.

In dieser Form ist hervorgehoben, worauf es Hegel ankommt: Die Gewichtskraft wirkt im Quadrat der Zeit.

Das Trägheitsprinzip und das d'Alembertsche Prinzip als Axiome der Mechanik

Als es gelungen war, für die Verlaufsform einer mechanischen Bewegung eine mathematische Formel aufzustellen und diese empirisch zu bestätigen, stellte sich die Frage, ob sich auch Axiome finden lassen, aus denen diese Gleichung hergeleitet werden kann, so wie beispielsweise in der Geometrie der Satz des Pythagoras auf die euklidischen Axiomen zurückgeführt werden kann. Anders gefragt: Können Axiome gefunden werden, aus denen sich die Bewegungsgleichungen von Kepler und Galilei ableiten lassen, die jeweils aus empirischen Beobachtungen hervorgegangen waren? Das war der Anspruch von Newton. Hegel bezeichnet das als »nicht-empirischen Beweis« (Enz. § 267, HW 9.75). Die euklidischen Axiome genügen nicht, denn sie kennen keinen Zeitbegriff. Die euklidische Geometrie gilt unabhängig von der Zeit. Eine geometrische Konstruktion kann zwar in eine Folge einzelner Konstruktionsschritte zerlegt werden, aber in den Gang der Konstruktion geht die Zeit nicht ein. Die Reihenfolge der Schritte ist rein logisch bestimmt. Sie können im Prinzip innerhalb eines einzigen Zeitmoments erfolgen.

Obwohl nur bei solchen Körpern, die über eine Masse verfügen, von Bewegung gesprochen werden kann, enthalten die Gleichungen von Galilei und Kepler keine Variable für die Masse. Sie gelten für alle Körper unabhängig davon, wie groß die Masse ist. Es wirkt wie ein mathematischer Trick, wenn beispielweise bei Aufstellung der Gleichung für den freien Fall die Masse »herausgekürzt« werden kann. Das liegt an einer Besonderheit der mathematischen Einheiten: Während es offenbar sinnlos ist, von einer Bewegung eines Körpers mit einer Masse von m = 0 zu sprechen, kann eine Einheitsmasse von m = 1 immer mitgedacht werden. Daraus ergeben sich zwei erste Anhaltspunkte, wie ein Axiomensystem schrittweise aufgebaut werden könnte:

(I) Raum-Axiome: Rein geometrische Axiome nach dem Vorbild von Euklid, die ausschließlich räumliche Verhältnisse beschreiben.

(II) Zeit-Axiome: Axiomatische Einführung der Zeit, aus der Bewegungsgesetze abgeleitet werden können, in denen unabhängig von der Masse der bewegten Körper Zeit und Raum verknüpft werden. Beispiele für Bewegungsgesetze dieser Art sind die genannte Bewegungsgleichung und die Keplerschen Gesetze, in denen noch nicht die Masse auftritt.

(III) Masse-Axiome: Axiomatische Einführung der Masse, um die Bewegungen zu beschreiben, für die die Masse der bewegten Körper bzw. des Mediums, durch das sie sich bewegen, von Bedeutung sind.

Dies Programm konnte jedoch bis heute nicht zufriedenstellend ausgeführt werden. Alle mechanischen Axiomensysteme gehen auf Newtons Mathematische Prinzipien der Naturphilosophie von 1687 zurück. Euler, d'Alembert, und Lagrange haben sie in ein vollständiges System gebracht, dessen unmittelbar vor der Französischen Revolution 1788 veröffentlichtes Lehrbuch Mécanique analytique bis heute grundlegend für alle weiteren Arbeiten ist (siehe den dort ausgeführten Lagrange-Formalismus). (Hegel erwähnt das Buch in seiner Darstellung des Falles, HW 9.77 Fußnote.)

Während Axiome des Raums seit Euklid in widerspruchsfreier Form formuliert werden konnten, ist es der Mechanik bis heute nicht gelungen, Axiome der Zeit und der Masse klar voneinander zu trennen. In allen Entwürfen werden sie letztlich zirkulär auseinander entwickelt (siehe dazu die Arbeiten von Max Jammer). Wer mit dem Raum beginnen will, muss dessen Eigenschaften aus der Verteilung der Materie im Raum erklären. Wer mit der Materie anfangen will, muss ihre räumliche Ausgedehntheit erklären. Wer mit der Zeit anfangen will, muss sich auf die Trägheit und ihre Dauerhaftigkeit beziehen und damit auf träge, massehaltige Objekte, an deren Bewegung Zeit erkennbar ist. Daraus hat sich auch der von Hilbert gewählte Ansatz nicht befreien können. Statt die euklidische Geometrie um Axiome zu erweitern, mit denen zeitliche Prozesse und Bewegungen massehaltiger Körper beschrieben werden können, wollte er den in der euklidischen Geometrie gebrauchen Abstand dahin verallgemeinern, dass mit ihm auch die Abstände zeitlicher Vorgänge (früher, später) und Veränderungen körperlicher Eigenschaften (leichter und schwerer, kompakter und durchlässiger) beschrieben werden können. Das hat den von der Physik verwendeten Formalismus zweifellos erheblich verbessert, letztlich jedoch keinen Ausweg aus der Zirkularität gezeigt. Es hat aber den Rahmen geschaffen, innerhalb dessen eine Lösung zu suchen ist.

Kant und Hegel haben sich mit dieser Situation niemals abgefunden und bis zu ihrem Tod nach einer von der Philosophie zu entwickelnden Lösung gesucht. Hegel hat zeitlebens – angefangen mit seiner Habilitation über die Planetengesetze bis zur zweiten Auflage des ersten Bandes der Wissenschaft der Logik kurz vor seinem Tod – versucht, hierauf eine eigene Antwort zu finden.

Die heutige Physik versucht einen Mittelweg. Am Beispiel eines typischen, über Internet verfügbaren Vorlesungsskripts soll gezeigt werden, wie üblicherweise die Ableitung der Bewegungsgleichung aus dem Trägheitsprinzip als Axiom der Mechanik erfolgt (Jörg Ihringer Experimentalphysik I in Tübingen, Link, Übersicht über das vollständige Skript: Link).

(6.1) FF = m · g	Ansatz: Es gibt eine beschleunigende, messbare Fundamentalkraft FF, in diesem Beispiel die auf der Erde wirkende Gewichtskraft. Die Gewichtskraft beschleunigt einen Körper, der sich frei im Raum oberhalb der Erde befindet, an jedem Punkt seiner Bewegungsbahn entsprechend seiner Masse m und der empirisch gemessenen Fallbeschleunigung g, bis er auf der Erde aufschlägt und dort liegen bleibt. Während die Fallbeschleunigung g konstant ist, ist die Kraft um so größer, je größer die Masse m des Körpers ist. Das entspricht der alltäglichen Erfahrung: Wer umgekehrt einen Körper von der Erde aufheben möchte, muss um so mehr Kraft aufwenden, je größer die Masse des Körpers ist. Warum die Konstante g eine Fallbeschleunigung beschreibt und die Geschwindigkeit während des freien Falls nicht immer gleich bleibt oder sogar kleiner wird, wird in diesem Ansatz nicht weiter begründet, sondern als empirisches Faktum hingenommen, welches zuerst von Galilei beobachtet worden war. ⏵ Diese Kraft ist in Figur 1 als blaue Linie eingezeichnet, die senkrecht zum Boden führt.
(6.2) FT = −m · a	Trägheitsprinzip: Entgegenwirkende Trägheitskraft FT Die Trägheitskraft wird an jeder Stelle der Bewegungsbahn durch die einwirkende Kraft hervorgerufen. Sie ist proportional zur Masse und zur Momentan-Beschleunigung im jeweiligen Zeitpunkt. Sie kann nicht für sich beobachtet werden, sondern muss als eine der Fundamentalkraft entgegenwirkende Kraft axiomatisch gesetzt werden. Wenn keine Kraft von außen einwirkt und der Bewegungszustand des Körpers erhalten bleibt, gibt es auch keine entgegenwirkende Kraft. Gedankenexperiment: Bei einem freien Fall im Fahrstuhl bewirkt die entgegenwirkende Trägheitskraft, dass der Fall nicht wahrgenommen werden kann. Experimentell wurde nachgewiesen, dass unabhängig von Gewicht und Masse alle Körper gleich schnell fallen. Wenn der Fahrstuhl auf den Boden aufschlägt, wird mit dem freien Fall zugleich die entgegenwirkende Trägheitskraft abrupt gestoppt. Das hat die gleiche Wirkung, als würde ein schnell fahrender Körper auf eine Mauer prallen. Hatten die Insassen im Fahrstuhl bis dahin den freien Fall nicht wahrgenommen, erleben sie jetzt einen massiven Zusammenstoß mit dem Boden unter ihren Füßen. ⏵ In Figur 1 ist für den Zeitpunkt t=0 durch einen blauen Kreis der Moment gezeichnet, in dem beide Kräfte 0 sind. Für die Zeit t0 ist eingetragen, wie der Gewichtskraft FF die Trägheitskraft FT entgegenwirkt.
(6.3) m · g − m · a = 0	d'Alembertsches Prinzip: Die Fundamentalkraft FF und die Trägheitskraft FT gleichen sich genau aus. ⏵ In Figur 1 bedeutet das, dass im Zeitpunkt t0 die beiden Kräfte, die entlang der blauen und hellblauen Linie einander entgegen wirken, genau gleich groß sind.
(6.4) m · a = m · g	Andere Darstellung des d'Alembertschen Prinzips. Die Trägheitskraft vergrößert bzw. verkleinert sich im gleichen Maß wie die jeweilige Fundamentalkraft. Gleichung (6.4) geht mathematisch aus Gleichung (6.3) hervor, wenn in Gleichung (6.3) auf beiden Seiten m · a addiert und anschließend die Seiten vertauscht werden.
(6.5) a = g	Gleichung (6.4) kann vereinfacht werden, indem auf beiden Seiten durch m geteilt wird. Die Bewegungsgleichung gilt unabhängig von der Masse des bewegten Körpers.
(6.6) v(t) = g · t + vA	Momentangeschwindigkeit nach Verlauf der Zeit t Gleichung (5) wird auf beiden Seiten über die Zeit integriert. Entsprechend den üblichen Ableitungsregeln ergibt sich auf der rechten Seite die lineare Funktion g · t und die Integrationskonstante vA. Die Konstante vA wird interpretiert als die Anfangsgeschwindigkeit des frei fallenden Körpers. Das bedeutet: Die Momentangeschwindigkeit ist die Summe der Anfangsgeschwindigkeit plus dem Produkt aus der Fallbeschleunigung g und der seit Beginn des freien Falls verstrichenen Zeit t. Durch die Anziehung erhöht sich die Geschwindigkeit fortlaufend. Auf der linken Seite wird das Integral der Beschleunigung a als Geschwindigkeit v bezeichnet.
(6.7) s(t) = ½ g · t² + vA· t + sA	Bewegungsgleichung Gleichung (6.6) wird nochmals auf beiden Seiten über die Zeit integriert. Das Ergebnis ist der Ort, an dem der fallende Körper nach Verlauf der Zeit t angekommen ist. Entsprechend den Regeln der Ableitung ergibt sich auf der rechten Seiten als Integral der linearen Funktion g · t die quadratische Funktion ½ g · t², als Integral der Anfangsgeschwindigkeit vA die lineare Funktion vA· t und die neue Integrationskonstante sA, die als der Ort interpretiert wird, an dem sich der Körper bei Beginn des Falls befunden hat. Auf der linken Seite wird das Integral der Geschwindigkeit v als Abstand (distance) s bezeichnet.

Mit dieser Entwicklung ist die gleiche Bewegungsgleichung hergeleitet, die bereits empirisch beobachtet worden war. Sie erscheint jetzt jedoch als notwendiges Ergebnis, wenn von der Theorie das Trägheitsprinzip und das d'Alembertsche Prinzip des Kräftegleichgewichts vorausgesetzt werden.

Die axiomatische Ableitung zeigt sehr deutlich, was empirisch beobachtet werden kann, und was im Verlauf der Geschichte der Physik theoretisch als Axiom gesetzt wurde.

Anmerkung 1 (Qualität und Relation): Die Trägheit erscheint auf den ersten Blick wie eine typische Eigenschaft eines Körpers, etwa seine Farbe, Größe, sein Geruch oder seine Gestalt. Es klingt ähnlich, wenn gesagt wird ›diese Kugel ist träge‹ oder ›diese Kugel ist schwarz‹, ›diese Kugel hat einen Durchmesser von 5 cm‹, ›diese Kugel ist 300 g schwer‹. Den Physikern wurde jedoch bald klar, dass die Trägheit eine besondere Eigenschaft ist, und sie unterschieden daher Masse und Trägheit. Während das Gewicht wahrgenommen und mit einer Waage gemessen werden kann, verhält es sich bei der Trägheit anders. Sie kann nicht mit einer Waage, einer Uhr oder einem Zollstock gemessen werden. Und doch ist sie körperlich zu spüren, wenn man z.B. von einem Ball oder einer Wasserwelle getroffen wird und diese einen umzuwerfen oder mitzureißen drohen. Ein ähnliches Phänomen ist der Rückstoß bei einem Gewehrschuss. – Wie groß ist die wahrgenommene Trägheit? Sie ist abhängig vom Gewicht und der Geschwindigkeit, mit der ein träger Gegenstand auftrifft oder abgefeuert wird. Ein Geschoss mit größerem Kaliber richtet größeren Schaden an, und dieser ist um so größer, je schneller er ist. – Und es zählt nur die relative Geschwindigkeit: Es ist ein Unterschied, ob ich frontal von einer Welle getroffen werde, wenn ich in das Wasser gehe, oder wenn ich vor der heranrollenden Welle fliehe und sie mich von hinten trifft. Das ist ein erster Hinweis, dass die Trägheit nur als Relation zwischen unterschiedlich bewegten Körpern wahrnehmbar ist, aber nicht unmittelbar an einem Körper. Sie ist relativ in Bezug auf den Bewegungszustand des Beobachters.

Anmerkung 2 (Träger und Substrat): Der Ausdruck »Trägheit« ist mit dem Wort »Träger« verwandt, worauf Wandschneider hinweist.

»Ohne äußeren Anstoß behält der Körper seinen jeweiligen Bewegungszustand bei. Er ist bloßer Träger des Bewegungszustands und insofern träge. (Fußnote 8: Wenn ich recht sehe, ist ein solches Wortspiel beim frühen Hegel intendiert, insofern die träge Materie als eine Substanz bestimmt wird, die den Begriff des Körpers, gegen Ruhe und Bewegung gleichgültig zu sein, 'trägt' (Jenaer Realphilosophie, ed. J. Hoffmeister, Hamburg 1931, 22)« (Wandschneider, 1987, S. 295).

Dieser Gedanke kann weitergeführt werden, wenn der Träger verglichen wird mit dem Substrat. Das Substrat ist der Träger der Zustände, in denen es auftritt: Zum Beispiel ist das Wasser der Träger seiner Zustände Eis, Flüssigkeit, Dampf. Das Wasser als solches kann nicht wahrgenommen werden, sondern nur im jeweiligen Zustand (Eis, Flüssigkeit, Dampf). Auf den ersten Blick wird jeder glauben, ein Eisblock, ein Eimer Wasser, eine Wolke Dampf seien unterschiedliche Gegenstände, so wie ein Baum, eine Blume und ein Haufen Sand unterschiedliche Gegenstände sind. Erst wenn beobachtet wird, wie Eis, Flüssigkeit und Dampf ineinander übergehen können, wird darüber indirekt verständlich, dass es eine gemeinsame Grundlage geben muss, die sich von dem einen Zustand in den anderen Zustand verändert. – Und so wie das Vorhandensein eines Substrats nur indirekt erschlossen werden kann, wenn es Zustände gibt, die sich ineinander umwandeln und hierbei ein unterliegendes Substrat erhalten, so zeigt sich die Trägheit nur indirekt darin, wenn sich unterschiedliche Bewegungszustände verändern und ineinander übergehen. An dieser Veränderung zeigt sich indirekt, wie über die Veränderung der Bewegungszustände hinweg eine innere Eigenschaft erhalten bleibt. Das ist die Trägheit, die in jedem Bewegungszustand gilt. Sie kann wie ein Substrat nur indirekt aus der Veränderung der Zustände erschlossen werden. Der Vergleich der Trägheit mit einem Substrat und seinen Zuständen wird im folgenden an weiteren Beispielen fortgeführt (siehe Anmerkung 4 zu Hegels Deutung der Planetenbewegung und das Kapitel über die Ordnung der Zeit).

Anmerkung 3 (Trägheitskraft und Trägheitsprinzip): Neuser unterscheidet in seiner Einleitung zur Neuübersetzung von Hegels Habilitationsschrift Philosophische Erörterung über die Planetenbahnen (1801) zwischen Trägheitskraft und Trägheitsprinzip. Bei Analyse der Planetenbewegung durch Newton hatte der Ausdruck ‘Trägheitskraft’ eine andere Bedeutung als später in der Darstellung durch d'Alembert, was zu einiger Verwirrung führen kann. Neuser betont, dass das d'Alembertsche Prinzip übergreifend gilt: Jede Fundamentalkraft ruft eine entgegenwirkende Kraft hervor. Beim freien Fall wirkt die Trägheitskraft der Gewichtskraft entgegen. Auf ähnliche Weise sind bei der Planetenbewegung die Zentripetal- und Zentrifugalkraft zu unterscheiden. Die Zentripetalkraft ist direkt zur Sonne hin gerichtet, während die Zentrifugalkraft von der Sonne weg weist. Das Trägheitsprinzip besagt, dass es zu jeder Kraft eine entgegengerichtete Trägheitskraft gibt, und das d'Alembertsche Prinzip, dass die entgegengerichtete Kraft in jedem Zeitmoment gleich groß ist wie die Fundamentalkraft. (Diese beiden Prinzipien sind in den Gleichungen (2) und (3) dargestellt.)

Wie ist dann zu erklären, warum auf der Erde die Gegenstände entsprechend Figur 1 auf einer Parabel zum Boden fallen, während die Planeten nicht in die Sonne stürzen, sondern auf ihren Bahnen verbleiben? Das kann aus den bisher genannten Axiomen nicht abgeleitet werden. Es muss eine zusätzliche dritte Kraft geben.

   

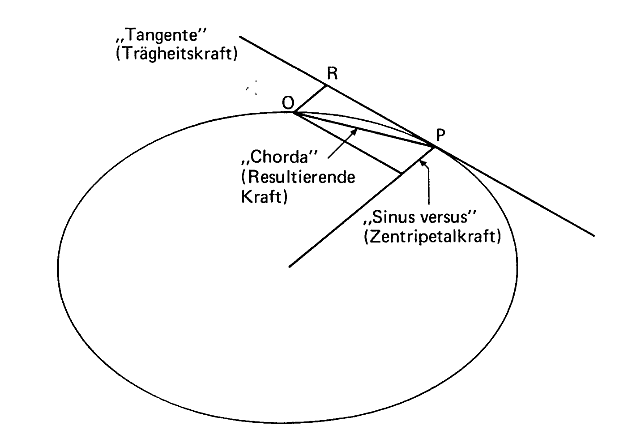
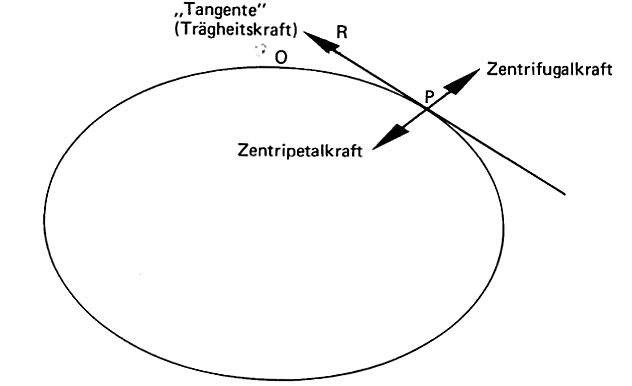
Figur 2a, 2b   Trägheitskraft nach Newton und Zentrifugalkraft nach d'Alembert
Quelle: Neuser, S. 14 und S. 15

Figur 2a: Newton zerlegt die Kraft der Planeten an jeder Stelle mit einem Kräfteparallelogramm in zwei Komponenten: Eine wirkt tangential entlang der Bahn und wird von ihm als »Trägheitskraft« bezeichnet, die andere ist zur Sonne gerichtet (»Sinus versus«, Zentripetalkraft). Hieraus bildet sich resultierend die Diagonale (»Chorda«), die zu dem nächsten Punkt auf der Bewegungsbahn verweist, den der Planet erreichen wird.

Figur 2b: Während Newton nur zwei Kräfte unterscheidet (die als Trägheitskraft gedeutete »Tangente« und den als Zentripetalkraft gedeuteten »Sins versus«), aus denen er die aus beiden »resultierende Kraft« ableitet und als »Chorda« bezeichnet, erkennt d'Alembert, dass drei Kräfte wirken müssen: Zwei Kräfte (die Zentripetal- und Zentrifugalkraft) wirken einander entgegen und gleichen sich in jedem Moment aus. Eine dritte zusätzliche Kraft hält den Planeten auf seiner Bahn und bewirkt, dass anders als beim freien Fall auf der Erde der Körper nicht im Verlaufe einer bestimmten Zeit entlang einer Spirale auf die Sonne stürzt, sondern die elliptische Bewegung beibehält.

Wenn diese dritte Kraft in Figur 2b in Anlehnung an Newton wiederum als Trägheitskraft bezeichnet wird, ist das allerdings missverständlich. Im Sinne von d'Alembert ist nur die Zentrifugalkraft ein Beispiel für die Trägheitskraft, die einer Fundamentalkraft (in diesem Beispiel der Zentripetalkraft) entgegenwirkt. Die in Figur 2b eingetragene »Trägheitskraft« ist dagegen von Newton übernommen und entspricht nicht der von d'Alembert gemeinten Trägheitskraft, sondern der zusätzlichen Kraft, die zur Zentrifugalkraft hinzukommen muss, um den Planeten nicht in die Sonne stürzen zu lassen.

Newton war sich dessen völlig bewusst und nahm an, dass in der von ihm gemeinten Trägheitskraft über die innere Trägheit hinaus eine zusätzliche äußere Kraftquelle wirkt, die den Planeten ständig »anschubst« und auf seiner Bahn hält. Er konstruierte daher zur Beschreibung der Planetenbewegung die Trägheitskraft so, dass sie nicht nur der Zentripetalkraft entgegenwirkt, die auf die Sonne gerichtet ist, sondern darüber hinaus den Planeten auf seiner elliptischen Bewegungsbahn verbleiben lässt.

Heute wird die dritte Kraft, – die zur Zentrifugalkraft hinzukommen muss, um die Planeten auf ihrer Bahn zu halten –, aus der Entstehung des Planetensystems in einer rotierenden Urwolke erklärt (so bereits 1755 Kant in Allgemeine Naturgeschichte und Theorie des Himmels). Das heute bekannte Planetensystem zehrt davon, dass der Schwung der Urwolke fortwirkt und die Rotation des Planetensystems aufrecht erhält. Das Fortwirken des ursprünglichen Drehimpulses wird aus einem zusätzlichen Erhaltungssatz erklärt, der axiomatisch gesetzt werden muss: Die Drehimpulserhaltung. Sie darf nicht verwechselt werden mit dem Trägheitsprinzip. Das Trägheitprinzip besagt, dass es zu jeder Kraft eine entgegenwirkende Trägheitskraft gibt. Die Drehimpulserhaltung ist einer von vielen Erhaltungssätzen, die empirisch beobachtet und axiomatisch gesetzt wurden. Wie bei einem Brummkreisel (einem Kreiselspiel) wird dank der Drehimpulserhaltung die rotierende Bewegung anfangs aufrecht erhalten bis sie vollständig an die Umgebung abgegeben wird und der Brummkreisel umkippt und am Boden liegen bleibt. Das gilt in gleicher Weise für das Planetensystem, jedoch in ganz anderen Zeiträumen.

Um das zu verstehen, sind wiederum die unterschiedlichen Bewegungszustände zu unterscheiden: (i) der sich schnell drehende Brummkreisel, (ii) der umkippende Brummkreisel, (iii) der am Boden liegende Brummkreisel. Offensichtlich verbraucht der am Boden liegende Brummkreisel am wenigsten Energie. Aber einen sich schnell drehenden Brummkreisel zu bremsen und umkippen zu lassen verbraucht mehr Energie, als wenn die schnelldrehende Bewegung des Brummkreisels aufrecht erhalten wird. Daher verbleibt er eine Zeitlang im Zustand (i), da der Übergang in den Zustand (ii) mehr Energie verbraucht, und erreicht noch nicht den Zutand (iii). Die innere Trägheit des Zustands (i) bewahrt ihn vor dem Umschlagen. Wer versucht, den Brummkreisel anzuhalten, spürt das. Hier zeigt sich deren Trägheit. Das ändert sich erst, wenn der Brummkreisel durch die Luftreibung Energie verliert und langsamer wird. Dadurch wird der Energievorteil des Zustandes (i) allmählich verringert, bis es zum Umkippen kommt und er über den Zustand (ii) in den Zutand (i) gelangen kann.

Die dritte Kraft ist diejenige Kraft, die den Übergang von einem Zustand in den anderen bewirkt. Das ist im Beispiel des Brummkreisels die Reibungskraft der umgebenden Luft. Ähnlich verhält es sich beim Planetensystem. Es behält wie der Brummkreisel seinen Zustand (i) aufrecht, gibt aber fortlaufend einen Teil seiner Energie als Wärme in das Weltall ab, bis es (ii) irgendwann zum Zusammenbruch des Systems kommen wird und (iii) die Rotation des Planetensystems zum Erliegen kommen wird.

Anmerkung 4 (Indifferenz als umgekehrtes Verhältnis ihrer Faktoren): Hegel spürt zwar, dass etwas an der Argumentation von Newton nicht stimmt, aber er kann es noch nicht exakt treffen, da er offenbar die weiterführenden Ideen von d'Alembert nicht kannte oder in ihrer Bedeutung nicht überschaut hat. Neuser will zeigen, dass Hegel zumindest in seiner Habilitationsschrift »Zentrifugalkraft und Newtonsche Trägheitskraft« verwechselt (Neuser, S. 7).

Hegel spürt, dass bei Newton zwei Gedanken durcheinander gehen. Zum einen hat Newton erkannt, dass bei allen mechanischen Bewegungen, für deren Verlauf Gesetze gefunden worden waren (das Gesetz des freien Falls durch Galilei und die Keplerschen Gesetze für die Planetenbewegung), etwas Gemeinsames vorliegt: In allen Fällen wird das Gegeneinander einer einwirkenden Kraft und einer Trägheitskraft betrachtet. Zum anderen hat Newton jedoch für die Planetenbewegung die Zentrifugalkraft und die Schwungkraft des aus der Urwolke entstandenen Sonnensystems miteinander gleichgesetzt, vermischt und gemeinsam als Trägheitskraft der Planeten angesehen. Das ließ sich nicht halten und musste von Newtons Nachfolgern seit d'Alembert korrigiert werden.

Mir scheint, dass Hegel zwar zutreffend bei Newton einen Fehler in dessen Bestimmung der Trägheitskraft der Planeten gesehen hat. Daraus hat er jedoch voreilig den falschen Schluss gezogen, auch dessen übergreifendes Konzept zu kritisieren. Daher spricht er sich sowohl gegen den Versuch von Newton aus, die verschiedenen mechanischen Gesetze auf einheitliche Axiome zurückzuführen, wie auch gegen Kant, der die Erhaltung der Planetenbewegung auf eine aus der Rotation der Urwolke herrührenden Schwungkraft erklärt hat.

Er sieht zwar richtig, dass die Darstellung von Newton unvollständig ist und für den Erhalt und die Umkehrung der elliptischen Bewegungsbahn der Planeten »eine fremde Kraft« notwendig wäre, welche Newton nicht erkennt (HW 5.453). Aber die auf Kant zurückgehende Lösung durch eine »Schwungkraft, [...], den sie von Haus aus erhalten hätten«, hält er für »läppisch« (Enz. § 269 Zusatz, HW 9.85). Während Kant 1755 ausdrücklich von der Allgemeine Naturgeschichte und Theorie des Himmels spricht und damit die Naturwissenschaft revolutioniert hat, hält Hegel an der von den Griechen überlieferten Vorstellung zeitloser, kosmologischer Vorgänge fest. Daher sieht er nicht die auf die historischen Anfänge des Planetensystems zurückgehende Schwungkraft des Urnebels. Er hat gegenüber Kant einen statischen Begriff der Zeit. Das ist tief in den Prinzipien seiner Philosophie verankert und für mich noch nicht abschließend geklärt. Ein erster Versuch liegt am Beispiel der Bewegungsbahn des Planeten Venus in der Arbeit Ruhende und bewegende Zeit vor, mit der 2013 diese Reihe der Hegel-Studien begonnen wurde. Weitere Ausarbeitungen sollen sich auf Jan van der Meulen Hegel. Die gebrochene Mitte (Hamburg 1958) beziehen, der den Zeitbegriff bei Kant, Hegel und Heidegger untersucht hat.

Darüber hinaus kritisiert Hegel grundsätzlich den Ansatz, die mechanischen Gesetze auf gemeinsame Axiome und Prinzipien zurückzuführen. Für ihn ist das der unzulässige Versuch, den einzelnen Bestandteilen der mathematischen Formeln eigenständige Kräfte zu unterschieben, aus denen sie hervorgegangen sein sollen.

»Die Voraussetzung bei diesem apriorischen Beweise ist, daß die Geschwindigkeit im Fall gleichförmig beschleunigt ist, der Beweis aber besteht in der Verwandlung der Momente der mathematischen Formel in physikalische Kräfte, in eine beschleunigende Kraft, welche in jedem Zeitmoment einen (denselben) Impuls mache, und in eine Kraft der Trägheit, welche die in jedem Zeitmomente erlangte (größere) Geschwindigkeit fortsetze, – Bestimmungen, die durchaus ohne empirische Beglaubigung sind, so wie der Begriff nichts mit ihnen zu tun hat. Näher wird die Größenbestimmung, welche hier ein Potenzenverhältnis enthält, auf die Gestalt einer Summe zweier voneinander unabhängiger Elemente gebracht und damit die qualitative, mit dem Begriffe zusammenhängende Bestimmung getötet« (Enz. § 267, HW 9.75f)

Hegel würdigt zwar »die unsterblichen Verdienste«, die sich Galilei und Kepler mit der Entdeckung ihrer Gesetze gemacht haben (HW 5.407), aber er ist nicht bereit anzuerkennen, dass es Newton gelungen ist, das Gemeinsame dieser Gesetze zu treffen und in übergreifenden Prinzipien der Mechanik zu formulieren, aus denen die Gesetze von Kepler und Galilei hergeleitet werden können. Stattdessen beschränkt sich für ihn die Leistung von Newton darauf, »jene Umformung des Ausdrucks und der den Anfängen nach eingeführten analytischen Behandlung« gefunden zu haben (HW 5.407).

Dagegen hat Hegel eine eigene Erklärung, warum die Planeten auf ihren Bahnen bleiben, die er aus dem 2. Keplerschen Gesetz entwickelt. Statt die Komponenten der mathematischen Bewegungsgleichung auf voneinander unabhängige Kräfte zurückzuführen, ist für Hegel die Planetenbewegung ein Beispiel für die »Indifferenz als umgekehrtes Verhältnis ihrer Faktoren« (Kapitelüberschrift, HW 5.446). Im 2. Keplerschen Gesetz sieht er die beiden Faktoren dargestellt, die im umgekehrten Verhältnis zueinander stehen: Der jeweilige Abstand des Planeten zur Sonne und seine Geschwindigkeit. Das sind nicht zwei Kräfte, sondern zwei Momente, die den jeweiligen Zustand des Planeten beschreiben.

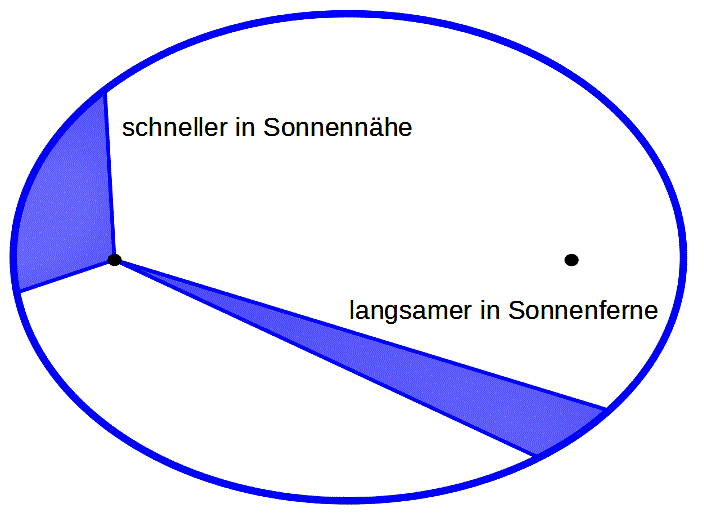
Figur 3 Zweites Keplersches Gesetz
»Zieht man einen Radiusvektor von der Sonne zum Planeten, so überstreicht dieser Fahrstrahl in gleichen Zeiten gleiche Flächen.« Das 2. Keplersche Gesetz beschreibt die Drehimpulserhaltung«. Je näher der Planet der Sonne ist, desto schneller ist er; je weiter entfernt, desto langsamer.
Quelle: Uni Würzburg, Physik Online)

Hegel deutet die Erhaltung gleicher Flächen, die in gleichen Zeiten überstrichen werden, als Beispiel für eine Indifferenz. Sie bleibt nach außen gleich, weil sich in ihrem Innern zwei Faktoren verändern, die in umgekehrten Verhältnis zueinander stehen und sich dadurch im Ganzen ausgleichen: Das sind der Abstand des Planeten zur Sonne und seine Geschwindigkeit. Der eine Faktor nimmt jeweils gerade so viel zu, wie sich der andere verringert. Mit dem 2. Keplerschen Gesetz ist für ihn »alles geleistet, was wahrhaft an die Theorie zu fordern ist« (HW 5.451, vgl. auch HW 9.95, siehe ergänzend die Ausführungen zum Zweiten Keplerschen Gesetz im Beitrag über den Widerspruch.). Das ist für Hegel der Theorie ohne Rückgriff auf Trägheits-, Zentripetal- oder Zentrifugalkräfte gelungen. Eine weitergehende Axiomatik hält er für unzulässig.

Die Deutung von Hegel kann so verstanden werden, dass das 2. Keplersche Gesetz eine Ordnung zeigt, die für einen bestimmten Zustand des Planetensystems gilt. Diese Ordnung wird aufrecht erhalten, obwohl sich die Bedingungen des Planetensystems langsam verändern. Ohne Zweifel gibt das Sonnensystem im Ganzen Energie an das Weltall ab und verliert allmählich seine ursprüngliche Schwungkraft. Dennoch bleibt die Bewegung der Planeten so lange erhalten, bis ein kritischer Schwellwert überschritten wird. Das ähnelt dem Zustand des flüssigen Wassers, das trotz leichter Erhöhung der Temperatur seine Ordnung aufrecht erhält, bis die kritische Marke von 100° überschritten ist.

Hegel legt zwar nahe, dass für ihn die Bewegung der Planeten ewig ist (»sie gehen, wie die Alten sagten, als selige Götter einher«, Enz. § 269 Zusatz, HW 9.85), aber seine Deutung des 2. Keplerschen Gesetzes kann auch so interpretiert werden, dass dies nur ein vorübergehender Zustand ist. Für mich kann dieser Ansatz als Vorläufer der Emergenztheorie verstanden werden. Die Emergenztheorie beschreibt, wie sich Zustände von hoher Ordnung bilden, die über eine genau definierte Bandbreite Bestand haben. Die heute geltende Ordnung des Planetensystems ist so gesehen eine Selbstorganisation, die für eine bestimmte Situation gilt. Hegels Ansatz kommt damit in Übereinstimmung mit ähnlichen Theorien seines Studienfreundes Schelling, als dieser von der Selbstorganisation sprach.

Anmerkung 5 (Trägheitsprinzip als Setzung): Hegels Erklärung des 2. Keplerschen Gesetzes als Indifferenz der zwei Faktoren Geschwindigkeit und Abstand zur Sonne hat für ihn systematische Bedeutung: Er will an diesem und weiteren Beispielen zeigen, wie die Seinslogik der kategorialen (messenden) Wissenschaft von sich aus in einen »allseitige[n] Widerspruch« gerät (HW 5.451), der durch keinerlei weitere empirische Arbeit aufgeklärt werden kann. Vielmehr müssen die Naturwissenschaftler im Verlaufe ihrer eigenen Arbeit erkennen, dass sie nicht ausschließlich aus wahrnehmbaren Eigenschaften induktiv oder abstraktiv die Naturgesetze ableiten können, sondern dass sie darüber hinaus Prinzipien wie das hier angesprochene Trägheitsprinzip und das d'Alembertsche Prinzip brauchen. Zwar nennt Hegel diese Prinzipien nicht oder kritisiert sie sogar, aber dennoch will er in meinem Verständnis zeigen, wie die Naturwissenschaft aus sich heraus der Erkenntnis nahekommt, dass für sie die empirische Arbeit nicht genügt, sondern dass sie Setzungen einführen muss, die sich – wie Hegel zeigen wird – letztlich nur zirkulär auf die mit ihnen mit-gesetzten Voraus-Setzungen berufen können. Ein Prinzip wie das Trägheitsprinzip kann nicht beobachtet werden, sondern es wird gesetzt.

Anmerkung 6 (Gesetze erster und zweiter Ordnung): Der Begriff des Gesetzes wird in der Wissenschaft der Logik an zwei Stellen entwickelt: In der Maßlogik in einer Anmerkung zum »Verhältnis beider Seiten (eines Maßes, t.) als Qualitäten« (HW 5.402, Zwischenüberschrift) und in der Wesenslogik im Unterkapitel mit der Überschrift »Das Gesetz der Erscheinung« (HW 6.150). Nach meinem Eindruck geht hier einiges durcheinander. Das liegt daran, dass Hegel zwar akzeptiert, wenn die Naturwissenschaft Gesetze wie z.B. das Fallgesetz von Galilei oder die Keplerschen Gesetze aufstellt, aber nicht, wenn sie weiter geht zu Axiomen und Prinzipien. In meinem Verständnis handelt es sich um Gesetze erster Ordnung, wenn auf der Objekt-Ebene die aus empirischer Forschung gewonnenen Daten in ein Gesetz gebracht werden, und um Gesetze zweiter Ordnung, wenn auf der Meta-Ebene Gesetze von Gesetzen gefunden werden. Das sind die Prinzipien. Für mich wird der übergreifende Gedankengang der Wissenschaft der Logik konsistent, wenn in der Maßlogik von Gesetzen ersten Ordnung und in der Wesenslogik von Gesetzen zweiter Ordnung gesprochen wird.

Gesetze erster Ordnung: Hegel führt die Gesetze erster Ordnung in der Maßlogik ein. Es handelt sich wie in der Unterüberschrift angekündigt um das Verhältnis zweier Seiten eines Maßes als Qualitäten. Das ist am deutlichsten beim Fallgesetz, wenn mit ihm Ort und Zeit in ein Verhältnis gesetzt werden und darüber das Maß des freien Falls gefunden wird. Ähnlich werden beim 2. Keplerschen Gesetz die lokale Geschwindigkeit und der Abstand zur Sonne in ein Verhältnis gesetzt. Systematisch beschreibt Hegel Gesetze dieser Art jedoch erst im Abschnitt über das Gesetz der Erscheinung, wo es jedoch inhaltlich nicht hingehört: Sie sind »aus der Erfahrung erkannt« und mit ihnen sind »zwei Inhaltsbestimmungen als wesentlich verbunden«, z.B. beim Fallgesetz »die Raumgröße und die Zeitgröße« (HW 6.155). Aber die Beziehung zwischen den beiden in einem Gesetz miteinander verbundenen Bestimmungen bleibt noch äußerlich. Zwar stellt die mathematische Bewegungsgleichung eine Beziehung zwischen Raum (der Strecke s) und der Zeit t her, aber sie begründet nicht, warum diese Beziehung gilt. Sie formuliert, dass die Zeit im Quadrat auftritt, aber sie vermag nicht zu erklären, warum das so ist. »So ist es nicht im Begriffe des im Falle durchlaufenen Raumes enthalten, daß ihm die Zeit als Quadrat entspricht.« Daher »erfordert (das Gesetz) noch einen Beweis« (HW 6.155).

Solange der Beweis fehlt, kann die mit dem Gesetz gegebene Einheit seiner beiden Seiten nur von außen hergestellt und in Hegels Ausdrucksweise »gesetzt« werden. »Der deutsche Ausdruck Gesetz enthält diese Bestimmung gleichfalls. In diesem Gesetztsein liegt die wesentliche Beziehung der beiden Seiten des Unterschiedes, die das Gesetz enthält.« (HW 6.152) Aus diesem Grund versteht Hegel das Gesetz als eine Wesensbestimmung. Das ließe sich genau so für alle anderen Maße sagen, bei denen ebenfalls die beiden Qualitäten ihres Verhältnisses als Gesetz formuliert, mit empirischen Beobachtungen erwiesen, aber nicht begründet werden. Mir scheint das Gesetz erster Ordnung noch zur Seinslogik gerechnet werden zu müssen, jedoch im Übergang zur Wesenslogik. Erst wenn das Gesetztsein für sich betrachtet wird, würde ich von einer wesentlichen Beziehung sprechen. Das geschieht mit dem Gesetz zweiter Ordnung.

Dieser Mangel war den Naturwissenschaftlern bewusst, und sie haben nach einer Lösung gesucht, wie Hegel durchaus würdigt:

»Es ist ein großes Verdienst, die empirischen Zahlen der Natur kennenzulernen, z.B. Entfernungen der Planeten voneinander, aber ein unendlich größeres, die empirischen Quanta verschwinden zu machen und sie in eine allgemeine Form von Quantitätsbestimmungen zu erheben, so daß sie Momente eines Gesetzes oder Maßes werden; – unsterbliche Verdienste, die sich z.B. Galilei in Rücksicht auf den Fall und Kepler in Rücksicht auf die Bewegung der himmlischen Körper erworben hat. Sie haben die Gesetze, die sie gefunden haben, so erwiesen, daß sie gezeigt haben, daß ihnen der Umfang der Einzelheiten der Wahrnehmung entspricht« (HW 5.406f).

Klarer lässt es sich nicht sagen, wobei auffällt, dass Hegel Gesetz und Maß im Grunde synonym gebraucht. Konsequent spricht er von »erweisen« und nicht von Beweis: Galilei und Kepler haben keinen Beweis für ihre Gesetze geliefert, sondern sie haben diese Gesetze intuitiv aufgestellt und nachgewiesen, dass sie mit den empirisch gegebenen Beobachtungsdaten übereinstimmen. Einen Beweis hat erst Newton geliefert, als er diese Gesetze aus seinen Axiomen hergeleitet hat. Das akzeptiert Hegel jedoch nicht und fordert stattdessen ein »höheres Beweisen dieser Gesetze [...] aus den Qualitäten oder bestimmten Begriffen, die bezogen sind (wie Zeit und Raum)« (HW 5.507). Die Leistung von Newton beschränkt er wie bereits zitiert auf »jene Umformung des Ausdrucks und der den Anfängen nach eingeführten analytischen Behandlung« (HW 5.407). Newton hat jedoch weit mehr als eine Umformung gefunden. Ihm ist es gelungen, die Gesetze von Galilei und Kepler einheitlich aus einem übergeordneten Ansatz herzuleiten. Das erfüllt zwar noch nicht Hegels Forderung nach einem höheren Beweisen aus den bezogenen Begriffen, aber es handelt sich um Gesetze zweiter Ordnung, aus denen die Gesetze erster Ordnung hergeleitet werden können. Leibniz und d'Alembert gingen nochmals einen Schritt weiter, als sie Prinzipien aufstellten, denen die Gesetze erster Ordnung folgen.

Gesetze zweiter Ordnung: Ein Prinzip wie das Trägheitsprinzip oder das Prinzip der kleinsten Wirkung bezieht sich dagegen nicht mehr wie das Maß auf einzelne gemessene Inhalte, sondern in einer höheren (zweiten) Ordnung auf die Gesetzmäßigkeiten der Gesetze. Ein Prinzip beschreibt, nach welchen inneren Gesetzen ein Gesetz aufgestellt werden kann. Alles, was Hegel in der Wesenslogik über die Gesetze schreibt, trifft daher in meiner Deutung auf die Prinzipien zu.

Erst mit der Unterscheidung von Gesetzen erster und zweiter Ordnung wird erkennbar, welche Bedeutung der Begriff des Quadrats erhält, auf den sich Hegel mehrfach bezieht, ohne ihn näher bestimmen zu können. Das Quadrat (und der Kubus) treten bei Gesetzen erster Ordnung rein empirisch auf: Galilei und Kepler haben buchstäblich durch Ausprobieren unterschiedlicher Ansätze für ihre Formeln intuitiv entdeckt, dass in ihren Gleichungen bestimmte Größen in der 2. und 3. Potenz auftreten, um die empirischen Daten zutreffend beschreiben zu können. Hegel hat vollständig recht, dass sie sich keinerlei Gedanken gemacht haben, warum das so ist. Aber wie soll aus dem Begriff des Quadrats das Fallgesetz von Galilei hergeleitet werden? Eine Lösung kann erst dann gefunden werden, wenn auf einer höheren Ebene die Prinzipien als Gesetze zweiter Ordnung verstanden werden. Es sind Prinzipien, wenn von Gesetzen erster Ordnung verlangt wird, dass sie nicht die Erhaltung der Energie und den Weg des geringsten Aufwandes verletzen dürfen. Gesetze erster Ordnung setzen jeweils zwei unabhängig Koordinaten in Beziehung (z.B. Raum und Zeit oder Abstand und Geschwindigkeit), Gesetze zweiter Ordnung legen fest, welche höhere (zweidimensionale) Ordnung erhalten bleiben muss. Das Wirkungsprinzip sagt aus, dass der Weg der kürzesten Wirkung gewählt wird. Die Wirkung ist über die Energie definiert, und diese ist das zweidimensionale Produkt über die Tangente und Cotangente entlang der Bewegungskurve. Auch dies lässt sich letztlich indirekt empirisch prüfen und bestätigen, wenn nachgewiesen wird, dass aus der Vielfalt möglicher Wege derjenige Weg mit dem geringsten Energieaufwand gewählt wird.

Wird mit Hegel eingesehen, dass die Gesetze zweiter Ordnung nicht direkt empirisch beobachtet werden können, sondern gesetzt werden müssen, dann wird verständlich, warum Gesetze zweiter Ordnung als Wesensbestimmungen anzusehen sind und traditionell in das Gebiet der Metaphysik fielen.

Die Mathematiker hatten ein Gespür dafür, als sie das elementare Beispiel eines solchen Raums als imaginären Raum bezeichneten und heute von virtuellen Räumen sprechen. Er lässt sich nur mit der Vorstellungskraft bilden. Anders als die aus der Natur bekannten bewegten Objekte hat er weder eine Substanz noch sonst eine zweite Kategorie (Qualität, Quantität, Maß), sondern besteht ausschließlich im reflektierenden Denken. Da die Vorstellungskraft nur mit Erscheinungen operiert, scheint es mir treffend, mit Hegel von Gesetzen der Erscheinung zu sprechen. Das unterscheidet sich vom üblichen Verständnis von Erscheinung, wenn damit gemeint ist, wie mir etwas erscheint. Hier ist dagegen darüber hinaus gemeint, welche eigenen Erscheinungen die Vorstellungskraft bilden kann, wenn sie ein gegebenes Objekt nicht nur aus unterschiedlichen Perspektiven betrachtet, sondern für sich eigene Erscheinungen bildet, wie dies Objekt aus virtuell angenommenen Perspektiven aussehen könnte. Hegel nähert sich diesem Verständnis, wenn er die Reflexionsbestimmung ‘Identität’ vor dem Hintergrund versteht, was etwas sein könnte, sich davon aber in seiner Identität unterscheidet. Er verfehlt dieses Verständnis jedoch wieder, wenn er das Gesetz lediglich von der Mannigfaltigkeit des ebenfalls Gegebenen, aber bloß Unwesentlichen unterscheidet, von dem für die Bildung eines Gesetzes abgesehen werden muss. Er schreibt in einer etwas undeutlichen Formulierung: »Die Erscheinung aber ist die seiende vielfache Verschiedenheit, die sich in unwesentlicher Mannigfaltigkeit herumwirft.« (HW 6.151) Mir geht es dagegen um die Mannigfaltigkeit der Möglichkeiten, die sich die Vorstellungskraft über einen gegebenen Sachverhalt hinaus entwerfen kann, und aus denen sie mit ihren Prinzipien herleiten kann, welche von ihnen wirklich wird.

Gesetze der freien Konstruktion: Mit den Gesetzen der zweiten Ordnung ist noch nicht das letzte Wort gesprochen, was unter einem Gesetz zu verstehen ist. Gesetze erster und zweiter Ordnung bringen in eine mathematische Gestalt, was empirisch beobachtet wurde. Bei Gesetzen zweiter Ordnung kommt bereits die Vorstellungskraft hinzu, die über die gegebenen empirischen Inhalte hinausgeht und sie aus einem Möglichkeitsfeld heraus deutet. Mit der Vorstellungskraft zeigt sich bereits die innere Freiheit des Wissenschaftlers, der sich vom gegebenen Phänomen lösen und es aus einer höheren Perspektive betrachten kann. Wird diese Fähigkeit für sich betrachtet, ist das für Hegel das Begreifen: "Das Begreifen eines Gegenstandes besteht in der Tat in nichts anderem, als daß Ich denselben sich zu eigen macht, ihn durchdringt und ihn in seine eigene Form, d. i. in die Allgemeinheit [...] bringt." (HW 6.255) Mit dem Begreifen befinden sich das Objekt und das Subjekt des Begreifens in Freiheit zueinander. Das Objekt kann so begriffen werden, wie es sich in seiner eigenen Freiheit bewegt. Es wird mit dem Begreifen keiner Macht unterworfen, sondern finden in der ihm eigenen Form zu seiner Freiheit. Das Subjekt unterliegt seinerseits im Begreifen keinerlei inneren oder äußeren Zwängen und erlebt seine eigene Freiheit in der freien Wechselwirkung mit dem Objekt. Das ist geradezu eine Utopie der Wissenschaft, das Ideal der Aufklärung.

Eine solche Wissenschaft kann in ihren Konstruktionen frei Gesetze entwerfen. Dies Ideal fand Hegel in der euklidischen Geometrie vor. Auf den ersten Blick erscheint es wie ein Fremdkörper, wenn er in seiner Lehre der Idee bis in Details die analytische und synthetische Methode der Geometrie ausführt. Erst der Geometrie gesteht er die axiomatische Methode zu, die er bei Newton, Leibniz und d'Alembert nicht angemessen würdigen mochte, weil sie ganz innerhalb der Kategorie der Größe bleibt (HW 6.506), und kritisiert, wenn sie »unpassenderweise [...] auch auf andere Wissenschaft, selbst auf die Philosophie angewendet worden« ist (HW 6.535).

Trotz dieser Bedenken kommt er einer axiomatischen Mechanik nahe. »Nur der freie Mechanismus hat ein Gesetz, die eigene Bestimmung der reinen Individualität oder des für sich seienden Begriffes.« (HW 6.427)

Die Freiheit der Konstruktion lohnt sich weiter ausgeführt zu werden. Sie kommt dem Spiel nahe, von dem Schiller in seinen Ästhetischen Briefen sprach, die das ursprüngliche Systemprogramm der seinerzeit noch befreundeten Studienkollegen Hegel, Hölderlin und Schelling anregten. Historisch hat die Freiheit der Konstruktion ihren höchsten Ausdruck im Satz des Pythagoras gefunden, den Hegel entsprechend würdigt. (Siehe den Beitrag Der Schluss von der Lebendigkeit über den Satz des Pythagoras auf die dialektische Methode)

Anmerkung 7 (Trägheitsgesetz als kausales Paradoxon): Ohne eine eigene Lösung anbieten zu können hat C.F. v. Weizsäcker 1985 – ausgehend von Kant und den neueren Erkenntnissen der Relativitäts- und Quantentheorie – nach einem neuen Aufbau der Physik gesucht. Anders als seine Physiker-Kollegen stellt er sich dem offenen Problem,

»dass in der klassischen Mechanik das Trägheitsgesetz eigentlich ein kausales Paradoxon darstellt: eine Bewegung ohne wirkende Kraft. Eben dieses Paradoxon trennt die neuzeitliche Physik von der aristotelischen; deshalb hatte man in der gesamten Neuzeit ein Interesse daran, seinen paradoxen Charakter zu verdrängen« (Weizsäcker, S. 400).

Aristoteles kannte keine Trägheit im neuzeitlichen Sinn, sondern eine natürliche Ordnung. Alle physischen Dinge sind Leben und Vergehen unterworfen und suchen in ihrer Lebensspanne den Zustand (und in engerem Sinn den Ort) zu erreichen, der ihrer Natur entspricht. Mechanische Bewegungen entstehen aus dem Mangel, wenn sich ein Körper nicht an seinem natürlichen Ort befindet – wenn z.B. ein Stein frei schwebend in der Luft hängt –, und sind abgeschlossen, sowie der Mangel behoben ist. Für Aristoteles war undenkbar, dass Bewegungen »grundlos« unendlich fortgeführt werden. Ewige Bewegungen gab es für ihn nur bei der Bewegung der Sterne, die sich unendlich auf ihren Bahnen halten. Doch gehörten die Sterne für ihn nicht zur physischen Welt. Sie sind nicht Entstehen und Vergehen unterworfen und sind aus einem eigenen Stoff gemacht (hyle topike, Met VIII 1, 1042b). Sie haben keine Schwere, und auf sie wäre ein Begriff wie die Trägheit nicht anwendbar.

Die Neuzeit gab die aristotelische Unterscheidung zwischen physischen und stellaren Körpern auf und sucht nach ihren gemeinsamen Bewegungsgesetzen. Auch wenn niemand an der Vergänglichkeit und Sterblichkeit jedes einzelnen physischen Körpers zweifelt, sollen seine Bewegungsabläufe mit Gesetzen beschrieben werden, die für alle Körper und für alle Zeiten gelten, d.h. als Gesetze unveränderbar und unvergänglich sind und gelten. Erst mit der Trennung des physikalischen Bewegungsbegriffs von der ursprünglichen Bedeutung des Physischen als Vergänglichem und Veränderlichem stellt sich die Frage nach der Trägheit. Es muss an den vergänglichen Dingen eine Eigenschaft geben, dank derer ihre Bewegungen trotz ihrer Sterblichkeit ewigen Gesetzen folgen. Das ist die Trägheit. Dank der Trägheit lassen sich die Bewegungsverläufe physischer Gegenstände mathematisch mit Formeln beschreiben, die für Aristoteles nur für die ewig bestehenden Himmelskörper gelten können.

Diese Trägheit enthält jedoch für v. Weizsäcker ein Paradox. Wird die Trägheit für sich betrachtet, handelt es sich um »eine Bewegung ohne wirkende Kraft«: Der träge Körper bewegt sich ewig auf seiner Bahn wie die Sterne in der Himmelslehre von Aristoteles. Es soll sich aber zugleich um einen physischen Körper handeln mit einer bestimmten Größe, Ausdehnung, Gewicht usf. Was hält die Bewegung eines trägen Körpers aufrecht?

Physiker machen sich darüber in der Regel keine Gedanken, da die von ihnen aufgestellten Formeln empirisch nachweisbar sind, womit für sie alle Fragen geklärt sind. Für v. Weizsäcker ist es dagegen »nichts als die Kapitulation vor einem ungelösten Problem«, wenn »man die Kraft zutreffend nicht Ursache der Bewegung, sondern Ursache der Beschleunigung nennt« (Weizsäcker, S. 235), wobei er sich auf die Definition der entgegenwirkenden Trägheitskraft bezieht, ›FT = m · a‹ (in Worten: ›Kraft ist Masse mal Beschleunigung‹). Mit der sprachlichen Unterscheidung in Beschleunigung und Bewegung ist zwar auf den ersten Blick das Paradox vermieden, eine Bewegung ohne wirkende Kraft zu konstruieren, da nur von einer Beschleunigung ohne wirkende Kraft gesprochen wird, doch sind das lediglich sprachliche Ausflüchte. Denn wie soll erklärt werden, dass es eine Beschleunigung ohne wirkende Kraft gibt und im Ergebnis eine Bewegung, die von dieser Beschleunigung hervorgerufen wird?

Wie schon bei Newtons Deutung der Planetenbewegungen stellt sich die Frage nach einer dritten Kraft. Es muss eine Kraft geben, dank derer die Bewegung aufrecht erhalten wird. Diese Kraft bekommt in der Neuzeit den Namen ‘Trägheit’. Das führt jedoch in einen Zirkel: Die Trägheit ist die Kraft, die sich zirkulär selbst erklärt.

Erst wer bereit ist, den Weg der Naturwissenschaft bis in diese »Höllenfahrt« mitzugehen, – wie Marx den Grenzübergang im Differentialkalkül bezeichnet hat (Marx, 110) –, oder ihren »Hexenkreis« durchschaut, »worin Bestimmungen des Daseins und Bestimmungen der Reflexion, Grund und Begründetes, Phänomene und Phantome in unausgeschiedener Gesellschaft durcheinanderlaufen und gleichen Rang miteinander genießen« (HW 6.102), wie es Hegel in seiner Wissenschaft der Logik auf den Punkt bringt, wird das Paradoxon von v. Weizsäcker verstehen und die Scheu aller Physiker, sich Fragen dieser Art zu stellen. An diesem Punkt stellt sich die Aufgabe einer begrifflichen Ableitung, um die es Hegel ging.

Anmerkung 8 (Io und Phaethon): Während sich die empirische Naturwissenschaft seit den frühesten Aufzeichnungen bei den Sumerern, Ägyptern und Babyloniern auf die in der jeweiligen Gegenwart gewonnenen Beobachtungsdaten verlässt und diese im Prinzip unendlich und zeitlos induktiv auf die Vergangenheit und Zukunft projiziert, geht das mythische Denken von unberechenbaren Ereignissen und Umbrüchen aus. Davon berichten zum Beispiel in kosmologischen Zusammenhängen die Mythen von Io und Phaethon. Während heute mit Io ein Jupiter-Mond bezeichnet wird, war in griechischen Zeiten Io die Mondkuh. Ihre Bahn geriet nicht weniger aus den Fugen als die Fahrt von Phaethon mit dem Sonnenwagen seines Vaters Helios (dem Sohn des Titanen Hyperion). Das wurde von den einen aus dem Wahnsinn von Io erklärt, von anderen aus der Eifersucht von Hera, oder als Zeichen eines Generationswechsels unter den Göttern, war doch ursprünglich Io die große Göttin und wurde erst später von Hera abgelöst. Wie auch immer: Entgleisende Bahnen wie die von Io und Phaethon zeigen, dass die Griechen ein klares Bewusstsein hatten, dass das kosmische Geschehen keineswegs immer so glatt verläuft wie wir es inzwischen voraussetzen. – Sicher sind Katastrophen auch der modernen Wissenschaft nicht ganz fremd. So gibt es eine Hypothese über die Entstehung des Mondes aus dem Zusammenstoß der Erde mit einem der Erde verwandten Protoplaneten Theia mit deutlich katastrophischen Zügen. Auch in dieser These wird jedoch von berechenbaren Bewegungsabläufen ausgegangen. Um diese Hypothese zu prüfen kann berechnet werden, auf welchen Bahnen sich Theia bewegt haben und welche Wechselwirkungen von ihr ausgegangen sein müssen. Wenn deren Spätwirkungen nachgewiesen werden können, gilt die Hypothese der Wissenschaft als nachgewiesen. – Zusammenfassend unterscheidet die Wissenschaft vom Mythos, dass die Wissenschaft von der Berechenbarkeit ihrer Objekte ausgeht. Die Berechenbarkeit ist nur möglich, wenn die Objekte über eine Trägheit verfügen, dank derer sie im zeitlichen Ablauf ihrer Bewegung identifiziert werden können. Das Trägheitsprinzip liegt der Wissenschaft zugrunde.

»Beweis aus dem Begriffe der Sache«

Für Hegel sind der empirische Nachweis der Bewegungsgleichungen durch die naturwissenschaftlichen Beobachtungen und der nicht-empirische Beweis durch die »mathematische Mechanik« zwar erfolgreiche und notwendige Schritte, aber sie reichen nicht aus. Das hat indirekt das von v. Weizsäcker genannte Paradoxon bestätigt. Was ist der Grund für dieses Paradoxon? Hegel will nicht die empirische Arbeit oder die Arbeit der mathematischen Physik ersetzen oder gar überbieten, sondern er fordert einen »Beweis aus dem Begriffe der Sache« (Enz. § 267, HW 9.78). Was ist hier der »Begriff der Sache«? Die empirischen Beobachtungen und die mathematischen Formeln erheben und untersuchen Messgrößen. Sie filtern aus der Mannigfaltigkeit aller Messgrößen diejenigen heraus, die für das jeweils betrachtete Phänomen von Bedeutung sind. Das sind für die Bewegung sicherlich nicht die Farbe oder der Geruch. Auf den ersten Blick könnte die Oberflächenstruktur (Porosität, Taktilität) einen Einfluss haben, da sich ein glatter oder ein windschnittiger Körper schneller bewegt als ein grobkörniger oder stark verwinkelter Körper. Doch wird schnell deutlich, dass dies nur Einfluss auf vernachlässigbare äußere Faktoren wie den Widerstand des Mediums hat. Auch das Material spielt keine Rolle. Zwar fällt eine Vogelfeder langsamer als ein Stein, doch auch dies hat mit dem Luftwiderstand zu tun. Die Feder schwebt hinab, der Stein stürzt direkt in die Tiefe. Schließlich erkannte die Physik, dass sogar die Masse unerheblich für das Bewegungsgesetz ist. Im Ergebnis sind ausschließlich der Raum (die Strecke) und die Zeit maßgeblich, um die Gesetze des Bewegungsverlaufs unabhängig von allen störenden Einflüssen erkennen zu können. Die einzige Überraschung liegt darin, dass die Zeit im Quadrat auftritt. Das lässt sich vorerst nicht erklären, sondern muss als empirisches Faktum hingenommen werden. Versteckt spielt jedoch das Quadrat eine Schlüsselrolle: Wird dem Differentialkalkül von Newton und Leibniz gefolgt, dann ergibt sich aus dem Auftreten der Zeit im Quadrat, dass zwei Ableitungsschritte möglich sind: Von der Bewegungsgleichung der Strecke, in der die Zeit in zweiter Potenz (dem Quadrat) steht, zum Impuls, der die Zeit in erster Potenz (linear) enthält, und vom Impuls zur Kraft, bei der die Zeit als Variable nicht mehr auftritt, d.h. formal in der Potenz Null aufgeschrieben werden kann. Siehe die oben ausgeführten Gleichungen (6.1) bis (6.7). Auch das wird als nicht weiter zu hinterfragendes Faktum hingenommen.

Hegel konzentriert sich daher auf die beiden kritischen Fragen:

(i) Er will zum einen nachweisen, warum das Gesetz des Falles erstmals »ein freies Naturgesetz« ist, »das eine Seite in ihm hat, die sich aus dem Begriffe des Körpers bestimmt« (Enz. § 267, HW 9.77), das ist die Seite der Freiheit. Wenn von allen Eigenschaften wie Farbe, Material, Masse abstrahiert werden kann, was ist es dann eigentlich, das sich bewegt? Und aufgrund welcher Eigenschaften kann es sich nicht nur bewegen, sondern gewinnt in seiner Bewegung Freiheit? Die Physik hat das erforderliche Datenmaterial geliefert, und die Mathematik hat die Verlaufsform der Bewegung beschrieben. Ohne sie zu verstehen, wäre es nicht möglich, im nächsten Schritt die begriffliche Bestimmung zu leisten. Der Begriff würde ins Leere gehen, wenn er sich nicht auf die maßgeblichen Seiten der Bewegung beziehen könnte, die die empirische Forschung für die Arbeit des Begriffs vorbereitet hätte, d.h. ohne zu verstehen, worin sich die Freiheit des freien Falls zeigen kann. Aber erst mit dem Begriff wird es möglich, die Freiheit der Bewegung als solche zu erkennen. Daher sucht Hegel nach einer begrifflichen Herleitung, die sich in letzter Instanz auf die mit dem Begriff gegebene Freiheit berufen kann und beide Seiten zusammen bringt: Die Ergebnisse der empirischen Arbeit und das Begreifen, das über ein bloßes Protokollieren hinausgeht. Begreifen bedeutet, etwas in seiner Freiheit zu erkennen, und nicht, es einfach einem Gesetz zu unterwerfen. Um das zu leisten, geht er gewissermaßen rückwärts vor: Er beginnt mit der Frage, was es eigentlich ist, das sich bewegt. Das ist ein Körper, und aus dem Begriff des Körpers ist zu bestimmen, was Bewegung bedeutet. Der Begriff des Körpers ist zu unterscheiden vom bloßen Volumen (dem geometrischen Körper), vom mathematischen Begriff des Körpers als einer Algebra, in der nach bestimmten Regeln addiert und multipliziert werden kann, und vom Körper als Leib, wie er in der Biologie und Medizin untersucht wird. Er liegt ihnen allen zugrunde. Statt den Begriff des Körpers aus einer Realwissenschaft zu übernehmen, geht Hegel zurück zum Begriff des Körpers, wie er ihn in der Philosophie vorgefunden hat, insbesondere bei Kant in dessen Metaphysischen Anfangsgründen der Naturwissenschaft: Ein Körper ist bestimmt durch seine Undurchdringlichkeit (Impenetrabilität) (siehe den Eintrag im Eisler-Lexikon), in wissenschaftlicher Sprachweise durch seine Elastizität. Das führt Hegel zur Kraft der Schwere und der Kraft der Trägheit, die als solche aus dem Begriff des Körpers hergeleitet werden sollen und aus denen sich die Bewegung ergibt. (Schelling hat den Begriff der Undurchdringlichkeit gleichsam emotionalisiert und moralisiert, wenn er in seiner Freiheits-Schrift vom Grimm und dem Verhangenen spricht. Hegel ist dieser Betrachtungsweise nicht grundsätzlich abgeneigt. Entsteht Freiheit, wenn sie sich vom Groll befreit, der die Bewegung stocken lässt, und sich als erstes innerlich befreit? Oder bleibt der Grimm die innerste Triebkraft der Freiheit? Um in diesen Fragen Klarheit zu finden, geht Hegel zurück bis auf den einfachsten Fall der Freiheit, dem freien Fall. Dort wird er mit der dynamis und der energeia die Begriffe finden, mit denen sich Freiheit bestimmen lässt.)

(ii) Zum anderen ist aus dem Begriff des Quadrats herzuleiten, warum sich das Quadrat in der Bewegungsgleichung zeigt. Allein diese Art zu fragen unterscheidet sich radikal von der gewohnten Naturwissenschaft. Genauer will Hegel zeigen, dass der Begriff der Sache, um die es bei der freien Bewegung geht, im Potenzenverhältnis liegt. Während die eindimensionale Bewegung rein der Notwendigkeit folgt und nicht von der vorgegebenen eindimensionalen Bahn abweichen kann, ist mit dem freien Fall ein Ausbruch von der Linie in die Freiheit der umgebenden Fläche gegeben. Dass das möglich ist, ergibt sich für Hegel aus dem Begriff des Quadrats. Das klingt für einen Naturwissenschaftler völlig abwegig, beginnt aber verständlich zu werden, wenn daran erinnert wird, dass der mathematische Ausdruck des Quadrats ursprünglich mit dem griechischen Ausdruck dynamis verbunden war. Dynamis ist sowohl die Möglichkeit wie auch das Vermögen oder gar die Gewalt (potentia), eine Möglichkeit ergreifen zu können. Der Dynamik steht die Energie gegenüber, die diese Möglichkeit ergreift und bis zum Ende, dem abgeschlossenen Werk (ergon) ausführt.

– Kraft der Trägheit und Kraft der Schwere

Wenn das Bewegungsgesetz des Falls begrifflich auf Kategorien zurückzuführen ist, die in der Seinslogik entwickelt sind, dann muss es dort möglich sein, auf rein logischer Ebene ein Gesetz der Trägheit und ein Gesetz der Schwere zu bestimmen, die den von der Naturphilosophie betrachteten mechanischen Gesetzen vorausgehen. Hegel sucht bereits in der Wissenschaft der Logik nach einer Erklärung, warum die Trägheitskraft mit der ersten Potenz der Zeit wirkt, die Schwerkraft dagegen in der zweiten Potenz der Zeit auftritt. Er fragt, welche Eigenschaften der Schwerkraft und der Trägheit dazu führen, dass in dieser Weise mit ihnen gerechnet werden kann.

»Wie s = at^², die Gleichung der Bewegung des Falles, analysiert wird, ist früher schon erinnert; – das erste Glied der Analyse ds/dt = 2at wird in die Sprache und resp. in die Existenz so übersetzt, es solle ein Glied einer Summe (welche Vorstellung wir längst entfernt haben) der eine Teil der Bewegung sein, und zwar solle dieser der Kraft der Trägheit, d. i. einer schlecht-gleichförmigen Geschwindigkeit so zukommen, dass in den unendlichkleinen Zeitteilen die Bewegung gleichförmig, in den endlichen Zeitteilen, d.h. in der Tat existierenden, aber ungleichförmig sei. Freilich ist fs = 2at und die Bedeutung von a und von t für sich bekannt, sowie dass hiermit die Bestimmung von gleichförmiger Geschwindigkeit einer Bewegung gesetzt ist; da a = s/t^², ist 2at = 2s/t überhaupt; damit aber weiß man im geringsten nichts weiter; nur die fälschliche Annahme, dass 2at ein Teil der Bewegung als einer Summe sei, gibt den fälschlichen Schein eines physikalischen Satzes. Der Faktor selbst, a, die empirische Einheit – ein Quantum als solches – wird der Schwere zugeschrieben; wenn die Kategorie der Kraft der Schwere gebraucht wird, so ist vielmehr zu sagen, dass eben das Ganze s = at^² die Wirkung oder besser das Gesetz der [347] Schwere ist. – Gleichmäßig ist der aus ds/dt = 2at abgeleitete Satz, dass, wenn die Schwere aufhörte zu wirken, der Körper mit der am Ende seines Falles erlangten Geschwindigkeit den doppelten Raum von dem, welchen er durchlaufen hat, in einer der Dauer seines Falles gleichen Zeit zurücklegen würde« (HW 5.346f).

Während die Physiker als Erfahrungstatsache hinnehmen, dass die Trägheitskraft mit der ersten Potenz der Zeit wächst und die Schwerkraft mit der zweiten Potenz, sieht Hegel ihr Verhältnis im Horizont von Endlichkeit und Unendlichkeit, von Kontinuität und Umkehr, Ausführung (Performation) und Selbstreflexion, erster und zweiter Ordnung. Die Kraft der Trägheit wächst mit »einer schlecht-gleichförmigen Geschwindigkeit« und ist Beispiel für das endliche Denken (wenn man so will: das träge Denken). Sie ist bloße Wiederholung der immer gleichen Handlung und kontinuiert sich über alle Grenzen hinweg ins Unermessliche. Die Kraft der Schwere dagegen bezieht ein gegebenes Element auf das ihn umgreifende System und lenkt seine Bewegung ab in Richtung auf dessen Zentrum, das ist bei allen Körpern im Schwerkraftsystem der Erde der Fall in Richtung auf den Erdmittelpunkt. Die schlechte Unendlichkeit ist das unendliche Entlanglaufen auf einer Geraden über alle Schranken hinweg, so wie es beim Zählen der natürlichen Zahlen geschieht (›eins, zwei, drei, …‹), während die höhere Unendlichkeit eine neue Dimension erreicht und diese mit einer Umkehr (Negation der Negation) im Innern der gegebenen schlechten Unendlichkeit entdeckt: Die Elemente der schlechten Unendlichkeit sind nicht nur zählbar (sortal), sondern bilden ein Kontinuum. Die Kraft der Trägheit und die Kraft der Schwere sind für Hegel jedoch nicht einfach Anwendungsbeispiele, sondern die Kraft der Trägheit ist die schlechte Unendlichkeit für sich gesehen, die mit innerer Trägheit in ihrer Bewegung verharrt, während die Kraft der Schwere die wahre Unendlichkeit für sich genommen ist: Mit der Schwere ist im Begriff der wahren Unendlichkeit gesetzt, dass diese sich nicht wie die Bahn des Phaethon überhebt und abstürzt, sondern ihr die sichere Umkehr gelingt. Es liegt für Hegel im Begriff der Idee, dass diese zirkulär zurückkehrt. Sie ist durch ihren eigenen Begriff vor Antinomien bewahrt und bedarf keiner von außen kommenden Anweisungen für eine regulative Disziplin, mit denen Kant sie vor einem überfliegenden Gebrauch schützen wollte.

Im gewöhnlichen Sprachgebrauch ist der Ausdruck »träge« häufig abwertend gemeint im Sinne von »stur, engstirnig, unbeweglich, pedantisch«, und so ist er auch bei Hegel oft zu finden. Wenn jedoch Trägheit ernst genommen wird als das Gesetz, wodurch etwas zusammengehalten wird, dann ist sie der entgegenwirkenden Kraft ebenbürtig. Ich würde so weit gehen und das Verhältnis von Trägheit und Schwere dem Verhältnis von Begriff und Ur-Teilung oder dem Verhältnis von Einheit und Unterschied analog zu setzen. Trägheit hält Einheit zusammen, Schwere zeigt den inneren Bezug etwas Einzelnen auf das Allgemeine, zu dem es gehört, und auf dessen Zentrum. Solange der Begriff der Trägheit mit einer abwertenden und für meinen Geschmack etwas überheblichen Bedeutung versehen bleibt, bleibt der Systementwurf in einer Schieflage. Insbesondere wird es nicht möglich sein, im weiteren das von Einstein eingeführte Äquivalenzprinzip von träger und schwerer Masse zu verstehen.

Wie weit dieser Gedanke reicht, wird sich im folgenden zeigen, wenn Hegel in einer weiteren Wendung der Kraft der Schwere das Licht gegenüberstellt, das nicht mehr nur den Ausbruch aus der Eindimensionalität erreicht, sondern innerhalb der höheren Dimension die freie Beweglichkeit. Die im freien Fall enthaltene innere Freiheit kommt für Hegel zu sich, wenn sie nicht mehr nur das Suchen nach einem Zentrum, sondern freie Beweglichkeit ist, die sich im Licht zeigt. Das mag mysteriös klingen, wird im weiteren jedoch in einer Deutung der Relativitätstheorie aus Sicht von Hegel näher betrachtet werden.

– Das Quadrat

Die Geometrie des Quadrats ist immer von Neuem faszinierend und unerschöpflich. Der Eintrag in Wikipedia hat wichtige Erkenntnisse zusammengestellt: Das Quadrat kann aus einer gegebenen Seitenlänge wie auch aus einer gegebenen Diagonale mit Lineal und Zirkel konstruiert werden. Es ist ein typisches Objekt der euklidischen Geometrie. Im Innern lässt sich das Quadrat auf vielfache Weise parkettieren, so auch mit den Penrose-Mustern.

Mit dem Begriff des Quadrats ist bei Hegel jedoch sicher weniger das in der Geometrie gleichsam empirisch gegebene Quadrat gemeint. Vielmehr ist angespielt auf die ursprüngliche Bedeutung des Quadrats als Dynamik und darüber als Energie.

Am Quadrat kann unterschieden werden:

1. Die empirisch gegebene Figur □
2. Die mathematische Operation des Quadrierens (x mal x, x²)
3. Das Übergehen in eine höhere Potenz und darüber in eine neue Zahlenklasse (Diagonale). Für Platon ist die Diagonale nur durch die Vernunft zu bestimmen. So gesehen sind die mit der Diagonale gegebenen Zahlen die ersten vernünftigen Zahlen, während die rationalen Zahlen nur verstandesmäßig sind.
4. In dieser Zahlenklasse gelten eigene Regeln. Imaginäre Zahlen.
5. Das Quadrat als Maß der Energie. Das Quadrat von Tangente und Cotangente entlang einer Kurve.
6. Die Wesenslogik als Logik zweiter Ordnung. Wird die zweite Ordnung für sich betrachtet, ist es der Begriff des Quadrats, um den es Hegel geht. Er wäre besser als Prinzip des Quadrat zu bezeichnen.

Für Hegel ist das Quadrat die Keimzelle, mit der eine eindimensionale Bewegung verlassen und die zweidimensionale Fläche erreicht wird. Während die Bewegung entlang einer Gerade keine Freiheit kennt, öffnen sich mit der Möglichkeit des Ausscherens in die Fläche unbegrenzt viele Möglichkeiten. Unter diesen Möglichkeiten ist Hegel die kreisförmige Umkehrung am wichtigsten. Das ist die Negation der Negation: Mit der Negation wird die Linie verlassen, mit der Negation der Negation wird zu ihr zurückgekehrt. Ähnlich versteht Spencer-Brown den Re-entry (die Wiederkehr nach einer freien Bewegung und deren Umkehrung im imaginären Raum) und spricht von Equations of the second degree.

"Das Gesetz des Falles ist gegen die abstrakte gleichförmige Geschwindigkeit des toten, von außen bestimmten Mechanismus ein freies Naturgesetz, d.h. das eine Seite in ihm hat, die sich aus dem Begriffe des Körpers bestimmt. Indem daraus folgt, daß es aus diesem muß abgeleitet werden können, so ist dieses sich vorzusetzen und der Weg / anzugeben, wie das Galileische Gesetz, daß die durchlaufenen Räume sich wie die Quadrate der verflossenen Zeiten verhalten, mit der Begriffsbestimmung zusammenhängt." (Enz. § 267, HW 9.77f)

Wie gelingt der von Hegel geforderte »Beweis aus dem Begriffe der Sache«? Ohne an dieser Stelle in Details zu gehen, begründet Hegel die Naturphilosophie mit dem Begriff der Natur (Enz. § 247), entwickelt aus ihr die Begriffe von Raum und Zeit (Enz. §§ 254 ff) und aus ihnen das in der Bewegungsgleichung auftretende Quadrat. Die nicht einfach zu lesende Stelle lautet:

»Die als der Form der Zeit, der Einheit, entgegengesetzte Form des Außereinander des Raums, und ohne daß irgendeine andere Bestimmtheit sich einmischt, ist das Quadrat, – die Größe außer sich kommend, in eine zweite Dimension sich setzend, sich somit vermehrend, aber nach keiner anderen als ihrer eigenen Bestimmtheit, – diesem Erweitern sich selbst zur Grenze machend und in ihrem Anderswerden so sich nur auf sich beziehend.
Dies ist der Beweis des Gesetzes, des Falls aus dem Begriffe der Sache. Das Potenzenverhältnis ist wesentlich ein qualitatives Verhältnis und ist allein das Verhältnis, das dem Begriffe angehört« (Enz. § 267, HW 9.78).

Wenn ich es richtig verstehe, sieht Hegel aus dem Begriff der Zeit den Begriff der Reihe und aus dem Begriff des Raums den Begriff des Quadrats hervorgehen. Er hat nicht zuerst den Begriff der eindimensionalen Reihe, um dann die Zeit als Beispiel für eine eindimensionale Reihe anzusehen, sondern versteht umgekehrt die eindimensionale Reihe als eine Eigenschaft der Zeit. Es entspricht dem Begriff der Zeit, dass sie eindimensional ist, eine Reihe bildet und entlang dieser Reihe Notwendigkeit und Kausalität gelten. Mit dem Begriff des Raums entsteht die Vielfalt der Möglichkeiten, in die sich entlang der Zeit (im Verlaufe der Zeit) die Bewegung entwickeln kann. Daher entsteht für Hegel aus dem Begriff des Raums der Begriff des Quadrats und mit ihm der Freiheit.

Hegel übernimmt in origineller Weise das von Kant ausgeführte Verständnis der Zeit und wendet es neu. Kant hatte an der Zeitreihe »das Schema der Ursache und der Kausalität« erkannt und am »Schema der Gemeinschaft (Wechselwirkung)«, dem »Zugleichsein [...] das Schema der Möglichkeit« (KrV, B 184) gefunden. Hegel zieht das alles in einen originellen Gedanken zusammen: Wenn die Zeit zum Quadrat erhoben wird, öffnet sie sich in den Raum und mit ihm in die Freiheit der Möglichkeiten. Für ihn ist der mit einer quadratischen Gleichung (Parabel) zu beschreibende Fall eine Ablenkung von der eindimensionalen Bewegung eines Körpers, der ohne äußere Einflüsse in Trägheit verharrt und seinen Bewegungszustand beibehält. Die Ablenkung ist für ihn in einem sehr anschaulichen, fast teleologisch klingenden Bild ein »Suchen des Zentrums« (Enz. § 267 Zusatz, HW 9.78). Während bei der trägen Bewegung ein einzelner Gegenstand für sich isoliert bleibt und nicht nach links oder rechts schaut, bewegt sich der fallende Körper auf ein Zentrum.

Wenn der Begriff des Quadrats seinerseits aus einem höheren Begriff hergeleitet werden soll, so ist das die Potentialität oder das Potenzenverhältnis. Platon gebraucht in seinem Dialog Theaitetos 147d4-5 ganz selbstverständlich das Wort dynameis für Quadratzahlen. Siehe hierzu den Beitrag über Dynamische Zahlen. In diesem Beitrag wird über die dynamischen Zahlen hinausgehend die Idee von ogkischen (gewichtigen) Zahlen eingeführt. Mit ogkischen Zahlen ließe sich der Grenzfall der Keplerschen Gesetze klären: Diese Gesetze sind zwar ohne Dimensionseinheit definiert, aber sie sind hergeleitet aus Beobachtungen, die nur an trägen Körpern erkannt werden konnten.

Anmerkung 1: Wenn Hegel vom Suchen des Zentrums spricht, steht er in der Tradition der antiken Philosophie. Als erstes ist Aristoteles zu nennen (siehe zum Folgenden HW 19.184). Aristoteles hat nicht nur die Bewegung der vergänglichen physischen Körper auf der Erde untersucht, die danach streben, ihren natürlichen Ort zu finden, – wobei auch in dieser Bewegung bereits ein »Suchen« enthalten ist und eine lebendige Kraft angenommen wird, mithilfe derer die Körper zu ihrem natürlichen Ort finden. Darüber hinaus hat Aristoteles gefragt, wie sich die unvergänglichen Körper am Himmel bewegen, für die es keine vergleichbaren natürlichen Orte gibt. Auch dort erkennt er Bewegungen, die zum Zentrum hin oder vom Zentrum weg gerichtet sind.

»Das Eine nämlich ist von Natur bestimmt, immer vom Mittelpunkt hinweg bewegt zu werden, das andere aber, immer zum Mittelpunkt hin. Von diesen beiden aber sage ich, dass das vom Mittelpunkt weg Bewegtwerdende nach oben bewegt werde, nach unten hingegen zum Mittelpunkt hin. Ungereimt aber ist es zu glauben, es gebe nicht Etwas im Himmelsgebäude, was das Oben, und Etwas, was das Unten sei« (Aristoteles, De caelo IV, 308a, Übersetzung von Prantl).

Dieser Bewegung entspricht der von Hegel gemeinte Fall, der zum Zentrum seines Systems strebt. Bei aller Kritik an Aristoteles ist dieser Gedanke der modernen Naturwissenschaft ganz selbstverständlich, wenn sie z.B. die Bewegung der im Weltall auseinander strebenden Galaxien daraus erklärt, dass sie sich von einem Mittelpunkt in der Raumzeit entfernen, der als Urknall bezeichnet wird.

Zum anderen ist Epikur zu nennen, der ungefähr 40 Jahre jünger als Aristoteles war. Epikur vertrat wie Demokrit eine rein materialistische Lehre und wandelte den Determinismus seines Vorgängers Demokrit um. Die Atome bewegen sich nach seiner Ansicht nicht ausschließlich auf starren, geradlinigen, völlig vorherbestimmten Bahnen, sondern können durch Zufall von ihnen abweichen. Bei aller Kritik durch Hegel (HW 19.312f) ist hier der Gedanke enthalten, dass und wie es zu Abweichungen von geradlinigen Bahnen kommen kann. Marx hat die Brisanz dieser Differenz erkannt und darüber seine Doktorarbeit geschrieben. Das ist keineswegs nur eine Spezialfrage innerhalb des entlegenen Gebiets verschiedener Atomisten in der Antike, sondern berührt zentral die Frage, was mit Bewegung gemeint ist.

Anmerkung 2: Ihmig hat in seiner 1989 veröffentlichten Studie Hegels Deutung der Gravitation nicht nur für das Gesetz des Falls, sondern allgemeiner für die Gravitation gezeigt, in welcher Weise Hegel eine philosophische Konstruktion anstrebt, indem er schrittweise in der Wissenschaft der Logik Begriffe entwickelt, die später in der Naturphilosophie herangezogen werden.

Ordnung der Zeit

– Die drei Dimensionen der Zeit

Für Hegel war nicht voraussehbar, dass es mit der Relativitätstheorie gelingen sollte, zunächst zwei und schließlich sogar drei Dimensionen der Zeit zu unterscheiden (die gewöhnliche Zeit, die Zeit des Alterns innerhalb eines Trägheitssystems, die Zeit der explosionsartigen Ausdehnung des Weltalls nach dem Urknall). Das soll im folgenden skizziert werden, um anschließend zu zeigen, dass damit eine Ordnung der Zeit konstituiert wird, die sich deuten lässt als ein Beispiel für die von Hegel im Kapitel über das Maßlose genannte »bloße Ordnung« (HW 5.445) und die Zerlegung der Zustände dieser Ordnung in innere Faktoren.

Die Zeit des Alterns Gemäß der Relativitätstheorie ist der Bewegungszustand eines Körpers in jedem Zeitmoment durch zwei zeitliche Dimensionen definiert:

(1) Die Geschwindigkeit vx, die ein Gegenstand benötigt, um in der Zeit t die Strecke x zurückzulegen. (Im Beispiel des Falls handelt es sich um die Strecke s, die ein Körper zu Boden fällt.) Diese Geschwindigkeit kann von jedem beliebigen Ort aus gemessen werden, indem die Lichtsignale verglichen werden, mit denen der Beginn und das Ende der Bewegung gesehen werden. Es wird vorausgesetzt, dass die Lichtgeschwindigkeit in allen Bezugssystemen gleich groß ist. Der Beobachter vergleicht, wann er das erste Signal und wann er das zweite Signal empfangen hat. Der Zeitabstand t zwischen den beiden Signalen wird durch die zurückgelegte Entfernung x geteilt und ergibt die Geschwindigkeit ›vx = x / t‹.

(2) Kritisch ist jedoch die Frage, wieviel Zeit zwischen den beiden Messungen zu Beginn und am Ende der Bewegung vergangen ist. Bewegt sich der Beobachter in einem Bezugssystem (Trägheitssystem, Inertialsystem), das sich schneller bewegt als das Bezugssystem der beobachteten Bewegung (wenn z.B. ein Weltraumreisender von einer von der Erde aus gestarteten Rakete auf die Erde schaut), dann gehen seine Uhren langsamer als die Uhren der beobachteten Bewegung. Paradox gesagt: Für ihn ist weniger Zeit vergangen als in der gleichen Zeit im langsameren Bezugssystem. Je langsamer ein Bezugssystem ist, desto schneller gehen in ihm die Uhren. Oder anders gesagt: Je langsamer ein Bezugssystem ist, desto schneller altern alle Gegenstände in diesem Bezugssystem. Die Geschwindigkeit des Alterns eines Bezugssystems wird mit vt bezeichnet.

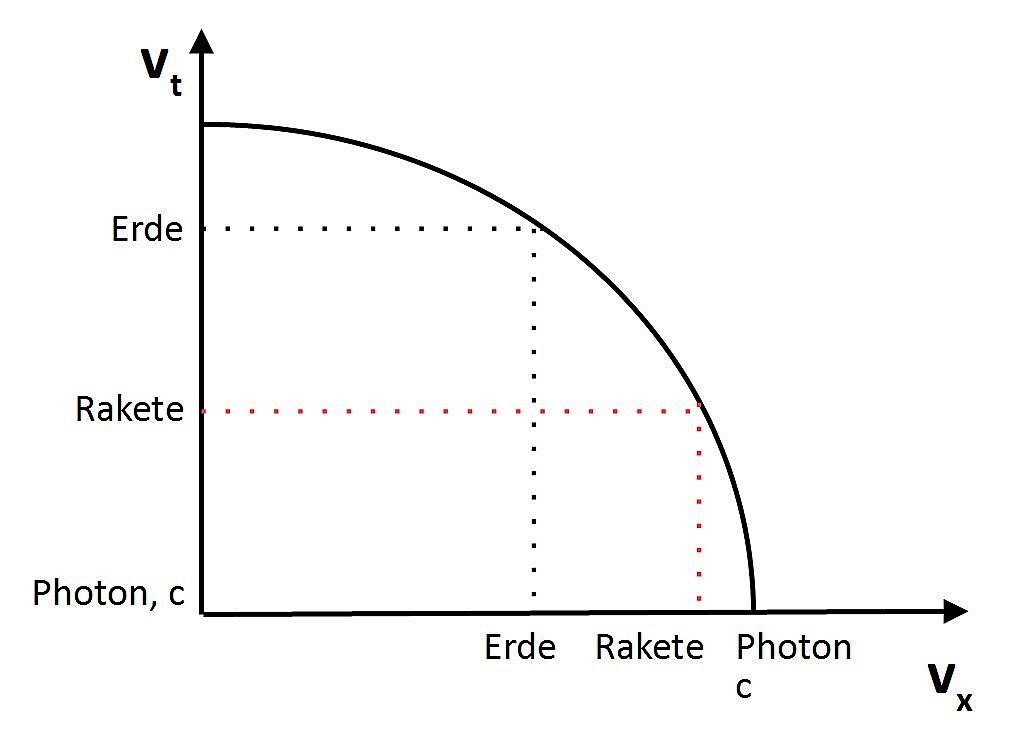
Figur 4  Epstein-Kreis: Geschwindigkeit im Raum und Altern der Zeit
Auf der waagerechten vx-Achse ist eingezeichnet: Die Erde (schwarz gepunktet) bewegt sich langsamer als eine von ihr gestartete Rakete (rot gepunktet), und beide bewegen sich langsamer als das Licht (Photon).
Die vt-Achse zeigt: Zugleich altert alles auf der Erde schneller als in der Rakete. Das Bezugssystems des Photons, das sich mit Grenzgeschwindigkeit c bewegt, altert gar nicht. Für das Photon gilt vt=0. – Die Zeichnung ist mit einigen Anpassungen übernommen aus: Helmut Hansen Linien des Alten, S. 51

Die waagerechte vx-Achse zeigt die übliche Geschwindigkeit, die vom jeweiligen Bezugssystem des Beobachters aus gemessen wird. Die senkrechte vt-Achse zeigt, wie schnell innerhalb des Bezugssystems die Uhren gehen. Startet auf der Erde eine Rakete und entfernt sich mit hoher Geschwindigkeit von ihr, dann ist die Geschwindigkeit vx der Rakete größer als die Geschwindigkeit der Erde, von der sie gestartet ist (siehe zur Eigengeschwindigkeit der Erde zum Beispiel DLR_next). Die Rakete entfernt sich im Verlaufe der Zeit von der Erde. Dieser Effekt wird dadurch ausgeglichen, dass auf der Rakete die Uhren langsamer gehen, so dass die Gesamtgeschwindigkeit, die sich aus der Summe von vx und vt ergibt, gleich bleibt.

Das Licht bewegt sich mit der Grenzgeschwindigkeit c und altert nicht. Die Aussage der Relativitätstheorie lässt sich daher in einem einzigen Satz zusammenfassen: Alles bewegt sich mit Lichtgeschwindigkeit, wenn sowohl die übliche messbare Geschwindigkeit vx wie das Altern des jeweiligen Bezugssystems vt berücksichtigt werden. Durch Einstein wurde daher die klassische Physik in keinem Punkt widerlegt, sondern er hat gezeigt, dass ihre Gesetze nur unter der Annahme gelten, dass sich alles innerhalb eines gemeinsamen Bezugssystems abspielt, also für alle Beteiligten die Uhren gleich schnell gehen.

In der Ausdrucksweise von Hegel kann dies als Zerlegung eines Bewegungszustandes in zwei innere Faktoren verstanden werden: Wird der eine Faktor größer, dann wird der andere Faktor entsprechend kleiner. Nach außen ergibt sich eine Indifferenz. Die Gesamtgeschwindigkeit ist immer gleich.

Daraus ergeben sich verschiedene Konsequenzen, die der gewöhnlichen Alltagserfahrung des Menschen widersprechen, da der Mensch mit seinen Augen weder Geschwindigkeiten verfolgen kann, die sich in der erforderlichen Größenordnung bewegen, noch kann er das Altern des eigenen oder anderer Bezugssysteme wahrnehmen. Dennoch ließen sich die von Einstein theoretisch vorausgesagten Effekte sehr gut nachweisen (Zeitdilatation bewegter Teilchen). Werden z.B. in Teilchenbeschleunigern Experimente durchgeführt, deren Geschwindigkeiten der Lichtgeschwindigkeit nahe kommen, dann können diese Bewegungen nicht mit bloßem Auge wahrgenommen werden, sondern müssen mit mathematischen Methoden in den Rechnungen berücksichtigt werden. Der Mensch »sieht« diese Bewegungen nur auf Fotos, die entsprechend aufbereitet sind.

Das Altern der Bezugssysteme ist wie das Trägheitsprinzip ein Beispiel, dass die Physik etwas  setzen  muss, das sich prinzipiell der Wahrnehmung entzieht. Insofern hat in einem höheren Sinn die moderne Naturwissenschaft Hegel nicht widerlegt, sondern bestätigt, weil sie zeigt, dass es Phänomene gibt, die nicht empirisch gemessen werden können, sondern indirekt vom Verstand gesetzt werden müssen. Daher stellt sich mit Hegel die Frage, mithilfe welcher Denkbestimmungen der Physik Setzungen dieser Art möglich sind. Sie selbst begnügt sich damit, dass ihre Ergebnisse nachprüfbar sind, und fragt nicht, wie sie zu solchen Ergebnissen kommen kann. Das wird letztlich mit der Intuition genialer Wissenschaftler vom Rang eines Einstein erklärt.

Anmerkung: Für jemanden, der bereits die Relativitätstheorie kennt, ist die einfache Darstellung durch Epstein überaus verblüffend. Auch die anderen Gesetzmäßigkeiten wie die berühmte Gleichung E = m · c^² ergeben sich in seiner Darstellung mithilfe einfachster Zeichnungen (siehe zum Beispiel die Darstellung durch Eckstein). Alle wissenschaftlichen Überprüfungen haben ergeben, dass es Epstein auf geniale Weise gelungen ist, den Grundgedanken der Speziellen Relativitätstheorie zu erfassen und zu treffen. Das zeigt nach meiner Meinung die Berechtigung des Ansatzes, Ordnungen und ihre Zustände und innerhalb der Zustände ihre inneren Faktoren zu erkennen.

Die Zeit der Expansion des Weltalls Die Astrophysik hat gezeigt, dass auch die Spezielle Relativitätstheorie nur unter bestimmten Annahmen gilt, die in frühen Entwicklungsstadien des Universums nicht gegeben waren. Daher werden die beiden von Einstein unterschiedenen Dimensionen der Zeit nochmals unterschieden von einer dritten Zeit, für die die Spezielle Relativitätstheorie nicht gilt. Im Gegenteil wird angenommen, dass sich das Universum in einer frühen Phase weit schneller als mit Lichtgeschwindigkeit ausgedehnt hat. Das wird so erklärt, dass es nicht um Bewegungen  in der Zeit, sondern um Bewegungen  der Zeit  geht. Während für jedes Bezugssystem gesagt wird, wie schnell es altert, soll für die Zeit im Ganzen gelten, dass es für sie kein Altern, d.h. keine Geschwindigkeit vt gibt. Und es gibt für sie auch keine Geschwindigkeit vx, mit der sie sich durch die Zeit, d.h. durch sich selbst bewegen könnte. Aber es gibt eine dritte Geschwindigkeit. Das ist die Geschwindigkeit, mit der sich die Zeit ausdehnt. Diese Geschwindigkeit sei mit ve bezeichnet, wobei der Buchstabe »e« für »Expansion« stehen soll. Die Urknall-Theorie beschreibt, wie sich im Verlaufe der Geschichte seit dem Urknall die Geschwindigkeit ve verändert hat, wobei ve in einigen Entwicklungsstadien weit größer als die Lichtgeschwindigkeit c ist.

Diese Unterscheidung ähnelt dem logischen Paradoxon, wenn Sprache und Meta-Sprache oder Logik und Meta-Logik ineinander verschlungen werden. Sie liegt dennoch allen Theorien der Astrophysik zugrunde. Die Urknall-Theorie besagt, dass der Urknall nicht als ein Ereignis  in der  Zeit zu verstehen ist, sondern als das Ereignis, mit dem  die Zeit  und damit auch die Möglichkeit und der Raum aller Ereignisse entstanden ist. Während die Spezielle Relativitätstheorie nur innerhalb der Zeit gilt, gelten für die Beschreibung der Zeit im Ganzen mit der Urknall-Theorie die klassischen Gesetze von Galilei und Newton, oder mathematisch gesprochen die euklidische Geometrie. Ohne es sich einzugestehen, wiederholt die neuzeitliche Physik auf dieser Ebene die gleiche Unterscheidung, die bereits Aristoteles mit dem sublunaren und dem supralunaren Raum getroffen hat. Was Aristoteles vorgeworfen wurde – dass er keine universellen Bewegungsgesetze aufstellen kann –, gilt daher auch für die neuzeitliche Physik. Für Bewegungen von Raum und Zeit im Ganzen gelten andere Bewegungsgesetze als für Bewegungen innerhalb von Raum und Zeit.

Zeitreisen Einem Logiker wie Kurt Gödel, der die logischen Paradoxa der Logik und der Mathematik durchschaut und mit ihnen zu operieren gewusst hat, ist das nicht entgangen. Ihm gelang es, streng nach den Regeln der Allgemeinen Relativitätstheorie ein Universum zu konstruieren, in dem Zeitreisen möglich sind, wodurch die klassischen Modi der Zeit, das sind Vergangenheit, Gegenwart und Zukunft (Hegel nennt sie Dimensionen) aufgehoben sind: Wer in einem solchem Universum aus seiner eigenen Sicht immer in die eigene Zukunft reist, kann am Ende des Weges einen Punkt in seiner eigenen Vergangenheit erreichen. Gödels Grundgedanke ist einfach: Er hat das Gödel-Universum so konstruiert, dass die Zeit im Ganzen rotiert. Da für die Zeit im Ganzen (und damit innerhalb des Gödel-Universums für die Rotation der Zeit) die Regeln der Speziellen Relativitätstheorie verletzt werden können, ist es möglich, sich die Rotation der Zeit im Ganzen zunutze zu machen und sich mit Überlichtgeschwindigkeit zu bewegen.

Anmerkung: Die Paradoxa von Zeitreisen können nach meiner Überzeugung überwunden werden, wenn die Rückkehr in die eigene Vergangenheit auf ähnliche Weise interpretiert wird wie die Mehrblättrigkeit in den komplexen Zahlen. Jede Zeitreise führt dann zwar in die Vergangenheit zurück, aber auf ein eigenes Blatt. Das führt zur Frage der Analytizität, die sich in ähnlicher Weise bei den Grundsatzfragen in der chemischen Sphäre ergibt (siehe den Beitrag zum realen Maß).

Zeitbewusstsein Von hier lässt sich ein Bogen schlagen zu den Ideen von Husserl über das Zeitbewusstsein. Auch er hat zwei Dimensionen der Zeit definiert, wenn es innerhalb der Lebenszeit möglich ist, sich an eine vergangene Zeit zu erinnern und eine künftige Zeit zu entwerfen und zu planen. Hier ist zu fragen, wie es dem Bewusstsein gelingt, die eigene Lebenszeit und die mithilfe der Einbildungskraft entworfene Zeit zu unterscheiden. (Siehe hierzu auch Hegel über die Vorstellungen etwa im Gedächtnis, die »isoliert von dem äußerlichen Orte, der Zeit und dem unmittelbaren Zusammenhang, in dem sie stand(en)«, gebildet werden können, Enz. § 452, HW 10.259. Hegel stellt jedoch nicht die Frage, wie die Zeit der Intelligenz, die Vorstellungen bildet – siehe Enz. § 453, HW 10.259f –, und die Zeit innerhalb dieser Vorstellungen miteinander verknüpft werden sollen. Das scheint für ihn selbstverständlich gewesen zu sein, da er offenbar von einem autonomen Subjekt ausgeht, das seine Autonomie sowohl von der Gesetzlichkeit seiner Umgebung wie von der Gesetzlichkeit der von ihm gebildeten Vorstellungen zu unterscheiden vermag.)

Anmerkung: Sambursky hat gezeigt, dass dieser Ansatz übereinstimmt mit verschiedenen Zeitideen des Neoplatonismus. Darauf soll im Rahmen der Aristoteles-Kommentare näher eingegangen werden.

– Wahlverwandtschaften und Knotenlinien von Bewegungszuständen und Ereignissen

Die begriffliche Schwierigkeit, wie die Bewegung der Zeit im Ganzen zu unterscheiden ist von den Bewegungen innerhalb der Zeit, und wie erklärt werden kann, warum für beide unterschiedliche Gesetze gelten, lässt sich meines Erachtens mithilfe der von Hegel diskutierten Begriffe der Wahlverwandtschaft und ihrer Knotenlinie lösen. Wahlverwandtschaft: Einstein ging in der Speziellen Relativitätstheorie von der Frage der Beobachtbarkeit und Messbarkeit unterschiedlicher Ereignisse aus. Zwei Ereignisse können gemessen werden, wenn ihre Lichtsignale von einem Dritten aufgefangen und miteinander verglichen werden können. Diese Situation lässt sich mit Hegel als Wahlverwandtschaft interpretieren: Zwei Ereignisse sind miteinander »verwandt«, wenn sie sich im Sinne der Speziellen Relativitätstheorie durch Signale abstimmen und aneinander gemessen werden können.

Wahlverwandtschaften gelten jedoch nicht absolut, sondern können sich in verschiedenen Zuständen ändern. Hegel bringt hierfür Beispiele aus der Chemie: Zwei chemische Stoffe gelten als wahlverwandt, wenn sie miteinander reagieren. Manche chemische Reaktionen treten jedoch nur in Flüssigkeiten auf, die eine bestimmte Temperatur oder eine bestimmte Zusammensetzung haben. Jeder Zustand ist durch Parameter wie Temperatur, Druck, Teilchenzahl, Zusammensetzung der Mischung bestimmt. Werden die Parameter geändert, entsteht eine Knotenlinie, die von einem Zustand in einen anderen führt. Jeder Zustand hat für eine gewisse Dauer eine innere Stabilität bis die Änderung des Parameters (z.B. eine Erhöhung der Temperatur) in den nächsten Zustand führt. Das kann übertragen werden auf die Zustände der Zeit, innerhalb derer die von der Speziellen Relativitätstheorie beschriebenen durch Lichtsignale vermittelten Wahlverwandtschaften unterschiedlichen Regeln folgen.

Die kosmologischen Beschreibungen der Entwicklungsstadien des Universums zeigen, dass nicht in allen Entwicklungsstadien des Universums Bedingungen gegeben sein können, unter denen die Spezielle Relativitätstheorie gilt. Vielmehr muss es Entwicklungsstadien gegeben haben, in denen sich der Raum und die Zeit weit schneller als mit Lichtgeschwindigkeit ausgedehnt haben, d.h., in denen für die Expansionsgeschwindigkeit ve gilt: ve > c. In diesen Stadien muss es andere Naturgesetze gegeben haben, mithilfe derer innerhalb von Raum und Zeit Ereignisse synchronisiert werden.

Die unterschiedlichen Gesamtzustände (und damit sind jetzt nicht gemeint die Bewegungszustände etwa eines bewegten Körpers, der verschiedene Phasen im Verlaufe seiner Bewegung durchläuft, sondern die verschiedenen Zustände, in denen im Ganzen die Regeln der Speziellen Relativitätstheorie oder andere Regeln für die Beschreibung mechanischer Regeln gelten) sind ihrerseits durch eine Knotenlinie verbunden, entlang derer sie auseinander hervorgehen. In der heutigen Physik werden Fragen dieser Art mit sehr komplexen mathematischen Methoden aus der Differentialgeometrie dargestellt (siehe zum Beispiel Geometrisierung von 3-Mannigfaltigkeiten).

Die Physiker spüren die hier auftretenden begrifflichen Schwierigkeiten und sprechen daher nicht von einer weiteren Dimension der Zeit, sondern von der »Zeit selbst«. Das derzeit am meisten diskutierte Beispiel ist die Inflationstheorie, mit der ein Entwicklungsstadium in der Frühgeschichte des Universums beschrieben wird, in dem die heute bekannten Gesetze nicht galten. Wird die Geschichte des Universums dargestellt, dann tritt hier die Zeit sowohl als Achse auf, entlang derer die Geschichte verläuft, wie auch als ein Objekt, dass sich innerhalb seiner eigenen Zeit verändert.

Die astrophysikalischen Theorien ändern sich zur Zeit sehr schnell und sind bisher in der Regel durch neue Entdeckungen widerlegt worden und mussten durch neue Modelle abgelöst werden. Es geht im folgenden daher nicht um ein besseres philosophisches Verständnis einzelner Theorien, die sicher in Kürze dank neuer Beobachtungen wieder fallen gelassen werden müssen, sondern um die zugrunde liegende Frage, in welcher Weise die verschiedenen Dimensionen (Ebenen) der Zeit miteinander vermittelt werden können.

Figur 5  Entwicklungsstadien des Universums
Jede vertikale Scheibe in dem dreidimensionalen, trichter-ähnlichen Raumzeit-Gebilde des Universums zeigt jeweils einen Zeitmoment, in dem sich unterschiedliche Bezugssysteme mit unterschiedlichen Geschwindigkeiten unterscheiden lassen. In jedem Zeitmoment sind am Himmel noch die Galaxien und Sterne vergangener Zeiten zu sehen, die bereits längst vergangen sind, aber deren Licht erst jetzt bei einem Betrachter der Gegenwart auf der Erde eintrifft. Alle Ereignisse, die sich innerhalb des Trichters gegenseitig sehen können, gelten als wahlverwandt oder sichtbar. Der Trichter im Ganzen zeigt die Zeit im Ganzen. Sein Ursprung und sein Rand sind vom Innern aus nicht sichtbar. Quelle: Wikipedia.

Innerhalb der Geschichte des Universums lassen sich verschiedene Entwicklungsstadien mit jeweils eigenen Eigenschaften unterscheiden. Zum Beispiel gab es am Anfang nach der Inflation einen Zustand des Universums, in dem es noch keine Galaxien und Sterne gab. Das Echo dieses Zustands ist heute als Hintergrundstrahlung nachzuweisen, die in Figur 5 durch eine grün-blaue Scheibe eingezeichnet ist.

Die Astrophysik sucht nach den Gesetzmäßigkeiten, aufgrund derer die verschiedenen Entwicklungsstadien ineinander übergegangen sind. Das ist im Sprachgebrauch von Hegel die Knotenlinie, die sich in diesem Trichter von links nach rechts zieht und entlang derer die Entwicklungsstadien auseinander hervorgehen. Um das zu veranschaulichen, sind in der folgenden Figur die in Figur 5 enthaltenen Zustände der Zeit schematisiert hervorgehoben:

Figur 6  Phasenmodell der Expansion des Universums

Figur 6 zeigt die Zustände der Zeit, wie sie sich aus heutiger Sicht entwickelt haben:

• Vor dem Urknall: Vor dem Urknall muss sich das Universum zusammengezogen haben, um den punktförmigen Urknall erreichen zu können. Die Expansionsgeschwindigkeit ve der Zeit war daher negativ: ve < 0. Es gibt verschiedene Theorien, wie diese Phase ausgesehen haben könnte, z.B. die Branenkosmologie.
• Quantenfluktuation: Im Moment des Urknalls bestand ein Zustand, in dem die uns vertrauten Gesetze der Zeit nicht galten. Für die kritische Größe kann sogar ein Zahlenwert angegeben werden: die Planck-Zeit. Sie beträgt ca. 5,391 · 10⁻⁴⁴ Sekunden. Auch hierfür gibt es verschiedene Theorien. Hier könnte es Zeitschlingen gegeben haben, aus denen sich die uns bekannte Zeit emergiert hat. Peter Eisenhardt spricht vom »Webstuhl der Zeit«.
• Inflation: In dieser Phase hat sich die Raumzeit mit extremer Geschwindigkeit ve ausgedehnt. Nach Überzeugung der Astrophysiker gilt für diese Phase: ve > c
• Expansion infolge Urknall: Das ist die Phase, in der die uns bekannte Physik gilt. Die Expansion der Zeit ist nur sehr mäßig. Der Raum ist annähernd perfekt euklidisch.
• Beschleunigte Expansion: Entgegen allen Vermutungen wird davon ausgegangen, dass sich die Expansion wieder beschleunigt hat.

Auch wenn sich das Verständnis dieser Zustände ohne Zweifel ändern wird und möglicherweise weitere Zustände hinzukommen und einige differenziert oder aufgegeben werden müssen, kann nach meiner Überzeugung dennoch grundsätzlich festgehalten werden: Es gibt verschiedene Zustände der Zeit, die im Einzelnen noch genauer zu erforschen sind, und die Entwicklung der Zustände der Zeit kann verglichen werden mit den Aggregatzuständen des Wassers. So wie Wasser in den Zuständen Eis, Flüssigkeit und Dampf auftreten kann, kann die Zeit auftreten in unterschiedlichen Zuständen, in denen jeweils eigene Wahlverwandtschaften von Ereignissen gelten. Das bedeutet, dass die Zeit vergleichbar dem Wasser ein Substrat ist. So wie Hegel bezogen auf ein jeweiliges Substrat die Gesamtheit seiner Zustände als ihre »bloße Ordnung« bezeichnet hat, zeigt diese Figur in einer ersten groben Annäherung die Ordnung der Zeit. Und so wie Hegel im weiteren die Zustände genauer beschrieben hat durch das »umgekehrte Verhältnis ihrer Faktoren« (HW 5.446), ist die Spezielle Relativitätstheorie dahin zu erweitern, dass jeder Zustand der Zeit in jeweils eigener Weise durch innere Faktoren zu beschreiben ist.

Vor allem steht sich die Frage, ob es in vergleichbarer Weise eine physikalische Erklärung gibt für die Übergänge zwischen den Zuständen der Zeit, so wie die Temperaturerhöhung die Übergänge zwischen den Aggregat-Zuständen des Wassers erklärt. Heute wird z.B. angenommen, dass für die aktuelle Phase der beschleunigten Expansion die Dunkle Energie verantwortlich ist. Im Grunde ist der Name »Dunkle Energie« nur eine Verlegenheitslösung, um nicht direkt zu sagen, dass die Ursache unbekannt ist.

– Die »Trägheit« von Zuständen

Auch wenn Zustands-Parameter wie die Temperatur kontinuierlich verändert werden, bilden sich im Verlaufe dieser Entwicklung einzelne Zustände heraus, die für eine bestimmte Dauer Bestand haben. Diese Stabilität kann als Trägheit bezeichnet werden. Physikalisch wird sie dadurch erklärt, dass innerhalb eines Zustands eine eigene Ordnung entsteht, die die Entropie vergrößert. Erst wenn die Veränderung des kritischen Systemparameters weit genug fortgeschritten ist, kann die mit der Ordnung des Zustands erreichte Optimierung überwunden und eine neue Ordnung erreicht werden, in der die Entropie nochmals erhöht ist. Trägheit beschreibt das Verharren, im jeweiligen Zustand zu bleiben, Schwere das Bestreben, den Zustand zu verlassen und einen anderen Zustand zu erreichen, der dem Zentrum der übergreifenden Bewegung näher liegt. Alle Beobachtungen deuten darauf hin, dass derzeit das Weltgeschehen danach strebt, die Entropie zu vergrößern. Zustände mit höherer Entropie liegen daher dem Zentrum näher, das mit vollständiger Entropie (Wärmetod) erreicht wäre. (Natürlich kann gefragt werden, ob auch dies nur eine vorübergehende Richtung ist, die abgelöst werden könnte von einer gegenteiligen Bewegung, die den Raum wieder kontrahieren und alle Temperaturen in ihm ansteigen lässt. Siehe hierzu die entsprechenden kosmologischen Modelle von einem zyklischen Universum.)

Es kann aber auch genau umgekehrt gesagt werden, dass ein einzelnes Element innerhalb eines Systems dank seiner Trägheit die Neigung hat, das System zu verlassen und ganz seiner Eigengesetzlichkeit (Autonomie, Eigenzeit) zu folgen, so wie entlang einer Ellipse jede Tangente die Richtung weist, entlang derer der Körper die Bahn und mit ihr das System verlassen könnte, oder wie einzelne Wassermoleküle das flüssige Wasser verlassen lange bevor das Wasser siedet. So verstanden enthält Trägheit ein Moment der Negation des Gesamtsystems (des Allgemeinen) und der Aktivität des einzelnen Elements innerhalb des Systems. – Die Schwere ist umgekehrt die Kraft, die den Ausbruch verhindert und das autonome System dahin drängt, sich weiter am Zentrum des vorhandenen Systems zu orientieren.

Trägheit kann als Kontinuation verstanden werden. Der träge Körper will seinen aktuellen Zustand in die Zukunft kontinuieren. Schwere ist dann die Kraft, die ihn von dieser Bahn wieder umkehren lässt und in der Umlaufbahn festhält.

Auf diese Weise beziehen sich Trägheit und Schwere wechselseitig aufeinander. Die Trägheit ist positiv der Eigengesetzlichkeit gegenüber und negativ gegen die Beharrungskräfte des Systems. Die Schwere ist positiv im Sinne der Systemerhaltung und negativ gegen alle Ausbruchsversuche. In dieser Weise entwickelt sich zwischen Trägheit und Schwere ein innerer Widerspruch, der als Figur bereits alles enthält, was Hegel in der Reflexionslogik über den Gegensatz von Positiv und Negativ beschreiben und in den Widerspruch treiben wird, bis dieser in einer neuen Dimension zugrunde geht.

Wenn Trägheit und Schwere in Widerspruch geraten und zu Grunde gehen, dann ist nach der Sache zu fragen, die dem zu Grunde liegt. Das ist nach heutiger Überzeugung die Steigerung der Entropie. Jeder Zustand ist nur eine lokale Stabilisierung, die so lange Bestand hat, bis sich die zugrunde liegende Sache durchsetzt und hervortritt.

Bezogen auf das Planetensystem bedeutet das, dass die Planeten deswegen nicht in die Sonne stürzen, weil sich derzeit das gesamte System bestehend aus Sonne und Planeten in einer stabilen Ordnung befindet, die aus sich heraus die Kraft enthält, kleine Abweichungen auszugleichen und sich zu stabilisieren. Die Aufrechterhaltung dieser Ordnung kostet dennoch Kraft. Irgendwann wird sich diese Kraft aufbrauchen und das System umschlagen in eine andere Ordnung. – Hegel war dagegen überzeugt, dass die Planetenbewegung direkter Ausdruck des Absoluten ist und sich niemals ändern wird. Er hält die Trägheit letztlich für die Kraft, mit der das Absolute seine Ewigkeit sichert. »Die Bewegung der Himmelskörper ist nicht ein solches Hin- und Hergezogensein, sondern die freie Bewegung; sie gehen, wie die Alten sagten, als selige Götter einher« (Enz. § 269, HW 9.85).

Figur 7  Phasenmodell der Expansion des Universums

Das Sonnensystem durchläuft nach heutiger Überzeugung unterschiedliche Zustände, in denen jeweils eigene Bewegungsmuster gelten. Am Anfang stand eine Urwolke, aus der sich das heute bekannte Planetensystem entwickelt hat. Dies wird sich dann wieder auflösen, wenn die Sonne ihre innere Energie so weit aufgebraucht hat, dass sie sich in einen Roten Riesen verwandelt, bis sich schließlich das Sonnensystem in Planetaren Nebel umwandelt.

Und so wie die Trägheitskraft in zwei Bedeutungen verstanden werden kann (als die der Fundamentalkraft entgegengerichtete Kraft und als die Kraft, die den aktuellen Zustand aufrecht erhält), lässt sich das auch für die Fundamentalkraft sagen: Sie weist zum einen in das Zentrum des aktuellen Systems und zieht zum Beispiel beim Fall auf der Erde alle Körper im Schwerefeld der Erde auf deren Oberfläche, und sie kann darüber hinaus als die weiterführende Kraft verstanden werden, die entlang der Knotenlinie die einzelnen Zustände in einer Richtung verändert, die dem Grundgesetz der Bewegung entspricht. In diesem erweiterten Sinn gilt heute die Entropie als die Fundamentalkraft.

– Wandschneider zu Licht und Masse

Kant wollte zeigen, wie aus den Eigenschaften der Zeit (Dauer, Kausalität und Wechselwirkung) elementare Fragen der transzendentalen Logik zu klären sind. Er unterscheidet die »Ordnung der Zeit« und ihren »Ablauf« (Kant, KrV, B 249). Hegel kehrte das um: Er will zeigen, wie im Verlaufe einer systematischen Entwicklung der Logik zunächst Dauer, Kausalität und Wechselwirkung als Begriffe der Logik entstehen, und dann mit ihnen der Begriff der Zeit erklärt werden kann. Dauer, Kausalität und Wechselwirkung sollen als eigenständige logische Begriffe eingeführt werden, die dem Begriff der Zeit vorausgehen. Sie können in diesem Sinn als Proto-Zeit verstanden werden, womit Hegel das Vorhaben des Neuplatonismus, die Zeit mithilfe einer Proto-Zeit zu erklären, aufgegriffen und neu ausgeführt hat.

Der Begriff der Dauer sollte sich aus dem Begriff der Trägheit ergeben. Wenn mit der Trägheit eine Kraft gefunden ist, die einen bestimmten Zustand für eine bestimmte Dauer erhält, dann liefern die Ausführungen zu Kraft und Schwere, Substrat und Zuständen und der Erhaltung von Zuständen im Verlaufe einer Knotenlinie einen Begriff der Dauer, der der Zeit vorangeht.

In diesem Sinn kann der Beitrag Licht und Masse verstanden werden, mit dem Wandschneider der Frage nachgeht, »was Masse ist, wodurch sie insbesondere befähigt ist, Dauer zu konstituieren« (Wandschneider 2008, S. 79). Er will zeigen, wie durch die Überlagerung zweier gegenläufiger Wellen eine Welle entsteht, innerhalb derer es stehende Punkte gibt, durch die »gewissermaßen ein raum-zeitliches Bezugssystems realisiert (ist): eine regelmäßige Abfolge ruhender Orte, verbunden mit synchronen Oszillationen« (Wandschneider 2008, S. 83).

Figur 8  Stehende Welle
»Eine stehende Welle (schwarz) als Überlagerung zweier gegenläufiger Wellen (rot und blau). Die Knoten der stehenden Welle befinden sich an den roten Punkten.« Quelle: Wikipedia

Wandschneider geht zwar in diesem Gedankenexperiment von Lichtwellen aus, aber sein Argument ist gültig für alle Wellen und ergibt sich aus der mathematischen Beschreibung des Wellenverlaufs und nicht aus bestimmten Eigenschaften von Licht oder Masse. Daher hat er nach meinem Eindruck etwas anderes und im Grunde Allgemeineres gezeigt: Bei jeder Überlagerung von Wellen wird ein System ruhender Orte konstituiert.

Gegenläufige Wellen können als eine geometrische Beschreibung des umgekehrten Verhältnisses zweier Faktoren verstanden werden, d.h. als geometrische Beschreibung der Indifferenz, mit der Hegel das »Werden des Wesens« ausführt. Wandschneider hat daher nach meiner Deutung ein Ergebnis gefunden, das über seine eigene Fragestellung hinausgeht: Er hat gezeigt, auf welche Weise innere Faktoren, die in umgekehrten Verhältnis zueinander stehen, eine Dauer konstituieren. Die Begriffe von Licht und Masse müssen dafür nicht herangezogen werden.

Dauer hat ohne Frage mit Trägheit zu tun. Das Argument von Wandschneider kann daher auch so verstanden werden, dass gezeigt ist, wie sich innerhalb des Verhältnisses der inneren Faktoren auf neue Weise eine Trägheit zeigt, die die Dauer konstituiert. Damit hat der Begriff der Trägheit eine neue Wende genommen, die es möglich macht, im Gegenzug auch den Begriff der Schwere neu zu verstehen. Das führt zur Allgemeinen Relativitätstheorie und ihrer Gleichsetzung von Trägheit und Schwere.

Es bleibt offen, wie in vergleichbarer Weise die beiden anderen von Kant diskutierten Eigenschaften der Zeit (Wechselwirkung und Kausalität) einzuführen sind. These: Wechselwirkung ist im Begriff der Wahlverwandtschaft vorbereitet. Zwei Dinge sind wahlverwandt, wenn es eine Wechselwirkung zwischen ihnen gibt. Es wäre noch im einzelnen auszuführen, wie Hegel schrittweise von der Wahlverwandtschaft zur Wechselwirkung und darüber zu Raum und Zeit kommt. – Die Knotenlinie zeigt eine Kausalität, wie ein Zustand in einen anderen übergeht. Auch hier ist zu fragen, wie die Übergänge entlang einer Knotenlinie im weiteren zu einem stärkeren Begriff der Kausalität führen.

Wenn es auf diese Weise gelingt, die in der Maßlogik entwickelten Begriffe als Keim der Eigenschaften zu verstehen, mit denen die Zeit charakterisiert ist, dann kann die Maßlogik als eine Proto-Physik verstanden werden, die dem Anliegen des Neuplatonismus gerecht wird. (Hiermit ist jedoch nicht die auf Dingler zurückgehende Protophysik gemeint, die im Rahmen des Konstruktivismus entstanden und von Lorenzen und Janich weiter ausgearbeitet worden ist, sondern eine der Physik vorausgehende Lehre, so wie bei Platon von einer Proto-Zeit – proton chronou – gesprochen wird und bei Aristoteles von einer prima materia – proto hyle die Rede ist. Siehe den Beitrag zum mathematischen und mythischen Symbol.)

Mit diesem Ansatz wird aus meiner Sicht auch der Aufbau der Wissenschaft der Logik von Hegel deutlicher: Hegel hat mit der Maßlogik die Grundlage gelegt, um anschließend die Reflexionsbegriffe ausführen zu können, die Kant letztlich aus den Eigenschaften der Zeit entwickelt hat (wenn Einerleiheit und Verschiedenheit auf Identität und Dauer, Einstimmung und Widerstreit auf Wechselwirkung und Inneres und Äußeres sowie Materie und Form auf Grund und Kausalität zurückgehen).

Der Widerstand im mechanischen Prozess

Der Widerstand ist für Hegel ein Phänomen des mechanischen Prozesses, bei dem autonome, mechanische Objekte aufeinander treffen und und gegenseitig ihren Bewegungszustand verändern. Das beginnt mit dem Widerstand, wenn das Eine und die Vielen in ihrem Fürsichsein einander abstoßen und anziehen (Repulsion und Attraktion) (HW 5.192, 203). Da kann von Wahlverwandtschaft noch keine Rede sein. Davon unterscheidet er das absolute Verhältnis der Substantialität, wenn die Substanz mit ihrer »Aktuosität [...] nicht tätig gegen Etwas, sondern nur gegen sich als einfaches widerstandsloses Element« ist (HW 6.220). Das verstehe ich so, dass nichts aus ihrem eigenen Inneren die Substanz aufhalten kann, zu ihrer eigenen Einheit zu finden. Diese Gedankenfigur wiederholt sich in den Ausführungen zur Teleologie und zur Idee. Wieder wird in doppelter Negation formuliert: Die in der Teleologie betrachteten Mittel verfügen über »keine Kraft des Widerstands gegen den Zweck« (HW 6.450). Das gilt entsprechend für die Idee des Guten: Für Hegel ist Prämisse des Handelns des Guten, dass »der Zweck ohne allen Widerstand sich der Wirklichkeit mitteilt« (HW 6.546). Und schließlich kann kein Objekt der Methode und ihrer »schlechthin unendliche(n) Kraft« Widerstand leisten (HW 6.551). – Dagegen würde Hegel vermutlich zustimmen, wenn heute beispielsweise vom elektrischen Widerstand gesprochen wird. – Anspielungen auf den politischen Widerstand können sowohl bei Fichte wie bei Hegel vermutet werden, siehe in Hegels Rechtsphilosophie die Hinweise auf den Widerstand der Materie in den §§ 52, 195 (HW 7.115, 352) und nahezu heroisch in der Phänomenologie des Geistes: »Diese ungeteilte Substanz der absoluten Freiheit erhebt sich auf den Thron der Welt, ohne daß irgendeine Macht ihr Widerstand zu leisten vermöchte.« (HW 3.433)

Die Aktuosität der Substanz gibt den wesentlichen Hinweis, worum es geht. Mit diesem vom Neuplatonismus und der Scholastik gebrauchen Ausdruck soll die innere Bewegung des Wortes (der Vernunft, der ratio, des logos, des Spiritus oder der Rationalität) bezeichnet werden, bevor sie das Fleisch (den Körper) ergriffen hat und sich in deren Bewegung zeigt. Für Aristoteles stellte sich die Frage, wie die Natur (physis) eines Körpers diesen dazu veranlassen kann, sich zu seinem natürlichen Ort zu bewegen. Bei lebendigen Körpern ist das die Frage, wie die Seele (psyche) bewirken kann, dass der Körper, dessen Seele sie ist, sich entsprechend ihren Zielen bewegt.

All diesen Fragen liegt das gemeinsame Thema zugrunde, in welcher Weise sich das Logische (Geistige) dem Stofflichen (Körperlichen) mitteilen oder theologisch gesprochen, wie sich das Göttliche dem Nicht-Göttlichen offenbaren kann. Hier erhält die Kraft der Trägheit eine neue Bedeutung: Dem Stofflichen kann nur etwas mitgeteilt werden, wenn es in sich eine Kraft des Widerstands hat, die weder die Mitteilung widerstands- und wirkungslos durch sich hindurchgehen lässt noch von der Gewalt der Mitteilung ausgelöscht wird. Hier droht in zweierlei Richtung eine Tragödie, wenn entweder der Mensch keinerlei Mitteilung mehr zu hören vermag und in Gottesferne und existenzielle Verlassenheit gerät, oder wenn er unter der Übermacht der göttlichen Botschaft jeden Halt verliert. In diesem Sinn hat Hölderlin die griechische Tragödie gelesen, und es kann angenommen werden, dass er darüber intensiv mit Hegel und Schelling gesprochen hat. In seinen Anmerkungen zur Antigonä deutet er die »tragische Darstellung« mit »Dialog und Chören«,

»die dem unendlichen Streite die Richtung oder die Kraft geben, [...] weil auch in tragischunendlicher Gestalt der Gott dem Körper sich nicht absolut unmittelbar mittheilen kann, sondern verständlich  gefasst, oder lebendig zugeeignet werden muß; vorzüglich aber besteht die tragische Darstellung in dem factischen Worte, das, mehr Zusammenhang, als ausgesprochen, schiksaalsweise, vom Anfang bis zu Ende gehet« (Hölderlin, Anmerkungen zur Antigonä, S. 374f).

Das ist der Seele nur möglich, wenn sie auf ihre Weise Widerstand leistet. Sie spürt, wie sie von etwas Größerem ergriffen wird, und reagiert zwiespältig darauf. Hölderlin sieht das in Antigone dargestellt. Sie begehrt sowohl gegen die bürgerliche Ordnung auf, als ihrem Bruder eine würdige Bestattung verwehrt wird, wie auch gegen die Götter, die das zulassen. Im Moment des Protestes wird sie von der göttlichen Mitteilung ergriffen.

»Der erhabene Spott, so fern heiliger Wahnsinn höchste menschliche Erscheinung, und hier mehr Seele als Sprache ist, übertrifft alle ihre übrigen Äußerungen; [...] Es ist ein großer Behelf der geheimarbeitenden Seele, daß sie auf dem höchsten Bewußtseyn dem Bewußtseyn ausweicht, und ehe sie wirklich der gegenwärtige Gott ergreift, mit kühnem oft sogar blasphemischem Worte diesem begegnet und so die heilige lebende Möglichkeit des Geistes erhält« (Hölderlin, Anmerkungen zur Antigonä, S. 371).

Heidegger ging in seiner Deutung der Freiheits-Schrift von Schelling so weit zu sagen, »jede Philosophie scheitert, das gehört zu ihrem Begriff«, weil sie sich nur im Widerstand gegen etwas Größeres entwickeln kann« (Heidegger, S. 118).

Hegel suchte auf diese Frage eine eigene Antwort und verlässt sich auf Unterstützung durch die neuzeitliche Naturwissenschaft. In der Mechanik findet er im mechanischen Prozess einen Weg, den er weit über ihre ursprüngliche Bedeutung innerhalb der Naturwissenschaft hinaus an die entscheidende Stelle seiner Wissenschaft der Logik aufnehmen möchte, um dort die Frage nach dem ontologischen Gottesbeweis beantworten zu können.

Das mechanische Objekt hat für ihn genau die gesuchte innere Spannung zwischen Widerstand und Aufnahmefähigkeit. Das ist seiner Meinung nach möglich, weil sich im mechanischen Prozess auf einzigartige Weise ein körperlicher und geistiger Prozess verbinden: Die äußere Bewegung der mechanischen Körper, die aneinander stoßen und sich dadurch gegenseitig beeinflussen, und darüber vermittelt die Mitteilung körperloser, »imponderabler Agentien«. Diese Mitteilung enthält zweierlei: Die unmittelbare Mitteilung (das ist im mechanischen Prozess der Impuls, in der geistigen Mitteilung die Nachricht) und darüber die Mitteilung, dass es eine übergreifende Ordnung gibt, die sich mitteilt (das sind die mechanischen Axiome, unter den Menschen die Sprache, in der Tragödie »der gegenwärtige Gott«, von dem Hölderlin gesprochen hatte).

Im einfachsten Fall berühren sich beim elastischen Stoß zwei bewegte Massen und ändern dadurch gegenseitig ihren Bewegungszustand:

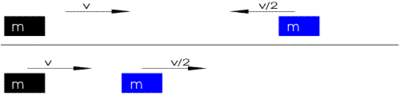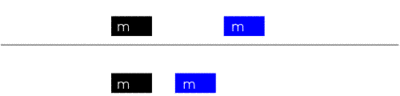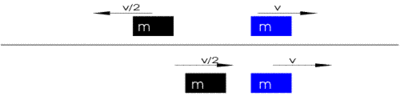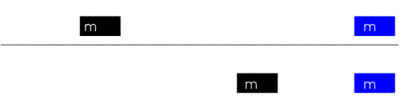
Figur 9  Elastische Stöße mit verschiedenen Anfangsgeschwindigkeiten

Zwei mechanische Körper mit gleicher Masse stoßen aufeinander. Im Moment des Zusammenstoßes kommt es zur Impulsübertragung, wodurch sich die Bewegungszustände der beiden Körper verändern. Wikipedia

Die beiden Massen bleiben jeweils völlig unverändert, nur ihre Bewegung ändert sich. Was ist übertragen worden? Hat eine Masse einen Teil ihrer Geschwindigkeit bzw. ihre Bewegungsrichtung abgegeben? Wie ist das möglich? Die Geschwindigkeit ist keine materielle Entität, die selbständig in einem mechanischen Objekt enthalten ist und an andere weiter gegeben werden kann, sondern eine Bewegungseigenschaft. Hegel versucht das zu beschreiben:

»Im Körperlichen sind es Bewegung, Wärme, Magnetismus, Elektrizität und dergleichen, die, wenn man sie auch als Stoffe oder Materien sich vorstellen will, als imponderable Agentien bestimmt werden müssen – Agentien, die dasjenige der Materialität nicht haben, was ihre Vereinzelung begründet« (HW 6.416).

Der Impuls ist kein eigener Körper, auch kein eigenes Teilchen, und es kann kein Impuls isoliert und für sich betrachtet werden, der wie ein Staffelholz von der einen Masse an die andere abgegeben wird. Die Bewegungsänderung nach dem Stoß  zeigt  das Wirken übergeordneter Naturgesetze, in diesem Beispiel die Impulserhaltung. Die Mitteilung ist nicht eine einzelne Botschaft, sondern das Wirken der Ordnung, in dem sich diese Massen befinden.

Die Physik des 20. Jahrhundert hat mit den Feynman-Diagrammen eine Veranschaulichung für die imponderablen Agentien gefunden. Den Ausdruck »imponderable Agentien« übernimmt die moderne Naturwissenschaft nicht, da er ihr zu sehr nach Mystik klingt, und ersetzt ihn durch den Ausdruck »virtuelle Teilchen«. Das ändert zwar nichts an der Sache, aber weil sie diesen Ausdruck neu definieren kann, glaubt sie, dass er wissenschaftlicher sei. Das Beispiel der Wechselwirkung von zwei Elektronen ist zwar insofern etwas problematisch, da Elektronen nicht als materielle Teilchen gedacht werden, aber dies Beispiel zeigt, worum es geht. Der Moment der Wechselwirkung wird nicht einfach als Berührung (Zusammenstoß) gedacht, sondern als Austausch eines virtuellen Photons. Zwei Elektronen nähern sich und tauschen ein Photon aus, wodurch sich ihr Bewegungszustand ändert:

Figur 10  Elektron-Elektron-Streuung durch Austausch eines virtuellen Photons
Die Zeitachse verläuft von unten nach oben. Wikipedia

Hier ist anschaulich unterschieden, wie es zum einen um materielle Prozesse geht, die mit durchgezogenen Linien gezeichnet sind, und zum anderen um eine Mitteilung, die mit der Wellenlinie gezeichnet ist. Daher zeigt diese Figur besonders gut, worum es Hegel geht: Einen Prozess, der sowohl auf einer körperlichen wie auf einer nicht-körperlichen (imponderablen, virtuellen) Ebene verläuft.

Dieser Prozess kann als Vorbild genommen werden, um auch »geistige Mitteilungen« zu beschreiben, die von einer Person an andere gegeben werden. Hegel wählt bewusst eine ungewohnte Formulierung, wenn er von einer »Beziehung« spricht,

»worin sich ungetrübt eine Bestimmtheit von einer Person in die andere kontinuiert und ohne alle Veränderung sich verallgemeinert« (HW 6.416).

Dem Kontinuieren der Mitteilung von Seiten des Sprechers stehen entgegen die Aufnahmefähigkeit und der Widerstand von seiten des Empfängers, das ist in einem umfassenden Sinn die Kunst des Hörens. Der Empfänger muss Widerstand leisten, um das Neue der Mitteilung zu verstehen. Andernfalls würde es sich um eine bloße Echokammer handeln. Er muss erkennen, inwiefern sein eigenes Vorwissen durch die Mitteilung erschüttert, in Frage gestellt und teilweise widerlegt bzw. verändert wird. Sein Vorwissen leistet Widerstand und sperrt sich zunächst gegen das Neue. Die erste Reaktion lautet: ›Das verstehe ich nicht‹. Diese Reaktion ist notwendig, denn sonst ließe sich das Neue der Mitteilung nicht erkennen. Auf der anderen Seite verfügt die Mitteilung über die Kraft der Kontinuation. Sie enthält in sich die Möglichkeit, sich zu verallgemeinern. Sie muss Züge tragen, dass sie von anderen verstanden werden kann. Andernfalls bliebe sie eine isolierte individuelle Äußerung, die niemandem sonst zugänglich ist, eine Privatsprache, die niemandem als dem Sprecher selbst verständlich ist und den anderen als Un-Sinn erscheint (siehe die 1937 erschienene Erzählung Dialog über die höchsten Systeme von Tommaso Landolfi).

Damit ist im mechanischen Prozess das Wechselverhältnis von Kontinuation und Umkehrung aufgehoben, das bereits als umgekehrtes Verhältnis der Faktoren der Indifferenz betrachtet worden war. Auch im mechanischen Prozess ergibt sich nach außen eine Indifferenz: Wird der körperliche physikalische Prozess betrachtet, dann bleibt die Summe der Impulse erhalten. In der sprachlichen Verständigung wird Indifferenz hergestellt, wenn der Hörer die Mitteilung übernimmt, sein Wissen anpasst und zugleich seine Reaktion dem Sprecher mitteilt (Feedback), der darüber seinerseits sein Wissen teilweise bestätigt sieht und teilweise entsprechend der Reaktion des Hörers anpasst.

Hegels Gedanke droht allerdings verzerrt zu werden, da er Beispiele nennt, die missverstanden werden können. Für ihn wird im mechanischen Prozess der Schwächere vom Stärkeren überwältigt.

»Wenn man sich ein ganz Dummes, Unedles vorstellen will, so kann auf dasselbe hoher Verstand, kann das Edle keinen Eindruck machen; das einzig konsequente Mittel gegen die Vernunft ist, sich mit ihr gar nicht einzulassen« (HW 6.420).

Auch wenn klar ist, wie das gemeint ist, klingt es arrogant und legt nahe, als würde sich im Gespräch der stärkere Gesprächspartner durchsetzen oder bei der Impulsübertragung die größere Masse. Doch gerade das ist nicht gemeint, wie Hegel im weiteren klarstellt. Stärker ist nicht die größere Kraft einer der beiden Objekte oder Personen (und schon gar nicht die größere Lautstärke dessen, der sich stimmlich am besten durchzusetzen weiß), sondern die in der  Mitteilung  enthaltene Kraft.

»Der Widerstand wird überwältigt, insofern seine Bestimmtheit dem mitgeteilten Allgemeinen, welches vom Objekte aufgenommen worden und sich in ihm singularisieren soll, nicht angemessen ist. Seine relative Unselbständigkeit manifestiert sich darin, daß seine Einzelheit nicht die Kapazität für das Mitgeteilte hat, daher von demselben zersprengt wird, weil es sich an diesem Allgemeinen nicht als Subjekt konstituieren, dasselbe nicht zu seinem Prädikate machen kann« (HW 6.420).

Wenn beim elastischen Stoß beide Massen ihre Bewegung ändern, dann nicht, weil die eine stärker ist, sondern beide der höheren Macht der Impulserhaltung unterworfen sind. Und wenn im Gespräch sich eine Mitteilung durchsetzen kann, dann aufgrund der Macht des Inhalts, den sie enthält. – Das widerspricht sicher der Alltagserfahrung, wenn sich häufig die Meinungen durchsetzen, deren Vertreter über die größeren Macht- und Einflussmittel verfügen. Hegels Bild einer idealen Kommunikation zeigt daher nicht unmittelbar die Realität, sondern das Maß, an der diese gemessen werden kann. Hegel ist davon überzeugt, dass seine ideale Position letztlich nur theologisch begründet werden kann, wenn sie sich ihrerseits orientiert an dem Bild der göttlichen Offenbarung, in der der Gott seine Macht zeigt. Es kommt zur Tragödie, wenn das misslingt.

Damit ist der Punkt berührt, an dem Objektivität über Subjektivität hinausgeht. Hegel stellt einander gegenüber den mechanischen Prozess, der für die Objektivität steht, und das unendliche Urteil, das für die formale Logik steht.

»Wenn sie sich nicht in einer Sphäre befänden, so wäre ihre Beziehung aufeinander ein unendliches Urteil und kein Prozess zwischen ihnen möglich« (HW 6.420).

Wie ist das gemeint? Wenn zum Beispiel etwas die Eigenschaft der Farbe hat, dann befindet es sich in der Sphäre des Farbigen und ihm kann aus dieser Sphäre eine bestimmte Farbe als Prädikat zugeschrieben werden, ›diese Rose ist rot‹. Das unendliche Urteil besagt dagegen, dass etwas nicht nur eine bestimmte Eigenschaft nicht hat, sondern darüber hinaus einer bestimmten Sphäre nicht angehört, z.B. haben Töne keinen Geschmack. Daher kann Tönen kein Geschmacksprädikat zugewiesen werden.

Von dieser Situation unterscheidet sich der mechanische Prozess. Es wird vorausgesetzt, dass die Objekte des mechanischen Prozesses sich in einer gemeinsamen Sphäre befinden. Zum Beispiel müssen die mechanischen Objekte elastisch sein (widerstandsfähig, undurchdringlich). Aber es ist nicht möglich, dass die mechanischen Objekte als formallogische Subjekte verstanden werden, denen das Mitgeteilte als Prädikat zugeschrieben werden kann. Das klingt auf den ersten Blick eigenartig und ist seinerseits eine Mitteilung, die Widerstand hervorruft. Zur Klärung sei auf das Beispiel des Impulses verwiesen: Wenn etwas mit blauer Farbe angestrichen wird, kann im Ergebnis gesagt werden, dass es blau ist. Wenn dagegen dem Objekt ein Impuls mitgeteilt wird, wird es dadurch weder elastisch, noch mechanisch, noch »impuls-artig«. Diese Eigenschaften hatte es bereits zuvor. Es wird ihm nur mitgeteilt, dass es sich innerhalb der Gesamtheit der mechanischen Objekte und ihres Systems der Impulserhaltung befindet, und in diesem System seinen Anteil am Gesamtimpuls mit dem mitteilenden Objekt austauscht. In dieser Weise verstehe ich Hegels Aussage, »daß seine Einzelheit nicht die Kapazität für das Mitgeteilte hat«. Das einzelne Objekt ist nicht Träger des Mitgeteilten, sondern nur ein einzelnes Objekt innerhalb eines übergreifenden Systems von Objekten, die in ihrer Gesamtheit Träger des Mitgeteilten sind.

Mit diesen Ausführungen wird ein erweiterter Begriff der Sphäre erreicht, der über die Sphären hinausgeht, die im Kapitel über das unendliche Urteil betrachtet worden waren. Das leitet über zum Chemismus, bei dem die Eigenschaften dieser Sphäre für sich betrachtet und als das  Medium  dargestellt werden, in dem sich die Mitteilung vollzieht.

Innerhalb des mechanischen Prozesses gelingt es nicht, eine formallogische Beziehung von Subjekt und Prädikat herzustellen. Die Mitteilung kann weder dem Sprecher noch dem Hörer, weder dem stoßenden Objekt noch dem angestoßenen Objekt als Prädikat zugewiesen werden. Daher versagt an dieser Stelle die Sprache, die auf Aussagesätzen beruht. So verstehe ich Hölderlins Deutung der Antigona, wenn er sagt, dass die Mitteilung »mehr Zusammenhang« als »faktisches Wort« ist. Obwohl die Mitteilung nur mithilfe der Sprache weiter gegeben werden kann, kann sie nicht zerlegt werden in atomare Aussagesätze. Damit ist beiläufig gezeigt, wie sich aus dem Verständnis des mechanischen Prozesses ergibt, dass alle Versuche fehlschlagen müssen, die die Sprache auf den Bereich der formalen Logik beschränken wollen.

Das lässt sich im Sinne von Kierkegaard und Wittgenstein interpretieren. Das Einzelne ist stark genug zu erkennen, dass es eine Mitteilung bekommen hat, und befindet sich so weit mit dem Mitteilenden in einer gemeinsamen Sphäre, dass es die Mitteilung verstehen kann. Aber es hat nicht die Kapazität, den vollen Hintergrund der Mitteilung zu überschauen. Der Mensch kann von Gott angesprochen werden, aber er wird nicht verstehen, warum Gott so gesprochen hat. Dieser Gedanke lässt sich mit Wittgenstein auch nicht-theologisch sagen: Der Mensch erfährt, dass er der Sprache fähig ist, aber er erkennt, dass er mit der Sprache an etwas stößt, was zu groß für ihn ist, was seine Kapazität überschreitet. – Aus der Literatur des 20. Jahrhunderts ist Franz Kafka zu nennen, dessen Werke die widersprüchliche Struktur der Sprache zeigen.

Es lässt sich kaum in geeignetere Worte bringen als es Hegel vermocht hat. Es gelingt dem Menschen nicht, sich als Subjekt der Sprache zu verstehen, oder formal-logisch gesprochen die Sprache dem Menschen als ein Prädikat zuzuweisen. Es kann nur gesagt werden, dass der Mensch sprachbegabt oder sprachfähig ist.

Hegel nennt weitere Beispiele.

»So ist das Schicksal des Lebendigen überhaupt die Gattung. [...] Ein eigentliches Schicksal hat nur das Selbstbewußtsein, weil es frei, in der Einzelheit seines Ich daher schlechthin an und für sich ist. [...] Damit also ein solches Gewalt über dasselbe haben könne, muß es irgendeine Bestimmtheit gegen die wesentliche Allgemeinheit sich gegeben, eine Tat begangen haben« (HW 6.421).

Der Mensch ist in seinem Leben frei, aber er kann nicht die Regeln der Gattung überspringen. Wenn er sich der existenziellen Tatsachen wie Geburt, Fortpflanzung oder Tod bewusst wird, wird er davon erschüttert, kann sich dieser Mitteilungen über seine Existenz bewusst werden, aber sie nicht überschauen. Er kann sagen ›der Mensch ist sterblich‹, aber dieser Satz sagt nicht im geringsten aus, was er für den einzelnen Menschen bedeutet, der sich damit auseinandersetzen muss. Der Mensch spürt in sich einen Widerstand, das zu akzeptieren. Niemand kommt über die »geistige Trägheit« hinaus, sich für unsterblich zu halten, das heißt, sein eigenes Leben nur in der Spanne des Lebens verstehen zu können.

Erst mit dem Widerstand ist der volle Begriff der Trägheit erreicht. Würde es keine Trägheit geben, dann würde alles instantan geschehen (so wie es sich im Grenzfall darstellt, wenn der Standort des Lichts eingenommen werden könnte). Der Begriff des Widerstands ist der gesuchte Begriff, um von den Axiomen der euklidischen Geometrie zu den mechanischen Axiomen zu gelangen. In der euklidischen Geometrie gibt es keinen Widerstand. Geraden und Kreise kreuzen sich in dimensionslosen Punkten ohne auf Widerstand zu treffen. Hier gibt es daher auch weder Zeit noch Bewegung, sondern lediglich logische Folgen von aufeinander folgenden Konstruktionsschritten. – In der Konsequenz bedeutet das, in der Mathematik den Begriff ogkischen (gewichtigen) Zahlen einzuführen, die den Übergang zur Physik denken lassen, und eine Neue Physik zu entwerfen, die nicht nach dem Vorbild der euklidischen Geometrie von Masse, Massepartikeln, Raum und Zeit ausgeht, sondern von dem für sie charakteristischen Gegensatz von Schwere (die der Träger von Trägheit und Widerstand ist) und dem Licht. So verstehe ich das Anliegen von Schelling, dem Hegel an diesem Punkt folgen kann. Von hier ergeben sich die Fragen an die Relativitätstheorie von Einstein.

Anmerkung 1: Michael Wolff spricht in Geschichte der Impetustheorie von »Übertragung« statt von »Mitteilung« und sieht sie in Verbindung mit sozialrevolutionären und ökonomischen Ideen. Er geht zurück auf Philoponos (490-570), der in einem Kommentar zur Physik von Aristoteles fast wortgleich wie später Hegel geschrieben hatte, »daß eine gewisse unkörperliche Bewegungskraft vom Werfenden dem Geworfenen mitgeteilt wird« (Philoponos, S. 139). Wenn Philoponos von der Übertragung der Kraft vom Menschen an das von ihm geschaffene Produkt spricht, gehört das für Wolff »einer spezifisch spätantiken Emanzipationsideologie« an und »soll die Tätigkeit der Produzenten als Entäußerung seiner eigenen Kraft« anerkennen (Wolff, S. 133). Bei Philoponos war das noch eingebettet in eine christliche Theologie, die die Ebenbildlichkeit des Menschen als Übertragung von Gott an den Menschen verstand. Im Mittelalter wurde die Impetus-Theorie erneut von radikalen Christen aufgenommen (den Franziskanern bzw. den Spiritualen), deren Theoretiker Petrus Olivi (1247/48-1296/98) den Kapital-Begriff begründete. Geld ist nicht mehr wie bei Aristoteles bloß ein Tauschmittel, sondern es zeigt einen Wert an, der durch Übertragung von Arbeitskraft vermehrt wurde. Wie Philoponos und Olivi entwickelten auch Nikolaus von Oresme (vor 1330-1382) und Johannes Buridan (1300-1358, Begründer der Impetus-Theorie) klare ökonomische Lehren von Kraft, Arbeit, Kapital, Wert und Geld mit der Stoßrichtung, die feudale Willkür (die sich zum Beispiel in Geldfälschungen zeigte) zu bekämpfen zugunsten einer Wirtschaftsordnung, in der nur Kraft und Leistung belohnt werden. – Der Übertragungsbegriff steht für Wolff zugleich am Beginn der neuzeitlichen Produktionstechniken, die Marx im 1. Band des Kapital beschrieben hat. Der Impetus ist ein Quantum, das weiter gegeben wird. Es ging darum, unterschiedliche Arbeitsprozesse mechanisch miteinander zu verknüpfen. Das Prinzip dieser vorindustriellen Zeit war der Transmissionsmechanismus. »Der Transmissionsmechanismus, zusammengesetzt aus Schwungrädern, Treibwellen, Zahnrädern, Kreiselrädern, Schäften, Schnüren, Riemen, Zwischengeschirr und Vorgelege der verschiedensten Art, regelt die Bewegung, verwandelt, wo es nötig, ihre Form, z.B. aus einer perpendikulären in eine kreisförmige, verteilt und überträgt sie auf die Werkzeugmaschinerie« (Marx Kapital, MEW 23, S. 393, Link).

Anmerkung 2: Der Gräzist Sven Müller hat dargestellt, wie sich die Kritik an Aristoteles historisch entwickelt hat. Es ging um Physik Kapitel VIII, 4. Aristoteles will klären, warum sich alle Körper zu den ihnen natürlichen Orten bewegen, also z.B. Feuer in die Höhe lodert und Wasser herabfällt und am Boden bleibt. Mögliche Antworten sind, dass (1) die unbeseelten Körper aufgrund einer eigenen innewohnenden Kraft zu ihrem Ort streben, oder (2) vom Ort aus eine anziehende Kraft auf die unbeseelten Körper ausgeht, oder (3) eine übergreifende Weltseele oder Allseele die Bewegung steuert, durch die alle unbeseelten Körper zu ihrem Ort finden. Christliche Philosophen haben seit Philoponos und möglicherweise bereits seit Alexander von Aphrodisias (ca. 200 n.Chr.) Aristoteles vorgeworfen, Position (1) zu vertreten, während nach ihrer Überzeugung die christliche Theologie für Position (3) steht. Das war auch das Argument von Newton gegen Aristoteles. Sven Müller will zeigen, dass Aristoteles missverstanden wurde und in Wahrheit Position (3) vertrat. Er hat nicht mit der Natur und der Seele der einzelnen Elemente argumentiert, die ihre Bewegung veranlasst, sondern mit der Natur im Ganzen, in der jedes Element seinen natürlichen Platz hat. Das scheint mir dem Verständnis von Hegel zu entsprechen, wonach im mechanischen Prozess dem einzelnen mechanischen Objekt der Anstoß zur Bewegungsänderung mitgeteilt wird, der aus den allgemeinen Gesetzen des Mechanismus hervorgeht. – Nicht einfach zu verstehen ist die Position von Newton. Bereits Philoponos hatte über die Ansicht seines Zeitgenossen Kosmas Indikopleustes gespottet, »dass Engel den Mond, die Sonne und jedes einzelne Gestirn bewegen, indem sie sie entweder vorwärts ziehen nach Art von Zugtieren oder von hinten stoßen wie diejenigen, die runde Lasten wälzen, oder auch beides oder indem sie sie auf ihren Schultern tragen« (Philoponos De opificio mundi, zitiert bei Müller S. 62), und dadurch die ewige Bewegung der Himmelskörper aufrecht erhalten. So etwas wollte Newton vermeiden und wandte sich daher sowohl gegen Aristoteles wie gegen die Impetus-Theorie. Ihnen allen warf er vor, dass sie die Bewegung erklärten aus »verborgene(n) Qualitäten, die, wie man erdichtet, aus den spezifischen Formen der Dinge entspringen sollten«, wogegen er »universale Gesetze der Natur« als Ursache sah, auch wenn »noch nicht erklärt worden (ist), welches die Ursachen ihrer selbst sind«, sondern sie zunächst nur mathematisch formuliert werden können (Newton Opticks 1706, zitiert bei Müller S. 200). Nach Müller missversteht Newton Aristoteles auf ähnliche Weise wie Philoponos. Zugleich will Müller mit zahlreichen Beispielen belegen, dass im Widerspruch hierzu Newton an einen Spiritus im Sinne der stoischen Philosophie denkt. Er hat diesen Gedanken übernommen von Lukrez und Cicero. Dieser Spiritus ist etwas Feinstoffliches.

Anmerkung 3: Bei aller Kritik kann Hegel von Kant ausgehen und sieht in dessen Metaphysischen Anfangsgründen der Naturwissenschaft den »Anstoß zur neueren Naturphilosophie« (HW 5.201). Kant hat dort in einer groß angelegten »Allgemeine(n) Anmerkung zur Dynamik« (MAN, AA 04: 523-535) eingeräumt, dass er eine Konstruktion der Materie »nicht zu leisten vermag«, sondern nur »Momente« nennen kann (MAN, AA 04: 525.21-22). Kant zählt recht intuitiv auf: (1) der Körper als die Figur der Materie, (2) der Zusammenhang innerhalb der Körper, der als »Zustand der Flüssigkeit« verstanden wird (MAN, AA 04: 526.28), (3) die Springkraft (Elastizität) und schließlich (4) die Wirkung der Körper durch Mitteilung.

Hervorzuheben ist Punkt 4 über Mitteilung und Medium. Bei einer Mitteilung wird eine Wirkung mitgeteilt, wobei die beiden Materien erhalten bleiben. Im Chemismus erfolgen dagegen Scheidung und Auflösung, also eine chemische Durchdringung.

»Die Wirkung bewegter Körper auf einander durch Mitteilung ihrer Bewegung heißt mechanisch; die der Materien aber, so fern sie auch in Ruhe durch eigene Kräfte wechselseitig die Verbindung ihrer Theile verändern, heißt chemisch. Dieser chemische Einfluß heißt Auflösung« (MAN, AA 04: 530.08-12).

Hegel hat von Kant die deutliche Betonung der Mitteilung übernommen, jedoch anders gewichtet. Kant will die Bewegung entsprechend der von ihm entwickelten drei Eigenschaften der Zeit verstehen: Dauer, Kausalität und Wechselwirkung. Mit ihnen erklärt er die drei von Newton eingeführten Axiome der Mechanik:

Substanz: Impuls-Erhaltung. Kant formuliert: »Erstes Gesetz der Mechanik. Bei allen Veränderungen der körperlichen Natur bleibt die Quantität der Materie im Ganzen dieselbe, unvermehrt und unvermindert« (MAN, AA 04: 541.28-30).

Kausalität: Trägheitsgesetz. »Zweites Gesetz der Mechanik. Alle Veränderung der Materie hat eine äußere Ursache« (MAN, AA 04: 543.16-17). Hier wird indirekt von Trägheit gesprochen: Ohne äußere Veränderung bleibt die Materie träge.

Gemeinschaft: Wechselwirkung. »Drittes mechanisches Gesetz. In aller Mitteilung der Bewegung sind Wirkung und Gegenwirkung einander jederzeit gleich« (MAN, AA 04: 544.32-33).

Das kommt Hegels Verständnis des mechanischen Prozesses bereits sehr nahe. Allerdings fasst Hegel die Begriffe weit klarer und löst sich von der engen Bindung an die drei Axiome von Newton. Statt von »Materien« (oder »Substanzen«) spricht er von »mechanischen Objekten« und vermeidet damit alle unklaren Abgrenzungen gegenüber den Begriffen von Substanz und Materie. Während Kant die Impuls-Erhaltung im Sinne seines Substanz-Begriffs als die Erhaltungsgröße deutet, durch die die Dauerhaftigkeit des mechanischen Prozesses gegeben wird, versteht Hegel die Impuls-Erhaltung als ein Beispiel für die höhere Allgemeinheit, die das einzelne mechanische Objekt dank seines Widerstands zwar aufnehmen, aber nicht überschauen oder als Prädikat aneignen kann. Das mechanische Objekt erfährt die Impuls-Erhaltung, kann aber nicht zu ihrem Subjekt werden.

Anmerkung 4: Der Ausdruck »imponderable Agentien« ist zur Zeit von Hegel vor allem im Bereich Medizin, Chemie und der entstehenden Elektrizitätslehre gebraucht worden. Die dort ablaufenden Prozesse wurden erst wenig verstanden, und es wurde vermutet, dass sie durch imponderable Agentien gesteuert werden. Zu dieser Zeit erschien es kaum vorstellbar, Medizin, Chemie, Elektrizität und Lebensprozesse auf ähnliche Weise zu beschreiben, wie es in der Mechanik möglich ist. Die Wende brachte erst in der zweiten Hälfte des 19. Jahrhunderts die neue medizinische Forschung von Physiologen wie dem Franzosen Claude Bernard (1813-1878), der als einer der Ersten eine experimentelle Medizin begründete und überzeugt war, dass im organischen und anorganischen Bereich die gleichen Gesetze gelten. Dagegen vertraten noch Gustav Theodor Fechner (1801-1887) und Ernst Haeckel (1834-1919) die Überzeugung, dass die Psychophysik (von Fechner 1860 begründet) und die Seelen-Substanz im Sinne der Welträtsel von Haeckel (1899) auf imponderablen Agentien beruhen. Im 20. Jahrhundert ist dieser Ansatz völlig fallen gelassen und von einem durchgreifenden Materialismus abgelöst worden. Erinnerten anfangs noch die um 1900 eingeführten Vorstellungen von Vitaminen oder Hormonen entfernt an imponderable Agentien, so sind sie mit dem biochemischen Nachweis 1909-41 völlig aufgegeben worden. Seither verstehen sich die Biowissenschaften als gleichrangige Naturwissenschaft wie Physik oder Chemie. Für imponderable Agentien ist kein Platz mehr. Das könnte sich erst wieder ändern, wenn sich die großen Erwartungen an medizinische Durchbrüche zur Heilung von physischen und psychischen Krankheiten, Planung von Wunschkindern und Verlängerung des Lebens nicht erfüllen.

Anmerkung 5: Das Zusammenwirken von körperlicher und imponderabler Ebene im mechanischen Prozess kann als Erzittern bezeichnet werden. Der Existenzialismus spricht von der Erschütterung, die den Menschen treffen kann. Umgangssprachlich wird vom Pfeil des Amor gesprochen, der den Verliebten trifft und verwandelt. Das führt weiter vom Mechanismus zum Chemismus. Es muss ein Medium geben, in dem Körperlichkeit und Virtualität miteinander verbunden sind. Davon handelt der Beitrag über die Sphäre des Begriffs (siehe dort die Anmerkung zu Hegels Ausführungen in der Phänomenologie des Geistes über das Erzittern, das den Menschen in der Entwicklung seines Selbstbewusstseins erfasst, HW 3.159).

Anmerkung 6: An der Grenze von Mechanismus und Chemismus steht die Relativitätstheorie. So wie Hegel im Verlaufe seiner Werke den Begriff »Äther« durch das »Medium« ersetzt hat, hat Einstein innerhalb der Physik eine Kritik an den Äther-Theorien entwickelt. Mit der Relativität wird gesetzt, dass es nicht möglich ist, Eigenschaften wie Raum, Zeit, Geschwindigkeit, Impuls oder Energie einzelnen Objekten als Prädikate zuzusprechen. Jede Aussage der Art ›das Objekt O hat den Ort x, die Zeit t, die Geschwindigkeit v, den Impuls p etc‹ muss relativiert werden durch zusätzliche Angaben über das jeweilige Bezugssystem, in dem sich das Objekt befindet. Die Relativitätstheorie hat umfassend die Grenzen eines formallogischen Systems gezeigt, das aus einzelnen Aussagesätzen, empirischen Beobachtungen und Messungen aufgebaut werden soll. Stattdessen ist zu fragen, wie innerhalb eines solchen Systems Zusammenhang und Kommunikation hergestellt werden.

Anmerkung 7: Kurt Gödel hat in seinen späten Jahren eine zunehmend deutliche Kritik an der vorherrschenden Richtung der mathematischen Grundlagenforschung vertreten. Diese ist entweder dem Empirismus verfallen, wenn sie sich nur noch auf die mathematische Formulierung vorgegebener physikalischer oder psychologischer Prozesse bezieht, oder dem Dogmatismus, wenn sie glaubt, ihre Objekte vollkommen frei aus sich selbst heraus schöpfen zu können. Diese Tendenz hat zu tun mit der Grundlagenkrise der Mathematik, zu der er mit seinem Unvollständigkeitssatz maßgeblich beigetragen hat. Doch deutet er die Ergebnisse seiner Arbeit völlig anders.

Für ihn bedeutet der Unvollständigkeitssatz, dass es nie gelingen wird, einen vollständigen Überblick über die Mathematik zu bekommen. Da dennoch die einzelnen Teile für sich jeweils Wahrheiten liefern, auch wenn sie vom Menschen nicht widerspruchsfrei zu einem Ganzen zusammengefügt werden können, schließt Gödel daraus, dass es einen Schöpfer der Mathematik geben muss, dessen Werk wir nicht überschauen. Wir müssen den Glauben aufgeben, die Mathematik sei unser eigenes Werk (»our own creation«).

»For the creator necessarily knows all properties of his creatures, because they can't have any others except those he has given to them. So this alternative seems to imply that mathematical objects and facts (or at least something in them) exist objectively and independently of our mental acts and decisions, that is to say [it seems to imply] some form or other of Platonism« (Gödel, S. 311).

Gödel beschreibt hier nach meinem Eindruck genau die Situation, um deren Verständnis es Hegel im Kapitel über den mechanischen Prozess geht. Der Mensch bekommt einen Anstoß, er kann einzelne Seiten der Mathematik entdecken und mit ihnen arbeiten, aber er muss einsehen, dass sie sich ihm in ihrer Gesamtheit entzieht. Das wäre nicht so, wenn er ihr Schöpfer wäre.

Anmerkung 8: Byung-Chul Han kommt in seiner Studie über Hegel und die Macht am Rande auf die Überwältigung des mechanischen Objekts im mechanischen Prozess. Er sieht bei Hegel ein einseitiges Verhältnis zwischen dem Absoluten und demjenigen, dem es erscheint. Vor allem das Kapitel über das »absolute Verhältnis« ist für ihn ein Beispiel, wie für Hegel das Absolute, wenn es sich zeigt, dennoch ganz bei sich bleibt. Mit dem Absoluten ist einseitig eine Macht gesetzt, die beim Absoluten liegt und der sich nichts entziehen kann. Grundsätzlich teile ich die Kritik von Han, sehe jedoch im Kapitel über den mechanischen Prozess wichtige Gedanken, die über diese einseitige Macht-Theorie hinausgehen und von Han nicht ausreichend berücksichtigt werden. Er zitiert daraus ausschließlich die Passagen, die von der Überwältigung des Widerstands handeln (Han, S. 84f mit Zitaten aus HW 6.420). – Die Kritik von Han ist wieder aufzunehmen, wenn der Frage nachgegangen wird, ob und warum die Mittel den Zwecken, von denen sie ergriffen werden, keinen Widerstand entgegensetzen können. Auch diese Formulierung ist zumindest missverständlich, wie Han zurecht betont. Ein Mittel kann nur eingesetzt werden, wenn es für den Zweck geeignet ist, andernfalls wird es die Erreichung des Zwecks erschweren oder gar unmöglich machen. Es wird zu fragen sein, welche Kraft (Potenz, dynamis) innerhalb eines Mittels vorhanden sein muss, um die gewünschten Ziele erreichen zu können. Das Verhältnis zwischen Zweck und Mittel wird sich als keineswegs so einseitig erweisen, wie es die Formulierung nahelegt, das Mittel könne dem Zweck keinen Widerstand leisten.

Offene Fragen

Objektivität und der spekulative Satz

Im Gesamtaufbau der Begriffslogik kann die Objektivität als Negation der Subjektivität verstanden werden, aus der dann in einer zweiten Negation die Idee hervorgeht. Wenn die Subjektivität als Lehre der formalen Logik gesehen wird, die den Begriff, die Aussagesätze und die Schlüsse enthält, ist dann die Objektivität als Negation der Aussagelogik zu verstehen? Wird also hier das Programm verwirklicht, das Hegel in der Vorrede zur Phänomenologie des Geistes formuliert hat, dass der spekulative Satz die »Natur des Urteils oder Satzes überhaupt ... zerstört« :

»Formell kann das Gesagte so ausgedrückt werden, daß die Natur des Urteils oder Satzes überhaupt, die den Unterschied des Subjekts und Prädikats in sich schließt, durch den spekulativen Satz zerstört wird und der identische Satz, zu dem der erstere wird, den Gegenstoß zu jenem Verhältnisse enthält. – Dieser Konflikt der Form eines Satzes überhaupt und der sie zerstörenden Einheit des Begriffs ist dem ähnlich, der im Rhythmus zwischen dem Metrum und dem Akzente stattfindet. Der Rhythmus resultiert aus der schwebenden Mitte und Vereinigung beider. So soll auch im philosophischen Satze die Identität des Subjekts und Prädikats den Unterschied derselben, den die Form des Satzes ausdrückt, nicht vernichten, sondern ihre Einheit [soll] als eine Harmonie hervorgehen. Die Form des Satzes ist die Erscheinung des bestimmten Sinnes oder der Akzent, der seine Erfüllung unterscheidet; daß aber das Prädikat die Substanz ausdrückt und das Subjekt selbst ins Allgemeine fällt, ist die Einheit, worin jener Akzent verklingt« (HW 3.59).

Hier sei die These vertreten, dass Hegel im Abschnitt über die Objektivität systematisch Begriffe entwickelt, die der in der Phänomenologie gemeinten »schwebenden Mitte« entsprechen und diese genauer ausführen. Während der Abschnitt über die Subjektivität in der Sphäre von Urteil, Satz und Schluss verbleibt, wird mit der Objektivität etwas erreicht, welches sich der räsonierenden Sprache entzieht und nur durch einen spekulativen Satz formuliert werden kann. Hinweise dafür gibt es bereits im Kapitel über den Mechanismus, wenn sich in der Mitteilung von einem mechanischen Objekt an ein anderes etwas Allgemeines zeigt, welches die Kapazität der jeweils einzelnen mechanischen Objekte sprengt, zwischen denen es mitgeteilt wird (HW 6.420).

Führt Hegel das im Abschnitt über die Objektivität in den Kapiteln über Chemismus und Teleologie fort? Einige Anhaltspunkte: Hegel schreibt zum chemischen Prozess:

»Diese Momente (des Schlusses, t.) sind hiermit die abstrakte, gleichgültige Basis einerseits und das begeistende Prinzip derselben andererseits, welches durch seine Trennung von der Basis ebenfalls die Form gleichgültiger Objektivität erlangt« (HW 6.433).

Das kann so verstanden werden, dass sich diese beiden Momente (Basis und begeistendes Prinzip) in ähnlicher Weise der Kapazität der am chemischen Prozess beteiligten Stoffe entziehen, wie sich das Mitteilbare den einander etwas mitteilenden mechanischen Objekten entzieht. So wie die Mitteilung gegenüber den einzelnen einander etwas Mitteilenden etwas Allgemeines enthält, das über ihre individuelle Kapazität hinausgeht, so enthält das Medium, in dem die chemischen Prozesse erfolgen, etwas Allgemeines, das nicht in den miteinander reagierenden Stoffen enthalten ist. Hegel versteht kursiv hervorgehoben die Sprache als ein Beispiel für ein Medium, in dem ein chemischer Prozess erfolgt (HW 6.431). Die Sprache hat damit sowohl als Mitteilbares für den mechanischen Prozess wie als Medium für den chemischen Prozess einen Rang, der sich nur durch spekulative Sätze erschließen lässt.

In Kapitel über die Teleologie spricht Hegel auf ähnliche Weise von der Allgemeinheit der Objektivität, die sich im Mittel gegenüber der Einzelheit der Zwecke zeigt, für die es eingesetzt wird:

»Umgekehrt hat das Mittel gegen den subjektiven Zweck, als unmittelbare Objektivität, Allgemeinheit des Daseins, welches die subjektive Einzelheit des Zweckes noch entbehrt« (HW 6.449f).

Im weiteren betont er, dass das Mittel keinen Widerstand gegen den Zweck leisten kann (HW 6.450), für den es eingesetzt wird. Aber gilt das nicht auch schon für das imponderable Agens, von dem im mechanischen Prozess die Rede ist, welches aufgrund seiner Masselosigkeit gegenüber den mechanischen Objekten ohne Widerstandskraft ist und nur dadurch als Mitteilung wirken kann, und für die neutrale Lösung, innerhalb derer die chemischen Prozesse ablaufen? Gleichwohl betont Hegel:

»Aber das Mittel hat auch eine Seite, nach welcher es noch Selbständigkeit gegen den Zweck hat«. Das nennt er »die im Mittel mit ihm verbundene Objektivität« (HW 6.451).

Zur Frage des Mediums siehe den Beitrag Die Sphäre des Begriffs und die Logik der Sphäre, in dem gezeigt werden soll, wie sich am Begriff des Mediums bzw. der Sphäre die Wege von Kant und Hegel trennen. Über den Begriff des Mittels ist ein Beitrag in Vorbereitung.

Die Kraft der Konstruktion

Wenn die Vermutung zutrifft, dass Hegel zwar in seiner Lehre der Subjektivität den überlieferten Regeln des Begriffs, des Satzes und des Schlusses eine neue Bedeutung gibt, aber sie dennoch im Abschnitt über die Objektivität letztlich auf ähnliche Weise negiert, wie sie in der Phänomenologie des Geistes durch den spekulativen Satz »zerstört« werden, dann ist damit eine Gegenüberstellung erreicht, die ihrerseits wiederum negiert werden muss. Die Objektivität hat sich gegen die Subjektivität gestellt. Die Negation dieser Gegenüberstellung führt zum Begriff der Idee, mit dem Hegel die Wissenschaft der Logik abschließt.

Dort nimmt er die Frage nach der Konstruktion nochmals auf. So wie er bereits zu den einzelnen Gesetzen der Erscheinung festgestellt hatte, dass sie einen Beweis erfordern (HW 6.155), so ist dies zu verallgemeinern auf die Objektivität im Ganzen. Für ihn sind »die Gesetze, Sitten, vernünftige Vorstellungen überhaupt« die »im Geistigen ... Mitteilbare(n)« (HW 6.416), und da liegt nahe, dass sie im Ganzen auf ähnliche Weise bewiesen werden müssen wie die mechanischen Gesetze im Einzelnen. Das wirft die Frage nach der Konstruktion auf, die im Abschnitt über die Idee entwickelt wird.

Hier ist zu fragen, wie sich die von Hegel gemeinte Konstruktion verhält zu der Konstruktion, von der Kant in den Metaphysischen Anfangsgründen der Naturwissenschaft spricht und zur Konstruktion, die Fichte in seiner Wissenschaftslehre ausführt, um den Weg zum Wissen zu finden. In diesem Zusammenhang soll der in diesem Beitrag aufgeworfenen Frage nachgegangen werden, welche Bedeutung die Mathematik für die Konstruktion hat. Wird eine Lehre in dem Maße wissenschaftlich, wie sie mathematisch wird und das heißt, ihre Begriffe zu konstruieren vermag? Und was bedeutet das für Hegels Anliegen, eine Wissenschaft der Logik zu schreiben? Hegel ist der Überzeugung, dass sich hier die Kreise schließen.

Mit der Kraft der Konstruktion wird Hegels Programm zuende geführt, ein Gegengewicht zur Kraft der Trägheit zu erhalten, welche die Kraft der Trägheit aufzuheben vermag. Ist die Trägheit verbunden mit Materie und Determinismus, dann öffnet sich für Hegel mit der Kraft der Konstruktion das Licht und die Freiheit.

Siglen

HW: Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971; Link

JLMN: Georg Wilhelm Friedrich Hegel: Jenenser Logik, Metaphysik und Naturphilosophie, Leipzig 1923

MAN: Immanuel Kant: Metaphysische Anfangsgründe der Naturwissenschaft (1786)
in: Akademie-Ausgabe, Bd. IV, Berlin 1911; Link Volltext

Literaturhinweise

David Gray Carlson: Hegel´s Theory of Measure, New York 2003; PDF

David Eckstein: Epstein erklärt Einstein, Online

Lewis Carroll Epstein: Relativity Visualized, San Francisco 1983

Michael Esfeld (Hg.): Philosophie der Physik, Berlin 2012

Kurt Gödel: Some Basic Theorems on the Foundations of Mathematics and their Implications (1952)
in: Kurt Gödel; Collected Works Bd. III, New York, Oxford 1995, S. 304-323

Byung-Chul Han: Hegel und die Macht, München 2005; Link

Helmut Hansen: Die Linien des Alten, Norderstedt 2009

Martin Heidegger: Schellings Abhandlung über das Wesen der menschlichen Freiheit (1809), Tübingen 1995

Friedrich Hölderlin: Anmerkungen zur Antigonä
in: Sämtliche Werke und Briefe (Knaupp-Ausgabe, Hanser-Ausgabe neu), Bd. 2, München 1992, S. 369-376

Karl-Norbert Ihmig: Hegels Deutung der Gravitation, Frankfurt 1989

Jörg Ihringer: Vorlesung zur Experimentalphysik I, Tübingen 2000; Link

Max Jammer: Das Problem des Raumes, Darmstadt 1960

Max Jammer: Der Begriff der Masse in der Physik, Darmstadt 1964

Tomasso Landolfi: Dialog über die höchsten Systeme
in: Viktoria von Schirach (Hg): Italienisches Lesebuch, München, Zürich 2003, S. 159-175

John McTaggart: A Commentary on Hegel's Logic, Cambridge 1910 (Neudruck durch "Forgotten Books" 2012); Link

Sven Müller: Naturgemäße Ortsbewegung – Aristoteles' Physik und ihre Rezeption bis Newton, Tübingen 2006

Wolfgang Neuser: Einleitung und Übersetzung von Georg Wilhelm Friedrich Hegel: Philosophische Erörterung über die Planetenbahnen, Weinheim 1986

Johannes Philoponos: Ausgewählte Schriften, hg. von Walter Böhm, München u.a. 1967

Georg Picht: Von der Zeit, Stuttgart 1999

Thomas Posch: Hegels Kritik am Newtonschen Kraftbegriff und seine Verteidigung Keplers
in: Sitzungsberichte der Leibniz-Sozietät der Wissenschaften zu Berlin 103(2009), S. 49-59; Link

Shmuel Sambursky: Der Begriff der Zeit im späten Neuplatonismus
in: Clemens Zintzen (Hg.): Die Philosophie des Neuplatonismus, Darmstadt 1977

Michael Schröder: Hegels Mechanik, der Jupitermond Io, und die Gezeitenkraft. Über Allgemeine und Besondernde Gravitation.
in: Jahrbuch für Hegelforschung, Band 18-20 (2017), 297-349

Renate Wahsner: Die Relativität des Raumes und der Zeit. Stürzte Einstein das Newtonsche Weltbild?
in: Revista de Filosofía, Vol. 30 Nr. 1 (2005), S. 25-48; Link

Dieter Wandschneider: Raum, Zeit, Relativität, Frankfurt am Main 1982

Dieter Wandschneider: Die Kategorien 'Materie' und 'Licht' in der Naturphilosophie Hegels
in: Michael John Petry (Hg.): Hegel und die Naturwissenschaften, 1987

Dieter Wandschneider: Licht und Masse – Absolutheit und Relativität als intrinsisch zusammengehörende Momente des kinematischen Relativitätsprinzips. Ein Beitrag zu einer Philosophie der Relativitätstheorie
in: Wolfgang Neuser und Jens Kohne: Hegels Licht-Konzepte, Würzburg 2008, S. 79-92; Link.

Carl Friedrich von Weizsäcker: Aufbau der Physik, München Wien 1985

Michael Wolff: Geschichte der Impetustheorie, Frankfurt 1978

2012-2020