Walter TydecksEmergenz und Higgs-Mechanismus |
|
Beitrag für das Philosophische Colloquium der Akademie 55plus Darmstadt am 28. Mai 2018, überarbeitete und erweiterte Version, Stand 31.5.2018
Inhaltsverzeichnis
Emergenz und Selbstorganisation
Dynamische Systeme
Higgs-Mechanismus: Festerkörperphysik und Emergenz von Materie
Emergenz und Selbstorganisation
Das Wort ‘Emergenz’ geht zurück auf das lateinische Verb emergere mit einem Bedeutungsspektrum wie erholen, emporkommen, befreien, losmachen, auftauchen, emporarbeiten, durchbrechen, zeigen, aufgehen, erheben, herausarbeiten, erwachen, herausziehen, freisprechen, durcharbeiten, entsprießen, durchwehen, herausdeuten und griechischen Wurzeln ananéo (emportauchen, come to the surface) und anakypto (den Kopf in die Höhe richten, sich aus Not und Gefahr emporarbeiten), in denen jeweils die Silbe ana (hinauf, auf, empor, gemäß) vorkommt und eine innere Beziehung zur Analogie andeutet.
Mit Emergenz werden Prozesse beschrieben oder einfach nur als Emergenz bezeichnet, die sich nicht reduktionistisch erklären lassen: Im Moment der Emergenz entsteht etwas Neues, das nicht auf das ursprüngliche System und dessen Elemente reduziert werden kann. Emergenz ist ein Konzept ganzheitlichen Denkens, des Holismus, der sich vom traditionellen Kausalitätsdenken, Determinismus und eindimensionalen Schlussketten befreien will. Einige sehen darin das Anzeichen einer neuartigen, aufgeklärten Spiritualität jenseits der überlieferten Religionen und empfinden Erfahrungen eines Flow und seiner Kreativität als das direkte persönliche Erleben von Emergenz, gewissermaßen die spirituelle Emergenz des eigenen Selbst in etwas Größerem, ein »ozeanisches Gefühl« (Freud). Andere verstehen die Emergenz als Naturgesetz in ausdrücklicher Kritik einer Neuauflage von Wunderglaube oder Magie. In diesem Sinn gibt Dedié seinem Buch über Emergenz den programmatischen Titel Die Kraft der Naturgesetze.
Emergenz ist verwandt mit Selbstorganisation und Autopoesis (wörtlich übersetzt: Selbsterschaffung). Streng genommen kann es keine Selbstorganisation geben, da sie den 2. Hauptsatz der Thermodynamik verletzen würde, wonach die Ordnung eines geschlossenen Systems im Ganzen nicht vergrößert werden kann. Spontane Selbstorganisation kann daher nur auftreten, wenn das System offen ist und es einen von außen kommenden Durchfluss gibt. Die doppelte Bedeutung von Hervortreten und Durchwehen ist bereits im lateinischen Verb emergere enthalten. Ilya Prigogine (1917-2003) spricht von dissipativen Strukturen (zerstreuten Strukturen) fern vom thermischen Gleichgewicht.
Heinz von Foerster (1911-2002) hat sich auf einer wegweisenden Tagung 1959 in Chicago gegen die Möglichkeit selbstorganisierender Systeme ausgesprochen. Für ihn kann Selbstorganisation nur auftreten, wenn sie aus der Umgebung Energie und Information zu gewinnen vermag. Er hat systematisch zwei Fälle von Selbstorganisation unterschieden:
'order from order' principle: Üblicherweise wird unter Selbstorganisation verstanden, dass es einer gegebenen Ordnung gelingt, sich aus sich selbst heraus in eine höhere Ordnung zu verwandeln. Nach dem Modell des Urknalls hat sich das Universum in mehreren Schritten entwickelt, die Dedié nachzeichnet: Aus purer Energie entstand ein Quark-Gluonen-Plasma, daraus Nukleonen, Atomkerne, Atome, Moleküle, Makromoleküle, lebende Systeme, und diese können Geist, Bewusstsein und gesellschaftliche Systeme entwickeln. Jeder Übergang gilt als eine Emergenz von einer niedrigeren in eine höhere Ordnung. Die traditionellen Begriffe der Metaphysik wie Seele, Welt und Gott bekommen einen neuen Inhalt, wenn sie als Emergenzen ihrer jeweiligen Träger gedeutet werden: Der Körper eines Lebewesens vermag bei höheren Lebewesen wie dem Menschen in eine Seele zu emergieren, die Gesellschaft in staatliche Ordnungen, das Denken in Geist und der Kosmos in eine übergreifende Ordnung, die traditionell als Gott verehrt wird.
Für den Mathematiker und Physiker Roger Penrose (* 1931) ist die extrem große Hitze des Urknalls bis heute Treiber der Selbstorganisations-Prozesse. Die Selbstorganisation wird energetisch ausgeglichen durch eine Abkühlung des Kosmos, wobei durch die Abkühlung in Summe trotz aller Selbstorganisation die Unordnung des Kosmos wächst. Er hält es jedoch für möglich, dass aus den Fluktuationen der Hintergrundstrahlung auf den Zustand vor dem Urknall geschlossen werden kann und eine übergreifende Bewegung vorliegt, die aus der Abkühlung des Kosmos in einer Art Wiedergeburt zu einer Erneuerung des Kosmos führen kann. Penrose ist ähnlich wie der Biologe Richard Dawkins (* 1943) Atheist. Seine mathematisch begründete Theorie kann als eine nicht-religiöse Schöpfungsgeschichte gelesen werden.
'order from noise' principle: Weil das 'order from order' principle in letzter Konsequenz das 2. Gesetz der Thermodynamik verletzt, betrachtet v. Foerster als zweiten Fall die Fähigkeit eines Systems, aus dem gegebenen Grundrauschen eine höhere Ordnung zu erzeugen (Foerster 1959, 13). Für ihn kann das Grundrauschen Keime enthalten, die zunächst nicht wahrgenommen werden, sich jedoch in ungewöhnliche Konstruktionen zusammenschließen können.
Dieser Gedanke wird leider nicht weiter ausgearbeitet. Er hat philosophische Vorläufer bei den von Platon im Timaios genannten Formspuren (wenn die Dinge vor ihrer Entstehung bereits als Spuren ihrer selbst präexistieren, ichnê men echonta hautô atta, Tim. 53b2), den kleinen Perzeptionen bei Leibniz (Monadologie, §§ 14, 21) und der Affinität, von der Kant in der ersten Auflage der Kritik der reinen Vernunft sprach (KrV, A 113). Wenn ich ihn richtig verstehe, bedeutet er, dass im Grundrauschen verborgene, rudimentäre Ordnungselemente enthalten sind, die danach streben, sich zusammen zu schließen und zur Emergenz in eine Ordnung führen können. Das kann als das Begehren verstanden werden, von dem Lacan sprach. Es gibt jedoch nie ein einseitiges Begehren, sondern eine wechselseitige Wahlverwandtschaft. »Das Begehren ist das Begehren des Anderen.« (Lacan Schriften I, 220, zitiert bei Rolf Nemitz Lacans Sentenzen, 14. Februar 2013). Das eine Begehren hört und reagiert auf das andere. So liegt im Grundrauschen der Bewegungskeim, der zwar noch im noise verborgen ist, jedoch aus sich heraus zur Emergenz in eine order drängt.
Bei komplexen und insbesondere lebendigen Systemen kann die Emergenz mithilfe der Kybernetik (vom griechischen Wort kybernesis, lenken, steuern, regieren) beschrieben werden. Die Kybernetik betrachtet Rückkoppelung (Zirkularität, Rekursion, feedback). Kommt es zu einer positiven Selbstverstärkung bei Rückkoppelung, dann kann daraus eine neue Ordnung emergieren. Rekursionen wiederholen sich schrittweise, bis sich in ihrem Ablauf Eigenwerte (Eigen-Verhalten) zeigen, die als gemeinsames Muster der Rekursionen hervortreten. Ein Beispiel ist das Immunsystem. Es gibt im Immunsystem eine Feedback-Schleife, wenn das Immunsystem auf äußere Einflüsse reagiert und zugleich Autoimmun-Erkrankungen vermeiden muss (was bekanntlich nicht immer gelingt). In einer Reihe fortlaufender Beobachtungen und Selbstbeobachtungen werden der innere und der äußere Zustand überprüft. Die Ergebnisse des eigenen Verhaltens und Handelns werden überwacht und angepasst, bis das Außen und das Innen in ein Fließgleichgewicht gebracht sind und der Organismus mit seiner eigenen Natur übereinstimmt (Gesundheit, hygieia). – Wenn ich es richtig verstehe, hat v. Foerster seinen früheren Gedanken des 'order from noise' principle zurückgestellt (oder aufgegeben) zugunsten der Theorien der Eigenformen.
Selbstorganisation entsteht aus Wechselwirkung benachbarter Elemente, bildet dann jedoch in einem »Prozess«, den Prigogine das »Werden» nennt, »erstaunlicherweise oft eine Fernordnung« (Dedié, 21). Der Ablauf erfolgt entlang von Keimen oder Inseln, so z.B. die Wolkenbildung an Staubkörnern, die als Kondensationskeime dienen (Dedié, 24). Dieser Vorgang kann synchron an verschiedenen, voneinander weit entfernten Stellen erfolgen und sogar Züge einer Quantenverschränkung annehmen (siehe hierzu den Beitrag über Quantenphysik).
Hier können Zwischenstufen auftreten, das sind jeweils Systemzustände, die für sich das Geschehen übergangsweise stabilisieren.
Bei der Selbstorganisation sind zahlreiche Naturkonstanten beobachtet worden. Sie lassen sich messen und in wiederholten Experimenten reproduzieren. Es ist zu vermuten, dass sich in den Naturkonstanten innere Zusammenhänge der Natur zeigen, die noch unbekannt sind. Ein schlagendes Beispiel ist die Klitzing-Konstante (siehe dazu unten). Das kann »eine bestimmte minimale Anzahl von Elementen bzw. eine minimale Größe des emergenten Systems« sein (Dedié, 24). Es kann auch ein Grenzwert sein. Wird ein Haufen Sand aufgeworfen, ist er flach und stabil. Das kippt um bei einem Böschungswinkel von etwa 34°. (Dedié, 87) Dann beginnt der Sand zu rutschen, bis eine Art fließende Abwärtsbewegung entsteht. Siehe auch Lawinenentstehung. Schließlich können für bestimmte Zustände Konstanten auftreten wie die Klitzing-Konstante, die später näher ausgeführt wird.
Besonders beeindruckend sind formale Automaten, die bisweilen erst nach tausenden von Schritten scheinbar chaotischer Bewegung in einen geordneten Prozess umschlagen: Ein verblüffendes Beispiel ist die 1987 von dem theoretischen Biologen und Computer-Wissenschaftler Christopher Langton (* 1949) entwickelte Turing-Maschine, mit der das Entstehen einer Ameisenstraße beschrieben wird (siehe faszinierende Animationen in YouTube). Ein Vorläufer dieser Art von Turing-Maschinen war das 1970 von John Conway (* 1937) entworfene Spiel des Lebens.
Dynamische Systeme
Auch wenn heute die ‘Dynamischen Systeme’ ein Fachbegriff für die mathematische System-Modellierung sind, erscheint mir kein anderer Ausdruck besser geeignet, um die Bedeutung der Emergenz zu verstehen. Die Dynamik von Systemen ist mit einem mehrstufigen Bild zu beschreiben, in dem auf unterschiedlichen Ebenen Bewegungen entstehen und ihrerseits miteinander wechselwirken. Für alle Ebenen ist der Rückbezug auf das System im Ganzen wesentlich. Daher kann in Erweiterung des mathematischen Fachbegriffs in einem präzisen Sinn von dynamischen Systemen gesprochen werden.
– Einzelne Elemente und ihre autonomen Bewegungsgesetze Beispiele: Mechanische Bewegung von Partikeln, Moleküle und ihre chemischen Reaktionen, Replikation (Vererbung) von Makromolekülen. Für diese elementare Stufe wird angenommen, dass die Umgebung keinen Einfluss hat, und dass es keine Wechselwirkung zwischen den voneinander unabhängig ablaufenden Bewegungen gibt. Jede Bewegung erfolgt für sich. Jedoch gilt für alle Bewegungen jeweils ein einheitliches Bewegungsgesetz wie z.B. die Stoßgesetze der Mechanik, die Reaktionsgleichungen für chemische Prozesse oder die Mechanismen der DNA-Replikation.
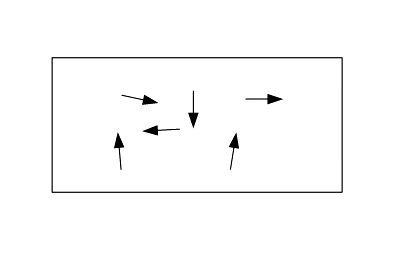
Stufe 1: Einzelne Partikel
Einzelne Partikel bewegen sich autonom in einer Gesamtheit. Wechselwirkungen der Partikel oder Systemeigenschaften erscheinen rein zufällig und lösen sich von allein wieder auf.
– Bewegtheit eines Systems Mit dem Nachweis des Grundrauschens kam es zu einem ersten Paradigmen-Wechsel. Das Grundrauschen ist eine Bewegtheit des Systems im Ganzen, die unabhängig von den Bewegungen der einzelnen Elemente im System gilt. Damit war erstmals der Reduktionismus infrage gestellt, da die Bewegtheit des Systems nicht reduziert (hergeleitet) werden kann auf die Bewegungen seiner einzelnen Elemente. Mit Entstehen der Thermodynamik und Quantendynamik führte das zu einer neuen Naturwissenschaft, die sich bis heute nicht in Übereinklang mit der klassischen, deterministischen Physik bringen lässt. Rückblickend wurde klar, dass zahlreiche elementare Begriffe der Naturwissenschaft wie Flüssigkeit, Kontinuität und Wärme nur als Bewegtheiten von Systemen verstanden werden können. Kein einzelner Wassertropfen ist für sich flüssig, und kein einzelnes Gasmolekül ist für sich warm oder kalt. Sie haben lediglich die Eigenschaft, als Keim einer umfassenden Systembewegtheit agieren zu können, die als Eigenschaft nur für das System im Ganzen gilt. Als dieser Weg einmal eingeschlagen war, wurden zahlreiche Bewegtheiten umfassender System untersucht und in mathematischen Modellen berücksichtigt: Das Grundrauschen der Information, die Wärme der Thermodynamik, Unschärfe-Relation in der Quantendynamik, Ausdehnung des Weltalls in der Allgemeinen Relativitätstheorie, die kosmische Hintergrundstrahlung als Nachhall des Urknalls
Im allgemeinen Bewusstsein ist diese Unterscheidung bis heute nicht präsent. Das naive – manche sagen auch ‘intuitive’ – Denken geht im Alltag von der Bewegung autonomer Objekte aus und übersieht die Bewegtheit des Systems.
Die Unterscheidung in Bewegtheit des Systems und Bewegung der einzelnen Elementen ist für mich letztlich die Begründung, warum in der bekannten Formel der Energie E = ½ m v² die Geschwindigkeit v im Quadrat auftritt. Im einfachsten Fall sind die Geschwindigkeit der einzelnen Elemente und die Geschwindigkeit der Bewegtheit des Systems in der gleichen Einheit v messbar und können miteinander multipliziert werden. v wird mit sich selbst multipliziert und bildet das Maß des Systems. Siehe dazu ausführlicher den Beitrag über Kraft, Energie, Impuls sowie über den Begriff des Quadrats.
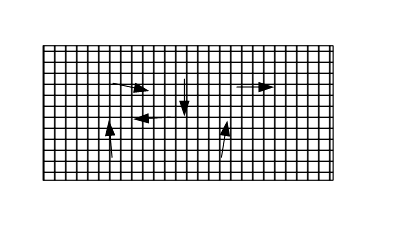
Stufe 2: Bewegtheit des Systems
Die Bewegtheit des Systems ist durch ein Muster angedeutet. Die Gesamtbewegung der Elemente ergibt sich aus dem Produkt ihrer Eigenbewegung und der Bewegtheit des Systems.
Wer möchte, kann bei diesem Bild an die Einschlüsse (Inklusen) von Insekten in Bernstein denken. Die Zähflüssigkeit des fossilen Harzes steht für die Bewegtheit eines Systems, die noch lebendig wirkende Bewegung der Insekten für die Eigenbewegung von Elementen, die aus dem Zustand der freien Luft in den Zustand des Bernsteins geraten sind.
– Emergenzen, Phasenübergänge von Systemzuständen Sind die Bewegtheit des Systems und die Bewegung seiner Elemente klar voneinander unterschieden, dann wird es möglich, für die Bewegtheit des Systems verschiedene Systemzustände zu unterscheiden. Das Wasser ist mit seinen Übergängen von Eis, Flüssigkeit und Gas das Standardbeispiel. In jedem Systemzustand verändern sich die Bewegtheit des Systems im Ganzen und die Regeln für die Bewegungen der einzelnen Elemente im System. Im einfachsten Fall – dem Wasser – werden die Übergänge klar erkennbar durch Aufwärmen bzw. Abkühlen des Systems erzeugt. Bei den beiden kritischen Schwellwerten von 0° bzw. 100° Celsius schlägt der Systemzustand um. Zugleich werden die einzelnen Elemente mit jedem Phasenübergang beweglicher: Im Eis sind sie fast starr, im flüssigen Wasser sind sie nur noch lose miteinander verbunden, und im Gas werden sie frei beweglich. Dies Modell lässt sich auf andere Situationen übertragen: Wird z.B. das Medium für chemische Prozesse durch Rühren oder Kneten mechanisch bewegt, durch fortlaufendes Hinzutropfen bestimmter Katalysatoren in seiner Zusammensetzung verändert oder aufgeheizt (oder eine Kombination dieser Einwirkungen), dann bilden sich bei bestimmten Schwellwerten jeweils eigene Zustände aus. Viele chemische Reaktionen werden erst bei bestimmter Wärme, Durchrühren des Mediums oder Zugabe von Katalysatoren möglich. Im Alltag kennt das jeder vom Kochen und Kuchenbacken.
Wenn Systeme ihren Systemzustand ändern können, spricht v. Foerster von nicht-trivialen Maschinen und unterscheidet sie von den trivialen Maschinen der Stufen 1 und 2, die jeweils nur einen einzigen Zustand kennen. Beispiele für triviale Maschinen sind die deterministischen Systeme und die Beweisketten nach Frege. Bei Schlussketten wie A → B → C → …, bei mathematischen Formeln wie a + b = c oder chemischen Reaktionsgleichungen a + b → c + d wird vorausgesetzt, dass sich die beteiligten Operanden A, B, C, …, a, b, c, d … während des Schließens bzw. Rechnens nicht ändern. Sie sind im Sinn von v. Foerster triviale Maschinen. Das galt als so selbstverständlich, dass es im Grunde erst durch v. Foerster explizit gemacht wurde. Aufgrund dieser Eigenschaft lässt sich das Verhalten trivialer Maschinen überschauen und vorhersagen. Dagegen sind die Möglichkeiten nicht-trivialer Maschinen schon in einfachen Fällen unüberschaubar und können nur beobachtet und gemessen werden.
Der Ausdruck ‘nicht-triviale Maschine‘ spielt mit einer rhetorischen Täuschung: Für gewöhnlich stellt sich jeder unter einer Maschine einen starren, mit einem Bewegungsmechanismus ausgestatteten Apparat vor, der sich in einem offenen System bewegt, z.B. in einer Fabrikhalle oder auf einer Straße. V. Foerster meint aber umgekehrt mit nicht-trivialen Maschinen die übergeordneten Systeme, in denen sich autonome Elemente bewegen können. Er gebraucht hierfür den Ausdruck ‘Maschine‘, da sich für ihn in diesen Fällen Systeme wie Maschinen beschreiben lassen, und kehrt damit die übliche Vorstellung von System und Maschine genau um.
V. Foerster hat durchgerechnet, dass bereits bei einer nicht-trivialen Maschine, die nur aus 4 Elementen besteht, 28192 = 102466 Möglichkeiten auftreten, was die Kapazitäten aller Rechenmaschinen weit übersteigt. (Foerster 1984, 65) In solchen Fällen besteht nur die Möglichkeit, kollektive Massenphänomene zu erkennen und zu formulieren. Wie sind diese großen Zahlen zu erklären?
Als Beispiel sei eine vereinfachte Uhr mit den 4 Ziffern 3, 6, 9 und 12 gewählt. Wenn die Uhr eine triviale Maschine ist, gilt die bekannte Regel, dass jeweils eine Zahl auf die andere folgt und nach der 12 mit der 3 ein neuer Zyklus begonnen wird: 3 - 6 - 9 - 12 - 3 - …. Wir können uns darauf verlassen, dass die Uhr nie von diesem trivialen Gang des Zeigers abweicht und entweder ganz stehen bleibt oder sich in ständig gleichen Zeiteinheiten weiter dreht. Sie kennt keinen anderen Systemzustand.
Gibt es 4 verschiedene, voneinander unabhängige Uhren, bei denen jeweils der Zeiger auf einer beliebigen Zahl steht, lässt sich mit der herkömmlichen Kombinatorik ausrechnen, welche Möglichkeiten für die unterschiedlichen Zeigerstellungen bestehen und wohin sie weiter wandern werden. So können alle auf 3 Uhr stehen, oder die erste auf 3 Uhr, die zweite auf 6 Uhr, die dritte auf 9 Uhr, die vierte wieder auf 3 Uhr usf. Das ergibt kombinatorisch insgesamt 256 Möglichkeiten, die in Quadrupeln aufgeschrieben werden können: (3333), (3336), … (6333) … ([12][12][12][12]).
Bei einer nicht-trivialen Uhr könnte sich zusätzlich der Zustand ändern. Im einfachsten Zustand geht die Uhr jeweils einen Schritt weiter. In einem anderen Zustand könnte sie z.B. jeweils einen Schritt rückwärts gehen, oder in einem weiteren Zustand erst 2 Schritte vor, dann 4 Schritte vor, dann 1 Schritt vor usf. Wird hierfür die Gesamtheit aller Möglichkeiten von Zuständen, Zustandswechseln und der mit ihnen erzeugten Reihenfolgen der Zeigerstellungen ausgerechnet, dann ergibt sich die von v. Foerster genannte, unvorstellbar große Zahl.
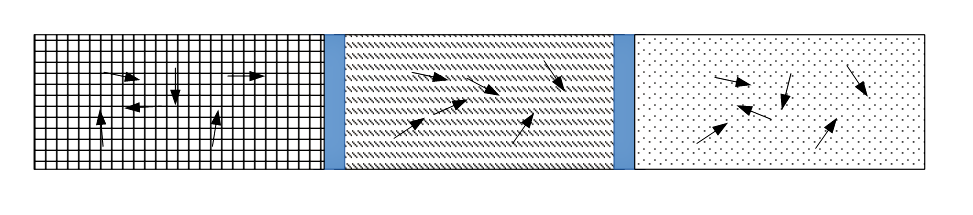
Stufe 3: Systemzustände und ihre Phasenübergänge
Wenn das System kontinuierlichen Einflüssen ausgesetzt ist, kann es bei kritischen Schwellwerten seine Bewegtheit verändern. Die Übergange sind hellblau hervorgehoben. Das ist die Emergenz, wenn ein Zustand aus dem anderen emergiert. – Mit den jeweils veränderten Pfeilrichtungen ist angedeutet, wie sich am Beispiel des Wassers die Beweglichkeit der Elemente mit den Phasenübergängen verändert.
– Knotenlinien Über die Phasenübergänge hinweg ist eine durchgehende Bewegung zu erkennen, die von einem Zustand in den nächsten führt. Das ist im Beispiel des Wassers die Wärmezufuhr oder Abkühlung. Ähnlich kann der Kosmos als eine Folge von Phasenübergängen verstanden werden, wenn die fortlaufende Abkühlung jeweils bestimmte Schwellwerte überschreitet. Hegel hat diese Entwicklungslinie in der Wissenschaft der Logik als Knotenlinie bezeichnet. Den Begriff hat er vermutlich von den Chladnischen Klangfiguren und ihren knotenartigen Strukturen übernommen (siehe hierzu Hegel Enz. § 301, HW 9.176). Für ihn sind das Beispiele für den Umschlag von Quantität in Qualität, wenn die quantitative Änderung eines Systemparameters zu einem qualitativ neuen Systemzustand führt. Sie zeigen, dass die elementaren Kategorien (wie Quantität und Qualität) nicht mehr wie bei Aristoteles und Kant unabhängig nebeneinander stehen, sondern auseinander hervorgehen und ineinander umschlagen.
– Lokale Keime und Fernwirkung Jeder einzelne Phasenübergang ist eine Emergenz. Die Emergenz kann für sich beschrieben werden über die Ausbildung von Keimen und die Ausbreitung lokaler Prozesse in die globale Fernwirkung. Neue Systemeigenschaften bilden sich zunächst nur in Inseln, bis sie das gesamte System einheitlich strukturieren.
– Resonanzen und Eigenwerte von Emergenzen Entlang der Knotenlinie zeigen sich Muster, deren Struktur zurückgeht auf die Binnenprozesse der Phasenübergänge (Emergenzen) und dem jeweiligen Prozess, der die Phasenübergänge auslöst (z.B. Wärmezufuhr). Möglicherweise treten zwischen den verschiedenen Emergenzen Resonanzen auf. Die Resonanzen können je nach ihrer qualitativen Beschaffenheit den Ablauf der Phasenübergänge stören oder stabilisieren. Mir ist nicht bekannt, ob und welche physikalischen Experimente in dieser Richtung durchgeführt werden.
Bei fortlaufenden Phasenübergängen (Emergenzen) können sich bestimmte Muster (Eigenwerte) wiederholen, die für alle Emergenzen gelten und eine Invariante darstellen. Um Eigenwerte dieser Art zu erkennen, ist die formale Struktur entlang der Knotenlinie und innerhalb der einzelnen Emergenzen zu erkennen. – V. Foerster unterscheidet daher Funktionen und Funktoren. Funktionen beschreiben, wie bei einer Emergenz die Elemente eines Systemzustands in den neuen Systemzustand übergehen: y = f(x), wobei x ein Element vor der Emergenz und y ein Element nach der Emergenz ist. Funktoren 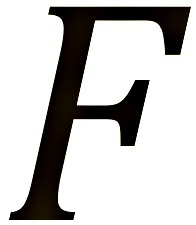 beschreiben eine Ebene höher das Verhältnis der Emergenzen zueinander: g =
beschreiben eine Ebene höher das Verhältnis der Emergenzen zueinander: g = 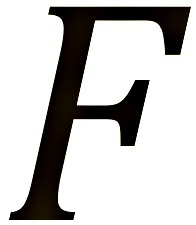 (f), wobei f eine Funktion einer Emergenz und g eine Funktion einer anderen Emergenz ist. (Dieser Gedanke ist bereits bei Frege angelegt, wenn er mehrstufig von Sättigungen spricht.)
(f), wobei f eine Funktion einer Emergenz und g eine Funktion einer anderen Emergenz ist. (Dieser Gedanke ist bereits bei Frege angelegt, wenn er mehrstufig von Sättigungen spricht.)
– Grenzwert von Eigenwerten Im Grenzübergang der Systemzustände lösen sich alle individuellen Besonderheiten der einzelnen Phasenübergänge und Systemzustände auf, doch zeigen sich Grenzwerte, die im Grenzübergang einen Grenzzustand bilden, der als solcher in der Realität nie erreicht werden kann. Gegenüber den einzelnen Systemzuständen erscheint der Grenzzustand maßlos und bildet für Hegel eine Unendlichkeit, die entlang der Knotenlinie angenähert wird. Ein Beispiel sind die Keplerschen Gesetze. Werden die Bewegungen der beobachtbaren Planeten gemessen, nähern sie sich den Keplerschen Gesetzen an ohne sie je ganz zu erreichen, da ihre Massen zu störenden gegenseitigen Anziehungen führen. Erst wenn im Grenzübergang angenommen wird, dass es keine Masse mehr gibt, treten die Keplerschen Gesetze in Reinform hervor. Die Keplerschen Gesetze setzen Abstand und Umlaufzeiten in Beziehung, enthalten jedoch keinen Term für die Masse und sind rein geometrisch formuliert. Sie können als die Eigenwerte des Grenzprozesses angesehen werden, bei dem fortlaufend kleinere Massen betrachtet oder in einer Störungsrechnung die Massen und deren Wirkungen herausgerechnet werden.
Diese Idee ist vom Funktionalismus verallgemeinert worden. Er spricht nicht nur von Eigenwerten, sondern auch von Eigenverhalten und systemischen Strukturen, die im Grenzübergang deutlich werden.
Eigenwerte müssen nicht eindeutig sein. Die Chaostheorie kennt Fälle von bistabilen Systemen, die ständig zwischen zwei Eigenwerten hin und her springen, oder die Attraktoren.
Unter einem abstrakten Gesichtspunkt kann wie bei den Keplerschen Gesetzen allgemein der Übergang physikalischer Räume in mathematische Räume als Eigenwert verstanden werden, oder noch allgemeiner mit Gödel die Mathematik als eine Syntax ohne Worte, die als Eigenwert innerhalb der Entwicklung der üblichen Sprachen hervortritt, in deren Verlauf sich die Worte schrittweise in Gesten und Symbole entleeren (siehe den Beitrag über Gödel und die Sprache der Kunst). Auch diese Entwicklung ist bereits bei Frege vorbereitet, wenn er nach einer Begriffssprache sucht, die nicht mehr gestört ist von den jeweiligen, meist ungenauen semantischen Bedeutungen der Worte. (Frege, vi-vii)
Die Eigenwerte können als diejenigen Beziehungen zwischen den jeweiligen Objekten verstanden werden, die im Grenzübergang als reine Beziehungen bestehen bleiben, wenn die Objekte mit ihren kategorialen (körperlichen, Substanz-)Eigenschaften in dimensionslose Punkte zusammengefallen sind. Der Prozess des Grenzübergangs stellt sicher, dass im Ergebnis Beziehungen übrig bleiben in einem Raum, in dem die mit den Beziehungen aufeinander Bezogenen nicht mehr vorhanden sind. Wird der Grenzübergang für sich betrachtet, ist die »Beziehung von Beziehung und Bezogenen« (Scheier, 107) zu untersuchen: Die Bezogenen verschwinden und bleiben dennoch implizit präsent in den Beziehungen, die erst im Grenzübergang rein hervortreten.
Wohin verschwinden die Bezogenen, wenn im Grenzzustand nur noch ihre Beziehungen in rein geometrischer Gestalt erhalten bleiben und deren Symmetrien in Reinform hervortreten? Das ist die Frage nach dem Higgs-Mechanismus, um den es im letzten Abschnitt gehen soll. Der Higgs-Mechanismus soll zeigen, in welchen Grund die Objekte und die Bezogenen zu Grunde gegangen sind, wenn dennoch ihre Beziehung erhalten geblieben ist.
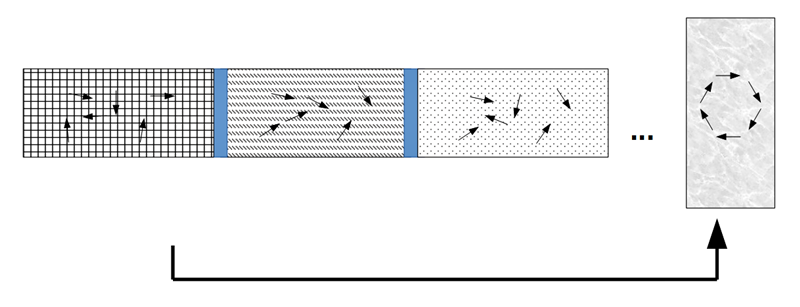
Stufe 4: Eigenwerte und ihr Grenzfall
Werden Phasenübergänge abzählbar oft wiederholt, dann können sich in ihrer Entwicklung Eigenwerte zeigen, an die sich das System asymptotisch annähert. Die Eigenwerte gehen in einen Grenzzustand über, in dem die Elemente des Systems keine Masse mehr haben und auf dimensionslose Punkte reduziert sind. – Der Grenzzustand ist marmoriert gezeichnet, um ihn von den vorangegangenen Systemzuständen zu unterscheiden. Im Grenzzustand kann eine rein symmetrische Bewegung auftreten, die in allen vorangegangenen Systemen aufgrund störender Einflüsse noch nicht zu sehen war.
– Re-entry von Eigenwerten Eigenwerte können bereits innerhalb einer Emergenz auftreten, wenn sich schrittweise lokale Inseln zu einer neuen globalen Struktur entwickeln. Genau genommen können innerhalb der Emergenz Sub-Emergenzen unterschieden werden, mit denen sich jeweils bestimmte Zwischenstufen kurzfristig stabilisieren. In diesem Fall kann die abschließende Emergenz als Grenzwert der Sub-Emergenzen angesehen werden.
Spencer-Brown sprach in seinen Laws of Form noch nicht von Emergenzen, sondern von einem Re-entry. Beim Re-entry erfolgt die Vernähung von Eigenwerten in einen neuen Systemzustand. Spencer-Brown geht noch weiter und entwirft komplette Schaltpläne, in denen mehrstufig Eigenwerte von Emergenzen auftreten und vernäht werden.
Um die graphische Darstellung nicht zu unübersichtlich werden zu lassen, wird der Re-entry im Folgenden nicht weiter berücksichtigt.
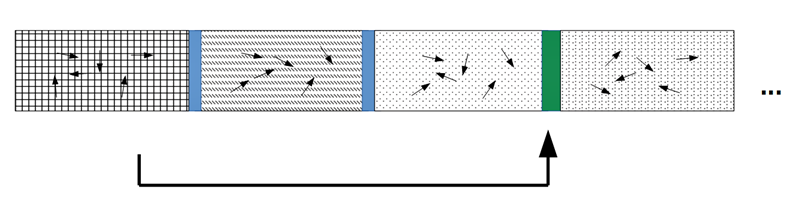
Stufe 4a: Eigenwerte und ihr Re-entry in einen neuen Systemzustand
Spencer-Brown betrachtet eine Variante. Die Eigenwerte führen nicht in einen fernen Grenzzustand, sondern werden durch ein Re-entry in die Reihenfolge der Systemzuständen aufgenommen und vernäht.
– Möglichkeitsräume Bisher wurde eine Reihenfolge von Systemzuständen betrachtet, die jeweils in der Wirklichkeit auftreten und nachweisbar sind wie z.B. Eis, Flüssigkeit und Gas beim Wasser. Es ist auch vorstellbar, dass es neben diesen wirklichen Zuständen eine Vielfalt von weiteren möglichen Zuständen gibt, die in der Wirklichkeit nicht nachweisbar sind, aber in ihrer Gesamtheit eigenen Gesetzen folgen. Das ist eine Verallgemeinerung der Quantenphysik. So wie dort vom Möglichkeitsraum aller Zustände eines Quantenobjekts gesprochen wird, so wird hier der Möglichkeitsraum aller Systemzustände betrachtet. Und so wie in der Quantenphysik die Eigenschaften eines Quantenobjekts an den Symmetrien erkannt werden, die erst über die wirklich messbaren Zustände hinaus als kollektive Phänomene im Raum aller Möglichkeiten dargestellt werden können, so gilt es auch hier. Und analog zur Quantenphysik ist zu vermuten, dass die Bewegungsgesetze im Raum aller möglichen Systemzustände mit imaginären Zahlen operieren vergleichbar der Schrödinger-Gleichung für die Quantenphysik.
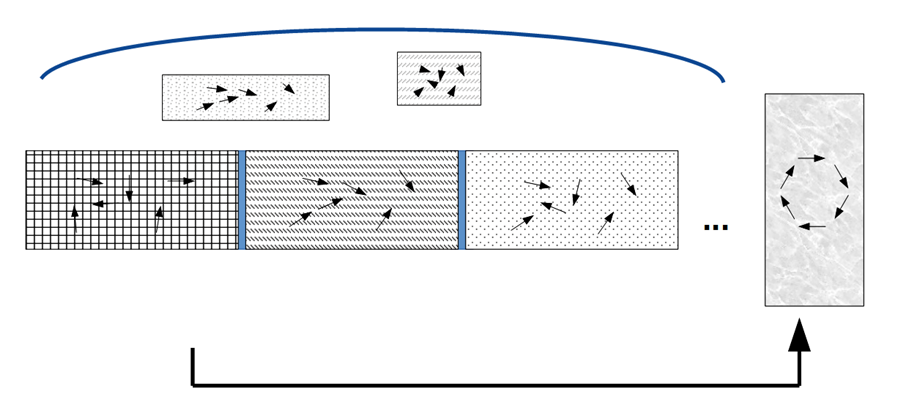
Stufe 5: Möglichkeitsraum und wirkliche Entwicklung
Die in der Wirklichkeit auftretenden Systemzustände erweisen sich als die gemessenen Fälle einer weit größeren Fülle von Alternativen, die in einem eigenen Möglichkeitsraum angeordnet sind. Diese virtuellen Fälle sind mit den kleinen Kästchen dargestellt, die sich oberhalb der Zustände befinden, die tatsächlich beobachtet und gemessen werden können.
– Beobachter Die Kybernetik zweiter Ordnung betrachtet aus einer Metaperspektive den Ablauf der rekursiven Selbstbeobachtung. Alle bisher genannten Systemtheorien müssen als Systeme auch den Beobachter mit einschließen. Wer sich dessen bewusst wird, trägt den eigenen Standort im System ein und von dort aus seinen Horizont.
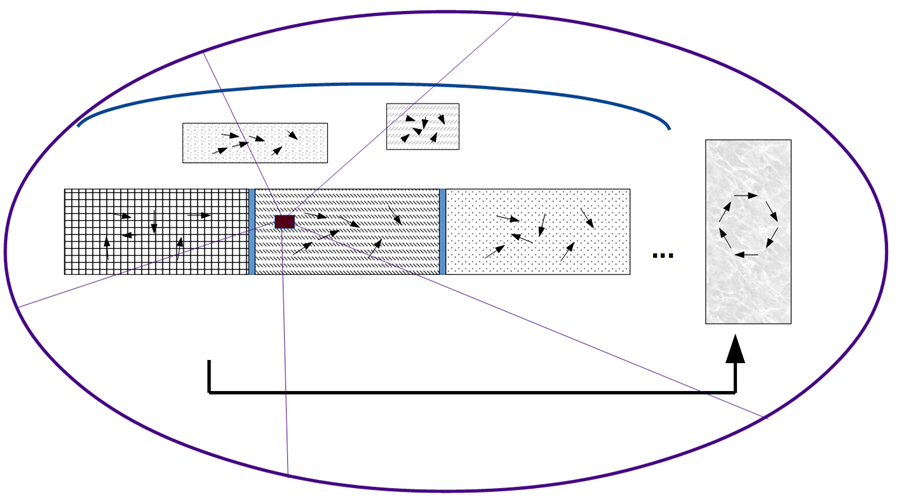
Stufe 6: Beobachter innerhalb des Systems
Der Beobachter befindet sich innerhalb des Systems, markiert durch ein dunkelrot hervorgehobenes kleines Rechteck. Er sieht das Geschehen von seinem Horizont aus, der durch die Ellipse dargestellt ist.
– Lebendigkeit Mit der rekursiven Selbstbeobachtung drohen die bekannten Antinomien der negativen Selbstbezüglichkeit. Für v. Foerster werden sie mit lebenden Systemen auf einer dritten Ordnungsstufe aufgelöst und stabilisiert. »A living organism is a third order relator which computes the relations that maintain the organism's integrity.« (Foerster 1972, 251). Lebende Systemen verfügen über die Fähigkeit, differenziert auf ihre Umgebung zu reagieren: Sie können zugreifen und sich zurückziehen. Erst mit lebenden Systemen entstehen Negation und Freiheit. Mit lebenden Systemen wird gegenüber der Emergenz etwas Neues erreicht.
Der Unterschied zwischen den lebendigen Systemen und den vorangegangenen Systemen zeigt sich am Re-entry. Wie Spencer-Brown ausgeführt hat, kann es in jedem ausreichend komplexen System zu einem Re-entry kommen. Im Re-entry bilden sich nicht nur Muster und Eigenwerte aus, sondern werden in dem zugrunde liegenden System vernäht und bilden einen neuen Systemzustand. Lebendige Systeme zeichnen sich dadurch aus, dass diese Systeme nicht nur einen Re-entry durchlaufen, sondern einen Re-entry planen und zielgerichtet durchführen können. Sie überschauen die Vielfalt der Möglichkeiten des Systems und wählt bewusst diejenigen aus, mit denen sie ihre Umgebung für sich optimieren. Zuende gedacht führt das für den Menschen in die Möglichkeit (oder die Gefahr) transhumaner Systeme, in denen die uns bekannten klaren Grenzen von Mensch und Umgebung aufgehoben werden.
Higgs-Mechanismus: Festkörperphysik und Emergenz von Materie
Festkörperphysik und Klitzing-Konstante
Mit der Festkörperphysik erlangte die Theorie der Emergenz einen völlig neuen Aufschwung. Dort entstand auch die Idee, die Existenz von etwas als Emergenz eines unterliegenden Systems (Grundes) zu verstehen und diese Emergenz zu formalisieren. Higgs hat das auf die Teilchenphysik übertragen, und seither ist es zurecht eine der populärsten Theorien der neueren Naturwissenschaft geworden.
Die Festkörperphysik erlebt seit den 1940ern einen beispiellosen Aufschwung und ist in den USA seit den 1960ern die größte Abteilung in der American Physical Society. Ein wesentlicher Durchbruch gelang 1980 mit der Entdeckung der Klitzing-Konstante, die bei auf −269° Celsius abgekühlten Festkörperkristallen nachgewiesen werden kann. Einer ihrer wichtigsten Pioniere ist der amerikanische Physiker Robert B. Laughlin (* 1950), der in seinem 2005 veröffentlichen Buch Abschied von der Weltformel in der Emergenz und insbesondere der Festkörperphysik einschließlich ihrer Anwendungen in der Nanotechnologie eine neue Leitwissenschaft sieht. Während im öffentlichen Bewusstsein nach wie vor die Raumfahrt und die Kernforschung einschließlich der Teilchenphysik als die frontiers der Wissenschaft gelten, sind sie in der Realität abgelöst worden von der Festkörperphysik und Materialwissenschaft. Weltweit wird an Projekten einer »Quanteninformationsverarbeitung in Festkörpern« gearbeitet (Leopoldina, 34-38) (solid state quantum information processing), die zu einer neuen Generation von Quantentechnologien und Computern führen könnten.
Für Laughlin ist entscheidend, dass die Klitzing-Konstante wie die Wärme oder die Flüssigkeit ein kollektives Phänomen ist, das nicht an einzelnen Elementen, sondern nur statistisch am Systemzustand des Elektronengases im Ganzen gemessen werden kann. Dieser Erfolg regte an, nach weiteren Systemzuständen zu suchen. »Seither hat man einen riesigen, kaskadenartigen verzweigten Baum solcher Phasen entdeckt.« (Laughlin, 125) So ist es nach Laughlin gelungen, nicht nur die drei bekannten Systemzustände des Wassers (Eis, Flüssigkeit, Gas), sondern insgesamt 11 Systemzustände nachzuweisen. Hier sind in den Übergängen der bisher bekannten Zustände eigene Zustände verborgen, die ihre eigene Zeit und ihre eigenen Gesetze haben. Das Erstaunliche ist, dass die Gesetze jeder Phase nicht davon abhängen, »woraus die Flüssigkeit besteht« (Laughlin, 67). Sie lassen sich wie ein mathematisches Modell beschreiben, das für unterschiedliche Stoffe gilt, wenn nur die entsprechenden Bedingungen wie eine bestimmte Kristallstruktur, die erforderliche Kälte etc. erfüllt sind. Das gilt ebenso für andere Systemzustände wie Kristallgitter, Superfluidität, Superfestigkeit.
Auf den ersten Blick erscheint die Klitzing-Konstante wie ein unbedeutendes Ereignis auf einem der zahlreichen Spezialgebiete der Physik: Das Elektronengas entsteht unter bestimmten Bedingungen an Grenzflächen innerhalb eines Festkörpers. Bei extremer Kälte von −269° Celsius nahe über dem absoluten Kältepunkt formieren sich die Elektronen der im Kristall eines Festkörpers miteinander verbundenen Atome zu einem ungewöhnlichen zweidimensionalen Elektronengas. Das bedeutet, dass sich die Elektronen in diesem Systemzustand nur in zwei Dimensionen bewegen können. In diesem Systemzustand verändert sich innerhalb eines bestimmten Temperaturbandes eine besondere elektrische Spannung (der Hall-Effekt) nicht wie üblich kontinuierlich, sondern ist gequantelt (Quanten-Hall-Effekt). Die Quantensprünge erfolgen gemäß der Klitzingkonstante RK, wobei R für Widerstand und K für Klitzing steht, h ist das Plancksche Wirkungsquantum und e die elektrische Elementarladung:
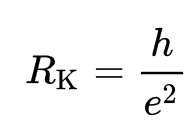
Offensichtlich wurde experimentell eine fundamentale Beziehung zwischen zwei der wichtigsten Naturkonstanten gefunden, die niemand theoretisch vorausgesagt hatte. Laughlin konnte nachweisen, dass unter anderen Bedingungen sogar gebrochene elektrische Elementarladungen auftreten, was bisher für völlig unmöglich galt. Die Klitzing-Konstante kann unvergleichlich genauer gemessen werden als das Plancksche Wirkungsquantum und die Elementarladung jeweils für sich und gilt daher inzwischen als reale Maßverkörperung (Etalon, Normal) für das physikalische Einheitensystem.
Higgs-Mechanismus
Gelingt es in der Festkörperphysik mit der fortlaufend feineren Unterscheidung von Zuständen und ihren Emergenzen genauer zu bestimmen, wie ein Grenzzustand auszusehen hat, in dem Materie aus einem materiefreien Feld emergiert, also der Übergang von materiellen Systemen in den materiefreien Grenzzustand rückwärts gelesen werden kann?
Aus der Festkörperphysik entstand in Arbeiten über die Supraleitung bereits 1960-61 mit dem Goldstonetheorem ein Modell, wie die Existenz fester Körper als Emergenz eines materiefreien Feldes beschrieben werden kann. Das soll nicht heißen, dass mit diesen Modellen oder dem Higgs-Mechanismus die Schöpfung von Materie möglich wird, – und im Feuilleton sogleich von Gottes-Teilchen gesprochen wurde, siehe dazu die radikale Gegenposition von Unzicker –, aber es handelt sich ohne Frage um eine der wichtigsten Neuentwicklungen der physikalischen Theorie der letzten Jahrzehnte. Was Hegel rein philosophisch in seiner Reflexionslogik entworfen hatte, könnte hier im Bereich der Realwissenschaft nachweisbar werden: Der Hervorgang der Existenz von Dingen aus einem Grund, welcher den Dingen unterliegt. Grund und Ding stehen weder in einem deterministischen Verhältnis (wonach der Grund eindeutig die Dinge bedingt), noch sind es voneinander unabhängige Begriffe, sondern so, wie in den Emergenzen Quantität und Qualität ineinander umschlagen, gelingt es zu beschreiben, wie die Dinge aus ihrem Grund emergieren.
Gerhard Samulat weist in einem Beitrag für Spektrum der Wissenschaft von 2013 darauf hin, dass der Higgs-Mechanismus ursprünglich in den frühen 1960ern von Festkörperphysikern wie Philip W. Anderson (1923-2020) entwickelt wurde, einem Physiker mit großem Interesse an Emergenz-Phänomenen. Peter Higgs (* 1929) und andere Teilchenphysiker erkannten sogleich die Tragweite des Mechanismus und übertrugen ihn 1964 auf die Teilchenphysik. Erst dort erhielt er den Namen Higgs-Mechanismus.
Mit dem Higgs-Mechanismus wird eine komplexe Bewegung zerlegt in ein Spektrum unendlich vieler, einzelner Bewegungen, die jeweils für sich eine regelmäßige Wellenstruktur aufweisen. Vorbild sind die aus der Musik bekannten Obertöne.
Obertonreihe
Urheber: Von Moodswingerscale.jpg: Y Landmanderivative work: W axell (talk) - Moodswingerscale.jpg, Gemeinfrei, Link
Die durchgehende Schwingung in der obersten Reihe steht für den physikalisch gemessenen Weg eines Teilchens von einem Zustand A in einen anderen Zustand B. Diese Bewegung wird erklärt als Aufnahme oder Abgabe eines Wechselwirkungsteilchens. An diesem Punkt droht die Physik in einen Widerspruch zu geraten: Obwohl eine Änderung der Masse gemessen wird, gibt es Bewegungsarten, bei denen das Wechselwirkungsteilchen keine Masse enthalten darf, weil mit ihr das Gleichgewicht der bekannten und empirisch überprüfbaren Prozesse gestört und der formale Mechanismus ausgehebelt werden würden. Es muss ein Weg gefunden werden, wie die Masse als Emergenzphänomen interpretiert werden kann.
Hierfür wird der einfache Weg zerlegt in die unendlich vielen Obertöne, von denen in dieser Darstellung die ersten 6 eingezeichnet sind. Hier wird angenommen: Während die Bewegungen der einzelnen Obertöne jeweils für sich materiefrei sind, emergiert aus ihrer Summe die Bewegung eines materiellen Teilchens, so wie sich in der Musik aus der Summe der Obertöne der Klang ergibt und in der Optik aus der Summe der Spektralfarben das natürliche Licht. Die Aufnahme bzw. Abgabe von Wechselwirkungsteilchen wird im Modell verlagert von der einfachen Bewegung vom Zustand A in den Zustand B auf die unendlich vielen Bewegungen der Obertöne, die für sich jeweils materiefrei sein sollen. Daher kann dort ein Mechanismus gefunden werden mit Wechselwirkungsteilchen, die keine Materie enthalten. Aus ihrer Gesamtheit emergiert der beobachtete Prozess. Dort wird nur noch die Bewegung des physikalischen Teilchens von Zustand A in Zustand B betrachtet, ohne auf dieser Ebene die Wechselwirkungsteilchen zu berücksichtigen.
Die Emergenz wird so erklärt, dass die Obertonschwingungen mit einem im Hintergrund präsenten Higgs-Feld wechselwirken. Die Wechselwirkung erfolgt an jedem Wellenknoten der Obertöne. Jeder einzelne Oberton zeigt ein Teilchen ohne Materie, das sich jedoch in Wechselwirkung mit dem Higgs-Feld befindet. In der Aufsummierung aller Obertöne ergibt sich ein Teilchen mit Materie. Die Materie verschwindet nicht und wird nicht erzeugt, sondern ist neu gedeutet als Summe der Wechselwirkungen der einzelnen, unendlich vielen Obertöne mit dem Higgs-Feld.
Aus der Musik ist bekannt, wie der gleiche Klang mit verschiedenen Obertönen klingt. Wird z.B. ein bestimmter Klang wie der Kammerton a (440 Hz) mal auf einer Violine und mal auf einem Klavier gespielt, ist der Unterschied hörbar. Die Qualität unterschiedlicher Violinen ist daran messbar, in welcher Weise die Obertöne mitklingen. Lässt sich das auf den Higgs-Mechanismus übertragen? Das würde bedeuten, dass die unterschiedlichen Frequenzen, mit denen Higgs-Teilchen aufgenommen oder abgegeben werden, in unterschiedlichen Intensitäten verknüpft werden. So kann in Analogie zur Musik von einer wohl- oder einer hässlichklingenden Materie gesprochen werden. Gibt es vergleichbar der Führungswelle in der Bohmschen Quantenmechanik eine Führungswelle, die das Verhältnis der verschiedenen Obertöne zueinander optimiert und in Harmonie bringt? Gibt es eine Wechselwirkung (ein Begehren), wie sich die Obertöne von sich aus in das optimale Verhältnis bringen? Von dieser Art zu fragen ist es nur noch ein kleiner Schritt zur Frage, in welchem Verhältnis die Higgs-Teilchen zu den Monaden und deren Harmonie nach Leibniz stehen.
Mit dem Higgs-Mechanismus wird nachvollziehbar, wie und wohin die Materie im Übergang aus den verschiedenen Systemzuständen in den Grenzzustand zu verschwinden scheint. Die in der Mathematik formulierbaren Gesetze erweisen sich als die sichtbare Seite eines Mechanismus, der im Hintergrund mit einem Higgs-Feld in Wechselbeziehung steht. Rein geometrische Erscheinungen wie die Annäherung einer Funktion durch eine Folge von Sinusfunktionen (der mathematischen Beschreibung von Wellen) werden gedeutet als Aufnahme und Abgabe von Higgs-Teilchen. Das ergibt ein prinzipiell neues Verständnis der Mathematik. Die mathematischen Konstruktionen und Rechenschritte können verglichen werden mit den Bewegungen der einzelnen Elemente in einem System, und in diesem Vergleich entspricht das Higgs-Feld der Bewegtheit des Systems im Ganzen. Die Mathematik kann nicht aus sich selbst heraus die Eigenschaften des Higgs-Feldes erkennen. Aber wenn es gelingt, in physikalischen Experimenten im Grenzübergang die Eigenwerte zu bestimmen und als Eigenschaften des Grenzzustands festzuhalten, werden mit den Eigenwerten die Eigenschaften des Higgs-Feldes gefunden und mit ihm öffnet sich die Perspektive auf eine neue Fundierung der Mathematik. Ein ähnlicher Gedanke lässt sich bereits aus Hegels Deutung des Satzes des Pythagoras ablesen, wenn er diesen Satz versteht als die Lebendigkeit eines Organismus, der sich in diesem Satz zeigt (siehe dazu den Beitrag).
‘Weniger als nichts‘ oder dynamische Logik von Möglichkeiten?
Wie kaum ein anderer Philosoph hat Slavoj Zizek (* 1949) ein waches Gespür für Neuentwicklungen. Als er an seinem Buch Weniger als nichts arbeitete, traf das zusammen mit den Berichten über die ersten erfolgreichen Nachweise der Higgs-Teilchen. Er nahm diese Ergebnisse sogleich in einem der abschließenden Teile auf und hat das Buch 2012 veröffentlicht. Für ihn ist das Higgs-Teilchen eine Facette des von Lacan eingeführten objet a.
»Das Teilchen bildet das Äquivalent zu Lacans objet a; dieses ist, als Objektursache des Begehrens, die Ursache, welche die Symmetrie eines Vakuums stört, [...] kurz: Es ist nichts weniger als die Ursache des Übergangs von nichts (dem Vakuum, der Leere reiner Potenzialitäten) zu etwas (wirklichen, verschiedenen Teilchen und Kräften).« (Zizek, 1282)
In dieser Sicht steht der mathematische Grenzzustand auf der Schwelle zwischen den physikalischen Systemen auf der einen Seite und einem Begehren auf der anderen Seite. So wie die Emergenzen aus lokalen Keimen erwachsen, ist jetzt die bisher betrachtete Entwicklung von der anderen Seite her zu lesen und der mathematische Raum als der Keim anzusehen, über den das im Hintergrund wirkende Begehren in die physikalische Existenz übergeht.
Stufe 5a: Das Begehren des objet a stört die Symmetrie des Grenzzustands, wodurch es zur Existenz kommt
Nach Zizek steht hinter dem Grenzzustand ein reines Begehren. Es ist hier als blaue Kugel dargestellt. Während bereits der Grenzzustand leer – und so gesehen ‘nichts‘ – ist, ist das Begehren des objet a ‘weniger als nichts‘.
Um das zu veranschaulichen, kann das unter Quantenphysikern beliebte Bild der Cheshire Cat (Grinsekatze, aus Lewis Carroll Alice im Wunderland) aufgenommen werden. Das Bild ›Stell dir eine grinsende Katze vor, und jetzt stell dir das Grinsen ohne Katze vor‹, wird nochmals fortgeführt: Und jetzt stell dir die Bereitschaft vor, grinsen zu können, ohne bereits zu grinsen. So ist es mit dem Weniger-als-nichts: Du siehst einen Schein und weißt, dass es etwas geben muss, das wie verzerrt auch immer im Schein zu sehen ist. Jetzt stell dir den Schein vor ohne das Sein, das in ihm zu sehen ist. Und dann stell dir das Bestreben vor, scheinen zu können, ohne dass es bereits den Schein gibt. Das ist weniger als nichts. – Was bisher nur wie ein von Wittgenstein eingeführtes Sprachspiel bekannt war, bekommt mit dem Higgs-Mechanismus eine mathematische Gestalt, die so weit ausgearbeitet werden kann, bis sie experimentell überprüfbar wird. Wenn das gelingt, ist die mit der Emergenz-Theorie in der Physik eingetretene Wende auch in der Philosophie nachvollzogen.
Zizek entwickelt seine Deutung des Higgs-Mechanismus in Anlehnung an Hegels Wissenschaft der Logik, von der er vor allem die Reflexionslogik ausführlich kommentiert hat. Nach Hegel und den darauf aufbauenden Ausführungen von Engels in Dialektik der Natur kann mit ein wenig Phantasie der mathematische Raum an der Stelle gesehen werden, an der nach den verschiedenen Umschlägen der unterschiedlichen Bewegungsformen der Materie (wie Mechanik, Chemie, Biologie) eine absolute Indifferenz und mit ihr nichts als Schein und dessen bloße Reflexion übrig geblieben ist. Mit der Reflexion ist in der Logik eine Sphäre erreicht, die sich nicht mehr auf die sinnliche Wahrnehmung und die mit ihr verbundenen Kategorien wie Qualität, Quantität, Raum, Zeit, Relation beziehen kann, sondern ausschließlich auf die Fähigkeit angewiesen ist, im und mit dem Denken etwas setzen zu können. Hegel versteht das Setzen als ein zirkuläres Voraus-Setzen, wenn das Denken in seiner Selbstanalyse erkennt, welche logischen Strukturen schon immer vorausgesetzt werden müssen, um denken und im Denken sich selbst erkennen zu können. Das führt das Denken bis an die Grenze eines Paradoxes. Zizek zitiert Hegel: »Die Reflexion also findet ein Unmittelbares vor, über das sie hinausgeht und aus dem sie die Rückkehr ist. Aber diese Rückkehr ist erst das Voraussetzen des Vorgefundenen. Dies Vorgefundene wird nur darin, daß es verlassen wird« (HW 6.27, zitiert bei Zizek, 259). Diese Bewegung, wie das Denken an sich selbst auf etwas stößt, das es vorfindet und aus dem es zurückkehrt in einer Bewegung, die offensichtlich jenseits des Denkens liegt, haben später sowohl Kierkegaard wie Wittgenstein aufgegriffen. Wenn ich ihn richtig verstehe, überträgt Zizek diesen Gedanken sowohl auf den Higgs-Mechanismus wie das objet a. Das Higgs-Teilchen wird sich an der Grenze zwischen Materie und materie-freien Symmetrien prinzipiell niemals nachweisen lassen, sondern ist eine Voraussetzung, ohne die der materiefreie Grenzzustand nicht gedacht werden kann. Es ist der Grund, in dem die Systembewegtheit eingeschrieben ist, oder im Sinne von Platon die chora (das Mütterliche), die die Formspuren enthält.
Soweit kann ich Zizek folgen. Aber ist es plausibel, den mathematischen Grenzzustand als Nichts und die ihm vorangehenden transzendentalen Voraus-Setzungen als Weniger-als-nichts zu bezeichnen und diese als zwei Vakua zu verstehen, in denen das Higgs-Feld »eingeschaltet« ist oder nicht (Zizek, 1283)? Was er mit Einschalten bezeichnet, ist offenbar ein anderer Name für die Emergenz. Mit dem Bild des Einschaltens wird ein Schöpfer nahegelegt, der in einem Akt vergleichbar dem biblischen ›Es werde Licht‹ den Sprung vom Weniger-als-nichts zum Nichts hervorruft und in dessen Folge die Materie erzeugt.
Stattdessen scheint es mir naheliegender, den Higgs-Mechanismus als ein mathematisches Modell zu verstehen, das der Mathematik zu Grunde liegt und den Weg für eine dynamische Logik öffnet, die in der Gesamtheit der Möglichkeiten Keimbahnen erkennt, die aus dem Raum der Möglichkeit in die Wirklichkeit führen. Hierfür lassen sich verschiedene Ideen aus der Quantenphysik aufnehmen, auf die sich der Higgs-Mechanismus mit seiner Zerlegung des Weges eines massehaltigen Teilchens in die Summe unendlich vieler Wege masseloser Teilchen ohnehin bereits bezieht.
Auch wenn Zizeks Deutung des Higgs-Teilchen als ein objet a als eine nicht ganz überzeugende Analogie erscheint, trifft er damit eine wichtige Frage: Wird wie oben dargestellt in der Gesamtheit aller Möglichkeiten nochmals der Beobachter-Standort hervorgehoben, dann kann der Hinweis auf das Begehren nach Lacan als Hinweis verstanden werden, den Beobachter nicht nur als einen dimensionslosen, neutralen, indifferenten Punkt anzusehen, sondern als einen Grund, der vergleichbar dem Willen nach Schopenhauer dem Denken vorausgeht, ihm Kraft und Richtung verleiht und für sich selbst immer eine Seite der Verborgenheit hat, die sich dem von ihm ausgehenden Denken entzieht und mit keiner zirkulären, selbstbezüglichen Bewegung des Denkens jemals voll erfasst werden kann. Hegel wählte dafür den schlichtesten Begriff, der sich denken lässt: Für ihn ist es das »Tun der Sache, sich zu bedingen und ihren Bedingungen sich als Grund gegenüberzustellen« (HW 6.119) mit dem scheinbar tautologischen Ergebnis: »Wenn alle Bedingungen einer Sache vorhanden sind, so tritt sie in die Existenz.« (HW 6.122)
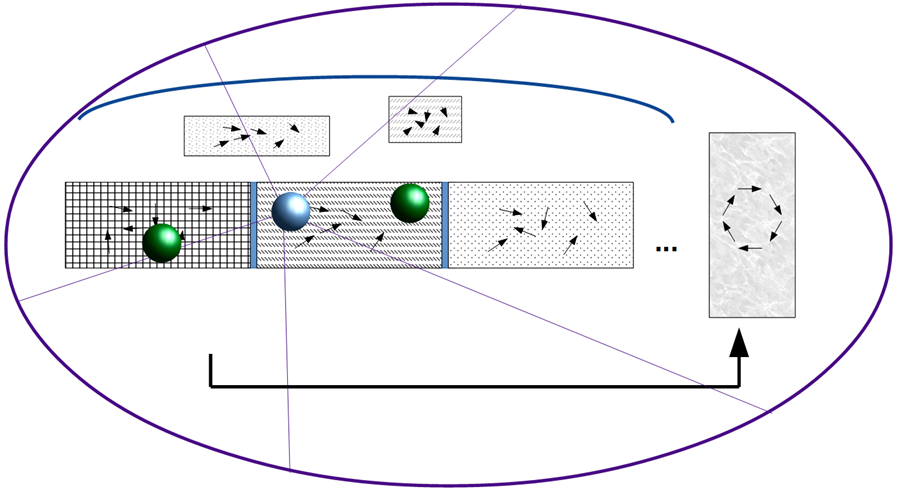
Stufe 7: Begehren innerhalb des Systems
Das Begehren befindet sich an der Stelle innerhalb des Systems, an der zuvor der Beobachter gesehen worden war. Es ist vergleichbar dem Willen nach Schopenhauer. Es befindet sich in Ausgleich mit dem Begehren der anderen, die durch grüne Kugeln symbolisiert sind.
Literatur
Günter Dedié: Die Kraft der Naturgesetze, Hamburg 2015 [2014]
Heinz von Foerster 1959: On Self-Organizing Systems and Their Environments
in: Heinrich von Foerster: Understanding understanding, New York u.a. 2003, 1-19
Heinz von Foerster 1972: Notes on an Epistemology for Living Thing
in: Heinrich von Foerster: Understanding understanding, New York u.a. 2003, 247-259
Heinz von Foerster 1984: Entdecken oder Erfinden
in: Heinz von Foerster u.a.: Einführung in den Konstruktivismus, München u.a. 2016 [1985], 41-88
Gottlob Frege 1879: Begriffsschrift, Halle 1879
Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971 (zitiert als HW)
Robert B. Laughlin: Abschied von der Weltformel, München 2010 [2005]
Nationale Akademie der Wissenschaften Leopoldina: Perspektiven der Quantentechnologie, Halle (Saale) 2015; Link
Roger Penrose: Computerdenken, Heidelberg 1991 [1989]
Gerhard Samulat: Ein Higgs im Kondensat, Interview mit Immanuel Bloch; Spektrum der Wissenschaft vom 22.5.2013
Claus-Artur Scheier: Die Selbstentfaltung der methodischen Reflexion als Prinzip der Neueren Philosophie, Freiburg, München 1973
George Spencer-Brown: Laws of Form, New York 1972 [1969]; Link
Alexander Unzicker: The Higgs Fake: Who Is Telling and Selling the Nonsense; Telepolis vom 31.10.2013
Slavoj Zizek: Weniger als nichts, Berlin 2014 [2012]
Bildnachweis: By Rusfuture - I photographed a car window with my Kodak digital cameraPreviously published: Published on Wikipedia, deleted by a vandal, unfortunately, CC BY-SA 3.0, Link



