Hegels Herleitung des Differentialkalküls aus der qualitativen Potenzbestimmung

- Rehabilitation der Hegelschen Deutung auf Grundlage der mathematischen Methoden des 20. Jahrhunderts

Einleitung

Hegels Deutung des Differentialkalküls ist absolut eigenständig und bis heute in der Mathematik nicht einmal ernsthaft zur Kenntnis genommen worden. Er sieht im Differentialkalkül ein völlig neues Verfahren, das unmöglich auf dem Boden der überlieferten Mathematik oder im Rahmen der formalen Logik begründet werden kann. In ihrem Bestreben nach formaler Strenge ist die Mathematik bis heute unfähig, das Neuartige des Differentialkalküls zu erkennen. Hegel will zeigen, dass sie sich buchstäblich eine neue Dimension erobert hat. Es ist ihr gelungen, nicht mehr nur mit Zahlen zu rechnen und geometrische Figuren zu konstruieren, sondern sie vermag unmittelbar vollständige Figuren miteinander zu verknüpfen und aus ihnen neue, höherdimensionale Figuren zu erzeugen. Im einfachsten Fall werden Linien miteinander multipliziert und erzeugen eine Fläche. Das wird meistens mit einer gewöhnlichen Rechenoperation verwechselt, wenn beispielsweise aus den beiden Zahlenwerten, die die Längen der Seiten eines Rechtecks beschreiben, der neue Zahlenwert errechnet wird, der den Flächeninhalt des Rechtecks darstellt. Hegel geht es dagegen nicht um die Multiplikation von Zahlen, die zu neuen Zahlen führt, sondern um die Multiplikation von Linien, die zu einer Fläche führt. Das geschieht, wenn z.B. im Koordinatenkreuz aus den beiden Achsen eine Fläche aufgespannt wird. Jeder kennt und versteht das, doch wird es meistens nur für eine Methode gehalten, die Anschaulichkeit zu verbessern. Hegel erkennt hier jedoch etwas qualitativ Neues. Hier gelingt es der Mathematik, aus Elementen mit mindestens einer Dimension Figuren in höheren Dimensionen zu erzeugen, während die Zahlen dimensionslos sind und als Punkte dargestellt werden. Diesen Übergang bezeichnet Hegel als Potenzierung. Wie ist er möglich, und was geschieht dabei? Das ist die Frage nach den Potenzbestimmungen, aus denen Hegel den Differentialkalkül herleiten will. Wie ist mit rein quantitativen Methoden ein solcher qualitativer Übergang zu bewerkstelligen?

Hegel will keineswegs über den Begriff der Größe oder der Dimension philosophieren, um mithilfe philosophischer Denkweisen der Mathematik von außen zu erklären, was sie tut. Sondern er begibt sich mitten hinein in das Gebiet der Mathematik und will anhand der von der Mathematik selbst aufgeworfenen Fragen zur Begründung des Differentialkalküls zeigen, wie der Differentialkalkül aus den Potenzbestimmungen, die zum Übergang in höhere Dimensionen führen, begründet werden kann. Das zwingt ihn, Begriffe zu gebrauchen, die bereits von der Mathematik und von der Philosophie genutzt werden. Was er sagen will, droht daher missverstanden zu werden oder unverständlich zu bleiben, wenn an den überlieferten Bedeutungen dieser Begriffe festgehalten wird. Hegel will zeigen, dass der Differentialkalkül aus qualitativen Potenzbestimmungen zu erklären ist. Was ist damit gemeint oder besser gesagt: nicht gemeint? In der überlieferten Bedeutung ist mit Potenz das rein quantitative Rechnen gemeint, das aus einer Zahl x eine neue Zahl y errechnet, z.B. x² = x · x. Hier ist x² die zweite Potenz von x. In dieser Bedeutung wird jedoch keine neue Dimension erreicht, sondern alles spielt sich zwischen Zahlen ab. Zum Beispiel wird aus der Zahl 3 die neue Zahl 3 · 3 = 3² = 9 ausgerechnet. Die Zahl 9 ist wie die Zahl 3 dimensionslos und liegt wie sie auf der eindimensionalen Zahlengerade, führt also in keine neue Dimension. Hegel geht es dagegen um eine Potenzbestimmung, die in höhere Dimensionen führt, zum Beispiel von Linien zu Flächen.

In diesem Beitrag soll sein Ansatz mithilfe der von der Mathematik im 20. Jahrhundert entwickelten neuen Verfahren der Tangentialbündel und allgemeiner der Faserbündel rekonstruiert werden. In einem Satz zusammengefasst wird die These vertreten, dass die Konstruktion von Tangential- und Faserbündeln die allgemeinste Methode ist, die Hegel als Potenzierung verstanden hat. Das hat im Grunde bereits zu einem neuen Verständnis des Differentialkalküls geführt, das jedoch noch nicht explizit gemacht ist, weil die Mathematik in ihren Lehrbüchern nach wie vor den im 19. Jahrhundert von Cauchy und Weierstraß eingeführten Definitionen des Grenzwerts folgt.

Wenn Hegels Deutung des Differentialkalküls gefolgt wird, dann wird es auch möglich, einen klareren Begriff der Bewegung zu finden. Daher trifft dieses Thema aus zwei Gründen in das Zentrum der Wissenschaft der Logik von Hegel: (1) Es wird sich im Weiteren zeigen, wie Hegel einen Begriff des Widerspruchs entwickelt, mit dem die Auflösung eines Widerspruchs aus seiner Verstocktheit verstanden werden kann. Der Widerspruch wird aufgelöst, indem er eine neue Dimension eröffnet, in der er sich bewegen kann. Während im Gegensatz die einander Entgegengesetzten auf einer Gerade einander gegenüberstehen, wie z.B. die positiven und negativen Zahlen auf der Zahlenachse, geht der Widerspruch zu Grunde, indem in einer neuen Dimension sein Grund gefunden wird. Die Auflösung in den Grund erfolgt entlang einer Linie, die senkrecht zur Achse steht, auf der der Gegensatz dargestellt ist. Es wird sich zeigen, wie diese Auflösung genau der Vorstellung folgt, die mit der Herleitung des Differentialkalküls aus den qualitativen Potenzbestimmungen gewonnen wird. (2) Zum anderen ist Hegel seit Trendelenburg zurecht vorgeworfen worden, dass seine Wissenschaft der Logik eine Vorstellung der Bewegung voraussetzt, aber nicht explizit zu entwickeln vermag. Nur über ein Verständnis der qualitativen Potenzbestimmungen scheint mir der bei Hegel fehlende oder nur implizit vorausgesetzte Begriff der Bewegung aufweisbar zu sein.

Statt Hegels Ideen aufzugreifen, hat sich in der Mathematik der 1821 von Cauchy eingeführte strenge Begriff der Ableitung durchgesetzt, den Bolzano und Weierstraß in der seither gültigen Form ausgearbeitet haben (Definition von Grenzwert und Stetigkeit durch das epsilon-delta-Kriterium, siehe z.B. den Eintrag in Wikipedia über die Stetige Funktion). Eine Rehabilitation Hegels führt daher notwendigerweise zu einer Auseinandersetzung mit Cauchy. Die von ihm und anderen vertretenen Definitionen und Formalisierungen haben zweifellos der Mathematik in einer bestimmten Entwicklungsphase geholfen und insbesondere ermöglicht, formal die Differentiation auf andere Zahlklassen wie die komplexen Zahlen zu erweitern, sind inzwischen aber zu einer Belastung geworden, die die weitere Entwicklung eher hemmt statt fördert. – Inhaltlich wird damit zugleich vorbereitet, ein anderes philosophisches Verständnis der Grundlagenbegriffe der Physik wie Energie und Kraft zu gewinnen. Das wird fortgeführt werden in Beiträgen zu Hegels Verständnis der Trägheit und des Systems der Naturwissenschaften (Mechanismus, Chemismus, Organismus).

Hegel kannte Cauchys Definition des Grenzübergangs mindestens in der ausführlichen Rezension von Dirksen, lehnte sie aber als zirkulär ab (HW 5.315 Fußnote). Sein eigener Deutungsansatz, die Besonderheiten des Differentialkalkül aus einer qualitativen Größenbestimmtheit herzuleiten, gilt dagegen als weltfremde Philosophie, sofern er überhaupt wahrgenommen wurde. Wichtigste Ausnahme ist die 1986 von Michael Wolff veröffentlichte Studie Hegel und Cauchy, von der im folgenden an vielen Punkten ausgegangen wird. Stattdessen beschäftigen sich die meisten Bücher über Philosophie der Mathematik nach wie vor mit der Grundsatzkrise des frühen 20. Jahrhunderts, dem Gegensatz von Formalismus und Intuitionismus (bzw. in dessen Nachfolge Konstruktivismus).

Wer heute Hegel zum Differentialkalkül liest, wird als erstes über seine gute Kenntnis der historischen Entwicklung überrascht sein. Innerhalb der Mathematik ist das Interesse an der eigenen Geschichte zu großen Teilen verloren gegangen, und es gilt als ausreichend, den jeweils aktuellen Stand zu kennen und daran weiter zu arbeiten. Die Regeln und Sätze des Differentialkalküls sind bekannt und werden bereits im Schulunterricht gelehrt. Kaum jemand macht sich mehr klar, aus welchen empirischen Studien sie entstanden sind. Das ist Hegel aber wichtig, denn nur wenn verstanden wird, wie diese Regeln aufgestellt werden konnten, kann auch erkannt werden, auf welche impliziten Annahmen die Mathematiker seinerzeit zurückgingen. Bei der Formulierung des Differentialkalküls wurden gewissermaßen naiv die qualitativen Gesichtspunkte genutzt, die Hegel erkennen und herausstellen will, um aus ihnen den Differentialkalkül herleiten zu können.

Wenn Hegel sich derart intensiv mit Grundlagenfragen der Analysis beschäftigt, geht es ihm keineswegs nur darum, in der Mathematik Beispiele für seine philosophischen Ideen zu finden oder als Philosoph der Mathematik bei der Klärung ihrer Grundlagenfragen zu helfen, sondern der Differentialkalkül ist für ihn die wichtigste Neuentwicklung der Wissenschaft seiner Zeit, aus deren Analyse er die Grundideen für seine eigene Philosophie finden wollte. Im folgenden soll gezeigt werden, wie zahlreiche Fragen seiner Wissenschaft der Logik ausgehend von seiner Deutung des Differentialkalküls verständlicher werden. Ein großes Vorbild hatte er sicher in Leibniz, der 1715 in den Metaphysischen Anfangsgründen der Mathematik den Beweis dafür gesucht hatte, »dass es eine Kunst der Analysis gibt, die umfassender ist als die Mathematik und aus der diese gerade ihre vollkommensten Methoden entlehnt« (Leibniz, Hauptschriften Bd. 1, S. 35).

Empirische Untersuchungen von Kurven und ihren Tangenten

Bis ins Detail malt Hegel aus, wie im 17. und 18. Jahrhundert für einzelne Probleme jeweils besondere, meist nur bedingt oder gar nicht übertragbare Lösungswege gesucht und gefunden wurden. Sie trafen nie das Problem im Kern, konnten es nicht aus allgemeinen Begriffen entwickeln, sondern lieferten ad-hoc-Lösungen, die gern als »Methoden« verkauft wurden. Die Mathematiker hielten ihre Methoden oft geheim, um sich bei öffentlich ausgeschriebenen Preisfragen einen Vorteil zu sichern.

»Es ist nicht ohne Interesse, von dem Historischen hierüber so viel zu bemerken, daß die ersten Entdecker ihren Fund nur auf eine ganz empirische Weise anzugeben wissen, ohne eine Rechenschaft von der völlig äußerlich gebliebenen Operation geben zu können. Ich begnüge mich hierüber mit der Anführung Barrows, des Lehrers Newtons. In seinen Lectiones opticae et geometricae, worin er Probleme der höheren Geometrie nach der Methode der unteilbaren behandelt, die sich zunächst von dem Eigentümlichen der Differentialrechnung unterscheidet, gibt er auch, 'weil seine Freunde in ihn gedrungen' (lect. X), sein Verfahren, die Tangente zu bestimmen, an. Man muß bei ihm selbst nachlesen, wie diese Aufgabe beschaffen ist, um sich eine gehörige Vorstellung zu machen, wie das Verfahren ganz als äußerliche Regel angegeben ist, – in demselben Stile, wie vormals in den arithmetischen Schulbüchern die Regeldetri oder noch besser die sogenannte Neunerprobe der Rechnungsarten vorgetragen worden ist. Er macht die Verzeichnung der Linienchen, die man nachher die Inkremente im charakteristischen Dreieck einer Kurve genannt hat, und gibt nun die Vorschrift als eine bloße Regel, die Glieder als überflüssig wegzuwerfen, die in Folge der Entwicklung der Gleichungen als Potenzen jener Inkremente oder Produkte zum Vorschein kommen (etenim isti termini nihilum valebunt), ebenso seien [337] die Glieder, die nur aus der ursprünglichen Gleichung bestimmte Großen enthalten, wegzuwerfen (das nachherige Abziehen der ursprünglichen Gleichung von der mit den Inkrementen gebildeten) und zuletzt für das Inkrement der Ordinate die Ordinate selbst und für das Inkrement der Abszisse die Subtangente zu substituieren. Man kann, wenn es so zu reden erlaubt ist, das Verfahren nicht schulmeistermäßiger angeben; – die letztere Substitution ist die für die Tangentenbestimmung in der gewöhnlichen Differentialmethode zur Grundlage gemachte Annahme der Proportionalität der Inkremente der Ordinate und Abszisse mit der Ordinate und Subtangente; in Barrows Regel erscheint diese Annahme in ihrer ganz naiven Nacktheit. Eine einfache Weise, die Subtangente zu bestimmen, war gefunden« (HW 5.336f).

Wer an Details interessiert ist, lese in der Encyclopaedia Britannica von 1911 den Eintrag über die Geschichte des Differentialkalkül (Wikisource). Barrow hat jedoch bereits sehr klar das Steigungsdreieck entwickelt, wovon Newton ausgehen konnte.

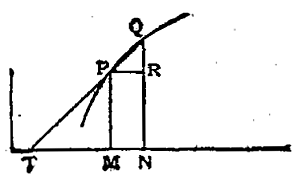
Figur 1: Barrows Steigungsdreiecke (Differential Triangle)
Das Diagramm zeigt deutlich die Grundidee, wie eine gekrümmte Kurve durch Steigungsdreiecke und im Grenzübergang durch eine geradlinige Tangente lokal angenähert wird. Es ist enthalten in: Lectiones opticae el geometricae, geschrieben vermutlich 1663-1664, veröffentlicht 1669, 1670. Quelle

Als trotz aller Widrigkeiten einmal der Durchbruch gelungen war, konnten recht schnell für alle einfachen Funktionen die Ableitungen gefunden werden. Damit ist die empirische Forschung jedoch keineswegs beendet. Die Analyse von Gradienten bleibt eine der wichtigsten Hilfsmittel der Naturwissenschaft. Wenn die Bewegungsgleichungen bestimmter Kräfte und damit die zu erwartende Entwicklung der Bewegung noch nicht bekannt sind, wird an zahlreichen Messpunkten gemessen, wie stark an diesen Stellen die Kraft ist und in welche Richtung sie weist. Gradienten werden durch Pfeile dargestellt. Hierfür ein aktuelles Beispiel aus der Medizin.

Nach Anbringen eines Bypass wird das Strömungsverhalten im Gefäß gemessen. Das wird graphisch dargestellt, indem mit Pfeilen die Messergebnisse eingetragen werden: Die Länge eines Pfeils zeigt die Stärke der Strömung an dieser Stelle, die Richtung des Pfeils, wohin die Strömung fließt. Aus diesen Messergebnissen wird ein zweites Diagramm entwickelt, indem entlang der jeweiligen Strömungsrichtung Kurven gezeichnet werden. Jeder Pfeil (Gradient) wird jetzt als Tangente an den verbindenden Kurven interpretiert. Die Kurven liegen um so dichter beieinander, je schneller sich die Strömung verändert. Das Diagramm zeigt anschaulich, an welchen Stellen Turbulenzen und mögliche Störungen auftreten. Zugleich sollte anschaulich deutlich sein, dass in der Regel zunächst nicht einmal offensichtlich ist, wie viele Dimensionen (Freiheitsgrade) zugrunde liegen. Es kann sein, dass es entlang einer Strömungslinie innere Beschleunigungen gibt. In diesem Fall muss das Diagramm dreidimensional veranschaulicht werden, vergleichbar einem Wollknäuel. In komplexeren Situationen sind noch mehr Freiheitsgrade denkbar.

Strömungslinien und Feldlinien stehen in jedem Punkt senkrecht aufeinander. Die Strömungslinie zeigt den Weg, entlang dessen die Strömung erfolgt. Die Feldlinie verbindet dagegen jeweils die Punkte, die die gleiche Feldstärke haben. Das anschaulichste Beispiel für Feldlinien sind die Höhenlinien eines Berges. Die Höhenlinien verlaufen entlang einer gleich bleibenden Höhe. Die Strömunglinien verlaufen senkrecht zu ihnen und zeigen, auf welchen Linien z.B. Wasser von der Bergkuppe den Berg hinabfließen würde. Meistens werden die Tangenten entlang der Feldlinien als »Tangenten«, und die senkrecht zu ihnen stehenden Tangenten entlang der Strömungslinien als »Cotangenten« bezeichnet. Gradienten und Cotangenten sind in dieser Sprachkonvention identisch. Dieser Sprachgebrauch kann natürlich zu einigen Missverständnissen führen.

Gesucht sind die Gleichungen, deren Ableitung die empirisch gefundenen Gradienten ergeben, um sie optimieren und daraus Konsequenzen für die medizinische Arbeit folgern zu können.

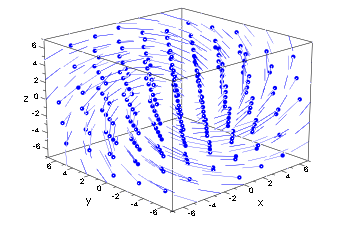
Figur 2: Vektorfeld und Stromlinien
»Darstellung eines Vektorfeldes anhand ausgewählter Punkte. Die Vektoren sind als Pfeile dargestellt, welche Richtung und Betrag (Pfeillänge) wiedergeben« (Wikipedia, abgerufen am 21.6.2017) Urheber: Mth77777 - Eigenes Werk, Gemeinfrei, https://commons.wikimedia.org/w/index.php?curid=12048094.

Fragestellungen dieser Art wurden bereits seit dem 17. Jahrhundert schrittweise komplexer. Eines der berühmtesten Beispiele ist die Brachistochrone: Gesucht ist »eine reibungsfreie Bahn zwischen einem höher und einem tiefer gelegenen Punkt, auf der ein Massenpunkt unter dem Einfluss der Gravitationskraft am schnellsten zum tieferen Endpunkt gleitet. Der Tiefpunkt der Bahn kann tiefer liegen als der Endpunkt« ( Wikipedia ). Diese Aufgabe hat schon 1696 Johann Bernouilli gelöst, also nur wenige Jahrzehnte nach den frühen Studien von Barrow.

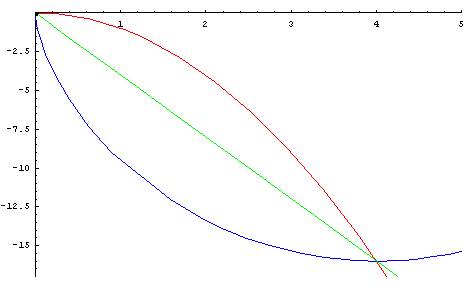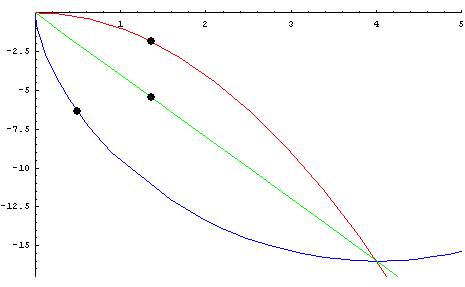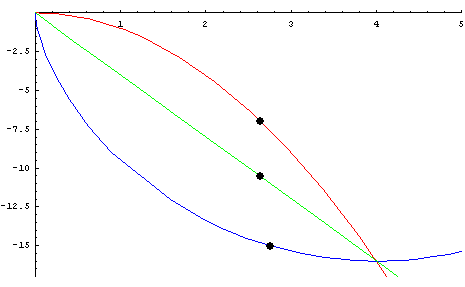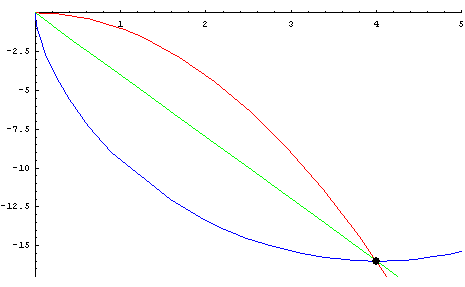
Figur 3: Brachistochrone;
Die blaue Linie zeigt den Weg, auf dem eine Kugel im freien Fall am schnellsten zum Punkt mit den Koordinaten x=4 und y=-15 gelangt; Quelle

Diese Beispiele sollen zeigen, wie bis heute empirische Analysen Grundlage weiterer Studien für den Differentialkalkül sind, dessen Ausarbeitung keineswegs abgeschlossen ist. Insbesondere die Medizin und die dort eingesetzten bildgebenden Verfahren liefern ständig neues Material, aber auch die experimentellen Ergebnisse aus der Teilchenphysik und den zahlreichen Anwendungsgebieten der Katastrophentheorie sowie das Beobachtungsmaterial der Astrophysik haben eine Datenmenge anwachsen lassen, durch die die Wissenschaft heute in eine ähnliche Situation gekommen ist wie nach den frühen Himmelsbeobachtungen von Tycho Brahe, für die Kepler die Lösungen gefunden hat.

Von empirischen Größen zu Regeln des Differentialkalküls

Die Suche nach algebraischen Regeln zum Bestimmen von Tangenten

Als die Steigungen der Tangenten entlang einer Kurve gemessen wurden, entstand die Frage, ob es irgendetwas gibt, woraus Regeln für die Steigung der Tangenten abgeleitet werden können. Zunächst konnte niemand erwarten, dass es überhaupt eine einheitliche Funktion gibt, die für jede Stelle x₀ die Steigung der Tangente an dieser Stelle liefert, und die Steigung der Tangenten nicht an jeder Stelle einzeln ermittelt werden muss. Heute erscheint das selbstverständlich. Um Hegels Deutung zu verstehen, ist jedoch zurückzugehen auf den historischen Moment, als Fragen dieser Art noch offen waren.

Noch weniger war zu erwarten, dass die Funktion zur Errechnung der Steigung der Tangenten aus der Funktion abgeleitet werden kann, deren Kurve betrachtet wird. Auch das erscheint erst heute selbstverständlich, seit die in einem mühsamen Forschungsprozess gefundenen Lösungen bekannt sind. Anfangs gab es die verschiedensten algebraischen Verfahren, die vorliegende Funktion zunächst für einzelne Stellen so umzurechnen, bis sie die empirisch gemessenen Steigungen der Tangenten lieferte und dadurch bestätigt wurde. In die Rechnungen gingen zahlreiche Tricks ein, Vermutungen und implizite Annahmen, die sich nicht begründen ließen und in Widerspruch zu den allgemeinen mathematischen Regeln stehen, sich aber in dem einen oder anderen Fall bewährt hatten und daher nach Möglichkeit verallgemeinert wurden. Auch für diese algebraischen Methoden gab es lange Zeit verschiedene Geheimverfahren. Sie dürfen nicht verwechselt werden mit den empirischen Verfahren, wie die Steigung der Tangenten zu messen sind. Hier handelt es sich um algebraische Verfahren, die Funktion geschickt umzurechnen, bis das gewünschte Ergebnis gefunden ist. Der Ansatz zur endgültigen Lösung der Umrechnungsverfahren wurde erst gefunden, als systematisch von Steigungsdreiecken ausgegangen wurde.

Hegel befand sich historisch auf einer Zwischenstufe. Zu seiner Zeit war das Konzept der Steigungsdreiecke noch nicht voll durchgesetzt, und erst recht waren die darauf aufbauenden Theorien noch unbekannt, einen Tangentialraum und ein Tangentialbündel (die Menge aller Tangentialräume) zu entwerfen. Aber dafür war es für ihn seinerzeit vielleicht leichter als heute zu erkennen, von welchen Ideen sich die Mathematiker leiten ließen, als sie eine Lösung suchten, die noch völlig unbekannt war. Diese leitenden Ideen zu erkennen, das war Hegels Ziel. Er wollte herausarbeiten, was bei den für den Differentialkalkül entwickelten mathematischen Verfahren neu ist im Vergleich zu den überlieferten Rechenverfahren des Addierens, Substrahierens, Multiplizierens und Dividierens. Seine Frage war, für das Neue die implizit bezogenen Qualitäten zu erkennen, die in den überlieferten traditionellen Rechenverfahren für endliche Größen noch fehlen oder nicht gebraucht werden, und die zugleich den Mathematikern verborgen blieben, da sie zu schnell mit den bloßen Ergebnissen zufrieden waren.

Im folgenden Zitat führt er den historischen Rückblick auf Barrow fort und bezieht sich weiter auf Subtangente und Ordinate. Diese Ausdrücke sind heute kaum mehr gebräuchlich, da die Mathematik seit dem 19. Jahrhundert möglichst vollständig auf geometrische Anschauung verzichtet und bestenfalls den Differenzenquotienten im Steigungsdreieck erwähnt. Mit Subtangente und Ordinate sind die Projektionen der Tangente auf die x- und y-Achse gemeint. Ihr Verhältnis ist das Grenzverhältnis, gegen das die Verhältnisse der Katheten in den Steigungsdreiecken konvergieren.

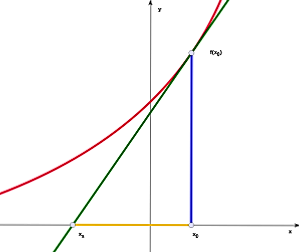
Figur 4: Subtangente und Ordinate

In dieser Figur ist die grün gezeichnete Tangente an der Stelle x₀ an die rot gezeichnete Kurve angelegt. Die Subtangente ist gelb gezeichnet, die Ordinate blau.
Urheber: McSush – hiesige png-Version "Subtan.png", Gemeinfrei, Link

»Das Verhältnis der Ordinate zur Subtangente ... hatten die Alten auf sinnreichem geometrischen Wege gefunden; was die neueren Erfinder entdeckt haben, ist das empirische Verfahren, die Gleichung der Kurve so zuzurichten, daß jenes erste Verhältnis geliefert wird, von dem bereits bekannt war, daß es einem Verhältnisse gleich ist, welches die Linie enthält, hier die Subtangente, um deren Bestimmung es zu tun ist. Teils ist nun jene Zurichtung der Gleichung methodisch gefaßt und gemacht worden – die Differentiation –, teils aber sind die imaginären Inkremente der Koordinaten und das imaginäre, hieraus und [aus] einem ebensolchen Inkremente der Tangente gebildete charakteristische Dreieck erfunden worden, damit die Proportionalität [339] des durch die Depotenzierung der Gleichung gefundenen Verhältnisses mit dem Verhältnisse der Ordinate und der Subtangente nicht als etwas empirisch nur aus der alten Bekanntschaft Aufgenommenes, sondern als ein Erwiesenes dargestellt werde. Die alte Bekanntschaft jedoch erweist sich überhaupt und am unverkennbarsten in der angeführten Form von Regeln als die einzige Veranlassung und respektive Berechtigung der Annahme des charakteristischen Dreiecks und jener Proportionalität« (HW 5.338f).

Hegel spricht an dieser Stelle zahlreiche Themen an, die Schritt um Schritt ausgeführt werden sollen, um im Ergebnis zu verstehen, warum er im Potenzenverhältnis den Begriff sieht, aus dem der Differentialkalkül hergeleitet werden kann.

Übergang von der Funktionskurve zu ihrem Tangentialbündel

Die entscheidende Idee war die Einführung der Steigungsdreiecke. Einen ersten, noch unvollkommenen Ansatz hatte Barrow gefunden, der im Weiteren systematisch ausgebaut wurde.

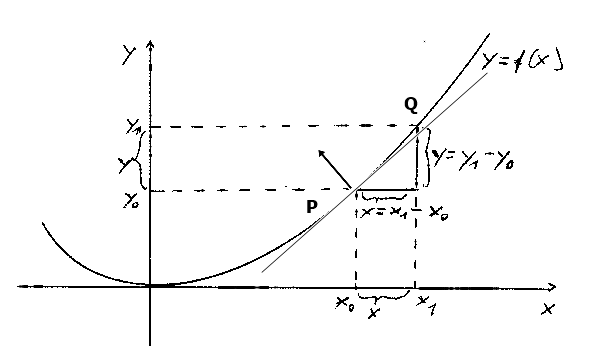
Figur 5: Steigungsdreieck

Freihandzeichnung

Beim Steigungsdreieck wird ein Wert x₁ in der Nähe von x₀ betrachtet. Wird der Abstand von x₁ zu x₀ als x bezeichnet, d.h. x₁ = x₀ + x, dann kann für den Abstand von f(x₁) zu f(x₀) gesetzt werden f(x₁) = f(x₀) + y. Das Verhältnis beider Seiten im Steigungsdreieck beträgt also:

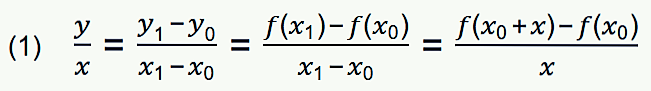
Mit dieser Gleichung war der allgemeine Ansatz gefunden, von dem aus algebraische Rechnungen begonnen werden konnten. In diesen Ansatz gehen keine Besonderheiten für bestimmte Funktionen f ein. Wenn eine Funktion f gegeben ist, kommt es darauf an, in dieser Gleichung auf der rechten Seite die Ausdrücke f(x₀ + x) und f(x₀) auszuschreiben und die Gleichung solange umzuformen, bis auf der linken Seite y / x stehen bleibt, während auf der rechten Seite weder x noch y im Nenner steht. Im einfachsten Beispiel wird die Funktion f(x) = x² betrachtet. In diesem Fall kann (1) in wenigen Schritten so umgeformt werden, dass auf der rechten Seite das Ergebnis steht (die Rechnung ist ausgeführt in Link ):

Im Grenzübergang werden x = 0 und y = 0 gesetzt. Dadurch entfällt auf der rechten Seite x und mit 2 · x₀ ist die Steigung der Tangente an der Stelle x₀ gefunden.

Bei dieser Vorgehensweise drohen jedoch Missverständnisse, da x und y in mehrfacher Bedeutung gebraucht werden. Die Längen des Steigungsdreiecks müssen mit x und y bezeichnet werden, um das Verhältnis x / y zu erhalten. Zugleich sind aber mit x und y auch die x-Achse und y-Achse im Ganzen gemeint sowie die betrachtete Funktion, die y = f(x) geschrieben wird.

Wenn auf diese Weise bis auf die ursprünglich durchgeführten Rechnungen zurückgegangen wird, mit denen die Ableitungen ausgerechnet wurden, sieht jeder sofort, dass hier etwas nicht stimmen kann. Während auf der linken Seite im Grenzübergang ausgehend von x / y der »verbotene« Ausdruck 0 / 0 festgehalten wird, der die arithmetische Regel verletzt, dass durch 0 nicht geteilt werden kann, wird auf der rechten Seite x einfach weggelassen. Das Ergebnis sieht nach dem Grenzübergang so aus:

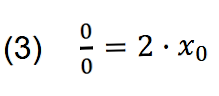
Bei komplexeren Funktionen sind die Ausdrücke weitaus komplizierter, aber im Prinzip geschieht im Grenzübergang immer das gleiche: Auf der linken Seite wird 0 / 0 stehen gelassen, während auf der rechten Seite alles wegfällt, wo x im Zähler auftritt. Dieses unterschiedliche Operieren auf beiden Seiten führt zur Depotenzierung: Wenn eine Funktion in der n-ten Potenz steht (in diesem Beispiel in der 2-ten Potenz), dann liefert die Ableitung einen Wert in der (n-1)-ten Potenz (in diesem Beispiel in der ersten Potenz). Dieses Vorgehen ist heute für niemanden mehr ein Skandalon, da die Ableitungsregeln als formaler Kalkül betrachtet werden, dessen Herkunft nicht mehr unterrichtet wird. Hegel hat es dagegen auf den Punkt gebracht:

»Allein bei der Methode ihres Unendlichen findet sie den Hauptwiderspruch an der eigentümlichen Methode selbst, auf welcher sie überhaupt als Wissenschaft beruht. Denn die Rechnung des Unendlichen erlaubt und erfordert Verfahrungsweisen, welche die Mathematik bei Operationen mit endlichen Größen durchaus verwerfen muß, und zugleich behandelt sie ihre unendlichen Größen wie endliche Quanta und will auf jene dieselben Verfahrungsweisen anwenden, welche bei diesen gelten« (HW 5.281).

Dieser Hauptwiderspruch kann nur aufgehoben werden, wenn verstanden wird, wie hier in einer rein quantitativen Gleichung zwei unterschiedliche Qualitäten aufeinandertreffen. Diese Situation so genau und so überzeugend wie möglich in ihrer Unvermeidlichkeit zu schildern, ist für Hegel mindestens so wichtig, wie in der Mathematik den höheren Begriff der Unendlichkeit zu entdecken. Denn diese Situation zeigt, wie innerhalb der Mathematik und Naturwissenschaft ein Widerspruch entsteht, der weder auf eine unvollkommene Erkenntnis noch auf ein falsches Urteil oder einen misslungenen Schluss zurückgeht, sondern notwendig zur Sache gehört. Damit hat Hegel am Beispiel der neueren Mathematik nachweisen wollen, dass es »wahre Widersprüche« gibt, und die weiteren Bücher der Wissenschaft der Logik bekommen die Aufgabe, daraus sowohl die Konsequenzen für den Begriff des Widerspruchs zu ziehen als schließlich eine geeignete neue Logik zu entwickeln, in der Widersprüche dieser Art ihren Platz finden können.

Der damalige Stand der Mathematik bot Hegel jedoch nur unzureichende Möglichkeiten, die höhere Qualität mathematisch zu beschreiben. Er sieht sie im Potenzenverhältnis. Das kann mit den inzwischen entwickelten neuen Erkenntnissen treffender dargestellt werden, wobei ich hoffe zeigen zu können, was Hegel vermutlich mangels einer besseren Darstellungsmöglichkeit mit dem Potenzenverhältnis gemeint hat.

Zunächst hat der hier dargestellte Weg der Ableitung einer Funktion f(x) zu einer neuen Funktion f '(x) geführt, die wiederum jedem x auf der x-Achse einen Funktionswert f '(x) auf der y-Achse zuordnet, der als die Steigung der Tangente an der entsprechenden Stelle verstanden wird. So führt in dem bereits genannten Beispiel die Funktion f(x) = x² zur abgeleiteten Funktion f '(x) = 2 · x. Das ist jedoch nur ein Zwischenschritt und noch keineswegs das Ergebnis des Differenzierens, wie es heute fälschlich in der Schule und in zahlreichen Lehrbüchern dargestellt wird. Das Ziel besteht darin, eine Regel zu finden, die für eine gegebene Funktion f an jeder Stelle x₀ die Tangente liefert. Jede einzelne Tangente ist ihrerseits eine Funktion. Die Aufgabe der Zwischenlösung f '(x) besteht nur darin, an jeder Stelle x₀ die Steigung der Tangente zu finden.

Im Ganzen führt die Ableitung einer Funktionskurve f(x) nicht nur zur abgeleiteten Funktion f '(x), sondern zum Tangentialbündel, das ist die Gesamtheit aller Tangenten an einer Kurve. Während f(x) und f '(x) Abbildungen von f: ℝ → ℝ sind (ℝ ist das Symbol für die reellen Zahlen, die anschaulich der eindimensionalen Zahlengerade entsprechen), die jeder reellen Zahl x eine andere reelle Zahl f(x) zuordnen, handelt es sich bei der Regel, alle Tangenten der Funktion zu finden um eine Abbildung, die jeder reellen Zahl x eine Tangente an der Kurve von f zuordnet. Wenn diese Regel Tf genannt wird und das Tangentialbündel an der Kurve von f mit Tf, dann kann sie so aufgeschrieben werden:

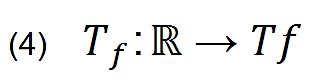
lies: Jedem Punkt x₀ aus der Menge der reellen Zahlen (ℝ) wird eine Tangente aus der Menge aller Tangenten (dem Tangentialbündel) zugeordnet, die an dieser Stelle x₀ an die gegebene Funktion f angelegt werden kann.

Ein sehr einfaches Beispiel für ein Tangentialbündel sind alle Tangenten, die an einen Kreis angelegt werden können.

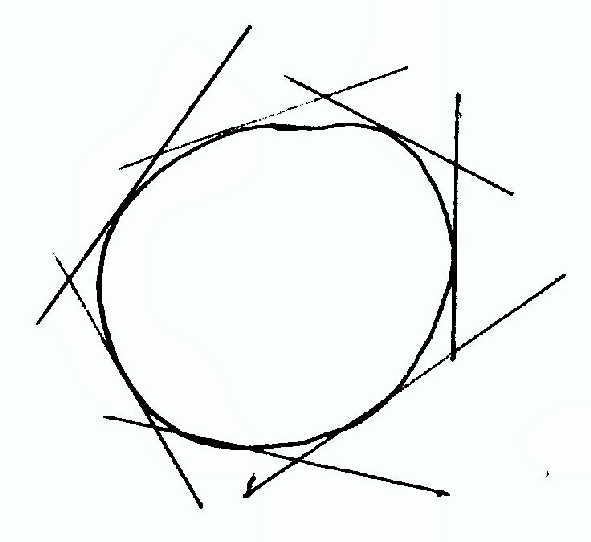
Figur 6 Kreis mit Tangenten

Freihandzeichnung

In diesem Beispiel wird eine Regel gesucht, die für jeden Punkt auf der Kreislinie die Tangente findet, die an dieser Stelle am Kreis angelegt ist. Anschaulich ist zu erkennen, dass alle Tangenten zusammen die vollständige zweidimensionale Ebene füllen mit Ausnahme des Inneren des Kreises. Anders gesagt: Jeder Punkt außerhalb des Kreises liegt auf mindestens einer Tangente, die an dem Kreis angelegt ist. Es lässt sich verallgemeinern: Während eine gekrümmte, differenzierbare Kurve eindimensional ist, ist ihr Tangentialbündel zweidimensional. im Weiteren soll dargelegt werden, wie dieser Übergang in die zweidimensionale Ebene Hegels Begriff des Potenzenverhältnisses zugrundeliegt.

Allerdings wird in der Mathematik bis heute die Ableitung nicht in dieser Weise als eine Abbildung von den Urbildern einer Funktion auf ihr Tangentialbündel eingeführt, sondern nur als die abgeleitete Funktion f '(x) verstanden. Dieses Verständnis steht quer zu dem völlig anderen Verständnis, das ich bei Hegel herauslese. Das erklärt, warum Hegels Deutung des Differentialkalküls bis heute alle Mathematiker ratlos läßt, da sie nicht sehen, wie sie ihrerseits das Grundanliegen des Differentialkalküls nicht festgehalten haben. (Das kann zu zahlreicher Verwirrung führen. Die Physiker denken dagegen wesentlich praktischer. Sie interessieren sich für Lösungen von Gradientenfeldern, wie es oben an dem medizinischen Beispiel dargestellt wurde. Jeder Gradient steht senkrecht auf der Tangente, die an einer Feldlinie angebracht wurde. Die Gesamtheit der Gradienten kann daher aus dem Tangentialbündel entlang der Feldlinien berechnet werden und wird als Cotangentialbündel bezeichnet. Wird gemessen und ausgewertet, wie dicht Feldlinien aneinander liegen und wie schnell daher der Übergang von einer Feldlinie zu einer benachbarten entlang des Gradienten erfolgt, ist nach heutigem Verständnis der Physik damit das Maß der Energie gefunden. Die Physik zeigt anschaulich, worum es Hegel geht: Er will den Übergang von der Kategorie ‘Quantität’, zu der auch die Größenbestimmungen der Funktionen und der Steigungen ihrer Tangenten gehören, zur Kategorie ‘Maß’ entwickeln.

Mathematisch ist jede einzelne Tangente eine eindimensionale Gerade, d.h. eine Abbildung vom Typ f: ℝ → ℝ. Jede Abbildung f bildet Punkte x ∈ ℝ auf andere Punkte y ∈ ℝ ab. Wenn die Fläche ℝ ✕ ℝ, die von der x-Achse und der y-Achse aufgespannt wird, als Menge von unendlich vielen Geraden verstanden wird, dann kann jede Tangente als ein Element aus ℝ ✕ ℝ dargestellt werden. Das Tangentialbündel aller Tangenten entlang einer Kurve für eine reell-wertige Funktion f ist daher eine Teilmenge aus dem Kreuzprodukt ℝ ✕ ℝ. Formel (4) kann entsprechend geschrieben werden:

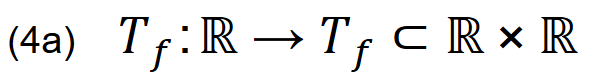
lies: Jeder Punkt x₀ ist eine reelle Zahl, die auf der Zahlenachse ℝ liegt. Diesem Punkt wird eine Gerade (die Tangente) zugeordet, die in der Fläche ℝ ✕ ℝ verläuft.

Mit ℝ ✕ ℝ ist hier die Ebene gefunden, auf die Hegel Bezug nehmen wird.

Steigungsdreiecke verschwinden, ihr Verhältnis bleibt bestehen

Bisher wurde gezeigt, wie die Steigungsdreiecke der beste Ansatz sind, um geometrisch und algebraisch die Tangenten zu einer Funktionskurve zu finden. Doch was geschieht beim Übergang, wenn die Steigungsdreiecke sich der Tangente annähern?

Die Steigungsdreiecke verschwinden in dem Moment, wenn das letzte Steigungsdreieck identisch ist mit der gesuchten Tangente. Dann gibt es keine zwei Katheten mehr, deren Verhältnis gemessen und ausgerechnet werden kann. Aus dem Verhältnis der beiden Katheten im Steigungsdreieck wird das Verhältnis von Ordinate und Subtangente, siehe Figur 4. Die Situation ähnelt dem später von den Quantenmechanikern gerne zitierten Bild, dass das Lächeln der Katze bleibt, obwohl die Katze verschwindet. Das Verhältnis der Seiten der Steigungsdreiecke bleibt, obwohl das Steigungsdreieck verschwindet.

In diesem Sinne wählt Hegel eine schwierige Formulierung, die Wolff intensiv analysiert.

»Die Gleichung dy/dx = P drückt gar nichts weiter aus, als daß P ein Verhältnis ist, und es ist dem dy/dx sonst kein reeller Sinn zuzuschreiben. Von diesem Verhältnis = P ist es aber ebenso noch unbekannt, welchem anderen Verhältnisse es gleich sei; solche Gleichung, die Proportionalität, gibt demselben erst einen Wert und Bedeutung« (HW 5.344, bei Wolff Hegel und Cauchy zitiert auf S. 225f).

Hier ist zweierlei zu beachten: (a) Der Grenzübergang der Steigungsdreiecke führt zum Verhältnis von Ordinate und Subtangente. Hegel behält – anders als die Mathematik heute – immer als das wesentliche Anliegen der Differentiation im Blick, an einer Stelle für eine Funktion eine Tangente zu finden. Das ist für ihn ihr »reeller Sinn«. Dazu dienten die empirischen Messungen und die algebraischen Umformungen der Funktionskurve. Daher ist für ihn das Ergebnis der Differentiation ein Verhältnis (von Subtangente und Ordinate), das die Tangente beschreibt. (b) Die mit der Ableitung gefundene Funktion f '(x) ist nur ein Hilfsmittel, um die Tangente zu bestimmen. Hegel lässt sich nicht davon irritieren, dass f '(x) formal auch eine Funktion ist. (Das sichert, dass er nicht auf eine rein formale Position zurückfällt, aber es verhindert, dass er auch die zweite Ableitung f ''(x) betrachtet. Er nimmt f '(x) nicht als vollwertige Funktion wahr, die ihrerseits abgeleitet werden kann.)

Damit zeigt sich der oben betrachtete Hauptwiderspruch im Grenzübergang von einer anderen Seite. Es muss etwas Übergreifendes geben, wodurch der Zusammenhang im Übergang vom Verhältnis der Katheten zur Steigung der Tangenten hergestellt und aufrecht erhalten wird. Während dort der Widerspruch nur konstatiert und nicht anders aufgelöst werden konnte als durch die bloße Setzung, dass beim Rechnen im Grenzübergang Regeln erlaubt sind, die sonst verboten sind, ist hier mithilfe der Darstellung der Steigungsdreiecke der gleiche Widerspruch in der Ebene dargestellt, in der die Steigungsdreiecke und Tangenten gezeichnet werden. Die Übertragung des gleichen Problems in einen anderen, erweiterten Kontext ermöglicht die Lösung. Sie liegt darin, hier die Gesamtheit aller Steigungsdreiecke zu betrachten und in deren Bewegung hin zur Tangente einen inneren Zusammenhang zu erkennen.

Damit nimmt Hegel intuitive Anschauungen vorweg, die in der Mathematik erst wesentlich später ausgearbeitet wurden. Der kontinuierliche Übergang von Figuren in eine Grenzfigur, wie es hier im Übergang von den Sekanten der Steigungsdreiecke zur Tangente geschieht, wird in einem Faserbündel dargestellt, das mathematisch dem Tangentialbündel sehr ähnlich ist. Wenn dort der Übergang kontinuierlich möglich ist, liegt ein innerer Zusammenhang vor. Das ist einer der seltenen Fälle, bei denen die Mathematik für einen neuen Begriff exakt den treffenden Ausdruck gefunden hat (siehe im Detail Vorlesungen zur Eichfeldtheorie, z.B. Link). – Die Technik der Übertragung eines Problems von einem Gebiet in ein anderes, so wie es hier bei der Übertragung von der algebraischen Methode der Ableitung zur geometrischen Methode der Ableitung geschieht, wird systematisch untersucht von der in den 1940ern entwickelten mathematischen Kategorientheorie. Die mathematische Kategorientheorie ist zu unterscheiden von der aristotelischen Kategorienlehre, aber es gibt starke innere Übereinstimmungen.

Veränderliche Größen im Potenzenverhältnis

Hegel erkennt sehr genau, wie der Übergang von den Steigungsdreiecken zur Tangente ein Beispiel für veränderliche Größen ist. Deren Maß ist für ihn das Potenzenverhältnis. Das soll an dieser Stelle abschließend vorgestellt werden.

Hegel unterscheidet direkte, umgekehrte und Potenzenverhältnisse. Bei direkten und umgekehrten Verhältnissen gibt es eine feste Konstante a, so dass für alle y gilt:

(5a) x = a · y

(5b) x = y / a

Das umgekehrte Verhältnis ergibt sich, wenn in (5a) zunächst der Faktor a auf die linke statt auf die rechte Seite geschrieben wird: a · x = y statt x = a · y, und dann auf beiden Seiten durch a geteilt wird.

Hegel bezeichnet abweichend vom heutigen Sprachgebrauch in der Mathematik in (5a) den Faktor a als Exponenten. Beim direkten Verhältnis beträgt die Steigung immer a, verändert sich also nicht. Damit umschreibt Hegel die Aussage, dass in (5a) die zweite Ableitung, das ist physikalisch die Beschleunigung, 0 ist. Von (5a) und (5b) unterscheidet er qualitativ das Potenzenverhältnis:

(5c) x = y · y

In diesem Verhältnis ist gegenüber (5a) der feste Wert a durch eine veränderliche Größe y ersetzt, die gleichmäßig mit dem Wert y mitwächst, zu dem x in Verhältnis gesetzt wird.

Vor diesem Hintergrund wird verständlich, wenn Hegel schreibt:

»Dadurch sind diese Seiten des Verhältnisses, x und y, erstens nicht nur keine bestimmten Quanta, sondern zweitens ihr Verhältnis ist nicht ein fixes Quantum (noch ist dabei ein solches wie bei a und b gemeint), nicht ein fester Quotient, sondern er ist als Quantum schlechthin veränderlich. Dies aber ist allein darin enthalten, daß x nicht zu y ein Verhältnis hat, sondern zum Quadrate von y. Das Verhältnis einer Größe zur Potenz ist nicht ein Quantum, sondern wesentlich qualitatives Verhältnis; das Potenzenverhältnis ist der Umstand, der als Grundbestimmung anzusehen ist« (HW 5.294).

Das Potenzenverhältnis ist für Hegel das Maß veränderlicher Verhältnisse. Daher will er nachweisen, dass aus dem Begriff des Potenzenverhältnisses der Differentialkalkül hergeleitet werden kann, der sich grundsätzlich auf veränderliche Größen bezieht, deren Bewegungskurve gekrümmt ist. Wenn sich etwas auf ähnliche Weise gleichmäßig verändert wie das Potenzenverhältnis, dann hat es die Eigenschaft, abgeleitet werden zu können.

Herleitung aus der Qualität (Potenzenverhältnis)

Hegel will die quantitativen Bestimmungen, die empirisch gemessen und mit den Regeln des Differentialkalküls algebraisch ausgerechnet werden, aus einer höheren Qualität herleiten. In einer komplexen Formulierung fasst er alles zusammen, was bisher Schritt für Schritt nachvollzogen wurde:

• Während die Bewegungskurve reeller Funktionen für sich eindimensional ist, befinden sich die Steigungsdreiecke und Tangenten, die an sie angelegt werden, in der sie umgebenden Ebene. Die Betrachtung wechselt daher von einer eindimensionalen Kurve in die zweidimensionale Ebene.

• Das Potenzenverhältnis x = y · y kann als Übergang in das Quadrat von y und damit in die Ebene interpretiert werden.

• Die Regeln des Differentialkalküls haben gezeigt, dass es beim Ableiten von Polynomen zu einer Depotenzierung kommt: Wenn eine Funktion in der n-ten Potenz steht, dann steht ihre Ableitung in der (n-1)-ten Potenz. f(x) = xⁿ ergibt abgeleitet f '(x) = n · xⁿ⁻¹

All dies packt Hegel in die folgende Formulierung:

»Die gerade Linie hat ein empirisches Quantum, aber mit der Ebene tritt das Qualitative, die Potenzenbestimmung ein; nähere Modifikationen, z.B. daß dies gleich auch mit den ebenen Kurven geschieht, können wir, insofern es zunächst um den Unterschied bloß im allgemeinen zu tun ist, unerörtert lassen. Hiermit entsteht auch das Bedürfnis, von einer höheren Potenzenbestimmung zu einer niedrigeren und umgekehrt überzugehen, indem z.B. lineare Bestimmungen aus gegebenen Gleichungen der Fläche usf. oder umgekehrt abgeleitet werden sollen. – Die Bewegung ferner, als an der das Größenverhältnis des durchlaufenen Raumes und der dazugehörigen verflossenen Zeit zu betrachten ist, zeigt sich in den verschiedenen Bestimmungen einer schlecht-gleichförmigen, einer gleichförmig beschleunigten, einer abwechselnd gleichförmig beschleunigten und gleichförmig retardierten, in sich zurückkehrenden Bewegung; indem diese unterschiedenen Arten der Bewegung nach dem Größenverhältnisse ihrer Momente, des Raums und der Zeit, ausgedrückt werden, ergeben sich für sie Gleichungen aus unterschiedenen Potenzenbestimmungen, und insofern es Bedürfnis sein kann, eine Art der Bewegung oder auch der Raumgrößen, an welche eine Art gebunden ist, aus einer anderen Art derselben zu bestimmen, führt die Operation gleichfalls das Übergehen von einer Potenzenfunktion zu einer höheren oder niedrigeren herbei« (HW 5.334).

Äußere Multiplikation (»Multiplikation von Linien«)

Während der Differentialkalkül in der Mathematik und erst recht der Philosophie der Mathematik intensiv diskutiert wird, – wenn auch Hegels Deutung weitgehend ignoriert bleibt –, hat das Potenzenverhältnis eine zweite Seite, die die Mathematik zwar kennt, über deren tiefe Bedeutung sich die Mathematik und die Philosophie der Mathematik jedoch noch nicht einmal bewusst geworden sind. Wenn im Potenzenverhältnis x = y · y gesetzt wird, entsteht ein neuer Ansatz für das Multiplizieren. Auch hier genügt es den Mathematikern, dessen formale Regeln aufzuschreiben und mit ihnen zu operieren, und ein Außenstehender wird wahrscheinlich gar nicht wissen, welche Wege Mathematik gefunden hat. In der Schule wird die äußere Multiplikation bis heute nicht unterrichtet, und wer nicht Mathematik, Physik oder Ingenieurwissenschaften studiert hat, hat noch nie etwas von ihr gehört. Wieder ist es erforderlich, auf die Ausgangsfrage zurückzugehen, die Hegel anders als alle anderen, die über die Mathematik nachgedacht haben, sehr genau trifft.

Seit Euklid und erst recht seit der Begründung der analytischen Geometrie durch Descartes erscheint es völlig selbstverständlich, zwei Längen miteinander zu multiplizieren, um daraus den Flächeninhalt zu berechnen, und dann in weiterer Verallgemeinerung aus dem Produkt von Breite, Höhe und Länge den Volumeninhalt. Wenn ein Rechteck die beiden Seitenlängen a und b hat, dann ergibt sich seine Fläche F als F = a · b. Jeder kann sich das veranschaulichen, indem die Fläche zerlegt wird in ein Raster von Einheitsquadraten, die abgezählt werden können.

    

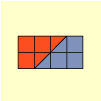
Figur 7a, 7b, 7c: Flächenberechnung durch Rasterung

»Zum Bestimmen des Flächeninhalts einer Figur kann diese mit Einheitsflächen, zum Beispiel mit Quadraten, ausgelegt werden. Die Maßzahl gibt dann die Anzahl der Einheitsquadrate an, die zum Auslegen der Figur benötigt werden« ( Schülerlexikon).

Aus der Formel für die Berechnung der Fläche eines Rechtecks ergibt sich direkt die Formel für die Berechnung eines Dreiecks: F = ½ · a · h, wobei a die Länge der Grundseite und h die Höhe des Dreiecks ist. Da sich alle Figuren mit geradlinigen Außenkanten in Dreiecke zerlegen lassen, ist damit ein allgemeines Verfahren für die Berechnung der Fläche gefunden.

Bei diesen Multiplikationen ist jedoch genau genommen keine Fläche das Ergebnis, sondern die Größe der Fläche, das ist die Anzahl der Einheitsquadrate, die in die Fläche passen. Diese Zahl besagt, um das Wievielfache die Fläche F größer ist als eine Einheitsfläche: Das ist ein Quadrat mit den Seitenlängen 1 · 1 und der Fläche 1. (Die Einheitslänge 1 ist wiederum gemessen am Pariser Urmeter, die Einheitsfläche beträgt damit 1 m², ein Quadratmeter.) Das bedeutet im einfachsten Fall des Rechtecks mit den Seitenlängen a und b:

(6) Die Größe der Seite a ergibt multipliziert mit der Größe der Seite b die Größe a · b der Fläche F.

Hier sind die Seitenlängen a und b reelle Zahlen jeweils mit der Dimensionsangabe m (für Meter), z.B. 4 m und 10 m, und F ist die Größe des Flächeninhalts in der Dimension m², in diesem Beispiel 40 m². Während sich die meisten damit zufrieden geben und ihnen alles klar zu sein scheint, unterscheidet Hegel sorgfältig die beiden Teiloperationen, aus denen sich das Multiplizieren der Seiten zusammensetzt: Zum einen werden reelle Zahlen multipliziert, zum anderen Dimensionen:

(6a) a · b = F  (z.B. 4 · 10 = 40)

(6b) m ⊗ m = m²

Während in (6a) aus zwei reellen Zahlen eine neue reelle Zahl errechnet wird, wird in (6b) aus zwei Längen eine Fläche gebildet. Das kann in ähnlicher Weise wie für den Differentialkalkül geschrieben werden:

(7a) ℝ, ℝ → ℝ (mit a,b,F ∈ ℝ)

lies: die reelle Zahl a ergibt multipliziert mit der reellen Zahl b die neue reelle Zahl a · b

(7b) ℝ, ℝ → ℝ ✕ ℝ (mit m ≡ ℝ und m² ≡ ℝ ✕ ℝ)

lies: Die in Metern (m) gemessene Länge a ergibt mit der ebenfalls in Metern gemessenen Länge b die in Quadratmetern gemessene Fläche a ⊗ b

Jedem Mathematiker ist zwar klar, dass die 1846 von Hermann Graßmann (1809-1877) eingeführte äußere Multiplikation (7b) anderen Regeln folgt als die gewöhnliche Multiplikation (7a), aber ähnlich wie bei dem von Hegel festgestellten »Hauptwiderspruch« des Differentialkalküls wird auch hier von der Mathematik lediglich formal definiert, wie die Regeln der äußeren und normalen Multiplikation verknüpft werden. Niemand fragt, was es eigentlich bedeutet, Linien mit Linien zu multiplizieren.

Hegels Text zu verstehen fällt daher aus dem Grund schwer, da mit Potenz in der Regel die gewöhnliche Multiplikation einer Zahl mit sich selbst gemeint ist, während hier aus dem Zusammenhang deutlich wird, dass Hegel die äußere Multiplikation meint. Das ist um so erstaunlicher, als die äußere Multiplikation in der Mathematik erst nach Hegel von Graßmann eingeführt worden ist, der Hegel gründlich studiert hat.

Dass sich die Mathematik hier am Rande des Paradoxes bewegt, wurde erst indirekt klar, als Cantor im Bereich der transfiniten Zahlen auf die verwandte Frage stieß, ob ein Produkt »unendlich mal unendlich« denkbar ist. Wenn das Symbol ∞ für ‘unendlich’ steht, muss dann nicht gelten?

(8) ∞ · ∞ = ∞

lies: unendlich mal unendlich ergibt wieder unendlich

Denn wenn ∞ die größtmögliche Zahl ist, wie kann dann etwas entstehen, das noch größer als die größtmögliche Zahl ist? Mit Formel (8) werden aber die Rechenregeln des Multiplizierens verletzt, nach denen nur für die beiden Zahlen 0 und 1 die Formel x · x = x gilt (0 · 0 = 0 bzw. 1 · 1 = 1). Cantor zog daraus den radikalen Schluss, dass es unterschiedliche Arten von Unendlichkeit geben muss. In Formel (8) gehören die beiden Unendlichkeiten auf der linken Seite der Gleichung einer anderen Art von Unendlichkeit an als die Unendlichkeit auf der rechten Seite. Er bezeichnete die Arten der Unendlichkeiten als ihre Mächtigkeit. Die Gleichung führt von einer einfachen Mächtigkeit in eine höhere Mächtigkeit, so wie bei der äußeren Multiplikation von Linien die höhere Potenz der Fläche erreicht wird. Cantor suchte nach einem Weg, im Bereich der transfiniten Zahlen auch mit ∞ formal ähnlich rechnen zu können wie mit endlichen Zahlen. Er erweiterte daher die Zahlklasse der natürlichen Zahlen um die transfiniten Zahlen und setzte, dass dort gelten soll:

(9) ∞ · ∞ = ∞²

Dieser Ausdruck ist rein formal aufgeschrieben, und es stellt sich die Frage, in welcher Zahlklasse ∞² liegt. Wenn sich ∞² von ∞ unterscheiden soll, aber beide auf der Zahlenachse liegen, muss es jenseits von ∞ einen eigenen Ort für ∞² geben. Die Kontinuumshypothese besagt, dass die reellen Zahlen mächtig genug sind, um auch Zahlen wie ∞² aufnehmen zu können. Dann würde zwar (9) gelten, aber nicht von der Zahlengerade in die Ebene führen, sondern irgendwo weit draußen ist auch Platz für ∞². Da bereits ∞ als die größte Zahl definiert worden war, bedeutet das, dass ∞ und ∞² ununterscheidbar sind oder in anderer Ausdrucksweise miteinander verschmiert (verfilzt, verschmolzen). Sie sind im Unendlich-Großen auf ähnliche Weise ununterscheidbar, wie im Unendlich-Kleinen beim Grenzübergang des Differentialkalküls die von Leibniz eingeführten Differentiale dx voneinander ununterscheidbar sind. Neuere Untersuchungen deuten jedoch darauf hin, dass sich die Kontinuumshypothese nicht halten lässt und Zahlen wie ∞² in der Ebene liegen, d.h. in einer Zahlenmenge, die gleichmächtig wie ℝ ✕ ℝ ist. Dann stellt sich die Frage, wie in (9) ein Sprung in die Ebene möglich ist, der nur durch die äußere Multiplikation erreicht werden kann, d.h. durch eine Formulierung wie:

(10) ∞ ⊗ ∞ = ∞²

Diese Formel ist nur möglich, wenn Linien mit Linien multipliziert werden. Das heißt aber, dass die unendlich große Zahl ∞ anders als alle endlichen Zahlen kein Punkt ist, sondern wie bereits vermutet weit draußen ein verschmiertes Intervall darstellt, dessen Elemente ununterscheidbar sind, und das mit sich selbst multipliziert in die Ebene führt. Hier ist exakt die Verlegenheit getroffen, auf die die Mathematik und Physik immer stoßen, wenn sie Grenzübergänge betrachten.

∞ liegt offenbar auf der Grenze zwischen der gewöhnlichen und der äußeren Multiplikation. Aristoteles sprach daher von Punkten, die sich berühren können (Aristoteles Physik, V.3, 227a), was wörtlich gesehen ein Widerspruch ist. An diese Grenze ist Hegel mit seinen Überlegungen zum Begriff des Unendlichen und der Herleitung des Differentialkalküls aus dem Potenzenverhältnis gestoßen.

Nach meiner Überzeugung wird die Mathematik auf großen Umwegen zu dem gleichen Ergebnis kommen, das Hegel bereits vorweggenommen oder mindestens vorausgeahnt hat, als er in diesem Zusammenhang vom »Übergang in eine höhere Dimension« (HW 5.360 und ähnlich HW 5.371) sprach, der »Multiplikation von Linien mit Linien« (HW. 5. 361). Es kann bis heute nicht besser in Worte gefasst werden als es ihm in der weit ausholenden Anmerkung zur »Qualitativen Größenbestimmtheit« gelungen ist:

»Die Multiplikation von Linien mit Linien bietet sich zunächst als etwas Widersinniges dar, insofern die Multiplikation überhaupt Zahlen betrifft, d. i. eine Veränderung von solchen ist, welche mit dem, in das sie übergehen, mit dem Produkte ganz homogen sind und nur die Größe verändern. Dagegen ist das, was Multiplizieren der Linie als solcher mit Linie hieße – es ist ductus lineae in lineam wie plani in planum genannt worden, es ist auch ductus puncti in lineam –, eine Veränderung nicht bloß der Größe, sondern ihrer als qualitativer Bestimmung der Räumlichkeit, als einer Dimension; das Übergehen der Linie in Fläche ist als Außersichkommen derselben zu fassen, wie das Außersichkommen des Punktes die Linie, der Fläche ein ganzer Raum ist« (HW 5.361).

Damit hat Hegel den entscheidenden Punkt getroffen. Das Potenzenverhältnis eröffnet eine neue Dimension. Bei quantitativen Größen werden Zahlen miteinander multipliziert und führen zu einer neuen Zahl. Beim Potenzenverhältnis werden Dimensionen miteinander multipliziert und führen in eine höhere Dimension. Im Differentialkalkül kommt beides zusammen.

Ich verstehe Hegel so, dass durch das Potenzenverhältnis der Übergang in eine höhere Dimension gelingt und dadurch eine neue qualitative Größenbestimmtheit erreicht wird gegenüber der üblichen Multiplikation, bei der das Produkt zweier Zahlen wiederum eine Zahl ist (und keine höhere Dimension). Ist der Wechsel der Dimensionen verstanden, dann können daraus die Eigenschaften des Differentialkalkül mit seiner Depotenzierung hergeleitet werden. Dieser Schritt ist hier noch nicht gelungen, sondern es ist nur die Richtung angegeben, in der weiter geforscht werden muß.

Aus Sicht der Mathematik des 20. Jahrhunderts bedeutet das für mich, dass die mit dem Potenzenverhältnis entstandene Ebene das Urbild des mehrdimensionalen Tangentialbündels ist. Das Tangentialbündel einer Funktion oder einer geometrischen Figur ist zunächst einfach die Menge aller Tangenten oder Tangentialflächen, die an die Funktion bzw. die Figur angelegt werden können. Während jede einzelne Tangente eine eindimensionale Gerade ist, bildet die Menge aller Tangenten entlang einer gekrümmten Kurve eine Fläche, die aus den Tangenten zusammengesetzt ist. Es war schwierig genug zu verstehen, wie die einzelnen Tangenten aus einem Grenzübergang aus den sie umgebenden Sekanten und deren Steigungsdreiecken hervorgehen. Daraus ergibt sich die weiterführende Frage, was geschieht, wenn nicht mehr nur miteinander benachbarte Punkte auf einer Funktion verglichen werden, sondern die an ihnen angelegten Tangenten. Schon anschaulich ist klar: Wenn die Punkte einer Funktion kontinuierlich miteinander verbunden sind und im Sinne von Aristoteles einander berühren, sollten auch die an ihnen angelegten Tangenten kontinuierlich miteinander verbunden sein. Mathematisch ist es erst mit der neueren Entwicklung der Differentialgeometrie seit den 1950ern gelungen, diese Verhältnisse klar zu fassen: Wenn beim Übergang von einer Tangente zur benachbarten Tangente Stetigkeit nachgewiesen werden kann, wird das mathematisch als die Eigenschaft des Zusammenhangs beschrieben. Dieser Zusammenhang ist nach meiner Hypothese die gesuchte höhere Qualität, aus der der Differentialkalkül hergeleitet werden kann.

Und auch hier ist es Newton gelungen, innerhalb der Mechanik die Lösung zu finden, die auf die Mathematik übertragen und dort verallgemeinert werden kann. Er unterscheidet drei Schritte: (i) Die empirisch beobachtbare Bewegungsbahn eines Körpers kann mathematisch mit einer Funktion s(t) beschrieben werden, wobei s für die Strecke steht, die ein Körper in einer Zeit t durchlaufen hat. Die Funktion wird graphisch in einer Ebene dargestellt, deren Achsen Raum und Zeit sind. Ein Punkt auf der Kurve zeigt, an welchem Ort s₀ der Körper zur Zeit t₀ angekommen ist. Beispiele sind die Bewegungskurve des freien Falls, die Parabelbahn einer Kanonenkugel oder die Bewegungsbahn der Planeten um die Sonne. So hat Newton alle Ergebnisse der ihm vorliegenden Physik in eine Einheit gebracht und das Koordinatenkreuz von Descartes als Raumzeit verstanden. (ii) Die Tangenten entlang der Bewegungsbahn beschreiben die jeweilige Momentangeschwindigkeit (und mit ihr den jeweiligen Impuls m · v, Masse mal Geschwindigkeit). (iii) Wird gefragt, wie eine Geschwindigkeit (Tangente an der Bewegungsbahn) in die benachbarte Geschwindigkeit übergeht, dann ergibt sich die kinetische Energie als ihr Zusammenhang (½ · m · v², einhalb mal Masse mal Geschwindigkeit zum Quadrat). ‘Zusammenhang’: Hier sind ausnahmsweise ein gewöhnlicher Begriff und ein mathematischer Begriff identisch. Newton hat daraus geschlossen, dass die Kraft das Produkt aus Masse und Beschleunigung ist (d.h. der Veränderung von einer Geschwindigkeit in eine andere Geschwindigkeit), und von ihm stammt die Erkenntnis, wie die Kraft, der Impuls und die Energie mathematisch auseinander hergeleitet werden können.

Der Schluss von der Quantität über die Energie zum Maß

[Dieser Abschnitt ist 2020 nach einer Zuschrift und Gesprächen mit Horst-Helmut Krause ergänzt worden.]

Im Grunde stand Hegel dicht vor der Lösung: Er hatte die Bedeutung des Grenzübergangs im Differentialkalkül erkannt, der zur Steigung der Tangenten führt. Und er hatte gesehen, wie mit der Multiplikation von Linien eine neue Art des Rechnens entsteht, die in höhere Dimensionen führt. Das kann als das mathematische Modell oder der Nukleus von Emergenz verstanden werden. Beides zusammengenommen erfordert, bei der Betrachtung einer Kurve nicht nur die Tangenten zu sehen, die an eine Gerade angelegt werden, sondern auch die Krümmung der Kurve. Während die Tangenten an die Bewegungskurve angelegt sind und ihre Steigung die lokale Steigung der Kurve zeigt, steht die Krümmung senkrecht zur Tangente. Mit der Krümmung bewegt sich die Kurve von der jeweils an ihr angelegten Tangente weg und unterscheidet sich von ihr. Die Krümmung öffnet daher gegenüber der Tangente eine weitere Achse. Die Richtung der Tangente und die Richtung der Krümmung sind im Unendlich-Kleinen die beiden Linien, über die eine äußere Multiplikation zu einer unendlich kleinen Fläche führt. Erst mit dieser Fläche kann das Maß der Kurve (bzw. in physikalischer Bedeutung das Maß der Bewegung) definiert werden. Wird das äußere Produkt aus Steigung und Krümmung physikalisch als Energie interpretiert, dann ist mit der Energie ein Begriff gefunden, der zugleich weit über die Physik hinausgeht. Aus der Philosophiegeschichte war Hegel der Begriff der Energie (energeia) bei Aristoteles vertraut. Im Grunde hatte er alles in der Hand, um den Zusammenhang oder in physikalischer Deutung die Energie als den terminus medius bestimmen zu können, über den auf das Maß geschlossen werden kann. Doch gelang es ihm noch nicht, dies alles (den Grenzübergang zur Tangente, die Krümmung der Kurve, die Multiplikation von Linien, die energeia nach Aristoteles) in einen übergreifenden Entwurf zu bringen.

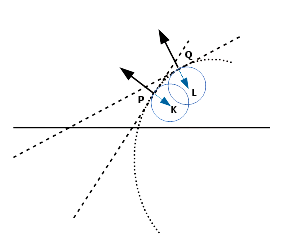
Figur 8a, 8b, 8c: Zahlenachse, gedrehte Gerade, gekrümmte Kurve mit Tangente und Cotangente

Das lässt sich in drei Schritten geometrisch veranschaulichen: (a) Die Zahlenachse ist eindimensional und hat keine Steigung. (b) Wird sie an einer beliebigen Stelle in die Ebene gedreht, hat sie überall die gleiche Steigung. Eine Gerade ist identisch mit den an sie angelegten Tangenten. (c) Erst bei einer gekrümmten Kurve unterscheiden sich die Tangenten von der Kurve und untereinander. Die Cotangente steht jeweils senkrecht auf der Tangente. Wird sie um 180° in das Innen der gekrümmten Kurve gedreht, verweist sie auf das Zentrum des lokalen Krümmungskreises. Mit der Tangente und der Krümmung entsteht die Differentialgeometrie, mit der das gewöhnliche Rechnen mit dimensionslosen Punkten verlassen und das Entstehen und die Konstruktion qualitativer Eigenschaften in höheren Dimensionen ermöglicht werden.

Rückkehr von der Quantität zur Qualität

Während Hegel an anderer Stelle keine Scheu hatte, Begriffe aus der Mathematik zu übernehmen und im Rahmen der Wissenschaft der Logik neu zu deuten, hat er an dieser Schlüsselstelle seines Werks darauf verzichtet. Er gebraucht den mathematisch-physikalischen Begriff der Energie weder in der Wissenschaft der Logik noch in der Naturphilosophie. Die Energie wird nur in den Vorlesungen über die Geschichte der Philosophie im Abschnitt über Aristoteles erwähnt. Dort gibt Hegel ihr jedoch den angemessenen Rang: Er versteht die Energie mit Aristoteles als »tätige Wirksamkeit« (HW 19.155), in einer anderen Wendung als Wirklichkeit und sieht sie wie die Möglichkeit als eine der »Weisen der Substanz (HW 19.156), d.h. als Modalität, und darüber hinausgehend gleichbedeutend mit der Entelechie als »freie Tätigkeit«, die »den Zweck in sich selbst hat« (HW 19.158). Insofern ist »beim Geist die Energie die Substanz selber« (HW 19.159). Das führt ihn zum Aphorismus: »Nicht das Gedachte ist das Vortrefflichere, sondern die Energie selbst des Denkens« (HW 19.163), der für mich das Motto meiner Studien über die Logik von Hegel ist. Entsprechend wird in der Phänomenologie des Geistes und der Enzyklopädie der philosophischen Wissenschaften im Grundrisse nur in diesem Sinn von der »Energie der Vernunft« gesprochen (so HW 9.222). An einer einzigen Stelle wird in der Enzyklopädie zum Begriff der Wirklichkeit gesagt, »seine Äußerlichkeit ist seine Energie« (Enz. § 142, HW 8.279).

Für mich liegt nahe, die Energie als die erste Form der Lebendigkeit zu sehen und sie im Entwicklungsgang der Logik schrittweise einzuführen: (i) Ausgehend vom Differentialkalkül im Übergang zum Maß, (ii) in der Wesenslogik im Übergang von der Erscheinung zum Begriff der Wirklichkeit, (iii) als Energie des lebendigen Begriffs, wodurch der Begriff zur Idee wird. An diesen drei Schritten ist zugleich die Kritik Hegels an Kant mitzuvollziehen:

(i) Während Kant in seiner Kategorientafel mit Aristoteles von Qualität (poion), Quantität (poson) und Relation (pros ti) spricht und die Modalität als vierte Kategorie ergänzt (KrV, B 106), spricht Hegel vom Maß (und nicht von der Relation) als der dritten Kategorie und bezieht sich auf den Maßbegriff in der Tradition der griechischen Philosophie. Das Maß ist mit Hegel eine selbstbezügliche Kategorie: Als Mitte ist das Maß nicht nur eine Kategorie wie die Qualität und die Quantität, die als »das Dritte der Qualität und Quantität« hinzugefügt wird (HW 5.388), sondern zugleich der terminus medius des Schließens. Wenn Hegel die Seinslogik mit der Kategorie des Maßes abschließt, hat er mit dem Maß den terminus medius gefunden, mit dem der Schluss begründet ist, wie die Kategorien über sich selbst hinaus zu gehen vermögen und der Schluss von den Kategorien an ihnen selbst (über das Maß) auf die Wesensbestimmungen gezogen werden kann. Mit diesem Schluss ist darüber hinaus bereits in nuce die Begriffslogik angesprochen, in deren Mitte wiederum die Lehre vom Schluss steht. Auf diese Weise gelingt es Hegel, nicht nur die Kategorien auseinander herzuleiten, – statt sie äußerlich in einer Tafel anzuordnen –, sondern über das Maß einen Schluss aus der traditionellen Lehre der Ontologie (die Lehre vom Sein und seinen Kategorien) auf die Metaphysik (die Sätze von Identität, Unterschied, Widerspruch und Grund) zu ziehen, und in einem abschließenden Schritt auf die traditionelle Logik (die Lehre vom Begriff, Urteil und Schluss). Bis dato standen sie äußerlich nebeneinander.

(ii) Hegel folgt Aristoteles und sieht die Modalität und mit ihr die Wirklichkeit nicht als Kategorie, sondern als Wesensbestimmung. Die Wirklichkeit kann für ihn nicht mit der Modalität als eine weitere Kategorie aufgezählt werden, sondern es muss gelingen, aus den Kategorien auf den Begriff der Wirklichkeit zu schließen. Nur wenn das gelingt, kann mit dem Begriff der Wirklichkeit die von Kant gesetzte Trennung von Erscheinung und Ding-an-sich aufgehoben und das Wirkliche als das Vernünftige gesehen werden. Ohne das an dieser Stelle weiter auszuführen, sei erinnert: In diesem Sinn kann Hegel in den Grundlinien der Philosophie des Rechts schreiben: »Was vernünftig ist, das ist wirklich; und was wirklich ist, das ist vernünftig.« (HW 7.24) Für ihn gilt: »Alles Vernünftige ist ein Schluß« (HW 6.352), d.h., es wird über einen terminus medius vermittelt und findet in ihm sein Maß.

(iii) Abschließend zieht er einen Schluss vom Begriff des Begriffs über dessen Objektivität auf den Begriff der Idee. Während Kant es als die Aufgabe der Vernunft angesehen hat, den Verstand vor überfliegenden Ideen und die mit ihnen verbundenen Antinomien zu bewahren, sieht Hegel die Idee als den Abschluss seiner Wissenschaft der Logik. Mit ihr findet die Logik ihr Maß. Und mit ihr zieht er die Summe aus der Geburt der Philosophie in Griechenland: Angefangen mit ihrem natürlichen Verständnis des Maßes im Sinne einer schlichten Weisheit, an das sich der Mensch sowohl bei der Betrachtung der Natur wie im eigenen Handeln zu halten hat, über die Ideenlehre von Platon bis zum Begriff der energeia bei Aristoteles. Dennoch bleibt er sich treu: So wie er im Übergang zum Maß die Energie nicht erwähnt, bleibt sie im Abschnitt über die Objektivität bei den Ausführungen über die Mechanik unbeachtet. Daher ergibt sich dort nach meinem Verständnis in seinem Gedankengang eine ähnliche Lücke wie in seinem Übergang zum Maß.

Diese Übersicht über Hegels Logik soll zeigen, warum aus meiner Sicht die Energie deren verborgener Schlüsselbegriff ist. Dass er ihn nicht zu ergreifen vermag, scheint mit einer oberflächlichen Kritik an Newton (und möglicherweise an Leibniz, der den neueren Entdeckungen der Naturwissenschaft weit offener gegenüberstand) zu tun zu haben. Ohne es in voller Klarheit formulieren zu können, hatte Newton den wesentlichen Punkt getroffen: Er hat gezeigt, wie mit der von ihm – gleichzeitig und unabhängig von Leibniz – neu eingeführten Differentialrechnung die Kraft als das Differential des Impulses und der Impuls als das Differential der Energie verstanden werden können. Statt das zu sehen und die Erkenntnisse von Newton und insbesondere dessen vorerst mathematisch-physikalisch bestimmten Begriff der Energie in seiner Wissenschaft der Logik aufzuheben, störte sich Hegel daran, dass bei Newton eine mathematische und physikalische Herangehensweise dem philosophischen Denken den Vorrang streitig zu machen schien. Statt wie Leibniz zu versuchen, die Ideen von Newton aufzugreifen und fortzuführen (wenn Leibniz über Newton hinausgehend die vis viva einführte und mit ihr das Prinzip des geringsten Energie-Aufwandes), und die Logik von Leibniz nochmals in einen größeren Horizont zu stellen, wollte Hegel dem Gedankengang von Newton eine rein begriffliche Ableitung gegenüberstellen. Er betrachtet rein formal (in seinem eigenen Verständnis: begrifflich) die Negation der Negation der verschwindenden Größe: In einem ersten Schritt wird die Qualität durch die Größe negiert, in einem zweiten Schritt wird mit der verschwindenden Größe im Differentialkalkül die Größe ihrerseits negiert und führt zum Maß. Wie ist das zu verstehen?

Erste Negation: Beim Dasein ist jedes Etwas qualitativ durch eine Grenze vom Anderen getrennt, mit dem es nichts gemeinsam hat. Mit dem Quantum wird diese Art von Unterscheidung negiert: Wird das Etwas als ein Quantum angesehen, dann befindet es sich gemeinsam mit dem Anderen in einem übergreifenden Medium, in dem sowohl am Etwas wie am Anderen nach den gleichen Regeln deren quantitative Größe gemessen und bestimmt werden kann. Innerhalb dieses Mediums gibt jenseits der Grenze nicht mehr einfach ein unbestimmtes Anderes, sondern jenseits der Grenze kann weitergezählt und weiter gemessen werden. Im Medium kann jede Grenze quantitativ überschritten werden: Ist z.B. ein Etwas 10 Meter groß, so gelten jenseits seiner räumlichen Ausdehnung und Begrenzung die gleichen Gesetze der Geometrie wie in seinem Innern. Das Etwas und das Andere befinden sich in einem gemeinsamen Raum und einer gemeinsamen Zeit. »Das Quantum ist aufgehobene qualitative Grenze, somit aufgehobene Negation.« (HW 5.277).

Negation der Negation: Doch liegt in diesem »unendliche[n] Progresse«, der jede Grenze überschreitet, die nachfolgende Größe immer im Jenseits (HW 5.277), jenseits des jeweils gegebenen Quantums. Mit dem Grenzübergang in das Unendlich-Kleine des Differentials wird dies Überschreiten in das weiter draußen liegende Jenseits seinerseits negiert: Das mit der Differentialrechnung neu gefundene Quantum (die Steigung P der Tangente) liegt nicht mehr im Jenseits, sondern im Diesseits. Daher spricht Hegel an dieser Stelle von der »Negation der Negation« und meint die Negation eines Hinausgehens in immer größere Größen (HW 5.278 und ähnlich nochmals HW 5.289) in eine Umkehr nach innen. Statt immer größere Werte zu finden, verschwinden die Steigungsdreiecke im Unendlich-Kleinen. Die Seitenlängen der Steigungsdreiecke werden im Grenzübergang fortlaufend kleiner, bis im Grenzübergang die Tangente gefunden ist, die nur noch aus einer Gerade und nicht mehr aus zwei Seitenlängen besteht. Im Ergebnis entsteht jedoch nicht die Null, sondern mit der Steigung der Tangente ein neuer endlicher Wert P. P ist die Proportionalität der Außenseiten der Steigungsdreiecke, die im Grenzübergang erhalten bleibt, wenn deren Längen verschwinden (HW 5.339 und 343f). Das ist für Hegel nur möglich, weil mit der Steigung eine neue Qualität gefunden wurde. Die Negation der Negation führt von der quantitativen Bewegung ins Jenseits zurück zu einer neuen Qualität im Diesseits, die ihrerseits mit P einen quantitativen Wert bekommt. Hegel spricht von der »Wiederherstellung« der Qualität (HW 5.279) und nennt die Qualität des Bogens gegenüber der Gerade (HW 5.318), die »Flächenqualität« gegenüber der Qualität der Linie (HW 5.360) und schließlich im Übergang zum Maß die Qualität des Potenzenverhältnisses (HW 5.382).

Im Ergebnis verweisen Qualität und Quantität wechselseitig aufeinander und bewegen sich in einem kunstvollen Zirkel der Selbstbezüglichkeit. Das Quantum »ist zu seinem Anderen, der Qualität, geworden, insofern jene Äußerlichkeit nun als vermittelst durch es selbst, so als ein Moment gesetzt ist, daß es eben in ihr auf sich selbst bezieht, Sein als Qualität ist.« (HW 5.383) Das ergibt einen »gedoppelte[n] Übergang«, erst den Übergang der Qualität in die Quantität und dann den »Rückgang« (HW 5.384).

Hegel versteht den Rückgang des Quantums zur Qualität jedoch nicht einfach als Rückkehr zu etwas bereits Bekanntem und im Denken Begriffenen, sondern zugleich als »Hinausgehen über sich selbst«, wodurch es eine »qualitative Totalität« wird, die sowohl eine Qualität ist, als auch »die Begriffsbestimmungen der Zahl, die Einheit und die Anzahl«, d.h. Bestimmungen der Quantität als Momente an sich enthält (HW 5.381). Erst wenn das Quantum zur Qualität geworden ist, – wie es am Beispiel der Steigung der Tangente gezeigt wurde, die sowohl eine genau bestimmbare Größe hat als auch eine neue Qualität –, »ist die Wahrheit des Quantums, Maß zu sein« erreicht. (HW 5.384)

Was ist die neue Qualität des »Hinausgehen über sich selbst«, die zum Maß führt? Hegel sieht nur die Umkehrung, die vom Hinausgehen in das Jenseits des Unendlich-Großen zum Grenzübergang der Steigungsdreiecke in das Unendlich-Kleine des Differentials und mit ihm zur Steigung P führt. Er sieht nicht den zweiten Grenzübergang, der in einer Negation der Negation des Unendlich-Kleinen der Differentiale den übergreifenden Zusammenhang beschreibt, der aus dem Übergang der Tangenten ineinander hervorgeht. Während die Differentiale lokal jeweils an einem Punkt x₀ der gegebenen Kurve bestimmt werden, ist mit dem Zusammenhang der Tangenten im Tangentialbündel eine Eigenschaft gefunden, die global für den Verlauf der Kurve im Ganzen gilt. Dies entspricht zugleich dem Begriff der energeia nach Aristoteles: Er meint mit energeia nicht den Impuls, der einer Bewegung während ihres Verlaufs in einem jeweils einzelnen Zeitmoment punktuell mitgeteilt wird und Punkt für Punkt gemessen werden kann, sondern die übergreifende Kraft (Energie), der es gelingt, eine Bewegung nicht nur zu beginnen, sondern bis zur Herstellung des Werks (ergon) aufrecht zu erhalten und niemals nachzulassen. Das ist für mich die inhaltliche Bestimmung des Hinausgehens der Quantität zum Maß. Hegel war dieser Einsicht bereits sehr nahe gekommen, als er die höhere Potenz (die Zweidimensionalität, die Fläche) der Gesamtheit aller Tangenten gesehen hatte, unter denen sich der Zusammenhang ergibt. Leibniz war sogar schon einen Schritt weiter gegangen: Er hatte die Frage nach der Gesamtheit aller Zusammenhänge gestellt, die zwischen den benachbarten Tangenten bestehen können, und mit dem Wirkungsprinzip die Antwort gefunden, dass unter ihnen diejenige mit dem geringsten Energieverbrauch wirklich wird.

Hegels Anmerkung: Philosophie »bedarf solche Hilfe nicht«

In einer Anmerkung lässt Hegel jedoch keinen Zweifel daran, dass er trotz allen Interesses an den neueren Entwicklungen in der Mathematik bei einer rein formalen (aus seiner Sicht: rein begrifflichen) Betrachtung stehen bleiben und keine Hilfe aus der Mathematik oder den Naturwissenschaften annehmen bzw. nur eingeschränkt würdigen will. Der Übergang zum Maß erfolgt für ihn nicht über die von Schelling angesprochenen Potenzen, nicht über die pythagoreische Potenz oder sonst ein mathematisches Symbol (HW 5.385f), und auch nicht über den Unterschied. »Die Philosophie bedarf solche Hilfe nicht.« (HW 5.386)

Der Begriff, die Differenz und die Rückkehr zu sich sollen nicht als erste, zweite und dritte Potenz gedacht werden (HW 5.385). Das ist wohl als Kritik an der Potenzenlehre von Schelling gemeint. Wenn ich ihn richtig verstehe, will Hegel sagen, dass diese Schritte nicht einfach aufgezählt werden können (erste, zweite, dritte Potenz), sondern eine begriffliche Bewegung zeigen, die weit über eine Aufzählung hinausgeht. So gesehen kann ihm sicher zugestimmt werden.

In einer missverständlichen Formulierung ergänzt er: »Es ist bei diesen Potenzen nicht an die potentia, dynamis des Aristoteles gedacht.« (HW 5.385) Das kann so verstanden werden, dass Hegel weder an die Potenzen im Sinne von Schelling denkt noch an die dynamis bei Aristoteles. Seine Formulierung kann aber auch genau entgegengesetzt so verstanden werden, dass er Schelling vorhält, nicht an die dynamis nach Aristoteles zu denken, während er sich anders als Schelling ausdrücklich auf die dynamis nach Aristoteles bezieht. Wird berücksichtigt, dass er sich nach einer intensiven Aristoteles-Lektüre in den Jahren der Entstehung der Phänomenologie des Geistes von Schelling getrennt hat, erscheint mir die zweite Deutung plausibler.

In diesem Sinn ist auch seine Kritik an Pythagoras zu verstehen. Für ihn befindet sich Pythagoras noch »in der Kindheit des Philosophierens« und konnte noch nicht anders, als »Zahlen [...] zur Bezeichnung allgemeiner, wesentlicher Unterschiede« heranzuziehen. »Erst [nach Pythagoras] sind die Gedankenbestimmungen selbst erfunden« worden, und er hält in einer boshaften Formulierung lediglich späteren Denkern wie Schelling vor, wenn mit ihnen »einem sich unvermögend fühlenden Denken« scheinbar kein Ausweg bleibt, als sich freiwillig auf die Stufe des frühesten Denkens zurück zu begeben.

Ähnlich missverständlich ist eine Passage über den Unterschied:

»Das Quantum enthält die Negativität, welche zur Natur des Begriffs gehört, noch gar nicht in dessen eigentümlicher Bestimmung gesetzt; Unterschiede, die dem Quantum zukommen, sind oberflächliche Bestimmungen für den Begriff selbst.« (HW 5.385)

Das kann so klingen, als wolle Hegel bei der Betrachtung des Differentialkalküls nicht von Unterschieden sprechen, obwohl diese eine entscheidende Bedeutung für dessen Verständnis haben. So sind die Unterschiede zwischen Sekanten und Tangenten, »zwischen Durchschnittssteigung und momentaner Steigung«, zwischen benachbarten Punkten x₁ und x₂ (Horst-Helmut Krause in einem unveröffentlichten Arbeitspapier Zur Abbildung des Absoluten Unterschiedes in der Mathematik), und zwischen benachbarten Tangenten zu erklären. Vermutlich meint Hegel diese Unterschiede jedoch gar nicht, wenn er von den »Unterschiede[n], die dem Quantum zukommen« spricht, sondern lediglich quantitative Unterschiede zwischen Zahlen, etwa den Unterschied zwischen den Zahlen 5 und 7 oder den Unterschied zwischen einem Volumen von 3 Kubikmetern und einem Volumen von 20 Kubikmetern. Wird der Abschnitt über die Quantität im Ganzen gesehen, besteht kein Zweifel, dass die im Differentialkalkül auftretenden Unterschiede einen anderen Charakter haben als der Unterschied zwischen einem daseienden Etwas und seinem Anderen oder als der Unterschied zwischen zwei endlichen Größen, und auf der Schwelle zu den Reflexionsbestimmungen stehen. Hegel trifft das sehr gut mit dem Ausdruck »Schweben eines Unterschieds« (HW 5.317).

Krümmung entsteht aus dem Verfilzen im Unendlich-Kleinen

Um zur Differentialgeometrie und ihren Maßen zu gelangen, ist die Krümmung entscheidend. Wie entsteht die Krümmung: Diese Frage kann sich an einzelnen Punkten auf Hegel beziehen, geht aber im Ganzen über seine Wissenschaft der Logik hinaus. Schrittweise ist zu zeigen, wie sich in der scheinbar völligen Unbestimmtheit und Ununterscheidbarkeit zwischen den unendlich kleinen Differentialen dx, dy dennoch keimhafte Strukturen herausbilden, die schließlich zum Maß führen. Es gibt zwei übergreifende Zusammenhänge, die voneinander unabhängig sind: (i) Das ist zum einen die übergreifende Bewegung des  Grenzübergangs  der verschwindenden Größen – »nicht ehe sie verschwinden und nicht nachher, sondern mit dem sie verschwinden (quacum evanescunt)« (HW 5.298 mit einem Zitat aus den Philosophiae Naturalis Principia Mathematica von Newton). Dieser Grenzübergang führt lokal zur Steigung der Tangenten. (ii) Und das ist zum anderen die übergreifende Bewegung, die durch den  Verlauf der Kurve  im Ganzen gegeben ist.

Was hier geschieht, lässt sich nicht mit endlichen Größen beschreiben, sondern im Bereich der unendlich kleinen Differentiale sind anschauliche Bilder zu finden. Die Mathematiker sprechen von unendlich kleinen ε-Kugeln, die Physiker von verschmierten Elektronen oder Elektronenwolken. Wird nach einem übergreifenden Begriff gesucht, kann davon gesprochen werden, wie die dimensionslosen Punkte im Unendlich-Kleinen zu einer Fläche verklumpen, verfilzen oder verschmelzen, deren Grenzen unbestimmbar sind. Sie gehen kontinuierlich ineinander über. Der lateinische Ausdruck Continuum geht zurück auf das griechische syneches und bedeutet verwachsen, zusammengewachsen. So hat es bereits Aristoteles gebraucht (siehe den Beitrag synecheia – der aristotelische Begriff des Continuums). In dieser Grauzone erweitert sich im Unendlich-Kleinen die gewöhnliche Multiplikation dimensionsloser Punkte zu einer Multiplikation verfilzter (zusammengewachsener) Punkte in einer Art von Proto-Linien, aus deren äußerer Multiplikation eine höhere Dimension hervorgehen kann, eine Art von Proto-Fläche. Diese Anschauung kann sich auf Platon berufen, der der Entstehung der dreidimensionalen, geometrischen Körper eine buchstäblich embryonale Phase vorschaltet: »Ehe das aber geschah, sei alles dies ohne Maß und Verhältnis (alogôs kai ametrôs) gewesen«, in einem Zustand von Proto-Elementen, »die aber bereits gewisse Spuren von sich selbst besaßen (ichnê men echonta hautô atta)«. »Diese von Natur also Beschaffenen formte zunächst Gott durch Gestaltungen und Zahlen (eidesi te kai arithmois).« (Platon Timaios, 53a-b) Platon geht es um die gleiche Frage wie Hegel: wie können aus einem Zustand »ohne Maß [...] Gestaltungen und Zahlen« entstehen. Das ist in moderner Sprachweise die Frage nach der Emergenz.

Mit Verklumpen und Verfilzen ist sowohl an den von Platon gebrauchten Ausdruck pilesis gedacht, (Platon Timaios 58b) in der Bedeutung ‘das Krämpen, Filzen, Zusammendrängen, Dichtmachen’ (nach Pape), oder auf englisch ‘compression, solidification, contraction, overloading’, wie auch an mathematische Untersuchungen von Zopfgruppen (Braid groups). Klumpen bezieht sich auf den griechischen Ausdruck ogkos, ‘Bug, Krümmung, Widerhaken, Masse, Gewicht’ (Pape), auf englisch ‘barb, bulk, size, mass, space filled by a body, volume, weight, particle, …’, und wird gelegenheitlich von den Neuplatonikern Plotin und Proklos gebraucht.

Hegel löst die Frage noch nicht, aber er gibt erste Anhaltspunkte, auch wenn er die entscheidende Bedeutung der Energie nicht sieht. Der Wendepunkt liegt in den beiden Schritten: (i) Erkenntnis der Ununterscheidbarkeit der Differentiale in einer dennoch wohldefinierten Bewegung (Hegel nennt das »Schweben eines Unterschieds«; HW 5.317) und (ii) Hervortreten einer inneren Struktur aus der Ununterscheidbarkeit, die sich als das Produkt von mindestens zwei senkrecht aufeinander stehenden Linien verstehen lässt.

(i) »Schweben eines Unterschieds«: Hegel bemerkt, wie sich in der Bewegung des Grenzübergangs das Verhältnis von Ordinate und Subtangente »unendlich, d.i. so nähern könne, daß der Unterschied kleiner als jeder gegebene werden könne« (HW 5.314). Siehe hierzu oben Figur 4. In diesem Übergang fällt aber nicht alles in 0 / 0 zusammen, sondern es entsteht im Bereich des Unendlich-Kleinen der Differentiale eine Linie, nämlich die Tangente mit einer festen Steigung P. Zugleich entsteht senkrecht zur Tangente die Cotangente, die die Krümmung der Kurve an dieser Stelle anzeigt. Mit Tangente und Cotangente wird lokal eine Fläche aufgespannt, und es kann gefragt werden, ob und wie sich diese Fläche ändert, wenn entlang der Kurve von einem Punkt zum benachbarten Punkt und damit von einer Tangente und Cotangente zur benachbarten Tangente und Cotangente fortgeschritten wird.

Diesen Übergang von dem kontinuierlich kleiner werdenden Unterschied zum Entstehen der Tangente und Cotangente bezeichnet Hegel als »das Schweben eines Unterschieds« (HW 5.317). Mit dem Schweben ist anschaulich gesagt, dass der Unterschied von einem Raum umgeben ist, innerhalb dessen er schweben kann.

(ii) Hervortreten einer inneren Struktur. Mit dem Schweben ist mindestens eine neue Dimension gegeben, innerhalb derer das Schweben den Freiheitsgrad seiner Bewegung findet. Die Tangente und die Cotangente sind zwei voneinander unabhängige Koordinaten, die lokal an jedem Punkt der Kurve eine Fläche erzeugen. Sie haben im Unendlich-Kleinen eine eigene Geometrie, die später von der Mathematik als Differentialgeometrie untersucht wurde. An Flächen oder höherdimensionalen Räumen dieser Art können die Erhaltungsgrößen der Bewegung dargestellt werden. Das ist in der klassischen Mechanik die Energie, in der Teilchenphysik sind es die Symmetriegruppen wie z.B. SU(2) für die starke Wechselwirkung oder SU(3) für das Quark-Modell und die Quantenchromodynamik.

Die neuzeitliche Physik der Differentialgeometrie wurde mit Keplers Untersuchung der Planetenbahnen begründet. Sie verlaufen auf Ellipsen. Anders als beim Kreis ändert sich bei der Ellipse die Krümmung von Punkt zu Punkt, doch erfolgt die Änderung gleichmäßig. Am Verlauf dieser Gleichmäßigkeit der Krümmung konnten erstmals die Erhaltungsgrößen der Mechanik abgelesen werden. Mathematisch gelang das bereits Newton, doch erst Leibniz erkannte hierin das Prinzip der Naturwissenschaft und sprach von der vis viva, dem Vorläufer des heutigen Energie-Begriffs. Mathematisch hat es Émilie du Châtelet (1706-1746) ausgearbeitet, die langjährige Freundin von Voltaire (den Hinweis gab mir Renate Quehenberger). Hegel hat diese Zusammenhänge nicht gesehen, aber er hat erkannt, wie seit Kepler innerhalb von Größen, die nach außen als Indifferenz erscheinen, innere Beziehungen nachgewiesen werden können, die sich der sinnlichen Wahrnehmung entziehen und nur von der Reflexion erfasst werden können. Er sprach von der Indifferenz als umgekehrtes Verhältnis ihrer Faktoren (HW 5.446) und beruft sich ausdrücklich auf Kepler. Diese inneren Faktoren der Indifferenz bestehen wie die Differentiale dx und dy, aus denen sie hervorgegangen sind, nur als Verhältnis ihrer Momente und bestimmen im jeweiligen Kontext die Erhaltungsgrößen einer Bewegung. Mit ihnen gelingt Hegel der Übergang vom Maß zur Reflexion und deren Reflexionsbestimmungen. Erst als Reflexionsbestimmungen lassen sich die Begriffe von Identität und Unterschied klären, die im Differentialkalkül noch ineinander verschwimmen. In der Reflexionslogik kann ihr In-einander-Scheinen erklärt werden.

An dieser Stelle schließen sich weiterführende Fragen an, die über den Rahmen der Wissenschaft der Logik hinausgehen: Entsteht im Unendlich-Kleinen der Differentiale ein zweidimensionaler Raum, oder handelt es sich um mehr Dimensionen? Das könnte die vierdimensionale Raumzeit oder ergänzt mit einem inneren Freiheitsgrad ihrer Krümmung ein fünfdimensionaler Raum sein. Ideen dieser Art gehen bis zu Pythagoras und Platon zurück und haben mit den im 20. Jahrhundert eingeführten fünfdimensionalen Mustern ein neues Forschungsgebiet eröffnet (siehe Renate Quehenberger Zur Hermeneutik der Penrose-Muster). In diesem Kontext könnte es vielleicht gelingen, Emergenz nicht nur als ein Phänomen zu beschreiben, das sich in der Natur beobachten lässt, sondern ihre inneren Bewegungsgesetze zu verstehen.

Ausblick

Für den Begriff der Energie ist der Nachweis entscheidend, dass die mathematischen Verhältnisse zwischen den Tangenten nicht einfach die gleichen Verhältnisse sind wie die mathematischen Verhältnisse zwischen den Zahlen, sondern etwas Neues enthalten. Das erwartete Hegel in seiner Maß-Logik von einer »Mathematik der Natur« (HW 5.406) und berief sich ausdrücklich auf Newton (HW 5.407), konnte es aber noch nicht an der Mathematik ausführen. Die Differentialgeometrie ist weitgehend erst im 20. Jahrhundert entstanden. Stattdessen hat er es an der Chemie gezeigt: Wenn er dort nachweist, wie sich die Knotenlinien der Systemzustände von den Wahlverwandtschaften der miteinander reagierenden chemischen Stoffe innerhalb eines Systemzustandes unterscheiden, stehen die Knotenlinien und Wahlverwandtschaften in einem ähnlichen Verhältnis zueinander wie die Krümmung der Kurve, die den Zusammenhang einer Kurve beschreibt, und die Steigung der Tangenten, die jeweils lokal an eine Kurve angelegt sind.

Es wird zu unterscheiden sein zwischen Größen innerhalb einer Dimension und Größen am Kreuzungspunkt verschiedener Dimensionen, oder zwischen der Bewegung eines einzelnen Punktes und der Beweglichkeit eines Systems, dem der Punkt angehört. Peter Ruben kommt darauf an entscheidender Stelle zurück, wenn er in seiner Prädikationstheorie die Analyse von Sätzen bis zu dem Verzweigungspunkt verfolgt, an der sie sich als Größen verstehen lassen. Allerdings hat er die ausgeführte Unterscheidung unterschiedlicher Mächtigkeiten nicht gesehen und konnte daher seinen wegweisenden Ansatz nicht zuende führen.

• Werden die Knotenlinien und Wahlverwandtschaften der Chemie näher untersucht, so geht es dort nicht nur um die äußere Multiplikation, mit der der Übergang in höhere Dimensionen gelingt, sondern auch um den Übergang von der Linearität der reellen Zahlen zur Zyklizität und Analytizität der komplexen Zahlen, Das reale Maß – die Logik der chemischen Sphäre.

• Gegensätze führen zu einer Achse (HW 6.61f), auf der sie einander gegenüber stehen. In deren Mitte steht senkrecht zu ihr die Symmetrie-Achse. Das Entstehen der Symmetrie-Achse senkrecht auf der Symmetrie-Ebene ist eine Fortführung des Übergangs von der Linie in die Ebene. Das ist näher ausgearbeitet im Beitrag Hegels Idee eines »höheren Widerspruchs«.

• Der Mechanismus betrachtet, wie Mitteilungen durch einen Impuls weitergegeben werden. Hier kann sich – Hegel fortführend – der Gedanke eines inneren Impulsraums mit seiner Vielfalt an Freiheitsgraden anschließen, von denen es möglicherweise unendlich viele gibt, auch wenn sich die Mechanik auf jeweils endlich viele beschränkt, nach heutigem Wissensstand auf sechs frei wählbare Bewegungsmöglichkeiten. Der Impulsraum ist ebenso an jedem Punkt angeheftet, wie die Tangenten des Tangentialbündels an der Kurve. Die Grundbegriffe sind ausgeführt in Kraft, Impuls, Energie.

• Die verborgene Kraft des Mediums erweist sich entsprechend der Allgemeinen Relativitätstheorie von Einstein als dessen Krümmung. Einstein versteht die Krümmung als einen Tensor, der wie ein Gradient oder eine Tangente an jedem Punkt des Raums ergänzt ist. Das führt zu weitreichenden Fragen über Die Sphäre des Begriffs und die Logik der Sphäre, wobei es um den philosophischen Begriff von Krümmung und Flüssigkeit geht.

• Die Prädikationstheorie von Ruben führt zur Proportionsgleichung: a : b und c : d sind proportional, wenn a · d = b · c gilt, d.h. wenn a · d und c · d die gleiche Fläche beschreiben. Das bedeutet aber, dass es ein Quadrat mit der Seitenlänge e gibt, e · e, dem beide gleich sind.

• Die Urteilslehre führt nach Peter Ruben und Bruno Hartmann in einen mehrdimensionalen Raum, dessen Achsen das Einzelne, das Besondere und das Allgemeine sind. Sie vergleichen ihn mit anderen mehrdimensionalen Räumen in der Physik und der Ökonomie. In allen Fällen liegen äußere Multiplikationen von eindimensionalen Achsen zugrunde. Ich vermute, dass das etwas Richtiges trifft, aber anders ausgearbeitet werden muß. Das ist die Frage nach der Architektur von formalen Kalkülen. Siehe zu Peter Rubens Prädikationstheorie die Ausführungen in Dialektische Theorie des Satzes.

• Die Differentiallogik soll nach dem Vorbild der Differentialgeometrie entworfen werden, die Grenzübergänge von Tangentialräumen betrachtet. Die Stetigkeit dieser Grenzübergänge ist meiner Meinung nach die höhere Qualität, aus der in Anlehnung an Hegel der Differentialkalkül hergeleitet werden kann, womit sich der Kreis wieder schließt.

• Hegel kommt in der Anmerkung 2 zur »Anwendung des Differentialkalkül« auf die physikalischen Gesetze von Schwerkraft und Trägheit zu sprechen. Siehe dazu Kraft der Trägheit.

Anhang 1: Vorläufer von Hegel (nach Wolff und Stekeler-Weithofer)

Hegel hat in zahlreichen, einander ähnlichen Formulierungen versucht, seine Herleitung des Differentialkalküls aus einer eigenen Qualität zu motivieren, aber sie bleiben ein wenig unbestimmt. Das dürfte auch mit den beschränkten mathematischen Mitteln zu tun haben, die zu seiner Zeit bekannt waren. Wolff und Stekeler-Weithofer suchen daher in der Philosophiegeschichte nach Vorläufern, an denen sich Hegel orientiert haben könnte, um seinen Ansatz in einen größeren Rahmen zu stellen und besser nachvollziehbar zu machen.

Ähnlichkeit

Wolff vermutet, dass Hegel mit seinem Begriff des Potenzenverhältnis auf Leibniz' Begriff der Ähnlichkeit zurückgeht. Er stellt einige Zitate von Leibniz zusammen, die das belegen sollen.

»Leibniz nennt 'ähnlich' allgemein das, 'was dieselbe Qualität hat', während 'gleich' ist, 'was dieselbe Quantität hat.' (Leibniz, Metaphysische Anfangsgründe der Mathematik, S. 55) ... 'Zur Erfassung der Quantität nämlich müssen die Gegenstände, die man vergleicht, unmittelbar nebeneinander gegeben sein oder doch durch irgendeine Art der Vermittlung tatsächlich einander gegenübergestellt werden können.' (Leibniz, Zur Analyse der Lage, S. 72) 'Die Qualität aber ist diejenige Bestimmtheit der Dinge, die sich an ihnen erkennen läßt, wenn man sie einzeln und für sich genommen betrachtet, auch ohne daß sie also in unmittelbarem Beisammensein gegeben zu sein brauchen.' (Leibniz, Metaphysische Anfangsgründe der Mathematik, S. 55) 'Die Qualität [...] stellt dem Geiste etwas dar, was sich in einem Gegenstand, auch wenn man ihn allein betrachtet, für sich erkennen und weiterhin zum Vergleich zweier Gegenstände unter sich brauchen läßt, ohne daß es nötig ist, die Vergleichsobjekte unmittelbar oder mittelbar, durch Beziehung auf ein drittes Objekt als Maßstab, aneinander heranzubringen. (Leibniz, Zur Analyse der Lage, S. 72)« (zitiert bei Wolff Hegel und Cauchy, S. 247)

Das ist unmittelbar anschaulich klar. Auch die Beziehung zum Potenzenverhältnis läßt sich einfach herstellen: Wenn in der Ebene Quadrate betrachtet werden, sind alle Quadrate einander völlig ähnlich unabhängig von ihrer jeweiligen absoluten Seitenlänge. Werden alle Quadrate der Größe nach geordnet, ergibt sich unmittelbar das Potenzenverhältnis x = y · y, wobei mit y die Seitenlänge der Quadrate gemeint ist. Es ist gut denkbar, dass Hegel auf diese Weise vom Begriff der Ähnlichkeit bei Leibniz auf seinen Begriff des Potenzenverhältnisses gekommen ist, den er ebenfalls als die Qualität interpretiert, aus dem der Differentialkalkül hergeleitet werden kann.

Wolff belegt durch ein weiteres Zitat, wie Leibniz ausgehend von der Ähnlichkeit das »wahre Unendliche« bestimmt hat, das Hegels »wahrhaftem Unendlichen« sehr nahe kommt.

»Das 'wahre Unendliche' läßt sich durch beliebig fortgesetzte Zusammensetzung oder Teilung eines Quantums nicht erfassen, wohl aber dadurch, daß man die Qualität oder Ähnlichkeit der Teile eines Ganzen in Betracht zieht, deren quantitatives Verhältnis eine stetige Proportion ergibt« (Wolff Hegel und Cauchy, S. 249 mit Zitat aus Leibniz Nouveaux Essays II 17, § 3).

Mit der »stetigen Proportion« hat Leibniz bereits die Idee gehabt, die Hegel aufgenommen und erweitert hat. Das »wahrhafte Unendliche« ist nicht die Vorstellung des irgendwie gearteten "größten", "unfassbar großen" oder sonstwie umschriebenen Großen, sondern die Einsicht in eine Regel, von der verstanden wird, dass sie unendlich fortgeführt werden kann. Historisch geht das im Grunde auf den Unendlichkeitsbegriff bei Aristoteles zurück.

Dynamis

Es kann auch sein, dass Hegel beim Begriff Potenzenverhältnis an das griechische dynamis dachte, siehe das oben angeführte Zitat über die Potenzen und die dynamis bei Aristoteles (HW 5.385). Dazu Stekeler-Weithofer:

»Die Operation der Bestimmung der Flächengröße a² eines Quadrats durch geometrische, insofern qualitative, Verwandlung in ein flächengleiches Rechteck mit vorgegebener Seite e heißt bei den Griechen 'dynamis', 'Potenz'. Sie ist die Basis für die quantitative Inhaltsangabe a · b/2 für des rechtwinkligen Dreiecks auf Grund der Länge a, b, und damit der gesamten Definition der Flächengröße überhaupt. Diese Multiplikation ist nicht nur für ganze oder rationale Zahlen arithmetisch definiert, sondern für alle elementargeometrisch konstruierbare ('euklidische') Längen. Durch die nur scheinbar triviale 'Identifikation' einer Einheitslänge e mit einer Einheitsfläche e · e hatte dann Descartes als erster Flächengrößen und damit zugleich auch Proportionen mit Längen identifiziert: Das war der zentrale Fortschritt gegenüber der antiken Mathematik. ... Die Operation des Quadrierens einer Längeneinheit ist somit in der Tat Basis der 'Arithmetisierung' bzw. 'Quantifizierung' der quantitativen Beziehungen von Größen (Längen, Flächen, Volumina) in einer geometrischen Form« (Stekeler-Weithofer, S. 243).

Anhang 2: Renate Wahsners Kritik an Hegels Lehre des Differentialkalküls

Renate Wahsner ist mit Michael Wolff einer Meinung, dass Hegel »von allen herkömmlichen und von allen bis heute üblichen Auffassungen« des Differentialkalküls abweicht (Wolff, Hegel und Cauchy, S. 252 Anm. 4, zitiert bei Wahsner, S. 290), doch hält sie Hegel diese Abweichung vor.

»Sie weicht ab, weil sie nur einzelne Aspekte des Differentialkalküls erfaßt und die fehlenden durch eigene Gedanken ausfüllt, die aber die mathematische-physikalische Verwendung des Kalküls nicht ermöglichen würden. Wenn es so wäre, daß der Differentialkalkül Operationen gestattet, durch die man von einer Gleichung zu etwas gelangt, was keine Gleichung mehr ist, dann widerspräche dies in der Tat - wie Hegel kritisiert - allen mathematischen Grundsätzen« (Wahsner, S. 290).

Gegenüber Hegel hält sie daran fest, dass die Ableitung von einer Funktion f(x) zu einer neuen Funktion f '(x) führt, der abgeleiteten Funktion. Sie stellt fest, dass Hegel davon abweicht, wenn er als Ergebnis der Ableitung nicht eine Funktion, sondern eine Gesamtheit von Tangenten findet, das »'mysteriöse' p« (Wahsner, S. 290 mit Verweis auf HW 5.313-316). (Hegel schreibt die Abkürzung P für Proportionalität als Großbuchstabe. Wahsner denkt an die Mathematik: Da sich die Steigungen von Punkt zu Punkt ändern können, würde ein Mathematiker einen Kleinbuchstaben p wählen und die Steigung als Variable ansehen. Variablen werden mit Kleinbuchstaben symbolisiert.)

Ohne es zu merken kommt sie jedoch im Weiteren inhaltlich auf den Ansatz von Hegel zurück und rechtfertigt ihn indirekt. Sie will erklären, warum es in der Bewegung nicht den Widerspruch gibt, dass etwas zugleich noch an einem Ort x und schon nicht mehr am Ort x ist. Sie bezieht sich auf Hegels Aussage, »daß die Bewegung der daseiende Widerspruch selbst ist« (HW 6.76), wobei Hegel wiederum ohne Aristoteles zu nennen auf die »alten Dialektiker« Bezug nimmt. Diesen Widerspruch will sie dadurch auflösen, dass die heutige Physik nicht nur den Ort, sondern auch die Geschwindigkeit v an diesem Ort betrachtet, und mit der Geschwindigkeit einen Bezug auf die Umgebung enthält. Was sie in physikalischer Anschauung als Geschwindigkeit v bezeichnet, sind genau die von Hegel gemeinten »mysteriösen« Verhältnisse P. Die Geschwindigkeiten liegen in dem Tangentialbündel, das Hegel durch die Ableitung erreicht.

»Dieses Mißverständnis entsteht dadurch, daß man glaubt, die Physik gebe den Bewegungszustand eines Körpers zum Zeitpunkt t nur durch seine Ortskoordinate x an. Das trifft aber nicht zu, denn die Physik beschreibt den Bewegungszustand eines Körpers zum Zeitpunkt t durch die Angabe zweier Größen, der Ortskoordinate x und der Geschwindigkeit v. Die Formulierung '... ist und ist nicht ...' bezieht sich also auf zwei verschiedene Größen, wobei die Geschwindigkeit (zum Zeitpunkt t am Orte x) tatsächlich einen Bezug auf Orte ungleich x impliziert. (Dies drückt Newton mit den Worten aus: '... die letzte Geschwindigkeit, mit welcher ...'). Daß es hierbei nicht zu einem logischen Widerspruch kommt, liegt daran, daß es sich um zwei verschiedene, algebraisch voneinander unabhängige Größen handelt, die man ein und demselben Körper zu ein und demselben Zeitpunkt t zuordnen kann. Für die geradlinig gleichförmige Bewegung ist die Größe Geschwindigkeit bekanntlich dadurch definiert, daß man eine Ortsdifferenz zu einer Zeitdifferenz in Verhältnis setzt (x' − x) / (t' − t), sich also auf zwei verschiedene Orte bezieht«. Im Grenzübergang gehen »die Zeit t' gegen die Zeit t und somit auch die entsprechenden Orte x' und x gegeneinander« (Wahsner, S. 297).

Besser lässt es sich nicht sagen. Wahsner hat auf den Punkt gebracht, wie der »daseiende Widerspruch« aufgelöst werden kann, in dem sich nach Hegel die Bewegung befindet. Nach meiner Überzeugung ist es aber nur konsequent, diesen Ansatz weiter zurück zu verfolgen bis zur Begründung des Differentialkalküls, und von dort aus die Grundsatzfragen der heutigen Mathematik und Physik neu und anders zu entwickeln. – Es versteht sich, dass mit der Auflösbarkeit des »daseienden Widerspruchs« der Bewegung zugleich der von Hegel entwickelte Begriff des Widerspruchs neu zu hinterfragen ist und damit das Zentrum seiner Philosophie.

Literatur

Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971 (zitiert als HW); Link

Gottfried Wilhelm Leibniz: Hauptschriften zur Grundlegung der Philosophie. Zusammengestellt von Ernst Cassirer. Hamburg 1996, 2 Bände

Pirmin Stekeler-Weithofer: Hegels Philosophie der Mathematik
in: Christoph Demmerling und Friedrich Kambartel (Hg.): Vernunftkritik nach Hegel, Frankfurt am Main 1992, 139-197

Renate Wahsner: »Der Gedanke kann nicht richtiger bestimmt werden, als Newton ihn gegeben hat.« Das mathematisch Unendliche und der Newtonsche Bewegungsbegriff im Lichte des begriffslogischen Zusammenhangs von Quantität und Qualität
in: Andreas Arndt, Christian Iber (Hg.): Hegels Seinslogik, Berlin 2000

Michael Wolff: Hegel und Cauchy
in: R.P. Horstmann & J.M. Petry (Hg.): Hegel und die Naturwissenschaften, Stuttgart 1986, S. 197 - 263

2012-2013, 2020