Walter Tydecks
Wie aus den Zahlen Pfeile wurden– Die graphische Wende zu einer dynamischen Mathematik |
|
Inhaltsverzeichnis
Einleitung
Vektoren (gerichtete Größen)
Prozessorientierte Karten
Kommutierende (vertauschende) Diagramme
Zirkuläre Zeit der Teilchenphysik
Abstract Seit den 1970ern gibt es in der Mathematik einen neuen Stil. Statt mit Zahlen zu rechnen, werden mit Pfeilen Rechen- und Lösungswege erklärt. Mathematische Formeln und Beweise sind nicht mehr wie gewöhnliche Texte in einer unübersichtlichen, durchgehenden Schrift geschrieben, vollgepackt mit Symbolen wie ∑, ∮, Γ und zahlreichen Indizes oben und unten, sondern in anschaulichen Diagrammen werden die Verbindungen zwischen Klassen, Mengen, Funktionen, abgeleiteten Funktionen, Strukturen und Modellen deutlich. Häufig werden Bewegungen auf zwei oder gar mehr Ebenen parallel betrachtet, die Rückkopplungs-Schleifen in die Vergangenheit und Zukunft ermöglichen (Resonanz). Die Mathematik beginnt nach ihrem eigenen Rhythmus zu schwingen.
Inzwischen hat sich dieser Stil auch in anderen Gebieten durchgesetzt, angefangen mit den Modellen der Informatik und des Ingenieurwesens bis zur Einführung der Präsentationssoftware Powerpoint. Das ist heute in allen Meetings, Vorträgen und Lehrbüchern so selbstverständlich geworden, dass es schwerfällt, die Anfänge und Beweggründe dieser Wende nachzuvollziehen, die nur wenige Jahrzehnte zurückliegen. In diesem Beitrag wird gezeigt, wie sie zu den Innovationsschüben der 1930er und 1960er zu rechnen sind, zu der auch die Wende der Psychologie von der Individualpsychologie zum systemischen Denken und der Physik von der Untersuchung isolierter Partikel und Objekte zu ganzheitlichen Theorien der Selbstorganisation (Autopoiesis) und Emergenz zählen.
Das wichtigste Ikon (Zeichen) der graphischen Wende ist der Pfeil ‘→’, wobei Ikon (von griechisch eikon) in der vielfachen Bedeutung von ‘Bild, Ähnlichkeit, Darstellung, Anschein, Muster, Archetyp’ gemeint ist. (Siehe zur Herkunft und zum Gebrauch des Wortes ‘Pfeil’ im Alltag und in der Literatur bis 1800 die umfassende Darstellung in Grimms Wörterbuch.) In der Physik und Mathematik hat sich der Pfeil mit der Vektorrechnung durchgesetzt, wenn der Ortsvektor  die Bewegung von A nach B und der Geschwindigkeitsvektor
die Bewegung von A nach B und der Geschwindigkeitsvektor  eine Geschwindigkeit v anzeigt, die in eine bestimmte Richtung weist. So gibt es für die graphische Wende zu einer dynamischen Mathematik drei Quellen: Der Pfeil als Ikon in Anwendungsgebieten wie Kartographie und Weg- und Verkehrszeichen, die Vektoren in der Physik, und als wichtigster Vorläufer die Verwendung von Pfeilen in den Reaktionsgleichungen der Chemie und den Feldern der Elektrodynamik. Im Ergebnis ist der Pfeil in der mathematischen Kategorientheorie zu der grundlegenden Entität geworden, das an die Stelle klassischer, starrer Objekte wie die Punkte, Zahlen oder die sortalen Elemente einer Menge tritt. Philosophisch kann von einer Umkehrung des Verhältnisses von Substanz und ihren Veränderungen gesprochen werden: Der Ausgangspunkt ist nicht mehr die Substanz mit ihren Akzidentien, zu denen ihre Veränderbarkeit und Relationalität gehören, sondern umgekehrt wird an den – mathematisch mit Pfeilen dargestellten – Prozessen auf deren Träger geschlossen, der sich möglicherweise als solcher niemals direkt nachweisen lässt, sondern in der Ausdrucksweise von Deleuze als dunkler Vorbote (précurseur sombre, dark precursor) erst in seinem Verschwinden an seinen Folgen indirekt erkennbar wird (Deleuze, 157). Der Träger muss nicht mehr ein fester Elementarbaustein sein (wie die Atome, Teilchen, Partikel), der für sich als ruhig angenommen und von außen in Bewegung versetzt wird, sondern das bewegte System ist selbst der Träger, und die Atome sind in einer ersten anschaulich gedachten Annäherung dessen Verdichtungen und Knotenlinien.
eine Geschwindigkeit v anzeigt, die in eine bestimmte Richtung weist. So gibt es für die graphische Wende zu einer dynamischen Mathematik drei Quellen: Der Pfeil als Ikon in Anwendungsgebieten wie Kartographie und Weg- und Verkehrszeichen, die Vektoren in der Physik, und als wichtigster Vorläufer die Verwendung von Pfeilen in den Reaktionsgleichungen der Chemie und den Feldern der Elektrodynamik. Im Ergebnis ist der Pfeil in der mathematischen Kategorientheorie zu der grundlegenden Entität geworden, das an die Stelle klassischer, starrer Objekte wie die Punkte, Zahlen oder die sortalen Elemente einer Menge tritt. Philosophisch kann von einer Umkehrung des Verhältnisses von Substanz und ihren Veränderungen gesprochen werden: Der Ausgangspunkt ist nicht mehr die Substanz mit ihren Akzidentien, zu denen ihre Veränderbarkeit und Relationalität gehören, sondern umgekehrt wird an den – mathematisch mit Pfeilen dargestellten – Prozessen auf deren Träger geschlossen, der sich möglicherweise als solcher niemals direkt nachweisen lässt, sondern in der Ausdrucksweise von Deleuze als dunkler Vorbote (précurseur sombre, dark precursor) erst in seinem Verschwinden an seinen Folgen indirekt erkennbar wird (Deleuze, 157). Der Träger muss nicht mehr ein fester Elementarbaustein sein (wie die Atome, Teilchen, Partikel), der für sich als ruhig angenommen und von außen in Bewegung versetzt wird, sondern das bewegte System ist selbst der Träger, und die Atome sind in einer ersten anschaulich gedachten Annäherung dessen Verdichtungen und Knotenlinien.
Die englische Sprache bietet die griffige Formel an: From point to pointers (Bühlmann, 37).
Pfeile Pfeil und Bogen sind so alt wie die Menschheit und sind in den Jagdszenen der ältesten Felszeichnungen dargestellt (Geschichte des Bogenschießen). In diesem Beitrag geht es um den daraus hergeleiteten Pfeil als Symbol. Eine gute, erste Übersicht des Pfeil-Symbols gibt das englisch-sprachige Wikipedia. Ein Vorläufer ist die pfeil-ähnliche Lilie (Fleur-de-Lys) aus der Heraldik, wie sie auf Wappen und Siegeln zu sehen ist, die bis in die Zeit um das Jahr 1000 zurückgehen. Der portugiesische Kartograph Pedro Reinel (1464-1542) zeichnete 1504 eine Windrose mit Verwendung der fleur-de-lys in 16 Richtungen. Im Weiteren kamen Pfeile zunächst nur vereinzelt in Karten vor, um die Fließrichtung von Flüssen anzudeuten (siehe Beispiele bei Finkel). Es folgte die Nutzung von Pfeilen für chemische Reaktionsgleichungen, Darstellung von Feldern des Magnetismus und der Elektrizität und überraschend erst 1922 durch David Hilbert für die logische Implikation (Miller Stichwort: "Implication") und seit den 1930ern für mathematische Operationen (Miller Stichwort: "Arrow notation"). Diese Neuentwicklung hat bis in die Kunst durchgeschlagen, als Paul Klee (1879-1940) Pfeile in seine Werke aufnahm, Zeichen einer technisch zivilisierten Welt (siehe eine Übersicht über GoogleBilder).
Chemische Affinität und Reaktionen Chemische Reaktionsgleichungen zeigen, welche Stoffe und Elemente sich zueinander hingezogen fühlen und miteinander reagieren. Einen guten historischen Überblick gibt die Website eoht.info, ein Projekt des Elektrochemie-Ingenieurs Libb Thims. Grundlegend sind die aus dem Lateinischen stammenden Begriffe der Affinitas in der Bedeutung von ‘Nachbarschaft, Verwandtschaft, Beziehung, Verbindung, Zusammenhang’, in englischer Übersetzung ‘relationship, bond/union, neighborhood’, mit Nachweisen bei Cicero, Livius, Plautus, Sueton, Terenz und anderen; und in verwandter Bedeutung Attraktion von attraho, at-traho, ‘heranziehen, anziehen, spannen, für sich gewinnen’ mit Nachweisen bei Cicero, Ovid und vielen anderen. Daraus wurde im Deutschen die ‘Wahlverwandtschaft’, zur Wortherkunft der entsprechende Eintrag in Grimms Wörterbuch. Der Begriff affinitas im Sinne chemischer Affinität geht bis zu Albertus Magnus De mineralibus 1250 zurück. Dort heißt es am Ende von Buch 4 Kapitel 5 in englischer Übersetzung: »But sulphur burns silver when it is sprinkled upon it in a molten condition; and the blackening of the silver shows that it is burnt by the sulphur, as we have said above. For sulphur, because of its affinity (propter affinitatem) for the nature of metal, burns it.» (archive.org). Der aus der Paracelsus-Schule stammende französische Chemiker Jean Beguin (1550-1620) hat 1610 im Tyrocinium Chymicum erstmals Diagramme von chemischen Reaktionen gezeichnet. Von dort war es nur noch ein kleiner Schritt zur Einführung von Pfeilen zur Darstellung chemischer Reaktionen, wie sie 1757 bei William Cullen (1710-1790) und seinem Schüler Joseph Black (1728-1799) zu sehen sind. In der uns heute gewohnten Weise wurden chemische Reaktionsgleichungen erstmals 1884 von Jacobus Henricus van't Hoff (1852-1911) in seinem Werk Studien zur chemischen Dynamik eingeführt.
Attraktion Auch wenn von der Alchemie bis zu Kant und der modernen Chemie der Begriff affinitas, Affinität dominiert, lohnt ein Blick auf den verwandten Begriff der Attraktion. Er wird zwar eher für mechanische Kräfte gebraucht, wenn von Attraktion und Repulsion (Anziehung und Abstoßung) gesprochen wird und seit den 1970ern als Attraktor in der Chaosforschung und Theorie dynamischer Systeme, aber er verweist über den griechischen Ursprung atraktos in der Bedeutung ‘Spindel, Pfeil, von ähnlicher Gestalt, oberster Teil der Segelstange’ auf das englische to draw, ursprünglich ‘tragen’ von ‘dragan’, heute vorrangig in der Bedeutung von ‘ziehen’, sowohl ‘eine Linie ziehen’ (‘eine Grenze ziehen’, ‘ein Unterscheidung treffen’) wie auch etwas ‘anziehen, zu sich hinziehen’, ‘anlocken’. Die Spindel gibt das Bild einer drehenden Bewegung, die einen Faden an sich heranzieht und aufrollt, und weiter gedacht der zirkulierenden Bewegung eines Strudels, der wie in einem Schwarzen Loch alles an sich heranzieht und einsaugt. In der griechischen Mythologie ist Klotho die Spinnerin, die für den Lebensfaden zuständig ist.
Affinität steht für eine Bereitschaft, eine Neigung, die aus sich heraus den Keim enthält, aus dem sich etwas entwickeln kann, während mit der Attraktion die Kraft gemeint ist, die bereits aktiv wirkt.
Das Digitale Wörterbuch der Deutschen Sprache DWDS gibt Statistiken über die Häufigkeit der Verwendung von Worten im deutschen Sprachgebrauch. Während der Gebrauch des Wortes Pfeil von 1650 bis heute auf ein Zehntel zurückgegangen ist, hat sich im gleichen Zeitraum der Gebrauch des Wortes Zahl mehr als verdreifacht. Das zeigt auf einer bewusst äußerst oberflächlich betrachteten statistischen Ebene eine Änderung des Denkstils hin zu quantitativen Betrachtungen. Diese Entwicklung könnte sich jetzt wieder umkehren und ist vermutlich zugleich an Indiz, dass Pfeile früher im Alltag bei Jagden oder als Kinderspiel eine weit größere Rolle gespielt haben als heute und entsprechend häufig genannt wurden.
Vektoren (gerichtete Größen)
– von der Mythologie über die Himmelsmechanik zur Elektrodynamik und Mathematik
Einen sehr guten Überblick über die Geschichte des Vektors als Begriff und Zeichen in der Mathematik gibt das französisch-sprachige Wikipedia (hier die von Google automatisierte Übersetzung).
Das lateinische Wort vector bedeutet sowohl aktiv ‘Träger, Fahrer’ als auch passiv ‘der Getragene’ und zugleich den Prozess des Fahrens. Es kommt von veho, ‘bewegen, führen, tragen, fahren, bringen’ oder auch substantiviert ‘Wagen’ mit einer Wurzel im Sanskrit vahami (siehe aus der gleichen Wurzel das Wort ‘Vehikel’), und ist inhaltlich verwandt mit atractos und to draw. Es ist bei allen bekannten römischen Dichtern nachgewiesen wie Cicero, Ovid und Vergil. Ursprünglich bezeichnete es göttliche Figuren, die in den dynamischen Himmelserscheinungen gesehen wurden, so steht der aureus vektor für den Goldenen Widder, der das Goldene Vlies nach Kolchis (heute Georgien) trug und zum Auslöser der Argonauten-Sage wurde, Apuleius spricht von Charon als Vektor, der die Toten in die Unterwelt fährt. Cicero nennt die Passagiere eines Schiffes die Vektoren, Vergil umgekehrt die Seefahrer, die für das Gelingen der Fahrt ihrer Passagiere verantwortlich sind.
Die Himmelsmechanik ist gleichsam selbstbezüglich die Überfahrt des Vektors vom Mythos und der Dichtung in die Naturwissenschaft und Mathematik. Die Astronomen bezeichneten mit dem Vektor den Fahrstrahl: Das ist die direkte Verbindungslinie von einem Zentralkörper zu einem umlaufenden Planeten. Um zu erklären, warum der Planet auf seiner Bahn bleibt und weder in den Zentralkörper stürzt noch in das Weltall ausbricht, wurde ein Fahrstrahl angenommen, der ihn wie ein Schiff entlang seiner Bewegung um den Zentralkörper trägt.
Das kann schrittweise verallgemeinert werden, bis rein mathematische Größenverhältnisse übrig bleiben: Der Ortsvektor  beschreibt eine Verschiebung von einem Ort A zu einem anderen Ort B. Der Geschwindigkeitsvektor v→ beschreibt eine Veränderung von einer Geschwindigkeit zu einer anderen. Und so fort. Jeder Vektor benennt einen Anfangs- und einen Endzustand sowie die Richtung vom ersten Zustand zum zweiten Zustand.
beschreibt eine Verschiebung von einem Ort A zu einem anderen Ort B. Der Geschwindigkeitsvektor v→ beschreibt eine Veränderung von einer Geschwindigkeit zu einer anderen. Und so fort. Jeder Vektor benennt einen Anfangs- und einen Endzustand sowie die Richtung vom ersten Zustand zum zweiten Zustand.
Aus dem Ortsvektor wurde der Kraftvektor. Seine Größe ist das Quantum der wirkenden Kraft und der Pfeil die Richtung, in die sie wirkt. Wenn mehrere Kräfte beteiligt sind, ergibt das das Kräfteparallelogramm. »Das Gesetz vom Kräfteparallelogramm wurde erstmals 1586 von Simon Stevin (1548-1620) formuliert. Genau hundert Jahre später gab Isaac Newton (1643-1727) es in seinen Principia Mathematica nicht als Axiom an, sondern als Zusatz.« (abgerufen am 5.5.2021)
Das Wirken von Kräften im Kräfteparallelogramm ist bis heute die maßgebliche Veranschaulichung eines Vektors. Das Rechnen mit Vektoren kann direkt an den Kräften veranschaulicht werden: Zwei Vektoren werden addiert, so wie sich zwei Kräfte zu einer resultierenden Kraft addieren.
Die Untersuchung der Kräfte entlang der Bewegungsbahn eines Planeten führte zur Differentialrechnung: Entlang der Bewegungskurve werden die Verbindung zum Zentralkörper (der Fahrstrahl) und die Tangente unterschieden. Die Steigungsdreiecke zeigen, wie entlang einer Kurve die tangentiale Kraft und die Kraft in Richtung zum Brennpunkt unterschieden werden können.
Während Kräfteparallelogramme und das Gravitationsfeld nicht unmittelbar beobachtet werden können, ist das möglich mit Magneten und kleinen magnetisierten Partikeln, die im Magnetfeld geordnet werden. Eine sehr klare Übersicht gibt die Seite magcraft. Fast gleichzeitig, als der flämische Mathematiker, Physiker und Ingenieur Simon Stevin die ersten Kräfteparallelogramme aufzeichnete, trägt der englische Arzt und Physiker William Gilbert (1544-1603) erstmals Pfeile zur Darstellung elektrischer und magnetischer Erscheinungen ein.
Isaac Newton (1642-1726) hat nicht nur alle vorgefundenen Gesetze der Mechanik vereinigt und vollendet, sondern steht an der Grenze der Mechanik zu den späteren Feldtheorien. Das von ihm untersuchte Grenzphänomen ist bis heute das Licht. Zum einen sind die Lichtstrahlen fast anschaulich Pfeile, die von der Lichtquelle zum Sensorium verlaufen, das den Lichtstrahl aufnehmen und umwandeln kann, zum anderen wird vermutet, dass es Lichtteilchen gibt, deren Bewegung mechanisch beschrieben werden kann. 1718 ergänzte Newton in seiner erstmals 1704 veröffentlichten Optik die legendäre Query 31, die seine tiefgehende Beschäftigung mit der Alchemie zeigt. Er vermutet, dass es neben der für die Mechanik bestimmenden Trägheit – »a passive Principle by which Bodies persist in their Motion or Rest« – weitere uns bisher unbekannte Kräfte gibt, aus denen sich die Anziehungen der Elemente untereinander erklären (Newton, 397). Er nennt die Aqua fortis, das Scheidewasser, um Gold und Silber zu trennen (die Salpetersäure) und den Lapis Calaminaris, den Galmei (Newton, 380). An vielen Beispielen zeigt er chemische Kräfte, die Stoffe zueinander bringen und bis zu katastrophenartigen Ereignissen führen können. Im Ergebnis ist er sich unsicher, wie sie zu beschreiben und zu bezeichnen sind und spricht von »hooked atoms« (wörtlich: »verhakte Atome«), »glued together by rest, that is, by an occult Quality, or rather by nothing« (»zusammengeklebt durch Ruhe«) oder »stick together by conspiring motions«, »Particles attract one another by some Force, which in immediate Contact is exceeding strong, at small distances performs the chymical Operations« (Newton, 388f). Er gebraucht nicht den Ausdruck ‘Affinität’, aber er erweitert das Verständnis von Attraktion weit über die Mechanik hinaus. Das hat zweifellos die nachfolgenden Generationen angeregt, für diese Art von Kräften nach ähnlichen mathematischen Formeln zu suchen wie für die Gravitation. Und so wie für die mechanischen Gesetze die Infinitesimalrechnung eingeführt werden musste, hat er den Weg für die Feldtheorie gebahnt.
Der Durchbruch gelang gut 100 Jahre später mit den 1831 begonnenen systematischen Forschungen durch Michael Faraday (1791-1841). Die Untersuchung elektrischer und magnetischer Phänomene geht bis in die Antike zurück (siehe die Geschichte der elektromagnetischen Theorie im englischsprachigen Wikipedia). Aber erst Faraday gelang es, sie auf ähnliche Weise zu beschreiben, wie zuvor die euklidische Geometrie und die neuzeitliche Mechanik gearbeitet hatten. Er prägte den Begriff der Kraftlinien (Line of Force) und zeichnete die von ihm untersuchten magnetischen und elektrischen Felder.
Aus diesen Beobachtungen entstand das systematische Studium von Feldlinien und physikalischen Feldern.
Was ist das Neue an elektrodynamischen Feldern? Schon das mechanische Feld ist kontinuierlich. Die Raumkrümmung ist kontinuierlich. Anziehungs- und Gravitationskräfte ändern sich kontinuierlich mit den Abständen der beteiligten mechanischen Körper. Aber erst im elektrischen Feld beginnt ein Strom zu fließen. Im Feld sind die elektrischen Quanta verteilt. Sie können nicht als Pakete fixiert werden, sondern aufgrund der Dynamik sind sie verteilt in Wahrscheinlichkeitsaussagen.
»Fließende Zahlen« sind für jeden traditionellen Mathematiker ein Unding. Nur unter Widerständen konnte die Vorstellung aufgegeben werden, die Mathematik atomar aus elementaren Einheiten wie Punkt und Eins aufzubauen und stattdessen in den Einheiten der Bewegung die Basis von dynamischen Bewegungsräumen zu sehen. Diese Einheiten sind keine statischen Elemente, sondern Keime, aus denen Bewegung entspringt. Mathematisch gesprochen sind die fließenden Zahlen imprädikativ: Sie lassen sich wie die Kontinuität, Flüssigkeit und Lebendigkeit nur über die übergreifenden Eigenschaften der Menge definieren, denen das jeweilige Element angehört. Mit imprädikativen Eigenschaften ist die übliche Zeitordnung in Frage gestellt: Was an einem Zeitpunkt des Hier und Jetzt gilt, ist nur zu verstehen aus dem in die Vergangenheit und Zukunft übergreifenden Zusammenhang. Für eine statische Betrachtung ergeben sich daraus die Paradoxa und Antinomien, dass wir heute die Erinnerung aus der Zukunft erleben und das in der Vergangenheit bereits verborgene, aber ihr noch nicht fassbare Wissen. Wer das darstellen will, benötigt Pfeile, die auf das verweisen, was heute aus der Vergangenheit und der Zukunft gegenwärtig ist. Das wirft die Frage nach dem ontologischen Status der Phänomene auf, die mit den Pfeilen beschrieben werden. (Die Psychologie lehrt, dass sich das Unbewusste dessen »bewusst« ist, wenn es etwa in der Traumlogik die übliche Zeitordnung aufgibt. Siehe hierzu die Arbeiten von Blanco.)
Bis dahin war es 1831 noch ein weiter Weg. Der irische Physiker und Mathematiker William Rowan Hamilton (1805-1865) gebrauchte 1834 den Ausdruck Vektor in der traditionellen Bedeutung aus der Astronomie, führte aber in seinen Arbeiten zu den vierdimensionalen Quaternionen (eine von ihm begründete Erweiterung der komplexen Zahlen) seit 1844 schrittweise die heute übliche Unterscheidung von Skalaren und Vektoren ein (Miller Stichwort "Vector, Vector Analysis and Vector Space"). Noch der Mathematiker Felix Klein (1849-1925) sprach bei den Vektoren von einem Entgegenkommen der abstrakten Mathematik an die anschaulicher operierenden Naturwissenschaften. Pfeile wurden in der Mathematik erst im 20. Jahrhundert eingeführt.
Prozessorientierte Karten
– Von Wetterkarten und Karten militärischer Operationen zu concept maps
Die Geschichte der Kartographie geht bis in die Ur- und Frühgeschichte zurück. Darstellung von gegenseitigen Beziehungen (Pfeilen) gibt es jedoch erst seit dem Entstehen von Thematischen Karten seit der Neuzeit, so z.B. 1607 die Designatio orbis christiani, die die Ausbreitung der Weltreligionen zeigt.
Aus dem Alltag ist jeder mit den Pfeilsymbolen auf den Karten der Wetterberichte und den Karten militärischer Operationen vertraut, in denen mit Pfeilen das Vorrücken und die Rückzüge von Luftmassen (Wärme- und Kaltfronten) und militärischer Verbände eingetragen sind. In Deutschland gibt es Generalstabskarten seit dem späten 18. Jahrhundert, bis sie im frühen 19. Jahrhundert standardisiert und allgemein eingeführt wurden. Nur wenig später entstanden in den 1840ern die ersten Wetterkarten.
Schmauks betrachtet die Pfeile in Karten unter dem Blickwinkel der Semiotik und der von Peirce eingeführten Unterscheidung in Ikone, Index und Symbol.
»Zu den indexikalischen Zeichen zählen die Pfeile für die Strömungsrichtungen der Luftmassen. Da ihre Länge nicht bedeutungstragend ist, handelt es sich nicht um Vektoren im formalen Sinne. Symbolische Zeichen sind die verstreut eingetragenen Temperaturwerte, die Buchstaben 'H' und 'T' im Zentrum der Druckgebiete und die Isobaren (Linien gleichen Luftdrucks). Als ikonisch gelten die Piktogramme des thematischen Teils, die in der Geographie als 'sprechende Signaturen' bezeichnet werden.« (Dagmar Schmauks Landkarten, Zeitschrift für Semiotik 1998, 18, zitiert bei Sick, 239)
Sick kommentiert: »Der Pfeil lokalisiert, organisiert eine gerichtete Beziehung. Seine indexikalische Wirkung wurde schon an anderer Stelle hervorgehoben. (Fn. 1: 'Dieser Baum / 'das Referenzobjekt wird durch die sprachliche Information kategorisiert und durch die begleitende Zeigegeste lokalisiert.' Schmauks, Multimediale 1996, 1)« (Sick, 240)
Für Präsentationen wurden zahlreiche Methoden entwickelt. Sie gehen auf frühe Arbeiten 1921 zurück und sind häufig bewusst formal, um eine maschinelle Auswertung mithilfe von Algorithmen zu ermöglichen. Für einen freien, nicht-formalisierten Gebrauch wird von Concept Map (Begriffslandschaft) gesprochen. Die grundlegenden Ideen gehen auf den Entwicklungspsychologen Jean Piaget (1896-1980) zurück, dessen Arbeiten der amerikanische Lerntheoretiker David Paul Ausubel (1918-2008) aufnahm. Für ihn erfolgt Lernen über das Erkennen von Verknüpfungen zwischen verschiedenen Begriffen. Daraus entwickelte der amerikanische Pädagoge Joseph D. Novak (* 1932) in den 1970ern die Concept-Map.
Dies bleibt nach meinem Eindruck im Ganzen noch »flach« auf eine Ebene beschränkt, in der die verschiedenen Begriffe gleichberechtigt wie auf einer großen Karten nebeneinander gelegt werden. Zwar gibt es Untersuchungen der Metacognition, die nach meinem Kenntnisstand weitgehend auf formale und neurophysiologische Fragen beschränkt sind und bei Weitem nicht den Stand erreichen, der in der Geschichte der Alchemie und Chemie gegeben ist. So bleiben die entsprechenden Techniken und der Gebrauch von Pfeilen weitgehend ein pädagogisches Mittel für bessere Präsentationen und haben bisher zu keiner eigenen Wissenschaft geführt, die bewusst provozierend als eine Alchemie der Ideen oder als Reaktionen und Reaktionsmuster unterschiedlicher Begriffe bezeichnet werden könnte. Dem steht bisher entgegen, dass nach wie vor einzelne Begriffe als autonome Entitäten gesehen werden, die zwar in Sätzen und Texten äußerlich miteinander verknüpft werden können, aber nicht unmittelbar miteinander reagieren.
Ausnahmen könnten die Untersuchungen von Träumen und Tagträumen sein. Der Gebrauch des Pfeils → ist für mich der erste Schritt, aus dem weitere Operatoren zu entwickeln sind, wodurch sich die bisher recht starren Begriffskarten in lebendige Systeme entwickeln könnten.
Kommutierende (vertauschende) Diagramme der Kategorientheorie
Seit Beginn der Neuzeit waren in den verschiedensten Wissenschaften und Anwendungsgebieten Pfeile eingeführt worden, um die Darstellung anschaulicher zu machen. Der Schwerpunkt lag jedoch auf dem jeweiligen Sachthema, und die Pfeile dienten vor allem als Hilfsmittel der besseren Orientierung, Hervorhebung und Vereinfachung. Für sich betrachtet galten sie eher als Fremdkörper, der möglichst unauffällig einzusetzen ist. Auch die ersten in der Mathematik eingeführten Pfeile hatten vor allem die Aufgabe, die zunehmend komplexere Schreibweise für logische und mathematische Folgerungen zu vereinfachen und übersichtlicher zu gestalten. Erst mit der in den 1940ern entstandenen mathematischen Kategorientheorie kehrt sich das um: Mit ihr werden die Pfeile unmittelbar zu den Objekten, mit denen mathematisch operiert wird. Das kann so weit führen, dass Pfeile mit Pfeilen aufeinander abgebildet werden.
Um die Grundidee der mathematischen Kategorientheorie zu verstehen, ist am besten vom Beispiel der Differentialrechnung auszugehen. Bei der Differentialrechnung muss der übliche Kalkül des arithmetischen Rechnens verlassen und ein eigener Differentialkalkül eingeführt werden, dessen Ergebnisse jedoch am Ende nicht in Widerspruch zum arithmetischen Kalkül geraten sollen. Die Zahlen des arithmetischen Kalküls werden mit Variablen wie x und y symbolisiert, der Differentialkalkül rechnet mit den Differentialen dx und dy. Um diese Verhältnisse darzustellen, werden Pfeile eingeführt, mit denen innerhalb der beiden Kalküle die Übergänge mit x → y und dx → dy bezeichnet werden und die Übergänge zwischen den Kalkülen mit x → dx und dy → y. Wenn sich das Diagramm der vier Übergänge schließt, ist das ein Beispiel für ein kommutierendes Diagramm.
Daraus entstand die Idee, das Beispiel der Differentialrechnung zu verallgemeinern und eine Mathematik der Diagramme zu entwerfen, deren Punkte mit Pfeilen verbunden sind (gerichtete Graphen). Das war die Geburtsstunde der Kategorien- und der Graphentheorie. Philosophisch stellt sich seither die Frage nach einer neuen Ontologie: Kehren sich die traditionellen Verhältnisse einer ruhenden Substanz und ihrer nachträglich eingeführten Bewegung um? Wird die Bewegung (symbolisiert durch Pfeile) zur neuen Substanz, und die ruhenden Einheiten sind nichts als ihre Verdichtungen und Knoten? Das führt zur Wende von einer statischen zu einer dynamischen Mathematik. Sie ist nicht mehr am Paradigma der Architektur (des Hausbaus) orientiert, die aus vorgegebenen Bausteinen Zug um Zug ihre Gebäude konstruiert und errichtet, sondern an der fließenden Strömung, innerhalb derer ihre Rhythmen und Eigenwerte abgelesen werden können. Zalamea spricht vom Einsteinian turn: Für Einstein sind der statische euklidische Raum und der statische, absolute Raum Newtons nur noch Grenzfälle eines dynamischen, gekrümmten Raums mit seiner nicht-euklidischen Geometrie (Zalamea 2009, 270). Ich würde von einem Leibnizian turn sprechen: Leibniz hat den Differentialkalkül eingeführt, und Einstein hat sich – wie Gödel – stets auf Leibniz als sein großes Vorbild berufen.
– Der Differentialkalkül als maßgebliches Beispiel
Um den Grundgedanken des Differentialkalküls zu erkennen, wird der Einfachheit halber von reellwertigen Funktionen y = f(x) ausgegangen. Das einfachste, nicht-triviale Beispiel ist die quadratische Funktion y = x². Die Differentiation kann mit einer geometrischen Zeichnung veranschaulicht werden:
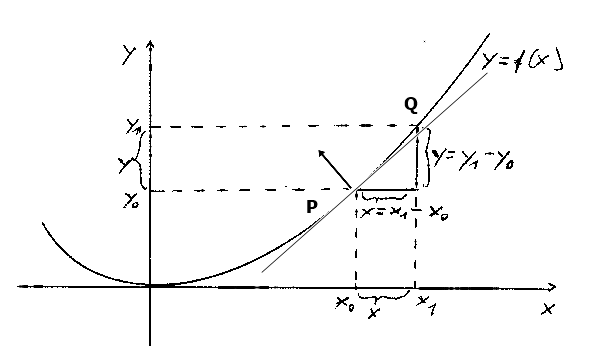
Figur 1: Steigungsdreieck
Freihandzeichnung. Der Pfeil steht an der Stelle x₀ senkrecht auf der dort angelegten Tangente und zeigt die Krümmung der Kurve.
Diese unmittelbar anschauliche geometrische Figur wird mit der Kategorientheorie aus einer neuen Perspektive betrachtet: Welche Operationen erfolgen bei der Ableitung, und wie ist sichergestellt, dass ihr Ablauf im Ganzen kohärent bleibt? Das ergibt das Diagramm der miteinander verbundenen Operationen.
| Beispiel | |||||
| Oben: Operation im Differentialkalkül (df) | dx | → | dy | dy = 2dx | |
| Übergang zum Differentialkalkül | ↑ | ↓ | |||
| Unten: Operation im üblichen arithmetischen Kalkül (f) | (x₀,x₁) | → | (y₀,y₁) | y = x² | |
| und daraus hergeleitete Steigungsdreiecke |
Figur 2: Diagramm der Operationen des Differentialkalküls
Das Diagramm ist von unten nach oben zu lesen:
- Unten: x₀ und x₁ stehen für übliche, reelle Zahlen auf der x-Achse. Sie werden mit einer Funktion f auf andere reelle Zahlen y₀ = f(x₀) und y₁ = f(x₁) abgebildet, die auf der y-Achse eingetragen sind. Das einfachste Beispiel ist die Funktion y = x²
- Um Steigungsdreiecke zeichnen zu können, wird die Funktion nicht auf einzelne Zahlen x₀ oder x₁ beschränkt, sondern es werden Intervalle (x₀,x₁) auf andere Intervalle (y₀,y₁) abgebildet. Anschaulich bedeutet das: Für jede gegebene Grundseite (x₀,x₁) wird die zugehörige Kathete (y₀,y₁) gezeichnet, die senkrecht auf ihr steht. Das ergibt die Steigungsdreiecke.
- Mit dem Grenzübergang erfolgt der Wechsel auf die obere Zeile.
- Oben: Nach den Regeln des Differentialkalküls wird berechnet, in welchem Verhältnis im Grenzübergang die verschwindende Größe dy zur verschwindenden Größe dx steht. Im Beispiel der quadratischen Funktion y = x² ergibt sich im Differentialkalkül, dass an jeder Stelle x₀ die Steigung der dort angelegten Tangenten 2x₀ beträgt.
Das Ergebnis der Differentialrechnung kann empirisch überprüft werden: Für Newton zeigt der Graph die Bewegungskurve eines Körpers, wobei die x-Achse für die räumliche Strecke steht, die der Körper durchläuft, und die y-Achse für die Zeit, die er dafür braucht. Die Steigung der Tangente ist die jeweilige Momentan-Geschwindigkeit des Körpers an einer Stelle x₀. Raum, Zeit und Geschwindigkeit können gemessen werden. Das ergibt die empirische Bestätigung. – Genauso gut kann das Ergebnis an der geometrischen Zeichnung überprüft werden: Wird in einer Zeichnung wie Figur 1 die Steigung der Tangente gemessen, wird sich das Ergebnis der Differentialrechnung bestätigen.
In diesen Beispielen wird der Einfachheit halber wie in der euklidischen Geometrie von einer ebenen Zeichenfläche und wie in der Physik von Newton von einem absoluten Raum ausgegangen. Um die gekrümmte Geometrie von Einstein zu erreichen, ist dieser Gedanke mit einer zweiten Ableitung nochmals zu wiederholen: Das Zeichenblatt ist im Ganzen gekrümmt, vergleichbar der gekrümmten Oberfläche auf einer Kugel. So wie die Krümmung einer Kurve durch die Steigung der Tangente bestimmt wird (die Krümmung wird durch einen Pfeil dargestellt, der senkrecht auf der Tangente steht und in das Innere der Kurve verweist), so kann die Krümmung des Raums durch eine Tangentialfläche bestimmt werden. Der Grundgedanke bleibt erhalten: Die Krümmung des Raums wiederholt die Krümmung der Kurve, wie sie an einem Beispiel in Figur 1 dargestellt ist.
– Von statischen zu dynamischen Analogien, die nicht Größen, sondern Strukturen erhalten
Bis heute werden die Kalküle (Rechenregeln) für die üblichen arithmetischen Rechnungen und der Differentialkalkül in verschiedenen mathematischen Disziplinen unabhängig voneinander untersucht: In der Arithmetik und in der Differential- und Integralrechnung (Analysis). Unausgesprochen (implizit) wird unterstellt, dass beide Rechenarten zusammenpassen und einander nicht widersprechen. Jeder hat sich so sehr daran gewöhnt, dass es schwer fällt sich vorzustellen, was damit gemeint sein könnte, dass irgendwann oder irgendwo die Rechenarten der Arithmetik und der Differentialrechnung auseinander laufen und sich voneinander entfernen können. Es waren exotische Beispiele von Monsterfunktionen, ineinander verschlungenen Kurven wie dem Möbiusband und anderen katastrophenartigen Verläufen notwendig, um zu verstehen, wie das geschehen kann. Mit Beispielen dieser Art drohte die Mathematik ihren festen Grund zu verlieren. Auf einmal wurde klar, dass es zwischen der Arithmetik und dem Differentialkalkül einen unauflösbaren, strukturellen Unterschied gibt: Während die Arithmetik ihre Zahlen aus einer festen Einheit aufbaut, – der Zahl Eins bzw. in der Geometrie dem dimensionslosen Punkt –, gibt es für die Differentiale keine vergleichbare Einheit. Ein Differential dx kann durch keinerlei arithmetische Operation aus gegebenen Zahlen berechnet werden. Stattdessen hat sich die negative Beschreibung durchgesetzt: Für jedes Differential dx, das seit dem Mathematiker Karl Weierstraß (1815-1897) als ε (Epsilontik) bezeichnet wird, gibt es ein kleineres Differential, das im Grenzübergang noch einen Schritt weiter ist. Droht sich das antike Paradoxon von Achilles und der Schildkröte zu wiederholen? Es ist unmöglich, im traditionellen Sinn zwischen den üblichen Zahlen und den Differentialen eine Analogie zu bilden. Es gibt nur ausnahmsweise zwei Zahlen x und y, die sich arithmetisch zueinander so verhalten wie dx und dy. Als Antwort darauf wurde die Kategorientheorie entwickelt. Mit ihr wird nicht einfach nur ein Diagramm wie in Figur 2 aufgezeichnet, sondern an dieses Diagramm wird die Forderung gestellt, dass es im Ganzen »kommutiert«. Das bedeutet: Die Rechnungen in beiden Kalkülen bleiben aufeinander bezogen. Das ist die Bedeutung des auf der rechten Seite des Diagramms nach unten weisenden Pfeils, der in diesem Beispiel von dy nach (y₀,y₁) verläuft.
Der Grundgedanke der Kategorientheorie bleibt die Analogie: Die obere und die untere Ebene verhalten sich analog. Die kategorientheoretische Analogie wird aber nicht mehr wie die traditionelle Analogie auf eine Größenerhaltung a : b = c : d (in Worten: ›a verhält sich zu b, wie sich c zu d verhält‹) beschränkt, sondern auf eine Erhaltung der Struktur verallgemeinert. In diesem Beispiel verhält sich von den Größen her x² sicher nicht zu x, wie sich 2x zu x verhält – und ist insofern keine traditionelle Analogie –, aber mit dem kommutierenden Diagramm ist aufgezeichnet, in welcher Weise dennoch von einer Analogie gesprochen werden kann. Der Differentialkalkül ist dem arithmetischen Kalkül strukturell analog.
Es muss einen bestimmbaren Unterschied zwischen beiden Arten der Analogie geben. Den hat im Prinzip bereits der amerikanische Mathematiker und Philosoph Charles Sanders Peirce (1839-1914) erkannt. Er hat noch nicht die Kategorientheorie entwickelt, aber er hat die entscheidenden Vorarbeiten geleistet. Er hat erkannt, dass die traditionellen Schlussformen der Induktion und Deduktion unvollständig sind: Der Differentialkalkül kann weder per Induktion noch per Deduktion aus dem Kalkül der Arithmetik hergeleitet werden. Stattdessen ist ein dritter Schluss notwendig: Das ist die von ihm eingeführte Abduktion. Die Abduktion stellt genau die Frage, um die es hier geht: In der Ausdrucksweise von Peirce kann der Differentialkalkül als eine Hypothese formuliert werden, die für eine gegebene Funktion f(x) ausgehend von bekannten Werten wie z.B. bei x₀ mit einer Abduktion voraussagt, welche Steigung an einer anderen Stelle x₁ gemessen werden kann. Wenn das bestätigt wird, kommutiert das Diagramm. Wenn es dagegen in bestimmten Situationen nicht zutrifft, kommutiert das Diagramm nicht, und es ist die Frage nach neuen Kalkülen zu stellen, in denen das gelingt. Diese Voraussage trifft zum Beispiel dann nicht ein, wenn die Parabel nicht auf einer Ebene, sondern auf einer Kugeloberfläche gezeichnet wird. Dort verändern sich die Krümmungen, während sie in der Ebene erhalten bleiben. Die nicht-euklidische Geometrie liefert die Lösung. Auch diese Lösungen gelten jedoch nicht immer: Wird die Parabel weder auf einem ebenen Blatt noch auf einer gleichmäßig gekrümmten Kugeloberfläche gezeichnet, sondern in einem Raum, der sich wie der Maelstrom (Edgar Allan Poe) eines Schwarzen Lochs unendlich eng verdrillt, versagt auch die nicht-euklidische Geometrie. Dafür gibt es bis heute keine Lösung. Aber die Kategorientheorie weist den Weg, auf dem nach Lösungen zu suchen ist: Es sind wiederum neue Kalküle zu entwerfen, die mit den bekannten Kalkülen kommutieren.
Erst mit den strukturerhaltenden Analogien ist es gelungen, die unvermeidlichen Antinomien und Paradoxa einer Wissenschaft zu verlassen, die auf statischen Elementen und ihren starren Beziehungen aufbaut. Georg Cantor (1845-1918) war von der Untersuchung solcher Situationen ausgegangen, in denen Arithmetik und Differentialkalkül auseinander zu fallen drohten (das waren Funktionen mit unendlich vielen Unstetigkeits-Stellen, an denen keine Ableitung möglich ist und der Differentialkalkül versagt). Er suchte eine Antwort mit einer Verallgemeinerung des klassischen Begriffs der Substanz: Statt von Zahlen und den aus ihnen arithmetisch zu berechnenden Vielfachen und Teilern sprach er von Mengen und ihren Elementen. Er hoffte, dass sich sowohl die Arithmetik wie der Differentialkalkül aus der Mengenlehre herleiten lassen und dadurch ihre innere Einheit gesichert ist. Die Paradoxien der Mengenlehre zeigten, dass das unmöglich ist. Erst als auch dieser Weg gescheitert war, musste mit der Kategorientheorie ein völlig neuer Ansatz gefunden werden.
Die Philosophie des 20. Jahrhundert scheint sich im Ganzen zumindest von den Fragen der Mathematik verabschiedet zu haben. Die analytische Philosophie beschäftigt sich seit Wittgenstein ausschließlich mit Fragen, die innerhalb des Kalküls der Arithmetik bleiben und sieht daher nicht einmal die hier genannte Problemstellung. Sie schläft gewissermaßen den Traum des mit sich zufriedenen, naiven Substanzdenkens. Nur Hegel hatte sich ernsthaft mit dem Differentialkalkül beschäftigt. Aber er hatte die Überlegungen zum Differentialkalkül in Anmerkungen ausgelagert, so dass sich viele Hegelianer damit zufrieden geben können, Hegels spekulatives Denken im Ganzen sei nicht dynamisch, sondern als das bisher anspruchsvollste Sprachspiel mit dem von ihm gewählten und definierten Begriffen anzusehen, die trotz aller Kritik am Verstandesdenken wie ein statisches »diamantene[s] Netz« (Enz. § 246Z, HW 9.20) von Worten miteinander verknüpft sind. Die einzigen Ausnahmen sind die französischen Philosophen Alain Badiou (* 1937) und Gilles Deleuze (1925-1995). Badiou hat als Einziger versucht, die von Hegel und Marx überlieferte Dialektik mit den Erkenntnissen der Mengenlehre weiter zu entwickeln und ist damit letztlich ebenso gescheitert wie Cantor. Er bestätigt, wie schwer es selbst denjenigen fällt, die sich in der revolutionären Tradition sehen, den Bruch von einer statischen zu einer dynamischen Wissenschaft zu vollziehen. So bleibt nur Deleuze und das von ihm angeregte nomadische Denken (siehe den Beitrag Das nomadische Subjekt nach Gilles Deleuze und Rosi Braidotti). Auf ihn berufen sich die wenigen Philosophen, von denen in dieser Arbeit auszugehen ist, wie z.B. Fernando Zalamea (* 1959), Manuel DeLanda (* 1952), Arkady Plotnitsky oder Simon Duffy und die von ihm in seinem Buch Deleuze and the History of Mathematics genannten »friends and colleagues« (Duffy 2013, 10f). Sie arbeiten überwiegend auf den Gebieten der Kultur-, Literatur- und Medienwissenschaft.
– Erweiterungen
Ist der Grundgedanke der Kommutation erfasst, dann können Diagramme dieser Art unabhängig von der jeweils konkreten Fragestellung (wie in diesem Fall das Beispiel der Differentialgleichung) als rein geometrische Objekte betrachtet werden. Der Phantasie sind keine Grenzen gesetzt. Figur 3 zeigt drei elementare Beispiele, die an eine ähnliche Darstellung im Wikipedia-Eintrag zum Groupoid angelehnt sind:
|
|
|
Figur 3 a,b,c: Einfachpfeile, Mehrfachpfeile, Eigendrehung
Figur 3a zeigt das elementare Diagramm. Seine wesentliche Bedeutung liegt im Auflösen von Paradoxien. Im Beispiel der Differentialrechnung liegt das Paradox in den verschwindenden Größen dx und dy im Moment des Grenzübergangs von Steigungsdreiecken zur Tangente. Statt die endlichen Seitenlängen im Steigungsdreieck unmittelbar den verschwindenden Seitenlängen der Tangente gegenüber zu stellen (die Tangente ist kein Dreieck mehr und seine nur noch fiktiv gedachten Seitenlängen der Katheten sind 0), gelingt mit dem kommutierenden Diagramm ein Weg, der den Sprung von dem einen Kalkül in den anderen Kalkül zeigt und formuliert, wie er aufrecht erhalten werden kann. Die Pfeile sind keine statischen Identitätsbeziehungen mit ihrer letztlich tautologischen Aussage A = A, sondern zeigen Prozesse und im Ergebnis Zuweisungen. Ihre Herkunft aus den Reaktionsgleichungen der Chemie ist unverkennbar. Kein Philosoph hat sich diesem Gedanken so weit genähert wie Hegel, als er es wagte, in seiner Wissenschaft der Logik chemische Reaktionsgleichungen in das Gebiet der Logik aufzunehmen (siehe den Beitrag Das reale Maß – die Logik der chemischen Sphäre).
Wird die Figur 3a von oben nach unten gelesen, kann gesagt werden, dass das Paradox der verschwindenden Größen »zu Grunde« geht. (Dieser Gedanke lässt sich weiter ausarbeiten mittels der Ausführungen von Hegel zum Differentialkalkül und den Reflexionsbestimmungen Widerspruch und Grund.)
Figur 3b soll andeuten, dass es in der Regel nicht eine einzige, eindeutige Lösung gibt, sondern eine Vielfalt unterschiedlicher Lösungen. Sie sind mit den parallel verlaufenden Doppelpfeilen angedeutet.
Wiederum ist der Differentialkalkül das beste Beispiel. Es gibt die unterschiedlichsten Wege, den Grenzübergang zu verstehen. Er kann mit Cauchy-Folgen, der Epsilontik oder Dedekind-Schnitten beschrieben werden. Ohne die von ihm gebrauchte Fachsprache weiter zu erläutern, sei Zalamea zitiert: »In the specific case of the category Sh(O(R)), the copies are different according the construction is done through Dedekind cuts (Rd) or through Cauchy sequences (Rc).« (Zalamea Peirce's Continuum, 40) Dieser Hinweis enthält in meinem Verständnis den Gedanken, dass mit der Kategorientheorie die unterschiedlichen Deutungen des Grenzgangs als strukturell analoge Wege kommutierender Diagramme beschrieben werden können,
In der Konsequenz bedeutet das, dass jeder Pfeil nicht einfach ein Lösungsweg ist, sondern verallgemeinert werden muss zu einem Lösungsraum, der eine Vielfalt von Lösungswegen enthält. Dieser Gedanke geht auf Evariste Galois (1811-1832) zurück, der von Deleuze und seinen Schülern zurecht häufig genannt wird.
Figur 3c deutet die Möglichkeit an, dass die mit Bullets • dargestellten Eckpunkte der Diagramme nicht statisch sein müssen, sondern ihrerseits bewegt sein können. Die Pfeile zeigen äußere Einflüsse und die auf sich selbst weisenden Kreise die innere Bewegtheit der mit den Pfeilen miteinander verbundenen Objekte.
In einem weiteren Schritt können die Diagramme vertikal auf mehr als 2 Ebenen und horizontal auf Bündel verallgemeinert werden:
|
|
… |
Figur 4 a,b: Mehrfach-Ebenen, Kette/Bündel
Figur 4a steht für drei übereinander gelagerte Ebenen. Ein Beispiel wurde bereits genannt: Die untere Ebene beschreibt klassische Objekte x und y, die mittlere Ebene die Differentiale dx und dy und die dritte Ebene nochmals deren Krümmung ddx und ddy. Dem entsprechen physikalisch die Bewegungen, ihre Geschwindigkeiten und deren Beschleunigungen. Das war der Ansatz von Newton, der mit diesen drei Ebenen Kraft, Impuls und Energie unterscheiden konnte. Wird nach der Energie von Formen gefragt, so wird dafür eine analoge Unterscheidung in drei Ebenen erforderlich sein: (i) die Formen, (ii) die Metamorphosen von Formen, (iii) die sich in den Metamorphosen der Formen äußernde Energie.
Mit Spencer-Brown können die drei Ebenen aus einer anderen Perspektive gedacht werden: (i) Dem void, dem leeren Medium, in das etwas eingetragen werden kann, z.B. ein Blatt Papier, (ii) dem Kalkül der Arithmetik, der in der leeren Ebene Unterschiede setzt, diese differenziert und wieder auslöscht, bis erneut das leere Medium erreicht ist, (iii) aus dem Kalkül der Arithmetik hervorgehende iterative Prozesse, die sich aus dem Kalkül verselbständigen und vergleichbar dem Differentialkalkül einen Grenzübergang vollziehen, dessen Grenzwert mit einem Re-entry in den Kalkül der Arithmetik aufgenommen wird. Spencer-Brown hat mit dem Re-entry den entscheidenden Begriff gefunden, mit dem der Abschluss der kommutierenden Diagramme bezeichnet werden kann.
Figur 4b zeigt die Grundidee von Faserbündeln. Das ist in drei Schritten eine Verallgemeinerung des Differentialkalküls:
(i) So wie im Differentialkalkül an einem einzelnen Punkt eines Graphen eine Tangente angelegt wird und die lokale Krümmung des Graphen senkrecht auf der Tangente steht und in das Innere der Kurve verweist (siehe den Pfeil in Figur 2), kann das auf alle Punkte entlang des Graphen verallgemeinert werden: An jedem Punkt werden eine Tangente und seine Krümmung bestimmt. Die Gesamtheit aller Tangenten ist das Tangentialbündel, die Gesamtheit aller Krümmungen das Cotangentialbündel.
(ii) Das lässt sich verallgemeinern von einer eindimensionalen Kurve in der Ebene auf mehrdimensionale Objekte in höherdimensionalen Räumen: Im einfachsten Fall wird an jedem Punkt auf der Oberfläche der Kugel eine Tangentialfläche angebracht. Im Beispiel der Kugel weist die Krümmung jeweils auf das Zentrum der Kugel. Was sich für die Kugel sagen lässt, kann wiederum verallgemeinert werden auf beliebige Objekte in n-dimensionalen Räumen. Die Energie wird im Cotangentialbündel als die Erhaltungsgröße der Krümmung definiert.
(iii) In einem letzten Schritt werden nicht nur an jedem Punkt auf der Oberfläche Tangentialräume betrachtet, sondern beliebige Räume, die jeweils eine gemeinsame Strukturgruppe haben. Nach dieser Vorstellung wird die Teilchenphysik interpretiert: Wird der Weg eines bewegten Teilchens betrachtet, dann beschreibt der Tangentialraum, in welche Richtung sich das Teilchen mechanisch bewegen kann. Darüber hinaus ist an jedem Punkt der Bewegungsbahn eine Symmetriegruppe angebracht, mit der beschrieben wird, gemäß welcher Symmetrien sich das Teilchen entlang seiner Bewegungsbahn verändern kann. Das sind die Symmetrien der Teilchenphysik wie z.B. die Symmetrie der Radioaktivität oder des Quarkmodells.
Figur 4b zeigt den Grundgedanken: Die untere Linie steht für den Basisraum B, in dem die mechanische Bewegungsbahn verläuft, die obere Linie für die an allen Basispunkten angebrachten Fasern F. Beim Übergang benachbarter Fasern kommt es zu den Metamorphosen des Teilchens. Mit ein wenig Phantasie lassen sich aus diesem einfachen Bild die mathematisch komplexeren Begriffe des Faserbündel ablesen, von denen der Eintrag in Wikipedia einen ersten Eindruck gibt. Dort finden sich alle Grundbegriffe der Kategorientheorie wieder. Die Teilchenphysik war das erste Anwendungsgebiet der Kategorientheorie.
Von der Vielfalt der hier dargestellten Diagramme ist es nur ein kleiner Schritt in weitere Anwendungsgebiete. Die Diagramme können als gerichtete Graphen verstanden werden, mit denen eine Anziehung und im Ergebnis ein Prozess von A nach B gezeichnet wird, der zugleich mehrstufig und in einer Kette einander nachfolgender Schritte betrachtet werden kann. Das kann sowohl in der systemischen Psychologie wie in der systemtheoretischen Soziologie dafür genutzt werden, Blockaden, Verknotungen und ihre Auflösungen darzustellen.
Mit Freud können die drei Ebenen in Figur 4a als Unbewusstes, Bewusstes und Über-Ich gedeutet werden. Das führt zum Entwurf der Traumlogik und allgemeiner zu einem Diagramm für das Wechselspiel von Realität und Phantasie. An dieser Stelle soll eine Skizze genügen, um anzudeuten, in welcher Richtung das weiter ausgearbeitet werden kann:
| Traum-Operation (Verdichtung, Verschiebung) | x' | → | y' | |
| Heraufführung, Bewusstwerdung | ↑ | ↓ | ||
| Reale Ereignisse | x | → | y |
Figur 5: Reale Logik und Traumlogik, Realität und Phantasma (Simulacrum)
Entscheidend ist die Heraufführung von x → x', die Abbildung des Realen auf das Imaginäre. In der Phantasie liegen zahlreiche Bilder bereit, auf die ein reales Ereignis abgebildet werden kann. Welche Auswahl getroffen wird, kann von unterschiedlichsten Faktoren abhängen. Möglicherweise gibt es kulturell und historisch vorgeprägte Bilder. Eventuell gilt auch im Traum eine eigene Sprache, die die Auswahl und Verarbeitung der Traumbilder beeinflusst. Insgesamt ist zu erkennen, wie mit der Kategorientheorie das Analogiedenken ernst genommen werden kann: Phantasie und Realität werden als Analogien gesehen, die dann wieder zusammengeführt werden können, wenn sie eine analoge Struktur erhalten.
– Die Gesetze der Form von Spencer-Brown
Die von Spencer-Brown eingeführten Formen können unmittelbar mit den Mitteln der Kategorientheorie dargestellt werden:
| → | → → | → ← |
|
||||||||||||
| Cross | Wiederholtes Cross | Cross und Recross | Re-entry |
Figur 6 a,b,c,d: Spencer-Brown
Figur 6a Statt eines Haken (cross) ⃧ wird ein Pfeil → gezeichnet: Der Pfeil ist wie das Cross die Grenze eines Innen und eines Außen und überschreitet sie. Er kann wie das Cross bei Spencer-Brown sowohl als Operand (Buchstabe, Zahl) wie auch als Operator verstanden werden, mit dem die Operationen der Grenzziehung und Überschreitung ausgeführt werden.
Figur 6b Wiederholtes Cross: Es wird nacheinander mehrfach das Überschreiten einer Grenze wiederholt.
Figur 6c Cross und Recross: Das Überschreiten einer Grenze wird rückgängig gemacht. Erst wird die Grenze überschritten und anschließend zurückgekehrt.
Werden die mit den Figuren 6 b,c gezeichneten Operationen mehrfach ausgeführt und ineinander verschachtelt, ergeben sich die von Spencer-Brown gezeichneten Formen und ihre Gesetzmäßigkeiten.
Figur 6d Der Re-entry ergibt sich unmittelbar als ein kommutierendes Diagramm: Aus der Protoalgebra heraus wird mit einer unendlichen Iteration ein neues Zeichen geschaffen. Mit diesem Zeichen kann – vergleichbar dem Differentialkalkül – seinerseits operiert werden. Wenn im Ergebnis der Re-entry in die Trägermenge gelingt, ist die Operation geschlossen.
– Analogien zweiter Stufe (Knotenlinien)
Die bisher betrachteten Diagramme sind endlich. Sie enthalten nur endlich viele Pfeile und Bullets. Sie können daher als endliche, gerichtete Graphen und aus der Perspektive der Informatik als endliche formale Automaten angesehen werden. Die Pfeile zeigen die Richtungen, in die sich der Automat verändern kann, und die Bullets die einzelnen Zustände des Automaten.
Das Beispiel der Faserbündel deutet den Übergang an. Die Fasern eines Faserbündel sind kontinuierlich miteinander verbunden. Jedoch wurde bisher angenommen, dass die Gesamtheit der Fasern auf einer euklidischen Ebene dargestellt werden kann. Es bleibt die Frage, ob sich dies System im Ganzen verändern kann. Anschaulich ist an das Beispiel zu denken, dass die Diagramme nicht auf einer ebenen Zeichenfläche eingetragen sind, sondern auf einer Kugeloberfläche. Weiter lässt sich vorstellen, dass die Kugeloberfläche wie im Beispiel der Erdkugel die Oberfläche tiefer liegender Veränderungen ist (Geologie). Das sind im Beispiel der Erde tektonische Verschiebungen, vulkanische Ausbrüche und andere Katastrophen. Die jeweils gültigen Diagramme auf der Kugeloberfläche gelten nur unter festen, gleichbleibenden Bedingungen, die als ein System mit seinen Symmetrien und Erhaltungsgrößen beschrieben werden können. Kommt es zu Umbrüchen, so führt das zu Systemwechseln mit veränderten Diagrammen. Die uns bekannten Diagramme auf der Zeichenebene erweisen sich als ein Grenzfall.
Hegel hat am Beispiel der chemischen Reaktionsgleichungen ausgeführt, wie zwischen den Wahlverwandtschaften innerhalb eines Systems (die mit chemischen Reaktionsgleichungen beschrieben werden) und der Knotenlinie unterschiedlicher Systeme zu unterscheiden ist. Physikalisch kann eine Knotenlinie durch fortlaufende Wärmezufuhr bzw. Wärmeentzug entstehen. Die Aggregatzustände des Wassers (Eis, Flüssigkeit, Gas) sind Beispiele für Systemzustände, die auf einer Knotenlinie angebracht sind. Im Grenzübergang führt die Knotenlinie in chaotische Systeme, die mathematisch mit dem Hilbertraum beschrieben werden und zur Quantenmechanik führen. (Siehe den Beitrag Hegel und Hilbert – das Maßlose (Substrat) als Keim der Quantenzahl.)
– Medialität und Beobachter
In den bisher dargestellten Diagrammen wird angenommen, dass mit den Pfeilen ein Prozess durch ein Medium erfolgt, das seinerseits neutral bleibt und keinen Einfluss auf den Prozess nimmt. Das ändert sich mit den Analogien zweiter Stufe. Wenn erkannt wird, dass die Prozesse sowohl von den Wahlverwandtschaften innerhalb eines gegebenen Systems wie von den Systemsprüngen entlang einer Knotenlinie von einem System in ein anderes abhängen, stellt sich die Frage nach den Eigenschaften des Mediums. Das klassische Beispiel für ein Medium ist das Wasser in seinen verschiedenen Aggregatzuständen. Die Systemänderungen entlang der Knotenlinie können als Änderungen des Mediums gedeutet werden, wodurch die Bedeutung und der Einfluss des Mediums hervortreten.
Wenn die Frage nach einer Mitwirkung durch das Medium gestellt wird, lässt sich ebenso fragen, ob der Beobachter eines solchen Systems neutral bleiben kann oder gewollt oder ungewollt Einfluss nimmt. Das wird seit 1927 mit der Kopenhagener Deutung der Quantenmechanik von Bohr und Heisenberg diskutiert. Ihre Ansicht erlebt derzeit bei Vertretern der Kategorientheorie wie Plotnitsky für mich überraschend eine Wiederkehr. Das lässt sich erklären aus der Sicht von Deleuze auf die Entwicklung der Mathematik:
| Nomadisches Denken | Ereignis | → | Problem | |
| Heraufführung | ↑ | ↓ | ||
| Königliche Wissenschaft | Axiome | → | Theorem |
Figur 7: Deleuze
Deleuze unterscheidet zwischen der königlichen Wissenschaft (royal or major science) und dem nomadischen Denken (minor science). Die königliche Wissenschaft ist seit Euklid bekannt: Sie formuliert Axiome, leitet aus ihnen ihre Theoreme ab und arbeitet induktiv und deduktiv. Jedoch kann es in der Wissenschaftsgeschichte zu Ereignissen kommen, die den Rahmen der jeweils gegebenen königlichen Wissenschaft sprengen. Das erfordert ein nomadisches Denken. Seine wichtigste Aufgabe ist, das mit dem Ereignis gegebene Problem als solches zu erkennen und zu formulieren. Wenn das gelingt, kann ein »Re-entry« in die königliche Wissenschaft erfolgen und diese mit einem Paradigmen-Wechsel reorganisiert werden.
Für das nomadische Denken sind die Subjektivität und damit die Bedeutung des Beobachters entscheidend. Er beobachtet nicht nur, sondern erkennt die neu auftretenden Ereignisse und die mit ihnen gegebenen Probleme. Im Sinne von Hegel ist das Problem die Negation der Negation: In einer ersten Negation sprengt das Ereignis das gegebene System. In einer zweiten Negation wird das Ereignis negiert: Es erscheint nicht mehr als eine von außen hereinbrechende Katastrophe, sondern es wird erkannt, wie das System aus sich selbst heraus das Ereignis hervorgebracht hat. Das führt in einem »Re-entry« zu einem neuen Verständnis des Systems. Dieser Vorgang wird sich stufenweise wiederholen.
Allerdings scheint mir die Kopenhagener Deutung noch zu naiv. Sie unterstellt, dass der Experimentator mit seinen Beobachtungen das von ihm beobachtete Objekt verändert. Da jedoch der Rahmen der Naturwissenschaft nicht verlassen wird, müsste diese Veränderung ihrerseits als ein physikalischer Prozess nachweisbar sein: Der Beobachter wird dann seinerseits ein Element des von ihm betrachteten Systems.
Die hier auftretende Paradoxie des sein eigenes Einwirken beobachtenden Beobachters kann nur aufgelöst werden, wenn das mechanische und das chemische Grundverständnis der Natur verlassen werden, die bis an diesen Punkt vorausgesetzt wurden: Stattdessen wird die Natur als ein organisches und in letzter Konsequenz gedacht politisches (soziologisches) System gesehen, in dem sowohl die Natur wie der Beobachter als Handelnde auftreten. Ihre Wechselwirkung wird sich auf einer grundlegenden Ebene immer mechanisch und chemisch beschreiben lassen, aber mit der Frage nach dem Beobachter geht es darüber hinaus um ein Handeln, das nicht auf die mechanische oder chemische Ebene sich selbstorganisierender Prozesse reduziert werden kann. Das ist in meinem Verständnis die Bedeutung, die mit dem nomadischen Denken gemeint ist. Es kann mit dem von Hegel eingeführten Verständnis des Selbstbewusstseins verglichen werden. Aber die Vorstellung eines Selbstbewusstseins droht noch zu sehr dem traditionellen, statischen Denken verpflichtet zu bleiben: Das Selbstbewusstsein wird meist als ein ruhiger Zustand verstanden, der im Verlaufe einer Entwicklung erreicht werden kann, wie es Hegel in der Phänomenologie des Geistes ausgeführt hat. Dagegen beschreibt das nomadische Denken deutlicher die Unruhe, die anders als bei Hegel nicht ein absolutes Wissen als ihr höchstes Gut vor Augen hat. (Hegel war sich der Schattenseite seiner Philosophie sehr bewusst, als er das absolute Wissen als »die Schädelstätte des absoluten Geistes« bezeichnete (Phän., das absolute Wissen; HW 3.591).
Zirkuläre Zeit der Teilchenphysik
Bisher wurde angenommen, dass alle Prozesse in einer übergreifenden Zeit ablaufen und synchronisiert werden können. Das hat sich mit der Quantenmechanik geändert. Bei Fritjof Capra (* 1937) werden Pfeile nötig, um Ereignisse anzuzeigen, die erst in der Zukunft stattfinden werden, aber bereits in der Gegenwart Teilchenumwandlungen verursachen. Um das tun zu können, versteht er den Pfeil als einen Operator, dessen Richtung umgedreht werden kann, wenn dies gemeinsam mit einem Vorzeichenwechsel von Quelle und Ziel erfolgt. Da hier Pfeile auf Pfeile abgebildet werden, sind zwei unterschiedliche Pfeilsymbole heranzuziehen:
(A⁺ → B⁺) ⮕ (A⁻ ← B⁻)
Das ist nur möglich, wenn es Operanden A und B gibt, für die in dieser Weise das Vorzeichen gewechselt werden kann. Das ist für ihn in der Teilchenphysik mit den Antiteilchen gegeben. Als Beispiel wählt er Experimente mit Elektronen, Positronen und Photonen. Elektronen werden mit e⁻, Positronen mit e⁺ und Photonen mit γ bezeichnet. (Hier ist zu beachten, dass das Positron e⁺ nicht mit dem Proton verwechselt werden darf, das aus der Nuklearphysik bekannt ist. Elektron und Proton haben zwar entgegengesetzte elektrische Ladung, unterscheiden sich aber ansonsten in zahlreichen Eigenschaften. Zum Beispiel verfügen die Protonen über eine weit größere Masse. Für Antiteilchen wird dagegen angenommen, dass sie sich ausschließlich in der Ladung unterscheiden.)
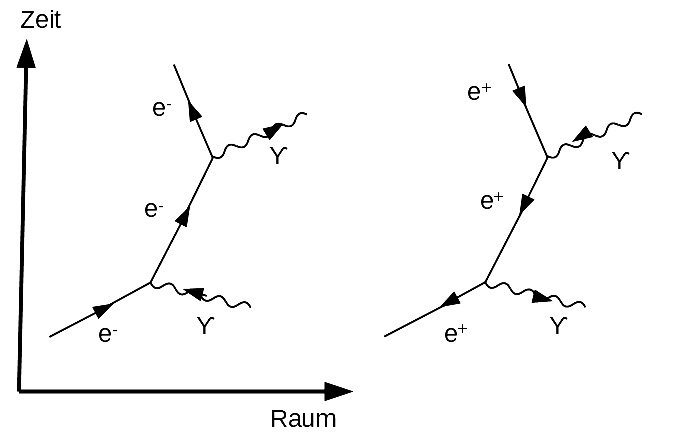
Figur 8 a,b: Zeitumkehr bei der Elektron-Photon- und Positron-Photon-Streuung
Quelle: Capra, 182, 184
Figur 8a: »Ein Elektron e⁻ stößt mit einem Photon γ zusammen; das Elektron absorbiert das Photon und setzt seinen Weg mit anderer Geschwindigkeit fort (andere Neigung der Weltlinie); nach einer Weile sendet das Elektron das Photon wieder aus und kehrt seine Bewegungsrichtung um.« (Capra, 182)
In dieser Beschreibung können sich Objekte im Raum in entgegengesetzte Richtungen bewegen. Das entspricht der klassischen Mechanik, wenn beispielsweise zwei Objekte aufeinanderprallen und ihren Impuls übertragen. Alle Prozesse erfolgen in der gleichen Zeitrichtung, in dieser Darstellung von unten nach oben.
Figur 8b: Das Positron e⁺ ist das Antiteilchen des Elektron mit positiver statt negativer elektrischer Ladung. Es wechselwirkt in analoger Weise mit einem Photon.
»Für die Darstellung des Positron-Photon-Streuprozesses brauchen wir im gleichen Diagramm nur die Richtung der Pfeile umzukehren.« (Capra, 184)
»Der mathematische Formalismus der Feldtheorie läßt für diese Linien zwei Deutungen zu: als Positron, das sich in der Zeit vorwärts bewegt, oder als Elektron, das sich in der Zeit rückwärts bewegt! Mathematisch sind beide Interpretationen identisch.« (Capra, 184f)
Mithilfe der Zeitumkehr von Teilchen und Antiteilchen werden virtuellen Teilchen definiert: Virtuelle Teilchen sind Paarbildungen eines Teilchen und eines Antiteilchen, die sich in der Zeit einander entgegen bewegen. Das eine Teilchen bewegt sich in die Zukunft, erzeugt dort sein Antiteilchen, das zugleich in die Vergangenheit wirkt und dort das ursprünglich erzeugende Teilchen auslöscht (annihiliert). Im Ergebnis scheint nichts geschehen zu sein, und es erscheint überflüssig, eine solche Operation einzuführen.
Virtuelle Teilchen sind zunächst ein reines Gedankenkonstrukt. Sie werden jedoch in der Teilchenphysik eingeführt, wenn dort an realen Teilchen Änderungen beobachtet werden, für die es keine nachweisbare Erklärung gibt. In diesen Fällen wird angenommen, dass virtuelle Teilchen auftreten, die unmittelbar wieder verschwinden und dennoch eine Änderung der realen Teilchen bewirken.
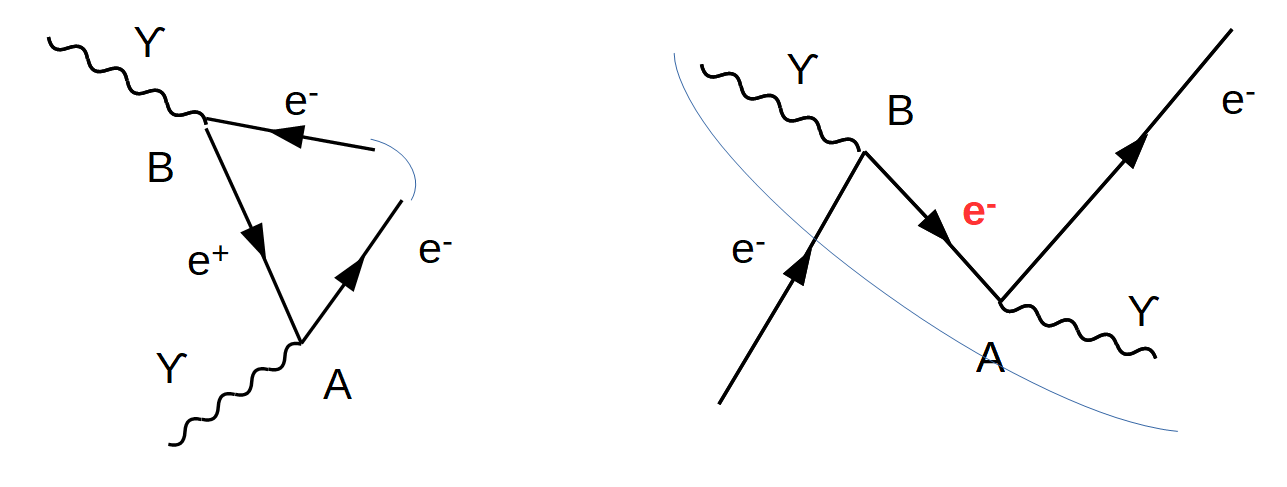
Figur 9 a,b: Streuprozess mit Photonen, Elektronen und einem Positron
Capra, 187
Figur 9a: Das Photon γ ändert in der Darstellung von unten links nach oben links seine Bewegung, ohne dass es dafür eine Erklärung gibt. Daher wird angenommen: »Das Photon γ erzeugt in Punkt A ein Elektron-Positron-Paar; das Elektron e⁻ fliegt nach rechts, das Positron e⁺ fliegt nach links; das Positron kollidiert mit dem ursprünglichen Elektron in Punkt B, und sie vernichten sich gegenseitig unter Erzeugung eines Photons, das nach links fliegt.« (186) Diese Interpretation lässt offen, warum und wo das ursprünglich erzeugte Elektron seine Richtung ändert, so dass das Positron mit ihm kollidieren kann. Diese Wegstrecke ist mit der hellblauen Kurve angedeutet. Möglicherweise ist eine höherdimensionale Geometrie anzunehmen, in der das Positron wie entlang einer Kugeloberfläche fliegt und auf das Elektron trifft.
Figur 9b: »Alternativ können wir den Prozess auch als Wechselwirkung zwischen den beiden Photonen und einem einzelnen Elektron deuten, das in der Zeit zuerst vorwärts, dann rückwärts und dann wieder vorwärts fliegt. Für diese Deutung folgen wir nur auf dem Weg den Pfeilen auf der Elektron-Linie. Das Elektron fliegt zu Punkt B, wo es ein Photon aussendet, seine Richtung umkehrt und zeitlich rückwärts nach Punkt A fliegt; dort absorbiert es das ursprüngliche Photon, kehrt wieder seine Richtung um und fliegt vorwärts durch die Zeit.« (Capra, 186) Die veränderte zeitliche Richtung des Elektrons auf dem Weg von B nach A ist durch die Farbe rot gekennzeichnet. Die elliptische, hellblaue Kurve deutet den Weg des Photons an.
»Diese Schwierigkeiten vermeidet man am besten dadurch, daß man Raum-Zeit-Diagramme wie das obige nicht als chronologische Aufzeichnungen des Weges von Teilchen durch die Zeit sieht, sondern als vierdimensionale Strukturen in der Raum-Zeit, die ein Netzwerk zusamenhängender Ereignisse darstellen, das keine definitive Richtung der Zeit enthält. Da sich alle Teilchen in der Zeit vorwärts und rückwärts bewegen können, genauso wie im Raum nach rechts und links, ist es nicht sinnvoll, auf den Diagrammen eine Zeitrichtung festzulegen.« (Capra, 187)
Mit der Umkehr der Zeitrichtung wird beschrieben, was in anderen Darstellungen als Vakuumfluktuation oder Borgen in die Zukunft bzw. aus der Vergangenheit bezeichnet wird. Das Bild rechts zeigt ein Borgen aus der Vergangenheit: Das Elektron fliegt zeitlich zurück, holt sich aus der Vergangenheit ein Photon, und gibt es wieder ab. Wird dieser Vorgang für das Antiteilchen betrachtet (das Positron), so kehren sich alle Pfeile um: Das Positron borgt sich ein Teilchen aus der Zukunft und gibt es anschließend wieder ab.
So zu denken droht in die Paradoxien von Zeitreisen in die Vergangenheit zu geraten. Ist es möglich, heute Bedingungen zu schaffen, die zugleich rückwirkend das gegenwärtige Handeln begründen, aus denen sie hervorgehen?
Wenn das geschieht, geht es für Capra um ein Ereignis, das sich der überlieferten Naturwissenschaft entzieht. Anders als Deleuze sucht er nicht nach einem nomadischen Denken, sondern er bezieht sich wie viele andere Naturwissenschaftler der 1960er auf den Buddhismus. Weitere prominente Beispiele sind der Logiker George Spencer-Brown (1923-2016), der Biologe Francisco Varela (1946-2001) und der Informatiker Joseph Goguen (1941-2006), dessen 1991 veröffentlichtes Categorical Manifesto maßgeblich zur Anwendung der Kategorientheorie auf die Computerwissenschaft beitrug. Sie spüren, dass die überlieferte Mathematik und Naturwissenschaft mit dem Übergang in eine dynamische Wissenschaft in eine Krise geraten ist, die bis in Fragen der Religion reicht. Darüber soll an dieser Stelle nicht weiter spekuliert werden. Für mich besteht die Gefahr, voreilig aus Fragen der Wissenschaft in das Gebiet der Religion zu wechseln, statt tiefer den Fragen nachzugehen, die innerhalb der Wissenschaft aufgetreten sind. Das schließt nicht aus, dass von der Wissenschaft aus so genau wie möglich Fragen an den Buddhismus gestellt werden, siehe dazu den Beitrag Drei Fragen der Quantenphysik an den Buddhismus und den Beitrag Das Licht, Vier Fragen der Relativitätstheorie an den Buddhismus.
Die Frage nach der zirkulären Zeit der Teilchenphysik ist mit den Streuexperimenten und der Idee virtueller Teilchen nicht abgeschlossen. Sie wird mit den Untersuchungen zur Quantenverschränkung fortgeführt und hat zu neuen philosophischen Ideen wie der Einführung von Hyperobjekten durch Timothy Morton (* 1968) angeregt, die derzeit im Kontext der wissenschaftlichen Untersuchung der Klimawende diskutiert werden.
Siglen
HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971; Link
Phän = Phänomenologie des Geiste (HW 3)
Enz = Enzyklopädie der philosophischen Wissenschaften (1830) (HW 8-10)
Literatur
Vera Bühlmann: Generic Mediality, On the Role of Ciphers and Vicarious Symbols in an Extended Sense of Code-based 'Alphabeticity'
in: Rosi Braidotti, Rick Dolphijn (Hg.): Philosophy After Nature, London, New York 2017 (Rowman & Littlefield International Ltd), 31-54
Fritjof Capra: Das Tao der Physik, Bern, München, Wien 1983 [1975]
Manuel DeLanda: Intensive Science and Virtual Philosophy, London 2002
Gilles Deleuze: Differenz und Wiederholung, München 1992 [1968]
Simon Duffy (Hg.) (Duffy 2006): Virtual Mathematics, the logic of difference, Manchester 2006
Simon Duffy (Duffy 2013): Deleuze and the History of Mathematics, London, New York 2013
Robert J. Finkel: History of the Arrow, in: printinghistoriy vom 1.4.2015
Ralf Krömer: Zur Geschichte des axiomatischen Vektorraumbegriffs, Wuppertal 2000
Ralf Krömer: Die Kategorientheorie: ihre mathematischen Leistungen, ihre erkenntnistheoretischen Implikationen, Wuppertal 2004
Ladislav Kvasz: Patterns of Change, Basel, Boston, Berlin 2008
Giuseppe Longo: Synthetic Philosophy of Mathematics and Natural Sciences Conceptual analyses from a Grothendieckian Perspective, in: Speculations 2015; PDF
Jeff Miller: Earliest Known Uses of Some of the Words of Mathematics; Link
Jeff Miller: Earliest Uses of Various Mathematical Symbols; Link
Isaac Newton: Opticks, 1730-Edition; PDF
Michel Serres: Atlas, Berlin 2005 [1994]
Andrea Sick: Kartenmuster. Bilder und Wissenschaft in der Kartografie, Hamburg 2003
George Spencer-Brown: Laws of Form, New York 1972 (Julian Press) [1969]; archive.org
Libb Thims: Encyclopedia of Human Thermodynamics, Hmolpedia 2020 (URL: EoHT.info); Link
Walter Tydecks: Hegel und Hilbert – das Maßlose (Substrat) als Keim der Quantenzahl, Bensheim 2013; Link
Walter Tydecks: Das reale Maß – die Logik der chemischen Sphäre, Bensheim 2013, 2019; Link
Walter Tydecks: Das nomadische Subjekt nach Gilles Deleuze und Rosi Braidotti, Bensheim 2015; Link
Walter Tydecks: Drei Fragen der Quantenphysik an den Buddhismus, Bensheim 2018; Link
Walter Tydecks: Das Licht, Vier Fragen der Relativitätstheorie an den Buddhismus, Bensheim 2019; Link
Fernando Zalamea (Zalamea 2009): Synthetic Philosophy of Contemporary Mathematics, Windsor Quarry, New York 2012 [2009]
Fernando Zalamea (Zalamea oj): Peirce's Continuum, ohne Ort, ohne Jahr
Slavoj Žižek: Disparitäten, Darmstadt 2018 [2016]
Bildnachweis des Titelbildes: Urheber Geek3; - Own work, CC BY-SA 3.0, Link
© tydecks.info 2021



