Re-entry by Spencer-Brown

Lecture for the formlabor in Berlin on January 31 2020 (substantially extended version), German original text

 

Introduction (Eigenvalues and Re-entry)

The theory of re-entry is at the heart of the Laws of Form. And it is also the only idea of Spencer-Brown that has got some attention. By re-entry is meant that, in a formally describable process, something dissociates itself from a given set, performs its own movement in a virtual space that is virtual from the point of view of the original set, changes in the process, and finally returns to the basic set as something new. The initial set not only takes up an element that could not previously be represented within its framework, but it is also changed as a whole by this process. It vibrates and is seized by a temporal process. The element taken up with the re-entry must be sewn.

To think in this way requires an imagination that was not common in traditional logic and mathematics and can only be historically proven at the place of its origin, but has been lost since then. It is therefore not surprising to me that ideas of this kind have so far only been taken up by psychology and sociology, but not by mathematics, computer science and academic philosophy. Precursors of re-entry exist in the poetry of the Romantic period, which revolted against the pure reason of the Enlightenment. Someone speaks of a lion, and suddenly a lion appears, stepping out of the realm of fantasy into reality and confusing the events and with them the confused reader of the story. »In such operations, the content of the text is ejected from the language itself, which is a specific feature of romantic texts.« (Gabriele Stumpp, email from October 20, 2019, my translation) The perspective is changed. »In general, one asks what someone means by what they say; E.T.A. Hoffmann asks what someone actually says when they mean something.« (ibid.) The same applies to mathematics, even if we no longer perceive it, because we have become accustomed to it. No one asks what it means when mathematicians speak of roots. Are these roots from which trees grow and which can be eaten? What imagination has led mathematicians to talk about roots? Why was imagination necessary to call such numbers roots and to insert them into the set of natural numbers?

This is the theme of the re-entry: (i) How does an infinite motion become independent from the natural numbers, leading to new numbers like the roots, and how are these numbers smoothly incorporated into the numbers? (ii) What causes these foreign objects not to evaporate into the unknown, but to turn around and return within their virtual space? Spencer-Brown does not only mean mathematics, but all linguistic processes that operate with signs.

This question goes back to the beginnings of Greek mathematics and philosophy. In his dialogue Theaitetos, Plato describes the roots as dynamic numbers, whereby dynamis means both that they exist only in the realm of the possible and that they have a power (dynamis) that leads them back from mere possibility to the usual calculation. If they not only move away from the natural numbers, but return, there must be an inner tension (tonos) in their movement that prevents them from vanishing into arbitrariness. In poetry, this is the creativity and empathy of the writer who knows how to form his fantasies so that they reach the reader and are understood by him.

It has to be shown step by step how the dynamic number that becomes independent has a law of its own that allows it in a double movement first to gain autonomy and then to reverse itself.

(i) Resonance. A vibrating body causes another body to resonate with it, which has an effect on the triggering body, changing its vibration and, in turn, the resonance. This can lead to a resonance disaster to complete self-destruction. If, on the other hand, the oscillation of both bodies stabilises to a harmony, one can speak of an eigenvalue, through which both meet and are connected to each other. Everybody knows this, who sings or makes music together with others or as listener perceives the leveling off.

(ii) Response. A person expresses a message and learns from the addressee how he or she has understood the message. Often enough this will amaze them and inspire them to further ideas. He will learn that he has said much more and often something different than he was aware of at the moment of utterance. Thanks to the feedback the communicator will check and adjust the comprehensibility and expressiveness of his message. In the course of the conversation both will get to know each other and after a while they will know almost in advance what the other person is getting at.

(iii) Feedback. The re-entry can be realized in a technical process. The simplest example is the thermostat: depending on the respective room temperature, the heat supply is increased or reduced. The steady state of a steam engine, for example, is somewhat more complex: the feedback changes the process. This can result in a tumbling movement. If the feedback becomes stable and the process moves smoothly, we can speak of an eigenvalue. It is not certain whether a system can reach an eigenstate or will remain in a chaotic motion.

(iv) Reflexivity. In the simplest case, I see myself in the mirror and begin to understand how others see me. The mirror image is the reflection of the object in front of the mirror. This can be extended in philosophical reflections: With them a model is created in which the reflected reality is mirrored.

These examples may lead to an understanding of the re-entry, and yet the re-entry differs from them in one essential point: The re-entry is created from within. It is not created by an external observer or an external entity and its feedback or an external influence (such as a heat input). There is no mirror from which anything is reflected and shows the process an image of itself. The re-entry returns of its own accord, and the question is how this reversal from within itself becomes possible. It lies in the laws of motion of the processes Spencer-Brown is looking at (intransitivity, cyclicity, algebraic rules of imaginary numbers).

Spencer-Brown transfers this to logic and mathematics and wants to show how self-reflexivity emerges from a formal system by itself. It does not have to be brought into the system afterwards by an observer. Gödel can be understood as a precursor of Spencer-Brown. Using prime numbers, he developed a method by which every proposition can be mapped to the elements of which it is composed (Gödelisation). This can also be a sentence like 'this sentence is wrong' or 'go one step further at the place where you are' (Turing machine). In the result, each element gets a double meaning: It can be a "normal" element or the image of a sentence formed by these elements. In an infinite regress, Gödelisation can also be gödelised. In their double meaning as element and sentence composed of elements, the elements contain within themselves the germ of a movement that starts from them and leads back to them: Sentences are formed from elements, and these in turn are mapped onto elements.

With the re-entry circularity and dynamics come into the logic. It is no longer limited to causal or conclusive chains with which one element of the system is concluded by another element, but the logic of the system-in-whole changes in interaction with its elements. Spencer-Brown thus also demonstrates a way out of Russell's paradox. He does not simply construct an alternative system in which, for example, the continuum hypothesis is dropped in order to test whether it is consistent, but rather, starting from the traditional systems of logic and mathematics, he develops how in them a movement between the system and the elements is set up, which is used by mathematicians in certain cases, and designs the general progression form which they satisfy. This leads to a new understanding of numbers.

As an introduction, the examples of the golden section from the Fibonacci series, the transfinite numbers and the irrational numbers will show how the re-entry as intended by Spencer-Brown can be read from them. Here is to be noted: If the numbers are understood as the objects of mathematics, then with the transfinite and irrational numbers new objects are added to the numbers. But it is not only about objects: New symbols must be created for the transfinite and irrational numbers. This is only possible if the object level is left and new names and symbols for numbers are introduced on the language level. Spencer-Brown goes one step further: He not only asks for new objects, but also for new language elements that are not included on the object level, but on the language level. This leads to a cyclical movement between the object and language levels. It is the thesis and the concern of this commentary to prove and execute this in detail.

Which properties of a given formal system enable re-entry? Spencer-Brown leaves this question open, but he gives hints for its solution. In his calculus he looks for a process that corresponds to the formation of transfinite numbers and irrational numbers and finds it in the echelon 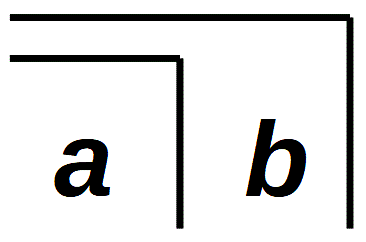. The graduation occurs in two places in his calculus of forms: (i) In consequence C7 he describes how a transitive echelon can be transformed into an intransitive figure. (ii) In the chapter on re-entry he chooses the staggering in order to demonstrate the formation of a new sign, which has to be taken up again by re-entry.

Can these two aspects be brought together? I want to show how staggering can be used to find an extended understanding of the arrangement of natural numbers, from which the emergence of a supplement and its re-entry can be explained. With intransitivity, the cyclicity is given, thanks to which the process first leads out of the given objects and can return again, without having to rely on an external influence for the reversal.

I got the inspiration for this idea from Donald Kunze (* 1947): He noticed how Spencer-Brown showed an equation (better: oscillation) of transitivity and non-transitivity in the figure of the echelon (Consequence C7 in LoF, 34). He compares this with examples from the history of urban planning and the wood engraving Der Zeichner des liegenden Weibes by Dürer, Nuremberg 1538.

Finally, the question of multivalence arises as well as an imaginary axis in which the dynamic numbers are entered. What is the relationship between this axis and Gotthard Günther's Kenogrammatik.

Iteration, Rekursion, Backtracking, Re-entry

What distinguishes iteration, recursion, reset and re-entry?

Iteration is the multiple repetition of the same calculation process, in programming a loop. The simplest iteration is counting, where the addition n + 1 is repeated continuously:

Iteration is the multiple repetition of the same calculation process, in programming a loop. The simplest iteration is counting, where the addition n + 1 is repeated continuously:

Initial number	1
Loop with fixed step increment 1	1 + 1 = 2 2 + 1 = 3 3 + 1 = 4 …

Counting is also a recursion: This means that each new calculation step takes the result of the previous calculation step as its starting point. The first counting step has led to the 2. Counting continues from the 2 and so on.

The recursion need not be limited to the last result. In the Fibonacci sequence, the sum of the last two elements of the sequence results in the new sequence element:

Initial numbers	0 1
Loop with variable step increment	0 + 1 = 1 1 + 1 = 2 2 + 1 = 3 3 + 2 = 5 5 + 3 = 8 8 + 5 = 13    …	2 / 1 3 / 2 5 / 3 8 / 5 13 / 8	= 2 = 1,5 = 1,66… = 1,6 = 1,625 → 1,618… (Φ, Golden Ratio)

Johannes Kepler had noticed that the ratio of two subsequent elements of the Fibonacci sequence aₙ₊₁ to aₙ approaches the Golden Ratio, but never reaches it. Since the golden ratio is not a common number, it is given its own symbolic name: Φ. Thus, from a sequence of natural numbers a number is approximated which is not natural and must be included in the set of all numbers by a re-entry. Since it is a ratio value within the series, it can be called an eigenvalue with some justification. Since then it has been regarded as the inner harmony of growth as well as beauty.

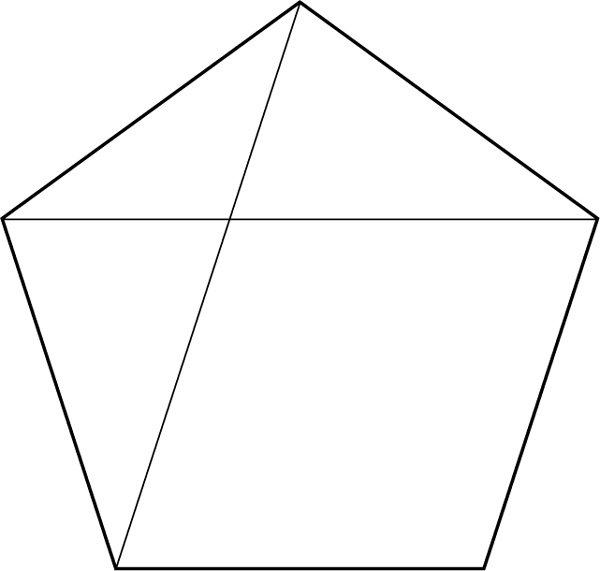
Where is the golden ratio, if it is not a natural number? Since Pythagoras it is known that in the pentagon the diagonals intersect in such a way that the two halves of a diagonal are in proportion to the golden ratio:

It becomes even more vivid when the Fibonacci series is unfolded as on a spiral in a plant where the golden angle occurs:

Phyllotaxis of the Aloe polyphylla
Author: By Stan Shebs, CC BY-SA 3.0, Link

If you want to calculate the root of 2 without a pocket calculator in writing, you can also use a recursive approach by calculating one decimal place after the other:

1st Digit:	1 · 1 = 1 2 · 2 = 4
	4 is too large, therefore the 1st digit is 1
2nd ditit:	1,5 · 1,5 = 2,25 1,4 · 1,4 = 1,96
	2,25 is too large, therefore the 2nd digit is 4
3rd digit:	1,41 · 1,41 = 1,9881 1,42 · 1,42 = 2,0164
	2,0164 is too large, therefore the 3rd digit is 1
…

A geometric example is the Pythagoras tree. At the upper edge of a square a right-angled triangle is created, at its catheters new squares, at their upper edges again right-angled triangles and so on.

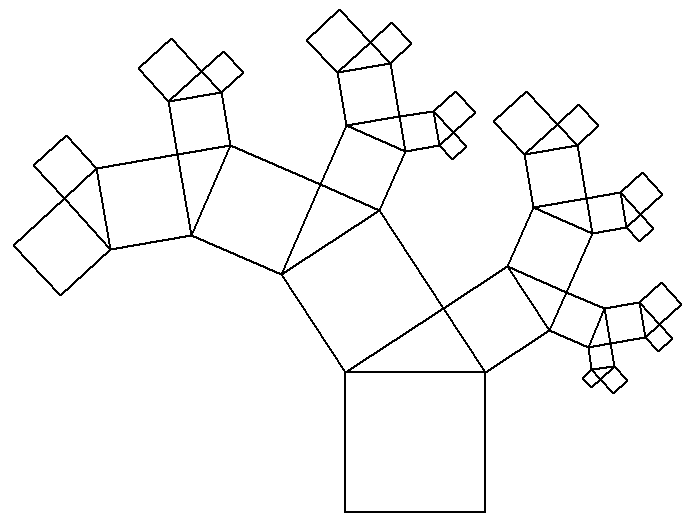
Pythagorasbaum
Author: Public domain, Link

» In programming terms, an iteration results in a loop, a recursion in the call of a method by itself.« (Uni Leipzig, my translation)

Backtracking. The elementary example is the way through a labyrinth.

Deep search of Backtracking
Author: Alexander Drichel - Eigenes Werk, CC BY-SA 3.0, Link

– The first step is to branch to the left at every bifurcation until a dead end is reached.
– The last step before the dead end is marked as a wrong way. From this bifurcation point, take the next possible path to the left.
– If all paths from a bifurcation point are marked as wrong paths, a step is taken to the previous bifurcation and from there a path is searched again.
– If the output is found, the procedure is ended.

The backtracking includes iterations and recursions: Individual steps, similar to each other, are executed, and after each dead end, the procedure is recursively recalled. However, backtracking contains more than just the simplest recursion, it also contains the marking of wrong paths. – Practical applications of backtracking are the Knight's tour, »to find a route for a knight on an empty chessboard, on which he visits each square exactly once«, the route search, various game programs or the programming language PROLOG.

What is the difference between the Re-entry and these algorithmic procedures? Wherever the three dots ›…‹ were previously entered, the three dots are replaced by a new number that was not contained in the previous number space and is taken up there by a re-entry. Mathematicians have always done this – without being aware of it – by introducing new number symbols and adding them to the original set of numbers. The default case are irrational numbers like the 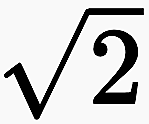, for which the new symbol is introduced.

In my understanding Spencer-Brown wants to solve three questions with the re-entry:

– What property does the original number space have so that a process can occur that leads out of it?

– What is the property of the space in which this movement takes its course? In the first place it is the space of the possible, the space of the imaginable (the imaginative power) and mathematically speaking the space of imaginary numbers. These properties must also explain why the movement reverses and returns to the initial space. In any case, these numbers are intransitive. This can already be seen at the imaginary numbers: The number i is neither larger nor smaller than 0. Although for complex numbers z their values |z|, – these are their distances from the zero point –, can be ordered transitively, but with them the identity is lost: i and 1 have the same value 1.

– What is the property of the initial space to take the returning dynamic numbers? It must be continuous. Thanks to its continuity, there are, graphically speaking, enough gaps between the already known numbers in which the re-entry can fit. If we look at this more closely, this is not a property of the numbers, but of the medium in which they are inscribed. The concept of the number is expanded: it is no longer just a matter of individual elements (the numbers), but of the continuum, which always contains more than the totality of its elements. Spencer-Brown has embedded the paradoxical question of the relationship between the set and its elements (Russell's question of the set of all sets that do not contain themselves as elements) in the broader question of the relationship between the medium and the forms registered in the medium (information).

Re-entry of the transfinite and irrational numbers

Prototypes (models) for the re-entry are, in my opinion, the construction of the first transfinite number ω with Cantor and the border crossing, which leads to the approximation of irrational numbers like .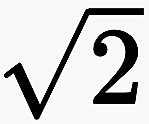

Transfinite numbers When counting ›1, 2, 3, … n, n+1, …‹, formally speaking, the same successor relation of ›n‹ to ›n + 1‹ is repeated infinitely often. Beyond all countable natural numbers lies the transfinite number ω. It can never be achieved by counting and has no predecessor, but it can be formally defined as the result of the rule of counting-in-whole. There must be an overlapping number class (a ground, a cause) in which the limit can be included by re-entry.

Where is ω, and how is ω included in the numbers? The mathematician Riemann had found a very vivid idea for this: If a sphere is placed on the straight line of numbers at the zero point, whose center is identical with the number zero and whose surface intersects the axis of the numbers at the two points −1 and 1, a point on the sphere can be uniquely assigned to each number by drawing a connecting line between the north or south pole and the respective number, which intersects the sphere at exactly one point. For numbers outside the sphere (in the following illustration, these are the numbers greater than 1 or smaller than −1), the intersection point is on the upper hemisphere, for numbers inside the sphere (these are the numbers in the interval [−1, 1]) on the lower hemisphere. The north pole corresponds to the number &omega on the number line infinitely far away; and with this construction method, it is included in the number class of all points on the sphere. The 0 is mapped onto the south pole.

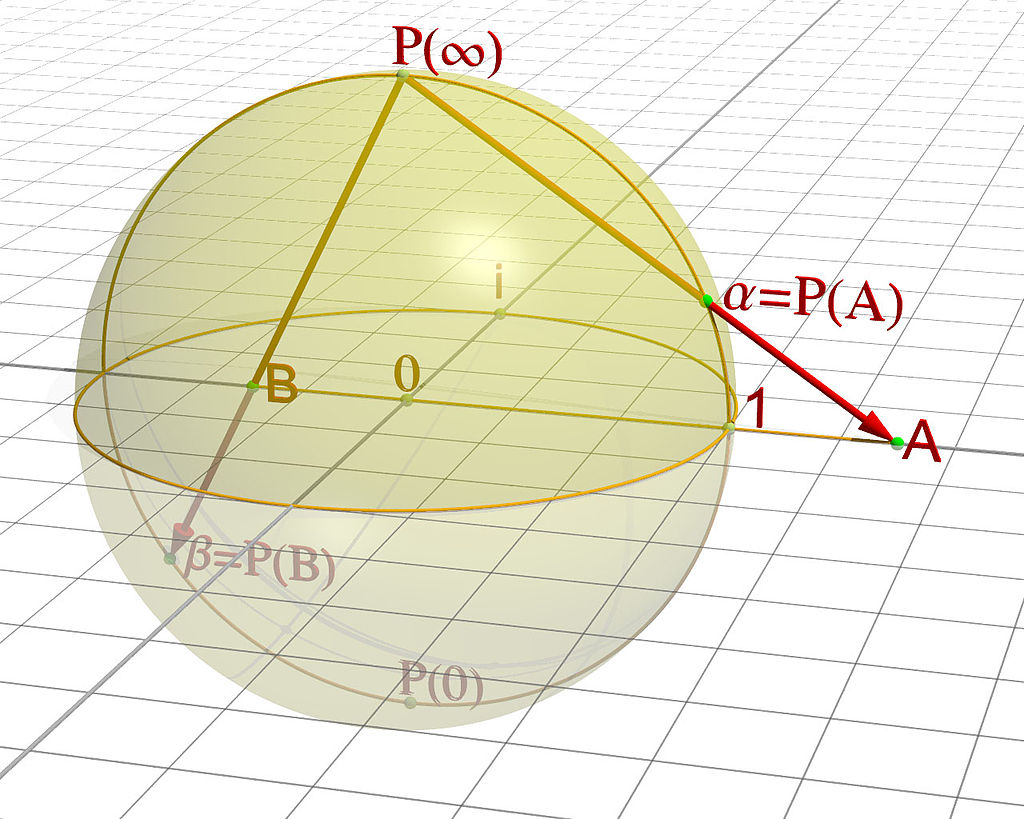
Source: Wikipedia, recalled on 4 March 2017
Author: Von Jean-Christophe BENOIST - Eigenes Werk. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV., CC BY-SA 3.0, Link

On the picture you can clearly see how ω lies infinitely far away on the number line, but finds its place on the number sphere at P(ω). How is this possible? The number sphere implicitly introduced new properties of the numbers, which are not yet present in the number line: The number sphere has a second, independent dimension (its height, which can also be interpreted as an imaginary axis or time axis), it is symmetrical to rotations (cyclic), and it is curved. These are properties that go beyond the previously known properties of numbers (transitivity, continuity) and already clearly suggest that an extension and new definition of numbers is necessary if processes leading to re-entry are to be allowed. (Spencer-Brown shows in the following chapters how this picture and these properties lead to the novel theory of observers).

Irrational numbers There is no decimal representation for irrational numbers such as 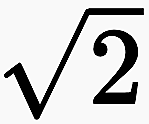. It is approximately 1.414… and can only be determined more precisely on a continuous basis. With each step, the interval in which it must lie is more precisely defined. For example, the expression 1,414… says that it lies somewhere in the interval [1,414, 1,415]. And just as Cantor had to find own symbols for the transfinite numbers with ω, for the irrational numbers with the root sign an own symbol had to be agreed.

Spencer-Brown mentions the irrational numbers in the Notes when he speaks of second-order equations. He demonstrates this with the square function x² or in his calculus aa = a and executes it on the elementary polynomial of second order. (LoF, 97f)

What happens at the two transitions to the transfinite and irrational numbers? It is no longer an ordinary arithmetical operation. An arithmetic operation such as ›7 + (10 · 3) / 91‹ can be arbitrarily complicated. In the end, however, it is a finite string consisting of operands and operators (in the simplest case, the natural numbers as operands and the usual calculation rules +, −, · and / as operators), which leads to a uniquely determined rational number. In contrast, in the case of infinite counting on and in the case of the approximation algorithms for determining irrational numbers, an arithmetic operation is  repeated  (iterated) infinitely often. It is only the repetition (iteration) that creates a process. Mathematics has remained unnoticed until today, or it does not want to admit that time is implicitly contained in the process of repetition. – Mathematics insists until today that its formulas are basically timeless. Only Spencer-Brown made the long overdue turnaround and consistently developed how time is implicitly contained in the process leading to re-entry.

With arithmetic operations, the respective number class is not left. It returns a new number and can be identified with it. It is the same whether one speaks of 12 or of ›5 + 7‹. With processes, on the other hand, a new number is defined which was not yet contained in the previously considered number class. Neither ω a natural number nor 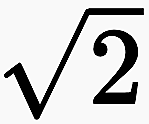is a rational number. With them a new concept of numbers is created: Numbers are all elements that can be used to calculate like natural and rational numbers. What a number is and what belongs to the totality of numbers will be developed step by step. The idea of the number is in itself infinite, and it can be assumed that new processes will always be found to recognize new numbers with properties that were previously unknown.

The re-entry in the Laws of Form and its language

How can Spencer-Brown transfer the infinite processes of counting or approximating an irrational number into his formal calculus? It would be most obvious to count the forms of proto-arithmetic in a similar way as natural numbers and to show that there must be an infinitely distant element that can be included in the set of all forms by a re-entry. But there is no unambiguous successor relation in his calculus like in the natural numbers, instead there are two possibilities of iteration of forms, which again can be combined arbitrarily:

Repetitive calling	⃧  ,  ⃧   ⃧  ,  ⃧   ⃧   ⃧   , …
Repetitive Crossing	⃧  ,, , …

A lexicographic order of all forms can look like this:

  

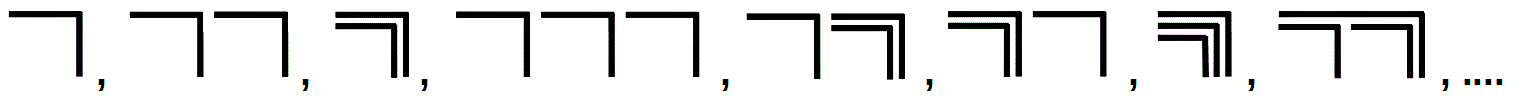
Bernie Lewin has examined the two iterations and understands them as the horizontal and vertical components of a holistic, two-dimensional gnomic development (gnomon, ‘pin, style, sundial’), which refers to the two-dimensional arrangement of the Tetractys with Pythagoras and can be systematically developed from it (Lewin, 185-193). He describes the horizontal component of the iterated callings as numbers and the vertical component of the iterated crossings as orders, which can be represented in a matrix (Lewin, 202). This approach seems very promising to me. Lewin gives numerous examples of how forms can be developed from the tectractys. I expect that an comprehensive development of numbers according to qualitative properties that go beyond current mathematics can be justified via the tectractys (dynamic, dreamed and imaginary numbers).

Spencer-Brown, however, has taken a different path. At first sight, he remains more conventional and has sought a one-dimensional (linear, transitive) process of forms emerging from each other, in order to include their limit value in his calculations by means of a re-entry. At the same time he goes beyond the classical examples of transfinite and irrational numbers and finds a re-entry that does not include a new number in a given set of numbers, but a new symbol f in the set of mathematical language symbols. He does not move on the object level of mathematics, – its numbers or geometric shapes – but on the meta-level of mathematical language. His re-entry is not about the numbers as the operands (objects) with which calculations (operations) are performed, but about the symbols with which the calculations (operations) and their properties are linguistically formulated and formally represented. These are symbols like the a (argument), which can stand as a variable for any number with which it is saturated, to use a descriptive expression of Frege. Symbols of this kind are usually used to describe the overall properties of sets of numbers as a whole, such as commutativity: ›a + b = b + a‹, regardless of the particular properties of the values used in a and b. It is now Spencer-Brown's novel idea to find a process for symbols of this kind, too, which leads to a limit value as in counting or approximating an irrational number and can be taken up by re-entry. This limit value shows at the individual elements (in this case the symbols of the mathematical language) a system property that is valid for the system as a whole (in this case the mathematical language). Thus, in simple terms, the system is created from the progressive order of its elements and can be included as a limit of this progressive order in itself as an element. In this way he succeeds in solving Russell's paradox: He shows how certain elements of a set can be ordered step by step in such a way that the inner law of this order emerges as the limit value of their progressive order and can be included in the set of elements ordered by him.

With these ideas he enters new ground, and it requires a complete rethinking to be able to follow him in this. First of all, a few milestones are highlighted, which will be dealt with in the following:

– Spencer-Brown chooses as a starting point a form that is both transitive and intransitive: the echelon.

– With it he succeeds in re-entry following the model of the re-entry of transfinite and irrational numbers.

– However, since he is not on the level of numbers but of language symbols used to describe arithmetical operations with numbers, he succeeds in generalizing the idea of Gödel, who showed the fundamental double character of all signs of a sufficiently complex formal system, which can be understood as operators as well as operands.

– The result is a calculus that objectively corresponds to the algebra of complex (imaginary) numbers, but which, from Spencer-Brown's perspective, take on a far more fundamental meaning than is known in ordinary mathematics. From this perspective, they can be understood as the mathematics of dynamic logic.

The following presentation is at the same time an appreciation of the work of Gotthard Günther (1900-1984), who, thanks to Warren McCulloch and Heinz v. Foerster, became aware of the newly emerging cybernetics in 1960-72 and began to look for an appropriate mathematics and logic for it. Even though, as far as I know, Günther and Spencer-Brown did not relate directly to each other anywhere, some basic ideas of Gotthard Günther are used, which in turn can be reinterpreted from Spencer-Brown's perspective (the role of reflection, the proemial relation of systems emerging from each other, and the blanks in which arguments a can be entered alternately with Spencer-Brown, such as the functions f formed via these arguments).

– The echelon without limit

Spencer-Brown chooses the echelon 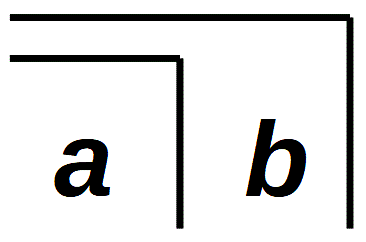as the starting point for a process that leads to re-entry within its calculation (LoF, 54).

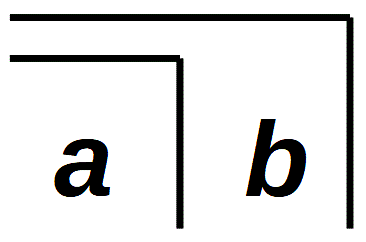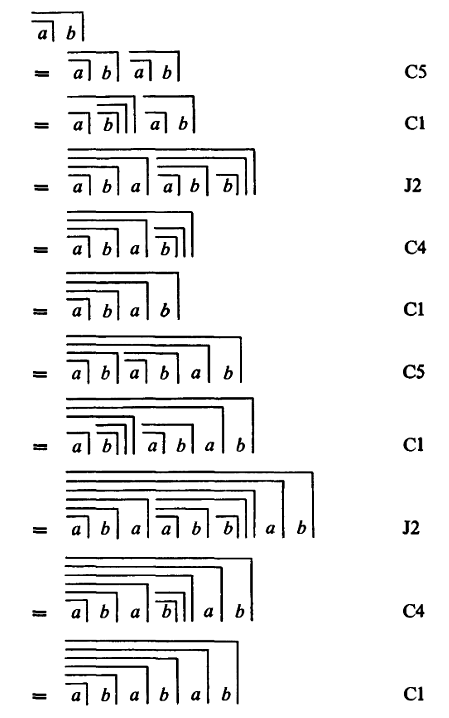
In the form calling and crossing are intuitively linked: The two variables a and b follow each other, and at the same time there is a double nesting. Spencer-Brown shows how a sequence of 5 transformations can be applied to the character , whereby the character is doubled after 5 steps, tripled after another 5 steps and so on. (LoF, 55). This representation is to be read like the step-by-step transformation of an ordinary equation until on one side the unknown x and on the other side its solution. Spencer-Brown uses the rules C5, C1, J2 and C4, which had been introduced in his calculus. (Instead of rules, he speaks of Initials and Consequences, in order to emphasize that the Consequences, in turn, can be derived from the Initials and are subsequently available as rules for operating in proto-algebra). The recalculation can be seen as a demanding exercise in dealing with Spencer-Brown's calculus. For details see the Appendix to Canon C9.

Or contracted (LoF, 56):

    ⇀ .

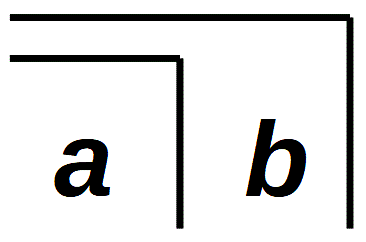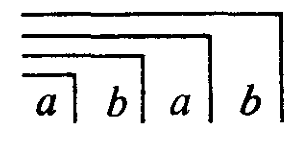The symbol ⇀ indicates that both signs (forms) are of equal value. The same sequence of 5 individual steps can be applied to the new character ( form ), thus extending it again. In this way, a sequence of steps is achieved which corresponds to the successor relation and can be repeated infinitely often. Although Spencer-Brown introduced the echelon within the Primary Algebra as Consequence C7 using three variables a, b and c (LoF, 34) and not as for two variables a and b as here, the result for him is » an echelon without limit« (LoF, 56).

The next crucial step is to imagine, if it is possible (let us imagine, if we can, LoF, 55), that the process of this sequence of steps will continue indefinitely or timelessly. In space this would result in an echelon of a's and b's without limit. [...] Since the determination of the value of an expression is bound to the rule of finite demonstrability, no statement can be made about the value of an echelon without limits.« (Schönwalder-Kuntze u.a., 175, my translation)

As a result, Spencer-Brown writes down a diagram that defines the form to be included in the proto-algebra by re-entry:

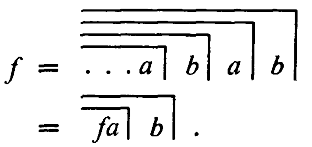
E1 Re-entry
(LoF, 56)

The formula E1, written down like a definition, highlights the recursion: The element reached in each case is called f and is recalled in the following step. The transition from a to b is repeated as often as required. He takes over the three dots from the corresponding processes known from ordinary arithmetic, if there beyond ›n‹ and ›n + 1‹ is counted further and further or an irrational number is approximated with arbitrary precision and describes with them the form resulting from the infinite process of echeloning.

The summary of the infinitely many crossings from a to b to a to b etc. in f is dependent on three conditions:

(a) »A clearly defined sequence of steps, so there is a clear construction instruction«,
(b) »it is to be repeated continuously«,
(c) and it contains a »pattern of the self-self-equality« (Schönwalder-Kuntze et al., 175, my translation).

»The key is to see that the crossed part of the expression at every even depth is identical with the whole expression, which can thus be regarded as re-entering its own inner space at any even depth.« (LoF, 56)

As a result, f has a multiple meaning:

– f describes in E1 the place where the recursion takes place and replaces the three undefined dots ›…‹.

– If the recursions are counted, then f is the name for the infinitely distant, last recursion. In this sense, f is comparable to the transfinite number ω. If f is understood as the name of the specific progression of all recursions executed in E1, it is comparable to the eigenvalues considered by v. Foerster.

– Finally, f in E1 is the name of the form used to describe the infinitely repeated recursion. E1 can be read as the self-referential written definition of f. This form with the name f stands for the element that is to be included in the proto-algebra via re-entry.

Spencer-Brown consistently keeps his idea of introducing symbols that can have multiple meanings  as well as an operation like the result of this operation. The multiple meaning of f is carefully introduced and bound by clear rules. It contains in itself a contradiction or, in the language of the early 20th century, a category mistake: f is, as the value progression of arguments a, both a set of elements, and is at the same time to be equated with the arguments a by the re-entry and included among them. This corresponds to the situation of Russell's antinomy, which speaks of the set of sets that are negatively self-referential (the set of all barbers that do not barber themselves, or mathematically: the set of all sets that do not contain themselves).

– The language of the re-entry

The 11th chapter of the Laws of Form, with its introduction of re-entry, time and networks, appears similar »dark« like the most complex aphorisms and texts by Heraclitus, Hegel or Heidegger (on dark languages, cf. Günther 1979, 3). When Spencer-Brown deals with the border crossing of symbolic forms of mathematical language, he asks the question of which language can be used self-reflectively to formulate a border crossing of this kind. It is not enough to have an external observer who sees and records this event from outside. Whoever records something uses the symbols whose border process Spencer-Brown is concerned with. Instead of an observer, one must speak of a higher language. This is the question of the language of re-entry.

Spencer-Brown describes a process that consciously evades the available characters and leads to new characters. In order to master this transition, something is needed for which the previous characters are not sufficient and the new characters are not yet available. To be able to close this gap (to make this jump successful), a specific language is necessary. This step is done in thinking with its specific imagination. The implicit language of thinking describes what takes place within the thinking process and what lies between the preconditions and their results. Since his earliest texts, Günther has taken the position that for this language of the thought process (of reflection) a value of its own is necessary, which cannot lie within the values with which the contents of thought are represented (the bivalence of logging thinking, or in the diction from Aristotle to Heidegger of categorical thinking). Is it possible with Spencer-Brown to describe this language far more precisely and possibly even to formalize it than has been possible so far with predominantly phenomenological approaches?

The specific language of the re-entry can be seen at two critical points:

– The point of the recursion gets the name f. Being able to give a name is a special language competence which, according to religious conviction, was given to man by God (Genesis 2,19). Did Spencer-Brown meet a special point with the naming of the recursion, about which this capability can be defined more precisely? Is the naming itself recursive and in a sense shows its intrinsic value in its ability to recognize and name recursive processes?

– For the re-entry of f there is no locality in the forms. f cannot be entered into a medium as a new form, but its re-entry is done by changing the medium as a whole. Spencer-Brown can find a suitable representation for this because he introduced the medium and the form as the two sides of the Laws of Form from the beginning. In the representation he has chosen, the re-entry has a certain existential effect on all forms that are inscribed in the medium. The change of the medium is neither a new form nor a new, so far unknown property of the forms, but can only be proven existentially on the forms. Spencer-Brown speaks of the oscillation of the medium, which can be felt in all forms inscribed in the medium, and the time in which the oscillation occurs. He thus succeeds in a much more precise and – if you like – less dark determination of the existential than was possible in the history of philosophy from Plato to phenomenology.

His distance to traditional philosophy can be measured best if it is presented in an analogy as a distance to traditional mathematics. How far Spencer-Brown has distanced himself from the mathematics he found can be clearly seen by comparing it with the re-entry of transfinite and irrational numbers. His kind of re-entry would mean for the transfinite and irrational numbers that not the limit ω is included in the numbers, but the successor relation with which the limit process is defined, and not the irrational number, but the limit process with which the irrational number is approximated. This is not the way today's mathematics sees it. In my view, Spencer-Brown wants to show that it does exactly that, – to include a boundary process and not a number – without realizing it or admitting it to itself. For example, when she talks about the irrational number 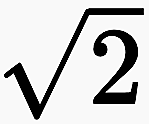, this is a symbol that does not describe a number but an approximation process. No one can say exactly where 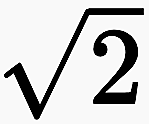is located on the number line, but it is possible to get closer and closer to its location. Geometrical considerations are of no help either: A unit square can be placed on the number line and a geometric operation can be used to draw a circle around the diagonal of the square that intersects the number line exactly where 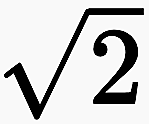is located. This clearly shows that 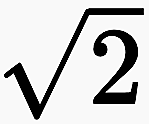has a unique location on the number line. The place is to »see«. But if you try to determine it by its numerical value, the geometric construction does not help and there is nothing left but to approximate this value more and more exactly.

There have been and still are attempts in mathematics to define real numbers in this way, which can only be determined by the process of their creation and not like fixed, static objects: The 1872 by Richard Dedekind (1831-1916; student of Gauss, friend of Riemann and Cantor) introduced cut (see Günther 1995, 9: »This cut and not the number obtained by it is the desired third value! «) and the 1974 by John Conway (* 1937; inventor of the Game of Life) defined surreal numbers. Lukáš Lánský has presented a very descriptive presentation in Wikipedia:

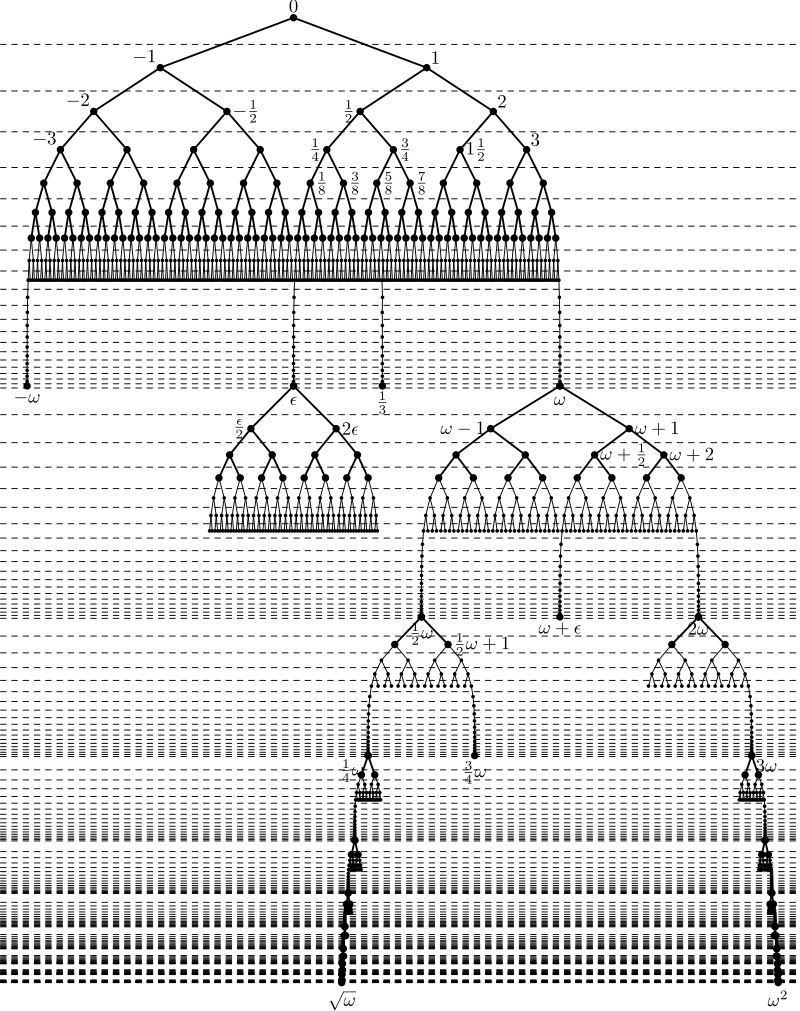
A visualization of the surreal number tree
Author: Von Lukáš Lánský - Eigenes Werk, CC BY-SA 3.0, Link

This drawing shows how the transfinite and irrational numbers can only be represented by infinite processes.

Spencer-Brown mentions Gödel several times. His idea of proof for the incompleteness theorem can be seen as a precursor to consider a number as a function and a function as a number at the same time.Gödel has shown how in any sufficiently complex formal system, in which addition as well as multiplication and by them prime numbers are introduced, every sign can be interpreted both as a number and as a function if the function is gödelised. The gödelisation is a translation: With a method based on prime numbers, each letter and each punctuation mark is assigned a number and above that, each complete sentence composed of letters and punctuation marks is also assigned a unique natural number, the gödel number. (Spencer-Brown rightly emphasizes that this consideration does not apply to his calculus, since addition, multiplication and prime numbers are not introduced there in a comparable way as with the natural numbers; LoF, 96; AUM, Session Two.).

Gödel looked at the self-contradictory sentence ›this sentence is wrong‹ and determined his Gödel number. Thus it is included as number in the formal system, although it contains an inner contradiction. Of course, this method can also be applied to any other sentence, such as the sentence ›n + 1 is the successor of n‹. If a gödel number is assigned to this sentence, then the method leading to the transfinite number ω, as method has been successfully included in the set of natural numbers.

With both re-entry and gödelisation, functions and arguments can be transformed into each other. Nevertheless, the differences are clear:

– In the case of Gödelisation, the transformation is in a way brought in from outside. Gödel has found a translation with which every sentence can be translated into a number and vice versa the number into the sentence. Spencer-Brown, on the other hand, wants to show how the function f emerges as a boundary process from the process of transformations forming an infinite series.

– The Gödelnumber is unique and is not outside or between the known natural numbers, but is a natural number whose location on the number line is uniquely determined. For the symbol f newly formed by Spencer-Brown, however, there is no place and its re-entry changes the medium in which the forms are entered.

– Conversely, Gödel's procedure gets into an endless loop when his assignment function is in turn gödelised, etc. This results in a similar infinite process as counting, whose limit value ω is not contained in the natural numbers, but must be taken up by a re-entry. This was irrelevant to Gödel's argument and was not further investigated by him, but it shows that his method is not excluded from the boundary processes either.

How does Spencer-Brown solve the problem? If there is no number to which the re-entry can fall and no place to which it can be uniquely assigned, the only way to do it is to change the properties of the medium in which all numbers are entered.

Spencer-Brown can only formulate the result of the re-entry in negative terms: It is undetermined in the given calculation where it can be included (»indeterminacy« LoF, 57). To find the right words, Spencer-Brown describes the transition from a to f in a more general sense as the transition from an expression e (for expression) to an expression e' to be taken up by re-entry:

»We have just introduced to e' a degree of indeterminacy in respect of its value which is not (as it was in the case of indeterminacy introduced merely by cause of using independent variables) necessarily resolved by fixing the value of each independent variable.« (LoF, 57)

f wanders around as it were and finds no fixed place. This wandering will lead Spencer-Brown to oscillation, with which he introduces the concept of time (LoF, 62-64). It will only be resolved when he turns from the wavelike progressions to the networks of the modulator function: In these networks a way is to be found to modulate the arguments a in functions f. (See the contribution for the The Unmarked State Conference celebrating the 50th Anniversary of the First Publication of George Spencer-Brown's ‘Laws of Form’ in Liverpool, August 9, 2019).

Transitivity and intransitivity of the Echelon according to Kunze

Did Spencer-Brown choose the form 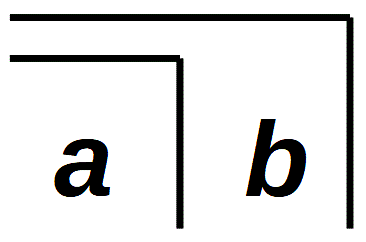just because its outer shape already points to a successor relation? Is there a hidden property of the echelon that makes it a suitable starting point for re-entry into proto-algebra? I got a hint from Donald Kunze (* 1947), who taught at Pennsylvania State University architecture theory and general arts criticism. He looks at Consequence 7 (C7), with which the echelon is transformed into another form (LoF, 34) and recognizes that with it an intransitivity is established. The echelon oscillates between transitivity and intransitivity.

Before going any further, the meaning of intransitivity should be pointed out. In everyday life we usually compare things that are evenly arranged and can be measured against a common standard. If, for example, the lengths of rolls of fabric are compared, they can be measured at the ell (ulna). They are transitive: if b is greater than a and c is greater than b, then c is even greater than a. This is no longer true for the intransitivity. The simplest example is the game Scissors, Rock, Paper: Although the scissors are stronger than the paper they cut and the rock is stronger than the scissors they dull, the rock is still weaker than the paper they wrap it in:

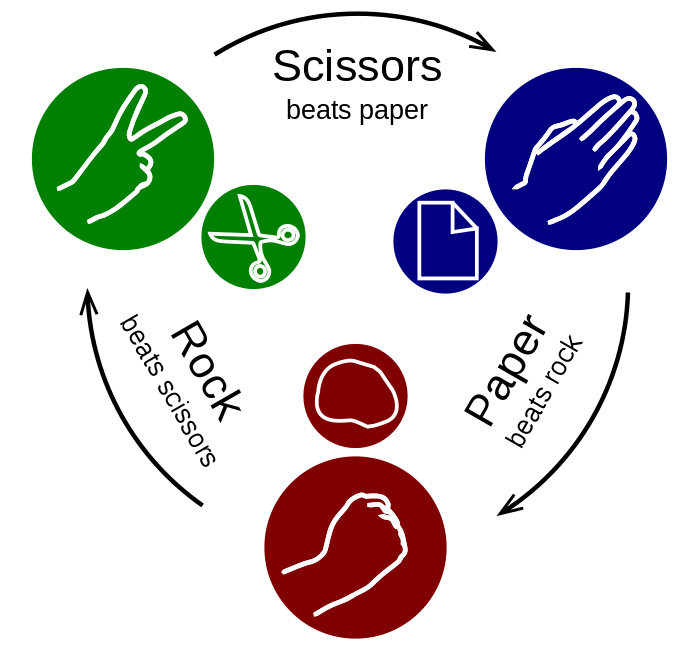
Rock-paper-scissors
Author: By Enzoklop - Own work, CC BY-SA 3.0, Link

When children play this game for the first time, they are amazed, don't understand at first what is actually happening, and then they are excited about it and can repeat it endlessly, as if they wanted to check whether it might change into a transitive order at some point. What they learn here is an example of mathematical creativity (see Spencer-Brown in AUM, Session 2). Intransitivity contains something that goes beyond ordinary mathematics: it is cyclical. An intransitive order returns to itself. And it is obviously non-hierarchical: every hierarchical higher development is a transitive order: the plants follow the stones, the animals follow them, the human being follows them, and at the highest level, depending on one's beliefs, God, the Spirit or the Absolute. In a cyclical order, the highest level returns to the lowest ground. (Every revelation has intransitive traits, e.g. when God appears in the form of a lily or in a burning thorn bush). It is this return that Spencer-Brown is concerned with when he wants to take the re-entry into the medium and not into a higher form of forms. If the language of the re-entry has been talked about so far, it will become clear how intransitivity and cyclicity are the mathematics of the re-entry. This explains the significance and the power of Spencer-Brown's re-entry for the design of heterarchic thinking, for cybernetics, and even for Luhmann's draft of a new sociology (theory of society) and a new understanding of imaginary numbers and analogy, to which this text on Spencer-Brown's re-entry is intended to contribute.

Kunze was fully aware of this. He sees the transformation of echelon into an intransitive form as no less than the key to understanding an epoch-making work by Dürer and, beyond that, the prehistory of mankind when the first cities were founded. There, as their inner logic, he wants to prove the same transformation from transitivity to intransitivity as that carried out in C7. In Spencer-Brown's work, Consequence 7 appears almost casually as one rule among many, which hardly plays a role in the rest.

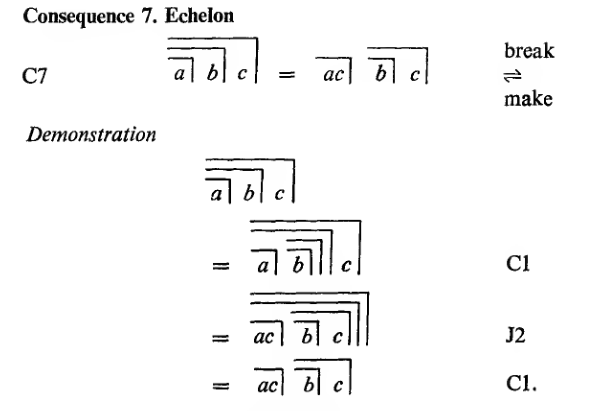
Kunze shows with an eminently vivid illustration of the ‘break’, with which the variable c is doubled and split in the echelon, where and how intransitivity occurs there: First, using C1, b becomes (a double crossing returns to the starting position). Then, according to the distributive law J2, c is placed next to a on the one hand and on the other hand in the space between the two crosses surrounding b. Thus on the one hand with ›a c‹ a transitive arrangement is created, on the other hand with ›b⃧   c‹ an intransitive arrangement. – A little confusingly, he renames the variables a, b and c written in lower case at Spencer-Brown to upper case A, B and C. In mathematics, constants are usually represented by capital letters. In the result he intuitively finds an analogy to Dürer's engraving Artist and Model in the Studio (Kunze, 333):

An architect's view is needed to understand what is happening here. Normally, the drawing is presented from the perspective of the painter: In the foreground stands or sits the painter, the observer of the painting looks over his shoulder and sees from his perspective both the object to be painted as well as the painting being created, so almost paradigmatic in the case of Jan Vermeer: he paints not simply a picture, but a picture with the title The Art of Painting.

Vermeer: The Art of Painting (1666/68)
Author: Von Jan Vermeer - lAHeqBoLaePtEA at Google Cultural Institute maximum zoom level, Gemeinfrei, Link

Dürer rotates that: Now the event is painted from the side to better illustrate which tools the painter uses for the central perspective drawing. In a similar way Kunze understands Consequence 7 in Spencer-Brown: The view is rotated, and for a viewer located to the right outside of the echelon, C appears from the side as seen from the perspective both next to A and next to B⃧  . (Kunze implicitly introduced and anticipated at this point for his interpretation of echelon the role of the observer, which Spencer-Brown will develop later after his investigation of re-entry, time and networks in chapter 12, see LoF, 69).

It remains to be explained how Kunze interprets the transition from B to B⃧  : For him, this is the transition from the object level to the meta level. With B, not only the tools of drawing are to be shown, but at the same time they are negated by B⃧   as mere tools at hand of the user and meta-linguistically stand for the term ‘drawing’. Thus a drawing is created which at the same time describes drawing as a process in a self-referential way and draws the term ‘drawing’ with it. The tools with which one draws are themselves drawn and become a metaphor for themselves: With the drawing tool a metaphor of drawing is found and in turn becomes a metaphor of drawing itself. This seems to me to be the best picture to illustrate what Spencer-Brown meant by the re-entry of the function f, which is self-referentially constituted from the process of its own arguments a and above that from the process described by it, and is taken up by re-entry. If this is seen again from a superordinate perspective (a second order meta-level), then this engraving is just as much a representation of the term ‘metaphor’, which is what all pictorial representations are about, as the engraving Melencolia I is a representation of the term ‘allegory’. On a third-order meta-level, it is a representation of geometry: thanks to its laws of perspective, drawing is possible. Geometry, in turn, builds on the analogy. On a forth-order meta-level, the analogy makes it possible to recognize the principle underlying geometry and with it both metaphor and allegory. Finally, at a highest, fifth order, one can ask about the principles that are themselves based on principles such as the principle of analogy. This leads into religious questions (see Walter Rella The Step into Analogy and the commentary Analogy Thinking according to Walter Rella). (At first glance, the orders of the meta levels are hierarchical and transitive. However, each order contains a surplus of interpretation possibilities for the respective superordinate level, from which a cyclical order results. Spencer-Brown has developed this exemplarily in the relationship between arithmetic and algebra).

To explain the special nature of Transformation C7, Kunze chooses as a further analogy the narrative of the historical origins of the cities and their trade with one another. Originally, the cities were separated from one another. As in the form 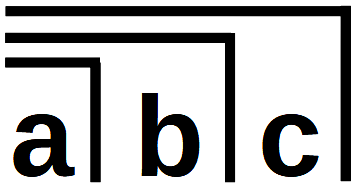all cities were separated from each other by borders, arranged transitively, one next to the other, without internal contact. Meetings and trade with strangers were frowned upon. Every household had its own gods. But there were crossroads between the cities: There some put down their surplus, which the others later picked up and put down their own surplus so that they never had to meet in person. In order to mark these trading places, stones and towers of stones were laid or erected at them. These were the original herms, for Hermes, the god of trade, theft and communication. These places became holy, and around them the first metropolises developed over time. They were connected to the first burial sites, which served the communication of the living with the dead. These meetings, like meetings between different cities, were also originally forbidden, and for these meetings Hermes was again the protecting God.

According to Kunze, the sanctification of B is the transition from B to B⃧  , in Spencer-Brown's notation the negation of B. The negation of B does not mean that the opposite of B is used, – for example black instead of white – but the real B is negated by a sacred B⃧  . The desired movement of trade becomes possible by turning three symbolic orders (negation, rotation) (Kunze, 334f):

– The motility of direct trade and commerce is interrupted by both tribes avoiding each other, but in accordance with an indirect, possibly unspoken agreement, they deposit and collect their goods at the same place in chronological order.

– The semblance of a direct trade is broken: According to their respective self-understanding, the real tribes A and C do not trade with each other at a real place B, but with the sanctification of place B, the products that are stored and exchanged there are also sanctified at this place. In this sense, the tribes do not exchange products, but the products are at the holy place where they were deposited, enclosed in images of gods B⃧  . A and C do not trade with each other, but with the herme B⃧  .

– The scalar is broken: Instead of a real trade with real goods, a holy transformation takes place at location B: What one tribe has deposited, takes on a special meaning through the sanctification, which is why the other tribe is allowed to collect these sacred products in the belief that they have not traded the other tribe's product, but have received the sacred products from the Herme.

– If this succeeds, C is split and connected to A on one side and to B⃧   hidden in a second hook. This results in a non-transitive operation.

Formal: First a double cross is placed around the B in the middle, which Kunze understands as pocket, as a sanctuary. Then C is divided according to the distributive law: One C is placed next to A, which results in a simple, transitive order with AC and allows the desired trade of A with C on the real level. The other C is placed in the gap between the two crosses, resulting in an intransitive order with B⃧  C. C is divided into two orders, but an inner relationship (an entanglement) of the two distributed C remains. This entanglement allows the later return. What has been sanctified at place B returns to the other tribe as real goods in everyday life and can be consumed there.

Is this just the intuitive view of an artist or art historian whose kind of thinking is far from mathematics and logic and whose historical truth is difficult to verify? For me, this intuition gives rise to a new view of natural numbers, which in terms of content goes back to Plato and, through him, to Pythagoras:

– Just as A and C exchange a product at place B, which was first sanctified there and later returns to economic life (re-entry), so in transitive counting a distinction must be made between the transitively consecutive numbers 1, 2, 3, … and that which lies between them and enables the process of counting and is exchanged and passed on in counting. This is the distance (the gap) between each two adjacent numbers. The distance takes on the meaning of B, at which the adjacent A and C can come together. Plato intertwines both aspects (here I follow Stenzel, 84-91 and the sources he mentioned, to whom McCulloch and with some reluctance also Günther came surprisingly close in the 1960s, see Günther 1995, 4-15): The distance is itself a number. For Plato, the odd (perissós) numbers are the numbers that are entered into a medium like isolated points, and the even (artios) numbers are the in-between (the medium) with which the distinction between two numbers and their distance from each other is possible. Why does Plato choose these terms: The first even number is 2, which not only follows 1 as a number and is itself entered on the number line, but which also defines the distance between two adjacent numbers: diastema in the multiple meaning of ‘distance, radius, interval, distinction’. The distinction with which Spencer-Brown bases his calculation goes back to this (»Draw a distinction«; LoF, 3). For his part, the distance has two aspects: It is a spatial distance between two numbers, which determines the in-between in which there are no other numbers within the natural numbers, and it has a value, which is the length of the distance, which in turn is 1. With each new number the distance is handed on when each number n is followed by a new number ›n + 1‹, which is again separated from n by a distance of length 1 and follows the measure given by the first distance between the numbers 1 and 2. Consequently, for Plato, the first odd number is 3, which follows 2, while 1 has no distance from itself. Unlike in modern mathematics, for Plato the 1 is not odd, but is outside the distinction between even and odd. The 1 is not divisible, while the even numbers can be divided into equal halves and the odd numbers only into unequal parts.

– The distance B is sanctified to B⃧  . This is recognizable at Plato only in the fact that the even numbers stand at the same time for the unlimited (apeiron) and its inner abyss. Aristotle interpreted it in such a way that for him the even numbers become the substance, which is general (katholou) and indeterminate (aoristos, Met. 1087a17), and the odd numbers become the form. Spencer-Brown has taken this further. His distinction between medium and form can be read as a new interpretation of the distinction between odd and even numbers in Plato's work.

– With the sanctification of distance B a curvature results, with Aristotle the formless (steresis) contained in the interior of the material, with Günther (even if he does not want to admit this in his criticism of Aristotle, which is incorrect for me) and Spencer-Brown the third value of a trivalent logic: The following C is connected both with its predecessor A and with the sanctified B. For me, this curvature is the inner tension (the inner degree of freedom) within the number line. It contains the possibility that processes can dissolve out of the number line and lead into an imaginary space, and vice versa, the place where this process leading out can be taken up again (re-entry).

– C splits up. On the one hand it connects transitively with A, on the other hand intransitively with B⃧  .

– However, the two divided C's remain entangled with each other. From this entanglement results the circularity and analyticity of the imaginary plane.

If the third value, given with the inner tension of the numbers, is considered on its own, it has led since the beginnings of mathematics to prominent numbers that are considered sacred. Examples are certain roots (such as 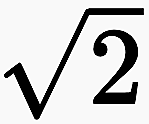, the diagonal in the square; the division of two diagonals in the pentagram ⛤, which stands for the golden section; the circle number 𝜋 and its close connection to the imaginary unit i through the Euler's formula ›ei · 𝜋 = −1‹; the first transfinite number ω. Its founders were aware of its holiness (according to Pythagoras and Cantor).

Trivalence of the re-entry and the proemial relation by Günther

»It is open whether the re-entry in Spencer-Brown's conception leads beyond the calculus and can only be absorbed by a structure of polyvalence, or whether it rather leads back into the calculus and supports the unfolding of the form there.« (Baecker 2013, 151 Fn. 23, my translation)

The trivalence is already given with the reciprocal relationship between transitivity and intransitivity: Within a transitive order, bivalence is valid when it is distinguished between greater and smaller, forward and backward. The transition to intransitivity is only possible along a third value. Initially, the question of trivalence is to be further differentiated. Above all, the question of a formal representation of the trivalence arises. After Günther has postulated a trivalence in many contributions without being able to justify and formalize it in more detail, he has made a breakthrough with the proemial relation. This is the subject of the second part of this section.

When and why does polyvalence occur?

(1) Is polyvalence needed in a given situation to initiate a movement that leads out of it and then returns through re-entry? Both the example of Kunze and the logical considerations of Gotthard Günther suggest that the impulse must come from outside by an observer. If the question is asked where the observer is located opposite the system, a third value is required to determine his location. In Kunze's case, Dürer's drawing, or the formal representation of the echelon, is in itself on a two-dimensional plane (the drawing sheet), while the observer is in three-dimensional space and can view the drawing from various perspectives. In Günther there is a rational observer who can look at the system that remains in bivalent logic and the opposites that apply in it, gain distance from this system, reflect on the situation and freely make the decision to reject the given bivalence and its oppositions (rejection) and to constitute a new, third value (tansjunction). Both Kunze and Günther implicitly presuppose the third value, by which they can distance themselves from bivalence, with the given observer, who is outside of bivalent logic. In contrast, Spencer-Brown wants to show how the process leading to the third value is initiated from the given bivalence from within and don't need an external impulse. If the third value is reached, then it becomes possible in a trivalent system to distinguish an observer, his object and the variety of the observer's perspectives on the object.

If there is no external observer at the beginning, but his/her location is only to be explained by further development, what triggers the process that separates from bivalence and returns by re-entry? For Spencer-Brown, this is the possibility of the infinite repetition of the echelon in the Canon C9.

»There is no limit to the possibility of continuing the sequence, and thus no limit to the size of the echelon of alternating a’s and b’s with which 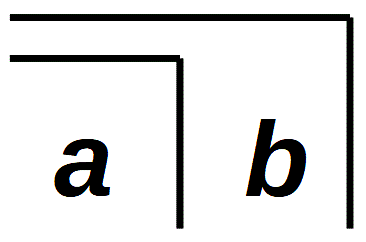can be equated.« (LoF, 55)

This infinity breaks the bivalence, and it is only important to give it a progression form in which it can express itself and develop into its own trivalence in the first step.

(2) Does an internal polyvalence arise during the course of the process, which dissolves from a bivalent base and returns by re-entry, which stabilises this process and leads to the result? That seems to be Spencer-Brown's view. He does not initially assume a third value, but rather shows how a process occurs within the bivalence that breaks away from the bivalence. The bivalence is left at the moment when the three dots are first used as auxiliary characters and then the new variable f is introduced for them. While the variables a are usually thought transitive and bivalent, the trivalence is constituted with f. Spencer-Brown does not speak of trivalence, however, but refers to the imaginary numbers. Thanks to the imaginary numbers, the transitivity of forms arranged on a straight line can be left (see LoF, 58, 61). With the imaginary axis, defined by the new unit i, the bivalence of the real axis is left, where only the negation of the positive and negative numbers is known.

(3) Does the re-entry induce a polyvalence in the receiving set through their trembling? Spencer-Brown shows the oscillation (the trembling) that is given with the re-entry. Time is created with it in a previously timelessly conceived bivalent logic. With time, a third value is introduced within the given logic: Time runs in the form of an oscillation, which differs in its ups and downs from a linear movement (LoF, 63). This process can be compared with Hegel's concept of contradiction and Husserl's remarks about inner time consciousness. For Hegel, a transitively conceived, simple opposition, which knows only plus and minus, evolves into a pulsation, through which the opposition perishes like in a whirl. The ground does not lie within the bivalence of the opposition, but as its ground in an axis perpendicular to the bivalence. At the point of intersection of the two axes lies, as with imaginary numbers, the zero. The opposition annihilates (becomes zero), and from the zero a new axis results, which founders to the ground (HW 6.67). In Husserl's view, time consciousness splits into two axes: Ordinary consciousness experiences the transitive order of the successive moments of the time stream, each moment present for a moment. The inner time consciousness can gain an inner freedom from being bound to the time stream, collect memories and formulate expectations for the future and act accordingly. The distinction between ordinary and inner time consciousness is only possible in a separate area that requires a third value.

(4) Why are networks needed to describe the modulation of a a into a f? Spencer-Brown emphasizes how in networks, when confronted with blocked paths, it is possible to choose redirections that bypass or tunnel the blockage. The initially unambiguous and fixed path is dispersed into a multitude of possibilities represented in a network, from which the most favorable one can be selected. The dispersion and its surplus compared to the linear path, where there is only a back and forth, requires a third value in which the branches can be represented. Spencer-Brown has explained this possibility of detours in a network with the imaginary numbers as well (LoF, 67, 99) and emphasized at the AUM conference in 1973 how his earliest programming of circuits goes back to this. – From the dispersion of paths in networks properties can be recognized which are not possible in a purely transitive order. While in a transitive order there is only one unambiguous, fixed path at a time and all sections of the path are strongly coupled to each other by this path, the diversity of a dispersed, intransitive order is characterized by the alterable coupling of its elements. A medium can change (emerge) into different states with specific degrees of coupling. Spencer-Brown shows this with the networks: There is not simply a multitude of equal, different paths, but the network emerges into different states, in which certain paths are favored. In my interpretation, this is based on the harmony principle formulated by Leibniz, by which the network is brought into the simplest state and optimized there. With its oscillation into different states, the network can react to the oscillation of different inputs. Spencer-Brown does not explicitly state this, but in this context he writes unambiguously: »We are now in difficulties through attempting to write in two dimensions what is clearly represented in three dimensions.« (LoF, 66) This is the point at which he explicitly mentions trivalence. – Water is the classic example of a substrate which, with its different states of aggregation, is able to react to the externally induced heat input or heat extraction and to optimize itself in each case. The starting point is the weak coupled aggregate state of the liquid, from which it can change in one direction into the crystal structure of the ice and in the other direction into the free movement of the gas. With a little imagination, each of the three states can be interpreted as a network in which the paths (connecting lines) between the units (molecules) of the substrate occur in different degrees of freedom of movement. – In summary: With Fritz Heider, a medium can be defined by the property of being able to emerge into different states of weak and strong coupling. If one asks for the dimension (axis of motion, degree of freedom) along which the states change, this is the third value, in Hegel's sense the nodal line. The medium is not simply determined by an inner motion, but the motion can assume different states. Motion is not a constant, but a third value that can change freely.

Günther looks at the process from a different angle. In classical bivalent thinking only the two relations (the interrelated ones, the arguments x and y) can be interchanged within a relation R(x,y): R(x,y) becomes R(y,x). On the straight line of numbers, the distinction between positive and negative numbers (x becomes −x) corresponds to this, on the linear way the forward and backward walking, in ordinary time the past and the future. On the other hand, it is not possible to interchange also the relation R with the arguments x and y, which would result in x(R,y), for example, just as it is not possible to leave the number axis in the case of transitively ordered numbers on a number axis. This is only possible with the introduction of the imaginary axis. If the relation R is interchanged with the arguments x and y, an argument x itself becomes a relation R and vice versa a relation R becomes an argument x or y. At first sight it is difficult to understand how this is supposed to be possible and what Günther means by this, but he gives a vivid example (Günther 1970, 227): In nature, different orders are nested in each other. Thus, an atom can be understood, on the one hand, as a form in which different elementary particles combine with each other and are brought into order, and, on the other hand, as the substance from which the atoms in a molecule are in turn brought into order. This can be formalized:

A = R(E₁, E₂)

read: the atom A is a relation of the elementary particles E₁ and E₂ of which it is composed

At a higher level the atoms sink to the level of the Relata:

M = R(A₁, A₂)

read: the molecule M is a relation of the atoms A₁ and A₂ of which it is composed

In this example, the molecule is a higher order (meta-order) than the atom, just as one level down the atom is a higher order than the elementary particles. Essential for Günther is the insight how the arguments and relations are interchanged in this example. The atom changes from the position as a relation to the position as an element.

This change from one order to a higher or lower order is somewhat misleadingly referred to by Günther as proemial relationship, »for it 'pre-faces' the symmetrical exchange relation and the ordered relation and forms, as we shall see, their common basis« (Günther 1970, 226). Günther refers to prooimion (Günther 1970, 226 Fn. 3). This literally means ‘introduction, prelude, beginning, preface, exordium’ with the language root oimos, ‘the path, stripes, one level’, also the ‘course of a song’. Günther understands as the preface or prelude the transition to a lower or higher level, which occurs first before the respective order can form (emerge) within this level, from emergere, literally ‘emerge, come out, ascend’. (Walter Rella suggests a different interpretation. For him, ‘proemial’ does not go to ‘prooimion’ but to the Latin root emo back in the meaning ‘acquire by purchase or auction’ and refers in the literal translation ‘before the purchase’ to the open state when a commodity enters the market and must find its buyer through price negotiation. An economy based on the division of labour can be understood as a network in the three states of production, exchange and consumption. While production and consumption each show a transitive order in which production or consumption can be carried out sequentially, the economy in the state of exchange moves in an imaginary order in which it must be shown whether producers and consumers can find each other and a social balance of all offers and demands can be achieved. At this moment, crises can occur such as the cyclical overproduction crises in capitalism or planning errors in socialist or state-organized economies. In this sense, the phase of exchange is a higher order than production and consumption, between which it mediates. Email from February 22, 2020.)

Kaehr and Mahler present a very clear presentation of the proemial relation introduced by Günther (Kaehr, Mahler, 5):

i + 1:	Rᵢ₊₂     →	xᵢ₊₁
		⇕
i:		Rᵢ₊₁     →	xᵢ
			⇕
i − 1:			Rᵢ    →     xᵢ₋₁

Legend
Rᵢ     Relator Rᵢ of the level i
x      Relatum xᵢ of the level i
→    Order relation between a Relator Rᵢ and a Relatum xᵢ₋₁
⇕      Exchange relation between a Relator Rᵢ and a Relatum xᵢ

With the two arrows → and ⇕ the trivalence is very clearly shown: Within a horizontal line, bivalence applies. For each number i there is also the negative number −i (order relation). The vertical double arrow ⇕ indicates the third value. At this point, a Relator is converted into a Relatum, or in equal reading from bottom to top, a Relatum is converted into a Relator (exchange relation). The double arrow indicates that it can be read from top to bottom or from bottom to top.

The proemial relation can be compared with the re-entry of Spencer-Brown:

– The process leading to re-entry goes beyond the originally given order. It leads into a space of its own. In this respect, Günther and Spencer-Brown can be united.

– In both cases there is a change of the relation and their Relata. Just as with Günther R and x, y change their places, so with Spencer-Brown a and f.

– The main difference is in the re-entry itself. With Günther there is no re-entry. However, with Günther, the idea of a re-entry is intended insofar as he – without being able to justify it – assumes that the proemial relation is cyclical as a whole and leads back into itself in a circular way.

Therefore, in my view, Günther and Spencer-Brown complement each other: Günther referred to the aspect of a trivalence with the proemial relation, which is not present in Spencer-Brown in this clarity. With the three characters Ɔ for the medium,  ⃧  for the boundary and for the re-entry a trivalence is created in Spencer-Brown, but not yet clearly pronounced. On the other hand, Spencer-Brown's reversal within the process leading to re-entry is the cyclicity that remains with Günther as an assertion and is more or less brought up from outside with reference to new empirical findings in neurophysiology (mediated by McCulloch).

In conclusion, it should be mentioned that the proemial relation provides a new understanding of the analogy, which also helps to formalize Walter Rella's approach. In the example of the two roles of the atom in relation to the molecules or elementary particles, the atom appears twice as a variable: as a relation and as a relator. If an analogy is formed for this, it leads to a change of level, which can either lead up to a higher level or down to a lower level. In this view, the analogy is therefore no longer a classical proportionality according to the pattern:

    A : B = C : D

read: A relates to B as C relates to D

Such an analogy is furthermore an ascending and descending. The figure of such an analogy is no longer, as in the intercept theorem, a proportion represented in the plane:

Intercept Theorem

Here the analogy applies: ZA behaves to ZA' like ZB to ZB', etc.

This analogy is linear and can be drawn in the plane. But in an analogy with higher or lower development, a screw is created that winds up or down.

Helix
Author: By RobHar - Own work using maple and inkscape (and a pass through gimp), Public Domain, Link

Examples are the Golden spiral, the helix and the Spiral of Theodorus, on which, according to Thedorus of Cyrene (4th century BC), the irrational numbers can be constructed geometrically apart:

Spiral of Theodorus (root snail)
Author: Von Pbroks13 in der Wikipedia auf Englisch, CC BY-SA 3.0, Link

The drawing clearly shows how the root snail has exhausted the first circuit at root of 17 and subsequently enters adjacent or higher circuits. Without going into further detail, these pictures clearly show the close inner relationship between irrational numbers, imaginary numbers (with which the circle is represented) and analogies that branch off to higher or lower levels.

From kenogrammatic blanks to abjection

Where in a given set of numbers can new values be added? According to the traditional idea, there must be  between  the known integers empty spaces: These are the distances defined by Plato (diastema) between the numbers in which, for example, between 1 and 2 the rational numbers ›3 / 2 = 1.5‹, ›4 / 3 = 1.33…‹ or Irrational numbers like ›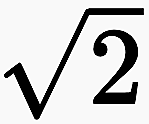 = 1.414…‹ or between 3 and 4 the transcendent number ›𝜋 = 3.141…‹ can find their place. Mathematically, the empty spaces are open intervals (n, n + 1): This is the set of all numbers greater than n and smaller than ›n + 1‹. Spencer-Brown, in contrast, takes a completely new approach. For him it is the inner  mobility  of the medium and the forms inscribed in it, in whose states of movement the re-entry finds its way in and can show itself. This mobility can also be understood as an inner void: The system (the medium and its forms) can be in different states of movement. In the simplest case it jumps back and forth between two different states (in the switching algebra the oscillation between ‘on’ and ‘off’, in the graphic representation of an oscillation between ‘up’ and ‘down’). The content of the higher-level term ‘state of movement’, which can be filled sometimes with this and sometimes with that value, but is empty for itself, can be regarded as a blank.

This is a surprising view, which goes back to Gottlob Frege (1848-1925) and was taken up and continued by Günther. Frege was looking for a deeper structure underlying both mathematics and language. He understood the classical expression of a function f(a) in a new way: The argument a is entered at a position where the function f contains a placeholder f( ), which is empty in itself and is filled by the respective arguments a. In this way of expression, mathematics can be applied to the study of language and its logic: A sentence like ›Caesar conquered Gallia‹ can be interpreted as a function with an empty space ›Caesar ( )‹ (Frege, 17). The predicate of the sentence is inserted into the blank. The value of this function describes all the properties of Caesar, and one of them is his conquest of Gallia. – In the same way the statements about the states of motion of a movement can be interpreted with blanks: ›the movement is in the state ( )‹. And just as Frege transferred the concept of blanks from the description of mathematical functions to linguistic sentences, the concept of blanks is suitable for describing both the distances between numbers as meant by Plato and the variety of states of motion in Spencer-Brown's work, in which the re-entry finds its place.

Günther is broadening that. He speaks with reference to the Greek word kenós in the meaning ‘empty, void, fruitless’ of a »kenogrammatic blank« (Günther 1979, 43). With this he goes far beyond Frege and approaches the original ideas of Plato by means of distance. For him, the blank is not only a placeholder, but at the blank the usual linear course of mathematical formulae and linguistic sentences is left behind. With the blank space a new dimension is opened up, which in an initially indeterminate way leaves the usual sentence and, from the point of view of ordinary language, goes into the void. This is exactly how I understand Spencer-Brown's idea: he leaves the usual linear sequence of numbers with the numbers and the spaces between the numbers and opens up a new dimension in which the respective states of movement of the medium and the forms inscribed in it can be represented.

In this sense the proemial relation is to be read anew. Günther understands the ascent or descent into higher or underlying relations as a kenogrammatic structure: »The proemial relation belongs to the level of the kenogrammatic structure because it is a mere potential.« (Günther 1970, 226) This can be illustrated with his visualizations: If, on the one hand, the atom is the substance of which the molecules are composed, on the other hand, it contains a degree of freedom to the inside, through which it can be understood as the composition (form) of elementary particles. What is meant by atom is no longer a fixed statement, but rather a kenogrammatic empty space which, depending on the context, can sometimes be understood as a relation and sometimes as a relatum, as substance or as form. And if the nesting of structural levels of matter is cyclic as a whole, i.e. recurs in itself, the same values are reassigned after each cycle. If, in this way, proemial relations are used to define kenogrammatic blanks, they denote a level that goes beyond the classical divisions into form and matter, inside and outside, relation and relata: something can – like the atom – in a changed context transform from a matter into a form, an inside into an outside, and vice versa. The transformation takes place inside the kenogrammatic void. This is what Günther is interested in: with Kenogrammatics he wants to overcome the traditional dualisms of a way of thinking that is bivalent for him up to metaphysics. Does this lead to a metaphysics that also undermines Spencer-Browns binary distinctions in form and medium, in »marked space« and »unmarked space« and opens a new horizon for the understanding of re-entry?

However, anyone reading Günther's explanations of Kenogrammatics with these expectations will be disappointed at first. The examples he gives for a Kenogrammatic approach seem banal and not very convincing. He restricts himself to pattern recognition and explains this using the example of truth tables. He notices that in truth tables overall patterns can be recognized, if e.g. in ›FFFW‹ and ›WWWF‹ in each case at the beginning a character appears three times and afterwards another character is added once. Günther therefore develops placeholders and writes overall: ∗∗∗□. Here, alternately for ∗ F or W and vice versa W or F in □ can be entered (Günther 1962, 215). This notation highlights the pattern. Similarly, for each word, a pattern of the letters contained in it can be found, e.g. for the German word ‘sonne’ (sun) the pattern ›□○⋄⋄△‹, by which it can be recognized that the first, second and fifth characters occur once and the character in the third position is repeated once (Matzka, 4).

Only his choice of words shows that he is interested in much more. Günther sees the kenogrammatic blanks as the smallest unit of an  negative language, while the usual characters such as the alphabet, punctuation marks and numbers are the smallest units of the  positive language  (Günther 1979, 20f). The characters of positive language are the values with which the spaces of negative language »can be saturated«. To speak and think like this is suggestive and enlightening, and goes far beyond the example of pattern recognition. It stimulates to understand the rupture that occurs at this point. For Günther, positive language is the area where bivalent logic applies. »It is the characteristic of positive language that it belongs to the domain of creation. Just as reality one day is there as an indisputable factum brutum, so is 'the word' as belonging to the real with it.« (Günther 1979, 20, my translation) It can also be understood as the categorial realm. Since Aristotle, categories have meant the basic elements of a positive language in which a recognizing subject can meet with an object recognized by him. Negative language leaves this area and opens up a third value.

However, these expressions are also ambiguous. For me, the blanks do not indicate that something disappears into nothingness, but they open the space of possibilities from which the real emerges and can be understood. They reach into the ground from which the real emerges (see Hegel's remarks on the contradiction that founders to the ground [zugrunde geht]; HW 6.67 and 76). They describe which possibilities are inherent in them in order to be able to prove them with real values. I want therefore to interpret Günther's distinction between negative and positive languages as a distinction between orders of the real and the possible. For the orders of the possible, one can speak of negative orders in the sense of Günther (see the article about the dynamic logic: »If, as usual, the real objects are described as zero order, the signs referring to them as first order, the metalanguage about these signs as second order and so on, then the virtual, unfinished objects of the possibility space can be called the first negative order, the totality of all possible names for possible objects as second negative order and so forth.«)

But it is not only about object and meta-languages of possibilities, but within the void there are stages to be distinguished. Just as Cantor distinguished between stages of infinity (cardinality), the stages of emptiness or nothingness are to be asked for. There is then not only one, clearly and uniquely determined transcendental logic that precedes all usual logics, but several stages with their specific cardinality and endangerments. Whether these can be described mathematically in a comparable way as the cardinal numbers introduced by Cantor is open to me. But questions can be asked e.g. like: From which stage orders like the Golden Ratio emerge, which can not only be proven in reality, but which develop their own creativity (fertility) and transcendently predefine all possibilities that are given with them. Where does the negativity, from which the negative languages and the nothingness (kenos) of Kenogrammatics emerge, have its ontological ground, if here it can be spoken of an ontological ground at all.

Outlook: So far we have only talked about the fact that every single empty space can be in different states of movement. In his consideration of networks, Spencer-Brown goes beyond this in two ways: There, the process leading from an argument a to the function f is no longer understood as the linear sequence of uniformly executed iterations, but as a network modulating an input a into an output f. Branching, concurrency and loops can occur within the network. There, not only the bifurcation points can assume different states, but the state of the network as a whole can change. The changes in the states of the network can be understood as an autonomous cybernetic system that is able to react to the different inputs in a steady state. See the lecture on networks in chapter 11 of the Laws of Form, presented and discussed at the Liverpool conference.

Silence

Which way leads from positive language to negative language? From a negative language to speak contains a contradiction in itself: negative language means what cannot be spoken of. In a first approximation, silence is a negative language, and negative language is reached when in the words of positive language it can be shown indirectly and negatively at which point it meets silence. The positive language changes from speaking to showing: it cannot speak about the negative language, it has no words for it, but it can show in the language game of its words at which point the negative language is created. This idea of Wittgenstein's is as fundamental to the idea of Kenogrammatics to be outlined here as Cantor's distinction of the different stages of infinity. (Hilbert: »From the paradise that Cantor created for us, no one should be able to drive us out.« Cantor's Paradise.) With equal justification, one can speak of Wittgenstein's paradise, which he created for the philosophy of language.

With the distinction between positive and negative language, i.e. with the paradox of talking about negative language, the horizon is opened in which the classical paradoxes like the liar paradox (›what I am saying now is wrong‹) can be understood.

Uncertainty

While Wittgenstein hopes to isolate the boundary of silence at the edge of thought, so to speak, positive language can also turn into negative language where it encounters uncertainties that it cannot resolve. It encounters uncertainties when a known solution fails. Instead of a fixed solution A, which has proved itself so far, a blank space should be inserted where other possible solutions can be entered. The constant A is replaced by a variable a, whereby it remains open whether there is a solution at all, i.e. a different value that can be entered at this position. Baecker describes as »the most important power of negation«:

»Not only can it imply blanks as indefinite outsides of a distinction and thus call for selectable determinations to be made where so far there are none, but it can also, by way of a detour through the conflict, produce a blank space where up to now one thought to be dealing with an unambiguous determination.« (Baecker 2013, 152, my translation)

With negation at this point it is only meant at first that the solution A, which has proven itself so far, is no longer tenable and must therefore be negated. What will replace it and whether there is anything at all that can take its place is open (uncertain) for the moment.

The real difficulty arises when not only the previously known solution but also the previously introduced methods of resolution fail. The decision-making process comes to a standstill: This begins with the question of whether the failure of a solution is seen by everyone and recognized as such. Often instead, people keep silent about the difficulties that arise. Could it be that only random, temporary events have caused the problem, which are so rare that they will disappear by themselves and can be neglected for further development? The problem is one level higher: Is the familiar judgement to be able to recognize and solve problems questioned? Is there a threat of a negative circle at this point: If you can no longer rely on your ability to judge, how can you get out of both the objective problem situation and the communication difficulty of being able to talk about the problem and find an answer?

At this point, Spencer-Browns distinction into linear processes and re-entries offers a way out. It can be assumed that in such a situation a higher-level process is at work, which has not yet been recognized and understood, and whose re-entry disrupts the normal course of the solution. Therefore, not only the previously known solution A has to be replaced by a variable a with a possible enumeration of alternatives, but also by a blank space, which can be filled by certain values as well as shaken by the effect of an re-entry coming from a higher level. At the empty space not only the respective variables that can be entered there, but also the states of movement of this empty space must be distinguished. Therefore, the only way out is to carefully examine all known re-entries and to recognize whether a further re-entry needs to be added, the non-consideration of which causes the given uncertainty. In the case of an organisation, this can mean not only finding a new solution to the specific problem at hand, but also recognising the values (visions) according to which possible solutions are assessed and decided upon, and the decision-making processes to recognise these values and give them the appropriate significance.

Such situations are associated with a typical form of silence. Difficulties of this kind cannot be spoken about openly, and those who do speak about them are not heard and may even be excluded. The silence is no longer on the boundary of the positive language, as in Wittgenstein's case, but rather it breaks out in the middle of it. Spencer-Brown's distinction into usual enumerations and re-entries has opened up the formal way to recognize and describe such situations. With each newly discovered re-entry, an area of questioning is solved about which previously it was only possible to remain silent.

(To see this kind of question at all I owe to the remarks of Florian Grote at various working conferences on the Laws of Form)

Opposition

This very general idea has to be differentiated more closely. The easiest way is to replace the previous solution A with its opposite ¬A. If this is always possible, we can speak of a digital world. A digital world is such that every question can be solved either by A or by ¬A (tertium non datur). As it looks today, robots and artificial intelligence can only move in a digital world. They only have the positive language at their disposal.

If both A and ¬A fail, the question can be extended: To which genus does solution A belong, and is there another species in this genus against which A can be exchanged? An example is the colours: If, for example, the color blue no longer works, you can ask for another color that is more suitable. This is usually how mathematics works: If it turns out that a certain number A is not a suitable solution, usually ¬A will not help, but A is replaced by a function f(a), where a can be any other number.

Rejection

This procedure can also fail. The classical example is the search of the Greek mathematics for the solution, which value the diagonal takes in a square. At first, individual solution proposals failed: At first glance, 1.5 could be a solution, but it fails. With every further approximation like 1.4 or 1.41 and so on, the solution seems to come within reach and is still missed.

If this happens, it is not possible to search further within the given context or within the genus in which previously known solutions were found. Günther speaks of rejection and means first of all only the special case, when it turns out that neither A nor ¬A is valid and the alternative A or ¬A must be rejected. I would like to extend this: In this case a context change is needed. Formally, it is about an ascent into a superior genus. This was Plato's solution to the question of irrational numbers: If it turns out that there is no rational number by which the length of the diagonal in the square can be determined, then a higher type of number must be sought with which to do so. Plato spoke of dynamic numbers. This is how mathematics went on afterwards: If no solution can be found within a given set of numbers, then superordinate number classes must be determined in which the solution is to be sought. These were the irrational numbers, the real numbers, the complex numbers or even more generally defined sets of numbers (algebras). – Surprisingly for me, Emanuel Seitz in his contribution Form and Philosophy at the formlabor 2020 in Berlin interpreted the distinction given by Spencer-Brown with the cross into an interior and an exterior (into the marked space and the unmarked space) as a transition from a species to its genus and in further steps to higher genera. The genus contains the species from which it originated and does not negate it. But it negates the hierarchical level on which the species is located and opens a higher level. In this regard, it can be said that the genus is located on the outside of the species.

However, there are also limits to these transitions. To recognize this was the great achievement of Cantor. After first expanding the number classes step by step, Cantor realized that there is a point where numbers appear which contradict themselves (to their own concept): He was able to show with the diagonal argument that the real numbers are not countable but over-countable. Non-countable numbers: Thus a negative self-reference is discovered. This situation is radically different from the well-known paradoxes like ›this sentence is wrong‹. These are artificial language expressions that nobody uses in everyday life, and which can therefore be neglected in normal scientific thinking. But what are uncountable numbers? With them, a contradiction occurs in the thing itself: A is no longer opposed to B, which claims the opposite of A (as Kant had demonstrated in his Antinomies), but contradicts itself. Whoever wants to reject this contradiction (rejection), at the same time rejects the subject at issue (the thing for which A stands) and comes to a deadlock.

Contradiction

With Cantor's proof of over-countable number classes and the resulting paradoxes, a new view of how Hegel understands the contradiction and distinguishes the contradiction from an opposition and an antinomy emerged from mathematics was possible. Robert Heiß (1903-1974) drew attention to this in 1932 in Logic of Contradiction : »It is the great advance of mathematical logic that it first noticed the self-objectiveness in the paradoxes. It is astonishing that it took this detour to induce philosophy to investigate self-applicable thinking.« (Heiß, 95, my translation)

Heiß has been able to achieve a new understanding of the Three Attitudes of Thought to Objectivity (the introducing part of Hegel's Encyclopaedia of the Philosophical Sciences). While Hegel distinguishes (i) metaphysics, (ii) empiricism and critical philosophy, and (iii) immediate or intuitive knowledge, Heiß distinguishes for me much more consistently (i) the positive knowledge of the academic disciplines, (ii) critical philosophy, (iii) the negative self-reference of contradiction. He does not oppose Hegel, but wants to elaborate towards Hegel too, what a philosopher like Hegel meant implicitly and was not yet able to formulate explicitly. »Above these larger tasks, Hegel has failed to clarify the basic phenomenon, precisely that of the self-reference of the concept, in its logical characteristics.« (Heiß, 55). The result will be that, from his point of view, Hegel's concept of the negation of negation will have to be reformulated: It does not simply lead into a new immediacy, but into negative self-reference. Once this has been recognized, the question that Hegel was hidden arises: how and why does the transition from negative self-reference to a new immediacy succeed, from which everything can begin anew? What ensures that with the negation of negation, negativity has not reached its end, but that a new circle can begin, which can lead to a new thesis (immediacy), its negation and a new negation of negation? What frees from the situation of negative self-reference? Mathematics has not yet found an answer to this question. The paradox of uncountable numbers has led to questions that are still undecidable to this day. (Meant is the continuum hypothesis: Is there a set of real numbers whose power is less than the power of the totality of all real numbers? For the practical work of mathematics, however, this question seems to be insignificant according to the current state of knowledge).

(i) The academic disciplines each find their specific subject and develop an appropriate method for exploring their field, approaching their subjects and gradually acquiring positive knowledge. Here there are no contradictions, but only incomplete knowledge that can be concluded in the course of further empirical work. The most prominent example is undoubtedly mathematics. It finds its subject in numbers and geometrical figures and its method in the rules of arithmetic and geometrical construction.

(ii) And yet antinomies may occur. Heiß quotes Kant's letter to Christian Garve on September 21, 1798: »Not the investigation of the existence of God, immortality etc. was the point from which I proceeded, but the antinomy of pure reason. [...] It was this that first woke me up from my dogmatic slumber and drove me towards the critique of reason itself, in order to remedy the scandal of the apparent contradiction of reason with itself.« (Kant, Academy Issue AA 12:257.32-258.03, quoted in Heiß, 25, my translation). In such situations philosophy cannot take the place of science and find a solution using new knowledge. But it can take a negative approach and examine what happens in a science that gets into antinomies. It examines the implicit presuppositions that are hidden to them, from which it proceeds without being aware of them. Their lack of understanding can lead to antinomies. This happens when science goes beyond the area of positive knowledge accessible to it without consciously wanting to do so and unnoticed by itself, leaves the positive language and makes statements that do not apply on the object level of positive knowledge, but on the meta level of the terminology used to talk about objects. More precisely, Kant had discovered and proved science is bound to time. It can investigate phenomena that are given in time and that can change and pass away in time. It can describe their developments, how they can be observed, recorded, mathematically represented and verified in the course of time, but with its methods it cannot look at time-in-itself as if time were an object like all others, which takes a temporal course. It cannot detect any self-referential (or even negatively self-referential) properties of time. The properties of time precede the method of science. Basically, Kant proceeds in the same way as Freud later followed him: Where It (the unconscious) was, I (the conscious) shall become. Science makes unconscious assumptions, which are investigated and made conscious by Kant. Today we find ourselves in the opposite situation: Quantum theory and the general theory of relativity, which has been expanded with it, are waiting almost eagerly for a corresponding clarification of their unsolved questions by philosophy.

In this way Critical Philosophy deepens step by step the understanding of the methods of science. From what these initially naively proceeded is not disproved, but enlightened. Step by step, their implicit assumptions become conscious. Kant showed that science remains in the horizon of time: Its concepts presuppose the properties of time (permanence, causality, interaction). The path of Kant was prepared by Descartes and continued by Husserl in particular. With his work of 1931, Heiß explicitly refers to his programme.

»What we see here is a deepening of the foundations of methodological philosophy. In each case the successor puts the approach further back. It is not the ascent of a thought that increases from positive to positive result as from step to step.« (Heiß, 47, my translation)

This anticipates in a more general way the idea of proemial relation and transfers it to the history of philosophical ideas: When the implicit knowledge of a science is recognized, this leads to an overarching context from which science can be understood and the antinomies occurring in it can be resolved. In other words, Critical Philosophy succeeds in finding a higher observer position from which the activity within science can be observed and explained. Heiß quotes from the Critique of Pure Reason by Kant the passage on the sphere of the concept (KrV B790, quoted by Heiß, 29). With it, it is suggested how the antinomies come across to see reason in a wider horizon and to recognize characteristics that had previously remained hidden: the curvature of the sphere. Science believes to move positively on an infinite plane that can be explored step by step. Critical Philosophy recognizes that it moves like on a sphere to which the respective horizon is principally limited and whose inner qualities (the curvature) remain hidden to science. (For further details see the contribution The sphere of the concept and the logic of the sphere.)

This idea corresponds to the example of the number sphere, which Riemann used to find a place for the infinite-distant natural number.

(iii) At first sight, Hegel has consistently followed the path of Critical Philosophy. He simply seems to have continued on Kant's path and to have uncovered, on an even deeper level, hidden implicit knowledge. This is how an influential movement of Hegelians sees it today, led by Robert Brandom (* 1950): »What Brandom omits in his attempt to 'normalize' Hegel is first and foremost the dimension of self-reference.« (Žižek, 110, my translation) This is the crucial point that Heiß first pointed out. »A completely different position on contradiction is the basis of Hegelian method.« (Heiß, 50, my translation) Before him, philosophy sought to resolve the contradictions (antinomies) found in the respective science. For Hegel, on the other hand, contradiction is not something that needs to be resolved, but the inner principle of movement in science. He recognizes in the contradiction, »that from the self-application of thinking, both the self-absorption and the self-expansion of thinking can be understood« (Heiß, 54, my translation).

Hegel carefully distinguishes between an opposition (an antinomy) and the contradiction. In the opposition, two somethings (two matters, in the physical realm two things) are opposed to each other. obiectus is literally ‘the opposition’. However they are judged, they can be clearly separated and distinguished. For Hegel, the opposition is the highest form of distinction.

The situation is completely different with the contradiction. Something is not in contradiction with something else (that would be a mere opposition), but with itself. The contradiction arises when the opposite (the opposition) is no longer outside but has returned to the thing itself. Hegel shapes the extremely descriptive term »the other of itself.« (HW 5.127, see the commentary by Richli). In the first step, the something has been defined by distinguishing and delimiting it from the other. But where is the boundary? Does it lie with the Something or with the Other or in an unexplained way between them? Hegel recognizes that the negation (the delimitation) must in turn be negated. Something can only be delimited from something else if it already carries the restlessness of being able to distinguish itself from something else. »The other determination is the unrest of the something in its limit in which it is immanent, the contradiction that propels it beyond itself.« (HW 5.138, translated by George di Giovanni) (See in more detail the study Antinomies of Existence and Infinity.) This is the elementary concept of negative self-reference: Something is only something if it has the property of referring in itself to something else from which it is different. Hegel completes a transition from difference to distinctiveness: the difference lies between something and the other. But distinctiveness is a property of something itself, which at the same time contradicts the something identical with itself.

When Hegel speaks of the restlessness of the something, he anticipates Spencer-Brown's idea of distinguishing the states of motion of the medium. The relation to Spencer-Brown is even closer: Hegel carries out the thought of the Other-On-Himself in all details. He distinguishes the double movement of continuity and reversal: with continuity, something has the quality of going beyond itself and referring to something else. By reversal is meant the characteristic that this distinction by something else does not call into question or even destroy the identity of something, but on the contrary makes us fully aware of our own identity. Hegel has explained this using numerous examples from the natural sciences. (See the contribution Hegel's idea of a »higher contradiction« – From continuity and reversal to »pulsation« of contradiction).

Baecker understands the double movement of continuity and reversal as communication: Something turns outwards into its environment (opens communication) and contains an answer from there. If the environment is understood as the excluded and the reception of the response from the excluded as its inclusion, then with Baecker the response can be interpreted as inversion and as a whole as a form of communication with the concept of contradiction introduced by Hegel as »the dynamics of the inclusion of the excluded« (Baecker 2005, 79, my translation) and written down with the re-entry in the most elementary and abbreviated form:

Communication, according Baecker 2005, 80

This is the formal form of the contradiction. From Something is distinguished something else by a border and this other is returning.

Does this take back the idea expressed at the beginning that re-entry is not a matter of resonance and feedback? In my understanding, Spencer-Brown does not yet assume that the re-entry is a communication (in his example, the form of echelon does not communicate with anything else). But the interpretation as communication is already the answer to the big question that arises with negative self-reference: The negative self-reference is not yet a communication in itself, but it can only be sustained if it can flourish in a communication.

(iv) How can Hegel manage the transition from the negation of negation in negative self-reference to a new immediacy, which opens a new cycle of immediacy, its negation and a new negation of negation? Hegel does not even ask this question, and it can only be assumed that he did not make the subject of negative self-reference explicit because he unconsciously shied away from this question. How else is it to be understood that although he has fully elaborated the concept of negative self-reference in terms of content, but has not introduced it as a concept?

With Spencer-Brown you can illustrate what it is all about: He distinguishes from the re-entry the re-crossing . Recrossing is a process of crossing a limit and then going back and wiping away the movement. This restores the original immediacy. An exact analysis of Hegel's negation of negation shows that he proceeds exactly in this way: He begins his logic by contrasting Being and Nothing. If their negation is negated, the result is Becoming. The negation of Becoming is Vanishing. Their negation is the »vanishing of vanishing itself« (HW 5.113). (More detailed again the work text Antinomies of Existence and Infinity.) The vanishing of the vanishing itself is the archetype of a negative self-reference. »The result is vanishedness, but it is not nothing.« (HW 5.113, translated by George di Giovanni) This is the critical point. When vanishing vanishes, it does not fall back into nothing, but reaches a new immediacy, which Hegel calls »existence« (Dasein). This movement corresponds formally to re-crossing: (i) A distinction is made. (ii) On the outside of the boundary, the original Something has vanished and has reached its Other. (iii) The distinction is reversed and vanishes in turn. Thus the original Something is restored in its immediacy. But it is no longer simply the old Something, but a Something that has passed the movement of re-crossing. In order to make this new state recognizable, on the Something its state of movement must be described: In this simple case only the two states of movement ‘before the crossing’ and ‘after the crossing’ can be distinguished. In this way, Spencer-Brown can not only graphically and formally describe the dialectical movement introduced by Hegel, but the implicit knowledge can be brought out, which Hegel tacitly presupposed in order to be able to differentiate between Being and Existence, which mean the same thing in common parlance. (Only Heidegger was able to put this difference more clearly into words, when he emphasized the variety of possibilities given with Being-There (Dasein), by which it differs from Being. In my interpretation, the variety of possibilities corresponds to the different states of movement that Spencer-Brown is concerned with).

In the language of Spencer-Brown, Hegel's dialectic, insofar as it leads to a new immediacy, has remained at the level of re-crossing. It does not reach the negative self-reference that is only described with the re-entry. Although Hegel has fully elaborated the content of negative self-reference, he has not yet been able to distinguish it from recrossing.

With the negative self-reference the thinking is at risk of coming to a deadlock. Hegel trusted that despite all the negation of the negation the negativity does not cease with it. There must be a force of its own to ensure this. In the Persian and Hebrew tradition, this power is personalised as the devil, Satan (literally the accuser and adversary) or, with Goethe, as Mephistopheles. This leads to a profound reflection on the nature of creation, which Lars Clausen addressed in his contribution Counting AND accounting for the formlabor 2020. A reader of the Old Testament must ask himself the question how the devil (or serpent) came into the world that contradicted God's prohibition to eat from the tree of knowledge. It can neither be created by God (a part of creation) nor be a side of God. In other words, it belongs neither to the positive language that encompasses the scope of creation, nor to the creator of positive language. With it, the objects of creation described by positive language can be replaced by empty spaces where the existing object can be negated and made room for an alternative. This possibility to replace a given positive object (even if it is a prohibition decreed by God) by a blank space is not itself an object made by Creation, but a principle on the meta-level preceding all objects and their places, in Günther's words the negative language.

Abjection

Hegel had assumed that with him philosophy was finished and the further history had come to an end. Contrary to his expectations, the risk endengered by negative self-reference and the negation of negation is evident in art and in various clinical pictures that have been investigated by a new generation of psychoanalysis since the 1970s. In 1980 Julia Kristeva (* 1941) published her Essay on Abjection on the topic Powers of Horror. abiectus comes from Latin and originally means ‘carelessly thrown down, pressed to the ground, low, mean, fainthearted, despondent, contemptuous, rejected’. In French l'abjection sounds far more drastic, translated as ‘depravity, deepest humiliation, baseness, ignominy, shame, infamy’ (dict.leo.org). For Kristeva, abjection describes a mental state in which subject and object, inside and outside, cannot be clearly separated and contrasted, and abject describes the monster-like phenomenon from which they feel seized and cannot release themselves. As examples she mentions panic attacks, phobias, borderline personality disorders, eating disorders, depression. In an almost literary language, she writes using the example of eating disorders:

»Loathing an item of food, a piece of filth, waste, or dung. The spasms and vomiting that protect me. The repugnance, the retching that thrusts me to the side and turns me away from defilement, sewage, and muck. The shame of compromise, of being in the middle of treachery. The fascinated start that leads me toward and separates me from them. Food loathing is perhaps the most elementary and most archaic form of abjection. « (Kristeva, 2)

Objects vital for survival such as food are perceived as a threat. The request to eat appears as a betrayal of one's own higher insight into the true, rejectable character of things. Eating disordered people get into a negative self-reference in their behaviour, which in many cases leads to death. The subject feels both driven from outside and proud of his supposed achievement. Objects can no longer be experienced and judged objectively, their own subject can no longer be experienced and judged in a subjectivity that is sure of itself. From the point of view of the outsider, all accustomed standards break down. »The object (is) from the space of symbolic community 'radically excluded and draws me toward the place, where meaning collapses'« (Žižek, 204 with quotation Kristeva, 2)

From the perspective of a psychoanalyst like Kristeva, who was educated in Freud's doctrine and with Lacan, the abject is even below the unconscious and the drives. Each drive manifests itself in the objects it desires or opposes, but the abject cannot be isolated as an object in itself and perceived as an Other facing the subject. The food is not rejected because it is negated for whatever reason, but it provokes disgust before any decision about acceptance or negation. What is experienced here is, in its own way, without question an immediacy of experience, but without the possibility of making distinctions.

The abject arises where in the usual development of the subject language is formed. Kristeva describes the psychoanalytical understanding of this situation: if the child has to learn that the mother is not always immediately available, it acquires the language with which it can put words in place of the physically experienced object, with which it begins to describe what it wants and learns to formulate consciously the object of its drives. The subject learns to find a new object. »Which one? Not the object of sexual drive; the mother, or her parts, or her representatives; no more than some neutral referent or other, but symbolic activity itself.« (Kristeva, 44) The child can feel erotic joy in its own language, which takes the place of the joy of immediate physical experience. In this »primordial sphere« (Husserl) everything is still intertwined: the awareness of one's own drives and their repression, temporal immediacy and displacement, subject and object, inside and outside, the separation of words from the things addressed with them. Everything is positive and negative self-referential: the subject emerges to the extent that it succeeds in separating itself from its objects. Objects can be recognized as such to the extent that they are related to the recognizing subject, but are separated from it.

Psychic constitutions such as the examples mentioned by Kristeva show how this can fail. Another example are the phobias. If an object (such as a dog or a horse) provokes a phobic reaction, it cannot be separated from the overwhelming storm of emotions unleashed in the subject. In panic, the categorical order of objects and subjects separated from one another collapses. – Those who are not familiar with examples from psychoanalysis and may find them problematic can choose examples from art. Kristeva mentions the horror experienced by the main characters in Dostoyevsky's novel The Demons such as Verkhovensky or Kirilov. In more recent times abject art is regarded as an art movement. »Cindy Sherman is seen as a key contributor to the abject in art, as well as many others including Louise Bourgeois, Helen Chadwick, Paul McCarthy, Gilbert & George, Robert Gober, Carolee Snowman, Kiki Smith, Sarah Lucas and Jake and Dinos Chapman.« (tate.org) Other examples are the paintings of Fancis Bacon, the films of David Cronenberg and David Lynch. In music, a work like I buried Paul by Michael Gordon can be mentioned (YouTube).

Art and religion meet the critical moment of the development of language and with it of human verbal communication. »It is within that undecidable space, logically coming before the choice of the sexual object, that the religious answer to abjection breaks in: defilement, taboo, or sin« (Kristeva, 48). Art and religion describe the phenomena of abjection. However, they cannot be objective towards them, just as it is not possible for those affected by abjection: Whoever suffers the fate of abjection is considered to be defiled by his environment and is seen in a state of shame and sin. This is an exclusion that knows no reconciliatory inclusion: They are not only excluded as human beings, but because of their limited ability to distinguish between I and you, subject and object, inside from almost all communication too. Therefore, for me the image of the devil (the snake) in the Fall of Man is ambivalent: he can embody the power of negativity, but also the danger of abjection, which is to be excluded. After having eaten the fruit of the tree of knowledge forbidden to him, man can distinguish between good and evil, as the serpent seductively promised him. But if he approaches the question of the reason for this distinction, he falls into an indissoluble negative self-reference: Is the distinction between good and evil itself good or evil? In the biblical narrative, God has warned against this negative self-reference, the serpent has seduced man. Is it good if man has chosen the freedom to transgress the prohibition, or evil if he has done so? The result was that man became aware of his disgrace (the literal translation of the abject) and began to feel shame.

In the face of the threatening abjection, how can we put into words that which makes it possible to move from the primordial sphere into a categorical order? In this sense, I understand the neologism which Baecker introduced: catjects. »Catjects are called catjects because they are neither objects nor subjects but complex categories giving rise to objects and subjects.« (Baecker 2018, 1) With catjects, that which fails in the abjection is to be formulated positively. For Baecker, Spencer-Brown hit the level with the Laws of Form where the catjects emerge and can be recognized in their emergence. How is this possible? The medium is not only the ground in which forms are inscribed, from which forms emerge and which can set into vibration in this process, but within the oscillation something new can emerge, with which the abjection can be avoided and the path of the catjects can be opened. If the vibration is referred to as the first emergence, the newness arising from it can be described with Scheier as »second emergence« which shows itself »in the moment, systema momentaneum, analogous to Leibniz' mens momentanea«.

»At the level of basal self-reference, it happens only this that time generates itself as a horizon (reflexivity) and immediately erases itself as this horizon. The product is only the vanishing moment of productivity, the identity only the vanishing moment of difference, the alêtheia only the vanishing moment of lêthê.« (Scheier, 121, my translation)

If this succeeds, not only is the negative self-reference of time found, which was indirectly addressed as an idea by Kant, but which could not yet be determined by him, since he did not yet know the concept of negative self-reference (time, which at the moment of its creation as a horizon immediately annihilates itself again), but with it one can speak of the fertility of the ground, thanks to which the forms inscribed in it can blossom. This leads to a second transformation of the processes of re-entry described so far. With the first transformation, the medium was set in vibration, with the second transformation, fertility emerges at the moment of vibration. Just as the abjection leads to the breaking off of communication, the communication that emerges in the blossoming is a sign of successful language ability. With the ability to speak, the question of the observer is raised. The observer not only has a spatial distance to the event, but also a language with which he can record the process and put it into words. With language the infinite variety of possible interpretations is given. The location of the observer is not only determined by the place from which he sees something and talks about what he sees, but by his inner condition, the conditio humana. This is a new topic that goes beyond the question of re-entry.

When asked about the place where abjection and linguistic ability are separated from each other, it is about the question of chora, which has been discussed since Plato. Paul Natorp translated: In the indefinite from which creation emerges, »something positive must be hidden« (Natorp, 365), and that is, in a first approximation, the »certainty of position« (ibid. ), »that, wherein> it becomes«, »the receptive of the mother« (Natorp, 367), the »seat«, »somehow a halt at being« (Natorp, 368, my translations), mathematically speaking the space. Or in the words of Plato (translated by B. Jowett):

»Being full of powers which were neither similar nor equally balanced, was never in any part in a state of equipoise, but swaying unevenly hither and thither (anômalôs pantê talantoumenên), was shaken by them, and by its motion again shook them.« (Plato Timaeus, 52e)

»At first, they were all without reason and measure. But when the world began to get into order, fire and water and earth and air had only certain faint traces of themselves (ichnê men echonta hautô atta), and were altogether such as everything might be expected to be in the absence of God; this, I say, was their nature at that time, and God fashioned them by form and number.« (53a-b)

Appendix on the Canon C9

Felix Lau gives some assistance in understanding canon C9 (Lau, 89). He explains the used rules C5 (iteration; LoF, 33; Lau, 79), C1 (reflection; LoF, 28; Lau, 77f), J2 (distributive law; LoF, 28; Lau, 77), C4 (occultation, concealment; LoF, 33; Lau, 79f). Above all, however, he focuses on the most difficult passage in this proof:

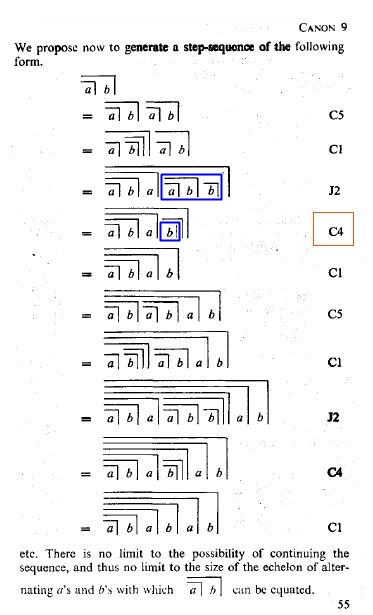
The critical point is highlighted with a blue border. Lau has shown their identity in an auxiliary calculation. He mentions – without elaborating further – the proof steps C1, J2, C5, C1, C4. Leon Conrad has succeeded in proving this (email from March 30, 2020 with my comments, see also on YouTube the Laws of Form Course by Leon Conrad, Session 14):

zurück zum Text: ⏴

Siglenverzeichnis

AUM = The G. Spencer-Brown – AUM-Conference 1973, Esalen 1973; Link

HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971; Link

LoF = George Spencer-Brown: Laws of Form, New York 1972 (Julian Press) [1969]; archive.org

Literatur

Dirk Baecker 1993 (Hg.): Kalkül der Form, Frankfurt am Main 2016 [1993]

Dirk Baecker 2005: Form und Formen der Kommunikation, Frankfurt am Main 2005

Dirk Baecker 2013: Beobachter unter sich: Eine Kulturtheorie, Darmstadt 2013

Dirk Baecker 2018: Why catjects? Version 3, Januar 2018; PDF

Ulrich Blau: Die Logik der Unbestimmtheiten und Paradoxien, Heidelberg 2008

Heinz von Foerster: Understanding understanding, New York u.a. 2003

Heinz von Foerster, Gotthard Günther: The Logical Structure of Evolution and Emanation
in: Ann.N.Y. Acad.Sci. 138 (1967) 874-891; PDF bei vordenker.de

Gottlob Frege: Funktion und Begriff, Jena 1891; Online

Gotthard Günther 1962: Das metaphysische Problem einer Formalisierung der transzendental dialektischen Logik
zuerst in: Heidelberger Hegeltage 1962, Hegel Studien Beiheft 1, p. 65-123
nachgedruckt in: ders.: Beiträge zur Grundlegung einer operationsfähigen Dialektik Bd. 1, Hamburg 1976, S. 189-247, Online: PDF bei vordenker.de

Gotthard Günther 1970: Cognition and Volition
in: ders.: Beiträge zur Grundlegung einer operationsfähigen Dialektik, Bd. 2, Hamburg 1979, S. 203-240, Online (deutsche Übersetzung) PDF bei vordenker.de

Gotthard Günther 1979: Identität, Gegenidentität und Negativsprache
in: Hegeljahrbücher 1979, S. 22-88; PDF bei vordenker.de

Gotthard Günther 1995: Number and Logos (Zahl und Begriff)
vermutlich kurz nach dem Tod von Warren McCulloch 1969 entstanden, zuerst veröffentlicht in: Axel Ziemke und Rudolf Kaehr (Hg.): Selbstorganisation - Jahrbuch für Komplexität in den Natur-, Sozial- und Geisteswissenschaften, Band 6 "Realitäten und Rationalitäten", Berlin 1995, 318-348; als PDF in deutscher Übersetzung abrufbar bei vordenker.de

Georg Wilhelm Friedrich Hegel: The Science of Logic, Edited and translated by George di Giovanni, Cambridge 2010

Fritz Heider: Ding und Medium, Berlin 2005 [1923]

Robert Heiß: Logik des Widerspruchs, Berlin Leipzig 1932

Rudolf Kaehr, Thomas Mahler: Proömik und Disseminatorik, vordenker.de (Sommer-Edition 2017) J. Paul (Ed.) PDF
ursprünglich in: R. Kaehr, A. Ziemke (Hg.): Selbstorganisation - Jahrbuch für Komplexität in den Natur-, Sozial- und Geisteswissenschaften, Bd. 6, Berlin 1995, S. 111-160

Julia Kristeva: Powers of Horror, An Essay on Abjection, New York 1982 [1980]

Daniel Kunze: Theory of the Metropolis
in: La Città Nuova, proceedings of ACSA International Conference, Rome (Washington DC: Association of Collegiate Schools of Architecture, 1999, 332-336; PDF

Felix Lau: Die Form der Paradoxie, Heidelberg 2012 [2005]

Bernie Lewin: Enthusiastic Mathematics, Melbourne 2018

Rudi Matzka: Klassische Kenogrammatik, Eine semiotische Ortsbestimmung, 2010; PDF auf rudolf-matzka.de

Paul Natorp: Platos Ideenlehre, Hamburg 1994 [1902]

Platon: Timaios, übersetzt von Friedrich Schleiermacher und Hieronymus Müller, Leipzig 1857; 12körbe.de

Plato: Timaeus, englisch translation by B. Jowett; onclick="window.open(this.href); return false;"ellopos.net

Walter Rella: Der Schritt in die Analogie
Teil I in Wiener Jahrbuch für Philosophie Band XVI/1984 S. 129-138
Teil II in Wiener Jahrbuch für Philosophie Band XVII/1985 S. 141-158

Urs Richli: Das Andere an ihm selbst
in: Max Gottschlich und Michael Wladika (Hg.): Dialektische Logik, Würzburg 2005, 62-71

Claus-Artur Scheier: Luhmanns Schatten – Zur Funktion der Philosophie in der medialen Moderne, Hamburg 2016

Tatjana Schönwälder-Kuntze, Katrin Wille, Thomas Hölscher: George Spencer Brown, Wiesbaden 2009 [2004]

Julius Stenzel: Zahl und Gestalt bei Platon und Aristoteles, Darmstadt 1959 [1924]

Walter Tydecks: Die Sphäre des Begriffs und die Logik der Sphäre, Bensheim 2014
unter: http://www.tydecks.info/online/logik_kraft_sphaere.html

Walter Tydecks: Antinomien des Daseins und der Unendlichkeit, Bensheim 2016
unter: http://www.tydecks.info/online/logik_kraft_dasein.html

Walter Tydecks: Hegels Idee eines »höheren Widerspruchs«, Bensheim 2012-19
unter: http://www.tydecks.info/online/logik_kraft_widerspruch.html

Walter Tydecks: Spencer-Brown Gesetze der Form – Einführung und weiterführende Ideen, Bensheim 2017-20
unter: http://www.tydecks.info/online/themen_spencer_brown_logik.html

Slavoj Žižek: Disparitäten, Darmstadt 2018 [2016]

 

© tydecks.info 2020