Re-entry nach Spencer-Brown

Beitrag für das formlabor in Berlin am 31.1.2020 (erheblich erweiterte Version)

 

Einleitung (Eigenwerte und Re-entry)

Die Lehre vom Re-entry (Wieder-Eintritt) ist das Herzstück der Laws of Form. Sie ist zugleich die einzige Idee von Spencer-Brown, die eine gewisse Beachtung gefunden hat. Mit Wieder-Eintritt ist gemeint, dass sich in einem formal beschreibbaren Prozess aus einer gegebenen Menge etwas herauslöst, in einem aus Sicht dieser Menge virtuellen Raum eine eigene Bewegung vollzieht, sich hierbei verändert, und am Ende als etwas Neues in die Ausgangsmenge zurückkehrt. Die Ausgangsmenge nimmt nicht nur ein Element auf, das bisher in ihrem Rahmen nicht darstellbar war, sondern sie wird durch diesen Vorgang im Ganzen verändert. Sie erzittert und wird von einem zeitlichen Prozess erfasst. Das mit dem Re-entry aufgenommene Element muss vernäht werden.

So zu denken verlangt eine Phantasie, die in der traditionellen Logik und Mathematik nicht üblich war und sich nur historisch am Ort ihrer Entstehung nachweisen lässt, seither aber verschüttet ist. Daher ist es für mich kein Zufall, wenn Ideen dieser Art bisher nur von der Psychologie und Soziologie aufgegriffen wurden, nicht aber von der Mathematik, Informatik und akademischen Philosophie. Vorläufer eines Re-entry gibt es in der Poesie der Romantik, die gegen die reine Vernunft der Aufklärung revoltierte. Jemand spricht von einem Löwen, und plötzlich tritt ein Löwe auf, der aus dem Reich der Phantasie in die Wirklichkeit tritt und das Geschehen und mit ihm den verwirrten Leser der Erzählung durcheinander bringt. »Der Inhalt des Textes wird bei solchen Operationen aus der Sprache selbst hervorgetrieben, das ist ein Spezifikum romantischer Texte.« (Gabriele Stumpp, E-Mail vom 20.10.2019) Der Blickwinkel wird verändert. »Gemeinhin fragt man, was jemand mit dem meint, was er sagt; E.T.A. Hoffmann geht der Frage nach, was eigentlich einer sagt, wenn er etwas meint.« (ebd.) Das gilt ebenso für die Mathematik, auch wenn wir das nicht mehr wahrnehmen, weil wir uns daran gewöhnt haben. Niemand fragt mehr, was es bedeutet, wenn Mathematiker von Wurzeln sprechen. Sind das Wurzeln, aus denen Bäume wachsen und die gegessen werden können? Welche Phantasie hat die Mathematik dazu gebracht, von Wurzeln zu sprechen? Warum war Phantasie notwendig, um solche Zahlen als Wurzeln zu bezeichnen und in die Menge der natürlichen Zahlen einzuschieben?

Das ist das Thema des Re-entry: (i) Wie kommt es aus den natürlichen Zahlen heraus zur Verselbständigung einer unendlichen Bewegung, die zu neuen Zahlen wie den Wurzeln führen, und wie werden diese nahtlos in die Zahlen aufgenommen? (ii) Was führt dazu, dass diese Fremdkörper sich nicht im Unbekannten verflüchtigen, sondern in ihrem virtuellen Raum umkehren und zurückkehren können? Spencer-Brown meint damit jedoch keineswegs nur die Mathematik, sondern alle mit Zeichen operierenden, sprachlichen Vorgänge.

Diese Frage reicht zurück bis zu den Anfängen der griechischen Mathematik und Philosophie. Platon bezeichnet in seinem Dialog Theaitetos die Wurzeln als dynamische Zahlen, wobei dynamis sowohl bedeutet, dass sie nur im Reich des Möglichen bestehen, als auch über eine Macht (Dynamik) verfügen, die sie aus der bloßen Möglichkeit in das übliche Rechnen zurückführt. Wenn sie sich nicht nur von den natürlichen Zahlen entfernen, sondern wieder zurückkehren, muss es in ihrer Bewegung eine innere Spannkraft (tonos) geben, die sie daran hindert, sich in die Beliebigkeit zu verflüchtigen. In der Poesie sind das die Kreativität und das Einfühlungsvermögen des Schriftstellers, der seine Phantasien so zu gestalten weiß, dass sie den Leser ergreifen und von ihm verstanden werden.

Es ist schrittweise zu zeigen, wie die sich verselbständigende dynamische Zahl eine Eigengesetzlichkeit hat, die sie in einer doppelten Bewegung zunächst Autonomie gewinnen und anschließend umkehren lässt.

(i) Resonanz. Ein schwingender Körper löst bei einem anderen Körper ein Mitschwingen aus, das auf den auslösenden Körper zurückwirkt, dessen Schwingung verändert und darüber wiederum auch die Resonanz. Das kann bei einer Resonanz-Katastrophe zu einer völligen Selbstzerstörung führen. Pendelt sich dagegen die Schwingung beider Körper auf eine Harmonie ein, kann von einem Eigenwert gesprochen werden, über den beide sich treffen und miteinander verbunden sind. Jeder kennt das, der gemeinsam mit anderen singt oder musiziert oder als Hörer das Einpendeln wahrnimmt.

(ii) Feedback. Jemand äußert eine Mitteilung und erfährt von seinem Adressaten, wie dieser die Mitteilung verstanden hat. Das wird ihn oft genug verblüffen und zu weitergehenden Ideen anregen. Er wird lernen, dass er weit mehr und oft etwas Anderes ausgesagt hat, als ihm im Moment des Aussprechens bewusst war. Dank des Feedback wird der Mitteilende die Verständlichkeit und Aussagekraft seiner Mitteilung überprüfen und anpassen. Im Verlaufe des Gesprächs werden beide einander kennenlernen und nach einer Weile fast schon im voraus wissen, worauf der Andere hinauswill.

(iii) Rückkopplung. Der Re-entry kann in einem technischen Prozess realisiert werden. Das einfachste Beispiel ist der Thermostat: Abhängig von der jeweiligen Raumtemperatur wird die Wärmezufuhr erhöht oder gedrosselt. Etwas komplexer ist das Fließgleichgewicht z.B. einer Dampfmaschine: Die Rückkopplung verändert den Prozess. Dadurch kann es zu einer taumelnden Bewegung kommen. Wenn die Rückkopplung stabil wird und der Prozess sich gleichmäßig bewegt, kann von einem Eigenwert gesprochen werden. Es ist nicht sicher, ob ein System in einen Eigenzustand gelangen kann oder in einer chaotischen Bewegung bleiben wird.

(iv) Reflexivität. Im einfachsten Fall sehe ich mich im Spiegel und beginne zu verstehen, wie andere mich sehen. Das Spiegelbild ist die Reflexion des Objekts vor dem Spiegel. Das kann in philosophischen Reflexionen erweitert werden: Mit ihnen wird ein Modell geschaffen, in dem die jeweils reflektierte Realität gespiegelt wird.

Diese Beispiele können zum Verständnis des Re-entry hinführen, und doch unterscheidet sich der Re-entry von ihnen in einem wesentlichen Punkt: Der Re-entry entsteht aus sich heraus. Er wird nicht von einem äußeren Beobachter oder einer äußeren Entität und deren Rückmeldung oder einem von außen kommenden Einfluss (wie z.B. einer Wärmezufuhr) erzeugt. Es gibt keinen Spiegel, von dem etwas zurückgeworfen wird und dem Prozess ein Bild seiner selbst zeigt. Der Re-entry kehrt von allein zurück, und es ist zu fragen, wie diese Umkehr aus sich selbst heraus möglich wird. Sie liegt in den Bewegungsgesetzen der von Spencer-Brown betrachteten Prozesse begründet (Intransitivität, Zyklizität, algebraische Regeln der imaginären Zahlen).

Spencer-Brown überträgt das auf die Logik und Mathematik und will zeigen, wie aus einem formalen System von sich aus Selbstreflexivität hervorgeht. Sie muss nicht erst nachträglich durch einen Beobachter in das System hineingetragen werden. Gödel kann als Vorläufer von Spencer-Brown verstanden werden. Er hat mithilfe von Primzahlen ein Verfahren entwickelt, mit dem jeder Satz auf die Elemente abgebildet werden kann, aus denen er zusammengesetzt ist (Gödelisierung). Das kann auch ein Satz sein wie ›dieser Satz ist falsch‹ oder ›gehe an der Stelle, an der du dich befindest, einen Schritt weiter‹ (Turing-Maschine). Im Ergebnis erhält jedes Element eine Doppelbedeutung: Es kann ein »normales« Element sein oder das Bild eines Satzes, der aus diesen Elementen gebildet ist. In einem unendlichen Regress kann auch die Gödelisierung gödelisiert werden. In ihrer Doppelbedeutung als Element und Satz, der aus Elementen zusammengesetzt ist, enthalten die Elemente in sich den Keim zu einer Bewegung, die von ihnen ausgeht und zu ihnen zurückführt: Aus Elementen werden Sätze gebildet, und diese werden wiederum auf Elemente abgebildet.

Mit dem Re-entry kommen Zirkularität und Dynamik in die Logik. Sie beschränkt sich nicht mehr auf Kausal- oder Schlussketten, mit denen von einem Element des Systems auf ein anderes Element geschlossen wird, sondern die Logik des Systems-im-Ganzen ändert sich in Wechselbeziehung mit ihren Elementen. Damit zeigt Spencer-Brown zugleich einen Ausweg aus der Russellschen Antinomie. Er konstruiert nicht einfach ein alternatives System, in dem z.B. die Kontinuum-Hypothese fallen gelassen wird, um zu prüfen, ob es konsistent ist, sondern er entwickelt ausgehend von den überlieferten Systemen der Logik und Mathematik, wie in ihnen eine Bewegung zwischen System und Elementen angelegt ist, die von den Mathematikern in bestimmten Fällen genutzt wird, und entwirft die allgemeine Verlaufsform, der sie genügen. Das führt zu einem neuen Verständnis der Zahlen.

Einleitend soll an den Beispielen des aus der Fibonacci-Reihe hervorgehenden Goldenen Schnitts, der transfiniten Zahlen und der Irrationalzahlen gezeigt werden, wie an ihnen der von Spencer-Brown gedachte Re-entry abgelesen werden kann. Hier ist zu beachten: Werden die Zahlen als die Objekte der Mathematik verstanden, dann werden mit den transfiniten und irrationalen Zahlen neue Objekte in die Zahlen aufgenommen. Aber es geht nicht nur um Objekte: Für die transfiniten und irrationalen Zahlen müssen neue Symbole gebildet werden. Das ist nur möglich, wenn die Objektebene verlassen und auf der Sprachebene neue Namen und Zeichen für Zahlen gebildet werden. Spencer-Brown geht noch einen Schritt weiter: Er fragt nicht nur nach neuen Objekten, sondern auch nach neuen Sprachelementen, die nicht auf der Objektebene, sondern auf der Sprachebene aufgenommen werden. Das führt zu einer zyklischen Bewegung zwischen Objekt- und Sprachebene. Es ist die These und das Anliegen dieses Kommentars, das im Einzelnen nachzuweisen und auszuführen.

Welche Eigenschaften eines gegebenen formalen Systems ermöglichen den Re-entry? Diese Frage lässt Spencer-Brown offen, aber er gibt Hinweise auf ihre Lösung. Er sucht in seinem Kalkül nach einem Prozess, der der Herausbildung transfiniter Zahlen und Irrationalzahlen entspricht und findet ihn in der Staffelung (echelon) 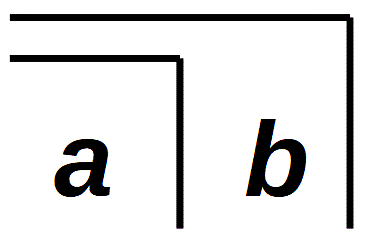. Die Staffelung kommt in seinem Formenkalkül an zwei Stellen vor: (i) In der Consequence C7 beschreibt er, wie eine transitive Staffelung in eine intransitive Figur umgewandelt werden kann. (ii) Im Kapitel über den Re-entry wählt er die Staffelung, um an ihr die Herausbildung eines neuen Zeichens zu demonstrieren, das per Re-entry wieder aufgenommen werden muss.

Können diese beiden Aspekte zusammengebracht werden? Ich möchte zeigen, wie mit der Staffelung ein erweitertes Verständnis der Anordnung der natürlichen Zahlen gefunden werden kann, aus dem sich das Entstehen eines Supplements und dessen Re-entry erklären lässt. Mit der Intransitivität ist die Zyklizität gegeben, dank derer der Prozess zunächst aus den gegebenen Objekten hinausführt und wieder zurückkehren kann, ohne für die Umkehr auf eine äußere Einwirkung angewiesen zu sein.

Den Anstoß für diesen Gedanken bekam ich von Donald Kunze (* 1947): Ihm ist aufgefallen, wie Spencer-Brown in der Figur der Staffelung (echelon) eine Gleichsetzung (besser: Oszillation) von Transitivität und Nicht-Transitivität gezeigt hat (Consequence C7 in LoF, 34). Das vergleicht er mit Beispielen aus der Geschichte des Städtebaus und dem Holzstich Der Zeichner des liegenden Weibes von Dürer, Nürnberg 1538.

Abschließend stellen sich die Frage nach der Mehrwertigkeit sowie nach einer imaginären Achse, in der die dynamischen Zahlen eingetragen sind. In welchem Verhältnis steht sie zur Kenogrammatik von Gotthard Günther.

Iteration, Rekursion, Backtracking, Re-entry

Was unterscheidet Iteration, Rekursion, Rücksetzverfahren und Re-entry?

Iteration ist die mehrfache Wiederholung des gleichen Rechenvorgangs, in der Programmierung eine Schleife (loop). Die einfachste Iteration ist das Zählen, bei der fortlaufend die Addition n + 1 wiederholt wird:

Anfangszahl	1
Schleife mit fester Schrittweite 1	1 + 1 = 2 2 + 1 = 3 3 + 1 = 4 …

Das Zählen ist zugleich eine Rekursion: Damit ist gemeint, dass jeder neue Rechenschritt das Ergebnis des vorherigen Rechenschritts als Ausgangspunkt übernimmt. Der erste Zählschritt hat zur 2 geführt. Von der 2 aus wird weiter gezählt usf.

Die Rekursion muss nicht auf das letzte Ergebnis beschränkt sein. Bei der Fibonacci-Folge ergibt die Summe der jeweils beiden letzten Folgenglieder das neue Folgeelement:

Anfangszahlen	0 1
Schleife mit variabler Schrittweite	0 + 1 = 1 1 + 1 = 2 2 + 1 = 3 3 + 2 = 5 5 + 3 = 8 8 + 5 = 13    …	2 / 1 3 / 2 5 / 3 8 / 5 13 / 8	= 2 = 1,5 = 1,66… = 1,6 = 1,625 → 1,618… (Φ, Goldener Schnitt)

Johannes Kepler hatte bemerkt, dass sich das Verhältnis zweier nachfolgender Elemente der Fibonacci-Folge aₙ₊₁ zu aₙ dem Goldenen Schnitt annähert, diesen jedoch nie erreicht. Da der Goldene Schnitt keine übliche Zahl ist, erhält er einen eigenen symbolischen Namen: Φ. So wird aus einer Folge natürlicher Zahlen eine Zahl angenähert, die nicht natürlich ist und durch einen Re-entry in die Menge aller Zahlen aufgenommen werden muss. Da sie sich als Verhältniswert innerhalb der Reihe ergibt, kann sie mit einiger Berechtigung als Eigenwert bezeichnet werden. Sie gilt seither als die innere Harmonie des Wachstums wie auch der Schönheit.

Wo liegt der Goldene Schnitt, wenn es sich um keine natürliche Zahl handelt? Seit Pythagoras ist bekannt, dass sich im Fünfeck die Diagonalen so schneiden, dass jeweils die beiden Hälften einer Diagonale im Verhältnis des Goldenen Schnitts zueinander stehen:

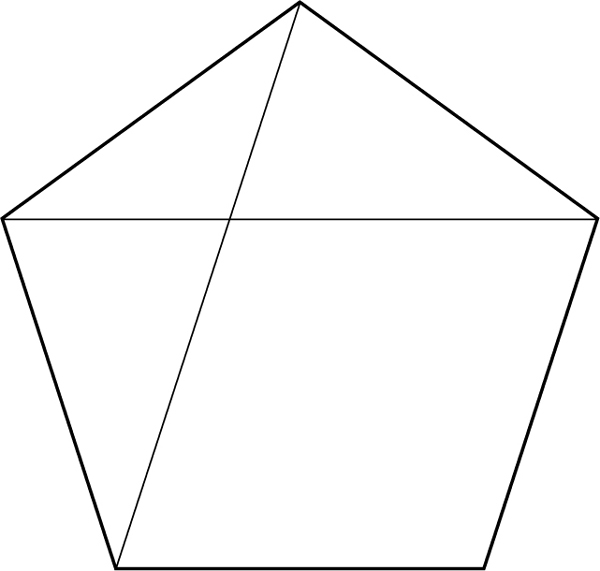
Noch anschaulicher wird es, wenn die Fibonacci-Reihe wie auf einer Spirale in einer Pflanze ent-wickelt wird, in der der Goldene Winkel auftritt:

Phyllotaxis der Aloe polyphylla
Urheber: By Stan Shebs, CC BY-SA 3.0, Link

Wer die Wurzel aus 2 ohne Taschenrechner rein schriftlich berechnen will, geht ebenfalls rekursiv vor, indem eine Nachkommastelle nach der anderen berechnet wird:

1. Stelle:	1 · 1 = 1 2 · 2 = 4
	4 ist zu groß, daher ist die 1. Stelle 1
2. Stelle:	1,5 · 1,5 = 2,25 1,4 · 1,4 = 1,96
	2,25 ist zu groß, daher ist die 2. Stelle 4
3. Stelle:	1,41 · 1,41 = 1,9881 1,42 · 1,42 = 2,0164
	2,0164 ist zu groß, daher ist die 3. Stelle 1
…

Ein geometrisches Beispiel ist der Pythagoras-Baum. An der Oberkante eines Quadrats wird ein rechtwinkliges Dreieck angelegt, an dessen Katheten neue Quadrate, an deren Oberkanten wiederum rechtwinklige Dreiecke usf.

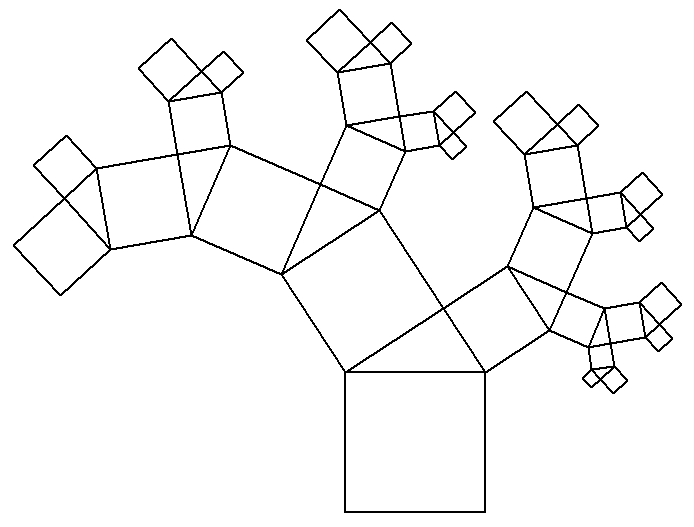
Pythagorasbaum
Urheber: Gemeinfrei, Link

»Programmtechnisch läuft eine Iteration auf eine Schleife, eine Rekursion auf den Aufruf einer Methode durch sich selbst hinaus.« (Uni Leipzig)

Backtracking (Rücksetzverfahren). Das elementare Beispiel ist der Weg durch ein Labyrinth.

Tiefensuche des Backtracking
Urheber: Alexander Drichel - Eigenes Werk, CC BY-SA 3.0, Link

– Im ersten Schritt wird an jeder Verzweigung nach links verzweigt bis eine Sackgasse erreicht ist.
– Der letzte Schritt vor der Sackgasse wird als Irrweg gekennzeichnet. Von diesem Verzweigungspunkt aus wird der nächstmögliche Weg nach links gegangen.
– Sind von einem Verzweigungspunkt aus alle Wege als Irrwege gekennzeichnet, wird einen Schritt zur vorherigen Verzweigung gegangen und von dort aus erneut ein Weg gesucht.
– Wenn der Ausgang gefunden ist, bricht das Verfahren ab.

Das Backtracking enthält Iterationen und Rekursionen: Es werden einzelne, untereinander ähnliche Schritte ausgeführt, und nach jeder Sackgasse wird das Verfahren rekursiv neu aufgerufen. Das Backtracking enthält jedoch über die einfachste Rekursion hinaus die Kennzeichnung von Irrwegen. – Praktische Anwendungen des Backtracking sind das Springer-Problem, »für einen Springer auf einem leeren Schachbrett eine Route zu finden, auf der dieser jedes Feld genau einmal besucht«, die Wegsuche, diverse Spielprogramme oder die Programmiersprache PROLOG.

Worin unterscheidet sich der Re-entry von diesen algorithmischen Verfahren? Überall dort, wo bisher die drei Pünktchen ›…‹ eingetragen wurden, werden die drei Pünktchen durch eine neue Zahl ersetzt, die im bisherigen Zahlenraum nicht enthalten war und dort durch einen Re-entry aufgenommen wird. Die Mathematiker machen das – ohne sich dessen bewusst zu sein – schon immer, indem sie neue Zahlensymbole einführen und in die ursprüngliche Zahlenmenge aufnehmen. Der Standardfall sind die irrationalen Zahlen wie die 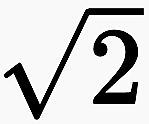, für die das neue Symbol eingeführt wird.

In meinem Verständnis will Spencer-Brown mit dem Re-entry drei Fragen lösen:

– Welche Eigenschaft hat der ursprüngliche Zahlenraum, damit es zu einem Prozess kommen kann, der aus ihn heraus führt?

– Welche Eigenschaft hat der Raum, in dem diese Bewegung ihren Verlauf nimmt? Das ist in erster Benennung der Raum des Möglichen, der Raum des Vorstellbaren (der Vorstellungskraft) und mathematisch gesprochen der Raum der imaginären Zahlen. Diese Eigenschaften müssen zugleich erklären, warum die Bewegung umkehrt und in den Ausgangsraum zurückfindet. Auf jeden Fall gilt, dass diese Zahlen intransitiv sind. Das ist schon an den imaginären Zahlen zu sehen: Die Zahl i ist weder größer noch kleiner als 0. Zwar lassen sich für komplexe Zahlen z ihre Beträge |z|, – das sind ihre Abstände vom Nullpunkt –, transitiv ordnen, doch geht mit ihnen die Identität verloren: i und 1 haben den gleichen Betrag 1.

– Welche Eigenschaft hat der Ausgangsraum, um die zurückkehrenden dynamischen Zahlen aufnehmen zu können? Er muss kontinuierlich sein. Dank seiner Kontinuität finden sich anschaulich gesprochen genügend Lücken zwischen den bereits bekannten Zahlen, in denen der Re-entry Platz findet. Wird das genauer betrachtet, ist dies nicht eine Eigenschaft der Zahlen, sondern des Mediums, in dem sie eingetragen sind. Der Begriff der Zahl wird erweitert: Es handelt sich nicht mehr bloß um einzelne Elemente (die Zahlen), sondern um das Kontinuum, das stets mehr enthält als die Gesamtheit seiner Elemente. Spencer-Brown hat die paradoxe Frage nach dem Verhältnis der Menge und ihrer Elemente (Russells Frage nach der Menge aller Mengen, die sich nicht selbst als Element enthalten) eingebettet in die übergreifende Frage nach dem Verhältnis des Mediums und der in das Medium eingetragenen Formen (Information).

Re-entry der transfiniten und irrationalen Zahlen

Vorbilder (Modelle) für den Re-entry sind nach meinem Eindruck die Konstruktion der ersten transfiniten Zahl ω bei Cantor und der Grenzübergang, der zur Annäherung von Irrationalzahlen wie 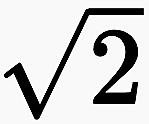führt.

Transfinite Zahlen Beim Zählen ›1, 2, 3, … n, n+1, …‹ wird formal betrachtet unendlich oft die jeweils gleiche Nachfolger-Relation von ›n‹ zu ›n + 1‹ wiederholt. Jenseits von allen abzählbaren natürlichen Zahlen liegt die transfinite Zahl ω. Sie kann nie durch Zählen erreicht werden und hat keinen Vorgänger, aber sie kann formal als Ergebnis der Regel des Zählens-im-Ganzen definiert werden. Es muss eine übergreifende Zahlenklasse (einen Grund) geben, in den der Grenzwert per Re-entry aufgenommen werden kann.

Wo liegt ω, und wie wird ω in die Zahlen aufgenommen? Der Mathematiker Riemann hatte dafür eine sehr anschauliche Vorstellung gefunden: Wenn auf der Zahlengerade im Nullpunkt eine Kugel aufgelegt wird, deren Mittelpunkt mit der Zahl Null identisch ist und deren Kugeloberfläche die Zahlenachse an den beiden Punkten −1 und 1 schneidet, kann eindeutig jeder Zahl ein Punkt auf der Kugel zugeordnet werden, indem eine Verbindungslinie zwischen dem Nord- bzw. Südpol und der jeweiligen Zahl gezogen wird, die an genau einer Stelle die Kugel schneidet. Für Zahlen außerhalb der Kugel (das sind in der folgenden Abbildung die Zahlen größer als 1 oder kleiner als −1) liegt der Schnittpunkt auf der oberen Halbkugel, für Zahlen innerhalb der Kugel (das sind die Zahlen im Intervall [−1, 1]) auf der unteren Halbkugel. Der Nordpol entspricht der auf der Zahlengerade unendlich-fernen Zahl ω und ist mit diesem Konstruktionsverfahren in die Zahlenklasse aller Punkte auf der Kugel aufgenommen. Auf den Südpol wird die 0 abgebildet.

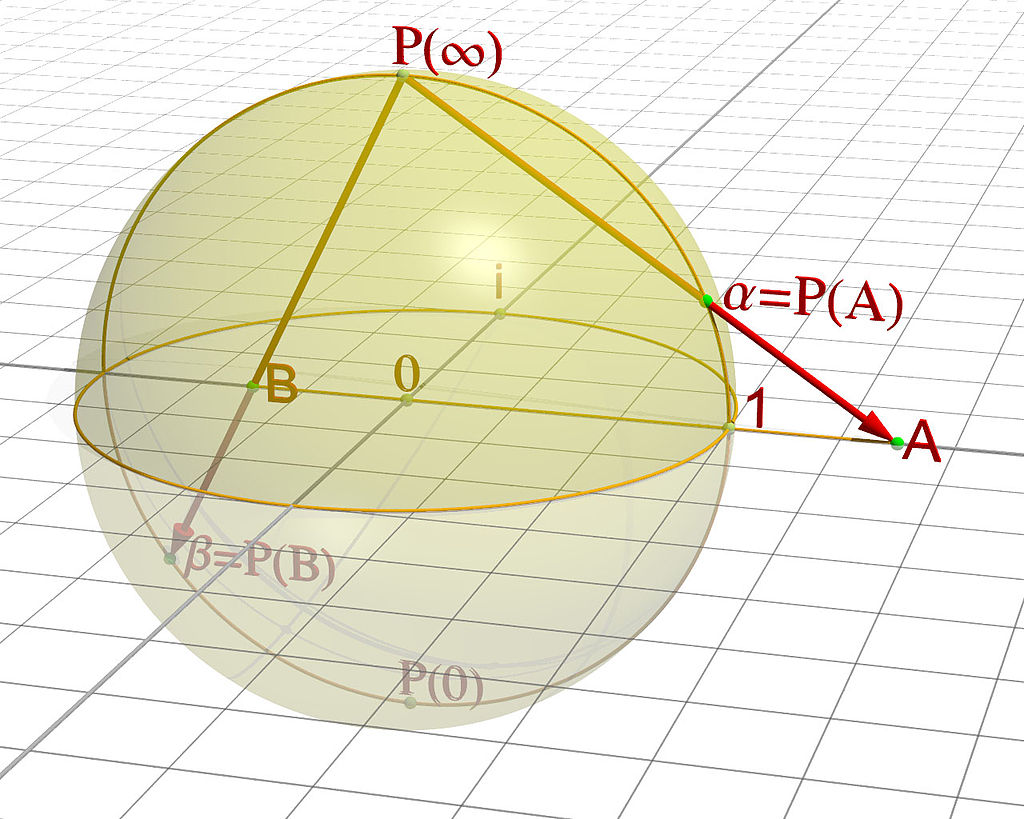
Quelle: Wikipedia, abgerufen am 4.3.2017
Urheber: Von Jean-Christophe BENOIST - Eigenes Werk. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV., CC BY-SA 3.0, Link

An dem Bild ist anschaulich zu sehen, wie ω auf der Zahlengerade unendlich weit weg liegt, jedoch auf der Zahlenkugel bei P(ω) ihren Ort findet. Wie ist das möglich? Mit der Zahlenkugel wurden implizit neue Eigenschaften der Zahlen eingeführt, die bei der Zahlengerade noch nicht gegeben sind: Die Zahlenkugel verfügt über eine zweite, unabhängige Dimension (ihre Höhe, die auch als imaginäre Achse oder als Zeitachse interpretiert werden kann), sie ist symmetrisch gegenüber Drehungen (zyklisch), und sie ist gekrümmt. Das sind Eigenschaften, die über die bisher bekannten Eigenschaften der Zahlen (Transitivität, Kontinuität) hinausgehen und bereits anschaulich nahelegen, dass eine Erweiterung und neue Definition der Zahlen notwendig wird, wenn Prozesse zugelassen werden sollen, die zu einem Re-entry führen. (Spencer-Brown zeigt in nachfolgenden Kapiteln, wie dieses Bild und diese Eigenschaften zu der neuartigen Theorie von Beobachtern führen.)

Irrationalzahlen Für Irrationalzahlen wie 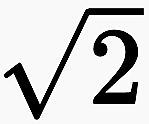gibt es keine Dezimaldarstellung. Sie beträgt ungefähr 1,414… und kann nur fortlaufend genauer bestimmt werden. Mit jedem Schritt wird das Intervall genauer eingegrenzt, in dem sie liegen muss. Zum Beispiel wird mit dem Ausdruck 1,414… gesagt, dass sie irgendwo im Intervall [1,414, 1,415] liegt. Und so wie Cantor mit ω für die transfiniten Zahlen eigene Symbole finden musste, musste für die Irrationalzahlen mit dem Wurzelzeichen ein eigenes Symbol vereinbart werden.

Spencer-Brown erwähnt die Irrationalzahlen in den Notes, wenn er dort von Gleichungen zweiten Grades spricht. Er demonstriert das an der Quadratfunktion x² oder in seinem Kalkül aa = a und führt es am elementaren Polynom zweiter Ordnung aus. (LoF, 97f)

Was geschieht bei den beiden Übergängen zu den transfiniten und den Irrationalzahlen? Es handelt sich nicht mehr um eine gewöhnliche arithmetische Operation. Eine arithmetische Operation wie z.B. ›7 + (10 · 3) / 91‹ kann zwar beliebig kompliziert sein. Letztlich handelt es sich jedoch um eine endliche Zeichenkette, die aus Operanden und Operatoren besteht (im einfachsten Fall aus den natürlichen Zahlen als Operanden und den üblichen Rechenregeln +, −, · und / als Operatoren), und die zu einer eindeutig bestimmten rationalen Zahl führt. Bei dem unendlichen Weiterzählen und bei den Annäherungs-Algorithmen zur Bestimmung von Irrationalzahlen wird dagegen eine arithmetische Operation unendlich oft  wiederholt  (iteriert). Erst die Wiederholung (Iteration) erzeugt einen Prozess. Der Mathematik blieb bis heute unbemerkt, oder sie will es nicht wahrhaben, dass im Prozess der Wiederholung implizit die Zeit enthalten ist. – Die Mathematik besteht bis heute darauf, dass ihre Formeln grundsätzlich zeitlos gelten. Erst Spencer-Brown vollzog die längst überfällige Wende und entwickelte konsequent, wie im Prozess, der zum Re-entry führt, implizit die Zeit enthalten ist.

Bei den arithmetischen Operationen wird die jeweilige Zahlenklasse nicht verlassen. Sie liefert eine neue Zahl und kann mit dieser identifiziert werden. Es ist gleichbedeutend, ob von 12 oder von ›5 + 7‹ gesprochen wird. Bei Prozessen wird dagegen eine neue Zahl definiert, die in der vorher betrachteten Zahlenklasse noch nicht enthalten war. Weder ist ω eine natürliche Zahl noch 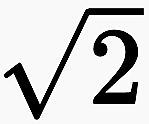eine rationale Zahl. Mit ihnen entsteht ein neuer Begriff von Zahlen: Zahlen sind alle Elemente, mit denen wie mit natürlichen und rationalen Zahlen gerechnet werden kann. Was eine Zahl ist und zur Gesamtheit der Zahlen gehört, wird schrittweise erschlossen. Die Idee der Zahl ist in sich unendlich, und es kann davon ausgegangen werden, dass immer neue Prozesse gefunden werden, um neue Zahlen mit Eigenschaften zu erkennen, die bisher unbekannt waren.

Der Re-entry in den Laws of Form und seine Sprache

Wie kann Spencer-Brown die unendlichen Prozesse des Zählens oder der Annäherung an eine Irrationalzahl in seinen Formenkalkül übertragen? Es wäre am naheliegendsten, die Formen der Proto-Arithmetik in ähnlicher Weise zu zählen wie die natürlichen Zahlen und zu zeigen, dass es ein unendlich-fernes Element geben muss, dass durch einen Re-entry in die Menge aller Formen aufgenommen werden kann. Aber es gibt in seinem Kalkül keine eindeutige Nachfolger-Relation wie bei den natürlichen Zahlen, sondern es gibt zwei Möglichkeiten der Iteration von Formen, die sich wiederum beliebig kombinieren lassen:

Wiederholtes Calling	⃧  ,  ⃧   ⃧  ,  ⃧   ⃧   ⃧   , …
Wiederholtes Crossing	⃧  ,, , …

Eine lexikographische Ordnung aller Formen kann so aussehen:

  

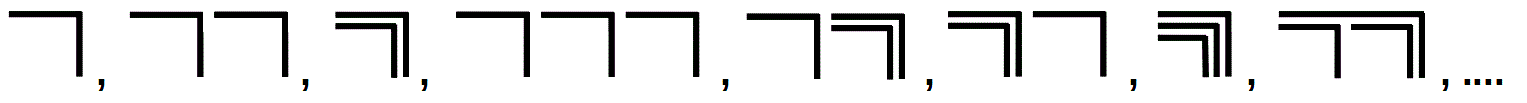
Bernie Lewin hat die beiden Iterationen untersucht und versteht sie als die horizontale und die vertikale Komponente einer ganzheitlichen, zweidimensionalen, gnomischen Entwicklung (gnomon, ‘Zeiger, Weiser auf der Sonnenuhr, Winkelmaß’, auf englisch ‘pin, style, sundial’), die auf die zweidimensionale Anordnung der Tetraktys bei Pythagoras zurückgeht und sich von ihr aus systematisch entwickeln lässt (Lewin, 185-193). Er bezeichnet die horizontale Komponente der iterierten Callings als Zahlen (number) und die vertikale Komponente der iterierten Crossings als Ordnung (order), die in einer Matrix dargestellt werden können (Lewin, 202). Dieser Ansatz erscheint mir sehr vielversprechend. Lewin gibt zahlreiche Beispiele, wie sich aus der Tektraktys Formen entwickeln lassen. Ich vermute, dass sich über die Tektraktys eine übergreifende Entwicklung der Zahlen nach qualitativen Eigenschaften begründen lässt, die über die derzeitige Mathematik hinausgehen (Dynamische, geträumte und imaginäre Zahlen).

Spencer-Brown ist jedoch einen anderen Weg gegangen. Auf den ersten Blick bleibt er konventioneller und hat einen eindimensional (linear, transitiv) darstellbaren Prozess auseinander hervorgehender Formen gesucht, um deren Grenzwert durch einen Re-entry in seinen Kalkül aufzunehmen. Zugleich geht er über die klassischen Beispiele der transfiniten und irrationalen Zahlen hinaus und findet einen Re-entry, der nicht eine neue Zahl in eine gegebene Zahlenmenge aufnimmt, sondern ein neues Symbol f in die Menge der mathematischen Sprachsymbole. Er bewegt sich nicht auf der Objektebene der Mathematik, – ihren Zahlen oder geometrischen Gebilden –, sondern auf der Meta-Ebene der mathematischen Sprache. Sein Re-entry handelt nicht von den Zahlen als den Operanden (Objekten), mit denen gerechnet (operiert) wird, sondern von den Symbolen, mit denen die Rechnungen (Operationen) und deren Eigenschaften sprachlich gefasst und formal dargestellt werden. Das sind Symbole wie das a (Argument), das als Variable für eine beliebige Zahl stehen kann, mit der es gesättigt wird, um einen anschaulichen Ausdruck von Frege zu gebrauchen. Mit Symbolen dieser Art werden gewöhnlich übergreifende Eigenschaften von Zahlenmengen-im-Ganzen beschrieben wie z.B. die Kommutativität: ›a + b = b + a‹, unabhängig von den jeweils besonderen Eigenschaften der in a und b eingesetzten Werte. Es ist nun der originelle Gedanke von Spencer-Brown, auch für Symbole dieser Art einen Prozess zu finden, der wie beim Zählen oder der Annäherung an eine Irrationalzahl zu einem Grenzwert führt und per Re-entry aufgenommen werden kann. Dieser Grenzwert zeigt an den einzelnen Elementen (das sind in diesem Fall die Symbole der mathematischen Sprache) eine Systemeigenschaft, die für das System als Ganze gilt (das ist hier die mathematische Sprache). So entsteht vereinfacht gesagt das System aus der fortschreitenden Ordnung seiner Elemente und kann als Grenzwert dieser fortschreitenden Ordnung in sich selbst als Element aufgenommen werden. Damit gelingt ihm die Lösung der Russellschen Antinomie: Er zeigt, wie sich bestimmte Elemente einer Menge schrittweise so ordnen lassen, dass als der Grenzwert ihrer fortschreitenden Ordnung das innere Gesetz dieser Ordnung hervortritt und in die Menge der Elemente aufgenommen werden kann, die von ihm geordnet werden.

Mit diesen Ideen betritt er Neuland, und es verlangt ein völliges Umdenken, um ihm hierin folgen zu können. Vorab seien einige Meilensteine genannt, um die es im Weiteren gehen wird:

– Spencer-Brown wählt als Ausgangspunkt eine Form, die zugleich transitiv und intransitiv ist: die Staffelung (echelon).

– Mit ihr gelingt ihm ein Re-entry nach dem Vorbild des Re-entry der transfiniten und irrationalen Zahlen.

– Da er sich jedoch nicht auf der Ebene der Zahlen, sondern der Sprachsymbole befindet, mit denen Rechenoperationen mit Zahlen beschrieben werden, gelingt ihm eine Verallgemeinerung der Idee von Gödel, der den grundsätzlichen Doppelcharakter aller Zeichen eines ausreichend komplexen formalen Systems gezeigt hat, die sich sowohl als Operatoren wie als Operanden verstehen lassen.

– Im Ergebnis entsteht ein Kalkül, der sachlich mit der Algebra der komplexen (imaginären) Zahlen übereinstimmt, die jedoch aus der Perspektive von Spencer-Brown eine weit grundsätzlichere Bedeutung bekommen, als sie in der gewöhnlichen Mathematik bekannt ist. Aus dieser Perspektive lassen sie sich verstehen als die Mathematik einer dynamischen Logik.

Die folgende Darstellung ist zugleich eine Würdigung der Arbeiten von Gotthard Günther (1900-1984), der 1960-72 über Warren McCulloch und Heinz v. Foerster die neu entstehende Kybernetik kennen gelernt und für sie nach einer angemessenen Mathematik und Logik gesucht hat. Auch wenn sich Günther und Spencer-Brown meines Wissens nirgends direkt aufeinander bezogen haben, werden einige Grundideen von Gotthard Günther herangezogen, die aus der Perspektive von Spencer-Brown ihrerseits neu gedeutet werden können (die Rolle der Reflexion, die Proemialrelation auseinander emergierender Systeme und die Leerstellen, in der mit Spencer-Brown wechselweise Argumente a wie die über diese Argumente gebildeten Funktionen f eingetragen werden können).

– Die unbegrenzte Staffelung (echelon without limit)

Spencer-Brown wählt das Echelon (Staffelung) 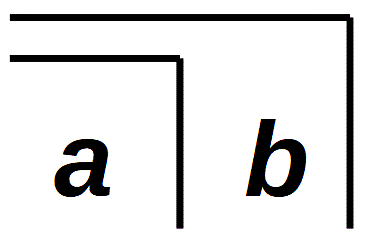als Ausgangspunkt für einen Prozess, der innerhalb seines Kalküls zum Re-entry führt (LoF, 54).

In der Form 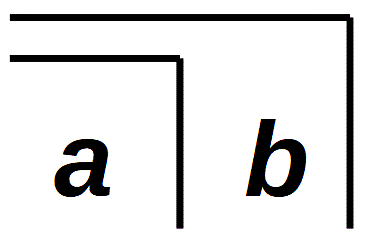sind Calling und Crossing intuitiv verknüpft: Die beiden Variablen a und b folgen einander, und zugleich gibt es eine doppelte Verschachtelung. Spencer-Brown zeigt, wie auf das Zeichen 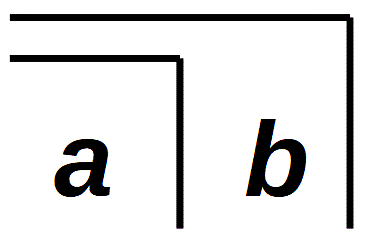eine Sequenz von 5 Transformationen angewandt werden kann, wodurch sich das Zeichen nach 5 Schritten verdoppelt, nach weiteren 5 Schritten verdreifacht usf. (LoF, 55). Diese Darstellung ist wie die schrittweise Umwandlung einer gewöhnlichen Gleichung zu lesen, bis auf der einen Seite die Unbekannte x und auf deren Seiten deren Lösung steht. Spencer-Brown nutzt die Regeln C5, C1, J2 und C4, die in seinem Kalkül eingeführt worden waren. (Statt von Regeln spricht er von Initialen und Consequences, um zu betonen, dass die Consequences ihrerseits aus den Initialen hergeleitet werden können und im Weiteren als Regeln für das Operieren in der Proto-Algebra bereit stehen.) Das nachzurechnen kann als eine anspruchsvolle Übungsaufgabe im Umgang mit dem Kalkül von Spencer-Brown angesehen werden. Für Details siehe den Anhang zum Canon C9.

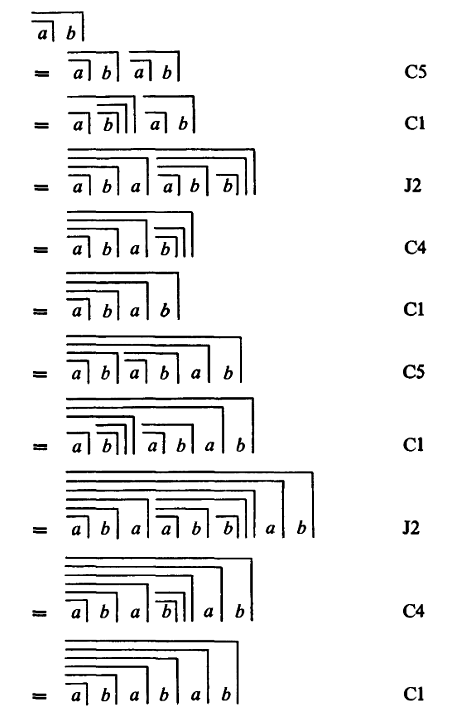
Oder zusammengezogen (LoF, 56):

    ⇀ .

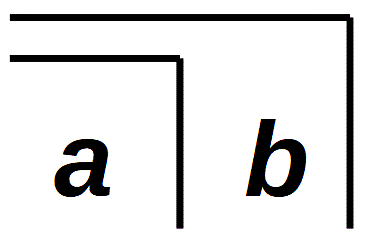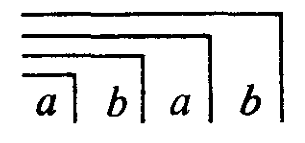Mit dem Symbol ⇀ ist ausgesagt, dass beide Zeichen (Formen) wertgleich sind. Auf das neue Zeichen (Form) kann wiederum die gleiche Sequenz aus 5 Einzelschritten angewandt werden, wodurch es sich erneut verlängert. Auf diese Weise gelingt eine Folge von Schritten, die der Nachfolger-Relation entspricht und unendlich oft wiederholt werden kann. Obwohl Spencer-Brown das Echelon innerhalb der Proto-Algebra (Primary Algebra) als Consequence C7 mit drei Variablen a, b und c eingeführt hat (LoF, 34) und nicht wie hier für zwei Variablen a und b, ist für ihn das Ergebnis »an echelon without limit« (LoF, 56).

»Der nächste entscheidende Schritt besteht darin, sich vorzustellen, wenn es möglich ist (let us imagine, if we can, LoF, 55), dass der Prozess dieser Schrittsequenz end- oder zeitlos (timelessly) weiterläuft. Im Raum würde das ein Echelon (Staffelung) von a's und b's ohne Grenze ergeben. [...] Da die Bestimmung des Wertes eines Ausdrucks an die Regel der endlichen Demonstrierbarkeit gebunden ist, kann über den Wert eines Echelons ohne Grenzen keine Aussage gemacht werden.« (Schönwalder-Kuntze u.a., 175)

Im Ergebnis schreibt Spencer-Brown ein Diagramm auf, mit dem die Form definiert wird, die per Re-entry in die Proto-Algebra aufgenommen werden soll:

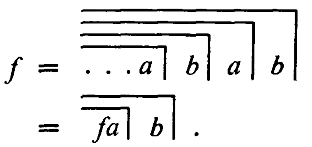
E1 Re-entry
(LoF, 56)

Die wie eine Definition aufgeschriebene Formel E1 hebt die Rekursion hervor: Das jeweils erreichte Element wird als f bezeichnet und im nachfolgenden Schritt neu aufgerufen. Der Übergang von a zu b wird beliebig oft wiederholt. Die drei Pünktchen übernimmt er von den entsprechenden, aus der gewöhnlichen Arithmetik bekannten Prozessen, wenn dort über ›n‹ und ›n + 1‹ hinaus immer weiter gezählt oder eine Irrationalzahl beliebig genau angenähert wird und beschreibt mit ihnen die Form, die aus dem unendlichen Prozess der Staffelung hervorgeht.

Die Zusammenfassung der unendlich vielen Crossings von a zu b zu a zu b usw. in f ist an drei Bedingungen gebunden:

(a) »Eine klar bestimmte Folge von Schritten, es gibt also eine klare Konstruktionsanweisung«,
(b) sie »soll kontinuierlich fortgesetzt werden«,
(c) und sie enthält ein »Muster der Sich-selbst-Gleichheit« (Schönwalder-Kuntze u.a., 175).

»The key is to see that the crossed part of the expression at every even depth is identical with the whole expression, which can thus be regarded as re-entering its own inner space at any even depth.« (LoF, 56)

Im Ergebnis hat f eine Mehrfachbedeutung:

– f beschreibt in E1 die Stelle, an der die Rekursion erfolgt, und ersetzt die drei unbestimmten Pünktchen ›…‹.

– Werden die Rekursionen mitgezählt, dann ist f der Name für die unendlich-ferne, letzte Rekursion. In dieser Bedeutung ist f vergleichbar mit der transfiniten Zahl ω. Wird f als der Name der spezifischen Verlaufsform aller in E1 ausgeführten Rekursionen verstanden, ist es vergleichbar mit den von v. Foerster betrachteten Eigenwerten.

– Schließlich ist f in E1 der Name der Form, mit der die unendlich-oft wiederholte Rekursion beschrieben wird. E1 kann als die selbstbezüglich geschriebene Definition von f gelesen werden. Diese Form mit dem Namen f steht für das Element, das per Re-entry in die Proto-Algebra aufgenommen werden soll.

Spencer-Brown hält konsequent seine Idee fest, Symbole einzuführen, die in Mehrfachbedeutungen  sowohl eine Operation wie das Ergebnis dieser Operation sein können. Die Mehrfachbedeutung von f ist sorgfältig eingeführt und an klare Regeln gebunden. Sie enthält in sich einen Widerspruch oder in der Sprache des frühen 20. Jahrhunderts einen Kategorienfehler: f ist als der Wertverlauf von Argumenten a sowohl eine Menge von Elementen, und soll zugleich durch den Re-entry den Argumenten a gleichgestellt und unter sie aufgenommen werden. Das entspricht der Situation der Russellschen Antinomie, die von der Menge von Mengen spricht, die negativ selbstbezüglich definiert sind (die Menge aller Barbiere, die sich nicht selbst barbieren, oder mathematisch: die Menge aller Mengen, die sich nicht selbst enthalten).

– Die Sprache des Re-entry

Das 11. Kapitel der Laws of Form erscheint mit seiner Einführung des Re-entry, der Zeit und der Netzwerke ähnlich »dunkel« wie die komplexesten Aphorismen und Texte von Heraklit, Hegel oder Heidegger (vgl. zu dunklen Sprachen Günther 1979, 3). Wenn Spencer-Brown von einem Grenzübergang symbolischer Formen der mathematischen Sprache handelt, stellt er die Frage, mit welcher Sprache selbstreflexiv ein Grenzübergang dieser Art formuliert werden kann. Es genügt nicht ein äußerer Beobachter, der dies Geschehen von außen sieht und protokolliert. Wer etwas protokolliert, gebraucht die Symbole, um deren Grenzprozess es Spencer-Brown geht. Statt von einem Beobachter muss von einer höheren Sprache gesprochen werden. Das ist die Frage nach der Sprache des Re-entry.

Spencer-Brown beschreibt einen Prozess, der sich bewusst den jeweils verfügbaren Zeichen entzieht und zu neuen Zeichen führt. Um diesen Übergang meistern zu können, ist etwas notwendig, für das die vorherigen Zeichen nicht ausreichend und die neuen Zeichen noch nicht verfügbar sind. Um diese Lücke schließen zu können (diesen Sprung erfolgreich gelingen zu lassen), ist eine eigene spezifische Sprache notwendig. Dieser Schritt wird im Denken mit seiner spezifischen Vorstellungskraft vollzogen. Die implizite Sprache des Denkens beschreibt das, was innerhalb des Denkprozesses erfolgt und zwischen den Voraussetzungen und ihren Resultaten liegt. Günther hat seit seinen frühesten Texten die Position vertreten, dass für diese Sprache des Denkprozesses (der Reflexion) ein eigener Wert notwendig ist, der nicht innerhalb der Werte liegen kann, mit denen die Inhalte des Denkens dargestellt werden (die Zweiwertigkeit des protokollierenden Denkens, oder in der Ausdrucksweise von Aristoteles bis Heidegger des kategorialen Denkens). Ist es mit Spencer-Brown möglich, diese Sprache weit genauer zu beschreiben und möglicherweise sogar zu formalisieren, als es bisher mit überwiegend phänomenologischen Ansätzen möglich war?

Die spezifische Sprache des Re-entry zeigt sich an zwei kritischen Stellen:

– Der Punkt der Rekursion erhält den Namen f. Einen Namen vergeben zu können, ist eine besondere sprachliche Fähigkeit, die nach religiöser Überzeugung dem Menschen von Gott verliehen wurde (Genesis 2,19). Hat Spencer-Brown mit der Benennung der Rekursion einen besonderen Punkt getroffen, über den diese Fähigkeit näher gefasst werden kann? Ist die Namensvergabe ihrerseits rekursiv und zeigt gewissermaßen ihren Eigenwert in ihrer Fähigkeit, an rekursiven Prozessen deren Namen zu erkennen und zu vergeben?

– Für den Re-entry von f gibt es in den Formen keinen Ort. f kann nicht als neue Form in ein Medium eingetragen werden, sondern sein Re-entry erfolgt über eine Veränderung des Medium-im-Ganzen. Spencer-Brown kann dafür eine geeignete Darstellung finden, da er von Anfang an das Medium und die Form als die beiden Seiten der Laws of Form eingeführt hat. In der von ihm gewählten Darstellung wirkt sich der Re-entry gewissermaßen existenzial auf alle Formen aus, die im Medium verwurzelt sind. Die Veränderung des Mediums ist weder eine neue Form noch eine neue, bisher unbekannte Eigenschaft der Formen, sondern kann an den Formen nur existenzial nachgewiesen werden. Spencer-Brown spricht von der Oszillation des Mediums, die in allen im Medium eingetragenen Formen zu spüren ist, und der Zeit, in der die Oszillation verläuft. Ihm gelingt damit eine wesentlich genauere und – wenn man so will – weniger dunkle Bestimmung des Existenzialen, als es in der Geschichte der Philosophie von Platon bis zur Phänomenologie möglich war.

Sein Abstand zur überlieferten Philosophie lässt sich am besten messen, wenn er in einer Analogie als Abstand zur überlieferten Mathematik dargestellt wird. Wie weit sich Spencer-Brown von der vorgefundenen Mathematik entfernt hat, kann ein Vergleich mit dem Re-entry der transfiniten und irrationalen Zahlen deutlich machen. Seine Art des Re-entry würde für die transfiniten und die irrationalen Zahlen bedeuten, dass nicht der Grenzwert ω in die Zahlen aufgenommen wird, sondern die Nachfolger-Relation, mit der der Grenzprozess definiert wird, und nicht die Irrational-Zahl, sondern der Grenzprozess, mit dem die Irrational-Zahl angenähert wird. So denkt die heutige Mathematik nicht. Aus meiner Sicht will Spencer-Brown zeigen, dass sie aber das der Sache nach genau tut, – einen Grenzprozess und nicht eine Zahl aufzunehmen –, ohne es zu merken oder sich einzugestehen. Wenn sie z.B. von der Irrationalzahl 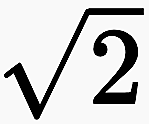spricht, ist dies ein Symbol, das keine Zahl, sondern ein Annäherungsverfahren beschreibt. Niemand kann exakt sagen, wo sich 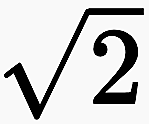auf der Zahlengerade befindet, sondern es besteht nur die Möglichkeit, ihren Ort immer genauer anzunähern. Es hilft auch keine geometrische Überlegung: So kann ein Einheitsquadrat auf die Zahlengerade gelegt werden und mit einer geometrischen Operation ein Kreis um die Diagonale des Quadrat geschlagen werden, der die Zahlengerade genau dort schneidet, wo 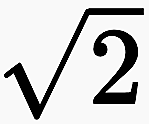liegt. Dann ist zwar anschaulich gezeigt, dass 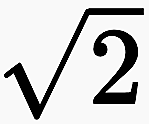einen eindeutigen Ort auf der Zahlengerade hat. Der Ort ist gewissermaßen zu »sehen«. Wird aber versucht, ihn durch seinen Zahlenwert zu bestimmen, hilft auch die geometrische Konstruktion nicht weiter und es bleibt nichts, als diesen Wert immer genauer anzunähern.

Es gab und gibt in der Mathematik Versuche, auf diese Weise die reellen Zahlen zu definieren, die nur durch den Prozess ihrer Erzeugung und nicht wie feststehende, statische Objekte bestimmt werden können: Die 1872 von Richard Dedekind (1831-1916; Schüler von Gauß, befreundet mit Riemann und Cantor) eingeführten Schnitte (siehe hierzu Günther 1995, 9: »Dieser Schnitt und nicht die Zahl, die man durch ihn erhält, ist der gewünschte dritte Wert!«) und die 1974 von John Conway (* 1937; Erfinder des Game of Life) definierten surrealen Zahlen. Lukáš Lánský hat in Wikipedia eine sehr anschauliche Darstellung präsentiert:

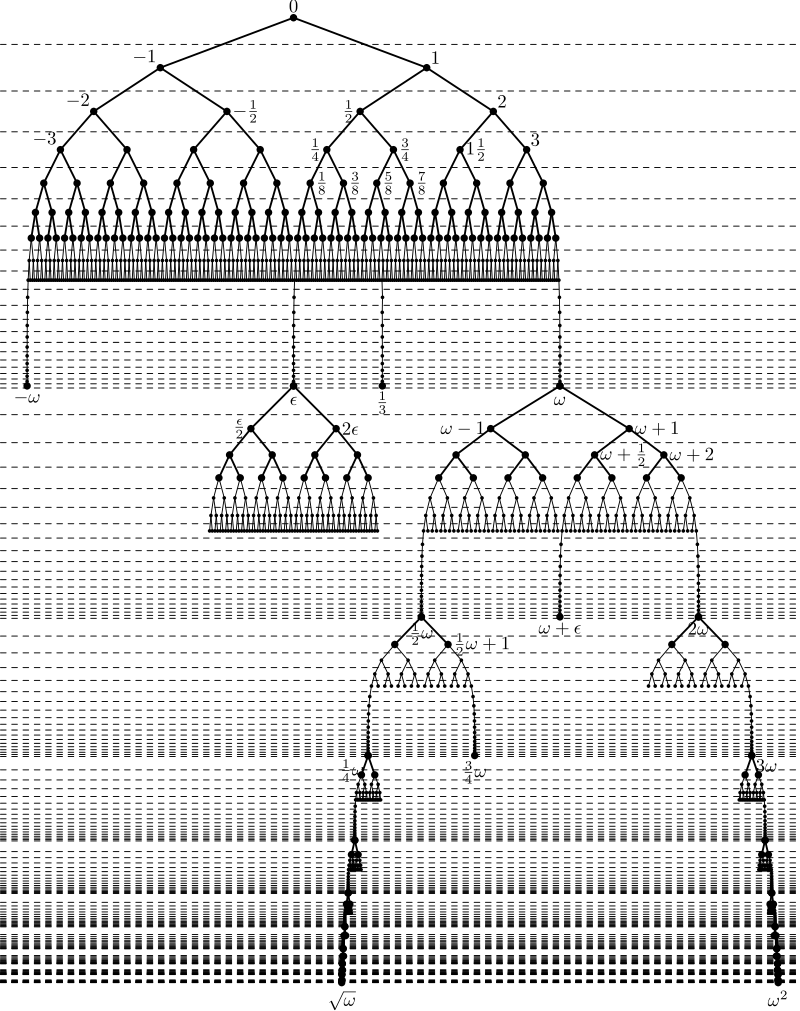
Surreale Zahlen
Urheber: Von Lukáš Lánský - Eigenes Werk, CC BY-SA 3.0, Link

In dieser Zeichnung ist angedeutet, wie sich die transfiniten und irrationalen Zahlen nur durch unendliche Prozesse darstellen lassen.

Spencer-Brown erwähnt mehrfach Gödel. Dessen Beweisidee für den Unvollständigkeitssatz kann als Vorläufer angesehen werden, eine Zahl zugleich als Funktion und eine Funktion als Zahl anzusehen. Gödel hat gezeigt, wie in jedem ausreichend komplexen formalen System, in dem sowohl die Addition wie die Multiplikation und darüber Primzahlen eingeführt sind, jedes Zeichen sowohl als Zahl wie auch als Funktion gedeutet werden kann, wenn die Funktion gödelisiert wird. Die Gödelisierung ist eine Übersetzung: Mit einem auf Primzahlen beruhenden Verfahren wird jedem Buchstaben und jedem Satzzeichen eine Zahl und darüber jedem aus Buchstaben und Satzzeichen zusammengesetzten vollständigen Satz ebenfalls eine eindeutige natürliche Zahl zugeordnet, die Gödelnummer. (Spencer-Brown betont zurecht, dass diese Überlegung für seinen Kalkül nicht gilt, da dort nicht in vergleichbarer Weise wie bei den natürlichen Zahlen Addition, Multiplikation und Primzahlen eingeführt sind; LoF, 96; AUM, Session Two.)

Gödel betrachtete den sich sich selbst widersprechenden Satz ›dieser Satz ist falsch‹ und bestimmte seine Gödelnummer. Dadurch ist er als Zahl im formalen System aufgenommen, obwohl er einen inneren Widerspruch enthält. Sein Verfahren lässt sich natürlich auch auf jeden anderen Satz anwenden wie z.B. den Satz ›n + 1 ist der Nachfolger von n‹. Wird diesem Satz eine Gödelnummer zugeordnet, dann ist es gelungen, das Verfahren, das zur transfiniten Zahl ω führt, als Verfahren in die Menge der natürlichen Zahlen aufzunehmen.

Sowohl mit dem Re-entry wie mit der Gödelisierung können Funktionen und Argumente ineinander umgeformt werden. Dennoch sind die Unterschiede deutlich:

– Bei der Gödelisierung wird die Umwandlung gewissermaßen von außen herangetragen. Gödel hat eine Übersetzung gefunden, mit der jeder Satz in eine Zahl und umgekehrt die Zahl in den Satz übersetzt werden können. Spencer-Brown will dagegen zeigen, wie aus dem Prozess der eine unendliche Reihe bildenden Umformungen die Funktion f als Grenzprozess hervorgeht.

– Die Gödelnummer ist eindeutig und liegt nicht außerhalb oder zwischen den bekannten natürlichen Zahlen, sondern ist eine natürliche Zahl, deren Ort auf der Zahlengerade eindeutig bestimmt ist. Für das bei Spencer-Brown neu gebildete Symbol f gibt es dagegen keinen Ort und sein Re-entry verändert das Medium, in dem die Formen eingetragen sind.

– Umgekehrt gerät Gödels Verfahren in eine Endlosschleife, wenn seine Zuordnungsfunktion ihrerseits gödelisiert wird usf. Das ergibt einen ähnlichen unendlichen Prozess wie das Zählen, dessen Grenzwert ω nicht in den natürlichen Zahlen enthalten ist, sondern durch einen Re-entry aufgenommen werden muss. Das war für Gödels Argument unerheblich und wurde von ihm nicht weiter untersucht, zeigt aber, dass auch sein Verfahren nicht den Grenzprozessen entzogen ist.

Wie löst Spencer-Brown das Problem? Wenn es keine Zahl gibt, auf die der Re-entry fallen kann und keinen Platz, dem er eindeutig zugewiesen werden kann, dann kann er nur auf dem Weg erfolgen, dass die Eigenschaften des Mediums geändert werden, in dem alle Zahlen eingetragen werden.

Spencer-Brown kann das Ergebnis des Re-entry nur negativ formulieren: Es ist in dem gegebenen Kalkül unbestimmt, wo es aufgenommen werden kann (»indeterminacy« LoF, 57). Um die treffenden Worte zu finden, bezeichnet Spencer-Brown den Übergang von a zu f in größerer Allgemeinheit als Übergang von einem Ausdruck e (für expression) zu einem Ausdruck e', der per Re-entry aufgenommen werden soll:

»We have just introduced to e' a degree of indeterminacy in respect of its value which is not (as it was in the case of indeterminacy introduced merely by cause of using independent variables) necessarily resolved by fixing the value of each independent variable.« (LoF, 57)

f irrt gleichsam umher und findet keinen festen Platz. Dies Umherirren wird Spencer-Brown zur Oszillation führen, mit der er den Begriff der Zeit einführt (LoF, 62-64). Es wird erst aufgelöst, wenn er von den wellenförmigen Verlaufsformen übergeht zu den Netzwerken der Modulator-Funktion: In diesen Netzwerken wird ein Weg gefunden, die Argumente a in Funktionen f zu modulieren. (Siehe hierzu den Beitrag für die The Unmarked State Conference celebrating the 50th Anniversary of the First Publication of George Spencer-Brown's ‘Laws of Form’ in Liverpool, 9.8.2019).

Transitivität und Intransitivität des Echelon nach Kunze

Hat Spencer-Brown einfach deshalb das Zeichen 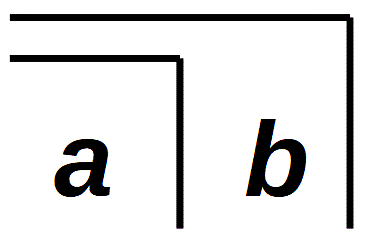gewählt, weil es bereits von seiner äußeren Gestalt auf eine Nachfolger-Relation deutet? Enthält das Echelon (die Staffelung) darüber hinaus eine verborgene Eigenschaft, dank derer es zum geeigneten Ausgangspunkt für den Re-entry in die Proto-Algebra wird? Einen Hinweis fand ich bei Donald Kunze (* 1947), der an der Pennsylvania State University architecture theory and general arts criticism gelehrt hat. Er betrachtet die Consequence 7 (C7), mit der das Echelon in eine andere Form umgewandelt (LoF, 34) und erkennt, dass mit ihr eine Intransitivität entsteht. Das Echelon oszilliert zwischen Transitivität und Intransivität.

Bevor dem weiter nachgegangen wird, ist auf die Bedeutung der Intransitivität aufmerksam zu machen. Im Alltag vergleichen wir in der Regel Dinge, die gleichmäßig angeordnet sind und sich an einem gemeinsamen Maßstab messen lassen. Werden z.B. die Längen von Stoffballen verglichen, lassen sie sich an der Elle messen. Sie sind transitiv: Wenn b größer ist als a und c größer ist als b, dann ist c erst recht größer als a. Das gilt bei der Intransitivität nicht mehr. Das einfachste Beispiel ist das Spiel Schere, Stein, Papier: Obwohl die Schere stärker ist als das Papier, das von ihr geschnitten wird, und der Stein stärker ist als die Schere, die er stumpf macht, ist dennoch der Stein schwächer als das Papier, von dem er eingewickelt wird:

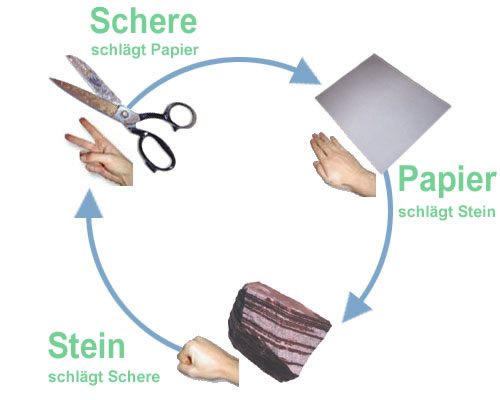
Die Figuren von Schere, Stein, Papier
Urheber: K-Maddin - Datei:Rock paper scissors.jpg, CC BY-SA 3.0, Link

Wenn Kinder dieses Spiel zum ersten Mal spielen, sind sie verblüfft, verstehen anfangs nicht, was hier eigentlich geschieht, und sind dann davon begeistert und können es endlos wiederholen, als wollten sie prüfen, ob es nicht doch irgendwann in eine transitive Ordnung umschlägt. Was sie hier lernen, ist ein Beispiel mathematischer Kreativität (vgl. Spencer-Brown in AUM, Session 2). Die Intransitivität enthält etwas, das über die gewöhnliche Mathematik hinaus geht: Sie ist zyklisch. Eine intransitive Ordnung kehrt zu sich selbst zurück. Und sie ist offensichtlich nicht-hierarchisch: Jede hierarchische Höherentwicklung ist eine transitive Ordnung: Auf die Steine folgen die Pflanzen, ihnen die Tiere, der Mensch und auf oberster Stufe je nach Glaubenseinstellung Gott, der Geist oder das Absolute. In einer zyklischen Ordnung kehrt die oberste Stufe zurück in den untersten Boden. (Jede Offenbarung trägt intransitive Züge, wenn sich z.B. Gott in der Gestalt einer Lilie oder in einem brennenden Dornbusch zeigt.) Um diese Rückkehr geht es Spencer-Brown, wenn er den Re-entry in das Medium und nicht in eine höhere Form von Formen aufnehmen will. War bisher von der Sprache des Re-entry die Rede, so wird sich zeigen, wie Intransitivität und Zyklizität die Mathematik des Re-entry sind. Von ihr aus erklärt sich die Bedeutung und Wirkungsmacht des von Spencer-Brown eingeführten Re-entry für die Entwürfe heterarchischen Denkens, für die Kybernetik bis hin zum Entwurf einer neuen Soziologie (Theorie der Gesellschaft) bei Luhmann und einem neuen Verständnis der imaginären Zahlen und der Analogie, zu dem dieser Text über den Re-entry bei Spencer-Brown beitragen soll.

Kunze war sich dessen voll bewusst. Er sieht in der Umwandlung des Echelon in eine intransitive Form nicht weniger als den Schlüssel zum Verständnis eines Epoche machenden Werkes von Dürer und darüber hinaus der Urgeschichte der Menschheit, als die ersten Städte entstanden. Dort will er als deren innere Logik die gleiche Umwandlung von Transitivität in Intransitivität nachweisen, wie sie in C7 ausgeführt ist. Bei Spencer-Brown erscheint die Consequence 7 fast beiläufig als eine Regel unter vielen, die im Weiteren kaum mehr eine Rolle spielt.

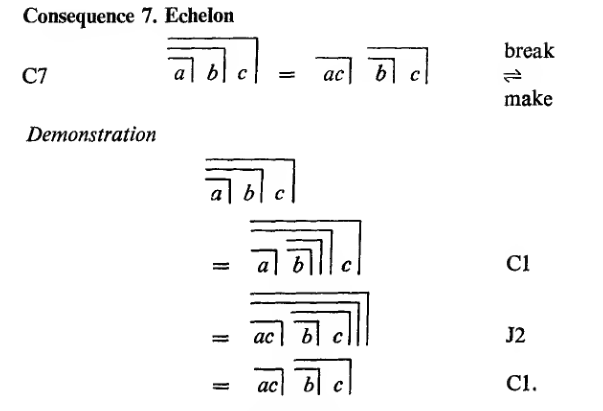
Kunze zeigt mit einer überaus anschaulichen Darstellung des Break, mit dem die Variable c im Echelon verdoppelt und aufgeteilt wird, wo und wie dort die Intransitivität auftritt: Zuerst wird unter Nutzung von C1 von b zu übergegangen (ein doppeltes Crossing führt zur Ausgangslage zurück). Anschließend wird c gemäß des Distributivgesetzes J2 zum einen neben a und zum anderen in den Zwischenraum zwischen den beiden Haken gelegt, die b umgeben. So entsteht zum einen mit ›a c‹ eine transitive Anordnung, zum anderen mit ›b⃧   c‹ eine intransitive Anordnung. – Ein wenig verwirrend nennt er die bei Spencer-Brown in Kleinbuchstaben geschriebenen Variablen a, b und c in Großbuchstaben A, B und C um. In der Mathematik werden gewöhnlich Konstanten mit Großbuchstaben dargestellt. Im Ergebnis findet er intuitiv eine Analogie zu Dürers Stich Der Zeichner des liegenden Weibes (Kunze, 333):

Es bedarf des Blicks eines Architekten, um zu verstehen, was hier geschieht. Normalerweise wird das Zeichnen aus der Perspektive des Zeichners dargestellt: Im Vordergrund steht oder sitzt der Zeichner, der Betrachter des Gemäldes schaut ihm über die Schulter und sieht aus seiner Perspektive sowohl das zu zeichnende Objekt wie das entstehende Gemälde, so geradezu paradigmatisch bei Jan Vermeer: Er malt selbstbezüglich nicht einfach ein Bild, sondern ein Bild mit dem Titel Die Malkunst.

Vermeer: Die Malkunst (1666/68)
Urheber: Von Jan Vermeer - lAHeqBoLaePtEA at Google Cultural Institute maximum zoom level, Gemeinfrei, Link

Dürer dreht (rotates) das um: Jetzt wird das Geschehen von der Seite gezeichnet, um besser darstellen zu können, welches Werkzeug der Zeichner für die zentralperspektivische Zeichnung nutzt. Auf analoge Weise versteht Kunze die Consequence 7 bei Spencer-Brown: Der Blick wird gedreht, und für einen Betrachter, der sich rechts außerhalb des Echelon befindet, erscheint dadurch C von der Seite aus gesehen perspektivisch sowohl neben A wie neben B⃧  . (Kunze hat an dieser Stelle für seine Deutung des echelon implizit die Rolle des Beobachters eingeführt und vorweggenommen, die Spencer-Brown erst später nach seiner Untersuchung des Re-entry, der Zeit und der Netzwerke in Kapitel 12 entwickeln wird, siehe LoF, 69.)

Es bleibt zu erklären, wie Kunze den Übergang von B zu B⃧   deutet: Das ist für ihn der Übergang von der Objekt-Ebene zur Meta-Ebene. Mit B sollen nicht nur die Werkzeuge des Zeichnens dargestellt werden, sondern sie werden zugleich durch B⃧   als bloße, zuhandene Werkzeuge negiert und stehen meta-sprachlich für den Begriff ‘Zeichnen’. So entsteht eine Zeichnung, die zugleich selbstbezüglich das Zeichnen als Prozess beschreibt und mit ihm den Begriff ‘Zeichnen’ zeichnet. Die Werkzeuge, mit denen gezeichnet wird, werden ihrerseits gezeichnet und werden selbstbezüglich zur Metapher ihrer selbst: Mit dem Zeichengerät wird eine Metapher des Zeichnens gefunden und ihrerseits gezeichnet. Das erscheint mir das gelungenste Bild um zu veranschaulichen, was Spencer-Brown mit dem Re-entry der Funktion f gemeint hat, die aus dem Prozess ihrer eigenen Argumente a und darüber aus dem von ihr beschriebenen Verfahren selbstbezüglich konstituiert und per Re-entry aufgenommen wird. Wird dies nochmals aus einer übergeordneten Perspektive (einer Meta-Ebene zweiter Stufe) gesehen, so ist dieser Stich ebenso eine Darstellung des Begriffs ‘Metapher’, um die es bei allen bildlichen Darstellungen geht, wie der Stich Melancolia I als Darstellung des Begriffs ‘Allegorie’ gilt. Auf einer Meta-Ebene dritter Stufe ist es eine Darstellung der Geometrie: Dank ihrer Gesetze der Perspektive ist das Zeichnen möglich. Die Geometrie baut wiederum auf der Analogie auf. Auf der vierten Meta-Ebene lässt sich mit der Analogie das Prinzip erkennen, das der Geometrie und mit ihr sowohl der Metapher wie der Allegorie zugrunde liegt. Schließlich lässt sich auf einer höchsten, fünften Ebene nach den Prinzipien fragen, denen selbstbezüglich Prinzipien wie das Prinzip der Analogie zugrunde liegen. Das führt in religiöse Fragen (siehe hierzu Walter Rella Der Schritt in die Analogie und den Kommentar Analogie-Denken nach Walter Rella). (Die Stufen der Meta-Ebenen sind auf den ersten Blick hierarchisch und transitiv. Jedoch enthält jede Stufe einen Überschuss an Deutungsmöglichkeiten für die jeweils übergeordnete Stufe, aus dem sich eine zyklische Ordnung ergibt. Spencer-Brown hat das exemplarisch am Verhältnis von Arithmetik und Algebra entwickelt.)

Um das Besondere der Transformation C7 zu erklären, wählt Kunze als weitere Analogie die Erzählung von der geschichtlichen Entstehung der Städte und ihres Handels untereinander. Ursprünglich waren die Städte voneinander getrennt. Wie in der Form 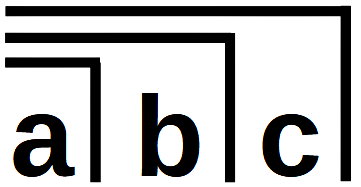waren alle Städte durch Grenzen voneinander abgesondert, transitiv angeordnet, eine neben der anderen, ohne inneren Kontakt. Treffen und Handel mit Fremden waren verpönt. Jeder Haushalt hatte seine eigenen Götter. Aber es gab Wegkreuzungen zwischen den Städten: Dort legten die einen ihren Überschuss ab, den die anderen später abholten und ihren eigenen Überschuss hinlegten, so dass sie sich nie persönlich treffen mussten. Um diese Handelsstätten zu kennzeichnen, wurden an ihnen Steine und Türmchen von Steinen abgelegt bzw. errichtet. Das waren die ursprünglichen Hermen, für Hermes, den Gott des Handels, Diebstahls und der Kommunikation. Diese Orte wurden heilig, und um sie herum entwickelten sich im Laufe der Zeit die ersten Metropolen. Sie verbanden sich mit den ersten Grabstätten, die der Kommunikation der Lebenden mit den Toten dienten. Auch diese Treffen waren ursprünglich wie die Treffen zwischen verschiedenen Städten verboten, und für diese Treffen war wiederum Hermes der beschützende Gott.

Die Heiligung von B ist nach Kunze der Übergang von B zu B⃧  , in der Schreibweise von Spencer-Brown die Negation von B. Mit der Negation von B ist nicht gemeint, dass das Gegenteil von B eingesetzt wird, – zum Beispiel schwarz statt weiß –, sondern das reale B wird negiert durch ein heiliges B⃧  . Die angestrebte Bewegung des Handels wird möglich, indem drei symbolische Ordnungen gewendet werden (negation, rotation) (Kunze, 334f):

– Die Beweglichkeit (motility) des direkten Handels und Handelns wird unterbrochen, indem sich beide Stämme aus dem Weg gehen, aber gemäß einer indirekten, möglicherweise unausgesprochenen Vereinbarung zeitlich nacheinander ihre Güter am gleichen Ort ablegen und abholen.

– Der Anschein (semblance) eines direkten Handels wird gebrochen: Nach ihrem jeweiligen Selbstverständnis handeln nicht die realen Stämme A und C an einem realen Ort B miteinander, sondern mit der Heiligung des Ortes B werden an diesem Ort auch die Produkte geheiligt, die dort gelagert und getauscht werden. So gesehen tauschen die Stämme nicht Produkte aus, sondern die Produkte sind am heiligen Ort, an dem sie abgelegt wurden, eingeschlossen in Götterbilder B⃧  . A und C handeln nicht miteinander, sondern jeweils mit der Herme B⃧  .

– Der Umfang (scalar) wird gebrochen: Statt eines realen Handels mit realen Gütern erfolgt am Ort B eine heilige Umwandlung: Was der eine Stamm abgelegt hat, bekommt durch die Heiligung eine besondere Bedeutung, weswegen der andere Stamm diese geheiligten Produkte abholen darf im Glauben, nicht mit dem anderen Stamm dessen Produkt gehandelt, sondern mit der Herme die von ihr geheiligten Produkte empfangen zu haben.

– Wenn das gelingt, wird C aufgeteilt und einerseits mit A verbunden und andererseits mit dem in einem zweiten Haken verborgenen B⃧  . Das ergibt eine nicht-transitive Operation.

Formal: Erst wird um das B in der Mitte ein doppelter Haken gelegt, den Kunze als pocket, als Heiligtum versteht. Anschließend wird C gemäß dem Distributivgesetz aufgeteilt: Ein C wird neben A gelegt, was mit AC eine einfache, transitive Ordnung ergibt und auf der realen Ebene den gewünschten Handel von A mit C ermöglicht. Das andere C wird in die Lücke zwischen den beiden Haken gebracht, wodurch mit B⃧  C eine intransitive Ordnung entsteht. C ist aufgeteilt in zwei Ordnungen, aber es bleibt eine innere Beziehung (eine Verschränkung) der beiden verteilten C erhalten. Diese Verschränkung ermöglicht die spätere Rückkehr. Was am Ort B geheiligt wurde, kehrt für den jeweils anderen Stamm als reale Ware in das alltägliche Leben zurück und kann dort konsumiert werden.

Ist das nur die intuitive Sicht eines Künstlers bzw. Kunsthistorikers, dessen Art zu denken der Mathematik und Logik fern und deren historische Wahrheit nur schwer zu überprüfen ist? Für mich ergibt sich aus dieser Intuition eine neue Sicht auf die natürlichen Zahlen, die inhaltlich auf Platon und über ihn auf Pythagoras zurückgeht:

– So wie A und C am Ort B ein Produkt austauschen, das dort erst geheiligt wurde und später in das Wirtschaftsleben zurückkehrt (Re-entry), so ist beim transitiven Zählen zu unterscheiden zwischen den transitiv einander nachfolgenden Zahlen 1, 2, 3, … und demjenigen, das zwischen ihnen liegt und den Vorgang des Zählens ermöglicht und im Zählen ausgetauscht und weitergegeben wird. Das ist der Abstand (die Lücke) zwischen je zwei benachbarten Zahlen. Der Abstand übernimmt die Bedeutung von B, an dem die einander benachbarten A und C zueinander kommen können. Platon verschränkt beide Aspekte (hier folge ich Stenzel, 84-91 und den von ihm genannten Quellen, dem McCulloch und mit einigen Widerwillen auch Günther in den 1960ern überraschend nahe kamen, siehe Günther 1995, 4-15): Der Abstand ist seinerseits eine Zahl. Für Platon sind die ungeraden (perissós) Zahlen die Zahlen, die wie isolierte Punkte in ein Medium eingetragen werden, und die geraden (artios) Zahlen das Zwischen, mit dem die Unterscheidung zweier Zahlen und ihr Abstand voneinander möglich sind. Warum wählt er diese Begriffe: Die erste gerade Zahl ist die 2, die nicht nur als eine Zahl der 1 nachfolgt und ihrerseits auf der Zahlengerade eingetragen wird, sondern mit der zugleich der Abstand definiert ist, mit der zwei benachbarte Zahlen voneinander getrennt sind: diastema in der vielfachen Bedeutung von ‘Distanz, Radius, Intervall, Distinktion’. Auf ihn geht die Unterscheidung (distinction) zurück, mit der Spencer-Brown seinen Kalkül begründet (»Draw a distinction«; LoF, 3). Der Abstand hat seinerseits zwei Aspekte: Es ist ein räumlicher Abstand zwischen zwei Zahlen, der das Zwischen bestimmt, in dem innerhalb der natürlichen Zahlen keine weiteren Zahlen liegen, und er hat einen Wert, das ist die Länge des Abstandes, der wiederum 1 beträgt. Mit jeder neuen Zahl wird der Abstand weitergegeben, wenn jeder Zahl n eine neue Zahl ›n + 1‹ nachfolgt, die von n wiederum durch einen Abstand der Länge 1 getrennt ist und sich an das Maß hält, das mit dem ersten Abstand zwischen den Zahlen 1 und 2 gegeben ist. Konsequenterweise ist bei Platon die erste ungerade Zahl die 3, die der 2 folgt, während die 1 sich selbst gegenüber keinen Abstand hat. Anders als in der heutigen Mathematik ist für Platon die 1 nicht ungerade, sondern steht außerhalb der Unterscheidung von gerade und ungerade. Die 1 ist nicht teilbar, während die geraden Zahlen in gleiche Hälften und die ungeraden Zahlen nur in ungleiche Anteile aufgeteilt werden können.

– Der Abstand B wird geheiligt zu B⃧  . Das ist bei Platon nur darin erkennbar, dass die geraden Zahlen zugleich für das Unbegrenzte (apeiron) und dessen innere Abgründigkeit stehen. Aristoteles deutete das so, das für ihn aus den geraden Zahlen der Stoff, der allgemein (katholou) und unbestimmt (aoristos, Met. 1087a17) ist, und aus den ungeraden Zahlen die Form wird. Spencer-Brown hat das weiter geführt. Seine Unterscheidung in Medium und Form kann als neue Deutung der Unterscheidung in gerade und ungerade Zahlen bei Platon gelesen werden.

– Mit der Heiligung des Abstandes B erfolgt eine Krümmung, bei Aristoteles das im Innern des Stoff enthaltene Formlose (steresis), bei Günther (auch wenn er das in seiner für mich unzutreffenden Kritik an Aristoteles nicht wahrhaben will) und Spencer-Brown der dritte Wert einer drei-wertigen Logik: Das nachfolgende C ist sowohl verbunden mit seinem Vorgänger A wie mit dem geheiligten B. Diese Krümmung ist für mich die innere Spannung (der innere Freiheitsgrad) innerhalb der Zahlengerade. Sie enthält die Möglichkeit, das sich aus der Zahlengerade Prozesse herauslösen und in einen imaginären Raum führen können, wie auch umgekehrt den Ort, an den dieser hinausführende Prozess wieder aufgenommen werden kann (Re-entry).

– C spaltet sich auf. Es verbindet sich zum einen transitiv mit A, zum anderen intransitiv mit B⃧  .

– Die beiden aufgeteilten C bleiben jedoch miteinander verschränkt. Aus dieser Verschränkung ergibt sich die Zirkularität und Analytizität der imaginären Ebene.

Wird der mit der inneren Spannung der Zahlen gegebene dritte Wert für sich betrachtet, führt er seit den Anfängen der Mathematik zu herausgehobenen Zahlen, die als heilig gelten. Beispiele sind bestimmte Wurzeln (wie 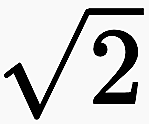, die Diagonale im Quadrat; die Teilung zweier Diagonalen im Pentagramm ⛤, die für den Goldenen Schnitt steht; die Kreiszahl 𝜋 und ihre enge Verbindung zur imaginären Einheit i durch die Eulersche Formel ›ei · 𝜋 = −1‹; die erste transfinite Zahl ω. Ihre Begründer waren sich ihrer Heiligkeit bewusst (so Pythagoras und Cantor).

Dreiwertigkeit des Re-entry und der Proemialrelation bei Günther

»Es ist offen, ob der Wiedereintritt in der Konzeption Spencer-Browns über den Kalkül hinausführt und nur durch eine Struktur der Mehrwertigkeit aufgefangen werden kann oder nicht vielmehr in den Kalkül zurückführt und dort die Entfaltung der Form mitträgt.« (Baecker 2013, 151 Fn. 23)

Die Dreiwertigkeit ist mit dem Wechselverhältnis von Transitivität und Intransitivität bereits gegeben: Innerhalb einer transitiven Ordnung gilt Zweiwertigkeit, wenn nach größer und kleiner, vorwärts und rückwärts unterschieden wird. Der Übergang zur Intransitivität ist nur entlang eines dritten Wertes möglich. Die Frage nach der Dreiwertigkeit soll einleitend weiter differenziert werden. Vor allem stellt sich die Frage nach einer formalen Darstellung der Dreiwertigkeit. Nachdem Günther in vielen Beiträgen lediglich eine Dreiwertigkeit postuliert hat, ohne sie näher begründen und formalisieren zu können, ist ihm mit der Proemialrelation ein Durchbruch gelungen. Das ist Gegenstand des zweiten Teils dieses Abschnitts.

Wann und warum kommt es zu Mehrwertigkeit?

(1) Ist in einer gegebenen Situation Mehrwertigkeit erforderlich, um eine Bewegung beginnen zu können, die aus ihr hinausführt und im Weiteren durch Re-entry zurückkehrt? Sowohl das Beispiel von Kunze wie die logischen Überlegungen von Gotthard Günther legen nahe, dass der Anstoß von außen durch einen Beobachter kommen muss. Wird gefragt, wo sich der Beobachter gegenüber dem System befindet, ist ein dritter Wert erforderlich, um seinen Standort bestimmen zu können. Bei Kunze ist die Zeichnung von Dürer bzw. die formale Darstellung des Echelon für sich auf einer zweidimensionalen Ebene gegeben (dem Zeichenblatt), während sich der Beobachter im dreidimensionalen Raum befindet und von dort aus die Zeichnung aus verschiedenen Perspektiven anschauen kann. Bei Günther gibt es einen vernunftbegabten Beobachter, der sich das in der zweiwertigen Logik verharrende System und die in ihr geltenden Gegensätze anschaut, gegenüber diesem System Distanz gewinnen, über die Situation nachdenken (reflektieren) und frei die Entscheidung treffen kann, die gegebene Zweiwertigkeit zu verwerfen (Rejektion) und einen neuen, dritten Wert zu konstituieren (Tansjunktion). Sowohl bei Kunze wie bei Günther wird mit der Gegebenheit des Beobachters, der sich außerhalb der zweiwertigen Logik befindet, der dritte Wert, durch den sie sich von der Zweiwertigkeit distanzieren können, implizit vorausgesetzt. Demgegenüber möchte Spencer-Brown zeigen, wie sich aus der gegebenen Zweiwertigkeit ohne einen äußeren Anstoß von innen her der Prozess loslöst, der zum dritten Wert führt. Ist dann der dritte Wert erreicht, dann wird es möglich, in einem dreiwertigen System einen Beobachter, seinen Gegenstand und die Vielfalt der Perspektiven des Beobachters auf den Gegenstand zu unterscheiden.

Wenn es anfangs keinen äußeren Beobachter gibt, sondern dessen Standort erst aus der weiteren Entwicklung erklärt werden soll, was löst dann den Prozess aus, der sich von der Zweiwertigkeit trennt und per Re-entry zurückkehrt? Für Spencer-Brown ist das die Möglichkeit der unendlichen Wiederholung des Echelon im Canon C9, und letztlich der Überschuss von unendlich vielen Möglichkeiten an Formen, der bereits in der Proto-Arithmetik gegeben ist.

»There is no limit to the possibility of continuing the sequence, and thus no limit to the size of the echelon of alternating a’s and b’s with which 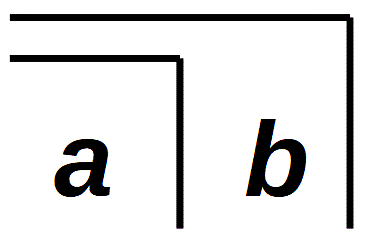can be equated.« (LoF, 55)

Diese Unendlichkeit sprengt die Zweiwertigkeit, und es kommt nur darauf an, ihr eine Verlaufsform zu geben, in der sie sich äußern und im ersten Schritt in seine eigene Dreiwertigkeit entwickeln kann.

(2) Entsteht im Verlaufe des Vorgangs, der sich aus einer zweiwertigen Menge löst und per Re-entry zurückkehrt, eine interne Mehrwertigkeit, die diesen Vorgang stabilisiert und zum Ergebnis führt? Das scheint mir die Ansicht von Spencer-Brown zu sein. Er setzt anfangs keinen dritten Wert voraus, sondern zeigt, wie es innerhalb der Zweiwertigkeit zu einem Prozess kommt, der sich aus der Zweiwertigkeit löst. Die Zweiwertigkeit wird in dem Moment verlassen, in dem zunächst die drei Pünktchen als Hilfszeichen eingesetzt und dann für sie die neue Variable f eingeführt wird. Während die Variablen a in der Regel transitiv und zweiwertig gedacht werden, ist mit f die Dreiwertigkeit konstituiert. Spencer-Brown spricht jedoch nicht von Dreiwertigkeit, sondern beruft sich auf die imaginären Zahlen. Dank der imaginären Zahlen kann die Transitivität der auf einer Gerade angeordneten Formen verlassen werden (siehe LoF, 58, 61). Mit der imaginären Achse, die durch die neue Einheit i definiert ist, ist die Zweiwertigkeit der reellen Achse verlassen, die nur die Negation der positiven und negativen Zahlen kennt.

(3) Löst der Re-entry in der ihn aufnehmenden Menge über deren Erzittern eine Mehrwertigkeit aus? Spencer-Brown zeigt die Oszillation (das Erzittern), die mit dem Re-entry gegeben ist. Mit ihr entsteht in einer zuvor zeitlos gedachten zweiwertigen Logik die Zeit. Mit der Zeit ist innerhalb der gegebenen Logik ein dritter Wert eingeführt: Die Zeit verläuft in der Form einer Oszillation, die sich in ihren Auf's und Ab's von einer linearen Bewegung unterscheidet (LoF, 63). Dieser Vorgang kann verglichen werden mit Hegels Begriff des Widerspruchs und Husserls Ausführungen über das innere Zeitbewusstsein. Für Hegel entwickelt sich ein transitiv gedachter, einfacher Gegensatz, der nur Plus und Minus kennt, in eine Pulsation, durch die der Gegensatz wie in einem Strudel zu Grunde geht. Der Grund liegt nicht innerhalb der Zweiwertigkeit des Gegensatzes, sondern als sein Grund in einer senkrecht zur Zweiwertigkeit liegenden Achse. Am Schnittpunkt beider Achsen liegt wie bei den imaginären Zahlen die Null. Der Gegensatz annihiliert sich (wird zu Null), und aus der Null geht eine neue Achse hervor, die zum Grund führt (HW 6.67). Bei Husserl trennt sich das Zeitbewusstsein in zwei Achsen auf: Das gewöhnliche Bewusstsein erlebt die transitive Ordnung der einander nachfolgenden, jeweils für einen Moment gegenwärtigen Augenblicke des Zeitstroms. Das innere Zeitbewusstsein kann gegenüber der Bindung an den Zeitstrom eine innere Freiheit gewinnen, Erinnerungen sammeln und Erwartungen für die Zukunft formulieren und entsprechend handeln. Die Unterscheidung des gewöhnlichen und inneren Zeitbewusstseins ist nur in einem eigenen Bereich möglich, der einen dritten Wert erfordert.

(4) Warum sind Netzwerke erforderlich, um die Modulation eines a in ein f beschreiben zu können? Spencer-Brown betont, wie in Netzwerken die Möglichkeit besteht, angesichts blockierter Wege Umleitungen zu wählen, die die Blockade umgehen oder untertunneln. Der zunächst eindeutig und fest vorgegebene Weg wird gestreut in eine Vielzahl von Möglichkeiten, die in einem Netzwerk dargestellt sind, aus denen der günstigste ausgewählt werden kann. Die Streuung und ihr Überschuss gegenüber dem linearen Weg, auf dem es nur ein Vor und Zurück gibt, erfordern einen dritten Wert, in dem die Verzweigungen dargestellt werden können. Auch diese Möglichkeit von Umwegen in einem Netzwerk hat Spencer-Brown mit den imaginären Zahlen erklärt (LoF, 67, 99) und 1973 bei der AUM-Konferenz betont, wie bereits seine frühesten Programmierungen von Schaltkreisen darauf zurückgehen. – An der Streuung von Wegen in Netzwerken können Eigenschaften erkannt werden, die in einer rein transitiven Ordnung nicht möglich sind. Während es in einer transitiven Ordnung nur jeweils einen eindeutigen, fest vorgegebenen Weg gibt und durch diesen Weg alle Abschnitte des Wegs stark miteinander gekoppelt sind, ist die Vielfalt einer gestreuten, intransitiven Ordnung durch die veränderbare Kopplung ihrer Elemente ausgezeichnet. Ein Medium kann sich in unterschiedliche Zustände mit jeweils spezifischen Graden ihrer Kopplung verändern (emergieren). Spencer-Brown zeigt das an den Netzwerken: Es gibt nicht einfach eine Vielzahl gleichberechtigter, unterschiedlicher Wege, sondern das Netzwerk emergiert in unterschiedliche Zustände, in denen jeweils bestimmte Wege favorisiert werden. In meiner Deutung liegt dem das von Leibniz formulierte Harmonie-Prinzip zugrunde, durch das das Netzwerk in den jeweils einfachsten Zustand gebracht und dort optimiert wird. Das Netzwerk kann mit seiner Oszillation in verschiedene Zustände auf die Oszillation unterschiedlicher Eingaben reagieren. Das ist bei Spencer-Brown nicht explizit ausgeführt, aber er schreibt in diesem Zusammenhang eindeutig: »We are now in difficulties through attempting to write in two dimensions what is clearly represented in three dimensions.« (LoF, 66) Das ist der Punkt, an dem er explizit auf die Dreiwertigkeit stößt. – Das Wasser ist das klassische Beispiel für ein Substrat, das mit seinen unterschiedlichen Aggregatzuständen auf die von außen induzierte Wärmezufuhr bzw. Wärmeentzug zu reagieren und sich jeweils zu optimieren vermag. Ausgangspunkt ist der lose gekoppelte Aggregatzustand der Flüssigkeit, von dem aus es sich in der einen Richtung in die Kristallstruktur des Eises und in der anderen Richtung in die freie Beweglichkeit des Gases verändern kann. Mit ein wenig Phantasie kann jeder der drei Zustände als ein Netzwerk gedeutet werden, in dem die Wege (Verbindungslinien) zwischen den Einheiten (Molekülen) des Substrats in unterschiedlichen Freiheitsgraden der Beweglichkeit auftreten. – Zusammenfassend: Mit Fritz Heider kann ein Medium durch die Eigenschaft definiert werden, in unterschiedliche Zustände loser und starker Kopplung emergieren zu können. Wird nach der Dimension (Bewegungsachse, Freiheitsgrad) gefragt, entlang derer die Zustände sich verändern, so ist dies der dritte Wert, im Sinne von Hegel die Knotenlinie. Das Medium ist nicht einfach durch eine innere Bewegtheit bestimmt, sondern die Bewegtheit kann unterschiedliche Zustände annehmen. Die Bewegtheit ist nicht eine Konstante, sondern ein dritter Wert, der sich frei verändern kann.

Günther betrachtet den Vorgang von einer anderen Seite. Im klassischen zweiwertigen Denken können innerhalb einer Relation R(x,y) lediglich die beiden Relata (die Aufeinander-Bezogenen, die Argumente x und y) miteinander vertauscht werden: Aus R(x,y) wird R(y,x). Dem entsprechen auf der Zahlengerade die Unterscheidung in positive und negative Zahlen (aus x wird −x), auf dem linearen Weg das Vorwärts- und Rückwärtsgehen, in der gewöhnlichen Zeit die Vergangenheit und die Zukunft. Es ist dagegen nicht möglich, auch die Relation R mit den Argumenten x und y zu vertauschen, wodurch z.B. x(R,y) entstehen würde, so wie es bei den transitiv geordneten Zahlen auf einer Zahlenachse nicht möglich ist, die Zahlenachse zu verlassen. Das gelingt erst mit der Einführung der imaginären Achse. Bei einer Vertauschung der Relation R mit den Argumenten x und y wird ein Argument x seinerseits zu einer Relation R und umgekehrt eine Relation R zu einem Argument x oder y. Auf den ersten Blick ist schwer zu verstehen, wie das möglich sein soll und was Günther damit meint, doch bringt er ein anschauliches Beispiel (Günther 1970, 227): In der Natur sind unterschiedliche Ordnungen ineinander verschachtelt. So kann ein Atom einerseits als eine Form verstanden werden, in der sich verschiedene Elementarteilchen miteinander verbinden und in eine Ordnung gebracht werden, und andererseits als der Stoff, aus dem in einem Molekül die Atome ihrerseits in eine Ordnung gebracht werden. Das lässt sich formalisieren:

A = R(E₁, E₂)

lies: das Atom A ist eine Relation der Elementarteilchen E₁ und E₂, aus denen es sich zusammensetzt

Auf einer höheren Stufe sinken die Atome auf die Ebene der Relata:

M = R(A₁, A₂)

lies: das Molekül M ist eine Relation der Atome A₁ und A₂, aus denen es sich zusammensetzt

In diesem Beispiel ist das Molekül gegenüber dem Atom eine höhere Ordnung (Meta-Ordnung) so wie eine Ebene tiefer das Atom eine höhere Ordnung gegenüber den Elementarteilchen ist. Wesentlich ist für Günther die Einsicht, wie sich in diesem Beispiel die Argumente und Relationen vertauschen. Das Atom wechselt aus der Position als eine Relation in die Position als ein Element.

Dieser Wechsel von einer Ordnung in eine höhere bzw. niedrigere Ordnung wird von Günther etwas missverständlich als Proemialrelation (proemial relationship) bezeichnet, »for it 'pre-faces' the symmetrical exchange relation and the ordered relation and forms, as we shall see, their common basis« (Günther 1970, 226). Günther bezieht sich auf prooimion (Günther 1970, 226 Fn. 3). Das bedeutet wörtlich ‘Eingang, Anfang, Vorrede, Vorspiel’ mit der Sprachwurzel oimos, ‘der Weg, Streifen, eine Ebene’, auch der ‘Verlauf eines Liedes’. Günther versteht als das Vorwort oder Vorspiel den Übergang in eine tiefer- bzw. höherliegende Ebene, der zuerst erfolgt, bevor sich innerhalb dieser Ebene die jeweilige Ordnung ausbilden (emergieren) kann, von emergere, wörtlich ‘auftauchen, herauskommen, emporsteigen’. (Walter Rella schlägt eine andere Deutung vor. Für ihn geht ‘proemial’ nicht auf ‘prooimion’, sondern auf die aus dem Lateinischen stammende Wurzel emo zurück in der Bedeutung ‘durch Kauf, Versteigerung oder Auktion erwerben’ und verweist in der wörtlichen Übersetzung ‘vor dem Kauf’ auf den offenen Zustand, wenn eine Ware auf den Markt tritt und über eine Preisverhandlung ihren Käufer finden muss. Eine arbeitsteilige Ökonomie kann als ein Netzwerk verstanden werden in den drei Zuständen Produktion, Austausch und Konsum. Während Produktion und Konsum für sich jeweils eine transitive Ordnung zeigen, in der die Herstellung bzw. der Verbrauch sequentiell ausgeführt werden können, bewegt sich die Ökonomie im Zustand des Austauschs in einer imaginären Ordnung, in der sich zeigen muss, ob die Produzenten und Konsumenten zueinander finden und ein gesellschaftlicher Ausgleich aller Angebote und Nachfragen erzielt werden kann. In diesem Moment können Krisen auftreten wie die zyklischen Überproduktionskrisen im Kapitalismus oder Planungsfehler in sozialistisch oder staatlich organisierten Wirtschaften. Die Phase des Austauschs ist so gesehen eine höhere Ordnung gegenüber Produktion und Konsum, zwischen denen sie vermittelt. E-Mail vom 22.2.2020.)

Kaehr und Mahler gestalten die von Günther eingeführte Darstellung der Proemialrelation sehr übersichtlich (Kaehr, Mahler, 5):

i + 1:	Rᵢ₊₂     →	xᵢ₊₁
		⇕
i:		Rᵢ₊₁     →	xᵢ
			⇕
i − 1:			Rᵢ    →     xᵢ₋₁

Legende
Rᵢ     Relator Rᵢ der Stufe i
x      Relatum xᵢ der Stufe i
→    Ordnungsrelation zwischen einem Relator Rᵢ und einem Relatum xᵢ₋₁
⇕      Umtauschrelation zwischen einem Relator Rᵢ und einem Relatum xᵢ

Mit den beiden Pfeilen → und ⇕ wird sehr klar die Dreiwertigkeit dargestellt: Innerhalb einer waagerechten Zeile gilt Zweiwertigkeit. Zu jeder Zahl i existiert auch die negative Zahl −i (Ordnungsrelation). Der senkrechte Doppelpfeil ⇕ zeigt den dritten Wert an. An dieser Stellen wird ein Relator in ein Relatum gewandelt bzw. in gleichberechtigter Leseweise von unten nach ein oben ein Relatum in einen Relator (Umtauschrelation). Mit dem Doppelpfeil wird angedeutet, dass von oben nach unten oder von unten nach oben gelesen werden kann.

Die Proemialrelation kann mit dem Re-entry von Spencer-Brown verglichen werden:

– Der Prozess, der zum Re-entry führt, geht über die ursprünglich gegebene Ordnung hinaus. Er führt in einen eigenen Raum. Insofern lassen sich Günther und Spencer-Brown vereinen.

– Bei beiden kommt es zu einem Wechsel der Relation und ihrer Relata. So wie bei Günther R und x, y ihre Plätze tauschen, so bei Spencer-Brown a und f.

– Der wesentliche Unterschied liegt im Re-entry selbst. Bei Günther gibt es keinen Re-entry. Doch ist bei Günther der Gedanke eines Re-entry insofern angelegt, als er – ohne es begründen zu können – davon ausgeht, dass die Proemialrelation im Ganzen zyklisch ist und kreisförmig in sich selbst zurückführt.

Daher ergänzen sich aus meiner Sicht Günther und Spencer-Brown: Günther hat mit der Proemialrelation auf den Aspekt einer Dreiwertigkeit verwiesen, der bei Spencer-Brown in dieser Klarheit nicht vorhanden ist. Mit den drei Zeichen Ɔ für das Medium, ⃧  für die Grenze und für den Re-entry ist bei Spencer-Brown zwar eine Dreiwertigkeit angelegt, aber noch nicht klar ausgesprochen. Auf der anderen Seite hat Spencer-Brown mit der Umkehrung innerhalb des Prozesses, die zum Re-entry führt, die Zyklizität angelegt, die bei Günther als Behauptung stehen bleibt und mehr oder weniger von außen mit Verweis auf neue empirische Erkenntnisse in der Neurophysiologie (vermittelt über McCulloch) herangetragen wird.

Abschließend ist zu erwähnen, dass mit der Proemialrelation ein neues Verständnis der Analogie gewonnen werden kann, das zugleich hilft, den Ansatz von Walter Rella zu formalisieren. Im Beispiel der beiden Rollen des Atoms gegenüber den Molekülen bzw. Elementarteilchen tritt das Atom als Variable doppelt auf: Als Relation und als Relator. Wird hierüber eine Analogie gebildet, dann führt sie zu einem Ebenenwechsel, der entweder in eine höhere Ebene hinauf- oder in eine tiefere Ebene hinabführen kann. Die Analogie ist daher in dieser Sicht nicht mehr eine klassische Proportionalität nach dem Muster:

    A : B = C : D

lies: A verhält sich zu B, wie sich C zu D verhält

Sondern eine Analogie ist darüber hinaus ein Hinauf- und Hinabsteigen. Die Figur einer solchen Analogie ist nicht mehr wie beim Strahlensatz eine in der Ebene dargestellte Proportion:

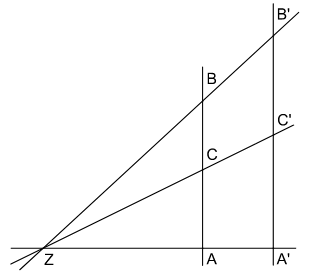
Strahlensatz

Hier gilt die Analogie: ZA verhält sich zu ZA' wie ZB zu ZB', usf.

Diese Analogie ist linear und lässt sich in der Ebene zeichnen. Sondern bei einer Analogie mit Höher- bzw. Tieferentwicklung entsteht eine Schraube, die sich nach oben bzw. nach unten windet.

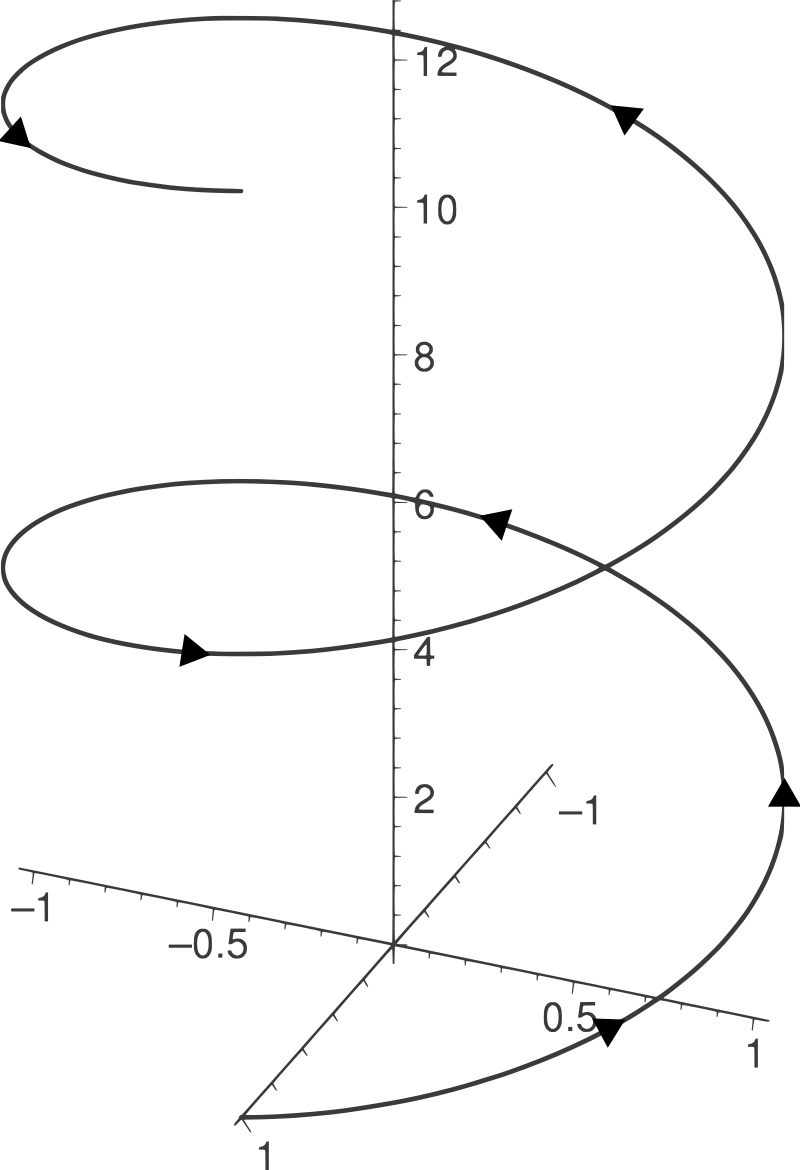
Helix
Urheber: By RobHar - Own work using maple and inkscape (and a pass through gimp), Public Domain, Link

Beispiele sind die Goldene Spirale, die von Albrecht Dürer gezeichnete Schraubenlinie und die Wurzelschnecke, auf der nach Thedoros von Kyrene (4. Jh. v. Chr.) die Irrationalzahlen geometrisch auseinander konstruiert werden können:

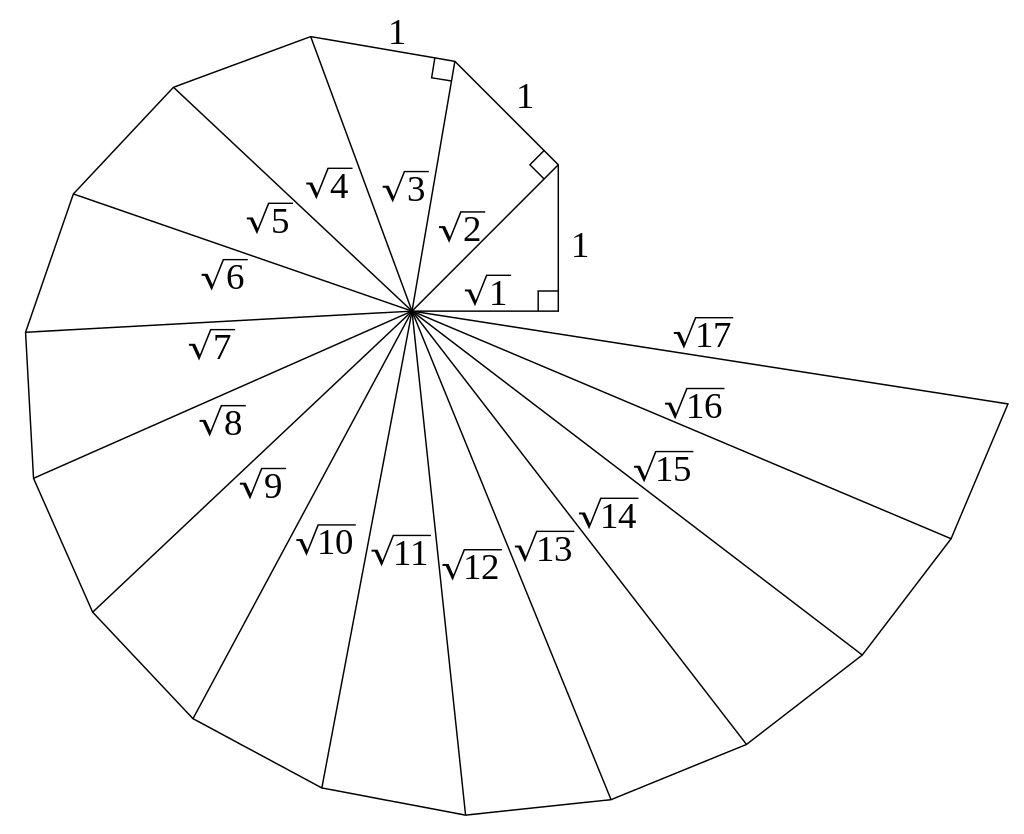
Wurzelschnecke
Urheber: Von Pbroks13 in der Wikipedia auf Englisch, CC BY-SA 3.0, Link

An der Zeichnung ist deutlich zu sehen, wie die Wurzelschnecke bei Wurzel aus 17 den ersten Kreislauf ausgeschöpft hat und im Weiteren in daneben oder darüber liegende Kreisläufe eintritt. Ohne es weiter auszuführen zeigen diese Bilder anschaulich die enge innere Beziehung zwischen Irrationalzahlen, imaginären Zahlen (mit denen der Kreis dargestellt wird) und Analogien, die auf höhere bzw. tiefere Ebenen verzweigen.

Von den kenogrammatischen Leerstellen zur Abjektion

Wo können in einer gegebenen Zahlenmenge neue Werte aufgenommen werden? Nach der traditionellen Vorstellung muss es  zwischen  den bekannten ganzen Zahlen Leerstellen geben: Das sind die mit Platon definierten Abstände (diastema) zwischen den Zahlen, in denen z.B. zwischen 1 und 2 die rationalen Zahlen ›3 / 2 = 1,5‹, ›4 / 3 = 1,33…‹ bzw. Irrationalzahlen wie ›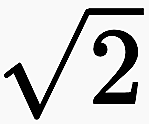 = 1,414…‹ oder zwischen 3 und 4 die transzendente Zahl ›𝜋 = 3,141…‹ ihren Platz finden. Mathematisch handelt es sich bei den Leerstellen um offene Intervalle (n, n + 1): Das ist jeweils die Menge aller Zahlen, die größer als n und kleiner als ›n + 1‹ sind. Spencer-Brown vertritt demgegenüber einen völlig neuen Ansatz. Für ihn ist es die innere  Beweglichkeit  des Mediums und der in ihm eingetragenen Formen, in deren Bewegungszuständen der Re-entry Eingang findet und sich zeigen kann. Auch diese Beweglichkeit kann als eine innere Leerstelle verstanden werden: Das System (das Medium und seine Formen) kann in der Bewegung unterschiedliche Zustände annehmen. Im einfachsten Fall springt es zwischen zwei verschiedenen Zuständen hin und her (in der Schalt-Algebra die Oszillation zwischen ‘an’ und ‘aus’, in der graphischen Darstellung einer Oszillation zwischen ‘oben’ und ‘unten’). Als Leerstelle kann der Inhalt des übergeordneten Begriffs ‘Bewegungszustand’ angesehen werden, der mal mit diesem und mal mit jenem Wert gefüllt werden kann, aber für sich selbst leer ist.

Das ist eine überraschende Sichtweise, die auf Gottlob Frege (1848-1925) zurückgeht und von Günther aufgenommen und fortgeführt wurde. Frege suchte nach einer tieferliegenden Struktur, die sowohl der Mathematik wie der Sprache zugrunde liegt. Er versteht den klassischen Ausdruck einer Funktion f(a) neu: Das Argument a wird an einer Stelle eingetragen, an der in der Funktion f ein Platzhalter f( ) vorgehalten ist, der für sich leer ist und durch die jeweiligen Argumente a gefüllt wird. In dieser Ausdrucksweise lässt sich die Mathematik auf die Untersuchung der Sprache und deren Logik übertragen: Ein Satz wie ›Caesar eroberte Gallien‹ kann als eine Funktion mit einer Leerstelle ›Caesar ( )‹ gedeutet werden (Frege, 17). In die Leerstelle wird das Prädikat des Satzes eingesetzt. Der Werteverlauf dieser Funkion beschreibt alle Eigenschaften von Caesar, und eine davon ist seine Eroberung von Gallien. – Ebenso lassen sich die Aussagen über die Bewegungszustände einer Bewegung mit Leerstellen deuten: ›die Bewegung befindet sich im Zustand ( )‹. Und so wie Frege den Begriff der Leerstelle von der Beschreibung mathematischer Funktionen auf sprachliche Sätze übertragen hat, ist der Begriff der Leerstelle geeignet, sowohl die von Platon gemeinten Abstände zwischen den Zahlen wie die Vielfalt der Bewegungszustände bei Spencer-Brown zu beschreiben, in denen der Re-entry seinen Platz findet.

Günther erweitert das. Er spricht mit Bezug auf das griechische Wort kenós in der Bedeutung ‘leer, Pause, entblößt, verlassen’, oder auf englisch ‘empty, void, fruitless’ von einer »kenogrammatische(n) Leerstelle« (Günther 1979, 43). Damit geht er weit über Frege hinaus und nähert sich den ursprünglichen Ideen von Platon über den Abstand. Die Leerstelle ist für ihn nicht nur ein Platzhalter, sondern an der Leerstelle wird der übliche lineare Gang mathematischer Formeln und sprachlicher Sätze verlassen. Mit der Leerstelle wird eine neue Dimension eröffnet, die auf zunächst unbestimmte Weise den üblichen Satz verlässt und aus Sicht der gewöhnlichen Sprache ins Leere geht. Genau so verstehe ich die Idee von Spencer-Brown: Er verlässt die übliche Zahlengerade mit den Zahlen und den Abständen zwischen den Zahlen und öffnet eine neue Dimension, in der die jeweiligen Bewegungszustände des Mediums und der in ihm eingetragenen Formen dargestellt werden können.

In diesem Sinn ist die Proemialrelation neu zu lesen. Günther versteht den Auf- oder Abstieg in höhere oder unterliegende Relationen als eine kenogrammatische Struktur: »The proemial relation belongs to the level of the kenogrammatic structure because it is a mere potential.« (Günther 1970, 226) Das lässt sich mit seinen Bildern veranschaulichen: Wenn das Atom zum einen der Stoff ist, aus dem sich die Moleküle zusammensetzen, so enthält es zum anderen nach innen einen Freiheitsgrad, über den es seinerseits als Zusammensetzung (Form) von Elementarteilchen verstanden werden kann. Was mit Atom gemeint ist, ist keine feste Aussage mehr, sondern eine kenogrammatische Leerstelle, die je nach Kontext mal als Relation und mal als Relatum, als Stoff oder als Form verstanden werden kann. Und wenn die Verschachtelung von Strukturebenen der Materie im Ganzen zyklisch ist, d.h. in sich selbst wiederkehrt, werden nach jedem Durchlauf des Zyklus die gleichen Werte neu belegt. Werden auf diese Weise mit der Proemialrelation kenogrammatische Leerstellen definiert, bezeichnen sie eine Ebene, die über die klassischen Aufteilungen in Form und Stoff, Innen und Außen, Relation und Relat hinausgreifen: Etwas kann sich – wie das Atom – in einem veränderten Kontext aus einem Stoff in eine Form wandeln, ein Innen in ein Außen, und umgekehrt. Die Wandlung erfolgt im Innern der kenogrammatischen Leerstelle. Darum geht es Günther: Er möchte mit der Kenogrammatik die traditionellen Dualismen einer für ihn bis in die Metaphysik zweiwertigen Denkweise überwinden. Führt das in eine Metaphysik, die auch Spencer-Browns binäre Unterscheidungen in Form und Medium, in »marked space« und »unmarked space« unterläuft und für das Verständnis des Re-entry einen neuen Horizont öffnet?

Wer mit diesen Erwartungen die Ausführungen von Günther über die Kenogrammatik liest, wird jedoch zunächst enttäuscht sein. Die von ihm genannten Beispiele für eine Kenogrammatik wirken banal und nicht recht überzeugend. Er beschränkt sich auf eine Mustererkennung und führt diese am Beispiel der Wahrheitstafeln aus. Ihm fällt auf, dass in Wahrheitstafeln übergreifende Muster erkannt werden können, wenn z.B. in ›FFFW‹ und ›WWWF‹ jeweils am Anfang ein Zeichen dreimal auftritt und anschließend ein anderes Zeichen einmal ergänzt wird. Daher entwickelt Günther Platzhalter und schreibt übergreifend: ∗∗∗□. Hier kann wechselweise für ∗ F oder W eingesetzt und jeweils umgekehrt W oder F in □ (Günther 1962, 215). Diese Schreibweise betont das Muster. Ähnlich lässt sich für jedes Wort ein Muster der in ihm enthaltenen Buchstaben finden, z.B. für das Wort ‘Sonne’ das Muster ›□○⋄⋄△‹, an dem zu erkennen ist, dass das erste, zweite und fünfte Zeichen einmalig auftreten und das an dritter Stelle stehende Zeichen einmal wiederholt wird (Matzka, 4).

Nur an seiner Wortwahl ist zu erkennen, dass es ihm um wesentlich mehr geht. Günther sieht in den kenogrammatischen Leerstellen die kleinste Einheit einer  Negativsprache, während die üblichen Zeichen wie das Alphabet, die Satzzeichen und die Zahlen die kleinsten Einheiten der  Positivsprache  sind (Günther 1979, 20f). Die Zeichen der Positivsprache sind die Werte, mit denen die Leerstellen der Negativsprache »gesättigt« werden können. So zu sprechen und zu denken ist suggestiv und erhellend, und geht weit über das Beispiel der Mustererkennung hinaus. Es regt an, den Bruch zu verstehen, der an dieser Stelle erfolgt. Die Positivsprache ist für Günther der Bereich, in dem die zweiwertige Logik gilt. »Es ist das Kennzeichen der Positivsprache, dass sie zum Bestand der Schöpfung gehört. So wie die Wirklichkeit eines Tages als unbestreitbares Faktum brutum da ist, so ist auch 'das Wort' als zum Wirklichen gehörend mit ihm da.« (Günther 1979, 20) Er kann auch als der kategoriale Bereich verstanden werden. Mit Kategorien sind seit Aristoteles die Grundelemente einer Positivsprache gemeint, in der sich ein erkennendes Subjekt mit einem von ihm erkannten Objekt zu treffen vermag. Mit der Negativsprache wird dieser Bereich verlassen und ein dritter Wert eröffnet.

Allerdings sind diese Ausdrücke auch missverständlich. Die Leerstellen zeigen für mich nicht an, dass etwas im Nichts verschwindet, sondern sie öffnen den Raum der Möglichkeiten, aus dem das Wirkliche hervorgeht und verstanden werden kann. Sie reichen in den Grund, aus dem das Wirkliche hervorgeht (siehe hierzu Hegels Ausführungen über den Widerspruch, der zu Grunde geht; HW 6.67 und 76). Mit ihnen wird beschrieben, welche Möglichkeiten in ihnen angelegt sind, um sie mit wirklichen Werten belegen zu können. Günthers Unterscheidung in Negativ- und Positivsprachen möchte ich daher als Unterscheidung in Ordnungen des Wirklichen und Möglichen deuten. Für die Ordnungen des Möglichen kann in Anlehnung an Günther von negativen Ordnungen gesprochen werden (siehe dazu den Beitrag über die dynamische Logik: »Wenn wie üblich die wirklichen Objekte als nullte Ordnung, die auf sie verweisenden Zeichen als erste Ordnung, die Metasprache über diese Zeichen als zweite Ordnung usf. bezeichnet werden, dann können die virtuellen, unfertigen Objekte des Möglichkeitsraums als erste negative Ordnung bezeichnet werden, die Gesamtheit aller möglichen Namen für mögliche Objekte als zweite negative Ordnung usf.«)

Doch geht es nicht nur um Objekt- und Metasprachen von Möglichkeiten, sondern innerhalb des Leeren sind Stufen zu unterscheiden. So wie Cantor zwischen Stufen des Unendlichen (den Mächtigkeiten, Kardinalzahlen) unterschieden hat, ist nach den Stufen des Leeren oder des Nichts zu fragen. Es gibt dann nicht nur eine, eindeutig und einmalig bestimmte transzendentale Logik, die allen gewohnten Logiken vorausgeht, sondern mehrere Stufen mit ihren jeweils spezifischen Mächtigkeiten und Gefährdungen. Ob diese sich auf vergleichbare Weise mathematisch beschreiben lassen wie die von Cantor eingeführten Kardinalzahlen, ist für mich offen. Aber es können z.B. Fragen gestellt werden wie: Aus welcher Stufe gehen Ordnungen wie der Goldene Schnitt hervor, die nicht nur in der Wirklichkeit nachgewiesen werden können, sondern eine eigene Kreativität (Fruchtbarkeit) entfalten und transzendental alle Möglichkeiten vorprägen, die mit ihnen gegeben sind. Wo hat die Negativität, aus der die Negativsprachen und das Nichts (kenos) der Kenogrammatik hervorgehen, ihrerseits ihren ontologischen Grund, wenn hier überhaupt noch von einem ontologischen Grund gesprochen werden kann.

Ausblick: Bisher wurde nur davon gesprochen, dass sich jede einzelne Leerstelle in verschiedenen Bewegungszuständen befinden kann. Bei seiner Betrachtung von Netzwerken geht Spencer-Brown in zweierlei Weise darüber hinaus: Dort wird der Prozess, der von einem Argument a zur Funktion f führt, nicht mehr als die lineare Folge gleichförmig ausgeführter Iterationen verstanden, sondern als Netzwerk, das einen Input a in einen Output f moduliert. Innerhalb des Netzwerks können Verzweigungen, Nebenläufigkeit und Schleifen auftreten. Dort können nicht nur die Verzweigungspunkte unterschiedliche Stati annehmen, sondern der Zustand des Netzwerks kann sich im Ganzen verändern. Die Änderungen der Zustände des Netzwerks können als ein autonomes kybernetisches System verstanden werden, das in einem Fließgleichgewicht auf die unterschiedlichen Inputs zu reagieren vermag. Siehe hierzu die bei der Konferenz in Liverpool vorgetragenen und diskutierten Ausführungen über die Netzwerke in Kapitel 11 der Laws of Form.

Schweigen

Welcher Weg führt von der Positivsprache zur Negativsprache? Von einer Negativsprache zu sprechen enthält einen Widerspruch in sich: Mit Negativsprache ist gemeint, wovon nicht gesprochen werden kann. In einer ersten Näherung ist das Schweigen eine Negativsprache, und die Negativsprache wird erreicht, wenn in den Worten der Positivsprache indirekt und negativ gezeigt werden kann, an welchem Punkt sie auf das Schweigen trifft. Die Positivsprache schlägt um vom Sprechen auf das Zeigen: Sie kann nicht über die Negativsprache sprechen, sie hat dafür keine Worte, aber sie kann im Sprachspiel ihrer Worte zeigen, an welchem Punkt die Negativsprache entsteht. Dieser Gedanke von Wittgenstein ist für die hier zu skizzierende Idee der Kenogrammatik ähnlich fundamental wie Cantors Unterscheidung der verschiedenen Stufen der Unendlichkeit. (Hilbert: »Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können.« Cantors Paradies. Mit gleicher Berechtigung lässt sich von Wittgensteins Paradies sprechen, das dieser der Sprachphilosophie bereitet hat.)

Mit der Unterscheidung von Positiv- und Negativsprache, d.h. mit dem Paradox, über Negativsprache zu sprechen, ist der Horizont geöffnet, in dem sich die klassischen Paradoxa wie das Lügner-Paradox (›was ich jetzt sage, ist falsch‹) verstehen lassen.

Unsicherheit

Während Wittgenstein hofft, die Grenze des Schweigens gewissermaßen am Rande des Denkens zu isolieren, kann die Positivsprache auch dort in die Negativsprache umschlagen, wo sie auf Unsicherheiten stößt, die sie nicht zu lösen vermag. Sie stößt auf Unsicherheiten, wenn eine bekannte Lösung versagt. An die Stelle einer festen Lösung A, die sich bisher bewährt hat, ist eine Leerstelle einzusetzen, an der andere Lösungsmöglichkeiten eintragbar sind. Die Konstante A wird durch eine Variable a ersetzt, wobei offen bleibt, ob es überhaupt eine Lösung gibt, d.h. einen anderen Wert, der an dieser Stelle eingesetzt werden kann. Baecker beschreibt als »die wichtigste Leistung der Negation«:

»Sie kann nicht nur Leerstellen als unbestimmte Außenseiten einer Unterscheidung implizieren und so dazu aufrufen, dort wählbare Bestimmungen vorzunehmen, wo es bislang keine gibt, sondern sie kann auf dem Umweg über den Widerstreit auch dort eine Leerstelle produzieren, wo man es bislang mit einer eindeutigen Bestimmung zu tun zu haben glaubte.« (Baecker 2013, 152)

Mit Negation ist an dieser Stelle zunächst nur gemeint, dass die bisher bewährte Lösung A nicht mehr haltbar ist und daher negiert werden muss. Was an ihre Stelle tritt und ob es überhaupt etwas gibt, das an ihre Stelle treten kann, ist vorerst offen (unsicher).

Die wahre Schwierigkeit entsteht dann, wenn nicht nur die bisher bekannte Lösung, sondern auch die bisher eingeführten Lösungswege versagen. Die Entscheidungsfindung gerät ins Stocken: Das beginnt mit der Frage, ob überhaupt das Scheitern einer Lösung von allen gesehen und als solches anerkannt wird. Oft wird stattdessen über die aufkommenden Schwierigkeiten geschwiegen. Haben möglicherweise nur zufällige, temporäre Ereignisse das Problem hervorgerufen, die so selten sind, dass sie von allein wieder verschwinden werden und für die weitere Entwicklung vernachlässigt werden können? Das Problem liegt daher eine Ebene höher: Ist die gewohnte Urteilsfähigkeit, Probleme erkennen und lösen zu können, in Frage gestellt? Droht an dieser Stelle ein negativer Zirkel: Wer sich nicht mehr auf seine Urteilsfähigkeit verlassen kann, wie soll der sowohl aus der objektiven Problemlage wie aus der kommunikativen Schwierigkeit herauskommen, über das Problem sprechen und eine Antwort finden zu können?

An dieser Stelle bietet Spencer-Browns Unterscheidung in lineare Prozesse und Re-entries einen Ausweg an. Es ist zu vermuten, dass in einer solchen Lage ein übergeordneter Prozess wirkt, der bisher nicht erkannt und verstanden wurde, und dessen Re-entry den normalen Gang der Lösung durcheinander bringt. Daher ist nicht nur die bisher bekannte Lösung A durch eine Variable a mit einer möglichen Aufzählung von Alternativen zu ersetzen, sondern durch eine Leerstelle, die sowohl durch bestimmte Werte gefüllt wie auch durch die Wirkung eines übergreifenden Re-entry erschüttert werden kann. An der Leerstelle sind nicht nur die jeweiligen dort eintragbaren Variablen, sondern zugleich die Bewegungszustände dieser Leerstelle zu unterscheiden. Daher ist der einzige Ausweg, alle bekannten Re-entries sorgfältig zu untersuchen und zu erkennen, ob ein weiterer Re-entry ergänzt werden muss, dessen Nicht-Berücksichtigung die gegebene Verunsicherung auslöst. Das kann bei einer Organisation bedeuten, nicht nur eine neue Lösung für den jeweils konkreten Problemfall zu finden, sondern auch die Werte (Visionen) zu erkennen, gemäß denen mögliche Lösungen beurteilt und unter ihnen entschieden wird, sowie die Entscheidungsprozesse, diese Werte zu erkennen und ihnen die angemessene Bedeutung zu verleihen.

Solche Situationen sind mit einer typischen Form von Schweigen verbunden. Über Schwierigkeiten dieser Art kann nicht offen gesprochen werden, und wer sie dennoch anspricht, wird nicht gehört und sogar möglicherweise ausgeschlossen. Das Schweigen befindet sich nicht mehr wie bei Wittgenstein am Rande der Positivsprache, sondern es bricht mitten in ihr auf. Spencer-Brown hat mit der Unterscheidung in übliche Aufzählungen und Re-entries den formalen Weg geöffnet, solche Situationen erkennen und beschreiben zu können. Mit jedem neu entdeckten Re-entry wird ein Fragebereich gelöst, über den zuvor nur geschwiegen werden konnte.

(Diese Art der Fragestellung überhaupt zu sehen verdanke ich den Ausführungen von Florian Grote bei verschiedenen Arbeitskonferenzen zu den Laws of Form.)

Gegensatz

Dieser sehr allgemeine Gedanke ist näher zu differenzieren. Am einfachsten ist es, die bisherige Lösung A durch ihr Gegenteil ¬A zu ersetzen. Wenn das immer möglich ist, kann von einer digitalen Welt gesprochen werden. Eine digitale Welt ist so beschaffen, dass jede Frage entweder durch A oder durch ¬A gelöst werden kann (tertium non datur). So wie es heute aussieht, können sich Roboter und die Künstliche Intelligenz nur in einer digitalen Welt bewegen. Sie verfügen ausschließlich über die Positivsprache.

Falls sowohl A wie auch ¬A versagen, kann die Frage erweitert werden: Welcher Gattung gehört die Lösung A an, und gibt es in dieser Gattung eine andere Art, gegen die A ausgetauscht werden kann? Ein Beispiel sind die Farben: Wenn sich z.B. die Farbe Blau nicht mehr bewährt, kann nach einer anderen Farbe gefragt werden, die besser geeignet ist. So verfährt üblicherweise die Mathematik: Wenn sich zeigt, dass eine bestimmte Zahl A nicht als Lösung infrage kommt, wird in der Regel auch ¬A nicht helfen, sondern A wird durch eine Funktion f(a) ersetzt, wobei a eine beliebige andere Zahl sein kann.

Rejektion

Auch dies Verfahren kann scheitern. Das klassische Beispiel ist die Suche der griechischen Mathematik nach der Lösung, welchen Wert die Diagonale in einem Quadrat annimmt. Zunächst schlugen einzelne Lösungsvorschläge fehl: Auf den ersten Blick könnte 1,5 eine Lösung sein, doch scheitert das. Mit jeder weiteren Annäherung wie 1,4 oder 1,41 usf. scheint die Lösung in greifbare Nähe zu rücken und wird doch nach wie vor verfehlt.

Wenn das geschieht, kann nicht weiter innerhalb des gegebenen Kontextes gesucht werden oder innerhalb der Gattung, in der sich bisher bekannte Lösungen befanden. Günther spricht von Rejektion und meint damit zunächst nur den Spezialfall, wenn sich zeigt, dass weder A noch ¬A gelten und die Alternative A oder ¬A verworfen werden muss (Rejektion). Das möchte ich erweitern: In diesem Fall ist ein Kontext-Wechsel notwendig. Formal geht es um einen Aufstieg in eine übergeordnete Gattung. Das war Platons Lösung der Frage nach den Irrationalzahlen: Wenn sich zeigt, dass es keine rationale Zahl gibt, mit der die Länge der Diagonale im Quadrat bestimmt werden kann, muss nach einem höheren Typ von Zahlen gesucht werden, mit denen das möglich ist. Platon sprach von dynamischen Zahlen. So ging im Weiteren die Mathematik vor: Wenn sich innerhalb einer gegebenen Zahlenmenge keine Lösung findet, sind übergeordnete Zahlenklassen zu bestimmen, in denen nach der Lösung zu suchen ist. Das waren die Irrationalzahlen, die reellen Zahlen, die komplexen Zahlen oder noch allgemeiner definierte Mengen von Zahlen (Algebren). – Für mich überraschend deutete Emanuel Seitz in seinem Beitrag Form und Philosophie beim formlabor 2020 in Berlin die von Spencer-Brown mit dem Cross gegebene Unterscheidung in ein Inneres und ein Äußeres (in den marked space und unmarked space) als Übergang von einer Art zu ihrer Gattung und in weiteren Schritten zu höheren Gattungen. Die Gattung enthält die Art, von der ausgegangen wurde, und negiert sie nicht. Aber sie negiert die hierarchische Stufe, auf der sich die Art befindet, und eröffnet eine übergeordnete Stufe. Insofern kann gesagt werden, dass sich die Gattung im Äußeren der Art befindet.

Auch für diese Übergänge gibt es jedoch Grenzen. Dies zu erkennen war die große Leistung von Cantor. Nachdem zunächst die Zahlenklassen schrittweise erweitert worden waren, erkannte Cantor, dass es einen Punkt gibt, an dem Zahlen auftreten, die zu sich selbst (zu ihrem eigenen Begriff) in Widerspruch geraten: Er konnte mit dem Zweiten Diagonalargument zeigen, dass die reellen Zahlen nicht zählbar, sondern überabzählbar sind. Nicht-zählbare Zahlen: Damit ist eine negative Selbstbezüglichkeit entdeckt. Diese Situation unterscheidet sich radikal von den bekannten Paradoxen wie ›dieser Satz ist falsch‹. Bei ihnen handelt es sich um künstliche Sprachausdrücke, die im Alltag niemand gebraucht, und die daher im üblichen wissenschaftlichen Denken vernachlässigt werden können. Aber was sind nicht-zählbare Zahlen? Bei ihnen tritt ein Gegensatz an der Sache selbst auf: A steht nicht mehr einem B gegenüber, welches das Gegenteil von A behauptet (wie es Kant in seinen Antinomien vorgeführt hatte), sondern tritt in Widerspruch mit sich selbst. Wer diesen Widerspruch verwerfen möchte (Rejektion), verwirft damit zugleich das Thema, um das es geht (die Sache, für die A steht), und gerät in einen Stillstand.

Widerspruch

Mit Cantors Nachweis überabzählbarer Zahlenklassen und den daraus folgenden Paradoxien ergab sich von der Mathematik her eine neue Sicht, wie Hegel den Widerspruch versteht und den Widerspruch von einem Gegensatz und einer Antinomie unterscheidet. Darauf hat 1932 Robert Heiß (1903-1974) in Logik des Widerspruchs aufmerksam gemacht: »Es ist der große Fortschritt der mathematischen Logik, dass sie die Selbstgegenständlichkeit in den Paradoxien allererst bemerkt hat. Es ist verwunderlich, dass es dieses Umweges bedurfte, um die Philosophie zur Untersuchung selbstanwendbaren Denkens zu veranlassen.« (Heiß, 95)

Heiß gelingt ein neues Verständnis der Drei Stellungen des Gedankens zur Objektivität. Während Hegel (i) Metaphysik, (ii) Empirismus und Kritische Philosophie und (iii) das Unmittelbare Wissen unterscheidet (so das Inhaltsverzeichnis des Vorbegriffs der Wissenschaft der Logik in der Enzyklopädie der philosophischen Wissenschaften im Grundrisse), unterscheidet Heiß für mich wesentlich konsequenter (i) das positive Wissen der Einzelwissenschaften, (ii) die Kritische Philosophie, (iii) die negative Selbstbezüglichkeit des Widerspruchs. Er stellt sich nicht gegen Hegel, sondern will auch Hegel gegenüber herausarbeiten, was Hegel implizit gemeint hat und noch nicht ausdrücklich zu formulieren vermochte. »Hegel hat über diesen größeren Aufgaben es unterlassen, das Grundphänomen, eben das der Selbstbezogenheit des Begriffes, in seinem logischen Charakter zu klären.« (Heiß, 55). Das Ergebnis wird sein, dass aus seiner Sicht Hegels Begriff der Negation der Negation neu gefasst werden muss: Er führt nicht einfach in eine neue Unmittelbarkeit, sondern in die negative Selbstbezüglichkeit. Wenn das eingesehen ist, stellt sich die Frage, die Hegel verborgen geblieben war: Wie und warum gelingt der Übergang von der negativen Selbstbezüglichkeit zu einer neuen Unmittelbarkeit, von der aus alles von vorn beginnen kann? Was stellt sicher, dass mit der Negation der Negation die Negativität nicht an ihr Ende gelangt ist, sondern ein neuer Kreis beginnen kann, der zu einer neuen These (Unmittelbarkeit), deren Negation und einer neuen Negation der Negation führen kann? Was befreit aus der Situation der negativen Selbstbezüglichkeit? Die Mathematik hat dafür bis heute keine Antwort gefunden. Das Paradox der überabzählbaren Zahlen hat zu Fragen geführt, die bis heute unentscheidbar sind. (Gemeint ist die Kontinuumshypothese: Gibt es eine Menge reeller Zahlen, deren Mächtigkeit kleiner ist als die Mächtigkeit der Gesamtheit aller reellen Zahlen? Für die praktische Arbeit der Mathematik scheint diese Frage jedoch nach heutigem Kenntnisstand unbedeutend zu sein.)

(i) Die Einzelwissenschaften finden jeweils ihr spezifisches Thema und entwickeln eine dafür angemessene Methode, mit der sie ihr Fachgebiet erkunden, sich ihren Gegenständen nähern und stufenweise positives Wissen erwerben. Hier gibt es keine Widersprüche, sondern nur unvollständiges Wissen, das im Laufe weiterer empirischer Arbeit geschlossen werden kann. Größtes Vorbild ist zweifellos die Mathematik. Sie findet in den Zahlen und geometrischen Figuren ihr Thema und mit den Regeln der Arithmetik und der geometrischen Konstruktion ihre Methode.

(ii) Und doch kann es zu Antinomien kommen. Heiß zitiert den Brief von Kant am 21.9.1798 an Christian Garve: »Nicht die Untersuchung vom Daseyn Gottes, der Unsterblichkeit etc. ist der Punct gewesen von dem ich ausgegangen bin, sondern die Antinomie der reinen Vernunft. [..] Diese war es welche mich aus dem dogmatischen Schlummer zuerst aufweckte und zur Critik der Vernunft selbst hintrieb, um das Scandal des scheinbaren Widerspruches der Vernunft mit ihr selbst zu beheben.« (Kant, Akademieausgabe AA 12:257.32-258.03, zitiert bei Heiß, 25). In solchen Situationen kann die Philosophie nicht an die Stelle der Naturwissenschaft treten und mit neuem Wissen eine Lösung finden. Aber sie kann negativ vorgehen und untersuchen, was in einer Wissenschaft geschieht, die in Antinomien gerät. Sie untersucht die ihnen selbst verborgenen, impliziten Voraussetzungen, von denen sie ausgeht, ohne sich dessen bewusst zu sein. Aus deren Unverständnis kann es zu Antinomien kommen. Das geschieht, wenn die Wissenschaft ohne es bewusst zu wollen und für sich selbst unbemerkt über den ihr zugänglichen Bereich des positiven Wissens hinausgeht, die Positivsprache verlässt und Aussagen trifft, die nicht auf der Objektebene des positiven Wissens gelten, sondern auf der Metaebene der Begrifflichkeit, mit der über Objekte gesprochen wird. Genauer gesagt hatte Kant entdeckt und nachgewiesen: Die Wissenschaft ist an die Zeit gebunden. Sie kann Phänomene untersuchen, die in der Zeit gegeben sind und sich in der Zeit ändern und vergehen können. Sie kann deren Entwicklungen beschreiben, wie sie im Verlaufe der Zeit beobachtet, protokolliert, mathematisch dargestellt und überprüft werden können, aber sie kann mit ihren Methoden nicht die Zeit-an-sich betrachten, als wäre die Zeit ein Objekt wie alle anderen, das einen zeitlichen Verlauf nimmt. Sie kann keine selbstbezüglichen (oder gar negativ selbstbezüglichen) Eigenschaften der Zeit erkennen. Die Eigenschaften der Zeit gehen der Methode der Wissenschaft voraus. Im Grunde geht Kant so vor wie später ihm folgend Freud: Wo Es (das Unbewusste) war, soll Ich (das Bewusste) werden. Die Wissenschaft macht unbewusste Annahmen, die von Kant untersucht und bewusst gemacht werden. Heute befinden wir uns in der umgekehrten Lage: Die Quantentheorie und die mit ihr erweiterte Allgemeine Relativitätstheorie warten geradezu sehnsüchtig auf eine entsprechende Klärung ihrer ungelösten Fragestellungen durch die Philosophie.

Auf diese Weise vertieft die Kritische Philosophie Schritt für Schritt das Methodenverständnis der Wissenschaft. Wovon diese anfangs naiv ausgegangen sind, wird nicht widerlegt, sondern aufgeklärt. Stufenweise werden ihre impliziten Annahmen bewusst. Kant zeigte, dass die Wissenschaft im Horizont der Zeit steht: Ihre Begriffe setzen die Eigenschaften der Zeit voraus (Beständigkeit, Kausalität, Wechselwirkung). Der Weg von Kant ist von Descartes vorbereitet und vor allem von Husserl fortgeführt worden. Heiß bezieht sich mit seiner Arbeit von 1931 ausdrücklich auf dessen Programm.

»Was sich hier zeigt, ist ein Absinken der Fundamente der methodischen Philosophie. Jeweils der Nachfolger legt den Ansatz weiter zurück. Es ist nicht das Aufsteigen eines Gedankens, der von positivem zu positivem Ergebnis wie von Stufe zu Stufe steigt.« (Heiß, 47)

Das nimmt in allgemeiner Weise den Gedanken der Proemialrelation vorweg und überträgt ihn auf die Geschichte der philosophischen Ideen: Wenn das implizite Wissen einer Wissenschaft erkannt ist, führt das in einen übergreifenden Kontext, von dem aus sich die Wissenschaft verstehen und die in ihr auftretenden Antinomien lösen lassen. Oder anders gesagt: Es gelingt der Kritischen Philosophie, einen jeweils höheren Beobachterstandort zu finden, von dem aus das Geschehen innerhalb der Wissenschaft beobachtet und erklärt werden kann. Heiß zitiert aus der Kritik der reinen Vernunft von Kant die Stelle über die Sphäre des Begriffs (KrV B790, zitiert Heiß, 29). Mit ihr wird nahegelegt, wie die Antinomien darauf stoßen, die Vernunft in einem größeren Horizont zu sehen und Eigenschaften zu erkennen, die vorher verborgen geblieben waren: die Krümmung der Sphäre. Die Wissenschaft glaubt, sich positiv auf einer unbegrenzten Ebene zu bewegen, die Schritt für Schritt erkundet werden kann. Die Kritische Philosophie erkennt, dass sie sich wie auf einer Kugel bewegt, auf der der jeweilige Horizont prinzipiell beschränkt ist und deren innere Eigenschaften (die Krümmung) der Wissenschaft verborgen bleiben. (Siehe hierzu weiterführend den Beitrag Die Sphäre des Begriffs und die Logik der Sphäre.)

Dieser Gedanke entspricht dem Beispiel der Zahlenkugel, mit dem Riemann für die unendlich-ferne natürliche Zahl einen Ort finden konnte.

(iii) Auf den ersten Blick hat Hegel den Weg der Kritischen Philosophie konsequent fortgeführt. Er scheint einfach den Weg von Kant weiter gegangen zu sein und auf einer nochmals tieferen Ebene verborgenes implizites Wissen aufgedeckt zu haben. So sieht es heute eine einflussreiche Strömung von Hegelianern, die von Robert Brandom (* 1950) ausgeht: »Was Brandom bei seinem Versuch, Hegel 'wieder zu normalisieren', wegfallen lässt, ist in erster Linie die Dimension der Selbstbezüglichkeit.« (Žižek, 110) Das ist der springende Punkt, auf den erstmals Heiß aufmerksam gemacht hat. »Eine vollkommen veränderte Stellung zum Widerspruch ist die Grundlage der Hegelschen Methode.« (Heiß, 50) Vor ihm suchte die Philosophie nach einer Auflösung der in der jeweiligen Wissenschaft vorgefundenen Widersprüche (Antinomien). Für Hegel dagegen ist der Widerspruch nicht etwas, das es aufzulösen gilt, sondern das innere Bewegungsprinzip der Wissenschaft. Er erkennt im Widerspruch, »dass aus der Selbstanwendung des Denkens sowohl die Selbstaufhebung, wie auch die Selbsterweiterung des Denkens begriffen werden kann« (Heiß, 54).

Hegel unterscheidet sorgfältig zwischen einem Gegensatz (einer Antinomie) und dem Widerspruch. Beim Gegensatz stehen zwei Etwase (zwei Sachen, im physischen Bereich zwei Dinge) einander gegenüber. obiectus ist wörtlich ‘das Entgegengeworfene’. Wie auch immer sie beurteilt werden, sie lassen sich klar voneinander trennen und unterscheiden. Der Gegensatz ist für Hegel die höchste Form der Unterscheidung.

Völlig anders verhält es sich beim Widerspruch. Etwas steht nicht zu etwas anderem in Widerspruch (das wäre ein bloßer Gegensatz), sondern mit sich selbst. Der Widerspruch entsteht, wenn das Entgegengesetzte (der Gegensatz) nicht mehr außen liegt, sondern in die Sache selbst zurückgekehrt ist. Hegel prägt den überaus anschaulichen Begriff »Das Andere an ihm selbst.« (HW 5.127, siehe hierzu den Kommentar durch Richli). Im ersten Schritt ist das Etwas definiert worden, indem es vom Anderen unterschieden und abgegrenzt wurde. Aber wo liegt die Grenze? Liegt sie beim Etwas oder beim Anderen oder in einer ungeklärten Weise zwischen ihnen? Hegel erkennt, dass die Negation (die Abgrenzung) ihrerseits negiert werden muss. Etwas kann nur von etwas Anderem abgegrenzt werden, wenn es bereits an-sich-selbst die Unruhe trägt, sich von etwas anderem unterscheiden zu können. »Die andere Bestimmung ist die Unruhe des Etwas in seiner Grenze, in der es immanent ist, der Widerspruch zu sein, der es über sich selbst hinausschickt.« (HW 5.138) (Siehe hierzu ausführlicher den Arbeitstext Antinomien des Daseins und der Unendlichkeit.) Das ist der elementare Begriff der negativen Selbstbezüglichkeit: Etwas ist nur ein Etwas, wenn es die Eigenschaft hat, an sich selbst auf etwas Anderes zu verweisen, von dem es sich unterscheidet. Hegel vollzieht einen Übergang vom Unterschied zur Unterscheidbarkeit: Der Unterschied liegt zwischen Etwas und dem Anderen. Aber die Unterscheidbarkeit ist eine Eigenschaft des Etwas selbst, die zugleich dem mit sich selbst identischen Etwas widerspricht.

Wenn Hegel von der Unruhe des Etwas spricht, nimmt er den Gedanken von Spencer-Brown vorweg, die Bewegungszustände des Mediums zu unterscheiden. Die Nähe zu Spencer-Brown ist noch enger: Hegel führt den Gedanken des Anderen-an-ihm-selbst in allen Einzelheiten aus. Er unterscheidet die doppelte Bewegung von Kontinuität und Umkehr: Mit der Kontinuität ist in Etwas die Eigenschaft angelegt, über sich selbst hinauszugehen und auf etwas Anderes zu verweisen. Mit Umkehr ist die Eigenschaft gemeint, dass diese Unterscheidung durch etwas Anderes das Etwas nicht in seiner Identität in Frage stellt oder sogar vernichtet, sondern buchstäblich umgekehrt die Identität ihrer selbst bewusst macht. Hegel hat das an zahlreichen Beispielen aus der Naturwissenschaft erläutert. (Siehe hierzu den Beitrag Hegels Idee eines »höheren Widerspruchs« – Von der Kontinuation und Umkehr zur »Pulsation« des Widerspruchs).

Baecker versteht die doppelte Bewegung von Kontinuität und Umkehr als Kommunikation: Etwas wendet sich nach außen in seine Umgebung (eröffnet die Kommunikation) und enthält von dort eine Antwort. Wird die Umgebung als das Ausgeschlossene verstanden und die Aufnahme der Antwort aus dem Ausgeschlossenen als dessen Einschluss, dann kann mit Baecker die Antwort als Umkehr und im Ganzen als Form der Kommunikation mit dem von Hegel eingeführten Widerspruchsbegriff als »die Dynamik des Einschlusses des Ausgeschlossenen« (Baecker 2005, 79) gedeutet und mit dem Re-entry in der elementarsten und abgekürztesten Form aufgeschrieben werden:

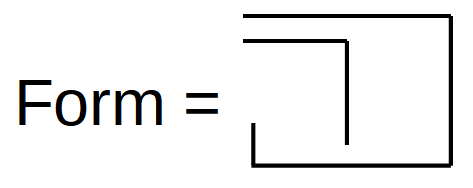
Kommunikation, nach Baecker 2005, 80

Das ist die formale Gestalt des Widerspruchs. Von Etwas wird durch eine Grenze sein Anderes unterschieden und kehrt zurück.

Ist damit der eingangs ausgeführte Gedanke zurückgenommen, beim Re-entry handele sich um keine Resonanz und kein Feedback? In meinem Verständnis geht Spencer-Brown beim Re-entry noch nicht von einer Kommunikation aus (in seinem Beispiel kommuniziert die Form des Echelon nicht mit etwas anderen). Aber die Deutung als Kommunikation ist bereits die Antwort auf die große Frage, die sich mit der negativen Selbstbezüglichkeit stellt: Die negative Selbstbezüglichkeit ist für sich noch keine Kommunikation, doch kann sie nur aufrecht erhalten werden, wenn sie in einer Kommunikation aufblühen kann.

(iv) Wie gelingt bei Hegel der Übergang von der Negation der Negation in der negativen Selbstbezüglichkeit zu einer neuen Unmittelbarkeit, die einen neuen Kreislauf von Unmittelbarkeit, deren Negation und einer erneuten Negation der Negation öffnet? Hegel stellt nicht einmal diese Frage, und es kann nur vermutet werden, dass er das Thema der negativen Selbstbezüglichkeit nicht explizit gemacht hat, weil er unbewusst vor dieser Frage zurückscheute. Wie ist sonst zu verstehen, dass er zwar den Begriff der negativen Selbstbezüglichkeit inhaltlich voll ausgearbeitet, aber nicht als Begriff eingeführt hat?

Mit Spencer-Brown lässt sich veranschaulichen, worum es geht: Er unterscheidet vom Re-entry das Recrossing . Beim Recrossing wird eine Grenze überschritten und anschließend das Überschreiten der Grenze wieder weggewischt. Dadurch wird die ursprüngliche Unmittelbarkeit wieder hergestellt. Eine genaue Analyse der Negation der Negation bei Hegel zeigt, dass er exakt auf diese Weise vorgeht: Er beginnt seine Logik, indem er Sein und Nichts einander gegenüberstellt. Wird ihre Negation negiert, ergibt sich daraus das Werden. Die Negation des Werdens ist das Verschwinden. Deren Negation ist das »Verschwinden des Verschwindens« (HW 5.113). (Ausführlicher wiederum der Arbeitstext Antinomien des Daseins und der Unendlichkeit.) Das Verschwinden des Verschwindens ist das Urbild einer negativen Selbstbezüglichkeit. »Das Resultat ist das Verschwundensein, aber nicht als Nichts.« (HW 5.113) Das ist der kritische Punkt. Wenn das Verschwinden verschwindet, fällt es nicht in das Nichts zurück, sondern erreicht eine neue Unmittelbarkei, die Hegel »Dasein« nennt. Diese Bewegung entspricht formal dem Recrossing: (i) Eine Unterscheidung wird getroffen. (ii) Im Äußeren der Grenze ist das ursprüngliche Etwas verschwunden und dessen Anderes erreicht. (iii) Die Unterscheidung wird rückgängig gemacht und verschwindet ihrerseits. Dadurch wird das ursprüngliche Etwas in seiner Unmittelbarkeit wiederhergestellt. Doch ist es nicht mehr einfach das alte Etwas, sondern ein Etwas, das die Bewegung des Recrossing hinter sich hat. Um diesen neuen Zustand kenntlich zu machen, ist am Etwas dessen Bewegungszustand zu beschreiben: In diesem einfachen Fall sind nur zu unterscheiden die beiden Bewegungszustände ‘vor dem Recrossing’ und ‘nach dem Recrossing’. Auf diese Weise kann mit Spencer-Brown nicht nur die von Hegel eingeführte dialektische Bewegung graphisch und formal beschrieben werden, sondern es kann das implizite Wissen herausgehoben werden, das Hegel stillschweigend vorausgesetzt hat, um Sein und Dasein unterscheiden zu können, die im gewöhnlichen Sprachgebrauch das gleiche bedeuten (Erst Heidegger hat diesen Unterschied klarer in Worte fassen können, als er am Dasein die mit ihm gegebene Vielfalt von Möglichkeiten hervorgehoben hat, wodurch es sich vom Sein unterscheidet. Die Vielfalt der Möglichkeiten entspricht in meiner Deutung den unterschiedlichen Bewegungszuständen, um die es Spencer-Brown geht.)

In der Sprache von Spencer-Brown ist Hegels Dialektik, sofern sie zu einer neuen Unmittelbarkeit führt, auf der Stufe des Recrossing stehen geblieben. Sie erreicht nicht die negative Selbstbezüglichkeit, die erst mit dem Re-entry beschrieben ist. Hegel hat zwar inhaltlich die negative Selbstbezüglichkeit vollständig ausgearbeitet, aber er hat sie noch nicht vom Recrossing abheben und unterscheiden können.

Mit der negativen Selbstbezüglichkeit droht das Denken in einen Stillstand zu geraten. Hegel vertraute darauf, dass trotz aller Negation der Negation mit ihr die Negativität nicht erlischt. Es muss eine eigene Kraft geben, die das sicherstellt. Diese Kraft wird in der persischen und hebräischen Tradition als Teufel, Satan (wörtlich der Ankläger und Widersacher) oder mit Goethe als Mephistopheles personalisiert. Das führt zu einer tiefgehenden Überlegung über das Wesen der Schöpfung, die Lars Clausen in seinem Beitrag Counting AND accounting für das formlabor 2020 angesprochen hat. Ein Leser des Alten Testaments muss sich die Frage stellen, wie der Teufel (oder die Schlange) in die Welt kam, die Gottes Verbot widersprochen hat, vom Baum der Erkenntnis zu essen. Sie kann weder von Gott geschaffen (ein Teil der Schöpfung) noch eine Seite an Gott sein. Oder anders gesagt: Sie gehört weder zur Positivsprache, die den Umfang der Schöpfung umfasst, noch zum Schöpfer der Positivsprache. Mit ihr können die von der Positivsprache beschriebenen Objekte der Schöpfung ersetzt werden durch Leerstellen, an denen das jeweils vorhandene Objekt negiert und Platz gemacht werden kann für eine Alternative. Diese Möglichkeit, ein gegebenes positives Objekt (und sei dies ein von Gott erlassenes Verbot) durch eine Leerstelle zu ersetzen, ist nicht ihrerseits ein Objekt, das mit der Schöpfung geschaffen wurde, sondern ein allen Objekten und ihren Orten vorausgehendes Prinzip auf der Meta-Ebene, in den Worten von Günther die Negativsprache.

Abjektion

Hegel war davon ausgegangen, dass mit ihm die Philosophie abgeschlossen ist und die weitere Geschichte ein Ende gefunden hat. Welche Gefährdung mit der negativen Selbstbezüglichkeit und der Negation der Negation verbunden ist, zeigt sich entgegen seinen Erwartungen in der Kunst und in verschiedenen Krankheitsbildern, die seit den 1970ern von einer neuen Generation der Psychoanalyse untersucht werden. 1980 veröffentlichte Julia Kristeva (* 1941) ihren Essay über Abjektion zum Thema Mächte des Horror. abiectus kommt aus dem Lateinischen und bedeutet ursprünglich ‘nachlässig hingeworfen, zu Boden gedrückt, niedrig, gemein, kleinmütig, verzagt, verächtlich, verworfen’. Im Französischen klingt l'abjection weit drastischer, übersetzt als ‘Verworfenheit, tiefste Erniedrigung, Niederträchtigkeit, Schändlichkeit, Schmach, Schandtat’ (dict.leo.org). Für Kristeva ist mit Abjektion eine psychische Verfassung beschrieben, in der sich Subjekt und Objekt, Innen und Außen nicht deutlich voneinander trennen und einander gegenüberstellen lassen, und mit Abjekt das monsterartige Phänomen, von dem sie sich ergriffen fühlen und nicht lösen können. Sie nennt als Beispiele Panikattacken, Phobien, Borderline-Persönlichkeitsstörungen, Essstörungen, Depressionen. In einer fast literarischen Sprache schreibt sie am Beispiel der Essstörungen:

»Verabscheuen eines Nahrungsmittels, eines Stückes Dreck, eines Abfalls oder Dungs. Die Krämpfe und das Erbrechen, die mich schützen. Die Abneigung, das Würgen, das mich zur Seite drängt und mich von Verunreinigungen (defilement, auch zu übersetzen als Schändung, Entweihung, Besudelung, t.), Abwässern und Dreck abhält. Die Scham über den Kompromiss, die Schande, inmitten des Verrats zu sein. Der faszinierte Start, der mit zu ihnen führt und mich von ihnen trennt. Die Abscheu vor der Nahrung ist vielleicht die elementarste und archaischste Form der Abjektion.« (Kristeva, 2, eigene Übersetzung)

Überlebenswichtige Objekte wie die Nahrungsmittel werden als Bedrohung empfunden. Die Aufforderung zum Essen erscheint als Verrat an der eigenen höheren Einsicht in den wahren, zu verwerfenden Charakter der Dinge. Essgestörte geraten in ihrem Verhalten in eine negative Selbstbezüglichkeit, die in vielen Fällen zum Tod führt. Das Subjekt fühlt sich zugleich von außen getrieben wie stolz auf seine vermeintliche Leistung. Objekte können nicht mehr objektiv, das eigene Subjekt nicht mehr in einer ihrer selbst sicheren Subjektivität erfahren und beurteilt werden. Aus Sicht des Außenstehenden brechen alle gewohnten Maßstäbe zusammen. »Das Abjekt (ist) aus dem Raum der symbolischen Gemeinschaft 'grundsätzlich ausgeschlossen und zieht mich zu dem Ort, wo die Bedeutung zusammenbricht'« (Žižek, 204 mit Zitat Kristeva, 2)

Aus Sicht einer an Freuds Lehre und mit Lacan geschulten Psychoanalytikerin wie Kristeva befindet sich das Abjekt noch unterhalb des Unbewussten und der Triebe. Jeder Trieb äußert sich in den Objekten, die er begehrt oder bekämpft, doch das Abjekt kann nicht als Objekt für sich isoliert und als ein dem Subjekt gegenüberstehendes Anderes wahrgenommen werden. Das Essen wird nicht abgelehnt, weil es aus welchen Gründen auch immer negiert wird, sondern es löst vor jeder Entscheidung über Annahme oder Negation Abscheu aus. Was hier erlebt wird, ist auf seine Art ohne Frage eine Unmittelbarkeit des Erlebens, doch ohne Möglichkeit, Unterscheidungen treffen zu können.

Das Abjekt entsteht dort, wo in der üblichen Entwicklung des Subjekts die Sprache gebildet wird. Kristeva beschreibt das psychoanalytische Verständnis dieser Situation: Wenn das Kind lernen muss, dass die Mutter nicht immer unmittelbar verfügbar ist, erwirbt es die Sprache, mit der es an die Stelle des körperlich erlebten Objekts Worte setzen kann, mit denen es das zu beschreiben beginnt, was es sich wünscht und als Objekt seiner Triebe bewusst zu formulieren lernt. Das Subjekt lernt, ein neues Objekt zu finden. »Which one? Not the object of sexual drive; the mother, or her parts, or her representatives; no more than some neutral referent or other, but symbolic activity itself.« (Kristeva, 44) Das Kind kann erotische Freude an der eigenen Sprache empfinden, die an die Stelle der Freude des unmittelbaren körperlichen Erlebens tritt. In dieser »primordialen Sphäre« (Husserl) ist noch alles miteinander verwachsen: Das Bewusstwerden der eigenen Triebe und ihrer Verdrängung, zeitliche Unmittelbarkeit und Verschiebung, Subjekt und Objekt, Innen und Außen, die Trennung der Worte von den mit ihnen angesprochenen Sachen. Alles ist positiv und negativ selbstbezüglich: Das Subjekt entsteht in dem Maß, wie es ihm gelingt, sich von seinen Objekten zu trennen. Objekte können in dem Maß als solche erkannt werden, wie sie zwar auf das erkennende Subjekt bezogen, aber von ihm gesondert werden.

Psychische Verfassungen wie die von Kristeva genannten Beispiele zeigen, wie das misslingen kann. Ein anderes Beispiel sind die Phobien. Löst ein Objekt (wie z.B. ein Hund oder ein Pferd) eine phobische Reaktion aus, dann kann es nicht vom überwältigenden Sturm der im Subjekt entfesselten Gefühle getrennt werden. In der Panik bricht die kategoriale Ordnung voneinander getrennter Objekte und Subjekte zusammen. – Wem Beispiele aus der Psychoanalyse nicht vertraut sind und möglicherweise problematisch erscheinen, kann Beispiele aus der Kunst wählen. Kristeva nennt den Horror, den in Dostojewskis Roman Die Dämonen die Hauptfiguren wie Werchowenskij oder Kirilow erfahren. In neuerer Zeit gilt abject art als eine Kunstrichtung. »Cindy Sherman is seen as a key contributor to the abject in art, as well as many others including Louise Bourgeois, Helen Chadwick, Paul McCarthy, Gilbert & George, Robert Gober, Carolee Schneemann, Kiki Smith, Sarah Lucas and Jake and Dinos Chapman.« (tate.org) Weitere Beispiele sind die Gemälde von Fancis Bacon, die Filme von David Cronenberg und David Lynch. In der Musik kann ein Werk wie I buried Paul von Michael Gordon genannt werden (YouTube).

Kunst und Religion treffen den kritischen Moment der Sprachentstehung und mit ihr der menschlichen verbalen Kommunikation. »In diesem unentscheidbaren Raum, der logischerweise vor der Wahl des Sexualobjekts liegt, bricht die religiöse Antwort auf die Erniedrigung ein: Verunreinigung (defilement), Tabu oder Sünde.« (Kristeva, 48, eigene Übersetzung). Kunst und Religion beschreiben die Phänomene der Abjektion. Sie können jedoch ihnen gegenüber ebenso wenig objektiv sein wie die das den von der Abjektion Betroffenen nicht möglich ist: Wer das Schicksal der Abjektion erleidet, gilt seiner Umgebung als verunreinigt und im Zustand der Schande und Sünde. Das ist ein Ausschluss, der keinen versöhnenden Einschluss kennt: Sie sind nicht nur als Menschen ausgeschlossen, sondern wegen ihrer eingeschränkten Unterscheidungsfähigkeit in Ich und Du, Subjekt und Objekt, Innen und Außenauch auch von fast jeder Kommunikation. Daher ist für mich das Bild des Teufels (der Schlange) in der Sündenfallgeschichte ambivalent: Er kann die Kraft der Negativität verkörpern, aber auch die auszuschließende Gefahr der Abjektion. Der Mensch kann nach dem ihm verbotenen Verspeisen der Frucht vom Baum der Erkenntnis zwischen gut und böse unterscheiden, wie es ihm die Schlange verführerisch versprochen hat. Aber wenn er sich der Frage nähert, worin diese Unterscheidung ihren Grund hat, gerät er in eine unauflösbare negative Selbstbezüglichkeit: Ist die Unterscheidung in gut oder böse ihrerseits gut oder böse? In der biblischen Erzählung hat Gott vor dieser negativen Selbstbezüglichkeit gewarnt, die Schlange hat den Menschen dazu verführt. Ist es gut, wenn der Mensch die Freiheit gewählt hat, das Verbot zu übertreten, oder böse, wenn er das getan hat? Das Ergebnis war, dass sich der Mensch seiner Schande (die wörtliche Übersetzung des Abjekten) bewusst wurde und Scham zu empfinden begann.

Wie kann gegenüber der drohenden Abjektion das in Worte gefasst werden, welches das Gelingen ermöglicht, aus der primordialen Sphäre heraus in eine kategoriale Ordnung zu gelangen? In diesem Sinn verstehe ich die von Baecker geprägte Wortschöpfung catjects: »Catjects are called catjects because they are neither objects nor subjects but complex categories giving rise to objects and subjects.« (Baecker 2018, 1) Mit catjects soll das positiv formuliert werden, was bei der Abjektion misslingt. Für Baecker hat Spencer-Brown mit den Laws of Form die Ebene getroffen, auf der die catjects hervortreten und in ihrem Hervortreten erkannt werden können. Wie ist das möglich? Das Medium ist nicht nur der Grund, in den Formen eingetragen werden, aus dem Formen hervorgehen und der in diesem Vorgang in Schwingung versetzen kann, sondern innerhalb der Schwingung kann es zu etwas Neuem kommen, mit dem die Abjektion vermieden und der Weg der catjects geöffnet werden kann. Wird die Schwingung als die erste Emergenz bezeichnet, kann das aus ihr entstehende Neue mit Scheier als »zweite Emergenz« bezeichnet werden, die sich »im Augenblick, systema momentaneum, analog zu Leibniz' mens momentanea« zeigt.

»Auf der Stufe der basalen Selbstreferenz ereignet sich nur dies, daß Zeit sich selbst erzeugt als Horizont (Reflexivität) und sich als dieser sofort wieder löscht. Das Produkt ist nur das verschwindende Moment der Produktivität, die Identität nur das verschwindende Moment der Differenz, die alêtheia nur das verschwindende Moment der lêthê.« (Scheier, 121)

Wenn das gelingt, ist nicht nur die negative Selbstbezüglichkeit der Zeit gefunden, die indirekt als Idee von Kant angesprochen, aber von ihm noch nicht bestimmt werden konnte, da er noch nicht über den Begriff der negativen Selbstbezüglichkeit verfügte (die Zeit, die sich im Augenblick ihrer Erzeugung als Horizont unmittelbar wieder löscht), sondern mit ihr ist von der Fruchtbarkeit des Grundes zu sprechen, dank derer die in ihm eingetragenen Formen aufblühen können. Das führt zu einer zweiten Verwandlung der bisher beschriebenen Prozesse des Re-entry. Mit der ersten Verwandlung war das Medium in Schwingung versetzt worden, mit der zweiten Verwandlung geht im Augenblick der Schwingung die Fruchtbarkeit hervor. So wie die Abjektion zum Abbruch der Kommunikation führt, ist die im Aufblühen hervortretende Kommunikation ein Zeichen der gelingenden Sprachfähigkeit. Mit der Sprachfähigkeit ist die Frage nach dem Beobachter aufgeworfen. Der Beobachter verfügt nicht nur über eine räumliche Distanz zum Geschehen, sondern über eine Sprache, mit der er den Vorgang protokollieren und in Worte fassen kann. Mit der Sprache ist die unendliche Vielfältigkeit möglicher Deutungen gegeben. Der Standort des Beobachters ergibt sich nicht nur aus dem Ort, von dem aus er etwas sieht und darüber spricht, was er sieht, sondern aus seiner inneren Verfassung, der conditio humana. Das ist ein neues Thema, das über die Frage des Re-entry hinausführt.

Wird nach dem Ort gefragt, an dem sich Abjektion und Sprachfähigkeit voneinander trennen, geht es um die seit Platon diskutierte Frage der chora. Paul Natorp übersetzt: Im Unbestimmten, aus dem die Schöpfung hervorgeht, muss »etwas Positives verborgen« liegen (Natorp, 365), und das ist in einer ersten Annäherung die »Ortsbestimmtheit« (ebd.), »das, worin es wird«, »das Aufnehmende der Mutter« (Natorp, 367), der »Sitz«, »irgendwie ein Halt am Sein« (Natorp, 368), mathematisch gesprochen der Raum. Oder in den Worten von Platon:

»Da sie aber weder mit ähnlichen noch mit im Gleichgewicht stehenden Kräften angefüllt wurde, befindet sich nichts in ihr im Gleichgewicht, sondern als überall ungleichmäßig schwebend (anômalôs pantê talantoumenên) wird sie selbst durch jene erschüttert und erschüttert, in Bewegung gesetzt, umgekehrt jene.« (Platon Timaios, 52e)

»Ehe das aber geschah, sei alles dies ohne Maß und Verhältnis (alogôs kai ametrôs) gewesen. Als jedoch Gott das Ganze zu ordnen unternahm, haben sich anfangs Feuer, Wasser, Luft und Erde, die aber bereits gewisse Spuren von sich selbst besaßen (ichnê men echonta hautô atta), durchaus in einem Zustande befunden, wie er bei allem, über welches kein Gott waltet, sich erwarten läßt. Diese von Natur also Beschaffenen formte zunächst Gott durch Gestaltungen und Zahlen (eidesi te kai arithmois).« (53a-b)

Anhang zum Canon C9

Felix Lau gibt einige Hilfestellungen zum Verständnis des Kanon C9 (Lau, 89). Er erläutert die herangezogenen Regeln C5 (Iteration; LoF, 33; Lau, 79), C1 (Reflexion; LoF, 28; Lau, 77f), J2 (Distributivgesetz; LoF, 28; Lau, 77), C4 (Occultation, Verbergung; LoF, 33; Lau, 79f). Vor allem aber konzentriert er sich auf die schwierigste Stelle in dieser Beweisführung:

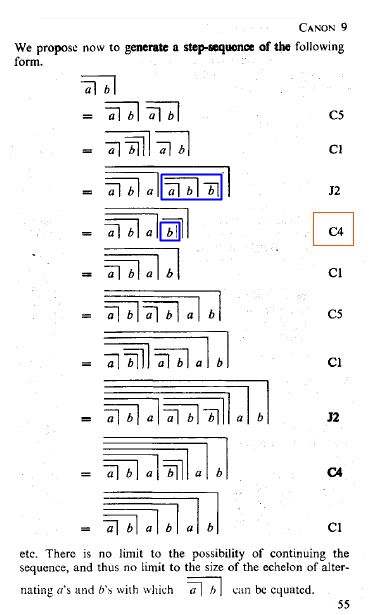
Die kritische Stelle ist blau umrandet hervorgehoben. Lau hat ihre Identität in einer Nebenrechnung gezeigt. Er nennt – ohne es weiter auszuführen – die Beweisschritte C1, J2, C5, C1, C4. Der Nachweis ist Leon Conrad gelungen (E-Mail vom 30. März 2020 mit meinen Kommentaren, siehe auch in YouTube den Laws of Form Course von Leon Conrad, Session 14):

zurück zum Text: ⏴

Siglenverzeichnis

AUM = The G. Spencer-Brown – AUM-Conference 1973, Esalen 1973; Link

HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971; Link

LoF = George Spencer-Brown: Laws of Form, New York 1972 (Julian Press) [1969]; Link

Literatur

Dirk Baecker 1993 (Hg.): Kalkül der Form, Frankfurt am Main 2016 [1993]

Dirk Baecker 2005: Form und Formen der Kommunikation, Frankfurt am Main 2005

Dirk Baecker 2013: Beobachter unter sich: Eine Kulturtheorie, Darmstadt 2013

Dirk Baecker 2018: Why catjects? Version 3, Januar 2018; PDF

Ulrich Blau: Die Logik der Unbestimmtheiten und Paradoxien, Heidelberg 2008

Heinz von Foerster: Understanding understanding, New York u.a. 2003

Heinz von Foerster, Gotthard Günther: The Logical Structure of Evolution and Emanation
in: Ann.N.Y. Acad.Sci. 138 (1967) 874-891; PDF bei vordenker.de

Gottlob Frege: Funktion und Begriff, Jena 1891; Online

Gotthard Günther 1962: Das metaphysische Problem einer Formalisierung der transzendental dialektischen Logik
zuerst in: Heidelberger Hegeltage 1962, Hegel Studien Beiheft 1, p. 65-123
nachgedruckt in: ders.: Beiträge zur Grundlegung einer operationsfähigen Dialektik Bd. 1, Hamburg 1976, S. 189-247, Online: PDF bei vordenker.de

Gotthard Günther 1970: Cognition and Volition
in: ders.: Beiträge zur Grundlegung einer operationsfähigen Dialektik, Bd. 2, Hamburg 1979, S. 203-240, Online (deutsche Übersetzung) PDF bei vordenker.de

Gotthard Günther 1979: Identität, Gegenidentität und Negativsprache
in: Hegeljahrbücher 1979, S. 22-88; PDF bei vordenker.de

Gotthard Günther 1995: Number and Logos (Zahl und Begriff)
vermutlich kurz nach dem Tod von Warren McCulloch 1969 entstanden, zuerst veröffentlicht in: Axel Ziemke und Rudolf Kaehr (Hg.): Selbstorganisation - Jahrbuch für Komplexität in den Natur-, Sozial- und Geisteswissenschaften, Band 6 "Realitäten und Rationalitäten", Berlin 1995, 318-348; als PDF in deutscher Übersetzung abrufbar bei vordenker.de

Fritz Heider: Ding und Medium, Berlin 2005 [1923]

Robert Heiß: Logik des Widerspruchs, Berlin Leipzig 1932

Rudolf Kaehr, Thomas Mahler: Proömik und Disseminatorik, vordenker.de (Sommer-Edition 2017) J. Paul (Ed.) PDF
ursprünglich in: R. Kaehr, A. Ziemke (Hg.): Selbstorganisation - Jahrbuch für Komplexität in den Natur-, Sozial- und Geisteswissenschaften, Bd. 6, Berlin 1995, S. 111-160

Julia Kristeva: Powers of Horror, An Essay on Abjection, New York 1982 [1980]

Daniel Kunze: Theory of the Metropolis
in: La Città Nuova, proceedings of ACSA International Conference, Rome (Washington DC: Association of Collegiate Schools of Architecture, 1999, 332-336; PDF

Felix Lau: Die Form der Paradoxie, Heidelberg 2012 [2005]

Bernie Lewin: Enthusiastic Mathematics, Melbourne 2018

Rudi Matzka: Klassische Kenogrammatik, Eine semiotische Ortsbestimmung, 2010; PDF auf rudolf-matzka.de

Paul Natorp: Platos Ideenlehre, Hamburg 1994 [1902]

Platon: Timaios, übersetzt von Friedrich Schleiermacher und Hieronymus Müller, Leipzig 1857; 12körbe.de

Walter Rella: Der Schritt in die Analogie
Teil I in Wiener Jahrbuch für Philosophie Band XVI/1984 S. 129-138
Teil II in Wiener Jahrbuch für Philosophie Band XVII/1985 S. 141-158

Urs Richli: Das Andere an ihm selbst
in: Max Gottschlich und Michael Wladika (Hg.): Dialektische Logik, Würzburg 2005, 62-71

Claus-Artur Scheier: Luhmanns Schatten – Zur Funktion der Philosophie in der medialen Moderne, Hamburg 2016

Tatjana Schönwälder-Kuntze, Katrin Wille, Thomas Hölscher: George Spencer Brown, Wiesbaden 2009 [2004]

Julius Stenzel: Zahl und Gestalt bei Platon und Aristoteles, Darmstadt 1959 [1924]

Walter Tydecks: Die Sphäre des Begriffs und die Logik der Sphäre, Bensheim 2014
unter: http://www.tydecks.info/online/logik_kraft_sphaere.html

Walter Tydecks: Antinomien des Daseins und der Unendlichkeit, Bensheim 2016
unter: http://www.tydecks.info/online/logik_kraft_dasein.html

Walter Tydecks: Hegels Idee eines »höheren Widerspruchs«, Bensheim 2012-19
unter: http://www.tydecks.info/online/logik_kraft_widerspruch.html

Walter Tydecks: Spencer-Brown Gesetze der Form – Einführung und weiterführende Ideen, Bensheim 2017-20
unter: http://www.tydecks.info/online/themen_spencer_brown_logik.html

Slavoj Žižek: Disparitäten, Darmstadt 2018 [2016]

 

© tydecks.info 2020