Dialektische Theorie des Satzes

– Interpretation und Weiterführung der Prädikationstheorie von Peter Ruben

 

Version 29.7.2015

Einleitung – Das Projekt »Hegel mit Frege« von Peter Ruben

Peter Ruben (* 1933) war zu DDR-Zeiten wissenschaftlicher Mitarbeiter und Oberassistent an der Humboldt-Universität und Arbeitsleiter am Zentralinstitut für Philosophie der Akademie der Wissenschaften der DDR. In dieser Zeit verfolgte er das von seinen Gegnern so genannte Projekt »Hegel mit Frege«, bis er seit 1981 nicht mehr lehren und öffentlich auftreten und nur noch eingeschränkt publizieren durfte. Seine Arbeiten sind heute nur noch in Fachzirkeln bekannt. Ich verdanke den Hinweis auf Bedeutung und Aktualität seines Werks Bernd Seestaedt und Werner Surek, die an Vorarbeiten des folgenden Beitrags beteiligt waren. Wichtig sind mir vor allem drei Themen:

(a) Rubens Prädikationstheorie kann helfen, auf einem neuartigen Weg eine Lösung für die Grundlagenkrise der Mathematik zu finden. Die Ergebnisse der auf Frege zurückgehenden mathematischen Logik werden zwar herangezogen und genutzt, aber sie werden im Kontext der Satzbildung und letztlich der allgemeinen Arbeit gesehen, aus der heraus die Satzbildung zu verstehen ist. Die verschiedenen symbolischen Zeichen und Abstraktionsebenen für Gegenstände, ihre Eigenschaften, Beziehungen, Operationen und Referenzmengen gelten nicht mehr als beliebig, gleichwertig und austauschbar, sondern bekommen durch ihre jeweilige Stellung im Satz ihren genauen Ort und ihre jeweils eigene Sphäre. Darüber können die in der Philosophie der Mathematik aufgetretenen Paradoxien, Unbestimmtheiten und Kategorien- und Satzfehler entwirrt und geordnet werden.

(b) Die Prädikationstheorie öffnet zugleich einen Weg, die Grundlagen der modernen Physik besser zu verstehen. Mit der Theorie des Satzes lassen sich die Logik der Messverfahren, der Beobachtungsprotokolle und der darauf aufbauenden neuen geometrischen Methoden der Physik einheitlich und durchgehend darstellen (Hilbert-Räume, Differentialgeometrie). Die Aufteilung des Satzes in Subjekt und Prädikat führt über ihre Deutung als Gegenstand und Eigenschaft zum mathematischen Ansatz der Faserbündel, mit denen heute physikalische Erkenntnisse beschrieben werden. Im Faserbündel entsprechen die Basis dem Subjekt der Satztheorie und die Fasern den Prädikaten.

(c) Schließlich liefert die Prädikationstheorie ein besseres Verständnis der Sprache und ihrer Wahrheit. Sie versteht die Namensbildung (Wertung) als das vermittelnde Element für den Schluss vom Einzelnen zum Allgemeinen. In der Namensbildung und der mit ihr gefundenen Anziehung und Verwandtschaft von Namen äußert sich die Produktivität des sprachbegabten Menschen. Für Hegel gilt sie als Medium des Geistigen, in der Tradition der Aufklärung und mit Marx als Werkzeug, das den Menschen vom Tier unterscheidet.

Ausgangspunkt ist die von Ruben formulierte dialektische Triade der Prädikation. Sie ist bewusst formal gehalten, um eine innere Verwandtschaft zwischen Hegel und Frege erkennen und aufzeigen zu können. Die Hegelsche Dialektik von Position, Negation und Negation der Negation wird übersetzt in die Grundbegriffe der Theorie des Satzes.

»Die Schritte dieser Triade sind:
(a) Position: S/P, Satzbildung;
(b) Negation: SP und PS mit !S/P, Terminusbildung;
(c) Negation der Negation: G = SP, und E = PS; Wertung.«
(P, S. 25, Indexierung dem üblichen Schreibgebrauch angepasst)

In dieser formalisierten Schreibweise sind zu lesen:
S/P als der elementare Satz ›S ist p‹,
SP als die Gesamtheit aller Subjekte S, für die das Prädikat P gilt,
PS als die Gesamtheit aller Prädikate P eines Subjekts S,
!S/P als das Urteil, dass der Satz ›S ist p‹ wahr ist,
G als Name für die Gesamtheit SP (G ist eine Abkürzung für ‘Gegenstand’),
E als Name für die Gesamtheit PS (E ist eine Abkürzung für ‘Eigenschaft’).

P wird groß geschrieben, wenn es um das Prädikat geht, und klein geschrieben, wenn es innerhalb des Satzes im Prädikativ steht. So wird z.B. gesagt ›die Rose ist rot‹ und nicht ›die Rose ist das Rote‹ oder ›(2 + 2 = 4) ist wahr‹ und nicht ›(2 + 2 = 4) ist die Wahrheit‹.

Zitate werden durch französische Anführungszeichen »Zitat« gekennzeichnet, Beispielsätze durch halbe Anführungszeichen ›Satz‹, Eigennamen mit Einfach-Anführungsstrichen ‘Eigenname’ und sinngleiche Namen mit Zweifach-Anführungsstrichen “Name”. Abweichend von Ruben werden für Gesamtheiten Großbuchstaben mit Doppelstrich (Mathematical Double Struck Capital) genutzt, um die formale Nähe zu Zahlklassen wie ℕ oder ℝ zu betonen. Daher wird für die Gesamtheit der Prädikate eines Subjekts ℙS statt PS geschrieben, und für die Gesamtheit der Subjekte, die in einem Prädikat P übereinstimmen, P statt SP. Ruben wählt für die Gesamtheit der Sätze bzw. der Subjekte kontextbezogen jeweils den Fraktur-Großbuchstaben und für die Gesamtheit der Prädikate , siehe P, S. 11, 23.) Hier steht dagegen für die Gesamtheit der Subjekte, ℙ für die Gesamtheit der Prädikate und für die Gesamtheit der Sätze (Aussagen).

Satzbildung, Sinnproduktion (Begriff des Satzes, der elementare Satz)

(1)    S ist p

Dieser scheinbar einfache und elementare Satz steckt voller Tücken und ist im Laufe der Philosophiegeschichte sehr kontrovers interpretiert worden. Ruben hat die wichtigsten Etappen dargestellt. Zum Verständnis seiner eigenen Prädikationstheorie möchte ich folgende Punkte hervorheben und weiter ausführen:

(a) Grammatik und analytische Philosophie. Der Satz ›S ist p‹ zeigt einen Perspektivwechsel, was mit einem Prädikat gemeint ist. Die Grammatik geht nicht von Sätzen wie ›S ist p‹ aus, sondern von Sätzen wie ›S macht etwas‹, den S-P-O-Sätzen: Sie unterscheidet Subjekt (S), Prädikat (P) und Objekt (O), wobei hier das Prädikat noch nicht für ein Merkmal, sondern für die  Tätigkeit  steht. In einem Satz wie ›der Gärtner pflanzt einen Baum‹ ist der ‘Gärtner’ das Subjekt, das etwas tut. Das, was er tut, ist das Prädikat (das Verb), in diesem Beispiel ‘pflanzt’ der Gärtner einen Baum. Und das, woran er etwas macht, ist das Objekt (in diesem Beispiel ‘der Baum’). Als Prädikat wird von der Grammatik das Verb verstanden, das Tätigkeitswort.

Auf den ersten Blick betrachtet die analytische Philosophie einfach den Sonderfall, wenn als Prädikat das Verb ‘ist’ eingesetzt wird, ›S ist p‹, z.B. ›Julia ist eine Studentin‹. Hier steht wieder an der ersten Stelle das Subjekt, doch gilt als Prädikat nicht mehr dasjenige, was dies Subjekt tut, sondern die Eigenschaft, die ihm mit diesem Satz zugeschrieben oder an ihm erkannt wird. In diesem Beispiel ist ‘Julia’ das Subjekt und ‘Studentin’ das Prädikat. Es ist nicht mehr das Subjekt, das handelt (in diesem Beispiel ‘Julia’), sondern derjenige, der erkennt, dass Julia eine Studentin ist. Es muss einen Vorgang gegeben haben, wodurch sie eine Studentin geworden ist. Ein solcher Satz könnte lauten ›Julia immatrikuliert sich an der Hochschule‹, wenn sie sich erfolgreich an der Hochschule einschreibt und dadurch zu einer Studentin wird.

Anders als die Grammatik bezeichnet die analytische Philosophie nicht das Verb eines Satzes (in diesem Beispiel ‘ist’) als Prädikat, sondern das Merkmal (‘Studentin’). Das Verb ‘ist’ wird stattdessen als Kopula bezeichnet, mit der Subjekt und Prädikat verbunden werden. Mit dieser Umdeutung verschiebt sich das Sprachverständnis grundlegend. Die Handlung liegt jetzt nicht mehr bei dem Subjekt, das etwas tut (Prädikat in der grammatischen Bedeutung, z.B. der Gärtner, der einen Baum pflanzt, oder Julia, die sich immatrikuliert), sondern beim Analytiker, der am Subjekt ein Merkmal feststellt (das Prädikat in der analytischen Bedeutung). Ausgangsfrage und Anfang der Philosophie ist nicht mehr die Bewegung (das Tun oder die Handlung, das Verb), sondern die Erkenntnis etwas Seienden (wie und was etwas ‘ist’).

Hegel nahm eine Sonderstellung ein. Zwar beginnt auch er seine Wissenschaft der Logik mit dem ‘Sein’, aber die Worte erhalten bei ihm eine spezifische Doppelbedeutung. Es kann sowohl gesagt werden, dass etwas der ‘Anfang’  ist, wie auch mit ‘Anfang’ die Bewegung des  Anfangens gemeint sein kann. Ähnlich bedeuten ‘Bestimmung’, ‘Unterscheidung’, ‘Entgegensetzung’ und ‘Messung’ sowohl den Vorgang des Bestimmens, Unterscheidens, Entgegensetzens und Messens wie auch ihr jeweiliges Resultat. Eine ‘Messung’ ist sowohl der Vorgang des Messens wie die Messung (das Mess-Ergebnis), die am Ende abgelesen wird. In diesem Sinn bedeutet der Satz ›S ist p‹ sowohl den Zustand, das Sein, dass S die Eigenschaft P hat, als auch die Bewegung, die dazu geführt hat, dass S diese Eigenschaft erhalten hat und fortdauernd behält. Das wird vielleicht deutlicher, wenn dieser Satz als Zuweisung verstanden wird, mit der sowohl einem Subjekt S die Eigenschaft P zugewiesen als auch das Ergebnis dieser Zuweisung protokolliert und festgehalten wird. Mit Aristoteles kann gesagt werden, es gehört zur Natur von S, die Eigenschaft P zu haben. (Siehe hierzu Ruben 1975, S. 79-84 und P, S. 2f sowie Guzzoni, S. 36.)

In seiner Urteilslehre neigt Hegel allerdings zu einem traditionellen Verständnis, das der analytischen Philosophie nahekommt. Statt auf den Bedeutungswandel des Prädikats von einer Tätigkeit zu einem Merkmal einzugehen, hebt er am Urteil dessen Zeitlosigkeit hervor, die er als Allgemeinheit versteht. Ein Satz, in dem das Prädikat als Tätigkeit verstanden wird, bezieht sich ausdrücklich auf den Zeitverlauf oder den Zeitpunkt, an dem das Ereignis eintritt, von dem gesprochen wird. Ein Urteil zeichnet sich für Hegel dagegen dadurch aus, dass es eine Allgemeinheit trifft, die nicht an die Zeit gebunden ist.

"Die Urteile sind von den Sätzen unterschieden; die letzteren enthalten eine Bestimmung von den Subjekten, die nicht im Verhältnis der Allgemeinheit zu ihnen steht, – einen Zustand, eine einzelne Handlung und dergleichen; ›Cäsar ist zu Rom in dem und dem Jahre geboren, hat 10 Jahre in Gallien Krieg geführt, ist über den Rubikon gegangen‹ usf. sind Sätze, keine Urteile. Es ist ferner etwas ganz Leeres, zu sagen, daß dergleichen Sätze, z.B. ›ich habe heute nacht gut geschlafen‹ oder auch ›Präsentiert das Gewehr!‹, in die Form eines Urteils gebracht werden können. Nur dann würde ein Satz [wie] ›es fährt ein Wagen vorüber‹ ein und zwar subjektives Urteil sein, wenn es zweifelhaft sein könnte, ob das vorüber sich Bewegende ein Wagen sei oder ob der Gegenstand sich bewege und nicht vielmehr der Standpunkt, von dem wir ihn beobachten; wo das Interesse also darauf geht, für [eine] noch nicht gehörig bestimmte Vorstellung die Bestimmung zu finden." (Enz. § 167, HW 8.319)

(b) Sinneinheit, Satzeinheit. Mit dem Bedeutungswandel des Prädikats von der Grammatik zur analytischen Philosophie geht das ursprüngliche Verständnis der  Sinneinheit  eines Satzes verloren. Solange entsprechend der Grammatik der Schwerpunkt auf dem Tun lag, das mit einem Satz beschrieben wird, war die Sinneinheit durch die Einheit und den Zusammenhang des Tuns gegeben, durch das eine Änderung begonnen, durchgeführt und abgeschlossen wird. Wenn gesagt wird ›der Gärtner pflanzt einen Baum‹, ist die Tätigkeit des Pflanzens die mit diesem Satz angesprochene Sinneinheit. Eine solche Sinneinheit kann auch noch in Sätzen wie ›Julia ist eine Studentin‹ erkannt werden, wenn diese Sätze als Zuweisung verstanden werden. Die Zuweisung kann sowohl in einer Gründung wie in einer Erkenntnis bestehen. In diesem Beispiel ist der Vorgang der Immatrikulation ein Gründungsakt (ein Tun), durch den Julia eine Studentin wird. Im Ergebnis wird nach der Einschreibung gesagt: ›Julia ist eine Studentin‹. Oder es erkennt später jemand, dass Julia eine Studentin ist, weil ihr Studentenausweis gültig ist und sie aktiv am Studium teilnimmt.

Was mit Sinneinheit gemeint ist, wird sich deutlicher zeigen, wenn die Einheit des Satzes aufgebrochen und der Satz in Subjekt und Prädikat geteilt wird (Ur-Teilung des Satzes) und schließlich in einer Negation der Teilung die Einheit mit der Namensbildung wieder hergestellt werden muß.

(c) Sinngleiche Sätze. Ausgehend von der Sinneinheit des Satzes kann eingesehen werden, was mit sinngleichen Sätzen gemeint ist. Sinngleiche Sätze stimmen in ihrer jeweiligen Sinneinheit miteinander überein. Ruben übernimmt von Frege die Unterscheidung in Sinn und Bedeutung von Eigennamen und überträgt sie auf Sätze. Freges Standardbeispiel für Eigennamen sind “Morgenstern” und “Abendstern”. Sie haben jeweils einen eigenen Sinn (der Morgenstern wird als letzter sichtbarer Stern am Morgenhimmel gesehen, der Abendstern als erster aufgehender Stern am Abendhimmel), aber die gleiche Bedeutung: Es handelt sich in beiden Fällen um den gleichen Planeten, der als ‘Venus’ bezeichnet wird. (Anmerkung 1: Es wären auch weitere Eigennamen möglich. Jemand mag die Venus als “Unglücksstern” bezeichnen, wenn er bei ihrem Auftreten häufig persönliches Unglück erlebt hat, ein anderer als “Liebesstern”, wenn er die Venus mit ihrer Verbindung von Tag und Nacht als Zeichen der Liebe sieht. So kann jeder der Venus einen eigenen Sinn verleihen, aber immer hat sie für Frege die gleiche Bedeutung: Der Planet mit dem Namen ‘Venus’). (Anmerkung 2: Warum mit ‘Venus’ aus der Vielzahl der Eigennamen ein bestimmter Eigenname als Bezeichnung der Bedeutung hervorgehoben wird, um die Bedeutung vom Sinn zu unterscheiden, ist eine vorgreifende Frage, die im Abschnitt über die Namensbildung weitergeführt wird. Mit diesem besonderen Eigennamen wird die Einheit wieder hergestellt, die in der Vielzahl der verschiedenen Eigennamen verloren zu gehen drohte.)

Das kann in ähnlicher Weise auf Sätze übertragen werden. Verschiedene Menschen können das gleiche meinen, aber mit jeweils eigenen Worten in unterschiedlichen Sätzen ausdrücken. Wer merkt, dass er oder jemand anders nicht verstanden wird, kann versuchen, das gleiche mit anderen Worten zu sagen. Daher will Ruben unter den Sätzen in ähnlicher Weise sinngleiche Sätze zusammenfassen wie Frege bedeutungsgleiche Eigennamen zusammengefasst hat.

»Wer Sätze bildet, vollzieht Sinnproduktion. Wer verschiedene Sätze hat, kann demzufolge den Sinnvergleich ausführen. Das Verstehen eines Satzes ist nichts anderes als die Feststellung seines Sinns. Man gibt den Sinn eines Satzes wieder, indem man ihn durch einen sinngleichen Satz ersetzt.« (P, S. 17)

(d) Die Gesamtheit der Sätze. Die Betrachtung sinngleicher Sätze legt nahe, alle einzelnen Sätze ›S ist p‹ als Elemente einer Gesamtheit von Sätzen anzusehen, die mit dem Symbol bezeichnet sei. (Hier wird der Buchstabe A für ‘Aussage’ verwendet und nicht S für ‘Satz’, um ihn unterscheiden zu können von den Gesamtheiten aller Subjekte und aller Prädikate ℙ.)

(2)    ›S ist p‹ ∈

lies: der Satz ›S ist p‹ ist Element der Gesamtheit aller Sätze

Die Zusammenfassung sinngleicher Sätze kann als Äquivalenzrelation innerhalb der Gesamtheit aller Sätze verstanden werden. Alle sinngleichen Sätze sind in jeweils einer Äquivalenzklasse zusammengefasst, die zur Gesamtheit aller Sätze gehört. Die Sätze innerhalb der Äquivalenzklasse sinngleicher Sätze unterscheiden sich nur in ihrer Formulierung und können eindeutig ineinander übersetzt werden.

Mit Formeln dieser Art nähert sich die Prädikationstheorie bewusst den Symbolen und der Formalisierung der Mathematik. Ruben folgt in dieser Vorgehensweise Frege. Frege wollte die Methoden der Arithmetik auf eine »Formelsprache des reinen Denkens« erweitern (so der Untertitel seiner Begriffsschrift), und es wird zu bestimmen sein, wie weit Ruben hier mit Frege mitgeht und an welchem Punkt sich ihre Wege trennen. Frege betrachtet eine Gesamtheit aller »Inhalte« oder genauer aller »beurteilbaren Inhalte« (Frege, Begriffsschrift, § 2, S. 2). Was Frege mit beurteilbaren Inhalten (oder oft auch einfacher mit den Inhalten) von Sätzen meint, entspricht den Äquivalenzklassen sinngleicher Sätze bei Ruben. Eine Äquivalenzklasse sinngleicher Sätze umfasst alle Sätze, die den gleichen Inhalt haben. Diesen Inhalt bezeichnet Frege als beurteilbaren Inhalt. (Auch hier gilt wie bei der Unterscheidung von Sinn und Bedeutung von Eigennamen, dass aus der Vielfalt von Sätzen, die den gleichen Inhalt meinen und sich in einer gemeinsamen Äquivalenzklasse befinden, ein bestimmter Satz aus dieser Äquivalenzklasse ausgewählt wird, der sowohl Element wie Name der Äquivalenzklasse ist. Der beurteilbare Inhalt ist sowohl ein bestimmter Satz in der jeweiligen Äquivalenzklasse aller sinngleichen Sätze wie auch übergreifend der Name dieser Äquivalenzklasse. Wie eine solche Namensbildung möglich ist, wird später näher ausgeführt.)

Eine solche Aufteilung in Äquivalenzklassen beurteilbarer Inhalte ist notwendig, wenn Frege im Weiteren logische Operationen erkennen will, die sich auf die formale Struktur von Sätzen beziehen unabhängig davon, wie die Sätze jeweils formuliert sind. Frege will mit ihnen die »Täuschungen« vermeiden, die im gewöhnlichen Sprachgebrauch oder bei sophistischen Spitzfindigkeiten auftreten können (Frege, Begriffsschrift, S. VIf). Ein Sophist gibt vor, für etwas nur eine andere Formulierung zu gebrauchen, und verändert dabei unter der Hand den Inhalt der Aussage. Frege unterscheidet daher konsequent zwischen Übersetzungen, mit denen der gleiche Inhalt mal so und mal anders ausgedrückt wird, und Operationen von Inhalten, mit denen sachliche Zusammenhänge zwischen den Inhalten beschrieben werden, unabhängig von der jeweiligen Formulierung. Wenn zum Beispiel zwischen den beiden Aussagen ›der Mond schiebt sich vor die Sonne‹ und ›die Sonnenscheibe ist nicht vollständig zu sehen‹ ein kausaler Zusammenhang besteht – ›weil der Mond sich vor die Sonne schiebt, ist sie nur noch teilweise zu sehen‹ –, soll die Kausalität ausschließlich in den Inhalten der beiden Sätze und nicht in der Art ihrer Formulierung begründet sein. Die Kausalität gilt genauso, wenn gesagt wird ›weil der Mond die direkte Verbindungslinie des menschlichen Auges und der Sonne kreuzt, sieht die Sonne wie angeknabbert aus‹.

Allerdings hat Frege später diese Bildung von Äquivalenzklassen von Sätzen gleichen Sinns oder gleichen Inhalts aufgegeben. Er unterscheidet in seinem Vortrag Funktion und Begriff von 1891 nur noch Sinn und Bedeutung eines Satzes und spricht nicht mehr von beurteilbaren Inhalten, die vom Sinn unterschieden werden. Er nimmt jedoch in diesem Vortrag auf seine frühere Schrift nicht Bezug, aber er scheint zu diesem Zeitpunkt jeden Satz mit einem eigenen Sinn verbunden zu sehen und fragt nur noch, ob ein Satz »Bedeutung« hat oder nicht, d.h. ob er wahr ist oder nicht. Diese scheinbar abwegige Position kann so verstanden werden, dass jetzt für ihn jede Formulierung, die von einer anderen Formulierung abweicht, dennoch ihren eigenen Sinn hat, selbst wenn sie sich auf den gleichen Inhalt bezieht. Auch wenn es um den gleichen Inhalt geht, betont jede Formulierung einen bestimmten Aspekt oder eine bestimmte Sicht, die sich von anderen Aspekten und Sichten unterscheidet. Daher kann und muss für jeden Satz gefragt werden, ob er wahr oder falsch ist (was Frege jetzt als ihre Bedeutung bezeichnet). – Es besteht die Gefahr eines Missverständnisses, da Frege den Begriff »Bedeutung« sowohl bei Eigennamen wie bei Sätzen gebraucht. Bei Eigennamen steht die Bedeutung dem Sinn gegenüber, bei Sätzen meint Frege mit Bedeutung die Wahrheitsfunktion, ob ein Satz wahr ist oder nicht. Er gebraucht hier den Ausdruck »Bedeutung« gemäß dem üblichen Sprachverständnis: Ein Satz hat nur dann Bedeutung, wenn er wahr ist. Andernfalls ist er wertlos.

(e) Sinn und Gebrauchswert. Mit dem Hinweis auf die Sinnproduktion legt Ruben nahe, an die Gebrauchswertproduktion zu denken. Er wird im Weiteren der Sinnproduktion die Wertung gegenüberstellen, die dem Tauschwertcharakter der Ware entspricht. Der Satz ›S ist p‹ hat daher für ihn nicht nur wie für Hegel die beiden genannten Bedeutungen von Sein und Bewegung (›S ist p‹ beschreibt die Bewegung, durch die S das Merkmal P  bekommt, wie auch das Resultat, dass S die Eigenschaft P  hat), sondern der Satz geht aus einer Bewegung (einer Praxis) hervor und bezieht sich auf sie. Jeder Satz ist nur zu verstehen aus dem Kontext, in dem er formuliert wurde, aus den Fragen, auf die er eine Antwort geben soll und den Lösungen, zu denen er beiträgt. Ruben führt damit den Gedanken von Frege weiter: Hatte Frege gesagt, dass ein Satz nur Bedeutung hat, wenn er wahr ist, so sagt Ruben, dass ein Satz nur Bedeutung hat, wenn es einen Handlungskontext gibt, innerhalb dessen er nicht nur wahr ist, sondern dazu beiträgt, die jeweilige Aufgabe zu lösen. Ein Satz hat nur Bedeutung, wenn er in einem ganz elementaren Sinn »gebraucht« wird, um eine Lösung zu finden und sich untereinander zu verständigen. Ruben kommt damit in die Nähe von Wittgenstein und dessen pragmatischem Sprachverständnis. Jeder Satz ist nur zu verstehen innerhalb eines »Sprachspiels«. Der Gebrauchswert eines Satzes kann daran gemessen werden, ob er seinen Sinn (seine Aufgabe) erfüllt, oder anders gesagt: ob und wie er gebraucht wird. Oder nochmals anders formuliert, im Sinne von Ockhams Rasiermesser: Sätze, die nicht gebraucht werden, sollten nicht gebraucht werden. Alles, was überflüssig ist zu sagen, braucht nicht gesagt zu werden.

Terminusbildung (Ur-Teilung des Satzes in zwei reduzierte Sätze)

Heutzutage ist es schwierig, die Terminusbildung als eine Ur-Teilung des Satzes zu verstehen, da wir uns völlig daran gewöhnt haben, Sätze als äußere Verknüpfung von Subjekt und Prädikat zu sehen und nicht als Sinneinheit, die der Terminusbildung vorausgeht. Nur in der Pädagogik taucht bisweilen die Frage auf, ob im ersten Schuljahr mit ganzen Sätzen oder mit einzelnen Worten zu beginnen ist. Fällt es Schülern leichter, zuerst ganze Sätze wie ›die Rose ist rot‹ zu verstehen, oder beginnen sie mit Worten wie ‘Rose’ und ‘rot’, um sie dann zu verknüpfen? Weiß ein Kind zuerst, was eine Rose ist und was die Farbe Rot bedeutet und entdeckt dann, dass die vorliegende Rose rot ist, oder hat es zuerst den ganzheitlichen Sinneseindruck einer roten Rose und erkennt dann, dass in dieser Wahrnehmung die Farbe Rot ein Merkmal der Pflanze Rose ist? Gelangt es zur Einsicht, dass zwar die Rose ihre Farbe ändern kann (zum Beispiel beim Aufblühen oder Verwelken), aber sich eine Eigenschaft wie die Farbe Rot für sich nie ändert (es bleibt immer gleich, was mit ‘rot’ gemeint ist, unabhängig davon, ob es eine Rose oder das Haltesignal der Ampel oder sonst etwas ist).

In diesem Kapitel soll gezeigt werden, wie die analytische und die dialektische Philosophie die Terminusbildung verstehen: Beide gehen davon aus, den Satz ›S ist p‹ in Subjekt und Prädikat aufzubrechen. Während die dialektische Philosophie Subjekt und Prädikat als Momente des Satzes versteht, die nur in der Satzeinheit zu verstehen sind und erst in einer nachträglichen, äußerlichen Reflexion voneinander getrennt und abstrakt aufeinander bezogen werden, die wiederum durch eine eine nachfolgende Negation der Ur-Teilung zu negieren ist, um die Einheit neu herzustellen, sieht die analytische Philosophie Subjekt und Prädikat als gleichwertige und austauschbare Termini, die durch Sätze frei miteinander verknüpft werden können. Es soll gezeigt werden, dass die analytische Philosophie dadurch in zwei Kategorienfehler gerät, die sich innerhalb der analytischen Philosophie als unlösbare Paradoxien zeigen:

• Die analytische Philosophie lässt Sätze zu, die als Subjekt oder als Prädikat ein Null-Element enthalten.
• Die analytische Philosophie hält erste und zweite Substanz (Träger und Merkmale) für austauschbar.

– Sätze als Relation von Subjekt und Prädikat

Ruben kann sich bei seiner Darstellung der Ur-Teilung, dem zweiten Schritt seiner dialektischen Triade, zunächst wiederum auf Frege berufen. Es ist ihm wichtig, den von Frege eingeschlagenen Weg der Formalisierung durchzuhalten und auf diesem Weg möglichst genau den Punkt zu treffen, an dem sich analytisches und dialektisches Denken voneinander trennen.

Frege übertrug in seinem Vortrag Funktion und Begriff den Funktionsbegriff von der Mathematik auf Behauptungssätze. So wie die Mathematik mit Funktionen nach dem Typ ›y = f(x)‹ jedem Wert x einen Wert y zuordnet, – zum Beispiel wird mit der Funktion ›f(x) = x2‹ jedem x das Quadrat x2 zugeordnet –, so verallgemeinerte Frege zum Beispiel den Satz ›Berlin ist die Hauptstadt des deutschen Reiches‹ in eine Funktion, die jedem Land x dessen Hauptstadt zuordnet, und bildet Ausdrücke wie ›die Hauptstadt des x‹ (Frege, Funktion und Begriff, S. 18).

Um Prädikationen formal beschreiben zu können, ist der Funktions-Begriff zur Relation zu erweitern. Eine Relation (x,y) beschreibt alle Elemente x und y, die durch eine bestimmte Beziehung (Relation) miteinander verbunden sind. Funktionen stellen einen Sonderfall von Relationen dar, bei denen jedem x genau ein einziges y zugeordnet wird (1:1-Beziehungen). In diesem Sinn ist das von Frege betrachtete Beispiel (Land, Hauptstadt) eine Funktion, da jedes Land nur eine Hauptstadt hat und jede Hauptstadt nur die Hauptstadt eines einzigen Landes sein kann. Dagegen ist (Land, Stadt) eine nicht-eindeutige (1:n)-Relation, da es in einem Land mehrere Städte geben kann und jede Stadt in genau einem Land liegt.

Der Relationsbegriff ist vermutlich aus der Beschreibung von Verwandtschaftsverhältnissen hervorgegangen. So ist (x, Mutter von x) eine (n:1)-Relation, da eine Mutter zwar mehrere Kinder, aber jedes Kind nur eine Mutter haben kann, während (x, Onkel von x) eine (m:n)-Relation ist, da jemand mehrere Onkel und ein Onkel mehrere Neffen haben kann. Das lässt sich beliebig erweitern auf Relationen wie (x, Verwandter n-ten Grades von x), mit denen Blutsverwandtschaften und daraus resultierende Pflichten, Rechte und Tabus beschrieben werden.

Ruben greift die Schreibweise der Relation auf, um die Mehrdeutigkeit der Prädikation formalisieren zu können und versteht die Prädikation als eine Relation (Subjekt, Prädikat), wobei sowohl einem Subjekt ein oder auch mehrere Prädikate zugeordnet werden können, wie auch ein Prädikat mehrere Träger haben kann. Daraus ergibt sich die Formalisierung. Wenn mit die Menge der Subjekte und mit ℙ die Menge der Prädikate symbolisiert wird, kann jede Aussage (S,P) als eine Relation zwischen der Gesamtheit der Subjekte und der Gesamtheit der Prädikate verstanden werden:

(3)    (S,P) ∈ ℙ

lies: Eine Verbindung (Relation) eines Subjekts mit einem Prädikat ist Element aus dem Kreuzprodukt der beiden voneinander unabhängigen Achsen der Gesamtheit aller Subjekte und der Gesamtheit aller Prädikate.

Mathematisch erzeugen die beiden voneinander unabhängigen Gesamtheiten aller Subjekte und aller Prädikate eine zweidimensionale Fläche, die als die Gesamtheit aller Aussagen bezeichnet werden kann.

(4)    = ℙ

lies: die Gesamtheit aller Sätze ›S ist p‹ ist eine Fläche, die von den beiden voneinander unabhängigen Achsen der Gesamtheiten der Subjekte und der Prädikate aufgespannt wird.

Wird jede Aussage ›S ist p‹ als ein Element der Gesamtheit verstanden, dann kann sie gemäß (3) als eine Relation (S,P) dargestellt werden, die Element aus dem Kreuzprodukt ℙ ist. Jeder Satz kann als ein Punkt (S,P) auf der Fläche aller Sätze veranschaulicht werden:

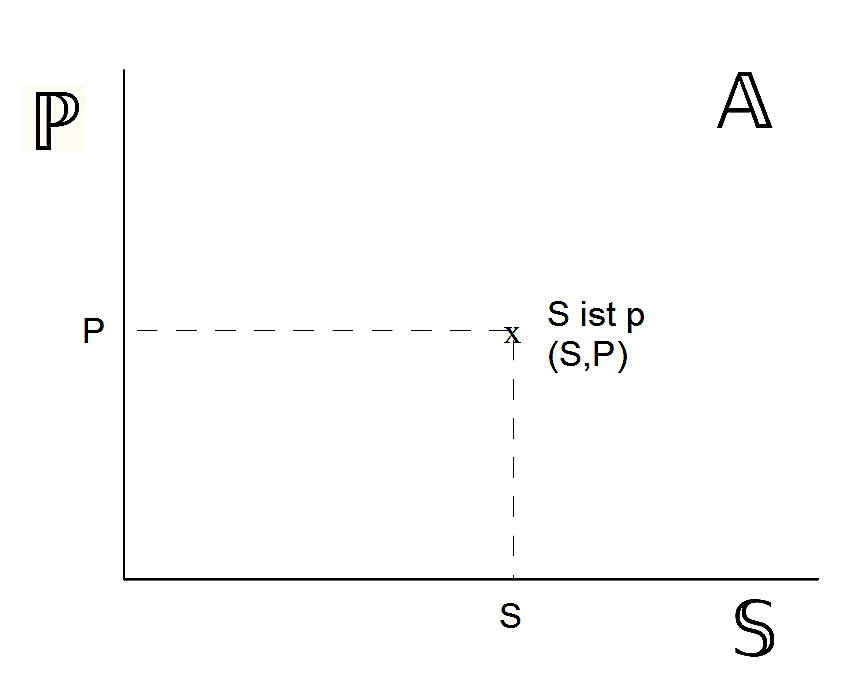
Figur 1: Satzbildung (Gesamtheit der Sätze )
Jeder Satz ist die kleinste Einheit (ein Punkt) in der Gesamtheit aller Sätze . Er wird jeweils durch zwei Koordinaten beschrieben (Subjekt, Prädikat), die auf der -Achse bzw. der ℙ-Achse liegen.

Diese Aufteilung kann mit Hölderlin und Hegel als Ur-Teilung verstanden werden: Die Sätze werden geteilt und auseinander gebrochen in Subjekt und Prädikat. Subjekte und Prädikate werden voneinander unabhängig betrachtet und in Sätzen äußerlich miteinander verknüpft. Wird die Satzbildung (Sinnproduktion) als der Begriff des Satzes angesehen, der die innere Einheit jedes einzelnen Satzes betont, dann wird mit der Terminusbildung ein Ur-Teil  über  den Satz gefällt. Beachte die Selbstreferentialität: Hier wird ein Satz über den Satz formuliert. Das entspricht der äußeren Reflexion, wenn mit einer Reflexion über die Reflexion reflektiert wird.

»Urteil   ist im höchsten und strengsten Sinne die ursprüngliche Trennung des in der intellektualen Anschauung innigst vereinigten Objekts und Subjekts, diejenige Trennung, wodurch erst Objekt und Subjekt möglich wird, die Ur=Teilung. Im Begriffe der Teilung liegt schon der Begriff der gegenseitigen Beziehung des Objekts und Subjekts aufeinander, und die notwendige Voraussetzung eines Ganzen, wovon Objekt und Subjekt die Teile sind.« (Hölderlin, S. 50)

Der Satz zerfällt in seine beiden Bestandteile. Formell kann jedes Subjekt mit jedem Prädikat verbunden werden, und es ist jeweils zu prüfen, welchen Sinn und welchen Wahrheitsgehalt (Bedeutung, Wert) diese Verbindung hat.

Anmerkung: Erst durch Dietrich Henrich wurde auf die weitreichende Bedeutung dieses kurzen Textes von Hölderlin aufmerksam gemacht. Hölderlin (1770-1843) hörte ab November 1794 in Jena Fichtes Vorlesung über die Wissenschaftslehre, traf ihn häufig und schrieb vermutlich im Frühjahr 1795 diese Notiz auf. Hegel und Schelling beschäftigten sich erst einige Jahre später intensiv mit Fichte. Vor allem Hegel war anfangs sicher durch Hölderlin beeinflusst, als beide 1797-1801 in Frankfurt waren, bevor Hegel nach Jena ging und dort 1801 Differenz des Fichteschen und Schellingschen Systems der Philosophie veröffentlichte.

– Reduzierte Sätze mit Null-Elementen

An Figur 1 kann gezeigt werden, wie und wo sich der dialektische und der analytische Weg trennen. Die dialektische Satztheorie hält die Satzeinheit ›S ist p‹ fest und unterscheidet prinzipiell zwischen solchen Sätzen, die innerhalb der von den beiden Achsen aufgespannten Fläche liegen und denjenigen Sätzen, die sich am Rand der Fläche auf einer der beiden Achsen befinden. Sätze auf der ℙ-Achse können formal als (0,P) geschrieben werden und enthalten als Subjekt das Null-Element. Es gibt kein Subjekt, dass diese Prädikate hat. Und umgekehrt können Sätze auf der -Achse formal als (S,0) geschrieben werden und enthalten als Prädikat das Null-Element. Das sind Subjekte, denen kein Prädikat zugewiesen werden kann.

Die analytische Philosophie sieht die Null-Elemente als gleichberechtigte Elemente an und unterscheidet formal nicht zwischen Sätzen innerhalb der Fläche und auf dem Rand. Dadurch handelt sie sich die Paradoxien ein, die mit dem Null-Element verbunden sind. Die dialektische Philosophie wird dagegen die Situation, in der Null-Elemente auftreten, als Widerspruch beschreiben, was jedoch aus Sicht der analytischen Philosophie zum »Zusammenbruch der Wissenschaft« führt und daher abgelehnt wird (Popper, S. 12).

Um das zu verstehen, ist Figur 1 weiter zu analysieren. In den Gesamtheiten und ℙ können Teilmengen gebildet werden, die jeweils alle Prädikate zusammenfassen, die Eigenschaften eines bestimmten Subjekts sind, bzw. alle Subjekte, die Träger einer bestimmten Eigenschaft sind. Ruben setzt implizit die Formeln (3) und (4) voraus, wenn er in dieser Weise die Terminusbildung formalisiert (P, S. 22f):

(5a)    ℙS = {P | (S,P)}

lies: ℙS ist die Menge aller P, die bezogen auf ein festes S in der Relation (S,P) stehen

ℙS ist die Menge aller Eigenschaften von S
Diese Menge ist gleichbedeutend mit der Funktion ›S ist (y)‹ bei Frege
Beispiel: ›die Rose ist (y)‹ ist die Funktion, die mit allen Eigenschaften der Rose »gesättigt« werden kann.
Inhaltslogik: S wird beschrieben durch die Gesamtheit seiner Eigenschaften (Intension von S)
ℙS gilt formal als die Realität von S

(5b)    P = {S | (S,P)}

lies: P ist die Menge aller S, die bezogen auf ein festes P in der Relation (S,P) stehen

P ist die Menge aller Gegenstände S mit der gemeinsamen Eigenschaft P
Diese Menge ist gleichbedeutend mit der Funktion ›(x) ist p‹ bei Frege
Beispiel: ›(x) hat eine Hauptstadt‹. Hier können für x alle Länder eingesetzt werden, die eine Hauptstadt haben.
Umfangslogik: P wird beschrieben durch den Umfang der Gegenstände, die diese Eigenschaft haben (Extension von P)
P gilt formal als das Substrat von P.

Ruben bezeichnet die Formeln (5a) und (5b) »als reduzierte Sätze« (P, S. 20), die durch das Auseinanderbrechen des Satzes ›S ist p‹ entstehen. Werden die von Frege genannten Beispiele ›die Rose ist (y)‹ bzw. ›(x) hat eine Hauptstadt‹ betrachtet, dann ist ein reduzierter Satz dadurch charakterisiert, dass entweder das Prädikat unbestimmt bleibt (wie in ›die Rose ist (y)‹) oder das Subjekt unbestimmt bleibt (wie in ›(x) hat eine Hauptstadt‹). Gegenüber einem vollständigen Satz ›S ist p‹ enthält der reduzierte Satz eine Unbestimmtheit.

Warum wird hier von »reduziert« gesprochen? Ein gewöhnlicher Satz wie ›die Rose ist rot‹ enthält eine Aussage, die das Ergebnis einer Beobachtung oder eines darauf bezogenen Gedankens ist. Dagegen kann ein reduzierter Satz eine offene Aufgabe enthalten, für die es keine Lösung gibt. Zum Beispiel gibt es für den reduzierten Satz ›(x) ist die größte natürliche Zahl‹ keine Lösung, denn es gibt keine größte Zahl. Es gibt für dieses Beispiel eines reduzierten Satzes nichts, was für x eingesetzt werden kann, x kann nicht gesättigt werden. Im Sinne von Frege ist ‘die größte natürliche Zahl’ ein Eigenname, der zwar einen Sinn, aber keine Bedeutung hat, da es nichts gibt, dem dieser Eigenname verliehen werden kann oder auf das er verweist. Gemäß Formel (5b) kann dies Beispiel geschrieben werden:

(5b.1)    P = {S | (S,größte natürliche Zahl)}

lies: P ist die Menge aller Subjekte S mit der Eigenschaft, dass S die größte natürliche Zahl ist

Offensichtlich gibt es keine derartige Zahl, und die Menge P ist leer. Mit reduzierten Sätzen lassen sich Sätze bilden, die als Subjekt oder als Prädikat die Leermenge enthalten.

Wenn diese Möglichkeit uneingeschränkt zugelassen wird, entstehen in der Konsequenz die aus der Mengenlehre bekannten Paradoxien. Sie können nicht durch Verbote gelöst werden, sondern es ist wie von Ruben vorgeschlagen die Wurzel zu erkennen, an welcher Stelle solche Paradoxien entstehen können und das Besondere dieser Situation zu untersuchen. Es ist zu verstehen, warum und wie reduzierte Sätze gebildet werden können, und im Weiteren kann dann die analytische Philosophie kritisiert werden, wenn sie das Besondere der reduzierten Sätze ignoriert und gewöhnliche und reduzierte Sätze einander gleichstellt. Darauf wird weiter unten näher eingegangen, wobei sich zeigen wird, dass Freges Hinweis auf die Eigennamen den Lösungsweg zeigt, auch wenn dieser dann von der analytischen Philosophie nicht mehr eingehalten wurde. (In gewissem Sinn wird Frege aus Sicht der dialektischen Philosophie gegenüber Russell rehabilitiert.) Es geht nicht darum, Sätze zu verbieten, die als Subjekt oder als Prädikat die Leermenge enthalten, sondern es ist zu verstehen, dass solche Sätze nur als reduzierte Sätze auftreten und zu erkennen, dass es ein Kategorienfehler ist, gewöhnliche und reduzierte Sätze einander gleichzusetzen. Als Aufgabe ist die Frage festzuhalten, ob überhaupt Sätze über die Leermenge gebildet werden können. Als Lösung wird sich erweisen, dass dies Sätze über den dialektischen Widerspruch sind.

Als Zwischenergebnis bleibt festzuhalten: Reduzierte Sätze können nur entstehen, wenn zuvor die Satzeinheit ›S ist p‹ aufgeteilt ist und dadurch formal Sätze möglich werden, die aus keiner Beobachtung und keiner darauf aufbauenden Schlussfolgerung, sondern aus einer formalen Verknüpfung der voneinander isolierten Subjekt- und Prädikat-Achse entstanden sind. Dieser Gedanke wird bisweilen dadurch erschwert, dass sehr knifflige Beispiele für Prädikate herangezogen werden, für die es kein Subjekt gibt, so zum Beispiel die Russell-Antinomie: »Man kann einen Barbier als einen definieren, der all jene und nur jene rasiert, die sich nicht selbst rasieren« Wikipedia. Es ist nicht unmittelbar evident, dass diese Definition in sich widersprüchlich ist. Doch ist mit dieser Definition ein Prädikat bestimmt, welches durch kein Subjekt erfüllt werden kann. Der genannte Wikipedia-Eintrag erläutert: »Angenommen der Barbier rasiert sich selbst, dann gehört er zu denen, die er laut Definition nicht rasiert, was der Annahme widerspricht. Angenommen es gilt das Gegenteil und der Barbier rasiert sich nicht selbst, dann erfüllt er selbst die Eigenschaft derer, die er rasiert, entgegen der Annahme.« – Der gemeinte reduzierte Satz lässt sich aufschreiben:

(5b.2)    P = {S | (S,Barbier im Sinne von Russell)}

lies: P ist die Menge aller Subjekte S mit der Eigenschaft, dass S all jene und nur jene rasiert, die sich nicht selbst rasieren

Diese Menge ist ebenso leer wie die in Formel (5b.1) betrachtete Menge aller natürlichen Zahlen, die größer als alle anderen natürlichen Zahlen sind. Reduzierte Sätze dieser Art sind nicht aus Beobachtungen gewonnen (denn es gibt kein beobachtbares Subjekt mit der Eigenschaft, dass es Russells Definition eines Barbiers erfüllt). Es sind keine gewöhnlichen Sätze, sondern mithilfe des Denkens konstruierte Sätze mit einem leeren Subjekt.

Um Kategorienfehler dieser Art zu vermeiden, ist von den in den Formeln (5a) und (5b) eingeführten Mengen ℙS und P überzugehen zu den jeweiligen Aussage-Sätzen, die diesen Mengen zugrunde liegen:

(6a)    S = {(S,P) für ein festes S}

Lies: S ist die Menge aller Sätze für ein bestimmtes Subjekt S. Das ist die Gesamtheit aller Beobachtungssätze, mit denen ein bestimmtes Subjekt S in allen seinen Prädikaten beschrieben wird.

(6b)    P = {(S,P) für ein festes P}

lies: P ist die Menge aller Sätze für ein bestimmtes Prädikat P. Das ist die Gesamtheit aller Beobachtungssätze, mit denen das Auftreten des Prädikats P protokolliert wird.

Die in (6a) und (6b) betrachteten Mengen enthalten ausschließlich Sätze, die sich jeweils auf ein bestimmtes Subjekt mit einem bestimmten Prädikat beziehen. Es wird sich zeigen, dass dieser Ansatz der tatsächlichen Forschungspraxis und ihren mathematischen Darstellungsverfahren wesentlich näher kommt als der Ansatz der analytischen Philosophie. Sie trägt alle Beobachtungssätze zusammen und sucht nach ihren inneren Regeln. Figur 2 ist daher zugleich der erste Schritt auf dem Weg, um von Figur 1 zu den Messprotokollen der messenden Wissenschaft zu gelangen.

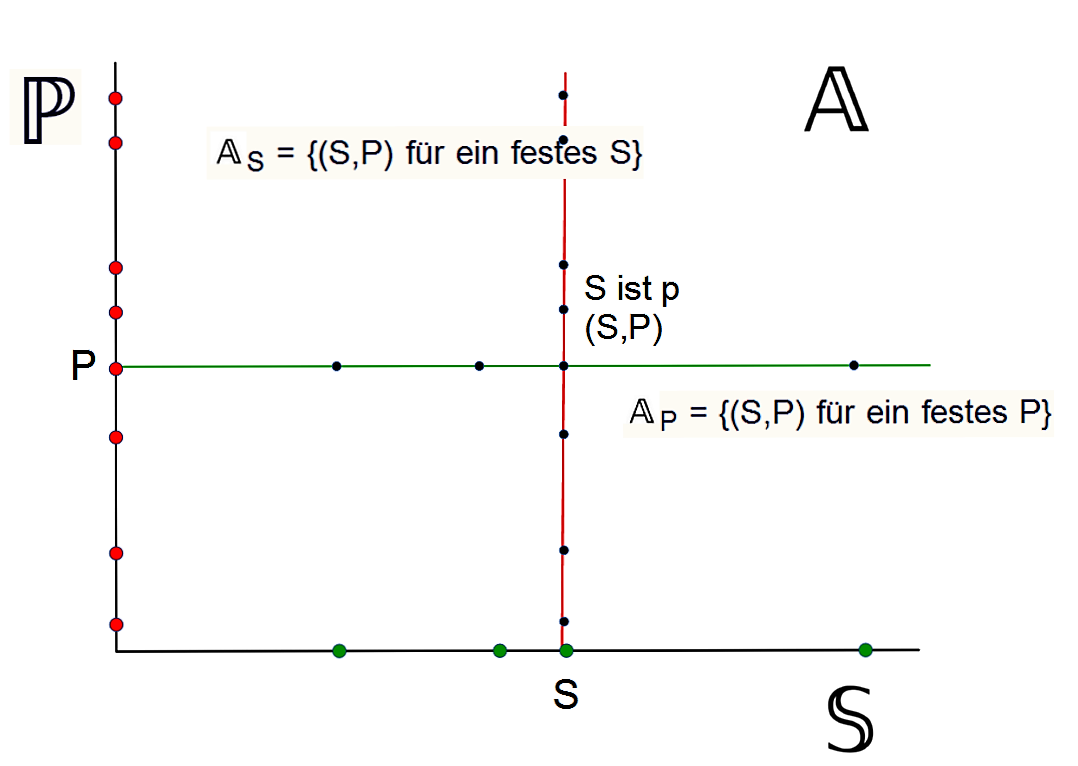
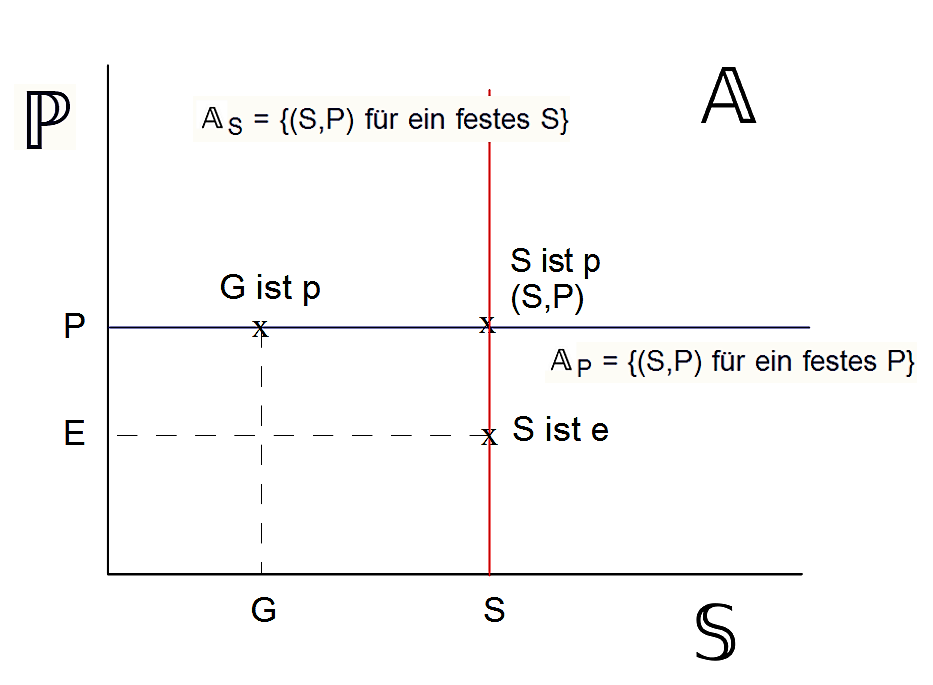
Figur 2: Terminusbildung
Die Fläche aller Sätze wird durch die Äquivalenzklassen S bzw. P horizontal bzw. vertikal aufgeteilt:
Für ein bestimmtes Subjekt S sind auf der ℙ-Achse alle Prädikate durch rote Punkte hervorgehoben, die für S zutreffen. Die entsprechenden Aussagen liegen auf der roten Geraden.
Analog sind für ein Prädikat P auf der -Achse alle Subjekte durch grüne Punkte hervorgehoben, auf die das Prädikat P zutrifft. Die entsprechenden Aussagen liegen auf der grünen Geraden.
Hier ist bereits die Grundidee der Physik zu erkennen, in weiteren Schritten zu untersuchen, ob die roten bzw. grünen Punkte symmetrisch angeordnet sind und ob es übergreifende Symmetrien gibt, die sowohl für die roten wie die grünen Punkte gelten.

Anmerkung: Beispiele wie ‘die größte natürliche Zahl’ oder die Russell-Antinomie zeigen buchstäblich die Grenzen der reduzierten Sätze. Die Russell-Antinomie enthält jedoch mehr. Weiter unten wird sie nochmals aufgenommen und als Satzfehler gedeutet.

– Erste und Zweite Substanz

Die beiden Formeln (5a) und (5b) sind völlig analog gebaut. Auf diese Weise zeigt Ruben, was Frege dazu gebracht haben könnte, den Unterschied von Subjekt und Prädikat ganz fallen zu lassen und stattdessen nur noch von Relationen zu sprechen. »Eine Unterscheidung von Subjekt und Prädikat findet bei meiner Darstellung nicht statt.« (Frege, Begriffsschrift, S. 2) Frege verweist auf das Beispiel, wie in Sätzen Subjekt und Prädikat vertauscht werden können ohne den Inhalt des Satzes zu ändern. Statt »Bei Platäa siegten die Griechen über die Perser« kann auch gesagt werden: »Bei Platäa wurden die Perser von den Griechen besiegt«. Beide Sätze sind inhaltsgleich, jedoch haben im Satz Subjekt und Prädikat ihre Position getauscht. (Frege, Begriffsschrift, S. 3).

Frege mischt zwei Betrachtungsweisen: Zum einen können in einem Satz Subjekt, Prädikat und Objekt jeweils als Worte bezeichnet werden und sind insofern gleich. (Aristoteles sprach von legomenon, das ist alles dasjenige, was sich in Worte fassen lässt. In dieser allgemeinen Hinsicht sind Subjekt, Prädikat und Objekt jeweils Worte und insofern gleich. Siehe Aristoteles, Cat. 2, 1a16-19). Zum anderen ist ein Subjekt dasjenige, das eine Eigenschaft hat, aber nicht seinerseits Eigenschaft an etwas anderem ist. (Aristoteles unterschied hypokeimenon und symbebekoi: hypokeimenon ist das Unterliegende, dem Eigenschaften zugesprochen werden. hypokeimenon ist für ihn die erste Substanz, prote ousia, und die Eigenschaften sind für ihn die zweiten Substanzen, deuterai de ousiai. Siehe Aristoteles, Cat. 5, 2a13ff. Scholastische Philosophen haben den Unterschied der ersten von der zweiten Substanz mit dem Begriff der Subsistenz zu bestimmen versucht, so auch später Kant.)

Was ist in den von Frege genannten Sätzen Subjekt, Prädikat und Objekt? Das ist schrittweise zu entwickeln: (a) So wie im Satz ›ein Gärtner pflanzt einen Baum‹ ein Tun beschrieben wird, bei dem eindeutig Subjekt, Prädikat und Objekt unterschieden werden können, gilt das auch für einen Satz wie ›die Griechen besiegten die Perser‹. (b) Dieser Satz kann auch durch eine Zuweisung dargestellt werden. ›Die Griechen sind Sieger der Schlacht bei Platäa‹ bzw. ›die Perser sind Verlierer der Schlacht bei Platäa‹. Erst in dieser Schreibweise wird deutlich, dass nicht einfach Subjekt und Prädikat vertauscht wurden, sondern dass in beiden Fällen verschiedene Subjekte mit verschiedenen Prädikaten gebraucht wurden. In dem einen Fall erhalten die Griechen das Prädikat ‘Sieger’, in dem anderen Fall die Perser das entgegengesetzte Prädikat ‘Verlierer’. (c) Die Verwechslungsmöglichkeit wird dadurch nahegelegt, dass anders als in einem Beispiel wie ›ein Gärtner pflanzt einen Baum‹ bei einer Schlacht zwischen zwei Völkern zwei Subjekte handeln und im Grunde Prädikate gesucht sind, die sich auf diese gemeinsame Handlung beziehen, also z.B. ›die Schlacht der Griechen und Perser fand bei Platäa statt‹, ›die Schlacht der Griechen und Perser dauerte 8 Stunden‹, ›die Schlacht der Griechen und Perser hatte die Griechen als Sieger‹.

Es war zwar das erklärte Ziel von Frege, »Täuschungen« zu vermeiden, aber er unterlag seinerseits einer Täuschung, als er bei dem Wechsel des Verbs von der Aktivform in die Passivform (von ‘siegten’ in ‘wurden besiegt’) nicht bemerkte, dass hierdurch auch implizit das Prädikat gewechselt wurde (von ‘Sieger’ zu ‘Verlierer’) und keineswegs frei vertauscht werden konnte.

Im Ergebnis sieht die analytische Philosophie Subjekt und Prädikat als prinzipiell gleichberechtigte Termini, die buchstäblich in einen Topf geworfen werden können, die Gesamtheit aller Termini. Statt = ℙ wird daher gesetzt:

(7)    ⊂ , ℙ ⊂

lies: die Gesamtheiten der Subjekte und der Prädikate sind jeweils Teilmengen der Gesamtheit der Termini.

Es ist dann nur konsequent, ausgehend von Sätzen ›S ist p‹ bzw. ihrer Darstellung als Relationen (S,P) eine dritte Gruppe von Termini zu ergänzen, die alle Operationszeichen wie z.B. ∈, ⊂, +, −, ¬, (, ), {, } etc. enthält. Wird die Gesamtheit der Operationszeichen mit bezeichnet, dann gilt:

(8)    = ⊕ ℙ ⊕

lies: Die Gesamtheit der Termini setzt sich zusammen aus den Gesamtheiten der Subjekte, Prädikate und Operationszeichen.

Die formale Logik spricht von der Sprache , mit der sie operiert, oder dem Vokabular . Ein Beispiel für einen ausformulierten Ansatz ist die Endliche Modelltheorie von Stefan Geschke:

»1.1. Strukturen. Ein Vokabular ist eine endliche Menge bestehend aus Relationssymbolen P, Q, R, …, Funktionssymbolen f, g, h, … und Konstantensymbolen c, d, … Jedes Relations- und Funktionssymbol trägt eine natürliche Zahl ≥ 1, seine Stelligkeit.
   Fixiere ein Vokabular . Eine Struktur für (eine -Struktur) ist eine Menge A zusammen mit
   (S1) Relationen ⊆ An für jedes n-stellige Relationssymbol ∈ ,
   (S2) Funktionen : Am → A für jedes m-stellige Funktionssymbol ∈ und
   (S3) Konstanten ∈ A für jedes Konstantensymbol ∈ .
   Oft identifiziert man eine Struktur mit ihrer unterliegenden Menge A, schreibt also A anstatt .« (Geschke, S. 1)

An dieser Stelle trennen sich die Wege der dialektischen und analytischen Philosophie. Beide untersuchen die Terminusbildung. Wenn die analytische Philosophie alle Zeichen in einer gemeinsamen Gesamtheit zusammenfasst und damit gleichrangig behandelt, führt kein Weg vorbei am Gödelschen Unvollständigkeitssatz. Gödel nutzte systematisch aus, dass Operationszeichen und Subjektzeichen gleichwertig geworden und damit im Prinzip austauschbar sind.

Die analytische Philosophie geht nicht auf die Satzeinheit als das kleinste (atomare) Element der Logik zurück, sondern sie geht einen Schritt weiter und sieht die kleinste (atomare) Einheit in den Termini, aus denen der Satz äußerlich zusammengesetzt wird. Die dialektische Philosophie sieht dagegen im Satz die kleinste Einheit. Sie betrachtet die gleichen Termini wie die analytische Philosophie, das sind Subjekte, Prädikate, Mengen von Prädikaten, die einem Subjekt zugeschrieben werden, und Mengen von Subjekten, für die ein bestimmtes Prädikat gilt. Aber sie vermeidet die formale Gleichstellung von Subjekten und Prädikaten zu Termini und hält an der aristotelischen Unterscheidung in erste und zweite Substanzen fest. Sie hält daran fest, dass der zweidimensionale Raum, in dem alle Sätze (S,P) dargestellt werden, nicht weiter reduziert werden kann auf einen eindimensionalen Raum aller Termini. Im Gegenteil ist für sie die Ur-Teilung des Satzes eine zwar notwendige, aber nicht endgültige Brechung der Einheit des Satzes. Die Satzeinheit ist auf einer neuen Ebene wieder herzustellen, und dort ist die Frage zu stellen, wie es zu Widersprüchen und leeren Subjekten und Prädikaten kommen kann. Davon handelt der dritte Schritt der von Ruben betrachteten dialektischen Triade.

Trotz dieser Kritik wird weiter unten gewürdigt, warum und wie Frege auf diese Gleichsetzung von Subjekt und Prädikat gekommen ist und welche neuen Erkenntnisse ihm auf diese Weise gelungen sind.

Wertung (Schluss des Satzes vom Einzelnen zum Allgemeinen über den Namen)

Während die analytische Philosophie die reduzierten Sätze als vollwertige Sätze versteht und anderen Sätzen formal gleichgestellt, sieht die dialektische Philosophie in ihnen einen  Schluss  vom Einzelnen zum Allgemeinen. So steht in Formel (5a) auf der rechten Seite eine Menge einzelner Prädikate {P | (S,P)}, von denen auf die Gattung (das Allgemeine) ℙS geschlossen wird. Die dialektische Philosophie fragt nach dem  terminus medius, über den dieser Schluss vermittelt werden kann. Das ist in der Deutung von Ruben der  Name.

So seltsam es klingen mag, aber für die analytische Philosophie gibt es keine Unterscheidung von Urteil und Schluss. Für sie gibt es nur sogenannte »Schlussketten«. Im einfachsten Fall werden die zwei Sätze verkettet ›A ist Vorgänger von B (oder gleichbedeutend: wenn A gilt, gilt auch B)‹ und ›B ist Vorgänger von C (oder gleichbedeutend: wenn B gilt, gilt auch C)‹. Daraus folgt durch Verkettung ›A ist Vorgänger von C (oder gleichbedeutend: wenn A gilt, gilt auch C)‹. Aber es kann nicht aus A und B auf C geschlossen werden. Als Vorbild dient der analytischen Philosophie seit Frege die Arithmetik. Jede natürliche Zahl hat einen Nachfolger, aber es ist unmöglich, aus zwei natürlichen Zahlen auf eine dritte natürliche Zahl zu schließen. Es ist nur möglich, zwei natürliche Zahlen durch eine arithmetische Operation zu verknüpfen und dadurch eine neue Zahl auszurechnen, wie in dem Standardbeispiel für einen analytischen Satz ›7 + 5 = 12‹. Hier wird nicht aus 7 und 5 auf 12 geschlossen, sondern 12 wird nach klar vorgegebenen Regeln als Summe aus 7 und 5 berechnet.

Um im Bereich der Arithmetik zu zeigen, was einen Schluss im Sinne von Hegel von einer Schlusskette unterscheidet, ist der reduzierte Satz zu bilden, der die Gesamtheit aller Subjekte enthält, die einen Nachfolger haben. Das ist ein Beispiel für Formel (5b).

(5b.3) Nachfolger = {S | (S,S hat einen Nachfolger)}

lies: Nachfolger ist die Gesamtheit aller Subjekte S, die einen Nachfolger haben

Für die analytische Philosophie ist Nachfolger ebenso ein Terminus in der Gesamtheit aller Termini wie jedes einzelne S, aus dem es zusammengesetzt ist. Für die dialektische Philosophie geht es dagegen darum zu verstehen, wie in diesem Beispiel der Schluss von den einzelnen Zahlen und ihrer Nachfolger-Eigenschaft zur Gesamtheit der natürlichen Zahlen gelingen kann. Erst dieser Übergang, der nicht wie im Beispiel ›7 + 5 = 12‹ von zwei einzelnen endlichen Zahlen 5 und 7 zu einer dritten endlichen Zahl 12 oder durch Induktion verallgemeinert von zwei einzelnen Zahlen n und m zu einer dritten einzelnen Zahl ›n + m‹ führt, sondern von den einzelnen endlichen Zahlen n zur unendlichen Zahlenmenge ℕ, kann aus Sicht der dialektischen Philosophie als Schluss bezeichnet werden. Alle üblicherweise genannten trivialen Schlüsse wie ›alle Menschen sind sterblich, Sokrates ist ein Mensch, also ist Sokrates sterblich‹ sind dagegen nichts als Tautologien, rein mechanische Operationen.

Für die dialektische Philosophie geht es daher darum, zunächst an den reduzierten Sätzen zu entwickeln, was ein Schluss ist, und dann zu zeigen, wie der von der analytischen Philosophie betrachtete Fall mit Schlussketten und wohldefinierten Verknüpfungen ein Grenzfall des schließenden Denkens ist.

Daraus ergeben sich auch zwei unterschiedliche Deutungen, was Sprache ist: Für die analytische Philosophie besteht die Sprache aus einer Gesamtheit von Termini und ihren Verknüpfungsregeln. Für die dialektische Philosophie ist die Sprache ein Medium, in dem von Einzelnem auf Allgemeines geschlossen werden kann (vgl. HW 6.431).

– Namen und Entitäten

Ohne weitere Erläuterung deutet Ruben kursiv hervorgehoben die reduzierten Sätze als Namen: »Ein Name ist stets ein reduzierter Satz.« (P, S. 23) Darin sehe ich drei Aussagen enthalten, um die es im Folgenden geht:

• Im reduzierten Satz steht der Name an der Position des Subjekts, ohne ein Subjekt zu sein. Wird z.B. gesagt ›Einstein lebte 1879 bis 1955‹, dann steht in diesem Satz der Name ‘Einstein’ an der Stelle eines Subjekts. Es ist aber offensichtlich nicht gemeint, dass der Name ‘Einstein’ von 1879 bis 1955 gelebt hat, sondern die mit diesem Namen gemeinte Person. Obwohl der Name im Satz die Position eines Subjekts einnimmt, ist er nicht das Subjekt, auf das sich die genannten Prädikate beziehen (wie in diesem Beispiel Geburts- und Todesjahr).
• Der Name vermittelt im reduzierten Satz von den einzelnen Subjekten bzw. Prädikaten, die auf der rechten Seite (der Prädikatseite) stehen, zur Gesamtheit, die auf der linken Seite (der Subjektseite) steht. Wird z.B. aus allen Sätzen ›(x) ist blau‹ auf den Terminus ‘Blau’ geschlossen, dann ist es der gemeinsame Name ‘Blau’, der in den jeweiligen Sätzen gebraucht wurde, über den dieser Schluss möglich ist. Die verschiedenen als ‘blau’ prädizierten Subjekte können aus völlig unterschiedlichen Gründen blau sein, und es gibt in der Regel auch keine Wechselbeziehung, dass die eine Sache deshalb blau ist, weil die andere blau ist. Sie stimmen nur darin überein, dass sie alle eine Eigenschaft haben, die mit dem Namen ‘blau’ bezeichnet wird. Die Gesamtheit aller blauen Gegenstände ist ihrerseits nicht blau, oder noch deutlicher: Der Name ‘Blau’ ist nicht seinerseits blau. Er ist anders als die blauen Gegenstände, denen ein Farbprädikat zugewiesen werden kann, kein Gegenstand, der eine Farbe hat.
• Die analytische Philosophie ignoriert diese Unterscheidungen. Sie reduziert die Unterschiede von Subjekt, Prädikat und Name, indem sie die mit den reduzierten Sätzen gebildeten Gesamtheiten als eigene Entitäten versteht. Oder anders gesagt: Für die analytische Philosophie sind Arten wie die einzelnen S oder die einzelnen P in einem reduzierten Satz als Termini gleichwertig den Gattungen ℙS und P, zu denen diese Arten gehören.

Wie können Namen gebildet werden? Sie wurden bisher rein formal als abkürzende Schreibweise eingeführt. Wenn zum Beispiel in Formel (5a) auf der rechten Seite der Ausdruck {P | (S,P)} steht, dann wird dieser Ausdruck abgekürzt, indem der Buchstabe S als Index herausgezogen und mit dem Buchstaben P verknüpft wird, der zur Unterscheidung von einzelnen Prädikaten P in eine andere Schriftform gebracht wird. Das Ergebnis ist der Ausdruck ℙS, der auf der linken Seite steht.

Was für ein Terminus ist das als Abkürzung eingeführte ℙS? Wenn Ruben ihn als Namen bezeichnet, enthält das implizit eine Kritik an der analytischen Philosophie, die in Ausdrücken dieser Art keine Namen, sondern eigene Entitäten sieht, die den zugrunde liegenden Termini wie S und P formal gleichgestellt sind. Die analytische Philosophie erweist sich hier als Nachfahre des Verstandesdenken, das Hegel kritisiert hat. Sie erkennt nicht, dass es sich hier "bloß" um Namen handelt.

Vom Verstandesdenken und ihm folgend der analytischen Philosophie wird gesagt, dass die mit den Formeln (5a) und (5b) formal eingeführten Zeichen ℙS und P  eigenständige Entitäten  sind, die  unabhängig  von den Elementen S und P bestehen, aus denen sie gebildet wurden. Sie werden ihnen als neugebildete Termini formal gleichgestellt und ihrerseits wie Subjekte angesehen, denen Prädikate beigelegt werden können.

Für Formel (5a) bedeutet das, dass die Gesamtheit der Prädikate eines bestimmten Subjekts im jeweiligen Kontext als dessen Gestalt, Organisation, Leib, Seele, Schema, Begriff, Idee, Form, Selbstmodell u.ä. bezeichnet wird, womit eine innere Einheit und ein innerer Zusammenhalt der Prädikate dieses Subjekts getroffen und hervorgehoben werden soll. Seit Platon und Aristoteles wird kontrovers diskutiert, ob eine solche Gesamtheit den Rang einer eigenen Entität hat, oder nur ein Name ist, den es lediglich im Denken des Menschen gibt. So kann zum Beispiel gefragt werden, ob es eine Seele gibt, die unabhängig und neben dem Körper besteht, dessen Seele sie ist.

Die Ansicht, Gesamtheiten seien eigene Entitäten, wird ungewollt von den skeptischen Kritikern philosophischen Denkens ad absurdum geführt, indem sie sie wörtlich nehmen. Sie wollen philosophisches Denken mit dem scheinbar wissenschaftlichem Argument lächerlich machen, es sei noch niemandem gelungen, im Körper die Seele als solche nachzuweisen. Daraus schließen sie, dass es keine Seele gibt, weil sie sich ebenso wie die analytischen Philosophen nicht vorstellen können, dass die Seele nur ein Name ist, der nur im Denken existiert und nicht körperlich nachweisbar ist. Aus dem gleichen Grund bestreiten sie, dass es das Denken als solches gibt, weil sie nie das Denken als solches nachweisen können, sondern nur körperliche Prozesse im Gehirn, die mit dem Denken korrelieren.

Ähnliche Fragen ergeben sich zu Formel (5b). Die Gesamtheit der Subjekte, die ein gemeinsames Prädikat haben, wird als dessen Substrat bezeichnet. Auf den ersten Blick scheint es schlicht absurd zu sein, Gesamtheiten dieser Art als eigene Entitäten anzusehen. Das ist so, als würde es eine eigene Entität der Tiere mit eigenen Eigenschaften geben, die unabhängig und neben den einzelnen Tieren (den Ameisen, Löwen oder Zebras) besteht, oder als wäre die Menge der natürlichen Zahlen ℕ wiederum so etwas wie eine natürliche Zahl, die neben den natürlichen Zahlen steht. (Cantor scheint in diese Richtung gedacht zu haben, wenn er künstlich der größten natürlichen Zahl den Namen ω gibt, wobei ω für ihn eher den üblichen natürlichen Zahlen wie 1, 2, 3, … vergleichbar ist als einer Menge. Er will hinter ω weiterzählen.)

Doch gibt es andere Beispiele, die zeigen, dass diese Frage schwieriger ist. So gilt seit der Antike das Wasser als eines der vier Elemente, aus denen sich jede Materie zusammensetzt. Das kann mithilfe von (5b) formalisiert werden:

(5b.4) wässrig = {S | (S,wässrig)}

lies: wässrig ist die Gesamtheit aller S, die wässrig sind

Damit ist die Gesamtheit der Meere, Flüsse, Wolken, des Grundwassers, der Eisberge, von Schweiß und Tränen etc. gemeint, wobei unterschiedliche Aggregatzustände wie Eis, Flüssigkeit und Dampf auftreten können. Jedes einzelne Subjekt kann wiederum mit Prädikaten beschrieben werden (Eis ist gefroren, kristallin, elastisch, starr, etc.; Tränen werden von den Tränendrüsen im Auge erzeugt; Meere sind stehende Gewässer auf der Erdoberfläche; …). Und auf ähnliche Weise scheint es möglich, das Substrat Wasser mit Prädikaten zu beschreiben (Wasser ist ein chemisches Molekül bestehend aus Wasserstoff und Sauerstoff-Atomen in einer bestimmten elektrischen Verteilung etc.). Das klingt sehr überzeugend, und darauf kann sich das Verstandesdenken beziehen. Es wird jedoch als widersinnig erkennbar, wenn z.B. gefragt wird, ob ein Eisblock Wasser  oder  Eis  oder  beides ist. Dann wird erkennbar, dass in grundsätzliche Paradoxien führt, über- und untergeordnete Termini gleichermaßen als Subjekte (oder als Gegenstände) anzusprechen.

Dennoch enthält dieser Ansatz einen rationalen Kern, der mit der Vererbungstechnik der Objektorientierung getroffen wird (die Objektorientierung ist eine Methode der Softwareentwicklung). Es können zum Beispiel in einem Objekt ‘Tier’ gemeinsame Eigenschaften zusammengestellt und beschrieben werden, die für alle Tiere gelten. Diese Eigenschaften werden an alle einzelnen Tiere »vererbt«. Für untergeordnete Arten wie Säugetiere, Schafe etc. können wiederum Objekte ‘Säugetier’ oder ‘Schaf’ gebildet werden, die jeweils die Eigenschaften enthalten, die für diese Abstraktionsstufe gelten. Bei der Vererbung der Objektorientierung erhalten jedoch die unterschiedlichen Abstraktionsstufen nicht den Rang eigener Entitäten, sondern sie beschreiben in einem Datenmodell Merkmale, die der jeweiligen Abstraktionsstufe gemeinsam sind. Sie werden in einem Klassendiagramm strukturiert aufgeschrieben. Objekte unterschiedlicher Abstraktionsstufen können auch nicht einander gleichgestellt werden. Wenn das irrtümlich geschieht, gibt das mit den Methoden der Objektorientierung geschriebene Programm zurecht eine Fehlermeldung aus, die auf einen Kategorienfehler verweist.

Der Unterschied zwischen den von der Vererbungstechnik beschriebenen Objekten und den reduzierten Sätzen, um die es hier geht, liegt darin, dass die Objektprogrammierung ausschließlich endliche Datenmengen betrachtet und in verschiedenen Abstraktionsstufen zusammenfasst, während bei den reduzierten Sätzen die Anzahl der zusammengefassten Subjekte bzw. Prädikate unendlich sein kann. Daher ist es für die Objektprogrammierung zum Beispiel nicht möglich, die Menge aller natürlichen Zahlen ℕ als ein Objekt zu betrachten, dessen Eigenschaften auf die einzelnen natürlichen Zahlen vererbt werden. Stattdessen kennt die Programmierung nur den Datentyp Integer, der grundsätzlich nur einen endlichen Wertebereich hat, dessen Grenzen durch die Speichergröße des Rechners und die Adressierbarkeit von Datenworten im jeweiligen Verarbeitungssystem bestimmt sind.

Wird der Ansatz der Entitäten zu Ende gedacht, zeigen sich seine Paradoxien besonders deutlich. So wie Eis, Flüssigkeit und Gas Zustände des Wassers sind, ist das Wasser ein Stoff, bis auf oberster Ebene metaphysische Begriffe übrig bleiben wie das Sein oder das Absolute. Wird versucht, auf dieser obersten Ebene die metaphysischen Begriffe als Subjekte zu verstehen und ihnen Prädikate zuzuschreiben, dann führt das in unlösbare Antinomien. Kant hat das an einigen Beispielen gezeigt wie der Frage, ob die Welt einen Anfang hat oder nicht, in kleinste Teile teilbar ist oder nicht etc. Hegel hat das weiter untersucht und erkannt, dass die von Kant genannten Beispiele durchweg darauf zurückgehen, dass versucht wird, Gesamtheiten, wie sie in reduzierten Sätzen gebildet werden, eine eigene Entität zu verleihen und sie ihrerseits als Satzsubjekte anzusehen, über die Sätze gebildet werden können.

»Jene Metaphysik setzte überhaupt voraus, daß die Erkenntnis des Absoluten in der Weise geschehen könne, daß ihm Prädikate beigelegt werden, und untersuchte weder die Verstandesbestimmungen ihrem eigentümlichen Inhalte und Werte nach, noch auch diese Form, das Absolute durch Beilegung von Prädikaten zu bestimmen.« (Hegel, Enz. § 28, HW 8.94)

Damit hat Hegel die Grenze der Sprache getroffen, an der später auch Wittgenstein anschlug. Dies radikale Argument gilt nicht nur für Grenzfragen, die auf das Gebiet des Glaubens abgeschoben werden können. Es gilt für alle reduzierten Sätze, wenn die dort gebildeten Gesamtheiten als eigene Entitäten angesehen werden, die formal allen anderen Termini gleich sind.

Es gilt für alle Sätze, mit denen aus Arten Gattungen gebildet werden. Das geschieht bei den reduzierten Sätzen, bei denen auf der rechten Seite eine Menge gebildet wird, die aus unterschiedlichen Subjekten bzw. Prädikaten eine Gattung bildet. So wird z.B. in (5b.4) aus der Gesamtheit aller wässrigen Subjekte die Gattung Wasser gebildet. Gattungen und Abstraktionen können keine neuen Eigenschaften (Prädikate, Merkmale) haben, die über die Eigenschaften der mit ihnen zusammengefassten Elemente (Arten) hinausgehen. Sie können gemeinsame Eigenschaften hervorheben, die bereits bei den einzelnen in der Gesamtheit zusammengefassten Subjekten gegeben sind. Mit ihnen können jedoch Symmetrien erkannt werden, die erst auf höheren Abstraktionsstufen sichtbar werden und bei den niedrigeren Abstraktionsstufen verborgen bleiben in der Fülle des Materials. Die Gattungen bestehen nicht neben oder unabhängig von den in ihnen zusammengefassten Arten, sondern sie werden im Denken gebildet, das ihnen nicht neue Eigenschaften beilegt, sondern mit ihnen bestimmte strukturelle Eigenschaften an den in ihnen enthaltenen Arten hervorhebt.

Statt Gattungen und Arten einander als Subjekte oder noch allgemeiner als Termini gleichzustellen, ist zu fragen, wie Gattungen gebildet werden können. Darum wird es im Folgenden gehen. Und es ist im Weiteren zu fragen, welche Beziehungen (Relationen, Verwandtschaften, Familienähnlichkeiten) zwischen Elementen bestehen.

Anmerkung: So wie in der Informatik in einem Modell Auszüge der Realität abgebildet und auf ihre inneren Strukturen untersucht werden, geht auch allgemein das Denken vor. So wie die Informatik ein virtuelles Abbild der Welt aufbaut und dies in einem Raum von Daten und ihren Beziehungen darstellt, schafft sich auch das Denken einen eigenen Raum des Erkennens, innerhalb dessen Gattungen und Arten unterschieden werden können. Hegel hat das in der Jenenser Logik klar ausgesprochen:

"Das Erkennen, als das Allgemeine, für welches ein anderes ist, ist zunächst auf dies andere einfach bezogen; es ist der indifferente Raum dieses andern, und seine Bewegung als die Reflexion in sich selbst ist, daß in ihm als der einfachen Beziehung dies andere sich bewegt, kommt und verschwindet, in dem Raum des Erkennens ein anderes gesetzt ist, und er wieder in sich zurückgeht, daß dies andere sich aufhebt. Das Erkennen als different zugleich gegen dies kommende und verschwindende ist selbst diese negative Beziehung desselben." (JLMN, S. 131, Hervorhebung d.V.)

Hegel hat gefragt, ob und welche Eigenschaften es in diesem Raum des Erkennens gibt. Darauf soll in einer geplanten Arbeit über die Idee des Erkennens und den Satz des Pythagoras näher eingegangen werden.

– Namen als terminus medius vom Einzelnen zum Allgemeinen

Während sich die analytische Philosophie in ihren Abstraktions- und Formalisierungverfahren notwendig in Paradoxien und Unvollständigkeiten verstrickt, wenn sie alle Termini und die mit ihnen gebildeten gewöhnlichen und reduzierten Sätze formal auf eine Stufe stellt und buchstäblich alles auf eine einzige Dimension der Termini projiziert und dort unabhängig voneinander stehen lässt, kann und will auch die dialektische Philosophie die notwendig eintretende Selbstreferentialität nicht leugnen oder vermeiden, sondern sie gibt ihr eine eigene  Bewegungsform: den Namen. Das ist ihr möglich, da sie anders als die analytische Philosophie von der Satzeinheit und mit ihr von dem zweidimensionalen Raum aller Sätze ausgeht (siehe Figur 1) statt von der unbestimmten Gesamtheit aller Termini.

Ein Name wird gebildet, indem aus den Gesamtheiten, die mit den reduzierten Sätzen entstanden sind, jeweils ein Element herausgezogen wird, einen Eigennamen erhält, und dieser Eigenname zugleich als Eigenname für die Gesamtheit steht.

Sowohl im gewöhnlichen wie im philosophischen Denken wird ständig so verfahren, allerdings ohne sich das immer bewußt zu machen. Aristoteles hat z.B. mit dem Namen ‘Holz (hyle)’ die Gesamtheit des Stofflichen bezeichnet. Hier steht ein bestimmter Stoff (das Holz) für die Gesamtheit alles Stofflichen. Auch der deutsche Name ‘Stoff’ ist auf diese Weise gebildet: ‘Stoff’ ist sowohl ein bestimmter Stoff (eine Textilie, z.B. aus Baumwolle), wie auch der Name für die Gattung, die außer Textilien alle anderen Stoffe enthält (Erde, Eisen, Stickstoff, Sauerstoff, Luft etc.). Ebenso hat in der gewöhnlichen Sprache jeder bei einem abstrakten Ausdruck einen bestimmten Vertreter im Blick. Das offenbart sich dann, wenn nach Piktogrammen gesucht wird. Zum Beispiel wird in der Regel ein Gänseblümchen (Maßliebchen, Tausendschön) als Zeichen aller Blumen verstanden.

In den meisten Fällen ist die Herkunft der Namen im Alltagsgebrauch nicht mehr bekannt oder unklar und muss etymologisch erschlossen werden. Zum Beispiel leitet sich das Wort ‘Wasser’ vom »althochdeutschen wazzar, das “Feuchte, Fließende”, ab« (Wikipedia, abgerufen am 26.3.2015), einer bestimmten Eigenschaft des Wassers, oder das Wort ‘Baum’ von Balken, der aus dem Holz eines Baumes hergestellt werden kann (Wiktionary, abgerufen am 26.3.2015).

Ähnlich verfahren die Physik und die Ökonomie. Aus der Gesamtheit aller Längen wird eine Länge herausgenommen – das Pariser Urmeter –, die sowohl eine einzelne Länge wie auch das Maß für alle Längen ist. In der Warengesellschaft wird aus der Gesamtheit der Waren, – das ist die Menge aller Gegenstände, die käuflich erworben werden können –, mit dem Geld eine bestimmte Ware herausgegriffen, die sowohl eine Ware wie alle anderen Waren ist und zugleich als Eigenname für alle Waren gilt: Der Wert jeder Ware misst sich in einer bestimmten Ware, dem Geld. (Dieses einzelne Beispiel aus der Ökonomie hat Ruben wiederum übernommen, um mit ihm dem allgemeinen Verfahren der Namensbildung einen übergreifenden Namen zu geben: die Wertung.)

Das lässt sich in Formeln schreiben, aus denen im Weiteren die Formeln für die geometrische und physikalische Größenbestimmung, das Tauschverhältnis und die Wahrheitsfunktion entwickelt werden sollen. Für die Gleichheit von Namen wird von mir anders als bei Ruben das Forcing-Symbol ⊩genutzt (siehe hierzu Anhang 1):

(9a)    ‘E’ ⊩ ‘ℙS’ mit E ∈ ℙS

lies: der Eigenname ‘E’ eines Elements E aus der Gesamtheit ℙS steht stellvertretend für den Eigennamen ‘ℙS’ der Gesamtheit ℙS
Eigennamen werden mit einfachen Anführungsstrichen gezeichnet. Es handelt sich um Eigennamen, wie sie von Frege als Bedeutungen eingeführt worden waren, zum Beispiel der Eigenname ‘Venus’.

(9b)    ‘G’ ⊩ ‘P’; mit G ∈ P

lies: der Eigenname eines Elements G aus der Gesamtheit P steht stellvertretend für den Eigennamen der Gesamtheit P
Beispiel: Der Eigenname ‘Stoff’ steht stellvertretend für alle Stoffe.

Figur 1 und 2 lassen sich entsprechend weiter differenzieren:

Figur 3: Namensbildung
In Figur 3 werden auf der ℙ-Achse ein besonderes Element E (für Eigenschaft) und auf der -Achse ein besonderes Element G (für Gegenstand) hervorgehoben. G ist sowohl ein Element von wie auch der Name der Gesamtheit P, die alle Subjekte enthält, die das Prädikat P haben. Für die analytische Philosophie ist G das Substrat von P.

Das Neue an Figur 3 gegenüber den Figuren 1 und 2 besteht darin, dass hier zwar die betrachteten Elemente wie E, G, S und P sowie die betrachteten Teilmengen wie S eingezeichnet sind, jedoch nicht die Namen wie ‘E’. Hier sind nur die Sachen zu sehen, die mit diesen Namen bezeichnet werden. Wo ist der Ort der Namen? Wiederholt sich hier das Dilemma der analytischen Philosophie, wenn jetzt allen Sachen in einer einheitlichen Achse ihre Namen zugewiesen werden? Führt die Namensbildung zur gleichen Vereinheitlichung wie die Gesamtheit der Termini?

Das lässt sich auch anders sagen: In den Formeln (9a) und (9b) treten Sätze auf, die sich von allen bisher eingeführten Sätzen unterscheiden, sowohl den elementaren Sätzen entsprechend Formel (1) als auch den reduzierten Sätzen entsprechend Formel (5a) und (5b). In den Formeln (9a) und (9b) steht sowohl an der Stelle des Subjekts ein Eigenname wie auch an der Stelle des Prädikats. Etwas umständlich kann formuliert werden: ›das Subjekt ‘Eigenname von E’ hat das Prädikat, ‘Eigenname von ℙS’ zu sein‹, oder einfacher: ›der Eigenname von E ist der Eigenname von ℙS‹. Hier werden nicht mehr Sätze über Sachen und ihre Eigenschaften, sondern über Namen gebildet.

Um den Bezug vom Namen zur Sache herzustellen, wird von den Eigennamen zu den Werten übergegangen. Was ist der Wert? Im Beispiel der Ökonomie ist der Wert einer Ware die durchschnittlich notwendige gesellschaftliche Arbeitszeit, die zu ihrer Herstellung erforderlich ist. Wird nun eine einzelne Ware wie das Geld hervorgehoben, um mit ihm die gesamte Warenwelt zu repräsentieren, führt das in folgenden Widerspruch: Der Gesamtwert aller Waren ist die gesamte Arbeitszeit, die für die Herstellung dieser Waren erforderlich ist. Das Geld ist eine Teilmenge dieser Waren. Auch für die Herstellung des Geldes ist eine bestimmte Arbeitszeit notwendig. Und dennoch soll der Wert des Geldes im Ganzen dem Wert der Waren im Ganzen gleichgesetzt werden. Dieser Widerspruch kann nur dadurch gelöst werden, dass das Geld einen zweiten, symbolischen Wert erhält, der ihm aufgedruckt oder eingestanzt wird: die Währung. Jedes einzelne Geldstück ist weniger wert als die Ware, die mit ihm eingetauscht werden kann, da für seine Herstellung weniger Arbeitszeit nötig war. Wenn dennoch beide im Tausch einander gleichgesetzt werden, ist das nur möglich, indem eine Instanz geschaffen wird, die das durchsetzt: der Staat. Er hat das Monopol, Geld als solches zu siegeln oder heutzutage zu drucken. Andernfalls wäre es möglich, dass sich jeder mit einem vergleichsweise geringen Arbeitsaufwand sein eigenes Spielgeld oder Falschgeld herstellt und mit ihm Waren kauft.

Dieser Widerspruch und seine symbolische Lösung erscheinen auf den ersten Blick verblüffend und falsch, sind aber unvermeidlich. Wenn ein einzelnes Element für die gesamte Menge stehen soll, der es als Element angehört, muss es zu diesem Widerspruch kommen. Er kann nur gelöst werden, wenn die einzelnen Waren nicht mehr voneinander isoliert stehen bleiben, sondern eine gesellschaftliche Übereinkunft erzielt wird, die die Währung festlegt. Auf diese Weise wird im Beispiel der Ökonomie von den einzelnen Waren auf die gesellschaftliche Einrichtung des Geldverkehrs geschlossen. Der Schluss wird nicht von einzelnen Waren auf eine andere Ware oder auf das Geld gezogen, sondern von den Waren auf die gesellschaftlich vereinbarte Währung. Daher ist es auch beliebig, wie die Währung bezeichnet und ihre Einheit benannt wird, als “Taler”, “Dollar”, “Renminbi” oder sonstwie. Entscheidend ist, dass es eine  gesellschaftlich anerkannte Macht  gibt, die die Währung zu garantieren vermag.

Für das Geld muss eine Standardtransformation zu mindestens einer anderen Ware festgelegt werden wie zum Beispiel der Goldstandard. Mit ihm garantiert der Staat, dass er bereit und fähig ist, für jedes Geldstück und jeden Geldschein eine bestimmte Menge Gold auszugeben. Die Aufhebung des Goldstandards 1971 zeigt, dass in diesem Beispiel der amerikanische Staat seine Macht zu verlieren beginnt, den Wert der Weltwährung zu garantieren. Seither befindet sich die Weltwirtschaft in einer dauerhaften Krise, die sich in der weltweiten Inflation und dem Aufblähen von Kreditgeld zeigt. Sie wird erst gelöst, wenn eine neue staatliche Macht etabliert ist, die einen Standard für das Geld zu setzen vermag.

Ist die Ökonomie ein Sonderfall, da in diesem Beispiel mit der Arbeitszeit ein zweiter Maßstab vorliegt, mithilfe dessen das Geld als namengebender Ware mit anderen Waren verglichen werden kann? Die Ökonomie zeigt lediglich besonders anschaulich, dass es zum einen eine gemeinsame Eigenschaft (Prädikat) geben muss, dank derer das namengebende Element mit allen anderen Elementen übereinstimmt. Das ist im Beispiel der Ökonomie die Arbeitszeit. Es werden nur Waren gehandelt, für deren Herstellung eine bestimmte Arbeitszeit notwendig ist. Und zum anderen muss eine Transformation Gültigkeit erlangen, mithilfe derer bei dem namengebenden Element (dem Geld) umgerechnet werden kann von der in ihr enthaltenen Arbeitszeit zur Währung. Mit dieser Umrechnung wird der Übergang vollzogen vom Geld als einer einzelnen Ware wie alle anderen Waren zum Geld als allgemeinem Äquivalent für alle Waren.

Im Beispiel der Länge gilt, dass der Wert der Länge des Pariser Urmeters, – das ist ein Meter – gleichgesetzt werden soll mit allen anderen Längen. Das setzt voraus, dass sich beim Vergleichen (dem Herantragen, Anlegen, ggf. Vervielfachen oder Verkürzen) der Länge die Längenmaße nicht ändern. In der uns vertrauten Alltagswirklichkeit ist das erfüllt. Jeder kann davon ausgehen, dass wenn er zum Beispiel seinen Zollstock nach Paris bringt und ihn dort mit dem Urmeter vergleicht, der Zollstock nicht unterwegs oder beim Anlegen an das Urmeter seine Länge verändert. Diese völlig selbstverständlich erscheinende Annahme gilt jedoch nicht mehr in der von Einstein entwickelten Speziellen Relativitätstheorie. Wenn dort unbewegte und bewegte Längen verglichen werden, wird die bewegte Länge relativ kürzer im Vergleich zur ruhenden Länge (Längenkontraktion). Wenn zum Beispiel jemand einen Zollstock von einem sehr schnell bewegten Raumschiff nach Paris bringt, muss er die Geschwindigkeit abbremsen, wodurch der Zollstock länger wird. Kehrt er in sein Raumschiff zurück, wird der Zollstock wieder kürzer. Obwohl also durch Anlegen an das Urmeter in Paris gezeigt wurde, dass der Zollstock im Raumschiff genau so lang ist wie das Pariser Urmeter, sind die mit ihm im Raumschiff gemessenen Längen dennoch kürzer als die Längen in Paris. So wie beim Geld eine Transformation notwendig ist von seinem Wert gemessen an der Arbeitszeit, die für seine Herstellung erforderlich war, in die Währung, für die es steht, ist auch hier eine Transformation notwendig.

Einstein erkannte, dass diese Transformationen bereits vor ihm entdeckt worden waren (die Lorentz-Transformation). Doch deutete er sie völlig neu. Er verstand, dass das Verfahren dieser Transformationen durch ihre Selbstbezüglichkeit auf ähnliche Weise zu kollabieren droht wie in der Logik die Russell-Antinomie, wenn es keine absolute Größe gibt, die für die Transformationen herangezogen werden kann. Die gesuchte Größe war für Einstein die Lichtgeschwindigkeit. Sie entspricht dem staatlichen Monopol, mit dem in der Ökonomie für alle bindend eine Währung festgesetzt wird. Daher kann gesagt werden, dass er erkannt hat, wie aus dem Vergleich einzelner Längen darauf geschlossen werden kann, dass es eine absolute Größe geben muss, mithilfe derer der Vergleich hergestellt werden kann. Es genügt nicht, alles am Pariser Urmeter zu messen, sondern es muss zusätzlich die überall gültige Lichtgeschwindigkeit geben, um alle Längen vergleichbar zu machen. Der Schluss von den einzelnen Längen auf eine von der Lichtgeschwindigkeit bestimmte Mechanik entspricht dem Schluss von den einzelnen Waren in der Warenökonomie auf die gesellschaftliche Übereinkunft, die die Transformation von der im Geld enthaltenen Arbeitszeit zur gesellschaftlich vereinbarten Währung setzt.

Wie nahe beieinander in dieser Frage Physik und Ökonomie liegen, ist daran zu sehen, dass Newton 1696 Münzmeister in England wurde und in dieser Funktion 1717 nach dem Vorbild der Perser, Alexander des Großen und Cäsars den Goldstandard einführte. Er hat offenbar verstanden, dass mit diesem Schachzug die nationale englische Währung zugleich den Rang einer Weltwährung bekam und damit das englische Imperium (Empire) solange seine Vorherrschaft sichern konnte, bis es durch die USA abgelöst wurde.

Warum ist Einstein in der Physik gelungen, was Russell und anderen Mathematikern in der Logik nicht gelungen ist? Aus dem einfachen Grund, weil dort bis heute keine allgemein anerkannte Übereinkunft besteht vergleichbar einer Weltwährung oder der in allen Inertialsystemen geltenden Lichtgeschwindigkeit. Im Folgenden soll gezeigt werden, dass es früher die Macht der Kirche war, die mit ihrem Recht der Auslegung heiliger Texte die Bedeutung der Namen festlegen konnte. Mit dem Sturz der Macht der Kirche durch die Französische Revolution ist diese Macht verloren gegangen. Hegel hat das erkannt und wollte mit seiner Philosophie des spekulativen Denkens die Macht des Absoluten rehabilitieren und auf neue Füße stellen. Worin besteht die Macht des Absoluten? Hegel sieht sie in der Objektivität der Offenbarung, der Sprache und der Mittel, dank derer Schlüsse gezogen werden können. Da in seiner Philosophie die Objektivität eng mit dem Absoluten verbunden ist, hat sich sein Ansatz nicht gegen den seither dominierenden Materialismus durchsetzen können. Aber es ist ihm gelungen, mit seinem Versuch gewissermaßen die Figur zu zeigen, wie ein solcher Maßstab auszusehen hat. Marx und ihm folgend Ruben übernehmen die Figur des spekulativen Denkens, aber sie nennen es nicht mehr spekulatives, sondern dialektisches Denken. Sie wollen die von Hegel in die Wissenschaft der Logik eingeführte Macht des Absoluten ersetzen durch die Macht des Produktions- und Lebensprozesses. Wird jedoch gefragt, worauf diese Macht beruht, führt das nach meiner Überzeugung letztlich wiederum auf die Objektivität. Daher soll im nächsten Kapitel gezeigt werden, dass für die Theorie der Sätze Wahrheits-Transformationen zu entwickeln sind, die den Werttransformationen des Geldes bzw. den Lorentz-Transformationen entsprechen und auf der Macht der Objektivität beruhen.

Der analytischen Philosophie ist es nur gelungen, die Problematik immer deutlicher aufzuzeigen. Solange jede Sache ihren eigenen Namen erhält, kann im Zweifel auf die Sache selbst verwiesen werden, wenn unklar ist, was mit dem Namen gemeint ist. Wer nicht weiß, was mit dem Namen ‘Bewegung’ gemeint ist, dem kann eine Bewegung vorgeführt werden, wie es Diogenes tat, als die Eleaten bezweifelten, dass es Bewegung gibt. Dennoch ist auch dies Verfahren nicht frei von möglichen Irrtümern. Quine hat das am Beispiel des Phantasiewortes “Gavagai” demonstriert. Wenn jemand in eine andere, ihm unbekannte Kultur kommt, und dort immer, wenn ein Hase zu sehen ist, das Wort “Gavagai” gesagt bekommt, bleibt unentscheidbar, ob damit ein Hase, der spezifische Bewegungsablauf eines Hasen, eine mit der Gegenwart eines Hasen verbundene Gefahr, ganz allgemein das Kommen und Gehen von etwas oder möglicherweise noch etwas Anderes gemeint ist. Nur wer sich innerhalb einer Kultur und ihrer Sprachgemeinschaft bewegt, kann die dort geltenden Namen verstehen. Innerhalb einer Kultur führt nichts daran vorbei, den Namen einen absoluten Charakter zu geben, weil ohne ihn keine Verständigung möglich wäre.

Die Bedeutung des Namen kann erst voll verstanden werden, wenn erkannt wird, dass der Name das verbindende Glied ist, um von einzelnen Sätzen auf Gesamtheiten schließen zu können. Der Name muß eine besondere Qualität, im Grunde eine eigene Macht haben, um diesen Schluss vermitteln zu können. Häufig wird davon gesprochen, dass Namen göttlich sind, von Engeln geschützt werden, und auf die von Gott dem Menschen verliehene Macht zurückgehen, den Dingen und Lebewesen einen Namen zu geben. Eltern zeichnen bestimmte Eigenschaften aus, wenn sie ihren Kindern einen Namen geben. Der Name symbolisiert bestimmte Eigenschaften, die die Eltern mit ihren Kindern verbinden und ihnen wünschen. Sie sind als Eigenname zugleich der Name der ganzen Persönlichkeit mit all ihren Eigenschaften und nicht nur derjenigen, die ursprünglich bei der Namensvergabe hervorgehoben wurden.

Ruben versteht die Vergabe von Namen als eine Fähigkeit des Menschen innerhalb des Produktions- und Lebensprozesses. Jeder Name ist Ausdruck einer »verständigen Abstraktion« (Ruben 1969, S. 8 mit Bezug auf Marx Einleitung zur Kritik der politischen Ökonomie 1857, MEW 13.617). Mit der Verständigkeit ist gemeint, dass jeder Name auf verständige Weise über sich selbst hinausweist. Wenn jemand etwas sagt, verstehen ihn die anderen, weil sich beide auf etwas Gemeinsames beziehen. Das ist für Ruben der gemeinsame Produktions- und Lebensprozess, an dem sie teilhaben. Für ihn ist der Produktions- und Lebensprozess die Macht, worauf sich die an ihm beteiligten Menschen beziehen und einander verstehen können. Der Staat kann lediglich als ein Machtorgan dieser übergreifenden Macht verstanden werden.

Wenn es gelungen ist, auf diese Weise die Bedeutung des Namens als terminus medius des Schlusses deutlich zu machen, dann ist als nächstes zu zeigen, wie sich einzelne Namen auf eine Weise zusammenschließen, dass sich aus ihnen eine zusammenhängende Sprache ergibt. Aus der Vielzahl der Schlüsse wird auf das gemeinsame Medium aller Schlüsse geschlossen, welches die Sprache ist, so wie innerhalb jedes einzelnen Schlusses aus den einzelnen Elementen auf die übergreifende Gesamtheit geschlossen wurde. Die Lehre des Schlusses wird auf sich selbst angewandt und geht im Sinne von Hegel über in die Objektivität, was in einem geplanten Beitrag näher ausgeführt werden soll.

Als Ergebnis dieser Überlegungen können die Formeln (9a) und (9b) nochmals umgeformt werden (siehe P, S. 23f):

(10a)    ‘E’ ⊩ ‘ℙS’ → [E] ≡ [ℙS]

lies: wenn der Eigenname von E der Eigenname der Gesamtheit ℙS ist, bedeutet das, dass der Wert von E identisch ist mit dem Wert von ℙS

andere Lesart: die mit dem Namen von E angesprochene Referenzmenge ist identisch mit der mit dem Namen von ℙS angesprochenen Referenzmenge, und das, obwohl E ein Element der mit dem Namen von ℙS angesprochenen Referenzmenge ist

(10b)    ‘G’ ⊩ ‘P’ → [G] ≡ [P]

Was Ruben an dieser Stelle als Äquivalenz bezeichnet und mit dem Zeichen ≡ symbolisiert, sind die jeweiligen Transformationsregeln wie zum Beispiel der Goldstandard oder die von Einstein in die Relativitätstheorie übernommenen Lorentz-Transformationen. Hier droht allerdings ein Missverständnis, da der Begriff Äquivalenz in zweierlei Sinne gebraucht wird. Zum einen werden in den reduzierten Sätzen gemäß den Formeln (5a) und (5b) auf der rechten Seite Äquivalenzklassen gebildet, wenn dort alle Prädikate zusammengefasst werden, die für ein Subjekt gelten, bzw. alle Subjekte, die in einem Prädikat übereinstimmen. Äquivalenz ist in (5a) und (5b) eine Beziehung zwischen den Elementen innerhalb der Mengen {P | (S,P)} bzw. {S | (S,P)}. In (10a) und (10b) wird dagegen eine Äquivalenz zwischen den Werten (Referenzmengen) gebildet, die mit dem Eigennamen des Standardobjekts und dem Eigennamen der Allgemeinheit besteht.

In der Ökonomie ist zum einen das Geld insofern allen anderen Waren äquivalent, weil es eine bestimmte Menge Arbeitszeit verkörpert. In Formel (10a) und (10b) ist aber die Äquivalenz gemeint, die zur Währungseinheit führt. Ähnlich gibt es in der Physik zum einen die Äquivalenz, die in dem Moment hergestellt wird, wenn eine Länge an das Pariser Urmeter angelegt wird, und zum anderen die Äquivalenz, die durch die Lorentz-Transformationen sichergestellt wird.

Statt von Transformation kann auch von  Wandlung  gesprochen werden. Das macht deutlicher, dass es eine Wandlungsmacht geben muss, dank derer die Wandlung vollzogen werden kann. Sie ist das heilige Sakrament der Eucharistie im christlichen Abendmahl, wenn symbolisch Brot und Wein in Körper und Blut Christi verwandelt werden und auf diese Weise die namengebende Macht der Kirche rituell bestätigt und erneuert wird. Diese Wandlungsmacht ist für Hegel das christlich verstandene Absolute und für den Materialisten Ruben der Produktions- und Lebensprozess.

Eine Wandlungsmacht ist in der Lage, eine Möglichkeit in eine Wirklichkeit zu überführen. Die gesellschaftliche Übereinkunft für eine Währung ermöglicht die Geschäfte der Warenökonomie. Die absolute Geltung der Lichtgeschwindigkeit in allen Inertialsystemen ermöglicht, bewegte und ruhende Längen aneinander zu messen und die Mechanik aufrecht zu erhalten. Die Namensbildung ermöglicht, aus unbestimmten Wesen mit einer abzählbaren Anzahl von Eigenschaften Persönlichkeiten zu machen, die über eine innere Freiheit verfügen und frei miteinander verkehren können.

Ruben trifft den kritischen Punkt, wenn er hier sprachlich den Übergang zum Dativ sieht. Das ist bereits an der für (10a) gebrauchten Formulierung zu sehen, dass der Wert von E identisch ist mit  dem Wert  von ℙS

»In diesen Sätzen treten die Subjekt- und Prädikattermini als Dativobjekte auf, während das Prädikat = (in Worten: 'ist gleichwertig') aus der Kopula und dem Prädikativ 'gleichwertig' (oder 'äquivalent' oder 'gleich') besteht. Diese Art der Satzbildung ist nicht mehr beschreibend, sondern wertend!« (P, S. 23)

Um den Raum der Möglichkeit zu unterscheiden von dem, was wirklich wird, sind ungewohnte Ausdrücke zu bilden. Um zu beschreiben, wie Namen gebildet werden, ist zu unterscheiden zwischen dem Wortbaren (dem in Worten Fassbaren), das von den Namensbildung aufgegriffen wird, und den vergebenen Namen. Das entspricht der Unterscheidung zwischen dem Zählbaren und den Zahlen, die als Ergebnis eines Zählens gefunden wurden, oder dem Wahrnehmbaren und der Wahrnehmung als Ergebnis des Wahrnehmens. Die Wandlungsmacht der Sprache ist ihre Fähigkeit, für alles dasjenige, wofür Worte gefunden können, auch die richtigen Worte zu treffen. Sie wandelt das Wortbare in Worte.

Für diese Deutung kann an Aristoteles erinnert werden.

»Was Gegenstand der Sprache ist, wird entweder in Verbindung oder ohne Verbindung gesprochen (ton legomenon ta men kata symploken legetai, ta de aneu symplokes); in Verbindung z.B.: der Mensch läuft; der Mensch siegt; ohne Verbindung z.B.: Mensch; Stier; läuft; siegt.« (Aristoteles, Cat. 2, 1a16-19) Im Englischen wird »aneu symplokes« mit »out of syntax« übersetzt.

Hier ist der Ausdruck »Gegenstand der Sprache«, d.h. das Wort, in den Dativ gesetzt: Statt von logos spricht Aristoteles von legomenon. Und zugleich betont er, dass diese Worte, die wörtlich als das »Wortbare« oder »Wortliche« übersetzt werden müssen, außerhalb der üblichen Verbindung in Sätzen stehen. Sie stehen nicht in Sätzen wie ›S ist p‹. Mit ihnen werden nicht Subjekten Prädikate zugeordnet, sondern sie gehen der Prädizierung voraus. Sie beschreiben noch einen unbestimmten Möglichkeitsraum, der durch die Namensbildung gefüllt wird. Erst wenn es Namen gibt, wird verständlich, wie eine Prädizierung ›S ist p‹ möglich ist. – Daher ist es auch verfehlt, wenn sich die analytische Philosophie bei ihrer Gleichsetzung von Subjekten und Prädikaten in Termini auf Gedanken wie diesen von Aristoteles beruft, dass Subjekte und Prädikate insofern einander gleich sind, als es sich bei beiden um Worte handelt. Es handelt sich zwar bei ihnen um Worte, aber bei Aristoteles ist damit eine Stufe gemeint, die noch der der Prädizierung vorausgeht.

Nach meinem Verständnis hat Aristoteles mit dem Übergang vom Wort zum »Wortbaren« oder »Wortlichen« den gleichen Übergang getroffen, um den es hier geht, wenn aus der Satz- und Terminusbildung die Namensbildung entwickelt werden soll. Mit einem Namen wird alles referenziert, was dem Inhalt des Namens entsprechen kann. – Das Zählbare ist alles, was gezählt werden kann. Das ist die entscheidende Erkenntnis, um die einführend aufgeworfene Frage zu beantworten, wie aus einzelnen natürlichen Zahlen und ihrer Eigenschaft, dass jede Zahl einen Nachfolger hat, auf die Menge der natürlichen Zahlen geschlossen werden kann. Die Menge der natürlichen Zahlen referenziert alles, was zählbar ist. – Die Referenzmenge eines Namens ist alles, was mit diesem Namen bezeichnet werden kann.

Heidegger macht darauf aufmerksam, dass der Name nicht willkürlich vergeben werden kann, sondern dass sich das Denken der Sache gegenüber in eine Position bringen muss, in der es die Sache hören und deren ‘Kundgabe’ verstehen kann. Mit ‘Kundgabe’ wählt Heidegger einen Begriff, der wie ‘Anfang’ oder ‘Messung’ sowohl einen Vorgang (das ‘Kundgeben’) wie das Ergebnis dieses Vorgangs (den Inhalt der Kundgabe) bedeuten kann. Er übersetzt daher in seiner Deutung von Aristoteles Met. 1046 b 7-15 und b 15-22 den Ausdruck logos bewußt doppeldeutig sowohl als Kundgabe wie als Kunde (Heidegger, S. 134ff und S. 149) und fasst damit, dass der Name die Kundgabe der Sache verstanden und als Kunde formuliert hat.

Der Name (die Kunde) darf nicht verwechselt werden mit der Sache, die kundgibt, einen Namen erhält und dann den Namen trägt. Nur in einem übertragenen Sinn wird der Name seinerseits zu einer Sache, wenn so wie hier über den Namen nachgedacht wird, also der Name zum Gegenstand des Denkens wird. Es geht um diese Selbstreferentialität des Namens, der auf eine Sache zurückgeht, auf sie verweist und seinerseits Sache des Denkens werden kann, wodurch er das schließende Denken ermöglicht.

Wenn Eltern ihren Kindern einen Namen geben, kann das nicht einfach ein willkürlicher Akt sein, sondern sie horchen bereits auf das Wesen, dessen Ankunft in die Welt bevorsteht, verstehen es und geben ihm seinen Namen. Diese Fähigkeit ist von einer größeren Macht getragen, die den jeweiligen Eltern ihre Macht der Namensvergabe verleiht. Das kann in religiöser Deutung eine göttliche Macht sein oder in materialistischer Deutung die für den Menschen charakteristische Macht seiner Menschlichkeit. Algorithmen, Schlussketten oder mechanische Schlussweisen unterscheiden sich dadurch vom Menschen, dass sie nicht über eine solche Macht verfügen. Ein Algorithmus kann keine Namen bilden, sondern nur nach einem Zufallsprinzip aus einer vorgegebenen Zeichenmenge eine willkürliche Zeichenfolge erzeugen, die als Name gilt.

An diesem Punkt vollendet sich die Unterscheidung von analytischer und dialektischer Philosophie:

»Die methodologische Operation besteht hier also darin, etwa in ‘G’ ⊩ ‘P’ den Subjektterminus P als den 'bekannten Wert' zum Standard zu erheben und das Wort G als einen Namen zu verstehen, der denselben Wert bezeichnet. In der metaphysischen Entgleisung des Erkennens passiert an dieser Stelle regelmäßig das Unglück, den Wert (d. i. das Abstraktum) mit dem sinnlichen Gegenstand zu verwechseln. Ein Naturgegenstand oder eine Natureigenschaft (eine Verhaltensart oder Reaktionsweise) ist nicht an sich ein Wert, sondern infolge seiner oder ihrer positiven Bedeutung für die Wertenden. In Bezug auf unsere Bedürfnisse werden Naturgegenstände zu Wertträgern!« (P, S. 24 mit Anpassung an die hier gewählte formale Schreibweise)

Das von Ruben genannte Unglück besteht darin, dass die Gesamtheit verwechselt wird mit dem einzelnen Element, mit dessen Eigennamen sie bezeichnet wird. Wenn alles Stoffliche von einem bestimmten Stofflichen, dem Stoff, seinen Namen bekommen hat, kann daraus der Irrtum entstehen, die Gesamtheit des Stofflichen sei ihrerseits wieder eine eigene Entität wie die einzelnen Stoffe. Im Beispiel der Mathematik bedeutet das, dass das Zählbare, das ist die Gesamtheit alles dessen, was gezählt werden kann, formal auf die gleiche Weise betrachtet werden soll wie eine Zahl, die gezählt wurde. Wenn das versucht wird, sind die Paradoxien der Mengenlehre unausweichlich.

An dieser Schlüsselstelle entscheidet sich Ruben mit Frege gegen Hegel, wenn er von Frege die Einsicht übernimmt, dass – so wie in dem vorliegenden Text die lesbaren Buchstaben G und E – die Zeichen von Gesamtheiten ihrerseits sinnlich sein müssen und nicht wie Hegel angenommen hat unsinnlich.

»'Wir würden uns ohne Zeichen auch schwerlich zum begrifflichen Denken erheben. Indem wir nämlich verschiedenen, aber ähnlichen Dingen dasselbe Zeichen geben, bezeichnen wir eigentlich nicht mehr das einzelne Ding, sondern das ihnen Gemeinsame, den Begriff. Und diesen gewinnen wir erst dadurch, dass wir ihn bezeichnen; denn da er an sich unanschaulich ist, bedarf er eines anschaulichen Vertreters, um uns erscheinen zu können. So erschließt uns das Sinnliche die Welt des Unsinnlichen.' (G. Frege: Über die wissenschaftliche Berechtigung einer Begriffsschrift. In: G. Frege: Funktion, Begriff, Bedeutung, Göttingen 1962. S. 90) Der so gemeinte 'Begriff' ist eben der, der durch Abstraktion gewonnen wird, die ja - unter vorausgesetzter Ähnlichkeitsbeziehung (Äquivalenzrelation) - die Zusammenfassung von Objekten in Bezug auf eine Eigenschaft (das ihnen Gemeinsame) ist. Frege hat hier übrigens mit tiefer dialektischer Einsicht das abstrakte Denken erfasst. Die Benutzung des Sinnlichen, um das Unsinnliche zu beherrschen - dies ist eine Erkenntnis, zu der Hegel leider gar keine Beziehung fand.« (Ruben 1966, S. 16)

– Der Begriff des Schlusses und der Schluss des Begriffs

Die von Hegel erarbeitete Wissenschaft der Logik enthält einen weiteren Selbstbezug: Es wird nicht nur in Sätzen entwickelt, was ein Satz, ein Urteil und ein Schluss ist, und es wird nicht nur innerhalb der Schlüsse nochmals ein Schluss gezogen, der von den einzelnen Schlüssen zur Sprache als dem allgemeinen Medium aller Schlüsse führt, sondern der Philosophie gelingt in dem Maße das schließende Denken, wie sie zeigt, dass der Schluss nur aus einem Schluss entstehen kann, sich also selbst als Sache enthält.

Auf die Einheit von Sache und Gedanke in der Wissenschaft der Logik hat vor allem Urs Richli aufmerksam gemacht. So trifft der Begriff ‘Anderes’ sowohl die Sache, was das Andere ist (die Sache des Anderen), das dem Etwas gegenübersteht, als auch das Andere des Begriffs (wenn Hegel sagt, »die physische Natur; sie ist das Andere des Geistes«, HW 5.127, zitiert bei Richli 1993, S. 144). Der Begriff des Anderen ist das Andere des Begriffs. Auf ähnliche Weise ist zu fragen, wie der Begriff des Schlusses zu verstehen ist als Schluss des Begriffes.

Die Begriffe des Anderen, des Namen und des Schlusses sind auseinander zu entwickeln. Der Satz ›S ist p‹, der bei Ruben als Position am Anfang der von ihm ausgeführten dialektischen Triade der Prädikation steht (P, S. 25), geht seinerseits auf die Daseinsanalyse zurück, mit der ein Daseiendes durch seine Qualitäten bestimmt wird. Jede Bestimmung beschreibt eine Qualität, jede Qualität ist eine Bestimmung. Sätze wie ›S ist p‹ können nur gebildet werden, wenn sie sich auf Etwas beziehen, das mit S bezeichnet wird, und das über Eigenschaften verfügt, die mit P bezeichnet werden. (Siehe zur Daseinslogik weiterführend den Arbeitstext Antinomien des Daseins und der Unendlichkeit.)

Jedes Etwas ist zunächst innerhalb seiner Grenzen endlich. Es hat eine Realität, die sich aus der Gesamtheit seiner Eigenschaften ergibt, und wodurch es sich unterscheidet von allen anderen Etwasen. Mit den Eigenschaften ist auf doppelte Weise eine Abgrenzung gegeben: Zunächst ist mit jeder Eigenschaft bestimmt, dass das Etwas anders ist alle anderen Etwase, die diese Eigenschaft nicht teilen. Was blau ist, ist nicht gelb, was im Norden liegt, liegt nicht im Süden. Mit dem Blauen ist das Etwas abgegrenzt von Anderem, das andere Farben hat oder farblos ist. Was im Norden liegt ist abgegrenzt von allem anderen, das in anderen Himmelsrichtungen liegt oder keinen geographischen Ort hat. Doch Hegel entwickelt einen Gedanken, der wesentlich darüber hinaus geht: Er differenziert nochmals den Begriff Eigenschaft in Beschaffenheit und Eigenschaft. Jede Beschaffenheit, die Etwas in seiner Realität hat, verfehlt die Eigenschaft, die es gemäß seiner Idealität haben könnte. Es ist anders beschaffen, als seiner Eigenschaft entsprechen würde. Diese Differenz erkennen zu können ist für Hegel die wahre Aufgabe der Philosophie. Sie vermag aus der unvollkommenen Beschaffenheit von Etwas auf die darin verborgene Idealität zu schließen.

Nach meinem Verständnis greift Hegel die aristotelische Unterscheidung zwischen Form und Natur auf. Wenn ich etwas vor mir sehe, kann ich an seiner Form untersuchen, welche Beschaffenheit es hat. Dann kann ich fragen, ob diese Beschaffenheit seiner Natur entspricht. So ist es möglich, dass etwas aufgrund äußerer Einflüsse anders beschaffen ist als es von Natur aus sein könnte. Eine Pflanze kann in ungünstigem Gelände wachsen und dort eine Gestalt ausbilden, die nicht ihrer Natur entspricht und verschiedene Möglichkeiten, die in ihr enthalten sind, verkümmern lassen. Jedem Etwas fehlt in seiner Realität etwas. Aristoteles bezeichnet dies Fehlen als steresis (siehe dazu den Aristoteles-Kommentar Steresis - eine Lehre des Fehlenden und Neinsagens).

"So oder anders beschaffen, ist Etwas nicht als in sich seyend, sondern als in äusserem Einfluß und Verhältnisse begriffen. Diese Bestimmtheit, die ihm zwar angehört, ist vielmehr sein Andersseyn, aber insofern es an ihm ist. Die äusserliche Beziehung, von der die Beschaffenheit abhängt, und das Bestimmtwerden durch ein Anderes erscheint als etwas Zufälliges, weil es als ein Anderes, Äusserliches erscheint. Aber das Etwas besteht darin, dieser Äusserlichkeit preisgegeben zu seyn, und eine  Beschaffenheit  zu haben." (Hegel, WdL 1812, S. 67, vgl. HW 5.133f)

Es geht Hegel um den  Schluss von der Beschaffenheit auf die Natur. Da alle vorhandenen Etwase immer in Umgebung mit etwas Anderem bestehen, kann keins von ihnen völlig frei seine Natur entwickeln. Bei jedem Etwas enthält seine Beschaffenheit einen Kompromiss zwischen seiner Natur und der Natur des Anderen.

Der Begriff ist die Erkenntnis der Natur einer Sache, die sich in dessen Realität nicht direkt zeigt, aber aus ihr geschlossen werden kann. Und der Begriff muss sich an dieser entscheidenden Stelle damit bescheiden, dass auch er die Natur einer Sache ebensowenig in ihrer vollen Idealität erfassen kann, wie das Etwas in seinem Sein niemals in volle Übereinstimmung mit seiner Idealität gelangen kann. Wenn Hegel gleichermaßen den Gedanken entwickelt, dass die Philosophie das Vermögen ist, von Etwas in seiner Unvollkommenheit auf die darin verborgene Idealität seiner Natur zu schließen und zugleich die Natur als das Andere des Geistes ansieht, ist damit sowohl die Größe wie die Grenze des Geistes beschrieben. Die Philosophie kann diese Differenz erkennen, und muss zugleich erkennen, dass sie sie immer verfehlen wird. (Anmerkung 1: Ob Hegel diesen Gedanken konsequent durchgehalten hat und an anderer Stelle nicht doch der Meinung war, das Denken könne das Absolute ergreifen und sich an die Stelle des Absoluten setzen, ist eine andere Frage.) (Anmerkung 2: Diese Interpretation Hegels unterscheidet sich weit von anderen Interpreten. So versteht z.B. Liebrucks Hegels Äußerung über die Natur als das Andere des Geistes nicht in dem hier vorgetragenen Sinne, dass der Geist zwar auf die Natur verweisen, aber sie immer verfehlen wird, sondern sagt umgekehrt, »Denken scheint dem Chaos erst logisch abgewonnen werden zu müssen«, Liebrucks, Bd. 6.1, S. 338. Für ihn ist die Natur in dem Sinne das Andere des Geistes, als der Geist sich von ihr als dem Chaos lösen muss. Er sieht daher Hegel in der Tradition von Platon und nicht von Aristoteles.) (Anmerkung 3: Wenn steresis mit “Mangel” übersetzt wird, kann das Missverständnis entstehen, dass das Fehlende ein fehlendes Teil ist, ein fehlendes Etwas, das einfach hinzugefügt werden muss, um den Mangel zu beseitigen. Wenn in der Suppe das Salz fehlt, ist nachzuwürzen. Dies Missverständnis hält Liebrucks der vorkantschen Metaphysik vor und entwickelt in Kritik daran einen Begriff der Negation, der die Verbindung zur aristotelischen steresis bewusst aufgibt; ebd., S. 322.)

Zum einen stehen jedem Etwas andere Etwase als das Andere gegenüber. Zugleich enthält jedes Etwas das Andere  an sich selbst  als seine Natur, die es in seiner Realität nicht ist, und die daher ihm gegenüber ebenfalls immer etwas Anderes bleibt, auf das hin es angelegt ist. Aristoteles bezeichnete diese Spannung von der Realität zur vollen Ausbildung der eigenen Natur als entelecheia. Das übernimmt Hegel. Der Übergang zur Unendlichkeit ist nicht, dass die vielen einzelnen Etwase in ihrer unendlichen Vielfalt zusammengezählt werden, sondern dass jedes auf die in ihm enthaltene Natur verweist. Die Fähigkeit einer solchen Philosophie kann auch als Liebe zu den Dingen bezeichnet werden, die selbst im Geringsten unter ihnen die darin verborgene Vollkommenheit zu sehen vermag. Die Phänomenologie nach Hegel ging einen Schritt weiter und fragte, was es an den Dingen ist, damit ihre innere Unendlichkeit an ihnen erkannt werden kann, obwohl sie diese in ihrer Realität verfehlen. Das ist ihr inneres Leuchten, ihr Er-Scheinen, das Sich-Zeigen, das phainómenon in seiner ursprünglichen Bedeutung.

Dieser Übergang kann nur im Namen vollzogen werden. Der Name einer Sache benennt das, was sie in ihrer Realität, in ihrer Beschaffenheit nie vollständig ist. (Hier übernimmt nach meinem Verständnis Hegel die Kritik von Aristoteles an Platon. Die Idealität ist nicht ein eigenes Etwas, auf das hin sich das noch unvollständige Etwas entwickeln soll und an dem es gemessen werden kann, sondern als Name ist es etwas, das nur mithilfe der Philosophie im Denken gebildet wird.) Wenn mit Ruben die Aufzählung aller Prädikate eines Subjekts oder aller Subjekte, die ein gemeinsames Prädikat haben, als reduzierter Satz bezeichnet wird, der nun seinerseits negiert wird, dann ist damit dieser Übergang gemeint, den Hegel bereits im Verhältnis von Etwas und Anderem, von Endlichkeit und Unendlichkeit angelegt hat. Erst wird das Etwas durch die unendliche Gesamtheit der Anderen negiert, die ihm äußerlich sind und ihm gegenüberstehen, und dann wird diese Gesamtheit wiederum negiert durch die innere Unendlichkeit, die das Andere an etwas selbst ist gegenüber dessen Endlichkeit.

Und nun zeigt sich, dass der Schluss, vom Begriff über das Urteil auf den Schluss zu schließen, der Begriff des Schlusses ist. Das soll in drei Schritten skizziert werden.

(a) Schluss von der Beschaffenheit zur Unendlichkeit

»Es ist also  die  Beschaffenheit als solche, die sich verändert; nicht  eine  Beschaffenheit, so daß die Beschaffenheit als solche bliebe; daher muß nicht sowohl gesagt werden, daß sie sich verändert, sondern ist selbst die Veränderung.« (Hegel, WdL 1812, S. 71, Hervorhebung bei Hegel, zitiert bei Richli 1993, S. 148)

Wenn etwas in der Realität anders beschaffen ist als es seiner Natur entspricht, muss es eine Sphäre geben, in der die reelle und die ideelle Beschaffenheit miteinander verglichen werden können. Wenn etwas zum Beispiel eine andere Farbe hat als seiner Natur entspricht, ist es die Sphäre der Farbe, in der diese beiden Beschaffenheiten miteinander verglichen werden können. Der Übergang von der einzelnen jeweiligen Beschaffenheit zu ihrer Sphäre ist für Hegel der Übergang vom Endlichen zum Unendlichen, da die Sphäre unendlich viele verschiedene Möglichkeiten für die Beschaffenheit enthält. Wenn gefragt wird, warum das so ist, ist nach meiner Überzeugung letztlich auf das Argument von Kant zurückzukommen, dass das Reale vor aller Unterscheidung in einzelne Qualitäten und Quantitäten über Kontinuität und Intensität verfügen muss (Kant, KrV, B 218). Jede Eigenschaft von Etwas ist als eine Sphäre zu verstehen, innerhalb derer die verschiedenen Möglichkeiten unterschieden werden können, welche Beschaffenheit es angenommen hat, welche es annehmen kann und welche Beschaffenheit seiner Natur entspricht.

Hegel geht es jedoch um einen weiteren Gedanken. Der Übergang von der vorliegenden Beschaffenheit zur Sphäre aller Ausprägungen, die diese Beschaffenheit annehmen kann, d.h. zu allen anderen möglichen Beschaffenheiten, kann als Negation der vorliegenden Beschaffenheit verstanden werden, die Schritt für Schritt alle anderen Möglichkeiten aufzählt. Doch ist auch diese Negation wiederum zu negieren. Wenn die Beschaffenheit von Etwas in seiner Realität unterschieden wird von der Eigenschaft, die es seiner Natur nach ist, heißt das nicht, dass es ein Standardobjekt gibt, dessen Beschaffenheit mit seiner Natur übereinstimmt und an dem das vorliegende Etwas gemessen werden kann. Die Natur von Etwas hat nicht ihrerseits eine eigene Realität, sondern besteht nur in Gedanken, ist Idealität, und wurde erschlossen mit dem Schluss von der Beschaffenheit auf die Natur.

Wenn daher die in der Realität gegebene Beschaffenheit verglichen wird mit der in der Idealität genannten Eigenschaft, hat sich verändert, was mit Beschaffenheit gemeint ist. Einmal ist die Beschaffenheit gemeint, wie sie in der Realität vorgefunden wird. Das andere Mal ist die Beschaffenheit gemeint, wie sie der Natur des Etwas entspricht, aber nur in Gedanken gebildet werden kann. Diese zweite Beschaffenheit ist in gewisser Weise eine Beschaffenheit des Denkenden, der in dem Etwas etwas anderes sehen kann als ihm die äußeren Sinne zeigen. So verstehe ich Hegels Aussage, dass sich bei bei diesem Übergang von Realität in Idealität nicht nur  eine  Beschaffenheit ändert (wenn zum Beispiel erkannt wird, dass etwas von Natur aus rot sein könnte, obwohl es in der vorliegenden Realität grün ist), sondern dass sich  die  Beschaffenheit ändert, weil es sich zum einen um eine Beschaffenheit in der Realität und zum anderen um eine Beschaffenheit im Gedanken, der auf die Natur des Etwas geschlossen hat, handelt. – Es gibt nicht neben den Sachen Doppelgänger, die ihre Natur zeigen, sondern ihre Natur ist das in ihnen enthaltene innere Telos in dem Sinn, wie Aristoteles von der entelecheia sprach. Es besteht nur in der Idee, es ist keine andere reelle Farbe, mit der die vorliegende reelle Farbe verglichen werden könnte. Vielleicht kann gesagt werden, dass es sich um Poesie handelt. Hegel bringt es kurz und knapp auf den Punkt, wenn er sagt, »die Idealität kann die Qualität der Unendlichkeit genannt werden« (HW 5.166). Er übersetzt damit nochmals den Gedanken von Aristoteles auf einen verwandten Gedanken von Spinoza: Statt von einer vorliegenden Beschaffenheit auf ihre Natur zu schließen, wird sie im Sinne von Spinoza sub specie aeternitatis (unter dem Gesichtspunkt der Ewigkeit) betrachtet.

Anmerkung: Die Frage der Beschaffenheit kann auch von einem systematischen Gesichtspunkt aus betrachtet werden: Wenn das reine Sein und das Dasein voneinander unterschieden werden, kann das Dasein auf selbstbezügliche Weise definiert werden, dass es die Beschaffenheit hat, Beschaffenheiten zu haben. Am reinen Sein lassen sich keine Beschaffenheiten bestimmen. Sowie Etwas vorliegt, dessen Beschaffenheiten erkannt werden können, handelt es sich um ein Etwas, das nicht mehr reines Sein ist. Und erst wenn Etwas vorliegt, das auf irgendeine Weise beschaffen ist, kann es sich verändern. Es gehört zur Beschaffenheit der Beschaffenheit, dass es sich ändern kann. Was völlig unveränderbar ist, kann nicht als Beschaffenheit bezeichnet werden. Nur bei einem Dasein, das sich verändern kann, lassen sich seine Realität und seine Idealität, seine Form und seine Natur voneinander unterscheiden. (Dieser Gedanke ergab sich aus einem Gespräch mit Urs Richli über sein Verständnis der Beschaffenheit.)

(b) Subjekt und Prädikat als Namen

Wenn das Argument von Aristoteles ernst genommen wird, dass die Natur von etwas nicht als eigenständige Idee neben dem Etwas besteht, sondern nur im Denken, ist die Frage zu stellen, wie dieses Denken beschaffen ist, mit dem das gedacht werden kann. Das Argument von Realität und Idealität gilt auch gegenüber dem Denken. Das Denken, das wir vorfinden, trägt auf vergleichbare Weise eine Beschaffenheit an sich, die von der Natur des Denkens zu unterscheiden ist und auf sie verweist. Das gewöhnliche, Verstandes- oder analytische Denken ist das Denken, wie jeder spontan denkt. Es geht nicht darum, ihm gegenüber eine Elite des Denkens abzuheben, die vergleichbar wäre den platonischen Ideen, die den mit Materie und Vergänglichkeit behafteten Dingen gegenüberstehen. Sondern auch das Denken ist als eine Sache zu verstehen, deren Beschaffenheit untersucht wird, um an ihr zu erkennen, wie sie ihre eigene Natur zwar verfehlt, aber als das Andere an ihr selbst enthält.

Wenn auf diese Weise die Beschaffenheit des Denkens untersucht werden soll, scheint sich alles zu wiederholen. Auf den ersten Blick scheint es immer dasselbe zu sein, wenn in der Daseinsanalyse zwischen dem Etwas und dem Anderen und den sie unterscheidenden Eigenschaften, in der Reflexionsanalyse zwischen Identität und Unterschied und schließlich in der Begriffsanalyse zwischen dem Subjekt und seinen Prädikaten unterschieden wird. Diese Wiederholung lässt sich nicht vermeiden, da es kein Denken gibt, das unabhängig von dem gedacht werden kann, was es denkt. Um die Beschaffenheit des Denkens zu verstehen, ist zu verstehen, wie es die von ihm gedachten Inhalte denkt. Daher müssen bei Untersuchung der Beschaffenheit des Denkens alle Inhalte neu aufgenommen werden, über die gedacht wird.

An der Stelle, an der Hegel in der Wissenschaft der Logik die Beschaffenheit des Denkens untersucht, trifft er jedoch eine wichtige Unterscheidung. Hier wird nicht mehr vom Etwas, sondern von  Namen  gesprochen. Um beim Denken eine vergleichbare Unterscheidung herausarbeiten zu können, wie sie beim Etwas zwischen dessen Beschaffenheit und seiner Natur besteht, ist zu untersuchen, wie das Denken mit Namen operiert.

»Es ist daher passend und Bedürfnis, für die Urteilsbestimmungen diese Namen, Subjekt und Prädikat, zu haben; als Namen sind sie etwas Unbestimmtes, das erst noch seine Bestimmungen erhalten soll; und mehr als Namen sind sie daher nicht.« (6.302)

Hegel ist gezwungen, für seine Untersuchung des Denkens fortlaufend Beispiele des Denkens heranzuziehen, die sich auf Etwase und deren Eigenschaften beziehen, weil sich das Denken nicht anders als mit solchen Beispielen beschreiben lässt. Daher kehrt auf den ersten Blick alles wieder. In der Urteilslehre werden die bereits in der Daseinsanalyse untersuchten Beispiele wie die Farbe Blau eines Etwas und so weiter neu aufgenommen. Es kann daher so scheinen, als wären Daseinsanalyse und Urteilslehre im Grunde identisch.

Doch geht es Hegel in der Urteilslehre nicht mehr um die Etwase, sondern um deren Namen, mit denen sie im Urteil aufgenommen werden. Das Subjekt und das Prädikat sind Namen, die auf Etwase und ihre Eigenschaften verweisen, aber nicht diese selbst. Hegel fragt in der Urteilslehre nicht nach der Beschaffenheit der Etwase, sondern nach der Beschaffenheit des Denkens, das mit den Namen von etwas an und über dieses denkt. Er will in der Urteilslehre nicht zeigen, wie die Etwase beschaffen sind und welche Natur sie haben, sondern wie das Denken beschaffen ist, was sich darin zeigt, wie es mit Subjekten und Prädikaten urteilt. An seinem Umgang mit den Namen soll gezeigt werden, dass das Denken zunächst so beschaffen ist, die von ihm gebrauchten Namen gleichzusetzen mit den von ihnen bezeichneten Etwasen. Das Denken ist so beschaffen, dass es zunächst nicht erkennt, dass es nur mit Namen operiert. Aber von seiner Natur her kann es nicht anders, als mit Namen zu operieren. Es ist daher an der Urteilsbildung (der Prädikation) zu zeigen, wie dessen Natur in der Namensbildung besteht, auch wenn das Denken so beschaffen ist, dies nicht unmittelbar zu erkennen.

So wie in der Daseinsanalyse unterschieden wurde zwischen der Beschaffenheit und der Idealität, so wird in der Urteilslehre unterschieden zwischen Urteilen des Daseins und Urteilen des Begriffs. Urteile des Daseins sind die protokollarischen Sätze, die das analytische Denken charakterisieren, wie ›diese Osterglocke ist gelb‹ oder ›heute ist Montag, der 30. März 2015‹. Das Denken ist so beschaffen, dass es mit Urteilen dieser Art anheben muss. Es gibt kein geheimes Denken, das hiervon unabhängig und einer Gemeinde von Eingeweihten vorbehalten ist, die zu spekulieren vermögen, wo die anderen bei bloßen Protokollen, Reflexionen, Meinungen (doxa) oder Räsonnements stehen bleiben und nicht weiter können. Auch hier folgt Hegel der Kritik von Aristoteles an Platon. Platon hat konsequent nicht nur die Existenz eines selbständigen Reiches der Ideen vertreten, sondern auch die Existenz einer hermetischen Lehre. Beides wurde von Aristoteles kritisiert. Aristoteles warf den Sophisten nicht vor, dass sie über keine geheime Lehre verfügen oder diese verraten oder verfälschen, sondern dass sie mit Benutzung falscher Namen und falscher Verweise von Namen auf Sachen oder untereinander rhetorisch ihre Gegner täuschen und von Urteilen überzeugen wollen, die in den ausgesagten Worten nicht oder anders enthalten sind.

Da es Hegel der Sache nach darum geht,  innerhalb  des gewöhnlichen, analytischen Denkens dessen wahre Natur zu erkennen, die dem gewöhnlichen Denken ebenso verborgen ist, wie die Natur der Etwase der rein sinnlichen Wahrnehmung, die nur deren Beschaffenheit sieht und nicht deren Natur, lässt sich kaum das Missverständnis vermeiden, als wolle Hegel wie Platon ein Denken entwickeln, dass in seiner Unterscheidung vom gewöhnlichen Denken elitär und nur Eingeweihten einsichtig ist. Die Sache selbst erfordert, dass dieser Schein entstehen musste, dem sowohl viele Hegelianer wie auch viele Kritiker an Hegel erlegen sind. Sie wollen entweder Hegel in seinem vermeintlichen elitären Denken folgen, oder werfen ihm dieses vor. Es scheint mir eine müßige Frage zu sein, ob Hegel absichtlich dazu beigetragen hat. Letztlich gilt auch für ihn, dass die Beschaffenheit seines Denkens unter äußeren Einflüssen stand und ihre eigene Natur verfehlen mußte, jedoch zugleich an sich trägt. – Angesichts dessen drängt sich die Frage auf, »ob Hegel mit der Anweisung, die Kategorien an ihnen selbst zu betrachten, nicht die Kapazität des endlichen Denkens überfordert« (Richli 1993, S. 145). Auch Hegel kann nicht anders, als so zu denken und ein solches Denken anzusprechen, wie das Denken beschaffen ist. Er kann nur versuchen, unter diesen Bedingungen die Idee verständlich zu machen, was das Denken von seiner Natur nach ist.

Genauer verstehe ich Hegels Urteilslehre so, dass Hegel an der Beschaffenheit des Denkens zeigen will, wie es aus sich heraus vom Urteil des Daseins übergeht zum Urteil des Begriffs und mit diesem zum Schluss. So wie in der Daseinsanalyse der Schluss von der Beschaffenheit zur Natur des Etwas gezogen werden sollte, ist hier der Schluss zu ziehen vom Urteil zum Schluss. Es ist zu verstehen, warum das analytische Denken, das nur Urteile des Daseins und keinen Schluss kennt, dennoch an sich selbst sein Anderes enthält, den Schluss. In diesem Sinn ist der Begriff des Schlusses der Schluss des Begriffs, der die Natur des Begriffs zeigt. So wie es in der Daseinsanalyse nicht möglich war, die Natur eines Etwas dem Etwas wie ein anderes Etwas gegenüber zu stellen, an dem es gemessen und mit dem es verglichen werden kann, und in das es idealerweise verändert werden könnte, so ist es hier nicht möglich, mit dem Schluss dem analytischen Denken ein anderes Denken gegenüberzustellen und damit die Aufforderung zu verbinden, dass die analytische Philosophie doch endlich anfangen sollte, auf diese Weise zu denken.

(c) Das Urteil des Begriffs

In der Urteilslehre scheint Hegel seine Methode zu verlassen. Er entwickelt das Urteil nicht wie alle anderen Begriffe in drei Schritten, sondern hält sich an die traditionelle vierteilige Urteilstafel, die die Urteile der Quantität, Qualität, Relation und Modalität unterscheidet. Offenbar will er das Denken in seiner Realität zeigen und an ihr darstellen, wie es von sich aus zum Schluss übergeht. Hegel tauscht entsprechend dem Aufbau seiner Seinslogik die Reihenfolge von Quantität und Qualität und spricht vom Urteil der Notwendigkeit statt vom Urteil der Relation und vom Urteil des Begriffs statt vom Urteil der Modalität, hält sich im Ganzen jedoch an die Tradition und entwirft in der Urteilslehre eine Abhandlung, die alle traditionell betrachteten Urteile enthält und ihnen gerecht wird.

Der kritische Punkt ist das Urteil der Modalität, ob etwas möglich, wirklich oder notwendig ist. Hier sieht Hegel innerhalb der Realität des gewöhnlichen Denkens die Frage verborgen, wie Beschaffenheit und Natur von etwas unterschieden werden können. Das gewöhnliche Denken erkennt, dass es nicht genügt zu urteilen, ob etwas möglich, wirklich bzw. notwendig ist, sondern dass jedes dieser Urteile zu verbinden ist mit einer Aussage über die jeweilige Beschaffenheit, warum etwas notwendig, wirklich oder nur möglich ist. Damit entsteht innerhalb des Urteils der Schluss. Die Beschaffenheit kann als der terminus medius verstanden werden, über den auf die Möglichkeit, Wirklichkeit oder Notwendigkeit geschlossen wird.

Hegel führt das an einfachen Beispielen vor. Wer mit einem assertorischen Urteil sagt, »dies Haus ist schlecht« (HW 6.346), sagt damit, dass es auch gut sein könnte. Es muss also eine bestimmte Beschaffenheit haben, weswegen es schlecht und nicht gut ist. Das zeigt sich noch deutlicher in dem darauf aufbauenden problematischen Urteil, das Haus ist gut oder schlecht »je nachdem es beschaffen ist« (HW 6.348), bis schließlich im apodiktischen Urteil direkt die Beschaffenheit als Grund angegeben wird »das Haus so und so beschaffen ist gut« (HW 6.349). Statt zu sagen ›das Haus ist gut‹, ist hier die Beschaffenheit ergänzt. »Durch diese Erfüllung der Kopula ist das Urteil zum Schlusse geworden« (HW 6.351). Es wird vom Haus über seine Beschaffenheit geschlossen, ob es gut oder schlecht ist.

Mit dem Urteil des Begriffs trifft Hegel wertende Urteile. Mit ihnen wird nicht nur über gut und schlecht, sondern auch über »wahr, schön, richtig usf.« geurteilt. Diese Urteile »drücken aus, daß die Sache an ihrem allgemeinen Begriffe als dem schlechthin vorausgesetzten Sollen gemessen und in Übereinstimmung mit demselben ist oder nicht« (HW 6.344).

Es ist Hegel wichtig, von innen heraus am Verstandesdenken zu zeigen, wie es auf den Schluss verweist. (i) Das Urteil der Qualität sind die üblichen Protokollsätze. (ii) Mit dem Urteil der Quantität kommt hinzu, dass eine gesamte Sphäre negiert werden kann, wenn zum Beispiel geurteilt wird, dass etwas nicht nur nicht-blau, sondern überhaupt keine Farbe hat, dass es nicht nur nicht im Norden liegt, sondern keinen geographischen Ort hat (wie z.B. die Hintergrundstrahlung des Universums). (iii) Das Urteil der Notwendigkeit schließt mit dem disjunktiven Urteil. Mit ihm werden innerhalb einer Sphäre die verschiedenen möglichen Ausprägungen aufgezählt, z.B. die unterschiedlichen Farben in der Sphäre der Farbe. Erst wenn innerhalb einer Sphäre verschiedene Ausprägungen unterschieden sind, kann geurteilt werden, welche von ihnen für ein bestimmtes Etwas möglich, wirklich oder notwendig ist.

(iv) Doch geht Hegel insofern über das Verstandesdenken hinaus, als er nicht eine beliebige Vielzahl von Urteilen der Modalität betrachtet (schön, gut, schlecht, wahr, usf.), sondern sie zusammenfassend als Urteil des Begriffs versteht, mit dem geurteilt wird, ob etwas seinem Begriff entspricht oder nicht. Für diese Urteil muss die Beschaffenheit herangezogen werden, womit Hegel zurückverweist auf die Ausführungen in der Daseinsanalyse über die Beschaffenheit und die Natur von etwas. So wie die Beschaffenheit in der Daseinsanalyse auf die Natur von Etwas verweist, verweisen die Urteile, die sich auf die Beschaffenheit beziehen, auf die Natur des Denkens, das im Schließen besteht.

Da Hegel dies sehr eng an der überlieferten Urteilstafel entwickelt, kommt möglicherweise nicht deutlich genug heraus, warum mit dem Urteil des Begriffs »das Urteil zum Schlusse geworden« ist und erst mit ihm »das Vernünftige« erreicht wird (HW 6.351). Es kann dem Verstand so scheinen, als habe er mit einer von ihm erkannten bestimmten Beschaffenheit einfach ein charakteristisches Merkmal getroffen, das allen Arten einer Gattung gemeinsam ist und wodurch die Gattung definiert wird (nach dem Muster »der Mensch ist Zweibeiner, nackt und ohne Federn«, so Platon ironisch in Politikos 261e-267c). So zu denken verfehlt zwar die Vernunft, aber es verweist auf die Natur des Denkens, den Begriff einer Sache zu erkennen. Damit schließt sich die Selbstbezüglichkeit: Wenn verstanden wird, was es heißt, von den positiven Urteilen über die Beschaffenheit von Etwas in mehreren Schritten überzugehen zum Schluss von der Beschaffenheit von Etwas auf dessen Natur, ist damit zu gleich verstanden, was es heißt, von der gewöhnlichen Beschaffenheit des Denkens überzugehen zur Natur des Denkens, die in dieser Fähigkeit besteht, den Schluss auf die Natur ziehen zu können.

Und so, wie sich die Beschaffenheit von Etwas wandelt, wenn übergegangen wird von der Realität zur Idealität und dort die Eigenschaft erkannt wird, die der Natur des Etwas entspricht, so wandeln sich auch die Urteile. Wenn Hegel schrittweise alle vier Arten der Urteile durchgeht, will er zugleich zeigen, wie auf diesem Weg nicht immer neue Urteile gefällt werden, sondern sich das Urteil selbst ändert vom Urteil des Daseins bis zum Urteil des Begriffs, mit dem es übergeht zum Schluss als der Natur des Urteils. Mit jedem Schritt auf diesem Weg verliert das Urteil etwas an Beliebigkeit und trifft die Sache immer besser, bis es in der Lage ist, deren Natur zu begreifen.

Das Wahrheitsmaß in der Gesamtheit der Sätze

Ist die Gesamtheit aller Sätze ein ähnliches System wie die Gesamtheit der physischen Körper oder der Waren, von denen die Mechanik bzw. die Ökonomie handeln? Das ist die abschließende These, auf die die Prädikationstheorie von Peter Ruben hinausläuft. So wie Längen an einer Standardlänge (dem Pariser Urmeter) in Metern und Waren an einer Standardware (Goldstandard) in einer gesellschaftlich vereinbarten Währung gemessen werden, sollte es möglich sein, Sätze an einem Standardsatz in einem für alle Sätze gültigen Maß zu "messen". Welche Vergleichs- und Bewertungsoperationen können für Sätze eingeführt werden, die dem Anlegen einer Länge an das Urmeter bzw. den Tauschoperationen der Warenökonomie entsprechen, mit denen der Wert (die Länge bzw. der Preis) von physischen Gegenständen und Waren bestimmt werden? Gibt es für die Gesamtheit der Sätze  Spielregeln, die den arithmetischen, geometrischen, mechanischen, ökonomischen etc. Systemen vorausgehen, die letztlich immer auf Sprache (Logik) angewiesen sind? Und reicht ein äußeres Maß aus, um Wahrheit nachzuweisen? Diese Fragen sind Gegenstand des folgenden Abschnitts, wobei Ideen von Hegel, Frege, Wittgenstein, der analytischen Philosophie und Ruben aufgenommen und mit dem neuen Entwurf mechanischer Systeme seit der Relativitätstheorie von Einstein zusammengeführt werden. Im Ergebnis soll die These vertreten werden, dass Wahrheit nicht einfach ein Prädikat ist, das an den jeweiligen Sätzen überprüft und nachgewiesen werden kann, sondern dass Sätze über eine innere Beschaffenheit verfügen müssen, durch die sie sich zu Gesamtheiten von Sätzen zusammenfügen lassen.

• Um Sätze zu bewerten, sind Sätze über Sätze zu bilden, mit denen Sätzen ein Wert zugewiesen wird. Ruben übernimmt von Frege den Gedanken, dass Sätze nach ihrem Wahrheitswert bewertet werden. Jeder Satz erhält das Prädikat ‘wahr’ oder ‘falsch’. Ein Satz gilt dann als wahr, wenn er in gleicher Weise wahr ist wie der Satz vom ausgeschlossenen Widerspruch ›S ist nicht zugleich p und nicht-p‹. Damit kann formal für Sätze über Sätze die dialektische Triade der Prädikation übernommen werden.
  
  
• Mit welchen Operationen kann nachgewiesen werden, dass ein Satz die gleiche Wahrheit hat wie der Satz vom Widerspruch? Ausgehend von den Wahrheitsoperationen, die Wittgenstein eingeführt hat, lässt sich formal ein rekursives Verfahren entwickeln, um innerhalb der Gesamtheit der Sätze die Geltung des Satzes vom Widerspruch sicherzustellen. Ein Satz ›S ist p‹ erfüllt den Satz vom Widerspruch, wenn sich zeigen lässt, dass er sich in einer Gesamtheit von Sätzen befindet, in der es keinen gegenteiligen Satz ›S ist nicht-p‹ gibt. – Hierbei wird implizit angenommen, dass die Gesamtheit der Sätze dem jeweiligen historischen Wissensstand entspricht und fortlaufend erweitert wird.
  
  
• Wie ist eine Gesamtheit von Sätzen zu strukturieren, um in dieser Weise auf ihr Wahrheitsoperationen ausführen zu können? Die Gesamtheit kann additiv aus endlich vielen Elementarsätzen aufgebaut oder subtraktiv aus der unübersehbaren Fülle aller Sätze entworfen werden. Es soll gezeigt werden, dass die additive Methode nur begrenzte Entwicklungsmöglichkeiten bietet. Bei allen Neuerungen ist subtraktiv vorzugehen. Das erfordert jedoch ein zweites Wahrheitsmaß. Die subtraktiv gesetzten Sätze lassen sich nicht am Standardsatz ›S ist p oder nicht-p‹ messen.
  
  
• So ergeben sich unterschiedliche Modi für die Gesamtheit der Sätze. Sie können starr und gültig in eine vollständige Ordnung gebracht werden, oder sich in einer Art flüssigem Zustand befinden, in dem es sowohl stabile wie auch lockere Verknüpfungen von Sätzen gibt, die mal bestehen und sich auch wieder auflösen und neu formieren können, und schließlich Ordnungen, die der Ausrichtung von Teilchen in einem Magnetfeld ähneln. Ebenso können sich einzelne Sätze jeweils in verschiedenen Modi befinden und nicht nur den Status eines gewöhnlichen oder spekulativen Satzes annehmen, wovon Hegel sprach, sondern auch den Status eines empirischen, konstruierbaren oder intuitiven (metaphorischen) Satzes. Das erinnert im Ganzen an die verschiedenen Aggregatzustände des Wassers. Nach diesem Vorbild soll die Idee eines  realen Maßes der Sätze entwickelt werden: Das Maß der Sätze ist dann nicht mehr ein Standardsatz, an dem alle Sätze gemessen werden, sondern das innere Maß für die Verknüpfung von jeweils zwei Sätzen, das Maß ihrer Verwandtschaft.

Der Grundaufbau dieses Abschnitts ist in zweifacher Hinsicht an Hegels Wissenschaft der Logik orientiert. Es wird sowohl der Gedankengang aus seiner Urteilslehre übernommen, als auch die Entwicklung vom spezifizierenden zum realen Maß von seiner Maßlogik auf die Urteilslehre übertragen. (1) Die einzelnen Sätze ›S ist p‹ können als positive Urteile oder gleichbedeutend mit der analytischen Philosophie als Protokollsätze verstanden werden. Die Wahrheitsoperationen decken sich inhaltlich weitgehend mit den Urteilen der Relation (Kant), die Hegel als Urteile der Notwendigkeit bezeichnet, das sind das kategorische, hypothetische und disjunktive Urteil. Wenn mit ihrer Hilfe ein Urteil über einen Satz gelingt, handelt es sich nach Hegel um Urteile des Begriffs, womit er die Urteile der Modalität (Kant) erweitert (das assertorische, apodiktische und problematische Urteil, mit denen über Möglichkeit, Wirklichkeit und Notwendigkeit geurteilt wird). (2) Der von Ruben nahegelegte Vergleich der Wahrheitsfunktion mit einer Messung von Sätzen an einem Standardsatz kann innerhalb der Urteilslehre als ein spezifizierendes Maß verstanden werden, mithilfe dessen etwas äußerlich an einem Maß verglichen wird (vgl. HW 5.398ff). Hiervon ausgehend soll weiter gegangen werden zur Frage nach dem realen Maß der Sätze. Das ist das Maß ihrer inneren Verwandtschaft, nach der sie sich ordnen lassen, und das sind die verschiedenen Zustände, innerhalb derer die Verwandtschaften zu verstehen sind. Was Hegel in der Maßlogik über Zustände und Knotenlinien des Substrats entwickelt hat, soll übertragen werden auf Zustände und Wahrheits-Transformationen zwischen diesen Zuständen von Sätzen.

Von Frege wird der Gedanke übernommen, die Urteile der Relation zu vereinfachen auf Schlussketten und Fallunterscheidungen. Mit Wittgenstein werden einzelne Urteile verallgemeinert auf Wahrheitsoperationen, die sich auf die Gesamtheit von Sätzen beziehen. Als wesentliche Eigenschaft der Wahrheitsoperationen wird sich zeigen, dass sie auf logisch voneinander unabhängigen Fallunterscheidungen beruhen, die sich zu einem rekursiven Wahrheitsbaum (»Pythagorasbaum«) erweitern lassen. Mit Hegel wird gefragt, nach welchen Prinzipien die Fallunterscheidungen getroffen werden. Das sind nach dem anschaulichen Vorbild der Farben die Additivität und die Subtraktivität. Das Prinzip der Subtraktivität führt zu den Wahrheits-Transformationen, während die Wahrheitsoperationen als additiv verstanden werden.

Die Unterscheidung in Wahrheitsoperationen und Wahrheits-Transformationen ist von den mechanischen Operationen und Lorentz-Transformationen übernommen, wie sie von Einstein in der Relativitätstheorie entwickelt wurden, und wird hier übertragen auf die Theorie der Sätze. Das ist das Anliegen, mit dem in diesem Beitrag die vorhandenen Theorien von Hegel, Frege, Wittgenstein und Ruben weitergeführt werden sollen.

Während sich die analytischen Wahrheitsoperationen auf die logische Gewissheit des Satzes vom Widerspruch berufen können, ist die Macht, von der die Wahrheits-Transformationen getragen werden, vergleichbar der staatlichen Macht, die die Geldtransformationen garantiert bzw. der Macht des Lichtes, dessen Konstanz in allen Trägheitssystemen zu den Lorentz-Transformationen führt. Die Frage nach der Macht, die sich in den Wahrheits-Transformationen zeigt, führt weiter zum nächsten Beitrag über die Objektivität. Die Wahrheits-Transformationen können sich nach Hegel berufen auf die Macht der Offenbarung, die Macht der Sprache und die Macht der vom Denken eingesetzten Mittel. Das sind die drei Kapitel des Abschnitts über Objektivität in der Wissenschaft der Logik.

– Dialektische Triade der Urteile des Begriffs

Sätze, die andere Sätze in ihrer Wahrheit bewerten, sind im Sprachgebrauch von Hegel Urteile des Begriffs. Es handelt sich im übertragenen Sinn um Prädikationen, wobei hier ein Urteil über einen Satz gefällt und der Satz als Subjekt angenommen wird, dem ein Prädikat zugeschrieben wird. Jeder Satz soll entweder das Prädikat ‘wahr’ oder ‘falsch’ erhalten. Für Ruben gilt auch in diesem Fall die von ihm entwickelte dialektische Triade der Prädikationstheorie.

Inhalt, Gedanke Um das Wahrheitsmaß von Sätzen zu finden, übertrug Frege seine Unterscheidung von Sinn und Bedeutung bei Eigennamen auf Sätze. Während jedoch für ihn Eigennamen auf Gegenstände verweisen und letztlich der Gegenstand selbst als Bedeutung des Eigennamen angesehen werden kann, verweisen Sätze wieder auf Sätze. Es wäre naheliegend, als Bedeutung eines Satzes seinen Inhalt anzusehen, den mit ihm ausgesprochenen Gedanken. Dieser Gedanke ist jedoch wiederum ein Satz. (Heutzutage wird versucht, für Gedanken einen materiellen Träger im Muster von Gehirnaktivitäten nachzuweisen. Das führt in eine andere Fragerichtung und soll an dieser Stelle nicht weiter diskutiert werden.) Daher bezeichnet Frege den Gedanken nicht als die Bedeutung des Satzes, sondern er schreibt: »Der Gedanke ist der Sinn eines Satzes« (Frege, Gedanke, S.61). Vom Sinn unterscheidet er die Wahrheit. Die Bedeutung eines Satzes liegt für Frege nicht in ihrem Inhalt, sondern darin, ob er wahr oder falsch ist. Er vergleicht das mit der Schönheit in der Kunst, dem Guten in der Ethik und überraschenderweise mit der Wärme und der Schwere: Die Logik »verhält sich zur Wahrheit etwa so wie die Physik zur Schwere oder zur Wärme« (Frege, Gedanke, S. 58). Statt der Wärme ließe sich auch die Länge nennen, um das bisher genannte Beispiel aufzugreifen. Frege versteht daher als die Bedeutung von Sätzen ihren »Wahrheitswert« (Frege, Funktion und Begriff, S. 20ff).

Anmerkung 1: Es ist bisweilen nicht einfach, sich in der Ausdrucksweise von Frege zurecht zu finden. Wenn er vom Wahrheitswert eines Begriffs spricht (Frege, Begriff und Funktion, S. 15), kann das so klingen, als wäre der Wahrheitswert des Subjekts oder des Prädikats gemeint, die als Begriffe in einem Satz verknüpft werden. Doch versteht Frege hier unter einem Begriff eine Funktion, und unter einer Funktion die Verallgemeinerung einer mathematischen Funktion auf Sätze, siehe die bereits genannten Beispiele wie ›die Hauptstadt des x‹. Ich verstehe Frege daher so, dass mit dem Wahrheitswert von Begriffen der Wahrheitswert gemeint ist, wenn in Sätzen wie ›die Hauptstadt des x‹ ein bestimmtes Beispiel wie ›die Hauptstadt von Deutschland ist Berlin‹ eingesetzt ist und danach bewertet wird, ob der jeweilige Satz wahr oder falsch ist.

Anmerkung 2: Zufriedenstellend ist diese Lösung nicht, weil offensichtlich bei Eigennamen und Sätzen auf unterschiedliche Weise Sinn und Bedeutung bestimmt werden. Wittgenstein führte daher den Begriff des Sachverhalts ein, um wenigstens für Protokollsätze einen analogen Verweis auf eine Sache herstellen zu können wie er bei Eigennamen gegeben ist. »Der Satz stellt das Bestehen und Nichtbestehen der Sachverhalte dar« (TLP 4.1). Um zu verstehen, was ein Satz wie ›die Rose ist rot‹ bedeutet, ist auf den entsprechenden Sachverhalt zu verweisen. In späteren Werken musste Wittgenstein jedoch einsehen, dass sich auch der Sachverhalt wiederum nur in Worten beschreiben lässt. Siehe hierzu das bereits genannte Beispiel von Quine. Mit dem künstlich gebildeten Eigennamen “Gavagai” und Sätzen wie ›das ist Gavagai‹ hat Quine demonstriert, dass es nicht möglich ist, sprachliche Ausdrücke eindeutig auf Gegenstände oder Sachverhalte zu beziehen. Es ist unvermeidlich, erläuternde Worte oder ein implizites Sprachverständnis innerhalb der jeweiligen Sprachkultur hinzuzunehmen. Auch bei Eigennamen kann letztlich nicht der Gegenstand selbst als Bedeutung dienen, sondern nur ein hervorgehobener und allgemein akzeptierter Eigenname wie zum Beispiel ‘Venus’, der als Benennung des entsprechenden Planeten anerkannt ist.

Anmerkung 3: Puntel hat daher 1990 als Lösung vorgeschlagen, dass ein Satz nicht auf einen anderen Satz oder auf ein Objekt verweist, sondern auf das der Sprache vorausgehende Artikulierbare. Inhalt eines Satzes ist weder ein anderer Satz noch ein Objekt, sondern das Ausdrückbare, das mit ihm ausgedrückt werden soll. Beispiel: Um einen Satz wie ›die Rose ist rot‹ verstehen zu können, muss es eine nicht-sprachliche Proposition geben, die die Eigenschaft hat, dass sie sprachlich ausgedrückt werden kann. Es genügt nicht, dass ein Sachverhalt vorliegt, über den gesprochen wird, sondern es muss ein Sachverhalt sein, der von sich aus die Eigenschaft hat, dass er sich in Worte fassen lässt. Puntel bezeichnet es als Proposition mit der Eigenschaft der »Artikulierbarkeit, Erkennbarkeit, Darstellbarkeit, Interpretierbarkeit« oder »Intelligibilität« (Puntel 1990, S. 278). Die Proposition ist »eine nicht-sprachliche, aber sprachabhängige Entität« (Puntel 1990, S. 318). Sie ist nicht-sprachlich, da sie der Sprache vorausgeht, und sie ist dennoch sprachabhängig, weil für sie die Eigenschaft der Ausdrückbarkeit wesentlich ist, die auf Sprache verweist, auch wenn sie noch nicht Sprache ist.

Nach meinem Eindruck hat Puntel die Grundaussage der aristotelischen Kategorienlehre getroffen, die den einzelnen Kategorien vorausgeht und weiter oben als das »Wortbare« (das in Worten Fassbare) übersetzt wurde. Puntel sieht richtig, dass dies nicht die erste Kategorie der Substanz, des Objekts oder des Gegenstands ist. Diese Einsicht versteht er jedoch als Kritik an Aristoteles, was ihn dazu veranlasst, sich insgesamt von Aristoteles abzuwenden. Im Ergebnis stimme ich ihm jedoch zu, dass Wahrheit nicht in der Korrespondenz von Gegenständen und Worten besteht, sondern darin, ob es gelingt, für das sprachlich Ausdrückbare die treffenden Ausdrücke zu finden. Nur von einem solchen Ansatz aus wird es möglich sein, nicht nach der Wahrheit einzelner Sätze zu fragen, sondern nach der Wahrheit, die mit einer Vielzahl von Sätzen intendiert und nie abschließend formuliert werden kann. Dieser Ansatz soll im Abschnitt über Wahrheits-Transformationen weiter ausgeführt werden.

Beurteilbare Inhalte Doch lässt sich nicht für alle Sätze ein Wahrheitswert bestimmen. So wie das Längenmaß in Metern nur für solche physikalischen Objekte anwendbar ist, die sich an einem Standardobjekt wie dem Urmeter in Paris anlegen lassen – und daher eine starre, durchgehende, ebene Kante haben müssen –, so sind unter allen Sätzen diejenigen auszuwählen, die an einem Standardsatz gemessen werden können. Das sind die Sätze, für die entschieden werden kann, ob sie wahr oder falsch sind. Frege unterscheidet daher Kunstgenuss und Streben nach Wahrheit.

»Beim Anhören eines Epos z.B. fesseln uns neben dem Wohlklange der Sprache allein der Sinn der Sätze und die davon erweckten Vorstellungen und Gefühle. Mit der Frage nach der Wahrheit würden wir den Kunstgenuß verlassen und uns einer wissenschaftlichen Betrachtung zuwenden. Daher ist es uns auch gleichgültig, ob der Name 'Odysseus' z. B. eine Bedeutung habe, solange wir das Gedicht als Kunstwerk aufnehmen. Das Streben nach Wahrheit also ist es, was uns überall vom Sinn zur Bedeutung vorzudringen treibt. Wir haben gesehen, daß zu einem Satze immer dann eine Bedeutung zu suchen ist, wenn es auf die Bedeutung der Bestandteile ankommt; und das ist immer dann und nur dann der Fall, wenn wir nach dem Wahrheitswerte fragen. So werden wir dahin gedrängt, den Wahrheitswert eines Satzes als seine Bedeutung anzuerkennen.« (Frege, Sinn und Bedeutung, S. 33f)

Der Bereich des Kunstgenusses kann ausgeweitet werden auf Träume, Phantasien, Scherze oder der Unterhaltung dienende Sprachspiele. Frege schränkt sich demgegenüber bewusst auf wissenschaftliche Sätze oder protokollarische Sätze ein. Sie haben nur einen Wert, wenn sie wahr sind oder eine Vermutung aussprechen, die auch im Falle der Widerlegung indirekt eine Wahrheit gewinnen lässt. – Vorausschau: Im Weiteren wird diese strikte Trennung von Kunst und Wahrheit relativiert werden müssen. In dem Maße, wie wissenschaftliche Wahrheit Neuland betritt, muss sie ebenfalls kreativ sein und Methoden der künstlerischen Gestaltung zu nutzen wissen, die im ersten Schritt aus dem Bereich der beurteilbaren Inhalte ausgeschlossen wurden.

Innerhalb der Gesamtheit aller Sätze seien die beurteilbaren Inhalte mit bezeichnet.

Die beurteilbaren Inhalte können als Argument der Wahrheitsfunktion dienen. Mit der Wahrheitsfunktion wird jedem Satz entweder der Wahrheitswert ‘wahr’ oder ‘falsch’ zugeordnet. Andere Wahrheitswerte werden ausgeschlossen (Bivalenzprinzip, Wahrheit kennt nur zwei Werte). Beurteilbare Inhalte sind diejenigen Sätze, bei denen eine solche Entscheidung möglich ist. Für alle anderen Sätze lässt sich kein Wahrheitsmaß ermitteln.

Anmerkung: Wittgenstein hat das übernommen und fortgeführt. Er unterscheidet im Tractatus logico-philosophicus Elementarsätze (TLP 4.21) und aus ihnen zusammengesetzte Sätze. Über die Sätze schreibt er: »Der Satz ist eine Wahrheitsfunktion der Elementarsätze« (TLP 5). Auch diese Aussage kann zu Missverständnissen führen. Nicht jeder Satz ist eine Wahrheitsfunktion, sondern nur solche Sätze, die andere Sätze als wahr oder falsch bewerten. Hegel hat das nach meinem Verständnis eindeutiger beschrieben: Die von Wittgenstein genannten Elementarsätze entsprechen den positiven Urteilen und die Wahrheitsfunktion ist ein Beispiel für ein Urteil des Begriffs.

Der Satz des Widerspruchs als Standardsatz Ruben erkennt, dass Frege mit dem Wahrheitswert eine Wertung findet, die formal dem dritten Schritt der Triade der Prädikationstheorie entspricht. Daher ist ein »logisches Standardobjekt« (P, S. 30) zu suchen, das den Wahrheits-Wert w repräsentiert, an dem die Wahrheit aller anderen Sätze gemessen wird. Das ist der Satz ›S ist nicht zugleich p und nicht-p‹. Ein Satz gilt als als wahr, wenn er den gleichen Wahrheitswert hat wie der Satz ›S ist nicht zugleich p und nicht-p‹.

»Dieser Term hat logisch eine ganz ähnliche Bedeutung wie früher das Pariser Urmeter, das die Längeneinheit repräsentierte« (P, S. 30).

Dialektische Triade Mit diesen Vorbereitungen lassen sich die drei Schritte der dialektischen Triade auf die Gesamtheit aller beurteilbaren Inhalte übertragen:

(a) Satzbildung: ›B ist w‹ bzw. ›B ist f‹

lies: der beurteilbare Inhalt B ist wahr bzw. falsch
In der Wissenschaft der Logik von Hegel werden Sätze dieser Art als »Urteile des Begriffs« bezeichnet (HW 6.345ff)

(b) Terminusbildung: w ist die Gesamtheit aller beurteilbaren Inhalte, auf die das Prädikat w (wahr) zutrifft.

Diese Gesamtheit wird üblicherweise als Referenzmenge bezeichnet, auf der der Kalkül der formalen Logik definiert werden kann, als Gesamtheit aller positiven Sätze oder mit Wittgenstein als alles, was der Fall ist.

(c) Wertung: Der Satz des Widerspruchs wird als stellvertretender Satz für die Wertung ausgewählt.

Die Wertung lässt sich gemäß Formel (10b) aufschreiben:

(11)    ‘›S ist nicht zugleich p und nicht-p‹’ ⊩ ‘w’
         → [›S ist nicht zugleich p und nicht-p‹] ≡ [w]

lies: Der Name des Satzes ›S ist nicht zugleich p und nicht-p‹ ist gleich dem Namen der Gesamtheit aller beurteilbaren Sätze, die wahr sind.

– Wahrheitsoperation von Sätzen

Im Ergebnis ist mit der dialektischen Triade der Urteile des Begriffs ein Ansatz gefunden, um formal eine Theorie der Sätze entwickeln zu können, die der Mechanik oder Ökonomie entspricht. Welche Operation entspricht bei der Wahrheits-Beurteilung (der Wertung) von Sätzen der Tauschoperation in der Ökonomie oder der Operation der Messung einer Länge an einem Standardobjekt? Mit welchen Operationen ist es möglich, einen Satz am Standardsatz ›S ist nicht zugleich p und nicht-p‹ zu messen? Diese und die darauf aufbauenden Fragen werden nicht mehr von Ruben in seiner Prädikationstheorie behandelt. Der folgende Unterabschnitt ist in drei Teile gegliedert: (a) Fragestellung, (b) Wahrheitsoperationen nach Frege und Wittgenstein und Wahrheitsbaum, (c) Additivität und Subtraktivität

– – Fragestellung

Der einfachste Weg, um die Wahrheit eines Satzes zu prüfen, wäre seine empirische Bestätigung. Die Korrespondenztheorie wird häufig mit Tarski verbunden: »x(p) ist eine wahre Aussage dann und nur dann, wenn p« (Tarski, S. 268). Gegen diesen Ansatz wurde überzeugend eingewandt, dass es dann einen zweiten – den empirischen – Zugang zu den Sachverhalten geben müsste und eine Meta-Sprache, mit der ein Vergleich des Sachverhalts und des Satzes, der ihn formuliert, möglich ist. Auch für diesen zweiten Zugang wäre zu prüfen, ob er zutrifft oder nicht. Der Empirismus beansprucht jedoch für sich, die letzte und nicht mehr hinterfragbare Klärung eines Sachverhalts liefern zu können. Darin sieht Quine das zweite Dogma des Empirismus (Quine 1951, S. 27). Wird der Empirismus gefragt, worauf er sich beruft, dann ist es letztlich die Objektivität, die er nur durch ein empirisches »Zurück zu den Sachen selbst« gewährleistet sieht. Dieser Beitrag soll helfen, einen Weg zu einem tieferem Verständnis zu finden, was mit Objektivität gemeint ist.

Wenn die unmittelbare Berufung auf die Sache oder den Sachverhalt nicht möglich ist, kann gefragt werden, ob alle Protokollsätze wie ›diese Rose ist rot‹ auf ähnliche Weise in einer axiomatisierbaren Gesamtheit von Sätzen dargestellt werden können wie es für die Sätze der Geometrie gelingt (Kohärenztheorie der Wahrheit). In der Geometrie sind Axiome und Konstruktionsverfahren festgelegt, mit denen sich jeder Satz auf seine Wahrheit prüfen lässt. Ein Satz wie z.B. ›die Winkelsumme des Dreiecks ist 180°‹ gilt als wahr, wenn eine Konstruktion gefunden werden kann, die ihn aus den Axiomen herleitet. – Ähnlich werden in der Arithmetik alle Gleichungen mit den anerkannten Rechenformeln solange umgeformt, bis sie auf einen Widerspruch oder auf eine wahre Gleichung wie ›0 = 0‹ zurückgeführt werden können. Das gilt für Sätze wie ›3 · 7 = 21‹, den Frege als Beispiel für einen wahren Satz nennt (Begriffsschrift, § 5, S. 5f). – Der französische Mathematiker Galois konnte 1832 diese Vorgehensweise wesentlich erweitern. Innerhalb der euklidischen Geometrie war z.B. der Satz ›jeder Winkel ist mit Lineal und Zirkel in drei gleich große Teile teilbar‹ ungeklärt geblieben. Galois gelang es, statt eines Beweises die Eigenschaften zu bestimmen, die jeder mögliche Beweis enthalten muss, und dann zu zeigen, dass kein Beweis dieses Satzes die erforderlichen Eigenschaften erfüllen kann. Damit war gezeigt, dass dieser Satz falsch ist.

Erfolge dieser Art ermutigten die Philosophie, für alle Sätze eine Enzyklopädie zu entwickeln, mit der schrittweise die Gesamtheit aller Sätze mit ihren Subjekten und Prädikaten axiomatisch aufgebaut werden kann. Daran hatten bereits die Enzyklopädisten der Aufklärung gearbeitet und gehofft, mit einfachen algorithmischen Methoden in der Enzyklopädie navigieren zu können. An der Basis einer solchen Enzyklopädie sollte der Satz vom Widerspruch stehen.

Jede Enzyklopädie bleibt jedoch an den jeweiligen Wissensstand ihrer Zeit gebunden und droht dogmatisch zu werden. Systematisch stellt sich die Frage, wie es gelingen soll, aus logischen Axiomen wie dem Satz vom Widerspruch ›S ist nicht zugleich p und nicht-p‹ einen Satz wie ›die Rose ist rot‹ zu konstruieren. Der Satz vom Widerspruch lässt sich nur tautologisch übersetzen in Anwendungsbeispiele wie ›die Rose ist nicht zugleich rot und nicht-rot‹, doch aus der Logik kann kein Satz abgeleitet werden, der auf die sinnliche Wahrnehmung angewiesen ist. Laut Quine hat Carnap den »Gedanken an Übersetzbarkeit von Aussagen über die physikalische Welt in Aussagen über direkte Erfahrung fallen« lassen müssen, wobei Quine unter »Aussagen über die physikalische Welt« die Protokollsätze versteht und diese in Annäherung an die Physik nicht mehr mit ›S ist p‹, sondern mit ›die Qualität q ist an dem Punkt x;y;z;t‹ aufschreibt (Quine 1951, S. 45).

Daher bleibt nur umgekehrt die Möglichkeit, für jeden Protokollsatz wie ›die Rose ist rot‹ fortlaufend sicherzustellen, dass es nicht gleichzeitig einen anderen Protokollsatz gibt, der die gegenteilige Beobachtung ›die Rose ist nicht rot‹ beinhaltet. Im Folgenden wird ausgehend von Frege und Wittgenstein schrittweise die Idee eines rekursiven Wahrheitsbaums entwickelt, mit dem jeder neue Protokollsatz danach geprüft wird, ob er im Baum aller Protokollsätze mit einem gegenteiligen Satz kollidiert. Zwei Kollisionen sind möglich: Er kann im Widerspruch zu einem anderen Protokollsatz oder im Widerspruch zu den Eigenschaften einer übergeordneten Gattung stehen.

Wenn es zum Beispiel gegenüber dem Protokollsatz ›die Rose ist rot‹ einen weiteren Protokollsatz ›die Rose ist gelb‹ gibt, dann sind zwei Auflösungen möglich:

(1) Die Rose wird als Gattung verstanden, die in zwei Arten unterteilt wird, von denen die eine rot und die andere gelb ist. Das positve Urteile ›die Rost ist rot‹ muss abgeschwächt werden in ein disjunktives Urteil ›die Rose ist rot oder gelb‹. Wird nach der Unterscheidung zwischen diesen beiden Arten gefragt, handelt es sich um die Beschaffenheit, durch die die roten von den gelben Rosen unterschieden werden können (das ist im Kern das Argument von Hegel, für den das disjunktive Urteil zum Begriff der Beschaffenheit und dieser zum Schluss führt).

(2) Oder es werden zusätzliche Bedingungen gefunden, warum eine identische Rose einmal rot erscheint und ein anderes Mal gelb. Zum Beispiel kann sich zwischen der Rose und dem Auge oder dem Meßgerät ein Medium befinden, welches die Farbe ändert. Das ist ein hypothetisches Urteil: ›Wenn das Medium A vorliegt, sieht die Rose rot aus. Wenn das Medium B vorliegt, sieht sie gelb aus.‹

Oder der Protokollsatz kann eine Eigenschaft enthalten, die mit den Eigenschaften der Gattung kollidiert. Das geschieht zum Beispiel häufig in der Teilchenphysik, wenn bei der näheren Untersuchung bestimmter Teilchen festgestellt wird, dass sie Eigenschaften enthalten, die der Gattung widersprechen. So wurden Teilchen mit der Eigenschaft Antimaterie entdeckt, was nach dem herkömmlichen Verständnis der Gattung Teilchen widerspricht, oder Teilchen, bei denen eine Paritätsverletzung auftritt, wobei die Parität als eine wesentliche Eigenschaft der Teilchen angesehen worden war. In solchen Fällen muss rekursiv die Hierarchie der Gattungen neu strukturiert werden, um formal die Verletzung des Satzes vom Widerspruchs zu vermeiden. In diesem Beispiel muss es gelingen, an einer geeigneten Stelle zwischen Gattungen zu unterscheiden, die die Parität verletzen oder nicht, und sie im Weiteren so in Arten aufzuteilen, dass Widersprüche vermieden werden.

Schließlich kann es möglich sein, dass für die Einführung neuer Ideen metaphorisch Eigenschaften von einem Bereich in einen anderen Bereich übertragen werden, in dem sie bisher ausgeschlossen wurden. Das sprengt den vorhandenen Rahmen und wird von den Vertretern der vorliegenden Wissenschaft kritisiert. Es kann jedoch zu einem Paradigmenwechsel führen. Auch ein Paradigmenwechsel ist entsprechend dem hier vorgeschlagenen Weg nichts anderes als eine Neuorganisation der Hierarchie von Gattungen und Arten. Mit dem neuen Paradigma werden neue Gattungen gebildet und innerhalb der Gattungen die Arten neu aufgeteilt.

Die hier vorgeschlagene Theorie der Wahrheitsoperationen kann als eine erweiterte, rekursive Kohärenztheorie bezeichnet werden, die sowohl auf neue Erkenntnisse wie auf neue theoretische Modelle Bezug nimmt. Ob und in welcher Weise rekursive Umbauten durchgesetzt werden können, wird an dieser Stelle nicht weiter diskutiert. Es lassen sich jedoch einige negative Abgrenzungen bestimmen: Es handelt sich nicht um eine Falsifikationstheorie. Wenn z.B. ein neuer Protokollsatz ›die Beta-Strahlung verletzt die Parität‹ nachgewiesen wird, sind damit die vorangegangen Sätze nicht widerlegt, sondern müssen in einen neuen Erklärungszusammenhang eingebettet werden. – Es ist auch zu wenig, den jeweiligen Wahrheitsbaum nur auf einen Konsens der jeweiligen Wissenschaftsgemeinde zu gründen.

Dagegen entspricht dieser Ansatz eher der Duhem-Quine-These, wonach jede Theorie mehr enthält als nur Protokollsätze. Sie enthält Prinzipien, nach denen die Protokollsätze in Gattungen und Arten aufgeteilt werden. Wenn es gelingt, sie explizit zu machen, dann wird mit ihnen die Objektivität herausgearbeitet, auf die sie sich letztlich beruft.

Ruben scheint sich diese Fragen nicht zu stellen, da für ihn gegenüber der analytischen Philosophie als Wahrheitskriterium ausreicht, ob und wie sich Theorien in der Praxis bewähren. Auch ihm gegenüber ist die Frage zu stellen, dank welcher Eigenschaften eine Theorie erfolgreich in der Praxis anwendbar ist. Ihre Anwendbarkeit wird wiederum aus ihrer Objektivität erklärt, und Hegel sieht konsequenterweise die Teleologie (das Handeln nach Zielen) als ein Kapitel in der Lehre von der Objektivität.

– – Wahrheitsoperationen nach Frege und Wittgenstein

– – – Übersicht

Was sind die Wahrheitsoperationen? Ausgehend von Frege und Wittgenstein soll gezeigt werden, dass sie sachlich übereinstimmen mit den Urteilen der Relation (Urteilen der Notwendigkeit, das sind das kategorische, hypothetische und disjunktive Urteil). Von Frege wird der Gedanke übernommen, die drei Urteile in zwei zusammenzufassen: Das sind Fallunterscheidungen (disjunktive Urteile) und Schlussketten (kategorische und hypothetische Urteile). Daraus entstehen im Ganzen Bäume von Urteilen, die horizontal in Arten und vertikal in Folgerungen gegliedert werden. Frege greift damit einen Ansatz von Kant auf und formalisiert ihn stärker (siehe KrV B 685ff).

Wittgenstein ging den nächsten Schritt, indem er nicht mehr nur einzelne Urteile betrachtet, die von einer einzelnen Gattung zu ihren Arten oder von einer einzelnen Bedingung zu ihren Folgerungen führen, sondern mit Wahrheitsoperationen einen Satz umwandelt in einen anderen, der ihm äquivalent ist. Anders als Frege betrachtet er zu Ende gedacht nicht mehr nur einzelne Urteile, die miteinander verknüpft werden, sondern Operationen, die auf der Gesamtheit der Sätze definiert werden. (Diese Konsequenz spricht er nicht explizit aus, sondern legt sie nahe durch Formulierungen wie »Der Satz bestimmt einen Ort im logischen Raum«, TLP 3.4 und den Hinweis auf Hertz, TLP 4.04.)

Als wesentliche Eigenschaft der Wahrheitsoperationen wird gezeigt, dass sie auf voneinander unabhängigen Fallunterscheidungen beruhen. Sie "funktionieren" nur, wenn Nebenwirkungen und versteckte Abhängigkeiten ausgeschlossen werden können. Mit jeder Wahrheitsoperation wird überprüft und sichergestellt, ob verborgene Wechselwirkungen zum Vorschein kommen. Jeder Programmierer kennt die Erfahrung, dass bisweilen erst auf einer sehr tiefen Stufe von Fallunterscheidungen Nebenwirkungen zwischen Elementen auftreten, die auf verschiedenen Ästen liegen und voneinander unabhängig sein sollten. Das erfordert eine Umstellung des gesamten Systems. Wahrheitsoperationen sind daher rekursiv zu gestalten: Mit jedem neuen Schritt kann es notwendig werden, wieder zurückzugehen und auf einer höheren Stufe die Fallunterscheidungen zu korrigieren. Mathematisch handelt es sich im Ergebnis um Operationen in einem System von kartesischen Koordinaten, die senkrecht aufeinander stehen, bzw. im Grenzübergang um kontinuierliche Felder voneinander entkoppelter Differentialgleichungen ohne gegenseitige Resonanz, mechanisch um ein System von Freiheitsgraden, die unabhängig voneinander variiert werden können.

– – – »Formelsprache des reinen Denkens« nach Frege

Unter welchen Bedingungen können aus gegebenen Sätzen neue Sätze gebildet werden, ohne dass sie unwahr werden? Um das zu klären, untersucht Frege die überlieferten traditionellen Urteile und erkennt in ihnen eine Binnenstruktur, die sich auf zwei Typen reduzieren lässt. Das führt im Ergebnis zu einer Vereinfachung und Formalisierung der Urteilslehre. (Es ist nicht ganz einfach, sich in den Ausführungen von Frege zurecht zu finden, doch lohnt sich der Aufwand, um seine überraschenden Ergebnisse und die Arbeiten seiner Nachfolger besser zu verstehen und einzuschätzen.)

• Kategorische Urteile. Ein Beispiel für ein kategorisches Urteil ist der Satz ›die Rose ist eine Pflanze‹. Während ein Satz wie ›die Rose ist rot‹ ein positives Urteil ist, das sich auf eine bestimmte vorliegende Rose bezieht, ist es wesentlich für alle Rosen, dass sie Pflanzen sind (HW 6.336).
  
  Frege zerlegt ein kategorisches Urteil wie ›die Rose ist eine Pflanze‹ in zwei beurteilbare Inhalte (A) ›S ist eine Pflanze‹ und (B) ›S ist eine Rose‹. Hier bezieht sich A auf eine Gattung und B auf eine Art, die in der in A genannten Gattung enthalten ist. Während der Sache nach die Gattung die Art enthält, ist es für die Formalisierung der Urteilslehre notwendig zu verstehen, dass umgekehrt das Urteil B ›S ist eine Rose‹ das Urteil A ›S ist eine Pflanze‹ enthält. Denn wenn von S nur bekannt ist, dass es eine Pflanze ist, ist noch offen, ob es auch eine Rose ist. Wenn dagegen mit B von S bekannt ist, dass es eine Rose ist, muss es auch eine Pflanze sein. Daher kann mit Frege dieser Fall formalisiert werden: ›A ⊂ B‹.
  
  Auf ähnliche Weise können auf Seite der Prädikate Gattungen und Arten gebildet werden. Beispiel: ›S ist farbig‹ und ›S ist blau‹. Die Folgerung ›wenn S blau ist, ist S farbig‹ gilt immer, dagegen gilt ›wenn S farbig ist, ist S blau‹ nur für einige S und nicht für alle S. Die beiden Aussagen A und B sind in diesem Beispiel durch das kategorische Urteil ›Blau ist eine Farbe‹ verbunden.
  
  
• Hypothetische Urteile. Das hypothetische Urteil ›wenn A ist, so ist B‹ (HW 6.337) enthält bereits zwei beurteilbare Inhalte A und B. Dies Urteil ist für Frege strukurell identisch mit den kategorischen Urteilen. Wenn die Folgerung B wahr ist, muss auch deren Bedingung A wahr sein, denn ohne sie könnte sie nicht gelten. Wenn dagegen B nicht wahr ist, kann nichts über die Wahrheit von A ausgesagt werden.
  
  Hypothetische Urteile werden ähnlich formalisiert wie die kategorischen Urteile: ›A ≺ B‹. Aus ihnen können Schlussketten gebildet werden ›A ≺ B ≺ C ≺ … ‹. Sie entsprechen formal den Hierarchien von Gattungen und Arten ›A ⊂ B ⊂ C ⊂ … ‹.
  
  
• Disjunktive Urteile. Wird umgekehrt gefragt, wann zwei Sätze A und B nicht gemeinsam wahr sein können, dann handelt es sich um Sätze, für die es auf höherer Stufe ein disjunktives Urteil gibt, mit dem zwischen einander ausschließenden Inhalten oder Sphären unterschieden wird. So können z.B. die beiden Sätze (A) ›S ist blau‹ und (B) ›S ist rot‹ nicht gleichzeitig wahr sein. Sie gehen zurück auf ein disjunktives Urteil wie ›die Farbe ist entweder violett, indigoblau, hellblau, grün, gelb, orange oder rot‹ (HW 6.343).
  
  Bei Frege finden sich häufig etwas komplexere Beispiele wie (A) ›S ist eine Zahl‹ und (B) ›S ist blau‹. Sollen A und B gleichzeitig gelten, muss es blaue Zahlen geben. Frege kennt zwar Konstruktionen dieser Art, lehnt sie aber ab. A und B sind voneinander unabhängig. Innerhalb der Gesamtheit aller Sätze muss es einen weit übergeordneten Punkt geben, an dem sich die unterschiedlichen Sphären trennen, zu denen A und B gehören, das sind in diesem Beispiel die Sphären der Qualität und der Quantität. Die Zahlen gehören zur Quantität, die Farben zur Qualität. An der Stelle, an der diese Sphären unterschieden werden, wird ein disjunktives Urteil gefällt. In diesem Beispiel ist es ein Urteil über die Kategorien, ›Kategorien sind Qualität oder Quantität oder Ort oder Zeit etc.‹.
  
  Aussagen wie (A) ›S ist grün‹ und (B) ›S ist bitter‹, die auf kein disjunktives Urteil mit Fallunterscheidungen zurückgehen, werden nicht weiter betrachtet.

Freges Idee war nun, von diesen drei Möglichkeiten die kategorischen und hypothetischen Urteile zusammenzufassen. Die Schlussketten ›A ≺ B‹ (›A ist Bedingung von B, und wenn B gilt, müssen auch die für B notwendigen Bedingungen A gelten‹) und die Gattungshierarchien ›A ⊂ B‹ (›wenn etwas zur Art B gehört und B eine Art innerhalb der Gattung A ist, dann gehört es auch zur Gattung A‹) sind für ihn formal identisch. Sie unterscheiden sich dagegen von disjunktiven Aufzählungen ›A ∨ B‹ (›entweder A oder B‹). Daher will Frege die Gesamtheit aller Verknüpfungen zweier Sätze auf zwei Typen reduzieren und diese geeignet formalisieren, um aus ihnen ein Gesamtnetz aller miteinander verknüpfbaren Sätze bilden zu können.

»Die Bedingtheit. Wenn A und B beurteilbare Inhalte bedeuten, so gibt es folgende 4 Möglichkeiten:
1. A wird bejaht und B wird bejaht;
2. A wird bejaht und B wird verneint;
3. A wird verneint und B wird bejaht;
4. A wird verneint und B wird verneint.

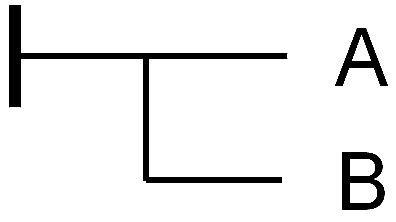
bedeutet nun das Urteil, dass die dritte dieser Möglichkeiten nicht stattfinde, sondern eine der drei andern. Wenn

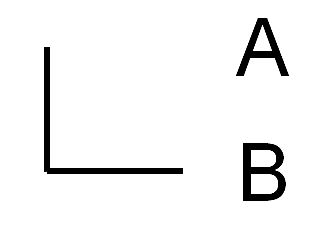
verneint wird, so besagt dies demnach, dass die dritte Möglichkeit stattfinde, dass also A verneint und B bejaht werde.« (Frege, Begriffsschrift, § 5, S. 5)

Hier ist zwar unmittelbar anschaulich zu sehen, wie Frege aus den vier Möglichkeiten zwei Verknüpfungstypen herausfiltert, wenn A und B graphisch entweder verbunden oder unverbunden sind. Doch es ist nicht unmittelbar einsichtig, wie er zu diesem Resultat gelangt, zumal er abweichend von der Aussage, dass das gleichzeitige Zutreffen von Möglichkeit (1), (2) und (4) eine Bedingung ergibt, im Weiteren Beispiele für eine rein formale Bedingtheit nennt, bei denen entweder nur (1) und (2) oder nur (3) und (4) gelten (Frege, Begriffsschrift, § 5, S. 5f). Aus dem Unterschied dieser beiden Arten von Bedingtheit wird sich ergeben, welche zusätzliche Bedingung Wittgenstein gewählt hat, um Wahrheitsoperationen zu definieren. Das sei an einigen charakteristischen Beispielen erläutert.

Fall 1: Frege will mit der ersten Figur 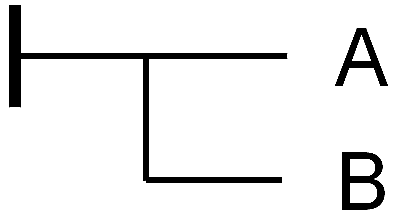die Bedingtheit definieren. Um das zu verstehen, sei ein einfaches Beispiel gewählt, in der ein Urteil das andere bedingt: A sei der beurteilbare Inhalt ›S ist farbig‹ und B der beurteilbare Inhalt ›S ist blau‹. (Frege wählt als Beispiel ›der Mond steht in Quadratur‹ und ›der Mond erscheint als Halbkreis‹, Begriffsschrift, § 5, S. 6. Dies Beispiel ergibt das gleiche Resultat, verlangt jedoch ein wenig Hintergrundwissen über die Bedeutung der Quadratur in der Astronomie.)

(1) A wird bejaht und B wird bejaht. Dann gilt in diesem Beispiel: ›S ist farbig‹ und ›S ist blau‹. Da die Farbe Blau in der Sphäre aller Farben liegt, ist das trivialerweise erfüllt und kann als Bedingung gedeutet werden: Nur wenn S farbig ist, kann S blau sein. In der Begriffspyramide folgt der Begriff Blau dem Begriff Farbe. Das ist ein Beispiel für ein kategorisches Urteil.
(2) A wird bejaht und B wird verneint. Dann gilt in diesem Beispiel: ›S ist farbig‹ und ›S ist nicht blau‹. Dies kann richtig sein, da zur Sphäre der Farben auch andere Farben als Blau gehören. Gilt z.B. ›S ist grün‹, dann sind die Bejahung von A und die Verneinung von B wahr. Die Aufteilung der Farben in blau, grün etc. ist ein Beispiel für ein disjunktives Urteil.
(3) A wird verneint und B wird bejaht. Dann gilt in diesem Beispiel: ›S ist nicht farbig‹ und ›S ist blau‹. Das ist offensichtlich nicht möglich. Wenn zwei Aussagen wahr sein sollen, von denen die erste verneint und die zweite bejaht wird, ist das nur möglich, wenn die zweite Aussage nicht innerhalb der Sphäre der ersten Aussage liegt.
(4) A wird verneint und B wird verneint. Das bedeutet in diesem Beispiel: ›S ist nicht farbig‹ und ›S ist nicht blau‹. Wenn S nicht farbig ist, kann es auch nicht blau sein. Das ist die formale Verneinung eines kategorischen Urteils

Fall 2: Es seien zwei Sätze gewählt, die einander nicht bedingen, sich jedoch auf ein gemeinsames Subjekt beziehen, zum Beispiel: ›S ist eine natürliche Zahl‹ und ›S ist blau‹. (Frege nennt Beispiele dieser Art in Grundlagen der Arithmetik, S. 27, 54.)

(1) A wird bejaht und B wird bejaht. Dann gilt in diesem Beispiel: ›S ist eine natürliche Zahl‹ und ›S ist blau‹. Da es keine blauen Zahlen gibt, ist diese Aussage falsch.
(2) A wird bejaht und B wird verneint. Dann gilt in diesem Beispiel: ›S ist eine natürliche Zahl‹ und ›S ist nicht blau‹. Dies ist richtig, da die Zahlen keine Farbe haben und daher auch nicht blau sind.
(3) A wird verneint und B wird bejaht. Dann gilt in diesem Beispiel: ›S ist keine natürliche Zahl‹ und ›S ist blau‹. Das ist richtig, da die blauen Gegenstände keine Zahlen sind.
(4) A wird verneint und B wird verneint. Das bedeutet in diesem Beispiel: ›S ist keine natürliche Zahl‹ und ›S ist nicht blau‹. Das kann richtig sein, da es z.B. rote Gegenstände gibt, die keine Zahlen sind.

Im Ergebnis stellt sich heraus, dass wiederum drei Möglichkeiten zutreffen und eine nicht. Während in Fall 1 die Möglichkeit (3) nicht galt, gilt hier Möglichkeit (1) nicht. Das zeigt indirekt, dass Frege unausgesprochen an ein Beispiel gemäß Fall 1 gedacht hat, da nur in diesem Fall seine Definition der Bedingtheit zutrifft, bei der Möglichkeit (1), (2) oder (4) gilt, nicht jedoch Möglichkeit (3).

Fall 3: Frege und ihm folgend die meisten Kommentare wählen beurteilbare Inhalte aus, die in keinerlei Bezug zueinander stehen. Frege nennt zwei Beispiele (Frege Begriffsschrift, § 5, S. 5f): (a) ›3 · 7 = 21‹ und ›die Sonne scheint‹. In diesem Beispiel ist der erste Satz wahr, unabhängig vom zweiten Satz. Daher gelten nur die beiden Fälle (1) und (2), in denen der erste Satz bejaht wird. (b) ›ein Perpetuum mobile ist möglich‹ und ›die Welt ist unendlich‹. Da der erste Satz falsch ist, treffen nur die Fälle (3) und (4) zu, in denen er verneint wird. – Auch diese Fälle sind für Frege Beispiele für Bedingtheit.

Überlegungen dieser Art haben Frege einen neuen Blick auf die Logik geöffnet. Für ihn sind nicht nur kategorische und hypothetische Urteile strukturell identisch, sondern er hält sowohl Subjekt und Prädikat wie auch kategorische, hypothetische und disjunktive Urteile für austauschbar und nur grammatisch unterschieden. Formal lässt sich jeder Satz so umformulieren, dass Subjekt und Prädikat getauscht werden. Beispiel: Aus ›der Ball ist blau‹ wird durch eine grammatische Operation ›die Farbe Blau ist Eigenschaft dieses Balles‹ (siehe Frege Begriffsschrift, § 3, S. 2, siehe auch das Slingshot-Argument, Steinschleuder-Argument).

Und ebenso lassen sich die unterschiedlichen Urteile der Relation grammatisch ineinander umwandeln (Frege, Begriffsschrift, § 4, S. 4). Das kategorische Urteil ›A ist B‹ kann geschrieben werden ›wenn A dann B‹ (Beispiel: Der Satz ›die Rose ist eine Pflanze‹ wird grammatisch umgewandelt in ›wenn dies eine Rose ist, dann ist es eine Pflanze‹). Das hypothetische Urteil ›wenn A dann B‹ wird von Frege konditional verstanden und geschrieben ›A ⊂ B‹. A ist eine notwendige, aber nicht unbedingt hinreichende Bedingung von B. Wenn B gegeben ist, müssen alle seine Bedingungen erfüllt sein, also auch A. Daher kann das hypothetische Urteil umgeschrieben werden in das kategorische Urteil ›mit B ist A gegeben‹. Das disjunktive Urteil ›A ist entweder B oder C‹ kann auseinander gelegt werden in zwei Bedingungen: ›wenn A B ist, dann ist A nicht D, und wenn A C ist, dann ist A nicht B‹ (Beispiel: ›wenn die Farbe einer Blume blau ist, dann ist sie nicht rot, und wenn sie rot ist, dann ist sie nicht blau‹). Mit diesen beiden Bedingungen ist gesetzt, dass entweder B oder C gilt. Das disjunktive Urteil ist damit zurückgeführt auf zwei hypothetische Urteile mit Verwendung des Verneinungszeichens. (Siehe hierzu auch die Darstellung durch Wolff 1995, S. 247)

Meines Erachtens kann kaum bestritten werden, dass Frege mit dieser Sicht der Logik eine Wende gegeben hat. Um die Wahrheitsoperationen von Wittgenstein zu verstehen, sind sie von grammatischen Operationen zu unterscheiden. Eine Wahrheitsoperation liegt nicht vor, wenn lediglich in der angegebenen Weise Subjekt und Prädikat vertauscht oder kategorische, hypothetische und disjunktive Urteile ineinander umgewandelt werden. Frege hat Wittgenstein den Blick geöffnet, was das Besondere einer Wahrheitsoperation ausmacht, die sich von rein grammatischen Operationen unterscheidet.

Doch führt es in die Irre, wenn die grammatischen Operationen überbewertet werden. Das kann das Ergebnis haben, dass zwischen Subjekt und Prädikat und möglicherweise sogar zwischen Subjekt, Prädikat und Operationszeichen nicht mehr unterschieden wird mit den bereits an früherer Stelle kritisierten Konsequenzen, siehe Formel (7) und (8) im Abschnitt über Terminusbildung.

– – – »Wahrheitsoperationen« nach Wittgenstein

Auf den ersten Blick hat Wittgenstein lediglich die Ideen von Frege neu formuliert und in den größeren Zusammenhang des Tractatus logico-philosophicus gebracht. Jedoch spricht er nicht mehr von einer »Formelsprache«, sondern führt den Begriff »Wahrheitsoperation« ein. Was ist daran das Neue? Während die Schlussketten von Frege Schritt für Schritt wahr sind, jedoch in der Regel den Geltungsbereich der wahren Aussage verkleinern (z.B. S ist eine Pflanze, eine Rose, eine Kletterrose, eine Abraham Darby, …), bleibt bei Wahrheitsoperationen der Geltungsbereich erhalten. In Formeln ausgedrückt: Frege betrachtet nach dem Vorbild der kleiner-als-Relation der natürlichen Zahlen Sätze, die in Ketten ›A ≺ B ≺ C … ‹ bzw. ›A ⊂ B ⊂ C … ‹ aufgeschrieben werden können, wogegen bei Wahrheitsoperationen ›A ⇔ B ⇔ C … ‹ gelten soll.

Wittgenstein definiert Wahrheitsoperationen als »Operationen, die die Elementarsätze als Basen haben« (TLP 5.234) und folgert weiter: »Alle Sätze sind Resultate von Wahrheitsoperationen mit den Elementarsätzen« (TLP 5.3). Konsequenz: »Wenn uns ein Satz gegeben ist, so sind  mit ihm  auch schon die Resultate aller Wahrheitsoperationen, die ihn zur Basis haben, gegeben« (TLP 5.442). Hier versteht Wittgenstein als Operation: »Die Operation ist das, was mit dem einen Satz geschehen muss, um aus ihm den anderen zu machen« (TLP 5.23). Damit leistet die Wahrheitsoperation genau das, was hier gesucht wird: Ein gegebener Satz kann mit Wahrheitsoperationen umgewandelt werden. Wenn es gelingt, ihn mit einer Kette von Wahrheitsoperationen in den Standardsatz ›S ist nicht zugleich p und nicht-p‹ umzuwandeln, dann ist gezeigt, dass er wahr ist.

Wittgenstein beruft sich ausdrücklich auf Frege, der in der Begriffsschrift elementare Beispiele von Wahrheitsoperatoren analysiert hat, auch wenn er dafür noch nicht den Ausdruck »Wahrheitsoperation« gebraucht.

Welche Wahrheitsoperationen gibt es? Aus Operationen entstehen Reihen (TLP 5.232), und im Einzelnen nennt Wittgenstein »Verneinung, logische Addition, logische Multiplikation, etc. etc.« (TLP 5.2341). Wittgenstein ist wie Frege sehr eng an den Rechenoperationen der natürlichen Zahlen orientiert. So wie Frege den Funktionsbegriff der Mathematik auf die Logik überträgt, überträgt Wittgenstein die Rechenoperationen auf die Wahrheitsoperationen. Die »etc. etc.« zeigen indes, dass Wittgenstein unsicher bleibt, ob bei dieser Übertragung etwas hinzukommen muss. Ich möchte zeigen, dass die Wahrheitsoperationen inhaltlich die Urteile der Notwendigkeit (Urteile der Relation) sind, das sind das kategorische, hypothetische und disjunktive Urteil, für die jedoch zusätzliche Bedingungen formuliert werden müssen, damit sie als Wahrheitsoperationen dienen können.

Wie können aus der von Frege analysierten formalen Struktur der Urteile der Relation Wahrheitsoperationen gewonnen werden? Wird ein Satz A durch eine Wahrheitsoperation in einen anderen Satz B überführt, dann soll gelten ›A ⇔ B‹. Es soll also nicht eine Gattung in eine einzelne Art überführt werden oder eine Bedingung in eine einzelne Folgerung, sondern jeweils in die Gesamtheit aller Arten oder die Gesamtheit aller Folgerungen. Statt ›A ⊂ B‹ ist daher zu schreiben ›A ⇔ ⋃Bi‹, wobei ⋃Bi die Vereinigungsmenge einer vollständigen Aufteilung der Gattung A in Arten bzw. einer Bedingung A in die Folgerungen Bi sein soll (oder symmetrisch einer Folgerung A in alle hierfür notwendigen Bedingungen Bi). Hierbei wird vorausgesetzt, dass die Arten jeweils voneinander unabhängig sind. Daher muss genauer geschrieben werden ›A ⇔ ⋁Bi‹, wobei das aus dem oder-Zeichen ∨ abgeleitete Symbol ⋁ die Aufteilung in voneinander unabhängige Arten darstellen soll.

Das ist der klassische induktive bzw. deduktive Schluss: Wenn etwas für alle Einzelfälle gezeigt werden kann, lässt es sich induktiv auf den allgemeinen Fall verallgemeinern, bzw. gleichbedeutend: Wenn etwas allgemein gilt, gilt es auch für alle untergeordneten Einzelfälle.

Doch das genügt noch nicht. Wittgenstein hat erkannt, dass Wahrheitsoperationen nur möglich sind, wenn mit den einzelnen Arten unabhängig voneinander operiert werden kann. Mir scheint daher der folgende Punkt eine Schlüsselstellung in seinem Entwurf zu haben:

»Eines kann der Fall sein oder nicht der Fall sein und alles übrige gleich bleiben« (TLP 1.21)

Damit trifft Wittgenstein genau das Unterscheidungsmerkmal, wodurch der oben erläuterte Fall 3 charakterisiert werden kann: In den von Frege genannten 4 Möglichkeiten gelten genau dann entweder nur die ersten beiden oder die zweiten beiden Möglichkeiten, wenn die miteinander verknüpften beurteilbaren Inhalte A und B in der von Wittgenstein genannten Weise voneinander unabhängig sind. Die Wahrheit von A bleibt auch dann erhalten, wenn sich die Wahrheit von B ändert, und umgekehrt.

Wenn eine Wahrheitsoperation auf einen zusammengesetzten Satz angewendet werden soll, dann müssen dessen Elemente in dieser Weise voneinander unabhängig sein. Daraus ergeben sich die elementaren Wahrheitsoperationen:

• Zerlegung (disjunktives Urteil): Ein Satz kann in Elementarsätze zerlegt werden, wenn sie im genannten Sinn voneinander unabhängig sind. Die Wahrheit des Satzes ergibt sich aus der Wahrheit der Elementarsätze, in die er zerlegt wurde.
  Beispiele für die Zerlegung sind die Aufteilung einer Gattung in Arten, die Aufteilung der Folgerungen aus einer Bedingung in voneinander unabhängige verschiedene Alternativen oder umgekehrt die Aufteilung der Bedingung einer Folgerung in voneinander unabhängige einzelne Bedingungen. Diese Aufteilungen müssen jeweils vollständig sein, um eine Wahrheitsoperation zu ergeben.
• Negation: Ein Satz kann negiert werden, indem alle seine Elemente negiert werden.
• Addition: Sätze können addiert werden, wenn sie sich ausschließlich aus Elementen zusammensetzen, die voneinander unabhängig sind. Der neue Satz wird gebildet, indem er aus den Elementen beider Sätze zusammengefügt wird. Kamen einzelne Elemente in beiden Sätzen vor, brauchen sie im Weiteren nicht mehr doppelt genannt zu werden. Der neue Satz hat den gleichen Geltungsbereich und die gleiche inhaltliche Aussage wie die beiden Sätze, aus denen er zusammengesetzt wurde.
• Multiplikation: Mehrfache Anwendung der Addition.

– – – Pythagorasbaum

Die Wahrheitsoperationen setzen voraus, dass es keine verborgenen Bedingtheiten gibt. Hier liegt nach meiner Überzeugung der Angelpunkt des Tractatus: Es bedeutet, dass eine Gattung auf solche Weise in Arten und eine Bedingung in solcher Weise auf Folgerungen aufgeteilt ist, dass zwischen den Arten bzw. den Folgerungen keine Wechselwirkung besteht. Wenn eine von ihnen wahr oder unwahr wird, hat das keine Nebenwirkung auf die anderen. Die Aufteilung ist  flach. Mathematisch gesprochen sind die einzelnen Elemente voneinander entkoppelt und bilden ein System von Freiheitsgraden, die unabhängig voneinander variiert werden können. Diese Voraussetzung entspricht dem Grundgedanken der euklidischen Geometrie, die nur in einem flachen Raum möglich ist. Sie bedeutet ausdrücklich, dass der logische Raum nicht gekrümmt und daher völlig übersichtlich ist. Wahrheitsoperationen sind nur in ebenen Räumen möglich.

Dieser Gedanke verallgemeinert den Reihen-Charakter von Schlussketten wesentlich. Im Reihen-Charakter, wie ihn Frege für Schlussketten herausgestellt hat, ist bereits eine Linearität enthalten, wenn linear eins aus dem anderen folgt und entlang der Schlusskette eine Nachfolger-Relation besteht. Aber die Schlussketten verfolgen an Verzweigungspunkten nur eine Richtung oder schließen in der Regel sogar implizit aus, dass es überhaupt Verzweigungspunkte gibt. Vorbild sind die natürlichen Zahlen, bei denen es für jede Zahl jeweils nur einen Nachfolger und keine Verzweigungen gibt. Bei einer zweidimensionalen Ebenheit wird dagegen prinzipiell an jeder Verzweigung die Gesamtheit aller Alternativen berücksichtigt. Ich vermute, dass Frege trotz seiner Orientierung an den natürlichen Zahlen dieser weitergehende Gedanke bereits vorschwebte, als er die Diagramme seiner Begriffsschrift entwarf, auch wenn ihm die Umsetzung noch nicht ganz gelungen war.

Die eindimensionale Linearität der Reihe verfolgt nur die Schlusskette entlang einer durchgehenden Kette von Bedingungen. Die zweidimensionale Betrachtung analysiert den vollständigen Begriffsbaum, das vollständige System aller Gattungen und Arten, die vollständige Pyramide aller Verzweigungen und ihnen untergeordneten Abhängigkeiten, die »Sphäre des Begriffs« im Sinne von Kant.

Demgegenüber bestehen sophistische Strategien (wie zum Beispiel Tricks beim Umgang mit Statistiken) immer darin, unübersichtliche Fallunterscheidungen zu treffen und verborgene Abhängigkeiten zwischen den Fällen oder Besonderheiten einzelner Fälle zu verwischen, aus denen Aussagen über den Allgemeinfall getroffen werden sollen.

Ich vermute daher, dass sich die Wahrheitsoperationen nur in einem Raum anwenden lassen, in dem im übertragenen Sinn der Satz des Pythagoras gilt. Das setzt voraus, dass es gelingt, im Raum der Wahrheitsoperationen Abstände und Quadrate zu definieren. (Davon wird die geplante Logik der Mittel handeln.)

Figur 4: Pythagorasbaum
Pythagorasbäume werden von der fraktalen Geometrie studiert, wobei die Aufteilung in rechtwinklige Dreiecke selbstähnlich wiederholt wird. Jeder einzelne Schritt stellt die Figur dar, an der der Satz von Pythagoras gezeigt werden kann (die Summe der Quadrate über die Katheten ist gleich der Summe des Quadrat über die Hypotenuse). Mir geht es jedoch weniger um die fraktale Geometrie, sondern um den Gedanken, dass durch die Rechtwinkligkeit der jeweils beiden neuen Katheten (Arten), die aus einer Gattung (Hypotenuse) abgeleitet werden, sichergestellt wird, dass mit jedem Schritt zwei neue Arten entstehen, die unabhängig voneinander sind. Ich kann mir vorstellen, dass ausgehend von Pythagorasbäumen weitere Eigenschaften erkannt werden können, die sich mithilfe der Mathematik, Informatik und Graphentheorie untersuchen lassen.
Quelle: „Pythagoras tree 1 1 13 Summer” von Guillaume Jacquenot Gjacquenot – Eigenes Werk. Lizenziert unter CC BY-SA 3.0 über Wikimedia Commons – Link http://commons.wikimedia.org/wiki/File:Pythagoras_tree_1_1_13_Summer.svg#/media/File:Pythagoras_tree_1_1_13_Summer.svg

Um die Idee der Wahrheitsoperationen von Wittgenstein zu Ende zu führen, ist daher nicht nur der Begriff der Funktion und der Rechenoperation in die Logik zu übertragen, wie es Frege und Wittgenstein gelungen ist, sondern darüber hinaus auch der Satz des Pythagoras. Erst mit ihm wird sichergestellt, dass Wahrheitsoperationen erfolgen, die nicht nur einzelne Arten oder einzelne Folgerungen bestimmen, sondern logische Aussagen im Ganzen ineinander umwandeln. Da im Pythagorasbaum jeder einzelne Schritt von einer Hypotenuse zu zwei rechtwinklig zueinander stehenden Katheten führt, ist mit der Rechtwinkligkeit sichergestellt, dass die beiden Katheten logisch voneinander unabhängig sind. Daher ist der Pythagorasbaum das formale Gerüst, entlang dessen Wahrheitsoperationen erfolgen. – Jeder einzelne Schritt von einer Hypotenuse zu zwei Katheten veranschaulicht ein disjunktives Urteil, mit dem eine Gattung in zwei Arten aufgeteilt wird. Sollte es mehr als 2 Arten geben, müssen diese formal weiter aufgeteilt werden, um einen Pythagorasbaum zu erhalten. So kann in diesem Sinne nicht gesagt werden, ›S ist rot oder blau oder grün‹, sondern z.B. ›S ist rot oder nicht-rot‹, und im Folgenden ist ‘nicht-rot’ weiter aufzuteilen in ‘blau oder nicht-blau’, ‘nicht-blau’ in ‘grün oder nicht-grün’ usf. Das zeigt anschaulicher, wie jeder einzelne Schritt des Pythagorasbaum eine Anwendung des Satzes vom Widerspruch ist.

Es geht jetzt "nur" noch darum, dies Gerüst mit Inhalt zu füllen. Rein geometrisch lässt sich der Pythagorasbaum beliebig weit verästeln, wobei auf jeder Stufe die Unabhängigkeit der neuen Arten (Katheten) gegeben ist. Werden Inhalte eingetragen, dann ist auf jeder Stufe zu prüfen, ob das aus inhaltlichen Gründen in eine Sackgasse führt oder Abhängigkeiten verschiedener Äste zum Vorschein kommen, die vorher nicht gesehen worden waren. Es kann zum Beispiel sein, dass in der Teilchenphysik Teilchen untersucht werden, die anfangs voneinander unabhängige Eigenschaften haben, bis sich auf einer tiefen Stufe zeigt, dass innerhalb einer Teilchenfamilie Eigenschaften auftreten, die für diese Familie ausgeschlossen worden waren. Dann ist es notwendig, rekursiv den Baum so weit zurückzugehen, bis die entsprechende Stelle gefunden wird, an der die Aufteilung in Arten neu vorgenommen und im Weiteren neu verästelt werden muss.

Mit diesem Gedanken soll intuitiv nahegelegt werden, warum der Satz des Pythagoras eine übergreifende objektive Eigenschaft beschreibt, die vorausgesetzt werden muss, um Wahrheitsoperationen ausführen zu können, so wie die Ebenheit des Raums Voraussetzung ist, damit die klassischen Galilei-Transformationen der Mechanik gelten.

Wenn es in dieser Weise gelingt, den Raum der Wahrheitsoperationen mit formalen Eigenschaften zu stabilisieren, dann ist in ihm eine Freiheit der Wahrheitsoperationen gesichert, die der Freiheit der mathematischen Konstruktion entspricht. Es ist für mich ein denkbares neues Gebiet der Mathematik, nicht nur wie in der euklidischen Geometrie Konstruktionen an einzelnen Gebilden wie Linien, Kreisen und Vielecken vorzunehmen, sondern auf übergreifenden Gebilden wie dem Pythagorasbaum. Die Figur des Pythagorasbaum zeigt schon anschaulich, dass dort Muster aufzutreten scheinen, die es lohnt näher zu analysieren. Diese Freiheit ermöglicht, sich von der Gefahr der Tautologie zu lösen. So wie die Geometrie und die Arithmetik keineswegs tautologisch sind, sondern überraschende und unerwartete Ergebnisse liefern können, obwohl sie strengen Axiomen folgen, gilt das auch für die Logik. Wittgenstein hat diese Grenze sehr klar genannt:

»Die Sätze der Logik sind Tautologien (TLP 6.1).
Das wirft ein Licht auf die Frage, warum die logischen Sätze nicht durch die Erfahrung bestätigt werden können, ebensowenig wie sie durch die Erfahrung widerlegt werden können. Nicht nur muss ein Satz der Logik durch keine mögliche Erfahrung widerlegt werden können, sondern er darf auch nicht durch eine solche bestätigt werden können (TLP 6.1222).
Der Beweis der logischen Sätze besteht darin, dass wir sie aus anderen logischen Sätzen durch successive Anwendung gewisser Operationen entstehen lassen, die aus den ersten immer wieder Tautologien erzeugen. (Und zwar  folgen  aus einer Tautologie nur Tautologien.)« (TLP 6.126).

Die Wahrheitsoperationen müssen in gewisser Weise tautologisch sein, da sie Äquivalenzen erzeugen sollen, die nichts am Wahrheitswert der Aussage ändern, die umgewandelt wird. Und doch können sie einen Erkenntnisgewinn enthalten. Die Kunst besteht darin, in einer auf den ersten Blick unübersehbaren und undeutlichen Gesamtmenge von Einzelaussagen eine Ordnung zu erkennen, indem es gelingt, geeignete Zerlegungen und die ihnen folgenden Schlussketten zu entdecken und herauszuarbeiten.

Das Vorbild für diese Art zu denken ist in der Physik die Quantentheorie. Deren Grundlagen wurden von Boltzmann entwickelt, bei dem Wittgenstein studieren wollte. Sie betrachtet für die physikalischen Objekte Zustandsräume, deren Eigenschaften voneinander unabhängig (das heißt mathematisch orthogonalisiert) sind. Für diesen Raum ist ausschließlich vorausgesetzt, dass dort in in verallgemeinerter Weise der Satz von Pythagoras gilt (Hilbert-Raum). Hier stellen sich prinzipielle Fragen des Raums wie insbesondere die Asymmetrie (Händigkeit) (TLP 6.36111). Damit benennt Wittgenstein innerhalb der Physik genau die Grenze, an die der Raum der Wahrheitsoperationen von innen stößt (siehe hierzu den Beitrag Hegel und Hilbert).

Daraus ergeben sich zwei weiterführende Fragen:

• Gibt es übergeordnete Eigenschaften, die allen Aufzählungen und Schlussketten zugrunde liegen, wenn diese den Wittgensteinschen Satz 1.21 erfüllen sollen? Diese Frage wird im Folgenden näher ausgeführt und wird im Ergebnis zur Objektivität führen, zur Frage der Mittel, mit der jede Logik zu arbeiten hat.
• Lässt sich die flache Logik verstehen als der Grenzfall eines gekrümmten Raums, deren Tangentialbündel sie darstellt? Ist es möglich, zu einer nicht-euklidischen Logik überzugehen? Erst dort lassen sich die von Kant mehr geahnten als im einzelnen ausgeführten Ideen einer Krümmung der Sphäre des Begriffs und der Affinität ihrer Elemente untereinander ausführen.

– – Additivität und Subtraktivität

Die Wahrheitsoperation der Zerlegung (das ist das disjunktive Urteil mit der zusätzlichen Bedingung TLP 1.21) führt zu einer Aufteilung einer Allgemeinheit in voneinander unabhängige Einzelfälle. Formal wird mit dieser Wahrheitsoperation keine neue Erkenntnis gefunden, sondern tautologisch eine Aussage in eine andere umgewandelt. Doch enthält sie eine verborgene Erkenntnis, das ist »das Prinzip ihrer Ordnung in Arten« (HW 6.343). Es wird nicht nur zum Beispiel die Sphäre der Farben aufgeteilt in die einzelnen Farben wie rot, blau, grün, violett etc., sondern es wird gefragt, nach welcher für alle Farben gültigen Eigenschaft diese Aufteilung erfolgen kann, und nach welchem Prinzip einzelne Farben herausgegriffen und mit Namen belegt werden, statt ein kontinuierliches Farbspektrum mit unendlich vielen Farben zu wählen.

Für Hegel erfolgt im disjunktiven Urteil der Umschlag, der zum Schluss führen wird. Wenn nicht nur mehr oder weniger intuitiv und willkürlich die Arten aufgezählt, sondern das Prinzip ihrer Ordnung erkannt ist, ist mit diesem Prinzip eine  Eigenschaft  der Gattung gefunden, eine bestimmte Beschaffenheit, die zu ihrer Aufteilung führt. Hegel betont, dass nicht nur (α) die Aufzählung der Arten inhaltlich identisch ist mit der Gattung – und aus diesem Grund als Wahrheitsoperation verstanden werden kann –, sondern dass (β) mit dem Prinzip der Aufteilung eine »negative Einheit« gegeben ist (HW 6.343). Die mit dem Prinzip der Aufteilung gefundene Eigenschaft der Gattung soll nicht neben oder außerhalb der Gattung liegen, sondern innerhalb der Gattung. Da die Gattung vollständig durch ihre Arten beschrieben werden soll, muss es herausgehobene Arten geben, die einerseits Arten wie alle anderen sind und andererseits Träger einer Eigenschaft, die übergreifend für alle Arten gilt. Dieser Doppelcharakter wird im Weiteren erklären, wie mithilfe solcher Arten und der von ihnen verkörperten Eigenschaften Schlüsse gezogen werden können. In ihrem Doppelcharakter ist die Objektivität enthalten, auf die sich die empirische und die praktische Wissenschaft beziehen.

Das soll an einigen Beispielen dargestellt und im Ergebnis auf die Wahrheitsheitsoperationen übertragen werden.

Farben Farben lassen sich nach dem Prinzip der Additivität oder der Subtraktivität aufteilen. Der Subtraktivität entspricht die Farbe Weiß als der Summe (der Fülle) aller Farben, von der alle anderen Farben durch Subtraktion abgezogen werden, bei der Addivität ist es die Farbe Schwarz, von der ausgehend alle anderen Farben abgehoben werden. Jede Farbe kann entweder subtraktiv aus der Fülle der Farben mit einem Farbfilter selektiert oder additiv mit einer Beleuchtung, die sich vom völlig dunklen Raum unterscheidet und diesen erhellt, aufgebaut werden. Hegel nennt diese Prinzipien nicht direkt, deutet sie aber innerhalb seiner Ausführungen zum disjunktiven Urteil mit der Unterscheidung in Helles und Dunkles an (HW 6.343).

Mit dem Prisma wird das weiße Licht in das Regenbogen-Spektrum zerlegt. Das kann als paradigmatisches Beispiel für den Übergang einer Gattung (Fülle der Farbe im weißen Licht) in ihre Arten dienen. Es widerspricht der Intuition, wonach umgekehrt das weiße Licht wie ein unbeschriebenes Stück Wachs das Leere ist, auf das etwas eingezeichnet werden muss, während das Schwarz als das Ergebnis erscheint, wenn viele unterschiedliche Öl- oder Wachsfarben übereinander gelegt wurden, bis sich ein dunkles, annähernd schwarzes Gemisch ergibt, aus dem sich durch Abkratzen einzelner Schichten die verschiedenen Farben zurückgewinnen lassen. Lange Zeit wurde angenommen, dass das Prisma nicht die Farben zerlegt, sondern auf eine noch unbekannte Art das Tageslicht färbt. Um das zu widerlegen legte Newton zwei Prismen hintereinander. Hätte das erste Prisma die Farbe gefärbt, dann könnte das zweite Prisma das Licht nur noch innerhalb des gefärbten Lichts brechen.

Newtons Experimentum Crucis
»Newtons Skizze seines experimentum crucis, bei dem Sonnenlicht durch eine Prisma gebrochen wird. Eine Farbe wird dann durch ein zweites Prisma gebrochen um zu zeigen, dass das Licht durch das erste Prisma nicht geändert wurde.« Quelle (eigene Übersetzung): bucknell.edu

Weiß bzw. Schwarz sind zum einen Farben wie alle Farben, zum anderen lässt sich jede Farbe durch ihr Verhältnis zur Farbe Weiß bzw. Schwarz bestimmen. Das führt dazu, dass es in der Realität niemals ein völlig reines Weiß oder ein völlig reines Schwarz geben wird, da jede Farbe, die dem Weiß bzw. dem Schwarz noch so nahekommt, dennoch notwendig eine Verunreinigung und Vermischung enthält. Ein völlig reines Weiß oder ein völlig reines Schwarz wäre nur möglich in einer völlig leeren Welt. – Vorausschau: Dies Beispiel, die Farbe Weiß bzw. Schwarz zu definieren, wird sich als Veranschaulichung zeigen, wenn die mathematische Methode der Erzwingung betrachtet wird. Die Farben Weiß und Schwarz lassen sich innerhalb der Sphäre der Farbe nur als Grenzwert definieren, für den es zwar einen Namen gibt, aber kein einziges Element innerhalb der Sphäre der Farbe, das tatsächlich dieser Farbe entspricht.

Die Sphäre der Farben ist offen. Die Farben Weiß und Schwarz befinden sich an ihrem Rand, gehören jedoch nicht zur offenen Menge. Sie werden durch einen Grenzübergang innerhalb der Sphären angenähert. Aus dem Doppelcharakter der Farben Weiß und Schwarz am Rande der Sphäre der Farben folgt, dass für jede Farbe innerhalb der Sphäre gilt, dass sie weder weiß noch nicht-weiß, und dass sie weder schwarz noch nicht-schwarz ist. Das kann verallgemeinert werden: Wenn es für eine Gattung G eine Eigenschaft p gibt, die auf diese Weise von einer Art am Rand der Gattung verkörpert wird, dann gilt für alle Arten A innerhalb der Gattung G das von Ruben formulierte zweite Wahrheitsmaß »A ist weder p noch nicht-p«.

Anmerkung 1: Meistens wird das Prinzip der Additivität der Farben mit den drei Grundfarben Rot, Grün und Blau verbunden. Das ist jedoch kein allgemeines Gesetz der Optik, sondern beruht auf der menschlichen Wahrnehmungsphysiologie. Das Auge filtert mithilfe der Zapfen subtraktiv aus dem weißen Licht die drei Grundfarben Rot, Grün und Blau heraus und überträgt das Ergebnis an das Gehirn, von dem die drei herausgefilterten Farben additiv zusammengesetzt werden und den Gesamtfarbeindruck ergeben. Andere Lebewesen wie die Bienen sehen die Farben der Natur ganz anders (siehe hierzu sehr anschaulich Bienen und Optik von Katharina Mondel, Link). Wer weiter darüber nachdenkt muss zu dem Schluss kommen, dass die Natur nicht so ist, wie wir sie sehen.

Anmerkung 2: Aus der konträren Struktur von Additivität und Subtraktivität ergibt sich, dass es auch ein »umgestülptes experimentum crucis in der Streulichtkammer« geben muss, »in dem die Rollen von Licht und Schatten genau ausgetauscht sind« (Rang und Müller Newton in Grönland; Link).

Anmerkung 3: Fichte wollte in seiner Wissenschaftslehre ein System entwickeln, das alle Sätze aus der Identität ›A = A‹ oder ›Ich = Ich‹ ableitet. Das könnte formal als ein Pythagorasbaum verstanden werden, der aus dem Satz der Identität herauswächst. Im Fortgang seiner Wissenschaftslehre wandelt sich der Satz der Identität in die »Wechselbestimmung«. Wenn versucht wird, das zu formalisieren, könnte dafür die hier beschriebene Aufteilung der Farben gewählt werden: Während zunächst alle schrittweise eingeführten Farben wie ‘rot’, ‘nicht-rot’, ‘blau’, ‘nicht-blau’, ‘grün’, ‘nicht-grün’ usf. einen Baum konstituieren, nähern sich an seinen beiden Rändern die Grenzfarben immer weiter ‘weiß’ und ‘schwarz’ an, ohne diese Farben je erreichen zu können. Wird das Verhältnis dieser beiden Grenzfarben zueinander betrachtet, dann ergibt sich eine Wechselbestimmung: Weiß und Schwarz schlagen ineinander um. Ein reines Weiß ist nicht von einem reinen Schwarz zu unterscheiden. Diese Wechselbestimmung ist in jeder einzelnen Farbe angelegt, die sowohl im Weiß enthalten und subtraktiv (durch ein Prisma) daraus erzeugt werden kann, wie auch umgekehrt im umgestülpten Experiment der Streulichtkammer aus der schwarzen Schattenwelt. – Wird das von den Farben übertragen auf die Sätze, sollte es möglich sein, aus einem einzelnen Satz wie dem Satz der Identität und seinen Zerlegungen schließlich zwei Grenzsätze abzuleiten, die in Wechselbestimmung zueinander stehen.

Relativitätstheorie Ein anderes Beispiel für Additivität und Subtraktivität ist die Relativitätstheorie. Wird die Gattung (Gesamtheit) der Inertialsysteme (Trägheitssysteme) in einzelne Inertialsysteme aufgeteilt, dann bewegen sie sich zwischen den Grenzwerten eines völlig ruhenden Systems (gewissermaßen das schwarze Inertialsystem) und eines Systems, das sich mit Lichtgeschwindigkeit bewegt (das weiße System). Die beiden Grenzwerte können beliebig angenähert, aber nicht erreicht werden. Sie können nur als Grenzwert der verschiedenen Inertialsysteme bestimmt werden. Im einen Grenzfall handelt es sich um reine Geometrie. Die Geometrie kann verstanden werden als völlig ruhendes Trägheitssystem. Im anderen Grenzfall wird ein System erreicht, das sich mit Lichtgeschwindigkeit bewegt. Dort gelten paradoxe, unmögliche Eigenschaften. Jedes Photon bewegt sich sowohl überall wie nirgendwo. Photonen haben untereinander sowohl keinen wie einen unendlichen Abstand. Sie können sich weder aufeinander zu noch voneinander weg bewegen, da in beiden Fällen Überlichtgeschwindigkeit gelten würde (die Eigengeschwindigkeit der Photonen plus ihrer Bewegung zueinander oder voneinander weg).

Während in der Geometrie ein starrer Abstandsbegriff definiert werden kann, lässt sich im System mit Lichtgeschwindigkeit kein Abstand bestimmen. Für alle Inertialsysteme gilt, dass sie sich zwischen diesen beiden Extremen befinden. Sie bewegen sich schneller als 0 und langsamer als das Licht.

Von einem sehr abstrakten Standpunkt aus kann gesagt werden, dass jedes Inertialsystem sowohl geometrisch als auch nicht-geometrisch ist, und dass seine Geschwindigkeit sowohl der Lichtgeschwindigkeit entspricht als auch nicht.

(a) Die Geometrizität eines Inertialsystem ist daran zu messen, wie sehr es sich der Lichtgeschwindigkeit nähert. Mit wachsender Geschwindigkeit beginnen die Abstände innerhalb des Inertialsystems unschärfer zu werden, aber sie lassen sich noch geometrisch beschreiben. Nur im ruhenden Inertialsystem gibt es reine Geometrie mit eindeutig bestimmbaren Abständen. Nur dort enthalten die geometrischen Gebilde (Punkte, Linien, Flächen, …) keinerlei Eigengewicht und beeinflussen sich nicht gegenseitig. Nur diese Geometrie ist vollkommen eben. Sobald sich das Inertialsystem mit Masse "auftankt", kommt Bewegung hinein. Aus geometrischen Punkten werden Massekörper, die sich gegenseitig anziehen und abstoßen. An die Stelle der geraden, rein geometrischen Verbindungslinien zwischen zwei Punkten treten die kürzesten, im Raum gekrümmten Verbindungslinien zwischen Massepunkten. Aus der euklidischen Geometrie wird die gekrümmte Differentialgeometrie. Die Differentialgeometrie ist nur noch in Annäherung eben.

(b) Im anderen Grenzfall gilt, dass jedes Inertialsystem zum einen die Lichtgeschwindigkeit verfehlt, sich also nie so schnell bewegen kann wie das Licht, und zum anderen die Eigenschaft der Lichtgeschwindigkeit in seinem Innern enthält. Um das zu verstehen, ist eine zweite Komponente der Geschwindigkeit zu erkennen, das Altern von Prozessen. Was sich schneller bewegt, altert langsamer, und was sich langsamer bewegt, altert schneller. Werden beide Geschwindigkeit berücksichtigt, dann gilt für die Gesamtgeschwindigkeit, dass sich alles mit Lichtgeschwindigkeit bewegt. Das ist mathematisch äquivalent zur Aussage, dass die Lichtgeschwindigkeit in allen Inertialsystemen konstant 300.000 km pro Sekunde beträgt, unabhängig davon, wie schnell sich das Inertialsystem bewegt. (Siehe hierzu das entsprechende Kapitel im Beitrag über die Kraft der Trägheit.)

Natürliche Zahlen Wird von der Relativitätstheorie zum anderen Extrem gewechselt, der ebenen Geometrie, und hier wiederum auf deren kleinste Einheit, die Menge der natürlichen Zahlen, dann zeigt sich, dass dort gewissermaßen im Kleinen ähnliche Verhältnisse herrschen. Das kann mit Cantor formalisiert werden: Es werde die Menge der natürlichen Zahlen als Gattung und jede einzelne natürliche Zahl als eine Art innerhalb dieser Gattung betrachtet. In diesem Fall gilt für die Aufteilung der Gattung in ihre Arten das Prinzip, dass es für jede natürliche Zahl einen Nachfolger gibt, das ist die Zahl, die ihr folgt und von ihr mit dem Abstand 1 unterschieden ist. Auf die Zahl n folgt die Zahl n+1.

Für das Prinzip der Aufteilung der Gattung der natürlichen Zahlen lassen sich diejenigen beiden Arten bestimmen, die Träger des Prinzips sind. Das sind die Zahlen 0 und ω, die kleinste von Cantor bestimmte transfinite Zahl. 0 ist Vorgänger jeder natürlichen Zahl und hat daher innerhalb der natürlichen Zahlen keinen Vorgänger mehr. ω ist Nachfolger jeder natürlichen Zahl. Es gibt innerhalb der natürlichen Zahlen keinen Nachfolger von ω. Cantor definiert formal ω+1 als den Nachfolger von ω in der Menge der transfiniten Zahlen. Sie entsprechen den infraroten Farben, die sich jenseits der Sphäre der Farben befinden. 0 kann als das ‘Schwarz’ und ω als das ‘Weiß’ der natürlichen Zahlen verstanden werden. Da die Begriffe Additivität und Subtraktivität der Lehre der natürlichen Zahlen entnommen sind, bekommen sie hier eine unmittelbar einsichtige Bedeutung: 0 ist die einzige Zahl, die sich selbst als Addition enthält: ›0 + 0 = 0‹. Oder umgekehrt: Wenn für eine Zahl x die Aussage ›x + x = x‹ gilt, so kann daraus gefolgert werden, dass es sich bei x um 0 handeln muss.

Auf der anderen Seite kann die von Cantor eingeführte Zahl ω formal definiert werden als ›ω = 1 + 2 + 3 + … + n + …‹, die Summe aller natürlichen Zahlen, und für jede Zahl n gilt die paradoxe Formel ›ω = ω − n‹. Anschaulich gesprochen ist zum einen jede natürliche Zahl n per Definition in ω enthalten, wenn ω als die Summe aller natürlichen Zahlen definiert wird, und zum anderen ist ω so groß, dass es nicht ins Gewicht fällt, wenn von ω eine beliebige endliche Zahl n abgezogen wird. ω hat keinen Vorgänger, und es gilt ›ω − 1 = ω‹. Es ist ohne Zweifel eine der größten Leistungen der Mathematikgeschichte, als Cantor gezeigt hat, wie sich dennoch mit Zahlen wie ω rechnen lässt.

Während sich im Sinne der Relativitätstheorie nur in einer absolut ruhenden Geometrie ein fester Abstand bestimmen lässt, der bei wachsender Geschwindigkeit des Inertialsystems zunehmend verwischt, gilt auf der anderen Seite für die natürlichen Zahlen, dass sich dort der Abstand einer Zahl nicht von ihrer Größe unterscheiden lässt. So ist z.B. die Zahl 5 definiert durch den Abstand 5 gegenüber der 0. Dem Punkt 5 auf der Zahlengerade entspricht eine Länge 5, die von dem Punkt für die 0 bis zum Punkt für die 5 reicht. Im Grenzfall gilt: Obwohl die 1 die kleinste natürliche Zahl ist, ist ihr Abstand 1 definiert zur 0, die nicht zu den natürlichen Zahlen gehört. Innerhalb der natürlichen Zahlen sind der Abstand zur 0 (das Ordnungsprinzip der natürlichen Zahlen) und die Größe der jeweilige Zahl nicht voneinander unterscheidbar.

Wird innerhalb der natürlichen Zahlen der Abstand für sich betrachtet, führt das zum Begriff des Betrages. Je zwei natürliche Zahlen sind durch den den Abstand 1 voneinander unterschieden, und jede einzelne Zahl n mit dem Abstand |n| (lies: Betrag von n) von der 0. Der Begriff des Abstandes wird den ersten Einstieg in die Lehre von der Objektivität ermöglichen. Er lässt sich übertragen vom Beispiel der Zahlen auf alle anderen Gattungen. (Abstand und Betrag sind für Hegel das mathematische Beispiel für den Widerspruch, siehe die entsprechenden Anmerkungen in den Kapitel zum Gegensatz und zum Widerspruch in der Wissenschaft der Logik.)

Anmerkung: Die paradoxe Formel ›ω = ω − n‹ zeigt, dass sehr große natürliche Zahlen auf ähnliche Weise miteinander verwachsen, wie die Abstände der Geometrie verschwimmen, wenn die Geometrie übergeht in immer schneller bewegte Inertialsysteme. Es wird intuitiv nahegelegt, dass sehr große natürliche Zahlen näher aneinander rücken, oder dass anders gesagt die Gerade der natürlichen Zahlen gekrümmt ist. Wer nahezu zwanghaft und bis an die Grenzen des Unendlichen hinein das Zählen wiederholt, wird möglicherweise auf verborgene innere Eigenschaften der Zahlen stoßen. Cantors Kontinuumshypothese, dass das Weiterzählen nach ω schließlich eine Menge von Zahlen erreicht, die die gleiche Mächtigkeit wie das Kontinuum hat, ist nur möglich, wenn bereits in den natürlichen Zahlen eine dort noch vernachlässigbare Krümmung angelegt ist. So wie die euklidische Geometrie und die auf sie aufbauenden bewegten Inertialsystem schließlich zum Grenzfall der Lichtgeschwindigkeit führen, führen nach der Hypothese von Cantor die natürlichen Zahlen und die durch Weiterzählen erreichten transfiniten Zahlen schließlich zum Grenzfall des Kontinuums und mit ihm zur Geometrie, die aus kontinuierlichen Strecken gebildet wird.

Fourier-Analyse Mit der Fourier-Analyse gelang es, für die Farben und Klänge Abstände zu definieren, die den Abständen zwischen den Zahlen auf der Zahlengerade entsprechen. Damit sind die einzelnen Farben und Klänge nicht mehr nur intuitiv durch ihre Eigennamen wie ‘rot’, ‘grün’ oder ‘gelb’ bestimmt, sondern jede Farbe und jeder Klang setzt sich zusammen aus den Intensitäten und Wellenlängen seines Grundtons und ihrer Obertöne. Mit den Wellenlängen kann auf vergleichbare Weise gerechnet werden wie mit den natürlichen Zahlen. Mathematisch definieren die Obertöne die voneinander unabhängigen Koordinaten eines Zustandsraums.

Verallgemeinert kann jede komplexe Funktion in eine Summe einfacher Wellenfunktionen zerlegt werden. Die einfachen Wellenfunktionen sind voneinander unabhängig. So lässt sich ein Klang zerlegen in die elementaren Sinusfunktionen, oder in der Ökonomie können die empirisch beobachtbaren komplexen Zyklen der Wirtschaft zerlegt werden in Zyklen mit unterschiedlicher Reichweite (kurzfristige Lagerzyklen, zehnjährige Überproduktionszyklen, 60-jährige Innovationszyklen, 150-jährige Preiszyklen).

Die Fourier-Analyse begründet mit den Zustandsräumen den übergeordneten Hilbertraum. Das ist der allgemeinste mathematische Raum, in dem der Satz von Pythagoras gilt, und er ist das mathematische Modell für den Tractatus von Wittgenstein.

Ökonomie In der Warenökonomie erfolgt eine Aufteilung der Gattung Ware in die vielen Arten, welche Waren es gibt. Eine Ware ist das Geld, das zugleich das Prinzip dieser Aufteilung ist, wenn alle Waren in der Warenökonomie am Geld gemessen werden. Der Wert allen Geldes soll sowohl gleich wie nicht gleich dem Wert aller Waren sein: Einerseits gilt: Wird das Geld wie jede andere Ware betrachtet, dann ist der Wert allen Geldes die Summe aller Herstellungskosten, um das Geld zu produzieren. Zum Beispiel wird geschätzt, dass im Jahr 2005 ein Geldstück ‘5 Schweizer Rappen’ seinerseits in der Herstellung 4,22 Rappen gekostet hat, oder ein Geldschein ‘5 Schweizer Franken’ 36,60 Rappen (siehe: 20min.ch). Daraus kann errechnet werden, wie viel die Herstellung der Gesamtheit aller Geldstücke und Geldscheine kostet. Zum anderen soll die gesamte Geldmenge die gesamte Warenmenge repräsentieren, wobei innerhalb der gesamten Warenmenge das Geld in Form von Geldstücken, Geldscheinen etc. mit enthalten ist.

Prädikationstheorie Auf analoge Weise können mit den Prinzipien der Additivität und Subtraktivität die einzelnen wahren Sätze als Arten der Gattung aller Sätze verstanden werden. In einem noch näher auszuführenden Sinn kann (a1) der Satz des Widerspruchs ›S ist nicht zugleich p und nicht-p‹ als das Schwarz und (a2) der Satz ›S ist weder p noch nicht-p‹ als das Weiß der Gattung der Sätze gelten. Das bedeutet, dass jeder Satz so zerlegt werden kann, dass er einen Anteil Weiß und einen Anteil Schwarz enthält. Um die Zerlegung vorzunehmen, wird (b1) ausgehend von einer Idee von Frege jeder Satz in eine Funktion erweitert. Werden (b2) die Eigenschaften der Funktion näher betrachtet, dann können ihre Tangential- und Radialkomponente (oder gleichbedeutend ihre Trägheit und ihre Krümmung) unterschieden werden. Sie verweisen auf die als Weiß und Schwarz bezeichneten Grenz-Sätze in der Theorie der Sätze und ermöglichen die gesuchte Aufteilung der Sätze. (b3) Während der Satz des Widerspruchs in der traditionellen Logik selbstverständlich ist, ist es weit weniger vertraut zu verstehen, in welcher Weise mit dem Satz ›S ist weder p noch nicht-p‹ eine Logik der Unbestimmtheit entsteht, in der analog zur Farbe Weiß oder der transfiniten Zahl ω gegenüber den natürlichen Zahlen etwas Ununterscheidbares in die Logik aufgenommen werden muss. Mit dieser These schließt Ruben seine Prädikationstheorie ab:

»Mit anderen Worten: der dialektische Widerspruch erscheint logisch als Unbestimmtheit! [...] Wer also die logische Fassung des dialektischen Widerspruchs im Unterschied zum logischen haben will, muß die Existenz der logischen Unbestimmtheit anerkennen! « (P, S. 31, 32)

(a1) Alle wahren Sätze haben nach Frege den gleichen Wahrheitswert ‘wahr’. So wie “Morgenstern” und “Abendstern” auf die ‘Venus’ referieren, referieren alle wahren Sätze auf den Satz des Widerspruchs ›S ist nicht zugleich p und nicht-p‹. Das hat 1967 Donald Davidson zu der ernüchternden Erkenntnis veranlasst:

»Any two sentences have the same reference if they have the same truth value. And if the meaning of a sentence is what it refers to, all sentences alike in truth value must be synonymous – an intolerable result« (Davidson Truth and Meaning, S. 306).

Was Davidson für »intolerable« hält, ist die Referenz aller wahren Sätze auf den einzigen Satz, der mit voller Gewissheit als wahr bezeichnet werden kann. Wer sagt ›die Rose ist rot‹ kann einer Sinnestäuschung unterliegen oder hat möglicherweise nicht verstanden, was mit einer Rose oder mit der Farbe rot gemeint ist. Fehler dieser Art sind beim Satz ›S ist nicht zugleich p und nicht-p‹ nicht möglich. Er ist für sich wahr und kann daher als Maß der Wahrheit gewählt werden. Alle wahren Sätze stimmen insofern, als sie wahr sind, mit ihm überein.

Das entspricht dem Tauschwert in der Warenökonomie. So wie alle Waren, die den gleichen Geldbetrag wert sind, untereinander gleich sind, und dennoch verschiedenen Gebrauchswert haben, gilt es auch für die wahren Sätze. Sie haben alle den gleichen Wahrheitswert ‘wahr’, aber unterschiedliche Inhalte.

Übertragen auf das Beispiel der natürlichen Zahlen bedeutet das: Wenn für alle natürlichen Zahlen n die Aussage ›n + 0 = n‹ gilt, ohne die die Additivität der Zahlen nicht definiert werden könnte (0 ist das neutrale Element bezüglich der Addition), sind sie bezüglich dieser Eigenschaft untereinander alle gleich, aber niemand würde sagen, dass deshalb alle Zahlen gleich sind. Der Satz ›S ist nicht zugleich p und nicht-p‹ ist das neutrale Element in der Gesamtheit aller wahren Sätze.

(a2) Zum anderen enthält jeder Satz etwas, das ihn von der leeren, wenn auch zweifellos wahren Aussage ›S ist nicht zugleich p und nicht-p‹ unterscheidet. So wie alle natürlichen Zahlen durch ihren jeweiligen Abstand von der 0 voneinander unterschieden sind (es gibt keine zwei natürlichen Zahlen mit gleichen Abstand zur 0), so muss es etwas geben, wodurch jeder Satz einen Abstand zum Satz ›S ist nicht zugleich p und nicht-p‹ gewinnt. Hierfür ist eine weitere Eigenschaft der wahren Sätze notwendig. Bis zu diesem Punkt geht Davidson mit. Er erkennt, dass er sich nur dann von »Frege's footsteps« (Davidson, S. 306) lösen kann, wenn sich zusätzlich zum Wahrheitswert w eine Eigenschaft p bestimmen lässt, durch die wahre Sätze wahr werden: ›S is T if and only if p‹ (Davidson, S. 309). Diese Formulierung ist allerdings missverständlich. Sie ist deutlich zu unterscheiden von der ähnlich klingenden Aussage von Tarski ›x(p) ist eine wahre Aussage dann und nur dann, wenn p‹, denn bei Tarski ist mit p das jeweilige besondere Prädikat gemeint, das in einem Satz ›S ist p‹ enthalten ist. Hier ist dagegen mit p eine übergreifende Eigenschaft aller wahren Sätze gemeint, die zum Wahrheitswert hinzukommen muss. In Analogie zur Ökonomie könnte p als der Gebrauchswert verstanden werden, womit nicht der jeweilige Gebrauchswert jeder einzelnen Ware gemeint ist, sondern die Aussage, dass jede Ware neben dem Tauschwert auch einen Gebrauchswert hat. – Und zum anderen ist es missverständlich, das von Davidson gesuchte p als Eigenschaft zu bezeichnen, wodurch etwas wahr wird und hierin gar einen truthmaker zu sehen. Es ist die Eigenschaft, durch die sich alle wahren Sätze vom ebenfalls wahren Satz ›S ist nicht zugleich p und nicht-p‹ unterscheiden, so wie sich alle natürlichen Zahlen durch ihren Betrag von der 0 unterscheiden.

Die von Davidson gesuchte Eigenschaft aller wahren Sätze ist in dem zweiten Satz, dem Weißen innerhalb der Gesamtheit der Sätze zu sehen, ›S ist weder p noch nicht-p‹. Jeder Satz enthält eine Unbestimmtheit, und je unbetimmter er ist, desto größer ist sein Abstand zum Satz ›S ist nicht zugleich p und nicht-p‹. Wenn das gelten soll, muss in einer nachvollziehbaren Weise jeder Satz im Satz der Unbestimmtheit enthalten sein, so wie jede Farbe im Weiß oder jede natürliche Zahl in der transfiniten Zahl ω enthalten ist. So wie beispielsweise für die Farbe Rot gezeigt wird, dass sie durch das Prisma aus dem Weiß hervorgeht, ist analog zu zeigen, wie alle Sätze aus dem Satz ›S ist weder p noch nicht-p‹ hervorgehen.

(b) Ich verstehe das so, dass jeder Satz zerlegbar sein muss in zwei Sätze, die zueinander konträr sind. So wie in der Mechanik jede Bewegung zerlegt wird in die Tangential- und Radialkomponente, ist jeder Satz zu zerlegen in zwei Komponenten.

(b1) Das wird auf den ersten Blick sehr weit hergeholt erscheinen, doch kommt Davidson in seiner Frege-Interpretation bereits dicht an diese Einsicht heran. Frege erweiterte jeden Satz ›S ist p‹ in eine Funktion f(x). Wenn x für ein bestimmtes Subjekt S betrachtet wird, wird es an dieser Stelle »gesättigt« (saturated) durch die Eigenschaft p. Davidson erläutert das an einem elementaren, allerdings nur unvollständig ausgeführten Beispiel. Der Satz ›John is the father of Annette‹ kann erweitert werden zu einer Funktion ›(x) is the father of Annette‹, die für ein bestimmtes Argument (wie in diesem Beispiel Annette) durch John »gesättigt« wird (Davidson, S. 304f).

Das sieht wie eine zirkuläre Spielerei aus, doch ist Frege in meiner Deutung der entscheidende Schritt gelungen: Wenn ein einzelner Satz verstanden wird als ein Element auf einer übergreifenden Funktion, dann kann nach den Eigenschaften der Funktion gefragt und mit ihnen die Wahrheit des Satzes erklärt werden. In diesem Beispiel wird vom Satz ›John is the father of Annette‹ übergegangen vom Begriff Vater (father) zur Vaterschafts-Funktion. Dann ist zu fragen, welche Eigenschaften die Vaterschafts-Funktion hat, um zu klären, ob der Satz ›John is the father of Annette‹ wahr ist oder nicht.

Die Schwierigkeit an diesem Beispiel liegt darin, dass es so einfach ist, dass es kaum gelingt, das Neue an diesem Übergang zu erkennen. Der Satz wird zerlegt in zwei Komponenten, zum einen eine Relation (Vater-von) und zum anderen eine Person (John). Diese beiden Komponenten sind unabhängig voneinander. Weder ist die Vater-von-Relation eine Person, noch kann eine Person eine Vater-von-Relation sein, sondern lediglich eine Vater-von-Relation sättigen. Beide Komponenten sind aber auch nicht einfach voneinander unabhängig, sondern im Sinne von Hegel Momente einer Satzeinheit, aus der sie hervorgegangen sind. Die Vater-von-Relation ist nur zu verstehen, wenn es Väter gibt, und das Vater-Sein enthält die Vater-von-Relation. Vielleicht wird das etwas deutlicher durch das andere, ebenfalls sehr einfache Beispiel ›die Rose ist rot‹. Dieser Satz kann mit Frege umgeformt werden in die Funktion ›die Rose hat die Farbe (x)‹, und von da ist es nur noch ein kleiner Schritt zu einer "echten" Funktion wie ›die Rose hat eine Farbe mit der Wellenlänge f(x)‹. Die Wellenlänge f(x) ist eine stetige Funktion, die kontinuierlich viele Farben enthält, und die Farbe der Rose ist ein bestimmter Wert im Verlaufe dieser Funktion.

(b2) Frege hat mit seiner Aufteilung von Sätzen in Funktionen und Inhalte, mit denen sie gesättigt werden, den Grundgedanken entwickelt, um den es mir geht. Es ist nur zu fragen, welche Bedingungen Frege implizit unterstellt hat, damit eine solche Zerlegung möglich ist. Ein Satz kann nur dann als eine bestimmte Stelle auf einer Funktion verstanden werden, wenn er nicht singulär ist, sondern im Zusammenhang steht mit anderen Sätzen, so dass eine übergreifende, zusammenhängende Funktion gebildet werden kann, die für viele einzelne Sätze gilt. Und es muss vorausgesetzt werden, dass die Funktion und die Werte, mit denen sie gesättigt wird, voneinander unabhängig sind. Wenn das nicht der Fall ist, trifft das von Gödel vorgebrachte Argument der Unvollständigkeit zu, mit dem Gödel gezeigt hat, was geschieht, wenn Relationen und ihre Relata als gleichberechtigte Terme angesehen werden und sich auf paradoxe Art wechselseitig beeinflussen und stören.

Um von einem Satz wie ›John is the father of Annette‹ zu einer Funktion wie ›(x) is the father of Annette‹ zu gelangen, muss mit der Unbekannten x ein Begriff gefunden werden, für den die weder-noch-Beziehung gilt: Weder ist x der Vater von Annette, noch ist x nicht der Vater von Annette. Im Begriff der  Unbekannten  x ist die Unbestimmtheit bereits enthalten, die durch den Übergang von einem einzelnen Satz zu der Funktion, in der er eingebettet ist, hervortritt.

Wird ein Satz auf diese Weise mit Frege zu einer Funktion erweitert, dann gilt im Moment der Erweiterung die gleiche Unbestimmtheit wie für alle Bewegungen. So wie für einen bewegten mechanischen Körper nicht gesagt werden kann, ob er noch an einer bestimmten Stelle x0 ist oder bereits an einer benachbarten Stelle, so enthält jede Funktion eine Unbestimmtheit. Sie ist bereits im Begriff des x enthalten, für das ein beliebiger Wert eingesetzt werden kann. Das x ist für sich unbestimmt und muss durch eine eigene Operation gesättigt werden.

Wird zurückgeschaut auf die vorangegangenen Beispiele, dann wurde dort genauso vorgegangen. Aus dem Satz ›diese Rose ist rot‹ wurde die Funktion ›diese Rose ist mit einer Wellenlänge x zu sehen‹. Aus dem Satz ›dieser Schuh ist zwei Hemden wert‹ wurde der Satz ›dieser Schuh ist x Geldeinheiten wert‹, wobei die Geldeinheiten eine Funktion sind, die auf alle Waren anwendbar ist. Der Geldwert kann nicht vom individuellen Produzenten oder von den beiden am Tausch beteiligten Verkäufer und Einkäufer ermittelt werden, sondern er ist eine gesellschaftliche Vereinbarung, in die zahlreiche andere Einflüsse eingehen. Daher kann sich niemand sicher sein, ob sein Besitz in Geld ausgedrückt an Wert verliert oder gewinnt, wenn es z.B. zu einer ökonomisch verursachten Inflation kommt. Die Geldwert enthält prinzipiell eine Unbestimmtheit, was von Waren- und Börsenspekulanten ausgenutzt wird.

Doch soll diese Frage nicht weiter ausgeführt oder mit Beispielen belegt werden, sondern grundsätzlicher ist zu fragen, welche Eigenschaften ein Satz haben muss, damit er in dieser Weise in Momente zerlegt werden kann. Das zu verstehen entfernt sich noch weiter von den gewöhnlichen Arbeiten zur Logik. Wenn im genannten Beispiel vom Satz ›John is the father of Annette‹ übergegangen wird zu einer Funktion ›(x) is the father of Annette‹, dann wird vorausgesetzt, dass die Eigenschaft Vater-von erhalten bleibt unabhängig von den jeweiligen Personen, auf die sie angewandt wird. Auch das scheint selbstverständlich zu sein, da aus dem Alltag gewählte Beispiele wie dieses an so viel Hintergrundwissen gebunden sind, welches als selbstverständlich vorausgesetzt wird, dass es schwierig wird, die tieferliegende Struktur der Sprache zu erkennen.

Damit ein Begriff von einem Träger und einer Situation auf eine andere übertragen und zu einer Funktion erweitert werden kann, muss er eine Art innere Trägheit haben, die sicherstellt, dass er sich bei der Übertragung nicht ändert. Diese Schwierigkeit wird deutlicher, wenn etwas aus einer Sprache in eine andere übersetzt werden soll. So kann es sein, dass unter Vaterschaft oder Mutterschaft in einer Gesellschaft und ihrer Sprache etwas anderes verstanden wird als in einer anderen. Jeder Begriff kann in jeder Sprache ein für die jeweilige Sprache eigentümliches Gewicht (Trägheit) haben, wodurch sich bei der Erweiterung eines Satzes, der mit diesem Begriff gebildet wurde, auf eine Funktion jeweils unterschiedliche Ergebnisse ergeben können.

In diesem Sinn kann nochmals das Beispiel von Quine aufgegriffen werden: Wenn jemand in einer fremden Sprache den Satz ›das ist Gavagai‹ hört, kann er ihn nur verstehen, wenn es ihm gelingt, ihn in eine Funktion ›das ist (x)‹ einzubetten, die durch “Gavagai” gesättigt wird. Nur wer versteht, was mit einer solchen Funktion gemeint ist, die den Satz ›das ist Gavagai‹ enthält, versteht, ob mit “Gavagai” ein bestimmtes Wesen, oder eine bestimmte Eigenschaft oder ein Verhalten dieses Wesens gemeint ist. Wenn Quine überzeugend ausgeführt hat, dass sich jeder Satz nur im Kontext einer bestimmten Sprache oder Theorie verstehen lässt, kann das bis in die kleinste Einheit heruntergebrochen werden, dass jeder Satz nur zu verstehen ist im Kontext einer Funktion, die durch ihn gesättigt wird. Wenn nie vermieden werden kann, dass ein Fremder die ihm mitgeteilten Worte missversteht, liegt das daran, dass unvermeidlich jeder Satz eine Unbestimmtheit enthält. Auf andere Weise zeigt sich das, wenn viele Menschen Fremdwörter oder Ausdrücke aus einer anderen Sprache gebrauchen, obwohl sie sie nicht übersetzen können und nur aus dem Umgang mit diesen Worten erschließen, was sie bedeuten sollen.

(b3) Gegenüber der absoluten Gewissheit des inhaltlich leeren Satzes ›S ist nicht zugleich p und nicht-p‹ enthält jede Funktion, in die ein Satz umgewandelt wurde, eine bestimmte Ungewissheit. Zum einen ist nie auszuschließen, dass unterschiedliche Menschen oder auch der gleiche Mensch in unterschiedlichen Situationen identische Begriffe mit jeweils eigener Bedeutung versteht. Zum anderen kann jede Funktion, die auf eine Gesamtheit unterschiedlicher Subjekte angewandt wird, innere Abhängigkeiten enthalten, wodurch der Verlauf einer reinen Funktion gestört wird und es zu Resonanzen und Obertönen kommen kann.

Etwas abrupt sei an dieser Stelle mit der Behauptung geendet, dass Sätze nur dann Wahrheitswerte enthalten können, wenn die mit ihnen gebrauchten Begriffe eine gewisse Trägheit enthalten, so dass die Erweiterung des Satzes in eine Funktion und eine Analyse der Eigenschaften der Funktion möglich ist. Daraus werden sich die beiden abschließenden Gedanken ergeben: Mit der Trägheit kann im Sinne der Relativitätstheorie gefragt werden, ob es unterschiedliche Trägheitssysteme gibt, zwischen denen in Analogie zur Lorentz-Transformation Wahrheits-Transformationen vermitteln müssen; und der Begriff der Trägheit kann seinerseits weiter untersucht werden, was zur Lehre der Objektivität führt. Siehe hierzu den Beitrag über die Kraft der Trägheit.

Im einen Extrem lässt sich jeder logisch wahre Satz mit dem leeren Satz des Widerspruchs gleichsetzen, der keine inhaltliche Aussage enthält. Auf der anderen Seite muss er sich unterscheiden von dem Satz ›S ist weder p noch nicht-p‹. Jeder wahre Satz liegt zwischen diesen beiden Extremen. Je gewisser, d.h. je formaler ein Satz ist, desto näher liegt er am Satz des Widerspruchs, der in äußerster Konsequenz gedacht der einzige Satz ist, der mit voller Gewissheit wahr ist. Je erkenntnisreicher, d.h. je inhaltlicher ein Satz ist, desto größere Unsicherheit enthält er – desto »chaotischer« und verworrener ist er – und nähert sich der Unbestimmtheit an, dass unentscheidbar bleibt, ob etwas diesen Inhalt erfüllt oder nicht. – Die Informationstheorie sagt: Je chaotischer eine Menge ist, desto mehr Informationen enthält sie.

Anmerkung 1 (Kant): Frege führt alle Verknüpfungen von zwei beurteilbaren Inhalten auf zwei Typen zurück: Entweder wird horizontal eine Schlusskette entwickelt, oder es wird vertikal mit einem disjunktiven Urteil ein Begriff in unterschiedliche, voneinander unabhängige Fälle zerlegt. Dies Verfahren ist bereits bei Kant im regulativen Gebrauch der Ideen angelegt (KrV, B 683ff). Kant konstruiert die Sphäre eines Begriffs mit den Prinzipien der Gleichartigkeit, Varietät und Affinität (KrV, B685). Die Gleichartigkeit entspricht den vertikalen Linien, entlang derer Schlussketten entwickelt werden. Die Varietät entspricht der horizontalen Aufteilung von Gattungen in voneinander unabhängige Arten. Jedoch ergänzt Kant als drittes Prinzip die Affinität. Anders als Frege untersucht Kant die Sphäre des Begriffs nicht rein formal, sondern hält für erforderlich, dass es in der jeweiligen Sache eine innere Affinität (Verwandtschaft) geben muss, wodurch dieser Aufbau in die Breite und in die Tiefe zusammengehalten wird. Die Affinität kann als die Eigenschaft verstanden werden, die das Prinzip enthält, wie ein Begriff aufgeteilt werden kann. Zum Beispiel sind alle Farben untereinander verwandt, da sie sich aus den Farben Weiß und Schwarz aufbauen. In der Physik sind alle Inertialsysteme miteinander verwandt, da sie durch das Prinzip der Konstanz der Lichtgeschwindigkeit verbunden sind. Frege hoffte dagegen, durch Verzicht auf jede Art von inhaltlichen Bezügen wie Affinität oder Verwandtschaft den Anwendungsraum der Logik erweitern zu können.

Anmerkung 2 (Hegel): Was zu Tarski und Davidson gesagt wurde, lässt sich auch auf Hegel beziehen: Wenn er in der Beschaffenheit einer Sache S den terminus medius vorgeprägt sieht, um aus einer Sache über ihre Beschaffenheit auf ihre Prädikate zu schließen, dann argumentiert er im Prinzip ähnlich wie Tarski. Es liegt in der Beschaffenheit der jeweiligen Sache, ob die Prädizierung wahr ist oder nicht. Das ist sicher zutreffend, doch geht es beim Urteil über ein Urteil um mehr: Es ist nicht nur die Frage, wie das ursprüngliche Subjekt beschaffen ist, sondern auch, wie das Urteil beschaffen ist, mit dem über das Subjekt geurteilt wurde. Es muss sich um einen Satz handeln, der sich in eine Funktion erweitern und in der angedeuteten Weise in zwei Momente zerlegen lässt. Fragen dieser Art sind nach meinem Eindruck erst durch die die Arbeiten von Frege wesentlich deutlicher geworden.

Anmerkung 3 (Russell-Antinomie): Die Russell-Antinomie berührt diese kritische Frage. Bisher war dagegen nur eingewandt worden, dass sie einen Kategorien-Fehler enthält, insofern sie ein leeres Subjekt konstruiert. Doch wie gelingt ihr dies? Offensichtlich liegt genauer gesehen ein Satz-Fehler vor. Sie konstruiert einen unmöglichen Satz.

Frege war davon ausgegangen, dass nicht-beurteilbare Inhalte nur dann entstehen können, wenn mit ihnen zwei Aussagen aus voneinander unabhängigen Sphären verbunden werden, wie zum Beispiel mit den beiden Sätzen ›S ist blau‹ und ›S ist eine Zahl‹. Er sah daher seinen Ansatz als gescheitert an, als Russell mit seiner Antinomie zeigen konnte, dass nicht-beurteilbare Inhalte auch anders gebildet werden können, indem auf unerfüllbare Weise ein negativer Selbstbezug hergestellt wird. In diesem Fall gibt es kein Subjekt, für das dieses Prädikat gilt. Ein Prädikat wie das von Russell lässt sich nicht in den von Frege intendierten Begriffsketten unterbringen. Wie kann darauf reagiert werden? Frege war überzeugt, dass das Bauprinzip seiner Begriffsschrift unvollkommen ist und zog seinen Ansatz zurück. Michael Wolff schlug vor, ein zusätzliches Prinzip zu ergänzen, wonach Sätze ausgeschlossen werden, bei denen die Menge aller Subjekte leer ist, die dieses Prädikat annehmen können (siehe hierzu Anhang 3). Eine andere Möglichkeit wäre herauszufinden, wie Russell die Konstruktion seiner Antinomie gelungen ist.

Diesen Weg ging Wittgenstein, der Frege in Jena besucht und von ihm ein Empfehlungsschreiben für Russell erhalten hatte. Für ihn beruht das Paradox darauf, dass Russell den Funktions-Begriff doppeldeutig verwendet: Wenn eine Funktion auf eine Funktion angewendet wird, kann es sich nicht in beiden Fällen um die gleiche Funktion handeln, was jedoch sprachlich verdeckt wird, da in beiden Fällen von »Funktion« gesprochen wird (TLP 3.333). Mir scheint diese Frage noch nicht ausreichend geklärt, doch zeigt Wittgenstein auf den entscheidenden Punkt: Es kann Satz-Fehler geben, wenn die Eigenschaft der Sätze, in Funktionen erweitert und als Funktionen in zwei Momente zerlegt werden zu können, fehlerhaft gebraucht wird. Fehler dieser Art liegen in der Natur des Satzes und nicht in den jeweiligen Inhalten, die mit einem Satz ausgesagt werden. Daher entziehen sie sich allen Ansätzen, die wie Hegel und im Grunde auch Frege von einer Sinn-Einheit des Satzes ausgehen und jeden Satz als Versuch verstehen, einen bestimmten außersprachlich gewonnenen Inhalt (einen Gegenstand oder Sachverhalt) in Worte zu bringen. So ist Russell nicht vorgegangen. Er hat sein Paradox konstruiert mithilfe der durch die Satz-Struktur gegebenen Möglichkeiten. Siehe hierzu Ruben (P, S. 6f), sowie neuere Arbeiten von Loomis, Leerhoff, Sutrop und einen anonymen Blog.

Anmerkung 4 (Kues): Die Additivität und Subtraktivität scheinen mir dem von Nikolaus von Kues ausgesprochenen Prinzip des Zusammenfalls der Gegensätze (Coincidentia oppositorum) zu entsprechen. In einer gegebenen Gesamtheit sind sowohl das Aller-Größte wie das Aller-Kleinste in allen Elementen enthalten: Das Aller-Größte, weil es alle umfasst, und das Aller-Kleinste, weil es so klein ist, dass es in allen enthalten ist. Aufgrund dieser Eigenschaft, in allem enthalten zu sein, sind das Aller-Größte und das Aller-Kleinste identisch. Weiß und Schwarz sind eins. Helmut Hansen hat in verschiedenen Arbeiten nachzuweisen versucht, dass dies Prinzip der Relativitätstheorie zugrunde liegt. Es lässt sich wie hier vorgeschlagen verallgemeinern auf alle Zerlegungen einer Gattung in Arten: Es gibt jeweils zwei Randelemente, die von den Arten angenähert, aber nicht erreicht werden. – Auch wenn Hegel Nikolaus von Kues nie erwähnt, ist in meinem Verständnis seine Begründung der Wissenschaft der Logik aus Sein und Nichts in diesem Sinn zu verstehen: Alles lässt sich additiv aus dem Nichts und subtraktiv aus dem Sein erkennen.

Anmerkung 5 (Ruben): Ruben formalisiert die Logik der Unbestimmtheit und integriert sie damit in seine Prädikationstheorie. Er will zeigen, wie die dialektische Logik, die er mit dem zweiten Wahrheitsmaß verbindet, und die formale Logik verknüpft werden können.

Entsprechend der bisher genutzten Nomenklatur können innerhalb der Gesamtheit aller Sätze diejenigen nicht-beurteilbaren Sätze, die eine Unbestimmtheit beschreiben, mit bezeichnet werden (wobei U für Unbestimmtheit steht). Dann lässt sich für ebenfalls ein Wahrheitsmaß angeben: Das ist für Ruben der Satz ›S ist weder p noch nicht-p‹ (P, S. 30f und 33). Mit ihm ergibt sich formal das Gegenstück zu Formel (11):

(12)    ‘›S ist weder p noch nicht-p‹’ ⊩ ‘w’
         → [›S ist weder p noch nicht-p‹] ≡ [w]

lies: Der Name des Satzes ›S ist weder p noch nicht-p‹ ist gleich dem Namen der Gesamtheit aller nicht-beurteilbaren (unbestimmten) Sätze, die wahr sind

Das zweite Wahrheitsmaß wird als Weder-Noch oder in der Sprachweise von Lorenzen als Negatkonjunktion definiert (P, S. 33), die formale Beschreibung des dialektischen Widerspruchs: ›S ist weder p noch nicht-p‹. Im Ergebnis ist Ruben überzeugt, dass die dialektische Logik nicht der formalen Logik widerspricht oder sie widerlegen und an ihre Stelle treten will, sondern die dialektische Logik umfasst die traditionelle formale Logik als ihren Grenzfall. Das unterscheidet sich nur wenig von der hier vertretenen Auffassung, wonach die beiden Wahrheitsmaße die Grenzfälle der Gattung der wahren Sätze sind.

Anmerkung 6 (vom spezifizierende zum realen Maß): Die von Ruben vorgetragene Analogie, jeder Satz könne am Satz des Widerspruchs gemessen werden wie ein physischer Körper am Pariser Urmeter, lässt sich letztlich nicht halten. Diese Analogie hat geholfen, das Verständnis der Gesamtheit der Sätze zu vertiefen, doch muss sie im Verlaufe der weiteren logischen Entwicklung negiert werden. Um im Bild des Pythagorasbaums zu bleiben: Wenn alle Sätze geordnet werden, liegen in ihrer Wurzel nicht der Satz vom Widerspruch, sondern die aristotelischen Kategorien und in deren Mittelpunkt das den Kategorien vorausgehende »Wortbare« oder die von Puntel genannte »nicht-sprachliche, aber sprachabhängige Entität« des Artikulierbaren. Werden hiervon ausgehend die weiteren Sätze entwickelt, dann ergeben sich der Satz des Widerspruchs und der Satz der Unbestimmtheit als die beiden unerreichbaren Grenzfälle vergleichbar dem Weißen und Schwarzen in der Sphäre der Farben. Aus dem leeren Satz ›S ist nicht zugleich p und nicht-p‹ lassen sich ebenso wenig Inhalte generieren wie mathematisch nichts aus der Identität ›0 = 0‹ erschlossen werden kann.

Das bedeutet in anderen Worten, dass es nicht genügt, den Satz des Widerspruchs als spezifizierendes Maß für die Wahrheit aller Sätze anzunehmen, an dem sie sich äußerlich messen oder von dem sie durch Wahrheitsoperationen abgeleitet werden können. Vielmehr wird verstanden, dass der Satz des Widerspruchs zum Grenzsatz wird, der dem Satz der Unbestimmtheit gegenübersteht und mit ihm in »Wechselbestimmung« gelangt. Die Wechselbestimmung zeigt sich innerhalb jedes einzelnen Satzes und ordnet ihn im Feld aller Sätze an. Damit ist der Übergang vom spezifizierenden Maß zum realen Maß gefunden. Die Wahrheit der Sätze liegt im realen Maß ihrer Verwandtschaft untereinander. Diese Verwandtschaft ist kein starres System, sondern geschieht in Prozessen vergleichbar den chemischen Reaktionen, durch die Sätze sich aufeinander beziehen, einander erläutern und mit der Erkenntnis neuer Sätze in ihrem Gefüge fortlaufend verändert werden.

– Wahrheits-Transformationen

Wie sieht die Gesamtheit der Sätze aus und wie lässt sie sich ordnen? Bisher ergaben sich intuitiv drei mögliche Ansätze: (α) Es handelt sich um ein Meer oder ein Gewimmel von Sätzen, von denen so viele wie möglich durch Schlussketten oder Gattung-Art-Hierarchien verbunden werden. Dies Bild kann mit Kant und Hegel erweitert werden zu einer gekrümmten, flüssigen Sphäre des Begriffs. (β) Die Sätze bilden einen völlig durchorganisierten Pythagorasbaum, der nach jeder neuen Erkenntnis überprüft und rekursiv angepasst werden muss. () Alle Sätze orientieren sich wie magnetisierte Teilchen in einem Magnetfeld an den beiden Polen des Satzes vom Widerspruch und der Unbestimmtheit, und für jeden Satz sollte bestimmt werden können, wie weit entfernt er von den beiden Polen ist und wie stark die Krümmung der Feldlinie ist, auf der er liegt. Die von Frege eingeführte Ausweitung eines Satzes in eine Funktion kann in diesem letzten Bild veranschaulicht werden, indem metaphorisch gesprochen jeder Satz dank der ihn einhüllenden Funktion ein Eigengewicht und einen inneren Kompass bekommt, mit denen er sich an den beiden Polen ausrichtet und an die geeignete Stelle im Feld aller Sätze einfügt.

In einer ersten Deutung scheint mir jedes dieser Bilder eine Teil-Wahrheit zu enthalten, die jeweils für sich entweder zu starr oder zu unpräzise sind. Doch scheint mir darüber hinaus der Gedanke naheliegend, dass diese unterschiedlichen Sichten auf die Gesamtheit der Sätze vergleichbar sind den verschiedenen Aggregat-Zuständen des Wassers oder allgemeiner den verschiedenen Zuständen eines Substrats. Die Gesamtheit der Sätze wird verstanden als das Substrat, das sich in verschiedenen Zuständen zeigen kann. Jeder Zustand ist eine eigene Ordnung mit ihren jeweils eigenen Wahrheitsoperationen. Zwischen den Zuständen und ihren Wahrheitsoperationen vermitteln die Wahrheits-Transformationen.

Um diesen Ansatz auszuführen ist es ohne Zweifel notwendig, die bisher teilweise nur intuitiv entwickelten Zustände der Gesamtheit genauer zu analysieren und möglicherweise weitere zu ergänzen. Doch soll bereits die These vertreten werden, dass die Wahrheits-Transformationen auf ähnliche Weise zwischen ihnen vermitteln wie die Knotenlinien zwischen den Zuständen des Substrats, siehe hierzu ausführlicher den Beitrag über das reale Maß.

Damit scheint sich wiederum wie im Beispiel der elementaren Prädikation alles zu wiederholen. So wie dort die Daseinsanalyse in der Lehre des positiven Urteils wiederkehrte, so hier die Analyse des realen Maßes in der Lehre des Urteils des Begriffs. Statt von Wahlverwandtschaften zwischen chemischen Stoffen, die miteinander chemisch reagieren, wird jetzt von Verwandtschaften zwischen Sätzen gesprochen, die durch Wahrheitsoperationen miteinander verbunden sind. Und statt einer Knotenlinie zwischen den Zuständen eines Substrats werden hier die Wahrheits-Transformationen untersucht. Das Russell-Paradoxon liegt genau auf der Grenze: Es sieht aus wie ein Kategorien-Fehler und verweist insofern noch auf die Daseins-Analyse (als würde es von daseienden Barbieren und ihren Eigenschaften sprechen), aber es ist ein Satz-Fehler, der auf Fehler innerhalb der Wahrheitsoperationen deutet. Es verletzt nicht die Denkbestimmungen des Seins (die Kategorien), sondern die formalen Denkbestimmungen des Begriffs (die formale Lehre des Urteilens und Schließens).

In diesem Sinne soll (a) motiviert werden, warum es ‘mittlere Strukturen’ innerhalb der Gesamtheit der Sätze geben sollte. Mit dem Ausdruck ‘mittlere Struktur’ wird ein Begriff gesucht, der an die Stelle des vielleicht missverständlichen Ausdrucks ‘Modus’ oder ‘Zustand der Gesamtheit der Sätze’ treten kann. (b) Das »Klarwerden von Sätzen« (Wittgenstein) kann als eine erste Beschreibung dienen, was mit Wahrheits-Transformationen erreicht werden soll. Wahrheits-Transformationen durchlaufen die verschiedenen Zustände der Gesamtheit der Sätze. (c) Schließlich werden erste Ideen entwickelt, wie die Wahrheits-Transformationen aussehen können. Das soll und muss an dieser Stelle genügen, um die Fragestellung an die Lehre der Objektivität so deutlich wie möglich zu bestimmen. Das wichtigste Anliegen wird sein, innerhalb der Lehre der Objektivität auf vergleichbare Weise die Macht zu erkennen, die den Wahrheits-Transformationen zugrunde liegt, wie das Licht den Lorentz-Transformationen und der Staat den Geld-Transformationen. Wenn das ein Stück weit gelungen ist, können sicher auch die hier entwickelten Ideen zu den Wahrheits-Transformationen genauer ausgeführt werden. Im Moment handelt es sich um eine möglichst genaue Beschreibung einer noch weitgehend offenen Fragestellung.

– – mittlere Struktur (Modi der Gesamtheit der Sätze)

Einige Beispiele sollen zeigen, was mit der fehlenden mittleren Struktur der Gesamtheit aller Sätze gemeint ist.

Farben Wie löst – salopp gesagt – die Natur solche Aufgaben? Ein Beispiel ist das Auge. In der Evolution haben sich im Auge die Stäbchen und Zapfen entwickelt, mit denen aus der Fülle des Lichts exemplarische Farben herausgegriffen und gefiltert werden, um aus ihnen anschließend ein internes Farbbild zusammensetzen zu können. Diese Vorgehensweise ist völlig anders als die der bisher beschriebenen Wahrheitsoperationen. Es ist kein disjunktives Urteil. Es kann nicht gesagt werden, weißes Licht ist blau, rot oder grün, sondern aus dem weißen Licht werden drei Bereiche herausgegriffen, die erst in der Summe das gesamte Farbspektrum abdecken, jedoch weder voneinander unabhängig sind, noch in der Summe einen gleichmäßigen Farbverlauf ergeben. Mithilfe der Aufteilung der Farben in drei Grundfarben kann sich der Mensch im unstrukturierten Meer aller Farben orientieren. Es kann mit der Evolutionstheorie angenommen werden, dass die Auswahl der drei Farben nicht willkürlich ist, sondern die Überlebenschancen des Menschen optimiert. Andere Lebewesen wie die Bienen nehmen die Farbwelt anders wahr. Nicht nur das Denken und Sprechen der Menschen muss sich in der Praxis bewähren und entsprechend fortlaufend angepasst und erweitert werden, sondern bereits die menschlichen Sinne werden auf ähnliche Weise entwickelt.

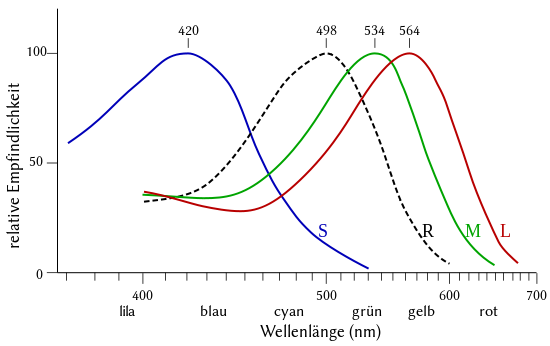
Figur 5: Spektrale Absorptionskurven der Zäpfchen im menschlichen Auge
»Die spektralen Absorptionskurven beschreiben die Reizantwort der drei Farbrezeptoren in Abhängigkeit von der Wellenlänge des einwirkenden Lichtreizes« ( Wikipedia, abgerufen am 8.5.2015).
Schwarzgestrichelt ist die Empfindlichkeitsverteilung der Stäbchen ergänzt, mit denen beim Nachtsehen Hell- und Dunkelwerte unterschieden werden können.
Quelle: „Cone-response-de” von Cone-response.svg: w:User:DrBob and w:User:Zeimusuderivative work: Sgbeer - Cone-response.svg. Lizenziert unter CC BY-SA 3.0 über Wikimedia Commons – Link

Mit dem Auge wird subtraktiv aus dem vollen Farbraum ein eingeschränkter Farbraum erzeugt, der den Bedürfnissen des Lebewesen optimal angepasst ist. Im Weiteren müssen Regeln gefunden werden, wie die Farben in diesem Farbraum sich übersetzen lassen in die Gesamtheit aller Farben. Das ist ein erstes Beispiel für Transformationen.

Klang Die unübersehbare Vielfalt der Klänge wird nicht einfach in kontinuierliche Funktionen von Grund- und Obertönen zerlegt, sondern nach bestimmten Gesetzen in Zusammenklänge und Melodien geordnet (Akkorde, Harmonien, Modi wie Dur und Moll). Jeder gehörte Ton muss übersetzt (transformiert) werden in einen Ton, der in das Tonsystem und seinen Regeln passt. Im Instrumentenbau kann das durch bestimmte Regeln unterstützt werden (z.B. bei der Spannung der Saiten für ein wohltemperiertes Klavier). Ähnlich wie beim Auge kann evolutionstheoretisch davon ausgegangen werden, dass das Ohr sich in einer Weise verändert hat, um die für den Menschen wichtigsten Klänge herauszuhören. Die mittlere Struktur der Zusammenklänge ist eine Entwicklung, die das erleichtert und beschleunigt.

Natürliche Zahlen Selbst die natürlichen Zahlen sind nicht einfach eine Menge von Zahlen, die ausschließlich nach der kleiner-als-Relation geordnet sind, sondern es gibt zahlreiche weitere Ordnungen. Das ist elementar das Stellenwertsystem, z.B. die Anordnung aller Zahlen in Binär-, Oktal-, Dezimal- oder Sexagesimal-Zahlen. Dadurch werden die Zahlen übersichtlicher und es kann leichter mit ihnen gerechnet werden. Für unterschiedliche Aufgabengebiete bestehen verschiedene Stellenwertsysteme nebeneinander: Für das kaufmännische und technische Rechnen hat sich das Dezimalsystem durchgesetzt, für Zeit-Angaben und Ordnungen im Kreis gilt das Sexagesimal-System (Stunden, Minuten, Sekunden). Wiederum sind Transformationen notwendig, um die verschiedenen Systeme ineinander zu übersetzen. (Siehe hierzu den Beitrag über die Entstehung der Zahlen.)

Inertialsysteme Inertialsysteme sind »Bezugssystem(e), in dem sich kräftefreie Körper geradlinig und gleichförmig bewegen« (Wikipedia, abgerufen am 13.6.2015). Mit den Inertialsystemen wird eine mittlere Struktur gefunden, die in Reinform nicht existiert, jedoch der Realität ausreichend nahekommt. Es gibt absolut gesehen weder kräftefreie Körper noch geradlinige Bewegungen, aber in einem Inertialsystem liegt ein Körper vor, dessen Masse so groß ist, dass alle Bewegungen in seiner Umgebung relativ auf seine Bewegung bezogen werden können. Das kann die Erde sein, auf der alles zu Boden fällt. Das kann innerhalb dieses Bezugssystem wiederum ein kleineres Bezugssystem sein wie ein Schiff. Wenn in einem fahrendem Schiff etwas von einem Tisch zu Boden fällt, dann fällt es senkrecht und macht die übergreifende Bewegung des Schiffes mit.

Es ist klar, dass sich die Grenzen eines Inertialsystems nicht absolut bestimmen lassen. Wer sich auf dem Deck eines Schiffes befindet, ist gleichzeitig so stark in das umgebende Inertialsystem eingebunden, dass die Eigenbewegung des Schiffs empfunden werden kann. Dennoch ist die Unterscheidung der Inertialsysteme notwendig, um ihnen gegenüber die Bedeutung der Konstanz der Lichtgeschwindigkeit erkennen und in Lorentz-Transformationen berechnen zu können.

Gesamtheit der Sätze Nur für die Gesamtheit der Sätze gilt ausschließlich das Bivalenzprinzip (wahr, falsch). Das ist, als würden die Farben nur in Schwarz- und Weiß-Töne unterschieden, die Klänge nur in Oktav-Intervalle, die Zahlen nur in ein Binärsystem oder die Mechanik nur in eine ruhende Geometrie und die Bewegung des Lichts. Und das, obwohl die Gesamtheit der Sätze wesentlich komplexer ist als die Gesamtheit der Farben, Klänge, natürlichen Zahlen und mechanischen Bewegungen.

Daher kann bis heute nicht zwischen Wahrheitsoperationen und Wahrheits-Transformationen unterschieden werden. Es gibt nur Wahrheitsoperationen, die einheitlich auf alle Sätze angewendet werden, und keine mittleren Strukturen, in denen sich Sätze in einem bestimmten Zustand befinden. Die Theorie des Satzes befindet sich noch auf einem Stand wie die Mechanik zur Zeit vor Galilei. Galilei kannte immerhin schon das Gedankenexperiment, dass sich Inertialsysteme innerhalb von umgebenden Inertialsystemen relativ bewegen (wie zum Beispiel ein Schiff auf der Erde), aber er konnte sich noch nicht vorstellen, dass es beim Übergang von einem Inertialsystem in ein anderes Transformationsregeln gibt. Die Theorie der Sätze hat bisher nicht einmal eine Vorstellung, ob und wie Gesamtheiten von Sätzen gebildet werden, die durch Transformationen ineinander zu übersetzen sind. Vergleichbar sind höchstens die verschiedenen Sprachen, die ineinander übersetzt werden müssen. (Und hier ist wiederum eine offene Frage, ob irgendwann alle Sprachen in eine einheitliche universale Sprache zusammengeführt werden können, oder ob es zum Wesen der menschlichen Sprache gehört, dass sie auseinanderfällt in verschiedene Sprachen. Es lässt sich vermuten, dass selbst bei Herausbildung einer universalen Sprache wie heutzutage in Richtung auf die englische Sprache notwendig Subsprachen entstehen, da keine Sprache ihren Universalitätsanspruch einhalten kann.)

– – »Klarwerden von Sätzen«

In dieser Situation kann versucht werden, statt einer Ordnung der Sätze eine Ordnung der Wahrheitsfindung zu erkennen, um sich in dieser nahezu ungeordneten Gesamtheit aller Sätze bewegen zu können.

Frege war sich dieser Problematik völlig bewusst. Um einen neuen Satz zu formulieren, ist ein theoretischer Entwurf notwendig, wie dieser Satz in die Gesamtheit der Sätze aufgenommen werden kann. Jeder neue Satz, der mehr ist als eine bloße Beobachtung, gründet in einer Vision, die zunächst nur schwer weiter ausgeführt werden kann. Um ihn von bloßen Glaubenssätzen zu unterscheiden, muss es gelingen, ihn in eine mittlere Gestalt zu bringen, d.h. in einen Satz, der zunächst unbewiesen und unter den gegebenen Paradigmen falsch ist, jedoch die Eigenschaft besitzt, an andere Sätze anschlussfähig zu sein.

»Das Erkennen einer wissenschaftlichen Wahrheit durchläuft in der Regel mehrere Stufen der Sicherheit. Zuerst vielleicht aus einer ungenügenden Zahl von Einzelfällen erraten, wird der allgemeine Satz nach und nach sicherer befestigt, indem er durch Schlussketten mit anderen Wahrheiten Verbindungen erhält, sei es dass aus ihm Folgerungen abgeleitet werden, die auf andere Weise Bestätigung finden, sei es dass er umgekehrt als Folge schon feststehender Sätze erkannt wird. Es kann daher einerseits nach dem Wege gefragt werden, auf dem ein Satz allmählich errungen werde, andererseits nach der Weise, wie er nun schließlich am festesten zu begründen ist.« (Frege, Begriffsschrift, S. III)

Klassische Beispiele sind die Bemühungen von Kepler, für die Bewegung der Planeten eine andere Bahn zu bestimmen als die verwickelten Epizyklen um die Erde, der Benzol-Ring oder das Bohrsche Atommodell, das sicher falsch war, jedoch die Wissenschaft beflügelt hat. Für Sätze dieser Art gilt offensichtlich ein eigenes Wahrheitsmaß. Sie befinden sich anfangs in einem Status, in dem sie weder wahr noch falsch sind. Sie können zunächst nicht anders, als in Bildern zu reden, um der Phantasie eine Anregung zu geben. »Die Metapher ist kein Ausdruck für Unbegriffliches, sondern die Erfindung eines Begriffs« (Holz, S. 287). Mit der Metapher soll bewusst ein Bruch herbeigeführt werden, eine »Sphärenvermengung« des bestehenden Systems (Carnap 1931, S. 235), doch wird sie nur erfolgreich sein, wenn es mit ihr gelingt, Anschluss an das vorhandene Wissen zu finden.

Wittgenstein sieht hier die Aufgabe der Philosophie. Die Ordnung des jeweiligen Wissens kann von der Fachwissenschaft geleistet werden. Die Philosophie soll helfen, in Zwischenzuständen, in denen ein Begriff neu gebildet wird, das Entstehen des Neuen zu fördern. Sie hat nicht nur die Aufgabe, bewusste Täuschungen (Sophismen) abzuwehren, sondern auch, das Denken zu öffnen.

»Das Resultat der Philosophie sind nicht 'philosophische Sätze', sondern das Klarwerden von Sätzen« (TLP 4.112).

Erst dann kann von einer philosophischen Theorie des Satzes gesprochen werden, wenn nicht nur im Sinne der Sprachtheorie ein Satz zerlegt und mit den verschiedenen Methoden der Grammatik, Syntax, Semantik usf. untersucht wird, sondern wenn es gelingt, die Transformationen von einer überlieferten zu einer neuen Wahrheit und ihren jeweiligen Sätzen zu verstehen.

– – Transformationen

Sätze, mit denen Transformationen von Sätzen erfolgen sollen, müssen nach dem Vorbild der Lorentz-Transformationen zwei Eigenschaften haben:

• Diese Sätze lassen sich prinzipiell nicht innerhalb des gegebenen Systems nachweisen.
• Sie können jedoch aus den innerhalb des gegebenen Systems geltenden Sätzen als deren Grenzfall erschlossen werden.

Diese Eigenschaften sind formal identisch mit der Methode der Erzwingung, mithilfe derer Cohen zeigen konnte, dass sich eine Gesamtheit von Mengen, in denen die üblichen Mengen-Axiome gelten, in eine Gesamtheit erweitern lässt, in der die Kontinuum-Hypothese nicht gilt (siehe Anhang 1).

Sätze dieser Art können nicht mit den bisher genannten Methoden mit anderen Sätzen verknüpft werden. Es gibt keine Wahrheitsoperationen wie Schlussketten oder disjunktive Zerlegung, um aus diesen Sätzen andere Sätze zu begründen. Stattdessen müssen diese Sätze eine Eigenschaft haben, die sich durch Wahrheits-Transformationen auf andere Sätze übertragen lässt, so wie mit Lorentz-Transformationen der Satz über die Konstanz der Lichtgeschwindigkeit auf die Beschreibung von Bewegungen in Inertialsystemen übertragen wird.

Mit den folgenden Schritten soll skizziert werden, wie Wahrheits-Transformationen eingeführt werden könnten. Übergreifend geht es darum, von leeren, aber formal sicheren Sätzen zu inhaltlich gehaltvolleren, aber unbestimmten (visionären, unsicheren, unverständlichen) Sätzen zu gelangen.

Zeit Alle formal sicheren Sätze verlieren ihre Sicherheit, wenn sie Aussagen über zeitliche Entwicklungen treffen. Ein Satz wie der Satz des Widerspruchs ist nur deswegen formal wahr, weil er zeitunabhängig gilt. Werden dagegen Prognosen getroffen oder Erinnerungen wachgerufen, dann sind sie im wörtlichen Sinn mit Visionen in der Zukunft oder Mythen aus der Vergangenheit verbunden. Nur das, was jetzt gegenwärtig gilt, ist absolut sicher.

Komplexität Fallunterscheidungen drohen verborgene Abhängigkeiten zu enthalten, wenn sie fortlaufend komplexer werden. Bei zunehmender Komplexität kann es zu unerwarteten Kombinationen (Datenkonstellationen) und Resonanzen kommen.

Das zeigt exemplarisch die Figur des Pythagorasbaums. Sie ist formal so aufgebaut, dass logische Wahrheit gewissermaßen garantiert ist, und doch ist intuitiv zu sehen, dass sie bei ausreichender Verästelung möglicherweise verborgene Figuren enthält, die mit dem Satz des Pythagoras noch nicht erreicht sind, der ausschließlich jeden einzelnen Schritt innerhalb der Figur beschreibt.

Mittel An dieser Stelle wird bei wachsender Komplexität der Einsatz von Mitteln notwendig. Der Begriff des Mittels ist ganz elementar zu verstehen: Die Zahlen wurden historisch eingeführt mithilfe solcher Mittel wie Kerbhölzer, Zählsteine, siehe hierzu ausführlicher den Beitrag über die ägyptischen und babylonischen Zahlen. Anfangs gab es nur diese Hilfsmittel, aber auch die aus ihnen entwickelten Zahlen lassen sich als Mittel verstehen, um komplexer werdende Aufgaben bearbeiten und lösen zu können.

In diesem Sinn sind auch die geometrischen Figuren, die euklidischen Konstruktionsmethoden, die Zahlengerade der natürlichen Zahlen und die Ebene der Geometrie Mittel. Die Frage nach den mittleren Strukturen kann nur gelöst werden, wenn die Mittel verstanden werden, mithilfe derer Sätze möglich sind.

Die Mittel lassen sich nicht ohne Paradoxien in ein gemeinsames System mit den Sätzen bringen, die mit ihnen dargestellt werden sollen. Das ist die formal korrekt bewiesene Erkenntnis des Unvollständigkeitssatzes von Gödel. Die Mittel müssen eigene Eigenschaften haben, die sich von den Eigenschaften der Fragen unterscheiden, die mit ihnen bearbeitet werden.

Ulrich Blau hat in seinem Werk Die Logik der Unbestimmtheiten und Paradoxien gezeigt, dass es zum Beispiel ganz elementar bis heute nicht gelungen ist, die besonderen Eigenschaften des geometrisch als Linie gezeichneten Linearkontinuums mit den Eigenschaften der mit seiner Hilfe dargestellten Zahlen zu vereinbaren.

Jede komplexe Aufgabe bedarf daher bestimmter Mittel, aber sie muss sich darauf verlassen, dass die Mittel gewissermaßen eine eigene Kraft haben, aus denen sich erklärt, warum sie erfolgreich eingesetzt werden können. Und nicht nur das. Es muß in der Natur der Mittel liegen, dass sie nicht zu unerwünschten Wechselwirkungen mit den Aufgaben führen, die mit ihnen gelöst werden sollen. Auch wenn die Diskussion über die Beeinflussung von Messergebnissen durch Messinstrumente in der Quantenphysik im Einzelnen möglicherweise auf philosophischen Irrtümern beruht, ist die Frage im Prinzip berechtigt: Wie kann garantiert werden, dass beim Lösen komplexer Aufgaben durch notwendig gewordene Mittel keine Verzerrung der Ergebnisse durch das Mittel entsteht?

Das ist die Stelle, an der Hegel erklären will, warum die Lehre der formalen Logik über sich hinausweist auf eine Lehre der Objektivität, an deren Ende die Frage nach der Objektivität der Mittel steht.

Die tiefste Erkenntnis der Wissenschaft der Logik von Hegel scheint mir darin zu bestehen, dass jeder Satz nicht nur als ein Urteil ›S ist p‹ für sich besteht, sondern in sich eine Neigung enthält, die über ihn hinausweist. Diesen Gedanken hat Hegel schrittweise in der Wissenschaft der Logik entwickelt, sei es im Verhältnis von Etwas und Anderem, von Endlichkeit und Unendlichkeit, oder in der formalen Logik, die im Ergebnis zum Schluss auf die Objektivität führt.

Vom Formalismus des Schließens zur Objektivität

Abstract     Die Lehre vom Schluss ist durch zwei selbstbezügliche Schlüsse bestimmt: So wie auf der einen Seite ein Schluss vom Urteil über das disjunktive Urteil zum Schluss führt, führt auf der anderen Seite ein Schluss vom Schluss über den disjunktiven Schluss zur Objektivität. Das vermittelnde Element in diesem Schluss ist in einer doppelten Bedeutung der terminus medius: Der terminus medius vermittelt nicht nur innerhalb eines jeden einzelnen Schlusses, sondern Hegel will zeigen, wie sich die unterschiedlichen von der Tradition überlieferten Schlüsse auseinander entwickeln lassen, wobei mit jedem Schritt der terminus medius so weit angereichert wird, bis aus ihm die Objektivität hervortritt. Der disjunktive Schluss stellt den Umschlagpunkt dar. Bei diesem Schluss lässt sich der terminus medius als neutrales Element verstehen, mit dem auf die Allgemeinheit aller Elemente einer gegebenen Sphäre geschlossen werden kann. Mit dem neutralen Element (gleichbedeutend mit dem Einselement der Mathematik, der Maßeinheit der messenden Wissenschaft oder der Quantenzahl in der Quantenmechanik) tritt die Objektivität des Schließens hervor und erweist sich als der Grund des wahren Schließens. – So wie in der Urteilslehre von einem Prädikat auf die Sphäre geschlossen wurde, der das im Urteil angesprochene Prädikat angehört, so wird hier von der Sphäre auf die Dimension geschlossen, innerhalb derer der Schluss gezogen werden kann: Das ist die Gesamtheit aller Elemente, die sich als die Vielfachen des jeweils neutralen Elements darstellen lassen. In der Mathematik sind das die reellen Zahlen als die Vielfachen der Eins und in der messenden Wissenschaft die jeweiligen Messgrößen (Quantenzahlen), die als die Vielfachen der jeweiligen Maßeinheit zu erschließen sind. Dieser Zusammenhang von Dimension, Einselement, Multiplikation und Schluss ist von Ruben eingeführt worden. In dieser Sicht wird verständlich, wie und warum die Dimensionen die Objektivität begründen und sich dort als Freiheitsgrade der Mechanik, als Medium des Chemismus und schließlich als der Wirkungsbereich organischer Systeme zeigen. – Als Motto sei erinnert: »Der Schluß ist das Vernünftige und alles Vernünftige« (Hegel, Enz. § 181, HW 8.331, zitiert bei Ruben 2003, S. 19).

Hegel beginnt die Lehre vom Schluss mit dem Schluss von der Einzelheit (E) über die Besonderheit (B) zur Allgemeinheit (A) und charakterisiert ihn durch eine Kurzformel:

»E – B – A ist das allgemeine Schema des bestimmten Schlusses.« (HW 6.355)

Damit kann ein trivialer Schluss gemeint sein wie »Diese Rose ist rot; Rot ist eine Farbe, also ist diese Rose ein Farbiges« (Enz. § 183 Zusatz, HW 8.335). In diesem Beispiel steht der Satz ›die Rose ist rot‹ für das Einzelne (die konkrete Rose), die Zuordnung ›Rot ist eine Farbe‹ für das Besondere, da die Farbe Rot eine besondere Eigenschaft der Rose ist, mit der sie auf die Sphäre der Farben verweist, innerhalb derer sie eine besondere Farbe ist, und der Schluss wird auf das Allgemeine gezogen: ›die Rose ist farbig‹. Ein solcher Schluss kann auch so formuliert werden, dass die Rose zum Roten und das Rote zum Farbigen und daher auch die Rose zum Farbigen gehört, und nimmt damit die von Frege betrachtete Form an: ›E ⊂ B ⊂ A‹ (in diesem Beispiel ›Rose ⊂ Rotes ⊂ Farben‹).

Auf diese Art zu schließen ist für Hegel ein »formeller Verstandesschluss« (Enz. § 182, HW 8.333) und »man wird sogleich von Langeweile befallen, wenn man einen solchen Schluß heranziehen hört« (HW 6.358). Wie gelingt der Weg von hier zum »vernünftiger Schluss« (ebd.)? Der Verstandesschluss setzt voraus, dass bereits die Hierarchie der Gattungen und Arten bekannt ist und wandert in diesem fertigen Gebäude hin und her. Der Vernunftschluss lebt davon, dass an Etwas etwas Neues erkannt wird und die Vernunft über den aktuellen Wissensstand hinausgeht. Diese Vorgehensweise kann bereits am bestimmten Schluss E – B – A mitvollzogen werden, wenn damit nicht gemeint ist, dass ein Einzelnes E durch eine besondere Eigenschaft B auf ein bereits bekanntes Allgemeines A bezogen wird, sondern bei der Untersuchung eines Einzelnen E an dessen besonderen Bestimmungen B etwas erkannt wird, wodurch es sich auf etwas Allgemeines bezieht, das aus diesen Eigenschaften des Einzelnen erschlossen werden kann. So geht zum Beispiel jeder Botaniker vor: Er bestimmt eine Pflanze, indem er sie nach Merkmalen untersucht, an denen er erkennt, zu welcher Gattung sie gehört. Hat er es mit einer bisher unbekannten Pflanze und bisher unbekannten Gattungen zu tun, dann wird er an dieser Pflanze das spezifische (besondere) Merkmal suchen, mit dem eine bisher noch nicht festgelegte, übergeordnete Gattung definiert werden kann. In den Worten von Hegel wird an diesen Merkmalen erkannt, wie das Einzelne »in die Allgemeinheit heraustritt, worin es nicht mehr nur sich selbst angehört, sondern in äußerem Zusammenhange steht« (HW 6.355).

Dennoch erscheint diese Art zu schließen in gewisser Weise beliebig und willkürlich. Hegel will daher schrittweise die Schlussformen komplexer und anspruchsvoller gestalten bis schließlich der disjunktive Schluss erreicht ist, mit dem »das Vermittelnde die objektive Natur der Sache ist« (HW 6.354, Hervorhebung von mir). Anders als die formale Logik sucht Hegel nicht nach dem allgemeinsten Mengen- oder Klassenbegriff, in dem alle Arten und Gattungen zusammenlaufen, sondern mit der »objektiven Natur der Sache« erreicht er den Punkt, an dem der Formalismus des Schließens aus seiner eigenen Entwicklung heraus übergeht in die Lehre von der Objektivität.

Wie kann dies Programm umgesetzt werden? Hegel entwickelt die Schlusslehre kunstvoll verschachtelt in drei mal drei Schritten. Sie setzt sich aus drei Stufen zusammen, die jeweils im Innern die drei Figuren E – B – A, B – E – A und E – A – B enthalten und ihrerseits für jeweils eine der drei Figuren stehen. Hier sind zwei Entwicklungen ineinander verwoben:

(a) Die drei Figuren gehen auf jeder Stufe und im Gesamtaufbau der drei Stufen auseinander hervor, indem im ersten Schritt an einem Einzelnen etwas Besonderes erkannt wird, durch das es auf ein Allgemeines verweist. Im Grunde verweist jedes Prädikat, das einem Subjekt zugeschrieben wird, auf die ganze Sphäre, in der sich dieses Prädikat befindet. Wird etwas als blau erkannt, gehört es über Blau zur Sphäre der Farben, wird es als bitter erkannt, gehört es zur Sphäre des Geschmacks etc. – Im zweiten Schritt wird unter diesen Besonderheiten, die zu etwas Allgemeinem führen, diejenige einzelne Besonderheit herausgesucht, mit der erkannt wird, warum die vorliegende Art zu einer Gattung gehört. So kann z.B. an der Rose erkannt werden, dass sie einen inneren Stoffwechsel hat und daher zur Gattung aller Lebewesen gehört. Dieser Schritt wird mit der Figur B – E – A beschrieben. Aus den vielen auf Allgemeines verweisenden Prädikaten ist eine einzelne herausgehoben, die nicht nur zu irgendeinem Allgemeinen führt, sondern zu einer Gattung, der die Rose angehört. Das ist der Schritt von der abstrakten zur objektiven Allgemeinheit (HW 6.369, 390). – Schließlich wird gefragt, ob dasjenige Merkmal getroffen ist, mit dem nicht nur der Schluss auf die Gattung gezogen werden kann, sondern das Allgemeine der Gattung getroffen ist. Bei Pflanzen genügt nicht zu sagen, dass sie über einen Stoffwechsel verfügen, was auch für die Tiere zutrifft, sondern sie sind photoautotroph (sie können Licht in Energie umwandeln und benötigen zum Aufbau organischer Stoffe ausschließlich anorganische Stoffe). Wird also z.B. an der Rose nachgewiesen, dass sie photoautotroph ist, dann ist an der Rose eine Eigenschaft gefunden, die zugleich die allgemeine Eigenschaft der Gattung aller Pflanzen ist. Den Schritt zu dieser Allgemeinheit bezeichnet Hegel als erfüllte Allgemeinheit (HW 6.398). Mit der erfüllten Allgemeinheit ist die Natur einer Sache gefunden.

Es ist deutlich, wie die Schlüsse mit jedem Schritt inhaltsvoller werden. Das liegt nicht nur daran, dass eine Aussage wie ›die Rose ist photoautotroph‹ komplexer ist als die Aussage ›die Rose ist rot‹, sondern auch der Anspruch an inhaltliche Aussagen hat sich erhöht. Es geht nicht mehr nur um beliebige Erscheinungen, die an einem Gegenstand beobachtet oder gemessen werden können, sondern um die Bestimmung seiner Natur. Es ist daher kein Zufall, wenn bis heute die üblichen den Verstandesschlüssen gewidmeten Lehrbücher über formale Logik bei den von Hegel belächelten trivialen Beispielen bleiben und sich nicht auf die schwierigeren Fragen der Naturwissenschaft begeben. Aber umgekehrt ist für Hegel auch nicht die Komplexität an sich Merkmal einer höheren Wissenschaft, sondern erst ihre Zielsetzung, nicht nur nach Merkmalen, sondern nach der Natur von etwas zu fragen. In diesem grundsätzlichen Sinne ist er Aristoteles verpflichtet, von dem er den Begriff der Natur übernehmen kann.

(b) Zum Zweiten will Hegel mit den drei Stufen entwickeln, worin sich Verstandes- und Vernunftschluss unterscheiden. Auf jeder Stufe ist der letzte Schritt maßgeblich, auf der es mit der Figur E – A – B gelingt, an einem Etwas das Allgemeine zu erkennen, das die charakteristische Eigenschaft der nächsthöheren Gattung ist. Dies Allgemeine verändert sich mit den drei Stufen von einer abstrakten Allgemeinheit beim Schluss des Daseins über das objektive Allgemeine beim Schluss der Reflexion zur erfüllten Allgemeinheit beim Schluss der Notwendigkeit (HW 6.369, 390, 398). Formal stimmen der Verstandes- und der Vernunftschluss überein. Aber erst mit der erfüllten Allgemeinheit ist der Vernunftschluss erreicht.

Im Mittelpunkt dieser Entwicklung steht der Analogie-Schluss, das ist der dritte Schluss auf der zweiten Stufe in der Figur E – A – B. Hegel ist sich bewusst, dass er hier der Naturwissenschaft sehr nahe kommt.

»Im Schluß der Analogie wird daraus, daß Dingen einer gewissen Gattung eine gewisse Eigenschaft zukommt, geschlossen, daß auch anderen Dingen derselben Gattung dieselbe Eigenschaft zukommt. So ist es z. B. ein Schluß der Analogie, wenn gesagt wird: Man hat bisher bei allen Planeten dies Gesetz der Bewegung gefunden, also wird ein neu entdeckter Planet sich wahrscheinlich nach demselben Gesetz bewegen. Die Analogie steht in den empirischen Wissenschaften mit Recht in großem Ansehen, und man ist auf diesem Wege zu sehr wichtigen Resultaten gelangt. Es ist der Instinkt der Vernunft, welcher ahnen läßt, daß diese oder jene empirisch aufgefundene Bestimmung in der inneren Natur oder der Gattung eines Gegenstandes begründet sei, und welcher darauf weiter fußt.« (Enz. § 190 Zusatz, HW 8.343)

Hegel spricht zwar noch nicht von Vernunft, sondern vom »Instinkt der Vernunft« und warnt vor zahlreichen Negativbeispielen, wenn ganz oberflächliche oder geradezu absurde Analogien gebildet werden. Dennoch ist der Analogie-Schluss der notwendige Zwischenschritt, um die »Natur« des Einzelnen (HW 6.387) zunächst gewissermaßen erraten zu können. Das Ergebnis muss abschließend gesichert werden. Was in einer einzelnen Analogie gilt, kann zufällig sein, im wörtlichen Sinn eine »bloße Ähnlichkeit« (HW 6.387). Wenn es jedoch gelungen ist nachzuweisen, auf welcher allgemeinen Grundlage der Analogie-Schluss beruht, also von einzelnen Analogien auf eine übergreifende allgemein-gültige Analogie zu schließen, ist die Objektivität erreicht (HW 6.401).

Um die Objektivität erreichen zu können, genügt es für mich jedoch nicht, den von Hegel eingeschlagenen Weg durch alle neun überlieferten traditionellen Schluss-Formen nachzuvollziehen, sondern es ist die Frage zu stellen, wie auf diesem Weg bereits keimhaft die Objektivität enthalten ist, die im Ergebnis klar hervortritt. Bei dieser Objektivität muss es sich um mehr handeln als den bloßen Formalismus, worauf sich nach Hegel Frege und die von ihm begründete Tradition konzentrierten. Um dies zu erkennen und herauszuheben hilft die ebenso einfache wie verblüffende Frage, die erstmals Ruben gestellt hat, was eigentlich mit den Querstrichen in den Schemata gemeint ist. Sind die Formeln wie E – B – A nur eine Abkürzung, um die verschiedenen Schluss-Figuren auf einfache Weise voneinander zu unterscheiden, oder deutet sich in den Querstrichen etwas Neues an, das im Weiteren näher zu bestimmen ist?

Die Formeln wie E – B – A zeigen zunächst nur sehr äußerlich, in welcher Reihenfolge das Einzelne, Besondere und Allgemeine in der jeweiligen Schlussfigur miteinander verknüpft sind. Für Ruben geht es dagegen nicht nur um die Reihenfolge, sondern er sieht in den Querstrichen eine inhaltliche Aussage enthalten.

»Wir haben aber in der ersten Schlussfigur weder Operations- noch Relationszeichen, die wir erwarten müssen, wenn ein ordentlicher logischer Satz mitgeteilt sein soll.« (Ruben 2003, S. 19)

Die Hegelsche Logik ist für ihn unvollendet, und er stellt etwas provokativ die Frage, wie »aus Hegels Dialektik-Torso eine akzeptable Theorie gemacht werden soll« (Ruben 2003, S. 20), d.h. in diesem Fall, welche Operationen und Relationen mit den Querstrichen im Schema des bestimmten Schlusses gemeint sind. Er versteht sie als mathematische Operation (Produkt, Vereinung) und als Relation der Gleichheit. Daraus ergibt sich seine Interpretation: E – B – A ist zu verstehen als E · B = A.

Mit diesem Ansatz wäre eine weitgehende Übereinstimmung von Hegel und Frege gefunden. Das von Hegel beschriebene Schließen ließe sich zurückführen auf die Formelsprache der Arithmetik. Das Ergebnis des Schlusses bliebe innerhalb eines Bereichs, der formal mit dem Aufbau der natürlichen Zahlen vergleichbar ist. Das würde aber bedeuten, dass noch nicht einmal ein Schluss möglich ist, der zur schlechten Unendlichkeit führt, und daher erst recht nicht zur wahren Unendlichkeit. In der Mathematik ist das Zeichen ∞ für die schlechte Unendlichkeit dadurch definiert, dass es keine zwei natürlichen Zahlen m und n gibt, für die ›m · n = ∞‹ gilt. Wenn E und B endlich sind, kann E · B nie unendlich und daher mit dem Ansatz von Ruben nie aus E und B auf ein Unendliches geschlossen werden.

Im Ansatz von Ruben scheint mir jedoch mehr enthalten zu sein. Wenn er danach fragt, wie die Bindestriche zu verstehen sind, ist das für mich die Frage nach der Objektivität, auf die sich die Schlüsse beziehen können. Die von ihm vorgeschlagene Formel E · B = A ist jedoch in mehrfacher Hinsicht zu revidieren und zu differenzieren.

(a) Mir erscheint der Grundgedanke von Ruben überzeugend, doch möchte ich ihn nicht auf das Schema E – B – A, sondern auf das Schema E – A – B beziehen. In diesem Schema wird nicht versucht, aus endlichen Größen auf das Allgemeine zu schließen, was meiner Meinung nach vorrangig im induktiven Schluss möglich ist, sondern es enthält die Allgemeinheit als Vermittlung. An dieser Stelle nach einer mathematischen Formel zu suchen, ist bereits bei Hegel vorbereitet. Er fasst auch den Schluss der Analogie und damit die auf Eudoxos zurückgehende Proportionenlehre mit ihrem neuen Begriff der Größe unter das Schema E – A – B, und er sieht mit dem disjunktiven Schluß in diesem Schema den Übergang zur Objektivität. Während nach meinem Eindruck bei Ruben der Ansatz E · B = A zunächst eine Intuition ist, die in die richtige Richtung geht, lässt sie sich überzeugender am Analogie-Schluss entwickeln und ausführen.

(b) Es soll gezeigt werden, dass eine wie von Ruben vorgeschlagene Formel nur innerhalb einer Dimension gilt. Wenn der Dimensionsbegriff gefunden ist, stellt sich die Frage, was im Kreuzungspunkt geschieht, an dem sich zwei voneinander unabhängige Dimensionen treffen und einen zweidimensionalen Raum aufspannen, wie es bereits am Beispiel der Subjekt- und Prädikat-Achse dargestellt worden ist. Im Kreuzungspunkt gilt eine Unbestimmtheit, und mit den voneinander unabhängigen Dimensionen wird ein Raum aufgespannt, der nicht aus der Multiplikation innerhalb einer Dimension erschlossen werden kann.

(c) Abschließend folgen eine Betrachtung der besonderen Rolle der Zeitdimension und (d) des Skalarprodukts, das von Ruben und Bruno Hartmann an anderer Stelle in die Logik eingeführt wurde.

Ruben versteht mit Berufung auf Helmholtz Zählen und Messen (1887) und Carnap Einführung in die symbolische Logik mit besonderer Berücksichtigung ihrer Anwendungen (1954) die Formel E · B = A als Verallgemeinerung der Grundformel der messenden Wissenschaft (Ruben 1997, S. 2f). Das gilt auch für die hier vorgeschlagene Formel E · A = B. Damit wird implizit vorausgesetzt, dass gemäß Kant eine Wissenschaft erst dann zu einer Wissenschaft wird, wenn sie über einen Messprozess verfügt, mit dem sie ihre Gegenstände zu messen und zwischen den Messergebnissen mathematische Beziehungen herzustellen vermag. Das gilt sowohl für die Naturwissenschaften wie für die Ökonomie. Rubens Ansatz ist aus seinen früheren Arbeiten entstanden, für die angewandte Ökonomie in einer planwirtschaftlichen, sozialistischen Wirtschaft die geeigneten Messverfahren zu entwickeln.

Die Formel E · A = B lässt sich zugleich als ein Satz in der Form ›S hat in der Dimension D den Messwert (S,D)‹ interpretieren, wobei S für das Einzelne in seiner Konkretheit und vielfältigen Messbarkeit steht, an dem die Messung vorgenommen wird, (S,D) für den besonderen Messwert, der gemessen wird, und die Dimension D für das Allgemeine, auf die in diesem Satz referenziert wird. – Es fällt auf, dass hier kaum mehr unterschieden werden kann, was das Einzelne und was das Besondere ist, denn ebensogut lässt sich sagen, dass S das Besondere ist, an dem eine Messung vorgenommen wird, und der Messwert (S,D) das Einzelne, das gemessen wird. Auch darauf weist bereits Hegel hin (HW 6.398f).

Anmerkung: Wenn die drei Stufen der Schluss-Lehre mit der Entwicklung von der formalen Logik über die Mathematik zu den Grundbegriffen der messenden Wissenschaft verknüpft wird, kann sich das nur bedingt auf Hegel stützen. Doch gibt es bei ihm Hinweise in diese Richtung. In der Enzyklopädie vergleicht er die dritte Stufe (den Schluss der Notwendigkeit, das sind der kategorische, hypothetische und diskursive Schluss) mit dem Hervortreten der Sache beim Übergang von der Reflexionslogik zur Logik der Erscheinung (Enz. § 193, HW 8.346). Vorbereitend steht im Zusatz des vorangehenden Paragraphen:

"Weiter ist nun aber diese Subjektivität mit ihren hier genannten Bestimmungen, dem Begriff, dem Urteil und dem Schluß, nicht als ein leeres Fachwerk zu betrachten, welches seine Erfüllung erst von außen, durch für sich vorhandene Objekte, zu erhalten hat, sondern die Subjektivität ist es selbst, welche, als dialektisch, ihre Schranke durchbricht und durch den Schluß sich zur Objektivität erschließt." (Enz. § 192 Zusatz, HW 8.345)

Innerhalb der Figuren der traditionellen Schlusslehre findet sich dieser Durchbruch, wenn im hypothetischen und diskursiven Schluss das hypothetische und diskursive Urteil erweitert wird mit der harmlos klingenden Formulierung »nun ist«, z.B. »Wenn A ist, so ist B, Nun ist A, Also ist B« (HW 6.395). Im Sinne der formalen Logik klingt das banal und wie eine leere Aussage. Doch wie kommt es zu der vermittelnden Aussage »Nun ist A«? Ist das eine willkürliche theoretische Option? Hegel sieht in dieser Formulierung die »Unmittelbarkeit des Seins hinzu(gefügt)« (HW 3.395, 399). Das »Nun ist A« ist eine Berufung auf die Unmittelbarkeit, die nur durch eine Beobachtung oder Messung erfolgen kann. Daher erscheint es mir gerechtfertigt, an dieser Stelle auf die messende Wissenschaft Bezug zu nehmen, wenn das »nun ist« im weitesten Sinn als Messergebnis verstanden wird. – Oder anders gesagt: Der disjunktive Schluss steht für Hegel unter dem Schema E – A – B (HW 6.398). E enthält eine disjunktive Aufzählung von Möglichkeiten. A ist eine Messung (oder, falls keine Messinstrumente eingesetzt werden, eine Wahrnehmung oder Beobachtung), durch die aus dem in E aufgezählten Möglichkeitsraum eine Auswahl getroffen wird (in der Sprachweise der Quantenmechanik ein Schnitt). Daraus wird auf B geschlossen. Es stellt sich die Frage, worin die Allgemeinheit besteht, die bei der Messung (Wahrnehmung) erfolgt. Die Antwort sehe ich in der Bestimmung der Dimension, in der gemessen (wahrgenommen) wird. Sie enthält bereits die Objektivität, die auf diese Weise aus der Lehre des Schlusses hervorgeht. – So gelingt mit dem disjunktiven Schluss zweierlei: Es wird aus E und A auf B geschlossen, und es wird durch die Art dieses Schließens auf die Objektivität geschlossen.

– E · A = B und die Grundformel der messenden Wissenschaft

Was ist die Grundformel der messenden Wissenschaft (Metrologie)? Wenn mit Ruben das Messobjekt (der zu messende Gegenstand, z.B. die Höhe eines Hauses) mit mi bezeichnet wird, der Messwert (der gemessene Wert) mit {mi} und die Maßeinheit (z.B. Meter) mit [m], dann lautet die Grundformel:

(13)   mi = {mi} · [m]

lies: am Messobjekt mi wird »die Größe oder bestimmte Quantität« {mi} bezogen auf eine Maßeinheit [m] gemessen (Ruben 1997, S. 2)
Beispiel: ›das Haus ist 7 Meter hoch‹ oder formal: ›Höhe des Hauses = 7 · m‹. Hier ist die Höhe des Hauses das Messobjekt, 7 der Messwert (die Größe) und Meter die Maßeinheit.
Es ist zu beachten, dass mit dem Buchstaben ‘m’ sowohl das Wort ‘Messung’ wie auch das Wort ‘Meter’ abgekürzt wird, was zu Missverständnissen führen kann.

Werden in (13) die Seiten vertauscht, dann ist dies in meiner Deutung bereits die gesuchte Formel für die Interpretation der Schluss-Schemata:

(14)   {mi} · [m] = mi

(15)   E · A = B

Hier steht die einzelne Messung {mi} für das Einzelne (E), die Maßeinheit [m] für das Allgemeine (A) und das gemessene Messobjekt mi für das Besondere (B). Die Deutung der Maßeinheit m als das Allgemeine der jeweiligen Messung wird für mich auch dadurch nahegelegt, dass dieser Faktor keinen Index hat und sich auf  alle  Messungen in der jeweiligen Messgröße bezieht.

Ruben deutet dagegen die Maßeinheit [m] als das Einzelne E, das Mess-Ergebnis {mi} als das Besondere B und das Messobjekt mi als das Allgemeine A. Für ihn wird von der Maßeinheit über das Mess-Ergebnis auf das Messobjekt geschlossen.

»Mit dieser Feststellung dürfen wir sagen: Hegels Querstriche in den Schlussfiguren sind Leerstellen für die Bezeichnung von Operationen und Relationen, was von einer theoretischen Logik natürlich zu erwarten ist. Somit gilt, wie schon bemerkt, für E - B - A vielmehr E · B = A.« (Ruben 2003, S. 27)

Trotz dieses Unterschieds in der Interpretation der Messformel halte ich den Grundgedanken von Ruben für überzeugend. Mit ihm können Verbindungen zur Axiomatik der natürlichen Zahlen, der Proportionenlehre von Eudoxos und damit dem Größenbegriff von Aristoteles und zum Analogie-Schluss und dem disjunktiven Schluss bei Hegel aufgezeigt werden.

Im Folgenden sollen (α) innerhalb der Zahlen das archimedische Axiom und (β) das Einselement definiert werden, um schließlich () in einer Analogie das Einselement in der Gesamtheit der Messobjekte zu definieren. Daraus soll im Ergebnis gezeigt werden, wie im disjunktiven Schluss die Maßeinheit als ein neutrales Element (Einselement) hervortritt, das vom Standardelement (dem stellvertretenden Element einer Sphäre) zum Objekt führt, das Grundlage der Lehre von der Objektivität ist.

(α) Archimedisches Axiom der natürlichen und reellen Zahlen

In der Grundformel (13) der messenden Wissenschaft sind weitreichende Voraussetzungen über die Gesamtheit der messbaren Gegenstände und ihre Mess-Ergebnisse verborgen, die auf den ersten Blick so selbstverständlich klingen, dass sie lange unbeachtet blieben. Es sei m die Gesamtheit aller messbaren Gegenstände. Dann gilt für die Mess-Ergebnisse von je zwei beliebigen messbaren Gegenständen mi und mj aus dieser Gesamtheit: Sie sind entweder gleich oder der eine ist größer als der andere. Formal aufgeschrieben:

(16)    Für alle mi, mj aus m gilt: {mi} < {mj} oder {mi} > {mj} oder {mi} = {mj}

Mit dieser Eigenschaft wird eine Ordnung der Mess-Ergebnisse sichergestellt. Sie müssen wie die natürlichen oder reellen Zahlen auf einer Reihe liegen. Andernfalls wäre es sinnlos, von Messung zu sprechen, wenn unterschiedliche Messungen nicht durchgängig miteinander verglichen werden können.

Mathematisch wird die in Formel (16) beschriebene Eigenschaft mit dem von Eudoxos eingeführten archimedischen Axiom formuliert. Hier wird eine Gesamtheit < betrachtet, wobei der Index anzeigen soll, dass auf dieser Gesamtheit die kleiner-als-Relation gilt. Die Gesamtheit m aller messbaren Gegenstände ist ein Beispiel für <.

Um das archimedische Axiom formulieren zu können, muss weiter vorausgesetzt werden, dass die Elemente dieser Gesamtheit miteinander multipliziert werden können. Das heißt, dass es sich um eine Menge von Zahlen handeln muss. (Arithmetische Operationen wie die Multiplikation sind nur für Zahlen möglich. Wenn umgangssprachlich vereinfacht gesagt wird, dass zwei Gegenstände oder eine Länge und die Zeit miteinander multipliziert werden, ist damit immer gemeint, dass die in Zahlen darstellbaren Größen dieser Gegenstände miteinander multipliziert werden.)

Die Gesamtheit einer archimedisch geordneten Zahlenmenge wird in diesem Zusammenhang mit bezeichnet, da sie im Weiteren als Index für die Analogie mit der Gesamtheit der messbaren Gegenstände dienen soll. (Siehe zur mathematischen Unterscheidung geordneter Mengen und geordneter Körper und wichtiger Gegenbeispiele den übersichtlichen Eintrag in Wikipedia. So sind zum Beispiel die komplexen Zahlen nicht geordnet.) Für sie soll das archimedische Axiom gelten:

(17)     Zu je zwei Größen a > b > 0 aus existiert ein weiteres Element n aus mit n · b > a

Dies Axiom ist trivialerweise für die natürlichen Zahlen ℕ erfüllt, da es sich aus der Nachfolger-Relation ergibt, mit der per Definition die natürlichen Zahlen konstruiert sind: Wenn a > b ist, muss a ein Nachfolger von b sein. b hat einen direkten Nachfolger ›b + 1‹, dieser Nachfolger hat wiederum einen direkten Nachfolger ›b + 1 + 1‹, bis irgendwann nach i Schritten a erreicht ist: ›b + i = a‹. Mit i ist eine natürliche Zahl gefunden, die auf jeden Fall ›i · b > a‹ erfüllt. Die natürlichen Zahlen sind das klassische Beispiel für eine Indexmenge.

Was für die natürlichen Zahlen gilt, gilt unmittelbar einsichtig auch für Zahlenmengen, die auf den natürlichen Zahlen basieren wie z.B. die Zahlenmenge {0, 1/2, 2/2, 3/2, …}, die für die Beschreibung des Spins gilt.

Bereits für die reellen Zahlen kann das archimedische Axiom nicht aus den sonstigen Axiomen der reellen Zahlen gefolgert werden, da für reelle Zahlen kein direkter Nachfolger bestimmt werden kann. Welche reelle Zahl ist der direkte Nachfolger von 1? Für jede reelle Zahl x, die der Nachfolger von 1 sein sollte, gibt es weitere Zahlen, die zwischen 1 und x liegen, z.B. die Zahl (1 + x) / 2, die größer als 1 und kleiner als x ist. Daher muss für die reellen Zahlen das archimedische Axiom als zusätzliches Axiom ergänzt werden.

Anmerkung: Mit dem archimedischen Axiom wird für die reellen Zahlen sichergestellt, dass das Paradox von Achilles und der Schildkröte nicht gilt. Wenn die Schildkröte dem Achilles voraus ist (also der Satz gilt: ›der Abstand a der Schildkröte von einem Startpunkt x0 ist größer als der Abstand b des Achilles von dem gleichen Startpunkt x0‹), dann muss es nach dem archimedischen Axiom ein n geben, für das ›n · b > a‹ gilt. Zenon argumentiert dagegen, dass Achilles nie die Schildkröte erreichen wird: Ist Achilles der Schildkröte näher gekommen, hat sie sich ihrerseits wiederum ein Stück weiter entfernt. Das veranschaulicht das formale Argument, warum es keinen Nachfolger der reellen Zahl a gibt, denn für jeden Nachfolger b gibt es eine weitere reelle Zahl, die zwischen a und b liegt. Zenon kann nicht "widerlegt" werden, sondern er hat zurecht gezeigt, dass die reellen Zahlen ein zusätzliches Axiom benötigen, um Paradoxien dieser Art auszuschließen.

(β) Einselement der natürlichen und reellen Zahlen

Gewissermaßen in Umkehrung des archimedischen Axioms wird das Einselement e definiert: Es gibt in einer archimedisch geordneten Zahlenmenge nicht nur für je zwei Zahlen a und b eine dritte Zahl n, für die ›n · b > a‹ gilt, sondern es gibt auch ein genau definiertes Einselement e aus , so dass die Multiplikation jeder Zahl mit dem Einselement sie selbst ergibt:

(18)    Es gibt ein e aus , so dass für alle x aus gilt: x · e = x

Für die reellen und natürlichen Zahlen ist trivialerweise die Zahl 1 das Einselement. Jede Zahl ergibt mulitipliziert mit 1 sich selbst. Mit dieser Zahl ist innerhalb der Zahlen ein Standardobjekt definiert, so dass alle anderen Zahlen formal ein Vielfaches dieses Standardobjekts sind.

Um von Formel (18) zur messenden Wissenschaft zu gelangen, ist die Eigenschaft der Indexmenge, dass dort die Zahl 1 das Einselement e ist, d.h. e = 1 gilt, wiederum formal aufzuschreiben. Das sieht auf den ersten Blick umständlich, tautologisch oder wie eine "Trickserei" der Mathematik aus, wird sich jedoch im nächsten Abschnitt erklären, wenn die Analogie zwischen den messbaren Objekten und einer archimedisch geordneten Zahlenmenge gebildet wird.

Formel (18) wird daher in folgende Gleichung erweitert, die eine Analogie enthält: Die archimedisch geordnete Indexmenge enthält ein Einheitselement e, so dass für alle Elemente x aus ein Element aus existiert, welches die Gleichung erfüllt:

(19)    1 · x = · e; oder gleichbedeutend: x : e = : 1

lies: In einer archimedisch geordneten Zahlenmenge gibt es ein Einselement e, so dass für jedes Element x aus eine Zahl aus existiert mit der Eigenschaft x = · e
oder gleichbedeutend: x verhält sich zu e wie zu 1, wobei die Größe von x und 1 die Größe von e ist.

Formel (19) ist für die natürlichen und reellen Zahlen trivialerweise erfüllt, da bei ihnen e = 1 gilt und daher = x gesetzt werden kann mit dem tautologischen Ergebnis: 1 · x = x · 1.

() Dimensionen (Messgrößen, Quantenzahlen) und Ausblick

Für die natürlichen und die reellen Zahlen erscheint es überflüssig, eigens ein Einselement zu definieren, da die 1 das Einselement ist. Doch lässt sich dieser Begriff auf die Gesamtheiten messbarer Objekte übertragen: An die Stelle des Einselements e tritt die Maßeinheit m0.

(20)    1 · {mi} = · {m0} oder gleichbedeutend: {mi} : {m0} = : 1
            mit m0, mi ∈ m und 1, ∈

lies: Innerhalb der Messobjekte mi gibt es ein Standardobjekt m0, so dass sich für jedes messbare Objekt mi ein Element aus der archimedisch geordneten Zahlenmenge finden lässt, für das gilt, dass der Messwert {mi} das -fache des Messwerts {m0} eines Standardobjekts m0 ist.
gleichbedeutend: Für alle Messobjekte mi gibt es eine Zahl aus der Indexmenge, so dass sich die Größe {mi} des Messobjekts zur Größe des Standardobjekts {m0} verhält wie zu 1

m0 ist das Standardobjekt, an dem alle Messobjekte gemessen werden. Beispiele sind das bereits genannte Pariser Urmeter, an dem alle Längen, Höhen und Breiten gemessen werden, der Elektronenspin, an dem der Spin gemessen wird, oder das Wahrheitsmaß in der Gesamtheit aller beurteilbaren Sätze, an dem die Wahrheit von Sätzen gemessen wird.

Wie verhält sich das Standardobjekt m0 in Formel (20) zu der in Formel (13) genannten Maßeinheit [m]? Mit dem Begriff des Standardobjekts wird gezeigt, dass innerhalb der Maßeinheit [m] nochmals eine Unterscheidung zu treffen ist: Die Maßeinheit verweist zum einen auf ein Standardobjekt m0 aus der Gesamtheit der messbaren Gegenstände wie auch auf die  Dimension, innerhalb derer gemessen wird. Die Dimension ist die Gesamtheit aller Zahlen, die sich aus den Produkten · {m0} ergibt, wobei alle Werte einer archimedisch geordneten Zahlenmenge durchläuft.

(21)    D = {x | x = · {m0}} mit ∈

lies: die Dimension D ist die Menge aller Produkte des Messwerts des Standardobjekts mit den Elementen aus einer archimedisch geordneten Zahlenmenge

Die Dimension umfasst sowohl die Größen aller Messobjekte, die innerhalb dieser Dimension tatsächlich gemessen werden, wie auch alle Größen, die sich rein mathematisch aus dem Messwert des Standardobjekts und einem beliebigen Element aus der archimedisch geordneten Zahlenmenge ergeben. Die Dimension umfasst alle  messbaren  Größen innerhalb einer gegebenen Dimension. Sie ist bezogen auf eine bestimmte Maßeinheit der Raum aller möglichen Messungen.

Die Dimension wird von der Messtheorie anschaulich als Messgröße bezeichnet. Das ist der kritische Punkt, an dem die Schluss-Lehre über die Urteils-Lehre hinausgeht. Bereits in der Urteils-Lehre war für das disjunktive Urteil erkannt worden, dass es innerhalb der jeweiligen Sphäre ein Element geben muss, das stellvertretend für alle anderen steht und hier als Standardobjekt wiederkehrt. Erst mit dem analogischen Schließen und der damit verbundenen Proportionenlehre wird jedoch klar, dass sich das Schließen innerhalb einer bestimmten Dimension (Messgröße) befindet.

In der Quantenmechanik wird von Quantenzahlen statt Messgrößen gesprochen. Eine Quantenzahl ist wiederum eine Dimension, jedoch mit der Besonderheit, dass in diesen Dimensionen nur diskrete Werte (die Quanten) auftreten. Während für Höhe, Länge, Breite, Wellenlängen von Farben etc. theoretisch alle reellen Zahlen möglich sind (also als Indexmenge die reellen Zahlen gewählt werden), können für Quantenzahlen nur ganze Vielfache eines elementaren Quantums auftreten. Zum Beispiel treten für den Spin nur ganze oder halbe Vielfache des reduzierten Planckschen Wirkungsquantums auf. Die Dimension ist gequantelt.

Ursprünglich war für jede Dimension ein eigener Größenbegriff entwickelt worden. Die frühen Naturforscher glaubten, dass für unterschiedliche Qualitäten wie Größe, Farbe, Geschmack etc. jeweils eigene Größenbegriffe und eigene Proportionen für den Größenvergleich bestehen. Erst als deutlich wurde, dass in allen Qualitäten beim Vergleich ihrer Größen übereinstimmende Regeln auftreten, konnte ein allgemeiner Größenbegriff entwickelt werden. Am Anfang stand ein Analogie-Schluss: Die Größen von Flächen verhalten sich zueinander wie die Größen von Längen, oder die Größen von Gewichten und so fort. Als erkannt war, dass es für alle Dimensionen einen allgemeinen Größenbegriff gibt, wurde damit umgekehrt klar, dass sich die verschiedenen Größen durch ihre jeweilige besondere Dimension unterscheiden.

Die gedankliche Schwierigkeit wirkt sich bis heute in sprachlichen Ungenauigkeiten und Missverständnissen aus. Wenn z.B. in der Quantenmechanik der Spin als Quantenzahl bezeichnet wird, ist das genau genommen falsch und führt in die Irre. Der Spin ist eine Dimension, innerhalb der Dimension ist das reduzierte Plancksche eine Maßeinheit, und nur die Größe der Maßeinheit und ihre Vielfachen sind Zahlen. In Texten über die Quantenmechanik ist bisweilen generell unklar, ob mit der Quantenzahl ein Merkmal eines Objekts gemeint ist, oder eine Maßeinheit, oder eine Dimension wie z.B. der Spin, oder der jeweilige Messwert, z.B. der Spin eines bestimmten Teilchens.

Auch in der Umgangssprache wird bisweilen die Ausdrucksweise nicht besonders genau genommen. Jeder versteht den Satz ›das Haus ist 7 Meter groß‹, obwohl in diesem Satz keine Dimension genannt wird, sondern lediglich von der Größe des Hauses die Rede ist. Die Unterscheidung von Größe und Dimension blieb lange verborgen, da der Mensch entsprechend seiner Wahrnehmungsphysiologie implizit bestimmte Dimensionen voraussetzt. Erst Vergleichssätze zeigen die Ungenauigkeit und mögliche Missverständnisse, wenn nicht explizit die jeweilige Dimension genannt wird:

›Das Haus ist 7 m groß‹
›Das Haus ist 7 Quadratmeter in der Grundfläche groß‹
›Das Haus ist 7 Quadratmeter in der Vorderansicht groß‹
›Das Haus ist 7 Kubikmeter im umbauten Raum groß‹
›Das Haus ist 7 m hoch.‹
›Das Haus ist 7 m breit‹

Diese Beispiele zeigen, wie die Aussage erst durch die jeweilige Dimensionsangabe Höhe, Länge, Breite, Grundfläche, Vorderansicht, umbauter Raum eindeutig wird. Mit Größe kann im jeweiligen Kontext mal die Höhe, die Breite, die Tiefe, die Grundfläche oder der umbaute Raum des Hauses gemeint sein. In der Umgangssprache versteht dennoch jeder, dass mit ›das Haus ist 7 m groß‹ gemeint ist ›das Haus ist 7 m hoch‹. Bei allen Gegenständen werden Größe und Dimension intuitiv im Kontext der üblichen Wahrnehmungssituation verstanden: Wer vor einem Haus steht, nimmt dessen Höhe als dessen Größe wahr.

Erst wenn in dieser Weise herausgestellt ist, was mit einem messbaren Gegenstand, einer Messgröße (Dimension) und einer Maßeinheit gemeint ist, kann der Begriff der Größe allgemein definiert werden. Ursprünglich gab es nur kontextbezogen Begriffe für Höhe, Breite, Dauer etc. Eudoxos hat als erster erkannt, dass alle Größenmessungen wie Höhe, Breite, Geschwindigkeit, Dauer etc. auf einen gemeinsamen Größen-Begriff zurückgehen.

Anmerkung 1: Mit Formel (20) ist die klassische Definition der antiken Proportionenlehre von Eudoxos erreicht. Aristoteles hat deren Tragweite erkannt und mit ihrer Hilfe seinen Begriff der Größe (megethos) gebildet. Das war der Durchbruch auf dem Weg von der Naturphilosophie zur Physik und zur euklidischen Geometrie (siehe dazu den Beitrag megethos – Größe und Krise der griechischen Mathematik). Erst mit einem klaren Begriff der Größe konnte die empirische Wissenschaft philosophisch begründet werden, was heute häufig vergessen wird, wenn polemisch die empirische Wissenschaft der theoretischen Wissenschaft gegenüber gestellt wird. Auf der einen Seite glauben die Empiriker, sie könnten sich allen theoretischen Spitzfindigkeiten entziehen und einfach "drauflos forschen". Sie vergessen, dass ihnen das nur dank einer intensiven philosophischen Arbeit möglich wurde. Und umgekehrt werfen manche Theoretiker oder Philosophen der empirischen Wissenschaft vor, sie würde nicht denken, sondern an der sinnlich erfahrbaren Oberfläche der Dinge bleiben. Diese herablassende Haltung geht auf das Höhlengleichnis von Platon zurück, wenn die empirische Wissenschaft mit der Wissenschaft der gefesselten Höhlenbewohner verglichen wird, die nur die Schatten an der Wand beobachten, aber nicht ins Licht treten können. Diese Haltung ignoriert, dass die empirische Wissenschaft aus einer komplexen Klärung philosophischer Grundbegriffe hervorgegangen ist, die erst nach Platon durch Eudoxos und Aristoteles geleistet wurde.

Anmerkung 2: Aufgrund der intensiven Verwendung mathematischer Methoden erscheint möglicherweise der hier eingeführte Begriff des Einselements und der Dimension als ärmer im Vergleich zum Begriff der Sphäre, der mit dem unendlichen und dem disjunktiven Urteil definiert wurde. Der Begriff der Dimension hat jedoch nicht weniger "tiefe" philosophische Grundlagen als der Begriff der Größe (megethos). Um das auszuführen, ist ein weiterer Kommentar zu Aristoteles geplant, mit dem die Begriffe der Dimension und der Austauschbarkeit näher ausgeführt werden sollen. Leider gibt es bisher so gut wie keine Arbeiten zu diesem Thema. Lediglich in der neuplatonischen Philosophie finden sich Anhaltspunkte, die sich in Ausdrücken wie Abstand (Lücke, diastema), Ausgedehntheit (Auseinanderstehen, diastasis), Umfang (parastasis) zeigen. Bei Hegel sind sie angedeutet in seinen Ausführungen zur Eins und dem Vielen in der Seinslogik. Ich möchte die These vertreten, dass sich eine Dimension dadurch auszeichnet, dass es für alle ihre Elemente eine einheitliche Abstandsfunktion gibt, durch die sie sich auf eine gemeinsame Einheit beziehen. Wieder besteht die Gefahr des Missverständnisses, dass sich in der Schluss-Lehre einfach zu wiederholen scheint, was in der Seinslogik bereits ausgeführt wurde. Es soll in einer geplanten Arbeit gezeigt werden, dass es eine Eigenschaft des schließenden Denkens ist, dass es einen gemeinsamen Bezugspunkt und eine allgemeingültige Abstandsfunktion gibt, über die auf alle Elemente in der Dimension geschlossen werden kann. Das erscheint mir als ein Fortschritt, der auf die gleiche Weise vom Begriff der Sphäre zum Begriff der Dimension führt, wie aus der Urteils-Lehre die Schluss-Lehre entwickelt wird.

Anmerkung 3: Aufgabe der messenden Wissenschaft ist es, das jeweilige Standardobjekt zu finden, welches als Einselement dient und die jeweilige Dimension definiert. Die Messungen müssen innerhalb dieser Dimension bleiben. In der praktischen Wissenschaft liegt anfangs nur eine ungeordnete Menge von Mess-Ergebnissen {mi} vor. Innerhalb dieser Gesamtheit wird nach einem Einselement m0 gesucht, als dessen Vielfache sich alle Mess-Ergebnisse deuten lassen. Wenn ein solches Einselement gefunden ist, dann kann daraus die physikalische Erkenntnis gewonnen werden, dass alle Mess-Ergebnisse in einer einheitlichen Dimension liegen. Im Alltagsleben erscheint dieser Schluss trivial, da aufgrund der natürlichen Wahrnehmungsfähigkeit Dimensionen wie Höhe, Breite, Tiefe, Farbe, Geruch, Geschmack oder Festigkeit bereits bekannt sind. Anders wird es, wenn die Wissenschaft unmittelbar sinnliche Erfahrungen verlässt. Sie sucht dann nach dem Vorbild der euklidischen Geometrie nach ihrem jeweils spezifischen Einheitselement und der daraus hervorgehenden Dimension, so die Massepartikel in der Mechanik, die elektrische Elementarladung in der Elektrostatik usw. Die Teilchenphysik spricht bei Deutung der experimentellen Mess-Ergebnisse von Quantenzahlen, wobei jede Quantenzahl auf ein Einselement zurückgeht, wie z.B. die Händigkeit, der Elektronenspin oder die verschiedenen Leptonenzahlen.

Anmerkung 4: Warum ist dieser technische Aufwand notwendig? Sehr häufig wird in erster Annäherung etwas für eine Maßeinheit gehalten, bis sich herausstellt, dass es sich durch eine zusätzliche Veränderung im Innern seinerseits ändern und daher nicht länger als Maßeinheit dienen kann. So war es, als erkannt wurde, dass die Atome nicht die kleinsten Einheiten sind, sondern aus Atomkern und Elektronen bestehen, die in weiteren Schritten ihrerseits weiter differenziert werden mußten. – In der Ökonomie ist es bis heute nicht gelungen, die kleinsten Einheiten zu erkennen, wie z.B. elementare Zyklus-Längen für Wirtschaftszyklen. Das macht bis heute Wirtschaftsprognosen so schwierig. – Die meisten sophistischen Tricks mit empirischen Studien und Zahlen etwas "objektiv" beweisen zu wollen, beruhen darauf, dass bewusst etwas als Standardeinheit ausgegeben wird, was sich in Wahrheit ändert. Häufig ist nicht zu entscheiden, ob das Unwissen oder Täuschungsabsicht war. So sehr einerseits die Möglichkeiten der Mathematik bewundert werden, wird andererseits dem mathematischen Rechnen prinzipiell Berechnung mit abwertender moralischer Bedeutung vorgeworfen (siehe dazu den Beitrag Mathematik des Bösen).

Anmerkung 5: In seinem ersten Systementwurf, der Jenenser Logik, Metaphysik und Naturphilosophie (wohl 1801-02 entstanden), sieht Hegel, dass der Schluss innerhalb einer eindimensionalen Kette verbleibt und kommt der hier von Frege und Ruben vertretenen Interpretation nahe:

»Der einfache Kreis des Begriffes hat sich in die Linie verengt und auseinandergeworfen, deren Mitte der verengte, in einen Punkt zusammengezogene Kreis selbst ist, und deren Extreme das Allgemeine und das Besondere sind.« (Hegel, JLM, S. 97)

Ausblick:    Allerdings ist die Logik nicht mit einem Schluss vollendet, der messbare Größen auf eine Maßeinheit bezieht. In weiteren Schritten sind voneinander unabhängige Dimensionen zu entwerfen und die Konstruktionsverfahren zu entwickeln, mit denen innerhalb dieser Räume Erkenntnisse gewonnen werden. Die linearen Schlüsse sind ein notwendiger Bestandteil, aber nur ein Grenzfall.

Die Dimensionen können ihrerseits in einem übertragenen Sinn wie Eigenschaften betrachtet werden, so wie es intuitiv und bisweilen missverständlich bereits in der Quantenmechanik mit den Quantenzahlen geschieht. Das leitet über zum nächsten Abschnitt.

Der disjunktive Schluss E – A – B lässt sich nach meiner Überzeugung nur verstehen als Schluss über eine allgemein-gültige Maßeinheit innerhalb der jeweiligen Messgröße. Daher gilt innerhalb dieser Dimension die Formel ›E · A = B‹. Mit dieser Deutung sollte gezeigt werden, wie aus der Schlusslehre die Objektivität hervorgeht: Begriffe wie Größe, Dimension, Standardobjekt, Multiplikation weisen bereits in die Objektivität. Die Lehre der Objektivität wird untersuchen, wie diese Begriffe, die aus dem disjunktiven Schluss hervorgehen, für sich betrachtet werden.

Mit dem Größenbegriff kehrt innerhalb der Begriffslogik der Begriff des Quantums und der Quantität wieder, der bereits in der Seinslogik eingeführt worden war, jedoch in einem völlig neuen Kontext. In der Schlusslehre erweist sich die Größe als das Allgemeine, über das im disjunktiven Schluss E – A – B geschlossen werden kann. Das wirft von einer neuen Seite die Frage nach dem Stellenwert und dem Status der Mathematik auf. Es ist zu fragen, dank welcher Eigenschaft die Mathematik fähig ist, eine Allgemeinheit (A) zu entwickeln, mithilfe derer geschlossen werden kann. Diese Frage führt zu einem abschließenden Durchgang durch die drei Schlussfiguren am Ende der Wissenschaft der Logik, wobei Hegel die geometrische Methode in der mittleren Position B – E – A sieht, mit der ein Schluss vom Besonderen über das Einzelne zum Allgemeinen erfolgt. Sie ist insofern systematisch in der gleichen Position wie bereits vorher das hypothetische und disjunktive Urteile (auf die sich Frege bezog) und der analogische Schluss, der der Proportionenlehre von Eudoxos korrespondiert. Am Satz von Pythagoras soll entwickelt werden, wie mit der geometrische Methode das Allgemeine gefunden wird, aus dem in einem letzten Schritt die dialektische Methode hervorgeht. Mathematik und Dialektik stehen nach dieser Idee in einem Verhältnis zueinander wie der analogische und der disjunktive Schluss. Die Mathematik entwickelt die Methoden, mit denen Analogie-Schlüsse gebildet werden können, aber erst der dialektischen Methode gelingt die vollständige Beschreibung des Wissens. Mit dieser Frage wird das Thema der einflussreichsten Veröffentlichung von Peter Ruben erreicht, Philosophie und Mathematik (1979).

– Das kartesische Produkt voneinander unabhängiger Dimensionen

So wie der Satz vom ausgeschlossenen Dritten nur ein Grenzfall innerhalb der Urteilslehre ist, so ist die soeben dargestellte Messung nur ein Grenzfall im Übergang zu weiterreichenden Methoden des Denkens. Sie zeigt, wie formalisiertes schließendes Denken entstanden ist und seine Gültigkeit und Bedeutung behält, wenn sich die Schlüsse innerhalb einer Dimension bewegen. Hegel hatte jedoch bereits in der Lehre vom Sein zahlreiche Beispiele genannt, in denen der Übergang in eine höhere Dimension erforderlich war (so bei der Herleitung des Differentialkalküls aus der qualitativen Potenzbestimmung und bei der Einführung von Knotenlinien in der Maßlogik, die gegenüber den Wahlverwandtschaften eine neue Dimension eröffnen). Daher reicht eine Formel wie E · A = B für seine Schluss-Lehre nicht aus, sondern bezeichnet den Grenzfall, an dem seine Schluss-Lehre in die Schluss-Lehre der formalen Logik übergeht.

Im Grunde ist auch Ruben an einer Schluss-Lehre interessiert, die nicht innerhalb einer Dimension verbleibt. Die Gesamtheit der Sätze ist ebenfalls ein Beispiel, in dem das Schließen innerhalb einer Dimension verlassen werden muss. Subjekte und Prädikate gelten als unabhängige Dimensionen, die zur höheren Dimension der Sätze führen (siehe Formel 3: › = ℙ‹). Das kann auf die Frage der Messung übertragen werden. Statt von Subjekten wird von Messgegenständen gesprochen, und statt von Prädikaten von Messgrößen. Dann geht es nicht mehr nur um eine einzige Messgröße (eine bestimmte Dimension), die gemessen wird, sondern um die Gesamtheit aller Messgrößen. Sie sei als bezeichnet, wobei D für Dimension steht. Daraus ergibt sich ein erweiterter Ansatz, die Messung zu verstehen: Der Gesamtheit der messbaren Gegenstände m wird die von ihr unabhängige Gesamtheit der Messgrößen gegenübergestellt. Jede einzelne Messung ist eine Messeinheit (S,D), wobei diese Einheit das Ergebnis der Messung von S in der Messgröße D zeigt. Sie entspricht der Satzeinheit (S,P). Weiter entspricht der Gesamtheit ℙS aller Prädikate eines Subjekts die Gesamtheit S aller Messgrößen eines Gegenstandes. Sie wird als  Zustand von S  bezeichnet. Der Begriff Zustand ist von der Quantenmechanik übernommen, die allerdings von Quantenzahlen statt von Dimensionen spricht, um auch Freiheitsgrade wie den diskreten Spin u.ä. ergänzen zu können. Die Gesamtheit aller Dimensionen ist wiederum identisch mit den Symmetrie-Gruppen, mit denen heute die Physik die Welt beschreibt.

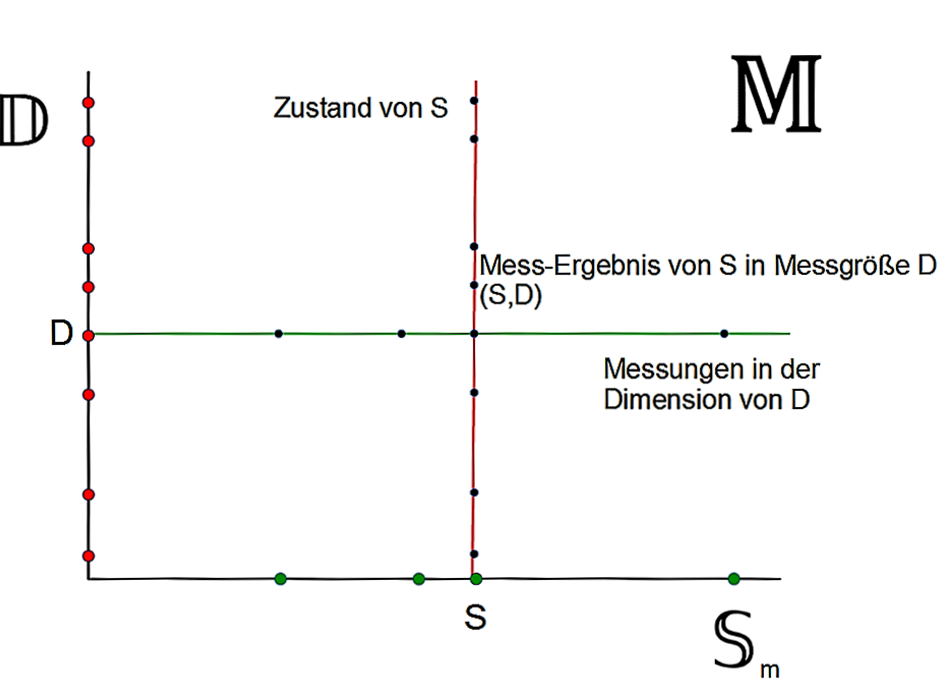
Figur 6: Messung (Gesamtheit der Mess-Ergebnisse )
(S,D) ist das Mess-Ergebnis, wenn ein Gegenstand S in der Messgrösse D gemessen wird.
Die rote Linie zeigt den Zustand von S, das ist die Gesamtheit S aller Messungen eines Gegenstandes S.
Die grüne Linie zeigt die Gesamtheit D der in der Dimension D durchgeführten Messungen.

Die Messung entspricht der Satzbildung, das Mess-Ergebnis dem Satz. Aus Formel (1) ›S ist p‹ wird daher:

(22)    S hat in der Dimension D den Messwert (S,D)

Wenn ein Raum aus voneinander unabhängigen Dimensionen gebildet wird, muss das "normale" Produkt · ersetzt werden durch das kartesische Produkt .

Anmerkung: Das Kartesische Produkt darf nicht verwechselt werden mit dem äußeren Produkt in der Vektorrechnung. Bei einem äußeren Produkt zweier Vektoren, die in einer Ebene liegen und in unterschiedliche Richtungen weisen, wird eine senkrecht zu dieser Ebene stehende dritte Dimension gegründet. Das wichtigste Anwendungsbeispiel des äußeren Produkts ist die Drei-Finger-Regel, nach der die Wirkung (Lorentz-Kraft) senkrecht zu den Richtungen des Stroms und des Magnetfelds steht.

Mit dem kartesischen Produkt werden die von Hegel gesuchten »höheren« Dimensionen gefunden, oder in der Sprachweise von Schelling die Potenzen. Das war bereits die Aussage von Formel (3) = ℙ. Entsprechend ist hier Formel (13) ›mi = {mi} · [m]‹ zu ersetzen durch:

(23)    = m

lies: die Gesamtheit aller Mess-Ergebnisse ist eine Fläche, die von den beiden voneinander unabhängigen Achsen der Gesamtheiten der messbaren Gegenstände und der Messgrößen aufgespannt wird.

Hier ist zu beachten, dass der Begriff der Dimension doppelt vorkommt, was zu Missverständnissen führen kann. Jede einzelne Messgröße definiert für sich eine Dimension, wie z.B. Länge, Höhe, Breite und in der heutigen Physik eine Quantenzahl, innerhalb derer es jeweils eine Maßeinheit gibt und die Messungen erfolgen. Zugleich bildet die Gesamtheit der Messgrößen ihrerseits eine Dimension, um die es hier geht. Die von den Messgrößen gebildeten Dimensionen sind eindimensionale Äquivalenzklassen in dem größeren Raum aller Mess-Ergebnisse. Sie sind in Figur 6 mit einer grünen Linie veranschaulicht und enthalten alle Messungen, die in dieser Dimension erfolgt sind. Die messbaren Gegenstände, die sich in dieser Dimension messen lassen, entsprechen formal dem Substrat eines Prädikats.

Anmerkung: Wird statt von einer Messung eines messbaren Gegenstands in einer Messgröße nur von der Zugehörigkeit zu dieser Dimension gesprochen, dann vereinfacht sich die Messung zur Bestimmung: Statt der messbaren Gegenstände m werden die bestimmbaren Gegenstände b betrachtet. Ihnen stehen statt der Dimensionen die Gattungen gegenüber. Die Bestimmung entspricht der Satzbildung bzw. der Messung. Mit der Bestimmung wird erkannt, ob das zu bestimmende Objekt ein spezifisches Merkmal (eine Familienähnlichkeit) trägt, wodurch es sich als eine Art der Gattung erweist. Das Ergebnis der Bestimmung entspricht dem Satz bzw. dem Messwert. Hier kommt es zu einer Doppeldeutigkeit, da sprachlich sowohl der Vorgang wie das Ergebnis als Bestimmung bezeichnet wird. Wie in der Prädikationstheorie entstehen Paradoxien, wenn nicht die Unabhängigkeit der Individuen und Gattungen sowie die unteilbare Einheit des Bestimmungs-Ergebnisses beachtet werden.

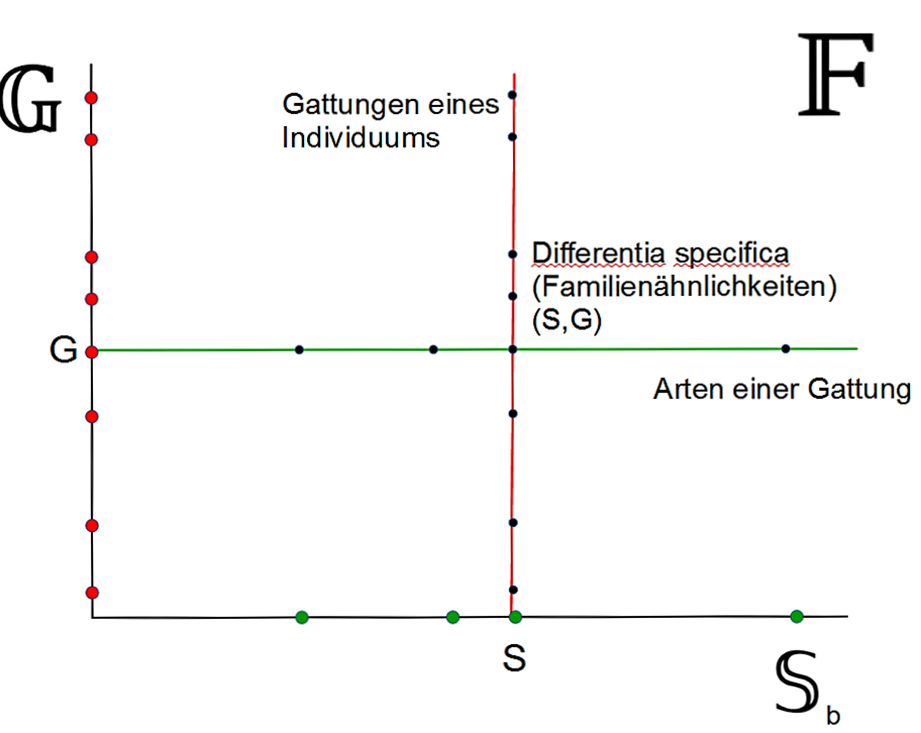
Figur 7: Bestimmungen (Gesamtheit der bestimmten Familienähnlichkeiten )
Im Bestimmungsprozess wird für bestimmbare Gegenstände S und Gattungen G nach spezifischen Merkmalen gesucht um zu erkennen, welche bestimmbaren Gegenstände innerhalb einer Gattung eine Art bilden.

Formel (23) ›S hat in der Dimension D den Messwert (S,D)‹ kann daher umgewandelt werden in:

(24)    S erfüllt in der Gattung G das spezifische Merkmal (S,G)

– Zeitdimension

Im Vorhergehenden wurde davon ausgegangen, dass Sätze und Messungen zeitunabhängig gelten. Da jede Messung in jeder Messgröße zeitlich wiederholt werden kann und sich zu unterschiedlichen Zeiten unterschiedliche Messungen ergeben können, ist die Zeit als dritte Achse zu ergänzen und nicht auf der Dimensions-Achse als eine weitere Dimension wie Höhe, Breite, Länge und andere Quantenzahlen einzutragen. Die Formeln (1) ›S ist p‹ und (19) ›S hat in der Dimension D den Messwert (S,D)‹ sind daher zu erweitern in:

(25)   S ist zum Zeitpunkt t p

(26)   S hat zum Zeitpunkt t in der Dimension D den Messwert (S,D,t)

Anmerkung: Hier wird die Zeitdimension mit bezeichnet, um Verwechslungen mit der Gesamtheit der Termini zu vermeiden.

 

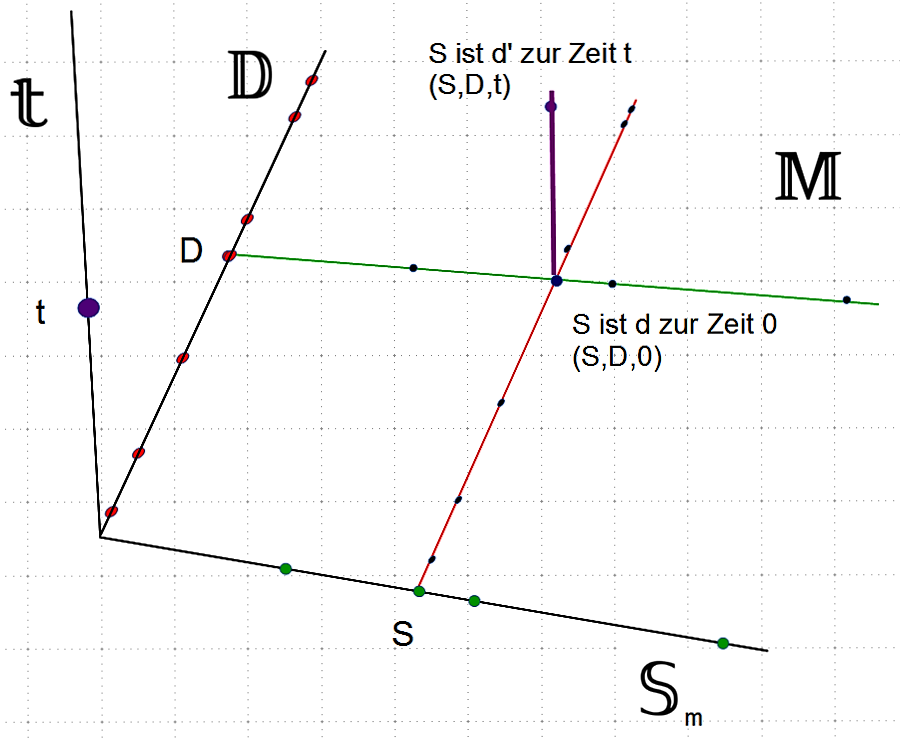
Figur 8: Messungen mit Zeitverlauf
Ein Messobjekt S wird in der Messgröße (Dimension) D fortlaufend gemessen. Die Messwerte zeigen im Verlaufe der Zeit bezüglich Dimension D eine Bewegungskurve, die violett eingetragen ist. Zur Zeit 0 wurde der Messwert d gemessen, zur Zeit T der Messwert d'.

In diesem äußerst verdichteten Bild hat die violett gezeichnete Bewegungskurve eine komplexe Bedeutung:

(a) Die messbaren Gegenstände auf der -Achse sind zu verstehen als die ausgedehnten Körper in der dreidimensionalen euklidischen Geometrie. Im einfachsten, idealisierten Fall ist ein messbarer Gegenstand S ein einzelner Punkt im euklidischen Raum. Im mechanischen Fall handelt es sich um dreidimensionale Objekte, die entsprechend dem Ansatz von Descartes durch ihre räumliche Ausgedehntheit charakterisiert sind. Kant verstand den euklidischen Raum im Ganzen als die Gleichzeitigkeit und Wechselwirkung aller in ihm enthaltenen Körper. Das entspricht der Anschauung der modernen Physik, die davon ausgeht, dass auch zwischen räumlich weit voneinander entfernten Körpern innere Symmetrien bestehen, die bewirken, dass Veränderungen des einen Körpers nur durch simultane, gegenläufig erfolgende Veränderungen des anderen Körpers erfolgen kann und beide Körper (bzw. größere Aggregate von Körpern) eine zusammenhängende Einheit bilden.

(b) So wie die eindimensional dargestellte -Achse in Wahrheit einen dreidimensionalen Raum bezeichnet, so steht jeder einzelne Punkt auf der -Achse wiederum für eine vollständige Dimension (Messgröße), die jeweils einen ganzen Messbereich möglicher Messwerte umfasst. Das können in einigen Fällen (wie z.B. dem Spin) sehr wenige einzelne Werte sein, in anderen Fällen kontinuierlich viele verschiedene Werte. Wenn die Bewegungskurve eines messbaren Gegenstands durch die Vielfalt der Dimensionen betrachtet wird, dann kann es sowohl vorkommen, dass sich innerhalb einer Dimension die Messwerte verändern, als auch, dass eine Dimension in eine andere umschlägt, in neuen Dimensionen Messwerte auftreten oder in ganzen Dimensionen Messwerte verschwinden. Die Vielfalt der Möglichkeiten wird durch die Katastrophentheorie klassifiziert.

Jeder messbare Gegenstand hat zu einem bestimmten Zeitpunkt T einen bestimmten Zustand D, der sich aus allen Mess-Ergebnissen zu diesem Zeitpunkt zusammensetzt. Die Quantenmechanik ermittelt die Wahrscheinlichkeiten, mit der sich dieser Zustand in einen anderen Zustand zu einer späteren Zeit verändert.

(c) Obwohl es seit der Speziellen Relativitätstheorie üblich geworden ist, die Zeitdimension in der Raumzeit mit den drei räumlichen Dimensionen zusammenzufassen, wird sie hier bewusst als eine dritte unabhängige Achse berücksichtigt. Die Zeitdimension hat spezifische Eigenschaften, die sie von allen anderen Dimensionen unterscheidet. Sie ist in die Zukunft gerichtet und enthält Eigenschaften wie Zufälligkeit, Wahrscheinlichkeit, Notwendigkeit und Unvorhersehbarkeit. Die Zukunft kann nie vollständig vorausgesagt werden. Bei einem Blick in die Zukunft treten daher notwendig Wahrscheinlichkeiten auf. Aus der gegebenen Situation kann nur mit Wahrscheinlichkeiten abgeschätzt werden, wie sich daraus die Zukunft entwickelt.

Bisher wurden die Subjekte den Prädikaten bzw. die messbaren Gegenstände den Dimensionen gegenübergestellt. Wenn die Zeitachse eine herausgehobene Bedeutung haben soll, die sie von allen anderen Dimensionen unterscheidet, dann muss es möglich sein, die Verhältnisse der beiden Achsen der messbaren Gegenstände und der Zeit für sich zu betrachten unabhängig von den Dimensionen der verschiedenen Merkmale, also insbesondere auch unabhängig von Schwere, Dichte, Farbe und allen anderen Eigenschaften, die eine Masse ausmachen. Das leistet die Spezielle Relativitätstheorie. Sie zeigt, welche allgemeinen Eigenschaften für ausgedehnte Körper gelten unabhängig von ihrer Masse. Wird nur die --Fläche betrachtet, dann gelten dort spezielle Beziehungen, die sich aus den besonderen Eigenschaften der Zeit erklären. Epstein hat gezeigt, dass die Spezielle Relativitätstheorie auf ähnliche Weise wie die hier vorgestellten Figuren veranschaulicht werden kann, wenn die Geschwindigkeiten in Richtung von Raum (Fortbewegung) und Zeit (Altern) betrachtet werden. Dort gilt, dass die Gesamtheit beider Geschwindigkeiten konstant sein muss. Das bedeutet, dass ein Körper, der sich schneller fortbewegt, langsamer altert und umgekehrt. Siehe dazu Link.

Diese Dreiteilung von drei ausgezeichneten Achsen kann sich auf eine lange philosophische Tradition berufen. Für die Subjekte steht bei Aristoteles die hervorgehobene Kategorie der Substanz (ousia), bei Descartes die Ausgedehntheit, bei Kant und Hegel das Quantum. Die Achse der Dimensionen hat ihr Vorbild in den sekundären Kategorien bei Aristoteles und den Qualitäten bei Kant und Hegel. Die dritte Achse schließlich wurde immer als etwas Besonderes betrachtet. Kant sah in der Zeit die übergreifenden Schemata der transzendentalen Analytik. Erst Hegel hat in dieser Achse das Zusammenspiel von Quantität und Qualität gesehen. In Bewegungsverläufen bzw. bei Verläufen, wenn ein bestimmter Parameter (wie die Temperatur oder der Anteil eines bestimmten Stoffs an einem Gemisch) kontinuierlich verändert wird, kommt es zu Umschlägen von Quantität und Qualität, die sich nur im Verlaufe der Zeit ereignen können.

Das bedeutet verallgemeinert, dass mit der Zeitachse auseinander hervorgehende Ebenen verbunden sind, die für sich jeweils als --Flächen angesehen werden können. Jede einzelne Ebene definiert für sich ihre eigene Geometrie und ihre eigenen Zustände. Die euklidische Geometrie stellt einen Grenzfall dar, wenn alle Dimensionen der -Achse auf ihrem Nullwert stehen, der ungefüllte, ruhende, materiefreie Raum. Das ist die Grundfläche, aus der alles weitere Geschehen hervorgeht. Im Verlaufe der zeitlichen Entwicklung erhalten die messbaren Objekte in den Dimensionen konkrete Werte, können von einem Zustand in einen anderen wechseln, wodurch die reine euklidische Geometrie verlassen und gekrümmt wird. Die Physik spricht vom Grundzustand, Ruben von der »Einsdimension« (Ruben 1997, S. 3).

– Skalarprodukt

In den Arbeiten von Ruben ist dieser Entwurf an zwei Stellen angesprochen. Er vermutet – ausgehend von den Arbeiten des Logikers Bruno Hartmann –, dass es eine übergreifende Dreidimensionalität gibt. »Zu zeigen bleibt noch, daß es zu einem Allgemeinen genau 3 Einzelne gibt (eine Inhaltsgattung also genau 3 Inhaltsarten hat).« (Ruben 1998, S. 39). Seinem Versuch, dies aus der Komplementarität verschiedener Ebenen innerhalb eines Allgemeinen zu begründen, kann ich zwar nicht folgen, stimme aber aus den vorgetragenen Überlegungen mit dem Resultat überein.

Ruben nennt aus verschiedenen Wissenschaften Beispiele, mit denen die Mess-Ergebnisse innerhalb eines dreidimensionalen Raums bewertet werden (Ruben 1998, S. 35):

(27a)   w = m · l · t

lies: Die Wirkung ist in der klassischen Mechanik das Produkt von Masse, Länge und Dauer

(27b)   w = K · l · t

lies: Die Wirkung ist in der technischen Mechanik das Produkt von Kraft, Länge und Dauer

Bruno Hartmann nennt weitere Beispiele (Hartmann, S. 164-170):

(27c)   w = k · n · t

lies: Der Wert ist in der Ökonomie das Produkt von Arbeitskraft, Nutzen und Arbeitsdauer

Das sind mathematisch gesehen Beispiele für Skalarprodukte. In einem dreidimensionalen Raum wird jedem Punkt mit den Koordinaten (x,y,z) eine reelle Zahl zugeordnet, ihr Skalarprodukt. Im Beispiel der klassischen Mechanik wird im Raum M L t an jedem Punkt die Wirkung eingetragen. (Es ist zu erkennen, wie hier die Länge stellvertretend für die Ausgedehntheit und die Masse stellvertretend für die Eigenschafts-Dimensionen steht.)

Damit wird der Übergang zum Mechanismus erreicht, mit dem Hegel die Schluss-Lehre fortführt. Im Mechanismus werden auf diese Weise Skalarprodukte definiert und nach Wirkungsprinzipien gefragt. Aus der Vielfalt aller Weltlinien durch den mechanischen Raum werden diejenigen ausgewählt, entlang derer die Wirkung minimiert ist.

Anhang 1: Name und Referenzmenge in der Mathematik

In der Mathematik wird von Erzwingung (Forcing) gesprochen, wenn in einer Situation auf eine genau definierte, also nicht willkürliche oder beliebige Weise ein Name gebildet werden kann, dessen Referenzmenge über die aktuelle Situation hinausgeht. Das heißt, dass dieser Name nicht nur Elemente aus der bekannten Situation bezeichnet, sondern auch Elemente, die in der gegebenen Situation unbekannt sind. Durch den Namen wird über die Situation hinausgegangen und ein übergreifender Horizont erreicht (»erzwungen«), der über die Referenzmenge des Namen gegeben ist.

– Erzwingung (Forcing)

In der Mathematik wurde die Methode der Erzwingung (Forcing) entwickelt, um eine Antwort auf die Kontinuumshypothese zu finden: Wenn 0 die Mächtigkeit (die Anzahl der Elemente) der Menge der natürlichen Zahlen und 1 die Mächtigkeit der Menge der reellen Zahlen bezeichnet, dann besagt die Kontinuumshypothese zweierlei: (a) Es gibt so viele reelle Zahlen, wie es Teilmengen von natürlichen Zahlen gibt. Es ist prinzipiell möglich, jeder reellen Zahl eineindeutig eine Teilmenge von natürlichen Zahlen zuzuordnen. (b) Es gibt keine Menge, die eine größere Mächtigkeit als die Menge der natürlichen Zahlen und eine kleinere Mächtigkeit als die Menge der reellen Zahlen hat. Das kann formal aufgeschrieben werden: 1 = 20. Hier bedeutet die Potenz 20 die Anzahl aller Teilmengen innerhalb der natürlichen Zahlen, und mit dem Index 1 in 1 soll ausgedrückt werden, dass dies die erste Mächtigkeit ist, die größer als 0 und folglich ihr direkter Nachfolger ist.

Kurt Gödel hat 1938 gezeigt, dass die Kontinuumshypothese nicht im Widerspruch zu den üblichen Axiomen der Mengenlehre steht. Seine Beweisidee war, innerhalb der unübersichtlichen Gesamtheit aller Mengen eine Teil-Gesamtheit zu bestimmen, die groß genug ist, um alle Axiome der Mengenlehre zu erfüllen und gleichzeitig klein genug, um in ihr die Kontinuumshypothese zu beweisen. Hierfür wählte er ein Konstruierbarkeitsaxiom, mithilfe dessen alle Mengen auf eine wohldefinierte Weise konstruiert werden können. Die Gesamtheit aller konstruierbaren Mengen erfüllt diese Eigenschaften. Sie liefert ein Modell der Gesamtheit aller Mengen, in der alle üblichen Axiome erfüllt sind und die Kontinuumshypothese widerspruchsfrei postuliert werden kann.

Die Erzwingung wurde eingeführt, um den umgekehrten Weg zu gehen: Ein abzählbares Modell 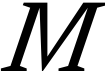der Gesamtheit aller Mengen 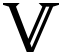wird in ein übergreifendes Modell erweitert, in dem nach wie vor alle Axiome der Mengenlehre gelten, aber nicht die Kontinuumshypothese. Diesen Weg ging 1963 Cohen. Er hat bewiesen: Wenn es gelingt, innerhalb des Modells 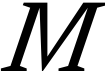mit den in diesem Modell verfügbaren Mitteln eindeutig zu beschreiben, welche Eigenschaften eine Menge G haben muss, die aus ununterscheidbaren Elementen besteht, dann kann zweierlei gezeigt werden: (a) Es gibt kein Element aus 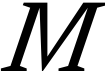, das zu G gehört. G ist innerhalb von leer. (b) Da aber die Eigenschaften von G eindeutig innerhalb von beschrieben werden können, ist es möglich, innerhalb von dieser Menge einen Namen zu geben, – den bereits genannten Namen G –, der innerhalb von verständlich ist. Dann kann nach der Referenzmenge aller Elemente gefragt werden, die die Eigenschaften von G erfüllen. Die Elemente dieser Referenzmenge können nicht in liegen, sondern liegen außerhalb von . Wird um diese Referenzmenge erweitert, liefert das das gesuchte Modell, für das gezeigt werden kann, dass dort die Axiome der Mengenlehre noch gelten, aber nicht die Kontinuumshypothese.

Es sei versucht, diesen komplexen Gedanken an dem berühmten Beispiel von Leibniz zu erläutern: Leibniz hatte behauptet, dass es keine zwei Blätter gibt, die völlig identisch und daher ununterscheidbar sind. Nun kann folgendermaßen vorgegangen werden: Schrittweise werden je zwei Blätter verglichen. Begonnen wird mit Blatt 1 und Blatt 2. Aus ihnen wird gedanklich ein Blatt ω0 konstruiert, das genau alle Eigenschaften enthält, in denen Blatt 1 und 2 übereinstimmen. Von diesen Eigenschaften wird eine beliebige gestrichen, so dass sich Blatt ω0 sowohl von Blatt 1 wie von Blatt 2 unterscheidet. Im nächsten Schritt wird Blatt ω0 verglichen mit Blatt 3, und aus der Liste der Eigenschaften von Blatt ω0 werden alle Merkmale gestrichen, die es nicht mit Blatt 3 teilt. Dies Verfahren kann unendlich fortgeführt werden. Unter der von Leibniz vorgegebenen Prämisse ist davon auszugehen, dass es in der Realität ein solches Blatt ω0 nicht gibt, aber das Verfahren, mit dem es konstruiert wird, ist in der Realität nachvollziehbar. Jeder versteht, was damit gemeint ist. Daher gibt es in der Realität alle die unterscheidbaren Blätter, wie wir sie kennen, und zusätzlich den Namen ω0 für ein Blatt, das es nicht gibt, dessen Konstruktion aber jeder versteht. Wird in Gedanken dieses Blatt der Realität hinzugefügt, dann ist eine Erweiterungsmenge gefunden, wie Cohen sie gemeint hat.

Badiou wählt ein etwas formaleres Beispiel, das inhaltlich den von Frege betrachteten Schlussketten sehr nahe kommt. Innerhalb einer Enzyklopädie kann jedes Wissen formal dargestellt werden, indem Elemente mit Mustern verglichen und diese fortlaufend verfeinert werden, so wie historisch Carl von Linné eine binäre Nomenklatur für alle Arten in der Biologie eingeführt hat, die fortlaufend bei Entdeckung neuer Arten ausgebaut wird. Muster sind im einfachsten Fall vom Typ ˂1,0,0,1,0,…˃. (Dieser Typ erinnert an die Diagonalgestalt der reellen Zahlen durch Cantor: Für jede reelle Zahl wird gesagt, ob sie an der i-ten Nachkommastelle die Ziffer 0 hat.) Die Muster bilden eine Menge, die lexikographisch geordnet werden kann. Komplexere Muster sind genauer, denn wenn sie gelten, gelten offensichtlich auch alle einfacheren Muster. Wenn z.B. ein Muster die Zeichen ˂1,0,0,1˃ enthält, so auch die darin enthaltenen Anfangszeichen ˂1,0˃. (Ein anderes Beispiel ist die alphabetische Ordnung. Wenn ein Wort mit den Buchstaben »BUCH« beginnt, ist es auch ein Beispiel für ein Wort, das mit den Buchstaben »BU« beginnt.)

Wenn die Muster schrittweise verfeinert werden, ist mit jedem Schritt eine Entscheidung zu treffen, ob das Muster durch »0« oder durch »1« erweitert werden soll. Beispiel: Das Muster ˂1,0,0,1,0˃ kann zu ˂1,0,0,1,0,0˃ oder zu ˂1,0,0,1,0,1˃ erweitert werden. Im Muster ˂1,0,0,1,0˃ ist noch unentschieden, welche Erweiterung gewählt werden wird. Jeder einzelne Schritt ist daher ein elementares disjunktives Urteil: ›das Muster ˂m˃ kann erweitert werden zu ˂m,0˃ oder ˂m,1˃‹, wobei ˂m˃ für ein beliebiges Muster steht, das im Verlaufe dieser Reihe gebildet wurde. Innerhalb jedes Muster m ist unentschieden, wie es ausgebaut wird.

Dies Verfahren ist offensichtlich der Nachfolger-Relation der natürlichen Zahlen nachgebildet mit einer wichtigen Erweiterung: Während auf jede natürliche Zahl ˂n˃ genau eine weitere natürliche Zahl ˂n+1˃ folgt, folgt hier auf jedes Muster ˂m˃ eine von den zwei Möglichkeiten ˂m,0˃ oder ˂m,1˃‹.

Daher kann für jede Bildung von Mustern eine Erweiterungsprozedur gefunden werden, die analysiert, welche Entscheidungen für dieses Muster getroffen wurden.

Umgekehrt kann daher entlang des gleichen Verfahrens innerhalb des Grundmodells eine Regel aufgestellt werden, die schrittweise jeweils das Ununterscheidbare festhält. Wichtig ist zu verstehen, dass das Ununterscheidbare kein Objekt ist, sondern eine Regel. Cohen nennt sie generische Prozedur, Badiou Wahrheitsprozedur oder Ermittlung.

Nun soll die Grundsituation um dies Ununterscheidbare in ein äußeres Modell erweitert werden. Das geht nur mithilfe des Namens und ihrer Referenzmenge. Innerhalb von kann die Ununterscheidbarkeit festgestellt werden. Der Menge aller ununterscheidbaren Elemente, die gemäß der genannten Regel fortlaufend erweitert wird, wurde von Cohen der Name gegeben, wobei G für »generische Erweiterung« steht. Badiou favorisiert mit seinem Sinn für das Dramatische das Venussymbol als Symbol der Ununterscheidbarkeit.

Was dieser Name im Ganzen bezeichnet, kann innerhalb der Grundsituation nicht geklärt werden, da die Regel fortlaufend weiterschreitet und ständig neue Ununterscheidbarkeiten produziert. Zugleich wurde aber die Regel der generischen Erweiterung innerhalb von aufgestellt. Daher ist es möglich, von zu einem neuen Modell [] überzugehen, welches die Referenzmenge von enthält. Dieser Schritt wird als Erzwingung bezeichnet. Der Schritt klingt fast tautologisch, aber es musste mit großem mathematischen Aufwand gezeigt werden, dass erstens auch die Erweiterung ein Modell der Mengenlehre ist, in dem alle Axiome der Mengenlehre gelten, dass dies Modell zweitens das Vorläufermodell enthält, und dass drittens innerhalb der Erweiterung die Menge unverändert existiert. Als das gelungen war, blieb "nur" noch nachzuweisen, dass in [] die Kontinuumshypothese nicht gilt.

Unmittelbar nach Cohen konnte gezeigt werden, dass generische Erweiterungen existieren, in denen die Kardinalzahl der Potenzmenge beliebig groß ist (Satz von Easton).

Badiou versieht das mit philosophischen Begriffen. Sein und Wissen gelten innerhalb der Grundsituation. Dem Wissen stehen alle bekannten enzyklopädischen Verfahren zur Verfügung. Das Ununterscheidbare ist dagegen der Anklang des Ereignisses (wobei Badiou zwar von Heidegger den Begriff Ereignis, aber nicht Anklang übernimmt). »Was über die Situation hinausschießt, ist die referentielle Bedeutung der Namen.« (Badiou, S. 449)

Den Satz von Easton interpretiert Badiou als das »Umherirren des Seins« (Badiou, S. 333). Es entsteht durch die nicht zu schließende Kluft zwischen Menge und Potenzmenge, ∈ und ⊂. Mit jedem Ereignis wird eine neue generische Prozedur (Wahrheitsprozedur) gefunden, die dort Namen vergibt, wo innerhalb der Grundsituation etwas ununterscheidbar ist.

Für Badiou ist es das Besondere des Subjekts, ein Ereignis zu ahnen, genauer einzugrenzen und schließlich konkret zu planen. Anschaulich besagt die Erzwingung, dass es gelingt, ein entscheidendes Experiment zu definieren, dessen Antwort im vorhandenen System offen ist. Wird dann eine Antwort gefunden, bekommt sie einen Namen und erzwingt die gewünschte Erweiterung. Beispiele: Newtons Physik war bestätigt, als aus den Abweichungen der bekannten Planetenbewegungen die Existenz eines neuen Planeten vorhergesagt und dieser entdeckt wurde. Erst die Entdeckung war das Ereignis, aber aus dem alten System heraus konnte ein solches Ereignis erzwungen werden. Allgemeiner ist das Ereignis eine Gründung, im politischen Bereich z.B. durch eine Revolution, in der Kunst durch die Präsentation eines radikal neuen Kunstwerks (etwa die Gedichte von Mallarmé oder das 2. Streichquartett von Schönberg).

Hegel beschreibt auf ähnliche Weise einen kritischen Übergang. Innerhalb der Reflexion können alle Bedingungen für eine Sache erkannt und aufgezählt werden, aber damit ist die Sache noch nicht eingetreten. Dazu bedarf es eines Schritts, der von der Sache ausgehen muss.

»Wenn alle Bedingungen einer Sache vorhanden sind, so tritt sie in die Existenz. Die Sache ist, ehe sie existiert; und zwar ist sie erstens als Wesen oder als Unbedingtes; zweitens hat sie Dasein oder ist bestimmt, und dies auf die betrachtete gedoppelte Weise: einerseits in ihren Bedingungen, andererseits in ihrem Grunde. In jenen hat sie sich die Form des äußerlichen, grundlosen Seins gegeben, weil sie als absolute Reflexion die negative Beziehung auf sich ist und sich zu ihrer Voraussetzung macht.« (HW 6.122)

Die Formulierung »so tritt sie in die Existenz« lässt unbestimmt, ob etwas aus sich heraus hervortritt, oder nur ein objektiver Prozess beschrieben ist. Hegel hat jedoch wenige Seiten zuvor unmissverständlich formuliert, dass es sich um ein »Tun der Sache« handelt (HW 6.119). Von der Sache her muss ein Ereignis erfolgen, wodurch die Sphäre erweitert wird, in der lediglich die Bedingungen für das Ereignis gegeben waren.

Abschließend bleibt anzumerken, dass die mathematische Theorie des Namens gut zur Namensbildung im Sinne von Ruben passt. Ruben hatte allgemein beschrieben, wie mit einem Namen eine Gesamtheit bezeichnet wird. Der für die Erzwingung gewählte Namen bringt auf den Punkt, in welcher Weise der Namen sich von einer Aufzählung bereits bekannter Elemente unterscheidet und ihr gegenüber etwas Eigenes bedeutet. Aufgrund seiner Fähigkeit, das Modell zu überschreiten, durch das er motiviert wurde, erhält der Name die Macht, den Schluss vom Einzelnen zum Allgemeinen zu vollziehen. Die Erzwingung ist der mathematisch kleinst-mögliche Schritt, von etwas Einzelnem (den einzelnen aufzählbaren Schritten der Ununterscheidbarkeit) zu etwas Allgemeinem (dem Modell, in dem alle Ununterscheidbarkeiten enthalten sind) zu schließen.

– Irrationale und reelle Zahlen

Die irrationalen und reellen Zahlen wurden auf ähnliche Weise eingeführt. An konkreten Beispielen ist zu »sehen«, was eine irrationale oder reelle Zahl ist: Wird in einem Quadrat die Diagonale gezogen, dann gilt für ihre Länge: d = √2 · e mit d für Diagonale und e für die Einheitsseite des Quadrats. Ebenso ist zu sehen, dass die Länge der Kreislinie u = 2 · · r mit u für Kreisumfang und r für Radius ein Grenzwert aller eingeschriebenen Polygone sein muss.

Mathematisch kann innerhalb der rationalen Zahlen nur ein Grenzwertverfahren entwickelt werden, das sich irrationalen und reellen Zahlen beliebig annähert, sie aber nie erreicht. Wird der Menge aller Elemente, die im Verlaufe des Grenzwertverfahrens dem Grenzwert immer näher kommen, ein Name vergeben, dann benennt dieser Name sowohl alle Elemente des Grenzwertverfahrens als auch den Grenzwert selbst, obwohl der Grenzwert nicht in der Menge der rationalen Zahlen liegt, mit deren Hilfe er angenähert wird, sondern in einer übergreifenden Zahlenmenge, die durch diesen Grenzübergang bestimmt wird. Der Grenzwert wird beliebig angenähert, und es kann und muss sogar gezeigt werden, dass der Grenzwert eindeutig ist, aber zur Existenz gebracht wird er erst durch ein eigenes Axiom (Grenzwert-Axiom) für die übergreifende Menge.

Es war die großartige Idee von Evariste Galois, die Eigenschaften der Menge zu untersuchen, die die einzelnen Schritte der Annäherung enthält, und für diese Eigenschaften auf einer höheren Ebene Kriterien zu erkennen, wann die Annäherung innerhalb des Modells den Grenzwert erreicht und wann nicht, in welchen Fällen also die Ausgangsmenge durch ein Grenzwertaxiom erweitert werden muss und in welchen nicht. Damit gelang es ihm, die offenen Fragen der griechischen Mathematik zu beantworten (wie z.B., ob innerhalb der euklidischen Geometrie der Kreis quadriert werden kann, oder ob es ein allgemeines Verfahren gibt, mithilfe der euklidischen Geometrie einen beliebigen Winkel in drei gleich große Teile zu unterteilen).

Anhang 2: Faserbündel in der Physik

– Faserbündel

Mathematisch gesehen ist der Raum der Messungen = ein Faserbündel.

Die allgemeine Definition des Faserbündels nach Jean Dieudonné, S. 83:

Unter einem differenzierbaren Faserbündel (oder einfach einem Faserbündel oder einer Faserung) versteht man ein Tripel λ = (X, B, ), wobei X und B differenzierbare Mannigfaltigkeiten sind und eine surjektive Abbildung der Klasse C∞ von X in B ist, die der folgenden Bedingung (der sogenannten lokalen Trivialität) genügt:
(LT) Zu jedem b ∈ B gibt es eine in B offene Umgebung U von b, eine differenzierbare Mannigfaltigkeit F und einen Diffeomorphismus
   φ: U F → -1(U)
derart, dass für alle y ∈ U und t ∈ F die Relation (φ(y,t)) = y erfüllt ist.

Wird in dieser Definition als Basismenge B die Gesamtheit der Messobjekte und als Faserung X über B die Gesamtheit der Messgrößen eingesetzt, dann besagt die Definition im wesentlichen, dass kontinuierliche Messungen möglich sind. Die lokale Trivialität bedeutet anschaulich, dass es in der Natur keine Sprünge gibt. Wenn ein Objekt gemessen wird, dann kann die Messung kontinuierlich und stetig auf seine Umgebung ausgedehnt werden.

Wenn angenommen wird, dass die Elemente D ∈ untereinander symmetrisch sind, d.h. dass eine Symmetrie-Gruppe ist, dann ist dies der Ansatz für alle Vereinheitlichungstheorien der Physik. Es wird danach gesucht, die geeigneten Messgrößen (Dimensionen) zu finden, so dass sich zum einen alle Eigenschaften mit ihnen darstellen lassen, und zum anderen eine möglichst einheitliche Symmetrie entsteht. Werden alle Elemente der Symmetriegruppe miteinander verknüpft, dann werden daraus Vorhersagen abgeleitet, dass es ein Messobjekt S geben muss, das genau diese Eigenschaften hat. Der Nachweis solcher vorhergesagter Teilchen ist die wesentliche Aufgabe, die mit den gigantischen Teilchenbeschleunigern angegangen wird. Häufig geschieht es dann jedoch, dass unvorhergesehene Zustände (Kombinationen von Mess-Ergebnissen) entdeckt werden, die nicht in das jeweilige Modell passen, so dass nach einer anderen Auswahl von Dimensionen gesucht werden muss, die auch diese Beobachtungen darstellen lassen.

Bei diesen Arbeiten treten Symmetrien von außerordentlicher Schönheit auf. Ein Beispiel sind die Calabi-Yau-Mannigfaltigkeiten. »Die besondere Bedeutung der Calabi-Yau-Eigenschaft ist, dass eine Kompaktifizierung der zehndimensionalen Stringtheorie auf einer Calabi-Yau-Geometrie zu einer vierdimensionalen Theorie im flachen Minkowski-Raum und mit ungebrochener Supersymmetrie führen kann.« (Wikipedia). Das bedeutet, dass eine Supersymmetrie betrachtet wird, um den kompletten Raum zu beschreiben, mit der Eigenschaft, dass innerhalb dieses Raums die Raumzeit als Grenzfall dargestellt werden kann, der den üblichen bekannten Merkmalen der Raumzeit entspricht.

Figur 9: Die Quintik, ein Schnitt durch eine Calabi-Yau-Mannigfaltigkeit
Graphik aus dem Beitrag in Wikipedia, siehe auch die Ausführungen von Dagmar Kuntz.

– Spezielle Relativitätstheorie

Nach meiner Überzeugung ist die Realität noch eine Stufe komplexer. Es ist nicht nur erforderlich, die Raumzeit (den flachen Minkowski-Raum) als Grenzfall des Faserbündels zu betrachten, mit der beschrieben wird, sondern innerhalb der Raumzeit sind wiederum die von der Speziellen Relativitätstheorie entwickelten Gesetzmäßigkeiten zu berücksichtigen. Die überzeugendste Darstellung stammt von Epstein, siehe hierzu Link.

Anhang 3: Die Prinzipien der von Frege begründeten mathematischen Logik nach Wolff

Aus einer anderen Richtung kommt Michael Wolff in seinen Arbeiten zur Logik zu ähnlichen Ergebnissen wie Peter Ruben. Beide haben bei Kant einen gemeinsamen Bezugspunkt. Wolff will zeigen, dass die von Frege begründete mathematische Logik innerhalb der Logik ein wohldefiniertes Teilgebiet ist, das eigenen Prinzipien folgt, die nicht für die gesamte Logik gültig sind. Er sieht daher die Logik von Frege dann in Paradoxien geraten, wenn sie übergreifende Gültigkeit beansprucht und glaubt, die Tradition von Aristoteles und Kant hinter sich gelassen zu haben.

»So betrachtet kann übrigens keine Rede davon sein, daß Freges Begriffsschrift zu so etwas wie einer Revolution der Logik geführt habe. [...] Freges Leistung dürfte wohl nicht herabgewürdigt werden, wenn man stattdessen sagt, er habe mit der Begriffsschrift die mathematische Logik als systematisches und sehr großes Teilgebiet der Logik etabliert.« (Wolff 1995, S. 310)

Von seiner Kritik an Frege sind drei Punkte hervorzuheben: (1) Weil Frege keinen Unterschied zwischen Subjekt und Prädikat macht, kann er die Besonderheit des Subjekts nicht erkennen und lässt inhalts-leere Subjekte zu. (2) Frege kann Situationen nicht erfassen, in denen zwei voneinander unabhängige Aussagen verbunden werden sollen. (3) Frege setzt implizit voraus, dass alle Operationssymbole der Logik abzählbar sind und die logischen Aussagen linear in einer durchgehenden Schlusskette angeordnet werden können.

(1) Bereits von Peter Strawson und anderen war darauf hingewiesen worden, dass konträre Sätze gültig sein können, wenn sie sich auf ein inhalts-leeres Subjekt beziehen. Wenn John keine Kinder hat, ist sowohl die Aussage wahr, ›Alle Kinder von John schlafen‹ wie auch die konträre Aussage ›Keins von Johns Kindern schläft‹ (siehe hierzu Wolff 1995, S. 288f).

Frege kannte inhalts-leere Subjekte, wie z.B. »ein blauer Begriff«, »schmelzbare Ereignisse, eine blaue Vorstellung, ein salziger Begriff, ein zähes Urteil« (Frege, Arithmetik, S. 27, 54), doch sind derlei Vermischungen von Sinnlichkeit und Begriff für ihn ein »Unding« oder schlicht »wunderbar« (ebd.) und fallen damit ganz aus der Logik heraus. Dass die Frage inhalts-leerer Subjekte keineswegs so einfach abgetan werden kann, belegt Wolff anhand anderer Beispiele. So ist sowohl die Aussage ›die größte Zahl ist größer als 10‹ wie auch ihr Gegenteil wahr, weil es keine größte Zahl gibt (Wolff 2006, S. 37).

In seinen späten Schriften ist sich Frege dessen offenbar bewußt geworden, nachdem er 1902 mit dem Russell-Paradoxon konfrontiert worden war. Wolff zitiert aus einem 1906 geschriebenen, jedoch erst posthum veröffentlichten Manuskript über das Buch von Schönflies Die logischen Paradoxien der Mengenlehre:

»Damit eine solche Bildung eines Eigennamens rechtmäßig sei, muß der Begriff, dessen Bezeichnung dabei gebraucht wird, zwei Bedingungen genügen: 1. er darf nicht leer sein, 2. es darf nur ein einziger Gegenstand unter ihn fallen.« (Frege Über Schönflies: Die logischen Paradoxien der Mengenlehre 1906, in: Nachgelassene Schriften, S. 193, zitiert in Wolff 2004, S. 129)

Daher schließt Wolff, dass die von Frege begründete Logik ein eigenes Prinzip enthalten muss, das inhalts-leere Subjekte ausschließt. Für eine Logik in der Tradition von Aristoteles und Kant ist dies Prinzip nicht notwendig, da es bereits in ihrem Begriff des Denkens enthalten ist. Als entscheidende Quelle bei Kant zitiert Wolff aus dessen Einführung der Urteilstafel:

»Denken ist das Erkenntnis durch Begriffe. Begriffe aber beziehen sich, als Prädikate möglicher Urteile, auf irgend eine Vorstellung von einem noch unbestimmten Gegenstande.« (Kant, KrV, B 94, zitiert in Wolff 1995, S. 47)

Selbst wenn der Gegenstand unbestimmt ist, ist mit dem Gegenstand als Bezug sichergestellt, dass er nicht inhalts-leer sein kann.

(2) Wolff unterscheidet zwischen dem üblichen und dem kartesischen Produkt, wählt dafür jedoch eine ungewöhnliche Schreibweise, die sich enger an den logischen Symbolgebrauch anlehnt. Statt zwischen ›p · q‹ und ›p q‹ unterscheidet er zwischen ›p & q‹ und ›(p,q)‹, womit die Darstellung in kartesischen Koordinaten gewählt ist.

Wird mit Wolff von dem alltagssprachlichen Gebrauch ›p und q‹ ausgegangen, dann ist die Unterscheidung anders zu formulieren: Befinden sich p und q innerhalb einer Dimension, dann kann ›p und q‹ als ›p + q‹ interpretiert werden. Sie lassen sich innerhalb der Dimension zusammenzählen. Befinden sie sich in verschiedenen Dimensionen, dann bedeutet ›p und q‹, dass sowohl ›p‹ wie auch unabhängig davon ›q‹ gilt. In diesem Fall lässt sich ›p und q‹ nur als Element ›(p,q) ∈ P Q‹ darstellen, wobei P und Q die beiden voneinander unabhängigen Dimensionen sind, innerhalb derer p und q liegen.

Wolff kritisiert an den von der formalen Logik eingeführten Wahrheitstafeln, dass sie diese Unterscheidung der beiden Bedeutungen von ›und‹ ignorieren.

»Ein solches Missverständnis drängt sich allerdings auf, wenn man meint, die logische Konstante ›... und ...‹ habe nun einmal keine andere Bedeutung als gerade die, die ihr durch die Wahrheitstafel für ›p & q‹ zugewiesen wird. Denn wenn man meint, ›... und ...‹ könne nur so gebraucht werden, wie es diese Tafel allgemein vorzuschreiben scheint, nämlich nur als wahrheitsfunktionaler Ausdruck, so muß man auch annehmen, daß aus der Konjunktion zweier beliebiger Sätze sogleich einer dieser Sätze abgeleitet werden darf. Die Meinung ist aber unbegründet, ›... und ...‹ könne nur im Sinne der Wahrheitstafel ›p & q‹ gebraucht werden. Ebenso wie ›nicht ...‹ hat ›... und ...‹ verschiedene Bedeutungen. Es läßt sich insbesondere zeigen, daß die Bedeutung des wahrheitsfunktionalen ›... & ...‹ nicht dieselbe ist wie die, mit der die Sätzverknüpfung in der Konklusion eines formal gültigen Schlusses der Form
      p,
      q,
      ∴ p und q (∴ bedeutet 'formal gültig', lies: 'deshalb', t.)
gebraucht wird. Das heißt, es lässt sich nachweisen, daß die in dieser Schlußformel auftretende Konstante ›... und ...‹ kein wahrheitsfunktionaler Ausdruck ist.« (Wolff 2006, S. 54f)

Vielmehr kann bei der Konklusion von p und q auch die Bedeutung im Sinne des kartesischen Produkts auftreten, wenn p und q voneinander unabhängig sind. Es wird so getan, als könne immer aus den beiden Einzelaussagen ›S ist p‹ und ›T ist p‹ zusammengefügt werden ›S und T ist p‹. Hier wird nicht analysiert, ob S und T in der gleichen Dimension liegen, also ein existiert mit ›S = · T‹, oder ob beide voneinander unabhängig in verschiedenen Dimensionen liegen. Siehe dazu Scherz-Beispiele wie ›Peter und ein Glas brechen‹. Mit Sätzen dieser Art wird mit der Mehrdeutigkeit der Sprache gespielt, von der auch die Logik nicht frei ist, wie Wolff zeigen will.

Ähnlich wie Ruben geht Wolff davon aus, dass in der Logik das übliche Produkt p · q als Grenzfall des kartesischen Produkt angesehen werden kann.

»Es ist nun von größtem logischen Interesse, daß die Bedeutung von ›... & ...‹ auf die Bedeutung von ›(..., ...) ‹ zurückgeführt werden kann.« (Wolff 2006, S. 58)

Wenn sich dagegen die mathematische Logik auf den Grenzfall beschränken will, bedarf sie dafür eines eigenen zusätzlichen Prinzips. Es besteht in der Behauptung, dass das Operationszeichen ›und‹ bzw. formal ›&‹ ausschließlich durch die Wahrheitstafeln definiert ist. Wolff analysiert, in welchen Prinzipien sich die universelle Gültigkeit der Wahrheitstafeln unterscheidet von einer Logik, die nicht von dieser Voraussetzung ausgeht. Er findet es im Prinzip, dass Wahres aus Beliebigem gefolgert werden kann. Das soll hier nicht im Detail nachvollzogen werden. Es lässt sich jedoch an den oben zitierten vier Fällen erkennen, mit denen Frege die beiden Aussagen A und B verknüpfen will. Wenn die Aussage B wahr ist, dann kann sie formal sowohl aus A wie aus nicht-A gefolgert werden. Dadurch wird der Sonderfall der dritten Möglichkeit, wenn A verneint und B bejaht wird, formal eingeordnet. Allerdings bleibt der wesentliche Unterschied unbeachtet, dass in dem einen Fall (wenn A bejaht und B bejaht werden) B in der Sphäre von A liegt, während in dem anderen Fall (wenn A verneint und B bejaht werden) A und B in verschiedenen Sphären liegen. Wenn dieser Unterschied ignoriert werden soll, ist dafür nach Wolff ein zusätzliches Prinzip erforderlich, das von der mathematischen Logik stillschweigend zugrunde gelegt, aber nicht wahrgenommen und ausgesprochen wird: Das Prinzip der Beliebigkeit des zureichenden Grundes ›Wenn etwas wahr ist, kann es aus Beliebigem begründet werden‹ (Verum sequitur ex quodlibet).

(3) Frege bezieht sich ausschließlich auf Gegenstände, die in einer Reihe angeordnet sind und für die die vollständige Induktion gilt. Kants transzendentale Logik lässt dagegen bewußt alle inhaltlichen Bestimmungen ihrer Gegenstände weg, auch deren Reihencharakter oder Erblichkeit.

»Es versteht sich dann auch von selbst, daß Prädikate wie 'folgt in einer Reihe' oder 'ist eine in einer Reihe erbliche Eigenschaft', wie sie in der Formelsprache der Begriffsschrift ausgedrückt werden können, für Kant zum 'Inhalt der Erkenntnis' gehören, von dem die formale Logik abzusehen hat.« (Wolff 1995, S. 227)

Wenn die mathematische Logik für ihre Formeln Buchstabenkonstanten wie p und q gebraucht, ist damit deren Abzählbarkeit und darüber ihre Anordnung auf einer Geraden entsprechend den natürlichen Zahlen vorausgesetzt. Die mathematische Logik gilt daher nur für diesen Bereich. (Siehe hierzu Wolff 2006, S. 159)

Ein Vergleich von Ruben und Wolff ergibt, dass Wolff innerhalb der logischen Symbolsprache argumentiert und nicht wie Ruben von einer sich auf Hegel berufenden Satzeinheit ausgeht, sondern von den Kategorien, wie sie von Aristoteles und Kant überliefert sind.

Siglenverzeichnis

HW = Georg Wilhelm Friedrich Hegel: Werke in 20 Bänden. Auf der Grundlage der Werke von 1832-1845 neu ediert. Red. E. Moldenhauer und K. M. Michel. Frankfurt/M. 1969-1971; Link

JLM = Georg Wilhelm Friedrich Hegel: Jenenser Logik, Metaphysik und Naturphilosophie, Leipzig 1923

KrV = Immanuel Kant: Kritik der reinen Vernunft (1781, 1787)

P = Peter Ruben: Prädikationstheorie und Widerspruchsproblem (1976, 2011); Link

TLP = Ludwig Wittgenstein: Tractatus logico-philosophicus
in: Werke Band 1, Frankfurt am Main 1984; Link

WdL 1812 = Georg Wilhelm Friedrich Hegel: Wissenschaft der Logik, Bd. 1, Nürnberg 1812; Link

Literatur

Aristoteles: Kategorien, in: Schriften Bd. 1, Hamburg 1995

Andreas Arndt u.a. (Hg.): Hegels Lehre vom Begriff, Urteil und Schluss, Berlin 2006

Alain Badiou: Das Sein und das Ereignis, Berlin 2005

Walter Benjamin: Über die Sprache überhaupt und über die Sprache des Menschen
in: Walter Benjamin: Angelus Novus, Ausgewählte Schriften Bd. 2, Frankfurt 1988; Link

Ulrich Blau: Die Logik der Unbestimmtheiten und Paradoxien, Heidelberg 2008

Rudolf Carnap 1931: Überwindung der Metaphysik durch logische Analyse der Sprache
in: Erkenntnis 2. 1931, S. 219-241; Link

Rudolf Carnap 1950: Empirismus, Semantik und Ontologie [1950]
in: ders.: Bedeutung und Notwendigkeit, Wien, New York 1972, S. 257-278; Link

Donald Davidson: Truth and Meaning
in: Synthese 17 (1967), S. 304-323; Link

Jean Dieudonné: Grundzüge der modernen Analysis, Bd. 3, Braunschweig 1976

Lewis C. Epstein: Relativity Visualized: The Gold Nugget of Relativity Books, San Francisco 1991 [1981]

Gottlob Frege: Begriffsschrift, Halle 1879

Gottlob Frege: Die Grundlagen der Arithmetik, Stuttgart 1987 [1884]

Gottlob Frege: Funktion und Begriff, Jena 1891

Gottlob Frege: Über Sinn und Bedeutung,
in: Zeitschrift für Philosophie und philosophische Kritik, NF 100, 1892, S. 25-50; Link

Gottlob Frege: Der Gedanke. Eine logische Untersuchung
in: Beiträge zur Philosophie des deutschen Idealismus. Band I: 1918-1919. S. 58-77; Link

Stefan Geschke: Endliche Modelltheorie, Link

Ute Guzzoni: Werden zu sich, Freiburg, München 1982 [1963]

Bruno Hartmann: Logik und Arbeit, St.Augustin 1994

Martin Heidegger: Aristoteles, Metaphysik Θ 1-3, Vom Wesen und Wirklichkeit der Kraft, Frankfurt am Main 2006, GA 33, Vorlesung in Freiburg 1931

Friedrich Hölderlin: Seyn, Urteil, Modalität (1795)
in: Sämtliche Werke und Briefe (Knaupp-Ausgabe, Hanser-Ausgabe neu), Bd. 2, München 1992, S. 49-50; Link

Douglas R. Hofstadter: Gödel, Escher, Bach – ein Endloses Geflochtenes Band, Stuttgart 1985

Hans Heinz Holz: Weltentwurf und Reflexion, Stuttgart, Weimar 2005

Holger Leerhoff: Some Remarks on Wittgenstein and Type Theory in the Light of Ramsey, Kirchberg am Wechsel 2008; Link

Bruno Liebrucks: Sprache und Bewusstsein, Bd. 6.1 bis 6.3, Frankfurt am Main, Bern 1974

Eric Loomis: Functions and Operations in the Tractatus
in: Rudolf Haller, Klaus Puhl (Hg.): Wittgenstein und die Zukunft der Philosophie, Kirchberg am Wechsel 2001, S. 26-32; Link

John McTaggart: A Commentary on Hegel's Logic, Cambridge 1910 (Neudruck durch "Forgotten Books" 2012); Link

Karl R. Popper: Was ist Dialektik?
original What is dialectic? in Mind Bd. 49 1940, deutsche Übersetzung online verfügbar Link

Lorenz Bruno Puntel 1973: Darstellung, Methode und Struktur, Bonn 1973

Lorenz Bruno Puntel 1990: Grundlagen einer Theorie der Wahrheit, Berlin, New York 1990

Willard Van Orman Quine 1951: Zwei Dogmen des Empirismus
in: ders.: Von einem Logischen Standpunkt, Frankfurt u.a. 1979, S. 27-50 [1951]; Link

Willard Van Orman Quine: Wort und Gegenstand, Stuttgart 1980 [1960]

Matthias Rang und Olaf L. Müller: Newton in Grönland
in: Philosophia naturalis 46 Heft 1 (2009), S. 61-114; Link

Urs Richli: Form und Inhalt in G.W.F. Hegels »Wissenschaft der Logik«, Wien, München 1982

Urs Richli 1993: Die Selbstbezüglichkeit der Kategorien in Hegels Wissenschaft der Logik
in: Hans-Dieter Klein und Johann Reikertstorfer (Hg.): Philosophia perennis, Frankfurt am Main u.a. 1993, S. 139-151

Peter Ruben 1966: Zum Verhältnis von Philosophie und Mathematik, Dialektik und Logik – dargestellt am Widerspruch
in: Deutsche Zeitschrift für Philosophie, 12(1966), Sonderheft Materialismus und moderne Naturwissenschaft, S. 167-188; Link

Peter Ruben 1969: Problem und Begriff der Naturdialektik ("Das blaue Buch")
in: A. Griese u. H. Laitko (Hg.): "Weltanschauung und Methode", Berlin: VEB Dt. Vlg. d. Wiss. 1969, S. 51-88; Link

Peter Ruben 1975: Widerspruch und Naturdialektik (1975); Link

Peter Ruben 1977: Dialektik und Analytik in der Naturforschung,
in: K.-F. Wessel (Hg.): Struktur und Prozess, Berlin 1977, S. 317-333; Link

Peter Ruben 1979: Philosophie und Mathematik, Leipzig 1979

Peter Ruben 1997: Vom Problem der ökonomischen Messung und seiner möglichen Lösung
in: F.u.G. Quaas (Hg.): Elemente zur Kritik der Werttheorie, Frankfurt am Main 1997 (Peter Lang), S. 53-77; Link

Peter Ruben 1998: Was bleibt von Marx' ökonomischer Theorie?
in: C. Warnke, G. Huber (Hg): Reflexionen nach dem Ende des euroäischen Kommunismus, Marburg 1998 (Metropolis), S. 13-66; Link

Peter Ruben 2003: Das Dialektikproblem zwischen Natur und Vernunft
gekürzt in: Hartwig Schmidt (Hg.): Figuren der Dialektik, S. 9-25, 2004 im BWV (Berliner Wissenschafts-Verlag); Link

Ralf Schindler: Forcing-Axiome und die Feinanalyse von Hω2, Vortrag an der LMU München 3.11.2010; Link

Urmas Sutrop: Wittgenstein's Tractatus 3.333 and Russell's Paradox
in: Trames, 2009, 13(63/58), 2, S. 179-197; Link

Alfred Tarski: Der Wahrheitsbegriff in den formalisierten Sprachen
in: Studia Philosophica, Lemberg Heft 1 1936, S. 261-405; Link

Hans-Joachim Waschkies: Von Eudoxos zu Aristoteles, Amsterdam 1977

Michael Wolff 1995: Die Vollständigkeit der kantischen Urteilstafel, Frankfurt am Main 1995

Michael Wolff 2004: Abhandlung über die Prinzipien der Logik, Frankfurt 2004

Michael Wolff 2006: Einführung in die Logik, München 2006

2012-2015